Summary
Inter-areal coherence between field potentials is a widespread phenomenon in cortex. Coherence has been hypothesized to reflect phase-synchronization between oscillators and flexibly gate communication according to behavioral and cognitive demands. We reveal an alternative mechanism where coherence is not the cause but the consequence of communication and naturally emerges because spiking activity in a sending area causes post-synaptic potentials both in the same and in other areas. Consequently, coherence depends in a lawful manner on power and phase-locking in the sender and connectivity. Changes in oscillatory power explained prominent changes in fronto-parietal and LGN-V1 coherence across behavioral conditions. Optogenetic experiments and excitatory-inhibitory network simulations identified afferent synaptic inputs rather than spiking entrainment as the principal determinant of coherence. These findings suggest that unique spectral profiles of different brain areas automatically give rise to large-scale coherence patterns that follow anatomical connectivity and continuously reconfigure as a function of behavior and cognition.
Keywords: coherence, phase locking, gamma, beta, V1, LGN, 7B, F5, mouse, macaque
Highlights
-
•
Synaptic projections from a sending to a receiving area explain long-range coherence
-
•
Inter-areal coherence can be predicted by power and connectivity
-
•
Power explains major changes in long-range coherence across behavioral states
-
•
Coherence emerges without spiking entrainment due to afferent synaptic inputs
Schneider et al. establish a mechanism for inter-areal coherence between field potentials, where it is the result and not the cause of communication. Consequently, coherence depends in a lawful manner on connectivity and power and does not require spiking entrainment. This mechanism explains behavior-related changes in fronto-parietal and LGN-V1 coherence.
Introduction
Behavior and cognition depend on coordinated interactions between brain areas (Buzsáki, 2006; Miller and Wilson, 2008; Engel et al., 2001; Nicolelis et al., 1995). Phase synchronization has been hypothesized to be a mechanism for coordinating these interactions and gating information transmission according to cognitive demands (Varela et al., 2001; Bressler et al., 1993; Bressler and Kelso, 2001; Roelfsema et al., 1997; Chrobak and Buzsáki, 1998). To test this hypothesis, studies have measured functional connectivity between brain areas using techniques like coherence and Granger causality. To circumvent the needle-in-the-haystack problem posed by examining spike-spike correlations, these analyses are most frequently based on meso- or macroscale field potentials (e.g., LFP, EEG), which are among the most widely used signals to relate brain activity to behavior (Buzsáki, 2006; Pesaran et al., 2018). Inter-areal coherence between field potentials correlates with many cognitive and behavioral processes (Grothe et al., 2012; Salazar et al., 2012; Fries, 2015; Colgin et al., 2009; Buschman and Miller, 2007; Bressler et al., 1993; Roelfsema et al., 1997). Evidence suggests that distinct oscillation bands play specific roles in inter-areal communication, e.g., gamma (30–80 Hz) and alpha/beta-frequencies (10–30 Hz) in feedforward and feedback communication, respectively (Buschman and Miller, 2007; Bastos et al., 2015; van Kerkoerle et al., 2014; Bressler et al., 2006). Yet, it is unclear to what extent coherence itself is of causal relevance for communication as, e.g., proposed by the Communication-through-Coherence (CTC) hypothesis (Fries, 2005; Chrobak and Buzsáki, 1998; Varela et al., 2001; Bressler and Kelso, 2001), and whether it is indeed a measure of effective communication and information transmission.
The functional relevance of coherence naturally depends on the mechanisms through which it arises, which remain not fully understood. In some cases, coherence may reflect bidirectional coupling between oscillators or synchronization by a common pacemaker, e.g., the thalamus, as in the case of sleep spindles (Lowet et al., 2017; Palmigiano et al., 2017; Timofeev and Steriade, 1996; Karbowski and Kopell, 2000). Phase synchronization may, in this case, align windows of excitability between areas and boost information transmission (Palmigiano et al., 2017). Yet, inter-areal LFP coherence might also result from a simpler, generic mechanism: cortical neurons form synaptic contacts both with other cells in their own area and through long-range connections with cells in target areas. Consequently, spiking activity in a sending area will cause synaptic potentials in the same area and highly correlated synaptic potentials in another receiving area at a delay. These synaptic activities will generate transmembrane currents that give rise to LFP signals. In the sender area, these reflect local activity, and in the receiver area, the consequences of the sender’s activity. Consequently, sender and receiver LFPs may naturally exhibit coherence and Granger causality (Pesaran et al., 2018; Buzsáki and Schomburg, 2015). Importantly, this should be the case even if afferent activity remains subthreshold in the target region.
Here, we describe a generic mechanism and mathematical model explaining the emergence of coherence from the dynamics of neuronal interactions in a sending area and the strength of the anatomical connections to a receiver. To test predictions of this model and dissociate the contributions of spiking entrainment and afferent synaptic inputs to coherence, we analyze simultaneous recordings of spikes and LFPs from multiple brain areas, perform optogenetic perturbation experiments, and simulate excitatory/inhibitory (E/I) networks.
Results
Beta coherence between areas F5 and 7B
We first analyzed data from two macaque brain areas showing clear LFP beta-coherence during a visually cued delayed grasping task. During motor holding and working memory periods, parietal cortex contains a prominent source of beta oscillations (Scherberger et al., 2005; Hagan et al., 2012; Murthy and Fetz, 1996; Donoghue et al., 1998), with strong Granger-causality influences toward visual and frontal areas (Brovelli et al., 2004; Bastos et al., 2015; Vezoli et al., 2020). These long-range interactions in the beta band are thought to play a role in working memory, attention, and predictive processing (Salazar et al., 2012; Buschman and Miller, 2007; Bastos et al., 2015; Roelfsema et al., 1997; Brovelli et al., 2004).
We recorded spikes and LFPs from areas 7B (parietal) and F5 (premotor) (Figure 1A), which are involved in tasks such as reaching and grasping objects (Dann et al., 2016). F5 is one of the main projection targets of area 7B. The 7B-to-F5 projection is strong and long range, as area F5 lies several centimeters away from area 7B (Johnson et al., 1996; Luppino et al., 1999; Markov et al., 2014).
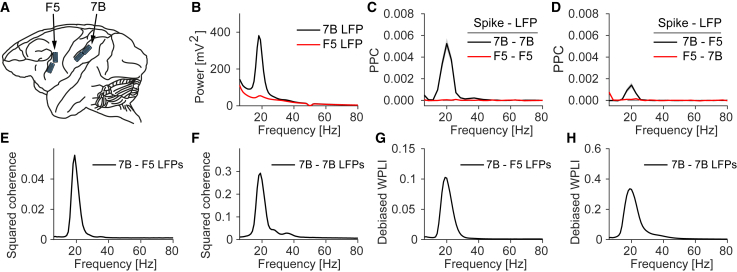
Figure 1.
Long-range beta coherence between macaque F5 and 7B in the absence of beta spike phase locking within F5
(A) Illustration of floating microelectrode array (FMA) recordings (total 128 channels).
(B) Power spectra during memory period.
(C and D) Spike-field phase locking within 7B and F5 (C) and between F5 and 7B (D). Locking was quantified with the PPC, which is unbiased and proportional to the squared spike-field coherence (Vinck et al., 2012). Phase-locking values were averaged over all electrodes in the corresponding grid. Spikes were pooled across all neurons in a session. Average number of neurons per session was 22.3 (7B) and 17.9 (F5). Standard error was computed across 4 conditions 6 recording sessions.
(E and G) Coherence and WPLI (weighted phase lag index) between 7B and F5. See Figure S1 for dependence of coherence on 7B beta power.
(F and H) Coherence and WPLI between medial and lateral 7B grids.
See also Figure S1.
During the memory period, 7B LFP power spectra showed a clear beta peak around 20 Hz (Figures 1B and S1). LFP beta activity within 7B was coherent between the medial and lateral grids (Figures 1F and 1H). To analyze locking between spikes and LFPs, we computed the unbiased PPC (pairwise phase consistency), which is proportional to the squared spike-field coherence (Vinck et al., 2012). Consistent with the LFP beta peak, 7B cells showed prominent spike phase locking with 7B LFPs in the beta band (Figures 1C and S1).
We then examined the coherence between areas 7B and F5. 7B LFPs showed relatively strong and narrow-band beta coherence with F5 LFPs (Figures 1E and S1). This suggests, prima facie, oscillatory coupling between 7B and F5. To rule out volume conduction, we computed the WPLI (weighted phase lag index), a synchronization measure that is not spuriously increased by volume conduction (see STAR Methods; Vinck et al., 2011). The WPLI spectrum showed beta synchronization between 7B and F5 LFPs, suggesting that LFP-LFP coherence was not due to volume conduction (Figures 1G and S1), consistent with the large physical distance between 7B and F5. Because of the beta coherence between 7B and F5 LFPs, we expected to also find beta oscillations in area F5, and inter-areal beta synchronization between spikes and LFPs. Surprisingly, we did not detect significant beta-band phase locking of F5 spikes with either F5 or 7B LFPs (Figures 1C, 1D, and S1). Furthermore, LFP-power in F5 was dominated by the component and showed only a small peak in the beta band (Figures 1B and S1).
Thus, there was clear beta oscillatory activity in area 7B and long-range beta coherence between 7B and F5 LFPs, but no beta synchronization within F5. How can this discrepancy be explained?
Coherence predicted from connectivity and power
To explain these observations, we developed the Synaptic-Source-Mixing (SSM) model of inter-areal coherence between field potentials (see STAR Methods). In this model, coherence itself has no functional consequence and arises as a product of communication, with a lawful dependence on connectivity and power. The model neither assumes coupling between oscillators, nor does it require that spiking in a receiver is phase-locked to the sender’s activity. We first explain the basic properties of the spectral coherence measure. (Magnitude) squared coherence is the frequency-domain equivalent of explained variance in linear regression. It can be understood as the fraction of variance in the power spectral density (PSD) that one signal explains about another signal at a frequency f. Coherence is a strictly linear measure and only captures relationships between signals at a given frequency. Frequency-resolved Granger causality (Geweke, 1982) can also be understood as explained variance of the PSD but, additionally, identifies directional influences by regressing out the extent to which one signal predicts itself. However, in the unidirectional case, Granger causality is approximately equal to squared coherence (see STAR Methods). The basic intuition of the SSM model is that the signal that is projected from a sender to a receiver will, by default, be correlated with the activity in the sender. Thus, the receiver’s LFP signal will result from the mixture of both local and afferent synaptic inputs, and part of the variance in this LFP signal can be explained by the sender activity. Starting from its basic definition, we will show that coherence depends on three main factors:
-
(1)
Inter-areal connectivity (w; Figure 2A), which is influenced by the number of active synapses and their conductances. Specifically, the larger the number of active afferent synaptic inputs, the larger the contribution of the sender to the receiver LFP, and the higher the explained variance.
-
(2)
The shape of the PSDs in the sender and the receiver. In particular, consider a case where the receiver’s PSD has a structure, but where at some frequency the sender exhibits oscillatory synchronization. Because the sender contains high power at that frequency, it makes a relatively strong contribution to the receiver signal. Consequently, the sender will also explain more variance in the receiver signal at that frequency (i.e., high coherence). Thus, even when connectivity is weak, a sender might explain a large fraction of variance at frequencies where it contains high power. This is not prevented by the fact that the coherence normalizes for signal power.
-
(3)
The coherence between (1) the LFP signal in the sender and (2) the signal that is projected from the sender to the receiver. We call this the source-projection coherence. The projections from a sending to a receiving area may originate from a relatively small subset of projection neurons (Markov et al., 2011, 2014). Hence, the projected signal may not be a fully coherent copy of the sender LFP (i.e., source-projection coherence lower than 1). We will show that the coherence between a sender and receiver scales with the source-projection coherence, and that the latter is determined by two factors: (1) The number of projecting neurons . If more neurons in the sender project to the receiver, then the projected signal will be more coherent with the sender. In the limit where equals the total number of neurons in the sender, then the signal will be fully coherent. (2) The coherence between the spiking of individual projecting neurons and the sender LFP. If individual projection neurons are highly coherent with the sender LFP, then the summed activity of a few projection neurons may already be highly coherent with the LFP (Vinck et al., 2011; Lepage et al., 2011). Consequently, inter-areal coherence can be suppressed at frequencies where a sender does not exhibit synchronized activity.
These dependencies are captured by two main analytical results. First, the squared coherence between a sender and receiver equals
| (1) |
(see STAR Methods: Theoretical analysis of SSM model without source-projection coherence and Theoretical analysis of SSM model with source-projection coherence for exact expression). Here, is the intrinsic power in the sender signal relative to the intrinsic power in the receiver signal. In case of unidirectional communication where only a sender exhibits oscillations, is the SOS (sender oscillation strength), defined as the oscillation power relative to the background fluctuations in the signal. Second, the source-projection coherence equals
| (2) |
(see STAR Methods: Theoretical analysis of source-projection coherence based on phase locking of projection neurons for exact expression). Here, is the squared spike-field coherence of the projection neurons, and is the number of projection neurons.
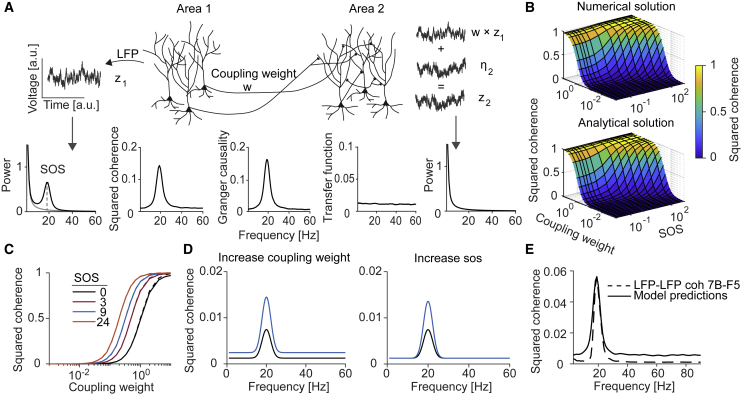
Figure 2.
Inter-areal coherence is predicted by connectivity and power
(A) In the Synaptic-Source-Mixing model, the receiver LFP is modeled as a linear superposition of intrinsic activity and afferent inputs from the sender, weighted by w. Shown are power, coherence, Granger-causality spectra, and the transfer function.
(B and C) Coherence as a function of the SOS (sender oscillation strength) and coupling weight.
(C) Data: dashes. Model: solid.
(D) Effect of coupling weight and SOS on coherence.
(E) SSM model fit of 7B-F5 coherence, with w = 0.069.
To further investigate the dependence of coherence on power, connectivity, and source-projection coherence, we performed numerical simulations. In the first simulations, we varied the factor and the connection weight w and set the source-projection coherence to 1 for all frequencies. The sender signal was modeled as the sum of an oscillatory process and a broad-band process, e.g., pink noise. We generated beta oscillations in the sender using dampened harmonic oscillators (AR(2); see STAR Methods), which are equivalent to a linear E/I circuit driven by stochastic noise (Spyropoulos et al., 2020). Yet, the precise model by which oscillations are generated does not matter for this simulation because only the PSD and connectivity are relevant. In contrast to the sender, the receiver’s intrinsic signal had no oscillatory component but only a component. Despite the absence of a beta peak in the receiver’s PSD, we found clear beta peaks in the coherence and Granger-causality spectra (Figure 2A). These peaks occurred although the transfer function from sender to receiver was flat, i.e., inputs at all frequencies impacted the receiver in the same manner. We further observed that the coherence was precisely predicted by our analytical expressions (Figures 2B and 2C). The SSM model shows that changes in coherence can either come from changes in connectivity or power in the sender area (Figure 2D).
We used the SSM model with a source-projection coherence of 1 to fit the coherence between 7B and F5 LFPs. Area 7B beta oscillations were modeled as dampened harmonic oscillators and the background processes as spectra (see STAR Methods). The model produced an LFP coherence spectrum with a clear beta peak. However, the model predicted stronger coherence outside the beta band than observed in the 7B-F5 data (Figure 2E). Below, we will show that this can be accounted for by the source-projection coherence.
Next, we performed simulations in which the source-projection coherence was included, which had three important consequences: (1) Coherence at frequencies outside the oscillation bands, where the source-projection coherence is weak, was strongly suppressed (Figures 3A and 3B). (2) Changes in coherence with inter-areal connectivity occurred in a very narrow frequency range at the oscillation frequency of the sender (Figure 3D). (3) A peak in the coherence spectrum emerged even when the sender and receiver had identical oscillation strengths (Figure 3E). Without the inclusion of the source-projection coherence, this would not be predicted if for all f. Thus, the observation of coherence between two brain areas that both show oscillations does not require oscillatory coupling. Finally, simulations showed a close match with the analytical expression for the source-projection coherence (Figure 3C; Equation 2; see STAR Methods: Theoretical analysis of source-projection coherence based on phase locking of projection neurons).
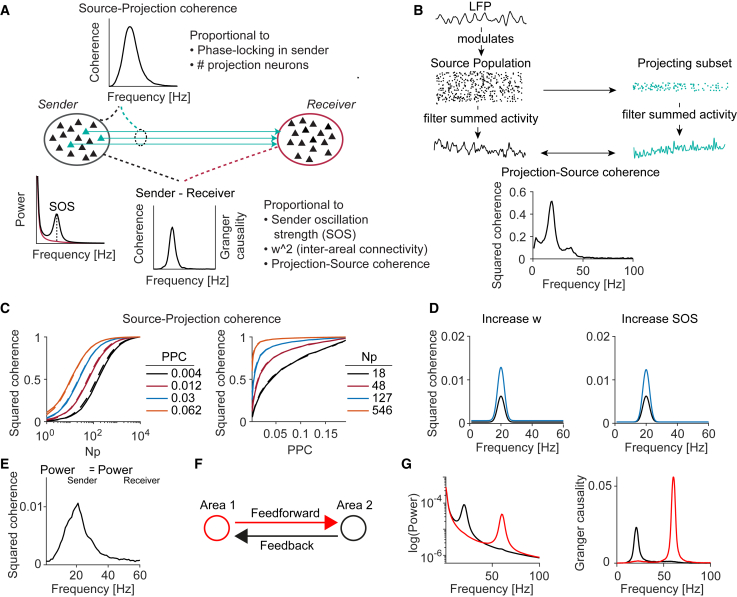
Figure 3.
The source-projection coherence and its effect on inter-areal coherence
(A) Illustration of different factors contributing to coherence. Inset plots show a simulation where the subset of area-1-to-2 projecting neurons is most coherent with the area-1 LFP at the oscillation frequency.
(B) LFP signals were generated as an oscillatory AR(2) process and modulated the activity of neurons according to inhomogeneous Poisson processes. 1,500/5,000 neurons were projection neurons. The activity of the projecting neurons (“projection”) and the entire population (“source”) were summed up. The resulting signals were used to calculate the source-projection coherence.
(C) Dependence of source-projection coherence on the number (Np) and phase locking (PPC) of projection neurons. Dashed: analytical fits. Solid: simulations, in which an AR(2) signal modulated spiking probability in 10,000 neurons according to inhomogeneous Poisson processes.
(D) Increases in coupling weight and SOS cause a narrow-band increase in inter-areal coherence.
(E) Coherence between two areas that have identical power spectra.
(F and G) Power and Granger-causality spectra for two bidirectionally coupled areas oscillating at gamma and beta frequencies.
See also Figures S2 and S3.
Predicting bidirectional influences
Next, we used the SSM model to study bidirectional influences. Among visuo-parietal areas, feedforward and feedback Granger-causal influences are, respectively, strong at gamma and beta frequencies (Bressler et al., 2006; Bastos et al., 2015; van Kerkoerle et al., 2014; Richter et al., 2018). Importantly, early visual areas and parietal cortex exhibit prominent gamma- and beta-oscillations, respectively (Bastos et al., 2015; Brovelli et al., 2004; Spyropoulos et al., 2020; Vezoli et al., 2021). Thus, the SSM model predicts that frequency-specific Granger causality is a byproduct of the presence of distinct oscillation bands in different cortical areas and not of frequency-specific transfer functions.
Indeed, the SSM model accurately reproduced previously reported feedforward and feedback Granger-causality spectra (Figures 3F and 3G). Similar findings were obtained in bidirectionally coupled networks of E/I neurons (Figure S2). To further test SSM model predictions, we reanalyzed the Bastos et al. (2015) data. We hypothesized that the strong gamma Granger causality from V1 to higher areas is due to the presence of a strong V1 gamma source. This predicts that gamma Granger values from V1 to other areas should increase by the same factor if V1 gamma power increases. It is known that V1 gamma power increases after the presentation of an attentional cue (post-cue period) (Richter et al., 2019; Bosman et al., 2012). Consistent with SSM model predictions, Granger-causal influences from V1 to higher areas increased by approximately the same factor across all areas in the post-cue period (1.76; Pearson’s R = 0.99; Figure S3).
Explaining task-related differences in 7B-F5 beta coherence
In Figure 2E, we showed that the coherence between 7B and F5 LFPs was not fully reproduced by the basic SSM model. Hence, we wondered if 7B-F5 coherence could be reproduced by including the source-projection coherence. Furthermore, we wished to determine if the SSM model explains task-related changes in long-range beta coherence, which is thought to play a role in cognitive functions like working memory and attention (Salazar et al., 2012; Buschman and Miller, 2007; Bastos et al., 2015). During our recordings, monkeys were cued to grasp a handle with one of two different grip types. Motor maintenance (hand in resting position) started during the fixation period. Subsequently, the monkey was visually instructed before the working memory period and had to execute a grip type in the movement period (for power and phase locking in the movement period, see Figure S1).
In both monkeys, beta coherence was most prominent during the fixation period, decreased during the memory period, and was strongly reduced during the movement period. This was accompanied by a corresponding decrease in beta power that was clearly visible in 7B but not in F5 LFPs (Figures 4A–4D). To infer the synaptic connectivity parameter w for both monkeys and all three task periods, we fitted the SSM model including the source-projection coherence (see STAR Methods). This analysis revealed three main findings:
-
(1)
Based on beta synchronization within area 7B, the model was able to explain the observed beta coherence between 7B and F5 (Figures 4C and 4D), including the absence of coherence at high frequencies. This held true for the different task periods and both monkeys.
-
(2)
In both monkeys, we found comparable connectivity weights around 0.05–0.07. Thus, despite large differences in coherence, the fitted connectivity weights were comparable between monkeys.
-
(3)
Connectivity weights did not differ significantly between task periods (Figures 4G and 4H).
We further modeled the inter-areal coherence based on spike-LFP PPC within area 7B, by using the analytical expression for the source-projection coherence based on spike-LFP PPC and the number of projecting neurons. This model accurately reproduced 7B-F5 LFP coherence (Figures 4E and 4F) and required fewer projection neurons than reported by Markov et al. (2011), 2014.
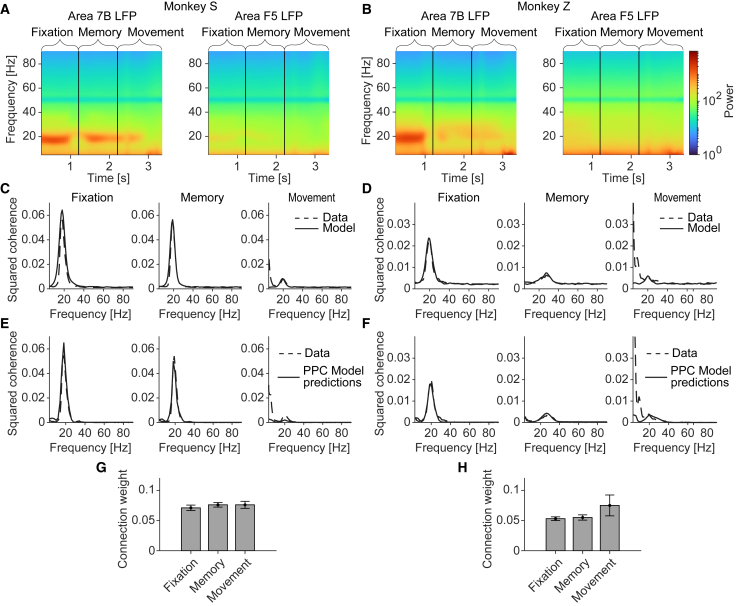
Figure 4.
7B-F5 coherence is predicted by 7B power
(A and B) Power spectra during different behavioral periods.
(C and D) 7B-F5 LFP coherence and the SSM model fits. Connectivity fits are shown in (G) and (H).
(E and F) SSM model predictions including estimates for the source-projection coherence based on the spike-LFP PPC within area 7B and using the coupling weights w of the model in (C) and (D).
(G and H) Coupling weights w for the different model fits in (C) and (D). Weights did not significantly differ between periods.
Significance of the coupling weights in (G) and (H) was estimated using Wilcoxon signed-rank test. Note that in (E) and (F), the model underestimates the low-frequency coherence in the movement period. The reason is that we modeled 7B-F5 coherence based only on the spike-field locking in 7B and ignored the locking in F5, which shows strong low-frequency phase locking and power. All error bars denote SEMs.
These findings suggest that: (1) 7B-F5 LFP beta coherence results from the synchronization of 7B spiking in the beta band, not because F5 neurons selectively respond to beta-rhythmic inputs; (2) differences in beta synchronization within 7B explain the state-dependent changes in LFP beta coherence between 7B and F5; and (3) changes in inter-areal beta coherence do not require changes in effective synaptic gain and can be predicted as a physiological consequence of 7B-to-F5 projections.
Laminar organization of LGN-V1 gamma coherence
Next, we analyzed LGN-V1 gamma coherence in mice. During locomotion and periods of high arousal, area V1 contains a narrow-band LFP peak in the 45–65 Hz gamma frequency range (Niell and Stryker, 2010; Storchi et al., 2017; Saleem et al., 2017). Evidence suggests that this gamma rhythm propagates from the LGN to V1 in a feedforward manner (Saleem et al., 2017). Furthermore, gamma-rhythmic excitatory postsynaptic currents in V1 layer-4 (L4) neurons are only weakly perturbed by silencing the activity of V1 excitatory neurons by activating GABAergic interneurons (Saleem et al., 2017). Here, we ask (1) whether the projection from LGN to V1, carrying gamma-rhythmic afferent synaptic inputs, can explain LGN-V1 gamma coherence; (2) whether state-dependent changes in LGN-V1 coherence are determined by LGN phase locking; and (3) whether LGN-V1 gamma coherence requires V1 spike phase locking.
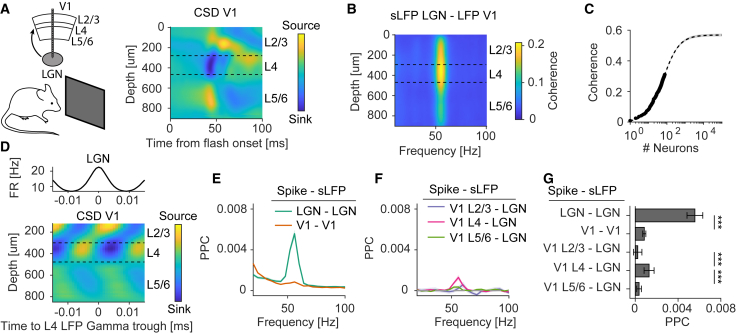
We analyzed Neuropixels recordings from LGN and V1 in awake, head-fixed mice placed on a radial treadmill (Allen Brain Observatory Data). Note that the LGN does not generate a meaningful LFP due to its geometric arrangement of principal neurons. We therefore generated a “surrogate LFP” (sLFP) for the LGN by superimposing all the LGN spikes together, similar to Okun et al. (2015) (see STAR Methods: Recordings from LGN and V1 in mice). V1 layers were identified based on depth and the laminar current source density (CSD) to visual flashes (Figure 5A).
Figure 5.
Layer-specific LGN-V1 gamma coherence
(A) Neuropixels recordings from V1 and LGN and the average V1 CSD.
(B) LGN-V1 coherence versus cortical depth. For LGN, we computed a surrogate LFP (sLFP) from the population LGN spiking activity.
(C) sLFP-LFP coherence between LGN and V1 versus the number of recorded LGN neurons. LGN-V1 coherence (dots) was underestimated because it was computed using a relatively small set of LGN neurons (compared to all LGN neurons). We directly quantified this by analytically deriving the asymptotic coherence between LGN and V1 (dashed line). Shaded area indicates 95% confidence interval.
(D) Average V1 CSD and LGN firing rates around detected gamma peaks in the LGN sLFP.
(E) Within-areal spike-sLFP phase locking (PPC), separately for LGN and V1 (LGN and V1: 1,219 and 1,912 neurons, respectively). To compare phase locking, we used the sLFP for both areas.
(F) PPC between spikes in different V1 layers and the LGN sLFP.
(G) Average gamma PPC values from (E). ∗∗∗p < 0.001; Wilcoxon Mann-Whitney test, comparisons between areas or layers. Error bars and shadings in (E), (F), and (G) indicate SEMs.
The LGN sLFPs showed narrow-band gamma coherence with the LFP in L4 of V1, consistent with the anatomical arrangement of LGN afferents (Figure 5B-C). This coherence tapered off slowly outside L4, most likely due to field spread of extracellular return currents. To identify the currents contributing to LGN-V1 gamma coherence, we analyzed the laminar CSD profile of V1 activity. We detected gamma peaks in LGN signals and computed an average V1 CSD around these peaks (van Kerkoerle et al., 2014). The peak in LGN firing was followed by a L4 current-sink and a L2/3 current-source in V1, with a clear alternating sink-source pattern in L4 (Figure 5D). (Note that a L2/3 current source is consistent with the observation that L5 principal cells have dendrites extending into L2/3 [Scala et al., 2019].)
Individual LGN neurons showed strong gamma phase locking to LGN population activity (Figure 5E). Individual V1 neurons only showed weak gamma phase locking to V1 population activity (Figure 5E) and were, on average, weakly phase locked to LGN population activity as compared to LGN spikes. V1 gamma phase locking was mostly restricted to L4 (9.8% of neurons significant), weaker in L5/6 (only 3.8% significant), and not significantly different from zero in L2/3 (Figures 5F and 5G).
These findings suggest that afferent synaptic inputs from LGN generate extracellular currents that give rise to LFP coherence between LGN and V1 and that, additionally, there is weak V1 phase locking to LGN afferents that is mostly restricted to L4.
Modeling state-dependent changes in LGN-V1 coherence
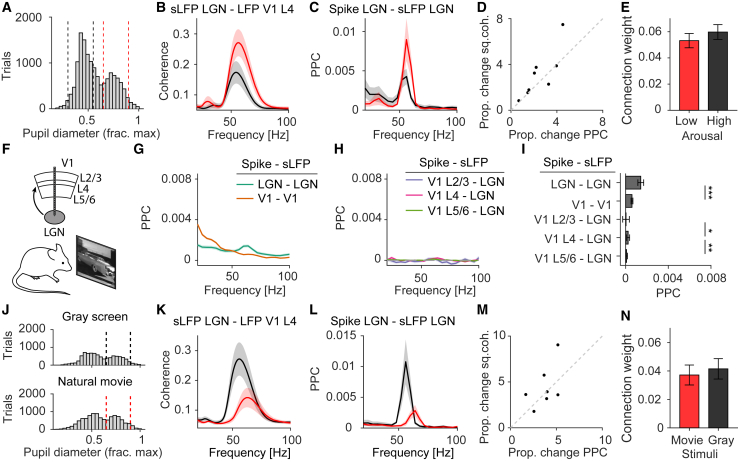
How does LGN-V1 coherence depend on different behavioral states? We first analyzed changes in LGN-V1 gamma coherence with pupil diameter, a measure of arousal (McGinley et al., 2015; Figure 6A). LGN-V1 coherence showed a strong increase with arousal (Figure 6B). This increase could suggest enhanced LGN-V1 communication or, alternatively, that during high arousal, the energy of LGN spiking is focused in the gamma frequency band.
Figure 6.
Changes in LGN-V1 gamma coherence with arousal states and visual stimulation explained by LGN gamma synchrony
(A) Histogram of pupil diameter, a measure of arousal (McGinley et al., 2015).
(B) LGN-V1 coherence for low and high arousal (n = 8 mice, p < 0.05; Wilcoxon signed-rank test).
(C) LGN-LGN phase locking for low and high arousal (n = 8 mice, p < 0.05; Wilcoxon signed-rank test).
(D) Arousal-related change in LGN-LGN spike-field locking versus change in LGN-V1 coherence. Regression : 0.68.
(E) Coupling weights w of the SSM model fits to the data in (B)–(D) (p > 0.05; Wilcoxon signed-rank test).
(F) V1 and LGN Neuropixels recordings during natural movie periods.
(G) As Figure 5E, but during natural movie periods.
(H) As Figure 5F, but during natural movie periods.
(I) As Figure 5G, but during natural movie periods (∗p < 0.05; ∗∗p < 0.01; ∗∗∗p < 0.001; Wilcoxon Mann-Whitney test, comparisons between areas or layers).
(J) Distribution of pupil diameters.
(K) LGN-V1 coherence for gray screen and natural movie periods (n = 7 mice,p < 0.05; Wilcoxon signed-rank test).
(L) LGN-LGN phase locking for gray screen and natural movie (n = 7 mice, p < 0.05; Wilcoxon signed-rank test).
(M) Stimulus-related change in LGN-LGN spike-field locking versus change LGN-V1 coherence. Regression : 0.28.
(N) As (E), but now for natural movie and gray screen periods (p > 0.05; Wilcoxon signed-rank test).
See also Figure S4. Error bars and shadings indicate SEMs.
To investigate this, we quantified changes in local LGN gamma phase locking, which showed a strong increase with arousal (Figure 6C). The SSM model predicts that the increase in local LGN phase locking (sender) should lead to a proportional increase in LGN-V1 coherence (sender and receiver). In particular, it predicts that when the source-projection coherence is 1, the change in squared spike-field coherence within LGN should lead to a proportional change in squared coherence between LGN and V1. Indeed, the increase in LGN-V1 coherence was proportional to the increase in LGN-LGN phase locking (slope 1.30; Figure 6D). Based on the local LGN-LGN phase locking and the LGN-V1 coherence, we then used the SSM model to infer inter-areal connectivity weights, which did not significantly differ between low and high arousal (Figure 6E). These findings indicate that the increase in LGN-V1 coherence with arousal was determined by an increase in LGN-LGN phase synchronization and occurred in the absence of a change in effective synaptic connectivity between LGN and V1.
Next, we asked how LGN-V1 gamma coherence depends on visual stimulation (Figure 6F). The LGN-V1 gamma coherence decreased during stimulation with natural movies as compared to a gray screen and shifted to a higher frequency. Single-unit V1 phase locking to LGN population activity decreased and was only significant for L4 (4.9% of neurons; Figures 6H and 6I). The decrease in LGN-V1 gamma coherence could indicate a decrease in transmission between LGN and V1, which seems difficult to reconcile with the fact that it occurred during stimulation with natural movies. Alternatively, the SSM model predicts that it results from a decrease in local LGN-LGN gamma phase synchronization. Consistent with the latter possibility, we found that the decrease in LGN-LGN gamma phase locking was proportional to the decrease in squared coherence between LGN and V1 (slope 0.98; Figures 6J–6M). Inferred LGN-V1 connectivity weights did not significantly differ between natural movie and gray screen periods (Figure 6N).
Finally, we wondered if communication between LGN and V1 depended on the ongoing gamma phase, as has been suggested in previous work for V1-V1 and V1-V4 communication (Womelsdorf et al., 2012, 2007; Rohenkohl et al., 2018; Ni et al., 2016). To analyze this, we performed reduced rank regression (Izenman, 1975; Semedo et al., 2019), predicting V1 from LGN firing rates. Similar to Womelsdorf et al. (2012), we created two “virtual” sets of spike trains from LGN activity, consisting of spikes that occurred during either the most or the least excitable phase of the LGN gamma cycle. We found that the prediction accuracy of V1 firing rates by LGN firing rates did not differ between the sets of spikes occurring during excitable and non-excitable gamma phases (Figure S4).
Dependence of LGN-V1 coherence on V1 spiking activity
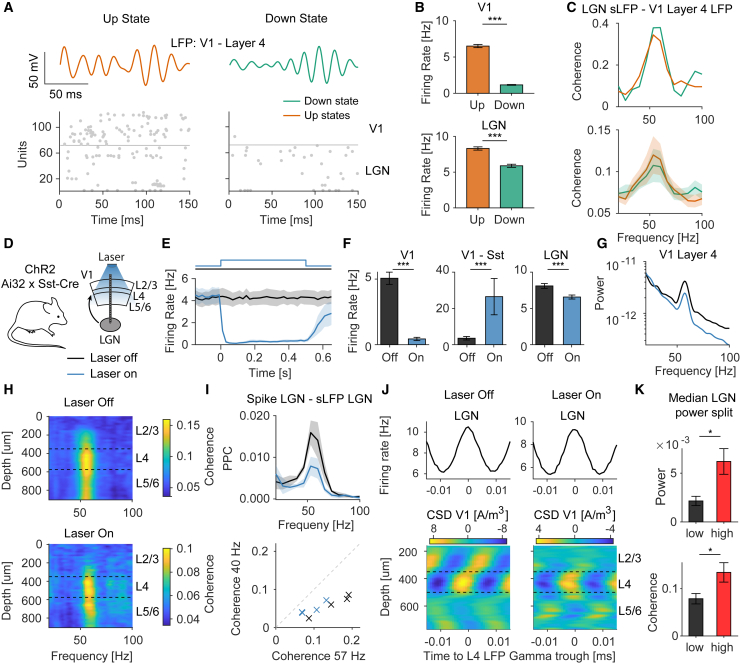
We then wished to isolate the contribution of LGN synaptic afferents to inter-areal coherence, because the weak spike phase locking of V1 neurons to the LGN gamma may have contributed to LGN-V1 coherence. To investigate this, we first analyzed local V1 DOWN-states, which occur spontaneously and during which V1 spiking activity is strongly suppressed. Importantly, LGN activity decreases only slightly during V1 DOWN states (Figures 7A and 7B), i.e., the UP and DOWN states are only weakly coordinated between V1 and LGN. We found that LGN-V1 gamma coherence had a similar magnitude during UP and DOWN states (Figure 7C), indicating that it was mainly determined by afferent synaptic inputs.
Figure 7.
Dissociating contributions of spiking activity and synaptic inputs to LGN-V1 gamma coherence
(A) Example of spontaneously occurring UP and DOWN states in area V1, with raster plots of simultaneously recorded units in LGN and V1 and LFPs in L4 of V1.
(B) Mean V1 and LGN firing rates for UP and DOWN states (LGN: N = 762 neurons, p < 0.001; V1: N = 1596 neurons, p < 0.001; Wilcoxon signed-rank test).
(C) Top: example of LGN-V1 gamma coherence during UP and DOWN states. Bottom: average gamma coherence during UP and DOWN states (n = 23 mice, p > 0.05; Wilcoxon signed-rank test).
(D) Simultaneous LGN-V1 Neuropixels recordings, together with optogenetic activation (laser-on) of V1 SST+ interneurons.
(E) Average firing activity of V1 neurons during laser-on and -off trials.
(F) Average firing rate changes in V1 and LGN neurons during laser-on trials (V1: N = 104; V1-SST+ opto-tagged: N = 15; LGN: N = 428 neurons; p < 0.001 for all groups; Wilcoxon signed-rank test).
(G) LFP power spectra in L4 of V1 for laser-on and -off.
(H) Average coherence between LGN and L4 of V1 for laser-on and -off (n = 4 sessions, p > 0.05).
(I) Top: phase locking (PPC) in LGN for laser-on and -off (n = 4 sessions, p > 0.05; Wilcoxon signed-rank test). Bottom: 40 Hz versus 57 Hz LGN-V1 coherence, separately for laser-on and -off. The weak suppression of LGN-V1 coherence may have been caused by the reduction in gamma phase locking of LGN neurons. This reduction was also observed in Saleem et al. (2017), who activated all subtypes of GABAergic interneurons. Hence LGN firing rates (F) and gamma-band activity may depend partially on corticothalamic feedback, which is unlikely to be gamma-rhythmic given the laminar phase-locking profile of V1 (Figure 5).
(J) Average CSD profile triggered on LGN gamma cycles, together with the concurrent firing rate modulation of the LGN.
(K) Median trial split based on the gamma-power of the LGN sLFP signal, showing LGN power and coherence between LGN and the LFP in L4 of V1 (power: p < 0.05; coherence LGN-V1, p < 0.05; paired t test). Error bars and shadings indicate SEMs.
Next, we recorded from LGN and V1 using Neuropixels and optogenetically activated somatostatin-positive (SST+) interneurons (Figure 7D). These SST interneurons inhibit both fast-spiking PV+ interneurons and excitatory neurons and receive only a weak input from LGN (Cruikshank et al., 2010; Pfeffer et al., 2013). Optogenetic activation (laser-on) of SST interneurons silenced almost completely the spiking of V1 neurons (Figures 7E and 7F). Activation of SST interneurons only weakly affected firing in the LGN (Figure 7F). The LFP power spectrum in L4 of V1 showed only a slight decrease in gamma power during laser-on periods, whereas higher frequencies showed a strong decrease (Figure 7G).
Both during laser-on and -off periods, LGN-V1 gamma coherence showed a characteristic peak around L4 of V1. Coherence was still observed when V1 activity was silenced and attained comparable values (Figures 7H and 7I). Finally, we observed that the CSD profile showed a similar structure during laser-on and -off periods (Figure 7J). We further expected that during optogenetic silencing of V1 spiking, the dependence of LGN-V1 coherence on LGN gamma power should be preserved. To test this, we split the laser-on trials into two groups based on the gamma power in LGN. Indeed, LGN-V1 gamma coherence increased with LGN gamma power (Figure 7K).
Thus, LGN-V1 coherence exhibited several characteristic features that are consistent with the SSM model: (1) Inter-areal coherence and CSD sink-sources were maximal in the anatomical location where synaptic (LGN) afferents terminate (L4 of V1) (Figures 5 and 7). (2) The state-dependence of inter-areal coherence could be explained by a change in the dynamics (i.e., phase locking) of the sending population (Figure 6). (3) Coherence was only weakly perturbed during periods where V1 neurons were spontaneously silent or optogenetically silenced, indicating that afferent synaptic inputs were the main determinant of coherence (Figure 7).
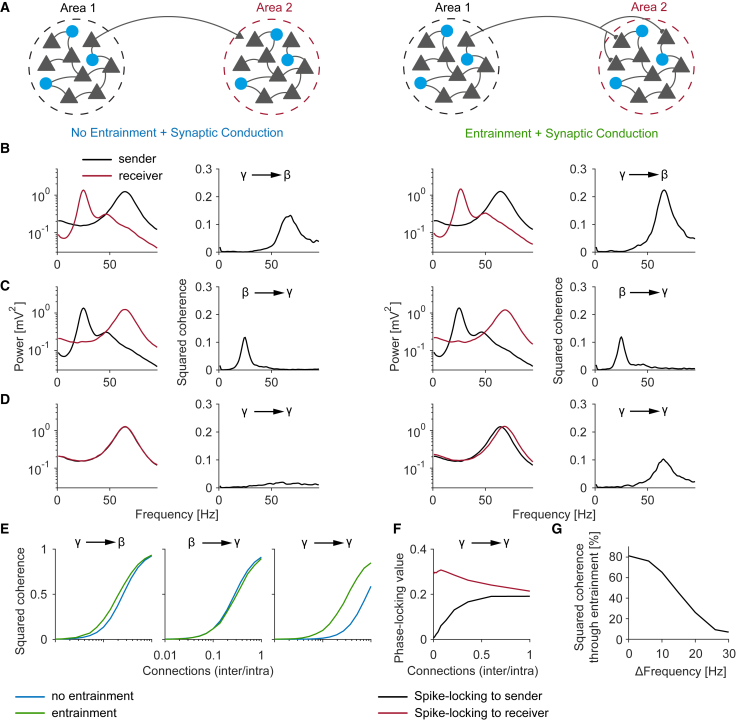
Dissociating the contribution of spike phase locking and afferent synaptic inputs in E/I networks
To further isolate the contribution of afferent synaptic inputs to LFP-LFP coherence, we modeled biophysically plausible networks of E/I neurons. In these networks, rhythms were not superimposed on background activity but were intrinsically, locally generated in both sender and receiver (stochastic Wilson-Cowan equations; see STAR Methods). The areas exhibited intrinsic noisy oscillations that mimic oscillatory behavior in the brain (Spyropoulos et al., 2020; Wallace et al., 2011; Mejias et al., 2016). The E/I networks did not contain dendritic low-pass filtering, which would have diminished the influence of E-E connections at higher frequencies (Buzsáki and Schomburg, 2015; Pike et al., 2000). By using these E/I network models, we performed an “in silico experiment” where we rendered the afferent synaptic inputs invisible to the receiver neurons. We compared two scenarios:
-
1.
No entrainment + synaptic conduction. Sender spikes generated afferent synaptic inputs and field potentials in the receiving area, but receiver neurons were “blind” to the afferent synaptic inputs (Figure 8A, left). That is, the spiking of receiver neurons was exclusively driven by local E/I interactions, which generated intrinsic oscillations. Thus, coherence should arise exclusively due to afferent synaptic inputs and follow the SSM model.
-
2.
Entrainment + synaptic conduction. Receiver neurons were now driven both by local and afferent synaptic inputs and could thus phase-lock to afferent inputs (Figure 8A, right). In this case, LFP-LFP coherence is not exclusively due to afferent synaptic inputs. Instead, afferent synaptic inputs influence the spiking of receiver neurons, which can in turn generate local synaptic currents that are coherent with the activity in the sender.
In both simulations, the sender and receiver areas could have a non-matching (e.g., gamma and beta) or a matching (gamma and gamma) oscillation frequency. In Figure 8, we only show coherence since Granger causality yielded qualitatively similar results (Figure S2).
Figure 8.
Distinct contributions of spiking activity and synaptic inputs to inter-areal coherence in E/I network models
(A) Each area consisted of a population of spiking neurons (stochastic Wilson-Cowan equations). Columns 1 and 2: neurons in area 2 were “blind” to the synaptic inputs from area 1, i.e., spiking entrainment was prohibited. Columns 3 and 4: inputs from area 1 could entrain the area-2 neurons.
(B–D) Power and coherence spectra for different sender-receiver oscillation frequencies.
(E) Coherence versus the ratio of inter- to intra-regional connections.
(F) Phase locking of receiver neurons to area-1 and area-2 oscillations versus connectivity weight.
(G) Percentage of coherence explained by spiking entrainment versus the frequency difference between sender and receiver oscillations.
See also Figures S2 and S5–S8.
We first analyzed the case in which the sender and receiver had non-matching intrinsic oscillation frequencies (gamma and beta). As predicted from the SSM model, we already observed strong LFP-LFP coherence when spike phase locking in the receiver was prohibited (Figures 8B and 8C, left). This coherence was maximal at the oscillation frequency of the sender. Coherence showed the stereotypical sigmoidal increase as a function of inter-areal connection strength that is predicted by the SSM model (Figure 8E). Including spike phase locking in the receiver only made a minor contribution to inter-areal LFP-LFP coherence (Figures 8B, 8C, right, and 8E).
This behavior changed when the sender and receiver had matching oscillation frequencies (Figure 8D). Without spike phase locking in the receiver, LFP-LFP gamma coherence was now weak (Figure 8D, left). This is predicted by the SSM model, because the oscillation strength (power) was now matched between sender and receiver, i.e., for all f. However, with spike phase locking in the receiver, we observed a strong increase in LFP-LFP gamma coherence (Figure 8D, right). This reflects the resonant properties of the receiving area, by which afferent oscillatory inputs are amplified through recurrent dynamics. Overall, the relative contribution of spike phase locking to LFP-LFP coherence decreased when there was a larger difference in oscillation frequency between sender and receiver (Figure 8G). In the presence of resonant interactions, spike phase locking explained more than 50% of the squared coherence. However, in the absence of resonance, spike phase locking made a minor contribution to inter-areal coherence, and afferent synaptic inputs explained the bulk of coherence.
To further understand the dependence of spike phase locking on connectivity in the gamma-to-gamma case, we computed phase locking of receiver spikes to the local and afferent gamma rhythms. Phase locking between receiver spikes and sender LFPs was initially weak, indicating that most spikes in the receiver were triggered by its local rhythm. With an increase in inter-areal connectivity, spike-field phase locking to the sender gradually increased (Figure 8F). Thus, there was no sudden phase transition where the local rhythm of the receiver was fully entrained by the sender.
Finally, we examined a scenario in which the receiver consisted out of two laminar compartments (L4 and L2/3). We found that there was essentially no propagation of the sender’s input rhythm to L2/3 in the receiver and that coherence was restricted to the “granular” compartment of the receiver. This occurred even in the case of communication with a resonant receiver (Figure S5). This is explained by the fact that the sender explains only a relatively small fraction of variance in the L4 receiver, which then subsequently explains only a relatively small fraction of variance in the L2/3 receiver.
Together, these findings show that the peak frequency of coherence and Granger causality is determined by the oscillatory properties of the sending area, not the receiving area (Figure 8). By contrast, the frequency at which spike phase locking (i.e., actual information transfer) will be prominent is determined by the resonant properties of the receiver (Figure S8). Yet, LFP-LFP coherence provided little information as to whether the sender frequency matched the resonant frequency of the receiver or not (compare gamma to beta with gamma to gamma in Figures 8B–8D). The reason for this is that when the sender oscillation is relatively large (non-matching frequencies), LFP-LFP coherence is dominated by afferent synaptic inputs (Figure S8). When the sender and receiver oscillation frequencies match, the direct contribution of afferent synaptic inputs decreases, and the contribution of phase-locked spikes increases (Figure S8).
Distinct contributions of spike phase locking and afferent synaptic inputs to coherence
In the previous figures, we showed how afferent (remote) synaptic inputs give rise to inter-areal LFP-LFP coherence according to the SSM model. However, as we showed, neurons in a receiver can, in addition, phase-lock to afferent synaptic inputs. Phase locking does not demonstrate that coherence itself has a functional consequence. Rather, it simply implies that the afferent synaptic inputs have a functional consequence and that neurons in the receiver integrate these inputs to some extent in a linear manner (since coherence is a linear measure). The phase-locked spikes in the receiver can in turn generate synaptic inputs in the receiving area, which can further increase the inter-areal LFP-LFP coherence. Thus, LFP coherence is determined by two factors, namely: (1) Coherence due to the direct contribution of afferent synaptic inputs, and (2) coherence between the sender LFP and the summed population spiking activity in the receiver.
Importantly, spike phase locking of receiver neurons to afferent synaptic inputs does not demonstrate intrinsic oscillatory activity in the receiver. We find that in the absence of resonance, the coherence between the sending area and the receiver’s spiking activity can be predicted by the SSM model equations. Hence it follows the inter-areal connectivity and oscillation power in the sender (Figures S6 and S7; see STAR Methods: Extension of SSM model to spike-field coherence). However, the coherence between sender and the receiver’s spiking activity will be reduced because neurons have non-linear input-output functions (see simulations using LIF or Poisson neurons in Figures S6 and S7). Hence, we generally expect that the sender will explain less variance in the receiver’s spiking activity than in the receiver’s synaptic activity (Figure S6). By extension, the same holds for the synaptic inputs that are in turn caused by the receiver’s spiking activity inside the receiver area through recurrent activity and thereby contribute to the LFP. Thus, afferent synaptic inputs should generally make a larger contribution to the inter-areal LFP coherence than spike phase locking in the receiver. This provides a theoretical explanation for our experimental findings and model results (Figure 8).
Discussion
We identified a generic mechanism for neuronal coherence, in which it is a consequence and not a cause of communication. Through mathematical analysis, we showed that coherence depends in a lawful manner on connectivity strength and oscillation power and does not require oscillatory coupling or spike phase locking in a receiver. The SSM model explained prominent changes in fronto-parietal and LGN-V1 coherence across behavioral conditions. Furthermore, we isolated the contribution of afferent synaptic inputs to inter-areal coherence by optogenetic perturbation of spiking activity and analysis of DOWN-states in a receiving area, as well as simulations of E/I networks. We found that afferent synaptic inputs rather than spike phase locking in a receiver area were the main determinant of inter-areal coherence. Finally, we showed that LFP coherence and Granger causality primarily reflect the dynamics of neuronal interactions in the sender. Yet, the extent to which the receiver is driven by the inputs of the sender, which is the relevant variable for communication, cannot be deduced from LFP coherence. Rather, the frequency at which the receiver will respond most strongly to synaptic inputs is determined by the resonant properties of the receiver.
Functional consequences for communication and information transmission
Our findings have several implications for the relationship between communication and coherence: (1) Because coherence results as a natural consequence of the oscillatory synchronization of afferent synaptic inputs, it does not require phase synchronization between the local rhythms in a sending and receiving area. (2) Coherence can emerge despite a flat transfer function (i.e., in the absence of any resonance) and does not by itself indicate that communication is more effective at a coherent frequency. (3) In the SSM model, coherence is not a mechanism for communication. Rather, it is a consequence of communication without having direct functional relevance for transmission gain.
Phase synchronization has been hypothesized to be a general mechanism for the gating of selective communication according to cognitive and behavioral demands (Chrobak and Buzsáki, 1998; Bressler and Kelso, 2001; Varela et al., 2001; Fries, 2005). This hypothesis is based on the basic observation that oscillatory coupling between local rhythms in a sender and receiver causes the inputs from a sender to consistently arrive at excitable phases of the receiver’s rhythm (Volgushev et al., 1998; Burchell et al., 1998; Buzsáki, 2006). Consequently, studies have taken coherence and Granger causality as proxies for the phase synchronization between local oscillators. However, coherence and Granger causality are strictly linear measures of frequency-resolved correlation and therefore show spectral peaks in the absence of phase synchronization between oscillators. In particular in the SSM model, coherence arises because the rhythmic activity in the sending area will by default be coherent with the synaptic inputs that the sender causes in the receiver. Importantly, this means that the sender’s synaptic inputs do not arrive at excitable phases of a local rhythm in the receiver. Rather, the sender spikes are simply coherent with the synaptic inputs that they cause themselves (source-projection coherence). Hence, the resulting coherence does not cause effective communication, but the communication causes coherence. The notion of communication that we adhere to is very basic and comprises the approximately linear transmission of a signal as an input to a receiver prior to further non-linear computation on the input and conversion to spiking outputs.
Coherence (and Granger causality) entails that the spectral energy from a sending region is focused in a specific frequency band and that the synaptic activity in a receiver has a relatively strong contribution from a sender at the coherent frequency. There are prominent differences between brain areas in the distribution of spectral energy and its modulation by behavior, which may reflect increases in intrinsic timescales across hierarchical levels (Murray et al., 2014; Gao et al., 2020; Buzsáki, 2006; Siegel et al., 2012). Hence, the unique power-spectral profiles of different brain areas will automatically give rise to large-scale inter-areal coherence and Granger-causality patterns that follow anatomical connectivity and continuously reconfigure as a function of behavior and cognition. Distinct coherence patterns may entail the separation of distinct input sources into a receiving area and thereby shape the way in which these sources interact in the local circuit. In the hippocampus, distinct inputs to dentate gyrus from medial and lateral entorhinal cortex, and from lateral entorhinal and CA3 to CA1, are carried by distinct gamma rhythms (Fernández-Ruiz et al., 2021; Schomburg et al., 2014; Colgin et al., 2009). In the visuo-parietal system, feedforward and feedback projections carry relatively strong energy in the gamma- and beta-frequency bands, respectively (Bastos et al., 2015; van Kerkoerle et al., 2014). In this sense, there is an interesting analogy with anatomy in that feedforward and feedback projections originate from different populations of neurons and layers and also target different layers and dendritic compartments (Vezoli et al., 2021). Distinct feedforward and feedback Granger-causality patterns may thus entail further separation of multiple input streams by occupying different frequency bands. This separation could, e.g., be important for a local recurrent circuit to process sensory evidence as distinct from sensory predictions (Bastos et al., 2012).
Yet, it remains unclear what kind of information is precisely carried by oscillatory activity and, by extension, the coherence and Granger causality that it gives rise to. Correlations can be information limiting in sensory systems (Ecker et al., 2010), and rhythms may emerge especially under stationary conditions and for low-dimensional sensory inputs. For example, beta coherence and power were most prominent during the fixation, rather than the memory and movement, period in which the monkey had to plan and execute sensorimotor transformations. LGN gamma was particularly strong when neurons were driven by the same stimulus (a uniform gray screen) but decreased for natural movies, which provided more heterogeneous and high-dimensional visual stimulation. These findings match with the recent observation that in macaque V1, gamma oscillations emerge for low-dimensional visual stimuli that are highly redundant across space and disappear for highly salient pop-out stimuli (Vinck and Bosman, 2016; Peter et al., 2019; Uran et al., 2021). On the other hand, other oscillatory states associated with wakefulness, like hippocampal theta, may be accompanied by information-rich neural sequences and exhibit genuine inter-areal phase-synchronization (Mizuseki et al., 2009; Dragoi and Buzsáki, 2006).
Inference of connectivity or communication from coherence
Previous work has shown correlations between functional and anatomical connectivity. Consistent with SSM model predictions, anatomical connection strength is linearly correlated with LFP coherence/Granger causality across brain areas in beta and gamma bands (Vezoli et al., 2020). Feedforward and feedback Granger causality in gamma and beta frequency bands correlate with the anatomical SLN measure (% of supragranular-labeled neurons) (Bastos et al., 2015). This is predicted by the SSM model, given the strength of gamma in superficial layers of early visual areas and beta in deep layers and parietal areas (Vezoli et al., 2021; Vinck and Bosman, 2016; Buffalo et al., 2011). Importantly, afferent synaptic inputs with strong oscillatory components can create the appearance of rhythmic components in a receiving area even when there is no local rhythm generated by E/I interactions in the receiver (Figure 7; Saleem et al., 2017; Schomburg et al., 2014). Thus, the presence of coherence and Granger causality between many area pairs does not provide evidence for the widespread presence of local rhythms.
Because coherence is strongly dependent on oscillatory power, it has major limitations as a measure of effective and anatomical connectivity. These limitations can be partially overcome by using the SSM model to correct for oscillation power and by estimating connectivity for different behavioral conditions (Figure 4). Several factors further complicate the problem of inferring anatomical and effective connectivity (see also Pesaran et al., 2018; Buzsáki and Schomburg 2015): (1) Spikes of neurons in a receiver can contribute to coherence (see below). (2) Volume conduction and third-party inputs can lead to coherence between areas that are not anatomically connected (Pesaran et al., 2018; Buzsáki et al., 2012; Sirota et al., 2008; Vinck et al., 2011). (3) Extracellular return currents from synaptic inputs at the basal and apical dendritic compartments cancel out. Hence, afferent axons that terminate exclusively either on the basal or apical dendrites will generate particularly strong LFPs (Lindén et al., 2011; Einevoll et al., 2013). Furthermore, if afferent synaptic inputs have a specific laminar termination zone, then coherence might not necessarily be observable at the ECoG level or in each cortical layer.
Likewise, changes in inter-areal coherence with cognition or behavior should be very carefully interpreted (e.g., Figures 4, 6, and S3). Task-related increases in coherence, e.g., with attention, have been interpreted to reflect increases in synaptic gain, or have even been postulated to represent a mechanism for synaptic gain increases (e.g., Bosman et al., 2012; Grothe et al., 2012). For example, attention to grating stimuli (which generate exceptionally strong gamma) increases V1-V4 gamma coherence from about 0.05 to 0.09 (which corresponds to explained power values <1%) (Ferro et al., 2021; Bosman et al., 2012; Grothe et al., 2012). These low coherence values are in line with the predictions of the SSM model, especially because V1 contains a very strong gamma source, which can show more than 100-fold power increases during visual stimulation (Onorato et al., 2020; Spyropoulos et al., 2020). An increase in V1-V4 gamma coherence may simply result from a combination of factors that are unrelated to synaptic gain, as demonstrated by the SSM model. These include increases in the firing rates and phase locking of V1 projection neurons and V1 gamma power. Because neurons have distinct firing rate patterns and stimulus correlates depending on their projection targets (Lur et al., 2016; Han et al., 2018), it is insufficient to control for average firing rates or spike-field coherence of single neurons when their projection patterns are unknown. An additional complication is the heterogeneity among excitatory neurons, e.g., the presence of distinct excitatory neurons showing different phase-locking patterns (e.g., Onorato et al., 2020), and the log-normal distribution of firing rates (Buzsáki and Mizuseki, 2014).
Contributions of spiking entrainment and afferent synaptic inputs to coherence
It is generally difficult to determine the relative contribution of afferent synaptic inputs and spike phase locking to inter-areal LFP coherence. It requires measurements of single neurons, CSDs, and causal perturbation experiments. We showed that if receiver neurons are phase locked to rhythmic afferent synaptic inputs, and they integrate these synaptic inputs in an approximately linear way, then the spike-field coherence can be predicted by the SSM model. Importantly, phase locking of spikes to afferent inputs does not indicate that there is resonance or a locally generated rhythm in the receiver. Further, it does not demonstrate that inter-areal coherence itself has a functional consequence. Rather, phase locking simply implies that afferent synaptic inputs have a functional consequence (not the coherence itself). The extent to which spikes can phase-lock to afferent synaptic inputs depends on numerous factors: (1) Passive dendritic filtering properties, which can prevent excitatory neurons to phase-lock to high-frequency inputs, in contrast to fast-spiking interneurons (Buzsáki and Schomburg, 2015; Pike et al., 2000). (2) Resonance, by which neurons or networks of neurons amplify synaptic inputs at certain frequencies (Izhikevich et al., 2003). (3) Non-linear input-to-output functions which reduce linear correlations (i.e., coherence), even though non-linearities are thought to be essential for cortical computation. (4) The number of presynaptic inputs that a neuron receives. Individual neurons in a receiver may be driven by a very small set of presynaptic neurons (Ringach, 2021), which may be only weakly coherent with the sender population rhythm (Figure 5F). This can prevent strong coherence between receiver spikes and a sender rhythm. Finally, it is critical to compute spike-field coherence in both directions (Buzsáki and Schomburg, 2015). If a sending area exhibits strong oscillations, then sender spikes can trivially show coherence with receiver LFPs, because their inputs contribute to the receiver LFPs (e.g., Figure 1D).
Outlook and recommendations
The mechanism for the generation of coherence identified in this study might not explain coherence in all model systems but is expected to always contribute to LFP coherence. We make several recommendations: (1) It is difficult to directly infer changes in effective communication and synaptic connectivity from coherence. To make progress, it is necessary to perform more sophisticated mathematical inferences on underlying circuit parameters and test different coherence models against each other. (2) It is critical to combine measurements of laminar CSDs and identified single units (Buzsáki and Schomburg, 2015). Yet, even if spike phase locking is observed, it remains difficult to dissociate contributions of local spiking and afferent inputs to coherence. (3) Causal perturbation techniques are necessary to circumvent the problems of correlational measures and distinguish different interpretations of coherence from each other. Combined with CSDs and spiking measures, causal techniques can disentangle the contribution of different afferent input streams to local phase-locking patterns (see, e.g., Fernández-Ruiz et al., 2021).
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Allen Brain Observatory Neuropixels dataset | Allen Brain Institute | https://portal.brain-map.org/explore/circuits/visual-coding-neuropixels |
| Experimental models: Organisms/strains | ||
| Rhesus macaque (Macaca mulatta) | German Primate Centrum, Germany & Aventis Pharma Deutschland GmbH, Germany | NA |
| Sst-IRES-Cre (SOM-IRES-Cre) mice | The Jackson Labaratory | Cat#013044 |
| Ai32(RCL-ChR2(H134R)/EYFP) mice | The Jackson Labaratory | Cat#024109 |
| Software and algorithms | ||
| MATLAB (version 2020a) | Mathworks | https://www.mathworks.com/ |
| FieldTrip | Oostenveld et al., 2011 | https://www.fieldtriptoolbox.org |
| Reduced Rank Regression | Semedo et al., 2019 | https://github.com/joao-semedo/communication-subspace |
| Stochastic Model of Spiking Neurons | Wallace et al., 2011 | https://github.com/ewallace/stochsimcode |
| Python version 3.6 | Python Software Foundation | https://www.python.org/ |
| AllenSDK pakage (version 2.3.1) | Allen Brain Institute | https://allensdk.readthedocs.io/en/latest/ |
| Kilosort 2.5 | Steinmetz et al., 2021 | https://zenodo.org/record/4482749#.YSjX4I4zaUk |
| Code for SSM model and E/I networks | This manuscript | https://zenodo.org/record/5507277 |
Resource availability
Lead contact
The Lead Contact of this study is Martin Vinck. Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Martin Vinck (martin.vinck@esi-frankfurt.de).
Materials availability
This study did not generate new unique reagents.
Experimental model and subject details
Experiments in macaque monkeys
For the data recorded in macaque neural activity was recorded simultaneously from many channels in two female rhesus macaque monkeys (Animals S and Z, body weight 9,7 and 7 kg, age 7 and 10 years, respectively). Detailed experimental procedures have been described previously (Dann et al., 2016). All procedures and animal care were in accordance with German and European law and were in agreement with the Guidelines for the Care and Use of Mammals in Neuroscience and Behavioral Research (National Research Council, 2003).
Visual coding neuropixels dataset in mice
We analyzed data from the publicly available Visual Coding - Neuropixels dataset, recorded and preprocessed by the Allen Institute of Brain Science (Siegle et al., 2021). The Dataset contains recordings from 30 C57BL/6J wild-type male and female (between 12 and 21 weeks old) mice, as well as 28 male and female (between 12 and 21 weeks old) mice from three transgenic lines (N = 8 Pvalb-IRES-Cre x Ai32, N = 12 Sst-IRES-Cre x Ai32, and N = 8 Vip-IRES-Cre x Ai32), implanted with up to six Neuropixels silicone probes each. Mice were maintained in the Allen Institute for Brain Science animal facility and used in accordance with protocols approved by the Allen Institute’s Institutional Animal Care and Use Committee. After surgery, all mice were single-housed on a reversed 12-hour cycle. Experiments were performed during the dark cycle. In each recording session mice passively viewed a battery of natural and artificial stimuli. We used default function in the Allen software development kit (AllenSDK) package to download the raw data files, containing the neuronal and behavioral data. The details on surgical procedures, stimulation protocols, recording techniques, preprocessing, and spike sorting can be found in the technical white paper (https://portal.brain-map.org/explore/circuits/visual-coding-neuropixels).
Experiments in mice with electrophysiology and optogenetics
For the second dataset collected in mice, adult male and female mice served as subjects (age range 5-6 months). All procedures complied with the European Communities Council Directive 2010/63/EC and the German Law for Protection of Animals, and were approved by local authorities, following appropriate ethics review. All mice were treated according to the approved research protocol V54–19c20/15–F149/1006. Mice were maintained on a 12/12 h light/dark cycle and recordings were performed their dark (awake) cycle. To identify the SST-positive neurons (SST+) during electrophysiological recordings, we crossed Sst-IRES-Cre mice (Ssttm2.1(cre)Zjh Stock, 013044, The Jackson Labaratory) to the Ai32(RCL-ChR2(H134R)/EYFP) mice, to allow Cre-dependent expression of ChR2 (SST-ChR2).
Method details
Recordings from macaque monkeys
The monkeys were trained to perform a delayed grasping task. In this task, the monkey was either instructed to grasp a target with one of the two possible grip types (power and precision) or was free to choose between the grip types, as described in detail in previous studies (Dann et al., 2016). During instructed trials, the monkey was visually cued by one of two discs displayed on a monitor to perform the associated grip type. During free-choice trials, both discs were displayed, and the monkeys could freely choose between grip types. To encourage switching behavior during consecutive free-choice trials, the reward was iteratively reduced every time the monkey repeatedly chose the same grip type. Note that delayed-instructed trials were also part of the task. These trials were not analyzed in this study and are therefore not further explained. The monkey learned to perform the task with high accuracy of 95 +- 0.01% SD successful trials on average.
Surgical procedures have been described in detail previously (Dann et al., 2016). In short, the monkey was implanted with four chronically implanted 32-channel microelectrode arrays (FMAs; Microprobes for Life Sciences; 32 electrodes; spacing between electrodes: 0.4mm; length: 1.5 to 7.1 mm monotonically increasing to target gray matter along the sulcus). Two arrays were positioned in part of the ventral premotor cortex (area F5) and two in area 7B, specifically around the anterior intraparietal area (AIP), yielding a total number of 128 channels. We will refer to the 7B/AIP recording simply as 7B, esp. because LFPs may pick up activity from a larger region of space. Electrode signals from the implanted arrays were amplified and digitally stored using a 128 channel recording system (Cerebus, Blackrock Microsystems; sampling rate 30 kS/s; 0.6-7500Hz band-pass hardware filter).
To detect spikes, electrode signals were first high-pass filtered with a median filter (window length 3ms) and then low-pass filtered with a non-causal Butterworth filter (5000Hz; 4th order). Next, common noise sources were eliminated by applying principal component (PC) artifact cancellation, and spike waveforms were detected and semi-automatically sorted using a modified version of the offline spike sorter Waveclus. Finally, redetection of the different average waveforms (templates) was used to detect overlaid waveforms. The exact procedures of spike detection are described previously (Dann et al., 2016). Only well-isolated single units were used for all analyses. To detect LFPs, electrode signals were first low-pass filtered with a median filter (window length 6.7 ms) and then high-pass filtered with a non-causal Butterworth filter (1 Hz; 4th order). In order to filter out line noise and their harmonics, additional band-stop filtering between 49 and 51 Hz and 98 and 102 Hz was applied. Subsequently, signals were down-sampled from 30000 to 1000Hz by averaging 30 consecutive frames. Broken channels and trials containing movement noise were removed from all further data analyses. For this purpose, the total power, the correlation and the maximum deflection of all channels, and trials were compared, and all outliers were discarded. Finally, to reduce the influence of the on-array ground and reference electrode on each array, the trimmed mean over all channels per array (leaving the highest two and the lowest two values per time point out) was removed by using linear regression. After spike and LFP detection, single-neuron spike events were binned in non-overlapping 1-ms windows to obtain an equal sampling rate of 1000 Hz for both signals. Subsequently, signals were aligned to cue and movement onset for the instructed- and free- choice-task.
Recordings from LGN and V1 in mice
For Figures 5, 6, and 7A–7C we used the publicly available Visual Coding - Neuropixels dataset, recorded and preprocessed by the Allen Institute of Brain Science (Siegle et al., 2021). The dataset contains LFP signals and single unit spikes recorded simultaneously in 4 to 6 visual areas of 58 awake mice during spontaneous activity and different visual stimuli. Gray screen and natural movie periods were chopped into 1 s trials.
Recordings from LGN and V1 combined with optogenetics
For Figures 7D–7K, we collected an additional dataset, where we performed Neuropixels recordings from LGN and V1 while activating SST+ interneurons using optogenetics. Thirty minutes prior to surgery antibiotic (Enrofloxacin, 10 mg/kg, sc, Bayer, Leverkusen, Germany) and analgesic (Metamizole, 200 mg/kg, sc) were administered. For the anesthesia, induction mice were placed in an induction chamber and briefly exposed to isoflurane (3 in oxygen, CP-Pharma, Burgdorf, Germany). Shortly after the anesthesia induction, the mice were fixated in a stereotaxic frame (David Kopf Instruments, Tajunga, California, USA) and the anesthesia adjusted to 0.8 – 1.5 in oxygen. To prevent corneal damage the eyes were covered with eye ointment (Bepanthen, Bayer, Leverkusen, Germany) during the procedure. A custom-made stainless steel head fixation bar was secured with dental cement (Super-Bond C & B, Sun Medical, Shiga, Japan) exactly above the bregma suture, while the area of the recording craniotomy (V1, AP: 1.3 mm anterior to the anterior border of the transverse sinus, ML: 2.0 to 2.5 mm) was covered with cyanoacrylate glue (Insta-Cure, Bob Smith Industries Inc, Atascadero, CA USA). Four to six days after the surgery, the animals were habituated for at least five days in the experimental conditions. The day before or the same day of the first recording session a 1 mm2 craniotomy was performed above V1 (AP: 1.3 mm anterior to the anterior border of the transverse sinus, ML: 2.0 to 2.5 mm) under isoflurane anesthesia. The craniotomy was covered with silicon (Kwik-Cast, World Precision Instruments, Sarasota, USA), and the mouse was allowed to recover for at least 2 hours. Recording sessions were carried out daily for a maximum of 5 days, depending on the quality of the electrophysiological signal. Awake mice were head-fixed and placed on the radial wheel apparatus. We recorded simultaneously from 384 recording sites on a single Neuropixels probe, from both LGN and V1. The probe was inserted in the brain tissue through the V1 craniotomy under a 15 degrees angle. We targeted SST+ interneurons using SST-ChR2 mice and activated them using optogenetic stimulation. During the optogenetic experiment, an optic fiber (Thorlabs, 200um, 0.39 NA) coupled to a diode laser (LuxX CW, 473nm, 100mW, Omicron-Laserage Laserprodukte GmbH, Germany) was used to illuminate V1 craniotomy. The optic fiber was positioned 0.2mm from the probe position, just above the surface of the brain. Continuous light square pulses were applied for 500ms interleaved by 3-6 s intervals. Light intensity on the tip of the fiber was 0.5-2mW/mm2.
Single units were isolated using the semi-automated spike sorting algorithm Kilosort 2.5 (Steinmetz et al., 2021). To obtain LFPs, electrode signals were first low-pass filtered at 400 Hz and then high-pass filtered at 0.1 Hz, using a third-order Butterworth filter. In order to filter out line noise, an additional band-stop filter between 49.5 and 50.5 Hz and 99 and 101 Hz was applied. Subsequently, signals were downsampled to 1200 Hz by averaging consecutive frames. For memory reasons, only every second electrode was used for the analysis of LFP signals.
Theoretical analysis of SSM model without source-projection coherence
In this section we describe our model of Synaptic-Source-Mixing and derive an analytical expression for coherence based on inter-areal connectivity and power. We start out from a unidirectional communication setting, where the sender projects to the receiving area. The measured signals of sender and receiver are denoted and . In the following derivations and our simulations, we assume that the signals are measured without the addition of extrinsic noise. That is we assume that all signals reflect neural activity, and we assume that there is no volume conduction.
We model the signal in the sender as the sum of an oscillatory process and a broad-band process, e.g., Pink noise, :
| (3) |
The intrinsic signal of the receiver has no rhythmic component and is modeled as a linear mixture of its own noise term and the projected input from the sender,
| (4) |
where w denotes the projection strength from sender to receiver and τ the transmission delay between the receiver and the sender area. We assume that the background processes and are linearly uncorrelated for all τ. For the purpose of mathematical derivation, we suppose that the power spectral densities of the broad-band processes are equal for all frequencies f, i.e., . We denote the spectral density of as . We define the SOS (“Sender Oscillation Strength”) as
| (5) |
The cross-spectral density between and equals
| (6) |
and is real-valued. Note that the other cross-terms fell out because we assumed that , and are uncorrelated. The squared coherence between sender and receiver is defined by
| (7) |
This simplifies as follows:
| (8) |
Since and are uncorrelated, we have
| (9) |
Equation 5 now reduces to
| (10) |
From Equation 5 it follows that
| (11) |
Hence reduces to the expression
| (12) |
Thus the coherence can be simplified to
| (13) |
where is the sigmoid function.
We can estimate the connectivity weight from the measurement variables by solving for w and ,
| (14) |
Here, the approximation is based on the first-order Taylor expansion of the coherence around . We can also take the Taylor expansion around for Equation 13 and obtain
| (15) |
Note that the same model derivations (and the derivations below) pertain to Granger causality, because for unidirectional coupling the following relationship holds between Geweke-Granger causality and coherence (Geweke, 1982):
| (16) |
where the approximation was made based on the first order Taylor-expansion around .
Theoretical analysis of SSM model with source-projection coherence
In the model above, we assumed that the signal received by the receiver is fully coherent with the signal in the sender. As explained in more detail in the Results Section, this is likely not the case for two reasons: 1) The sender consists of sub-populations that are not fully coherent with each other, especially for frequencies where there is no oscillatory synchronization. 2) The number of projecting neurons in the sender may be small. Therefore, the coherence between the summed potential of sender-to-receiver projection neurons and the sender LFP (the source-projection coherence) may not be 1.
We first derive an expression of the inter-areal coherence that includes a linear dependence on the source-projection coherence. We model the signals as
| (17) |
| (18) |
Here, is the projected oscillatory signal into the receiver, and is the projected background signal into the receiver. The coherence between and is denoted . The coherence between and is denoted . We assume that and have the same power spectral densities. Likewise we assume that , and have the same power spectral densities.
We now obtain
| (19) |
The squared coherence now simplifies as
| (20) |
Plugging in for all f we obtain
| (21) |
| (22) |
where the first-order Taylor expansion was made around . Thus, the squared coherence between areas scales with the coupling weight and the squared inter-areal coherence in the sender. For the oscillatory part, assuming the background fluctuations have coherence close to zero, we have
| (23) |
Following the same derivation, we can also obtain an expression for the squared coherence that combines both the noise and the oscillatory term as
| (24) |
Here is the source-projection coherence. The variable is defined as the ratio of power of the intrinsic signal in the sender over the intrinsic signal in the receiver.
Theoretical analysis of source-projection coherence based on phase locking of projection neurons
We then derive the expression for the source-projection coherence based on active (i.e., firing spikes) projecting neurons as follows. Let be the activity of a single neuron in the sender with power spectral density for all i. The cross-spectral density of the projecting neurons with the signal based on all neurons in the sender equals
| (25) |
Here is the coherence between two individual neurons,
| (26) |
The factor accounts for the fact that each projecting neuron is fully coherent with itself. For simplicity, we assume that the cross-spectral density between any two neurons is real-valued (i.e., all neurons are on average coherent at zero-phase). The power of the signal in the source (sender) equals
| (27) |
The power of the signal of the projection equals
| (28) |
The squared coherence now equals
| (29) |
This simplifies further to
| (30) |
Plugging in , where g is the fraction of projecting neurons, we obtain
| (31) |
By taking the Taylor expansion around , because the coherence between two individual neurons will be small, we obtain the first-order approximation
| (32) |
Here we removed the term because we can assume that g is typically close to zero. Hence the source-projection coherence is proportional to the fraction of projecting neurons, plus the coherence times the total number of projecting neurons. We can furthermore relate to the coherence of an individual neuron with the total signal in the sender (the spike field coherence). The squared-magnitude spike-field coherence can be expressed in terms of as
| (33) |
Note that we used
| (34) |
because we assumed all cross-spectra to be real-valued. Furthermore the total power in the source can be decomposed as
| (35) |
Solving Equation 33 for yields
| (36) |
where . Plugging this into Equation 32 we obtain the approximation
| (37) |
We thus obtain
| (38) |
Theoretical analysis of the relation between power and spike-field coherence
We further expect to be proportional to : Let be here is the consistency of single spikes (estimated by spike-field PPC; Pairwise Phase Consistency, Vinck et al. (2011)) and divide the population into spike trains of single spikes. The power due to the oscillation that is projected equals
| (39) |
The power due to the background equals
| (40) |
Here, is the spike-field coherence related to the background fluctuations, which may be non-zero. We note that if is large enough, we have
| (41) |
However, for small , we obtain the first-order Taylor expansion
| (42) |
In this case, the SOS depends on . The reason for this dependence is that when is small, the contribution of the phase consistency across neurons is relatively small and the intrinsic power due to the individual energy contributions weighs in.
Because the connection weight w should be proportional to the total number of projection neurons (Markov et al., 2011), we therefore expect coherence to be proportional to w and φ. Combining all results we obtain:
| (43) |
The factor follows from the dependence of α on and on . The factor follows from the dependence of on , the dependence of on and therefore w, and the dependence of on and therefore w. When the number of projection neurons and is sufficiently high, the source-projection coherence should converge to one, and to . In that regime we obtain
| (44) |
Simulations of SSM model without source-projection coherence
We summarize the simulations shown in Figure 2 (see Methods: Theoretical analysis of SSM Model without source-projection coherence). We modeled the LFP signal in the sender and receiver area using (3), (4). The simulation of the different components are described in Simulations: 1/f processes and AR(2) models. The details of the simulations were as follows:
-
•
For Figure 2A the SOS (Sender Oscillation Strength) at the oscillatory frequency was and .
-
•
In Figure 2D the parameters were: (blue and black - left), (black - left), (blue - left) and (black - left), (blue - left), .
-
•
For the fits of 7B-LFP data shown in Figure 2E, power spectra were fitted as a linear mixture of an AR(2) model with background fluctuations ().
Simulations of SSM model with source-projection coherence
In this subsection we summarize the model simulations shown in Figures 3A, 3D, 3E, and 3G, as well as the model fits of 7B-LFP data shown in 4C-D (see Methods: Theoretical analysis of SSM model with source-projection coherence for the mathematical derivation).
For the purpose of simulations, we modeled the signal in the sender as follows:
| (45) |
The intrinsic signal of the receiver is defined as a linear mixture of its own background fluctuations, and the input from the sender:
| (46) |
The transmission delay is denoted by and was set to in all simulations. For the purpose of simulations, we assumed that the projected oscillatory component is fully coherent with the oscillatory process in the sending area. We used the following parameters:
-
•
For Figure 3A the SOS at the oscillatory frequency was , and .
-
•
For the model fits of 7B-F5 coherence shown in Figure 3D the parameters were: (blue and black - left), (black - left), (blue - left) and (black - right), (blue - right), (blue and black - right). for all panels in Figure 3D. The background fluctuations in Area-1 were only partially transmitted, with a weight of , .
-
•
For Figure 4C the parameters were the following (memory-period), (fixation-period) and (movement-period) and . For Figure 4D the parameters were the following (memory-period), (fixation-period) and (movement-period) and .
Simulations for source-projection coherence based on phase locking of projection neurons
For Figure 3B we generated an LFP signal as an oscillatory AR(2) process (see Methods: Simulations: processes and AR(2) models) and used it to modulate the activity of 200000 neurons according to an inhomogeneous Poisson process. The average PPC peak between the neurons and the modulation signal was 0.007. A subset of 100 neurons represents the projecting neurons. The activity of the projecting and the source population were summed up and filtered with a 100Hz low pass filter. The resulting signals were used to calculate the source-projection coherence.
To fit the 7B-F5 coherence in Figures 4E and 4F, the model predictions were inferred from the spike-LFP PPC within area 7B, the SOS and the coupling weight w of the model in 4C. As spike-LFP PPC has no trial bias, while LFP-LFP squared coherence has a trial bias for low number of trials we subtracted the trial bias from the squared coherence of the data. The trial bias was estimated by generating uncorrelated signals with the same number of trials and evaluating their coherence. The peaks in the spike-LFP PPC spectra were fitted using a Gaussian function. The inter-areal coherence was inferred using (24), (31). For Figure 4E the total number was (which was arbitrarily chosen) and the number of projecting neurons was . For Figure 4F the parameters were and . Note that low-frequency synchronization in the movement period was not captured by our model, as it was unidirectional and not optimized for spectral resolution at low frequencies.
Simulations: processes and AR(2) models
The background fluctuations in Figure 2, 3, and 4 were simulated as pink-noise processes. For every trial we generated a trace of white noise sample points. Each trace was Fourier transformed. The complex coefficients of the positive frequencies were multiplied by the -function. By concatenating the resulting coefficients with a flipped version of their complex conjugate, we obtained a spectrum following the -function. By inverse Fourier transforming the resulting spectrum we obtained a time series. The oscillatory processes in Figures 2, 3, and 4 were simulated using an AR(2)-model. The AR(2)-model is defined as
| (47) |
where is a white noise process with zero mean. To obtain a stationary signal, the roots must lie within the unit circle. If the AR process has complex conjugated roots it becomes a stochastic noise driven oscillator. The eigenvalues determine the strength of the oscillations.
Simulations of E/I networks
In this section we summarize the population model from Figure 8. All simulations of the Wilson Cowan model were performed using code from Wallace et al. (2011). The Wilson Cowan Model is a stochastic network model of nonlinear neuron models. It is often used to demonstrate the appearance of oscillations on a network scale (Powanwe and Longtin, 2019; Wallace et al., 2011; Wilson and Cowan, 1972). Each area shown in Figures 8, S2, and S5 was modeled by a Wilson-Cowan model, composed of fully connected excitatory and inhibitory neurons. The neurons were modeled as two-state Markov processes (one active and one quiescent state). In this model, the transition probability of the ith neuron to change from the active to the quiescent state is equal to
| (48) |
The transition probability of the ith neuron to change from the quiescent to the active state is equal to
| (49) |
Here the activation function is defined:
| (50) |
The total input current to excitatory neurons and to inhibitory neurons is defined:
| (51) |
and
| (52) |
Here and are the external input current to the correspondent neuron types. The number of active excitatory neurons is referred to as and the number of active inhibitory neurons as . The synaptic strength from excitatory neurons to inhibitory neurons is denoted , and is the synaptic strength from inhibitory neurons to excitatory neurons. The total synaptic weight between excitatory neurons is referred to as , whereas the total synaptic weight between inhibitory neurons is referred to as .
The model determines the rates of transition between states by the variables α and β. However, since biological networks are stochastic processes, it is necessary to randomize the time of the next event. We achieved this by running the simulation with a Gillespie algorithm (Gillespie, 1977). In the scenario of “synaptic-source-mixing with entrainment,” the excitatory neurons from the sender formed connections with the excitatory neurons of the receiver. This changed Equation 51 for region 2 as follows:
| (53) |
Whereas the neurons within an area were all-to-all connected, the inter-regional connection rate in 8B-D (right), S2B-D (right) and S5B,C (right) was 10%. For simplification, each connection is represented in the LFP signal as one synapse. We calculated the LFP signal by convolving every incoming spike to an area with an alpha function . Here, the variable t is defined as the time relative to the spike onset and for . The factor g was equal to for inhibitory synapses and for excitatory synapses. In Figures 8B–8D (left), S2B-D (left) and S5B,C (left) we used Equation 51 instead of Equation 53, in order to make receiver neurons blind to inter-areal connections. For the calculation of the LFP signal in Area 2 we still considered an inter-areal connection rate of 10% (Figures 8B–8D left) to dissociate the contribution of spike phase locking and afferent synaptic inputs in E/I networks.
Finally, the synaptic potentials of all input connections within an area were summed up to calculate an overall LFP signal of the corresponding area. In the simulations we used the following parameters:
-
•
Each simulated area consisted of 800 excitatory and 200 inhibitory neurons. The neurons within one area were fully connected.
-
•
In Figures 8A–8D, S2B–S2D, S5B, and S5C, each neuron in the receiver received inputs from 80 randomly chosen excitatory neurons within the sender.
-
•
All simulations in Figures 8, S2, and S5 had the following parameter values, , , , , , .
-
•
Areas oscillating in the beta-frequency band had parameter values , , .
-
•
Areas oscillating in the gamma-frequency band had parameter values , , , .
-
•
For Figure 8G the coherence peaks were integrated between and .
Simulations of Poisson modulated neurons
To investigate the consequences of a sigmoidal input-output relationship on inter-areal coherence, we simulated a population of inhomogeneous Poisson neurons (Figure S7). The receiver was modeled as a population of up to 1000 neurons. The firing of the neurons was modulated by a synthetic LFP signal according to an inhomogeneous Poisson process. The modulation signal was a mixture of the afferent oscillatory inputs and the intrinsic fluctuations. This mixed modulation signal was passed through a sigmoid function and normalized on the standard deviation of the signal. We implemented the inhomogeneous Poisson process by applying the time-rescaling theorem (Brown et al., 2002). In the first step, we generated spike times from a homogeneous Poisson process with unit firing rate. Thereupon we applied the inverse of the cumulative rate function to each event time (Nawrot et al., 2008). The average firing rate of the neurons across trials was 2Hz. There was no input from the sender area, i.e., the coherence followed the extended synaptic mixing model shown in Figure 3C.
Simulations of leaky-integrate-and-fire neurons
In this section, we describe the simulations shown in Figure S6. In order to investigate the effects of spiking entrainment on inter-areal coherence in a biologically realistic way, we modeled the receiver population as N leaky integrate-and-fire (LIF) neurons. Each neuron received an input current, which consisted of an afferent oscillatory signal and a local, intrinsic input . The local input is modeled as a pink-noise process described before, and defined as
| (54) |
Here, represents the shared fluctuations across receiver neurons, whereas represents local fluctuations that are specific to neuron i. The parameter γ scales the temporal correlation between the neurons in the receiver population. The oscillatory signal was generated using the AR(2) model that we described above. We denote the power spectral density of the total background fluctuations in the receiver, , as . The power spectral density of oscillatory input is defined as . We define the SOS of a population of N neurons as
| (55) |
The dynamics of the membrane potential of neuron i is defined by
| (56) |
Here, is the membrane time constant, the membrane resistance, and the input current.
The input current of neuron i is defined as
| (57) |
where w denotes the projection strength from the sender to the receiver. At the membrane voltage is set to the resting potential . Whenever the membrane potential passes a threshold , the neuron elicits a spike and the membrane potential is reset to . The LIF neurons in Figure S6 had the following parameters: , , , and .
Extension of SSM model to spike-field coherence
The same model developed for field-field coherence should apply to spiking activity, if spiking relates in a linear or sigmoidal way to synaptic inputs. Consider that represents the average voltage fluctuations in the receiver. If population spiking activity is a linear function of , i.e., , then the same equation for coherence applies. Because spiking activity is stochastic and sparse for a single neuron, a population of neurons will contain additional variance that suppresses the coherence, i.e., we can write
| (58) |
where is the intrinsic signal in the receiver. This distortion , which should decrease with the number of neurons, will decrease the inter-areal spike-field coherence by increasing the intrinsic power in the receiver (see Figures S6 and S7). Next, consider the case where the population spiking activity is a standard sigmoidal activation function of , i.e.
| (59) |
where . In analogy to the data processing equality, we expected that the coherence after the transformation should always be lower than in the linear case, because the signal gets distorted by the sigmoid transformation, and coherence expresses the amount of variance that can be explained by linear prediction (see Figure S7). Assuming that w is relatively small, we use the Taylor-expansion around and obtain
| (60) |
Here, denotes the first derivative of the sigmoid function at x. Note that
| (61) |
We can thus scale the signal as follows. Define a new transformation function by scaling inside the sigmoid as
| (62) |
Assuming that and are statistically independent, we can see that the resulting coherence between and now equals
| (63) |
where is the spectral density function of . Here, we can recognize that the equation has the same form above and is scaled by the weight and the source-projection coherence.
Quantification and statistical analysis
Spectral analysis of the macaque monkey data
All analyses of macaque data were performed in MATLAB (Mathworks) using custom scripts and the FieldTrip toolbox (Oostenveld et al., 2011). Power and coherence spectra were computed using integration windows of 0.35 s, which were moved over the whole data in steps of 0.05 s. The weighted phase lag index (WPLI) between LFPs was calculated using adaptive windows of 5 cycles per time-window, with a maximum window length of 0.75 s (Vinck et al., 2011). The epochs were Hann-tapered to avoid spectral leakage. The pairwise phase consistency (PPC) between spikes and LFPs was calculated using windows of 0.35 s around each spike (Vinck et al., 2012), using the spiketriggeredspectrum functions in the FieldTrip SPIKE toolbox. To compute the spike-LFP PPC, we first pooled all neurons in the area together, which gives the most sensitive estimate of entrainment in an area by increasing the number of pairwise phase comparisons (Vinck et al., 2013).
Layer Assignment of mouse V1 data
The layer assignment was carried out using current source density (CSD) analysis on the average LFP signal during whole screen flash stimulation. The current source density was computed by taking the second discrete spatial derivative across the different electrode sites (Mitzdorf, 1985). Single units were assigned to a layer based on the location of the electrode with the highest amplitude during AP depolarization. To avoid incorrect layer assignment, the peak amplitude electrode of a unit needed to be at least 50 m apart from the intersection of two cortical layers.
Spectral analysis of V1 and LGN data
Power and coherence spectra were computed using integration windows of 0.25 s, which were moved over the whole data in steps of 50ms. The epochs were Hann-tapered to avoid spectral leakage. The pairwise phase consistency (PPC) between spikes and LFPs was calculated using windows of 0.25 s around each spike (Vinck et al., 2012), using the spiketriggeredspectrum functions in the FieldTrip SPIKE toolbox. Only neurons firing at least 150 spikes were considered for the calculation of spike-LFP PPC. Because LGN is a nucleus and the neurons are not aligned, the LFP signal in LGN does not reflect the oscillatory activity of the neurons in LGN. For this reason, we used a surrogate LFP (sLFP) derived from the spiking activity of the neurons in LGN. The sLFP was derived by summing the spikes of all individual isolated units in the LGN. Subsequently, the population spike activity was filtered between 1 and 100Hz. In order to get a meaningful sLFP only sessions with at least 10 recorded single units in LGN were analyzed. The asymptote of the sLFP - LFP coherence between LGN and V1 as a function of recorded neurons in LGN was estimated based on the following equation:
| (64) |
Here denotes the coherence between the sLFP of LGN and the LFP of V1, N the number of LGN neurons used to infer the sLFP, the coherence between single units in LGN and the LFP signal in V1 and the average coherence between the units in LGN. In order to estimate the asymptote of the coherence between the sLFP in LGN and the LFP in V1 we computed and and subsequently fitted Equation 64. For Figures 6A–6E and 6J–6N we only included session with at least 150 trials per condition.
Laminar profile of gamma oscillations in mouse V1
In order to infer the delay between LGN gamma peaks and LFP signals across the laminar structure of V1 we used peaks of oscillatory gamma activity in the sLFP of LGN (van Kerkoerle et al., 2014). To detect genuine oscillatory gamma activity we filtered the sLFP of LGN with a bandpass filter between 45 and 65 Hz. Thereupon we detected gamma peaks exceeding 0.5 standard deviations of the filtered signal. Time windows around the gamma peaks in LGN were used to align the broadband LFP signals in V1, calculate the average LFP response as well as the average CSD in V1. Subsequently, we aligned the CSD of the different mice to calculate an average CSD profile.
Up and down state detection in mouse V1
Up and down states during spontaneous activity were detected based on the average firing rate across all V1 neurons for each mouse. The average V1 firing rate was z-scored, binned into 0.01 s windows, and smoothed using Gaussian windows of 0.4 s. This analysis was only carried out on stationary periods, where the running speed was constantly below 1 cm/s. Subsequently, we used a 3 state hidden Markov model to detect the different brain states of V1. The state with the highest average firing rate was considered as up state, while the state with the lowest average firing rate as down state. The subsequent analyses were only carried out on identified states with a minimum length of 0.15 s (McFarland et al., 2011).
Reduced rank regression using phase-binned population activity in LGN-V1 data
Spike trains of LGN units were split into two subsets based on the gamma phase of the sLFP in LGN. One subset of spike trains containing spikes from the most excitable gamma phase and one of the opposite phase. The widths of the phase bins were adjusted such that spike counts were kept constant across phase bins (Womelsdorf et al., 2012). Spike virtual LGN spike trains and V1 spike trains were counted into 100 ms bins. The average Peri-stimulus time histogram (PSTH) was subtracted from every single trial response. Reduced rank regression was carried out using the implementation of Semedo et al. (2019).
Statistical Testing
Statistical details, including the specific statistical tests and p values are specified in the corresponding figure legends or results section. In general, paired t test, Wilcoxon-Mann-Whitney and Wilcoxon signed-rank test were performed. Throughout the whole paper data are presented as the mean SEM, unless otherwise indicated. All statistical analyses were conducted using MATLAB 2020a (Mathworks).
Acknowledgments
This was supported by an ERC Starting Grant (SPATEMP, 850861) and a BMF grant (Bundesministerium fuer Bildung und Forschung, Computational Life Sciences, project BINDA, 031L0167). We thank Wolf Singer, Georgios Spyropoulos, Conrado Bosman, Quentin Perrenoud, Patrick Jendritza, Jarrod Dowdall, and Craig Richter for helpful comments, edits, and insightful discussions.
Author contributions
Conceptualization, M.S. and M.V.; mathematical analysis, M.S. and M.V.; simulations and data analysis, M.S.; macaque surgeries, recordings, and data preprocessing, B.D., S.S., and H.S.; mouse recordings and surgeries, A.C.B. and A.T.; software and methods for mouse data, M.S., A.C.B., A.T., C.U., and M.V.; writing, M.S. and M.V.; supervision, M.V.
Declaration of interests
The authors declare no competing interests.
Published: October 11, 2021
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.neuron.2021.09.037.
Contributor Information
Marius Schneider, Email: marius.schneider@esi-frankfurt.de.
Martin Vinck, Email: martin.vinck@esi-frankfurt.de.
Supplemental information
Data and code availability
-
•
All data reported in this paper will be shared by the lead contact upon request.
-
•
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the Key resources table.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
References
- Bastos A.M., Usrey W.M., Adams R.A., Mangun G.R., Fries P., Friston K.J. Canonical microcircuits for predictive coding. Neuron. 2012;76:695–711. doi: 10.1016/j.neuron.2012.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastos A.M., Vezoli J., Bosman C.A., Schoffelen J.-M., Oostenveld R., Dowdall J.R., De Weerd P., Kennedy H., Fries P. Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron. 2015;85:390–401. doi: 10.1016/j.neuron.2014.12.018. [DOI] [PubMed] [Google Scholar]
- Bosman C.A., Schoffelen J.M., Brunet N., Oostenveld R., Bastos A.M., Womelsdorf T., Rubehn B., Stieglitz T., De Weerd P., Fries P. Attentional stimulus selection through selective synchronization between monkey visual areas. Neuron. 2012;75:875–888. doi: 10.1016/j.neuron.2012.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressler S.L., Kelso J.A. Cortical coordination dynamics and cognition. Trends Cogn. Sci. 2001;5:26–36. doi: 10.1016/s1364-6613(00)01564-3. [DOI] [PubMed] [Google Scholar]
- Bressler S.L., Coppola R., Nakamura R. Episodic multiregional cortical coherence at multiple frequencies during visual task performance. Nature. 1993;366:153–156. doi: 10.1038/366153a0. [DOI] [PubMed] [Google Scholar]
- Bressler S.L., Richter C.G., Chen Y., Ding M. The 2006 IEEE International Joint Conference on Neural Network Proceedings. IEEE; 2006. Top-down cortical influences in visual expectation; pp. 384–390. [Google Scholar]
- Brovelli A., Ding M., Ledberg A., Chen Y., Nakamura R., Bressler S.L. Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by Granger causality. Proc. Natl. Acad. Sci. USA. 2004;101:9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown E.N., Barbieri R., Ventura V., Kass R.E., Frank L.M. The time-rescaling theorem and its application to neural spike train data analysis. Neural Comput. 2002;14:325–346. doi: 10.1162/08997660252741149. [DOI] [PubMed] [Google Scholar]
- Buffalo E.A., Fries P., Landman R., Buschman T.J., Desimone R. Laminar differences in gamma and alpha coherence in the ventral stream. Proc. Natl. Acad. Sci. USA. 2011;108:11262–11267. doi: 10.1073/pnas.1011284108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burchell T.R., Faulkner H.J., Whittington M.A. Gamma frequency oscillations gate temporally coded afferent inputs in the rat hippocampal slice. Neurosci. Lett. 1998;255:151–154. doi: 10.1016/s0304-3940(98)00676-4. [DOI] [PubMed] [Google Scholar]
- Buschman T.J., Miller E.K. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 2007;315:1860–1862. doi: 10.1126/science.1138071. [DOI] [PubMed] [Google Scholar]
- Buzsáki G. Oxford University Press; 2006. Rhythms of the Brain. [Google Scholar]
- Buzsáki G., Mizuseki K. The log-dynamic brain: how skewed distributions affect network operations. Nat. Rev. Neurosci. 2014;15:264–278. doi: 10.1038/nrn3687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G., Schomburg E.W. What does gamma coherence tell us about inter-regional neural communication? Nat. Neurosci. 2015;18:484–489. doi: 10.1038/nn.3952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G., Anastassiou C.A., Koch C. The origin of extracellular fields and currents--EEG, ECoG, LFP and spikes. Nat. Rev. Neurosci. 2012;13:407–420. doi: 10.1038/nrn3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chrobak J.J., Buzsáki G. Operational dynamics in the hippocampal-entorhinal axis. Neurosci. Biobehav. Rev. 1998;22:303–310. doi: 10.1016/s0149-7634(97)00016-x. [DOI] [PubMed] [Google Scholar]
- Colgin L.L., Denninger T., Fyhn M., Hafting T., Bonnevie T., Jensen O., Moser M.B., Moser E.I. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Cruikshank S.J., Urabe H., Nurmikko A.V., Connors B.W. Pathway-specific feedforward circuits between thalamus and neocortex revealed by selective optical stimulation of axons. Neuron. 2010;65:230–245. doi: 10.1016/j.neuron.2009.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dann B., Michaels J.A., Schaffelhofer S., Scherberger H. Uniting functional network topology and oscillations in the fronto-parietal single unit network of behaving primates. eLife. 2016;5:e15719. doi: 10.7554/eLife.15719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoghue J.P., Sanes J.N., Hatsopoulos N.G., Gaál G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. J. Neurophysiol. 1998;79:159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Dragoi G., Buzsáki G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron. 2006;50:145–157. doi: 10.1016/j.neuron.2006.02.023. [DOI] [PubMed] [Google Scholar]
- Ecker A.S., Berens P., Keliris G.A., Bethge M., Logothetis N.K., Tolias A.S. Decorrelated neuronal firing in cortical microcircuits. Science. 2010;327:584–587. doi: 10.1126/science.1179867. [DOI] [PubMed] [Google Scholar]
- Einevoll G.T., Kayser C., Logothetis N.K., Panzeri S. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nat. Rev. Neurosci. 2013;14:770–785. doi: 10.1038/nrn3599. [DOI] [PubMed] [Google Scholar]
- Engel A.K., Fries P., Singer W. Dynamic predictions: oscillations and synchrony in top-down processing. Nat. Rev. Neurosci. 2001;2:704–716. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
- Fernández-Ruiz A., Oliva A., Soula M., Rocha-Almeida F., Nagy G.A., Martin-Vazquez G., Buzsáki G. Gamma rhythm communication between entorhinal cortex and dentate gyrus neuronal assemblies. Science. 2021;372:eabf3119. doi: 10.1126/science.abf3119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferro D., van Kempen J., Boyd M., Panzeri S., Thiele A. Directed information exchange between cortical layers in macaque V1 and V4 and its modulation by selective attention. Proc. Natl. Acad. Sci. USA. 2021;118 doi: 10.1073/pnas.2022097118. e2022097118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci. 2005;9:474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- Fries P. Rhythms for Cognition: Communication through Coherence. Neuron. 2015;88:220–235. doi: 10.1016/j.neuron.2015.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao R., van den Brink R.L., Pfeffer T., Voytek B. Neuronal timescales are functionally dynamic and shaped by cortical microarchitecture. eLife. 2020;9:e61277. doi: 10.7554/eLife.61277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geweke J. Measurement of linear dependence and feedback between multiple time series. J. Am. Stat. Assoc. 1982;77:304–313. [Google Scholar]
- Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- Grothe I., Neitzel S.D., Mandon S., Kreiter A.K. Switching neuronal inputs by differential modulations of gamma-band phase-coherence. J. Neurosci. 2012;32:16172–16180. doi: 10.1523/JNEUROSCI.0890-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagan M.A., Dean H.L., Pesaran B. Spike-field activity in parietal area LIP during coordinated reach and saccade movements. J. Neurophysiol. 2012;107:1275–1290. doi: 10.1152/jn.00867.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Y., Kebschull J.M., Campbell R.A.A., Cowan D., Imhof F., Zador A.M., Mrsic-Flogel T.D. The logic of single-cell projections from visual cortex. Nature. 2018;556:51–56. doi: 10.1038/nature26159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izenman A.J. Reduced-rank regression for the multivariate linear model. J. Multivariate Anal. 1975;5:248–264. [Google Scholar]
- Izhikevich E.M., Desai N.S., Walcott E.C., Hoppensteadt F.C. Bursts as a unit of neural information: selective communication via resonance. Trends Neurosci. 2003;26:161–167. doi: 10.1016/S0166-2236(03)00034-1. [DOI] [PubMed] [Google Scholar]
- Johnson P.B., Ferraina S., Bianchi L., Caminiti R. Cortical networks for visual reaching: physiological and anatomical organization of frontal and parietal lobe arm regions. Cereb. Cortex. 1996;6:102–119. doi: 10.1093/cercor/6.2.102. [DOI] [PubMed] [Google Scholar]
- Karbowski J., Kopell N. Multispikes and synchronization in a large neural network with temporal delays. Neural Comput. 2000;12:1573–1606. doi: 10.1162/089976600300015277. [DOI] [PubMed] [Google Scholar]
- Lepage K.Q., Kramer M.A., Eden U.T. The dependence of spike field coherence on expected intensity. Neural Comput. 2011;23:2209–2241. doi: 10.1162/NECO_a_00169. [DOI] [PubMed] [Google Scholar]
- Lindén H., Tetzlaff T., Potjans T.C., Pettersen K.H., Grün S., Diesmann M., Einevoll G.T. Modeling the spatial reach of the LFP. Neuron. 2011;72:859–872. doi: 10.1016/j.neuron.2011.11.006. [DOI] [PubMed] [Google Scholar]
- Lowet E., Roberts M.J., Peter A., Gips B., De Weerd P. A quantitative theory of gamma synchronization in macaque V1. eLife. 2017;6:e26642. doi: 10.7554/eLife.26642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luppino G., Murata A., Govoni P., Matelli M. Largely segregated parietofrontal connections linking rostral intraparietal cortex (areas AIP and VIP) and the ventral premotor cortex (areas F5 and F4) Exp. Brain Res. 1999;128:181–187. doi: 10.1007/s002210050833. [DOI] [PubMed] [Google Scholar]
- Lur G., Vinck M.A., Tang L., Cardin J.A., Higley M.J. Projection-Specific Visual Feature Encoding by Layer 5 Cortical Subnetworks. Cell Rep. 2016;14:2538–2545. doi: 10.1016/j.celrep.2016.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markov N.T., Misery P., Falchier A., Lamy C., Vezoli J., Quilodran R., Gariel M.A., Giroud P., Ercsey-Ravasz M., Pilaz L.J., et al. Weight consistency specifies regularities of macaque cortical networks. Cereb. Cortex. 2011;21:1254–1272. doi: 10.1093/cercor/bhq201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markov N.T., Vezoli J., Chameau P., Falchier A., Quilodran R., Huissoud C., Lamy C., Misery P., Giroud P., Ullman S., et al. Anatomy of hierarchy: feedforward and feedback pathways in macaque visual cortex. J. Comp. Neurol. 2014;522:225–259. doi: 10.1002/cne.23458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFarland J.M., Hahn T.T.G., Mehta M.R. Explicit-duration hidden markov model inference of up-down states from continuous signals. PLoS One. 2011;6:1–16. doi: 10.1371/journal.pone.0021606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGinley M.J., Vinck M., Reimer J., Batista-Brito R., Zagha E., Cadwell C.R., Tolias A.S., Cardin J.A., McCormick D.A. Waking State: Rapid Variations Modulate Neural and Behavioral Responses. Neuron. 2015;87:1143–1161. doi: 10.1016/j.neuron.2015.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mejias J.F., Murray J.D., Kennedy H., Wang X.-J. Feedforward and feedback frequency-dependent interactions in a large-scale laminar network of the primate cortex. Sci. Adv. 2016;2:e1601335. doi: 10.1126/sciadv.1601335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller E.K., Wilson M.A. All my circuits: using multiple electrodes to understand functioning neural networks. Neuron. 2008;60:483–488. doi: 10.1016/j.neuron.2008.10.033. [DOI] [PubMed] [Google Scholar]
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol. Rev. 1985;65:37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- Mizuseki K., Sirota A., Pastalkova E., Buzsáki G. Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron. 2009;64:267–280. doi: 10.1016/j.neuron.2009.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray J.D., Bernacchia A., Freedman D.J., Romo R., Wallis J.D., Cai X., Padoa-Schioppa C., Pasternak T., Seo H., Lee D., Wang X.J. A hierarchy of intrinsic timescales across primate cortex. Nat. Neurosci. 2014;17:1661–1663. doi: 10.1038/nn.3862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy V.N., Fetz E.E. Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J. Neurophysiol. 1996;76:3949–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
- Nawrot M.P., Boucsein C., Rodriguez Molina V., Riehle A., Aertsen A., Rotter S. Measurement of variability dynamics in cortical spike trains. J. Neurosci. Methods. 2008;169:374–390. doi: 10.1016/j.jneumeth.2007.10.013. [DOI] [PubMed] [Google Scholar]
- Ni J., Wunderle T., Lewis C.M., Desimone R., Diester I., Fries P. Gamma-rhythmic gain modulation. Neuron. 2016;92:240–251. doi: 10.1016/j.neuron.2016.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolelis M.A., Baccala L.A., Lin R.C., Chapin J.K. Sensorimotor encoding by synchronous neural ensemble activity at multiple levels of the somatosensory system. Science. 1995;268:1353–1358. doi: 10.1126/science.7761855. [DOI] [PubMed] [Google Scholar]
- Niell C.M., Stryker M.P. Modulation of visual responses by behavioral state in mouse visual cortex. Neuron. 2010;65:472–479. doi: 10.1016/j.neuron.2010.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun M., Steinmetz N., Cossell L., Iacaruso M.F., Ko H., Barthó P., Moore T., Hofer S.B., Mrsic-Flogel T.D., Carandini M., Harris K.D. Diverse coupling of neurons to populations in sensory cortex. Nature. 2015;521:511–515. doi: 10.1038/nature14273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onorato I., Neuenschwander S., Hoy J., Lima B., Rocha K.-S., Broggini A.C., Uran C., Spyropoulos G., Klon-Lipok J., Womelsdorf T., et al. A distinct class of bursting neurons with strong gamma synchronization and stimulus selectivity in monkey v1. Neuron. 2020;105:180–197.e5. doi: 10.1016/j.neuron.2019.09.039. [DOI] [PubMed] [Google Scholar]
- Oostenveld R., Fries P., Maris E., Schoffelen J.M. FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011;2011:156869. doi: 10.1155/2011/156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmigiano A., Geisel T., Wolf F., Battaglia D. Flexible information routing by transient synchrony. Nat. Neurosci. 2017;20:1014–1022. doi: 10.1038/nn.4569. [DOI] [PubMed] [Google Scholar]
- Pesaran B., Vinck M., Einevoll G.T., Sirota A., Fries P., Siegel M., Truccolo W., Schroeder C.E., Srinivasan R. Investigating large-scale brain dynamics using field potential recordings: analysis and interpretation. Nat. Neurosci. 2018;21:903–919. doi: 10.1038/s41593-018-0171-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter A., Uran C., Klon-Lipok J., Roese R., van Stijn S., Barnes W., Dowdall J.R., Singer W., Fries P., Vinck M. Surface color and predictability determine contextual modulation of V1 firing and gamma oscillations. eLife. 2019;8:e42101. doi: 10.7554/eLife.42101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeffer C.K., Xue M., He M., Huang Z.J., Scanziani M. Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nat. Neurosci. 2013;16:1068–1076. doi: 10.1038/nn.3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pike F.G., Goddard R.S., Suckling J.M., Ganter P., Kasthuri N., Paulsen O. Distinct frequency preferences of different types of rat hippocampal neurones in response to oscillatory input currents. J. Physiol. 2000;529:205–213. doi: 10.1111/j.1469-7793.2000.00205.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powanwe A.S., Longtin A. Determinants of brain rhythm burst statistics. Sci. Rep. 2019;9:18335. doi: 10.1038/s41598-019-54444-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richter C.G., Coppola R., Bressler S.L. Top-down beta oscillatory signaling conveys behavioral context in early visual cortex. Sci. Rep. 2018;8:6991. doi: 10.1038/s41598-018-25267-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richter C.G., Bosman C.A., Vezoli J., Schoffelen J.-M., Fries P. Brain rhythms shift and deploy attention. bioRxiv. 2019 doi: 10.1101/795567. [DOI] [Google Scholar]
- Ringach D.L. Sparse thalamocortical convergence. Curr. Biol. 2021;31:2199–2202.e2. doi: 10.1016/j.cub.2021.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roelfsema P.R., Engel A.K., König P., Singer W. Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature. 1997;385:157–161. doi: 10.1038/385157a0. [DOI] [PubMed] [Google Scholar]
- Rohenkohl G., Bosman C.A., Fries P. Gamma synchronization between v1 and v4 improves behavioral performance. Neuron. 2018;100:953–963.e3. doi: 10.1016/j.neuron.2018.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salazar R.F., Dotson N.M., Bressler S.L., Gray C.M. Content-specific fronto-parietal synchronization during visual working memory. Science. 2012;338:1097–1100. doi: 10.1126/science.1224000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saleem A.B., Lien A.D., Krumin M., Haider B., Rosón M.R., Ayaz A., Reinhold K., Busse L., Carandini M., Harris K.D. Subcortical Source and Modulation of the Narrowband Gamma Oscillation in Mouse Visual Cortex. Neuron. 2017;93:315–322. doi: 10.1016/j.neuron.2016.12.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scala F., Kobak D., Shen S., Bernaerts Y., Laturnus S., Cadwell C., Hartmanis L., Froudarakis E., Castro J., Tan Z., et al. Layer 4 of mouse neocortex differs in cell types and circuit organization between sensory areas. Nat. Commun. 2019;10:4174. doi: 10.1038/s41467-019-12058-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherberger H., Jarvis M.R., Andersen R.A. Cortical local field potential encodes movement intentions in the posterior parietal cortex. Neuron. 2005;46:347–354. doi: 10.1016/j.neuron.2005.03.004. [DOI] [PubMed] [Google Scholar]
- Schomburg E.W., Fernández-Ruiz A., Mizuseki K., Berényi A., Anastassiou C.A., Koch C., Buzsáki G. Theta phase segregation of input-specific gamma patterns in entorhinal-hippocampal networks. Neuron. 2014;84:470–485. doi: 10.1016/j.neuron.2014.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semedo J.D., Zandvakili A., Machens C.K., Yu B.M., Kohn A. Cortical areas interact through a communication subspace. Neuron. 2019;102:249–259.e4. doi: 10.1016/j.neuron.2019.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel M., Donner T.H., Engel A.K. Spectral fingerprints of large-scale neuronal interactions. Nat. Rev. Neurosci. 2012;13:121–134. doi: 10.1038/nrn3137. [DOI] [PubMed] [Google Scholar]
- Siegle J.H., Jia X., Durand S., Gale S., Bennett C., Graddis N., Heller G., Ramirez T.K., Choi H., Luviano J.A., et al. Survey of spiking in the mouse visual system reveals functional hierarchy. Nature. 2021;592:86–92. doi: 10.1038/s41586-020-03171-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirota A., Montgomery S., Fujisawa S., Isomura Y., Zugaro M., Buzsáki G. Entrainment of neocortical neurons and gamma oscillations by the hippocampal theta rhythm. Neuron. 2008;60:683–697. doi: 10.1016/j.neuron.2008.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spyropoulos G., Dowdall J.R., Schölvinck M.L., Bosman C.A., Lima B., Peter A., Onorato I., Klon-Lipok J., Roese R., Neuenschwander S., et al. Spontaneous variability in gamma dynamics described by a linear harmonic oscillator driven by noise. bioRxiv. 2020 doi: 10.1101/793729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz N.A., Aydin C., Lebedeva A., Okun M., Pachitariu M., Bauza M., Beau M., Bhagat J., Böhm C., Broux M., et al. Neuropixels 2.0: A miniaturized high-density probe for stable, long-term brain recordings. Science. 2021;372:eabf4588. doi: 10.1126/science.abf4588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storchi R., Bedford R.A., Martial F.P., Allen A.E., Wynne J., Montemurro M.A., Petersen R.S., Lucas R.J. Modulation of Fast Narrowband Oscillations in the Mouse Retina and dLGN According to Background Light Intensity. Neuron. 2017;93:299–307. doi: 10.1016/j.neuron.2016.12.027. [DOI] [PubMed] [Google Scholar]
- Timofeev I., Steriade M. Low-frequency rhythms in the thalamus of intact-cortex and decorticated cats. J. Neurophysiol. 1996;76:4152–4168. doi: 10.1152/jn.1996.76.6.4152. [DOI] [PubMed] [Google Scholar]
- Uran C., Peter A., Lazar A., Barnes W., Klon-Lipok J., Shapcott K.A., Roese R., Fries P., Singer W., Vinck M. Predictive coding of natural images by v1 activity revealed by self-supervised deep neural networks. bioRxiv. 2021 doi: 10.1101/2020.08.10.242958. [DOI] [Google Scholar]
- van Kerkoerle T., Self M.W., Dagnino B., Gariel-Mathis M.-A., Poort J., van der Togt C., Roelfsema P.R. Alpha and gamma oscillations characterize feedback and feedforward processing in monkey visual cortex. Proc. Natl. Acad. Sci. USA. 2014;111:14332–14341. doi: 10.1073/pnas.1402773111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varela F., Lachaux J.P., Rodriguez E., Martinerie J. The brainweb: phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2001;2:229–239. doi: 10.1038/35067550. [DOI] [PubMed] [Google Scholar]
- Vezoli J., Vinck M., Bosman C.A., Bastos A.M., Lewis C.M., Kennedy H., Fries P. The role of anatomical connection strength for interareal communication in macaque cortex. bioRxiv. 2020 doi: 10.1101/2020.12.15.422902. [DOI] [Google Scholar]
- Vezoli J., Magrou L., Goebel R., Wang X.-J., Knoblauch K., Vinck M., Kennedy H. Cortical hierarchy, dual counterstream architecture and the importance of top-down generative networks. Neuroimage. 2021;225:117479. doi: 10.1016/j.neuroimage.2020.117479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinck M., Bosman C.A. More gamma more predictions: Gamma-synchronization as a key mechanism for efficient integration of classical receptive field inputs with surround predictions. Front. Syst. Neurosci. 2016;10:35. doi: 10.3389/fnsys.2016.00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinck M., Oostenveld R., van Wingerden M., Battaglia F., Pennartz C.M. An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias. Neuroimage. 2011;55:1548–1565. doi: 10.1016/j.neuroimage.2011.01.055. [DOI] [PubMed] [Google Scholar]
- Vinck M., Battaglia F.P., Womelsdorf T., Pennartz C. Improved measures of phase-coupling between spikes and the Local Field Potential. J. Comput. Neurosci. 2012;33:53–75. doi: 10.1007/s10827-011-0374-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinck M., Womelsdorf T., Fries P. In: Principles of Neural Coding. Quiroga-Quia R., Panzeri S., editors. CRC Press; 2013. Gamma-band synchronization and information transmission; pp. 449–470. [Google Scholar]
- Volgushev M., Chistiakova M., Singer W. Modification of discharge patterns of neocortical neurons by induced oscillations of the membrane potential. Neuroscience. 1998;83:15–25. doi: 10.1016/s0306-4522(97)00380-1. [DOI] [PubMed] [Google Scholar]
- Wallace E., Benayoun M., van Drongelen W., Cowan J.D. Emergent oscillations in networks of stochastic spiking neurons. PLoS ONE. 2011;6:e14804. doi: 10.1371/journal.pone.0014804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson H.R., Cowan J.D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Womelsdorf T., Schoffelen J.M., Oostenveld R., Singer W., Desimone R., Engel A.K., Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T., Lima B., Vinck M., Oostenveld R., Singer W., Neuenschwander S., Fries P. Orientation selectivity and noise correlation in awake monkey area V1 are modulated by the gamma cycle. Proc. Natl. Acad. Sci. USA. 2012;109:4302–4307. doi: 10.1073/pnas.1114223109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
-
•
All data reported in this paper will be shared by the lead contact upon request.
-
•
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the Key resources table.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.