Learning and Segmenting Dense Voxel Embeddings for 3D Neuron Reconstruction

Abstract

We show dense voxel embeddings learned via deep metric learning can be employed to produce a highly accurate segmentation of neurons from 3D electron microscopy images. A “metric graph” on a set of edges between voxels is constructed from the dense voxel embeddings generated by a convolutional network. Partitioning the metric graph with long-range edges as repulsive constraints yields an initial segmentation with high precision, with substantial accuracy gain for very thin objects. The convolutional embedding net is reused without any modification to agglomerate the systematic splits caused by complex “self-contact” motifs. Our proposed method achieves state-of-the-art accuracy on the challenging problem of 3D neuron reconstruction from the brain images acquired by serial section electron microscopy. Our alternative, object-centered representation could be more generally useful for other computational tasks in automated neural circuit reconstruction.

I. Introduction

NEURONAL connectivity can be reconstructed from a 3D electron microscopy (EM) image of a brain volume [1], [2]. A challenging and important subproblem is the segmentation of the image into neurons. One state-of-the-art approach applies a convolutional network to detect neuronal boundaries [3]-[6], which are postprocessed to yield a segmentation. Impressive accuracy has been obtained via this approach, and it has proven hard to beat. For example, the boundary detection net of [5] has remained at the top of the leaderboard of the SNEMI3D neuron segmentation challenge¹ for the past three years. All the leading entries of the CREMI challenge² are also boundary detection nets [6], [7].

Alternatives to boundary detection have been proposed. For example, one can train a convolutional net to iteratively extend one object at a time, as in flood-filling nets (FFNs, [8], [9]) and MaskExtend [10]. Cross-classification clustering [11] introduces a multi-object tracking technique based on convolutional/recurrent nets. Among such alternative approaches, FFNs have successfully been employed to densely reconstruct neurons from several real world datasets [9], [12], [13], and follow very closely the boundary detection net of [5] on the SNEMI3D leaderboard. Nevertheless, none of them have so far displaced boundary detection nets from the top of the SNEMI3D and CREMI leaderboards.

This paper will show that dense voxel embeddings from deep metric learning can be segmented to significantly outperform the state-of-the-art strong boundary detection net of [5], the same architecture that leads the SNEMI3D challenge. Convolutional nets are trained to assign similar embedding vectors to voxel pairs within the same objects and well-separated vectors to voxels from different objects [14], [15]. This general approach is by now well-known, but has most often been applied to segment images that contain only a few objects, or a few well-separated instances of each object. Brain images from serial section EM, in contrast, contain many densely intertwined branches of neurons.

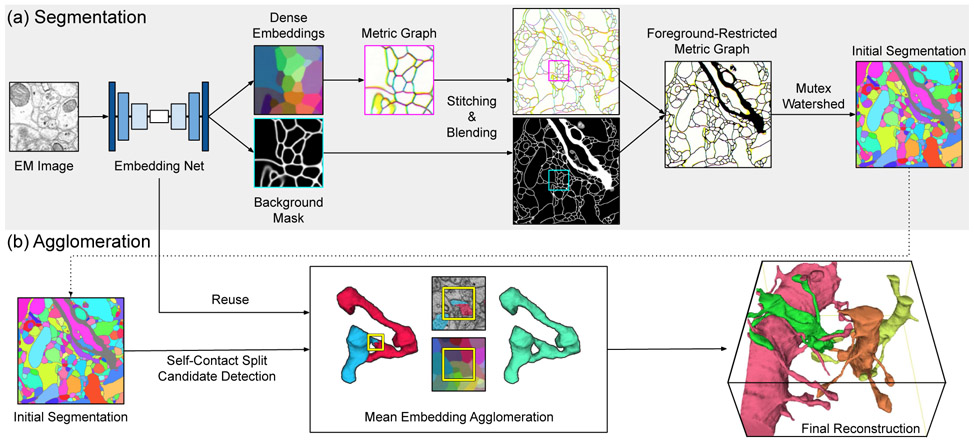
Our postprocessing of the voxel embeddings from deep metric learning contains several key elements. First, affinities between voxel pairs are computed from embeddings generated by a convolutional net operating on 3D patches of limited size. The affinities from overlapping patches are stitched and blended to cover the entire image volume (Fig. 1). Following [16], we use the term “metric graph” to refer to an affinity graph generated by deep metric learning. Second, the metric graph is segmented by the recently proposed Mutex Watershed [17], which exploits long-range as well as short-range affinities. Third, the segmentation is improved by agglomerating pairs of objects with similar mean embedding vectors. Combining these three elements significantly outperforms the state-of-the-art boundary detection net of [5].

Fig. 1.

Overview of the proposed method. Dense voxel embeddings generated by a convolutional net (Sec. III-A) are employed at two subtasks for 3D neuron reconstruction: (a) neuron segmentation via metric graph [16] (Sec. III-B) and (b) agglomeration based on mean embeddings (Sec. III-C). All graphics shown here (images and 3D renderings) are drawn from real data. Although depicted in 2D for clarity, each 2D image represents a 3D volume. To visualize embeddings, we used PCA to project the 24-dimensional embedding space onto the three-dimensional RGB color space. For brevity, we only visualize nearest neighbor affinities on the metric graph by mapping x, y, and z-affinity to RGB, respectively.

The rationale for the above elements is as follows. The restriction to patches of limited size is required by the memory constraint of the GPU. It also has the effect of making the problem easier for the net by limiting the number, size, and complexity of objects contained in the patch.

Naively, one might attempt to stitch and blend embeddings rather than affinities, but this is problematic if the embeddings from two patches are inconsistent in the overlap region.

A great deal of previous work has relied solely on nearest neighbor affinities for segmentation [5], [6]. For example, even when long-range affinities were predicted during training, segmentation at test time was based only on nearest neighbor affinities [5]. A previous application of deep metric learning to 2D neuron segmentation used only nearest neighbor affinities at test time [16], but we found that this did not yield state-of-the-art segmentation accuracy in 3D. By employing the Mutex Watershed [17] we were able to leverage long-range affinities to improve segmentation accuracy.

The Mutex Watershed and mean affinity agglomeration [5], [6] suffer from a failure mode caused by self-contact. For example, a dendritic spine occasionally bends back and contacts the shaft or an adjacent dendritic spine. Such self-contact is problematic because the existence of a boundary there is local evidence that the two contacting parts of the neuron should lie in two different segments. This local evidence may cause the segmentation algorithm to make a split error. We show that many of the self-contact errors can be corrected by agglomerating segments with similar mean embedding vectors.

Our work has three novelties. First, we apply deep metric learning to 3D neuron reconstruction (Sec. III-A), building on previous work in 2D [16]. Second, we combine the Mutex Watershed with a convolutional net trained to generate voxel embeddings (Sec. III-B), whereas it was originally combined with a net trained to directly predict affinities [17]. Third, we recognize the self-contact failure mode, and propose a method of correction using mean embedding agglomeration (Sec. III-C).

Remarkably, we find that deep metric learning outperforms boundary detection by a wide margin, when quantified by variation of information [18] or number of errors. Qualitatively, the accuracy gains come from avoiding split errors for very thin objects and for objects with self-contact.

II. Related Work

A. Boundaries vs. Objects

State-of-the-art methods for serial section EM images (reviewed in [2]) employ convolutional nets to detect neuronal boundaries [5], [6], for which affinity graphs [19] have been widely adopted as underlying representations.

One could argue that the task of detecting boundaries does not force the net to learn about objects, and that more object-centered representations could be critical for further improvements in accuracy. FFNs [8], [9] and MaskExtend [10] extend a single object at a time. Cross-classification clustering [11] extends multiple objects simultaneously. Deep metric learning can also be seen as object-centered, but all objects in the image are processed simultaneously.

B. Postprocessing of Affinity Graphs

Affinity graphs are partitioned to produce an oversegmentation into supervoxels, typically using watershed-type algorithms [20]. Supervoxels can be greedily agglomerated based on simple statistics such as mean affinity [5] or percentiles of binned affinity [6]. Supervoxels can also be agglomerated by optimizing a global objective for graph partitioning, as in the Multicut problem [4].

Recently, [17] has proposed the Mutex Watershed, a greedy algorithm for partitioning signed graphs with both attractive/repulsive edges. This algorithm obviates the need for explicit seeds and tunable thresholds for partitioning, and directly produces a deterministic segmentation, bypassing supervoxel generation. The Mutex Watershed has more recently been integrated into GASP [7], a generalized framework for signed graph partitioning, and has also been extended to incorporate semantics for joint graph partitioning and labeling [21].

C. Refinement of Neuron Segmentation

Biological domain knowledge such as geometric [22] or semantic [23], [24] properties of neurons can be leveraged for agglomeration of supervoxels. Further refinement of segmentation is possible with error detection and correction based on convolutional nets [25], [26]. Unsupervised embeddings of neuronal morphology [27] and supervised classification of neuronal compartments [28] have recently been proposed to detect and correct certain types of merge errors.

We propose mean embedding agglomeration (Sec. III-C) to refine segmentation by agglomerating pairs of objects with similar mean embedding vectors. Independently of our work,³ [30] has proposed to use mean embeddings as one of the several features for agglomerating supervoxels in the 3D instance segmentation of indoor scene. Unlike their method, mean embeddings are our sole feature for agglomeration, and our computation of mean embeddings is restricted to a focused region at the contact between objects, thereby increasing agglomeration accuracy.

D. Deep Metric Learning for 2D Neuron Segmentation

Our work builds on a previous application of deep metric learning to 2D neuron segmentation [16]. Using the loss function of [15], they train a 2D convolutional net to generate dense embeddings, from which nearest neighbor affinities between pixels are computed. The resulting affinity graph, called “metric graph,” [16] is then partitioned with connected components to yield a segmentation.

We extend their method to 3D neuron reconstruction, which requires fundamental changes in the way we generate and exploit the dense embeddings. While they trained a 2D convolutional net to generate dense embeddings on the entire 2D image slice, the extent of 3D dense embeddings is severely limited by the memory constraint of the GPU during both training and inference.

Moreover, a 2D image slice contains neuronal cross sections of relatively simple shape, which are often locally confined within a small space and thus well-isolated. In contrast, a 3D image volume contains intertwined branches of neurons with complex morphology, which extend from one end of the volume to another most of the time. As a consequence, increasing the input size in 2D would not necessarily increase the size and complexity of contained objects, whereas doing so in 3D would obviously increase the both. This poses a fundamental challenge to learning dense embeddings in 3D.

E. Dense Embeddings via Deep Metric Learning

The concept of learning dense embeddings with convolutional nets first appeared in [31]. The core idea is to densely map each pixel in the image to a vector in the embedding space, such that the learned embeddings are useful for downstream tasks. The first applications of dense embeddings include semantic segmentation [31] and multi-person pose estimation [32].

Dense embeddings soon started to gain popularity in the problem of semantic instance segmentation [14], [15]. In this approach, the loss function encourages the embedding vectors to form discriminative clusters for each object instance, and the clustered embeddings are directly utilized to produce an instance segmentation. While [14] implements an embedding loss by randomly sampling image pixel pairs, the loss function proposed by [15] is centered around mean embeddings and their interactions. The latter has extensively been applied to a wide variety of computer vision problems [30], [33]-[36].

Instead of the Euclidean embedding of [14], [15], the hyper-spherical embedding based on cosine similarity has also been proposed in several applications [37]-[41]. Notably, [39]-[41] show that locally exerting inter-cluster repulsive forces only to spatially neighboring instances is effective at cell segmentation and tracking from light microscopy images, which contain sparsely dispersed and well-isolated cells as opposed to the densely packed and intertwined neurons in EM images.

Our proposed method bears similarities with the method of [42] for instance segmentation of fibers in polymer material. Using the loss of [15], they train a 3D convolutional net to learn dense voxel embeddings for local patches of 3D CT scans. The main difference is in postprocessing; they directly segment each patch-wise embeddings and then iteratively stitch the segmentations between neighboring patches with overlap. Their simple stitching strategy based on the distance between segmented fibers was prone to merge errors [42].

III. Methods

A. Loss Function

We use the loss function of [15], which was applied by [16] to 2D neuron segmentation. They refer to it as “means-based loss,” because the mean embeddings of distinct objects act as cluster centers. The “internal” term of (1) pulls embeddings toward the respective cluster centers, the “external” term of (2) pushes distinct cluster centers apart from each other, and the regularization term of (3) prevents all cluster centers from deviating too far from the origin:

$${\mathcal{L}}_{\text{int}}=\frac{1}{C}\sum _{c=1}^C\frac{1}{N_c}\sum _{i=1}^{N_c}\Vert {\mu }_c-x_i{\Vert }^2,$$ (1)

$${\mathcal{L}}_{\text{ext}}=\frac{1}{C(C-1)}\underset{c_A\ne c_B}{\sum _{c_A=1}^C\sum _{c_B=1}^C}\max (2{\delta }_d-\Vert {\mu }_{c_A}-{\mu }_{c_B}\Vert ,0{)}^2,$$ (2)

$${\mathcal{L}}_{\text{reg}}=\frac{1}{C}\sum _{c=1}^C\Vert {\mu }_c\Vert .$$ (3)

Here C is the number of ground truth objects, N_c is the number of voxels in object c, μ_c is the mean embedding for object c, x_i is an embedding for voxel i, ∥·∥ is the L1 norm, δ_d is the margin for the external loss term (2). We choose δ_d = 1.5 following [15], [16]. Note that only those voxels that belong to the ground truth objects (i.e., foreground objects) are taken into account in (1)-(3). The embeddings for background voxels are not included in the loss.

The embedding loss ${\mathcal{L}}_{\text{embedding}}$ is a weighted sum of the three terms, ${\mathcal{L}}_{\text{embedding}}=\alpha {\mathcal{L}}_{\text{int}}+\beta {\mathcal{L}}_{\text{ext}}+\gamma {\mathcal{L}}_{\text{reg}}$, where α = β =1 and γ = 0.001 as in [16].

Besides the embedding loss, we additionally predict a voxel-wise background mask (Fig. 1) using the standard binary cross-entropy loss. The total loss is a sum of the embedding and background losses, ${\mathcal{L}}_{\text{total}}={\mathcal{L}}_{\text{embedding}}+{\mathcal{L}}_{\text{background}}$.

It is challenging for a convolutional net to generate embedding vectors that are uniform across neurons, because of their complex and extended morphologies. For achieving approximate uniformity in 3D, we found the means-based loss of [15] to be superior to other proposed loss functions for deep metric learning, much as [16] found in 2D.

Sometimes parts of the same neuron may seem to be distinct objects when they are restricted to a local patch of limited context. For achieving better generalization performance, [16] found it critical to locally recompute connected components of the ground truth objects in each training patch, and then remove from (2) the pairwise interactions between the locally split object parts. We confirmed their finding in our preliminary experiment, and therefore used the same trick.

B. Segmentation with Metric Graph

We define an affinity a_ij ∈ [0, 1] between a pair of voxels i and j by

$$a_{ij}=\max {\left(\frac{2{\delta }_d-\Vert x_i-x_j\Vert }{2{\delta }_d},0\right)}^2,$$ (4)

where x_i and x_j are embeddings for the voxel i and j, respectively. Note that this definition is directly derived from the term max (2δ_d − ∥μ_CA − μ_CB∥, 0)² in (2); we simply normalize it to [0, 1] after replacing the mean embeddings μC_A, μC_B with the voxel embeddings x_i, x_j. The affinity a_ij approaches 1 as x_i and x_j get closer in the embedding space, whereas a_ij approaches 0 as x_i and x_j become more distant.

Once the embedding net generates dense voxel embeddings for a local image patch, we can construct a patch-wise metric graph [16] whose nodes are voxels and edge weights are metric-derived affinities between voxel pairs.

Reference [16] explored only the simplest possible form of metric graph and postprocessing, i.e., nearest neighbor metric graph partitioned by connected components clustering. However, we found in our 3D experiments that nearest neighbor affinities are occasionally noisy, primarily due to the noisy embeddings for the background voxels, which were excluded from the embedding loss and thus did not receive explicit training signals (Supp. Fig. S6).

To address this issue, and to push the segmentation accuracy further, we augmented our metric graph and its postprocessing by (a) incorporating long-range affinities into the metric graph and exploiting them as repulsive constraints during graph partitioning, and (b) removing noisy affinities from the metric graph using a voxel-wise background mask predicted by the embedding net (Fig. 1).

To mask out noisy affinities, we first defined background voxels by thresholding the predicted real-valued background mask with θ_mask (empirically chosen on the validation set), and then removed the background voxels (nodes) along with every incident affinities (edges) from the metric graph.

The resulting “foreground-restricted” metric graph (Fig. 1) was used as input to the Mutex Watershed [17], a recently proposed algorithm for partitioning a graph with both attractive/repulsive edges. They trained a 2D convolutional net to directly predict affinities on a small predefined set of short and long-range edges, thus only a fixed graph could be generated. We have no such limitation; affinities on any edge can be dynamically computed from the dense voxel embeddings, being much more flexible.

C. Mean Embedding Agglomeration

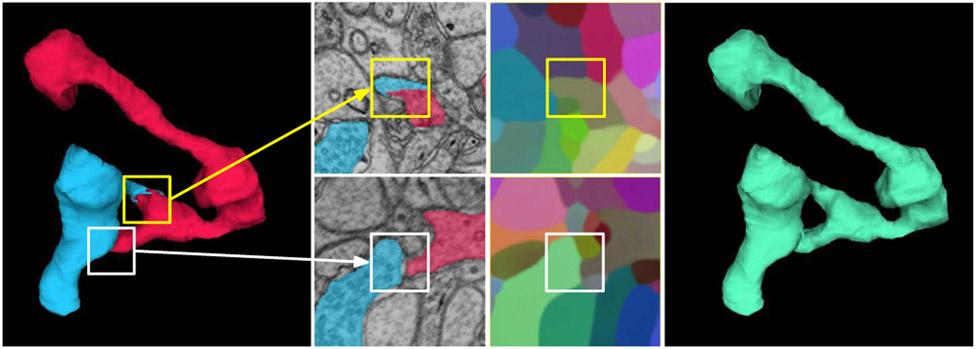
We observed that both the Mutex Watershed [17] for our proposed method and mean affinity agglomeration [5] for the baseline (Sec. III-D) make systematic split errors on objects with self-contact (Fig. 2). These greedy clustering/agglomeration algorithms suppress localized mistakes in the input graph by averaging out noisy affinities (mean affinity agglomeration) or by putting long-range repulsive constraints as a safeguard in locations with more certainty (the Mutex Watershed). However, they often fail to reconcile the local evidence for disconnectivity at self-contacts (e.g., white box in Fig. 2) with the evidence for connectivity elsewhere (e.g., yellow box in Fig. 2), if the former precedes the latter in greedy decision making.

Fig. 2.

Mean embedding agglomeration (Sec. III-C). Shown here is a real example of self-contacting axon from the validation set. Left: a false split error (yellow box) in the Mutex Watershed [17] segmentation caused by a self-contact (white box). Middle top: PCA visualization reveals homogeneous embeddings across the false split. Middle bottom: each side of the self-contact receives distinct embedding vectors (white box). Note that the both sides appear to be distinct objects in the limited local context. Right: mean embedding agglomeration correctly heals the false split.

To address this systematic failure mode, we detected the candidates for self-contact split errors based on a simple and intuitive heuristic. Specifically, we first constructed a region adjacency graph (RAG) from the initial segmentation, where nodes are segments and edges represent spatial adjacency, i.e., whether two segments are contacting each other. Then the foreground-restricted metric graph was reused to compute an agglomeration score S of each individual contact between adjacent segments. To compute S, we averaged nearest neighbor affinities between interfacing voxels at each contact.

We selected a pair of adjacent segments as candidate if (a) they have multiple contacts, and (b) the highest S among the multiple contacts is above a certain threshold θ_self-contact (chosen empirically on the training and validation sets). Intuitively, self-contact splits should have at least two contacts, false split and self-contact (Fig. 2), and the false split is likely to have high agglomeration score.

Each candidate is a triplet (s₁, s₂, (x, y, z)), where s₁ and s₂ are the pair of candidate segments and (x, y, z) is the centroid coordinate of the contact with the highest S. Given a list of candidates detected by the heuristic, we reused the embedding net without any modification to make an agglomeration decision (Fig. 2). Specifically, we generated dense voxel embeddings on each local image patch centered on (x, y, z), and then computed mean embeddings μ_s1 and μ_s2 of the restrictions of s₁ and s₂ to a central “focal” widow of size p_x × p_y × p_z (e.g., yellow box in Fig. 2). The two candidate segments were agglomerated if the L1 distance d = ∥μ_s1 − μ_s2∥ is below a predetermined threshold θ_d. The parameters p_x, p_y, p_z, and θ_d were determined empirically on the training and validation sets.

D. Establishing a Strong Baseline

As a strong baseline, we reproduced the state-of-the-art result of [5], which is currently leading the SNEMI3D benchmark challenge. They train a 3D variant of U-Net [43] to directly predict nearest neighbor affinities as a primary training target [19], and long-range affinities as an auxiliary training target. The predicted nearest neighbor affinities are then partitioned with a variant of watershed algorithm [20] to produce an initial oversegmentation. Although the costly 16× test-time augmentation [3], [5] produced the best result (the top entry of the SNEMI3D leaderboard), mean affinity agglomeration without test-time augmentation was shown to be competitive while being efficient [5]. Therefore, we included both postprocessing methods in our strong baseline results.

Additionally, we performed a preliminary experiment with baseline models to test the following hypothesis: can we obtain segmentation with comparable accuracy from the images with lower resolution? This is an important question because connectomics is facing an imminent challenge of scaling up to petascale data [44]. We performed dual experiments with the original images (voxel resolution: 6 × 6 × 29 nm³) and 2 × in-plane-downsampled images (voxel resolution: 12 × 12 × 29 nm³), and found no significant drop in accuracy (Supp. Fig. S13). Therefore, we performed our main experiment exclusively using the 2× in-plane-downsampled images.

IV. Experimental setup

A. Dataset

Since its 2013 launch, the SNEMI3D benchmark challenge has catalyzed remarkable progress in automated neuron reconstruction algorithms [3]-[5], [11]. As mentioned earlier, self-contact is a major failure mode for one of the leading SNEMI3D submissions [5]. We noticed a qualitative difference in neuronal morphology between SNEMI3D’s training and test sets. While the test set contains large spiny dendrites with many self-contacting spines, the training set barely contains them. Therefore we decided to create a training set containing more examples of self-contact.

We used the publicly available AC3/AC4 dataset,⁴ which is a superset of SNEMI3D. AC3 and AC4 are human-labeled subvolumes from the mouse somatosensory cortex dataset of [45], which was acquired by serial section EM. The sizes of AC3 and AC4 are 1024 × 1024 × 256 and 1024 × 1024 × 100 voxels, respectively, at 6 × 6 × 29 nm³ voxel resolution. We used AC4 and the bottom 116 slices of AC3 for training, the middle 40 slices of AC3 for validation, and the top 100 slices of AC3 for testing.

The SNEMI3D training set is AC4 only, and the SNEMI3D test set is the top 100 slices of AC3. In other words, this paper’s training set is the SNEMI3D training set plus some of AC3. This paper’s test set is the same as the SNEMI3D test set, except that extra image padding was obtained from the full image stack of [45],⁵ and used at test time only to provide enough image context for preventing systematic drop in accuracy near the dataset edge.

Since this paper uses an enlarged training set, we are retraining the leading SNEMI3D submission [5] and using it as a strong baseline for comparison in our main experiment (Sec. V). We note that SNEMI3D has not, strictly speaking, been a blind challenge since the publication of AC3/AC4 [45]. Submissions to SNEMI3D are on an honor system. To enable objective comparison with other methods, we have also retrained our proposed method strictly under the SNEMI3D challenge setup and submitted the result to the leaderboard (Supp. Note). Our code and data will be made available at https://github.com/seung-lab/devoem.

B. Network Architecture

We used a modified version of the “Residual Symmetric U-Net” architecture of [5]. We used a 128 × 128 × 20 voxel input patch for both training and inference, using 2× in-plane-downsampled images. The net produces as output 24-dimensional dense voxel embeddings, as well as a single channel background mask. These outputs are then spatially cropped to 96 × 96 × 16 in order to reduce uncertainty near the patch border. To give more expressive power, we linearly scaled the embeddings with a learnable scalar parameter, which was initialized to 0.1 at the beginning of training. For upsampling, we used the bilinear resize convolution [46], i.e., bilinear upsampling followed by a pointwise (1 × 1 × 1) convolution. Further details are illustrated in Supp. Fig. S8.

C. Data Augmentation

We used the same training data augmentation as in [5]. This includes flip & rotation by 90°, brightness & contrast perturbation, warping, simulated misalignment, simulated out-of-focus and missing sections.

Additionally, we introduced a novel “slip interpolation” that substitutes the slip-type simulated misalignment of [5] (Supp. Fig. S10). Specifically, we simulated the slip-type misalignment only in the input, not in the target. The mismatch between the input and target forces the nets to ignore any slip misalignment in the input and produce smoothly interpolated target prediction.

D. Training Details

We performed all experiments with PyTorch. We trained our nets on four NVIDIA Titan X Pascal GPUs using synchronous gradient update. We used the AMSGrad variant [47] of the Adam optimizer [48], with α = 0.001, β₁ = 0.9, β₂ = 0.999, and ϵ = 10⁻⁸. We used a single training patch (i.e., minibatch size of 1) for each model replica on GPUs at each gradient step. We trained the baseline and embedding nets for three and five days, respectively, and selected the model checkpoints at the lowest validation error.

E. Inference

We used the overlap-blending inference of [5]. Both the baseline and embedding nets used the most conservative output overlap of 50% in x, y, and z-dimension. The embedding net’s output cropping incurred nearly 2× overhead relative to the baseline, which did not use output cropping. This is because the 50% overlap between cropped outputs amounts to the overlap higher than 50% between inputs, thus increasing the coverage factor for each input voxel.

F. Metric Graph & Postprocessing

To construct the metric graph as input to the Mutex Watershed [17], we used three nearest neighbor attractive edges and nine long-range repulsive edges. Specifically, each edge is characterized by an offset vector. An affinity map for a given edge is constructed by computing a map of metric-derived affinities (using (4) in Sec. III-B) between a reference grid of voxels and another grid of voxels shifted by the characteristic offset vector. The list of (x, y, z) offset vectors we used is (−1,0,0), (0,−1,0), (0,0,−1), (0,0,−2), (−5,0,0), (0,−5,0), (−5,−5,0), (−5,5,0), (−5,0,−1), (0,−5,−1), (−5,0,1), and (0,−5,1). These 12 edges (or offset vectors) yield 12 affinity maps that comprise the resulting metric graph (Supp. Fig. S12).

We grid searched the postprocessing parameters strictly on the training and validation sets. Selected parameters were θ_mask = 0.6, θ_self-contact = 0.25, θ_d = 1.5, and p_x × p_y × p_z = 32 × 32 × 5.

G. Evaluation

For quantitative evaluation of segmentation quality, we adopted the widely-used variation of information (VI), [18], [49], VI = VI_split + VI_merge = H(S∣T) + H(T∣S), where H (·∣·) is the conditional entropy, S is the segmentation proposal, and T is the ground truth segmentation.

V. Results

A. Quantitative Analysis

Table I shows the quantitative evaluation of different methods on the test set. To evaluate segmentation quality, we adopted the widely-used variation of information (VI) error metric [18]. Metric graph followed by the Mutex Watershed produced an initial segmentation with high precision, which is indicated by the low VI_merge of 0.0163. However, the initial segmentation largely suffered from the systematic self-contact split errors (Sec. V-C), which are reflected in the high VI_split of 0.1025.

TABLE I.

Test Set Evaluation Result

Method	Postprocessing	VI ↓	VIsplit ↓	VImerge ↓
Baseline†	Watershed [20]	0.0798	0.0574	0.0224
Baseline*†	Watershed [20] + Test-Time Augmentation (16×) [3], [5]	0.0610	0.0475	0.0135
Baseline	Watershed [20] + Mean Affinity Aggl. [5]	0.1049	0.0877	0.0172
Hybrid	Watershed [20] + Mean Affinity Aggl. [5] + Mean Embedding Aggl. (Sec. III-C)	0.0572	0.0399	0.0173
Proposed	Mutex Watershed [17]	0.1188	0.1025	0.0163
Proposed	Mutex Watershed [17] + Mean Embedding Aggl. (Sec. III-C)	0.0470	0.0276	0.0194

^†For these baselines, we chose the best possible operating point by optimizing postprocessing parameters directly on the test set, giving advantage over our proposed method.

^↓The lower, the better.

Remarkably, mean embedding agglomeration healed almost all of these self-contact split errors (Sec. V-C), resulting in a precipitous drop in VI_split from 0.1025 to 0.0276. With this substantial improvement, our proposed method outperformed all baselines in VI. We found that the slight increase in VI_merge from 0.0163 to 0.0194 after mean embedding agglomeration was caused by the correct agglomeration of a self-contacting glia fragment, which already contained a small merge error. As exemplified by this, VI is sensitive to the size of erroneous objects, and thus tends to hide underlying qualitative difference especially when comparing highly accurate methods. Therefore, we will present rigorous qualitative analyses in the following sections.

B. Improvements on Very Thin Objects

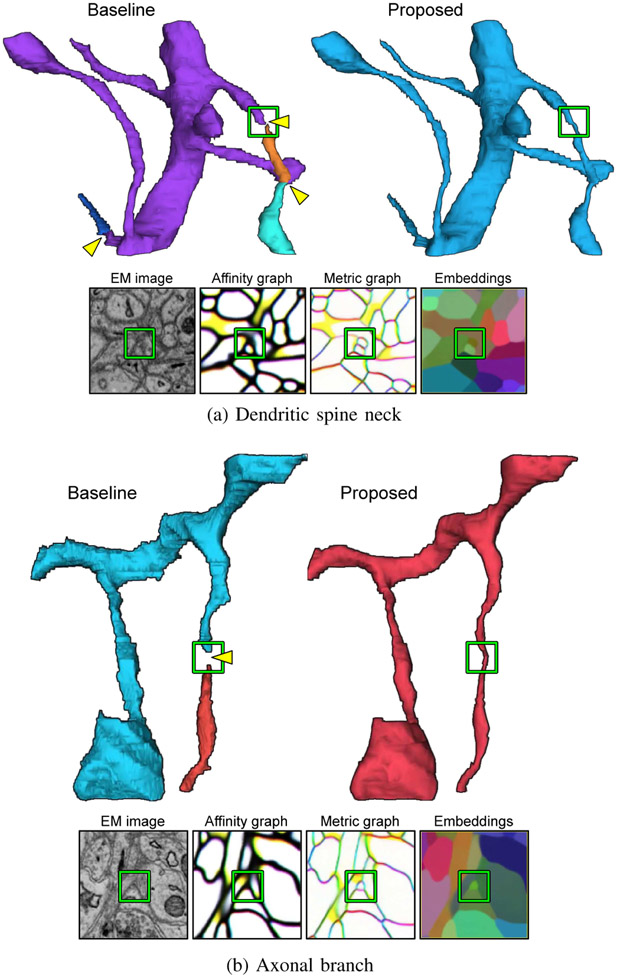
Neuronal branches, or neurites, can become very thin, such as in the thinnest part of axons and dendritic spine necks [50]. Being capable of tracing such thin neurites is crucial for reconstructing neuronal connectivity. Qualitatively, we observed that our proposed method performs substantially better on very thin objects compared to the baseline. Visualization reveals how the object-centered representation of dense voxel embeddings could outperform the boundary-centered representation of the baseline on the thin objects (Fig. 3-4).

Fig. 3.

Our proposed method (bottom row) correctly segments a very difficult thin spine neck that is parallel to the imaging plane.

Fig. 4.

Comparison on the thinnest parts of neurites. Yellow arrowheads indicate split errors.

Fig. 3 compares segmentation accuracy of the baseline and proposed methods on a very thin spine neck that is parallel to the imaging plane. The thinnest parts (yellow arrowheads in Fig. 3) are so severely constricted that it is extremely difficult for the boundary-centered baseline to learn and represent the object continuity. In contrast, our embedding net was able to assign similar vectors across the constricted parts, yielding a metric graph that could represent the object continuity adequately (Fig. 3).

Further examples of extremely thin parts of neurites in different orientations are shown in Fig. 4a (oblique spine neck) and Fig. 4b (vertical axonal branch). The thinnest parts are again so severely constricted that their cross sections are barely recognizable in the EM images. The boundary-centered baseline totally failed at recognizing the cross sections, whereas our embeddings and metric graph captured them successfully (Fig. 4a, 4b). It is remarkable that learning about object rather than boundary enables the net to virtually “imagine through” the input image that lacks much evidence for object continuity.

C. Effectiveness of Mean Embedding Agglomeration

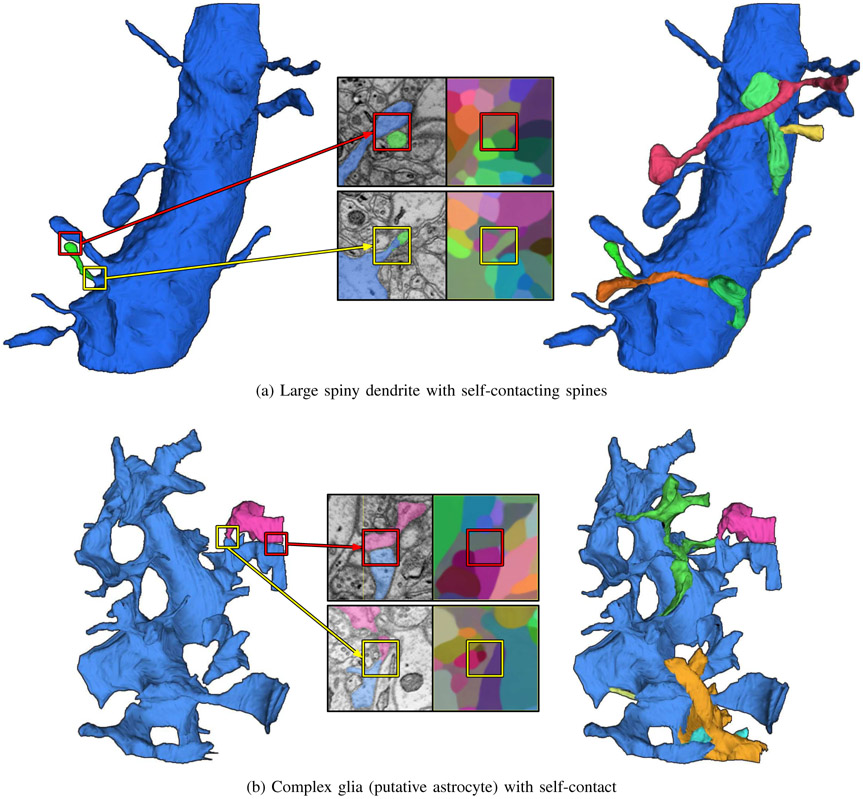
As we mentioned earlier, our initial segmentation produced with the Mutex Watershed contained systematic split errors caused by objects with complex self-contact. They were found mostly in large spiny dendrites (Fig. 5a) and astrocytes, a kind of glia (Fig. 5b). Since our proposed method is based on dense voxel embeddings for local image patches, their limited context may make a self-contact seem like a boundary between two distinct objects (e.g., red boxes in Fig. 5a, 5b). Consequently, the Mutex Watershed may put long-range repulsive constraints across the self-contact, making a false split error.

Fig. 5.

Mean embedding agglomeration successfully corrects most of the self-contact split errors. Left: one of the self-contact split errors (top: green spine, bottom: pink glia fragment) is displayed along with the main object (top: dendritic shaft, bottom: glia body). Middle: visualization of embeddings at the self-contact (red box) and false split (yellow box). Right: final reconstruction after applying mean embedding agglomeration.

We found that mean embedding agglomeration (Sec. III-C) is highly effective at agglomerating the self-contact split errors, without introducing new merge errors. Examples from the test set are shown in Fig. 5a, 5b.

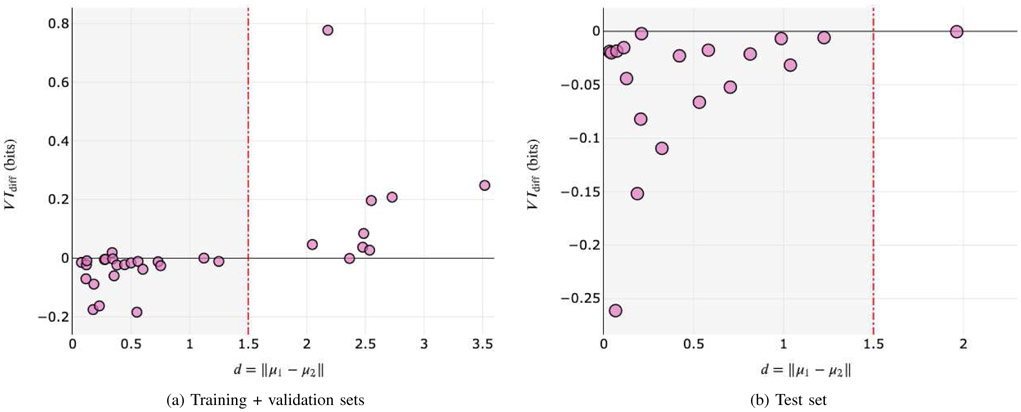
Fig. 6a shows an analysis on how we selected the decision boundary θ_d for mean embedding agglomeration on the training and validation sets. Pink circles represent individual agglomeration candidates selected by the heuristic described in Sec. III-C. Horizontal axis represents the L1 distance d = ∥μ₁ − μ₂∥ between the mean embeddings of two agglomeration candidates, and vertical axis represents VI_diff, which is the change in VI when the two candidates are forced to be agglomerated. Here we computed VI_diff within each local patch for agglomeration.

Fig. 6.

Analysis on individual decisions made by mean embedding agglomeration on (a) training + validation sets and (b) test set. Pinky circles represent individual agglomeration candidates selected by the heuristic described in Sec. III-C. Vertical axes represent the change in VI after agglomeration, and horizontal axes represent the distance between mean embeddings. See main text for details.

We grid searched the agglomeration decision boundary θ_d on the training and validation sets. Fig. 6a shows that the resulting θ_d = 1.5 nicely separates the true positive self-contact splits (left to the decision boundary in Fig. 6a) from the false positives (right to the decision boundary in Fig. 6b). Although determined empirically, the optimal θ_d = 1.5 turned out to be equivalent to the δ_d = 1.5 of (2) in Sec. III-A, being theoretically reasonable.

Next, we performed a similar postmortem analysis on how effective mean embedding agglomeration was on the test set (Fig. 6b). Among 19 candidates selected by the heuristic, 18 were agglomerated correctly (true positives, left to the decision boundary in Fig. 6b) and one was rejected incorrectly (true negative, right to the decision boundary in Fig. 6b). The true negative rejection was caused by a self-contact within the field of view of the embedding net. We found it hard to fix this particular failure mode, which is illustrated with a representative example in Supp. Fig. S16.

To further demonstrate the effectiveness of mean embedding agglomeration, we additionally applied it to the baseline segmentation that was postprocessed with mean affinity agglomeration, which was also reported to suffer from systematic self-contact split errors [5]. Remarkably, mean embedding agglomeration significantly reduced VI_split without any increase in VI_merge (“Hybrid” in Table I), outperforming all baselines in VI. Nevertheless, this hybrid approach was still slightly inferior to our proposed method (Table I).

D. Further Evaluation on Extra Test Sets

We questioned whether the difference between our proposed method and the baselines could still hold outside the dataset used for our experiments. This is a critical question because we divided the single volume of AC3 into training, validation, and test sets. The outstanding test set performance of our proposed method could have been attributable, at least partly, to statistical similarity between the training, validation, and test sets due to their spatial proximity.

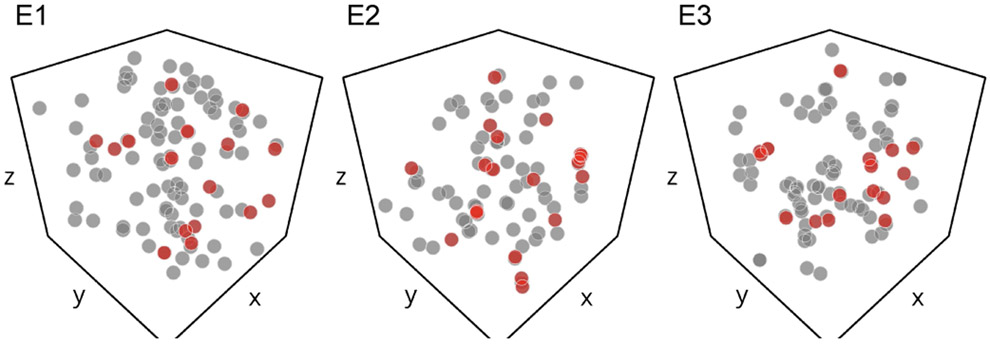
To address this question, three extra image volumes (namely E1, E2, and E3) of the same size as the test set were obtained from randomly chosen locations in the full dataset of [45] (Supp. Fig. S2). We applied both our proposed method and the best baseline (“Baseline*” in Table I) on these volumes, and four expert brain image analysts exhaustively examined every single segment to find out remaining errors.

Fig. 7 visualizes the spatial distribution of individual merge/split errors from the baseline and proposed method in E1–E3. There were 17.3 ± 1.33 and 75.0 ± 7.23 remaining errors (mean ± S.E., N = 3) from the proposed and baseline method, respectively (Table II). These results suggest that our proposed method produces a significantly lower number of errors compared to the strong baseline (p = 0.0014, paired sample t-test), although one should be cautious about the small number of sample volumes (N = 3).

Fig. 7.

Spatial distribution of remaining errors in three extra test volumes E1–E3. Gray circles: remaining errors in the best baseline segmentation. Red circles: remaining errors in the proposed segmentation.

TABLE II.

Number of Errors in Extra Test Sets

	E1	E2	E3	Mean ± S.E.
Baseline	87	62	76	75.0 ± 7.23
Proposed	16	20	16	17.3 ± 1.33

Qualitatively, we observed a similar tendency that our proposed method performs substantially better at very thin objects while mean embedding agglomeration successfully healed most of the self-contact split errors. However, we also found that there remained some uncaught self-contact split errors, mostly due to the heuristic’s failure in detecting them (Supp. Fig. S14).

VI. Discussion

Learning dense voxel embeddings can be viewed as learning a “panoptic” representation of all objects in a scene. While being similar in learning an object-centered representation, our approach is contrasted with FFNs [8], [9], which focus on a single object in a scene. This difference may make the two approaches complementary to each other. For instance, [9] employs FFNs for agglomeration as well as for generating an initial oversegmentation. Their FFN-based agglomeration could possibly be complemented with the panoptic representation of dense voxel embeddings.

In principle, our proposed method is not linearly scalable due to the supra-linear time complexity of the Mutex Watershed [17] algorithm, not to mention the obvious limitation in memory. In practice, such limitations can be overcome by partitioning an entire dataset into tractable subvolumes, which can be independently segmented in parallel and then stitched together to produce a global segmentation.

Although such a “block-stitching” approach has been shown to work in practice [9], [51], introducing stitching errors may be inevitable especially when using simplistic stitching algorithms, e.g., that are based solely on segmentation overlap between blocks (i.e, subvolumes). To reduce stitching errors while limiting computation overhead, dense voxel embeddings could be selectively employed to resolve only those ambiguous cases in stitching.

We have seen that the self-contact motifs can cause problems in segmentation because they present opposing local and global connectivity depending on the size of context. We found that they also raise a tricky technical issue when preparing local training patches. As we briefly mentioned in Sec. III-A, recomputing connected components of the ground truth objects in a local training patch of limited context is an important preprocessing step. With this preprocessing, the self-contacting parts of a neuron should be cleaved into distinct pieces if they are connected outside the local training patch. However, we observed that locally recomputing connected components occasionally fails to cleave such self-contact, depending on whether background voxels properly form a separating “gap” at the self-contact (Supp. Fig. S15).

Consequently, numerous self-contacts in glia (e.g., see Fig. 5b) became a significant source of inconsistency that confuses the embedding net during training, resulting in occasional generalization failures specific to glia. Therefore, it would be necessary to carefully remove such inconsistency in the future. Alternatively, targeted detection and special handling of glia could be a remedy to this problem. For instance, the Semantic Mutex Watershed [21] combined with glia detection could be effective at preventing merge errors between neurons and glia.

VII. Conclusion

We have presented a novel application of dense voxel embeddings for 3D neuron reconstruction. We have demonstrated that our proposed method outperforms the state-of-the-art method based on boundary detection [5], and that learning an object-centered representation enables substantial improvements on very thin objects. Future work will include scale-up of the proposed method with block-stitching [9], [51] and large-scale evaluation on real world datasets. Our dense voxel embeddings could be more generally useful for other computational tasks in the connectomics pipeline. For instance, the error detection and correction system of [25] could be further enhanced with the rich information in dense voxel embeddings.