Modeling and analysis of the macronutrient signaling network in budding yeast

Abstract

Adaptive modulation of the global cellular growth state of unicellular organisms is crucial for their survival in fluctuating nutrient environments. Because these organisms must be able to respond reliably to ever varying and unpredictable nutritional conditions, their nutrient signaling networks must have a certain inbuilt robustness. In eukaryotes, such as the budding yeast Saccharomyces cerevisiae, distinct nutrient signals are relayed by specific plasma membrane receptors to signal transduction pathways that are interconnected in complex information-processing networks, which have been well characterized. However, the complexity of the signaling network confounds the interpretation of the overall regulatory “logic” of the control system. Here, we propose a literature-curated molecular mechanism of the integrated nutrient signaling network in budding yeast, focusing on early temporal responses to carbon and nitrogen signaling. We build a computational model of this network to reconcile literature-curated quantitative experimental data with our proposed molecular mechanism. We evaluate the robustness of our estimates of the model’s kinetic parameter values. We test the model by comparing predictions made in mutant strains with qualitative experimental observations made in the same strains. Finally, we use the model to predict nutrient-responsive transcription factor activities in a number of mutant strains undergoing complex nutrient shifts.

INTRODUCTION

In yeast and other eukaryotes, the sensing and transmission of distinct classes of macronutrient signals are carried out by specialized signaling pathways (Conrad et al., 2014). These environmental signals, which may be synergistic or antagonistic, are processed within the cell by cross-talk among the signal-transduction pathways in order to produce an adaptive and robust response to the nutritional environment of the cell. This response ultimately manifests itself physiologically in a modulation of the growth rate of the cell, by regulation of global transcriptional and translational activities (Schaechter et al., 1958; Metzl-Raz et al., 2017). Adaptive modulation of the global cellular growth state is crucial for the survival of unicellular organisms that are exposed to fluctuating environments.

Budding yeast Saccharomyces cerevisiae is an ideal eukaryotic organism in which to study nutrient signaling for three reasons: it is a unicellular “model” organism whose metabolism has been thoroughly characterized from many angles, its genetic constitution is well known and easily manipulated by standard techniques, and there is a large degree of molecular homology between yeast and mammalian nutrient signaling systems (Virgilio and Loewith, 2006b; Chantranupong et al., 2015). Despite this high degree of homology, the nutrient signaling system plays divergent roles in yeast and in mammals. In budding yeast cells, the default state is exponential growth, and nutrient starvation signals inhibit cell growth. In mammalian cells, on the other hand, the default state is the inhibition of growth, despite abundant and continuous availability of nutrients in the bloodstream. Cell growth and division is stimulated by hormonal signals that trigger growth pathways in competent cells. Dysregulation of the default state in mammalian cells leads to a (yeast-like) growth and proliferation state that is characteristic of cancer cells.

In yeast, distinct pathways sense and signal the sufficiency of the two major classes of macronutrients, carbon and nitrogen. The Ras/cAMP/Protein Kinase A (PKA) pathway largely conveys the glucose status of the environment, suppressing carbon adaptation and general stress responses when glucose is plentiful, while up-regulating ribosome biogenesis and the overall growth rate (Mbonyi et al., 1988, 1990; Verstrepen et al., 2004; Zaman et al., 2009). When glucose is in short supply, the Snf1 pathway shuts off catabolite repression and up-regulates carbon adaptation responses (Schöler and Schüller, 1994; Cherkasova et al., 2010). In the presence of rich nitrogen sources, the TORC1 pathway activates nitrogen catabolite repression (NCR) and up-regulates ribosome biogenesis via the Sch9-kinase branch (Powers and Walter, 1999; Magasanik and Kaiser, 2002; Martin et al., 2006; Cipollina et al., 2008). In response to declining nitrogen status, the Tap42-Sit4/PP2A phosphatase branch activates nitrogen adaptation responses (Como and Arndt, 1996).

While the upstream sensing mechanisms are nutrient specific, the downstream signal-processing network is characterized by cross-talk among the signaling pathways just described. Consequently, how the cell responds to specific combinations of nutrients depends on complex interactions among key regulatory enzymes in the network (Mayordomo et al., 2002; Jorgensen, 2004; Roosen et al., 2005; Yorimitsu et al., 2007; Deprez et al., 2018). In yeast, the pathways responsive to particular nutrients have been well studied, but the molecular decision-making carried out by the network as a whole remains unclear. The complexity of the system obfuscates the interpretation of experimental observations, based on genetic and environmental perturbations that interrogate the nutrient adaptation responses (Hallett et al., 2014).

In the study of such complex biochemical control systems, dynamical modeling has proven to be useful in determining cellular behaviors that result from entangled molecular interactions (Kim et al., 2010; Gunawardena, 2014; Kraikivski et al., 2015). These dynamical models are often presented as systems of nonlinear ordinary differential equations (ODEs) built from biochemical rate laws describing the reaction steps that constitute the biochemical interaction network. Previous authors have published ODE models (see Box 1) of nutrient signaling in yeast cells in restricted physiological contexts. In this paper, we construct a model of broader scope based on a literature-curated diagram of carbon and nitrogen signaling, focusing on the short-term response of yeast cells to nutrient stresses. The nonlinear ODE model based on this diagram is calibrated with time-series measurements of key regulatory proteins as well as perturbation experiments carried out on wild-type and mutant strains. Finally, we use the calibrated model to predict nutrient responses of yeast cells under novel conditions.

Box 1. Previously published models.

The cAMP-PKA pathway. Using a nonlinear ODE model, Garmendia-Torres et al. (2007) investigated the PKA-mediated regulation of Msn2/4 nucleocytoplasmic oscillations, capturing the essential feedback loops in the PKA activation mechanism (Garmendia-Torres et al., 2007). Gonze et al. (2008) proposed a stochastic version of this model (Gonze et al., 2008). Cazzaniga et al. (2008) investigated the guanine nucleotide exchange reactions in the PKA activation mechanism but failed to capture the short time-scale behavior of cAMP dynamics (Cazzaniga et al., 2008; Pescini et al., 2012). Stewart-Ornstein et al. (2017) presented a simplified mechanism to investigate, both computationally and experimentally, the upstream mechanism of cAMP activation (Stewart-Ornstein et al., 2017). Williamson et al. (2009) created a full model of the PKA pathway, incorporating substantial mechanistic details with respect to alternative PKA activation mechanisms, with a focus on understanding features of cAMP regulation (Williamson et al., 2009). In order to account for experimental observations not captured by these models, Gonzales et al. (2013) used a simplified mechanism to investigate strain-specific cAMP oscillatory dynamics (Gonzales et al., 2013). All the models described in this paragraph have focused on the mechanism of cAMP regulation, or the regulation of Msn2/4 nucleocytoplasmic oscillations purely in response to glucose abundance or starvation.

The Snf1 pathway. Garcia-Salcedo et al. (2014) systematically explored a series of hypothetical interactions in the Snf1 pathway in order to identify a high confidence network topology that recapitulated experimentally observed phenotypes (García-Salcedo et al., 2014). More recently Welkenhuysen et al. (2017) (Welkenhuysen et al., 2017) have investigated the structure of the Snf1 pathway in the context of glucose starvation.

The TORC1 pathway. Many mathematical models of mTOR signaling have been proposed. Of particular relevance to our work, Vinod investigated the role of mTOR in metabolic regulations in response to insulin signaling (Vinod and Venkatesh, 2009). Sonntag carried out a systematic investigation of regulatory mechanisms underlying the interactions between AMPK and mTORC2 (Sonntag et al., 2012). Pezze expanded this model to study its response to amino acids (Pezze et al., 2016). Thobe studied the regulation of mTORC2 using logical modeling (Thobe et al., 2017).

Integrated pathway models. Sengupta et al. (2007) studied the steady-state properties of an integrated model of the cAMP-PKA pathway and the MAPK signaling system in regulating the pseudohyphal transition of yeast cells to response to nitrogen starvation (Sengupta et al., 2007). Recently Welkenhuysen et al. (2019) created a Boolean model of the crosstalk between various signaling pathways (Welkenhuysen et al., 2019), to show how the network confers robustness to diverse nutrient environments.

RESULTS

A proposal for the nutrient signaling network in budding yeast

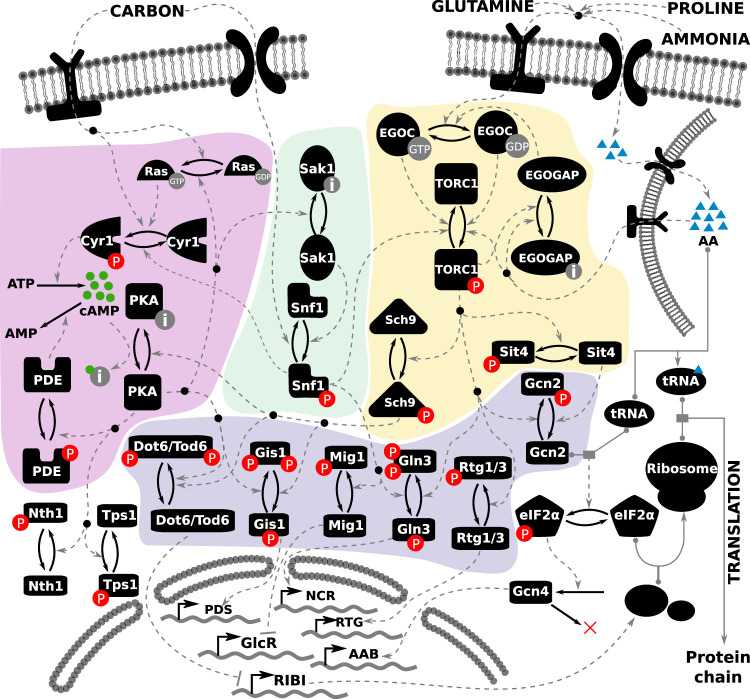
To construct a coherent and comprehensive regulatory network that is consistent with a broad range of experimental results, we first gathered relevant data on nutrient signaling from the published literature along with hypotheses about the underlying molecular mechanisms. On the basis of this information, we propose a molecular regulatory network for nutrient signaling in budding yeast in Figure 1.

FIGURE 1:

Literature-curated molecular regulatory network of nutrient signaling in yeast cells. The cAMP-PKA pathway is depicted on the left (highlighted in purple), the Snf1 pathway in the middle (highlighted in green), and the TORC1 pathway on the right (highlighted in yellow). The readouts of the model are the activities of the transcription factors toward the bottom of the diagram (highlighted in blue), whose target genes at the bottom of the figure comprise various regulons: GlcR, glucose-repressed genes; PDS, post–diauxic shift element; NCR, nitrogen catabolite repression genes; RTG, retrograde genes; AAB, amino acid biosynthesis; and RIBI, ribosome biogenesis. Each black icon represents a molecular species. Posttranslational modifications are represented by a pair of solid arrows pointing in opposite directions. Phosphorylation is indicated by “P” in a red circle. The inactive form of a species is indicated by the letter “i” in a gray circle. Guanidylation is indicated by “GTP” in a gray circle. Regulatory signals are represented by dashed gray lines. Complex formation is indicated by a solid gray line, with the binding partners indicated by gray circles. The inputs to the model are shown at the top of the figure, represented by one carbon input, and three nitrogen inputs: glutamine, ammonia, and proline. The intracellular amino acid pool stored in the vacuole is represented by the membrane-bound structure at the top right.

In yeast, a set of nutrient-specific membrane-bound receptors sense and transduce signals to the downstream signaling pathways within the cell (Conrad et al., 2014). In our model, the nutrient receptors are abstracted away; the notion of nutrient sufficiency of carbon and nitrogen is represented on a scale from 0 to 1, where 0 represents starvation and 1 represents abundance. There are four such nutrient inputs for “Carbon” (i.e., glucose) and three classes of nitrogen: “Glutamine” (high quality), “Proline” (poor quality), and “Ammonia” (which requires a carbon source). The output of the network is the regulation of transcription factors governing global metabolic transitions (shown at the bottom of Figure 1). Because the activities of these transcriptional regulators will determine the growth status of the cell, they are used as readouts of the cellular state in response to a nutrient input. Table 1 summarizes the interacting components of the model, their regulators, and their targets.

TABLE 1:

The molecular interactions in our proposed nutrient signaling model.

Variable	Regulators	Targets
Carbon	Model input	Cyr1, Ras
Glutamineext	Model input	Glutamine
NH4	Model input	Glutamine
Proline	Model input	Glutamine
Glutamine	Glutamineext, NH4, proline	TORC1, EGOC
Ras	Glucose ( Colombo et al., 2004), PKA ( Jian et al., 2010)	Cyr1
Cyr1	Ras, glucose ( Mbonyi et al., 1988)	cAMP
cAMP	Cyr1, PDE ( Ma et al., 1999)	PKA
PKA	cAMP ( Colombo, 1998), Sch9 ( Zhang and Gao, 2012)	Gis1, Dot6, Sak1, PDE, Mig1, Tps1, trehalase, Ras
PDE	PKA ( Colombo, 1998)	cAMP
EGOC	Glutamine, N sources, EGOGAP ( Stracka et al., 2014)	TORC1
EGOGAP	Glutamine, TORC1 ( Hatakeyama and Virgilio, 2016)	EGOC
TORC1	Glutamine, EGOC, EGOGAP, Snf1 ( Hallett et al., 2014)	Sch9, Gln3, Rtg1/3
Sch9	TORC1 ( Urban et al., 2007)	PKA, Dot6, Gis1, Gcn2
Sak1	PKA ( Nicastro et al., 2015b)	Snf1
Snf1	Sak1, carbon ( Nicastro et al., 2015a)	Mig1, Gln3, Cyr1
Gis1	PKA, Sch9 ( Pedruzzi et al., 2000)	Post–diauxic shift genes
Mig1	Snf1 ( Welkenhuysen et al., 2017), PKA (via Reg1/Glc7) ( Castermans et al., 2012)	Fermentation
Gln3	Snf1, TORC1 ( Bertram et al., 2002)	NCR genes
Rtg1/3	TORC1 ( Crespo et al., 2002)	Retrograde genes
Gcn2	Sch9 ( Cherkasova and Hinnebusch, 2003), Snf1 ( Cherkasova et al., 2010)	Gcn4
Gcn4	tRNA, Gcn2, glutamine ( Hinnebusch, 2005)	Amino acid biosynthesis genes
Dot6	Sch9, PKA ( Virgilio and Loewith, 2006a)	RIBI
Tps1	PKA ( Hirimburegama et al., 1992)	Model output
Nth1	PKA ( Hirimburegama et al., 1992)	Model output
Rib	Dot6 ( Chaillot et al., 2019)	Model output

For each model variable, the corresponding upstream regulators and downstream targets are listed.

In view of the large number of interacting components and the relative paucity of high-resolution data on their dynamics, we are compelled to simplify the model to make the problem more manageable without—we hope—sacrificing its most important details. In the following sections, we describe the key simplifications we have made.

Storage molecules.

In yeast, amino acids are stored both in the cytosol and in a vacuole (Halvorson, 1955; Wiemken and Durr, 1974; Messenguy et al., 1980; Li and Kane, 2009). The regulation of these distinct, dynamic nutrient pools is complex. Because glutamine has been shown to be the primary nutrient input to TORC1 (Stracka et al., 2014), a single variable representing the intracellular glutamine level, depicted as AA in Figure 1, is used to quantify intracellular nitrogen sufficiency. In the absence of external glutamine, but in the presence of sufficient carbon sources, yeast cells can synthesize glutamine from ammonia. The uptake of ammonia is regulated by ammonia transporters that are expressed in response to declining glutamine levels (Boeckstaens et al., 2014). Finally, in the presence of poor nitrogen sources such as proline, yeast cells activate amino acid biosynthesis pathways. Nitrogen stores are depicted at the top right of Figure 1, where the lipid bilayer depicts the yeast vacuole membrane.

To achieve maximal growth rate, the cell requires a sufficient amount of ATP. Instead of modeling the dynamic regulation of cellular energy charge, we assume that energy charge is proportional to the carbon sufficiency of the environment, while acknowledging that the true relationship is highly nonlinear (Özalp et al., 2010). Finally, in response to carbon starvation, the activity of trehalose synthase (Tps1) is up-regulated in order to synthesize the storage molecule trehalose, and upon relief from starvation, the PKA pathway activates trehalase (Nth1) in order to consume the stored trehalose (Hirimburegama et al., 1992). The activities of Tps1 and Nth1 are used as readouts to characterize the yeast cell’s response to carbon shifts. We do not model the changing levels of trehalose or glycogen because they are not directly relevant to the short-term responses of the carbon signaling pathway.

Nitrogen sensing.

See the area of Figure 1 that is highlighted in yellow. The precise mechanism of nitrogen sensing in yeast by TORC1 remains controversial. The TOR complex has been shown to interact at the vacuolar membrane with multiple G-proteins, which sense the levels of distinct intracellular amino acid pools (Conrad et al., 2014; Hatakeyama and Virgilio, 2016). The EGO complex, composed of the G-proteins Gtr1/2 and their membrane anchors Ego1/2/3, is activated by various subunit-specific GTPase-activating proteins (GAPs). For example, Lst4/7 has been shown to be a GAP specific to Gtr2 (Péli-Gulli et al., 2015), while the SEACIT complex is the Gtr1-GAP (Panchaud et al., 2013). We simplify this mechanism by letting one variable (EGOC) represent the activity of the EGO complex and another (EGOGAP) represent the activity of a generic GAP protein.

PKA activation.

See the area of Figure 1 that is highlighted in pink. Several published models have explored the complexity of PKA activation via the Ras-cAMP mechanism with a focus on cAMP dynamics (Box 1). In our version of this pathway, we include reactions for cAMP synthesis (by adenylate cyclase, Cyr1) and degradation (by phosphodiesterase, PDE) and shift our attention to the interactions between the PKA pathway and the rest of the nutrient signaling system. Glucose has been shown to stimulate Cyr1 both directly (Matsumoto et al., 1982; Thevelein, 1991) and indirectly, via Ras2 (Colombo et al., 2004). cAMP activates the PKA heterotetramer, here represented by a single species “PKA.” PKA activates PDE, which converts cAMP to AMP. The two isoforms of phosphodiesterase have been shown to have distinct characteristics (Ma et al., 1999). In our model the “PDE” variable represents Pde1.

The Snf1 pathway.

See the area of Figure 1 that is highlighted in green. Snf1 is inhibited by the glucose-dependent phosphatase Reg1/Glc7; however, the exact mechanism remains unclear. Hence, in our regulatory network we simply assume a carbon source–dependent inhibition of Snf1 activity. During glucose starvation, Snf1 is activated by Sak1/Tos3/Elm1 kinases (García-Salcedo et al., 2014), which are represented by a single variable “Sak1” in our model.

Cross-talk between pathways.

PKA and Snf1 have been shown to mutually inhibit each other: Snf1 inhibits Cyr1 activity, thereby inhibiting PKA; while PKA inhibits Sak1 kinase, thereby inhibiting Snf1 (Barrett et al., 2011; Nicastro et al., 2015b). While Castermans et al. (2012) have speculated that glucose-activated phosphatases might be regulated by the PKA pathway, Nicastro et al. (2015b) propose that PKA might inhibit Sak1 kinase activity. Here, we assume that PKA-dependent Snf1 dephosphorylation occurs via the inhibition of Sak1/Tos3/Elm1 activity. The relationship between Snf1 and TORC1 is less clear. While glucose-dependent TORC1/Sch9 kinase activity has been reported in multiple publications, the mechanism by which TORC1 activity is modulated by the presence of glucose remains unclear (Urban et al., 2007). On the basis of data from Hallett et al. (2015) and Prouteau et al. (2017), we assume that Snf1 inhibits TORC1. Finally, the relationship between Sch9 and PKA is confounded by the complex and overlapping regulation of their many shared downstream targets  (Roosen et al., 2005). While early studies on the PKA pathway found an apparent negative interaction between Sch9 and PKA (Crauwels et al., 1997), the exact relationship between these kinases remains unclear. Zhang et al. claim that Sch9 interacts with and inhibits PKA at multiple levels  (Zhang et al., 2011; Zhang and Gao, 2012). Here, we assume a direct inhibition of PKA by Sch9.

Creating a mathematical model

The component parts of the network (discussed above) are derived from experimental evidence in the literature. When we assemble these components into a comprehensive signaling network (Figure 1), it is not clear that the full network is still consistent with all the individual experiments. To answer this question, we converted our proposed regulatory mechanism into a system of ODEs using the Standard Component Modeling framework (Methods; Supplemental Section S1). The full set of 25 ODEs along with details of the representation of certain abstract variables (like the intracellular nutrient levels) are presented in Supplemental Section S1.1. The ODEs contain 128 parameters (Supplemental Section S2). Before we can simulate the behavior of the model equations, we must estimate the values of these parameters. To make these estimates, we need some experimental data on the time courses of molecular variables in the model and some observations of the steady-state characteristics of the signaling network under a variety of conditions. In the next section, we describe the experimental data sets that we collected and how we estimate the parameter values, and in later sections we use the parameterized model to make predictions about nutritional responses of yeast cells under novel conditions.

Parameterizing the model with experimental data

In the following two subsections, we describe the two types of quantitative data used to calibrate the model: 1) time-course measurements and 2) steady-state nutrient-shift data, related to the abundance/activity of particular molecules in the nutrient signaling pathway in both wild-type (wt) and mutant backgrounds. From these data, we derived a set of parameter values that provides a “best” fit to the experimental observations, using parameter-estimation tools that minimize the sum of squared differences between experimental measurements and model simulations (see Methods). In the third subsection, we find alternative sets of parameter values that fit the quantitative data nearly as well as the best-fitting, “optimal” parameter set.

Comparing simulation results with experimental time-course data.

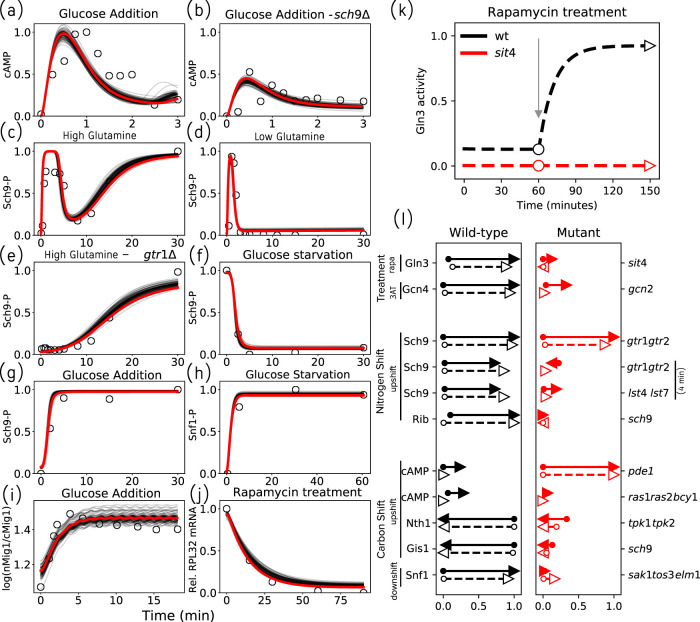
First, we combed the literature for experimental time-course measurements of molecular species in our model (see Supplemental Table S2). In Figure 2, a–j , we compare the experimental data (open circles) to time-series simulations (in red) of the model using the optimal parameter values.

FIGURE 2:

The model successfully explains experimental data. (a–j) Time-series fits to literature-curated time-course data. The red lines represent simulated trajectories from the best-fit parameter set, while the gray lines represent simulations from 100 parameter sets with comparable sums of squared errors. The experimental measurements are shown as open circles. (a, b) Relief from glucose starvation. (c–e) Relief from nitrogen starvation by glutamine addition. (f, h) Glucose starvation. (g, i) Relief from glucose starvation. (j) Rapamycin treatment of well-nourished cells. (k) Comparing model simulations with data from a shift experiment (Beck and Hall, 1999) measuring Gln3 phosphorylation in response to rapamycin treatment in well-nourished wt and sit4Δ strains. In the wt simulation (black dashed line), we calculate the steady-state value of Gln3 in rich medium in the absence of rapamycin (black circle). Next, rapamycin is introduced (at the gray arrow), and the new, postshift steady state is recorded (black triangle). The same simulation was repeated for sit4Δ cells to yield preshift (red circle) and postshift (red triangle) steady states. (l) Visualization of perturbation analyses. The perturbations are drug treatments or nutrient shifts carried out in wt cells (left column, black arrows) and mutant strains (right column, red arrows). The labels on the left indicate the molecular species being assayed, and the labels on the far right indicate the gene(s) deleted in the mutant strains. Experimental results are represented by solid arrows and model simulations by dashed arrows. For each molecular species under consideration, the arrow’s tail and head indicate (respectively) the pre- and postperturbation steady-state values, as measured on the relative scale (0–1) at the bottom of the column. As an example, the rapamycin treatment in panel k is reproduced in the first line of panel l. Note that the y-axis in panel k is now the x-axis in panel l.

FIGURE 3:

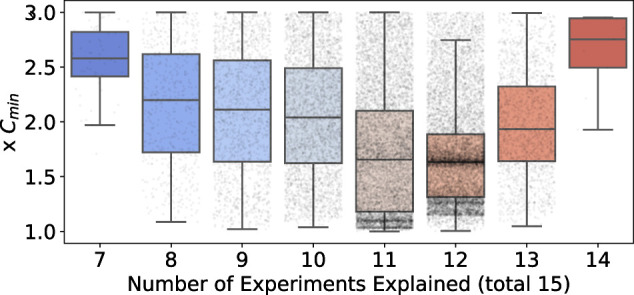
Dependence of model cost on explanatory capacity, across the entire collection of 18,000 alternative sets of parameter values. Model predictions of the 15 qualitative phenotype experiments were repeated for the collection of acceptable parameter sets. Each boxplot shows the distribution of cost-of-fit (to the quantitative measurements) for a given level of explanatory capacity (i.e., the number of qualitative phenotypes explained). Each point represents a parameter set. The cost, on the y-axis, is reported as a multiple of C_min, the best observed cost across all parameter sets. The boxplot shows the median cost, and the whiskers extend to 1.5 times the interquartile range (IQR), or the last data point less than 1.5×IQR. Note that only parameter sets with a cost less than or equal to twice the C_min are reported.

Our model includes molecular species that are common readouts in experiments investigating nutrient signaling. cAMP is a standard readout for the activity of the PKA pathway. cAMP shows rapid transient changes, on the timescale of minutes, upon relief from glucose starvation. Model simulations successfully capture the cAMP dynamics in wt cells as well as sch9Δ mutant cells (Figure 2, a and b). Sch9 phosphorylation is a widely accepted readout for TORC1 activity and displays changes on the timescale of tens of minutes upon relief from nitrogen starvation (Stracka et al., 2014). Model simulations successfully capture the transient as well as steady-state behavior of Sch9 phosphorylation in wt and in gtr1,2Δ strains (Figure 2, c–e). Moreover, we are able to capture changes in Sch9 phosphorylation in response to glucose starvation and readdition (Figure 2, f and g), as reported by Prouteau et al. (2017). Snf1 kinase activity is typically measured indirectly, by examining the phosphorylation of the SAMS peptide, a Snf1 target sequence  (Wilson et al., 1996). The model successfully captures the activation of Snf1 during glucose downshift (Figure 2h), leading to the expression of glucose-repressed genes. Apart from assays of biochemical activities, subcellular localization measured by fluorescence microscopy provides indirect information about the activity of transcription factors. Mig1 nuclear localization upon relief from glucose starvation was recently reported by Welkenhuysen et al. (2019) (Figure 2i). Model simulations successfully capture this response if we identify Mig1 transcriptional activity with the experimentally observed translocation of Mig1 into the nucleus. Direct information about transcription factor activity can also be obtained by measuring mRNA levels of the transcription factor’s target genes. For example, RPL32 mRNA, encoding the large ribosomal subunit, is down-regulated in response to rapamycin treatment, and our model captures this effect nicely (Figure 2j).

Capturing phenotypes of wt and mutant strains in response to nutrient shifts.

To investigate the roles of regulators in nutrient signaling, experimentalists typically characterize the phenotype of a strain in response to perturbations (nutrient shifts or drug treatments). To parameterize our model, we collected data from direct biochemical assays of molecular responses to perturbations (see Supplemental Table S3).

An example of the type of perturbation data used to calibrate our model is illustrated in Figure 2k, where model simulations are compared with data reported by Beck and Hall (1999), who studied the phosphorylation of Gln3 by TORC1 and Sit4. Using Western blots of Gln3 pull downs, Beck and Hall (1999) found that Gln3 is phosphorylated (inactive) in untreated wt cells (black dashed line), while treatment with rapamycin led to Gln3 dephosphorylation. In contrast, Gln3 remained phosphorylated (inactive) in a sit4Δ strain even after rapamycin treatment (red dashed line). The figure shows simulated time courses of active (dephosphorylated) Gln3 under these conditions, and the markers (empty circles and empty triangles) indicate the (pre- and postshift) steady-state values of active Gln3 used to compare against the experimental measurements.

Figure 2l visualizes such comparisons for a representative sample of experimental perturbations. For example, the results in Figure 2k are summarized in the first line of Figure 2l. The second line shows the results of 3-amino-1,2,4-triazole (3AT) treatment on Gcn4 activity in wt cells (black) and in a gcn2 deletion strain (red). 3AT inhibits histidine synthesis, resulting in induction of Gcn4 and an amino acid starvation response. There is no induction of Gcn4 expression in a gcn2Δ strain.

The second and third blocks of Figure 2l show the results of “nitrogen shifts” and “carbon shifts”; either a downshift (nutrient starvation) or upshift (relief from starvation). The first two rows in the “Nitrogen Shift” block (call them N1 and N2) repeat the results in panels c and e, which report the phosphorylation of Sch9 in wt and gtr1Δgtr2Δ strains in response to relief from starvation (i.e., addition of glutamine to nitrogen-starved cells). Row N1 compares the preshift steady state (at time 0) to the postshift steady state (at time 30 min). Row N2 compares the preshift steady state to the transient state (at time 4 min). Row N3 makes a similar comparison of wt cells to lst4Δlst7Δ cells. Row N4 compares expression levels of RPL25 (a ribosomal protein), as measured by Crauwels et al. (1997) in wt and sch9Δ strains, with model simulations.

In the “Carbon Shift” block, the first four rows report the results of readdition of glucose to carbon-starved cells, while the last row summarizes a glucose starvation experiment. Row C1, left column, repeats the results in panel a. The pde1Δ strain shows an increase in cAMP levels compared with wt (Ma et al., 1999), while the ras1Δras2Δbcy1Δ strain shows a diminished amount of cAMP compared with wt (Mbonyi et al., 1988). Row C3 depicts trehalase (Nth1) levels after a glucose upshift; trehalase levels remain low in a strain containing either a single TPK1 or TPK3 catalytic subunit (Mbonyi et al., 1990). Row C4 demonstrates that a mutation in the nitrogen signaling pathway (sch9Δ) has a significant effect on the carbon stress response factor Gis1 (Crauwels et al., 1997). Finally, row C5 shows that Snf1 activity increases in response to a carbon downshift in wt cells, but this response is absent in sak1Δtos3Δelm1Δ cells (Hong et al., 2003).

Alternative sets of parameter values.

In the preceding subsections, quantitative data obtained from the literature were used to estimate the numerical values of the parameters in the model. Because the available data are sparse and the number of parameters is large, we expect that many parameter values will be poorly constrained by the data. Because any particular set of parameter estimates will be unreliable in this situation, we would like to obtain a representative ensemble of sets of parameter values that all give acceptable fits to the data. One approach to obtaining such an ensemble would be to randomly sample parameter values, evaluate the model for goodness-of-fit, and accept those parameter sets that meet some standard of acceptable fit. However, sampling parameter values in a completely random manner is not an efficient way to find alternative parameter sets because small random perturbations will not effectively explore the parameter space, whereas large random perturbations are not likely to find an acceptable set of parameter values. Instead, we use the fact that the region of acceptable parameter values in a high-dimensional parameter space is characterized by “stiff” and “sloppy” directions (Gutenkunst et al., 2007), and a random parameter search has to respect these directions. To carry out this search, we used a method of “model robustness analysis” described by Tavassoly et al. (2015).

The mathematical details of this method are provided in Supplemental Section S2. In short, we first construct a quadratic cost function that quantifies the goodness-of-fit between model predictions and the curated data (Supplemental Section S2.1). The cost is a function of the model’s parameter values. We then used a Markov chain Monte Carlo (MCMC) sampling scheme to improve our initial “hand-tuned” set of parameter values (Supplemental Section S2.2). The resulting parameter set with the smallest cost we designate as the “optimal” parameter set. In the neighborhood of this optimal parameter set, we expect the cost function to be bowl shaped, such that any deviation from the optimal set will lead to an increase in cost. The curvature of the cost surface is described by the Hessian matrix of second derivatives of the cost function with respect to the parameter values. The eigenvectors of the Hessian matrix differentiate between the directions in parameter space along which the cost increases rapidly (i.e., the stiff directions) and the directions along which the cost function hardly changes (i.e., the sloppy directions). Knowledge of these directions helps us to constrain the search for alternative parameter sets.

Using this approach, we obtained a large collection (18,000) of acceptable parameter sets (with cost less than twice the minimum). For this analysis, we varied 81 of 125 parameters, considering only parameters that affected the kinetics of the variables, fixing the rest of the parameters to their default values in the optimal parameter set (Supplemental Section S2.5). We used this representative collection of parameter sets to investigate the robustness of model predictions, as described in the next section. We also used this collection to investigate the robustness of our estimates of parameter values as described in Supplemental Section S2.8.

Testing the model against observed phenotypes of mutant strains

In the preceding section, we used quantitative data (time courses and steady-state measurements) on specific molecular components of the nutrient signaling network to estimate parameter values in our mathematical model. In this section, we test the behavior of the parameterized model against qualitative experimental observations of the responses of wt and mutant strains to environmental perturbations. These “test case” data were not used in the preceding section to constrain the parameters.

From the literature, we collected a list of 37 experiments (provided in Supplemental Table S4; Supplemental Section S5) describing the qualitative phenotypes of mutant strains, typically colony growth phenotypes. We selected strains whose cellular states under nutrient shifts can be adequately characterized in terms of the transcription factors (TFs) in our model. To compare these experiments with our model predictions, we used the following strategy. For each colony growth experiment, we interpreted the observed phenotype in terms of the state (ON or OFF) of the nutrient-responsive TFs in our model. Next we simulated each nutrient-shift or drug-treatment protocol for the specific mutant strain. We recorded the predicted steady-state values of the six TFs in our model and converted these values into binary form (0 or 1) using thresholds corresponding to the half-maximal values in the wt simulation, thereby obtaining a Boolean vector of predicted TF states. Finally, we compared the predicted states of the relevant TFs to those interpreted from the experiment.

An important assay in the investigation of the nutrient signaling response is rapamycin treatment, constituting 22 of the 37 experiments in our collection. In wt cells, rapamycin treatment inhibits TORC1 activity, consequently activating nitrogen stress responses via TFs like Gln3, Gcn4, and Rtg1/3 (via the Tap42-Sit4 branch), inhibiting ribosome biogenesis via transcriptional repressors like Dot6/Tod6 (via the Sch9 branch), and indirectly causing a cell cycle arrest in the G1 phase. It appears that decoupling either one of these branches from TORC1 is sufficient to confer rapamycin resistance (cf. rapamycin treatment of gln3Δgcn4Δ double mutant [ Valenzuela et al., 2001], and the Sch^DE and tap41-11 TORC1 insensitive strains [ Staschke et al., 2010]). Taking these observations into account, we attempted to carry out in silico experiments to explain our collection of experiments by examining different potential effects of rapamycin treatment, including up-regulation of nitrogen adaptation responses and down-regulation of ribosome biogenesis. Using either of these definitions, the model could explain only about half of the rapamycin experiments that we have collected. We present this investigation in Supplemental Section S3. Below, we focus on the remaining 15 experiments not involving rapamycin treatment.

To characterize our confidence in model predictions, we recorded statistics on the number of times an experiment is predicted correctly across the representative collection of parameter sets (Table 2). Across all parameter sets, the model is able to correctly simulate up to 12 of 15 experiments. Four of these 15 experiments are explained by all of the parameter sets, and three of 15 are predicted by fewer than half of the parameter sets. The following paragraphs discuss some of the experimental observations that our model succeeds in explaining and some that our model fails to explain. The predictions described here are made using the optimal parameter set. Details of simulations are provided in Supplemental Section S5.

TABLE 2:

Confidence in qualitative predictions expressed as the percentage of parameter sets that make the correct prediction.

Exp ID	Confidence	Exp ID	Confidence
12-gln3 gat1	100.00	3-rtg1	87.39
24-gcn2	100.00	1-rho0	84.63
26-gcn2 snf1	100.00	23-wt	83.51
41-sch9 gis1	100.00	11-gln3	56.56
13-wt	95.89	5-snf1	14.78
2-rho0	94.54	40-sch9	13.07
30-rph1 gis1	94.34	4-rtg1	1.39
29-rph1 gis1	89.24

The experiments are ordered in decreasing order of prediction confidence. The in silico experiments corresponding to the experiment IDs are presented in Supplemental Section S5.

Nitrogen adaptation responses.

An important function of the tricarboxylic acid cycle (TCA cycle) in central carbon metabolism is diverting the carbon backbone to amino acid biosynthesis pathways via α-ketoglutarate. Because the genes coding for the TCA cycle enzymes are present in the mitochondrial genome, mitochondrial dysfunction can severely affect respiration, resulting in the so-called ρ⁰ petite strains. Conceivably, these strains have a diminished capacity to divert carbon flux into amino acid biosynthesis. In yeast, the Rtg1/3 transcription factors control the expression of the CIT2 gene, a TCA cycle enzyme encoded by the nuclear genome, which allows the diversion of carbon flux to amino acid biosynthesis pathways, under nuclear control (the so-called retrograde pathway). Liu and Butow (1999) studied wt(ρ⁺) and ρ⁰ to characterize the activity of the Rtg1/3 transcription factors by systematically varying the carbon and nitrogen content in the growth medium. While the ρ⁰ strains can grow on media containing glucose only, raffinose only, and glucose supplemented with glutamate, the rtg strains in a ρ⁰ background show growth only on glucose + glutamate medium.

We simulated wt and rtg strains in such ρ⁰ petite strains. We assume that ρ⁰ strains have a lower level of glutamine pool replenishment than ρ⁺ strains. The rtg1Δ, rtg3Δ, and rtg1Δrtg3Δ strains in ρ⁰ backgrounds do not grow on media lacking glutamate, while supplementing the medium with glutamate results in wt growth (Liu et al., 2003). Model predictions recapitulate the observations made by Liu et al. in media with and without glutamate (Supplemental Sections S5.1–S5.3).

Model mismatches.

The majority of parameter sets (>50%) in our model succeed in explaining 12 of the 15 “test-case” experiments (Table 2 and Figure 3). We discuss the reasons for the three model mismatches below.

Gasmi et al. (2014) reported that a snf1Δ strain cultured on minimal medium supplemented with ethanol grows slowly. In our model the glucose repression factor Mig1 will remain active in a snf1Δ strain, inhibiting any carbon adaptation responses, indicating no growth (Supplemental Section S5.5). Liu and Butow (1999) showed that an rtg1Δ single deletion strain does not grow on medium containing a small amount of glutamate (0.02%). Our model predicts that this strain will still mount an Rtg1/3 response (Supplemental Section S5.4). This might indicate a problem with the representation of nitrogen sufficiency in the model. Roosen et al. (2005) showed that an sch9Δ strain grows when cultured on medium containing glycerol as a carbon source. To grow on glycerol, the Gis1 transcription factor must be activated via inhibition of PKA. Because our model assumes an inhibition of PKA by Sch9, an sch9Δ strain with hyperactive PKA will result in repression of Gis1 (Supplemental Section S5.37).

Predictions of global cellular responses to nutrient states

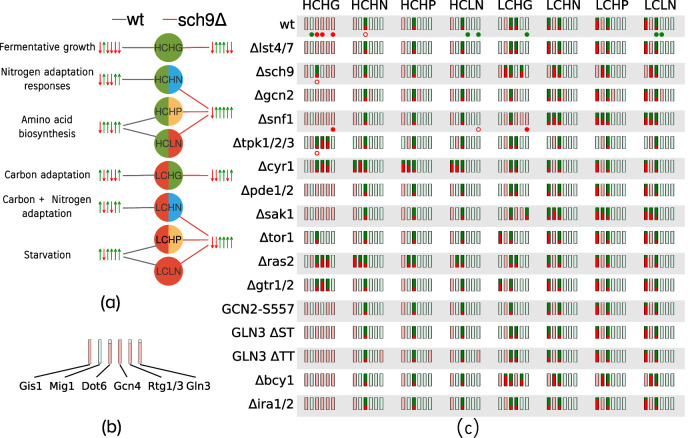
Motivated by our model’s success in predicting the qualitative phenotypes of 12 of 15 experimentally studied mutant yeast strains, we used it to predict global cellular responses to nutrient conditions in a variety of mutant strains. We chose a list 16 mutant strains affecting all three nutrient signaling pathways: 13 of these strains are gene deletion mutants including lst4Δlst7Δ, sch9Δ, gcn2Δ, snf1Δ, tpk1Δtpk2Δtpk3Δ, cyr1Δ, pde1Δ, sak1Δ, tor1Δ, ras2Δ, gtr1Δgtr2Δ, bcy1Δ, and ira1Δira2Δ. Three are protein-sequence mutants: GCN2-S577A has lost the phosphorylation site for TORC1, and the two hypothetical strains GLN3-ΔST and GLN3-ΔTT lack the phosphorylation sites for Snf1 and TORC1, respectively (see Figure 4). The model representations of these mutants are summarized in Supplemental Table S4 in Supplemental Section S4.

FIGURE 4:

Global cellular responses to nutrient conditions. (a) Illustration of cellular states in response to various nutrient environments. The nutrient input is shown in the circles: L and H indicate low and high, respectively; C, G, N, and P represent carbon, glutamine, ammonia, and proline, respectively. The cellular state, defined by the set of transcription factor (TF) readouts, is shown by the upward-pointing green (on) and downward-pointing red arrows (off). The order of TFs is Gis1, Mig1, Dot6, Rtg1/3, Gcn4, Gln3. Each nutrient input is connected to a cellular state by an edge. The figure shows a comparison between the predicted states for two strains, wt (black edges) and sch9Δ (red edges), using the optimal parameter set. Qualitative descriptions of the cellular states in the wt simulations are provided at the far left. (b) Representation of the consensus prediction of cellular state across 18,000 alternative parameter sets. The example shows the prediction for wt cells under the HCHG condition. The height of a red/green bar represents the fraction of parameter sets that predicted the corresponding state to be off and on, respectively. We consider the prediction to be robust if greater than 90% of parameter sets are in agreement, shown using light green or red. As shown, most parameter sets are in agreement regarding the states of the readouts for wt cells under high carbon, high glutamine. (c) The robustness of global state predictions across 17 strains and eight nutrient conditions. Fragile predictions are indicated in bright green and red. Additionally, direct measurements of TF activities obtained from the literature are indicated using filled and empty circles below the corresponding readouts; a filled circle indicates that the model prediction agrees with experimental data, while empty circles represent a model mismatch. Green and red circles indicate that the readout is on or off, respectively.

We characterized each strain’s response to eight nutrient conditions (qualitatively low and high inputs for “Carbon,” “Glutamine,” “Ammonia,” and ‘Proline”). In Figure 4, these qualitative states are denoted using “H” and “L,” respectively, for high and low, and the nutrient input is denoted using “C,” “G,” “N,” and “P” for carbon, glutamine, ammonia, and proline, respectively. (Note that “LN” represents nitrogen starvation.) For each simulation, we recorded the steady-state values of the six TFs in our model and thresholded the TF activities using their half-maximal values in the wt simulations. We thus obtained a Boolean vector describing the phenotypic state of a cell under different nutrient conditions, with each TF taking a value 0 (off) or 1 (on). The predicted states for the 17 strains (including wt) over all nutrient conditions (as predicted by the model using the optimal parameter set) are provided in Supplemental Table S5.

Figure 4a provides an example of the predicted cellular states for wt and sch9Δ cells for each of the eight nutrient conditions. We observed that, for each nutrient input, the state of the wt strain was different from that of the sch9Δ strain. Repeating these simulations across the 17 strains and the eight nutrient conditions yielded a total of 136 predicted cellular states. To gain confidence regarding model predictions, we repeated these in silico experiments for each of the 18,000 alternative parameter sets. Using two parameter sets, if the predicted states of a particular TF in a given experiment are identical, the two sets are considered to agree on the prediction. We define fragile predictions to be the experiments where fewer than 90% of the parameter sets were in agreement about the outcome of a simulation. The results of this analysis are summarized in panel c of Figure 4, where the consensus of the predictions across all tested parameter sets is indicated by the brightness of the bars. We observed that in the HCHG simulations, the predictions exhibited consensus across most strains for all TFs. Note that in Figure 4c there is significant disagreement between the predictions made by the parameter sets regarding the state of Dot6, the repressor of RIBI, in all conditions except rich media (HCHG). This is likely due to the lack of experimental data constraining Dot6 dynamics. Furthermore, we observe that the HP and LN columns are identical for both HC and LC, implying that the model fails to distinguish between the high proline and nitrogen starvation conditions, whereas proline, a poor source of nutrients, would still be expected to serve as a substrate in order to maintain intracellular amino acid reserves. We believe that this failure is a consequence of the fact that our model does not include the effects of metabolic feedback on nutrient signaling, thus rendering the two poor-nitrogen conditions indistinguishable.

Finally, we observe that the alternative parameter sets disagree about the state of Gis1 across most strains during nitrogen stress under carbon starvation (LCHN, LCHP, and LCLN columns in Figure 4c). Gis1 is jointly regulated by Sch9 and PKA. However, the data used to calibrate the model come from experiments related to the PKA pathway only (Crauwels et al., 1997). To refine our predictions for Gis1, the model will need to be recalibrated with Gis1 data obtained from nitrogen-shift experiments, when they become available.

DISCUSSION

Because the default state of yeast cells in the presence of nutrients is exponential growth, the coordination of various nutrient levels within the cell is of paramount importance. The integration of extracellular nutrient signals is distributed broadly across the cAMP/PKA (glucose signaling), Snf1 (carbon adaptation), and TORC1 (nitrogen signaling) pathways, along with many cross-talk interactions among members of these pathways and their downstream targets. These interactions comprise the nutrient signaling and decision-making system in budding yeast. In this paper we have proposed a mathematical model of this system, based on well-studied interactions of the individual pathways and less-studied cross-talk between the pathways (Figure 1). Our results demonstrate that the proposed mechanism can account for many aspects of nutrient signaling in budding yeast, as observed in diverse nutrient-shift experiments (Figure 2).

Cross-talk interactions between the carbon and nitrogen signaling pathways

In Figure 1 we include two well-documented interactions by which the carbon and nitrogen signaling pathways cross-talk: Snf1 inhibition of the TORC1 complex, and Sch9 inhibition of PKA. In the preceding section we investigated how deletions of Snf1 and Sch9 affect global metabolic responses in terms of regulatory signals impinging on transcription factor readouts. In this section, by looking more closely at the role of Snf1 in communicating carbon status to the nitrogen signaling pathway through TORC1, we conclude that our model oversimplifies the interaction and needs to be revised when further experimental studies resolve the discrepancy between the formation of TORC1 protein aggregates and the inhibition of TORC1 kinase activity on Sch9.

The effects of glucose starvation and refeeding on the activity of the TORC1 complex have been studied by Hallett et al. (2015) and by Prouteau et al. (2017). Both groups observe that, in response to glucose starvation, 1) components of TORC1 complexes rapidly form dense protein aggregates and 2) Sch9 protein is rapidly dephosphorylated (indicating a loss of TORC1 activity). Hallett et al. (2015) reported that YFP-Kog1 dissociates from TORC1 complexes (monitored by GFP-Tor1), forming “Kog1-foci.” The formation of Kog1-foci was slowed considerably in snf1Δ mutants and, even more so, in cells expressing Kog1 proteins with serine-to-alanine mutations at Snf1-phosphorylation sites, clearly indicating Snf1 involvement in the formation of Kog1-foci. Nonetheless, the dephosphorylation and rephosphorylation of Sch9 in response to glucose withdrawal and readdition was no different in these mutant cells compared with wild type (Figure 5 in Hallett et al., 2015), suggesting a complicated relationship between Kog1 aggregation and TORC1 activity. Prouteau et al. (2017) confirmed the formation of TORC1 foci microscopically, using GFP-Kog1– and GFP-Tor1–labeled cells. In electron micrographs they observed large, toroidal aggregates of TORC1 forming under glucose-starvation conditions. Nonetheless, they observed (in Extended Data Figure 3 of Prouteau et al., 2017) no appreciable differences between wild type and snf1Δ mutants in terms of either GFP-TOR1 foci formation or Sch9 dephosphorylation in response to glucose starvation (and reversed by glucose refeeding). These results suggest that the formation of “Kog1-foci” but not “Tor1-foci” is strongly dependent on Snf1 signaling, but TORC1 activity (in terms of Sch9 phosphorylation) is not dependent on Snf1.

FIGURE 5:

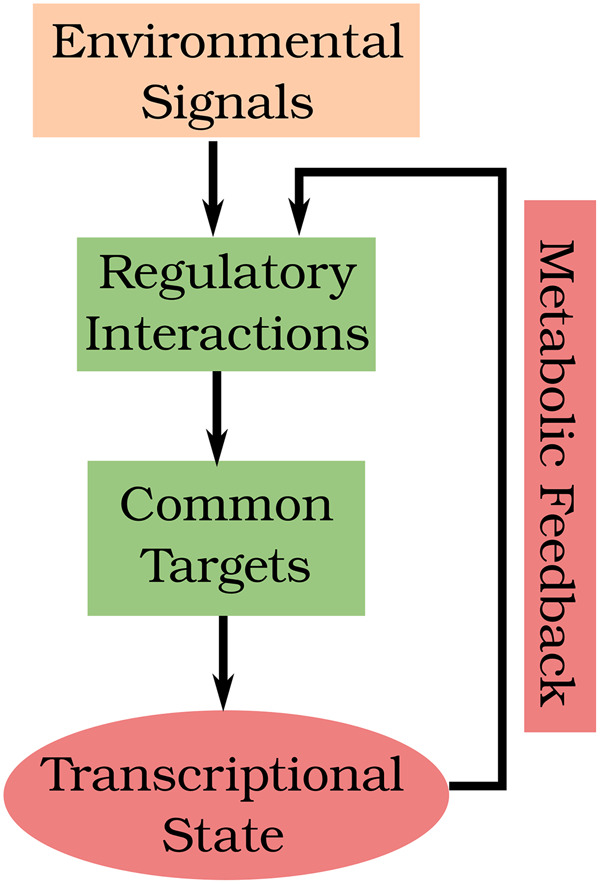
During nutrient stress, upstream sensing mechanisms transduce stress signals to downstream transcription factors. Stress signals can originate from both the extracellular environment and intracellular nutrient reserves. The latter are sensed indirectly via the levels of uncharged tRNAs (in the case of amino acids) or metabolic intermediates that are directly sensed by signaling molecules. The drops in flux through metabolic pathways result in up-regulation of specific biosynthetic pathways and other adaptation responses, indicated in red at the bottom of the figure. Subsequently, metabolic fluxes are remodeled, leading to inactivation of stress responses. This “metabolic feedback,” which is currently not included in our model, determines the long-term responses of the nutrient signaling network.

Our model, at present, cannot account for these complex relationships because it does not distinguish between TORC1 aggregation and TORC1 kinase activity. In our network diagram (Figure 1), the signal from Snf1 to TORC1 seems to represent the formation of Kog1 foci but not the inhibition of TORC1 kinase activity. There seems to be some other signal(s) from carbon sensing to TORC1 signaling that is not included in our model; perhaps a direct link from glucose receptors in the cell membrane to the guanine exchange factor that converts EGOC-GDP (an activator of TORC1 kinase) into EGOC-GTP. Until we have more convincing experimental evidence of the molecular identity of this “other signal,” it seems premature to model these interactions based on speculative assumptions.

Global cellular responses to nutrient shifts

Two experimental observations highlight the cross-talk between nutrient signaling pathways: 1) cells facing nitrogen stress in the context of carbon abundance can redirect carbon flux from the TCA cycle into amino acid biosynthesis (Butow and Avadhani, 2004), and 2) acute nitrogen starvation results in down-regulation of glucose fermentation (Brauer et al., 2007). These interactions are regulated by metabolic enzymes that are under the regulation of various TFs included in our model. To get a sense of the cell’s response to complex nutrient shifts, we thus need to examine the activities of the TFs spanning carbon and nitrogen responses.

In our model, we use the Boolean states of the TFs to define the state of a cell. Each of these predicted states is deemed “robust” or “fragile” based on the consensus among predictions from a representative collection of 18,000 alternative sets of parameter values (see Figure 4c). Robust predictions that are subsequently shown to be incorrect indicate parts of the model that need further refinement. Fragile predictions, on the other hand, indicate those parts of the model that are poorly constrained by available data. Experimental tests of a fragile prediction can invalidate those “alternative” parameter sets that make the incorrect prediction. Hence, both robust and fragile predictions suggest potentially informative experiments that can be used to further constrain the model. In the following paragraphs, we propose experiments that we deem informative based on some fragile predictions.

The Rtg1/3 transcription factors play the crucial role of diverting carbon flux into amino acid biosynthesis. Rtg1/3 are expected to be activated during nitrogen stress in carbon-rich conditions. Interestingly, Figure 4c indicates that the model makes fragile predictions for Rtg1/3 activity in the HCHG condition in three mutant strains, namely tpk1/2/3Δ, cyr1Δ, and ras2Δ. In these three strains PKA is inactive. Because, in our model, PKA activates TORC1 (via Sak1 and Snf1), TORC1 activity should be low in these mutants. However, because high glutamine activates TORC1, this protein receives contradictory signals from the carbon and nitrogen pathways. As a result, Rtg1/3 may be either active or inactive, depending on the values of the parameters in our model simulations. Hence, data pertaining to Rtg1/3 activity in these strains will help to narrow down the acceptable sets of parameter values.

The Mig1 transcriptional repressor implements glucose repression, that is, in the presence of glucose, Mig1 inhibits expression of genes involved in carbon adaptation responses. During glucose starvation, Snf1 inhibits Mig1 by localizing it to the cytoplasm. Interestingly, our model predictions for the state of Mig1 are fragile in LCHN, LCHP, and LCLN conditions in two separate strains, sch9Δ and bcy1Δ. (Note that Sch9 inhibits PKA via Bcy1.) In this case, the fragile predictions of Mig1 activity are consequences of contradictory signals received by Snf1. In LC, Snf1 should be active and Mig1 inactive. However, in these mutants, despite LC conditions, PKA is active, Sak1 is inactive, and there is little or no activation of Snf1. Hence, whether Snf1 is active or inactive depends sensitively on precise parameter values. Therefore, measurements of Mig1 activity under glucose starvation conditions in the bcy1Δ strain will also help to narrow down the acceptable sets of parameter values.

An important determinant of cell growth under diverse nutrient conditions is ribosome biogenesis, which in our model is regulated by the Dot6/Tod6 repressors. Interestingly, Figure 4c shows that Dot6 predictions are fragile in most conditions across a majority of mutant strains, indicating that the strength of cross-talk between carbon and nitrogen signaling pathways is crucial in determining Dot6 activity. Measurements of Dot6 activity in the mutant strains identified by Figure 4c will provide important constraints on these cross-talk interactions. However, we must bear in mind that other factors controlling ribosome biogenesis, such as Sfp1, are not yet included in our model.

Nutrient adaptation responses and global metabolic feedback

Our proposed mechanism successfully recapitulates many features of the nutrient response system in budding yeast over short timescales (30 min). During nutrient stress, the cell mounts a variety of adaptation responses in order to maintain intracellular nutrient pools. Our model captures the activation of stress TFs immediately after a nutrient shift. However, on longer timescales of ∼50 min, data from Granados et al. (2018) reveal that many of these stress TFs are eventually turned off. Our model simulations do not capture this feature. How can this inactivation of TFs be explained? The stress TFs activate various biosynthetic pathway enzymes that restore the flux of metabolites through anabolic processes. Consequently, the starvation signals are turned down, inactivating the stress TFs themselves. Metabolic processes are known to play important roles in cell growth and division (Ewald, 2018). Because the mechanisms by which metabolic responses feed back on the nutrient signaling network are complex and poorly understood, we have not yet tried to include these effects in our model (Figure 5).

In general, how to incorporate metabolic fluxes in nutrient signaling networks is a difficult challenge. Three aspects stand out: 1) the accurate representation of intracellular nutrient pools, 2) the metabolic fluxes spanning carbon and nitrogen metabolism, and 3) the dynamics of regulation of metabolic enzymes by the upstream signaling network. By providing a mechanistic model of the nutrient signaling system in yeast, our model is well poised to serve as a bridge between global metabolism and a wide range of cellular adaptation responses ranging from ribosome biogenesis to autophagy.

METHODS

Request a protocol through Bio-protocol.

Ideally, dynamical models of biological regulatory systems are based on biochemical details of the system under consideration, but oftentimes these details are obscure. Furthermore, the rate constants of enzyme-catalyzed reactions in a detailed mechanism are difficult to measure experimentally, posing a major hurdle for model parameterization. In this paper, we employ a general framework that circumvents these problems by using generic functions to describe biochemical reactions that occur on three different timescales: slow (e.g., gene expression, protein synthesis and degradation), intermediate (e.g., posttranslational modifications) and fast (e.g., complex formation and dissociation). This approach is called the Standard Component Modeling strategy (Laomettachit et al., 2016; Tyson et al., 2019). We provide a brief description of this strategy in Supplemental Section S1 and a full list of the model equations in Supplemental Section S1.1.

To estimate numerical values of a parameter in the model, we need quantitative experimental data from the literature. We focused on published measurements of molecular species as functions of time, which we digitized using WebPlotDigitizer (Rohatgi, 2017), and on data from electrophoretic gels, which we digitized using the “Analyze Gels” option in ImageJ (Schneider et al., 2012). As described in Results, all values obtained from a given publication are scaled between 0 and 1 with respect to the lowest and highest reported values in a particular experiment.

To represent a nutrient shift, we first simulate the model to steady state using parameters representing the preshift condition. For example, in order to represent an amino acid–replete but carbon-poor preshift condition, we first set the “Carbon” parameter to 0 and the “Glutamine” parameter to 1, simulate the model, and record the steady state. Then, in order to simulate the shift to a carbon-rich environment, we set the “Carbon” parameter to 1 while maintaining the “Glutamine” parameter at 1, continuing the simulation from the previous steady state.

Parameter estimation and robustness analysis

During the model construction phase, we parameterized individual parts of the network corresponding to each signaling pathway with time-course data relevant to that pathway. We defined a quadratic cost function, as described in Supplemental Section S2.1, and used the Levenberg–Marquardt Least Squares Optimization method (the leastsq function in the Scipy Python library) to minimize the cost (i.e., to improve the goodness-of-fit of the simulated trajectories to the experimental data). Next, we combined the subnetworks and supplemented the cost function with additional time-course and “perturbation” data (see Figure 2) relevant to regulators across the signaling pathways. We observed that the quality of the least-squares fit declined as the complexity of the model and the data increased. Hence, after an initial manual tuning of the full set of 128 parameters, we used an MCMC sampling procedure (described in Supplemental Section S2.2) to find an “optimal” (least-cost) parameter set at the end of 10,000 steps of MCMC sampling. The parameter values constituting the optimal set are presented in Supplemental Table S2.

To better understand the reliability of the optimal parameter values, we performed a global parameter-robustness analysis, as described in Supplemental Section S2. The goodness-of-fit cost function defined in the preceding paragraph is known to have a characteristic “stiff” and “sloppy” shape in the neighborhood of the best-fitting parameter set. Our goal was to characterize the shape of the cost function and, in the process, obtain a large collection of alternative parameter sets that provide a “good” fit (if not the “best” fit) to the data. To this end, we started by calculating the cost function on a Latin hypercube sample around the optimal set of parameter values obtained from the MCMC procedure. Then we constructed a quadratic approximation (the Hessian matrix) of the cost function around the local minimum. Using this approximate Hessian, we proposed new sets of parameter values constrained by the directions in parameter space corresponding to the largest eigenvalues of the Hessian, namely the “stiff” directions. By limiting parameter variations in the stiff directions and permitting large variations in the sloppy directions, we were able to generate thousands of potential parameter sets that differed significantly from the optimal set but still might provide an acceptable fit to the experimental data. For each of these proposed parameter sets, we evaluated the model cost, accepting the set if its associated cost was less than three times the lowest cost. Next, we recomputed the Hessian matrix using the cost evaluations over the “accepted” sets of parameter values, and we repeated the procedure of proposing new parameter sets based on the stiff and sloppy directions of the Hessian. At the end of four iterations of this process, we had collected 26,000 parameter sets with cost <3C_min. We winnowed this collection down to 18,000 parameter sets with cost <2C_min. Using this large collection of “acceptable” parameter sets, we studied the robustness of our parameter estimates, and the results of this analysis are presented in Supplemental Section S2.

Availability

The data curated from the literature are provided in five Supplemental Microsoft Excel files.

The code and data used in the construction, calibration, and analysis of the model are available at https://github.com/amoghpj/nutrient-signaling. The model is additionally provided in the SBML format. To enable ease of interaction with code, the Excel data sets are also provided as YAML files in this repository.

Abbreviations used:

AA

amino acids

AAB

amino acid biosynthesis

EGOC

EGO complex

GAP

GTPase activating protein

GlcR

glucose repression

MCMC

markov chain monte carlo

NCR

nitrogen catabolite repression

ODE

ordinary differential equation

PDE

phosphodiesterase

PDS

post-diauxic shift

PKA

protein kinase A

Rib

ribosome

RIBI

ribosome biogenesis

RTG

retrograde signaling

TCA

tricarboxylic acid cycle

TF

transcription factor

TORC1

target of rapamycin complex 1

wt

wild type.