Momentum-resolved electronic structure and band offsets in an epitaxial NbN/GaN superconductor/semiconductor heterojunction

Addressing design of future quantum devices, the study uncovers electronic structure of a superconductor-semiconductor interface.

Abstract

The electronic structure of heterointerfaces is a pivotal factor for their device functionality. We use soft x-ray angle-resolved photoelectron spectroscopy to directly measure the momentum-resolved electronic band structures on both sides of the Schottky heterointerface formed by epitaxial films of the superconducting NbN on semiconducting GaN, and determine their momentum-dependent interfacial band offset as well as the band-bending profile. We find, in particular, that the Fermi states in NbN are well separated in energy and momentum from the states in GaN, excluding any notable electronic cross-talk of the superconducting states in NbN to GaN. We support the experimental findings with first-principles calculations for bulk NbN and GaN. The Schottky barrier height obtained from photoemission is corroborated by electronic transport and optical measurements. The momentum-resolved understanding of electronic properties of interfaces elucidated in our work opens up new frontiers for the quantum materials where interfacial states play a defining role.

INTRODUCTION

The metal-semiconductor junction—also known as the Schottky junction—is one of the earliest solid-state devices discovered by Braun (1) as early as in 1874. It was used for rectification of electronic current flow even before the discovery of the electron (2). In the 1930s and 1940s, Schottky (3), Mott (4), and Bethe (5) uncovered the reason for the characteristic current rectification using the then newly formulated quantum mechanical picture of electronic bands in metals and semiconductors. The offset in electron energies between the Fermi level (E_F) of the metal and the conduction band minimum (CNM) of the semiconductor was found to be responsible for the very large rectification of electronic current flow across the junction. Despite the long history, Schottky junctions remain at the forefront of many technological applications ranging from high-speed terahertz electronics to low-power digital electronics and high-voltage power electronics (6–9). Latest generations of these devices are based on newer families of semiconductors and metals or superconductors, often using quantum confinement and correlation effects in low-dimensional structures. Even with the ubiquity of Schottky junctions in modern electronics, a full quantum mechanical understanding of their workings remains far from complete. An important and still elusive piece is the momentum (k)–dependent electronic band alignment across the junction as characterized by their individual electronic dispersions E(k).

Angle-resolved photoemission spectroscopy (ARPES) provides the most direct pathway for scrutiny of electron states resolved in k space. Its use to probe buried interfaces is, however, hampered by a relatively small probing depth of typically less than 0.5 nm, limited by the photoelectron mean free path (10). This constraint can be removed by the use of soft x-ray photon energies (hv ~ 1 keV), whereby the probing depth increases to several nanometers (11) to access buried interfaces. Such applications of soft x-ray ARPES (SX-ARPES) have recently been demonstrated, for example, for semiconductor/semiconductor interfaces AlN/GaN in high electron mobility transistor heterostructures (12), ferromagnetic/semiconductor interfaces EuO/Si (13) and EuS/InAs (14) where the band offset is crucial for the spin injection functionality, ferromagnetic/topological interfaces EuS/Bi₂Te₃ (15), metal/strong spin-orbit coupling semiconductor interfaces Al/InAs and Al/InSb prototypic of the Majorana fermionic systems for quantum computing (16), etc. [for a recent review, see (17)]. Measurement of k-resolved energy states at heterojunctions using SX-ARPES requires interfaces of high elemental and structural purity and ultrathin overlayer films to allow photoelectrons generated at the interface to escape.

Nitride materials host a rich palette of semiconducting and superconducting properties, and also host piezoelectricity, ferroelectricity, and magnetism (18). Semiconducting GaN and its heterostructures are used in blue light-emitting diodes and high-power electronic devices such as diodes and transistors. Metallic NbN becomes superconducting below 17 K, enabling applications such as single-photon detectors (19), bolometers (20), and Josephson junctions (21) as building blocks for low-temperature electronics and quantum computing (22, 23). Although the first study of NbN dates back nearly 100 years (24), its electronic band structure, unexpectedly, has never been measured directly. Recently, NbN was epitaxially integrated with gallium and aluminum nitride (25, 26), positioning it as an important material for future electronics integrating superconductivity with semiconducting behavior. Properties of the NbN/GaN heterostructure are attractive for potential applications in the latest devices for quantum computation. For example, the typically incompatible integer quantum Hall effect and superconductivity was recently found to exist concurrently in this material family (27). Other properties include reduction of phonon escape time (28) and high operating frequency (29) in hot electron bolometers. Critical to progress in this field is a detailed understanding of the k-resolved electronic structure of the interface between NbN and the group III nitride materials.

Here, we explore the k-resolved electronic structure of a Schottky junction of epitaxially grown ultrathin, nearly lattice-matched superconducting NbN interfaced to the semiconducting GaN. By taking advantage of the larger probing depth of SX-ARPES, we directly measure the k-resolved band structure of the highly crystalline NbN overlayer and the band structure on the GaN side of the ultrashallow heterojunction buried ~2 nm below. This information allows us to determine not only the band bending in GaN but also the Schottky barrier height and k-resolved interfacial alignment of the NbN and GaN band structures, which defines the main quantum-mechanical properties of this metal-semiconductor junction. The experimental band structures and alignments are compared with first-principles calculations. The success of our experimental methodology can be carried over to other epitaxial junctions of metals and superconductors with semiconductors and other heterojunctions.

RESULTS

Structural and transport properties of the NbN/GaN heterostructures

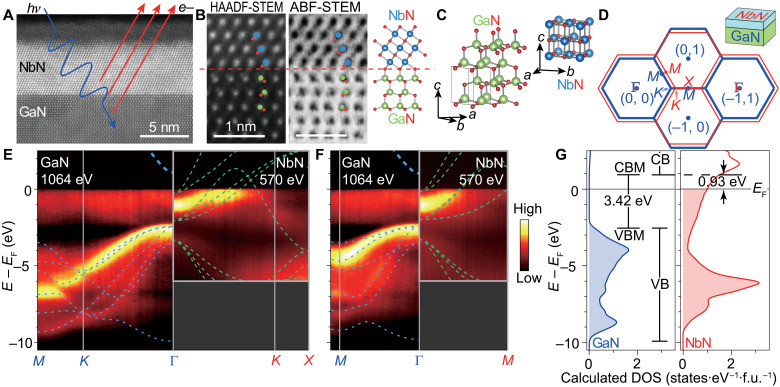
The structural properties of the molecular beam epitaxy (MBE)–grown NbN/GaN heterojunction with an NbN thickness of 5.5 nm are shown in Fig. 1 (A to C). A high-resolution scanning transmission electron microscopy (STEM) image of the NbN/GaN interface in Fig. 1A is superimposed with a schematic of SX-ARPES, illustrating how this technique probes the interface electronic structure for NbN/GaN. Figure 1B shows high-angle annular dark field (HAADF)–STEM and annular bright field (ABF)–STEM image of the GaN/NbN interface in atomic scale. The GaN is metal (Ga)–polar and aligned along the [0001] direction. The NbN [111] axis aligns with the [0001] crystal direction of GaN. Both the Nb and N sublattices can be resolved in Fig. 1B. The atomic arrangement of the two crystalline layers is indicated by the ball-and-stick models in Fig. 1 (B and C). The NbN/GaN interface is atomically sharp, with no evidence of disorder, contamination, or intermixing across the interface.

Fig. 1. Characterization of the MBE-grown NbN/GaN heterojunction.

(A) STEM image showing high-quality NbN film and sharp interface of NbN/ GaN. A thin oxidized layer (~2 nm) is observed on top of NbN. (B) Simultaneously acquired HAADF-STEM and ABF-STEM images showing the interface quality and the polarity. Nb, Ga, and N from the atomic ball-and-stick model correspond to blue, green, and red spheres, respectively. (C) Bulk crystal lattice of NbN and GaN. The NbN [111] direction is aligned with the GaN [0001] direction in (A) and (B). (D) Surface BZs of (0001) GaN and (111) cubic NbN. (E and F) Measured band structure of the NbN/GaN heterojunction along the Γ-K and Γ-M directions. GaN data were taken at hv = 1064 eV, while NbN data were taken at hv = 570 eV. Calculated band structure for GaN (blue dashed lines) and NbN (green dashed lines) has been superimposed on the intensity data. (G) Density of electronic states in bulk GaN and NbN calculated using DFT indicating a barrier height of 0.93 eV.

Introducing our electronic structure results, Fig. 1D sketches the k-space configuration as a superposition of the surface Brillouin zones (BZs) of (0001) GaN and (111) cubic NbN. As a quick start into our essential SX-ARPES results to be unfolded below, Fig. 1 (E and F) shows the k-resolved band structure of the NbN/GaN heterointerface represented as the experimental band structure of GaN matched at the interface to that of the NbN overlayer. In the GaN band structure, the valence band maximum (VBM) is seen at the Γ point, and the dispersions along both the Γ-K-M and the Γ-M directions are clearly resolved. For NbN, the experimental band structure shows bands dispersing upward from the Γ point and crossing E_F at about halfway along the Γ-K and Γ-M lines. The dashed lines are the energy bands of GaN and NbN calculated using density functional theory (DFT), with the bands above E_F being unoccupied and thus inaccessible to photoemission. One of the key results of our study is that the valence band offset (the energy difference between the VBM of GaN and E_F of NbN) is determined to be 2.49 eV. With the fundamental GaN bandgap of 3.42 eV, this figure implies a conduction band offset of 0.93 eV at the Γ point of the interface. This is summarized in the density-of-states calculations in Fig. 1G. We emphasize that the k-space separation of the superconducting states of NbN at E_F from the GaN states at the VBM, about a quarter of the BZ, results in their entire electronic decoupling. We will expand on the SX-ARPES measurements and its implications for the physics of the NbN/GaN heterojunction later on, after describing our measurements of the structural, transport, and optical properties of our NbN/GaN samples.

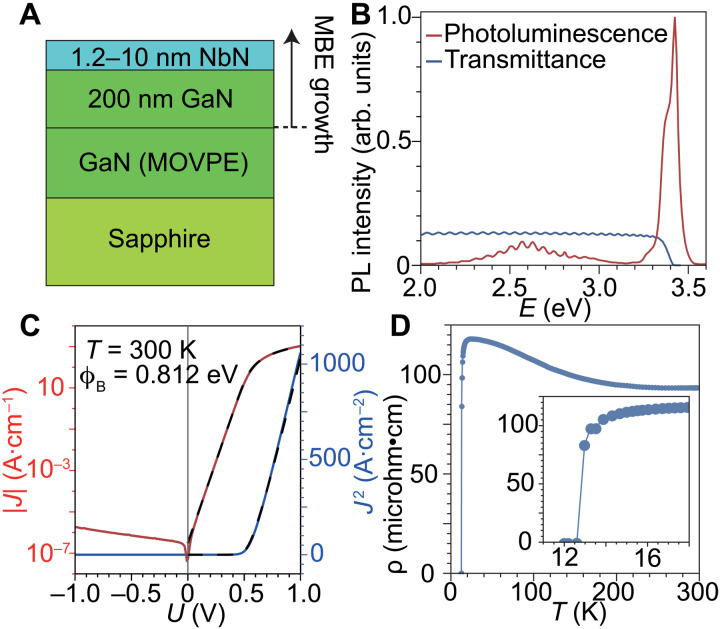
A series of NbN thin films of differing thickness were grown on GaN, as shown in Fig. 2A, to ensure that the NbN would retain its structural and electronic properties when the films were scaled to the thicknesses of a few nanometers tailored to the probing depth of the SX-ARPES measurements. Reflection high-energy electron diffraction (RHEED), x-ray diffraction (XRD), and atomic force microscopy (AFM) were also used to confirm that all NbN films in this thickness series are epitaxial, with uniform thickness and smooth surfaces. Using XRD, we determined that the lattice constant of the rock-salt cubic NbN is a = b = c ~ 4.34 Å, while that of the hexagonal GaN is a = b ~ 3.19 Å and c ~ 5.19 Å (crystal structures are shown in Fig. 1C). The in-plane Nb-Nb spacing is therefore ~3.07 Å along the (111) orientation, which results in a 3.8% lattice misfit at the interface. Photoluminescence measurement (Fig. 2B) of a sample with a 5.5-nm NbN film on GaN indicates that the MBE-grown GaN underneath the NbN exhibits a photoluminescence peak at 3.42 eV. This value is in good agreement with previously reported values for GaN and provides confidence that the electronic properties of the MBE-grown GaN film are preserved through the growth of the NbN thin film, a process that occurs at high temperature. Additional details of the heterostructure growth and characterization as well as removal of the in situ indium cap needed to protect sample quality until SX-ARPES measurement are described in Methods.

Fig. 2. Properties of the NbN/GaN films.

(A) Illustration of the MBE growth of the samples. (B) Photoluminescence (PL) and optical transmittance measurements of a 5.5-nm NbN on GaN sample performed at 300 K. (C) IV data for an NbN/GaN Schottky barrier diode performed at 300 K. The dashed line represents the best-fit thermionic emission model with a series resistance. (D) Resistance versus temperature of a 2.8-nm NbN on GaN film. A clear and sharp transition to the zero-resistance state is seen around 13 K.

Electronic transport across the NbN/GaN interfaces was studied by fabricating circular Schottky barrier diode devices with a diameter of 50 μm. A current-voltage (IV) measurement of such a device performed at 300 K is shown in Fig. 2C. The diode exhibits strong rectification, demonstrating an exponential increase in the current of seven orders of magnitude in forward bias. This behavior is modeled well using thermionic emission theory

$$I=a{A}^{**}{T}^2{e}^{-\frac{q}{k\mathrm{T}}{\mathrm{\varphi }}_{\mathrm{b}}}(e^{-\frac{q}{\mathrm{\eta }k\mathrm{T}}(V-\mathit{IR})}-1)$$

where I is the current, a is the device area, A^** is the Richardson constant for GaN, T is the temperature, q is the elementary charge, k is the Boltzmann constant, ϕ_b is the effective barrier height, η is the ideality factor, V is the voltage, and R is a resistance in series with the diode. In this model, ϕ_b, η, and R are used as fitting parameters.

Using the GaN effective mass (m*) in the CBM of 0.222 m₀ (m₀ is the free-electron mass) (30) to calculate the Richardson constant for GaN of 26.64 A K⁻² cm⁻², the effective NbN/GaN barrier height is calculated from the best-fit thermionic emission model to be 0.7660 ± 0.002 eV. Using capacitance-voltage measurements of the same NbN/GaN diode in reverse bias, we determine the donor concentration in the GaN to be ~2 × 10¹⁷ cm⁻³. Using this value for the donor concentration in the GaN, the Schottky barrier height lowering due to electric fields within the GaN is calculated (31). Thereby, we determine the fundamental Schottky barrier height of the NbN/GaN junction to be 0.812 ± 0.003 eV. We see a 0.12-eV difference in the barrier height determined using IV measurements and that determined by SX-ARPES (0.93-eV barrier height). This may be traced to several of the simplifying assumptions of the thermionic emission model, such as the assumption of a spatially homogeneous Schottky barrier, which ignores the effects of threading dislocations or other defects in the semiconductor, the assumption of an absence of tunneling current, and the neglect of effects related to the band structure of the materials and the interfacial reconstruction of the electronic structure.

Resistance versus temperature measurements of an NbN film with a thickness of 2.8 nm exhibit both a low normal state resistivity of 94 microhm·cm and a superconducting critical temperature of 12.8 K, as shown in Fig. 2D. These values compare favorably to other reports of superconducting and normal metal properties of ultrathin NbN films, which we ascribe to the high quality of the MBE-grown interface and films (32).

Electronic structure of the NbN/GaN interface

Comparing the different samples of the NbN/GaN heterostructure, we find that neither the NbN band structure nor that of GaN shows any changes with the film thickness within the experimental resolution. The highest-quality SX-ARPES data on NbN were found for the sample with its largest thickness of 10 nm (Figs. 1, E and F, and 3). The GaN band structure could be seen in the hv range of our experiment through an NbN film thickness of less than 2 nm, with the strongest signal recorded in the 1.2-nm-thick NbN film (Figs. 1, E and F, and 4).

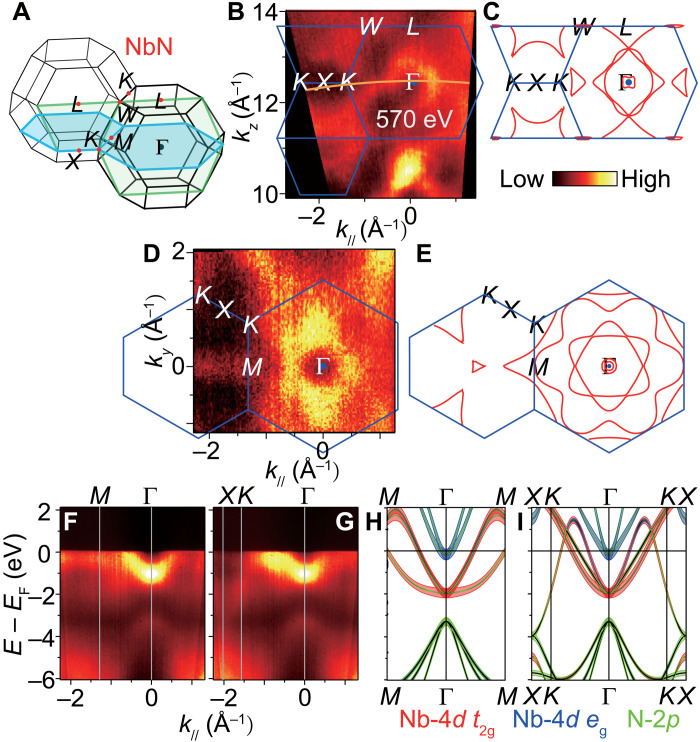
Fig. 3. The electronic structure of NbN.

(A) BZ, where the green and blue planes indicate the position of the measured out-of-plane and in-plane FS cuts, respectively. (B to E) Experimental out-of-plane and in-plane FSs and corresponding calculated FSs. The orange curve marked by 570 eV indicates the experimental k_z across the Γ point. The blue boundaries represent the BZ edges shown as planes in (A). (F and G) SX-ARPES intensity along M-Γ and X-K-Γ measured at hv = 570 eV. (H and I) DFT-calculated band structure, with atomic orbital projections, along the directions measured in (F) and (G).

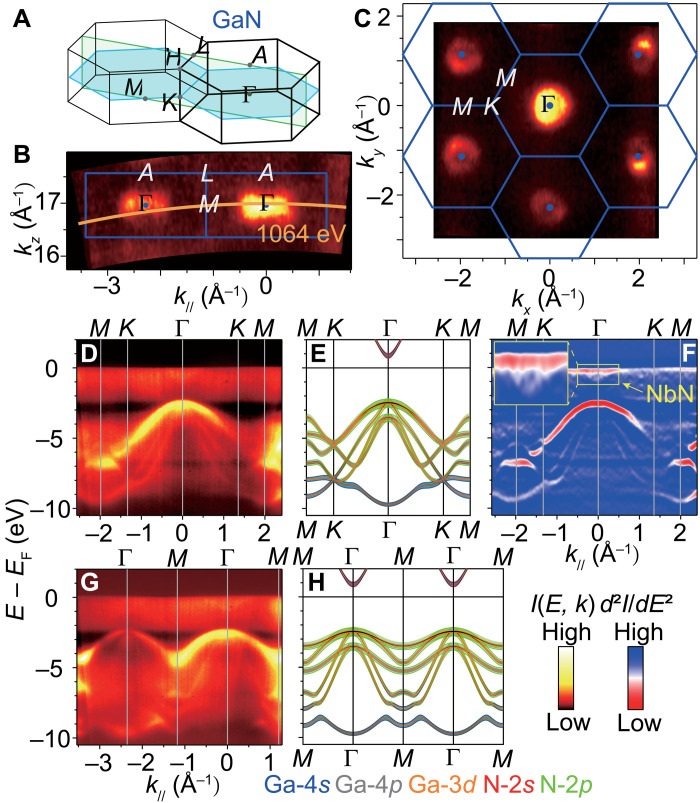
Fig. 4. The electronic structure of GaN.

(A) BZ. The green and blue planes indicate the position of the out-of-plane and in-plane isoenergy maps, respectively. (B and C) Experimental out-of-plane and in-plane isoenergy maps at E_F −2.6 eV. The orange curve marked at 1064 eV indicates the experimental k_z across the Γ point. (D) SX-ARPES intensity showing the valence bands of GaN along M-K-Γ-K-M. (E) DFT-calculated bands along M-K-Γ-K-M. (F) Second-derivative representation for (D) (positive values set to zero). The conduction band of NbN near E_F is zoomed in. (G and H) Same as (D) and (E) but along M-Γ-M-Γ-M.

Our results for NbN, the first direct measurement of the k-resolved electronic structure of this material, are presented in Fig. 3. The experimental in-plane and out-of-plane Fermi surface (FS) maps and the corresponding calculated FS cuts (Fig. 3, B to E) show large electron pockets of the NbN conduction bands centered at the Γ and X points of the extended BZ. The Γ-centered FS pocket in the in-plane map has a sixfold symmetry, consistent with the NbN growth direction of [111] and reproduced in the calculations (Fig. 3E). There is no spectral weight in the FS of NbN at the Γ point where the CBM and VBM of GaN are located. The dispersive FS contours in the out-of-plane map identify the three-dimensional (3D) character of the electron states formed in the 10-nm-thick NbN film. The broad spectral width of the experimental bands contributing to the FS (Fig. 3, F and G) does not directly allow us to distinguish the number of separate bands, but the band structure calculated from DFT for bulk NbN gives a useful starting point for the interpretation of the SX-ARPES dispersions. An electron-like band centered about Γ with a binding energy (E_B) of −1.1 eV is expected to be Nb-4d t_2g in orbital character based on our DFT calculations presented in Fig. 3 (H and I) and fig. S1. We verify the d t_2g character of these bands by their x-ray polarization dependence presented in fig. S2. The octahedral crystal field due to the N atoms is expected to split the Nb-4d orbitals, pushing the e_g bands up toward E_F. The bands starting near E_B = −3.4 eV at the Γ point are calculated to be N-2p in orbital character. DFT underestimated the energy difference between the N-2p and Nb-4d t_2g states by ~1 eV, where it is clear that the measured Nb-4d t_2g bands are pushed up relative to the N-2p bands. This disagreement could be due to the approximations made in DFT or due to nitrogen vacancies in the NbN film, which are known to reduce E_F (33). The two dispersion branches along Γ-M are consistent between the experiment and theory. The three branches predicted by DFT along Γ-K are not resolved independently in the experimental data; however, the Fermi momentum (halfway the Γ-K line) is consistent between the experiment and theory. The experimental dispersion range of these bands is notably smaller than that predicted by DFT, which may indicate a strong renormalization of the Nb-4d t_2g bands due to yet unknown many-body effects. The ~1-eV scale of these changes is suggestive of electron-electron interactions. The increase in the density of states near E_F associated with the enhanced m* may contribute to the robust superconductivity and high critical temperature known for NbN. While a dispersive band of Nb-4d character can be seen clearly at the K point, low intensity at the X point prevents a direct comparison with theory (Fig. 3G). DFT predicts that this band changes character from Nb-4d to N-2p, becoming degenerate with the N-2p manifold at the X point (Fig. 3I). Overall, our experiment confirms the characteristic features of the DFT band structure for bulk NbN.

We now focus on the GaN band structure measured by SX-ARPES in the 1.2-nm sample (Fig. 4). We note that zero E_B of the heterostructure is defined by E_F of the NbN film. Both in-plane and out-of-plane isoenergy maps taken 2.6 eV below E_F (Fig. 4, B and C) display the expected hole-like pockets of the Γ-centered valence bands of GaN. The VBM of GaN is 2.49 eV below E_F at the Γ point probed at hv = 1064 eV (Fig. 4, D and F). Although the M-Γ-M and M-K-Γ images taken at hv = 1064 and 1216 eV (see fig. S3) correspond to k_z values different by the reciprocal lattice vector 2π/c (where c is the [0001] lattice constant of GaN) and are therefore equivalent, the photoemission dipole selection rules in the nonsymmorphic crystal structure of GaN for these k_z are different and light up different sets of bands (34). Apart from an energy shift, the measured band structure is identical to that observed in other GaN-based heterostructures (12). The calculated bulk band structure of GaN, including the orbital projections of the bands, is shown in Fig. 4 (E and H). (Additional orbitally projected band structure can be found in fig. S3.) The heavy-hole m* is estimated from a fit to the SX-ARPES data to be ~1.82 ± 0.04 m₀ compared to the DFT value of 2.1 m₀ [the light-hole m* cannot be evaluated accurately from our SX-ARPES data because this band is much obscured by the heavy-hole band’s spectral weight at the Γ point and, in addition, its apparent dispersion can be flattened by the intrinsic k_z broadening of the ARPES final states (35)]. Overall, the agreement between the theoretical and experimental band structure of GaN can be regarded as excellent. We note, however, that the measured ARPES dispersions reflect the band structure of GaN in the thin interfacial layer. Because of band bending in the semiconducting GaN, the bulk band structure is slightly shifted in energy and can be recovered from energy shifts of core-level peaks as a function of hv. On the basis of the Ga 3d core levels, we have measured an upward band-bending profile varying by ~300 meV over a distance of ~6 nm from the interface. This band bending is comparable to the expected electric field due to depletion of carriers in the GaN at the interface. We note that the measured band bending in this NbN/GaN structure is much smaller than previously reported photoemission measurements of band bending in a GaN/AlGaN structure (12) and the band bending at the Ga-polar n-GaN surface (36) (see Methods and fig. S4).

Concurrently with the GaN valence bands, our SX-ARPES data resolve NbN conduction bands in the vicinity of E_F, which are best resolved in the second derivative d²I/dE² of the spectral intensity (Fig. 4F and fig. S3). Their difference from the NbN bands in Fig. 3 indicates the 3D character of the electron states formed in NbN. The hv values used in Fig. 4 set k_z to the Γ points of GaN but miss the Γ points of NbN because of the different c lattice constants of these materials in our heterostructure. Because of large electron concentration and thus small Thomas-Fermi screening length in NbN, only 4.5 monolayers stacked within the 1.2-nm thickness of the NbN film are already sufficient to form its 3D band structure, with quantum size effects suppressed by an inhomogeneity of the film thickness.

Last, to visualize the k-dependent band alignment, we bring together the NbN experimental band structure measured at hv = 570 eV (Fig. 3) and the GaN one measured at 1064 eV (Fig. 4), both corresponding to k_z tuned to the Γ point. The energy scale of these band structures is matched via the E_F position. These plots, displayed in Fig. 1 (E and F), are the key result of our work. We directly observe that the energy separation of the GaN states from E_F, where the superconducting states of NbN are located, markedly varies across the BZ and attains its minimum value of 2.49 eV at the VBM of GaN. The superconducting states of NbN are separated in k space from this point as much as about a quarter of the BZ. The consequences of these experimental results for physics of the NbN/GaN heterojunction are discussed below.

DISCUSSION

Interfacial band offsets are key ingredients in design of technologically important heterostructures. However, they are not often directly measured (37–39) and almost never k-resolved. Direct measurement of the band offset between NbN and GaN along with the k-resolved band structures of the constituent materials and their heterointerface enables integration of NbN into the general electronic materials framework; this sets the stage for streamlined design, modeling, and understanding of fully integrated NbN-based superconductor/semiconductor devices (Josephson junctions with integrated gain, single-photon detectors, etc.). Furthermore, the first direct measurement of the NbN band structure enables a greater understanding of the properties of this widely studied and used material.

The k-resolved electronic structure at the NbN/GaN interface, directly determined in our SX-ARPES experiments, bears an important consequence on its functional properties. In its normal metal state, moving electrons from the CBM of GaN in the Γ point into the superconducting states of NbN would require a larger lateral momentum because NbN does not have electronic states at the BZ center. Superconductivity is an effect dictated by electronic structure within the pair potential energy (several millielectron volts) from E_F of the junction. Because the GaN valence/conduction bands are separated from E_F by a much larger energy difference of hundreds of millielectron volts in the VBM/CBM due to the large energy denominator in this second-order perturbative picture, the hybridization between the superconducting states in NbN at E_F and the GaN states is negligible. Furthermore, the superconducting states of NbN at E_F are displaced in k space from the Γ point by about a quarter of the BZ, where the dispersion of the GaN bands away from E_F further increases their energy separation from NbN and thus the strength of their already negligible hybridization. The absence of such hybridization is crucial to protect the superconductivity on the NbN side of the interface from potential poisoning by an admixture of the states on the GaN side. This property establishes the NbN/GaN interfaces as an important route toward integration of superconductivity into semiconductor technology for electronic devices with important functionalities.

On the other hand, the Cooper pair formation in the conventional superconductor NbN can be affected on the electron-phonon interaction (EPI) side through interfacial cross-talk of the phonon modes. It has been reported that such interfacial EPI is crucial to the enhancement of T_c by almost 20 K in the monolayer FeSe/SrTiO₃ (40), when compared to the optimally doped bare FeSe (41). Another example is the LaAlO₃/SrTiO₃ interface, where the deposition of LaAlO₃ increases the LO3 phonon energy in SrTiO₃ from 100 to 120 meV (42, 43). In NbN/GaN, there are optical phonon modes stretching from 18 to 92 meV (44). Interfacial EPI in the NbN side of the interface, if notable, could manifest as replica bands shifted from the quasiparticle bands by the phonon energy (41–43) or as electron dispersion kinks at this energy (45, 46). Our ARPES experiment could not resolve such signatures of the EPI because of the relatively large width of the spectral peaks, insufficient energy resolution, or fundamentally weak interfacial EPI. These considerations call for studies of monolayer-thick NbN/GaN heterostructures by the vacuum ultraviolet (VUV) in an attempt to resolve the effects of interfacial EPI.

Additional important functionalities of the NbN/GaN junction may be envisaged if Cooper pairs can be injected from NbN to GaN. However, the large ~0.9-eV band offset implies that, for such an injection, a heavily doped GaN tunnel junction is necessary. For enhanced transparency, the growth of thin intervening layers of graded bandgap InGaN that remove the measured energy band offset is needed. This sort of careful interfacial engineering is critical, for example, to seamlessly interface superconducting and integer quantum Hall states in this superconductor/semiconductor heterojunction.

From a methodological perspective, our results highlight the advantages of SX-ARPES as the only spectroscopic technique capable of directly visualizing k-resolved electronic structure of buried interfaces and heterostructures. Our present study uses tunable synchrotron radiation to determine band structure of NbN and GaN at different photon energies as dictated by their different out-of-plane lattice constants. The direct measurement of the k-resolved electronic states across the NbN/GaN interface has been enabled by the fusion of SX-ARPES technique with the development of MBE growth techniques capable of producing crystalline, coalesced NbN films on GaN down to 1.2 nm in thickness. Applications of such ultrathin epitaxial superconducting NbN films for advanced electronic devices such as single-photon detectors (47) are currently being investigated.

In conclusion, we have measured the momentum-resolved band structure of the all-epitaxial NbN/GaN heterointerface—a system allowing integration of superconductivity into nitride semiconductor technology—using SX-ARPES. Advances in crystal growth and resulting crystal quality of the GaN and NbN heterointerface allowed us to measure the GaN band structure at the interface while concurrently resolving the band structure of the nearly century-old superconductor NbN. Both GaN and NbN band structures are well described by DFT studies of the bulk materials. This study of the electronic structure of the heterointerface gives a direct measure of the band alignment between two constituent materials. A large separation of the superconducting NbN states from the GaN states in energy and k space excludes their hybridization, thereby protecting the superconductivity from potential poisoning by the GaN electrons. The materials advances, methods, and the momentum-resolved understanding of the electronic properties of heterojunctions presented in this work highlight the power of combining MBE and SX-ARPES and further position nitrides as a scalable, industrially capable platform for future hybrid superconductor/semiconductor electronics.

METHODS

The NbN/GaN heterostructures were grown by nitrogen plasma-assisted MBE (PAMBE) on commercially available hydride vapor phase epitaxy (HVPE) GaN on sapphire wafers. Ga (99.99999% purity) was provided by a Knudsen cell, and active nitrogen species were provided using a radio frequency plasma source. n-type GaN films of approximately 200 nm in thickness were grown by PAMBE on the HVPE GaN. The GaN was grown in Ga-rich conditions, and upon completing the GaN growth, the substrate temperature was increased to a surface temperature of 710°C to thermally desorb excess Ga that had accumulated on the film surface for 5 min before the NbN was nucleated. Nb (99.95% purity) was supplied by an electron beam evaporator; Nb flux is measured using an electron impact energy spectroscopy system measuring the optical emission of the Nb. During growth, the nitrogen flux exceeds the Nb flux by a factor of approximately 3.5; the NbN film growth rate is 1.8 nm/min. The final NbN film thickness covered 1.2, 1.5, 2.0, 2.5, and 10 nm for the SX-ARPES experiments and was 2.8 nm for the resistance and 5.5 nm for photoluminescence measurements. In situ RHEED measurements during and after growth confirmed that the rock-salt cubic NbN grows in the (111) orientation. For characterization of the NbN/GaN heterostructure in atomic scale, a cross-sectional TEM specimen was prepared using focused ion beam milling, with carbon and platinum layers sputtered on the sample surface before the milling and a final milling step of 5 keV to reduce damage. The sample was then examined by STEM, using an aberration-corrected Titan Themis operating at 300 keV. To prevent contamination during the ex situ sample transfer to the ARPES experiment, all samples were capped with indium films of approximately 800 nm in thickness grown before removing the samples from the growth reactor. The indium films were grown with the sample at room temperature to aid agglomeration of the film. AFM was used to confirm that the indium capping film was coalesced.

SX-ARPES experiments were performed in the hv range of 350 to 1250 eV at the SX-ARPES end station (48) of the ADRESS (Advanced Resonant Spectroscopies) beamline of the Swiss Light Source, Paul Scherrer Institute, Switzerland (49). The indium capping films were removed via annealing at 690° to 730°C by electron beam heating method for 1 to 2 hours in situ. The photoelectrons were detected with the analyzer PHOIBOS 150 from SPECS GmbH at an angular resolution of ~0.1°. The combined energy resolution was set to 80 to 250 meV. The isoenergetic maps were integrated within ±50 meV. The experiments were performed in vacuum <9 × 10⁻¹¹ mbar. To minimize suppression of the coherent spectral component caused by the thermal atomic motion (50), the experiments were performed at a base sample temperature of ~20 K. In all presented SX-ARPES data, the coherent component was accentuated by subtracting angle-integrated spectral intensity. All the data shown in this study are probed with p-polarized photons. The photoelectron kinetic energies and emission angles were converted into E_B and k by using the kinematic formulas compiled in (48), which take into account the photon momentum. For the second-derivative data representation d²I/dE², the intensity data were denoised by Gaussian smoothing along the energy axis with the full width of 700 meV. We note that although laser ARPES at ultralow hv might provide better energy resolution and, in principle, larger probing depth than SX-ARPES, its limited span in k space and E_B would be insufficient for complete characterization of the NbN/GaN electronic structure.

DFT calculations are performed using the VASP (Vienna Ab initio Simulation Package) (51, 52) code with projector augmented wave pseudopotentials and plane wave basis sets. For NbN, we use the generalized gradient approximation as implemented in the Perdew-Burke-Ernzerhof (PBE) functional (53) with Methfessel-Paxton smearing for the occupation of the electronic states of 0.1 eV with an electron-momentum grid of 18 × 18 × 18 and a kinetic energy cutoff of 700 eV. For GaN, we use the range-separated hybrid functional HSE06 (54) with Gaussian smearing of 0.01 eV with an electron-momentum grid of 10 × 10 × 6 and a kinetic energy cutoff of 600 eV. For the energy convergence, a threshold on the change in total energy of 10⁻⁸ eV is used for all calculations. For both materials, atomic coordinates and lattice parameters are relaxed using the PBE functional with a 10⁻³ eV/Å force convergence condition. The relaxed lattice constants overestimate the experimental values, as expected in PBE. We find a = 4.418 Å for NbN and a = 3.218 Å and c = 5.243 Å for GaN. An additional scissor cut was applied to the calculated GaN conduction band to match the experimental bandgap measured in this study. The orbital projections and FS cuts were calculated on the DFT-relaxed NbN and GaN structures.

The method to extract the band-bending profile is as described elsewhere (55, 56). The Ga 3d core-level peaks were modeled as a sum of several reference spectra with their own E_B shift and intensity. The effective attenuation length was calculated using TPP-2M formula (57). The reference spectra were simulated as an ideal asymmetric Voigt doublet, where the peaks area ratio and separation were taken from literature; Lorentz broadening was taken from the optimal fitting of all obtained spectra, and the Gauss broadening was calculated from beamline and spectrometer resolution.

Supplementary Materials

This PDF file includes:

Supplemental Text

Figs. S1 to S4

References