Abstract
Motivation
Single-cell RNA sequencing (scRNA-seq) enables transcriptome-wide gene expression measurements at single-cell resolution providing a comprehensive view of the compositions and dynamics of tissue and organism development. The evolution of scRNA-seq protocols has led to a dramatic increase of cells throughput, exacerbating many of the computational and statistical issues that previously arose for bulk sequencing. In particular, with scRNA-seq data all the analyses steps, including normalization, have become computationally intensive, both in terms of memory usage and computational time. In this perspective, new accurate methods able to scale efficiently are desirable.
Results
Here, we propose PsiNorm, a between-sample normalization method based on the power-law Pareto distribution parameter estimate. Here, we show that the Pareto distribution well resembles scRNA-seq data, especially those coming from platforms that use unique molecular identifiers. Motivated by this result, we implement PsiNorm, a simple and highly scalable normalization method. We benchmark PsiNorm against seven other methods in terms of cluster identification, concordance and computational resources required. We demonstrate that PsiNorm is among the top performing methods showing a good trade-off between accuracy and scalability. Moreover, PsiNorm does not need a reference, a characteristic that makes it useful in supervised classification settings, in which new out-of-sample data need to be normalized.
Availability and implementation
PsiNorm is implemented in the scone Bioconductor package and available at https://bioconductor.org/packages/scone/.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Gene expression data exhibit a scale-free power-law distribution () with the exponent fluctuating from 1 to 3. This result holds independently of experimental techniques (such as SAGE, microarray and RNA-seq experiments) and across different organisms (Awazu et al., 2018; Furusawa and Kaneko, 2003; Kuznetsov et al., 2002; Nacher and Akutsu, 2006; Ueda et al., 2004).
A power-law distribution has the property that large numbers are rare, while smaller numbers are more common. In transcriptomics, this translates to the presence of a relatively low number of genes with high expression levels along with many low-abundant genes. This suggests the presence of a complex organization conserved among species (Barabási and Albert, 1999).
Supported by this observation, Lu et al. (2005) and Wang (2020) proposed two normalization methods based on Zipf’s law, a type of power law, for microarray and RNA-seq data, respectively, showing promising results. Zipf’s law (also known as Z distribution) is a discrete variant of the Pareto distribution that in turn is a continuous power law.
Many between-sample normalization methods have been proposed for bulk and single-cell RNA-Seq data, and several attempts have been made to determine the best normalization procedure (Cole et al., 2019; Dillies et al., 2013; Evans et al., 2018; Tian et al., 2019). The general conclusion of these studies is that different datasets require different normalization strategies, and that the performance of normalization is influenced by many dataset-specific characteristics, such as sample heterogeneity, library preparation protocol and sequencing depth.
Apart from the statistical aspects, single-cell RNA sequencing (scRNA-seq) has posed new considerable computational challenges. The increase in the number of cells per experiment translates into a dramatic increase in the data points to be analyzed, requiring methods able to efficiently scale to millions of cells, both in terms of memory usage and computational time. Typically, each step of the analysis, from normalization to clustering and functional analyses, can be highly demanding when dealing with hundreds of thousands or even millions of cells (Hicks et al., 2021; Lähnemann et al., 2020). In this perspective, a desirable normalization method should be able to scale efficiently with the number of cells, while simultaneously maintaining a good performance.
In the analysis of bulk and single-cell RNA-seq data, two major classes of between-sample normalization methods have been proposed: global scaling and non-linear approaches. The simplest scaling method is the Count Per Million (CPM) transformation, which simply scales the observed read [or unique molecular identifiers (UMI)] counts by the total number of sequenced reads (or UMIs) per sample. More robust scaling procedures have been proposed in the bulk RNA-seq literature, such as TMM (Robinson and Oshlack, 2010), geometric mean scaling (DESeq2; Anders and Huber, 2010) and upper-quartile scaling (Bullard et al., 2010). In the context of single-cell data, a popular scaling approach is the deconvolution strategy proposed in Lun et al. (2016a) and implemented in the scran Bioconductor package (Lun et al., 2016b). Linnorm (Yip et al., 2017), a linear model-based scaling algorithm, although not as popular as scran, has been shown to outperform other methods in a recent benchmark (Tian et al., 2019). More recently, sctransform (Hafemeister and Satija, 2019) has gained popularity due to its good performance and its integration in the popular Seurat package (Stuart et al., 2019). Briefly, sctransform uses the Pearson residuals of a regularized negative binomial model as normalized data.
While CPM is scalable to millions of cells, its performance is not always optimal (Hafemeister and Satija, 2019; Robinson and Oshlack, 2010; Tian et al., 2019); on the other hand, more robust normalizations, such as scran and sctransform, require a large amount of time and/or memory in big datasets.
Here, we propose PsiNorm, a new scRNA-seq scaling normalization method, inspired by the Pareto power-law distribution. We compare PsiNorm to state-of-the-art methods in terms of concordance, scalability and computational efficiency, as well as in terms of the accuracy of downstream clustering. We show that PsiNorm is the most scalable normalization among those that show good accuracy, being highly efficient in terms of memory usage and computational time. In particular, PsiNorm leads to comparable and sometimes better results in terms of clustering and cell markers detections than state-of-the-art methods, such as scran and Linnorm, that either take longer or need more RAM. Finally, the ability of PsiNorm to work with out-of-memory data, such as HDF5 files, allows it to efficiently normalize datasets that may not even fit in RAM memory.
2 Approach and rationale
scRNA-seq data structures substantially differ from bulk. Potential gene dropouts and shallow sequencing make single-cell data highly sparse. Moreover, the ‘large p, small n’ paradigm (p being the number of genes, n the number of samples) that is typical of bulk data, is quickly moving toward the opposite scenario (n > p) with recent indexing-based experimental protocols. With the dramatic increase in the number of cells, all the analyses steps, including normalization, have become computationally intensive.
While some evidence showed a good fit of power-law distributions on bulk gene expression data, only few attempts have been made to fit such distributions to single-cell data (Townes and Irizarry, 2020). Motivated by these observations, here we investigate if and how power-law distributions could resemble scRNA-seq data empirical distributions with the goal of normalization in mind.
In the following, (i) we investigate the goodness-of-fit of the Pareto (type I) and Z (Zipf’s law) distributions on scRNA-seq data and (ii) we propose a new method, called PsiNorm, to normalize raw read counts based on this fit. Then, (iii) we compare our normalization in terms of cluster identification, concordance and computational resources required (time and memory usage) with other methods, proposed for bulk RNA-seq, such as logCPM, TMM and DESeq2, compositional data, such as the Centered Log Ratio (CLR), and scRNA-seq, such as Linnorm, sctransform and scran. The choice of these normalization methods represents a comprehensive set of methods that either have shown good performance in benchmark studies (e.g. Tian et al. 2019) or are popular among practitioners for the ease-of-use of their implementation. In addition, they are representative of both global scaling approaches (logCPM, TMM, DESeq2, scran and CLR) and non-linear approaches (Linnorm and sctransform).
Finally, we present a case study to evaluate the top performing methods, not only in terms of clustering but also in terms of differential expression and marker detection.
3 Materials and methods
3.1 The Pareto distribution
The Pareto (type I) distribution is a continuous power-law probability distribution with support on the positive real axis. Its cumulative distribution function (cdf) is:
where α is the shape parameter and m is the minimum value of X.
The Pareto’s density function can be expressed as a power-law
Given a sample of n independent observations, the parameter α can be estimated using the maximum likelihood method obtaining
| (1) |
One important problem of fitting such distribution to sequencing data is that the Pareto distribution is defined only for m > 0, a condition not met since we always expect some genes with zero mapped reads.
There are two possible solutions to this problem. The first one (that we called Pareto0) estimates α on non-zero counts, while the second one (called Pareto + 1) fits the model on pseudo-counts (raw counts + 1). In this second approach, can be seen as the inverse of the log geometric mean of the pseudo-sample:
| (2) |
3.2 The Zipf’s law and its relation to Pareto
The Zipf’s power-law distribution originates from the observation that the frequencies of words in a text are inversely proportional to their ranks (Powers, 1998). It is a discrete distribution based on ranks and its probability mass function is given by:
where I is the number of elements, k the vector of their ranks and s the coefficient characterizing the distribution. H(I, s) is the generalized harmonic series. Both Pareto and Zipf distributions are simple power laws with negative exponent and Zipf can be derived from the Pareto distribution if X values are binned into I ranks (Arnold, 2015; Meintanis, 2009).
Given the relationship between the two distributions, we can derive that (see Supplementary Text for details) (Arnold, 2015; Meintanis, 2009). However, while the maximum likelihood estimator of the Pareto α parameter has a closed-form, Zipf’s distribution parameter does not. Hence, numerical optimization methods are required.
3.3 The PsiNorm normalization
The Pareto parameter α is inversely proportional to the sequencing depth, it is sample specific and its estimate can be obtained for each cell independently. Denoting by X the I × J matrix of read counts, with I genes and J cells, then the vector of normalized counts of cell j, , is equal to:
| (3) |
Given the inverse relationship between α and the sequencing depth, here is used as a multiplicative normalization factor. We note that this essentially reduces to dividing each count by the sum of the log-counts of each cell, rescaled by a constant, a very similar approach to the CPM normalization. Note that often (e.g. in clustering and dimensionality reduction) it is useful to work with log-normalized counts. In the following, we will denote with log-normalized counts the quantity .
In the following, PsiNorm is compared with seven state-of-the-art methods (see Supplementary Text), in terms of clustering performance, concordance and computational efficiency.
3.4 Evaluation criteria
3.4.1 Cluster analyses
To evaluate the ability of normalization to remove technical bias and reveal the true cell similarity structure, we used both an unsupervised and a supervised approach, since we know the labels of the datasets used for the comparison (see Section 3.5 for details).
In the unsupervised approach, we applied principal component analysis (PCA) on the log-normalized counts and, using the first 50 PCs, we identified clusters using a partitional method (clara in the cluster R package) with k (number of groups) equal to the known number of clusters. Then, we computed the Adjusted Rand Index (ARI) to compare the known and the estimated partitions (Hubert and Arabie, 1985).
In the supervised approach, we computed the silhouette index of the known partition in the reduced dimensional space obtained by PCA of the log-normalized counts. The rationale is that a normalization that properly reduces technical noise should lead to compact clusters with high cohesion and separation that correspond to the known cell populations.
3.4.2 Concordance analyses
We estimated within-method concordance (replicability) by randomly splitting each dataset into two equally sized parts and evaluating the Jaccard index between the two lists of the 500 most variable genes (defined by the function FindVariableFeature of the Seurat package with method vst) after normalization. The splitting is repeated 10 times and the average within-method concordance is reported. Between-dataset concordance (reproducibility) has been evaluated using scRNA-seq data of the same samples obtained with different experimental techniques. As a measure of concordance, we used the Jaccard index between the two lists of the 500 most variable genes after normalization across datasets.
3.5 Real datasets
We used two sets of data to compare methods: the scRNA-seq mixed human cell lines experiments from Tian et al. (2019), which we refer to as the mixology dataset, and the mouse primary motor cortex datasets generated by the BRAIN Initiative Cell Census Network (BICCN) (Yao et al., 2020), which we refer to as the BICCN dataset.
In the mixology dataset, five human lung adenocarcinoma cell lines were cultured separately, single cells from each cell line were mixed in equal proportions, with libraries generated using three different protocols CEL-seq2, Drop-seq with Dolomite equipment and 10× Chromium (Tian et al., 2019).
In the BICCN dataset, over 600,000 cells were characterized via single-cell and single-nucleus RNA-seq (using 10X and SMART-seq protocols) to comprehensively identify all cell types in the adult mouse primary motor cortex (Yao et al., 2020).
To compare the normalization approaches in terms of concordance and clustering performance, we selected a random subset of 500 cells from both single-cell and single-nucleus samples for each sequencing protocols 10X v2, 10X v3 and SMART-Seq. All datasets were filtered to keep only those genes with more than 1 read in more than 5 cells and discarding cells without labels. For further details see Supplementary Table S1.
3.6 Case study
As a case study, we use the complete 10X v2 BICCN dataset. After our filtering procedure, we obtained a matrix with 7171 genes and 124,330 cells. Cell labels were provided by Yao et al. (2020) with three different degree of details: cluster (a fine-grained partition that contains cell sub-populations), sub-class (which defines the major cell types of the adult mouse motor cortex) and class (which partitions the cells in broad classes, i.e. excitatory neurons, inhibitory neurons and non-neuronal cells). We used the sub-class label as our ground truth.
Clusters were identified as in Section 3.4.1. Then, we used the ARI to compare the cluster identified after each normalization with the known labels.
We selected two contrasts, Parvalbumin GABAergic neurons (Pvalb) versus Somatostatin GABAergic neurons (Sst) and Astrocytes (Astro) versus Oligodendrocytes (Oligo), to evaluate normalization methods in terms of their ability to identify cell-type markers. These contrasts were selected because of their biological interest, as they are closely related cellular populations, yet distinct enough to be a reliable test. Ample literature exists on validated marker genes for these populations, specifically, we used the Sst and Pvalb genes for the first contrast and Mbp, Rorb and Aqp4 for the second (Huang and Paul, 2019; Yao et al., 2021).
The lists of 100 most differentially expressed genes were obtained using edgeR with normalization factors derived from the global scaling methods evaluated in this study, including PsiNorm (i.e. the estimated alpha parameters). We evaluated the degree of overlap among methods and the rank of the known markers genes. In principle, the lower the rank the better the result.
3.7 Simulated datasets
We used simulations to compare normalization methods in terms of their computational efficiency (RAM usage and CPU time). To simulate data, we used the splatSimulateSingle function of the splatter R/Bioconductor package (Zappia et al., 2017), with default parameters. We set the number of genes equal to 10 000 with increasing number of cells: 25,000, 50,000, 75,000 and 100,000 cells. RAM usage and computational time were recorded for a single core usage.
3.8 Software and data availability
An implementation of PsiNorm is available in the scone Bioconductor package available at https://bioconductor.org/packages/scone/. The code to generate the analysis and figures of this manuscript is available at https://github.com/MatteoBlla/PsiNorm-plot.
The raw data of the mixology dataset are available in GEO with accession code GSE118767. The processed data, used in this article, are available at https://github.com/LuyiTian/sc_mixology. The BICCN dataset, generated by the Brain Initiative Cell Census Network, is available at the NeMO archive with identifier dat-ch1nqb7 and can be downloaded from https://assets.nemoarchive.org/dat-ch1nqb7.
4 Results
4.1 Goodness-of-fit
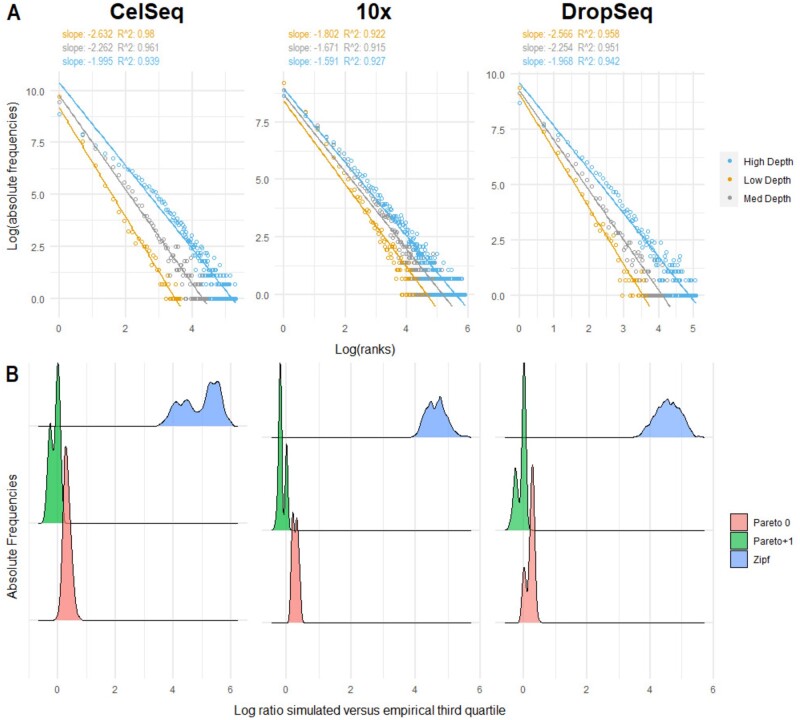
To evaluate the goodness of fit of the Pareto and Zipf models on single-cell data, we evaluated two distinct aspects: i) the power-law fit and ii) the differences between expected and observed counts. We first visually inspected the log-log plot of the frequency of expression versus rank (ordered from the lowest to the highest expression) to check the approximation to a power law for three cells representative of the minimum, median and maximum sequencing depths and for different technologies (Fig. 1A and Supplementary Fig. S1A). Secondly, for each cell, we estimated the parameters of Pareto0, Pareto + 1 and Zipf distributions. Using these estimates, we compared the log ratio between the theoretical and the empirical third quartiles; the closer this ratio is to 0, the better the goodness of fit (Fig. 1B and Supplementary Fig. S1B).
Fig. 1.
Goodness of fit. (A) Log-frequency versus log rank plot of three cells representative of the minimum, median and maximum depth for each technology. The rank is based on the unique expression values ordered from the lowest to the highest. Each dot in the plot represents more than one gene, namely all the genes that share the same expression value in that cell. Linear fit is reported along with least-squares estimates of the slopes and R2 values of the linear fit. (B) Distribution of the log ratios between simulated and empirical third quartiles per cell across different technologies. Supplementary Figure S2 shows the same quantity for other quantiles. The figure shows that the Zipf simulated quantiles are far from the empirical ones, while the Pareto distribution (especially when applied to x + 1) provides a much better fit given that values are closer to zero
Single-cell data are well approximated by a power-law () independently of the sequencing depths (Fig. 1A and Supplementary Fig S1A and S2A). However, while Zipf’s law largely overestimates counts, the Pareto distribution is more flexible and better fits scRNA-seq data, as shown by the distribution of the log ratios of the simulated versus empirical quartiles (Fig. 1B and Supplementary Fig. S1B for the third quartile and Supplementary Fig. S2 for the other quantiles). Indeed, while Zipf’s law uniformly over-estimates distribution values, the log ratio between simulated and empirical quantiles obtained from Pareto distribution approaches decrease with the increasing of the quantiles (Supplementary Fig. S2). In particular, the use of the pseudo-counts for parameter estimation (Pareto + 1) shows a better goodness-of-fit than the removal of zero counts (Pareto0; Fig. 1B, Supplementary Fig S1B and 2).
While, our analysis shows a reasonable goodness of fit of power laws also for SMART-Seq data (Supplementary Fig. S3B), confirming Pareto + 1 as the most appropriate model, there are some concerns on the fit for cells with large counts (Supplementary Fig. S3A and C). This is reasonable, since technologies that do not include UMIs may exhibit very large counts, leading to less skewed distributions for the most deeply sequenced cells.
Taken together, our results indicate that the Pareto distribution on pseudo-counts well resembles scRNA-seq data, especially those from UMI-based platforms, independently of sequencing depths and technology.
4.2 PsiNorm leads to comparable distributions across cells
Supplementary Figures S4A and S5A show the effect that PsiNorm has on the expression distribution on three representative cells (with low, moderate and high depths). After normalization, the distributions of the highly expressed genes (those with small ranks) are aligned. The effect on the entire dataset can be appreciated in Supplementary Figures S4B and S5B where the slope and intercept distributions are reported for raw and normalized data. As expected, after normalization the variability of both distributions is greatly reduced.
These findings confirm that PsiNorm is able to effectively scale the data making the distribution of highly expressed genes comparable across cells.
4.3 Impact of normalization on cell clustering
Organizing cells into groups is the first intermediate result of any single-cell analysis. Here we wonder whether PsiNorm transforms the data maintaining the similarity structure among cells, allowing a downstream clustering algorithm to detect cell populations.
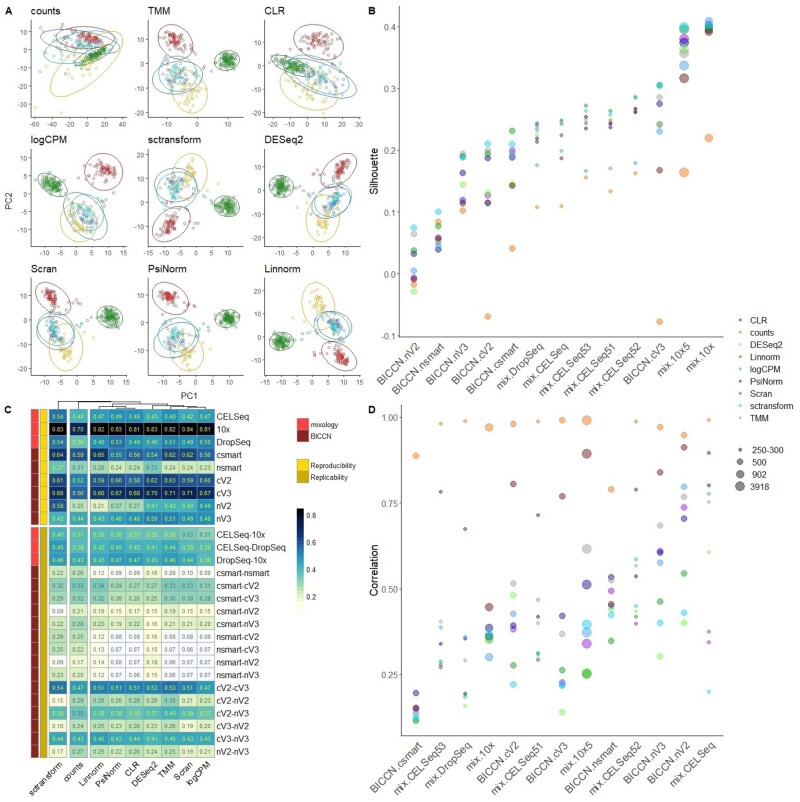
Figure 2A shows an example of principal component analysis (PCA) obtained with different normalizations in the mixology dataset with five groups (CELSeq2_5cl_p3). See Supplementary Figures S6–S8 for the other datasets.
Fig. 2.
(A) Principal component analysis (PC1 versus PC2) of the CELSeq dataset composed of 5 groups (highlighted with different colors, data ellipses were generated by using multivariate t-distribution). See Supplementary Figures S6–S8 for PCA analyses of the other datasets. (B) Silhouette index across different datasets and different normalization methods. Datasets are sorted by the silhouette index obtained with PsiNorm normalized data. The dot dimension is proportional to the dimension of the datasets in terms of number of cells. See Supplementary Figure S9 for individual panels for each normalization methods. (C) The upper and the lower blocks of the heatmap show respectively the degree of reproducibility and replicability in colour scale. The number within cells is the concordance (namely the average Jaccard index) between the top 500 variable genes obtained in (i) random split of the same dataset (replicability) and in (ii) different datasets with the same samples but obtained with different technologies (reproducibility). (D) The maximum correlation index between PC1 and PC2 and cell sequencing depths is reported for each dataset, see Supplementary Figure S10 for individual panels for each normalization methods
Apart from CLR that hardly recognizes the similarity structure of some known groups, all the other methods are able to identify the major differences among the cell lines (Fig. 2A). This is confirmed in most of the other datasets. Interestingly, the first two components of logCPM and sctransform normalized data did not separate well the five classes of the 10X dataset (Supplementary Fig. S7B). However, when looking at the full 50 components, these methods still performed reasonably well in the 5 class 10X dataset (Supplementary Fig. S9).
We computed the ARI of all partitions to compare the inferred clusters and the real cell-line classification. Linnorm and sctransform lead to the highest ARI, followed by PsiNorm and scran (Table 1).
Table 1.
Normalization evaluation: each column reports the average values across all datasets (see Supplementary Table S2 for median values)
| Average ARI | Average silhouette | Average correlation PCA-depth | Average within concordance | Average between concordance | computational costs (s) | RAM usage (Gb) | HDF5 ready | |
|---|---|---|---|---|---|---|---|---|
| sctransform | 0.756 | 0.244 | 0.310 | 0.712 | 0.417 | 1154 | 43 | No |
| Linnorm | 0.767 | 0.241 | 0.323 | 0.641 | 0.424 | 446 | 23 | No |
| PsiNorm | 0.734 | 0.218 | 0.476 | 0.638 | 0.388 | 112 | 17 | Yes |
| Scran | 0.720 | 0.212 | 0.369 | 0.674 | 0.375 | 1838 | 16 | Yesa |
| TMM | 0.711 | 0.228 | 0.491 | 0.651 | 0.378 | 506 | 25 | No |
| logCPM | 0.696 | 0.180 | 0.450 | 0.676 | 0.368 | 64 | 12 | Yes |
| DESeq2 | 0.695 | 0.204 | 0.329 | 0.692 | 0.414 | 192 | 20 | No |
| CLR | 0.626 | 0.191 | 0.714 | 0.661 | 0.270 | 122 | 40 | No |
Note: Computational costs and RAM usage are referred to the simulation matrix with 100 000 cells and single core mode. ‘HDF5 Ready’ means that the method takes full advantage of the on-disk data representation and doesn’t merely work on HDF5 input by loading the full matrix in memory.
When used with clusters, loads entire cluster in memory.
Exploiting known cell labels, we used the silhouette width to quantify the cohesion of the clusters and the separation of the cell lines. Figure 2B and Supplementary Figure S9 show the average silhouette widths for each normalization-dataset combination. In general, single-nucleus datasets show a lower average silhouette, independently of the normalization (Fig. 2B). This is probably due to the higher level of sparsity that characterize these data. Furthermore, the average silhouette depends on the number of cells (the more cells the higher the silhouette) and, perhaps unsurprisingly, on the complexity of the dataset: the simple mix of cell lines from the mixology dataset showed a higher silhouette than the complex BICCN data (Fig. 2B). In terms of normalization performance, our analysis confirmed that no single method outperforms all others in all datasets: for instance scran, which was among the top performers in the mixology 10× datasets, did not perform as well in the BICCN 10× v2 datasets (both single-cell and single-nucleus). Overall, Linnorm, sctransform, TMM and PsiNorm showed the most consistent performance (Table 1).
When a normalization fails to reduce unwanted variation within a dataset (due for instance to differences in sequencing depth), the factors computed by the dimension reduction technique might capture technical noise rather than biological variability. To check whether the first two PCs are capturing technical variance, we computed the maximum correlation obtained between PC1 and PC2 and cell sequencing depths (Fig. 2D and Supplementary Fig. S10). A higher correlation indicates that the normalization was not able to properly remove noise.
While we observed a general high correlation for CLR (and no normalization), TMM shows high correlations only for some datasets confirming that these methods do not remove enough technical variation (Fig. 2D and Supplementary Fig. S10). All other methods performed similarly, with sctransform, DESeq2 and Linnorm as top performers (Fig. 2D, Supplementary Fig. S10 and Table 1).
4.4 Concordance analyses
Replicability and reproducibility are two important aspects when dealing with data transformations. Here, we defined replicability as the ability to maintain the order of the most variable genes between two random split of the same dataset (within-dataset concordance) and reproducibility as the ability to maintain the order of the most variable genes between two independent datasets measuring the same samples (between-dataset concordance).
As expected, we observed a general higher concordance within than between datasets (Fig. 2C). Indeed, the mean of the within-dataset concordance was 0.59 for the mixology dataset and 0.49 for the BICCN data. On the other hand, the average between-dataset concordance was 0.41 for the mixology dataset and 0.24 for the BICCN data. Single-nucleus datasets showed the lowest within-dataset concordance while the 10× mixology dataset showed the highest (Fig. 2C). We observed similar results for the between-dataset concordance. As expected, between-dataset concordance was higher for datasets from similar platform, e.g. 10× and Dropseq showed a higher concordance than 10× and SMART-seq (Fig. 2C). Interestingly, the concordance between single-cell 10× V2 and V3 was higher than that between single-cell 10× V2 and single-nucleus 10× V2 (and between single-cell 10× V3 and single-nucleus 10× V3), suggesting that the 10× chemistry was less important than the RNA provenance in determining concordance (Fig. 2C).
In terms of normalization performance, methods fell into two main groups: raw counts and sctransform showed a high between-dataset concordance; and PsiNorm, CLR, Linnorm, TMM, Scran, DESeq2 and logCPM performed well both in term of within- and between-dataset concordance (Fig. 2C and Table 1).
4.5 Computational performance
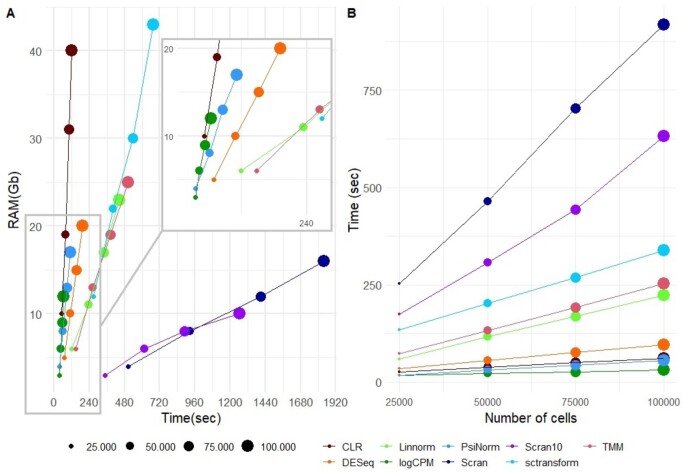
To complete our benchmark, we performed a comparative analysis of computational performances in different simulated settings. Figure 3A and Table 1 show the RAM usage and the elapsed time for each method on single-core mode, except for scran, the only method supporting multi-core parallel computing, for which we tested the performance in the case of single- and 10-core mode. As expected, logCPM, PsiNorm and DESeq2 are the most scalable methods (Fig. 3B). Indeed these methods only need simple operations (such as averages and multiplications) to scale the data. While CLR is as fast as the above-mentioned methods, it is much more demanding in terms of memory usage. At the other end of the spectrum, scran and sctransform are not as scalable. sctransfrom requires the highest amount of RAM among the tested methods, exceeding 40 GB for 100 000 cells (Fig. 3A). While scran is much more memory-efficient, it is the slowest method, requiring at least 20 min for 100 000 cells (Fig. 3A). Overall, PsiNorm is very scalable, being only slightly slower than the simplest strategy (logCPM) (Fig. 3A and B).
Fig. 3.
Computational performance. (A) Comparative evaluation of RAM usage and computational time on simulated data with increasing number of cells using a single core. scran10 refers to scran with 10 cores. (B) Method scalability in terms of computational time versus number of cells
4.6 Case study
As a case study, we analyzed the full 10× V2 single-cell data from the BICCN study (Yao et al., 2020). These data consists of 124 330 cells and 7171 genes.
We applied the four methods that showed the best performance among those with a limited memory footprint, i.e. Linnorm, scran, logCPM and PsiNorm. For scran, we used both the default setting and the use of clustering before the normalization, an option suggested in Lun et al. (2016a). Although sctransform performed well in our benchmark, its memory usage prevents its use in very large datasets.
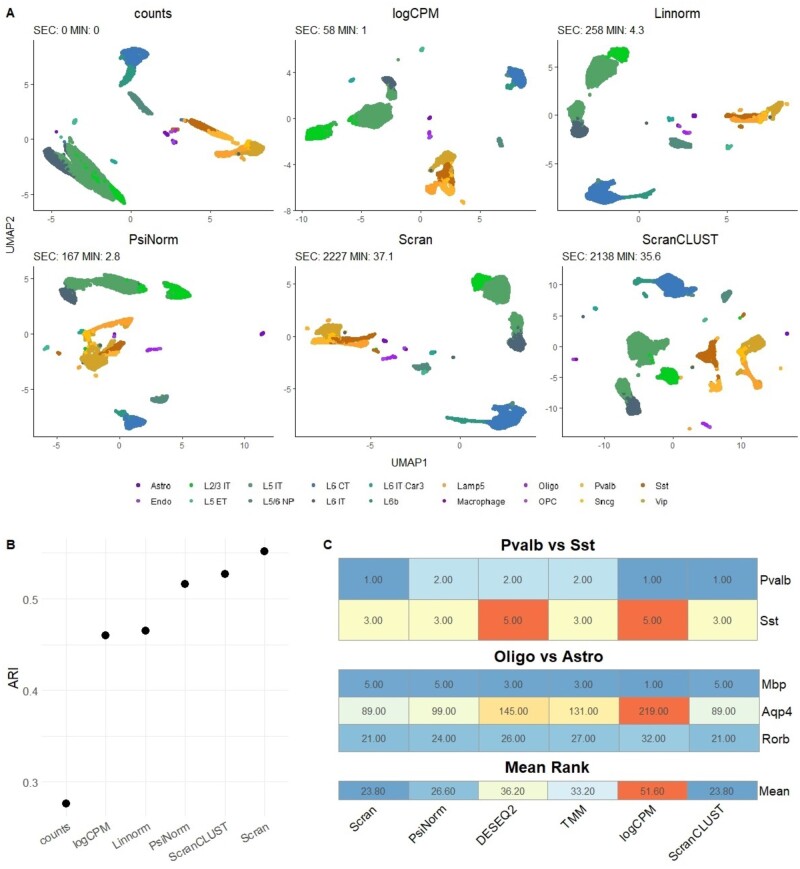
Figure 4A shows the UMAP plot obtained using the first 50 Pcs after each normalization. While all methods are able to separate the major cell types, the comparison with the BICCN labels showed that scran and PsiNorm lead to the best agreement in terms of ARI (Fig. 4B).
Fig. 4.
(A) UMAP plots based on the first 50 PCs of the 10× V2 single-cell data from the BICCN study (Yao et al., 2020) obtained with raw data and after the four best performing normalizations. (B) ARI comparing the inferred versus known groups. See Section 3.6 for details on the preprocessing of the data. (C) Rank of known cell-type markers for each normalization in the two considered contrasts. Differential expression analysis between Sst and Pvalb and between Oligo and Astro was performed with edgeR and the rank of five canonical marker genes was computed. The lower the rank the better the normalization
Scran is confirmed to be the most time consuming method, taking more than 30 min to normalize the matrix. On the other hand, PsiNorm is almost as fast as logCPM, completing the task in just under 3 min.
Exploiting the information on the available cell types annotations and the presence of known marker genes, we evaluated the selected methods in terms of overlapping of differential expressed gene lists and ranks of marker genes. We compared Pvalb versus Sst neurons and Astrocytes versus Oligodendrocytes. We observed a high agreement (81% of genes common among all methods) among the top 100 ranked genes in Pvalb versus Sst, and a moderate agreement (56% of common genes) in Astro versus Oligo. In the latter contrast, PsiNorm’s performance is very similar to scran’s (Supplementary Fig. S11).
To investigate the similarity between PsiNorm and scran, we compared each method’s estimated size factors, which show a fairly large correlation (Supplementary Fig. S12A). However, there is a cell-type-specific effect, e.g. oligodendrocytes have consistently lower size factor estimates in PsiNorm (Supplementary Fig. S12A). The difference between the two size factors are more pronounced in rare cell populations with low sequencing depths (Supplementary Fig. S12 B and C).
Moreover, the rank of the known marker genes confirms that scran and PsiNorm are the top performing methods, as they lead to lower ranks for the known markers compared to the other methods (Fig. 4C).
5 Discussion
In single-cell experiments, computational efficiency in terms of time and memory usage is a key aspect. The massive number of cells, combined with the large number of genes, make even simple scaling normalization demanding. For instance, scran applied to a dataset of 1.3 million datasets take more than 5 h (Hicks et al., 2021).
Based on the Pareto distribution scale parameter estimate, , we derived a simple and scalable global between-sample normalization method, called PsiNorm. PsiNorm is fast and memory efficient. Moreover, through the integration with the Bioconductor DelayedArray framework (Pagès et al., 2019), it can be applied to dense or sparse in-memory matrices as well as out-of-memory data representations, such as data stored in HDF5 files (The HDF Group, 1997), a feature that cannot be exploited by some of the best performing methods (Table 1).
PsiNorm does not need a reference and is performed independently for each cell. This is useful for supervised classification settings, in which it can be useful to apply normalization to new out-of-sample data. The final goal of the transformation is to align the gene expression distribution especially for those genes characterized by high expression. Note that, similar to other global scaling methods, our method does not remove batch effects, which can be dealt with downstream tools (e.g. Butler et al., 2018; Haghverdi et al., 2018; Risso et al., 2014).
Globally, our results are summarized in Table 1, where the best method for each task is reported in bold. We observed that, as expected, normalizations specifically designed for scRNA-seq data are among the best performing. Among them, we found that PsiNorm and scran show good performances in six features.
To conclude, normalization for the purpose of clustering and cell type discovery seems less critical than normalization for differential expression, and even very simple methods, such as logCPM, work well in several cases. Hence, methods’ scalability becomes an important aspect to consider in the choice of normalization. Our proposed PsiNorm normalization showed a good trade-off between accuracy and scalability, exhibiting better performance than logCPM with only a small increase in computational time, making it a promising method for very large datasets.
Supplementary Material
Acknowledgements
The authors thank Hongkui Zeng and the members of the BICCN consortium for sharing the BICCN dataset. They thank Ilaria Billato for her help with testing the PsiNorm function.
Funding
D.R. was supported by ‘Programma per Giovani Ricercatori Rita Levi Montalcini’ granted by the Italian Ministry of Education, University and Research and by the National Cancer Institute of the National Institutes of Health [2U24CA180996]. C.R. was supported by the Italian Association for Cancer Research (AIRC) [Grant N. IG 21837]. G.M. is supported by grants from the Giovanni Armenise-Harvard Foundation and ERC Starting Grant (MetEpiStem). This work was supported in part by CZF2019-002443 (D.R.) from the Chan Zuckerberg Initiative DAF, an advised fund of Silicon Valley Community Foundation. M.B. was supported by the National Cancer Institute of the National Institutes of Health [2U24CA180996] and Italian Association for Cancer Research (AIRC) [IG21837].
Conflict of Interest: none declared.
Contributor Information
Matteo Borella, Department of Biology, University of Padova, Padua 35121, Italy.
Graziano Martello, Department of Biology, University of Padova, Padua 35121, Italy.
Davide Risso, Department of Statistical Sciences, University of Padova, Padua 35121, Italy.
Chiara Romualdi, Department of Biology, University of Padova, Padua 35121, Italy.
References
- Anders S., Huber W. (2010) Differential expression analysis for sequence count data. Genome Biol., 11, R106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold B.C. (2015) Pareto Distribution. American Cancer Society, pp. 1–10, doi: 10.1002/9781118445112.stat01100.pub2.
- Awazu A. et al. (2018) Broad distribution spectrum from Gaussian to power law appears in stochastic variations in RNA-seq data. Sci. Rep., 8, 8339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási A.-L., Albert R. (1999) Emergence of scaling in random networks. Science, 286, 509–512. [DOI] [PubMed] [Google Scholar]
- Bullard J.H. et al. (2010) Evaluation of statistical methods for normalization and differential expression in mRNA-seq experiments. BMC Bioinformatics, 11, 94–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler A. et al. (2018) Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol., 36, 411–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole M.B. et al. (2019) Performance assessment and selection of normalization procedures for single-cell RNA-seq. Cell Syst., 8, 315–328.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillies M.-A. et al. ; French StatOmique Consortium. (2013) A comprehensive evaluation of normalization methods for Illumina high-throughput RNA sequencing data analysis. Brief. Bioinf., 14, 671–683. [DOI] [PubMed] [Google Scholar]
- Evans C. et al. (2018) Selecting between-sample RNA-Seq normalization methods from the perspective of their assumptions. Brief. Bioinf., 19, 776–792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furusawa C., Kaneko K. (2003) Zipf’s law in gene expression. Phys. Rev. Lett., 90, 088102. [DOI] [PubMed] [Google Scholar]
- Hafemeister C., Satija R. (2019) Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biol., 20, 296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haghverdi L. et al. (2018) Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nat. Biotechnol., 36, 421–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hicks S.C. et al. (2021) mbkmeans: fast clustering for single cell data using mini-batch k-means. PLoS Comput. Biol., 17, e1008625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z.J., Paul A. (2019) The diversity of gabaergic neurons and neural communication elements. Nat. Rev. Neurosci., 20, 563–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubert L., Arabie P. (1985) Comparing partitions. J. Classif., 2, 193–218. [Google Scholar]
- Kuznetsov V.A. et al. (2002) General statistics of stochastic process of gene expression in eukaryotic cells. Genetics, 161, 1321–1332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu T. et al. (2005) Can Zipf’s law be adapted to normalize microarrays? BMC Bioinformatics, 6, 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lun A.T. et al. (2016a) Pooling across cells to normalize single-cell RNA sequencing data with many zero counts. Genome Biol., 17, 75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lun A.T. et al. (2016b) A step-by-step workflow for low-level analysis of single-cell RNA-seq data with bioconductor. F1000Research, 5, 2122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lähnemann D. et al. (2020) Eleven grand challenges in single-cell data science. Genome Biol., 21, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meintanis S.G. (2009) A unified approach of testing for discrete and continuous Pareto laws. Stat. Papers, 50, 569–580. [Google Scholar]
- Nacher J., Akutsu T. (2006) Sensitivity of the power-law exponent in gene expression distribution to mRNA decay rate. Phys. Lett. A, 360, 174–178. [Google Scholar]
- Pagès H. et al. (2019) DelayedArray: Delayed Operations on Array-Like Objects, doi: 10.18129/B9.bioc.DelayedArray.
- Powers D.M.W. (1998) Applications and explanations of Zipf’s law. In: New Methods in Language Processing and Computational Natural Language Learning.
- Risso D. et al. (2014) Normalization of RNA-seq data using factor analysis of control genes or samples. Nat. Biotechnol., 32, 896–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M.D., Oshlack A. (2010) A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol., 11, R25–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart T. et al. (2019) Comprehensive integration of single-cell data. Cell, 177, 1888–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The HDF Group. (1997) Hierarchical Data Format, version 5.
- Tian L. et al. (2019) Benchmarking single cell RNA-sequencing analysis pipelines using mixture control experiments. Nat. Methods, 16, 479–487. [DOI] [PubMed] [Google Scholar]
- Townes F.W., Irizarry R.A. (2020) Quantile normalization of single-cell RNA-seq read counts without unique molecular identifiers. Genome Biol., 21, 160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ueda H.R. et al. (2004) Universality and flexibility in gene expression from bacteria to human. Proc. Natl. Acad. Sci. USA, 101, 3765–3769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B. (2020) A Zipf-plot based normalization method for high-throughput RNA-seq data. PLoS One, 15, e0230594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao Z. et al. (2020) An integrated transcriptomic and epigenomic atlas of mouse primary motor cortex cell types. bioRxiv, doi: 10.1101/2020.02.29.970558. [DOI]
- Yao Z. et al. (2021) A taxonomy of transcriptomic cell types across the isocortex and hippocampal formation. Cell, 184, 3222–3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yip S.H. et al. (2017) Linnorm: improved statistical analysis for single cell RNA-seq expression data. Nucleic Acids Res., 45, e179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zappia L. et al. (2017) Splatter: simulation of single-cell RNA sequencing data. Genome Biol., 18, 174. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.