Abstract
Over the last two decades, intrinsically disordered proteins and protein regions (IDRs) have emerged from a niche corner of biophysics to be recognized as essential drivers of cellular function. Various techniques have provided fundamental insight into the function and dysfunction of IDRs. Among these techniques, single-molecule fluorescence spectroscopy and molecular simulations have played a major role in shaping our modern understanding of the sequence-encoded conformational behavior of disordered proteins. While both techniques are frequently used in isolation, when combined they offer synergistic and complementary information that can help uncover complex molecular details. Here we offer an overview of single-molecule fluorescence spectroscopy and molecular simulations in the context of studying disordered proteins. We discuss the various means in which simulations and single-molecule spectroscopy can be integrated, and consider a number of studies in which this integration has uncovered biological and biophysical mechanisms.
1. Introduction
A structure-centric perspective has dominated our models of molecular function since the first folded proteins were visualized over 60 years ago [1–4]. Despite this, over a third of the eukaryotic proteome consists of regions or entire proteins that do not adopt a stable structure but instead sample a conformationally heterogeneous collection of structurally distinct states referred to as a conformational ensemble (Fig. 1) [5–8]. These intrinsically disordered proteins and protein regions (collectively referred to hereafter as IDRs) play a wide variety of roles that are critical for biological function [9–11]. As a result, the classical view that protein function is determined by folded proteins has expanded to recognize that function is driven by the combination of structure, conformation, and dynamics. There exists a continuum of structural heterogeneity, with well-folded hyper-stable proteins at one end and heterogeneous disordered regions at the other (Fig 1) [12]. While well-folded proteins lend themselves to various functions, including mechanical strength or enzymatic activity, disordered proteins are ideally suited for molecular recognition or biological self-assembly [9,13]. It is this repertoire of conformational plasticity that provides cells with a complex molecular toolkit, through which adaptive and responsive function can be encoded.
Figure 1.
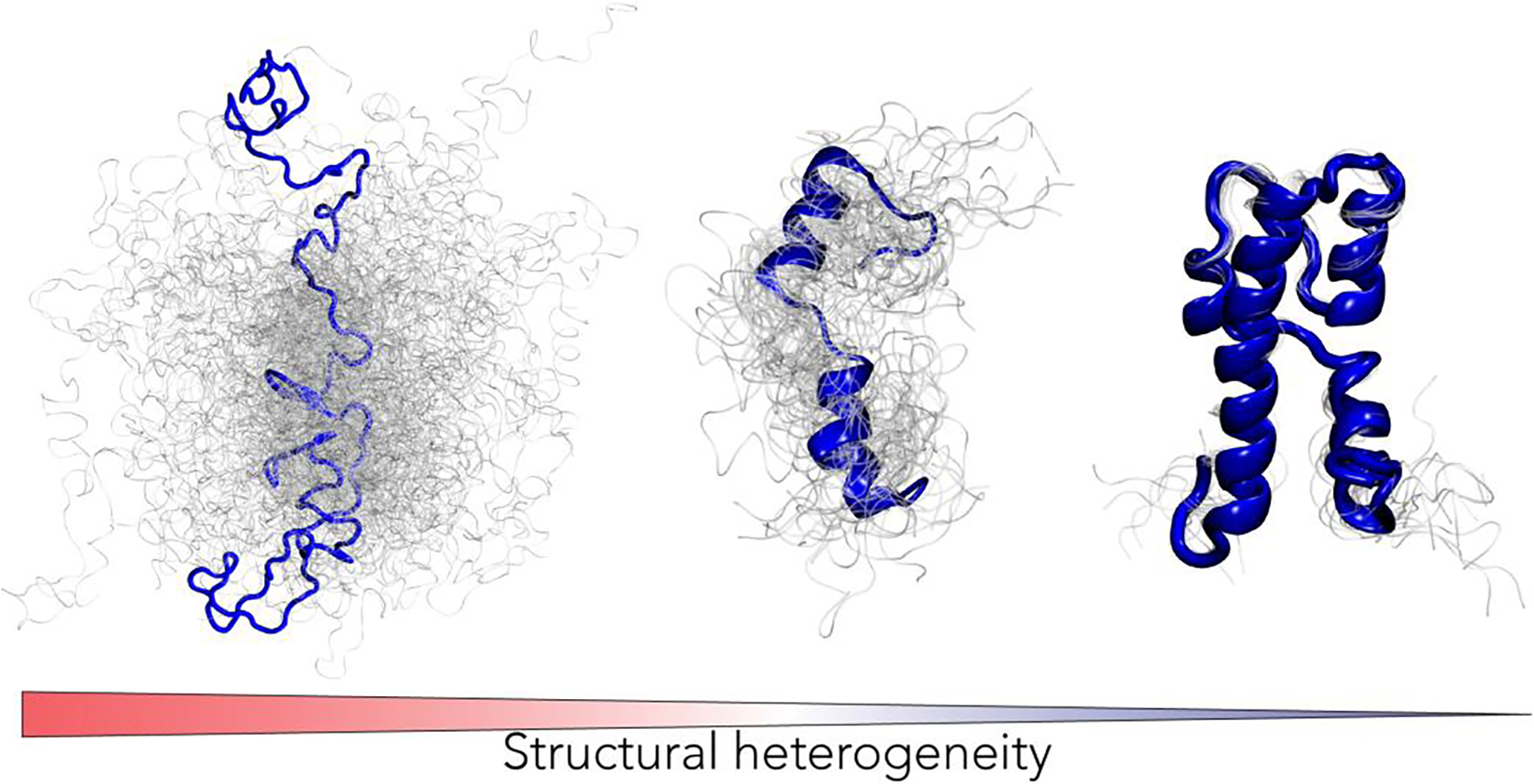
Proteins exist along a continuum of structural heterogeneity. While some proteins adopt well-defined tertiary structures (far right), intrinsically disordered protein regions (IDRs) lack a defined reference state (far left). Importantly, all proteins are defined by an ensemble, where function is ultimately determined by the combination of chain dynamics and preferential conformations [11,12,14]. IDRs are not fundamentally different from folded proteins but are distinguished by conformational fluctuations so large that a single native-state reference frame is no longer applicable nor useful.
The three-dimensional structure of a folded domain is encoded by its primary sequence, an observation that has generally been referred to as the sequence-to-structure relationship [15–17]. Although IDRs do not adopt a set three-dimensional structure, they are far from “featureless random noodles.” As such, an analogous sequence-to-ensemble relationship exists for IDRs in which the amino acid sequence of an IDR determines the conformational biases associated with its ensemble [10,18,19]. Just as the last four decades have focused immense attention on understanding the physical principles that map sequence to structure, the same types of questions are now being asked of disordered regions. Beyond merely an exercise in understanding physical chemistry, the conformational biases in IDRs are a central determinant of their biological function [20–24]. As such, our ability to interpret IDR function rests at least partially on how well we understand their sequence-encoded conformational biases and transient structure.
A major challenge in studying conformational behavior in IDRs is posed by the structural heterogeneity and rapid dynamics associated with their ensembles. Due to the absence of a standard ‘reference’ structure, techniques such as X-ray crystallography are inherently limited in their ability to provide molecular information in the context of IDRs. Similar limitations can be extended to cryogenic electron microscopy (cryoEM), where class averaging across multiple particles is often limited to a few conformational subsets. While various techniques have been instrumental in elucidating the conformational behavior of IDRs, single-molecule fluorescence spectroscopy and all-atom simulations have played essential roles in contributing to our understanding of IDR conformational behavior and IDR dynamics. In this review, we focus on how combining single-molecule fluorescence spectroscopy and computational methods can provide quantitative and complementary insights into the solution state behavior of IDRs.
Single-molecule fluorescence spectroscopy offers a high-resolution readout of molecular behavior, making it ideal for investigating the complexities and heterogeneity of disordered proteins [25–27]. Specifically, single-molecule fluorescence spectroscopy enables measurements of intra- and inter-chain distances and protein dynamics with high temporal and spatial resolution. Paired with an understanding of the physics that underlie protein interactions, single-molecule approaches can be used to dissect the molecular mechanisms that drive protein behavior, dynamics, and binding. As an example, fluorescence correlation spectroscopy (FCS) allows the diffusion coefficient of an IDR to be measured, from which the overall hydrodynamic radius of the protein can be estimated. Single-molecule Förster Resonance Energy Transfer (smFRET) provides a molecular ruler to quantify intramolecular distances within the protein [27–29], which can be directly tied to fundamental descriptors of polymer physics.
Finally, many single-molecule fluorescence approaches provide access to protein dynamics, over a broad range of times, from nanoseconds to hundreds of seconds, depending on the method of choice. Readouts of protein dynamics are often essential for adequately interpreting measured transfer efficiencies in smFRET experiments, particularly when discriminating whether a population reflects a static or dynamic conformation. More generally, experimentally-derived molecular dynamics offer an additional lens through which perturbations to an IDR (mutation, binding partners, solution changes) can be examined.
Molecular simulations include a robust set of tools that provide structural insight at an effectively infinite spatial resolution [30–33]. By generating large conformational ensembles, protein conformation and dynamics can be directly assessed (in the case of molecular dynamics), or ensemble-averaged properties can be computed (in the case of molecular dynamics and Monte Carlo simulations). Essentially any property that can be derived from the collection of conformations can be calculated, offering a window into a wide array of molecular information. Of particular relevance in the context of disordered proteins, all-atom simulations are especially well-poised to enable a structural interpretation of experimental data as a function of some perturbations, such as mutations, post-translational modification, and changes in solution properties such as temperature, ion concentrations, or pH. [20,34–40].
Single-molecule fluorescence spectroscopy and all-atom simulations are highly complementary. Both techniques can, in principle, provide information at the resolution of a single molecule and do so at high temporal resolution. As such, the types of information available from single-molecule fluorescence spectroscopy and all-atom simulations are simultaneously overlapping, yet the assumptions and limitations are inherently orthogonal. As such, results from simulations can help interpret measurements made by single-molecule fluorescence spectroscopy, and vice versa.
The remainder of this review is laid out as follows. We provide a brief description of all-atom simulations and single-molecule fluorescence spectroscopy approaches used in the context of disordered proteins. We discuss theoretical approaches through which results from simulations and experiments can be formally integrated. We then consider specific examples in which simulation and experiment have been integrated to provide complementary insight. Finally, we conclude by summarising the outstanding questions and challenges.
2. Materials and Methods
2.1. Overview of all-atom simulations
Molecular simulations represent a large class of methods in which one or more molecules are explicitly described in terms of their spatial coordinates and their associated chemical and physical properties. All physics-based molecular simulations require two different components: a representation scheme and an update scheme.
The representation scheme reflects how a biomolecule is described within a simulation framework. This is typically achieved using a force field – a collection of equations, reference values, and rules that converts each three-dimensional conformation of a protein into a potential energy value [41,42]. The granularity of a representation scheme reports on the degrees of freedom that are explicitly encoded within that scheme (Fig. 2). We broadly categorize all-atom simulations here as those in which every biomolecule in the system is represented with atomistic detail, providing a one-to-one mapping between a simulated and real molecule. This would include representations that encode implicit and explicit hydrogens, given in both cases a clear mapping between a given biomolecule and atomic position are present. Commonly used modern forcefields that have shown good agreement in the context of disordered proteins include Amber ff03w, Amber ff03ws, Amber ff99SBws, a99SB-disp, DES-Amber, Amber ff99SBws-STQ, CHARMM36m, and the ABSINTH implicit solvent model [43–51].
Figure 2.
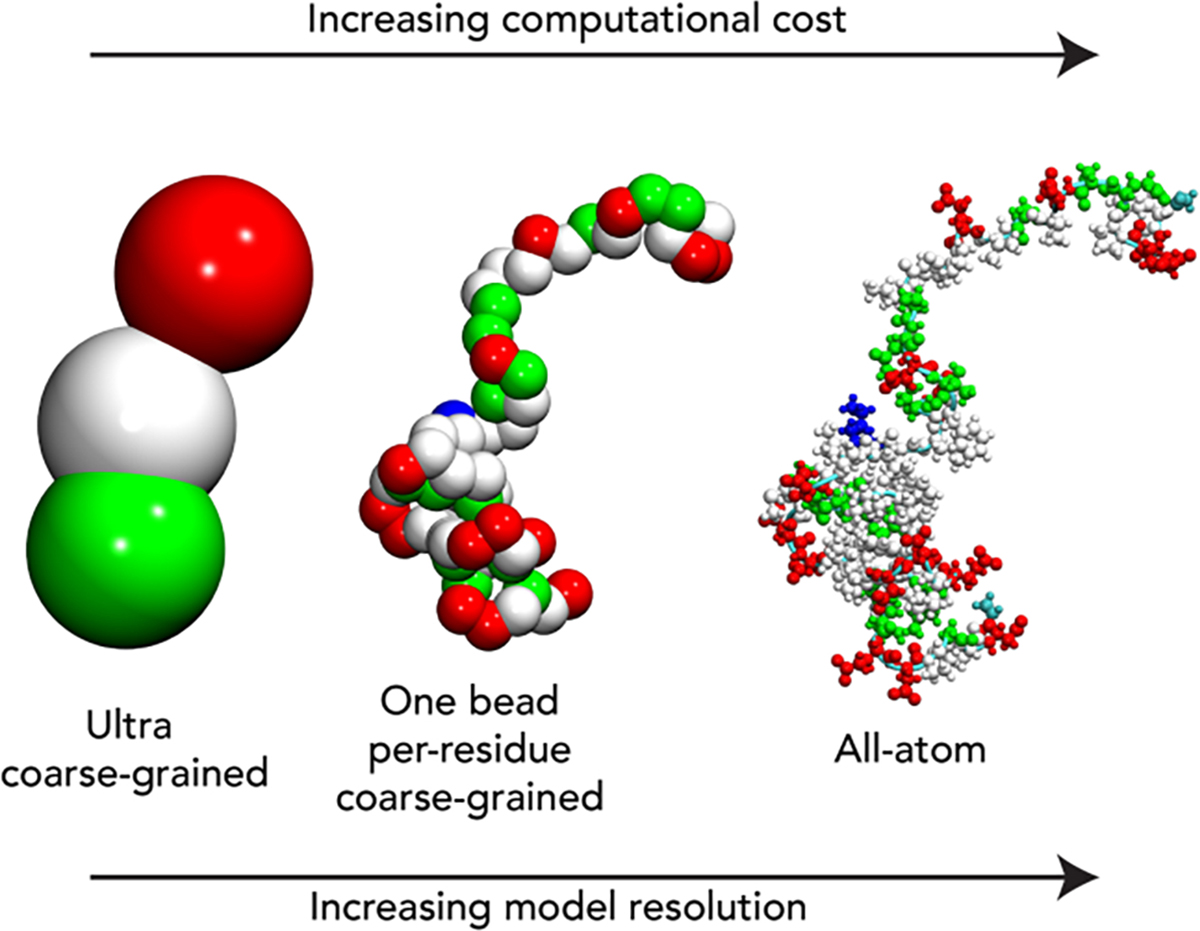
Examples of distinct levels of granularity of the representation schemes. As the number of degrees of freedom increases (from left to right), as does the computational cost. In principle, more degrees of freedom should yield a higher accuracy model, although this depends on the actual fidelity of the model. A model with many degrees of freedom is only more accurate if those degrees of freedom and described correctly.
In contrast to all-atom simulations, coarse-grained simulations sacrifice accuracy for a reduced number of degrees of freedom, facilitating larger, longer, and faster simulations. Disordered proteins have been well-described by a range of different coarse-grained models, including ultra-coarse-grained models, one-bead-per residue models, or mixed-resolution models [52–65]. While coarse-grained simulations have had remarkable success in capturing conformational behavior in disordered proteins, here we focus on all-atom simulations [66–71].
Not only must the protein of interest be represented, so too must the solution environment. The solvent can be represented using an explicit solvent model (in which water is described as individual molecules) or an implicit solvent (in which the solvation effects are ‘felt’ by the molecules through a mean-field interaction) [72]. Explicit solvents are generally computationally expensive but benefit from directly capturing information related to the local solvent structure. While implicit solvents sacrifice molecular detail, the performance enhancement by reducing the number of atoms in the system by 90–99% is substantial. In the context of disordered proteins, the strength of attractive protein-water interactions has been the subject of substantial investigation, and may be one of the most important factors that determines forcefield accuracy in the context of disordered proteins [46,47,50,73,74].
The update scheme reflects how the molecules defined by the representation scheme evolve as the simulation proceeds. In Molecular Dynamics (MD) simulations, the update scheme converts changes in energy with respect to the atomistic position into force [41,75,76]. This force dictates the evolution of the system through a series of timesteps in which new forces are calculated and used to alter the velocity of each atom in a sequential manner. MD simulations can be used to obtain both ensemble-average values for observables of interest (e.g., end-to-end distance, the radius of gyration, local transient structure) as well as information on chain dynamics [39,44,77,78].
Monte Carlo (MC) simulations differ from MD simulations with respect to the update scheme. For MC simulations, changes to the protein conformation are made in a series of Monte Carlo steps [79]. During each step, i) a random perturbation (move) to the system is applied, leading to a temporary change in protein conformation ii) the potential energy associated with the new conformation is calculated, and iii) the new conformation is either accepted or rejected depending on the change in energy compared to an acceptance criterion. Typically Monte Carlo moves include rigid body moves (e.g., translation or rotation of a molecule of interest), local moves that act on a single degree of freedom (e.g., a single dihedral angle rotation or bond stretching), or more complex moves that perturb several degrees of freedom simultaneously (e.g., in the context of concerted pivot moves or moves to perturb systems in specific ways [80–84].)
The acceptance criterion determines how moves are accepted or rejected. The most commonly used criterion here is Metropolis-Hastings, and when combined with an ergodic moveset that maintains detailed balance, this approach ensures that the collection of conformations generated sample the canonical (NVT) distribution [85,86]. Standard MC simulations cannot provide information on chain dynamics as there is no time component involved in the update scheme. However, if well-sampled ensembles are generated, equilibrium distributions of various ensemble properties such as global dimensions, average distances between residues, or transient structure can be obtained [24,35,87].
2.2. Limitations of all-atom simulations
There are several caveats associated with the interpretation of intrinsically disordered proteins with all-atom simulations. One area that has received considerable attention is that of force field accuracy [44,50,74,88]. Obtaining the correct balance of attractive and repulsive atomic interactions and dihedral angle distributions is an inherently challenging problem. For IDRs in particular, small inaccuracies can have a substantial impact on the final conformational ensemble due to the metastable nature of residual structure in IDRs. Many standard force fields lead to over-compaction of IDRs, influencing both final ensemble behavior and introducing local kinetic traps that can impair conformational sampling [46,47,88]. There has been a substantial effort over the last decade to address this challenge with IDRs in mind, with notable work from several key players including Best, Mittal, and Piana on this challenging problem [31,43–50,73,74,88–91].
A related but distinct challenge is that of conformational sampling. The heterogeneous conformational landscape of an IDR means that the total number of energetically accessible conformations is vast - much larger than there are for the same folded protein. Given conformational rearrangement takes time, there is a real and practical challenge in that for MD simulations, adequate sampling in unbiased simulations will typically require many microseconds of simulation time, even in the best-case scenario where there are no kinetic traps. Unfortunately, this requirement is often forgotten, with simulations run as a single replica for just a few hundred nanoseconds. These simulations can inherently only explore a small slice of conformational space and will inevitably lead to biased or noisy conclusions.
As mentioned above, simulations of IDRs also often experience “kinetic” traps - long-lived metastable states that impede conformational exploration. Both MD and MC simulations can suffer from these metastable states (Fig. 3). In the context of MC simulations, structurally-cooperative energetic minima raise a specific challenge, whereby the probability of the specific move(s) necessary for escape becomes vanishingly small. In the context of MD simulations, large energetic barriers between distinct states can yield slow conformational rearrangements that lead to locally trapped states domination ensembles. Even long MD or MC simulations may only sample a small region of phase space due to spending large fractions of simulations in a single state. In both cases, local conformational traps can lead to disparate levels of conformational sampling along a single polypeptide, with locally trapped structural ‘nuggets’ that may give the illusion of good sampling. All told, substantial care should be taken when assessing ensembles for goodness of sampling [92,93].
Figure 3.
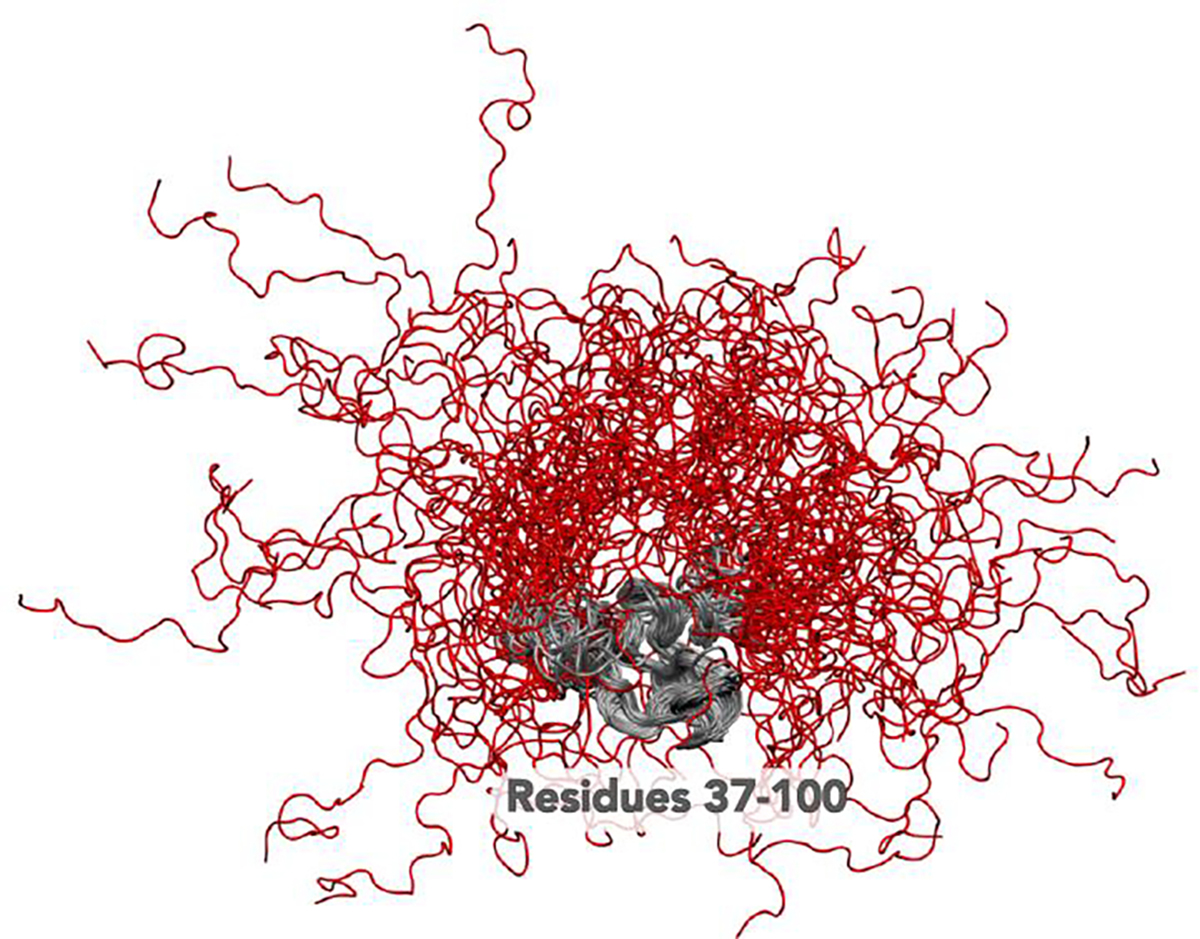
Snapshots taken from a simulation trajectory of α-synuclein reveal a scenario in which a subregion of the protein is kinetically trapped while the N and C-termini explore a diverse collection of conformational states.
2.3. Single-molecule Förster Resonance Energy Transfer
Förster Resonance Energy Transfer (FRET) is a non-radiative energy transfer that can occur when the emission band of one fluorophore (the donor) overlaps in part with the absorption band of the other fluorophore (the acceptor), and the two fluorophores are in proximity to one another. FRET provides a spectroscopic ruler to measure distances between specific positions on a molecule of interest [94], such as a disordered protein (Fig. 4a). As derived by Förster, the rate of energy transfer, denoted here as kFRET, is dependent on the sixth power of the distance r between the two fluorophores [95],
| (1) |
Here kD is the inverse of the fluorescence lifetime of the intrinsic donor lifetime τD (i.e., in the absence of the acceptor) and R0 is the Förster radius,
| (2) |
where QD is the fluorescence quantum yield of the donor, n is the refractive index of the solution, J is the spectral overlap integral, NA is Avogadro’s constant, and κ is the dipole orientation factor which reports on the relative orientation of the dyes.
Figure 4.
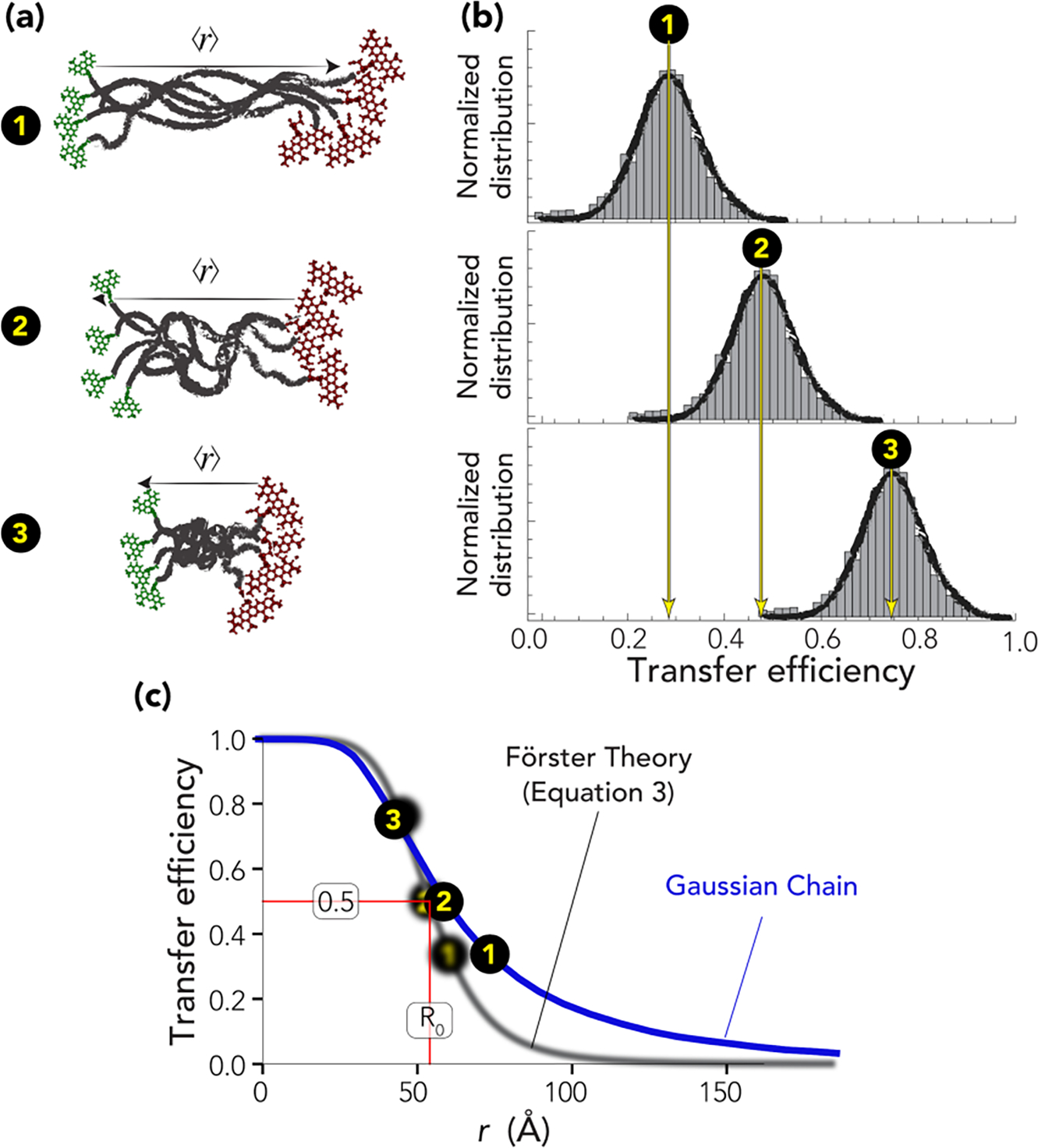
Overview of single-molecule FRET experiment and data (a) Schematic representation of disordered proteins with different mean end-to-end distances. (b) Histograms of photon bursts for the hypothetical ensembles in corresponding panels in (a). (c) The black curve represents the dependence of the mean transfer efficiency on the inter-dye distance as predicted by Förster’s theory (eq. 3), shown with conformations annotated. The blue curve depicts the transfer efficiency of a fluctuating Gaussian chain as a function of the average root mean square inter-dye distance.
The efficiency of the energy transfer E(r) can be computed by comparing the rate of the transfer kFRET with the other radiative and non-radiative relaxation rates (in the absence of acceptor) from the excited state to the ground state of the donor, krad and knrad,
| (3) |
using Eq. 1 and the fact that krad + krnad = kD.
In single-molecule experiments, the transfer efficiency can be measured by comparing the number of acceptor photons nA over the total number of acceptor (nA) and donor (nD) photons,
| (4) |
or by measuring the change in the lifetime of the donor in the presence and absence of the acceptor,
| (5) |
where
| (6) |
It is important to note that only a small number of photons are detected in a typical experiment. The low number of photons is determined by the relatively long interval between the detection of two consecutive photons (interphoton time), which is largely due to the fluorophores being trapped in long-lived dark states (e.g., triplets state on the microsecond timescale) after excitation. Therefore, the measurement of transfer efficiencies is affected by shot-noise [96]. This means that, even when measuring a rigid distance across a folded domain where one single transfer efficiency is expected, a distribution of transfer efficiencies will be determined, and the mean and width of the distribution can usually be extracted.
The mean value of a shot-noise limited distribution reports on the configuration of the chain. For a rigid protein, this will coincide with a single distance as follows from Eq. 3. For IDRs, this mean value reports on the average value of transfer efficiency across the multiple conformations of the protein, and the factors that determine the average transfer efficiency are detailed below.
The width of a shot-noise limited distribution depends on the average total number of detected photons according to,
| (7) |
where ⟨1/N⟩ is the average of the inverse number of photons in a burst and NT is the minimum number of photons in a burst (usually determined as acceptance threshold for burst identification) [97]. This implies that to determine whether a single population in the transfer efficiency distribution represents a static, rigid distance (as for folded domains) or a dynamic, flexible polymer (as for IDRs), an orthogonal measure is required. Particularly helpful in this context are measurements that report on chain dynamics, and many single-molecule fluorescence approaches provide access to protein dynamics, including the analysis of transfer efficiencies vs. fluorescence lifetimes, transfer efficiencies vs. time binning, burst variance [98], the use of Probability Distribution Analysis (PDA) [99–101], and analysis of photon trajectories of immobilized molecules [23,102–107].
Since the measured transfer efficiency is an average of a given interval of time, the measured dynamics will reflect the conformational changes occurring on the characteristic timescale of observation. The diffusion time of molecules in the confocal volume and the camera detection rate in TIRF microscopy set an intrinsic timescale of reference for the corresponding measurements, usually in the range of milliseconds. Another timescale is given by the time-data bin used to analyze the data. There are no special limitations in the range of binning times that can be applied besides the intrinsic limitations due to the detection rate, whether related to the acquisition rate of the instrument (e.g., camera frame rate) or to the emission rate of the fluorophores (e.g., only a limited number of photons are observed in freely diffusing molecules). However, the choice of bin width dictates the averaging of FRET information over the selected time range. As a tangible example of what this assumption can mean, let us assume the case of two different conformational states with distinct conformations. When exchange dynamics are slower than the binning time, the two states will appear as separated peaks with distinct mean transfer efficiencies and widths. When dynamics are faster than the binning time, the transfer efficiencies associated with the two states will be averaged out together, giving rise to a single population. When using intermediate binning times, a partial averaging of the two populations occurs. Therefore, analysis of transfer efficiency histograms as a function of time binning can provide insights on conformational changes and dynamics [103,108,109].
When the distribution of transfer efficiencies is broader than shot-noise, Photon Distribution Analysis (PDA) can provide insights into the underlying populations as well as interconversion between different states [99–101]. The method appears to be more sensitive to interconversion occurring between 0.01 and 10 times of the burst duration [110]. Whereas PDA considers the differences in transfer efficiency among all the detected molecules, Burst Variance Analysis (BVA) quantifies how the transfer efficiency changes inside each molecule (burst) over time [98]. Consequently, BVA provides a measure of dynamics on timescale longer than the minimum binning of photons required to compute the transfer efficiency variance within the burst. Analysis of the photon trajectory with maximum likelihood methods do not require time binning and can provide access to fast dynamics (up to the microsecond timescale) by studying the statistics of detected photons [111].
Another intrinsic timescale in single-molecule measurements is the fluorescence lifetime of the fluorophore, which is typically in the nanosecond range. Therefore, contrasting the donor lifetime in the presence of the acceptor (Eq. 5) with the transfer efficiency determined from the number of acceptor and donor photons detected in a burst (Eq. 4) provides a useful test for the occurrence of fast dynamics compared to the burst duration. Indeed, Eq. 5 provides information on the transfer efficiency adopted by the system on the lifetime timescale [112–115]. Instead, Eq. 4 computes transfer efficiencies from the number of donor and acceptor photons detected in a burst and, therefore, probes the transfer efficiency on the timescale associated with burst duration (or with the data binning time). The burst duration of freely diffusing species is commonly on the millisecond timescale. In the case of a rigid distance, we expect an identical transfer efficiency on the nanosecond and millisecond timescale probed by lifetime and bursts, respectively, as indicated by the linear relation between the two terms in Eq. 4 and 5. As a result, the measured static distribution should fall on the corresponding predicted linear trend. A deviation from this linear behavior is expected when the molecule of interest samples a broad conformational ensemble on a timescale longer than nanoseconds but shorter than milliseconds, as in the case of many IDRs [111,116,117]
| (8) |
where σ represents the variance of transfer efficiency due to fluctuations in the donor-acceptor distance.
A similar dependence can also be found when studying the characteristic delay acceptor emission [111]. If we denote P(r) as the distribution of conformations adopted by the interdye distance and we assume the interdye dynamics are slower than the dye tumbling but significantly faster than the interphoton times, we can compute the average τDA from the dynamic distribution as defined by,
| (9) |
where I(t) is the time-dependent fluorescence intensity and is given by [115],
| (10) |
By integrating over the distance r, Eq. 10 assumes that the lifetime decay occurs faster than the conformational change in r as sampled by the distribution of distances given by P(r).
The corresponding mean transfer efficiency is computed as,
| (11) |
where lc is the contour length between the dyes if the protein segment was fully extended.
Dye orientation is commonly described in terms of a parameter defined as κ, with the typical result of “κ2 = ⅔” for isotropic orientation of the fluorophores[25,27]. This is commonly valid if the dye tumbling is faster than the protein dynamics. However, if the dynamics of the protein are instead much faster than the tumbling of the dyes, the relative orientation of the dyes becomes coupled to the transfer efficiency. Under this regime, the mean transfer efficiency is given by the combination of the distribution of distances sampled by the protein and of k sampled by the fluorophores with the transfer efficiency dependence of distance and k:
| (12) |
where a is contact radius between the dyes, P(r) is the inter-dye probability distribution as described previously, E(r, κ2) is the transfer efficiency dependence on κ is as given by,
| (13) |
and the probability distribution p(κ2) is given by:
| (14) |
and,
| (15) |
Analogously, if the chain dynamics are faster or comparable to the fluorescence lifetime, the energy transfer rate will depend on the distribution of states sampled by labeled molecules,
| (16) |
where, as before, lc is the contour length of the chain and a the dye-dye contact radius.
Experimentally, time-resolved lifetime and anisotropy measurements can provide information on the tumbling rate of the fluorophores [118], and more extensive discussion of the influence of the different timescales at play on transfer efficiency histograms can be found in the fundamental works of Gopich and Szabo [96,97,112,119].
Finally, the functional form of the inter-dye probability distribution P(r) is typically approximated using simple polymer models or inferred from molecular simulations. While the mean transfer efficiency can be used to constrain the mean value of the distribution, the variance of transfer efficiency fluctuations σ can be used as a further constraint [120] for the distribution given that,
| (17) |
Various closed-form analytical and numerical models have been applied to describe FRET data, including the freely jointed (or Gaussian) chain, worm-like chain, and the self-avoiding walk [27,121–124]. Popularity of these models is largely due to the fact that they rely on single fitting parameters, enabling association of the mean transfer efficiency with a mean square distance, persistence length, or excluded volume term. While the worm-like chain and self-avoiding walk distributions provide descriptive parameters to capture excluded volume effects (and repulsive interaction in general), more advanced polymer models are required to capture the transition from good to poor solvent often observed by tuning solution conditions (e.g., denaturant), temperature, or by altering the sequence [125–129]. Ziv et al. adapted the coil-to-globule theory of Sanchez, introducing a conversion factor between the mean radius of gyration and the corresponding distribution of end-to-end distances [121,130,131]. More recently, by comparing single-molecule FRET and small-angle X-ray scattering (SAXS) data with simulations, Zheng et al. have proposed an empirical adaptation of the self-avoiding walk distance distribution that depends on the solvent quality through the scaling exponent ν [120,132]. These polymer models have been employed extensively to study disordered and unfolded proteins in many different contexts, where they have shown remarkable success [34,35,133–136].
2.4. Fluorescence correlation spectroscopy
Fluorescence correlation spectroscopy (FCS) is a powerful complementary tool to smFRET that measures the correlations of fluorescence fluctuations caused by diffusion and dynamics of labeled molecules as well as other photophysical effects [137–141]. This correlation can be computed as,
| (18) |
where ⟨...⟩t represents the average over all measured times, τ is the lag time at which the correlation is computed, and I(t) and I(t + τ) is the fluorescence intensity at times t and (t+τ).
When applied to single-photon counting measurements, the expression in Eq. 18 can be interpreted as the joint probability of observing a photon at time t and (t + τ) compared to the joint probability of observing two photons at any time,
| (19) |
Eq. 19 provides an intuitive way to understand how the correlation decays of FCS relates to molecular diffusion through the confocal volume or other physical properties. If the lag time is shorter than the average residence time of a molecule in the confocal volume, the joined probability of observing two photons that are separated by that given lag time will be high since they are emitted by the same molecule. When the lag time increases and approaches the average residence time of the molecule in the confocal, the decrease in the joined probability reflects the increased probability of the emitting molecule exiting the confocal volume without being immediately replaced by a new one. Ultimately, if the lag time is much longer than the average residence time of the molecule, the joined probability of observing two photons at times t and (t + τ) will be identical to the probability of observing two photons at any time. Therefore, for very long lag times, the correlation (as described by Eq. 18 and Eq. 19) tends to unity. The same reasoning can be applied to understand the correlation decay connected to photophysical effects that result in dark states (e.g., quenching or triplet states).
To better understand the properties of the correlation function, we can express the intensity as,
| (20) |
with ijand Ibg being the intensity of a single fluorophore and the background intensity at time t, respectively. Under this description, the correlation function from Eq. 18 adopts the form,
| (21) |
Assuming that ⟨ Ibg(t) ⟩t has a negligible contribution compared to other quantities, Eq. 21 reduces to,
| (22) |
where the amplitude of the correlation clearly depends on the inverse of the average number of molecules Nobserved in the confocal volume. As implied by Eq. 22, FCS is not exclusively restricted to the single-molecule regime and is often applied in conditions under which multiple molecules diffuse through the confocal volume. Importantly, when measurements are performed at sufficiently low concentrations of N molecules, the background term may contribute to the correlation amplitude and, if not accounted for, can affect a proper determination of N. Importantly, the ability to function at extremely low concentrations makes FCS an ideal technique in the context of IDRs that are prone to undergo self-assembly [142,143].
Nanosecond FCS (nsFCS) extends conventional FCS to sub-microseconds timescales by distributing photons across multiple detectors. The application of multiple detectors circumvents the intrinsic limitations (deadtime after pulse) that affect the correlation on individual detectors. Access to the sub-microsecond timescales allows the assessment of the contribution of static quenching (e.g., caused by dye-residues and dye-dye stacking), protein dynamics, and other photophysical effects [134,144,145]. Of particular interest in the context of IDRs is the application of nsFCS to provide an estimate of chain conformational dynamics. ns-FRET-FCS provides a measure of the protein dynamics through the characteristic correlated relaxation in the donor-donor and acceptor-acceptor correlations and the anti-correlated relaxation of the donor-acceptor cross-correlation. The anti-correlated decay directly reflects the anticorrelated intrinsic nature of FRET, where an increase in acceptor emission corresponds to a decrease in the donor emission and vice versa. When performed at the single-molecule level in a subpopulation specific way, the amplitude of the dynamic component (in the absence of quenching) of the correlation is directly related to the variance of transfer efficiency fluctuations in the solution, according to [146,147],
| (23) |
Here, Aij is an amplitude component related to the number of fluorescent molecules in the confocal volume, cAB is the antibunching amplitude, τ is the lag time between the two detected photons, τAB is the correlation time of the antibunching component, cT is the amplitude of the triplet component, τT is the correlation time of the triplet component, and τb is the correlation time associated with chain dynamics.
It is important to stress that the relaxation time τb of these three correlations represents a FRET-filtered value of the real reconfiguration time of the protein. Gopich et al. determined a simple correction factor that enables the extraction of the reconfiguration time of the protein [146]. This reconfiguration time can be directly linked to polymer quantities such as the characteristic times derived in Rouse and Zimm models [148–152]. Finally, since this approach provides access to the variance in the transfer efficiency fluctuations, it can be combined with single-molecule FRET and lifetime measurements to infer properties of the distribution of transfer efficiencies.
Single-molecule contact formation dynamics can also be probed using photon-electron transfer (PET) between a single fluorophore and an aromatic residue (or other quencher attached to the protein) [134,143,145,153,154]. In PET-FCS experiments, the fluorophore forms transient static complexes with the quencher. Therefore, the amplitude cq and characteristic time τq associated with the static quenching in the correlation contains information on both the on- and off-rate of contact formation: τq = 1/(kon + koff) and cq = kon/koff. Importantly, static quenching is not diffusion limited, such that the on-rate must be calibrated with a known diffusion-limited quenching process to extract the real on-rate of contact formation. For comparison, the dynamic quenching between dyes and aromatic residues, as measured by changes in the fluorescence lifetime, has been found very close to the diffusion-limited regime and offers a convenient strategy for extracting correction factors for reaction-limited quenching.
Furthermore, the on-rate of contact formation as measured in PET-FCS experiments can be related to the reconfiguration time measured by ns-FRET-FCS when computing the first passage time of the corresponding polymer model [134,155,156]. In the scenario where internal friction dominates the protein dynamics, Cheng et al. proposed a convenient equation where the contact time is computed by using the Szabo-Schulten-Schulten theory[157] in terms of 1D diffusion in a potential of mean force for the Rouse and Zimm model for internal friction [150]. This leads to the remarkably simple expression,
| (24) |
Where τi is the internal friction characteristic time, R is the root-mean-square separation between the dye and the quencher and Rc is the contact radius for quenching.
2.5. Challenges and practical considerations in single-molecule fluorescence spectroscopy
Recent cross-lab verification demonstrated that smFRET can provide highly reproducible results across different laboratories when the instruments are properly calibrated [158]. Calibration of experimental setups can be obtained by measuring reference samples that provide an estimate of the excitation and detection efficiency of the detectors and correct for the different quantum yields of the fluorophores [25,27]. An elegant solution has recently been proposed [158–161] and relies on the use of alternating-laser excitation (ALEX) [162,163] or pulsed interleaved excitation (PIE) [164,165]. In brief, fluorescence detection of donor-only and acceptor-only molecules provides insights on the direct excitation of acceptor and cross talk, while a comparison of the stoichiometry ratio of donor-acceptor labeled molecules as a function of transfer efficiency (e.g., polyproline or other systems of interest) enables estimates of the relative corrections for detection efficiency and quantum yield across the donor and acceptor channels. Investigating the dependence of the stoichiometry ratio vs. transfer efficiency requires either multiple samples with different mean transfer efficiency or altering transfer efficiency by changing the solution conditions of the same sample, although it should be noted that altered solution conditions may alter the quantum yield of the fluorophores or introduce quenching, which may further complicate this analysis.
An important decision in designing smFRET experiments is the choice of the experimental strategy, e.g., whether one is investigating freely diffusing or immobilized molecules. Which approach to take is determined by several factors, including the accessible experimental setup and the biophysical or biochemical question being addressed. A common solution for the investigation of immobilized molecules is the use of Total Internal Reflection Fluorescence (TIRF). TIRF microscopy relies on evanescent illumination of samples tethered to the surface [166,167], reducing background fluorescence from labeled molecules in solution. TIRF microscopy often uses camera-based detection, enabling the simultaneous observation of multiple molecules and the study of out of equilibrium kinetics. Confocal single-molecule fluorescence microscopy enables measurements of both freely diffusing and immobilized molecules.
The use of single-photon counting avalanche photodiodes and Time Correlated Single Photon Counting (TCSPC) electronics provide access to fast dynamics, kinetics, and photophysical properties of the systems such as triplet and fluorescence lifetimes. Owing to the high temporal resolution, confocal single-molecule fluorescence experiments have captured even rare events such as the transition path time from a folded to unfolded state or from a bound to unbound state [23,168]. Several approaches have been developed to enable the investigation of higher concentrations regimes and out of equilibria phenomena in confocal setups. For example, zero-mode waveguides have been used to extend the concentration boundaries of single-molecule confocal detection up to micromolar concentrations [169,170]. Similarly, microfluidic devices with fast mixing allows following the kinetics of the system of interest, at the single-molecule level, from hundreds of microseconds up to tens of seconds. [171–177]. Recurrence analysis of single particles (RASP) also captures the kinetics of freely diffusing molecules by identifying those molecules that after passing through the confocal volume re-enter in the confocal volume. By studying how the conformations of these molecules changes at different lag times, information on kinetics can be reconstructed [178,179]
Once the experimental setup and strategy have been chosen, the next step is the selection of appropriate labeling positions. The average Förster radius across the fluorophores suitable for single-molecule FRET lies between 5 and 7 nm, limiting the sensitivity of the method to distances approximately larger than 2–3 nm and smaller than 10 nm (see Fig. 4c). While knowledge of the protein structure allows for the tailoring of dye placement in folded proteins, more difficult is the choice of label position when studying IDRs, since the sequence properties of the chain can significantly alter the root-mean-square interdye distance. A distance of approximately 50 – 60 amino acids provides an appropriate dynamic range for sequences with a broad range of charge compositions, ranging from expanded polyelectrolytes to collapsed polyampholytes [180]. It is important to note that proline-rich sequences can adopt very extended configurations [38,181]. Sampling different interdye positions within the same IDR can further improve the ability to to quantify the dependence of the related interdye distance with the sequence length of the measured segment, providing access to the associated scaling exponent [20,65,133,182]. As mentioned, an estimate of the expected distance between two pairs of residues can be derived using appropriate polymer models or simulations [66,67,109,180,181,183–187].
The amino acid sequence raises additional constraints with respect to the optimal strategy for labeling. Both FCS and FRET measurements rely on covalently labeling proteins of interest with one or more fluorescent dyes. The labeling strategies typically take advantage of endogenous cysteine residues or introduce novel cysteines via mutation. These cysteine residues can be covalently modified with fluorescent dyes via maleimide chemistry [188]. Given the general scarcity of cysteine residues in most protein sequences, it is not uncommon for an IDR of interest to contain one or even zero endogenous cysteines. In this scenario, mutations that convert small polar amino acids (e.g., serine or glutamine) to cysteine (or vice versa when removing unwanted endogenous cysteines) are generally expected to have minimal impact on the conformational behavior of a disordered protein owing to the approximate chemical equivalence of the residues. Nevertheless, scenarios in which altering the number of cysteine residues in the protein can arise, in which case alternative labeling strategies are required.
The introduction of non-natural amino acids and enzymatic reactions for site-specific labeling presents a set of approaches that move beyond the intrinsic limitations of cysteine-based labeling methods. For example, the use of the enzyme sortase A has enabled site specific labeling of proteins that contain substantial cysteines and would be otherwise unamenable to site specific labeling by maleimide chemistry [189,190]. Sortase A catalyzes the ligation of an “LPETG” motif with a “GGG” motif [191,192]. In this way, a linker containing a fragment of a protein that harbors a single cysteine can be utilized to enable maleimide chemistry on the sole cysteine residue [193]. The rest of the protein that contains multiple cysteines can be ligated to the singular-cysteine containing protein fragment. Conversely, the use of split-inteins can enable maleimide labeling of multiple cysteine residues across a protein that has been separated into fragments that contain one cysteine each, followed by ligation of the fragments with native chemical ligation [194,195]. Non-natural amino acids, alone and in conjunction with Click chemistry, can enable site specific labeling which can be critical in the context of three- or four-color smFRET experiments, although the incorporation of non-natural amino acids can lead to complications in protein expression yields [135,196–202]. Additionally, in sequences where mutating endogenous cysteine residues is likely to disrupt protein conformation, non-maleimide chemistry methods offer an alternative labeling strategy. For example, short peptide sequences (A4/Q-Tags) have been used to site-specifically label several proteins [203–207]. Q tags utilize a transglutaminase catalyzed reaction to ligate cadaverine functionalized fluorophores to the glutamine residue present in Q-tag motifs (PNPQLPF, PKPQQFM, GQQQLG) [203]. Unlike sortase or maleimide chemistry, the A4 tag utilizes a phosphopantetheinyl transferase reaction to conjugate CoA conjugated substrates to the serine present in the A4 motif (DSLDMLEM) [205,208–210]
The subsequent key step rests on the choice of dye. With the advent of superresolution microscopy, a broad range of fluorophores and donor-acceptor combinations have become available, each with different photophysical and chemical properties. It is worth mentioning that, when targeting the cellular environment in single-molecule experiments, a choice of red-shifted fluorophores (compared to the often used 480–520 nm range of excitation) has proven to reduce the fluorescence contribution originated by the cellular background [179]. Each fluorophore differs not only in excitation and emission wavelengths, but also in terms of geometry, hydrophobicity, net charge and linker flexibility and length. As a result, different dyes have different possible impacts on protein conformation, depending on the sequence-encoded physical chemistry of the given protein.
Although several studies have implicated dyes as a source of non-native interactions that can alter conformational behavior [211–214], with careful dye selection and validation, these issues can be minimized, and a number of studies have found that dyes can have a minimal impact on ensemble behavior [35,65,215,216]. However, some relevant examples do require attention. Due to the high hydrophobicity, the popular ATTO 647N dye has been reported to cause a substantial collapse of an IDR, at variance with many other dyes [34]. This result suggests that caution must be taken when using this fluorophore on IDRs. Focusing on the role of dye charges, many of the commonly used fluorophores, such as Alexa 488 and 594, carry a −2 negative charge each. This net charge may become particularly relevant when investigating polyampholytic sequences with local regions of net positive charge, or with proteins that possess a net positive charge, such that these electrostatic effects must be accounted for when modeling or interpreting the experimental data [180]. Finally, the choice of the dye may also depend on the specific environment in which the protein is located: recent work has revealed preferential interaction of specific fluorophores with lipids [217].
The reality is that there is no “one-size fits all” solution for choosing dyes. For some proteins, certain dyes will likely have an impact on molecular details, while in others they will not. The determinants of dye effects reflect the physicochemical properties of dyes and the sequence-encoded physical chemistry present in a given protein. As such, due diligence is required when considering if and how dyes may be impacting conformational behavior. This may include testing different combinations of dye pairs to ascertain if different dyes reveal different results. Ideally, orthogonal verification with other techniques (either computational and/or experimental) offers a convenient route to refute or confirm findings [215].
When approaching the data analysis of smFRET experiments, several assumptions undergo transforming the measured transfer efficiency into a distance distribution. The most commonly cited assumption is the isotropic orientation of the fluorophores described by the κ2 parameter in the definition of the Förster radius (R0). Although simulations may achieve a quantitative estimate of κ2, a measurement of the steady-state and/or time resolved anisotropy of the two fluorophores provides quantitative insight into possible conformational restrictions of fluorophores orientation [118,218].
Less discussed but equally important when comparing results from single-molecule fluorescence experiments with simulations is an appropriate estimate of the characteristic timescales at play. It is crucial to consider the timescales’ impact on the interpretation of the mean transfer efficiency, with particular attention needed with respect to the rate of fluorophore tumbling and fluorescence lifetime, as well as chain dynamics. As mentioned in section 2.3, Eq. 6 assumes that the dynamics of the chain are faster compared to the interphoton time, but slower than both dye tumbling and the fluorescence lifetime (Fig. 5). This behavior is a precondition for invoking the approximation that fluorophores are experiencing isotropic orientation.
Figure 5. Experiments and simulations inform over a broad range of timescales.
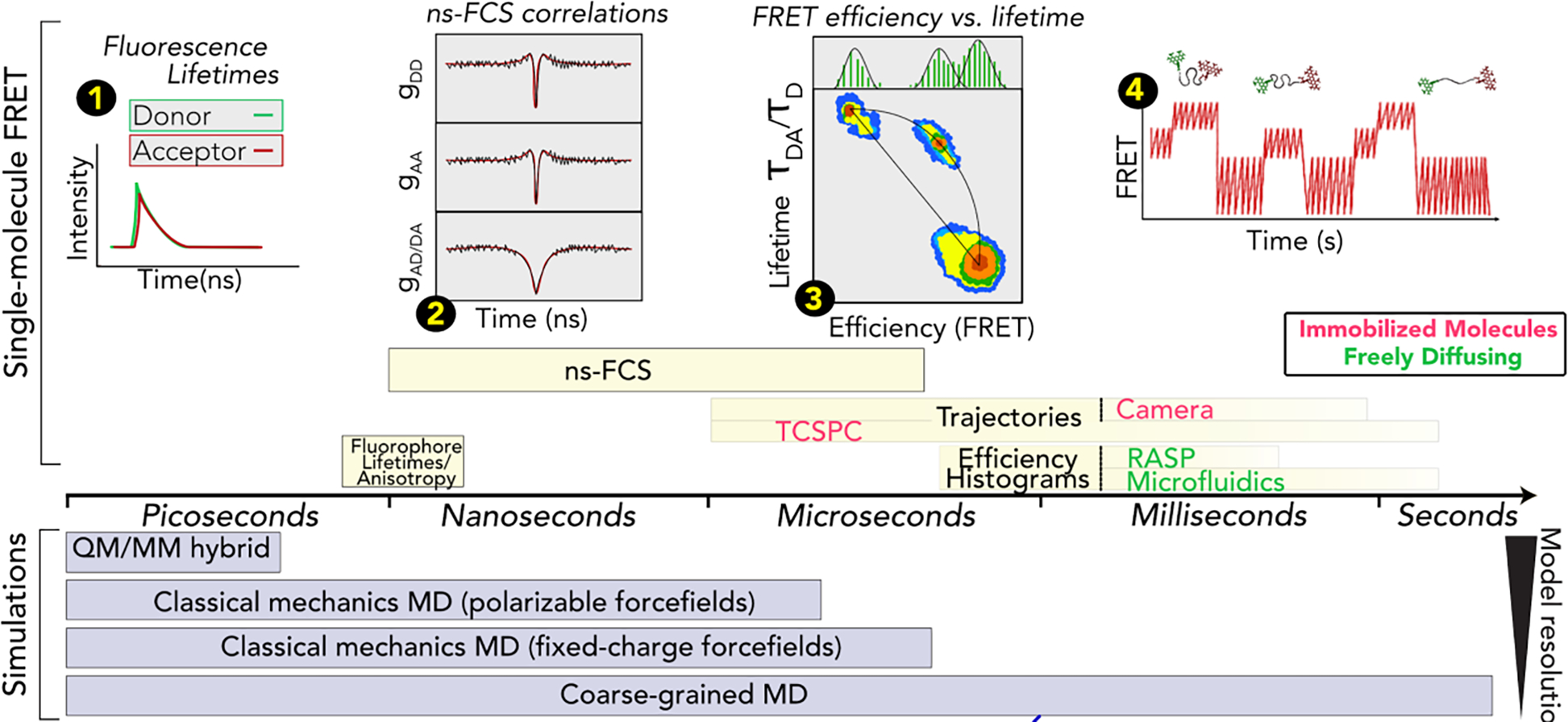
Schematic detailing the different timescales accessible to single-molecule fluorescence spectroscopy and simulations. (1) Time-resolved fluorescence provides access to donor and acceptor lifetimes (which are influenced by the FRET process) and to anisotropies (which reports about tumbling of the dyes and of the overall molecule. (2) The correlate decay in the donor (DD) and acceptor (AA) autocorrelations as well as the anticorrelated rise in the donor-acceptor (AD/DA) cross-correlation reports about protein dynamics. (3) 2D-histogram of donor lifetime in the presence of the acceptor (normalized by the donor lifetime in the absence of the acceptor) vs. transfer efficiency. The diagonal line represents the result for a static configuration of the protein and the curved line represents dynamics exchange in the protein conformational ensemble. (4) Transfer efficiency trajectory of immobilized molecules can reveal slow conformational changes of the protein up to minutes.
Once all these aspects are considered, a root mean square distance is extracted based on the mean transfer efficiency ⟨E⟩. The measured distances provide a readout on the separation of the fluorophore, as opposed to a direct readout on the residue-residue distance between labeling positions and fluorophores linker needs to be accounted for [118]. For the dye pair Alexa 488 and 594, the dye linkers’ contribution to the root-mean-square interdye distance for an unstructured protein corresponds to an increase in the protein sequence length of about nine amino acids [184,185,219].
2.7. Approaches for the integration of single-molecule fluorescence spectroscopy and simulations
Various theoretical frameworks appropriate for the integrations of single-molecule fluorescence spectroscopy with results from atomistic simulations have emerged over the last decade, with many of these being directly applicable to the study of disordered proteins. Rather than providing an exhaustive technical description of these methods, we will briefly overview the conceptual approaches and practical methodologies available.
The most straight-forward approach involves performing unbiased molecular simulations of a protein of interest without dyes, computing relevant observables from the simulations, and then comparing those observables with the analogous values obtained from experiment [20,220,221]. In the context of smFRET experiments, this would involve computing distributions of inter-residue distances and then comparing those distances with the analogous distribution obtained from experiments [161]. For FCS, this would involve computing a hydrodynamic radius (Rh) from simulations and comparing that value with the apparent Rh obtained from the diffusion constant [222,223]. For nsFCS, this would involve computing molecular reconfiguration times and comparing those times with timescales measured by experiment [134,224,225]. This approach makes two key assumptions. Firstly, it assumes that the dyes do not significantly contribute to the conformational ensemble obtained from simulations, such that the ensemble generated in the presence/absence of dyes is equivalent. Secondly, it assumes that analytical models (i.e., P(r), for determining inter-dye distance, see section 2.3) offer an appropriate route to back-calculate molecular properties that can also be obtained from simulations. Both these assumptions are reasonable, well established for many systems, and often taken to be true irrespective of if a comparison between simulation and experiment is to be performed. This naive comparison offers a convenient first approach to demonstrate agreement between simulation and experiment. Moreover, if the agreement is poor, it provides a starting point to diagnose the origin of discrepancies.
While simulations lacking fluorophores are – by definition – reporting on the naturally occurring state of the protein, for a quantitative comparison with single-molecule spectroscopy, this approach has some shortcomings. For one, the absence of explicit dyes ignores their conformationally heterogeneous nature, and as such, these simulations are unable to interpret/assess dye-protein interactions, should they occur. Furthermore, a simulation that lacks explicit dyes does not generally take dye photophysics into account. Consequently, an alternative approach involves the explicit inclusion of dyes in the simulations [147,161,215,226]. Here, simulations of biomolecules with fluorescent dyes are run, and then relevant observables (e.g., FRET transfer efficiencies) are calculated from ensembles using dye orientation directly. The resulting computationally-derived FRET results can then be directly compared with mean transfer efficiencies obtained from smFRET experiments. While conceptually appealing, the inclusion of fully parameterized dyes in all-atom simulations is somewhat less common than one might expect. This reflects several challenges that dyes introduce in the context of all-atom simulations.
One challenge in the inclusion of explicit dyes is the appropriate forcefield parameters. As mentioned, even for protein-only systems, correctly parameterized force fields that accurately describe IDR configurational rearrangement and dynamics are challenging. This is despite the wealth of data surrounding protein physical chemistry and structure. In contrast, large heterocyclic aromatic dyes are comparatively less well-studied. Consequently, the validity of dye parameters is less clear. Furthermore, there is good reason to expect that fixed-charge force fields may struggle to correctly capture the physical chemistry of large heterocyclic dyes due to the complex delocalized electron systems that are distributed across them. Finally, interpreting transfer efficiencies directly from dyes requires consideration of the dye photophysics, including the orientational dependence of the dipole-induced energy transfer that gives rise to FRET [161,226]. In principle, the explicit inclusion of fluorophores allows the impact of dye-protein interactions and the associated photophysics to be directly taken into account when computing transfer efficiencies, which, on the surface, appears ideal. However, in practice, it also introduces many potentially poorly-defined parameters that may bias or confound the calculation of FRET transfer efficiencies if done incorrectly. Moreover, given fluorescent lifetimes are inherently stochastic, this necessitates sufficient sampling to capture both IDR conformational rearrangement and dye-rearrangement. Taken together, the inclusion of explicit dyes is certainly the appropriate long-term strategy. However, with the exception of a small number of groups who have pioneered the aforementioned technical and theoretical issues, in the absence of well-characterized parametrization of dye and protein force fields, it remains unclear if the additional challenges introduced by including explicit dyes is more of a help or hindrance.
A final approach is one in which simulations are performed initially without dyes, but in a post hoc processing step the resulting ensemble has dyes (or clouds of dyes per protein conformation) rebuilt [35,87,118,227–230]. Using this approach, transfer efficiencies (or dye-dye distances) can be back-calculated. This offers a convenient middle-ground in that dye geometry and size are explicitly taken into account, yet the challenges associated with dye parameters are avoided. It does, however, operate under the assumption that the presence of dyes has no impact on the conformational ensemble explored in the simulations. Depending on the implementation details, this approach also runs the risk of over-representing conformations in which dye-attachment residues are more exposed, given only conformers where dyes can be added are included in the calculations of transfer efficiencies. Finally, this type of reconstruction requires further assumptions regarding the timescales associated with the fluorophores tumbling. The reconstruction of dye ensembles can be achieved in a number of ways and is facilitated by specific software tools [187,228,231].
The three approaches described above far operate under the assumption that simulation and experiment will agree “out of the box”. In reality simulations and experiments frequently do not show quantitative (and sometimes even qualitative) agreement. This is generally taken (fairly or unfairly) to reflect weaknesses on the side of the simulations, specifically due to force field errors and/or limited sampling. One solution to this challenge is development and improvements in both force fields (as mentioned) and the development of more powerful supercomputers [232–234]. In parallel, a number of approaches for ensemble re-weighting (also known as ensemble refinement) have emerged. These reweighting strategies alter the probability of each conformation in the ensemble to shift the expected values to better match the experiment. While a mismatch between simulations and experiments is generally taken to mean the simulation is at fault, this need not necessarily be the case, and scrutiny with respect to possible experimental artifacts (e.g., fluorophore quenching altering transfer efficiencies) should be taken [144].
To summarize briefly, reweighting involves the process of re-defining the probability of each conformation in an ensemble. For clarity, we define conformation here in terms of a frame or snapshot of the simulation - i.e., in the case of a non-reweighted, correctly sampled set of n conformations taken from an NVT ensemble it is assumed that any conformation i selected at random from the ensemble is present with probability,
| (25) |
Where, as for any discretized probability distribution,
| (26) |
As such, the ensemble-average value for any given observable with an instantaneous value (e.g., end-to-end distance, ⟨Re⟩) can be computed as,
| (27) |
where reflects the end-to-end distance of conformation i. There is nothing complex about Eq. 27 - in fact, this is simply a reformatted version of the arithmetic mean. When we calculate the mean we inherently assume every element in that calculation is equally important, such that every element appears with the same probability of 1/n. Reweighting reflects a change in this assumption where we instead re-define the probabilities such that not every element is equally likely, under the constraint that the probabilities must sum to 1.
Several key factors must be considered for ensemble refinement. Firstly, when re-weighting a large ensemble of states, we typically wish to apply systematic changes that simultaneously alter our observable to match some experiment while doing so in a manner that minimizes the loss of entropy. As such, maximum entropy-based methods have emerged as a key component of most reweighting schemes [235–237].
During maximum entropy reweighting, the collection of conformation-specific probabilities are altered such that the resulting probability distribution of an observable matches a prescribed distribution, or the reweighted ensemble average matches some experimentally observed value.
This requirement is reached under a constraint in which probabilities must sum to 1 and the entropy S(p), defined as,
| (28) |
is maximized.
Entropy-maximization does not explicitly take uncertainty into account. This uncertainty can lie on the side of the experiment in terms of precision or accuracy but can also reflect uncertainty in the simulation. This uncertainty is often considered through some kind of Bayesian approach that allows fine-tuning of uncertainty in a variety of ways [238–243]. Specifically, Bayesian inference provides a general framework through which a posterior model can be generated based on a prior model and the inclusion of newly observed data [235]. Several modern frameworks have emerged to facilitate simulation reweighting with large ensembles of disordered proteins in mind. These include Bayesian Inference of Ensembles (BioEn), Convex OPtimization for Ensembl Reweighting (COPER), Bayesian/Maximum Entropy (BME), and Extended Experimental Inferential Structure Determination (X-EISD) [238,240,241,243]. Although these tools have been recently developed and applied to disordered proteins, a large number of additional tools have been developed over the years (as reviewed by Bonomi et al. [236]). An in-depth discussion of the theoretical and practical differences between these methods goes beyond the scope of this review. However, each approach offers distinct advantages and disadvantages, and in principle are compatible with the integration of multiple different types of experimental data with distinct uncertainties.
An important caveat with respect to reweighting strategies reflects the fact that these approaches are ultimately limited by the quality of the starting ensemble [244,245]. Put another way - you cannot reweight what is never observed in the original simulations. Consequently, when starting ensembles are sufficiently large and sufficiently close to reality, reweighting can be a powerful approach to fine-tune simulation results to improve the signal-to-noise. However, if a starting ensemble is sufficiently incorrect, no amount of reweighting can rescue it. The gold standard here is to include two orthogonal methods and show that re-weighting simulation results with respect to one experimental dataset improves agreement with the other [135,245]. In this context, small-angle X-ray scattering is a good complementary technique to verify reweighted ensembles generated when ensembles are reweighted based on results from single-molecule spectroscopy.
As a final note, rather than reweighting unbiased simulations to match experimentally measured distributions, an alternative set of methodologies involve applying restraints or bias terms directly to the simulation. In this approach, a cost function that penalizes conformational behavior that deviates from experimentally compatible results is applied [66,246–249]. The nature of the cost function, how it is applied over long-timescale simulations, or how experimental uncertainty is dealt with vary depending on the implementation. While this approach has been used extensively in the context of structure determination, it has been used less frequently in the context of integrating single-molecule spectroscopy with all-atom simulations. For a comparison between restraints and reweighting in molecular simulations see work by Rangan et al. [250]
The preceding section introduced maximum entropy and Bayesian inference as theoretical frameworks through which reweighting or restraining can be achieved. It is worth noting that the alternative and complementary approaches including maximum parsimony, maximum likelihood, and maximum caliber provide alternative theoretical frameworks for ensemble selection and reweighting. These approaches can be applied either to bias simulations or as a post-facto reweighting strategy, as reviewed by Bonomi, Gaalswyk, and Ghosh, respectively [236,246,251].
3. Results
Having established the key features of all-atom simulations, single-molecule spectroscopy, and the integration of these methods, we will finish by considering a number of examples in which integrative experimental and computational modeling has revealed synergistic insight.
3.1. Single-molecule spectroscopy and solvent quality
The impact of solvent quality on denatured proteins was evident already in early studies of protein denaturation with single-molecule FRET [109,252] as a shift in the transfer efficiency population associated with the unfolded state. The work of Sherman & Haran directly implied a coil to globule transition in the conformations of the unfolded state [131]. In this context, important early work that integrated single-molecule spectroscopy and simulations was performed by Best, Gopich, Eaton, and Schuler [185,253]. Using both all-atom MD simulations and simple coarse-grained Langevin simulations, Merchant et al. showed a continuous transition in global dimensions of Protein L and cold shock protein CspTm observed by smFRET is reproduced as a function of solvent quality by simulations [253]. The integration of simulation and experiment here played a crucial role in helping to interpret smFRET data by demonstrating that the inferred radius of gyration (Rg) obtained from smFRET matched the Rg values obtained from simulations. This study represents one of the earliest examples in which all-atom simulations and smFRET were combined, and in many ways, defined the template for this class of study. Subsequent work using coarse-grained models has arrived at similar conclusions and shows good agreement with extant smFRET data [68,254].
The importance of solvent quality for disordered and unfolded proteins was again the topic of further study by Best and Schuler. In a series of papers, a comprehensive investigation of chain dimensions in response to denaturant concentration combined several different disordered proteins and a collection of methods including all-atom simulations, FCS, smFRET [34,78,220]. In work by Zheng et al., unbiased all-atom simulations without explicit dyes were performed as a function of denaturant concentrations [220]. Using these ensembles, intermolecular distances were then back-calculated, revealing a modest but continuous expansion in IDR global dimensions as a function of denaturant concentration. These computational results compared favorably with analogous measurements made by smFRET and SAXS. In a separate study by Borgia & Zheng et al., smFRET and SAXS data were used to reweight ensembles generated from all-atom simulations using a Bayesian approach. The resulting ensembles were compared against changes in global dimension obtained by FCS and dynamic light scattering (DLS) [34]. This study also identified a modest but meaningful chain ‘contraction’ as denaturant concentration is decreased (Fig. 6). In parallel, analogous integrative biophysical studies made on several other systems came to similar conclusions, supporting a model in which the solvent quality tunes the dimensions of unfolded protein ensembles, but that these ensembles do remain relatively expanded [135,255,256]. This is in reasonable agreement with measurements made by SAXS that inferred that if any chain-compaction occurred at all, it would be modest [257,258]. Taken together, these results have helped establish that as unfolded polypeptides transition from high concentrations of denaturant into native conditions, there is a sequence-dependent contraction in global and local chain dimensions. The magnitude of this contraction depends on the chemical nature of the denaturant and protein sequence. In many foldable proteins, this contraction appears to be in the range of 10–25% in global dimensions prior to bona fide folding [256]. For disordered proteins the extent of compaction (or lack thereof) this contraction can range from a few percent to over 50%, depending on the amino acid sequence and denaturant [24,34,38,133,220,259,260].
Figure 6.
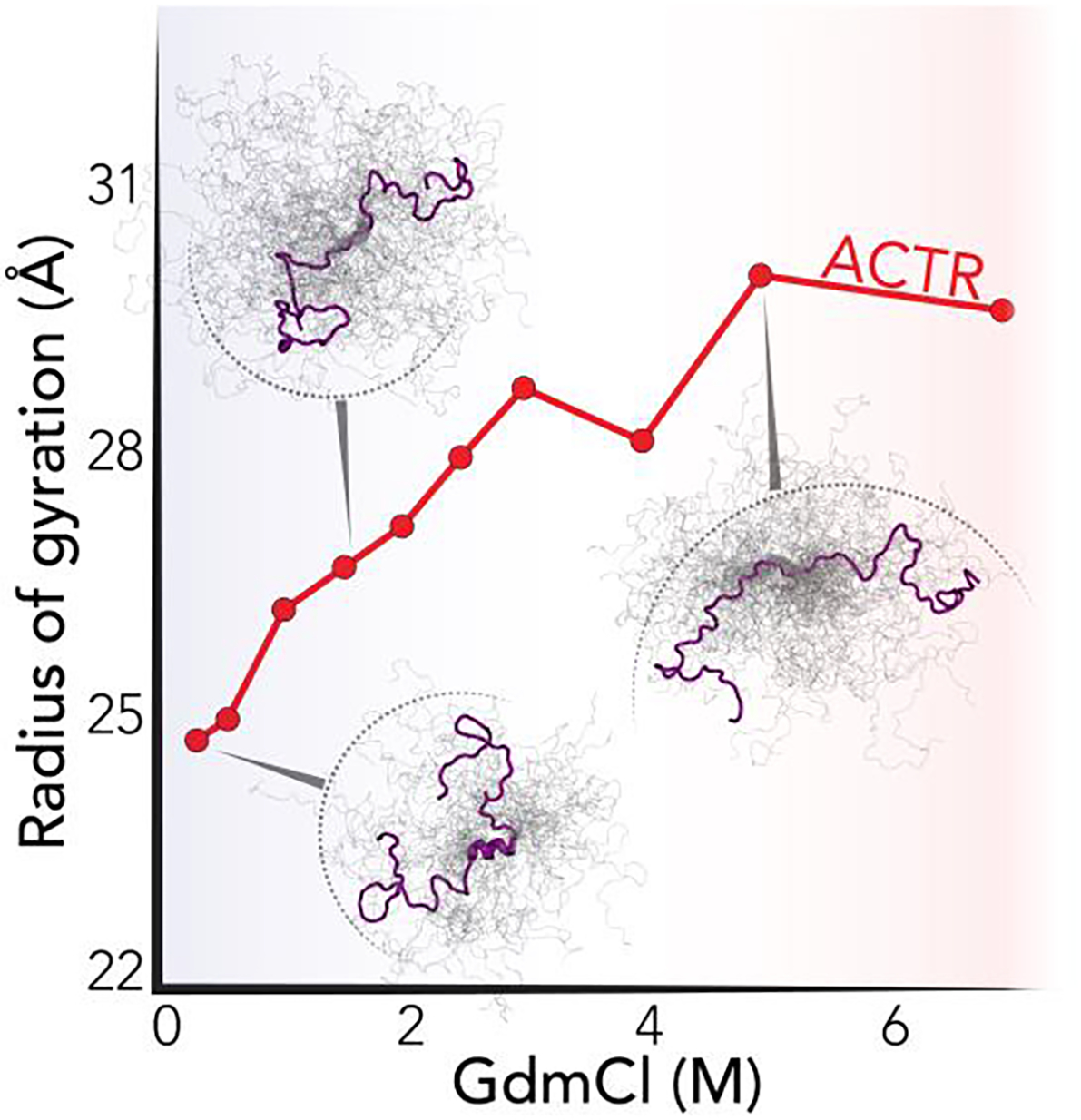
The conformational ensemble of the 71-residue ACTR as a function of denaturant, as obtained from smFRET and all-atom simulation by Borgia & Zheng et al. [34].
Despite this substantial effort, a quantitative and absolute agreement between SAXS and FRET-derived measurements remains contentious for at least some systems [211,212,256]. Despite the valid and important concerns regarding the impact of dyes, a general consensus that disordered/unfolded proteins are sensitive to changes in their solution environment seems undeniable [256]. These conclusions need not be at odds with the observation that foldable proteins undergo a sharp folding transition when solution condition conditions permit [261].
As a final point, the magnitude, modality, and physical origin of solution-dependent changes in IDR conformational behavior will depend on the amino acid sequence and the chemical nature of the co-solute [255,262–265]. This sequence-encoded sensitivity has been proposed to offer IDRs a mechanism to act as biological actuators and sensors of cellular state [36,260].
3.2. Reconciling length-scale dependent conformational heterogeneity with smFRET and simulations
The apparent discrepancy between SAXS and smFRET has an additional possible origin: residual structure leading to deviations from homopolymer models used to infer smFRET-derived distances [35,69,70,266]. Analytical homopolymer models are remarkably good at quantitatively describing the conformational behavior of IDRs [20,133,136]. However, for IDRs with a substantial amount of residual structure or peculiar sequence patterning, there is an expectation that homopolymer models will become progressively less reliable [67,266].
The possible impact of structural heterogeneity was examined simultaneously and independently in two studies. Song et al. applied simulations and theory to analyze extant smFRET data for unfolded proteins to argue that anisotropic biases in the underlying conformational ensemble could explain apparent discrepancies between SAXS and smFRET data [69–71]. Using coarse-grained simulations to construct transfer efficiency distributions, the authors show that even relatively small but persistent conformational biases can have a substantial impact on distances derived from transfer efficiencies.
In independent but complementary work, Fuertes & Ruff et al. performed an integrative study that combined all-atom simulations, smFRET, and SAXS of both labeled and unlabelled IDRs under native and strongly denaturing conditions. In this work, a dye-reconstruction approach was applied in which clouds of dyes were rebuilt around simulations run in the absence of dyes. A key result from this study reflects the fact that homopolymeric models are better equipped to describe conformational behavior under denaturing conditions. This result reflects the fact that in the limit of high denaturant concentration, the chain has - in effect - become a bona fide homopolymer. In contrast, under native conditions, sequence-dependent residual structure can lead to deviations from true homopolymeric behavior, limiting the accuracy when pairwise intra-chain distances are used to inform on global dimensions.
An analogous study by Gomes et al. integrated smFRET with nuclear magnetic resonance (NMR) spectroscopy, SAXS, and simulations and came to similar conclusions [216]. Here, coarse-grained simulations in which explicit dyes with modeled photophysics were used to construct realistic transfer efficiency histograms. In agreement with Fuertes & Ruff, the authors found that integrative modeling is necessary to fully reconcile seemingly discordant observations due to local conformational biases. The need for several distinct methods that provide unfolded-state behavior across distinct length-scales has also emerged in other systems [24,135,267].
Taken together, the application of homopolymer models remains a critical tool for the analysis and interpretation of IDRs. As it turns out, the specific choice of polymer models often introduces only small systematic variations on the extracted root-means-square distances from single-molecule data [27,120]. However, underlying assumptions baked into polymer models may not hold true across various interdye distances of the protein due to long-range anisotropic interactions or local residual structure [22,35,268]. It is therefore important to test whether the assumptions associated with a given model are robust across multiple interdye distances. Polymer models can be assessed by comparing the persistence length for a wormlike chain model or the Kuhn segment for a Gaussian Chain. The origins of any observed deviations must then be examined. At the same time, heteropolymer theories often describe the local contribution of compositional heterogeneity over a specific inter-residue distance in terms of an effective bond segment that rescales the second moment of the ideal chain distribution. Different segments of the chain will adopt different effective bond lengths, such that no single effective bond length is expected to fit an entire chain. The expected heterogeneity in the effective bond lengths along a heteropolymeric protein provides a possible explanation for the empirical success of using freely jointed chain (or similar) homopolymer models on systems that are clearly far from theta-solvent conditions. As such, one should carefully consider the physical meaning of the extracted distance in the context of appropriate theories and models. In this respect, the application of homopolymer models to the interpretation of heteropolymeric IDRs should be used under the guise of “What is the homopolymer that best describes my data?” as opposed to “Does my heteropolymer behave as a homopolymer?”. [267].
3.3. Conformational dynamics as assessed by single-molecule spectroscopy and simulations
The ability of single-molecule spectroscopy to provide direct insight into the molecular dynamics of a given IDR has opened up additional avenues of experimental characterization and comparison between simulation and experiment.
Soranno et al. combined simulations, single-molecule spectroscopy, and theory to build a complete molecular dissection of the determinants of internal friction in unfolded proteins [115,134]. By combining smFRET and ns-FCS, the authors were able to probe how fast chain dynamics depends on the interdye sequence length and solvent viscosity, demonstrating that under native condition protein dynamics are often not dictated only by solvent conditions, but more significantly by internal friction effects, where internal refers to intrinsic properties of the protein, such as transient intramolecular interactions and dihedral angle constraints. These results were in remarkable agreement with extant simulation data performed by Piana et al. [73,134]. Moreover, the conclusions drawn in this study were further confirmed via integrative analysis of alpha-synuclein dynamics using smFRET, NMR, and MD simulations [224]. The integration of simulation and experiments provided a comprehensive molecular readout that implicates non-local intramolecular interactions and a second contribution from the retardation of dihedral rotation, although these two effects may be inherently coupled.
Integrating smFRET with simulations allowed Metskas & Rhoades to reconcile apparent discrepancies between published structures of the intrinsically disordered C terminal domain of troponin-1 [269]. Multiple high-resolution structures lacked agreement with each other and with NMR based measurements, highlighting the conformational heterogeneity that exists in the system. MD simulations performed with discordant published structures as starting points allowed them to gain an understanding of the conformational landscape the protein adopted. Interestingly, although good agreement between smFRET measurements and MD simulations was obtained when comparing folded subregions, substantial disagreement was arrived at when smFRET measurements of the intrinsically disordered C terminal domain were compared with MD simulations. Hypothesizing that this discrepancy reflected a difference in the timescales of the techniques, the authors applied MC simulations to construct a large ensemble of conformations for the disordered region. This ensemble showed good agreement between smFRET, MD, and MC simulations, and the most populated conformations present in the MC simulations matched the three published structures that were ‘incongruent.’ This study elegantly demonstrates that if distinct timescales are probed, it is possible to obtain apparently contradictory yet entirely valid results.
Zosel et al. integrated extensive single-molecule fluorescence data and all-atom simulations to assess complex binding kinetics between the disordered protein ACTR and its conformationally heterogeneous folded partner NCBD [23]. Single-molecule experiments revealed that an evolutionarily conserved proline in NCBD undergoes slow cis-trans isomerization. The binding affinity of NCBD for ACTR depends heavily on the isomerization state of this slow-switching proline. MD simulations provided a cogent molecular explanation for the proline-dependent affinities and demonstrated that the molecular structure of the bound complexes differs depending on the proline isomerization state. The ability to reconcile complex and counterintuitive kinetic behavior was entirely dependent on the ability to observe conformational rearrangement on a range of timescales and length scales. Similarly, the ability to offer a cogent structural explanation for this behavior rests on the application of molecular simulations to the binding event. Taken together, this study offers an example in which simulations and experiments offer complementary insights into the structure and dynamics of a complex molecular mechanism.
Medina et al. utilized MD simulations paired with smFRET and hydrogen-deuterium exchange mass spectrometry to probe the conformational heterogeneity and dynamics present within intermediate binding steps of FOXP1 [270]. This approach allowed the authors to probe low-population conformations that would be hidden if ensemble experiments were used exclusively. By applying single-molecule spectroscopy and simulations, this complex structural landscape was disentangled, enabling the development of a model in which domain switching involves intermediate states populated by a heterogeneous population of conformations.
Finally, while not strictly an IDR, Chung et al. utilized a combination of long-timescale simulations and single-molecule spectroscopy to determine the physical basis for slow protein folding in a small triple-helix designed protein [168]. By first analyzing photon trajectories from FRET histograms using a maximum likelihood method [271] to obtain relaxation rates, the authors reveal a sharp pH dependence on the folding rates, where folding is dramatically faster at low pH. A similar pH dependence on folding is also observed in all-atom molecular dynamics simulations. By strengthening or weakening the non-bonded interactions associated with salt bridges by altering the underlying forcefield, the authors are able to perform a computational experiment to decouple the observed rate effects on salt-bridge strength vs. net charge of the molecule. This ingenious analysis revealed that salt-bridge strength is the key determinant of the transition time, providing a clear example in which the types of theoretical experiments that simulations afford offers direct insight into a physical process that would otherwise be impossible to measure.
3.4. Multi-molecular assemblies as measured by single-molecule spectroscopy and simulations.
The integration of single-molecule spectroscopy and simulations has more recently played key roles in providing a high-resolution window into dynamic protein:protein and protein:RNA complexes [65,230,272]. Ensemble methods typically hide the heterogeneous nature of IDPs, masking dynamic interactions that may underlie biological function. In a series of papers exploring polyelectrolytic complexes, the integration of smFRET, nsFCS, and MD simulations has been essential to deconvolve complex heterogeneous systems.
In a landmark study, Borgia, Borgia, & Bugge et al. demonstrated that a binary complex formed between the negative polyelectrolyte prothymosin alpha (ProTα) and the positive polyelectrolyte linker histone H1.0 (H1) formed a high-affinity complex in which both proteins remain fully disordered [65]. Using a bespoke coarse-grained model that is directly compared against 28 distinct intra- and inter-molecular distances measured by smFRET, the authors demonstrate remarkably good agreement and provide a comprehensive molecular picture of the resulting high-affinity complex. Importantly, on the experimental side, the authors compare results with two different sets of dye pairs, and on the computational side, simulations are run both with and without explicit dyes. In addition to smFRET and simulations, extensive NMR data corroborate the disordered nature of the complex and provide additional key insights.
In two subsequent studies, Holmstrom and Heiðarsson & Mercadante probed the dynamic nature of intrinsically disordered proteins in the context of protein:protein, protein:RNA, and protein:DNA interaction [272,273]. In both of these studies, single-molecule spectroscopy was combined with coarse-grained MD simulations were able to capture the dynamic nature of the association of an IDP with another protein or nucleic acid. In the bound state, the IDP in question remains both disordered and dynamic upon association with its ligand, where this dynamic association underlies the biological function. For Holmstrom et al. this dynamic association enhanced the folding of an RNA hairpin, providing an electrostatic screening effect analogous to high concentrations of monovalent salts. For Heiðarsson & Mercadante et al. a ternary electrostatic competition mechanism driven through a dynamic protein assembly enabled the dissociation of Histone H1 from the nucleosome.
In addition to providing insight into individual molecules or small complexes in a dilute solution, single-molecule fluorescence spectroscopy can be used to peer into the interior of biomolecular condensates formed through liquid-liquid phase separation [24,274,275]. Martin, Holehouse, & Peran et al. combined turbidity, FCS, and coarse-grained simulations to calculate full phase diagrams of the low-complexity domain of the RNA binding protein hnRNPA1 [24]. More broadly, both smFRET and FCS offer a means to examine the conformational behavior of IDRs inside and around phase-separated droplets [274,275].
3.5. The application of simulations and single-molecule spectroscopy to offer molecular insight into biophysical mechanism
The true power of integrating molecular simulations with single-molecule spectroscopies lies in the ability to uncover novel biophysical mechanisms. In our final results section, we consider a collection of studies in which specific molecular details have been unraveled through the combination of single-molecule fluorescence spectroscopy and simulations.
A long-standing question in cell biology pertains to the molecular basis of recognition and translocation of nuclear transport receptors by the phenylalanine and glycine-rich (FG) disordered regions that line the interior of the nuclear pore complex [276–279]. An integrative study by Milles & Mercadante et al. combined all-atom simulations with smFRET, NMR, and SAXS to offer a direct molecular picture of the nature of FG interactions with their associated cargo proteins [280]. This work revealed a degenerate network of transient molecular contacts between a nuclear pore protein and its corresponding nuclear transport receptors. These interactions were encoded by distributed adhesive phenylalanine residues in FG motifs where they interact in a multivalent fashion across the surface of the cognate transportin proteins. Despite the lack of specific binding sites and the microscopically weak binding affinities of individual motifs, the resulting macroscopic binding affinity is remarkably high. As such, nuclear transport receptors are tightly bound, yet relatively free to diffuse. This work provides a molecular explanation for the selective partitioning and rapid translocation of transportin-bound cargo proteins across the nuclear pore complex.
The physical basis for temperature-induced collapse of disordered and unfolded proteins has been examined via smFRET interpreted via all-atom replica exchange molecular dynamics simulations, pointing to the role of sidechain solvation in driving compaction [183]. This observation was confirmed in subsequent work where temperature-dependent free energies of solvation were used with all-atom implicit-solvent Monte Carlo (MC) simulations to explain corresponding smFRET experiments for a number of different IDRs [281]. In both cases, unbiased simulations without explicit dyes were performed and the radius of gyration (Rg) from simulations compared with the apparent Rg calculated from smFRET-derived inter-dye distances.
Beyond these classic examples, there are many cases in which single-molecule spectroscopy and simulations have been combined to address specific mechanistic questions. In the context of protein folding, all-atom MD simulations have been used to identify transient non-native salt bridges that are the dominant determinant of transition-path times along the folding barrier [168]. All-atom simulations have been used in conjunction with smFRET of aggregation-prone polyglutamine (polyQ) to demonstrate that – contrary to naive expectation – the biophysical behavior of polyglutamine tracts do not show a discontinuous transition as polyQ length extends between physiological and disease-associated lengths [87,142]. In a similar vein, residual structure in the monomeric state of the aggregation-prone amyloid-beta peptide was examined through an in-depth study that combined smFRET will all-atom MD simulations where explicit dyes were included [147]. By combining FCS and simulations, Mao et al. demonstrated that the sequence net charge plays a crucial role in determining the global dimensions of disordered regions [221]. Similarly, FCS, smFRET, and simulations help demonstrate that sufficiently long polyglutamine and polyglycine repeats undergo chain collapse to form compact yet heterogeneous ensembles [87,142,255]. By combining MD simulations and an extensive set of smFRET experiments, Vancraenenbroeck et al. showed that IDR-binding affinity can be directly modulated by solution-dependent changes to conformational behavior, hinting at a complex, environmental-dependent protein:protein interaction network inside cells, a conclusions supported by more recent work that combines simulations and ensemble FRET [20,260].
IDRs are frequently involved in molecular recognition, and single-molecule spectroscopy and molecular simulations are well-poised to provide molecular detail on those interactions. A crucial aspect of microtubule function in axons is their ability to undergo dynamic instability, where they experience periods of elongation and depolymerization, a process that is highly regulated by a family of intrinsically disordered Tau proteins[282,283]. To better understand the first step of microtubule assembly, where tau protein binds soluble tubulin heterodimers, Melo et al. completed an extensive mapping of free and tubulin-bound tau conformations using smFRET [284]. Subsequently, they generated an ensemble of possible tau conformations using Monte Carlo simulations constrained by distances generated from their smFRET measurements. When modeled in proximity of coarse grained tubulin dimers it was possible to visualize how tau binding to multiple dimers could be accomplished. Importantly, this gave insight into the dynamic nature of the interaction. Instead of adopting a fixed structure upon tubulin binding, a “fuzzy complex” is observed, where the disordered nature of Tau allows for the binding of multiple tubulin dimers and highlighted the significance of conformational flexibility upon binding, a phenomena later seen with other IDP binding interactions as well [65,272,273].
Finally, in an integrative study that combined MD and MC simulations with single-molecule spectroscopy, Cubuk et al. performed a comprehensive dissection of the three disordered regions in the SARS-CoV-2 nucleocapsid protein [136]. This work revealed distinct structural features that provide a molecular explanation for several previously described binding interactions.
In short, the ability to ascribe atomistic-level insight from simulations with analogous observations for a specific subset of intramolecular distances affords high-resolution physical descriptions of complex phenomena in a way that most other techniques do not.
3. Discussion
The integration of single-molecule spectroscopy and simulations has emerged as a fruitful approach to provide molecular insight into the complex and heterogeneous behavior of disordered proteins. A recurrent theme in many of the studies described above is the need to consider a range of length-scales and time-scales to construct a holistic understanding of IDR conformational behavior. While smFRET provides high spatial accuracy and precision with respect to specific pairs of distances, it is largely blind to conformational behavior that occurs distally to the labeling positions. In contrast, while simulations provide high-precision insight into both global and local conformational behavior, they are limited by possible force field or sampling inaccuracies. As such, the most comprehensive – and arguably informative – studies are those in which smFRET empowers confidence in the simulations (either by confirming simulated results or providing a means to refine them), which in turn allows simulations to report on features that are not directly captured by smFRET [34,35,65,134,168,253,272]. When smFRET and simulations can be combined to make predictions that can be tested via orthogonal methods such as FCS, SAXS, NMR, DLS, or any additional method, the accuracy of inferences made through integrative studies can be directly assessed [65,73,216,240,280].
Despite substantial successes, several open challenges remain for the effective integration of single-molecule spectroscopy and simulations. A significant challenge is the need for better methods to describe dyes and their photophysics. A number of groups have pioneered work in this arena, yet despite notable successes, the inclusion of dyes in all-atom or coarse-grained simulation simulations is by no means standard practice [65,120,161,226]. As mentioned in the introduction, large heterocyclic dyes are inherently challenging for fixed-charge force fields due to their aromatic nature. The emergence of polarizable force fields offers a potential solution to this challenge [285–288]. While in fixed-charge all-atom force fields, each atom has a fixed partial charge, in polarizable force fields the local charge density is responsive and variable, depending on the local chemical environment. As a result, polarizable dyes models may offer a more realistic route to describe their physicochemical effects and, potentially, help identify scenarios in which protein:dye interactions are likely. Beyond facilitating better interpretation of smFRET data, an accurate and transferable description of fluorescent dyes would allow experimental groups to computationally screen distinct pairs of dyes to help identify those which are least likely to interact with a given protein. While polarizable models (such as AMOEBA) have historically been viewed as substantially slower than fixed-charge models, recent major efforts to improve performance have yielded simulation times on the order 10–30 ns/day in AMOEBA [289,290]. As a result timescales relevant for comparison with single-molecule spectroscopy are firmly within reach, suggesting further application of polarizable forcefields is a promising future avenue.
A more general challenge for simulations of disordered proteins represents robust methods for the quantification and assessment of conformation sampling. While limitations in standard molecular force fields persist with respect to disordered proteins, even if a perfect forcefield existed, it would not guarantee that accurate estimates of chain conformations and dynamics could be reached. Recent work from Lincoff et al. has argued that while over compaction of standard force fields when describing IDRs is a known problem if better conformational sampling was available, some of the force field limitations may be less severe than they appear [291,292]. This is not to suggest that forcefield limitations are overblown, but simply to urge a critical assessment of local and global conformational heterogeneity when performing molecular simulations of disordered proteins. Simulations of a few hundred nanoseconds are rarely sufficient for even modestly sized disordered proteins. General best-practices for assessing conformational sampling in IDRs are lacking but would help to guide researchers to understand if poor agreement between simulation and experiment is due to forcefield weaknesses, insufficient conformational sampling, or a combination of the two
4. Conclusions
The integration of single-molecule fluorescence spectroscopy and all-atom simulations has been instrumental in our modern understanding of sequence-encoded conformational behavior in disordered proteins. As more advanced methods for multi-dimensional data integration emerge, integrative studies in which multiple experimental techniques are used to better understand a specific system will likely become more commonplace and more effective. The ability to obtain insight over multiple length-scales and timescales is an essential feature that integrative studies provide. For disordered proteins especially, the need to consider a range of length scales and timescales reflects the inherently heterogeneous and stochastic nature of the conformational transition. Given the fact that molecular simulations and single-molecule fluorescence spectroscopy offer a comparative spatial and temporal resolution, they are an inherently complementary and powerful combination.
Highlights.
Single-molecule spectroscopy offers a collection of methods that provide high-resolution insight into the conformational and dynamical behavior of disordered proteins
Molecular simulations can provide atomistic insight into both local and global conformational biases and dynamics
Despite their strengths, single-molecule spectroscopy and molecular simulation have a number of limitations
When combined and integrated together, these tools offer complimentary insight with largely orthogonal weaknesses
Acknowledgements
This work was supported by NIGMS R25 IMSD Training Grant GM103757 (J.J.A.), the Longer Life Foundation - RGA/Washington University Collaboration (A.S.H.) and the NIA AG062837 (A.S.).
We thank Priya Banerjee, Alessandro Borgia, Robert Best, Greg Bowman, Osman Bilsel, Hue Sun Chan, Ashok Deniz, Roberto Galletto, Gilad Haran, Hagen Hofmann, Jay Ponder, Edward Lemke, Dmitrii Makarov, Davide Mercadante, Erik Martin, Tanja Mittag, Ivan Peran, Rohit Pappu, David De Sancho, Ben Schuler, Shahar Sukenik, Dan Raleigh and Maxwell Zimmerman for many stimulating discussions over the years on the topics of single-molecule spectroscopy, all-atom simulations, and intrinsically disordered proteins.
References
- [1].Kendrew JC, Bodo G, Dintzis HM, Parrish RG, Wyckoff H, Phillips DC, A three-dimensional model of the myoglobin molecule obtained by x-ray analysis, Nature. 181 (1958) 662–666. [DOI] [PubMed] [Google Scholar]
- [2].Pauling L, Corey RB, Branson HR, The structure of proteins; two hydrogen-bonded helical configurations of the polypeptide chain, Proc. Natl. Acad. Sci. U. S. A. 37 (1951) 205–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Pauling L, Corey RB, Configurations of polypeptide chains with favored orientations around single bonds: two new pleated sheets, Proc. Natl. Acad. Sci. 37 (1951) 729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Perutz MF, Rossmann MG, Cullis AF, Muirhead H, Will G, North ACT, Structure of hæmoglobin: a three-dimensional Fourier synthesis at 5.5-Å. resolution, obtained by X-ray analysis, Nature. 185 (1960) 416–422. [DOI] [PubMed] [Google Scholar]
- [5].van der Lee R, Buljan M, Lang B, Weatheritt RJ, Daughdrill GW, Dunker AK, Fuxreiter M, Gough J, Gsponer J, Jones DT, Kim PM, Kriwacki RW, Oldfield CJ, Pappu RV, Tompa P, Uversky VN, Wright PE, Babu MM, Classification of intrinsically disordered regions and proteins, Chem. Rev. 114 (2014) 6589–6631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Wright PE, Dyson HJ, Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm, J. Mol. Biol. 293 (1999) 321–331. [DOI] [PubMed] [Google Scholar]
- [7].Dunker AK, Obradovic Z, Romero P, Garner EC, Brown CJ, Intrinsic protein disorder in complete genomes, Genome Inform. Ser. Workshop Genome Inform. 11 (2000) 161–171. [PubMed] [Google Scholar]
- [8].Uversky VN, Gillespie JR, Why are “natively unfolded” proteins unstructured under physiologic conditions?, Proteins: Struct. Funct. Bioinf. (2000). . [DOI] [PubMed] [Google Scholar]
- [9].Dyson HJ, Wright PE, Intrinsically unstructured proteins and their functions, Nat. Rev. Mol. Cell Biol. 6 (2005) 197–208. [DOI] [PubMed] [Google Scholar]
- [10].Forman-Kay JD, Mittag T, From sequence and forces to structure, function, and evolution of intrinsically disordered proteins, Structure. 21 (2013) 1492–1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Davey NE, The functional importance of structure in unstructured protein regions, Curr. Opin. Struct. Biol. 56 (2019) 155–163. [DOI] [PubMed] [Google Scholar]
- [12].Babu MM, Kriwacki RW, Pappu RV, Structural biology. Versatility from protein disorder, Science. 337 (2012) 1460–1461. [DOI] [PubMed] [Google Scholar]
- [13].Wright PE, Dyson HJ, Intrinsically disordered proteins in cellular signalling and regulation, Nat. Rev. Mol. Cell Biol. 16 (2014) 18–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Henzler-Wildman K, Kern D, Dynamic personalities of proteins, Nature. 450 (2007) 964–972. [DOI] [PubMed] [Google Scholar]
- [15].Sadowski MI, Jones DT, The sequence–structure relationship and protein function prediction, Curr. Opin. Struct. Biol. 19 (2009) 357–362. [DOI] [PubMed] [Google Scholar]
- [16].Guzzo AV, The influence of amino-acid sequence on protein structure, Biophys. J. 5 (1965) 809–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Lesk AM, Chothia C, How different amino acid sequences determine similar protein structures: the structure and evolutionary dynamics of the globins, J. Mol. Biol. 136 (1980) 225–270. [DOI] [PubMed] [Google Scholar]
- [18].Das RK, Ruff KM, Pappu RV, Relating sequence encoded information to form and function of intrinsically disordered proteins, Curr. Opin. Struct. Biol. 32 (2015) 102–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Mittag T, Forman-Kay JD, Atomic-level characterization of disordered protein ensembles, Curr. Opin. Struct. Biol. 17 (2007) 3–14. [DOI] [PubMed] [Google Scholar]
- [20].Vancraenenbroeck R, Harel YS, Zheng W, Hofmann H, Polymer effects modulate binding affinities in disordered proteins, Proc. Natl. Acad. Sci. U. S. A. 116 (2019) 19506–19512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Dahal L, Kwan TOC, Hollins JJ, Clarke J, Promiscuous and Selective: How Intrinsically Disordered BH3 Proteins Interact with Their Pro-survival Partner MCL-1, J. Mol. Biol. 430 (2018) 2468–2477. [DOI] [PubMed] [Google Scholar]
- [22].Borcherds W, Theillet F-X, Katzer A, Finzel A, Mishall KM, Powell AT, Wu H, Manieri W, Dieterich C, Selenko P, Loewer A, Daughdrill GW, Disorder and residual helicity alter p53-Mdm2 binding affinity and signaling in cells, Nat. Chem. Biol. 10 (2014) 1000–1002. [DOI] [PubMed] [Google Scholar]
- [23].Zosel F, Mercadante D, Nettels D, Schuler B, A proline switch explains kinetic heterogeneity in a coupled folding and binding reaction, Nat. Commun. 9 (2018) 3332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Martin EW, Holehouse AS, Peran I, Farag M, Incicco JJ, Bremer A, Grace CR, Soranno A, Pappu RV, Mittag T, Valence and patterning of aromatic residues determine the phase behavior of prion-like domains, Science. 367 (2020) 694–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Brucale M, Schuler B, Samorì B, Single-molecule studies of intrinsically disordered proteins, Chem. Rev. 114 (2014) 3281–3317. [DOI] [PubMed] [Google Scholar]
- [26].Zheng W, Chung HS, Chapter 4 - Single-molecule fluorescence studies of IDPs and IDRs, in: Salvi N (Ed.), Intrinsically Disordered Proteins, Academic Press, 2019: pp. 93–136. [Google Scholar]
- [27].Schuler B, Soranno A, Hofmann H, Nettels D, Single-Molecule FRET Spectroscopy and the Polymer Physics of Unfolded and Intrinsically Disordered Proteins, Annu. Rev. Biophys. 45 (2016) 207–231. [DOI] [PubMed] [Google Scholar]
- [28].LeBlanc SJ, Kulkarni P, Weninger KR, Single Molecule FRET: A Powerful Tool to Study Intrinsically Disordered Proteins, Biomolecules. 8 (2018). 10.3390/biom8040140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Metskas LA, Rhoades E, Single-Molecule FRET of Intrinsically Disordered Proteins, Annu. Rev. Phys. Chem. (2020). 10.1146/annurev-physchem-012420-104917. [DOI] [PubMed] [Google Scholar]
- [30].Huang J, MacKerell AD Jr, Force field development and simulations of intrinsically disordered proteins, Curr. Opin. Struct. Biol. 48 (2018) 40–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Best RB, Computational and theoretical advances in studies of intrinsically disordered proteins, Curr. Opin. Struct. Biol. 42 (2017) 147–154. [DOI] [PubMed] [Google Scholar]
- [32].Baker CM, Best RB, Insights into the binding of intrinsically disordered proteins from molecular dynamics simulation, WIREs Comput Mol Sci. 4 (2014) 182–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Levine ZA, Shea J-E, Simulations of disordered proteins and systems with conformational heterogeneity, Curr. Opin. Struct. Biol. 43 (2017) 95–103. [DOI] [PubMed] [Google Scholar]
- [34].Borgia A, Zheng W, Buholzer K, Borgia MB, Schüler A, Hofmann H, Soranno A, Nettels D, Gast K, Grishaev A, Best RB, Schuler B, Consistent View of Polypeptide Chain Expansion in Chemical Denaturants from Multiple Experimental Methods, J. Am. Chem. Soc. 138 (2016) 11714–11726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Fuertes G, Banterle N, Ruff KM, Chowdhury A, Mercadante D, Koehler C, Kachala M, Estrada Girona G, Milles S, Mishra A, Onck PR, Gräter F, Esteban-Martín S, Pappu RV, Svergun DI, Lemke EA, Decoupling of size and shape fluctuations in heteropolymeric sequences reconciles discrepancies in SAXS vs. FRET measurements, Proc. Natl. Acad. Sci. U. S. A. 114 (2017) E6342–E6351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Holehouse AS, Sukenik S, Controlling Structural Bias in Intrinsically Disordered Proteins Using Solution Space Scanning, J. Chem. Theory Comput. 16 (2020) 1794–1805. [DOI] [PubMed] [Google Scholar]
- [37].Ignacio Gutierrez J, Brittingham GP, Karadeniz YB, Tran KD, Dutta A, Holehouse AS, Peterson CL, Holt LJ, SWI/SNF senses carbon starvation with a pH-sensitive low complexity sequence, Cold Spring Harbor Laboratory. (2021) 2021.03.03.433592. 10.1101/2021.03.03.433592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Martin EW, Holehouse AS, Grace CR, Hughes A, Pappu RV, Mittag T, Sequence Determinants of the Conformational Properties of an Intrinsically Disordered Protein Prior to and upon Multisite Phosphorylation, J. Am. Chem. Soc. 138 (2016) 15323–15335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Murthy AC, Dignon GL, Kan Y, Zerze GH, Parekh SH, Mittal J, Fawzi NL, Molecular interactions underlying liquid-liquid phase separation of the FUS low-complexity domain, Nat. Struct. Mol. Biol. 26 (2019) 637–648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Zheng W, Dignon GL, Jovic N, Xu X, Regy RM, Fawzi NL, Kim YC, Best RB, Mittal J, Molecular Details of Protein Condensates Probed by Microsecond Long Atomistic Simulations, J. Phys. Chem. B. (2020). 10.1021/acs.jpcb.0c10489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Leach AR, Molecular modelling: principles and applications, Pearson education, 2001. [Google Scholar]
- [42].Best RB, Atomistic Force Fields for Proteins, Methods Mol. Biol. 2022 (2019) 3–19. [DOI] [PubMed] [Google Scholar]
- [43].Huang J, Rauscher S, Nawrocki G, Ran T, Feig M, de Groot BL, Grubmüller H, MacKerell AD Jr, CHARMM36m: an improved force field for folded and intrinsically disordered proteins, Nat. Methods. 14 (2017) 71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Robustelli P, Piana S, Shaw DE, Developing a molecular dynamics force field for both folded and disordered protein states, Proc. Natl. Acad. Sci. U. S. A. 115 (2018) E4758–E4766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Piana S, Robustelli P, Tan D, Chen S, Shaw DE, Development of a Force Field for the Simulation of Single-Chain Proteins and Protein-Protein Complexes, J. Chem. Theory Comput. 16 (2020) 2494–2507. [DOI] [PubMed] [Google Scholar]
- [46].Best RB, Mittal J, Protein simulations with an optimized water model: cooperative helix formation and temperature-induced unfolded state collapse, J. Phys. Chem. B. 114 (2010) 14916–14923. [DOI] [PubMed] [Google Scholar]
- [47].Best RB, Zheng W, Mittal J, Balanced Protein-Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association, J. Chem. Theory Comput. 10 (2014) 5113–5124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Tang WS, Fawzi NL, Mittal J, Refining All-Atom Protein Force Fields for Polar-Rich, Prion-like, Low-Complexity Intrinsically Disordered Proteins, J. Phys. Chem. B. (2020). 10.1021/acs.jpcb.0c07545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Vitalis A, Pappu RV, ABSINTH: A new continuum solvation model for simulations of polypeptides in aqueous solutions, J. Comput. Chem. 30 (2009) 673–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Mercadante D, Milles S, Fuertes G, Svergun DI, Lemke EA, Gräter F, Kirkwood-Buff Approach Rescues Overcollapse of a Disordered Protein in Canonical Protein Force Fields, J. Phys. Chem. B. 119 (2015) 7975–7984. [DOI] [PubMed] [Google Scholar]
- [51].Ploetz EA, Bentenitis N, Smith PE, Developing Force Fields from the Microscopic Structure of Solutions, Fluid Phase Equilib. 290 (2010) 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Saunders MG, Voth GA, Coarse-graining methods for computational biology, Annu. Rev. Biophys. 42 (2013) 73–93. [DOI] [PubMed] [Google Scholar]
- [53].Ruff KM, Harmon TS, Pappu RV, CAMELOT: A machine learning approach for coarse-grained simulations of aggregation of block-copolymeric protein sequences, J. Chem. Phys. 143 (2015) 243123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Wu H, Wolynes PG, Papoian GA, AWSEM-IDP: A Coarse-Grained Force Field for Intrinsically Disordered Proteins, J. Phys. Chem. B. 122 (2018) 11115–11125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Dignon GL, Zheng W, Kim YC, Best RB, Mittal J, Sequence determinants of protein phase behavior from a coarse-grained model, PLoS Comput. Biol. 14 (2018) e1005941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Ruff KM, Khan SJ, Pappu RV, A coarse-grained model for polyglutamine aggregation modulated by amphipathic flanking sequences, Biophys. J. 107 (2014) 1226–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Perdikari TM, Jovic N, Dignon GL, Kim YC, Fawzi NL, A coarse-grained model for position-specific effects of post-translational modifications on disordered protein phase separation, Biophys. J. (2021). https://www.sciencedirect.com/science/article/pii/S0006349521001351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Dignon GL, Zheng W, Kim YC, Mittal J, Temperature-Controlled Liquid–Liquid Phase Separation of Disordered Proteins, ACS Cent. Sci. 5 (2019) 821–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Baul U, Chakraborty D, Mugnai ML, Straub JE, Thirumalai D, Sequence Effects on Size, Shape, and Structural Heterogeneity in Intrinsically Disordered Proteins, J. Phys. Chem. B. 123 (2019) 3462–3474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Zhao Y, Cortes-Huerto R, Kremer K, Rudzinski JF, Investigating the Conformational Ensembles of Intrinsically Disordered Proteins with a Simple Physics-Based Model, J. Phys. Chem. B. 124 (2020) 4097–4113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Cragnell C, Rieloff E, Skepö M, Utilizing Coarse-Grained Modeling and Monte Carlo Simulations to Evaluate the Conformational Ensemble of Intrinsically Disordered Proteins and Regions, J. Mol. Biol. 430 (2018) 2478–2492. [DOI] [PubMed] [Google Scholar]
- [62].Klein F, Barrera EE, Pantano S, Assessing SIRAH’s Capability to Simulate Intrinsically Disordered Proteins and Peptides, J. Chem. Theory Comput. 17 (2021) 599–604. [DOI] [PubMed] [Google Scholar]
- [63].Ramis R, Ortega-Castro J, Casasnovas R, Mariño L, Vilanova B, Adrover M, Frau J, A Coarse-Grained Molecular Dynamics Approach to the Study of the Intrinsically Disordered Protein α-Synuclein, J. Chem. Inf. Model. 59 (2019) 1458–1471. [DOI] [PubMed] [Google Scholar]
- [64].Latham AP, Zhang B, Maximum Entropy Optimized Force Field for Intrinsically Disordered Proteins, J. Chem. Theory Comput. 16 (2020) 773–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Borgia A, Borgia MB, Bugge K, Kissling VM, Heidarsson PO, Fernandes CB, Sottini A, Soranno A, Buholzer KJ, Nettels D, Kragelund BB, Best RB, Schuler B, Extreme disorder in an ultrahigh-affinity protein complex, Nature. 555 (2018) 61–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Nath A, Sammalkorpi M, DeWitt DC, Trexler AJ, Elbaum-Garfinkle S, O’Hern CS, Rhoades E, The conformational ensembles of α-synuclein and tau: combining single-molecule FRET and simulations, Biophys. J. 103 (2012) 1940–1949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].O’Brien EP, Morrison G, Brooks BR, Thirumalai D, How accurate are polymer models in the analysis of Forster resonance energy transfer experiments on proteins?, J. Chem. Phys. 130 (2009) 124903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].O’Brien EP, Ziv G, Haran G, Brooks BR, Thirumalai D, Effects of denaturants and osmolytes on proteins are accurately predicted by the molecular transfer model, Proc. Natl. Acad. Sci. U. S. A. 105 (2008) 13403–13408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Mazouchi A, Zhang Z, Bahram A, Gomes G-N, Lin H, Song J, Chan HS, Forman-Kay JD, Gradinaru CC, Conformations of a Metastable SH3 Domain Characterized by smFRET and an Excluded-Volume Polymer Model, Biophys. J. 110 (2016) 1510–1522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Song J, Gomes G-N, Shi T, Gradinaru CC, Chan HS, Conformational heterogeneity and FRET data interpretation for dimensions of unfolded proteins, Biophys. J. 113 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Song J, Gomes G-N, Gradinaru CC, Chan HS, An Adequate Account of Excluded Volume Is Necessary To Infer Compactness and Asphericity of Disordered Proteins by Forster Resonance Energy Transfer, J. Phys. Chem. B. 119 (2015) 15191–15202. [DOI] [PubMed] [Google Scholar]
- [72].Onufriev AV, Izadi S, Water models for biomolecular simulations, WIREs Comput Mol Sci. 8 (2018) e1347. [Google Scholar]
- [73].Piana S, Donchev AG, Robustelli P, Shaw DE, Water dispersion interactions strongly influence simulated structural properties of disordered protein states, J. Phys. Chem. B. 119 (2015) 5113–5123. [DOI] [PubMed] [Google Scholar]
- [74].Zerze GH, Zheng W, Best RB, Mittal J, Evolution of All-Atom Protein Force Fields to Improve Local and Global Properties, J. Phys. Chem. Lett. 10 (2019) 2227–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Braun E, Gilmer J, Mayes HB, Mobley DL, Monroe JI, Prasad S, Zuckerman DM, Best Practices for Foundations in Molecular Simulations [Article v1.0], Living J Comput Mol Sci. 1 (2019) 5957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Karplus M, McCammon JA, Molecular dynamics simulations of biomolecules, Nat. Struct. Biol. 9 (2002) 646–652. [DOI] [PubMed] [Google Scholar]
- [77].Conicella AE, Dignon GL, Zerze GH, Schmidt HB, D’Ordine AM, Kim YC, Rohatgi R, Ayala YM, Mittal J, Fawzi NL, TDP-43 α-helical structure tunes liquid–liquid phase separation and function, Proc. Natl. Acad. Sci. U. S. A. 117 (2020) 5883–5894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Zheng W, Borgia A, Borgia MB, Schuler B, Best RB, Empirical Optimization of Interactions between Proteins and Chemical Denaturants in Molecular Simulations, J. Chem. Theory Comput. 11 (2015) 5543–5553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Vitalis A, Pappu RV, Chapter 3 Methods for Monte Carlo Simulations of Biomacromolecules, in: Wheeler RA (Ed.), Annual Reports in Computational Chemistry, Elsevier, 2009: pp. 49–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Ulmschneider JP, Jorgensen WL, Monte Carlo backbone sampling for polypeptides with variable bond angles and dihedral angles using concerted rotations and a Gaussian bias, J. Chem. Phys. 118 (2003) 4261–4271. [Google Scholar]
- [81].Dodd LR, Boone TD, Theodorou DN, A concerted rotation algorithm for atomistic Monte Carlo simulation of polymer melts and glasses, Mol. Phys. 78 (1993) 961–996. [Google Scholar]
- [82].Favrin G, Irbäck A, Sjunnesson F, Monte Carlo update for chain molecules: Biased Gaussian steps in torsional space, J. Chem. Phys. 114 (2001) 8154–8158. [Google Scholar]
- [83].Whitelam S, Geissler PL, Avoiding unphysical kinetic traps in Monte Carlo simulations of strongly attractive particles, J. Chem. Phys. 127 (2007) 154101. [DOI] [PubMed] [Google Scholar]
- [84].Gelb LD, Monte Carlo simulations using sampling from an approximate potential, J. Chem. Phys. 118 (2003) 7747–7750. [Google Scholar]
- [85].Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E, Equation of State Calculations by Fast Computing Machines, J. Chem. Phys. 21 (1953) 1087–1092. [Google Scholar]
- [86].Hastings WK, Monte Carlo Sampling Methods Using Markov Chains and Their Applications, Biometrika. 57 (1970) 97–109. [Google Scholar]
- [87].Warner JB 4th, Ruff KM, Tan PS, Lemke EA, Pappu RV, Lashuel HA, Monomeric Huntingtin Exon 1 Has Similar Overall Structural Features for Wild-Type and Pathological Polyglutamine Lengths, J. Am. Chem. Soc. 139 (2017) 14456–14469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Rauscher S, Gapsys V, Gajda MJ, Zweckstetter M, de Groot BL, Grubmüller H, Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment, J. Chem. Theory Comput. 11 (2015) 5513–5524. [DOI] [PubMed] [Google Scholar]
- [89].Henriques J, Cragnell C, Skepö M, Molecular Dynamics Simulations of Intrinsically Disordered Proteins: Force Field Evaluation and Comparison with Experiment, J. Chem. Theory Comput. 11 (2015) 3420–3431. [DOI] [PubMed] [Google Scholar]
- [90].Nerenberg PS, Jo B, So C, Tripathy A, Head-Gordon T, Optimizing Solute–Water van der Waals Interactions To Reproduce Solvation Free Energies, J. Phys. Chem. B. 116 (2012) 4524–4534. [DOI] [PubMed] [Google Scholar]
- [91].Mercadante D, Wagner JA, Aramburu IV, Lemke EA, Gräter F, Sampling Long- versus Short-Range Interactions Defines the Ability of Force Fields To Reproduce the Dynamics of Intrinsically Disordered Proteins, J. Chem. Theory Comput. 13 (2017) 3964–3974. [DOI] [PubMed] [Google Scholar]
- [92].Grossfield A, Zuckerman DM, Quantifying uncertainty and sampling quality in biomolecular simulations, Annu. Rep. Comput. Chem. 5 (2009) 23–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Grossfield A, Patrone PN, Roe DR, Schultz AJ, Siderius DW, Zuckerman DM, Best Practices for Quantification of Uncertainty and Sampling Quality in Molecular Simulations [Article v1.0], Living J Comput Mol Sci. 1 (2018). 10.33011/livecoms.1.1.5067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Stryer L, Fluorescence energy transfer as a spectroscopic ruler, Annu. Rev. Biochem. 47 (1978) 819–846. [DOI] [PubMed] [Google Scholar]
- [95].Förster T, Zwischenmolekulare Energiewanderung und Fluoreszenz, Ann. Phys. 437 (1948) 55–75. [Google Scholar]
- [96].Gopich I, Szabo A, Theory of photon statistics in single-molecule Förster resonance energy transfer, J. Chem. Phys. 122 (2005) 14707. [DOI] [PubMed] [Google Scholar]
- [97].Gopich IV, Szabo A, Single-molecule FRET with diffusion and conformational dynamics, J. Phys. Chem. B. 111 (2007) 12925–12932. [DOI] [PubMed] [Google Scholar]
- [98].Torella JP, Holden SJ, Santoso Y, Hohlbein J, Kapanidis AN, Identifying molecular dynamics in single-molecule FRET experiments with burst variance analysis, Biophys. J. 100 (2011) 1568–1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99].Kalinin S, Valeri A, Antonik M, Felekyan S, Seidel CAM, Detection of structural dynamics by FRET: a photon distribution and fluorescence lifetime analysis of systems with multiple states, J. Phys. Chem. B. 114 (2010) 7983–7995. [DOI] [PubMed] [Google Scholar]
- [100].Ingargiola A, Weiss S, Lerner E, Monte Carlo Diffusion-Enhanced Photon Inference: Distance Distributions and Conformational Dynamics in Single-Molecule FRET, J. Phys. Chem. B. 122 (2018) 11598–11615. [DOI] [PubMed] [Google Scholar]
- [101].Antonik M, Felekyan S, Gaiduk A, Seidel CAM, Separating structural heterogeneities from stochastic variations in fluorescence resonance energy transfer distributions via photon distribution analysis, J. Phys. Chem. B. 110 (2006) 6970–6978. [DOI] [PubMed] [Google Scholar]
- [102].Chung HS, McHale K, Louis JM, Eaton WA, Single-molecule fluorescence experiments determine protein folding transition path times, Science. 335 (2012) 981–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103].Chung HS, Gopich IV, McHale K, Cellmer T, Louis JM, Eaton WA, Extracting rate coefficients from single-molecule photon trajectories and FRET efficiency histograms for a fast-folding protein, J. Phys. Chem. A. 115 (2011) 3642–3656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Rhoades E, Cohen M, Schuler B, Haran G, Two-state folding observed in individual protein molecules, J. Am. Chem. Soc. 126 (2004) 14686–14687. [DOI] [PubMed] [Google Scholar]
- [105].Rhoades E, Gussakovsky E, Haran G, Watching proteins fold one molecule at a time, Proc. Natl. Acad. Sci. U. S. A. 100 (2003) 3197–3202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Pirchi M, Ziv G, Riven I, Cohen SS, Zohar N, Barak Y, Haran G, Single-molecule fluorescence spectroscopy maps the folding landscape of a large protein, Nat. Commun. 2 (2011) 493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Chung HS, Cellmer T, Louis JM, Eaton WA, Measuring ultrafast protein folding rates from photon-by-photon analysis of single molecule fluorescence trajectories, Chem. Phys. 422 (2013) 229–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108].Gopich IV, Szabo A, FRET efficiency distributions of multistate single molecules, J. Phys. Chem. B. 114 (2010) 15221–15226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [109].Schuler B, Lipman EA, Eaton WA, Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy, Nature. 419 (2002) 743. [DOI] [PubMed] [Google Scholar]
- [110].Santoso Y, Torella JP, Kapanidis AN, Characterizing single-molecule FRET dynamics with probability distribution analysis, Chemphyschem. 11 (2010) 2209–2219. [DOI] [PubMed] [Google Scholar]
- [111].Chung HS, Gopich IV, Fast single-molecule FRET spectroscopy: theory and experiment, Phys. Chem. Chem. Phys. 16 (2014) 18644–18657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Gopich IV, Szabo A, Theory of the energy transfer efficiency and fluorescence lifetime distribution in single-molecule FRET, Proc. Natl. Acad. Sci. U. S. A. 109 (2012) 7747–7752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Widengren J, Kudryavtsev V, Antonik M, Berger S, Gerken M, Seidel CAM, Single-molecule detection and identification of multiple species by multiparameter fluorescence detection, Anal. Chem. 78 (2006) 2039–2050. [DOI] [PubMed] [Google Scholar]
- [114].Kühnemuth R, Seidel CAM, Principles of single molecule multiparameter fluorescence spectroscopy, Single Mol. 2 (2001) 251–254. [Google Scholar]
- [115].Soranno A, Buchli B, Nettels D, Cheng RR, Müller-Späth S, Pfeil SH, Hoffmann A, Lipman EA, Makarov DE, Schuler B, Quantifying internal friction in unfolded and intrinsically disordered proteins with single-molecule spectroscopy, Proc. Natl. Acad. Sci. U. S. A. 109 (2012) 17800–17806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Chung HS, Louis JM, Gopich IV, Analysis of Fluorescence Lifetime and Energy Transfer Efficiency in Single-Molecule Photon Trajectories of Fast-Folding Proteins, J. Phys. Chem. B. 120 (2016) 680–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [117].Nettels D, Gopich IV, Hoffmann A, Schuler B, Ultrafast dynamics of protein collapse from single-molecule photon statistics, Proc. Natl. Acad. Sci. U. S. A. 104 (2007) 2655–2660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Sindbert S, Kalinin S, Nguyen H, Kienzler A, Clima L, Bannwarth W, Appel B, Müller S, Seidel CAM, Accurate distance determination of nucleic acids via Förster resonance energy transfer: implications of dye linker length and rigidity, J. Am. Chem. Soc. 133 (2011) 2463–2480. [DOI] [PubMed] [Google Scholar]
- [119].Gopich IV, Szabo A, Single-Macromolecule Fluorescence Resonance Energy Transfer and Free-Energy Profiles, J. Phys. Chem. B. 107 (2003) 5058–5063. [Google Scholar]
- [120].Zheng W, Zerze GH, Borgia A, Mittal J, Schuler B, Best RB, Inferring properties of disordered chains from FRET transfer efficiencies, J. Chem. Phys. 148 (2018) 123329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Sanchez IC, Phase Transition Behavior of the Isolated Polymer Chain, Macromolecules. 12 (1979) 980–988. [Google Scholar]
- [122].Kratky O, Porod G, Röntgenuntersuchung gelöster Fadenmoleküle, Recl. Trav. Chim. Pays-Bas. 68 (1949) 1106–1122. [Google Scholar]
- [123].Flory PJ, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, 1953. [Google Scholar]
- [124].Lord Rayleigh XXXI. On the problem of random vibrations, and of random flights in one, two, or three dimensions, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 37 (1919) 321–347. [Google Scholar]
- [125].Lin Y-H, Brady JP, Chan HS, Ghosh K, A unified analytical theory of heteropolymers for sequence-specific phase behaviors of polyelectrolytes and polyampholytes, J. Chem. Phys. 152 (2020) 045102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Firman T, Ghosh K, Sequence charge decoration dictates coil-globule transition in intrinsically disordered proteins, J. Chem. Phys. 148 (2018) 123305. [DOI] [PubMed] [Google Scholar]
- [127].Huihui J, Firman T, Ghosh K, Modulating charge patterning and ionic strength as a strategy to induce conformational changes in intrinsically disordered proteins, J. Chem. Phys. 149 (2018) 085101. [DOI] [PubMed] [Google Scholar]
- [128].Sawle L, Ghosh K, A theoretical method to compute sequence dependent configurational properties in charged polymers and proteins, J. Chem. Phys. 143 (2015) 085101. [DOI] [PubMed] [Google Scholar]
- [129].Lin Y-H, Forman-Kay JD, Chan HS, Sequence-Specific Polyampholyte Phase Separation in Membraneless Organelles, Phys. Rev. Lett. 117 (2016) 178101. [DOI] [PubMed] [Google Scholar]
- [130].Ziv G, Thirumalai D, Haran G, Collapse transition in proteins, Phys. Chem. Chem. Phys. 11 (2009) 83–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [131].Sherman E, Haran G, Coil–globule transition in the denatured state of a small protein, Proc. Natl. Acad. Sci. U. S. A. 103 (2006) 11539–11543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132].Schäfer L, Excluded Volume Effects in Polymer Solutions: as Explained by the Renormalization Group, Springer Science & Business Media, 2012. [Google Scholar]
- [133].Hofmann H, Soranno A, Borgia A, Gast K, Nettels D, Schuler B, Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy, Proc. Natl. Acad. Sci. U. S. A. 109 (2012) 16155–16160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [134].Soranno A, Holla A, Dingfelder F, Nettels D, Makarov DE, Schuler B, Integrated view of internal friction in unfolded proteins from single-molecule FRET, contact quenching, theory, and simulations, Proc. Natl. Acad. Sci. U. S. A. 114 (2017) E1833–E1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [135].Peran I, Holehouse AS, Carrico IS, Pappu RV, Bilsel O, Raleigh DP, Unfolded states under folding conditions accommodate sequence-specific conformational preferences with random coil-like dimensions, Proc. Natl. Acad. Sci. U. S. A. 116 (2019) 12301–12310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [136].Cubuk J, Alston JJ, Incicco JJ, Singh S, Stuchell-Brereton MD, Ward MD, Zimmerman MI, Vithani N, Griffith D, Wagoner JA, Bowman GR, Hall KB, Soranno A, Holehouse AS, The SARS-CoV-2 nucleocapsid protein is dynamic, disordered, and phase separates with RNA, Nat. Commun. (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137].Magde D, Elson E, Webb WW, Thermodynamic fluctuations in a reacting system—measurement by fluorescence correlation spectroscopy, Phys. Rev. Lett. (1972). 10.1103/PhysRevLett.29.705. [DOI] [Google Scholar]
- [138].Magde D, Elson EL, Webb WW, Fluorescence correlation spectroscopy. II. An experimental realization, Biopolymers. 13 (1974) 29–61. [DOI] [PubMed] [Google Scholar]
- [139].Elson EL, Magde D, Fluorescence correlation spectroscopy. I. Conceptual basis and theory, Biopolymers: Original Research on. (1974). 10.1002/bip.1974.360130102. [DOI] [PubMed] [Google Scholar]
- [140].Axelrod D, Koppel DE, Schlessinger J, Elson E, Webb WW, Mobility measurement by analysis of fluorescence photobleaching recovery kinetics, Biophys. J. 16 (1976) 1055–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [141].Elson EL, Fluorescence correlation spectroscopy: past, present, future, Biophys. J. 101 (2011) 2855–2870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [142].Crick SL, Jayaraman M, Frieden C, Wetzel R, Pappu RV, Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions, Proc. Natl. Acad. Sci. U. S. A. 103 (2006) 16764–16769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [143].Neuweiler H, Löllmann M, Doose S, Sauer M, Dynamics of unfolded polypeptide chains in crowded environment studied by fluorescence correlation spectroscopy, J. Mol. Biol. 365 (2007) 856–869. [DOI] [PubMed] [Google Scholar]
- [144].Zosel F, Haenni D, Soranno A, Nettels D, Schuler B, Combining short- and long-range fluorescence reporters with simulations to explore the intramolecular dynamics of an intrinsically disordered protein, J. Chem. Phys. 147 (2017) 152708. [DOI] [PubMed] [Google Scholar]
- [145].Doose S, Neuweiler H, Sauer M, Fluorescence quenching by photoinduced electron transfer: a reporter for conformational dynamics of macromolecules, Chemphyschem. 10 (2009) 1389–1398. [DOI] [PubMed] [Google Scholar]
- [146].Gopich IV, Nettels D, Schuler B, Szabo A, Protein dynamics from single-molecule fluorescence intensity correlation functions, J. Chem. Phys. 131 (2009) 095102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [147].Meng F, Bellaiche MMJ, Kim J-Y, Zerze GH, Best RB, Chung HS, Highly Disordered Amyloid-β Monomer Probed by Single-Molecule FRET and MD Simulation, Biophys. J. 114 (2018) 870–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [148].Soranno A, Zosel F, Hofmann H, Internal friction in an intrinsically disordered protein—comparing Rouse-like models with experiments, J. Chem. Phys. (2018). 10.1063/1.5009286. [DOI] [PubMed] [Google Scholar]
- [149].Khatri BS, McLeish TCB, Rouse Model with Internal Friction: A Coarse Grained Framework for Single Biopolymer Dynamics, Macromolecules. 40 (2007) 6770–6777. [Google Scholar]
- [150].Cheng RR, Hawk AT, Makarov DE, Exploring the role of internal friction in the dynamics of unfolded proteins using simple polymer models, J. Chem. Phys. 138 (2013) 074112. [DOI] [PubMed] [Google Scholar]
- [151].de Gennes P-G, Gennes P-G, Scaling Concepts in Polymer Physics, Cornell University Press, 1979. [Google Scholar]
- [152].Doi M, Edwards SF, Edwards SF, The Theory of Polymer Dynamics, Clarendon Press, 1988. [Google Scholar]
- [153].Sauer M, Neuweiler H, PET-FCS: probing rapid structural fluctuations of proteins and nucleic acids by single-molecule fluorescence quenching, Methods Mol. Biol. 1076 (2014) 597–615. [DOI] [PubMed] [Google Scholar]
- [154].Doose S, Neuweiler H, Sauer M, A close look at fluorescence quenching of organic dyes by tryptophan, Chemphyschem. 6 (2005) 2277–2285. [DOI] [PubMed] [Google Scholar]
- [155].Wang Z, Makarov DE, Nanosecond Dynamics of Single Polypeptide Molecules Revealed by Photoemission Statistics of Fluorescence Resonance Energy Transfer: A Theoretical Study, J. Phys. Chem. B. 107 (2003) 5617–5622. [Google Scholar]
- [156].Makarov DE, Spatiotemporal correlations in denatured proteins: The dependence of fluorescence resonance energy transfer (FRET)-derived protein reconfiguration times on the location of the FRET probes, J. Chem. Phys. 132 (2010) 035104. [DOI] [PubMed] [Google Scholar]
- [157].Szabo A, Schulten K, Schulten Z, First passage time approach to diffusion controlled reactions, J. Chem. Phys. 72 (1980) 4350–4357. [Google Scholar]
- [158].Hellenkamp B, Schmid S, Doroshenko O, Opanasyuk O, Kühnemuth R, Rezaei Adariani S, Ambrose B, Aznauryan M, Barth A, Birkedal V, Bowen ME, Chen H, Cordes T, Eilert T, Fijen C, Gebhardt C, Götz M, Gouridis G, Gratton E, Ha T, Hao P, Hanke CA, Hartmann A, Hendrix J, Hildebrandt LL, Hirschfeld V, Hohlbein J, Hua B, Hübner CG, Kallis E, Kapanidis AN, Kim J-Y, Krainer G, Lamb DC, Lee NK, Lemke EA, Levesque B, Levitus M, McCann JJ, Naredi-Rainer N, Nettels D, Ngo T, Qiu R, Robb NC, Röcker C, Sanabria H, Schlierf M, Schröder T, Schuler B, Seidel H, Streit L, Thurn J, Tinnefeld P, Tyagi S, Vandenberk N, Vera AM, Weninger KR, Wünsch B, Yanez-Orozco IS, Michaelis J, Seidel CAM, Craggs TD, Hugel T, Precision and accuracy of single-molecule FRET measurements-a multi-laboratory benchmark study, Nat. Methods. 15 (2018) 669–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [159].Kudryavtsev V, Sikor M, Kalinin S, Mokranjac D, Seidel CAM, Lamb DC, Combining MFD and PIE for accurate single-pair Förster resonance energy transfer measurements, Chemphyschem. 13 (2012) 1060–1078. [DOI] [PubMed] [Google Scholar]
- [160].Lee NK, Kapanidis AN, Wang Y, Michalet X, Mukhopadhyay J, Ebright RH, Weiss S, Accurate FRET measurements within single diffusing biomolecules using alternating-laser excitation, Biophys. J. 88 (2005) 2939–2953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [161].Holmstrom ED, Holla A, Zheng W, Nettels D, Best RB, Schuler B, Accurate Transfer Efficiencies, Distance Distributions, and Ensembles of Unfolded and Intrinsically Disordered Proteins From Single-Molecule FRET, Methods Enzymol. 611 (2018) 287–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162].Kapanidis AN, Laurence TA, Lee NK, Margeat E, Kong X, Weiss S, Alternating-laser excitation of single molecules, Acc. Chem. Res. 38 (2005) 523–533. [DOI] [PubMed] [Google Scholar]
- [163].Hohlbein J, Craggs TD, Cordes T, Alternating-laser excitation: single-molecule FRET and beyond, Chem. Soc. Rev. 43 (2014) 1156–1171. [DOI] [PubMed] [Google Scholar]
- [164].Müller BK, Zaychikov E, Bräuchle C, Lamb DC, Pulsed interleaved excitation, Biophys. J. 89 (2005) 3508–3522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [165].Hendrix J, Lamb DC, Pulsed interleaved excitation: principles and applications, Methods Enzymol. 518 (2013) 205–243. [DOI] [PubMed] [Google Scholar]
- [166].Niaki AG, Sarkar J, Cai X, Rhine K, Vidaurre V, Guy B, Hurst M, Lee JC, Koh HR, Guo L, Fare CM, Shorter J, Myong S, Loss of Dynamic RNA Interaction and Aberrant Phase Separation Induced by Two Distinct Types of ALS/FTD-Linked FUS Mutations, Mol. Cell. 77 (2020) 82–94.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [167].Holden SJ, Uphoff S, Hohlbein J, Yadin D, Le Reste L, Britton OJ, Kapanidis AN, Defining the limits of single-molecule FRET resolution in TIRF microscopy, Biophys. J. 99 (2010) 3102–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [168].Chung HS, Piana-Agostinetti S, Shaw DE, Eaton WA, Structural origin of slow diffusion in protein folding, Science. 349 (2015) 1504–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [169].Levene MJ, Korlach J, Turner SW, Foquet M, Craighead HG, Webb WW, Zero-mode waveguides for single-molecule analysis at high concentrations, Science. 299 (2003) 682–686. [DOI] [PubMed] [Google Scholar]
- [170].Zhu P, Craighead HG, Zero-mode waveguides for single-molecule analysis, Annu. Rev. Biophys. 41 (2012) 269–293. [DOI] [PubMed] [Google Scholar]
- [171].Polinkovsky ME, Gambin Y, Banerjee PR, Erickstad MJ, Groisman A, Deniz AA, Ultrafast cooling reveals microsecond-scale biomolecular dynamics, Nat. Commun. 5 (2014) 5737. [DOI] [PubMed] [Google Scholar]
- [172].Zhi Z, Liu P, Wang P, Huang Y, Zhao XS, Domain-specific folding kinetics of staphylococcal nuclease observed through single-molecule FRET in a microfluidic mixer, Chemphyschem. 12 (2011) 3515–3518. [DOI] [PubMed] [Google Scholar]
- [173].Lemke EA, Gambin Y, Vandelinder V, Brustad EM, Liu H-W, Schultz PG, Groisman A, Deniz AA, Microfluidic device for single-molecule experiments with enhanced photostability, J. Am. Chem. Soc. 131 (2009) 13610–13612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [174].Horrocks MH, Rajah L, Jönsson P, Kjaergaard M, Vendruscolo M, Knowles TPJ, Klenerman D, Single-molecule measurements of transient biomolecular complexes through microfluidic dilution, Anal. Chem. 85 (2013) 6855–6859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [175].Tyagi S, VanDelinder V, Banterle N, Fuertes G, Milles S, Agez M, Lemke EA, Continuous throughput and long-term observation of single-molecule FRET without immobilization, Nat. Methods. 11 (2014) 297–300. [DOI] [PubMed] [Google Scholar]
- [176].Benke S, Nettels D, Hofmann H, Schuler B, Quantifying kinetics from time series of single-molecule Förster resonance energy transfer efficiency histograms, Nanotechnology. 28 (2017) 114002. [DOI] [PubMed] [Google Scholar]
- [177].Segal M, Ingargiola A, Lerner E, Chung S, White JA, Streets A, Weiss S, Michalet X, High-throughput smFRET analysis of freely diffusing nucleic acid molecules and associated proteins, Methods. 169 (2019) 21–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [178].Hoffmann A, Nettels D, Clark J, Borgia A, Radford SE, Clarke J, Schuler B, Quantifying heterogeneity and conformational dynamics from single molecule FRET of diffusing molecules: recurrence analysis of single particles (RASP), Phys. Chem. Chem. Phys. 13 (2011) 1857–1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [179].König I, Zarrine-Afsar A, Aznauryan M, Soranno A, Wunderlich B, Dingfelder F, Stüber JC, Plückthun A, Nettels D, Schuler B, Single-molecule spectroscopy of protein conformational dynamics in live eukaryotic cells, Nat. Methods. 12 (2015) 773–779. [DOI] [PubMed] [Google Scholar]
- [180].Müller-Späth S, Soranno A, Hirschfeld V, Hofmann H, Rüegger S, Reymond L, Nettels D, Schuler B, Charge interactions can dominate the dimensions of intrinsically disordered proteins, Proc. Natl. Acad. Sci. U. S. A. 107 (2010) 14609–14614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [181].Schuler B, Lipman EA, Steinbach PJ, Kumke M, Eaton WA, Polyproline and the “spectroscopic ruler” revisited with single-molecule fluorescence, Proc. Natl. Acad. Sci. U. S. A. 102 (2005) 2754–2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [182].Aznauryan M, Delgado L, Soranno A, Nettels D, Huang J-R, Labhardt AM, Grzesiek S, Schuler B, Comprehensive structural and dynamical view of an unfolded protein from the combination of single-molecule FRET, NMR, and SAXS, Proc. Natl. Acad. Sci. U. S. A. 113 (2016) E5389–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [183].Nettels D, Müller-Späth S, Küster F, Hofmann H, Haenni D, Rüegger S, Reymond L, Hoffmann A, Kubelka J, Heinz B, Gast K, Best RB, Schuler B, Single-molecule spectroscopy of the temperature-induced collapse of unfolded proteins, Proc. Natl. Acad. Sci. U. S. A. 106 (2009) 20740–20745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [184].McCarney ER, Werner JH, Bernstein SL, Ruczinski I, Makarov DE, Goodwin PM, Plaxco KW, Site-specific dimensions across a highly denatured protein; a single molecule study, J. Mol. Biol. 352 (2005) 672–682. [DOI] [PubMed] [Google Scholar]
- [185].Best RB, Merchant KA, Gopich IV, Schuler B, Bax A, Eaton WA, Effect of flexibility and cis residues in single-molecule FRET studies of polyproline, Proc. Natl. Acad. Sci. U. S. A. 104 (2007) 18964–18969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [186].Dimura M, Peulen TO, Hanke CA, Prakash A, Gohlke H, Seidel CA, Quantitative FRET studies and integrative modeling unravel the structure and dynamics of biomolecular systems, Curr. Opin. Struct. Biol. 40 (2016) 163–185. [DOI] [PubMed] [Google Scholar]
- [187].Dimura M, Peulen T-O, Sanabria H, Rodnin D, Hemmen K, Hanke CA, Seidel CAM, Gohlke H, Automated and optimally FRET-assisted structural modeling, Nat. Commun. 11 (2020) 5394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [188].Renault K, Fredy JW, Renard P-Y, Sabot C, Covalent Modification of Biomolecules through Maleimide-Based Labeling Strategies, Bioconjug. Chem. 29 (2018) 2497–2513. [DOI] [PubMed] [Google Scholar]
- [189].Teng F-Y, Jiang Z-Z, Huang L-Y, Guo M, Chen F, Hou X-M, Xi X-G, Xu Y, A Toolbox for Site-Specific Labeling of RecQ Helicase With a Single Fluorophore Used in the Single-Molecule Assay, Front Mol Biosci. 7 (2020) 586450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [190].Chen L, Cohen J, Song X, Zhao A, Ye Z, Feulner CJ, Doonan P, Somers W, Lin L, Chen PR, Improved variants of SrtA for site-specific conjugation on antibodies and proteins with high efficiency, Sci. Rep. 6 (2016) 31899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [191].Levary DA, Parthasarathy R, Boder ET, Ackerman ME, Protein-protein fusion catalyzed by sortase A, PLoS One. 6 (2011) e18342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [192].Popp MW-L, Site-specific labeling of proteins via sortase: protocols for the molecular biologist, Methods Mol. Biol. 1266 (2015) 185–198. [DOI] [PubMed] [Google Scholar]
- [193].Sarpong K, Bose R, Efficient sortase-mediated N-terminal labeling of TEV protease cleaved recombinant proteins, Anal. Biochem. 521 (2017) 55–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [194].Lee TC, Moran CR, Cistrone PA, Dawson PE, Deniz AA, Site-Specific Three-Color Labeling of α-Synuclein via Conjugation to Uniquely Reactive Cysteines during Assembly by Native Chemical Ligation, Cell Chem Biol. 25 (2018) 797–801.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [195].Yang J-Y, Yang WY, Site-specific two-color protein labeling for FRET studies using split inteins, J. Am. Chem. Soc. 131 (2009) 11644–11645. [DOI] [PubMed] [Google Scholar]
- [196].Lai W-JC, Ermolenko DN, Ensemble and single-molecule FRET studies of protein synthesis, Methods. 137 (2018) 37–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [197].Chinnaraj M, Barrios DA, Frieden C, Heyduk T, Flaumenhaft R, Pozzi N, Bioorthogonal Chemistry Enables Single-Molecule FRET Measurements of Catalytically Active Protein Disulfide Isomerase, Chembiochem. 22 (2021) 134–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [198].Lee NK, Kapanidis AN, Koh HR, Korlann Y, Ho SO, Kim Y, Gassman N, Kim SK, Weiss S, Three-color alternating-laser excitation of single molecules: monitoring multiple interactions and distances, Biophys. J. 92 (2007) 303–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [199].Barth A, Seidel CAM, Lamb DC, Studying Complex Biomolecular Dynamics by Single-Molecule Three-Color FRET, Biophysical Journal. 116 (2019) 476a–477a. 10.1016/j.bpj.2018.11.2574. [DOI] [Google Scholar]
- [200].Yoo J, Louis JM, Gopich IV, Chung HS, Three-Color Single-Molecule FRET and Fluorescence Lifetime Analysis of Fast Protein Folding, J. Phys. Chem. B. 122 (2018) 11702–11720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [201].Hohng S, Joo C, Ha T, Single-molecule three-color FRET, Biophys. J. 87 (2004) 1328–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [202].Clamme J-P, Deniz AA, Three-color single-molecule fluorescence resonance energy transfer, Chemphyschem. 6 (2005) 74–77. [DOI] [PubMed] [Google Scholar]
- [203].Lin C-W, Ting AY, Transglutaminase-catalyzed site-specific conjugation of small-molecule probes to proteins in vitro and on the surface of living cells, J. Am. Chem. Soc. 128 (2006) 4542–4543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [204].Lu M, Uchil PD, Li W, Zheng D, Terry DS, Gorman J, Shi W, Zhang B, Zhou T, Ding S, Gasser R, Prévost J, Beaudoin-Bussières G, Anand SP, Laumaea A, Grover JR, Liu L, Ho DD, Mascola JR, Finzi A, Kwong PD, Blanchard SC, Mothes W, Real-Time Conformational Dynamics of SARS-CoV-2 Spikes on Virus Particles, Cell Host Microbe. 28 (2020) 880–891.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [205].Yin J, Lin AJ, Golan DE, Walsh CT, Site-specific protein labeling by Sfp phosphopantetheinyl transferase, Nat. Protoc. 1 (2006) 280–285. [DOI] [PubMed] [Google Scholar]
- [206].Lu M, Ma X, Reichard N, Terry DS, Arthos J, Smith AB 3rd, Sodroski JG, Blanchard SC, Mothes W, Shedding-Resistant HIV-1 Envelope Glycoproteins Adopt Downstream Conformations That Remain Responsive to Conformation-Preferring Ligands, J. Virol. 94 (2020). 10.1128/JVI.00597-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [207].Lu M, Ma X, Castillo-Menendez LR, Gorman J, Alsahafi N, Ermel U, Terry DS, Chambers M, Peng D, Zhang B, Zhou T, Reichard N, Wang K, Grover JR, Carman BP, Gardner MR, Nikić-Spiegel I, Sugawara A, Arthos J, Lemke EA, Smith AB 3rd, Farzan M, Abrams C, Munro JB, McDermott AB, Finzi A, Kwong PD, Blanchard SC, Sodroski JG, Mothes W, Associating HIV-1 envelope glycoprotein structures with states on the virus observed by smFRET, Nature. 568 (2019) 415–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [208].Mofid MR, Finking R, Marahiel MA, Recognition of hybrid peptidyl carrier proteins/acyl carrier proteins in nonribosomal peptide synthetase modules by the 4’-phosphopantetheinyl transferases AcpS and Sfp, J. Biol. Chem. 277 (2002) 17023–17031. [DOI] [PubMed] [Google Scholar]
- [209].Flugel RS, Hwangbo Y, Lambalot RH, Cronan JE Jr, Walsh CT, Holo-(acyl carrier protein) synthase and phosphopantetheinyl transfer in Escherichia coli, J. Biol. Chem. 275 (2000) 959–968. [DOI] [PubMed] [Google Scholar]
- [210].Gehring AM, Lambalot RH, Vogel KW, Drueckhammer DG, Walsh CT, Ability of Streptomyces spp. acyl carrier proteins and coenzyme A analogs to serve as substrates in vitro for E. coli holo-ACP synthase, Chem. Biol. 4 (1997) 17–24. [DOI] [PubMed] [Google Scholar]
- [211].Riback JA, Bowman MA, Zmyslowski AM, Plaxco KW, Clark PL, Sosnick TR, Commonly used FRET fluorophores promote collapse of an otherwise disordered protein, Proc. Natl. Acad. Sci. U. S. A. 116 (2019) 8889–8894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [212].Watkins HM, Simon AJ, Sosnick TR, Lipman EA, Hjelm RP, Plaxco KW, Random coil negative control reproduces the discrepancy between scattering and FRET measurements of denatured protein dimensions, Proc. Natl. Acad. Sci. U. S. A. 112 (2015) 6631–6636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [213].Fuertes G, Banterle N, Ruff KM, Chowdhury A, Pappu RV, Svergun DI, Lemke EA, Comment on “Innovative scattering analysis shows that hydrophobic disordered proteins are expanded in water,” Science. 361 (2018). 10.1126/science.aau8230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [214].Riback JA, Bowman MA, Zmyslowski A, Knoverek CR, Jumper J, Kaye EB, Freed KF, Clark PL, Sosnick TR, Response to Comment on “Innovative scattering analysis shows that hydrophobic disordered proteins are expanded in water,” Science. 361 (2018). 10.1126/science.aar7949. [DOI] [PubMed] [Google Scholar]
- [215].Zerze GH, Best RB, Mittal J, Modest influence of FRET chromophores on the properties of unfolded proteins, Biophys. J. 107 (2014) 1654–1660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [216].Gomes G-NW, Krzeminski M, Namini A, Martin EW, Mittag T, Head-Gordon T, Forman-Kay JD, Gradinaru CC, Conformational Ensembles of an Intrinsically Disordered Protein Consistent with NMR, SAXS, and Single-Molecule FRET, J. Am. Chem. Soc. 142 (2020) 15697–15710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [217].Zhang Z, Yomo D, Gradinaru C, Choosing the right fluorophore for single-molecule fluorescence studies in a lipid environment, Biochim. Biophys. Acta Biomembr. 1859 (2017) 1242–1253. [DOI] [PubMed] [Google Scholar]
- [218].Sisamakis E, Valeri A, Kalinin S, Rothwell PJ, Seidel CAM, Accurate single-molecule FRET studies using multiparameter fluorescence detection, Methods Enzymol. 475 (2010) 455–514. [DOI] [PubMed] [Google Scholar]
- [219].Schröder GF, Alexiev U, Grubmüller H, Simulation of Fluorescence Anisotropy Experiments: Probing Protein Dynamics, Biophysical Journal. 89 (2005) 3757–3770. 10.1529/biophysj.105.069500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [220].Zheng W, Borgia A, Buholzer K, Grishaev A, Schuler B, Best RB, Probing the action of chemical denaturant on an intrinsically disordered protein by simulation and experiment, J. Am. Chem. Soc. 138 (2016) 11702–11713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [221].Mao AH, Crick SL, Vitalis A, Chicoine CL, Pappu RV, Net charge per residue modulates conformational ensembles of intrinsically disordered proteins, Proc. Natl. Acad. Sci. U. S. A. 107 (2010) 8183–8188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [222].Fleming PJ, Fleming KG, HullRad: Fast Calculations of Folded and Disordered Protein and Nucleic Acid Hydrodynamic Properties, Biophys. J. 114 (2018) 856–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [223].Nygaard M, Kragelund BB, Papaleo E, Lindorff-Larsen K, An Efficient Method for Estimating the Hydrodynamic Radius of Disordered Protein Conformations, Biophys. J. 113 (2017) 550–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [224].Rezaei-Ghaleh N, Parigi G, Soranno A, Holla A, Becker S, Schuler B, Luchinat C, Zweckstetter M, Local and Global Dynamics in Intrinsically Disordered Synuclein, Angew. Chem. Int. Ed. 57 (2018) 15262–15266. [DOI] [PubMed] [Google Scholar]
- [225].Echeverria I, Makarov DE, Papoian GA, Concerted dihedral rotations give rise to internal friction in unfolded proteins, J. Am. Chem. Soc. 136 (2014) 8708–8713. [DOI] [PubMed] [Google Scholar]
- [226].Best RB, Hofmann H, Nettels D, Schuler B, Quantitative interpretation of FRET experiments via molecular simulation: force field and validation, Biophys. J. 108 (2015) 2721–2731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [227].Walczewska-Szewc K, Corry B, Accounting for dye diffusion and orientation when relating FRET measurements to distances: three simple computational methods, Phys. Chem. Chem. Phys. 16 (2014) 12317–12326. [DOI] [PubMed] [Google Scholar]
- [228].Kalinin S, Peulen T, Sindbert S, Rothwell PJ, Berger S, Restle T, Goody RS, Gohlke H, Seidel CAM, A toolkit and benchmark study for FRET-restrained high-precision structural modeling, Nat. Methods. 9 (2012) 1218–1225. [DOI] [PubMed] [Google Scholar]
- [229].Woźniak AK, Schröder GF, Grubmüller H, Seidel CAM, Oesterhelt F, Single-molecule FRET measures bends and kinks in DNA, Proc. Natl. Acad. Sci. U. S. A. 105 (2008) 18337–18342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [230].Lehmann K, Felekyan S, Kühnemuth R, Dimura M, Tóth K, Seidel CAM, Langowski J, Dynamics of the nucleosomal histone H3 N-terminal tail revealed by high precision single-molecule FRET, Nucleic Acids Res. 48 (2020) 1551–1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [231].Craggs TD, Kapanidis AN, Six steps closer to FRET-driven structural biology, Nat. Methods. 9 (2012) 1157–1158. [DOI] [PubMed] [Google Scholar]
- [232].Zimmerman MI, Porter JR, Ward MD, Singh S, Vithani N, Meller A, Mallimadugula UL, Kuhn CE, Borowsky JH, Wiewiora RP, Hurley MFD, Harbison AM, Fogarty CA, Coffland JE, Fadda E, Voelz VA, Chodera JD, Bowman GR, Citizen Scientists Create an Exascale Computer to Combat COVID-19, bioRxiv. (2020). 10.1101/2020.06.27.175430. [DOI] [Google Scholar]
- [233].Shirts M, Pande VS, Screen Savers of the World Unite!, Science. 290 (2000) 1903–1904. [DOI] [PubMed] [Google Scholar]
- [234].Shaw DE, Deneroff MM, Dror RO, Kuskin JS, Larson RH, Salmon JK, Young C, Batson B, Bowers KJ, Chao JC, Eastwood MP, Gagliardo J, Grossman JP, Ho CR, Ierardi DJ, Kolossváry I, Klepeis JL, Layman T, McLeavey C, Moraes MA, Mueller R, Priest EC, Shan Y, Spengler J, Theobald M, Towles B, Wang SC, Anton, a Special-purpose Machine for Molecular Dynamics Simulation, Commun. ACM. 51 (2008) 91–97. [Google Scholar]
- [235].Jaynes ET, Information Theory and Statistical Mechanics, Phys. Rev. 106 (1957) 620–630. [Google Scholar]
- [236].Bonomi M, Heller GT, Camilloni C, Vendruscolo M, Principles of protein structural ensemble determination, Curr. Opin. Struct. Biol. 42 (2017) 106–116. [DOI] [PubMed] [Google Scholar]
- [237].Boomsma W, Ferkinghoff-Borg J, Lindorff-Larsen K, Combining experiments and simulations using the maximum entropy principle, PLoS Comput. Biol. 10 (2014) e1003406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [238].Hummer G, Köfinger J, Bayesian ensemble refinement by replica simulations and reweighting, J. Chem. Phys. 143 (2015) 243150. [DOI] [PubMed] [Google Scholar]
- [239].Köfinger J, Różycki B, Hummer G, Inferring Structural Ensembles of Flexible and Dynamic Macromolecules Using Bayesian, Maximum Entropy, and Minimal-Ensemble Refinement Methods, Methods Mol. Biol. 2022 (2019) 341–352. [DOI] [PubMed] [Google Scholar]
- [240].Lincoff J, Haghighatlari M, Krzeminski M, Teixeira JMC, Gomes G-NW, Gradinaru CC, Forman-Kay JD, Head-Gordon T, Extended experimental inferential structure determination method in determining the structural ensembles of disordered protein states, Communications Chemistry. 3 (2020) 74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [241].Bottaro S, Bengtsen T, Lindorff-Larsen K, Integrating Molecular Simulation and Experimental Data: A Bayesian/Maximum Entropy Reweighting Approach, Methods Mol. Biol. 2112 (2020) 219–240. [DOI] [PubMed] [Google Scholar]
- [242].Crehuet R, Buigues PJ, Salvatella X, Lindorff-Larsen K, Bayesian-Maximum-Entropy Reweighting of IDP Ensembles Based on NMR Chemical Shifts, Entropy. 21 (2019) 898. [Google Scholar]
- [243].Leung HTA, Bignucolo O, Aregger R, Dames SA, Mazur A, Bernèche S, Grzesiek S, A Rigorous and Efficient Method To Reweight Very Large Conformational Ensembles Using Average Experimental Data and To Determine Their Relative Information Content, J. Chem. Theory Comput. 12 (2016) 383–394. [DOI] [PubMed] [Google Scholar]
- [244].Larsen AH, Wang Y, Bottaro S, Grudinin S, Arleth L, Lindorff-Larsen K, Combining molecular dynamics simulations with small-angle X-ray and neutron scattering data to study multi-domain proteins in solution, PLoS Comput. Biol. 16 (2020) e1007870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [245].Camilloni C, Langkilde AE, Lindorff-Larsen K, Refinement of α-synuclein ensembles against SAXS data: Comparison of force fields and methods, bioRxiv. (2021). 10.1101/2021.01.15.426794v2.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [246].Gaalswyk K, Muniyat MI, MacCallum JL, The emerging role of physical modeling in the future of structure determination, Curr. Opin. Struct. Biol. 49 (2018) 145–153. [DOI] [PubMed] [Google Scholar]
- [247].Morrone JA, Brini E, MacCallum JL, Blind protein structure prediction using accelerated free-energy simulations, Science. (2016). https://advances.sciencemag.org/content/2/11/e1601274.short. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [248].Perez A, MacCallum JL, Dill KA, Accelerating molecular simulations of proteins using Bayesian inference on weak information, Proc. Natl. Acad. Sci. U. S. A. 112 (2015) 11846–11851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [249].MacCallum JL, Perez A, Dill KA, Determining protein structures by combining semireliable data with atomistic physical models by Bayesian inference, Proc. Natl. Acad. Sci. U. S. A. 112 (2015) 6985–6990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [250].Rangan R, Bonomi M, Heller GT, Cesari A, Bussi G, Vendruscolo M, Determination of Structural Ensembles of Proteins: Restraining vs Reweighting, J. Chem. Theory Comput. 14 (2018) 6632–6641. [DOI] [PubMed] [Google Scholar]
- [251].Ghosh K, Dixit PD, Agozzino L, Dill KA, The Maximum Caliber Variational Principle for Nonequilibria, Annu. Rev. Phys. Chem. 71 (2020) 213–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [252].Deniz AA, Laurence TA, Beligere GS, Dahan M, Martin AB, Chemla DS, Dawson PE, Schultz PG, Weiss S, Single-molecule protein folding: diffusion fluorescence resonance energy transfer studies of the denaturation of chymotrypsin inhibitor 2, Proc. Natl. Acad. Sci. U. S. A. 97 (2000) 5179–5184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [253].Merchant KA, Best RB, Louis JM, Gopich IV, Eaton WA, Characterizing the unfolded states of proteins using single-molecule FRET spectroscopy and molecular simulations, Proc. Natl. Acad. Sci. U. S. A. 104 (2007) 1528–1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [254].Thirumalai D, Samanta HS, Maity H, Reddy G, Universal Nature of Collapsibility in the Context of Protein Folding and Evolution, Trends Biochem. Sci. 44 (2019) 675–687. [DOI] [PubMed] [Google Scholar]
- [255].Holehouse AS, Garai K, Lyle N, Vitalis A, Pappu RV, Quantitative assessments of the distinct contributions of polypeptide backbone amides versus side chain groups to chain expansion via chemical denaturation, J. Am. Chem. Soc. 137 (2015) 2984–2995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [256].Best RB, Emerging consensus on the collapse of unfolded and intrinsically disordered proteins in water, Curr. Opin. Struct. Biol. 60 (2020) 27–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [257].Riback JA, Bowman MA, Zmyslowski AM, Knoverek CR, Jumper JM, Hinshaw JR, Kaye EB, Freed KF, Clark PL, Sosnick TR, Innovative scattering analysis shows that hydrophobic disordered proteins are expanded in water, Science. 358 (2017) 238–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [258].Yoo TY, Meisburger SP, Hinshaw J, Pollack L, Haran G, Sosnick TR, Plaxco K, Small-Angle X-ray Scattering and Single-Molecule FRET Spectroscopy Produce Highly Divergent Views of the Low-Denaturant Unfolded State, J. Mol. Biol. 418 (2012) 226–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [259].Bowman MA, Riback JA, Rodriguez A, Guo H, Li J, Sosnick TR, Clark PL, Properties of protein unfolded states suggest broad selection for expanded conformational ensembles, Proc. Natl. Acad. Sci. U. S. A. (2020). 10.1073/pnas.2003773117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [260].Moses D, Yu F, Ginell GM, Shamoon NM, Koenig PS, Holehouse AS, Sukenik S, Revealing the Hidden Sensitivity of Intrinsically Disordered Proteins to their Chemical Environment, J. Phys. Chem. Lett. (2020) 10131–10136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [261].Clark PL, Plaxco KW, Sosnick TR, Water as a Good Solvent for Unfolded Proteins: Folding and Collapse are Fundamentally Different, J. Mol. Biol. 432 (2020) 2882–2889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [262].Diehl RC, Guinn EJ, Capp MW, Tsodikov OV, Record MT Jr, Quantifying additive interactions of the osmolyte proline with individual functional groups of proteins: comparisons with urea and glycine betaine, interpretation of m-values, Biochemistry. 52 (2013) 5997–6010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [263].Record MT Jr, Anderson CF, Lohman TM, Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity, Q. Rev. Biophys. 11 (1978) 103–178. [DOI] [PubMed] [Google Scholar]
- [264].Wang Y, Sukenik S, Davis CM, Gruebele M, Cell Volume Controls Protein Stability and Compactness of the Unfolded State, J. Phys. Chem. B. 122 (2018) 11762–11770. [DOI] [PubMed] [Google Scholar]
- [265].Sukenik S, Salam M, Wang Y, Gruebele M, In-Cell Titration of Small Solutes Controls Protein Stability and Aggregation, J. Am. Chem. Soc. 140 (2018) 10497–10503. [DOI] [PubMed] [Google Scholar]
- [266].Ruff KM, Holehouse AS, SAXS versus FRET: A Matter of Heterogeneity?, Biophys. J. 113 (2017) 971–973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [267].Stenzoski NE, Zou J, Piserchio A, Ghose R, Holehouse AS, Raleigh DP, The Cold-Unfolded State Is Expanded but Contains Long- and Medium-Range Contacts and Is Poorly Described by Homopolymer Models, Biochemistry. 59 (2020) 3290–3299. [DOI] [PubMed] [Google Scholar]
- [268].Das RK, Pappu RV, Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues, Proc. Natl. Acad. Sci. U. S. A. 110 (2013) 13392–13397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [269].Metskas LA, Rhoades E, Conformation and Dynamics of the Troponin I C-Terminal Domain: Combining Single-Molecule and Computational Approaches for a Disordered Protein Region, J. Am. Chem. Soc. 137 (2015) 11962–11969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [270].Medina E, Villalobos P, Hamilton GL, Komives EA, Sanabria H, Ramírez-Sarmiento CA, Babul J, Intrinsically Disordered Regions of the DNA-Binding Domain of Human FoxP1 Facilitate Domain Swapping, J. Mol. Biol. 432 (2020) 5411–5429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [271].Gopich IV, Szabo A, Decoding the pattern of photon colors in single-molecule FRET, J. Phys. Chem. B. 113 (2009) 10965–10973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [272].Heidarsson PO, Mercadante D, Sottini A, Nettels D, Borgia MB, Borgia A, Kilic S, Fierz B, Best RB, Schuler B, Disordered Proteins Enable Histone Chaperoning on the Nucleosome, bioRxiv. (2020) 2020.04.17.046243. 10.1101/2020.04.17.046243. [DOI] [Google Scholar]
- [273].Holmstrom ED, Liu Z, Nettels D, Best RB, Schuler B, Disordered RNA chaperones can enhance nucleic acid folding via local charge screening, Nat. Commun. 10 (2019) 2453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [274].Alshareedah I, Moosa MM, Raju M, Potoyan DA, Banerjee PR, Phase transition of RNA−protein complexes into ordered hollow condensates, Proc. Natl. Acad. Sci. U. S. A. 117 (2020) 15650–15658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [275].Kaur T, Raju M, Alshareedah I, Davis RB, Potoyan DA, Banerjee PR, Sequence-encoded and composition-dependent protein-RNA interactions control multiphasic condensate morphologies, Nat. Commun. 12 (2021) 872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [276].Wente SR, Rout MP, The nuclear pore complex and nuclear transport, Cold Spring Harb. Perspect. Biol. 2 (2010) a000562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [277].Görlich D, Kutay U, Transport between the cell nucleus and the cytoplasm, Annu. Rev. Cell Dev. Biol. 15 (1999) 607–660. [DOI] [PubMed] [Google Scholar]
- [278].Görlich D, Mattaj IW, Nucleocytoplasmic transport, Science. (1996). https://science.sciencemag.org/content/271/5255/1513.abstract. [DOI] [PubMed] [Google Scholar]
- [279].Schmidt HB, Görlich D, Transport Selectivity of Nuclear Pores, Phase Separation, and Membraneless Organelles, Trends Biochem. Sci. 41 (2016) 46–61. [DOI] [PubMed] [Google Scholar]
- [280].Milles S, Mercadante D, Aramburu IV, Jensen MR, Banterle N, Koehler C, Tyagi S, Clarke J, Shammas SL, Blackledge M, Gräter F, Lemke EA, Plasticity of an ultrafast interaction between nucleoporins and nuclear transport receptors, Cell. 163 (2015) 734–745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [281].Wuttke R, Hofmann H, Nettels D, Borgia MB, Mittal J, Best RB, Schuler B, Temperature-dependent solvation modulates the dimensions of disordered proteins, Proc. Natl. Acad. Sci. U. S. A. 111 (2014) 5213–5218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [282].Drubin DG, Kirschner MW, Tau protein function in living cells, J. Cell Biol. 103 (1986) 2739–2746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [283].Weingarten MD, Lockwood AH, Hwo SY, Kirschner MW, A protein factor essential for microtubule assembly, Proc. Natl. Acad. Sci. U. S. A. 72 (1975) 1858–1862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [284].Melo AM, Coraor J, Alpha-Cobb G, Elbaum-Garfinkle S, Nath A, Rhoades E, A functional role for intrinsic disorder in the tau-tubulin complex, Proc. Natl. Acad. Sci. U. S. A. 113 (2016) 14336–14341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [285].Nerenberg PS, Head-Gordon T, New developments in force fields for biomolecular simulations, Curr. Opin. Struct. Biol. 49 (2018) 129–138. [DOI] [PubMed] [Google Scholar]
- [286].Shi Y, Xia Z, Zhang J, Best R, Wu C, Ponder JW, Ren P, The Polarizable Atomic Multipole-based AMOEBA Force Field for Proteins, J. Chem. Theory Comput. 9 (2013) 4046–4063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [287].Rackers JA, Wang Q, Liu C, Piquemal J-P, Ren P, Ponder JW, An optimized charge penetration model for use with the AMOEBA force field, Phys. Chem. Chem. Phys. 19 (2016) 276–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [288].Lemkul JA, Huang J, Roux B, MacKerell AD Jr, An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications, Chem. Rev. 116 (2016) 4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [289].Lagardère L, Jolly L-H, Lipparini F, Aviat F, Stamm B, Jing ZF, Harger M, Torabifard H, Cisneros GA, Schnieders MJ, Gresh N, Maday Y, Ren PY, Ponder JW, Piquemal J-P, Tinker-HP: a massively parallel molecular dynamics package for multiscale simulations of large complex systems with advanced point dipole polarizable force fields, Chem. Sci. 9 (2018) 956–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [290].Inizan TJ, Célerse F, Adjoua O, El Ahdab D, Jolly L-H, Liu C, Ren P, Montes M, Lagarde N, Lagardère L, Monmarché P, Piquemal J-P, High-resolution mining of the SARS-CoV-2 main protease conformational space: supercomputer-driven unsupervised adaptive sampling, Chem. Sci. (2021). 10.1039/D1SC00145K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [291].Brown S, Head-Gordon T, Cool walking: a new Markov chain Monte Carlo sampling method, J. Comput. Chem. 24 (2003) 68–76. [DOI] [PubMed] [Google Scholar]
- [292].Lincoff J, Sasmal S, Head-Gordon T, The combined force field-sampling problem in simulations of disordered amyloid-β peptides, J. Chem. Phys. 150 (2019) 104108. [DOI] [PMC free article] [PubMed] [Google Scholar]


