Two-Phase Sampling Designs for Data Validation in Settings with Covariate Measurement Error and Continuous Outcome

Abstract

Measurement errors are present in many data collection procedures and can harm analyses by biasing estimates. To correct for measurement error, researchers often validate a subsample of records and then incorporate the information learned from this validation sample into estimation. In practice, the validation sample is often selected using simple random sampling (SRS). However, SRS leads to inefficient estimates because it ignores information on the error-prone variables, which can be highly correlated to the unknown truth. Applying and extending ideas from the two-phase sampling literature, we propose optimal and nearly-optimal designs for selecting the validation sample in the classical measurement-error framework. We target designs to improve the efficiency of model-based and design-based estimators, and show how the resulting designs compare to each other. Our results suggest that sampling schemes that extract more information from the error-prone data are substantially more efficient than SRS, for both design- and model-based estimators. The optimal procedure, however, depends on the analysis method, and can differ substantially. This is supported by theory and simulations. We illustrate the various designs using data from an HIV cohort study.

1 |. INTRODUCTION

Measurement error is common in clinical practice, particularly with the increased use of routinely collected and readily available data (e.g., electronic health records) for biomedical research. It is well known that if not addressed, covariate measurement error can lead to biased results and potentially misleading conclusions (Fuller, 2009). Many different analysis approaches have been proposed to address covariate measurement error, including but not limited to, moment-based estimation, regression calibration, simulation and extrapolation, instrumental variables, corrected scores, multiple imputation, likelihood-based approaches, and design-based approaches (Carroll et al., 2006). These approaches can be applied with a validation sample, i.e., the availability of a subset of records where the true value of the covariate is known.

The two-phase sampling literature is also broad. A classical two-phase sample is one in which the outcome and inexpensive covariates are available for all subjects in the first phase sample, and then that information is used to select a subsample of subjects for measurement of an expensive covariate during the second phase. Different sampling schemes for the second phase have been studied to improve efficiency over simple random sampling (SRS), including outcome-dependent sampling (which includes case-control sampling as a special case), residual sampling, and weighted residual sampling (Lin et al., 2013; Tao et al., 2019). It has been recognized that obtaining a validation sample to address measurement error is a specific case of two-phase sampling (Lawless et al., 1999; Chatterjee and Wacholder, 2002). The error-prone covariate and outcome are measured in all subjects (phase 1), but the expensive-to-obtain, true value of the covariate is only sampled in a subset of subjects (phase 2).

Several works have investigated study designs for validation sampling with measurement error or for two-phase sampling in general. Reilly and Pepe (1995) developed an optimal design specific for the mean score method and Holcroft and Spiegelman (1999) compared different designs to estimate the odds ratios between exposure and outcome. Tosteson et al. (1994) also focused on binary outcomes with measurement errors and propose a two-phase sampling scheme, stratified by the error-prone case status of the phase-1 data; their goal was to minimize the variance of estimators of sensitivity and specificity. Shoukri et al. (2003) and Berglund et al. (2007) have also discussed designs beyond SRS for reliability studies (i.e., repeated measures of error-prone covariate) that lead to more efficient estimates of the parameter of interest. Other works focused on estimation of correlation coefficients (Rosner and Willett, 1988) or on the optimality between the number of measurements per subject and the number of subjects with one single measurement (Kaaks et al., 1995; Stram et al., 1995).

In practice, however, validation samples in the context of measurement error are still almost always obtained via SRS schemes or SRS stratified within levels of any error-free covariate. Blattman et al. (2016), for example, discuss an intervention study designed to reduce crime and violence, directly and indirectly, in Monrovia, Liberia. Because of the high chance of inaccurately reporting data due to social stigma and discouragement on sensitive outcomes, a subsample was randomly selected from each treatment group and key variables that were believed to be more prone to error were validated. Another example is given by Holford and Stack (1995). The authors discuss the Nurses’ Health Study (Willett et al., 1987, 1985), which aimed to estimate the effect of nutrition on risk of cancer and cardiovascular disease. A semi-quantitative food frequency questionnaire was used in the original study, which was later validated for 194 women who were selected via an age-stratified random sample. Other examples can be found in Wong et al. (1999) and Bound et al. (2001), to name a few. None of these validation studies were designed to increase the precision of the parameter of interest. Two-phase designs, on the other hand, target the parameter of interest and extract more information from the phase-1 data (Zhou et al., 2007), leading to better estimates. The same idea can be applied to validation studies.

The literature for optimal sampling with two-phase designs is relevant to measurement error settings, but there are subtle differences that can impact the designs. For example, in classical two-phase designs, observed variables in the phase-1 sample are typically assumed to be predictive of the expensive variable only measured in phase-2, but they are rarely assumed to be surrogates for the expensive variable. With measurement error problems, the correlation between the true and observed covariates is often much higher than we would expect in other settings and is often treated as a surrogate, such as in the work by Reilly and Pepe (1995). This information can be exploited to improve efficiency, as will be seen below.

In this article, we study two-phase sampling schemes for measurement error settings. We focus on settings with classical covariate measurement error and a continuous outcome, focusing on the precision of the linear regression coefficient for a target variable. We study designs for two general types of estimators that represent a wide variety of commonly employed methods for addressing measurement error: model-based estimators (e.g., likelihood-based estimators) and design-based estimators (e.g., inverse-probability weighted estimators). We focus on estimators that are consistent under the missing at random assumption (Little and Rubin, 2002), leaving out the traditional regression calibration technique (Prentice, 1982), which requires further modifications (Oh et al., 2019). We review existing designs and principles and propose additional designs that can be particularly efficient for errors-in-variables settings. Through simulations, we show that the efficiency of estimators can be greatly improved by performing targeted probabilistic sampling. We show that the optimal design is highly dependent on the choice of estimator and we demonstrate the (minor) loss in efficiency by designing a validation sample based on a design-based estimator but performing estimation using a model-based estimator. The paper is organized as follows. In Section 2 we introduce the problem and notation. In Sections 3 and 4 we describe model-based and design-based estimators, respectively, and provide motivation for how each favors certain sampling schemes. In Section 5, we empirically compare several sampling schemes using extensive simulations, followed by a case study and discussion in Sections 6 and 7, respectively.

2 |. SET-UP AND NOTATION

Let Y and (X, Z) denote a continuous outcome and a vector of covariates, respectively. Assume that they are related through the linear model Y = α + β^t X + γ^t Z + ϵ, where ϵ is normally distributed with mean zero and constant variance. Let X* = X + U be the error-prone variables; we assume that U has expectation zero and is independent of ϵ. X is only observed in the validation (i.e., phase-2) sample, while the error-prone X*, correctly-measured Z, and outcome Y are observed for all subjects and are denoted as the phase-1 data. Let R_i = 1 indicate that the ith subject was selected for validation (phase-2) and R_i = 0 otherwise. Let N denote the sample size of the phase-1 data and $n={\sum }_{i=1}^N{R}_i$ denote phase-2 sample size. We assume that the probability of being selected for validation depends only on the fully observed/phase-1 data, specifically p(R | Y, X*, Z, X, U) = p(R | Y, X*, Z), so that X are assumed to be missing at random (Little and Rubin, 2002). We are interested in assessing the association between X (with X ∈ X) and Y conditional on Z and the other elements in X. That is, our goal is to select the validation sample so that the variance of β, the parameter associated with a particular covariate of interest X, is minimized.

3 |. MODEL-BASED ESTIMATORS

Let (Y, Z, X*, U, R) follow the joint density

$$p\left(Y,Z,X^{*},\mathit{U},R\right)=f\left(Y\mid Z,X^{*},U;\beta \right)g_1\left(U\mid X^{*},Z\right)g_2\left(X^{*},Z\right)\pi {\left(Y,X^{*},Z\right)}^R{\left[1-\pi \left(Y,X^{*},Z\right)\right]}^{(1-R)}$$

where f(·; β) is a normal distribution, π(·) = P (R = 1 | Y, Z, X*) is the probability of being selected for validation and is known by design, and g₁(·) and g₂(·) are the conditional and joint densities of U | (X*, Z) and (X*, Z), respectively. Note that f (Y | Z, X*, U; β) = f (Y | X, Z; β).

The observed-data log-likelihood takes the form

$$\sum _{i=1}^N{R}_i\left\{\text{log}f\left(Y_i\mid X_i,Z_i;\beta \right)+\text{log}{g}_1\left(U_i\mid X_i^{*},Z_i\right)\right\}+\sum _{i=1}^N\left(1-R_i\right)\text{log}\int f\left(Y_i\mid X_i^{*}-u,Z_i\right)g_1\left(u\mid X_i^{*},Z\right)du,$$ (1)

under the assumption that Y ⫫ X* | X, Z. Estimation of β is fully parametric if a parametric model is used for g₁(·). However, this is often undesirable, as inference will be dependent on correct model specification. Semi-parametric maximum likelihood estimation, on the other hand, leaves g₁(·) unspecified, leading to more robust estimates (Tao et al., 2017).

Alternatively, measurement error can be addressed using multiple imputation (Rubin, 1987; Freedman et al., 2008). We start by fitting a model for the distribution of X given (X*, Y, Z) in the validation subsample. Specifically, we fit the linear model $E\left(X\mid X^{*},Y,Z\right)={\gamma }_0+{\mathit{\gamma }}_1^t{X}^{*}+{\gamma }_{2}Y+{\mathit{\gamma }}_3^{t}Z$ among those with R = 1. The fitted model is then used to impute values for those subjects not selected for phase-2. Specifically, for those with R = 0, $X_{imp}=\widehat{E}\left(X\mid X^{*},Y,Z\right)+e^{*}$, where e* is a random draw from the distribution of the residuals and $\widehat{E}\left(X\mid X^{*},Y,Z\right)$ is a random draw from the fitted distribution that accounts for uncertainty in the estimates of the regression parameters (γ₀, γ₁, γ₂, γ₃) by drawing from their multivariate distribution. Inference is then carried out as if all data had been observed in the first place, by maximizing the phase-1 likelihood with X′ replacing X, where X′ = X_imp if R = 0 and X′ = X if R = 1. This procedure is repeated m times, leading to a total of m estimates of β. All m estimates are finally combined following Rubin’s rule (Rubin, 1987). In our simple measurement error set-up, this procedure results in proper multiple imputation under most settings (details in the Supplementary Material), such that for large m resulting estimates of β are consistent and asymptotically normal, and resulting confidence intervals have correct coverage.

3.1 |. Model-based sampling strategies

Let $\widehat{\beta }$ be the estimator that maximizes the log-likelihood (1) and let $\mathbb{V}$ denote its variance. Our goal is to find designs that make ${\mathbb{V}}_{[j,j]}$ smaller, where ${\mathbb{V}}_{[j,j]}$ denotes the jth row and jth column of the matrix $\mathbb{V}$, corresponding to the variance of $\widehat{\beta }$ for our covariate of interest X. The optimal design minimizes ${\mathbb{V}}_{[j,j]}$ for a fixed phase-2 sample size, n. The general form of $\mathbb{V}$ has been derived by Bickel et al. (1993) and Robins et al. (1994), but it involves an integral that makes the expression for $\mathbb{V}$ analytically intractable. Here we describe a few sampling strategies proposed in the two-phase literature and introduce a new one.

Outcome-dependent sampling:

Outcome-dependent sampling (ODS) has been widely used as a cost-effective way to enhance study efficiency. In ODS designs, the probability of sampling a unit in phase-2 depends on the outcome Y, i.e., π(·) = P (R = 1 | Y). Examples include case-control sampling; for a discrete outcome, and continuous outcome ODS designs (Zhou et al., 2002, 2011). For the latter, subjects with extreme values of the outcome Y are sampled for further observation. The rationale behind ODS designs is that subjects in the tails of the distribution of Y provide greater influence on the parameter under study, so by oversampling them we expect to increase efficiency of the estimator.

Residual sampling:

When there are auxiliary variables W observed in phase-1, which may contain (X*, Z) among other variables, we could discretize both Y and W and randomly select units from each stratum Y × W in such a way that n subjects are selected into phase-2. This, however, becomes impractical if W is multidimensional. Alternatively, we can calculate the residuals ${\widehat{ϵ}}^{*}=Y-\widehat{Y}$, where fitted values $\widehat{Y}$ are obtained by regressing Y on W, and sample subjects with extreme values of ${\widehat{ϵ}}^{*}$ (e.g., the largest ${\widehat{ϵ}}^{{*}^2}$). Moreover, if Y ⫫ W, residual sampling (RS) reduces to outcome-dependent sampling.

Weighted residual sampling:

For β = o(1), i.e., in a neighborhood of 0, Tao et al. (2019) derived an analytically tractable expression for $\mathbb{V}$:

$$\mathbb{V}={\left\{{\Sigma }_1+E\left[R\text{var}\left(\frac{\partial }{\partial \beta }\text{log}(f(Y\mid Z;\beta ))\mid R=1,Z\right)\text{var}\left(X\mid X^{*},Z\right)\right]\right\}}^{-1},$$ (2)

where Σ₁ denotes the Fisher information for the regression model f (Yi | Xi, Zi; β). Since Σ₁ does not depend on R, Tao et al.’s optimal sampling rule is obtained by maximizing the second term of (2). With normally distributed Y, this corresponds to assigning R to maximize (Y − μ(Z))²var(X | X*, Z), with μ(Z) denoting the linear predictor of Y (noting that β = 0). Following standard practice in two-phase designs (Tao et al., 2019), we do this by selecting the n/2 subjects with highest and n/2 with lowest (Y − μ(Z))var(X | X*, Z)^1/2. We call this a weighted residual sampling design (WRS). The inclusion of var(X | X*, Z) makes intuitive sense because this variance is larger if there are more errors in X and those errors are more extreme. For example, if X ≈ X* for certain Z (say a particular study site), then var(X | X*, Z) is close to zero and one would not need to perform extensive validation sampling for those levels of Z. However, var(X | X*, Z) is not known from the phase-1 sample, so applying this design requires either some preliminary knowledge about data errors or dividing n into a simple random sample (SRS) to estimate var(X | X*, Z), and then a targeted sample based on the optimal sampling rule once var(X | X*, Z) has been estimated. It is also important to reiterate that this weighted residual design is optimal when β = o(1), but may not be optimal as β deviates from the null.

Score function sampling:

An ad hoc sampling scheme can be constructed based on the expression provided by Tao et al. (2019). Note that [Y − μ(Z)]²var(X | X*, Z) is the variance of the score function of the fully observed data if Y ⫫ X given Z. An ad hoc design can be considered by ignoring the conditional independence at this last step and instead selecting phase-2 to maximize var{[Y − μ(Z)]X | X*, Z}. Since X is not known but X* is often a good surrogate for it, one could thus plug in X* for X and sample to maximize var{[Y − μ(Z)]X*}. Therefore, one would sample the n/2 largest and n/2 smallest values of [Y − μ(Z)]X*. We call this score function sampling (SFS). This sampling procedure has the advantage that it does not require preliminary knowledge of the var(X | X*, Z). SFS is feasible in our measurement error problem because the error-prone X* may be a good approximation for X, whereas in traditional two-phase designs, there is often no good surrogate for X in the phase-1 sample. As the WRS method of Tao et al. (2019) is guaranteed to have optimal performance in a region close to the null, we expect that sampling based on the score function will lead to less efficient estimates around that neighborhood, but might have advantages as β deviates from 0.

4 |. DESIGN-BASED ESTIMATORS

Design-based estimators depend on the sampling probabilities used to obtain the phase-2 data and weight phase-2 data based on the inverse of these probabilities. The goal is to estimate the quantity that would have been estimated if we had the entire dataset, instead of only the validated sample (Lawless et al., 1999). Design-based models are semiparametric models when the sampling scheme is known by design. They are more robust than model-based approaches since they do not require estimating nuisance parameters related to the distribution of X* and have fewer distributional assumptions. Design-based estimators are the estimators consistent under these models (Robins et al., 1994).

The most popular design-based estimator is the Horvitz-Thompson estimator (Horvitz and Thompson, 1952). The Horvitz-Thompson estimator, often called the inverse probability weighted (IPW) estimator, maximizes the weighted log-likelihood ${\ell }^w(\beta )=\sum _i{R}_i\text{log}f(Y\mid X,Z;\beta )/{\pi }_i$ with respect to β where ${\pi }_i=P\left(R_i=1\mid Y_i,Z_i,X_i^{*}\right)>0$.

Another design-based estimator, generalized raking, is growing in popularity because it is more efficient than the Horvitz-Thompson estimator (Lumley, 2010). Generalized raking maximizes a similar weighted log-likelihood, except it uses a new set of “calibrated” weights g_i/π_i. Here, g_i is obtained by minimizing the distance ${\sum }_{i=1}^N{R}_{i}d\left(1/{\pi }_i,g_i/{\pi }_i\right)$ under the constraint that ${\sum }_{i=1}^N{R}_i{g}_i{W}_i/{\pi }_i={\sum }_i{W}_i$, where d(·) is a distance function and W is an auxiliary variable known at phase-1. For a list of distance functions d(·) and properties of generalized raking, the reader is referred to Deville and Särndal (1992), Särndal et al. (2003), Lumley (2010); for connections between generalizing raking and augmented inverse probability weights, we refer to Lumley et al. (2011). In this manuscript we use the distance function d(a, b) = a[log(a) − log(b)] + (b − a). Breslow et al. (2009a) showed that the optimal auxiliary variable is the expectation of the efficient influence function for the phase-2 data given the observed phase-1 data; this is unknown, so a natural choice is to use the expectation of the influence function plugging in the observed, error-prone variables. Specifically, for the normal linear model case, the influence function IF is given by ${\mathbb{I}}^{-1}\mathbb{S}$, where

$$\mathbb{S}=X^t(Y-\mu (X,Z))\text{\hspace{1em}and\hspace{1em}}\mathbb{I}=E{\left(X^{t}X\right)}^{-1}.$$ (3)

Since X is only available for the phase-2 subsample and because X* is often highly correlated with X, the influence function may be approximated by simply replacing X by X* in equation (3).

4.1 |. Design-based sampling strategies

4.1.1 |. Optimal allocation

For model-based estimators, an efficient sampling strategy is to sample subjects with extreme values, irrespective of the approach (ODS, RS, WRS, SFS). Clearly, sampling only from the extremes does not work for design-based estimators because π_i must be non-zero for all subjects. As in the outcome-dependent design of Zhou et al. (2002), consider stratifying the phase-1 sample into K mutually exclusive groups and sampling n_k subjects from the kth stratum, for k = 1, …, K. The stratification can be based on the outcome (as in Zhou et al. (2002)), covariates, or any other quantity that is available for all subjects in phase-1. Once the stratification variable and number of strata are defined, we compute the optimal design for the IPW estimator by minimizing the asymptotic variance of the estimator under the constraint that n subjects are selected for validation.

To this end, let β₀ denote the truth and ${\widehat{\beta }}_w$ denote the IPW estimator that solves $S_w={\sum }_i^N{S}_{w,i}={\sum }_i^N{R}_i{S}_i/{\pi }_i=0$ for β, where S is the score function for β and S_w,i is the score contribution from the ith person, for i = 1, …, N. Assuming that π_i is known by design for all i, from Hsieh et al. (1985) we have that

$$\sqrt{N}\left({\widehat{\beta }}_w-{\beta }_0\right)\stackrel{d}{\to }N\left(0,{\Sigma }_w\right),$$ (4)

where Σ_w = A⁻¹BA^t with $A=-\mathbb{E}\left\{\partial S_{w,i}(\beta )/\partial \beta \right\}$ and B = Var{S_w,i(β)}. Let N_k denote the number of individuals in stratum k, n_k be the number of subjects from stratum k that were selected for validation, S_i,k be the score contribution from the ith person allocated to the kth stratum, and R_i,k be an indicator variable corresponding to whether the ith person from the kth stratum was selected for validation. Let p_k = n_k /N_k denote the probability of sampling a subject from stratum k and assume that subjects from the same stratum are equally likely to be sampled for validation. Then $S_w={\sum }_{k=1}^K{\sum }_{i=1}^{N_k}{R}_{i,k}{S}_{i,k}/p_k=0$, with the constraint that a total of n subjects are selected for validation. Our goal is to find n_k, for k = 1, …, K, that minimize

$${\Sigma }_{w,[j,j]}+\lambda \left(\sum _{k=1}^K\frac{N_k}{N}{p}_k-\frac{n}{N}\right),$$ (5)

where λ is a Lagrange multiplier and [j, j] denotes the element in the jth row and jth column of Σ_w, corresponding to the variance of our parameter of interest.

Equation (5) actually admits a closed-form solution, giving us the optimal proportions. Notice that

$$A=-\mathbb{E}\left\{\frac{\partial }{\partial \beta }{S}_{w,i}(\beta )\right\}=-\mathbb{E}\left\{\frac{R_{i,k}}{p_k}\frac{\partial }{\partial \beta }{S}_{i,k}(\beta )\right\}=-\mathbb{E}\left\{\frac{\partial }{\partial \beta }{S}_{i,k}(\beta )\right\}.$$ (6)

In addition,

$$B=\text{Var}\left\{S_{w,i}(\beta )\right\}=\mathbb{E}\left\{S_{w,i}(\beta )S_{w,i}^t(\beta )\right\}=\mathbb{E}\left\{\frac{R_{i,k}}{p_k^2}{S}_{i,k}(\beta )S_{i,k}^t(\beta )\right\}=\mathbb{E}\left\{\frac{1}{p_k}{S}_{i,k}(\beta )S_{i,k}^t(\beta )\right\}.$$

and by taking another iterated expectation, we have that

$$B=\mathbb{E}\left\{\frac{1}{p_k}\mathbb{E}\left[S_{i,k}(\beta )S_{i,k}^t(\beta )\mid K\right]\right\},$$ (7)

Let $\mathcal{V}=A^{-1}\mathbb{E}\left\{S_{i,k}(\beta )S_{i,k}{(\beta )}^t\mid K\right\}{A}^{-1}$ and $s_k^2={\mathcal{V}}_{[j,j]}$. Minimizing (5) with respect to p_k gives

$$p_k=\frac{n{s}_k}{{\sum }_{k=1}^K{N}_k{s}_k},$$ (8)

where s_k is the standard deviation of the influence function associated with the parameter of interest, restricted to the kth stratum. Moreover, as p_k = n_k/N_k, we have that

$$\frac{n_k}{n}=\frac{N_k{s}_k}{{\sum }_{k=1}^K{N}_k{s}_k}.$$ (9)

This is the optimal sampling proportion from stratum k. A similar result has also been shown by McIsaac and Cook (2014) and previously by Reilly and Pepe (1995), but in the setting of two-phase studies with a discrete outcome and expensive covariates.

This result is actually similar to Neyman allocation (Neyman, 1934) which is the optimal way to sample from mutually exclusive strata with a fixed sample size. Neyman allocation focuses on minimizing the variance of the population total. It shows that the optimum number of subjects sampled from stratum k should be proportional to the number of subjects in that stratum multiplied by the standard deviation of the total. Our setting is slightly different as we are not interested in a population total, but rather in estimating the regression parameter β. Since ${\widehat{\beta }}_w$ can be written as

$$\sqrt{N}\left({\widehat{\beta }}_w-\beta \right)=\sqrt{N}\left(\frac{1}{N}\sum _{i=1}^N\frac{R_i}{{\pi }_i}\mid {\text{F}}_i\right)+o_p(1),$$ (10)

that is, as ${\widehat{\beta }}_w$ is asymptotically equivalent to the sum of the influence functions IF_i, i = 1, …, N (Breslow et al., 2009b; Breslow and Wellner, 2007), we have that equation (9) is the translation of Neyman allocation to our two-phase regression setting.

Notice that while likelihood-based estimators lead to designs that focus on extreme values and ignore observations from the middle of the distribution, design-based estimators may still sample considerably from the middle. For example, consider a symmetric distribution stratified into 3 regions such that s₁ = s₃ ≠ s₂. The optimal allocations for likelihoodand design-based estimators in this setting become more similar as s₁ (as well as s₃) becomes larger compared to s₂, and will coincide only in the limit in which the ratio s₂/s₁ → 0. If s₂/s₁ = 1 instead, that is s₁ = s₂ = s₃, design-based samples favor sampling proportionally to the size of each stratum. For example, if we selected equal-sized strata, we should sample n₁ = n₂ = n₃ = n/₃, resembling stratified simple random sampling. This is considerably different than the likelihood-based designs discussed in section 3.

4.1.2 |. Optimal stratification variable

Any variable observed in phase-1 can be used as a stratification variable. The better variable, however, would lead to smaller variance for the estimator of the parameter of interest β. Since the variance of the estimator is proportional to the variance of its influence function (Breslow et al., 2009a), stratification on this influence function will lead to strata that are more similar with respect to this variable and, as a result, a smaller overall variance for ${\widehat{\beta }}_w$. Recall that in two-phase designs we cannot compute the influence function for the regression parameter for the target variable because X is not known. However, in our case we can again approximate this target influence function using the error-prone variable X*, which is expected to be highly correlated with X. Once the strata are created, we use Neyman allocation to select the validation data.

Särndal et al. (2003) discussed a similar problem, but aimed to estimate a population total. Since the outcome is not known, the authors suggested using an auxiliary variable that is highly correlated with the outcome as the stratification variable and later to compute the optimal allocation following Neyman allocation. The authors provided a general rule of thumb that a correlation greater than or equal to 0.90 between the outcome and the stratification variable will lead to efficient estimation, whereas a correlation less than or equal to 0.80 will no longer be an efficient stratification. Translated to our setting, this suggests that X* and X should be highly correlated so that the influence function plugging in X* should be highly correlated with the true influence function.

4.1.3 |. Optimal boundaries

Knowing the stratification variable as well as the sampling ratios within strata is still not enough to derive an optimal design. Neyman allocation, for example, assumes a fixed number of strata and fixed boundaries. Different boundaries will lead to different strata and different sampling proportions, which will affect the efficiency of the design. Therefore, an optimal design should also address the selection of the strata thresholds. These should be chosen such that the asymptotic variance of the IPW estimator is again minimized. Here we give an approximate view of how these boundaries should be obtained. As the variance of the parameter of interest is proportional to the variance of its influence function, combining equations (6) to (8), we have that

$$\text{Var}\left({\widehat{\beta }}_{w,j}\right)\propto \frac{1}{N}{\left(\sum _{k=1}^K{N}_k{s}_k\right)}^2.$$

Thus, minimizing $\text{Var}\left({\widehat{\beta }}_{w,j}\right)$ should be equivalent to minimizing ${\sum }_{k=1}^K{N}_k{s}_k$. Reddy et al. (2018) discussed a similar problem and provided a numerical algorithm to find the optimal boundaries. A similar problem, but for estimating a population total, has been discussed by Dalenius (1950), Dalenius and Hodges Jr (1957) and Dalenius and Hodges Jr (1959), to name a few. Särndal et al. (2003) also discuss this problem, again for estimating a population total, and suggest equal allocation in all strata as a feasible strategy to estimate strata boundaries. The goal is therefore to find boundaries that allows for equal sampling, recalling that sampling is based on Neyman allocation. This means that strata should be chosen such that N_k s_k ≈ N_k′ s_k′ for all k ≠ k′. Note that, for this particular problem of finding optimal boundaries, estimating a population total and a regression parameter is mathematically equivalent (see equation (10)). For the former, the outcome is not known for all subjects and some auxiliary variable that is highly correlated to the outcome is used as as a stratification variable. In the regression setting, the estimated influence function should be highly correlated with the parameter of interest, of course assuming that X* is highly correlated with X.

Selecting optimal boundaries, however, becomes more computationally intensive as the number of strata increases. Increasing the number of strata should lead to more homogeneous strata and therefore reduce the total variance of the IPW estimator (Lumley et al., 2011). However, the computational power required to find the optimal boundaries increases as K becomes larger, and the gains in efficiency are potentially not worth this extra effort. This will be investigated via simulations in Section 5.

4.1.4 |. Summary of Design-Based Sampling Strategies

Summarizing Sections 4.1.1 - 4.1.3 to compute the optimal designs for design-based estimators we propose using the influence function associated with β, replacing X with X*, as the stratification variable. The strata boundaries should be chosen such that N_k s_k ≈ N_k′ s_k′, where N_k and s_k are the number of subjects and the standard deviation of the influence function for β in stratum k. Notice that this can lead to designs that are considerably different from those obtained for likelihood-based estimators, highlighting the importance of having a solid analysis plan in the early stages of the study. Both classes of estimators, in addition, suggest designs that differ from simple random sampling and can lead to substantial gains in efficiency. This will be explored in the next section.

5 |. EMPIRICAL COMPARISONS

5.1 |. General setting

We performed a series of simulations to investigate the proposed designs. The outcome Y was generated from the normal linear model Y = β₀ + β₁ X + β₂ Z + ϵ, where Z was Bernoulli distributed with success probability equal to 1/2 and ϵ followed a standard normal distribution. Z can be thought of as representing study site and X is the main covariate of interest, with X ~ N ((1 − Z)/2, σ_X), so that the mean of X depended on Z. We assumed additive error, X* = X + U, with U ~ N (0, σ_U), where ${\sigma }_U^2={\sigma }_{U,1}^{2}I(Z=0)+{\sigma }_{U,2}^{2}I(Z=1)$, so that the error mechanism could differ across sites. We show results from four settings based on the values of ${\sigma }_U^2$: scenario 1, ${\sigma }_U^2=(0.5,0.5)$; scenario 2, ${\sigma }_U^2=(1,1)$; scenario 3, ${\sigma }_U^2=(3,3)$; scenario 4, ${\sigma }_U^2=(0.5,1)$. We set σ_X = 1 for settings 1, 2 and 3 and σ_X = 0.5 if Z = 0 and σ_X = 1, otherwise for setting 4. That is, X* is expected to be a good surrogate for X in scenario 1, a fair surrogate in scenario 2, and a poor surrogate in scenario 3. In scenario 4 we allowed X and the error to vary across a covariate (e.g. study site), resembling what is often seen in practice.

Our goal was to estimate β₁, the parameter associated with X. The triplet (Y, X*, Z) were observed at phase-1, for all N = 2000 subjects in the study, while X was validated for only a subset of size n = 500. We compared several different designs for selecting the validation sample and compared the variance of estimators of β₁ under various model-based and design-based estimators.

For model-based estimators we considered simple random sampling (SRS); a balanced simple random sample stratified on Z (SSRS), in which we randomly selected n/2 observations from Z = 0 and n/2 from Z = 1; and (following Section 3) sampling the n/2 smallest and the n/2 largest values of the following:

1. Y (outcome-dependent sampling; ODS)

2. ${\widehat{ϵ}}_r=Y-\left({\widehat{\beta }}_0+{\widehat{\beta }}_{2}Z\right)$ (residual sampling; RS)

3. ${\widehat{ϵ}}_w=\left\{Y-\left({\widehat{\beta }}_0+{\widehat{\beta }}_{2}Z\right)\right\}\text{var}{\left(X\mid X^{*},Z\right)}^{1/2}$ (weighted residual sampling; WRS)

4. ${\widehat{ϵ}}_s=\left\{Y-\left({\widehat{\beta }}_0+{\widehat{\beta }}_{2}Z\right)\right\}{X}^{*}$ (score function sampling; SFS).

For WRS we plugged in the known var(X | X*, Z). Our model-based estimators were multiple imputation estimators (MI) and semi-parametric maximum likelihood estimators (SPMLE). Multiple imputation estimators fit a normal linear model of X on X*, Y, Z for those in the phase-2 sample and then imputed X based on this model for the remaining subjects; 40 imputation replications were used. SPMLE followed the approach of Tao et al. (2017); a normal linear model was specified for f (Y | X, Z) in (1) and g₁(U | X*, Z) was flexibly estimated using B-splines sieves. We used 10–15 cubic sieves, equally spaced, for each value of Z.

For design-based designs, we considered SRS, SSRS, and (following Section 4.1) samples based on Neyman allocation with different stratification variables. Specifically, we considered stratification based on Y, ${\widehat{ϵ}}_r$, and ${\widehat{ϵ}}_w$ (as defined above), and the influence function, ${\widehat{ϵ}}_I={\widehat{\sigma }}_x{X}^{*}\left\{Y-\left({\widehat{\beta }}_0+{\widehat{\beta }}_1{X}^{*}+{\widehat{\beta }}_{2}Z\right)\right\}$, where ${\widehat{\sigma }}_x={\sum }_{i=1}^N{\left(x_i^{*}\right)}^2/N$. We refer to these designs as ODS-D, RS-D, WRS-D, and IFS to link and distinguish them from the analogous model-based designs. For each stratification variable we first fixed the number of strata (typically K = 3). Then, following Neyman allocation, we found strata boundaries such that N_k s_k ≈ N_k′ s_k′ for all strata, where s_k denotes the standard deviation of the estimated influence function based on the phase-1 data. The phase-2 sample was then selected from each stratum, based on Neyman allocation procedures as explained in previous sections. Design-based estimators were Horvitz-Thompson (IPW) and generalized raking, with the latter using the error-prone influence function as the auxiliary variable (as explained in Section 4).

For both model-based and design-based sampling strategies, we compared the empirical variance of our estimates based on 1,000 Monte Carlo simulations. All estimators, unless stated otherwise, were approximately unbiased (data not shown).

Table 1 shows the empirical variance for model-based estimates of β₁ under various sampling strategies. First consider the results for the MI estimators (top half of Table 1). Under all simulation scenarios and values of β₁, SRS (or SSRS) was the least efficient design. The efficiency gains (i.e., reduction in the empirical variance) of SFS, WRS, or RS designs were at least 20% for all scenarios and as high as 60% (Scenario 3, β₁ = 0). As expected, WRS led to the most efficient estimates when β₁ = 0. However, consistent with theory, RS had similar efficiency when the variance of X was independent of Z (scenarios 1–3). It is important to stress once again that WRS requires knowledge of var(X | X*, Z), which was known in our simulations but in most practical situations is unknown; all other designs only used information readily available from the phase-1 data. When β₁ deviated substantially from the null (i.e., β₁ = 1), SFS outperformed all other designs, being at least 10% more efficient than WRS and RS. These gains in efficiency were present even when X* was a poor surrogate for X (scenario 3). With less substantial deviation from the null (β₁ = 0.5), the efficiency of SFS designs was similar to that of WRS and RS designs, with somewhat better efficiency when X* was a good surrogate (scenario 1) and similar efficiency when X* was a poor surrogate (scenario 3).

TABLE 1.

Empirical variance (×10³) for β₁ of the MI and SPMLE estimators under SRS, SSRS, and extreme-tail sampling of ODS, RS, WRS, and SFS.

β 1	SRS	SSRS	ODS	RS	WRS	SFS	SRS	SSRS	ODS	RS	WRS	SFS
MI
Scenario 1, ${\sigma }_U^2=(0.5,0.5)$							Scenario 2, ${\sigma }_U^2=(1,1)$
0	1.001	1.004	0.709	0.568	0.568	0.641	1.287	1.244	0.812	0.593	0.593	0.733
0.5	1.054	1.024	0.924	0.850	0.850	0.742	1.279	1.185	1.093	1.010	1.010	0.901
1	1.113	1.051	1.129	1.098	1.098	0.844	1.200	1.194	1.246	1.186	1.186	0.921
Scenario 3, ${\sigma }_U^2=(3,3)$							Scenario 4, ${\sigma }_U^2=(0.5,1)$
0	1.753	1.737	1.008	0.690	0.690	0.884	1.209	1.170	0.767	0.631	0.619	0.704
0.5	1.490	1.466	1.216	1.040	1.040	0.992	1.213	1.124	1.044	0.961	0.947	0.812
1	1.401	1.280	1.307	1.251	1.251	1.138	1.284	1.187	1.173	1.140	1.128	0.922
SPMLE
Scenario 1, ${\sigma }_U^2=(0.5,0.5)$							Scenario 2, ${\sigma }_U^2=(1,1)$
0	0.648	0.644	0.580	0.513	0.513	0.564	0.742	0.749	0.605	0.502	0.502	0.636
0.5	0.791	0.755	0.842	0.806	0.806	0.662	1.000	0.941	1.057	0.941	0.941	0.779
1†	1.015	0.876	1.413	1.404	1.404	0.843	1.168	1.150	1.831	1.618	1.618	0.954
Scenario 3, ${\sigma }_U^2=(3,3)$							Scenario 4, ${\sigma }_U^2=(0.5,1)$
0	1.040	1.044	0.645	0.463	0.463	0.473	0.728	0.725	0.608	0.550	0.529	0.613
0.5	1.202	1.222	1.148	0.833	0.833	0.754	0.907	0.848	0.982	0.896	0.880	0.736
1†	1.380	1.259	2.153	2.016	2.016	1.408	1.167	1.111	1.657	1.587	1.528	0.941

Note:

^†,bias varying from 5 to 8% overall in scenrion 3; non-convergence rate varying from 6 to 20% for SFS, across all 4 scenarios.

Abbreviations: SRS: Simple random sampling; SSRS: stratified simple random sampling; ODS: Outcome-dependent sampling; RS: Residual sampling; WRS: Weighted residual sampling; SFS: Score function sampling; MI: Multiple imputation; SPMLE: Semiparametric maximum likelihood estimator.

Results were fairly similar with SPMLE (lower half of Table 1). Under β₁ = 0, WRS and RS were most efficient and as β₁ deviated from the null, the SFS became relatively more efficient. It should be noted that we had issues with convergence when computing the SPMLEs with large values of β₁, particularly with SFS designs. Convergence improved by reducing the number of sieves, but bias increased. Interestingly and as a side note, SPMLE was more efficient than MI when β₁ was close to the null, but comparable or less efficient when β₁ = 1, in particular when more complex designs were used. This may be partially explained by different model assumptions: the SPMLE assumes conditional independence of Y and X* given X, while multiple imputation did not make this assumption, leading to a wider class of estimators. This is further discussed in the Supplementary Material.

5.2 |. Simulation results for design-based estimation

5.2.1 |. IPW estimators

The upper half of Table 2 shows the empirical variance of IPW estimators based on various sampling schemes. In this table, ODS-D, RS-D, WRS-D, and IFS designate Neyman-allocation sampling from three optimally divided strata based on the outcome, residuals, weighted residuals, and influence functions, respectively. By ‘optimally divided’ we mean that the product of the sample size and the standard deviation of the estimated influence function based on phase-1 data was approximately equal between strata. As expected from theory, with IPW estimators IFS led to the smallest variance when X* was a strong surrogate for X, as seen in scenario 1. Under scenario 1 with β₁ = 0, the IFS design led to estimates that were about 40% more efficient than SRS. However, as X* became less correlated with X, the full-data influence function was no longer well approximated, affecting the performance of IFS; it worsened as β₁ increased. For scenarios 2 and 3, for example, we saw that IFS performed well for smaller effect sizes, but as β₁ got bigger, IFS was comparable to other complex designs or slightly less efficient; e.g., 5% less efficient than ODS-D when β₁ = 1 and ${\sigma }_U^2=(1,1)$. Compared to SRS, however, IFS still showed efficiency gains irrespective of effect size for settings 1, 2 and 4. For setting 3, when X* was very weakly correlated with X, IFS performed better than SRS when β₁ = 0, but had similar performances otherwise. In scenario 3, the other designs that did not depend on X* (ODS-D, RS-D, and WRS-D) performed better than IFS.

TABLE 2.

Empirical variance (×10³) for β₁ of the Horvitz-Thompson (IPW) and generalized raking estimators under SRS, SSRS, and Neyman allocation sampling from 3 strata based on ODS-D, RS-D, WRS-D, or IFS.

β 1	SRS	SSRS	ODS-D	RS-D	WRS-D		IFS	SRS	SSRS	ODS-D	RS-D	WRS-D	IFS
IPW
Scenario 1, ${\sigma }_U^2=(0.5,0.5)$								Scenario 2, ${\sigma }_U^2=(1,1)$
0	2.109	1.986	1.716	1.553	1.553		1.235	2.058	1.982	1.719	1.617	1.617	1.419
0.5	2.009	1.919	1.660	1.737	1.737		1.314	2.094	2.010	1.775	1.630	1.630	1.597
1	2.016	2.015	1.748	1.835	1.835		1.582	2.060	2.028	1.698	1.738	1.738	1.793
Scenario 3, ${\sigma }_U^2=(3,3)$								Scenario 4, ${\sigma }_U^2=(0.5,1)$
0	1.994	2.042	1.758	1.478	1.478		1.675	2.766	2.802	2.218	2.037	2.005	1.801
0.5	1.936	2.113	1.850	1.714	1.714		1.849	2.669	2.533	2.425	2.289	2.250	2.051
1	1.962	1.971	1.716	1.829	1.829		2.087	2.699	2.817	2.303	2.304	2.294	2.292
Generalized Raking
Scenario 1, ${\sigma }_U^2=(0.5,0.5)$								Scenario 2, ${\sigma }_U^2=(1,1)$
0	1.051	1.045	0.997	0.857		0.857	0.985	1.255	1.269	1.169	1.062	1.062	1.238
0.5	1.134	1.037	1.070	1.086		1.086	1.100	1.397	1.383	1.299	1.264	1.264	1.457
1	1.251	1.326	1.281	1.372		1.372	1.381	1.561	1.585	1.481	1.484	1.484	1.657
Scenario 3, ${\sigma }_U^2=(3,3)$								Scenario 4, ${\sigma }_U^2=(0.5,1)$
0	1.653	1.724	1.504	1.243		1.243	1.589	1.788	1.675	1.514	1.433	1.385	1.664
0.5	1.671	1.821	1.621	1.582		1.582	1.779	1.793	1.732	1.730	1.759	1.768	1.832
1	1.775	1.816	1.659	1.812		1.812	2.035	2.073	2.128	1.757	2.075	2.078	2.041

Note: SRS: Simple random sampling; SSRS: Stratified simple random sampling; ODS-D: Stratification based on the outcome; RS-D: Stratification based on the phase-1 residuals; WRS-D: Stratification based on the phase-1 weighted residuals; IFS: Stratification based on the phase-1 influence function of the target parameter with X* replacing X; IPW: Inverse probability weight.

Figure 1 compares the empirical variance of IPW estimates of β₁ when 1, 3, 4, 5 and 10 strata were used. We simulated data as before under scenario 1 and considered only IFS designs for simplicity. (One stratum corresponds to a SRS design.) To compute the optimal strata cut points we used a built-in algorithm in the stratifyR package (Reddy and Khan, 2018). Due to its complexity, the algorithm had difficulties converging when 10 strata were used; in this case, we manually selected strata boundaries such that approximately the same number of subjects were sampled from each stratum, as discussed in Section 4.1.3. The empirical variance was substantially reduced when we moved from 1 stratum (SRS) to 3 strata (as already seen in Table 2). The empirical variance also decreased when going from 3 to 4 to 5 strata, but to a lesser extent. For all values of β₁, efficiency using 10 strata was slightly better than 5 strata, but 10 strata were much more computationally challenging to create.

FIGURE 1.

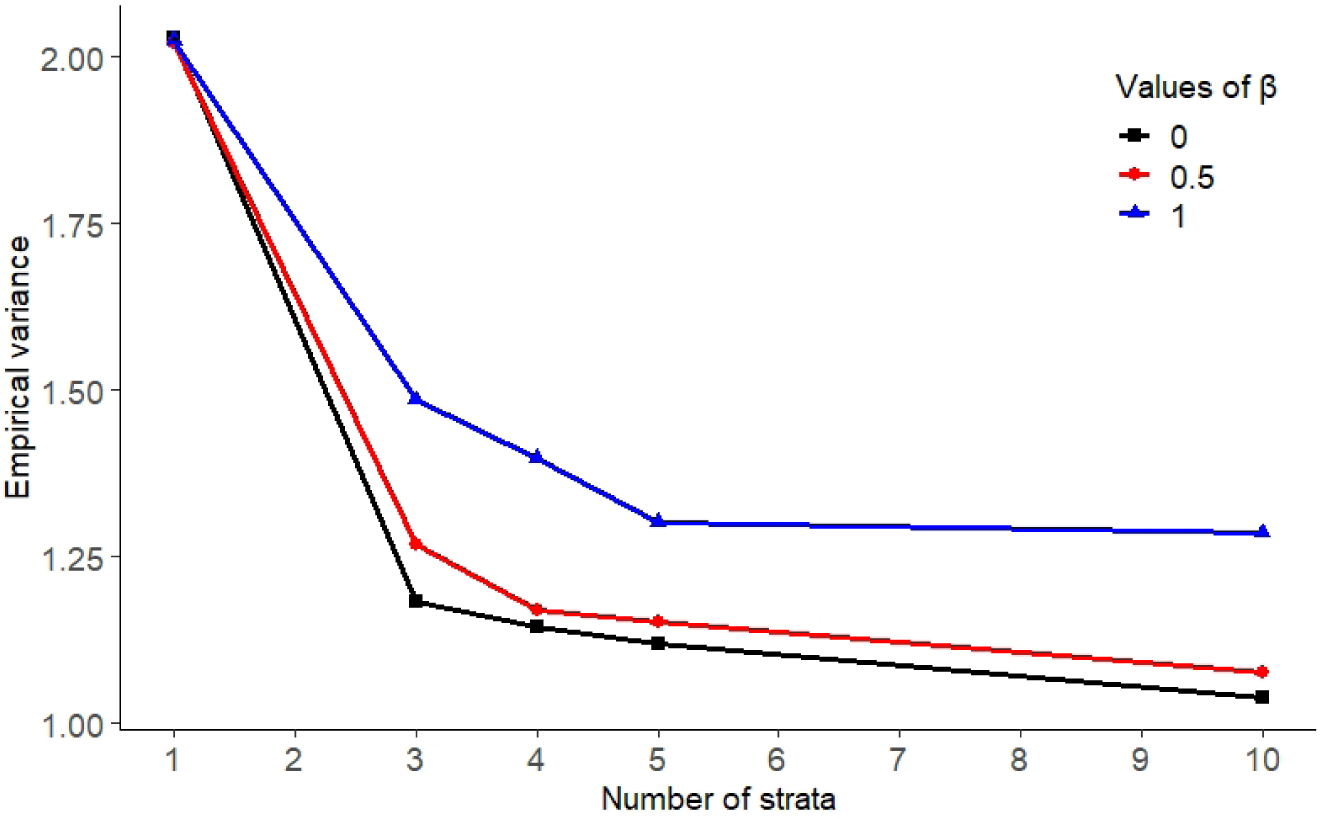
Empirical variance (×10³) for IPW estimator for different values of β₁ and different number of strata.

We also varied strata boundaries to investigate optimal strata cut-points / boundaries. We generated data as before under scenario 1 and fixed the number of strata to 3. We focused on IPW with IFS sampling. The strata boundaries were selected to be symmetric with respect to the percentiles of the stratification variable. They varied from (10%, 90%) to (25%, 75%), with increments of 2.5%. The empirical variances of ${\widehat{\beta }}_1$ after 3,000 Monte Carlo simulations are displayed in Figure 2. We see that there is a clear minimum around the percentiles (17.5%, 82.5%). This setting corresponds, as expected from Subsection 4.1.3, to the cut-off points in which the product of N_k s_k, the number of subjects in stratum k and the standard deviation of the phase-1 influence function, is approximately constant for k = 1, 2, 3.

FIGURE 2.

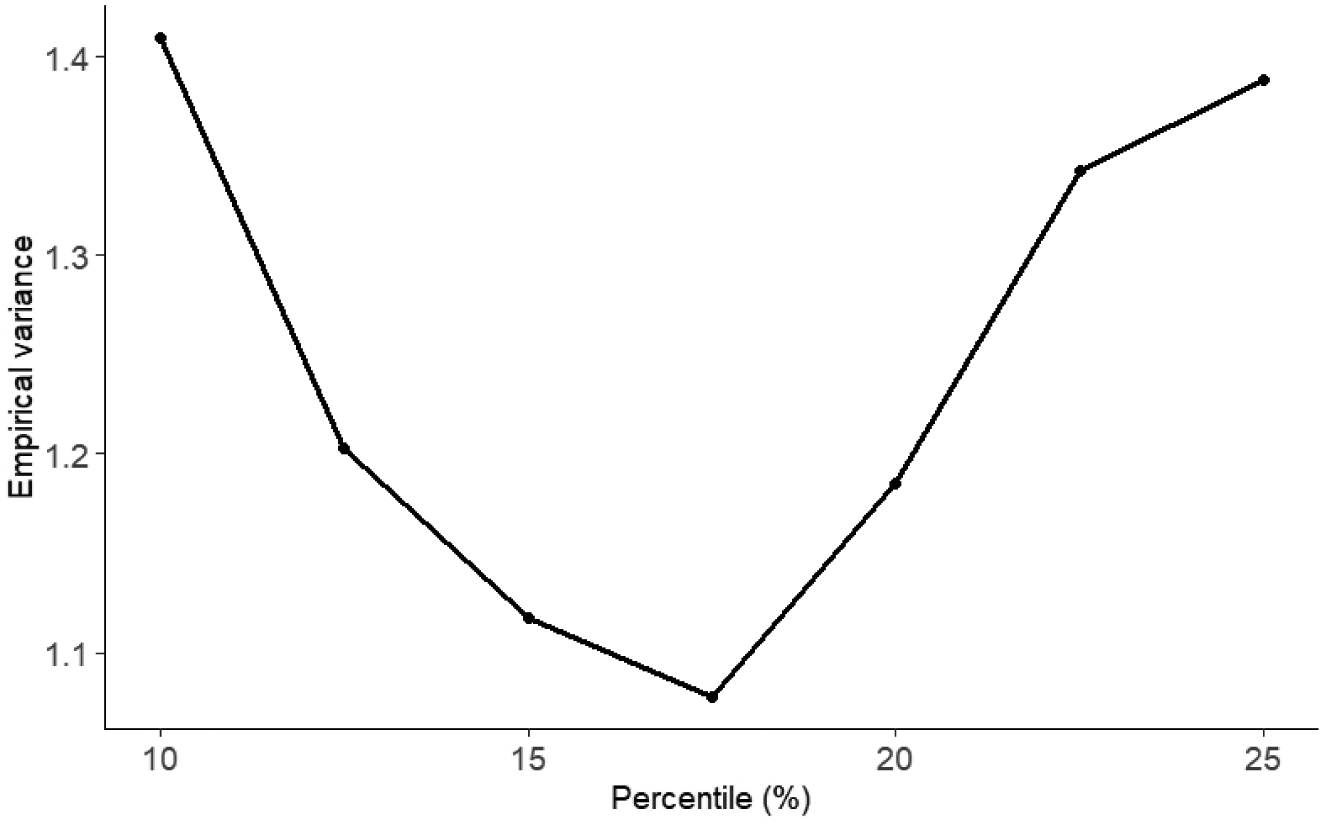
Empirical variance (×10³) for IPW estimator for 3 strata, for β = (1, .5, 1) and different strata boundaries. We considered symmetrical strata, with cut-off points at the qth and (1 − q)th percentiles.

5.2.2 |. Generalized raking estimators

Table 2 also shows the empirical variance of generalized raking estimators for the various design-based sampling schemes. As expected, generalized raking estimators were much more efficient than their IPW counterparts except in scenario 3, where there was little correlation between X* and X so the benefits of raking were expected to be minimal. However, it is a little more difficult to see patterns in the results comparing sampling designs when using generalized raking estimators. Stratifying based on the residuals (RS-D), weighted residuals (WRS-D) or outcomes (ODS-D) seemed to result in the most efficient estimators.

The lack of efficiency when stratifying on IFS may be due in part because information from the phase-1 influence function is already being used in the analysis as an auxiliary variable to calibrate the design weights so that, in a sense, stratifying on this variable is redundant. However, it may also be due to the relatively poor correlation between the error-prone phase-1 influence function and the true (typically unknown) influence function. For example, in scenario 1 where X and X* are highly correlated, the correlation between the two influence functions is about 0.83 when β = 0 and below 0.70 when β = 1. These are well below the correlation of 0.90 recommended by Särndal et al. (2003) for efficient stratification. To verify, we investigated performance of generalized raking estimators using the phase-1 influence function as the auxiliary variable but stratifying using the true influence function. We simulated data under scenarios 1 and 2 with β₁ = 0 and 1. Estimates using the true influence function as the stratification variable were substantially more efficient with empirical standard errors that were 30% to 50% smaller than those using the phase-1 influence function (see Table 3). Further investigation showed that stratifying on the error-prone IF often led to strata there were very different than those that we would have obtained had the true influence function be used as a stratification variable (see Figure 3).

TABLE 3.

Empirical variance (×10³) for ${\widehat{\beta }}_1$ estimated via generalized raking under IFS and IFS_r, where cor(IF_r, IF_true) = r, for β = 0 and 1, respectively.

β 1	IFS	IFS70	IFS80	IFS90	ifs TRUE	IFS	IFS70	IFS80	IFS90	ifs TRUE
Scenario 1, ${\sigma }_U^2=(0.5,0.5)$						Scenario 2, ${\sigma }_U^2=(1,1)$
IPW
0	1.235	1.483	1.287	1.065	0.821	1.419	1.527	1.277	1.092	0.819
1	1.582	1.527	1.334	1.075	0.804	1.793	1.828	1.341	1.121	0.812
Generalized Raking
0	0.985	0.977	0.920	0.851	0.711	1.238	1.169	1.037	0.919	0.748
1	1.381	1.169	1.062	0.909	0.738	1.657	1.518	1.189	1.027	0.783

FIGURE 3.

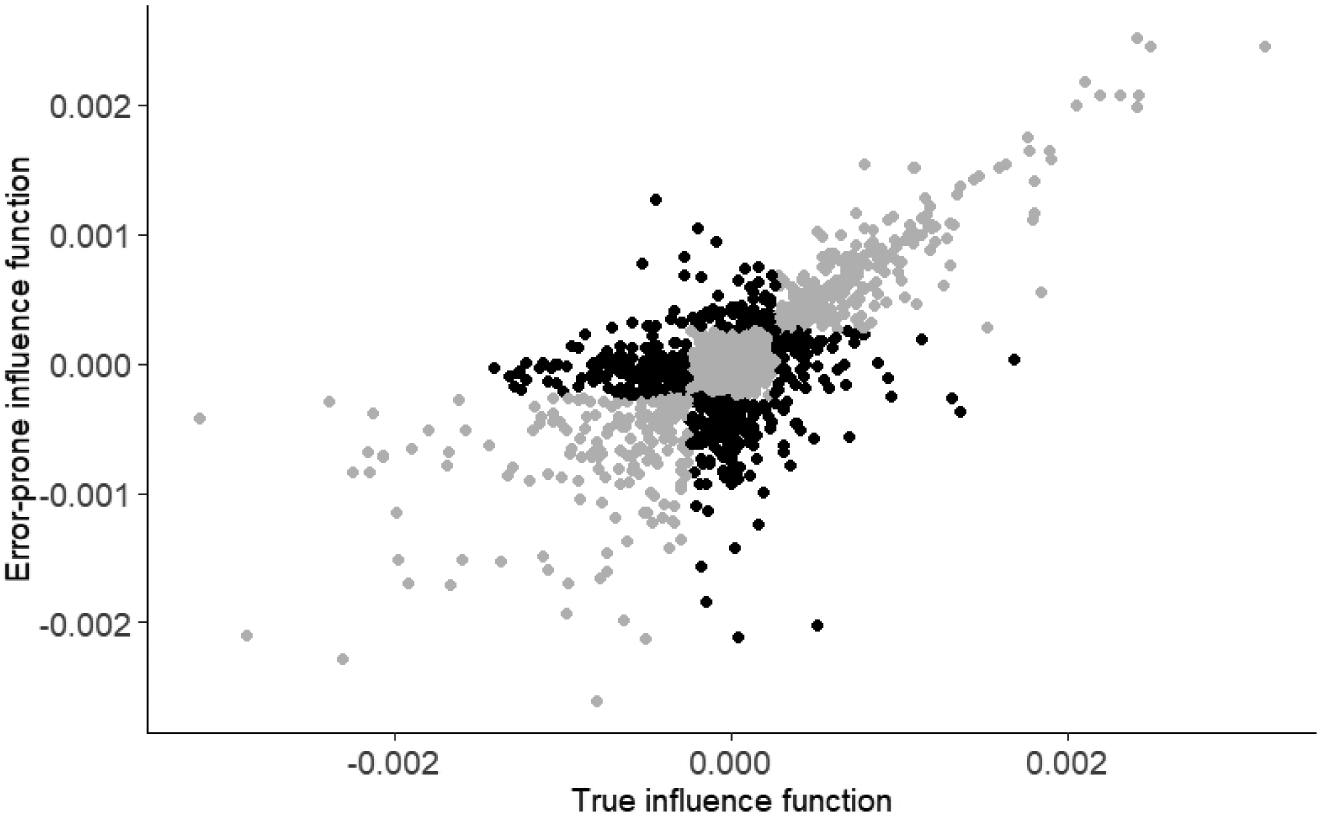
Overlap between the true and error-prone influence functions. Grey dots represent observations that were classified into the correct strata, with respect to the unknown true IF, by the error-prone IF.

Of course, the true influence function is not known and without prior information we cannot compute a better estimated influence function than that based on the error-prone phase-1 data. However, these results suggest that more efficient designs may be possible if we employ multi-wave sampling schemes (McIsaac and Cook, 2015; Chen and Lumley, 2020). In short, one could sample and validate n′ subjects (for n′ < n), compute the influence function for these subjects, use this information to estimate the influence function for the remaining N − n′ subjects, and then select the remaining n − n′ records to validate based on these estimated influence functions. This strategy may potentially lead to influence functions that are closer to the truth than the error-prone ones and therefore more efficient estimation. Multi-wave sampling could also be useful in conjunction with other designs. However, as multi-wave sampling schemes require an extra step and may differ substantially from those discussed in this manuscript, we do not pursue them further here.

5.3 |. Simulation results for model-based estimators under sampling schemes constructed for design-based estimators

Both the theory and simulations show that the optimal design is specific to the inference procedure. As the optimal sampling for design-based estimators will sample roughly the same amount of data from each stratum, the validation data may differ substantially from that obtained via model-based designs. An interesting comparison is to see how much efficiency is lost if we apply model-based estimators for sampling schemes that were constructed for design-based estimators. Figure 4 shows the results for scenarios 1 − 4 described above for IPW, Raking and MI estimators. We restrict the figure to MI only, as the results were generally similar to those obtained from SPMLE. IPW and Raking estimators are computed under designs that were optimal for IPW estimators as well as under SRS. MI is computed for SRS as well as for designs that were optimal for IPW and for likelihood-based estimators.

FIGURE 4.

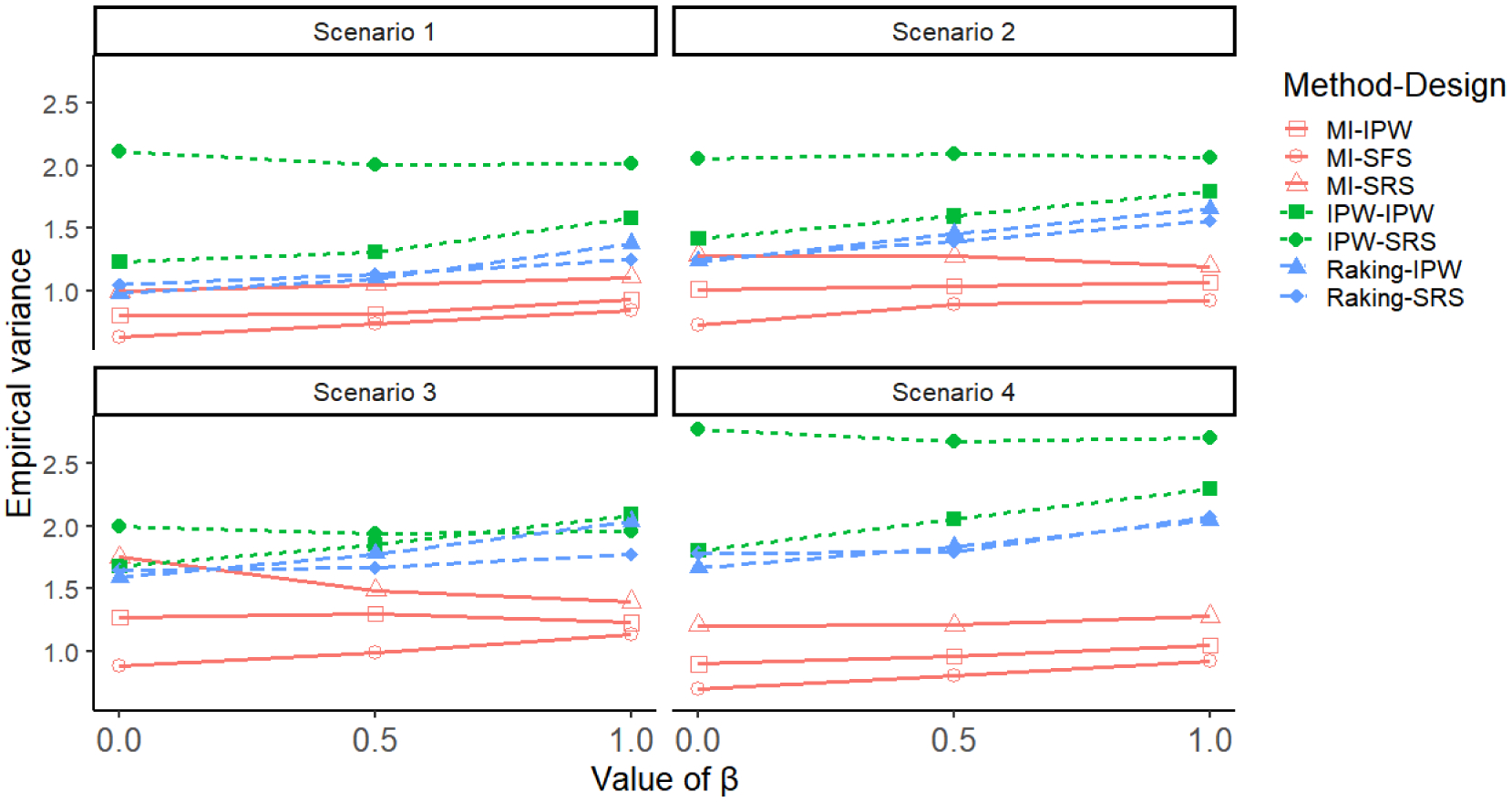
Empirical variances for MI, IPW and raking estimators, for all 4 settings. IPW, raking and MI were applied to data collected via the IPW optimal design discussed in Section 4 and are denoted by IPW-IPW, raking-IPW and MI-IPW, respectively. IPW-SRS, raking-SRS and MI-SRS denote IPW, raking an MI applied to data obtained via simple random sampling (SRS), respectively. MI-SFS corresponds to MI applied to data obtained from the model-based SFS design discussed in Section 3.

As depicted in Figure 4, MI was more efficient than the IPW and generalized raking estimators under properly specified models, even when the sampling scheme was optimal for IPW estimators. As expected, applying MI under SFS led to the most efficient estimates, in particular when the effect size was close to 0. However, applying MI to data obtained from designs that were optimal for IPW still led to efficient estimation, without too much loss in efficiency when compared to those using SFS, and improvements in efficiency when compared to MI applied to the commonly employed SRS. Raking was more efficient than IPW, and its efficiency was impacted less by the sampling strategy than that of other estimators.

These results illustrate the well-known efficiency loss of design-based estimators. However, design-based estimators are more robust to model misspecification, and have been shown to have lower mean squared error than model-based estimators under minor misspecifications (Han et al., 2019). In our simulations the true model was correctly fitted in all cases. A study of the impact of model misspecification on the various designs and estimators is beyond the scope of this manuscript. Because model-based estimators can be applied to optimal design-based designs with little loss in efficiency, whereas design-based estimators cannot be applied to optimal model-based designs, one might favor using design-based designs because they allow the analyst more flexibility while still improving efficiency (McIsaac and Cook, 2014).

6 |. CASE STUDY

The Vanderbilt Comprehensive Care Clinic (VCCC) is an outpatient clinic for people living with HIV. Patient information including demographics, laboratory values, medications, and clinical outcomes are entered into an electronic health record (EHR) system. The VCCC validates all of their EHR data that is used for research, meaning that a team goes through all key variables and checks the validity of data extracted from the EHR by comparing it to source file documents. All VCCC patient records have been validated, leading to two complete datasets: one with error-prone variables directly pulled from the EHR and another with fully-validated variables based on chart review. These two datasets allow us to explore settings in which some variables are assumed to be observed with no errors (so that only validated values are used), while some other variables are assumed to be observed with errors and validated for a subsample only (so that both unvalidated and validated values are used for analysis).

We aim to estimate the association between viral load at antiretroviral therapy (ART) initiation (baseline) (VL₀) and CD4 count at 1 year after ART initiation (CD4₁), adjusted for CD4 at baseline (CD4₀) and race (white or non-white). Viral load is log₁₀-transformed and CD4 at baseline and 1 year are both square root-transformed. We assume for this exercise that CD4 counts and race were correctly observed, with no errors. That is, only the validated values are used. On the other hand, we use the error-prone, unvalidated values of baseline viral load, ${\text{VL}}_0^{*}$. Therefore, the phase-1 sample consists of N = 1518 records of $Y=\sqrt{CD{4}_1}$, $X^{*}={\text{log}}_{10}\left(V{L}_0^{*}\right)$, $\left(Z_1,Z_2\right)=\left(\sqrt{CD{4}_0},\text{race }\right)$. Our goal is to estimate β₁ in the model

$$E\left(Y\mid X,Z_1,Z_2\right)={\beta }_0+{\beta }_{1}X+{\beta }_2{Z}_1+{\beta }_3{Z}_2,$$

where X =log₁₀(VL₀) is the validated baseline viral load, which we assume is unknown except for some phase-2 sample of records.

To estimate β₁, we consider various phase-2 sample designs for obtaining n (for n = 250 and n = 500) validated values of the baseline viral load. All designs will be compared in terms of bias (defined as the difference from the estimate based on full data validation) and width of the associated 95% confidence intervals. For model-based estimators we consider SRS, ODS, RS, WRS, and SFS. For design-based estimators we consider SRS, ODS-D, RS-D, WRS-D, and IFS. Recall that for model-based methods, ODS means sampling the extremes of the outcome, RS means sampling the extreme of the phase-1 residuals, etc. For design-based methods, ODS-D means that the outcome variable was used to stratify the data, RS-D means that the phase-1 residuals were used to stratify, etc. For design-based designs, once the stratification variable and the number of strata were chosen, strata boundaries were defined as described in Section 4.1.3 using the standard deviation of the error-prone influence function, and subjects were then selected via Neyman allocation. As before, the error-prone influence function was used to calibrate the weights in generalized raking. The results based on 3 strata and 1000 Monte Carlo simulations are displayed in Tables 4 and 5.

TABLE 4.

Bias and width of confidence interval for estimating β₁ for designs based on model-based estimators.

	n	SRS	ODS	RS	WRS	SFS
		MI
bias	250	−0.046	−0.001	−0.006	−0.008	0.003
95% CI width		0.263	0.233	0.180	0.179	0.185
bias	500	0.028	0.056	−0.015	−0.016	−0.000
95% CI width		0.204	0.204	0.169	0.169	0.168
		SPMLE
bias	250	0.015	−0.049	−0.010	−0.010	−0.002
95% CI width		0.211	0.204	0.185	0.185	0.196
bias	500	−0.039	−0.019	−0.017	−0.017	−0.006
95% CI width		0.204	0.193	0.176	0.176	0.173

Note: For n = 250, 15 sieves (8 and 16 for SFS, for Z₂ = 0 and 1 respectively), cubic, equally spaced; for n = 500, 20 sieves (10 and 20 for SFS, for Z₂ = 0 and 1 respectively), cubic, equally spaced. Abbreviations: SRS: Simple random sampling; ODS: Outcome-dependent sampling; RS: Residual sampling; WRS: Weighted residual sampling; SFS: Score function sampling; MI: Multiple imputation; SPMLE: Semiparametric maximum likelihood estimator.

TABLE 5.

Bias and width of confidence interval for estimating β₁, for designs based on design-based estimators.

	n	SRS	ODS-D	RS-D	WRS-D	IFS
		IPW
bias	250	−0.012	0.002	0.001	−0.000	−0.002
95% CI width		0.429	0.416	0.372	0.376	0.349
bias	500	−0.034	−0.006	0.004	0.010	−0.004
95% CI width		0.306	0.296	0.266	0.261	0.245
		Generalized Raking
bias	250	0.008	−0.005	−0.003	0.001	−0.005
95% CI width		0.255	0.252	0.216	0.221	0.225
bias	500	−0.007	0.010	0.001	−0.000	0.001
95% CI width		0.212	0.205	0.183	0.178	0.176

Note: SRS: Simple random sampling; ODS-D: Stratification based on the outcome; RS-D: Stratification based on the phase-1 residuals; WRS-D: Stratification based on the phase-1 weighted residuals; IFS: Stratification based on the influence function of the target parameter with X* replacing X; IPW: Inverse probability weight.

To provide context, in the full validated analysis using all 1518 validated records ${\widehat{\beta }}_1=0.24(95\%\text{CI}=(0.16,0.33))$. The associated residual plots are depicted in the Supplementary Material and suggest that the proposed linear regression is likely appropriate. The naive analysis regressing X* instead of X results in ${\widehat{\beta }}_1=0.19(95\%\text{CI}=(0.11,0.28))$. The estimated standard deviations of X, U = X* − X, and Y | X, Z₁, Z₂ are 2.48, 1.13, and 3.88, respectively, suggesting that the measurement error for baseline viral load was moderate and X* was a fair surrogate for X (cor(X, X*) = 0.894).

For MI and SPMLE estimators (Table 4), WRS, RS, and SFS all resulted in efficient estimation. For the IPW estimators, IFS was the most efficient (Table 5). For the generalized raking estimators, IFS, RS-D, and WRS-D were all comparable. Again, it is worth noting that WRS and WRS-D required extra information from the whole population to estimate var(X | X*, Z₁, Z₂), so it is arguably not fair to compare these designs to the others which only depend on phase-1 data. As we saw in our simulations, of all the designs, simple random sampling (SRS) was the least efficient. This highlights once again the benefits of better study design, which come with no added costs and may lead to substantial efficiency gains. As expected, the model-based estimators resulted in the narrowest confidence intervals, followed by generalized raking, and IPW. Bias was fairly small for all settings, although it was particularly low for the generalized raking estimators.

7 |. CONCLUSION

In this paper we focused on the classical measurement error problem with a mismeasured covariate. Unlike most studies in the literature, we did not focus on estimation, but on design of the validation study. In practice, a simple random sample is usually used to select observations for validation, but this design is typically suboptimal. We considered various sampling schemes that were motivated by the close relationship between validation studies and classical two-phase studies, and compared their precision to estimate the parameter of interest. Our simulations suggest that careful consideration at the design stage can lead to much more precise estimates of the parameter of interest than simple random sampling. These gains in efficiency come at no extra cost to the study.

Not surprisingly, the search for efficient designs is highly dependent on the method used for analysis. Different methods have different estimating procedures and thus lead to different designs to optimize efficiency. We considered model-based (i.e., MI and SPMLE) and design-based (i.e., IPW and generalized raking) methods in this paper. For model-based estimators, extreme tail sampling of the weighted residuals (WRS) was most efficient when β₁ = 0 (Tao et al., 2019). However, the weighted residuals cannot be computed without prior data or a pilot sample, so in their absence we recommend sampling the extremes of the residuals (RS) or sampling the extremes of the score function (SFS), which are both computable using only the phase-1 data. RS would be favored if β₁ is thought to be close to zero or if X* is a poor surrogate for X. SFS would be favored if β₁ is likely away from zero and X* is a fair surrogate. For design-based designs, we recommend creating 3–5 strata based on the phase-1 influence function, selecting strata boundaries such that the standard deviation of the phase-1 IF times the number of subjects in each stratum is approximately constant across strata, and then randomly sampling an equal number of subjects to validate in each stratum. The closer the phase-1 IF is to the true IF, i.e., the closer X* is to X, the closer this sampling strategy will be to the optimal sampling strategy.

There is clearly room for additional research in this area. The optimal sampling strategy for model-based designs is not analytically tractable without simplifying assumptions. Our proposed SFS is somewhat ad hoc and other designs may be better in other settings. For design-based estimators, we studied optimal designs for IPW estimators; focusing on generalized raking may lead to different designs. Multi-wave sampling with an intermediate validation step of size n′, before validating all n subjects, seems like a particularly promising direction for future research given that the optimal design often depends on information that can only be known from prior data or a pilot sample (McIsaac and Cook, 2015; Han et al., 2020; Chen and Lumley, 2020). Multi-wave sampling could improve IFS and SFS designs by using the pilot sample to improve estimation of the influence function. It also provides a way to estimate var(X | X*, Z)^1/2, allowing the weighted-residual designs to be applied in practice. As pointed out by an anonymous referee, having this intermediate step could also allow a combination of IFS/SFS and WRS-D/WRS designs, which may lead to efficiency gains, in particular when β₁ is close to the null. Adding this intermediate sampling step also raises interesting questions with respect to sample size allocation, for example determining what fraction of the data should be used to construct this intermediate step. Thus, a multi-wave sampling scheme may lead to different designs from those addressed in this manuscript and warrants additional investigation.