Abstract
Increasingly, medical research is dependent on data collected for non-research purposes, such as electronic health records data. Health records data and other large databases can be prone to measurement error in key exposures, and unadjusted analyses of error-prone data can bias study results. Validating a subset of records is a cost-effective way of gaining information on the error structure, which in turn can be used to adjust analyses for this error and improve inference. We extend the mean score method for the two-phase analysis of discrete-time survival models, which uses the unvalidated covariates as auxiliary variables that act as surrogates for the unobserved true exposures. This method relies on a two-phase sampling design and an estimation approach that preserves the consistency of complete case regression parameter estimates in the validated subset, with increased precision leveraged from the auxiliary data. Furthermore, we develop optimal sampling strategies which minimize the variance of the mean score estimator for a target exposure under a fixed cost constraint. We consider the setting where an internal pilot is necessary for the optimal design so that the phase two sample is split into a pilot and an adaptive optimal sample. Through simulations and data example, we evaluate efficiency gains of the mean score estimator using the derived optimal validation design compared to balanced and simple random sampling for the phase two sample. We also empirically explore efficiency gains that the proposed discrete optimal design can provide for the Cox proportional hazards model in the setting of a continuous-time survival outcome.
Keywords: Mean score method, Neyman allocation, pilot study, measurement error, surrogate variable, auxiliary information
1. Introduction
Error-prone exposures are common in many epidemiological settings, such as clinical studies relying on electronic health records (EHR), medical claims data, or large observational cohort studies where a gold standard measure was not collected on the full cohort. In EHR settings, data are not collected for research purposes and exposures of interest frequently must be derived using a computer-derived algorithm that is prone to error. For example, whether someone has a co-morbid condition, such as hypertension or diabetes, can be difficult to classify correctly with EHR data, since biomarkers used to determine disease status need to be taken in context of other information (e.g. whether the patient fasting or on medications that affect the biomarker) and that may be difficult to abstract accurately in an automated fashion. However, it may be possible to obtain a validated or gold standard exposure on a subset of subjects by a careful examination of records or by enrolling a subset in a research study. In large studies, a gold standard measure for an exposure of interest may be too expensive or impractical to obtain on everyone, and cheaper surrogate information may be obtained instead. For example, self-reported family history of a certain disease is collected on a cohort when genotype is truly of interest, but due to cost is only available on a subset.
When measurements of key exposures are prone to errors, statistical estimation of disease-related risk factors can be biased and inference unreliable. Performing validation on a subset of individuals, on which both the error-prone and validated data are obtained, can be a cost-effective way to obtain the data necessary to inform measurement error correction methods. Two-phase sampling has been widely used for a number of settings in clinical and epidemiological studies with budgetary constraints. The first sampling phase includes readily available data (e.g. electronic health records data) on all study subjects, and the second phase includes additional information on a subsample of records (e.g. extensive chart validation of a key exposure variable).
The efficiency of two-phase sampling can vary substantially based on the selection of the second phase sample. For logistic regression, Breslow and Chatterjee1 showed stratification of the phase two sample on the outcome and covariates with equal numbers per stratum performed well and better than stratifying on the outcome or covariates alone. When the outcome and error-prone exposure are categorical, the mean score method2,3 can be used to derive regression parameter estimates that have been corrected for measurement error and can improve efficiency over the complete case analysis by incorporating information from auxiliary data. For subjects not included in the phase two sample, the mean score approach imputes the average score contribution from those validated subjects whose observed phase one data match that of the unvalidated subjects. Further, the mean score approach provides a closed-form expression for the optimal phase two sampling strategy by providing the proportion of the validation sample that should be allocated into each outcome-exposure stratum to minimize the variance of a target regression parameter for a fixed validation subset size.3 McIsaac and Cook4 compared response-dependent two-phase sampling designs for the setting of a binary outcome when both the true and auxiliary covariates were also binary. They found that the mean score estimator was an efficient approach, even when the model used to derive the optimal design was misspecified. They also found that the mean score optimal design improved the efficiency of other estimation approaches, such as maximum likelihood.
For survival outcomes, however, the focus of most of the previous work on two phase sampling has been on estimation and hypothesis testing and not design. Lawless5 reviewed two-phase estimators for outcome dependent sampling and failure time data, and mentioned that efficiency can be gained by sampling extremes of the outcome, those with early events and late censoring. Tao et al.6 developed optimal two-phase sampling designs for full likelihood estimators of general regression models, but these designs are only optimal under the null assumption that the regression coefficient for the expensive/mis-measured exposure of interest is zero. While this framework in principle applies to the Cox proportional hazards regression model, they require estimation of several nuisance parameters related to the conditional distribution of expensive covariate given the surrogate, as well as a potentially infinite-dimensional nuisance parameter related to the partial likelihood, and their performance have not yet been studied for survival outcomes.6,7
In this study, we consider an extension of the mean score method to handle survival outcomes, in which error-prone exposures are treated as auxiliary variables. Specifically, we first collect phase one data that consist of survival data plus auxiliary information available on the full cohort. Next, the phase two subset of individuals is selected to precisely measure key exposures of interest, where we can exploit the complete data likelihood. To take advantage of the mean score approach, we will consider a discrete-time survival model. Discrete survival data are natural for settings where the occurrence of an event is monitored periodically and occur frequently in clinical studies where there is routine follow-up at fixed intervals. We develop an application of the mean score method to the discrete proportional hazards model.
We will also extend the work of Reilly et al.3 to derive an optimal sampling design for the mean score approach, which minimizes the variance of the regression parameter estimation for a given size of the validation subset. This approach requires an estimate of several nuisance parameters, which, in the absence of external estimates, can be estimated with internal pilot data. We consider a multi-wave sampling strategy that in the first wave obtains a pilot phase two sample to estimate the parameters necessary to derive the optimal design and then for the second wave adopts an adaptive sampling strategy for the remaining phase two subjects to achieve the optimal allocation. McIsaac and Cook8 considered a similar approach for binary outcomes. Finally, we will consider how the derived optimal design can be advantageous for a continuous time analysis.
We compare the relative efficiency of our mean score estimator under simple random sampling, balanced sampling and the proposed optimal design in numerical simulations. We also examine the mean squared error and its bias-variance decomposition, illustrating the efficiency gains of the mean score approach over the complete case estimator that is based only on the subset of individuals in the phase two sample. The proposed method is further illustrated with data from the National Wilms Tumor Study (NWTS), in which a validated and error-prone exposure were available on everyone, which enables us to subsample the validation data repeatedly, so that we evaluate the performance of different two-phase sampling strategies in the applied setting. In the context of this example, which had a continuous survival outcome, we study the efficiency gains of using the proposed optimal design of the discretized outcome for the usual continuous-time analysis. We also investigate how different allocations of the pilot sample affect the efficiency gains of the mean score estimator, depending on how individuals with censored versus observed outcomes are sampled. Finally, we provide some concluding remarks on the advantages of the mean score estimator in this setting and discuss directions for future work.
2. The mean score method for discrete-time survival models
2.1. Setup and notation for the discrete-time model
Let T be a discrete random variable. Denote the j-th discrete value of T by tj and write λ0j = λ0(tj), where λ0 is the baseline hazard function for T defined by λ0(tj) = P(T = tj∣T ≥ tj) for j ∈ J, where J is the index set for the discrete times with positive mass. We assume the time to event response T is associated with a d-dimensional time-fixed covariate vector X = (X1,…, Xd)⊤ such that the conditional hazard function λ(t∣x) = P(T = t∣T ≥ t, X = x) is given by
| (1) |
for some coefficient vector β = (β1,…, βd)⊤, where g : [0, 1] → R is a monotone transformation and . For example, the odds transformation yields the logit hazard model, where logit(λj(x)) = αj + β⊤x for αj = logit(λ0j) and λj(x) = λ(tj∣x). It follows that the likelihood function under the logit hazard model has the same representation as the logistic regression model such that the number of events at a time tj represents binomial outcomes with probability λj(x) for each j ∈ J.9 The complementary log transformation g2(u) = −log(1 − u) gives a proportional log-survival model log(Sj(x)) = log(S0j)exp(β⊤x), where Sj(x) = P(T ≥ tj∣X = x) and S0j = S0(tj) for the baseline survival function S0 for T. Kalbfleisch and Prentice10 provide further details.
We consider that T may be subject to random censoring prior to the finite maximum follow-up time of τ < ∞. For a random censoring time C, independent of T, let Y = min{T, C} be the observed censored survival time and be the event indicator. We assume that are independent and identically distributed and will not be completely observed on all subjects as N-random copies of (Y, Δ, X). Instead, are the data available for all subjects in the first phase of a study, where Z = (Z1,…, Zq)⊤ are discrete surrogates or auxiliary variables associated with X. Complete data for the likelihood are observed on the phase two sample, denoted by , where is a subset of {1,…,N} having the cardinality of n. For example, the auxiliary variables Z might be error-prone discrete measures of X while X may or may not be discrete.
We allow for settings where some components of X are available on all subjects, such as sex or other demographic information ascertained in the first phase of the study. For this setting, we may introduce a slight abuse of notation writing X = (XC, XI) and Z = (XC, A), where XC are the components of Xi observed on everyone, XI are the incomplete components of X not observed at the phase one, and A indicates a generic notation for auxiliary variables in the first phase of the study. In this case, denotes the set of subject indices for which the true covariates X are fully observed, with XI sampled in the second phase of the study, and the auxiliary phase one variables are limited to A.2,8
Unlike previous literature,7,11-13 we note that the model (1) does not include auxiliary variables as predictors, but rather Z is a surrogate by the Prentice criterion.14 That means the likelihood function L1 (θ; Y, Δ, X, Z) equals L1(θ; Y, Δ, X), where θ is the collection of parameters involved in (1). Thus, the complete information for θ is carried by (Y, Δ, X), while E{logL1 (θ; Y, Δ, X) ∣ Y, Δ, Z} may represent extra information of (Y, Δ, Z) compared to likelihood-based inference using only complete case data for (Y, Δ, X). In this paper, we consider the mean score method, which is valid when the validation subset for the phase two sample is a random sample from the full cohort, possibly stratified on the information obtained by the phase one study.2,8 Therefore, we use the log-likelihood from all available observations written by
| (2) |
where h(x∣z) denotes the conditional density function of X given Z = z and indicates a set of (N – n) indices for individuals whose complete covariates are not available. For an individual i and time j, we define the observed event indicator and denote subject i’s censored survival time index by J(i) = argmin{j ∈ J : Yi = tj} for 1 ≤ i ≤ n. Thus, Dik = 0 for all k < J(i). Then, it follows that the log-likelihood function given (Yi, Δi, Xi) can be written by
| (3) |
for each 1 ≤ i ≤ n. In the above equation, we used the fact that L1(θ; Y, Δ, X) = S(Y∣X)λ(Y∣X)Δ(1 – λ(Y∣X))1–Δ and the conditional survival function Sj(x) = P(T ≥ tj∣X = x) was calculated by for j ≥ 2, together with S1 (x) = 1 by definition.
2.2. The mean score method
We apply the mean score method2,3 to the conditional hazard model (1) when auxiliary variables are discrete. Employing the Expectation-Maximization (EM) technique15 with equations (2) and (3), we may find the maximum likelihood estimator of θ. However, h(x∣z) is generally unknown and a parametric approach for the estimation of h(x∣z) may result in inconsistent inference of θ in likelihood-based methods. Lawless et al.11 introduced a semi-parametric method, estimating the conditional density function h(x∣z) nonparametrically, such that the integration in (2) is replaced with a single-step approximation.4 Following the mean score approach, for those not in the phase two subset, we can replace the unobserved score contribution based on X with its expected value based on the observed phase one data. By replacing the expected value with an empirical mean, the semi-parametric estimation of θ can then be achieved by maximizing an inverse probability weighted log-likelihood
| (4) |
where is an empirical estimate of π(Yi, Δi, Zi), the sampling probability of the i-th individual selected into the validation subset, which can be consistently estimated by n(Yi, Δi, Zi)/N(Yi, Δi, Zi) as n and N increase.16 Here, n(y, δ, z) is the number of subjects in who have the same observations with (y, δ, z) in the first phase study; N(y, δ, z) is defined similarly to n(y, δ, z) with replacement of the index set with {1,…,N} of the full sample. We note a similar estimating equation was proposed based on the pseudo-likelihood method.17
Depending on the choice of transformation g in equation (1), different forms of score equations follow from the above weighted log-likelihood (equation (4)). In Supplementary Material Section A.2, we provide the detailed forms of the mean score equations and the associated Hessian matrices when the logit transformation g1 and the complementary log transformation g2 are used.
2.3. Connection to the Cox model for a continuous-time outcome
Our expectation that the optimal design for our discrete time proportional hazards model will also be advantageous for the continuous time Cox model is based on the connection between the parameters in these two models. For this, we briefly review this connection. For further discussion, see Kalbfleisch and Prentice.10
From the log-likelihood (3), we note that the logit hazard model is the canonical form of the discrete-time survival model (1) under the odds transformation , such that logit(λj(x)) = αj+β⊤x, where αj=logit(λ0j) is the logit transformation of the baseline hazard. However, we also note that any model with an arbitrary monotone transformation in equation (1) leads to a reparameterization of the logit hazard model. For example, suppose the complementary log transformation g2(u) = −log(1 – u) defines the true survival model. Then it can be easily seen that logit(λj(x)) = exp(eαj+β⊤x) – 1, where αj = log(−log(1 – λ0j)) is the complementary log-log transformation of the baseline hazard, and the application of the chain rule to equation (3) is followed by likelihood-based estimation of θ = (α, β), which is also equivalent to reparameterization of the logit hazard model.
In particular, if usual continuous-time survival outcomes are grouped into discrete disjoint intervals, this will lead to the conditional hazard model (1) for discrete-time outcomes with the complementary log transformation. To be specific, let λC(t∣x) be the conditional hazard function in the Cox model for the continuous-time survival outcome such that , where is the associated baseline hazard function. Suppose continuous-time survival events or censoring outcomes are grouped at one of a set of pre-determined disjoint time intervals (tj–1, tj], where t0 ≡ 0. Then, we may consider statistical inference for the conditional hazard on each interval. The conditional hazard on the j-th interval can be written as
| (5) |
for each j ∈ J.10 Since the conditional survival function SC(t∣x)= P(T > t∣X = x) is equivalent to in the Cox model, we note that represents the cumulative conditional hazard on the interval (tj–1, tj] and, under the proportional hazards assumption, it can be shown that
| (6) |
where is the associated cumulative baseline hazard on (tj–1, tj]. Thus, the cumulative hazard model (6) is directly connected with the discrete-time survival model (1) under the complementary log transformation, and the two models have the same regression coefficient β.
3. Adaptive sampling design for optimal estimation
We now consider phase two sampling designs that incorporate phase one data to improve efficiency. Specifically, we extend the optimal design for the mean score method derived by Reilly et al.3 to the discrete-time survival analysis setting. Furthermore, in the spirit of McIsaac and Cook,8 we propose an adaptive phase two sampling strategy. In Theorem 1, we first establish that the asymptotic variance of the mean score estimator depends on the sampling probability for the phase two validation subset.
Theorem 1 For each j ∈ J, let αj = g(λ0j) ∈ R be transformation of baseline hazards in equation (1). Suppose that the censoring time is bounded, that is P(C ≤ τ) = 1 for some fixed constant τ > 0, and that the conditional hazard functions λj(x) = λ(tj∣x) are bounded away from 0 and 1 for all x ∈ Rd. Under the regularity conditions in Supplementary Material Section A.1, the mean score estimator of θ = (α, β) solving the score equation of (4) is asymptotically normal such that as N → ∞, where with and Ω = E[{π(Y, Δ, Z)−1 – 1}Var(U1(θ)∣ Y, Δ, Z)] for the score function .
Suppose that we fix the sample probability for the validation subset by πV = E[π(Y, Δ, Z)], or empirically n/N. Then, the mean score estimator of θk, the k-th component of θ, is asymptotically efficient when the validation sampling probability π(Y, Δ, Z) is proportional to , so that we empirically assign the optimal sampling size for each (y, δ, z)-stratum
| (7) |
satisfying , where M[j,k] denotes the (j, k)-element of a matrix M. We note that equation (7) can be viewed as Neyman allocation maximizing the survey precision in stratified sampling.18 Such an optimal design can be also obtained by the Lagrangian multiplier method to minimize Σ[k,k] in Theorem 1, which equivalently minimizes the variance of the target parameter θk with respect to π(y, δ, z) under the constraint of a fixed-validation rate πV = E[π(Y, Δ, Z)], or empirically .
Note that the optimal sampling design depends on external information about population structure, namely IV and Var(U1(θ)∣y, δ, z), which are usually unknown. McIsaac and Cook8 introduced an adaptive procedure for multi-phase analyses such that one first draws a pilot sample for validation and then adaptively draws an additional validation set, write and , respectively. That is, the overall validation corresponds to the optimal design, where . Similarly, we consider an adaptive constraint on the final validation size, , where nPilot(y, δ, z) and nAdapt(y, δ, z) are sampling sizes on each (y, δ, z)-stratum for the pilot and adaptive validation, respectively.
We apply the Lagrangian multiplier method to minimize Σ[k, k] in Theorem 1 with respect to π(Y, Δ, Z) under the adaptive constraint. Then, the adaptive sampling design is given by
| (8) |
where is the estimated optimal sampling size of equation (7). Here, the information matrix IV and the conditional variance of the score function Var(U1(θ)∣y, δ, z) can be consistently estimated using the individuals in the phase two pilot sample. We employ inverse probability weighting to estimate IV by
| (9) |
The above equation (9) is also known as a Horvitz-Thompson type estimator,19 commonly used in survey sampling when there is a probability-based sample, such as outcome-dependant sampling.11,20 The Var(U1 (θ)∣y, δ, z) is estimated by the sample covariance matrix of the score function within each (y, δ, z)-stratum such that
| (10) |
where , for ℓ = 1, 2. The expressions for the score function and Hessian matrix of equation (3) for two discussed choices of the survival models can be found in Supplementary Material Section A.2.
Due to sparse observations or oversampled pilot data on some strata, we may not achieve practically the optimal design with equation (8) when or . In either case, we set nAdapt(y, δ, z) = 0 ∨ {N(y, δ, z) – nPilot(y, δ, z)} for the saturated strata and distribute the remaining validation allocation to the other strata proportional to the estimated optimal sampling sizes. This approach for handling saturated strata is similar to that of McIsaac and Cook,8 originally introduced by Reilly and Pepe.2
4. Numerical illustrations
In this section, we examine the performance of our proposed mean score estimator and adaptive phase two sampling procedure first by a computer simulation study. We then further illustrate the method with an analysis of data from the National Wilms Tumor Study (NWTS). For this example, the original survival outcome was continuous and so in addition to presenting the discrete time analysis, we consider whether the proposed phase two sampling procedure provided efficiency gains for the analysis of the continuous time outcome. We also provide further discussion on phase two sampling in the setting of intermittently censored outcomes. Data and source code in R (version 3.6.1) for our numerical studies are provided at https://github.com/kyungheehan/mean-score.
4.1. Simulation study
Here, we evaluate the empirical performance of the proposed mean score estimator for the discrete survival time setting via a simulation study. We also evaluate the degree to which the proposed adaptive validation design improves estimation performance compared to simple random sampling and a balanced design for several scenarios.
We consider the conditional hazard model (1) with the complementary log transformation g2(u) = −log(1 – u), where β = (log(1.5),log(0.7), log(1.3), −log(1.3))⊤. We assume survival status is observed at discrete times 0 < t1 < t2 < ⋯ < t10 < ∞. As previously mentioned in section 2.3, this model will estimate the same β as in the underlying continuous-time Cox proportional hazards model. We first generate a four-dimensional covariate vector X = (X1,…,X4)⊤, which consists of both continuous and binary variables. We simulate correlated covariates with a unit scale between 0 and 1, by first considering a multivariate normal random vector W = (W1,…,W4)⊤ with zero mean and Cov(Wj, Wk) = 0.3∣j–k∣, so that we put Xj = Qj(Φ(Wj)) for j = 1, 2 and Xj~Bernoulli(Φ(Wj)) for j = 3, 4, where Φ is the cumulative standard normal distribution function, and Q1 and Q2 are quantile functions of the beta distribution with pairs of the shape and rate parameters (2, 1.5) and (3, 3), respectively. By doing this, all Xj’s are correlated with each other, and particularly X1 and X2 are marginally beta random variables with Corr(X1, X2)≈0.290. Since continuous covariates are generally bounded in practice, the simulated continuous covariates (X1, X2)⊤ represent standardized covariates over the range of observations into unit intervals.
For discrete survival outcomes, we note that enables us to generate the discrete survival outcomes as multinomial random variables associated with covariates. To simplify the censoring mechanism in our simulation, we set a fixed censoring time C = t6 as the maximum follow-up for all subjects, so that we observe a truncated survival time Y = min{T, t6} and . It is worth mentioning that the proposed method also allows random censoring. An application of the method with a more complex censoring mechanism will be considered in section 4.2.
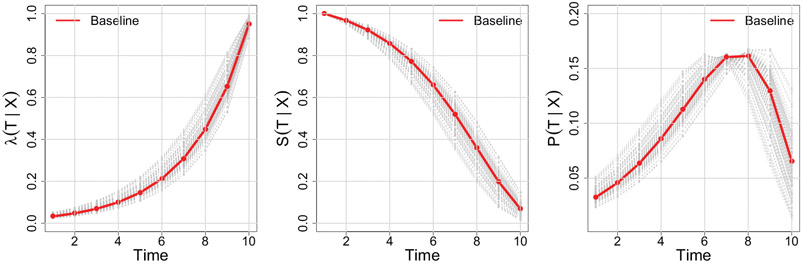
Next, we generate N-random copies of (Y, Δ, X), which will inform the benchmark full cohort analysis. We consider full cohort sizes N = 2000, 4000, 8000 in the simulation. By choosing different baseline hazards, we considered three scenarios of overall censoring rates with 30%, 50% and 70%. Here, we mainly refer to simulation results when the censoring rate is 50%, since we found that this setting fundamentally provides similar lessons with the other scenarios which can be found in the Supplementary Material Tables B.1 and B.2. Figure 1 illustrates the conditional hazard, survival and probability functions in our simulation settings.
Figure 1.
Illustrations of the simulation setting for the discrete-time survival model. The conditional hazard λ(tj∣x) (left) is demonstrated together with its associated survival S(tj∣x) and probability mass P(tj∣x) (middle and right), where λ(tj∣x) = P(T = tj∣T ≥ tj, X = x), S(tj∣x) = P(T ≥ tj∣X = x) and P(tj∣x) = P(T = tj∣X = x). The baseline functions are illustrated in red and gray solid lines show realization of conditional hazards, survival and probability functions associated with covariates for randomly chosen 100 subjects. The marginal rate of censoring over the maximum follow-up period t6 is P(T > t6)≈0.5.
We assume that direct observations of X1 are not available in the phase one sample of the cohort, but instead one observes a discretized and error-prone exposure Z such that
| (11) |
where is perturbation of X1 with an independent measurement error ε~N(0, 0.12). Let Zo be the true discretization of X1 defined similarly to Z by replacing with X1. For the assumed parameter values, the discordance or misclassified rate between Zo and Z was P(Zo ≠ Z)≈0.284 and this shows that Z is not only a discrete but also an error-prone surrogate of X1, and potentially associated with (X2, X3, X4). Finally, we set to be the phase one sample available on all subjects.
Efficient estimation of the regression coefficient of X1 is of interest and the optimal sampling allocations are designed to minimize the variance of the β1 estimate in our simulation study. Since the optimal sampling design (7) depends on nuisance parameters defined by the population structure, namely IV and Var(U1(θ)∣y, δ, z) in Theorem 1, we approximate their true values with empirical estimates obtained from an externally generated large sample of size N0 = 104 that was independent from the full cohort . We define the optimal sampling strategy based on these values as the oracle procedure and refer to Supplementary Material Section A.2 for some technical details for the derived optimal allocation. In practice, however, the oracle procedure is infeasible and so we are interested in evaluating the adaptive sampling design as described in Section 3. For this, we first sample a pilot validation subset and estimate the optimal sampling design together with the phase one sample . To accommodate all possible strata information in the first phase sample, we employ balanced sampling for the pilot study, with nPilot(Yi, Δi, Zi) equal for all {Yi, Δi, Zi}. We then estimate IV and Var(U1(θ)∣y, δ, z), as outlined at the end of the previous section. Next, we draw an additional validation subset for each stratum following equation (8), and the mean score method is finally applied to the two-stage analysis for the phase one sample and the adaptive phase two sample . We considered validation subset sizes of n = 200, 400, and 800 and took equal proportions for the pilot and adaptive samples.
Due to saturated strata, there might be some remaining validation size to be allocated, for example in the pilot study. In this case, we randomly select unvalidated subjects for the remaining allocation, which is also similarly applied to the adaptive sample. We note that the proportion of the pilot sample size to the adaptive entails a trade-off between precision of the nuisance parameters needed for optimal sampling design and efficiency gains from the adaptive validation when the final phase two sample size is fixed. Some preliminary simulations showed that the adaptive sampling design with nearly equal sizes of the pilot and adaptive samples usually produced robust and efficient estimates (data not shown), which is similar to observations made by McIsaac and Cook8 for the two-stage analysis with binary outcomes.
We compare our proposed adaptive sampling method, which we refer to here as mean score adaptive (MS-A), to the mean score method using the oracle procedure (MS-O) and to some other standard estimation methods for two-phase designs. The complete case analysis of fully randomly selected n-validation sample (CC-SRS) will give unbiased results. Since CC-SRS does not use auxiliary information of the first stage sample, we examine if the optimal design for the mean score method improves estimation performance of CC-SRS and evaluate efficiency gains from the two-stage analysis (MS-SRS). We also conduct design-based estimation with balanced sampling such that validation size is equally allocated to each (y, δ, z)-stratum of the first stage sample. Similarly to the proposed adaptive procedure, if there are some remaining individuals to be allocated after balanced sampling, due to saturated strata, we randomly sample the remaining from the unvalidated subjects to yield a final total phase two sample of n individuals. The design-based estimation with balanced sampling is given by a Horvitz-Thompson type estimator (MS-BAL), where sampling proportions of validation within strata are used for inverse probability weights as in equation (4). For our setting, we note that the inverse probability weighted (IPW) estimator is technically the same with the design-based mean score estimator which incorporates the balanced sampling weights pre-specified in the two-phase analysis.4 We implement the proposed mean score estimator with the adaptive sampling described above, estimating the necessary nuisance parameters from the validation subset (MS-A), and with the oracle procedure, plugging in the information obtained from a large dataset independently generated from the simulation (MS-O). Finally, we consider the full cohort analysis (Full-CC) based on fully observed data, as the benchmark performance, which empirically gives the upper bound of efficiency for the two-phase analysis, since the Full-CC uses the complete covariate information on all subjects.
We investigated two different aspects of varying sample sizes and conducted five simulation scenarios: (i) increasing the phase two sample size from n = 200, 400, 800 with a fixed full cohort size N = 4000, (ii) increasing the full cohort size from N = 2000, 4000, 8000 when the phase two sample size is fixed by n = 400. Table 1 summarizes the relative performance for estimation of β1. Compared to CC-SRS, MS-SRS had a reduction of the variance, which demonstrates efficiency gains of the mean score method from employing auxiliary information of the phase one sample. For n = 400 and 800, MS-A was more efficient than MS-SRS, whereas for n = 200, MS-SRS was more efficient. This suggests that n = 200 is too small in this setting to gain efficiency using adaptive sampling; this is reasonable as the optimal sampling allocation is based on estimates derived from a pilot sample half that size. MS-BAL had relatively inferior performance compared to MS-SRS and MS-A, and this was true across all scenarios studied. The MS-O had the smallest mean squared error (MSE) in all scenarios, as expected, and it turned out that the superior performance of MS-O mostly came from variance reduction. As the cohort sample size increased, the associated adaptive sampling design (MS-A) behaved closely to MS-O, which indicates that the proposed adaptive approach consistently approximates the oracle procedure. In the scenarios studied, increasing the phase two sample size was much more beneficial for efficiency gains for MS-A and MS-O, compared to the sample size increment of the phase one study. For example, MS-A achieved 60.7% (≈1 – 0.147/0.374) variance reduction while the validation rate increased four-fold from n = 200 to n = 800 given N = 4000 in the left three columns of Table 1. On the contrary, increasing the phase one sample size from N = 2000 to N = 8000 only produced 11.2% (≈1 – 0.190/0.214) improvement in the right three columns when n = 400 is fixed. This suggests that the performance of the proposed MS-A procedure is sensitive to the size of the phase two study, more so than the total cohort size for a fixed n.
Table 1.
Relative performance for the estimation of β1 is compared for (i) the complete case analysis with simple random sampling (CC-SRS); (ii) the mean score method with simple random sampling (MS-SRS); (iii) a design-based estimation with balanced sample, equivalent to the mean score (MS-BAL); (iv, v) the mean score estimation with adaptive sampling (MS-A) and the oracle sampling design (MS-O), for varying sample sizes.
| Sampling | Estimation | Criterion | Estimation performance by sample sizes |
|||||
|---|---|---|---|---|---|---|---|---|
|
N = 4000 |
n = 400 |
|||||||
| n = 200 | n = 400 | n = 800 | N = 2000 | N = 4000 | N = 8000 | |||
| Full cohort | CC | 0.094 | 0.094 | 0.094 | 0.129 | 0.094 | 0.067 | |
| Bias | 0.003 | 0.003 | 0.003 | 0.004 | 0.003 | 0.000 | ||
| 0.094 | 0.094 | 0.094 | 0.129 | 0.094 | 0.067 | |||
| SRS | CC | 0.470 | 0.330 | 0.228 | 0.324 | 0.330 | 0.321 | |
| Bias | 0.017 | 0.014 | 0.005 | 0.011 | 0.014 | −0.010 | ||
| 0.470 | 0.329 | 0.228 | 0.324 | 0.329 | 0.321 | |||
| MS | 0.332 | 0.220 | 0.155 | 0.237 | 0.220 | 0.200 | ||
| Bias | 0.053 | 0.035 | 0.004 | 0.020 | 0.035 | 0.027 | ||
| 0.330 | 0.217 | 0.155 | 0.236 | 0.217 | 0.198 | |||
| Balanced | MS | 0.400 | 0.278 | 0.194 | 0.276 | 0.278 | 0.265 | |
| Bias | 0.042 | 0.024 | 0.010 | 0.026 | 0.024 | 0.021 | ||
| 0.398 | 0.277 | 0.194 | 0.275 | 0.277 | 0.264 | |||
| Adaptive | MS | 0.374 | 0.197 | 0.147 | 0.214 | 0.197 | 0.190 | |
| Bias | 0.049 | 0.007 | 0.006 | 0.004 | 0.007 | 0.002 | ||
| 0.371 | 0.197 | 0.147 | 0.214 | 0.197 | 0.189 | |||
| Oracle | MS | 0.253 | 0.182 | 0.133 | 0.202 | 0.182 | 0.174 | |
| Bias | 0.009 | 0.003 | 0.005 | 0.012 | 0.003 | −0.005 | ||
| 0.252 | 0.182 | 0.133 | 0.202 | 0.182 | 0.174 | |||
Note: Results for the full cohort estimator based on complete data (Full-CC) are provided as a benchmark. Mean squared error (MSE) and its bias-variance decomposition are estimated from 1000 Monte Carlo replications, where the censoring rate was 50%. The adaptive and optimal sampling designs were for efficient estimation of X1 with β1 = log(1.5)≈0.405. In all adaptive sampling scenarios, we took equal proportions for the pilot and adaptive samples.
Simulation results for all regression parameters and various combinations of n = 200, 400, 800 and N = 2000, 4000, 8000 can be found in Supplementary Material Tables B.3-B.7. Comparing the relative performance of the methods for the other regression parameters, including those for the discrete baseline hazards, we found that the MS-O outperformed the other estimators for all model parameters. The oracle sampling design is infeasible in most practical situations; however, the two mean score estimators consistently showed the best performance for the target parameter among all other practical competitors. MS-A generally achieved the minimum mean squared errors for all parameters when the phase two sample size exceeded 200, compared to the other practical estimators, for the scenarios studied. For the setting where n = 200, the MS-SRS performed the best amongst the practical estimators. These results suggest that MS-A will perform well with respect to MSE for all model parameters, particularly the target and discrete proportional hazard parameters, for robust phase two sample sizes. For small phase two samples and similar censoring rates, the MS-SRS may be preferred.
4.2. Data example: The National Wilms Tumor Study
Wilms tumor is a rare renal cancer occurring in children, where tumor histology and the disease stage at diagnosis are two important risk factors for relapse and death. We consider data, reported by Kulich and Lin,21 on 3915 subjects from two randomized clinical trials from the National Wilms Tumor Study (NWTS).22,23 There are two measures of tumor histology, classified as either favorable (FH) or unfavorable (UH), one by a local pathologist and the other by an expert pathologist from a central facility. Because of the rarity of disease, local pathologists may be less familiar with Wilms Tumor and their assessment is subject to misclassification. The central assessment is considered to be the gold standard, or true histology in our analysis, and the local evaluations are considered surrogate observations for the central evaluation (sensitivity = 0.738, specificity = 0.983). Since histology for all subjects was validated by the central laboratory, NWTS data has been widely used to evaluate two-phase sampling methodology.1,21,24
We demonstrate our proposed mean score method for discrete-time survival in an analysis of relapse in this NWTS cohort. We assume that the local histology is available for all subjects in a first phase sample and that only a sub-cohort was sampled for evaluation by the central pathologist in a second phase sample. Specifically, we are interested in the proportional hazards discrete-time survival model (1) for time to relapse, under the complementary log transformation g2(u) = −log(1 – u), in order to evaluate the risk associated with unfavorable central histology, late (III/IV) disease stage versus the early (I/II) stage, age at diagnosis (year), and tumor diameter (cm). For this model, we also include an interaction between histology and stage of disease.
In this cohort, 90% of the 669 events occurred within the first three years of diagnosis, while less than 5% of non-relapsed subjects were censored in the same period. Based on this observation, we first define a modified, or reduced, cohort to include only patients who had an event or were fully followed up in the first three years, so that censoring only occurs at the third year (82.2%), the assumed end of the study. This modified cohort included N = 3757 subjects and is used in our NWTS data analysis. We took this approach first out of concern that the large number of nuisance parameters introduced by the small number of individuals with intermittent censored outcomes, due to the added strata for a binary outcome at each failure time interval, might adversely affect the mean score method. Here, the nuisance parameters include the sample covariance matrices of the score function (10) for each combination of the relapsing time and the local histology examination among the censored group, which increases the number of strata for the phase two sample. We now consider the regression coefficients from the discrete-time survival analysis of the modified full cohort as the reference values. We will evaluate efficiency gains of the optimal mean score design, based on the discretized survival outcomes, for the continuous-time analysis in section 4.3. Finally, we also conducted an analysis of all individuals, regardless of the time of censoring, and discuss design issues regarding how to handle intermittent censoring in our framework in section 4.4.
We first discretize the continuous event time into six 6-month intervals, so that we model the hazard of relapse during the first three years after diagnosis. Where necessary, we rounded the event time to the nearest six-month interval. As in Section 4.1, we consider four different sampling scenarios for the phase two subsample: simple random sampling, balanced allocation across strata, the adaptive and optimal (oracle) mean score designs, where the last three employ stratified sampling based on the phase one sample. To evaluate the efficiency gains of the proposed mean score approach, we performed the two-stage analysis, with a phase two sample of n = 400, 1000 times. For implementation of the optimal design, we estimate parameters in equation (7) using the oracle procedure by using the central histology records of the full cohort. We refer to section 4.1 for further details of implementation. Bias and efficiency are calculated using the estimates of the full cohort analysis with the central histology as the reference.
Table 2 demonstrates the performance of the different methods, where efficient estimation of the interaction between unfavorable histology and late stage of the disease is of main interest. MS-A outperformed the other practical competitors: CC-SRS, MS-SRS and MS-BAL. For example, MS-A had a 38.7% (≈1 – 0.425/0.693) variance reduction compared to CC-SRS for estimating the interaction term. We also note that performance of MS-A was pretty close to the oracle procedure, MS-O; MS-A was only 7% less efficient than MS-O for estimating the regression coefficient of interest. Furthermore, across all parameters, MS-A achieved the smallest mean squared error among the practical competitors, not only for baseline hazards estimation but also regression coefficients. Overall, the proposed method performed better than the other two-phase estimators, with both an efficient design and by incorporating auxiliary information from the phase one sample. In general, the efficiency gains for estimating other parameters depend on the joint distribution between all variables and will vary across settings.
Table 2.
For the discrete-time survival analysis of the National Wilms Tumor Study, we compare five different methods: (i) complete case analysis with simple random sampling (CC-SRS), (ii) mean score estimation with simple random sampling (MS-SRS), (iii) mean score estimation with a balanced sample (MS-BAL), also equivalent to the Horvitz-Thompson estimator, (iv) mean score estimation with adaptive sampling (MS-A) and (v) mean score estimation with the oracle sampling design (MS-O).
| Baseline hazard in complementary log–log scale |
Regression coefficienta |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sampling | Estimation | Criterion | 0.5 yr | 1yr | 1.5 yr | 2yr | 2.5 yr | 3yr | UHb | Stagec | Aged | dTmre | U*Sf |
| Full cohort | CC | Estimate | −4.028 | −3.876 | −4.336 | −5.005 | −5.353 | −5.719 | 1.058 | 0.280 | 0.063 | 0.032 | 0.636 |
| SRS | CC | 0.452 | 0.456 | 0.458 | 0.666 | 1.459 | 2.468 | 0.555 | 0.317 | 0.046 | 0.031 | 0.693 | |
| Bias | −0.071 | −0.065 | −0.077 | −0.096 | −0.278 | −0.649 | −0.015 | 0.018 | −0.002 | 0.001 | 0.032 | ||
| 0.446 | 0.451 | 0.452 | 0.659 | 1.432 | 2.381 | 0.555 | 0.317 | 0.046 | 0.031 | 0.692 | |||
| MS | 0.420 | 0.414 | 0.411 | 0.558 | 1.375 | 2.441 | 0.548 | 0.337 | 0.047 | 0.034 | 0.732 | ||
| Bias | −0.041 | −0.034 | −0.042 | −0.101 | −0.291 | −0.757 | −0.091 | 0.017 | −0.001 | 0.002 | 0.094 | ||
| 0.418 | 0.412 | 0.409 | 0.549 | 1.344 | 2.320 | 0.541 | 0.337 | 0.047 | 0.034 | 0.726 | |||
| Balanced | MS | 0.410 | 0.404 | 0.396 | 0.391 | 0.389 | 0.388 | 0.370 | 0.353 | 0.056 | 0.035 | 0.554 | |
| Bias | −0.109 | −0.096 | −0.084 | −0.076 | −0.072 | −0.070 | 0.043 | 0.007 | 0.013 | 0.005 | 0.004 | ||
| 0.396 | 0.393 | 0.387 | 0.383 | 0.382 | 0.382 | 0.368 | 0.353 | 0.054 | 0.035 | 0.554 | |||
| Adaptive | MS | 0.315 | 0.309 | 0.303 | 0.299 | 0.297 | 0.296 | 0.284 | 0.254 | 0.042 | 0.025 | 0.425 | |
| Bias | −0.065 | −0.058 | −0.052 | −0.048 | −0.046 | −0.045 | 0.003 | −0.007 | 0.008 | 0.003 | 0.034 | ||
| 0.308 | 0.304 | 0.298 | 0.295 | 0.294 | 0.293 | 0.284 | 0.254 | 0.041 | 0.025 | 0.424 | |||
| Oracle | MS | 0.311 | 0.306 | 0.301 | 0.296 | 0.299 | 0.295 | 0.250 | 0.256 | 0.038 | 0.025 | 0.396 | |
| Bias | −0.048 | −0.043 | −0.038 | −0.035 | −0.042 | −0.036 | 0.010 | 0.003 | 0.004 | 0.001 | 0.013 | ||
| 0.307 | 0.303 | 0.298 | 0.294 | 0.296 | 0.293 | 0.250 | 0.256 | 0.037 | 0.025 | 0.396 | |||
Note: The optimal sampling design was estimated using the full cohort data. The MS-A and MS-O designs are for efficient estimation of the interaction effect between unfavorable histology and disease stage. Results from the full cohort analysis with complete data (Full-CC) are presented as a benchmark. Mean squared error and its bias-variance decomposition are estimated using 1000 phase two samples of n = 400 from the reduced full cohort (N = 3757). We took equal proportions for the pilot and adaptive samples.
Log-hazard ratio.
Unfavorable histology versus favorable.
Disease stage III/IV versus I/II.
Year at diagnosis.
Tumor diameter (cm)
Interaction effect between UH and Stage.
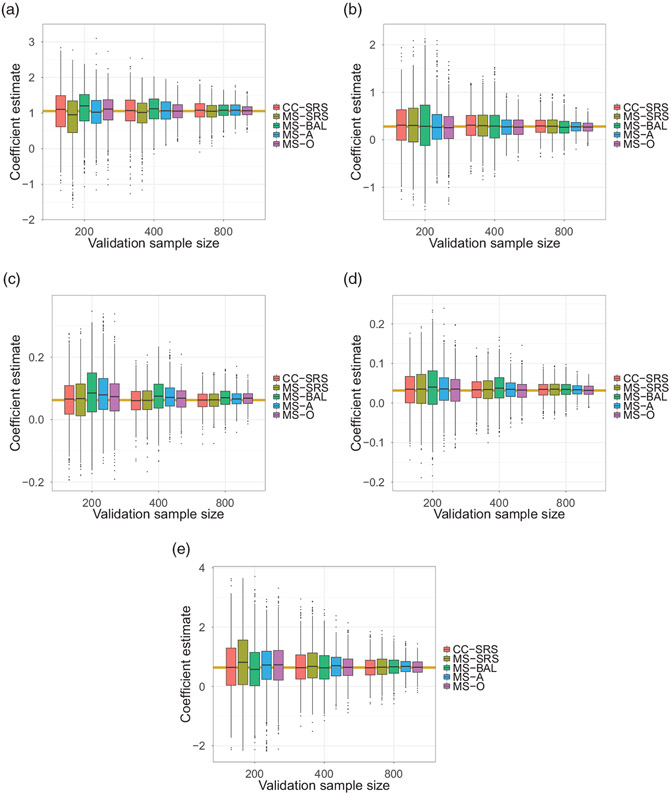
In Figure 2, we examine the relative performance of the different estimators for each of the regression parameters and phase two sample sizes n = 200, 400, 800. In the top-left panel (a), we show the estimation results for the regression coefficient for unfavorable histology (UH) over 1000 repetitions of subsampling, when the adaptive and optimal mean score allocations were designed for the efficient estimation of UH. The rest of the panels are similar, showing results for the other regression coefficients they were set as targets, namely when the MS-A and MS-O designs were for efficient estimation of (b) late stage of the disease, (c) age of diagnosis (year), (d) tumor diameter (cm) and (e) the interaction between UH and stage of the disease, respectively. MS-O consistently showed superior performance for all phase two ample sizes; however, MS-A again had the smallest mean squared error among the practical methods. Further, the performance of MS-A tended to be close to MS-O as the validation size increased.
Figure 2.
The relative performance of different methods by repeatedly subsampling the phase two sample 1000 times from the reduced full cohort (N = 3757) of the NWTS data. For each validation sample size, the bundle of five box plots: complete case with simple random sampling (CC-SRS) and mean score with simple random sampling, balanced sampling, adaptive sampling and the oracle design (MS-SRS, MS-BAL, MS-A, and MS-O, respectively); shows relative performance. Efficient estimation results for each targeted covariate are shown in each panel; (a) unfavorable histology, (b) late stage of the disease, (c) age of diagnosis (year), (d) tumor diameter (cm), and the interaction between the histology and late stage, respectively, when validation sizes are n = 200, 400, 800. The yellow horizontal lines represent the reference parameter estimates obtained from the full cohort analysis.
4.3. Continuous-time survival analysis with the mean score design
In many practical settings, the continuous-time Cox model will be the analysis of primary interest. We further investigate benefits of the proposed mean score sampling design, when the phase two estimating equation employs the continuous-time Cox proportional hazards model. In Section 2.3, we discussed the direct connection between the continuous-time Cox model (1) and the analogous grouped discrete-time model with the complementary log transformation, in the sense that the two models have the same regression coefficient β. This allows for a pragmatic approach to improve efficiency of a two phase design for a continuous survival outcome, where we conduct the two-phase analysis of the Cox model with the proposed optimal mean score sampling method derived for the parameter of interest in the discretized model. This design can be used for the phase-two sample and the analysis can still be conducted on the original continuous time scale.
In this section, we study the numerical performance of different sampling methods when they were applied to the two-phase analysis of the usual Cox model in both numerical simulation and the data example with NWTS. Unlike sections 4.1 and 4.2, we assume that continuous survival times were observed for the full cohort in the phase one study and employ the previously developed optimal and adaptive mean score design for the discrete-time survival model (1) only to design the allocation of the phase two sample. That is, we first calculated the sampling probabilities and associated inverse probability weights for the phase two sample, and then the design-based estimates of the continuous-time Cox model were investigated. We used the survival package in R25 and applied the inverse probability weights of the phase two sample with the weights option of the coxph function.
Table 3 compares performance of different sampling methods when they were applied to the two-phase analysis of the usual Cox model in the numerical simulation. We employed the same simulation setting that was used in section 4.1, except continuous-time responses were generated from an exponential survival function. Specifically, the survival outcome T associated with the covariate vector X = (X1, X2, X3, X4)⊤ was generated by the exponential distribution with the conditional hazard rate . The baseline hazar was fixed during the 1000 Monte Carlo simulation, which led to the average censoring rate of 70%. The phase two sample was designed for the efficient estimation of β1. We found that the two-phase analysis with the adaptive sampling design was more efficient than with simple random sampling or with balanced sampling designs, except when the phase two sample size was small (n = 200). Similarly to Table 1, this also suggests that n = 200 is too small in this simulation setting to gain efficiency using the adaptive sampling design. We also note that although the oracle sampling design is optimal for mean score estimation of discrete-time survival model (1), it remained the most efficient of all designs considered for continuous-time estimation. Again, with larger phase two sample sizes, the adaptive design’s loss of efficiency compared to the oracle design was not substantial. We examined the performance comparison tables with censoring rates for 30% and 50%, and the lesson was similar (data not shown).
Table 3.
Performance of the two-phase continuous-time Cox model analysis with exponential baseline survival.
| Sampling | Criterion | Estimation performance by sample sizes |
|||||
|---|---|---|---|---|---|---|---|
|
N = 4000 |
n = 400 |
||||||
| n = 200 | n = 400 | n = 800 | N = 2000 | N = 4000 | N = 8000 | ||
| Full cohort | 0.128 | 0.128 | 0.128 | 0.179 | 0.128 | 0.088 | |
| Bias | 0.000 | 0.000 | 0.000 | 0.010 | 0.000 | −0.002 | |
| 0.128 | 0.128 | 0.128 | 0.178 | 0.128 | 0.088 | ||
| SRS | 0.396 | 0.279 | 0.202 | 0.289 | 0.279 | 0.266 | |
| Bias | −0.010 | 0.001 | 0.003 | 0.027 | 0.001 | −0.001 | |
| 0.396 | 0.279 | 0.202 | 0.288 | 0.279 | 0.266 | ||
| Balanced | 0.544 | 0.344 | 0.250 | 0.349 | 0.344 | 0.338 | |
| Bias | 0.083 | 0.035 | 0.020 | 0.058 | 0.035 | 0.023 | |
| 0.537 | 0.342 | 0.249 | 0.344 | 0.342 | 0.338 | ||
| Adaptive | 0.413 | 0.242 | 0.184 | 0.271 | 0.242 | 0.230 | |
| Bias | 0.007 | 0.007 | 0.002 | 0.021 | 0.007 | 0.012 | |
| 0.413 | 0.242 | 0.184 | 0.270 | 0.242 | 0.230 | ||
| Oracle | 0.306 | 0.234 | 0.174 | 0.247 | 0.234 | 0.215 | |
| Bias | 0.002 | −0.001 | −0.001 | 0.014 | −0.001 | −0.006 | |
| 0.306 | 0.234 | 0.174 | 0.247 | 0.234 | 0.215 | ||
Note: We used inverse probability weights (IPW) for the two-phase analysis for four different sampling designs for the second phase; (i) simple random sampling (SRS), (ii) balanced sampling, (iii, iv) the proposed adaptive and oracle sampling designs, respectively, determined by the mean score method for the discrete-time survival analysis. Mean squared error (MSE) and its bias-variance decomposition are estimated from 1000 Monte Carlo replications, where the censoring rate was 70%. The adaptive and optimal sampling designs were for efficient estimation of X1 with β1 = log(1.5)≈0.405. In all adaptive sampling scenarios, we took equal proportions for the pilot and adaptive samples.
In Table 4, we applied a similar strategy to the two-phase analysis of the usual Cox model based on 1000 repeated phase two samples in the NWTS data. Unlike the previous analysis in Table 2 or Figure 2, we assumed that the continuous relapse times were observed for the full cohort in the phase one study and that efficient estimation of the interaction effect between unfavorable histology and disease stage was of primary interest in the adaptive and oracle sampling designs. It is worth mentioning that the full cohort analysis with the continuous-time outcomes yielded very similar regression estimates to that of the discrete-time model. This indicates that the discretization of event times had a minor impact. As shown in Table 4, the adaptive sampling design for the discrete-time analysis also provided efficiency gains for the continuous-time analysis. For example, the variance reduction was about 26% compared to both the simple random sampling and the balanced design. In this example, the adaptive design happened to slightly outperform the oracle design, but we note that these two allocations were for the optimal design for the discrete-time and not the continuous survival model (1). We found that the proposed adaptive sampling design provided 20–25% of efficiency gains in each case varying the target parameter to be (a) unfavorable histology (UH), (b) late stage of the disease, (c) age of diagnosis (year) or (d) tumor diameter (cm) (data not shown).
Table 4.
Performance of the two-phase continuous-time Cox model analysis of time to relapse in the National Wilms Tumor Study.
| Sampling | Criterion | Estimation performance by regressor |
||||
|---|---|---|---|---|---|---|
| UHa | Stageb | Agec | dTmrd | U*Se | ||
| Full cohort analysis | Ref. | 1.027 | 0.292 | 0.064 | 0.022 | 0.620 |
| SRS | 0.388 | 0.313 | 0.046 | 0.033 | 0.600 | |
| Bias | −0.018 | 0.014 | −0.002 | 0.001 | 0.028 | |
| 0.387 | 0.312 | 0.046 | 0.033 | 0.599 | ||
| Balanced | 0.413 | 0.421 | 0.061 | 0.043 | 0.622 | |
| Bias | 0.057 | 0.020 | 0.010 | 0.006 | −0.008 | |
| 0.409 | 0.420 | 0.060 | 0.042 | 0.622 | ||
| Adaptive | 0.308 | 0.297 | 0.048 | 0.030 | 0.461 | |
| Bias | −0.000 | −0.006 | 0.007 | 0.003 | 0.039 | |
| 0.308 | 0.296 | 0.048 | 0.029 | 0.459 | ||
| Oracle | 0.313 | 0.332 | 0.046 | 0.031 | 0.477 | |
| Bias | −0.001 | 0.001 | 0.000 | 0.000 | 0.035 | |
| 0.313 | 0.332 | 0.046 | 0.031 | 0.476 | ||
Note: We used inverse probability weights (IPW) for the two-phase analysis for four different sampling designs for the second phase; (i) simple random sampling (SRS), (ii) balanced sampling, (iii, iv) the proposed adaptive and oracle sampling designs, respectively, determined by the mean score method for the discrete-time survival analysis. We took equal proportions for the pilot and adaptive samples. The target parameter for the mean score design was the interaction between unfavorable histology and late stage disease. Mean squared error and its bias-variance decomposition are estimated from 1000 phase two subsamples of n = 400 from the reduced full cohort (N = 3757). Reference parameters estimates are from the full cohort analysis using the continuous-time Cox model with complete data on all subjects.
Unfavorable histology versus favorable.
Disease stage III/IV versus I/II.
Year at diagnosis.
Tumor diameter (cm).
Interaction effect between UH and Stage.
4.4. Design considerations for general censoring patterns
The proposed method in Section 3 can be applied without modification for the setting where there is random intermittent censoring, as well as censoring at the end of the study, the only difference being that there will be more strata at the intermittent event times. The mean score estimation depends on nonparametric estimation of the probability distribution for the phase two variables conditional on each discrete value of the phase one surrogate. We note that in section 2.2 is the empirical estimate of the sampling probability of the i-th individual selected into the validation subset, which may suffer from the curse of dimensionality as the number of phase one strata (Yi, Δi, Zi) increases. One could consider an increasing number of discretized intervals to approximate the continuous-time points, but the number of unique continuous-time survival outcomes observed will increase as the sample size increases. For this reason, in our data example we first studied the two-phase analyses of the discrete-time survival models in the previous sections where individuals were right-censored only at the sixth time point, an induced end of follow-up, which is equivalent to a fixed Type I censoring when individuals who were intermittently censored were excluded from analysis. Even in this simple setting in section 4.1, there were (7 × 4)-strata for the phase two sampling, resulting from a discrete surrogate Z having four categories. If we further considered random right-censoring for this setting, we would have to estimate sampling probabilities for (6 × 2 × 4)-strata. The larger number of associated nuisance parameters in this case for MS-A estimator may require larger phase two samples to achieve the expected efficiency gains due to unstable nuisance parameter estimation in small strata.
We suggest a simple strategy for the proposed adaptive mean score design aimed at under-sampling less informative strata in the pilot study, which may preserve efficiency gains by providing more precise nuisance parameters for the more informative strata. For example, under the random right-censoring assumption, individuals censored before the end of the follow-up period should generally be less informative than non-censored individuals with similar covariates for that same period. For a fixed phase two sample size, such under-sampling may enable us to re-allocate the pilot sample for the MS-A so that relatively more informative groups can be up-weighted.
For the numerical assessment, we investigated the numerical performance of the two-phase analysis with the modified sampling design in the NWTS data analysis. Supplementary Material Tables B.8 and B.9 provide analogous results for the discrete-time analysis in Table 2 and continuous time analysis of Table 4 for the NWTS, but we analyzed the full cohort (N = 3915) and under-sampled the censored individuals not relapsing before the end of the follow-up period in the balanced and the pilot samples. Specifically, we allocated a small number of the pilot sample size for individuals censored before the end of the follow-up period (i.e. y < 3 and δ = 0) at each level of histology, and the remaining allocation was equally distributed to the other strata in the pilot sample. In this particular example, we set the under-sampling size to 4, which was approximately half of the balanced sampling size for each stratum in the pilot study with n = 400. Indeed, we found that the naive balanced sampling of all strata in the pilot often over-sampled censored-groups compared to the oracle design (data not shown), and consequently this simple remedy made the modified adaptive sampling design closer to the oracle design than did the balanced pilot sample with the proposed adaptive design. As seen in Supplemental Material Table B.8, the modified approach produced a 14% variance reduction compared to both the fully balanced and the MS-A with a balanced pilot sample. Additionally, the precision for all estimates, relative to the analogous estimates in Tables 2 and 4, benefited from including the intermittently censored 158 (= 3915 – 3757) individuals who had been excluded as discussed in section 4.2, with more gains seen for the MS-BAL and MS-A estimators.
We also simulated the same simulation setting considered in Table 3 but the 20% of individuals were randomly censored before the maximum follow-up period t6, i.e. P(Y < t6, Δ = 0) = 0.2. For the modification of the pilot sample, we set the under-sampling size for these strata following the same manner of choosing the allocation number with the NWTS data analysis, which depends on the phase two sample size. Supplementary Material Tables B.10 demonstrates that the modification of the balanced and the pilot samples improved the numerical performance of the two-phase analysis. In Supplementary Material Table B.11, we also reported the phase two sampling design for a single dataset with N = 4000 and n = 400 among simulation scenarios. As anticipated in the NWTS data analysis, the optimal sampling design would allocate very few individuals randomly censored before the follow-up period, so we seek to avoid putting too many individuals into these strata in the pilot sample.
From these numerical observations, we hypothesize that this modification will allow for more robust efficiency gains for the proposed adaptive design in other settings with intermittent censoring. Supportive simulation studies that examine the performance of MS-A given the anticipated phase two sample size and other study parameters may provide useful insights to guide refinements of this strategy for a given setting.
5. Discussion
The mean score method is a practical approach for two-phase studies that allows for a relatively straightforward derivation of an optimal design for a phase two study, one that can minimize the variance of a target parameter given a fixed phase two sample size.2 In this study, we extended the mean score estimation method for the two-phase analysis of discrete-time survival outcomes. We also derived an adaptive sampling design approach that first draws a pilot phase two sample in order to estimate the nuisance parameters necessary to derive the optimal sampling proportions, similar to the approach of McIsaac and Cook8 for binary outcomes.
Through numerical studies with simulated data and the National Wilms Tumor Study data, we found that the proposed mean score estimator with an adaptive sampling design provided efficiency gains over the complete case estimator, as well as the mean score estimator with simple random or balanced stratified sampling, for selection of the phase two sample. For the studied settings, as the phase two sample size increased, the proposed adaptive sampling design not only outperformed the simple random sampling and balanced designs consistently but also behaved very close to the oracle design, which depends on the true (generally unknown) population parameters. When the phase two sample was small, the mean score estimator with the adaptive sampling design was less efficient than with simple random sampling, likely because the pilot sample was too small to adequately estimate parameters needed to optimize the phase two sample. Our simulations suggest that for small phase two samples, simple random sampling, together with mean score estimation, is preferred.
The mean score adaptive optimal design also provided efficiency gains for the two-phase analysis of the continuous-time outcome using the usual Cox proportional hazards model. This design offers a practical and straightforward approach to improve the efficiency of the two-phase estimator for the continuous survival time setting and can be applied for settings with both type I and random right censoring.
There are some limitations of our proposed method. First, the error-prone covariate is assumed to be categorical. While this may be the case in many biomedical settings, future work is needed to understand the value of the proposed method for continuous surrogate variables. For continuous surrogates, a kernel smoothing approach proposed by Chatterjee and Chen13 may be useful. Further, the adaptive design requires estimating nuisance parameters to estimate the strata-specific sampling probabilities that minimize the variance of the target parameter, whose number increases with the number of strata. Many small strata could lead to instability in the necessary estimated nuisance parameters, which in turn could threaten the efficiency of the design. In the case of the Wilms Tumor data, undersampling the early censored individuals in the pilot was an advantageous approach that was compatible with the subsequent derived optimal sample, in that it avoided oversampling uninformative strata, and improved the performance of the adaptive design. In some settings, one may consider changing the information used to estimate the sampling weights. In survival analysis, one may replace the two variables that define the outcome (observed follow-up time and censoring/event status) by a martingale residual that captures the information on both, while taking into account the relevant covariates. Burne and Abrahamowicz proposed to use the martingale residual to impute missing values of confounders measured only in a validation sample.26,27 Formalization of this strategy needs further study and is a subject for future work. Incorporation of prior information regarding the sampling priorities for certain strata may be an additional way to improve the performance of the adaptive design, particularly in the case of a small phase two sample. Recently, Chen et al.28 have considered a method for incorporation of prior information into multi-wave sampling in a regression framework. Also, further extension to time-dynamic models that introduce time-varying covariates and their time-dependent effects will also provide flexible tools for the two-phase analysis of a broader class of survival models.
Interval censoring is also a practically important setting in the continuous-time survival analysis for many real-life applications. Although the generic notation λj(x) in equation (1) represents the discrete-time hazard censored at fixed times tj commonly for all subjects, it can be applied to the continuous-time survival analysis by modeling the cumulative hazard, which accumulates the Cox proportional hazard with the integral over the interval [tj–1, tj) as in equation (5). This means that the discrete-time survival model can also handle grouped survival outcomes.10 However, discretization of interval censored data requires careful consideration of how to discretize time, as there may be some uncertainty as to which discretized time an interval-censored event should be assigned, particularly when periods of time without observation in the interval censored data are large. Further, having too many distinct observations times can lead to an impractical number of nuisance parameters. This challenging topic requires further study.
Two-phase studies are used in a variety of settings. In the era where the analysis of error-prone electronic health records data are of increasing interest, a phase two sample in which data can be validated to understand the error structure is a critical step towards valid inference. The proposed method and two-phase study design offer a practical and easy to implement framework for the common setting of survival outcomes, in which both the validated and error-prone exposures can be efficiently combined so that analyses are adjusted for errors in the surrogate data. Future work is needed to expand this method to also handle settings where there is error in both the exposure and survival outcome.
Supplementary Material
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported in part by the U.S. National Institutes of Health (NIH) grant R01-AI131771 and Patient Centered Outcomes Research Institute (PCORI) Award R-1609-36207. The statements in this manuscript are solely the responsibility of the authors and do not necessarily represent the views of PCORI or NIH.
Footnotes
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Supplemental Material
Supplemental material for this article is available online.
References
- 1.Breslow NE and Chatterjee N. Design and analysis of two-phase studies with binary outcome applied to Wilms tumour prognosis. J Royal Stat Soc: Ser C (Appl Stat) 1999; 48: 457–468. [Google Scholar]
- 2.Reilly M and Pepe MS. A mean score method for missing and auxiliary covariate data in regression models. Biometrika 1995; 82: 299–314. [Google Scholar]
- 3.Reilly M. Optimal sampling strategies for two-stage studies. Am J Epidemiol 1996; 143: 92–100. [DOI] [PubMed] [Google Scholar]
- 4.McIsaac MA and Cook RJ. Response-dependent two-phase sampling designs for biomarker studies. Can J Stat 2014; 42: 268–284. [Google Scholar]
- 5.Lawless J. Two-phase outcome-dependent studies for failure times and testing for effects of expensive covariates. Lifetime Data Analys 2018; 24: 28–44. [DOI] [PubMed] [Google Scholar]
- 6.Tao R, Zeng D and Lin DY. Optimal designs of two-phase studies. J Am Stat Assoc. Epub ahead of print 29 October 2019. DOI: 10.1080/01621459.2019.1671200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tao R, Zeng D and Lin DY. Efficient semiparametric inference under two-phase sampling, with applications to genetic association studies. J Am Stat Assoc 2017; 112: 1468–1476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.McIsaac MA and Cook RJ. Adaptive sampling in two-phase designs: a biomarker study for progression in arthritis. Stat Med 2015; 34: 2899–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Meier AS, Richardson BA and Hughes JP. Discrete proportional hazards models for mismeasured outcomes. Biometrics 2003; 59: 947–954. [DOI] [PubMed] [Google Scholar]
- 10.Kalbfleisch JD and Prentice RL. The statistical analysis of failure time data, vol. 360. Hoboken, NJ: John Wiley & Sons, 2011. [Google Scholar]
- 11.Lawless J, Kalbfleisch J and Wild C. Semiparametric methods for response-selective and missing data problems in regression. J Royal Stat Soc: Ser B (Stat Methodol) 1999; 61: 413–438. [Google Scholar]
- 12.Chatterjee N, Chen YH and Breslow NE. A pseudoscore estimator for regression problems with two-phase sampling. J Am Stat Assoc 2003; 98: 158–168. [Google Scholar]
- 13.Chatterjee N and Chen YH. A semiparametric pseudo-score method for analysis of two-phase studies with continuous phase-I covariates. Lifetime Data Analys 2007; 13: 607–622. [DOI] [PubMed] [Google Scholar]
- 14.Prentice RL. Surrogate endpoints in clinical trials: Definition and operational criteria. Stat Med 1989; 8: 431–440. [DOI] [PubMed] [Google Scholar]
- 15.Dempster AP, Laird NM and Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J Royal Stat Soc: Ser B (Methodol) 1977; 39: 1–22. [Google Scholar]
- 16.Pepe MS, Reilly M and Fleming TR. Auxiliary outcome data and the mean score method. J Stat Plan Inference 1994; 42: 137–160. [Google Scholar]
- 17.Flanders WD and Greenland S. Analytic methods for two-stage case-control studies and other stratified designs. Stat Med 1991; 10: 739–747. [DOI] [PubMed] [Google Scholar]
- 18.Neyman J On the two different aspects of the representative method: the method of stratified sampling and the method of purposive selection. J Royal Stat Soc 1934; 97: 558–625. [Google Scholar]
- 19.Horvitz DG and Thompson DJ. A generalization of sampling without replacement from a finite universe. J Am Stat Assoc 1952; 47: 663–685. [Google Scholar]
- 20.Binder DA and Patak Z. Use of estimating functions for estimation from complex surveys. J Am Stat Assoc 1994; 89: 1035–1043. [Google Scholar]
- 21.Kulich M and Lin D. Improving the efficiency of relative-risk estimation in case-cohort studies. J Am Stat Assoc 2004; 99: 832–844. [Google Scholar]
- 22.D’angio GJ, Breslow N, Beckwith JB, et al. Treatment of Wilms’ tumor. Results of the third national Wilms’ tumor study. Cancer 1989; 64: 349–360. [DOI] [PubMed] [Google Scholar]
- 23.Green DM, Breslow NE, Beckwith JB, et al. Comparison between single-dose and divided-dose administration of dactinomycin and doxorubicin for patients with Wilms’ tumor: a report from the National Wilms’ Tumor Study Group. J Clin Oncol 1998; 16: 237–245. [DOI] [PubMed] [Google Scholar]
- 24.Lumley T. Complex surveys: a guide to analysis using R, vol. 565. Hoboken, NJ: John Wiley & Sons, 2011. [Google Scholar]
- 25.Therneau TM and Lumley T. survival: Survival Analysis, 2019, https://CRAN.R-project.org/package=survival. R package version 3.1–8. [Google Scholar]
- 26.Burne RM and Abrahamowicz M. Martingale residual-based method to control for confounders measured only in a validation sample in time-to-event analysis. Stat Med 2016; 35: 4588–4606. [DOI] [PubMed] [Google Scholar]
- 27.Burne RM and Abrahamowicz M. Adjustment for time-dependent unmeasured confounders in marginal structural cox models using validation sample data. Stat Meth Med Res 2019; 28: 357–371. [DOI] [PubMed] [Google Scholar]
- 28.Chen T, Lumley T and Rivera-Rodriguez C. Optimal multi-wave sampling for regression modelling, https://www.otago.ac.nz/nzsa/programme-and-speakers/otago720017.pdf (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.