Abstract
Mixture theory models continua consisting of multiple constituents with independent motions. In constrained mixtures, all constituents share the same velocity but they may have different reference configurations. The theory of constrained reactive mixtures was formulated to analyze growth and remodeling in living biological tissues. It can also reproduce and extend classical frameworks of damage mechanics and viscoelasticity under isothermal conditions, when modeling bonds that can break and reform. This study focuses on establishing the thermodynamic foundations of constrained reactive mixtures under more general conditions, for arbitrary reactive processes where temperature varies in time and space. By incorporating general expressions for reaction kinetics, it is shown that the residual dissipation statement of the Clausius–Duhem inequality must include a reactive power density, while the axiom of energy balance must include a reactive heat supply density. Both of these functions are proportional to the molar production rate of a reaction, and they depend on the chemical potentials of the mixture constituents. We present novel formulas for the classical thermodynamic concepts of energy of formation and heat of reaction, making it possible to evaluate the heat supply generated by reactive processes from the knowledge of the specific free energy of mixture constituents as well as the reaction rate. We illustrate these novel concepts with mixtures of ideal gases, and isothermal reactive damage mechanics and viscoelasticity, as well as reactive thermoelasticity. This framework facilitates the analysis of reactive tissue biomechanics and physiological and biomedical engineering processes where temperature variations cannot be neglected.
Keywords: thermodynamics, constrained reactive mixtures, energy of formation, heat of reaction, thermoelasticity, ideal gas mixtures
1 Introduction
Biological tissues and cells undergo biochemical reactions that may consume or release chemical energy. The standard approach in biochemistry is to assess this energy using the Gibbs potential of reactants and products, usually under the assumption that these reactions occur at constant temperature and pressure. Most commonly, this constant temperature is body temperature, and the constant pressure is ambient pressure. The Gibbs potential is commonly used to assess whether these reactions may proceed spontaneously or require the addition of chemical energy, such as that provided by the dephosphorylation of adenosine triphosphate, or thermal energy (heating). While many processes in mammalian physiology may be suitably modeled to take place under these isothermal and isobaric conditions, there are circumstances where it may be necessary to allow for spatiotemporal variations in temperature and pressure. In the context of continuum mechanics, we may alternatively model variations in pressure using strain as a state variable, then relate pressure (or more generally stress) to strain using appropriately selected functions of state. For tissues and cells that are subjected to loading, the state of pressure or strain may significantly influence the kinetics and thermodynamics of reactive processes. Moreover, biological tissues and cells may interact with an environment at a different temperature or pressure, such as ambient air flowing in the lungs, injurious heating (e.g., burning) or cooling (freezing) of skin by external fluids or solids, or potentially detrimental thermal effects of medical procedures, such as laser ablation or cryotherapy. To better understand how to model such processes, it becomes necessary to update the standard thermodynamic methodologies for assessing energy exchanges during reactive and thermal processes involving biological tissues and cells.
Moreover, biomedical devices typically employ nonbiological materials whose thermomechanical properties may also matter significantly in some biomechanical modeling contexts. For example, vascular stents may undergo large plastic deformation, ultrahigh molecular weight polyethylene used in joint arthroplasty may undergo significant viscoelastic deformation, thus these materials may heat up during normal function, potentially affecting the progression of wear, or the viability of cells that come in contact with these heated materials. Despite the potential importance of these phenomena, the classical training of bioengineers rarely encompasses this wider range of conditions for understanding and modeling the mechanics and thermodynamics of biological processes and nonbiological materials in a unified framework. The primary objective of this study is to present a framework that facilitates the modeling of this wide range of thermomechanical and reactive processes using mixture theory.
Mixture theory is the framework first introduced by Truesdell [1] to model the mechanics of mixtures of multiple constituents. In his original formulation, this author described a general framework where all constituents that coexist in an elemental volume may have independent motions. More detailed formulations were subsequently developed by other authors, notably including reactions that may take place among the various constituents [2–7]. This general mixture theory framework has been popular in the field of biomechanics, where it has been used to describe the mechanics of biological tissues and cells as a mixture of a porous permeable solid matrix and an interstitial fluid [8–10], later expanded to incorporate solutes and osmotic effects [11–15]. In these studies, the relative motion and frictional interactions between solute, solvent, and solid constituents gave rise to the classical relations known as Fick's law of diffusion and Darcy's law of permeation, which played an important role in the phenomena being examined. Reactive processes have also been incorporated in this mixture framework to model biological growth [7]. In this approach, growth is modeled as a set of reactions that convert solute constituents in the interstitial fluid into solid matrix constituents, governed by the mass supply term in the mass balance equation. Since growth is modeled as the interstitial addition of solid mass to a porous solid matrix, there is no obligatory concomitant change in volume; however, volumetric changes may take place when growth reactions alter the osmotic environment [16,17].
In an effort to accommodate growth mechanics without the added complexity of independent constituent motions (such as solute diffusion and solvent permeation), Humphrey and Rajagopal [18] proposed to specialize the reactive mixture framework to the case where all constituents are solids constrained to move together, even though these constituents may not share the same reference configuration. They used this constrained solid mixture approach to model vascular tissue consisting of collagen, elastin, and smooth muscle cells. As recognized by earlier authors [19], growth mechanics poses an intriguing challenge to the classical field of solid mechanics because growth causes the solid mass content to evolve over time; since new solid mass may be added interstitially to an existing porous solid matrix, it becomes necessary to specify the reference configuration of the constrained solid mixture as growth evolves. Baek et al. [20] proposed to keep track of this evolution using a time-dependent tensor that represents the prestretch of the newly added solid constituent at the time it is being added to the mixture, based on the original concept presented by Wineman and Rajagopal [21]. Ateshian and Ricken [22] adopted this constrained mixture framework; however, they proposed that each generation of newly deposited solid matrix represents a distinct mixture constituent with a distinct, time-invariant, reference configuration.
In their earlier work, Rajagopal and co-workers used their constrained mixture approach to describe the mechanics of inelastic materials [23–27] along with the thermomechanics of viscoelasticity and plasticity [28], with an emphasis on the evolution of the natural configuration of such materials. However, these studies did not explicitly adopt a reactive framework to describe this type of inelastic behavior. In contrast, in our own prior work, we proposed that viscoelasticity, damage mechanics, and plasticity could all be modeled using reactive constrained mixtures where intact bonds (mixture reactants) may break permanently (damage) or reform into stress-free bonds (viscoelasticity) or stressed bonds (plasticity) [29–32], by postulating different types of constitutive relations for the reference configuration of newly formed mixture products. We also showed that this framework could be easily extended to accommodate elastoplastic damage, by modeling three types of reactions (intact to broken bonds for elastic damage, intact to yielded bonds for plasticity, and yielded to broken bonds for plastic damage) [32]. Here again, in contrast to Rajagopal and co-workers, our approach proposed a time-invariant reference configuration for each mixture product, postulated by constitutive assumption, while recognizing that an infinite number of products could emerge in a continuously evolving viscoelastic or plastic deformation. This distinction implies that the theoretical formulations for these alternative approaches differ at a fundamental level, even though both approaches adopt the same conceptual constrained mixture framework.
In the studies of reactive mixtures from our group [7,22,29–32], the stoichiometry of reactions was based on a standard textbook approach [33], consistent with earlier mixture theory presentations [4,5], and thus capable of also modeling standard biochemical reactions as they may occur in biological systems. However, our prior studies were restricted to isothermal processes. More general formulations of reactive mixtures have been presented before, allowing for temperature to vary in time and space, within unconstrained [2,4–6,34,35] or constrained [36] mixtures.
Among these studies, there is a distinction between those that allow each constituent to have its own distinct temperature [2,5,6,35] and those that assume a common temperature for all constituents [4,34,36]. When each mixture constituent has its own temperature, a separate energy equation must be used for that constituent to provide a well-posed mathematical problem that can be solved for all the unknown temperatures. In mixture theory, this means that constitutive relations for energy supplies between each pair of constituents must be formulated, based on the specific type of energy transfer mechanism being considered in a model (such as phase transformation in two-phase flow). Unfortunately, few studies have proposed specific constitutive relations for this type of energy supply in unconstrained mixtures, thus limiting their usage in practice. Even those studies that presented the more general thermodynamic framework with constituent-specific temperatures chose to present isothermal problems as illustrative examples, with all constituents sharing the same temperature [35].
In this study, we present a complete framework for constrained reactive mixtures, which also accounts for their thermodynamics. Whereas the principal constraint in the original constrained mixture formulation was kinematic, requiring all constituents to move together (i.e., to share the same velocity), in this presentation we also assume that all mixture constituents are thermally constrained to share the same temperature. Indeed, there is a distinctive analogy between the concept of constraining all mixture constituents to share the same velocity, with that of sharing the same temperature: In the former case, we forgo the ability to formulate constitutive models for the momentum exchange between pairs of constituents in a mixture; in the latter case, we lose the ability to formulate constitutive relations for the energy exchange. However, these constraints produce a considerable simplification of the governing mixture equations; thus, we adopt both of them in the presentation of this study. This assumption is consistent with the thermodynamic framework for chemically reacting systems presented by Kannan and Rajagopal [36] and adopted by other investigators [37,38]. The main distinctions between this prior work and the current presentation are twofold: First, as mentioned above, Rajagopal and co-workers adopt a single evolving natural configuration for their constrained mixture, requiring a constitutive model for this evolution, whereas we assume that each product of a reaction has a time-invariant reference configuration postulated by constitutive assumption. Second, they adopt the Gibbs potential as the fundamental function of state from which constitutive models for stress, chemical potential, and entropy are derived, whereas we adopt the Helmholtz free energy, consistent with classical mixture approaches [2,4,39]. This distinction is nontrivial because their novel Gibbs potential formulation depends on the stress tensor, but in general the stress may have contributions from nondissipative and dissipative mechanisms, of which only the former depends on the free energy. This distinction is clarified in the current presentation.
The ability to combine chemical reactions in biological systems with inelastic processes in solid and fluid materials under the same reactive framework makes it possible to examine a broad range of thermodynamic processes using the same set of equations. In particular, it is noteworthy that engineering thermodynamic textbooks do not provide the fundamental equations for evaluating the heat produced in a reactive process under arbitrary conditions of temperature and pressure (or strain). In this study, we show that a reactive framework, which models the evolution of the apparent densities of reactants and products, necessarily introduces the chemical potential of reacting species in the axioms of energy balance and entropy inequality. Terms involving these chemical potentials in the energy balance are shown to represent the reactive heat supply. The corresponding terms in the entropy inequality determine whether the reaction is exergonic or endergonic.
Finally, in the Appendix, we illustrate how this framework of constrained reactive solid mixtures may be used to model reactive mixtures of ideal gases, and heat dissipation in damage mechanics, viscoelasticity, and thermoelasticity.
2 Governing Equations
2.1 Kinematics.
A mixture may consist of any number of constituents, each denoted by α. The motion of constituent α is given by , where denotes material points of constituent α in their referential configuration. At the current time t, all constituents that occupy an elemental region at the spatial position x may thus have originated from different referential positions , such that for all α. The velocity of each constituent is given by , whereas the deformation gradient is given by . Let represent the master constituent whose reference configuration is determined by the material point positions .
A constrained mixture represents the special case when all mixture constituents share the same velocity in the current (spatial) configuration
| (2.1) |
even though the respective referential configurations may be different.
Remark 1. In a strict sense, we should differentiate between the material and spatial representations of a function , such as . However, for notational simplicity, we assume that and .
For any pair of constituents α and β, it follows that , explicitly establishing the constraint equation between constituent deformation gradients. Since the mixture is constrained, a unique, time-invariant mapping may be defined between the reference configurations of α and s, such that
| (2.2) |
where maps the pair of material points and that satisfy in the current configuration. It follows that volume ratios similarly satisfy
| (2.3) |
where and .
Remark 2. In constrained mixtures, only a single deformation gradient such as of the master constituent is observable and thus available as a state variable. For remaining constituents α, the mapping represents a function of state that must be postulated by constitutive assumption; by definition, this function of state is not observable. Thus, the position extracted by integrating the constitutive model for is not observable either.
2.2 Mass Balance Relations.
The axiom of mass balance for each constituent is given by
| (2.4) |
where is the apparent density of α (mass of α per volume of the mixture in the current configuration), is the mass density supply describing mass supply to α due to reactions with all other mixture constituents, and is the material time derivative of . In the spatial frame, it is given by
| (2.5) |
From the kinematics of the continuum, we recall that
| (2.6) |
Substituting this expression into Eq. (2.4) produces a simplified form of the mass balance for α
| (2.7) |
where
| (2.8) |
From this expression, we understand that represents the mass of constituent α per volume of the mixture in the reference configuration of the master constituent s. In the form given in Eq. (2.7), the axiom of mass balance clearly shows that the referential apparent density remains invariant when constituent α is nonreactive ( ).
Since the mixture includes all constituents present in an elemental region, the net mass supply for the mixture must reduce to zero
| (2.9) |
implying that mass gained by products of a reaction must balance the mass lost by reactants. Therefore, the mass balance for the mixture, which may be evaluated by summing Eq. (2.4) over all constituents, reduces to
| (2.10) |
where
| (2.11) |
is the mixture density and
| (2.12) |
is the mixture velocity [1,2]. According to Eq. (2.8), we may rewrite Eq. (2.11) as
| (2.13) |
Similarly, Eq. (2.9) may be rewritten as ; when combined with Eq. (2.7), we conclude that , so that ρr is constant.
2.3 Stoichiometry of Reactions.
When examining the stoichiometry of reactions, we find it convenient to express the amount of each constituent α in the mixture in terms of its number of moles. We may relate the mass concentration (apparent density) of constituent α to its molar concentration via , where is its molar mass. Since is constant, the mass balance equation (2.4) may be rewritten as , where is the molar density supply to α from reactions with all other constituents.
Reactions may occur among the constituents of a mixture which result in a temporal evolution of the mass content of reactants and products. Following standard textbook presentations [33], a forward reaction between mixture constituents may be written down as
| (2.14) |
where is the chemical (molecular) species associated with constituent α, represents the stoichiometric coefficient of reactant α, and is that of the corresponding product. Similarly, a reversible reaction may be written as
| (2.15) |
The summations are taken over all mixture constituents, though constituents that are not reactants in that particular reaction will have , and those that are not products will have . The stoichiometry of the reaction imposes constraints on the molar density supplies such that we may define a molar production rate (units of mole per volume, per time)
| (2.16) |
where
| (2.17) |
is the net stoichiometric coefficient of α in the reaction. Using the above relation between and , Eq. (2.16) may be substituted into the constraint on mass supplies, Eq. (2.9) to produce . This relation may be recognized as the classical requirement to balance the molar mass of reactants and products in a reaction. Thus, the constraint (2.9) produces a classical outcome when applied to the mass balance.
Combining the relation between and with Eq. (2.16) yields a relation between the mass density supply and molar production rate
| (2.18) |
Thus, for each reaction, a single constitutive relation for the molar production rate is required to evaluate for all α. We may rewrite Eq. (2.18) as , where as per Eq. (2.8).
2.4 Mixture Momentum Balance.
As shown previously [22], the state of stress in each constituent α remains indeterminate in a constrained mixture, since the absence of relative motion precludes the formulation of constitutive relations for momentum exchanges between constituents. However, this indeterminacy is inconsequential, since these internal forces cancel out. Hence, the mixture Cauchy stress may be obtained by solving the mixture momentum balance
| (2.19) |
where is the mixture acceleration, and b represents external body forces per mixture mass. Therefore, given a constitutive relation for , only one unknown deformation gradient may be obtained from this momentum equation, such as . All other deformation gradients may be related to by Eq. (2.2), where is prescribed by constitutive assumption based on the nature of the constrained mixture [22], as illustrated in the examples presented in the Appendix. For nonpolar continua, the axiom of angular momentum requires to be symmetric.
2.5 Mixture Energy Balance.
As noted in the Introduction, we now propose to construct our constrained mixture framework such that all constituents also share the same temperature θ. Under this constraint, energy exchanges between constituents remain indeterminate, and the only equation we may solve is the mixture energy balance
| (2.20) |
where is the specific mixture internal energy, is the rate of deformation tensor, q is the heat flux in the mixture, and r is a specific heat supply representing interior sources of heat [39], which we propose are those resulting from mechanisms not accounted for explicitly in a model (such as radiation in a framework that does not include electromagnetism, or Joule heating in a model that does not account explicitly for the flow of electrically charged constituents and their frictional interactions with fixed charge constituents). Accordingly, given constitutive relations for ε and q, only one unknown temperature θ may be obtained from this energy equation. Note that , which appears on the right-hand side of the energy balance, is known as the stress power density.
2.6 Mixture Entropy Inequality.
The axiom of entropy inequality for a constrained reactive mixture takes the form described by Truesdell and Toupin [39] which they named after Clausius and Duhem
| (2.21) |
where is the specific mixture entropy. By using the energy balance (2.20) to eliminate r, we may rewrite this inequality as
| (2.22) |
where
| (2.23) |
emerges naturally as the specific free energy, commonly named after Helmholtz. We may also introduce the mixture free energy density , representing the free energy per volume of the mixture in the master reference configuration. Since as explained in Sec. 2.2, it follows that . We may also express the specific free energy of each constituent α as , such that
| (2.24) |
3 State Variables for Reactive Constrained Mixtures
3.1 State Variables and Functions of State.
In our continuum mechanics and thermodynamics treatment, we consider that state variables represent observable variables derived from measurements of three-dimensional space (length, area, and volume) and time. Thus, velocity, acceleration, gradient of velocity, and other similar measures relating space and time are all considered to be observable. Similarly, force is measured from the change of length of a standard material; mass is measured from force and acceleration; and temperature is measured from the change of length of a standard fluid (e.g., mercury). Functions of state are measures of a material's behavior, i.e., , ε, η, ψ, q, and , that cannot be observed directly but must be calculated from suitably formulated constitutive relations that are functions of observable state variables. In particular, the complete state of stress (a tensorial measure) cannot be determined exclusively from force and area measurements (a vectorial measure) at every point inside a material without cutting the material and altering that state of stress.
3.2 Constraints on Constitutive Relations.
To formulate constitutive relations that satisfy the entropy inequality, we extend the approach of Coleman and Noll [40] by taking into account that state variables are always observable, and that functions of state are not observable, and thus they should not be arbitrarily interchanged with observable state variables. Keeping in mind that our principal applications for constrained reactive mixtures include growth mechanics, damage mechanics, thermoelasticity, viscoelasticity, heat transfer, and other dissipative processes using only observable variables, we select a set of state variables that can accommodate a wide range of phenomena in these fields. Including the temperature θ allows us to define material functions (e.g., elastic moduli and viscosities) that vary with temperature. Including the temperature gradient allows us to model heat conduction. The deformation gradient of the master constituent is also included to account for the elastic response. The rate of deformation D may also be included to account for rate effects when significant, as in the case of viscous flow. Since the axiom of mass balance in Eq. (2.7) shows that the referential mass densities evolve over time in a reactive framework, they also need to be included in the list of state variables for a reactive mixture. According to the principle of equipresence, all functions of state ( , ε, η, ψ, q, , and ) are nominally dependent on this entire list of state variables ; in this list, α spans all constituents in the mixture. Using the chain rule of differentiation, and the kinematic relation where , we find that
| (3.1) |
We use the axiom of mass balance (2.7) to substitute for above, and the resulting expression is substituted into the entropy inequality (2.22), using Eqs. (2.8), (2.13), and (2.24), to produce
| (3.2) |
Note that we substituted L with D knowing that is symmetric (thus, ). This inequality must hold for arbitrary changes in , D, , and g (all of which are observable and independent variables of state), under our self-imposed constraint that ψ, η, , q, and cannot depend on , or . For example, looking at the first term, which is the only one that involves , we expect that this term must be positive regardless of the algebraic sign of ; however, since the coefficient multiplying is independent of it, this inequality can be satisfied if and only if the coefficient is zero. Applying the same reasoning to the terms involving and , we conclude that
| (3.3) |
| (3.4) |
| (3.5) |
The remaining terms in Eq. (3.2) involve functions of D and g, preventing us from simplifying this expression further. Thus, we are left with the residual dissipation statement
| (3.6) |
where
| (3.7) |
and
| (3.8) |
is the definition of the chemical potential of constituent α (with units of specific energy). The chemical potential always makes an appearance in a reactive framework, since the composition of reactants and products may evolve.
According to Eqs. (3.4) and (3.5), ψ (thus, ) cannot depend on the temperature gradient g nor the rate of deformation
| (3.9) |
Therefore, based on Eqs. (2.23), (3.3), and (3.8), the mixture specific entropy η, the specific internal energy ε, and the chemical potentials must also be independent of g and D. Moreover, η, ε, and are entirely determined by ψ. Thus, a suitable constitutive relation for the specific free energy suffices to also evaluate the specific entropy, the specific internal energy, and the chemical potential of all mixture constituents.
In contrast, the list of state variables for , q, and is still the complete set where β spans all α. Since these functions of state persist in the residual dissipation statement (3.6), they represent dissipative processes by definition. In particular, we may refer to as a dissipative stress, since it represents the dissipative part of the stress tensor in Eq. (3.7). Furthermore, according to Eq. (2.18), the molar production rate is a function of all those state variables. Thus, the rate at which a reaction evolves is determined not only by temperature and concentrations of reactants and products (the conventional assumption in chemistry) but also by the temperature gradient, the state of strain, and the rate of deformation.
The relation of Eq. (3.7), when combined with the restriction of Eq. (3.9), shows that
| (3.10) |
where
| (3.11) |
Thus, the stress tensor includes the dissipative contribution and the nondissipative contribution .
3.3 Residual Dissipation.
The residual dissipation statement in Eq. (3.6) provides necessary and sufficient constraints on the constitutive models we may adopt for the dissipative stress , the heat flux q, and the molar production rate . Thus, any constitutive model for these functions of state must satisfy Eq. (3.6), as illustrated here. As we shall also discuss in greater detail, terms that remain in the residual dissipation represent the irreversible processes for the material being modeled, whereas terms from the entropy inequality that reduce to zero (such as the coefficients of , and ) may be associated with reversible processes.
In the absence of reactions ( , implying that 's are all constant), the residual dissipation statement (3.6) reduces to . Necessary and sufficient conditions for satisfying this inequality are not generally available due to dependencies of and q on D and g. However, constitutive relations for functions of state are guided by experimental observations, while the axiom of entropy inequality only needs to place constraints on specific choices of such relations. In practice, it has been common to satisfy this residual dissipation statement using the sufficient (but not necessary) conditions and . To satisfy for arbitrary temperature gradients g, the heat flux must have the general form , where is the thermal conductivity tensor, which must be positive semidefinite and symmetric for all to uniquely satisfy that inequality constraint. This constitutive model represents a generalization of Fourier's law of heat conduction as it also allows a dependence on g and D. The precise mathematical dependence of the material function K on its state variables must be informed by experimental observations of each desired material.
Similarly, the relation may be used to place a constraint on the choice of constitutive relations for . It follows that must be a function of D or else this inequality may not be satisfied for arbitrary values of D; therefore, the dissipative stress represents a viscous stress [40]. The stress in Eq. (3.7) must reduce to zero when the material is at rest in its reference configuration. Thus, the free energy density should be formulated such that in Eq. (3.11) reduces to zero when there is no strain; simultaneously, the constitutive relation for the dissipative stress should be constructed such that it reduces to zero when the rate of deformation is zero (i.e., when the material is at rest in a strain-free state).
Example 1. For example, for an isotropic material, we may formulate as a Taylor series expansion of D. Using the Cayley–Hamilton theorem, we can show that powers of D higher than two may be expressed in terms of lower powers, so that the general form of is
| (3.12) |
where (i = 0, 1, 2) are scalar functions of their arguments. In particular, since the material is assumed to be isotropic in this example, may be functions of the invariants of D. In order for to reduce to zero in the reference state should reduce to zero when . For a material with a linear response, we may choose , where is the dynamic shear viscosity and is the dynamic bulk viscosity; this is equivalent to setting , , and . According to the residual dissipation constraint , these material functions must satisfy and for all . Moreover, in a Newtonian fluid, μ and κ are assumed to depend neither on D nor g. Since is the stress power density, we may refer to as the viscous stress power density.
The last term in the residual dissipation statement (3.6) represents dissipative mechanisms resulting from reactions. It may be denoted by
| (3.13) |
where we used Eq. (2.18) and defined as the chemical potential of α on a molar basis (with units of molar energy). Here, has units of power density, and we may refer to it generically as the reactive power density. In the absence of net heat supplies generated by the viscous stress and the heat flux q (i.e., when ), the residual dissipation statement reduces to . Thus, a reaction may proceed spontaneously (i.e., in the absence of net heat supplies) if and only if is negative. Since the constitutive relation for the chemical potentials is completely determined from according to Eq. (3.8), in practice the constraint on represents a constraint on the algebraic sign of the constitutive relation for the molar production rate . If a reaction is observed experimentally to take place spontaneously, and if is negative for that reaction, the constitutive model postulated for must produce a positive function (i.e., a net forward reaction). In practice, however, this argument is generally flipped: a forward reaction ( ) may proceed spontaneously if and only if . Conversely, when is positive, a nonspontaneous reaction may be induced by supplying a sufficient amount of heat to satisfy .
In classical chemistry and thermodynamics, the argument regarding the spontaneity of chemical reactions is expressed in terms of a net change in (Helmholtz) free energy for processes under constant volume and temperature or a net change in Gibbs energy for processes under constant pressure and temperature [41]. In our continuum treatment using reactive mixtures, this argument is given in rate form, valid for any process (not necessarily at constant temperature, nor volume, nor pressure). By analogy to the classical framework, we may state that processes for which are exergonic, those for which are endergonic, and represents isergonic processes. Moreover, we may define the energy of formation (with units of molar energy) as
| (3.14) |
by analogy to the classical definition of as the Gibbs energy of formation in a reaction. Contrary to and , which depend on the complete list of state variables , the right-hand side of Eq. (3.14) shows that the energy of formation is only a function of .
3.4 Implications for Energy Balance.
Using the thermodynamically restricted dependencies on state variables presented in Sec. 3.2, the material time derivative of the specific internal energy ε becomes
| (3.15) |
Employing Eq. (3.3), as well as Eqs. (2.23), (3.7), and (3.8), this expression may be used to evaluate
| (3.16) |
where
| (3.17) |
is the definition of the isochoric specific heat capacity. Substituting Eq. (3.16) into the energy balance in Eq. (2.20) produces its alternative form commonly described as the heat equation
| (3.18) |
where, using Eq. (2.18), we define
| (3.19) |
The form of the axiom of energy balance in Eq. (3.18) represents the specialization of the general form (2.20) to the case of reactive processes in constrained mixtures, for the choice of state variables adopted in Sec. 3.2. Based on the definition in Eq. (3.19), the term on the right-hand side of Eq. (3.18) evidently represents the reactive heat supply density (heat supply from reactions, in units of power density), for any type of system that may be modeled as a constrained reactive mixture. When heat is supplied by reactions to the continuum, implying that the net effect of all reactions is exothermic; conversely, implies that heat is lost by the mixture due to endothermic reactions; describes an adiabatic reaction.
We may now define the heat of reaction (units of molar energy) as
| (3.20) |
This definition differs from that of the enthalpy of formation of the product of a reaction in classical thermodynamics, which is defined in terms of the enthalpies of reactants and products at constant temperature and pressure (or volume). The expression given in Eq. (3.20) encompasses transient and steady-state processes under any set of conditions for temperature, pressure, or volume. Contrary to the enthalpy of formation, the relation of Eq. (3.20) does not include the heat supply density contributed by on the right-hand side of Eq. (3.18), which arises from the dependence of the elastic stress (thus, elastic or thermodynamic pressure) on temperature. The heat of reaction is defined in terms of the intrinsic properties (the chemical potential) of reactants and products. Contrary to and , which depend on the complete list of state variables , the right-hand side of Eq. (3.20) shows that the heat of reaction is only a function of .
Yet another form of the energy balance may be obtained by taking the material time derivative of Eq. (2.23) and expressing it as , substituting Eq. (3.1) into this expression, and making use of the constraints (3.3)–(3.5) and (3.11) to produce . Substituting this relation into the energy balance (2.20) produces
| (3.21) |
This relation clarifies which mechanisms increase the entropy of a reactive mixture, namely, the heat generated by viscous stresses, a converging heat flux, the loss of reactive power density, and other heat supplies not modeled explicitly. It can be verified that substituting Eq. (3.21) into the general entropy inequality (2.21) recovers the residual dissipation (3.6).
Finally, combining Eq. (2.20) with Eqs. (2.23) and (3.21) produces another alternative form of the energy balance
| (3.22) |
This expression could also be obtained from Eq. (3.1) by substituting into it the relations (2.7), (2.8), (3.8), and the constraints (3.3) and (3.9). This form of the energy balance shows that gains to the free energy density occur due to losses in , the gain of elastic stress power density , and the gain of reactive power density . The elastic stress power is the rate of work of the conservative part of the stress tensor.
3.5 Irreversible, Reversible, and Isentropic Processes.
We found two types of constraints resulting from the Clausius–Duhem inequality: Constraints that reduce the corresponding terms to zero, such as those in Eqs. (3.3)–(3.5), and constraints that persist in the residual dissipation, as in Eq. (3.6). We deduce that the processes associated with terms that vanish from the residual dissipation are reversible, since they produce no dissipation, whereas processes that persist in the residual dissipation are irreversible. In the derivations presented above, it becomes apparent that processes which only alter the temperature ( ) while maintaining zero dissipation, , are reversible processes. A process is irreversible if the sum of terms on the left-hand side of the residual dissipation (3.6) is strictly positive. In practice, this means that any process which exhibits a nonzero viscous stress , or nonzero heat conduction q, or undergoes an exergonic or endergonic reaction, is irreversible. (We may theoretically conceive of a reversible process where none of these individual terms is zero but their sum remains zero; however, this type of construct is mostly hypothetical.) Conversely, when (implying the material is idealized as inviscid; or rigid, with zero rate of deformation), and (implying no temperature gradient, , or that the material is idealized as a perfect heat insulator, ), and (no reactions, or only isergonic reactions), the process is reversible. For example, nonreactive perfectly elastic materials ( ) and rigid materials ( ) undergo reversible processes under isothermal conditions ( ).
By definition, a process is isentropic ( ) when the right-hand side of Eq. (3.21) is zero. Therefore, a reversible process that satisfies , , r = 0, and is always isentropic. However, the requirement for isentropic processes is slightly less restrictive than that for reversible processes. When , r = 0, and , a process is isentropic if , which is less stringent than requiring . For example, one-dimensional steady-state heat conduction in a rigid body satisfies but , implying that it represents an isentropic process which is irreversible. (In other words, heat can never conduct from low temperature to high temperature, even under one-dimensional steady-state conditions.)
Recall that we eliminated the heat supply r from the entropy inequality (2.21) by combining it with the energy balance. As a result, r does not appear in the residual dissipation statement (3.6), and we may wonder whether this user-specified heat supply term is dissipative or not. This apparent ambiguity arises from the fact that we introduced r to simulate various potential sources of heat supplies, such as microwave heating, Joule heating, etc., without explicitly accounting for the mechanisms that give rise to these phenomena. In reality, these illustrative phenomena are dissipative, as shown for frictional interactions between electrically neutral or charged species in unconstrained mixtures [7], which can represent Joule heating. Therefore, the absence of r in the residual dissipation statement represents a simplifying idealization of actual dissipative processes. In effect, r is a generic placeholder for processes that have not been modeled explicitly via the adoption of suitable state variables. For example, when processes in a material are assumed a priori to be isothermal ( ) or the material is assumed to be inviscid ( ), or when reactive processes are not modeled explicitly ( ), ρr may serve as a placeholder for any of the irreversible processes embodied by viscous heat dissipation, a converging heat flux, or exothermic/endothermic reactions, as per Eq. (3.18).
In summary, reversible processes and isentropic processes are not interchangeable concepts under general conditions, and the specific heat supply r is a generic placeholder for dissipative processes that are not modeled explicitly due to the exclusion of selected state variables, such as g to model q, D to model , or to model . As a final point on the subject of residual dissipation, we can define the concept of thermodynamic equilibrium of a system as the set of conditions when all the terms in the residual dissipation (3.6) are identically equal to zero.
3.6 Specialized Mixtures
3.6.1 Formulation in Terms of .
In some applications, we may propose a constitutive model for the mixture where is expressed in terms of the specific free energy of each of the mixture constituents, as per Eq. (2.24). In that case, we may find it more suitable to set the list of state variables for to , such that it depends on the deformation gradient of that constituent relative to its own reference configuration ; here, β spans all constituents. Using the relation (2.2) and the chain rule of differentiation, it follows that
where we also used (a time-invariant fourth-order tensor).
Remark 3. Using Cartesian components, the tensor dyadic product ⊘ is defined such that (A ⊘ .
Combining this relation with Eq. (2.24), and recalling that and are mutually independent state variables, the elastic stress in Eq. (3.11) may be evaluated from
| (3.23) |
where is in the standard hyperelastic form of a constitutive model for stress evaluated using a strain measure based on . To maintain frame indifference for constrained mixtures, we must satisfy , where Q is an orthogonal transformation that maintains the symmetry group of . Here, we abbreviated the list of state variables for from to just , for notational simplicity. This frame indifference is automatically satisfied for based on the hyperelasticity relation of Eq. (3.11) and the invariance of ψ to Q. By the same argument, as given in Eq. (3.23) satisfies for transformations that maintain the symmetry group of . Since the symmetry transformations Q of ψ must also belong to the symmetry groups of all , we need to ensure that and also satisfy the kinematic constraint of Eq. (2.2) for those transformations Q, namely, . This can be achieved if and only if is invariant under a change of frame.
3.6.2 Mixture of Fluids.
If mixture constituents are all fluids, the only measure of strain needed to describe their elastic response is the volume ratio (see Sec. 2.1). We may thus substitute the state variable for throughout our treatment and use
| (3.24) |
Moreover, for fluid mixtures, we may pick a common reference configuration for all constituents α, so that Js is the only needed measure of volumetric strain. Now, the elastic stress in Eqs. (3.11) and (3.23) reduces to
| (3.25) |
We may define the fluid pressure p as
| (3.26) |
such that . By this definition it should be evident that p represents a gauge pressure, not the absolute pressure, since it reduces to zero in some arbitrary reference configuration. The energy balance for a mixture of fluids may be reduced from Eq. (3.18) to
| (3.27) |
3.6.3 Ideal Simple Mixtures.
We define ideal simple mixtures as those whose constituents have specific free energies that are independent of concentrations
| (3.28) |
For ideal simple mixtures, it follows from Eq. (3.8) that the chemical potential of each constituent is equal to its specific free energy
| (3.29) |
According to Eq. (3.14), the energy of formation simplifies to
| (3.30) |
where is the molar free energy, and the heat of reaction (3.20) simplifies to
| (3.31) |
where and are the molar entropy and molar internal energy, respectively, of each constituent. In other words, for ideal simple mixtures the energy of formation represents the net gain or loss of molar free energy, and the heat of reaction represents the net loss or gain of molar internal energy. Thus, a reaction is exergonic (endergonic) when the net free energy of products is less (greater) than that of reactants. A reaction is endothermic (exothermic) when the net internal energy of products is less (greater) than that of reactants.
4 Discussion
The objective of this study was to present a complete framework for constrained reactive mixtures of solids or fluids which accounts for their thermodynamics using observable state variables. The framework of constrained reactive mixtures was originally formulated to analyze growth and remodeling mechanics in biological tissues [18,20,22]. More recently, it has been shown to be capable of also describing classical dissipative mechanics phenomena such as viscoelasticity, damage mechanics, plasticity, and elastoplastic damage [29–32].
In this study, we presented the general equations of mass, momentum, and energy conservation, as well as the axiom of entropy inequality, for constrained mixtures undergoing reactive processes, accounting for spatiotemporal changes in temperature. An important element of this framework was the assumption that the temperature must be constrained to be the same for all constituents of such mixtures in order to produce a well-posed system of equations. As usual for mixture theory, an equation of mass balance was posed for each constituent which includes a function of state for the mass density supply resulting from reactions with all other constituents, making it possible to solve for the evolving composition of reactive mixture constituents. However, in contrast to general mixture theory, the theory of constrained mixtures only requires a single momentum and a single energy balance equation to solve for the motion and temperature of the mixture. An essential aspect of this constrained mixture approach is that each constituent may have its own reference configuration, which represents a function of state that should be postulated by constitutive assumption as illustrated in the Appendix.
To illustrate the application of this constrained reactive mixture framework to familiar problems in mechanics, we selected a broad set of observable state variables in Sec. 3 that allowed us to consider a wide range of examples as presented in the Appendix. Using those state variables we extended the approach of Coleman and Noll [40] to show that the Clausius–Duhem inequality (2.22) produced familiar constraints on the functions of state as presented in Sec. 3.2. Most notably, as in our previous presentation of general reactive mixtures [7], we found that the chemical potential of the constituents in Eq. (3.8) emerges naturally to play a critical role in the thermodynamics of constrained reactive mixtures. It enters into the expression for the reactive power density in Eq. (3.13), which appears in the residual dissipation statement (3.6). As usual, the residual dissipation statement places thermodynamic constraints on the constitutive models for the viscous stress and the heat flux. It also places a constraint on which embodies the classical concept from chemistry that spontaneous reactions may only take place when there is a net decrease in Helmholtz free energy for processes under constant volume and temperature, or a net decrease in Gibbs energy for processes under constant pressure and temperature [41].
However, in this continuum mechanics framework, the meaning of in the residual dissipation statement is more significant: It represents a constraint in rate form, valid for any process, not just those taking place at constant temperature, or volume, or pressure. The sign of determines if a reaction is exergonic, endergonic, or isergonic. Moreover, by accounting for the stoichiometry of reactions as presented in Sec. 2.3, it becomes apparent that the residual dissipation constraint on actually places a constraint on the molar production rate , which determines the mass density supplies (2.18) for all constituents in a reaction. This is consistent with our expectation that the Clausius–Duhem inequality should place constraints on the constitutive relations of all functions of state. This study shows that the thermodynamic feasibility of classical dissipative mechanics processes, such as viscoelasticity and damage mechanics, may be determined by the contribution of to the residual dissipation statement, just like the feasibility of chemical reactions. Thus, classical concepts from chemical kinetics extend to the mechanics of solids, as long as we recognize that dissipative processes in solid mechanics may be modeled by letting also depend on the state of deformation ( and D).
In our constrained mixture approach, we emphasize that the mapping between the reference configurations of constrained mixture constituents α and s is a nonobservable function of state, instead of an observable (or hidden) state variable. As such, one may wonder why the entropy inequality in Eq. (3.2) does not impose an explicit constraint on this function of state. In fact, the residual dissipation statement (3.6) indirectly imposes a constraint on , as illustrated in the reactive damage framework, Appendix A.2, and the reactive viscoelasticity framework, Appendix A.3. In the damage reaction , we made the constitutive assumption that the specific free energy of broken bonds b is zero, whereas that of intact bonds i is positive (since the free energy is the strain energy in an isothermal framework); in the viscoelasticity reaction , we made the constitutive assumption that the specific free energy of reformed bonds v is zero at the time of reformation, whereas that of the breaking bonds u is positive. These constitutive assumptions led to the formulation of associated functions (arbitrary for damage mechanics, and given by at time when bonds α are formed for isotropic viscoelasticity). Had we formulated such that the specific free energy of the product of a reaction was higher than that of the reactant, we would have violated the residual dissipation statement in those isothermal frameworks. Thus, the axiom of entropy inequality does indeed constrain our choices of constitutive models for .
Another important finding of this study is that an expression emerged naturally for the reactive heat supply density in a constrained reactive mixture, as presented in Sec. 3.4 and Eq. (3.19). The reactive heat supply density is proportional to the molar production rate ; it also depends on the chemical potential and its rate of change with temperature. The sign of determines if the reaction is exothermic, endothermic, or adiabatic. To the best of our knowledge, this study gives the first presentation of this simple and elegant formula for the reactive heat supply in a continuum thermodynamics framework. In other words, the formulation of constitutive relations for the specific free energy of each mixture constituent, using experimental measurements of its elastic stress versus strain and temperature (or elastic pressure versus volume ratio and temperature in the case of a fluid) along with experimental characterization of its isochoric specific heat capacity, makes it possible to calculate the reactive heat supply density in rate form. For many fluids, may be calculated from Eq. (2.23) using internal energy and entropy values available from thermodynamic tables, even though engineering thermodynamic textbooks do not tell how to evaluate . The formulation given in Eq. (3.19) now provides this capability, thereby allowing engineers to solve the energy balance (3.18) in rate form using known constitutive models for and similarly characterized constitutive models for .
Since both and are proportional to , we could define the ratios of these measures as the energy of formation in Eq. (3.14) and the heat of reaction in Eq. (3.20). The concepts of energy of formation and heat of reaction are well recognized in thermodynamics and chemistry, but the general form of the equations presented in this study differs from the various process-specific forms given for these concepts in the classical literature. For example, in these classical approaches, the energy of formation is typically associated with the Gibbs potential, whereas the heat of reaction is often associated with the change of enthalpy in a reactive thermoelastic fluid undergoing steady flow at constant pressure and temperature. As can be seen in Secs. 2 and 3, neither Gibbs potential nor enthalpy emerge naturally in the general governing equations of continuum thermodynamics presented here. We believe that the concepts presented in the classical literature lack the generality of our formulation.
In this context, it is noteworthy that the classical thermodynamics literature is based on frameworks that long predate the formulation of the Clausius–Duhem inequality in the form given by Truesdell and Toupin [39]. Their form of this axiomatic inequality has been adopted by many in the continuum mechanics community, but it does not enjoy universal acceptance as reviewed by Müller [42]. In particular, Truesdell and Toupin [39] chose to include the specific heat supply r in the inequality (2.21), as explained in a subsequent historical note by Truesdell [43], which differentiated their approach from that of other continuum formulations [42]. In our treatment, we go one step further and explain that r is a generic placeholder for mechanisms of internal heat generation that cannot be accounted for due to the self-restricted choice of observable state variables adopted in an analysis. Thus, as explained in Sec. 3.5, ρr could serve as a placeholder for when one wants to model reactive heat supplies without explicitly accounting for evolving compositions . This point is further illustrated by our adoption of a constrained mixture framework in this study, which prevented us from explicitly accounting for frictional heat supplies arising from the relative motion of mixture constituents since we could not include such relative motions as state variables.
To illustrate this novel approach to the thermodynamics of dissipative processes, in the Appendix, we provided explicit expressions for the heat of reaction in reactive mixtures of ideal gases (A15), in damage mechanics of solids (A20), and in viscoelasticity (A28). We also showed that the heat of reaction is zero in thermoelasticity (A47). In a recent study, we demonstrated that the thermodynamic framework presented here could also be used to evaluate these measures of heat production for elastoplastic processes, with or without damage [32].
One of the greatest challenges in modeling reactive mixtures is the dependence of the mixture free energy density on the constituent concentrations as per Eq. (2.24), especially when the specific free energy of each constituent depends on of all mixture constituents. For a pure substance (single constituent), ψ is characterized experimentally by performing stress–strain (or pressure–volume) experiments at various temperatures, and extracting the isochoric specific heat capacity cv, to fully characterize all the functions of state for that material, as illustrated for a pure ideal gas in Appendix A.1.1 and for a thermoelastic neo-Hookean solid in Appendix A.4.2. These stress–strain or pressure–volume experiments are generally conducted under quasi-static conditions. Methods for obtaining cv may rely on experimental measurements of the spatiotemporal evolution of temperature in the material under various strains, which would be temporally constrained by the thermal diffusivity and characteristic dimensions of a sample. In practice, the experimental characterization of ψ over a wide range of deformations and temperatures may be a very time-consuming process, constrained by the characteristic time constant of the experiments being conducted.
When multiple constituents are mixed, their specific free energies could vary significantly due to the presence of other constituents; a simple example is the case of fluid solutions, where the solvent free energy may be significantly affected by solute concentrations. To model such mixtures, one would also need to characterize as a function of for all constituents β in the mixture, preferably over a wide range of their concentrations. For reasons given above, this effort would be typically prohibitive from an experimental perspective, especially if spontaneous reactions take place in the mixture at some pressures and temperatures, creating a fleeting presence of some of the reactants and products that would prevent the performance of quasi-static measurements at constant values of . In practice, investigators may postulate a constitutive model (often motivated by microstructural theories) to account for the influence of constituent concentrations in mixtures. In Sec. 3.6.3, we adopted the simplest such model, namely, that is independent of any of the concentrations ; we called such mixtures ideal and simple, and provided an illustration using simple mixtures of ideal gases in Appendix A.1.
Even for the standard models of ideal gases and neo-Hookean solids, our continuum framework emphasizes that the functions of state for the stress , or the pressure p in thermoelastic fluids, represent a gauge stress and pressure, which are set to zero at an arbitrary absolute ambient pressure Pr and temperature θr. While this concept is well-accepted in solid mechanics and fluid mechanics, it is much more common to use the absolute pressure P and temperature θ in conventional thermodynamics. In this study, our illustration of pure ideal gases and their mixtures in Appendix A.1 provides a formulation that employs the gauge pressure relative to Pr, also allowing a nonzero referential absolute temperature θr.
Because of our ability to completely characterize the functions of state of ideal gas mixtures, we were able to evaluate the energy of formation in Eq. (A13) and the heat of reaction in Eq. (A15) for such mixtures, serving as a practical illustration of these fundamental concepts as presented in their novel form in this study. These relations may be combined with constitutive relations for the kinetics (the molar production rate ) of various reactions in such ideal gas mixtures. This type of framework can be very useful in studies of reactive processes in air, such as respiratory exchanges in the lung.
Finally, we illustrated the application of this thermodynamics framework to problems in solid mechanics, notably damage mechanics in Appendix A.2, viscoelasticity in Appendix A.3, and thermoelasticity in Appendix A.4. The first two reactive frameworks were described in our earlier studies [29,30] where we assumed that isothermal conditions prevailed. Here, we showed that the dissipative mechanisms of damage mechanics and viscoelasticity, which arise from the breaking of intact bonds, produce reactive power densities and heat supplies that can be characterized in a straightforward manner. To maintain this hypothetical isothermal condition, the exothermic supply has to radiate out of the continuum to satisfy the axiom of energy balance.
Evidently, more general theories of thermodamage mechanics, thermoviscoelasticity and phase transformations could be formulated, where the dissipative heat supply changes the temperature of the continuum, driving heat conduction. However, the starting point for such theories would need to account for the thermal expansion of the solid in response to changes in temperature. Therefore, in Appendix A.4, we developed a novel formulation of reactive thermoelasticity that can serve as a foundation for more general thermal theories of dissipative solid mechanics. We treated the change in temperature as a reactive process that transforms a substance by altering its reference configuration and material properties. As for ideal gases, damage mechanics, and viscoelasticity, we demonstrated that reactive thermoelasticity recovers standard models in the classical literature. Moreover, we examined the conditions under which thermoelastic processes satisfy the residual dissipation statement.
The fact that constrained reactive mixture theory can reproduce such a broad range of classical material responses, while also clarifying many thermodynamic concepts associated with these materials, suggests that this framework is a suitable generalization of classical continuum mechanics frameworks for pure substances. Indeed, in future studies, we will demonstrate that constrained reactive mixtures can be used to model fatigue failure in biological tissues and metals; we will also demonstrate that this framework can be used to examine liquid–gas phase transformations across an interface, where the Gibbs potential (free enthalpy) emerges naturally as a function of state. We believe that this constrained reactive mixture framework provides a powerful and intuitive approach for modeling material responses within a unified framework. This study has provided the broad foundations of the thermodynamics of such mixtures, along with several illustrations for solids and fluids.
Acknowledgment
The authors would like to thank Professor Michael Burke of Columbia University for his insightful comments.
Appendix: Examples
A.1 Ideal Gas Mixtures
In this section we model a mixture of compressible fluids where each fluid is modeled as an ideal gas. We start by reviewing the governing equations for a pure ideal gas (a single constituent).
A.1.1 Pure Substance.
Our approach for modeling thermodynamics defines a reference configuration (such as a reference absolute pressure Pr and temperature θr) for evaluating the volume ratio. Therefore, the pressure p (elastic stress ) in our treatment represents a gauge pressure (stress) acting on top of the reference pressure Pr (stress ). For a pure ideal gas with molar mass M, its gauge pressure is given by
| (A1) |
where R is the universal gas constant, θr is the reference temperature, and ρr is the gas density in the reference configuration (when J = 1 and ). The reference absolute pressure Pr is
| (A2) |
and the absolute pressure is . In practice, we may pick the desired reference Pr and θr and evaluate the corresponding value of ρr from Eq. (A2); then according to Eq. (2.13). Equation (A1) may be integrated with respect to J to produce an expression for the specific free energy
| (A3) |
where ψr and ηr are, respectively, the specific free energy and entropy of the gas at the reference temperature θr and reference pressure Pr. This expression for ψ also accounts for Eq. (3.17), where is evaluated from the gas isobaric specific heat capacity as
| (A4) |
This form for ψ was derived such that the term on the right-hand side of Eq. (A3) represents that part of the specific free energy which varies with pressure, since this term reduces to zero when p is zero at any temperature, i.e., when according to Eq. (A1). The specific internal energy of a pure ideal gas may be evaluated from Eqs. (2.23) and (A3) as
| (A5) |
where and . The specific entropy of an ideal gas may be obtained by substituting ψ in Eq. (A3) into Eq. (3.3) to produce
| (A6) |
A.1.2 Mixture.
Now consider that we formulate a mixture of ideal gases α which all share the same reference configuration (same absolute reference pressure Pr and temperature θr, and for all α), for which the mixture free energy density is constructed to produce an ideal simple mixture
| (A7) |
In other words, we have assumed that the specific free energy of each ideal gas constituent is not altered by the presence of other constituents in the mixture; thus, it keeps the same form (A3) as that of a pure substance. According to Eq. (3.26), the gauge pressure in this mixture is
| (A8) |
where ρr is given in Eq. (2.13) and M is the mixture molar mass, evaluated from
| (A9) |
Note that M may evolve during a reaction, since evolves according to Eq. (2.7), while ρr remains constant. The expression for the mixture pressure in Eq. (A8) has the exact same form as that of a pure ideal gas as shown in Eq. (A1); therefore, an ideal constrained mixture of ideal gases is also an ideal gas. We may express Eq. (A8) as , where
| (A10) |
is called the partial pressure of each ideal gas constituent α.
Remark 4. In a strict sense, as mentioned at the start of this presentation on constrained mixtures, the pressure in each mixture constituent remains indeterminate. In reality, the true pressure of constituent α has the form , where 's are indeterminate pressures that satisfy .
Note that this expression for the partial pressure satisfies where
| (A11) |
is the molar fraction of constituent α in the mixture.
Remark 5. In classical chemistry of ideal gas mixtures, this relation is expressed in terms of absolute pressures, ; these two forms are equivalent.
Now, using Eq. (3.29), the chemical potential of each constituent is
| (A12) |
In other words, the chemical potential of each constituent is equal to its specific free energy, as anticipated in Eq. (3.29) for ideal simple mixtures. Therefore, the energy of formation for an ideal reactive mixture of ideal gases may be evaluated from Eq. (3.30) as
| (A13) |
where , and . As is evident here, the energy of formation in an ideal gas mixture is not a function of the constituent concentrations.
In particular, for an isobaric process at some gauge pressure p0, we may evaluate Js from Eq. (A8)
| (A14) |
and substitute it into the expression for in Eq. (A13). Since M and θ may evolve during a reaction, it follows that Js may similarly evolve under a constant pressure reactive process. If the process takes place at the reference pressure Pr (i.e., when ), this expression for the volume ratio simplifies further to and . Conversely, we may consider an isochoric and isothermal process under the reference conditions ( ), in which case the energy of formation simplifies to .
Similarly, we may evaluate the heat of reaction (3.31) using in the form of Eq. (A5) to produce
| (A15) |
where is the molar internal energy of constituent α. As seen here, the heat of reaction for an ideal mixture of ideal gases is not a function of the constituent concentrations. We may similarly simplify when modeling isobaric, isochoric, or isothermal processes.
For this fluid mixture, the heat supply contributed by the fluid pressure (A3) on the right-hand side of Eq. (3.27) reduces to
| (A16) |
where is the absolute pressure. For an isochoric process (constant Js), this term reduces to zero.
In summary, we have presented the constitutive relations relevant to ideal simple mixtures of ideal gases, and we have evaluated the chemical potential of each constituent in Eq. (A12), as well as the energy of formation in Eq. (A13) and the heat of reaction in Eq. (A15) for reactions involving these ideal gas constituents. These relations are not generally given in engineering thermodynamics textbooks. A key aspect of this formulation is that the constitutive relations for the mixture constituents are all expressed relative to the same reference configuration at absolute pressure Pr and absolute temperature θr (e.g., the standard state, or the standard temperature and pressure). Therefore, , and for each constituent α must be determined for this specific reference configuration.
A.2 Reactive Damage Mechanics
In our previously reported formulation for reactive damage mechanics [30], it was proposed that an elastic material ( ) undergoing damage from loading could be modeled as an ideal constrained mixture of a constituent with intact bonds and another with broken bonds ( and , respectively). In that presentation, a simplifying constitutive assumption was made that the specific free energy of each constituent was only a function of deformation, , implying an isothermal process ( ) where the specific free energy only represents the specific strain energy stored in constituents α, which is a positive semidefinite function of the strain. Here, we examine the energy of formation and heat of reaction for this damage model.
The net free energy density of this ideal mixture is
| (A17) |
and the chemical potential of each constituent reduces to its specific free energy, as predicated in Eq. (A12). The damage reaction, , is a forward reaction derived from Eq. (2.14) with and . It requires the formulation of a constitutive relation for the molar production rate . Consider that damage occurs when some scalar damage measure (e.g., the von Mises stress in the material) causes a mass fraction of the constituent with intact bonds to break at that value of . The cumulative mass fraction of the constituent with broken bonds at is , where . Then, according to Eqs. (2.7) and (2.18)
| (A18) |
where M is the molar mass of i and b, and is the maximum value of achieved so far in the loading history. Since the bond concentrations satisfy according to Eq. (2.13), a natural damage variable D emerges from that framework, representing the mass fraction of broken bonds, .
Since broken bonds cannot store strain energy, it follows that . Therefore, it is not necessary to specify a function of state for the mapping of broken bonds in a reactive damage framework. The reactive power density in Eq. (3.13) and the energy of formation in Eq. (3.14) reduce to
| (A19) |
To satisfy the residual dissipation statement (3.6) for this process, , we must have (implying a forward, bond-breaking reaction), since is always positive, implying that the reaction is exergonic (i.e., in this context, it can occur spontaneously from loading, without the addition of heat). By examining the constitutive model for the molar production rate in Eq. (A18), we find that must always be positive, implying that must be a monotonically increasing function of . Therefore, the functions f and F may be represented by a probability density function and its associated cumulative distribution function, respectively, with f representing the probability of bonds breaking at the value of . In this context, it makes further sense to interpret F as a damage measure bounded by . As usual, the Clausius–Duhem inequality has placed a constraint on our choice of constitutive models; in this case, the constraint is placed on the constitutive relation for the molar production rate.
For this isothermal damage mechanics framework, using Eqs. (3.19) and (3.20) produces
| (A20) |
Thus, since the molar strain energy of intact bonds is always positive, and since when bonds break, it follows that for a damage reaction. In other words, as expected, damage mechanics is an exothermic process.
The elastic stress may be evaluated from Eq. (3.23) using Eq. (A17). Evidently, since in a damage model, the only contribution to arises from in Eq. (A17), which decreases with decreasing concentration of the constituent with intact bonds. Since we also assumed that the specific free energy is not a function of temperature in this idealized damage model, it follows that in the energy balance (3.18), which now reduces to for this isothermal process. This relation implies that the reactive heat supply must be emitted as some form of radiation in order to maintain isothermal conditions. Of course, this mechanism of radiation is a hypothetical construct arising from our imposition of the isothermal constraint.
A.3 Reactive Viscoelasticity
The complete framework for nonlinear reactive viscoelasticity was presented in our earlier study [29], and the special case of linear viscoelasticity was reviewed by Nims and Ateshian [31]. In this isothermal framework, a viscoelastic solid includes constituents associated with two bond families: Strong bonds ( ) that do not break in response to loading and produce the equilibrium elastic response; and weak bonds ( ), which break in response to loading and immediately reform into a stress-free state. Loading is represented by a change in any strain measure derived from the deformation gradient . Constituents with weak bonds are the reactive constituents in this mixture, responding to this change in strain; those that reform in a stress-free state at time t = u are denoted by and called generation bonds. Similarly, those that break and reform in a stress-free state at a subsequent time t = v are denoted by . The reaction describing bond breaking and reforming as a result of consecutive changes in strain at times u and v is (with and ). The earliest generation in this reactive mixture is where ; it represents the master constituent for the reactive mixture, while also represents the stress-free reference configuration of strong bonds.
The strain energy density of this mixture of constituents with strong and weak bonds thus takes the form
| (A21) |
where is the strain energy density of the elastic constituent with strong bonds. Here, we have assumed that all generations u of weak bonds share the same functional form ψ for the specific strain energy of their associated constituent u; however, the value of ψ for each generation u depends on the deformation gradient for that generation. For example, suppose that the first step increase in strain occurs at time u and is given by . Starting at time u, weak bonds that belonged to generation s start breaking and reforming immediately into generation bonds whose reference configuration is the current configuration . Thus, by constitutive assumption (i.e., by assuming that bonds break and immediately reform in a stress-free state), we postulate that (i.e., the right stretch tensor of ) for isotropic materials, from which it follows that is equal to the rotation tensor of for , until the next change in deformation. The concentration of the constituent associated with generation bonds is zero at time u but progressively increases for t > u due to the time-dependent reaction which increases at the expense of , while maintaining according to Eq. (2.13).
The energy stored in constituents with strong bonds for is ; the specific strain energy in the constituent with generation weak bonds is , while that in generation bonds is (stress-free state). Upon loading ( ), the temporal evolution of in Eq. (A21) is now governed by the temporal evolutions of and . At a subsequent time v, another step change in strain occurs given by , causing bonds from generation u and remaining bonds from generation s to start breaking and reforming into generation bonds with a stress-free configuration .
The bond breaking-and-reforming reaction is governed by Eq. (2.7); thus, for generation bonds, we may write , where M is the molar mass of the constituent associated with weak bonds, whereas . For a first-order reaction, we may propose a constitutive model where is proportional to the evolving concentration of generation bonds
| (A22) |
where τ is a time constant for the temporal evolution of this reaction. As presented in earlier studies [29,31], these constitutive assumptions (first-order reaction with strain-independent time constant τ) reproduce the framework of quasi-linear viscoelasticity; a recursive solution is found from these equations for each consecutive pair of generations
| (A23) |
where is the total referential density of weak bonds. In particular, this solution shows that all generations of loaded weak bonds in a loading history have decaying concentrations that eventually reduce to zero, leaving only reformed weak bonds in a stress-free state. Thus, as under steady loading, the free energy density reduces to that stored in the strong bonds, , reducing to the elastic response for this viscoelastic mixture.
For continuous time increments between consecutive generations (i.e., when ), and assuming that loading starts at t = 0, it was shown earlier [29] that the above recursive relation leads to
| (A24) |
where is the deformation gradient at t relative to time u. The elastic stress may be evaluated from this expression for using Eqs. (3.11) and (3.23). Since we assumed that the specific free energy is not a function of temperature in this idealized isothermal viscoelasticity model, it follows that in the energy balance (3.18).
For example, consider the simplest case of stress relaxation, where a step change in deformation occurs at . In this case, , where is the Heaviside unit step function, and for . Since , the strain energy density in Eq. (A24) reduces to
| (A25) |
which clearly shows that the strain energy density decays from its peak value of to its equilibrium value of as a result of the viscous dissipation caused by bonds breaking and reforming. The elastic stress becomes
| (A26) |
These two expressions clearly show that the time-dependent response of a reactive viscoelastic material is governed by the time-dependent decrease in the concentration of loaded weak bonds. It is of particular interest that this reactive viscoelasticity framework does not involve time derivatives of the stress tensor.
Since the constrained mixture of weak bonds in this reactive viscoelasticity framework represents an ideal mixture, it follows that the chemical potential of each weak mixture constituent is equal to its specific free energy, as per Eq. (3.29). According to Eq. (3.30) and the above relations, the energy of formation for each reaction is
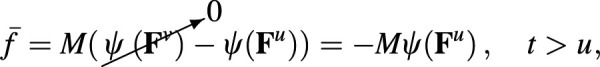 |
(A27) |
where we have recognized that generation bonds form in a stress-free state for this reaction. Since ψ represents the specific strain energy (always positive), this expression shows that is negative. To satisfy the residual dissipation statement (3.6), which reduces to in this isothermal framework (exergonic process), it follows from Eq. (3.13) that the molar production rate must be positive, hence producing a forward reaction. This constraint is satisfied in our constitutive model (A22) for by assuming that the parameter τ (the time constant for the bond-breaking reaction) is positive.
The heat of reaction is given by Eq. (3.31), which reduces to
| (A28) |
for the breaking-and-reforming reaction . The reactive heat supply for this reaction is which becomes
| (A29) |
Using the recursive relation (A23) in the limit of continuous time increments, it follows that the net reactive heat supply for all the breaking-and-reforming reactions is
| (A30) |
This quantity is always positive; thus, the bond breaking-and-reforming reaction is exothermic as expected. For this isothermal problem, the energy balance in Eq. (3.18) reduces to , once again implying that this heat supply must be radiated out of the continuum to maintain isothermal conditions.
A.4 Reactive Thermoelasticity
In elasticity theory the reference configuration of a material is defined as the traction-free configuration that also produces a stress-free state. This reference configuration is unique. In thermoelasticity, a traction-free material subjected to temperature changes exhibits a change in mass density due to its thermal expansion, even while it may remain in a stress-free state. Therefore, at each temperature the material has a different stress-free reference configuration and a different referential (stress-free) mass density. It may also have different material properties, such as elastic moduli that vary with temperature. Thus, it would be natural to consider that a pure substance at temperature θu is a different material than the same substance at temperature θv, even though both materials (call them and ) share the same chemical formula. This assumption makes it possible to treat each material as having its own unique reference configuration and intrinsic referential mass density. Then, changes in temperature may be treated as reactions that convert the substance from material to material . From this perspective it becomes possible to analyze thermoelasticity using constrained reactive mixtures. Here, the reaction is triggered by a change in temperature. In this treatment of reactive thermoelasticity we exclude phase transformations.
We adopt as the reference temperature for a thermoelasticity analysis, such that the corresponding stress-free configuration is the master reference configuration, corresponding to material . Importantly, the “stress-free” state should be understood to be the state of the material under an arbitrary, uniform constant ambient absolute pressure Pr. Therefore, throughout this treatment, represents the state of stress relative to this ambient condition (gauge stress). The density of the material in this referential stress-free state is .
As the temperature changes from θs to θu, we assume that the referential density goes from ρr to zero, while goes from zero to ρr. Similarly, for the temperature change from θu to θv, the reaction causes the density to go from ρr to zero, while goes from zero to ρr. The corresponding referential mass densities at these three consecutive temperatures are given by
| (A31) |
These expressions satisfy . In that case, using Eqs. (2.7) and (2.18), the molar production rate for is given by
| (A32) |
where δ is the Dirac delta function, and is the material time derivative of the temperature. In the limit of an infinitesimal temperature increment from θu to θv, this expression for reduces to zero.
For the specialization presented in this section, we use as our list of state variables and exclude the rate of deformation D, thus setting the viscous stress to zero. Even though the emergence of in Eq. (A32) might suggest that it should be included in the list of state variables, we use the fact that the right-hand side of Eq. (A32) is actually equal to zero in the limit of continuous temperature changes. Assuming that the mixture is ideal, the mixture free energy density (3.28) for this reactive thermoelasticity framework takes the form
| (A33) |
where we also assume that the specific free energy for all constituents α share the same functional form , such that . The stress is related to this mixture free energy density via Eq. (3.11).
A.4.1 Thermal Expansion.
Based on our constrained mixture framework, the stress-free configuration at θu is achieved when (a pure rotation) and ; according to Eq. (2.2), it follows that when the temperature is θu and the material is in a stress-free state. Thus, describes the stress-free thermal expansion of the mixture between temperatures θs and θu. This constitutive model makes it possible to characterize experimentally for a specific material.
For example, for isotropic thermal expansion, the general form for is that of an isotropic stretch tensor
| (A34) |
where λus is the stretch ratio at θu, relative to θs, representing the unconstrained (stress-free) thermal expansion. According to Eq. (2.2), it follows that .
In particular, the line element is stretched to . Experimental measurements of the stretch ratio resulting from stress-free thermal expansion of a material may be performed relative to a reference temperature θs, producing a function , such that . In the special case of a constant (temperature-invariant) linear thermal expansion coefficient αL, it follows that . More generally, for temperature-dependent thermal expansion, the linear thermal coefficient is .
For orthotropic materials whose mutually orthogonal symmetry planes have unit normals in the reference configuration (i = 1, 2, 3 and ), the general form for remains that of a stretch tensor
| (A35) |
where is the stretch ratio resulting from unconstrained thermal expansion along ; in general, . According to Eq. (2.2), it follows that
At lower symmetries, thermal expansion produces a combination of stretch and rotation. For example, for monoclinic materials, thermal expansion may be described along three unit vectors that satisfy , and , such that defines the single plane of symmetry. In this case
| (A36) |
where is the thermal stretch along . Under general conditions (i.e., when and ), the polar decomposition theorem shows that this deformation gradient is not a pure stretch, as it also involves a rotation. The deformation gradient for thermal expansion of a triclinic material may be similarly constructed by finding such that (no sum) for nonorthogonal and noncollinear unit vectors . The combination of stretch and rotation is the expected behavior in the thermoelasticity of monoclinic and triclinic materials. A transformation Q in the symmetry group of this monoclinic material satisfies and . It is straightforward to verify that such transformations keep invariant.
A.4.2 Thermoelastic Neo-Hookean Solid.
This example illustrates the application of this reactive framework to model thermoelasticity for a solid substance; it also demonstrates that we can recover the classical thermoelastic stress response of a linear isotropic elastic solid in the limit of infinitesimal deformations.
Consider that an isotropic solid material is tested for its stress–strain response at a constant temperature θu. The experimental data show that the material behaves as a compressible neo-Hookean elastic solid, so that its strain energy density has the form [44]
| (A37) |
where and νu are the measured material coefficients at that temperature, corresponding to Young's modulus and Poisson's ratio in the limit of infinitesimal strains. This strain energy density is expressed in terms of the deformation gradient describing the deformations at this temperature, with , such that reduces to zero when . The mass density of the material at this temperature, under stress-free conditions, is measured to be . By definition, measures the strain energy per volume of the material in its stress-free reference configuration at temperature θu (which is generally different from the referential volume at θs due to thermal expansion). From this expression, we may easily evaluate the specific strain energy as , which would produce an expression similar to Eq. (A37), with replaced by (with units of specific energy). At this fixed temperature θu, the specific free energy may be offset from this value by a constant representing the thermal free energy, , where needs to be determined using additional experiments.
Consider that these experiments are repeated at multiple temperatures , producing corresponding experimental values of (or ), , and . In the absence of phase transformations we assume that the functional form of remains the same but the material coefficients vary with temperature. Thus, we may formulate continuous functions of temperature , , and , such that , and . Then, the specific free energy takes the form
| (A38) |
such that . We may also express the specific free energy as by substituting into this relation.
We can differentiate Eq. (A38) with respect to θ, while keeping F constant since θ and F are independent state variables, to evaluate the remaining functions of state, such as the specific entropy using Eq. (3.3), and the isochoric specific heat capacity using Eq. (3.17), which is needed in the energy balance. The general expression for is too cumbersome to present here, but under stress-free conditions ( ) it reduces to
| (A39) |
It is evident from this relation that depends on ; thus, additional experimental measurements that characterize the stress-free isochoric specific heat capacity as a function of temperature may be used to extract , which may be integrated subject to arbitrary referential constraints, such as and at the reference temperature, as shown for ideal gases in Sec. A.1.1. In practice, for solids, it is expected that cv will be nearly independent of deformation, in which case we may simply set .
Given that and the fact that at and zero at all other temperatures, we may evaluate the elastic stress using Eqs. (3.23) and (A38) to produce
| (A40) |
where , and we used . To recover the classical thermoelastic stress response of a linear isotropic elastic solid in the limit of infinitesimal deformations, consider that , where . Then, according to Eqs. (2.2) and (A34), , from which we get and . Furthermore, under infinitesimal strains and rotations, , where is the symmetric infinitesimal strain tensor and is the infinitesimal rotation tensor, and is antisymmetric; then, and . Substituting these relations into Eq. (A40) produces the classical thermoelastic stress response of a linear isotropic elastic solid
| (A41) |
where , and , since small changes in temperature are assumed to have a negligible effect on the material properties.
This example also allows us to illustrate how we may evaluate , as required for the energy balance (3.18). We may rewrite the general nonlinear relation (A40) more conveniently in terms of Lamé coefficients
| (A42) |
where
| (A43) |
Then
| (A44) |
Here again, we may express this formula for as a function of using .
A.4.3 Thermoelastic Processes.
Since we are using an ideal simple mixture, the chemical potential is equal to the specific free energy according to Eq. (3.29). For the reaction , the net stoichiometric coefficients are and . Thus, the reactive power density in Eq. (3.13) evaluated at time v reduces to
| (A45) |
However, as explained earlier, the expression for in Eq. (A32) reduces to zero when we consider that consecutive temperatures θu and θv differ by an infinitesimal increment. In that case, and the residual dissipation statement for our proposed thermoelastic process simplifies from Eq. (3.6) to
| (A46) |
As shown in Sec. 3.3, this residual dissipation statement is satisfied unconditionally when the constitutive model for q is constructed properly.
The reactive heat supply for may now be evaluated from Eq. (3.19) as
| (A47) |
where we have also used the relations of Eqs. (2.23) and (3.3). Since reduces to zero in our reactive thermoelasticity framework, we conclude that . In other words, the change in temperature does not produce a reactive heat supply.
Funding Data
National Institute of General Medical Sciences (Grant No. GM083925; Funder ID: 10.13039/100000057).
National Science Foundation Graduate Research Fellowship Program (DGE-1644869; Funder ID: 10.13039/100000082).
References
- [1]. Truesdell, C. , 1957, “ Sulle basi della termomeccanica,” Rend. Accad. Lincei, 22(8), pp. 33–38. [Google Scholar]
- [2]. Kelly, P. D. , 1964, “ A Reacting Continuum,” Int. J. Eng. Sci., 2(2), pp. 129–153. 10.1016/0020-7225(64)90001-1 [DOI] [Google Scholar]
- [3]. Eringen, A. C. , and Ingram, J. D. , 1965, “ A Continuum Theory of Chemically Reacting Media—I,” Int. J. Eng. Sci., 3(2), pp. 197–212. 10.1016/0020-7225(65)90044-3 [DOI] [Google Scholar]
- [4]. Bowen, R. M. , 1968, “ Thermochemistry of Reacting Materials,” J. Chem. Phys., 49(4), pp. 1625–1637. 10.1063/1.1670288 [DOI] [Google Scholar]
- [5]. Nunziato, J. W. , and Walsh, E. K. , 1980, “ On Ideal Multiphase Mixtures With Chemical Reactions and Diffusion,” Arch. Ration. Mech. Anal., 73(4), pp. 285–311. 10.1007/BF00247672 [DOI] [Google Scholar]
- [6]. Bedford, A. , and Drumheller, D. S. , 1983, “ Theories of Immiscible and Structured Mixtures,” Int. J. Eng. Sci., 21(8), pp. 863–960. 10.1016/0020-7225(83)90071-X [DOI] [Google Scholar]
- [7]. Ateshian, G. A. , 2007, “ On the Theory of Reactive Mixtures for Modeling Biological Growth,” Biomech. Model. Mechanobiol., 6(6), pp. 423–445. 10.1007/s10237-006-0070-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8]. Kenyon, D. E. , 1979, “ A Mathematical Model of Water Flux Through Aortic Tissue,” Bull. Math. Biol., 41(1), pp. 79–90. 10.1016/S0092-8240(79)80055-5 [DOI] [PubMed] [Google Scholar]
- [9]. Mow, V. , Kuei, S. , Lai, W. , and Armstrong, C. , 1980, “ Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments,” ASME J. Biomech. Eng., 102(1), pp. 73–84. 10.1115/1.3138202 [DOI] [PubMed] [Google Scholar]
- [10]. Oomens, C. W. , van Campen, D. H. , and Grootenboer, H. J. , 1987, “ A Mixture Approach to the Mechanics of Skin,” J. Biomech., 20(9), pp. 877–885. 10.1016/0021-9290(87)90147-3 [DOI] [PubMed] [Google Scholar]
- [11]. Lai, W. , Hou, J. , and Mow, V. , 1991, “ A Triphasic Theory for the Swelling and Deformation Behaviors of Articular Cartilage,” ASME J. Biomech. Eng., 113(3), pp. 245–258. 10.1115/1.2894880 [DOI] [PubMed] [Google Scholar]
- [12]. Huyghe, J. M. , and Janssen, J. , 1997, “ Quadriphasic Mechanics of Swelling Incompressible Porous Media,” Int. J. Eng. Sci., 35(8), pp. 793–802. 10.1016/S0020-7225(96)00119-X [DOI] [Google Scholar]
- [13]. Gu, W. , Lai, W. , and Mow, V. , 1998, “ A Mixture Theory for Charged-Hydrated Soft Tissues Containing Multi-Electrolytes: Passive Transport and Swelling Behaviors,” ASME J. Biomech. Eng., 120(2), pp. 169–180. 10.1115/1.2798299 [DOI] [PubMed] [Google Scholar]
- [14]. Mauck, R. L. , Hung, C. T. , and Ateshian, G. A. , 2003, “ Modeling of Neutral Solute Transport in a Dynamically Loaded Porous Permeable Gel: Implications for Articular Cartilage Biosynthesis and Tissue Engineering,” ASME J. Biomech. Eng., 125(5), pp. 602–614. 10.1115/1.1611512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Ateshian, G. A. , Likhitpanichkul, M. , and Hung, C. T. , 2006, “ A Mixture Theory Analysis for Passive Transport in Osmotic Loading of Cells,” J. Biomech., 39(3), pp. 464–475. 10.1016/j.jbiomech.2004.12.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Ateshian, G. A. , Costa, K. D. , Azeloglu, E. U. , Morrison, B. , and Hung, C. T. , 2009, “ Continuum Modeling of Biological Tissue Growth by Cell Division, and Alteration of Intracellular Osmolytes and Extracellular Fixed Charge Density,” ASME J. Biomech. Eng., 131(10), p. 101001. 10.1115/1.3192138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Ateshian, G. A. , Morrison, B., III , Holmes, J. W. , and Hung, C. T. , 2012, “ Mechanics of Cell Growth,” Mech. Res. Commun., 42, pp. 118–125. 10.1016/j.mechrescom.2012.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Humphrey, J. , and Rajagopal, K. , 2002, “ A Constrained Mixture Model for Growth and Remodeling of Soft Tissues,” Math. Models Methods Appl. Sci., 12(03), pp. 407–430. 10.1142/S0218202502001714 [DOI] [Google Scholar]
- [19]. Rodriguez, E. K. , Hoger, A. , and McCulloch, A. D. , 1994, “ Stress-Dependent Finite Growth in Soft Elastic Tissues,” J. Biomech., 27(4), pp. 455–467. 10.1016/0021-9290(94)90021-3 [DOI] [PubMed] [Google Scholar]
- [20]. Baek, S. , Rajagopal, K. R. , and Humphrey, J. D. , 2006, “ A Theoretical Model of Enlarging Intracranial Fusiform Aneurysms,” ASME J. Biomech. Eng., 128(1), pp. 142–149. 10.1115/1.2132374 [DOI] [PubMed] [Google Scholar]
- [21]. Wineman, A. , and Rajagopal, K. , 1990, “ On a Constitutive Theory for Materials Undergoing Microstructural Changes,” Arch. Mech., 42(1), pp. 53–75.https://www.semanticscholar.org/paper/On-a-constitutive-theory-for-materials-undergoing-Wineman-Rajagopal/346d45859f49bf7bc53e167323701f0feff83ad4 [Google Scholar]
- [22]. Ateshian, G. A. , and Ricken, T. , 2010, “ Multigenerational Interstitial Growth of Biological Tissues,” Biomech. Model. Mechanobiol., 9(6), pp. 689–702. 10.1007/s10237-010-0205-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Rajagopal, K. , and Srinivasa, A. , 1998, “ Mechanics of the Inelastic Behavior of Materials—Part 1, Theoretical Underpinnings,” Int. J. Plast., 14(10–11), pp. 945–967. 10.1016/S0749-6419(98)00037-0 [DOI] [Google Scholar]
- [24]. Rajagopal, K. , and Srinivasa, A. , 1998, “ Mechanics of the Inelastic Behavior of Materials. Part II: Inelastic Response,” Int. J. Plast., 14(10–11), pp. 969–995. 10.1016/S0749-6419(98)00041-2 [DOI] [Google Scholar]
- [25]. Mollica, F. , Rajagopal, K. , and Srinivasa, A. , 2001, “ The Inelastic Behavior of Metals Subject to Loading Reversal,” Int. J. Plast., 17(8), pp. 1119–1146. 10.1016/S0749-6419(00)00082-6 [DOI] [Google Scholar]
- [26]. Rajagopal, K. , and Srinivasa, A. , 2015, “ Inelastic Response of Solids Described by Implicit Constitutive Relations With Nonlinear Small Strain Elastic Response,” Int. J. Plast., 71, pp. 1–9. 10.1016/j.ijplas.2015.02.007 [DOI] [Google Scholar]
- [27]. Rajagopal, K. , and Srinivasa, A. , 2016, “ An Implicit Three-Dimensional Model for Describing the Inelastic Response of Solids Undergoing Finite Deformation,” Z. Angew. Math. Phys., 67(4), pp. 1–14. 10.1007/s00033-016-0671-x [DOI] [Google Scholar]
- [28]. Rajagopal, K. R. , and Srinivasa, A. R. , 2004, “ On the Thermomechanics of Materials That Have Multiple Natural Configurations Part I: Viscoelasticity and Classical Plasticity,” Z. Angew. Math. Phys. ZAMP, 55(5), pp. 861–893. 10.1007/s00033-004-4019-6 [DOI] [Google Scholar]
- [29]. Ateshian, G. A. , 2015, “ Viscoelasticity Using Reactive Constrained Solid Mixtures,” J. Biomech., 48(6), pp. 941–947. 10.1016/j.jbiomech.2015.02.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Nims, R. J. , Durney, K. M. , Cigan, A. D. , Dusséaux, A. , Hung, C. T. , and Ateshian, G. A. , 2016, “ Continuum Theory of Fibrous Tissue Damage Mechanics Using Bond Kinetics: Application to Cartilage Tissue Engineering,” Interface Focus, 6(1), p. 20150063. 10.1098/rsfs.2015.0063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Nims, R. J. , and Ateshian, G. A. , 2017, “ Reactive Constrained Mixtures for Modeling the Solid Matrix of Biological Tissues,” J. Elasticity, 129(1–2), pp. 69–105. 10.1007/s10659-017-9630-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Zimmerman, B. K. , Jiang, D. , Weiss, J. A. , Timmins, L. H. , and Ateshian, G. A. , 2021, “ On the Use of Constrained Reactive Mixtures of Solids to Model Finite Deformation Isothermal Elastoplasticity and Elastoplastic Damage Mechanics,” J. Mech. Phys. Solids, 155, p. 104534. 10.1016/j.jmps.2021.104534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Prud'homme, R. , 2010, Flows of Reactive Fluids (Fluid Mechanics and Its Applications, Vol. 94), Springer, New York. [Google Scholar]
- [34]. Liu, I.-S. , and Müller, I. , 1984, “ Thermodynamics of Mixtures of Fluids,” Rational Thermodynamics, Springer, Berlin, pp. 264–285. [Google Scholar]
- [35]. Passman, S. L. , Nunziato, J. W. , and Walsh, E. K. , 1984, “ A Theory of Multiphase Mixtures,” Rational Thermodynamics, Springer, Berlin, pp. 286–325. [Google Scholar]
- [36]. Kannan, K. , and Rajagopal, K. , 2011, “ A Thermodynamical Framework for Chemically Reacting Systems,” Z. Angew. Math. Phys., 62(2), pp. 331–363. 10.1007/s00033-010-0104-1 [DOI] [Google Scholar]
- [37]. Pullela, M. , and Ravindran, P. , 2014, “ Aging in Soft Tissues: Influence of Chemical Reactions on Mechanical Response,” ASME Paper No. IMECE2014-37801. 10.1115/IMECE2014-37801 [DOI]
- [38]. Mythravaruni, P. , and Ravindran, P. , 2019, “ The Effect of Oxidation on the Mechanical Response of Isolated Elastin and Aorta,” ASME J. Biomech. Eng., 141(6), p. 061002. 10.1115/1.4043355 [DOI] [PubMed] [Google Scholar]
- [39]. Truesdell, C. , and Toupin, R. , 1960, “ The Classical Field Theories,” Encyclopedia of Physics, Vol. III/1, Springer-Verlag, Berlin. [Google Scholar]
- [40]. Coleman, B. D. , and Noll, W. , 1963, “ The Thermodynamics of Elastic Materials With Heat Conduction and Viscosity,” Arch. Ration. Mech. Anal., 13(1), pp. 167–178. 10.1007/BF01262690 [DOI] [Google Scholar]
- [41]. Atkins, P. W. , 1978, Physical Chemistry, W. H. Freeman, San Francisco, CA. [Google Scholar]
- [42]. Müller, I. , 2007, A History of Thermodynamics: The Doctrine of Energy and Entropy, Springer, Berlin. [Google Scholar]
- [43]. Truesdell, C. , 1984, Rational Thermodynamics, 2nd ed., Springer-Verlag, New York. [Google Scholar]
- [44]. Bonet, J. , and Wood, R. D. , 1997, Nonlinear Continuum Mechanics for Finite Element Analysis, Cambridge University Press, Cambridge, UK. [Google Scholar]


