Abstract
COVID-19 vaccination in Brazil required a phased program, with priorities for age groups, health workers, and vulnerable people. Social distancing and isolation interventions have been essential to mitigate the advance of the pandemic in several countries. We developed a mathematical model capable of capturing the dynamics of the SARS-CoV-2 dissemination aligned with social distancing, isolation measures, and vaccination. Surveillance data from the city of Rio de Janeiro provided a case study to analyze possible scenarios, including non-pharmaceutical interventions and vaccination in the epidemic scenario. Our results demonstrate that the combination of vaccination and policies of transmission suppression potentially lowered the number of hospitalized cases by 380+ and 66+ thousand cases, respectively, compared to an absence of such policies. On top of transmission suppression-only policies, vaccination impacted more than 230+ thousand averted hospitalized cases and 43+ thousand averted deaths. Therefore, health surveillance activities should be maintained along with vaccination planning in scheduled groups until a large vaccinated coverage is reached. Furthermore, this analytical framework enables evaluation of such scenarios.
Keywords: SARS-CoV-2, Vaccination, COVID-19
1. Introduction
Since the emergence of the SARS-CoV-2 virus, the COVID-19 pandemic has reached many countries causing millions of severe cases and deaths (Tangcharoensathien et al., 2021). The need for interventions was necessary to mitigate the pandemic by reducing dissemination and in the next phase by starting vaccination (Brauner et al., 2021; Perra, 2021). Even with a phased vaccination, some measures remain essential such as social distancing and isolation of cases until extensive vaccine coverage is achieved. Many authors in the literature have pointed out the importance of combining non-pharmaceutical and pharmaceutical interventions to hinder the pandemic (Borchering et al., 2021; Gumel et al., 2021; Huang et al., 2021; Patel et al., 2021). However, these interventions are geographically determined, depending on diverse factors from each city to be applied, having different outcomes in different regions and populations.
Several models studied the impact of social distancing (Matrajt & Leung, 2020). Models range from understanding the epidemiological mechanisms behind SARS-CoV-2 and also to predict the dynamics of the epidemic. Schematic and extensive reviews by Wynants et al. (2020) and Padmanabhan et al. (2021) evaluates diverse models against their predictive capabilities. As SARS-CoV-2 is a challenging disease in terms of modelling due to its diverse epidemiological mechanisms that involve different comorbidities (Gude-Sampedro et al., 2021), heavy dependence on public health capacity (Garcia et al., 2020), different impact by age groups (Wu & McGoogan, 2020), the role of asymptomatic individuals (Day, 2020), and is heavily affected by several interventions (Zamir et al., 2020; Lai et al., 2020). Models in the literature have been specializing in understanding not only the general dynamics but also the impact of each factor to tackle each problem assertively. Regarding the diverse epidemiological scenario, models have been developed to enlighten the question of which are the high-risk population where public health authorities could focus resources (Gude-Sampedro et al., 2021; Das, Upadhyay, et al., 2021,a).
Several non-pharmaceutical interventions require prior careful analysis since they involve not only the number of cases and deaths, but many also address psychological issues (Adeniyi et al., 2022; Rahaman et al., 2020), the necessary resources for their application, and other health issues related to them, due to the emergence of other diseases during the pandemic (Rana et al., 2021; Shimizu et al., 2021; Torner, 2020). Nonetheless, these interventions have been of paramount necessity in reducing the number of deaths and hospitalizations worldwide (Spinelli et al., 2021; Perra, 2021; Lai et al., 2020; Flaxman et al., 2020; Zamir et al., 2020; Jorge et al., 2021).
Since the beginning of the pandemic, vaccination and other pharmaceutical interventions have been an object of study (Huang et al., 2021). However, only recently more thorough vaccination has been reached in various countries. Understanding the specific dynamics that separate the impacts of non-pharmaceutical and pharmaceutical interventions is still debated in the literature. It demands a modelling task that requires careful exploration of different classes of individuals through age groups, and their specificities (Wu & McGoogan, 2020).
In this work, we develop and evaluate how a model can capture the dynamics of the SARS-CoV-2 pandemic and compare scenarios with and without interventions to better deal with the ongoing SARS-CoV-2 pandemic and understand the real impact of these measures. Results consider specifically the dynamics of the pandemic in the city of Rio de Janeiro, Brazil, as a case study. However, implications of the results are general, such that they could be extended to other similar cities. Also, as non-pharmaceutical measures are essential to mitigate the effects of the pandemic, the perspective of controlling it comes with vaccination. However, its policies and methods for application need yet to be systematically addressed. Health surveillance should be maintained along with the planning for effective vaccination.
2. Methods
2.1. Model
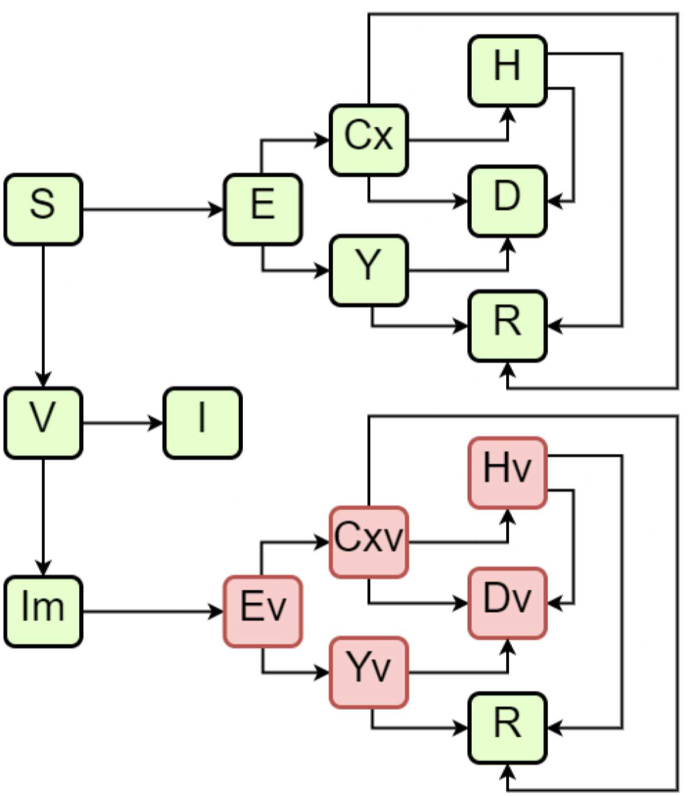
We modelled different scenarios with an ODE-based compartmental model. In the model, susceptible individuals (S) can evolve to exposed (E) condition when in contact with infected individuals. The group of infected individuals is divided between asymptomatic cases (Y), symptomatic cases (C), which includes both mild and moderate cases (Cx), which can evolve to severe cases (H). This last group occurs from the evolution of the symptomatic group and, therefore, is considered to represent hospitalized individuals. All infected individuals can evolve to death (D) or recovered (R). We have also included the dynamics of vaccination for a single dose. Vaccination individuals (V) can evolve into Immunized (I) or non-immunized individuals (Im). Each of these model classes is stratified by age groups, from 0 to 100 years, in 5-year intervals, added by one last age group of higher than 100 years, in a total of 21 groups of distinct age ranges for each compartment of the model.
Vaccination is included in the model as susceptible individuals are vaccinated at a coverage rate of η. These vaccinated individuals will take a pre-determined time τimmun to develop immunity at a probability of ρI when they evolve to immunized status (I). Due to incomplete vaccine efficacy, we included the possibility of the vaccinated individual not developing the required immunization and still being susceptible (Im). Although some individuals are to be considered non-immunized, as reported by other authors (Hogan et al., 2020), these individuals are less likely to be infected, develop symptoms, be hospitalized, and die. Therefore, these individuals evolve to different but relatable classes of individuals, as shown in Fig. 1 with the classes that end with the letter “v”. The reduced parameters related to these different degrees of severity were previously reported (Hogan et al., 2020).
Fig. 1.
Schematic diagram of the model compartments.
The infection rate between susceptible individuals and symptomatic is β, and with asymptomatic individuals is βA. When they become exposed individuals, the time to evolve to infected is the incubation time τinc. At the end of this time, the individual has a probability ρS of developing symptoms.
The time required for an asymptomatic individual to evolve to death is , whereas for the symptomatic individuals is α−1. It is expected that α > αA due to higher morbidity in the former case, besides the fact that asymptomatic individuals do not present themselves as clinical cases. Symptomatic individuals can evolve to a severe case with a risk probability of αH. The symptomatic (C) and severe cases (H) individuals are modeled separately due to their different epidemiological mechanisms (Liu et al., 2020; Siordia Jr, 2020), and to allow the test of non-pharmaceutical methodologies that target these individuals separately. The separation between these individuals is mainly based on their symptoms, e.g., mild/symptomatic and symptoms requiring hospitalization. Severe cases exhibit clinical conditions for hospitalization, such as oxygen saturation lower than 93%, dyspnea, or multiple organ failure (Wu & McGoogan, 2020; Betti & Heffernan, 2021; Musa et al., 2021; Chevrier et al., 2021). Both can evolve to death (or the symptomatic case can evolve to the severe case) separately with different case-fatality ratios, as shown in the literature (Wu & McGoogan, 2020). It is vital to understand whether isolating only the severe cases is an adequate measure to mitigate the pandemic or if we should apply a broader approach when applying non-pharmaceutical interventions.
The parameters related to asymptomatic individuals, such as βA and αA are calculated through a product between a reducing factor (Byambasuren et al., 2020) fA and the original parameter for symptomatic individuals β and α, respectively. Regarding the individuals that were vaccinated but are not immunized, another reducing factor is considered (Palacios et al., 2021), fv. This factor applies to reduce the infection rate β with the product β ⋅ fv. These individuals also have a reducing factor applied to their hospitalization risk (Palacios et al., 2021), fv,H.
The recovery of infected individuals (symptomatic and severe) is controlled by the recovery rate (Zhou et al., 2020) γ, being modified to γH in the case of severe cases. Severe cases are hospitalized and thus receiving proper assistance confronting the sickness. The hospitalized individuals can recover after a determined period, controlled by the discharge time τdisc and dyspnea time τdysp. The discharge time is a median time where individuals who present a clinical recovery are therefore termed as recovered individuals and are no longer hospitalized. In contrast, the dyspnea time is the time from illness onset to dyspnea clinical condition (Zhou et al., 2020). We calculated the recovery rate of individuals () using both the discharge and dyspnea time, as we considered a stochastic implementation of our model.
The ODE system which resumes this model is:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
2.1.1. Social distancing interventions
The model enables the application of intervention measures with the social distancing of specific age groups. Social distancing affects people in reducing the probability of encounters between infected and susceptible individuals. Thus, we simulate this condition by reducing the infection rates β, βA, βI and βIm for the specific age groups. Due to imperfect application of social distancing intervention, each intervention is controlled by a success rate.
The fact that the model is stratified by age groups opens a new range of different scenarios, e.g. when applying the social distancing intervention to younger age groups, we can simulate limitation of school activities. The reduction is applied to the R0 value, from which the infection rates are calculated, by multiplying it with the reduction factor κ = 0.65. The social distancing applied to the 0–20 years old age groups is labeled SD-Y, when applied to the age groups higher than 60 years old is labeled SD-E, and when we apply the reduction to all age groups, we label this condition as SD-A.
2.1.2. Isolation interventions
The application of isolation interventions is made by reducing the encounter probability between susceptible and infected individuals. Different scenarios are tested in this work. In the lockdown scenario (L), we alter the susceptible flow equation to
| (11) |
Another intervention possibility is when tests are applied to the individuals, and a quarantine is applied where symptomatic cases are isolated with a probability σ and asymptomatic with a probability σA, this condition is labeled as TQ-C. In this scenario, we modify the susceptible flow equation to
| (12) |
If we only isolate the symptomatic cases (scenario TQ), we change the susceptible individuals flow equation to
| (13) |
The scenario where we only isolate the severe cases is termed TQ-S, and we modify the susceptible flow equation to
| (14) |
The exposed, vaccinated, and partially immunized compartments are also changed as the susceptible flow, depending on the applied scenario. Table 1 summarizes the parameters used in the model with their respective values and references. Only four parameters were fitted to represent the SARI notification data for the city of Rio de Janeiro: the basic transmission rate (β) via R0, and the three probabilities of isolation (for symptomatic cases (σ), asymptomatic cases (σA) and lockdown scenario (σL)). The other parameters are recovered from the literature (Table 1).
Table 1.
Description of parameters in the model and values used in simulations with references.
| Parameter | Description | Value |
|---|---|---|
| β | Infection rate | Calculated using R0 |
| fA | Asymptomatic factor | 0.42 (Byambasuren et al., 2020) |
| βA | Asymptomatic infection rate | fA ⋅ β |
| σ | Probability of successful isolation of symptomatic individuals | 0.60 |
| σA | Probability of successful isolation of asymptomatic individuals | 0.20 |
| σL | Probability of successful isolation during lockdown | 0.75 |
| ρS | Probability of developing symptoms | 0.83 (Byambasuren et al., 2020) |
| α | Death risk | Depends on age group (Wu and McGoogan, 2020) |
| αH | Hospitalization risk | Depends on age group (Stokes et al., 2020) |
| αA | Death risk of asymptotic individuals | fA ⋅ α |
| τdysp | Time for dyspnea | 7 days (Zhou et al., 2020) |
| τdisc | Discharge time | 22 days (Zhou et al., 2020) |
| τinc | Incubation time | 5.1 days (Lauer et al., 2020) |
| γ | Recovery rate | 1/6.5 (Zhou et al., 2020) |
| γH | Recovery rate for hospitalized individuals | Calculated using τdisc and τdysp |
| γI | Immunization probability | 0.493 (Palacios et al., 2021) |
| τI | Time to immunization | 14 days (Palacios et al., 2021) |
| fv | β reducing factor for Im individuals | 0.163 (Palacios et al., 2021) |
| fv,H | αH reducing factor for Im individuals | 0.0 (Palacios et al., 2021) |
The parameter β is calculated from the previous definition of R0 value, the asymptomatic value (Byambasuren et al., 2020) fA, the probability of developing symptoms (Byambasuren et al., 2020) ρS, and the incubation time (Lauer et al., 2020) τinc with
| (15) |
Fig. 1 depicts a schematic diagram showing the model compartments.
2.1.3. Stochastic implementation
The model is implemented in a discrete-time fashion. Days were applied as the time units since cases are reported on a daily basis and the change of interventions could be simulated on specific dates. However, the algorithm can use other time units such as weeks, if adjusted parameters are applied. The algorithm requires initial values for the variables used in the model. The transitions given in the equations in the ODE system are used to obtain the transition probabilities (Allen, 2017). Typically, for each time step, all transitions are evaluated as probabilities and the number transitioning from a compartment to the other linked compartments, including keeping the state, are drawn from a multinomial distribution. Multiple simulations generate multiple sample paths, which are evaluated allowing to obtain mean values and intervals. Since the transitions follow distributions with the parameters used in the model, after multiple simulations the mean values are expected very close to the deterministic realization. A stochastic simulation code was implemented using Rstudio (Racine, 2012) Version 1.2.5 042 with R software version 4.0.0 (http://www.r-project.org) was used for all calculations, data importation, and curation.
2.2. Case study
Parameters of the model were adjusted to the number of cases and the dynamics observed in the municipality of Rio de Janeiro. Data from Severe Acute Respiratory Illness (SARI) are compared to the results of new daily hospitalizations. In contrast, data from Acute Respiratory Illness (ARI) notified cases are compared to the results of new daily cases. All notified data is retrieved from the public database OpenDataSus (available at https://opendatasus.saude.gov.br/dataset).
Throughout the pandemic, the scenario was altered several times due to governmental decisions of applying the interventions or making them more flexible and the incomplete adherence of the population. We evaluate how the model behaves when we use the same quarantine severity as applied by the government for each period while comparing the results to real-time data. Our approach is based on the Rio de Janeiro municipality and state real pandemic decrees, with slight adjustments, as the accordance of the population to governmental decisions is not straightforward. We consider no intervention done between 01 January 2020 and 15 March 2020 (day 1 to day 74). Starting from 16 March 2020 until 27 March 2020 (day 75 to day 86), we consider that this is the beginning of the pandemic, where the government started to apply some intervention measures. The population's adherence to non-pharmaceutical interventions of the government in Brazil was not strictly followed (de Moura Villela et al., 2021; Jorge et al., 2021; Szwarcwald et al., 2020), decreasing with the temporal advance of the pandemic. Therefore, to model the notification data, we have considered the non-pharmaceutical interventions during 2021 after the vaccination as adjustable when necessary. The different isolation and social distancing scenarios are summarized in Table 2.
Table 2.
Isolation and social distancing scenarios for the different data ranges throughout the years of 2020 and 2021.
| Data range (DD.MM.YY) | Isolation | Social Distancing |
|---|---|---|
| 16.03.2020–27.03.2020 | TQ-S | SD-Y + SD-E |
| 28.03.2020–03.04.2020 | TQ-S | SD-A |
| 05.04.2020–14.05.2020 | TQ-C | SD-A |
| 15.05.2020–29.05.2020 | L | SD-A |
| 30.05.2020–02.06.2020 | TQ | SD-A |
| 03.06.2020–12.07.2020 | TQ-C | SD-A |
| 13.07.2020–02.09.2020 | TQ-C | SD-Y + SD-E |
| 03.09.2020–22.09.2020 | TQ-C | SD-A |
| 23.09.2020–31.10.2020 | TQ-C | SD-Y + SD-E |
| 01.11.2020–16.11.2020 | TQ-S | SD-A |
| 17.11.2020–21.11.2020 | TQ-C | SD-A |
| 22.11.2020–01.12.2020 | TQ | SD-A |
| 02.12.2020–30.01.2020 | TQ-C | SD-A |
| 31.01.2021–07.03.2021 | TQ-S | SD-A |
| 08.03.2021–18.03.2021 | TQ-S | SD-Y + SD-E |
| 19.03.2021–02.04.2021 | TQ | SD-A |
| 03.04.2021–06.04.2021 | – | SD-A |
| 07.04.2021–18.04.2021 | TQ-S | SD-A |
| 19.04.2021–22.04.2021 | TQ-C | SD-A |
| 23.04.2021–30.04.2021 | TQ-S | SD-A |
| 01.05.2021–04.05.2021 | TQ-C | SD-A |
| 04.05.2021–14.05.2021 | TQ-S | SD-Y + SD-E |
| 15.05.2021–19.05.2021 | TQ-C | SD-Y + SD-E |
| 20.05.2021–30.06.2021 | TQ-S | SD-A |
To better fit the model to the real notification data, we estimated initially R0 = 2.6, the reduction factor of the social distancing during lockdown to be 0.75, the success in isolating symptomatic cases to be 0.60, while 0.20 for the asymptomatic cases. Also, we considered that the first cases were imported on 11 February 2020. Reporting rate of severe cases (SARI) is 96% of the real cases, accounting for small under-reporting, whereas under-reporting of notified ARI disease cases is 20% of the actual number of ARI cases. The number of SARI cases notified in the city of Rio de Janeiro, daily aggregated, is evaluated from January to the end of June of 2021. This data range is considered an acceptable range to avoid the effect of dramatic sub notification due to notification delay.
In order to evaluate the vaccination program, we used real vaccination data notification from the city of the Rio de Janeiro applied to each group at the specific dates on which they were applied. Figures containing the reported vaccination data are available in the supplementary material of this work. As our model accounts for only one dose of vaccination, we applied to the simulations the dates of first dose to reach the different scenarios, using data from all applied vaccines. In Brazil, the vaccination program covers both two-dose and single dose vaccines (Hung & Poland, 2021; Ranzani et al., 2021; Villela et al., 2021). To capture the general mechanism provided by the pharmaceutical interventions, our approach has only the application of a single dose program that also includes the infection-rate reduction (Hogan et al., 2020) and hospitalization risk reduction (Palacios et al., 2021). Furthermore, the protection provided by the vaccination starts after the first dose (Iacobucci & Mahase, 2021; Tuite et al., 2021), although not full nor long-lasting, as these mechanisms help to represent the notification data using only a single dose program simulation. Also, we analyzed the prevention of deaths and hospitalizations for different scenarios considering the cumulative curves of each case using the equation for number of prevented (deaths or hospitalizations) λ(t),
| (16) |
where λ(t) represents cumulative deaths or hospitalization at time t, specific refers to the specific scenario studied scenario, and non represents the scenario without vaccination and restrictions.
3. Results
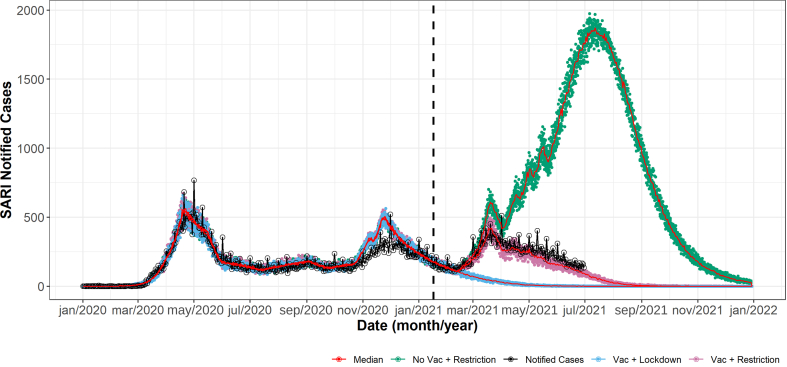
The model captured the dynamics of the epidemics in Rio de Janeiro successfully regarding the hospitalizations compared to SARI notified cases (Fig. 2). As the model does not account for all the influenza-like illness, but it is limited to the SARS-CoV-2 cases, there should be a difference between the notification data and the SARI notified cases, also due to some natural errors within notification systems. To cover this problem, we considered a reporting parameter of 0.95 to data.
Fig. 2.
Model results for new daily hospitalizations and cases of SARI in Rio de Janeiro. Notified cases of SARI in Rio de Janeiro are represented by black lines, other colors represent the different simulated vaccination scenarios: vaccination with the applied restrictions (pink), no vaccination but applying the same restrictions as the pink case (green), and vaccination with lockdown scenario (blue). Red lines represents the median values in each scenario.
The model also presented a good fit to notification data when using the vaccination data. As expected, the combination of vaccination, social distancing and isolation measures was responsible to significantly lower the number of SARI notified cases throughout the years of 2020 and 2021 in Rio de Janeiro. However, if more restrictive measures were applied, the resulting effect was clearly stronger.
After the beginning of the vaccination program, the downfall of the pandemic is advanced and accelerated, which is evidenced by the observed inflection point. Abandoning social distancing, however, generates an increase in the number of expected SARI cases as shown. As shown by a last peak of simulation data, the advancement of vaccination dates is responsible to reduce the number of cases in a downward direction in conditions where a new peak would rise. If there were no flexibilization during vaccination, no peaks would be observed. The number of cumulative and prevented deaths and hospitalizations, are shown in Fig. 3.
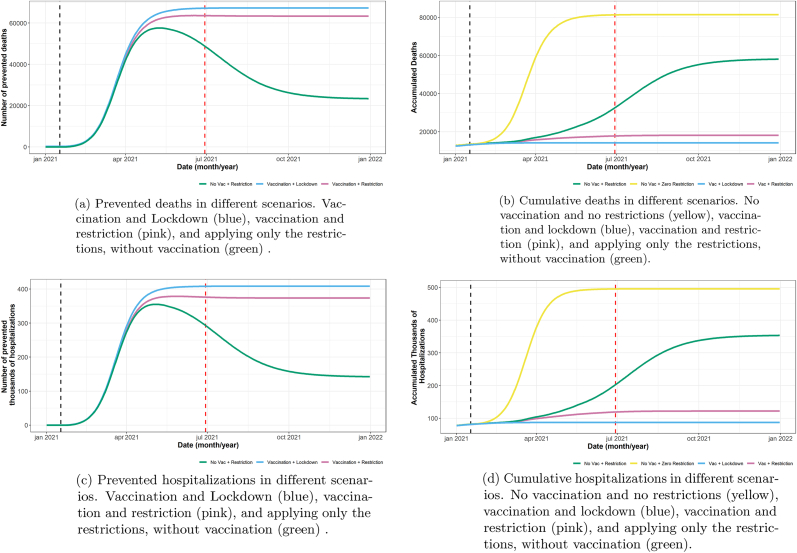
Fig. 3.
Different scenarios comparing prevented deaths and hospitalizations, and cumulative deaths and hospitalizations due to SARI. To calculate the prevented deaths and hospitalizations, we used our model to calculate a scenario where no restrictions and no vaccination were applied, the cumulative deaths and hospitalization curves of this scenario was our reference to calculate the absolute the number of prevention.
As shown in Fig. 3, the vaccination had a major role in reducing the number of hospitalizations and deaths due to SARI. The reduction in number of cases after vaccination and suppression policies, compared to a no-policy scenario, was 380+ thousand hospitalized cases and 66+ thousand cases, considering until June 2021. Vaccination is expected in this case to avert more than 230+ thousand hospitalized cases and 43+ thousand deaths.
The prevented deaths and hospitalizations are only observed to remain high when the vaccination is applied, which is a direct result of the long-term protection provided by the vaccine. The contrary is observed when only social distancing or other non-pharmaceutical interventions are applied, as new peaks maintain high number of deaths and hospitalizations.
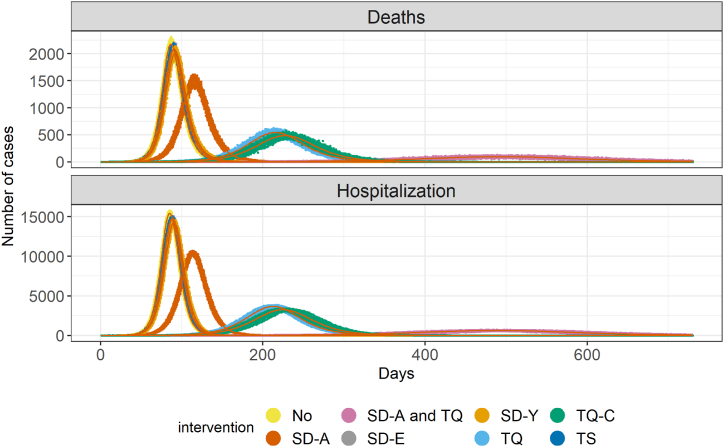
As shown in Fig. 4, there is a marked difference in the effectiveness of each intervention alone. Social distancing alone had a less pronounced effect than the quarantine of cases, except for the quarantine of only the severe cases (TS), which had a minimal delaying effect at the peak. A combination of mitigation policies makes significant impact in the peak of number of cases.
Fig. 4.
Different scenarios model comparison. A different color identifies each intervention. The points represent the stochastic calculation done with the model considering the given probabilities with 100 iterations per day. The red lines are means of each intervention. The used parameters are given in Table 1, with the exception of R0, which is 3.5.
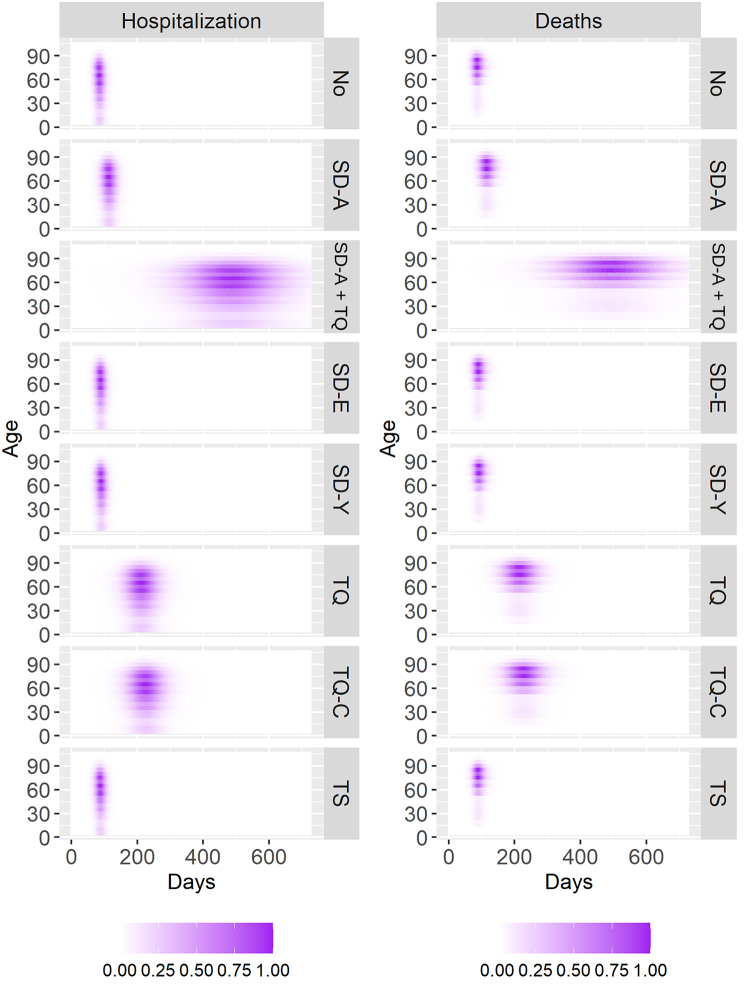
As our model is stratified by age groups, we also observe how the different interventions change the number of deaths and hospitalizations by age, as shown by Fig. 5. The quarantine of all cases, the social distancing of all individuals, and the combination of this intervention with the quarantine of symptomatic cases are the three most effective interventions, as also seen by Fig. 4. In all cases, despite isolating or distancing different age groups, the pattern of hospitalizations and deaths regarding age groups is very similar. The major difference is observed in delaying the pandemic peak and the pandemic's length, broadening its profile through time but not through age groups. Hospitalizations are centered around older groups, mainly individuals around 60 years old and older, in all interventions.
Fig. 5.
Normalized death and hospitalization profiles for different intervention scenarios. Normalized values are calculated by the quotient of each daily new hospitalization or death by the highest hospitalization or death of the group with most hospitalizations or death through the pandemic.
Also, in Fig. 5, despite profile similarity across age groups, some age groups are more affected since the beginning of the pandemic and at the end. There is a distortion of the profile's rectangular shape observed in almost all scenarios in favor of a more oval-oriented shape, which is more pronounced in the SD-A and TQ, only TQ, and only TQ-C scenarios.
4. Discussion
The main objective of NPI interventions is to mitigate the effect of the pandemic for proper health care attention to mild and severe cases. Independently from the nature of the intervention (social distancing or isolation of cases), as expected and seen in many studies (Matrajt & Leung, 2020; Ferguson et al., 2020; Flaxman et al., 2020; Prem et al., 2020), delaying the epidemic peak is a consequence of the reduction in transmission intensity.
As demonstrated, when comparing different interventions, there is a considerable difference between the isolation of both symptomatic and asymptomatic cases and isolating only the symptomatic cases, with the former intervention being a more successful application. Further, if we combine isolation with social distancing interventions, a better result is reached in reducing the number of hospitalizations and delaying the peak of new cases. This result highlights the importance of an enforced isolation measure, as the asymptomatic cases also impact the transmission dynamics. The correct identification and consequently isolation of these cases pose a problem which has been discussed in the actual pandemic (Gandhi et al., 2020; Nishiura et al., 2020), in some cases, following the correct procedure to identify and isolate these cases were responsible for ending the pandemic (Day, 2020). The isolation of only the severe cases did alter significantly the dynamics, demonstrating the importance of having a model in which mild and severe cases are studied separately, as they have marked differences in their epidemiology (Liu et al., 2020; Siordia Jr, 2020) besides having some studies indicating some similarities (Wu & McGoogan, 2020; Yilmaz et al., 2020). The isolation of only symptomatic cases was more effective when applied together with the social distancing of all age groups. Therefore, it is imperative to recognize the importance of transmission by asymptomatic individuals.
Comparing the applied social distancing measures, results here show a very marked difference between the isolation of all age groups against the isolation of only young or elderly individuals and the severity of SARS-CoV-2 among elderly individuals higher than younger individuals (Siordia Jr, 2020; Wu & McGoogan, 2020). However, there must be a very careful distinction between the severity of cases and the epidemiological dynamic imposed by the different groups, the isolation of only the elder individuals is not sufficient to significantly halter the pandemic. As shown in the model, isolating the elderly group may give a false impression of protection to these individuals, as this intervention is not sufficient to effectively control the epidemic. Therefore, only the social distancing of all age groups at an early stage acts to avoid severe cases.
The social distancing of all age groups had similar performance compared to the isolation of both symptomatic and asymptomatic cases, as shown by Fig. 4. This interesting result indicates that the early recognition and application of broad interventions to the population are the most effective measures to be studied. In regard to the social distancing, all age groups should be taken into account, in agreement with other modeling studies (Ferguson et al., 2020; Flaxman et al., 2020). Regarding the isolation intervention, all cases should be included in the measure, including asymptomatic cases, which can only be reached through successful testing. This highlights the importance of mass testing individuals exposed to the SARS-CoV-2 pandemic.
The value of 2.6 for the R0 is within the range of the estimated value for other studies and even other areas (Abbott et al., 2020; Coelho et al., 2020; Li et al., 2020; Wu et al., 2020; Yue et al., 2021). Despite the significant number of interventions, either a social distancing or isolation intervention, the best approach is clearly the combination of both measures. This is shown where the SD-A intervention combined with the TQ isolation measure produced the best results.
Despite all of the interventions, combined or not, there is a growing concern about the social and economic distress of a population during interventions (Ashraf, 2020; Fernandes, 2020). It is also imperative to develop pharmaceutical interventions to reduce the posed threat by the virus infections. Also, initiatives such as the vaccines being developed and the fundamental understanding of how the virus acts biologically are essential to this end. Therefore, it is crucial to model beyond the dynamics of only non-pharmaceutical interventions.
Non-pharmaceutical interventions also demonstrate through Fig. 2 that they have the merit of controlling the direction, evolution, and severity of the pandemic and should be studied and applied whenever possible. However, pharmaceutical and non-pharmaceutical interventions need to be considered altogether during the pandemic. Considering these results, it is clear that the vaccine has a long-term effect on the population. Comparing the last peaks obtained by the results, although vaccination did not control the direction of the pandemic, it was directly responsible to diminish the number of cases and deaths effectively.
In all scenarios, the phased rollout of the vaccination program should be along with maintaining social distancing and case isolation. Abandoning the quarantine shows to be a most critical scenario, in which there is a considerable increase in the number of hospitalizations. The only condition where the pandemic maintains its downward strategy during the vaccination program is combining social distancing and isolation.
This is a crucial moment to study and show that we must yet consider the application of strict interventions of social distancing, isolation, and vaccination as the risk of SARS-CoV-2 transmission is present in multiple countries. The modelling in this work shows that effective control of the COVID-19 pandemic requires a combination of these efforts.
Funding statement
This study was partially supported by the Coordination for the Improvement of Higher Education Personnel (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-CAPES) -Finance Code 001. DV is grateful to Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq Refs 441 057/2 020-9, 309 569/2 019-2).
Data availability statement
All SARI and ARI notification data are publicly available at OpenDataSUS database, maintained by the Ministry of Health, located at https://opendatasus.saude.gov.br/.
Ethics statement
No approval by an ethics committee was necessary, since the work involved only simulations and secondary anonymized data which are publicly available.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Daniel A.M. Villela has a grant for modeling COVID-19 scenarios in Brazil, funded from the National Council for Scientific and Technological Development, a funding agency from the Brazilian federal government. Daniel A.M. Villela is Research Scientist, working for Fiocruz, the biggest research institution in public health in Brazil, which has a vaccine producing unit. All authors declare no financial benefits.
Handling editor: Dr Lou Yijun
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.idm.2021.12.007.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Abbott S., Hellewell J., Munday J., Funk S., nCoV working group C., et al. The transmissibility of novel Coronavirus in the early stages of the 2019-20 outbreak in Wuhan: Exploring initial point-source exposure sizes and durations using scenario analysis. Wellcome Open Research. 2020;5 doi: 10.12688/wellcomeopenres.15718.1. The Wellcome Trust. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adeniyi M.O., Oke S.I., Ekum M.I., Benson T., Adewole M.O. Modeling, control and drug development for COVID-19 outbreak prevention. Springer; 2022. Assessing the impact of public compliance on the use of non-pharmaceutical intervention with cost-effectiveness analysis on the transmission dynamics of COVID-19: Insight from mathematical modeling; pp. 579–618. [Google Scholar]
- Allen L.J. A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis. Infectious Disease Modelling. 2017;2(2):128–142. doi: 10.1016/j.idm.2017.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashraf B. Economic impact of government interventions during the COVID-19 pandemic: International evidence from financial markets. Journal of Behavioral and Experimental Finance. 2020;27(1):10037. doi: 10.1016/j.jbef.2020.100371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betti M., Heffernan J.A. Simple model for fitting mild, severe, and known cases during an epidemic with an application to the current SARS-CoV-2 pandemic. Infectious Disease Modelling. 2021;6:313–323. doi: 10.1016/j.idm.2021.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borchering R., Viboud C., Howerton E., Smith C., Truelove S., Runge M., Reich N., Contamin L., Levander J., Salerno J., Modeling O. Modeling of future COVID-19 cases, hospitalizations, and deaths, by vaccination rates and nonpharmaceutical intervention scenarios— United States, April–September 2021. Morbidity and Mortality Weekly Report. 2021;70:719. doi: 10.15585/mmwr.mm7019e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brauner J.M., Mindermann S., Sharma M., Johnston D., Salvatier J., Gavenčiak T., et al. Inferring the effectiveness of government interventions against COVID-19. Science. 2021;371(6531) doi: 10.1126/science.abd9338. American Association for the Advancement of Science. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byambasuren O., Cardona M., Bell K., Clark J., McLaws M.-L., Glasziou P. Estimating the extent of asymptomatic COVID-19 and its potential for community transmission: Systematic review and meta-analysis. Official Journal of the Association of Medical Microbiology and Infectious Disease Canada. 2020;5(4):223–234. doi: 10.3138/jammi-2020-0030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevrier S., Zurbuchen Y., Cervia C., Adamo S., Raeber M., Souza N., Sivapatham S., Jacobs A., Bachli E., Rudiger A., Others A. A distinct innate immune signature marks progression from mild to severe COVID-19. Cell Reports Medicine. 2021;2(6):10016. doi: 10.1016/j.xcrm.2020.100166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coelho F.C., Lana R.M., Cruz O.G., Villela D.A., Bastos L.S., Pastore y Piontti A., Davis J.T., Vespignani A., Codeço C.T., Gomes M.F. Assessing the spread of COVID-19 in Brazil: Mobility, morbidity and social vulnerability. PLoS One. 2020;15(9) doi: 10.1371/journal.pone.0238214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das P., Nadim S., Das S., Das P. Dynamics of COVID-19 transmission with comorbidity: A data driven modelling based approach. Nonlinear Dynamics. 2021:1–15. doi: 10.1007/s11071-021-06324-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das P., Upadhyay R., Misra A., Rihan F., Das P., Ghosh D. Mathematical model of COVID-19 with comorbidity and controlling using non-pharmaceutical interventions and vaccination. Nonlinear Dynamics. 2021:1–15. doi: 10.1007/s11071-021-06517-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day M. COVID-19: Identifying and isolating asymptomatic people helped eliminate virus in Italian village. BMJ British Medical Journal. 2020;368 doi: 10.1136/bmj.m1165. [DOI] [PubMed] [Google Scholar]
- Ferguson N., Laydon D., Nedjati-Gilani G., Imai N., Ainslie K., Baguelin M., et al. Vol. 10. Imperial College London; 2020. p. 77482. (Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand). [Google Scholar]
- Fernandes N. 2020. Economic effects of coronavirus outbreak (COVID-19) on the world economy; p. 3557504. Available at SSRN. [Google Scholar]
- Flaxman S., Mishra S., Gandy A., Unwin H., Coupland H., Mellan T., et al. Imperial College; London: 2020. Report 13: Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries. [Google Scholar]
- Gandhi M., Yokoe D.S., Havlir D.V. Asymptomatic transmission, the Achilles' heel of current strategies to control COVID-19. New England Journal of Medicine. 2020;382(22):2158–2160. doi: 10.1056/NEJMe2009758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia P., Alarcón A., Bayer A., Buss P., Guerra G., Ribeiro H., Rojas K., Saenz R., Snyder N., Solimano G., Covid-19 O. COVID-19 response in Latin America. The American Journal of Tropical Medicine and Hygiene. 2020;103:1765. doi: 10.4269/ajtmh.20-0765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gude-Sampedro F., Fernandez-Merino C., Ferreiro L., Lado-Baleato O., Espasandin-Dominguez J., Hervada X., Cadarso C., Vaedes L. Development and validation of a prognostic model based on comorbidities to predict COVID-19 severity: A population-based study. International Journal of Epidemiology. 2021;50:64–74. doi: 10.1093/ije/dyaa209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gumel A., Iboi E., Ngonghala C., Ngwa G. Mathematical assessment of the roles of vaccination and non-pharmaceutical interventions on COVID-19 dynamics: A multigroup modeling approach. medRxiv. 2021:2021. [Google Scholar]
- Hogan A.B., Winskill P., Watson O.J., Pgt W., Whittaker C., Baguelin M., et al. Report 33: Modelling the allocation and impact of a COVID-19 vaccine. Imperial College report; 2020. Response team. [Google Scholar]
- Huang B., Wang J., Cai J., Yao S., Chan P., Tam T., Hong Y., Ruktanonchai C., Carioli A., Floyd J., Integrated O. Vaccination and physical distancing interventions to prevent future COVID-19 waves in Chinese cities. Nature Human Behaviour. 2021;5:695–705. doi: 10.1038/s41562-021-01063-2. [DOI] [PubMed] [Google Scholar]
- Hung I., Poland G. Single-dose Oxford–AstraZeneca COVID-19 vaccine followed by a 12-week booster. The Lancet. 2021;397:854–855. doi: 10.1016/S0140-6736(21)00528-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacobucci Gareth, Mahase Elisabeth. Covid-19 vaccination: What’s the evidence for extending the dosing interval? BMJ. 2021;372 doi: 10.1136/bmj.n18. British Medical Journal Publishing Group. [DOI] [PubMed] [Google Scholar]
- Jorge D.C., Rodrigues M.S., Silva M.S., Cardim L.L., da Silva N.B., Silveira I.H., et al. Assessing the nationwide impact of COVID-19 mitigation policies on the transmission rate of SARS-CoV-2 in Brazil. Epidemics. 2021;35:100465. doi: 10.1016/j.epidem.2021.100465. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai S., Ruktanonchai N., Zhou L., Prosper O., Luo W., Floyd J., Wesolowski A., Santillana M., Zhang C., Du X., Yu H., Tatem A. Effect of non-pharmaceutical interventions to contain COVID-19 in China. Nature. 2020;585:410–413. doi: 10.1038/s41586-020-2293-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A., Reich N., Lessler J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Annals of Internal Medicine. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. New England Journal of Medicine. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. Mass Medical Soc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Yan L.-M., Wan L., Xiang T.-X., Le A., Liu J.-M., Peiris M., Poon L.L., Zhang W. Viral dynamics in mild and severe cases of COVID-19. The Lancet Infectious Diseases. 2020;20(6):656–657. doi: 10.1016/S1473-3099(20)30232-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matrajt L., Leung T. Evaluating the effectiveness of social distancing interventions to delay or flatten the epidemic curve of coronavirus disease. Emerging Infectious Diseases. 2020;26(8) doi: 10.3201/eid2608.201093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Moura Villela E.F., López R.V.M., Sato A.P.S., de Oliveira F.M., Waldman E.A., Van den Bergh R., Fodjo J.N.S., Colebunders R. COVID-19 outbreak in Brazil: Adherence to national preventive measures and impact on people's lives, an online survey. BMC Public Health. 2021;21(1):1–10. doi: 10.1186/s12889-021-10222-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musa S., Qureshi S., Zhao S., Yusuf A., Mustapha U., He D. Mathematical modeling of COVID-19 epidemic with effect of awareness programs. Infectious Disease Modelling. 2021;6:448–460. doi: 10.1016/j.idm.2021.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H., Kobayashi T., Miyama T., Suzuki A., Sm J., Hayashi K., et al. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19) International Journal of Infectious Diseases. 2020;94:154. doi: 10.1016/j.ijid.2020.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padmanabhan R., Abed H., Meskin N., Khattab T., Shraim M., Al-Hitmi M.A. Review of mathematical model-based scenario analysis and interventions for COVID-19. Computer Methods and Programs in Biomedicine. 2021:106301. doi: 10.1016/j.cmpb.2021.106301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palacios R., Batista A.P., Albuquerque C.S.N., Patiño E.G., Santos J.d.P., Tilli Reis Pessoa Conde M., et al. Efficacy and safety of a COVID-19 inactivated vaccine in healthcare professionals in Brazil: The PROFISCOV study. SSRN Electronic Journal. 2021;14:4. Published Online. [Google Scholar]
- Patel M.D., Rosenstrom E., Ivy J.S., Mayorga M.E., Keskinocak P., Boyce R.M., Lich K.H., Smith R.L., Johnson K.T., Delamater P.L., Swann J. Association of simulated COVID-19 vaccination and nonpharmaceutical interventions with infections, hospitalizations, and mortality. JAMA Network Open. 2021;4(6) doi: 10.1001/jamanetworkopen.2021.10782. e2110782–e2110782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perra N. Non-pharmaceutical interventions during the COVID-19 pandemic: A review. Physics Reports. 2021;913:1–52. doi: 10.1016/j.physrep.2021.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prem K., Liu Y., Russell T.W., Kucharski A.J., Eggo R.M., Davies N., et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. The Lancet Public Health. 2020;5(5):e261–e270. doi: 10.1016/S2468-2667(20)30073-6. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahaman M., Islam M., Khan A., Sarker B., Mumtaz A. Understanding ”quarantine”, ”Social distancing”, and ”Lockdown” during COVID-19 Pandemic in Response to Global Health: A Conceptual Review. Open Journal of Social Sciences. 2020;8(10) [Google Scholar]
- Rana M., Alam M., Ikram A., Salman M., Mere M., Usman M., Umair M., Zaidi S., Arshad Y. Emergence of measles during the COVID-19 pandemic threatens Pakistan's children and the wider region. Nature Medicine. 2021;27:1127–1128. doi: 10.1038/s41591-021-01430-6. [DOI] [PubMed] [Google Scholar]
- Ranzani O.T., dos Santos Leite R., Castilho L.D., Gonçalves C.C.M., Resende G., de Melo R.L., Croda J. medRxiv; 2021. Vaccine effectiveness of Ad26. COV2. S against symptomatic covid-19 and clinical outcomes in Brazil: A test-negative study design. [Google Scholar]
- RStudio J.R. A platform-independent IDE for R and Sweave. Journal of Applied Econometrics. 2012;27 [Google Scholar]
- Shimizu K., Teshima A., Mase H. Measles and Rubella during COVID-19 pandemic: Future challenges in Japan. International Journal of Environmental Research and Public Health. 2021;18(9) doi: 10.3390/ijerph18010009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siordia J.A., Jr. Epidemiology and clinical features of COVID-19: A review of current literature. Journal of Clinical Virology. 2020;127:104357. doi: 10.1016/j.jcv.2020.104357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spinelli M.A., Glidden D.V., Gennatas E.D., Bielecki M., Beyrer C., Rutherford G., Chambers H., Goosby E., Gandhi M. The Lancet Infectious Diseases; 2021. Importance of non-pharmaceutical interventions in lowering the viral inoculum to reduce susceptibility to infection by SARS-CoV-2 and potentially disease severity. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes E.K., Zambrano L.D., Anderson K.N., Marder E.P., Raz K.M., Felix S.E.B., Tie Y., Fullerton K.E. Coronavirus disease 2019 case surveillance — United States, January 22– May 30, 2020. Morbidity and Mortality Weekly Report. 2020;69(24):759. doi: 10.15585/mmwr.mm6924e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szwarcwald C.L., Souza P.R. B.d., Malta D.C., Barros M.B.d.A., Magalhães M.d.A.F. M., Xavier D.R., et al. Adherence to physical contact restriction measures and the spread of COVID-19 in Brazil. Epidemiologia e Serviços de Saúde. 2020;29 doi: 10.1590/S1679-49742020000500018. SciELO Brasil. [DOI] [PubMed] [Google Scholar]
- Tangcharoensathien V., Singh P., Mills A. COVID-19 response and mitigation: A call for action. Bulletin of the World Health Organization. 2021;99(2):78. doi: 10.2471/BLT.20.285322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torner N. Collateral effects of COVID-19 pandemic emergency response on worldwide immunizations. Vacunas. 2020;21(73) doi: 10.1016/j.vacun.2020.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuite A.R., Zhu L., Fisman D.N., Salomon J.A. Alternative dose allocation strategies to increase benefits from constrained COVID-19 vaccine supply. Annals of Internal Medicine. 2021;174(4):570–572. doi: 10.7326/M20-8137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villela D.A., de Noronha T.G., Bastos L.S., Pacheco A.G., Cruz O.G., Carvalho L.M., et al. Effectiveness of mass vaccination in Brazil against severe COVID-19 cases. medRxiv. 2021 Cold Spring Harbor Laboratory Press. [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. The Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z., McGoogan J.M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: Summary of a report of 72 314 cases from the Chinese center for disease control and prevention. JAMA. 2020;323(13):1239–1242. doi: 10.1001/jama.2020.2648. [DOI] [PubMed] [Google Scholar]
- Wynants L., Van Calster B., Collins G.S., Riley R.D., Heinze G., Schuit E., et al. Prediction models for diagnosis and prognosis of COVID-19: Systematic review and critical appraisal. BMJ. 2020;369 doi: 10.1136/bmj.m1328. British Medical Journal Publishing Group. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yilmaz A., Marklund E., Andersson M., Nilsson S., Andersson L.-M., Lindh M., Gisslén M. The Journal of Infectious Diseases; 2020. Upper respiratory tract levels of SARS-CoV-2 RNA and duration of viral RNA shedding do not differ between patients with mild and severe/critical COVID-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yue T., Fan B., Zhao Y., Wilson J.P., Du Z., Wang Q., et al. Dynamics of the COVID-19 basic reproduction numbers in different countries. Science Bulletin. 2021;66(3):229. doi: 10.1016/j.scib.2020.10.008. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamir M., Shah Z., Nadeem F., Memood A., Alrabaiah H., Kumam P. Non pharmaceutical interventions for optimal control of COVID-19. Computer Methods and Programs in Biomedicine. 2020;196 doi: 10.1016/j.cmpb.2020.105642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. The Lancet. 2020;395(10229):1054–1062. doi: 10.1016/S0140-6736(20)30566-3. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All SARI and ARI notification data are publicly available at OpenDataSUS database, maintained by the Ministry of Health, located at https://opendatasus.saude.gov.br/.