Defined core–shell particles as the key to complex interfacial self-assembly

Significance

The spontaneous self-organization of matter is ubiquitous in nature and an attractive technological approach to create defined nanostructured materials from the bottom-up. Spherical colloidal particles are among the most widely used building blocks, but their self-assembly is limited to hexagonal symmetries as the densest sphere packing. Here, we demonstrate that this limitation in structural versatility can be overcome using soft core–shell particles self-assembling at a liquid interface. The propensity of the polymer shell to spread at such interfaces allows tailoring their interactions, which in turn affords a complex, nonintuitive phase behavior upon compression. The observed structures agree with theoretical predictions of particles interacting via two length-scale Jagla potentials, which have been predicted decades ago but remained elusive in experiments.

Abstract

The two-dimensional self-assembly of colloidal particles serves as a model system for fundamental studies of structure formation and as a powerful tool to fabricate functional materials and surfaces. However, the prevalence of hexagonal symmetries in such self-assembling systems limits its structural versatility. More than two decades ago, Jagla demonstrated that core–shell particles with two interaction length scales can form complex, nonhexagonal minimum energy configurations. Based on such Jagla potentials, a wide variety of phases including cluster lattices, chains, and quasicrystals have been theoretically discovered. Despite the elegance of this approach, its experimental realization has remained largely elusive. Here, we capitalize on the distinct interfacial morphology of soft particles to design two-dimensional assemblies with structural complexity. We find that core–shell particles consisting of a silica core surface functionalized with a noncrosslinked polymer shell efficiently spread at a liquid interface to form a two-dimensional polymer corona surrounding the core. We controllably grow such shells by iniferter-type controlled radical polymerization. Upon interfacial compression, the resulting core–shell particles arrange in well-defined dimer, trimer, and tetramer lattices before transitioning into complex chain and cluster phases. The experimental phase behavior is accurately reproduced by Monte Carlo simulations and minimum energy calculations, suggesting that the interfacial assembly interacts via a pairwise-additive Jagla-type potential. By comparing theory, simulation, and experiment, we narrow the Jagla $g$-parameter of the system to between 0.9 and 2. The possibility to control the interaction potential via the interfacial morphology provides a framework to realize structural features with unprecedented complexity from a simple, one-component system.

Two-dimensional (2D) colloidal self-assembly enables fundamental studies of structure formation and has the potential to yield defined surface patterns from simple and inexpensive building blocks. The ideal template to experimentally study 2D colloidal self-assembly are liquid interfaces (1–3). Colloidal particles strongly adsorb to such liquid interfaces (4, 5) and are therefore inherently confined in two dimensions, yet retain the mobility required to form ordered arrangements. The interfacially assembled colloidal monolayer can be subsequently transferred to a solid substrate, providing nanoscale surface patterns with useful functionalities in a range of technologies (6, 7), including photonics (8, 9), phononics (10, 11), plasmonics (12, 13), solar cell engineering (14), cell-surface interactions (15, 16), or liquid repellency (17, 18).

The structural motifs accessible to 2D colloidal assembly are typically determined by the shape of the particles via their most efficient packing. In particular, the general propensity of spherical particles to assemble into hexagonal lattices limits the versatility of using spherical building blocks to create complex structures. Surface patterns with increasing complexity have been achieved by multiple deposition steps (19, 20), deformation of preassembled lattices upon transfer to a solid substrate (21), or mechanical stretching of the underlying substrates (22). While these approaches can provide practical solutions, they do not alter the fundamental self-assembly process itself.

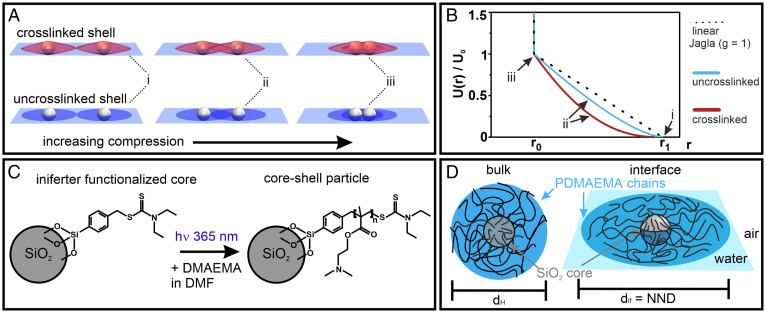
An elegant solution to directly decouple particle shape from the resulting self-assembled phases has been theoretically proposed decades ago. In 1998, Jagla showed that a simple addition of a soft repulsive shell surrounding a hard sphere introduces a second length scale in the interaction potential, which allows for the creation of nonhexagonal minimum energy configurations (MECs) such as chains, squares, and rhombic phases (23). The formation of such counterintuitive phases results from the competition between the two length scales in the interaction: when the core–shell particles are compressed such that their shells begin to touch, the system can minimize its energy by fully overlapping neighboring shells in some directions in order to prevent the overlap of shells in other directions (24–26). Jagla further showed that the generic potential, shown in Fig. 1A and Eq. 1, provides flexibility to tune the resultant self-assembly behavior. In particular, the minimum energy phase in such core–shell systems is determined by three parameters: the ratio of the shell-to-core diameter ($r_1/r_0)$, the shape of the soft repulsive potential, expressed by the parameter $g$, and the area fraction of the system ($\text{η}$), which determines the total amount of shell overlap (23, 27). Since this initial discovery, many theoretical reports have shown that dozens of different structures can originate from simple spherical particles interacting via such Jagla-like potentials, including honeycombs, or quasicrystals of various symmetries for relative small shell-to-core ratios ($r_1/r_0\lesssim 2)$ (26–30), as well as defined particle clusters and complex chains phases at higher shell-to-core ratios ($r_1/r_0\gtrsim 2)$ (24, 31–35).

Fig. 1.

Interfacial morphology of soft particle systems and hypothesized interaction potentials. (A) While a crosslinked shell retains a quasi–three-dimensional character at the interface (red), the noncrosslinked polymer shell of hairy particles can spread efficiently into a two-dimensional corona (blue). (B) Interaction potentials of the two different interfacial morphologies, calculated using a simple model where the repulsive potential is assumed to be proportional to the volume of shell overlap. A linear ramp Jagla potential ($g=1$) is also shown for comparison. (C) Reaction scheme to synthesize hairy particles with controllable shell thickness. A silica core is functionalized with an iniferter molecule, from which defined poly(2-dimethylaminoethyl) methacrylate (PDMAEMA) polymer chains are grafted in a controlled radical polymerization. (D) PDMAEMA@SiO2 core–shell particle and its dimensions in bulk and at the interface.

In contrast to this theoretical understanding, the experimental progress of such systems has remained largely elusive. The fundamental bottleneck that has impeded the experimental realization of such complex assembly phases is the difficulty of engineering suitable interaction potentials. For a system to form Jagla phases, two stringent requirements need to be met. First, the particle interaction potential requires two distinct length scales as described earlier and, in particular, a soft repulsive shell with a nonconvex shape (23, 25, 26), meaning that the repulsion should have at least a linear ramp profile (i.e., the Jagla parameter $g\mathrm{\gtrsim }1$). Second, the interaction potentials need to be strictly pairwise additive (i.e., many-body effects where the interaction between two core–shell particles is influenced by the presence of other neighboring particles need to be avoided).

In principle, interaction potentials satisfying the two length-scale criteria can be implemented using core–shell particles consisting of a solid, incompressible core and a compressible shell. Microgels (36) are ideally suited as shell material because of their soft nature and their ability to deform under the influence of surface tension (3, 37–39). In particular, when adsorbed at a liquid interface, microgels with and without a solid core exhibit a pronounced, very thin corona at the periphery, which is formed by the interfacial spreading of dangling chains (5, 40–43). This corona acts as a compressible spacer between the cores, effectively introducing a repulsive shoulder to the interaction potential.

However, despite their interfacial core–corona morphology, we note that for pure microgels (44, 45) and typical core–microgel shell systems (46–49), only an isostructural hexagonal non–close packed to hexagonal close-packed transition is observed. This behavior has been rationalized by the quasi–three-dimensional shape that these particle systems retain despite their deformation at the interface (Fig. 1A, Top). Due to their crosslinked nature, the shell protrudes significantly into the water subphase (38, 49, 50). This interfacial morphology causes a rapid increase in shell overlap upon compression. Assuming that that the energy penalty associated with the compression of the polymer shell scales with the overlap volume, this interfacial morphology therefore can be assumed to form a convex shape for the interaction potential (Fig. 1B and SI Appendix, Supplementary Discussion). In the terminology of the Jagla potential, the $g$ parameter for the shell interaction is much smaller than 1, which is not sufficient for observing complex assembly phases (25–27). The ability to expand at a liquid interface is intimately connected to the molecular architecture of the microgel. Microgels with low or ultralow crosslinking densities can spread particularly well at the interface, as the individual chains are less hindered by mutual crosslinking points (44, 51). While such systems may exhibit a larger $g$ parameter, they lack a hard core and therefore do not possess the required two length scales in the potential and do not form any unconventional phases (49). In contrast, the only reports of anisotropic chain phases to date were observed in interfacial systems with extremely flat coronae, formed by binary mixtures of polystyrene microspheres and very small microgels (25), and core–shell particles with a pronounced crosslinker gradient (49). These examples indicate that the ideal interfacial morphology to achieve Jagla-type interaction potentials with sufficiently large $g$-parameters is a core–shell system with an effectively 2D shell, where the overlap volume increases nearly linearly with compression. Again assuming that the overlap volume is proportional to the resultant energy penalty, this results in a near-linear ramp potential (i.e., $g\approx 1$) (Fig. 1A and SI Appendix, Supplementary Discussion). Even though they pinpoint at important structural requirements, both initial experimental systems are limited in their ability to probe the wealth of theoretically predicted Jagla phases because they lack proper control of the shell dimensions. In particular, an experimental realization of more complex chains and defined clusters, predicted for larger shells, remains elusive.

The interconnected nature of a crosslinked microgel shell not only limits the interfacial spreading but also forces the polymer chains in the corona to react in a concomitant manner. This implies that upon compression, cross-linked shells are forced to distribute stress across the entire shell. As a consequence, a collapse of the shell with one neighboring particle also facilitates the collapse of the same shell with other neighboring contacts. It has been shown that such many-body interactions destabilize the formation of anisotropic Jagla phases and bias the system toward the conventionally observed isostructural phase transitions (49).

Here, we circumvent the problems associated with conventional core–shell particles by using hairy particles consisting of an inorganic silica core functionalized with individual, noncrosslinked, and surface-active polymer chains (Fig. 1 C and D). As we will see, at a liquid interface, the polymer chains in these hairy particles spread very efficiently and form an effectively 2D corona, which we assume to translate into a near-linear repulsive potential. Using controlled radical polymerization to grow these polymer chains from the particle surface (Fig. 1C) (52–54), our method further provides uniform shell structures and control over their dimensions. By completely avoiding any crosslinking in the shell, we also ensure that mechanical stress, arising from a local shell collapse upon compression, is not translated throughout the entire microgel shell. This, in turn, facilitates the partial and anisotropic collapse of a single shell in the vicinity of a neighboring particle. In the Jagla terminology, this behavior reflects a pairwise-additive character of the interaction potential. Our experimental particle system thus fulfils both the stringent conditions required for the formation of Jagla phases. As we will show, upon compression these particles indeed form a series of complex 2D phases that are quantitatively reproduced by minimum energy calculations and Monte Carlo (MC) simulations based on the Jagla potential.

Results

Defined Core–Shell Particles.

We use an iniferter-based controlled radical polymerization scheme to synthesize the targeted particle architecture shown in Fig. 1 C and D (52–55). We functionalize silica core particles (d = 170 nm) with the iniferter using silane chemistry (56, 57) (Fig. 1C and SI Appendix, Fig. S1). Subsequently, we graft poly(2-dimethylaminoethyl) methacrylate (PDMAEMA) polymer chains from these cores in a ultraviolet (UV) light ($\text{λ}$ = 365 nm)–initiated controlled radical polymerization. The key advantage of this reaction is that it allows a convenient yet precise control of the shell thickness via the exposure time. The length of the polymer chains controls the interfacial dimensions of the particles and, therefore, the radius of the repulsive shell (r₁) in the assumed interaction potential.

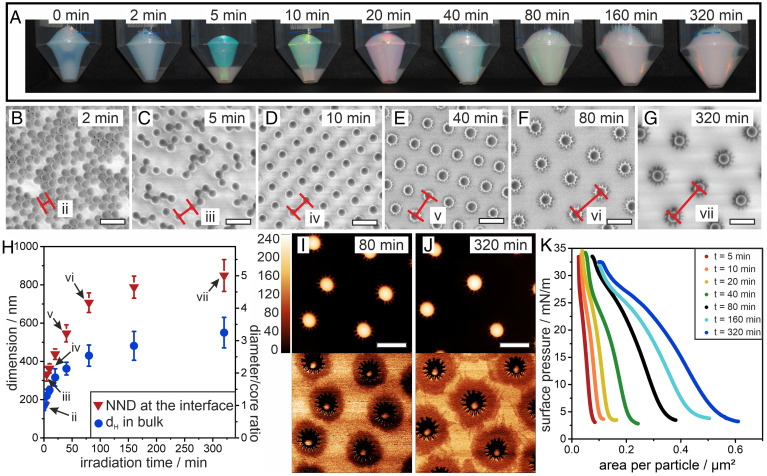
Fig. 2A shows photographs of dispersions of hairy particles after increasing UV exposure time up to 320 min. The increase in shell thickness can be directly observed by the color change of the colloidal crystal formed upon centrifugation (2, 58) (Fig. 2A). The photonic stop band shifts through the visible spectrum as the spacing of the silica cores in the formed crystal increases. The shell growth can also be seen in the increase in hydrodynamic diameter ($d_H)$ measured by dynamic light scattering in Fig. 2H. The diameter increases from 170 nm at 0 min of irradiation to 550 nm at 320 min of irradiation, corresponding to a shell thickness of 190 nm in bulk. The increasing presence of organic polymer shell material is further verified by thermogravimetric analysis (TGA) and infrared (IR) spectroscopy (SI Appendix, Fig. S1).

Fig. 2.

Shell growth for PDMAEMA@SiO2 core–shell particles. (A) Photographs of core–shell particles after centrifugation in 50-mL falcon tubes. An increase in mass and particle dimensions can be observed from the color change with increasing irradiation time. (B–G) SEM images of the core–shell particles transferred to a solid substrate from the air/water interface at a surface pressure of 5 mN/m. The distance between two particles is marked in red. (H) Dimension of the core–shell particles with increasing irradiation time, measured by dynamic light scattering in the bulk (i.e., the hydrodynamic diameter d_H, polydispersity index width as error bars) and by determination of the NND from SEM images (SD as error bars). (I and J) AFM height (Top) and phase (Bottom) images of particles irradiated for 80 (I) and 320 (J) min. (K) Surface pressure-area isotherms for the different core–shell particle systems (Scale bar: 500 nm).

We form colloidal monolayers by spreading the particles at an air/water interface and investigate the resulting interfacial morphologies using the simultaneous compression–deposition technique on a Langmuir trough (59). Fig. 2 B–G shows scanning electron microscopy (SEM) images of the different particle monolayers after transfer to a solid substrate at a low surface pressure of 5 mN/m. For very short irradiation times up to 2 min, the monolayer consists of silica cores, which are mostly in direct contact (Fig. 2B). For 5 min irradiation, the image shows particles in core–core contact as well as separated particles (Fig. 2C). Core separation results from coronae formed by the interfacially adsorbed polymer chains. However, the coronae do not yet seem sufficiently stable to fully prevent core–core attractions by capillary forces. Note that from our characterization, it is not possible to deduce whether the core–core contact is already formed at the interface or arises from capillary forces during transfer and drying. Stable nonclose packed phases with increasing interparticle distance emerge from irradiation times of 10 min or more (Fig. 2 D–G), indicating that the corona now reliably separates the individual cores at the liquid interface. Note that the absence of particles in direct contact indicates that the transferred colloidal monolayer retains its interfacial arrangement as immersion capillary forces upon drying would inherently push particles together, as is the case for shorter irradiation. These findings corroborate previous reports and demonstrate that this ex situ analysis can yield an accurate picture of their interfacial morphology and phase behavior (42, 43, 45, 49). Using image analysis, we extract the average nearest-neighbor distance (NND), which we take as a proxy for the interfacial corona dimensions, since the particles can be assumed to be in corona–corona contact at the interface at this surface pressure (Fig. 2H) (3, 5).

Atomic force microscopy (AFM) phase contrast images, shown in Fig. 2 I and J for core–shell particles from irradiation times of 80 and 320 min, respectively, give direct evidence of the interfacial morphology. The solid core is surrounded by a pronounced, extended 2D corona. The very thin, quasi-2D nature of this corona is obvious from the fact that it is revealed in phase contrast but not visible in the height image. The star-shaped appearance of core–shell particles with longer polymer chains (Fig. 2 F, G, I, and J) indicates a bundling of polymer chains close to the core, presumably by collapse of polymer chains protruding into the water subphase upon drying. The increasing dimensions of the coronae is also reflected in the surface pressure-area isotherms shown in Fig. 2K, which show a continuous shift to larger areas per particle and an increasing compressibility of the interfacial assembly for samples with increasing exposure times.

Phase Transitions at the Interface.

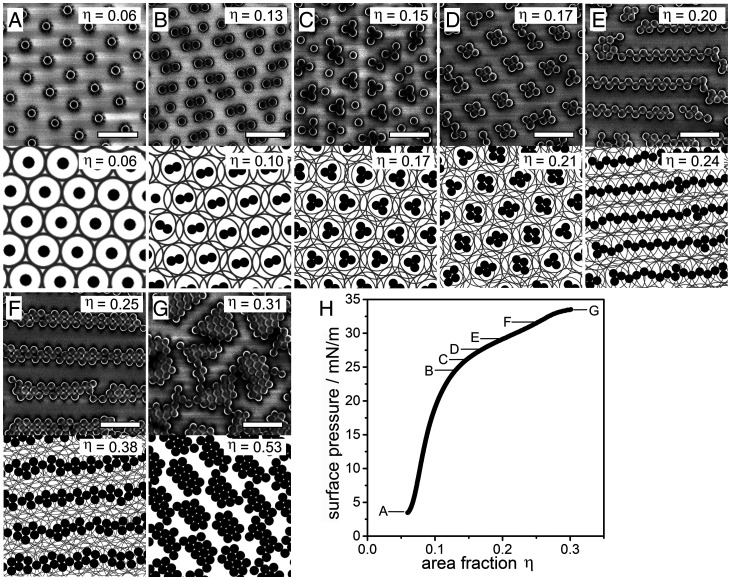
Next, we investigate the interfacial phase behavior as a function of the particle area fraction on a Langmuir trough using the example of core–shell particles from 80 min irradiation (Fig. 2 F and I). Experimentally, we determine the $r_1/r_0$ ratio from the NND at the interface (Fig. 2H) and the core diameter to be $r_1/r_0=4.1$. The core–shell particles form a hexagonal non–close packed monolayer at surface pressures below 5 mN/m. Upon compression, both surface pressure and the area fraction of the particles ($\text{η}$) increases, as seen in Fig. 3H. The hexagonal non–close packed phase prevails up to $\text{η}=0.11$, and the compression only results in a decreasing lattice constant (Fig. 3A). Above this area fraction, the system undergoes phase transitions into cluster phases. First, lattices of defined particle dimers are observed (Fig. 3B), which are increasingly replaced by trimers (Fig. 3C) and tetramers (Fig. 3D). At even higher area fractions, the lattices of small clusters collapse into larger clusters and complex chain phases with characteristic morphologies. These morphologies include well-defined zig-zag chains (Fig. 3E), observed around $\text{η}=0.2$, and braided chains (Fig. 3F) which emerge at $\text{η}=0.25$. At $\text{η}>0.3$, the chains and clusters merge to form a less defined network of very large clusters at the highest compressions achievable in experiments (Fig. 3G and SI Appendix, Fig. S2).

Fig. 3.

Phase behavior of the core–shell system upon compression in experiment and MC simulations based on particles interacting via a Jagla potential with a linear ramp potential and shell-to-core ratio $r_1/r_0=4$. (A–G) Representative SEM image of characteristic phases observed in experiment (Top row) and snapshots of the MC simulations (Bottom) at different area fractions specified in the images. (H) Surface pressure-area fraction isotherm indicating the regions in which the phases are observed (Scale bar: 1 µm).

In order to elucidate the driving force behind these phase transitions, we perform MC simulations of core–shell particles interacting via the Jagla potential [i.e., Eq. 1 [shown in (MMCs)]. We choose $r_1/r_0=4$ to match the shell-to-core ratio of the experimental system. The shape of the soft repulsive shoulder and hence the value of $g$ is not known a priori. However, from our arguments in the introduction (Fig. 1 A and B), we hypothesize that the repulsion for the effectively 2D soft shells in the experimental system should be reasonably approximated by a linear ramp, and we therefore choose $g=1$ (SI Appendix, Supplementary Discussion). As we will elaborate in the Discussion, by comparing both MC simulations and minimum energy calculations for varying $g$ with the experimental data, we are also able to bracket $g$ to be in the range $0.9\le g\mathrm{\lesssim }2$, which again is consistent with our choice of $g=1$. In order to more closely mimic the kinetic history of the experimental system, the different area fractions $\eta$ were accessed through a slow uniaxial compression of the simulation box starting from the hexagonal non–close packed phase at a reduced temperature of $T^{*}=k_{B}T/U_0=0.005$, where $k_B$ is the Boltzmann constant, and $U_0$ is the soft shoulder height in the Jagla potential (see Materials and Methods for details).

Snapshots of the phase behavior resulting from the MC simulations are shown in Fig. 3 A–F below their experimental counterparts. The size of the soft shell ($r_1$) is shown as a gray circle surrounding the black hard cores to help visualize the degree of shell overlap in the different phases. Our MC simulations accurately reproduce all the characteristic phases observed in the experiments. There is also excellent agreement between simulation and experiment in the area fractions for the cluster phases but slightly larger discrepancies in the area fractions for the complex chain phases. The close agreement between experiment and simulation provides evidence that the complex self-assembly observed experimentally can indeed be rationalized by Jagla-type interactions. Note that the highest-density simulation data shown in Fig. 3G was obtained using a more conventional slow cool equilibration protocol (i.e., system started at the required area fraction then slowly cooled from $T^{*}=\infty$ to $T^{*}=0.005$) to avoid finite size effects in the simulation box occurring during the uniaxial compression. Interestingly, this slow cool protocol also reliably reproduces the cluster phases but not the zig-zag chains or braided chains (SI Appendix, Fig. S2), suggesting that these complex chain phases are sensitive to the kinetic history of the sample and can only be accessed via specific kinetic pathways. This sensitivity is confirmed by the fact that in both the compression MC simulations and experiments, the complex chains are aligned along the compression axis. We note that the general phase behavior with chain and cluster formation agrees with literature results using similar potentials (24, 34), with the important exception of the complex zig-zag and braided chains (see Discussion section for more details), corroborating the importance of kinetic pathway for their formation.

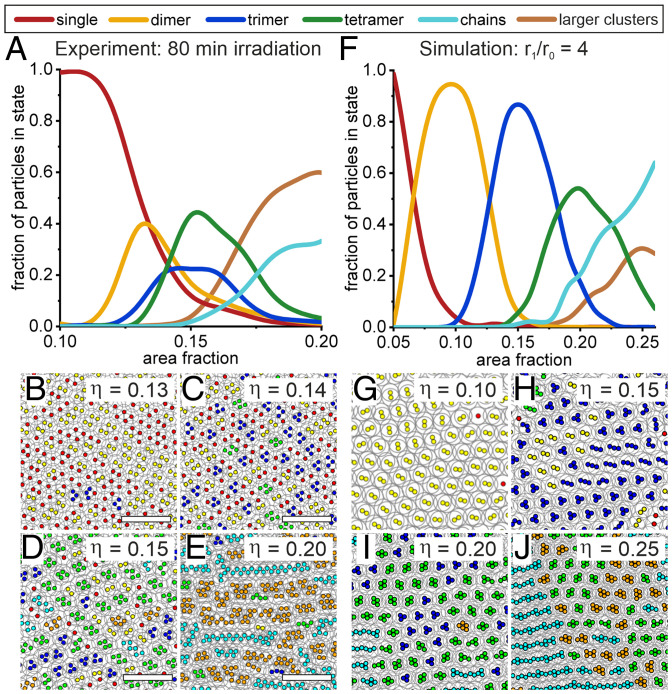
In the evolution of the experimental interfacial assembly, characteristic phases often coexist, as evidenced by lower-magnification SEM images (SI Appendix, Fig. S3). Similarly, larger area simulation snapshots show the presence of multiple phases in the MC simulations (SI Appendix, Fig. S4). This behavior is expected for area-controlled experiments (i.e., a canonical or NVT ensemble) but also hints at small energetic differences between the different phases. We use image analysis to detect and analyze the characteristic phases as the system evolves with increasing compression. Fig. 4 shows the statistical evaluation of the phase behavior as well as large area snapshots of characteristic area fractions where different phases are dominant for both experiment (Fig. 4 A–E) and simulation (Fig. 4 F–J). Considering the complexity of the phase behavior and the experimental system and the simplicity of the theoretical model, the qualitative agreement between the statistical analysis for experiment and simulations is surprising. In particular, the statistical data from both experiment and simulation supports the qualitative picture shown in Fig. 3 and clearly shows that with increasing compression, the system evolves from a non–close packed hexagonal phase, via defined clusters to chains and large clusters in both experiments and simulation (see Materials and Methods for details). This evolution of phases is also observed in the animation of the color-coded compression simulation (Movie S1) and the animated postprocessed SEM images (Movie S2). Interestingly, using the slow cool protocol instead of the compression protocol in our MC simulations led to much poorer agreement of the distribution of the different phases compared to experiment (SI Appendix, Fig. S2), further underlining the contributions of kinetic pathways in forming the complex phases.

Fig. 4.

Statistical evaluation of the phase transitions in experiment and simulation. (A) Fraction of particles in different phases as a function of area fraction in experiment. (B–E) Postprocessed SEM images with color-coded cores (d = 170 nm) detected in image analysis (Scale bar: 2 µm). (F) Fraction of particles in different phases as a function of area fraction in compression-type MC simulation. (G–J) Simulation snapshots with color-coded phases detected in image analysis.

The nonergodic nature of the system provides a post-hoc justification for using our compression MC method rather than a MC method that is more efficient at finding the ground state in a rugged energy landscape [e.g., parallel tempering, simulated annealing, etc. 60)] since the former mimics the kinetic history of the experimental system more accurately. Interestingly, we did not find any evidence of a glass transition either in our simulations or experiments, and we therefore conclude that the soft shells in our system are soft enough to allow local rearrangements of the colloidal particles into (at least locally) ordered structures so that they are not trapped in an amorphous, glassy state.

While our compression MC simulations capture the key features of the phase distribution, a closer examination of Fig. 4 A and F reveals subtle differences between experiment and simulations. First, the area fraction range over which the phase transitions take place is larger, and the peaks for the individual phases are better separated in the simulations compared to in the experiments. This difference can be attributed to an underestimation of the experimentally determined area fraction, which is based on the nominal area of the silica cores and ignores the presence of highly compressed polymer chains between cores in contact (Materials and Methods). Secondly, the peak population of the particles in the different phases is higher in the simulations (dimers 93%, trimers 83%, and tetramers 52%) compared to in the experiments (dimers 43%, trimers 30%, and tetramers 42%). This difference may be attributed to particle polydispersity and the presence of minor amounts of impurities in the experimental system (61). To assess the effect of polydispersity, we included the experimental polydispersities for both the core and shell diameters in our MC simulations and further increased these values to probe the evolution of the system (SI Appendix, Fig. S5). These simulations reveal that polydispersity does not change the phase behavior of the system qualitatively, though it suppresses the peak population for clusters. The latter result confirms that the smaller peak populations for the different phases observed in the experiments compared to the simulations of monodisperse particles is at least partially due to polydispersity. Finally, at high area fractions, the dominant phase is observed to be large clusters in the experiments but predicted to be chains in the simulations. The latter is in fact an artifact due to finite size effects in the simulations at high compressions. Specifically, for large area fractions above $\text{η}\mathrm{\gtrsim }0.25$, the largest chain length in the simulation is equal to the dimension of the simulation box along the compression axis. At higher area fractions, periodic boundary conditions start to connect clusters into chains, artificially driving up the proportion of chains relative to clusters.

MECs.

In order to gain a deeper understanding of the phase transitions occurring in our system, we calculate the zero-temperature phase diagram and MECs for an ensemble of core–shell particles interacting via the generic core–shell potential proposed by Jagla (27)

$$U\left(r\right)=\{\begin{array}{cc}\begin{array}{c}\infty ,\\ \end{array}& \begin{array}{c}r<{\text{r}}_0\\ \end{array}\\ \begin{array}{c}{U}_0\frac{g+ {\left( \left(\frac{r/r_0-1}{r_1/r_0-1}\right)\left(g-g^{-1} \right)-g\right)}^{-1}}{g-g^{-1} },\\ \end{array}& \begin{array}{c}{r}_0\le r\le r_1\\ \end{array}\\ 0,& r>r_1\end{array},$$ [1]

where $r$ is the separation between the interacting particles, $r_0, r_1$ are the range of the hard-core and soft-shell repulsion, respectively, $U_0$ is the height of the soft-shell potential, and the parameter $g$ controls the profile of the soft-shell interactions (Fig. 5A). Note that although our core–shell system is not globally ergodic as discussed in the previous section, we are justified in using minimum energy calculations to determine the local structure of the different phases since the experimental system is effectively in the zero-temperature regime ($U_0\gg k_{B}T$) as demonstrated in the SI Appendix.

Fig. 5.

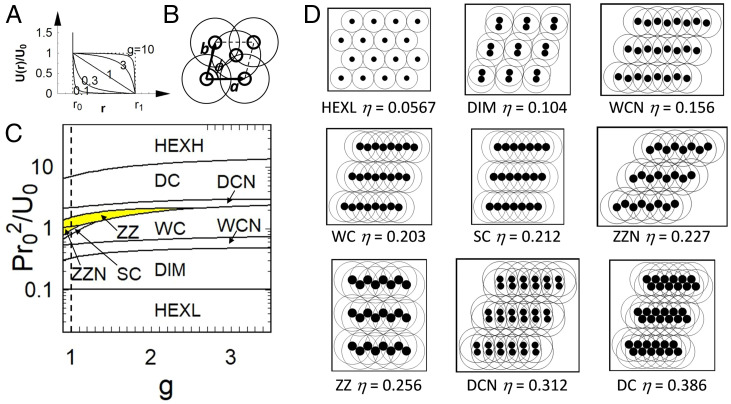
M ECs of core–shell particles with $r_1/r_0=4$. (A) Jagla potential for different values of $g$. The dotted lines on the Left and the Right correspond to $g=0$ (no shoulder) and $g=\infty$ (square shoulder), respectively. (B) Two-particle unit cell used in the calculations, where $\mathit{a},\mathit{b}$ are the lattice vectors, $\varphi$ is the unit cell angle, and the thick and thin circles represent the particle core and shell, respectively. (C) Zero-temperature phase diagram for the core–shell particles in the $g-P$ plane, where $P$ is surface pressure. The vertical dashed line represents $g=1$. The region for zig-zag phases (i.e., ZZN and ZZ) is highlighted in yellow in the phase diagram. (D) Representative MECs and their corresponding area fractions $\eta$. The full set of MECs (including the hexagonal close-packed phase HEXH) is shown in SI Appendix, Fig. S6.

Following the experiments in Figs. 3 and 4, we fix $r_1/r_0=4$. To simplify the discussion, we only consider 2D structures containing up to two particles per unit cell (Fig. 5B) as this model is simple enough to allow us to perform a comprehensive exploration of the all the MECs but complex enough to generate the representative phases and their approximants seen in the experiments and simulations such as clusters (i.e., dimers) and complex chains (e.g., zig-zag chains and double chains). Working in the NPT (i.e. isobaric-isothermal) ensemble, we calculate the MECs for each value of $g$ and reduced pressure $P^{*}=r_0^{2}P/U_0$ by minimizing the enthalpy per particle $H$ with respect to the lattice parameters (26). Note that the value of $U_0$ is not relevant to the phase behavior in the low-temperature regime $T^{*}=k_{B}T/U_0\ll 1$ that we are considering here.

Fig. 5C shows the phase diagram in the $g-P^{*}$ plane, while Fig. 5 D–M shows a subset of representative MECs together with their area fractions (see SI Appendix, Fig. S6 for the complete set). The dashed line in Fig. 5C corresponds to $g=1$ considered in our simulations. With increasing pressure, corresponding to increasing $\eta$ in the experiments and simulations, the system evolves from a low-density hexagonal phase (HEXL), via defined dimers (DIM) to a series of distinct chain phases, including non–close packed and close-packed wavy chains (WCN, WC), straight chains (SC), non–close packed and close-packed zig-zag chains (ZZN, ZZ), non–close packed and close-packed double chains (DCN, DC), and finally a series of higher-density compact structures culminating in the close-packed hexagonal phase HEXH (SI Appendix, Fig. S6). Note that within the framework of our two-particle calculation, trimer and tetramer clusters and braided chains cannot be formed and are therefore absent in the MECs. However, if we consider the double-chain phases as approximants for the braided chain phase (which is reasonable; see figure 5 of ref. 35), the evolution of the minimum energy phases in our simplified model closely mimics the phases observed in the experiments and simulations (Fig. 3), going from the non–close packed hexagonal phase, to defined clusters, zig-zag chains, and complex double chains. There is also excellent agreement in the area fractions of these phases between theory and simulation.

Discussion

The agreement between experiment, simulation, and theory on the observed phases and their evolution suggests that the developed particle system with its tailored interfacial morphology indeed exhibits an interaction potential that can be described via pairwise-additive Jagla potentials. Unfortunately, the small particle dimensions prevent the direct measurement of the interfacial interaction potential to confirm this conclusion. Existing methods, such as optical tweezer experiments (62) or the inversion of pair distribution functions (63) require larger particles with µm dimensions that can be directly observed at the interface. However with increasing core radius, the core–shell particles will experience stronger attraction due to floatation capillary forces, which destabilizes the core–corona morphology required for the two–length scale interaction potential (44, 46). In addition, even for stable monolayers of µm-sized core–shell particles, the inversion method only works when the interaction energy scales are of the order of $k_{B}T$ (63) and is therefore not applicable to our experimental system, where the interaction energy scales are much greater than $k_{B}T$ (SI Appendix, Supplementary Discussion). An alternative method for determining the interaction potential from first principles is to use monomer-resolved simulations (64, 65), but such a calculation is nontrivial and requires a separate and substantial study, which lies outside the scope of this paper.

However, while it is not possible to determine the interaction potential directly, it is possible to constrain the effective values of $g$ and $U_0$ for these particles by comparing the experimentally observed morphology of the different characteristic phases with those predicted by theory and simulation. In SI Appendix, Supplementary Discussion, we determine the value of $U_0$ from the coexistence pressure between the low-density hexagonal phase and the dimer phase. Here, we focus on the $g$ parameter. Our minimum energy calculations predict that the zig-zag chain phases (ZZN and ZZ) are only stable for $g\mathrm{\lesssim }2$ (Fig. 5C, yellow highlighted region). At first sight, this seems to contradict the minimum energy calculation results of Fornleitner and Kahl, who observed a zig-zag chain phase for core–shell particles with a square shoulder profile $g=\infty$ and $r_1/r_0=5$ (35). However, a closer examination of bond angles and density of the phase reveals that the zig-zag chain phase in ref. 35 is in fact essentially equivalent to what we have called the double-chain phase (DC) in Fig. 5 (SI Appendix, Supplementary Discussion). Our experimental observation of zig-zag chains therefore puts an upper boundary of $g\approx 2$ for the $g$ parameter.

The lower boundary for $g$ is more difficult to access via minimum energy calculations because the complex energy landscape when $g<1$ makes the calculation of the zero-temperature phase diagram challenging (26, 27). We therefore determine the lower bound for $g$ by performing MC simulations for $g$ values varying between 0.85 and 1 and comparing the resultant phase behavior to our experimental observations (SI Appendix, Fig. S7). These simulations reveal that the characteristic dimer phase at low area fractions, which is pronounced in experiments, is absent for $g<0.9$. Based on these indirect evaluations from theory and simulation, we therefore bracket the effective $g$ parameter for our experimental system to be $0.9\le g\mathrm{\lesssim }2$. This range is consistent with our simple model of overlapping 2D shells, which suggests that the soft shoulder repulsion should be reasonably approximated by a linear ramp profile [i.e., $g=1$ (Fig. 1 A and B)].

It is important at this point to compare the Jagla potentials we have used in our MC simulations with those derived from previous monomer-resolved simulations on similar systems. For example, Schwenke et al. found the interaction potential between polymer-coated colloids at a liquid interface to be a Gaussian (64), while Camerin et al. found the interaction potential between microgels at a liquid interface to be a Hertzian (65). Both these potentials clearly have a convex shape (effective $g<1$) which is qualitatively different from the linear ramp Jagla potential ($g=1$) we have used in this paper (SI Appendix, Fig. S8A). In order to assess whether these convex potentials are applicable to our experimental system, we used them in place of the Jagla potential in our MC simulations and compared the resultant phase behavior with what we find in our experiments (SI Appendix, Fig. S8). We see that neither the Gaussian potential nor the Hertzian potential could reproduce the phase behavior seen in our experiments, indicating that our experimental system does not interact via these potentials.

We believe the reason why the effective potential for our polymer-coated colloids is different from that studied by Schwenke et al. is because although the two systems appear to be similar, they are in fact in different regimes (64). Specifically, in the simulations that gave rise to Gaussian interaction potentials, both bulk phases were assumed to act as a good solvents for the grafted polymer chains, so the majority of the polymer chains were stretched out into the bulk and only a small fraction are stretched out along the interface [i.e., those grafted close to the equatorial plane (64)]. In addition, the polymer chains along the interface are only stretched out slightly more compared to the chains that are stretched out into the bulk. As a result, the interactions in their system are dominated by the swollen chains in the bulk rather than the interfacial chains, leading to Gaussian interactions, as predicted for dilute polymer solutions in the bulk (66–68). In contrast, our polymer-coated particles are at an air–water interface, where all the polymer chains on the air side and presumably a significant fraction of the polymer chains on the water side are adsorbed at the interface. In addition, the polymer chains along the interface are stretched out around 60% more compared to polymer chains in the bulk (Fig. 2H). As a result, the interactions in our system are dominated by interfacial chains rather than swollen chains in the bulk, which as we have argued earlier, leads to a ramp-like potential (Fig. 1A, SI Appendix, Supplementary Discussion). In order to gain further insight into the relative contribution of the different terms to the total interaction, we performed MC simulations using a composite potential consisting of a Gaussian potential (with weighting $w$, $0\le w\le 1$) and a linear ramp potential (with weighting $1-w$) (SI Appendix, Fig. S9). We find that cluster formation, which is pronounced in the experimental system, only occurs when $w<10\%$. This behavior suggests that the interactions in our system are dominated by the pronounced and extended corona formed by the interfacially adsorbed polymer chains.

Finally, a major limitation in existing experimental approaches based on microgel/microsphere mixtures (25) and shells with a pronounced crosslinker gradient (49) is the inability to accurately control the dimensions and structure of the shell. These limitations prevent the formation of more complex Jagla phases and limit the system to the formation of single chains. In contrast, the iniferter-based controlled radical polymerization scheme produces hairy polymer chains with tailored dimensions (Fig. 2) and affords shells with large dimensions. The ability to engineer the shell dimensions allows us to study the impact of varying the shell-to-core ratio on interfacial phase behavior. Similar to the $r_1/r_0=4.0$ case, the observed phase behavior agrees between experiment and simulations for $r_1/r_0=2.5$ and $r_1/r_0=5.0$ (SI Appendix, Figs. S10 and S11, respectively). As expected, the onset of phase transitions is shifted to larger area fractions for smaller $r_1/r_0$ ratios and to smaller area fractions for larger $r_1/r_0$ ratios. One small discrepancy that occurs for the thin shell case $r_1/r_0=2.5$ is that simulations show that chain phases start to appear together with the trimer phase, which is not seen in experiments (SI Appendix, Figs. S10 and S11). We hypothesize that this discrepancy is due to the fact that attractive capillary forces cannot be completely ignored in thin shell experimental systems, and these may suppress the emergence of the chain phase until we reach higher area fractions. Indeed, for even thinner shells—or larger core particle dimensions— capillary forces dominate over the soft-shell repulsion and lead to aggregation and the formation of close-packed structures (SI Appendix, Fig. S12). In contrast, we can safely ignore capillary forces for thicker shells because the cores are separated by much larger distances, leading to increasingly better agreement between experiment and simulation as we increase shell thickness.

Conclusion

We use controlled radical polymerization to synthesize defined core–shell particles consisting of a silica core surface functionalized with individual polymer chains. Due to their noncrosslinked nature, these polymer chains can spread efficiently at a liquid interface to form a near-ideal 2D corona and behave independently of each other. Upon compression, these particle systems undergo a series of phase transitions and form complex self-assembled phases, including defined cluster lattices and chains with distinct morphologies. The evolution of these experimentally observed phases accurately coincides with results of MC simulations and minimum energy calculations based on pairwise-additive Jagla potentials with a linear ramp potential. This agreement between experiment, simulation and theory indicates that control of the interfacial morphology of soft particles can be used to realize Jagla-type phases, provided the following criteria are fulfilled:

• 1.The interfacial corona formed by the polymer chains approaches a 2D shape around an incompressible core. This interfacial morphology affords the required two–length scale interaction potential with sufficiently large g parameter.
• 2.The polymer chains are not crosslinked and therefore allow different degrees of shell overlap with neighboring particles. This independent behavior effectively ensures pairwise-additive interactions without biasing a collapse in all spatial directions, enabling the formation of anisotropic structures (49).
• 3.The polymer shell is uniform to afford a regular interfacial structure in all directions. This uniformity is enabled by the controlled radical polymerization (56).

This demonstration of a single component, spherical system to form a series of defined, anisotropic interfacial assembly phases provides a paradigm to experimentally realize the vast variety of theoretically predicted Jagla phases. The combination of available predictive theoretical models with the ability to use functional core materials and to tailor the chemical nature, chain architecture, density, structure, and dimensions of the polymer shell will spark discoveries in functional, self-assembled materials.

Materials and Methods

Materials.

All chemicals were obtained from commercial sources and used as received if not stated otherwise. Ethanol (EtOH; 99.9%; Merck), (p-chloromethyl)phenyltrimethoxysilane (95%; Gelest Inc.), dimethylformamide (DMF, anhydrous, 99.8%; Sigma Aldrich), tetraethyl orthosilicate (TEOS; 98%; Sigma Aldrich), and ammonium hydroxide solution (28 to 30% NH3 basis; Sigma Aldrich) were used as received. (2-Dimethylaminoethyl) methacrylate (DMAEMA; 99%; Merck) was passed over neutral Aluminum Oxide (Al2O3; Carl Roth) for deinhibition. Sodium diethyldithiocarbamate trihydrate (Sigma Aldrich) was recrystallized from methanol (99.8%; Sigma Aldrich). Tetrahydrofuran (THF; 99.9%; Sigma Aldrich) was dried by storage over activated molecular sieves. Water (H₂O) was double deionized using a Milli-Q system (18.2 M.cm; Elga PURELAB Flex).

Synthesis of the Photoiniferter, N,N-(diethylamino) dithiocarbamoylbenzyl-(trimethyoxy)silane (SBDC).

The photoiniferter SBDC was synthesized according to literature (56). In short, 10.6 g sodium diethyldithiocarbamate was dissolved in 100 mL dry, degassed THF and then dropwise added to a solution of 15.4 g (p-chloromethyl)phenyltrimethoxysilane in 100 mL dry, degassed THF under nitrogen atmosphere. After a reaction time of 4 h under stirring, the sodium chloride precipitate was removed by filtration and the THF by applying vacuum. The crude SBDC was purified by vacuum distillation at 160 °C, yielding 23 mol% of SBDC, which was stored under inert gas atmosphere in a fridge.

Synthesis of the Iniferter Functionalized Silicon Dioxide Cores.

The silicon dioxide (SiO₂) cores were synthesized according to the Stöber method (47, 69). A total of 12.5 mL H₂O, 250 mL EtOH, and 25 mL ammonium hydroxide solution were added to a 500-mL round-bottom flask and heated to 50 °C in an oil bath. Under stirring at 1,100 rpm, a solution of 18.75 mL TEOS in 75 mL EtOH, preheated to 50 °C, was added. After a reaction time of 18 h, 150 mL Stöber dispersion was removed and purified. A total of 100 mg SBDC in 10 mL EtOH was added to the remaining 231 mL Stöber dispersion, and the dispersion was diluted with 170 mL DMF. After another 24 h, the functionalized cores were purified by centrifugation and redispersion four times in EtOH and four times in dry DMF. The yield was 2.6 g functionalized silica particles with a diameter of 170 nm (±7 nm SD).

Synthesis of the SiO2@DMAEMA Core–Shell Particles.

A dispersion of 0.9 g functionalized cores in 162 mL dry DMF was mixed with 18 mL DMAEMA in a 250-mL round-bottom flask. The dispersion was treated with ultrasound and flushed with argon four times to remove oxygen. Then, the dispersion was placed in a UV crosslinker (Vilber Bio-Link 365) and irradiated with 365 nm UV radiation for up to 320 min under stirring. After 0, 2, 5, 10, 20, 40, 80, 160, and 320 min, 20 mL dispersion was removed and purified by centrifugation and redispersion 10 times in EtOH.

Simultaneous Compression and Deposition using a Langmuir–Blodgett Trough.

We used the simultaneous compression and deposition method as described previously (59). A Teflon Langmuir trough (KSV NIMA) (area = 243 cm², width = 7.5 cm) with Delrin barriers, filled with Milli-Q water was used, and the surface pressure was measured by a Wilhelmy plate. We used 5 × 0.5 cm² N-type silicon wafers (LG Silicon Inc.) as substrates, which were cleaned with ethanol and oxygen plasma (Diener) prior to use. The substrate was mounted to the dipper at a 45° angle.

The core–shell particle dispersion in ethanol was mixed with an equal volume of water before spreading. A 100-μL pipette was used to conduct the dropwise spreading of the particles. After an equilibration time of 20 min, the barriers were closed at a speed of 4 mm/min, and the substrate was lifted at a speed of 0.8 mm/min. The substrate with the core–shell lattice was further characterized by SEM (Zeiss Gemini 500) and AFM (JPK Nano Wizard, cantilever: Anfatec NSC 18). The AFM images were postprocessed using Gwyddion.

TGA.

For TGA measurements, the Hi-Res TGA 2950 Thermogravimetric Analyzer by TA Instruments was used. The samples, dispersed in ethanol, were pipetted into the TGA-crucible and dried under air at room temperature of 1 h. Inside the TGA, they were heated to 120 °C at 5 °C/min under nitrogen and kept isothermal for 40 min for further drying. Subsequently, they were cooled to 30 °C and then heated to 700 °C at 5 °C/min under air.

SEM Image Analysis.

The SEM images used for illustration were taken at a voltage of 1 kV, and the contrast was enhanced with CorelDraw. The SEM images used for statistical analysis were taken at a voltage of 4 kV for better core contrast. The SEM images were analyzed using a custom-written image analysis software, which is described in detail in our previous work (42). In short, the Matlab algorithm “imfindcircles” was used to identify circular objects in the SEM images, which were previously converted to black and white images. The extracted coordinates were used for a Voronoi tessellation, which gave the NNDs of each particle in the assembly. The area fraction was calculated by multiplying the number of particles with the area of the core with a diameter of 170 nm and subsequently dividing this overall core area by the overall image are. For highly coordinated lattices at high compressions, the contrast in the SEM images was not sufficient to automatically track all particles. Under those circumstances, the missing particles were tracked manually.

MC Simulation.

NVT Metropolis simulations were performed on an ensemble of 1,024 core–shell particles interacting via the Jagla potential (Eq. 1) with periodic boundary conditions and adjustable MC step lengths to achieve an acceptance probability of 30%. Two different kinetic pathways were used to access the different area fractions $\text{η}$. For the slow cool MC simulations, we used a fixed rectangular simulation box with aspect ratio of 2:$\surd 3$ starting with particles in a hexagonal lattice at the desired area fraction. The particles were first disordered at the reduced temperature of $T^{*}=100$, then brought to the final temperature $T^{*}=0.005$ through a slow cool process by successively quenching to $T^{*}=$ 0.5, 0.3, 0.2, 0.1, 0.08, 0.06, 0.04, 0.03, 0.02, 0.01, and 0.005. The system was equilibrated for ${10}^5$ attempted moves per particle at each temperature. For the compression MC simulations, an elongated rectangular simulation box with aspect ratio 8:$\surd 3$ was used instead. The particles were first prepared in the HEXL phase at an area fraction of $\eta =\pi r_0^2/\left(2\sqrt{3}{r}_1^2\right)$ through the slow cool protocol described in the Results section. Higher area fractions were then accessed by slowly reducing the length of the simulation box along its long dimension by steps of $r_0/5$ and affinely displacing all particles at each compression step. The system was equilibrated by $3\times {10}^4$ attempted moves per particle between each compression. A reduced temperature of $T^{*}=k_{B}T/U_0=0.005$ was used throughout these simulations, where $k_B$ is the Boltzmann constant and $U_0$ is the soft shoulder height in the Jagla potential (Fig. 5A), as this represents a good compromise between satisfying the experimental condition that $U_0\gg k_{B}T$ (SI Appendix, Supplementary Discussion) while still being computationally accessible in terms of system equilibration times. A higher temperature of $T^{*}=0.02$ was used for the thin shell case $r_1/r_0=2.5$ to account for the fact that in the experimental system, attractive capillary forces cannot be ignored in the thin shell regime, and these lead to a softening of the thin shell repulsion. Multiple compression runs (around 10) were carried out to increase the effective sample size from which to identify the different defined phases. To remove any core overlaps arising from the affine displacement of the particles, the hard-core region $r<r_0$ of the potential in Eq. 1 was replaced with a very high inverse power law potential $U_0{\left(r/r_0\right)}^{-30}$, which led to a very efficient removal of core overlaps when the Metropolis acceptance criteria was applied. Note that the compression MC simulations produced severe finite size effects at high compressions as the uniaxial compression from low-density results in very small dimensions of the simulation box along the compression axes.

Cluster Analysis.

In both experiments and simulations, particle cores which according to visual inspection are in contact generally have particle separations greater than $r_0$. To correctly capture particle aggregates from the snapshots, we therefore define a threshold separation below which cores are considered to be in contact. For our MC simulations, we define this threshold separation to be $1.4r_0$ for the particles with thicker shells ($r_1/r_0=4.0, 5.0$) and $1.25r_0$ for the particles with thinner shells ($r_1/r_0=2.5$). For our experiments, we define this threshold separation to be $1.4r_0$ for particles with thin shells (20-min irradiation). For particles with thicker shells (i.e., 80- and 320-min irradiation), a fixed threshold separation did not accurately capture clusters since with increased area fraction, there is a greater proportion of collapsed polymer chains between contacting cores leading to a larger core–core separation. To account for this effect, we define the threshold separation to be $(1.4+2\eta )r_0$ for the thicker shell experimental systems. Having defined the threshold separation, we define an aggregate as a group of particles where each particle is in contact with at least one other particle in the group. For aggregates containing five or more particles, we differentiate between chains and clusters by calculating the gyration tensor of the aggregate

$$S_{mn}=\frac{1}{2N^2}{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N(r_m^{\left(i\right)}-r_m^{\left(j\right)})(r_n^{\left(i\right)}-r_n^{\left(j\right)}),$$ [2]

where $N$ is the number of particles in the aggregate, and $r_n^{(i)}$ is the $x$ or $y$ coordinate of the $i^{th}$ particle in the aggregate ($n=x,y$). The eigen values of the symmetric $2\times 2$ gyration tensor give the mean squared separation of particle pairs in the aggregate along the long and short axes of the aggregate (i.e., along the eigen vectors). We define an aggregate to be a chain if the ratio of the eigen values exceeds 10 (i.e., long axis/short axis $\ge \sqrt{10}$). For the compression MC simulations, this scheme for classifying chains and clusters breaks down at high compressions when the length of chains become comparable to the shortest dimension of the simulation box and periodic boundary conditions start to interfere with the calculation of the gyration tensor. To get around this problem, we classify any aggregate containing more than 100 particles to be a chain, as we observe from our MC simulations that there are no clusters containing more than 100 particles. The resulting particle categorization is used for statistical analysis of the phases and for the creation of colorized monolayer representations, where the cores are represented by circles with a radius of $r_0/2$ in simulation and 85 nm in experiment.

Data Availability

All study data are included in the article and/or supporting information.