Summary
How tissues acquire complex shapes is a fundamental question in biology and regenerative medicine. Zebrafish semicircular canals form from invaginations in the otic epithelium (buds) that extend and fuse to form the hubs of each canal. We find that conventional actomyosin-driven behaviors are not required. Instead, local secretion of hyaluronan, made by the enzymes ugdh and has3, drives canal morphogenesis. Charged hyaluronate polymers osmotically swell with water and generate isotropic extracellular pressure to deform the overlying epithelium into buds. The mechanical anisotropy needed to shape buds into tubes is conferred by a polarized distribution of actomyosin and E-Cadherin-rich membrane tethers, which we term cytocinches. Most work on tissue morphogenesis ascribes actomyosin contractility as the driving force, while the extracellular matrix shapes tissues through differential stiffness. Our work inverts this expectation. Hyaluronate-pressure shaped by anisotropic tissue stiffness maybe a widespread mechanism for powering morphological change in organogenesis and tissue engineering.
Graphical Abstract
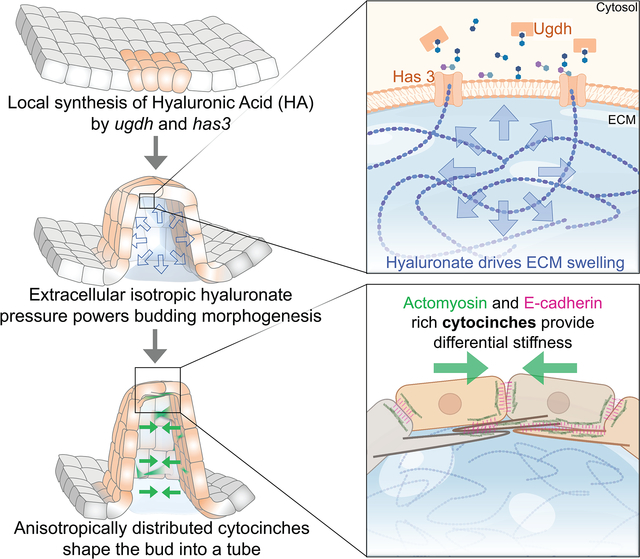
In Brief
Munjal et al. present evidence that the extracellular matrix can provide the driving force to shape tissue morphogenesis. Specifically, they show that hyaluronate-pressure, shaped by anisotropic tissue stiffness, is a mechanism for powering morphological change.
Introduction
Most organs including kidney, vasculature, lung, gut and heart begin as simple epithelia that then undergo morphogenesis to create elaborate shapes necessary for their function (Lubarsky and Krasnow, 2003). How this occurs is a fundamental question in biology with important implications in disease and regenerative medicine. Most research across tissues and species impute actomyosin networks as the central producers of mechanical forces that power cell deformations during tissue morphogenesis (Heisenberg and Bellaiche, 2013; Munjal and Lecuit, 2014). Actomyosin networks generate active contractile tension through the pulling of Actin filaments (F-Actin) by non-muscle Myosin II motor proteins (Myosin II) using ATP hydrolysis (Hartman and Spudich, 2012). The F-actin cortex is anchored to the plasma membrane and transmits forces across the tissue through cell adhesion (e.g. Cadherins and Integrins) (Lecuit et al., 2011). In this paradigm, developmental signals and biochemical information pattern tissue dynamics by locally activating actomyosin contractility and/or modulating cell adhesion to drive cellular morphogenesis. Classic examples include apical constriction during the invagination of the presumptive mesoderm (Dawes-Hoang et al., 2005), and the planar polarization of cell-cell junction strength to control cell arrangements during convergence- extension (Bertet et al., 2004).
The extracellular matrix (ECM), that is attached to most tissues, has long been recognized as an important determinant of tissue mechanics by integrating tissue forces and by providing stiffness. The ECM gets its stiffness from fibrous protein polymer networks such as fibronectins, laminins and collagens. In this regime, the key mechanical aspect of the ECM is its elasticity and ability to transmit tensile force across cells in an epithelium. During tissue morphogenesis, the ECM can create anisotropic shapes by resisting isotropic forces through differential stiffness (Dzamba and DeSimone, 2018). For instance, the circumferentially aligned collagen fibers in the ECM of the Drosophila egg constrain isotropic tissue growth to facilitate elongation in the anterior-posterior axis (Crest et al., 2017). The ability of collagen fibers to assemble into gels with high tensile strength, especially after cross-linking, is key to the regime where the ECM plays a passive, elastic role in morphogenesis (Chaudhuri et al., 2020).
Hyaluronic acid (HA) is another widespread ECM component, but its physical properties differ greatly from collagens, fibronectin and laminins. HA is a long, flexible polysaccharide with a high density of carboxylate groups that are mostly negatively charged and balanced by sodium ions under physiological conditions. As a result of this chemistry, HA polymers tend to swell with water and form viscoelastic hydrogels with a low mass fraction, low tensile strength but high propensity to generate compressive osmotic forces by swelling (Cowman et al., 2015; Toole, 1981). Despite its abundance, the role of HA in tissue morphogenesis due to its biophysical properties has not been fully investigated. Rather, the biophysical HA literature is dominated by medical applications such as cosmetic surgery as a dermal filler, drug delivery and joint lubrication (Borzacchiello et al., 2015).
We investigated how morphogenic forces are generated to deform a simple epithelium in an understudied yet exemplary system common to all vertebrate organisms, semicircular canal (SCC) development (Higuchi et al., 2019). All jawed vertebrates have three mutually orthogonal SCCs in each inner ear whose well-conserved shape is required for their function of sensing balance and acceleration (Groves and Fekete, 2012) (Figure 1B). Head movement results in fluid movement in the canals, which is transduced by the hair cells to sense motion. Morphogenesis of the SCCs is among the most geometrically complex and precise events in vertebrate development (Figure 1A). The vertebrate inner ear forms from a thickening of the embryonic ectoderm located lateral to the hindbrain, called the otic placode (Whitfield, 2015). The otic placode cavitates or invaginates to form a tight epithelial fluid-filled structure called the otic vesicle (OV) (Whitfield, 2015). The single-layered OV then undergoes a dramatic topological change to form the SCCs (Alsina and Whitfield, 2017) (Figure 1A). The mechanisms underlying SCC morphogenesis remain poorly understood due to their inaccessibility in most model organisms. Zebrafish lack middle and outer ears, and the inner ear forms before ossification of the skull, which encases the inner ear, making it both optically and physically accessible, and thereby an excellent model organism to study SCC morphogenesis.
Figure 1-. In toto imaging of the developing zebrafish inner ear reveals multi-scale dynamics during semicircular canal morphogenesis.
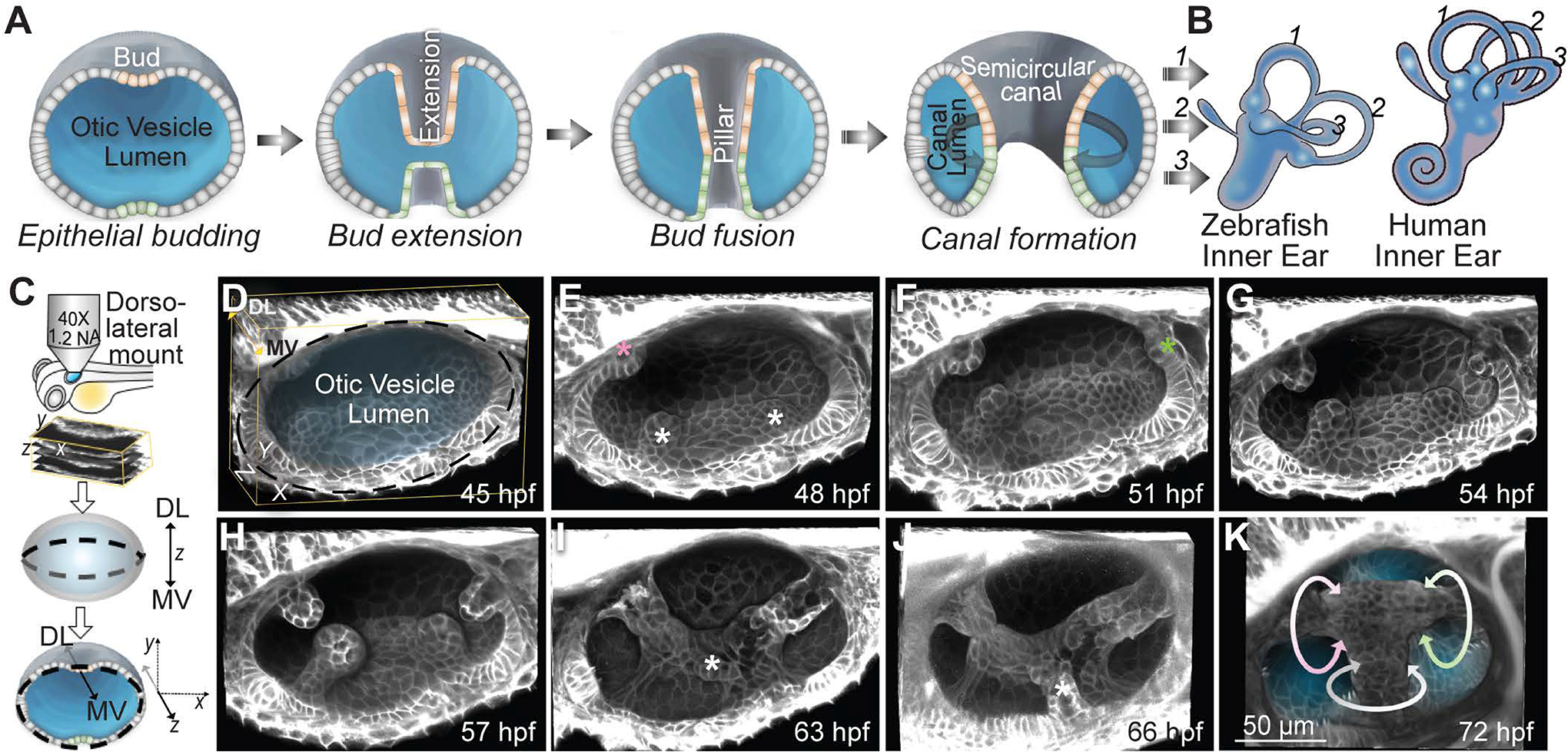
(A) Illustrations showing the formation of a SCC.
(B) Illustrations of the inner ears from adult zebrafish and human comparing the conserved structures of the SCCs. Anterior, posterior and lateral SCCs are labelled as 1, 2 and 3 respectively. (C) Workflow for zebrafish embryo mounting, image acquisition and visualization.
(D-K) 3D rendered otic vesicles (OVs) at select time points using Tg(βActin:membrane-Citrine). Anterior to the left and dorso-lateral (DL) into plane of view. Lateral, anterior and posterior buds are marked by white, pink and green asterisks respectively. The buds extend (G and H), and fuse (I). Ventro-lateral and ventral buds form and extend (marked by white asterisks) (I and J). Bud fusion demarcates the hubs for the anterior, posterior and lateral SCC (marked by pink, green and white circular arrows respectively) (K). Scale bar, 50 μm.
Using in toto imaging of transparent zebrafish embryos, perturbation approaches and biophysical modelling, we discovered unexpected roles of the ECM and actomyosin networks in SCC morphogenesis. Patterned cells in the otic epithelium locally generate extracellular HA, which in turn actively reshapes the tissue through osmotic swelling. Thus, the driving force is ultimately ECM-derived osmotic pressure rather than actomyosin contractility. Actomyosin networks instead, play a role in directing anisotropic morphogenesis through differential tissue stiffness provided by E-cadherin linked intercellular tethers we term cytocinches.
Results
Long-term imaging of the developing zebrafish inner ear reveals multi-scale dynamics during semicircular canal morphogenesis
All prior studies on SCC development have been done with either low resolution live microscopy or static imaging by fluorescence, paint-fills or micro-CT images (Chang et al., 2004; Groves and Fekete, 2012; Nishitani et al., 2017; Whitfield et al., 1996). To perform long-term imaging at high spatiotemporal resolution, of zebrafish SCC development, we take advantage of transgenic zebrafish expressing a bright membrane-localized fluorescent protein (Swinburne et al., 2018). Embryos were mounted dorso-laterally as shown in Figure 1C, in a cast agarose mount that secures the head and the yolk, and positions the ear just beneath the cover slip.
SCCs form from the topological remodeling of the OV sandwiched between the skin and the hindbrain and surrounded by mesenchymal cells (Figure 1D, Figure S1A and Video S1). Morphogenesis initiates when cells from six different regions of the otic epithelium sequentially form buds projecting into the lumen (Figures 1E, 1F, 1I, 1J, S1A–S1C and Video S1). Cells in lateral (antero-lateral and postero-lateral) and anterior regions form buds first (45 hpf), followed by cells in the posterior region (51 hpf), and lastly in the ventro-lateral and the ventral regions (63 hpf) (Figures 1E, 1F, 1I, 1J, S1A–S1C, and Video S1). The six buds extend anisotropically in their longitudinal axis (Figures 1F–1J, S1B–S1F, and Video S1). Topology change occurs when the buds fuse to one another to form three pillars through the OV lumen demarcating the hubs of the future anterior, posterior and lateral SCCs (Figures 1I–1K and Video S1).
Stereotypical morphogenic behaviors are not responsible for SCC morphogenesis
To investigate the mechanisms underlying SCC development, we tested existing models for morphogenesis, including elevated proliferaton of bud cells compared to the neighboring cells (Figure 2K). Localized increase of cell proliferation has been observed in nascent epithelial buds during branching morphogenesis in a number of organs including kidney, salivary gland and lung (Varner and Nelson, 2014). Using a proliferative marker, 5-ethynyl-2′-deoxyuridine (EdU) staining, we find a low rate of proliferation during SCC morphogenesis (45 – 54 hpf) with 25% of cells in the lateral region of the OV, and less than 10% of the bud forming cells in S phase (Figures 2A and 2C). Inhibiting S phase with Hydroxyurea and Aphidicolin between 48–54 hpf reduced EdU incorporation down to 10% in the lateral OV and to 0% in bud cells, yet their morphogenesis continued normally with a slight delay (Figures 2B–2D). We conclude that localized cell proliferation is not responsible budding.
Figure 2-. Stereotypical morphogenic behaviors are not responsible for SCC morphogenesis.
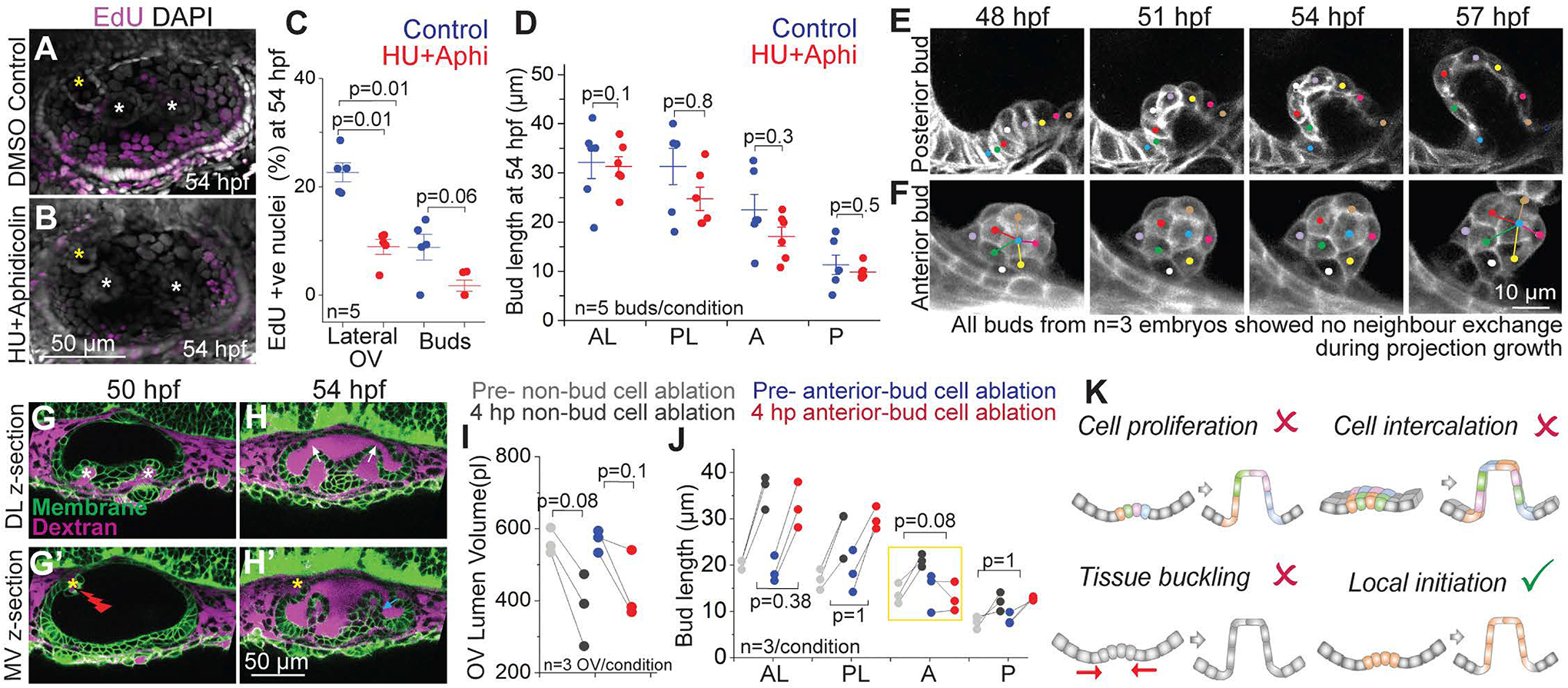
(A and B) 3D rendered representative examples of OVs with DAPI and EdU staining marking all nuclei (grey) and nuclei in S phase (purple) respectively, in control (A), and Hydroxyurea (HU)+Aphidicolin treated embryos (B) at 54 hpf. Lateral buds are marked by white asterisks and anterior bud is marked by yellow asterisks. Anterior to the left and DL into the plane of view. Scale bar, 50 μm.
(C) Individual data points and mean±s.d. of percentage of EdU positive nuclei in the lateral region of the OV, and only in the buds. ‘n’ denotes the number of OVs. p values as labelled (Mann Whitney- U test).
(D) Individual data points and mean±s.d. of bud lengths in control and HU+Aphidicolin treated embryos at 54 hpf. In the absence of buds, lengths correspond to cell lengths. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(E and F) 2D sections (E) and 3D rendering (F) of a posterior and an anterior bud respectively from membrane-labeled transgenic embryo at select time points with individual cells tracked (colored dots). Scale bar, 10 μm.
(G and H) 2D sections from two different z-depths of an ablated OV (marked by red flash) using Tg(βActin:membrane-Citrine) (green) and Texas-red dextran (magenta) in the periotic space. Lateral buds (marked by white asterisks) can be seen in the DL section (L). Anterior bud (marked by yellow asterisk) can be seen in the MV section (L’). Dextran dye enters the OV lumen upon ablation (M-M’). Lateral buds continue to extend in the ablated OV (marked by white arrows) (M’). Posterior bud also forms and extends (cyan arrow). Anterior bud ablation blocks its extension (yellow asterisk) (M’). Scale bar, 50 μm.
(I), OV lumen volume in control and experiment before and after ablation. ‘n’ denotes the number of OVs per condition. p values as labelled (Mann Whitney- U test).
(J) Bud lengths in control and experimental embryos before and 4 hours post (hp) ablation. ‘n’ denotes number of buds measured per condition. p values as labelled (Mann Whitney- U test).
(K) Illustrations show the models tested for budding morphogenesis.
We next investigated whether cell-rearrangement based convergence-extension drives otic epithelial bud extension (Figure 2K). Convergence-extension is a widely employed mechanism for tissue elongation during embryonic development (Wallingford et al., 2002). During Drosophila salivary gland morphogenesis, cells exhibit circumferential convergence and radial extension to form a narrow tube from a round and flat epithelium (Sanchez-Corrales et al., 2018). Given the geometrical similarity, we tested this model in the otic epithelium by tracking cells in the morphogenic regions. We observe that as buds extend, cells adjacent to the bud become part of the bud (Figure 2E). However, both the cells adjacent to and within the bud, maintain their neighbors during bud extension, thereby refuting a cell-rearrangement based model for budding morphogenesis (Figures 2E and 2F).
We next examined tissue-scale mechanisms such as buckling in SCC morphogenesis (Figure 2K). Compressive stresses from the differential growth of apposed tissues can cause tissues to buckle or fold (Nelson, 2016). Examples include villi formation in the small intestine (Shyer et al., 2013) and branching in the airways of the lung (Nelson, 2016). Besides tissue growth, osmotic pressure from interstitial and lumenal fluids can also apply stresses on the surrounding epithelium (Chan et al., 2019; Navis and Bagnat, 2015), including in the OV (Mosaliganti et al., 2019). As reported above, cell proliferation is low during SCC morphogenesis and blocking it does not affect bud extension (Figures 2A–2D). To reduce lumen pressure, we used a laser-mediated targeted ablation of single cells in the OV to disrupt the epithelial barrier causing loss of lumen volume and pressure (Mosaliganti et al., 2019) (Figure 2G and 2I). Ablation-mediated loss of lumen pressure neither affected initiation of new buds nor the extension of existing buds (Figures 2H and 2J). Together these data are inconsistent with a buckling-based model for morphogenesis (Figure 2K). Interestingly, ablation of one or two bud cells was sufficient to block extension of that bud, while the adjacent non-ablated buds continued morphogenesis normally (Figures 2G–2J), showing that morphogenesis of each bud is locally initiated.
Semicircular canal morphogenesis requires patterned expression of hyaluronan synthesis enzymes ugdh and has3
We next examined a role for the extracellular matrix (ECM) in the local initiation of each bud (Figure 2K). In mouse gut explants, mesenchymal condensates have been shown to align the surrounding Collagen I fibers causing the overlying epithelium to bend (Hughes et al., 2018). In the frog inner ear, hyaluronic acid (HA) was shown to be required for SCC formation (Haddon and Lewis, 1991). Yet, which cells are responsible for HA-production and how HA generates morphological change during SCC formation remains unclear. HA is a secreted, unbranched and non-sulfated glycosaminoglycan composed of repeating disaccharide subunits. HA is synthesized by the enzymes uridine 5′-diphosphate dehydrogenase (ugdh), which participates in subunit synthesis, and hyaluronan synthase (has) that polymerizes subunits at the cell membrane to extrude out chains directly into the extracellular space (Vigetti et al., 2014). This is similar to how plants spin out their cell wall using cellulose synthases present on the membrane (Keegstra, 2010). However, unlike HA, cellulose-based plant cell walls are extremely stiff and do not swell.
We investigated whether HA synthesis enzymes are expressed by the mesenchymal cells that surround the OV, or by the cells of the otic epithelium, using multiplexed fluorescent in situ hybridization (Choi et al., 2018). We observed local and uniform expression of ugdh and has3 in the bud cells of the OV, except the cells at the corner of the bud that have slightly lower expression (Figures 3A–3C, S2A and S2B). In contrast, Collagen 2 (col2a1a), a major component of the ECM, is not exclusive to the buds and is instead expressed in all the cells of the OV (Figures 3A–3C and S2C), while has2, known for its role in cardiac morphogenesis (Patra et al., 2011), is not expressed in the OV (C. Thisse, 2005). Moreover, in contrast to col2a1a, ugdh and has3 expression were not observed after the buds fused (Figures S2A–S2C). We conclude that ugdh and has3 are locally, uniformly and transiently expressed in the bud cells of the OV during morphogenesis.
Figure 3-. SCC morphogenesis requires patterned expression of hyaluronan synthesis enzymes ugdh and has3.

(A and B) Maximum intensity projections of OVs at select time points stained with multiplex in situ probes against ugdh (green) and col2a1a (white) (A), and has3 (purple) and col2a1a (white)
(B). The z-volume is different across time points to capture all the buds, and hence the contrast of each time point is individually set for better visualization. Scale bar, 50 μm.
(C) Mean intensities±standard error (s.e.) of various genes across the illustrated region of interest (ROI) in the anterior bud at 57 hpf.
(D and E) Representative examples of 3D-rendered OVs at 54 hpf from sibling control and ugdhm151/m151 mutant embryos labelled with membrane-NeonGreen mRNA (D), and Tg(βActin:membrane-Citrine) embryos injected with control morpholino (MO) and has3-specific MO-1 (E). Buds in controls are marked by asterisk (white, yellow and cyan for lateral, anterior and posterior buds respectively). Genetically perturbed embryos have no buds. Anterior to the left and DL into the plane of view. Scale bar, 50 μm.
(F) Individual data points and mean±standard deviation (s.d.) of bud lengths in controls and genetic perturbations at 54 hpf. In the absence of buds, bud lengths correspond to cell lengths. ‘n’ denotes the number of buds measured per condition. p values as labelled (Mann Whitney- U test).
We next tested the function of these enzymes in SCC morphogenesis. A point mutation that disrupts ugdh (Driever et al., 1996; Neuhauss et al., 1996; Walsh and Stainier, 2001) blocked OV budding at 54 hpf (Figures 3D and 3F) and caused aberrant bud morphologies at 72 hpf (Figure S2H). Morpholino-mediated knockdown of has3 (Ouyang et al., 2017) (Figures S2D–S2G) also abrogated SCC formation with no budding at 54 hpf (Figures 3E and 3F) and aberrant bud morphologies at 72 hpf (Figures S2I and S2J). We conclude that ugdh and has3 are required for zebrafish SCC formation. The requirement of HA for SCC development is potentially conserved across species as specific expression of has2 is observed in the SCCs during mouse development (Tien and Spicer, 2005).
The ECM of the buds is rich in hyaluronan and dense
We examined the localization of endogenous HA using a HA- binding protein (HABP) (Kohda et al., 1996). During bud formation, HABP is restricted to and fills up the extracellular space beneath the buds (hereafter referred to as the bud-ECM) (Figures 4A–4C, 4E and S3B). In contrast, Collagen2 was detected in the ECM surrounding the entire OV with slightly higher expression in the bud-ECM (Figures 4A–4C, 4E and S3B). Interestingly, the basement membrane (BM) component, Laminin, was present in the entire OV prior to budding (Figure S3A), and was subsequently depleted from the BM of the budding cells during morphogenesis, except the cells at the corner of the bud (Figure S3A) (which are also the cells that express lower HA synthesizing enzymes (Figure 3C)). These immuno-stainings suggest that HA-producing bud cells detach from the BM, while the cells at the boundary of the bud remain attached.
Figure 4-. The ECM of the buds is rich in hyaluronan and dense.
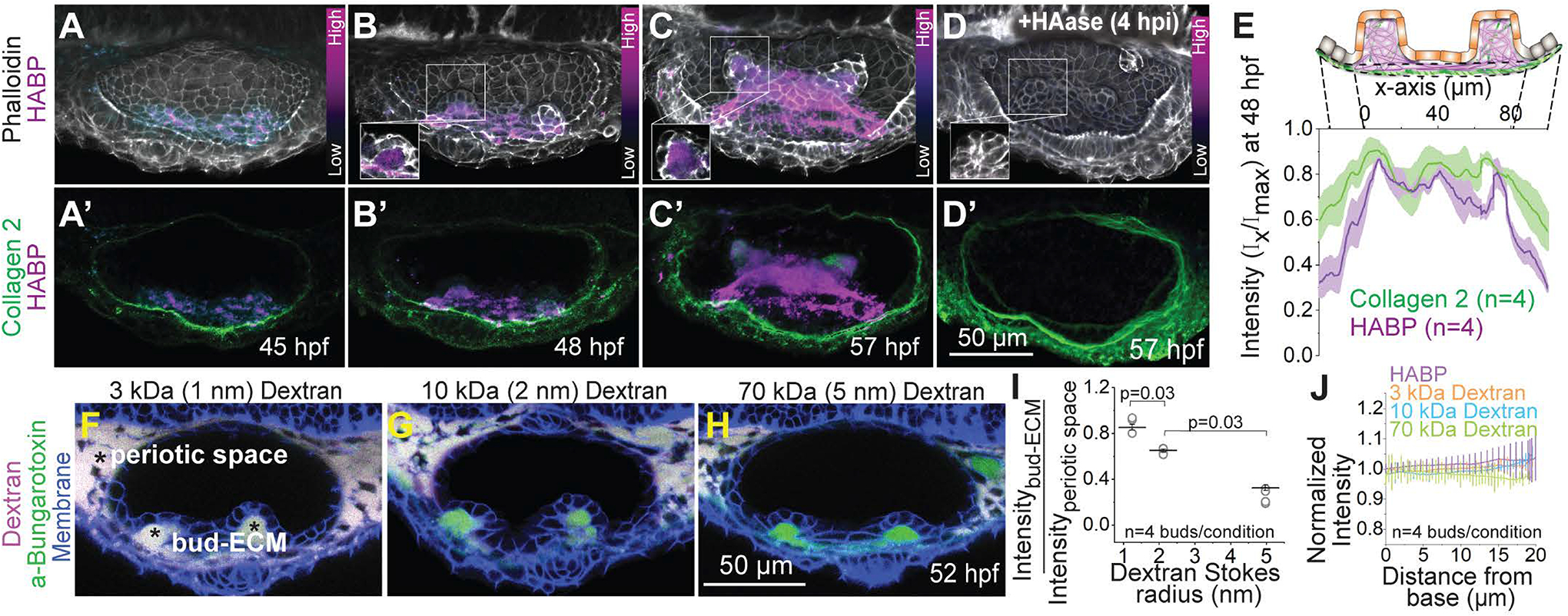
(A-D) 3D rendered OVs showing HA, F-actin and Collagen 2 staining using HA-Binding Protein (HABP), Phalloidin and Anti-Col2a1a respectively, at select time points in uninjected (A-C) and hyaluronidase (HAase) treated embryos (D). Anterior to the left and DL into the plane of view. The contrast of each time point is individually set to capture the dynamic range of HABP. Insets show 2D sections of the antero-lateral buds. Scale bar, 50 μm. ‘n’ denotes the number of buds.
(E) Mean intensities±s.e. of various stains across the illustrated ROI in the lateral buds at 48 hpf.
(F-H) 2D sections showing percolation of dextran from the periotic space into the bud-ECM 2 hours post injection (hpi). Different sizes of Texas-red dextran (in magenta)-3 kDa (F), 10 kDa (G) and 70 kDa (H) with approximate Stokes radii 1 nm, 2 nm and 5 nm respectively, were co-injected with aBt (green) in Tg(βActin:membrane-citrine) embryos (blue). aBt colocalizes with all three sizes of dextran in the periotic space (white). Contrast is same across embryos. Scale bar, 50 μm.
(I) Individual data points and mean±s.e. of fluorescent intensities of different sizes of dextran in the bud ECM normalized to their intensities in the periotic space. ‘n’ denotes the number of buds per condition. p values as labelled (Mann Whitney- U test).
(HJ) Mean±s.e. of the normalized fluorescent intensities of different sizes of dextran and HABP in the bud ECM from the base to the tip (as show in the illustration Figure S3C). ‘n’ denotes the number of buds per condition.
We next perturbed HA by injecting hyaluronidase (HAase), an enzyme that breaks down HA polymers, in the space surrounding the OV (periotic space). HAase treatment inhibited HA accumulation in the bud-ECM (Figures 2D and S3C) showing that local accumulation of HA depends on its polymeric properties. To probe the physical properties of HA, we measured the percolation of different sizes of fluorescent dextran (molecular weights 3 kDa, 10 kDa, and 70 kDa and approximate Stokes radii 1.3, 2.4 and 5 nm respectively (Granath, 1958)) into the bud-ECM when injected in the periotic space surrounding the OV (Figures S3D and 4F–4H). Fluorescent labelled aBt was co-injected with dextran as a control. After 2 hours, aBt equilibrated in the bud-ECM relative to the periotic space, while 85% of 3 kDa, 65% of 10 kDa, and only 30% of 70 kDa dextran percolated in the bud-ECM (Figures 4F–4I). Low percolation of large dextrans shows that the HA-rich bud-ECM is dense with a pore size in the range of at most a few tens of nanometer. We find the intensity of HABP and percolation of dyes to be uniform within the bud-ECM suggesting uniform distribution and structure of the HA-rich bud-ECM (Figures S3D and 4J) consistent with the long flexible structure of HA.
Hyaluronate drives cellular and tissue morphogenesis through osmotic pressure
We investigated the mechanical basis of HA-dependent morphogenesis. In physiological conditions, HA is made as long charged polymers (0.5–6MDa) behaving as a polyelectrolyte, which imbibes and retains large amounts of water to a form a viscoelastic solution (Cowman et al., 2015). We distinguished between two hypotheses. First, a propellant model, where HA pushes the overlying epithelium to form buds through localized secretion (as suggested in frog SCC morphogenesis, (Haddon and Lewis, 1991)). Interestingly, this model is similar to how most raphid diatoms glide over surfaces through polysaccharide-rich mucilage strand secretion (Chen et al., 2019). Key evidence against the propellent model is the uniform expression of HA synthesis genes, has3 and ugdh, rather than just at the tip (Figure 3C).
The second hypothesis is a pressure model, where HA actively applies stresses on the surrounding tissues due to osmotic-swelling (Li et al., 2020; Toole, 1981). As the buds form and extend, the volume of the bud-ECM increases (Figures 5A, 5C). Inhibition of HA with HAase treatment led to a significant reduction of bud-ECM volume (Figures 5B and 5D), and in agreement with previous results (Geng et al., 2013), arrested bud extension (Figures 5B and 5E). We examined whether the osmotic swelling of the HA confined in the bud-ECM applies hydrostatic pressure on the overlying bud cells causing cell strain (Figure 5F). Consistent with our hypothesis, during bud extension, the HA- producing bud cells thin in the radial axis and stretch in the circumferential and longitudinal axes, while maintaining their volume (Figures 5C, 5G, 5H and Video S2). Strikingly, HAase treatment causes loss of cell stretching in the buds (Figures 5G and 5I). These data are consistent with a hyaluronate pressure-based model for powering cell stretching and epithelial budding.
Figure 5 -. Hyaluronate drives tissue and cellular morphogenesis through isotropic pressure.
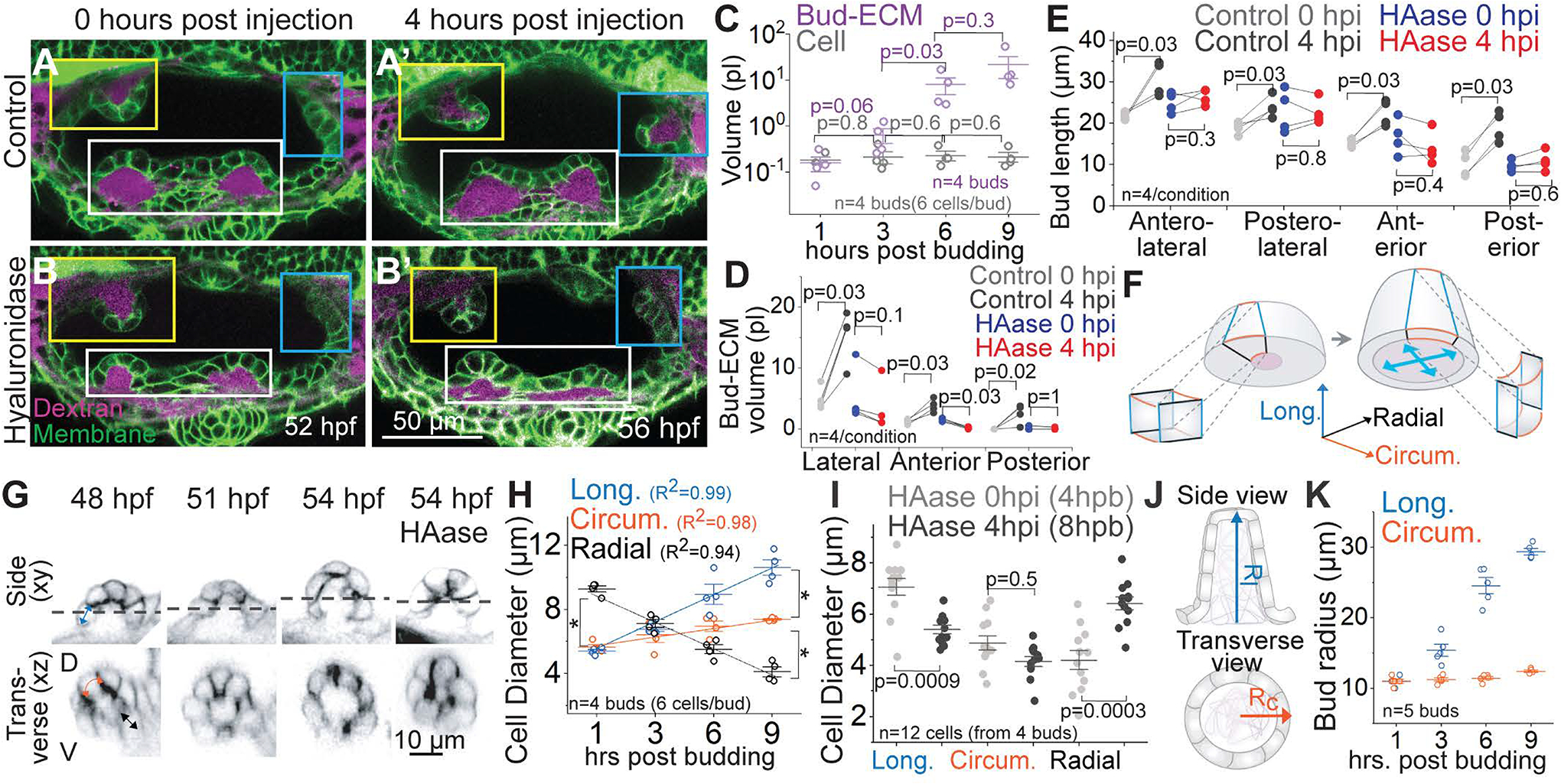
(A and B) Composite of 2D sections of representative examples from controls (A) and HAase injected (B) embryos at 0 and 4 hours post injection (hpi) using Tg(βActin:membrane-Citrine) (green) and Texas-red dextran (magenta) in the periotic space. Lateral, anterior and posterior buds from different z-depths are framed in white, yellow and cyan respectively. Scale bar, 50 μm.
(C) Individual data points and mean±s.d. of bud-ECM and cell volume across time. Each data point for cell volume is an average from 6 cells in a bud. ‘n’ denotes the number of buds per condition. p values as labelled (Mann Whitney- U test).
(D and E) Bud-ECM volume (D) and bud lengths (E) in control and HAase injected embryos at 0 and 4 hpi. In the absence of buds, lengths correspond to cell lengths. ‘n’ denotes the number of bud-ECMs or buds respectively. p values as labelled (Mann Whitney- U test).
(F) Illustration showing the longitudinal (blue), circumferential (orange) and radial (black) axes of cells during budding. Deposition of HA in the bud-ECM is shown in purple. Cyan arrows show hydrostatic pressure from HA swelling. Notice the change in aspect ratio of the cells before and after HA-swelling.
(G) Side and transverse sections of an anterior bud from an uninjected embryo at select time points, and HAase treated embryo at 54 hpf, using Tg(βActin:membrane-Citrine). Dotted line in side view (xy) marks the y position for transverse view (xz). Scale bar, 10 μm.
(H) Individual data points and mean±s.d. of cell diameters across time (hours post budding, hpb). *denotes p=0.03 (Mann Whitney- U test). Each data point is an average from 6 cells per bud. ‘n’ denotes the number of buds.
(I) Individual data points and mean±s.d. of cell diameters in HAase-treated embryos at 0 and 4 hpi. Each data point is the diameter of a single cell. ‘n’ denotes the number of cells. p values as labelled (Mann Whitney- U test).
(J) Illustration showing the longitudinal (Rl) and circumferential radius (RC) of the bud.
(K) Individual data points and mean±s.d. of bud radii across time. ‘n’ denotes the number of buds.
We next investigated how buds can grow anisotropically in the longitudinal axis. Time-lapse observation showed that cell stretching is greater in the longitudinal than the circumferential axis (Figure 5H and Video S2). Similarly, buds first have an isotropic aspect ratio (1:1, longitudinal: circumferential radius) between 1–3 hours post budding (hpb), and then extend only in the longitudinal axis to acquire an anisotropic aspect ratio (2.5:1) (Figure 5K and Video S2). We considered whether anisotropic bud extension could be mediated by HA. Pascal’s law states that pressure is spatially uniform within a static fluid. For HA to exert anisotropic stresses on the overlying epithelium, either pressure would need to be non-equilibrated at these time-scales, or HA would need to form a stiff gel rather than a fluid. However, HA forms a viscoelastic solution in vitro (Cowman et al., 2015) and pressure equilibration in viscoelastic gels with similar pore sizes (Figure 4F–4I) has been shown to be on timescales ~10 seconds across length-scales 15–30 μm (Charras et al., 2005). The bud-ECM size is comparable (Figure 5K) and the morphogenic deformations are much slower (30 mins to a few hours, Figures S1F and 5K), strongly suggesting uniform isotropic pressure in the bud-ECM. In addition, intensity of HABP and percolation of dyes is uniform within the bud-ECM suggesting isotropic structural properties of the matrix (Figure 4J). Taken together, these data support an active pressure-based model whereby HA drives morphogenesis through osmotic swelling, but that HA alone cannot be responsible for the anisotropy of bud extension.
Adhesive and tension-rich membrane tethers (cytocinches) resist hyaluronate-pressure
We examined whether the bud epithelium itself provides the anisotropic stiffness needed to shape the isotropic hyaluronate pressure. Epithelial cells can alter their stiffness by increasing actomyosin network assembly to generate high internal tension (Lecuit et al., 2011; Tee et al., 2009). Using live reporters, we find that during bud extension, both F-actin and Myosin II accumulate on the lateral and basal (ECM-facing) cell surfaces relative to the apical surface (OV lumen-facing) (Figures S4A–S4D and Video S3). Remarkably, using high-resolution imaging and confirmed by mosaic membrane labelling, we observe actomyosin-rich protrusive membrane tethers extending tangentially at the basal surface (Figures 6A–6C, S4E, and Video S4). While protrusive activity is commonly observed in migratory epithelia, protrusions in non-migratory epithelia have also been reported. Examples include cytonemes involved in chemical signaling in a number of tissues (Ramírez-Weber and Kornberg, 1999)), E-cadherin-rich filopodia involved in mechanical compaction of mouse blastocyst (Fierro-González et al., 2013), and E-cadherin-rich membrane tethers at the dissolving contact of separating cells during zebrafish gastrulation (Caneparo et al., 2011; Maître et al., 2012). We therefore examined E-cadherin localization using a live BAC reporter (Yamaguchi et al., 2019), and detected signal in lateral membranes as well as in tethers linking adjacent cells (Figure 6D and Video S5).
Figure 6-. Adhesive and tension-rich membrane tethers resist hyaluronate-pressure.
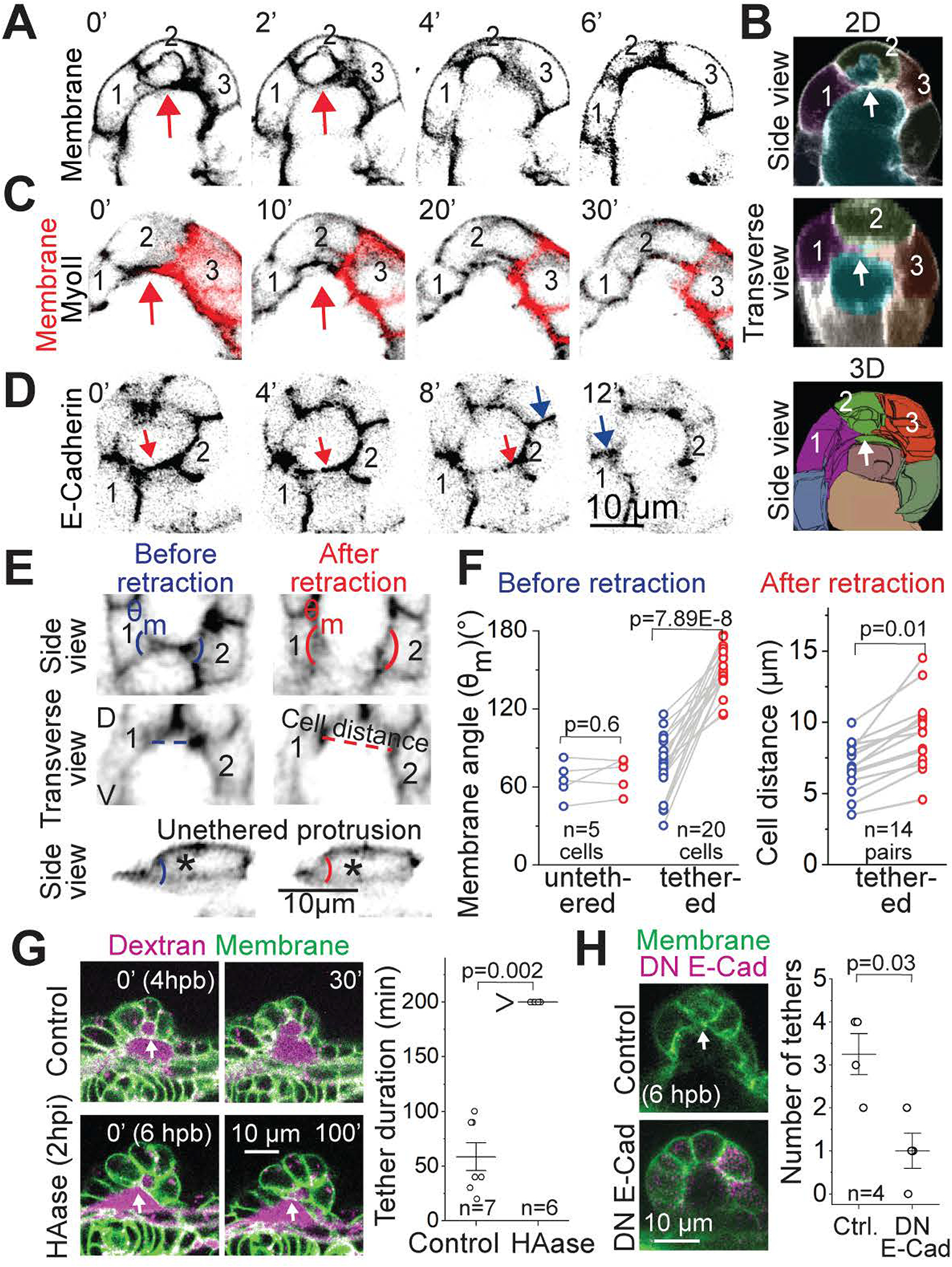
(A) 2D sections of an anterior bud showing cells (1, 2 and 3) engaged in a tether (red arrow) that eventually breaks and retracts. Scale bar, 10 μm.
(B) Two-dimensional (2D) and three-dimensional (3D) views of segmented cells showing membrane tether between cells 1,2 and 3 using side and transverse sections.
(C) 2D sections of a lateral bud showing cells (1, 2 and 3) engaged in a tether (red arrow) using mosaic membrane labelling in red and Myosin II (black) reporter. Scale bar, 10 μm.
(D) 2D section of an anterior bud showing accumulation of E-Cadherin (black) on the lateral membrane (blue arrows) and in the tether between cells 1 and 2 (red arrow)
(E) Side and transverse views of 2D sections showing tethered and unmembrane tether retraction with membrane labelling. The cell forming an unmembrane tether (top) is marked with an asterisk. The cells forming membrane tethers (bottom) are tracked with numbers 1 and 2. Adjacent membrane angles and adjacent cell distance are shown in blue and red before and after retraction respectively. Scale bar, 10 μm.
(F) Adjacent membrane angles (G) and cell distance (H) before and after retraction. ‘n’ denotes the number of cells. p values as labelled (Mann Whitney- U test).
(G)Left: 2D sections of lateral buds from controls (top) and HAase (bottom) injected embryos using Tg(βActin:membrane-Citrine) and Texas-red dextran in the periotic space. Membrane tethers (marked by white arrow) retract in control (top) but not in HAase treated embryo (bottom). Scale bar, 10 μm. Right: Individual data points and mean±s.d. of the duration of membrane tethers in control and HAase-treated embryos. n denotes the number of tethers. p values as labelled (Mann Whitney- U test).
(H) Left: 2D sections of anterior buds from controls (top) and DN E-Cadherin (bottom) expressing embryos using Tg(βActin:membrane-Citrine). Membrane tether (marked by white arrow) is present in control (top) but not in perturbed embryo (bottom). Scale bar, 10 μm. Right: Individual data points and mean±s.d. of the number of membrane tethers in control and DN E-cad mutant expressing embryos. n denotes the number of buds. p values as labelled (Mann Whitney- U test).
Using time-lapse imaging we observe that tethers eventually break and retract on time-scales of minutes (Figures 6A, 6C, 6D6E, and Videos S4 and S5). Akin to laser ablation-induced recoil of cell-cell apical junctions to probe tension (Fierro-González et al., 2013; Rauzi and Lenne, 2015), breaking of tethers served as a natural tension probe (Figure 6E). Tether retraction was associated with significant widening of adjacent membrane angles and an increase in neighboring cell distance (Figure 6E–6F). In contrast, untethered membrane protrusion retraction (observed using mosaic membrane labeling), did not associate with membrane angle change (Figure 6E and 6F). These measurements show that tethers are under tension. Notably, breaking of tethers was not observed in HAase treated embryos resulting in longer tether duration (Figure 6G), thereby showing that HA-induced pressure generates the epithelial stresses needed to break the tethers. Conversely, expression of a heat-shock inducible dominant-negative mutant (DN) of E-cadherin, which cannot engage in trans-clusters, results in a significant decrease in the number of tethers (Figure 6H). Together these data show that adhesive and tension-rich cinched tethers resist ECM pressure. We therefore termed them “cytocinches”.
Anisotropic distribution of cytocinches drives the bud-to-tube transition
We tested whether cytocinches are responsible for the anisotropy in bud shape. During bud extension, cytocinch tether numbers progressively increased with an orientation that was strongly biased towards the circumferential axis (Figures 7A, 7B and Videos S4 and S5). Strikingly, cytocinch anisotropy (measured as the product of number and orientation) correlated with the anisotropic aspect ratios of the bud (Figure 7C). If cytocinches resist pressure from HA, the anisotropic stiffness from this directional bias could explain the elongation of buds into tubes. To further explore this hypothesis, we built a theoretical model to examine if a cytocinch-based bias in resistance in the circumferential axis can result in bud extension in the orthogonal (longitudinal) axis (Figures 7D). A 2D vertex model (Alt et al., 2017; Hannezo et al., 2014) representing a longitudinal “slice” of the epithelial monolayer, enclosing a gradually increasing volume of bud-ECM and attached to the BM at the boundaries, was used (See STAR Methods and Data S1 for further details). The equilibrium configuration via energy minimization for a given volume was then calculated. Geometrical parameters and epithelial surface tension were estimated using membrane image data and actomyosin localization respectively (Figure S4A–S4D and STAR Methods). The only free parameter was the inward tension from cytocinches applied to the basal vertices (Figures 7E, S5A–S5D and STAR Methods). Consistent with our hypothesis, increasing the tension of circumferential cytocinches increased the anisotropy of the buds (Figures 7E, 7F, S5E, S5F and Video S6). Interestingly, for intermediate values of cytocinch tensions, the bud short-axis remained roughly constant during 3-fold volume inflation, while the long-axis increased 3-fold (Figures 7F and S5E), as observed experimentally (Figure 5K). A good fit for bud anisotropy can be reached in simulations either by slowly increasing volume to a given level or simply starting at that level (Figures S5F and S5G), corroborating our conclusion that the bud-ECM is important for bud swelling, but not for its anisotropy. On the other hand, a progressive increase in cytocinch number was required for a good fit with experimental data, otherwise the model would overestimate early bud anisotropy (Figures S5F and S5H), corroborating the observed scaling between cytocinch and bud anisotropies (Figure 7C). Furthermore, the model predicted a relaxation of the bud to a hemispherical shape upon removal of cytocinch tension (Figure 7G and Video S6).
Figure 7-. Anisotropic distribution of cytocinches drives bud-to-tube transition.
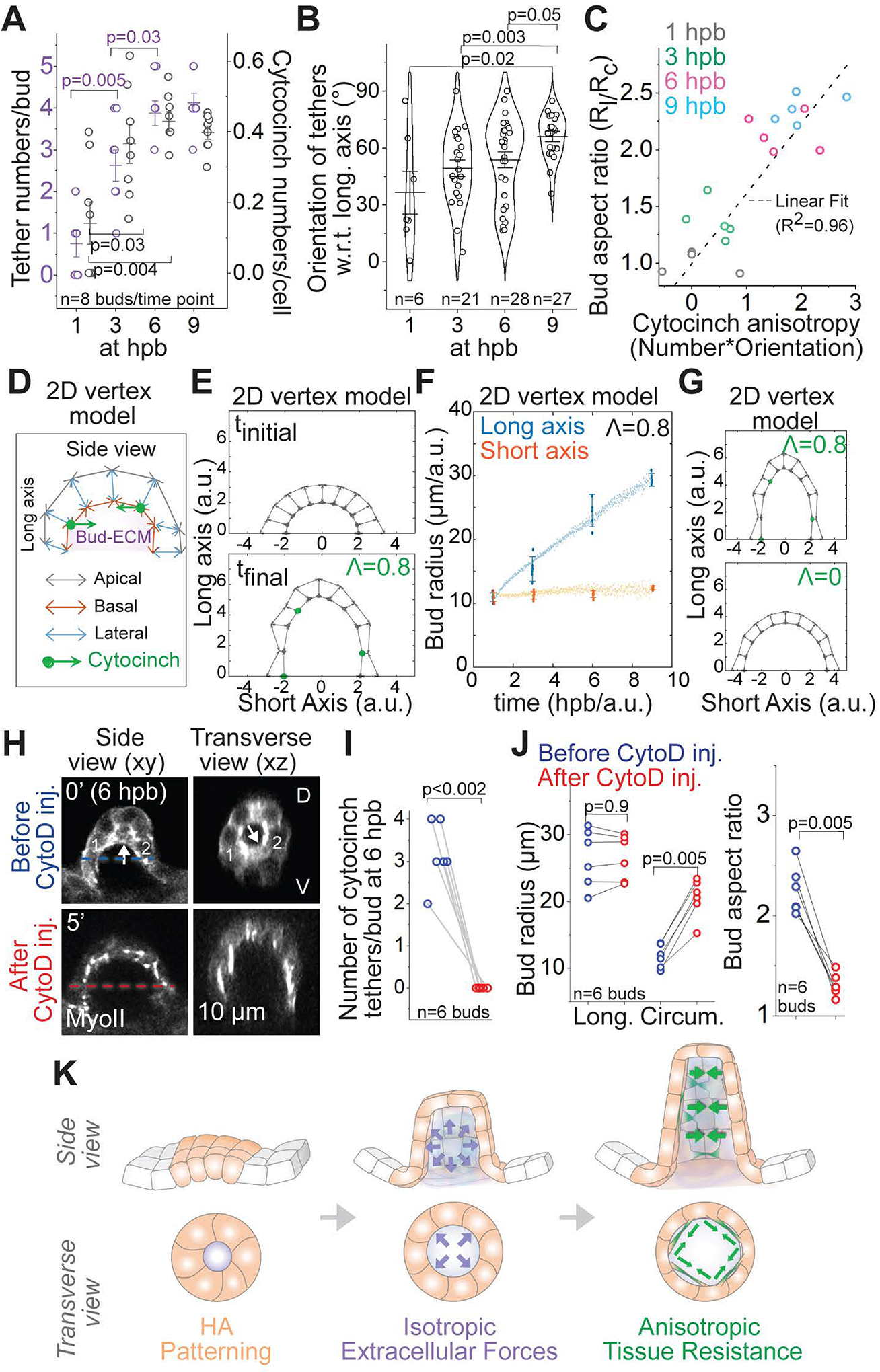
(A) Individual data points and mean±s.d. of the number of tethers per bud (left axis, purple) and the number of cytocinches per cell (right axis, gray) at given time points. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(B) Individual data points, mean± s.d. and violin plot of cytocinch tether orientation measured with respect to (w.r.t) the longitudinal bud axis at given time points. ‘n’ denotes the number of tethers. p values as labelled (Mann Whitney- U test).
(C) Bud aspect ratio plotted as a function of cytocinch anisotropy (number*orientation) at different stages. Grey line is a linear fit with R2=0.96.
(D) Schematic of the 2D vertex model with apical, lateral and basal surface tension, enclosing a prescribed bud-ECM volume, with addition of inward forces from circumferential cytocinches (Λ).
(E) Equilibrium configurations of a bud section, using the 2D vertex model (n=10 cells, grey arrows for basal, lateral and apical surfaces and green dots for cytocinches) at 1 hpb (Λ=0) and 9 hpb (Λ=0.8/cytocinch).
(F) Predicted evolution of bud radii in the long (blue) and short (orange) axes (experimental: big dots, predictions: little dots) assuming the experimentally observed increase of bud-ECM volume and cytocinch fraction in time.
(G) 2D vertex model configuration with (Λ=0.8) and without (Λ=0) cytocinches.
(H) 2D sections of an anterior bud at 6 hpb using Myosin II reporter before and after Cytochalasin D (CytoD 1mM) treatment. Cytocinch is marked by white arrow before treatment. Cytocinch is lost after CytoD treatment. Before (blue) and after (red) circumferential bud diameter is labelled.
(I and J) Number of cytocinch tethers per bud (I), bud radii and aspect ratios (J) before and after CytoD treatment. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(K) Illustration of the mechanism underlying budding morphogenesis for SCC formation. Patterned cells in the OV (in orange) synthesize HA. HA drives budding through isotropic extracellular forces (in purple). Anisotropic resistance from cytocinches (in green) mediate anisotropic bud extension.
To experimentally test if cytocinches direct bud extension via mechanical anisotropy, we inhibited their tension using either Cytochalasin D (CytoD), an antagonist of F-actin polymerization, or SMIFH2, an inhibitor of formin (an actin polymerization protein). Injecting a mild drug dose (1mM) in the periotic space did not affect OV integrity on short time-scales, but resulted in complete loss of cytocinches and subsequent widening of adjacent membrane angles (Figures 7H, 7I and S6A–S6E). Loss of cytocinches caused the bud radii to increase in the circumferential axis and the aspect ratio of the buds to become significantly isotropic (Figures 7H, 7J, S6A, S6C, S6D, S6F, Video S6), showing that cytocinches restrain extension in this axis. In addition, loss of epithelial tension resulted in a significant increase in the bud-ECM volume, further corroborating a hyaluronate-pressure based model of epithelial budding (Figure S6G). Together with theory and experiments, we conclude that biased circumferential orientation of cytocinches constrain the isotropic hyaluronate-pressure into an anisotropic bud extension (Figure 7K, Figure S7, and Video S6).
Discussion
Previous studies of tissue morphogenesis typically impute actomyosin contractility as the force producing process. The ECM is deemed as a passive mechanical element that might help shape those forces. Our observations challenge this standard model. In the inner ear, we propose an active and isotropic hyaluronate pressure-based model wherein the patterned synthesis of HA-rich ECM powers bud growth by osmotic swelling. The data that support our model include: 1) HA-dependent stretch experienced by the bud cells; 2) Uniform expression of HA synthesis genes across the bud and uniform structural properties of the HA-rich bud-ECM; 3) HA-dependent breaking and retraction of cytocinches; 4) Increase of HA-rich bud-ECM volume upon cytocinch inhibition; and finally, 5) Pressure equilibration of hyaluronate in the time-scales of morphogenetic deformations. HA-driven morphogenesis of the bud is shaped by the biased orientation of E-cadherin and actomyosin-rich cytocinches in the circumferential axis that result in greater tissue stiffness in this axis, thereby directing the bud towards a tube. Spatial patterning of extracellular hyaluronate-pressure combined with anisotropic tissue material properties from cytocinches may serve as a broadly applicable mechanism for sculpting tissues during development.
Remarkably, hyaluronan synthases are locally expressed in a variety of morphogenic epithelia such as the tooth placode, the endocardium and the lens placode (Felszeghy et al., 2001; Haack and Abdelilah-Seyfried, 2016; Kwan, 2014; Tien and Spicer, 2005). Similar to the otic epithelium, HA may be creating pressure to drive morphogenesis of these tissues. Furthermore, local expression of HA is conserved in the otic epithelial cells of mice (Tien and Spicer, 2005), suggesting a conserved mechanism for SCC morphogenesis across species. The upstream developmental signals that pattern the otic epithelial cells for HA-expression and budding remain to be investigated.
HA is involved in a number of cellular processes including migration, adhesion and differentiation due to binding with cell surface receptors and interactions with other ECM components such as proteoglycans (Chanmee et al., 2015; Cyphert et al., 2015; Toole, 2001). For example, in mouse, covalent modification of HA by the enzyme Tsg-6 is required for mid-gut laterality (Sivakumar et al., 2018). In zebrafish, the bud cells of the otic epithelium express Versican (vcana and vcanb) (Geng et al., 2013), a proteoglycan that can regulate the structural properties of HA (Wight, 2017). The contribution of HA- mediated signaling and binding with proteoglycans in SCC morphogenesis still remains to be explored.
Our work shows that actomyosin-rich cytocinches resist hyaluronate-pressure. Most literature on actomyosin attributes its role in morphogenesis to contractility gradients that power local cell deformations (Salbreux et al., 2012). However, there is an important role of actomyosin networks in stiffening tissues without powering morphogenesis. For instance, actomyosin-dependent tissue stiffening has been observed during axis elongation in frogs and suggested to maintain tissue architecture (Barriga et al., 2018; Zhou et al., 2009). Developmental biologists tend to equate a high local density of Myosin II with active contractility (Streichan et al., 2018). Our data suggest this assumption should always be questioned. Resistance to forces by anisotropic tissue material properties from cytocinches may serve as a broadly applicable mechanism in tissue morphogenesis.
HA-dependent breaking of cytocinches suggests that adjacent contacts in the budding cells are fractured by hyaluronate pressure, leaving behind cytocinches due to stable E-cadherin trans-clusters. Hydraulic fracturing of cell-cell junctions has been reported in epithelial monolayers by extracellular pressures (Casares et al., 2015). In the mouse blastocyst, fluid pressure fractures cell-cell contacts into microlumens that eventually form a single dominant lumen (Dumortier et al., 2019). Whether HA results in protrusion and cytocinch formation through hydraulic fracking or other means still remains to be explored. Moreover, further investigation is needed to determine how cytocinches relate to other cellular protrusions (Chauhan et al., 2009; Fierro-González et al., 2013; Jacinto et al., 2000; Ramírez-Weber and Kornberg, 1999), and how they are polarized.
With our work, it is now clear that sources of force production can be cellular (e.g. actomyosin contractility), tissue-scale (e.g. global proliferation), or ECM-derived (e.g. hyaluronate-pressure). Sources of anisotropic stiffness can also be cellular (e.g. cortical tension), tissue-scale (e.g. cytocinches), or ECM-derived (aligned collagen fibres). Our data compels a unifying paradigm for tissue morphogenesis, whereby any or a combination of these sources of force production and anisotropic stiffness can sculpt intricate organs from simple embryonic tissues.
Limitations of the study
While we provide indirect evidence and cite supporting literature, we do not provide a direct measurement for hyaluronate pressure in the bud-ECM as this has been technically challenging in vivo. In addition, while the data point towards a fracking-based mechanism for cytocinch formation, our study lacks experiments to test this model.
STAR Methods
RESOURCE AVAILABILITY
Lead contact
Further information for reagents and resources should be addressed to and will be fulfilled by the lead contact, Sean Megason (megason@hms.harvard.edu).
Materials availability
Plasmids generated and transgenic fish used in this study are available upon request.
Data and code availability
Source code for the 2D vertex model is included in this paper’s supplemental information. Additional information needed to reanalyze the data reported in this paper will be available from the lead contact upon request.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Zebrafish (Danio rerio) AB wild-type strain was used. Adult fish were kept at 28.5°C on a 14 hours light/ 10 hours dark cycle. Embryos were collected by crossing female and male adults (3–24 months old). Fish husbandry and fish-related experimental procedures were carried out with approved guidelines from the Animal Welfare Assurance on file with the Office of Laboratory Animal Welfare. The Assurance number on file is #D16–00270.
METHOD DETAILS
Zebrafish strains and lines:
Transgenic- Tg(βActin:membrane-Citrine): Tg(actb2:mem-citrine-citrine)hm30 (Megason lab (Xiong et al., 2013)) used in Figures 1D–1K, S1A–S1E, 2G, 2H, 3E, S2I, 4F–4H, S4A, 5A, 5B, 5G, 6A, 6G, 6H and Videos S1– S4.
AB wildtype: Figures 2A, 2B and S2D–F
Pigmentation triple mutant- ((roy−/−; nacre−/−; fms−/−) (Parichy et al., 2000; White et al., 2008)) used in Figures S2A–S2C, 3A, 3B, S3A–S3C. The triple mutant lacks all pigmentation in skin rendering the OVs optically clear for fluorescent imaging.
ugdh mutant: ugdhm151/m151 is a missense point mutation that disrupts ugdh (Driever et al., 1996; Neuhauss et al., 1996) used in Figures 3D and S2H. Homozygous mutants (25%) were screened from heterozygous parents through characteristic pericardial edema phenotype22. Unaffected sibling embryos (75%) could either be homozygous wild-type (25%) or heterozygous for the mutation (50%).
Transgenic- Tg(βActin:Utrophin-mCherry): Tg(actb1:mCherry–utrCH) (Heisenberg lab (Behrndt et al., 2012)) used in Figures S4A, S4E, S6A, S6C, Videos S3 and S4.
Transgenic- Tg(βActin:Myl12.1-eGFP): Tg(actb2:myl12.1-EGFP)e2212 (Heisenberg lab (Behrndt et al., 2012)) Figures 6C, S4B, S4E, S6D, 7H and Videos S3 and S4.
Transgenic- Tg(βActin:membrane-mCherry): Tg(actb2:mem-mcherry2)hm29(Megason lab (Xiong et al., 2014)) in Figures 6C, 6E, S4B, S4E, S6A, S6C and Video S3.
E-Cadherin BAC transgenic: Tg (cdh1:cdh1-sfGFP) ((Yamaguchi et al., 2019) used in Figure 6D and Video S5.
Construct generation and injection of mRNAs and plasmids
• actb2:mem-neongreen-neongreen
The actb2:mem-neongreen-neongreen construct was made using previously reported membrane localization tags with two copies of moxNeonGreen subcloned downstream of the actb2 promoter into a pMTB backbone (described here (Collins et al., 2018) in detail). mRNA was synthesized from a linearized plasmid using the mMessage mMachine T7 transcription kit (Ambion) and injected in single cell stage embryos using a Nanoject system calibrated to 2.3nl of injection volume. ugdh mutant embryos were injected with 90pg of membrane-neongreen mRNA (Figures 3D and S2D). For mosaic membrane labelling, 90 pg of Tol2 mRNA was injected with either actb2:mem-neongreen-neongreen or actb2:mem-mcherry2 (15ng/ul final concentration) into embryos from either Tg(βActin:Utrophin-mCherry) or Tg(βActin:Myl12.1-eGFP) respectively (Figures 6A, 6B(bottom), 6F (untethered), S4E and S4F).
• Cloning of dominant negative E-Cadherin plasmid
The hsp70l:DN-Cdh1-Cardinal plasmid was constructed in two steps. We first constructed the dominant negative E-Cadherin (DN-Cdh1), missing the bulk of the extracellular domain, including the ectodomains (EC1-EC4) important for homophilic binding. DNA sequence containing the first 107 amino acid of cdh1 was amplified from cDNA of 14hpf AB strain zebrafish by PCR reaction with the following pair of primers: forward primer: agctacttgttctttttgcagga; reverse primer: ttttatggtcctttcattaataacaggactggagtcccaggcatg. DNA sequence containing the last 286 amino acid of cdh1 was amplified from cDNA of 14hpf AB strain zebrafish by PCR reaction with the following pair of primers. Forward primer: catgcctgggactccagtcctgttattaatgaaaggaccataaaa; Reverse primer: tgtatcttatcatgtctggatcacc
The plasmid backbone containing heat-shock inducible promoter (hsp70l) was digested by BamHI and AgeI, gel purified, and assemble with the two PCR products by isothermal assembly. After obtaining the dominant negative Cdh1 (DN-Cdh1), we further tagged it with fluorescent protein mCardinal. The DN-Cdh1 construct was PCR amplified with the following primers: forward primer: agctacttgttctttttgcagga; reverse primer: ccagctggcgctccatcctctcctcctccatacatgt. The mCardinal DNA was s amplified from a previously made construct ((Liu et al., 2018)) with the following primers: forward primer: ggagaggatggagcgccagctggaggtgcaggtgcagcaatggtttcaaaaggggaagag; reverse primer: tgtatcttatcatgtctggatcaccggttcacttgtacagctcgtccatgc. The plasmid backbone containing heat-shock inducible promoter (hsp70l) was digested by BamHI and AgeI, gel purified, and assemble with the two PCR products by isothermal assembly to make the final plasmid hsp:DN-cdh1-cardinal.
90 pg of Tol2 mRNA was injected with plasmid DNA for hsp:DN-cdh1-cardinal (15ng/ul final concentration) into embryos from Tg(βActin:membrane-Citrine) at single cell stage. 50 hpf embryos (with their chorion) were heat shocked at 38°C for 20 mins in pre-warmed 1X Danieau buffer. Embryos were kept at 28°C post heat-shock to allow DN E-Cad expression and imaged after 2 hours (52 hpf).
Morpholino injection and validation
Two previously characterized morpholino oligonucleotides (MO) (Ouyang et al., 2017) targeting either has3 start codon (MO-1) or the intron 2-exon 3 splice junction (MO-2) were purchased from Gene Tools along with their Standard Control MO. 7ng of either has3 MO-1 or has3 MO-2 or control MO was injected with 3.5ng of p53 MO (to control for phenotypic variability (Gerety and Wilkinson, 2011)) at single cell stage (Figures 3E and S2E). The efficiency of MO-2 mediated mis-splicing was verified by RT-PCR using the primers: 5’CCTGATGTGGGAGGA-GTTGGAGGA-3’ (forward) and 5’-GGACGCGGTTGGTGAGATGTCG-3’ (reverse) (Figure 2G).
Confocal Imaging
Dechorionated embryos were mounted dorso-laterally (as shown in Figure 1C) using a canyon mount cast in 1% agarose filled with 1X Danieau buffer as previously described in detail (Swinburne et al., 2018). Confocal z-stacks were acquired with an upright Zeiss LSM 710 laser scanning confocal microscope using a C-Apochromat 40X 1.2 NA objective for all fluorescence microscopy data, except Figures S3A, 6A, 6B, 6D and 6H, where Zeiss LSM 980 laser scanning confocal microscope with C-Apochromat 40X 1.2 NA objective and Airy Scan 2 module was used. For single time points, embryos were immobilized by soaking in 1% tricaine. For long-term time lapse imaging, embryos were immobilized with 500 μM α-bungarotoxin protein (aBt from Tocris) (Swinburne et al., 2015) injected into the heart ~30 minutes prior to imaging (at variable stages depending on the experiment). Time-lapse imaging took place in a home-built incubator at 28.5°C. In a typical experiment using Zeiss LSM 710, ~250 μm × 250 μm × 150 μm volume with a voxel size ~0.2 μm × 0.2 μm × 0.5 μm captured the entire OV within ~3 minutes. With the better resolution of the Zeiss LSM 980 Airy Scan 2, the voxel size improved to ~0.12 μm × 0.12 μm × 0.35 μm. The volume and speed of acquisition was adjusted depending on the experiment.
Two-photo laser ablation
Ablation of cells in the OV were performed using a Mai-Tai HP 2-photon laser (Spectra-Physics, Santa Clara, CA) as previously described in detail (Mosaliganti et al., 2019). Briefly, the 2-photon laser was tuned to 800 nm at 50–75% power. The pinhole was opened completely and a spot scan at the target cell was performed for 10,000 cycles. To monitor ablation, 3 kDa Texas red-Dextran dye was injected into the heart to label the periotic space. Successful ablation disrupted the otic epithelium causing the dye to enter the OV lumen.
Edu Staining, and Hydroxyurea and Aphidicolin drug treatments
45 hpf dechorionated AB wildtype embryos were kept in 500 uM 5-ethynyl-2′-deoxyuridine (EdU), a proliferative marker (Salic and Mitchison, 2008), without (control), or with 20 mM Hydroxyurea (Thompson Coon, 2010) and 300 μM Aphidicolin (DNA replication inhibition (Ikegami et al., 1978)), and a final concentration of 10% Dimethyl sulfoxide (DMSO), in 1X Danieau buffer on a shaker at 4°C for 1 hour. The embryos were transferred back at 28.5°C in fresh 1X Danieau buffer containing 50 uM EdU, without (control) or with 20 mM Hydroxyurea and 300 μM Aphidicolin, and a final concentration of 1% DMSO for 9 hours (45–54 hpf). Embryos were fixed with 4% paraformaldehyde (PFA) in 1X phosphate buffered saline solution (PBS) at room temperature (RT) for 2 hours. Embryos were then permeabilized in pre-chilled acetone at -20°C for 7min, rinsed in 1% Triton in 1X PBS for 5 minutes (thrice) and blocked with 2% Bovine Serum Albumin (BSA) in 1X PBS for 30 minutes. For EdU detection, embryos were transferred to a freshly prepared click-iT® reaction mixture (Thermo Fisher Scientific) for 30mins, at room temperature (RT) in dark. Embryos were washed with 0.1% Tween-20 in 1X PBS (PBT) for 5 mins (5 times) and stained overnight at 4°C with 4′,6-diamidino-2-phenylindole (DAPI) to detect DNA.
Multiplex in situ hybridization chain reaction (HCR)
HCR probes, amplifiers, and hybridization, wash and amplification buffers were bought from Molecular Instruments (Choi et al., 2018). Dechorionated embryos at various stages were fixed with 4% PFA in 1X PBS at RT for 2 hours, followed by PBS washing for 5 mins (five times) and permeabilization in pre-chilled acetone at −20°C for 7 min. Embryos were washed with PBS again, and pre-hybridized in hybridization buffer, followed by incubation in hybridization solution containing 1 pg of probes overnight at 37°C. Embryos were then washed in wash buffer followed by washes with 0.1% of Tween-20 in 5X SSC buffer (5X SSCT) for 5 minutes, twice. Embryos were then incubated in amplification buffer for 30 minutes at RT. Meanwhile, hairpin mixtures were prepared by heating 12 pmol of hairpin 1 and 2 per sample to 95°C for 90 seconds, and snap-cooled in the dark. The prepared hairpins were added to the amplification buffer. Embryos were incubated in the hairpin mixture overnight, at RT in dark. Embryos were then washed in 5X SSCT (5 times) and mounted for confocal microscopy (or stored at 4°C). For each embryo, two HCR probes were used and visualized with amplifiers conjugated with AlexaFlour™ (AF) 546 and AF647.
Hyaluronan Binding Protein, Phalloidin, Laminin and Collagen 2 staining
Dechorionated embryos (either uninjected or treated as described below) at various stages were fixed with 4% PFA in 1X PBS at RT for 2 hours, followed by PBS washing for 5 mins (thrice), and permeabilization in pre-chilled acetone at -20°C for 7 min. Embryos were then rinsed in 1X PBT for 5 minutes, thrice, and blocked with 5% BSA in 1X PBT for 60 minutes. Embryos were then incubated with primary solution containing either Laminin antibody (from Sigma-Aldrich, polyclonal, rabbit, 1:200 dilution) or Collagen 2 antibody (from GeneTex, polyclonal, rabbit, 1:200 dilution), and biotinylated- Hyaluronan Binding Protein (HABP from EMD Millipore, 1:100 dilution) at 4°C, overnight. Embryos were washed with 1X PBS (Tween-20 was avoided as HABP binds to HA with lower affinity compared to antibody-immunogen binding) for 15 mins, thrice. Embryos were incubated with a cocktail of fluorescent labelled secondary antibody (against rabbit), Streptavidin (against Biotin) and Phalloidin (to label F-Actin) at 4°C, overnight. Embryos were washed with PBS for 15 mins, thrice and mounted for confocal microscopy (or stored at 4°C).
Hyaluronidase, Cytochalasin-D and SMIFH2 treatments
Dechorionated embryos (at various stages) were soaked in 1X tricaine and immobilized in a 1% canyon mount filled with 1X Danieau buffer. All injection solutions were made with 1X PBS/0.5% Phenol Red. Streptomyces hyaluronidase (HAase from Sigma dissolved in 1X PBS, 300 unit/ml from 3000unit/ml stock) was injected in the periotic space (anterior and posterior to the OV). Control injection solution did not contain HAase. To monitor injections, 3 kDa Texas-red Dextran (from Thermo Fisher dissolved in 1X PBS, 0.5 mg/ml from 20 mg/ml stock) was injected with HAase or control. Cytochalasin D (from Tocris suspended in DMSO, 1 mM from 10 mM stock) (Burke, 1978) or SMIFH2 (from EMD Millipore suspended in DMSO, 1 mM from 10 mM stock) (Rizvi et al., 2009) or DMSO control (1:10 dilution) were injected in the cardiac chamber.
Dextran Percolation Assay
Dechorionated embryos (at 50 hpf) were soaked in 1X tricaine and immobilized in 1% canyon mount cast filled with 1X Danieau buffer. All injection solutions were made with 1X PBS/ 0.5% Phenol Red. Neutral Texas-red dextran (either 3 kDa, 10 kDa or 70 kDa from Thermo Fisher dissolved in 1X PBS, 500 μM from 10 mM stock) was co-injected with AF647 conjugated aBt (from Thermo Fisher dissolved in 1X PBS, 500 μM from 1 mM stock) into the periotic space (anterior and posterior to the OV). Embryos were imaged 2 hours post injection.
QUANTIFICATION AND STATISTICAL ANALYSIS
Quantification
3D visualization-
FluoRender (Wan et al., 2012), an open source software was used for 3D renderings. Monochrome heatmap represents z-depth with darker greys into the plane of view in Figures 1D–1K, 2A, 2B, 2F, 3D, 3E, S2D, S2E, S6A, S6C, Videos S1 and S2. Fire heatmap represents fluorescent intensities in Figures S2A–S2C and 4A–D. Image analysis was not performed on 3D renderings.
Bud length measurements-
Bud lengths were measured manually using the “straight-line” tool in Fiji (Schindelin et al., 2012). Lines were drawn in the middle sections of the bud and averaged from three different planes for each bud. Where budding had not started or in perturbations where budding was affected, bud lengths correspond to average cell lengths distinguished by their unique taller morphology (visible in Figures S1A–S1C).
Volume measurements-
Manual segmentations of the OV lumen volume and bud-ECM volume were performed in ITK-SNAP (Yushkevich et al., 2006) to create meshes. The number of voxels that belong to the mesh were converted to picolitre using the known voxel resolution.
EdU positive nuclei-
Total number of nuclei and EdU positive nuclei were manually counted in a fixed volume of 3D rendered OVs (z depth 80 μm starting from the dorsal most plane) in Fiji.
Aberrant morphogenesis-
Number of embryos injected with either membrane-NeonGreen mRNA or morpholinos with visible aberrant morphologies by the total number of embryos measured at 72 hpf.
Intensity analysis of multiplex in situ HCR -
Fluorescent intensity measurements of the two HCR probes per embryo were made in Fiji using maximum intensity z-projections covering the entire anterior bud at 57 hpf (25 μm z-depth). Using the “freehand-line” tool (width 20 pixels), region of interest (ROI) was drawn manually as illustrated in Figure 3C, and the mean intensity traces across the line were obtained using the “plot profile” tool. Embryos were carefully staged and mounted, and lines of equal length were drawn and registered at the first cell of the bud to allow comparison between embryos. Intensity traces were normalized to the maximum value, smoothed and averaged.
Intensity analysis of Collagen 2 and HABP staining-
Fluorescent intensity measurements of Collagen 2 and HABP staining were made in Fiji using maximum intensity z-projections covering both lateral buds at 48 hpf (20 μm z-depth). Using the “freehand-line” tool (width 10 pixels), ROI was drawn manually as illustrated in Figure 4E and the mean intensity traces across the line were procured using the “plot profile” tool. Embryos were carefully staged, and lines of equal length were drawn and registered at the first cell of the antero-lateral bud to allow comparison between embryos. Intensity traces were normalized to the maximum value, smoothed and averaged.
Dextran percolation-
Percolation of different sizes of dextran was measured in Fiji using maximum intensity z-projections covering all lateral bud-ECM at 52 hpf (10 μm z-depth). ROIs in the bud ECM and the periotic space were drawn manually (as illustrated in Figure S3C). Mean intensity in the red channel (Texas-red Dextran) was normalized to the mean intensity in the far-red channel (aBt). Percolation was measured as a ratio of the normalized intensity in the bud-ECM to the normalized intensity in the periotic space.
Structural uniformity of the bud-ECM-
Structural uniformity of the bud ECM was measured by drawing a line of width 10 pixels the from base to the tip of the bud (as illustrated in Figure S3C). Mean intensity trace across the line was obtained using the “plot profile” tool for various sizes of dextran and HABP staining. Intensity traces were normalized to their mean, averaged and smoothed.
Cell diameters and bud radii-
Longitudinal cell diameters and longitudinal bud radii were manually measured in Fiji using the “straight-line” tool in the middle XY plane (side view) of either anterior or posterior buds. Line was drawn across the length of the cell for measuring cell diameter, or across the length of the bud for measuring bud radius. Circumferential and radial cell diameters, and circumferential bud radii were measured in the middle XZ plane (transverse view) (as illustrated by the dotted line in Figure 5G) of either anterior or posterior buds. Circumferential and radial cell diameters were measured using the “line” tool by manually drawing a line across the length and the width of the cell respectively. Circumferential bud radii were measured manually by drawing a polygon outlining the apical circumference of the bud. The polygon was fit to an ellipse by Fiji to obtain the radius (since the short and the long axis of the ellipse were comparable).
Intensity analysis of F-actin and Myosin II-
Fluorescent intensity measurements of F-Actin (Tg(βActin:Utrophin-mCherry) and Myosin II (Tg(βActin:Myl12.1-eGFP)) were made in Fiji using maximum intensity z-projections covering the cells in the middle plane of either anterior or posterior buds (8 μm z-depth). Using the “line” tool (width 5 pixels), ROI was drawn manually inside the cell at the apical, lateral or basal surface to obtain mean intensities.
Cytocinch measurements
Tether duration was calculated by measuring the time spent by the protrusions in tethered-form before retraction. The start was the first frame of the time-lapse.
Distance between cells from which tethers originate a time frame before and immediately after tether retracts, were measured manually using the Fiji “line” tool as illustrated in Figure 6E.
Membrane angles of cells from which cytocinches originate a time frame before and immediately after tether retracts, were measured manually using the Fiji “angle” tool.
To accurately estimate the total number of cytocinch tethers at a given time point, tethers were tracked in time-lapses using their tension signatures (membrane angle and recoil distances as described above).
Cytocinch number per cell was calculated by dividing the total number of cytocinches in tethers (i.e. number of tethers in Figure 7A multiplied by 2) by the total number of the cells in the bud (counted manually from 3D renderings) at a given time point.
Cytocinch tether angles were measured with respect to the longitudinal axis of the bud using the Fiji “angle” tool. Cytocinches were detected using their tension signatures (membrane angle and recoil distances as described above).
Cytocinch anisotropy- Cytocinch anisotropy was calculating by decomposing tether angles into their x (circumferential) and y (longitudinal) components. y component was then subtracted from x, averaged for all cytocinch tethers in a bud at a given time point, multiplied by the total tether numbers at that time point, and plotted against the aspect ratio of the bud at that time point.
Theoretical modeling
Here we provide additional information into the modelling approach, parameter fitting, and data-theory comparisons used to understand bud extension during ear morphogenesis. The complete code in Python is provided (Data S1).
Model derivation
• 2D vertex model without cytocinches
We start by considering the equilibrium of a single cell, under differential tensions on its apical, lateral and basal areas (respectively denoted γa, γl and γb). The energy of a single cell of height h, apical length ra and basal length rb then reads (Fouchard et al., 2020; Krajnc et al., 2013; Okuda et al., 2015; Osterfield et al., 2013):
Because the bud that we model is axisymmetric, we restrict ourselves here to a 2D vertex description, which will describe well the bud aspect ratio and cellular shapes as assessed by 2D axial sections along the axis of elongation of the bud. Moreover, epithelial cells may be considered incompressible, with constant volume (or here 2D area A = A0, which we implement by taking very large compressibility values K → ∞), given the small forces generated by actomyosin structures, compared to osmotic forces (Salbreux et al., 2012). This is valid since cell volume does not change appreciably over the time scales considered (Figure 5C). We thus consider the ear as consisting of N identical such cells (all having the same volume/area and tension parameters γl,a,b. Finally, given the experimental findings of a key role for ECM-driven pressure for bud growth, we consider that the epithelial monolayer encloses an incompressible fluid of fixed volume VM (Yang et al., 2021)(which we similarly implement by a quadratic terms around a fixed (but changing in time) area in our 2D description, with high compressibility KM → ∞), such that the total energy of the monolayer reads
There are therefore two types of control parameters in the system: ECM-controlled temporal changes of volume and cellular-level changes in tensions γl,a,b (largely controlled by actomyosin contractility, which can change the shape of the bud at constant overall volume (Salbreux et al., 2012)).
Finally, this model is complemented with boundary conditions for the border cells i = 1 and i = N, which are the ones remaining in contact with the flat monolayer at position y = 0 surrounding the bud. To simulate the rest of the monolayer and ECM attachment, we fix the position of their basal/apical vertex to the plane y = 0 while still allowing translations on the plane. Denoting and the (x, y) positions of the basal and apical vertices, this translate into . We impose a constant lateral distance for the boundary vertices (as otherwise, the absence of a next cell promotes lateral junction collapse).
We also tested an alternative, fully clamped boundary conditions (where both x and y displacements of boundary vertices are forbidden, and found very similar results).
From past theoretical study, we know that such cytocinch-free model will display a buckling transition if there is a mismatch between the preferred area of cells and the volume of the monolayer. For larger hemi-spherical buds (which are indeed observed experimentally when inhibiting cytocinches, see Figures 7H and S6), we can calculate from Eq. S1 that ra ≈ rb and the equilibrium configuration of a single cell is . The stress-free state of the bud is one where the ECM volume exactly matches the equilibrium configuration of the monolayer, so that , so that for larger , the epithelium will be in a tensile configuration, while being compressed for lower , which can trigger monolayer buckling (Figure S5A) (Trushko et al., 2020). Numerical simulations of the equilibrium configurations of the bud for different and/or different γl confirmed this. Here however, we find no evidence of buckling in the system (see discussion in main text). Instead, ECM volume increase causes a marked flattening of cells, which go from being columnar early on to flattened and squamous like (Figure S4A), as expected in the model for cells with near constant volume. Furthermore, we do not find folding/buckling either upon pharmacological reduction of ECM volume (Figures 5A and 5G), with cells instead going back to cuboidal/columnar, again in agreement with the hypothesis of ECM-driven pressure putting the bud under tension.
Next, we asked whether boundary conditions could be enough to bias the orientation of bud growth, and give rise to elongated structures. We reasoned for instance that a supracellular contractile ring, forming at the base of the buds by cytocinches, could constrain their growth to the axial direction (Turlier et al., 2014). However, in such a model, the local tension within the rest of the monolayer would still be isotropic, which is then predicted to give rise to identical curvatures in both directions (see Figure S5B for example of a numerical simulations with cytocinches only for the vertices at the base), similar to the wetting-de-wetting transitions of droplets.
However, given the anisotropy observed in cytocinch tension, we reasoned that this could provide a mechanism to give rise to anisotropic tensions within the monolayer, and therefore proceeded to incorporated them into our model.
• 2D vertex model with cytocinches
We now consider the consequence of cytocinches exclusively in the orthoradial direction (i.e. perpendicular to the 2D section that we model). This induces an additional contribution to surface tension, which tends to shrink locally the radius of the bud (a “purse-string” mechanism), which adds an energy term on basal vertex for each cytocinch:
where Λ is the cytocinch tension (which tends to minimize the local radius of the bud in the plane), and we note pc the probability of a given vertex displaying a cytocinch (which increases in time experimentally as well as becoming more directed radially, see Figures 7A and 7B). For the sake of simplicity, we do not include in the model cytocinches in the other, tangential direction, as this simply adds a term which rescales the basal tension γb.
Before proceeding to run full simulations, we first proceeded to constrain the parameters of the model. From a qualitative perspective, as the bud short-axis is of the order of cell size, and that the tethered cytocinches cause large deflection of vertices (with typical angles θm ≈ 90° from Figures 6E–6G), this means from local force balance that cytocinch tension Λ should be of comparable magnitude as the surface tensions γb.
To make this more quantitative, we computed the equilibrium shape of a bud with constant, time-invariant volume and a single cytocinch exerting forces on a single basal vertex (Figures S5A–S5D) - first considering the simplified case of all surface tensions being equal γa,l,b = 1. As expected, we found that increasing cytocinch tension increased the local angle of the basal surfaces at the point of force application (Figure S5A), up to a point where cytocinch forces are large enough to pinch off the bud (similar to modelling of cytokinesis). Interestingly, this is something that was observed experimentally, arguing that cytocinch tension is in the high regime.
However, we also found that maintaining γa + γb constant (and thus the global stretching resistance of the epithelium, (see (Yang et al., 2021)), but changing separately the balance of γa and γb modified the response of the epithelium with respect to local force application. In particular, increased basal tension led to higher bud stability (because this stabilizes the interface on which forces are directly applied, see Figure S5A) whereas increase apical tension led to pinching/collapse of the lateral surfaces (which can occur even for little apical deformation) as shown in Figure S5D. Interestingly, we observe experimentally a relocation of actomyosin from the apical to the basal side in time, as the fraction of cytocinches increases (Figure 7A and S4) - which we conjectured would be an adaptive response giving additional stability to ear bud morphogenesis.
Finally, as an additional control of our simulations, we tested the effect of alternative boundary conditions, in particular to relax our strong assumption of having the bottom-most vertices tightly bound along the y-axis (see above). In particular, we also modelled the cells surrounding the bud, which we take to have exactly the same active tensions (although we do not implement cytocinch forces for these cells), and which we assume to be linked to the underlying BM (based on the experimental findings shown in Figure S3A and modelled as an elastic force in the y-direction acting on the basal vertices of the surrounding cells: . Note that the total cross-sectional area controlled by hyaluronan pressure AM is now calculated taking into account all cell positions. Thus, for very low binding to the BM kBM, surrounding cells are pulled upwards by the pressure, giving rise to poorly defined, non-experimentally observed bud shapes (Figure S5I). However, for large values of kBM (compared to the scale of other active tensions), we recovered very similar shape to the previous modelling of bud cells alone (Figure S5J)
Parameter estimation, numerical simulations and predictions
• Parameter estimation and numerical simulations
From these observations and measurements, we then proceeded to constrain further the parameters of the model. After actomyosin relocation (i.e. the relevant anisotropic growth phase with cytocinches), we measured the relative intensities of Myosin on the lateral, basal and apical surfaces (resp. ml, mb and ma), as a proxy to the tension ratios. We found ma/mb = 0.4 ± 0.08 and ma/ml = 0.7 ± 0.3 (see Figure S4).
In the following, we therefore non-dimensionalize all forces by γl = 1 and take γa = 0.7, γb = 1.75. Unless specified, we simulate N = 10 cells with varying ECM volume (although we tested different numbers of cells, which did not give rise to significantly different results). We non-dimensionalize all cell length by the preferred cell area (note that with these values, the equilibrium apical length of a flat cell is , which is close to the experimental value, with a cellular aspect ratio initially around 2: 1 at the early bud stage.
We use a Metropolis algorithm with small temperature to minimize the total energy of the system, performing the simulations multiple times to check that we converge towards the same steady state. Briefly, at each time point, we select N times at random a basal vertex at random, move it by a random small change δr = 0.05 and calculate the resulting difference in total energy ΔE (accepting the move always if ΔE < 0 or with a probability e−ΔE/T if ΔE > 0 (with T = 10−4). We then do the same on the adjacent apical vertex. With K = 10 and KM = 0.1, we find that we find all cell areas and ECM area close to their target configuration, while allowing for a non-negligible number of rejected Monte-Carlo steps, so that structures robustly converge to a steady-state for T = 103 steps (we found that doubling the number of steps did not change the results). For numerical stability, we prohibited moves that shrank junctions to values smaller than a small cut-off (lmin = 0.3).
Moreover, in simulations where we vary the ECM volume , we do so in a slow manner, so that the monolayer is near equilibrium throughout the simulation (T = 5. 104 steps, although we again found that doubling the step number did not change the results). Such quasi-static approximation is justified by the fact that ECM growth occurs very slowly at time scale of hours, which are much larger than the timescales of actomyosin-driven shape changes (minutes to tens of minutes). We thus define (where we normalized time to be 1 at the end of the simulation, so that ai and af are respectively the initial and final volumes/areas (measured experimentally to be af ≈ 3ai between 1hpb and 9hpb, as shown on Figure 5K).
Furthermore, guided by the increase in frequency of cytocinches in time, to a maximal value of around 0.5 cytocinch per cell (Figure 7A), we define the probability of a cytocinch on a given basal vertex as (zero at the beginning of the simulation and 0.5 at the end, with a build-up time of τc ≈ 1.5h based on Figure 7A, although the results were weakly sensitive to this value). We also tested the effect of a constant, non-time-varying fraction of cytocinches (with Λ = 0.8), and found, as expected that although the long-term effect was unchanged, this would predict smaller, early bud to be already highly anisotropic (Figure S5G and S5H), in contrast to the experimental data. This validates our hypothesis that cytocinch (and more specifically the increase of oriented cytocinches as a function of time) is crucial for the growing anisotropy of the buds. On the other hand, we also tested the converse scenario of increasing probabilities of cytocinches (as in WT simulations), but with a constant ECM volume. This led to anisotropies very similar to WT with volume increase (despite long and short axis being much shorter), also validating our hypothesis of ECM-bud volume growth being mainly responsible for overall bud inflation, but not anisotropic growth (Figure S7).
One particular assumption here is that the tension in a given tethered cytocinch is constant in time (and thus that the increased anisotropy of the structure is driven by the increase in cytocinch number), an assumption motivated by the angle of basal deformation caused by cytocinches (Figure 6E), which we found to be comparable in early vs. late buds. With this, as well as the various parameters constrained as described above, the main key parameter controlling the bud anisotropy that remains to be fitted is thus the tension Λ.
• Comparison with data
For this, we computed the short a and long axis b of the bud in time during our simulation for different values of Λ, as this provides a direct comparison to Figure 5J and 5K. As expected, for Λ = 0, the structure was growing spherically, with the ratio of short and long axis converging towards 1 a/b → 1 for large volumes, while the anisotropy increased for larger values of Λ. Interestingly, we found that for intermediate values of Λ ≈ 0.8, the short-axis remained roughly constant in width, while the long-axis increased (3-fold to match the 3-fold increase in volume, see Figure S5E and Video S6), very close to the experimental observations as shown on Figure 7F. We also plot the anisotropy of the bud in time (calculated as the long axis length divided by the short axis at the base) for different values of Λ, overlaying the points from 10 different runs of a simulation with identical parameters, to show the stochastic variability (due to the fact that cytocinch formation is a random event in the model) and robustness.
This behavior at intermediate Λ = 0.8 (Figures 4E–4G) contrasts with lower values of Λ, for which the short-axis markedly increase in size (Figure S5E) and larger values of Λ, characterized in particular by mechanical instabilities which the bud is locally pinched off (and in particular at the base as we have not imposed boundary stresses in the x direction). This argues that the data can be well-fitted (Figure 7F) by these intermediary values of constant Λ (also consistent with the basal deformation angles observed in the data, as discussed above), and increasing number of cytocinches as a function of time. The model also showed near-uniform transition from a columnar epithelium to a squamous one upon bud-ECM volume growth, an effect which stems from the approximation of constant cell volume together with uniform cytocinch distribution in space, and which was reversed upon volume reduction as expected (Figures 5G–5I).
We then proceeded to test this further in the data, by directly comparing cytocinch number and anisotropy ratio a/b, with the prediction that these should strongly correlate in a quasi-linear manner (see prediction for different Λ on Figures S5E and S5F). Importantly, this was in close agreement with the data (Figure 7C). We also performed several pharmacological experiments to test the model. Disrupting cytocinches via CytoD decreases the aspect ratio a/b back to a value close to 1, as a expected for Λ ≈ 0 in the model (Figures 7H–7J and Video S6 for a simulation where we turned off cytocinches to Λ = 0 at 8h). Similar behavior was obtained by disrupting cytocinches with SMIFH2 (Figures S6 and S7). Conversely, reducing volume as constant cytocinch strength/numbers is predicted to retain high anisotropy while shrinking (Figures 5G, S5G, S7 and Video S6 for a simulation where we go back to the initial ECM area ai at 8h) as experimentally observed upon hyaluronidase treatment which causes a collapse of the ECM (Figure 5G).
Statistics
Statistical methods were not used to predetermine sample size. Sample size was chosen such that statistical variability between experiments was captured and did not change significantly when more data points were added. No data were excluded. No experiments were randomized and the investigator was not blinded to any data set. Each experiment was replicated at-least thrice. Statistics were done on all replicates pooled together.
Average values are calculated from ‘n’, where ‘n’ represents numbers of OVs, buds, bud-ECM, cells, cytocinch tethers, or cytocinches (as labelled in each figure). Plots show individual data points, mean values and error bars (standard deviation or standard error of mean, as labeled). Non-parametric Mann–Whitney U-test was used to determine p values wherever mentioned. All statistical tests and plots were made in OriginPro.
Supplementary Material
Zip file containing the source code in Python for the 2D vertex model, a Readme file describing usage, and sample output.
3D rendered time-lapse images of the otic vesicle (OV) showing semicircular canal morphogenesis involving bud formation (black asterisks), extension and fusion using two Tg(βActin:membrane-Citrine) embryos (change at 59 hpf). OV lumen is coloured (blue) in the first and last frame. Bud fusion demarcates the hubs for the anterior, posterior and lateral semicircular canals (marked by pink, green and white circular arrows respectively). Anterior to the left and dorso-lateral into the plane of view. Scale bar, 50 μm.
Side and transverse views of 3D rendered time-lapse images of an anterior bud using Tg(βActin:membrane-mCherry) embryo. Longitudinal (blue), circumferential (orange) and radial (white) axes are labelled at 5 hpb. Scale bar, 10 μm.
Side and transverse views (maximum intensity projections) of time-lapse images showing localization of F-actin (using Tg(βActin:Utrophin-mCherry)) and Myosin II (using Tg(βActin:myl12.1-eGFP)) in green. Membrane (in magenta) is labelled using Tg(βActin:membrane-Citrine) with F-Actin, and Tg(βActin:membrane-mCherry) with Myosin II. Scale bar, 10μm.
2D sections of lateral buds showing membrane tethers (white arrows) with mosaic membrane labelling (magenta), and the corresponding localization of F-actin (using Tg(βActin:Utrophin-mCherry)) and Myosin II (using Tg(βActin:myl12.1-eGFP)) in green at 4 hpb. Scale bar, 10 μm.
2D sections of two anterior buds showing tethers (red arrows) with E-Cadherin accumulation using Tg (Cdh1:Cdh1-sfGFP) at 6 hpb. Scale bar, 10 μm.
Equilibrium configurations of a bud section over ‘time’ (hours post budding), modelled via the 2D vertex model representing apical, lateral and basal tensions on the cell surfaces (grey arrows), and inward forces from cytocinches (green dots). ECM-bud volume and cytocinch frequency increase in time (as experimentally measured). X and Y axes are short and long respectively. Left panel is control, middle panel represents Hyaluronidase treatment (through reduction in bud-ECM volume), and right panel represents Cytochalasin D treatment (through removal of cytocinches), each at 7 hpb.
(A-E) Select time points of the OV using Tg(βActin:membrane-Citrine) showing 2D sections from two different z-depths. Dorso-lateral (DL) section shows formation of lateral buds (marked by white asterisks) and their extension (white arrows). Medio-ventral (MV) section shows anterior and posterior bud formation (pink and green asterisks respectively) and their extension (pink and green arrows respectively). Scale bar, 50 μm.
(F) Individual data points and mean±s.d. of bud lengths across time. In the absence of buds, lengths correspond to cell lengths. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(A-C), Representative examples of 3D-rendered OVs at select time points, stained with fluorescent in situ probes against ugdh (A), has3 (B), and col2a1a (C). Heat map represents fluorescent intensity with the same contrast for each probe across time points. Lateral buds are marked with white asterisks. Anterior and posterior buds are marked with yellow and cyan asterisks respectively. Anterior to the left and DL into the plane of view. Scale bar, 50 μm.
(D-F) Brightfield images of AB embryos injected with control morpholino (MO) and has3-specific MO-1 (E and E’) and MO-2 (F and F’). Scale bar, 500 μm.
(G) RT-PCR verification of has3-specific MO-2
(H-I) Representative examples of 3D-rendered OVs at 72 hpf from sibling control and ugdhm151/m151 mutant embryos labelled with membrane-NeonGreen mRNA (D and D’), and Tg(βActin:membrane-Citrine) embryos injected with control morpholino (MO) and has3-specific MO-1 (E and E’). Anterior and posterior pillars have formed and the ventro-lateral bud is extending (white arrow) in sibling control (D). All three pillars have formed in the control MO
(E). Genetically perturbed embryos do not have pillars (D’-E’). Anterior to the left and DL into the plane of view. Scale bar, 50 μm.
(J) Table showing the number of embryos over the total number measured with aberrant SCC morphogenesis in MO injections at 72 hpf.
(A) Composite of 2D sections of OVs showing Phalloidin and Laminin staining at 45, 51 and 57 hpf. Lateral, anterior and posterior buds from different z-depths are framed in white, yellow and cyan respectively. Contrast is different at different z depths to capture the dynamic range, and the same across control and treated embryos at the same z-depth. Scale bar, 50 μm.
(B-C) Composite of 2D sections of OVs showing HA, F-actin and Collagen 2 staining using HA-Binding Protein (HABP), Phalloidin and Anti-Col2a1a respectively, in control and HAase treated embryos at 57 hpf. Lateral, anterior and posterior buds from different z-depths are framed in white, yellow and cyan respectively. Contrast is different at different z depths to capture the dynamic range, and the same across control and treated embryos at the same z-depth. Scale bar, 50 μm.
(D) Illustration showing different sizes of dextran and alpha-Bungarotoxin (aBt) injected in the periotic space percolating into the bud-ECM.
(A and B) Maximum intensity projections at select time points from posterior buds showing localization of F-actin (using Tg(βActin:Utrophin-mCherry)) (A) and Myosin II (using Tg(βActin:myl12.1-eGFP)) (B) in green. Membrane (in magenta) is labelled using Tg(βActin:membrane-Citrine) in (A) and Tg(βActin:membrane-mCherry) in (B). Apical cell surfaces face OV lumen and basal cell surfaces face the bud-ECM. Scale bars, 10 μm.
(C and D) Individual data points and mean±s.d. of F-actin and Myosin II intensities at the basal and lateral surface normalized to the intensities at the apical surface over time. Each data point is an average from 3–6 cells per bud. ‘n’ denotes the number of buds.
(E) 2D sections showing protrusive membrane tethers (white arrows) in lateral buds using either F-actin (top) or Myosin II (middle and bottom) reporters and mosaic membrane labelling. Scale bar, 10 μm.
(A) Equilibrium configurations of a section of a bud, modelled via a 2D vertex model (n=10 cells) representing the apical, lateral and basal tensions on the cell surfaces (grey arrows, taken all as equal to unity), as well as inward forces (black arrows) from cytocinches (green dots) with increasing tension (Λ=0, Λ=1 and Λ=2 from left to right panels).
(B) Equilibrium configurations of a section of a bud with cytocinches only at the base (Λ=1), showing that this is not sufficient to drive anisotropic bud extension, as the monolayer is predicted to be locally spherical (due to isotropic tensions everywhere but at the base).
(C) Equilibrium configurations of a section of a bud with cytocinches (Λ=1), increased basal tension and decreased apical tension (same parameters as panel a otherwise), showing a better resistance of the epithelium to local deformations.
(D) Equilibrium configurations of a section of a bud with cytocinches (Λ=1), decreased basal tension and increased apical tension (same parameters as panel a otherwise), showing a worsened resistance of the epithelium to local deformations, and associated bud pinching.
(E and F) Predicted evolution of the bud radii in the long (blue) and short (orange) axes (experimental: dots, predictions: lines) (E), and their ratios representing bud anisotropy (F) (data in red, model in black, assuming a linear bud-ECM volume increase (3-fold) and temporal increase in fraction of cytocinches (see STAR Methods for details)), for different values of cytocinch tension Λ (left to right panels)). For low cytocinch tension Λ, the bud retains low anisotropy during growth under-estimating experimental anisotropy (left panels), while for high cytocinch tension (Λ=1.5), the model over-estimates bud anisotropy (right panels). Intermediate values of cytocinch tensions provide a good fit for the data (middle panel, Λ=1.0, to be compared to the best-fit value of Λ=0.8 shown in Figures 7E and 7F). Error bars show mean and s.d.
(G and H) Predicted evolution of bud anisotropies (data in red, model in black), assuming either a constant, non-varying ECM volume and temporal increase in fraction of cytocinches (see STAR Methods for details) for intermediate cytocinch tension Λ=0.8 (G), or a linear bud-ECM volume increase in time (3-fold) and constant fraction of cytocinches (see STAR Methods for details) for intermediate cytocinch tension Λ=0.8 (H). Error bars show mean and s.d.
(I and J) Same vertex model simulations under different boundary conditions, considering cells surroundings the bud as well as non-infinitely stiff binding kBM to the underlying basement membrane (BM) for these surrounding cells. For low binding to the BM, the surrounding cells can be pulled upwards to the hyaluronan-derived pressure, giving rise to unphysiological poorly defined bud shapes (I, kBM =0.1), however for higher binding we recover similar bud shapes to previous simulations (J, kBM = 1).
(A and C) 3D-rendered OVs using Tg(βActin:Utrophin-mCherry) at 54 hpf before and after Cytochalasin D (CytoD 1mM) treatment (A), and SMIFH2 (1mM) treatment (C). Anterior to the left and into the plane of view. Scale bar, 50 μm.
(B) Adjacent membrane angle change before and after CytoD injection. ‘n’ denotes the number of cell membrane angles. p values as labelled (Mann Whitney- U test).
(D) 2D sections of an anterior bud at 8 hpb using Tg(βActin:myl12.1-eGFP) before and after SMIFH2 treatment. Cytocinch is marked by white arrow before treatment. Cytocinch is lost after treatment. Scale bar, 10 μm.
(E and E’) Total number of cytocinch tethers (E) and adjacent membrane angles (E’) before and after SMIFH2 treatment. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(F and F’) Bud radii (F) and aspect ratios (F’) before and after SMIFH2 treatment. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(G) Anterior bud volume before and after CytoD treatment. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
2D vertex model (top) and illustrations (bottom) showing the effects of HA-mediated isotropic extracellular pressure (purple arrows) and cytocinch-mediated anisotropic tissue resistance (green arrows) on bud and cell morphologies in control and perturbed conditions.
KEY RESOURCE TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Rabbit Polyclonal Anti-Col2a1a | Gene-Tex | Cat# GTX127988 |
| Rabbit Polyclonal Anti-Laminin | Sigma-Aldrich | Cat# L9393 |
| Chemicals, Peptides, and Recombinant Proteins | ||
| α-Bungarotoxin | Thermo Fisher | Cat# B1601 |
| α-Bungarotoxin, Alexa Fluor™ 647conjugate | Thermo Fisher | Cat# B35450 |
| Biotinylated HA- Binding Protein | EMD Millipore | Cat# 385911 |
| Streptavidin, Alexa Fluor™ 594 conjugate | Thermo Fisher | Cat# S11227 |
| Hyaluronidase from Streptomyces hyalurolyticus | Sigma Aldrich | Cat# H1136 |
| Cytochalasin D | Tocris | Cat# 1233 |
| Click-iT™ EdU Cell Proliferation Kit for Imaging, Alexa Fluor™ 488 dye | Thermo Fisher | Cat# C10337 |
| Hydroxyurea | Sigma Aldrich | Cat# H8627 |
| Aphidicolin (readymade solution) | Sigma Aldrich | Cat# A0781 |
| Alexa Fluor™ 488 Phalloidin | Thermo Fisher | Cat# A12379 |
| Formin FH2 Domain Inhibitor, SMIFH2 | Calbiochem | Cat# CAS3403 |
| HCR v3.0 Probe Sets, Amplifiers, and Buffers | Molecular Instruments | https://www.molecularinstruments.com/products |
| Dextran, Texas Red™,3000 MW,Neutral | Thermo Fisher | Cat# D3329 |
| Dextran, Texas Red™,10,000 MW,Neutral | Thermo Fisher | Cat# D1828 |
| Dextran, Texas Red™,70,000 MW,Neutral | Thermo Fisher | Cat# D1830 |
| DMSO | Sigma Aldrich | Cat# 472301 |
| Experimental Models: Organisms/Strains | ||
| Zebrafish: Tg(actb2:mem-citrine-citrine)hm30 | (Xiong et al., 2014) | ZDB-TGCONSTRCT-130114-2 |
| (roy−/−; nacre−/−; fms−/−) | (Parichy et al., 2000; White et al., 2008) | N/A |
| Zebrafish: AB wildtype strain | Zebrafish International Resource Centre | ZDB-GENO-960809-1 |
| Zebrafish: ugdhm151/m151 | (Driever et al., 1996; Neuhauss et al., 1996) | ZDB-GENO-200828-1 |
| Zebrafish: Tg(actb1:mCherry–utrCH) | (Behrndt et al., 2012) | RRID:ZFIN_ZDB-TGCONSTRCT-130206-3 |
| Zebrafish: Tg(actb2:myl12.1-EGFP)e2212 | (Behrndt et al., 2012) | RRID:ZFIN_ZDBTGCONSTRCT-130108-2 |
| Zebrafish: Tg(actb2:mem-mcherry2)hm29 | (Xiong et al., 2014) | ZDB-TGCONSTRCT-130625-1 |
| Recombinant DNA | ||
| pMTB actb2:mem-neongreen-neongreen plasmid for mRNA synthesis | (Collins et al., 2018) | N/A |
| pMTB actb2:mem-mcherry2 plasmid for mRNA synthesis | (Xiong et al., 2014) | N/A |
| pMTB hsp70l:DN-Cdh1-Cardinal plasmid | This study | N/A |
| Oligonucleotides | ||
| has3 MO-1 5’ CCGCAGTGCCAAAGCGAGAGGGCAT 3’ | Gene Tools | N/A |
| has3 MO-2 5’ATCTGAAGGAAACAATGAACAGAGA 3’ | Gene Tools | N/A |
| Control MO-1 5’ CCTCTTACCTCAGTTACAATTTATA 3’ | Gene Tools | N/A |
| p53 MO 5’GCGCCATTGCTTTGCAAGAATTG 3’ | Gene Tools | N/A |
| has3 HCR in situ probe NM_173220.2 | Molecular Instruments | N/A |
| col2a1a HCR in situ probe NM_131292 | Molecular Instruments | N/A |
| ugdh HCR in situ probe NM_001110402.1 | Molecular Instruments | N/A |
| Software and Algorithms | ||
| Image J | (Schindelin et al., 2012) | https://fiji.sc/ |
| Origin Pro | Origin(Pro), Version 2020. OriginLab Corporation, Northampton, MA, USA. | https://www.originlab.com/origin |
| Excel | Microsoft | https://www.microsoft.com/en-us/microsoft365/excel |
| ITK Snap | (Yushkevich et al., 2006) | http://www.itksnap.org/pmwiki/pmwiki.php |
| FluoRender | (Wan et al., 2012) | https://www.sci.utah.edu/software/fluorender.html |
| BioRender | biorender.com | https://biorender.com/ |
HIGHLIGHTS.
The ECM, rather than actomyosin forces, drives semicircular canal morphogenesis.
The ECM component hyaluronan is locally synthesized by the enzymes ugdh and has3.
Isotropic hyaluronate pressure deforms the overlying epithelium into buds.
Differential stiffness from polarized tethers (cytocinches) shape buds into tubes.
Acknowledgements:
We thank Ian Swinburne, Sandy Nandagopal and Toru Kawanishi for support, discussions and reagents. We thank Vanessa Barone, Joseph Nasser and members of the Megason lab for useful comments on the manuscript and general feedback. We are grateful to the Heisenberg and Knaut labs for transgenic fish. Diagrams on the right in the graphical abstract were created using BioRender. This work was supported by R01DC015478 to S.G.M. A.M. was supported by Human Frontiers Science Program LTF and K99HD098918.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Competing interests: The authors declare no competing interests.
References
- Alsina B, and Whitfield TT (2017). Sculpting the labyrinth: Morphogenesis of the developing inner ear. Semin Cell Dev Biol 65, 47–59. [DOI] [PubMed] [Google Scholar]
- Alt S, Ganguly P, and Salbreux G (2017). Vertex models: from cell mechanics to tissue morphogenesis. Philos Trans R Soc Lond B Biol Sci 372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barriga EH, Franze K, Charras G, and Mayor R (2018). Tissue stiffening coordinates morphogenesis by triggering collective cell migration in vivo. Nature 554, 523–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrndt M, Salbreux G, Campinho P, Hauschild R, Oswald F, Roensch J, Grill SW, and Heisenberg C-P (2012). Forces Driving Epithelial Spreading in Zebrafish Gastrulation. Science 338, 257. [DOI] [PubMed] [Google Scholar]
- Bertet C, Sulak L, and Lecuit T (2004). Myosin-dependent junction remodelling controls planar cell intercalation and axis elongation. Nature 429, 667–671. [DOI] [PubMed] [Google Scholar]
- Borzacchiello A, Russo L, Malle BM, Schwach-Abdellaoui K, and Ambrosio L (2015). Hyaluronic Acid Based Hydrogels for Regenerative Medicine Applications. Biomed Res Int 2015, 871218–871218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke DC (1978). Cytochalasins — biochemical and cell biological aspects Edited by S. W. Tanenbaum. Pp. 564. North-Holland Research Monographs Frontiers of Biology No. 46. 1978. Biochemical Education 6, 95–95. [Google Scholar]
- Thisse C, T. B (2005). High throughput expression analysis of ZF-models consortium clones. (ZFIN direct data submission).
- Caneparo L, Pantazis P, Dempsey W, and Fraser SE (2011). Intercellular bridges in vertebrate gastrulation. PloS one 6, e20230–e20230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casares L, Vincent R, Zalvidea D, Campillo N, Navajas D, Arroyo M, and Trepat X (2015). Hydraulic fracture during epithelial stretching. Nat Mater 14, 343–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan CJ, Costanzo M, Ruiz-Herrero T, Mönke G, Petrie RJ, Bergert M, Diz-Muñoz A, Mahadevan L, and Hiiragi T (2019). Hydraulic control of mammalian embryo size and cell fate. Nature 571, 112–116. [DOI] [PubMed] [Google Scholar]
- Chang W, Brigande JV, Fekete DM, and Wu DK (2004). The development of semicircular canals in the inner ear: role of FGFs in sensory cristae. Development 131, 4201. [DOI] [PubMed] [Google Scholar]
- Chanmee T, Ontong P, and Itano N (2015). Hyaluronan: Cancer and Cancer Metastasis. In Glycoscience: Biology and Medicine, Taniguchi N, Endo T, Hart GW, Seeberger PH, and Wong C-H, eds. (Tokyo: Springer Japan; ), pp. 1411–1417. [Google Scholar]
- Charras GT, Yarrow JC, Horton MA, Mahadevan L, and Mitchison TJ (2005). Non-equilibration of hydrostatic pressure in blebbing cells. Nature 435, 365–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri O, Cooper-White J, Janmey PA, Mooney DJ, and Shenoy VB (2020). Effects of extracellular matrix viscoelasticity on cellular behaviour. Nature 584, 535–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chauhan BK, Disanza A, Choi S-Y, Faber SC, Lou M, Beggs HE, Scita G, Zheng Y, and Lang RA (2009). Cdc42- and IRSp53-dependent contractile filopodia tether presumptive lens and retina to coordinate epithelial invagination. Development 136, 3657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, Weng D, Du C, Wang J, and Cao S (2019). Contribution of frustules and mucilage trails to the mobility of diatom Navicula sp. Scientific Reports 9, 7342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi HMT, Schwarzkopf M, Fornace ME, Acharya A, Artavanis G, Stegmaier J, Cunha A, and Pierce NA (2018). Third-generation in situ hybridization chain reaction: multiplexed, quantitative, sensitive, versatile, robust. Development 145, dev165753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins Z, Ishimatsu K, Tsai T, and Megason S (2018). A Scube2-Shh feedback loop links morphogen release to morphogen signaling to enable scale invariant patterning of the ventral neural tube. bioRxiv. [Google Scholar]
- Cowman MK, Schmidt TA, Raghavan P, and Stecco A (2015). Viscoelastic Properties of Hyaluronan in Physiological Conditions. F1000Research 4:622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crest J, Diz-Muñoz A, Chen D-Y, Fletcher DA, and Bilder D (2017). Organ sculpting by patterned extracellular matrix stiffness. eLife 6, e24958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cyphert JM, Trempus CS, and Garantziotis S (2015). Size Matters: Molecular Weight Specificity of Hyaluronan Effects in Cell Biology. International Journal of Cell Biology 2015, 563818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawes-Hoang RE, Parmar KM, Christiansen AE, Phelps CB, Brand AH, and Wieschaus EF (2005). folded gastrulation, cell shape change and the control of myosin localization. Development 132, 4165. [DOI] [PubMed] [Google Scholar]
- Driever W, Solnica-Krezel L, Schier AF, Neuhauss SC, Malicki J, Stemple DL, Stainier DY, Zwartkruis F, Abdelilah S, Rangini Z, et al. (1996). A genetic screen for mutations affecting embryogenesis in zebrafish. Development 123, 37. [DOI] [PubMed] [Google Scholar]
- Dumortier JG, Le Verge-Serandour M, Tortorelli AF, Mielke A, De Plater L, Turlier H, and Maître J-L (2019). Hydraulic fracturing and active coarsening position the lumen of the mouse blastocyst. Science 365, 465–468. [DOI] [PubMed] [Google Scholar]
- Dzamba BJ, and DeSimone DW (2018). Chapter Seven - Extracellular Matrix (ECM) and the Sculpting of Embryonic Tissues. In Current Topics in Developmental Biology, Litscher ES, and Wassarman PM, eds. (Academic Press; ), pp. 245–274. [DOI] [PubMed] [Google Scholar]
- Felszeghy S, Módis L, Tammi M, and Tammi R (2001). The distribution pattern of the hyaluronan receptor CD44 during human tooth development. Archives of Oral Biology 46, 939–945. [DOI] [PubMed] [Google Scholar]
- Fierro-González JC, White MD, Silva JC, and Plachta N (2013). Cadherin-dependent filopodia control preimplantation embryo compaction. Nature Cell Biology 15, 1424–1433. [DOI] [PubMed] [Google Scholar]
- Fouchard J, Wyatt TPJ, Proag A, Lisica A, Khalilgharibi N, Recho P, Suzanne M, Kabla A, and Charras G (2020). Curling of epithelial monolayers reveals coupling between active bending and tissue tension. Proceedings of the National Academy of Sciences 117, 9377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng F-S, Abbas L, Baxendale S, Holdsworth CJ, Swanson AG, Slanchev K, Hammerschmidt M, Topczewski J, and Whitfield TT (2013). Semicircular canal morphogenesis in the zebrafish inner ear requires the function of gpr126 (lauscher), an adhesion class G protein-coupled receptor gene. Development 140, 4362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerety SS, and Wilkinson DG (2011). Morpholino artifacts provide pitfalls and reveal a novel role for pro-apoptotic genes in hindbrain boundary development. Developmental Biology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granath KA (1958). Solution properties of branched dextrans. Journal of Colloid Science 13, 308–328. [Google Scholar]
- Groves AK, and Fekete DM (2012). Shaping sound in space: the regulation of inner ear patterning. Development 139, 245–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haack T, and Abdelilah-Seyfried S (2016). The force within: endocardial development, mechanotransduction and signalling during cardiac morphogenesis. Development 143, 373. [DOI] [PubMed] [Google Scholar]
- Haddon CM, and Lewis JH (1991). Hyaluronan as a propellant for epithelial movement: the development of semicircular canals in the inner ear of Xenopus. Development 112, 541. [DOI] [PubMed] [Google Scholar]
- Hannezo E, Prost J, and Joanny J-F (2014). Theory of epithelial sheet morphology in three dimensions. Proceedings of the National Academy of Sciences 111, 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartman MA, and Spudich JA (2012). The myosin superfamily at a glance. Journal of Cell Science 125, 1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heisenberg CP, and Bellaiche Y (2013). Forces in tissue morphogenesis and patterning. Cell 153, 948–962. [DOI] [PubMed] [Google Scholar]
- Higuchi S, Sugahara F, Pascual-Anaya J, Takagi W, Oisi Y, and Kuratani S (2019). Inner ear development in cyclostomes and evolution of the vertebrate semicircular canals. Nature 565, 347–350. [DOI] [PubMed] [Google Scholar]
- Hughes AJ, Miyazaki H, Coyle MC, Zhang J, Laurie MT, Chu D, Vavrušová Z, Schneider RA, Klein OD, and Gartner ZJ (2018). Engineered Tissue Folding by Mechanical Compaction of the Mesenchyme. Dev Cell 44, 165–178.e166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikegami S, Taguchi T, Ohashi M, Oguro M, Nagano H, and Mano Y (1978). Aphidicolin prevents mitotic cell division by interfering with the activity of DNA polymerase-alpha. Nature 275, 458–460. [DOI] [PubMed] [Google Scholar]
- Jacinto A, Wood W, Balayo T, Turmaine M, Martinez-Arias A, and Martin P (2000). Dynamic actin-based epithelial adhesion and cell matching during Drosophila dorsal closure. Current Biology 10, 1420–1426. [DOI] [PubMed] [Google Scholar]
- Keegstra K (2010). Plant cell walls. Plant physiology 154, 483–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohda D, Morton CJ, Parkar AA, Hatanaka H, Inagaki FM, Campbell ID, and Day AJ (1996). Solution Structure of the Link Module: A Hyaluronan-Binding Domain Involved in Extracellular Matrix Stability and Cell Migration. Cell 86, 767–775. [DOI] [PubMed] [Google Scholar]
- Krajnc M, Štorgel N, Brezavšček AH, and Ziherl P (2013). A tension-based model of flat and corrugated simple epithelia. Soft Matter 9, 8368–8377. [Google Scholar]
- Kwan KM (2014). Coming into focus: The role of extracellular matrix in vertebrate optic cup morphogenesis. Developmental Dynamics 243, 1242–1248. [DOI] [PubMed] [Google Scholar]
- Lecuit T, Lenne P-F, and Munro E (2011). Force Generation, Transmission, and Integration during Cell and Tissue Morphogenesis. Annual Review of Cell and Developmental Biology 27, 157–184. [DOI] [PubMed] [Google Scholar]
- Li Y, Konstantopoulos K, Zhao R, Mori Y, and Sun SX (2020). The importance of water and hydraulic pressure in cell dynamics. Journal of Cell Science 133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T-L, Upadhyayula S, Milkie Daniel E, Singh V, Wang K, Swinburne Ian A, Mosaliganti Kishore R, Collins Zach M, Hiscock Tom W, Shea J, et al. (2018). Observing the cell in its native state: Imaging subcellular dynamics in multicellular organisms. Science 360, eaaq1392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubarsky B, and Krasnow MA (2003). Tube morphogenesis: making and shaping biological tubes. Cell 112, 19–28. [DOI] [PubMed] [Google Scholar]
- Maître J-L, Berthoumieux H, Krens SFG, Salbreux G, Jülicher F, Paluch E, and Heisenberg C-P (2012). Adhesion functions in cell sorting by mechanically coupling the cortices of adhering cells. science 338, 253–256. [DOI] [PubMed] [Google Scholar]
- Mosaliganti KR, Swinburne IA, Chan CU, Obholzer ND, Green AA, Tanksale S, Mahadevan L, and Megason SG (2019). Size control of the inner ear via hydraulic feedback. eLife 8, e39596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munjal A, and Lecuit T (2014). Actomyosin networks and tissue morphogenesis. Development 141, 1789–1793. [DOI] [PubMed] [Google Scholar]
- Navis A, and Bagnat M (2015). Developing pressures: fluid forces driving morphogenesis. Curr Opin Genet Dev 32, 24–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson CM (2016). On Buckling Morphogenesis. J Biomech Eng 138, 021005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuhauss SCF, Solnica-Krezel L, Schier AF, Zwartkruis F, Stemple DL, Malicki J, Abdelilah S, Stainier DYR, and Driever W (1996). Mutations affecting craniofacial development in zebrafish. Development. [DOI] [PubMed] [Google Scholar]
- Nishitani AM, Ohta S, Yung AR, Del Rio T, Gordon MI, Abraira VE, Avilés EC, Schoenwolf GC, Fekete DM, and Goodrich LV (2017). Distinct functions for netrin 1 in chicken and murine semicircular canal morphogenesis. Development (Cambridge, England) 144, 3349–3360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okuda S, Inoue Y, and Adachi T (2015). Three-dimensional vertex model for simulating multicellular morphogenesis. Biophys Physicobiol 12, 13–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osterfield M, Du X, Schüpbach T, Wieschaus E, and Shvartsman SY (2013). Three-dimensional epithelial morphogenesis in the developing Drosophila egg. Dev Cell 24, 400–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ouyang X, Panetta NJ, Talbott MD, Payumo AY, Halluin C, Longaker MT, and Chen JK (2017). Hyaluronic acid synthesis is required for zebrafish tail fin regeneration. PLOS ONE 12, e0171898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parichy DM, Ransom DG, Paw B, Zon LI, and Johnson SL (2000). An orthologue of the kit-related gene fms is required for development of neural crest-derived xanthophores and a subpopulation of adult melanocytes in the zebrafish, Danio rerio. Development 127, 3031. [DOI] [PubMed] [Google Scholar]
- Patra C, Diehl F, Ferrazzi F, van Amerongen MJ, Novoyatleva T, Schaefer L, Mühlfeld C, Jungblut B, and Engel FB (2011). Nephronectin regulates atrioventricular canal differentiation via Bmp4-Has2 signaling in zebrafish. Development 138, 4499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramírez-Weber F-A, and Kornberg TB (1999). Cytonemes: Cellular Processes that Project to the Principal Signaling Center in Drosophila Imaginal Discs. Cell 97, 599–607. [DOI] [PubMed] [Google Scholar]
- Rauzi M, and Lenne PF (2015). Probing cell mechanics with subcellular laser dissection of actomyosin networks in the early developing Drosophila embryo. Methods in Molecular Biology vol 1189. [DOI] [PubMed] [Google Scholar]
- Rizvi SA, Neidt EM, Cui J, Feiger Z, Skau CT, Gardel ML, Kozmin SA, and Kovar DR (2009). Identification and Characterization of a Small Molecule Inhibitor of Formin-Mediated Actin Assembly. Chemistry & Biology 16, 1158–1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salbreux G, Charras G, and Paluch E (2012). Actin cortex mechanics and cellular morphogenesis. Trends in Cell Biology 22, 536–545. [DOI] [PubMed] [Google Scholar]
- Salic A, and Mitchison TJ (2008). A chemical method for fast and sensitive detection of DNA synthesis in vivo. Proceedings of the National Academy of Sciences 105, 2415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Corrales YE, Blanchard GB, and Röper K (2018). Radially patterned cell behaviours during tube budding from an epithelium. eLife 7, e35717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012). Fiji: an open-source platform for biological-image analysis. Nature Methods 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shyer AE, Tallinen T, Nerurkar NL, Wei Z, Gil ES, Kaplan DL, Tabin CJ, and Mahadevan L (2013). Villification: How the Gut Gets Its Villi. Science 342, 212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivakumar A, Mahadevan A, Lauer ME, Narvaez RJ, Ramesh S, Demler CM, Souchet NR, Hascall VC, Midura RJ, Garantziotis S, et al. (2018). Midgut Laterality Is Driven by Hyaluronan on the Right. Dev Cell 46, 533–551.e535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Streichan SJ, Lefebvre MF, Noll N, Wieschaus EF, and Shraiman BI (2018). Global morphogenetic flow is accurately predicted by the spatial distribution of myosin motors. eLife 7, e27454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swinburne IA, Mosaliganti KR, Green AA, and Megason SG (2015). Improved Long-Term Imaging of Embryos with Genetically Encoded α-Bungarotoxin. PLOS ONE 10, e0134005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swinburne IA, Mosaliganti KR, Upadhyayula S, Liu T-L, Hildebrand DGC, Tsai TYC, Chen A, Al-Obeidi E, Fass AK, Malhotra S, et al. (2018). Lamellar projections in the endolymphatic sac act as a relief valve to regulate inner ear pressure. eLife 7, e37131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tee S-Y, Bausch AR, and Janmey PA (2009). The mechanical cell. Current Biology 19, R745–R748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson Coon J (2010). Goodman and Gilman’s the Pharmacological Basis of Therapeutics. Focus on Alternative and Complementary Therapies.
- Tien JYL, and Spicer AP (2005). Three vertebrate hyaluronan synthases are expressed during mouse development in distinct spatial and temporal patterns. Developmental Dynamics 233, 130–141. [DOI] [PubMed] [Google Scholar]
- Toole BP, ed. (1981). Glycosaminoglycans in Morphogenesis (In: Hay ED (eds) Cell Biology of Extracellular Matrix. Springer, Boston, MA.). [Google Scholar]
- Toole BP (2001). Hyaluronan in morphogenesis. Semin Cell Dev Biol 12, 79–87. [DOI] [PubMed] [Google Scholar]
- Trushko A, Di Meglio I, Merzouki A, Blanch-Mercader C, Abuhattum S, Guck J, Alessandri K, Nassoy P, Kruse K, Chopard B, et al. (2020). Buckling of an Epithelium Growing under Spherical Confinement. Dev Cell 54, 655–668.e656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turlier H, Audoly B, Prost J, and Joanny J-F (2014). Furrow Constriction in Animal Cell Cytokinesis. Biophysical Journal 106, 114–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varner VD, and Nelson CM (2014). Cellular and physical mechanisms of branching morphogenesis. Development 141, 2750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vigetti D, Karousou E, Viola M, Deleonibus S, De Luca G, and Passi A (2014). Hyaluronan: biosynthesis and signaling. Biochim Biophys Acta 1840, 2452–2459. [DOI] [PubMed] [Google Scholar]
- Wallingford JB, Fraser SE, and Harland RM (2002). Convergent Extension: The Molecular Control of Polarized Cell Movement during Embryonic Development. Dev Cell 2, 695–706. [DOI] [PubMed] [Google Scholar]
- Walsh EC, and Stainier DYR (2001). UDP-Glucose Dehydrogenase Required for Cardiac Valve Formation in Zebrafish. Science 293, 1670. [DOI] [PubMed] [Google Scholar]
- Wan Y, Otsuna H, Chien CB, and Hansen C (2012). FluoRender: An Application of 2D Image Space Methods for 3D and 4D Confocal Microscopy Data Visualization in Neurobiology Research. IEEE Pac Vis Symp, 201–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White RM, Sessa A, Burke C, Bowman T, LeBlanc J, Ceol C, Bourque C, Dovey M, Goessling W, Burns CE, et al. (2008). Transparent Adult Zebrafish as a Tool for In Vivo Transplantation Analysis. Cell Stem Cell 2, 183–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitfield TT (2015). Development of the inner ear. Current Opinion in Genetics & Development 32, 112–118. [DOI] [PubMed] [Google Scholar]
- Whitfield TT, Granato M, van Eeden FJ, Schach U, Brand M, Furutani-Seiki M, Haffter P, Hammerschmidt M, Heisenberg CP, Jiang YJ, et al. (1996). Mutations affecting development of the zebrafish inner ear and lateral line. Development 123, 241. [DOI] [PubMed] [Google Scholar]
- Wight TN (2017). Provisional matrix: A role for versican and hyaluronan. Matrix Biol 60–61, 38–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong F, Ma W, Hiscock Tom W., Mosaliganti Kishore R., Tentner Andrea R., Brakke Kenneth A., Rannou N, Gelas A, Souhait L, Swinburne Ian A., et al. (2014). Interplay of Cell Shape and Division Orientation Promotes Robust Morphogenesis of Developing Epithelia. Cell 159, 415–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong F, Tentner Andrea R., Huang P, Gelas A, Mosaliganti Kishore R., Souhait L, Rannou N, Swinburne Ian A., Obholzer Nikolaus D., Cowgill Paul D., et al. (2013). Specified Neural Progenitors Sort to Form Sharp Domains after Noisy Shh Signaling. Cell 153, 550–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamaguchi N, Colak-Champollion T, and Knaut H (2019). zGrad is a nanobody-based degron system that inactivates proteins in zebrafish. eLife 8, e43125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q, Xue S-L, Chan CJ, Rempfler M, Vischi D, Maurer-Gutierrez F, Hiiragi T, Hannezo E, and Liberali P (2021). Cell fate coordinates mechano-osmotic forces in intestinal crypt formation. Nature Cell Biology 23, 733–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, and Gerig G (2006). User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. NeuroImage 31, 1116–1128. [DOI] [PubMed] [Google Scholar]
- Zhou J, Kim HY, and Davidson LA (2009). Actomyosin stiffens the vertebrate embryo during crucial stages of elongation and neural tube closure. Development 136, 677. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Zip file containing the source code in Python for the 2D vertex model, a Readme file describing usage, and sample output.
3D rendered time-lapse images of the otic vesicle (OV) showing semicircular canal morphogenesis involving bud formation (black asterisks), extension and fusion using two Tg(βActin:membrane-Citrine) embryos (change at 59 hpf). OV lumen is coloured (blue) in the first and last frame. Bud fusion demarcates the hubs for the anterior, posterior and lateral semicircular canals (marked by pink, green and white circular arrows respectively). Anterior to the left and dorso-lateral into the plane of view. Scale bar, 50 μm.
Side and transverse views of 3D rendered time-lapse images of an anterior bud using Tg(βActin:membrane-mCherry) embryo. Longitudinal (blue), circumferential (orange) and radial (white) axes are labelled at 5 hpb. Scale bar, 10 μm.
Side and transverse views (maximum intensity projections) of time-lapse images showing localization of F-actin (using Tg(βActin:Utrophin-mCherry)) and Myosin II (using Tg(βActin:myl12.1-eGFP)) in green. Membrane (in magenta) is labelled using Tg(βActin:membrane-Citrine) with F-Actin, and Tg(βActin:membrane-mCherry) with Myosin II. Scale bar, 10μm.
2D sections of lateral buds showing membrane tethers (white arrows) with mosaic membrane labelling (magenta), and the corresponding localization of F-actin (using Tg(βActin:Utrophin-mCherry)) and Myosin II (using Tg(βActin:myl12.1-eGFP)) in green at 4 hpb. Scale bar, 10 μm.
2D sections of two anterior buds showing tethers (red arrows) with E-Cadherin accumulation using Tg (Cdh1:Cdh1-sfGFP) at 6 hpb. Scale bar, 10 μm.
Equilibrium configurations of a bud section over ‘time’ (hours post budding), modelled via the 2D vertex model representing apical, lateral and basal tensions on the cell surfaces (grey arrows), and inward forces from cytocinches (green dots). ECM-bud volume and cytocinch frequency increase in time (as experimentally measured). X and Y axes are short and long respectively. Left panel is control, middle panel represents Hyaluronidase treatment (through reduction in bud-ECM volume), and right panel represents Cytochalasin D treatment (through removal of cytocinches), each at 7 hpb.
(A-E) Select time points of the OV using Tg(βActin:membrane-Citrine) showing 2D sections from two different z-depths. Dorso-lateral (DL) section shows formation of lateral buds (marked by white asterisks) and their extension (white arrows). Medio-ventral (MV) section shows anterior and posterior bud formation (pink and green asterisks respectively) and their extension (pink and green arrows respectively). Scale bar, 50 μm.
(F) Individual data points and mean±s.d. of bud lengths across time. In the absence of buds, lengths correspond to cell lengths. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(A-C), Representative examples of 3D-rendered OVs at select time points, stained with fluorescent in situ probes against ugdh (A), has3 (B), and col2a1a (C). Heat map represents fluorescent intensity with the same contrast for each probe across time points. Lateral buds are marked with white asterisks. Anterior and posterior buds are marked with yellow and cyan asterisks respectively. Anterior to the left and DL into the plane of view. Scale bar, 50 μm.
(D-F) Brightfield images of AB embryos injected with control morpholino (MO) and has3-specific MO-1 (E and E’) and MO-2 (F and F’). Scale bar, 500 μm.
(G) RT-PCR verification of has3-specific MO-2
(H-I) Representative examples of 3D-rendered OVs at 72 hpf from sibling control and ugdhm151/m151 mutant embryos labelled with membrane-NeonGreen mRNA (D and D’), and Tg(βActin:membrane-Citrine) embryos injected with control morpholino (MO) and has3-specific MO-1 (E and E’). Anterior and posterior pillars have formed and the ventro-lateral bud is extending (white arrow) in sibling control (D). All three pillars have formed in the control MO
(E). Genetically perturbed embryos do not have pillars (D’-E’). Anterior to the left and DL into the plane of view. Scale bar, 50 μm.
(J) Table showing the number of embryos over the total number measured with aberrant SCC morphogenesis in MO injections at 72 hpf.
(A) Composite of 2D sections of OVs showing Phalloidin and Laminin staining at 45, 51 and 57 hpf. Lateral, anterior and posterior buds from different z-depths are framed in white, yellow and cyan respectively. Contrast is different at different z depths to capture the dynamic range, and the same across control and treated embryos at the same z-depth. Scale bar, 50 μm.
(B-C) Composite of 2D sections of OVs showing HA, F-actin and Collagen 2 staining using HA-Binding Protein (HABP), Phalloidin and Anti-Col2a1a respectively, in control and HAase treated embryos at 57 hpf. Lateral, anterior and posterior buds from different z-depths are framed in white, yellow and cyan respectively. Contrast is different at different z depths to capture the dynamic range, and the same across control and treated embryos at the same z-depth. Scale bar, 50 μm.
(D) Illustration showing different sizes of dextran and alpha-Bungarotoxin (aBt) injected in the periotic space percolating into the bud-ECM.
(A and B) Maximum intensity projections at select time points from posterior buds showing localization of F-actin (using Tg(βActin:Utrophin-mCherry)) (A) and Myosin II (using Tg(βActin:myl12.1-eGFP)) (B) in green. Membrane (in magenta) is labelled using Tg(βActin:membrane-Citrine) in (A) and Tg(βActin:membrane-mCherry) in (B). Apical cell surfaces face OV lumen and basal cell surfaces face the bud-ECM. Scale bars, 10 μm.
(C and D) Individual data points and mean±s.d. of F-actin and Myosin II intensities at the basal and lateral surface normalized to the intensities at the apical surface over time. Each data point is an average from 3–6 cells per bud. ‘n’ denotes the number of buds.
(E) 2D sections showing protrusive membrane tethers (white arrows) in lateral buds using either F-actin (top) or Myosin II (middle and bottom) reporters and mosaic membrane labelling. Scale bar, 10 μm.
(A) Equilibrium configurations of a section of a bud, modelled via a 2D vertex model (n=10 cells) representing the apical, lateral and basal tensions on the cell surfaces (grey arrows, taken all as equal to unity), as well as inward forces (black arrows) from cytocinches (green dots) with increasing tension (Λ=0, Λ=1 and Λ=2 from left to right panels).
(B) Equilibrium configurations of a section of a bud with cytocinches only at the base (Λ=1), showing that this is not sufficient to drive anisotropic bud extension, as the monolayer is predicted to be locally spherical (due to isotropic tensions everywhere but at the base).
(C) Equilibrium configurations of a section of a bud with cytocinches (Λ=1), increased basal tension and decreased apical tension (same parameters as panel a otherwise), showing a better resistance of the epithelium to local deformations.
(D) Equilibrium configurations of a section of a bud with cytocinches (Λ=1), decreased basal tension and increased apical tension (same parameters as panel a otherwise), showing a worsened resistance of the epithelium to local deformations, and associated bud pinching.
(E and F) Predicted evolution of the bud radii in the long (blue) and short (orange) axes (experimental: dots, predictions: lines) (E), and their ratios representing bud anisotropy (F) (data in red, model in black, assuming a linear bud-ECM volume increase (3-fold) and temporal increase in fraction of cytocinches (see STAR Methods for details)), for different values of cytocinch tension Λ (left to right panels)). For low cytocinch tension Λ, the bud retains low anisotropy during growth under-estimating experimental anisotropy (left panels), while for high cytocinch tension (Λ=1.5), the model over-estimates bud anisotropy (right panels). Intermediate values of cytocinch tensions provide a good fit for the data (middle panel, Λ=1.0, to be compared to the best-fit value of Λ=0.8 shown in Figures 7E and 7F). Error bars show mean and s.d.
(G and H) Predicted evolution of bud anisotropies (data in red, model in black), assuming either a constant, non-varying ECM volume and temporal increase in fraction of cytocinches (see STAR Methods for details) for intermediate cytocinch tension Λ=0.8 (G), or a linear bud-ECM volume increase in time (3-fold) and constant fraction of cytocinches (see STAR Methods for details) for intermediate cytocinch tension Λ=0.8 (H). Error bars show mean and s.d.
(I and J) Same vertex model simulations under different boundary conditions, considering cells surroundings the bud as well as non-infinitely stiff binding kBM to the underlying basement membrane (BM) for these surrounding cells. For low binding to the BM, the surrounding cells can be pulled upwards to the hyaluronan-derived pressure, giving rise to unphysiological poorly defined bud shapes (I, kBM =0.1), however for higher binding we recover similar bud shapes to previous simulations (J, kBM = 1).
(A and C) 3D-rendered OVs using Tg(βActin:Utrophin-mCherry) at 54 hpf before and after Cytochalasin D (CytoD 1mM) treatment (A), and SMIFH2 (1mM) treatment (C). Anterior to the left and into the plane of view. Scale bar, 50 μm.
(B) Adjacent membrane angle change before and after CytoD injection. ‘n’ denotes the number of cell membrane angles. p values as labelled (Mann Whitney- U test).
(D) 2D sections of an anterior bud at 8 hpb using Tg(βActin:myl12.1-eGFP) before and after SMIFH2 treatment. Cytocinch is marked by white arrow before treatment. Cytocinch is lost after treatment. Scale bar, 10 μm.
(E and E’) Total number of cytocinch tethers (E) and adjacent membrane angles (E’) before and after SMIFH2 treatment. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(F and F’) Bud radii (F) and aspect ratios (F’) before and after SMIFH2 treatment. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
(G) Anterior bud volume before and after CytoD treatment. ‘n’ denotes the number of buds. p values as labelled (Mann Whitney- U test).
2D vertex model (top) and illustrations (bottom) showing the effects of HA-mediated isotropic extracellular pressure (purple arrows) and cytocinch-mediated anisotropic tissue resistance (green arrows) on bud and cell morphologies in control and perturbed conditions.
Data Availability Statement
Source code for the 2D vertex model is included in this paper’s supplemental information. Additional information needed to reanalyze the data reported in this paper will be available from the lead contact upon request.


