Connectivity-informed adaptive regularization for generalized outcomes

Abstract

One of the challenging problems in neuroimaging is the principled incorporation of information from different imaging modalities. Data from each modality are frequently analyzed separately using, for instance, dimensionality reduction techniques, which result in a loss of mutual information. We propose a novel regularization method, generalized ridgified Partially Empirical Eigenvectors for Regression (griPEER), to estimate associations between the brain structure features and a scalar outcome within the generalized linear regression framework. griPEER improves the regression coefficient estimation by providing a principled approach to use external information from the structural brain connectivity. Specifically, we incorporate a penalty term, derived from the structural connectivity Laplacian matrix, in the penalized generalized linear regression. In this work, we address both theoretical and computational issues and demonstrate the robustness of our method despite incomplete information about the structural brain connectivity. In addition, we also provide a significance testing procedure for performing inference on the estimated coefficients. Finally, griPEER is evaluated both in extensive simulation studies and using clinical data to classify HIV+ and HIV− individuals.

1. INTRODUCTION

Neuroimaging data usually include multiple data types, but most commonly, the analysis is performed separately for each data type. Implicit in the work of Randolph, Harezlak, & Feng (2012) is a framework for the simultaneous use of multiple data types. For instance, structural and/or functional connectivity measures can be viewed as prior knowledge about the structure of dependencies between brain regions in a linear model that estimates the association between brain region properties (e.g., cortical thickness) and a scalar outcome. Karas et al. (2019) demonstrated that using correct prior information significantly increases estimation accuracy. The statistical methodology, ridgified Partially Empirical Eigenvectors for Regression (riPEER) (Karas et al., 2019), incorporates such a predefined structure into a regression model, which minimizes the use of incorrect information. However, the estimation procedure in Karas et al. (2019) assumes that the response variable is normally distributed, which excludes, for instance, a binary response that indicates the presence/absence of a condition such as a disease or phenotype.

To fill this gap, we developed a variant of riPEER, named generalized ridgified Partially Empirical Eigenvectors for Regression (griPEER), which handles the outcomes coming from the exponential family of distributions. In the context of brain imaging, our approach can incorporate information from either a structural or functional connectivity matrix. Similar to the riPEER precursor, griPEER uses the predefined information across a whole range of scenarios—from full inclusion to complete exclusion. To achieve this, griPEER employs a penalized optimization approach with a flexible, parametrized penalty term with parameters chosen in a fully automated, data-driven manner.

Here, we work with a generalized linear regression model where the ith scalar outcome, y_i, belongs to the exponential family of distributions with the parameter θ_i. We consider only the canonical link functions and assume that θ = Xβ + Zb. Here, X denotes a matrix of covariates (e.g., demographic data) for which the prior information is not used, and Z is a matrix whose columns correspond to variables with at least a partially known structure. In this work, β includes the intercept and demographic data, and b represents the coefficients of the average cortical thickness of 66 brain regions. The associations between these cortical thickness measures are represented by a connectivity matrix that encodes a density of connections or the average fractional anisotropy (FA).

The use of structural information in image reconstruction and estimation has been implemented for over 50 years (Phillips, 1962; Bertero & Boccacci, 1998; Engl, Hanke, & Neubauer, 2000). If the object of interest is a function belonging to a class of, for example, differentiable functions, a differential operator-based penalty may be used to “regularize” or impose smoothness on the estimates (Huang, Shen, & Buja, 2008). This may improve the prediction and interpretability and is “efficient and sometimes essential” when many highly correlated predictors (Hastie, Buja, & Tibshirani, 1995) are present. When the object of estimation is a vector, the penalties are very often constructed based on ℓ₁ and ℓ₂ norms as implemented in LASSO (Tibshirani, 1996), adaptive LASSO (Zou, 2006), ridge regression (Tikhonov, 1963) and elastic net (Zou & Hastie, 2005), to name just a few.

There is no unique method or approach to regularize a particular model in different applications, and the final construction depends strongly on the context. If the coefficients are sparse or they occur in blocks, using the ℓ₁ norm to constrain them (as in the LASSO) or constrain the difference of adjacent coefficients (as in the fused LASSO) is useful (Tibshirani et al., 2005). A more generalized fused LASSO with two ℓ₁ norms could also be applied: one constraining the coefficients and one their pairwise differences (Xin et al., 2016).

When structure among the variables is more intricate, and some (possibly imprecise) knowledge is available, less generic penalization schemes are more appropriate (Slawski, Castell, & Tutz, 2010; Tibshirani & Taylor, 2011), for example, a p × p adjacency matrix representing known connections, or “edges,” between p nodes in a graph. This matrix can inform a model that aims to estimate the relationship between an outcome and a vector of p values at the graph nodes. More specifically, the adjacency matrix is used to define the graph Laplacian matrix, which represents differences between nodes (Chung, 2005) and may be used to penalize the process of estimating regression coefficients, b.

For any p × p matrix Q, defining a penalty of the form λb^⊤Qb, where λ is a nonnegative regularization parameter, constitutes the essence of the methods of Li & Li (2008) and Karas et al. (2019). Using a penalty of this form also links the considered optimization problem with the theory of mixed-effects models in which b is assumed to be a random-effects vector with distribution $\mathcal{N}(0,{\sigma }_b^2{Q}^{-1})$, for some ${\sigma }_b^2>0$. This, in turn, reveals a connection with the Bayesian approach, where the distribution is treated as a prior on b, as in Maldonado (2009).

However, Q may not be invertible as is the case when Q is defined as Laplacian or normalized Laplacian (Chung, 2005). In addition, a single multiplicative parameter, λ, adjusts the trade-off between model fit and penalty terms but cannot change the regularization pattern, that is, the shape of the set {b: penalty(b) = const} is preserved. When Q is misspecified (i.e., is not informative), this lack of adaptivity may significantly degrade performance below that offered by an uninformed penalty such as ridge regression or LASSO (Karas et al., 2019).

Both these issues were considered in Karas et al. (2019), which does not assume that Q is exactly the true signal precision matrix, $\mathbb{Q}$, but is merely “close.” It is important to notice that brain connectivities are rather rough approximations to the truly complex brain network structure, and it is unrealistic to assume that all the entries reflect some universal “truth” in any given sample. Moreover, the multistep procedure of quantifying the diffusion tensor imaging-based structural brain connectivity itself can produce a significant number of false positives. Increasing the flexibility of the regularization process is therefore a natural step, and Karas et al. (2019) achieve that by extending the space of possible precision matrices and assuming $b\sim \mathcal{N}\left(0,{\sigma }_b^2(Q+a{I}_p{)}^{-1}\right)$. For a > 0, such modification of Q is invertible and can therefore be directly used in the estimation procedure. The resulting penalty, λb^⊤(Q + aI_p)b, has an equivalent form ${\lambda }_Q{b}^{\mathsf{T}}Qb+{\lambda }_R\Vert b{\Vert }_2^2$, and the connection with a specific linear mixed model enables the selection of λ_Q and X_R.

The approach by Karas et al. (2019) assumes the response variable to be normally distributed and hence not suitable for categorical outcomes. Here, we extend the concept of riPEER’s penalty function to the case when the distribution of the response variable is a member of a one-parameter exponential family of distributions. The proposed estimation method, griPEER, is of the form:

$$\left[\begin{array}{c}\hfill {\widehat{\beta }}^{\text{gP}}\hfill \\ \hfill {\widehat{b}}^{\text{gP}}\hfill \end{array}\right]≔\underset{\beta ,b}{\text{argmin}}\left\{-2loglik\left(\beta ,b\mid y\right)+{\lambda }_Q{b}^{T}Qb+{\lambda }_R\Vert b{\Vert }_2^2\right\},$$ (1)

where loglik(β, b ∣ y) is a log-likelihood. Here, the term −2loglik(β, b ∣ y) is used to fit the model to the response distribution, while the parameters λ_Q and λ_R are chosen based on the connection between the optimization problem and the generalized linear mixed model; this is formulated explicitly in Section 2. It is important to emphasize that these parameters not only determine the trade-off between the model fit and the penalty term but also the form of the penalty. More precisely, if λ_Q is large relative to λ_R, then the connectivity information has a large role in the estimation process. Conversely, when λ_Q is small relative to λ_R, the penalty is equal in all coordinates, as with ridge regression.

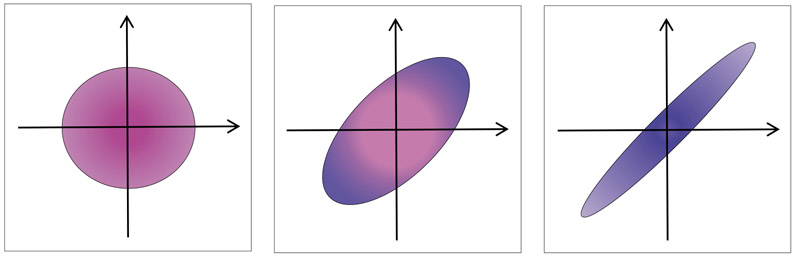
We illustrate this in a simple example with p = 2 variables and prior information stating that these variables are connected. The solution structure depends on the shape of level curve of penalty function as illustrated by three scenarios shown in Figure 1. If the relationship between variables, as represented in Q, is reflected in the data and related to the outcome y, then griPEER will tend to choose relatively large λ_Q, which links the coefficients in b (see Figure 1c). The other extreme is when the structure in Q is not informative for the relationship between y and Z. In such cases, griPEER will select a relatively large λ_R inducing a ridge-like penalty that ignores Q (see Figure 1a).

Figure 1:

Shapes of the set $\{b:{\lambda }_Q{b}^{\mathsf{T}}Qb+{\lambda }_R\Vert b{\Vert }_2^2=1\}$ (level curve) for various pairs of regularization parameters: (a) assumed strong connections between variables is neglected, (b) moderate tendency for coefficients of the solution to be similar to each other and (c) strong tendency for coefficients of the solution to be similar to each other.

The remainder of this work is organized as follows. In Section 2, we formulate our statistical model, investigate the special case of binomial distribution and discuss the equivalence between generalized linear mixed models (GLMMs) and penalized optimization problems. We also describe the penalty term construction from the graph theory point of view. The estimation procedure used to select the optimal regularization parameters is introduced in Section 3, while Section 4 addresses the selection of response-relevant variables. The extensive simulations showing very good performance of griPEER in the context of estimation accuracy and variables selection (under various scenarios illustrating the impact of inaccurate prior information) are reported in Section 5. Finally, in Section 6, we apply our methodology to study associations between cortical thickness and HIV disease. The conclusions and a discussion are summarized in Section 7.

2. STATISTICAL MODEL

We address the problem of estimation in a penalized generalized linear model where the penalty term is derived using structural connectivity information. This information is represented by a p × p symmetric matrix whose nondiagonal elements are nonnegative and whose diagonal elements are set to zero. This adjacency matrix or connectivity matrix is denoted by $\mathcal{A}$. The corresponding graph Laplacian matrix, Q, which defines the penalty term of (1) is explained next, followed by specific details about the considered statistical model.

2.1. The Graph Laplacian, Q

We are interested in modelling the association between a scalar outcome, y, and a set of p predictor variables that are measured at each graph node. We assume that information about connections between these variables—that is, strengths of the connections between the nodes—can be summarized by a (symmetric) p × p adjacency matrix $\mathcal{A}=[a_{ij}]$, 1 ≤ i, j≤ p that has nonnegative entries and zeros on the diagonal. We denote the jth node degree as $d_j≔{\sum }_i{a}_{ij}$ and define the degree matrix as D: = diag(d₁, … , d_p).

Following Chung (2005), we define the unnormalized Laplacian, Q_u, corresponding to $\mathcal{A}$ simply as $Q_u≔D-\mathcal{A}$. This matrix is always positively semidefinite. It is also singular as, for the vector of ones, 1 := [1, …, 1]^⊤, we have $1^{\mathsf{T}}{Q}_{u}1=1^{\mathsf{T}}D1-1^{\mathsf{T}}\mathcal{A}1={\sum }_i{d}_i-{\sum }_i{d}_i=0$.

A penalty of the form b^TQ_ub, as in (1), can be intuitively understood by the following simple formula: for any adjacency matrix, $\mathcal{A}$, and its unnormalized Laplacian, Q_u,

$$b^T{Q}_{u}b=\sum _{i,j}{a}_{ij}{\left(b_i-b_j\right)}^2.$$ (2)

That is, if the term b^TQ_ub is used in the optimization problem (1), the squared differences of coefficients are penalized in a manner that is proportional to the strengths of connections between them. Consequently, coefficients corresponding to nodes having many stronger connections (i.e., higher degree nodes) are constrained more than others.

In order to allow a smaller number of nodes with larger d_i to have more extreme values, we employed the normalized Laplacian, Q, which is obtained by dividing each column and row of Q_u by the square root of the corresponding node’s degree. As a result, the property (2), with Q instead of Q_u, takes the form $b^{T}Qb={\sum }_{i,j:a_{ij}\ne 0}{a}_{ij}{\left(\frac{b_i}{\sqrt{d_i}}-\frac{b_j}{\sqrt{d_j}}\right)}^2$. Q has ones on the diagonal and, just like the unnormalized Laplacian, is a symmetric, positive semidefinite, and singular matrix.

2.2. Statistical Model in General Form

Consider the general setting where y is an n × 1 vector of observations, and the design matrices, X and Z, are n × p and n × m matrices, respectively. The columns of X represent the p covariates, and the rows are denoted by X_i. Similarly, the columns of Z correspond to m variables, or graph nodes, for which some connectivity information may be available; the rows are denoted by Z_i. We assume that unknown vectors b and β exist such that, for each i∈{1, … , n}, y_i is the member of a one-parameter exponential family of distributions described by

$$f(y_i)=\text{exp}\{y_i{\theta }_i-\psi ({\theta }_i)+c(y_i,\phi )\},$$ (3)

where θ_i := X_iβ + Z_ib is a subject-specific parameter. The expression in (3) includes exponential, binomial, Poisson and Laplace densities.

It can be shown that, for the exponential family of distributions, the mean of y_i is simply given by the first derivative of ψ at the point θ_i, while the variance could be expressed as the second derivative of ψ, that is,

$$\mathbb{E}\left(y_i\right)={\psi }^{\prime }({\theta }_i),\text{var}\left(y_i\right)={\psi }^{″}({\theta }_i).$$ (4)

Moreover, the log-likelihood function is

$${\text{loglik}}_{\psi ,c}\left(\beta ,b\mid y\right)=\sum _{i=1}^n\{y_i(X_i\beta +Z_{i}b)-\psi (X_i\beta +Z_{i}b)+c(y_i)\}$$ (5)

and it provides a core for the methodology presented in this work. Indeed, we define griPEER as a solution to the following optimization problem

$$\left[\begin{array}{c}\hfill {\widehat{\beta }}^{\text{gP}}\hfill \\ \hfill {\widehat{b}}^{\text{gP}}\hfill \end{array}\right]≔\underset{\beta ,b}{\text{argmin}}\left\{-2l_{\psi }\left(\beta ,b\mid y\right)+{\lambda }_Q{b}^{\mathsf{T}}Qb+{\lambda }_R\Vert b{\Vert }_2^2\right\},$$ (6)

where $l_{\psi }\left(\beta ,b\mid y\right)≔{\sum }_{i=1}^n\left\{y_i(X_i\beta +Z_{i}b)-\psi (X_i\beta +Z_{i}b)\right\}$ consists of the terms of log-likelihood function (5) depending on b and β. Here, λ_Q and λ_R are regularization parameters, which are selected automatically, as described in Section 3.

2.3. The Special Case: Binomial Distribution

This subsection focuses on one special choice of a density function, the binomial distribution. This case is further outlined in Sections 5 (binomial outcome in the simulations) and 6 (binomial distribution application to neuroimaging data).

Similar to the classical logistic regression theory, we assume that the response, y_i, takes the value 1 with probability e^θ_i/(e^θ_i + 1) and 0 with probability 1/(e^θ_i + 1). Consequently, the density function, f(y_i), is given by

$$f\left(y_i\right)=\text{exp}\left\{y_i{\theta }_i-\text{ln}(1+e^{{\theta }_i})\right\},$$ (7)

which is a member of the exponential family of distributions (3) with ψ(θ_i) = ln(1 + e^θ_i) and c(y_i) = 0. We also have

$$\{\begin{array}{c}\mathbb{E}\left(y_i\right)={\psi }^{\prime }({\theta }_i)=e^{{\theta }_i}∕(e^{{\theta }_i}+1)\hfill \\ \text{var}\left(y_i\right)={\psi }^{″}({\theta }_i)=e^{{\theta }_i}∕(e^{{\theta }_i}+1{)}^2\hfill \end{array}\phantom{\}}$$ (8)

.

From this, ${\theta }_i=\text{ln}\left(\frac{\mathbb{E}(y_i)}{1-\mathbb{E}(y_i)}\right)$ that, with the assumption θ = Xβ + Zb adopted earlier, yields the canonical link for logistic regression, the logit function.

2.4. Equivalence Between GLMM and Two Optimization Problems

The optimization problem in (6) can be strongly connected with the specific GLMM formulation. Indeed, suppose that β and b are vectors of fixed and random effects, respectively. Moreover, y_i ∣ b are independent, and consequently, $f(y\mid b)={\prod }_{i=1}^{n}f\left(y_i\mid b\right)$, f(y_i∣b) = exp {y_i(X_iβ + Z_ib)–ψ(X_iβ + Z_ib) + c(y_i)}, for some (known) functions ψ, c and i = 1, … , n. Moreover, $b\sim \mathcal{N}\left(0,{\tilde{Q}}_{\lambda }^{-1}\right)$, where ${\tilde{Q}}_{\lambda }≔{\lambda }_{Q}Q+{\lambda }_R{I}_p$ for some unknown, positive parameters λ_Q and λ_R.

To see this correspondence, assume that the parameters λ_Q and λ_R have been estimated, say as $\widehat{\lambda }≔[{\widehat{\lambda }}_Q,{\widehat{\lambda }}_R{]}^{\mathsf{T}}$, and these values are used to obtain β and b. One can proceed by treating both fixed and random effects as parameters and finding maximum likelihood estimates by maximizing (with respect to β, b) the density function

$$\begin{gathered} f(y,b)=f(y\mid b)f(b)=\prod _{i=1}^n\{f(y_i\mid b)\}f(b) \\ \propto \text{exp}\left\{\sum _{i=1}^n\left[y_i{\theta }_i-\psi ({\theta }_i)\right]-\frac{1}{2}{b}^{\mathsf{T}}{\tilde{Q}}_{\widehat{\lambda }}b\right\}, \end{gathered}$$ (9)

where θ_i = X_iβ + Z_ib, for i = 1, … , n. Taking the logarithm of the above leads directly to the objective of the optimization problem (6).

We now derive a constrained optimization problem that is equivalent to (6) and reveals the impact of the regularization parameters on the solution from a slightly different perspective. For this, suppose that $\left[\begin{array}{c}\hfill \widehat{\beta }\hfill \\ \hfill \widehat{b}\hfill \end{array}\right]$ is the solution to (6) for given parameters λ_Q and λ_R. Then, we can define $c≔{\lambda }_Q{\widehat{b}}^{\mathsf{T}}Q\widehat{b}+{\lambda }_R\Vert \widehat{b}{\Vert }_2^2\ge 0$. One can check that $\left[\begin{array}{c}\hfill \widehat{\beta }\hfill \\ \hfill \widehat{b}\hfill \end{array}\right]$ also solves the problem

$$\begin{gathered} \underset{\beta ,b}{\text{argmin}}\left\{-2l_{\psi }\left(\beta ,b\mid y\right)+{\lambda }_Q{b}^{\mathsf{T}}Qb+{\lambda }_R\Vert b{\Vert }_2^2\right\} \\ \text{subject to}{\lambda }_Q{b}^{\mathsf{T}}Qb+{\lambda }_R\Vert b{\Vert }_2^2=c. \end{gathered}$$ (10)

The multiplicative factor may be neglected, as well as the term ${\lambda }_Q{b}^{\mathsf{T}}Qb+{\lambda }_R\Vert b{\Vert }_2^2$, which is constant in the feasible set. This yields

$$\begin{gathered} \underset{\beta ,b}{\text{argmax}}{l}_{\psi }\left(\beta ,b\mid y\right) \\ \text{subject to}{\lambda }_Q{b}^{\mathsf{T}}Qb+{\lambda }_R\Vert b{\Vert }_2^2=c. \end{gathered}$$ (11)

This formulation quantifies our intuition presented in the introduction and the corresponding Figure 1, where griPEER selects the estimates by taking the maximal likelihood value on a set whose shape is explicitly regularized by the parameters λ_Q and λ_R.

3. A NEW ESTIMATION ALGORITHM

To select the optimal values of λ_Q and λ_R, we employ the corresponding GLMM. The likelihood function, $\mathcal{L}\left(\beta ,\lambda \mid y\right)$, is given by

$$\begin{gathered} \mathcal{L}\left(\beta ,\lambda \mid y\right)={\int }_{{\mathbb{R}}^p}{f}_{\beta ,\lambda }(y\mid b)f_{\beta ,\lambda }(b)db \\ ={\int }_{{\mathbb{R}}^p}{\mid 2\pi {\tilde{Q}}_{\lambda }\mid }^{-\frac{1}{2}}\text{exp}\left\{\sum _{i=1}^n\left[y_i(X_i\beta +Z_{i}b)-\psi (X_i\beta +Z_{i}b)-c(y_i)\right]-\frac{1}{2}{b}^{\mathsf{T}}{\tilde{Q}}_{\lambda }b\right\}db. \end{gathered}$$ (12)

Unfortunately, obtaining the maximum of $\mathcal{L}$ with respect to β and λ is complicated by the fact that there is no closed-form solution to the multidimensional integral in (12). However, several approaches to find a solution have been proposed. Breslow & Clayton (1993) proposed a general method based on penalized quasilikelihood (PQL) for the estimation of fixed effects and the prediction of random effects. Wolfinger & O’connell (1993) investigated the pseudolikelihood (PL) approach, which is closely related to the Laplace approximation of $\mathcal{L}$. Other proposals include the Adaptive Gaussian Quadrature to approximate integrals with respect to a given kernel (Pinheiro & Chao, 2006) and an Markov chain Monte Carlo-based procedure (Zeger & Karim, 1991).

In this work, we focus on the Wolfinger PL approach, which is recognized as being fast and computationally efficient. It relies on the first-order Taylor series approximation and uses the linear mixed model (LMM) proxy in the iterative process: At each iteration, the updates of β and b are based on the variance–covariance parameters of random effects. The steps are repeated until the convergence criteria are met.

The procedure used here differs from Wolfinger & O’connell (1993) in how the updates of β and b are obtained. Unlike the Wolfinger PL approach, which uses the solution to the mixed-model equations to update β and b, we employ the correspondence between GLMM and the griPEER optimization problem, as described in Section 2.4. Specifically, the (k – 1)-step estimates of λ_Q and λ_R (i.e., $\stackrel{[\mathrm{k}-1]}{{\lambda }_{\mathrm{Q}}}$ and $\stackrel{[\mathrm{k}-1]}{{\lambda }_{\mathrm{R}}}$) are used to obtain the (k – 1)-step estimates of β and b (i.e., $\stackrel{[\mathrm{k}-1]}{\beta }$ and $\stackrel{[\mathrm{k}-1]}{b}$) via the solution to (6). Consequently, we can define $\stackrel{[\mathrm{k}-1]}{{\theta }_i}≔X_i\stackrel{[\mathrm{k}-1]}{\beta }+Z_i\stackrel{[\mathrm{k}-1]}{b}$.

Details of our estimation procedure are as follows. Using the Taylor approximation of function ψ′ at point $\stackrel{[\mathrm{k}-1]}{{\theta }_i}$, we get

$${\psi }^{\prime }({\theta }_i)\approx {\psi }^{\prime }(\stackrel{[\mathrm{k}-1]}{{\theta }_i})+{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_i})\cdot ({\theta }_i-\stackrel{[\mathrm{k}-1]}{{\theta }_i})$$ (13)

and therefore, from (4)

$$[{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_i}){]}^{-1}\cdot (\mathbb{E}\left(y_i\mid \beta ,b\right)-{\psi }^{\prime }(\stackrel{[\mathrm{k}-1]}{{\theta }_i}))+\stackrel{[\mathrm{k}-1]}{{\theta }_i}\approx {\theta }_i.$$ (14)

We now define a random variable $\stackrel{[\mathrm{k}]}{y_i}≔[{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_i}){]}^{-1}\cdot (y_i-{\psi }^{\prime }(\stackrel{[\mathrm{k}-1]}{{\theta }_i}))+\stackrel{[\mathrm{k}-1]}{{\theta }_i}$. The main step now is the assumption that the distribution of $\stackrel{[\mathrm{k}]}{y_i}$ can be well approximated by a normal density. Computation of mean and variance of $\stackrel{[\mathrm{k}]}{y_i}$ immediately yields

$$\mathbb{E}(\stackrel{[\mathrm{k}]}{y_i}\mid b)\approx {\theta }_i=X_i\beta +Z_{i}b,\text{and}\text{var}(\stackrel{[\mathrm{k}]}{y_i}\mid b)=[{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_i}){]}^{-2}{\psi }^{″}({\theta }_i)\approx [{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_i}){]}^{-1}.$$ (15)

The assumption that $\stackrel{[\mathrm{k}]}{y_i}$ is approximately normally distributed allows us to replace the GLMM formulation in the kth step by an LMM where β is a vector of fixed effects and b is a vector of random effects, $\stackrel{[\mathrm{k}]}{y}=[XZ]\left[\begin{array}{c}\hfill \beta \hfill \\ \hfill b\hfill \end{array}\right]+\stackrel{[\mathrm{k}]}{\epsilon }$, $\stackrel{[\mathrm{k}]}{\epsilon }\sim \mathcal{N}(0,\stackrel{[\mathrm{k}]}{W})$, where $\stackrel{[\mathrm{k}]}{W}≔diag([{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_1}){]}^{-1},\dots ,[{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_n}){]}^{-1})$, $b\sim \mathcal{N}(0,{\tilde{Q}}_{\lambda }^{-1})$, where ${\tilde{Q}}_{\lambda }$ was defined before.

We denote by $\stackrel{[\mathrm{k}]}{\mathcal{P}}≔I-X(X^{\mathsf{T}}\stackrel{[\mathrm{k}]}{W^{-1}}X{)}^{-1}{X}^{\mathsf{T}}\stackrel{[\mathrm{k}]}{W^{-1}}$ the $\stackrel{[\mathrm{k}]}{W}$-weighted projection onto the orthogonal complement of the columns of X. Now, defining $\stackrel{[\mathrm{k}]}{\tilde{y}}≔\stackrel{[\mathrm{k}]}{\mathcal{P}}\stackrel{[\mathrm{k}]}{y}$, $\stackrel{[\mathrm{k}]}{X}≔\stackrel{[\mathrm{k}]}{\mathcal{P}}X$ and $\stackrel{[\mathrm{k}]}{Z}≔\stackrel{[\mathrm{k}]}{\mathcal{P}}Z$ we assume that

$$\stackrel{[\mathrm{k}]}{\tilde{y}}\sim \mathcal{N}\left(0,\stackrel{[\mathrm{k}]}{V}{}_{\lambda }\right),\text{for}\stackrel{[\mathrm{k}]}{V}{}_{\lambda }≔\stackrel{[\mathrm{k}]}{Z}{\tilde{Q}}_{\lambda }^{-1}\stackrel{[\mathrm{k}]\mathsf{T}}{Z}+\stackrel{[\mathrm{k}]}{W}.$$ (16)

Maximizing the log-likelihood for $\stackrel{[\mathrm{k}]}{\tilde{y}}$, that is, the function $l(\stackrel{[\mathrm{k}]}{\tilde{y}};\lambda )≔-\frac{n}{2}\text{ln}2\pi -\frac{1}{2}\text{ln}\mid \stackrel{[\mathrm{k}]}{V}{}_{\lambda }\mid -\frac{1}{2}\stackrel{[\mathrm{k}]}{{\tilde{y}}^{\mathsf{T}}}\stackrel{[\mathrm{k}]}{V_{\lambda }^{-1}}\stackrel{[\mathrm{k}]}{\tilde{y}}$, leads directly to the optimization problem

$$\left[\begin{array}{c}\hfill \stackrel{[\mathrm{k}]}{{\lambda }_Q}\hfill \\ \hfill \stackrel{[\mathrm{k}]}{{\lambda }_R}\hfill \end{array}\right]≔\underset{\lambda \underset{¯}{\succ }0}{\text{armin}}\left\{\text{ln}\mid \stackrel{[\mathrm{k}]}{V}{}_{\lambda }\mid +\stackrel{[\mathrm{k}]}{{\tilde{y}}^{\mathsf{T}}}\stackrel{[\mathrm{k}]}{V_{\lambda }^{-1}}\stackrel{[\mathrm{k}]}{\tilde{y}}\right\},$$ (17)

where λ ≽ 0 refers to {(λ_Q, λ_R) : λ_Q ≥ 0, λ_R ≥ 0}. The following proposition helps us to rewrite the objective of (17). We provide proof in the Supplementary Material of section 8.

Proposition 1. Let $\stackrel{[\mathrm{k}]}{\Omega }≔\stackrel{[\mathrm{k}]\mathsf{T}}{Z}\stackrel{[\mathrm{k}]-1}{W}\stackrel{[\mathrm{k}]}{Z}$ and $\stackrel{[\mathrm{k}]}{q}≔\stackrel{[\mathrm{k}]\mathsf{T}}{Z}\stackrel{[\mathrm{k}]-1}{W}\stackrel{[\mathrm{k}]}{\tilde{y}}$. Then

• $\text{ln det}\stackrel{[\mathrm{k}]}{V_{\lambda }}=\text{det}({\tilde{Q}}_{\lambda }+\stackrel{[\mathrm{k}]}{\Omega })-\text{ln det}{\tilde{Q}}_{\lambda }+\text{ln det}(\stackrel{[\mathrm{k}]}{W})$,

• $\stackrel{[\mathrm{k}]\mathsf{T}}{\tilde{y}}\stackrel{[\mathrm{k}]}{V_{\lambda }^{-1}}\stackrel{[\mathrm{k}]}{\tilde{y}}=-\stackrel{[\mathrm{k}]\mathsf{T}}{q}({\tilde{Q}}_{\lambda }+\stackrel{[\mathrm{k}]}{\Omega }{)}^{-1}\stackrel{[\mathrm{k}]}{q}+\stackrel{[\mathrm{k}]}{{\tilde{y}}^{\mathsf{T}}}\stackrel{[\mathrm{k}]}{W^{-1}}\stackrel{[\mathrm{k}]}{\tilde{y}}$.

This proposition makes it possible to reformulate (17) and define the kth step update, $\stackrel{[\mathrm{k}]}{{\lambda }_Q}$ and $\stackrel{[\mathrm{k}]}{{\lambda }_R}$, as

$$\underset{\lambda ⪰0}{\text{armin}}\{\text{ln det}\{({\tilde{Q}}_{\lambda }+\stackrel{[\mathrm{k}]}{\Omega }){\tilde{Q}}_{\lambda }^{-1}\}-\stackrel{[\mathrm{k}]\mathsf{T}}{q}({\tilde{Q}}_{\lambda }+\stackrel{[\mathrm{k}]}{\Omega }{)}^{-1}\stackrel{[\mathrm{k}]}{q}\}.$$ (18)

It is important to use an efficient and accurate method to solve (18) as this problem appears in every step k and determines when the entire algorithm is terminated (i.e., when $\Vert \stackrel{[\mathrm{k}]}{\lambda }-\stackrel{[\mathrm{k}-1]}{\lambda }\Vert$ is sufficiently small). To achieve this, we have analytically derived the gradient and the Hessian of the objective function as detailed in the Supplementary Material. The final algorithm for selecting the regularization parameters is outlined here:

Algorithm 1. Finding regularization parameters in griPEER

$$\begin{gathered} \begin{array}{cc}\hfill & \mathrm{Input}:\text{matrices:}Z,X\text{and}Q;\text{vector:}y;\text{initial point:}\stackrel{[0]}{\lambda }≔[\stackrel{[0]}{{\lambda }_Q},\stackrel{[0]}{{\lambda }_R}{]}^{\mathsf{T}};\text{stop criterion:}\delta >0;\hfill \\ \hfill & \text{function which defines the density:}\psi ;k≔1\hfill \\ \hfill & \mathbf{do}\hfill \\ \hfill & \\ 1.\text{define}\stackrel{[\mathrm{k}-1]}{\beta }\text{and}\stackrel{[\mathrm{k}-1]}{b}\text{by solving:}\hfill \\ \hfill & \\ \underset{\beta ,b}{\text{argmin}}\left\{-2{\sum }_{i=1}^n\left[y_i(X_i\beta +Z_{i}b)-\psi (X_i\beta +Z_{i}b)\right]+\stackrel{[\mathrm{k}-1]}{{\lambda }_Q}{b}^{T}Qb+\stackrel{[\mathrm{k}-1]}{{\lambda }_R}\Vert b{\Vert }_2^2\right\};\hfill \\ \hfill & \\ 2.\stackrel{[\mathrm{k}-1]}{\theta }≔X\stackrel{[\mathrm{k}-1]}{\beta }+Z\stackrel{[\mathrm{k}-1]}{b},\stackrel{[\mathrm{k}]}{W}≔\text{diag}\left([{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_1}){]}^{-1},\dots ,[{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_n}){]}^{-1}\right);\hfill \\ \hfill & \\ 3.\text{define}\stackrel{[\mathrm{k}]}{y}\text{by putting}\stackrel{[\mathrm{k}]}{y_i}≔[{\psi }^{″}(\stackrel{[\mathrm{k}-1]}{{\theta }_i}){]}^{-1}\cdot (y_i-{\psi }^{\prime }(\stackrel{[\mathrm{k}-1]}{{\theta }_i}))+\stackrel{[\mathrm{k}-1]}{{\theta }_i},\text{for}i=1,\dots ,n;\hfill \\ \hfill & \\ 4.\stackrel{[\mathrm{k}]}{\mathcal{P}}≔\mathrm{I}-X(X^{\mathsf{T}}\stackrel{[\mathrm{k}]}{W^{-1}}X{)}^{-1}{X}^{\mathsf{T}}\stackrel{[\mathrm{k}]}{W^{-1}};\hfill \\ \hfill & \\ 5.\stackrel{[\mathrm{k}]}{\tilde{y}}≔\stackrel{[\mathrm{k}]}{\mathcal{P}}\stackrel{[\mathrm{k}]}{y},\stackrel{[\mathrm{k}]}{X}≔\stackrel{[\mathrm{k}]}{\mathcal{P}}X,\stackrel{[\mathrm{k}]}{Z}≔\stackrel{[\mathrm{k}]}{\mathcal{P}}Z;\hfill \\ \hfill & \\ 6.\stackrel{[\mathrm{k}]}{\Omega }≔\stackrel{[\mathrm{k}]}{TZ}\stackrel{[\mathrm{k}]-1}{W}\stackrel{[\mathrm{k}]}{Z},\stackrel{[\mathrm{k}]}{q}≔\stackrel{[\mathrm{k}]\mathsf{T}}{Z}\stackrel{[\mathrm{k}]-1}{W}\stackrel{[\mathrm{k}]}{\tilde{y}};\hfill \\ \hfill & \\ 7.\stackrel{[\mathrm{k}]}{\lambda }≔\underset{\lambda \underset{¯}{\succ }0}{\text{argmin}}\left\{\text{ln}\mid \left({\lambda }_{Q}Q+{\lambda }_R{\mathrm{I}}_p+\stackrel{[\mathrm{k}]}{\Omega }\right){\left({\lambda }_{Q}Q+{\lambda }_R{\mathrm{I}}_p\right)}^{-1}\mid -\stackrel{[\mathrm{k}]\mathsf{T}}{q}{\left({\lambda }_{Q}Q+{\lambda }_R{\mathrm{I}}_p+\stackrel{[\mathrm{k}]}{\Omega }\right)}^{-1}\stackrel{[\mathrm{k}]}{q}\right\};\hfill \\ \hfill & \\ 8.k\leftarrow k+1;\hfill \\ \hfill & \mathbf{while}\left\{\Vert \stackrel{[\mathrm{k}]}{\lambda }-\stackrel{[\mathrm{k}-1]}{\lambda }\Vert ∕\Vert \stackrel{[\mathrm{k}-1]}{\lambda }\Vert >\delta \right\}\hfill \end{array} \end{gathered}$$

To find the numerical solutions to problems in 1. and 7., we employed, respectively, the penalized (McIlhagga, 2016) and fsolve functions from the MATLAB Optimization Toolbox.

4. PROCEDURES FOR SIGNIFICANCE TESTING

Unlike the LASSO estimation procedure that produces a sparse set of regression coefficients but does not (without additional theory such as (Buhlmann, 2013; Zhao & Shojaie, 2016)) provide statistical significance testing, we employ two methods to identify variables that are significantly related to the response. In this section, we describe two such approaches that were implemented in our analysis. Both use the knowledge about the optimal regularization parameters described in the previous section. The first approach takes advantage of asymptotic properties of generalized linear model (GLM) estimates and constructs the asymptotic variance–covariance matrix in a similar fashion as proposed by Cessie & Houwelingen (1992) in the context of ridge-penalized logistic regression. The second approach applies the bootstrap method. Subsequently, we will refer to these two approaches as griPEER_asmp (the asymptotic-based approach) and griPEER_boot (the bootstrap-based approach). The numerical experiments presented in Section 5 suggest that griPEER_boot can achieve significantly greater power than griPEER_asmp when applied to structural brain imaging metrics. As the false discovery rates among variables labelled as relevant were similar in this brain imaging application, we applied only griPEER_boot in the analysis of cortical thickness in HIV-positive and HIV-negative participants (Section 6).

4.1. Asymptotic Variance–Covariance Matrix

We start by introducing some notations. Denote by $\mathcal{B}$ the m + p dimensional vector of true coefficients and by $\widehat{\mathcal{B}}$ its estimate given by the solution to (6). We will also need the matrix $\mathcal{X}≔[X,Z]$ and the vector $\theta ≔\mathcal{X}\mathcal{B}$. Moreover, we define a (m + p) × (m + p) penalty matrix as $\mathcal{Q}≔\phantom{[}[\frac{0_{m\times m}}{0_{p\times m}}\mid \frac{0_{m\times p}}{{\lambda }_{Q}Q+{\lambda }_R{I}_p}]$, where the nonnegative parameters λ_Q and λ_R are adjusted by Algorithm 1. To summarize, $\widehat{\mathcal{B}}$ is the solution to ${\text{argmin}}_{B\in {\mathbb{R}}^{p+m}}\left\{2{\sum }_i\psi ({\mathcal{X}}_{i}B)-2y^{\mathsf{T}}\mathcal{X}B+B^{\mathsf{T}}\mathcal{Q}B\right\}$, with ψ being a function from the definition of exponential family of distributions (3). Furthermore, the expressions we derive in this section include the diagonal matrix Ψ, defined as Ψ := diag{ψ″(θ₁), … , ψ′(θ_n)}.

Using the first-order Taylor approximation, as well as asymptotic properties of a GLM estimate, one can find that estimated asymptotic variance for $\widehat{\mathcal{B}}$ has a form ${\text{var}}_a\widehat{\mathcal{B}}={\left({\mathcal{X}}^{\mathsf{T}}\Psi \mathcal{X}+\mathcal{Q}\right)}^{-1}{\mathcal{X}}^{\mathsf{T}}\Psi \mathcal{X}{\left({\mathcal{X}}^{\mathsf{T}}\Psi \mathcal{X}+\mathcal{Q}\right)}^{-1}$. The derivation is based on Cessie & Houwelingen (1992), and it is described in Section 8.3 of the Supplementary Material. Based on the above formula, we propose a simple decision-making strategy where the ith covariate is labelled as statistically relevant if 0 is excluded from the confidence interval for its respective regression coefficient, that is, $0\notin \left({\widehat{\mathcal{B}}}_i-1.96\cdot \sqrt{({\text{var}}_a\widehat{\mathcal{B}}{)}_{ii}},{\widehat{\mathcal{B}}}_i+1.96\cdot \sqrt{({\text{var}}_a\widehat{\mathcal{B}}{)}_{ii}}\right)$. The entire procedure was presented as Algorithm 2.

Algorithm 2. Asymptotic confidence interval

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{matrices:}X,Z\text{and}Q,\text{estimate:}\widehat{\mathcal{B}}=\left[\begin{array}{c}\hfill {\widehat{\beta }}^{\text{gP}}\hfill \\ \hfill {\widehat{b}}^{\text{gP}}\hfill \end{array}\right],\text{optimal parameters:}{\lambda }_Q\text{and}{\lambda }_R,\text{function:}\psi \hfill \\ \hfill & 1.\text{Define:}\mathcal{X}≔[X,Z],\theta ≔\mathcal{X}\widehat{\mathcal{B}}\text{and}\Psi ≔\text{diag}\left\{{\psi }^{″}({\theta }_1),\dots ,{\psi }^{″}({\theta }_n)\right\}\hfill \\ \hfill & 2.\text{Construct}m+p\text{by}m+p\text{matrix:}\mathcal{Q}≔\phantom{[}[\frac{0_{m\times m}}{0_{p\times m}}\mid \frac{0_{m\times p}}{{\lambda }_{Q}Q+{\lambda }_R{\mathrm{I}}_p}]\hfill \\ \hfill & 3.\text{Calculate the variance of}\widehat{\mathcal{B}}:{\text{var}}_a\widehat{\mathcal{B}}≔{\left({\mathcal{X}}^{\mathsf{T}}\Psi \mathcal{X}+\mathcal{Q}\right)}^{-1}{\mathcal{X}}^{\mathsf{T}}\Psi \mathcal{X}{\left({\mathcal{X}}^{\mathsf{T}}\Psi \mathcal{X}+\mathcal{Q}\right)}^{-1}\hfill \\ \hfill & 4.\text{Define the asymptotic confidence interval (CI) for}{\mathcal{B}}_i\text{as}\hfill \\ \hfill & C{I}_{asmp}({\mathcal{B}}_i)≔\left({\widehat{\mathcal{B}}}_i-1.96\cdot \sqrt{({\text{var}}_a\widehat{\mathcal{B}}{)}_{ii}},{\widehat{\mathcal{B}}}_i+1.96\cdot \sqrt{({\text{var}}_a\widehat{\mathcal{B}}{)}_{ii}}\right)\hfill \end{array}$$

4.2. Bootstrap-Based Approach

Here, the variances of $\widehat{\mathcal{B}}$ coefficients were estimated based on bootstrap samples. Each such sample was created from n elements of y and n corresponding rows of Z and X, where indices were selected randomly by sampling with replacement. The dataset obtained in the jth repetition, X^[j], Z^[j] and y^[j], was then substituted according to (6) with λ_Q and λ_R selected by Algorithm 1 applied to the original dataset (i.e., λ_Q and λ_R were estimated only once). The percentile bootstrap confidence intervals, with the significance level α = 0.05, were defined based on all s estimates, ${\widehat{\mathcal{B}}}^{[1]},\dots ,{\widehat{\mathcal{B}}}^{[s]}$. The default value of s was set to 500 in this analysis and used in simulations performed in Section 5.3. Coefficients from the griPEER estimate whose confidence intervals do not contain zero are then considered response-related discoveries. We summarize this procedure as Algorithm.

Algorithm 3. Bootstrap confidence interval

$$\begin{gathered} \begin{array}{cc}\hfill & \mathrm{Input}:\text{matrices:}X,Z\text{and}Q,\text{column matrix of responses:}y,\text{optimal parameters:}{\lambda }_Q\text{and}{\lambda }_R,\hfill \\ \hfill & \text{the number of bootstrap samples:}s(\text{by defaults}s=500)\hfill \\ \hfill & \mathbf{For}j\in (1,\dots ,k)\mathrm{do}:\hfill \\ \hfill & \\ 1.\text{generate}j\text{th bootstrap sample},X^{[j]},Z^{[j]}\text{and}{y}^{[j]},\text{by sampling with replacement from}\hfill \\ \hfill & [X,Z,y]\hfill \\ \hfill & \\ 2.\text{get}j\text{th griPEER estimate},{\widehat{\mathcal{B}}}^{[j]},\text{for}Q,X^{[j]},Z^{[j]},y^{[j]}\text{and tuning parameters}{\lambda }_Q\text{and}{\lambda }_R\hfill \\ \hfill & \mathbf{End}\hfill \\ \hfill & \text{Define}C{I}_{boot}({\mathcal{B}}_i)-\text{the bootstrap CI for}{\mathcal{B}}_i-\text{as the percentile bootstrap confidence interval}\hfill \\ \hfill & \text{for}{\widehat{\mathcal{B}}}_i^{[1]},\dots ,{\widehat{\mathcal{B}}}_i^{[s]}\text{with the significance level}\alpha =0.05\hfill \end{array} \end{gathered}$$

5. NUMERICAL EXPERIMENTS

We conducted a simulation study to investigate the performance of griPEER when responses are modelled by binomial distribution and compared the results with the logistic ridge estimates.

5.1. Definitions

5.1.1. Matrix density

For a p × q matrix A, density is defined as a proportion of nonzero entries,

$$\text{dens}(A)≔\frac{1}{pq}\sum _{i,j}1\left\{\mid A(i,j)\mid >0\right\}.$$ (19)

5.1.2. Matrix dissimilarity

To quantify a dissimilarity between two p × q matrices, A and B, with dens(A) = dens(B), we defined

$$\text{diss}(A,B)≔\left(\sum _{i,j}1\left\{\mid A(i,j)-B(i,j)\mid >0\right\}\right)∕\left(2\sum _{i,j}1\left\{B(i,j)>0\right\}\right),$$ (20)

with values in the interval [0, 1]. If diss(A, B) = 0, then A = B, while diss(A, B) = 1 indicates that the positions of nonzero entries do not overlap.

5.2. Model Coefficient Estimation

5.2.1. Settings

5.2.1.1. “Informativeness” of the penalty term—

The simulation settings were designed to evaluate performance in a variety of situations ranging from an “observed” (available in estimation) connectivity matrix, ${\mathcal{A}}^{obs}$, that is fully informative to one that is completely noninformative. Here, “informativeness” refers to the amount of true dependencies among the variables that are represented in the matrix.

We denote ${\mathcal{A}}^{true}$ to be a matrix representing true connections between variables and ${\mathcal{A}}^{obs}$ to be a matrix that is observed and used in an estimation via griPEER. To express “informativeness” of ${\mathcal{A}}^{obs}$ with respect to ${\mathcal{A}}^{true}$, we used a measure of dissimilarity, $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})$, defined in (20). We have

• $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})=0$ indicates that ${\mathcal{A}}^{obs}$ is fully informative;

• $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})=1$ indicates that ${\mathcal{A}}^{obs}$ is noninformative;

• $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})\in (0,1)$ indicates that ${\mathcal{A}}^{obs}$ is partially informative.

5.2.1.2. Brain region connectivity context—

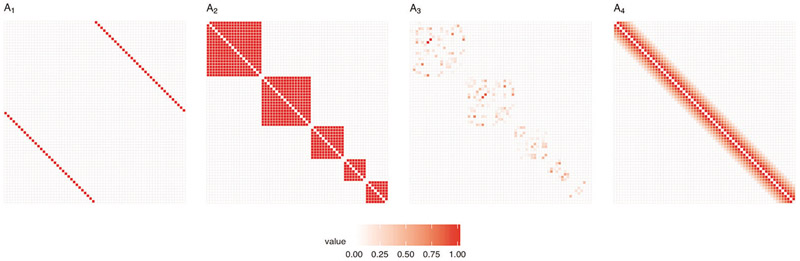
One may view ${\mathcal{A}}^{true}$ as an adjacency matrix of a graph representing the connections between brain regions, and our simulations scenarios are based on the following four interpretations regarding this structure.

• ${\mathcal{A}}_1$: “homologous regions.” ${\mathcal{A}}_1$ represents a case when brain regions, i and j, are connected (i.e., ${\mathcal{A}}_1(i,j)=1$) if and only if i and j are homologous brain regions from different hemispheres (Figure 2, first panel).

• ${\mathcal{A}}_2$: “modularity.” ${\mathcal{A}}_2$ represents a case when brain regions i and j are connected if and only if they belong to the same module with ${\mathcal{A}}_2(i,j)=1$ within the module and 0 otherwise (Figure 2, second panel).

• ${\mathcal{A}}_3$: “density of connections, masked.” ${\mathcal{A}}_3$ is defined based on the brain-imaging measure—density of connections between brain regions (see, Section 6)—and is then “masked” by modularity information. Here, ${\mathcal{A}}_3(i,j)$ equals the median of a density of connections between regions i and j if they belong to the same module. Otherwise, ${\mathcal{A}}_3(i,j)≔0$ (Figure 2, third panel)

• ${\mathcal{A}}_4$: “neighbouring regions.” ${\mathcal{A}}_4$ represents a case when brain regions i and j are connected if they are in close spatial proximity $({\mathcal{A}}_4(i,j)>0)$. Otherwise, they are not connected $({\mathcal{A}}_4(i,j)≔0)$ (Figure 2, last panel).

Figure 2:

Matrices used in the simulation study to construct ${\mathcal{A}}^{true}$. Presented are variants for p = 66 (based on the Desikan–Killiany atlas (Desikan et al., 2006)). ${\mathcal{A}}_1$ “homologous regions,” ${\mathcal{A}}_2$ “modularity”, ${\mathcal{A}}_3$ “density of connections, masked” and ${\mathcal{A}}_4$ “neighbouring regions.”

A homologous regions matrix ${\mathcal{A}}_1$ reflects the situation where we assume that only homologous regions from two hemispheres are assumed to be connected. A modularity matrix ${\mathcal{A}}_2$, in turn, represents an adjacency-defining division of the brain cortical regions into five modules (Sporns, 2013; Cole et al., 2014; Sporns & Betzel, 2016). Next, a “density of connections, masked” matrix ${\mathcal{A}}_3$ is based on the estimated density of connections between brain cortical regions, as described in Section 6). Finally, the “neighbouring regions” matrix ${\mathcal{A}}_4$ models the situation where adjacent brain regions are connected, that is, the strength of connection between brain regions depends on the physical distance between them.

5.2.1.3. Simulation scenarios—

We evaluated three simulation scenarios to express different sources of “uninformativeness” of ${\mathcal{A}}^{obs}$ that loosely reflect real-life scenarios. For each scenario, we tested all four types of matrices, ${\mathcal{A}}_1,\dots ,{\mathcal{A}}_4$. In addition, we consider the number of observations that is commonly encountered in the imaging studies, ranging from n = 100 to n = 400, and the number of predictors ranging from p = 66 to p = 528 corresponding to common parcellations of the cortex (Eickhoff et al., 2015; Eickhoff, Yeo, & Genon, 2018).

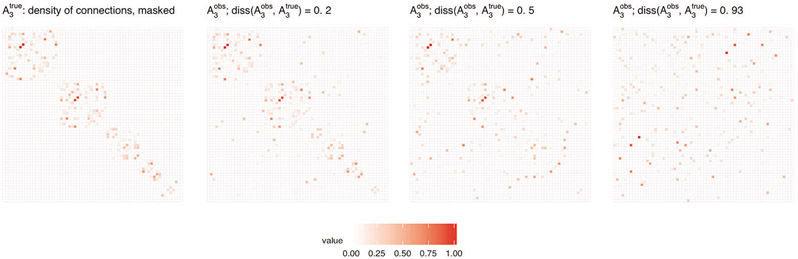
• Scenario 1. The observed connectivity matrix, ${\mathcal{A}}^{obs}$, represents connections (partially) permuted with respect to connections represented by ${\mathcal{A}}^{true}$. Based on one of the four considered matrices, the corresponding ${\mathcal{A}}^{obs}$ matrix is constructed by randomizing edges of a graph given by A^true until a desired dissimilarity, diss(${\mathcal{A}}^{obs}$, ${\mathcal{A}}^{true}$), is achieved. The randomization technique preserves graph size, density, strength and graph degree sequence (and hence degree distribution). Figure 13 in Section 8.5 of the Supplementary Material shows a visualization of the permutation effect for all four matrices considered, ${\mathcal{A}}_1^{true},\dots ,{\mathcal{A}}_4^{true}$; Figure 3 below shows a visualization of permutation effect for one selected matrix ${\mathcal{A}}_3^{true}$.

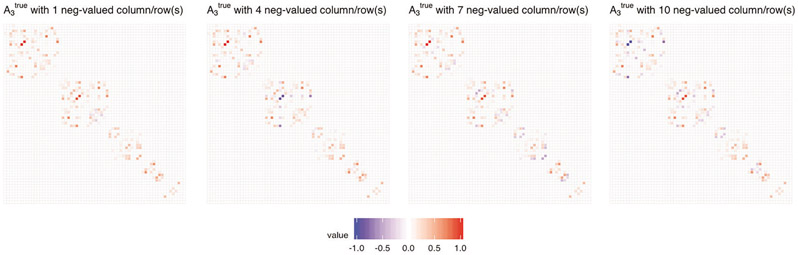
• Scenario 2. We investigate the impact of incorrect information of strong similarity between variables (and consequently an incorrect assumption about closeness of their regression coefficients) while, in fact, their influence on the response variable is very distinct. To model such situations, the true signal was generated by also taking into account the dissimilarity between some coefficients, which was accomplished by setting some entries in ${\mathcal{A}}^{true}$ to negative values. Specifically, for i ∈ {1, … , 4}, matrix ${\mathcal{A}}_i^{true}$ was defined by changing entries of k columns and corresponding k rows (with k ∈ {1, 4, 7, 10}) of ${\mathcal{A}}_i$ into their negative values. Such a structure of ${\mathcal{A}}^{true}$ yields the tendency that k coefficients of the true signal will be separated from others. Here, ${\mathcal{A}}^{obs}(i,j)=\mid {\mathcal{A}}^{true}(i,j)\mid$, and hence, ${\mathcal{A}}^{obs}$ contains only nonnegative values. Figure 14 in Section 8.5 of the Supplementary Material shows a visualization of the sign alteration effect for all ${\mathcal{A}}^{true}$ matrices considered, ${\mathcal{A}}_1^{true},\dots ,{\mathcal{A}}_4^{true}$; Figure 4 below shows a visualization of the sign alteration effect for one selected matrix a true ${\mathcal{A}}_3^{true}$.

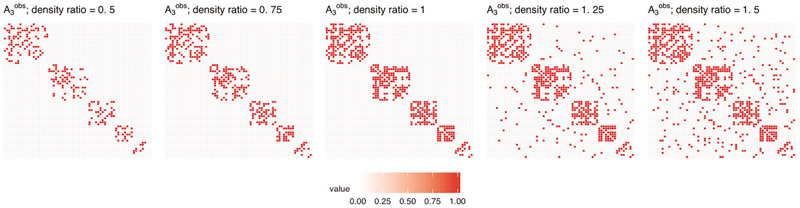
• Scenario 3. The observed connectivity matrix ${\mathcal{A}}^{obs}$ has lower or higher matrix density than ${\mathcal{A}}^{true}$. For ${\mathcal{A}}^{true}$ defined based on one of the four considered matrices, the corresponding ${\mathcal{A}}^{obs}$ is then constructed by randomly removing or adding edges to the graph of connections represented by ${\mathcal{A}}^{true}$ until the desired ratio of matrix densities, $\text{dens}({\mathcal{A}}^{obs})∕\text{dens}({\mathcal{A}}^{true})$, is reached. Figure 15 in Section 8.5 of the Supplementary Material shows a visualization of edges removing and adding effect for all ${\mathcal{A}}^{obs}$ matrices considered, ${\mathcal{A}}_1^{obs},\dots ,{\mathcal{A}}_4^{obs}$; Figure 5 below shows a visualization of the removing and adding effects of edges for one selected matrix ${\mathcal{A}}_3^{obs}$.

Figure 3:

${\mathcal{A}}_3^{true}$ connectivity graph adjacency matrix (first column) and ${\mathcal{A}}_3^{obs}$ connectivity graph adjacency matrices (second to fourth columns) used in Scenario 1.

Figure 4:

Visualization of sign alteration effect for ${\mathcal{A}}_3^{true}$ connectivity graph adjacency matrix used in Scenario 2.

Figure 5:

Visualization of removing and adding effects of edges for matrix ${\mathcal{A}}_3^{obs}$ used in Scenario 3.

5.2.1.4. Simulation procedure—

In each numerical experiment, we performed the following procedure.

• For graph adjacency ${\mathcal{A}}^{true}$, we computed its normalized Laplacian, Q^true (in Scenario 2, the node’s degree is defined as $d_i≔{\sum }_j\mid a_{ij}\mid$; see Section 2.1).

• Replaced the zero singular values of Q^true by 0.01 · s, where s is the smallest nonzero singular value of Q^true (to obtain an invertible matrix required in 6. (a)).

• For graph adjacency matrix, ${\mathcal{A}}^{obs}$, we computed its normalized Laplacian, Q^obs.

• Generated $Z\in {\mathbb{R}}^{n\times p}$, where the rows are independently distributed by ${\mathcal{N}}_p(0,\Sigma )$, where Σ is variance–covariance matrix estimated from a real data study (see: Sect. 6); standardized columns of Z have zero mean and unit ℓ₂ norm.

• Generated X as n-dimensional column of ones.

• Performed the following steps 100 times:

  • generated $b\in {\mathbb{R}}^p$ as $b\sim \mathcal{N}(0,{\sigma }_b^2(Q^{true}{)}^{-1})$ and set β = 0,
  • defined θ : = Xβ + Zb,
  • defined pr^Binom := [e^θ1 /(1 + e^θ₁), …, e^θ_n/(1 + e^θ_n)]^⊤,
  • generated y ~ Binom(pr^Binom), $y\in {\mathbb{R}}^{n\times 1}$,
  • estimated model coefficients b, β using (i) griPEER, assuming the binomial distribution of y and using Q^obs in a penalty term and (ii) logistic ridge estimator
  • computed b estimation error, $MSEr≔\Vert \widehat{b}-b{\Vert }_2^2∕\Vert b{\Vert }_2^2$, for two b estimates, (i) ${\widehat{b}}^{griPEER}$ and (ii) ${\widehat{b}}^{l.ridge}$.

• Computed mean relative relative Mean Squared Error (MSEr) out of the 100 runs from (5), for the two estimation methods.

Importantly, a “true” coefficient vector b obtained as $b\sim \mathcal{N}(0,{\sigma }_b^2(Q^{true}{)}^{-1})$ reflects the connectivity structure represented by ${\mathcal{A}}^{true}$. Example vectors b generated using ${\mathcal{A}}_1,\dots ,{\mathcal{A}}_4$ are presented in Figure 12 in the Section 8.4 of the Supplementary Material.

5.2.1.5. Simulation parameters—

We consider the following experiment settings:

• number of predictors: p ∈ {66, 198, 528},

• number of observations: n ∈ {100, 200, 400},

• ${\mathcal{A}}^{true}$ matrix constructed based on ${\mathcal{A}}_i\in \{{\mathcal{A}}_1,\dots ,{\mathcal{A}}_4\}$,

• (Scenario 1.) dissimilarity between ${\mathcal{A}}^{obs}$ and ${\mathcal{A}}^{true}:diss({\mathcal{A}}^{obs},{\mathcal{A}}^{true})\in [0,1]$,

• (Scenario 2.) number of columns (and corresponding rows) of ${\mathcal{A}}^{true}$ that have signs switched: k ∈ {0, 1, 4, 7, 10},

• (Scenario 3.) density ratio: $\text{dens}({\mathcal{A}}^{obs})∕\text{dens}({\mathcal{A}}^{true})\in [0.5,1.5]$.

The number of predictors, p = 66, was selected to match the imaging analysis of the 66 brain regions as described in Section 6. To investigate the situations with a larger number of predictors for ith type of connectivity pattern, we created block-diagonal adjacency matrices with ${\mathcal{A}}_i$ as blocks. Specifically, adjacency matrices in cases with p = 198 and p = 528 were defined as $\text{diag}\{{\mathcal{A}}_i,\dots ,{\mathcal{A}}_i\}$ with a number of repetitions selected, so the resulted dimension matches the target p.

5.2.2. Results

5.2.2.1. Scenario 1—

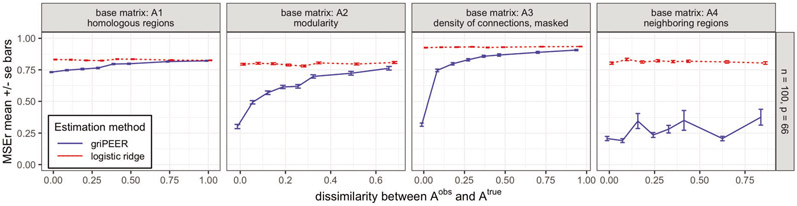
In Scenario 1, we compare griPEER and logistic ridge estimation methods when an observed connectivity matrix ${\mathcal{A}}^{obs}$ contains connections that are permuted with respect to connections represented by ${\mathcal{A}}^{true}$. We consider the following simulation parameter values: number of predictors p ∈ {66, 198, 528}; number of observations n ∈ {100, 200, 400}, ${\mathcal{A}}^{true}$ base matrix ${\mathcal{A}}_1,\dots ,{\mathcal{A}}_4$; and dissimilarity between ${\mathcal{A}}^{obs}$ and ${\mathcal{A}}^{true}$ $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})\in [0,1]$. Figure 16 in the Section 8.6 of the Supplementary Material displays the aggregated (mean) values of the relative estimation error based on 100 simulation runs for all experiment settings considered; Figure 6 below shows visualization of a selected subset of experiment settings for n = 100 and p = 66.

Figure 6:

MSEr for estimation of b as a function of dissimilarity between ${\mathcal{A}}^{obs}$ and ${\mathcal{A}}^{true}$ as measured by $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})$ (Scenario 1) for griPEER (blue line) and logistic ridge (red line). Standard errors of the mean from 100 experiment runs are shown.

MSEr of griPEER is lower or equal to the MSEr of the logistic ridge regression in all cases. The utility of griPEER is particularly apparent when ${\mathcal{A}}^{obs}$ is fully or largely informative, which corresponds to the low values of dissimilarity $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})$. As ${\mathcal{A}}^{obs}$ becomes less informative about the true connections between the model coefficients, that is, values of $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})$ become high, the MSEr of griPEER approaches the MSEr of logistic ridge. The result illustrates the adaptiveness of griPEER to the amount of true information in an observed ${\mathcal{A}}^{obs}$ matrix. When ${\mathcal{A}}^{obs}$ is largely informative, incorporating ${\mathcal{A}}^{obs}$ into the estimation is clearly beneficial, but even when ${\mathcal{A}}^{obs}$ carries little or no information, griPEER still yields an MSEr no larger than the MSEr of logistic ridge estimator.

The performance of griPEER and logistic ridge regression depends on the structure of connections imposed by ${\mathcal{A}}^{true}$ on the true b. We can observe that a difference between the MSErs for griPEER and logistic ridge is smaller when ${\mathcal{A}}^{true}$ is defined using ${\mathcal{A}}_1$: homologous regions matrix (Figure 16, left column panel). Indeed, ${\mathcal{A}}_1$ has smaller density than ${\mathcal{A}}_2$, ${\mathcal{A}}_3$ and ${\mathcal{A}}_4$ and imposes fewer connections between true coefficients in a model. Therefore, utilizing (full or partial) connectivity information ${\mathcal{A}}^{obs}$ in estimation for ${\mathcal{A}}_1$-based signals is less beneficial compared to other considered patterns of coefficients dependencies. Furthermore, when each node is connected to every other by a path consisting of strong connections, as in the case when ${\mathcal{A}}^{true}$ is created based on ${\mathcal{A}}_4$ (fourth column panel in Figure 16), it is expected that all “true” model coefficients in a generated vector b will be strongly dependent on each other; see Figure 12 in the Section 8.4 of the Supplementary Material. In such cases, even inaccurate information about the connections (high $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})$ values) may still be beneficial. Finally, if we compare the results within each column panel of Figure 16, we observe, as expected, that the estimation error becomes smaller as number of predictors p becomes smaller and as the number of observations n becomes larger.

5.2.2.2. Scenario 2—

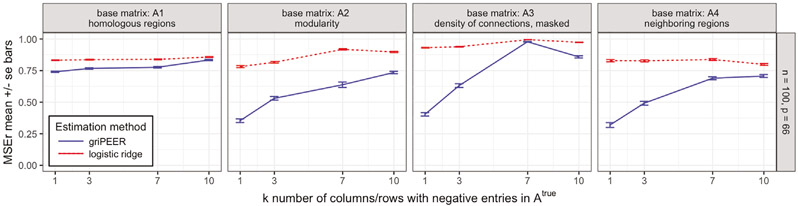
In Scenario 2, we compare griPEER and logistic ridge estimation methods in a situation when some coefficients of the true signal are separated from the others much more than suggested by the observed connectivity matrix, ${\mathcal{A}}^{obs}$. To generate such a design, ${\mathcal{A}}^{true}$ has some columns and rows of negative values, which “pushes” the corresponding coefficients away, while the signal is randomized. We run the simulation for number of observations, n = 100; number of variables, p = 66; and for ${\mathcal{A}}^{true}$ based on four connectivity patterns inducing matrices, $\{{\mathcal{A}}_1,\dots ,{\mathcal{A}}_4\}$. Matrix ${\mathcal{A}}^{true}$ was generated from ${\mathcal{A}}_i$ by switching signs in k columns (and corresponding rows), where k ∈ {1, 4, 7, 10}. Figure 7 displays the aggregated (mean) values of the relative estimation error based on 100 simulation runs.

Figure 7:

MSEr for estimation of b for four true connectivity patterns described by matrices, ${\mathcal{A}}_1,\dots ,{\mathcal{A}}_4$ (Scenario 2). Results for griPEER and logistic ridge (blue and red lines, respectively). Presented are the average values of MSEr from 100 runs for n = 100 and p = 66. The number of columns (and corresponding rows) of ${\mathcal{A}}_i$, for which signs of entries were switched in ${\mathcal{A}}^{true}$ construction, is represented by the x-axis values. Error bars indicate standard errors of the mean.

With increasing k, ${\mathcal{A}}^{obs}$ differs more from the connectivity pattern used in the true signal, and so, the relative difference between MSEr for logistic ridge regression and griPEER decreases for nearly all settings. Notably, MSEr values for griPEER remain below or equal to MSEr values for logistic ridge. These results suggest that even some incorrect information (accomplished by introducing negative dependencies between variables) is not detrimental.

5.2.2.3. Scenario 3—

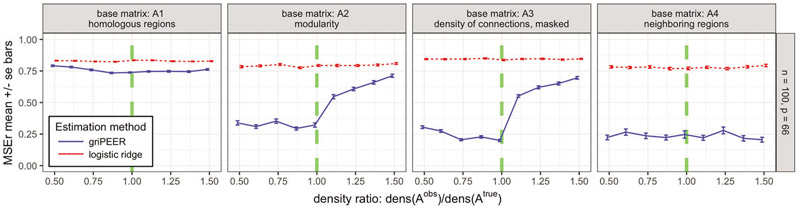
In this scenario, we compare griPEER and logistic ridge estimation methods when ${\mathcal{A}}^{obs}$ is of lower and higher matrix density than ${\mathcal{A}}^{true}$. We again consider n = 100 and p = 66. This time, we generated ${\mathcal{A}}^{true}$ by adding/removing some connections to/from ${\mathcal{A}}_i$, which influences the density of the resulting matrix. Here, we consider $\text{dens}({\mathcal{A}}^{obs})∕\text{dens}({\mathcal{A}}^{true})\in [0.5,1.5]$ as a range of density ratios. Figure 8 illustrates the mean values of the relative estimation error based on 100 simulation runs.

Figure 8:

MSEr for estimation of b as a function of the matrix density ratio (Scenario 3). Results for griPEER and logistic ridge (blue and red lines, respectively). Presented are the average values of MSEr from 100 runs for n = 100, p = 66 and four true connectivity patterns inducing matrices, ${\mathcal{A}}_1,\dots ,{\mathcal{A}}_4$. Ratio of densities, $\text{dens}({\mathcal{A}}^{obs})∕\text{dens}({\mathcal{A}}^{true})$ was varied from 0.5 to 1.5. Standard errors of the mean are shown. Green dashed vertical lines denote ratio of matrix densities of 1, when ${\mathcal{A}}^{obs}$ is identical to ${\mathcal{A}}^{true}$.

Similar to Scenario 1, incorporating information on only a few connections (${\mathcal{A}}_1$ case) yields the smallest gain in the estimation accuracy measured by MSEr among all considered connectivity patterns. If ${\mathcal{A}}^{true}$ is set to ${\mathcal{A}}_4$, then (again, analogously to Scenario 1) the information about the strong coefficients’ dependence is provided through ${\mathcal{A}}^{obs}$. This results in substantially lower MSEr for griPEER across the full considered density ratio range. When ${\mathcal{A}}^{true}$ is one of the module-based matrices, ${\mathcal{A}}_2$ or ${\mathcal{A}}_3$, we still benefit from using ${\mathcal{A}}^{obs}$ of lower density than ${\mathcal{A}}^{true}$ as ${\mathcal{A}}^{obs}$ contains unaffected information about five separated modules in connectivity structure (values lower than 1 on the x-axis). Including the false connections in ${\mathcal{A}}^{obs}$ (values greater than 1 on the x-axis) provides the incorrect message of some dependencies between modules. A loss in griPEER’s estimation accuracy is apparent at the transition point x = 1. It remains, however, significantly better than the estimation accuracy for logistic ridge regression over the entire range of considered densities ratios.

Table 3 in the Section 8.6 of the Supplementary Material summarizes obtained regularization parameter values and griPEER estimation execution time in numerical experiments across three simulation scenarios. The median execution time varied from 3.8 to 1,277 seconds per run depending on the simulation scenario; the longest execution times were attained for p = 528 settings. It is worth noting that the computational time depends on a few factors with longer computation times for: (a) larger sample sizes, (b) smaller ratios of the number of observations to the number of predictors and (c) fewer sparse connectivity matrices.

5.3. Model Coefficient Significance Testing

5.3.1. Settings

We designed a simulation study to evaluate the performance of the two procedures from coefficient significance testing for griPEER, introduced in Section 4: asymptotic variance–covariance matrix-based approach, griPEER_asmp, and bootstrap-based approach, griPEER_boot.

5.3.1.1. Simulation scenario—

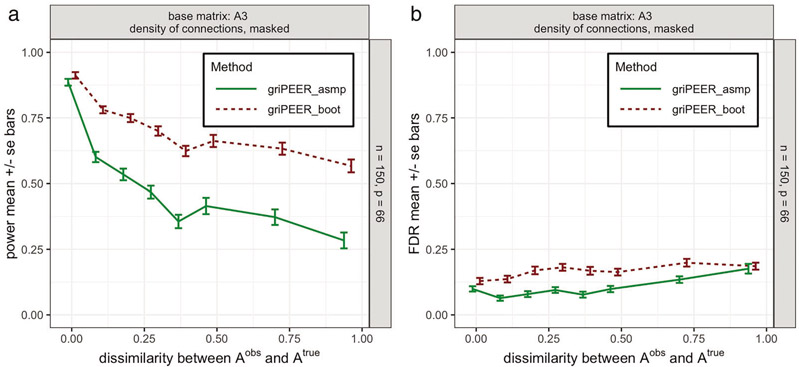
We followed the simulation setting from Scenario 1, described in Section 5.2. Specifically, we assumed that ${\mathcal{A}}^{obs}$ represented connections (partially) permuted with respect to connections represented by ${\mathcal{A}}^{true}$, that is, the corresponding ${\mathcal{A}}^{obs}$ is constructed by randomizing entries in ${\mathcal{A}}^{true}$ until a desired dissimilarity, $\text{diss}({\mathcal{A}}^{obs},{\mathcal{A}}^{true})$, is achieved (see: Figure 13). The randomization technique preserves graph size, density, strength and graph degree sequence (and hence degree distribution). Here, we confined our evaluation to p = 66 and specific ${\mathcal{A}}^{true}$ based on ${\mathcal{A}}_3$. The median of a density of connections was masked by modularity information, which corresponds to an adjacency matrix in the brain imaging analysis Section 4.

The adopted simulation scheme starts by generating the true signal and responses as in Section 5.2. We generated a large number of observations, n = 1,000, but in the estimation, only 150 records were used to emulate a real data setting. The large sample size was used only to label the variables that were “truly relevant” so that the performance of griPEER_asmp and griPEER_boot in the context of variables selection could be assessed. Defining “truly relevant” variables was accomplished by using the asymptotic confidence interval for the logistic model estimate (nonregularized estimation), which is unbiased and asymptotically normal (Fahrmeir & Kaufmann, 1985). The details are described below.

5.3.1.2. Simulation study procedure—

Here, we perform the following steps.

• Applied Steps 1–5 from the simulation study procedure described in Section 5.2 with n = 1,000.

• Ran the following steps 100 times:

  • generated p-dimensional vector of true coefficients, b, as well as n-dimensional vectors, θ and y, by following steps 2(a)–2(d) described in Section 5.2,
  • calculated the asymptotic standard deviations, ${\delta }_i≔\sqrt{{\left[{\left(Z^{\mathsf{T}}\Psi Z\right)}^{-1}\right]}_{ii}}$, for i = 1, … , p, where $\Psi ≔diag\left\{\frac{e^{{\theta }_1}}{(e^{{\theta }_1}+1{)}^2},\dots ,\frac{e^{{\theta }_n}}{(e^{{\theta }_n}+1{)}^2}\right\}$ (see, Section 8.3 of the Supplementary Material),
  • divided the set of indices, {1, … , p}, into two separated groups: I_T, corresponding to the variables defined as relevant and I_F, corresponding to the variables defined as irrelevant, by using the criterion i ∈ I_T ⇔ 0 ∉ [b_i – 1.96 δ_i, b_i + 1.96 δ_i],
  • generated the data for estimation, y*, X* and Z*, by taking the first 150 rows of y, X and Z; centered and normalized the columns of Z* to zero means and unit ℓ₂ norms,
  • applied griPEER_asmp and griPEER_boot on y*, X* and Z* to indicate response-related variables defined by each of methods,
  • based on information about “truly relevant” and “truly irrelevant” variables, that is, the known division into I_T and I_F; for each method identified: S, the number of true discoveries and V, the number of false discoveries,
  • for each method collected measures $po{w}^{\ast }≔\frac{S}{\mid I_T\mid }$ and, $fd{r}^{\ast }≔\frac{V}{V+S}$,

• Defines the estimates of power and false discovery rate (FDR) as the averages of pow* and fdr* (across 100 repetitions of the step 2), respectively.

5.3.2. Results

The values of power and false discovery rate (FDR) (Figure 9, left and right, respectively) were estimated based on the simulation procedure described in Section 5.3.1. As expected, for both methods, power decreases as ${\mathcal{A}}^{obs}$ becomes less informative regarding the true connections between model coefficients. We observe, however, that griPEER_boot can reach substantially higher power than griPEER_asmp. The estimated FDRs are fairly similar for both methods, particularly when connectivity information is less accurate.

Figure 9:

The estimated values for power (left panel) and FDR (right panel) obtained with an asymptotic variance–covariance matrix-based approach (griPEER_asmp, green line) and a bootstrap-based approach (griPEER_boot, red line). Values are aggregated (mean) over 100 runs with number of observations n = 150, number of variables p = 66 and ${\mathcal{A}}_3$ (Figure 2, middle right plot) as a true connectivity pattern. The extent of dissimilarity between ${\mathcal{A}}^{obs}$ and ${\mathcal{A}}^{true}$ is shown on the x-axis. Standard errors of the mean are used.

These results suggest that utilizing griPEER_boot for coefficient significance testing produced greater power compared to the griPEER_asmp approach without a substantial increase of FDR. Consequently, we employ griPEER_boot in the real data application in Section 6.

5.4. The Software Used in Simulations

Our analyses were performed using software built in MATLAB, available at GitHub at https://github.com/martakarass/gripeer-numerical-experiments. This repository also contains all scripts used in numerical simulations and to generate figures.

6. BRAIN IMAGING DATA APPLICATION

We model the association between the presence or absence of HIV and the properties of the cortical structural brain imaging data. More specifically, we employ cortical thickness measurements obtained using FreeSurfer software (Fischl, 2012) to classify the binary response indicating the status of HIV infection, where 0 indicates an HIV-uninfected (HIV−) individual and 1 an HIV-infected (HIV+) individual.

6.1. Data and Preprocessing

6.1.1. Study sample

The analyzed sample consisted of 162 men aged 18-42 years, where 108 were HIV+ and 54 were HIV−. The demographic and clinical characteristics are summarized in Table 1.

Table 1:

Characteristics for 162 men included in the study. Table includes the information about subjects’ age (Age), recent CD4 cell count (Recent CD4), nadir CD4 cell count (Nadir CD4) and recent viral load (Recent VL).

HIV status	Variables	Min	Median	Max	Mean	StdDev
	Age	18	24	41	26.31	6.45
HIV+ (108)	Recent CD4	20	446	1179	461.83	243.81
	Nadir CD4	15	293	690	289.13	158.31
	Recent VL	20	50	555495	30232.22	78827.35
HIV− (54)	Age	18	23	41	24.8	6.45

6.1.2. Cortical measurements

The FreeSurfer software package (version 5.1) was used to analyze the structural magnetic resonance imaging data, including gray – white matter segmentation, reconstruction of cortical surface models, labelling of regions on the cortical surface and analysis of group morphometry differences. The resulting dataset has cortical measurements for 68 cortical regions with parcellation based on the Desikan-Killiany atlas (Desikan et al., 2006). However, in this analysis, we used 66 variables describing average cortical gray matter thickness (in millimeters), which did not incorporate left and right insula due to their exclusion from the structural connectivity matrix.

6.1.3. Structural connectivity information

We used two adjacency matrices, which were incorporated in the griPEER estimation through the normalized Laplacian matrix. The adjacency matrices were based on two structural connectivity metrics: density of connections (DC) and fractional anisotropy (FA). For each of these matrices, we performed two steps to obtain the final adjacency matrix, $\mathcal{A}$. In the first step, we computed the entry-wise median (across participants) of DC or FA connectivity matrices. The second step relied on “masking by modularity partition”, that is, limiting the information achieved in the first step to only the connections between brain regions that were in the same module (i.e., we set ${\mathcal{A}}_{ij}≔0$ if regions i and j were not in the same module). For this purpose, we used the modularity connectivity matrix (Sporns, 2013; Cole et al., 2014; Sporns & Betzel, 2016), which defines the division of the brain into five separated communities. The modularity matrix was obtained using the Louvain method Blondel et al. (2008) and was based on model proposed by Hagmann et al. (2008). More details on this procedure can be found in Karas et al. (2019).

6.2. Estimation Methods

We employed griPEER_boot and logistic ridge to classify the HIV+ and HIV− individuals based on the estimated cortical thickness measurements. All analyses were adjusted for Age with its respective coefficient nonpenalized. Consequently, X was an n × 2 matrix containing the column of ones (representing the intercept) and the column corresponding to participants’ age. Columns of design matrices (other than the intercept) were zero mean-centered and normalized to unit standard deviation before the estimation. The selection of regularization parameter in logistic ridge regression was performed within the GLMM framework. For all presented results, we used a bootstrap-based approach with 50,000 samples to define the subset of statistically significant variables.

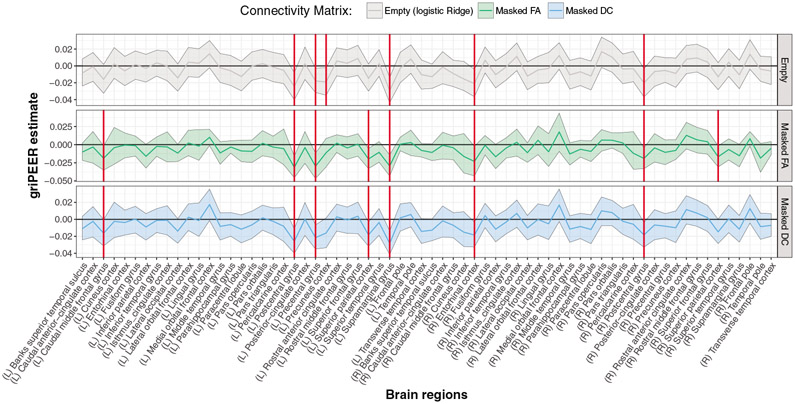
6.3. Results

The estimates obtained from the griPEER_boot and logistic ridge regression for the sample in Table 1 are presented in Figure 10. Brain regions labelled as response related are indicated by solid red vertical lines. In Table 2, we summarize the estimated values corresponding to brain regions tagged as response related by at least one considered approach. Note that all significant associations are negative, indicating that thinner cortical areas are indicative of HIV-positive status. Significant estimates obtained from the griPEER for both (FA and DC) connectivity matrices agree for seven of eight cortical brain regions. The significant logistic ridge findings disagree with the FA-based griPEER estimates in four regions and with the DC-based griPEER estimates in three regions. The corresponding tuning parameters are (λ_Q = 192.4, λ_R = 482.7) for FA and (λ_Q = 168.9, λ_R = 133.5) for the DC matrix. For the logistic ridge, the selected parameter is λ_R = 277.

Figure 10:

griPEER_boot results in a sample of 162 participants, of whom 108 were HIV-infected. Here, the binary response variable was defined as the disease indicator, and 66 cortical brain regions were considered—33 from each hemisphere. Regions labelled as response related are indicated by red vertical lines. Confidence intervals were calculated based on 50,000 bootstrap samples.

Table 2:

Estimates of the cortical brain region coefficients obtained by the logistic ridge regression and griPEER_boot with two different connectivity matrices—fractional anisotropy (Masked FA) and density of connections (Masked DC). Both matrices were masked by the modularity matrix before the analysis. Values corresponding to regions tagged to be response related are shown in bold font. Regions are listed in the table if they were found to be significant by at least one of the three considered methods.

Connectivity	CaudMF	PostCen	PreCen	PreCun	SupPar	SupraMar	Entor	PostCen	SupPar
type	[L]	[L]	[L]	[L]	[L]	[L]	[R]	[R]	[R]
Empty	−0.016	−0.025	−0.018	−0.019	−0.015	−0.029	−0.021	−0.020	−0.013
Masked FA	−0.019	−0.031	−0.030	−0.011	−0.020	−0.029	−0.023	−0.019	−0.017
Masked DC	−0.016	−0.026	−0.022	−0.016	−0.018	−0.028	−0.018	−0.018	−0.015

The discovered regions are primarily located in the left hemisphere’s frontal and parietal lobes. Two regions, the postcentral gyrus and superior parietal lobule, were detected in both hemispheres. All considered approaches identified the right entorhinal cortex as being significantly thinner in HIV-infected individuals.

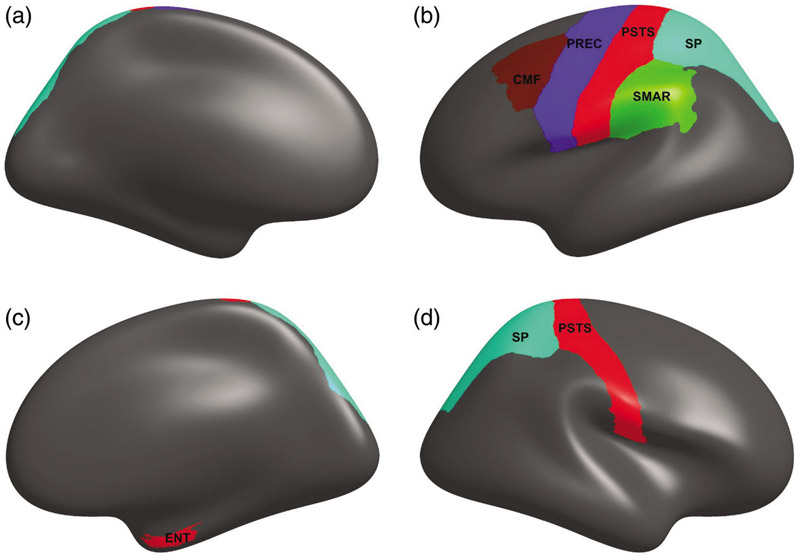
Brain regions identified by griPEER_boot using an FA matrix restricted to modules (Masked FA) are shown in the Figure 11.

Figure 11:

Brain regions associated with HIV disease for Masked FA connectivity matrix. Here, five left-hemisphere (LH) and three right-hemisphere (RH) regions were identified griPEER_boot. Brain region abbreviations: CMF = Caudal middle frontal, PREC = Precentral, PSTS = Postcentral, SP = Superior parietal, SMAR = Supramarginal, ENT = Entorhinal.

7. DISCUSSION

In this work, we presented a rigorous, computationally feasible method to incorporate additional information in the estimation of regression parameters in the GLM setting. The method presented here, griPEER, extends our previous work performed in the linear model setting of Karas et al. (2019). We utilized known structural connectivity information (assessed by different diffusion weighted imaging (DWI) metrics) to inform the association between the cortical thickness covariates and a generalized outcome (e.g., binary indicator of HIV infection). The structural connectivity information was used to create a Laplacian matrix, which in turn allowed us to specify the regularization penalty. The simulation study showed that, in each of the presented scenarios, the griPEER method outperformed logistic ridge in a binomial model coefficient estimation—griPEER yielded a smaller or similar relative estimation error, $MSEr=\Vert \widehat{b}-b{\Vert }_2^2∕\Vert b{\Vert }_2^2$, when compared to the logistic ridge. Performance of griPEER is significantly better when the observed connectivity information was either fully or largely informative about the true connectivity structure between model coefficients. Notably, even in the cases when the observed connectivity information was only partially informative or completely noninformative, griPEER yielded MSEr that was no larger than the logistic ridge estimator. Our method has therefore the same desirable properties as its precursor, riPEER, in the continuous outcomes case. Moreover, the performed simulations showed that our implementation produces stable regression coefficient estimates. In addition, we did not encounter convergence problems even when the binary response variables were highly unbalanced.

griPEER simultaneously estimates the associations between the predictors (region-specific cortical thickness) and binary outcome variables in the GLMM framework. This constitutes a huge advantage over widely used approaches relying on testing variables individually. Such procedures are then followed by a multiple testing correction leading to an increased number of false negatives and, consequently, to reduced power. For instance, after multiple testing correction was applied in MacDuffie et al. (2018), there were no brain regions found with cortical thickness significantly related to the HIV diagnosis, although smaller global cortical area and volume were observed in HIV-positive participants with lower nadir CD4 count.

Application of griPEER to classify individuals as HIV+ and HIV− resulted in the discovery of eight and seven cortical regions when FA and DC matrices were used, respectively. Applying logistic ridge regression (i.e., performing the analysis with no external information arising from brain connectivity) to the same dataset provided six discoveries. Interestingly, all regression coefficients identified as statistically significant were estimated as negative by all three considered approaches. Our results therefore confirm the belief, strongly supported by the literature (Thompson et al., 2005; Sanford et al., 2018), that HIV infection is associated with reduced cortical thickness.

All considered approaches discovered regions located mostly in left parietal and frontal brain lobes. The cortical thickness of these brain regions is often reported as being significantly reduced by HIV infection (MacDuffie et al., 2018; Sanford et al., 2018). In particular, changes in mean cortical thickness in the left precentral and the supramarginal gyrus were found to be significantly associated with HIV infection Kallianpur et al. (2012), while significantly lower cortical thickness in the bilateral postcentral region in HIV patients was observed by Yadav et al. (2017). In addition, all considered methods revealed regions in the left primary sensory and motor cortex where cortical thickness differences between HIV-positive and HIV-negative subjects were detected by Sanford et al. (2018).

Employing griPEER with FA matrix revealed three additional cortical regions compared to logistic ridge regression, namely, the left frontal gyrus and the bilateral superior parietal lobes, that were thinner in the HIV+ individuals. These additional findings are consistent with the literature cited above and suggest that using DWI-based information may indeed increase the power of statistical techniques applied to investigate the association between cortical thickness and HIV-related outcome variables.

By providing a fully data-adaptive tool, we extend the existing approaches and show how the external information can be employed in the estimation when binary responses are considered. In future work, we plan to extend our methodology in two directions. First, we will utilize other cortical structural metrics, such as the cortical area and its curvature, to create structural connectivity matrices. Second, we will incorporate multiple sources of information in the regularization procedures. This will enable simultaneous inclusion of both structural and functional brain connectivity information, as well as allow us to divide the connectivity information into parts corresponding to different brain modules and let the algorithm automatically determine their impact on the regression coefficient estimates.