Spatially distributed infection increases viral load in a computational model of SARS-CoV-2 lung infection

Melanie E Moses; Steven Hofmeyr; Judy L Cannon; Akil Andrews; Rebekah Gridley; Monica Hinga; Kirtus Leyba; Abigail Pribisova; Vanessa Surjadidjaja; Humayra Tasnim; Stephanie Forrest

doi:10.1371/journal.pcbi.1009735

. 2021 Dec 23;17(12):e1009735. doi: 10.1371/journal.pcbi.1009735

Spatially distributed infection increases viral load in a computational model of SARS-CoV-2 lung infection

Melanie E Moses ^1,^2,^*, Steven Hofmeyr ³, Judy L Cannon ⁴, Akil Andrews ¹, Rebekah Gridley ⁴, Monica Hinga ¹, Kirtus Leyba ⁵, Abigail Pribisova ¹, Vanessa Surjadidjaja ¹, Humayra Tasnim ¹, Stephanie Forrest ^2,⁵

Editor: Amber M Smith⁶

¹Department of Computer Science, University of New Mexico, Albuquerque, New Mexico, United States of America

²Santa Fe Institute, Santa Fe, New Mexico, United States of America

³Lawrence Berkeley National Laboratory, Berkeley, California, United States of America

⁴Department of Molecular Genetics and Microbiology, University of New Mexico School of Medicine, Albuquerque, New Mexico, United States of America

⁵Biodesign Institute, Arizona State University, Tempe, Arizona, United States of America

⁶University of Tennessee Health Science Center College of Medicine Memphis, UNITED STATES

The authors have declared that no competing interests exist.

^✉

* E-mail: melaniem@unm.edu

Roles

Melanie E Moses: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Writing – original draft, Writing – review & editing

Steven Hofmeyr: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing

Judy L Cannon: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Writing – original draft, Writing – review & editing

Akil Andrews: Investigation, Methodology, Software, Validation, Visualization, Writing – original draft

Rebekah Gridley: Investigation, Methodology, Validation

Monica Hinga: Investigation, Methodology, Validation, Writing – original draft

Kirtus Leyba: Investigation, Methodology, Software, Validation, Visualization, Writing – original draft

Abigail Pribisova: Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing

Vanessa Surjadidjaja: Investigation, Methodology, Software, Validation, Visualization

Humayra Tasnim: Investigation, Methodology, Software, Validation, Writing – original draft

Stephanie Forrest: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Writing – original draft, Writing – review & editing

Amber M Smith: Editor

PMCID: PMC8740970 PMID: 34941862

Abstract

A key question in SARS-CoV-2 infection is why viral loads and patient outcomes vary dramatically across individuals. Because spatial-temporal dynamics of viral spread and immune response are challenging to study in vivo, we developed Spatial Immune Model of Coronavirus (SIMCoV), a scalable computational model that simulates hundreds of millions of lung cells, including respiratory epithelial cells and T cells. SIMCoV replicates viral growth dynamics observed in patients and shows how spatially dispersed infections can lead to increased viral loads. The model also shows how the timing and strength of the T cell response can affect viral persistence, oscillations, and control. By incorporating spatial interactions, SIMCoV provides a parsimonious explanation for the dramatically different viral load trajectories among patients by varying only the number of initial sites of infection and the magnitude and timing of the T cell immune response. When the branching airway structure of the lung is explicitly represented, we find that virus spreads faster than in a 2D layer of epithelial cells, but much more slowly than in an undifferentiated 3D grid or in a well-mixed differential equation model. These results illustrate how realistic, spatially explicit computational models can improve understanding of within-host dynamics of SARS-CoV-2 infection.

Author summary

A key question in SARS-CoV-2 infection is why viral loads and patient outcomes are so different across individuals. Because it’s difficult to see how the virus spreads in the lungs of infected people, we developed Spatial Immune Model of Coronavirus (SIMCoV), a computational model that simulates hundreds of millions of cells, including lung cells and immune cells. SIMCoV simulates how virus grows and then declines, and the simulations match data observed in patients. SIMCoV shows that when there are more initial infection sites, the virus grows to a higher peak. The model also shows how the timing of the immune response, particularly the T cell response, can affect how long the virus persists and whether it is ultimately cleared from the lungs. SIMCoV shows that the different viral loads in different patients can be explained by how many different places the virus is initially seeded inside their lungs. We explicitly add the branching airway structure of the lung into the model and show that virus spreads slightly faster than it would in a 2D layer of lung cells, but much slower than in traditional mathematical models based on differential equations. These results illustrate how realistic spatial computational models can improve understanding of how SARS-CoV-2 infection spreads in the lung.

Introduction

Reducing the spread, severity, and mortality caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection is an urgent global priority. A key question is why viral loads and patient outcomes vary so dramatically among infected individuals. While severe COVID-19 disease is correlated with some known risk factors, such as age, co-morbidities, and some immune response characteristics [1–3], it remains challenging to understand why some patients develop high viral loads and others do not.

We developed a scalable computational model to study the role of spatial effects in determining the time course of viral load within patients, which has been shown to affect disease severity [4] and transmission [5]. Most prior work uses Ordinary Differential Equation (ODE) models to represent within-host virus dynamics, e.g., [6–12]. Such models are useful for studying the onset and duration of the infective period [13] and the effect of various therapeutics given at different times [14–16]. However, they have limited ability to fully account for dynamics in the large and complex structure of the lung [12, 17]. The Spatial Immune Model of Coronavirus (SIMCoV) is an agent-based model (ABM) that simulates infection dynamics and CD8⁺ T cell responses in tissue consisting of hundreds of millions of epithelial cells. Our model results highlight the importance of spatial viral dispersion in the lung and how this affects peak viral load. We focus on CD8⁺ T cells because they are a key player in the immune response to SARS-CoV-2 and because spatial dynamics are important for these cells that move in the lung to kill virally infected cells. Earlier studies report that T cell levels are correlated with disease severity [18], and there is mounting evidence that T cells are critical for protection from severe illness and for preventing subsequent infection [19–22]. These studies collectively suggest that an early and strong T cell response is correlated with less severe disease, but they do not provide a quantitative understanding of how T cell response impacts viral dynamics.

SIMCoV and other ABMs are appealing because they can represent and visualize the complex heterogeneous movements of individual cells and diffusing fields of small particles (i.e., virions or cytokines) [23]. Our prior work analyzed how key factors such as spread of infection, signals, and cells affect search efficiency, timing of immune response, and clearance of infection; this work showed that interactions that depend on movement and physical cell-cell contact require a spatially explicit modeling framework [24, 25]. The SIMCoV simulation of SARS-CoV-2 reinforces the importance of spatial effects as drivers of viral dynamics in the lung.

Our simulations replicate the viral dynamics reported from infected patients and explain differences among those patients in terms of the initial number of foci of infection (FOI) and the magnitude and timing of the CD8⁺ T cell response. SIMCoV demonstrates how the spatial structure of the lung can affect viral spread in the tissue and contribute to the wide diversity of outcomes and infection dynamics observed in COVID-19 patients.

Results

SIMCoV model overview

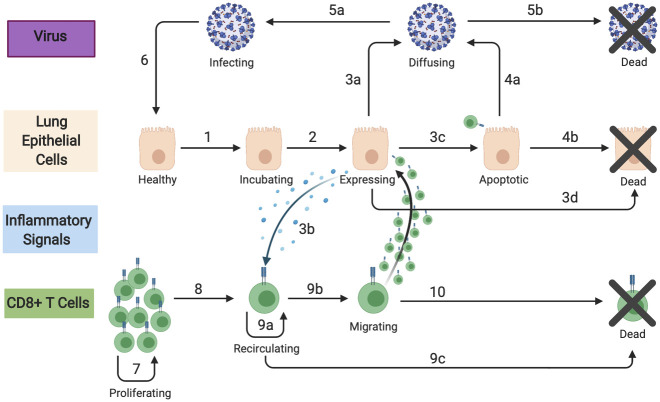
We initialize SIMCoV with SARS-CoV-2 virus that can infect lung epithelial cells. In most of our experiments, epithelial cells are modeled as a 2D grid, where each grid point represents a 5 x 5 x 5 μm³ volume. Upon infection, epithelial cells incubate virus in what is often called an eclipse phase, and then they express virus until they die. Expressing cells produce both virus and an inflammatory signal, which is an abstraction of the cytokines that influence T cell extravasation into tissue. The virus and inflammatory signal both diffuse through tissue. After a delay, an abstract pool is created that represents CD8⁺ cytotoxic T cells that are activated in lymph nodes and then circulate in the vasculature. When T cells reach the lung and encounter a concentration of inflammatory signal above a threshold, they extravasate and are then explicitly represented as mobile agents in SIMCoV. We adjust the probability of T cell extravasation according to the fraction of the lung that is modeled in the simulation. T cells that have extravasated move at random across the 2D grid until they either die or encounter an epithelial cell incubating or expressing virus, in which case the T cells cause apoptosis of the infected epithelial cell with some probability. SIMCoV extends an ABM developed for influenza [25–27] by adding the ability to simulate viral spread through the 3D branching structure of lung epithelial cells and parameterizing the model for SARS-CoV-2. Each transition in Fig 1 is parameterized with estimates or probabilities detailed in Materials and Methods and in configuration files provided with the SIMCoV code in https://github.com/AdaptiveComputationLab/simcov.

Fig 1 — Epithelial and T cells are represented as agents; virions and inflammatory signals are represented as concentrations. Numbered transitions are described in Materials and Methods.

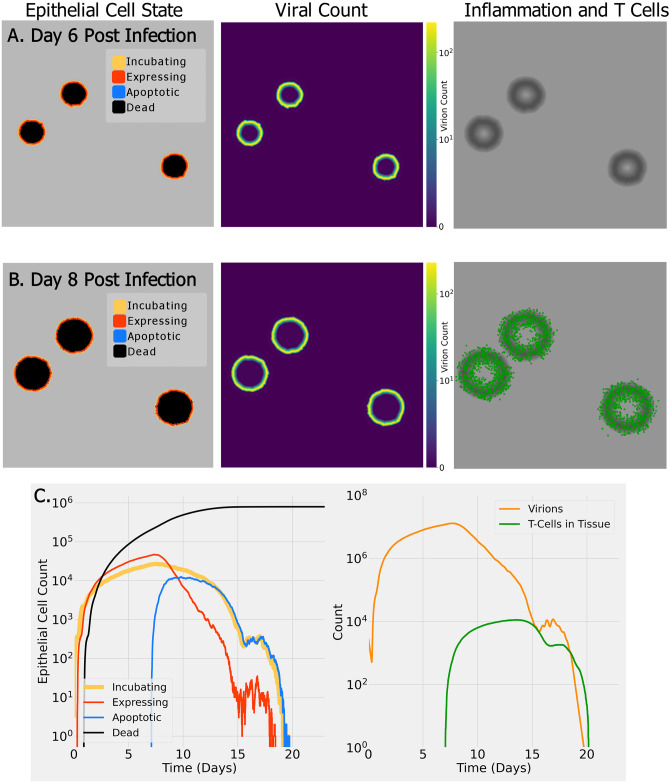
Fig 2 shows the results of a small run of SIMCoV representing infection spreading over a 15 mm x 15 mm x 5 μm layer of lung epithelial tissue (9 million cells). The top row (Fig 2A) shows the state of epithelial cells (left), virion concentration (center), and inflammatory signal (right) at six days post infection (dpi), and the second row (Fig 2B) shows the same including extravasated T cells at eight dpi. The dynamics of the epithelial cells, the count of virions, and the number of T cells moving through the tissue are shown in the bottom row (Fig 2C). The number of epithelial cells incubating and expressing virus (Fig 2C, left) and viral load (Fig 2C, right, orange line) all rise quickly after infection and then increase more slowly until seven dpi. The CD8⁺ T cell response begins at seven dpi, and when T cells encounter infected cells, the infected cells become apoptotic. This reduces both the the number of incubating and expressing epithelial cells and the viral load, and the cumulative number of dead cells levels off. In this example, by approximately 15 dpi, the T cells have induced apoptosis in nearly all expressing epithelial cells, which leads to a reduction in produced inflammatory signals and consequently fewer T cells entering the lung. Then, the virus level begins to rebound. However, once incubating and newly infected cells express more virus and inflammatory signals, more T cells enter the tissue, encounter these expressing cells, and reinstate control over the infection.

Peak viral load is proportional to the number of initial FOI

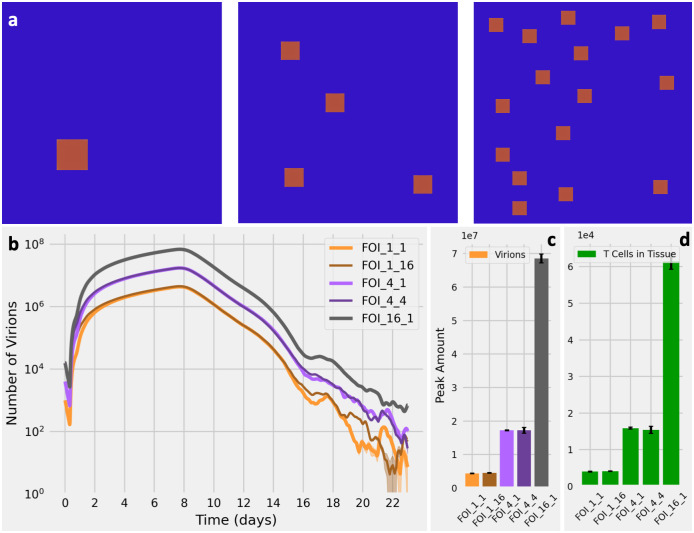
We used SIMCoV to test how spatially differentiated locations of initial infection affect viral dynamics. Images of the lungs of SARS-CoV-2 patients and experimental animal models suggest that there may be multiple sites of viral infection [28–30]. We tested the effect of seeding SIMCoV with multiple FOI on viral dynamics. We initialized simulations with one, four, and 16 spatially dispersed FOI (Fig 3A, square size not to scale). We found that each four-fold increase in the number of FOI increases both the peak viral load (Fig 3C) and number of extravasated T cells (Fig 3D) by a factor of approximately four (Fig 3B). This remains true when the absolute number of initially infected cells is held constant across all experiments, i.e., by creating a single FOI with a cluster of 16 adjacent infected cells and four FOI with four adjacent infected cells, so that all three experiments contain 16 initially infected cells but with varying number of FOI (Fig 3C). The initial number of infected cells only affects the peak viral load if those initial infections are dispersed across multiple FOI; peak viral load depends on the number of FOI, not the number of infected cells within each initial FOI. Virus diffuses from each spatially dispersed FOI independently, and with a larger number of FOI, there are more infectable cells available for virus to contact and infect. Greater spatial dispersion of infected cells also results in more inflammatory signal produced at more sites of infection, and T cells respond by entering the tissue in greater numbers, as seen in the correspondence between T cells and virions in (Fig 3C and 3D).

The replicated runs shown in Fig 3 are highly consistent for a fixed number of FOI for several reasons. Because the simulated tissue size is large relative to the FOI, even at their peak extent, it is statistically unlikely that randomly placed FOI will grow to overlap in the simulations. In Fig 3, each FOI, even at its peak extent, comprises less than 0.2% of the entire simulated tissue in our default configuration that represents 225 million cells. In addition, we located all FOI in the inner 80% of the simulated tissue to avoid boundary effects.

Effect of CD8⁺ T cell response on viral clearance

CD8⁺ T cells that kill virally infected cells are another key factor that varies among patients [19, 22]. The CD8⁺ T cell response depends on interactions in physical space: CD8⁺ T cells are activated in lymph nodes, circulate in the blood, and migrate to the lung, where they extravasate into lung tissue at locations with sufficient inflammatory signal. After extravasation, they move through infected tissue until they directly interact with infected cells and cause cell death [31–34]. T cells likely play an important role in controlling SARS-CoV-2 infection; elderly individuals and patients suffering from severe COVID-19 disease have fewer circulating CD8⁺ T cells [19, 35]. However, because it is difficult to study T cell responses in the lungs of infected patients, relatively little is known about how the presence of T cells in infected lung tissue might impact viral dynamics and control.

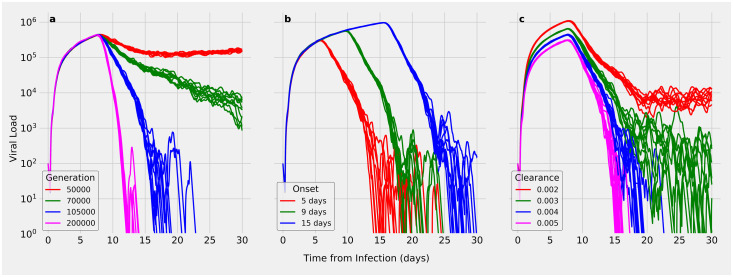
We used SIMCoV to test how the magnitude of the immune response affects viral control. We found that varying the number of circulating T cells in the blood dramatically affects viral control (Fig 4A). Even a two-fold decrease in the production rate of circulating T cells can delay the timing of viral control by several days (compare 100,000 to 200,000 T cells/minute) or even change the outcome from viral control to viral persistence (compare 100,000 to 50,000 T cells/minute).

When the arrival of CD8⁺ T cells in infected tissue is delayed, the time it takes to reach peak viral load is also delayed, which allows a slightly higher peak load to be reached (Fig 4B). Delayed T cell arrival also increases the time until the infection is controlled, but it does not dramatically change the rate at which viral load is reduced. Even when T cell arrival is delayed from five to 15 days, viral control can eventually be achieved, albeit later in the infection. A delay in viral control allows a longer period of elevated viral load, which may increase both the window of transmission and the extent of tissue damage, possibly leading to more severe disease.

The viral clearance rate is a parameter that captures the strength of the innate immune response, and, as can be seen in Fig 4C, changes in the viral clearance rate have a small effect on peak viral load and a much larger effect on viral dynamics in the later days of the infection. The magnitude of the innate immune response can make the difference between rapid viral control versus viral persistence leading to an infection that drags on indefinitely.

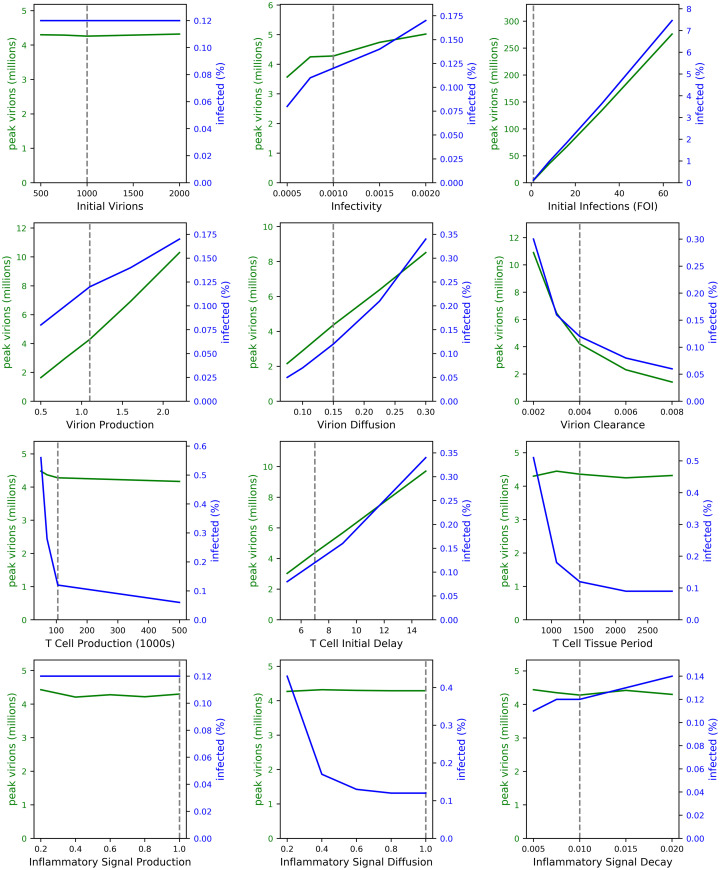
We performed a more complete analysis of how peak viral load and the percentage of infected cells vary given variations in individual parameters. We find that increasing viral production, viral diffusion, and the delay in T cell arrival into the lung each cause an approximately linear increase in viral load and percent of infected cells (Fig 5). The number of FOI has a particularly strong linear correlation with viral load and percent of infected cells. Our sensitivity analysis also confirms our findings in Fig 3 showing no effect of the number of virions within a single FOI. Similar to results in Fig 4, we find that varying parameters that affect the number of T cells in infected tissue, including T cell production, T cell lifespan in the tissue, and the inflammatory signal responsible for recruiting T cells into lung tissue show a threshold effect. That is, beyond a certain threshold, the viral load and percentage of infected cells are not sensitive to changes in these parameters. Our results suggest that below a certain number of CD8⁺ T cells, infection control is not achieved.

Fig 5 — Each line is the average of five runs. Dashed lines indicate SIMCoV default values. The left axes (green lines) show how each parameter affects peak viral load and the right axes (blue lines) show the effect on the percent of cells in the simulation that become infected. The one-at-a-time sensitivity analysis is detailed in Materials and Methods.

SIMCoV viral loads compared to patient data

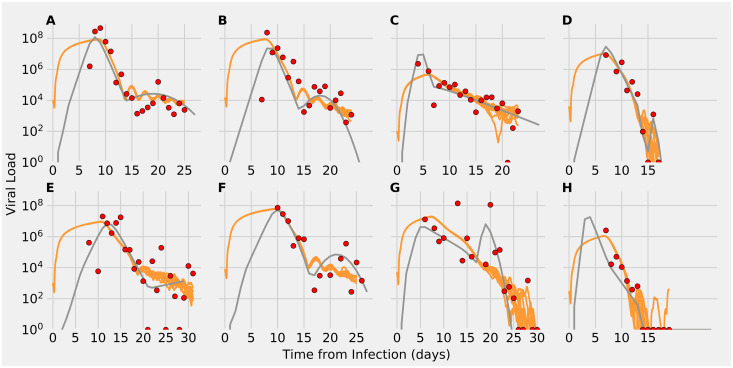
Having shown how the number of initial FOI and the timing and number of responding CD8⁺ T cells affect viral dynamics, we next consider how these factors affect SIMCoV fits to time courses of viral load in COVID-19 patients. Following previous ODE models, e.g. [7, 8, 12, 14], we use data from sputum samples reported in Wolfel et. al. [36]. This study collected sputum from the lower respiratory tract, in contrast to most viral swabs that are collected from the nasal cavity. The lung contains vastly more tissue than the nasal cavity; the epithelial lining of the branching airways and alveoli forms a large and complex surface area of up to 80 m² [37]. Most earlier models of the Wolfel et al. patient data used a target cell limited (TCL) framework, in which viral load peaks when the virus infects all infectable “target” epithelial cells and runs out of targets. These models typically predict viral peaks within the first four or five dpi. However, SARS-CoV-2 peak viral load occurs later in the lung than in the upper respiratory tract (URT) [38], and the patient data have complex dynamics that last 15 to 30 dpi (Fig 6). Although the viral peak may be reached earlier in the URT, in the lung, it may not be achieved before the adaptive immune response begins [17]. Thus, TCL models may not be the most suitable approach for capturing infection dynamics in the lung, which is larger and has more complex organization.

Fig 6 — For each simulation, 10 random runs are shown.

We tested whether SIMCoV can explain the substantial variation in patient viral load data by varying only the initial FOI, timing and strength of T cell response, and viral clearance rates that include other immune activity. We began with default model parameters (Materials and Methods—Table 2 and Fig 2) and varied the number of FOI from one to 220 sites. We also varied the timing of first T cell arrival (from five to 10 days), T cell generation rate (from 90,000 to 200,000 cells per minute), and the viral clearance term (from 0.003 to 0.005) to account for variations in other components of the immune response.

We find that SIMCoV simulates the dynamics of patient viral load over the full 25-30 day time courses with fits that are quantitatively similar to those of the extended ODE described in Ke et al. [12] (Fig 6). Table 1 shows that the goodness-of-fit is similar between SIMCoV and the ODE as measured by the Root Mean Squared Log Error (RMSLE). SIMCoV was parameterized manually, as described in the subsection “Manually Parameterizing SIMCoV to Fit Patient Data” of the Methods section. When we varied the initial FOI, SIMCoV replicated the several order-of-magnitude differences in viral load observed across the eight patients. Compared to the ODE model, SIMCoV produced a less pronounced peak with higher viral loads early in infection that persisted for several days. The SIMCoV curves are consistent with the observation that individuals infected with SARS-CoV-2 are most infectious early in infection before symptom onset [39, 40]. The SIMCoV runs also predict that elevated viral titers persist for more days, which agrees with patient viral load data.

Table 1. SIMCoV parameter settings used for each patient; RMSLE for the simulation averaged over 10 runs and RMSLE for the ODE.

Patient	T Cell Generation Rate (1000 T cells/min)	T Cell Onset (days)	Initial Sites of Infection	Viral Clearance	SIMCoV RMSLE	ODE RMSLE
A	200	8	220	0.003	1.98	1.79
B	160	7	150	0.003	2.58	2.55
C	90	5	1	0.003	2.31	2.05
D	120	6	40	0.005	2.65	1.62
E	120	10	10	0.003	3.75	3.40
F	150	9	80	0.003	2.30	1.92
G	90	6.5	50	0.004	3.54	2.88
H	160	6	3	0.004	2.30	1.82

Open in a new tab

Varying the T cell generation rate and first day of arrival captures the unique shapes of viral load trajectories after seven dpi. SIMCoV exhibits both oscillations in viral load and second peaks that are seen in some patients [36]. These results support the hypothesis that decreased T cell numbers can account for viral persistence and inability to control viral load in some individuals [19, 20]. The fit to Patient A also shows that a high initial and peak viral load, which we fit by setting the number of FOI to 220, is not quickly controlled by even a high T cell response (in this case, a T cell production rate of 200,000 T cells/min beginning on 8 dpi). This suggests that initial infection in a large number of FOI could overwhelm even a robust T cell response.

Previous TCL models have replicated the data in Wolfel et al. [36] by expanding the availability of target cells later in infection and varying many parameters in each patient [7, 12]. For example, the extended ODE model in [12] achieves good fits by varying infectivity, infected cell death rate, virion production rate, number and timing of new target cells introduced to represent newly seeded infections, and the exponential increase of the infected cell death rate to account for the adaptive immune response. By incorporating spatial interactions, SIMCoV provides a more parsimonious explanation for the dramatically different viral load trajectories among SARS-CoV-2 positive individuals by varying only the number of FOI in the initial infection and the magnitude and timing of the immune response, particularly the CD8⁺ T cell response. These factors are consistent with hypothesized explanations for highly variable patient outcomes. Elderly individuals have lower T cell counts, and our model suggests that fewer T cells along with slower T cell response could help explain why elderly individuals have increased disease severity [19, 22]. More speculatively, the number of FOI might be larger if a larger amount of virus is inhaled into the lungs; a larger initial viral dose has been shown to increase disease severity in macaques [41] and has been suggested in humans [42, 43]. Variation in FOI and T cell response may also account for the long infectious period in some patients [4–6].

Modeling viral spread over branching airways

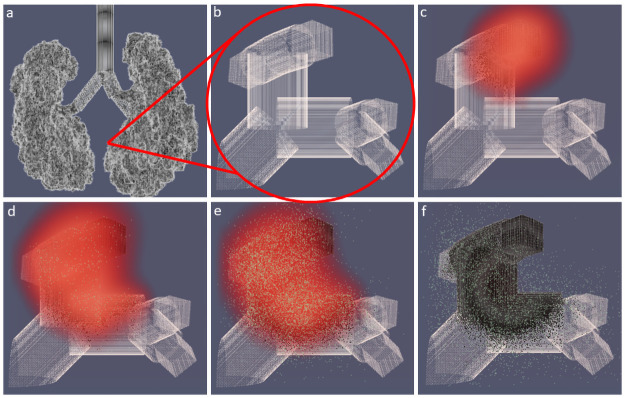
The SIMCoV experiments described above simulate a single layer of epithelial cells (Figs 2–6). However, the lung is a highly complex structure of branching airways descending from large bronchioles down to alveoli lined by epithelial cells, with much of the volume consumed by alveolar space for gas exchange [37]. To investigate how the lung airway structure impacts viral spread and T cell control, we developed a bifurcating fractal branching algorithm and integrated it into SIMCoV simulations to form the surface of the epithelial layer. Following Yeh et al. [44], we model 26 branching generations (from the trachea to alveolar sacs) in all five lobes of the lung. The 3D branching model incorporates trachea, bronchi, bronchioles, and ducts, represented as cylinders of epithelial cells with length, diameter, branching angle, and gravity angle calculated at each level of the branching hierarchy, and each terminal alveolar sac is represented as a hollow 200 x 200 x 200 μm³ cube of epithelial cells. Fig 7A shows the full model of the branching structure, and Fig 7B–7F show how virus spreads over a small region of bronchioles and alveoli in a 1500 x 1500 x 1500 μm³ volume.

Fig 7 — **(A)** shows the full lung model; **(B)**–**(F)** show T cells (green), virions (red), and a small region of epithelial cells (gray) at **(B)** 0 dpi, **(C)** 4.2 dpi, **(D)** 6.3 dpi, **(E)** 6.9 dpi, and **(F)** 8.3 dpi. Dead epithelial cells are indicated in black. A video corresponding to these images is available at https://youtu.be/ychAmDU4qFM.

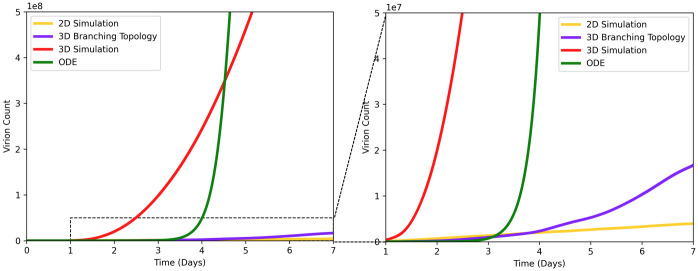
Fig 8 shows how different topologies of epithelial cells modeled in SIMCoV affect the predicted rate of viral spread in the first seven dpi and before the T cell response. The default model parameters are used for all topologies, and each simulation was run with sufficient numbers of epithelial cells to avoid reaching target cell limitation. The branching network model (Fig 7) best captures the spatial arrangement of epithelial cells. However, viral spread over the branching network (blue line in Fig 8) shows only four times greater growth than spread over the simple 2D layer (yellow line) used in our earlier simulations. In contrast, an undifferentiated 3D grid of cells (red line) generates 66 times more infected cells than the branching model at the end of the first week of infection, and the TCL ODE from [12] (green line) generates thousands of times more infected cells before reaching target cell limitation within the first week.

We hypothesize that the 2D model slightly underestimates viral growth because it is constrained by the circumference of the circle of infection, which grows linearly with the total number of cells in the FOI (Fig 2). In (non-branching) 3D grid simulations, infection spreads from the faster growing sphere of infected cells. ODE models assume all infected cells can infect all other infectable cells, and without spatial constraints, the virus spreads even faster. At least at the scale of the hundreds of millions of cells modeled here, the simple 2D model is computationally efficient and captures the dynamics of the branching model well (although small differences are visible in the right panel of Fig 8). Future work can incorporate more detailed movement of virus and immune cells through the epithelium and branching airways as well as the percent and locations of infectable cells in simulations at the full scale of the human lung.

Discussion

Summary

SIMCoV models the spread of SARS-CoV-2 through the lung and subsequent immune control by CD8⁺ T cells. There are three main findings from our simulations. First, variation in the initial number of sites of infection (or FOI) can dramatically change the peak viral load. Second, variation in the magnitude and timing of the CD8⁺ T cell response can explain why some patients clear infections quickly while viral load oscillates and lingers in others. Third, modeling the spatial spread in a 2D layer of tissue, or more realistically, in a fractal branching model of airway epithelial tissue, results in much slower viral spread than in mathematical models that do not consider spatial constraints.

Fig 3 shows that the number of initial FOI determines peak viral load, but the actual number of virions causing initial infection does not independently affect the viral peak. However, in real infections, the likelihood of virus taking hold in more FOI might increase if more virus is inhaled. The number of inhaled virions and their spatial dispersion may be a key explanation for why viral load and disease outcome can be so different in demographically similar patients. An important insight from SIMCoV is that spatial dispersion of virus may be particularly important for SARS-CoV-2 and other lung infections because the epithelial surface area of the lung is so large; this contrasts with the smaller surface areas of the nasopharynx, where TCL can be reached quickly even with a small initial infection [17].

Fig 6 shows that varying T cell arrival time by only a few days (from five to 10 dpi, consistent with [45]) and the magnitude of the T cell and other immune responses by two-fold accounts for the variability and oscillations in viral clearance of the patients from [36]. This is consistent with studies that show CD8⁺ T cells in particular are critical for clearance and control of SARS-CoV-2 infection [18, 19, 22, 46, 47].

Fig 8 shows how the branching topology of the lung (shown in Fig 7) impacts viral spread compared to a simple 2D or 3D grid and a non-spatial ODE model. The 2D model (which we used to simulate viral dynamics in Figs 2–6) produces fits most similar to the more realistic branching airway model. In contrast, the 3D and ODE models both predict much faster viral growth than the branching model. ODE models assume well-mixed (also called “mass action”) interactions in which any infected cell can infect any other infectable cell regardless of the physical distance between them. ODE models with TCL require extremely fast viral replication (e.g., R₀ ≈ 27 in [12]) to reach TCL and fit the timing of the viral peak.

The relatively slow viral spread over surfaces (either the branching airway surface or the simpler 2D layer of cells) means that it is unlikely that TCL can explain the peak viral load. Our hypothesis that not all lung cells are infected is consistent with observed mild illness in many patients, including those in [36]. It is also consistent with CT scans showing damage in only a small percentage of tissue in most patients [28, 48]. Because SIMCoV includes spatial constraints on viral spread, it suggests that immune response, particularly CD8⁺ T cell response, determines the timing of the peak viral load, rather than the time at which virus infects all infectable cells.

Relationship to other models

Several earlier SARS-CoV-2 ODE models were tuned to fit the same lung viral load data from [36] that we fit here. Some included an implicit immune response incorporated in the cell clearance term and an explicit adaptive immune response, e.g. [8, 14–16, 49], similar to the approach we took with SIMCoV. SIMCoV complements these earlier ODE models but makes different predictions. For example, earlier models predict a sharp early peak in viral load in the first few days of infection, while SIMCoV predicts a broader peak which rises rapidly for the first few days post infection and then continues to increase slowly until the T cell response begins between day seven and 10 [45]. Viral levels then decline gradually but continue to oscillate as infected cells continue to produce virus and as T cells discover pockets of hidden infection. The viral dynamics predicted by SIMCoV are consistent with observations that the viral load in the lung peaks later than in the upper respiratory tract and can persist for much longer [16, 17, 50]. In contrast to ODE models, SIMCoV suggests a parsimonious, mechanistic explanation that peak viral load in the lung is determined by the number of FOI and the magnitude and timing of the CD8⁺ T cell response.

Other spatially explicitly models of viral spread through the lung have been developed. SIMCoV replicates many of the features of the CyCells ABM that modeled the spatial spread of tuberculosis [26] and influenza [25] over a 2D grid. Sego et al. [51] built a multi-scale model of SARS-CoV-2 that connects a 2D spatial grid that, like SIMCoV and CyCells, represents epithelial cells as a static 2D layer with virus and signals diffusing as fields over that grid. Quirouette et al. [52] used partial differential equations to model diffusion and advection of influenza along the single dimension from the lower to upper regions of the lung. Each of these attempts to model spatial dynamics has strengths and limitations.

SIMCoV is unique in its ability to explicitly model the spread of virus from multiple FOI as well as the recruitment of T cells to those locations. To do this, SIMCoV uses a highly scalable architecture to represent hundreds of millions of cells that can contain multiple growing FOI. T cell killing of infected cells requires direct cell to cell contact [31, 33, 53]. Because SIMCoV represents spatial positioning and T cell movement explicitly, their physical co-location with infected cells arises naturally in the model. This modeling strategy provides a mechanistic explanation that shows how even a small decrease in the number of responding T cells changes viral dynamics from a smooth decline to an oscillating decline to uncontrolled viral persistence. Interestingly, later arrival of T cells into the infected lung delays viral control but otherwise has little effect on viral dynamics or clearance.

Caveats, limitations, and future work

SIMCoV, like any model, focuses on only a subset of possible factors. In this paper, we focused on the CD8⁺ T cell response and not innate, antibody, B cell, or CD4⁺ T cell immunity, and we focused on spread through the lung and not the nasal cavity. Some parameters in the model are not well characterized in the biological literature, i.e. rates of production, diffusion and decay of inflammatory signals. Fig 5 shows that peak viral load and the extent of infection are largely insensitive to these parameters.

When fitting the model to patient viral loads, we kept parameters related to virus characteristics (i.e. viral infectivity and production rates) constant because we do not expect viral characteristics to vary across patients. However, these parameters might vary significantly between different SARS-CoV-2 variants. A logical avenue for future work is to better understand the dynamics of different SARS-CoV-2 variants, particularly Delta and Omicron, by modeling its properties, such as increased viral production and increased infectivity. Future studies could also explicitly represent antibody responses and CD4⁺ T cell responses, either as time varying components of the clearance term or by modeling their ability to neutralize virus or reduce viral replication or entry into cells. This would enable comparisons of naive patients with vaccinated and previously infected patients. Lipsitch et al. speculate that a higher viral inoculum might reduce vaccine efficacy [54]; future SIMCoV experiments can assess how the number of FOI impact T cell control of infection in vaccinated people. SIMCoV could also be used to study other respiratory diseases, such as influenza, or even be extended to model infection in other organs. The SIMCoV platform could be used to simulate other spatial interactions, like predator prey dynamics between immune and infected cells or collective action dynamics [11], such as the collective search strategies of T cells [55] or the movement patterns of T cells within the lung [32, 34].

Previous spatial models were limited both by data on infection dynamics and the computational power required to explicitly represent spatial interactions among large numbers of cells [23]. SIMCoV overcomes these limitations by leveraging data shared in response to the COVID-19 pandemic and a model design and implementation that takes advantage of HPC capabilities. To enable open and reproducible science, SIMCoV is freely available under an open-source license, and it was designed to be easily extensible. Future extensions of the model could scale up to a full lung, investigate the effects of mucus and the complex dynamics of airflow in the respiratory tract [56], and incorporate more detailed topological models of the airways and alveoli, including the fraction and distribution of epithelial cells with receptors susceptible to infection. By predicting the time course of viral loads within individuals, SIMCoV can help to identify factors that determine windows of transmission between individuals and thereby improve understanding of epidemic spread.

Materials and methods

Model description

SIMCoV is an Agent Based Model (ABM). The SIMCoV source code is available at https://github.com/AdaptiveComputationLab/simcov. Space is represented by a discrete Cartesian grid that can be either two or three-dimensional. For clarity, we describe the model with reference to a 2D layer of epithelial cells, although the mechanisms apply to other topologies, in particular, a 3D grid and a 3D branching structure of lung airways.

Grid points are spaced five microns apart (roughly the diameter of a T cell), and components of the model occur only at these discrete locations. The model is run as a discrete-time simulation, where each time step represents one minute, approximately the time it takes for a T cell to move five microns (one grid point) [34, 57]. At each time step, the model components are updated according to their states and interactions. Grid boundaries are fixed, not periodic.

There are four main components of SIMCoV: epithelial cells, CD8⁺ T cells, virions, and inflammatory signals, representing the subset of cytokines that cause T cell extravasation into the lung tissue. The interactions between these components are shown in Fig 1. Each epithelial cell has a fixed grid location with no more than one cell per location. However, some locations can be empty, representing airways (as can be seen in Fig 7). In addition, a single T cell may also occupy a grid point, and every grid point has a concentration of virions and inflammatory signals. The number of virions per grid point is represented explicitly but capped at 125,000 virions, which is the maximum number estimated to fit within 125 μm³. The concentration of inflammatory signal is represented as a floating point number between 1 × 10⁻⁶ and one.

Each simulation run begins with a number of sites of infection (parameter b in Table 2), which are grid points with an initial number of virions (parameter c). At each time step, the virions diffuse uniformly at a given rate (parameter j) to neighboring grid points, both those with and without epithelial cells, and some fraction (parameter i) of the virions are cleared, reducing the concentration.

Table 2. Table of SIMCoV parameters.

Default values are COVID-19 parameters assembled from a variety of sources. Time periods are Poisson distributions, defined by the mean, λ. Each time step is one minute, and grid points are five microns apart. Unless stated otherwise, the default parameters were used for all experiments. Parameters marked with (*) were not taken from the literature—see Parameter Derivation.

Parameter	Description	Default	Reference
(a) Dimensions	Simulation size in x, y, and z dimensions	15000x15000x1	*
(b) Initial Infections	Number of grid points with initial infections	1	*
(c) Initial Virions	Number of virions at initial infection locations	1000	*
(d) Incubation Period	Average minutes until an infected cell starts expressing virions	480	[58]
(e) Expressing Period	Average minutes after expressing starts until cell death	900	[10]
(f) Apoptosis Period	Average minutes after apoptosis is induced until cell death	180	[59]
(g) Infectivity	Probability of one virion infecting one cell per minute	0.001	[25]
(h) Virion Production	Number of virions produced by expressing cell per minute	1.1	[60]
(i) Virion Clearance	Fraction by which virion count drops per minute	0.004	[25]
(j) Virion Diffusion	Fraction of virions that diffuse into all neighboring grid points per minute	0.15	[25]
(k) Inflammatory Signal Production	Concentration of inflammatory signal produced by expressing cells per minute	1	*
(l) Inflammatory Signal Decay	Fraction by which inflammatory signal concentration drops per minute	0.01	*
(m) Inflammatory Signal Diffusion	Fraction of inflammatory signal that diffuses into all neighboring grid points per minute	1	[25]
(n) T Cell Production	Number of T cells generated per minute into circulation	105000	[25, 61]
(o) T Cell Initial Delay	Average minutes before T cells start to be produced	10080	[45, 62, 63]
(p) T Cell Vascular Period	Average minutes before death for a T cell in the vasculature	5760	[25]
(q) T Cell Tissue Period	Average minutes before death for a T cell after it extravasates	1440	[64]
(r) T Cell Binding Period	Average minutes T cell is bound to an epithelial cell	10	[33]

Open in a new tab

Initially, all epithelial cells are healthy (uninfected) and susceptible to infection. At the end of each time step, if there are virions in the same location as a healthy epithelial cell, that cell becomes infected (transition 1 in Fig 1) with probability proportional to the virion concentration multiplied by infectivity (parameter g). An infected epithelial cell is initially incubating and remains in this state for a number of time steps, which is sampled from a Poisson distribution (parameter d). An expressing epithelial cell produces virions at a constant rate per time step (parameter h, transition 3a), which are added to the local concentration and diffuse (transition 4a) until they are cleared (transition 4b). Expressing cells that avoid contact with a T cell eventually die (parameter e, transition 3c).

When epithelial cells are expressing (and apoptotic, described below), they produce inflammatory signal at a constant rate (parameter k) per time step (transition 3b). Those signals diffuse to neighboring grid points and decay at a constant rate (parameters m and l, respectively). Inflammatory signal is represented as a floating point number (concentration) with a minimum value (1 × 10⁻⁶), below which it is considered eliminated. In the current implementation, inflammatory signals only affect T cell extravasation, although future extensions could incorporate other chemokines and cytokines.

After some delay (parameter o), activated antigen-specific CD8⁺ T cells enter the blood from (unmodeled) lymph nodes (transition 7) at a constant rate (parameter n). T cells in the vasculature extravasate when they detect inflammatory signal (transition 9b). T cell movement through the vasculature is not explicitly modeled; instead, a random location is chosen for each T cell at every time step, and if that location contains inflammatory signal, then the T cell extravasates. The random location is chosen from among all of the possible locations for a complete lung, but when only a fraction of the lung is being modeled, the probability of extravasation is reduced accordingly. Since only one T cell can occupy any single location in the tissue at a time, T cells are blocked from extravasating if the location already contains a T cell. T cells that do not extravasate continue to circulate (transition 9a); those that fail to extravasate before the vascular T cell lifespan (parameter p) die and are removed from the simulation (transition 9c).

T cells residing in lung tissue can bind to epithelial cells at the same location or at an immediate neighboring location (transition 10a). Binding probability is proportional to how long the cell has been incubating, with a maximum of one if the cell is expressing. Multiple T cells can bind to a single infected cell (respecting the occupancy rules outlined earlier). When binding occurs, the T cell transitions to apoptotic (transition 3d) and after some time (parameter f), it dies (transition 6b). Apoptotic epithelial cells produce virions (transition 6a) and inflammatory signals at the same rates as expressing cells. T cells remain bound for a fixed time (parameter r), after which they continue moving in the tissue. During each time step, the T cell moves one step to a randomly selected adjacent location that is not occupied by another T cell. Hence, T cells move at a maximum rate of five microns per minute [34]. After moving, if a T cell is adjacent to or colocated with an infected cell, it can bind again. This process of random movement and possible binding continues until the T cell dies (transition 10b, parameter q). T cells residing in lung tissue never return to the vasculature.

Parameter derivation

Where possible, parameter settings were derived from published data, as described below:

a
Dimensions: In general, each dimension is set large enough to avoid target cell limitation during the first week post-infection; for the default 2D simulation, the dimensions are 15,000 x 15,000 x 1, representing a 75mm x 75mm layer of 225 million cells.
b
Initial Infections: Set to one to represent the minimum number of infections to simulate viral spread.
c
Initial Virions: Set according to infectivity (g), so as to ensure a successful initial infection of at least one cell.
d
Incubation Period: Roughly, the eclipse period; estimated to be 7-8 hours or 480 time steps in [58].
e
Expressing Period: Estimated to be about 15 hours or 900 minutes in [10], which is similar to the expressing period of the influenza virus (about 1000 minutes [25]).
f
Apoptosis Period: Estimated to range between 48 minutes and 168 minutes in mice [59]; we estimate a slightly longer period, 180 minutes, for humans.
g
Infectivity: Set to 0.001, which is the probability of infection per cell per minute, i.e. it will take on average 1,000 minutes for a virion to infect a single cell. This is within the range of 12 to 1,200 minutes estimated for influenza [25], although this value is largely unknown and almost certainly varies between diseases and viral variants.
h
Virion Production: Calculated by dividing the burst size by the expressing period (e); the burst size is the total number of virions produced by an infected cell, which was found to be 1,000 virions [60].
i
Virion Clearance: Set to 0.004 virions per minute, which is within prior calculations of the virion decay rate of the influenza virus, ranging from 7e-7 to 0.07 virions per minute [25]. We vary this parameter from 0.003 to 0.005 to fit patient data.
j
Virion Diffusion: Calculated from the Einstein-Smoluchowski equation for particle movement, D ≈ αx²/(2t), where x is the mean distance diffused in one direction along one axis in time t, and α is the SIMCoV parameter. Hence, for a mean distance of five microns (one grid point), a time of one minute (one simulation time step), and a virion diffusion parameter of 0.15, the diffusion coefficient is 0.0312μm²/s. This diffusion coefficient is similar to the diffusion coefficient calculated for influenza [25], which is 0.0318μm²/s.
k
Inflammatory Signal Production: The concentration of inflammatory signal produced per minute is not a value explicitly available from the literature because it is an abstraction of the production rates of multiple signaling molecules, each of which varies for different pathogens. For example, in [25, 27] production of CXCL10 (IP-10) and CCL5 (RANTES) vary by several orders of magnitude for different strains of influenza. Therefore, we model inflammatory signals as an abstract quantity with a production rate of 1 unit per time step. The effect of this parameter on T cell extravasation then depends on inflammatory signal decay and diffusion parameters. The inflammatory production, decay, and diffusion parameters result in an area or volume containing inflammatory signals that is two to three times that of infected cells in simulations with default parameters.
l
Inflammatory Signal Decay: We estimate a half life of 70 minutes, which is similar to the half life of 30 minutes estimated in earlier work for influenza [25].
m
Inflammatory Signal Diffusion: Calculated from the Einstein-Smoluchowski equation for particle movement, D ≈ α.x²/(2t), where x is the mean distance diffused in one direction along one axis in time t, and α is the SIMCoV parameter. Hence, for a mean distance of five microns (one grid point), a time of one minute, and an inflammatory signal diffusion parameter of 1, the diffusion coefficient is 0.210μm²/s, which is within the range of the chemokine diffusion coefficient calculated in [25] (from 0.00318μm²/s to 318μm²/s).
n
T Cell Production: The number of T cells produced by replication in the mediastinal lymph nodes of the lung is calculated by scaling up the T cell production rate in Levin et al. [25], which was estimated from mouse models [61]. That previous calculation assumed that a single virus-specific T cell encounters an antigen-presenting cell and begins to replicate on day 0 post infection, doubling every eight hours. After five days, those activated CD8⁺ T cells could generate approximately 30,000 new T cells per day (or 21 per minute) into circulation. For SIMCoV, we assume a linear 5,000-fold increase from mouse to human, which reflects the approximate increase in lung and blood volume and gives a rate of 105,000 T cells per minute entering circulation.
o
T Cell Initial Delay: Estimated from [45] for SARS-CoV-2. The SIMCoV default is seven dpi, which we vary from five to ten dpi to fit patient data. We note that T cell delay is related to the T cell production rate. If T cells double every eight hours and replication in humans lasts 2.3 days longer than in mice (seven versus five dpi), this would cause a 128-fold increase in T cell production. With 40 times greater SARS-CoV-2 specific T cell precursors, this would generate 5,000 times greater T cell production in humans. Alternatively, exponential replication of a single T cell precursor for nine days would generate 5,000 times greater production in humans compared to mice.
p
T Cell Vascular Period: Equivalent to the T cell age in the blood used in a model of T cell responses to influenza [25].
q
T Cell Tissue Period: Largely unknown, but estimates were provided in Keating et al. [64].
r
T Cell Binding: Taken from Halle et al. [33].

Fig 5 explores the impact of varying model parameters. We used a one-at-a-time (OAT) approach for sensitivity analysis, similar to the method reported in Hoertel et al. [65]. OAT is useful when it is computationally expensive to run many simulations and when some parameters are predetermined or have a small acceptable range [66]. Thus, our analysis varied one parameter at a time while holding the others at their default values. We report the size of the peak viral load during the run and the percentage of infected cells at the end of the run (including dead cells). Several of the parameters have only a small impact on disease progression: initial virions (b), T cell tissue period (q), and inflammatory signal production and decay (k, l). Other parameters have clear and expected effects; for example, there is a linear relation between peak viral load and virion production (h).

Manually parameterizing SIMCoV to fit patient data

We developed the fits to patient data manually, using an approach based on plausible biological mechanisms related to the immune response. We hypothesized that the differences among individual patients arose as a consequence of different immune responses and initial viral exposure, rather than from changes in the nature of the virus from one patient to the next. We also focused on adjusting the subset of model parameters that are expected to vary from patient to patient, depending on age, health, etc., and initial viral exposure. First, there are the parameters that control the extent of the immune response, including T cell production and onset delay and viral clearance rate. Second are the parameters that capture the size of the initial exposure: the number of FOI and initial virions parameters (the latter has no impact, as seen in Fig 5, so we ignored it in the fitting process). All other parameters were kept constant at the default values because we do not expect them to vary between patients. For example, several parameters define disease characteristics, such as virion production and diffusion and infectivity. In the future, these could be varied to explore the impact of different variants or different pathogens; we hypothesized that those factors are unlikely to vary substantially across patients in the Wolfel dataset [36].

In all cases, the four selected parameters were adjusted to obtain the fit as follows. We set the T cell initial delay according to the timing of peak viral load, using a value one day (1440 minutes) before the empirical peak. Second, we set the initial infections (the number of FOI) to obtain a matching peak viral load. Because the model produces a count of virions deep within the lungs, and for the patients we only have sputum samples with counts of RNA copies, we do not expect a one-to-one mapping between empirical viral load and the model virion counts. To address this, we used a scaling factor of 0.1, chosen to minimize the number of FOI required for matching (and hence the computational cost). This scaling factor is the same for all patients; we match the peak scaled values by adjusting the number of FOI. As can be seen in Fig 5, there is a linear relationship between the number of FOI and the size of the peak viral load, so it is a simple matter to adjust the FOI to match the observed peak. As can be seen in Fig 4A, the T cell generation rate affects the shape of the curve after the T cell response begins. Hence, we adjusted this value to match the post-peak curve observed in the patient data. If the viral load continues to oscillate for some period after the initial drop (patients A, B, C, E, F), then we reduced the clearance rate from the default of 0.004 down to 0.003. This results in more “hidden” pockets of incubating virus that evade detection and cause repeated surges in the later stages of disease progression. Finally, there is one case (patient D) where the infection is cleared very rapidly, and in this case, we increased the clearance rate to 0.005.

Model implementation

The SIMCoV model is implemented in UPC++ [67], which is a library extension to the C++ programming language with state-of-the-art HPC capabilities for parallel computation. UPC++ runs on a variety of platforms, including distributed memory supercomputers and networked clusters. Consequently, the SIMCoV application can run on systems from laptops up to high performance supercomputers without requiring any code changes. Because the computational cost of the simulation is substantial, only small areas can be simulated on smaller systems with one or a few compute nodes. Simulations of significant fractions of the human lung require hundreds or thousands of compute nodes.

Massively parallel simulation

SIMCoV was designed by composing parallelizable functions to create a highly scalable simulation framework. Running immense agent-based simulations of this type would not be computationally feasible without the application of high performance computing techniques (HPC). For SIMCoV, we relied on the HPC primitives and multi-process communication techniques provided by UPC++. We reduced the communication and computational work load of running large SIMCoV simulations using different approaches. To mitigate expensive cross-process calculation, we maintain two- or three-dimensional blocks of closely spaced grid points in contiguous single process memory. This lowers the chance that for any given update of agents in the simulation that two processes have to share memory. To prevent unnecessary computation costs, we maintain an active list of agents and grid points that are updated at each iteration of the simulation. Some grid points can be predicted to remain constant from one iteration to the next, so there is no need to update their behavior for that step.

SIMCoV can be used to run large simulations in minutes on suitable supercomputers. For example, we simulated an infection seeded with multiple initial FOI in a 285000 x 285000 x 5 μm³ tissue, comprising over three billion epithelial cells, which is equivalent to a single slice of tissue through the full human lung. On the NERSC Cori supercomputer, it took 15 minutes to complete a two-week simulation on 32 nodes.

ODE model implementation

Our ODE implementation replicates the model in [12], which was fit to the published sputum swab viral load data of the patients in [36]. Most parameters are similar to our SIMCoV parameters, such as the virion clearance rate and virion production rate. The ODE parameters were fit to the population of patients using non-linear mixed effects modeling in [12]. To account for the variation in patients, they fit each individual patient, varying cell death rate, infectivity, and virion production rate. The model relies on target cell limitation to fit the viral peak for each patient, and fits were assessed using AIC. The ODE fits in Fig 6 use the parameters selected as best fits for each individual patient. We implemented this ODE model using the scipy odeint Python package, the model description in [12], and the fit model parameters for patient A in [12].

Acknowledgments

We thank Ruian Ke for sharing insights and an early draft of his ODE model; Matthew Fricke, UNM CARC, and ASU RC for HPC support; and Greg Forest for helpful discussions.

Data Availability

All code can be accessed at https://github.com/AdaptiveComputationLab/simcov. Configuration files to reproduce each figure in the paper are available in the configs folder in that repository.

Funding Statement

This project was funded by NSF (www.nsf.gov) 2030037 and 2029696 which includes Coronavirus Aid, Relief, and Economic Security (CARES) Act funding (MEM, JLC, AA, RG, MH, KL, AP, VS, HT, SF). DARPA (www.darpa.mil) provided partial funding through AFRL FA-8650-18-C-6898 (JLC, MM, HT and AA). JLC is also supported by the Autophagy Inflammation and Metabolism Center of Biomedical Research Excellence (AIM CoBRE, NIH NIGMS P20GM121176). This work is also partly supported by the Advanced Scientific Computing Research (ASCR) program within the Office of Science of the DOE (www.energy.gov) under contract number DE-AC02-05CH11231 (SH) and the Exascale Computing Project(17-SC-20-SC), a collaborative effort of the U.S. Department of Energy Office of Science (SH). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1. Moderbacher CR, Ramirez SI, Dan JM, Grifoni A, Hastie KM, Weiskopf D, et al. Antigen-specific adaptive immunity to SARS-CoV-2 in acute COVID-19 and associations with age and disease severity. Cell. 2020;183(4):996–1012. doi: 10.1016/j.cell.2020.09.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Arunachalam PS, Wimmers F, Mok CKP, Perera RA, Scott M, Hagan T, et al. Systems biological assessment of immunity to mild versus severe COVID-19 infection in humans. Science. 2020;369(6508):1210–1220. doi: 10.1126/science.abc6261 [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Yang J, Zheng Y, Gou X, Pu K, Chen Z, Guo Q, et al. Prevalence of comorbidities and its effects in patients infected with SARS-CoV-2: a systematic review and meta-analysis. International Journal of Infectious Diseases. 2020;94:91–95. doi: 10.1016/j.ijid.2020.03.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
4. Fajnzylber J, Regan J, Coxen K, Corry H, Wong C, Rosenthal A, et al. SARS-CoV-2 viral load is associated with increased disease severity and mortality. Nature Communications. 2020;11(1):1–9. doi: 10.1038/s41467-020-19057-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Marks M, Millat-Martinez P, Ouchi D, Roberts Ch, Alemany A, Corbacho-Monné M, et al. Transmission of COVID-19 in 282 clusters in Catalonia, Spain: a cohort study. The Lancet Infectious Diseases. 2021;. doi: 10.1016/S1473-3099(20)30985-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Néant N, Lingas G, Le Hingrat Q, Ghosn J, Engelmann I, Lepiller Q, et al. Modeling SARS-CoV-2 viral kinetics and association with mortality in hospitalized patients from the French COVID cohort. Proceedings of the National Academy of Sciences. 2021;118(8). doi: 10.1073/pnas.2017962118 [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Wang S, Pan Y, Wang Q, Miao H, Brown AN, Rong L. Modeling the viral dynamics of SARS-CoV-2 infection. Mathematical biosciences. 2020;328:108438. doi: 10.1016/j.mbs.2020.108438 [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Hernandez-Vargas EA, Velasco-Hernandez JX. In-host mathematical modelling of covid-19 in humans. Annual reviews in control. 2020;. doi: 10.1016/j.arcontrol.2020.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Gonçalves A, Bertrand J, Ke R, Comets E, De Lamballerie X, Malvy D, et al. Timing of antiviral treatment initiation is critical to reduce SARS-CoV-2 viral load. CPT: pharmacometrics & systems pharmacology. 2020;9(9):509–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Kim KS, Ejima K, Ito Y, Iwanami S, Ohashi H, Koizumi Y, et al. Modelling SARS-CoV-2 dynamics: Implications for therapy; 2020. [Google Scholar]
11. Metcalf CJE, Grenfell BT, Graham AL. Disentangling the dynamical underpinnings of differences in SARS-CoV-2 pathology using within-host ecological models. PLoS pathogens. 2020;16(12):e1009105. doi: 10.1371/journal.ppat.1009105 [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Ke R, Zitzmann C, Ribeiro RM, Perelson AS. Kinetics of SARS-CoV-2 infection in the human upper and lower respiratory tracts and their relationship with infectiousness. medRxiv. 2020. [Google Scholar]
13. Ejima K, Kim KS, Ludema C, Bento AI, Iwanami S, Fujita Y, et al. Estimation of the incubation period of COVID-19 using viral load data. Epidemics. 2021;35:100454. doi: 10.1016/j.epidem.2021.100454 [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Goyal A, Cardozo-Ojeda EF, Schiffer JT. Potency and timing of antiviral therapy as determinants of duration of SARS-CoV-2 shedding and intensity of inflammatory response. Science advances. 2020;6(47):eabc7112. doi: 10.1126/sciadv.abc7112 [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Kim KS, Ejima K, Iwanami S, Fujita Y, Ohashi H, Koizumi Y, et al. A quantitative model used to compare within-host SARS-CoV-2, MERS-CoV, and SARS-CoV dynamics provides insights into the pathogenesis and treatment of SARS-CoV-2. PLoS biology. 2021;19(3):e3001128. doi: 10.1371/journal.pbio.3001128 [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Perelson AS, Ke R. Mechanistic modelling of SARS-CoV-2 and other infectious diseases and the effects of therapeutics. Clinical Pharmacology & Therapeutics. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Du SQ, Yuan W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID-19 and implications for viral pathogenesis. Journal of medical virology. 2020;92(9):1615–1628. doi: 10.1002/jmv.25866 [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Zhang X, Tan Y, Ling Y, Lu G, Liu F, Yi Z, et al. Viral and host factors related to the clinical outcome of COVID-19. Nature. 2020;583(7816):437–440. doi: 10.1038/s41586-020-2355-0 [DOI] [PubMed] [Google Scholar]
19. Sette A, Crotty S. Adaptive Immunity to SARS-CoV-2 and COVID-19. Cell. 2021; doi: 10.1016/j.cell.2021.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Tan AT, Linster M, Tan CW, Le Bert N, Chia WN, Kunasegaran K, et al. Early induction of functional SARS-CoV-2-specific T cells associates with rapid viral clearance and mild disease in COVID-19 patients. Cell reports. 2021;34(6):108728. doi: 10.1016/j.celrep.2021.108728 [DOI] [PMC free article] [PubMed] [Google Scholar]
21. Grifoni A, Weiskopf D, Ramirez SI, Mateus J, Dan JM, Moderbacher CR, et al. Targets of T cell responses to SARS-CoV-2 coronavirus in humans with COVID-19 disease and unexposed individuals. Cell. 2020;181(7):1489–1501. doi: 10.1016/j.cell.2020.05.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Bertoletti A, Tan AT, Le Bert N. The T-cell response to SARS-CoV-2: kinetic and quantitative aspects and the case for their protective role. Oxford Open Immunology. 2021;2(1). doi: 10.1093/oxfimm/iqab006 [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Bauer AL, Beauchemin CAA, Perelson AS. Agent-based modeling of host–pathogen systems: The successes and challenges. Information sciences. 2009;179(10):1379–1389. doi: 10.1016/j.ins.2008.11.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Fricke GM, Letendre KA, Moses ME, Cannon JL. Persistence and adaptation in immunity: T cells balance the extent and thoroughness of search. PLoS Computational Biology. 2016;12(3):e1004818. doi: 10.1371/journal.pcbi.1004818 [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Levin D, Forrest S, Banerjee S, Clay C, Cannon J, Moses M, et al. A spatial model of the efficiency of T cell search in the influenza-infected lung. Journal of Theoretical Biology. 2016;398. doi: 10.1016/j.jtbi.2016.02.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Warrender C, Forrest S, Koster F. Modeling intercellular interactions in early Mycobacterium infection. Bulletin of mathematical biology. 2006;68(8):2233–2261. doi: 10.1007/s11538-006-9103-y [DOI] [PubMed] [Google Scholar]
27. Mitchell H, Levin D, Forrest S, Beauchemin CA, Tipper J, Knight J, et al. Higher level of replication efficiency of 2009 (H1N1) pandemic influenza virus than those of seasonal and avian strains: kinetics from epithelial cell culture and computational modeling. Journal of virology. 2011;85(2):1125–1135. doi: 10.1128/JVI.01722-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Kassin MT, Varble N, Blain M, Xu S, Turkbey EB, Harmon S, et al. Generalized chest CT and lab curves throughout the course of COVID-19. Scientific reports. 2021;11(1):1–13. doi: 10.1038/s41598-021-85694-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Zhang K, Liu X, Shen J, Li Z, Sang Y, Wu X, et al. Clinically applicable AI system for accurate diagnosis, quantitative measurements, and prognosis of COVID-19 pneumonia using computed tomography. Cell. 2020;181(6):1423–1433. doi: 10.1016/j.cell.2020.04.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Imai M, Iwatsuki-Horimoto K, Hatta M, Loeber S, Halfmann PJ, Nakajima N, et al. Syrian hamsters as a small animal model for SARS-CoV-2 infection and countermeasure development. Proceedings of the National Academy of Sciences. 2020;117(28):16587–16595. doi: 10.1073/pnas.2009799117 [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Harris TH, Banigan EJ, Christian DA, Konradt C, Wojno EDT, Norose K, et al. Generalized Lévy walks and the role of chemokines in migration of effector CD8+ T cells. Nature. 2012;486(7404):545–548. doi: 10.1038/nature11098 [DOI] [PMC free article] [PubMed] [Google Scholar]
32. Ariotti S, Beltman JB, Borsje R, Hoekstra ME, Halford WP, Haanen JBAG, et al. Subtle CXCR3-dependent chemotaxis of CTLs within infected tissue allows efficient target localization. The Journal of Immunology. 2015;195(11):5285–5295. doi: 10.4049/jimmunol.1500853 [DOI] [PubMed] [Google Scholar]
33. Halle S, Keyser KA, Stahl FR, Busche A, Marquardt A, Zheng X, et al. In Vivo Killing Capacity of Cytotoxic T Cells Is Limited and Involves Dynamic Interactions and T Cell Cooperativity. Immunity. 2016;44(2):233–245. doi: 10.1016/j.immuni.2016.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
34. Mrass P, Oruganti SR, Fricke GM, Tafoya J, Byrum JR, Yang L, et al. ROCK regulates the intermittent mode of interstitial T cell migration in inflamed lungs. Nature communications. 2017;8(1):1–14. doi: 10.1038/s41467-017-01032-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
35. Zhang X, Tan Y, Ling Y, Lu G, Liu F, Yi Z, et al. Viral and host factors related to the clinical outcome of COVID-19. Nature. 2020. [DOI] [PubMed] [Google Scholar]
36. Wölfel R, Corman VM, Guggemos W, Seilmaier M, Zange S, Müller MA, et al. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020. [DOI] [PubMed] [Google Scholar]
37. Wiebe BM, Laursen H. Lung morphometry by unbiased methods in emphysema: bronchial and blood vessel volume, alveolar surface area and capillary length. Apmis. 1998;106(1-6):651–656. doi: 10.1111/j.1699-0463.1998.tb01395.x [DOI] [PubMed] [Google Scholar]
38. Regan J, Flynn JP, Rosenthal A, Jordan H, Li Y, Chishti R, et al. Viral Load Kinetics of SARS-CoV-2 In Hospitalized Individuals with COVID-19. In: Open Forum Infectious Diseases; 2021. doi: 10.1093/ofid/ofab153 [DOI] [PMC free article] [PubMed] [Google Scholar]
39. Hart WS, Maini PK, Thompson RN. High infectiousness immediately before COVID-19 symptom onset highlights the importance of continued contact tracing. Elife. 2021;10:e65534. doi: 10.7554/eLife.65534 [DOI] [PMC free article] [PubMed] [Google Scholar]
40. Tindale LC, Stockdale JE, Coombe M, Garlock ES, Lau WYV, Saraswat M, et al. Evidence for transmission of COVID-19 prior to symptom onset. Elife. 2020;9:e57149. doi: 10.7554/eLife.57149 [DOI] [PMC free article] [PubMed] [Google Scholar]
41. Dabisch PA, Biryukov J, Beck K, Boydston JA, Sanjak JS, Herzog A, et al. Seroconversion and fever are dose-dependent in a nonhuman primate model of inhalational COVID-19. PLoS pathogens. 2021;17(8):e1009865. doi: 10.1371/journal.ppat.1009865 [DOI] [PMC free article] [PubMed] [Google Scholar]
42. Gandhi M, Beyrer C, Goosby E. Masks do more than protect others during COVID-19: reducing the inoculum of SARS-CoV-2 to protect the wearer. Journal of general internal medicine. 2020;35(10):3063–3066. doi: 10.1007/s11606-020-06067-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
43. Guallar MP, Meiriño R, Donat-Vargas C, Corral O, Jouvé N, Soriano V. Inoculum at the time of SARS-CoV-2 exposure and risk of disease severity. International Journal of Infectious Diseases. 2020;97:290–292. doi: 10.1016/j.ijid.2020.06.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
44. Yeh HC, Schum GM. Models of human lung airways and their application to inhaled particle deposition. Bulletin of Mathematical Biology. 1980;42(3):461–480. doi: 10.1007/BF02460796 [DOI] [PubMed] [Google Scholar]
45. Kalimuddin S, Tham CYL, Qui M, de Alwis R, Sim JXY, Lim JME, et al. Early T cell and binding antibody responses are associated with Covid-19 RNA vaccine efficacy onset. Med. 2021;. doi: 10.1016/j.medj.2021.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Ni L, Cheng ML, Feng Y, Zhao H, Liu J, Ye F, et al. Impaired cellular immunity to SARS-CoV-2 in severe COVID-19 patients. Frontiers in immunology. 2021;12. doi: 10.3389/fimmu.2021.603563 [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Lucas C, Wong P, Klein J, Castro TBR, Silva J, Sundaram M, et al. Longitudinal analyses reveal immunological misfiring in severe COVID-19. Nature. 2020;584(7821):463–469. doi: 10.1038/s41586-020-2588-y [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Shan F, Gao Y, Wang J, Shi W, Shi N, Han M, et al. Abnormal lung quantification in chest CT images of COVID-19 patients with deep learning and its application to severity prediction. Medical physics. 2021;48(4):1633–1645. doi: 10.1002/mp.14609 [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Xavier MP, Reis RF, dos Santos RW, Lobosco M. A simplified model of the Human Immune System response to the COVID-19. In: 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). IEEE; 2020. p. 1311–1317.
50. Cevik M, Tate M, Lloyd O, Maraolo AE, Schafers J, Ho A. SARS-CoV-2, SARS-CoV, and MERS-CoV viral load dynamics, duration of viral shedding, and infectiousness: a systematic review and meta-analysis. The Lancet Microbe. 2020;. doi: 10.1016/S2666-5247(20)30172-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
51. Sego T, Aponte-Serrano JO, Ferrari Gianlupi J, Heaps SR, Breithaupt K, Brusch L, et al. A modular framework for multiscale, multicellular, spatiotemporal modeling of acute primary viral infection and immune response in epithelial tissues and its application to drug therapy timing and effectiveness. PLoS computational biology. 2020;16(12):e1008451. doi: 10.1371/journal.pcbi.1008451 [DOI] [PMC free article] [PubMed] [Google Scholar]
52. Quirouette C, Younis NP, Reddy MB, Beauchemin CA. A mathematical model describing the localization and spread of influenza A virus infection within the human respiratory tract. PLoS computational biology. 2020;16(4):e1007705. doi: 10.1371/journal.pcbi.1007705 [DOI] [PMC free article] [PubMed] [Google Scholar]
53. Hickman HD, Reynoso GV, Ngudiankama BF, Cush SS, Gibbs J, Bennink JR, et al. CXCR3 chemokine receptor enables local CD8+ T cell migration for the destruction of virus-infected cells. Immunity. 2015;42(3):524–537. doi: 10.1016/j.immuni.2015.02.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
54. Lipsitch M, Krammer F, Regev-Yochay G, Lustig Y, Balicer RD. SARS-CoV-2 breakthrough infections in vaccinated individuals: measurement, causes and impact. Nature Reviews Immunology. 2021. doi: 10.1038/s41577-021-00662-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
55. Moses ME, Cannon JL, Gordon DM, Forrest S. Distributed adaptive search in T cells: lessons from ants. Frontiers in immunology. 2019;10:1357. doi: 10.3389/fimmu.2019.01357 [DOI] [PMC free article] [PubMed] [Google Scholar]
56. Levy R, Hill DB, Forest MG, Grotberg JB. Pulmonary fluid flow challenges for experimental and mathematical modeling; 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
57. Looney MR, Thornton EE, Sen D, Lamm WJ, Glenny RW, Krummel MF. Stabilized imaging of immune surveillance in the mouse lung. Nature Methods. 2011;8(1):91–96. doi: 10.1038/nmeth.1543 [DOI] [PMC free article] [PubMed] [Google Scholar]
58. Schneider M, Ackermann K, Stuart M, Wex C, Protzer U, Schätzl HM, et al. Severe Acute Respiratory Syndrome Coronavirus Replication Is Severely Impaired by MG132 due to Proteasome-Independent Inhibition of M-Calpain. Journal of Virology. 2012;86(18):10112–10122. doi: 10.1128/JVI.01001-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
59. Ganusov VV, De Boer RJ. Estimating In Vivo Death Rates of Targets due to CD8 T-Cell-Mediated Killing. Journal of Virology. 2008;82(23):11749–11757. doi: 10.1128/JVI.01128-08 [DOI] [PMC free article] [PubMed] [Google Scholar]
60. Bar-On YM, Flamholz A, Phillips R, Milo R. SARS-CoV-2 (COVID-19) by the numbers. 2020;9:e57309. [DOI] [PMC free article] [PubMed] [Google Scholar]
61. Miao H, Hollenbaugh JA, Zand MS, Holden-Wiltse J, Mosmann TR, Perelson AS, et al. Quantifying the early immune response and adaptive immune response kinetics in mice infected with influenza A virus. J Virol. 2010;84(13):6687–6698. doi: 10.1128/JVI.00266-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
62. Mohn KGI, Brokstad KA, Islam S, Oftung F, Tøndel C, Aarstad HJ, et al. Early Induction of Cross-Reactive CD8+ T-Cell Responses in Tonsils After Live-Attenuated Influenza Vaccination in Children. The Journal of Infectious Diseases. 2020;221(9):1528–1537. doi: 10.1093/infdis/jiz583 [DOI] [PMC free article] [PubMed] [Google Scholar]
63. Powell T, Peng Y, Berthoud T, Blais ME, Lillie P, Hill A, et al. Examination of Influenza Specific T Cell Responses after Influenza Virus Challenge in Individuals Vaccinated with MVA-NP+M1 Vaccine. PloS one. 2013;8:e62778. doi: 10.1371/journal.pone.0062778 [DOI] [PMC free article] [PubMed] [Google Scholar]
64. Keating R, Morris MY, Yue W, Reynolds CE, Harris TL, Brown SA, et al. Potential killers exposed: tracking endogenous influenza-specific CD8+ T cells. Immunology & Cell Biology. 2018;96(10):1104–1119. doi: 10.1111/imcb.12189 [DOI] [PMC free article] [PubMed] [Google Scholar]
65. Hoertel N, Blachier M, Blanco C, Olfson M, Massetti M, Rico MS, et al. A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nature medicine. 2020;26(9):1417–1421. doi: 10.1038/s41591-020-1001-6 [DOI] [PubMed] [Google Scholar]
66. Ten Broeke G, Van Voorn G, Ligtenberg A. Which sensitivity analysis method should I use for my agent-based model? Journal of Artificial Societies and Social Simulation. 2016;19(1):5. doi: 10.18564/jasss.2857 [DOI] [Google Scholar]
67.Bachan J, Baden SB, Hofmeyr S, Jacquelin M, Kamil A, Bonachea D, et al. UPC++: A High-Performance Communication Framework for Asynchronous Computation. In: Proceedings of the 33rd IEEE International Parallel & Distributed Processing Symposium. IPDPS. IEEE; 2019. Available from: https://escholarship.org/uc/item/1gd059hj.

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1009735.r001

Decision Letter 0

Rob J De Boer, Amber M Smith

19 Aug 2021

Dear Dr. Moses,

As with all papers reviewed by the journal, your manuscript was reviewed by members of the editorial board and by several independent reviewers. In light of the reviews (below this email), we would like to invite the resubmission of a significantly-revised version that takes into account the reviewers' comments.

We cannot make any decision about publication until we have seen the revised manuscript and your response to the reviewers' comments. Your revised manuscript is also likely to be sent to reviewers for further evaluation.

When you are ready to resubmit, please upload the following:

[1] A letter containing a detailed list of your responses to the review comments and a description of the changes you have made in the manuscript. Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

[2] Two versions of the revised manuscript: one with either highlights or tracked changes denoting where the text has been changed; the other a clean version (uploaded as the manuscript file).

Important additional instructions are given below your reviewer comments.

Please prepare and submit your revised manuscript within 60 days. If you anticipate any delay, please let us know the expected resubmission date by replying to this email. Please note that revised manuscripts received after the 60-day due date may require evaluation and peer review similar to newly submitted manuscripts.

Thank you again for your submission. We hope that our editorial process has been constructive so far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Amber M Smith

Associate Editor

PLOS Computational Biology

Rob De Boer

Deputy Editor

PLOS Computational Biology

***********************

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #1: Full review is uploaded as attachment.

Reviewer #2: In this study, the authors present a large-scale agent-based model to simulate and investigate infection and immune dynamics in lung epithelial tissue during SARS-CoV-2 infection. The Spatial Immune Model of Coronavirus (SIMCoV) considers the dynamics of lung epithelial cells, SARS-CoV-2 viral load, inflammation signals and CD8+ T cells within a spatio-temporal context. Analyzing their modeling environment they find that heterogeneity in patient outcomes could be explained by the number of initial fields of infection within lung tissue, as well as the timing of the T cell response.

The article is generally well written and structured. However, some aspects regarding the analyses and methodology are only insufficiently explained and would need some further explanations. This especially relates to the parameterization of the agent-based model, which is a key aspect for such highly complex models and its comparison to patient data. In addition, the analysis seems a bit limited in terms of making use of the stochasticity that an ABM, especially one considering the spatial distribution of cells, can provide.

# Major points:

(1.) SIMCoV represents an extended agent-based modeling environment to simulate and study viral infection within tissue in a spatially defined context. It is claimed that considering infection dynamics in a spatially-resolved context helps to explain the variation observed in individual patient outcome to SARS-CoV-2 infection, with the number of initially infected sites being an important factor determining disease progression. To which extent could this not also be covered by different initial viral loads within an ODE-model, as well as different timing of the T cell responses? While it is investigated how the distribution of the same number of infected cells within different numbers of initial fields of infection influence the dynamics, I could not follow the claim that this analysis might provide a better explanation of variation in patient outcome than the analysis provided by the ODE model. Both seem to explain the data comparably well, judged from the RMSE (see also point 3).

(2.) Agent-based models usually provide stochastic outputs given repeated simulations with the same parameter set. However, in each of the figures (e.g. Figure 3,4,5,7) only a single line for the model simulations of a particular scenario is shown. It is not clear or specified within the figure legends if this is the mean over several simulation runs or a single representation. In any case, it would be very important to know how much variation in the dynamics can occur from one given model parameterization. Especially the distribution of the initial fields of infection will potentially have a substantial impact on the observed dynamics in such a spatial modeling environment. In this regard, the authors should investigate how non-equidistant distribution of FOI (see Fig. 3a) would affect the model outcome and variation. The authors need to report the variation in model outcomes to corroborate their claims, i.e. that the initial number of FOI partly determines disease outcome.

(3.) Figure 5: How was SIMCoV adapted to the patient data? On page 6, bottom, the phrasing leaves the impression that SIMCoV was actually “fitted” to the data. What kind of fitting procedure was used for this task? From the Materials and Methods section, I get more the impression that several parameters were varied and manually adapted according to values and parameter ranges from the literature. But it is not clear which parameters were fixed and which ones were varied/fitted/adapted. If only the initial FOI was varied to explain the patient data in Figure 5 (p.6/7) it is also not clear if FOI were always equidistantly (as shown in Figure 3a) or randomly placed within the grid. If several parameters were varied, are the parameters identifiable or are they correlated given the complexity of the model? If the simulations were manually adapted, the authors might want to consider automatic parameter inference methods, such as approximate Bayesian computation (ABC-methods), as they have been used before for agent-based models to analyze multi-cellular systems and infection dynamics (e.g. Jagiella et al. Cell Systems 2017, Imle et al. Nat Com. 2019). Parameterizations of such modeling environments is one of the key aspects for obtaining reliable predictions and simulations.

(4.) Some details on how the ABM was implemented are missing. While the different processes are explained and introduced, it is not fully specified how these processes are actually parameterized, i.e. how probabilities of events were calculated and simulated. While it is very applaudable that the authors make their simulation environment publicly available, appropriate details on how the parameters were used within the code seem to be missing, if I did not miss this within the text.

(5.) The ODE-model used to explain the individual patient data is not introduced, nor the methods how this was fitted to the data (e.g. mixed-effect model?, individual fits?). Even though this might be published previously, I think the details have to be repeated within the manuscript to compare the different modeling approaches and evaluate the outcomes. In addition, confidence intervals should be given for the estimates within Table 1.

# Minor points:

- page 2, bottom: If epithelial cells are modeled as a 2D grid, it is not clear why they have to be represented as a volume. Does this play a role for e.g. diffusion?

- Figure 7: How comparable are the different scenarios when studied in 2D and 3D? Were the same number of cells/ target cell densities used, as well as the same number of T cells able to infiltrate the tissue?

- Figure 3d: I am not sure how much informative the peak number of T cells would be on viral control in order to compare the different settings. The peak might occur at different time points and the overall level of the T cell responses might be similar. Wouldn’t the cumulative T cell concentration up to a certain time point, and potentially a ratio between T cells and Viral load be more informative for a comparison between the different scenarios, i.e, clearly indicating that the spatial distribution of the number of locations and not the magnitude of initial infection determines disease progression?

- There have been other studies that introduced multi-cellular modeling environments for studying viral infections within epithelial tissues (Sego et al. PLos Comp Biol. 2020). The authors might want to discuss how their approach relates to those. In addition, the authors should discuss why their model is especially a modeling environment for coronaviruses, and not viral infections per se. Only in the last part when studying lung structure, the modeling environment seems to become lung specific.

Reviewer #3: In this paper, Moses et. al. propose a nicely designed mathematical model that includes spatial aspects of infection to recapitulate the SARS-CoV-2 viral load variability among infected individuals. The model is an agent-based one that simulates infection dynamics and CD8 responses in the space of millions of epithelial cells. This approach is relevant as it may explain how more heterogenous virus dynamics could be produced as a function of the spatial parameters, something that ordinarily differential equations are limited to do in this context. Below are my comments:

1. Regarding the peak viral load as a function of the initial FOI, I was wondering if the proportionality is also affected by spatial distribution of the virions. In other words, if the initial FOI and initial virions on them are randomly distributed in the grid—and not just equally dispersed—would the peak viral load still be proportional? What if all the initial FOI is in a specific place in the grid? In a target cell-limited model, or even those that include effector cells, the peak viral load wouldn’t change as a function of the initial viral load. In that sense, it would be helpful to have a more elaborated mechanistic explanation of why this is not the case in the spatial model. Examples of this would be to have spatial simulations of infected cells and CD8 cells per each case illustrating the possible mechanisms. Is the proportionality only due to more infection sites or due to something else like the dispersion of CD8 cells that decrease the chances to attack the infection?

2. Although authors present the effect of two parameters related to the CD8 response with respect to the virus dynamics, it would be also helpful to do a sensitivity analysis on how that compares to the effect of other parameters in Table 2. Which parameters are driving each phase of the virus dynamics? If there are multiple parameters that drive one aspect of the dynamics, which one is more significant? This is relevant in the sense that it would highlight in which aspects the spatial aspects (diffusion rates, initial distribution of variables in the grid, etc) are more significant in the virus dynamics than the non-spatial ones.

3. After having a set of estimated parameters from the model fits, it would be more convincing, in terms of viral load variability, if the model could be simulated multiple times to show that it does allow for more heterogeneity in terms of peak levels, time to peak, time to shoulder phase and time to control.

4. It seems to me the paper is lacking a section (in the Materials and Methods) describing the fitting procedure in detail.

5. Would the model be able to reproduce multiple viral peaks as in figure 5G?

6. The github page did not work when I tried to open it.

**********

Have the authors made all data and (if applicable) computational code underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data and code underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data and code should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data or code —e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: No: The link to the code repository was broken. "page not found".

Reviewer #2: Yes

Reviewer #3: Yes

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

Figure Files:

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org.

Data Requirements:

Please note that, as a condition of publication, PLOS' data policy requires that you make available all data used to draw the conclusions outlined in your manuscript. Data must be deposited in an appropriate repository, included within the body of the manuscript, or uploaded as supporting information. This includes all numerical values that were used to generate graphs, histograms etc.. For an example in PLOS Biology see here: http://www.plosbiology.org/article/info%3Adoi%2F10.1371%2Fjournal.pbio.1001908#s5.

Reproducibility:

To enhance the reproducibility of your results, we recommend that you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. Additionally, PLOS ONE offers an option to publish peer-reviewed clinical study protocols. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols

Attachment

Submitted filename: ReviewOf_PCOMPBIOL-D-21-01181.docx

Click here for additional data file.^{(16KB, docx)}

PLoS Comput Biol. 2021 Dec 23;17(12):e1009735. doi: 10.1371/journal.pcbi.1009735.r002

Author response to Decision Letter 0

20 Oct 2021

Attachment

Submitted filename: PloSCompBioSIMCoVReviewerResponse.pdf

Click here for additional data file.^{(164.9KB, pdf)}

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1009735.r003

Decision Letter 1

Rob J De Boer, Amber M Smith

16 Nov 2021

Dear Dr. Moses,

Thank you very much for submitting your manuscript "Spatially distributed infection increases viral load in a computational model of SARS-CoV-2 lung infection" for consideration at PLOS Computational Biology. As with all papers reviewed by the journal, your manuscript was reviewed by members of the editorial board and by several independent reviewers. The reviewers appreciated the attention to an important topic. The reviews lie between major and minor with important points raised by Reviewer 2 that require addressing.

Please prepare and submit your revised manuscript within 30 days. If you anticipate any delay, please let us know the expected resubmission date by replying to this email.

When you are ready to resubmit, please upload the following:

[1] A letter containing a detailed list of your responses to all review comments, and a description of the changes you have made in the manuscript. Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out

[2] Two versions of the revised manuscript: one with either highlights or tracked changes denoting where the text has been changed; the other a clean version (uploaded as the manuscript file).

Important additional instructions are given below your reviewer comments.

Thank you again for your submission to our journal. We hope that our editorial process has been constructive so far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Amber M Smith

Associate Editor

PLOS Computational Biology

Rob De Boer

Deputy Editor

PLOS Computational Biology

***********************

A link appears below if there are any accompanying review attachments. If you believe any reviews to be missing, please contact ploscompbiol@plos.org immediately:

[LINK]

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #2: In this revised version, the authors have addressed all of my previous comments by performing additional analyses and extending previous explanations on the used methods within the manuscript. This clearly has improved and clarified the manuscript. However, I still would have some comments that I would be happy to see addressed by the authors.

# Major points:

(1.) Figure 3b): It is quite surprising that even given random positioning of individual initial foci, the variation between different simulation runs is basically non-existent. Given the large dependency of the infection dynamics on the initial foci number this is difficult to believe. As indicated in Figure 2, given the chosen parameterization of viral diffusion and infectivity, the infection seems to be largely spreading to directly neighboring cells, i.e. no seeding of new foci by diffusing virions. This means infection spread depends on the combined “surface area” of all foci. However, if foci were seeded randomly, I would expect that at least some foci are initiated closely together, merge early or are initialized close to the boundary of the grid, so that this effectively decreases the “spread surface”, and, thus, should lead to some variation between the simulations. Did the authors also had a look at the corresponding plot for Figure 3b for the number of infected/uninfected epithelial cells? Did this also not reveal any variation in the dynamics? At least for 16 randomly placed, initial foci, I would expect this.

(2.) Although this might be only semantic, I would recommend to speak of “adapting” the model to data rather than “fitting”. In my view, fitting always implies an automatic/algorithmic approach to minimize a difference between model and data. “Manual fitting” could be misleading in this sense. Although it is indicated that some ordered way of adjusting the parameters for each individual patient is used (novel paragraph in M&M), it is still not an elaborated search of the possible parameter space (i.e. fixed parameter ranges for all patients), as has been acknowledged by the authors.

# Minor points:

- Related to point 1 above: I couldn’t find within the text if for the 2D simulations in Figure 2D and 3, periodic or fixed boundaries were used for the simulations.

- p8 bottom: “… controlled by a even a high ….”

- Fig. 7: How many foci were used to start the infection in the different topologies? I would assume this should be a single infected cell to allow comparison.

Reviewer #3: The authors have addressed all my comments successfully.

My only comment is that the results of Figure 8 seemed a little out of place. It was odd to see results of peak viral load in CD8/viral clearance results and the methods section. My suggestion would be to divide Figure 8 in two:

-The first figure would include how parameters affect the viral peak only and include a reference to those results in the second section of the results, "Peak viral load is proportional...". In this way, it would show better how the effect of FOI in the viral peak is more prominent than the other parameters in the same section. The figure related to the viral peak could be part of Figure 3.

-The second figure would include how parameters affect the final percentage of infected cells (as a measure for viral clearance) and could be part of Figure 4. This figure would be referenced in the "Effect of CD8+ T cell response on viral clearance" section.

In this way, Figure 8 is not at the end/methods, and its results would follow the flow of the paper.

**********

Have the authors made all data and (if applicable) computational code underlying the findings in their manuscript fully available?

Reviewer #2: Yes

Reviewer #3: Yes

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #2: No

Reviewer #3: No

Figure Files:

Data Requirements:

Reproducibility:

References:

Review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript.

If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

PLoS Comput Biol. 2021 Dec 23;17(12):e1009735. doi: 10.1371/journal.pcbi.1009735.r004

Author response to Decision Letter 1

25 Nov 2021

Attachment

Submitted filename: ResponseToReviewers2_SIMCoV.pdf

Click here for additional data file.^{(61.6KB, pdf)}

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1009735.r005

Decision Letter 2

Rob J De Boer, Amber M Smith

9 Dec 2021

Dear Dr. Moses,

We are pleased to inform you that your manuscript 'Spatially distributed infection increases viral load in a computational model of SARS-CoV-2 lung infection' has been provisionally accepted for publication in PLOS Computational Biology.

Before your manuscript can be formally accepted you will need to complete some formatting changes, which you will receive in a follow up email. A member of our team will be in touch with a set of requests.

Please note that your manuscript will not be scheduled for publication until you have made the required changes, so a swift response is appreciated.

IMPORTANT: The editorial review process is now complete. PLOS will only permit corrections to spelling, formatting or significant scientific errors from this point onwards. Requests for major changes, or any which affect the scientific understanding of your work, will cause delays to the publication date of your manuscript.

Should you, your institution's press office or the journal office choose to press release your paper, you will automatically be opted out of early publication. We ask that you notify us now if you or your institution is planning to press release the article. All press must be co-ordinated with PLOS.

Thank you again for supporting Open Access publishing; we are looking forward to publishing your work in PLOS Computational Biology.

Best regards,

Amber M Smith

Associate Editor

PLOS Computational Biology

Rob De Boer

Deputy Editor

PLOS Computational Biology

***********************************************************

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #2: The authors have clarified all the previous issues. I have no further comments.

**********

Have the authors made all data and (if applicable) computational code underlying the findings in their manuscript fully available?

Reviewer #2: None

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #2: No

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1009735.r006

Acceptance letter

Rob J De Boer, Amber M Smith

21 Dec 2021

PCOMPBIOL-D-21-01181R2

Spatially distributed infection increases viral load in a computational model of SARS-CoV-2 lung infection

Dear Dr Moses,

I am pleased to inform you that your manuscript has been formally accepted for publication in PLOS Computational Biology. Your manuscript is now with our production department and you will be notified of the publication date in due course.

The corresponding author will soon be receiving a typeset proof for review, to ensure errors have not been introduced during production. Please review the PDF proof of your manuscript carefully, as this is the last chance to correct any errors. Please note that major changes, or those which affect the scientific understanding of the work, will likely cause delays to the publication date of your manuscript.

Soon after your final files are uploaded, unless you have opted out, the early version of your manuscript will be published online. The date of the early version will be your article's publication date. The final article will be published to the same URL, and all versions of the paper will be accessible to readers.

Thank you again for supporting PLOS Computational Biology and open-access publishing. We are looking forward to publishing your work!

With kind regards,

Livia Horvath

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Attachment

Submitted filename: ReviewOf_PCOMPBIOL-D-21-01181.docx

Click here for additional data file.^{(16KB, docx)}

Attachment

Submitted filename: PloSCompBioSIMCoVReviewerResponse.pdf

Click here for additional data file.^{(164.9KB, pdf)}

Attachment

Submitted filename: ResponseToReviewers2_SIMCoV.pdf

Click here for additional data file.^{(61.6KB, pdf)}

Data Availability Statement

All code can be accessed at https://github.com/AdaptiveComputationLab/simcov. Configuration files to reproduce each figure in the paper are available in the configs folder in that repository.

[pcbi.1009735.ref001] 1. Moderbacher CR, Ramirez SI, Dan JM, Grifoni A, Hastie KM, Weiskopf D, et al. Antigen-specific adaptive immunity to SARS-CoV-2 in acute COVID-19 and associations with age and disease severity. Cell. 2020;183(4):996–1012. doi: 10.1016/j.cell.2020.09.038 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref002] 2. Arunachalam PS, Wimmers F, Mok CKP, Perera RA, Scott M, Hagan T, et al. Systems biological assessment of immunity to mild versus severe COVID-19 infection in humans. Science. 2020;369(6508):1210–1220. doi: 10.1126/science.abc6261 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref003] 3. Yang J, Zheng Y, Gou X, Pu K, Chen Z, Guo Q, et al. Prevalence of comorbidities and its effects in patients infected with SARS-CoV-2: a systematic review and meta-analysis. International Journal of Infectious Diseases. 2020;94:91–95. doi: 10.1016/j.ijid.2020.03.017 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref004] 4. Fajnzylber J, Regan J, Coxen K, Corry H, Wong C, Rosenthal A, et al. SARS-CoV-2 viral load is associated with increased disease severity and mortality. Nature Communications. 2020;11(1):1–9. doi: 10.1038/s41467-020-19057-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref005] 5. Marks M, Millat-Martinez P, Ouchi D, Roberts Ch, Alemany A, Corbacho-Monné M, et al. Transmission of COVID-19 in 282 clusters in Catalonia, Spain: a cohort study. The Lancet Infectious Diseases. 2021;. doi: 10.1016/S1473-3099(20)30985-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref006] 6. Néant N, Lingas G, Le Hingrat Q, Ghosn J, Engelmann I, Lepiller Q, et al. Modeling SARS-CoV-2 viral kinetics and association with mortality in hospitalized patients from the French COVID cohort. Proceedings of the National Academy of Sciences. 2021;118(8). doi: 10.1073/pnas.2017962118 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref007] 7. Wang S, Pan Y, Wang Q, Miao H, Brown AN, Rong L. Modeling the viral dynamics of SARS-CoV-2 infection. Mathematical biosciences. 2020;328:108438. doi: 10.1016/j.mbs.2020.108438 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref008] 8. Hernandez-Vargas EA, Velasco-Hernandez JX. In-host mathematical modelling of covid-19 in humans. Annual reviews in control. 2020;. doi: 10.1016/j.arcontrol.2020.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref009] 9. Gonçalves A, Bertrand J, Ke R, Comets E, De Lamballerie X, Malvy D, et al. Timing of antiviral treatment initiation is critical to reduce SARS-CoV-2 viral load. CPT: pharmacometrics & systems pharmacology. 2020;9(9):509–514. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref010] 10. Kim KS, Ejima K, Ito Y, Iwanami S, Ohashi H, Koizumi Y, et al. Modelling SARS-CoV-2 dynamics: Implications for therapy; 2020. [Google Scholar]

[pcbi.1009735.ref011] 11. Metcalf CJE, Grenfell BT, Graham AL. Disentangling the dynamical underpinnings of differences in SARS-CoV-2 pathology using within-host ecological models. PLoS pathogens. 2020;16(12):e1009105. doi: 10.1371/journal.ppat.1009105 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref012] 12. Ke R, Zitzmann C, Ribeiro RM, Perelson AS. Kinetics of SARS-CoV-2 infection in the human upper and lower respiratory tracts and their relationship with infectiousness. medRxiv. 2020. [Google Scholar]

[pcbi.1009735.ref013] 13. Ejima K, Kim KS, Ludema C, Bento AI, Iwanami S, Fujita Y, et al. Estimation of the incubation period of COVID-19 using viral load data. Epidemics. 2021;35:100454. doi: 10.1016/j.epidem.2021.100454 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref014] 14. Goyal A, Cardozo-Ojeda EF, Schiffer JT. Potency and timing of antiviral therapy as determinants of duration of SARS-CoV-2 shedding and intensity of inflammatory response. Science advances. 2020;6(47):eabc7112. doi: 10.1126/sciadv.abc7112 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref015] 15. Kim KS, Ejima K, Iwanami S, Fujita Y, Ohashi H, Koizumi Y, et al. A quantitative model used to compare within-host SARS-CoV-2, MERS-CoV, and SARS-CoV dynamics provides insights into the pathogenesis and treatment of SARS-CoV-2. PLoS biology. 2021;19(3):e3001128. doi: 10.1371/journal.pbio.3001128 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref016] 16. Perelson AS, Ke R. Mechanistic modelling of SARS-CoV-2 and other infectious diseases and the effects of therapeutics. Clinical Pharmacology & Therapeutics. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref017] 17. Du SQ, Yuan W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID-19 and implications for viral pathogenesis. Journal of medical virology. 2020;92(9):1615–1628. doi: 10.1002/jmv.25866 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref018] 18. Zhang X, Tan Y, Ling Y, Lu G, Liu F, Yi Z, et al. Viral and host factors related to the clinical outcome of COVID-19. Nature. 2020;583(7816):437–440. doi: 10.1038/s41586-020-2355-0 [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref019] 19. Sette A, Crotty S. Adaptive Immunity to SARS-CoV-2 and COVID-19. Cell. 2021; doi: 10.1016/j.cell.2021.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref020] 20. Tan AT, Linster M, Tan CW, Le Bert N, Chia WN, Kunasegaran K, et al. Early induction of functional SARS-CoV-2-specific T cells associates with rapid viral clearance and mild disease in COVID-19 patients. Cell reports. 2021;34(6):108728. doi: 10.1016/j.celrep.2021.108728 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref021] 21. Grifoni A, Weiskopf D, Ramirez SI, Mateus J, Dan JM, Moderbacher CR, et al. Targets of T cell responses to SARS-CoV-2 coronavirus in humans with COVID-19 disease and unexposed individuals. Cell. 2020;181(7):1489–1501. doi: 10.1016/j.cell.2020.05.015 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref022] 22. Bertoletti A, Tan AT, Le Bert N. The T-cell response to SARS-CoV-2: kinetic and quantitative aspects and the case for their protective role. Oxford Open Immunology. 2021;2(1). doi: 10.1093/oxfimm/iqab006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref023] 23. Bauer AL, Beauchemin CAA, Perelson AS. Agent-based modeling of host–pathogen systems: The successes and challenges. Information sciences. 2009;179(10):1379–1389. doi: 10.1016/j.ins.2008.11.012 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref024] 24. Fricke GM, Letendre KA, Moses ME, Cannon JL. Persistence and adaptation in immunity: T cells balance the extent and thoroughness of search. PLoS Computational Biology. 2016;12(3):e1004818. doi: 10.1371/journal.pcbi.1004818 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref025] 25. Levin D, Forrest S, Banerjee S, Clay C, Cannon J, Moses M, et al. A spatial model of the efficiency of T cell search in the influenza-infected lung. Journal of Theoretical Biology. 2016;398. doi: 10.1016/j.jtbi.2016.02.022 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref026] 26. Warrender C, Forrest S, Koster F. Modeling intercellular interactions in early Mycobacterium infection. Bulletin of mathematical biology. 2006;68(8):2233–2261. doi: 10.1007/s11538-006-9103-y [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref027] 27. Mitchell H, Levin D, Forrest S, Beauchemin CA, Tipper J, Knight J, et al. Higher level of replication efficiency of 2009 (H1N1) pandemic influenza virus than those of seasonal and avian strains: kinetics from epithelial cell culture and computational modeling. Journal of virology. 2011;85(2):1125–1135. doi: 10.1128/JVI.01722-10 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref028] 28. Kassin MT, Varble N, Blain M, Xu S, Turkbey EB, Harmon S, et al. Generalized chest CT and lab curves throughout the course of COVID-19. Scientific reports. 2021;11(1):1–13. doi: 10.1038/s41598-021-85694-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref029] 29. Zhang K, Liu X, Shen J, Li Z, Sang Y, Wu X, et al. Clinically applicable AI system for accurate diagnosis, quantitative measurements, and prognosis of COVID-19 pneumonia using computed tomography. Cell. 2020;181(6):1423–1433. doi: 10.1016/j.cell.2020.04.045 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref030] 30. Imai M, Iwatsuki-Horimoto K, Hatta M, Loeber S, Halfmann PJ, Nakajima N, et al. Syrian hamsters as a small animal model for SARS-CoV-2 infection and countermeasure development. Proceedings of the National Academy of Sciences. 2020;117(28):16587–16595. doi: 10.1073/pnas.2009799117 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref031] 31. Harris TH, Banigan EJ, Christian DA, Konradt C, Wojno EDT, Norose K, et al. Generalized Lévy walks and the role of chemokines in migration of effector CD8+ T cells. Nature. 2012;486(7404):545–548. doi: 10.1038/nature11098 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref032] 32. Ariotti S, Beltman JB, Borsje R, Hoekstra ME, Halford WP, Haanen JBAG, et al. Subtle CXCR3-dependent chemotaxis of CTLs within infected tissue allows efficient target localization. The Journal of Immunology. 2015;195(11):5285–5295. doi: 10.4049/jimmunol.1500853 [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref033] 33. Halle S, Keyser KA, Stahl FR, Busche A, Marquardt A, Zheng X, et al. In Vivo Killing Capacity of Cytotoxic T Cells Is Limited and Involves Dynamic Interactions and T Cell Cooperativity. Immunity. 2016;44(2):233–245. doi: 10.1016/j.immuni.2016.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref034] 34. Mrass P, Oruganti SR, Fricke GM, Tafoya J, Byrum JR, Yang L, et al. ROCK regulates the intermittent mode of interstitial T cell migration in inflamed lungs. Nature communications. 2017;8(1):1–14. doi: 10.1038/s41467-017-01032-2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref035] 35. Zhang X, Tan Y, Ling Y, Lu G, Liu F, Yi Z, et al. Viral and host factors related to the clinical outcome of COVID-19. Nature. 2020. [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref036] 36. Wölfel R, Corman VM, Guggemos W, Seilmaier M, Zange S, Müller MA, et al. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020. [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref037] 37. Wiebe BM, Laursen H. Lung morphometry by unbiased methods in emphysema: bronchial and blood vessel volume, alveolar surface area and capillary length. Apmis. 1998;106(1-6):651–656. doi: 10.1111/j.1699-0463.1998.tb01395.x [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref038] 38. Regan J, Flynn JP, Rosenthal A, Jordan H, Li Y, Chishti R, et al. Viral Load Kinetics of SARS-CoV-2 In Hospitalized Individuals with COVID-19. In: Open Forum Infectious Diseases; 2021. doi: 10.1093/ofid/ofab153 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref039] 39. Hart WS, Maini PK, Thompson RN. High infectiousness immediately before COVID-19 symptom onset highlights the importance of continued contact tracing. Elife. 2021;10:e65534. doi: 10.7554/eLife.65534 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref040] 40. Tindale LC, Stockdale JE, Coombe M, Garlock ES, Lau WYV, Saraswat M, et al. Evidence for transmission of COVID-19 prior to symptom onset. Elife. 2020;9:e57149. doi: 10.7554/eLife.57149 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref041] 41. Dabisch PA, Biryukov J, Beck K, Boydston JA, Sanjak JS, Herzog A, et al. Seroconversion and fever are dose-dependent in a nonhuman primate model of inhalational COVID-19. PLoS pathogens. 2021;17(8):e1009865. doi: 10.1371/journal.ppat.1009865 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref042] 42. Gandhi M, Beyrer C, Goosby E. Masks do more than protect others during COVID-19: reducing the inoculum of SARS-CoV-2 to protect the wearer. Journal of general internal medicine. 2020;35(10):3063–3066. doi: 10.1007/s11606-020-06067-8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref043] 43. Guallar MP, Meiriño R, Donat-Vargas C, Corral O, Jouvé N, Soriano V. Inoculum at the time of SARS-CoV-2 exposure and risk of disease severity. International Journal of Infectious Diseases. 2020;97:290–292. doi: 10.1016/j.ijid.2020.06.035 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref044] 44. Yeh HC, Schum GM. Models of human lung airways and their application to inhaled particle deposition. Bulletin of Mathematical Biology. 1980;42(3):461–480. doi: 10.1007/BF02460796 [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref045] 45. Kalimuddin S, Tham CYL, Qui M, de Alwis R, Sim JXY, Lim JME, et al. Early T cell and binding antibody responses are associated with Covid-19 RNA vaccine efficacy onset. Med. 2021;. doi: 10.1016/j.medj.2021.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref046] 46. Ni L, Cheng ML, Feng Y, Zhao H, Liu J, Ye F, et al. Impaired cellular immunity to SARS-CoV-2 in severe COVID-19 patients. Frontiers in immunology. 2021;12. doi: 10.3389/fimmu.2021.603563 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref047] 47. Lucas C, Wong P, Klein J, Castro TBR, Silva J, Sundaram M, et al. Longitudinal analyses reveal immunological misfiring in severe COVID-19. Nature. 2020;584(7821):463–469. doi: 10.1038/s41586-020-2588-y [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref048] 48. Shan F, Gao Y, Wang J, Shi W, Shi N, Han M, et al. Abnormal lung quantification in chest CT images of COVID-19 patients with deep learning and its application to severity prediction. Medical physics. 2021;48(4):1633–1645. doi: 10.1002/mp.14609 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref049] 49.Xavier MP, Reis RF, dos Santos RW, Lobosco M. A simplified model of the Human Immune System response to the COVID-19. In: 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). IEEE; 2020. p. 1311–1317.

[pcbi.1009735.ref050] 50. Cevik M, Tate M, Lloyd O, Maraolo AE, Schafers J, Ho A. SARS-CoV-2, SARS-CoV, and MERS-CoV viral load dynamics, duration of viral shedding, and infectiousness: a systematic review and meta-analysis. The Lancet Microbe. 2020;. doi: 10.1016/S2666-5247(20)30172-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref051] 51. Sego T, Aponte-Serrano JO, Ferrari Gianlupi J, Heaps SR, Breithaupt K, Brusch L, et al. A modular framework for multiscale, multicellular, spatiotemporal modeling of acute primary viral infection and immune response in epithelial tissues and its application to drug therapy timing and effectiveness. PLoS computational biology. 2020;16(12):e1008451. doi: 10.1371/journal.pcbi.1008451 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref052] 52. Quirouette C, Younis NP, Reddy MB, Beauchemin CA. A mathematical model describing the localization and spread of influenza A virus infection within the human respiratory tract. PLoS computational biology. 2020;16(4):e1007705. doi: 10.1371/journal.pcbi.1007705 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref053] 53. Hickman HD, Reynoso GV, Ngudiankama BF, Cush SS, Gibbs J, Bennink JR, et al. CXCR3 chemokine receptor enables local CD8+ T cell migration for the destruction of virus-infected cells. Immunity. 2015;42(3):524–537. doi: 10.1016/j.immuni.2015.02.009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref054] 54. Lipsitch M, Krammer F, Regev-Yochay G, Lustig Y, Balicer RD. SARS-CoV-2 breakthrough infections in vaccinated individuals: measurement, causes and impact. Nature Reviews Immunology. 2021. doi: 10.1038/s41577-021-00662-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref055] 55. Moses ME, Cannon JL, Gordon DM, Forrest S. Distributed adaptive search in T cells: lessons from ants. Frontiers in immunology. 2019;10:1357. doi: 10.3389/fimmu.2019.01357 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref056] 56. Levy R, Hill DB, Forest MG, Grotberg JB. Pulmonary fluid flow challenges for experimental and mathematical modeling; 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref057] 57. Looney MR, Thornton EE, Sen D, Lamm WJ, Glenny RW, Krummel MF. Stabilized imaging of immune surveillance in the mouse lung. Nature Methods. 2011;8(1):91–96. doi: 10.1038/nmeth.1543 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref058] 58. Schneider M, Ackermann K, Stuart M, Wex C, Protzer U, Schätzl HM, et al. Severe Acute Respiratory Syndrome Coronavirus Replication Is Severely Impaired by MG132 due to Proteasome-Independent Inhibition of M-Calpain. Journal of Virology. 2012;86(18):10112–10122. doi: 10.1128/JVI.01001-12 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref059] 59. Ganusov VV, De Boer RJ. Estimating In Vivo Death Rates of Targets due to CD8 T-Cell-Mediated Killing. Journal of Virology. 2008;82(23):11749–11757. doi: 10.1128/JVI.01128-08 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref060] 60. Bar-On YM, Flamholz A, Phillips R, Milo R. SARS-CoV-2 (COVID-19) by the numbers. 2020;9:e57309. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref061] 61. Miao H, Hollenbaugh JA, Zand MS, Holden-Wiltse J, Mosmann TR, Perelson AS, et al. Quantifying the early immune response and adaptive immune response kinetics in mice infected with influenza A virus. J Virol. 2010;84(13):6687–6698. doi: 10.1128/JVI.00266-10 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref062] 62. Mohn KGI, Brokstad KA, Islam S, Oftung F, Tøndel C, Aarstad HJ, et al. Early Induction of Cross-Reactive CD8+ T-Cell Responses in Tonsils After Live-Attenuated Influenza Vaccination in Children. The Journal of Infectious Diseases. 2020;221(9):1528–1537. doi: 10.1093/infdis/jiz583 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref063] 63. Powell T, Peng Y, Berthoud T, Blais ME, Lillie P, Hill A, et al. Examination of Influenza Specific T Cell Responses after Influenza Virus Challenge in Individuals Vaccinated with MVA-NP+M1 Vaccine. PloS one. 2013;8:e62778. doi: 10.1371/journal.pone.0062778 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref064] 64. Keating R, Morris MY, Yue W, Reynolds CE, Harris TL, Brown SA, et al. Potential killers exposed: tracking endogenous influenza-specific CD8+ T cells. Immunology & Cell Biology. 2018;96(10):1104–1119. doi: 10.1111/imcb.12189 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1009735.ref065] 65. Hoertel N, Blachier M, Blanco C, Olfson M, Massetti M, Rico MS, et al. A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nature medicine. 2020;26(9):1417–1421. doi: 10.1038/s41591-020-1001-6 [DOI] [PubMed] [Google Scholar]

[pcbi.1009735.ref066] 66. Ten Broeke G, Van Voorn G, Ligtenberg A. Which sensitivity analysis method should I use for my agent-based model? Journal of Artificial Societies and Social Simulation. 2016;19(1):5. doi: 10.18564/jasss.2857 [DOI] [Google Scholar]

[pcbi.1009735.ref067] 67.Bachan J, Baden SB, Hofmeyr S, Jacquelin M, Kamil A, Bonachea D, et al. UPC++: A High-Performance Communication Framework for Asynchronous Computation. In: Proceedings of the 33rd IEEE International Parallel & Distributed Processing Symposium. IPDPS. IEEE; 2019. Available from: https://escholarship.org/uc/item/1gd059hj.

PERMALINK

Spatially distributed infection increases viral load in a computational model of SARS-CoV-2 lung infection

Melanie E Moses

Steven Hofmeyr

Judy L Cannon

Akil Andrews

Rebekah Gridley

Monica Hinga

Kirtus Leyba

Abigail Pribisova

Vanessa Surjadidjaja

Humayra Tasnim

Stephanie Forrest

Roles

Abstract

Author summary

Introduction

Results

SIMCoV model overview

Fig 1. SIMCoV model components and their interactions.

Fig 2. Example SIMCoV simulation on a small 15 x 15 mm2 layer of epithelial tissue.

Peak viral load is proportional to the number of initial FOI

Fig 3. Effect of the number of FOI on virus and T cell dynamics.

Effect of CD8+ T cell response on viral clearance

Fig 4. Effect of varying key immune response simulation parameters.

Fig 5. The effect of varying model parameters, one at a time.

SIMCoV viral loads compared to patient data

Fig 6. Viral load predictions from SIMCoV simulations (orange) compared to the extended ODE in [12] (gray), and patient data from [36] (red points).

Table 1. SIMCoV parameter settings used for each patient; RMSLE for the simulation averaged over 10 runs and RMSLE for the ODE.

Modeling viral spread over branching airways

Fig 7. Simulated 3D branching airway with a single FOI.

Fig 8. Viral spread from a single FOI given different model topologies.

Discussion

Summary

Relationship to other models

Caveats, limitations, and future work

Materials and methods

Model description

Table 2. Table of SIMCoV parameters.

Parameter derivation

Manually parameterizing SIMCoV to fit patient data

Model implementation

Massively parallel simulation

ODE model implementation

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Rob J De Boer

Amber M Smith

Roles

Author response to Decision Letter 0

Decision Letter 1

Rob J De Boer

Amber M Smith

Roles

Author response to Decision Letter 1

Decision Letter 2

Rob J De Boer

Amber M Smith

Roles

Acceptance letter

Rob J De Boer

Amber M Smith

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Fig 2. Example SIMCoV simulation on a small 15 x 15 mm² layer of epithelial tissue.

Effect of CD8⁺ T cell response on viral clearance