Skip to main content
PMC home page
NIST Author Manuscripts logoLink to NIST Author Manuscripts
. Author manuscript; available in PMC: 2022 Jan 11.
Published in final edited form as: Radiat Phys Chem Oxf Engl 1993. 2021;180:10.1016/j.radphyschem.2020.109319. doi: 10.1016/j.radphyschem.2020.109319

H2 Production in the 10B(n,α)7Li Reaction in Water

Travis C Dietz a, Alan Thompson b, Mohamad Al-Sheikhly a, Marcin Sterniczuk c, David M Bartels c,*
PMCID: PMC8751655  NIHMSID: NIHMS1701367  PMID: 35023888

Abstract

We demonstrate a method for measuring the H2 produced in water from the 10B(n,α)7Li fission reaction. Low energy neutrons from the NIST Center for Neutron Research interact with borate-containing water in a temperature-controlled high pressure cell made from titanium. After exposure for one to several hours, the water is extracted and sparged with argon. H2 entrained in the sparging gas is sampled with a small mass spectrometer. To determine the neutron exposure, a small amount of sodium is included in the borate solution. The water is collected and 24Na activation is measured in a counting apparatus on the following day. The G-value for H2 at room temperature is found to be (1.18 ± 0.10) molecules H2/100eV, in good agreement with previous estimates and recent modeling calculations.

Keywords: water radiolysis, 10B, neutron capture

1. Introduction

The boron-10 (10B) nucleus in the chemical form of boric acid is injected into commercial nuclear reactor cooling water as a neutron “shim” to even out the neutron flux over the course of a fuel cycle.(EPRI, 2014) The 10B(n,α)7Li fission reaction usually produces a 4He ion with kinetic energy 1.472 MeV and 7Li ion with kinetic energy 0.840 MeV (with emission of a 0.478 MeV gamma ray); there is a 6.3 % branch of the reaction that produces a 1.776 MeV 4He ion and a 1.015 MeV 7Li ion and no gamma.(Barth et al., 1990) These high-LET (LET = linear energy transfer) particles quickly lose energy by ionization of the water medium, resulting in water radiolysis and production of H2, H2O2, .OH radicals, .H atoms, and hydrated electrons in dense tracks. (Mozumder, 1999) It is straightforward to estimate the total energy deposited into the cooling water from this reaction given the nuclear cross-sections, (Brown et al., 2018; Carlson, 2011; Carlson et al., 2018) the neutron flux, and the boron concentration in the water (EPRI, 2014). At the beginning of a fuel cycle, dose from the 10B(n,α)7Li fission can amount to 30 % of the total radiation dose in the core. (Christensen, 1994; Garbett et al., 2000)

The majority of radiation dose in reactor cooling water occurs via low-LET gamma radiolysis, producing a large yield of the free radicals .OH, .H, and (e-)aq which escape immediate recombination because of their low initial density. In stark contrast, the great preponderance of “escape” product from the high-LET 4He and 7Li tracks, is H2 and H2O2 (in nearly equal amounts) produced by prompt recombination of the radicals in the dense tracks. (LaVerne, 2000; LaVerne, 2004) Given the importance of this source for corrosive (Lin, 2000; Macdonald, 1992; Raiman et al., 2017) H2O2, it ought to be accurately included in models of the cooling water radiation chemistry (Elliot and Bartels, 2009). However a literature search indicates there exist no measurements of any product yields for this radiolysis event in high temperature water, and almost no measurements at room temperature (Barr and Schuler, 1959; Yokohata and Tsuda, 1974). H2O2 is very difficult to measure accurately at high temperature and pressure because it catalytically decomposes on metal oxide surfaces and is lost to corrosion reactions (Kanjana et al., 2013; Lin et al., 1991; Satoh et al., 2004). By mass balance, the H2 yield should be virtually identical to the H2O2 yield, and is far easier to measure reliably (Edwards et al., 2007; Janik et al., 2007; Sterniczuk et al., 2016). In this paper we demonstrate a methodology for measuring the H2 yield from the 10B(n,α)7Li reaction at room temperature that can easily be extended to reactor temperatures in future work.

Unless otherwise noted, uncertainties in this paper are k=1, i.e., they define intervals around the central value within which the actual value is believed to lie with a level of confidence of approximately 68 percent.

2. Experimental Method

Neutron irradiations were carried out on the Beam Tube 2 (BT-2) Neutron Imaging Facility at the NIST Center for Neutron Research (NCNR). This facility has been described elsewhere (Hussey et al., 2005; J. M. LaManna, 2017). The beamline consists of a neutron beam flight tube containing a neutron beam shutter and collimator. In the present study the facility was used without any neutron imaging equipment in place and the sample cell was placed directly in the path of the ca. 6 cm diameter neutron beam as close to the exit window as possible. The irradiations were timed based on the opening and closing action of the beam shutter.

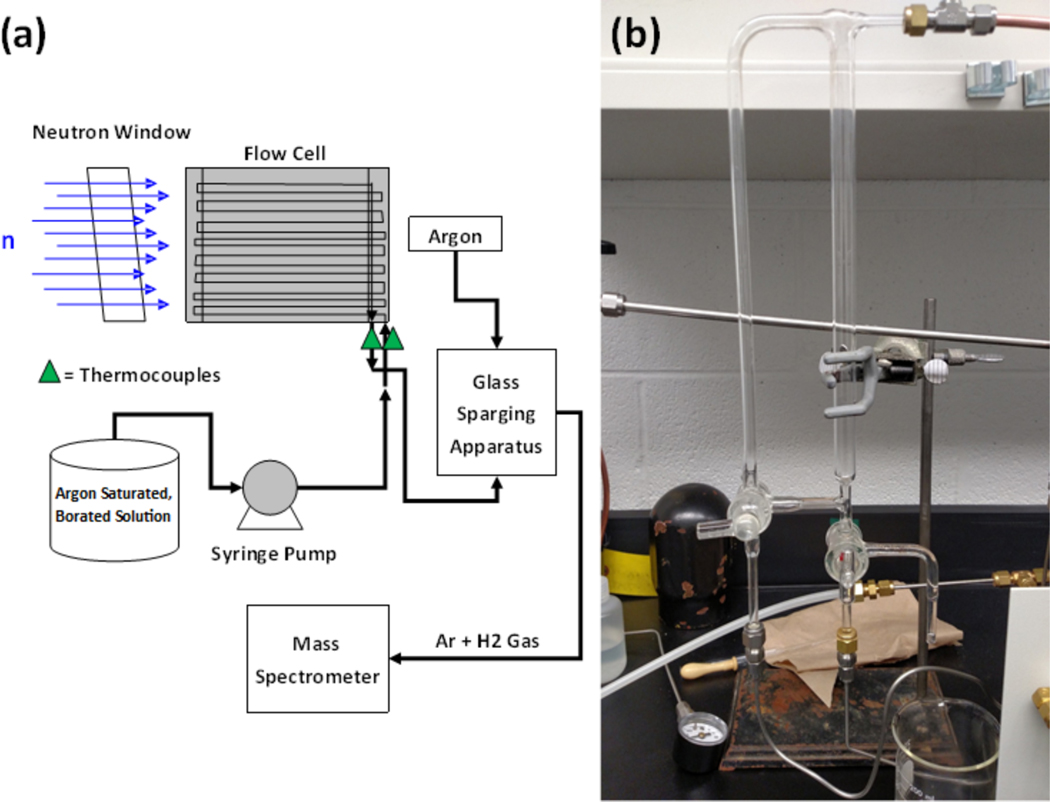
A schematic of the apparatus used to irradiate solution, collect it, and test it for H2 is shown in Figure 1. The irradiation cell, schematically illustrated in Figure 2, is designed for high temperature and pressures, but in this initial experiment was used at ambient conditions. It is welded together from Grade 3 titanium as a three-part “sandwich” with a close-packed honeycomb of 3.2 mm dia flow channels machined in the center section, to present the maximum liquid target to the neutron beam, but still allow fast quantitative removal of the irradiated liquid. Connecting channels are machined into the top and bottom sections of the sandwich to provide a flow-through geometry. Total liquid volume of the flow cell is ca. 90 mL. Thermocouples at the entrance and exit of the cell monitored the temperature of the water during all irradiations. All tubing used in the flow system was composed of either 316 stainless steel or Hastelloy, except for about 60 cm of tubing connected to the inlet and outlet of the flow cell which was composed of titanium. Titanium was used for the components that would be in the direct line of neutron irradiation to reduce the total activity produced by neutron activation.

Fig. 1.

Fig. 1.

Open in a new tab

A block diagram (a) of the experimental set-up for the flow system to irradiate and collect samples of borated water and an image of the glass sparging apparatus (b) used to collect the irradiated water and sparge out H2 from the water sample.

Fig 2.

Fig 2.

Open in a new tab

Schematic illustration of the three-part sandwich construction of the high pressure titanium flow cell. The close-packed flow channels (in green) contain the aqueous boric acid, and are exposed to neutrons from the end as shown.

In order to check the contribution of gamma radiolysis to the production of H2 in the flow cell, gamma dosimetry was performed on the water-filled (no boron) flow cell using alanine pellets whose response to gamma radiation has been described previously (Sleptchonok et al., 2000). Seven alanine pellets were placed at various locations around the outside of the flow cell, specifically two near the front of the cell facing the neutron beam, one on top of the cell, one on each side of the flow cell, and two at the back of the flow cell. This setup was irradiated for 26.6 hours, after which the highest average dose recorded was (158±11) Gy from the two alanine pellets positioned at the front of the cell facing the neutron beam. This result was unexpected, as the dose is of similar order of magnitude to the fission energy released by the 10B, and there is virtually no gamma incident on the cell with the neutron beam.

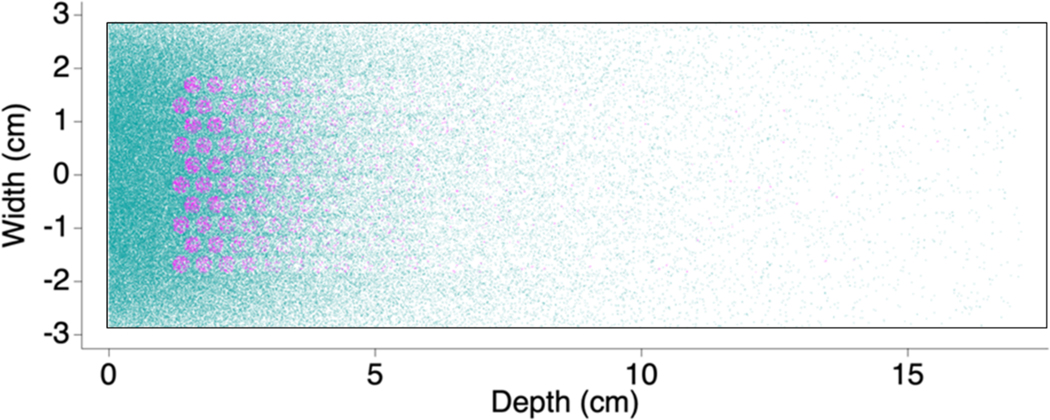
To determine energy deposited into the boric acid solution from the products of the 10B(n,𝛼)7Li reaction vs. energy released in other reactions, a geometrically-simplified model of the experimental cell and neutron beam was modeled using the Monte Carlo neutron transport code MCNP 6.2 (Werner, 2017). Figure 3 illustrates the neutron-capture events in a cross-section of the cell by either titanium (blue dots) or 10B (magenta dots). The quantitative analysis relies on two F6 tallies, which sum energy deposition probabilities vs. energy throughout the length of a particle track. One of the F6 tallies included energy deposited in the boric acid solution from all particles, and the other included only energy deposited from the 𝛼 particle and 7Li. The ratio of integrals of the F6 tallies over energy showed the fraction of the energy deposited in the boric acid solution from the boron fission nuclei (𝛼 particle and 7Li) is 0.71 ± 0.02 (this uncertainty is the 95 % confidence interval). Almost all of the gamma dose originates from neutron absorption and prompt fluorescence from the major (75 %) titanium isotope 48Ti. The fraction of total deposited energy from the 0.478 MeV 10B gamma is approximately 1 %. Energy deposition from any absorption reactions other than titanium and boron are negligible. The MCNP calculation is used to correct the experimental result as described below.

Fig 3.

Fig 3.

Open in a new tab

Plot of neutron captures in the high pressure cell by titanium (blue/green) and 10B (magenta) in a center cross-section. Because there are absorptions in titanium above and below the channels there are a mixture of absorptions in those regions of the image. (See Figure 2 for a schematic drawing of the cell.)

The experimental procedure is similar to that used in a number of previous publications for both gamma and neutron radiolysis studies (Edwards et al., 2007; Janik et al., 2007; Sterniczuk et al., 2016), except that in the present case the flow is stopped during the irradiation. The borated solution was generated by mixing 40.0 g of boric acid (Sigma, BioReagent grade, ≥99.5 %), 0.156 g of lithium hydroxide monohydrate (Aldrich, 99.95 % trace metal basis), and 1 L of 18.2 MΩ deionized water. This solution was sparged with UHP argon for at least 30 minutes while being stirred by a magnetic stir bar. The solution was sucked out of the bottle using a Teledyne ISCO 260D syringe pump. Initially, 50 mL of solution was sent to waste out the secondary port of the syringe pump to remove any air from the pump and 200 mL of solution was flushed through the flow system to replace any solution remaining from previous runs. The total volume of the flow system is estimated to be about 120 mL from the exit port of the syringe pump to the glass sparging apparatus.

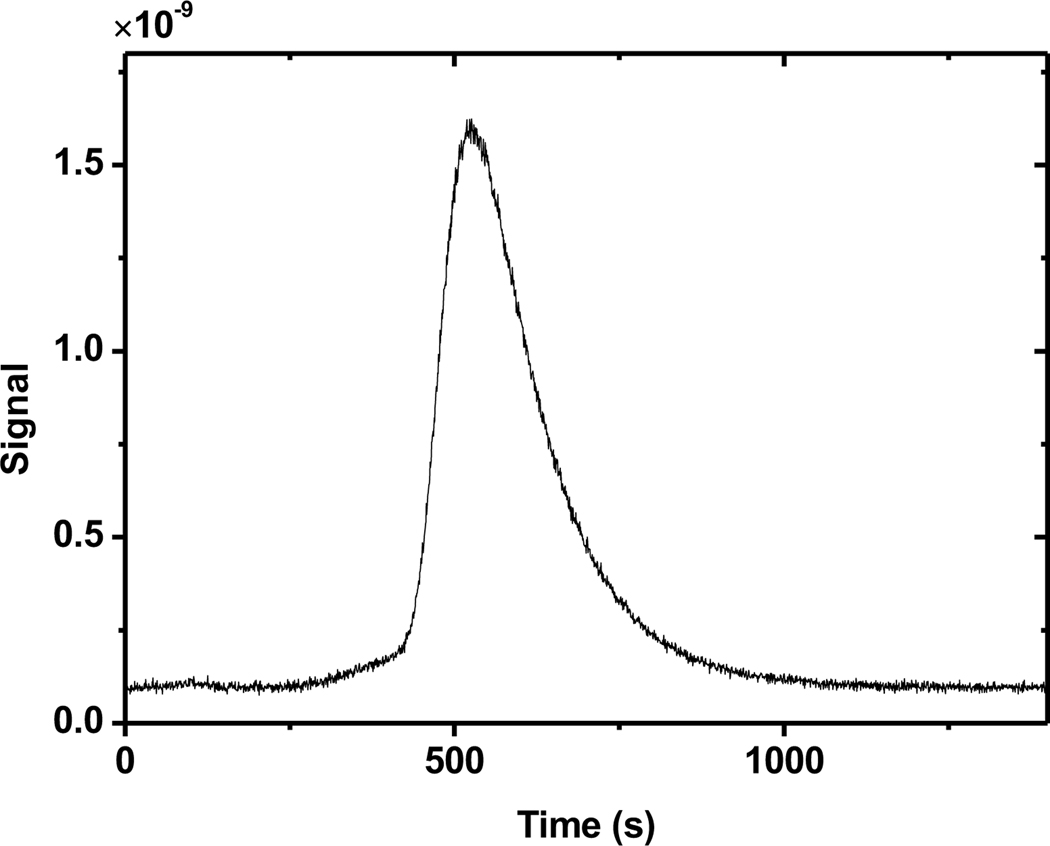
Once an irradiated solution was ready for analysis, the syringe pump was used to pump precisely 150ml of solution, including all of the irradiated volume, into a glass sparging apparatus, shown in Figure 1b. The left portion of the glass tubing allows for a continuous stream of 99.999 % argon carrier gas to bypass the solution as it is collecting in the right hand side of the apparatus. When the collection is complete, the three-way glass valve is turned to send the argon gas flow bubbling through the solution and up to the exit port. The argon and any stripped gases pass through two Restek Molecular Sieve S-Traps in parallel to remove moisture from the gas. This gas flow then passes through a T-junction which allows sampling by an Inficon Transpector2 Compact Process Monitor Residual Gas Analyzer (RGA). Characteristic masses (typically mass 2, 28, and 32 for H2, N2, and O2) are monitored as a function of time to determine the gas content of the water. Integration of the ion current over the peak is proportional to the aqueous concentration of that particular gas species. A typical signal for H2 can be seen in Figure 4. Following complete analysis of the dissolved gas, the solution is sent to waste through a spigot on the glass sparging apparatus in preparation for the next run.

Fig. 4.

Fig. 4.

Open in a new tab

A representative current signal (amps) from the mass spectrometer for 4.57 μmol of H2 dissolved in deionized water.

To calibrate the mass spec detection of H2, water was saturated with a gas mixture of 4.76 % H2 in argon, obtained from Roberts Oxygen Company Inc. Different volumes of 4.76 % H2-saturated water were collected in the sparging apparatus by controlling the flow rate and the pumping time of the syringe pump. Volumes from 25 mL to 150 mL of solution were collected and sparged. The resulting mass-2 current signals were integrated to establish a linear relationship between moles of H2 in the sample and the area of the signal peak.

The determination of the total neutron dose was carried out via sodium activation analysis. In place of lithium hydroxide, 5.299 g of sodium carbonate (Fisher, anhydrous, Certified ACS) was dissolved with 40.0 g of boric acid in 1 L of 18.2 MΩ deionized water. This solution was sparged for at least 30 minutes with UHP argon gas while being stirred. The sodium-containing solution was irradiated for varying lengths of time from one to three hours. 150 mL of solution was collected in the glass sparging apparatus, tested for hydrogen concentration, and then collected in a plastic container. This solution was later placed in a 1 L Marinelli beaker along with 850 mL of water. Activity of the Marinelli beaker was then counted for 20 minutes on an Ortec GEM Series HPGe Coaxial Detector System gamma spectrometer (two models were used, a GEM60200–5 and a GEM40–83). These spectrometers were calibrated for activity measurements using a 1 L Marinelli activity standard provided by the National Institute of Standards and Technology. The total 24Na activity was based on the weighted average value of the area under peaks located at 1368.5 and 2754.1 keV. Based on the total 24Na activity produced during the neutron exposure, the average neutron flux density on the flow cell could be calculated from the following equation:

NNa−24=NNa−23σNa−23Φ(1−e−λNa−24*t)λNa−24

Here NNa-24 is the number of atoms of 24Na generated in the irradiation volume, NNa-23 is the number of initial atoms of 23Na in the irradiated volume, σNa-23 is the thermal absorption cross section of 23Na (0.533 barns(Brown et al., 2018)), Φ is the neutron flux density, λNa-24 is the decay rate of 24Na (1.287 × 10−5 s−1), and t is the total time of irradiation. Using the exponential decay rate, the activity (NNa-24 x λNa-24) at the end of neutron exposure was precisely back-calculated from the activity measured at the time of analysis on the following day.

Results

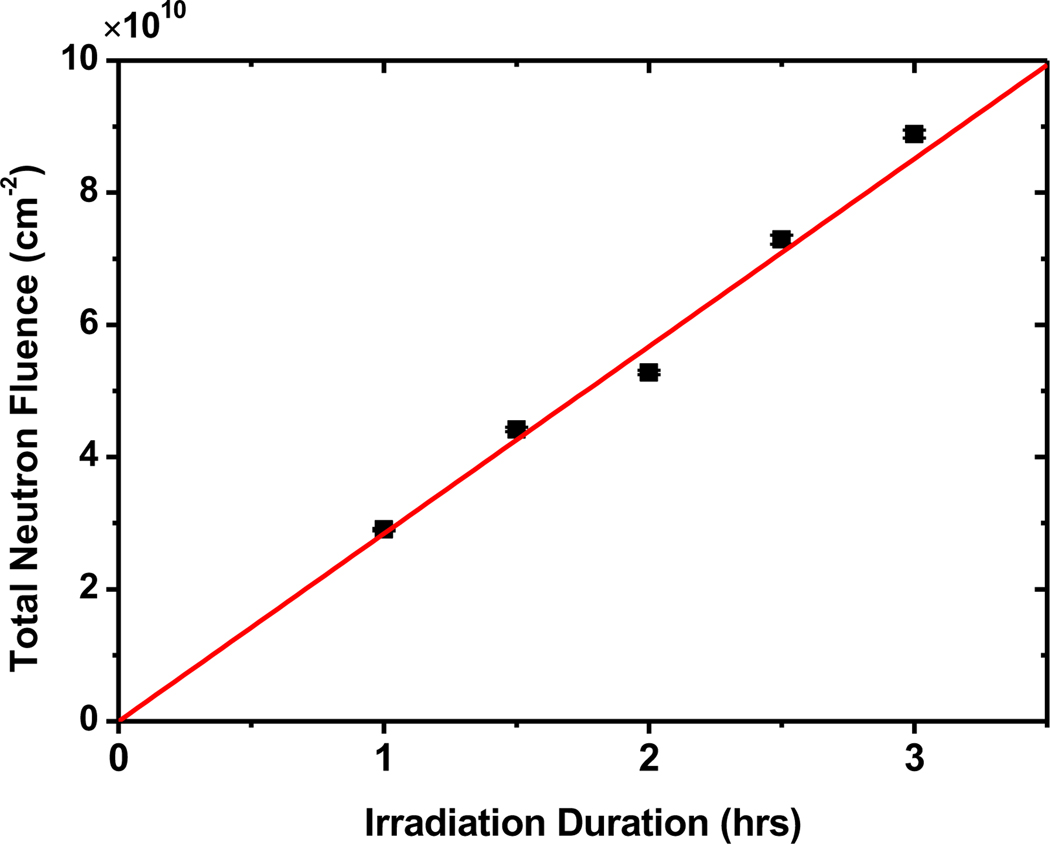
A several-day experimental run was carried out first with several H2 measurements vs. exposure time, and then with simultaneous H2 and sodium activation measurements vs. exposure time. Successful calibration of the neutron flux density by the 24Na activation analysis is illustrated in Figure 5, showing the good linearity between the total neutron fluence and the duration of exposure for five separate exposures.

Fig. 5.

Fig. 5.

Open in a new tab

Calibration of the neutron fluence versus time of irradiation. Graph shows the calculated total neutrons incident upon the cell versus irradiation time. The average neutron flux density is (7.73±0.59) × 106 cm−2 sec−1 from the slope. Statistical uncertainties are similar to the size of the plot symbols.

In order to calculate the value of G(H2) for this system, the total quantity of H2 produced must be divided by the energy deposited in the system from the 10B(n,α)7Li reaction. The 10B(n,α)7Li reaction can proceed through two pathways: 6.3 % of the reactions release 2.791 MeV and 94 % of the reactions release 2.312 MeV as ion kinetic energy (Barth et al., 1990). The weighted average of these two energy values gives the average energy deposited in the irradiated medium per event, or 2.342 MeV. Additionally, a 0.478 MeV gamma is produced during 93.7 % of the 10B(n,α)7Li reactions. The mean free path of these gammas is estimated to be 30 cm through water and 8 cm through titanium, so not surprisingly our simulation showed very little absorbed dose from this gamma. We therefore omit them from the G-value calculation.

The thermal capture cross section of the 10B(n,α)7Li reaction is 3869 barns according to the Evaluated Nuclear Data File neutron library (Brown et al., 2018). Due to the fact that the boric acid used in these experiments is at the natural isotopic concentration of 20 % 10B, the effective thermal capture cross section is 774 barns. By using the following equation, the total energy deposited in the solution from 10B(n,α)7Li reaction can be calculated:

E=ΦtσB−natNB−nat

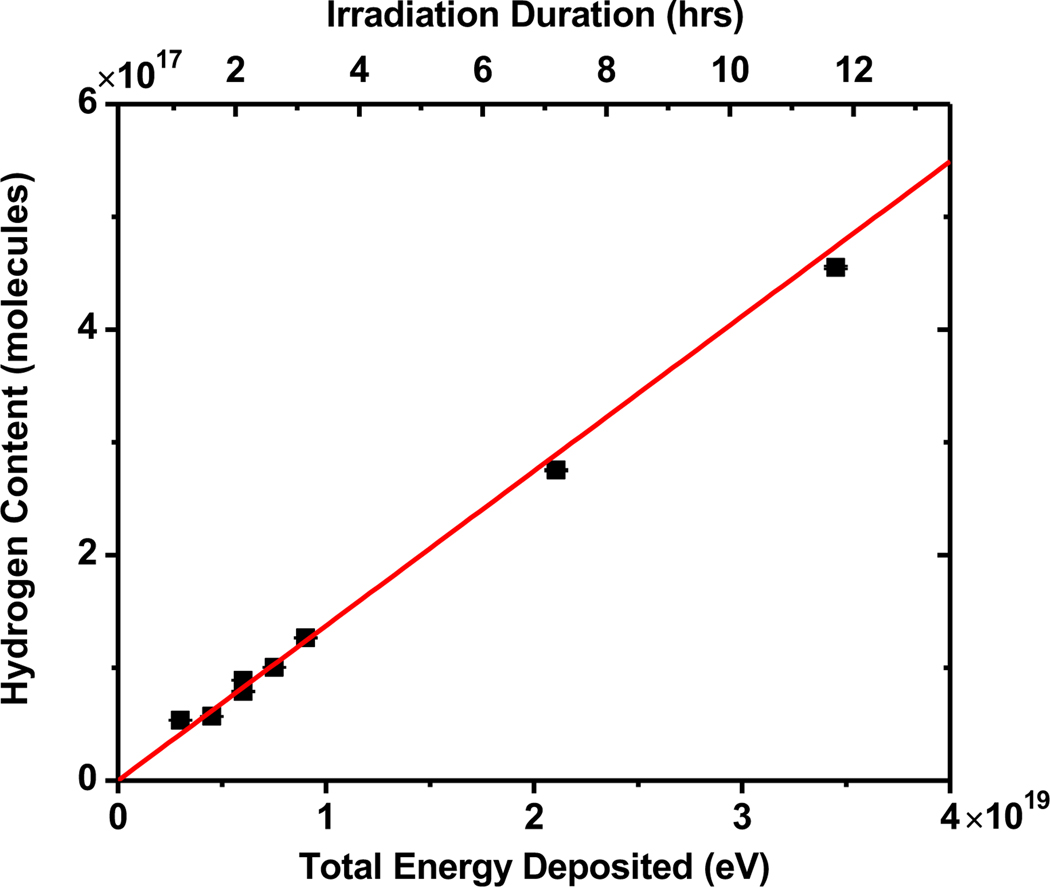
where Φ is the average neutron flux density, (7.73 ± 0.59) × 106 cm−2 s−1, t is the irradiation time, σB-nat is the thermal neutron cross section of boron-natural isotopic concentration, 774 barns, and NB-nat is the number of boron atoms present in the irradiated boron solution prior to the irradiation. The number of hydrogen molecules sparged out of the borated solution following each irradiation can be calculated based on the calibration described previously. Figure 6 shows the hydrogen content in the borated solution versus the exposure time (upper axis) and versus total energy deposited in the solution via the B10(n,α)7Li reaction (lower axis). The slope of the data presented in Figure 6 can be converted to a G-value for H2 of (1.37 ± 0.05) molecules/100 eV. However, the simulations presented earlier suggest that gamma dose from 48Ti neutron capture is 29 % of the total energy deposition in this experiment. Gamma G(H2) is well-known to be 0.45 ± 0.01 molecules/100eV (uncertainty is estimated from the consistent literature number) (Elliot and Bartels, 2009; Spinks and Woods, 1990; Sterniczuk et al., 2016). If we subtract this hydrogen from the measured total, the G-value for just 10B neutron capture becomes (1.18 ± 0.10) molecules/100eV.

Fig. 6.

Fig. 6.

Open in a new tab

Relationship between the molecules of H2 obtained from sample versus total energy deposited in the sample via the B10(n,α)7Li reaction.

Discussion

As indicated in the introduction, there are very few product yield measurements for the 10B(n,α)7Li fission reaction in aqueous solution. Barr and Schuler reported yields in the Fricke dosimeter solution (Fe2+, 0.8N sulfuric acid) with and without oxygen, and Ce4+ reduction with and without oxygen (Barr and Schuler, 1959). The (Fe3+,Ce3+) products can be detected spectrophotometrically, and the four solutions allow estimates of yields G(H2O2), G(H), G(OH), and G(-H2O), where the last G-value is for decomposition of water. Much later, LaVerne and Schuler (LaVerne and Schuler, 1987) reported that the sum of oxidation yields of Fe3+ in 0.8N sulfuric acid from individual accelerator-produced 4He and 7Li ions gave good agreement with the 10B(n,α)7Li fission work. To our knowledge the only 10B(n,α)7Li radiolysis yield measurement in neutral water was a measurement of N2 from hydrated electrons reacting with N2O (Yokohata and Tsuda, 1974). G(e-)aq was thereby estimated as 0.36 per 100 eV.

The 10B(n,α)7Li fission product yields have been calculated recently up to 350°C with a Monte Carlo model at Sherbrooke University for both neutral water and the acidic Fricke solution (Islam et al., 2017). The assumption is made that the 10B(n,α)7Li fission is just the sum of the individual 4He and 7Li tracks. Rather than calculate the energy-dependent differential product yields and integrate over these quantities from the initial energy down to zero (Edwards et al., 2007), the authors estimate a “representative” energy and charge for each ion, and just calculate ion radiolysis yields for that single condition at each temperature. The calculation gives yields qualitatively similar to the very limited measurements found in the literature. G(e-)aq at room temperature was calculated as nearly zero at one hundred nanoseconds after the fission event, which seems to disagree with the N2O experiment of Yokohata, and Tsuda (Yokohata and Tsuda, 1974). (This latter experiment might suffer from unexpected gamma dose much like our own.) At room temperature G(H2O2) and G(H2) are both calculated to be ca. 1.35 molecules/100eV, in reasonable agreement with our measurement of the H2.

The Monte Carlo simulation(Islam et al., 2017) suggests G(OH) is about 0.1 molecules/100 eV at 1 microsecond after the fission, much less than the G(H2), but not zero. More importantly, the unexpected gamma dose from 48Ti neutron capture will produce .OH radicals with G-value of 2.6 molecules/100eV. Our initial experiment can be faulted for not including a specific .OH scavenger, as this radical is capable of reacting with H2 and reducing the measured yield. However it is likely that in the presence of concentrated 0.45M borate, enough impurity is also present to react with the .OH instead of the H2. The free radical product of .OH reaction with nearly any impurity is unlikely to react with H2, so our G(H2) measurement is probably correct in spite of this experimental flaw. In fact, the 0.05M CO3= counterion present in the sodium activation runs serves as an efficient .OH scavenger, and the H2 yield of these runs falls on the same line in Figure 6, confirming that .OH production is unimportant. Any additional H2 production from recombination of gamma-produced (e-)aq and .H atoms is also likely prevented by impurities as well as the H2O2 yield (nearly equal to the H2 yield) from 10B fission.

For the moment the simulations of Jay-Gerin and coworkers remain the best 10B(n,α)7Li yield estimates for use in reactor modeling at high temperature (Islam et al., 2017). As these authors suggest, future experiments to measure the G(H2) and radical yields in high temperature water are essential to test the model predictions. Both simulations and experience with low-LET electron radiolysis (Elliot and Bartels, 2009) suggest that the free radical escape yields will tend to increase at high temperature, so a scavenger system that accounts for all of these species (Sterniczuk et al., 2016) will be essential for future experiments.

Acknowledgement

The authors would like to thank Timothy Barvitskie of the NIST Center for Neutron Research for his assistance with the sodium activation measurements and the productive discussions concerning these measurements. We would also like to thank Eli Baltic for his assistance in the set-up of the flow system at the NCNR. Travis Dietz was supported by the Nuclear Regulatory Commission Fellowship Program under fellowship NRC-HQ-12-G-38-0023. Alan Thompson was supported by the Physical Measurements Laboratory of NIST. David Bartels and Marcin Sterniczuk were supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under award number DE-FC02-04ER15533. This is manuscript number 5293 of the Notre Dame Radiation Laboratory.

ABBREVIATIONS

LET

linear energy transfer

G(x)

molecules of x produced per unit of radiation energy absorbed by the system

Footnotes

DISCLAIMER

Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by NIST, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.

REFERENCES

  1. Barr NF, Schuler RH, 1959. The Dependence of Radical and Molecular Yields on Linear Energy Transfer in the Radiation Decomposition of 0.8 N-Sulfuric Acid Solutions. Journal of Physical Chemistry 63, 808–812. [Google Scholar]
  2. Barth RF, Soloway AH, Fairchild RG, 1990. Boron Neutron Capture Therapy of Cancer. Cancer Research 50, 1061–1070. [PubMed] [Google Scholar]
  3. Brown DA, Chadwick MB, Capote R, Kahler AC, Trkov A, Herman MW, Sonzogni AA, Danon Y, Carlson AD, Dunn M, Smith DL, Hale GM, Arbanas G, Arcilla R, Bates CR, Beck B, Becker B, Brown F, Casperson RJ, Conlin J, Cullen DE, Descalle MA, Firestone R, Gaines T, Guber KH, Hawari AI, Holmes J, Johnson TD, Kawano T, Kiedrowski BC, Koning AJ, Kopecky S, Leal L, Lestone JP, Lubitz C, Damian JIM, Mattoon CM, McCutchan EA, Mughabghab S, Navratil P, Neudecker D, Nobre GPA, Noguere G, Paris M, Pigni MT, Plompen AJ, Pritychenko B, Pronyaev VG, Roubtsov D, Rochman D, Romano P, Schillebeeckx P, Simakov S, Sin M, Sirakov I, Sleaford B, Sobes V, Soukhovitskii ES, Stetcu I, Talou P, Thompson I, van der Marck S, Welser-Sherrill L, Wiarda D, White M, Wormald JL, Wright RQ, Zerkle M, Zerovnik G, Zhu Y, 2018. ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. Nuclear Data Sheets 148, 1–142. [Google Scholar]
  4. Carlson AD, 2011. The neutron cross section standards, evaluations and applications. Metrologia 48, S328–S345. [Google Scholar]
  5. Carlson AD, Pronyaev VG, Capote R, Hale GM, Chen ZP, Duran I, Hambsch FJ, Kunieda S, Mannhart W, Marcinkevicius B, Nelson RO, Neudecker D, Noguere G, Paris M, Simakov SP, Schillebeeckx P, Smith DL, Tao X, Trkov A, Wallner A, Wang W, 2018. Evaluation of the Neutron Data Standards. Nuclear Data Sheets 148, 143–188. [Google Scholar]
  6. Christensen H, 1994. Calculations of Radiolysis in PWR, Chemistry in Water Reactor. French Nuclear Energy Society, p. 153.
  7. Edwards EJ, Wilson PPH, Anderson MH, Mezyk SP, Pimblott SM, Bartels DM, 2007. An apparatus for the study of high temperature water radiolysis in a nuclear reactor: Calibration of dose in a mixed neutron/gamma radiation field. Review of Scientific Instruments 78, 124101. [DOI] [PubMed] [Google Scholar]
  8. Elliot AJ, Bartels DM, 2009. The Reaction Set, Rate Constants and g-Values for the Simulation of the Radiolysis of Light Water over the Range 20° to 350°C Based on Information Available in 2008. AECL; 153–127160-450–001 [Google Scholar]
  9. EPRI, 2014. Pressurized Water Reactor Primary Water Chemistry Guidelines: Revision 7. EPRI; report 3002000505 [Google Scholar]
  10. Garbett K, Henshaw J, Sims HE, 2000. Hydrogen and oxygen behaviour in PWR primary coolant, Water Chemistry in Nuclear Reactor Systems 8. British Nuclear Energy Society, p. 85.
  11. Hussey DS, Jacobson DL, Arif M, Huffman PR, Williams RE, Cook JC, 2005. New neutron imaging facility at the NIST. Nuclear Instruments & Methods in Physics Research Section a-Accelerators Spectrometers Detectors and Associated Equipment 542, 9–15. [Google Scholar]
  12. Islam MM, Lertnaisat P, Meesungnoen J, Sanguanmith S, Jay-Gerin JP, Katsumura Y, Mukai S, Umehara R, Shimizu Y, Suzuki M, 2017. Monte Carlo track chemistry simulations of the radiolysis of water induced by the recoil ions of the B-10(n, alpha)Li-7 nuclear reaction. 1. Calculation of the yields of primary species up to 350 degrees C. Rsc Advances 7, 10782–10790. [Google Scholar]
  13. LaManna JM, D.S.H., Baltic E, Jacobson DL, 2017. Neutron and X-ray Tomography (NeXT) system for simultaneous, dual modality tomography. Review of Scientific Instruments 88, 113702. [DOI] [PubMed] [Google Scholar]
  14. Janik D, Janik I, Bartels DM, 2007. Neutron and beta/gamma Radiolysis of Water up to Supercritical Conditions. 1. Beta/gamma yields for H2, H atoms, and Hydrated Electrons. Journal of Physical Chemistry A 111, 7777–7786. [DOI] [PubMed] [Google Scholar]
  15. Kanjana K, Haygarth KS, Wu W, Bartels DM, 2013. Laboratory Studies in Search of the Critical Hydrogen Concentration. Radiation Physics and Chemistry 82, 25–34. [Google Scholar]
  16. LaVerne JA, 2000. Track effects of heavy ions in liquid water. Radiation Research 153, 487–496. [DOI] [PubMed] [Google Scholar]
  17. LaVerne JA, 2004. Radiation chemical effects of heavy ions, in: Mozumder A, Hatano Y. (Ed.), Charged Particle and Photon Interactions with Matter. Chemical, Physicochemical, and Biological Consequences with Applications. Marcel Dekker, New York, pp. 403–429. [Google Scholar]
  18. LaVerne JA, Schuler RH, 1987. Radiation Chemical Studies with Heavy-Ions - Oxidation of Ferrous Ion in the Fricke Dosimeter. Journal of Physical Chemistry 91, 5770–5776. [Google Scholar]
  19. Lin CC, 2000. Hydrogen water chemistry technology in boiling water reactors. Nuclear Technology 130, 59–70. [Google Scholar]
  20. Lin CC, Smith FR, Ichikawa N, Baba T, Itow M, 1991. Decomposition of Hydrogen Peroxide in Aqueous solutions at Elevated Temperatures. International Journal of Chemical Kinetics 23, 971–987. [Google Scholar]
  21. Macdonald DD, 1992. Viability of Hydrogen Water Chemistry for Protecting in-Vessel Components of Boiling Water-Reactors. Corrosion 48, 194–205. [Google Scholar]
  22. Mozumder A, 1999. Fundamentals of Radiation Chemistry. Academic Press. [Google Scholar]
  23. Raiman SS, Bartels DM, Was GS, 2017. Radiolysis driven changes to oxide stability during irradiation-corrosion of 316L stainless steel in high temperature water. Journal of Nuclear Materials 493, 40–52. [Google Scholar]
  24. Satoh T, Uchida S, Sugama J, Yamashiro N, Hirose T, Morishima Y, Satoh Y, Iinuma K, 2004. Effects of Hydrogen Peroxide on Corrosion of Stainless Steel (I)—Improved Control of Hydrogen Peroxide Remaining in A High Temperature High Pressure Hydrogen Peroxide Loop. J. Nucl. Sci. Technol. 41, 610. [Google Scholar]
  25. Sleptchonok OF, Nagy V, Desrosiers MF, 2000. Advancements in accuracy of the alanine dosimetry system. Part 1. The effects of environmental humidity. Radiation Physics and Chemistry 57, 115–133. [Google Scholar]
  26. Spinks JWT, Woods RJ, 1990. An Introduction to Radiation Chemistry, 3rd Edition. Wiley Interscience, New York. [Google Scholar]
  27. Sterniczuk M, Yakabuskie PA, Wren JC, Jacob JA, Bartels DM, 2016. Low LET radiolysis escape yields for reducing radicals and H2 in pressurized high temperature water. Radiation Physics and Chemistry 121, 35–42. [Google Scholar]
  28. Werner CJ, 2017. MCNP User’s Manual - Code Version 6.2. LA-UR-17–29981
  29. Yokohata A, Tsuda S, 1974. Solvated Electron Formed From Water by Irradiation of Recoil Particles of 10B(n,a)7Li and 6Li(n,a)T. Bulletin of the Chemical Society of Japan 47, 2869–2870. [Google Scholar]

RESOURCES