Abstract
What proportion of the risk in a given population is attributable to a risk factor? The population attributable fraction (PAF) answers this question. “Attributable to” is understood as “due to”, which makes PAFs closely related to the concept of potential impact or potential benefits of reducing the exposure. The PAF is a tool at the border between science and decision making. PAFs are estimated based on strong assumptions and the calculations are data intensive, making them vulnerable to gaps in knowledge and data. Current misconceptions include summing up PAFs to 100% or subtracting a PAF for a factor from 100% to deduce what proportion is left to be explained or prevented by other factors. This error is related to unrecognised multicausality or shared causal responsibility in disease aetiology. Attributable cases only capture cases in excess and should be regarded as a lower bound for aetiological cases, which cannot be estimated based on epidemiological data alone (exposure-induced cases). The population level might not be relevant to discuss prevention priorities based on PAFs, for instance when exposures concentrate in a subgroup of the population, as for occupational lung carcinogens and other workplace hazards. Alternative approaches have been proposed based on absolute rather than relative metrics, such as estimating potential gains in life expectancy that can be expected from a specific policy (prevention) or years of life lost due to a specific exposure that already happened (compensation).
Short abstract
Attributable fractions inform research priorities and guide public policies. They are constructs subject to misconceptions, data gaps and misuses. Potential impact metrics should be carefully selected and interpreted based on their intended use. https://bit.ly/3kEJtlk
Epidemiologists interested in disease aetiology produce indicators of the increase in risk within a group of people exposed to a particular factor, compared to a non-exposed group. The ratio between these two quantities is the relative risk (RR), which, when higher than one, identifies factors that increase the risk of developing the disease, i.e. potential “risk factors”. The higher the RR, the stronger the risk factor. Now, a powerful risk factor to which only a small proportion of the population is exposed may generate a lower disease burden than a weaker risk factor to which a large proportion of the population is exposed [1]. It is precisely that kind of information, beyond RRs, that decision-makers in public health are asking for: quantitative tools designed to rank problems based on disease burden or number of cases related to different risk factors in the target population.
One such instrument of great importance is the concept of “attributable risk proportion” or “population attributable fraction” (PAF). Historically, PAFs were promoted by epidemiologists in the early 1950s [2, 3] to quantify the proportion of people afflicted by lung cancer who would not have developed the disease in the absence of exposure to active smoking. Various measures and related procedures followed in the 1970s and 1980s [4–6], and the topic has since been part of most epidemiology textbooks, although generally taught at the basic level. Usually reported as proportions (e.g. percentages) of cases of a disease that might be avoided, were the exposure of interest reduced or removed, PAFs have “become increasingly popular to carry out estimation of the burden of disease with the aim of identifying major risk factors contributing to important morbidity burdens as an aid to prioritizing risk reduction strategies” [7]. They now play a crucial role in the justification of public health decisions. Respiratory health is no exception, as exemplified by the recent figures published by the American Thoracic Society and the European Respiratory Society, estimating a substantial contribution of workplace exposures to the current burden of multiple chronic respiratory diseases [8].
Being familiar with such metrics and learning their proper uses, as much as their eventual misuses, is key to avoiding misinterpretation and grasping their clinical, research and policy implications. This article will: 1) define the metric, its main formulas and core assumptions; 2) summarise the pitfalls and misconceptions that may alter the validity and interpretation; and 3) highlight some of the complexities of chronic respiratory disease epidemiology that call for a cautious selection and use of figures to define public health problems in that field.
Attributable fractions: what is it about?
Formal definitions and preferred terminology
The PAF answers the question “What proportion of the risk in a given population is attributable to a risk factor?” In practice, the PAF is defined as the difference between the risk in the whole population (Rtot) and the risk in the unexposed group (R0), divided by the risk in the whole population (equation 1 in table 1). “Attributable to” is understood as “due to”, which makes PAFs closely related to the concept of potential impact or potential benefits. Indeed, if x% of the current disease load is due to a particular risk factor, it retrospectively means that had the exposure prevalence been lower, fewer people would have developed the disease in that population (up to x% less, if no one had been exposed). By extension, PAFs are often interpreted as answering a prospective question: “By how much would the disease load be lowered in the future (over a specified period) if the exposure to this risk factor were reduced from now on, while nothing else were to change?” It may also be of interest to quantify that load and potential reduction specifically among the at-risk or exposed group; the corresponding metric is called attributable fraction in the exposed (AFE). It is defined as the difference between the risk in the exposed group (Re) and the risk in the unexposed group (R0), divided by the risk in the exposed group (equation 1′).
Table 1.
Summary definitions and usual formulas for the attributable fraction
| PAF | AFE | |
| Population of interest | The whole target population, irrespective of exposure to the risk factor | People exposed to the risk factor in the target population |
| Question answered | What proportion of the disease burden in a given (target) population is attributable to a given risk factor? | What proportion of the disease burden in those exposed in a given (target) population is attributable to a given risk factor? |
| Definition |
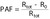 (Equation 1) (Equation 1) |
 (Equation 1′) (Equation 1′) |
| Alternative formulas | Levin's 1953 formula [3]: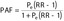 (Equation 2) (Equation 2)Miettinen's 1974 formula [4]: 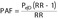 (Equation 3) (Equation 3) |
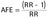 (Equation 2′) (Equation 2′) |
Note that to express PAFs and AFEs as proportions (%), formulas should be further multiplied by 100. The RR for PAF should be based on the same exposure definition as the prevalence, and for AFE on the same exposure definition as for defining the exposed group, and in both cases should be transportable to the target population. Pe: prevalence of exposure in the target population; PeD: prevalence of exposure in diseased people; AFE: attributable fraction in the exposed.
In 2015, Poole [6] noted, in a historical review of the PAF concept and its formulas, that some authors have used interchangeably “population attributable risks” (PARs) and “attributable risks” (ARs) for PAFs. Now, ARs are also used to denote the risk difference. Following Rothman et al. [9] in 2008 and Poole [6] in 2015, we suggest using the term PAF to avoid confusion in terminology.
Main calculations
As studies directly allowing estimation of unbiased Rtot and R0 in the target population are rare, a PAF is often calculated by combining 1) prevalence of exposure (or distribution of exposure) to the risk factor, estimated from representative cross-sectional surveys, with 2) RR estimated from cohort studies, case–control studies (under the rare disease assumption) and their meta-analysis. The typical formula by which RR is weighted by the prevalence of exposure in the target population (Pe) is presented in equation 2, often referred to as the Levin's formula. For a fixed value of RR, the PAF can range from zero (no one is exposed) to a maximum value bound by RR minus one over RR (if everyone is exposed), meaning if RR=2, PAF would be at most 50% if the whole population is exposed. The latter situation corresponds to estimating the AFE (equation 2′).
One important condition to apply equations 1 and 2 (respectively 1′ and 2′) is that no factor confounds the relationship between the risk factor and the disease. This condition is actually never met in practice. In case of confounding, it is not possible to simply use the adjusted RR in equations 2 and 2′; this would produce biased estimates [10]. It is instead possible to use the adjusted RR in equation 3, but it requires a valid estimate of the prevalence of exposure in diseased people (PeD). Adjusted methods dealing with confounding and effect modification are beyond the scope of the current article, but details can be found in articles by Gefeller [11] and Benichou [12], who review adjusted PAF (or AR) estimators based on cross-sectional, cohort and case–control studies. Defining and interpreting attributable fractions based on right-censored survival data require further caution [13].
Another important issue in deriving and interpreting PAFs is the precision of estimates. Calculating the variance of a PAF and then deriving (95%) confidence intervals have long been topics of interest to methodologists. In their article from 2006, Steenland and Armstrong [14] provide a good summary of formulas matching with equations 2 and 3, also mentioning advanced approaches like Monte Carlo simulations [15]. Some statistical softwares now provide computation tools, such as the AF [16] and stdReg [17] R-packages or the PUNAF, PUNAFCC and REGPAR packages in Stata [18], which allow derivation of attributable fractions and their confidence intervals from different study designs.
Core assumptions
The term “attributable” has a causal interpretation. The first and foremost assumption is therefore that the risk factor is a causal one. It means there must be enough evidence and a scientific consensus that the observed association between the exposure and disease of interest can be interpreted as reflecting causation. This may take decades, as is usually the case for occupational and environmental carcinogens, precluding the introduction of the risk factor in scenarios of risk reduction strategies. It is thus important to keep in mind that understudied or complex (although actual) causes will be less likely to be included in the scope of the calculations. In practice, this condition may be applied based on a stringent definition of causation, or a broader one. In a recent estimation of cancers attributable to occupational exposures in France, conducted by the International Agency for Research on Cancer (IARC), only group 1 (definite) carcinogens were considered in the main analysis [19, 20], while the prior UK comprehensive study also included group 2A (probable) human carcinogens [21].
The second assumption is that data used to estimate the PAF in the target population are valid and accurate. “Ideally, the attributable fraction should be estimated from a lifetime follow-up of exposed and non-exposed cohorts in the population of interest. In practice, the attributable fraction is usually based on one or more epidemiologic studies of specific exposed and non-exposed populations with incomplete follow-up, and results are often applied to a larger general population” [14]. While precision is reflected in confidence intervals (be it for prevalence, RR or PAF itself), uncertainty should also be carefully discussed by listing potential confounding, selection and information bias. It is therefore key to assess transportability to the target population in terms of exposure distribution, timeline, sociodemographic characteristics and other factors that may influence estimates. Hutchings and Rushton [22] provide an innovative example of how Monte Carlo sensitivity analysis may be used to weigh the main sources of uncertainty against each other. Their analysis of lung cancer and respirable crystalline silica exposure among men in Britain yields a PAF of 3.9% with a credibility interval of 2.0–16.2%. The uncertainty was mainly driven by the choice of RR and, to a lesser extent, by the employment turnover used as input to estimate the prevalence of occupational exposure over the relevant time window. Such approaches are important to identify input parameters that are critical to improve the relevance of PAF estimates.
Additional assumptions are required when PAFs are used to predict potential benefits from lowering exposure to a risk factor. The natural history of the disease and causal mechanisms involved should be at least minimally understood in terms of latency, existing threshold, dose–response relationship, and interaction with other factors to cause the disease. Interpreting PAFs as potential impact fractions requires that the intervention will work quickly and that other factors that affect risk will not be affected over the same period, which are both questionable. Reversibility of damage is also key. For instance, if the damage is irreversible, then prevention will be successfully achieved only by avoiding new-onset exposures. If it is instead reversible, then reducing or eliminating ongoing exposures will also be efficient in reducing the risk in those ever exposed, as was evidenced with smoking. Finally, the underlying exposure reduction scenario should be plausible based on identifiable actions. For example, assuming that every current smoker in a population will quit shortly and that no one will ever become a smoker any more is not realistic. In contrast, banning asbestos and imposing lower exposure limits to silica dust in the workplace have proved feasible (although achieved through decades of social mobilisation) and efficient to prevent asbestosis, silicosis, lung cancer and other specific respiratory diseases in countries where those regulations were adopted. This makes the choice of realistic risk reduction scenarios instrumental in giving a comparative (and social) value to these metrics [6].
Properties
The magnitude of PAFs is highly dependent on exposure definition and the choice of a reference level. Both will determine the prevalence of exposure as well as the risk in the exposed and unexposed groups. In the absence of a (clear) threshold, more restrictive definitions of the reference level will in particular lead to higher prevalence of exposure, while a broader definition of the reference group will play in the opposite direction. The interpretation of PAFs should be accompanied by a clear statement of that reference level and a discussion of how it applies to the target population.
Another important feature of PAFs is their distributive property. This means that, conditional on keeping the reference level constant, the total PAF equals the sum of PAFs (or rather “components of attributable fractions” (CAFs) [23]) for different exposure groups. If the reference group is non-exposed, and three exposure levels have been defined based on mutually exclusive bounds, then the total PAF for the risk factor is the sum of the three CAFs corresponding each to one level of exposure (compared to the same non-exposed group). This property is particularly interesting when partial rather than total elimination of the exposure is considered.
Finally, a tricky property of the PAF is that it will take the same value for two populations with the same RR and same exposure prevalence. Yet, if incidence is lower in one of the two populations, then the same PAF would lead to a substantially lower potential impact in terms of number of avoided disease load and/or saved lives. This draws our attention to the importance of considering different metrics, both in terms of relative importance, e.g. PAFs, and absolute burden, e.g. attributable or excess cases, while comparing potential benefits of the same intervention applied in two different populations, or in relation to two different health outcomes [24].
On attributing disease burden to causal factors: mind the knowledge gap
What does attribution really mean?
Although attributable cases are usually interpreted as aetiological cases, i.e. cases of disease that were caused by a specific exposure of interest, they are estimated based on excess cases, i.e. cases that would not have occurred during the study period, had the exposure been absent [25]. While all excess cases are aetiological cases, the reverse is not true. In fact, for an attributable fraction to equal an aetiological caseload, conditions should be met that are not easily warranted. Every time the exposure hastens disease onset among people who would anyway have got the disease during the study period, or some of the caused cases are balanced with prevented cases (by the same exposure), the aetiological caseload will be underestimated. The attributable fraction should therefore be seen as a plausible lower bound for the aetiological fraction [26]. Authors need to be careful in wording the interpretation of PAFs in order not to confuse the excess and aetiological fractions [6, 27]. Although this terminology has not been proposed so far, we personally would find more suitable the use of “attributed fraction” (or cases) in place of “attributable fraction”, which makes clear that attribution is not given by directly measurable facts, but constructed based on partially observable facts interpreted in the light of scientific theory. Another important distinction is between attributable (or attributed) cases at the group or population level and the decision (sometimes made by courts or legal compensation systems) that the disease was caused by the risk factor in a particular person. Other metrics have been proposed to quantify the probability of a causal contribution at the individual level, in particular the probability of causation (the probability of being an exposure-induced case), which has been extensively discussed by Greenland and Robins [25, 26, 28, 29].
Do not sum up… or subtract!
The problem of wrongly summing up PAFs calculated for single risk factors, or conversely trying to deduce the upper bound of the PAF for a particular risk factor by subtracting the PAF for another risk factor from 100%, has been repeatedly pointed out in the epidemiology and public health literature over the last two decades [27, 30]. In 2005, Rothman and Greenland [31] explained nicely why this could not be done, based on multicausality, or shared causal responsibility [32]. That model of causation acknowledges that “a given disease can be caused by more than one causal mechanism, and every causal mechanism involves the joint action of a multitude of component causes” [31].
Let's consider three causal mechanisms that involve five causal factors in total. The first causal mechanism involves the combined action of risk factors A, D and E; the second involves A, B and C, while the third involves B, D and E. Suppose that the PAFs for each causal mechanism distribute this way: 40% for the first, 35% for the second, and 25% for the third. As shown in table 2 for causal factors A and B, the PAF for each causal factor will be given by the sum of PAFs for causal mechanisms in which each risk factor is involved. In this example, causal factor A that is involved in two causal mechanisms has a PAF of 75%, while the PAF for B is 60%. This makes clear that summing up PAFA and PAFB would yield a PAF higher than 100%. The error of thinking that PAFs sum up to 100% stems from not understanding that A and B are being involved in a common mechanism. When we are summing PAFA and PAFB we are in fact counting twice the 35% of cases that occur through causal mechanism 2: once for causal factor A, once for causal factor B. This multicausality model allows us to understand in practice that “every case of every disease has some environmental and some genetic component causes [causal factors], and therefore every case can be attributed both to genes and to environment” [31]. For the same reason, it is not right to consider the complement of a PAF (e.g. 100%−PAF) as the proportion of a risk that can be attributed to other causes.
Table 2.
Theoretical example of multicausality and how it affects PAFs for single causal factors
| Causal mechanism | |||
| 1 | 2 | 3 | |
| Risk factors causally involved | A, D, E | A, B, C | B, D, E |
| PAF for each causal mechanism | 40% | 35% | 25% |
| PAF for causal factor A | 40%+35%=75% | NA | |
| PAF for causal factor B | NA | 35%+25%=60% | |
NA: not applicable.
This has strong implications; in particular, the fact that the PAF for a causal factor is high does not mean that every other causal factor necessarily has a low PAF and minor impact. It just means that removing/reducing exposure to that particular factor would have a potential high impact on lowering the disease burden. It does not say anything about other factors being unimportant. In fact, even another factor with a lower PAF but more feasible or ethical exposure reduction actions could well be preferred as a target for prevention, in the end. Therefore, the fact that a single risk factor (or the combination of known risk factors) has a high PAF does not directly mean that there are interventions able to improve population distributions of those risk factors; neither can it be used to plead for a reduced priority on the search for new causes.
The other thing is that removing one of the component causes through prevention will prevent every case in which that component cause might have been involved. If A is completely eliminated, then only causal mechanism 3 will remain, and the PAF for B, D and E would then rise to 100%, although relative to a lower burden of disease (in number of incident cases).
From “no data, no problem”…
In spite of conceptual clarity provided by methodologists in epidemiology, those attempting to apply PAFs are often faced with important empirical knowledge and data gaps. “No data, no problem” is a key issue regarding PAFs, which require the gathering of a large amount of knowledge prior to any estimation and are data- and computer-intensive. A causal link must be established between the risk factor of interest and the selected disease outcome. We already mentioned that meeting this assumption is a long process: it took more than 20 years between the first classification of diesel exhaust as a probable carcinogen to humans (group 2A) and its upgrade as a proved human carcinogen (group 1). Then an unbiased estimate of the RR must be available in the target population (or transportable from other populations) using a compatible disease definition. A valid prevalence of the exposure of interest in the same population is also needed, based on a definition of exposure consistent with available RRs and over a period relevant to disease aetiology (notably in terms of latency). In the French occupational cancer burden study conducted by IARC, 15 out of 68 group 1 occupational carcinogens could not be considered due to lack of proper cancer incidence or exposure prevalence data [19]. Also, as the prevalence of the ever-exposed population over the relevant (long-term) exposure period was not directly available for most of the considered carcinogens, it was estimated either through modelling (simulation) or correction of cross-sectional data based on expert decisions [20]. The implications may differ by population subgroups. For lung cancer, the joint PAF for 13 established (group 1) occupational lung carcinogens was estimated at 19.3% among adult French men and only 2.6% among women. It is, however, not clear to what extent the difference is due mainly to lower exposures among women or to more extensive data gaps about occupational lung carcinogens in women [33].
In the end, even when important hypotheses are met and calculation algorithms are robust, a metric will just be as good as the knowledge and data assembled to build it. Indeed, a metric is a construct that is based on numerous steps, each one bearing its part of uncertainty. The more complex or aggregate the metric, the more cautious we should be, at least in reviewing potentially important blind spots or distortions. This is all the more important if we intend to use the metric to define high-risk groups and target prevention, or even compensation.
…to “wrong question, wrong problem”
We have pointed out already that multicausality is difficult to take into account in the derivation of PAFs and should always be kept in mind at the interpretation stage. Multiple exposures and their eventual synergism or inhibition is another area in which important knowledge gaps can mislead us. We now know that on top of smoking, asbestos, crystalline silica dust, polycyclic aromatic hydrocarbons and diesel exhaust are established causal factors (or component causes) for lung cancer. But we know very little about how much co-exposures occur, quantitatively, which they obviously do in some population subgroups, like construction workers. And we know even less about eventual interactions between those factors, with some exceptions: notoriously asbestos and smoking do interact to synergistically increase the risk, beyond mere addition [34], although even this apparently robust statement has been challenged by a recent review [35]. Formulas have been proposed to estimate joint PAFs, i.e. summary PAFs for several risk factors taken together, but they are generally based on the assumption of no interaction or independent effects. Joint PAFs can also be directly derived from case–control studies where co-exposure prevalence, RRs, confounding and eventual effect modification can be taken into account. For example, Wild et al. [36] assessed that, among middle-aged men in a former industrial region in France, the joint PAF of asbestos, silica dust, polycyclic aromatic hydrocarbons and diesel exhaust for lung cancer amounted to 52–56% after adjusting for smoking. As pointed out by the authors, this suggests that beyond smoking, which is a powerful lung carcinogen, occupational exposures should be taken into account to identify relevant target groups for prevention.
This important comment raises the broader issue of the relevant target population for estimating attributable fractions, depending on how the risk factor distributes (or is distributed) within the general population. In the case of occupational carcinogens that concentrate within specific occupations, it would make sense to provide estimates by activity sector or even broader socio-occupational groups, rather than reporting a diluted PAF at the scale of the whole population [37]. In a population-based case–control study, the joint PAF for asbestos, silica and diesel exhaust among middle-aged men was 29.3% for lung cancer; however, the decomposition of the PAF by socio-occupational group showed that blue-collar workers contributed 92% of the attributed caseload [38]. In the case of occupational carcinogens, the population level estimates (overall 2–8% of incident cancers) are too often interpreted as confirming a posteriori their lesser aetiological importance or lower priority for prevention, whereas they are amenable to interventions beyond individual behaviours (banning or restrictions in use) and such interventions could help reduce social inequalities considerably.
Specific challenges and new avenues
Facing the complexities of chronic respiratory disease epidemiology
Some features of specific respiratory diseases should be further considered while estimating and interpreting PAFs, in particular in relation to disease definition and aetiology [39]. The heterogeneity of COPD and asthma phenotypes makes it challenging to consolidate disease definitions. This also implies that studies on which we rely to estimate attributable fractions are themselves heterogeneous. Their disease definitions are not necessarily in line with the latest internationally agreed definitions and, most importantly, with the intended use of the impact measures (e.g. for discussing complex aetiology, prevention priorities or compensation rules). For example, contrary to primary cancer of the lung, which can be clearly defined based on first diagnosis, “current asthma” definitions reflect the intermittent course of the disease, which requires accounting for incidence but also remission and persistence. COPD, on the other hand, is defined based on lung function levels that determine stages of severity. Another crucial aspect pertains to disease aetiology, which is key to selecting established causal factors. While respiratory diseases like lung cancer and COPD fit narrowly the causality paradigm supported by Bradford Hill's viewpoints [40], the aetiology of asthma is by far less well understood. More generally, while many risk factors have been established during adulthood, there is growing evidence that in utero and early-life exposures, and typically a wide range of environmental or parental occupational exposures, may affect lung function later in life. We hence should keep these complexities in mind while interpreting attributable fractions in relation to single exposures captured at one point in time (or for a limited period contingent on available data) rather than multiple exposures during critical time windows of susceptibility or over the life course.
Keeping up with meaningful methodological innovations
Beside the application of standard methods within a growing body of burden of disease studies, some important conceptual and statistical innovations were introduced that yet failed to be reproduced and appropriated by the wider audience. For instance, a stepwise procedure aiming at apportioning PAFs to individual risk factors and subpopulations was introduced in 1995 by Eide and Gefeller [23] and further developed [41]. This method allows estimation of sequential attributable fractions that are interpreted in terms of an additional reduction in disease occurrence when an exposure is eliminated in a given sequence, after having removed other risk factors. Newer approaches and metrics that have not yet been extensively discussed include pathway-specific attributable fractions [42] and degrees of necessity and of sufficiency [43]. Such recent developments in methodology are linked to the current shift in causal theory towards the potential outcomes framework [44] that stimulates many discussions among academics in epidemiology (see for example the special section on Causality in Epidemiology of the International Journal of Epidemiology, Volume 45, Issue 6, December 2016).
Matching metrics and interpretations with their intended use
We pointed already towards some pitfalls and misuses of PAFs regularly seen among clinicians, epidemiologists and, even more so, people involved in public health decision making. We warned not to deduce from the value of a PAF for a single (or a combination of) factor(s) that other causal factors would be less important. We also discussed that the potential impact of reducing the exposure depends on how far the exposure is modifiable among the relevant subgroups in the population, through ethical and timely interventions.
At stake is the adequate selection and interpretation of metrics and their estimates to answer a particular, explicit question. The question may be about aetiology: “How much do we know about the causes of a disease? What further research is needed?” As pointed out by Poole [6] in 2015, “the greater the PAF for a given cause or set of causes, the more advisable it is to look for new causes among exposed persons, especially if the cause or cause(s) with the high PAF are resistant to favorable change at the population level”. We may instead wish to assess the importance of a particular causal factor (or group of causal factors) within a defined population, with the idea that the considered exposure(s) is amenable to interventions, and this would sustain advocacy towards moving ahead in that direction. Such exercise may be performed at different scales, from international [45] to regional [8] or national [20] levels, with their respective strengths and limitations. PAFs may also be estimated within a specific occupation rather than the general population. For example, in 2019, Dumas et al. [46] estimated that the attributable fraction of weekly use of disinfectants on COPD risk among a large cohort of registered female nurses in the USA was 12%. The authors concluded that this estimate, if confirmed by other studies, would call for the development of exposure-reduction strategies in healthcare settings.
The aim may more specifically be to model the burden that will arise from current exposures, or the benefits that could be achieved in the future through specific interventions or regulations adopted at the country level, as for the UK [47], or at the European Union level [48]. Recently, innovative approaches adopting a comparative risk assessment perspective have been proposed to facilitate communication between scientists, managers and workers’ representatives. Building on previous suggestions to prefer absolute risk metrics such as years of life lost [49], in 2020 Richardson et al. [50] developed a set of estimates and graphical outputs comparing the potential impact of two policies on a cohort of Ontario uranium workers. The results show that removing occupational exposure to radon progeny could increase life expectancy by an average of 6 months per worker (depending on age), also shifting the causes of death towards a different composition, in particular a lower contribution of lung cancer.
Conclusion
We have shown that calculating attributable fractions is partly a theoretical exercise, based on assumptions not all warranted in many settings, and that the metric should therefore be interpreted cautiously. An in-depth presentation of other methodological complexities can be found elsewhere [6, 26]. The estimates provided by PAFs are imperfect. They are nevertheless widely used to pose disease aetiology and research needs, to debate alternative actions to reduce the disease burden in a target population, as well as (in particular) to set occupational or environmental disease compensation rules. The later misuse of PAFs or the more specific probability of causation metric may raise even greater problems where knowledge on biological mechanisms as well as epidemiological/exposure data are not sufficient to frame the question and answer it adequately. Beyond the scientific difficulties in documenting complex industrial and environmental hazards over long periods of time, we should keep in mind what science and technology studies have taught us: that undone science and the production of ignorance are narrowing the definition of problems and shaping blind spots that complicate the improvement of public health, PAFs being one good example [51].
Footnotes
Conflict of interest: E. Counil reports grants or contracts from Fondation de France, outside the submitted work.
References
- 1.Rose G. Sick individuals and sick populations. Int J Epidemiol 1985; 14: 32–38. doi: 10.1093/ije/14.1.32 [DOI] [PubMed] [Google Scholar]
- 2.Doll R. On the aetiology of cancer of the lung. Acta Unio Int Contra Cancrum 1951; 7: 39–50. [PubMed] [Google Scholar]
- 3.Levin ML. The occurrence of lung cancer in man. Acta Unio Int Contra Cancrum 1953; 9: 531–541. [PubMed] [Google Scholar]
- 4.Miettinen OS. Proportion of disease caused or prevented by a given exposure, trait or intervention. Am J Epidemiol 1974; 99: 325–332. doi: 10.1093/oxfordjournals.aje.a121617 [DOI] [PubMed] [Google Scholar]
- 5.Walter SD. The estimation and interpretation of attributable risk in health research. Biometrics 1976; 32: 829–849. doi: 10.2307/2529268 [DOI] [PubMed] [Google Scholar]
- 6.Poole C. A history of the population attributable fraction and related measures. Ann Epidemiol 2015; 25: 147–154. doi: 10.1016/j.annepidem.2014.11.015 [DOI] [PubMed] [Google Scholar]
- 7.Rushton L. Occupational cancer: recent developments in research and legislation. Occup Med 2017; 67: 248–250. doi: 10.1093/occmed/kqx020 [DOI] [PubMed] [Google Scholar]
- 8.Blanc PD, Annesi-Maesano I, Balmes JR, et al. The occupational burden of nonmalignant respiratory diseases. An official American Thoracic Society and European Respiratory Society statement. Am J Respir Crit Care Med 2019; 199: 1312–1334. doi: 10.1164/rccm.201904-0717ST [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. 3rd Edn. Philadelphia, Lippincott Williams & Wilkins; , 2008. [Google Scholar]
- 10.Greenland S. Bias in methods for deriving standardized morbidity ratio and attributable fraction estimates. Stat Med 1984; 3: 131–141. doi: 10.1002/sim.4780030206 [DOI] [PubMed] [Google Scholar]
- 11.Gefeller O. Comparison of adjusted attributable risk estimators. Stat Med 1992; 11: 2083–2091. doi: 10.1002/sim.4780111606 [DOI] [PubMed] [Google Scholar]
- 12.Benichou J. A review of adjusted estimators of attributable risk. Stat Methods Med Res 2001; 10: 195–216. doi: 10.1177/096228020101000303 [DOI] [PubMed] [Google Scholar]
- 13.Samuelsen SO, Eide GE. Attributable fractions with survival data. Stat Med 2008; 27: 1447–1467. doi: 10.1002/sim.3022 [DOI] [PubMed] [Google Scholar]
- 14.Steenland K, Armstrong B. An overview of methods for calculating the burden of disease due to specific risk factors. Epidemiology 2006; 17: 512–519. doi: 10.1097/01.ede.0000229155.05644.43 [DOI] [PubMed] [Google Scholar]
- 15.Greenland S. Interval estimation by simulation as an alternative to and extension of confidence intervals. Int J Epidemiol 2004; 33: 1389–1397. doi: 10.1093/ije/dyh276 [DOI] [PubMed] [Google Scholar]
- 16.Dahlqwist E, Zetterqvist J, Pawitan Y, et al. Model-based estimation of the attributable fraction for cross-sectional, case-control and cohort studies using the R package AF. Eur J Epidemiol 2016; 31: 575–582. doi: 10.1007/s10654-016-0137-7 [DOI] [PubMed] [Google Scholar]
- 17.Sjölander A. Estimation of causal effect measures with the R-package stdReg. Eur J Epidemiol 2018; 33: 847–858. doi: 10.1007/s10654-018-0375-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Newson RB. Attributable and unattributable risks and fractions and other scenario comparisons. Stata J 2013; 13: 672–698. doi: 10.1177/1536867X1301300402 [DOI] [Google Scholar]
- 19.Marant Micallef C, Shield KD, Baldi I, et al. Occupational exposures and cancer: a review of agents and relative risk estimates. Occup Environ Med 2018; 75: 604–614. doi: 10.1136/oemed-2017-104858 [DOI] [PubMed] [Google Scholar]
- 20.Marant Micallef C, Shield KD, Vignat J, et al. Cancers in France in 2015 attributable to occupational exposures. Int J Hyg Environ Health 2019; 222: 22–29. doi: 10.1016/j.ijheh.2018.07.015 [DOI] [PubMed] [Google Scholar]
- 21.Van Tongeren M, Jimenez AS, Hutchings SJ, et al. Occupational cancer in Britain. Exposure assessment methodology. Br J Cancer 2012; 107: Suppl. 1, S18–S26. doi: 10.1038/bjc.2012.114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hutchings S, Rushton L. Estimating the burden of occupational cancer: assessing bias and uncertainty. Occup Environ Med 2017; 74: 604–611. doi: 10.1136/oemed-2016-103810 [DOI] [PubMed] [Google Scholar]
- 23.Eide GE, Gefeller O. Sequential and average attributable fractions as aids in the selection of preventive strategies. J Clin Epidemiol 1995; 48: 645–655. doi: 10.1016/0895-4356(94)00161-I [DOI] [PubMed] [Google Scholar]
- 24.Poole C. On the origin of risk relativism. Epidemiology 2010; 21: 3–9. doi: 10.1097/EDE.0b013e3181c30eba [DOI] [PubMed] [Google Scholar]
- 25.Greenland S, Robins JM. Conceptual problems in the definition and interpretation of attributable fractions. Am J Epidemiol 1988; 128: 1185–1197. doi: 10.1093/oxfordjournals.aje.a115073 [DOI] [PubMed] [Google Scholar]
- 26.Greenland S. Concepts and pitfalls in measuring and interpreting attributable fractions, prevented fractions, and causation probabilities. Ann Epidemiol 2015; 25: 155–161. doi: 10.1016/j.annepidem.2014.11.005 [DOI] [PubMed] [Google Scholar]
- 27.Rockhill B, Newman B, Weinberg C. Use and misuse of population attributable fractions. Am J Public Health 1998; 88: 15–19. doi: 10.2105/AJPH.88.1.15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Greenland S, Robins JM. Epidemiology, justice, and the probability of causation. Jurimetrics 2000; 40: 321–340. [Google Scholar]
- 29.Greenland S. Relation of probability of causation to relative risk and doubling dose: a methodologic error that has become a social problem. Am J Public Health 1999; 89: 1166–1169. doi: 10.2105/AJPH.89.8.1166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Krieger N. Health equity and the fallacy of treating causes of population health as if they sum to 100%. Am J Public Health 2017; 107: 541–549. doi: 10.2105/AJPH.2017.303655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rothman KJ, Greenland S. Causation and causal inference in epidemiology. Am J Public Health 2005; 95: Suppl. 1, S144–S150. doi: 10.2105/AJPH.2004.059204 [DOI] [PubMed] [Google Scholar]
- 32.Rothman KJ. Causes. Am J Epidemiol 1976; 104: 587–592. doi: 10.1093/oxfordjournals.aje.a112335 [DOI] [PubMed] [Google Scholar]
- 33.Betansedi C-O, Vaca Vasquez P, Counil E. A comprehensive approach of the gender bias in occupational cancer epidemiology: a systematic review of lung cancer studies (2003–2014). Am J Ind Med 2018; 61: 372–382. doi: 10.1002/ajim.22823 [DOI] [PubMed] [Google Scholar]
- 34.Ngamwong Y, Tangamornsuksan W, Lohitnavy O, et al. Additive synergism between asbestos and smoking in lung cancer risk: a systematic review and meta-analysis. PLoS One 2015; 10: e0135798. doi: 10.1371/journal.pone.0135798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.El Zoghbi M, Salameh P, Stücker I, et al. Absence of multiplicative interactions between occupational lung carcinogens and tobacco smoking: a systematic review involving asbestos, crystalline silica and diesel engine exhaust emissions. BMC Public Health 2017; 17: 156. doi: 10.1186/s12889-017-4025-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wild P, Gonzalez M, Bourgkard E, et al. Occupational risk factors have to be considered in the definition of high-risk lung cancer populations. Br J Cancer 2012; 106: 1346–1352. doi: 10.1038/bjc.2012.75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Counil E, Henry E. Is it time to rethink the way we assess the burden of work-related cancer? Curr Epidemiol Rep 2019; 6: 138–147. doi: 10.1007/s40471-019-00190-9 [DOI] [Google Scholar]
- 38.Counil E, Henry E, Ismail W. Relier mesures d'impact en population et inégalités sociales de santé. L'exemple des liens entre travail et cancer [Linking population impact measures and social inequalities in health: the example of work-related cancer]. Environnement Risques & Santé 2020; 19: 267–272. doi: 10.1684/ers.2020.1456 [DOI] [Google Scholar]
- 39.Antó JM. Teaching chronic respiratory disease epidemiology. In: Olsen J, Greene N, Saracci R, Trichopoulos D, eds. Teaching Epidemiology: A Guide for Teachers in Epidemiology, Public Health and Clinical Medicine. 4th Edn. Oxford, Oxford University Press; , 2015; pp. 390–408. [Google Scholar]
- 40.Hill AB. The environment and disease: association or causation? Proc R Soc Med 1965; 58: 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Eide GE, Heuch I. Average attributable fractions: a coherent theory for apportioning excess risk to individual risk factors and subpopulations. Biom J 2006; 48: 820–837. doi: 10.1002/bimj.200510228 [DOI] [PubMed] [Google Scholar]
- 42.Ferguson J, O'Connell M, O'Donnell M. Revisiting sequential attributable fractions. Arch Public Health 2020; 78: 67. doi: 10.1186/s13690-020-00442-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gleiss A, Schemper M. Quantifying degrees of necessity and of sufficiency in cause-effect relationships with dichotomous and survival outcomes. Stat Med 2019; 38: 4733–4748. doi: 10.1002/sim.8331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Glass TA, Goodman SN, Hernán MA, et al. Causal inference in public health. Annu Rev Public Health 2013; 34: 61–75. doi: 10.1146/annurev-publhealth-031811-124606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Loomis D. Estimating the global burden of disease from occupational exposures. Occup Environ Med 2020; 77: 131–132. doi: 10.1136/oemed-2019-106349 [DOI] [PubMed] [Google Scholar]
- 46.Dumas O, Varraso R, Boggs KM, et al. Association of occupational exposure to disinfectants with incidence of chronic obstructive pulmonary disease among US female nurses. JAMA Netw Open 2019; 2: e1913563. doi: 10.1001/jamanetworkopen.2019.13563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hutchings S, Rushton L. Toward risk reduction: predicting the future burden of occupational cancer. Am J Epidemiol 2011; 173: 1069–1077. doi: 10.1093/aje/kwq434 [DOI] [PubMed] [Google Scholar]
- 48.Cherrie JW, Hutchings S, Gorman Ng M, et al. Prioritising action on occupational carcinogens in Europe: a socioeconomic and health impact assessment. Br J Cancer 2017; 117: 274–281. doi: 10.1038/bjc.2017.161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Robins J, Greenland S. Estimability and estimation of expected years of life lost due to a hazardous exposure. Stat Med 1991; 10: 79–93. doi: 10.1002/sim.4780100113 [DOI] [PubMed] [Google Scholar]
- 50.Richardson DB, DeBono NL, Berriault C, et al. Innovations in applied decision theory for health and safety. Occup Environ Med 2020; 77: 520–526. doi: 10.1136/oemed-2019-106303 [DOI] [PubMed] [Google Scholar]
- 51.Counil E, Henry E. When scientific knowledge and ignorance make it difficult to improve occupational health: a French and European perspective. New Solut 2021; 31: 141–151. doi: 10.1177/10482911211019135 [DOI] [PubMed] [Google Scholar]


