Escherichia coli chemotaxis is information limited

Abstract

Organisms acquire and use information from their environment to guide their behaviour. However, it is unclear whether this information quantitatively limits their behavioural performance. Here, we relate information to the ability of Escherichia coli to navigate up chemical gradients, the behaviour known as chemotaxis. First, we derive a theoretical limit on the speed with which cells climb gradients, given the rate at which they acquire information. Next, we measure cells’ gradient-climbing speeds and the rate of information acquisition by their chemotaxis signaling pathway. We find that E. coli make behavioural decisions with much less than the one bit required to determine whether they are swimming up-gradient. Some of this information is irrelevant to gradient climbing, and some is lost in communication to behaviour. Despite these limitations, E. coli climb gradients at speeds within a factor of two of the theoretical bound. Thus, information can limit the performance of an organism, and sensory-motor pathways may have evolved to efficiently use information acquired from the environment.

Organisms’ survival depends on their ability to perform behavioral tasks. These tasks require that the organism measure signals in its environment and respond appropriately. Information theory is a natural language for quantifying the fidelity of measurements and responses, but it is unclear how an abstract quantity like information might limit an organism’s performance at real-world tasks. Past studies have used information theory to understand the maximum amount of information biological systems can acquire and transmit about environmental signals^1–6 and have shown that they can approach biophysical limits^6–9. But high information transfer is not sufficient for high performance because not all of the information contained in the signal is relevant (i.e. contributes to performing the task), and not all of it is appropriately acted on¹⁰. What limits does information place on performance, and how efficiently do organisms use the information they acquire relative to these limits?

We address these questions using one of the best-understood behaviors in biology: bacterial chemotaxis. The bacterium Escherichia coli alternates between “runs,” which propel the cell forward, and “tumbles,” which randomly reorient its swimming direction¹¹ (Fig. 1). E. coli continuously sense the concentration c(t) of chemoattractant they encounter using transmembrane receptors. Relative changes in concentration¹² $s(t)=\frac{d}{dt}\text{log}(c)$, which we define to be the “signal”, induce changes in activity a(t) of receptor-associated CheA kinases. Thus, CheA kinase activity encodes E. coli’s estimate of the signal. CheA activity then modulates transitions in the cell’s swimming behavior m(t) between run and tumble states via a signal transduction pathway^13,14. If the attractant concentration is increasing (s(t) > 0), the cell runs for longer on average, thereby biasing its random motion up the gradient¹¹. However, noise in sensing and signal transduction corrupt the signal^15–18. Since the goal of chemotaxis is to climb chemical gradients, we quantify performance as the cell’s drift velocity v_d up a static gradient. E. coli chemotaxis has been studied extensively, but how much information a cell acquires about chemical signals^19–22 and its relationship to chemotactic performance are unknown.

Figure 1. Information sets an upper limit on chemotaxis performance.

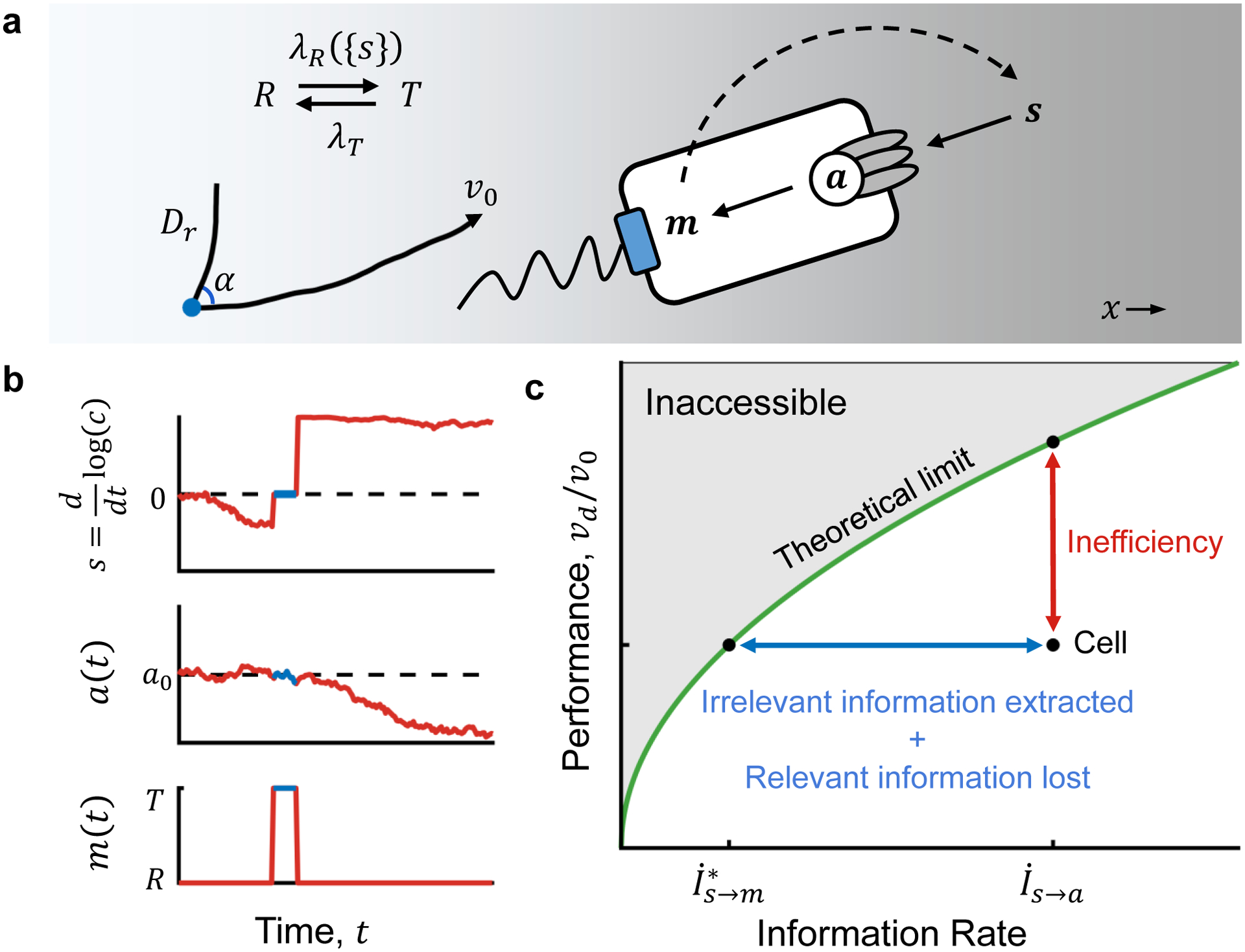
A) In our model, a cell navigates chemical gradients by sensing relative changes $s(t)=\frac{d\text{log}(c)}{dt}$ in attractant concentration c over time using receptors, which influence the activity a of receptor-associated kinases. a encodes E. coli’s estimate of the signal, i.e. whether it’s going up or down the gradient. a then modulates stochastic transitions between behavioral states m: a run state R, in which the cell swims with constant speed v₀ and rotational diffusion D_r; and a tumble state T, in which it reorients randomly with directional persistence a (see Supplementary Fig. S1). Responses to past signals {s} that are transduced from a to m are described by changes in the cell’s transition rate λ_R({s}) from run to tumble states. The cell’s motion creates the signal that it experiences (dashed arrow). B) Signals the cell experience s(t) (top) are encoded in noisy kinase activity a(t) (middle), which influences stochastic behavioral state transitions m(t) (bottom). The flow of information from s(t) to a(t) to m(t) implies that ${\dot{I}}_{s\to a}\ge {\dot{I}}_{s\to m}$. C) Given an information rate ${\dot{I}}_{s\to a}$, there is an upper limit on chemotaxis performance (green line), defined as the cell’s up-gradient drift speed v_d relative to v₀ (Eqn. 1). The cell’s performance is ultimately set by how much relevant information contained in ${\dot{I}}_{s\to a}$ is communicated to its behavior, quantified by ${\dot{I}}_{s\to m}^{*}$. Thus, real cells cannot reach the limit because of two factors (quantified by the length of the blue line): some of the information they encode in CheA kinase activity is irrelevant for climbing the gradient, and some of the relevant information in a is lost during transfer to the motors. These factors result in reduced performance (quantified by the length of the red line) and reduced efficiency of information usage.

To use information efficiently, a cell must only encode information in CheA that is relevant to gradient-climbing and act on that information appropriately at the motors to guide behavior. An inefficient cell may acquire abundant information about the signal, but it is either irrelevant to chemotaxis or goes unused. To determine how efficiently E. coli use information to navigate, we first must derive the maximum gradient-climbing speed a cell can achieve given the amount of information available in CheA. Second, we need to quantify how close to this theoretical bound E. coli cells operate by measuring both the amount of information available in CheA and cells’ performance with that information (Fig. 1C). In doing so, we will quantify information transfer on two different length scales: the information about signals available in kinase activity, and the information used to perform behaviors.

To do this, we must define a measure of information acquisition. Bacteria continuously encode chemical signals they experience. Thus, unlike most studies in biological systems^1–3,5,6, we cannot use the one-shot mutual information²³ between signal s(t) and kinase activity a(t) as a measure of information transfer because it is blind to past signals the cell has experienced. Instead, we need to quantify information transfer between signal and kinase trajectories, in this case using a steady state information rate²⁴. Furthermore, signals are generated by the cell’s own motion in the gradient²⁵. This makes a natural extension, the mutual information rate ṀI(s; a) between s(t) and a(t), also unsuitable because kinase activity and signal are correlated even for cells that don’t respond to the signal (Fig. 1AB). We address these challenges by decomposing the mutual information rate into the sum of two directed information terms (SI Section 1; see also^26,27): the transfer entropy^21,28 rates from kinase activity to signal ${\dot{I}}_{a\to s}$ and from signal to kinase activity ${\dot{I}}_{s\to a}$, or $\dot{M}I(s;a)={\dot{I}}_{a\to s}+{\dot{I}}_{s\to a}$. The first term ${\dot{I}}_{a\to s}$ quantifies the feedback of kinase activity onto signal via the behavior. The second term ${\dot{I}}_{s\to a}$ measures the influence of the signal on kinase activity, in bits/s, and must be nonzero for the cell to climb the gradient.

Next, we need to derive the theoretical limit on gradient-climbing performance v_d imposed by information ${\dot{I}}_{s\to a}$. The drift speed depends on how the cell’s motors use information about past signals that is provided by CheA. While information at the motors ${\dot{I}}_{s\to m}$ cannot exceed the information in kinase activity ${\dot{I}}_{s\to a}$²⁹, at best, all information in kinase activity is preserved at the motors, in which case ${\dot{I}}_{s\to m}={\dot{I}}_{s\to a}$. Therefore, to derive the bound, we sought to determine how ${\dot{I}}_{s\to m}$, and thus ${\dot{I}}_{s\to a}$, bounds performance v_d.

To do this, we constructed a mathematical model of run-and-tumble navigation (Fig. 1A; SI Section 2). During runs, cells swim with a constant speed v₀ and lose direction with rotational diffusion coefficient D_r. During tumbles, they randomly reorient with directional persistence α. In the absence of a gradient, cells switch from run to tumble and vice versa with rates λ_R0 and λ_T. The fraction of time the cell spends running is $P_{run}=\frac{{\lambda }_T}{{\lambda }_{R0}+{\lambda }_T}$. In shallow gradients, like those we consider here, the tumble rate λ_R({s}) depends approximately linearly on the history of signals experienced {s}^30–33.

Using the model above, we derived how v_d and ${\dot{I}}_{s\to m}$ depend on the behavioral response λ_R({s}). While any response to signal implies information transfer, it does not imply high drift speed. To find the limit, we derived the maximum drift speed v_d possible given an information rate ${\dot{I}}_{s\to m}$ by optimizing over responses λ_R({s}). This revealed that the optimal behavioral response only depends on the current rate of change of log-concentration, s(t) (SI Section 4). Thus, information about the current signal is relevant to gradient-climbing (SI Section 5). Bacteria can’t implement the optimal behavioral response because they must make comparisons of concentrations over a finite time to infer s(t)¹⁵. Nevertheless, the performance achieved by any behavioral response is bounded by (Fig. 1C):

$$v_d/v_0\le f(\theta ){\left(\frac{\text{log}(2){\dot{I}}_{s\to a}}{12D_r}\right)}^{\frac{1}{2}},\text{ where }0\le f(\theta )\le 1,\theta =\left\{{\lambda }_{R0},P_{run},\alpha \right\},$$ (1)

where we have used that ${\dot{I}}_{s\to m}={\dot{I}}_{s\to a}$, and $f(\theta )=\frac{(1-\alpha ){\lambda }_{R0}}{(1-\alpha ){\lambda }_{R0}+2D_r}{\left(8\frac{D_r}{{\lambda }_{R0}}{P}_{run}\right)}^{\frac{1}{2}}$. This expression makes rigorous the intuition that information transfer sets a limit on chemotaxis performance^{15,20,22,24,34,35}. Of the information contained in ${\dot{I}}_{s\to a}$, the amount that is both relevant and transferred to behavior, ${\dot{I}}_{s\to m}^{*}$, ultimately determines performance: $v_d/v_0=f(\theta ){\left(\frac{\text{log}(2){\dot{I}}_{s\to m}^{*}}{12D_r}\right)}^{1/2}$ (SI Section 5). Thus, the green line in Fig. 1C directly maps a cell’s performance to ${\dot{I}}_{s\to m}^{*}$. Furthermore, the length of the blue line in Fig. 1C measures the amount of irrelevant information encoded in CheA plus the amount of relevant information lost in communication to the motors. These factors lower the cell’s performance relative to the theoretical limit by an amount quantified by the length of the red line. With this, we define the efficiency of information usage as the cell’s actual drift speed relative to the maximum possible with the information available in CheA, $\eta =\frac{v_d}{v_0}/\left[f(\theta ){\left(\frac{\text{log}(2){\dot{I}}_{s\to a}}{12D_r}\right)}^{\frac{1}{2}}\right]={\left({\dot{I}}_{s\to m}^{*}/{\dot{I}}_{s\to a}\right)}^{1/2}$.

We next set out to measure how efficiently E. coli use information to navigate, η. First, we quantified the bound by measuring the rotational diffusion coefficient D_r and behavioral parameters θ from trajectories of swimming E. coli (Supplementary Figs. S1, S2). Individual cells in a clonal population exhibit nongenetic differences in behavioral parameters^36–39, which in E. coli are highly correlated with P_run^36,38. From this data, we find f(θ) = 0.531 ± 0.005 for the median P_run (± one standard error throughout; Supplementary Table S1). This quantifies the minimum amount of information needed to climb a gradient. Surprisingly, the bound predicts that run-and-tumble navigation is theoretically possible with very small information rates: a hundredth of a bit per second is sufficient to climb gradients at ~6% of the run speed. This is far less than the 1 bit per run (~1 bit/s) required to distinguish whether concentration is currently increasing or decreasing before every tumble decision²⁴.

To compare E. coli to the theoretical limit, we measured the rate at which cells encode information about signals in their CheA kinase activity, ${\dot{I}}_{s\to a}$, during chemotaxis. Directly measuring kinase activity in individual swimming cells is infeasible. Instead, we quantified the mutual information rate^24,40 between signal and kinase activity, ṀI(s; a), in immobilized cells by measuring their kinase response and noise properties and by separately measuring the signal statistics they would experience during navigation (Fig. 2A). In these immobilized cells, $\dot{M}I(s;a)={\dot{I}}_{s\to a}$ since there is no feedback of kinase activity onto the signal. ${\dot{I}}_{s\to a}$ quantified this way in immobilized cells differs from ${\dot{I}}_{s\to a}$ in a swimming cell because it does not take into account higher-order correlations between s and a. However, these correlations contribute terms that are multiplied by higher powers of the gradient steepness g = d log(c)/dx, and thus can be neglected in shallow gradients (SI Section 8).

Figure 2. Measuring the rate of information transfer from signal to intracellular kinase.

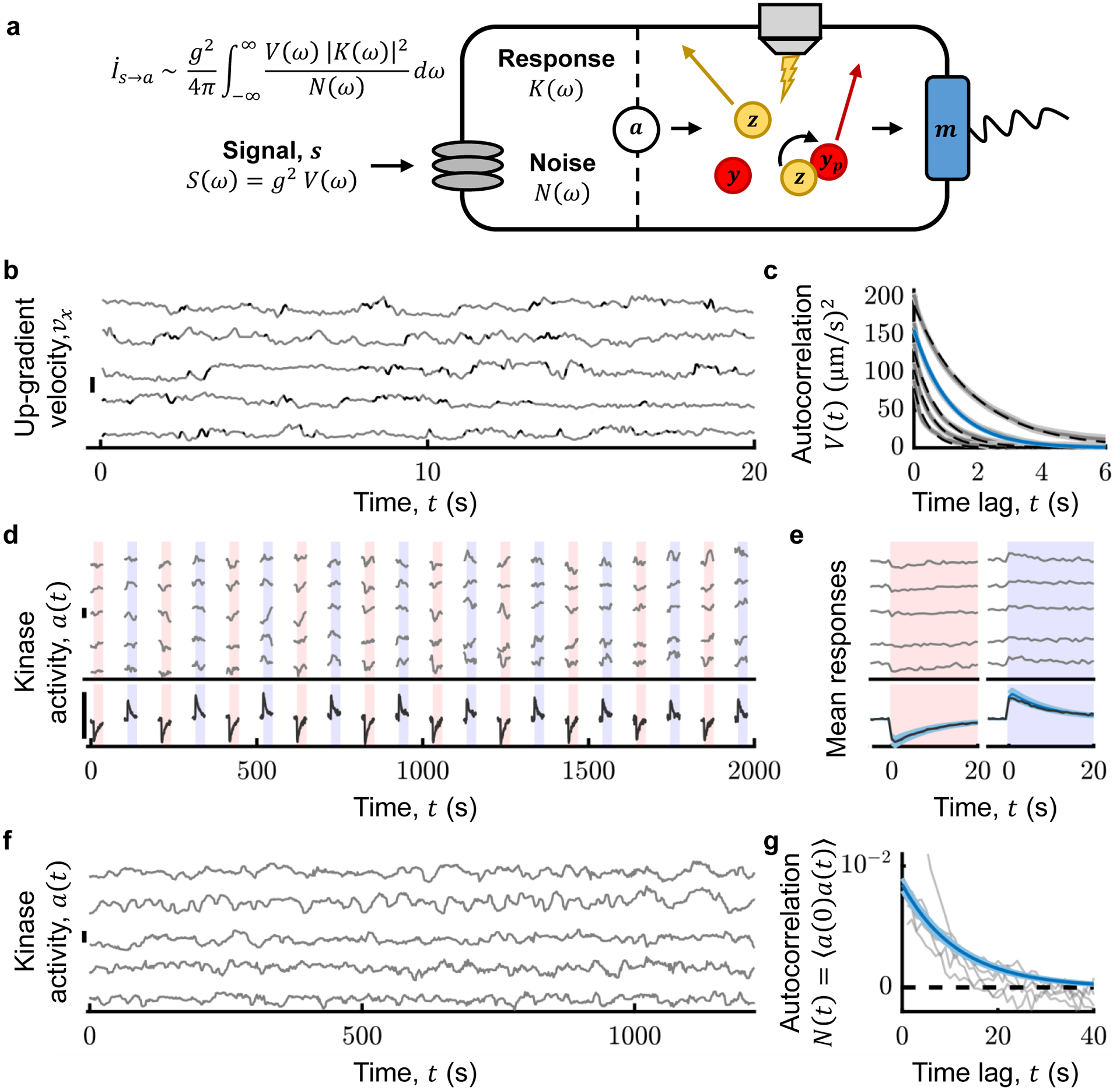
A) Information rate ${\dot{I}}_{s\to a}$ from signal s to kinase activity a depends on the signal power spectrum S(ω), the kinase frequency response K(ω), and the kinase noise power spectrum N(ω). The signal is s(t) = g v_x(t), where g is the gradient steepness and v_x is the cell’s up-gradient velocity. Thus, S(ω) = g² V(ω), where V(ω) is the power spectrum of v_x. Kinase activity a was quantified from the FRET between the substrate of the kinase, CheY-mRFP, and its phosphatase, CheZ-mYFP (Methods; SI Sections 10–15; Supplementary Figs. S3–S6). All experiments were performed in a background of 100 μM MeAsp. B) (Gray) Individual cells’ v_x(t). (Black: tumbles; scale bar 40 μm/s.) C) (Gray) Average autocorrelation of v_x, V(t), for P_run = 0.93, 0.89, 0.84, 0.79, 0.74 (top to bottom; throughout, shading is ± one standard error; black dashed lines are fits to V(t) = a_v exp(−λ_tot |t|)). (Blue) Best fit to the median bin, P_run~0.89 (Supplementary Fig. S2; SI Section 21). D) Immobilized cells were delivered 10 μM steps up (red shading) and down (blue shading). (Top, gray) a(t) for five cells (here and in (F), smoothed with 10^th order median filter, and scale bars represent Δa = 0.3; Methods; SI Section 16; Supplementary Fig. S5). (Bottom, black) Population average a(t) (n = 442 cells). E) Single-cell average (top, gray) and population-average (bottom, black) response functions K(t) to positive and negative stimuli. (Blue line) K(t) = G exp(−t/τ₂)(1 − exp(−t/τ₁)) H(t), where H(t) is the Heaviside step function and G, τ₁, and τ₂ are the median parameters extracted from fits to single-cell responses. F,G) (Gray) Kinase activity (F) and corresponding autocorrelations (G) in single cells (Methods; SI Section 17; Supplementary Fig. S6). (Blue, G) $N(t)=\langle a(t)a(0)\rangle ={\sigma }_n^2\text{exp}\left(-|t|/{\tau }_n\right)$, where σ_n and τ_n are the median parameters extracted from fits to single-cell traces (n = 262 cells). V(ω), K(ω), and N(ω) shown in Supplementary Fig. S7.

The signal statistics are characterized by their power spectrum S(ω). It is often difficult to know the natural signal statistics an organism experiences^7,41. But during bacterial chemotaxis in static gradients, the signal is generated from the cell’s own motion. Thus, the signal power spectrum is S(ω) = g² V(ω), where V(ω) is the power spectrum of the cell’s up-gradient velocity v_x(t). Furthermore, in shallow gradients, the statistics of v_x(t) are nearly identical to those in the absence of a gradient (SI Sections 8,9). To quantify the autocorrelation function of v_x, V(t), and thus V(ω), we tracked individual swimming cells in a 100 μM background of the attractant α-methyl-aspartate (MeAsp) (Fig. 2BC; Supplementary Fig. S2; Methods; SI Sections 18–21). For each value of P_run, we fit the measured V(t) with a decaying exponential, $V\text{(}t\text{)=}{a}_v{e}^{-{\lambda }_{tot}|t|}$, giving a_v = 157.1 ± 0.5 (μm/s)² and λ_tot = 0.862 ± 0.005 s⁻¹ for the median phenotype (~10⁴ s total trajectory time, 7s average duration; Supplementary Table S1).

Next, we measured the response and noise properties of CheA kinase activity using Förster resonance energy transfer (FRET) between the kinase’s substrate CheY and the phosphatase CheZ inside single cells^17,18,42 (Fig. 2A). In the linear regime, the kinase response is characterized by its frequency-response function, K(ω), or its response K(t) to an impulse of signal $\left(s(t)=\frac{d}{dt}\text{log}(c)\right)$. To measure K(t), we used a microfluidic device that can rapidly switch (in ~100 ms) the concentration of attractant delivered to hundreds of immobilized cells⁴² (Supplementary Figs. S3–S4). To ensure cells were in the log-sensing regime^12,43, we first adapted them to a background of 100 μM MeAsp. We then delivered 10 positive and 10 negative 10% step changes of MeAsp concentration (impulses of s) (Fig. 2D; Methods), which were small enough to be in the linear-response regime^44,45 (Supplementary Fig. S5). Cell responses exhibited a stereotypical shape (Fig. 2E) described by a phenomenological model $K\left(t\right)=G{e}^{-t/{\tau }_2}\left(1-e^{-t/{\tau }_1}\right)H(t)$, with gain G, rise time τ₁, and adaptation time τ₂, and H(t) is the Heaviside step function. We fit this model to each cell’s responses to the positive and negative stimuli simultaneously (SI Section 16) and then determined the population-median parameter values (n = 442 cells) (Supplementary Table S1; Supplementary Fig. S5): G = 1.73 ± 0.03, τ₁ = 0.22 ± 0.01 s, and τ₂ = 9.9 ± 0.3 s. This value of τ₁ includes the stimulus switching time and CheY/CheZ binding kinetics, making it longer than the kinase response time, which was previously measured to be τ₁ ~ 1/60 s^46,47. After verifying that our results are insensitive to the value of τ₁ (SI Section 9; Supplementary Fig. S8), we used the literature value in our estimate of ${\dot{I}}_{s\to a}$.

We quantified the statistics of noise in kinase activity by measuring FRET in single cells in a constant background of 100 μM MeAsp (Fig. 2F; Supplementary Fig. S6). These fluctuations were well-approximated by an Ornstein-Uhlenbeck process, consistent with previous measurements^16,18. Using Bayesian filtering (SI Section 17), we inferred the single-cell parameters of the noise model directly from the time series. These parameters determined the noise autocorrelation function $N(t)={\sigma }_n^2{e}^{-|t|/{\tau }_n}$ (Fig. 2G; SI Section 9) and power spectrum N(ω) (Supplementary Fig. S7). The population-median parameter values (n = 262 cells) were σ_n = 0.092 ± 0.002 AU (standard deviation of the noise) and τ_n = 11.75 ± 0.04 s (noise correlation time) (Supplementary Table S1). These measurements include the effects of all noise sources upstream of CheA, including stochastic ligand arrivals at the cells’ receptors¹⁵.

With the signal statistics, response function, and noise, we then computed the information rate from the signal to kinase activity ${\dot{I}}_{s\to a}$ (Fig. 3A). Since the signal power is proportional to g², the information rate is, as well: ${\dot{I}}_{s\to a}=\beta g^2$. Using our measurements above, we estimated that the E. coli chemotaxis system transfers information to the kinases at a rate β = 0.22 ± 0.03 bits/s/mm⁻² (SI Sections 8,9). Thus, in shallow gradients, where concentration varies on millimeter to centimeter length scales, cells only get ~10⁻² bits/s. The bound in Eqn. 1 predicts that this is sufficient for a run-and-tumble navigator to climb gradients at a few percent of its swimming speed. However, it is unclear how much of this information is relevant to chemotaxis, communicated to the motors, and used to navigate.

Figure 3. E. coli use information efficiently to navigate.

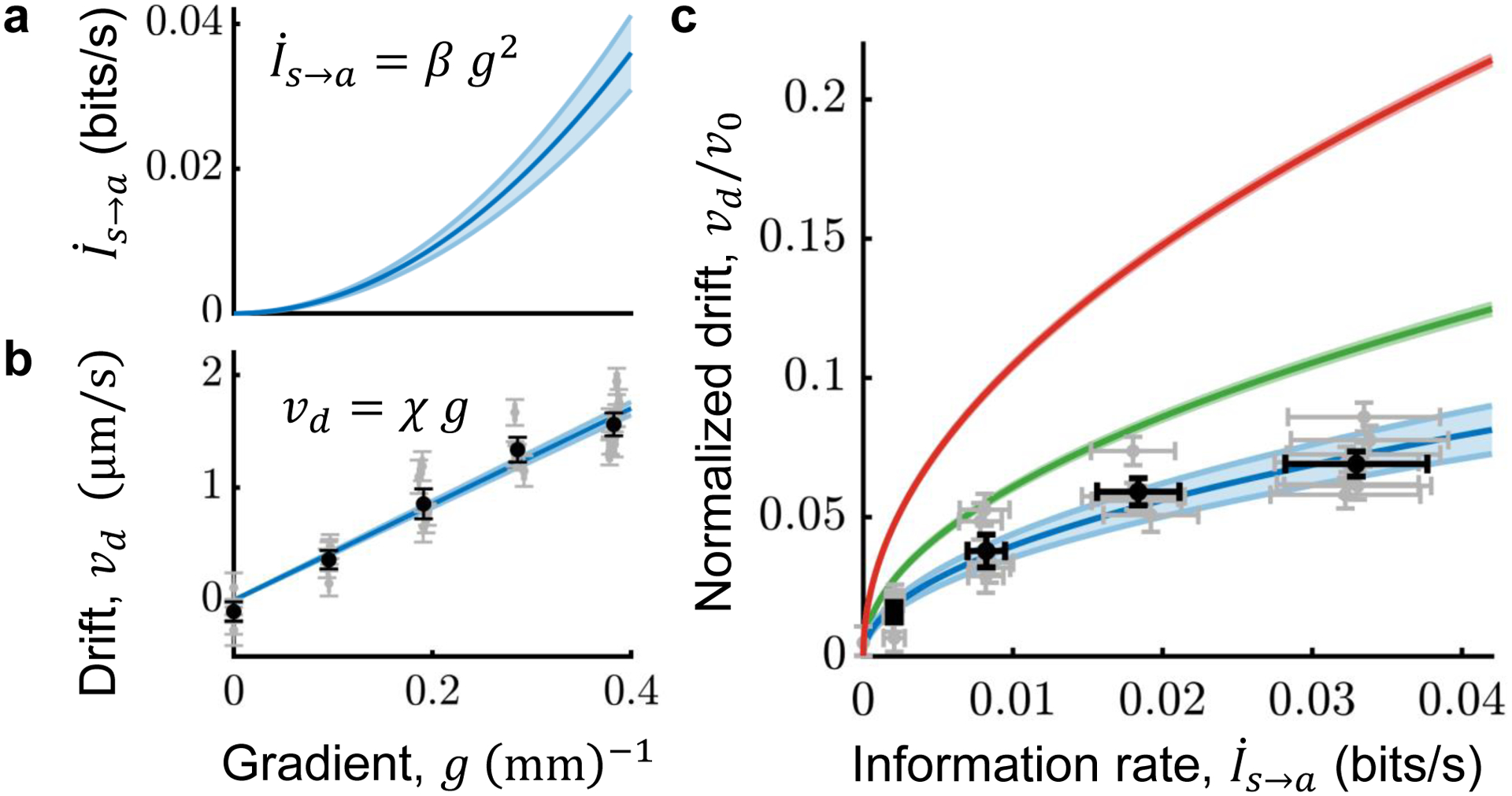
A) The rate of information transfer from signal to kinase activity depends on gradient steepness $g:{\dot{I}}_{s\to a}=\beta g^2(\beta =0.22\pm 0.03\text{bits}/\text{s}/{\text{mm}}^{-2}$; Fig. 2; SI Section 8). Throughout, shading and error bars indicate ± one standard error. B) Chemotactic performance as a function of gradient steepness g, in a background of 100 μM MeAsp. Gray dots: average drift speeds in individual experiments. Black dots: averages over experiments. Error bars on g are smaller than the markers. Population average drift speed increases linearly with gradient steepness, v_d = χ g (χ = 4300 ± 150 μm²/s; blue line and shading; SI Section 22). C) From measurements of E. coli cells’ information rates and chemotactic drift speeds, we compared their performance to the theoretical bound (Eqn. 1). Green: predicted maximum performance given information acquisition rate ${\dot{I}}_{s\to a}$ (Eqn. 1), with measured behavioral parameters θ = {λ_R0, P_run, α} (f(θ) = 0.531 ± 0.005). Blue: measured performance v_d/v₀ (v₀ = 22.61 ± 0.07 μm/s) versus information rate ${\dot{I}}_{s\to a}$, obtained by eliminating g from the fits of v_d(g) = χ g and ${\dot{I}}_{s\to a}(g)=\beta g^2$ to plot $v_d/v_0=\chi /v_0{\left({\dot{I}}_{s\to a}/\beta \right)}^{1/2}$. Black and gray dots are data points from (B) plotted against ${\dot{I}}_{s\to a}(g)=\beta g^2$. Taking the ratio of the blue and green curves, we find that E. coli achieve drift speeds within a factor η = 0.65 ± 0.05 of the theoretical limit. Red: Theoretical bound (Eqn. 1) if λ_R0 is optimized, and all other behavioral parameters are held fixed at their measured values (f(θ) = 0.914 ± 0.006, just below the maximum value of 1).

To answer this, we measured E. coli’s average drift speeds by tracking individual cells’ motion in gradients of varying steepness. Static, linear MeAsp gradients were constructed (Methods) in a 100 μM background, with length scales ranging from 10 mm (g = 0.1 mm⁻¹) to 2.5 mm (g = 0.4 mm⁻¹). From >10⁵ seconds of trajectories in each condition, we estimated the drift speed v_d as the time-averaged up-gradient velocity over all cells in each experiment (SI Section 22). As expected from theory in shallow gradients, drift speed increased linearly with gradient steepness v_d = χ g, with “chemotactic coefficient” χ ~ 4.30 ± 0.15 μm/s/mm⁻¹ (Fig. 3B; Supplementary Fig. S9), consistent with previous measurements⁴⁸.

With measurements of both their information acquisition rate and performance, we were in a position to quantify how efficiently E. coli use information, η. For each gradient g, we plotted the drift speed v_d(g) against the information rate ${\dot{I}}_{s\to a}(g)$ (blue in Fig. 3C). On the same plot, we show the maximum drift speeds, given by the bound in Eqn. 1 (green in Fig. 3C). The ratio of these two curves is the efficiency $\eta =\chi /\left[v_{0}f(\theta ){\left(\frac{\text{log}(2)\beta }{12D_r}\right)}^{\frac{1}{2}}\right]$, which is independent of g in shallow gradients. We find that E. coli achieve an efficiency of η = 0.65 ± 0.05—that is, they climb gradients at ~65% of the maximum possible speed given the rate at which their kinases encode information about environmental signals. Equivalently, comparing information rates (blue and green lines) at the same drift speed in Fig. 3C indicates that ${\eta }^2={\dot{I}}_{s\to m}^{*}/{\dot{I}}_{s\to a}$ ~ 42% of the total information available in kinase activity is relevant, preserved in communication with the motors, and used to navigate.

Many studies of information theory in biology have focused on the maximum amount of information signaling pathways can transmit^{1–6,49–51}. Here, we instead asked how the information an organism transmits limits its performance at functional tasks, using E. coli chemotaxis as a model system. Whereas previous works measured one-shot information transfer by biochemical networks^{1–6,49–51}, in bits, we measured the rate at which E. coli transfer information, in bits/s, between time-varying inputs and outputs, with natural input statistics. Combining this with measurements of E. coli’s chemotactic performance and the theoretical limit (Eqn. 1), we found that about half of the information about concentration changes that flows through CheA is both relevant to and used for navigation.

Achieving high efficiency requires that cells acquire, transmit, and act on information that is relevant to their task¹⁰, but which bits are relevant is often not clear. Using rate-distortion theory^6,52,53, we found that the relevant bits for bacterial chemotaxis are those that indicate how fast the attractant concentration is currently changing (SI Section 5). Responding to signals experienced multiple signal correlation times, ${\tau }_v^{-1}=(1-\alpha ){\lambda }_{R0}+2D_r$, in the past transmits a significant amount of irrelevant information (SI Section 5). But in typical gradients, which are much longer than their body lengths, E. coli must swim and time integrate to infer signals from stochastic ligand arrivals^15,54. This forces E. coli to respond to past signals to learn about the current signal, thus transmitting irrelevant information and preventing them from reaching the bound in Eqn. 1. Between the green and blue lines in Fig. 3C, there is a tighter bound on performance that accounts for the need to time integrate, relative to which E. coli are even more efficient.

The information-performance bound in Eqn. 1 depends on the cell’s swimming behavior. We quantified this bound for a typical cell from a laboratory strain, but behavioral parameters θ vary across individual cells^{16,36–38,55,39}, strains, and growth conditions⁵⁶. This raises the question of what behavioral phenotype can achieve the highest performance with a given information rate. Maximizing f(θ) with respect to θ (SI Section 6), we find that the optimal agent changes direction by tumbling at the same rate as rotational diffusion^33,57,58, (1 − α) λ_R0 = 2 D_r. Our median phenotype tumbles more frequently than this and misses out two-fold. First, the bound on its performance (green in Fig. 3C) is about half as high as it could be (red in Fig. 3C). Second, a lower average tumble rate λ_R0 would lengthen the signal correlation time τ_v, increasing the fraction of relevant information the cell would transfer, and thus increasing η relative to the higher bound. Laboratory strains of E. coli were historically selected for motility in semisolid agar^59–61, and our strain’s frequent reorientations may be optimized to navigate that environment^62–64. Alternatively, their behavioral parameters may optimize other objectives^31,33. While E. coli’s behavioral strategy thus appears sub-optimal for gradient-climbing in liquid, they nevertheless use biochemical information in CheA efficiently to carry it out.

A hallmark of E. coli’s chemotactic response to many ligands—including MeAsp used here—is precise adaptation⁶⁵: following a stimulus, the kinase activity responds transiently before relaxing back to the pre-stimulus activity (Fig. 2E). However, for some attractants, such as serine, adaptation is imperfect, causing the average tumble rate to decrease with increasing concentration of attractant in the background^{30,37,57,66–68}. By lowering λ_R0 closer to the optimal value, a background of serine both increases the bound and causes cells to climb gradients of MeAsp faster⁶⁷ (SI Section 7). However, from an information-usage perspective, if the cell could choose λ_R0 and its response function independently, our theory shows that it should match its average tumble rate to rotational diffusion, (1 − a) λ_R0 = 2 D_r, and its response function should adapt perfectly. Imperfect adaptation implies that the cell is responding to concentration changes that occurred far in the past, which transfers irrelevant information.

Because we measured signal statistics and kinase activity in different cells, our estimate of the information rate does not account for the long tail in the run-length distribution that can arise from fluctuations in kinase activity^16,69–71. In theory, these fluctuations can improve performance in shallow gradients^72,73. However, they only contribute corrections to the information rate that are higher order in g and can be neglected in shallow gradients (SI Section 8).

This work relied on linear theory, which is only valid in shallow gradients. In steep gradients, behavioral feedback can drive large deviations in the tumble rate, leading to ratchet-like gradient climbing²⁵. In this regime, the signal statistics gain multiple time scales due to the very different run durations up and down the gradient. In future studies, it will be interesting to examine how these factors, combined with nonlinearities in the signaling pathway, alter cells’ information-acquisition rates and efficiencies.

Here, we measured information transfer at two very different length scales. The first is the relevant information contained in behavior, which is quantified by the drift speed and behavioral parameters. The second is the total information available in CheA kinase activity. Considering how different these measurements are, there is no reason to expect that they must be similar in magnitude. But their agreement to about a factor of two is a strong indication that information is a limitation on chemotaxis performance. Information transfer is not necessarily the end-goal of biological tasks, but it is needed to perform many of them. Our results suggest organisms may be under selective pressure to efficiently use information from environmental cues to perform tasks necessary for their survival.

Methods

Strains and plasmids

The strain used for the FRET experiments is a derivative of E. coli K-12 strain RP437 (HCB33), a gift of T. Shimizu, and described in detail elsewhere^18,42. In brief, the FRET acceptor-donor pair (CheY-mRFP and CheZ-mYFP) is expressed in tandem from plasmid pSJAB106¹⁸ under an isopropyl β-D-thiogalactopyranoside (IPTG)-inducible promoter. The glass-adhesive mutant of FliC (FliC*) was expressed from a sodium salicylate (NaSal)-inducible pZR1 plasmid¹⁸. The plasmids are transformed in VS115, a cheY cheZ fliC mutant of RP437¹⁸ (gift of V. Sourjik). The crosstalk coefficient for spectral bleedthrough was measured using a strain expressing CheZ-YFP from a plasmid, and that for cross-excitation was measured using a strain expressing CheY-mRFP from a plasmid, both of which are gifts from T. Shimizu. RP437, the direct parent of the FRET strain and also a gift from T. Shimizu, was used to measure behavioral parameters and chemotactic drift speeds. A mutant that can’t tumble due to an in-frame deletion of the cheY gene, VS100 (gift of V. Sourjik), was used to measure the rotational diffusion coefficient D_r. All strains are available from the authors upon request.

Cell preparation

Single-cell FRET microscopy and cell culture was carried out essentially as described previously^18,42. In brief, cells were picked from a frozen stock at −80°C and inoculated in 2 mL of Tryptone Broth (TB; 1% bacto tryptone, 0.5 % NaCl) and grown overnight to saturation at 30°C and shaken at 250 RPM. Cells from a saturated overnight culture were diluted 100X in 10 mL TB and grown to OD600 0.45–0.47 in the presence of 100 μg/ml ampicillin, 34 μg/ml chloramphenicol, 50 μM IPTG and 3 μM NaSal, at 33.5°C and 250 RPM shaking. Cells were collected by centrifugation (5 min at 5000 rpm, or 4080 RCF) and washed twice with motility buffer (10 mM KPO4, 0.1 mM EDTA, 1 μM methionine, 10 mM lactic acid, pH 7), and then were resuspended in 2 mL motility buffer. Cells were left at 22°C for 90 minutes before loading into the microfluidic device. All experiments, FRET and swimming, were performed at 22–23°C.

For swimming and chemotaxis experiments, cells were prepared identically. Saturated overnight cultures were diluted 100X in 5 mL of TB. After growing to OD600 0.45–0.47, 1 mL of cell suspension was washed twice in motility buffer with 0.05% w/v of polyvinylpyrrolidone (MW 40 kDa) (PVP-40) added. Washes were done by centrifuging the suspension in an Eppendorf tube at 1700 RCF (4000 RPM in this centrifuge) for 3 minutes. After the last wash, cells were resuspended with varying concentrations of MeAsp (see below).

Microfluidic device fabrication and loading for FRET measurements

Microfluidic devices for the FRET experiments⁴² were constructed from polydimethylsiloxane (PDMS) on 24 × 60 mm cover glasses (#1.5) following standard soft lithography protocols⁷⁴. Briefly, the master molds for the device were created with a negative SU-8 photoresist on 100-mm silicon wafers. Approximately 16-μm-high master molds were created. To fabricate the device, the master molds were coated with a 5-mm-thick layer of degassed 10:1 PDMS:curing agent mixture (Sylgard 184, Dow Corning). The PDMS layer was cured at 80 °C for 1 hour, and then cut and separated from the wafer, and holes were punched for the inlets and outlet. The punched PDMS layer was further cured at 80 °C for > 2 hours. Then, the PDMS was cleaned with transparent adhesive tape (Magic Tape; Scotch) followed by rinsing with (in order) isopropanol, methanol, and Millipore-filtered water. The glass was rinsed with (in order) acetone, isopropanol, methanol, and Millipore-filtered water. The PDMS device was tape-cleaned an additional time before the surfaces of the device and coverslip were treated in a plasma bonding oven (Harrick Plasma). After 1 min of exposure to plasma under vacuum, the device was laminated to the coverslip and then baked at 80°C hotplate for > 30 min to establish a covalent bond.

Sample preparation in the microfluidic device was conducted as follows. Five inlets of the device (Supplementary Fig. S3) were connected to reservoirs (Liquid chromatography columns, C3669; Sigma Aldrich) filled with motility buffer containing various concentrations of α-methyl-aspartate (MeAsp) through polyethylene tubing (Polythene Tubing, 0.58 mm id, 0.96 mm od; BD Intermedic). The tubing was connected to the PMDS device through stainless steel pins that were directly plugged into the inlets or outlet of the device (New England Tubing). Cells washed and suspended in motility buffer were loaded into the device from the outlet and allowed to attached to the cover glass surface via their sticky flagella by reducing the flow speed inside the chamber. The pressure applied to the inlet solution reservoirs was controlled by computer-controlled solenoid valves (MH1; Festo), which rapidly switched between atmospheric pressure and higher pressure (1.0 kPa) using a source of pressurized air. Only one experiment was conducted per device.

Single-cell FRET imaging system

FRET imaging in the microfluidic device was performed using an inverted microscope (Eclipse Ti-E; Nikon) equipped with an oil-immersion objective lens (CFI Apo TIRF 60X Oil; Nikon). YFP was illuminated by an LED illumination system (SOLA SE, Lumencor) through an excitation bandpass filter (FF01–500/24–25; Semrock) and a dichroic mirror (F01–542/27–25F; Semrock). The fluorescence emission was led into an emission image splitter (OptoSplit II; Cairn) and further split into donor and acceptor channels by a second dichroic mirror (FF580-FDi01–25×36; Semrock). The emission was then collected through emission bandpass filters (FF520-Di02–25×36 and FF593-Di03–25×36; Semrock) by a sCMOS camera (ORCA-Flash4.0 V2; Hamamatsu). RFP was illuminated in the same way as YFP except that an excitation bandpass filter (FF01–575/05–25; Semrock) and a dichroic mirror (FF593-Di03–25×36; Semorock) were used. An additional excitation filter (59026x; Chroma) was used in front of the excitation filters. To synchronize image acquisition and the delivery of stimulus solutions, a custom-made MATLAB program controlled both the imaging system (through the API provided by Micro-Manager⁷⁵) and the states of the solenoid valves.

Procedure for measuring the linear response functions

All experiments were performed in a background MeAsp concentration of c₀ = 100 μM. Measurements were made in single cells. First, the FRET level at minimum kinase activity was measured by delivering a saturating stimulus (1 mM MeAsp plus 100 μM serine⁷⁶) for 10 seconds. Immediately afterwards, the FRET level at maximum kinase activity was measured by delivering motility buffer with no attractant (0 μM MeAsp, 0 μM serine) for 5 seconds. When cells are adapted to 100 μM MeAsp, removing all attractant is sufficient to elicit a maximal response^18,44. Donor excitation interval (i.e., measurements of I_DD and I_DA; see SI Section 10) was 0.5 seconds and acceptor excitations (i.e., measurements of I_AA) were done before and after the set of donor excitations. After this, the concentration of MeAsp was returned to the background c₀, and no serine was delivered to the cells for the rest of the experiment. Imaging was then stopped and cells were allowed to adapt to the background for 120 seconds.

After this, a series of stimuli were delivered to the cells in the microfluidic device (see Figure 2E for stimulus protocol). Importantly, the cells were only illuminated and imaged for part of the experiment in order to limit photobleaching. First, cells were imaged for 7.5 seconds in the background concentration c₀. Then, the concentration of MeAsp was shifted up to c₊ = 110 μM for 30 seconds and imaging continued. Donor excitation interval was 0.75 seconds and acceptor excitations were done before and after the set of donor excitations. After this time, imaging was stopped and the MeAsp concentration returned to c₀ for >60 seconds to allow cells to adapt. Then, the same process was repeated, but this time shifting MeAsp concentration down to c₋ = 90 μM. Alternating up and down stimuli were repeated 10 times each.

The change in concentration experienced by cells in this experiment is significantly larger than the changes experienced by cells swimming in our gradient experiments. Ideally, we could deliver the same magnitude of stimulus to cells in both conditions. However, to detect the responses to stimuli as small as the ones experienced in the gradient experiments above the noise, we would need to deliver and average over responses to many more instances of the stimulus. The photon budget is a major constraint when imaging in single cells, making this impossible. We chose the 10% stimuli to balance the need to measure responses above noise, while also keeping the response in the linear regime^44,45 (Supplementary Fig. S5).

FRET levels at minimum and maximum kinase activity were measured again at the end of the experiment. The whole imaging protocol lasted <2200 seconds. In total, cells spent <60 minutes in the device, from loading to the end of imaging. Analyses of these data are described in SI Sections 10–16.

Procedure for measuring the noise statistics

Spontaneous fluctuations in kinase activity were also measured in a background MeAsp concentration of c₀ = 100 μM. Measurements were made in single cells. FRET levels at minimum and maximum kinase activity were measured at the beginning and the end of each experiment, as described above. As above, after these measurements, imaging was then stopped and cells were allowed to adapt to the background for 120 seconds. After this, cells were imaged for about 1200 seconds. Throughout, donor excitations (i.e., measurements of I_DD and I_DA; see SI) were done every 1.0 second, except when it was interrupted by acceptor excitations (i.e., measurements of I_AA; see SI), which were conducted every 100 donor excitations. The whole imaging protocol lasted <1400 seconds. In total, cells spent about < 60 minutes in the device, from loading to the end of imaging. Analyses of these data are described in SI Section 10–15, 17.

Procedure to measure swimming and behavioral parameters

After the second wash, cells were centrifuged again and resuspended in motility buffer containing 100 μM MeAsp. Then, the cell suspension was diluted to an OD600 of 0.00025. The cell suspension was then loaded into μ-Slide Chemotaxis devices (ibidi; Martinsried, Germany), the same type of device used to create static gradients, described below. However, instead of tracking cells in the gradient region, we tracked their swimming in one of the large reservoirs, which are roughly 750 μm deep. 1000-s movies of swimming cells were recorded on a Nikon Ti-E Inverted Microscope using a CFI Plan Fluor 4X objective (NA 0.13). This objective’s depth of field is about ±18 μm, much shorter than the depth of the chamber. Adjusting the focal plane to the middle of the chamber made cells that were swimming near the ceiling or floor of the device, which could experience hydrodynamic interactions that affect their behavior^77,78, not visible in the movie. At the same time, this lower magnification objective allowed us to collect relatively longer swimming trajectories. Movies were captured around 30 minutes after loading cells into the chamber to mimic the gradient experiments below. Images here and below were captured using a sCMOS camera (ORCA-Flash4.0 V2; Hamamatsu). Analyses of these data are described in SI Sections 18–21. Five biological replicates were done for behavioral parameter measurements, and four biological replicates were done for measuring D_r.

Procedure to measure chemotactic drift speeds

Chemotaxis experiments were performed in μ-Slide Chemotaxis devices (ibidi; Martinsried, Germany). These devices generate a linear gradient between two concentration reservoirs that is stable for a long time. After the second wash, the cell suspension was split into two Eppendorf tubes, 0.5 mL each. After one more centrifugation, one tube of cells was resuspended in 1 mL of motility buffer with 100 μM of MeAsp, to be injected into the “low-concentration reservoir”, and the other was resuspended in 1 mL of motility buffer with 2 μM of fluorescein and varying concentrations of attractant, to be injected into the “high-concentration reservoir”. Cells in both tubes were diluted to OD 0.001 for each experiment. Loading cells in both reservoirs ensured that the concentration of cells throughout the experimental device was approximately uniform. This limited the effects of potential biases that could arise from observing a finite field of view.

Using a background concentration of at least 100 μM MeAsp ensured that the cells were in the log-sensing regime¹². The “high” concentrations of MeAsp used were 110.5 μM, 122.1 μM, 135.0 μM, and 149.2 μM. With 1 mm separating the two reservoirs, these concentrations produced linear gradients that approximated shallow exponentials gradients with steepness of roughly: g = {0.1, 0.2, 0.3, 0.4} mm⁻¹. g was calculated from $g=\frac{\Delta \text{log}c}{\Delta x}$, where Δ log c is the difference in log concentrations between the two reservoirs, and Δx is the distance between them. This is exactly the average steepness of log-concentration across with the width of the channel. To see this, the steady state concentration profile is linear, $c(x)=\frac{\Delta c}{\Delta x}\left(x-x_0\right)+c_0$, where Δc is the difference in concentration between the two reservoirs, x₀ is the midpoint between them, and c₀ is the concentration at x = x₀. From this, the gradient of log concentration depends on position x and can be computed from $g(x)=\frac{d\text{log}(c(x))}{dx}=\frac{1}{\frac{1\Delta c}{c_0\Delta x}x+1}\frac{1}{c_0}\frac{\Delta c}{\Delta x}$, where we have defined a reference frame where x₀ = 0. Averaging over the channel by integrating over x from −Δx/2 to Δx/2 and dividing by Δx gives, $\langle g\rangle =\frac{\text{log}\left(1+\frac{1\Delta c}{2c_0}\right)-\text{log}\left(1-\frac{1\Delta c}{2c_0}\right)}{\Delta x}=\frac{\text{log}\left(c_0+\frac{1}{2}\Delta c\right)-\text{log}\left(c_0-\frac{1}{2}\Delta c\right)}{\Delta x}=\frac{\Delta \text{log}c}{\Delta x}=g$. Close to the low-concentration reservoir, g(x) is larger than g, and vice versa near the high-concentration reservoir, but these errors are small and approximately cancel each other out when we average drift speeds of cells across the channel.

To load the device, first the reservoirs were sealed with the manufacturer’s tabs. Cell suspension with 100 μM MeAsp was injected into the channel where the gradient would form. Excess liquid in the inlets was removed. Then one tab from each reservoir was removed, and the gradient channel was sealed with tabs. The left reservoir was then fully unsealed, and the right reservoir was sealed with tabs. 60–65 μL of cell suspension with 100 μM MeAsp was injected into the left reservoir, and then both inlets of that reservoir were sealed with tape or tabs. Care was taken to make sure there were no bubbles in reservoir at the inlets. Then, the right reservoir was unsealed, and 60–65 μL of cell suspension with the higher concentration of MeAsp was injected. A timer was then immediately started. The right reservoir was then sealed.

Cells were imaged by phase contrast with a CFI Plan Fluor 10X objective (NA 0.30). The depth of the gradient region of the device is 70 μm, and the depth of field of the objective is about ±4 μm. Focusing on the middle of the chamber with this objective filtered out cells that could be interacting with the ceiling or floor surfaces. Images of fluorescein were taken every 5 minutes using a CFI Plan Fluor 4X objective (NA 0.13) through a YFP filter cube (Chroma 49003), illuminated by a LED (SOLA SE, Lumencor) with an exposure time of 100 ms. Since the diffusivity of fluorescein is similar to (slightly lower than) that of MeAsp (MW of fluorescein is 376 kDa; MW of MeAsp is 147 kDa; Sigma Aldrich), we used fluorescein as an indication of when the attractant gradient was stable and linear in the observation region between the two reservoirs, as has been done before^55,79. Once the fluorescein profile was stable for several time points (typically around 50–60 minutes after loading), a 1000-second phase contrast movie was recorded at 20 FPS using the 10X phase contrast objective. Before the recording, the transmitted light illumination was adjusted to minimize the number of saturated pixels. After the recording, an additional image of the fluorescein profile was recorded, and the cells were observed to check that they were still swimming normally. Analyses of these data are described below. At least five biological replicates were performed for each gradient steepness.

Data availability:

Source data for the main text figures are provided online with the manuscript. Source data for the Supplementary Figures are contained in a Supplementary Data file.