Metabolic signatures of regulation by phosphorylation and acetylation

Summary

Acetylation and phosphorylation are highly conserved posttranslational modifications (PTMs) that regulate cellular metabolism, yet how metabolic control is shared between these PTMs is unknown. Here we analyze transcriptome, proteome, acetylome, and phosphoproteome datasets in E. coli, S. cerevisiae, and mammalian cells across diverse conditions using CAROM, a new approach that uses genome-scale metabolic networks and machine learning to classify targets of PTMs. We built a single machine learning model that predicted targets of each PTM in a condition across all three organisms based on reaction attributes (AUC>0.8). Our model predicted phosphorylated enzymes during a mammalian cell-cycle, which we validate using phosphoproteomics. Interpreting the machine learning model using game theory uncovered enzyme properties including network connectivity, essentiality, and condition-specific factors such as maximum flux that differentiate targets of phosphorylation from acetylation. The conserved and predictable partitioning of metabolic regulation identified here between these PTMs may enable rational rewiring of regulatory circuits.

Graphical abstract

Highlights

• •CAROM predicts PTM targets in a condition based on enzyme & reaction properties
• •Growth-limiting enzymes are preferential targets of acetylation
• •Isozymes and futile-cycles are associated with phosphorylation
• •CAROM reveals a ‘division of labor’ and a unique regulatory role for each PTM

Machine learning; Metabolic flux analysis; Metabolic regulation; Omics; Systems biology

Introduction

A key challenge in systems biology is to predict how various regulatory processes orchestrate cellular response to perturbations. Numerous mechanisms regulate metabolic adjustment to new environments. Nevertheless, it is unclear why or when some enzymes are regulated by acetylation while others are regulated through phosphorylation in a given condition (Chubukov et al., 2014; Heinemann and Sauer, 2010). Several advantages of regulation by PTMs have been proposed over the past five decades (Fell and Cornish-Bowden, 1997; Holzer and Duntze, 1971; Stadtman and Chock, 1978). These include low energy requirements, rapid response, and signal amplification. Yet these characteristics do not differentiate between PTMs such as acetylation and phosphorylation.

The staggering complexity of each regulatory process has limited the comparative analysis of metabolic regulation at a systems level (Chubukov et al., 2014). Existing studies have focused on a single regulatory process, usually transcriptional regulation (Brunk et al., 2018; Chandrasekaran and Price, 2010; Covert et al., 2004; Daran-Lapujade et al., 2007; Heinemann and Sauer, 2010; Lee et al., 2008; Oliveira et al., 2012; Shen et al., 2019a; Zaslaver et al., 2004; Zhao et al., 2010). Such studies have revealed reaction reversibility and metabolic network structure to be predictive of regulation (Almaas et al., 2004; Hackett et al., 2016; Stadtman, 1970; Stelling et al., 2002, 2004; Zaslaver et al., 2004). Hubs in the metabolic network and essential genes are frequent targets of transcriptional regulation (Orth et al., 2010). Yet these studies do not shed light on the differences between each regulatory process, especially PTMs. In sum, although some general network principles of regulation are known, how it is partitioned among various regulatory mechanisms is unclear.

Proteomics surveys have found PTM sites on almost all metabolic enzymes (Sharma et al., 2014; Zhao et al., 2010). But it is unclear if all the PTM sites are ‘functional’, i.e., they have an impact on metabolism and are not an artifact of biological and technical noise (Beltrao et al., 2013). PTMs can regulate metabolism in multifarious ways. Prior studies on the role of PTMs have focused on in vitro enzyme activity and do not consider the impact of PTMs on the operation of the metabolic network as a whole. Apart from impacting enzyme activity, PTMs can also impact protein-protein interactions (PPIs), protein stability, or localization. PTMs like phosphorylation are enriched in proteins that occupy central positions in the PPI network in various organisms (Duan and Walther, 2015). Hence the impact of PTMs could be more easily uncovered using systems level phenotypes like metabolic fluxes rather than enzyme activity assays. Consistent with this idea, Oliveira et al. found that fluxes are better representative of functional phosphorylation regulation than in vitro enzyme activities (Oliveira et al., 2012). There are over 200 different PTMs and it is impossible to determine their distinct roles in metabolic regulation individually using experimental methods.

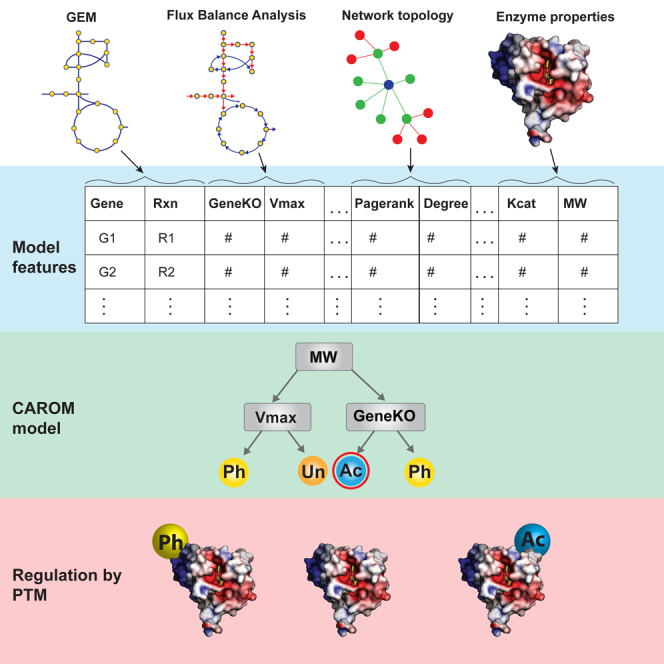
We hence developed a data-driven approach, called Comparative Analysis of Regulators of Metabolism (CAROM), to identify the unique regulatory role of each PTM. CAROM achieves this by comparing various properties of the metabolic enzyme targets of PTMs, including essentiality, flux, molecular weight, and topology. It identifies properties that are more highly enriched among targets of each regulatory process than expected by chance. We selected these properties as they each reflect on the potential functional role of PTMs based on the placement of their targets within the metabolic network, extent of impact on systems level properties like flux and growth rate, and fundamental biochemical properties of enzymes like catalytic activity and molecular weight. Furthermore, we investigated whether characteristics of PTM targets are conserved across different species. The distinct roles of PTMs may become apparent when inspected from evolutionary and systems biology viewpoints.

Using CAROM, we found features that were significantly associated with each PTM. Nevertheless, no single feature on its own is completely predictive of PTM targets in a condition. CAROM hence uses machine learning to uncover how features in combination influence regulation. Here we use the term ‘regulation’ broadly to account for the numerous ways in which PTMs can impact metabolism in vivo rather than focusing on enzyme activity alone.

We used CAROM to understand PTM dynamics during well-characterized fundamental processes in microbes and mammalian cells, namely the cell cycle, transition to stationary phase, and response to nutrient alterations. Although we focus on acetylation and phosphorylation here as they are the most well-studied PTMs with available omics datasets, our approach can be applied to any regulatory process.

The manuscript is organized as follows: we first analyze various multi-omics datasets in E. coli, yeast, and mammalian cells and reveal properties that are either enzyme-specific (molecular weight) or context-specific (flux) that correlate with regulation by each PTM. These common observations across various organisms allowed us to build a multi-organism machine learning model that explains regulation in each condition using these features. The feature importance from CAROM is highly consistent across numerous studies in all organisms studied here. These results suggest that this approach is applicable to a wide range of model systems. CAROM can shed light on how metabolic changes impact PTMs. Overall, CAROM provides evidence for a context-specific, enzyme property-based regulation by PTMs.

Results

Comparing regulation using CAROM

The CAROM approach takes as input a list of proteins that are the targets of one or more PTMs. Here we define PTM ‘targets’ as those proteins whose PTM levels change significantly in a condition compared to a reference condition. We assumed that PTM targets that are dynamic and conditionally regulated are likely to be functional (Beltrao et al., 2013).

CAROM analyzes the properties of the targets of PTMs in the context of a genome-scale metabolic network model. CAROM compares the properties of the targets statistically using Analysis of Variance (ANOVA). It also builds a machine learning model capable of classifying regulation using boosted decision trees. Overall, CAROM compares the following 13 properties:

• •Impact of gene knockout on biomass production, ATP synthesis, and viability across different conditions obtained from experimental knockout screens or computationally using Flux Balance Analysis (FBA)
• •Flux through the network measured through Flux Variability Analysis, Parsimonious flux balance analysis (PFBA), and reaction reversibility
• •Enzyme molecular weight and catalytic activity
• •Topological properties, including the total pathways each reaction is involved in, its degree, betweenness, closeness, and PageRank

These properties were chosen based on the hypothesis that target preferences of PTMs can be inferred from biochemical, topological, and flux properties of the targets. This hypothesis stems from prior experimental and computational flux studies that have found an association between regulation by phosphorylation and changes in reaction fluxes (Oliveira et al., 2012). Analysis of PPI networks has revealed that phosphorylation occupies central nodes in the PPI network (Duan and Walther, 2015). However, these studies do not predict or differentiate metabolic regulation by PTMs. Here we first demonstrate a quantitative link between these properties and PTM regulation, and then use these properties to identify condition-specific PTM regulation sites in the metabolic network.

These properties were also chosen based on ease of calculation using FBA. FBA and its related methods have been shown to be predictive of metabolic behavior in a wide range of organisms, and discrepancies with experiments can point to missing biochemical knowledge (Lewis et al., 2012; O'Brien et al., 2015). By identifying potential targets of PTMs, our approach can help ultimately enhance the predictive power of FBA and uncover principles of metabolic regulation (Chung et al., 2021). Overall, CAROM can help interpret the properties of PTM targets in a condition and forecast targets of PTMs in novel conditions using these features above. The CAROM source code is available from the Synapse bioinformatics repository https://www.synapse.org/CAROM.

Shared features of enzymes targets of acetylation and phosphorylation in yeast

We first analyzed metabolic regulation during a well-characterized process in yeast, namely, transition to stationary phase. To differentiate PTM targets from those regulated at the transcriptional and posttranscriptional level, we also analyzed differentially expressed genes and proteins from transcriptomics and proteomics data. We obtained RNA sequencing, time course proteomics, acetylomics, and phospho-proteomics data from the literature (Murphy et al., 2015; Treu et al., 2014; Weinert et al., 2014). Targets for each process (transcriptomic, proteomic, and PTMs) were determined based on differential levels between stationary and exponential phase (STAR Methods).

Proteins and transcripts were mapped to corresponding metabolic reactions using the gene-protein-reaction annotations in the genome-scale metabolic network model of yeast (Aung et al., 2013). There was significant overlap among reactions that were differentially expressed in both the transcriptome and proteome, and transcriptome and acetylome (hypergeometric p value = 5 × 10⁻²⁵ and 1 × 10⁻¹⁵, respectively, Table S1A). In contrast, there was little overlap between targets of phosphorylation (i.e., differential phosphoproteins) with other mechanisms (p value > 0.1; Table S1A). Although prior studies found higher overlap between targets of PTMs (Beltrao et al., 2012; Oliveira and Sauer, 2012), they used all possible sites that can be acetylated or phosphorylated. However, only a fraction of PTM sites is likely to be active and functional in a single condition. Overall, each regulatory mechanism had a distinct set of targets (Figure 1A). The targets of each regulatory mechanism (i.e., differentially expressed transcripts, proteins, or PTMs between stationary and exponential phase) were then used as input to CAROM.

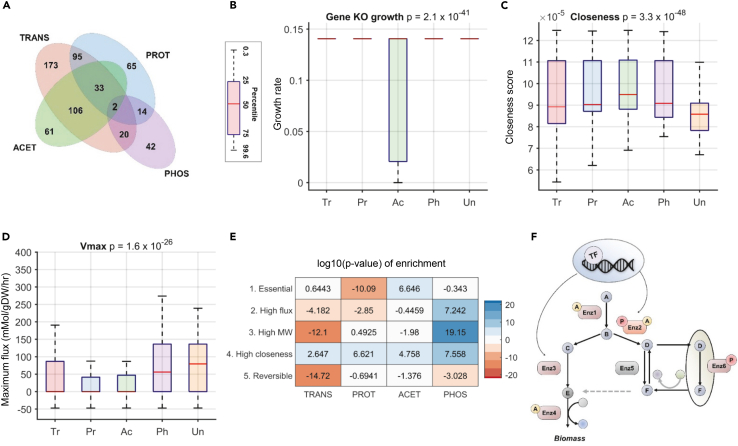
Figure 1.

Comparison of the properties of PTM targets in yeast

(A) The ANOVA p value comparing the differences in means is shown in the title of the boxplots (Abbreviation: Targets of transcription (Tr), posttranscription (Pr), acetylation (Ac), phosphorylation (Ph), and unknown regulation (Un)). (A) The Venn diagram shows the extent of overlap between targets (i.e., differentially expressed genes/proteins) of each process in the stationary phase. Only 2 genes were found to be targeted by all four mechanisms. Targets of phosphorylation did not show any significant overlap with other mechanisms, whereas transcriptome and proteome showed the highest overlap (Table S1A).

(B) Enzymes that impact growth when knocked out are highly likely to be acetylated. The plot shows the growth rates predicted by FBA knockouts of the targets.

(C) Enzymes with poor connectivity, as measured through the network connectivity metric - closeness, are more likely to be underrepresented among the targets of all 4 mechanisms.

(D) Enzymes catalyzing reactions with high maximum flux are likely to be either targeted by phosphorylation or to be unregulated/unknown regulation.

(E) The heatmap shows the statistical enrichment (positive sign) and depletion (negative sign) of the targets of each process among reactions that are - (1) essential, (2) have high maximum flux (Vmax > 75^th percentile), (3) catalyzed by enzymes with high molecular weight (MW > 75^th percentile), (4) highly connected (Closeness >75^th percentile), and (5) reversible.

(F) A schematic pathway summarizing the division of labor in metabolic regulation. Essential reactions (Enz1 and Enz4) are preferentially acetylated; reactions in futile cycles and in different compartments (Enz6) are phosphorylated, and reactions with high connectivity are targeted by multiple mechanisms (Enz2). Reversible reactions are predominantly unregulated or regulated by unknown mechanisms (Enz5).

We used CAROM to find common features of enzyme targets of each PTM. We first analyzed the regulation of enzymes that are essential for growth in minimal media. Essential enzymes in the yeast metabolic model were determined using FBA (Growth <0.01 units, STAR Methods). Surprisingly, this set of enzymes was highly enriched among targets of acetylation but not for other processes (ANOVA p value < 10⁻¹⁶; Figure 1B; Table S1B). Because regulation can be optimized for fitness across multiple conditions (Schuetz et al., 2012), we identified enzymes that impact growth in 87 different nutrient conditions comprising various carbon and nitrogen sources using FBA. This set of essential enzymes was once again enriched for acetylation targets relative to other mechanisms (ANOVA p value < 10⁻¹⁶; Figure S1). This trend was observed using an experimentally derived list of essential genes as well (hypergeometric p value = 2 × 10⁻⁷ for acetylation). Thus, essential enzymes are likely to be constitutively expressed and their activity modulated through acetylation. This may explain why transcriptional regulation has minimal impact on fluxes in central metabolism, which contain several growth-limiting enzymes (Chubukov et al., 2014; Daran-Lapujade et al., 2007).

We next determined the impact of reaction position in the network on its regulation. We counted the number of pathways each reaction is involved in, along with other topological metrics, such as the closeness, degree, and PageRank. All these metrics are based on graph theory and calculate the importance of a given node in the network. For example, the degree metric quantifies the number of links to each node (i.e., reaction). Betweenness quantifies the number of times a node lies on the shortest path between other nodes. Closeness assigns a score based on the shortest path to all other nodes, whereas PageRank also takes into account the node's connections' connections (Freeman, 1978).

We found that the regulation of enzymes differed significantly based on network topology (Figures 1C and S2). First, reactions with low connectivity, measured through any of the topological metrics, were highly likely to be under-represented among the targets of all these mechanisms. In contrast, highly connected enzymes linking multiple pathways were more likely to be targets of either PTMs. However, connectivity metrics were unable to differentiate between the two PTMs. Interestingly, reactions that were targets of both PTMs had the highest connectivity (Figures S2 and S3). Several key hubs, such as hexokinase and phosphofructokinase are targets of both PTMs (Table S1C).

We next assessed how PTM targets were distributed based on the magnitude and direction of flux through the corresponding reactions. We inferred the full range of fluxes possible through each reaction using flux variability analysis (FVA) (Mahadevan and Schilling, 2003). Because yeast cells may not optimize their metabolism for biomass synthesis during transition to stationary phase, we also performed FVA without assuming biomass maximization. We found that reversible reactions were underrepresented among the targets of all mechanisms (i.e., PTMs, transcriptional, and posttranscriptional regulations) (Figure S4). A recent study found the same trend for allosteric regulation as well (Hackett et al., 2016). However, reversibility alone did not differentiate between regulatory mechanisms.

Interestingly, reactions that have high predicted maximum flux (Vmax) from FVA, such as ATP synthase and phosphofructokinase, were predominantly enriched among the targets of phosphorylation (Figure 1D; ANOVA p value < 10⁻¹⁶). Using data from experimentally constrained fluxes from the Hackett et al study (Hackett et al., 2016) revealed similar patterns of regulation (Figure S5). This set of phosphorylated reactions comprise several kinase-phosphatase pairs, enzymes that are part of loops that consume energy (“futile cycles”), or reactions that have isozymes in compartments such as vacuoles or nucleus (Table S1D). Thus, we speculate that phosphorylation selectively toggles reactions to avoid futile cycling between antagonizing reactions or those operating in different compartments. In a futile cycle, there is interconversion of the same substrates and products, but these interconversions consume energy (Qian and Beard, 2006). Hence there is an upper limit for the fluxes in these cycles because of energetic constraints. In contrast, there can be erroneous cycles in the metabolic models that involve interconversion of metabolites without consuming energy (Fritzemeier et al., 2017). These reactions can attain the maximum possible upper bound flux values in FVA simulations. To differentiate these two types of cycles, the first one being biological and the second an artifact of the metabolic model, we used a threshold on the Vmax value to separate out erroneous cycles from futile cycles (Table S1I). Analysis using a different approach for inferring fluxes – PFBA, did not reveal any significant difference between the PTMs as PFBA eliminates futile cycles and redundancy by minimizing total flux through the network (Lewis et al., 2010) (Figure S5).

Finally, we compared regulation based on fundamental enzyme properties: catalytic activity, and molecular weight. Although catalytic activity was similar across the targets of all mechanisms, targets of phosphorylation had the highest molecular weight (p value < 10⁻¹⁶) (Figure S6). There is no correlation between molecular weight and maximum flux (Pearson's correlation R = 0.02), suggesting that both maximum flux and molecular weight are likely to be independent predictors of regulation by phosphorylation.

In sum, our results suggest a distinct target preference and a unique regulatory niche for each PTM (Figures 1E and 1F). Of note, our classification of targets of PTMs based on differential levels is condition specific. Hence to check if this pattern of target preferences of PTMs is observed in other conditions, we analyzed data from nitrogen starvation response and cell cycle in yeast, where both phospho-proteomics and transcriptomics data are available (Kelliher et al., 2016; Oliveira et al., 2015b; Oliveira et al., 2015a; Touati et al., 2018). A similar trend was observed in this condition (Figure S6), with phosphorylation targets enriched for isozymes and enzymes that have high Vmax (futile cycles). Overall, these results are robust to the thresholds used for finding PTM targets, using data from different sources, and other modeling parameters (Tables S1E–S1I).

Context specific metabolic regulation by PTMs in E. coli

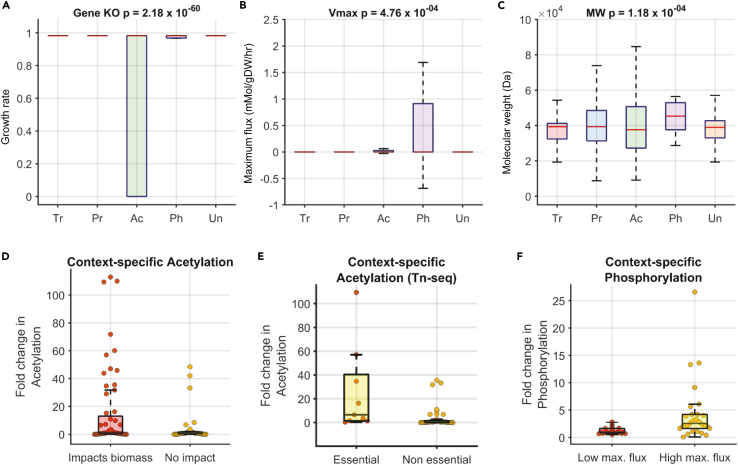
Because many mechanisms of metabolic regulation are evolutionarily conserved (Chubukov et al., 2014), we next analyzed multi-omic data from E. coli cells during stationary phase (Houser et al., 2015; Soares et al., 2013; Weinert et al., 2013). By analyzing transcriptomics, proteomics, acetylomics, and phosphoproteomics data using the E. coli metabolic network model, we uncovered that the pattern of regulation observed in yeast was also observed in E. coli (Figures 2A–2C and S7A). Essential reactions were enriched among targets of acetylation, and reactions with high maximum flux or large enzyme molecular weight were enriched among targets of phosphorylation. However, in contrast to yeast, phosphorylation impacted very few metabolic genes in E. coli, and may play a relatively minor role in this specific context. Phosphorylation had 20-fold fewer targets compared to other mechanisms, and its targets overlapped significantly with other processes (Tables S1J and S1K). Interestingly, the number of reactions with high maximum flux was considerably lower in E. coli compared to yeast (1,282 in Yeast and 100 in E. coli), which correlates with the difference in phosphorylation between the species (Figure S7).

Figure 2.

Comparison of the properties of PTM targets in E. coli

(Abbreviation: Enzyme targets of transcription (Tr), posttranscription (Pr), acetylation (Ac), phosphorylation (Ph), unknown regulation (Un))

(A) Enzymes that impact growth when knocked out are highly likely to be acetylated. The ANOVA p value comparing the differences in means is shown in the title of the boxplot.

(B) Enzymes catalyzing reactions with high maximum flux are likely to be targets of phosphorylation. The ANOVA p value comparing the differences in means is shown in the title of the boxplot.

(C) Enzymes with high molecular weight are likely to be targets of phosphorylation. Similar to yeast, reaction essentiality (A), maximum flux (B), and molecular weight (C) are predictive of regulation by acetylation and phosphorylation (Vmax, MW) respectively during transition to stationary phase. Analysis of condition-specific PTM targets across 11 growth conditions.

(D–F) Proteins that were found to be conditionally essential (growth < wild type glucose) based on FBA (D) or Transposon sequencing (Z score < −2) (E) were more likely to be acetylated (p value = 0.02 & 0.0011 for FBA and Tn-seq respectively). (F) Enzymes that are predicted to have high maximal flux (Vmax > 90^th percentile) in a condition were likely to be phosphorylated compared to those with low maximal flux (p value = 0.008).

Acetylation in E. coli can also occur nonenzymatically through the transfer of acetyl group from the metabolite acetyl phosphate to an accessible lysine. Only a small fraction of these acetylation events is known to directly alter enzyme activity and their systems level function is unclear. To account for this issue of functionality, we next analyzed acetylation sites that are targets of the deacetylase enzyme cobB, the only known deacetylase in E. coli (Weinert et al., 2017). We hypothesized that sites targeted by cobB have a higher chance of being functional. We used acetylomics data from Weinert study that measured the impact of cobB deletion on proteome wide acetylation in both exponential and stationary phase cultures (Weinert et al., 2017). Sites that increase by at least 2-fold in acetylation stoichiometry were considered to be targets of cobB. We find a similar enrichment of essential genes among the subset of protein targets of cobB as compared to the targets derived from the entire acetylome data (Figure S7B).

Regulation by acetylation and phosphorylation are strongly associated with factors such as reaction flux and essentiality that change significantly between conditions. To further understand the condition-specific regulation of enzymes by PTMs, we used data from the Schmidt et al study that measured PTM levels for a small set of proteins in E. coli (Schmidt et al., 2016). From this dataset we used 11 growth conditions in distinct nutrient sources that could be modeled using FBA. There were 10 proteins that were both part of the metabolic model and had acetylation data. Similarly, there were 5 proteins in the metabolic model with phosphorylation data in this study. Despite the small sample size, we found that enzymes that impact biomass when deleted using FBA were more likely to be targets of acetylation in that condition (p value = 0.02; Figure 2D). This trend was also observed using experimental gene essentiality data from transposon mutagenesis screens (TN-seq) across these growth conditions (Figure 2E). For example, isocitrate lyase (aceA) shows a consistent increase in acetylation as it becomes more essential (Figures S8 and S9). Similarly, we observed a significant association between phosphorylation levels and the maximal flux through a reaction in each condition (Figure 2F). For example, phosphorylation of isocitrate dehydrogenase (icd) increased up to 20-fold in conditions with the highest maximal flux (Figure S10).

These results suggest that the metabolic features like essentiality and flux are predictive of both the regulation of different enzymes in a condition and for the same enzyme between conditions. Nevertheless, even though the maximal reaction flux and essentiality were associated with regulation by PTMs for many proteins in both organisms, there were exceptions that did not show this trend, suggesting that various factors identified earlier likely influence regulation by PTMs in a combinatorial fashion.

Classifying metabolic regulation by PTMs using CAROM-ML

Although our statistical analysis has revealed various metabolic features of PTM targets, each feature on its own is a weak predictor. We next sought to uncover how these features in combination determine the regulation of each enzyme. We used machine learning (ML) to build a CAROM-ML model that accounts for all these features and quantifies their interrelationship in influencing regulation by PTMs. Although metabolic network models are more mechanistic, ML methods outperform metabolic models in prediction tasks (Zampieri et al., 2019). Integrating metabolic network outputs with ML can enable mechanistic interpretation without compromising predictive accuracy (Kim et al., 2020; Yang et al., 2019). We used the decision trees ML algorithm in CAROM-ML because of its ease of interpretation and created an ensemble of decision trees using the XGBoost framework (Chen and Guestrin, 2016). Traditional machine learning studies using transcriptomics or genomics data have thousands of features (>20,000 genes) and hence require a large number of samples (>1,000) (James et al., 2013). The use of fewer samples than features can lead to overfitting. In contrast, by rationally selecting a small set of 13 features, here we have a lot more observations (>1,000) than features. Hence this combination of mechanistic feature prioritization and use of boosted decision trees allows us to build a more robust model and avoid overfitting.

We reanalyzed the E. coli and yeast genome-wide omics datasets using CAROM-ML. We further augmented this with phosphorylation and acetylation datasets from HeLa cells (the most commonly used model human cell line) to assess if a similar pattern of PTM regulation exists in mammalian cells. Time course acetylation data was taken from the Kori et al. study (Kori et al., 2017), which identified 702 proteins whose acetylation levels changed significantly over time (Mann-Kendall test p value < 0.05). Similarly, time course phosphorylation data from HeLa cells undergoing mitosis were obtained from Olsen et al. (Olsen et al., 2010).

We created a single CAROM-ML model using data from all organisms with the goal of identifying conserved patterns among PTM targets. A ternary classification algorithm was built to identify proteins that are targets of acetylation, phosphorylation, or were not targeted by these PTMs. The input to CAROM-ML was the list of 13 features (STAR Methods; Figures 3A and 3B). The model was trained using known examples of proteins that are targets of the two PTMs. The trained CAROM-ML model was then used to predict the regulators of new proteins based on their feature values.

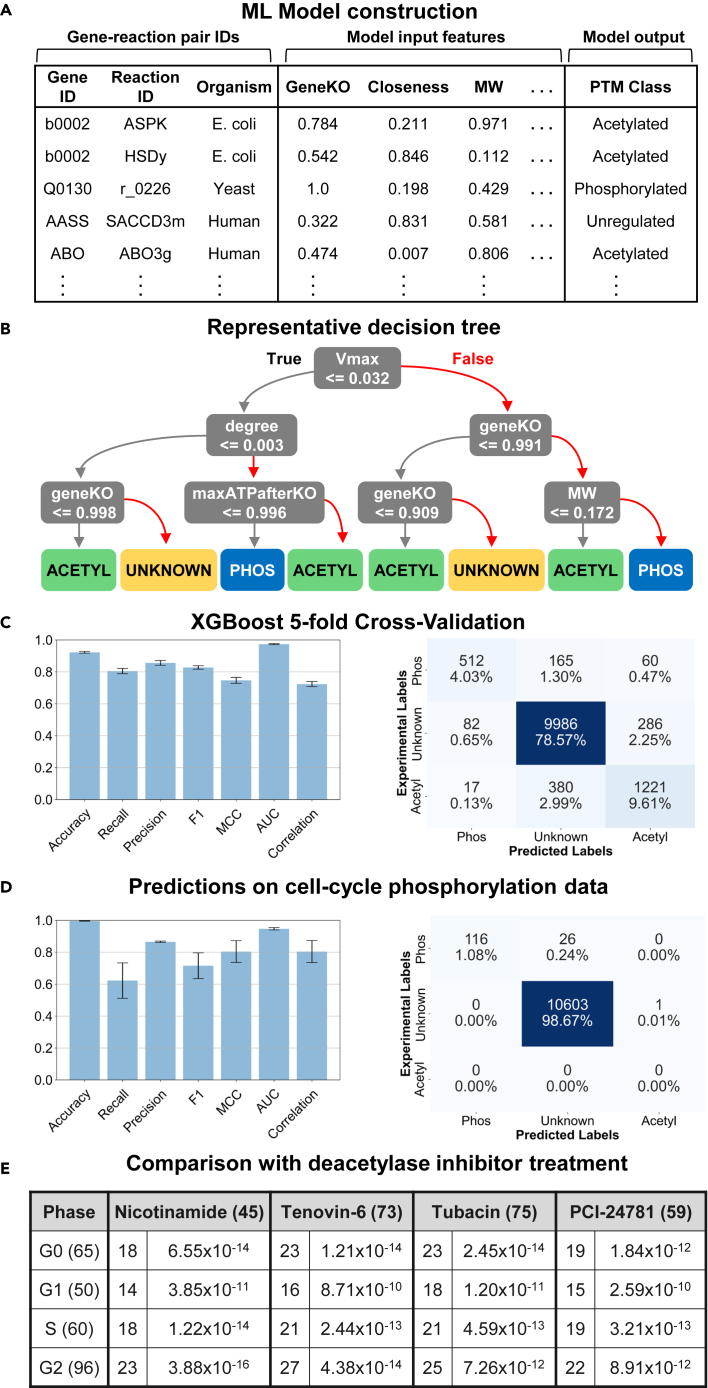
Figure 3.

Construction and validation of the CAROM-ML model

(A) Table of inputs for CAROM-ML. The input features comprise 13 gene, reaction, and enzyme properties. The target column includes the posttranslational modification class. Each gene-reaction pair is marked as either phosphorylated, acetylated, or unknown.

(B) A single decision tree model was built by training on the observations from all organisms, while only using the top 50% most important features as identified in the SHAP analysis. The complexity of the tree was constrained by limiting the tree depth to enable ease of interpretation and visualization. The XGBoost model is made of an ensemble of such decision trees.

(C) The results from the CAROM-ML model from 5-fold cross validation are shown in the bar graph (left) with the 95% confidence intervals represented by the error bars. The cross-validation results are also shown in the confusion matrix.

(D) Comparison of model predictions for the G1, S, and G2 phases of the cell cycle with experimental phospho-proteomics data for those phases. Confusion matrix shows predictions from the main CAROM-ML model, whereas the bar graph shows the standard deviation for five models trained with different random seeds.

(E) Comparison of cell cycle acetylation predictions with experimental acetylomics data from HeLa cells treated with pan-deacetylase inhibitors. The number of unique acetylated genes for each group are displayed in parentheses. Within the table, the number of overlapping genes between each phase and drug is shown, along with the p value of the hypergeometric test.

CAROM-ML showed very high accuracy in predicting PTM target proteins in all three systems based on five-fold cross-validation, wherein a portion of the dataset (20%) is hidden from the model. Specifically, the model was trained using feature data for 80% of the proteins along with class labels (i.e., acetylation, phosphorylation, or none of these), and predicted class labels for the hidden 20% of the proteins based on their features. We used a range of metrics to quantify accuracy including the Pearson's Correlation Coefficient (R), Matthews Correlation Coefficient (MCC), the F1 score, precision, and recall. The ML models performed accurately based on all these metrics and significantly better than random shuffling of the data (Figures 3C and S26).

To test the generalizability of this approach in novel conditions, we used the model to predict phosphorylation during a mammalian cell cycle. We used time course phosphoproteome data for the first cell cycle from a murine lymphocyte cell line in response to a cytokine activation (STAR Methods). We focused on the cell cycle as it is a fundamental process and is known to involve coordination of kinases and phosphorylase cascades (Fisher et al., 2012). Importantly, this model system was previously used by Lee et al. to measure metabolomics changes during the cell cycle (Lee et al., 2017). Phospho-proteomes were obtained at the same time points as the metabolomics data from the Lee et al. study. We used the extracellular and intracellular metabolomics data from the Lee et al. study to build metabolic models for each phase of the cell cycle. We used the DFA approach, a variation of dynamic FBA, to fit the rate of change of metabolites in FBA to experimental measurements from time course metabolomics (Campit and Chandrasekaran, 2020; Chandrasekaran et al., 2017). We used this approach to create four different models corresponding to different phases of the cell cycle (G0/G1, G1, G1/S, and G2/M) (Figure 4A, STAR Methods). The resulting models correctly recapitulated known metabolic differences between the cell cycle phases, including peak methionine consumption during G1/S phase, and nucleotide metabolism during G0, confirming the accuracy of the flux predictions (Table S1AC). Our flux predictions are also consistent with phase-specific changes in lysine metabolism (Jang et al., 2020), fatty acid elongation (Gimple et al., 2019), and heme biosynthesis (Pran Babu et al., 2020) during the cell cycle observed in other systems.

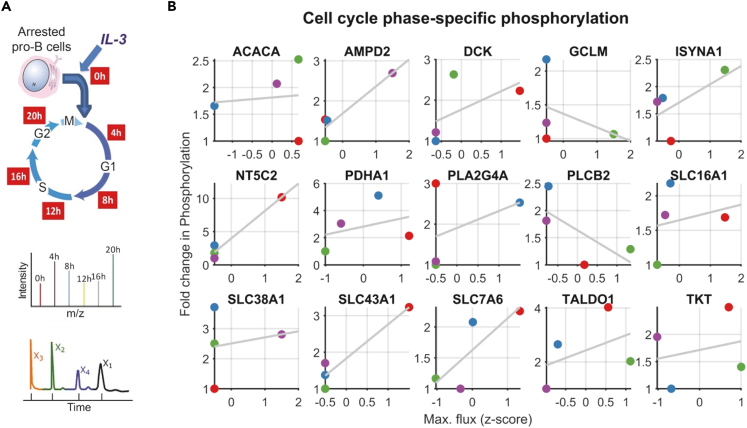
Figure 4.

Enzyme phosphorylation across the cell cycle correlates with maximum flux

(A) Pro-B cells were synchronized by growing in media without IL-3 for 36 h and then released from G0 by regrowingthem in the presence of IL-3. Phosphoproteomics data were collected at each phase. In addition, metabolomics data from the same system from Lee et al. was used to build metabolic models for each phase.

(B) All proteins that show at least two-fold change in phosphorylation are shown. For those proteins associated with multiple reactions, the reaction with the highest flux change is shown. Markers are colored by cell cycle phase (red G0/G1, blue G1, green G1/S, and violet G2/M). Among the proteins that showed at least 5-fold difference in phosphorylation between phases, the average correlation was 0.56 between the normalized maximum flux and fold change in phosphorylation. The correlation increases to 0.9 for proteins that show a tenfold difference and is 0.17 for proteins that show 2-fold difference.

The feature data (i.e., fluxes, topology) from the phase-specific metabolic models were used as input for the CAROM-ML model to predict reaction targets of phosphorylation. The G0/G1 phase data was used for additional training of the model to learn cell-type specific phosphorylation patterns, and the G1, G2/M, and G1/S phase were used for testing the CAROM-ML model. CAROM-ML achieved high MCC, AUC, and Pearson correlation (AUC > 0.8, MCC > 0.8, R > 0.6) in all conditions tested, and the accuracy of the model is significantly better than random shuffling of the data (MCC & R ∼ 0, p value comparing CAROM-ML with random = 7.59 × 10⁻⁶⁷). 116 out of 142 predictions on phase-specific phosphorylated enzymes/reactions were also observed experimentally (Table S1L). These results are robust to noise in metabolomics data based on parameter sensitivity analysis (Figure S24).

Similar to E. coli and yeast, there was a significant correlation between the maximum flux of a reaction in a condition and the change in phosphorylation of the corresponding enzyme during the mammalian cell cycle (Figure 4B). For example, AMP deaminase (AMPD2) shows a threefold increase in phosphorylation in G2/M phase wherein it also shows a corresponding increase in maximal flux. These results together suggest that knowledge of fluxes can be predictive of regulation by phosphorylation in mammalian systems as well.

CAROM-ML also predicted several reactions to be targets of acetylation in various phases (Table S1M). The predicted list includes enzymes such as ATP-citrate lyase whose activity is known to be regulated by acetylation during the cell cycle (Icard et al., 2020; Lin et al., 2013). As we lack proteome-wide time course acetylation data to systematically confirm these predictions, we compared predictions with data from cells treated with deacetylase inhibitors (Schölz et al., 2015). Deacetylase inhibitors prevent the removal of acetylation marks. Hence new acetylation marks progressively accumulate over time resulting in cell death. We hypothesized that acetylation sites predicted by the CAROM-ML model during the cell cycle will be enriched among the proteins with increased acetylation after deacetylase inhibitor treatment. Indeed, there was a significant overlap between CAROM-ML predicted acetylated enzymes and those found to increase significantly (>1.5-fold) after treatment with four different pan-deacetylase inhibitors – nicotinamide, tenovin-6, tubacin, and PCI24781. Interestingly, even though the experimental proteomics data was not phase specific, we observed the highest overlap for nicotinamide targets with CAROM-ML predictions in the G2/M phase of the cell cycle (hypergeometric p value = 3 × 10⁻¹⁶), which also had the highest number of acetylated reactions (Figure 3E; Table S1N). This overlap suggests that growth inhibition likely occurs in the G2/M phase, which is consistent with the experimental data from nicotinamide treatment in various mammalian cell types that have observed growth arrest at G2 (Hassan et al., 2020; Kim et al., 2017; Saldeen et al., 2003).

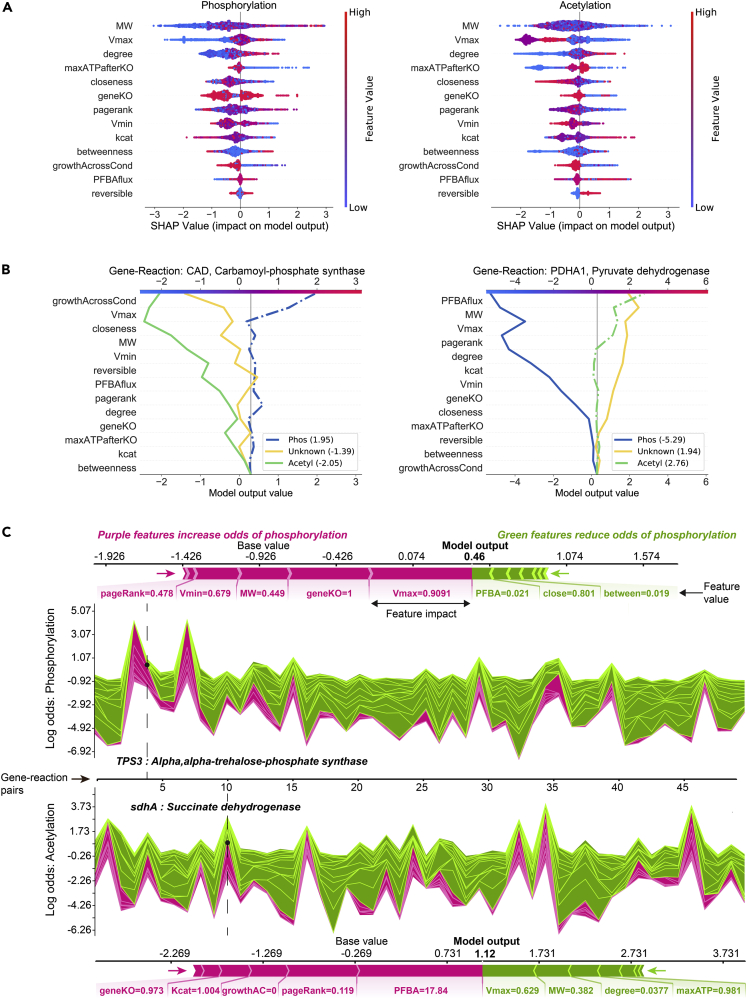
Interpreting the machine learning model using Shapley analysis

To understand how CAROM-ML predicted each PTM target, we used a game-theoretic framework called Shapley analysis to quantify the contribution of each feature to the model accuracy using the SHAP (SHapley Additive exPlanation) Python package (Lundberg et al., 2018, 2020). The Shapley ‘feature importance’ values are computed by sequentially adding one feature at a time and measuring the feature's contribution to the model output. To account for the order in which the features are added to the decision trees, this process is repeated for all possible orderings. The Shapley value represents the average impact for each feature across all orders (STAR Methods).

All 13 features contributed to the CAROM-ML predictions, albeit to various extents. Molecular weight and maximum flux had two of the highest importance scores, and higher values favored phosphorylation, which is consistent with the high enrichment we observed using our statistical analysis (Figure 5A).

Figure 5.

Interpretation of the CAROM-ML model using Shapley analysis

(A) SHAP summary plot for the phosphorylation class (left) and acetylation class (right). The summary plot shows how a feature's effect on the output changes with its own value. For each feature, high values are shown in red and low values in blue. For example, it appears that Vmax is positively and negatively correlated with the log odds of phosphorylation and acetylation, respectively. Features are ordered on the y axis by their average SHAP importance value across the three classes.

(B) SHAP decision plots for a phosphorylated enzyme (left) and acetylated enzyme (right) show how the model's prediction was made for a single observation. Each line represents the log odds for a single class. The features are on the y axis and are sorted by the average SHAP value for that specific observation. The lines intercept the top x axis at their final log odds value. The class with the maximum log odds value is used as the model's output.

(C) SHAP force plots show the features which significantly pushed the model output from its expected value to its final prediction. Features that push the prediction higher for the respective class are shown in purple and features that pushed it lower are shown in green. Single force plots for a phosphorylated reaction (top; TPS3) and an acetylated reaction (bottom; sdhA) are shown. The collective force plots are made up of many single force plots rotated 90° and stacked together horizontally and are shown for phosphorylation (upper middle) and acetylation (bottom middle) for the same 50 random observations. The model output, f(x), is on the y axis and observations on the x axis. The dashed lines show where the single force plot observations appear in the collective force plot. For both the single and collective force plots, the model output is read where the purple and green areas intersect.

Growth-related features, such as impact of gene knockout on biomass and ATP, were found to have opposite Shapley values for acetylation and phosphorylation, respectively (Figure 5A). Thus, high growth values after knockout favor phosphorylation, whereas low growth values favor acetylation. Similar to E. coli and yeast, the set of proteins acetylated in HeLa cells were highly enriched for essential genes identified by both FBA simulations and experimental genome-wide CRISPR knockdown studies (hypergeometric test comparing acetylated metabolic genes to all metabolic genes, p value = 1 × 10⁻³ & 9 × 10⁻⁷ for FBA and CRISPR respectively). Because the functionality of many of the experimentally measured acetylation sites is unknown, we performed this analysis again using a curated list of known functional acetylation sites in mammalian cells from ∼550 studies (Narita et al., 2019). Once again, we find that this list of curated functional acetylation sites is also enriched for essential enzymes based on CRISPR screens (p value < 0.01). These results show that changes in fluxes and essentiality between conditions are associated with a corresponding change in regulation by PTMs.

Molecular weight, topological features and reversibility were used by CAROM-ML to prioritize putative targets of either PTMs, but do not bias the prediction toward a specific PTM (Figures 5A, 3B, and S11). Gene knockout growth and maximum flux likely aid in differentiating between PTMs based on their opposing Shapley values for each PTM. These observations help explain why using both acetylation and phosphorylation in a single model improves performance compared to ML models built separately for each PTM (Figure S13). The SHAP decision plots and force plots show how these features influence the prediction outcome for any given protein (Figures 5B and 5C). This also allowed us to identify factors that led to incorrect predictions by the ML model. Notably, a majority of the incorrect phosphorylation predictions were on proteins that had high molecular weight (Figure S12). Our ability to predict context specific fluxes and gene essentiality more accurately in the future may help rectify these incorrect predictions.

To tease out organism specific differences, we next built CAROM-ML models separately for each organism. Overall, the model accuracy and feature importance were similar for both the pan-organism CAROM-ML model and organism-specific models (Figures S14–S17). This suggests that a similar template involving the same set of features is used for partitioning regulation. Vmax, molecular weight, topology, and gene knockout values are used in the same way in all three organisms for partitioning regulation. However, the specific parameters (the threshold for Vmax or molecular weight) were organism specific. Nevertheless, these parameters can be learned by CAROM-ML using a small subset of data. Although the accuracy is very low when an entire organism's data is removed from the model and used as a test set, a substantial increase is observed when just 10% of the test organism's data is used for additional training (Figure S23). These results suggest that the model is generalizable across datasets and organisms. Patterns learned by CAROM-ML from one model system can be transferred to make predictions in a new organism or model system with a relatively small training dataset.

The distribution of these top features from CAROM-ML may explain the differences in distribution of PTMs observed between different species and metabolic conditions. We observed that the number of reactions with high Vmax was an order of magnitude higher in yeast compared to E. coli for the same condition (stationary phase). A concordant difference in the number of targets of phosphorylation was observed between the two species (Figures S7C and S7D). A similar trend was observed in phosphorylation levels in different conditions within the same species, namely the phases of the mammalian cell cycle and nutrient adaptation in E. coli (Figures 4 and S10). In addition, the total reactions targeted by acetylation correlated with the number of growth-limiting enzymes across conditions or species (Figures S7–S9).

Discussion

There are several ways to regulate an enzyme's activity in a cell. Yet, the factors that determine when an enzyme is regulated by different PTMs are unknown. Here we systematically analyze the properties of the targets of PTMs in model microbes and mammalian cells using a new approach called CAROM. Our approach explains why some proteins are targeted by specific PTMs in a condition based on their biochemical properties, activity in a condition, and location in the metabolic network.

We find that a small set of 13 features can distinguish the targets of each PTM. The importance of these features is highly consistent across numerous datasets suggesting that these features may play a role in influencing regulation. Although prior studies have associated features such as topology with transcriptional regulation, here we report an association between regulation by PTMs and condition-specific attributes such as maximal flux.

The key features identified by CAROM may be related to specific functions performed by each PTM. For example, phosphorylation may represent a mechanism of feedback regulation to control futile cycles and high flux reactions that consume ATP (Humphrey et al., 2015; Kochanowski et al., 2015). The differences in the total number of isozymes and high flux enzymes between species may explain the varying number of phosphorylation targets observed between the species. Because isozymes arise frequently from gene duplication, our results may also explain the observation that duplicated genes are more likely to be targeted by phosphorylation (Amoutzias et al., 2010). However, it is unclear how the maximum flux is sensed by cells. These regulatory interactions may have been shaped by evolution to avoid drain of ATP. Cells may also utilize ‘flux sensors’ to identify such reactions (Kochanowski et al., 2013).

Similarly, we find that enzymes are likely to be acetylated in conditions where their activity is growth limiting. The number of acetylated enzymes correlates with the number of essential genes between organisms or between conditions. During transition to the stationary phase, essential genes do not show significant changes in transcript and protein levels but show significant changes in acetylation in both yeast and E. coli. By regulating growth limiting enzymes, acetylation may play an evolutionarily conserved role in determining the balance of biosynthetic and catabolic processes in a cell.

Each PTM also has distinct chemical properties. The systems level functions of phosphorylation and acetylation we predict here may be related to their distinct chemical properties. For example, the chemical stability and relatively longer half-life of acetylation may make it better suited for regulating essential enzymes and other essential proteins such as histones that also have long half-lives (Kori et al., 2017). Phosphorylation, on the other hand, is less stable, and can enable rapid switching between isozymes and control high flux reactions.

Limitations of the study

Our approach does have limitations because of the underlying algorithms and datasets used. The accuracy of the metabolic reconstruction strongly influences CAROM-ML accuracy. False positive gene knockout essentiality predictions can lead to incorrect assignment of regulation by acetylation. Using experimental gene deletion screens can improve accuracy but may not be available for all conditions. Similarly, phosphorylation predictions by CAROM-ML can also be impacted by flux predictions by FBA. FBA is currently the most powerful approach to obtain genome-wide fluxes. Several studies have shown that fluxes from FBA are strongly correlated with experimental fluxomics datasets (McCloskey et al., 2013). Discrepancies with experiments also pinpoint to missing regulation in the metabolic models. Hence uncovering design principles of metabolic regulation as done in this study will further improve FBA models and their predictive power. Building upon established methods like FBA will eventually allow us to fill the gaps in our knowledge on metabolic regulation, and eventually construct a whole cell model. Although our model has been built using data from FBA simulations, we have also demonstrated that using analogous experimentally generated data, such as from gene essentiality screens and flux tracing can provide similar results (e.g., Figures S5 and 2E). Hence our approach could be directly informed by experimental data if available.

The set of features used in CAROM-ML, although most of them were significantly associated with regulation, are unlikely to be exhaustive. These features were selected based on prior knowledge and ease of prediction using FBA. Other features such as presence of other PTMs may provide additional information to improve accuracy. Finally, ML methods require numerous measurements for training and may not perform well in cases with small sample sizes. Choosing a small set of mechanistic features and using boosted decision trees allowed us to build a robust CAROM-ML model and avoid overfitting issues that arise because of the number of features (James et al., 2013). The accuracy of our model was verified through both cross validation and testing in unseen datasets in the cell cycle.

Another limitation is that the datasets used by CAROM do not provide direct evidence of functional regulation by these PTMs. It is unclear if all the PTM targets are functional. For example, acetylation is predominantly predicted to occur nonenzymatically (Christensen et al., 2019; Weinert et al., 2013). Only a small fraction of acetylation events is known to alter enzyme activity. Yet here we observe a robust statistical association across numerous conditions and organisms between acetylation and these metabolic properties. We have also addressed the issue of functionality by confirming the observed pattern of regulation in a smaller subset of experimentally validated functional acetylation targets in mammalian cells and cobB targets in E. coli. Although nonenzymatic acetylation may not affect enzyme activity, it might still have a functional role (Christensen et al., 2019). For example, acetylation can impact protein stability, protein interactions, or may act as a storage mechanism for excess carbon by associating with essential proteins with long lifetimes. Acetylation may also serve as a protective PTM that shields essential proteins from harmful modifications like carboxylation. Further, low stoichiometry PTMs may help precisely tune enzyme activity, in contrast to large-scale adjustments through transcriptional changes.

In sum, our analysis reveals a unique distribution of regulation by PTMs within the metabolic network. This can help identify PTMs that will likely orchestrate flux adjustments based on reaction attributes. By identifying condition-specific factors that are associated with regulation by PTMs, CAROM can complement sequence-based approaches for identifying PTM sites. It is well established that individual regulators such as transcription factors or kinases have their own unique set of targets. Here we find that similar specialization likely occurs at a higher scale, between PTMs. Our approach can guide drug discovery and metabolic engineering efforts by identifying regulators that are dominant in different parts of the network (Choi et al., 2019). CAROM can also be used to uncover the impact of metabolic alterations on PTMs in normal and pathological processes. Given the conservation of these principles in E. coli, yeast, and mammalian cells, it provides a path toward a detailed understanding of posttranslational regulation in a wide range of organisms and to uncover target specificities of other PTMs. This approach may help define the basic regulatory architecture of metabolic networks.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
COBRA	https://doi.org/10.1038/s41596-018-0098-2	https://opencobra.github.io/cobratoolbox/stable/
SHAP	https://www.nature.com/articles/s42256-019-0138-9	https://shap.readthedocs.io/en/latest/
CAROM source code and data	https://www.synapse.org/CAROM	https://doi.org/10.7303/syn20843407

Resource availability

Lead contact

Sriram Chandrasekaran, Department of Biomedical Engineering, University of Michigan, Ann Arbor, MI, USA, 48109, csriram@umich.edu.

Materials availability

No materials were generated in this study.

Method details

Compilation of omics data

We used RNA-sequencing data from Treu et al. (2014) that compared the expression profile of S. cerevisiae between mid-exponential growth phase with early stationary phase (Treu et al., 2014). A 2-fold change threshold was used to identify differentially expressed genes. Lysine acetylation and protein phosphorylation data were obtained from the Weinert et al. (2014) study that compared PTM levels between exponentially growing and stationary phase cells using stable isotope labeling with amino acids in cell culture (SILAC) (Weinert et al., 2014). A 2-fold change threshold of the protein-normalized PTM data was used to identify differentially expressed PTMs. Proteomics data was taken from Murphy et al time course proteomics study (Murphy et al., 2015). The hoteling T2 statistic defined by the authors was used to identify proteins differentially expressed during diauxic shift; the top 25% of the differentially expressed proteins were assumed to be regulated at the proteomic level. Proteomics data from Weinert et al was also used as an additional control and we observed the same trends using this data as well (Table S1G). Further, we repeated the analysis after removing genes that were not expressed during transition to stationary phase; the transcripts for a total of 12 genes out of the 910 in the model were not detected by RNA-sequencing in the Treu et al study (Treu et al., 2014). Removing the 12 genes did not impact any of the results (Table S1F).

As additional validation, we used periodic data from the yeast cell cycle. Time course SILAC phospho-proteomics data was obtained from Touati et al. (Touati et al., 2018). Phospho-sites whose abundance declined to less than 50% or increased by more than 50% at least two consecutive timepoints were considered dephosphorylated or phosphorylated respectively as defined by the authors. Transcriptomics data was taken from Kelliher et al study that identified 1,246 periodic transcripts using periodicity-ranking algorithms (Kelliher et al., 2016). The phospho-proteomics and transcriptome data during nitrogen shift was obtained from Oliveira et al. (Oliveira et al., 2015b; Oliveira et al., 2015a). The nitrogen shift studies compared the impact of adding glutamine to yeast cells growing on a poor nitrogen source (proline alone or glutamine depletion) with cells growing on a rich nitrogen source (glutamine plus proline). A 2-fold change threshold was used to identify differentially expressed transcripts and phospho-sites.

E. coli acetylation data was taken from the Weinert et al study comparing actively growing exponential phase cells to stationary phase cells (Weinert et al., 2013). Proteomics and transcriptomics were from Houser et al study of E. coli cells in early exponential phase and stationary phase (Houser et al., 2015). Phospho-proteomics data for exponential and early stationary phase E. coli cells was taken form Soares et al. (Soares et al., 2013). We used a 2-fold change (p < 0.05) threshold for all studies.

Condition specific PTM data for E. coli was taken from Schmidt et al. (2016) study (Schmidt et al., 2016). Among the 22 different experimental conditions measured, those conditions that involved change in carbon sources that could be modeled using FBA were chosen. The following carbon sources were used: acetate, fumarate, galactose, glucose, glucosamine, glycerol, pyruvate, succinate, fructose, mannose and xylose. Out of 44 unique lysine acetylation and 21 serine/threonine phosphorylation sites identified in the study (FDR < 0.01), 11 and 5 proteins were mapped to the metabolic model for the subset of conditions analyzed here. Protein modifications were normalized by their corresponding protein levels, a standard procedure in proteomics studies to ascertain the variation in PTM levels relative to the total protein levels.

Acetylated proteins in HeLa cells were taken from Kori et al. (2017) which measured time course acetylation levels in HeLa cells grown on 13C labeled glucose with samples collected at 0.5, 1, 4, 8, 12, 16, and 24 hours (Kori et al., 2017). A total of 702 unique target proteins were identified based on significance of acetylation incorporation as monotonic trend across the time points using the Mann-Kendall statistical test (p value < 0.05) as defined by the authors. For the phosphorylation data for HeLa cells, phosphorylation sites that are up-regulated during mitosis and show more than 50% occupancy as defined by the authors were used (Olsen et al., 2010).

Phosphoproteomics data from the mammalian cell cycle contained a total of 5,861 identified phosphopeptides (Lee et al., 2021). Phospho-peptides whose abundance intensities (or signal to noise ratios) are zero at any channel (or any time point sample), those with Ascore <13, and those that were identified by a decoy dataset in a reverse manner were removed, resulting in a set of 3,095 phosphopeptides that correspond to 1,552 unique proteins. A Z score normalization was performed to identify phase specific differential levels of phosphorylated proteins (z threshold of +/− 2).

Gene essentiality based on CRISPR knockout screens was obtained from Hart et al. (2015) study that measured essentiality across all 5 cell lines (HeLa, RPE1 DLD1, GBM and HCT116) (Hart et al., 2015). Growth limiting genes with FDR < 0.05 were considered to be essential, as defined by the authors. In addition, essential genes from Hart et al. (2017) study using genome-wide knockout screens in 17 human cell lines also showed similar enrichment among acetylated proteins (p value = 1.7 × 10⁻⁷) (Hart et al., 2017).

The results are robust to the thresholds used for identifying differentially expressed genes or proteins (Tables S1F–S1H). In all studies, proteins that are either up or down regulated were considered to be targets of a regulatory mechanism. The final dataset table used for all comparative analyses is provided as a supplemental information (Tables S1Q–S1T).

Genome scale metabolic modeling

We used the yeast metabolic network reconstruction (Yeast 7) by Aung et al, which contains 3,498 reactions, 910 genes and 2,220 metabolites (Aung et al., 2013). The analysis of E. coli data was done using the IJO1366 metabolic model (Orth et al., 2011) and the mammalian cell cycle modeling was done using the human metabolic reconstruction (Recon1) (Duarte et al., 2007). All analyses were performed using the COBRA toolbox for MATLAB (Becker et al., 2007).

The impact of gene knockouts on growth was determined using flux balance analysis (FBA). FBA identifies an optimal flux through the metabolic network that maximizes an objective, usually the production of biomass. A minimal glucose media (default condition) was used to determine the impact of gene knockouts. Further, gene knockout analysis was repeated in different minimal nutrient conditions to identify genes that impact growth across diverse conditions; these conditions span all carbon and nitrogen sources that can support growth in the metabolic models. The number of times each gene was found to be lethal (growth <0.01 biomass units, measured as millimolar per gram dry weight per hour or mM/gDW/hr) across all conditions was used as a metric of essentiality.

To infer topological properties, a reaction adjacency matrix was created by connecting reactions that share metabolites. We used the Centrality toolbox function in MATLAB to infer all network topological attributes including centrality, degree, and PageRank. Removing highly connected metabolites did not affect the associations between topology and regulation (Figure S2B). Since ATP and NADH are involved in thousands of reactions, some network analysis studies remove these metabolites in their topology calculations, as including them could lead to a reduced path length between distant reactions that utilize ATP or NADH. Hence repeating this analysis after removing these metabolites suggests that our analysis is robust to the approach used for calculating the topology metrics.

Flux Variability Analysis (FVA) was used to infer the range of fluxes possible through every reaction in the network. Two sets of flux ranges were obtained with FVA – the first with optimal biomass and the latter without assuming optimality. In the second case, the fluxes are limited by the availability of nutrients and energetics alone, thus it reflects the full range of metabolic activity possible in a cell. Reactions with maximal flux above 900 units (mM/gDW/hr) were assumed to be unconstrained and were excluded from the analysis, as they are likely due to thermodynamically infeasible internal cycles (Schellenberger et al., 2011); the choice of this threshold for flagging unconstrained reactions did not impact the distribution between regulators over a wide range of values (Table S1I). FVA fluxes could also be potentially biased by the size of the metabolites catalyzed by each reaction, with reactions involving smaller metabolites predicted to have very high FVA fluxes. In our case, we did not find a consistent pattern of correlation between molecular weight of the metabolites and the predicted fluxes across all the organisms studied here (Figure S25).

For fitting experimentally derived flux data from Hackett et al. (Hackett et al., 2016), reactions were fit to the fluxes using linear optimization and the flux through remaining reactions that do not have experimentally derived flux data were inferred using FVA (Lewis et al., 2010) (Figure S5).

Reaction reversibility was determined directly from the model annotations. We also used additional reversibility annotation from Martinez et al based on thermodynamics analysis of the Yeast metabolic model (Martínez et al., 2014). Pathway annotations and enzyme molecular weight values were obtained from Sanchez et al. The catalytic activity values were obtained from Sanchez et al, Heckman et al, and Yeo et al for Yeast, E. coli and mammalian cells respectively (Heckmann et al., 2018; Sánchez et al., 2017; Yeo et al., 2020). The comparative analysis of regulatory mechanisms was also repeated using the updated Yeast 7.6 model and yielded similar results (Table S1E) (Sánchez et al., 2017).

Models for each cell cycle phase were built using the Dynamic Flux Activity (DFA) approach (Chandrasekaran et al., 2017; Shen et al., 2019b). The cell cycle metabolomics data contains 155 intracellular metabolites and 173 extracellular metabolites and was used as inputs for DFA. The time points were grouped in to different phases as follows: 0–4 h for G0-G1, 4–8–12 h for G1, 12–16 h for G1-S, and 16–20 h for G2-M. DFA utilizes time course metabolomics data and calculates the rate of change of each metabolite level over time (dM/dt). The rate of change of each metabolite is calculated using linear regression in DFA. Based on the regression line for a metabolite i, one calculates ϵ_i which is the slope divided by the intercept which is a normalization factor at the initial time point. Then, together with a known metabolic network for the stoichiometry matrix, S, and by introducing flux activity coefficients, α and β, the DFA equation becomes a modified version of the conventional FBA: S⋅v + α - β = ϵ. α and β are both positive values. This equation is then solved by minimizing α + β and maximizing the biomass objective function, yielding a flux vector or distribution of all reactions for time course data. We have also performed a sensitivity analysis to study the impact of noise in the metabolomics data on the inferred fluxes. This suggests that the default settings for the DFA algorithm, which we had identified from prior studies (Shen et al., 2019b), provides an optimal tradeoff between overfitting the model and learning useful information. This suggests that only the strongest signals in metabolomics data are picked up by the model to infer fluxes (Figure S24C).

For validating the CAROM-ML model, the fluxes from the G0/G1 phase were used in the training set and the remaining phases were used for testing. This analysis was repeated by training on different phases of the cell cycle. The accuracy from the G1, G1/S and G2/M phases was lower compared to training on G0/G1. suggesting that these conditions have a distinct phosphorylation pattern from the G0/G1 condition (Figure S18).

The comparative analysis of target properties was done using gene-reaction pairs rather than genes or reactions alone. The gene-reaction pairs accounts for regulation involving all possible combinations of genes and associated reaction. This includes isozymes that may involve different genes but the same reaction, or multi-functional enzymes involving same the gene associated with different reactions. For example, the 910 genes and 2,310 gene-associated reactions resulted in 3,375 unique gene-reaction pairs in yeast.

Machine learning

The CAROM-ML model was built using the XGBoost package in Python. XGBoost is a gradient boosting algorithm that uses decision trees as its weak learners (Chen and Guestrin, 2016). Unlike bagging algorithms, such as random forest, which train their learners independently in parallel, boosting algorithms train their predictors sequentially. Each weak learner uses gradient descent to minimize the error of the previous learner. XGBoost is unique among boosting algorithms due to its speed and regularization abilities, which help prevent over-fitting, and provided robust performance in our independent study (Lee, 2021). Importantly this machine learning model is especially suited for the (relatively) small training size used here.

We used a randomized search with an internal cross validation in the training set to tune hyperparameters. A stratified split was employed to ensure the class balance was preserved between the training and test sets. To measure the model robustness and generalization, we performed 5-fold cross-validation. The hyperparameters were re-tuned on each iteration. The hyperparameters from the fold with the best performance were then used to fit a final model to the entire training set. To assess predictive power in novel conditions, the model was also assessed using data from G1, G2/M & G1/S phase conditions. Note that for the acetylation predictions during the cell cycle, no additional training data was available for the G0/G1 phase (in contrast to phosphorylation).

To assess the impact of using other ML algorithms on CAROM-ML accuracy, additional models were built using Random Forests and AdaBoost. Similar accuracy to XGBoost was obtained using these approaches (Figure S19) (Freund and Schapire, 1996). AdaBoost is also a gradient boosting algorithm that can use decision trees as its base learners. For each learner, weights are assigned to its errors and these weights are used to adjust the next learner's predictions.

For model interpretation, a single decision tree model was created to visualize the typical prediction path that an observation follows when its class is being decided. The decision tree was built using the scikit-learn Python package. The decision tree was trained on the entire dataset and the RandomizedSearchCV function was used to tune hyperparameters, including maximum depth. To address the class imbalance, synthetic minority oversampling (SMOTE) was used for training the decision tree model.

To build the ML model, each gene-reaction pair is assigned a class of −1, 0, or 1, corresponding to phosphorylated, unknown regulation and acetylated, respectively. For cases where genes/proteins were targeted by both PTM types in the training data, phosphorylation was assigned, as this was the minority class. This overlap occurred in 25 gene-reaction pairs in the E. coli dataset, 67 pairs for yeast and 2 for HeLa. Any genes that were included in the metabolic network, but not found in the corresponding PTM dataset, were assumed to be not-regulated by these PTMs. Any missing feature data was replaced with the median value. To account for the differences between organism characteristics, we normalized the features for each condition table on a scale of 0–1 for each condition. The catalytic activity and PFBA flux features showed unique organism-specific signatures when normalized, so these two attributes were scaled using their mean values. Reaction reversibility is a binary variable and therefore was not scaled. Prior to scaling, the maximum and minimum reaction flux features were limited to 100 to reduce feature range, as opposed to the value of 900 used in the statistical portion of the study. This step did not significantly affect the model accuracy (Figure S24).

Proteins that were not annotated to be acetylated or phosphorylated in any condition in the protein lysine modification database or the UniProt database were removed from the ML model (Huang et al., 2016; The UniProt Consortium, 2019). However, this step did not significantly alter the accuracy as most metabolic proteins were annotated to be targets of these PTMs (Figure S20; Table S1AA). The final data used to train the CAROM-ML model included 2,427 gene-reaction pairs for E. coli, 3,039 for yeast, 3,661 for HeLa, and 3,582 for the G0/G1 condition of the mammalian cell cycle dataset, for a total of 12,709 observations (Figure S22; Tables S1Q–S1Z). The validation set, which includes the G1, G1/S, and G2/M phases, contained 10,746 pairs (3,582 for each phase).

Shapley analysis

For determining features that have the largest influence in the ML models, we used the SHAP (SHapley Additive exPlanation) package in Python. SHAP uses the game theory concept of Shapley values for calculating each feature's contribution to the model output (Lundberg et al., 2020). The Shapley analysis was completed using TreeExplainer from the SHAP package. TreeExplainer is specifically designed for use with tree-based models. The Shapley value represents the average impact for each feature across for all possible orderings. This process is represented by the following equation:

$${\phi }_i(f,x)=\sum _{S\subseteq S_{all/\left\{i\right\}}}\frac{\left|S\right|!(M-|S|-1)!}{M!}[f_x(S\cup \left\{i\right\})-f_x\left(S\right)]$$

The Shapley value is the ${\phi }_i(f,x)$ term, or the effect that feature i has on model f, given the independent variable data, x. M is the total number of features, and M! represents the number of possible feature combinations. S is a subset of the features excluding feature i, |S| is the number of features in subset S, and f_x(S) is the model output for subset S. The SHAP values are relative to the average model output, called the base value. The base value can also be thought of as the null model output. Therefore, the sum of the SHAP values for a given observation is equal to the difference between the model prediction and the base value. Considering the SHAP values across all observations in a dataset provides insight into the overall feature importance, direction of a feature's impact on the model output and relationships between the predictor features. For model interpretation using SHAP, the final XGBoost model and its training data were used as inputs to the TreeExplainer function.

Quantification and statistical analysis

All statistical tests were performed using MATLAB. Significance of overlap between lists was estimated using the hypergeometric test. The ANOVA test and the non-parametric Kruskal-Wallis test were used to compare target properties between regulatory mechanisms and determine statistical significance of the observed differences. The p values were corrected for multiple hypothesis testing and assessed for significance (Table S1E).

Published: January 21, 2022

Data and code availability

• •All data have been deposited at Synapse and are publicly available as of the date of publication at https://www.synapse.org/CAROM. DOIs are listed in the key resources table.
• •All original code has been deposited at Synapse and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.