Detecting Selection in Multiple Populations by Modeling Ancestral Admixture Components

Abstract

One of the most powerful and commonly used approaches for detecting local adaptation in the genome is the identification of extreme allele frequency differences between populations. In this article, we present a new maximum likelihood method for finding regions under positive selection. It is based on a Gaussian approximation to allele frequency changes and it incorporates admixture between populations. The method can analyze multiple populations simultaneously and retains power to detect selection signatures specific to ancestry components that are not representative of any extant populations. Using simulated data, we compare our method to related approaches, and show that it is orders of magnitude faster than the state-of-the-art, while retaining similar or higher power for most simulation scenarios. We also apply it to human genomic data and identify loci with extreme genetic differentiation between major geographic groups. Many of the genes identified are previously known selected loci relating to hair pigmentation and morphology, skin, and eye pigmentation. We also identify new candidate regions, including various selected loci in the Native American component of admixed Mexican-Americans. These involve diverse biological functions, such as immunity, fat distribution, food intake, vision, and hair development.

Introduction

The emergence of population genomic data has facilitated fine-scale detection of regions under recent positive selection in humans and other species. There are multiple different methods for carrying out such selection scans. Some of these rely on patterns of long-range linkage disequilibrium (Voight et al. 2006; Sabeti et al. 2007), one of the characteristic genomic footprints left by a selective sweep (Kim and Stephan 2002; Kim and Nielsen 2004; McVean 2007). However, this pattern fades rapidly over time, and these methods are, consequently, best suited for detecting very recent selective sweeps from de novo mutations. Other techniques, based on distortions in the allele frequency spectrum caused by positive selection, can allow for the detection of more ancient events, but are generally only applicable to one population at a time (Tajima 1989; Fu and Li 1993; Fay and Wu 2000; Nielsen 2005; DeGiorgio et al. 2016; Huber et al. 2016).

A different class of methods for detecting selection involves analyzing patterns of allele frequency differentiation between populations. The basic idea is that regions that have experienced episodes of positive selection will display frequency differences between populations that are stronger than what would be expected under pure genetic drift. For example, one can compute Wright’s fixation index (F_ST) locally across different regions of a genome and look for extreme outliers (Beaumont and Nichols 1996; Akey et al. 2002; Beaumont and Balding 2004). Population differentiation methods can detect more ancient selective events than linkage disequilibrium-based methods (Sabeti et al. 2006), and are sensitive to different types of positive selection events, including sweeps from a de novo mutation, sweeps from standing variation, incomplete sweeps, and adaptive introgression (Bonhomme et al. 2010; Yi et al. 2010; Fumagalli et al. 2015; Racimo et al. 2017). Recent methods have allowed researchers to detect excess local differentiation on particular branches of a three-population tree (Yi et al. 2010; Racimo 2016), a four-population tree (Cheng, Xu, et al. 2017), or an arbitrarily large tree (Librado and Orlando 2018), albeit without modeling postsplit admixture events.

A generalization of these approaches was developed by Coop et al. (2010), Günther and Coop (2013), and Gautier (2015). It involves the detection of genomically local distortions from a genome-wide covariance matrix, which is used as a neutral baseline. An advantage of this approach is that one can apply it to an arbitrary number of populations. Other researchers have used hierarchical Bayesian models (Foll and Gaggiotti 2008; Foll et al. 2014) or principal component analysis (Duforet-Frebourg et al. 2016; Luu et al. 2017) to model patterns of population differentiation to identify local distortions across the genome. Another method extended single-locus differentiation-based methods to the analysis of haplotype differentiation (Fariello et al. 2013). More recently, Mathieson et al. (2015) developed an admixture-aware selection test based on a linear model and applied it to human data. The analysis took advantage of the fact that present-day European populations could be modeled as a mixture of three highly differentiated ancestral components. Regions of the genome that exhibited strong deviations from the genome-wide mixture proportions were therefore strong candidates for positive selection. Finally, Refoyo-Martínez et al. (2019) developed a method to test for selection on an admixture graph, which represents the history of divergence and admixture events among populations. Although useful for detecting selection in the presence of admixture, it still requires the user to specify which individuals belong to which populations, and to infer the graph in advance.

Here, we introduce a new selection detection framework that can explicitly model admixture and detect selection from populations of admixed ancestries. It can simultaneously compare arbitrarily many populations and ancestry components and is encoded in a flexible framework for testing selection on a specific lineage or set of lineages. The method allows the user to identify signals of positive selection via population differentiation, without relying on self-reported ancestry or admixture correction to group individuals into populations. The method can also determine if a selective event is specific to a particular population or shared among different populations.

Unlike previous methods, we fully take advantage of admixed populations, and we do not require the user to a priori categorize samples into populations, or to correct allele frequencies to account for recent admixture. Thus, the selection scan does not rely on user-supplied sample labels or ancestry compositions. These methods identify positive selection by searching for loci showing distortions in the population covariance matrix, relative to the genome-wide baseline. It provides a flexible framework to specifically test for selection on individual components or sets of components. This functionality allows researchers to accommodate specific evolutionary scenarios into the range of testable hypotheses, including local adaptation, adaptive introgression, and convergent selection. The method first coestimates the population structure of the input panel and the allele frequencies of the ancestral admixture components through an unsupervised learning process (Cheng, Mailund, et al. 2017), before testing for selection on the ancestral components themselves. Researchers can also use the method to examine estimated population structure and visualize trees connecting the ancestral components using plotting functionalities provided by our software package, Ohana, as part of the analysis pipeline.

Results

Simulations

Power to Detect Selection

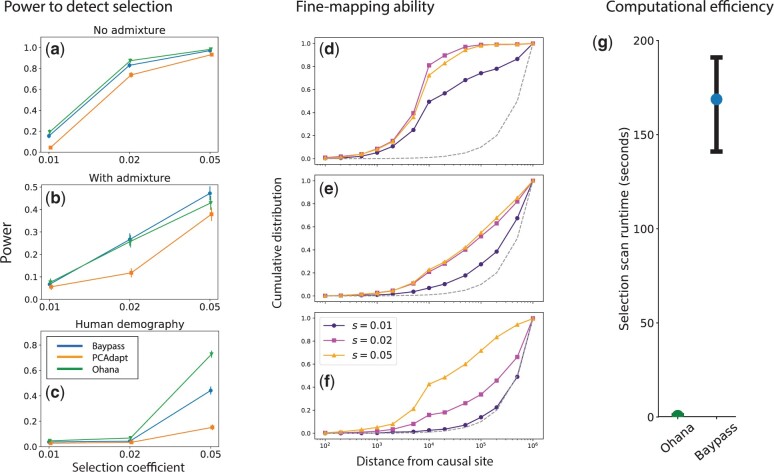
We first evaluated the performance of our method against comparable methods in detecting whether a locus has evolved under positive selection (fig. 1a–c). For all tests, we use the empirical null distribution to find the threshold associated with 5% false positive rate (FPR). We compute power as the proportion of simulations with test statistic exceeding this threshold. For all three methods, the test statistic was the site statistic with the maximum value across the whole 2 Mbp locus; with Ohana, the test statistic used was the log-likelihood ratio (testing for selection in the specified ancestry group); with BayPass, the test statistic was the “XtX” statistic; and with pcadapt, the test statistic was the selection test P value, using K = 3 PCs (because there are four ancestral populations in each case). For all three methods, power increased uniformly with the value of the selection coefficient (fig. 1a–c). However, different demographic scenarios result in different power levels; for example, all methods were better-powered under the simple demographic scenario (model 1, figs. 1a and 2a) compared with selection preadmixture (model 1, figs. 1b and 2b) or in the human demographic model (model 3, figs. 1c and 2c).

Fig. 1.

Simulation tests of Ohana performance and efficiency in detecting and mapping selected sites. (a–c) Power to detect selection relative to two comparable methods, BayPass and pcadapt. Error bars are 95% CIs; (d–f) efficacy of Ohana to fine-map the causal site; (g) computational efficiency compared with that of BayPass. Error bars are 5th to 95th percentiles.

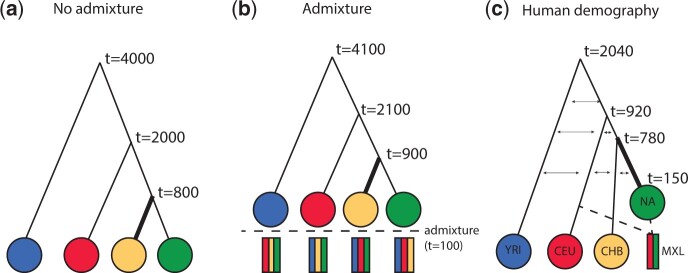
Fig. 2.

Illustration of simulation models. (a) Model 1, a basic model of four-population split with no admixture. (b) Model 2, a four-population split with subsequent admixture. (c) Model 3, a four-population model mimicking human demographic models. Population size changes in model 3 are omitted from the visualization for simplicity. Selection is simulated to operate on the branch that has a larger width.

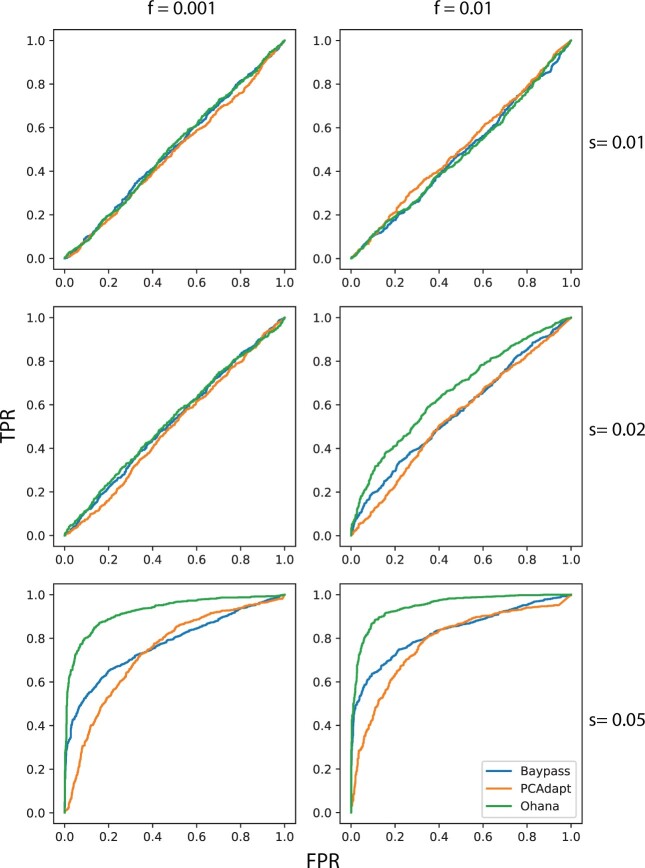
pcadapt was significantly less well-powered than Ohana in most scenarios, for example, 72% versus 88% and 90% versus 98% power under moderate and strong selection, respectively (see fig. 1a). In most scenarios, we found Ohana to have power equivalent to or greater than that of BayPass; for example, in models 1 and 2, we fail to reject that Ohana and BayPass have different power curves with 95% confidence (fig. 1a and b). However, in one simulation scenario, we found Ohana had significantly higher power than Baypass, under a model of human demography (fig. 1c). However, we note that although BayPass and Ohana have similar power, Ohana’s test is by design more specific, as it is testing for selection in a specified ancestry group; hence power calculations are inherently more lenient for BayPass than Ohana. In figure 1a–c, we show results assuming $0.001\le f<0.01$, and present full results illustrating the entire ROC curve (i.e., not conditioned on FPR = 0.05) and for other values of f, in figure 3 and supplementary figures S1 and S2, Supplementary Material online. Also note the overall low power in figure 3. The main reason for this low power is that selection is acting in a relatively short period in the past, and that the population has experienced 50% admixture after selection. The strong admixture after selection tends to obscure much of the selection signal.

Fig. 3.

ROC curves for Ohana versus state-of-the-art methods, assessed using simulations with various values of the initial allele frequency at the beginning of selection (f) and different selection coefficients (s). Here the demographic model used was our human model (with selection in the Native American lineage), versus other demographic models considered (i.e., basic tree without and with admixture, supplementary figs. S1 and S2, Supplementary Material online, respectively).

Efficacy for Fine-Mapping the Causal Site

We also considered the performance of Ohana for fine mapping the position of the causal site (fig. 1d–f). We considered the distribution of the distance between the site of the test statistics described above (i.e., the locus-wide max statistic) and the causal site (in the center of the 2 Mbp locus). We plot the empirical cumulative distribution of these distances for different values of the selection coefficient under each demographic model. We found that in cases where Ohana is well-powered to detect selection, there is considerable power to narrow the position of the causal site down to ±10 kb of the max test statistic (e.g., >40% power for $s\ge 0.01$ under model 1 and $25\%$ power for s = 0.05 under models 2 and 3; see fig. 1d–f). Interestingly, under models 1 and 2, there is similar power to fine-map sites with moderate and strong selection (s = 0.02 vs. 0.05, see fig. 1d and e); in contrast, under model 3, there is significantly higher power to fine-map sites with strong selection (fig. 1f); this dramatic difference may be due to the effects of demography on the pattern of hitchhiking surrounding the causal site. In figure 1d–f, we show results assuming $0.001\le f<0.01$ and present full results illustrating other values of f in supplementary figures S3–S5, Supplementary Material online.

Computational Efficiency

In addition to comparing power to detect selection, we compared computational efficiency of Ohana and BayPass, which we showed in previous sections was the most competitive method in terms of statistical power (fig. 1g). We found that Ohana was >250× faster than BayPass (mean selection scan runtimes: Ohana, 0.626 s [±0.008 s]; BayPass, 168 s [±2 s]; N = 1,000 replicates). We reiterate that our power comparison revealed Ohana to generally have comparable power to that of BayPass, despite multiple orders of magnitude improvement in computational efficiency.

Analysis of Real Data

We identified regions in the genome that are likely to have been under the influence of positive selection using a merged data set containing several population panels from phase 3 of the 1000 Genomes Project (1000 Genomes Project Consortium et al. 2015). We randomly selected 64 genomes from each of four populations from the 1000 Genomes project: the British from Great Britain (GBR), the Han Chinese from Beijing (CHB), the Yoruba Africans (YRI), and the admixed Mexican-Americans from Los Angeles (MXL) (the number 64 was chosen because it was the size of the smallest panel). We only included variable sites with no missing data and a minimum allele frequency of 0.05 across the entire merged panel. In total, we analyzed 5,601,710 variable sites across the autosomal genome. We inferred genome-wide allele frequencies and covariances for the latent ancestry components as described in Materials and Methods section, using K = 4. To scan for covariance outliers, we performed four hypothesis-driven scans, in which we specifically searched for selection separately in each of the four inferred ancestry components in our data set (fig. 4 and table 1).

Fig. 4.

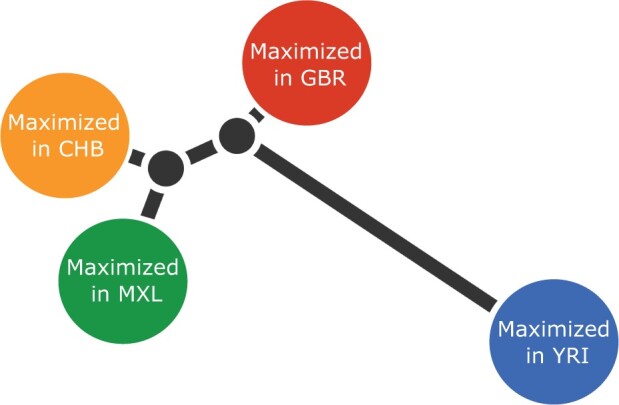
Inferred unrooted tree of latent ancestry components for the analysis including the CHB, YRI, MXL, and GBR genomic panels. We label each component by the population in which it is maximized, but emphasize that the components and the populations are not equivalent entities.

Table 1.

Top Ten Most Differentiated SNPs from Each of the Ancestry-Specific Scans.

Chr	Pos	Rsid	LLRS	Target Ancestry	Nearest Gene
5	33951693	rs16891982	22.085902	European	SLC45A2
15	48426484	rs1426654	19.707464	European	SLC24A5
15	28356859	rs1129038	19.290553	European	HERC2
15	28495956	rs12912427	18.270213	European	HERC2
9	16792200	rs10962596	15.819739	European	BNC2
1	1385211	rs1312568	15.066101	European	ATAD3C
2	136407479	rs1446585	14.957582	European	R3HDM1
2	136616754	rs182549	14.629386	European	MCM6
1	204784969	rs3940119	14.393216	European	NFASC
4	38798648	rs5743618	14.38681	European	TLR1
16	48258198	rs17822931	23.271759	CHB	ABCC11
16	48375777	rs6500380	22.474103	CHB	LONP2
1	234635790	rs2175591	20.95541	CHB	TARBP1
4	100142780	rs75721934	20.453247	CHB	LOC100507053
11	61579427	rs72643557	20.114033	CHB	FADS1
11	120154631	rs12224052	19.696284	CHB	POU2F3
21	43974948	rs228088	19.518001	CHB	SLC37A1
11	133043841	rs79802711	19.157192	CHB	OPCML
5	128016573	rs79478220	18.476104	CHB	FBN2
19	51441759	rs11084040	18.158963	CHB	KLK5
14	46745012	rs140736443	32.730697	Native American	LINC00871
9	82968379	rs6559543	27.584847	Native American	LINC01507
16	80619307	rs2316155	27.399123	Native American	LINC01227
14	21647765	rs77549780	27.355769	Native American	LINC00641
12	14189549	rs12425115	25.867367	Native American	GRIN2B
10	8150713	rs10508343	25.609772	Native American	GATA3
15	34936250	rs16959274	25.424824	Native American	GOLGA8B
8	4490837	rs71523639	24.59957	Native American	CSMD1
1	14301862	rs72640512	24.455822	Native American	PRDM2
12	29817716	rs12580697	23.967094	Native American	TMTC1
8	145639681	rs1871534	11.906794	Yoruba/Ancestral Non-African	SLC39A4
5	178626609	rs6869589	11.541667	Yoruba/Ancestral Non-African	ADAMTS2
15	29427400	rs10152250	11.48232	Yoruba/Ancestral Non-African	FAM189A1
1	1106112	rs6670693	11.447873	Yoruba/Ancestral Non-African	TTLL10
4	3666494	rs58827274	11.341367	Yoruba/Ancestral Non-African	LOC100133461
17	2631985	rs4790359	11.118134	Yoruba/Ancestral Non-African	PAFAH1B1
9	136769888	rs2789823	11.031687	Yoruba/Ancestral Non-African	VAV2
6	169656029	rs6930377	10.824098	Yoruba/Ancestral Non-African	THBS2
17	29350769	rs8073072	10.794224	Yoruba/Ancestral Non-African	RNF135
5	173642871	rs10067518	10.787147	Yoruba/Ancestral Non-African	HMP19

LLRS = log-likelihood ratio score for positive selection.

After running these scans, we queried the CADD server (Rentzsch et al. 2019) to obtain functional, conservation, and regulatory annotations for the top candidate SNPs, including SIFT (Sim et al. 2012), PolyPhen (Adzhubei et al. 2013), GERP (Davydov et al. 2010), PhastCons (Siepel et al. 2005), PhyloP (Pollard et al. 2010), and Segway (Hoffman et al. 2012) annotations, so as to find the changes most likely to be disruptive. We discuss some of these below. We also queried the GTEx cis-eQTL database (Lonsdale et al. 2013), the UK Biobank GeneATLAS (Canela-Xandri et al. 2018), and the GWAS catalog (MacArthur et al. 2017), to look for trait-associated SNPs. We particularly focus on SNPs that have both high log-likelihood ratios in favor of positive selection (LLRS > 15) and high CADD scores in favor of functional disruption (>10).

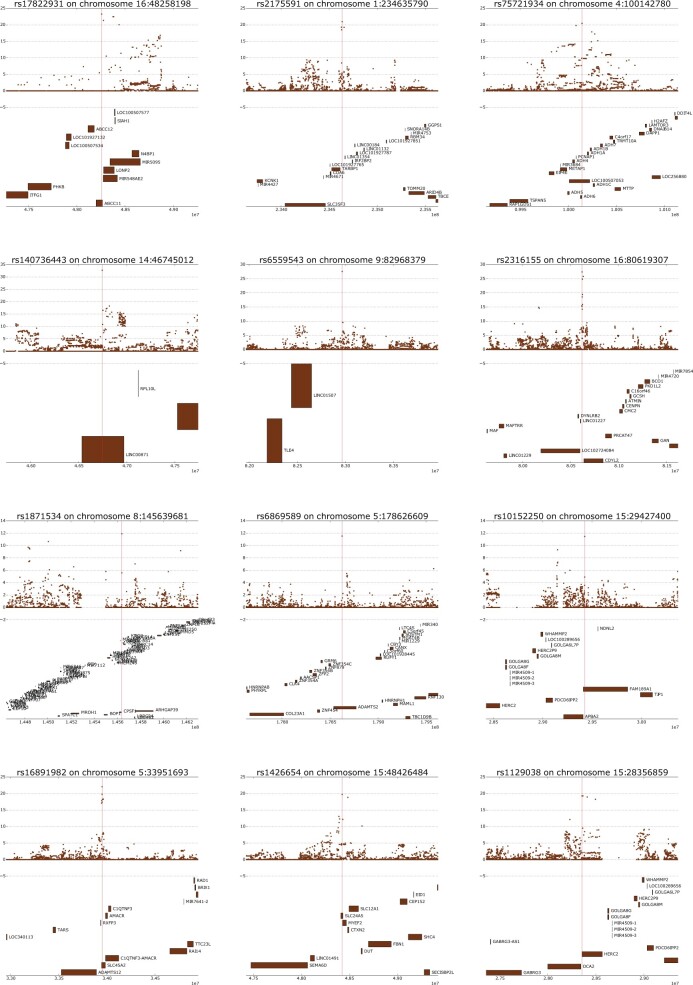
Below, we describe some of the top SNPs with high LLRS and their surrounding regions, for those cases in which available genic, expression, or regulatory information can provide us some clue as to the possible organismal function that may have been affected by the selective event. We particularly focus on the Native American ancestry scan (fig. 5), as few selection scans have been performed in this population, but also briefly summarize the results from the other scans.

Fig. 5.

Top 5 annotated peaks in each of the ancestry-specific selection studies. MXL-specific = scan for selection in Native American ancestry of MXL. GBR-specific = scan for selection in European ancestry of GBR. CHB-specific = scan for selection in CHB ancestry of CHB. YRI-specific = scan for selection in Yoruba African ancestry or ancestral non-African ancestry. We analyzed 5,601,710 variable sites across the autosomal genomes. We inferred genome-wide allele frequencies and covariances as described in Materials and Methods section. We applied a likelihood model for each SNP by rescaling all variances and covariances by a scalar multiplier α. Descriptions of each candidate region are in table 1. LLR, log-likelihood ratio score.

European Ancestry Scan

Results for the top 30 loci in the European ancestry scan are presented in supplementary table S1, Supplementary Material online. Most loci have been previously shown to be under selection in Europeans populations, including SLC45A2, SLC24A5, BNC2, the OCA2/HERC2 region, the LCT/MCM6 region, and the TLR region (Bersaglieri et al. 2004; Voight et al. 2006; Barreiro et al. 2009; Vernot and Akey 2014; Mathieson et al. 2015). We notice that, in several cases, the presumed causal SNP previously identified in the literature coincides with the SNP with the strongest selection signal. This is the case, for example, for rs1426654 (SLC24A5) (Lamason et al. 2005; Kimura et al. 2009) and for rs16891982 (SLC45A2) (Branicki et al. 2008). This suggest that the top SNPs for other loci, for which the causal SNPs are not yet known, may be good candidates for further tests of functional effects.

East Asian Ancestry Scan

We also performed a scan where we sought to recover SNPs that were candidates for selection in the ancestry component that is prevalent among our CHB samples. Results for the top 30 loci in this scan are in supplementary table S2, Supplementary Material online. Here, we also recover several candidate regions that have been previously reported in East Asian selection scans, including ABCC11, POU2F3, ADH1B, FADS1, and TARBP1 (Peng et al. 2010; Ohashi et al. 2011; Vernot and Akey 2014; Liu et al. 2018; Refoyo-Martínez et al. 2019). Here, as in the previous scan, the top-scoring SNPs also tend to have the strongest phenotypic associations. For example, the highest scoring SNP (rs17822931) is the well-known missense variant in ABCC11, which is involved in sweat and earwax production (Yoshiura et al. 2006).

Yoruba/Ancestral Non-African Ancestry Scan

Because our algorithm relies on an unrooted tree of the ancestry components (fig. 4), we cannot distinguish between SNPs under positive selection in the terminal branch leading to the Yoruba/Sub-Saharan Africans and the ancestral non-African branch (supplementary table S3, Supplementary Material online). Nevertheless, more careful study of the allele frequencies of these SNPs in other populations may serve to distinguish among these scenarios in the future. As in the other ancestry scans, we also retrieve several genes that have been previously reported in positive selection studies. For example, the highest-scoring SNP is a missense variant in SLC39A4 (rs1871534) that has been reported to be under selection in Sub-Saharan Africa and to be causal for zinc deficiency (Engelken et al. 2014).

Native American Ancestry Scan

The Native American ancestry scan yielded several novel candidates for positive selection (supplementary table S4, Supplementary Material online). As this ancestry has been less studied than the other aforementioned populations in the selection scan literature, we highlight some of the more interesting regions here.

The top SNP (rs140736443) is located in an intron of LINC00871. This SNP does not have a high CADD score (=1.125), but is very close to an SNP (rs10133371) with a very high LLRS (=16.54) and CADD score (=15.99). This SNP is also intronic but is highly conserved in primates (PhastCons = 0.972) and is located in a GERP conserved element (P = 1.92e−21). LINC00871 is a long noncoding RNA gene that has been associated with number of children born (Barban et al. 2016), although the specific trait-associated SNP in that study does not have a high LLRS. This gene also contains a suggestive association to longevity in females (Zeng et al. 2018), although this study was under-powered to retrieve genome-wide significant associations.

The third top SNP (rs2316155) has a low CADD score (=0.633) but is located near two SNPs with high LLRS (rs1466182, rs1466183) that overlap a regulatory region (ENSR00000088366) and have high CADD scores (=16.8 and 19.5, respectively). Both of these SNPs have high PhastCons conservation scores across primates, mammals and vertebrates, and both overlap a GERP conserved element.

The sixth top SNP (rs10508343) has a low CADD score but lies very close to another SNP (rs17143255) with a high LLRS and a very high CADD score (=14.16). The latter is an intergenic SNP overlapping a GERP conserved element between LINC00708 and GATA3, which has been shown to lead to abnormal hair shape and growth in mice when mutated (Kaufman et al. 2003). Interestingly, SNPs overlapping LINC00708 have been recently associated with hair shape in a GWAS of admixed Latin Americans (Adhikari et al. 2016). There is also a high-LLRS SNP in this region that is significantly associated with the response to treatment for acute lymphoblastic leukemia (rs10508343) (Yang et al. 2009).

The seventh top SNP (rs16959274) is a GTEx eQTL for GOLGA8A for tibial artery and skeletal muscle, and for GOLGA8B in pancreas. These two genes are members of the same gene family, and code for an autoantigen localized in the surface of the Golgi complex (Eystathioy et al. 2000).

The tenth top SNP (rs12580697) is a GTEx eQTL for TMTC1 in whole blood and has a moderately high CADD score (=8.676). TMTC1 codes for an endoplasmic reticulum transmembrane protein that is involved in calcium homeostasis (Sunryd et al. 2014).

The 11th top SNP (rs75607199) has a low CADD score but lies near three other SNPs (rs41325445, rs4901738, and rs59250732) with almost equally high LLRS and high CADD scores (=13.49, 19.7, and 12.67, respectively). All of these SNPs are intronic and overlap OTX2-AS1, a long noncoding RNA gene. The SNP with the highest CADD score (rs4901738) is located in a GERP conserved element and has high PhastCons conservation scores across primates and mammals (>0.98). They all lie upstream of OTX2, coding for a developmental transcription factor implicated in microphthalmia (Ragge et al. 2005), retinal dystrophy (Vincent et al. 2014), and pituitary hormone deficiency (Diaczok et al. 2008). In mice, this gene has been found to be involved in the embryonic development of the brain (Boncinelli et al. 1993), photoreceptor development (Nishida et al. 2003), and susceptibility to stress (Peña et al. 2017).

The 14th top SNP (rs78441257) has a fairly high CADD score (=12.72) and lies in a GERP conserved element of the 3′ UTR of LRAT. This gene is implicated in retinal dystrophy (Thompson et al. 2001) and retinitis pigmentosa (Sénéchal et al. 2006).

The 15th top SNP (rs1919550) is a GTEx eQTL for FBXO40 in whole blood, but does not have a high CADD score. However, it lies near an SNP (rs9813391) with a high LLRS that leads to a nonsynonymous change (R145Q) in ARGFX—a homeobox gene—and another SNP (rs4676737) with both a high LLRS and high CADD score (=14.07) overlapping a repressor region in an intron of FBXO40. The latter SNP is a GTEx eQTL for IQCB1 in fibroblasts, muscular esophagus, and thyroid. IQCB1 is associated with Senior-Loken syndrome (Otto et al. 2005), a ciliopathic eye disorder.

The 22nd top SNP (rs4946567) is an eQTL of TBC1D32 in cerebellar brain. This SNP has a high CADD score (=11.02) and is conserved across vertebrates (vertebrate PhyloP = 0.916 and vertebrate PhastCons = 0.747). Interestingly, the region in which it is located also harbors signature of selection in Yucatan miniature pigs (Kim et al. 2015; Kwon et al. 2019). TBC1D32 plays a role in cilia assembly (Ko et al. 2010) and may be involved in ciliopathic congenital abnormalities, including midline cleft, microcephaly, and microphthalmia (Adly et al. 2014).

The 23rd and 24th top SNPs (rs5758430 and rs4822061) are close to each other and lie in a large region with several high-LLRS SNPs. They are both linked GTEx eQTLs to several genes in a variety of different tissues. They are also both significantly associated with several traits related to body fat, food intake and white blood cells in the UK Biobank GeneATLAS (P$<{10}^{-8}$). Although these SNPs do not have particularly high CADD scores, there are several neighboring linked high-LLRS, high-CADD SNPs with significant associations to the same traits, including splice site and missense mutations. We also find two significantly associated SNPs in the GWAS catalog in this region (P$<{10}^{-8}$): rs4822024 is associated with Vitiligo (Jin et al. 2012) and rs13054099 is associated with neuroticism (Nagel et al. 2018).

We also repurposed our aforementioned neutral simulations under human demography to estimate the false discovery rate (FDR) of these selected variants in aggregate. We estimate the expected number of SNPs to exceed a threshold log LR T, assuming a genome length of $3\times {10}^9$ bp, a simple LD structure of 2 Mbp blocks, and ascertaining the SNP with the top log LR within each block. Under this approach, we find that at the cutoffs of top 1, 5, 10, 20, and 30 SNPs, the FDR is approximately 0.0% (i.e., up to simulation precision), 15.1%, 22.6%, 30.1%, and 42.6%, respectively. We encourage users of the program to do similar simulations for estimating FDRs for inferences made on their specific data sets.

Signals of Selection in Mexican Ancestry

We wanted to verify that our method was picking up signals of selection that were supported by alternative methods not explicitly relying on single-SNP patterns of population differentiation. For this, we used the program CLUES (Stern et al. 2019), which relies on a likelihood approach based on reconstructed approximation to the ancestral recombination graph along the genome (supplementary table S5, Supplementary Material online). We applied CLUES using parameters corresponding to the demographic history of Mexican-ancestry (MXL) individuals in the 1000 Genomes Project (i.e., effective population size inferred by the method Relate [Speidel et al. 2019]) to the set of hits identified using Ohana with selection acting on the Native American branch. We found that nine out of the ten tested SNPs showed significant (P < 0.05) signals of positive selection in MXL, under the asymptotic interpretation of the log-likelihood ratio statistics, supporting the evidence that these top hits in Native American ancestry have been targets of selection.

To learn more about the mode and time-frame of selection in these loci, we also used CLUES (Stern et al. 2019) to estimate the trajectory of allele frequency changes for the ten loci in the Native American component mentioned in table 1 (supplementary fig. S6, Supplementary Material online). In all cases, the estimated allele frequency trajectory was compatible with relative old selection leading to alleles with current day intermediate frequencies, typically between 0.4 and 0.6, that is, incomplete sweeps. The fact that we only detect incomplete sweep might be related to the filtering procedure we have used to eliminate SNPs with small MAF. The fastest change in allele frequency is found for the SNP in CSMD1 (s71523639), which currently is at frequency close to 0.5 but was at a frequency of approximately zero 700 generation ago, suggesting relative strong selection on a de novo mutation.

Discussion

We describe a new modeling framework that can detect signals of positive selection on ancestry components, using allele frequency patterns across admixed populations. It models admixture explicitly and works with an arbitrary number of populations with or without admixed ancestries. It also does not rely on labeling of samples into particular populations, and allows for testing of different positive selection models reflecting different historical adaptive hypotheses. It is in many ways similar to the Bayesian methods by Coop et al. (2010) and Günther and Coop (2013) in the structure of the likelihood function. The major differences being the use of optimization of the likelihood function in Ohana instead of Markov Chain Monte Carlo (MCMC) used by Coop et al. (2010) and Günther and Coop (2013), which provides some computational advantages. The methods also differ in other ways, including the enforcement of a tree-structure in Ohana, the use of ancestry components to model selection in hypothesized ancestral populations in Ohana, and the functionality to perform branch-specific detection of selection, or detection of selection in multiple branches if one has an a priori selection hypothesis one wants to test.

The run-time complexity of our method is linear in the number of markers, but we still recommend a high-performance cluster to be used in a typical genomic analysis. With parallelization, a selection scan takes <10 min to analyze a 6 Mbp genome for <10 ancestry components using 100 cores. An example of how to perform this parallelization can be found on the project’s wiki page on GitHub: https://github.com/jade-cheng/ohana.

Our method works by testing for selection in specific components of the ancestry covariance matrix. We also explored what would occur if we used a likelihood model in which the ancestry covariance matrix was multiplied by a scalar, so as to find “global” candidates for selection rather than testing for selection in particular ancestries. We found, however, that this was not an optimal way to detect candidates for selection, as it is biased toward finding many variants in highly drifted populations, likely because the excess variance in the Wright–Fisher process is not well modeled by the multivariate Gaussian assumption, especially at the boundaries of fixation and extinction.

We note, however, that the latent ancestry components inferred by Ohana and other similar programs cannot be strictly interpreted as corresponding to existing populations (now or in the past) and that the labels we assign to them (“European,” “Asian,” “African,” etc.) are largely for convenience. This is especially true when the studied individuals are not descended from recent admixture events among highly differentiated populations, so care should be taken in the interpretation of the identity of these components. We refer the reader to Lawson et al. (2018); Mathieson and Scally (2020) for more in-depth studies and discussions on the assumptions and limitations of latent ancestry inference methods.

We note that there is currently some debate in the field on the possibility that F_ST outliers could be caused by negative selection in various forms (see, e.g., Matthey-Doret and Whitlock 2019; Johri et al. 2020; Schrider 2020). Although it has been argued that such an effect is unlikely to explain F_ST outliers in real data (Matthey-Doret and Whitlock 2019; Schrider 2020), our method will be similarly challenged by this effect, as the information used is very similar to that of F_ST outlier scans.

When specifically testing for candidates for selection in the “European,” “East Asian,” and “Sub-Saharan African” components, we identified several well-known candidates under positive selection, including OCA2, SLC24A5, SLC45A2, ABCC1, and SLC39A4. Many of our top scoring SNPs were also previously known to be causal for particular traits, as in the case of rs17822931 in ABCC11 in East Asians, rs16891982 in SLC45A2 in Europeans, rs1426654 in SLC24A5 in Europeans, and rs1871534 in SLC39A4 in Sub-Saharan Africans.

Our scan for positive selection in the Native American ancestry component of Latin Americans yielded several novel candidates for adaptation in the human past. We found signatures of selection near genes involved in fertility (LINC00871), hair shape and growth (LINC00708), immunity (GOLGA8A/GOLGA8B and IRAK4), vision (OTX2 and LRAT), the nervous system (MDGA2), and various ciliopathies (IQCB1 and TBC1D32). Several of the highest-scoring SNPs in the candidate regions are known to be cis-eQTLs to their nearby genes, as is the case for rs12580697/TMTC1 (involved in calcium homeostasis) and rs4676737/IQCB1 (involved in ciliopathies). We also found individual SNPs with high likelihood ratio scores in favor of selection that are associated with a variety of phenotypes, including rs12426688 (fat percentage), rs10508343 (response to leukemia treatment), rs34670506 (insomnia), and the cluster of high-scoring SNPs that include rs5758430 and rs4822061, among other SNPs. This particular cluster is especially interesting, as the SNPs in the region are associated with a variety of traits related to body fat distribution, food intake and white blood cells, suggesting a possible underlying phenotype related to these traits that may have driven an adaptive event. Estimates of the FDR suggest that the lion’s share of these SNPs are selected, especially toward the higher end (e.g., the top eight SNPs have an FDR of <10%).

We provide a list of functional annotations for all the SNPs with high LLRS (>15) within a 2 Mb region surrounding each of the top genome-wide SNPs, including CADD, conservation, regulatory, and protein deleteriousness scores, which we hope will guide future functional validation studies in these regions of the genome (supplementary table S6, Supplementary Material online).

In conclusion, Ohana provides a fast and flexible selection–detection and hypothesis-testing framework. It is easy to use and has in-built visualization functionalities to explore patterns on a genome-wide and locus-specific scale. We believe that it will be a useful tool for biologists aiming to study positive selection and understanding the genomic basis of adaptation, particularly in cases where demographic histories are complex or not well characterized.

Materials and Methods

Basic Model

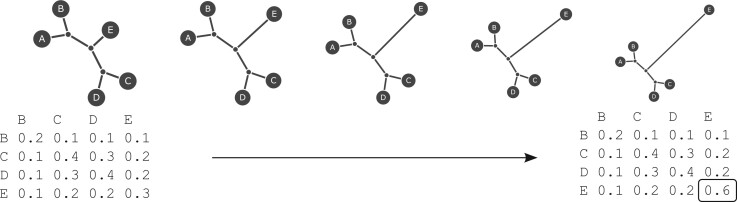
The new method is based on the Ohana inference framework (Cheng, Mailund, et al. 2017), which works with both genotype calls and genotype likelihoods. In brief, the classical structure model (Pritchard et al. 2000) is used to infer allele frequencies, ancestry components, and admixture proportions using maximum likelihood (ML). Then a covariance matrix among components is inferred using a multivariate Gaussian distribution while enforcing constraints imposed by the assumption of a tree structure. The covariance between leaf nodes is proportional to the amount of shared phylogenetic history between the nodes. Consider, for example, the example of the matrix and corresponding tree in the left side of figure 6. In this tree, all branches have length 0.1 and the tree is rooted in node A. The covariance between node E and node B is then 0.1, because B and E share one edge in the path from A. However, the covariance between node C and E is 0.2 because they share two edges in common in the path from A. The covariance matrix, $\Omega =\left\{{\Omega }_{ij}\right\}$, can be converted into a distance matrix, $d=\left\{d_{ij}\right\}$, using the rule $d_{ij}={\Omega }_{ii}+{\Omega }_{jj}-2{\Omega }_{ij}$. Treeness can then be tested using the four point condition applied to d.

Fig. 6.

Selection hypotheses and their encodings as covariance matrices. In this example, the ancestry component E is assumed to be the potential target of selection. The entry E: E in the covariance matrix is therefore allowed to deviate from the globally estimated value.

This system is underdetermined because the tree can be rooted in any node (see, e.g., Felsenstein 1985), and the same joint probability distribution is obtained no matter which rooting is chosen. We root the tree in one of the ancestry components and condition on the allele frequencies in this component when calculating the joint distribution of allele frequencies in the other components. This idea is similar to Felsenstein’s restricted ML approach (Felsenstein 1985). We emphasize that the rooting is arbitrary but that it does not imply any assumptions about this component actually being ancestral.

We estimate the covariance matrix Ω via ML. This matrix has size $(K-1)\times (K-1)$, where K is the number of populations assuming a joint density of allele frequencies given by

$$\begin{array}{c}P\left(f_j|\Omega , {\mu }_j,f_{aj}\right) \sim \mathcal{N}\left(f_{aj}, {\mu }_j\left(1-{\mu }_j\right)\left[\begin{array}{ccc}{\Omega }_{1,1}& \cdots & {\Omega }_{1,k-1}\\ ⋮& & ⋮\\ {\Omega }_{k-1,1}& \cdots & {\Omega }_{1,k-1}\end{array}\right]\right)\hfill \end{array},$$ (1)

where f_aj is the allele frequency in the ancestry component arbitrarily assigned as ancestral and f_j is a vector of the allele frequencies in the other K− 1 components, at SNP j. μ_j is the mean allele frequency for SNP j (averaged over all components). Note that this model of joint allele frequencies is similar to the model implemented in TreeMix (Pickrell and Pritchard 2012) which also uses a Gaussian approximation to allele frequency change. The full-likelihood function is obtained by taking the product of equation (1) over all SNPs in the genome. The method for optimizing this function is described in a subsequent section.

Selection Model

Following the genome-wide estimation of Ω, a natural extension of this framework is to detect SNPs that deviate strongly from the globally estimated covariance structure. The idea of testing for deviations from a Gaussian distribution follows Günther and Coop (2013), but differs in the use of an enforced tree-structure, an ML inference framework and fast optimization algorithms, thereby avoiding some of the computational challenges associated with MCMC. We also note that admixture is incorporated into the inference framework, thereby enabling the possibility to test for positive selection that acted on the ancestral components of a panel, before interbreeding occurred between the ancestors of the sampled individuals.

Ohana uses a likelihood ratio test that identifies SNPs with allele frequency patterns that are poorly described by the genome-wide pattern. After estimating Ω jointly for all SNPs, each SNP is then independently tested for deviations from this model, using a scalar factor introduced to certain elements of the covariance matrix. This scalar factor can be introduced in different ways depending on which selection hypotheses are tested. In our analyses, we chose to scale the covariance matrix such that one of its diagonal values is multiplied by a scalar, α, corresponding to differences in allele frequency in one of the ancestry components relative to the rest, for example:

$$\begin{array}{c}{\Omega }_{\alpha }=\left[\begin{array}{ccc}{\Omega }_{\mathrm{1,1}}& \cdots & {\Omega }_{1,k-1}\\ ⋮& & ⋮\\ {\Omega }_{k-\mathrm{1,1}}& \cdots & \alpha ·{\Omega }_{1,k-1}\end{array}\right]\end{array}.$$ (2)

The value of α is then estimated via ML using equation (1) (assuming all other values in ${\Omega }_{\alpha }$ is fixed at the genomic ML estimates) and a likelihood ratio is formed by testing the hypothesis of α = 1 against the alternative of $\alpha >1$. A significantly high likelihood ratio indicates a larger deviation in allele frequency in a focal component than expected under the globally estimated null-model. Figure 6 shows an example. This test can also be implemented to test selection on ancestral nonterminal lineages by multiplying the corresponding values in the covariance matrix by a scaling factor.

Under the null-hypothesis, the likelihood ratio test statistic is expected to approximately follow a 50:50 mixture between a ${\chi }_1^2$-distribution and a point mass at zero (Self and Liang 1987) because α is bounded at 1, and we use this asymptotic distribution to calculate P values.

In summary, we estimate a scaling factor for one or more components of the covariance matrix in a multivariate normal model of allele frequency distribution among populations. For each candidate SNP, we then compare the estimated covariance matrix to that obtained genome-wide, using a likelihood ratio test.

Optimization

To estimate allele frequencies, we assume a classical structure/admixture model (Pritchard et al. 2000) and first estimate Q, a matrix of admixture proportions for each individual, and F, the matrix of allele frequencies for all loci, using a quadratic programming algorithm described in full detail in Cheng, Mailund, et al. (2017) and we refer the reader to the description in this paper. This method can also incorporate genotype likelihoods.

Conditional on these estimates of values of f_j and f_aj for all j, we then maximize the likelihood in equation (1) for Ω. This optimization is done using the Nelder–Mead simplex method (Nelder and Mead 1965). It uses Cholesky decomposition (Cholesky 1910) to determine the positive semidefiniteness of a matrix and to compute matrix inverses and determinants. For the initial starting point, we use sample covariances:

$$S_c=\frac{1}{J}{\sum }_j^J\left(x_j-{\overline{x}}_j\right)(x_j-{\overline{x}}_j{)}^T\begin{array}{cc}{x}_j& =\left[\begin{array}{c}{f}_1\\ ⋮\\ f_{K-1}\end{array}\right]\end{array}\begin{array}{cc}{\overline{x}}_j& =\left[\begin{array}{c}{f}_A\\ ⋮\\ f_A\end{array}\right]\end{array}.$$ (3)

To enforce treeness, instead of using a costly constrained optimization, we convert the covariance matrix into a distance matrix, $d=\left\{d_{ij}\right\}$, which is converted into a tree using the Neighbor-Joining algorithm (Saitou and Nei 1987). We then use the covariance matrix induced by this procedure. For estimating α during a selection scan for a single SNP, conditionally on the globally estimated value of Ω, we use a simple Golden-section search algorithm (Kiefer 1953).

Simulations

We conducted population genetic simulations using the forward simulator SLiM 3 (Haller and Messer 2019). We consider three distinct demographic models (fig. 2):

• A basic four-population tree with no admixture (fig. 2a): An ancestral population splits into four subpopulations at times 4,000, 2,000, and 800 generations before present, following the topology in figure 2a. Selection is simulated on the yellow branch in figure 2a. Tests for selection are conducted for yellow ancestry (i.e., the main ancestry component in the third branch).

• A four-population tree with admixture (fig. 2b): The same model as in (1), but split times are shifted backwards in time by 100 generations; at 100 generations before present, selection is turned off, and each population is supplanted by a (1/3,1/3,1/3) mixture of the other three populations. Tests for selection are conducted for yellow ancestry (i.e., the most depleted ancestry component in the third branch).

• A model based on human demography of Mexican (MXL), Northwestern European (CEU), CHB (EAS), and African Yoruba (YRI) populations (fig. 2c): The model is based on parameter estimates from Gravel et al. (2011) and Gutenkunst et al. (2009). MXL is modeled as a (1/2,1/2) mixture of CEU and Native American (NA) ancestry. We simulate selection only in the ancestral NA population (i.e., no ongoing selection in MXL). We use Ohana to test for selection in this NA ancestry component, which is only observed in the admixed MXL individuals.

In simulations (1) and (2), we assume all populations are constant in size with $N_e=10,000$. For all simulations, we simulate a locus of 2 Mbp with mutation and recombination rates $\mu =r={10}^{-8}$ per bp per generation. In all cases, we sample 20 diploid individuals from each extant population (i.e., 160 chromosomes sampled). We simulate a single selected site occurring within a ±10 kb window of the center of the simulated locus. In order to simulate selection during particular time periods, we simulate sweeps from standing variation (an initial frequency f), although we consider such low frequencies (down to f = 0.0001) that these should produce indistinguishable patterns from those produced by hard sweeps (Przeworski et al. 2005). For each demographic scenario, we consider four different selection coefficients (s = 0, 0.01, 0.02, and 0.05) and three different ranges of starting frequencies for the selected allele (f in $[0.0001,0.001), [0.001,0.01)$, and $[0.01,0.1)$). (Simulations under model (3) exclude sweeps with f < 0.001 because the ancestral NA population size is too small for any such variation at that low frequency.) We use a neutral burn-in phase of 100,000 generations. For all simulations, as is typical in forward simulations, we scale times down by a factor of 10, and scale up the selection coefficients and mutation and recombination rates by a factor of 10, in order to ease computational burden. In all simulation scenarios we use 1,000 independent replicates. Open-source implementations of each model are provided at https://github.com/35ajstern/ohana_simulation_models.

We compared Ohana’s performance to that of two other state-of-the-art methods: pcadapt and BayPass (Gautier 2015; Duforet-Frebourg et al. 2016). Like Ohana, both methods depend on some sort of empirical null model. To this end, we simulated three 20 Mb-long neutral regions under otherwise the same settings as previously described, with s = 0, in order to generate a null data set for calibrating each method. In the case of Ohana and BayPass, this null data set is used to estimate the covariance matrix for each population; in pcadapt, we append this null data set to each region we test for selection (we do this because the pcadapt package does not have an equivalent two-step process for calculating PCs in one region and testing for deviation from these PCs in a separate region). In all cases, we filter out SNPs with MAF <0.05 prior to any analysis. In Ohana, we test for selection in specific ancestry groups; in contrast, BayPass and pcadapt test for any significant deviation from the empirical covariance matrix (BayPass models population-level covariance, whereas pcadapt models individual-level covariance). In this sense, it is important to keep in mind that Ohana is performing a more specific test for selection, and can be used to methodologically attribute selection to a particular ancestral component/branch.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.