Beyond t-Test and ANOVA: applications of mixed-effects models for more rigorous statistical analysis in neuroscience research

Abstract

In basic neuroscience research, data are often clustered or collected with repeated measures, hence correlated. The most widely used methods such as t-test and ANOVA do not take data dependence into account, and thus are often misused. This Primer introduces linear and generalized mixed-effects models that consider data dependence, and provides clear instruction on how to recognize when they are needed and how to apply them. The appropriate use of mixed-effects models will help researchers improve their experimental design, and will lead to data analyses with greater validity and higher reproducibility of the experimental findings.

1. Overview

The importance of using appropriate statistical methods for experimental design and data analysis is well recognized across scientific disciplines. The growing concern over reproducibility in biomedical research is often referred to as a “problem of inadequate rigor” (Kilkenny et al., 2009; Prinz et al., 2011). The reproducibility crisis has been attributed to various factors that include lack of adherence to good scientific practices, underdeveloped experimental designs, and the misuse of statistical methods (Landis et al., 2012; Steward and Balice-Gordon, 2014). Further compounding these challenges, we are in the midst of an ever-expanding biomedical research revolution. “Big Data” are being produced at an unprecedented rate (Margolis et al., 2014). Proper analysis of Big Data requires up-to-date statistical methodologies that take complex features of data such as explicit and implicit data dependencies into consideration. Better matching of statistical models that take data characteristics into account will allow for better interpretation of data outcomes. It will also boost the confidence in biomedical research of all stakeholders in the scientific enterprise, including the industry and the taxpaying public (Alberts et al., 2014; Freedman et al., 2015; Macleod et al., 2014). Despite recent advances in statistical methods, current neuroscience research is often conducted using a limited set of well-known statistical tools. Many models and tests assume that the observations are independent of each other. Failure to account for this dependency in the data often leads to an increased number of false positives, a major cause of the irreproducibility crisis (Aarts et al., 2014).

The t-test and ANOVA are familiar methods to all neuroscience researchers. Both methods assume that individual observations are independent of each other. For example, data measurements from multiple mice observed under different conditions, e.g., different mouse genetic models, are taken to be unique. However, this assumption of independence is false for animals clustered into cages or litters and for neuroanatomical and neurophysiological studies that rely on large scale longitudinal recordings and involve repeated measurements over time of the same neurons and/or animals (Aarts et al., 2014; Galbraith et al., 2010; Wilson et al., 2017). In those cases, data are structured as clusters of multiple measurements collected from single units of analyses (neurons and/or animals), leading to natural dependence and correlation between the observations (Figure 1).

Figure 1. Sources of correlation.

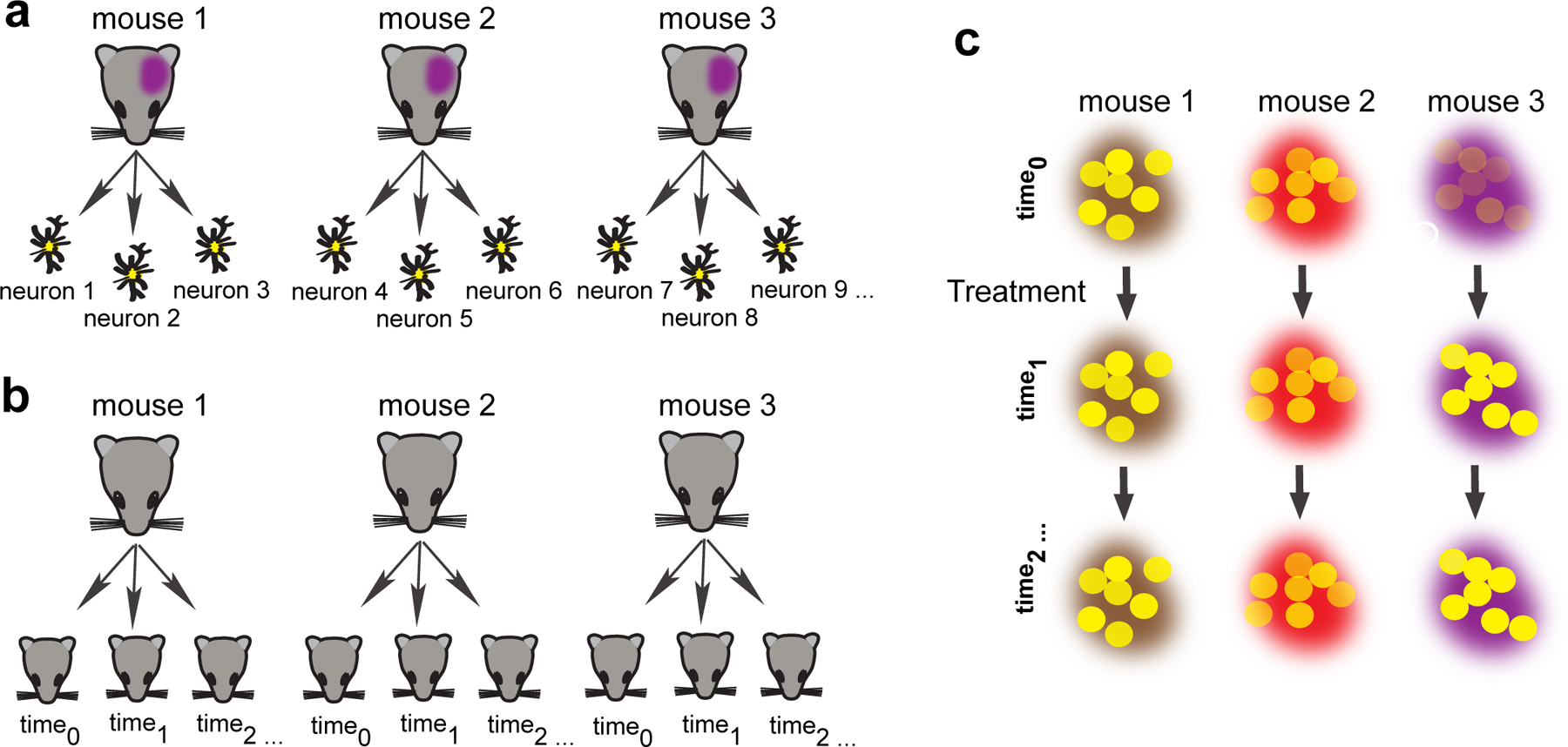
A graphical representation shows potential sources of correlated data. (A) The data are correlated because neurons from the same animal tend to be more similar to each other than neurons from different animals. (B) The observations are dependent when they are taken from the same animal temporally, while the data from different animals are independent. (C) Correlation arises from two sources: individual observations are made from neurons from three different mice before and after a drug treatment.

A quick examination of recently published articles indicate that reported results in basic neuroscience research often use inappropriate statistical methods for which the experimental designs and the ensuing/resulting data dependencies are not taken into account (Aarts et al., 2014; Boisgontier and Cheval, 2016). Our conclusion is supported by our survey of the studies published in prestigious journals over the past few years. In total we identified over 100 articles where recordings of individual neurons from multiple animals were pooled for statistical testing. Alarmingly, about 50% of these articles accounted for data dependencies in any meaningful way. Our finding is in agreement with an investigation published a few years ago (Aarts et al., 2014), which found that 53% of neuroscience articles failed to account for the dependence in their data. Representative descriptions of the inappropriate analyses read, “t(28656)=314 with p<10⁻¹⁰ over a total of n=28657 neurons pooled across six mice”, “n=377 neurons from four mice, two-sided Wilcoxon signed rank test …”, “610 A cells, 987 B cells and 2584 C cells from 10 mice, one-way ANOVA and Kruskal–Wallis test”, “two-sided paired t-test, n=1597 neurons from 11 animals, d.f.=1596”, among numerous others. Such analyses can lead to astonishingly high type I error (false positive) rates (see below). Even in cases for which data dependencies are obvious, investigators continue to use repeated ANOVA, paired t-test, or their nonparametric versions. In many cases, errors due to the use of inappropriate statistics affect the article’s main conclusion (Fiedler, 2011).

Statisticians have developed effective methods to analyze correlated data. Several widely used statistical tools that take data dependencies into account are the linear and generalized mixed-effects models, which include t-test and ANOVA as special cases. Although the value of analyzing correlated data has been increasingly recognized in many scientific disciplines, including clinical research, genetics, psychological science studies, mixed-effects (ME) models have been under-utilized in basic neuroscience research.

The purpose of our article is to provide a readable primer to neuroscience experimentalists, who do not have extensive training in statistics. We illustrate and discuss what features of the experimental questions require an appropriate consideration of adequate design and data structure, and how the proper use of mixed-effects models will lead to more rigorous analysis, reproducibility and richer conclusions. We provide concrete data examples on how to properly use mixed-effects models. In addition to providing an improved perspective on appropriate statistical analyses, we provide easy-to-follow instructions for the implementation of mixed-effects models with access to code and practice data sets to all interested users. See Glossary Box 1 for a useful glossary related to this Primer.

Box 1: Glossary.

Clustered data: In neuroscience research, the data from a study are often obtained from a number of different experimental units (referred to as clusters). The key feature of clustered data is that observations from the same cluster tend to be correlated with each other.

Dependent versus independent: For dependent samples, the selection of subjects for consideration (e.g., neurons, animals) in one sample is affected by the selection of subjects in the other samples. For independent samples, the selection of subjects for consideration (e.g., neurons, animals) is not affected by the selection of subjects in the other sample.

Effect size: An effect size is a numerical quantity for the magnitude of a certain relationship such as the difference between population means or the association between two quantitative variables.

Fixed versus random effects: Fixed effects often refer to fixed but unknown population parameters such as coefficients in the traditional linear model (LM). Random effects often refer to effects at the individual or subject level that are included in the model to take into account the heterogeneity/variability of individual observations but are usually not of direct interest.

Frequentist versus Bayesian approaches in mixed-effects models: In frequentist analysis, a fixed effect is a fixed but unknown population parameter, whereas a random effect is a value drawn from a distribution to capture individual variability. In Bayesian analysis, both fixed and random effects are random variables drawn from distributions (priors); the inference is conducted by computing the posterior distribution for the fixed effects and the variance-covariance of the random effects. The posterior distribution updates the prior information using the observed data.

Hypothesis testing: A hypothesis is a statement about a parameter (or a set of parameters) of interest. Statistical hypothesis testing is formalized to make a decision between rejecting or not rejecting a null hypothesis, on the basis of a set of experimental observations and measurements. Two types of errors can result from any decision rule (test): 1) rejecting the null hypothesis when it is true (a Type I error, “false positive”), and 2) failing to reject the null hypothesis when it is false (a Type II error, “false negative”).

Independently and identically distributed: A set of random variables are independently and identically distributed (i.i.d.) if they are mutually independent and each of them follows the same distribution.

Linear regression model (or linear model): A linear regression model is an approach to model the linear relationship between a response variable and one or more explanatory variables.

Linear mixed-effects model (LME) and generalized linear mixed model (GLMM): The LME is an extension of the linear regression model to consider both fixed and random effects. It is particularly useful when the data are clustered or have repeated measurements. The GLMM is an extension to the generalized linear model, in which the linear predictor contains random effects in addition to the fixed effects.

Parameters: Parameters are the characteristic values of an entire population, such as the mean and standard deviation of a normal distribution. Samples can be used to estimate population parameters.

Parametric versus nonparametric tests: A parametric test assumes that the data follow an underlying statistical distribution. A nonparametric test does not impose a specific distribution on data. Nonparametric tests are more robust than parametric tests as they are valid over a broader range of situations.

2. Introduction to linear and generalized linear mixed-effects (LME, GLMM) models

2.1. Important concepts and definitions related to statistical testing

To understand the practical issues of mixed-effects models in the context of neuroscience research, we next introduce several important concepts and definitions using real-world data illustrations. Considering 5000 cells measured from five mice, what is the effective sample size in this study? Is it 5000 or 5? Perhaps it is neither. The number of biological units, experimental units, and observational units can be quite distinct from each other. A detailed discussion of sample size in cell cultures and animal experiments is provided by an earlier paper (Lazic et al., 2018). Here we will use an example data set collected from our laboratory to illustrate the concept and definition of intra-class-correlation (ICC), which is a metric to quantify the degree of correlation due to clustering. We also introduce the concepts of “design effect” and “effective sample size,” and discuss why conventional methods such as t-test and ANOVA are not appropriate for this example.

ICC is a widely used metric to quantify the degree to which measurements from the same group are correlated. Depending on the specific settings that are concerned, different definitions have been proposed. For simplicity, let us consider the simple one-way ANOVA setting, where each animal is considered as a class. The total variance of data can be partitioned into the between- (inter-) and within- (intra-) class variances. The population ICC (Fischer, 1944) is defined as the ratio of the between-class variance to the total variance:

$$ICC=\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }_e^2},$$

where ${\sigma }_b^2$ denotes the between-class variance and ${\sigma }_e^2$ denotes the within-class variance. For naturally occurring clusters, ICC often falls between 0 and 1. If ICC=0, the data can be treated as uncorrelated; if ICC=1, all the observations in each cluster are perfectly correlated.

In our study of ketamine effects on neuroplasticity (Example 1, see detailed information in Section 3 below), we measured pCREB immunoreactivity of 1200 putative excitatory neurons of mouse visual cortex at different time points: collected at baseline (saline), 24, 48, 72 hours, and 1 week following ketamine treatment from 24 mice (Figure 2). The original data and full description of the experiments can be found in (Grieco et al., 2020). For this example, a large ICC suggests that neurons from the same mouse tend to be more similar to each other than neurons from different mice. For larger values of ICC, there is greater homogeneity within clusters and greater heterogeneity between clusters. As shown in Figure 2, the pCREB values of the 357 neurons in the saline group tend to cluster into groups indexed by the seven mice. The estimated ICC (Wolak and Wolak, 2015a) is 0.61, which implies that the 357 observations should not be treated as independent data points.

Figure 2. Avoiding false positives that arise from correlated measurements taken from the same animals.

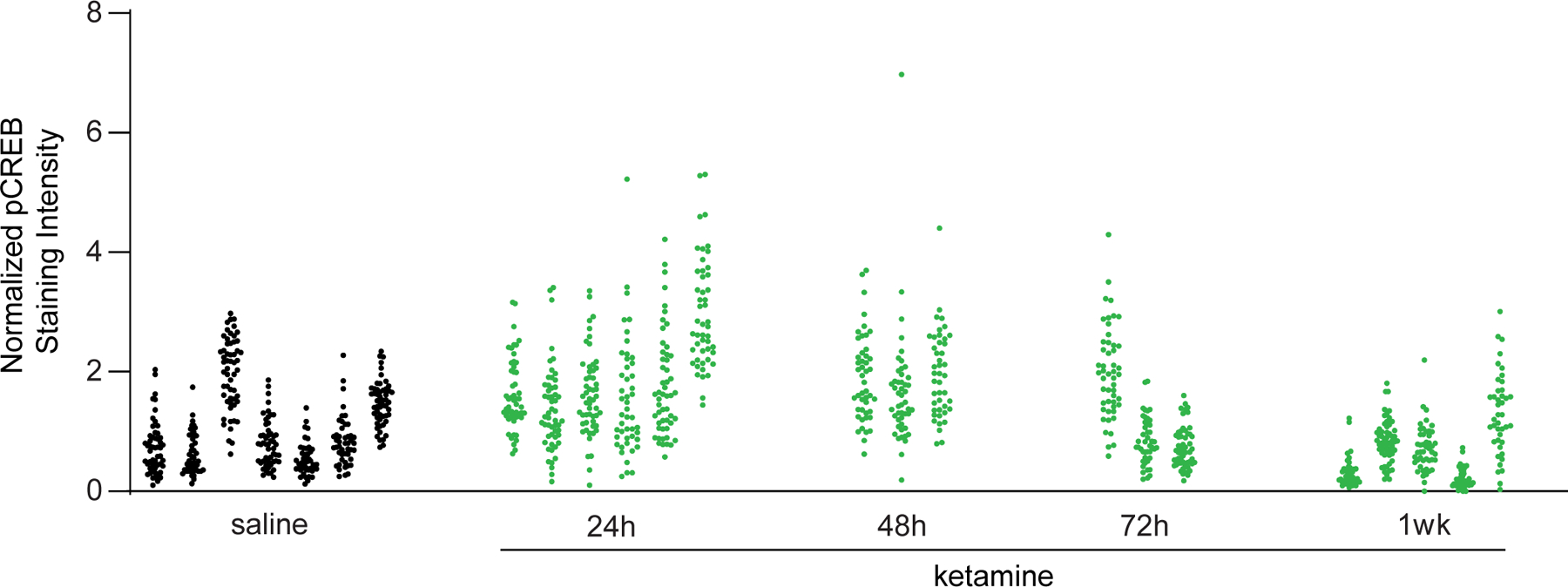
Normalized pCREB staining intensity values from 1200 neurons (Example 1). The values in each cluster were from one animal. In total, pCREB values were measured for 1200 neurons from 24 mice at five conditions: saline (7 mice, ICC=0.61), 24h (6 mice, ICC=0.33), 48h (3 mice, ICC=0.02), 72h (3 mice, ICC=0.63), 1wk (5 mice, ICC=0.54) after treatment. According to ICC, observations at 48h and 72h show the smallest and largest intra-class correlations, respectively.

To understand why conventional methods (t-test, ANOVA) fail when data dependencies are not taken into account, it is helpful to quantify the magnitude of clustering of an experiment using the design effect (D_eff) (Kish, 1965), which is defined as:

$$D_{eff}=1+\left(M-1\right)ICC$$

where M denotes the average cluster size of an experiment design. It is a useful metric to recalibrate the standard error of an estimate in the presence of clustering or adjusting sample size when designing an experiment. For the saline group, with n=357 and ICC=0.61, the design effect is 32, i.e., on average 32 neurons under the current design are equivalent to one uncorrelated neuron. This experimental design may call for more measurements, but how many should be made?

Another closely related concept that helps answer this question is the effective sample size (n_eff), which is the equivalent sample size if there is no clustering / correlation. It is defined as n_eff =n/D_eff, where n is the total sample size (number of observations). This definition is also an interpolation of the two extreme cases of ICC=0 or 1, with ICC=0 leading to n_eff =n (no correlation) and ICC=1 leading to n_eff =n/M (complete correlation). In sample size calculations, the design effect can be interpreted as a multiplying factor to obtain the desired sample size under the assumption of independence. With D_eff=32 in the saline example, the effective sample size based on the 357 neurons is n_eff=357/32≈11, which is only about 50% more than the number of mice. The ICC, design effects, and effective sample sizes for the five groups are shown in Table 1. The results indicate that there is substantial dependence in data. Unfortunately, when researchers analyze data under such circumstances, the methods they choose often make the wrong assumption that all the observations are independent from each other. One well known consequence of ignoring correlations in data is an increased number of false positives, which will be discussed in the next sub-section.

Table 1.

ICC, design effect, and effective sample size for the five groups in Example 1. ICC and the design effect were the lowest at 48h, when the data were relatively homogeneous across animals. At baseline and 72h, the data are noticeably heterogeneous across animals, leading to high ICC.

	Saline (7 mice)	24h (6 mice)	48h (3 mice)	72h (3 mice)	1wk (5 mice)
# of cells	357	209	139	150	245
ICC	0.61	0.33	0.02	0.63	0.54
Design effect	32.0	17.7	1.8	31.8	26.8
Effective sample size	11.1	17.5	76.9	4.7	9.1

2.2. Failing to account for data dependence leads to high type I error (false positive) rates

When dependence is ignored in the data analysis, null hypotheses can be erroneously rejected and confidence intervals do not have enough coverage. In the statistical literature, the action of erroneously rejecting a null hypothesis (see Glossary Box 1 and Appendix 1 of the Supplemental Materials) is called a “false positive”. For a given test, its size, or type I error rate, is defined as the probability that the null hypothesis is erroneously rejected. We say that a test has an inflated type I error rate when its type I error rate is greater than its significance level, which is often denoted as α. To evaluate the severity of inflated type I error rates due to failure to consider data dependencies in realistic scenarios, we simulated data using the dependence structure of Example 1. The number of neurons from each of the 24 animals, the number of animals from each of the five groups, and the ICCs from Example 1, illustrated in Figure 2 and Table 1, were used to generate simulated data. To ensure that the data were simulated under the null hypothesis, the responses in each of the five groups were simulated from a multivariate normal distribution with mean 0 and correlation structure based on the ICC of that group. Thus, the a priori known ground truth is that the five groups (baseline (saline), 24, 48, 72 hours, and 1 week) share the same population mean.

We simulated 10,000 data sets, and each of which were analyzed using the linear model (LM) by pooling all neurons, or were analyzed using the linear mixed-effects (LME) model, to test equal population means of the five groups. The histogram of LM p-values indicates most of the p-values are small (Figure 3a, left panel); the type I error rate is about 90% when α = 0.05 is used. Thus, with no difference between the five groups, the probability that LM will reject the null hypothesis is 90%. This strikingly large type I error rate of LM confirms that when substantial data dependency exists, the cost of failure to take data dependency into account is very serious due to the higher probability of false positives.

Figure 3.

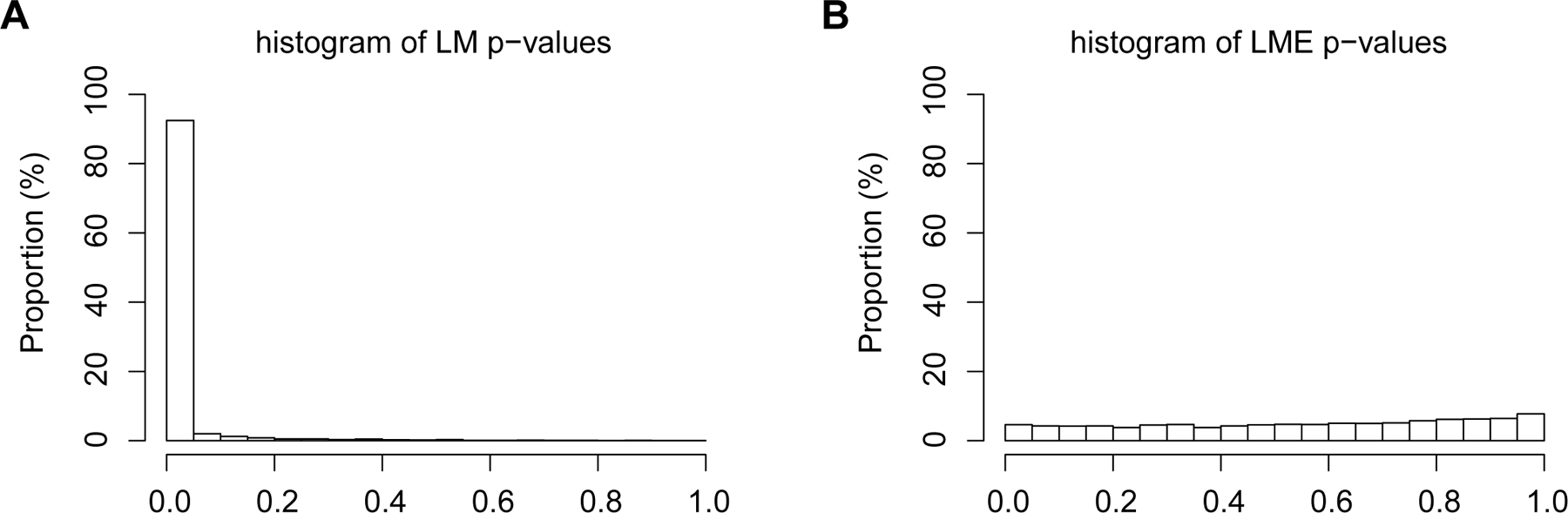
Histograms of p-values using simulated data that assume (1) no treatment effects and (2) the same sample sizes and correlation structure with Example 1. (A) Histogram of the p-values from the inappropriate method (LM) shows that ignoring the correlation structure of the data lead to surprisingly high type I error rate (90%) at significance level α=0.05. (B) Histogram of the p-values from LME.

In comparison, the histogram of LME p-values is approximately uniform between 0 and 1 (Figure 3b, right panel); if the significance level is chosen at α=0.05, the estimated type I error rate is 8.6%, which indicates that the LME test is effective in accounting for data dependency. This convincingly illustrates the need for use of the LME in neuroscience research. Next, we provide some background and describe the method of linear mixed-effects model (LME).

2.3. Linear mixed-effects model

The word “mixed” in linear mixed-effects (LME) means that the model consists of both fixed and random effects. Fixed effects refer to fixed but unknown coefficients for the variables of interest and the explanatory covariates, as identified in the traditional linear model (LM) developed by Francis Galton more than a century ago. Random effects, first proposed in (Fisher, 1919), refer to variables that are not of direct interest - however, they may potentially lead to correlated outcomes. A major difference between fixed and random effects is that the fixed effects are considered as unknown parameters whereas the random effects are considered as random variables drawn from a distribution (e.g., a normal distribution). LME was pioneered by C. R. Henderson in his series of work on animal breeding (Henderson, 1949). It is now widely accepted and has been successfully applied in various scientific disciplines such as economics, genetics, psychology, medicine and sociology (Fitzmaurice et al., 2012; Jiang and Nguyen, 2021; Laird and Ware, 1982). Depending on the disciplines and application domains, alternative names have been used for LME, including random-effects model, multi-level model, hierarchical model, and variance component model. In order to apply LME, it is necessary to understand its assumptions and representation in sufficient detail, especially with respect to simpler methods. We start by reviewing the two-sample t-test, one-way ANOVA, and the linear model, and then introduce the linear mixed-effects model.

2.3.1. Background: Two-sample t-test, one-way ANOVA, and linear model

We start from the familiar two-sample case with n₀ observations (Y₁, …, Y_n0) from a control group and n₁ observations from a treatment group (Y_n0+1, …, Y_n0+n1). Under independence and normality assumptions, the t-test statistic, which standardizes the difference of the sample means by its standard error, follows a t distribution. Equivalently, one can use a simple linear model (LM) to model the difference between treatment and control.

Let x_i denote a covariate (predictor) variable such that x_i = 1 if the observed outcome Y_i is from a subject assigned to the treatment group and x_i =0 otherwise. Then, we can assume a linear relationship between the outcome and the treatment assignment as follows:

$$Y_{\text{i}}={\beta }_0+x_{\text{i}}\times {\beta }_1+{\epsilon }_{\text{i}},i=1,\dots ,n_0,n_0+1,\dots ,n_0+n_1.$$ (1)

In this model, β₀ is the mean of the control group and (β₀+ β₁) is the mean of the treatment group. The null hypothesis of no effect of the treatment versus control is expressed as H₀: β₁ = 0 and the test statistic of the well-known t-test is identical to the least square estimate of the coefficient β₁ divided by its standard error. The Ԑ_i is the random error term. The generalization from one treatment to p treatments is e p indicator variables, also known as dummy variables, for each of the treatment labels:

$$Y_{\text{i}}={\beta }_0+x_{\text{i,1}}\times {\beta }_1+\dots +x_{\text{i,}p}\times {\beta }_p+{\epsilon }_{\text{i}},i=1,\dots ,n,$$ (2)

where n is the total number of observations. In the above multiple linear regression, β₀ indicates the population mean of the reference group (which is often just the control group). Then each coefficient β_k is the difference in population means between the k^th treatment and the reference group, since x_i,k = 1 if observation i belongs to the k^th treatment group and x_i,k =0 otherwise. Most often, we are interested in whether there is any difference in population means among all the (p +1) groups, i.e., H₀: β₁ = … = β_p = 0. If the random errors (Ԑ_i) are independently and identically distributed (i.i.d.) from a normal distribution, we can use an F-test to assess the null hypothesis H₀. The same F-test is probably more familiar to practitioners from the one-way analysis of variance (ANOVA). The idea is to decompose the total variance of the data into different sources. The two sources modeled in the multiple linear regression are the variation due to different treatments and the variation due to randomness. The F statistic used in the F-test characterizes the variation due to treatments relative to the variation due to randomness. Thus, ANOVA, in a broad sense, is a method of understanding the contributions of different factors to an outcome variable by studying the proportion of variance explained by each factor (Gelman, 2005).

Unfortunately, ANOVA is frequently misused in neuroanatomical and neurophysiological studies due to a failure of the practitioner to account for the collection of multiple observations from the same animal. Many investigators tend to use the default setup in statistical software or packages, and may not be familiar with more advanced regression framework. Mixed-effects models are a generalization of the previous methods (t-test, ANOVA, LM) and provide researchers with an effective strategy to analyze correlated data by taking dependence into account.

2.3.2. A practical guidance to the linear mixed-effects model

We consider the data in Example 1. The data consist of 1200 observed pCREB immunoreactivity values from 24 mice under five groups, which include the baseline group (7 mice) and 24 hours (6 mice), 48 hours (3 mice), 72 hours (3 mice), and 1 week after ketamine treatment (5 mice), as shown in Table 1 and Figure 2. Here the data are recorded as multiple measurements from each mouse, which represents a single unit (cluster) of analysis. Let Y_ij indicate the j^th observation of the i^th mouse, and (x_ij,1, …, x_ij,4) are the dummy variables for the treatment labels with x_ij,1 = 1 for 24 hours, x_ij,2 = 1 for 48 hours, x_ij,3 = 1 for 72 hours, and x_ij,4 = 1 for 1 week after ketamine treatments, respectively. Because there are multiple observations from the same animal, the data are naturally clustered by animal. We account for the resulting dependence by adding an animal-specific effect to the regression framework discussed in the previous section, as follows:

$$Y_{\text{ij}}={\beta }_0+x_{\text{ij,1}}\times {\beta }_1+\dots +x_{\text{ij,4}}\times {\beta }_{\text{4}}+u_{\text{i}}+{\epsilon }_{\text{ij}},i=1,\dots ,24;j=1,\dots ,n_{\text{i}};$$ (3)

where n_i is the number of observations from the i^th mouse, u_i indicates the deviance between the overall intercept β₀ and the mean specific to the i^th mouse, and Ԑ_ij represents the deviation in pCREB immunoreactivity of observation (cell) j in mouse i from the mean pCREB immunoreactivity of mouse i. Among the coefficients, the coefficients of the fixed-effects component, (β₀, β₁, β₂, β₃, β₄), are assumed to be fixed but unknown, whereas (u₁, …, u₂₄) are treated as independent and identically distributed random variables from a normal distribution with mean 0 and a variance parameter that reflects the variation across animals. It is important to notice that the cluster/animal-specific means are more generally referred to as random intercepts in an LME. Equivalently, one could write the previous equation by using a vector (z_ij,1, …, z_ij,24) of dummy variables for the cluster/animal IDs such that z_ij,k=1 for i=k and 0 otherwise:

$$Y_{\text{ij}}={\beta }_0+x_{\text{ij,1}}\times {\beta }_1+\dots +x_{\text{ij,4}}\times {\beta }_{\text{4}}+z_{\text{ij,1}}{u}_{\text{1}}+\dots +z_{\text{ij,24}}{u}_{\text{24}}+{\epsilon }_{\text{ij}},I=1,\dots ,24;j=1,\dots ,n_{\text{i}}.$$ (4)

In the model above, Y_ij is modeled by four components: the overall intercept β₀, which is the population mean of the reference group in this example, the fixed-effects from the covariates (x_ij,1, …, x_ij,4), the random-effects due to the clustering (z_ij,1, …, z_ij,24), and the random errors Ԑ_ij’s, assumed to be i.i.d. from a normal distribution with mean 0.

In the application of these methods, one practical issue is to determine which effects should be treated as fixed and which should be considered as random. A number of definitions of fixed-effects and random-effects have been given (Gelman and Hill, 2006). It is generally agreed that a fixed effect captures a parameter at the population level; as such, it should be a constant across subjects / clusters. Population-level treatment effects, which are often of direct scientific interest, are included in the fixed-effects. When scientifically relevant, predictors (such as age and gender) whose effects are not expected to change across subjects should also be treated as fixed effects. In contrast, a random effect captures cluster-specific effects (e.g., due to the animal or the cell considered), which are only relevant for capturing the dependence among observations and are typically of no direct relevance for assessing scientific hypotheses. Indeed, the mice in a study are a sample from a large population and they are randomly chosen among all possible mice. Thus, the animal-specific effects are often not of primary interest; hence, they are added to the random-effects component. In Example 1, the mean in pCREB immunoreactivity from a particular mouse is not relevant for the final analysis; however, including the mouse-specific means accounts for the correlation between observations from the same animal.

In addition to cluster-specific means, a linear mixed effects model may include additional terms that describe the variability observed within a cluster (e.g., an animal or cell). Most often, this is the case when measurements are taken at different times from within the same animal and cell and it may be important to account for possibly different cluster-specific trajectories over time. We will discuss this in more detail as it pertains to Example 3 in Section 3 below.

2.3.3. The LME in a matrix format

It is often convenient to write the LME in a very general matrix form, which was first derived in (Henderson et al., 1959). This format gives a compact expression of the linear mixed-effects model:

$$Y=\text{1}{\beta }_0+X\beta +Zu+\epsilon ,$$ (5)

where Y is an n-by-1 vector of individual observations, 1 is the n-by-1 vector of ones, the columns of X are predictors whose coefficients β, a p-by-1 vector, are assumed to be fixed but unknown, the columns of Z are the variables whose coefficients u, a q-by-1 vector, are random variables drawn from a distribution with mean 0 and a partially or completely unknown covariance matrix, and Ԑ is the residual random error.

In addition to being compact, the matrix form is convenient from a data analysis perspective, since many software packages for LMEs often require that the data are organized according to the so-called “long format”, i.e., each row of the dataset contains only the values for one observation. For example, using the long format, the data in Example 1 can be stored in a matrix with 1200 rows; the dummy variables introduced in Section 2.3.2 for the treatment labels and the cluster / animal IDs are used as the columns for X and Z, respectively. Because many software packages such as Matlab and R can take categorical variables and convert them to dummy variables automatically in their internal computation, the data for Example 1 can be stored in a 1200-by-3 matrix, with the first column being the pCREB immunoreactivity values, the second column being the treatment labels, and the last column being the animal identification numbers (see the Supplemental Materials Part I).

Since the LME model consists of both fixed and random effects, it is highly versatile and includes the traditional linear regression model (LM), the random effects model, t-test, paired t-test, ANOVA, and repeated ANOVA as special cases. In fact, software implementing the LME model can also be used to implement the LM, ANOVA, two-sample t-test, paired t-test, and other methods. In order to determine whether and which LME model should be used, one needs to understand the sources of correlation. Data visualization, as depicted in Figure 2, is the first step we recommend to have a good understanding of the data. It is helpful to have a visual inspection of model assumptions, especially regarding whether there is any data dependency due to factors that should be modeled. The decision chart in Figure 4 provides a user friendly guide to determine whether some variables should be included in the matrix Z to model the correlation in animal experiments appropriately. Please also refer to our sections below for implementation details.

Figure 4. A decision chart for setting up mixed-effects model analysis.

This basic decision chart shows in a step-wise fashion how to identify the ME application scenarios and random effects.

2.4. Generalized linear mixed-effects model (GLMM)

In this section we discuss how to model data dependency for a broader range of outcome types. Traditional linear models and the LME are designed to model a continuous outcome variable with a fundamental assumption that its variance does not change with its mean. This assumption can be violated for commonly collected outcome variables, such as the choice made in a two-alternative forced choice task (binary data), the proportion of neurons activated (proportional data), the number of neural spikes in a given time window, and the number of behavioral freezes in each session (count data). For example, a natural choice of distribution for count data is the Poisson distribution, for which its mean and variance are equal. This violates the homoscedasticity (meaning “constant variance”) assumption that is a fundamental assumption of a standard linear regression model. In addition, negative predictive values might occur in a linear model, which is undesirable for count or proportional data. These issues can be addressed by the generalized linear model framework, which is an important extension of the linear model.

We first present a unified framework to analyze various outcome types, known as the generalized linear model (GLM) (McCullagh and Nelder, 2019; Nelder and Wedderburn, 1972). It includes the conventional linear regression (for continuous variables), logistic regression (for binary outcomes), and Poisson regression (for count data) as special cases. Let Y_i be the i^th outcome variable and X_i=(X_i,1, …, X_i,p) be the corresponding covariates. The critical operation of GLM is to link the expected value of Y_i and a linear predictor (i.e., a linear combination of the covariates) through a “link” function g:

$$g\left(\text{E}\left(Y_{\text{i}}|X_{\text{i}}\right)\right)={\beta }_0+X_{\text{i,1}}\times {\beta }_1+\dots +X_{\text{i,p}}\times {\beta }_{\text{p}};$$ (6)

The link function g connects the expected mean of the outcome variable to a linear predictor. An equivalent expression is E(Y_i | X_i)=g⁻¹(β₀+X_i,1 x β₁ +… + X_i,p x β_p), where g⁻¹ denotes the inverse function of g. For example, the link function of the liner regression model is the identity function, which implies that

$$\text{E}\left(Y_{\text{i}}|X_{\text{i}}\right)={\beta }_0+X_{\text{i,1}}\times {\beta }_1+\dots +X_{\text{i,p}}\times {\beta }_{\text{p}}.$$ (7)

To further help understand the link function g, we then consider the situation when the outcome variable is binary, which is often modeled using a logistic regression. Note that a logistic regression is a special GLM with the link function g being the logit function; in other words, we model the logit-transformed success probability using a linear combination of the covariates:

$$\text{logit}\left({\pi }_i\right)=\log \left(\frac{{\pi }_i}{1-{\pi }_i}\right)={\beta }_0+X_i{}_{\text{,1}}\times {\beta }_1+\dots +X_{i\text{,}p}\times {\beta }_p$$ (8)

where the success probability πi= E(Y_i | X_i)=Pr(Y_i =1| X_i), with the last equation due to the fact that Y_i is either 0 or 1. The logit function ensures that the estimated success probabilities are always between 0 and 1, thus preventing negative predictive values or predictive values greater than 1. To complete the specification of the model, a data generating mechanism for the outcomes is needed. One natural choice is the Bernoulli distribution, i.e.:

$$Y_i|{\pi }_i~Bernoulli\left({\pi }_i\right).$$ (9)

The corresponding likelihood function can then be used to make inference on parameters using the maximum likelihood. The distributional assumptions can be relaxed by specifying the relationship between mean and variance, rather than the full distribution, which is expected to have good robustness. This approach is known as the quasi-likelihood method. We refer the interested readers to this publication (Wedderburn, 1974). The GLM generalizes the conventional LM for various types of outcomes by using appropriate link functions and by distributional assumptions of the outcomes. Like the conventional LM, all coefficients in the GLM are assumed to be unknown but fixed parameters. Next, we further extend GLM to generalized linear mixed-effects models so that the data dependence due to the underlying experimental design can be appropriately accounted for by including random effects.

To account for data dependency, the GLM has been extended to the generalized linear mixed-effects model (GLMM) (Breslow and Clayton, 1993; Liang and Zeger, 1986; Stiratelli et al., 1984; Wolfinger and O’connell, 1993; Zeger and Karim, 1991; Zeger and Liang, 1986):

$$g\left(\text{E}\left(Y_{\text{ij}}|X_{\text{i}}\right)\right)={\beta }_0+X_{\text{ij,1}}\times {\beta }_1+\dots +X_{\text{ij,p}}\times {\beta }_{\text{p}}+{\text{Z}}_{\text{ij,1}}\times u_1+\dots +{\text{Z}}_{\text{ij,q}}\times u_{\text{q}};$$ (10)

The random-effects terms in LME (equation 4) and GLMM (equation 10) play the same role; they explicitly model the dependence structure by specifying subject-specific or other relevant random effects and their joint distribution. With appropriate assumptions on the distribution of the outcome variables Y_ij’s and the mean assumption specified in equation (10), likelihood-based approaches are often used for parameter estimation. Compared to LME, the computation involved in GLMM with non-normal data is substantially more challenging, both in computational speed and stability. As a result, several strategies have been developed to approximate the likelihood (Bolker et al., 2009).

A robust alternative is the generalized estimating equation (GEE) (Zeger et al., 1988)-approach. GEE makes assumptions based on the first two moments rather than imposing explicit distributional assumptions. The idea of GEE is to estimate coefficients using a “working” correlation structure, which does not have to be identical to the unknown underlying true correlation. An incorrect correlation structure, while it would not bias the estimates, would affect the estimate of the variance. Thus, a correction approach is applied to obtain consistent estimates of variance and covariance. However, caution is merited, as GEE and GLMM might lead to different estimates and interpretations (Fitzmaurice et al., 2012). Moreover, the correction procedure in GEE relies on aggregated information across subject-level data, but for cases of animal studies that only use a few animals in an experiment, the accuracy of GEE results may be questionable.

2.5. Bayesian analysis

In the LME and GLMM framework, the random-effects coefficients are drawn from a given distribution (typically Gaussian). Therefore, Bayesian analysis provides a natural alternative for analyzing the data considered in this Primer. One inherent advantage of Bayesian analysis is that it is easy to incorporate prior information on all the parameters in the model, including both the fixed-effects coefficients and the parameters involved in the variance-covariance matrices. In particular, the Bayesian framework allows practitioners to consider distributions of the random effects that are far from Gaussian, or to consider more flexible covariance structures needed to characterize the underlying data generating process. In the frequentist framework (see Glossary Box 1 and Appendix 1 of the Supplemental Materials), computational algorithms can become formidably complex and prohibitive in those cases. The Bayesian framework obtains inference on the parameters of interest by means of the posterior distribution, which results from combining the prior information with the data using the Bayes’ theorem. Therefore, Bayesian inference does not rely on asymptotic approximations that may be invalid with limited sample sizes.

To describe how Bayesian analysis works for mixed-effects model, consider again the model (equation 4) in Section 2.3:

$$Y_{\text{ij}}={\beta }_0+X_{\text{ij,1}}\times {\beta }_1+\dots +X_{\text{ij,p}}\times {\beta }_{\text{p}}+Z_{\text{ij,1}}\times u_1+\dots +Z_{\text{ij,q}}\times u_{\text{q}}+{\epsilon }_{\text{ij}}.$$ (11)

For simplicity of presentation and to avoid advanced statistical and mathematical details required for more general models, we assume independently and identically distributed (i.i.d.) random effects, i.e., the random effects are i.i.d. from N(0, σ²_u). We also assume the errors are i.i.d. from N(0, σ²). While we focus here for simplicity on the linear model (equation 4) from Section 2.3, our discussion can also be extended to the generalized linear framework of Section 2.4. Using the Bayes’ theorem, the posterior distribution, f(β₀, β₁, …, β_p,σ²_u, σ²|Y), is proportional to the product of the likelihood function $f\left(Y|{\beta }_0,{\beta }_1\dots ,{\beta }_p,{\sigma }_u^2,{\sigma }^2\right)$ and the prior distribution $\pi \left({\beta }_0,{\beta }_1,\dots ,{\beta }_p,{\sigma }_u^2,{\sigma }^2\right)$ (summarizing the available knowledge on the parameters):

$$f\left({\beta }_0,{\beta }_1,\dots ,{\beta }_p,{\sigma }_u^2,{\sigma }^2|Y\right)=\frac{f\left(Y|{\beta }_0,{\beta }_1\dots ,{\beta }_p,{\sigma }_u^2,{\sigma }^2\right)\pi \left({\beta }_0,{\beta }_1,\dots ,{\beta }_p,{\sigma }_u^2,{\sigma }^2\right)}{f\left(Y\right)},$$ (12)

where f(Y) is a constant that depends only on the observed data but does not depend on the model parameters. If possible, the prior distribution $\pi \left({\beta }_0,{\beta }_1,\dots ,{\beta }_p,{\sigma }_u^2,{\sigma }^2\right)$ should be chosen to reflect the beliefs or information investigators may have about the parameters. In the absence of prior knowledge about the parameters, uninformative prior distributions are often employed. These types of priors are also known as flat, weak, objective, vague, or diffuse priors. For example, a uniform distribution over a wide range or a normal distribution with a very large variance can be regarded as a weak prior for the fixed-effects coefficients.

Once the likelihood and the priors have been specified, Bayesian inference often requires the use of sophisticated sampling methods to get quantities from the posterior distribution, generally denoted as Markov chain Monte Carlo (MCMC) algorithms like the Gibbs sampling (Gelfand and Smith, 1990), the Metropolis-Hastings algorithm (Casella and George, 1992; Hastings, 1970; Metropolis et al., 1953), and the Hamiltonian Monte Carlo algorithm (Betancourt, 2017; Duane et al., 1987; Hoffman and Gelman, 2014; Neal, 2011; Shahbaba et al., 2014). However, in practical applications, it is possible to employ existing software packages to conduct Bayesian analysis of mixed-effects models without the necessity of an in-depth knowledge of the underlying computational details (Bürkner, 2017; Bürkner, 2018; Fong et al., 2010; Hadfield, 2010). Inference on a parameter can then be conducted using its marginal posterior distribution. For example, one can consider the mean of the posterior distribution as a point estimate of the unknown parameter as well as a 95% credible interval to obtain the Bayesian counterpart of a confidence interval in frequentist analysis. In a Bayesian framework, the 95% credible interval is an uncertainty estimate that identifies the shortest interval containing 95% of the posterior distribution of the parameter of interest (highest posterior density interval). Hypothesis testing on the parameters of the mixed-effects models can be conducted by comparing the marginal likelihoods under two competing models, via the so-called Bayes factor. The use of a Bayesian approach and Bayes factors has been sometimes advocated as an alternative to p-values since the Bayes factor represents a direct measure of the evidence of one model versus the other (Benjamin and Berger, 2019; Held and Ott, 2018; Kass and Raftery, 1995).

3. Practical applications of the linear mixed-effects model (LME) and generalized linear mixed-effects model (GLMM)

We provide practical examples to demonstrate why conventional LM, including t-test and ANOVA fail for the analysis of correlated data, and why LME should be used instead, with its advantages in each practical example explained.

3.1. Example 1.

As described in Section 2.1, we measured pCREB immunoreactivity of 1200 putative excitatory neurons in mouse visual cortex at different time points: collected at baseline (saline), 24, 48, 72 hours, and 1 week following ketamine treatment, collected from 24 mice (Figure 2). If we use ANOVA or a linear model (LM) to compare each time point to the baseline (saline), as shown in Table 1, we find that the p-values of all comparisons are less than 0.05 and the overall difference between the five groups is highly significant (p=1.2×10⁻⁷⁸). However, recall that the 1200 neurons are clustered in 24 mice. The ICC, design effect, and effective sample sizes (Table 1) indicate that the dependency due to clustering is substantial. Therefore, the 1200 neurons should not be treated as 1200 independent cells. The lesson from this example is that the number of observational units is much larger than the number of experimental units (see reference (Lazic et al., 2018) for helpful discussion). We used an LME with animal-specific random effects to handle the dependency due to clustering. The p-values are much larger than those from LM, thus less likely to reach the threshold of significance (Table 2). Note that the difference between saline and 72h or 1wk by LME analysis is not significant after accounting for dependency of the data.

Table 2.

P-values for comparing pCREB immunoreactivity at each time point (24, 48, 72 hours, and 1 week) after ketamine treatment to the baseline (saline). The “Overall” column corresponds to the null hypothesis of no difference among the five groups (Example 1). The LME p-values are based upon the lme function in the nlme package, in which the denominator degrees of freedom are determined by the animal grouping level (Pinheiro and Bates, 2006). The methods for obtaining more accurate p-values with adjustments for multiple comparisons can be found in the Supplemental Materials.

	Overall	24h	48h	72h	1wk
Linear Model (ANOVA)	1.2×10−78	6.0×10−38	6.8×10−26	0.0291	1.1×10−08
LME	0.0029	0.0049	0.0164	0.5601	0.2525

3.2. Example 2.

Data were derived from an experiment designed to determine how in vivo calcium (Ca⁺⁺) activity of PV cells (measured longitudinally) changes over time after ketamine treatment (Grieco et al., 2020). Ca⁺⁺ event frequencies were measured from brain cells of four mice at 24h, 48h, 72h, and 1 week after ketamine treatment; Ca⁺⁺ event frequencies at 24h were compared to the other three time points. In total, Ca⁺⁺ event frequencies of 1724 neurons were measured. The boxplot in Figure 5A and LM (or ANOVA, t-test) analysis results in Table 3 indicate significantly reduced Ca⁺⁺ activity at 48h relative to 24h with p=4.8×10⁻⁶, and significantly increased Ca⁺⁺ event frequency at 1 week compared to 24h with p=2.4×10^-3. However, if we account for repeated measures due to cells clustered in mice using LME with random intercepts (the model is similar to Equation (4) in Section 2.3.2), most of the p-values are greater than 0.05 and thus fail to reach significance except that the overall p-value is 0.04.

Figure 5. Weighting effects from single animals.

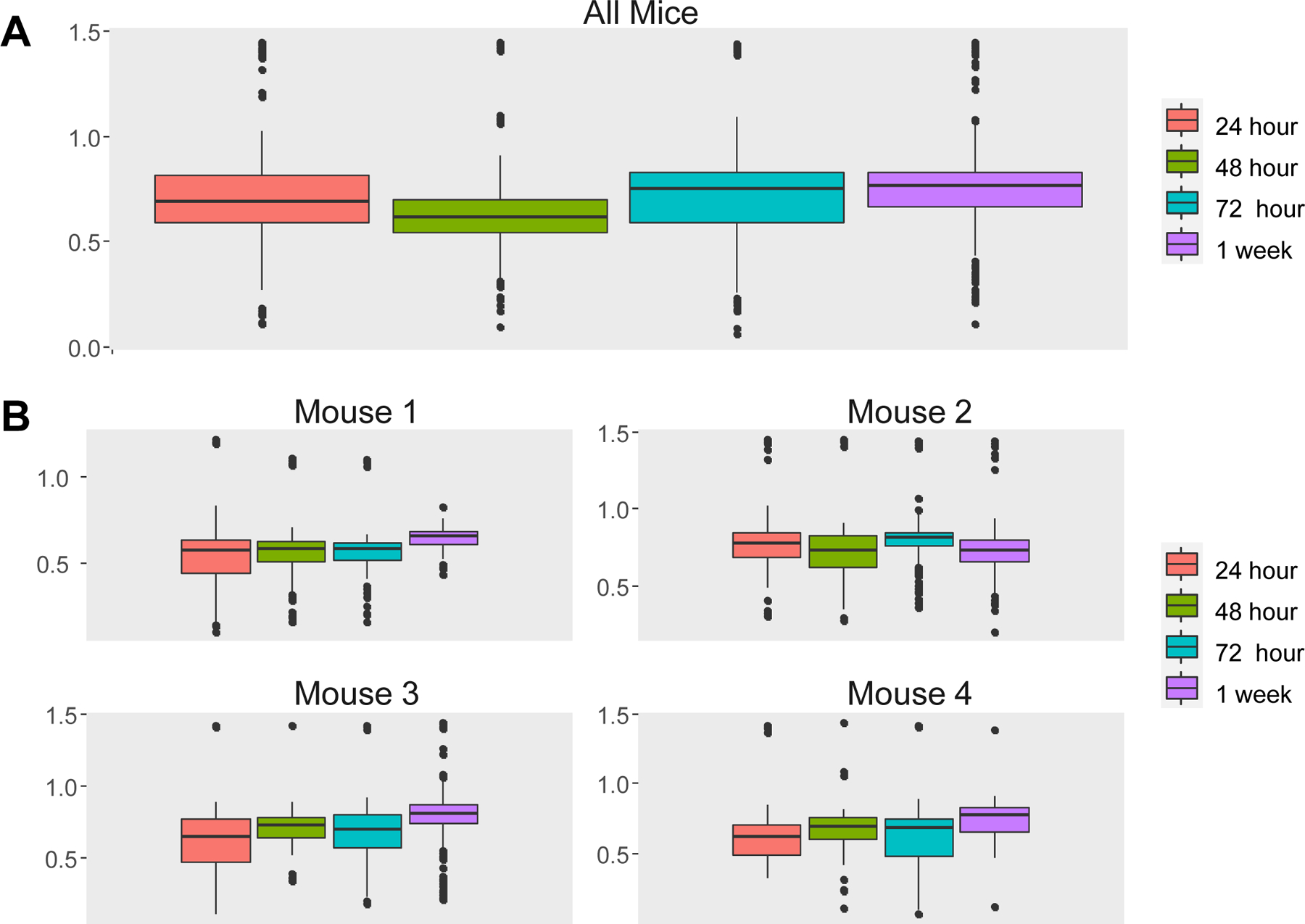
When data from different animals are naively pooled, the result can be dominated by the data from a single animal (Example 2). To illustrate this point, we present the boxplots of Ca++ event frequencies measured at four time points using two different ways: (A) Boxplot of Ca++ event frequencies using the pooled neurons from four mice. ANOVA or t-test showed that Ca++ activity was significantly reduced at 48h relative to 24h with p=4.8×10⁻⁶, and significantly increased Ca++ activity at 1wk compared to 24h with p=2.4×10^-3. However, when looking at (B) boxplots of Ca++ event frequencies stratified by individual mice, these changes occur only in mouse 2. This is because Mouse 2 contributed 43% cells, which likely explains why the pooled data are more similar to Mouse 2 than to other mice. Note that the comparisons are not significant if we account for repeated measures due to cells clustered in mice using LME, thus avoiding an erroneous conclusion.

Table 3.

The results (estimates ± s.e., and p-values) for the Ca⁺⁺ event frequency data using LM and LME (Example 2).

	48h	72h	1wk
LM (est)	−0.078±0.017	0.009±0.017	0.050±0.016
LM (p)	4.8×10−6	0.595	2.4×10−3
LME (est)	−0.011±0.014	0.020±0.014	0.025±0.014
LME (p)	0.424	0.150	0.069

To understand the discrepancy between the results from LM and LME, we created boxplots for the pooled data and for each mouse (Figure 5B). Although the pooled data (Figure 5A) and the corresponding p-value from the LM show significant reduction in Ca⁺⁺ activities from 24h to 48h, we noticed that the only mouse showing a noticeable reduction was Mouse 2. In fact, close examination of Figure 5B suggests that there might be small increases in the other three mice. To examine why the pooled data follow the pattern of Mouse 2 and not that of other mice, we checked the number of neurons in each of the mouse-by-time combinations (Table 4). The last column of Table 4 shows that Mouse 2 contributed 43% of all cells, which likely explains why the pooled data are more similar to Mouse 2 than to the other mice. The lesson from this example is that naively pooling data from different animals is a potentially dangerous practice, as the results can be dominated by a single animal that can misrepresent a substantial proportion of the measured data. Investigators limited to using LM often notice outlier data of a single animal and they may agonize about whether they are justified in “tossing that animal” from their analysis, sometimes by applying “overly creative post-hoc exclusion criteria”. The other way out of this thorny problem is the brute force approach of repeating the experiment with a much larger sample size – a more honest, but expensive solution. The application of LME solves this troubling potential problem as it takes dependency and weighting into account.

Table 4.

The number of neurons by mouse and time in Example 2. In total, Ca⁺⁺ event frequencies at 1,718 neurons were measured. When splitting the number by mouse, Mouse 2 has the largest number of measured neurons (43%). Thus, when pooling the cells naïvely, the overall results would be dominated by the results observed in Mouse 2.

	24h	48h	72h	1wk	Total
Mouse 1	81	254	88	43	466 (27%)
Mouse 2	206	101	210	222	739 (43%)
Mouse 3	33	18	51	207	309 (18%)
Mouse 4	63	52	58	37	210 (12%)
Total	383	425	407	509	1,724 (100%)

In this example there are only four mice. This number may be smaller than the one recommended for using random-effects models. However, as discussed in (Gelman and Hill, 2006), using a random-effects model in this situation will not provide much gain versus simpler analyses, but probably will not do much harm either. An alternative would be to include the animal ID variable as a factor with fixed animal effects in the conventional linear regression. However, a recent study suggests that clusters should be modeled using random effects as long as the software does not incur any computational issue such as flags due to convergence (Oberpriller et al., 2021). Note that neither of the two analyses is the same as fitting a linear model to the pooled cells together, which erroneously ignores the between-animal heterogeneity and fails to account for the data dependency due to the within-animal similarity. In a more extreme case, for an experiment using only two monkeys for example, naively pooling the neurons from the two animals faces the risk of making conclusions mainly from one animal and unrealistic homogeneous assumptions across animals, as discussed above. A more appropriate approach is to analyze the animals separately and check whether the results from these two animals “replicate” each other. Exploratory analysis such as data visualization is highly recommended to identify potential issues.

3.3. Example 3.

In this experiment, Ca⁺⁺ event integrated amplitudes are compared between baseline (saline) and 24h after ketamine treatment (Grieco et al., 2020). 1248 cells were sampled from 11 mice and each cell was measured twice (baseline and after ketamine treatment). As a result, correlation arises from both cells and animals, which creates a three-level structure: repeated measurements (baseline and after treatment) within cells, and cells within animals. It is clear that the ketamine treatment should be included as a fixed effect. The choice of the random effects deserves more careful consideration. The hierarchical structure, i.e., two observations per cell and multiple cells per animal, suggests that the random effects of the cells should be nested within individual mice. We first consider a basic model that includes random intercepts at both cell and animal levels:

$$Y_{\text{ijk}}={\beta }_0+x_{\text{ijk}}\times {\beta }_1+u_{\text{i}}+u_{\text{ij}}+{\epsilon }_{\text{ijk}},i=1,\dots ,11;j=1,\dots ,n_{\text{i}};k=0,1;$$ (13)

where the indices i, j, k stand for the i^th mouse, the j^th cell, and the k^th measurement of neuron j from mouse i. Similarly, x_ijk = 1 if the measurement is taken after treatment and 0 if it is taken at baseline. By including the cell variable in the random effect, we implicitly capture the change from “before” to “after” treatment for each cell. This is similar to how paired data are handled in a paired t-test. Moreover, by specifying that the cells are nested within individual mice, we essentially model the correlations within both mouse and cell levels. As explained in the Supplemental Materials (Part II Example 3), when the cell IDs are not unique, specifying nested random effects is necessary; otherwise two cells with the same cell ID from two different mice will be considered as sharing a cell-specific effect (known as crossed random effects, in comparison to nested random effects), which does not make sense. We recommend that users employ unique cell IDs across animals to avoid confusion and mistakes in the model specification.

For the treatment effect, LME and LM produce similar estimates; however, the standard error of the LM was larger. Thus, the p-value based on LME was smaller (0.0036 for LM vs 0.0001 for LME). In this example, since the two measures from each cell are positively correlated (Figure 6), the variance of the differences is smaller when treating the data as paired than as independent. As a result, the more rigorous practice of using cell effects as random effects leads to lower but more accurate p-values. The lesson in this example is that the LME can actually yield lower p-values than conventional approaches. This is opposite to Example 1 and Example 2 and dispels the potential notion that LME incurs a “cost” by always leading to greater p-values. Rigorous statistical analysis is not a hunt for the smallest p-value (commonly known as p-hacking or significance chasing); the objective of the experimenter should be always to use the most appropriate and thorough analysis method.

Figure 6. LME does not always lead to larger p-values than methods that ignore data dependencies.

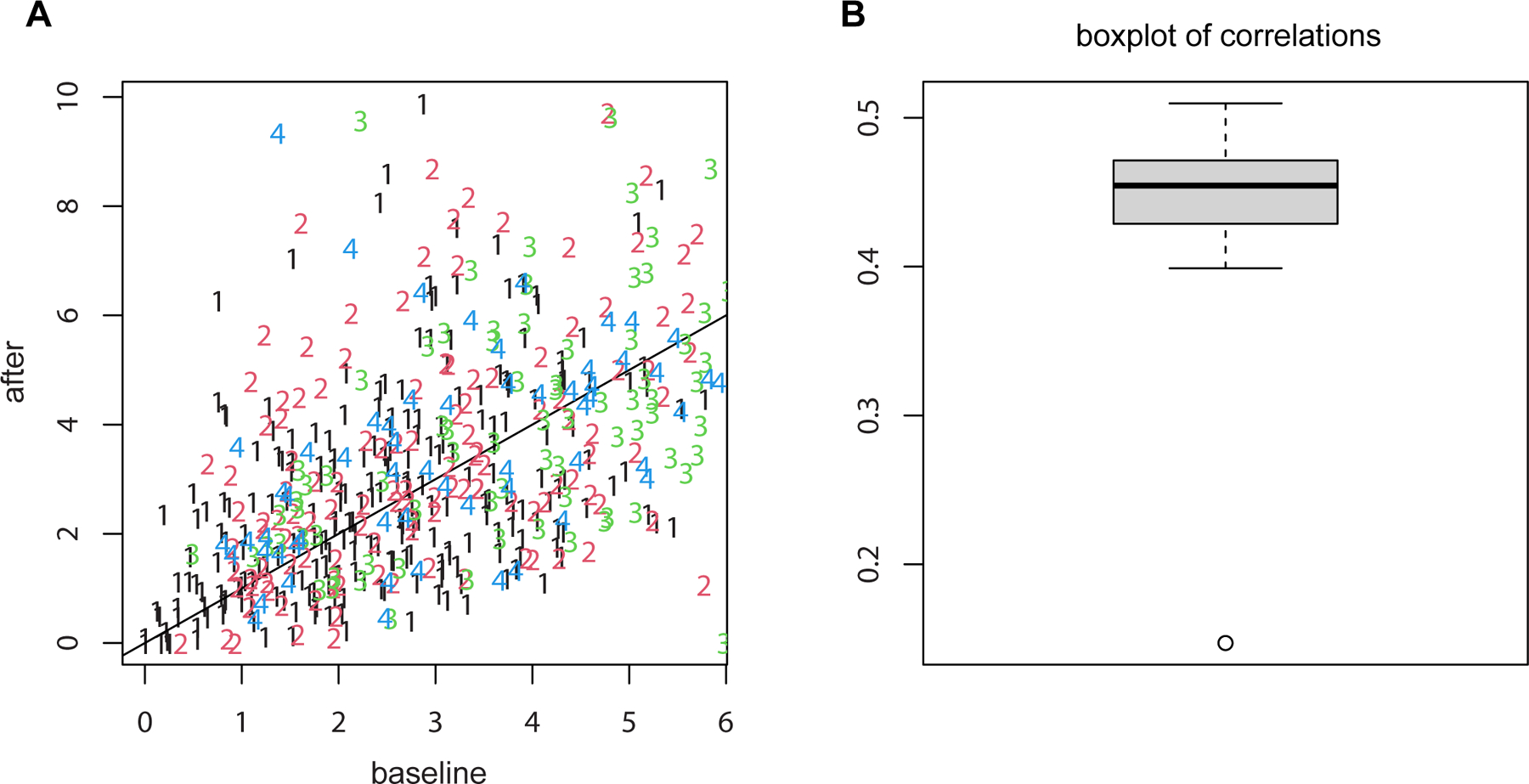
(A) the scatter plot of Ca++ event integrated amplitude at baseline vs 24h after treatment for the neurons from four example mice (labeled as 1, 2, 3 and 4) indicates that the baseline and after-treatment measures are positively correlated. (B) boxplot of the baseline and after-treatment correlations of all the 11 mice. Due to the positive correlations shown in the data, the variance of differences is smaller when treating the data as paired than independent. As a result, LME produced a smaller p-value than t-test.

In this example, the random effects involve more than one level and the LME model we fit includes neuron-specific and animal-specific random intercepts. Sometimes, models incorporating additional random effects might be appropriate to account for additional sources of variability (Barr et al., 2013; Ferron et al., 2002; Heisig and Schaeffer, 2019; Kwok et al., 2007; Matuschek et al., 2017). For example, both the overall mean levels and the treatment effects may vary across animals and neurons. A mouse may have a higher (lower) treatment response than the average population response, e.g., due to unobserved individual physiology. The plausibility of including extra random effects can often be assessed visually by linearly interpolating the observed response over the values of the predictor of interest in each cluster (e.g., all the recorded Ca⁺⁺ event integrated amplitudes pre- and post-treatment within a specific animal); that is, by conducting an LM regression within each cluster. Suppose the interpolation suggests that the slopes of the regression differ across clusters/animals along with their intercepts. In that case, the LME may incorporate both random intercepts and random slopes to capture how each mouse responds differently to the treatment. It might also be helpful to allow correlations between the different random-effect components. In the example considered here, there is a nested structure of clusters: cells within animals. Therefore, it is possible to conceive three other models with additional random effects: a model that includes random slopes only at the neuron level, a model with random slopes only at the animal level, and a model with random slopes for both neurons and animals. By conducting likelihood ratio tests to compare these models, we find that including random slopes at the neuron level leads to substantial improvement in the likelihood. On the other hand, random slopes at the animal level seem unnecessary. More detailed analyses and technical remarks are provided in our accompanying Supplemental Materials. It should be noted that the modeling decisions should not be based on tests and p-values alone, as the result might be significant even with a very small effect size if the sample size is large enough or be insignificant with a moderate or large effect size for small sample sizes. Rather, the modeling decision should always be guided by the combined information provided by the study design, scientific reasoning, and previous evidence. For example, different animals are expected to have different mean levels on outcome variables; thus, it is reasonable to model the variation due to animals by considering animal-specific random effects. A similar argument is the inclusion of baseline covariates such as age in many biomedical studied even when they are not significant. Also, when random slopes are included, it is typically recommended to include the corresponding random intercepts. If random slopes (for treatment) are included at the animal level, it is sensible to also include the animal-specific random intercepts.

3.4. Example 4.

In this example, we will illustrate how to use both frequentist and Bayesian GLMM approaches to analyze binary outcomes. The data set analyzed here is simulated based on a published study (Wei et al., 2020), in which eight mice were trained in a tactile delayed response task to use their whiskers to predict the location (left or right) of a water pole and report it with directional licking (lick left or lick right). The behavioral outcome we are interested in is whether the animals made the correct predictions. Therefore, we code correct left or right licks as 1 and erroneous licks as 0. In total, 512 trials were generated in our simulation, which includes 216 correct trials and 296 wrong trials. One question we would like to answer is whether a particular neuron is associated with the prediction. For this purpose, we analyze the prediction outcome and mean neural activity levels (measured by neuronal calcium signal changes, dF/F) from the 512 trials using a GLMM. The importance of modeling correlated data by introducing random effects has been shown in the previous examples. In this example, we focus on how to interpret results from a GLMM model for the mouse behavioral and imaging experiment.

The result from a frequentist approach shows that with the increase of one percent of mean calcium intensity (dF/F), the odds that the mice will make a correct prediction will increase by 6.4% (95% confidence interval: 2.4%−10.7%) and the corresponding p-value is 0.0016 based on the large-sample Wald test. The large-sample likelihood ratio test and a parametric bootstrap test give similar p-values.

The Bayesian analysis requires the specification of the prior distributions for the model parameters. Due to the lack of prior information, we select priors that are relatively non-informative, i.e., those have large variances around their means. More specifically, we use a normal prior with mean 0 and large standard deviation 10 for the fixed-effect coefficients. For the variances of the random intercept and the errors, we imposed a half-Cauchy distribution with a scale parameter of 5. The results showed that the odds that the mice will make a correct prediction increase by 6.2% (95% credible interval: 2.0%−10.6%) with 1% increase in dF/F. The Bayes factor of the model with dF/F versus the null model is 5.02, i.e., the posterior odds of the model with dF/F to the null model is five times of the prior odds, suggesting moderate association of dF/F with prediction (Held and Ott, 2018; Kass and Raftery, 1995). These results are comparable to those from the frequentist GLMM in the preceding paragraph.

4. Resources

We provide effective and easy-to-follow instructions for the implementation of LME and GLMM with access to the R code, with practice data sets to help with such analysis and results interpretation in the Supplemental Materials. We choose R because it is a free and open source software (CRAN) (R Development Core Team, 2020), widely adopted by the data science community. One major advantage of R over other open source or commercial software is that R has a rich collection of user-contributed packages (over 15,000), greatly facilitating a programing environment for developers and the access to cutting-edge statistical methods. There are many statistical packages. A selected (but not complete) list of packages that provide statistical inference and tools for mixed-effects models is summarized in Table 5. Our sample code, explanations and interpretations of results from lme4 (Bates et al., 2014), nlme (Pinheiro et al., 2007), icc (Wolak and Wolak, 2015b), pbkrtest (Halekoh and Højsgaard, 2014), brms (Bürkner, 2017; Bürkner, 2018), lmerTest (Kuznetsova et al., 2017), emmeans (Lenth et al., 2019), car (Fox and Weisberg, 2018), and sjPlot (Lüdecke, 2018) are provided in the Supplemental Materials.

Table 5.

Selected R packages and functions for mixed-effects modeling and statistical inference.

Package name	Functions related to mixed-effect modeling
nlme	lme: fit a linear mixed-effects model
lme4	lmer: fit a linear mixed-effects model glmm: fit a generalized linear mixed-effects model
brms	It can conduct Bayesian mixed-effects modeling.
lmerTest	It can perform hypothesis testing on fixed and random effects based on models from lme4::lmer.
emmeans	It can provide adjusted p-values for pairwise and treatments versus control comparisons.
pbkrtest	It can perform the F test (Kenward-Roger and Satterthwaite-type), and parametric bootstrap test.
car	car::Anova provides large-ample Wald test or F test with Kenward-Roger denominator degrees of freedom.
sjPlot	It can provide visualization and create manuscript-style tables.

5. Discussion and Conclusions

Our goal is to raise awareness of the widespread issue in correlated data analysis by t-test and ANOVA and to introduce effective solutions and provide clear guidance on how to analyze data that are clustered or have repeated measurements. We note that the issues raised in our article should be considered ideally in the first steps of experimental design, rather than as post-hoc applications. Prior knowledge based on direct experience, information from published literature, or pilot studies on possible ranges of ICC are useful for optimizing statistical power with fixed available resources. For repeated measurements involving a single level of clusters, formulas to obtain the optimal number of clusters (such as animals) and the number of observations per cluster (such as cells) can be determined (Aarts et al., 2014). For more complicated scenarios, simulation-based methods seem to be more suitable for accurate power analysis and sample size calculations (Green and MacLeod, 2016).

One might be tempted to use summary statistics such as cluster means to remove correlations due to animal effects. These approaches are not applicable to all experimental designs, such as those involving crossed random effects (Baayen et al., 2008). When methods based on summary statistics work, they give correct type I error rates, but they often have lower power than LME (Aarts et al., 2014; Galbraith et al., 2010). Compared to LME, the paired t-test and repeated ANOVA are far more familiar to most researchers. For simple designs such as paired samples or balanced designs, they are still valuable tools; however, they can be less efficient in the presence of missing data. For example, repeated ANOVA implements list-wise deletion, i.e., the entire list or case will be deleted if one single measure is missing. Since an incomplete case still provides information about the parameters we are interested in, deleting the entire case does not make full use of data. As a comparison, by using a likelihood approach, LME is still able to capture information provided by incomplete cases.

As generalizations of linear models, mixed-effects models (LME and GLMM) also share many of the same challenges: model selection and diagnostics, heterogeneous variances, and adjustments for multiple comparisons. What if the outcome data are severely skewed? How will one jointly analyze multiple features? Statisticians have developed methods to address these challenges. For example, resampling methods have been proposed as robust alternatives to LME (Halekoh and Højsgaard, 2014; Zeger et al., 1988). To relax the Gaussian assumption of random errors, statisticians have proposed semiparametric methods where treatment effects remain parametric and the distributions of random effects are estimated using nonparametric methods (Datta and Satten, 2005; Dutta and Datta, 2016; Rosner et al., 2006; Rosner and Grove, 1999). In addition, it is important to conduct model diagnostics on the random effects when conducting LME. Due to the limited space, it is overambitious to cover all the practical issues one may encounter in handling dependent data, including the issue of multiple testing and the misuse and misinterpretation of p-values. We refer the interested reader to specialized research articles (Aickin and Gensler, 1996; Altman and Bland, 1995; Benjamin and Berger, 2019; Benjamini and Hochberg, 1995; Gelman and Stern, 2006; Goodman, 2008; Holm, 1979; McHugh, 2011; Storey, 2002; Wasserstein and Lazar, 2016) or consult with experienced statisticians.

We believe that proper use of linear and generalized mixed-effects models will help neuroscience researchers to improve their experimental design and leverage the advantages of more recently developed statistical methodologies. The recommended statistical approach introduced in this article will lead to data analyses with greater validity, and will enable accurate and informative interpretation of results toward higher reproducibility of experimental findings in the neurosciences.

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.