Longer CAG repeat length is associated with shorter survival after disease onset in Huntington disease

Summary

It is well known that the length of the CAG trinucleotide expansion of the huntingtin gene is associated with many aspects of Huntington disease progression. These include age of clinical onset and rate of initial progression of disease severity. The relationship between CAG length and survival in Huntington disease is less studied. To address this, we obtained the complete Registry HD database from the European Huntington Disease Network and reanalyzed the time from reported age of disease onset until death. We conducted semiparametric proportional hazards modeling of 8,422 participants who had experienced onset of clinical Huntington disease, either retrospectively or prospectively. Of these, 826 had a recorded age of death. To avoid biased model estimates, retrospective onset ages were represented by left truncation at study entry. After controlling for onset age, which tends to be younger in those with longer CAG repeat lengths, we found that CAG length had a substantial and highly significant influence upon survival time after disease onset. For a fixed age of onset, longer CAG expansions were predictive of shorter survival. This is consistent with other known relationships between CAG length and disease severity. We also show that older onset age predicts shorter lifespan after controlling for CAG length and that the influence of CAG on survival length is substantially greater in women. We demonstrate that apparent contradictions between these and previous analyses of the same data are primarily due to the question of whether to control for clinical onset age in the analysis of time until death.

Introduction

Huntington disease (HD) (MIM: 143100) is an autosomal-dominant nervous system disease caused by abnormally long expansion of CAG trinucleotide repeats within the huntingtin (HTT) gene (MIM: 613004). The age of onset is well known to be strongly influenced by CAG expansion-length¹ (hereafter referred to as CAG length). Within the typically encountered range of approximately 40 to 50 CAG repeats, onset age ranges from 30 to 65 years² for most affected individuals. CAG lengths above this range are often associated with juvenile or young adult onset,³ whereas partial penetrance and late disease onset occurs for CAG lengths of 36 to 39.²

HD manifests by onset of cognitive decline, abnormal involuntary motor movements, and a less predictable range of behavioral-psychiatric problems that include severe apathy, impulsivity, and deterioration of executive function. HD develops insidiously within an affected individual, with brain changes detectable several decades before onset4, 5, 6 (and possibly from birth⁷). Upon careful examination, subtle loss of motor and cognitive function is often detectable a number of years prior to the point of clinically significant disease.^8,9

Confusingly, several overlapping and imprecise terms are used to discuss the onset of frank clinical illness (e.g., HD onset, motor onset, clinical diagnosis, motor diagnosis with 100% certainty). These differences have often been ignored in the HD literature regarding onset age. The issue is further confused because, as noted above, the onsets of many aspects of HD are gradual. Thus, there is some subjectivity in determining the degree of severity that constitutes “onset.” Within large clinical HD databases, the most commonly reported of these measures is the age of motor symptom onset as either self-reported or as estimated by a clinician. This is usually a retrospective determination and is frequently listed as between 1 and 3 years prior to “diagnosis” of significantly limiting disease.¹⁰ Although imprecise, because of its widespread reporting, this onset age has been the measure most often used to document the relationship of HD “onset” to CAG repeat length and to secondary genetic factors.

CAG length has been shown to strongly influence not only onset age but also the rate of brain changes and motor and cognitive progression in the years before and shortly after onset.11, 12, 13 However, there is little literature addressing potential relationships between CAG length and the course of late-stage disease and death. Kieburtz and colleagues¹⁴ saw little or no relationship between CAG length and loss of functional capacity in moderately advanced HD. They did not, however, consider interactions of CAG length and patient age. In contrast, in a similarly advanced sample of patients, Rosenblatt and colleagues⁴ reported a strong relationship between CAG length and continuing progression when disease duration and onset age were controlled.

We are aware of only one large-scale study examining the relationship between CAG length and death in HD. Keum and colleagues¹⁵ have reported that CAG length in HD does not predict the duration of illness from the time of disease onset until death. This finding, which the authors described as “counter-intuitive,” was based on separate statistical analyses of two datasets and did not control for onset age. The first set of data was a mixture from a variety of academic brain and tissue banks. The second was a subset of 1,314 participants from the Registry-HD observational database of the European Huntington Disease Network (EHDN),¹⁶ 115 of whom had a recorded age of death. This represents but a fraction of more than 8,000 relevant participants available within the EHDN Registry study. The criteria for choosing this subset are not explained within the referenced work.

In analyses of early disease progression, the effect of CAG length is primarily manifested by its interaction with age.^9,11,12 It thus seems relevant to ask whether CAG length influences time until death among patients who experienced onset at the same age. This overlooked consideration would potentially align our understanding of the effect of CAG length on post-onset survival with models of CAG length and disease progression. In this report, we reanalyze the length of time from HD onset until death using the complete Registry database. We use statistical modeling techniques that control for the age of onset, as well as for the retrospective reporting of onset ages before entry into the Registry study.

Subjects and methods

Upon application to the EHDN Executive Committee, we were granted access to pertinent data from the entire Registry database. The data was anonymized, including all information identifying subjects, sites, and countries. This anonymization exempted this project from local Human Subjects approval. The original study was approved by local institutional review boards at each particpating cite.

Registry was a multi-center, multi-national, prospective, observational study of HD with data collected between June 2004 and June 2017 (see web resources for clinicaltrials.gov description). Participants were recruited from HD-affected families who were known to study sites throughout Europe and thus are not a true epidemiological random sample. (To our knowledge, no such samples exist for this rare genetic disorder.) The observations used in the present analyses were collected at 156 different sites within 19 countries. Our analyses are based on 8,422 participants with expanded CAG repeat measurements (>35) with reported age of HD onset either prior to study entry (n = 8,205) or during the study (n = 217). Within this sample, 826 (9.8%) had an age of death reported. In addition to the 8,422 participants analyzed, the database contained 275 participants with onset age reported later than their age at last Registry visit. These were excluded from analyses, as there is no meaningful post-onset survival to analyze. No deaths were reported among these. We also excluded two participants with HD onset age listed as 0.

The database consists of two subsets, labeled R2 and R3 by the original investigators, with some overlap of participants. R2 data were collected earlier than R3. There were 3,507 participants with data only in R2 and 2,111 participants with data only in R3. The other 2,808 participants had data in both R2 and R3. In the earlier subset R2, the only available HD onset age values were from the “study rater’s best estimate of onset age.” In the later R3 subset, values were potentially reported for both the “rater’s best estimate of onset age” and the “age of motor onset.” The latter of these may also be the rater’s estimate but is often based on reports from the participant or a secondary informant. (The source of the estimate is not given within the database.) There is no criterion by which to judge whether the “rater’s best estimate” is objectively the better of the two onset measures. Regardless, the estimates are highly correlated. For the 6,582 participants from R3 for whom both rater and motor ages were recorded, the Pearson correlation between the two was 0.949 and the standard deviation of the age differences was 3.976 years. The correlation between R2 rater onset and R3 motor onset ages was 0.962 among 807 overlapping participants with ages recorded in both data subsets. The standard deviation of that difference was 3.302 years.

Our analyses used one observation per person after combining the two subsets. For participants included only in R2, we necessarily used the rater’s best onset estimate. In the R3 data we used the age of motor onset because of its greater inclusiveness. There were 498 participants (5.9%) more with a reported motor age than with a rater age. For 22 deaths (2.7%) in which no rater age of onset was listed, the participants had substantial HD signs and symptoms recorded prospectively within the database. For participants with inconsistent onset age reported in R2 and R3, the earlier of the ages was used. During analyses, we verified that this decision had no notable effect on the key statistical estimates of age and CAG effects within the survival models. (Details are described later in this methods section.)

We performed Cox proportional hazards survival analyses of time from HD symptom onset until death. We checked plausibility of the proportional hazard assumption using Harrell’s “zph” method¹⁷ of collapsing estimators containing a common term and then plotting and testing smoothed, scaled Schoenfeld residuals. As is customary, statistical inference and confidence intervals for proportional hazards were calculated using the log transform.

The predictor variables in the models were CAG repeat length, age of HD symptom onset, and sex. We also examined all potential two-way interactions among these variables. Further, we explored possible nonlinearity of onset age and CAG length using restricted cubic splines with up to four degrees of freedom.¹⁷ Final model selection was based on best AIC value within a predefined ordering of model complexity.

For those with reported onset earlier than their study entry, their data was considered left-truncated¹⁸ at the point of study entry. This means that the portion of their survival period before entry into Registry did not contribute to the statistical evidence used to estimate the survival model. The opportunity to observe such participants is conditional on the fact that they had already survived from the time of HD onset until entering the study. We cannot observe how often a potential participant with similar predictive characteristics would have died before having the chance to enroll. Left truncation avoids the bias that would arise from this discrepancy.

Nearly half of the analyzed sample (49.2%) had age of onset prior to the Registry study and only a single visit within the study. A participant’s age at that visit is statistically informative because it indicates that the participant survived from their onset age up to at least their age at this observation. These participants were credited with a left-truncated interval of 1 day of survival before right censoring. (It can be shown that survival model estimates are insensitive to the precise length of this short observation interval.)

Model robustness was tested in a variety of ways. We refit the model excluding small amounts of data of doubtful validity: (1) onset less than 10 years of age when CAG length was 47 or less (n = 6); (2) study enrollment within 1 month of death (potentially biasing study entry, n = 10); (3) HD onset reported but no UHDRS motor scores of five or greater within the database (n = 105). We also checked model sensitivity by reanalysis after we controlled for data subset R2 versus R3 (earlier versus later data collection), after we used age of rater onset instead of motor onset age within the R3 subset, and after we controlled for minor allele length. Consistent with exclusions in analyses reported by Langbehn and colleagues,² we refit the final model excluding 774 individuals with CAG lengths less than 41 (because of suspected enrollment bias with short repeat lengths) and 216 individuals with CAG larger than 56 (due to potentially outsized influence on model estimates of CAG effect). Finally, we examined potential confounding effects of anonymized study site and country by refitting the models with cluster effects for either of these.

To assess the robustness of our analyses to imprecise determinations of onset age, we performed a simulation study in which we perturbed the reported onset ages with normally distributed random variation. The standard deviation was 3 years, which we derived as a plausible value based on discrepancies between the rater onset and motor onset ages within the R3 Registry subset. Discrepancies between the mean simulation results and the original analysis allowed estimation of possible bias due to measurement error in model parameters and their statistical significance. Full details of the simulation methods and results are given in the supplement.

All analyses were performed using base R 3.5.3 or 4.0.2, with the survival 2.43-3, and rms 5.1-3 packages added. Initial data processing and some descriptive statistics were done using SAS 9.4.

Results

Descriptive statistics are given in Table 1. The mean age at death or last censored observation is only slightly higher than the mean age of the first observation because nearly half of the sample (49.2%) had only one observation in the data. The role of these left-truncated observations, which still contain relevant survival information, is discussed in the Subjects and methods section above.

Table 1.

Registry descriptive statistics

Measure	Mean	SD	5%ile	95%ile	Frequency (%)
HD onset age	44.68	12.70	23.96	65.00	–
Age of first observation	51.40	13.17	29.55	72.80	–
Time from onset until first observation	6.76	5.48	0.76	17.14	–
Age of death or of last observation	52.97	13.22	30.86	74.36	–
Right censoring time after onset	8.52	5.83	1.65	19.38	–
Age at death (n = 826)	58.73	13.52	37.38	80.78	–
Time from onset until death (n = 826)	13.35	6.27	4.47	24.07	–
CAG expansion length	44.58	4.72	40.00	53.00	–
Male	–	–	–	–	51.2 (n = 4108)
Death	–	–	–	–	9.8 (n = 826)

Abbreviations: %ile, percentile; HD, Huntington disease.

Controlling only for sex, we initially tested the otherwise unadjusted influence of CAG repeat length on time from symptom onset until death. The estimated hazard ratio was modest, but statistically significant. The estimated hazard ratio was 1.022, per increase in CAG, p value = 0.0014 (95% confidence interval 1.009 to 1.036) (see Table 2, model 1). Controlling for age of symptom onset (Table 2, model 2), the estimated influence of CAG length increased notably to a hazard ratio of 1.087 (95% confidence interval 1.068 to 1.105, p = 8 × 10⁻²²) per increase in CAG.

Table 2.

Proportional hazard models for time from HD onset until death

Variable	log HR	SE	z	p val	HR	95% CI
Model 1
CAG (per repeat)	0.022	0.007	3.195	1.40E−03	1.022	1.009	1.036
Men versus women	0.359	0.071	5.066	4.07E−07	1.432	1.246	1.645
Model 2
CAG (per repeat)	0.083	0.009	9.604	7.69E−22	1.087	1.068	1.105
Men versus women	0.369	0.071	5.201	1.98E−07	1.446	1.259	1.662
Age of HD onset (per year)	0.036	0.004	8.980	2.71E−19	1.036	1.028	1.044
Model 3
CAG (per repeat)	0.1227	0.0134	9.157	5.34E−20	1.131	1.101	1.161
Age of HD onset	0.0704	0.0124	5.677	1.37E−08	1.073	1.047	1.099
Age of HD onset′	−0.1191	0.0265	−4.494	6.99E−06	0.888	0.843	0.935
Age of HD onset′′	0.5751	0.1113	5.167	2.38E−07	1.777	1.429	2.211
Men versus women	2.2965	0.5782	3.972	7.13E−05	9.939	3.200	30.868
CAG by (M versus W)	−0.0422	0.0127	−3.323	8.91E−04	0.959	0.935	0.983

Abbreviations: HR, hazard ratio; SE, standard error; CI, confidence interval; p val, p value; M, men; W, women. For age of HD onset in model 3, restricted cubic spline knots were placed at 23.05, 40.00, 50.00 and 65.00 years of age. Age of HD onset′ and age of HD onset′′ are the nonlinear restricted cubic spline coefficients for age of HD onset. In model 3, the Wald test for the joint significance of the nonlinear cubic spline terms for age of HD onset = 30.62 (2 df), p = 2.24E−7. In model 3, the Wald test for the overall significance of the age of HD onset = 129.55 (3 df), p < 1E−16.

Results of these initial models (Table 2, models 1 and 2) are very strong evidence against the null hypothesis assertion that CAG length had no influence on the length of time from symptom onset until death in HD. Having rejected this hypothesis, we wanted to describe the nature of these risk relationships in as much detail as the data would allow without over-fitting. We fit models with nonlinear restricted cubic spline terms of up to four degrees of freedom for CAG length and onset age. We also tested potential interactions of these spline transformations of onset age with linear CAG effects and of linear onset-age effects with nonlinear CAG effects. Among this hierarchy of models, AIC was maximized by a three degree-of-freedom spline transformation of the main effect of onset age. The main effect of CAG length and the CAG by onset-age interaction terms involved only linear terms in the final model (Table 2, model 3).

This final model also contained a significant interaction between sex and CAG length (hazard ratio 0.959 for men versus women [95% confidence interval = 0.935 to 0.983], p = 0.00089), with men having a lower decline in survival per CAG length. Potential interactions between CAG length and onset age (either linear or in spline form) were non-significant. Model diagnostics showed that proportional hazard assumptions for the final model were consistent with the data (Figure S1 and Table S1).

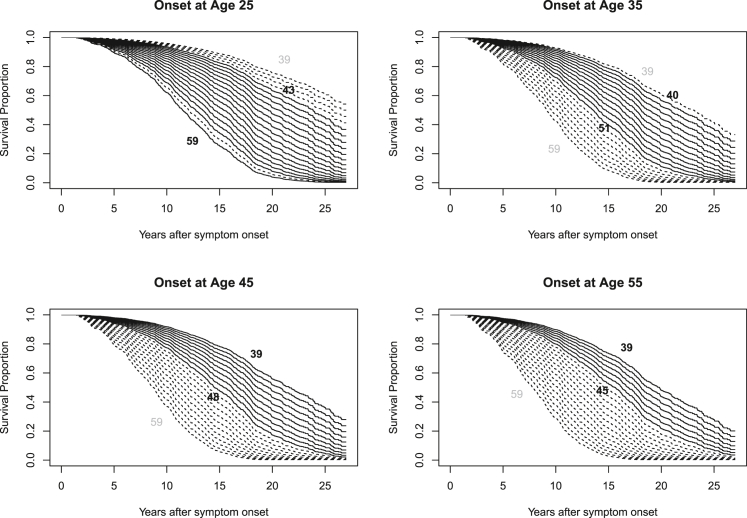
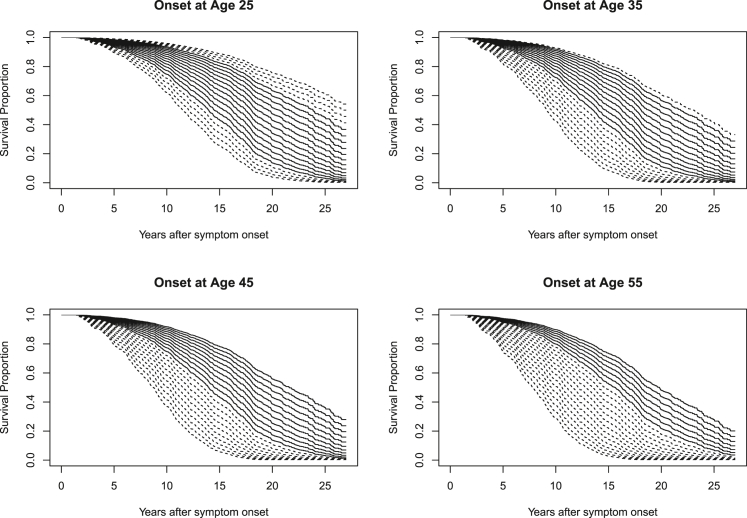
The estimated survival effect of CAG length at different onset ages is illustrated in Figure 1 for women and in Figure 2 for men. Underlying statistical tables generated from model 3 of Table 2 for these plots, including confidence intervals, are contained within Tables S3–S10. Extrapolated predictions for hypothetical CAG lengths observed in fewer than 1% of cases at these onset ages are shown with dashed lines. Because the CAG hazard ratio does not vary significantly with onset age, all CAG-specific curves in Figure 2 show a similar shape that shifts with onset age. There is, however, clear separation of the CAG-specific survival curves, which is greater for women than for men.

Figure 1.

Estimated CAG-specific survival curves in women for HD onset at ages 25, 35, 45, and 55

Estimated survival curves for the CAG repeat range 39 to 59 are shown in each plot. Dashed lines represent CAG lengths present in fewer than 1% of observations (sexes combined) in the 5-year period around the stated onset ages (e.g., 42.5 to 47.5 for the onset age 45 plot). The values of the minimum and maximum CAG lengths occurring with at least 1% frequency are printed in black within each plot. Also see Table S2.

Figure 2.

Estimated CAG-specific survival curves in men for HD onset at ages 25, 35, 45, and 55

Estimated survival curves for the CAG repeat range 39 to 59 are shown in each plot. Dashed lines represent CAG lengths present in fewer than 1% of observations (sexes combined) in the 5-year period around the stated onset ages (e.g., 42.5 to 47.5 for the onset age 45 plot). The values of the minimum and maximum CAG lengths occurring with at least 1% frequency are printed in black within each plot.

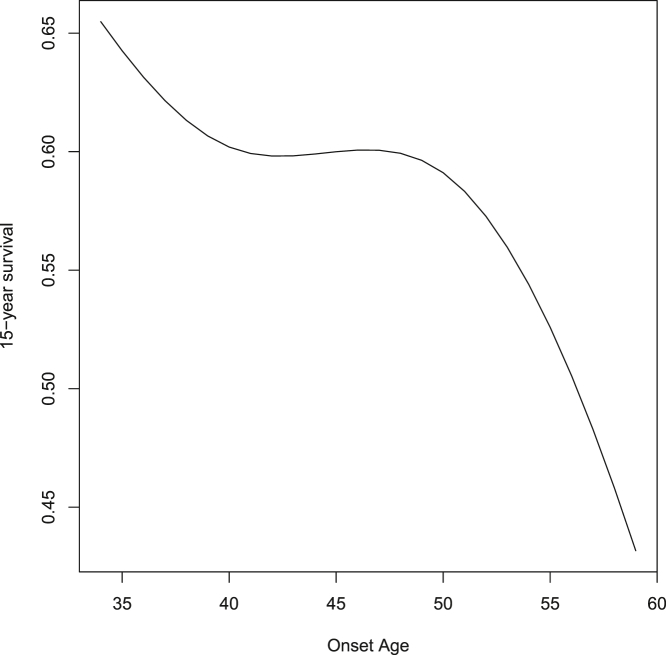
The nonlinear effect of onset age on hazard ratios is difficult to interpret from inspection of either Figure 2 or of the spline coefficients in model 3 of Table 2. Instead, in Figure 3, we illustrate the predicted effect on 15-year survival for the commonly encountered HD CAG length of 43. Note that, because of the lack of interaction between CAG length and onset age, the pattern shown is the same, regardless of CAG length. The notable nonlinear aspect is that variation in symptom onset between approximately 40 and 50 years of age has little effect on survival. However, nearly linear effects are present both below and above this range. The magnitude of the negative slope is notably greater for onset greater than age 50 than for onset less than age 40.

Figure 3.

The nonlinear effect of onset age on 15-year HD survival

The general shape of the onset age effect remains the same regardless of CAG length or survival period. There is essentially no age effect between 40 and 50 years. However, outside of that range there is a marked negative relationship between onset age and survival.

As described in the Subjects and methods, we used a variety of model alterations to test the robustness of our final model (repeated in Table S11 for convenient reference). None of these alterations substantially affected the model parameters of primary interest. We refit the model after deletion of 105 questionable age-of-onset determinations (Table S12). We then refit after restricting the CAG range to 41 to 56 (Table S13). We demonstrate no appreciable effect of minor allele CAG length (Table S14). We then checked possible effects of cohort and onset definition differences between the earlier R2 versus later R3 Registry subsets. We refit the model controlling for data subset (Table S15) and after using rater-estimated age of onset in place of motor onset for the R3 as well as the data (Table S16). Finally, we re-estimated the model after clustering adjustment for potential country effects (Table S17) or site effects (Table S18). The estimated hazard ratios for both CAG length and CAG length interaction with sex were little changed by any of these model adjustments (Tables S19 and S20).

Our simulations of potential bias due to inaccurate age of onset also showed little effect on the model results (Table S21). Most critically, the simulation suggested that the estimated log hazard ratio coefficient for the CAG-length effect in our final model (model 3 of) had an expected inflation of 6.9% and that the CAG-length interaction with sex had an expected under-estimation of 1.6%. The mean adjusted p value for the main CAG effect was 9 × 10⁻¹⁶ while the mean p value for the interaction with sex was 0.0012.

Discussion

We have demonstrated that the expansion length of the HTT CAG trinucleotide mutation has a substantial influence on time until death as measured from the onset of HD motor symptoms. The CAG influence is clearly present when age of HD onset is considered as a covariate, and we believe this is the context relevant for most clinical and research questions. However, with a larger sample than was available to Keum and colleagues,¹⁵ we have also detected a small but significant influence of CAG length on survival even before controlling for onset age. The previously reported absence of association seems likely due to lack of statistical power and may represent an example of the difficulty of asserting the truth of a null hypothesis.

The data include participants with different CAG lengths who experience onset at the same age. The current analysis demonstrates that, under this circumstance, those with longer CAG repeats typically have shorter disease duration until death. We must caution, however, that the overlapping range of CAG repeat lengths at any fixed age is limited. For example, it would be a substantial extrapolation beyond the observed data if we were to estimate the impact of CAG length 59 instead of 39 for those with onset at age 55. We have emphasized the observed CAG ranges for various ages in Figures 1 and 2.

Our findings are consistent with the well-documented influence of CAG length upon both the age of clinical onset and rate of preclinical and early clinical progression. Although some important extrinsic risk factors (e.g., quality of care) and end-stage pathological processes that hasten death are unrelated to CAG length, the present analysis provides very strong evidence that the length of life after HD onset is not independent of CAG length.

We found an interaction with sex, showing that CAG length has a stronger influence on the age of all-cause mortality in women than in men. The only outcome we could analyze was death due to any cause, including deaths unrelated to HD. Matching for age, men are well known to have higher general mortality rates. This may dilute the apparent CAG effect in men and be the source of the statistical interaction. It is therefore unclear whether there is a sex difference in the CAG influence on the HD disease processes that lead to death.

Baseline age is often an important predictor in survival analyses of the time from a disease-related event until death. A classic example is the prognostic modeling of the Mayo Clinic primary biliary cirrhosis data,¹⁹ which is often used as a teaching case for survival analysis methodology.^17,18,20 Age does not become irrelevant just because it is not the metric used as the survival outcome. In the present case, if ignored, age of onset is a confounder because it is an additional important predictor of HD survival and is not independent of CAG length. Those with higher CAG lengths tend to become ill at an earlier age. One could hypothesize that more aggressive illness, driven by longer CAG repeat lengths, is imposed on a younger and essentially healthier body. This may approximately counterbalance the adverse effect on mortality of longer CAG repeats such that the apparent CAG length influence is small when onset age is not considered.

HD age of onset determination is somewhat subjective. Indeed, the underlying concept is imprecise, given the insidious initial presentation of HD signs and symptoms. One might question whether the idea of onset age is even meaningful. Despite a high correlation, there is not perfect agreement between the patient’s, the caregiver’s, and clinician’s estimate of this age, all usually reported retrospectively. There is no standardized objective definition of “onset,” and this age determination would vary somewhat from clinician to clinician as well. The underlying reality is that the clinically significant signs and symptoms of HD typically develop as a transition over a period of a very few years, while the range of ages when this happens varies over decades. Furthermore, death typically occurs 10 to 20 years after this onset transition. Considering these relative timescales, the ages of onset, though imperfectly defined and imprecise, nonetheless reflect information meaningful to the questions at hand.

The imprecision of onset age is seldom discussed and is perhaps underappreciated within the HD genetic literature. We have addressed the potential impact of rater discrepancies from the perspective of measurement error. This is a special case of such error because survival length is measured from the age of onset. There is therefore a perfect negative correlation between measurement errors in age of onset (predictor) and length of survival (outcome). If onset is reported too early, then survival after onset is exaggerated. This may partially explain the fact that, for a constant CAG length, earlier reported onset predicts longer survival. Our simulation study suggested that measurement error tends to cause a slightly exaggerated bias in the estimated effect of CAG length, but this bias is far too weak to affect the conclusion that survival after onset has a substantial dependence upon CAG repeat length. With this conclusion in mind, we do not report simulation-adjusted estimates (Table S21) as our final best estimates, as they are only averages of a range of plausible but unmeasurable small biasing effects.

Consistent with the interpretation of Keum and colleagues,¹⁵ we found no notable evidence of a survival effect for the short allele CAG length. Despite earlier claims to the contrary,²¹ minor allele length has been convincingly shown to play no substantial role in determining age of HD onset.²² Our sensitivity analysis further supports the assertion that variation of minor CAG allele length within its usual range has no bearing on the course of HD.

Although we did not have access to the brain bank database studied by Keum and colleagues,¹⁵ it seems reasonable to hypothesize that lack of control for onset-age also confused the interpretation of that data. The use of standard linear regression methods may also have contributed to the lack of a detectable CAG effect. In many cases (including all cases when the proportional hazards assumption is correct), a statistical model based only on observed failures (i.e., deaths) biases the estimated magnitude of risk factor effects toward zero. If using a simple regression model, this can be avoided only if a prospectively identified sample is followed until all members have died. Indeed, this bias is the motivation for survival analysis models that properly account for censored data from those who have not yet died.

Despite the overwhelming statistical significance of CAG length in the current analysis, Registry is not a random sample from the HD population. Rather, it is a sample drawn from willing HD research participants. Therefore, models based on this data may be biased relative to the general HD population. Replication is quite a challenging proposition, given the rarity of HD and its slow disease course. However, the ongoing, world-wide ENROLL-HD study²³ may eventually provide adequate mortality data to attempt such a confirmation.

The CAG association with survival is strong enough to suggest the presence of CAG-length-dependent pathological mechanisms, even in the later stages of disease. Ongoing pathological research should account for this instead of focusing on explanations of why end-stage disease is unrelated to CAG length. The relationship between CAG length and survival will also have relevance to future disease-modifying clinical trials. As these trials begin to target more advanced diseases stages, age-CAG combinations may help define patient risk groups appropriate for specific therapeutic approaches. The results also confirm that, as with current trials involving earlier disease stages, statistical control and balanced randomization of age and CAG length will be important in assuring unbiased and maximally powered trials.

As with other HD phenomena associated with CAG repeat length, we caution against clinical overinterpretation. Our findings suggest that clinicians should provide ongoing care with some expectation that adult-onset Huntington disease will progress more aggressively with longer CAG lengths. However, much individual variation in survival remains after accounting for CAG length. Despite the association of HD disease course with trinucleotide expansion length, within the contexts of personalized medicine and genetic counseling, we must continue to emphasize that CAG length is not destiny.

Published: December 22, 2021

Web resources

• OMIM, https://www.omim.org/

• Registry investigators of the European Huntington Disease Network, http://www.ehdn.org/wp-content/uploads/REGISTRY-contributors-full-list.pdf

• Registry study registration and description, https://clinicaltrials.gov/ct2/show/NCT01590589