STRUCTURED CORRELATION DETECTION WITH APPLICATION TO COLOCALIZATION ANALYSIS IN DUAL-CHANNEL FLUORESCENCE MICROSCOPIC IMAGING

Abstract

Current workflows for colocalization analysis in fluorescence microscopic imaging introduce significant bias in terms of the user’s choice of region of interest (ROI). In this work, we introduce an automatic, unbiased structured detection method for correlated region detection between two random processes observed on a common domain. We argue that although intuitive, using the maximum log-likelihood statistic directly suffers from potential bias and substantially reduced power. Therefore, we introduce a simple size-based normalization to overcome this problem. We show that scanning using the proposed statistic leads to optimal correlated region detection over a large collection of structured correlation detection problems.

1. Introduction

Most, if not all, biological processes are characterized by complex interactions between biomolecules. A common way to decipher such interactions is to use multichannel fluorescence microscopic imaging, where each molecule is labeled with the fluorescence of a unique emission wavelength. Then, their biological interactions can be measured by the correlations between the fluorescently labeled proteins in user-selected regions of interest (ROIs). Although it is an ad hoc approach, a visual inspection of the overlayed image from both channels is a common first step in determining colocalization in multichannel fluorescence microscopy, especially in terms of the spatial location of the colocalization. However, the potential pitfalls of this naïve strategy are well documented, showing that merged images are heavily influenced by factors such as bleed-through, cross-talk, and the relative intensities between channels; see, for example, Bolte and Cordeliéres (2006), Comeau, Costantino and Wiseman (2006), and Dunn, Kamocka and McDonald (2011).

Since the pioneering work of Manders and his collaborators in the early 1990s, quantitative methods have been added to colocalization analysis; see, for example, Manders et al. (1992) and Manders, Verbeek and Aten (1993). These approaches typically proceed by first manually selecting a region of interest (ROI), where the two molecules are considered likely to colocalize. The degree of colocalization is determined using various correlation coefficients, most notably, Pearson’s correlation coefficient or Manders’ correlation coefficients, computed specifically within the chosen ROI; see Manders, Verbeek and Aten (1993), Costes et al. (2004), Adler, Pagakis and Parmryd (2008), and Herce, Casas-Delucchi and Cardoso (2013), among others. Obviously, the calculated outcomes of these approaches depend on the manually selected ROI, making the analysis subjective, and creating a bottleneck for high-throughput microscopic image processing. Moreover, even if a region is selected following particular principles, colocalization cannot be inferred directly from the value of the correlation coefficient computed within the ROI, because the value of the coefficient does not translate into statistical significance. This problem can be alleviated using permutation tests, as suggested by Costes et al. (2004). However, this still neglects the fact that the ROI is selected based upon the plausibility of colocalization within the region, thus introducing significant bias. Thus, the resulting p-value may appear significant merely because of our failure to adjust for the selection bias. The present work is motivated by the clear need for an automated, objective, and statistically valid way to detect regions of colocalization.

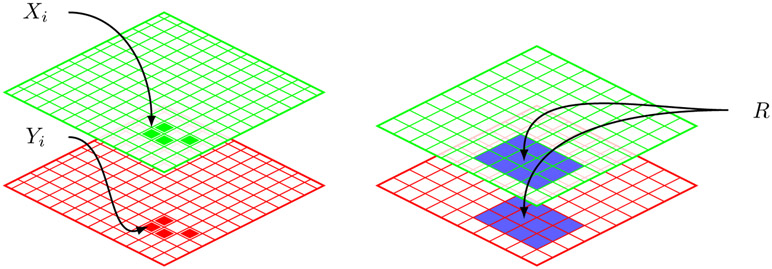
Colocalization analyses can be formulated naturally as a broad class of problems that we refer to as “structured correlation detection.” Here, we observe collections of random variables within a common domain to determine whether there is a region in which a subset of these variables are correlated. These types of problems arise naturally in many fields. For example, in finance, detecting periods in which two common stocks show unusual correlation is essential to the so-called pairs trading strategy (see, e.g., Vidyamurthy (2004)). Other potential examples of structured correlation detection problems can be found in Chen and Gupta (1997), Robinson, de la Pena and Kushnir (2008), Wieda, Krämera and Dehling (2011), and Rodionov (2015), among others. We build a novel mathematical model for structured correlation detection within the context of a colocalization analysis. Specifically, denote the index set of all pixels in the field of view by $\mathbb{I}$. In a typical two- or three- dimensional image, $\mathbb{I}$ could be a lattice of the corresponding dimension. In practice, it is also possible that $\mathbb{I}$ is a certain subset of a lattice. For example, when investigating intracellular activities, $\mathbb{I}$ only includes pixels that correspond to the interior of a cell or a compartment (e.g., nucleus) within the cell. For each location i ∈ $\mathbb{I}$, let X_i and Y_i be the intensities measured at the two channels, respectively, as illustrated in the left panel of Figure 1. Hereafter, (X_i, Y_i) are assumed to be independent across i.

Figure 1.

Pixel view of dual channel images.

In the absence of colocalization, we assume that X_i and Y_i are uncorrelated. This can be modeled as

$$\left[\begin{array}{c}\hfill X_i\hfill \\ \hfill Y_i\hfill \end{array}\right]\sim N\left(\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_2\hfill \end{array}\right],\left[\begin{array}{cc}\hfill {\sigma }_1^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_2^2\hfill \end{array}\right]\right),$$ (1.1)

where the marginal means μ₁ and μ₂ and the variances ${\sigma }_1^2$ and ${\sigma }_2^2$ may be unknown. In the presence of colocalizaton, X_i and Y_i are correlated. In this case, we treat them as observations from a correlated bivariate normal distribution,

$$\left[\begin{array}{c}\hfill X_i\hfill \\ \hfill Y_i\hfill \end{array}\right]\sim N\left(\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_2\hfill \end{array}\right],\left[\begin{array}{cc}\hfill {\sigma }_1^2\hfill & \hfill \rho {\sigma }_1{\sigma }_2\hfill \\ \hfill \rho {\sigma }_1{\sigma }_2\hfill & \hfill {\sigma }_2^2\hfill \end{array}\right]\right).$$ (1.2)

When colocalization occurs, it typically does not occur at isolated locations. As a result, a colocalization region R is more structured than an arbitrary subset of $\mathbb{I}$. For example, colocalization may be observed frequently within a contiguous region R, as illustrated in the right panel of Figure 1. Let $\mathcal{R}$ be a library containing all possible regions in which correlation may be present. For example, $\mathcal{R}$ could be the collection of all ellipses or polygons on a two-dimensional lattice ($\mathbb{I}$). The primary goal of correlation detection in general, and colocalization analysis in particular, is to determine whether there is an unknown region R ∈ $\mathcal{R}$, such that (1.1) holds for all i ∈ $\mathbb{I}$ \ R, and (1.2) holds for all i ∈ R and for some ρ ≠ 0.

Because we do not know which region R ∈ $\mathcal{R}$ includes correlations, this requires structured multiple testing. Such tests have been studied extensively; see, for example, Lepski and Tsybakov (2000), Dümbgen and Spokoiny (2001), Desolneux, Moisan and Morel (2003), Pacifico et al. (2004), Arias-Castro, Donoho and Huo (2005), Dümbgen and Walther (2008), Hall and Jin (2010), Walther (2010), Arias-Castro, Candès and Durand (2011), Fan, Han and Gu (2012), Chan and Walther (2013), Cai and Yuan (2014), and Enikeeva, Munk and Werner (2015), among others. However, a colocalization analysis is unique in at least two aspects. First, most, if not all, existing works focus exclusively on signals at the mean or variance, with a single observation at every location. In contrast, we examine the correlation coefficient between two observations at each pixel. Not only do we want to detect signals in terms of the correlation, but we also want to do so in the presence of unknown marginal means and variances as nuisance parameters. Second, prior works tend to treat $\mathbb{I}$ as one dimensional and $\mathcal{R}$ as a collection of segments. These assumptions promote statistical analyses, and may improve the computation time. The few exceptions include Arias-Castro, Donoho and Huo (2005), who studied classes of geometrical shapes on a lattice, and Walther (2010), who considered rectangles on a two-dimensional lattice. However, in the case of a colocalization analysis, the index set $\mathbb{I}$ is multidimensional, and the set $\mathcal{R}$ usually contains more complex geometric shapes. To address both challenges, we have developed a general methodology for correlation detection on a broad domain that is readily applicable to colocalization analyses.

Our method is motivated by the observation that, for a relatively general family of $\mathcal{R}$, likelihood ratio statistics exhibit a subtle dependence on the size of a candidate region. As a result, using such statistics directly for correlation detection may lead to nontrivial bias and substantially reduced power. Similar observations have been made on the detection of signals at the mean level (e.g., Dümbgen and Spokoiny (2001); Dümbgen and Walther (2008); Walther (2010); Chan and Walther (2013)). To overcome this problem, we introduce a size-corrected likelihood ratio statistic. We show that scanning using the proposed statistic yields optimal correlation detection for a large family of $\mathcal{R}$, in the sense that it can detect elevated correlations at a level that no other detectors could improve upon significantly. We show that a scan based on the proposed statistic can be computed efficiently for a large collection of geometric shapes in arbitrary dimensions, characterized by their covering numbers under a suitable semimetric. This includes, among others, convex polygons or ellipses, arguably two of the most commonly encountered ROI shapes in practice.

The rest of the paper is organized as follows. In the next section, we introduce our size-corrected likelihood ratio statistic for a general index set $\mathbb{I}$ and a collection $\mathcal{R}$. Then, we discuss how the statistic can be used to automatically detect regions of colocalization. We investigate its efficient implementation, as well as the theoretical properties of the proposed method. Section 3 gives several concrete examples of $\mathbb{I}$ and $\mathcal{R}$ that show how to apply the general methodology to these specific situations, and Section 4 discusses the optimality of our approach. Numerical experiments are presented in Section 5 to further illustrate the merits of the proposed methods. All proofs are relegated to the Supplementary Material, for brevity. We believe the proposed method can greatly improve current colocalization analysis workflows, removing the bias introduced by the pre-selection of ROIs, and replacing it with an automatic, robust means of selecting colocalization regions.

2. Structured Correlation Detection

In a general correlation detection problem, $\mathbb{I}$ can be an arbitrary index set, and $\mathcal{R}\subset 2^{\mathbb{I}}$ is a given collection of subsets of $\mathbb{I}$. We are interested in testing the null hypothesis H₀, that (1.1) holds for all i ∈ $\mathbb{I}$, against a composite alternative H_a, that (1.2) holds for all i ∈ R, whereas (1.1) holds for all i ∉ R, for some R ∈ $\mathcal{R}$. We argue here that the usual maximum log-likelihood ratio statistic may not be suitable for correlation detection and, thus, introduce a size-based correction to address the problem.

2.1. Likelihood ratio statistics

A natural test statistic for our purpose is the scan, or maximum log-likelihood ratio statistic:

$$L^{\ast }=\underset{R\in \mathcal{R}}{\max }{L}_R,$$

where L_R is the log-likelihood ratio statistic for testing H₀:

$$L_R=-(\mid R\mid -2)\log (1-r_R^2).$$ (2.1)

Here, ∣R∣ is the cardinality of R, and r_R is the Pearson correlation within R:

$$r_R=\frac{{\sum }_{i\in R}(X_i-{\overline{X}}_R)(Y_i-{\overline{Y}}_R)}{\sqrt{{\sum }_{i\in R}(X_i-{\overline{X}}_R{)}^2{\sum }_{i\in R}(Y_i-{\overline{Y}}_R{)}^2}},$$

where

$${\overline{X}}_R=\frac{1}{\mid R\mid }\sum _{i\in R}{X}_i,\text{and}{\overline{Y}}_R=\frac{1}{\mid R\mid }\sum _{i\in R}{Y}_i.$$

Strictly speaking, L_R defined by (2.1) is not the genuine likelihood ratio statistic, which would replace the factor ∣R∣ −2 on the right-hand side of (2.1) by ∣R∣. Our modification accounts for the correct degrees of freedom so that, for a fixed uncorrelated region R,

$$L_R\approx (\mid R\mid -2)\frac{r_R^2}{1-r_R^2}\sim t_{\mid R\mid -2}^2;$$

see, for example, Muirhead (2008). Obviously, when ∣R∣ is large, L_R approximately follows a ${\chi }_1^2$ distribution, and the effect of such a correction becomes negligible.

Using scan or maximum log-likelihood ratio statistics to detect spatial clusters or signals is a common practice in many fields; see, for example, Fan (1996), Fan, Zhang and Zhang (2001), and Glaz, Naus and Wallenstein (2001), and the references therein. The statistics are popular because it is well known that they are minimax optimal if ∣R∣ is small relative to $\mid \mathbb{I}\mid$; see, for example, Lepski and Tsybakov (2000). However, it is also known that when considering changes in the mean, these methods may lead to nontrivial bias (e.g., Dümbgen and Spokoiny (2001); Dümbgen and Walther (2008)). We show here that this is also the case for our task, and that such a strategy may not be effective for correlation detection unless ∣R∣ is very small. In particular, we show that, in the absence of a correlated region, the magnitude of L_R depends critically on its size ∣R∣. Therefore, the maximum L_R over regions of different sizes is typically dominated by those evaluated on smaller regions. As a result, using L* for correlation detection could be substantially conservative in detecting larger correlated regions.

We now examine the behavior of the maximum of L_R for R ∈ $\mathcal{R}$ of a particular size. Note that it is possible that there is no element in $\mathcal{R}$ that is of a particular size. To avoid lengthy discussion to account for such trivial situations, we consider instead the subset

$$\mathcal{R}(A)=\left\{R\in \mathcal{R}:\mid R\mid \in \left(\frac{A}{2},A\right]\right\},$$

for some positive A. In other words, $\mathcal{R}(A)$ is the collection of all possible correlated regions of size between A/2 and A. The factor of 1/2 is chosen arbitrarily, and can be replaced by any constant in (0,1). Basically, $\mathcal{R}(A)$ includes elements of $\mathcal{R}$ that, roughly speaking, are of size A. It is clear that

$$L^{\ast }=\underset{A}{\max }\left\{\underset{R\in \mathcal{R}(A)}{\max }{L}_R\right\}.$$

We argue that the magnitude of ${\max }_{R\in \mathcal{R}(A)}$ L_R may vary with As under the null hypothesis. In particular, we show that for a large collection of $\mathcal{R}(A)$, ${\max }_{R\in \mathcal{R}(A)}$ L_R can be characterized precisely.

Obviously, the behavior of ${\max }_{R\in \mathcal{R}(A)}$ L_R depends on the complexity of $\mathcal{R}(A)$. More specifically, we first assume that the possible correlated regions are indeed more structured than arbitrary subsets of $\mathbb{I}$, in that there exist constants c₁, c₂ > 0 independent of A, and n := $\mid \mathbb{I}\mid$, such that

$$\mid \mathcal{R}(A)\mid \le c_{1}n{A}^{c_2}.$$ (2.2)

In other words, (2.2) dictates that $\mid \mathcal{R}(A)\mid$ increases with A only polynomially. In contrast, a completely unstructured setting, where $\mathcal{R}=2^{\mathbb{I}}$ and the collection of all subsets of $\mathbb{I}$ and the number of all subsets of $\mathbb{I}$ of size A are of order n^A, depends on A exponentially. Condition (2.2) essentially requires that $\mathcal{R}$ be a much smaller subset of $2^{\mathbb{I}}$ and, therefore, imposes structures on the possible regions of correlation.

Naïve counting of the size of $\mathcal{R}(A)$, as above, however, may not reflect its real complexity. To this end, we also need to characterize the dissimilarity of the elements of $\mathcal{R}(A)$. For any two sets R₁, R₂ ∈ $2^{\mathbb{I}}$, write

$$d(R_1,R_2)=1-\frac{\mid R_1\cap R_2\mid }{\sqrt{\mid R_1\mid \mid R_2\mid }}.$$

It is easy to see that d(·, ·) is a semimetric on $2^{\mathbb{I}}$. We now consider the covering number of sets of a particular size in $\mathcal{R}$ under d. Let N(A, ϵ) be the smallest integer such that there is a subset, denoted by ${\mathcal{R}}_{\text{app}}(A,ϵ)$, of $\mathcal{R}$ with

$$\mid {\mathcal{R}}_{\text{app}}(A,ϵ)\mid =N(A,ϵ)$$

and

$$\underset{R_1\in \mathcal{R}(A)}{\text{sup}}\underset{R_2\in {\mathcal{R}}_{\text{app}}(A,ϵ)}{\text{inf}}d(R_1,R_2)\le ϵ.$$

Note that we require the covering set ${\mathcal{R}}_{\text{app}}(A,ϵ)\subset \mathcal{R}$. It is clear that N(A, ϵ) is a decreasing function of ϵ and N(A, 0) = $\mid \mathcal{R}(A)\mid$. We shall also adopt the convention that N(A, 1) represents the largest number of non-overlapping elements from $\mathcal{R}(A)$. Clearly, without any structural assumption, we can always divide $\mathbb{I}$ into n/A subsets of size A. We assume that the collection $\mathcal{R}(A)$ is actually rich enough that

$$N(A,1)\ge c_3\frac{n}{A},$$ (2.3)

for some constant c₃ > 0. Furthermore, we assume there are not too many “distinct” sets in $\mathcal{R}(A)$, in that there are certain constants c₄, c₅, c₆ > 0 independent of A and N, such that

$$N(A,ϵ)\le c_4\frac{n}{A}{\left(\log \frac{n}{A}\right)}^{c_5}{\left(\frac{1}{ϵ}\right)}^{c_6}.$$ (2.4)

Conditions (2.2), (2.3), and (2.4) are fairly general, and hold for many common choices of $\mathcal{R}$. Consider, for example, the case when $\mathbb{I}=\{1,2,\dots ,n\}$ is a one-dimensional sequence, and

$$\mathcal{R}=\{(a,b]:0\le a<b\le n\}$$

is the collection of all possible segments on $\mathbb{I}$. It is clear that there are at most n – ℓ segments of length ℓ for any ℓ ∈ (A/2, A], which means

$$\mid \mathcal{R}(A)\mid \le \frac{1}{2}nA.$$

In addition, for any A, there are at least ⌊n/A⌋ distinct segments

$$\left\{((i-1)A,iA]:i=1,\dots ,\lfloor \frac{n}{A}\rfloor \right\},$$

of length A, implying that (2.3) also holds. On the other hand, it is not hard to see that the collection of all segments starting at (i – 1)ϵA/2 (i = 1, 2, …) of length between A/2 and A can approximate any segment of length between A/2 and A, with approximation error ϵ. Therefore,

$$N(A,ϵ)\le \left(\frac{A∕2}{ϵA∕2}\right)\left(\frac{n}{ϵA∕2}\right)=2\frac{n}{A}{\left(\frac{1}{ϵ}\right)}^2,$$

so that (2.4) also holds. In the next section, we consider more complex examples, motivated by colocalization analysis, and show that these conditions are expected to hold in relatively general settings.

We now show that if $\mathcal{R}(A)$ satisfies these conditions, ${\max }_{R\in \mathcal{R}(A)}$ L_R concentrates sharply around 2log(n/A).

Theorem 1. Suppose that (1.1) holds, for all i ∈ $\mathbb{I}$. Furthermore, assume that (2.2) and (2.4) hold. Then,

$$\underset{R\in \mathcal{R}(A)}{\text{max}}{L}_R\le 2\log \left(\frac{n}{A}\right)+O_p\left(\log \log \left(\frac{n}{A}\right)\right),\text{as}n\to \infty .$$ (2.5)

If, in addition, (2.3) holds, then

$$\underset{R\in \mathcal{R}(A)}{\text{max}}{L}_R=2\log \left(\frac{n}{A}\right)+O_p\left(\log \log \left(\frac{n}{A}\right)\right),\text{as}n\to \infty .$$ (2.6)

We adopt a generic chaining (see, e.g., Talagrand (2000)) argument for the proof of Theorem 1. A similar technique is used by Dümbgen and Spokoiny (2001) to establish bounds for likelihood ratio statistics in detecting mean shifts in a sequence. One of the main difficulties in using this type of argument is to quantify the dependence between the likelihood ratio statistics evaluated on two overlapping regions, which is considerably more involved for correlation coefficients than it is for normal means. More recently, Rivera and Walther (2013) argued that, instead of generic chaining, one could take advantage of the classical result on the maximum of sub-Gaussian random variables by considering the square root of the likelihood ratio statistics. Moreover, they show that if $\mathcal{R}$ consists of one-dimensional segments, it may be possible to simplify the technical argument by explicitly using the properties of an approximation set of $\mathcal{R}$. Similar arguments are made by Walther (2010) to treat rectangles on a two-dimensional lattice. However, it is not immediately clear to what extent their techniques can be applied in our setting, owing to the difficulty of characterizing the dependence structure among L_Rs and the generality of the library $\mathcal{R}$.

2.2. Size-corrected likelihood ratio statistics

An immediate consequence of Theorem 1 is that the value of L* alone may not be a good measure of evidence of correlation. Furthermore, it depends critically on the size of R for which L_R is maximized. As such, when using L* as a test statistic, the critical value is driven largely by ${\max }_{R\in \mathcal{R}(A)}$ L_R, corresponding to smaller A. Therefore, a test based on L* may be too conservative when correlation is present in a region with a large cardinality. Several remedies have been proposed in the literature to overcome this hurdle when considering detecting mean shifts (e.g., Dümbgen and Spokoiny (2001); Dümbgen and Walther (2008); Chan and Walther (2013)). Following a similar spirit, we normalize ${\max }_{R\in \mathcal{R}(A)}$ L_R, leading to the following size-corrected log-likelihood ratio statistic:

$$\begin{gathered} T^{\ast }=\underset{A}{\max }\left\{\frac{1}{\log \log (n∕A)}\left[\underset{R\in \mathcal{R}:\mid R\mid =A}{\text{max}}{L}_R-2\log \left(\frac{n}{A}\right)\right]\right\} \\ =\underset{R\in \mathcal{R}}{\max }\left\{\frac{1}{\log \log (n∕\mid R\mid )}\left[L_R-2\log \left(\frac{n}{\mid R\mid }\right)\right]\right\}. \end{gathered}$$

For brevity, we henceforth assume that ${\max }_{R\in \mathcal{R}}$ ∣R∣ ≤ n/4. In general, we can always replace log x by log₊(x) := log(max{x, 1}) to avoid the trivial cases where the logarithms may not be well defined. After size correction, Theorem 1 suggests that T* is bounded almost surely when n → ∞, and is not dominated by statistics evaluated on small regions.

It is clear that under the null hypothesis, the distribution of T* is invariant to the nuisance parameters and, therefore, can be evaluated using a Monte Carlo simulation. More specifically, we simulate $(X_i^{\ast },Y_i^{\ast }{)}^{\mathsf{T}}$ ~ N(0,I₂) independently for i ∈ $\mathbb{I}$, and compute T* for the simulated data. The distribution of T* can be approximated by the empirical distribution of the test statistics estimated by repeating this process. Denote by q_α the (1 – α)-quantile of T* under the null hypothesis. We reject H₀ if and only if T* > q_α. The complete test procedure is summarized in Algorithm S1 in the Supplementary Material. This clearly is an α-level test, by construction. We show in Section 4, that it is also a powerful test for detecting correlation.

One of the potential challenges for scan statistics is computation. To compute T*, we need to enumerate all elements in $\mathcal{R}$, which could be quite burdensome. To reduce the computational cost, Arias-Castro, Donoho and Huo (2005) suggested evaluating L_R on a carefully chosen approximation set of $\mathcal{R}$, for several specific examples of $\mathcal{R}$. See also Walther (2010), where $\mathcal{R}$ is a collection of rectangles on a two-dimensional lattice. A key insight obtained from studying T* suggests an alternative to T* that is more amenable for computation. Specifically, although numerous, regions of large size, that is $\mathcal{R}(A)$ with a large A, may have fewer “distinct” elements. As such, we do not need to evaluate L_R on each R ∈ $\mathcal{R}(A)$, but rather on a smaller covering set $\mathcal{R}(A)$.

With a slight abuse of notation, write

$${\mathcal{R}}_k=\{R\in \mathcal{R}:\mid R\mid \in (2^{-k}n,2^{-(k-1)}n]\},k=2,\dots ,\lfloor {\log }_{2}n\rfloor +1.$$

It is clear that $T^{\ast }={\max }_k{T}_k^{\ast }$, where

$$T_k^{\ast }=\underset{R\in {\mathcal{R}}_k}{\max }\left\{\frac{1}{\log \log (n∕\mid R\mid )}\left[L_R-2\log \left(\frac{n}{\mid R\mid }\right)\right]\right\}.$$

It turns out that for

$$k\le k_{\ast }≔\lfloor {\log }_{2}n-2{\log }_2\log n\rfloor ,$$

we can approximate $T_k^{\ast }$ very well by scanning through only a small number of R from ${\mathcal{R}}_k$. In particular, let ${\tilde{\mathcal{R}}}_k$ be a 1/(4k²) covering set of ${\mathcal{R}}_k$, with

$$\mid {\tilde{\mathcal{R}}}_k\mid =N\left(2^{-(k-1)}n,\frac{1}{4k^2}\right).$$

We approximate $T_k^{\ast }$ by

$${\tilde{T}}_k^{\ast }=\underset{R\in {\tilde{\mathcal{R}}}_k}{\max }\left\{\frac{1}{\log \log (n∕\mid R\mid )}\left[L_R-2\log \left(\frac{n}{\mid R\mid }\right)\right]\right\},$$

where k ≤ k*. Denote

$${\tilde{T}}^{\ast }=\underset{k}{\max }{\tilde{T}}_k^{\ast },$$

where, with a slight abuse of notation, ${\tilde{T}}_k^{\ast }=T_k^{\ast }$ for k > k*. Rather than use T*, we now consider ${\tilde{T}}^{\ast }$ as our test statistic; see Algorithm S2 in the Supplementary Material. As before, we compute the 1 – α-quantile ${\tilde{q}}_{\alpha }$ of ${\tilde{T}}^{\ast }$ under the null hypothesis using the Monte Carlo method, and reject H₀ if and only if ${\tilde{T}}^{\ast }>{\tilde{q}}_{\alpha }$.

Compared with T*, the new statistic ${\tilde{T}}^{\ast }$ is much more computationally friendly. More specifically, under the complexity condition (2.4), it amounts to computing the corrected likelihood ratio statistic on a total of

$$\begin{gathered} \sum _{k\le k_{\ast }}N\left(2^{-(k-1)}n,\frac{1}{4k^2}\right)+\sum _{k>k_{\ast }}N\left(2^{-(k-1)}n,0\right) \\ \le c_4(\log 2{)}^{c_5}{4}^{c_6}n(\log n{)}^{c_5+2c_6+1}+c_{1}n(\log n{)}^{2c_2+1} \end{gathered}$$

sets. In other words, the number of size-corrected likelihood ratio statistics we need to evaluate in computing ${\tilde{T}}^{\ast }$ is linear in n, up to a certain polynomial of logarithmic factor.

3. Correlation Detection on a Lattice

In the previous section, we presented a general methodology for correlation detection under a generic domain. We now examine more specific examples, motivated by colocalization analysis in microscopic imaging, and discuss the operating characteristics of the proposed approach. In particular, we focus on correlation detection in a two-dimensional lattice, where $\mathbb{I}=\{(i,j):1\le i,j\le m\}$, such that n = m², although the discussion can be extended straightforwardly to more general situations, such as rectangular or higher-order lattices.

Most imaging tools allow users to visually identify areas of colocalization, allowing either a convex polygonal or ellipsoidal ROI to be selected by the user prior to colocalization calculations. Motivated by this, we consider the automatic, objective detection of correlated ROIs on either an unknown convex polygonal or an ellipsoidal region on a two-dimensional lattice. We show that, in both cases, the collection $\mathcal{R}$ of all possible correlated areas satisfies conditions (2.2), (2.3), and (2.4); thus, the size-corrected scan statistic ${\tilde{T}}^{\ast }$ can be computed efficiently.

3.1. Polygons

We first examine convex k-polygons. Any k-polygon can be indexed by its vertices {(a_i, b_i) : 1 ≤ i ≤ k}, and is therefore denoted by K({(a_i, b_i) : 1 ≤ i ≤ k}). For expositional ease, we focus on the case in which the vertices are located on the lattice, although the general case can also be examined with further care. The convexity of a polygon allows us to define its center as ($\overline{a}$, $\overline{b}$), where

$$\overline{a}=\frac{1}{k}\sum _{i=1}^k{a}_k,\text{and}\overline{b}=\frac{1}{k}\sum _{i=1}^k{b}_i.$$

Denote by

$$r_i=\sqrt{(a_i-\overline{a}{)}^2+(b_i-\overline{b}{)}^2}$$

the distance from the ith vertex to the center. Thus, we focus on nearly regular polygons, where all r_i are of the same order. In this case, the collection of possible correlated regions is:

$${\mathcal{R}}_{\text{polygon}}(k,M)=\left\{K(\{(a_i,b_i):1\le i\le k\}):\frac{{\max }_i{r}_i}{{\text{min}}_i{r}_i}\le M\right\}.$$

Recall that

$${\mathcal{R}}_{\text{polygon}}(A;k,M)=\left\{R\in {\mathcal{R}}_{\text{polygon}}(k,M):\mid R\mid \in \left(\frac{A}{2},A\right]\right\}.$$

The following result states that (2.2) holds for ${\mathcal{R}}_{\text{polygon}}$(k, M).

Proposition 1. There exists a constant c > 0, depending on k and M only, such that

$$\mid {\mathcal{R}}_{\text{polygon}}(A;k,M)\mid \le cn{A}^k.$$

We now verify (2.3) for ${\mathcal{R}}_{\text{polygon}}$(k, M). To this end, note that any convex k-polygon can be identified using a minimum bounding circle, as shown in Figure 2. Clearly, if two polygons intersect, so do their minimum bounding circles. This immediately implies that (2.3) holds, because we can always place ⌊m/r⌋² mutually exclusive circles of radius r over an m × m lattice.

Figure 2.

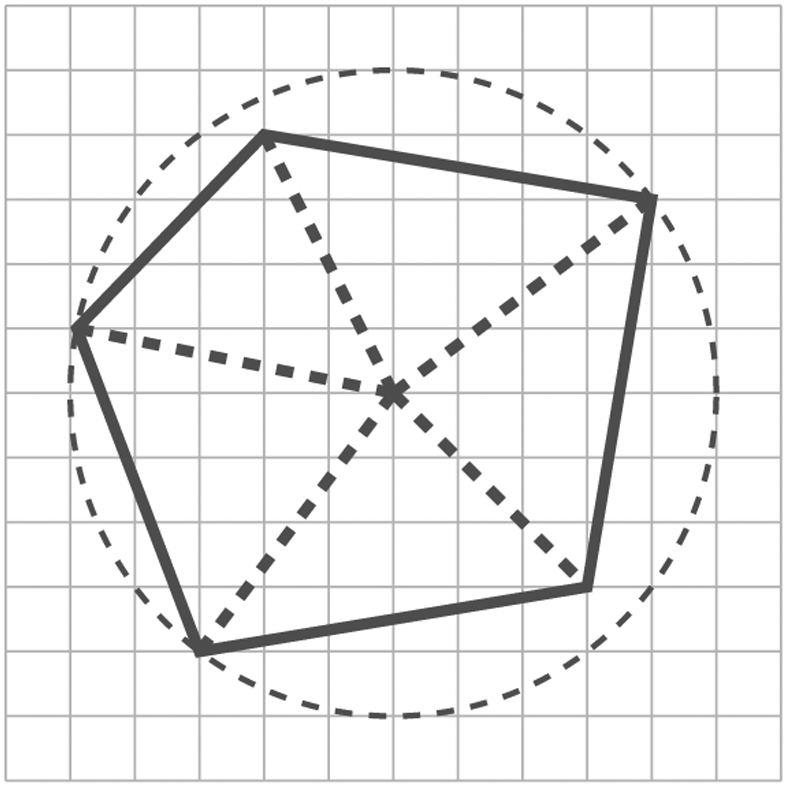
Convex polygon and its minimum bounding circle.

Finally, we show that (2.4) holds for ${\mathcal{R}}_{\text{polygon}}$(k, M) as well. To do so, we construct an explicit covering set. The idea is fairly simple, we apply a local perturbation to each vertex:

$${\pi }_s(K(\{(a_i,b_i):1\le i\le k\}))=K(\{(2^s\lfloor 2^{-s}{a}_i\rfloor ,2^s\lfloor 2^{-s}{b}_i\rfloor ):1\le i\le k\}).$$

Thus, we have the following proposition.

Proposition 2. Let π_s be defined above. Then, there exists an absolute constant c > 0, such that

$$d(K(\{(a_i,b_i):1\le i\le k\}),{\pi }_s(K(\{(a_i,b_i):1\le i\le k\})))\le c(\underset{i}{\text{min}}{r}_i{)}^{-1}{2}^s.$$

It is clear that there exist constants 0 < c₇ < c₈, depending on k and M only, such that

$${\mathcal{R}}_{\text{polygon}}(A;k,M)\subset \left\{K\in {\mathcal{R}}_{\text{polygon}}(k,M):c_7{A}^{1∕2}\le r_i\le c_8{A}^{1∕2},i=1,2,\dots ,k\right\}.$$

Therefore, by taking s = log₂ (ϵA^1/2), we obtain

$$N(A,ϵ)\le c_9\frac{n}{A}{\left(\log \left(\frac{n}{A}\right)\right)}^{k-1}{\left(\frac{1}{ϵ}\right)}^{2k+2}.$$

In addition, this argument suggests a simple strategy of using digitalization (π_s) to construct a covering set for $\mathcal{R}$.

From this particular case, we can see the tremendous computational benefit of ${\tilde{T}}^{\ast }$ over T*. To evaluate T*, we need to compute the size-corrected likelihood ratio statistics for a total of $\mid \mathcal{R}\mid =O(n^k)$ possible regions. In contrast, computing ${\tilde{T}}^{\ast }$ involves O (npolylog(n)) regions only, as shown in the previous section. Here, polylog(·) stands for a certain polynomial of log(·).

3.2. Ellipses

Next, we consider the case when $\mathcal{R}$ is a collection of ellipses on a two-dimensional lattice. Recall that any ellipse can be indexed by its center (τ₁, τ₂)^T, and a positive-definite matrix $\Sigma \in {\mathbb{R}}^{2\times 2}$:

$$\mathcal{E}(({\tau }_1,{\tau }_2{)}^{\mathsf{T}},\Sigma )=\left\{(x_1,x_2{)}^{\mathsf{T}}\in {\mathbb{R}}^2:(x_1-{\tau }_1,x_2-{\tau }_2){\Sigma }^{-1}\left(\begin{array}{c}\hfill x_1-{\tau }_1\hfill \\ \hfill x_2-{\tau }_2\hfill \end{array}\right)\le 1\right\}.$$

For brevity, we consider the case in which Σ is well conditioned in that its condition number, that is the ratio between its eigenvalues, is bounded. In this way, we avoid a lengthy discussion about the effect of discretization. In this case,

$${\mathcal{R}}_{\text{ellipse}}=\left\{\mathcal{E}(({\tau }_1,{\tau }_2{)}^{\mathsf{T}},\Sigma )\cap \mathbb{I}:1\le {\tau }_1,{\tau }_2\le m,\Sigma \succ 0,\frac{{\lambda }_{\max }(\Sigma )}{{\lambda }_{\text{min}}(\Sigma )}\le M\right\}.$$

First, note that any ellipse can be identified by its circumscribing rectangle, as shown in Figure 3. Therefore, from the bound on the number of rectangles on a lattice, for example by Proposition 1 with k = 4, we obtain

$${\mathcal{R}}_{\text{ellipse}}\le cn{A}^4,$$

for some constant c > 0. Similarly, if two ellipses intersect, then so do their minimum bounding rectangles. By the argument for polygons, we therefore know that (2.3) and (2.4) also hold for ${\mathcal{R}}_{\text{ellipse}}$.

Figure 3.

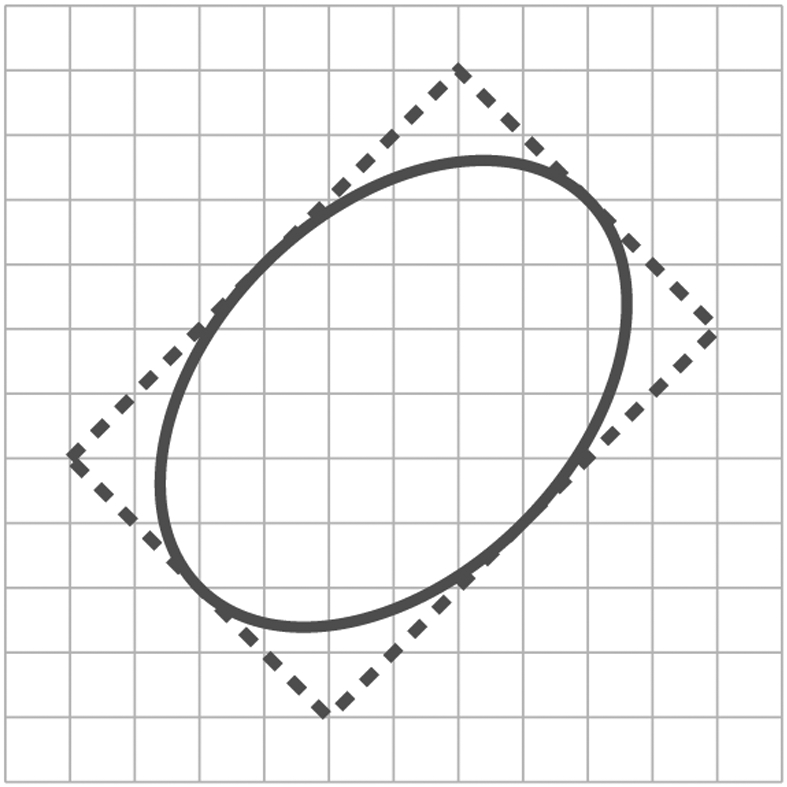
Circumscribing rectangle of an ellipse

4. Optimality

We now study the power of the proposed test T* and its variant ${\tilde{T}}^{\ast }$. We first investigate the required strength of correlation so it can be detected using the proposed tests.

Theorem 2. Assume that (2.2) and (2.4) hold. If there exists a correlated region R ∈ $\mathcal{R}$, with ∣R∣ → ∞ such that (1.1) holds for i ∉ R and (1.2) holds for i ∈ R, and

$$\mid R\mid \log \left(\frac{1}{1-{\rho }^2}\right)\ge (2+{\delta }_n)\log \left(\frac{n}{\mid R\mid }\right),$$ (4.1)

for some δ_n > 0, such that δ_n log^1/2(n/∣R∣) → ∞ then T* > q_α and ${\tilde{T}}^{\ast }>{\tilde{q}}_{\alpha }$ with probability tending to one as n → ∞.

Theorem 2 shows that whenever a correlation on a region R satisfies (4.1), our tests will consistently reject the null hypothesis and have power tending to one. The detection boundary of the proposed tests for a correlated region R can therefore be characterized by (4.1). More specifically, depending on the cardinality ∣R∣, there are three different regimes.

• For large regions, where ∣R∣ ≍ n, correlation is detectable if ∣R∣p² → ∞. Recall that, from the Neyman–Pearson lemma, even if the correlated region R is known in advance, we can detect it consistently only under the same requirement. Put differently, the proposed method is as powerful as if we knew the region in advance.

• For regions of intermediate sizes, such that log n ≪ ∣R∣ ≪ n, the detection boundary becomes ρ² ≥ (2 + δ_n)∣R∣⁻¹ log(n/∣R∣), provided that ${\delta }_n\sqrt{\log (n∕\mid R\mid )}\to \infty$. Here, we can see that a weaker correlation can be detected over larger regions.

• Finally, for small regions, where ∣R∣ ≪ log(n), detection is only possible in the case of a nearly perfect correlation, in that ρ² ≥ 1 – exp(−(2 + δ_n) log(n)/∣R∣), where ${\delta }_n\sqrt{\log n}\to \infty$.

It turns out that the detection boundary achieved by T* and ${\tilde{T}}^{\ast }$, as shown in Theorem 2, is indeed sharply optimal, following the similar arguments of Dümbgen and Spokoiny (2001), Dümbgen and Walther (2008), and Walther (2010).

Theorem 3. Assume that (2.3) holds. For any α-level test Δ, there exists an instance in which correlation occurs on some R ∈ $\mathcal{R}$, obeying

$$\mid R\mid \log \left(\frac{1}{1-{\rho }^2}\right)\ge (2-{\delta }_n)\log \left(\frac{n}{\mid R\mid }\right),$$ (4.2)

for a certain δ_n > 0, with δ_n log^1/2(n/∣R∣) → ∞, such that the type-II error of Δ converges to 1 – α as n → ∞. Moreover, if there exists an α-level test Δ for which the type-II error converges to 0 as n → ∞, on any instance where correlation occurs on some R ∈ $\mathcal{R}$ obeying

$$\mid R\mid \log \left(\frac{1}{1-{\rho }^2}\right)\ge c_{n}and\mid R\mid \to \infty ,$$ (4.3)

then it is necessary to have c_n → as n → ∞.

In other words, Theorem 3 shows that any test is essentially powerless in terms of detecting correlation with

$$\mid R\mid \log \left(\frac{1}{1-{\rho }^2}\right)\le (2-{\delta }_n)\log \left(\frac{n}{\mid R\mid }\right),$$

for any δ_n > 0, such that δ_nlog^1/2(n/∣R∣) → ∞. Together with Theorem 2, we see that when n/∣R∣ → ∞, the optimal detection boundary for colocalization for a general index set $\mathbb{I}$ and a large collection of $\mathcal{R}$ that satisfy certain complexity requirements is

$$\mid R\mid \log \left(\frac{1}{1-{\rho }^2}\right)=2\log \left(\frac{n}{\mid R\mid }\right),$$

where the size-corrected scan statistic is sharply optimal.

The second statement of Theorem 3 deals with the case when lim sup n/∣R∣ is finite. Together with Theorem 2, (4.3) implies that this correlated region can be detected if and only if

$${\rho }^2\mid R\mid \to \infty ,$$

and size-corrected scan statistic is again optimal.

To better appreciate the effect of the size of a correlated region on its detectability, it is instructive to consider cases where ∣R∣ = n^α, for some 0 < α < 1, or ∣R∣ = (log n)^α, for some α > 1. In the former case, when ∣R∣ = n^α, the detection boundary is

$${\rho }^2=2(1-\alpha )n^{-\alpha }\log n.$$

In the latter case, when ∣R∣ = (log n)^α, the detection boundary is

$${\rho }^2=2(\log n{)}^{1-\alpha }.$$

In both cases, it is clear that a much weaker correlation can be detected on larger regions.

5. Numerical Experiments

We now conduct numerical experiments to further demonstrate the practical merits of the proposed methodology.

5.1. Simulation

We begin with a series of four sets of simulation studies that focus on two-dimensional lattices. The first set of simulations is designed to show the flexibility of the general method by considering a variety of different shapes of correlated regions, namely, the choice of the library $\mathcal{R}$, including axis-aligned rectangles, triangles, and axis-aligned ellipses. We compare the performance of size-corrected likelihood ratio statistic and the uncorrected likelihood ratio statistic to demonstrate the necessity and usefulness of the proposed correction. The second set of simulations is carried out to compare the full scan statistic T* and the nearly linear time scan ${\tilde{T}}^{\ast }$. As such, we illustrate the similar performance between the two methods, and, at the same time, demonstrate the considerable computation gain from using ${\tilde{T}}^{\ast }$. The third and fourth sets of simulation studies are conducted to confirm qualitatively our theoretical findings about the effect of the size $\mid \mathbb{I}\mid$ of the lattice and the area A of the correlated region on its detectability. In each case, we assume that only the shape of the correlated region is known; thus, $\mathcal{R}$ is the collection of all regions of a particular shape. In addition, we simulate the null distribution and identify the upper 5% quantile of the distribution based on 1,000 Monte Carlo simulations. We reject the null hypothesis for a simulation run if the corresponding test statistic, T*, ${\tilde{T}}^{\ast }$, or L*, exceeds the respective upper quantile. This ensures that each test is at level 5%, up to the Monte Carlo simulation error.

As argued in the previous sections, our methods can handle a variety of geometric shapes. We now demonstrate this versatility through simulation, where we consider detecting a correlated region in the form of a triangle, an ellipse, and a rectangle. In particular, we simulate data on a 32 × 32 lattice. Correlation is imposed on a right triangle with sides 10, 20, and 10$\sqrt{5}$, an axis-aligned ellipse with short axis 4.94 and long axis 6.36, and a rectangle of size 10×10, respectively. The location of these correlated regions is selected uniformly over the lattice.

To assess the power of T*, we consider two relatively small values of correlation coefficient ρ: 0.2 and 0.4. For comparison purposes, for each simulation run, we compute both T* and the uncorrected maximum likelihood ratio statistic L*. The experiment is repeated 500 times for each combination of shape and correlation coefficient. The results are summarized in Table 1. These results not only show the general applicability of our method, but also demonstrate the improved power of the size correction we apply.

Table 1.

Power comparison between T* and L* for different combinations of shape and correlation coefficient.

Shape	Rectangle		Ellipse		Triangle
ρ	0.2	0.4	0.2	0.4	0.2	0.4
T*	0.16	0.42	0.25	0.6	0.21	0.58
L*	0.04	0.20	0.03	0.51	0.03	0.26

We now compare the full scan statistic T* with its more computationally efficient variant ${\tilde{T}}^{\ast }$. We focus on the case in which the correlated region is known to be an axis-aligned rectangle. The true correlated region is a randomly selected 10×10 rectangle on a 64×64 lattice. We consider a variety of different correlation coefficients: 0.2, 0.4, 0.6, and 0.8. The performance and computing times (all tests are implemented in Java and the experiments are run on an Intel Core i7 @2.2 GHz/16GB computer) of both tests are reported in Table 2, based on 500 runs for each value of the correlation coefficient. It is clear from Table 2 that the two tests enjoy similar performance, with T* being slightly more powerful. However, ${\tilde{T}}^{\ast }$ is much more efficient, to evaluate, as expected.

Table 2.

Comparison between T* and ${\tilde{T}}^{\ast }$.

	Correlation Coefficient	0.2	0.4	0.6	0.8
Power	T*	0.108	0.228	0.502	0.708
	${\tilde{T}}^{\ast }$	0.106	0.214	0.410	0.606
Time (ms)	T*	444.084	447.236	452.634	453.064
	${\tilde{T}}^{\ast }$	139.026	139.344	140.554	142.144

Note that the computing gain of ${\tilde{T}}^{\ast }$ over T* becomes more significant for larger images. In particular, we ran similar scans over lattices of size 256 × 256, 256 × 512, and 512 × 512. The computing time for a typical data set in each case is presented in Table 3.

Table 3.

Comparison of computing times for T* and ${\tilde{T}}^{\ast }$.

Size of Lattice	256 × 256	256 × 512	512 × 512
Computing time of T* (s)	129.942	487.238	1934.996
Computing time of ${\tilde{T}}^{\ast }$ (s)	16.59	45.117	144.206

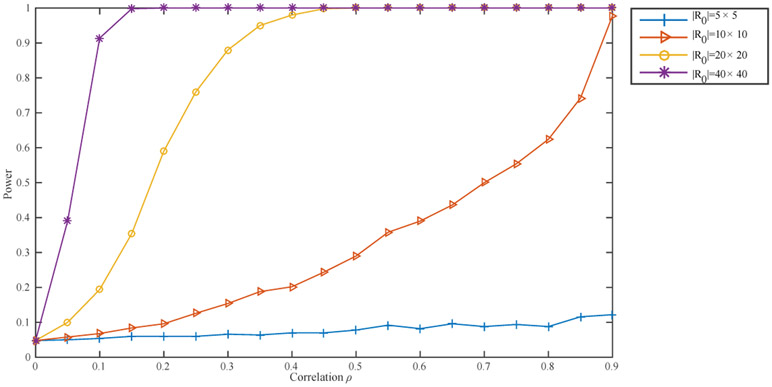
We now evaluate the effect of the size of a correlated region on its detectability. Given the results of the earlier experiments, we use ${\tilde{T}}^{\ast }$ to detect a correlated rectangle on a 64 × 64 lattice. We consider four sizes for the correlated rectangle: 5 × 5, 10 × 10, 20 × 20, and 40 × 40. For each size, we vary the correlation coefficient to capture the relationship between the power of our detection scheme and ρ. The results, summarized in Figure 4, are again based on 500 runs for each combination of size and correlation coefficient of the correlated region. The observed effect of A on its detectability is consistent with the results established in Theorem 2 and Theorem 3: larger regions are easier to detect using the same correlation coefficient.

Figure 4.

Power plot for detecting a correlated rectangle of different sizes on a 64 × 64 lattice.

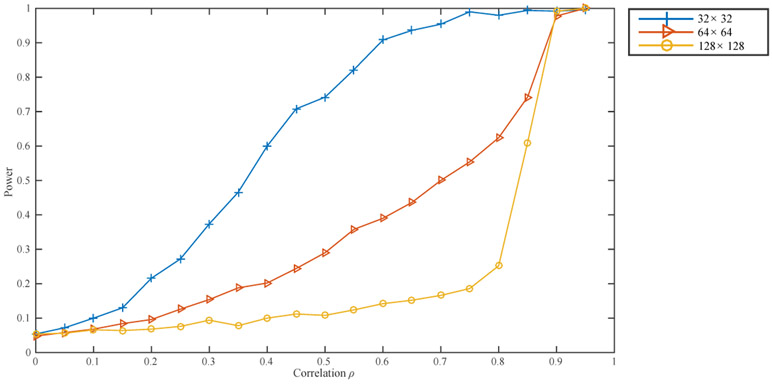
Our final set of simulations is designed to assess the effect of $\mathbb{I}$. To this end, we consider identifying a 10 × 10 correlated rectangle on a squared lattice of size 32 × 32, 64 × 64, and 128 × 128. As in the previous example, we repeat the experiment 500 times for each combination of $\mathbb{I}$ and a variety of values of ρ. The results are presented in Figure 5. The observed effect of $\mid \mathbb{I}\mid$ is consistent with our theoretical findings: as the size of the lattice increases, detection becomes more difficult for a region of the same size and correlation.

Figure 5.

Power plot for detecting a 10 × 10 correlated rectangle on squared lattices of different sizes.

5.2. Real-data example

For illustration purposes, we consider a biological data set to examine the post-transcriptional process of human immunodeficiency virus type 1 (HIV-1) using imaging-based approaches. HIV uses the host cellular factor chromosome region maintenance 1 (CRM1) mRNA nuclear export pathway to initiate the post-transcriptional stages of the viral life cycle. It is well established that a viral Rev trafficking protein recruits CRM1 nuclear export receptors (Fukuda et al. (1997)), thus having high levels of colocalization during the viral life cycle (Daelemans et al. (2005)). HIV-1 genomic RNAs (gRNAs) frequently exhibit burst nuclear export kinetic events (Pocock et al. (2016)) that are characterized by en masse evacuations of gRNAs from the nucleus to the cytoplasm; burst nuclear export is regulated through interactions between Rev and CRM1. Therefore, colocalization analyses of Rev and CRM1 binding provide insight into the role of Rev in viral gene expression and virus particle assembly.

Previous studies have shown a strong association between the viral protein Rev and the CRM1 in the nucleolus (Adler, Pagakis and Parmryd (2008); Daelemans et al. (2005)). Therefore, the colocalization between Rev and CRM1 in the nucleolus was compared to a mutant form of Rev (Rev M10) that cannot bind CRM1. This method provides a measurable way to describe the degree of association between the viral protein Rev and the host protein CRM1 in order to help ascertain their combined roles in the nuclear export of viral genomic RNA (Pocock et al. (2016)).

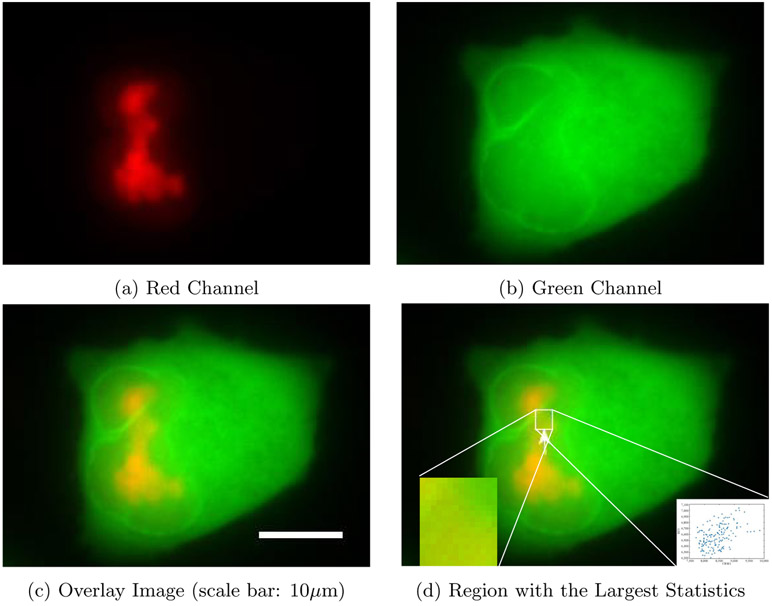
A specific data example is provided in Figures 6 and 7 as dual-channel images of a cell expressing wild type (WT) Rev (Figure 6) and a cell expressing the Rev M10 mutant, which is unable to bind CRM1 (Figure 7). Imaging experiments were performed on a Nikon Ti-Eclipse inverted wide-field epifluorescent deconvolution microscope (Nikon Corporation) using a 40x Plan Apo (N.A. 0.95) objective with a pixel size of 0.16 μm per pixel. Single images were typically acquired either every 30 minutes using the following excitation/emission filter sets (wavelengths in nm): 490-520/520-550 (YFP) and 565-590/590-650 (mCherry). Their respective sizes are 172 × 255 and 201 × 281.

Figure 6.

Colocalization between CRM1 and wild type Rev

Figure 7.

No colocalization between CRM1 and Rev M10 mutant

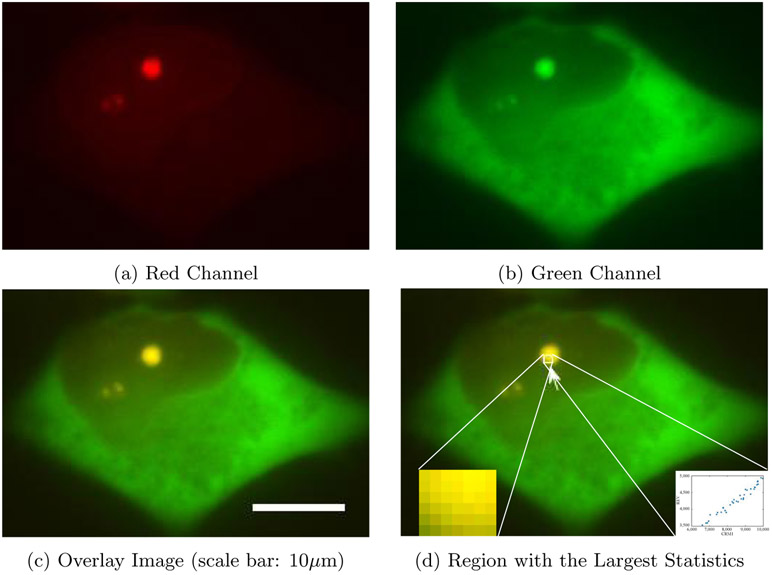
CRM1 is represented as red, and Rev by green. While the “burst” gRNA nuclear export phenotype occurs for the WT Rev condition (Figure 6), it does not occur for the condition in which Rev can no longer bind CRM1 (Figure 7). Therefore, the ability of Rev to bind to CRM1 is essential for “burst” nuclear export. To show the degree of association between Rev or RevM10 and CRM1, we apply our method to this example following the standard pre-processing steps. These include applying a threshold using Otsu’s method for each channel in order to segment the cell, and then identify the spatial compartments within which both channels are significantly expressed. On the post-processed images, we computed the test statistic T* and evaluated its corresponding p-value by simulating the null distribution through 1,000 Monte Carlo experiments. For the wild-type cell, we obtained T* = 3.93 × 10³, which is larger than any of the 1,000 values from the Monte Carlo simulations under the null hypothesis, suggesting a p-value < 0.1%, up to a Monte Carlo simulation error. In Figure 6d, we display the region with the largest log-likelihood ratio statistics, its zoomed-in version (left bottom corner), and corresponding scatter plot in this region (right bottom corner). The pixel intensities within the region showed a clear linear relationship. On the other hand, the test statistic for the mutant cell was 77.53, which corresponds to a p-value of 0.664. This data aligns with the expected levels and, more importantly, the spatial location of colocalization between Rev/Rev M10 and CRM1. This confirms the applicability of this region-finding method on biological data sets. Note that no existing method is able to identify the location of colocalization automatically.

6. Discussion

In this paper, we propose a new automated, objective colocalized region-detection method for colocalization analysis on dual-channel fluorescence microscopic imaging. When colocalized region detection is formulated as a structure correlation detection problem, our investigation shows that the maximum of the log-likelihood ratio statistics is dominated by those evaluated on small regions and, thus, is conservative when detecting large correlated regions. To overcome this problem, a size-corrected log-likelihood ratio statistic is proposed that will yield optimal correlation detection. The optimal detection statistic can be computed very efficiently, as long as some mild complexity conditions on the shape of correlated regions are satisfied.

The formulation of the colocalization analysis we consider here can be viewed as a generalization of traditional methods. More specifically, most existing colocalization analysis methods, such as the Pearson correlation coefficient and Manders’ split coefficients, can be cast as a statistic for testing hypotheses within a fixed region of interest in an image (see, e.g., Wang et al. (2018)). In contrast, the goal of a structure correlation detection problem is to test for the existence of a small colocalized region, without any location information input. Because of the new formulation, the proposed method does not need the user to input the region of interest (ROI), which avoids the selection bias brought by subjective ROI. Moreover, the proposed method is also able to provide unique information on the location of colocalization, which no existing methods can provide.

Although our theoretical analysis focuses on the detection of a single correlated region, the analysis can be extended to multiple regions if some regularity assumptions on the regions are satisfied (see e.g., Jeng, Cai and Li (2010)). In practice, we recommend adopting the multiple regions detection strategy in Jeng, Cai and Li (2010). Let ${\mathcal{R}}_1$ be the collection of all significant regions, that is, the regions statistics which are larger than the critical value, q_α. First, we identify the most significant region R_s from ${\mathcal{R}}_1$ (i.e., the region with the largest statistics). Second, we remove all regions overlapping with R_s from ${\mathcal{R}}_1$. The two steps above can be repeated until ${\mathcal{R}}_1$ is empty; that is, there are no significant regions. In this way, multiple regions can be detected.

Our results are mainly presented under a Gaussian distribution assumption. However, when the Gaussian assumption is violated, the proposed method is still applicable. More specifically, under a non-Gaussian distribution, the parameter of interest ρ is no longer a parameter of the bivariate gaussian distribution. However, the linear correlation coefficient between X_i and Y_i

$$\rho ≔\frac{\mathbb{E}(X_i-\mu (X))(Y_i-\mu (Y))}{\sqrt{\mathbb{E}(X_i-\mu (X){)}^2\mathbb{E}(Y_i-\mu (Y){)}^2}},$$

where μ(X) and μ(Y) are expectations for X_i and Y_i, respectively. The concentration inequalities suggest that the key lemmas, including Lemma 4 and Lemma 5, still hold on a large enough region when the underlying distributions are sub-Gaussian or sub exponential distribution (see, e.g.,Vershynin (2010)). Thus, we can apply the same size correction technique, and derive similar detection upper bound in Theorem 1 and Theorem 2, up to a constant, by the generic chaining. To illustrate this, we conducted a small experiment to compare ${\max }_{R\in \mathcal{R}(A)}$ L_R when the distributions of (X_i, Y_i) are Gaussian and Poisson distribution, respectively. Specifically, we generate 2,000 pairs of random variables on a line, and let $\mathcal{R}$ be a collection of segments. Here, (X_i, Y_i) is generated from an independent standard Gaussian distribution or an independent Poisson distribution with mean 10. We repeat the simulation 5,000 times, and summarize the distribution of ${\max }_{R\in \mathcal{R}(A)}$ L_R, when A = 50, in Figures S1a and S1b. The figures show that the distributions are almost the same and confirm our arguments. On the other hand, when the region size is sufficiently small, the form of L_R is specifically designed for a Gaussian distribution, and Lemma 1 does not always hold. In Figures S1c and S1d, we repeat the above simulation to examine the distribution of ${\max }_{R\in \mathcal{R}(A)}$ L_R when A = 10. The results suggest there is little difference between the two distributions. Hence, our newly proposed method is a robust approach to detecting linear correlation on large regions.

In this study, our focus is to detect the existence of colocalization in microscopic images, which can be viewed as a one sample hypothesis test problem. However, in many applications, biologists wish to determine whether the level of colocalization differs under different conditions (e.g., experiment group vs. control group), which is basically a two-sample hypothesis test problem. Applying the proposed technique to the two-sample problem is not straightforward because registration issues between cells under different conditions arise when scanning. Nevertheless, extending the application to two-sample cases offers a promising direction for future research.