Cell-type modeling in spatial transcriptomics data elucidates spatially variable colocalization and communication between cell-types in mouse brain

Summary

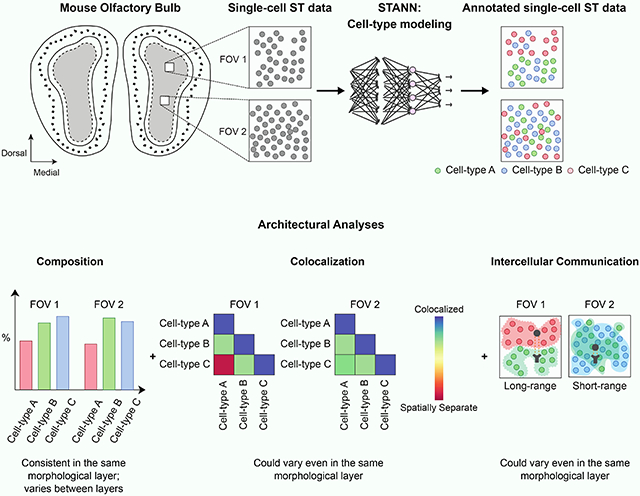
Single-cell spatial transcriptomics (sc-ST) holds the promise to elucidate architectural aspects of complex tissues. Such analyses require modeling cell-types in sc-ST datasets through their integration with single-cell RNA-Seq datasets. This integration, however, is non-trivial since the two technologies differ widely in the number of profiled genes and the datasets often do not share many marker genes for given cell-types. We developed a neural network model, STANN (Spatial Transcriptomics Cell-Types Assignment Using Neural Networks), to overcome these challenges. Analysis of STANN’s predicted cell-types in mouse olfactory bulb (MOB) sc-ST data delineated MOB architecture beyond its morphological layer-based conventional description. We find that cell-type proportions remain consistent within individual morphological layers but vary significantly between layers. Notably, even within a layer, cellular colocalization patterns and intercellular communication mechanisms show high spatial variations. These observations imply a refinement of major cell-types into subtypes characterized by spatially localized gene regulatory networks and receptor-ligand usage.

Graphical Abstract

eTOC blurb

Grisanti Canozo et al. developed a neural network, STANN, to model cell-types in single-cell resolution spatial transcriptomics (sc-ST) data. They deployed STANN within a pipeline for careful feature selection and class imbalance-aware model fitting. STANN’s predicted cell-types in mouse olfactory bulb (MOB) sc-ST data revealed high spatial variations in cellular colocalization and intercellular communication, and suggested that major cell-types may have spatially localized subpopulations that differ in receptor-ligand usage. This work delineates MOB architecture beyond its conventional morphological layer-based description.

Introduction

Mammalian brain architecture is commonly defined in terms of morphological layers. Each layer comprises a complex mixture of cell-types; and an accurate understanding of brain architecture requires locating its cell-types in situ and determining their spatial organization, colocalization, and intercellular communication mechanisms (Nagayama, Homma and Imamura, 2014; Moffitt et al., 2018; Tepe et al., 2018; Zeisel et al., 2018). Although the premise for these goals was set by Ramon y Cajal and others nearly 150 years ago (see (Lein, Borm and Linnarsson, 2017)), they have remained challenging due to the lack of technologies and methods to profile individual cells’ transcriptome in situ in the brain. Recent advances in spatial transcriptomics and single-cell transcriptomics (single-cell RNA-seq) show the promise to overcome these challenges (Lein, Borm and Linnarsson, 2017; Filipp, 2019; Stuart and Satija, 2019).

Spatial transcriptomics (ST) and single-cell RNA-seq (scRNA-seq) are complementary technologies, each with its strengths and weaknesses, for studying the transcriptomes of complex tissues (Lein, Borm and Linnarsson, 2017). While scRNA-seq can profile the transcriptome of individual cells and characterize transcriptionally distinct cell-types in a tissue, it does not record the spatial location of cells within the tissue (Crosetto, Bienko and van Oudenaarden, 2015; Lein, Borm and Linnarsson, 2017; Stuart and Satija, 2019). In this regard, the ST technologies complement scRNA-seq by profiling spatially resolved gene expression (Stuart and Satija, 2019). Current ST technologies fall into two broad categories, and notably, neither category profiles the transcriptome of single-cells. The spot-based ST technologies (spot-ST) use spatially resolved spots (or beads) where each spot captures the transcriptome of a variable number of cells (Stuart and Satija, 2019; Liao et al., 2020). The commercially available Visium technology, for example, captures 5 to 10 cells (on average) per spot. Because of this “pseudo-bulk” nature of the spot-ST technologies, it becomes challenging to use these datasets to investigate the above questions that require locating single-cells in situ. In particular, although recent methods have used spot-ST data to compute the proportion of different cell-types in each spot (Andersson et al., 2020; Kleshchevnikov et al., 2020; Biancalani et al., 2021; Cable et al., 2021; Elosua-Bayes et al., 2021), since the number of cells in each spot is variable and is difficult to determine, the estimated cell-type composition of a given tissue region that comprises multiple spots is not as accurate as could be derived from single-cell resolution spatial data. For the same reason, it is challenging to compute the colocalization of cell-types or their intercellular communications from spot-ST data. One practical solution is to first make a binary presence-absence call in the spots for each cell-type using a predefined threshold on the cell-type’s proportion per spot. On the one hand, it is unclear how to define this threshold and whether one should use a cell-type-specific threshold; on the other hand, the conclusions from such binarized analyses would arguably be sub-optimal than those that a single-cell resolution ST data could offer.

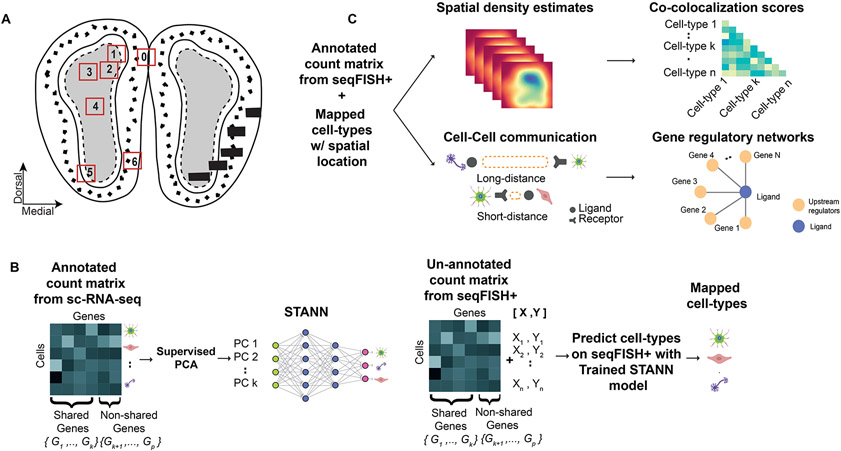
In contrast to the spot-ST technologies, the single-cell ST (sc-ST) technologies record the location of single-cells. Such datasets are, in principle, more well-suited to locate the individual cell-types in situ and study cellular colocalization and intercellular communication. However, because of their technological design, current sc-ST technologies profile the transcriptional expression of only about half as many genes as commonly profiled by scRNA-seq and spot-ST (1,000-10,000 compared to 20,000) (Stuart and Satija, 2019; Vieth et al., 2019), an issue that can make it problematic to identify cell-types in the sc-ST datasets. In particular, when the marker genes of different cell-types are absent in an sc-ST dataset, it is challenging to assign correct types to the cells in that dataset (Dumitrascu et al., 2021). Errors in cell-type assignment, in turn, may lead to inaccurate biological conclusions. Thus, utilizing sc-ST data to their full potential requires accurate cell-type modeling even when the marker genes of different cell-types are missing in the data. To elucidate the architectural aspects of complex tissues at single-cell resolution, Eng et al.’s recent sc-ST technology seqFISH+ (sequential FISH), a highly multiplexed FISH (fluorescence in situ hybridization) based technology (Eng et al., 2019), combined with machine learning based cell-type modeling could be effective. Eng et al.’s pilot seqFISH+ data showed high quality and reproducibility (high concordance between replicates and also with other bulk and single-cell transcriptomics datasets). Therefore, to study the mammalian brain architectural layers at single-cell resolution, here we opted to use Eng et al.’s mouse olfactory bulb (MOB) seqFISH+ data. MOB architecture is classically described in terms of morphological layers (Nagayama, Homma and Imamura, 2014; Tepe et al., 2018; Zeisel et at., 2018). A coronal image of MOB shows five distinct layers appearing from the center to the outside: granule cell layer (GCL), internal plexiform layer (IPL), mitral cell layer (MCL), external plexiform layer (EPL), and glomerular layer (GL) (Fig. 1A). Eng et al. featured MOB sc-ST data from six 0.20 mm X 0.20 mm sized sections (field of view; FOV) (Fig. 1A). The dataset, therefore, offers an exciting opportunity to study MOB architecture in a detail that goes beyond morphological layers. For example, the three FOVs from GCL (FOVs 2, 3, and 4; Fig. 1A) could help investigate spatial variations of cellular colocalization and intercellular communication even within a morphological layer.

Figure 1.

Mouse olfactory bulb (MOB) architecture and an outline of the STANN model with the downstream analyses. A) A schematic showing the layered architecture of MOB. The numbered boxes show the locations of the six fields of views (FOVs) in the MOB seqFISH+ data. B) Learning stage of STANN, model training on annotated scRNA-seq data. C) Downstream analyses on cell-type annotated seqFISH+ data: spatial density maps of locations of cell-types, colocalization scores, intercellular communication, and gene regulatory networks.

Consistent with the general characteristic of sc-ST datasets, the MOB seqFISH+ dataset profiles only about 10,000 genes that cover a small subset of the marker genes of different MOB cell-types. Depending on the reference scRNA-seq dataset and the number of cell-types being studied, these subsets comprise 33%-53% of the marker genes (Supplementary Table S1), making it challenging to assign cell-types in seqFISH+ data. To mitigate this shortcoming, we developed a neural network model, STANN (Spatial Transcriptomics Cell-Types Assignment Using Neural Networks) (Fig. 1B,C). Given the transcriptional expression of genes shared between an scRNA-seq and a seqFISH+ datasets, STANN first learns the mapping of cell-types to the scRNA-seq cells (Fig. 1B). STANN next predicts each cell’s type in the seqFISH+ dataset given the transcriptional expression of the shared genes in that cell (Fig. 1B). We applied STANN to integrate the seqFISH+ dataset with our previously published MOB scRNA-seq data (Tepe et al., 2018). Our analysis of STANN’s outputs revealed that the cellular composition (the proportions of cell-types) in FOVs remain consistent within a morphological layer but can vary significantly across layers. Colocalization analysis of different cell-types further showed that colocalization patterns between a cell-type pair vary significantly between different FOVs, but also when the FOVs are within the same morphological layer (Fig. 1C). We also find spatially localized sub-types of the major cell-types in MOB (Fig. 1C). These sub-types are distinguished by spatially localized expression of receptors and ligands and underlie a high variation in intercellular communication mechanisms between the same pair of cell-types across different FOVs, even when the FOVs are in the same morphological layer. Besides developing these approaches to study cellular colocalization and intercellular communication, we also benchmarked STANN against alternative models. The benchmarking showed STANN’s better performance and suggested that methods for integrating spot-ST and scRNA-seq data are likely to produce suboptimal results if applied to integrate sc-ST and scRNA-seq data (Discussion). Altogether, our work offers important insights into brain architecture and intercellular communication principles and for developing the necessary computational tools for similar investigations.

Results

STANN: a deep neural network model for mapping cell-types from scRNA-seq to single-cell ST (sc-ST) data

Assigning cell-types to sc-ST data, such as seqFISH+, becomes challenging when the datasets do not profile the marker genes of cell-types in that tissue. The seqFISH+ data of mouse olfactory bulb (MOB), for example, profiles only 33-53% of the marker genes of different MOB cell-types (Supplementary Table S1). In such cases, it is essential to integrate the seqFISH+ data with scRNA-seq data. Since scRNA-seq profiles the transcriptome, including the marker genes, we can assign cell-types unambiguously to the cells in scRNA-seq data. Using these cell-type assignments in the scRNA-seq data, we can build models that learn to map a cell to its cell-type, i.e., classify the cell, given the transcriptional expression of only the shared genes between scRNA-seq and seqFISH+. We can then apply the classification model on each cell in the seqFISH+ data to determine its type.

Deep neural networks have recently shown remarkable performance in classification tasks (Angermueller et al., 2016). The models can efficiently deal with high dimensional data and learn sufficiently complex, non-linear functions in a data-driven manner to map data points to their respective classes. With proper statistical measures, one can identify the architecture and the parameters that yield an accurate and generalizable model (Yu and Zhu, 2020). The STANN (Spatial Transcriptomics Cell-Types Assignment Using Neural Networks) model in this work implements a fully connected deep neural network with additional steps to select the most relevant features (inputs), reduce the effect of noise in model fitting, and minimize the chances of inflated performance originating from class imbalance (Fig. 1B; Methods). We select the most relevant input features for STANN by performing a procedure akin to supervised principal components (sPCA) (Methods). Given these input features for a cell, STANN learns to assign the correct cell-type to it. Each intermediate layer in STANN comprises neurons (linear functions) that combine inputs from the neurons of the previous layer and propagate the result through a nonlinear activation function to the next layer. STANN also uses a class-imbalance aware loss function that adjusts for under- or over-represented cell-types. This makes STANN robust against being biased by the majority classes, which will lead to a model with inflated average performance but the model will fail on rare cell-types. Parameters of STANN are optimized using the backpropagation algorithm (Rumelhart, Hinton and Williams, 1986).

STANN learns an accurate model for mapping mouse olfactory bulb cell-types from scRNA-seq data

We applied STANN to learn cell-types from our recent scRNA-seq data of the mouse olfactory bulb (MOB) (Tepe et al., 2018). This dataset provides transcriptional expression of 17,840 genes from 11,744 cells of 15 cell-types in MOB (Fig. S1). To be able to integrate this dataset with the MOB seqFISH+ data, we trained the model using only the 9,031 genes shared between the two datasets. In order to build a robust model, we first identify the genes that are most informative for the classification task and input to the model only the necessary number of principal components summarizing the expression of these genes. In order to identify an accurate and generalizable model, we perform a ten-fold cross-validation based hyper-parameter search for the optimal number informative genes, principal components, and STANN’s number of intermediate layers, numbers of neurons in each layer, and the activation function for neurons in each layer (Methods). The optimal STANN model showed an average accuracy of 99.413 ± 0.059% on training data and 95.150% ± 0.325% on separately held-out test data.

STANN performs better than alternative models in benchmarking across different datasets

We note that two other classes of tools, namely tools to combine multiple scRNA-seq datasets and tools to integrate spot-ST with scRNA-seq data, could apply to achieve STANN’s goal for integrating sc-ST with scRNA-seq data. However, STANN aims to solve the computational problem of mapping cell-types from a fewer number of genes than a transcriptome scale data would capture, often from genes that were not used in the first place to define the cell-types. To test the suitability of the other two classes of tools for solving this computational problem, we ran the following benchmarking analyses.

On Mouse Olfactory Bulb (MOB) scRNA-seq

The majority of the alternative methods noted above rely on marker genes to assign cell-types in the sc-ST dataset (Moncada et al., 2020; Qian et al., 2020; Zhang et al., 2019). However, the MOB seqFISH+ dataset shares only 33% marker genes of Tepe et al.’s scRNA-seq data (Tepe et al. 2018) (Supplementary Table S1), which makes it unlikely that marker gene-based methods will be effective in this case. This lack of shared marker genes was independent of the dataset selected. For example, only ~50% of the marker genes in the Mouse Brain Atlas (http://mousebrain.org/) scRNA-seq data (Zeisel et al., 2018) are shared with the MOB seqFISH+ data (Supplementary Table S1). We note that, this increase in the number of marker genes (from 33% in Tepe et al. data to 53% in mousebrain.org data) is mainly because the mousebrain.org data features fewer clusters, i.e., cell-types (15 vs. 6).

For benchmarking, we therefore used the widely used method Seurat (Butler et al., 2018), which integrates two datasets by computing anchor genes from the datasets’ low dimensional embeddings, and scPred (Alquicira-Hernandez et al., 2019), another method that combines unbiased feature selection from a reduced-dimensional space with support vector machine based classification.

We compared Seurat and scPred against STANN over 50 independent runs. In each run, we simulated an ST dataset by taking a random subsample of 2500 cells and ~9k genes (equal to the number of shared genes between scRNA-seq and seqFISH+ datasets) from the original scRNA-seq data and tested each method on this subsampled data. In two additional benchmarking analyses described in the following sections, we also used Tangram (Biancalani et al., 2021), a recently proposed method for transferring annotations from a source scRNA-seq dataset (S) to a target ST dataset (G). To this end, Tangram learns a mapping matrix, M, by maximizing the similarity of gene expression distribution and cell-densities between M^TS and G. However, given the high memory and runtime requirements of Tangram’s current implementation, we did not use Tangram in this first benchmarking of 50 independent runs.

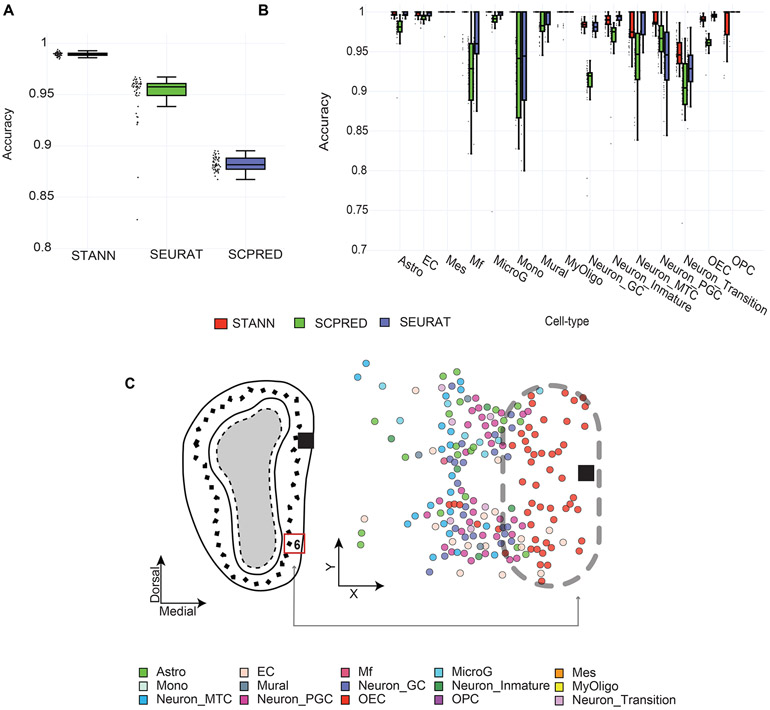
STANN performed better than both Seurat and scPred by margins of 4.57% and 10.67%, respectively (Fig. 2A, Methods). STANN showed accuracies of 98.9% ± 0.18% vs. Seurat’s 94.4% ± 4.51% and scPred’s 88% ± 0.64% (Fig. 2A). STANN’s performance was consistently high in rare cell types (< 30 cells). For example, for monocytes (Mono), macrophages (MF), oligodendrocyte progenitor cells (OPC), and mural cells, STANN showed improvements of 0.4 – 17% over Seurat and scPred (Fig. 2B).

Figure 2.

STANN’s performance compared to alternative methods. Boxplots showing (A) overall accuracy and (B) cell-type specific accuracies for STANN, Seurat and scPred over 50 independent runs. Horizontal lines in the boxplots mean the following: center line, median; box limits, upper and lower quartiles; whiskers, 1.5x interquartile range; points, outliers. C) Spatial distribution of predictions in FOV 6, located in the glomerular layer and external plexiform layer (cf. Fig. 4F in Eng. et al (Eng et al., 2019)), with the grey arrow pointing to the spatial location of FOV 6 in the MOB. Astro: Astrocytes, EC: Endothelial Cells, OECs: Olfactory Ensheathing Cells, MicroG: Microglia Cells, Neuron_Inmature: Neuron Immature Cells, Neuron_Mature: Neuron Mature Cells, Neuron_GC: Neuron Granule Cells, MyOligo: Myelinating-Oligodendrocyte Cells, Mes: Mesenchymal Cells, Mural: Mural Cells, Mono: Monocytes Cells, Neuron_MTC: Neuron M/T cells, Mf: Macrophages, OPC: Oligodendrocyte Progenitor Cells, Neuron_PGC: Periglomerular Cells.

On Two Different scRNA-sea Tabula Sapiens Samples

The validation and the training data in the above analysis were from the same sample. To further benchmark STANN when the validation data is taken from a different sample, we took two publicly available lung scRNA-seq samples from Tabula Sapiens (The Tabula Sapiens Consortium and Quake, 2021). We trained STANN and other methods on one sample and made predictions on the second sample to compare the methods’ accuracies. We found that STANN outperformed Seurat and scPred in this task, with accuracy of 96.66% vs Seurat’s 85.33% and scPred’s 78.37%. The recently proposed method Tangram (Biancalani et al., 2021) showed an accuracy of 41.85%.

On MERFISH Data

To benchmark STANN on other types of sc-ST data, we applied STANN and the other methods on MERFISH (Multiplexed error-robust fluorescence in situ hybridization) data of hypothalamic preoptic region (Moffitt et al. 2018) (Fig. S2). Compared to the original cell-type assignment (Moffitt et al. 2018) we found that STANN outperformed Seurat and scPred in this task, with an accuracy of 87.62% vs Seurat’s 82.52%, scPred’s 52.08%, and Tangram’s 41.86%. STANN’s mapping revealed similar spatial localization and composition of different cell-types to Moffitt et al.’s results (Fig. S2C,D). STANN’s assigned cell-types also showed similar cell-type colocalization as reported by Moffitt et al. For example, we find mutual separation of mature oligodendrocytes and inhibitory cells and colocalization of immature oligodendrocytes and microglia associated with development and modulation of social behaviors and reproduction (Moffitt et al. 2018) (Fig. S2E,F).

Overall, STANN consistently performed better than the available alternative methods in our benchmarking runs, suggesting that tools to integrate multiple scRNA-seq datasets or spot-ST with scRNA-seq datasets might give suboptimal results when applied to integrating sc-ST with scRNA-seq datasets (see Discussion).

STANN provides a spatially resolved annotation of cell-types in the mouse olfactory bulb

The mouse olfactory bulb (MOB) seqFISH+ dataset (Eng et al., 2019) comprises six 0.2 mm X 0.2 mm sized fields of view (FOV) from a slice of adult MOB (Fig. 1A). As we noted in the Introduction, the MOB is structured into several morphological layers, such as the granule cell layer (GCL) and the glomerular layer (GL), and the seqFISH+ data feature FOVs from all of these layers with three FOVs collected from the same layer (GCL) (Eng et al., 2019) (Fig. 1A; Supplementary Table S2). As noted earlier, the data are highly reproducible and in accordance with other transcriptomic methods. The dataset reports 2050 single cells, 10000 genes from each cell, 9031 of which are in common with our previously published MOB scRNA-seq data (Tepe et al., 2018). In the rest of this manuscript, we refer to these genes as the “shared” genes. As noted above, the shared genes include only 33% of the marker genes for MOB cell-types (Supplementary Table S1).

We trained STANN on our scRNA-seq dataset (Tepe et al., 2018) and utilized the trained model to assign cell-types to the seqFISH+ data. As noted above, this scRNA-seq dataset had 15 major cell-types (Supplementary Table S3; Fig. S1). STANN found examples of all 15 cell-types in the seqFISH+ data. Consistent with previous studies (Zeisel et al., 2018; Ortiz et al., 2020), STANN showed an abundance of olfactory ensheathing cells in FOVs originating from the GL (Fig. 2C). STANN also predicted neuronal granule cells as the most abundant cell-type when the seven FOVs are considered together. This is expected since the majority of the FOVs are located within the GCL or map to an extension of it (Fig. 1A). Furthermore, neuronal granule cells have previously been reported as the most abundant interneuron in the MOB and GCL (Lein et al., 2007; Nagayama, Homma and Imamura, 2014; Burton, 2017; Tepe et al., 2018; Vickovic et al., 2019) . Overall, STANN revealed a high imbalance in the proportions of cell-types in seqFISH+ data (all FOVs considered together; Fig. 3A). This likely reflects MOB biology and is not an artifact of STANN, since the MOB scRNA-seq data has a similar imbalance of cell-type proportions (Fig. 3B). However, STANN found subtle differences between the two datasets in terms of the relative abundance of cell-types. For example, the most abundant cell-type across the seven FOVs of seqFISH+ data is neuronal granule cells, which is the second most abundant cell-type in the scRNA-seq data. Such variations are expected since the seqFISH+ FOVs constitute a small sample of the scRNA-seq data. Notably, these variations imply that STANN did not overfit the scRNA-seq data or its training was not biased by the more abundant cell-types. STANN also highlighted the importance of explicitly learning the complex non-linear relationships between shared genes to ensure accurate cell-type assignments. Conventional methods mentioned above for integrating multiple scRNA-seq datasets may miss such relationships (Zheng et al., 2017; Luecken and Theis, 2019; Moncada et al., 2020; Qian et al., 2020). However, the seqFISH+ data embeddings built from the shared genes did not converge to a good separation of neuron clusters (Fig. S3). This implies that ignoring the complex non-linear relationships between shared genes will fail to capture the necessary variation to classify these cell-types.

Figure 3.

MOB cell-type compositions are similar in scRNA-seq data and in STANN’s predictions on seqFISH+ data. Shown are the compositions according to (A) STANN’s predictions in seqFISH+ data and (B) in the scRNA-seq data.

Cell-type compositions differ significantly between FOVs from different layers but remain consistent within a layer

With STANN’s predictions of cell-type for each individual cell in the seqFISH+ data, we then asked a series of questions regarding MOB architecture. Cell-type composition of a tissue, defined as the proportions of different cell-types in it, is a fundamental property of its architecture and function. Altered composition of cell-types is a hallmark of diseased and damaged tissues. However, the extent to which cell-type composition changes spatially within a tissue, and potentially encodes for physiological functions, is still unclear.

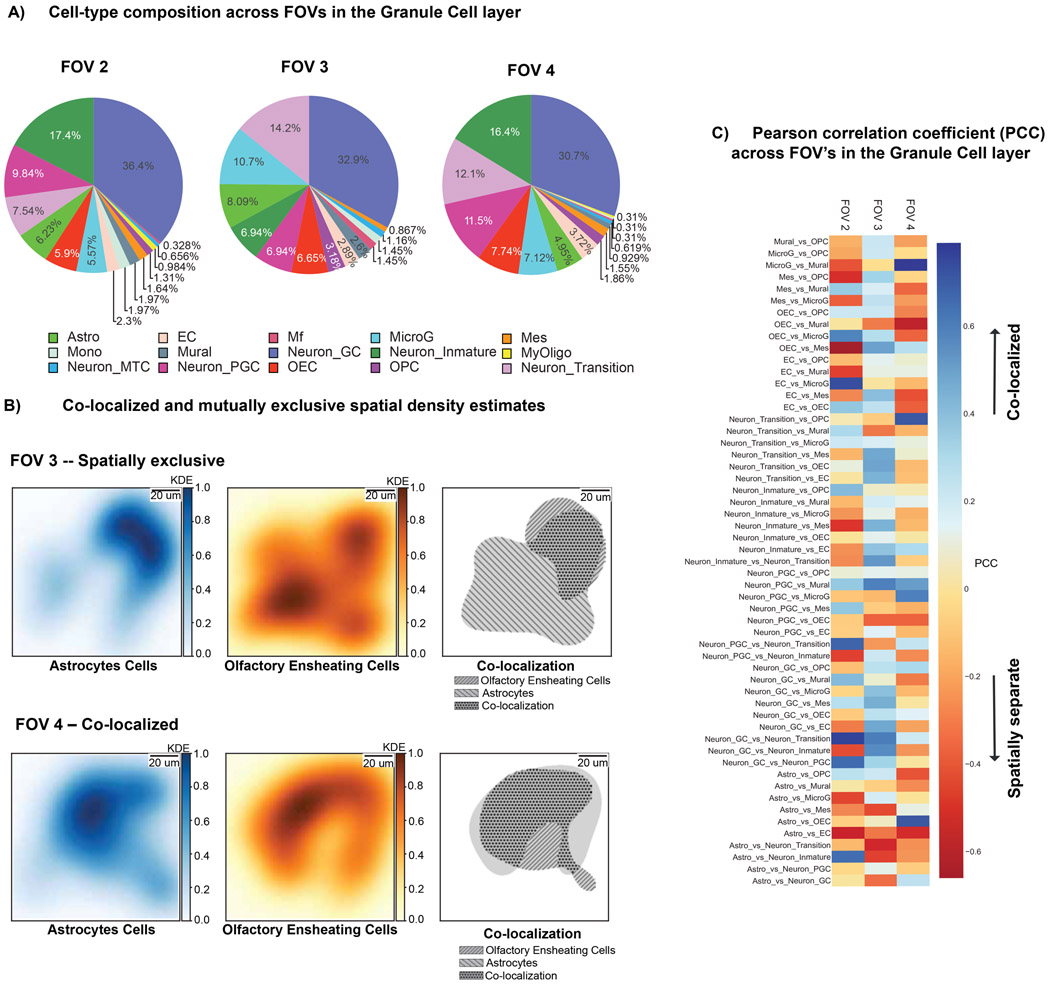
To study spatial variation of cell-type compositions within the MOB, we used STANN’s cell-type predictions in each FOV. We first find that closely located FOVs within a morphological layer have very similar cell-type compositions (based on both Chi-square test and relative entropy; Methods; Supplementary Table S4). For example, the three FOVs located within the GCL have nearly identical cell-type compositions (FOVs 2, 3, and 4 in Fig. 4A; Supplementary Table S4). However, FOVs significantly differ in cell-type compositions when they span different morphological layers. For example, FOV 1 (spanning GCL and IPL) and FOV 5 (spanning GCL, IPL, EPL and MPL) have significantly different cell-type compositions (Fig. S4, Supplementary Table S4). The same applies for the FOVs 0 (spanning GL and EPL) and 4 (spanning GCL).

Figure 4.

Consistency of cell-type composition and variation of cellular colocalization in the same MOB layer. A) Composition of cell-types across different FOVs in the Granule Cell Layer (GCL). B) Kernel density maps of Neuronal Transition cells vs. Olfactory Ensheathing cells in two different FOVs located in the GCL layer, showing completely opposite co-colocalization patterns. Color bar represents in linear scale the Pearson Correlation Coefficients (PCC). C) Heatmap of PCC scores of cellular colocalization within FOVs located in the GCL.

To have an orthogonal validation of these observations, we utilized an HDST (High-definition spatial transcriptomics) (Vickovic et al., 2019) dataset of MOB. This high throughput sequencing based technique by Vickovic et al. captures mRNAs from spatially resolved beads, where each bead is small enough to accommodate a single-cell. The HDST data is highly sparse and not particularly suitable to investigate the questions on cell-subtypes and intercellular communications that we asked below. However, we could use Vickovic et al.’s cell-type annotations to investigate our questions on cell-type compositions. To this end, we selected regions from Vickovic et al.’s MOB HDST data where each region’s size was the same as an FOV of the seqFISH+ data. Based on a random selection of 100 regions, we indeed found that cell-type compositions are very similar for FOVs located within the same layer, but they change significantly for FOVs sampled from different morphological layers (Fig. S5).

Colocalization patterns between cell-types vary substantially both within and between morphological layers

Colocalization or spatial separation between cell-types is another fundamental aspect of tissue architecture, and is known to change in disease and injured tissues (Holubarsch and Hasenfuss, 1992; Martin and Blaxall, 2012). To quantify the colocalization between any pair of cell-types in a given FOV, we performed the following analysis building upon previous studies of colocalized fluorescence probes (Manders, Verbeek and Aten, 1993). For each cell-type predicted by STANN in an FOV, we first calculated a multivariate kernel density map (Chacón and Duong, 2018) using cross-validation from its locations within the FOV (Fig. 4B; see Methods). We then computed the Pearson correlation coefficient between the probabilities of observing the two cell-types across all spatial coordinates in that FOV. This colocalization analysis identified cell-type pairs with significant colocalization (strong positive correlation) or cell-type pairs that were spatially separate (strong negative correlation) in each FOV (Fig. 4B,C). Interestingly, we found a high variation in colocalization patterns between every pair of cell-types across the FOVs, even when the FOVs are located in the same morphological layer (Fig. S6). The three FOVs located within the GCL (FOV 2, 3, and 4) demonstrate this point. The most conservative prediction will be that FOVs that share the same morphological layer or are adjacent, will be more similar than FOVs located in different morphological layers or at a distance. While this conservative prediction holds for 49.51 % of cell-type pairs in FOVs 2, 3, and 4, we found that 50.48% of the cell-type pairs in these FOVs show highly variable colocalization patterns, ranging from spatial separation to significant colocalization across the FOVs (Fig. 4C).

Widespread spatial variation in intercellular communication mechanisms give rise to spatially localized gene regulatory networks

Intercellular communication is critical for tissue function (Cohen et al., 2018; Skelly et al., 2018; Ximerakis et al., 2019; Xiong et al., 2019; Li et al., 2020; Wang et al., 2020) and is also associated with disease states (Tirosh et al., 2016; Ji et al., 2020; Moncada et al., 2020). Identifying the communicating cell-type pairs and their communication mechanisms (in terms of receptors and ligands) is a major focus of single-cell transcriptomic studies. Recent studies suggest that the communications between certain cell-types may be enriched within specific parts of a tissue (commonly termed microenvironments or niches (Tirosh et al., 2016; Baccin et al., 2020)). However, to what extent and how intercellular communication varies across a tissue is still an open question (Efremova et al., 2020).

We applied CellPhoneDB (Efremova et al., 2020), an intercellular communication analysis tool for scRNA-seq data, on STANN’s predicted cell-types in each FOV of the seqFISH+ data (Methods). For every pair of cell-types in an FOV, CellPhoneDB identifies the receptors and ligands that are significantly and specifically enriched between those two cell-types. However, CellPhoneDB does not take the spatial location of cell-types into account and could incorrectly infer communication between two cell-types when they each communicate with a third cell-type but not with each other (Fig. 5A). To make our analysis robust against this type of incorrect inferences, at least for the spatially separate cell-types, we have applied an additional filtering on the intercellular communications computed by CellPhoneDB (Methods).

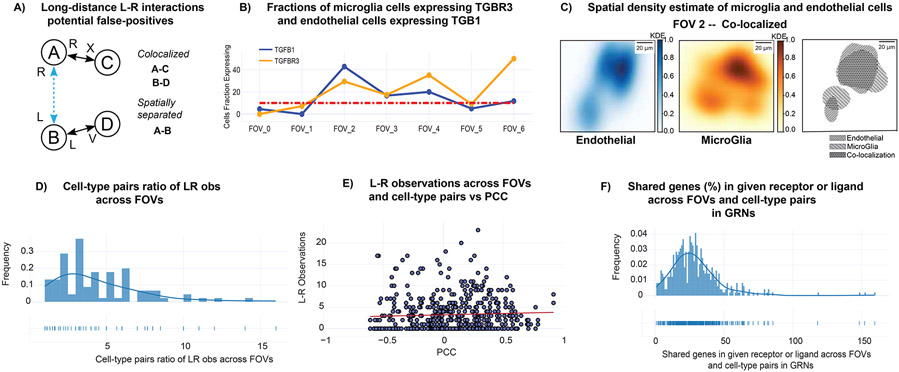
Figure 5.

Spatial variation of intercellular communication in MOB. A) Outline of the scheme to identify potential false-positive long-range ligand-receptor communications. B) Variability in expression of TGF β ligand in microglia cells and type III TGF β receptor in endothelial cells. The Y-axis represents the fraction of cells of the given cell-type expressing TGF β and type III TGF β receptor. The X-axis represents FOV (Field of View). C) Kernel density maps of endothelial cells and microglia, and their co-colocalization pattern in FOV 2 (located within the GCL layer). Color bar represents in linear scale the kernel density estimates (KDE) values. D) Ratio between the maximum and the minimum numbers of ligand-receptor pairs utilized by each pair of cell-types across FOVs. E) Number of ligand-receptor used across FOVs and cell-type pairs vs Pearson Correlation Coefficient (PCC) F) Shared genes in receptor or ligand GRNs across FOVs and cell-type pairs.

This analysis discovered widespread intercellular communication in MOB while capturing bona fide receptors and ligands. For example, we found endothelial and microglial cells communicating through the Type 3 TGF-β receptor and the Type 1 TGF-β ligand in FOV 4 (Fig. 5B, S7). Previous work, including Eng et al.’s seqFISH+ study, have experimentally validated this TGF-β family receptor-ligand pair in MOB (Yousef et al., 2015; Eng et al., 2019). These two cell-types are also colocalized in this FOV (Pearson correlation coefficient for colocalization = 0.74) (Fig. 5C, S6), further supporting the possibility of their communication. Similarly, we found neuronal periglomerular cells and olfactory ensheathing cells to communicate through the BMP pathway ligand Bmp7 and the receptor Ptprk in FOV 6, although the two cell-types are spatially separated in this FOV (Pearson correlation coefficient for colocalization = −0.53). The BMP pathway is classically known to mediate long-range intercellular communication (Zakin and De Robertis, 2010; Ramel and Hill, 2012). As expected overall, we found the most abundant receptors and ligands are from the well-known signaling pathways such as Fibroblast growth factor (FGF), Notch, Bone morphogenetic protein (BMP), Transforming growth factor beta (TGF-β), and Wnt (Hébert et al., 2003; Maier et al., 2011; Marei et al., 2012; Bialas and Stevens, 2013).

The analysis also found spatial variation of intercellular communication in the MOB. On average, a given cell-type pair communicates in three FOVs (range: 1-7). We observe this variation even when we focus on FOVs from the same morphological layer. For FOVs 2, 3, and 4, which are from the GCL layer, we see that 37% of cell-type pairs communicate in one FOV, 17% in two and 29% in all three FOVs. Some intercellular communications are specific to an FOV or to a particular morphological layer. For example, endothelial cells and neuronal granule cells communicate only in FOVs 2, 3, and 4 located specifically in the GCL layer. Similarly, astrocytes cells and endothelial cells communicate only in FOV 0 that covers the GL, EPL layers. On the other hand, certain pairs of cell-types communicate in nearly every FOV and their communications appear to be a common aspect of MOB. These examples include the intercellular communication between astrocytes and olfactory ensheathing cells, and olfactory ensheathing cells and endothelial cells.

Interestingly, we found that a cell-type pair often uses different sets of receptors and ligands in different FOvs. On average, the number of receptors and ligands used by two cell-types in different FOVs can change by two-fold (Fig. 5D; ratio of the maximum and the minimum number of receptors-ligands used across different FOVs; range: 1-16), with minimal overlap between the sets of receptors and ligands across FOVs (median Jaccard Index similarity between cell-type pairs in receptor-ligand usage: 2%, range: 0-13%). We observed this variation even across FOVs where the two cell-types colocalize. For example, astrocytes and microglial cells colocalize in FOVs 0 and 6 (Pearson Correlation Coefficient > 0.5), but only one of their 10 ligand-receptor pairs are common in these FOVs. We found that a higher colocalization between cell-types shows a positive trend with a higher number of ligands and receptors (Fig. 5E), although there are instances when cell-types colocalize but do not communicate.

The above analyses implied spatially variable usage of receptors and ligands for intercellular communication. We next asked if the gene regulatory network (GRN) of a receptor or ligand, i.e., the genes in regulatory relationships with it, in a given cell-type may change across FOVs. This concept of spatially localized GRNs has been noted in the literature (Yang, Fang and Shen, 2019) and aligns with previous observations on spatial variation of gene expression because of intercellular communication (Arnol et al., 2019). However, to our knowledge, the existence and role of spatially localized GRNs of different cell-types in mediating their intercellular communications have never been discussed.

We applied SCENIC (Aibar et al., 2017), a GRN construction algorithm, on STANN’s predicted cell-types in each FOV (Methods). We found that the GRN of a receptor or ligand in every cell-type often changes across FOVs, suggesting that spatially localized GRNs are very common in MOB. For example, endothelial cells use the TGFβ-1 ligand to communicate with microglia cells in FOVs 2 and 4 (Fig. S8), yet only 5.5% of genes in the GRN of TGFβ-1 in endothelial cells are shared in these two FOVs. On average, only 19.7% (Fig. 5F; range 0.8%-49.5%) genes in the GRN of a receptor or ligand in a cell-type were common across FOVs. Overall, our analyses in this section revealed widespread spatial variation in intercellular communications. A pair of cell-types often interacts in a region-specific manner and may communicate through utilizing very different sets of receptors and ligands.

Spatially localized ligands and receptors refine cell-subtypes and are predictive of their colocalization patterns

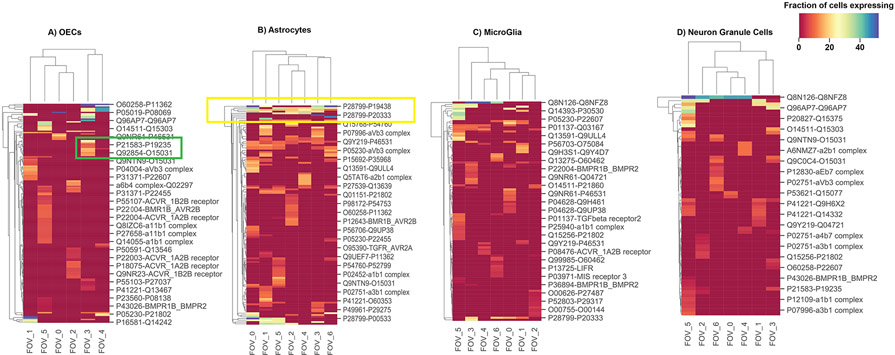
Since the above analysis revealed widespread spatial variation in ligand and receptor usage, we asked if ligand-receptor expressions define distinct subpopulations of a cell-type in different FOVs. We indeed found that the subpopulations of a cell-type in different FOVs often use distinct ligand-receptor pairs (Fig. 6). For example, olfactory ensheathing cells use KITLG ligand and EPOR receptor (Grebien et al., 2008) in FOV 3, while they use BMP6 ligand and BMPR1B-ACVR2A (Mueller and Nickel, 2012) receptor in FOV 5. Since the previous section showed that spatially varying usage of ligands and receptors also induce spatially localized gene regulatory networks, we posit that such spatial variations in ligand-receptor usage refines cell-subtypes in the MOB. Finally, we asked if ligand-receptor usage could also be predictive of spatial separation or colocalization of cell-type pairs in different FOVs. Indeed, for every cell-type pair, we found it to use a different set of ligands-receptors in FOVs where they are colocalized compared to FOVs where they are spatially separate (median Jaccard Index similarity between cell-type pairs in receptor-ligand usage: 9%, range: 0-20.8%).

Figure 6.

Subpopulations of a cell-type in different FOVs may use distinct ligand-receptor pairs. Shown are the hierarchically bi-clustered heatmaps of the fractions of cells expressing ligand-receptors pairs across FOVs on the outgoing (selected cell type ligand communicating with rest of cell types receptors) communication of cell types. The selected cell types are: A) OECs, B) Astrocytes, C) Microglia and D) Neuron Granule Cells. The selected green box highlights examples of distinct ligand-receptor usage across FOVs, and the yellow box highlights consistent ligand-receptor usage across FOVs. Color bar represents in linear scale the percentage fraction of cells expressing a particular ligand-receptor pair.

The above analyses not only revealed spatially variable GRNs regulating receptors and ligands and how variation in receptor-ligand usage could refine cell-subtypes, it also enabled us to identify the spatially consistent up-stream regulators of cell-type specific marker genes (Fig. S9). Consistent with the literature, we found that certain upstream regulators are key for overall cell-type specific functionality. For example, we found Rorb is an upstream regulator of astrocytes’ marker genes across all FOVs. This is consistent with previous studies reporting a major role for Rorb in astrocyte maturation (Clarke et al., 2021). Similarly, we found that Sox10 regulates the olfactory ensheathing cell marker genes, as was previously reported (Barraud et al., 2013); and Larp1 regulates the markers of neuronal granule cells -- Larp1 has been associated previously with neuronal proliferation and differentiation (Gower-Winter et al., 2013).

Discussion

Mammalian brains are complex ecosystems of several millions to hundreds of billions of cells (Herculano-Houzel, 2009; Herculano-Houzel et al., 2015). Brains exhibit a high degree of architectural principle in terms of the spatial organization (Defelipe, 2011; Glasser et al., 2016) of cell-types, their colocalization and intercellular communication (Lein, Borm and Linnarsson, 2017). These aspects of brain architecture are disrupted in nearly every brain disease (Patel et al., 2014; Keren-Shaul et al., 2017). A critical step toward understanding the pathophysiology of the brain is to gain a deeper understanding of its architecture. However, our current understanding of brain architecture is largely limited to descriptions of morphological layers and does not offer the single-cell level insights mentioned above.

By integrating scRNA-seq (single-cell transcriptomics) with seqFISH+ (single-cell resolution spatial transcriptomics) data, and performing a series of systematic analyses, we have charted the spatial organization of cell-types, their colocalization and communications in mouse olfactory bulb (MOB). Our analyses revealed both consistent and variable aspects of cell organization and intercellular communications in the MOB. On the one hand, as we had expected, we found that the proportions of cell-types vary across different morphological layers of MOB, but remain consistent when they are spatially close within a given morphological layer. On the other hand, we found remarkable variations in their colocalization patterns and intercellular communication mechanisms throughout MOB even when we studied tissue regions (fields of views; FOVs) from the same morphological layer. Our analyses point to a widespread use of spatially localized gene regulatory networks in the MOB. Overall, we find that spatially localized usage of ligands and receptors is a signature of spatially varying cell-subtypes and underlie their colocalization patterns.

As we have noted in the Introduction, our aim was to fill in a critical gap in this realm since previous studies have described brain architecture using spot-ST data in terms of the proportion of different cell-types in the spots (Andersson et al., 2020; Biancalani et al., 2021; Cable et al., 2021). However, since the number of cells in each spot of spot-ST data is difficult to determine and variable between spots, one cannot comment on a tissue region’s cell-type composition, colocalization of cell-types or their intercellular communications from spot-ST data as accurately as one could from sc-ST data. For those analyses, one practical solution is to first make a binary presence-absence call in the spots for each cell-type using a predefined threshold on the cell-type’s proportion per spot. On one hand, it is not clear how to define this threshold and whether one should use a cell-type specific threshold, on the other hand, the conclusions from such binarized analyses would arguably be sub-optimal than those that an sc-ST data could offer. That is why, we posited that sc-ST data are better suited to reveal the consistent and the variable aspects of the architecture and intercellular communication mechanisms in MOB beyond its layer-based architectural description, and developed STANN to tackle the associated computational challenges. To this end, we also developed the necessary statistical approaches to quantify cellular colocalization, detect potential long-range intercellular communications, and check for spatially localized gene regulatory networks. Altogether, the STANN model, the downstream analyses and the benchmarking offer important insights toward delineating the principles of brain architecture and intercellular communication and developing the necessary computational tools.

We have shown in our benchmarking analysis that STANN outperforms alternative models and we also found that methods for integrating spot-ST and scRNA-seq data are likely to produce suboptimal results if applied to integrate sc-ST and scRNA-seq data. This is not unexpected since although both sc-ST and spot-ST require integration with scRNA-seq, the methods require solving two different computational problems. In the case of sc-ST, a tool like STANN needs to find a mapping to cell-types from a fewer number of genes, even from genes that were not used in the first place to define the cell-types in the scRNA-seq data. In the case of spot-ST, since each spot contains a variable number of cells, the problem is to deconvolve the data into proportions of different cell-types. Since sc-ST data do not require deconvolution, when applied to sc-ST datasets, the algorithms developed for spot-ST data essentially optimize linear correlations of gene expression between the given sc-ST and scRNA-seq datasets. However, as our benchmarkings suggest, explicitly learning a non-linear high dimensional mapping function, as STANN does, is potentially more useful than that for sc-ST data.

Although we attribute STANN’s success primarily to its ability to identify complex nonlinear functions that map the expression values of shared genes in a cell to its cell-type, STANN also benefited from a careful selection of input features through supervised PCA (Methods). Another aspect boosting STANN’s performance was its class imbalance aware approach, both in the sPCA step and the deep learning optimization through a class imbalance aware loss function (Methods). Class imbalance is common in single-cell transcriptomics and may compound the challenges for integrating sc-ST with scRNA-seq data. Our analyses suggest that in these situations, it would be necessary to carefully assess the outputs of scRNA-seq data integration methods that do not account for class imbalance (Butler et al., 2018; Ma and Pellegrini, 2020; Zhao et al., 2020). In our comparisons, for example, although the widely used method Seurat performed better than more complex models, it suffered from misclassifying rare cell-types.

The STANN model and the downstream analyses have shown the feasibility and value of studying the consistent and variable aspects of cell-type composition, colocalization, and intercellular communication. We see this as an initial step toward comparative spatial transcriptomics between healthy and diseased samples. We anticipate future studies will characterize the spatially aberrant transcriptomics of diseased samples enabling the design of targeted therapies.

STAR Methods

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Dr. Md. Abul Hassan Samee (samee@bcm.edu).

Materials availability

This study did not generate new materials

Data and code availability

• Source data statement

This paper analyzes existing, publicly available data (Moffitt et al., 2018; Tepe et al., 2018; Eng et al., 2019; Vickovic et al., 2019; The Tabula Sapiens Consortium and Quake, 2021)(Tepe et al., 2018; Eng et al., 2019). These accession numbers for the datasets are listed in the key resources table.

KEY RESOURCES TABLE

RESOURCE	SOURCE	IDENTIFIER
Deposited data
Single-cell RNA sequencing	Tepe et al. 2018	GEO: GSE121891
Single-cell Spatial Transcriptomics	Eng et al. 2019	https://github.com/CaiGroup/seqFISH-PLUS
Single-cell RNA sequencing	The Tabula Sapiens Consortium and Quake, 2021	https://tabula-sapiens-portal.ds.czbiohub.org/
Single-cell RNA sequencing	Moffitt et al. 2018	GEO: GSE113576
Single-cell Spatial Transcriptomics	Moffitt et al. 2018	DOI: 10.5061/dryad.8t8s248
Spot-based Spatial Transcriptomics	(Vickovic et al., 2019)	https://portals.broadinstitute.org/single_cell/study/SCP420
Software and algorithms
STANN	This paper	DOI: 10.5281/zenodo.5227626;https://doi.org/10.5281/zenodo.5227626
Tensorflow	Abadi et al. 2016	https://github.com/tensorflow/tensorflow
Scikit-Learn	Pedregosa et al., 2011	https://github.com/scikit-learn
KS	Duong 2020	https://github.com/cran/ks
CellPhoneDB	Efremova et al. 2020	https://github.com/Teichlab/cellphonedb
SCENIC	Aibar et al. 2017	https://github.com/aertslab/pySCENIC
Scanpy	Wolf, Angerer, and Theis 2018	https://github.com/theislab/scanpy
Seurat	Butler et al. 2018	https://github.com/satijalab/seurat
scPred	Alquicira-Hernandez et al. 2019	https://github.com/powellgenomicslab/scPred
Tangram	Biancalani et al., 2021	https://github.com/broadinstitute/Tangram
Scipy	Virtanen et al., 2020	https://github.com/scipy/scipy

• Code statement

All original code has been deposited at https://github.com/sameelab/STANN and is publicly available as of the date of publication. DOIs are listed in the key resources table.

• Any additional information required to reproduce this work is available from the lead contact upon request.

METHOD DETAILS

Cell type annotation in scRNA-seq data

We collected the annotated cell-types from our previous scRNA-seq dataset of mouse olfactory bulb (MOB) (Tepe et al., 2018). Following the common steps for cell-type annotation in scRNA-seq data (Zheng et al., 2017; Butler et al., 2018), we ran Scanpy’s highly_variable_genes function (v1.5.0) and selected the top 4000 genes based on the variance-to-mean ratio of their expression values. Then, using principal component analysis, we computed a low dimensional manifold that best explains the variance in the data (Number of PCs=50), and further reduced the dimensionality into two dimensions using uniform manifold approximation and projection (UMAP). We then clustered cells in this two-dimensional space using the Louvain community detection algorithm (Traag, Waltman and van Eck, 2019). Finally, based on marker genes detected using the Wilcoxon rank-sum test and original annotation (Tepe et al., 2018), we annotated the clusters (Fig. S1).

Data normalization

For all scRNA-seq datasets, Scanpy toolkit 1.3 (Wolf, Angerer and Theis, 2018) was used to perform standard pre-processing, including normalization of library-size with 10000 reads per cell, log transformation, regression of effects of total counts per cell and the percentage of mitochondrial gene expression. We finally scaled the data to unit variance (clipping values exceeding standard deviation greater than 10).

Following the original seqFISH+ manuscript, STANN performs a quantile normalization on the normalized count matrix of each gene in the scRNA-seq and seqFISH+ datasets to correct for cross-platform differences (Bolstad et al., 2003; Zhu et al., 2018; Eng et al., 2019). STANN also applies Min-Max scaling to scale the data between 0 and 1. This final step was used to ensure efficient updates in the gradient descent optimization of our neural network model.

Supervised Principal Component Analysis (sPCA)

We implement supervised principal component analysis (Bair et al., 2006) (sPCA), a feature selection approach that performs PCA while taking the labels of a prediction task (such as classification) into account (Jolliffe and Cadima, 2016). Briefly, we first score each feature according to the accuracy of a weighted logistic regression model that uses only the given feature to solve the classification task at hand. Under the weighted scheme, a weight w_j is applied to the loss function for the j − th class as follows:

$$w_j=\frac{N}{k\cdot N_j}$$

Where N is total number of observations, N_j is the number of observations in class j, and k is the number of classes. This scheme ensures that the logistic regression model minimizes the loss while accounting for class imbalance. After estimating the predictive accuracy score for each feature, we ranked and selected the top features as discussed below in the section on hyperparameter search.

STANN Architecture

We implemented STANN as a multi-layer fully connected neural network model and searched for its optimal architecture using hyper-parameter search under 10-fold cross-validation (see below). The input layer of this model has size equal to the number of supervised principal components (sPCs) that we learned from the shared genes (i.e., the genes profiled by both scRNA-seq and sc-ST). The output layer is a softmax layer with size equal to the number of cell-types detected above from the scRNA-seq data.

The softmax value for the i-th output node is defined as:

$$\text{Softmax}(x_i)=\frac{\text{exp}(x_i)}{{\sum }_{j=1}^k\text{exp}(x_j)}$$

Where all the x_i values are the elements of the output of the fully connected layer immediately preceding it, k is the number of classes and $\sum _{j=1}^k\text{exp}(x_j)$ is the normalization term, which ensures that all output will sum to one, and thus constitute a probability distribution. The vector x_i are the elements of the output of the fully connected layer immediately preceding it, where k is the number of classes.

We used categorical cross-entropy (CE) as the loss function to train the model. CE is defined as:

$$\text{CE}=-\sum _{i=1}^N\sum _{j=1}^k{t}_{i,j}\cdot \log (p_{i,j})$$

Where N is number of observations (single-cells), k is the number of classes, t_i,j is the binary indicator whether class j is the correct classification for observation i. Finally, p_i,j is the predicted probability that observation i belongs to class j (STANN’s sigmoid output in the j − th node of the output layer). Since single-cell datasets are usually imbalanced, we used an alternative loss function that adjusts the loss function for under or over-represented cell-types based on their number of cells in the dataset, defined as:

$$\text{Weighted CE}=-\sum _{i=1}^N\sum _{j=1}^k{w}_j\cdot t_{i,j}\cdot \log (p_{i,j})$$

Where w_j is class weight balance defined previously.

STANN Implementation

STANN is implemented in Python 3 through high level API Keras library (Chollet, 2015), using the TensorFlow library back-end for backpropagation using automatic differentiation (Abadi et al., 2016). The model training and prediction takes less than an hour for a dataset of ~10K cells and ~10K genes. All analyses were run in a personal computer with 16-GB RAM memory and a 3-GHz Intel Core i5 processor. Training on CPU or GPU is supported using Keras and TensorFlow. The hyperparameter optimization is implemented using KerasTuner (O’Malley et al., 2019) using the Hyperband algorithm (Li et al., 2018).

Fitting STANN through Hyper-parameter Search under a 10-fold Cross-Validation Scheme

We performed a stratified 10-fold cross validation setup using scikit-learn (Pedregosa et al., 2011), in this setup, each fold preserves the percentage of samples for each class (cell-type). We first split the data into 10 folds (each containing about 10% of the data) and at the i-th iteration, we hold out the i-th fold as our test data. On each iteration, the model is trained on nine partitions (90% of the data) and subsequently tests the model on the unseen partition that was held out (10% of the data). The average performance metrics for training and testing across 10 iterations is then reported. Over the 10 folds, the model showed an average accuracy of 99.413 ± 0.059% on the training data and 95.150% ± 0.325% on the separately held-out test data (Fig. S10).

We implemented hyperparameter optimization using KerasTuner (O’Malley et al., 2019). Specifically, we used the hyperband algorithm (Li et al., 2018) which performs a computationally efficient random search through adaptive resource allocation and early stopping. We evaluated 2000 random models with varying the following parameters within the shown ranges or sets.

• Dense layers neurons: Min: 10, Max: 500

• Activation functions: Relu, Sigmoid and Tanh

• Learning rates: Min: 1e-4, Max: 1e-2, and

• Optimizers: Adam, SGD, and RMSprop.

The optimal model found had two hidden layers (with 160 and 145 neurons), the hyperbolic tangent function as the nonlinear function and a learning rate of 0.01. We performed the above hyperparameter search using the first 5000 principal components (PCs) of the top 8000 features (genes). These numbers for features and PCs were fixed using an initial exploratory search over 6000, 7000, and 8000 features, and 3000, 4000, and 5000 PCs, and randomly sampling the other hyperparameter values five times from the above ranges (or sets).

Comment on runtime and memory usage of STANN and other benchmarked methods

All benchmarking runs were conducted in a server equipped with 80x Intel(R) Xeon(R) Gold 6148 CPU @ 2.40GHz processors and with 256GB of DDR4 memory. From the benchmarked methods, we found that STANN had similar runtime as Seurat and scPred and significantly lower memory usage than the three other benchmarked methods. Seurat and Tangram had the highest peak memory usage. STANN and Tangram were run on a single processor, Seurat and scPred were run on 10 processors to leverage functions that supported multithreading.

Training a model with ~10K cells and ~150 genes (MERFISH benchmarking) and predicting on ~90K cells and ~150 genes took both STANN and Seurat runtime took < 20min, scPred and Tangram > 1hr. Training a model with ~10K cells and ~10K genes (Tabula Sapiens and MOB runs) and predicting in ~10K cells and ~10K genes took STANN, Seurat and scPred < 1hr and > 1hr for Tangram.

Colocalization analysis

The method is based on principles of co-colocalization analysis in microscopy images (Manders, Verbeek and Aten, 1993). Briefly, we first use kernel density estimation to estimate the density of each cell-type in each FOV. Kernel density estimation is a method to estimate the density of a random variable from a finite sample size (Chacón and Duong, 2018). For any pair of cell-types, we then used the Pearson’s Correlation Coefficient (PCC) (Manders, Verbeek and Aten, 1993) between their kernel densities in an FOV as a measure of their colocalization in that FOV. Details of the kernel density estimation step is as follows.

The kernel density estimator is defined as

$$\widehat{f}(\mathbf{x};\mathbf{H})=n^{-1}\sum _{i=1}^n{K}_{\mathbf{H}}(\mathbf{x}-{\mathbf{X}}_{{}_i})$$

where K_H is a kernel function that depends on H, the symmetric and positive-definite bandwidth matrix. x is an estimation point and X_i is an observation point (Chacón and Duong, 2018). We use the scaled and translated normal kernel function:

$$K_{\mathbf{H}}(\mathbf{x}-{\mathbf{X}}_{{}_i})=(2\pi {)}^{-1∕2}\mid H{\mid }^{-1∕2}\text{exp}\{-\frac{1}{2}(\mathbf{x}-{\mathbf{X}}_{{}_i}{)}^{\mathsf{T}}{H}^{-1}(\mathbf{x}-{\mathbf{X}}_{{}_i})\}$$

which is a normal density centered at X_i and with variance matrix H. Normal Kernel is the most widely used multivariate kernel function. We used the kernel density estimator from the R package ks (Duong, 2020). This package estimates H through cross-validation.

We used Pearson’s Correlation Coefficient (PCC) (Manders, Verbeek and Aten, 1993) to measure the similarity between the kernel densities of two cell-types in an FOV. It is the covariance normalized by the product of their standard deviations:

$$\text{PCC}=\frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n(x_{{}_i}-\overline{x}{)}^2}\sqrt{{\sum }_{i=1}^n(y_i-\overline{y}{)}^2}}$$

where x_i represents the probability of observing cell-type x at the i − th location in that FOV, as estimated in the kernel density for x. Similarly, y_i represents the probability of observing cell-type y at the i − th location in that FOV, as estimated in the kernel density for y. Here n is the number of discrete locations in this FOV. We did not apply PCC on the overall kernel densities, we selected only those locations where probabilities are greater or equal to the 2-quantiles of the kernel densities.

Ligand-Receptor analysis

With STANN’s predictions of cell-types in each FOV of the seqFISH+ data, we identified every pair of communicating cell-types and the receptor-ligands that they use. We used the tool CellPhoneDB (Efremova et al., 2020) for this analysis. CellPhoneDB uses a curated database of receptor-ligand pairs and constrains that a receptor or ligand should be expressed in at least 10% cells of a cell-type to be considered for this analysis. Based on an empirical null distribution, the tool then identifies receptors-ligands that are significantly and specifically enriched within a pair of cell-types.

Eliminating potential false-positive predictions of long-range intercellular communication

To flag potential false-positive predictions of intercellular communication between spatially separated cell-types, we checked if the predicted ligand-receptor pairs are used for communication with other colocalized cell-types. In particular, we perform the following check for each spatially separated but communicating cell-type pair A-B (PCC < 0). Let the communication between A and B is mediated by the ligand L and the receptor R. We eliminate this ligand-receptor pair from consideration if A is colocalized with cell-type C and communicates with C using L, and if B is colocalized with cell-type D and communicates with D using R. We outline this scheme in Fig. 5A. We reported the remaining ligand-receptors between A-B as potential mediators of long distance communication between A-B (Supplementary Table S5). This eliminated 78.26% of the communications between spatially separate cell-types inferred by CellPhoneDB. Although we were over-conservative in this step, the possibility of such a large fraction of inferences being incorrect underscores the importance of studying intercellular communication with spatial information.

To check if the above approach works, we simulated spatial colocalization/separation patterns and checked if the number of long-range communications marked as false-positives by this approach increases or decreases as we introduce more spatial colocalization or separation, respectively. We note that we can represent the spatial colocalization/separation pattern in an FOV using a graph where nodes represent cell-types and edges represent pairs of colocalized cell-types. The absence of an edge between two nodes represents a spatial separation of the corresponding cell-types.

Thus, we first compute seven graphs representing the spatial colocalization/separation patterns of cell-types in the seven FOVs of this seqFISH+ data. We then create 100 synthetic patterns of spatial colocalization/separation for the seven FOVs as follows. For 50 patterns, we increased spatial separation by randomly removing k edges from the seven graphs, where we sampled k uniformly from the range [10, 50% of the total number of edges in the seven graphs]. Similarly, 50 times we increased spatial colocalization by randomly adding k new edges to the seven graphs, again sampling k uniformly from the range [10, 50% of the number of node-pairs that did not have an edge in the original seven graphs].

For each of the 100 spatial colocalization/separation patterns generated above, we repeat our analysis and record the fraction of intercellular communications between spatially separate cell-types (i.e., long-range communications) that our approach marks as false-positives and filters out. This analysis showed that the number of false-positives marked by our approach increases or decreases as we simulate more spatial colocalization or separation, respectively (Fig. S11).

Orthogonal validation using HDST data

In order to check whether the observation spatial organization principles are dataset-dependent, we analyzed cell type composition and colocalization in HDST MOB data (Vickovic et al., 2019). We focused only on the region of HDST data marked as granule cell layer and subsampled from it 100 regions of similar size of a seqFISH+ FOV. For each region we proceed to calculate cell-type proportions and colocalization of cell-type pairs following the same methodology we used for seqFISH+ data.

Gene Regulatory Networks

We used SCENIC (Aibar et al., 2017) to compute gene regulatory networks for each cell-type within each region of the tissue. Based on these networks, we identified the genes having regulatory relationships with the receptors and ligands mediating intercellular communication.

Jaccard Similarity coefficient

We used the Jaccard similarity coefficient (also known as Jaccard Index) to gauge similarity between two finite sample sets A and B, e.g., between sets of receptors and ligands across FOVs. The Jaccard index is defined as the size of the intersection (N(A∩B)) divided by the size of the union (N(A∪B)) of the sample sets, it’s expressed as:

$$\text{Jaccard similarity}(A,B)=N(A\cap B)∕N(A\cup B)$$

Statistical comparison of cell-type compositions

To compare cell-type compositions between a pair of FOVs, we used the chi-square test of independence on the counts of different cell-types in those FOVs, across all pairwise comparisons of FOVs. We used a p-value cutoff of 0.01 after Bonferroni correction (Supplementary Table S4). We further corroborated these results using the Jensen-Shannon divergence and relative entropies as follows. Let x and y denote the compositions of cell-types in the two FOVs. We then computed the Jensen-Shannon divergence between x and y. We also computed the KL-divergences of x given y and also of y given x. Let p and q denote these two relative entropy terms. We checked both the arithmetic and the harmonic means of p and q, and the Jensen-Shannon divergence values and confirmed that the results are in agreement with our chi-square test, i.e., we confirmed that the cases where we could not reject the null hypothesis are indeed the cases where the two FOVs differ the least in terms of x and y.

All analyses were performed using Scipy v1.5.2 (Virtanen et al., 2020).

Mouse Models

Wild-type mice C57BL/6J of post-natal day P40 (male) was used for the olfactory bulb seqFISH+ experiments (Eng et al., 2019). The olfactory bulb scRNA-seq data (Tepe et al., 2018) was generated from wild-type male and female C57BL/6NJ mice at 14 weeks of age.

Supplementary Material

3

Supplementary Table S1. Marker genes from Tepe et al, 2018 & Zeisel et al. 2018 with their intersection with the genes profiled in seqFISH+, Related to Figure 2 and Figure 3.

4

Supplementary Table S2. Morphological layer annotation of each Field of Views (FOVs), Related to Figure 1.

5

Supplementary Table S3. Acronyms of each cell-type referred in this study, Related to Figure 2, Figure 3, Figure 4, Figure 5, and Figure 6.

6

Supplementary Table S4. Statistical comparison of cell-type compositions results, Related to Figure 4.

7

Supplementary Table S5. Ligand-receptors potentially mediating long-range intercellular communication, Related to Figure 5.

Highlights.

• A neural network, STANN, models cell-types in single-cell spatial transcriptomics data

• Subsequent analyses reveal mouse brain architecture beyond conventional layers

• Cellular colocalization and communications could show high variations within a layer

• Spatially localized subpopulations of cell-types differ in receptor-ligand usage