The Cortical Connectome of Primate Lateral Prefrontal Cortex

SUMMARY

The lateral prefrontal cortex (LPFC) of primates plays an important role in executive control, but how it interacts with the rest of the cortex remains unclear. To address this, we densely mapped the cortical connectome of LPFC, using electrical microstimulation combined with functional MRI (EM-fMRI). We found isomorphic mappings between LPFC and five major processing domains comprising most of the cerebral cortex except early sensory and motor areas. An LPFC grid of ~200 stimulation sites topographically mapped to separate grids of activation sites in the five domains, coarsely resembling how the visual cortex maps the retina. The temporal and parietal maps largely overlapped in LPFC, suggesting topographically organized convergence of the ventral and dorsal streams, and the other maps overlapped at least partially. Thus, the LPFC contains overlapping, millimeter-scale maps that mirror the organization of major cortical processing domains, supporting LPFC’s role in coordinating activity within and across these domains.

eTOC Blurb

By building a dense connectome using EM-fMRI, Xu et al. find layout-preserving, surface-to-surface mappings between macaque LPFC and other major association cortices, coarsely resembling how visual cortex maps retina. Thus, LPFC contains overlapping, millimeter-scale maps that parallel the organization of other cortices, which may help integrate representations at appropriate levels.

INTRODUCTION

In primates, the LPFC is strongly implicated in executive control (Desimone and Duncan, 1995; Fuster, 2001; Goldman-Rakic, 2011; Miller and Cohen, 2001; Petrides, 2005), including working memory, attention to stimulus attributes, and the selection of context-dependent responses. How these functions arise from the interactions between LPFC and the rest of the brain remains unclear.

The LPFC contains numerous major cytoarchitectonic regions (Barbas and Pandya, 1989; Neubert et al., 2014; Petrides, 2005; Sallet et al., 2013), including areas 9, 46, 8, 45, and 12, and even finer subdivisions by some parcellations. Tracing studies in monkeys found extensive connectivity of these areas, with some specificity. Dorsal and ventral LPFC preferentially connect with medial and lateral cortical areas, respectively (Barbas and Pandya, 1989; Petrides, 2005; Saleem et al., 2014; Yeterian et al., 2012). Caudal LPFC tends to connect with higher-order sensory areas and rostral LPFC with limbic areas (Barbas, 2015; Barbas and Pandya, 1989; Petrides, 2005). Besides the broader trends, topography at a smaller scale has been reported in some parts of LPFC. For example, in the most caudal LPFC, dorsal and ventral areas mainly connect with dorsal and ventral sensory cortices, respectively (Petrides, 2005). In the principal sulcus (PS), caudal to mid areas mainly connect with oculo- and skeleto-motor areas, respectively (Borra et al., 2019; Gerbella et al., 2013). Finally, areas from the dorsal bank to the ventral bank of the PS topographically connect with caudal to rostral areas, respectively, in the posterior parietal convexity (Cavada and Goldman-Rakic, 1989; Petrides and Pandya, 1984).

In addition to anatomical organization, many studies have examined the functional organization of LPFC. A dorsal-ventral axis has been proposed for spatial vs. object working memory (Levy and Goldman-Rakic, 2000; but see O’Reilly, 2010; Petrides, 2005), respectively, and a posterior-anterior axis has been proposed for stimulus and action selection to more complex functions (Badre and D’Esposito, 2009; Petrides, 2005), respectively. However, mounting evidence suggests that neurons throughout LPFC process many types of information (Chen et al., 2020; Kadohisa et al., 2015; Rainer et al., 1998; Rao et al., 1997), and reflect multiple aspects (Mante et al., 2013; Siegel et al., 2015) and levels (Crittenden and Duncan, 2014; Premereur et al., 2018) of executive control. At a smaller scale, some studies report more regional specialization in the LPFC, with face processing patches (Haile et al., 2019; Ku et al., 2011; Tsao et al., 2008) and auditory and audiovisual responsive regions (Romanski and Goldman-Rakic, 2002; Sugihara et al., 2006) in parts of LPFC. But stimulus preferences may not fully explain the functional organization of LPFC. Currently, one dominant theory of prefrontal function (Miller and Cohen, 2001) focuses on its integrative, flexible nature, and largely relegates functional organization and differential connectivity within LPFC to second-order effects. In line with this idea, the observed mixed selectivity of LPFC neurons might be computationally beneficial (Rigotti et al., 2013), and consistent with recurrent network architectures (Mante et al., 2013; Song et al., 2016).

More recently, our own work (Bichot et al., 2015, 2019) found evidence for differential roles of the frontal eye field (FEF) (Ekstrom et al., 2008; Moore and Armstrong, 2003) and an adjacent, ventral prearcuate region (VPA) in spatial and feature-based attention, respectively. Are separable executive functions the exception or the rule for LPFC? We believe anatomical connectivity may give some clues, but the existing tracing studies have limitations. The studies relied largely on parcellation of cytoarchitectonic areas, which are coarse in size and location (Patel et al., 2014) and may themselves contain spatially segregated functional clusters (Kiani et al., 2015). In addition, sparseness of injections within single animals and individual differences in anatomical landmarks make it difficult to integrate data across studies and animals.

To gain a better understanding of LPFC connectivity, we created a dense (Van Essen and Ugurbil, 2012), parcellation-free connectome between the LPFC and the cerebral neocortex using EM-fMRI (Tolias et al., 2005) in two monkeys. The EM-fMRI technique has several features that meet our need. The elicited activations are largely restricted to areas with known monosynaptic connections to the stimulation site (Logothetis et al., 2010; Sultan et al., 2011); the spatial specificity of EM is high (Klein et al., 2016; Robinson, 1972; Stoney et al., 1968; Tehovnik, 1996); experiments can be conducted repeatedly in the same animal in vivo, with full-brain coverage at millimeter-resolution; a large number of sites can be stimulated, and MRI lends itself to streamlined data processing. EM-fMRI activations may be restricted to anterograde projection targets of the stimulation site (Klein et al., 2016; Logothetis et al., 2001, 2010), although retrograde connections cannot be ruled out (Klink et al., 2021; Petkov et al., 2015). In either case, the directionality may not be critical for mapping cortico-cortical connections as they are often reciprocal (Felleman and Van Essen, 1991), though the connectivity strength can be asymmetric (Markov et al., 2014).

Through dense connectivity mapping, we found topographic patterns that are evident in each animal and repeated across animals. The connections of LPFC are organized on a much finer scale than cytoarchitectonic areas. Rather, the spatial layout of stimulation sites in LPFC determines the connections observed across multiple cortical domains, in a fashion that is coarsely analogous to retinotopic mapping in visual areas (Tootell et al., 1982). What is mapped onto the LPFC is not the visual field, but the cortical surface of respective domains, i.e., the LPFC contains overlapping “maps” of the major processing domains of the cortex.

RESULTS

Mapping dense connectome using EM-fMRI

We stimulated an array of sites in caudal to mid LPFC of two macaques under anesthesia (Figures 1C and 1D). The sites covered 366 and 328 mm² of the cortex (see STAR Methods) from the anterior bank of the arcuate sulcus (AS) to caudal to mid PS in monkeys J and N, respectively, with a median spacing of ~2 mm mapped onto the surface. The EM-fMRI parameters, including voxel size and current amplitude, were optimized to maximize effect size as quantified by contrast-to-noise ratio or CNR (Figure S1; see STAR Methods). Under optimized parameters, the effect size of EM-fMRI was large at the level of single voxels (Figure S2A), and was consistent across sessions (Figure S2C). By stimulating a site, we usually found several clusters (Xu et al., 2010) of activated voxels, and within a cluster the effect size was high for the more strongly activated voxels, which implies robustness to overall gain/loss of effect size (Figure S2B). Indeed, although the size of the activated regions increased with stimulation intensity up to a limit, the pattern of mapped connections did not change much beyond 500 μA, the amplitude we settled on (Figure S1D). CNR was used as the metric of fMRI activations elicited from stimulating a single site, whereas log-normalized CNR (more Gaussian; see STAR Methods) was used for purposes that require combining results from multiple sites. We projected both metrics onto the cortical surface (i.e., from voxels to vertices; see STAR Methods), and will refer to them as “connections”.

Figure 1. EM-fMRI Experiments and Overall Connectivity Patterns.

(A) Left, from top to bottom, medial, top, and lateral views of inflated cortical surface of left hemisphere (ipsilateral to stimulation sites) of monkey N. Right, the same surface flattened. White contour encloses the MDS planes in (C) and (D). Dark gray, sulci; light gray, gyri. D, dorsal; L, lateral; R, rostral. Abbreviation of sulci: as, arcuate s.; cas, calcarine s.; cgs, cingulate s.; cs, central s.; ios, inferior occipital s.; ips, intraparietal s.; ls, lateral s.; lus, lunate s.; ots, occipitotemporal s.; ps, principal s.; sts, superior temporal s.

(B) As in (A), with colored, transparent overlay of the six cortical domains connecting with the LPFC.

(C and D) Stimulation sites of monkey J/N ([C]/[D]). Left, sites projected onto individual pial surface as blue/orange beads. Right, sites as blue/orange circles on a plane generated by multidimensional scaling (MDS), within matching extent in both monkeys. Black contours indicate borders of areas in CBCetal15 parcellation. Scale bar (for MDS plane of both monkeys; as in all figures), 5 mm.

(E and F) Cortical connections of all sites combined in monkey J/N ([E]/[F]). The color of overlay indicates how many stimulation sites were connected with a vertex. Throughout the paper, color scaling is linear between denoted min and max (1 and half of the total sites in a monkey in this case, respectively). Blue contour encloses the MDS planes in (C) and (D). Black contours indicate gyri-sulci boundaries.

(G1) Overall LPFC-TEMP connectivity. Left, mean connectivity of vertices, averaged over sites of both monkeys. Center/right, mean connectivity of sites in monkey J/N, averaged over TEMP vertices. Percentile of mean connectivity (log-normalized CNR) within domain and type (of vertices/sites) is indicated by color, for vertices (as overlay) and sites (as circles). Area of circle also indicates mean connectivity, and small black circle indicates no connection.

(G2-G6) As in (G1), overall LPFC connectivity with PPC ([G2]), ORBINS ([G3]), DMPFC ([G4]), PMC ([G5]), and within LPFC ([G6]). Cropped views are scaled differently across domains.

Although the total area of the zone of dense stimulation covered only 3.5% and 2.7% of the cortex, they collectively had connections with 69% and 53% of the ipsilateral neocortex in monkeys J and N (Figures 1A, 1E and 1F), respectively, or about a 20X expansion. Consistent with previous EM-fMRI studies (Sultan et al., 2011; Tolias et al., 2005), the ipsilateral cortical connections excluded areas known to be polysynaptically connected with LPFC, such as the primary visual cortex. Consistent with tracing studies (Cavada and Goldman-Rakic, 1989; Hedreen and Yin, 1981; Innocenti, 1986), the contralateral cortical connections of LPFC were much more confined than the ipsilateral connections, mostly found in LPFC areas homotopic as well as heterotopic to the stimulation sites, and areas in medial prefrontal and orbitofrontal cortices (Figures 1E and 1F). This paper focuses on the ipsilateral cortical connections. Subcortical (Amemori et al., 2020) and contralateral cortical connections will be reported separately.

Validation of connectivity mapping using EM-fMRI

To confirm the validity of connectivity mapping using EM-fMRI, we compared the results to a tracing dataset (Markov et al., 2014). At the level of cytoarchitectonic areas (MERetal14 parcellation; see Figures 2A and 2B), the non-parametric correlation (Spearman’s ρ) between downsampled EM-fMRI data (see STAR Methods; also see Figures S4A–S4C for the site-vertex-level data) and tracing data was high (Figure 2C, left-top). The correlation largely held for long-range connections (see Figure 2C, right-top for number of area pairs at various minimal distances), which is important for mapping connections of the LPFC. The correlation was more moderate if we excluded the area pairs that were not connected (Figure 2C, left-bottom), in part because the EM-fMRI connectivity decayed more slowly than connectivity measured with tracing as the inter-areal distance increased (Figure 2D). In other words, the EM-fMRI responses showed that the functional activation over long distances was stronger than one would expect from the weaker anatomical connectivity (e.g., see Figure 2B, top vs. middle). Nonetheless, the results suggest that EM-fMRI is able to both detect the existence of even long-distance connections, and indicate the relative strength of these connections. This supports an implicit assumption that the connectivity metric of EM-fMRI is monotonically related to anatomical connection weights. In contrast, the LPFC-cortical connections reported in a state-of-the-art diffusion MRI (dMRI) dataset (Donahue et al., 2016) showed much lower consistency compared to tracing, which dropped to near zero for long-range connections (Figure 2; see STAR Methods). An alternative analysis based on receiver operating characteristics (ROC) confirmed that EM-fMRI was consistent with tracing in mapping both near and long-distance connections, whereas dMRI was not (Figure S4D).

Figure 2. Interareal LPFC-cortical connectivity mapped by MRI methods vs. tracing.

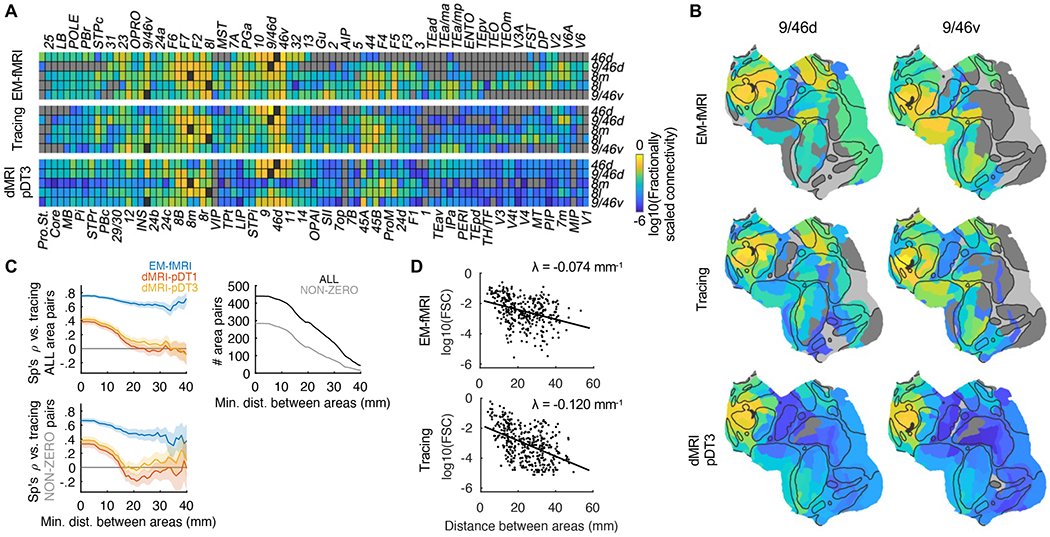
(A) Area-level 5 × 89 connectivity matrices of EM-fMRI (top), tracing (middle), and dMRI-pDT3 (bottom), using MERetal14 parcellation. We built the EM-fMRI matrix by pooling data of both monkeys. pDT3 and pDT1 are two very similar variants based on the same dMRI data. Logarithm base 10 of fractionally scaled connectivity (FSC) is shown. Gray, no connectivity; black, intrinsic connectivity (undefined).

(B) Areal level 1 × 89 connectivity vectors of example row areas 9/46d (left) and 9/46v (right) visualized on flattened surface, of EM-fMRI (top), tracing (middle), and dMRI-pDT3 (bottom), using the same color scaling as (A). Black mask indicates respective row areas.

(C) Consistency (Spearman’s ρ) between interareal connectivity matrices mapped by EM-fMRI (blue), dMRI-pDT1 (red), and dMRI-pDT3 (yellow) vs. tracing, using all area pairs (left-top) or those with non-zero connectivity (left-bottom). X axis is the minimum distance between pairs of areas included in calculating consistency. Solid lines and shadings denote mean and standard deviation (SD) of bootstrap distributions, respectively. Right-top, number of all (black) and non-zero (gray) area pairs at varying minimum interareal distance.

(D) log10(FSC) plotted against interareal distance, of EM-fMRI (top) and tracing (bottom). Dots denote area pairs, and line denotes fitted FSC (Ercsey-Ravasz et al., 2013) as c × exp(− λ × d), where exp() denotes natural exponential (not base 10, to be comparable to literature), d is interareal distance, and c is interception term. FSC mapped by EM-fMRI declined with distance more slowly than tracing, indicated by a smaller λ of the former.

The interareal connectivity mapped by EM-fMRI also showed several major regularities that are comparable to tracing (Ercsey-Ravasz et al., 2013; Markov et al., 2011, 2014). First, it followed a log-normal distribution, and showed variations of ~5-order of magnitude across area pairs (Figure S4E). Second, it declined exponentially as interareal distance increased (Figure 2D). Finally, while it was highly variable across area pairs (the first regularity), two observations suggest that it was also consistent across individuals (Figures S4F and S4G): (i) cross-animal variability for any pair of areas was much smaller than the full range of variability across area pairs; (ii) we rarely found areas connected in only one monkey, except in a few cases where the connectivity was weak. Below we describe detailed, heretofore unknown parcellation-free patterns of LPFC-cortical connections, which is yet intractable to standard anatomical tracing.

Overall connectivity patterns between LPFC and cortical domains

The connections with LPFC appeared to fall within six cortical domains: temporal cortex (TEMP), posterior parietal cortex (PPC), orbitofrontal and insular cortices (ORBINS), dorsomedial prefrontal cortex (DMPFC), posteromedial cortex (PMC), and within LPFC itself, which were parcellated according to an MRI-based atlas (Calabrese et al., 2015) projected to individual brains (Figures 1A, 1B, and S5; see STAR Methods). Because the variation of LPFC connections may not be well captured by such an atlas, we performed structured clustering (Figure S5; see STAR Methods) to find clusters of vertices that are adjacent on the cortical surface and share similar connections with stimulation sites, and used these clusters to refine the boundaries between domains.

We first examined the domain-level connectivity (Figure 1G). Individual stimulation sites connected with a median of four domains, although there was some specificity in the connections to the different domains. Specifically, connections with the TEMP and PPC domains were found within AS and immediately rostral to it, except that the PPC domain didn’t connect with the most ventral LPFC; connections with DMPFC and PMC domains were mainly found in the dorsal LPFC, avoiding most parts of the LPFC that connected with TEMP and PPC domains, except for the PS and the dorsal tip of AS; and connections with the ORBINS domain were concentrated in the ventral LPFC.

Topographic gradients across individual LPFC sites

We next characterized the LPFC-cortical connections at a finer scale, i.e., across individual stimulation sites and within cortical domains. According to the widely reported linear relationship between threshold current and square of distance from the electrode tip to neural element (Stoney et al., 1968; Tehovnik, 1996), the 200-μs, 500-μA, cathodal current pulses used in this study may have directly (instead of synaptically) activated cell bodies of pyramidal neurons within a radius of 0.38-1.36 mm from the electrode tip, based on reported current-distance constant (272-3460 μA/mm²), or axons of pyramidal neurons within a radius of 0.69-1.64 mm (current-distance constant = 186-1040 μA/mm²). Consistent with the idea that the directly stimulated areas were small, we routinely found substantial differences between connectivity patterns of stimulation sites a few millimeters apart. Crucially, these differences were not random, but revealed a surprising degree of topography between the LPFC and every domain. There was often a systematic and nearly one-dimensional progression of connections on the cortical surface resulting from a displacement of the stimulation sites along a particular direction in the LPFC. We refer to the latter as a topographic gradient. For example, if one follows stimulation sites (gradient A of sites 1-3, 7 in Figures 3A and 3B) from rostroventral LPFC toward the intersection of AS and PS, the TEMP connections (Figure 3C) in both monkeys move from the most rostral to progressively more caudal regions in the superior temporal sulcus (STS). In other words, a rostroventral to caudal gradient of stimulation sites in the LPFC maps to a rostral to caudal progression of connection zones within the STS.

Figure 3. Connections of LPFC Sites Along Example Topographic Gradients.

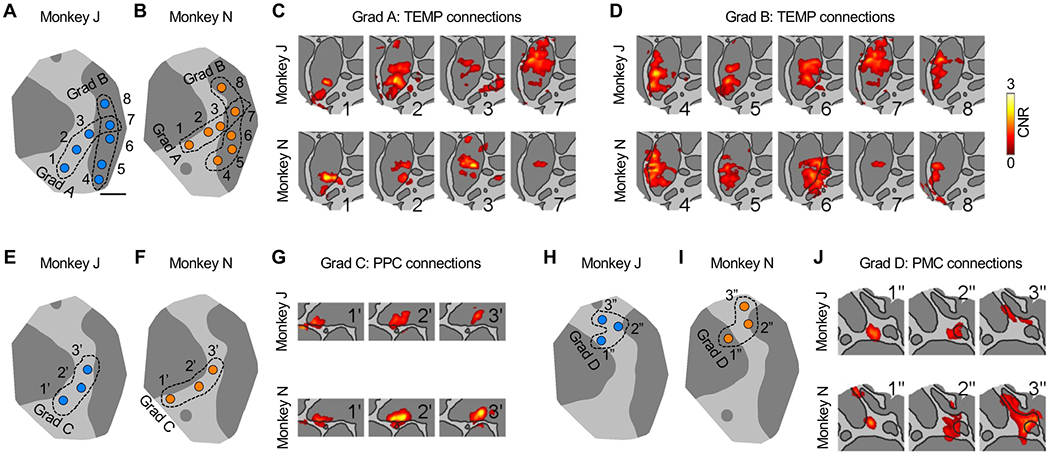
(A and B) Example gradients A and B consisting of sites 1-3, 7, and 4-8, respectively, in monkey J/N ([A]/[B]). Gradients are enclosed by black dotted contours. Scale bar, 5 mm.

(C and D) TEMP connections of stimulation sites in gradient A ([C]) and gradient B ([D]). CNR of significant vertices from stimulating these sites are shown as overlay on cropped views of flattened surface, labeled by site number as in (A) and (B). Connections outside of the domain of interest were masked. Top, monkey J; bottom, monkey N.

(E and F) As in (A) and (B), example gradient C (sites 1’ to 3’) in monkey J/N ([E]/[F]).

(G) As in (C) and (D), PPC connections of sites in gradients C.

(H and I) As in (A) and (B), example gradient D (sites 1” to 3”) in monkey J/N ([H]/[I]).

(J) As (C) and (D), PMC connections of sites in gradients D.

A contrasting pattern is found as one follows another gradient of sites (gradient B of sites 4-8 in Figures 3A and 3B) along the AS, from ventrolateral to dorsomedial, the TEMP connections (Figure 3D) mainly move along a dorsal-ventral arc, from the dorsal bank of STS, to more ventral regions in STS, and then back again to the dorsal bank of STS. Sites 6 and 7 might be within the FEF based on both their locations and characteristic connections consistent with the connections of ventrolateral and dorsomedial FEF mapped by tracing respectively (Schall et al., 1995; Stanton et al., 1995), whereas site 2 might be within the VPA based on its location (Bichot et al., 2015, 2019). The connections of these putative FEF and VPA sites seemed to fit the general topography of connections across stimulation sites in and near the AS.

We found such orderly progressions of connections in other domains too. From sites 1’ through 3’ in gradient C (Figures 3E and 3F), going from the rostroventral to caudodorsal surface in the LPFC, the PPC connections (Figure 3G) progressed from rostral to caudal in the intraparietal sulcus (IPS) and adjacent posterior parietal gyrus, and also progressed deeper into the IPS. As another example in more dorsal LPFC, gradient D consisted of an arc of stimulation sites (1”-3”, Figures 3H and 3I) which mapped to a progression of connections forming an arc from dorsal to mid-caudal then to ventral in the PMC (Figure 3J).

Principal dimensions of LPFC-cortical connectome

These topographic gradients suggested that they may be fragments of an overarching scheme for prefrontal organization. In the previous examples, we identified the gradients by manually and locally reducing the dimensionality of connections to one, i.e., the direction along which connections progress along on cortical surface. Here we used principal component analysis (PCA) as an unbiased method to extract the dimensions that best capture the variations of connections across all LPFC sites in both monkeys, which was performed for each domain separately. Taking vertices as features and stimulation sites as samples (see STAR Methods), PCA represents the multi-vertex connectivity pattern of a site as a weighted sum of a series of basis patterns of connections (Figure 4A), and reduces the dimensionality of connections from number of vertices to number of weights or basis patterns (# dimensions). In some sense, the weight reflects how well a site’s connections match the basis pattern of a particular principal dimension.

Figure 4. Principal Dimensions of LPFC-Cortical Connectome.

(A) Schematic of PCA-based approach for finding principal dimensions of LPFC-cortical connectome. Connections of any site (black row vector in left matrix) are decomposed as weighted sum of a series (# dimensions) of basis multi-vertex patterns of connections (green row vectors in right matrix). Weights of all sites form multi-site patterns (purple column vectors in center matrix), one for each basis pattern. TEMP connections of example site J-047 are shown.

(B) Percent variance explained by dimensions 1 to 5 (2^nd to 6^th PCA dimension) in each domain separately. Dim 1 and dim 2 are the focus here and labeled as red.

(C) Basis pattern of connections of TEMP dim 0 (top, as overlay) and weight for this basis of monkey J/N (middle/bottom, as circles). Color denotes value of basis (vertices) and weight (sites), the latter of which is also denoted by size of circle. Scale bar, 5 mm.

(D) Basis patterns of connections (top) and corresponding weight of monkey J/N (middle/bottom), of TEMP dim 1 (left) and dim 2 (right). Sites are shown as circles, of which color indicates weight, and area indicates mean connectivity to same-domain vertices. Color also indicates value in basis patterns. (E-I) As in (D), of PPC ([E]), ORBINS ([F]), DMPFC ([G]), PMC ([H]), and LPFC ([I).

In all domains, the first principal dimension (dim 0) reflected the domain-level connectivity rather than finer, within-domain topography. For example, in the TEMP domain, the basis pattern of connections (Figure 4C, top) was highly similar to the mean connectivity with LPFC (Figure 1G1, left), whereas the weight for this basis pattern (Figure 4C, middle and bottom) was highly similar to the mean connectivity of stimulation sites to TEMP (Figure 1G1, center and right). Similar observations were made in other domains (data not shown).

In contrast, the second (dim 1) and third (dim 2) dimensions revealed within-domain topography (Figures 4D–4I), and we focused on these dimensions. In TEMP (Figure 4D, top), going from vertices with negative to positive values in the basis patterns of dim 1 and dim 2, one moves from the dorsal to ventral bank of STS, and from rostral to caudal STS, respectively. In PPC (Figure 4E, top), basis patterns of dimensions 1&2 (from negative to positive values) represented caudal to rostral and superficial (gyrus) to deep (sulcus) axes, respectively. In ORBINS (Figure 4F, top), DMPFC (Figure 4G, top), and PMC (Figure 4H, top), the two basis patterns also represented roughly perpendicular axes, although less clearly.

Within LPFC itself (Figure 4I, top), the basis patterns represented clear ventral to dorsal and rostral to caudal axes, which reflect a tendency of stimulation sites to connect heavily with their adjacent locations. This tendency reflects the actual organization of connectivity within LPFC, rather than passive spread of current around the electrode tips. Each stimulation site connected with 475 and 507 mm² of the cortex within LPFC in monkeys J and N, respectively, which was far beyond the amount of tissue that could be directly activated by passively spread current (within 1.64-mm radius according to our estimations), and might be synaptically driven (Tolias et al., 2005). Thus, the two basis patterns in each domain corresponded to perpendicular axes on the cortical surface, which is non-trivial because the location of vertices was not fed into the PCA. On a related note, swapping the choice of features vs. samples would not alter the multi-vertex/site patterns (see STAR Methods). Dimensions after the third explained less variance (Figure 4B), and their basis patterns didn’t correspond to clear, one-dimensional axes on the cortical surface (Figure S6I), which may reflect more idiosyncratic details of connectivity patterns.

We confirmed that the basis patterns were highly indicative of how connectivity patterns progressed across individual sites (Figures S6A–S6H), in the sense that a site’s weight for a basis pattern indicated where the bulk of its connections is along the cortical axis associated with this pattern. For example, site J-047 in Figure 4A had positive (ventral) weight of dimension 1 (W1) and negative (rostral) weight of dimension 2 (W2) for the TEMP domain, and connected with rostroventral STS.

The spatial layout of W1 and W2 formed meaningful spatial patterns in the LPFC (Figures 4D–4I, middle and bottom for monkeys J and N respectively). For example, stimulation sites with negative TEMP W1 were in more dorsal LPFC and most ventral AS, and those with positive W1 were in mid to ventral LPFC; negative to positive TEMP W2 was located in rostroventral to caudal LPFC. We refer to the LPFC patterns of W1 and W2 as topographic maps, as they are the PCA version of manually identified topographic gradients (see Figure 3).

The topographic maps were in general similar between monkeys. Some differences could be attributed to less coverage of the dorsal surface and mid PS in monkey N (e.g., Figures 4G and 4H, middle vs. bottom). However, the exact location of stimulation sites (relative to sulcal landmarks) with similar weights could also differ between monkeys. For example, positive PPC W1 was found mostly just ventral to PS in monkey J but shifted further within PS in monkey N (Figure 4E, middle vs. bottom). This is consistent with recent studies of human neuroimaging (Glasser et al., 2016) suggesting that sulcal patterns are not always good landmarks for functional correspondence across individuals. However, folding variability is not as great in macaques as in humans (Van Essen et al., 2019).

LPFC preserves organization of cortical domains

We have established a 2D-to-2D correspondence between the organizations of LPFC and the cortical domains it connects with: the 2D layout of LPFC sites is associated with both coordinates along two orthogonal axes of their connections in each domain. To further characterize this correspondence, we compared the layout of LPFC stimulation sites (Figures 5A–5D and 6A–6H, right) with that of their connections indicated by the center-of-mass location (CoM, mean location of vertices weighted by connectivity; Figures 5A–5D and 6A–6H, center). We used a 2D colormap to jointly indicate W1&2 and help identify correspondence between the sites and their CoMs. They were displayed in two complementary forms, circles and arrows (top and bottom rows of Figures 5A–5D and 6A–6H, respectively). The circles contain information about the mean connectivity to the domain of interest (by area, as in Figures 4 and S6). The arrows (2D vectors) represent W1&2 more directly, since their horizontal and vertical projections are proportional to the values of W1 and W2, respectively, which together specify both direction and length of the arrows. We adopted the arrows from retinotopy studies (Sereno et al., 1994). To aid comparison, in Figures 5 and 6 we used alphabetic labels (A to D or A to C) to coarsely indicate W1&2 relative to the main axes of their distribution across both monkeys’ sites (white lines in Figures 5A–5D and 6A–6H, left-top; see STAR Methods).

Figure 5. Cortical Layouts of LPFC Sites and Their Connections in TEMP/PPC.

(A) 2D distribution of W1&2 (left), CoM of connections (center), and Joint 2D topographic map (right) for TEMP, of stimulation sites in monkey J. Top (3 views), sites and CoMs were shown as circles, of which color indicates joint value of W1&2 using a 2D colormap (inset), and area indicates mean connectivity to same-domain vertices. Bottom (2 views), sites and CoMs were shown as arrows, which are 2D vectors proportional to W1&2 and share the same colors and center locations as corresponding circles. Size of circle/arrow is scaled differently across types of display (left/center/right). In left-top, black lines are axes of W1&2, and white lines denote main axes of variations in the 2D distribution of W1&2 across sites of both monkeys. In all types of display, white alphabetic labels coarsely indicate W1&2 relative to the main axes. In right, black label indicate sites that have similar W1&2 but are at different locations from sites indicated by white label of the same alphabet. Scale bar, 5 mm.

(B) As in (A), of PPC.

(C and D) As in (A) and (B), of stimulation sites in monkey N.

Figure 6. Cortical Layouts of LPFC Sites and Their Connections in ORBINS/DMPFC/PMC/LPFC.

(A-H) As in Figure 5, 2D distribution of W1&2 (left), CoM of connections (center), and joint 2D topographic map (right) for ORBINS ([A]/[C]), DMPFC ([B]/[D]), PMC ([E]/[G]), and LPFC ([F]/[H]), of stimulation sites in monkey J/N. In center-bottom of (F) and (H), white contour encloses the MDS planes in Figures 1C and 1D.

Consistent with the observations of each weight alone (Figures S6A–S6H), W1&2 jointly were a good indicator of the 2D location of a stimulation site’s connections in all domains. The cloud of sites in the virtual plane of W1&2 (Figures 5A–5D and 6A–6H, left-top) closely matched the cloud of the CoMs of their connections (Figures 5A–5D and 6A–6H, center). For example, a small clockwise rotation of the sites in the virtual plane of W1&2 would match the CoMs of their connections in the TEMP domain (Figures 5A and 5C, left-top and center, respectively).

Importantly, the LPFC sites preserved the layout of the CoM of their connections. For example, in both TEMP and LPFC (Figures 5A and 5C, center and right) one can travel from label A (red) to label D (blue) in a counterclockwise order. Moreover, the cortical layout of both LPFC sites and their CoMs tracked W1&2 (and each other) beyond the level of quadrants, especially in TEMP, PPC, and PMC, which is consistent with the millimeter-scale topographic gradients in Figure 3. For example, gradual changes of W1&2 (small-step, almost monotonic morphing of colors and arrows) were evident in parallel for both LPFC sites and their TEMP CoMs, from label D to label A (blue through purple to red) in monkey J (Figure 5A, center and right).

The most ventral sites in and near the AS (indicated by black label D in Figures 5A–5D, right-top) didn’t fit into the layout-preserving organizations of TEMP and PPC, which could mean that the organizations of these domains are folded, or that these sites belong to a different map in the LPFC, and our stimulation sites did not extend ventral enough in LPFC to derive the map. We also found sites that didn’t fit into the layout-preserving organizations of ORBINS, DMPFC, and PMC (indicated by black label C, C, D in Figures 6A and 6C, 6B and 6D, and 6E and 6G, right-top, respectively).

Quantification of layout-preserving LPFC-cortical mappings

Thus, except for some idiosyncrasies, the LPFC seems to hold layout-preserving, or isomorphic “representations” (through connectivity) of other cortices. To quantify the isomorphism between the layouts of sites and their connection zones, we calculated the correlation between inter-site distance and inter-CoM distance of all site pairs, per domain/monkey. In TEMP as an example, the two distances were clearly positively associated with each other in both monkeys (Figures 7A and 7B), although there was variability. We found significantly positive correlation (Spearman’s ρ; two-sided) between inter-site and inter-CoM distances in all domains of both monkeys (Figure 7D), which verifies the isomorphic nature of LPFC-cortical mappings. The correlation was stronger for TEMP, PPC, and PMC, suggesting that the cortical layout of CoM in these domains was preserved by LPFC sites in higher fidelity.

Figure 7. Correlation Between Cortical Layouts of LPFC Sites and Their Connections.

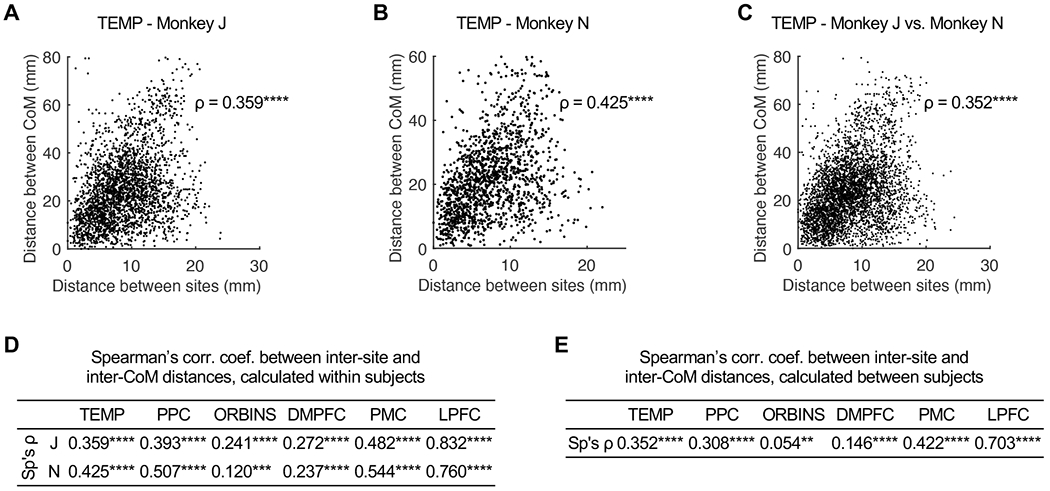
(A and B) Distance between CoM of TEMP connections plotted against distance between stimulation sites in LPFC, of all site pairs in monkey J/N ([A]/[B]).

(C) Similar as (A) and (B), but calculated with pairs of sites in different monkeys.

(D) Spearman’s correlation coefficient (Sp’s ρ) between same-subject inter-site and inter-CoM distances.

(E) As in (D), for cross-subject correlation coefficient.

**, p < 0.01; ***, p < 0.001; ****, p < 0.0001.

We further assessed the between-subject consistency of LPFC-cortical mappings by calculating the correlation between inter-site and inter-CoM distances using cross-subject site pairs, i.e., two sites in a pair were from different monkeys (e.g., see Figure 7C for TEMP). The variability was expected to be larger in this case, since LPFC sites with similar connections may have shifted cortical locations across monkeys. Despite this caveat, the between-subject correlation was significantly positive in all domains (two-sided; Figure 7E), suggesting similar LPFC-cortical mappings in the two monkeys.

A mapping-based summary of LPFC-cortical connectome

The layout-preserving correspondence between LPFC sites and their connections allowed a summary of the LPFC-cortical connectome, as multiple overlapping surface-to-surface mappings (Figure 8A). Specifically, for each vertex in a domain, we calculated the mean of W1&2 over all sites in both monkeys, weighted by connectivity between the vertex and sites. For every vertex, connectivity-weighted W1&2 should indicate which LPFC sites it connected with, providing more details on LPFC-cortical connectivity omitted in the site-CoM mappings (see Figures 5 and 6). By examining the detailed connectivity patterns of sites with varying W1&2 (Figures S7 and S8), we confirmed that connectivity-weighted W1&2 works as intended, i.e., a vertex mainly connected with sites of W1&2 similar to its connectivity-weighted W1&2. We chose to show connectivity-weighted W1&2 as colored overlays in Figure 8A, for clear separation between domains. However, we caution that regions with similar color in the colormap (indicated by black contours in Figure 8A) may have different connectivity profiles with LPFC, and that the sharp transitions in color may not necessarily indicate sharp changes of connectivity. The arrows in Figures S7 and S8 better convey the fine differences in connectivity between vertices. We propose Figures S7 and S8 as an index system for the dense LPFC-cortical connectome, which for this purpose also included the arrow diagrams of LPFC sites from Figures 5 and 6. In comparison, Figure 8A provides more of a bird’s eye view to the connectome.

Figure 8. Summary of LPFC-Cortical Connectome: Overlapping Surface-to-Surface Mappings.

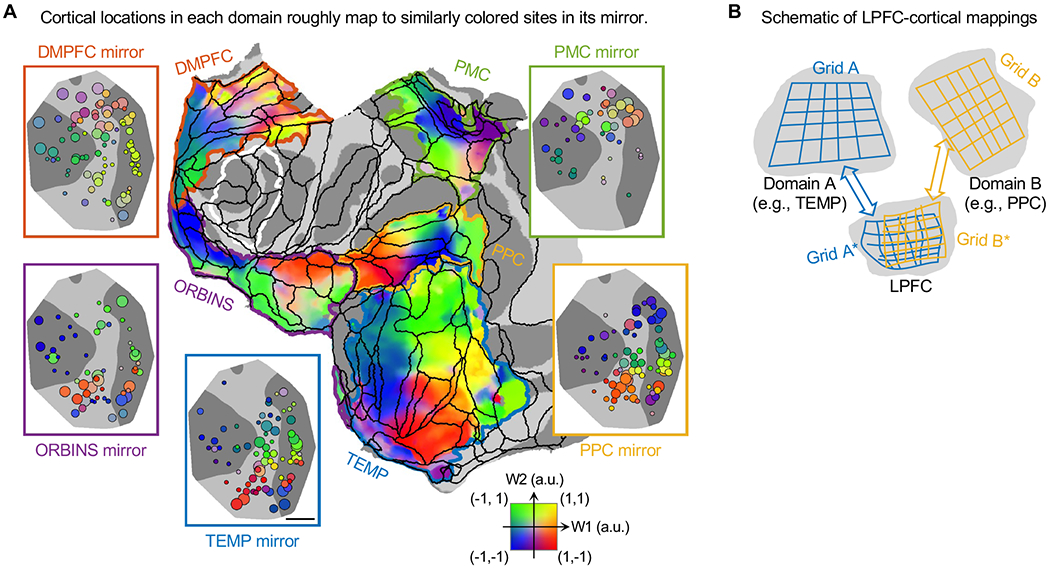
(A) Surface-to-surface mappings between LPFC and other cortical domains. Each non-LPFC domain (on flattened surface) and its mirror organization in LPFC (on MDS plane) are enclosed by curved and rectangle contours of the same color, respectively. The mirror organizations in LPFC are W1&2 maps of monkey J from Figures 5 and 6. The same 2D colormap indicates both W1&2 of LPFC sites (as circles) and W1&2 mapped to vertices (as overlay). On flattened surface, white contour encloses the MDS planes in Figures 1C and 1D, and black contours indicate borders of areas in CBCetal15 parcellation. Scale bar, 5 mm.

(B) Schematic of overlapping isomorphic mappings between LPFC and other cortical domains.

DISCUSSION

Using EM-fMRI, this study performed the first dense, parcellation-free characterization of primate LPFC-cortical connections. We sampled the LPFC in individual macaques much more densely than recent comprehensive connectome studies in macaque and other species (Harris et al., 2019; Hayashi et al., 2021; Lin et al., 2019; Majka et al., 2020; Markov et al., 2014), extrapolating to ~2500 sites/hemisphere/animal if applied to the entire cortex. The connectome can be summarized as consisting of overlapping, isomorphic LPFC-cortical mappings (Figure 8B). The LPFC stimulation sites can be considered to be members of multiple, overlapping 2D grids, each of which maps to a roughly layout-preserving grid of locations in a major cortical domain, in the sense that the connections of an LPFC site concentrate around its corresponding location in the latter grid. Among the domains, the LPFC grids seemed to preserve the layout of TEMP, PPC, and PMC better than DMPFC and ORBINS (Figure 7D). However, for all domains, overlapping, isomorphic LPFC-cortical mappings offer a unified account of the connectome of a large portion of LPFC spanning multiple cytoarchitectonic areas.

Strengths and limitations of dense connectivity mapping using EM-fMRI

The dense, parcellation-free sampling was able to capture significant and systematic differences of connections across adjacent LPFC sites, whereas sparse sampling could have missed such differences, or worse, could have been misleading due to aliasing. It also revealed the similarities between the topographic maps of individual monkeys, despite inter-subject variability relative to sulcal landmarks and potentially areal boundaries. The variability would make it more difficult to create composite topographic maps from multiple animals with one or a few samples or anatomical tracer injections in each. To better understand this variability, it might be useful to compare the sub-area location of small tracer injections vs. EM-fMRI sites with matching connections.

The fMRI signal is noisy, and the results could potentially vary depending on the thresholding used. To minimize this variability, we optimized the parameters of EM-fMRI and achieved a large effect size at the level of single voxels, allowing stricter thresholding and robust connectivity mapping of single stimulation sites (Figures S1 and S2). The anesthetized preparation was helpful in minimizing head-motion induced artifact, which also simplified distortion correction. Anesthesia may also have reduced variability from spontaneous fMRI activity (Huang et al., 2016), which is noise to EM-fMRI. Both suppressing and enhancing effects of propofol on functional, fronto-parietal interactions have been reported (Lee et al., 2013; Ma et al., 2019), and so it is unclear if propofol itself might also have influenced the EM-fMRI signal. When down-sampled, our findings were consistent with the gross connectivity established in anatomical tracing studies (Figures 2A–2C and S4D), taking into account that these studies typically have, at most, only a small number of injections per animal. The inter-subject variability at the area level was also comparable between EM-fMRI and anatomical tracing (Figures S4F and S4G). Interestingly, the EM-fMRI connectivity was found to be relatively strong between long-distance areas, compared to anatomical tracing (Figure 2D).

One caution is that the neurovascular response measure by fMRI may not reflect all neuronal changes elicited by EM (Logothetis et al., 2001), and could fail to detect some sparse connections. Another limitation of this study is that our resolution (2-mm) was not fine enough to capture the finer-scaled regularities of connectivity, including columnar (Cavada and Goldman-Rakic, 1989; Schwartz and Goldman-Rakic, 1984; Selemon and Goldman-Rakic, 1988; Seltzer et al., 1996), laminar (Barbas, 2015), and layer-specific, stripe-like (Levitt et al., 1993; Lund et al., 1993) patterns observed in tracing studies. High-resolution fMRI (Huber et al., 2017; Yacoub et al., 2020) and ultrafast whole-brain fluorescence imaging (Xu et al., 2021) in primates will help better link connectivity patterns mapped by EM-fMRI and tracing in the future.

Comparing isomorphic LPFC-cortical mappings to previously reported topographic connections

It is well known that different LPFC areas preferentially connect with different parts of other cortices (Borra et al., 2019; Gerbella et al., 2013; Petrides, 2005; Schall et al., 1995; Stanton et al., 1995), i.e., that there is some topography to connections. In a few cases, another level of regularity was found: a series of adjacent areas in LPFC preferentially connected with a parallel series of areas in other cortices (Cavada and Goldman-Rakic, 1989; Petrides and Pandya, 1984), which is similar to the topographic gradients shown in Figure 2. Such topography was also reported between human language-related areas, using resting-state fMRI (Van Essen and Glasser, 2018; Glasser et al., 2016).

However, the mere presence of local, inherently 1D topographic gradients doesn’t put enough constraints on the 2D cortical organization of connectivity throughout LPFC. It is the ubiquitous, multi-directional (Figures 3A–3D) nature of such gradients that supports an overarching scheme for LPFC connections. A data-driven analysis (PCA) revealed that topographic connections formed two perpendicular axes on the cortical surface, for each of the five major domains. This analysis then aided us in characterizing the isomorphic, 2D-to-2D mappings between LPFC and the other domains.

The isomorphic LPFC-cortical mappings might be analogous to how the striate and extrastriate cortices map the retina, in the sense that they are both 2D-to-2D mappings. The analogy is coarse, because the early visual cortices represent the retinal image in polar coordinates due to the central role of the fovea, whereas the LPFC seems to represent other domains in Cartesian coordinates. Instead, the LPFC-cortical mappings might more closely resemble the interconnections between early visual cortical areas. Regions in early visual cortices tend to interconnect if their receptive fields overlap (Angelucci et al., 2002), resulting in cortico-cortical mappings (Rockland and Pandya, 1981) of a similar aspect to those observed for LPFC. Alternatively, the LPFC-cortical mappings may also resemble the interconnections within IT cortex (DiCarlo et al., 2012), where many neurons have large receptive fields, and there is no clear retinotopic organization. Recent studies have found that IT cortex is organized as a series of patches or stripes, repeated several times as one proceeds anteriorly through the temporal cortex (Bao et al., 2020), with patches or stripes each representing object or feature categories such as faces, bodies, colors, scenes and 3D object properties. Connections may be strongest between patches of the same type within IT (Bao et al., 2020; Borra et al., 2010; Grimaldi et al., 2016; Moeller et al., 2008; Premereur et al., 2016). The LPFC-cortical mappings may reflect even higher-order, yet unknown dimensions; but they could, in principle, be driven by similar factors mediating the isomorphic connections in the visual system.

Functional implications of isomorphic LPFC-cortical mappings

There now seems to be a consensus that both spatial and feature selectivity for visual stimuli are well represented in both dorsal and ventral regions of LPFC (Kadohisa et al., 2015; Meyer et al., 2011; Rainer et al., 1998; Rao et al., 1997; Riley et al., 2017; Tang et al., 2021). Consistent with the functional findings, we find that at least the posterior portions of LPFC (Bullock et al., 2017; Hussar and Pasternak, 2013; Mendoza-Halliday et al., 2014; Zaksas and Pasternak, 2006) have connections with visual areas in both PPC and TEMP (Felleman and Van Essen, 1991). The anatomical connections of these posterior portions of LPFC may support topographically organized convergence of the dorsal and ventral streams for spatial and object vision.

Going beyond the convergence of the dorsal and ventral streams, topographic connectivity may help us predict yet unknown axes of functional organization in the LPFC, and, by extension, candidates for dissociable components of executive control. To take just one example, a caudoventral to rostroventral gradient in TEMP and a caudal/sulcal to rostral/superficial gradient in PPC seem to map to a largely overlapping gradient in the LPFC. This latter gradient extends from the intersection of AS and PS towards the rostroventral surface. A clue into the nature of these converging gradients is that along the TEMP gradient, there is increasingly complex and invariant object representations (e.g., invariant to image transforms) with more extended processing time (Bao et al., 2020; DiCarlo et al., 2012). Along the corresponding PPC gradient, there is a transition from ocular to manual sensorimotor integration (Andersen and Buneo, 2002; Rozzi et al., 2008) and increasingly higher-order spatial information, with fixation-invariant spatial relationships between objects (Chafee and Crowe, 2013). Considering these TEMP and PPC inputs, the gradient from caudal to rostroventral LPFC might operate on increasingly invariant object and spatial representations and recruit fast to slow motor effectors. More hypotheses can be generated by the details of LPFC-cortical mappings, which may also help guide future experimental work.

Our findings implicate a novel architecture for how the LPFC interacts with other cortices, which might be related to the idea of distributed networks (Goldman-Rakic, 1988; Selemon and Goldman-Rakic, 1988; Stepniewska et al., 2020; Yeo et al., 2011). Instead of staying on “top”, the LPFC might actually be organized in a parallel fashion to other domains, which often have a spatially orderly organization of function. Topographic connectivity rather than divergent or uniform connectivity may allow LPFC regions to specialize in various aspects of executive control that require them to interact with specific levels of other domains (Schall et al., 1995). If a function of LPFC is to integrate (bottom-up anatomy) and also bias (Miller and Cohen, 2001) (top-down anatomy) representations in other domains, the topographic connections of LPFC could ensure that these functions are carried out at the appropriate level of each domain.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Rui Xu (ruix@mit.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

The data and code that support the findings of this study is available from the Lead Contact upon request. Any additional information required to reanalyze the data reported in this work paper is available from the Lead Contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Two macaque monkeys were used (J and N; Macaca mulatta; one female, J; 8-9 kg and 7-10 years old during the study). All procedures were in full compliance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and the guidelines of the MIT Animal Care and Use Committee.

METHOD DETAILS

Surgical procedures

Implant surgery

For each monkey, a headpost and a chamber that allowed access to left LPFC were designed to fit the shape of the skull inferred from structural MRI (sMRI) images, and made in polyether ether ketone (PEEK) with 5-axis CNC machining (Mulliken et al., 2015). While the monkeys were anesthetized, both implants were secured to the skull by ceramic screws (SA10, Thomas RECORDING) without acrylic, under aseptic conditions. In monkey J, hydroxyapatite paste (Directlnject, Stryker) was used to compensate an imperfect fit. In the surgery, general anesthesia was initiated with atropine (0.04 mg/kg), ketamine (10 mg/kg), and dexdomitor (18 μg/kg), and maintained with sevoflurane (1.5-2%). As a prophylactic measure, antibiotics and analgesics were administered after surgery. A craniotomy was created during the implant surgery to allow penetration of electrodes for microstimulation, and we covered it with biocompatible silicon (Kwik-Sil, WPI), which seemed beneficial in reducing the growth rate of granulation tissue. In monkey J, an additional layer of Kwik-Sil was applied to serve as a temporary gasket of the chamber’s cap made in polyetherimide (Ultem). Under aseptic conditions, both layers of Kwik-Sil were replaced during cleaning of the chamber.

Anesthesia for EM-fMRI experiments

In the EM-fMRI experiments, general anesthesia was initiated with dexdomitor (18 μg/kg) and a low dosage of ketamine (2-4 mg/kg), and was maintained with propofol (0.1-0.4 mg/kg/min and occasional bolus). Dexdomitor was fully reversed with atipamezole at least 1 hour before the MRI scans began. To achieve a steady state of anesthesia and reduce extraneous fluctuations of the fMRI signal, we monitored the animals’ heart rate and oxygen saturation continuously, and body temperature intermittently, and kept them within each monkey’s normal ranges. Both eyes of monkeys were covered to block visual stimulation. Because of the lengthy procedure (4-6 hours of MRI scans plus preparation and clean-up per session), we scanned each monkey no more frequently than once every two weeks.

Data acquisition

Pre-implant and in-session sMRI

To guide implant design and reconstruct cortical surfaces, T1-weighted sMRI images (MPRAGE, 0.5 mm isotropic) were collected from both monkeys before implant surgery under anesthesia (following the same protocol as in implant surgery except not using sevoflurane), inside a 3T MRI scanner (Prisma/Trio, Siemens for monkey J/N) using a saddle-shaped, single-loop receive coil (diameter = 10.2/12.7 cm for monkey J/N). In each monkey, four runs of T1 scans were collected and averaged to achieve a two-fold increase of signal-to-noise ratio (SNR). To validate the positioning of electrodes, in-session T1-weighted sMRI images (MPRAGE, 0.5 mm isotropic) were collected at the beginning of every EM-fMRI session and often at the end too. During both pre-implant sMRI and EM-fMRI sessions, animals were put in an MRI-compatible stereotaxis frame (David Kopf Instruments).

Positioning of electrodes

Machined (PEEK) and 3D printed (Projet 3500 HD Plus with VisiJet Crystal, 3D Systems) grids were used to guide positioning of electrodes for microstimulation. For clear visualization of the grid tracks, we filled them with gel-like mixture of gadolinium (Gd, 5 mg/mL) and agar (10 mg/mL) in saline, and collected T1-weighted sMRI images (MPRAGE, 0.39 mm isotropic) of animals under anesthesia with the grids put in chamber, following the same anesthesia protocol of pre-implanted sMRI. Compared to Gd, often used mineral oil has a chemical shift that could misplace the grid tracks (by a few voxels, depending on the readout bandwidth) in T1-weighted images. To correct distortion of T1-weighted images along the readout direction, we collected two sets of data with opposite readout directions along the orientation of grid tracks, and merged the images using FSL’s topup (Jenkinson et al., 2012). The merged images containing grid tracks were then co-registered to pre-implant sMRI images via rigid transformation, and were visualized in 3D sheer (Fedorov et al., 2012) along with reconstructed cortical surfaces to guide the planning of stimulation sites. The goal of planning was to evenly sample the cortical surface of caudal-to-mid LPFC.

Before each EM-fMRI session, we loaded up to 8 Platinum/Iridium (Pt/Ir) microelectrodes (~100 kΩ after penetrating the dura; FHC) for stimulation and 2 ground electrodes into a custom-made, MRI-compatible microdrive attached to the grid. After being sterilized using vaporized hydrogen peroxide (STERIS), the assembly was put into the freshly cleaned chamber at the beginning of a session. All stimulation electrodes were pushed through the dura to their planned depth, and ground electrodes were lowered to touch dura. A small amount of saline was left in the chamber to assure good grounding. Electrode tips were then examined in in-session T1 images, and were manually adjusted with the microdrive to approach mid thickness of planned cortical locations. In preliminary experiments (data not shown), we found excessively wide-spread and strong fMRI activations from stimulating the white matter, and no activation from stimulating outside of dura, and we didn’t find reliable differences between stimulations at the same cortical location but aimed for deep vs. superficial layers, possibly because the range of passive current spread was sufficient to cover most layers (see Results for estimations).

EM-fMRI experiments

In total, we had 99 and 76 “good” sites from 17 and 14 sessions in monkeys J and N, respectively. From these sites, we collected up to eight 8.5-min EM-fMRI runs per site (83/66 four-run sites, 13/8 two-run sites, 3/2 other in monkey J/N) using “standard” parameters, and sometimes extra data for parameter testing as presented in Figure S1. In the same sessions, a small portion of “bad” sites (28/13 in monkey J/N) were discarded for one of the following reasons: 1) no data was collected using “standard” (see below) parameters (0/1 in J/N); 2) sites weren’t placed in gray matter (11/12 in J/N); 3) sites were placed too distant (6/0 in J/N) from the majority of sites, so that including them would make spatial sampling uneven; 4) stimulation didn’t elicit reliable fMRI responses (11/0 in J/N), due to broken insulation of electrodes or excessive electrical/physiological noise.

We adopted a standard blocked design similar to what has been used in EM-fMRI studies (Matsui et al., 2011), in which each run included eight blocks with EM and nine blocks without (no-EM), each 30 seconds long. In an EM block, 70 square-shaped pulses were delivered as a pulse train at the rate of 1 train per second. A single pulse consisted of cathodal and then anodal phases of equal amplitude and duration (200 μs), separated by a 100-μs null phase with no current. The inter-pulse-interval was 2500 ps, setting the frequency of EM pulses to 333 Hz. Figure S1 presented data using varying levels of amplitude from 100 to 750 μA, and all other figures presented data using 500 μA (“standard”). Monopolar microstimulation was performed with battery-powered, constant-current isolators (A365, WPI), driven by a programable stimulator (DS8000, WPI) and each connected to a pair of stimulation and ground electrodes. The stimulator was in turn controlled by a desktop PC using Matlab (MathWorks) and Psychtoolbox (Brainard, 1997), and was synchronized with fMRI data acquisition. To attenuate RF noise which may cause excessive heating and noise in the MRI images, low-pass filters (BLP-1.9+, Mini-Circuits) were placed between the isolators and electrodes on the penetration panel between MRI scanner and control room, and custom-made low-pass filters consisting of a series of inductors were used inside the MRI bore.

For the majority of data we presented, single-shot gradient-echo EPI images of fMRI activity (“standard”) were collected using a 5-channel receive coil, the shape of which better fits the head, in monkey J (3T, Prisma, Siemens; TR = 1.5 s, TE = 18 ms, bandwidth = 2230 Hz/pixel, flip angle = 90 degrees, field of view = 128 × 128 mm², matrix = 64 × 64, slice thickness = 2 mm, no gap, partial FFT = 7/8), and a saddle-shaped, single-loop receive coil (diameter = 12.7 cm) in monkey N (3T, Trio, Siemens; TR = 2 s, TE = 30 ms, bandwidth = 1662 Hz/pixel, flip angle = 90 degrees, field of view = 128 × 128 mm², matrix = 64 × 64, slice thickness = 2 mm, no gap, partial FFT off). For data presented in Figure S1, EPI images with higher spatial resolution were also collected in monkey J using the 5-channel coil (3T, Prisma, Siemens; TR = 2.5 s, TE = 17 ms, bandwidth = 1685 Hz/pixel, flip angle = 90 degrees, field of view = 100 × 100 mm², matrix = 76 × 76, slice thickness =1.3 mm, no gap, partial FFT = 7/8). We employed linear and second-order shimming before most fMRI data acquisitions, to minimize the shim offsets in structures with very low spatial frequencies; the built-in Siemens sequence was used, and echo time was chosen to minimize phase errors from fat found in skin and scalp tissue; the fieldmap was fitted to spherical harmonics and shim coil current was adjusted to minimize the residual field offsets. Fieldmap images were always acquired to compensate for (not completely remove) geometric distortion of EPI images due to inhomogeneity of magnetic field, with FSL’s PRELUDE and FUGUE (wrapped in Freesurfer’s epidewarp.fsl), which geometrically unwarp the EPI images while ignoring areas of signal loss; a phase image was calculated as the phase difference between complex signals collected at two different echo times; Jacobian intensity modulation wasn’t applied. No acceleration (e.g., GRAPPA) was used because it would reduce SNR, and it was feasible to correct the distortion base on fieldmap since little head motion was present during anesthesia. A Prisma scanner became available for the data acquisition of monkey J, which allowed faster TE and shorter TR, and thus improved effect size with contrast agent (measured by contrast-to-noise-ratio, CNR; see “Volume-based processing of fMRI data”) and larger temporal degree of freedom, respectively, compared to the Trio scanner used in data collection of monkey N. Nevertheless, we found similar overall patterns of results across monkeys, which suggests that the effect size was sufficient in both monkeys.

To enhance the effect size of the EM-fMRI activations, ferumoxytol (Feraheme, AMAG Pharmaceuticals), a contrast agent similar to monocrystalline iron oxide nanoparticles (Leite et al., 2002) (MION, which we used to denote the signal) was injected to the monkeys before fMRI scans (“standard”), and the dosage was adjusted (8-10 mg/kg) to reduce overall intensity of standard-resolution EPI image to half of pre-injection level. The half-life of ferumoxytol was usually long enough to maintain a steady level till the end of a session, and in rare cases we injected again to retain half of pre-injection EPI image intensity. To mitigate iron accumulation, chelation was performed after every session by injecting deferoxamine. For data presented in Figure S1, we also collected EM-fMRI responses of regular blood-oxygen-level-dependent (BOLD) signal before injection of ferumoxytol.

QUANTIFICATION AND STATISTICAL ANALYSIS

First-level data analysis

Semi-automatic reconstruction of cortical surfaces

Surface reconstruction provides compact visualization of cortex with anatomically valid topology (e.g., two voxels next to each other in volume may belong to the opposite sulcus banks, but correctly correspond to distant vertices on surface). However, standard automatic surface reconstruction doesn’t work for the macaque brain without labor-intensive and bias-prone manual labeling. Here we performed semi-automatic reconstruction by utilizing the recently available NIMH Macaque Template (NMT) (Seidlitz et al., 2018). Using NMT’s script based on AFNI (Cox, 1996) and ANTs (Avants et al., 2009), each monkey’s pre-implant sMRI volume (individual sMRI volume; cropped to a 0.5-mm isotropic, 256 × 256 × 256 grid) was warped to the NMT template using a nonlinear transformation, and masks of brain and white matter were generated for each monkey taking NMT’s brain mask inversely warped to individual sMRI volume as prior. By taking the individual sMRI volumes and individualized masks as input, white (white-gray boundary) and pial (gray-pial boundary) surfaces (75344/75269/84028/82495 vertices in monkey J’s left/right and N’s left/right hemispheres, respectively) were reconstructed using FreeSurfer (Fischl, 2012) almost automatically, except for manually setting up a few parameters. Note the line going through matched white and pial vertices is a surface normal of cortex. A mid-thickness surface (mid) built by averaging white and pial surfaces was inflated and flattened for overlaying results on it, and was used to calculate the center-of-mass location of connections. Piriform cortex and subiculum weren’t well represented in the reconstructed surface, and their connections with LPFC will be reported separately.

To create surface-based labels of gyri and sulci, we calculated mean curvature in the volumetric space using ANTs, and assigned each pial vertex the value averaged over its nearby voxels (including those outside of cortex), which provided a good index of gyri/sulci separation utilizing the fact that voxels between sulci bank had high concavity. Labels of anatomical areas in main parcellation schemes (including Paxinos et al. or CBCetal15 parcellation (Calabrese et al., 2015), Saleem and Logothetis or RGYetal17 parcellation (Reveley et al., 2017), and MERetal14 parcellation of the tracing dataset (Markov et al., 2014) to be compared to EM-fMRI connectome) were warped from respective template volumes to the NMT template, which were then inversely warped to individual sMRI volumes. To project label onto surface, we used a winner-take-all strategy to combine labels over each vertex’s neighboring cortical voxels found by Surfing toolbox (Oosterhof et al., 2011).

Visualization of stimulation sites in LPFC

Because of brain deformation from electrode insertion during the EM-fMRI experiments, we localized each stimulation site by manually finding the coordinate in the individual sMRI volume corresponding to the tip of electrode in the in-session T1 volume, via iterative inspection of coronal, sagittal, and axial views of both volumes. The coordinate was then projected onto the surface by finding its nearest mid vertex.

To create a flat representation of LPFC that reflects the cortical layout of stimulation sites, in each monkey we performed 2D metric multidimensional scaling (MDS) on geodesic distance (distance along shortest path on a surface; code.google.com/p/geodesic) between mid vertices of LPFC. The MDS planes covered roughly matched cortical surface across monkeys, in which 2D distance well reflected geodesic distance on non-flattened surfaces (stress = 0.037/0.037, r = 0.996/0.997 in monkey J/N). Voronoi diagram of stimulation sites on the MDS plane was used to calculate area covered by sites.

Volume-based processing of fMRI data

We used Nipype (Gorgolewski et al., 2011), a Python interface to tailor a pipeline of volume-based processing steps, which combines tools from numerous packages of neuroimaging software, including AFNI, ANTs, FreeSurfer/FsFast, and FSL. Preprocessing was performed for individual runs separately in the native space of EPI volumes (2-mm or 1.3-mm isotropic), including slice time correction, motion correction, fieldmap-based distortion correction, skull stripping, and detection of outlier time points with large motion or deviation of image intensity (using FSL; norm_threshold = 0.5, zintensity_threshold =3). No spatial smoothing was performed. We refer to preprocessed data belonging to the same stimulation site (S) and EM-fMRI parameters (P) as an SP-combo. Runs of the same SP-combo were aligned using rigid transformation (to address minor displacement between runs) and concatenated together. Separate GLM models were built for each SP-combo, which used canonical hemodynamic response functions designed for MION and BOLD signals respectively, high-pass filtered the data (cutoff = 0.008 Hz), regressed out six parameters obtained from rigid-body motion correction, fit and removed polynomial of order two, and discarded outlier time points.

The output volumes of GLM models were used in the following analyses, including t-statistic (t) and p value (sig) of the EM vs. no-EM contrast, CNR, and temporal SNR (tSNR). In the simple blocked design of this study, CNR indicates the ratio of peak signal change induced by EM vs. baseline (no-EM) and residual standard deviation (SD, across TRs) in the GLM model (unaccounted noise), and can therefore be interpreted as effect size (e.g., Cohen’s d) (Welvaert and Rosseel, 2013), and tSNR indicates the ratio of mean signal intensity and residual SD. Thus, the peak percent signal change induced by EM equals CNR divided by tSNR and multiplied by 100. Note the effect we want to measure is actually the difference (“contrast”) of “signal” between EM and no-EM conditions; whereas tSNR indicates the inverse of noise level, which affects how easy a given contrast would be detected, but doesn’t tell the actual strength of this contrast. FDR correction was performed on the sig volume using a small q (0.01) to suppress detection of spurious responses, taking advantage of the large effect size of EM-fMRI. Across SP-combos using standard parameters, FDR-adjusted p threshold was 10^−4.8 to 10^−3.1 and 10^−4.5 to 10^−3.5 (median = 10^−3.9 and 10^−4.0) in monkeys J and N, respectively, depending on significance level across all voxels of each SP-combo.

For better functional-structural alignment, nonlinear transformation from aligned EPI images of each SP-combo to in-session T1 volume was computed multiple times using various algorithms implemented in AFNI and ANTs. This step was useful to further reduce functional-structural distortion, which was often visible even after fieldmap-based correction (for examples, see Figure S3A). The multiple results were manually inspected, and the best version was combined with nonlinear transformation from in-session to individual sMRI volumes calculated using ANTs. The combined transformation was applied to warp the GLM output to the space of individual sMRI volume in a 1-mm isotropic, 128 × 128 × 128 grid, using cubic spline (t, CNR, tSNR) and nearest-neighbor (sig) interpolations depending on the data type. To properly warp the results of FDR correction, for each SP-combo we found the absolute t value (t_threshold) in the pre-warping GLM output that corresponded to FDR-corrected threshold of p value, and created a binary mask in the post-warping grid by thresholding the absolute value of warped t volume with t_threshold.

Building surface-based connectivity matrix

The metric we used to quantify the EM-fMRI activations is based on CNR. Compared to alternatives like t or −log₁₀(p), CNR is not systematically biased by the amount of data (depending on number of runs and number of TRs per run) fed into the GLM model. Because the activations were predominantly positive in the form of increase (decrease) of BOLD (MION) signal and we didn’t observe reliable patterns of negative activations (Logothetis et al., 2010; Sultan et al., 2011), we inverted the sign of CNR if MION was used and removed negative activations if present. It was shown that low-frequency delivery of EM pulses can elicit a decrease of BOLD signal (Logothetis et al., 2010), but we did not observe this in our preliminary experiments (data not shown). A possible reason is that the baseline activation in our study may have been lower than that in the previous study, which maintained lighter anesthesia. For each SP-combo, we further removed 26-connected clusters of fewer than sixteen 1-mm activated voxels (taking the same volume as two 2-mm voxels), which we considered spurious for cortical connections.

The residual structural-functional misalignment (despite our best effort) and the relatively large, 2-mm voxel size, could make locating the volumetric activations on cortical surface challenging and error-prone. Occasionally, a cluster overlapped with multiple anatomically separated structures, like two opposite banks of a sulcus or adjacent subcortical and cortical regions. We therefore designed an automated procedure in the following steps, which we called disambiguation, to mimic how one would typically manually detect and remove the spurious activations based on local maximums (Figure S3C). A small portion of relatively weak activations were removed by the disambiguation (Figure S3D).

1. The disambiguation required separating between subcortical and cortical activations, for which masks of subcortical voxels (based on CBCetal15 and RGYetal17 parcellations) and cortical (one per hemisphere) voxels (based on CBCetal15 parcellation) were down-sampled into the 128 × 128 × 128 grid of functional data. The masks were slightly dilated without overlapping with each other, to compensate for functional-structural misalignment.

2. In each SP-combo, the inter-connectivity between activated voxel was pruned, so that a voxel only connected with its most strongly activated neighbor, to separate multiple local maximums within the same cluster.

3. Within each 26-connected cluster after pruning, the disambiguation process detected spurious activations based on the location of the local maximum, in the order below.

   1. Subcortical activations were removed if they together didn’t contain local maximum.
   2. In each hemisphere, cortical voxels were removed if they together didn’t contain local maximum.
   3. In each hemisphere, voxels that survived step b were further separated into subclusters, by considering two voxels as inter-connected if their nearest mid vertices were within 2 mm apart (on surface). Subclusters not containing local maximum were removed.

After the disambiguation, because the distribution of CNR was heavily positively skewed (Figure S2A), we took its logarithm to make the distribution more Gaussian. We then linearly scaled the logarithm to [0.05 1] across SP-combos of the same monkey. We used raw CNR as the metric for visualizing fMRI activations elicited from stimulating a single site, and log-normalized CNR as the metric for further connectome-level analyses that require combining results from multiple sites.

We next project both raw and log-normalized CNR from volume to surface (Figure S3B) through following steps, as cortical activations may fall outside of structurally defined gray matter ribbon.

1. Initiate transformation matrix T_vol2surf of # vertices × # voxels zero entries, one per hemisphere, including cortical vertices (outside of mid-wall) and voxels only.

2. For each voxel, find its nearest mid vertex in the respective hemisphere.

3. For each vertex i that is the nearest neighbor to n>=1 voxels j₁ to j_n, set the entries (i, j₁ to (i, j_n) of T_vol2surf to 1/n.

4. For each vertex p that is not the nearest neighbor of any voxel, find its neighbor vertices q₁ to q_m within 1 mm, and if m>=1 set the entry (p, s) to the mean value of entries (q₁, s) to (q_m, s), where each vertex from q₁ to q_m is the nearest neighbor of at least 1 voxel and s ranges from 1 to # voxels.

5. Multiply T_vol2surf with volume-based connectivity of each SP-combo (# voxels × 1) to get surface-based connectivity (# vertices × 1).

6. Smooth the surface-based connectivity with Freesurfer’s mri_surf2surf (FWHM = 1 mm), which were then concatenated over sites (or SP-combos for data presented in Figure S1) and transposed to get surface-based connectivity matrix of # sites × # vertices entries.

7. After smoothing, values smaller than one fourth of minimal positive value in volume-based connectivity of each SP-combo was set to zero.

Finally, for processing data of both monkeys in the same space, we projected monkey J’s connectivity onto monkey N’s surfaces, as the morphology of the latter is more “canonical” and thus easier to read. To this aim, we followed modified steps I to IV described above to build transformation matrix T_surfJ2surfN of # vertices_N × # vertices_J entries. In step II, we warped the mid coordinate of each vertex in J to the NMT template and then inversely to N, and found its nearest vertex in N. We then multiplied T_surfJ2surfN with surface-based connectivity of monkey J, smoothed the projected connectivity on N’s surfaces (FWHM = 1 mm), and set values smaller than the threshold in step VII to zero (for each SP-combo separately). Further analyses were performed at the vertex level on monkey N’s surface.

Connectome-level data analysis

Area-level comparison of MRI and tracing connectomes

At a macro scale, we compared the LPFC-cortical connectome mapped by EM-fMRI to a tracing dataset (Markov et al., 2014). A state-of-the-art ex vivo dMRI dataset (Donahue et al., 2016) was compared to tracing as a control, from which we took 29 × 91 pDT1/pDT3 ISA matrices of subject PM1. pDT1 and pDT3 matrices were built from the same tractography data using different seeding strategies. Both tracing and dMRI datasets were at the level of cytoarchitectonic areas using MERetal14 parcellation, based on which we built 5 × 89 LPFC-cortical connectivity matrices (Figure 2A), taking 5 LPFC areas injected with tracer (Markov et al., 2014) and covered by at least two stimulations sites per monkey in this study as rows, and all 89 cortical areas in MERetal14 parcellation as columns. In these matrices, intrinsic connectivity (between one area and itself) was undefined, and the connectivity metric (count of labeled neurons or tractography streamlines) was fractionally scaled, i.e., divided by total extrinsic connectivity of each row area (Donahue et al., 2016; Markov et al., 2014).

Dense surface-based EM-fMRI connectivity matrices (# sites × # vertices; see Figures S4A–S4C) were downsampled and then combined to get 5 × 89 area-level matrices. Specifically, we took the multiplication of log-normalized CNR and surface area (which varies across vertices) and summed the product over vertices within a column area, and then added this sum over all stimulation sites of a row area as the unsealed metric of interareal connectivity. We chose to multiply by surface area, based on the observation that the number of neurons per unit surface area is relatively constant across most cortical areas (Rockel et al., 1980). We then divided the unsealed connectivity by the sum over 88 column areas (with intrinsic connectivity left undefined) for each row area separately, to derive fractionally scaled connectivity (FSC) comparable to the aforementioned studies. By using sites in each monkey separately or pooled from both monkeys, we built individual vs. pooled connectivity matrices for EM-fMRI, which were used in Figures S4D, S4F, and S4G, and in Figures 2, S4D, and S4E, respectively. Calculating FSC based on raw instead of log-normalized CNR didn’t alter the overall pattern of results (data not shown), since the operation of multiplication by surface area and then summation over vertices rendered both metrics following similar log-normal distributions (Figure S4E).

For better visualization, we performed hierarchical clustering on 5 row areas and 89 column areas separately, based on similarity between their respective column/row vectors of both tracing and EM-fMRI mapped connectivity concatenated. Similarity was defined as the cosine of angle between vectors. Both row and column areas were then sorted according to the order of leaves in the cluster trees. The interareal distance was provided by a public dataset (Markov et al., 2013) from the same authors of the tracing dataset, which is calculated based on minimal white matter trajectories between areas.

Consistency of interareal connectomes mapped by MRI methods vs. tracing was quantified non-parametrically by Spearman’s correlation coefficient (ρ) between all (Figure 2C, left-top) or non-zero (Figure 2C, left-bottom) entries of 5 × 89 matrices. Non-zero entries indicate pairs of areas of which the connectivity was deemed present in all MRI and tracing matrices. As an alternative way to assess consistency, we built receiver operating characteristics (ROC) curves of MRI methods, with tracing data as reference, which used all entries. We examined the consistency at various levels of minimum distance between areas of which the connectivity was used in calculating the correlation coefficient. At each distance, we built bootstrap distributions of Spearman’s ρ and area under the ROC curve, calculated with randomly resampled (with replacement) entries for 1000 times.

Structured clustering of vertices

To refine parcellation of cortical domains (Figure S5), we sought to identify clusters of adjacent vertices with similar LPFC connections (connectivity patterns across all stimulation sites). To this aim, we performed structured hierarchical clustering in which vertices or clusters that are adjacent on surface are iteratively merged if they are the most similar to each other among all neighbors (Blumensath et al., 2013). Similarity to merged clusters was updated based on Ward’s linkage rule using a Python implementation (sklearn.cluster.ward_tree). On the surface mesh, two clusters were considered adjacent if at least two vertices (one from each cluster) belong to the same triangulate face. Similarity between two clusters was defined as the cosine of angle between their multi-site connectivity patterns, in which stimulation sites of both monkeys were concatenated. For robust clustering, we limited its scope to vertices connecting with at least two sites in both monkeys (four sites in total), which represented 90.0% and 97.6% of positive entries in the surface-based connectivity matrix of monkeys J and N, respectively. We decided the total number of clusters using the elbow method, by manually finding the “elbow” of the curve of vertex-level variance of connectivity explained by clusters against number of clusters (n = 133; Figure S5A). Out of the 133 clusters, 7 clusters may reflect incorrectly localized activations not fully addressed by the disambiguation (e.g., with weaker yet highly similar connectivity patterns to clusters in the opposite bank of a sulcus) and 8 clusters were too small compared to the majority, and these clusters were discarded from further analyses.

Finding principal dimensions of connectome

We performed non-centered PCA on surface-based connectivity matrices (# sites × # vertices) of each domain separately, based on singular value decomposition. Non-centered PCA means we didn’t normalize the samples to have zero mean, which we would consider inappropriate for non-negative connectivity matrices. We concatenated data from both monkeys into a single matrix per domain, and took vertices as features and stimulation sites as samples. We then perform reduced singular value decomposition on each concatenated connectivity matrix (X):

$$\text{X}=\text{U}\times \text{S}\times {\text{V}}^{\text{T}}$$

where U and V are # sites × # dimensions and # verticesx # dimensions matrices consisting of mutually orthogonal, unitary columns, and S is # dimensions × # dimensions diagonal matrix. The connectivity matrix was thus decomposed as multiplication of a weight matrix (U × S, # sites × # dimensions) and a basis matrix (V^T, # dimensions × # vertices). Each row of the basis matrix represents a multi-vertex basis patterns of connections, and each column of the weight matrix represents weight for the basis pattern of corresponding dimension, of sites of the two monkeys. The dimensions of basis and weight matrices were ordered by importance, i.e., how much variance of the connectivity matrix a dimension explains. Note the choice of features and samples doesn’t affect the resulting multi-vertex/site patterns, since to swap the choice, we simply transposed the above equation as:

$${\text{X}}^{\text{T}}=\text{V}\times \text{S}\times {\text{U}}^{\text{T}}$$

where V × S becomes the new weight matrix (# vertices × # dimensions), and U^T becomes the new basis matrix (# dimensions × # sites). Thus, after transposition, the multi-vertex pattern (now as weight) of each dimension is scaled by the same factor (diagonal entry of respective dimension in S) for each vertex, which doesn’t change the spatial pattern. The same is true for multi-site patterns (now as basis).

For our purpose, a caveat of PCA is that a site’s weight of all dimensions is positively associated with its overall connectivity to the domain of interest. To address this, we divided the weight after the first dimension (e.g., W1&2) by a site’s overall connectivity to the domain of interest, so that the normalized weight better reflects how well a site’s connections match the corresponding basis pattern.

We did further rescaling for visualizations based on 1D and 2D (Steiger et al., 2015) colormaps. Specifically, in each domain, three types of numbers, i.e., basis value (of vertices), weight (of sites, normalized), and connectivity-weighted weight mapped to vertices (Figures 8, S7, and S8) of the second and third dimensions (dim 1&2) were pooled within type, and then divided by the absolute value of 90^th or 10^th percentile, whichever was large. For dim 0, the numbers of basis value (of vertices) and weight (of sites, unnormalized) were pooled within domain and type, and then divided by the 90^th percentile. We then capped the rescaled value within [−1 1] (dim 1&2) or [0 1] (dim 0), to utilize the full range of colormaps for better discernability between colors, and the area of circle in the circle diagrams was proportional to 0.1+0.90.9x(capped(capped value). For purposes other than these two, we always used uncapped value, e.g., to plot W1&2 coordinate (Figures 5A–5D and 6A–6H, left-top), to determine angle and length of arrows in all arrow diagrams, and to perform the analysis of Figure S6H.

Finding main axes of 2D distribution of weights

Because W1&2 were normalized after PCA, the main axes of their joint distribution were generally shifted and rotated relative to the cardinal axes. The proper shift and rotation were found by performing centered PCA, in which mean was subtracted before PCA, taking W1&2 as features and stimulation sites of both monkeys combined as samples.

Supplementary Material

2

Figure S1. Related to STAR Methods

Figure S2. Related to STAR Methods

Figure S3. Related to STAR Methods

Figure S4. Related to Figure 2 and STAR Methods

Figure S5. Related to Figure 1

Figure S6. Related to Figure 4

Figure S7. Related to Figures 5,6, and 8

Figure S8. Related to Figures 5,6, and 8

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental models: Organisms/strains
Rhesus macaque (Macaca mulatta)	Alpha Genesis; California National Primate Research Center	N/A
Software and algorithms
MATLAB	MathWorks	R2017a (9.2.0.538062)
Python	Python Software Foundation	2.7
Nipype	https://nipype.readthedocs.io (Gorgolewski et al., 2011)	0.13.0
FreeSurfer	https://surfer.nmr.mgh.harvard.edu (Fischl, 2012)	6.0.0
AFNI	https://afni.nimh.nih.gov (Cox, 1996)	16.3.08
ANTs	https://stnava.github.io/ANTs/ (Avants et al., 2009)	2.1.0
FSL	https://fsl.fmrib.ox.ac.uk/fsl/fslwiki (Jenkinson et al., 2012)	5.0.9
3D Slicer	http://slicer.org (Fedorov et al., 2012)	4.6.2
Psychtoolbox	http://psychtoolbox.org (Brainard, 1997)	3.0
Surfing toolbox	http://surfing.sourceforge.net (Oosterhof et al., 2011)	N/A
Other
Interareal connectivity matrix (tracing)	core-nets.org (Markov et al., 2014)	https://core-nets.org/download/Cercor_2012%20Table.xls
Interareal connectivity matrix (dMRI)	BALSA (Donahue et al., 2016)	https://balsa.wustl.edu/study/show/W336
Interareal distance matrix	core-nets.org (Markov et al., 2013)	https://core-nets.org/download/PNAS_2013_Distance_Matrix.xlsx
NIMH Macaque Template (NMT)	NIMH (Seidlitz et al., 2018)	https://afni.nimh.nih.gov/pub/dist/doc/htmldoc/nonhuman/macaque_tempatl/template_nmtv1.html#nmt-v1-2
CBCetal15 parcellation (Paxinos et al.) on CIVM_rhesus_v1 template	Scalable Brain Atlas (Calabrese et al. 2015)	https://scalablebrainatlas.incf.org/macaque/CBCetal15
MERetal14 parcellation (Markov et al.) on F99 template	Scalable Brain Atlas (Markov et al. 2014)	https://scalablebrainatlas.incf.org/macaque/MERetal14_on_F99
RGYetal17 parcellation (Saleem and Logothetis) on D99 template	NIMH (Reveley et al., 2017)	https://afni.nimh.nih.gov/pub/dist/atlases/macaque/macaqueatlas_1.2b/
2D colormap	https://github.com/dominikjaeckle/Color2D (Steiger et al., 2015)	ziegler
Platinum/iridium microelectrodes	FHC	RD5, RD6, RD15, RD16 (adapted from UEPLGCSEBN4G)
Programable stimulator	World Precision Instruments	DS8000
Constant-current isolator	World Precision Instruments	A365
Low-pass filters	Mini-Circuits	BLP-1.9+

Highlights.

• EM-fMRI maps cortical connections of densely sampled LPFC sites

• LPFC has topographically organized connections with five major processing domains

• EM-fMRI connectivity is consistent with classic tract-tracing but at a finer scale

• LPFC sites mirror the layout of their connections in major association cortices