Effect of Diffusion on Resonance Energy Transfer Rate Distributions: Implications for Distance Measurements

Abstract

Intrinsically disordered protein regions and many other biopolymers lack the three-dimensional structure that could be determined by X-ray crystallography or NMR, which encourages the application of alternative experimental methods. Time-resolved resonance energy transfer data are often used to measure distances between two fluorophores attached to a flexible biopolymer. This is complicated by the rotational and translational diffusion of the fluorophores and by non-monoexponential donor decay in the absence of the acceptor. Equation $I_{\text{DA}}(t)=I_{\text{D}}(t)\cdot F(t)$ is derived here, which is applicable regardless of whether I_D(t) is monoexponential. I_D(t) and I_DA(t)are the δ-excitation donor emission decays in the absence and in the presence of the acceptor; F(t) contains information about energy transfer, donor–acceptor distance distribution, and diffusion dynamics. It is shown that in the absence of rotational and translational diffusion, F(t) is a continuous distribution of exponentials, whereas in the presence of rotational and translational diffusion, F(t) is a sum of discrete exponentials. For each case it is shown how F(t) is related to the distance distribution. Experimental data obtained with a flexible tetradecapeptide in aqueous solution clearly demonstrate that F(t) is a sum of discrete exponential terms. A partial differential equation describing resonance energy transfer in the presence of both rotational and translational diffusion of the donor and acceptor tethered to the ends of a semiflexible chain is solved in this work using a combination of analytical and numerical methods; the solution is used to fit time-resolved emission of the donor, which makes it possible to determine the model parameters: contour length, persistence length, and the end-to-end translational diffusion coefficient.

Graphical Abstract

1. INTRODUCTION

Nonradiative resonance transfer of electronic excitation energy between two fluorescent molecules was first described by Perrin.¹ A quantitative theory of this phenomenon was developed by Förster.² According to Förster’s theory, the rate of energy transfer (ET) is inversely proportional to the sixth power of the distance between the centers of the fluorophores that play the roles of the energy donor and acceptor. This distance dependence has been widely used to measure intramolecular and intermolecular distances in the range between 10 and 100 Å. In most energy transfer studies the original steady-state or time-resolved fluorescence emission data are first converted to the energy transfer efficiency, which is then used to calculate the donor–acceptor distance. By definition, the energy transfer efficiency E represents the quantum yield of energy transfer:³

$$E=\frac{k_{\text{ET}}}{{{\tau }_{\text{D}}}^{-1}+k_{\text{ET}}}$$ (1.1)

where k_ET is the energy transfer rate as defined by Förster² and τ_D is the lifetime of the donor in the absence of the acceptor; the inverse of τ_D equals the sum of the radiative and nonradiative decay rate. The definition eq 1.1 implicitly assumes that the donor decay is monoexponential; from this assumption it also follows that³

$$E=\frac{{R_0}^6}{{R_0}^6+r^6}$$ (1.2)

where r is the distance between the donor and the acceptor (measured between the centers of their π-orbital systems) and R₀ is the Förster radius, which, among other things, depends on the orientation of the fluorophores. If both r and R₀ have the same value for all donor–acceptor pairs, then it is possible to calculate the r value by solving eq 1.2 with respect to r. To ensure that the distances and orientations are identical for all donor–acceptor pairs, the donor and the acceptor must be incorporated into a rigid three-dimensional structure, e.g., in the structure of a globular protein that has a unique conformation under experimental conditions. Indeed, for the donor–acceptor pairs naturally present in human γD-Crystallin, a rigid globular protein with a known X-ray structure, the experimental values of the energy transfer efficiency are in reasonable agreement with the ones calculated theoretically.⁴ However, if the donor and acceptor are in a rigid globule, then the distance r can be determined by X-ray diffraction crystallography, which undermines the need for energy transfer experiments.

Energy transfer data are indispensable in the case where there is no rigid structure and the distance r can be different for different donor–acceptor pairs. In this case the solution of eq 1.2 with respect to r is often called the mean donor–acceptor distance. The following example is intended to show how far this can be from the truth. For simplicity, consider a distribution of donor–acceptor distances that consists of just two discrete narrow peaks at r = 0.62R₀ and r = 2.36R₀, accounting for 53% and 47% of the donor–acceptor pairs, respectively. The mean distance equals 0.53 × 0.62R₀ + 0.47 × 2.36R₀ = 1.44R₀. Substituting this mean distance for r in eq 1.2 yields E = 0.10, which is a low efficiency value. The actual energy transfer efficiency value depends on the rate of exchange between the two conformations corresponding to r = 0.62R₀ and r = 2.36R₀. If there is no exchange during the excited-state lifetime, then we should calculate two separate efficiencies by substituting r = 0.62R₀ and r = 2.36R₀ in eq 1.2 and then take their weighted mean, which yields E = 0.50, a medium efficiency value. In the opposite case, where the exchange is much faster than the excited-state population decay, we should first calculate the mean energy transfer rate and then substitute it in eq 1.1, which yields E = 0.90, a high efficiency value. This example clearly shows that if there is a distance distribution rather than just one donor–acceptor distance, then (i) the energy transfer efficiency strongly depends on the dynamics of distance variations and (ii) from the value of the energy transfer efficiency alone it is not possible to calculate the mean donor–acceptor distance.

Steady-state fluorescence data can be used only to calculate the energy transfer efficiency E and provide no additional information that could be used to draw conclusions about the shape of the distance distribution or the dynamics of distance variations. Time-resolved fluorescence data contain lots of additional information as compared to the steady-state data. The first theoretical study that showed the possibility of determining distance distributions from time-resolved fluorescence data was published in 1972 by Grinvald, Haas, and Steinberg.⁵ In 1975 Haas et al. published the first experimental study of donor–acceptor distance distributions.⁶ Since then, a few other experimental studies based on the same theory have been published.^7–13 Three common drawbacks characterize these studies. First, in most of these studies it was assumed that the decay of the donor in the absence of the acceptor was monoexponential.^5–9,12,13 Second, the dynamics of distance variations was assumed to be infinitely slow; this implied no translational diffusion of the donor and the acceptor.^5–13 Third, it was assumed that the value of the orientation factor κ² = 2/3 could be used for every donor–acceptor pair,^5–13 which implied that not only the orientations of both fluorophores were completely random but also their rotational dynamics was faster than the time resolution of the experimental setup.

The effect of rotational dynamics of the donor and acceptor on energy transfer was thoroughly considered in 1974 by Dale and Eisinger.¹⁴ They pointed out that the same mean value of the orientation factor κ² can be applied to all donor–acceptor pairs only in the case where the rotational dynamics is very fast. In the opposite extreme case, where there is no fluorophore rotation at all, the energy transfer efficiency must be calculated separately for every κ² value between 0 and 4 and then the efficiency (and not the κ²) must be averaged over the κ² distribution. For the same donor–acceptor distance and the same orientation distribution, the energy transfer efficiency can change several fold depending on whether the rotational dynamics is fast or slow. This important fact was ignored in many energy transfer studies, which assumed that the rotational dynamics was very fast (κ² = 2/3) and the translational dynamics was infinitely slow. In this connection it is worthwhile to evaluate the characteristic times of rotational and translational diffusion of a fluorophore. For simplicity, we assume that the fluorophore is a sphere and that it is allowed to rotate about its center. For the characteristic time of rotational diffusion t_R we will take the anisotropy decay time³

$$t_{\text{R}}=\frac{1}{6D_{\text{R}}}=\frac{\eta V_{\text{l}}}{k_{\text{B}}T}$$ (1.3)

where D_R is the rotational diffusion coefficient, η is the dynamic viscosity of the solvent, V₁ is the volume of one fluorescent molecule, k_B is Boltzmann constant, and T is the absolute temperature. For the characteristic time of translational diffusion t_T we will take the time during which the root-mean-square translational displacement of the two fluorophores relative to each other in one dimension (along the donor–acceptor line) equals the root-mean-square width W of the distance distribution:

$$t_{\text{T}}=\frac{W^2}{2D_{\text{T}}}$$ (1.4)

where D_T is the translational diffusion coefficient of the two fluorophores relative to each other, which equals the sum of the translational diffusion coefficient of the donor and acceptor D_T = D_TD + D_TA. Note that here we consider translational diffusion in one dimension only (along the donor–acceptor line), because translational diffusion in the two directions normal to the donor–acceptor line does not change the donor–acceptor distance (see Appendix A in Supporting Information for details). This explains why there is 2D_T rather than 6D_T in the denominator of 1.4. Stokes’ law expresses the translational diffusion coefficient for each fluorophore in terms of the radius R_S of the sphere:

$$D_{\text{TD}}=D_{\text{TA}}=\frac{k_{\text{B}}T}{6\pi \eta R_{\text{S}}}$$ (1.5)

For the purpose of estimate we assumed that both fluorophores have the same size and the same diffusion coefficient. The volume of a sphere is related to its radius:

$$V_1=\frac{4}{3}\pi {R_S}^3$$ (1.6)

From eqs 1.4, 1.5, and 1.6 follows the final expression for t_T:

$$t_{\text{T}}=\frac{9}{8}{\left(\frac{W}{R_{\text{S}}}\right)}^2\frac{\eta V_1}{k_{\text{B}}T}$$ (1.7)

Now from eqs 1.3 and 1.7 we obtain the ratio

$$\frac{t_{\text{T}}}{t_{\text{R}}}=\frac{9}{8}{\left(\frac{W}{R_{\text{S}}}\right)}^2$$ (1.8)

Because the ratio in eq 1.8 is a rough estimate (in reality the fluorophores are not spheres and, on top of this, they are usually tethered to a biopolymer, which increases both t_T and t_R, but not in equal proportion), we can omit the multiplier 9/8 and state that the ratio of the characteristic translational diffusion time to the characteristic rotational diffusion time approximately equals the squared ratio of the distance distribution full width 2W to the fluorophore linear dimension 2R_S. Considering that 2W is usually just a fraction of the Förster radius R₀ and does not exceed 50 Å, whereas the linear dimensions of smallest fluorophores (such as indole or naphthalene) are at least 7 Å, the ratio t_T/t_R is not expected to exceed 50. This means that if, by using κ² = 2/3 for all donor–acceptor pairs, rotational relaxation is implicitly assumed to be faster than the time resolution of the experimental equipment, then translational relaxation must take place on the nanosecond time scale, and therefore translational diffusion cannot be ignored.

In 1978 Haas et al. published the first theoretical and experimental study that considered not only a distribution of donor–acceptor distances but also translational diffusion of the fluorophores.¹⁵ The theoretical model resulted in partial differential equations that were solved numerically; the numerical solution was then fit to experimental time-resolved fluorescence data. A similar approach was later used in a number of other studies.^16–32 In some of these studies the decay of the donor without the acceptor was considered monoexponential.^{15,17–19,23,25–28,30,31} Other studies took into account that the decay of the donor without the acceptor can be multiexponential but falsely assumed that the value of the Förster radius R₀ is the same for every lifetime.^16,20,22,24

In this work we do not use the Förster radius R₀ to calculate the rate of energy transfer. The expression for the energy transfer rate introduced in section 2 is applicable to both heterogeneous donor ensembles (where different donors have different decay rates) and to relaxing donor ensembles (where the decay rate varies with time after excitation). In section 3 we describe a simple method for separating the effect of the complex donor decay without the acceptor from that of a dynamics-dependent energy transfer. In section 4 we present a model describing the energy transfer rate distribution for the case of no rotational and no translational diffusion. In section 5 we present a model for the case where the rotational and translational diffusion are present. In section 6 we describe experimental methods. In section 7 we describe numerical data analysis techniques. In section 8 we compare the experimental time-resolved fluorescence data with the predictions of the models described in sections 4 and 5.

Two significant new theoretical results are presented in this work. First, a simple equation describing fluorescence emission decay of the donor in the presence of energy transfer is derived in section 3; this equation is applicable whether or not the donor emission decay in the absence of energy transfer is monoexponential. Second, a partial differential equation describing resonance energy transfer in the presence of both rotational and translational diffusion of the donor and acceptor tethered to the ends of a semiflexible chain is solved in section 5 using a combination of analytical and numerical methods. A well-known method of time-correlated single-photon counting (TCSPC) is employed in this work to measure the decay of the donor fluorescence emission in the absence and in the presence of the acceptor. The finding that the theoretical model developed in section 5 actually fits the experimental data very well, which makes it possible to determine the shape of the donor–acceptor distance distribution and the translational diffusion coefficient, represents the new experimental result.

Throughout this work and in refs 5–42 it is assumed that the energy donor and acceptor are two different fluorophores and that there exists a spectral range in which all fluorescence emission is contributed by the donor and none by the acceptor; fluorescence emission at wavelengths within this spectral range is used by us and by the authors of refs 5–42 to monitor the excited-state donor population decay. Energy transfer between two identical fluorophores has been considered elsewhere.^43–48 In the case of identical donor and acceptor the total fluorescence emission at any wavelength is insensitive to energy transfer; thus, time-resolved fluorescence anisotropy must be measured to obtain useful information.^43–48 There is one common feature and four differences between the work described here and that of the other authors.^43–48 Equations describing rotational diffusion of the two fluorophores involved in energy transfer were solved by the authors of refs ^43–48 and in section 5 of the present work, which represents the common feature. In refs ^43–48 the authors consider energy transfer between two identical fluorophores, whereas the theory developed in this work applies only when the donor and acceptor are different, which is the first difference. The second difference is that in refs ^43–48 the authors measure fluorescence emission anisotropy whereas in this work we measure the magic-angle fluorescence emission intensity at a wavelength where only the energy donor emits. In refs ^43–48 the authors consider a single donor–acceptor distance rather than a distance distribution, whereas in this work the main purpose is to determine the shape of the donor–acceptor distance distribution, which makes the third and the most important difference. At last, the physical description of the system of two interacting fluorophores is different: in refs ^43–48 the authors solve the equation describing the evolution of the quantum-statistical density matrix, whereas in this work we solve the rate equation describing the excited-state donor population. The equation of motion for the density matrix is usually called the quantum Liouville equation or the von Neumann equation or the Liouville–von Neumann equation by analogy to the equation derived by Liouville in the framework of classical (nonquantum) statistics.⁴⁹ The density matrix description takes into account not only the populations of different quantum states but also the phase relations between their wave functions; in the case of two interacting fluorophores, this difference becomes essential when the energy of the dipole–dipole coupling (between the electronic transition dipoles) is greater than both the emission bandwidth and the difference in the electronic excitation energies between the donor and the acceptor. If this condition is satisfied, a phenomenon known as reverberating energy migration^43,45,47,48 may be observed under the right conditions (when the system is somehow prepared at time zero with one of the two fluorophores in its excited state and the other one in its ground state, although, because of excitonic splitting,⁵⁰ this is not a stationary state of the system). The difference in the electronic excitation energies between the donor and the acceptor considered in this work is significantly greater that the energy of dipole–dipole coupling between them at the shortest possible distance (i.e., when the two fluorophores are in van der Waals contact); therefore, in our case, the phase relations, represented by the off-diagonal elements of the density matrix, are unimportant and it is sufficient to solve the rate equations describing the populations (the diagonal elements). Furthermore, because the energy transfer is irreversible, we are interested in only one diagonal element, which describes the excited-state donor population.

2. MODIFIED FÖRSTER RADIUS

Time-resolved energy transfer experiments are in essence the measurements of donor decay rates in the presence and in the absence of the acceptor. The difference between these decay rates represents the energy transfer rate k_ET. It is therefore important to have an accurate expression for k_ET in terms of the donor–acceptor distance r and the relative orientations. In most published work the authors used the expression

$$k_{\text{ET}}=\frac{1}{{\tau }_{\text{D}}}{\left(\frac{R_0}{r}\right)}^6$$ (2.1)

where R₀ is the Förster radius,

$${R_0}^6=\frac{9{\kappa }^{2}Q}{128{\pi }^5{\eta }^4}\times \frac{\ln (10)C_L}{N_{\text{A}}}\times J$$ (2.2)

κ² is the squared orientation factor,

$$\kappa =\sin {\theta }_{\text{D}}\sin {\theta }_{\text{A}}\cos \left({\phi }_{\text{D}}-{\phi }_{\text{A}}\right)-2\cos {\theta }_{\text{D}}\cos {\theta }_{\text{A}}$$ (2.3)

to define the angles θ_D, φ_D, θ_A, and φ_A we introduce a floating reference frame with the Z axis passing through the centers of both fluorophores; the direction of the transition electric dipole moment of each fluorophore with respect to the floating reference frame is characterized by two spherical angles, θ and φ, with the subscripts D for the donor and A for the acceptor; Q is the quantum yield,

$$Q=\frac{\mathrm{\Gamma }}{\mathrm{\Gamma }+k_{\text{nr}}}=\mathrm{\Gamma }{\tau }_D$$ (2.4)

Γ is the spontaneous emission rate of the donor, also known as the radiative decay rate, k_nr is the nonradiative decay rate of the donor in the absence of the acceptor, ${\tau }_{\text{D}}={\left(\mathrm{\Gamma }+k_{\text{nr}}\right)}^{-1}$ is the lifetime of the donor in the absence of the acceptor, n is the refractive index of the medium in which the values of Q, Γ, k_nr, τ_D, and the spectra of the donor and the acceptor were measured and the calculated value of R₀ is applicable, the multiplier ln(10)C_L/N_A converts from the units of decadic molar extinction coefficient ε to the units of natural molecular extinction coefficient σ, C_L = 1000 cm³/L, N_A is Avogadro’s number, and J is the overlap integral,

$$J=\frac{{\int }_0^{\infty }{F}_{\text{D}}(\nu ){ϵ}_{\text{A}}(\nu ){\nu }^{-4}\text{d}\nu }{{\int }_0^{\infty }{F}_{\text{D}}(\nu )\text{d}\nu }$$ (2.5)

$F_{\text{D}}(\nu )$ is the corrected emission spectrum of the donor, ${\epsilon }_{\text{A}}(\nu )$ is the decadic molar extinction coefficient spectrum of the acceptor, and ν is the wavenumber in cm⁻¹ (all spectra must be measured in the same medium of the refractive index n).

Consider the use of eq 2.1 in the case where the donor without the acceptor has a multiexponential decay that is entirely attributable to heterogeneity; i.e., there are M donor subpopulations, each having a different lifetime τ_Dm, where m = 1, 2, ..., M. In this case most of the authors substituted τ_Dm for τ_D in eq 2.1 to calculate k_ETm for each subpopulation, while assuming that the same value of R₀ applies to all subpopulations.^{16,20,22,24,33–42} The latter was a false assumption. According to eq 2.2 R₀⁶ is directly proportional to Q, which, in turn, is directly proportional to τ_Dm according to eq 2.4. Thus, any difference in τ_Dm between the subpopulations should have canceled out, but it did not, because the authors of the above cited studies forgot that R₀ is not a constant: among other things, it depends on τ_Dm and on κ².

To avoid problems of this nature in the present work and in the future, we need to define a true constant that can be used instead of R₀. Toward this goal, we start from the equation that Förster originally derived for k_ET, before he introduced the definition of Förster radius:²

$$k_{\text{ET}}=\frac{9{\kappa }^2\mathrm{\Gamma }}{128{\pi }^5{n}^4{r}^6}\times \frac{\ln (10)C_{\text{L}}}{N_{\text{A}}}\times J$$ (2.6)

Equation 2.6 differs from eq 1 in Förster’s paper² in notation only: Förster’s notation $n_{{\text{S}}^{*}\to {\text{A}}^{*}}$ corresponds to k_ET in this work, Förster’s ${{\tau }_{\text{S}}}^0$ corresponds to ${\mathrm{\Gamma }}^{-1}$ in this work, instead of J, Förster’s original equation explicitly contained the integral from the numerator of the fraction on the right-hand side of eq 2.5, and the integral from the denominator of that fraction did not enter in Förster’s original equation because Förster normalized $F_{\text{D}}(\nu )$ in such a way that the integral in the denominator equaled 1. It is important that Förster derived eq 2.6 first, and then from it he obtained eqs 2.1 and 2.2. The variable lifetime τ_D does not enter in eq 2.6, which proves that it should not enter in the final expression for k_ET either. The fact that k_ET is independent of τ_D has also been emphasized by other authors.^21,31 The next step is to split the constants and the variables in eq 2.6. The product of most constants will be denoted R₁⁶ and R₁ will be named the modified Förster radius:

$${R_1}^6=\frac{9}{128{\pi }^5{n}^4}\times \frac{\ln (10)C_{\text{L}}}{N_{\text{A}}}\times J$$ (2.7)

In terms of the modified Förster radius eq 2.6 can be rewritten as

$$k_{\text{ET}}=\mathrm{\Gamma }{\kappa }^2{\left(\frac{R_1}{r}\right)}^6$$ (2.8)

Note that eq 2.8 equally applies to all donor subpopulations, regardless of the fact that they have different lifetimes τ_Dm. The modified Förster radius R₁ has the same value for all donor–acceptor pairs as long as the spectra $F_{\text{D}}(\nu )\text{and}{\epsilon }_{\text{A}}(\nu )$ remain unchanged (solvatochromic fluorophores may change their spectra when moved to a solvent of a different polarity). In most cases the spontaneous emission rate Γ also has the same value for all donor–acceptor pairs: it depends only on the intrinsic properties of the fluorophore, the shape of the spectrum $F_{\text{D}}(\nu )$, and the refractive index n.⁵¹

An equation similar to eq 2.8 was introduced by Jacob et al.;³¹ see eq 22 in that reference. The notation R_F⁶ in the notation of Jacob et al. is equivalent to the product κ²R₁⁶ in our notation. Haas in a review article²⁹ also used a similar approach, see eq 11 in that article; the second term on the right-hand side of that equation is equivalent to the right-hand side of eq 2.8 here. Likewise, the second term on the right-hand side in eq 13 of Orevi et al.,³² is equivalent to the right-hand side of eq 2.8 here.

3. SEPARATION OF THE COMPLEX DONOR DECAY FROM THE DYNAMICS-DEPENDENT ENERGY TRANSFER

In 1975, when the first experimental determination of donor–acceptor distance distribution was attempted, the time resolution of a typical time-correlated single-photon counting (TCSPC) instrument was about 5 ns and the integral number of photons in an experimental decay curve was under one million.⁶ With that quality of experimental data it was difficult to tell the difference between a monoexponential and a multiexponential (or nonexponential) decay. With the invention of picosecond lasers, microchannel plate photo-multipliers, and new nuclear electronics modules, the time resolution improved by about 2 orders of magnitude. Using the excitation pulse rate of 4 × 10⁶ Hz and two emission wings in parallel, one can now register 2 × 10⁸ photons during a 3 h experiment.⁵² With this data quality it is easy to see that any fluorophore attached to a protein or a polypeptide exhibits nonexponential fluorescence decay, which usually can be approximated by a linear combination of four or more exponential terms. A rigid aromatic dye, such as anthracene, in a low-viscosity nonpolar solvent still has a monoexponential decay law because all relaxation times in such solvent–solute system are much faster than the time resolution of a modern TCSPC instrument. The relaxation of proteins and other biopolymers is considerably slower, which results in nonexponential (aka multiexponential) decay. For solvatochromic fluorophors, such as tryptophan, dansyl, IAEDANS, etc., the instantaneous emission spectrum shifts to the red during the relaxation process, which implies that the decay law varies with the emission wavelength at which the TCSPC data are collected.^53–55 The decay law at any one emission wavelength is nonexponential and can be mathematically described in terms of a time-variant decay rate,

$$k(t)=-\frac{1}{I(t)}\frac{\text{d}I(t)}{\text{d}t}=-\frac{\text{d}\ln [I(t)]}{\text{d}t}$$ (3.1)

where I(t) is the δ-excitation decay law measured at one emission wavelength.

The other important source of deviations from a monoexponential law is heterogeneity. For example, the decay rate of a tryptophan residue depends on the presence of proton donors in the vicinity of its side chain.⁵⁶ The protonation state of potential proton donors (histidine, lysine, cysteine, amino terminus) is pH-dependent; within some pH ranges it is possible to find both protonated (quenching) and deprotonated (nonquenching) forms, which explains why different tryptophan residues may have different decay rates. In this work we will not consider the heterogeneity resulting from multiple tryptophan residues in the polypeptide sequence or multiple extrinsic labels attached to one biopoymer: this would result in different donor–acceptor distance distributions for different fluorophore positions. Here we consider only the case where for all donor–acceptor pairs there is the same distance distribution, the same orientation distribution, and the same conformation dynamics. The heterogeneity (if present) may be due to differences in the protonation states, side chain conformations, or similar small local changes.

Consider the case where there are M donor subpopulations, numbered with the index m = 1, 2, ..., M. Each subpopulation has a different decay rate k_m in the absence of the acceptor (heterogeneity). Furthermore, due to relaxation each decay rate may explicitly vary with time t after excitation, which means that we have M different functions k_m(t). Now we will write the partial differential equation describing the decay, energy transfer, rotational diffusion, and translational diffusion for just one donor subpopulation

$$\frac{\partial }{\partial t}{\xi }_m(\mathrm{\Omega },r,t)=\left(-k_m(t)-\mathrm{\Gamma }{\kappa }^2(\mathrm{\Omega })\frac{{R_1}^6}{r^6}+{\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}+{\widehat{\mathrm{\Xi }}}_r\right){\xi }_m(\mathrm{\Omega },r,t)$$ (3.2)

where ${\xi }_m(\mathrm{\Omega },r,t)$ is the distribution function, Ω denotes the collection of the angles θ_D, φ_D, θ_A, φ_A, t is the time after δ-excitation, k_m(t) is the decay rate for the mth donor subpopulation in the absence of the acceptor, Γ and R₁ are the radiative decay rate and the modified Förster radius for all donor subpopulations, κ(Ω) is defined in eq 2.3, ${\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}$ is the rotational diffusion operator (a linear differential operator acting on the set of the angles Ω only), and ${\widehat{\mathrm{\Xi }}}_r$ is the translational diffusion operator (a linear differential operator acting on r only). The specific form of these diffusion operators will be considered later. It is important, however, that these operators are the same for all donor subpopulations.

In the general case, the solution of eq 3.2 can be represented as a product of two functions,

$${\xi }_m(\mathrm{\Omega },r,t)=d_m(t)\cdot f(\mathrm{\Omega },r,t)$$ (3.3)

where d_m(t) and f(Ω,r,t) are the solutions of the following differential equations:

$$\frac{\partial }{\partial t}{d}_m(t)=-k_m(t)d_m(t)$$ (3.4)

$$\frac{\partial }{\partial t}f(\mathrm{\Omega },r,t)=\left(-\mathrm{\Gamma }{\kappa }^2(\mathrm{\Omega })\frac{R_1^6}{r^6}+{\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}+{\widehat{\mathrm{\Xi }}}_r\right)f(\mathrm{\Omega },r,t)$$ (3.5)

Note that eq 3.5 equally applies to all donor subpopulations. This is a direct result of the fact that in this work we consider only the case where for all donor–acceptor pairs there is the same distance distribution, the same orientation distribution, and the same conformation dynamics. We do not consider, for instance, a mixture of different-length biopolymers labeled with a donor and an acceptor on the opposite ends. Likewise, we do not consider mixtures of biopolymers with donors and acceptors attached to different positions at random. The case considered here also implies that the initial distribution f(Ω,r,0) is the same for all donor subpopulations. If the initial condition is the same and the differential equation is the same, then the solution f(Ω,r,t) must be also the same for all donor subpopulations; this explains why the function f is missing the subscript m.

The total fluorescence emission intensity of the donor is directly proportional to the size of the excited donor population, which can be obtained by integrating ${\xi }_m(\mathrm{\Omega },r,t)$ over all the angles and the distance r and summing over all subpopulations:

$$I(t)=\sum _{m=1}^M{\int }_0^{\infty }{\int }_{\mathrm{\Omega }}{\xi }_m(\mathrm{\Omega },r,t)\text{d}r\text{d}\mathrm{\Omega }$$ (3.6)

In eq 3.6 we employed the integration sign with the letter Ω under it and the symbol dΩ. These notations will be used throughout the present work for space economy; their meaning is defined as

$$\begin{gathered} {\int }_{\mathrm{\Omega }}\dots \text{d}\mathrm{\Omega }={\int }_0^{\pi }{\int }_0^{2\pi }{\int }_0^{\pi }{\int }_0^{2\pi }\dots \sin {\theta }_{\text{D}}\text{d}{\theta }_{\text{D}}\text{d}{\phi }_{\text{D}}\sin {\theta }_{\text{A}}\text{d}{\theta }_{\text{A}} \\ \text{d}{\phi }_{\text{A}} \end{gathered}$$ (3.7)

where the ellipses denote any mathematical expression. Substituting the expression for ${\xi }_m(\mathrm{\Omega },r,t)$ from eq 3.3 into eq 3.6 and using the fact that d_m(t) is independent of all integration variables and f(Ω,r,t) is the same for all m, we obtain

$$I(t)=\left(\sum _{m=1}^M{d}_m(t)\right)\cdot F(t)$$ (3.8)

where

$$F(t)={\int }_0^{\infty }{\int }_{\mathrm{\Omega }}f(\mathrm{\Omega },r,t)\text{d}r\text{d}\mathrm{\Omega }$$ (3.9)

Note that the sum on the right-hand side of eq 3.8 represents the total fluorescence emission intensity from all donor subpopulations in the absence of the acceptor, when no energy transfer takes place. Equation 3.8 can be rewritten using the notation I_DA(t) for fluorescence emission intensity of the donor in the presence of the acceptor and I_D(t) for that in the absence of the acceptor,

$$I_{\text{DA}}(t)=I_{\text{D}}(t)\cdot F(t)$$ (3.10)

If the donor is at least slightly solvatochromic, then it is essential that I_DA(t) and I_D(t) are measured at the same emission wavelength (all fluorescent probes that can be covalently attached to a biomolecule lack a center of inversion and therefore are solvatochromic at least to some extent). It is also important that I_DA(t) and I_D(t) are measured through a magic angle polarizer, in the solvent of the same refractive index, the same polarity, the same pH, and at the same temperature.

As a side note, it is interesting to point out that eq 3.10 directly supports the conclusion of Jacob et al.³¹ regarding the uselessness of quenching in the studies of distance distributions and dynamics. The addition of a quencher would change both I_DA(t) and I_D(t), but not the function F(t), which contains all the information about the distance distributions and dynamics. Thus, no additional information is obtained by varying the quencher concentration. The most accurate information about the function F(t) is actually obtained when fluorescence intensity is the highest, i.e., at zero quencher concentration.

4. ENERGY TRANSFER RATE DISTRIBUTION IN THE ABSENCE OF DIFFUSION

An expression for the function F(t) in eq 3.10 is derived here for the case where there is an arbitrary-shape donor–acceptor distance distribution, the fluorophore orientations are random, and both rotational and translational diffusion are infinitely slow (the distance r and the angles Ω do not change on the time scale of TCSPC measurements). Because there is neither rotational nor translational diffusion, the corresponding operators can be omitted from eq 3.5, which becomes

$$\frac{\partial }{\partial t}f(\mathrm{\Omega },r,t)=-\mathrm{\Gamma }{\kappa }^2(\mathrm{\Omega })\frac{{R_1}^6}{r^6}f(\mathrm{\Omega },r,t)$$ (4.1)

The solution of eq 4.1 is

$$f(\mathrm{\Omega },r,t)=f(\mathrm{\Omega },r,0)\exp \left[-\mathrm{\Gamma }{R_1}^6{\kappa }^2(\mathrm{\Omega })r^{-6}t\right]$$ (4.2)

For completely random orientations of the donor and the acceptor

$$f(\mathrm{\Omega },r,0)=\frac{1}{16{\pi }^2}p(r)$$ (4.3)

where p(r) is the equilibrium donor–acceptor distance distribution in the absence of energy transfer (or in the ground state). To obtain F(t), we substitute the expression from eq 4.3 into eq 4.2, then substitute f(Ω,r,t) into eq 3.9 and integrate. The result can be represented as follows

$$F(t)={\int }_0^{\infty }{\int }_0^{4}p(r)q\left({\kappa }^2\right)\exp \left(-\mathrm{\Gamma }{R_1}^6{\kappa }^2{r}^{-6}t\right)\text{d}r\text{d}{\kappa }^2$$ (4.4)

where q(κ²) is the distribution of κ² values for a random orientation of the donor and the acceptor,

$$\begin{gathered} q(x)=\frac{1}{16{\pi }^2}{\int }_{\mathrm{\Omega }}\delta (x-[\sin {\theta }_{\text{D}}\sin {\theta }_{\text{A}}\cos \left({\phi }_{\text{D}}-{\phi }_{\text{A}}\right) \\ {-2\cos {\theta }_{\text{D}}\cos {\theta }_{\text{A}}]}^2)\text{d}\mathrm{\Omega } \end{gathered}$$ (4.5)

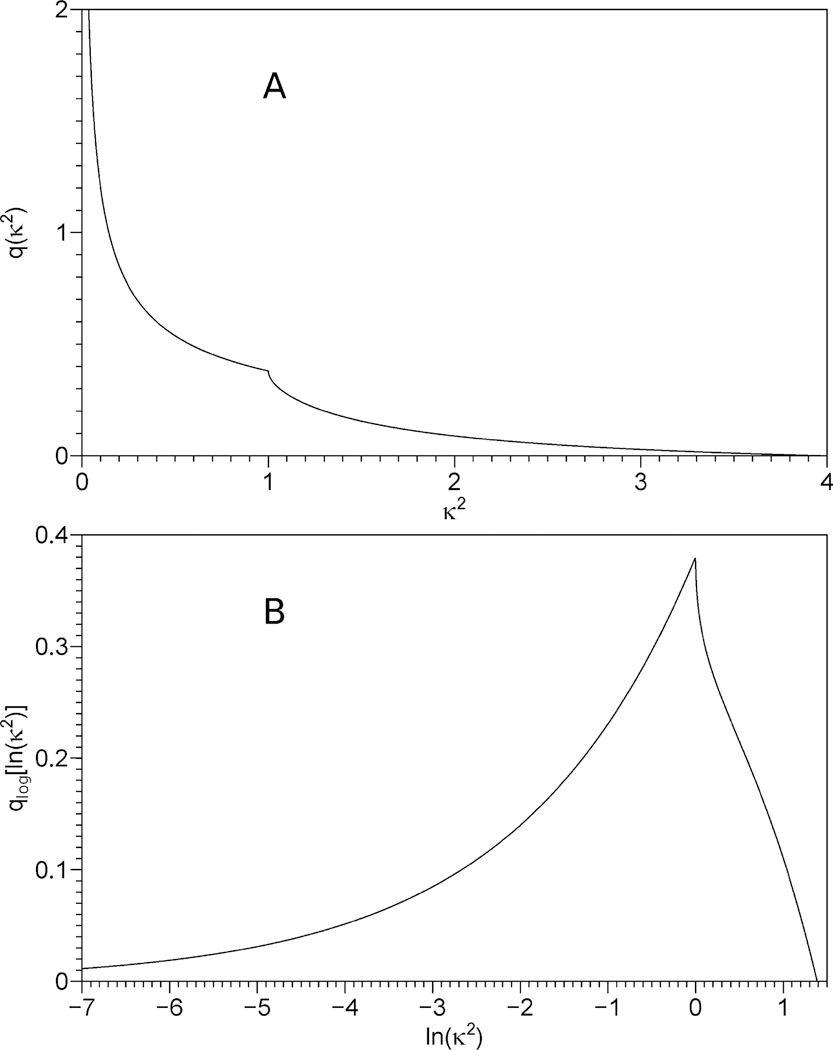
δ(...) is Dirac’s delta function, and integration by dΩ is defined in eq 3.7. The κ² distribution calculated in accordance with eq 4.5 is shown in Figure 1A; an analytical expression for q(κ²) can be found in eq 4.12 of Van Der Meer et al.⁵⁷

Figure 1.

Panel A: distribution of κ² values for a random orientation of the donor and the acceptor, calculated according to eq 4.5. Panel B: distribution of ln(κ²) values for a random orientation of the donor and the acceptor. The distributions on the linear and logarithmic κ² scales are related via eq 4.10.

Equation 4.4 can be rewritten as

$$F(t)={\int }_0^{\infty }\exp \left(-k_{\text{ET}}t\right)\rho \left(k_{\text{ET}}\right)\text{d}{k}_{\text{ET}}$$ (4.6)

where ρ(k_ET) is the energy transfer rate distribution,

$$\rho \left(k_{\text{ET}}\right)=\mathrm{\Gamma }{R_1}^6{\int }_0^{\infty }{r}^{-6}p(r)q\left(k_{\text{ET}}{r}^6{\mathrm{\Gamma }}^{-1}{R_1}^{-6}\right)\text{d}r$$ (4.7)

Equation 4.7 establishes the relationship between the energy transfer rate distribution ρ(k_ET) on the linear k_ET scale and the distance distribution p(r) on the linear r scale. Analysis of experimental data (section 7) yields the energy transfer rate distribution ${\rho }_{\text{log}}[\text{ln}(k_{\text{ET}})]$ on the logarithmic k_ET scale. It is interesting that converting all three distributions $\rho (k_{\text{ET}}),p(r),\text{and}q({\kappa }^2)$ to logarithmic scales,

$$\rho \left(k_{\text{ET}}\right)={k_{\text{ET}}}^{-1}{\rho }_{\log }\left[\ln \left(k_{\text{ET}}\right)\right]$$ (4.8)

$$p(r)=r^{-1}{p}_{\log }[\ln (r)]$$ (4.9)

$$q({\kappa }^2)={({\kappa }^2)}^{-1}{q}_{\log }\left[\ln \left({\kappa }^2\right)\right]$$ (4.10)

reduces eq 4.7 to

$${\rho }_{\log }(y)=\frac{1}{6}{\int }_{-\infty }^{+\infty }{p}_{\log }\left(-\frac{1}{6}z+\ln R_1+\frac{1}{6}\ln \mathrm{\Gamma }\right)q_{\log }(y-z)\text{d}z$$ (4.11)

Equation 4.11 shows that ρ_log(y) is merely a convolution of two functions: (i) q_log(y), and (ii) p_log(x) that was expanded (−6)-fold and shifted by ln Γ + 6 ln R₁ on the x axis prior to the convolution, i.e., y = −6x + 6 ln R₁ + ln Γ. A plot of the distribution q_log(y) is shown in Figure 1B; this is clearly a continuous function (although its first derivative is discontinuous). Because one of the two functions under the convolution integral is a continuous function, the convolution must be a continuous function regardless of whether the second function under the convolution integral is continuous or not. Due to the relations 4.8 and 4.9 this applies not only to the distributions on the logarithmic scales but also to the distributions on the linear sales: regardless of whether the distance distribution is a continuous function or not, the energy transfer rate distribution must be a continuous function. In summary, this means that in the absence of rotational and translational diffusion we expect to see a continuous distribution of energy transfer rates regardless of the actual form of the donor–acceptor distance distribution.

5. FUNCTION F(T) IN THE PRESENCE OF ROTATIONAL AND TRANSLATIONAL DIFFUSION

In the presence of rotational and translational diffusion, the function F(t) should be obtained by the integration in accordance with eq 3.9 of the solution f(Ω,r,t) of the partial differential eq 3.5, which is repeated here:

$$\frac{\partial }{\partial t}f(\mathrm{\Omega },r,t)=\left(-\mathrm{\Gamma }{\kappa }^2(\mathrm{\Omega })\frac{{R_1}^6}{r^6}+{\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}+{\widehat{\mathrm{\Xi }}}_r\right)f(\mathrm{\Omega },r,t)$$ (5.1)

One important conclusion about F(t) can be made before we proceed to solve eq 5.1. First, we note that

$$\widehat{H}=\mathrm{\Gamma }{\kappa }^2(\mathrm{\Omega })\frac{{R_1}^6}{r^6}-{\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}-{\widehat{\mathrm{\Xi }}}_r$$ (5.2)

represents a linear differential operator. We define the eigenfunctions Ψ_n(Ω,r) and corresponding eigenvalues Λ_n of the operator $\widehat{H}:$

$$\widehat{H}{\mathrm{\Psi }}_n(\mathrm{\Omega },r)={\mathrm{\Lambda }}_n{\mathrm{\Psi }}_n(\mathrm{\Omega },r)$$ (5.3)

It should be noted that in eqs 5.3–5.6 one subscript n enumerates all eigenfunctions and eigenvalues; however, in practice it may be convenient to use a larger number of subscripts; because we have not found yet how many subscripts will be needed, the subscript n in eqs 5.3–5.6 should be treated as a placeholder for multiple subscripts that will be defined later. The subscript n should not be confused with the refractive index, for which we used the symbol n in section 2 only. Any solution of eq 5.1 can be represented in terms of the eigenfunctions and eigenvalues,

$$f(\mathrm{\Omega },r,t)=\sum _n{a}_n{\mathrm{\Psi }}_n(\mathrm{\Omega },r)\exp \left(-{\mathrm{\Lambda }}_{n}t\right)$$ (5.4)

Substituting this into eq 3.9 yields

$$F(t)=\sum _n{a}_n{b}_n\exp \left(-{\mathrm{\Lambda }}_{n}t\right)$$ (5.5)

where

$$b_n={\int }_0^{\infty }{\int }_{\mathrm{\Omega }}{\mathrm{\Psi }}_n(\mathrm{\Omega },r)\text{d}r\text{d}\mathrm{\Omega }$$ (5.6)

From eq 5.5 it follows that in the presence of rotational and translational diffusion F(t) is a sum of discrete exponential terms, i.e., a discrete spectrum of energy transfer rates is observed in the presence of rotational and translational diffusion. In the absence of diffusion the theory predicted a continuous spectrum of energy transfer rates; see section 4.

Historically, the idea to employ eigenfunctions and eigenvalues to solve energy transfer-with-diffusion problem belongs to Steinberg,²⁵ although the equation he solved was not identical to eq 5.1. Unfortunately, Steinberg did not emphasize the significance of the fact that the solution is a discrete rather than a continuous spectrum of energy transfer rates, probably because this distinction was unimportant in 1994, when it was experimentally impossible (or very difficult) to tell the difference between a discrete and a continuous spectrum of exponential terms. With the data quality available to us today it is possible to tell the difference (see section 8).

Equations 5.3–5.6 are too general and therefore are of little practical use in reconstructing the shape of the donor–acceptor distance distribution from experimental data. To derive practically useful expressions, we must first define the specific form of the diffusion operators ${\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}\text{and}{\widehat{\mathrm{\Xi }}}_r.$ If we assume that the rotational diffusion of the donor and the acceptor with respect to the floating reference frame is completely isotropic and independent of each other, then

$${\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}={\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }D}+{\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }A}$$ (5.7)

where

$${\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }\text{D}}=\frac{D_{\text{RD}}}{\sin {\theta }_{\text{D}}}\frac{\partial }{\partial {\theta }_{\text{D}}}\sin {\theta }_{\text{D}}\frac{\partial }{\partial {\theta }_{\text{D}}}+\frac{D_{\text{RD}}}{{\sin }^2{\theta }_{\text{D}}}\frac{{\partial }^2}{\partial {{\phi }_{\text{D}}}^2}$$ (5.8)

$${\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }\text{A}}=\frac{D_{\text{RA}}}{\sin {\theta }_{\text{A}}}\frac{\partial }{\partial {\theta }_{\text{A}}}\sin {\theta }_{\text{A}}\frac{\partial }{\partial {\theta }_{\text{A}}}+\frac{D_{\text{RA}}}{{\sin }^2{\theta }_{\text{A}}}\frac{{\partial }^2}{\partial {{\phi }_{\text{A}}}^2}$$ (5.9)

D_RD is the rotational diffusion coefficient of the donor and D_RA is that of the acceptor. The translational diffusion operator explicitly depends on the equilibrium donor–acceptor distance distribution p(r)

$${\widehat{\mathrm{\Xi }}}_r=D_{\text{T}}\frac{\partial }{\partial r}p(r)\frac{\partial }{\partial r}\frac{1}{p(r)}$$ (5.10)

where D_T equals the sum of the translational diffusion coefficient of the donor and that of the acceptor. With these expressions for the rotational and translational diffusion operator the problem of finding the eigenfunctions and eigenvalues of the combined operator $\widehat{H}$ from eq 5.2 is not trivial. A simplification can be achieved if we follow the recipe of Born and Oppenheimer,⁵⁸ who separated the eigenfunctions of a molecular Hamiltonian operator into electronic eigenfunctions (calculated in the fixed-nuclei approximation) and nuclear vibrational eigenfunctions. Following this recipe, we first seek the rotational eigenfunctions in the fixed r approximation

$$\widehat{V}(r){\psi }_{jklm}(\mathrm{\Omega };r)={\lambda }_{jklm}(r){\psi }_{jklm}(\mathrm{\Omega };r)$$ (5.11)

where

$$\widehat{V}(r)=\frac{\mathrm{\Gamma }{R_1}^6}{r^6}{\kappa }^2(\mathrm{\Omega })-{\widehat{\mathrm{\Xi }}}_{\mathrm{\Omega }}$$ (5.12)

and then seek the translational eigenfunctions

$${\widehat{W}}_{jklm}{\chi }_{jklmn}(r)={\mathrm{\Lambda }}_{jklmn}{\chi }_{jklmn}(r)$$ (5.13)

where

$${\widehat{W}}_{jklm}={\lambda }_{jklm}(r)-{\widehat{\mathrm{\Xi }}}_r$$ (5.14)

Note that the eigenfunctions ${\psi }_{jklm}(\mathrm{\Omega };r)$ are functions of the angles Ω only, the distance r plays here the role of a constant parameter, which is separated by the semicolon from the variables Ω for clarity. The operator $\widehat{V}(r)$ and the eigenvalues ${\lambda }_{jklm}(r)$ also depend on the constant parameter r. It is easy to define the eigenfunctions ${\psi }_{jklm}(\mathrm{\Omega };r)$ and eigenvalues ${\lambda }_{jklm}(r)$ for the limiting case r → ∞:

$${\psi }_{jklm}(\mathrm{\Omega };\infty )=Y_j^k\left({\theta }_{\text{D}},{\phi }_{\text{D}}\right)Y_l^m\left({\theta }_{\text{A}},{\phi }_{\text{A}}\right)$$ (5.15)

$${\lambda }_{jklm}(\infty )=j(j+1)D_{\text{RD}}+l(l+1)D_{\text{RA}}$$ (5.16)

where $Y_j^k\left({\theta }_{\text{D}},{\phi }_{\text{D}}\right)\text{and}{Y}_l^m\left({\theta }_{\text{A}},{\phi }_{\text{A}}\right)$ are spherical harmonics defined in accordance with the Condon−Shortley phase convention and D_RD and D_RA are the rotational diffusion coefficients of the donor and acceptor, respectively. Indices j and l assume non-negative integer values, j = 0, 1, 2, ..., l = 0, 1, 2, .... Index k assumes integer values from −j to +j. Index m assumes integer values from −l to +l. The eigenfunctions ${\psi }_{jklm}(\mathrm{\Omega };r)$ and eigenvalues ${\lambda }_{jklm}(r)$ for r < ∞ will be calculated in the framework of the quantum mechanical perturbation theory,⁵⁹ by considering the first term on the right-hand side of eq 5.12 as the perturbation operator,

$$\widehat{U}=\frac{\mathrm{\Gamma }{R_1}^6}{r^6}{\kappa }^2(\mathrm{\Omega })$$ (5.17)

Toward this goal we first express κ²(Ω) in terms of spherical harmonics,

$${\kappa }^2(\mathrm{\Omega })=4\pi \sum _{j=0,2}\sum _{l=0,2}\sum _{m=-\min (j,l)}^{+\min (j,l)}{c}_{jlm}{Y}_j^{-m}\left({\theta }_{\text{D}},{\phi }_{\text{D}}\right)Y_l^m\left({\theta }_{\text{A}},{\phi }_{\text{A}}\right)$$ (5.18)

Here indices j and l assume only two values: 0 and 2. If at least one of the indices j and l equals 0, then m assumes only one value m = 0. However, if j = l = 2, then m assumes five different values from m = −2 to m = +2. The values of the coefficients $c_{jlm}$ corresponding to all eight possible index combinations are given in Table 1. Using eq 5.18, the perturbation operator is expressed in terms of spherical harmonics:

$$\widehat{U}=4\pi \frac{\mathrm{\Gamma }{R_1}^6}{r^6}\sum _{j=0,2}\sum _{l=0,2}\sum _{m=-\min (j,l)}^{+\min (j,l)}{c}_{jlm}{Y}_j^{-m}\left({\theta }_{\text{D}},{\phi }_{\text{D}}\right)Y_l^m\left({\theta }_{\text{A}},{\phi }_{\text{A}}\right)$$ (5.19)

Table 1.

Coefficients c_jlm Defined in Eq 5.18^a

j	l	m	cjlm
0	0	0	2/3
0	2	0	2√5/15
2	0	0	2√5/15
2	2	−2	2/15
2	2	−1	4/15
2	2	0	2/5
2	2	+1	4/15
2	2	+2	2/15

^aAll non-zero c_jlm are included.

Matrix elements of the perturbation operator $\widehat{U}$ in the unperturbed eigenfunctions ${\psi }_{jklm}(\mathrm{\Omega };\infty )$ possess eight indices,

$$U_{j_1{l}_1{m}_1{j}_2{k}_2{l}_2{m}_2}={\int }_{\mathrm{\Omega }}{\psi }_{j_1{k}_1{l}_1{m}_1}^{*}(\mathrm{\Omega };\infty )\widehat{U}{\psi }_{j_2{k}_2{l}_2{m}_2}(\mathrm{\Omega };\infty )\text{d}\mathrm{\Omega }$$ (5.20)

Two kinds of matrix elements will be used below: the diagonal elements $U_{jklmjklm}$ and off-diagonal elements $U_{jklm0000}.$ The latter can be obtained directly from eq 5.19:

$$U_{jklm0000}=\frac{\mathrm{\Gamma }{R_1}^6}{r^6}{\delta }_{k,-m}{c}_{jlm}$$ (5.21)

Where ${\delta }_{k,-m}$ is Kronecker delta, it equals 1 if k = −m and 0 if k ≠ −m. The diagonal elements $U_{jklmjklm}$ can be expressed in terms of coefficients $d_{jklm},$

$$U_{jklmjklm}=\frac{\mathrm{\Gamma }{R_1}^6}{r^6}{d}_{jklm}$$ (5.22)

that are defined in terms of the coefficients c_jlm and Wigner 3j symbols,

$$\begin{gathered} d_{jklm}={(-1)}^{k+m}(2j+1)(2l+1) \\ \times \sum _{J=0,2}\sum _{L=0,2}\sqrt{(2J+1)(2L+1)}{c}_{JL0} \\ \times \left(\begin{array}{ccc}j& J& j\\ -k& 0& k\end{array}\right)\left(\begin{array}{ccc}j& J& j\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}l& L& l\\ -m& 0& m\end{array}\right)\left(\begin{array}{ccc}l& L& l\\ 0& 0& 0\end{array}\right) \end{gathered}$$ (5.23)

The values of the relevant coefficients d_jklm are given in Table 2. Note that Table 2 includes only those combinations of j, k, l, m that will be used in this work. An extended version, Table 2X, that includes all coefficients d_jklm with j ≤ 4 and l ≤ 4 has been included in Supporting Information. On the contrary, Table 1 already includes all nonzero values of c_jlm; therefore, there is no extension of Table 1.

Table 2.

Coefficients d_jklm Defined in Eq 5.23^a

j	k	l	m	djklm
0	0	0	0	2/3
2	0	0	0	6/7
0	0	2	0	6/7
2	−2	2	+2	22/49
2	−1	2	+1	44/49
2	0	2	0	178/147
2	+1	2	−1	44/49
2	+2	2	−2	22/49

^aOnly relevant d_jklm are included.

The diagonal matrix elements U_jklmjklm represent the first-order corrections to the unperturbed eigenvalues λ_jklm(∞).⁵⁹ Adding up the unperturbed eigenvalues from eq 5.16 and the first-order corrections from eq 5.22 gives the corrected eigenvalues,

$${\lambda }_{jklm}(r)=j(j+1)D_{\text{RD}}+l(l+1)D_{\text{RA}}+\frac{\mathrm{\Gamma }{R_1}^6}{r^6}{d}_{jklm}$$ (5.24)

As the next step, λ_jklm(r) from eq 5.24 must be substituted into eq 5.14, which should be followed by the search of the eigenfunctions and eigenvalues of the operator ${\widehat{W}}_{jklm}$ in accordance with eq 5.13. Equation 5.13 is rewritten below, including the explicit form of the translational diffusion operator ${\widehat{\mathrm{\Xi }}}_r,$ which is defined in eq 5.10:

$$\begin{gathered} {\lambda }_{jklm}(r){\chi }_{\mathit{\text{jklmn}}}(r)-D_{\text{T}}\frac{\partial }{\partial r}\left[p(r)\frac{\partial }{\partial r}\left(\frac{{\chi }_{j\mathit{\text{klmn}}}(r)}{p(r)}\right)\right] \\ ={\mathrm{\Lambda }}_{jklmn}{\chi }_{jklmn}(r) \end{gathered}$$ (5.25)

Note that the linear differential operator on the left-hand side of eq 5.25 is not Hermitian; therefore, its eigenfunctions ${\chi }_{jklm}(r)$ are not orthogonal, which would present a serious problem down the road. To correct this problem, we define

$$s(r)=\frac{\sqrt{p(r)}}{4\pi }$$ (5.26)

The old eigenfunctions are expressed as products of s(r) times the new eigenfunctions,

$${\chi }_{jklmn}(r)=s(r)v_{jklmn}(r)$$ (5.27)

Substituting ${\chi }_{jklm}(r)$ from eq 5.27 into eq 5.25 and dividing both sides by s(r) results in

$$\begin{gathered} {\lambda }_{jklm}(r){\upsilon }_{jklmn}(r)-\frac{D_T}{s(r)}\frac{\partial }{\partial r}\left[s^2(r)\frac{\partial }{\partial r}\left(\frac{{\upsilon }_{jklmn}(r)}{s(r)}\right)\right] \\ ={\mathrm{\Lambda }}_{jklmn}{\upsilon }_{jklmn}(r) \end{gathered}$$ (5.28)

The operator on the left-hand side of eq 5.28 is Hermitian; therefore, its eigenfunctions ${\upsilon }_{j\mathit{\text{klm}}}(r)$ are orthogonal, which is used below. Equation 5.28 can be solved numerically, which requires discretization of the continuous variable r. The minimum and maximum donor–acceptor distance, r_min and r_max, must be selected so that all nonzero values of the function p(r) correspond to the argument values from the range r_min < r < r_max. For example, the semiflexible chain model⁶⁰ results in the following equilibrium end-to-end distance distribution:

$$p(r)=\frac{4}{{\pi }^{1/2}}\frac{{\omega }^{3/2}}{1+3{\omega }^{-1}+\frac{15}{4}{\omega }^{-2}}\frac{r^2{L}^6}{{\left(L^2-r^2\right)}^{9/2}}\exp \left(-\frac{\omega r^2}{L^2-r^2}\right)$$ (5.29)

where L is the contour length of the chain, and parameter ω equals three-quarters of the ratio of the contour length to the persistence length L_p:

$$\omega =\frac{3L}{4L_{\text{p}}}$$ (5.30)

The distance distribution in eq 5.29 is normalized to a unit integral, for details see Appendix B in Supporting Information. For this distance distribution it is natural to take r_min = 0 and r_max = L, because for every r from the range 0 < r < L the value of p(r) is positive, whereas for r ≤ 0 as well as for r ≥ L, p(r) = 0. The interval between r_min and r_max is divided into N_discr + 1 equal steps,

$$\mathrm{\Delta }=\frac{r_{\max }-r_{\min }}{N_{\text{discr}}+1}$$ (5.31)

$$r_i=\text{i}\mathrm{\Delta }+r_{\min }$$ (5.32)

Index $i=1,2,\dots ,N_{\text{discr}}$ enumerates equally spaced points r_i. The number N_discr should not be too small, because this would decrease the accuracy of the numerical solution, and it should not be too large, because this would increase the computing time. For the semiflexible chain model N_discr + 1 = 2048 appears to be an excellent compromise. Discretization of eq 5.28 results in the matrix equation

$$\mathbf{G}{\mathbf{v}}_n={\mathrm{\Lambda }}_{jklmn}{\mathbf{v}}_n$$ (5.33)

where we have omitted for brevity the indices j, k, l, and m in the notation of the matrix G and vector ${\mathbf{v}}_n.$ In terms of the numerical algorithm, the omission of these indices makes direct sense: the N_discr × N_discr matrix G and N_discr vectors ${\mathbf{v}}_n$ of N_discr components each are stored in the same two N_discr × N_discr arrays for every combination of j, k, l, and m; the calculation of eigenvalues and eigenvectors is carried out for one combination at a time. Nonzero elements of the matrix G are

$$G_{i,i-1}=G_{i,i+1}=-\frac{D_{\text{T}}}{{\mathrm{\Delta }}^2}$$ (5.34)

$$G_{i,i}=\frac{D_{\text{T}}}{{\mathrm{\Delta }}^2}\frac{s\left(r_{i-1}\right)+s\left(r_{i+1}\right)}{s\left(r_i\right)}+{\lambda }_{jklm}\left(r_i\right)$$ (5.35)

Equation 5.35 defines the diagonal elements of the matrix G. Equation 5.34 defines all nonzero off-diagonal elements. Note that by definition matrix G is symmetrical, which means that it has only one set of eigenvectors. An asymmetrical matrix would have a set of right eigenvectors and a set of left eigenvectors, which would complicate the numerical calculation of eigenvectors. Note that discretization of eq 5.25 would result in an asymmetrical matrix. The transition from eq 5.25 to eq 5.28 using the function s(r) resulted in the symmetrical matrix G. All eigenvalues of the matrix G are positive because all ${\lambda }_{jklm}\left(r_i\right)$ are positive. Numerical algorithms for calculating eigenvectors and eigenvalues of a positive-definite symmetrical matrix are available. Any of them can be used as long as the computer subroutine employes REAL(8) arithmetic, outputs eigenvalues in the ascending order, and normalizes eigenvectors to unit sum of squared components,

$$\sum _{i=1}^{N_{\text{discr}}},{v_{in}}^2=1$$ (5.36)

Eigenvalues ${\mathrm{\Lambda }}_{jklmn}$ of the matrix G represent the discrete decay rates that can be directly substituted into eq 5.5. Equation 5.5 also contains amplitudes $a_{jklmn}$ and integrals $b_{jklmn}$ that need to be calculated. Amplitudes $a_{jklmn}$ can be calculated only if we know the angular-and-distance distribution of the donor–acceptor pairs immediately after δ-excitation at t = 0. If we assume that the excitation probability of the energy donor is independent of r and Ω, then the distribution at t = +0 is the same as the ground-state distribution, which equals the product of the distance distribution p(r) and the isotropic angular distribution 1/16π². If the angular-and-distance distribution at t = 0 is p(r)/16π², then

$$\sum _{j=1}^{\infty }\sum _{k=-j}^{+j}\sum _{l=1}^{\infty }\sum _{m=-j}^{+j}\sum _n{a}_{jklmn}{\psi }_{jklm}(\mathrm{\Omega };r){\chi }_{jklmn}(r)=\frac{p(r)}{16{\pi }^2}$$ (5.37)

Multiplying both sides of eq 5.37 by the complex conjugate of ${\psi }_{jklm}(\mathrm{\Omega };r)$ and integrating by dΩ as defined in eq 3.7, using the orthogonality of the eigenfunctions ${\psi }_{jklm}(\mathrm{\Omega };r),$ results in

$$\sum _n{a}_{jklmn}{\chi }_{jklmn}(r)=\frac{p(r)}{16{\pi }^2}{\int }_{\mathrm{\Omega }}{\psi }_{jklm}^{*}(\mathrm{\Omega };r)\text{d}\mathrm{\Omega }$$ (5.38)

Substituting for ${\chi }_{jklmn}(r)$ in eq 5.38 the expression from eq 5.27 and then dividing both sides by s(r) results in

$$\sum _n{a}_{jklmn}{\upsilon }_{jklmn}(r)=s(r){\int }_{\mathrm{\Omega }}{\psi }_{jklm}^{*}(\mathrm{\Omega };r)\text{d}\mathrm{\Omega }$$ (5.39)

Multiplying both sides of eq 5.39 by the complex conjugate of ${\upsilon }_{jklmn}(r)$ and integrating from 0 to ∞ by dr, using the orthogonality of the eigenfunctions ${\upsilon }_{jklmn}(r),$ results in

$$a_{jklmn}={\int }_0^{\infty }{\int }_{\mathrm{\Omega }}{\psi }_{jklm}^{*}(\mathrm{\Omega };r){\upsilon }_{jklmn}^{*}(r)s(r)\text{d}r\text{d}\mathrm{\Omega }$$ (5.40)

By substituting ${\psi }_{jklm}(\mathrm{\Omega };r)\cdot s(r)\cdot {\upsilon }_{jklmn}(r)\text{for}{\mathrm{\Psi }}_{jklmn}(\mathrm{\Omega },r)$ in eq 5.6, we obtain

$$b_{jklmn}={\int }_0^{\infty }{\int }_{\mathrm{\Omega }}{\psi }_{jklm}(\mathrm{\Omega };r){\upsilon }_{jklmn}(r)s(r)\text{d}r\text{d}\mathrm{\Omega }$$ (5.41)

Comparing eqs 5.40 and 5.41, taking into account that s(r) is real by definition, leads to the conclusion that a_jklmn equals the complex conjugate of b_jklmn. This is not a coincidence; this is a direct result of our definition of s(r) in eq 5.27 and the assumption that the probability of excitation of the donor is independent of Ω and r. If the probability of excitation depended on Ω and/or r, then a_jklmn would not be equal to the complex conjugate of b_jklmn. To calculate the integrals b_jklmn, we first need to calculate

$$g_{jklm}(r)={\int }_{\mathrm{\Omega }}{\psi }_{jklm}(\mathrm{\Omega };r)\text{d}\mathrm{\Omega }$$ (5.42)

For ${\psi }_{jklm}(\mathrm{\Omega };r)$ we will use the expressions obtained in the framework of the first-order perturbation theory.⁵⁹ Because we used ${\psi }_{jklm}(\mathrm{\Omega };\infty )$ defined in eq 5.15 as the unperturbed eigenfunctions, it is important to point out that

$${\int }_{\mathrm{\Omega }}{\psi }_{jklm}(\mathrm{\Omega };\infty )\text{d}\mathrm{\Omega }=\{\begin{array}{ll}4\pi \hfill & \text{if}j=k=l=m=0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (5.43)

From eq 5.43 it follows that from all the terms in the sum that represents the first-order correction for ${\psi }_{jklm}(\mathrm{\Omega };r)$ we only need to know the term containing ${\psi }_{0000}(\mathrm{\Omega };\infty ).$ In the case where at least one of the indices j, k, l, m is not equal to zero this gives

$$g_{jklm}(r)=4\pi \frac{U_{jklm0000}^{*}}{{\lambda }_{jklm}(\infty )-{\lambda }_{0000}(\infty )}$$ (5.44)

Using the expressions for the off-diagonal matrix elements U_jklm0000 from eq 5.21, we arrive at

$$g_{jklm}(r)=\frac{4\pi \mathrm{\Gamma }{R_1}^6}{\left[j(j+1)D_{\text{RD}}+l(l+1)D_{\text{RA}}\right]r^6}{\delta }_{k,-m}{c}_{jlm}$$ (5.45)

Note that eqs 5.44 and 5.45 were derived for the case where at least one of the indices j, k, l, m is not equal to zero. If all four indices are equal to zero, then the first-order correction for ${\psi }_{0000}(\mathrm{\Omega };r)$ lacks the term containing ${\psi }_{0000}(\mathrm{\Omega };\infty ),$ thus, in the framework of first-order perturbation theory $g_{0000}(r)$ equals $g_{0000}(\infty )$, which, in accordance with eq 5.43, equals 4π,

$$g_{0000}(r)=4\pi$$ (5.46)

Equation 5.41 can be rewritten using the definition of $g_{jklm}(r)$ from eq 5.42,

$$b_{jklmn}={\int }_0^{\infty }{g}_{jklm}(r){\upsilon }_{jklmn}(r)s(r)\text{d}r$$ (5.47)

Switching from continuous eigenfunctions ${\upsilon }_{jklmn}(r)$ to discrete eigenvectors ${\mathbf{v}}_{jklmn}$ and from integration by dr to summation over the index i results in

$$b_{jklmn}=\sum _{i=0}^{N_{\text{discr}}}{g}_{jklm}\left(r_i\right){\mathbf{v}}_{ijklmn}s\left(r_i\right)$$ (5.48)

For $g_{jklm}(r)$ in eq 5.48 one must substitute the expression from eq 5.46 if all four indices are equal to zero or the expressionfrom 5.45 otherwise. There is a total of eight combinations of j, k, l, m for which the integrals b_jklmn are not equal to zero. Using that fact that a_jklmn equals the complex conjugate of b_jklmn, we rewrite the expression for F(t) from eq 5.5 in the form

$$F(t)=\sum _{j=0,2}\sum _{k=-j}^{+j}\sum _{l=0,2}\sum _{m=-l}^{+l}\sum _{n=1}^{N_{\text{discr}}}{\left|b_{jklmn}\right|}^2\exp \left(-{\mathrm{\Lambda }}_{jklmn}t\right)$$ (5.49)

where nonzero coefficients b_jklmn occur only if k + m = 0, which, in principle, makes it possible to eliminate one of the summation signs (but we have not done it to preserve the symmetry of the final expression). Furthermore, in eqs 5.49 the terms with m = −k ≠ 0 have identical twins, because changing the signs of both m and k at the same time does not change the values of ${\left|b_{jklmn}\right|}^2\text{or}{\mathrm{\Lambda }}_{jklmn}.$ The latter makes it possible to calculate just one of the two identical terms and then multiply the result by 2. Following these recipes, one needs to calculate only six terms for every value of index n.

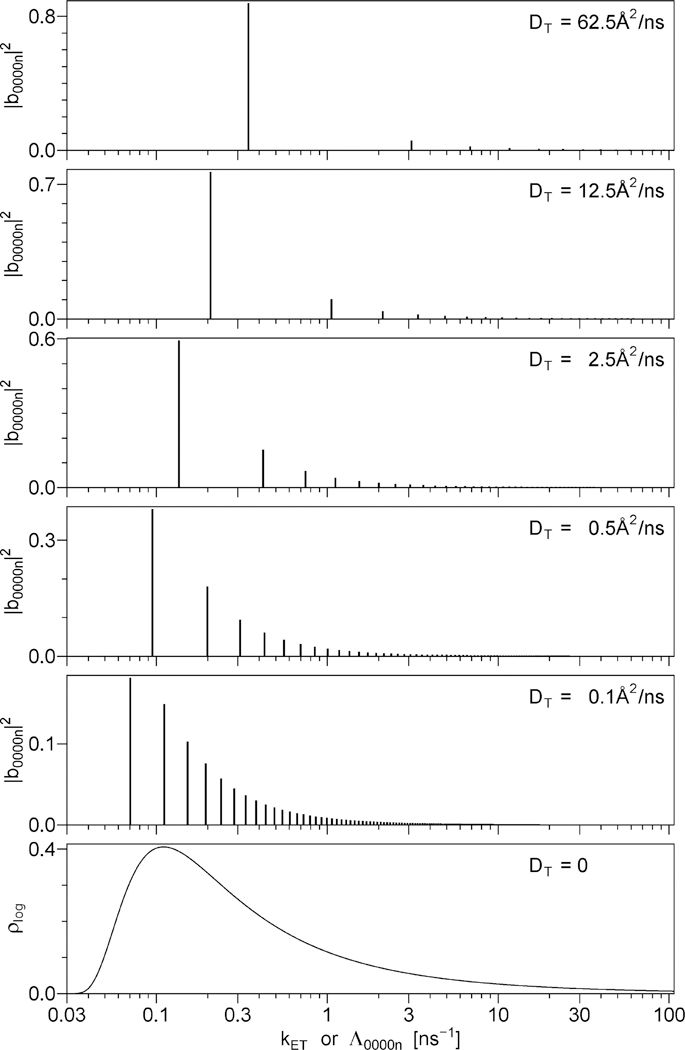
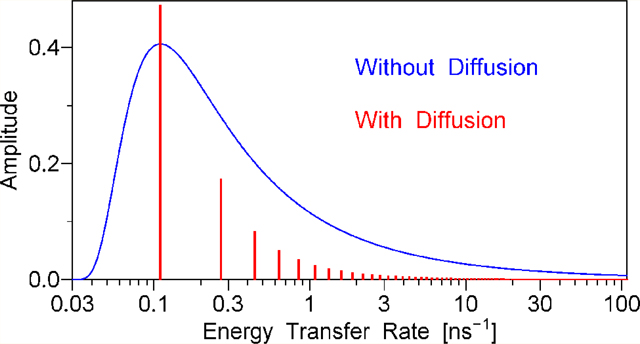
Sums of discrete exponentials, such as the one in eq 5.49, can be represented graphically as vertical bars on a logarithmic rate scale, where the placement of the base of each bar on the X axis is determined by $\log \left({\mathrm{\Lambda }}_{jklmn}\right),$ whereas the height (Y) of each bar is directly proportional to the amplitude ${\left|b_{jklmn}\right|}^2.$ Five such series of bars are shown in Figure 2, the only difference between the series is in the value of the translational diffusion rate D_T. For comparison, Figure 2 also contains a continuous distribution of energy transfer rates on the logarithmic rate scale, which represents the case where D_T = 0. For all six data sets shown in Figure 2, both D_RD and D_RA are assumed to be high, so that the rates 6D_RD and 6D_RA are both outside of the range of the rate scale of Figure 2. This was done in part to avoid unnecessary complication of Figure 2 and in part because the amplitudes ${\left|b_{jklmn}\right|}^2$ for nonzero indices j, k, l, or m are small and therefore difficult to show on the same vertical scale as the amplitudes ${\left|b_{0000n}\right|}^2.$ The results shown in Figure 2 were calculated using the following values of the model parameters: the contour length L = 50 Å, the ratio of the contour length to the persistence length $L/L_{\text{p}}=3.0,$ the product $\mathrm{\Gamma }\cdot {\left(R_1/L\right)}^6=0.0345{\text{ns}}^{-1}$ (this value was calculated using the experimental spontaneous emission rate Γ for the donor and the modified Förster radius R₁ for donor–acceptor pair, see section 8), and the translational diffusion rates D_T between 0 and 62.5 Å/ns, with the corresponding D_T value shown in each panel. Because the rates ${\mathrm{\Lambda }}_{0000n}$ and amplitudes ${\left|b_{0000n}\right|}^2$ are independent of the rotational diffusion rates D_RD and D_RA, the data for Figure 2 were obtained using D_RD = D_RA = ∞.

Figure 2.

Top five panels: series of discrete exponentials that represent the function F(t) in the presence of rotational and translational diffusionl. See eq 5.49. The placement of the base of each vertical bar on the X axis is determined by the decay rate, ${\mathrm{\Lambda }}_{jklmn},$. whereas the height (Y) of each bar is directly proportional to the amplitude ${\left|b_{jklmn}\right|}^2$. Bottom panel: the continuous distribution of exponentials that represent the function F(t) in the absence of translational diffusion. The translational diffusion rate D_T increases from the bottom panel to the top panel, the corresponding value of D_T is printed in each panel. The remaining model parameters are the same for all panels: L = 50 Å, L/L_p = 3.0, Γ·(R₁/L)⁶ = 0.0345 ns⁻¹, D_RD = D_RA = ∞.

The top panel of Figure 2 demonstrates that a high translational diffusion rate D_T = 62.5 Ų/ns results in F(t) dominated by one exponential, which contributes 88% of the total amplitude; the second- and the third-significant exponentials being responsible for 6% and 2% of the total amplitude, respectively. The ratio of the rates corresponding to the first two exponentials, Λ₀₀₀₀₂/Λ₀₀₀₀₁, equals 9.01, which ensures that these exponentials can be easily resolved from the experimental decay data. As the diffusion rate D_T decreases from 62.5 to 12.5, 2.5, 0.5, and 0.1 Ų/ns, all rates Λ_0000n decrease their values; the rate ratios Λ₀₀₀₀₂/Λ₀₀₀₀₁ decrease as well, and the amplitudes corresponding to the dominant exponential also decrease. At the translational diffusion rate of 0.1 Ų/ns the amplitude of the dominant exponential equals only 18% of the total and the rate ratio Λ₀₀₀₀₂/Λ₀₀₀₀₁ equals 1.58, which means that these exponentials can hardly be resolved from the experimental decay data. As D_T approaches zero, the density of discrete exponentials per unit log(k_ET) approaches infinity, which results in the continuous distribution of energy transfer rates, see the bottom panel of Figure 2. The data for the bottom panel were obtained using eq 4.11 with one important modification: because all equations in section 4 were derived for the case where D_RD = D_RA = 0, whereas Figure 2 represents the case where D_RD = D_RA = ∞, to obtain the data for the bottom panel instead of $q_{\log }(y)$ depicted in Figure 1B we substituted in eq 4.11 $q_{\log }(y)=\delta [y-\ln (2/3)]$ where δ[...] denotes Dirac’s delta-function.

Of all physical parameters on which the rates and amplitudes of the discrete exponentials in eq 5.49 depend it is convenient to make five combinations:

$${\beta }_1=\frac{L}{L_{\text{p}}}$$ (5.50)

$${\beta }_2=\frac{D_{\text{T}}{L}^4}{\mathrm{\Gamma }{R_1}^6}$$ (5.51)

$${\beta }_3=\frac{\mathrm{\Gamma }{R_1}^6}{L^6}$$ (5.52)

$${\beta }_4=\frac{D_{\text{RD}}{L}^6}{\mathrm{\Gamma }{R_1}^6}$$ (5.53)

$${\beta }_5=\frac{D_{\text{RA}}{L}^6}{\mathrm{\Gamma }{R_1}^6}$$ (5.54)

where L and L_p denote the contour length and the persistence length of the semiflexible chain, see eqs 5.29 and 5.30. These parameter combinations have useful properties listed below. The quantities β₁, β₂, β₄, and β₅ are dimensionless, whereas β₃ has the units of rate, i.e., ns⁻¹. All the amplitudes ${\left|b_{jklmn}\right|}^2$ are independent of β₃, whereas all the rates Λ_jklmn scale in direct proportion to β₃ when the values of β₁, β₂, β₄, and β₅ are kept constant. The rates Λ_0000n and amplitudes ${\left|b_{0000n}\right|}^2$ are independent of β₄ and β₅. The amplitudes ${\left|b_{0000n}\right|}^2$ are also independent of β₃. The ratio of any rate Λ_0000n to β₃ is also independent of β₃. Thus, just two parameters, β₁ and β₂, determine all amplitudes ${\left|b_{0000n}\right|}^2$ and all ratios Λ_0000n/β₃. The variation of the amplitudes ${\left|b_{0000n}\right|}^2$ and ratios Λ_0000n/β₃ with β₁ and β₂ is depicted in Figures 1S–6S in the Supporting Information. Figures 1S and 2S show the plots of Λ₀₀₀₀₁/β₃ versus β₁ (Figure 1S) and β₂ (Figure 2S). Figures 3S and 4S show the plots of Λ₀₀₀₀₂/Λ₀₀₀₀₁ versus β₁ (Figure 3S) and β₂ (Figure 4S). Figures 5S and 6S show the plots of ${\left|b_{00002}\right|}^2/|{b_{00001}|}^2$ versus β₁ (Figure 5S) and β₂ (Figure 6S).

6. EXPERIMENTAL METHODS

Experimental data were obtained with the tetradecapeptide TAU-PT, amino acid sequence CAKTPPAPKTPPAW. The side chain of the tryptophan residue (W) located at the C-terminus of the tetradecapeptide played the role of the energy donor. For the energy acceptor we used the dye 7-(diethylamino)-3-(4′-maleimidylphenyl)-4-methylcoumarin (CPM), LifeTechnologies catalog number D-346, that was attached to the N-terminal cysteine residue (C) by maleimide reaction. A separate study of the effects of phosphorylation of the two tyrosine residues (T) on the end-to-end distance distribution in this peptide and other similar peptides will be published elsewhere. In the present study we show just one data set, in which both tyrosine residues (T) were phosphorylated. This one data set is sufficient to demonstrate the possibilities and limitations of the data analysis.

Time-correlated single-photon counting data were obtained using the instrument that has been previously described in great detail.⁵² The time resolution estimated as the full width at half-maximum of the impulse response function (IRF) was equal to 65 ps. The integral number of photons in one decay curve representing either I_DA(t) or I_D(t) was typically about 10⁸. The decay curve I_D(t) was measured using the peptide with no CPM attached; the decay curve I_DA(t) was measured using the same peptide with CPM attached to the cysteine residue. All measurements were done through magic-angle polarizers, using 295 nm excitation wavelength and 350 nm emission wave-length, at 20 °C temperature. Peptide concentration was 20 μM, mean exciting power did not exceed 10 μW, and mean power density at the center of the exciting beam did not exceed 5 W/m².

7. DATA ANALYSIS

Equation 3.10 was derived here for the case where every energy donor has an acceptor attached to the same biopolymer. In practice, the labeling of the biopolymer (in our case, the tetradecapeptide) with the acceptor (CPM) is not 100% efficient; therefore, there is a subpopulation of donors that have no acceptor. Equation 3.10 can be modified to accommodate this situation:

$$I_{\text{DA}}(t)=A_1{I}_{\text{D}}(t)+A_2{I}_{\text{D}}(t)\cdot F(t)$$ (7.1)

where A₁ and maybe A₂ are the additional fitting parameters. Depending on the specific model function used for F(t), it may be that F(0) = 1 for any combination of the parameters on which F(t) depends; in this case A₂ should be treated as a free fitting parameter. However, if the parameters on which F(t) depends make it possible to vary the value of F(0) from 0 to ∞, then A₂ should be fixed at a constant value, for example, A₂ = 1. In either case, the efficiency of acceptor labeling reaction can be estimated as

$$E_{\text{LAB}}=\frac{A_{2}F(0)}{A_1+A_{2}F(0)}$$ (7.2)

Experimental TCSPC data are convolutions of the δ-excitation decays I_DA(t) and I_D(t) with the impulse response function (IRF) and also contain random noise.⁵² This suggests the following two steps that are always used to calculate F(t). In step one, the experimental decay of the donor without the acceptor is fit by a numerical convolution of the experimentally measured IRF with the linear combination of many exponentials,

$$I_{\text{D}}(t)=\sum _{i=1}^{N_{\text{ES}}}{\alpha }_i^{\text{ES}}\exp \left(-t/{\tau }_i^{\text{ES}}\right)$$ (7.3)

where ${\alpha }_i^{\text{ES}}$ are free fitting parameters (allowed to be negative and positive) and the values of ${\tau }_i^{\text{ES}}$ are evenly spaced on the logarithmic scale and fixed, with ${{\tau }_{i+1}}^{\text{ES}}\approx 1.743\cdot {\tau }_i^{\text{ES}},{\tau }_1^{\text{ES}}$ equal to one-half of the fwhm time resolution, and ${{\tau }_N}^{\text{ES}}$ equal to the time difference between the last channel of the multichannel analyzer (MCA) and the channel corresponding to the IRF peak. Typically, N_ES = 13. This is known as the exponential series (ES) model, it fits any decay curve with unbeatable accuracy (judging by the reduced χ² value), regardless of the origin of the nonexponential decay. Furthermore, because eq 7.3 is linear in all fitting parameters ${\alpha }_i^{\text{ES}},$ the fitting is done using the method of linear least-squares, which requires no successive iterations.

In step two, the experimental decay of the donor with the acceptor is fit by a numerical convolution of the experimentally measured IRF with the function I_DA(t) from eq 7.1, in which we substitute I_D(t) from eq 7.3 and F(t) corresponding to a specific model (see sections 4 and 5). In this fitting all ${\alpha }_i^{\text{ES}}$ and ${\tau }_i^{\text{ES}}$ are fixed at the values obtained in the first step, while A₁, maybe A₂, and the fitting parameters on which the function F(t) depends are adjusted using a nonlinear least-square method (requires successive iterations) to obtain the best fit to the experimental TCSPC data. Specifics of step two associated with the use of the models without diffusion (section 4) and with diffusion (section 5) are discussed separately below.

In the case of a model without diffusion (section 4), eq 4.6 defines F(t) that should be used in the second step of the data fitting. Instead of the rate distribution ρ(k_ET) on the linear k_ET scale, it is more convenient to use the distribution ${\rho }_{\log }\left[\ln \left(k_{\text{ET}}\right)\right]$ on the logarithmic k_ET scale; the relationship between the two distributions is given by eq 4.8. For the purpose of nonlinear least-squares fitting we must switch from the continuous variable ln(k_ET) to a discrete set of equally spaced ln(k_n) values, which must be closely spaced to ensure that the discretized function ${\rho }_{\log }\left[\ln \left(k_n\right)\right]$ still resembles a continuous function. Forty discrete k_n values per one decade works fine in most cases,

$$k_n=k_1\cdot {10}^{(n-1)/40}$$ (7.4)

where k₁ = 0.001 ns⁻¹ and the total number of different rates N_EXP = 201, which makes k₁₆₁ = 100 ns⁻¹. This effectively covers the lifetime range from 0.01 to 1000 ns. Function F(t) is expressed as a linear combination of N_EXP exponentials,

$$F(t)=\sum _{n=1}^{N_{\text{EXP}}}{\alpha }_n\exp \left(-k_{n}t\right)$$ (7.5)

where all parameters α_n as well as A₁ from eq 7.1 represent fitting parameters, and A₂ = 1. A high density of exponentials with closely spaced rates k_n results in a singular Hessian matrix, which means that exactly the same quality of fit can be achieved with different combinations of parameters α_n, most of which do not represent smooth functions. To define a unique set of parameters α_n, some constraint must be imposed. The algorithm used here requires that (i) all α_n must be positive, and (ii) the following penalty function must be minimal

$$\begin{gathered} \text{penalty}=w_1\sum _{n=2}^{N_{\text{EXP}}}{\left(\ln {\alpha }_n-\ln {\alpha }_{n-1}\right)}^2 \\ +w_2\sum _{n=3}^{N_{\text{EXP}}}{\left(\ln {\alpha }_n-2\ln {\alpha }_{n-1}+\ln {\alpha }_{n-2}\right)}^2 \end{gathered}$$ (7.6)

where the weights w₁ and w₂ define the contributions to the penalty of the squared first and second derivatives of the distribution ${\rho }_{\log }\left[\ln \left(k_n\right)\right],$ The penalty is added to the χ² (not to the reduced χ²), which is calculated as previously described;⁵² the sum χ² + penalty is minimized by varying the values of all α_n and A₁. The values of w₁ and w₂ are then adjusted so that the value of the χ² (without the added penalty) obtained with these values of w₁ and w₂ would be equal to 1 plus the minimum χ² achieved in the case where w₁ → 0 and w₂ → 0. The relative increase in the χ² approximately equals $\left(N_{\text{D}}-N_{\text{EXP}}\right)/(N_{\text{D}}-N_{\text{EXP}}-1),$ where N_D is the number of usable channels of the multichannel analyzer (MCA), in our case N_D = 1926, and N_D − N_EXP − 1 represents the number of degrees of freedom as defined in statistics. The technique described here is conceptually similar to the method of maximum entropy (MEM). Once the shape of the continuous function ${\rho }_{\log }[\ln \left(k_{\text{ET}}\right)]$ is determined using the technique described above, one can try to use a deconvolution algorithm to recover the shape of the distance distribution $p_{\log }[\ln (r)],$ which is related to ${\rho }_{\log }[\ln (k_{\text{ET}})]$ by eq 4.11.

In the case of a model with diffusion (section 5), two different approaches were used. In the first approach F(t) from eq 5.49 was directly substituted in eq 7.1. Parameters A₁, A₂, contour length L, persistence length L_p, and translational diffusion coefficient D_T played the roles of free fitting parameters. The values of modified Förster radius R₁ and the radiative decay rate Γ were measured experimentally and fixed in the analysis. Unambiguous determination of the rotational diffusion coefficients D_RD and D_RA from the energy transfer data alone appears to be impossible: nonlinear least-squares algorithm always fails to find the best fit, regardless of the initial guesses, when D_RD and D_RA play the roles of free fitting parameters. This suggests that it may be necessary to first determine the values of D_RD and D_RA from time-resolved anisotropy data and then fix these values during the analysis of the energy transfer data. To determine the D_RD value, one could use the sample without the acceptor label, excited in the donor absorption band, and collect both vertically and horizontally polarized TCSPC data at the donor emission wavelength. To determine the D_RA value, one would have to use the sample containing the acceptor label, excited in the acceptor absorption band, and collect both vertically and horizontally polarized TCSPC data at the acceptor emission wavelength. In this work no vertically or horizontally polarized TCSPC data were collected; only the magic-angle polarizer orientation was used. This means that accurate determination of D_RD and D_RA is impossible; to determine the values of the other model parameters (contour length, persistence length, translational diffusion coefficient), we have set D_RD = D_RA = ∞.

The second (simplified) method uses the model function F(t) from eq 7.5 with a small number of N_EXP, typically not exceeding five. Parameters A₁, α_n, and k_n all play the roles of free fitting parameters in this case, while the value of A₂ is fixed at A₂ = 1. Once the smallest number N_EXP necessary for an adequate fit is determined and the rates k_n are numbered in the ascending order, the rates and amplitudes corresponding to the first two exponentials are used to determine the model parameters. The ratio of the amplitudes ${\left|b_{00002}\right|}^2/{\left|b_{00001}\right|}^2$ and the ratio of the rates Λ₀₀₀₀₂/Λ₀₀₀₀₁ depend on just two dimensionless combinations of model parameters β₁ and β₂; see eqs 5.50 and 5.51. Using a lookup table and interpolation the values of β₁ and β₂ that result in the ratio ${\left|b_{00002}\right|}^2/{\left|b_{00001}\right|}^2$ equal to the experimental α₂/α₁ and the ratio Λ₀₀₀₀₂/Λ₀₀₀₀₁ equal to the experimental k₂/k₁ are found. Then the rate Λ₀₀₀₀₁ is calculated for the values of β₁ and β₂ obtained as described above and β₃ = 1, after which the final value of β₃ is calculated as k₁/Λ₀₀₀₀₁. Using the known values β₁, β₂, and β₃, and the independently obtained values of Γ and R₁, the system of eqs 5.50, 5.51, and 5.52 is solved with respect to L, L_p, and D_T. This simplified method is dependent on our ability to reliably separate the first two exponentials from the remaining ones, which requires that Λ₀₀₀₀₂/Λ₀₀₀₀₁ ≥ 3.0 and Λ₀₀₀₀₃/Λ₀₀₀₀₂ ≥ 3.0.

8. RESULTS AND DISCUSSION

The value of the modified Förster radius R₁ for the tryptophan-CPM donor–acceptor pair equals 45.86 Å, calculated using eqs 2.5 and 2.7 from the corrected spectra measured in aqueous buffer and the refractive index of water n = 1.333. Figure 7S in Supporting Information presents the extinction coefficient spectrum of CPM and the corrected emission spectrum of tryptophan in water at 20 °C; these spectra were used to calculate the integral in 2.5. The radiative decay rate Γ = 0.0578 ns⁻¹ for tryptophan in water with no added glycerol or sucrose was taken from previously published work.⁶¹

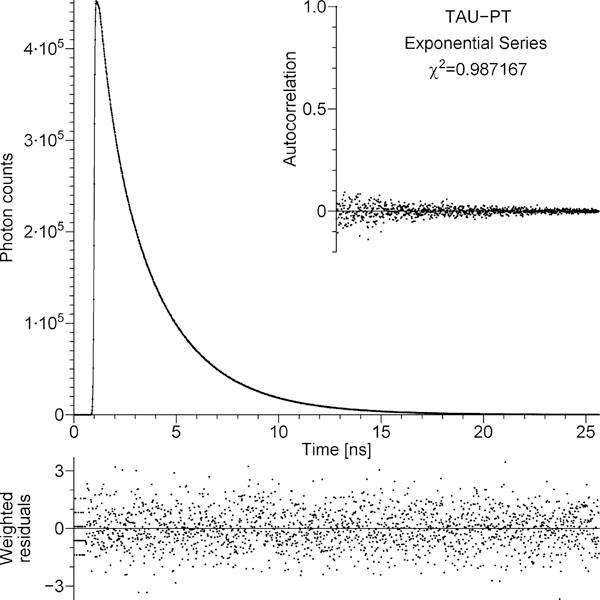
The TCSPC data that represent the decay of the donor in the absence of the acceptor, I_D(t), are depicted by dots in the main panel of Figure 3. The continuous line in the main panel represents the fit to the TCSPC data by the convolution of the experimentally measured IRF with exponential series, eq 7.3. All the dots fall directly on the continuous line; therefore, it may be difficult to see the two elements of the main panel separately. The strip below the main panel represents the weighted residuals. The inset represents the autocorrelation of unweighted residuals. Weighting, residuals, autocorrelation, and reduced χ² were strictly defined elsewhere.⁵² The value of the reduced χ² for the exponential series fit to the data in Figure 3 equals 0.987. For about 2000 degrees of freedom the reduced χ² value must be less than 1.052 with the probability of 95% and less than 1.081 with the probability of 99.5%. The reduced χ² = 0.987 satisfies both of these requirements, which, together with the residuals and autocorrelation in Figure 3, prove that the fit by the exponential series is adequate. Just to prove that the decay of the donor without the acceptor is not monoexponential, we also attempted to fit the same TCSPC data by the convolution of the experimental IRF with a single exponential. The fit is presented in Figure 8S in Supporting Information. The residuals, autocorrelation, and the reduced χ² value of 317.2 reliably prove that the decay of the donor without the acceptor is not monoexponential, which justifies the use of the theory in section 3. A minimum of five discrete exponentials with adjustable lifetimes τ_i is required for an adequate fit to the data (reduced χ² = 0.986). The values of τ_i and α_i are listed in Table 1S in Supporting Information. The amplitude-weighted mean lifetime $\langle \tau \rangle$ equals 2.252 ± 0.006 ns. Using the previously published⁶¹ value Γ = 0.0578 ns⁻¹ and the amplitude-weighted mean lifetime, it is possible to calculate the quantum yield $\mathrm{\Gamma }\cdot \langle \tau \rangle =\mathrm{0.130.}$ Experimentally measured quantum yield of free tryptopnan in water at 20 °C equals 0.13 ± 0.01,³ which is close to the calculated quantum yield of the tryptophan residue in TAU-PT.

Figure 3.

Main panel: dots, the TCSPC data that represent the decay of the donor in the absence of the acceptor (unlabeled tetradecapeptide TAU-PT); solid line, the best fit obtained using exponential series model. Bottom strip: weighted residuals. Inset: autocorrelation of unweighted residuals. The figure is automatically generated by the program that fits TCSPC data; the χ² shown in the figure has been divided by the number of degrees of freedom (the reduced χ²).

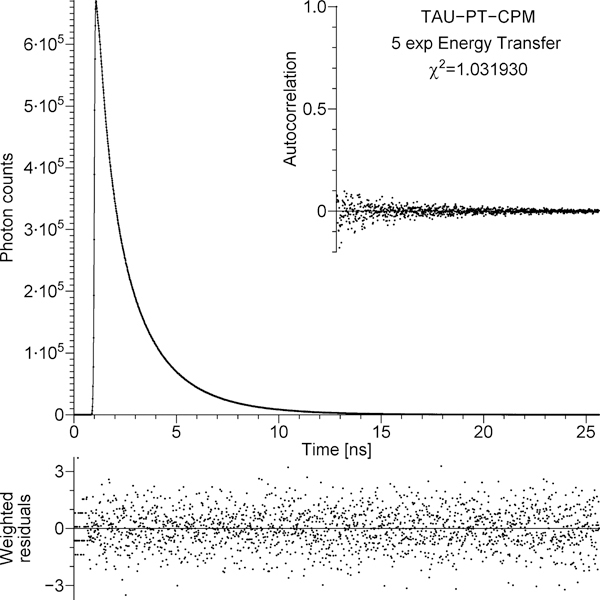
The TCSPC data that represent the decay of the donor in the presence of the acceptor, I_DA(t), are shown by dots in the main panel of Figure 4. The continuous line in the main panel represents the fit to the TCSPC data by the convolution of the experimentally measured IRF with I_DA(t) from eq 7.1, in which for I_D(t) we substituted the function obtained by fitting the data in Figure 3, and for F(t) we used the function from eq 7.5 with N_EXP = 5, where all α_n and k_n were free fitting parameters. This approach will be referred to as the model of free discrete exponentials, where the word free emphasizes that α_n and k_n do not have to comply with the theory in section 5. The residuals, autocorrelation, and reduced χ² = 1.032 prove that the fit is adequate. The five rates k_n that resulted in the χ² minimum are represented by the positions of five blue vertical bars in Figure 5; the height of each bar represents corresponding amplitude α_n. The values of k_n and α_n are also listed in Table 2S in Supporting Information.

Figure 4.

Main panel: dots, the TCSPC data that represent the decay of the donor in the presence of the acceptor (tetradecapeptide TAU-PT labeled with CPM); solid line, the best fit obtained using I_DA(t) from eq 7.1, where I_D(t) was obtained in the analysis of the data shown in Figure 3 and F(t) represents the model of free discrete exponentials. Bottom strip: weighted residuals. Inset: autocorrelation of unweighted residuals. The figure is automatically generated by the program that fits TCSPC data; the χ² shown in the figure has been divided by the number of degrees of freedom (the reduced χ²).

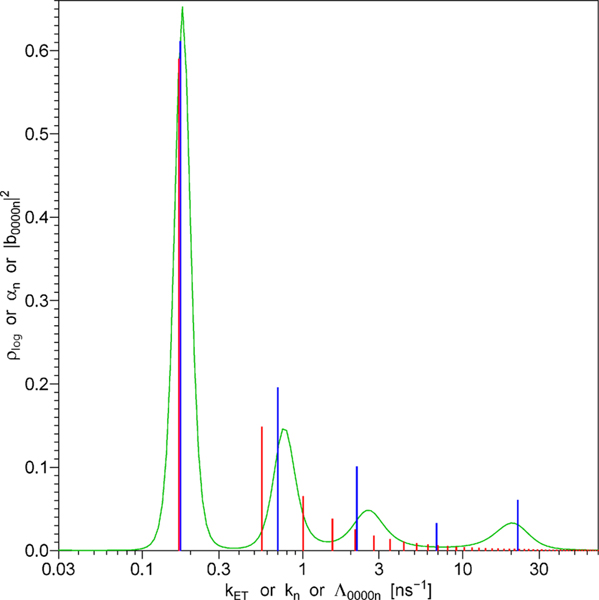
Figure 5.

Green line: the continuous distribution of energy transfer rates that represents the function F(t) in the case of no diffusion. Blue vertical bars represent the model of free discrete exponentials. Red vertical bars represent the model of dependent discrete exponentials; the rates and amplitudes of these exponentials are determined by just three model parameters, L, L_p, and D_T, in accordance with the theory of the energy transfer in the presence of rotational and translational diffusion, section 5.

The same TCSPC data as in Figure 4 were also fit using the function F(t) from eq 5.49, which is strictly based on the theory of energy transfer in the presence of rotational and translational diffusion (section 5). The fit is shown in Figure 9S in the Supporting Information. The weighted residuals and autocorrelation in Figure 9S are quite similar to those in Figure 4, which is the reason for placing one of the two near-identical figures in the Supporting Information instead of the main text. The reduced χ² equals 1.041, which is slightly higher than that in the case of five discrete exponentials, but the difference is not statistically significant. Because the reduced χ² is less than 1.052, this fit is also statistically adequate. The series of rates Λ_0000n and amplitudes |b_0000n|² that resulted in the χ² minimum are depicted by by red vertical bars in Figure 5 and also listed in Table 3S in the Supporting Information. These rates and amplitudes are not free: their values depend on three variable physical parameters (L, L_p, D_T) and two constants (Γ, R₁); therefore, this approach will be referred to as the model of dependent discrete exponentials. The χ² minimum was achieved with the following parameter values: contour length L = 49.94 Å, persistence length L_p = 14.84 Å, translational diffusion coefficient D_T = 3.833 Ų/ns. The distance distribution p(r) defined by these values of L and L_p is shown by the red line in Figure 6. The efficiency of acceptor labeling reaction calculated using eq 7.2 equals 83%. The values of the rotational diffusion coefficients D_RD and D_RA could not be determined by fitting the TCSPC data presented here (the χ² surface did not possess a minimum with respect to D_RD and D_RA when these parameters were varied within the physically possible range); therefore, in the data analysis we set D_RD = D_RA = ∞, which corresponds to the model of very fast rotation. The same TCSPC data as in Figures 4 and 9S were also fit using a continuous distribution of energy transfer rates for the function F(t), which corresponds to the case of energy transfer in the absence of rotational and translational diffusion (section 4). The fit is shown in Figure 10S in Supporting Information. The weighted residuals and autocorrelation in Figure 10S are practically indistinguishable from those in Figure 4. The reduced χ² value was not calculated because this method uses over 200 fitting parameters, which are not completely free (see section 7). Because it is not clear how to calculate the number of degrees of freedom when the fitting parameters are not free, we will compare the unreduced χ² sums. The χ² sum equals 1974.1 in the case of five free discrete exponentials (Figure 4) and 1976.1 in the case of the continuous distribution of exponentials (Figure 10S). This demonstrates that the fit obtained with the continuous distribution of exponentials is almost as good as that obtained with five free discrete exponentials. The continuous distribution of exponentials that resulted in the χ² minimum is depicted by the green line in Figure 5.

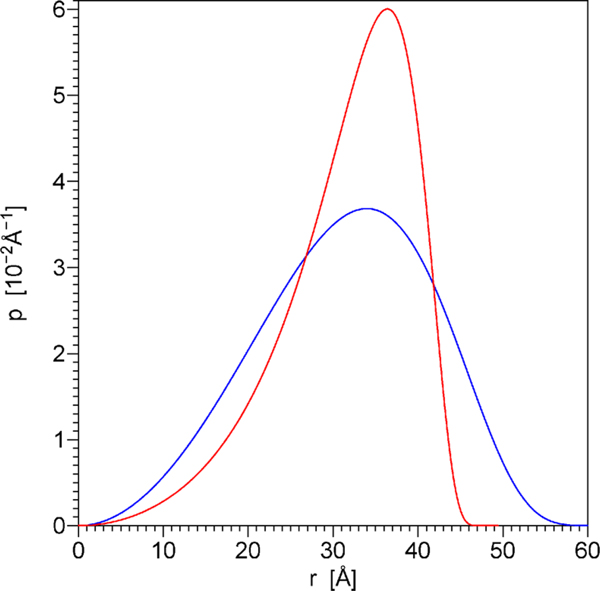
Figure 6.

Distance distributions p(r) calculated using eqs 5.29 and 5.30 with the parameter values L = 49.94 Å, L_p = 14.84 Å (red line) and L = 69.52 Å, L_p = 8.91 Å (blue line). The former parameter combination was obtained by fitting the TCSPC data by the model of dependent discrete exponentials, which is strictly based on the theory of energy transfer in the presence of diffusion. The latter parameter combination was obtained using the simplified method from the values α_n and k_n that represent the model of free discrete exponentials. Note that the latter parameter combination (blue line) does not result in adequate fit to the experimental TCSPC data. The mean donor–acceptor distances equal 31.72 and 31.44 Å for the distributions shown by the red and blue lines, respectively.

As shown above, the model of free discrete exponentials, the model of dependent discrete exponentials, and the continuous distrubution model produce statistically adequate fits to the experimental TCSPC data. Now we have to decide which of these three models are physically meaningful. Consider the continuous distribution model, which corresponds to the case of no translational and no rotational diffusion. The energy transfer rate distribution on the logarithmic k_ET scale, ${\rho }_{\log }\left[\ln \left(k_{\text{ET}}\right)\right],$ is related to the distance distribution on the logarithmic r scale by eq 4.11; on the right-hand side of this equation we have a convolution of two functions, one of which, $q_{\log }\left[\ln \left({\kappa }^2\right)\right],$ is depicted in Figure 1B. Numerical deconvolution makes it possible to calculate the other function, $p_{\log }[\ln (r)],$ which represents the distance distribution on the logarithmic r scale. The distance distribution calculated using numerical deconvolution is shown in Figure 11S in Supporting Information; this distance distribution contains several regions where the density of probability p_log assumes negative values, which is physically impossible. The negative values result from the fact that each of the four peaks in the ${\rho }_{\text{log}}\left[\ln \left(k_{\text{ET}}\right)\right]$ distribution (depicted by the green line in Figure 5) is narrower than the $q_{\log }\left[\ln \left({\kappa }^2\right)\right]$ distribution (depicted in Figure 1B). In the convolution of any non-negative function with $q_{\log }\left[\ln \left({\kappa }^2\right)\right]$ all the peaks would be at least as wide as $q_{\log }\left[\ln \left({\kappa }^2\right)\right]$ or wider. The peaks of the energy transfer rate distribution ${\rho }_{\log }\left[\ln \left(k_{\text{ET}}\right)\right]$ can be made wider by increasing the coefficients w₁ and w₂ in eq 7.6, which increases the penalty for the first and the second derivative during the nonlinear least-squares fitting; however, this also worsens the fit to the original TCSPC data. The smallest coefficients w₁ and w₂ that wiped off almost all negative values in the distance distribution $p_{\log }[\ln (r)]$ were found by the method of trial and error; this increased the unreduced χ² sum by more than 1 order of magnitude: from 1976 to 23512. The resulting fit is shown in Figure 12S in the Supporting Information. The drastic increase in the χ² sum as well as completely unacceptable residuals and autocorrelation in Figure 12S prove beyond any doubt that in the absence of negative probability densities in the distance distribution it is not possible to achieve adequate fit to the experimental TCSPC data using the theoretical model that does not take into account rotational and translational diffusion. Thus, the continuous distribution depicted by the green line in Figure 5 is not really a continuous distribution, but rather a fuzzy (due to limited resolution) image of a series of infinitely narrow discrete spikes. Consider, for instance, the tallest and narrowest left peak in the continuous distribution. This peak is almost centered around the blue bar at k = 0.173 ns⁻¹ and the red bar at k = 0.169 ns⁻¹. Clearly, the sharp green peak, the blue bar, and the red bar represent the same discrete exponential that is well resolved from the rest of the discrete exponentials. The remaining three peaks in the continuous distribution also tend to be nearly centered around three blue bars; however, the correlation with the red bars is not so great. The red bars represent the exponentials that are too closely spaced on the log(k) scale, which makes it impossible to resolve them.

Now the continuous distribution model has been ruled out. Of the two discrete models the dependent one is strictly based on the theory in section 5 and therefore is physically meaningful. The free discrete exponentials model is not based on a physical model. The question we ask here is whether useful information can be extracted from the values of the parameters α_n and k_n. The simplified method described in the last paragraph of section 7 makes it possible to calculate the contour length, persistence length, and translational diffusion rate from the ratios α₂/α₁ and k₂/k₁ and from the value of k₁. From the values in Table 2S in the Supporting Information follows that α₂/α₁ = 0.320, k₂/k₁ = 4.044, and k₁ = 0.173 ns⁻¹. The first problem arises during the search for the values of β₁ and β₂ that would result in the ratio ${\left|b_{00002}\right|}^2/{\left|b_{00001}\right|}^2$ equal to α₂/α₁ and the ratio Λ₀₀₀₀₂/Λ₀₀₀₀₁ equal to k₂/k₁: no such combination of β₁ and β₂ exists. It is possible to find β₁ and β₂ for which Λ₀₀₀₀₂/Λ₀₀₀₀₁ = 4.044, but in this case ${\left|b_{00002}\right|}^2/{\left|b_{00001}\right|}^2$ is always less than 0.320. It is also possible to find β₁ and β₂ for which ${\left|b_{00002}\right|}^2/{\left|b_{00001}\right|}^2=0.320,$ but in this case Λ₀₀₀₀₂/Λ₀₀₀₀₁ is always less than 4.044. The compromise is found when the standard deviations in the values of α₂, α₁, k₂, and k₁ are taken into consideration. It is possible to find a combination of β₁ and β₂ for which ${\left|b_{00002}\right|}^2/{\left|b_{00001}\right|}^2$ equals α₂/α₁ within the experimental errors and Λ₀₀₀₀₂/Λ₀₀₀₀₁ equals k₂/k₁ within the experimental errors. The values are β₁ = 7.803, β₂ = 0.6676. From these values and k₁ follows that β₃ = 0.00476 ns⁻¹. Solving eqs 5.50–5.52 gives the contour length L = 69.52 Å, persistence length L_p = 8.91 Å, and translational diffusion coefficient D_T = 15.36 Ų/ns. The distance distribution p(r) defined by these values of L and L_p is shown by the blue line in Figure 6. These parameter values differ significantly from those obtained using the model of dependent discrete exponentials. For the final check we use the values of L, L_p, D_T obtained by the simplified method to generate the function F(t) in accordance with the theory in section 5 and then see how well this function fits the experimental TCSPC data. The fit, residuals, and autocorrelation are shown in Figure 13S in the Supporting Information. The reduced χ² equals 5.069. The fit is clearly inadequate, which demonstrates that the simplified method, which is described in the last paragraph of section 7, does not work as expected. The reason for the failure of the simplified method is in the close spacing of the rates Λ_0000n on the logarithmic scale. The ratio Λ₀₀₀₀₃/Λ₀₀₀₀₂ equals 1.81, which is too close to be resolved. This explains both why the blue bars in Figure 5 do not exactly coincide with the red bars and why the simplified method does not work.

The dependent discrete exponentials model remains the only approach that yields physically meaningful results. The parameter values obtained using this model are discussed below. Because in this work r is measured from the center of the tryptophan side chain π-orbital system to the center of CPM π-orbital system, the contour length L, should be also measured between these points. The contour length can be roughly approximated as the sum of two parts. The first part is the distance from the tryptophan side chain to the cysteine side chain, which will be calculated as (14–1) × L₁, where 14 and 1 are the sequence numbers for the tryptophan and cysteine, and L₁ is the contour length per amino acid, 3.4 Å ≤ L₁ ≤ 4.0 Å.⁶² The second part is the distance from the CPM attachment point to the center of CPM π-orbital system, which we estimate to be near 8.5 Å. By adding the two parts together, we calculate that L can be anywhere between 52.7 and 60.5 Å. The experimental value obtained here, L = 49.95 Å, is slightly less than the theoretically estimated lower limit. The experimental value was calculated from the parameter combination β₃ defined in eq 5.52. With 99% probability the value of β₃ falls in the range between 0.0325 and 0.0370 ns⁻¹. If we assume that the values of Γ and R₁ are absolutely accurate, then this translates into the following 99% confidence interval for the contour length: 49.40 Å ≤ L ≤ 50.48 Å. One possibility is that the Γ or R₁ values may contain systematic errors. For example, the R₁ value depends on the overlap integral in eq 2.5, which, in turn, depends on the extinction coefficient spectrum of CPM. In this work we relied on the value of ε = 29 700 cm⁻¹ M⁻¹ at 387 nm wavelength for CPM in DMSO.⁶³ This ε value was used to determine the concentration of CPM in our samples. If the actual ε value is 1.38-fold greater, then the value of R₁ will increase from 45.86 to 48.39 Å, and the value of L will increase from 49.95 to 52.70 Å, which equals the theoretically estimated lower limit. A similar result can be achieved if the actual value of the spontaneous emission rate Γ for tryptophan in water is 1.38-fold greater than the reported value Γ = 0.0578 ns⁻¹.⁶¹

The discrepancy between the measured and theoretically estimated contour length may also have a different explanation. The data analysis in this work shows that the donor–acceptor distance distribution p(r) described by eqs 5.29 and 5.30 with L = 49.95 Å and L_p = 14.83 Å is consistent with the experimental data. If the persistence length had the same value at every point along the chain, starting from the center of the donor and ending at the center of the acceptor, then the parameters L and L_p would exactly comply with the definitions of the contour length and the persistence length. Because in our case the persistence length of the polypeptide is not equal to that of the linker and the acceptor fluorophore, or in other words, the chain is inhomogeneous along its length, L and L_p are just mathematical parameters describing the shape of the distance distribution p(r) rather than the contour length and the persistence length in their original sense. For example, in the case where the linker between the polypeptide and the acceptor fluorophore is extremely flexible and therefore has near-zero persistence length, the donor–acceptor distance distribution differs little from the distance distribution between the side chains of tryptophan and cysteine. In the other case, where the linker between the polypeptide and the fluorophore is rigid and makes a 90° angle, the donor–acceptor distance distribution also differs little from the distance distribution between the side chains of the residues 1 and 14. In both of these cases the parameters L and L_p are close to the contour length and the persistence length of 13 amino acids of the polypeptide TAU-PT, without the additional 8.5 Å. In this interpretation L = 49.95 Å corresponds to L₁ = 3.84 Å per amino acid, which falls well within the accepted range 3.4 Å ≤ L₁ ≤ 4.0 Å.⁶²

The values of the translational diffusion coefficients for the donor (D_TD) and the acceptor (D_TA) can be estimated using eqs 1.5 and 1.6, assuming that the fluorophores are free spheres of 1 g/cm³ density. Using the molecular weight of 204.23 g/mol for tryptophan and 402.45g/mol for CPM, we obtain D_TD = 49.5 Ų/ns and D_TA = 39.5 Ų/ns. Thus, if the donor and acceptor were free and spherical, then their relative translational diffusion coefficient D_T would be equal to 89.0 Ų/ns. Deviations from the spherical shape can decrease the isotropic translational diffusion coefficients D_TD and D_TA a few times, but not by an order of magnitude. The experimental value D_T = 3.833 Ų/ns is 23-fold lower than the theoretical estimate for free spheres, which implies that the relative translational diffusion of the fluorophores is slowed down by the conformational changes in the polypeptide that must accompany any change in the end-to-end distance.

The distance distribution p(r) that resulted in the best fit to the experimental data (red line in Figure 6) is characterized by the mean distance $\langle r\rangle$ the full width at half-maximum (fwhm) of 15.24 Å, and the root-mean-square width W = 7.51 Å. The latter is defined as the square root of $\langle {(r-\langle r\rangle )}^2\rangle ;$; in the case of a near-Gaussian p(r) shape fwhm to W ratio equals 2(2 ln(2))^1/2 or about 2.355. Substituting W = 7.51 Å and D_T = 3.833 Ų/ns in eq 1.4 yields the characteristic translational diffusion time t_T = 7.36 ns. This characteristic time is of great importance for single-molecule resonance energy transfer measurements, where the steady-state energy transfer efficiency is measured through a microscope for a single donor–acceptor pair and recorded as a function of time. The time resolution of the single-molecule instrument must be at least 1 order of magnitude faster than t_T, or otherwise the measured distance distribution p(r) will appear significantly narrower than the actual one. This means that for the CPM labeled TAU-PT one would need a single-molecule instrument with 0.7 ns time resolution or 1.4 GHz sampling rate. No such instrument exists at present. The value of t_T can be made longer by using bulky fluorophores with slow translational diffusion rates, such as the green fluorescent protein (GFP) and its derivatives. For the molecular weight of 27 × 10³ g/mol and 1.35 g/cm³ density eqs 1.5 and 1.6 give the translational diffusion rate 1.075 Ų/ns, which represents D_TD and/or D_TA. When the donor and the acceptor are both GFP derivatives, their relative translational diffusion coefficient D_T equals 2.15 Ų/ns. If the bulky fluorophores are combined with a very wide distance distribution, for example, W = 42.47 Å, which corresponds to 100 Å fwhm, then, in accordance with eq 1.4, t_T = 0.42 μs and the required sampling rate equals 24 MHz, which is achievable at present.

In the case of time-resolved resonance energy transfer measurements small fluorophores have significant advantages. As the rotational diffusion rates D_RD and D_RA increase, not only the rates Λ_jklmn with nonzero indices j, k, l, m increase and almost exceed the experimental time resolution but also the corresponding amplitudes ${\left|b_{jklmn}\right|}^2$ decrease and become negligible. This is what made it possible to essentially ignore all the exponential terms with nonzero indices j, k, l, m in our data analysis. It is also important to note that the separation of rotational and translational eigenfunctions in eqs 5.11–5.14 is valid only when both 6D_RD and 6D_RA are greater than (2/3)·$\mathrm{\Gamma }·{\left(R_1/\langle r\rangle \right)}^6,$ which represents the rate of energy transfer at $r=\langle r\rangle$ and κ² = 2/3. This situation can be directly compared to Born and Oppenheimer’s separation of electronic and vibrational wave functions,⁵⁸ which is valid only when the gaps between electronic energy levels are greater than the gaps between vibrational energy levels. For tryptophan 6D_RD = 11.9 ns⁻¹, for CPM 6D_RA = 6.0 ns⁻¹, and $(2/3)\cdot \mathrm{\Gamma }\cdot {\left(R_1/\langle r\rangle \right)}^6=0.35{\text{ns}}^{-1};$ therefore, the condition for eigenfunction separation is perfectly satisfied for these small fluorophores. If, however, GFP derivatives were used for the donor and the acceptor, then 6D_RD and 6D_RA would be equal to 0.12 ns⁻¹, which would make the eigenfunctions inseparable and most of the theory in section 5 inapplicable to those fluorophores. The inverse values (6D_RD)⁻¹ and (6D_RA)⁻¹ represent the characteristic rotational diffusion times t_RD and t_RA and are of great importance in the case of single-molecule resonance energy transfer measurements. Because t_RD and t_RA represent the correlation times of the noise in the steady-state signal, the integration time in a single-molecule measurement must be at least 1 order of magnitude longer than the longest of t_RD and t_RA. For GFP derivatives eq 1.3 yields t_RD = t_RA = 8.2 ns; therefore, the integration time must be at least 82 ns, which implies that the sampling rate must be less than 12 MHz. If the integration time is shorter than the greater of 10∙t_RD and 10∙t_RA, then the assumption that κ² = 2/3 cannot be used and one has to consider the effects of both distance and orientation on the energy transfer efficiency.

9. CONCLUSIONS

Resonance energy transfer rate k_ET depends on the spontaneous emission rate (aka radiative decay rate) of the donor but is independent of the donor’s nonradiative decay rate and lifetime. This makes it possible to prove that the equation $I_{\text{DA}}(t)=I_{\text{D}}(t)\cdot F(t)$ is applicable regardless of whether the decay of the donor in the absence of the acceptor, I_D(t), is monoexponential or not. The function F(t) contains all the information about energy transfer, donor–acceptor distance distribution, and diffusion dynamics. In the absence of rotational and translational diffusion F(t) is a continuous distribution of exponentials, whereas in the presence of rotational and translational diffusion F(t) is a sum of discrete exponentials. Experimental data obtained with a flexible tetradecapeptide in aqueous solution demonstrate that F(t) is inconsistent with the theory of energy transfer in the absence of diffusion and consistent with the theory of energy transfer in the presence of diffusion. Using the functional form of the end-to-end distance distribution p(r) that represents semiflexible chain model, eqs 5.29 and 5.30, the contour length, persistence length, and the end-to-end translational diffusion coefficient have been determined from the experimental data. The experimental value of the contour length is in reasonable agreement with the physical estimates based on the structure of the flexible tetradecapeptide. The translational diffusion coefficient is 23-fold slower than the estimate obtained for free spherical fluorophores, which implies that the tetradecapeptide conformation changes required for a change in its end-to-end distance slow down the relative translational diffusion of the donor and the acceptor.