Abstract
Diversity indices are useful single-number metrics for characterizing a complex distribution of a set of attributes across a population of interest. The utility of these different metrics or sets of metrics depend on the context and application, and whether a predictive mechanistic model exists. In this topical review, we first summarize the relevant mathematical principles underlying heterogeneity in a large population before outlining the various definitions of ‘diversity’ and providing examples of scientific topics in which its quantification plays an important role. We then review how diversity has been a ubiquitous concept across multiple fields including ecology, immunology, cellular barcoding studies, and socioeconomic studies. Since many of these applications involve sampling of populations, we also review how diversity in small samples is related to the diversity in the entire population. Features that arise in each of these applications are highlighted.
Keywords: diversity indices, ecology, barcoding, immunology, wealth distributions, microbiota, sampling
1. Introduction
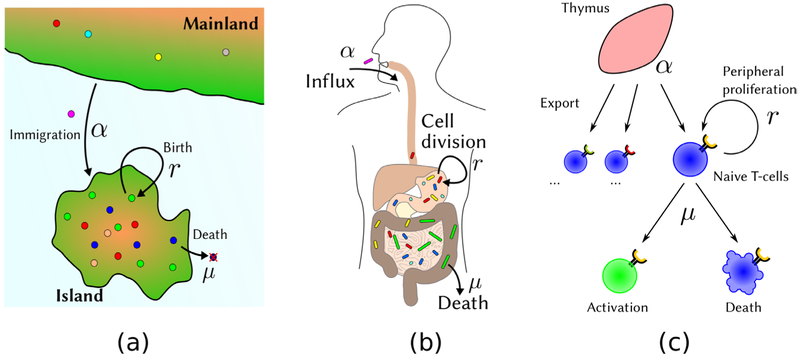
Diversity is a frequently used concept across a broad spectrum of scientific disciplines, ranging from biology [1-5] and ecology [6-11], over investment and portfolio theory [12-16], to linguistics [17, 18] and sociology [19-24]. In each of these disciplines, diversity is a measure of the range and distribution of certain features within a given population. It is considered a key attribute that can be dynamically varying, influenced by intra-population interactions, and modified by environmental factors. The concept of diversity, variety, or heterogeneity can be applied to any population. The evolution of the population can also be highly correlated with its diversity. Some examples of biological population dynamics occurring at different scales are shown in figure 1. At first sight, diversity seems to be an intuitively simple concept, but since certain population attributes require a full distribution function to quantify, it can be rather complex and difficult to capture using a single metric [3, 4, 25, 26]. We could for example think of a community with a total of four species, with one of the species dominating the total population. Consider a second community that consists of two equally common species. Which one of the two communities exhibits a higher diversity? The first one, because it harbors a larger number of species? Or the second one, because a sample is more likely to contain two species? This example shows that diversity is intrinsically linked to the total number of extant species (richness) and how the population is distributed throughout the species (evenness), and thus cannot be captured by a single number [3]. As a result, there are numerous different diversity indices and associated concepts used in different applications [3, 4, 25-29]. Nonetheless, diversity measures are important for assessing the current condition of ecosystems, to quantify the influence of environmental factors on different species, and in the context of conservation planning [2, 5, 9, 10, 29-31]. In addition, the concept of diversity is important for the quantitative description of wealth distributions and, more generally, to identify mechanisms leading to variations in societies [32-36]. In a broader sense, diversity indices may be helpful for the design of robust energy distribution systems [37] or even to assemble well-performing teams [23]. Thus we see that, despite the ambiguity in the definition of diversity, the concept is very relevant to many different disciplines and applications.
Figure 1.
Examples of complex, multicomponent populations in which diversity may be a meaningful quantitative concept. (a) Diversity in island ecology. A large number of species may migrate onto an island. Organisms can proliferate and die, leading to a specific time-dependent pattern of species diversity on the island. (b) Microbes are ingested and form a community in the gut by proliferating, competing, and dying. They can also be cleared from the gut. (c) Naive T cell generation in vertebrates. Naive T cells develop in the thymus. Each T cell expresses only one type of T cell receptor (TCR). Naive T cells can proliferate and die in the peripheral blood. The possible number of T cell receptors that can be expressed is enormous > 1015, but only perhaps 106−108 different TCRs usually exist in an organism. The diversity of the T cell receptor repertoire is an important determinant of the organism ’s response to antigens. (a) Island biodiversity. (b) Gut microbiota. (c) T cell production.
In this topical review, we start by summarizing the basic concepts from information theory which are necessary for a quantitative treatment of diversity. We continue with describing aspects of populations and diversity that are common to many applications in biology. In the next section, we present the common mathematical descriptions of diversity in terms of both number and species counts. Moreover, in most applications, only a small sample of a population is available. Thus, we place particular emphasis on the effects of sampling on diversity measures in section 5. In section 6 and subsections within, we survey a number of biological systems in which concepts of diversity play a key role in understanding the dynamics of the population. These include ecological populations, stem cell barcoding experiments, immunology, cancer, and societal wealth distributions. Each of these systems carry their unique attributes and thus require specific diversity measures. Finally, in section 7 we summarize the advantages and disadvantages of some common diversity measures and conclude with a discussion of possible future applications of concepts of diversity.
2. Mathematical concepts
2.1. Entropy, relative entropy, KL divergence, KS statistic, mutual information and all that
We first provide a summary of the fundamental mathematical structures that arise in the analysis of populations in which one naturally seeks to quantitatively compare distributions or frequencies of subpopulations. These mathematical notions invariably involve ideas from information theory such as entropy and mutual information which have a rich history and deep connections to thermodynamics, coding theory, cryptography, inference, and communication [38]. To review the necessary information-theoretic concepts, we consider a discrete random variable X which takes on values from the set {x1, x2, …, xN} with probability Pk = Pr (X = xk) such that
| (1) |
where the sum is taken over all possible values xk. This probability mass function may represent the relative frequency that the attribute X takes on the value xk in a large population. In the case of species diversity, we may interpret Pk as the proportion or frequency of species with X = xk in a certain population. The entropy, or ‘Shannon entropy’ is defined by
| (2) |
and can be thought of as the expected uncertainty or surprise .
The continuous limit of Shannon entropy, or differential Shannon entropy has also been defined, but care must be taken if X carries physical dimensions. If the probability of X taking on values in the interval [x, x + dx] is denoted by P(x) dx, the differential Shannon entropy is
| (3) |
These expressions are synonymous with the ‘Shannon index’ of species diversity with some freedom in the choice of the base of the logarithm. Without any constraints on the distributions other than being compactly supported, the form of Pk or P(x) that maximizes H(X) is a uniform distribution. With additional constraints there are classes of distributions that maximize the Shannon index. For example, for a fixed mean and variance on an unbounded domain, the Shannon index- or entropy-maximizing distribution is Gaussian. Within Gaussian distributions, the Shannon index increases logarithmically with the variance. In fact, within a specific class of distributions, the Shannon index is larger for flatter distributions [39, 40]. As such, the Shannon index has been used as a measure of diversity [41].
The problem with the differential entropy of equation (3) is that P(x) carries dimensions X−1, because the cumulative distribution function has to be dimensionless. Therefore, the argument of the logarithm in equation (3) is not dimensionless as required. To avoid such an issue, one can define a point-density function P0(x) according to [39]
| (4) |
Given that the limit is well-behaved, we can express the difference between two adjacent points xk+1 and xk in terms of
| (5) |
We now consider the continuum limit of the discrete Shannon entropy as defined in equation (2), and set
| (6) |
In this way, it is possible to derive a continuous Shannon entropy
| (7) |
that is invariant under parameter changes and whose logarithm depends on the dimensionless quantity P(x)/P0(x). We subtracted log(N) in equation (7) to obtain a finite HN(X).
To characterize the diversity between two communities, we consider two discrete random variables X and Y with the corresponding joint probability mass function PX,Y(xk, yℓ) = Pr(X = xk, Y = yℓ). Given the joint distribution PX,Y(xk, yℓ), we can compute the marginal distributions and by summing over the complementary variable. These definitions enable us to define the joint entropy
| (8) |
which may be also written as . Moreover, the conditional entropy
| (9) |
| (10) |
describes the expected uncertainty in the random variable Y given X. It can be also expressed as where PX∣Y is the conditional probability mass function. For independent random variables X and Y, we find that H(Y∣X) = H(Y) and H(X∣Y) = H(X).
While the Shannon index is a measure of the absolute entropy of a distribution, the relative entropy or Kullback–Leibler (KL) divergence
| (11) |
quantifies the distance between two probability mass functions P and Q. In the case of continuous distributions P(x) and Q(x), we obtain DKL(P∥Q) = ∫ P(x) log(P(x)/Q(x)) dx.
The KL divergence is the relative entropy of P with respect to the reference distribution Q. Note that the limiting Shannon entropy is simply the KL divergence between the distribution P(x) and the associated invariant measure P0(x). Usually, P is an experimental or observed distribution and Q is a model that represents P. Furthermore, the KL divergence is nonnegative and equals zero if and only if P = Q [38]. It is not symmetric, DKL(P∥Q) ≠ DKL(Q∥P), and is thus not a metric. In addition, a special case of the KL divergence is the ‘mutual information’
| (12) |
Note that I(X; Y) = I(Y; X) is symmetric and quantifies how much knowing one variable reduces the uncertainty in the other. If X and Y are completely independent, I(X, Y) = 0. According to equation (12) and the definitions of joint and conditional entropy in equations (10) and (8), the mutual information can be written in terms of marginal, conditional, and joint entropies [38]:
| (13) |
A symmetric version of the KL divergence is provided by the Jensen–Shannon divergence [42]
| (14) |
where M = (P + Q)/2 defines the mean distribution of P and Q. These divergences can be extended to include multiple and higher-dimensional distributions. The square-root of the Jensen–Shannon divergence is a distance metric between two distributions.
Another useful distance metric is the Kolmogorov–Smirnov (KS) distance, which is defined as
| (15) |
where F(x) is a cumulative reference distribution and G(x) is an empirical distribution function. The distribution G(x) is based on different samples with cumulative distribution function that can be F(x) or another distribution to be tested against F(x). The KS metric is the maximum distance between the two cumulative distributions F(x) and G(x). We outline in section 6.6 that the KS metric is related to the Hoover index which is used to quantify diversity, or inequity, in wealth or income distributions relative to a uniform distribution.
3. Commonly used measures of diversity
The notions of entropy and information are naturally related to the spread of a distribution P(x), and can be subsumed into a general metric for quantifying diversity. Usually, a population is measured and can be thought of as one realization of an underlying distribution. Consider a realization n = {n1, n2, … , nR} describing the number ni of entities of a discrete and distinguishable group/species/type (1 ⩽ i ⩽ R). The total population is . This given realization constitutes a ‘distribution’ across all possible types. Thus, any realization is completely described by a set of R numbers. Diversity measures are reduced representations of the distribution. An example would be a single parameter which captures the spread of the distribution of realizations {ni}. This is not different than, for example, defining a Gaussian distribution by its mean and standard deviation. Realizations {ni}, however, usually are not described by specific functions that can be defined by one or two parameters such as Gaussians. However, many different diversity indices can be unified into a single formula called ‘Hill numbers’ of order q [43-45]:
| (16) |
where fi ≡ ni/N is the relative abundance of types i. This general formula represents different classes of ‘diversity indices’ for different values of q. It is also useful because one can consistently define an effective proportional abundance
| (17) |
that corresponds to an average abundance with increasing weighting towards the larger-population species as q increases [45, 46].
Note the similarity of this definition to the standard mathematical p-norm
| (18) |
except that the exponent is 1/p instead of 1/(1 − q). Another diversity measure is provided by the Renyi index [47]
| (19) |
which is a generalization of the Shannon entropy defined in equation (2). The order q describes the sensitivity qD and qH to common and rare types [48]. Below, we provide an overview of the most commonly used indices which result from the generalized diversity qD for different values of q:
3.1. Richness
In the limit of q → 0+, the probabilities are equal to unity and 0D is simply the total number of types in the population, or the ‘richness’ R. The richness is often used in quantifying the diversity of T cells and species counts in ecology [3] and represents a metric that weights the smallest subpopulations the most.
3.2. Shannon index
For q = 1 − ε in the limit ϵ → 0+, the generalized diversity as defined by equation (16) becomes
| (20) |
which is the exponential of the Shannon index
| (21) |
that parallels the Shannon entropy defined in equations (2) and (10). This index is also sometimes called the Shannon–Wiener index (H) and can be defined using any logarithmic base. Usually measured values are Sh ~ (1). Qualitatively, eSh can be thought of as a rule of thumb for the number of effective species in a population.
3.3. Evenness
Evenness is another class of diversity indices often invoked in ecological and sociological studies. One definition (‘Shannon’s equitability’) is based on simply normalizing the Shannon diversity by the maximum Shannon diversity that arises if every species is equally likely [49]:
| (22) |
3.4. Simpson’s index with replacement
When q = 2, we find
| (23) |
Simpson’s diversity index is defined as
| (24) |
which carries the interpretation that upon drawing an entity from a given population the same type is selected twice.
3.5. Simpson’s index without replacement.
A related index that cannot be directly constructed from qD is Simpson’s index without replacement:
| (25) |
Here, when an entity is drawn, it is not replaced before the second entity is drawn. The differences between Sr and S are significant only for systems with small numbers of entities ni for all types i.
3.6. Berger–Parker diversity index
In the q → ∞ limit, we find
| (26) |
where fmax = maxi∈{1,…,R}(fi). The Berger–Parker diversity index
| (27) |
is defined as the maximum abundance in the set {fi}, i.e. the abundance of the most common species. It is equivalent to the optimal solution of an ∞-norm of f= n/N.
4. Clone count representation
An alternative way of quantifying a population is through the species abundance distribution or ‘clone counts’ defined by
| (28) |
where the discrete indicator function if n = k and zero otherwise. The sum is usually taken over all species for which ni ⩾ 1. Clone counts can also be defined over only a certain special subset of species. Clone counts, or species abundance distributions, in the language of computational mathematics, can be thought of as the measure of the level-sets [50] of the discrete function ni, or, in the language of condensed matter physics, the density of states if ni are thought of as energies of states i [51]. The clone counts also satisfy
| (29) |
where N and R are the discrete total population and the total number of species (richness) present.
Clone counts are commonly used in the theory of nucleation and self-assembly [52-54], where all particles are identical and ck represents the number of clusters of size k. They are equivalent to ‘species abundance distributions’ or sometimes ambiguously described as ‘clone size distributions.’ Clone counts have been recently used to quantify populations in barcoding studies [55] described below.
Clone counts do not depend on the specific labeling of the different types i and do not contain any identity information. However, since the common diversity indices are only a summary of the vector {ni} and also do not retain species identity information, qD can be written in terms of ck rather than ni:
| (30) |
which leads to corresponding expressions at specific values of q, e.g. 0D = R,
| (31) |
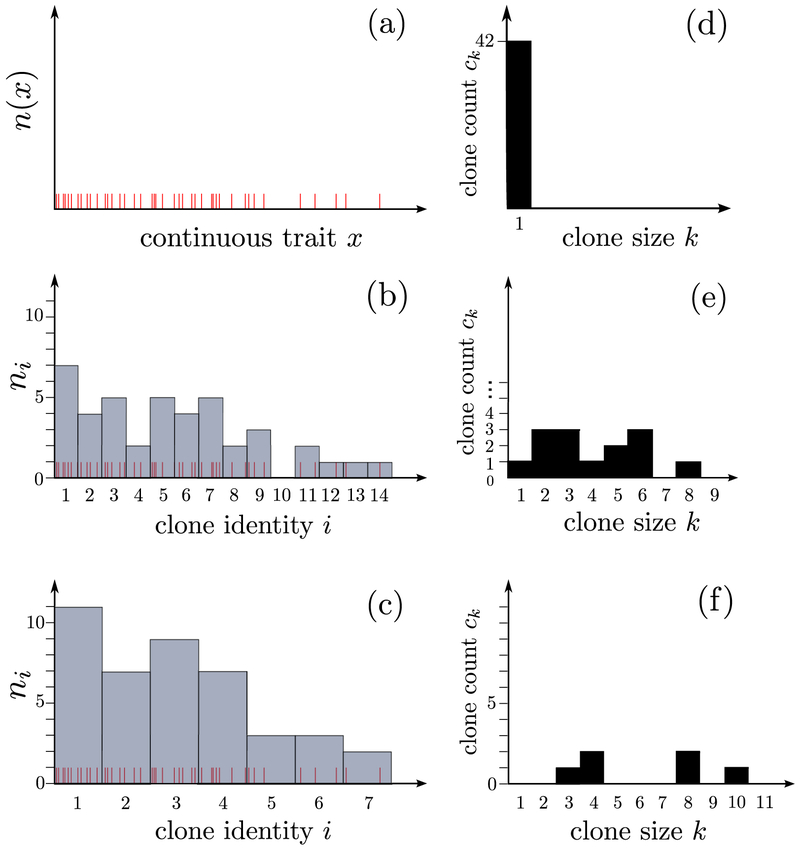
While the definitions of qD are well-defined when the discrete species are delineated, for more granular or continuous traits, the delineation of different species will affect the values of ni and ck. Figure 2 shows population counts ordered by a continuous trait x. By defining the discrete species i according to different binning windows over x, we find different sets of number and clone counts. Thus, measures of diversity can be highly dependent on the resolution and definition of traits and species.
Figure 2.
Number counts and clone counts vary depending on the definition and thresholding of discrete species. This consideration arises in designing experimental measurements.
5. Sampling
In most applications, including all the ones we will discuss below, the entire population is not accessible for identification and measurement. In an ecology, all animals of the population cannot be tracked. In blood samples, only a small fraction of the cell types in the whole organism is drawn for identification/sequencing. Thus, inferring the diversity in the entire system from the diversity in the sample is a key problem encountered across many fields.
There are numerous ways to randomly sample a population. One approach is to draw one individual, record its attributes, return it back into the system, and allow it to well-mix or equilibrate before again randomly drawing the next individual. This process can be repeated M times. To indicate this type of sampling, we use the subscript 1 × M in the corresponding distributions and expectation values. Similar sampling approaches are used in the ‘mark-release-recapture’ experiments to estimate population size [56], survival, and dispersal of mosquitos [57]. For a given configuration {ni} and total population size N [58], the probability that the configuration {mi} is drawn after M samples is simply
| (32) |
where fj ≡ nj/N is the relative population of species i, ni is the total population and mi is the total number of samples.
We can now use P1×M to compute the statistics of how the system diversity is reflected in the diversity in the samples. For example, the mean population in the sample in terms of ni is . The lowest moments of the populations in the sample are
| (33) |
An alternative random sampling protocol is to draw a fraction α ≡ M/N < 1 of the entire population once. This type of sampling arises in biopsies such as laboratory blood tests. To be able to distinguish between this sampling protocol and the previous one, we now use the notation M × 1. In this case the combinatorial probability of a specific sample configuration, given n, N, and M is
| (34) |
where the discrete indicator function enforces the constraint between mi and the sampled population M. In this single-draw sampling scenario, we use the Fourier decomposition to find
| (35) |
| (36) |
Results using p1×M and PM×1 rely on perfectly random sampling, where certain clones/species are not more likely sampled or captured than others. The moments can be directly used to evaluate the expected Simpson’s diversities, Sr (with replacement) and S (without replacement) defined by equations (24) and (25), in the corresponding sample. In the case of 1×M sampling, we find
| (37) |
and
| (38) |
while for M×1 sampling, we find
| (39) |
and
| (40) |
Note that for both types of random sampling, we find that the expected Simpson’s diversity (without replacement) in the samples are equal to the Simpson’s diversity in the full system. In general, the expectations do not commute and .
Effects of sampling on clone counts ck can be similarly calculated by averaging the definition for the sampled clone count
| (41) |
over the sampling probabilities PM×1(m∣n, M, N) or P1×M(m∣n, M, N). For clone counts, the calculations of moments of sampled quantities bk are more involved, and explicitly noncommutative . One advantage of working in the bk representation is that diversity indices such as the expected sampled richness are difficult to extract from but is simply . Some related results are given in [59, 60].
The above results provide expected diversities in the sample assuming full knowledge of {ni} in the system. They represent solutions to the forward problem, the so-called mean ‘rarefaction’ in ecology. However, the problem of interest is usually the inverse problem, or extrapolation in ecology. In the simplest case, we wish to infer the expected diversity (or {ni} and ck) in the system from a given configuration {mi} or clone count bk. Extrapolation is a much harder problem and is the subject of many research papers [61-65].
One may wish to use the observed sample diversity qD(M) to approximate the population diversity qD(N). For any q, the underestimation of qD(N) using qD(M) decreases as the sample size M increases. The deviation of qD(M) from qD(N) is smaller for larger q, as higher-order Hill numbers are more heavily weighted by large species, which are less sensitive to subsampling.
Chao and others have shown that for q ⩾ 1 and in the N → ∞ limit nearly unbiased approximations can be obtained and when q ⩾ 2, these unbiased estimates are very insensitive to sample size M [59, 60]. Using clone counts in a sample of population M, Chao et al [66] obtained for q = 1 (in terms of Shannon’s index):
| (42) |
where A = 2d2/[(M − 1)d1 + 2d2].
For q ⩾ 2, Gotelli and Chao [59] obtained
| (43) |
where x(j) = x(x − 1)…(x − j + 1). For example, , the inverse of Simpson’s index without replacement (equations (23) and (25)).
The ill-conditioning of the inverse problems is particularly severe for the richness 0D. The general formula for an estimate of the system richness is
| (44) |
and reduces to the unseen species problem for determining d0 [67, 68]. Since the sample size M and the richness R in the system are uncorrelated, rigorously, one must use information contained in the species fractions fi or the clone counts ck in the full system [69, 70]. However, a popular estimate for the system richness R(N) is the ‘Chao1’ estimator [59, 71]
| (45) |
which is actually a lower bound and gives reliable estimates for systems of size only up to approximately double or triple the sample size M. The uncertainty of the Chao1 estimator has also been derived via a variance that is also a function of d1 and d2 [72]. The ‘Chao2’ estimator gives the system richness as a function of measured incidence [59]
| (46) |
where q1, q2 are the number of species found in 1 or 2 samples out of many (as in the 1 × M sampling method). Shen et al [73] derived another estimate
| (47) |
which is only reliable if the sample size M is more than half of the system size N. Many of these estimators have been coded into analysis software such as R and iNEXT [74].
Regardless of the estimator, the major limitation is an insufficient sample size M ⪡ N. Models predicting species abundances as a function of system size can help bridge this gap. For example a log-normal relationship for the clone count ck [75] has been used to find agreeable results [76, 77]. In general, models can be extremely useful analyzing the effects of sampling, particularly when a Bayesian prior is desired.
We have outlined the basic mathematical frameworks for quantifying diversity that have utility across applications in different disciplines. The above summary of sampling assumes a well-mixed population, precluding any spatial dependence of the distribution of individual species. Spatially dependent sampling has been proposed for the origin of relationships between the number of species detected and the total area occupied by the population (see below).
6. Fields in which diversity play a key role
Below, we summarize a few modern applications in which diversity is important. By no means exhaustive, the following are simply examples of specific systems in modern biology that reflect the authors’ intellectual biases.
6.1. Ecology, paradox of the plankton
The classic problem in the context of biological diversity is dubbed the paradox of the plankton and was originally discussed in a paper of the same title [78]. It describes diverse populations of plankton in environments of limited number of resources or nutrients. Sampled populations of plankton exhibit a large number of species even in low nutrient conditions during which one expects strong competition for resources. This observation runs counter to the competitive exclusion principle arising in many settings [79].
Perhaps the most common application of diversity arises in biological population studies, specifically in ecology [6-11]. Possible areas of application include the monitoring of ecosystems and the development of efficient species conservation strategies [2, 5, 9, 10, 29-31]. Multiple overlapping and nebulous definitions of ecological diversity have been advanced [3, 4, 25-29]. Early work by Fisher [6] introduced a logarithmic series model to mathematically describe empirical species diversity data. Here, the diversity index referred to a free parameter in the corresponding model. In a later study, MacArthur defined species diversity based on the size of the sampled area [80]. In the ecological setting, multiple layers of subpopulations are an important feature of populations. These subpopulations may be delineated by another property of the individual species, such as size, weight, behavioral attributes, etc. Subpopulations can also be distinguished through their spatial distribution or occupation of different habitats. Whittaker [81, 82] qualitatively defined four types of diversity (point, alpha, beta, and gamma) conditioned on habitat or spatial distribution of the subpopulations [82]. Fundamentally, these differences arise from different methods of sampling, leading to different Hill numbers qD. We summarize a few often-used descriptions below:
‘Point diversity’ refers to samples taken at a single point or ‘microhabitat.’ This quantity is usually operationally measured by trapping organisms at one or more specific points.
‘Alpha diversity’ is defined as the diversity within an individual location or specific area. In general, one can define a Hill number derived from measurements at a specific location as qDα, while the index α ≡ 0Dα is the richness encountered within a defined area or specific location. A few subtle variations in the definition of the index α exist, mostly related to the sampling process [45, 46]. For example, in relation to beta diversity (discussed below), alpha diversity is the mean of the specific-location diversities across all locations within a larger landscape.
‘Gamma diversity’ is the diversity index qDγ determined from the entire dataset, the total landscape, or entire ecosystem. The index γ ≡ qDγ usually denotes the total number of different species or clones at the largest scale. Note that the mean or sum of the alpha diversities is in most cases not equal to the gamma diversity. The nonlinearity of the Hill numbers as well as the intersection or exclusion of species amongst the different sites suggests a need for indices that connect alpha and gamma diversities.
‘Beta diversity’ was devised to describe the difference in diversity between two habitats or between two different levels of ecosystems. While the different levels of diversity are designed to the spatial aspects of diversity, different habitats overlap, leading to some amount of arbitrariness in determining, or sampling of the β-diversity. Moreover, beta diversity was initially described in different ways [45, 81, 82], leading to confusion about its mathematical definition and use [45, 46, 48]. One possible definition is Whittaker’s [81] multiplicative law qDγ ≡ qDα qDβ where here, α is defined as the mean of the diversities across all micro-habitats. Whittaker’s definition describes beta diversity qDβ = qDγ/qDα as a measure to quantify the diversity in the total population relative to the mean diversity across all micro-habitats [45]. In the limit of q → 1−, we obtain the Shannon diversity relationship Shγ = Shα + Shβ according to equation (21). Another definition of β is given by Lande’s [83] additive law γ ≡ α + β according to which diversity indices are measured in the same units. One concept associated with β in terms of the additive partitioning is ‘species turnover’ quantifying the difference in richness between the entire and the local population. As an example, consider two distinguishable or spatially separate habitats A and B. If A contains species {a, b, c, d, e} and B contains {b, c, f, g}, we find βA,B = 5 associated with the set {a, d, e, f, g}. The laws of Whittaker and Lande sparked debates about how to properly define beta diversity, and led to the distinction between multiplicative and additive diversity measures [45, 46, 48].
‘Delta, epsilon, omega diversity’ are other hierarchical definitions of diversities proposed by Whittaker [82]. Delta diversity is analogous to beta diversity but defined at the larger among-landscape scale, while epsilon diversity corresponds to gamma diversity, but at the regional scale that contains many landscapes. Omega diversity is measured at the biosphere scale, and thus characterizes the diversity of all ecosystems [84].
‘Zeta diversity’ was introduced by Hui and McGeoch [85], and is defined by a set of ζ indices that mathematically describe the species numbers between different partitions of a certain habitat. Specifically, ζi is the mean number of species shared by i partitions. In particular, ζ1 is the mean richness across all sites. For example, between two samples A and B or sets of data, the average number of species is ζ1 := (RA + RB)/2, while the intersection is ζ2 := A ∩ B. Generalizations to multiple samples can be defined using a series of zeta diversity indices ζi.
Many other indices have been defined for different applications. The Jaccard index [45, 81, 85, 86] is defined as J(A, B) = ∣A ∩ B∣/∣A ∪ B∣, and is a general measure for quantifying the similarity in richness between two sets of populations A and B. Margalef’s index [87] and Menhinick’s index [88] are relative richness measures given by R/ ln N and , respectively. Other indices include the Bray–Curtis dissimilarity [89], the Berger–Parker diversity index [90] as defined in equation (27), Fager’s index [91], Keefe and Bergersen’s index [92], McIntosh’s index [93], and Patil and Taillie’s index [94].
A myriad of different definitions of diversity indices arise from specific cases of the Hill numbers and consideration of different spatial scales of ecosystems. There is potential to further unify these definitions in a more systematic way using mathematical norms and more general mathematical structures of spatial dispersal of particles.
6.2. Area-species law and Island biodiversity
A particularly consistent, albeit qualitative feature observed in ecology is the species-area relationship (SAR) which relates the measured number of species (richness) with the relevant area. These areas can represent distinct habitats, such as mountain tops, or islands. For the latter, much work has been done in the subfield of island biodiversity.
The SAR is usually expressed as a power-law relationship between the number of species (or richness) R and the habitat/island area:
| (48) |
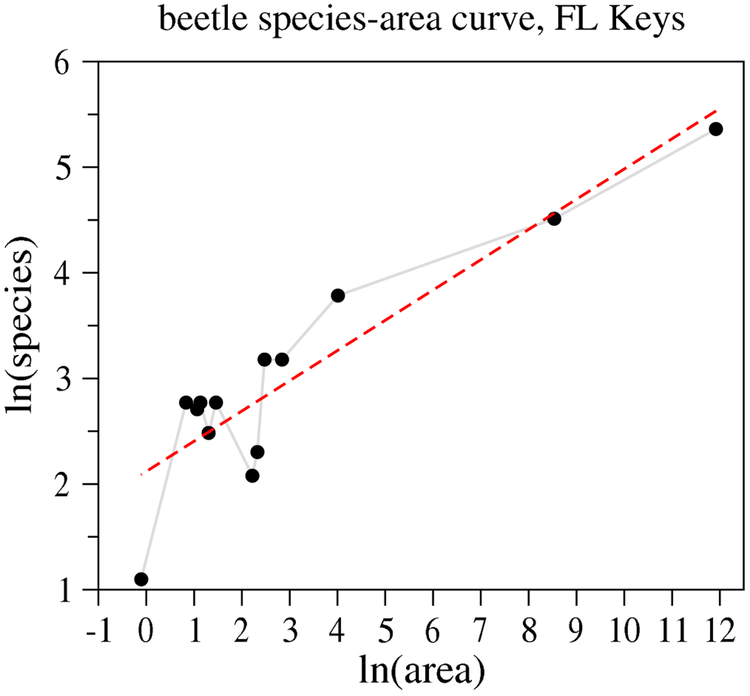
where c is a constant prefactor and z is an exponent. On a log–log plot, log R = log c + z log A defines a line with slope z. An example of the area-species law for species counts of long-horned beetles in the Florida Keys is shown in figure 3, yielding a slope z = 0.29. An alternative species-area relationship is eR = cAz [95], which is a straight line on a semi-log plot.
Figure 3.
Plot of ln R versus ln A with area A measured in terms of km2. Species counts of long-horned beetles in the Florida Keys are plotted against the island size [98]. The linear regression line yields a slope of z = 0.29. Usually, fits of the species-area exponent z yield a small number.
The classic book by MacArthur and Wilson [96] and many subsequent analyses have promoted and extensively analyzed the SAR idea. In MacArthur and Wilson’s neutral equilibrium theory, immigration to and death on an island are monotonically decreasing and increasing functions of the number of species already on the island, respectively. Usually, measured values of the exponent fall in the range z ~ 0.1−0.4. Field work has also found relationships between the parameters c and z and system-specific attributes such as the island distance to the mainland, habitat type, etc [96, 97]. Nonetheless, reasonable predictions based on equation (48) are ubiquitous across many ecological examples.
Mechanistic origins of the robustness of the SAR have been proposed [99-101]. Different models for species populations ni or clone counts ck were surveyed and the corresponding species-area laws were derived by He and Legendre [100]. Spatial clustering of species and the averaging of random measurements was shown to robustly generate a power-law species-area curve [100, 101], highlighting the fundamental importance of sampling.
6.3. Gut microbiome
Another ecological system that has recently received much attention is the human microbiome, especially in the gut. The gut bacterial ecosystem is important for health and can impact cardiovascular disease, diabetes, neuropsychiatric diseases, inflammatory bowel disease (IBD), digestive and metabolic function to the point that fecal transplantation (bacteriotherapy) has become an effective treatment for recurrent C. difficile colitis infections [103]. This type of infection often occurs after antibiotics disrupt the gut microbiome. Transplants have also shown to be effective in treating slow-transit constipation [104].
Recent efforts to collect and curate gut microbiome data have included NIH’s Human Microbiome Project (HMP) [105, 106] and the European Metagenomics of the Human Intestinal Tract (MetaHIT) [107-109], as well as the integration of the data in [110]. Each dataset contains sequence data from samples from different body regions of hundreds of individuals, both healthy and diseased.
Bacterial species are usually determined by sequencing of the 16S ribosomal RNA (rRNA), a component of prokaryotic ribosomes that contain hypervariable regions that are species-specific. However, closely related taxa can have very similar sequences, making separation imperfect [111]. Nonetheless, with numerous public databases [102, 112-114], estimates of species abundances in samples are readily available. In the gut, there are usually on the order of 103 bacterial species, with Bacteroidetes and Firmicutes being the dominant phyla [115, 116]. Indeed, lower gut diversity is seen to be associated with conditions such as Crohn’s disease [115]. For example, the frequency distribution of bacterial species in healthy and irritable bowel syndrome patients are shown in figure 4. The quantification of diversity of human microbiome is an essential step in ongoing research and the diversity indices have been applied to microbiome data, including α-diversity and β-diversity across the microbiome from different anatomical regions and different patients. As with island biodiversity, the gut microbiome can be modeled as birth-death-immigration (BDI) process.
Figure 4.
Frequencies of approximately 200 species of bacteria distributed across about a dozen phyla. (a) Group 1 depicts the relative abundance distribution for healthy individuals while (b) Group 2 shows the pattern for irritable bowel syndrome (IBD) patients. The differences in abundance patterns are apparent and have been quantified using the Shannon index for each individual plotted in (c). From Park et al [102]. (a) Group 1. (b) Group 2.
6.4. Barcoding experiments
Besides taxonomy of gut bacteria, the accurate identification of animal and plant species from samples is an essential task in ecology. In the early 2000’s a DNA barcoding method was developed to read relatively short DNA regions specific to certain species [120, 121]. These barcodes are usually found in mitochondrial DNA and often derived from a region in the cytochrome oxidase gene [120]. By sequencing samples and comparing with a sequence database such as The Barcode of Life Data System [122, 123], one can infer the number of species present within a sample. Detecting specific species within samples using DNA barcoding and DNA libraries have been used in many applications including identification of birds [121], identification of flowering plants [124], detecting contaminants [125], and tracking plant composition in processed foodstuffs [126].
Recently, a number of barcoding or tagging protocols [127-129] have been developed to genetically label a large population of cells to study how they differentiate and proliferate, especially in the context of hematopoiesis [117, 118, 130, 131] and cancer progression [132-134].
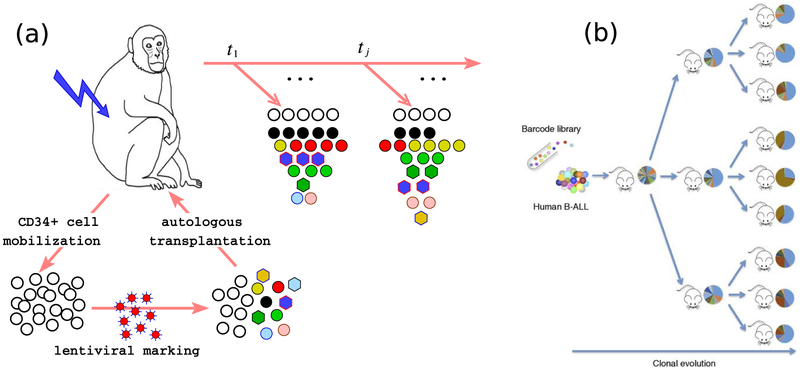
A novel approach used to investigate hematopoiesis exploits in situ barcodes [130]. Mice were engineered with an enzyme (Sleeping Beauty Transposase) that randomly moves DNA sequences (transposons) to different parts of the genome. The transposase is designed to be controllable by doxycycline, an antibiotic that can be used to switch on or off gene regulation. When the transposase is briefly activated, transposons within cell are randomly rearranged within a brief period. Since the genome length ⪢ transposon length, the new locations of the transposons will be distinct across the founder cells. After switching off the transposase, proliferation of founder cells will impart, except for rare DNA replication events, the same genomic sequence to its daughter cells. These collections of cells constitute a multiclonal population that proliferates and differentiates.
Analysis of the clonal population within differentiated cell pools show that granulocytes derive from stem cells at particular time points during the life of the mouse [130]. Comparing clonal abundance structure within different cell lineages showed that clones originally predominant in the lymphoid lineages eventually arise in myeloid cells, indicating that multipotent progenitor cells continually produce cells of both lineages. These conclusions arise after statistical analysis of the clone (defined by their transposon sites) abundance distribution within different groups of cells.
In another recent series of studies on hematopoiesis, stem cells (HSCs) were extracted from rhesus macaques and infected with a lentiviral vector. The lentivirus integrates its genome randomly in the genome of the HSCs. Since the lentivirus genome is much shorter than that of mammalian cells, nearly every successful infection results in a new viral integration site (VIS) or clone. The infected stem cells are autologously transplanted into the animal and some of them resume differentiation into progenitor cells that transiently proliferate and further differentiate. Descendant cells carry the same genetic sequence, including the lentivirus integration locations, or the viral integration sites (VIS). Another approach is to use libraries of synthesized DNA/RNA as tags. Here, the different sequences, rather than their integration sites, serve as the distinguishing feature. This process avoids the need to determine VISs.
In all the above approaches, each successive generation of cells will acquire the same tag, VIS or specific DNA barcode sequence, as their parent and ultimately the founder HSC. Compared to the Sleeping Beauty Transposon protocol, the VIS or barcoding experiments require an additional viral transfection step. Nonetheless, these VIS and barcoding experiments are equally effective in dissecting the differentiation process and quantifying lineage bias with age. For example, the variation (in time) of the abundances of a clone across different lineages indicates the level of fate switching of a stem cell [117, 135].
These experiments also enabled observation of biological mechanisms on a finer scale compared to traditional studies, allowing inference of parameters that are difficult to measure directly such as the initial HSC differentiation rate and the proliferative potential (number of generations) accessible to progenitor cells [55, 136].
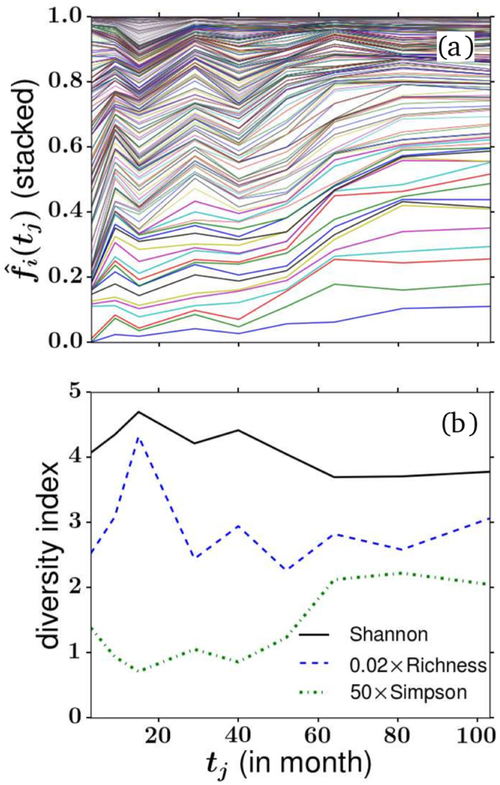
After sampling, PCR amplification, and sequencing (each process exhibiting their specific errors), the relative species populations and clone counts within defined cell types can be quantified. Figure 6(a) shows frequencies of barcode i as a function of sampling times tj in rhesus macaque. The fraction of each clone is depicted by the vertical distance between two neighboring curves. Here, it is important to note that the ‘diversity’ is a measure of the distribution of clone ID (barcodes) instead of lineages (cell types). In figure 6(b), we plot three different and rescaled diversity indices associated with the data in (a). The sampled richness is initially low at month 3 when barcoded clones have not fully differentiated and emerged in the peripheral blood. The sampled richness then peaks at month 9 before stabilizing after month 29. Simpson’s diversity seems to continue to increase after month 29 which may indicate more unevenness and coarsening (fewer clones dominating the total population). Shannon’s index is shown to decrease slightly, suggesting a decrease in the effective number of barcodes.
Figure 6.
(a) The fractional populations of the largest clones (barcodes) detected in granulocyte blood samples from rhesus macaque. Relative populations are described by the distances between neighboring curves. (b) Diversity indices derived from the data in (a). The Simpson’s index and Shannon diversity are rescaled to fit on the same plot.
Sun et al [130] and Kim et al [117] also used simple clustering algorithms that identified similar clones according to their activity patterns across time. They identified distinct groups of clones that are featured by different time points of contribution to hematopoiesis. Koelle et al [135] calculated Shannon diversity to ensure comparability between animals, different cell types, and across time.
The employment of neutral barcodes to study blood cell populations is statistically insensitive to spatial partitioning (different tissues in the organism). Nonetheless, small sampling M ⪡ N makes inference difficult. Thus, mechanistic simplifications and mathematical models have been used to quantify clonal evolution. Assuming a multispecies birth-death-immigration process (figure 7) Dessalles et al [137] found explicit steady-state distribution functions for ni (log series) and ck (Poisson) for constant r and μ, as well as formulae for the expected Shannon’s and Simpson’s diversities. Goyal et al [55] derived a master equation for the evolution of and then extended the solution to expected clone counts in the progenitor cell and sampled cell pools. By comparing results to the expected clone count in the sample at steady-state, they were able to infer kinetic parameters of the differentiation process. Biasco et al [139] proposed two candidate stochastic models for ni and used Bayesian Information Criterion (BIC) to assess the likelihood of each.
Figure 7.
A simple multispecies birth-death-immigration (BDI) process [55, 136-138]. A constant source (i.e. stem cells with slow dynamics) generated by 16 cells, each of a different clone, undergo asymmetric differentiation with rate α to produce differentiated cells that can undergo birth or death with rates r(N) and μ(N) that may depend on the total population in the differentiated pool. In this example, the differentiated population contains N = 30 cells, R = 9 different clones (barcodes), thus leaving c0 = 7 unseen species.
6.5. Cells of the adaptive immune system
Another intra-organism system for which diversity is often quantified is the adaptive immune system in vertebrates. The simplest immune subsystem consists of lymphoid cells (e.g. B and T cells) and tissues. B and T cells originate from common lymphoid progenitors (CLPs) that differentiate from HSCs in the bone marrow. B cells develop from CLPs in multiple stages in the bone marrow and spleen while T cells are formed from CLPs in the thymus. During T cell development in the thymus, T cell receptors (TCRs) are generated by random recombination of the associated receptor gene. TCRs are heterodimeric proteins that usually consist of an alpha chain and a beta chain. After a specific genetic sequence–corresponding to a specific amino acid sequence–is chosen and then selected for, the naive T cell is exported from the thymus into peripheral tissue (such as circulating blood and lymph nodes) where they can further proliferate or interact with antigens presented on the surface of antigen-presenting cells (APCs) and become activated. Naive T cells (those that have not previously strongly interacted with an antigen) can be activated through association of the surface T cell receptors (TCRs) with antigens presented by major histocompatibility complex (MHC) molecules on the surface of APCs. Similarly, naive B cells are generated in the bone marrow. The B cell receptors (BCRs) are comprised of heavy and light chains and an antigen-binding region, which is generated by the same recombination processes as TCRs. B cells are subsequently activated within tissues by binding to an antigen via their B-cell receptors (BCRs).
The mechanism responsible for creating very diverse repertoires of both BCRs and TCRs is V(D)J recombination [140]. In developing B cells, this mechanism involves the random recombination of diversity (D) and joining (J) gene segments of the heavy chain (DJ recombination). In the following step, a variable (V) gene segment joins the previously formed DJ complex to create a VDJ segment. In light chains, D segments are missing and therefore only VJ segments are generated. During T cell development and TCR generation, gene segments of the alpha chain and beta chain, the VJ and VDJ segments, respectively, also undergo random recombination. In the case of the beta chain, one of two different D regions of thymocytes recombine with one of six different joining J regions first, followed by rearrangement of the variable V region connecting it to the now-combined DJ segment. Due to the missing D segments in alpha chains, only VJ recombination is taking place. The recombination and joining processes in B cells and T cells involve many different genetic deletions and insertions that result in many different BCR and TCR protein sequences and a very large theoretical total number of possible clones with R ≳ 1014–1015 [141, 142].
In the end, each T or B cell expresses only one TCR or BCR type (an ‘immunotype’ or ‘clonotype’). TCR sequences are preserved during proliferation, while BCR sequences can further evolve [143]. Since the space of antigens (the different amino acid sequences, or epitopes, presented by MHCs) is large, a large number of different TCR and BCR sequences should be present in the organism in order to mount an effective response to a wide range of infections. However, before T cell export from the thymus, a complex selection process occurs [144]. Positive selection eliminates T cells that interact too weakly with MHC molecules. Subsequently, negative selection eliminates those T cells and TCRs that bind too strongly to epitopes. Cells that escape negative selection may lead to autoimmune disease as they react to self-proteins. Thus, the total number of different distinct immunoclones realized in an organism (the richness) defines its T cell repertoire and is estimated to range from 106−108 [145], with the lower range describing mice and the higher range an estimate for humans. B cell richness in man is estimated to be 108−109 [146, 147]. These values are much lower than the theoretical repertoire size R ≳ 1014−1015. TCR and BCR diversity is an important factor in health. For example, TCR diversity it has been shown to influence the tumor microenvironment and survival in lymphoma [148].
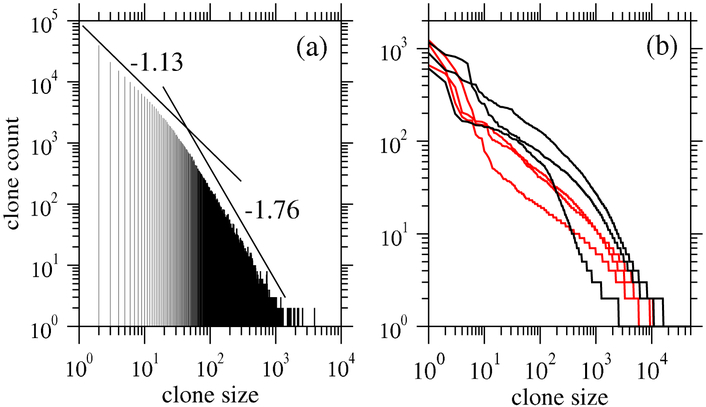
Although specific TCR sequences i can be determined, and their populations ni measured and estimated, the TCR identities vary significantly across individuals (private sequences) so clone counts are usually studied. Figure 8(a) shows T cell clone counts bk sampled from mice [142] that exhibit a biphasic power-law behavior. Figure 8(b) shows preliminary clone counts for six individuals, three HIV-negative patients and three HIV-infected patients [151].
Figure 8.
Examples of recently published clone count data. (a) Clone counts derived from a small sample (105 sequences) of T cells [142]. Note the broad distribution described by a biphasic power-law curve. Ignoring the largest clones, power-law fits for each regime yield slopes of – 1.13 and – 1.76. However, one should be cautious describing sampled TCR (and BCR) clone counts using power laws as they hold typically for far less than two decades. (b) Human TCR clone counts for three HIV-infected (red) and three uninfected (black) individuals show qualitative differences between the distributions (unpublished). Other data from mice and humans, under different conditions and in different cell types, have been recently published [149, 150].
Quantifying T cell diversity is confounded by a number of technical limitations. Usually, the complete T cell repertoire in an animal cannot be directly measured. Rather, as in most other applications, small samples of the entire population are usually drawn. In sampling from animals, the fraction of cells drawn and sequenced is perhaps only M/N ~ 10−5−10−2. Thus, clones that have small populations may be missed in the sample. Besides sampling, sequencing requires PCR amplification of the sample, leading to PCR bias, especially in the larger-sized clones [150]. Finally, as in many other applications, there are multiple subclasses of the T cell population. Naive T cells that are activated by antigens develop into memory T cells that carry the same TCR and that can further proliferate. Thus, it is difficult to separate the clone counts of different subpopulations such as naive or memory T cells [150].
Many mathematical models for the development and maintenance of the immune systems have been developed [136, 137, 141, 144, 152, 153]. For the multiclonal naive T cell population, rudimentary insights can also be gleaned from a birth-death-immigration process, much as in the modeling of hematopoiesis. Here, the thymus mediates the immigration of a large number of clones, which undergo homeostatic proliferation and death in the periphery. Immigration rates can be different for different clones, depending on the likelihood of specific recombination patterns which may be inferred from probabilistic models of VDJ recombination [154, 155].
Proliferation in the periphery depends on interactions between self-peptides with T cell receptors and is thus clone-dependent. Recently, it has been shown that TCR-dependent thymic output and proliferation rates (a nonneutral BDI model) influence the measured clone count patterns [156]. These processes form and maintain a diverse T cell receptor repertoire, which is usually characterized by its richness. Unlike the barcode abundances in arising during hematopoiesis, the neutral BDI processes are not able to capture the shapes of the measured TCR clone counts.
It is also known that T cell residence times depend on interactions between tissues and T cell receptors. Thus, different clones of T cells are expected to be differentially spatially distributed in the body. Hence, diversity metrics should be defined within and between habitats, much like that in ecology.
Finally, it is known that T cell richness decreases with age [157-160]. Qualitatively, a loss of diversity has been predicted within the multispecies BDI process by assuming a decreasing thymic output rate with age. Even when the thymus is completely shut down, the diversity of the T cell repertoire slowly decreases as successive clones go extinct and the clone abundance distribution coarsens. In humans, since the overall T cell population is primarily maintained by proliferation rather than thymic immigration [161], the reduction in diversity is fortunately a slow process.
6.6. Societal applications of diversity: wealth distributions
Metrics associated with diversity have been naturally applied in human social contexts [19-21, 162], including physical, cultural, educational [24, 32], and economic settings. For example, the distribution of wealth is the chief metric in many economic and political studies. As with all applications, data collection, sampling, and delineating differences in attributes are main research challenges.
Wealth or income, unlike species, are essentially continuous and ordered quantities, and can be described by many indices designed by economists to measure different wealth attributes of a population. Distinct from cellular or ecological contexts, socio-economic diversity is also often discussed in terms of ‘inequality,’ ‘evenness,’ or ‘polarization.’ Diversity or ‘inequality’ indices in the socioeconomic setting usually invoke a number of additional assumptions
Individual identities are irrelevant: this is analogous to barcoding studies of a singular cell type in which the barcode identity is not important.
Size and total wealth invariance: the diversity is invariant to the total population size. Only proportions of the total population that are associated with a proportion of the total wealth are relevant.
Dalton principle: any inequality index should increase if any amount of wealth is transferred from an entity to one with higher existing wealth.
Mathematically, one starts by ordering the wealth or income of a population of N entities w1 ⩽ w2 … ⩽ wi ⩽ wi+1, … ⩽ wN. For large N, the rescaled wealth distribution w(f) ≡ WfN is a function of the relative fraction of the total population f = n/N ∈ [0, 1]. Furthermore, we can define a normalized wealth distribution or density
| (49) |
and the corresponding cumulative distribution
| (50) |
or
| (51) |
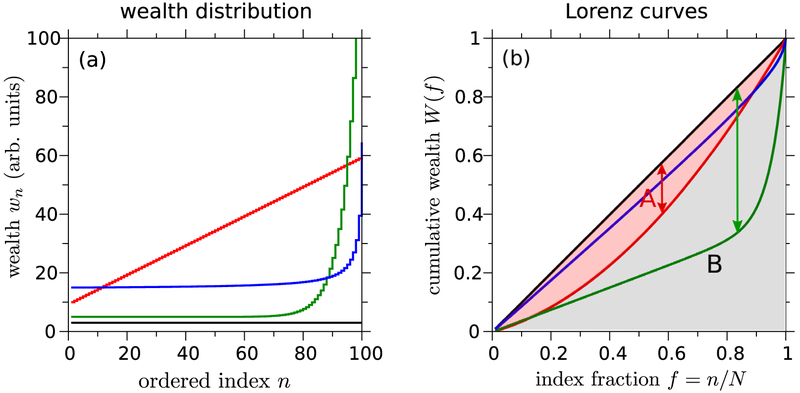
The functions W (f) are known as ‘Lorenz-consistent’ if they satisfy the above assumptions [33]. Four representative Lorenz consistent raw wealth distributions are shown in figure 9(a) as functions of the individual index. In figure 9(b), we plot the continuous cumulative rescaled wealth distribution W (f) as a function of the relative population fraction f corresponding to the wealth distributions shown in figure 9(a). From any ordered distribution, we can define a so-called ‘Lorenz curve’ that illustrates many indices graphically. The Lorenz curve is defined as the cumulative wealth of all individuals of a relative index f = n/N and lower.
Figure 9.
(a) Ordering of all N = 100 individuals in increasing wealth or income. The hypothetical wealth distributions plotted are wi = 3 (equal wealth, black curve), wi = 10 + (i − 1)/2 (linear distribution, red), Wi = 5 + ei/5−15 − e−14.8 (green), and wi = 14.5 + 50/(101 − i) (blue). The latter three represent distributions with some amount of inequity. (b) These inequalities can be visually quantified by their corresponding Lorenz curves, plotted as the relative fraction of the population f. The Lorenz curve for a perfectly uniform wealth distribution is given by the straight diagonal line. The area between the diagonal equality line and any other Lorenz curve can be used to visualize the Gini coefficient of the associated wealth distribution. The Gini coefficient, Gini = A/(A + B), is calculated by dividing the difference in areas between the equality line and the Lorenz curve in question (A) by the total area (A + B = 1/2) under the equality curves. The ‘Robin Hood’ index is defined as the maximum difference between the equality line and a given Lorenz curve, and is indicated by arrow for the red and green Lorenz curves.
Many indices can be visualized by the Lorenz curves. For example, the Gini index [163, 164] for the red distribution (linear wealth) in figure 9(a) is calculated by the area of the red shaded region (A) divided by the area under the equality curve (A + B = 1/2): Gini = A/(A + B) = 2A. In a society where every person receives the same income, the Gini index equals zero. However, if the total wealth is concentrated in only one out of N entities, Gini = 1 – 2/N. This motivates one to define the Gini index for discrete cumulative wealth values Wi according to
| (52) |
while the ‘Hoover’ or ‘Robin Hood’ index defined by [34, 165, 166]
| (53) |
is the Legendre transform at f*, the fraction of individuals corresponding to dW(f)/df∣f=f* = 1. For the two Lorenz curves in figure 9(b), the Robin Hood index is indicated by the two corresponding arrows.
The Robin Hood index happens to be a specific case of the Kolmogorov–Smirnoff statistic as defined in equation (15) for two cumulative distributions. For convex functions W(f) such that W(0) = 0, W (1) = 1, the index H corresponds to the fraction of the total wealth that needs to be distributed in order to achieve uniform wealth. This can be seen by considering the wealth wi up to an index n* such that Wi ⩽ N−1 for all i ⩽ n*. The total wealth that needs to be redistributed to obtain equal wealth fractions N−1 for every individual is
| (54) |
Another possibility is to sum over all entities wi according to
| (55) |
The specific, local redistribution is not specified but it would be intriguing to cast it in the language of optimal transport and Wasserstein distances [167]. This way, one might also define costs to wealth redistribution.
It is also possible to quantify inequity according to the Theil index [168-170]
| (56) |
which corresponds to a relative entropy as defined in equation (11). In this case, the entropy of the distribution of Wi is measured with respect to the expectation value . If , we may interpret wi as the probability of finding an individual in income class i, and corresponds to the relative share of equally distributed wealth. Naturally, many others measures for inequality have been defined my numerous authors focussing on specific socioeconomic areas [171].
However, typical inequality indices do not convey any judgment, belief system, or behavioral propensity on measured inequity and thus may not capture typical social concepts. In an effort to better quantify concepts such as inequity or ‘polarization’ [172], a sociologists have proposed a number of polarization indices that are argued to be more directly correlated with social tension and unrest. For example, Esteban and Ray [35, 36] developed a measure of polarization to account for clusters within which individuals are more similar in an attribute x (such as wealth) than they are between clusters. While there may be many ways to define polarization, imposing a few reasonable features and constraints can narrow down the allowable forms. First, they assume an ‘identity-alienation framework’ in which an individual also identifies with his own distribution f (x) at value x. An effective ‘antagonism’ of an individual with attribute x towards those with attribute y is defined as T[f(x), d] where a simple form for the distance is d = ∣x – y∣. The polarization P is then assumed to take the form
| (57) |
By imposing axioms that the polarization (i) cannot increase if the distribution is squeezed (compressed towards its peak), (ii) must increase if two non-overlapping distributions are moved farther apart, and (iii) the polarization should be invariant to scalings of the total population. Using these constraints, the polarization can be more explicitly defined as
| (58) |
where 1/4 ⩽ α ⩽ 1 [36] (Esteban and Ray [35] and Kawada, Nakamura, and Sunada [173] find 0 ⩽ α < 1.6 using slightly different assumptions). The parameter α describes the amount of ‘polarization sensitivity.’ It measures identification of a population with its distribution and distinguishes polarization from other standard inequity measures such as the Gini index (when α = 0 [35]) or Simpson’s index. Also, note that when α = 0, the form of P[f] resembles the total potential energy of a system of particles which is distributed according to f (x) and exhibits an interaction energy ∣x – y∣. The discrete analogue of equation (58) is , for which the individuals i, j can be generalized to groups. In empirical studies, the Esteban and Ray polarization measure is given by
| (59) |
where
| (60) |
are the relative frequency and the mean of the wealth in group i, respectively [174]. D’Ambrosio and Wolff suggested replacing the difference of mean wealths in equation (59) by the Kolmogorov measure of variation distance [174, 175]
| (61) |
to obtain
| (62) |
Additional indices have been proposed, including a class of polarizations by Tsui and Wang [176] of the form
| (63) |
where ψ is a smooth function of the rescaled distance di. The median income m(x) is computed from the individual incomes xi (1 ⩽ i ⩽ N).
Many of these polarization metrics can in fact be expressed in terms of the Gini coefficient. For example, the Foster–Wolfson polarization index is defined as [177]
| (64) |
where μ(x) is the corresponding mean income, and the subscript indices B and W denote the between and within group Gini coefficients. According to the definition of PFW (x), inequity differs from polarization in the following way: the Gini index as the sum of GiniB and GiniW quantifies the unequal distribution of wealth in a society whereas polarization is measured in terms of the difference of GiniB and GiniW. Thus, an increase in within-group inequality leads to a larger total inequality, but to a lower polarization. A more refined understanding of socioeconomic diversity will need to consider multiple classes of attributes, including possible geographic or spatial distributions.
The described polarization measures are relevant not only in the context of wealth distributions, but they are also able to provide important insights in other sociological phenomena associated with the notion of diversity. As one example, quantitative measures of polarization are applicable to examine factors that influence the cohesiveness of groups [23]. In addition, diversity measures may help to identify mechanisms which lead to inequality among different social groups in our education system [24]. In this context, the social entropy theory aims to quantitatively compare diversity across social systems such as societies, organizations, and individual groups [19, 20, 178].
7. Summary and discussion
Quantifying the diversity of a given population in terms of a single measure such as richness does not fully describe the underlying distribution of species or other properties. Various diversity measures have been developed and tailored to specific applications in different fields including ecology, biology, and economics. Mathematically, one can describe populations in terms of species numbers ni (number of entities of type i) or clone counts ck (number of species of size k). Hill numbers qD provide a framework to unify some common diversity indices that are based on a species-number description. Hill numbers with large values of q put more weight on common species whereas small values of q yield measures that are more sensitive to rarer species. This implies that measures such as richness (q = 0) and evenness (q = 1) are more prone to sampling effects than Simpson’s diversity index (q = 2) or Hill numbers with q > 2 [180]. In table 1, we summarize some common diversity measures, their applications, and advantages and disadvantages.
Table 1.
Summary of fundamental, commonly used diversity measures. The variable q indicates the order of the corresponding Hill number qD as defined in equation (16).
| Measure | Interpretation | Application | Advantages | Disadvantages |
|---|---|---|---|---|
| Species number ni | Number of entities of type i | Evolutionary and population models | Straightforward interpretation in models | Keeping track of species identity may be unrealistic |
| Species abundance (clone count) ck. | Number of species of size k | Models of self-assembly/nucleation [52-54]; characterization of population in barcoding studies [55] | Directly related to richness, useful when clone identity is not important | No clone identity information, insensitive to exchange of populations between clones |
| Richness (0D) | Total number of distinguishable species | Conservation planning; assessment of ecosystems [3] | Straightforward mathematical definition and interpretation | Maximally affected by small sampling; all species are treated equally |
| Evenness (1D) | Uniformity of relative abundances of species in a population | Characterization of ecosystems and inequity in societies; Theil index [3, 168-170] | Straightforward mathematical definition and interpretation; similar to entropy | Affected by sampling |
| Simpson’s diversity (2D) | Probability that two randomly drawn entities are of the same species | Characterization of cell populations [147, 179] | Less affected by sampling | More intricate mathematical definition & Less interpretability |
| qD, q > 2 | N/A | Characterization of more frequent species in a population; Berger–Parker index [90] | Significantly less affected by sampling | No intuitive interpretation |
| Lorenz curve | Cumulative relative wealth | Economics, wealth distributions | Fundamental mathematical object | No identity information (like ordered clone counts) |
| Gini index | Deviation of Lorenz curves from absolute equality | Population-level wealth inequality | Easily understood | No identity information, Values are subjectively interpreted |
| Hoover/Robin Hood index | KS statistic between Lorenz curve and equality line | Population-level wealth inequality | Easily understood | No identity information, values are subjectively interpreted |
In conclusion, we have provided an overview of the most relevant measures of diversity and their information-theoretic counterparts. We then summarized common applications of diversity indices in biological and ecological systems. Despite the ambiguity in the definitions and the variety of different diversity measures [3, 4, 25-29], the concept is of great importance for the monitoring of ecosystems and in the context of conservation planning [2, 5, 9, 10, 29-31].
We also described the importance of a quantitative treatment of diversity for experiments in the study of the gut microbiome, stem cell barcoding, and the adaptive immune system. Finally, we discussed examples of the application of diversity measures in human social systems including the characterization of wealth distributions in societies and measures of political or cultural polarization. Scientific conclusion in these fields, and in ecology, are particularly sensitive to sampling and measurements. However, accurate measurements [181], meaningful classification, spatial resolution [101], and informative sampling protocols [69, 76] remain elusive across almost all fields. Sometimes, as shown for example in figure 6(b), different measures even lead to contradictory conclusions [182]. There is no golden rule in choosing a unique metric for a specific situation, as the sampling effects also depend on the underlying unknown clone-count distribution [180]. It is recommended that one considers different metrics and cross-checks their values while bearing in mind how sampling effects may impact diversity measures differently.
Figure 5.
(a) Protocol for Viral Integration site (VIS) barcoding studies of hematopoiesis in rhesus macaque [55, 117, 118]. Here, ‘barcodes’ are defined by the random integration sites of a lentiviral vector. (b) Xenograft barcode experiments using mice [119] in which a library of barcodes was used to tag leukemia-propagating cells before direct transplantation into mice.
Acknowledgments
This work was supported in part by grants from the NSF through Grant DMS-1814364, the Army Research Office through Grant W911NF-18-1-0345, and the National Institutes of Health through Grant R01HL146552. The authors also thank Greg Huber for insightful discussions.
References
- [1].Nei M 1973. Analysis of gene diversity in subdivided populations. Proc. Natl Acad. Sci 70 3321–3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Heywood VH et al. 1995. Global Biodiversity Assessment vol 1140 (Cambridge: Cambridge University Press; ) [Google Scholar]
- [3].Purvis A and Hector A 2000. Getting the measure of biodiversity Nature 405 212. [DOI] [PubMed] [Google Scholar]
- [4].Whittaker RJ, Willis KJ and Field R 2001. Scale and species richness: towards a general, hierarchical theory of species diversity J. Biogeogr 28 453–70 [Google Scholar]
- [5].Sala OE et al. 2000. Global biodiversity scenarios for the year 2100 Science 287 1770–4 [DOI] [PubMed] [Google Scholar]
- [6].Fisher RA, Corbet AS and Williams CB 1943. The relation between the number of species and the number of individuals in a random sample of an animal population J. Animal Ecol 42–58 [Google Scholar]
- [7].Magurran AE 1988. Ecological Diversity and its Measurement (Princeton, NJ: Princeton University Press; ) [Google Scholar]
- [8].Benton MJ 1995. Diversification and extinction in the history of life Science 268 52–8 [DOI] [PubMed] [Google Scholar]
- [9].Courtillot V and Gaudemer Y 1996. Effects of mass extinctions on biodiversity Nature 381 146 [Google Scholar]
- [10].Alroy J 2004. Evolutionary faunas dynamically coherent? Evolutionary Ecol. Res 61–32 [Google Scholar]
- [11].Stollmeier F, Geisel T and Nagler J 2014. Possible origin of stagnation and variability of Earth’s biodiversity. Phys. Rev. Lett 112 228101. [DOI] [PubMed] [Google Scholar]
- [12].Blume ME, Crockett J and Friend I 1974. Stock ownership in the united states: characteristics and trends Surv. Curr. Bus 54 16–40 [Google Scholar]
- [13].Blume ME and Friend I 1975. The asset structure of individual portfolios and some implications for utility functions J. Finance 30 585–603 [Google Scholar]
- [14].Rajan R, Servaes H and Zingales L 2000. The cost of diversity: the diversification discount and inefficient investment J. Finance 55 35–80 [Google Scholar]
- [15].Goetzmann WN and Kumar A 2008. Equity portfolio diversification Rev. Finance 12 433–63 [Google Scholar]
- [16].Haldane AG and May RM 2011. Systemic risk in banking ecosystems Nature 469 351. [DOI] [PubMed] [Google Scholar]
- [17].Greenberg JH 1956. The measurement of linguistic diversity Language 32 109–15 [Google Scholar]
- [18].Yule CU 2014. The Statistical Study of Literary Vocabulary (Cambridge: Cambridge University Press; ) [Google Scholar]
- [19].Bailey KD 1990. Social Entropy Theory (SUNY Press; ) [Google Scholar]
- [20].Balch T 2000. Hierarchic social entropy: an information theoretic measure of robot group diversity Auton. Robots 8 209–38 [Google Scholar]
- [21].Neckerman KM and Torche F 2007. Inequality: causes and consequences Annu. Rev. Sociol 33 335–57 [Google Scholar]
- [22].Ostrom E 2009. Understanding Institutional Diversity (Princeton, NJ: Princeton University Press; ) [Google Scholar]
- [23].Mäs M, Flache A, Takács K and Jehn KA 2013. In the short term we divide, in the long term we unite: demographic crisscrossing and the effects of faultlines on subgroup polarization Organ. Sci 24 716–36 [Google Scholar]
- [24].Domina T, Penner A and Penner E 2017. Categorical inequality: schools as sorting machines Annu. Rev. Sociol 43 311–30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Sepkoski JJ 1988. Alpha, beta, or gamma: where does all the diversity go? Paleobiology 14 221–34 [DOI] [PubMed] [Google Scholar]
- [26].Ricotta C 2005. Through the jungle of biological diversity Acta Biotheoretica 53 29–38 [DOI] [PubMed] [Google Scholar]
- [27].Simpson EH. Measurement of diversity. Nature. 1949;163:688. [Google Scholar]
- [28].Hurlbert SH 1971. The nonconcept of species diversity: a critique and alternative parameters Ecology 52 577–86 [DOI] [PubMed] [Google Scholar]
- [29].Sarkar S 2006. Ecological diversity and biodiversity as concepts for conservation planning: comments on ricotta Acta Biotheoretica 54 133–40 [DOI] [PubMed] [Google Scholar]
- [30].John Sepkoski J Jr 1998. Rates of speciation in the fossil record Phil. Trans. R. Soc. B 353 315–26 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Margules CR and Pressey RL 2000. Systematic conservation planning Nature 405 243. [DOI] [PubMed] [Google Scholar]
- [32].Herrnstein RJ and Murray C 1994. Bell Curve (New York: Free Press; ) [Google Scholar]
- [33].Lorenz MO 1905. Methods of measuring the concentration of wealth Publ. Am. Stat. Assoc 9 209–19 [Google Scholar]
- [34].Edgar Malone Hoover J 1936. The measurement of industrial localization Rev. Econ. Stat 18 162–71 [Google Scholar]
- [35].Esteban J-M and Ray D 1994. On the measurement of polarization Econometrica 62 819–51 [Google Scholar]
- [36].Duclos J-Y, Esteban J and Ray D 2004. Polarization: concepts, measurement, estimation Econometrica 72 1737–72 [Google Scholar]
- [37].Grubb M, Butler L and Twomey P 2006. Diversity and security in UK electricity generation: the influence of low-carbon objectives Energy Policy 34 4050–62 [Google Scholar]
- [38].Cover TM and Thomas JA 2012. Elements of Information Theory (New York: Wiley; ) [Google Scholar]
- [39].Jaynes ET 1963. Information theory, statistical mechanics Statistical Physics ed Ford K (New York: Benjamin; ) p 181 [Google Scholar]
- [40].Lazo A and Rathie P 1978. On the entropy of continuous probability distributions IEEE Trans. Inf. Theory 24 120–2 [Google Scholar]
- [41].Spellerberg IF and Fedor PJ 2003. A tribute to claude shannon (1916–2001) and a plea for more rigorous use of species richness, species diversity and the ‘shannon–wiener’ index Glob. Ecol. Biogeogr 12 177–9 [Google Scholar]
- [42].Lin J 1991. Divergence measures based on the shannon entropy. IEEE Trans. Inf. Theory 37 145–51 [Google Scholar]
- [43].Hill MO 1973. Diversity and evenness: a unifying notation and its consequences Ecology 54 427–32 [Google Scholar]
- [44].Tuomisto h 2010. a consistent terminology for quantifying species diversity? Yes, it does exist Oecologia 164 853–60 [DOI] [PubMed] [Google Scholar]
- [45].Tuomisto H 2010. A diversity of beta diversities: straightening up a concept gone awry. Part 1. Defining beta diversity as a function of alpha and gamma diversity Ecography 33 2–22 [Google Scholar]
- [46].Jost L 2007. Partitioning diversity into independent alpha and beta components Ecology 88 2427–39 [DOI] [PubMed] [Google Scholar]
- [47].Rényi A et al. 1961. On measures of entropy and information Proc. 4th Berkeley Symp. on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics (The Regents of the University of California; ) [Google Scholar]
- [48].Jost L 2006. Entropy and diversity Oikos 113 363–75 [Google Scholar]
- [49].Heip C 1974. A new index measuring evenness J. Mar. Biol. Assoc. United Kingdom 54 555–7 [Google Scholar]
- [50].Sethian JA 1999. Level Set Methods, Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision and Materials Science (Cambridge: Cambridge University Press; ) [Google Scholar]
- [51].Kittel C 1996. Introduction to Solid State Physics 7th edn (New York: Wiley; ) [Google Scholar]
- [52].Wattis JAD and King JR 1998. Asymptotic solutions of the Becker–Döring equations J. Phys. A: Math. Gen 31 7169 [Google Scholar]
- [53].D’Orsogna MR, Lakatos G and Chou T 2012. Stochastic self-assembly of incommensurate clusters J. Chem. Phys 136 084110. [DOI] [PubMed] [Google Scholar]
- [54].D’Orsogna MR, Lei Q and Chou T 2015. First assembly times and equilibration in stochastic coagulation-fragmentation J. Chem. Phys 139 014112. [DOI] [PubMed] [Google Scholar]
- [55].Goyal S, Kim S, Chen ISY and Chou T 2015. Mechanisms of blood homeostasis: lineage tracking and a neutral model of cell populations in rhesus macaques BMC Biol. 13 85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Villela DAM, Garcia GDA and Maciel-de Freitas R 2017. Novel inference models for estimation of abundance, survivorship and recruitment in mosquito populations using mark-release-recapture data PLoS Neglected Tropical Dis. 11 1–20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Epopa PS, Millogo AA, Collins CM, North A, Tripet F, Benedict MQ and Diabate A 2017. The use of sequential mark-release-recapture experiments to estimate population size, survival and dispersal of male mosquitoes of the anopheles gambiae complex in bana, a west african humid savannah village Parasites Vectors 10 376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Cianci D, Broek JVD, Caputo B, Marini F, Torre AD, Heesterbeek H and Hartemink N 2013. Estimating mosquito population Size from mark release recapture data J. Med. Entomol 50 533–42 [DOI] [PubMed] [Google Scholar]
- [59].Gotelli NJ and Chao A 2013. Measuring and estimating species richness, species diversity and biotic similarity from sampling data Encyclopedia of Biodiversity vol 5 (New York: Academic; ) pp 195–211 [Google Scholar]
- [60].Chao A, Gotelli NJ, Hsieh T, Sander EL, Ma K, Colwell RK and Ellison AM 2014. Rarefaction and extrapolation with Hill numbers: a framework for sampling and estimation in species diversity studies Ecological Monogr. 84 45–67 [Google Scholar]
- [61].Fisher RA, Corbet AS and Williams CB 1943. The relation between the number of species and the number of individuals in a random sample of an animal population J. Animal Ecol 12 42–58 [Google Scholar]
- [62].Bunge J and Fitzpatrick M 1993. Estimating the number of species: a review J. Am. Stat. Assoc 88 364–73 [Google Scholar]
- [63].Hsieh TC and Chao A 2016. Rarefaction and extrapolation: making fair comparison of abundance-sensitive phylogenetic diversity among multiple assemblages Systematic Biol. 66 100–11 [DOI] [PubMed] [Google Scholar]
- [64].Cox KD et al. 2017. Community assessment techniques and the implications for rarefaction and extrapolation with Hill numbers Ecol. Evol 7 11213–26 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Budka A, Lacka A and Szoszkiewicz K 2019. The use of rarefaction and extrapolation as methods of estimating the effects of river eutrophication on macrophyte diversity Biodiversity Conservation 28 385–400 [Google Scholar]
- [66].Chao A, Wang Y and Jost L 2013. Entropy and the species accumulation curve: a novel entropy estimator via discovery rates of new species Methods Ecol. Evol 4 1091–100 [Google Scholar]
- [67].Efron B and Thisted R 1976 Estimating the number of unseen species: how many words did Shakespeare know? Biometrika 63 435–47 [Google Scholar]
- [68].Orlitsky A, Suresh AT and Wu Y 2016. Optimal prediction of the number of unseen species Proc. Natl Acad. Sci 113 13283–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Willis A and Bunge J 2015. Estimating diversity via frequency ratios Biometrics 71 1042–9 [DOI] [PubMed] [Google Scholar]
- [70].Willis A. Extrapolating abundance curves has no predictive power for estimating microbial biodiversity. Proc. Natl Acad. Sci. 2016;113:E5096. doi: 10.1073/pnas.1608281113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Chao A 1984. Nonparametric estimation of the number of classes in a population Scand. J. Stat 265–70 [Google Scholar]
- [72].Chao A 1987. Estimating the population size for capture-recapture data with unequal catchability Biometrics 783–91 [PubMed] [Google Scholar]
- [73].Shen T-J, Chao A and Lin C-F 2003. Predicting the number of new species in further taxonomic sampling Ecology 84 798–804 [Google Scholar]
- [74].Hsieh TC, Ma KH and Chao A 2016. iNEXT: an R package for rarefaction and extrapolation of species diversity (Hill numbers) Methods Ecol. Evol 7 1451–6 [Google Scholar]
- [75].Curtis TP, Sloan WT and Scannell JW 2002. Estimating prokaryotic diversity and its limits Proc. Natl Acad. Sci 99 10494–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Locey KJ and Lennon JT 2016. Scaling laws predict global microbial diversity Proc. Natl Acad. Sci 113 5970–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Locey KJ and Lennon JT 2016. Reply to Willis: Powerful predictions of biodiversity from ecological models and scaling laws Proc. Natl Acad. Sci 113 E5097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Hutchinson GE 1961. The paradox of the plankton Am. Naturalist 95 137–45 [Google Scholar]
- [79].Hardin G 1960. The competitive exclusion principle Science 131 1292–7 [DOI] [PubMed] [Google Scholar]
- [80].MacArthur RH 1965. Patterns of species diversity Biol. Rev 40 510–33 [Google Scholar]
- [81].Whittaker RH 1960. Vegetation of the siskiyou mountains, oregon and california Ecol. Monogr 30 279–338 [DOI] [PubMed] [Google Scholar]
- [82].Whittaker RH 1977. Evolution of species diversity in land communities Evol. Biol 10 1–67 [Google Scholar]
- [83].Lande R 1996. Statistics and partitioning of species diversity, and similarity among multiple communities Oikos 5–13 [Google Scholar]
- [84].Contoli L and Luiselli L 2015. Contributions to biodiversity theory: the importance of formal rigor Web Ecol. 15 33–7 [Google Scholar]
- [85].Hui C and McGeoch MA 2014. Zeta diversity as a concept and metric that unifies incidence-based biodiversity patterns Am. Naturalist 184 684–94 [DOI] [PubMed] [Google Scholar]
- [86].Jaccard P 1900. Contribution au problème de l’immigration post-glaciare de la flore alpine Bull. Soc. Vaudoise Sci. Nat 36 87–130 [Google Scholar]
- [87].Margalef DR 1957. Information theory in ecology Mem. Real Acad. ciencias y artes de Barcelona 32 374–559 [Google Scholar]
- [88].Menhinick EF 1964. A comparison of some species-individuals diversity indices applied to samples of field insects Ecology 45 859–61 [Google Scholar]
- [89].Bray J and Curtis J 1957. An ordination of upland forest communities of southern Wisconsin Ecol. Monogr [Google Scholar]
- [90].Berger WH and Parker FL 1970. Diversity of planktonic foraminifera in deep-sea sediments Science 168 1345–7 [DOI] [PubMed] [Google Scholar]
- [91].Fager EW 1957. Determination and analysis of recurrent groups Ecology 38 586–95 [Google Scholar]
- [92].Keefe TJ and Bergersen EP 1977. A simple diversity index based on the theory of runs Water Res. 11 689–91 [Google Scholar]
- [93].McIntosh RP 1967. An index of diversity and the relation of certain concepts to diversity Ecology 48 392–404 [Google Scholar]
- [94].Patil G and Taillie C 1982. Diversity as a concept and its measurement J. Am. Stat. Assoc 77 548–61 [Google Scholar]
- [95].Gleason HA 1922. On the relation between species and area Ecology 3 158–62 [Google Scholar]
- [96].MacArthur R and Wilson EO 1967. The Theory of Island Biogeography (Princeton, NJ: Princeton University Press; ) [Google Scholar]
- [97].Volkov I, Banavar JR, Hubbell SP and Maritan A 2003. Neutral theory and relative species abundance in ecology Nature 424 1035–7 [DOI] [PubMed] [Google Scholar]
- [98].Browne J and Peck SB 1996. The long-horned beetles of south Florida (Cerambycidae: Coleoptera): biogeography and relationships with the Bahama Islands and Cuba Can. J. Zool 74 2154–69 [Google Scholar]
- [99].Connor EF and McCoy ED 1979. The statistics and biology of the species area relationship Am. Naturalist 113 791–833 [Google Scholar]
- [100].He F and Legendre P 2002. Species diversity patterns derived from species-area models Ecology 83 1185–98 [Google Scholar]
- [101].Martín HG and Goldenfeld N 2006. On the origin and robustness of power-law species-area relationships in ecology Proc. Natl Acad. Sci 103 10310–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Park SY, Nanda S, Faraci G, Park Y and Lee HY 2019. CCMP: software-as-a-service approach for fully-automated microbiome profiling J. Biomedi. Inf. X 2 100040. [DOI] [PubMed] [Google Scholar]
- [103].Wilson BC, Vatanen T, Cutfield WS and O’Sullivan JM 2019. The super-donor phenomenon in fecal microbiota transplantation Frontiers Cell. Infection Microbiol 9 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Tian H, Ge X, Nie Y, Yang L, Ding C, McFarland LV, Zhang X, Chen Q, Gong J and Li N 2017. Fecal microbiota transplantation in patients with slow-transit constipation: a randomized, clinical trial PLoS One 12 e0171308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105].Proctor LM et al. 2014. The integrative human microbiome project: dynamic analysis of microbiome-host omics profiles during periods of human health and disease Cell Host & Microbe 16 276–89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Human Microbiome Project (https://hmpdacc.org/)
- [107].Qin J et al. 2010. A human gut microbial gene catalogue established by metagenomic sequencing Nature 464 59–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108].Ehrlich SD and the MetaHIT Consortium 2011. MetaHIT: the European Union Project on Metagenomics of the human intestinal tract Metagenomics of the Human Body ed K Nelson ch 15 (Berlin: Springer; ) [Google Scholar]
- [109].MetaHIT Website (www.metahit.eu)
- [110].Li J et al. 2014. An integrated catalog of reference genes in the human gut microbiome Nat. Biotechnol 32 834–41 [DOI] [PubMed] [Google Scholar]
- [111].Vetrovský T and Baldrian P 2013. The variability of the 16S rRNA gene in bacterial genomes and its consequences for bacterial community analyses PLoS One 8 e57923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Metabolomic Workbench (https://metabolomicsworkbench.org/)
- [113].Ribosome Database Project (https://rdp.cme.msu.edu/)
- [114].EZBioCloud (https://ezbiocloud.net/)
- [115].Shreiner AB, Kao JY and Young VB 2015. The gut microbiome in health and in disease Curr. Opin. Gastroenterol 31 69–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Thursby E and Juge N 2017. Introduction to the human gut microbiota Biochem. J 474 1823–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [117].Kim S et al. 2014. Dynamics of HSPC repopulation in nonhuman primates revealed by a decade-long clonal-tracking study Cell Stem Cell 14 473–85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Wu C et al. 2014. Clonal tracking of rhesus macaque hematopoiesis highlights a distinct lineage origin for natural killer cells Cell Stem Cell 14 486–99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Belderbos ME, Koster T, Ausema B, Jacobs S, Sowdagar S, Zwart E, de Bont E, de Haan G and Bystrykh LV 2017. Clonal selection and asymmetric distribution of human leukemia in murine xenografts revealed by cellular barcoding Blood 129 3210–20 [DOI] [PubMed] [Google Scholar]
- [120].Hebert PD, Cywinska A, Ball SL and deWaard JR 2003. Biological identifications through DNA barcodes Proc. R. Soc. B 270 313–21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Hebert PDN, Stoeckle MY, Zemlak TS and Francis CM 2004. Identification of Birds through DNA Barcodes PLoS Biol. 2 e312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [122].Ratnasingham S and Hebert PDN 2007. BOLD: the barcode of life data system (www.barcodinglife.org) Mol. Ecol. Notes 7 355–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [123].The barcode of life data system (www.barcodinglife.org)
- [124].Kress WJ, Wurdack KJ, Zimmer EA, Weigt LA and Janzen DH 2005. Use of DNA barcodes to identify flowering plants Proc. Natl Acad. Sci 102 8369–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Sgamma T, Masiero E, Mali P, Mahat M and Slater A 2018. Sequence-specific detection of aristolochia DNA a simple test for contamination of herbal products Frontiers Plant Sci. 9 1828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Bruno A, Sandionigi A, Agostinetto G, Bernabovi L, Frigerio J, Casiraghi M and Labra M 2019. Food tracking perspective: DNA metabarcoding to identify plant composition in complex and processed food products Genes 10 248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [127].Hawkins JA, Jones SK, Finkelstein IJ and Press WH 2018. Indel-correcting DNA barcodes for high-throughput sequencing Proc. Natl Acad. Sci 115 E6217–26 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128].Thielecke L, Aranyossy T, Dahl A, Tiwari R, Roeder I, Geiger H, Fehse B, Glauche I and Cornils K 2017. Limitations and challenges of genetic barcode quantification Sci. Rep 7 43249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129].Tambe A and Pachter L 2019. Barcode identification for single cell genomics BMC Bioinform. 20 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130].Sun J, Ramos A, Chapman B, Johnnidis JB, Le L, Ho Y-J, Klein A, Hofmann O and Camargo FD 2014. Clonal dynamics of native haematopoiesis Nature 514 322–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [131].Perié L and Duffy KR 2016. Retracing the in vivo haematopoietic tree using single-cell methods FEBS Lett. 590 4068–83 [DOI] [PubMed] [Google Scholar]
- [132].Blundell JR and Levy SF 2014. Beyond genome sequencing: lineage tracking with barcodes to study the dynamics of evolution, infection, and cancer Genomics 104 417–30 [DOI] [PubMed] [Google Scholar]
- [133].Rogers ZN, McFarland CD, Winters IP, Seoane JA, Brady JJ, Yoon S, Curtis C, Petrov DA and Winslow MM 2018. Mapping the in vivo fitness landscape of lung adenocarcinoma tumor suppression in mice Nat. Genet 50 483–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [134].Akimov Y, Bulanova D, Abyzova M, Wennerberg K and Aittokallio T 2019. DNA barcode-guided lentiviral CRISPRa tool to trace and isolate individual clonal lineages in heterogeneous cancer cell populations bioRxiv [Google Scholar]
- [135].Koelle SJ, Espinoza DA, Wu C, Xu J, Lu R, Li B, Donahue RE and Dunbar CE 2017. Quantitative stability of hematopoietic stem and progenitor cell clonal output in rhesus macaques receiving transplants Blood 129 1448–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [136].Xu S, Kim S, Chen IS and Chou T 2018. Modeling large fluctuations of thousands of clones during hematopoiesis: the role of stem cell self-renewal and bursty progenitor dynamics in rhesus macaque PLoS Comput. Biol 14 e1006489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137].Dessalles R, D’Orsogna M and Chou T 2018. Exact steady-state distributions of multispecies birth–death–immigration processes: effects of mutations and carrying capacity on diversity J. Stat. Phys 173 182–221 [Google Scholar]
- [138].Xu S. Mathematical modeling of clonal dynamics in primate hematopoiesis. PhD Thesis UCLA 2018 [Google Scholar]
- [139].Biasco L. et al. In vivo tracking of human hematopoiesis reveals patterns of clonal dynamics during early and steady-state reconstitution phases. Cell Stem Cell. 2016 doi: 10.1016/j.stem.2016.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [140].Alt FW, Oltz EM, Young F, Gorman J, Taccioli G and Chen J 1992. Vdj recombination Immunol. Today 13 306–14 [DOI] [PubMed] [Google Scholar]
- [141].Lythe G, Callard RE, Hoare RL and Molina-París C 2016. How many TCR clonotypes does a body maintain? J. Theor. Biol 389 214–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [142].Zarnitsyna V, Evavold B, Schoettle L, Blattman J and Antia R 2013. Estimating the diversity, completeness, and cross-reactivity of the T cell repertoire Frontiers Immunol. 4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [143].Hoehn KB, Fowler A, Lunter G and Pybus OG 2016. The diversity and molecular evolution of B-cell receptors during infection Mol. Biol. Evol 33 1147–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [144].Yates AJ 2014. Theories and quantification of thymic selection Frontiers Immunol. 5 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [145].Casrouge A, Beaudoing E, Dalle S, Pannetier C, Kanellopoulos J and Kourilsky P 2000. Size estimate of the αβ TCR repertoire of naive mouse splenocytes J. Immunol 164 5782–7 [DOI] [PubMed] [Google Scholar]
- [146].DeWitt WS, Lindau P, Snyder TM, Sherwood AM, Vignali M, Carlson CS, Greenberg PD, Duerkopp N, Emerson RO and Robins HS 2016. A public database of memory and naive b-cell receptor sequences PLoS One 11 e0160853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [147].Rosenfeld AM, Meng W, Chen DY, Zhang B, Granot T, Farber DL, Hershberg U and Luning Prak ET 2018. Computational evaluation of B-cell clone sizes in bulk populations Frontiers Immunol. 9 1472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [148].Keane C et al. 2017. Biology of human tumors the T-cell receptor repertoire influences the tumor microenvironment and is associated with survival in aggressive B-cell lymphoma Clin. Cancer Res 23 1820–8 [DOI] [PubMed] [Google Scholar]
- [149].Sethna Z, Elhanati Y, Dudgeon CR, Callan CG, Levine AJ, Mora T and Walczak AM 2017. Insights into immune system development and function from mouse T-cell repertoires Proc. Natl Acad. Sci 114 2253–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [150].Oakes T et al. 2017. Quantitative characterization of the T cell receptor repertoire of Naïve and memory subsets using an integrated experimental and computational pipeline which is robust, economical, and versatile Frontiers Immunol. 8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [151].Aguilera-Sandoval CR et al. 2017. Supranormal thymic output up to two decades after HIV-1 infection AIDS 30 701–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [152].Lythe G and Molina-París C 2018. Some deterministic and stochastic mathematical models of naive T-cell homeostasis Immunol. Rev 285 206–17 [DOI] [PubMed] [Google Scholar]
- [153].Xu S and Chou T 2018. Immigration-induced phase transition in a regulated multispecies birth-death process J. Phys. A: Math. Theor 51 425602 [Google Scholar]
- [154].Marcou Q, Mora T and Walczak AM 2018. High-throughput immune repertoire analysis with IGoR Nat. Commun 9 561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [155].Sethna Z, Elhanati Y, Callan J, Curtis G, Walczak A M and Mora T 2019. OLGA: fast computation of generation probabilities of B- and T-cell receptor amino acid sequences and motifs Bioinformatics [DOI] [PMC free article] [PubMed] [Google Scholar]
- [156].Dessalles R, D’Orsogna M and Chou T 2019. How heterogeneous thymic output and homeostatic proliferation shape naive t cell receptor clone abundance distributions submitted to PLoS Comput. Biol [Google Scholar]
- [157].Johnson P, Yates A, Goronzy J and Antia R 2012. Peripheral selection rather than thymic involution explains sudden contraction in naive CD4 T-cell diversity with age Proc. Natl Acad. Sci. USA 109 21432–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [158].Rane S, Hogan T, Seddon B and Yates A J 2018. Age is not just a number: naive T cells increase their ability to persist in the circulation over time PLoS Comput. Biol 16 e2003949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [159].Lewkiewicz S, Chuang Y-L and Chou T 2018. A mathematical model predicting decay of naive T-cell diversity with age Bull. Math. Biol [DOI] [PubMed] [Google Scholar]
- [160].Egorov ES et al. 2018. The changing landscape of naive T cell receptor repertoire with human aging Frontiers Immunol. 9 1618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [161].den Braber I et al. 2012. Maintenance of peripheral naive T cells is sustained by thymus output in mice but not humans Immunity 36 288–97 [DOI] [PubMed] [Google Scholar]
- [162].Maignan C, Ottaviano G, Pinelli D and Rullani F 2003. Bio-ecological diversity versus socio-economic diversity: a comparison of existing measures Fond. Eni Enrico Mattei [Google Scholar]
- [163].Gini C 1912. Variabilità e mutabilità Reprinted in Memorie di Metodologica Statistica ed Pizetti E and Salvemini T (Rome: Libreria Eredi Virgilio Veschi; ) [Google Scholar]
- [164].Gastwirth JL 1972. The estimation of the Lorenz curve and Gini index Rev. Econ. Stat 54 306–16 [Google Scholar]
- [165].Atkinson AB and Micklewright J 1992. Economic Transformation in Eastern Europe and the Distribution of Income (Cambridge: Cambridge University Press; ) [Google Scholar]
- [166].Kennedy BP, Kawachi I and Prothrow-Stith D 1996. Income distribution and mortality: cross sectional ecological study of the Robin hood index in the United States Br. Med. J 312 1004–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [167].Galichon A 2017. Optimal Transport Methods in Economics (Princeton, NJ: Princeton University Press; ) [Google Scholar]
- [168].Theil H. Statistical decomposition analysis; with applications in the social and administrative sciences. Technical Report 1972 [Google Scholar]
- [169].Novotný J 2007. On the measurement of regional inequality: does spatial dimension of income inequality matter? Ann. Reg. Sci 41 563–80 [Google Scholar]
- [170].Lasarte E. et al. Decomposition of regional income inequality and neighborhood component: a spatial Theil index. Technical Report Instituto Valenciano de Investigaciones Economicas, SA (Ivie) 2014 [Google Scholar]
- [171].Maio FGD 2007. Income inequality measures J. Epidemiol. Commun. Health 61 849–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [172].Böttcher L, Montealegre P, Goles E and Gersbach H 2019. Competing activists-political polarization (arXiv:1910.14531) [Google Scholar]
- [173].Kawada Y, Nakamura Y and Sunada K 2018. A characterization of the Esteban-ray polarization measures Econ. Lett 169 35–7 [Google Scholar]
- [174].D’Ambrosio C and Wolff EN 2006. Is wealth becoming more polarized in the United States? Int. Perspectives on Household Wealth Chapters (Edward Elgar Publishing; ) ch 12 [Google Scholar]
- [175].D’Ambrosio C 2001. Household characteristics and the distribution of income in Italy: an application of social distance measures Rev. Income Wealth 47 43–64 [Google Scholar]
- [176].Wang Y-Q and Tsui K-Y 2000. Polarization orderings and new classes of polarization indices J. Public Econ. Theory 2 349–63 [Google Scholar]
- [177].Wolfson MC 1994. When inequalities diverge Am. Econ. Rev 84 353–8 [Google Scholar]
- [178].Bailey KD 1990. Social entropy theory: an overview Syst. Pract 3 365–82 [Google Scholar]
- [179].Venturi V, Kedzierska K, Turner SJ, Doherty PC and Davenport MP 2007. Methods for comparing the diversity of samples of the T cell receptor repertoire J. Immunol. Methods 321 182–95 [DOI] [PubMed] [Google Scholar]
- [180].Soetaertl K and Heip C 1990. Sample-size dependence of diversity indices and the determination of sufficient sample size in a high-diversity. Mar. Ecol. Prog. Ser 59 305–7 [Google Scholar]
- [181].Lewis JE, DeGusta D, Meyer MR, Monge JM, Mann AE and Holloway RL 2011. The mismeasure of science: Stephen jay gould versus samuel george morton on skulls and bias PLoS Biol. 9 1–60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [182].Nagendra H 2002. Opposite trends in response for the shannon and simpson indices of landscape diversity Appl. Geogr 22 175–86 [Google Scholar]