FiberSim: A flexible open-source model of myofilament-level contraction

Abstract

FiberSim is a flexible open-source model of myofilament-level contraction. The code uses a spatially explicit technique, meaning that it tracks the position and status of each contractile molecule within the lattice framework. This allows the model to simulate some of the mechanical effects modulated by myosin-binding protein C, as well as the dose dependence of myotropes and the effects of varying isoform expression levels. This paper provides a short introduction to FiberSim and presents simulations of tension-pCa curves with and without regulation of thick and thin filament activation by myosin-binding protein C. A myotrope dose-dependent response as well as slack/re-stretch maneuvers to assess rates of tension recovery are also presented. The software was designed to be flexible (the user can define their own model and/or protocol) and computationally efficient (simulations can be performed on a regular laptop). We hope that other investigators will use FiberSim to explore myofilament level mechanisms and to accelerate research focusing on the contractile properties of sarcomeres.

Significance

Myotropes, such as omecamtiv mecarbil and mavacamten, are new therapeutics that bind directly to sarcomeric proteins. Their clinical development has reenergized interest in mechanistic understanding of sarcomere level function. FiberSim is an open-source spatially explicit computer model that simulates myofilament level mechanics and can predict how modulating the function of a sarcomeric protein will impact contractility. The software was specifically designed to be flexible and user friendly and may help to further accelerate myofilament research.

Introduction

Different approaches exist to model myofilament-level contraction. For example, Andrew Huxley's original work (1) simulated myofilament dynamics using a system of partial differential equations to determine the time evolution of a two-state model for myosin (bound or unbound to actin). Classical Huxley-type models describe the time-dependent probability that a given myosin molecule is in a particular biochemical state, and the dynamic changes in those probabilities are governed by partial differential equations (2,3). Extensions of Huxley's initial model have been implemented to add multiple actin binding sites (4) or cooperativity between myosin heads (2,3). Our laboratory developed MyoSim (5), a Huxley-type model that can reproduce many features of contractile dynamics (6,7). However, models based on Huxley's approach do not incorporate the three-dimensional configuration of the sarcomere lattice and do not implement all of the spatial constraints on protein interactions.

Spatially explicit models of myofilaments track the position and status of each contractile protein in the sarcomere lattice. These models typically run more slowly than Huxley-type systems and are more complicated to program. However, they may provide a more accurate description of contractile function, as the spatial arrangement of proteins within the sarcomere is likely to impact the underlying biophysics (8). Even if the spatial constraints can be implemented in Huxley-type models, this requires additional assumptions. A simple comparison of the strengths and weaknesses of each approach (Huxley-type and spatially explicit) is provided in Table 1.

Table 1.

Simple comparison of Huxley-type and spatially explicit models

	Huxley type	Spatially explicit
Spatial constraints	Possible (with additional calculations)	Implicit
Computational time	Fast	Slow
Number of parameters	Low	High
Numerical algorithm	Partial differential equations	Stochastic and force-balance

To the authors' knowledge, Daniel, Trimble, and Chase (9) developed the first spatially explicit model of a half-sarcomere. This initial model introduced the concept of compliant realignment of myosin heads and actin binding sites and spurred further work (10), including Fenwick et al.’s study of the spatial distribution of thin filament activation (11). Arguably the most sophisticated model to date is MUSICO, developed by Mijailovich et al. (12). This important model simulates the activation of both thin and thick filaments and has provided important new insights into sarcomere-level function (13).

FiberSim (https://campbell-muscle-lab.github.io/FiberSim/) builds on the pioneering work described above (9, 10, 11, 12, 13), but was developed with a special emphasis on usability and flexibility. The user can vary the biophysical properties of each contractile protein and simulate different types of protocols. Many types of simulations, including those included as demonstrations on the website, can be run in a few minutes on a standard laptop. This makes FiberSim more accessible to most users than prior spatially explicit models.

The following sections provide additional details about the FiberSim model and present example simulations demonstrating how myosin-binding protein C (MyBP-C) can modulate contractile function via localized effects within the sarcomere lattice. Another example shows the dose-dependent response to mavacamten, a myosin-targeting drug. Finally, slack/re-stretch maneuvers are also presented.

Methods

FiberSim describes the contractile properties of a half-sarcomere composed of thick and thin filaments. The underlying framework is similar to that described by groups led by Daniel, Chase, Tanner, and Mijailovich (9,10,12). The code tracks the position and status of each myosin head, each binding site on actin, and each MyBP-C molecule. The software is separated into two components:

• •FiberCpp is the core model and implements the calculations underlying the myofilament system. It is written in C++ and designed solely to run quickly and efficiently. The results of the simulations are written to files using standard formats for portability and efficiency.
• •FiberPy is the interface. This part of the software is written in Python to facilitate rapid development and flexibility. It provides options to run simulations, analyze simulation outputs, visualize the FiberSim framework, make figures and fit simulations to experimental data.

Computational structure

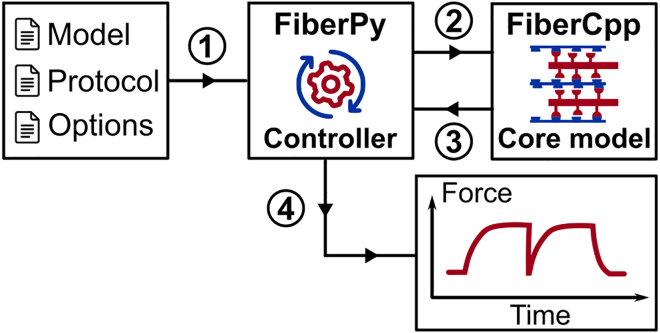
As shown in Fig. 1, FiberSim requires three input files to run a simulation:

• 1.The protocol file is a tab-delimited text file with four columns: the time step, the pCa value $(\text{pCa}=-{\log }_{10}\left[{\text{Ca}}^{2+}\right]),$ the imposed length change (held at 0 for isometric), and the mode of contraction (length-control or force-control mode). Each new line of the protocol file represents an additional time step.
• 2.The model file is a JSON file that describes the half-sarcomere lattice structure and the filament kinetics (see below). JSON is a file format for storing and transporting data that is simple and human-readable. Each parameter value comes with a key, which simplifies the process of adding new features to FiberSim as understanding of sarcomere biology evolves.
• 3.The options file is a JSON file that provides settings, such as the tolerance limit for the force-balance calculations and whether to create log files that track the status of the filaments throughout the simulations.

Fig. 1.

The FiberSim framework. FiberPy is the Python code that handles communication with the core model. FiberCpp is the C++ code that simulates the myofilament level biophysics. Once the simulation is complete, FiberCpp writes the results of the calculations to an output file. FiberPy analyzes the results, summarizes the data, and creates figures such as those presented in Fig. 4. FiberPy can also create lattice snapshots such as the one shown in Fig. 2A.

Sarcomere lattice and filament structure

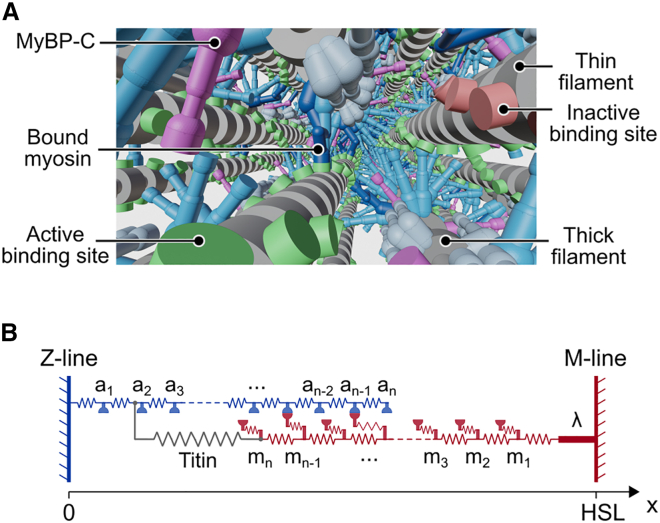
Fig. 2A shows a rendering of the half-sarcomere lattice. Myosin heads are arranged in dimers and can attach to available binding sites on the nearest thin filaments. Thick and thin filaments located at the edge of the lattice are mirrored on the opposite side to minimize edge effects (10,11).

Fig. 2.

Half-sarcomere lattice. (A) Rendering of the half-sarcomere lattice. Myosin heads from the thick filament can attach to binding sites on the surrounding thin filaments. This sarcomere lattice snapshot is generated using Blender (an open-source visualization software available at https://www.blender.org/). (B) A two-dimensional representation of a thin and a thick filament from the half-sarcomere lattice. Each filament is compliant, and represented as a series of nodes connected by linear springs. Actin binding sites are located on the thin filament nodes. Myosin heads and MyBP-C are located on the thick filament nodes. The thick filament is linked to the M-line by a rigid link of length λ to represent the bare zone. HSL is the half-sarcomere length.

FiberSim tracks the location of filament nodes, where either actin binding sites, myosin heads, or MyBP-C molecules are located. (To our knowledge, FiberSim is the first spatially explicit model to incorporate MyBP-C.) Fig. 2 B shows a simplified two-dimensional representation of a single thin and a single half-thick filament. Nodes on each filament are joined by linear springs to account for the filaments' compliance. The thick filament is connected to the M-line by a rigid link to represent the bare zone. In 3D, titin springs link each thick filament to the six nearest thin filaments.

The model file defines the number of filaments in the simulation as well as structural and biophysical properties, including the number of binding sites per filament, the stiffness of the compliant link, and the rate functions defining binding site and myosin kinetics. The models provided in the demonstrations on the website are intended to mimic striated muscle structure so that:

• •Each thin filament node holds two diametrically opposed binding sites, each of which can be available (active) or not available (inactive) for myosin binding.
• •Each thick filament node holds six myosin heads arranged in three dimer pairs. Each myosin head can bind to a nearby active actin binding site. Again, to our knowledge, FiberSim is the first spatially explicit in which paired myosin heads can interact to form a super-relaxed state (14).

Force-balance calculations

FiberSim stores the distance of each node from the Z-line in an x-position vector. Thus, this vector holds information about the position of each molecule within the lattice structure. At each simulation time-step, the x-position vector is calculated by assuming that forces are balanced at each node (9).

FiberSim performs this calculation using an iterative approach based on the conjugate gradient method (15). This approach takes advantage of the sparsity of the stiffness matrix originally described by Daniel et al. (9). The iterative approach is much faster and requires less memory than solving the full matrix equation using direct methods.

The complexity of the calculations depends on the total number of nodes (N). The conjugate gradient method solves the force-balance calculation using an algorithm where the number of calculations and the memory required scale linearly with N. This is normally written as O(N). In contrast, the most efficient direct methods scale as O(N³) and require O(N²) memory (15). For a system with 100 thick filaments, the conjugate gradient method is approximately 100² = 10,000 times faster.

An example of an isometric twitch simulation (with 196 thick filaments) is provided in Fig. S1 in the Supporting material. This simulation runs in approximately 30 min on a standard Windows laptop, using three of the four processors to perform the calculations. (Simulations with a smaller number of thick filaments, including those demonstrated on the project website, run much faster but have more stochastic noise.) As a comparison, MUSICO takes approximately 10 h on a system with 192 processors to simulate a comparable experiment (13).

The constant time step that is defined in the protocol file also impacts the computational time. Fig. S2 compares FiberSim simulations run with different time steps. The results show that a time step of 10⁻⁴ s is enough to provide numerical accuracy for the time evolution of thin and thick filaments activation under the conditions used in our demonstrations.

Thin filament and thick filament kinetics

In FiberSim, the two actin strands forming the thin filament are composed of regulatory units. Each thin filament regulatory unit consists of seven consecutive active binding sites which switch simultaneously between an inactive or active state, depending on the calcium concentration and on the transition rate constants ${\text{k}}_{\text{on}}$ and ${\text{k}}_{\text{off}}$. Those parameters are defined by the user. A cooperative mechanism is also implemented such that:

$$\{\begin{array}{l}{\text{k}}_{\text{activate}}={\text{k}}_{\text{on}}.\left(1+\text{n}.{\mathrm{\gamma }}_{\text{coop}}\right)\\ {\text{k}}_{\text{deactivate}}={\text{k}}_{\text{off }}.\left(1+\left[2-\text{n}\right].{\mathrm{\gamma }}_{\text{coop}}\right)\end{array}$$

where n is the number of adjacent regulatory units in the active state (n = 0, 1 or 2), and γ_coop defines how the status of each unit is influenced by its immediate neighbors.

In FiberSim, a single bound myosin prevents all seven of the binding sites in a regulatory unit from inactivating. Although the model only has two explicit thin filament states, it mimics some of the features of the biochemical open state of thin filament, which cannot return to the blocked state, even in the absence of calcium (16). Fig. S3 shows activation curves for the thin filament as a function of calcium concentration. These curves are in good agreement with experimental data of thin filament activation measured with fluorescent probes (17).

The kinetic scheme and the rate constants for individual myosin heads are defined by the user. The stochastic approach described in (18) is used to determine which transitions occur during each time step.

Software availability

FiberSim is available for free download under the GPL3 license. Full documentation and examples are available at the project home page, https://campbell-muscle-lab.github.io/FiberSim/. Source code, bug reports, and development plans are provided at https://github.com/campbell-muscle-lab/FiberSim/. This article describes release version 2.0.2, which is archived at https://doi.org/10.5281/zenodo.4929389.

Results

The results presented in this section are reproduced from examples posted at https://campbell-muscle-lab.github.io/FiberSim/pages/manuscripts/2021a/2021a.html and https://campbell-muscle-lab.github.io/FiberSim/pages/manuscripts/2021b/2021b.html.

MyBP-C

The first set of simulations investigate how one potential action of MyBP-C impacts contractile dynamics. Specifically, the calculations predict how contractile force is changed if MyBP-C stabilizes the super-relaxed state of myosin and/or binds to actin (19, 20, 21).

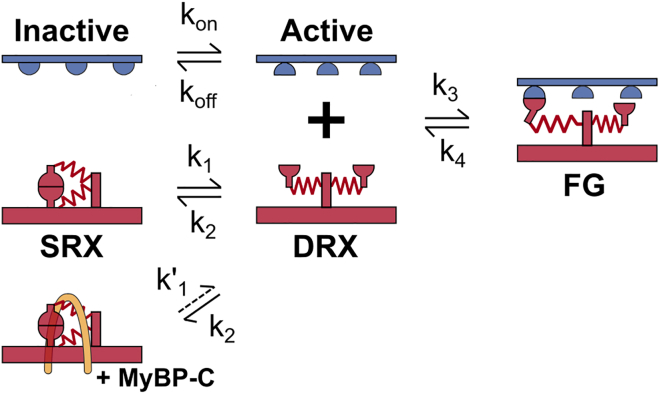
The calculations simulate a half-sarcomere lattice containing 100 thick and 200 thin filaments. Myosin heads cycle through the three-state model (6) shown in Fig. 3 that includes a super-relaxed (SRX) state.

Fig. 3.

Example of a three-state myosin kinetic model. Myosin dimers (red) can transition together between the SRX state and the DRX. Then they can transition independently to a force-generating state. Attachment to actin (blue) and force generation are only allowed if the binding site is available for binding (active state). Rate constants (k_i) can be constant or depend on stretch, node force, and/or on the MyBP C status.

Dimers of myosin heads can transition together from the SRX state (gray structures in Fig. 2 A) to the disordered-relaxed state (DRX, light blue structures in Fig. 2 A). Then, each myosin head is able to bind to an available actin binding site and transition to a force-generating state (dark blue structures in Fig. 2 A).

Two sets of simulations are presented. In the base model, MyBP-C molecules (pink structures in Fig. 2 A) are assumed to have no effect. Thus, k′₁ in Fig. 3 is equal to k₁. In the MyBP-C stabilized model, k′₁ for myosin dimers in the C-zone is reduced by 30%.

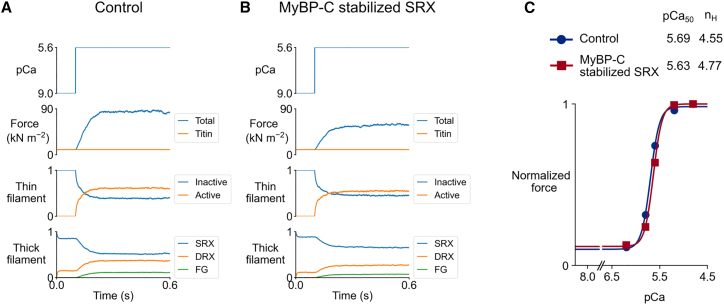
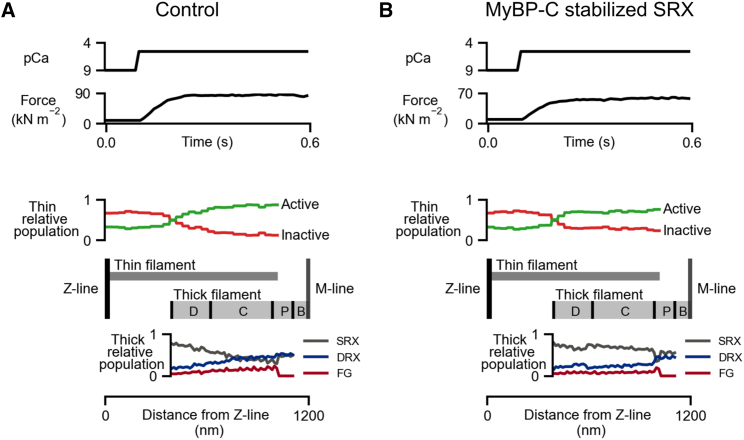
Fig. 4A and B show simulations for an isometric activation protocol at pCa = 5.6 in the base case and in the MyBP-C stabilized SRX case. Fig. 4 C shows normalized tension-pCa curves generated by running the isometric activation protocols with different pCa values. Each tension-pCa curve simulation runs in approximately 15 min on a regular laptop. Interestingly, there is a rightward shift of the tension-pCa curve when MyBP-C stabilizes SRX heads in the C-zone (pCa₅₀ = 5.63 compared with pCa₅₀ = 5.69 in the base case).

Fig. 4.

Isometric contractions at constant calcium activation and tension-pCa curves. Isometric contraction at pCa = 5.6 and half-sarcomere length (HSL) = 1.2 μm for the (A) base and (B) MyBP-C stabilized SRX case. (C) Tension-pCa curves built from isometric contractions at different pCa values.

Since the model is spatially explicit, the proportion of binding sites and myosin heads in each state can be calculated as a function of their distance from the Z-line. Fig. 5 shows snap shots at steady state along with a schematic representation of the half-sarcomere.

Fig. 5.

Intra-half-sarcomere heterogeneity. Panels show the relative populations of the actin and myosin states at steady state plotted against distance from the Z-line for (A) base and (B) MyBP C stabilized SRX conditions. pCa = 5.6 where isometric force is approximately 70% of maximum.

In this model, k₁ and k′₁ are assumed to be force dependent (6). Force increases toward the M-line in a spatially explicit model so the relative population of the DRX state increases with the x-coordinate in the base simulation. This underlies a parallel increase in the number of force-generating heads at the M-line end.

In the MyBP-C-stabilized SRX condition, the SRX to DRX transition is slowed in the C-Zone. Consequently, the number of force-generating heads is reduced and force-pCa curves are shifted to the right (lower pCa₅₀, reduction in Ca²⁺ sensitivity, Fig. 4 C).

Movies showing the time evolution of the spatial population distribution with and without MyBP-C stabilization are available at https://campbell-muscle-lab.github.io/FiberSim/pages/manuscripts/2021a/2021a.html.

There is also experimental evidence suggesting that MyBP-C can bind to actin (21). Fig. 6 A shows simulations investigating some of the contractile consequences of this mechanism. MyBP-C can compete with myosin heads for binding sites on actin. If an MyBP-C molecule binds, it acts as an additional cross-link with stiffness k_pc and, thus, creates a drag force during interfilamentary movement. Similar to bound myosin heads, bound MyBP molecules also prevent the regulatory unit from deactivating. MyBP-C can thus contribute to myofilament cooperativity. When MyBP-C is attached, it is assumed that it is not stabilizing the SRX state of myosin dimers anymore.

Fig. 6.

MyBP-C potential roles on thick and thin filaments, and its impact on tension-pCa curves. (A) MyBP-C interaction with the thick and thin filaments. MyBP-C stabilizes the SRX state of myosin dimers. MyBP-C is also able to bind to nearby active binding sites. (B) Tension-pCa curves for the four situations (base, MyBP-C stabilized SRX only, MyBP-C binding only, and MyBP-C stabilized SRX + MyBP-C binding).

The four tension-pCa curves shown in Fig. 6 B correspond with four situations. The first two are the base case and the MyBP-C stabilized SRX case described earlier. The last two correspond with MyBP-C binding to actin only (unbound MyBP-Cs do not stabilize SRX), and to MyBP-C stabilized SRX together with actin binding (unbound MyBP-Cs stabilize SRX). When the only MyBP-C effect is actin binding, there is an increase in calcium sensitivity, but no substantial change in maximal isometric force. When MyBP-C can bind to actin and also stabilize the SRX when unbound, Ca²⁺ sensitivity is enhanced but maximum force is reduced.

Mavacamten

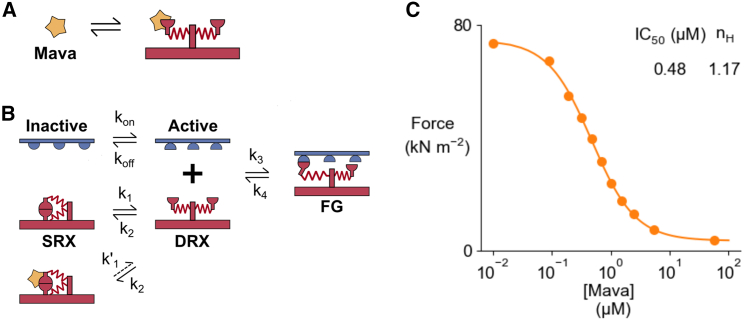
Myotropes, such as omecamtiv mecarbil and mavacamten, are new therapeutics that bind directly to sarcomeric proteins (22). The next set of simulations show that it is possible to produce a dose-dependent curve associated with a drug such as mavacamten (Mava). This myotrope has been shown to stabilize the SRX state of myosin (23). In the model, Mava-free myosins have the same kinetics scheme as the one presented in Fig. 3, and Mava-bound myosins have a decreased k₁ (k′₁ = 0.1 k₁) (Fig. 7). More precisely, as both myosin heads form a dimer transition together in and out of the SRX state, a Mava molecule bound to the first myosin head of any dimer will decrease the rate of transition to the DRX state for this dimer.

Fig. 7.

Mava's role on myosin kinetics and dose-dependent response. (A) Mava is assumed to be in rapid equilibrium with myosin. (B) Kinetics model. Mava stabilizes the SRX state of myosin. (C) The maximal isometric force is computed for different fractions of Mava-bound myosins. It is then possible to plot the isometric force as a function of Mava concentration.

The steady-state proportion of myosin heads bound by Mava can be calculated as a function of the Mava concentration using the experimental data from (24). This prediction can then be integrated into FiberSim to predict a dose-response curve for maximum isometric force (Fig. 7 C). This curve qualitatively compares to the ATPase dose-dependent curve shown in Fig. 4 from (24).

k_tr Maneuvers

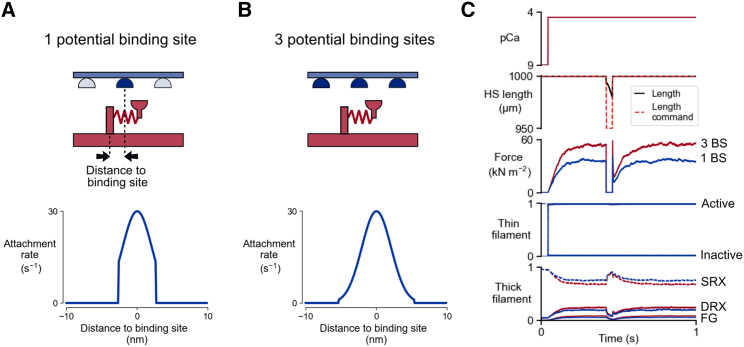
The last demo shows a slack/re-stretch (or k_tr) maneuver simulation. Results from two different simulations at full calcium activation are provided in Fig. 8. In the first simulation, myosin heads can only bind to the nearest binding site (number of potential binding sites set to 1, see Fig. 8 A). In the second simulation myosin heads can bind to one of the three nearest binding sites (number of potential binding sites set to 3, see Fig. 8 B).

Fig. 8.

Slack/re-stretch maneuvers for different numbers of potential binding sites. (A) Myosin heads are allowed to bind to the nearest binding site (top). The gaussian attachment rate profile is thus zero outside of the nearest binding site distance range (bottom). (B) Myosin heads are allowed to bind to one of the three nearest binding sites (top). The gaussian attachment rate profile is thus wider than for the “1 potential binding site” case (bottom). (C) Slack/re-stretch protocols. The half-sarcomere length is suddenly shortened by 5%, then stretched back to its initial value. Immediately after the rapid shortening, the half-sarcomere shortens against zero load (force is zero). During the re-stretch, there is a sudden increase in force, followed by a force drop that does not reach zero (force residual). The isometric and residual forces are greater for simulations with 3 potential binding sites (red) than for 1 potential binding site (blue).

For the slack/re-stretch protocol, the half-sarcomere length is suddenly decreased by 5%, held constant for 40 ms and then stretched back to its initial value. The imposed variations in half-sarcomere during this maneuver are shown in Fig. 8 C (“Length command”, dashed lines), but they do not always match the real half-sarcomere length (“Length”, solid line). This is because, during rapid shortening, the force falls to zero and the half-sarcomere becomes slack. FiberSim tracks the moment at which the force reaches zero and switches the contraction mode from isometric to isotonic. The half-sarcomere then shortens against no load, until force redevelops. As soon as this occurs, FiberSim switches to the isometric mode again, and the “Length command” and “Length” curves match. This mimics the experimental situation in which a fiber that becomes slack falls out of plane so that the distance between the ends of the preparation is no longer indicative of the half-sarcomere length.

Force recovery traces are shown in Fig. 8 C. Each curve reproduces the typical residual force (force not dropping to zero) observed experimentally during the re-stretch phase (25). The simulation with three potential binding sites shows a greater force residual, as well as greater isometric force compared with the simulation with one potential binding site.

Discussion

FiberSim runs on standard PCs and can simulate typical experiments in a few minutes. The software was designed to be flexible and users can define their own simulation protocols, adjust the structural details of the filament models, and implement different types of myosin and MyBP-C kinetics. It is also possible to simulate the action of myotropes. More demonstrations, including isometric twitch contractions and simulations of force-velocity relationships, are provided on the FiberSim website.

The spatially explicit aspect of FiberSim allows for the precise description of local behaviors at the molecular level. For instance, myosin heads can only bind to nearby sites and may be blocked by competitive binding. Similarly, SRX to DRX transitions can depend on the local force in the thick filament. This leads to intra-half-sarcomere effects such as in Fig. 5 A where the DRX population increases toward the M-line as the force in the thick filament backbone accumulates.

MyBP-C also exhibits local effects due to its restricted location within the sarcomere, such as the decrease in DRX and force-generating myosin populations in the C-zone upon MyBP-C stabilization of the SRX (Fig. 5 B). This action of MyBP-C on the thick filament leads to a decrease in calcium sensitivity and maximal isometric force (Figs. 4 C and 6 B, red curves). In contrast, when the sole MyBP-C effect is actin binding, there is an increase in calcium sensitivity. This is due to bound MyBP-C molecules activating the thin filament via its intrinsic cooperativity. However, at full calcium activation, where almost all binding sites are activated, enhancing cooperativity has no additional effect (Fig. 6 B, light blue curve). Thus, maximum force is comparable with that calculated for the base condition. When MyBP-C can bind to actin and also stabilize the SRX when unbound (Fig. 6 B, pink curve), Ca²⁺ sensitivity is enhanced but maximum force is decreased (because more heads remain in the SRX state). This illustrates the complex role of MyBP-C that can act both as a cross-bridge inhibitor and a calcium sensitizer (21). It is worth mentioning that a model with a set of ordinary differential equations published by Walcott et al. (26) also investigated the potential role of MyBP-C binding to actin and competing with myosin heads, and it also showed that complex effects can arise from this regulatory mechanism. It is important to note that this model is based on motility assays data with solubilized MyBP-C fragments, and not on intact myofilaments.

The k_tr maneuvers shown in Fig. 8 qualitatively reproduce the typical force recovery pattern observed experimentally (25). More important, the simulations show that the number of potential binding sites for myosin impacts (1) the isometric force and (2) the residual force. This can be explained as follows: as additional binding sites are made available for myosin binding, more cross-bridges attach, and isometric force increases. During the re-stretch phase of the k_tr, force increases transiently as the attached heads are rapidly extended. This strains the links and the myosins detach quickly. However, in FiberSim, the detached heads are replaced almost immediately because the interfilamentary movement increases the probability of new myosin heads coming within range of an available binding site. Thus, rather than force dropping to near zero, FiberSim-based simulations of k_tr produce a large residual force (similar to that measured in experiments) that reflects an increased rate of myosin attachment during rapid interfilamentary movement. This type of effect can be built into Huxley-based models (27), but arises naturally in FiberSim because of its spatially explicit framework.

Spatially explicit frameworks are also useful for simulating the potential effects of MyBP-C. Since these regulatory molecules are localized to the C-zone of the half-sarcomere they can only exert a direct influence on a portion of the myosin heads. FiberSim handles this explicitly; some myosin heads are controlled by MyBP-C and others are not.

In summary, FiberSim is a new, open source computational tool for studying myofilament contraction. To the authors' knowledge, it is the first spatially explicit model to incorporate MyBP-C and to describe myosin dimers interacting to form a SRX state. The software is user friendly and the calculations run quickly enough that it can be used effectively on standard laptops. We hope that other investigators will use FiberSim to explore myofilament level mechanisms and would be excited to collaborate with researchers who want to add additional features.

Author contributions

SK wrote the manuscript, helped develop the website and demonstrations, and optimized and tested FiberCpp. DC worked on prototypes of the code-base and developed the website and GitHub repository. QY helped optimize the force-balance algorithm in the core model. KC planned the overall project, wrote the first versions of FiberCpp and FiberPy, helped develop the demonstrations, and edited the final manuscript.

Editor: Samantha Harris.

Supporting citations

Reference (28) appears in the Supporting material.