Significance
Spillover of infectious diseases from wildlife populations into humans is an increasing threat to human health and welfare. Current approaches to manage these emerging infectious diseases are largely reactive, leading to deadly and costly time lags between emergence and control. Here, we use mathematical models and data from previously published experimental and field studies to evaluate the scope for a more proactive approach based on transmissible vaccines that eliminates pathogens from wild animal populations before spillover can occur. Our models are focused on transmissible vaccines designed using herpes virus vectors and demonstrate that these vaccines—currently under development for several important human pathogens—may have the potential to rapidly control zoonotic pathogens within the reservoir hosts.
Keywords: transmissible vaccines, zoonoses, emerging infectious disease, spillover, emergence
Abstract
Transmissible vaccines have the potential to revolutionize how zoonotic pathogens are controlled within wildlife reservoirs. A key challenge that must be overcome is identifying viral vectors that can rapidly spread immunity through a reservoir population. Because they are broadly distributed taxonomically, species specific, and stable to genetic manipulation, betaherpesviruses are leading candidates for use as transmissible vaccine vectors. Here we evaluate the likely effectiveness of betaherpesvirus-vectored transmissible vaccines by developing and parameterizing a mathematical model using data from captive and free-living mouse populations infected with murine cytomegalovirus (MCMV). Simulations of our parameterized model demonstrate rapid and effective control for a range of pathogens, with pathogen elimination frequently occurring within a year of vaccine introduction. Our results also suggest, however, that the effectiveness of transmissible vaccines may vary across reservoir populations and with respect to the specific vector strain used to construct the vaccine.
Pathogen transmission at the human–wildlife interface is a fundamental threat to human health. Examples of the detrimental effects that zoonotic spillover has on humans include the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic (1), the 2014–2015 Ebola virus epidemic (2), and the persistent threat of Lassa virus (LASV) in West Africa (3, 4). These spillover events illustrate the significant burden that zoonotic pathogens can impose on human populations and emphasize the importance of controlling zoonotic pathogens before spillover occurs.
Historically, mass vaccination and culling have been the two most prominent methods for controlling zoonotic pathogens within wildlife reservoirs. However, the success of these traditional control measures relies on the ability to vaccinate or remove a high proportion of the target animal population, a requirement that may often be infeasible (5, 6). As a consequence, wildlife vaccination has generally proven successful at limiting spillover only in special cases where mass distribution of vaccine-laced baits can be regularly accomplished (e.g., rabies carried by raccoons and foxes in North America and Europe, respectively) (7). An approach that could overcome the challenges faced by traditional wildlife vaccination programs is to use recombinant vector vaccines capable of self-dissemination (8, 9). Transmissible recombinant vector vaccines are constructed by engineering a benign vector virus to carry and express an immunogenic transgene from a specific target pathogen (10). In theory, the resulting vaccine takes on the transmission characteristics of the vector virus, while triggering an immune response specific to the target pathogen. Leading candidates to serve as vectors for transmissible vaccines are betaherpesviruses (e.g., murine cytomegalovirus [MCMV]), due to their broad taxonomic distribution across important groups of reservoir species, high species specificity, and mild or undetectable virulence in most natural reservoirs (11, 12).
Although previous modeling efforts have demonstrated the potential benefits of vaccine transmission (9, 13–17), these models have been general and not parameterized for specific candidate vaccine vectors or zoonotic pathogens. Further, existing models have focused almost exclusively on steady-state solutions and have not addressed the timescale over which zoonotic pathogens can be eliminated. Consequently, we do not yet know how well transmissible vaccines developed using betaherpesvirus vectors such as MCMV are likely to work in practice. To address this gap, we develop a mathematical model describing the spread of an MCMV-vectored transmissible vaccine through a reservoir population and parameterize it using data from captive and free-living mouse populations. We use this parameterized model to predict how rapidly MCMV-vectored transmissible vaccines can eliminate pathogens with different properties and to quantify the scope for variable outcomes across reservoir populations and across vaccines developed from different vector strains.
Results
Pathogens That Generate Acute Viral Infections Are Vulnerable to Transmissible Vaccines.
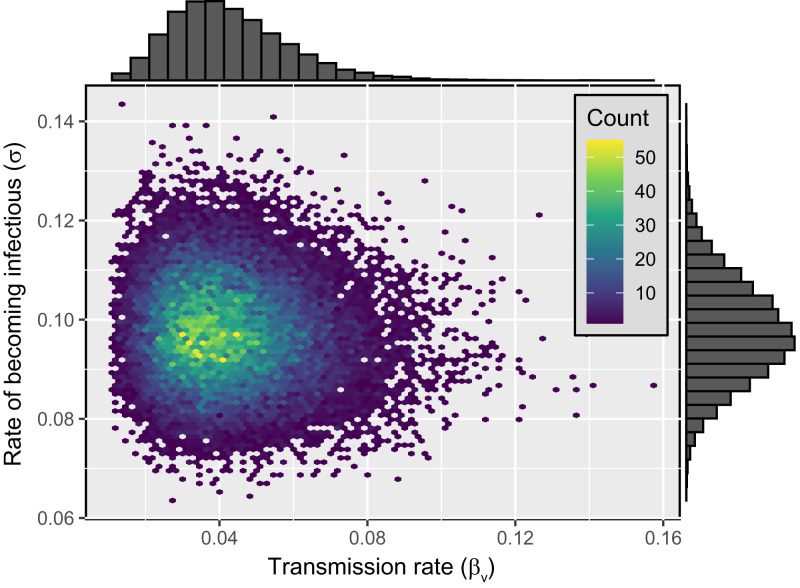
We used approximate Bayesian computation (ABC) to parameterize an epidemiological model tuned to the biology of betaherpesviruses such as MCMV. Our approach capitalized on a unique dataset that tracked the spread of MCMV through naive mouse populations inhabiting seminatural enclosures (18). Applying our ABC algorithm to these time series data allowed us to estimate the transmission rate of MCMV (βv) and the rate at which exposed individuals become infectious (σ) as the mode of the bivariate posterior distribution (Fig. 1).
Fig. 1.
Bivariate posterior distribution of the transmission rate (βv) and the rate at which individuals exposed to the virus transition into the infectious class (σ). The marginal distribution of the transmission rate and rate of becoming infectious are displayed on the top and right of the density plot, respectively. The modal values of the distribution are and .
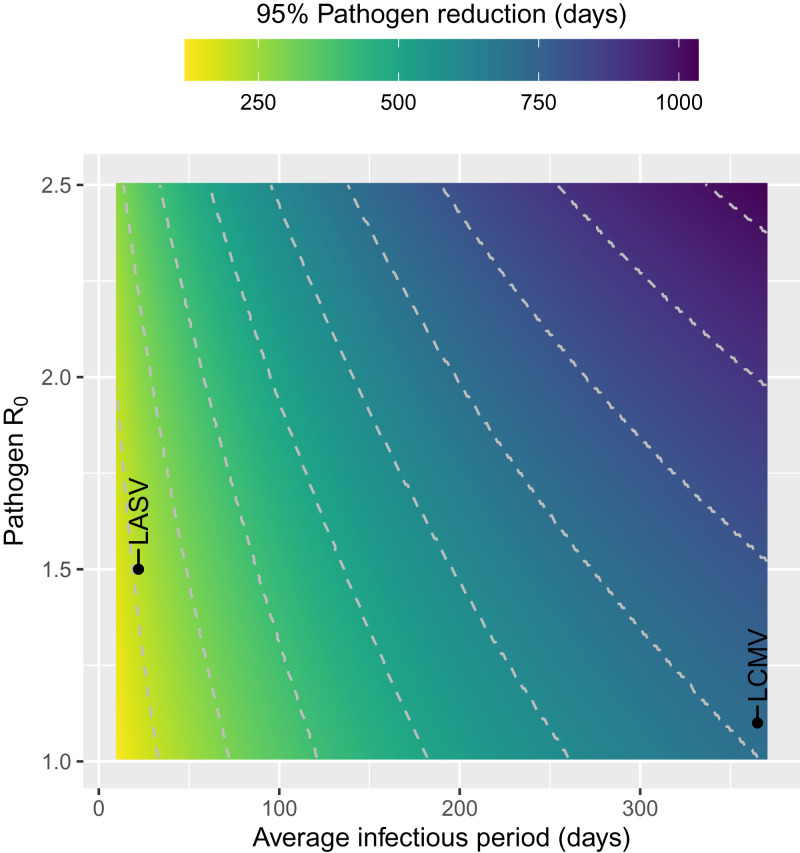
Next, we used these parameter estimates to predict how rapidly an MCMV-vectored transmissible vaccine could reduce pathogen prevalence. Specifically, simulating the interaction between the transmissible vaccine and pathogen revealed that the time required to reduce pathogen prevalence by 95% varies widely across pathogens and depends on the pathogen’s basic reproductive number (R0) and infectious period. For example, our model predicts an MCMV-vectored transmissible vaccine will reduce pathogen prevalence by 95% in 156 d if the pathogen has an R0 of 1.5 and infectious period of 10 d, but will require 1,028 d to accomplish an identical reduction for a pathogen with an R0 of 2.5 and infectious period of 365 d (Fig. 2).
Fig. 2.
Time to 95% pathogen reduction as a function of pathogen R0 and the infectious period (). Simulations start at the steady-state quantities for susceptible and pathogen-infected individuals, and 10% of the susceptible population is exposed to the transmissible vaccine. The pathogens highlighted in this figure include LASV and LCMV.
To better ground our predictions in the biology of specific pathogens, we used our model to predict the impact of an MCMV-vectored transmissible vaccine on LASV and lymphocytic choriomeningitis virus (LCMV). Both pathogens regularly spill over into the human population from rodent reservoirs and cause significant morbidity (19, 20). Although the primary reservoir of LASV, the multimammate rat Mastomys natalensis, is only distantly related to the domestic mouse, both LASV and LCMV do infect species within the genus Mus (21). Using published estimates for the seroprevalence and infectious period of these pathogens (22, 23) we developed models describing their response to an MCMV-vectored transmissible vaccine. These models were used to simulate the introduction of a transmissible vaccine into a reservoir population where the target pathogen was endemic. These simulations suggest that LASV is very susceptible to control with an MCMV-vectored transmissible vaccine, with 95% reduction achieved in only 212 d. In contrast, our model predicts that LCMV is more recalcitrant and requires 716 d for 95% reduction to be achieved (Fig. 2). The greater resistance to the vaccine exhibited by LCMV is mostly due to its increased infectious period which we have assumed is, on average, lifelong. In contrast, the infectious period for LASV has been estimated to be 22 d, on average (22, 23). These results highlight that pathogens that generate acute, short-term infections and have relatively low R0 are most readily controlled using MCMV-vectored transmissible vaccines.
We further explored the uncertainty in our predictions for the impact of an MCMV-vectored transmissible vaccine by conducting simulated vaccination campaigns where the vaccine parameters were drawn at random from the bivariate posterior distribution (i.e., Fig. 1). Performing 100 simulated vaccine releases for LASV and for LCMV revealed considerable uncertainty in the timescale over which each pathogen can be locally eliminated. Specifically, our results show that, when 10% of the susceptible population is directly vaccinated, the time required for LASV to be reduced by 95% ranges from 121 d to 371 d post vaccine introduction, whereas the time required for LCMV to be reduced by 95% ranges from 609 to 940 d post vaccine introduction (Fig. 3). In cases where vaccine introduction is more challenging, the time required to reduce the pathogen is increased. For instance, if only 1% of the susceptible population can be vaccinated, we find that the time to reduce LASV by 95% ranges from 176 d to 762 d, and the time to reduce LCMV by 95% ranges from 652 d to 1,197 d (SI Appendix, Fig. S2).
Fig. 3.
Temporal dynamics of (A) LASV and (B) LCMV reduction as a result of using an MCMV-vectored transmissible vaccine. Simulations are initialized at the steady-state quantities for susceptible and pathogen infected individuals, with 10% of the susceptible population exposed to the transmissible vaccine. For each pathogen, we randomly sampled βv and σ from the posterior distribution 100 times, and simulated our model forward in time for each set of parameters. The gray region represents the range of values observed across the 100 replicate simulations, where the orange dashed line is the mean. The gray vertical lines indicate the minimum, mean, and maximum time to 95% pathogen reduction (in A, min = 121 d, mean = 194 d, max = 371 d; in B, min = 609 d, mean = 701 d, max = 940 d).
Transmissible Vaccines Are Robust to Variation in Efficacy.
The preceding results are predicated on the development of an MCMV-vectored transmissible vaccine that blocks 100% of pathogen transmission. In practice, however, vaccines for wild animal populations will rarely block 100% of transmission, as demonstrated by vaccination campaigns using oral rabies vaccine (24). To account for imperfect vaccine efficacy, we extended our basic model to allow partial blocking of pathogen transmission (SI Appendix). With the extended model, we explored how vaccine efficacy, quantified as the reduction in pathogen transmission rate in vaccinated animals (ρ), impacts a transmissible vaccine’s ability to protect a reservoir population from pathogen invasion, and also how it impacts the time required to effectively eliminate an endemic pathogen.
We began our analysis by deriving the critical vaccine efficacy that must be achieved for a transmissible vaccine to protect a reservoir population from pathogen invasion. Specifically, results derived in SI Appendix show that the efficacy of an MCMV-vectored transmissible vaccine must exceed the critical value
| [1] |
to prevent the spread of a pathogen, where and are the basic reproductive numbers of the pathogen and vaccine, respectively. Numerical analyses suggest this critical value also represents the vaccine efficacy required for a transmissible vaccine to eliminate an endemic pathogen (SI Appendix, Fig. S1). Without reintroduction of the vaccine, this result demonstrates that transmissible vaccines with lower vaccine efficacy must be more transmissible to control a pathogen.
Although vaccine efficacy plays an important role in determining the success or failure of pathogen control, it has only a modest influence on the timescale over which pathogen elimination occurs. Specifically, numerical simulations of MCMV-vectored transmissible vaccines show that, if vaccine efficacy exceeds the critical value for eliminating LASV and LCMV, the timescale over which pathogen elimination occurs is relatively insensitive to vaccine efficacy (Fig. 4).
Fig. 4.
Temporal dynamics of pathogen prevalence for (A) LASV and (B) LCMV for three levels of vaccine efficacy. Here, pathogen prevalence is defined as the fraction of individuals that are actively infectious with the pathogen. Simulations are initialized at the steady-state quantities for susceptible and pathogen-infected individuals, where 10% of the susceptible population is exposed to the transmissible vaccine.
Reservoir Population and Vector Strain May Matter.
An additional source of uncertainty in our predictions arises from our reliance on data from MCMV introductions into naive, captive mouse populations using a single genetic variant of MCMV. Although the time series data from these experimental introductions is invaluable for the opportunities it provides for robust parameter estimation, these parameters may vary across wild mouse populations and MCMV strains used as vaccine vectors. To evaluate the scope for local adaptation of vector strains to restrict the spatial scale over which any specific vector strain can be used effectively to construct a transmissible vaccine, we analyzed published data describing the prevalence of two MCMV strains, as defined by the genotype of ie1, a major immunodominant T cell epitope (25, 26), within four populations of free-living wild mice (27). This analysis rests on two important assumptions. First is that the prevalence of these MCMV sequences represents their strain and population-specific equilibrium. Second is that all strains are independent. To the extent that these assumptions hold, we can use classical epidemiological theory to predict the maximum R0 of a pathogen that could be eliminated by a transmissible vaccine constructed from each MCMV strain within each reservoir population (28). Specifically, we know that the fraction of a population that must be vaccinated to protect against a pathogen with basic reproductive number R0 is equal to
| [2] |
Rearranging Eq. 2 and substituting in the strain and location specific values for MCMV prevalence for p allows us to calculate the range of pathogen R0 that an MCMV-vectored transmissible vaccine with perfect efficacy could protect against (Table 1). The results of this simple analysis suggest the potential for considerable variation in the protective ability of transmissible vaccines constructed from different MCMV strains and used in different reservoir populations, with the pathogen R0 that can be suppressed ranging from 1.17 to 11.72. We extended this simple equilibrium analysis to the timescale of pathogen elimination by combining our ABC estimate for σ () with the prevalence of the MCMV variants within each of the four free-living mouse populations to yield estimates for the transmission rate of each MCMV strain within each reservoir population.
Table 1.
Parameter estimates
| Maximum pathogen control | ||||
| Location | Strain | () | Method | Data source |
| Outdoor enclosure | N1 | 11.72 | ABC | (18) |
| Boullanger Island | G4 | 1.29 | Steady state | (27) |
| Macquarie Island | G4 | 11.35 | Steady state | (27) |
| Canberra | G4 | 1.75 | Steady state | (27) |
| Walpeup | G4 | 1.69 | Steady state | (27) |
| Boullanger Island | K181 | 7.83 | Steady state | (27) |
| Macquarie Island | K181 | 1.17 | Steady state | (27) |
| Canberra | K181 | 2.60 | Steady state | (27) |
| Walpeup | K181 | 1.62 | Steady state | (27) |
MCMV parameter estimates were found using a combination of ABC and steady-state methods. Because the N1 strain was not found in any of the natural populations that were sampled across Australia, the only N1 sample comes from the enclosure study. Further, to account for possible sampling error during the capture of rodents, we calculated the Clopper–Pearson 95% CI on MCMV sampling data. To be conservative in our parameter estimates, we used the minimum βv value calculated from the 95% CI to estimate R0.
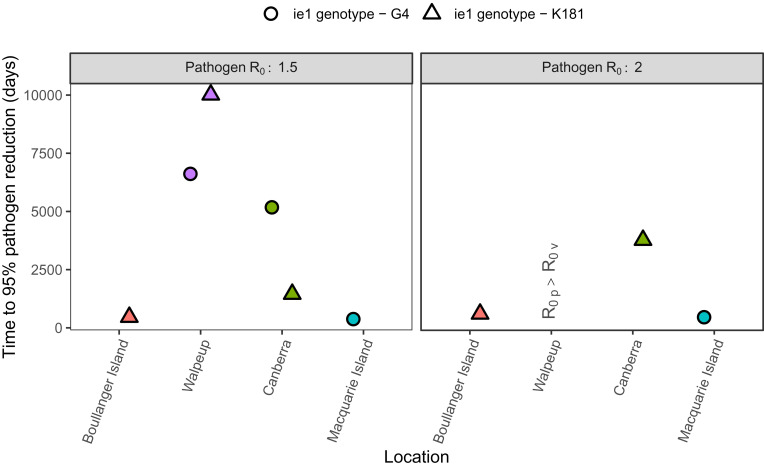
Our results reveal potentially important spatial variation in the time required for a transmissible vaccine to reduce pathogen prevalence by 95%. For example, the prevalence of a pathogen with an is reduced by 95% in only three of the four locations when using the parameter estimates from our equilibrium analysis of strain prevalence (Fig. 5). Even in the three locations where a 95% reduction is achieved, the time it takes to reach this objective differs by thousands of days between the three locations and the two MCMV strains defined by their ie1 genotype.
Fig. 5.
Time to 95% pathogen reduction when parameters are estimated from equilibrium analyses of strain prevalence. Simulations start at the steady-state quantities for susceptible and pathogen-infected individuals (SI Appendix), where 10% of the susceptible population is exposed to the transmissible vaccine. represents the scenario when the vaccine fails to reduce the pathogen.
Discussion
We have developed a parameterized model predicting how much, and how rapidly, a betaherpesvirus-vectored transmissible vaccine can be expected to reduce the prevalence of a target pathogen. Our results demonstrate that the most vulnerable pathogens are those with relatively short infectious periods and a modest R0. Pathogens that maintain a greater R0, or that generate long-term chronic infections, take longer to eliminate or, in some extreme cases, may be impervious to betaherpesvirus-vectored transmissible vaccines altogether. Further, our results demonstrate that MCMV-vectored transmissible vaccines remain effective against a broad range of pathogens even when they provide less than perfect blocking of pathogen transmission. Perhaps most importantly, however, our results suggest that the effectiveness of MCMV-vectored transmissible vaccines may depend on the virus strain used to construct the vaccine and the target population into which the vaccine is ultimately deployed. If this prediction is borne out, it complicates the design of transmissible vaccines, and suggests it may be difficult to develop “universal” transmissible vaccines that transmit well across geographically distinct reservoir populations.
Although our results support betaherpesvirus-vectored transmissible vaccines as effective tools, these results are tempered by several important assumptions. First, and of critical importance, is our assumption that MCMV is capable of superinfection. This assumption is supported by studies showing that betaherpesviruses like MCMV can superinfect animals already infected with MCMV (27, 29). At the same time, however, other studies have suggested superinfection is much more challenging (30–32) and may be achievable only by genetically differentiated MCMV strains. If superinfection requires genetic divergence, transmissible vaccines constructed from locally common betaherpesvirus strains or constructed in a way that results in the rapid loss of their immunogenic cargo are unlikely to succeed (15, 16, 33). Second, our inferences drawn from wild populations assume the geographic distribution of MCMV prevalence represents an equilibrium state and that differences in equilibrium prevalence thus reflect location specific transmission rates. There are, of course, many reasons this may not be true, including the possibility that geographic variation in MCMV prevalence is shaped by seasonal fluctuations in the population size of the target reservoir (34). Third, we have assumed betaherpesvirus-vectored transmissible vaccines will transmit to the same degree as the wild-type virus vector. This may not be the case, as genetically engineering the vector virus to carry an immunogenic transgene may alter the transmissibility of the self-disseminating vaccine (35).
A clear but unavoidable limitation of our work is our reliance on data from Australian populations of Mus musculus (18, 27). We focused on these populations due to the availability of unique experimental and field datasets that do not yet exist for other betaherpesviruses and reservoir populations. The limitation, of course, is that our results may not generalize well to other geographic regions or rodent reservoir populations of greater concern for viral spillover. In addition, we have defined a strain based on a 126–base pair sequence of the ie1 gene (27). And, while this is a dominant T cell epitope, there are other genes within MCMV that could be expected to modulate geographical penetrations. Unfortunately, data on the prevalence of betaherpesviruses within natural populations of important reservoir species are extremely scarce (29), and experiments tracking the spread of betaherpesviruses through important reservoir populations are absent altogether. Until these data become available, our results represent the most robust possible assessment of the future utility of betaherpesviruses for transmissible vaccine design.
Recombinant vector transmissible vaccines show promise for revolutionizing how we mitigate the risk of zoonotic disease. Our results support the pursuit of betaherpesviruses, such as MCMV, as vaccine vectors but also highlight critical assumptions about the dynamics of reinfection on which this optimistic outlook rests. Conclusive judgment on the utility of betaherpesviruses as transmissible vaccine vectors will require more extensive study of the interactions between vector strain diversity and superinfection in the wild. Combining this information with the predictive framework developed here will help ensure that the first recombinant vector transmissible vaccines realize their promise.
Materials and Methods
Epidemiological Model of MCMV.
To evaluate the effectiveness of an MCMV-vectored transmissible vaccine, we rely on an SEI model as defined in the following sentence, similar to that previously described by Arthur et al. (36). In the model, individuals can belong to one of three classes: susceptible to the vaccine (S), exposed to the MCMV-vectored transmissible vaccine via rodent transmission (E), and actively infectious with the MCMV-vectored transmissible vaccine (I). We do not model a recovered or immune class, because infection with MCMV is thought to be lifelong (11, 37). Throughout, we assume that the total population size, denoted N, is constant. Individuals are introduced into the susceptible class through a constant birth rate denoted b and die at a constant per capita rate d. Further, individuals transition from the susceptible class to the vaccine-exposed class based on frequency-dependent transmission with transmission coefficient βv, and transition from being exposed to actively infectious at rate σ. The deterministic model is as follows:
| [3] |
| [4] |
| [5] |
MCMV Model Parameterization Using Time Series Data.
To parameterize the model of MCMV spread, we rely on a detailed time course study conducted by Farroway et al. (18) that was later presented in Arthur et al. (36). Together, these studies detail the time course and spread of MCMV in seminatural enclosures of naive house mice (M. musculus). The studies detail the transmission of MCMV within six outdoor enclosures at four time points (days 35, 49, 63, and 84). Each enclosure consisted of 22 individuals, where 6 individuals were initially inoculated with MCMV via intraperitoneal injection, and 16 individuals remained initially susceptible.
We used ABC to parameterize a stochastic version of our epidemiological model Eqs. 3–5 (SI Appendix) with the time series data. Because the initial founder population size remained relatively constant across the 12-wk study period, the birth rate and death rate were set to zero. Mechanistically, ABC estimates a posterior distribution for the remaining parameters βv and σ by 1) drawing parameters at random from prior distributions informed by previous studies, 2) using the sampled parameters to simulate the model forward in time, and 3) including the sampled parameters in the posterior distribution if the simulated data are sufficiently close to the real data (38, 39). Repeating steps 1 through 3 a sufficient number of times and for an appropriate acceptance threshold results in a posterior probability distribution for the model’s parameters. To determine whether a simulation was sufficiently close to the real data, we calculated the total sum of squared residuals for the predicted prevalence of MCMV for a given time point across all enclosures. We then averaged this value across all time points, and compared the result to the critical threshold (0.10). We repeated steps 1 through 3 until the posterior distribution contained 25,000 parameter sets defining a multivariate probability distribution for the transmission rate (βv) and the rate of becoming infectious with MCMV (σ). We used the mode of the multivariate distribution as the estimate for these parameters (, ).
Model Parameterization Using MCMV Prevalence and Steady-State Assumptions.
Although the time series dataset is ideal for developing parameter estimates, its generality may be limited by focusing on only a single geographic location and strain of MCMV. To generalize our parameter estimates to other locations, we used published estimates of MCMV prevalence from four Australian locations and two MCMV strains defined by their ie1 genotype (27). A total of 117 M. musculus were live trapped, and qPCR was utilized to identify the presence of the two MCMV strains. For our modeling purposes, we assume that all individuals positively identified by qPCR are in the infectious or exposed classes (I, E) and that only qPCR negative individuals are in the susceptible class (S). Further, we refer to the fraction of individuals that tested positive for a particular MCMV strain as pi, where i is the genotype of ie1 (i.e., K181, G4). To account for possible sampling error when testing M. musculus, we calculate the Clopper–Pearson 95% CI (40) for the prevalence of MCMV at each geographic location and use the lower bound.
We use the prevalence data from Gorman et al. (27) to estimate a transmission rate for each geographic location and MCMV strain. We start by solving for the steady-state solution of Eqs. 3–5 when MCMV is endemic. We then rewrite the susceptible steady-state expression in terms of the fraction of susceptible individuals, and solve the resulting expression for the transmission rate, βv. The result is as follows:
| [6] |
Obtaining a numerical value for βv requires knowledge of σ and d. We use the σ value derived in the ABC fitting process, and we choose to describe an average lifespan of 365 d, typical of free-living M. musculus (41).
Predicting Time to 95% Pathogen Reduction.
To explore a transmissible vaccine’s ability to reduce pathogen prevalence in a host population, we extend the model of MCMV spread to include a target pathogen. In the extended model, P is a state variable that describes the number of hosts that are infected with the pathogen. Individuals that have been infected by the pathogen transmit at a frequency-dependent rate βp. Further, individuals recover from the pathogen at rate δ, and remain in the recovered class (R) for the remainder of their lives. The full model is as follows:
| [7] |
| [8] |
| [9] |
| [10] |
| [11] |
To calculate the time to 95% pathogen reduction, we simulate the model forward in time, starting at the pathogen endemic steady state (SI Appendix) with the following parameter values: and . We chose the value of d to reflect the typical lifespan of individuals in the Mus genus (41) and chose b to reflect a constant population size of 500 individuals. Each simulation was initialized with a number of exposed individuals set to 10% of the susceptible population. Model simulations were carried out until the number of pathogen-infected individuals is equal to 5% of the starting value.
Estimating Epidemiological Parameters for LASV and LCMV.
We estimated epidemiological parameters for LASV and LCMV using published serological data and duration of infection estimates from previous studies (22, 23). Similar to the methods used in Model Parameterization Using MCMV Prevalence and Steady-State Assumptions, we find the steady-state solutions to our general pathogen model, and identify the solution where the pathogen is endemic. We then solve this quantity for the fraction of individuals that are susceptible, and input our LASV and LCMV seroprevalence data to get estimates for the transmission rate within each population. The solution is
| [12] |
where p is the prevalence for the given pathogen, , and δ is assigned a value based on LASV and LCMV literature [LASV: 1/δ = 22 d (22), LCMV: 1/δ = 365 d (23)].
Supplementary Material
Acknowledgments
We thank James Bull and Nathan Layman for helpful suggestions on this work. This work was funded by Defense Advanced Research Projects Agency Grant D18AC00028 (S.L.N.) and NIH Grant R01GM122079 (S.L.N.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. O.B. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2108610119/-/DCSupplemental.
Data Availability
Previously published data were used for this work: refs. 18, 27, and 36. Code can be accessed via GitHub (https://github.com/tvarrelman/betaherpesvirus_vectored_trans_vax).
References
- 1.Guo Y. R., et al., The origin, transmission and clinical therapies on coronavirus disease 2019 (COVID-19) outbreak –An update on the status. Mil. Med. Res. 7, 11 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Centers for Disease Control and Prevention, Ebola (Ebola virus disease). https://www.cdc.gov/vhf/ebola/outbreaks/2014-west-africa/cost-of-ebola.html. Accessed 3 May 2021.
- 3.Centers for Disease Control and Prevention, Lassa fever. https://www.cdc.gov/vhf/lassa/index.html. Accessed 3 May 2021.
- 4.Bagcchi S., Lassa fever outbreak continues across Nigeria. Lancet Infect. Dis. 20, 543 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mariën J., et al., Evaluation of rodent control to fight Lassa fever based on field data and mathematical modelling. Emerg. Microbes Infect. 8, 640–649 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gortazar C., et al., The wild side of disease control at the wildlife-livestock-human interface: A review. Front. Vet. Sci. 1, 27 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Freuling C. M., et al., The elimination of fox rabies from Europe: Determinants of success and lessons for the future. Philos. Trans. R. Soc. Lond. B Biol. Sci. 368, 20120142 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Murphy A. A., Redwood A. J., Jarvis M. A., Self-disseminating vaccines for emerging infectious diseases. Expert Rev. Vaccines 15, 31–39 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nuismer S. L., Bull J. J., Self-disseminating vaccines to suppress zoonoses. Nat. Ecol. Evol. 4, 1168–1173 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bull J. J., Smithson M. W., Nuismer S. L., Transmissible viral vaccines. Trends Microbiol. 26, 6–15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shellam G. R., The potential of murine cytomegalovirus as a viral vector for immunocontraception. Reprod. Fertil. Dev. 6, 401–409 (1994). [DOI] [PubMed] [Google Scholar]
- 12.Jarvis M. A., Hansen S. G., Nelson J. A., Picker L. J., Früh K., “Vaccine vectors using the unique biology and immunology of cytomegalovirus” in Cytomegaloviruses From Molecular Pathogenesis to Intervention, Reddehase M. J., Lemmermann N. A., Eds. (Caister Academic, Norfolk, United Kingdom, 2013), vol. 2, pp. 450–461. [Google Scholar]
- 13.Nuismer S. L., et al., Eradicating infectious disease using weakly transmissible vaccines. Proc. Biol. Sci. 283, 20161903 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Varrelman T. J., Basinski A. J., Remien C. H., Nuismer S. L., Transmissible vaccines in heterogeneous populations: Implications for vaccine design. One Health 7, 100084 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nuismer S. L., Basinski A., Bull J. J., Evolution and containment of transmissible recombinant vector vaccines. Evol. Appl. 12, 1595–1609 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Layman N. C., Tuschhoff B. M., Nuismer S. L., Designing transmissible viral vaccines for evolutionary robustness and maximum efficiency. Virus Evol. 7, veab002 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Basinski A. J., Nuismer S. L., Remien C. H., A little goes a long way: Weak vaccine transmission facilitates oral vaccination campaigns against zoonotic pathogens. PLoS Negl. Trop. Dis. 13, e0007251 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Farroway L. N., Singleton G., Lawson M. A., Jones D. A., The impact of murine cytomegalovirus (MCMV) on enclosure populations of house mice (Mus domesticus). Wildl. Res. 29, 11–17 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.McCormick J. B., Webb P. A., Krebs J. W., Johnson K. M., Smith E. S., A prospective study of the epidemiology and ecology of Lassa fever. J. Infect. Dis. 155, 437–444 (1987). [DOI] [PubMed] [Google Scholar]
- 20.Blasdell K. R., Becker S. D., Hurst J., Begon M., Bennett M., Host range and genetic diversity of arenaviruses in rodents, United Kingdom. Emerg. Infect. Dis. 14, 1455–1458 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Olayemi A., et al., Widespread arenavirus occurrence and seroprevalence in small mammals, Nigeria. Parasit. Vectors 11, 416 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nuismer S. L., et al., Bayesian estimation of Lassa virus epidemiological parameters: Implications for spillover prevention using wildlife vaccination. PLoS Negl. Trop. Dis. 14, e0007920 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tagliapietra V., et al., Spatial and temporal dynamics of lymphocytic choriomeningitis virus in wild rodents, northern Italy. Emerg. Infect. Dis. 15, 1019–1025 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mähl P., et al., Twenty year experience of the oral rabies vaccine SAG2 in wildlife: A global review. Vet. Res. (Faisalabad) 45, 77 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Del Val M., et al., Molecular basis for cytolytic T-lymphocyte recognition of the murine cytomegalovirus immediate-early protein pp89. J. Virol. 62, 3965–3972 (1988). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Reddehase M. J., Rothbard J. B., Koszinowski U. H., A pentapeptide as minimal antigenic determinant for MHC class I-restricted T lymphocytes. Nature 337, 651–653 (1989). [DOI] [PubMed] [Google Scholar]
- 27.Gorman S., et al., Mixed infection with multiple strains of murine cytomegalovirus occurs following simultaneous or sequential infection of immunocompetent mice. J. Gen. Virol. 87, 1123–1132 (2006). [DOI] [PubMed] [Google Scholar]
- 28.Anderson R., May R., Infectious Diseases of Humans: Dynamics and Control (Oxford University Press, 1992). [Google Scholar]
- 29.Griffiths M. E., et al., Epidemiology and biology of a herpesvirus in rabies endemic vampire bat populations. Nat. Commun. 11, 5951 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gorman S., et al., Prior infection with murine cytomegalovirus (MCMV) limits the immunocontraceptive effects of an MCMV vector expressing the mouse zona-pellucida-3 protein. Vaccine 26, 3860–3869 (2008). [DOI] [PubMed] [Google Scholar]
- 31.Nikolovski S., et al., Overcoming innate host resistance to vaccination: Employing a genetically distinct strain of murine cytomegalovirus avoids vector-mediated resistance to virally vectored immunocontraception. Vaccine 27, 5226–5232 (2009). [DOI] [PubMed] [Google Scholar]
- 32.Farroway L. N., et al., Transmission of two Australian strains of murine cytomegalovirus (MCMV) in enclosure populations of house mice (Mus domesticus). Epidemiol. Infect. 133, 701–710 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Basinski A. J., et al., Evaluating the promise of recombinant transmissible vaccines. Vaccine 36, 675–682 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Singleton G. R., Smith A. L., Krebs C. J., The prevalence of viral antibodies during a large population fluctuation of house mice in Australia. Epidemiol. Infect. 125, 719–727 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Redwood A, et al., Prospects for virally vectored immunocontraception in the control of wild house mice (Mus domesticus). Wildl. Res. 34 530–539 (2007). [Google Scholar]
- 36.Arthur A. D., Krebs C. J., Pech R. P., Farroway L. N., Singleton G. R., The transmission rate of mcmv in house mice in pens: Implications for virally vectored immunocontraception. Wildl. Res. 36, 386–393 (2009). [Google Scholar]
- 37.Osborn J. E., “Cytomegalovirus and other herpesviruses” in Diseases: The Mouse in Biomedical Research, H. L. Foster, Small J. D., Fox J. G., Eds. (Academic, 1982), vol. 2, pp. 267–292. [Google Scholar]
- 38.Beaumont M. A., Approximate Bayesian computation in evolution and ecology. Annu. Rev. Ecol. Evol. Syst. 41, 379–406 (2010). [Google Scholar]
- 39.Sunnåker M., et al., Approximate Bayesian computation. PLOS Comput. Biol. 9, e1002803 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Clopper C. J., Pearson E. S., The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 26, 404–413 (1934). [Google Scholar]
- 41.Ballenger L., Mus musculus. Animal Diversity Web. https://animaldiversity.org/accounts/Mus_musculus/. Accessed 6 June 2021.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Previously published data were used for this work: refs. 18, 27, and 36. Code can be accessed via GitHub (https://github.com/tvarrelman/betaherpesvirus_vectored_trans_vax).