A Doubly Robust Method to Handle Missing Multilevel Outcome Data with Application to the China Health and Nutrition Survey

Summary

Missing data are common in longitudinal cohort studies and can lead to bias, particularly in studies with informative missingness. Many common methods for handling informatively missing data in survey samples require correctly specifying a model for missingness. Although doubly robust methods exist to provide unbiased regression coefficients in the presence of missing outcome data, these methods do not account for correlation due to clustering inherent in longitudinal or cluster-sampled studies. In this work, we developed a doubly robust method to estimate the regression of an outcome on a predictor in the presence of missing multilevel data on the outcome, which results in consistent estimation of regression coefficients assuming correct specification of either (1) the probability of missingness or (2) the outcome model. This method involves specification of separate hierarchical models for missingness and for the outcome, conditional on observed auxiliary variables and cluster-specific random effects, to account for correlation among observations. We showed this proposed estimator is doubly robust and derived its asymptotic distribution, conducted simulation studies to compare the method to an existing doubly robust method developed for independent data, and applied the method to data from the China Health and Nutrition Survey, an ongoing multilevel longitudinal cohort study.

1 |. INTRODUCTION

The China Health and Nutrition Survey (CHNS) is an ongoing longitudinal cohort study, consisting of a diverse population-based sample¹. The CHNS was implemented to study the effects of various government programs and the rapidly changing social and economic environments in China on the nutrition and health of the population. The original CHNS cohort included households from eight provinces in China, with households from additional provinces and municipalities added in later waves of data collection, resulting in a cohort of about 7,200 households with over 30,000 people from 15 provinces and municipalities, with nine waves of data collection that started in 1991. A diverse set of individual-level and household-level data was collected via household-based surveys and physical exams, in addition to the collection of community-level data.

The CHNS cohort includes entire households (i.e., all participants from a given household) and multiple households per community (i.e., geographic neighborhood), resulting in natural clusters in the data. In addition, repeated measures from multiple study visits are clustered within individuals. This natural clustering introduces correlation to the data, which can complicate statistical analysis. Similarly to most long-term, longitudinal studies, CHNS suffers from a substantial amount of missing data due to individual- or household-level non-response at particular years of data collection. It can be of interest to estimate the effect of an independent variable on an outcome variable via regression analysis. However, estimating this regression based only on the subset of the sample with non-missing outcome data may result in biased effect estimates if the missing values of the outcome variable differ systematically from the observed values after conditioning on the observed variables in the model, including observed model covariates and observed outcome data within the same cluster². The CHNS collected a rich set of variables, and so if there is a set of observed (i.e., non-missing) variables that are related either to the outcome variable or to whether an individual provides outcome data, then it may be possible to use these auxiliary variables to adjust for the missing data in certain situations.

Many methods currently exist to accommodate missing data in regression analysis. One commonly used method is multiple imputation, which involves imputing (i.e., filling-in) the missing data multiple times, performing identical analyses on each set of imputed data using standard statistical methods for complete data, and combining the results³. Another common method for handling missing data is inverse probability weighting (IPW), which involves estimating the probability of data being non-missing for each record, and performing statistical analysis among the sub-sample with non-missing data, weighted by the inverse of this estimated probability⁴. However, the validity of multiple imputation depends on correct specification of the imputation model³, and IPW requires correct specification of a model for the probability of missingness⁴. Therefore, there is need for missing data methods that have the double robustness property, meaning that the method is unbiased if either the imputation model (i.e., model for the missing variable) or the probability of missingness model, but not necessarily both, is specified correctly. Several doubly robust methods have been developed to estimate a regression of an outcome variable on a predictor variable in the presence of missing outcome data for independent records. Scharfstein et al.⁵ proposed estimating the probability that the outcome is observed (i.e., non-missing) for each data record based on a specified working model for missingness, estimating the predicted outcome for each data record based on a specified working model for the outcome, and solving a set of estimating equations that depends on the predicted non-missing probabilities and predicted outcomes to estimate the regression coefficients of interest. In addition, Zeng and Chen⁶ also proposed estimating the non-missing probability and predicted outcome for each data record based on specified working models, and estimating the regression estimator of interest based on these predicted non-missing probabilities and predicted outcomes and a partition of the support of the predictor variable(s) of interest. When the working model for either missingness or the outcome (or both) is specified correctly, both the Scharfstein et al.⁵ estimator and the Zeng and Chen⁶ estimator are consistent for the true effect of the predictor on the outcome. However, both of these methods were developed for independent data, and therefore estimate the non-missing probabilities and predicted outcomes from working models that would ignore any multilevel data structure.

We build upon the Scharfstein et al.⁵ method to propose a new doubly robust approach to estimate the association between a predictor and outcome variable for multilevel data, when the outcome variable is missing for some records. Since the CHNS data contain natural clusters, it is expected that missingness for different records within the same cluster may be correlated, and similarly the outcome variable may be correlated among different records within the same cluster. Therefore, we propose estimating the probability of missingness and the mean of the outcome variable conditional on cluster-specific random effects (in addition to observed data), which differs from existing doubly robust methods^5,6 that estimate these quantities conditional on observed variables only. Allowing cluster-specific random effects in the working models may improve the plausibility that one or both of the working models will be specified correctly, particularly when there is high within-cluster correlation in the missingness and/or the outcome variable beyond what can be explained by observed covariates.

The rest of the paper is organized in the following way. Section 2 provides details for regression estimation using our new approach, and shows that this approach is doubly robust. Section 3 provides results from a simulation study comparing the numerical performance of this new approach with other existing methods. Section 4 illustrates the use of this approach on data from the CHNS. Section 5 concludes with a discussion.

2 |. DOUBLY ROBUST METHOD FOR SEMIPARAMETRIC REGRESSION WITH MISSING DATA

2.1 |. Notation

Without loss of generality, let us focus on the case with two-level data (e.g., repeated measures data on independent individuals), where j = 1, …, m denotes the cluster (i.e., level 2), i = 1, …, n_j denotes the data record within cluster j (i.e., level 1), and $n={\sum }_{j=1}^m{n}_j$ (a discussion of the extension to more than two levels is included in Section 5). Let Y_ij denote an outcome of interest, R_ij denote an indicator that Y_ij is observed (i.e., non-missing), X_ij denote a vector of predictors for Y_ij, and Z_ij denote a high-dimensional vector of auxiliary variables related to missingness and/or the outcome variable (including all variables in X_ij). Let ${\mathbf{Y}}_{\mathbf{j}}={\left(Y_{1j},\dots ,Y_{n_{j}j}\right)}^{\prime }$, ${\mathbf{R}}_j={\left(R_{1j},\dots ,R_{n_{j}j}\right)}^{\prime }$, ${\mathbf{X}}_{\mathbf{j}}={\left[{\mathbf{X}}_{\mathbf{1}\mathbf{j}}\dots {\mathbf{X}}_{{\mathbf{n}}_{\mathbf{j}}\mathbf{j}}\right]}^{\prime }$ be a matrix of dimension n_j by p where p equals the number of predictor variables, ${\mathbf{Z}}_{\mathbf{j}}={\left[{\mathbf{Z}}_{\mathbf{1}\mathbf{j}}\dots {\mathbf{Z}}_{{\mathbf{n}}_{\mathbf{j}}\mathbf{j}}\right]}^{\prime }$ be a matrix of dimension n_j by q where q equals the number of auxiliary variables, and the data (R_j, Y_j, Z_j) be independent and identically distributed for j = 1, …, m. Let Y = (Y₁, …, Y_m)′ and R = (R₁, …, R_m)′ be vectors of length n, $\mathbf{X}={\left[{\mathbf{X}}_{\mathbf{1}}^{\prime }\dots {\mathbf{X}}_{\mathbf{m}}^{\prime }\right]}^{\prime }$ be a matrix of dimension n by p, and $\mathbf{Z}={\left[{\mathbf{Z}}_{\mathbf{1}}^{\prime }\dots {\mathbf{Z}}_{\mathbf{m}}^{\prime }\right]}^{\prime }$ be a matrix of dimension n by q. Let

$$E\left[Y_{ij}\mid {\mathbf{X}}_{\mathbf{i}\mathbf{j}}\right]=\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })$$ (1)

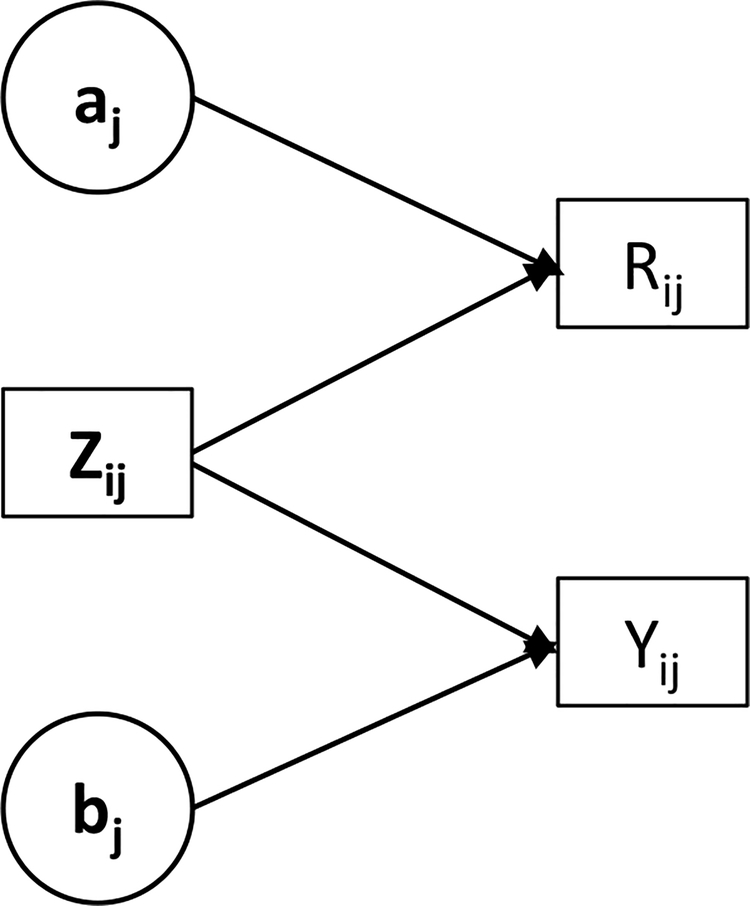
be the semi-parametric regression model of interest, where β is an unknown vector of constant regression coefficients with dimension p, β* is the true value of β, and μ(·) is some known function of X^Tβ. Throughout the remainder of the paper, assume that R_ij and Y_ij are independent conditional on the auxiliary variables Z_ij and independent cluster-specific random vectors a_j and b_j (i.e., R_ij ⊥ Y_ij|Z_ij, a_j, b_j), that R_ij depends on Z_ij and a_j only (i.e., R_ij ⊥ b_j|Z_ij, a_j) and Y_ij depends on Z_ij and b_j only (i.e., Y_ij ⊥ a_j|Z_ij, b_j), and that the parameters for the joint distributions for (R_j, a_j) and (Y_j, b_j) conditional on Z_j are distinct (i.e., the model for the joint distribution for (R_j, a_j) conditional on Z_j and the model for the joint distribution for (Y_j, b_j) conditional on Z_j do not share the parameters); see assumption (A1) in Web Appendix A in the Supplementary Materials. Note that taken together, these assumptions imply that the outcome data are missing at random (MAR)²; in other words, these assumptions imply that the outcome variable is independent of missingness, conditional on the observed data (i.e., R_ij ⊥ Y_ij|Z_ij). These assumed relationships between the different variables described here are illustrated in Figure 1.

FIGURE 1.

A directed acyclic graph (DAG) to illustrate the assumed relationships between all variables based on Assumption (A1) in Web Appendix A in the Supplementary Materials.

2.2 |. Proposed Doubly Robust Method for Multilevel Data

First, specify hierarchical working models for [R_j, a_j|Z_j] and [Y_j, b_j|Z_j], where a_j and b_j are independent vectors of cluster-specific random effects to account for within-cluster correlation in missingness and the outcome variable respectively; let the cluster-specific random effects (a_j, b_j) be independent and identically distributed for j = 1, …, m. For example, generalized linear mixed effect models may be specified for [R_j, a_j|Z_j] and [Y_j, b_j|Z_j], with linear predictors ${\mathbf{Z}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\alpha }$ and ${\mathbf{Z}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\gamma }$ and cluster-specific random intercepts a_j and b_j respectively. If the random effects were known, then the predicted values from these working models, ${\widehat{\pi }}_{ij}\left({\mathbf{a}}_{\mathbf{j}}\right)=\tilde{\mathit{P}}\left[{\mathit{R}}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}}\right]$ and $\mid {\widehat{v}}_{\mathbf{i}\mathbf{j}}\left({\mathbf{b}}_{\mathbf{j}}\right)=\tilde{E}\left[Y_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};{\widehat{\mathit{\gamma }}}_{\mathit{m}}\right]$, could be substituted in the set of doubly robust estimating equations for independent data introduced by Scharfstein et al.⁵, resulting in the following estimating equations conditional on the random effects:

$$0=S_m(\mathit{\beta }\mid {\mathbf{a}}_{\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})=\sum _{i,j}\left[\frac{{\mathit{R}}_{ij}}{{\widehat{\pi }}_{ij}({\mathbf{a}}_{\mathbf{j}})}(Y_{ij}-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })){\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathbf{\beta })-\left(\frac{{\mathit{R}}_{ij}}{{\widehat{\pi }}_{ij}({\mathbf{a}}_{\mathbf{j}})}-1\right)({\widehat{v}}_{ij}({\mathbf{b}}_{\mathbf{j}})-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathbf{\beta })){\partial }_{\beta }\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\beta )\right].$$ (2)

Solving this set of conditional estimating equations would result in a doubly robust estimator for β if the random effects a_j and b_j were known⁵. However, the random effects a_j and b_j are unknown in practice, but rather are assumed to be randomly distributed according to some specified working distribution. Therefore, it is necessary to integrate the estimating equations over the posterior distribution of the random effects conditional on the observed data that is implied by the working models, $\tilde{p}\left({\mathbf{a}}_{\mathbf{j}},{\mathbf{b}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathbf{\alpha }}}_{\mathit{m}},{\widehat{\mathbf{\tau }}}_{\mathit{m}},{\widehat{\mathbf{\gamma }}}_{\mathit{m}},{\widehat{\mathbf{\varphi }}}_{\mathit{m}}\right)$, to obtain a revised set of estimating equations that depend on observed data only. Let $\tilde{p}\left({\mathit{R}}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}};\mathit{\alpha }\right)$ be the working density for [R_ij|Z_ij, a_j], $\tilde{p}\left(Y_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};\mathit{\gamma }\right)$ be the working density for [Y_ij|Z_ij, b_j], $\tilde{p}\left({\mathbf{a}}_{\mathbf{j}};\mathit{\tau }\right)$ be the working density for the random effects a_j, and $\tilde{p}\left({\mathbf{b}}_{\mathbf{j}};\mathit{\varphi }\right)$ be the working density for the random effects b_j. The posterior densities for the random effects (a_j, b_j) are conditioned on the observed data in cluster j. Assumption (A1) (see Web Appendix A in the Supplementary Materials) implies that the random effects a_j and b_j are independent conditional on the observed data, that the working posterior distribution for a_j depends only on the working model [R_j, a_j|Z_j; α, τ], and that the working posterior distribution for b_j depends only on the working model [Y_j, b_j|Z_j; γ, ϕ]:

$$\begin{gathered} \tilde{p}({\mathbf{a}}_{\mathbf{j}},{\mathbf{b}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}) \\ \propto \tilde{p}({\mathbf{a}}_{\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}) \\ \prod _{i=1}^{n_j}\tilde{p}({\mathit{R}}_{ij},{\mathit{R}}_{ij}{Y}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}) \\ =\left\{\tilde{p}({\mathbf{a}}_{\mathbf{j}};{\widehat{\mathit{\tau }}}_{\mathit{m}})\prod _{i=1}^{n_j}\tilde{p}({\mathit{R}}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}})\right\}\left\{\tilde{p}({\mathbf{b}}_{\mathbf{j}};{\widehat{\mathit{\varphi }}}_{\mathit{m}})\prod _{i=1}^{n_j}\tilde{p}{(Y_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{b}}_{\mathbf{j}},{\widehat{\mathit{\gamma }}}_{\mathit{m}})}^{{\mathit{R}}_{ij}}\right\} \\ \propto \tilde{p}({\mathbf{a}}_{\mathbf{j}}|{\mathbf{R}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}})\tilde{p}({\mathbf{b}}_{\mathbf{j}}|{\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\gamma }}}_{\mathit{m}}{\widehat{\mathit{\varphi }}}_{\mathit{m}}), \end{gathered}$$ (3)

where $\tilde{p}\left({\mathbf{a}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}}\right)$ is the posterior density of a_j conditional on the observed data based on the working model for [R_j, a_j|Z_j] and the estimated α and τ, and $\tilde{p}\left({\mathbf{b}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}\right)$ is the posterior density of b_j conditional on the observed data based on the working model for [Y_j, b_j|Z_j] and the estimated γ and ϕ.

Therefore, we obtain the following set of estimating equations:

$$\begin{gathered} 0=S_m(\mathit{\beta };{\widehat{\mathbf{\alpha }}}_{\mathit{m}},{\widehat{\mathbf{\tau }}}_{\mathit{m}},{\widehat{\mathbf{\gamma }}}_{\mathit{m}},{\widehat{\mathbf{\varphi }}}_{\mathit{m}}) \\ =\sum _{i,j}\int \left[\frac{R_{ij}}{{\widehat{\mathbf{\pi }}}_{ij}({\mathbf{a}}_{\mathbf{j}})}(Y_{ij}-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })){\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })-\left(\frac{R_{ij}}{{\widehat{\mathbf{\pi }}}_{ij}({\mathbf{a}}_{\mathbf{j}})}-1\right)({\widehat{v}}_{ij}({\mathbf{b}}_{\mathbf{j}})-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })){\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })\right] \\ \tilde{p}({\mathbf{a}}_{\mathbf{j}},{\mathbf{b}}_{\mathbf{j}}\mid R,RY,\mathbf{Z};{\widehat{\mathbf{\alpha }}}_{\mathit{m}},{\widehat{\mathbf{\tau }}}_{\mathit{m}},{\widehat{\mathbf{\gamma }}}_{\mathit{m}},{\widehat{\mathbf{\varphi }}}_{\mathit{m}})d{\mathbf{a}}_{\mathbf{j}}d{\mathbf{b}}_{\mathbf{j}} \\ =\sum _{i,j}\int \left[\frac{{\mathit{R}}_{ij}}{{\widehat{\mathbf{\pi }}}_{ij}({\mathbf{a}}_{\mathbf{j}})}(Y_{ij}-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })){\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })-\left(\frac{{\mathit{R}}_{ij}}{{\widehat{\mathbf{\pi }}}_{ij}({\mathbf{a}}_{\mathbf{j}})}-1\right)({\widehat{v}}_{ij}({\mathbf{b}}_{\mathbf{j}})-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })){\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })\right] \\ \tilde{p}({\mathbf{a}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathbf{\alpha }}}_{\mathit{m}},{\widehat{\mathbf{\tau }}}_{\mathit{m}})\tilde{p}({\mathbf{b}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathbf{\gamma }}}_{\mathit{m}},{\widehat{\mathbf{\varphi }}}_{\mathit{m}})d{\mathbf{a}}_{\mathbf{j}}d{\mathbf{b}}_{\mathbf{j}} \\ \equiv \sum _{\mathbf{j}=1}^{\mathit{m}}g({\mathbf{R}}_{\mathbf{j}},{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};\mathbf{\beta },{\widehat{\mathbf{\alpha }}}_{\mathit{m}},{\widehat{\mathbf{\tau }}}_{\mathit{m}},{\widehat{\mathbf{\gamma }}}_{\mathit{m}},{\widehat{\mathbf{\varphi }}}_{\mathit{m}}). \end{gathered}$$ (4)

Since these estimating equations are a function of the observed data (R, RY, Z) only, we propose to estimate β by solving these estimating equations.

Since the working model parameters (α, τ, γ, ϕ) are unknown in practice, in order to solve the estimating equations, it is necessary to obtain estimates of these parameters, such as by maximizing the observed data likelihoods for Y and R. For example, if the models [R_j, a_j|Z_j] and [Y_j, b_j|Z_j] are generalized linear mixed effects models, then the observed data likelihoods for R and Y are of the form ${\prod }_{j=1}^m\int {\prod }_{i=1}^{n_j}\tilde{p}\left({\mathit{R}}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}};\mathit{\alpha }\right)\tilde{p}\left({\mathbf{a}}_{\mathbf{j}};\mathbf{\tau }\right)d{\mathbf{a}}_{\mathbf{j}}$ and ${\prod }_{j=1}^m\int {\prod }_{i=1}^{n_j}\tilde{p}{\left({\mathit{Y}}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};\mathit{\gamma }\right)}^{R_{ij}}\tilde{p}\left({\mathbf{b}}_{\mathbf{j}};\mathit{\varphi }\right)d{\mathbf{b}}_{\mathbf{j}}$ respectively, and the working model parameter estimates (${\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}$) are the values that maximize these observed data likelihoods. After estimating the working model parameters, these estimates are substituted into the estimating equations $0=S_m\left(\mathit{\beta };{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}\right)$, and these estimating equations are solved for β to obtain the effect estimate of interest,${\widehat{\mathit{\beta }}}_{\mathit{m}}$. The observed data likelihood functions for the working models and the final set of estimating equations can be maximized or solved by EM algorithm, Markov Chain Monte Carlo, or Gauss-Hermite quadrature.

2.3 |. Asymptotic Properties

We now present arguments to justify the consistency and asymptotic normality of the proposed estimator ${\widehat{\mathit{\beta }}}_{\mathit{m}}$ when at least one of the hierarchical working models, [R_j, a_j|Z_j] and/or [Y_j, b_j|Z_j], is specified correctly. For example, the working model for [R_j, a_j|Z_j] would be specified correctly if both the working model for R_ij conditional on a_j, $\tilde{p}\left(R_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}};\mathit{\alpha }\right)$, and the working density for a_j, $\tilde{p}\left({\mathbf{a}}_{\mathbf{j}};\mathit{\tau }\right)$, are specified correctly; similarly, the working model for [Y_j, b_j|Z_j] would be specified correctly if both the working model for Y_ij conditional on b_j, $\tilde{p}\left({\mathit{Y}}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};\mathit{\gamma }\right)$, and the working density for b_j, $\tilde{p}\left({\mathbf{b}}_{\mathbf{j}};\mathit{\varphi }\right)$, are specified correctly. Let ∂_α,τ denote a vector of partial derivatives and ${\partial }_{\alpha ,\tau }^2$ denote a matrix of second-order derivatives with respect to α and τ; let ∂_γ,ϕ and ${\partial }_{\gamma ,\mathit{\varphi }}^2$ denote the corresponding operations with respect to γ and ϕ.

Generally, note that the proposed estimating equations 4 can be re-written as the following:

$$\begin{gathered} 0=S_{\mathit{m}}(\mathit{\beta };{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}) \\ =\sum _{i,j}\int \left\{\left[\frac{{\mathit{R}}_{ij}}{{\widehat{\mathit{\pi }}}_{ij}\left({\mathbf{a}}_{\mathbf{j}}\right)}{Y}_{ij}-\left(\frac{{\mathit{R}}_{ij}}{{\widehat{\mathit{\pi }}}_{ij}\left({\mathbf{a}}_{\mathbf{j}}\right)}-1\right){\widehat{v}}_{ij}\left({\mathit{b}}_{\mathbf{j}}\right)\right]\tilde{p}({\mathit{a}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}}) \\ \tilde{p}({\mathbf{b}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})d{\mathbf{a}}_{\mathbf{j}}d{\mathbf{b}}_{\mathbf{j}}-\mathit{\mu }({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })\right\}{\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta }) \\ =\sum _{i,j}\left\{Q_{ij}-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta })\right\}{\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta }), \end{gathered}$$ (5)

where $Q_{ij}=\int \left[\frac{R_{ij}}{{\widehat{\pi }}_{ij}\left({\mathbf{a}}_{\mathbf{j}}\right)}{Y}_{ij}-\left(\frac{R_{ij}}{{\widehat{\mathit{\pi }}}_{ij}\left({\mathbf{a}}_{\mathbf{j}}\right)}-1\right){\widehat{v}}_{ij}\left({\mathbf{b}}_{\mathbf{j}}\right)\right]\tilde{p}({\mathbf{a}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}})\tilde{p}({\mathbf{b}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})d{\mathbf{a}}_{\mathbf{j}}d{\mathbf{b}}_{\mathbf{j}}$. The estimating equations (5) are equivalent to a generalized estimating equations (GEE) model to estimate β. Therefore, it follows that this set of proposed estimating equations inherits the properties of standard GEE models (e.g., unique solution for β, identifiability of β from the observed data distribution) under some mild regularity conditions.

According to maximum likelihood theory for generalized linear mixed effect models⁷, $\left({\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}\right)$ converge in probability to a constant (α*, τ*, γ*, ϕ*), where (α*, τ*) are the true parameter values if the working model [R_j, a_j|Z_j; α, τ] is correct, and (γ*, ϕ*) are the true parameter values if the working model [Y_j, b_j|Z_j; γ, ϕ] is correct. Let ${\pi }_{ij}^{\ast }\left({\mathbf{a}}_{\mathbf{j}}\right)=\tilde{P}\left[{\mathit{R}}_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}};\mathit{\alpha }\ast \right]$ and $v_{ij}^{\ast }\left({\mathbf{b}}_{\mathbf{j}}\right)=\tilde{E}\left[Y_{\mathbf{i}\mathbf{j}}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};\mathit{\gamma }\ast \right]$ based on the specified working models. It can be shown by Taylor series expansion of the log-likelihood for each working model around the limits of the maximum likelihood estimates of the parameters that

$$\begin{gathered} {\mathit{m}}^{1/2}\left(\begin{array}{c}{\widehat{\mathit{\alpha }}}_{\mathit{m}}-{\mathit{\alpha }}^{*}\\ {\widehat{\mathit{\tau }}}_{\mathit{m}}-{\mathit{\tau }}^{*}\end{array}\right)=-{\mathit{m}}^{-1/2}E{\left[{\partial }_{\mathit{\alpha },\mathit{\tau }}^{2}l\left(\mathit{\alpha }*,\mathit{\tau }*\right)\right]}^{-1}\sum _{j=1}^{\mathit{m}}{\partial }_{\mathit{\alpha },\mathit{\tau }}{l}_j\left({\mathit{\alpha }}^{*},{\mathit{\tau }}^{*}\right)+o_p(1) \\ \equiv {\psi }_{\mathit{\alpha },\mathit{\tau }}\left(\mathbf{R},\mathbf{Z};\mathit{\alpha }*,\mathit{\tau }*\right)+o_p(1) \end{gathered}$$ (6)

Where $l_j(\mathit{\alpha },\mathit{\tau })=log\left[\int {\prod }_{i=1}^{n_j}\tilde{p}\left(R_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{a}}_{\mathbf{j}};\mathit{\alpha }\right)\tilde{p}\left({\mathbf{a}}_{\mathbf{j}};\mathit{\tau }\right)d{\mathbf{a}}_{\mathbf{j}}\right]$, and

$$\begin{gathered} {\mathit{m}}^{1/2}\left(\begin{array}{c}{\widehat{\mathit{\gamma }}}_{\mathit{m}}-\mathit{\gamma }*\\ {\widehat{\mathit{\varphi }}}_{\mathit{m}}-\mathit{\varphi }*\end{array}\right)=-{\mathit{m}}^{-1/2}E{[{\partial }_{\mathit{\gamma },\mathit{\varphi }}^{2}l\left(\mathit{\gamma }*,\mathit{\varphi }*\right)]}^{-1}\sum _{j=1}^{\mathit{m}}{\partial }_{\gamma ,\varphi }{l}_j\left(\mathit{\gamma }*,\mathit{\varphi }*\right)+o_p(1) \\ \equiv {\psi }_{\gamma ,\varphi }\left(\mathbf{R},\mathbf{R}\mathit{Y},\mathbf{Z};\mathit{\gamma }*,\mathit{\varphi }*\right)+o_p(1) \end{gathered}$$ (7)

where $l_j(\mathit{\gamma },\mathit{\varphi })=log\left[\int {\prod }_{i=1}^{n_j}\tilde{p}{\left(Y_{ij}\mid {\mathbf{Z}}_{\mathbf{i}\mathbf{j}},{\mathbf{b}}_{\mathbf{j}};\gamma \right)}^{R_{ij}}\tilde{p}\left({\mathbf{b}}_{\mathbf{j}};\varphi \right)d{\mathbf{b}}_{\mathbf{j}}\right]$.

The following results show that the proposed estimating equations are unbiased for β if at least one of the working models is correct, and therefore ${\widehat{\mathit{\beta }}}_{\mathit{m}}$ is consistent for the true value β*. It is also shown that ${\mathit{m}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\mathit{m}}-\mathit{\beta }*\right)$ is asymptotically normally distributed.

Lemma 1.

Let $E\left[Y_{ij}\mid {\mathbf{X}}_{\mathbf{i}\mathbf{j}}\right]=\mu \left({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\beta *\right)$, and either the working model [R_j, a_j|Z_j] or the working model [Y_j, b_j|Z_j] be correct. Then E[S_m(β*; α*, τ*, γ*, ϕ*)] = 0.

An outline of the proof is presented in the Supplementary Materials (Web Appendix B). In particular, this proof follows from (1) the independence of the posterior distributions of the random effects a_j and b_j, (2) $\int \frac{R_{ij}}{{\pi }_{ij}^{*}\left({\mathbf{a}}_{\mathbf{j}}\right)}\tilde{p}\left({\mathbf{a}}_{\mathbf{j}}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};\mathit{\alpha }*,\mathit{\tau }*\right)d{\mathbf{a}}_{\mathbf{j}}$ $=E\left[\frac{R_{ij}}{{\pi }_{ij}^{*}\left({\mathbf{a}}_{\mathbf{j}}\right)}\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}}\right]$ if working model [R_j, a_j|Z_j; α, τ] is correct, and (3) $\int (v_{ij}^{*}({\mathbf{b}}_{\mathbf{j}})-\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta }*)){\partial }_{\mathit{\beta }}\mu ({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta }*)\tilde{p}({\mathbf{b}}_{\mathbf{j}}\mid {\mathbf{R}}_{\text{j}},{\mathbf{R}}_{\text{j}}{\mathbf{Y}}_{\text{j}},{\mathbf{Z}}_{\text{j}};\mathit{\gamma }*,\mathit{\varphi }*)d{\mathbf{b}}_{\text{j}}=E\left[(v_{ij}^{*}({\mathbf{b}}_{\mathbf{j}})-\mathit{\mu }({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta }*)){\partial }_{\mathit{\beta }}\mathit{\mu }({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta }*)\mid {\mathbf{R}}_{\mathbf{j}},{\mathbf{R}}_{\mathbf{j}}{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}}\right]$ if working model $[{\mathbf{Y}}_{\mathbf{j}},{\mathbf{b}}_{\mathbf{j}}|{\mathbf{Z}}_{\mathbf{j}};\mathit{\gamma },\mathit{\varphi }]$ is correct.

Theorem 1.

Let $E\left[Y_{ij}\mid {\mathbf{X}}_{\mathbf{i}\mathbf{j}}\right]=\mathit{\mu }\left({\mathbf{X}}_{\mathbf{i}\mathbf{j}}^{\mathbf{T}}\mathit{\beta }*\right)$, and either the working model [R_j, a_j|Z_j] or the working model [Y_j, b_j|Z_j] be correct. Under assumptions (A1)-(A8) (see Web Appendix A in the Supplementary Materials), ${\widehat{\mathit{\beta }}}_{\mathit{m}}$ converges in probability to the true parameter value β*, and ${\mathit{m}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\mathit{m}}-\mathit{\beta }*\right)$ converges to a normal distribution with mean zero and a covariance matrix that can be estimated by

$$\begin{array}{l}\frac{1}{{\mathit{m}}^2}{\left\{\widehat{E}\left[{\partial }_{\beta }g(\mathbf{R},\mathbf{Y},\mathbf{Z};{\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})\right]\right\}}^{-1}\\ \sum _{j=1}^m\{-g({\mathbf{R}}_{\mathbf{j}},{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}},{\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})\\ +\widehat{E}\left[{\partial }_{\alpha ,\tau }g(\mathbf{R},\mathbf{Y},\mathbf{Z};{\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})\right]\widehat{E}{\left[{\partial }_{\mathit{\alpha },\mathit{\tau }}^{2}l({\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}})\right]}^{-1}{\partial }_{\mathit{\alpha },\mathit{\tau }}{l}_j({\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}})\\ {+\widehat{E}\left[{\partial }_{\gamma ,\varphi }g(\mathbf{R},\mathbf{Y},\mathbf{Z};{\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})\right]\widehat{E}{\left[{\partial }_{\mathit{\gamma },\mathit{\varphi }}^{2}l({\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})\right]}^{-1}{\partial }_{\mathit{\gamma },\mathit{\varphi }}{l}_j({\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})\}}^{\otimes 2}\\ {\left\{\widehat{E}\left[{\partial }_{\beta }g(\mathbf{R},\mathbf{Y},\mathbf{Z};{\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})\right]\right\}}^{-1},\end{array}$$ (8)

where $\widehat{E}[\cdot ]$ indicates empirical mean, and u^⊗2 = uu^T for a px1 vector u.

An outline of the proof is presented in the Supplementary Materials (Web Appendix B). Essentially the proof involves applying the asymptotic properties of $({\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}})$, Lemma 1, and a Taylor series expansion of $S_{\mathit{m}}({\widehat{\mathit{\beta }}}_{\mathit{m}};\mathit{\alpha }*,\mathit{\tau }*,\mathit{\gamma }*,\mathit{\varphi }*)$ around β* to obtain that

$$\begin{array}{l}{\mathit{m}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\mathit{m}}-\beta *\right)={\mathit{m}}^{-1/2}{\left\{E\left[{\partial }_{\beta }g\left(\mathbf{R},\mathbf{Y},\mathbf{Z};\mathit{\beta }*,\mathit{\alpha }*,\mathit{\tau }*,\mathit{\gamma }*,\mathit{\varphi }*\right)\right]\right\}}^{-1}\\ \sum _{j=1}^{\mathit{m}}\{-g\left({\mathbf{R}}_{\mathbf{j}},{\mathbf{Y}}_{\mathbf{j}},{\mathbf{Z}}_{\mathbf{j}};\beta *,\mathit{\alpha }*,\mathit{\tau }*,\mathit{\gamma }*,\mathit{\varphi }*\right)\\ +E\left[{\partial }_{\mathit{\alpha },\mathit{\tau }}g\left(\mathbf{R},\mathbf{Y},\mathbf{Z};\mathit{\beta }*,\mathit{\alpha }*,\mathit{\tau }*,\mathit{\gamma }*,\mathit{\varphi }*\right)\right]E{\left[{\partial }_{\mathit{\alpha },\mathit{\tau }}^{2}l\left(\mathit{\alpha }*,\mathit{\tau }*\right)\right]}^{-1}{\partial }_{\mathit{\alpha },\mathit{\tau }}{l}_j\left(\mathit{\alpha }*,\mathit{\tau }*\right)\\ +E\left[{\partial }_{\mathit{\gamma },\mathit{\varphi }}g\left(\mathbf{R},\mathbf{Y},\mathbf{Z};\mathit{\beta }*,\mathit{\alpha }*,\mathit{\tau }*,\mathit{\gamma }*,\mathit{\varphi }*\right)\right]E{\left[{\partial }_{\mathit{\gamma },\mathit{\varphi }}^{2}l\left(\mathit{\gamma }*,\mathit{\varphi }*\right)\right]}^{-1}{\partial }_{\mathit{\gamma },\mathit{\varphi }}{l}_{\mathbf{j}}\left(\mathit{\gamma }*,\mathit{\varphi }*\right)\}+o_p(1).\end{array}$$ (9)

The covariance estimator for ${\widehat{\mathit{\beta }}}_{\mathit{m}}$ can be obtained based on the empirical covariance of this expression for ${\mathit{m}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\mathit{m}}-\mathit{\beta }*\right)$ substituting $\left({\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{\alpha }}}_{\mathit{m}},{\widehat{\mathit{\gamma }}}_{\mathit{m}},{\widehat{\mathit{\tau }}}_{\mathit{m}},{\widehat{\mathit{\varphi }}}_{\mathit{m}}\right)$ for (β*; α*, γ*, τ*, ϕ*), and substituting empirical means for expected values.

3 |. SIMULATION STUDY

3.1 |. General Set-Up

We conducted simulation studies to examine the performance of our proposed estimator and to compare its performance to existing methods in finite samples. One thousand datasets were simulated, each with 1000 clusters with 2 data records each (i.e., 1000 individuals with data for 2 time-points each). Let j indicate the individual and i = 1, 2 indicate the time-point. One time-varying predictor variable of interest, ${\mathbf{X}}_{\mathbf{j}}=\left(\begin{array}{l}{X}_{1j}\hfill \\ X_{2j}\hfill \end{array}\right)$, was generated for each cluster from a multivariate normal distribution, $N_2\left(\left(\begin{array}{c}1.5\\ 1.5\end{array}\right),\left(\begin{array}{cc}1& 0.3\\ 0.3& 1\end{array}\right)\right)$, where the first element of the random vector X_j corresponded to the first time-point and the second element corresponded to the second time-point. Similarly, three time-varying auxiliary variables were generated for each cluster based on the value of ${\mathbf{X}}_{\mathbf{j}}:{\mathbf{Z}}_{\mathbf{1},\mathbf{j}}=\left(\begin{array}{c}{Z}_{1,1j}\\ Z_{1,2j}\end{array}\right)~N_2(\left(\begin{array}{c}0.2+0.2X_{1j}\\ 0.2+0.2X_{2j}\end{array}\right),\left(\begin{array}{cc}1& 0.5\\ 0.5& 1\end{array}\right))$, ${\mathbf{Z}}_{2,\mathbf{j}}=\left(\begin{array}{l}{Z}_{2.1j}\hfill \\ Z_{2,j}\hfill \end{array}\right)~N_2\left(\left(\begin{array}{c}0.7+0.2X_{1j}\\ 0.7+0.2X_{2j}\end{array}\right),\left(\begin{array}{cc}1& 0.1\\ 0.1& 1\end{array}\right)\right)$, and Z_3,ij ~ Exp(mean = |0.7 + 0.2X_ij |). In addition, one time-invariant auxiliary variable was generated for each cluster: Z_4,1j = Z_4,2j ~ Bernoulli(0.5). Two random intercepts, a_j (used to generate missingness R_ij) and b_j (used to generate the outcome Y_ij), were independently generated from a normal distribution with mean 0 and variance 1.We considered the outcome variable Y_ij to be continuous (presented in this section) and binary (see Web Appendix C in the Supplementary Materials).

For the proposed method, separate mixed effects models were fit for missingness R_ij (logistic mixed effect model) and the outcome Y_ij (linear mixed effect model) to estimate the working model parameters, each with a cluster-specific intercept specified as normally distributed with mean zero; in other words, the working model for missingness was logit{P (R_ij = 1|Z_ij, a_j)} = Z_ijα + a_j and a_j ~ N(0, τ), and the working model for the outcome was E[Y_ij |Z_ij, b_j ] = Z_ijγ + b_j and b_j ~ N(0, ϕ), where Z_ij is a vector of covariates for data record i from cluster j. Since the random effects were assumed to be normally distributed, all intractable integrals were evaluated using Gauss-Hermite quadrature. The Newton-Raphson algorithm was used to solve the estimating equations S_m(β) for β. Mixed effects models were fit using PROC GLIMMIX in SAS. An R function written by the authors was used to solve the estimating equations and estimate the covariance matrix, using the estimated working model parameters.

The proposed method was also compared to an available case analysis (i.e., dropping missing records from the dataset prior to statistical analysis) and the method introduced by Scharfstein et al.⁵ for independent data (marginal approach). For the available case analysis, generalized estimating equations with an exchangeable working correlation matrix were used to estimate the marginal effect of X_ij on Y_ij (ignoring the additional information provided by the auxiliary variables Z_ij). For the marginal approach, independent-data regression models were fit for R_ij (logistic regression) and Y_ij (linear regression) conditional on Z_ij (ignoring the clustering in the data), and β was estimated as the solution to the estimating equations introduced by Scharfstein et al.⁵, where ${\widehat{\mathit{\pi }}}_{\mathbf{i}\mathbf{j}}$ was predicted from the estimated independent-data model for R_ij and ${\widehat{v}}_{\mathbf{i}\mathbf{j}}$ was predicted from the estimated independent-data model for Y_ij. Note that for the working models with a non-identity link function (e.g., logistic regression for R_ij), even the marginal working model fit with the correct set of fixed effects was misspecified since R_ij and Y_ij were generated based on models conditional on a random intercept.

3.2 |. Misspecification of Working Models by Omitting an Important Covariate

First, we considered the performance of the proposed method when either working model was misspecified by omitting an important covariate. The outcome variable Y_ij was generated from a normal distribution with mean (1 + Z_1,ij + Z_2,ij + γ₃ ∗ Z_3,ij + Z_4,ij + X_ij + b_j) and variance 1, where γ₃ equaled 0.2 (weak effect) or 1 (strong effect). An indicator that Y_ij was observed (R_ij) was generated from a Bernoulli distribution with probability logit⁻¹(α₀ − Z_1,ij + Z_2,ij + α₃ ∗ Z_3,ij − Z_4,ij + X_ij + a_j), where α₀ equaled 0.5 (20% missing) or −1 (35% missing), and α₃ equaled 0.2 (weak effect) or 1 (strong effect). For both the proposed multilevel approach and the marginal approach, each working model was either fit using the correct set of fixed effects, or by excluding Z_3,ij from the model.

Table 1 presents bias, empirical standard deviation of the estimates (SDE), average estimated standard errors (ESE), mean square error (MSE), and coverage rates for 95% confidence intervals (CP) for the proposed multilevel approach. Table 2 presents ratios of the empirical variance and MSE for the multilevel approach to the available case and marginal approaches. The proposed multilevel approach exhibited essentially no bias when either the working model for [R_j, a_j|Z_j] and/or the working model for [Y_j, b_j|Z_j] were specified correctly, confirming the double robustness property. Bias for the multilevel approach tended to decrease as the percent missing decreased. Also, bias when the [Y_j, b_j|Z_j] working model was misspecified tended to decrease as the magnitude of the omitted effect decreased. The 95% confidence interval coverage rates were nearly at the nominal level when at least one working model was specified correctly.

TABLE 1.

Results from simulation study for the multilevel approach with a continuous outcome where working models were misspecified by omitting an important covariate

				β 0					β 1
Effect strength	% Miss.	Ra	Ya	Bias	SDE	ESE	MSE	CP	Bias	SDE	ESE	MSE	CP
Weak	20	T	T	0.003	0.104	0.103	0.011	95.0	−0.002	0.055	0.054	0.003	95.0
		T	F	0.006	0.104	0.103	0.011	94.7	−0.002	0.055	0.054	0.003	95.3
		F	T	0.003	0.104	0.103	0.011	94.7	−0.002	0.055	0.054	0.003	95.2
		F	F	0.011	0.104	0.103	0.011	94.7	−0.003	0.055	0.054	0.003	95.3
	35	T	T	0.005	0.127	0.123	0.016	95.4	−0.002	0.064	0.062	0.004	95.6
		T	F	0.011	0.128	0.124	0.016	95.3	−0.003	0.065	0.062	0.004	95.4
		F	T	0.005	0.127	0.123	0.016	95.2	−0.002	0.064	0.061	0.004	95.6
		F	F	0.019	0.127	0.123	0.017	95.0	−0.003	0.065	0.062	0.004	95.1
Strong	20	T	T	−0.001	0.107	0.105	0.011	95.1	0.000	0.059	0.057	0.003	94.3
		T	F	0.026	0.111	0.109	0.013	93.7	−0.006	0.060	0.059	0.004	94.4
		F	T	−0.001	0.106	0.105	0.011	95.1	0.000	0.058	0.057	0.003	94.6
		F	F	0.112	0.112	0.111	0.025	80.6	−0.026	0.060	0.060	0.004	91.5
	35	T	T	−0.004	0.125	0.163	0.016	95.1	0.001	0.065	0.080	0.004	94.7
		T	F	0.060	0.142	0.195	0.024	92.8	−0.011	0.073	0.084	0.006	93.5
		F	T	−0.004	0.120	0.159	0.014	94.6	0.001	0.063	0.079	0.004	94.7
		F	F	0.246	0.137	0.151	0.079	58.5	−0.045	0.070	0.077	0.007	89.6

^aT = Working model specified correctly. F = Working model misspecified by excluding the covariate Z_3,ij.

TABLE 2.

Comparison of multilevel approach with the marginal approach and the available case approach from simulation study for continuous outcome where working models were misspecified by omitting an important covariate

				β 0				β 1
				Emp var ratiob		MSE ratiob		Emp var ratiob		MSE ratiob
Effect strength	% Miss.	Ra	Ya	Available case approach	Marginal approach	Available case approach	Marginal approach	Available case approach	Marginal approach	Available case approach	Marginal approach
Weak	20	T	T	0.994	0.844	0.992	0.845	1.103	0.858	1.104	0.858
		T	F	0.993	0.847	0.994	0.850	1.104	0.861	1.106	0.862
		F	T	0.993	0.846	0.991	0.847	1.101	0.861	1.102	0.861
		F	F	0.993	0.848	1.002	0.851	1.102	0.863	1.105	0.864
	35	T	T	1.002	0.671	0.971	0.672	1.042	0.667	1.040	0.667
		T	F	1.009	0.679	0.983	0.684	1.054	0.676	1.053	0.677
		F	T	0.997	0.671	0.966	0.671	1.037	0.668	1.036	0.669
		F	F	1.003	0.679	0.991	0.684	1.050	0.676	1.049	0.677
Strong	20	T	T	0.901	0.891	0.626	0.891	0.965	0.907	0.905	0.907
		T	F	0.964	0.935	0.707	0.985	1.023	0.954	0.968	0.963
		F	T	0.892	0.913	0.620	0.912	0.951	0.928	0.892	0.928
		F	F	0.996	0.937	1.385	0.973	1.021	0.953	1.136	0.965
	35	T	T	0.877	0.739	0.398	0.738	0.915	0.762	0.824	0.762
		T	F	1.123	0.857	0.602	1.010	1.151	0.866	1.061	0.886
		F	T	0.811	0.795	0.368	0.795	0.848	0.819	0.764	0.819
		F	F	1.044	0.890	2.016	1.007	1.058	0.896	1.338	0.946

^aT = Working model specified correctly. F = Working model misspecified by excluding the covariate Z_3,ij.

^bRatio comparing multilevel approach to corresponding comparison method.

The proposed standard error estimator for the multilevel approach approximated the SDE well in most cases. One exception was the scenario with 35% missing data and a strong omitted effect, where the estimated standard errors largely over-estimated the SDE for a few simulated datasets, resulting in an ESE that was considerably larger than the SDE; when the simulated datasets with the largest estimated standard errors were removed (≤5 datasets), the ESE approximated the SDE similarly well as the other scenarios. Additionally, when the proportion of missing data in each dataset was reduced to 30% (results not shown), the ESE approximated the SDE well, suggesting that although the proposed standard error estimator performs well for moderate amounts of missing data (e.g., ≤30%), it may be over-estimated in some situations when the proportion of missing data is particularly high. Both the empirical variance and MSE were almost always smaller for the proposed multilevel approach than the marginal approach that ignored the clustering, and this difference in the empirical variance and MSE between those two approaches was generally greater for increased percent missing. Analogous simulation results considering a binary outcome variable (Y) are presented in the Supplementary Materials (Web Tables 1 and 2); results from simulations with a binary outcome variable were similar to simulations with the continuous outcome presented here except that the reductions in the empirical variance and MSE for the proposed method compared to the marginal method were smaller for the binary outcome than for the continuous outcome.

3.3 |. Misspecification of Working Models by Omitting a Non-Linear Effect

We also considered the performance of the proposed method when either working model was misspecified by omitting a quadratic term. The outcome variable Y_ij was generated from a normal distribution with mean (1 + Z_1,ij + Z_2,ij + Z_3,ij + Z_4,ij + γ₅ ∗ $Z_{2,ij}^2$ + X_ij + b_j) and variance 1, where γ₅ equaled 0.1 (weak effect) or 0.5 (strong effect). An indicator that Y_ij was observed (R_ij) was generated from a Bernoulli distribution with probability logit⁻¹(α₀ − Z_1,ij + Z_2,ij + Z_3,ij − Z_4,ij + α₅ ∗ $Z_{2,ij}^2$ + X_ij + a_j), where α₀ equaled 0.5 (20% missing) or −1 (35% missing) and α₅ equaled −0.1 (weak effect) or −0.5 (strong effect). For both the proposed multilevel approach and the marginal approach, each working model was either fit using the correct set of fixed effects, or by excluding the quadratic term $Z_{2,ij}^2$ from the model.

Table 3 presents bias, SDE, ESE, MSE, and CP for the proposed multilevel approach. Table 4 presents ratios of the empirical variance and MSE for the multilevel approach to the available case and marginal approaches. The proposed multilevel approach exhibited essentially no bias when either the working model for [R_j, a_j|Z_j] and/or the working model for [Y_j, b_j|Z_j] were specified correctly, confirming the double robustness property. Bias for the multilevel approach tended to decrease as the percent missing decreased. Also, bias when the [Y_j, b_j|Z_j] working model was misspecified tended to decrease as the magnitude of the omitted effect decreased. The 95% confidence interval coverage rates were nearly at the nominal level for almost all cases where at least one working model was specified correctly. The proposed standard error estimator for the multilevel approach approximated the SDE well in most cases. Both the empirical variance and MSE were almost always smaller for the proposed multilevel approach than the marginal approach, and this difference in the empirical variance and MSE between those two approaches was generally greater for increased percent missing. Analogous simulation results considering a binary outcome variable (Y_ij) are presented in the Supplementary Materials (Web Tables 3 and 4); results from simulations with a binary outcome variable were similar to simulations with the continuous outcome presented here except that the reductions in the empirical variance and MSE for the proposed method compared to the marginal method were smaller for the binary outcome than for the continuous outcome.

TABLE 3.

Results from simulation study for the multilevel approach with a continuous outcome where working models were misspecified by omitting a quadratic term

				β 0					β 1
Effect strength	% Miss.	Ra	Ya	Bias	SDE	ESE	MSE	CP	Bias	SDE	ESE	MSE	CP
Weak	20	T	T	−0.001	0.110	0.109	0.012	95.2	0.001	0.060	0.059	0.004	94.9
		T	F	−0.010	0.111	0.109	0.012	95.2	0.004	0.061	0.060	0.004	94.8
		F	T	−0.001	0.110	0.108	0.012	95.2	0.001	0.060	0.059	0.004	95.2
		F	F	−0.014	0.110	0.109	0.012	95.0	0.006	0.060	0.060	0.004	95.1
	35	T	T	−0.002	0.128	0.124	0.016	95.0	0.001	0.067	0.065	0.004	94.8
		T	F	−0.017	0.128	0.125	0.017	94.5	0.006	0.067	0.066	0.005	94.2
		F	T	−0.002	0.126	0.122	0.016	95.0	0.001	0.066	0.065	0.004	94.6
		F	F	−0.024	0.127	0.123	0.017	94.4	0.008	0.067	0.065	0.005	94.2
Strong	20	T	T	0.001	0.134	0.130	0.018	94.3	−0.001	0.075	0.073	0.006	94.2
		T	F	−0.059	0.148	0.143	0.025	91.1	0.015	0.081	0.079	0.007	93.6
		F	T	0.000	0.132	0.129	0.017	94.8	−0.000	0.074	0.072	0.005	94.7
		F	F	−0.163	0.133	0.131	0.044	75.1	0.037	0.075	0.073	0.007	91.6
	35	T	T	0.008	0.156	0.149	0.024	93.8	−0.004	0.083	0.080	0.007	94.9
		T	F	−0.091	0.186	0.170	0.043	88.8	0.019	0.098	0.091	0.010	93.0
		F	T	0.008	0.150	0.144	0.022	94.7	−0.004	0.080	0.078	0.006	95.2
		F	F	−0.215	0.156	0.149	0.071	67.4	0.038	0.083	0.080	0.008	91.1

^aT = Working model specified correctly. F = Working model misspecified by excluding the quadratic term $Z_{2,ij}^2$.

TABLE 4.

Comparison of multilevel approach with the marginal approach and the available case approach from simulation study for continuous outcome where working models were misspecified by omitting a quadratic term

				β 0				β 0
				Emp var ratiob		MSE ratiob		Emp var ratiob		MSE ratiob
Effect strength	% Miss.	Ra	Ya	Available case approach	Marginal approach	Available case approach	Marginal approach	Available case approach	Marginal approach	Available case approach	Marginal approach
Weak	20	T	T	0.825	0.905	0.612	0.905	0.873	0.911	0.842	0.911
		T	F	0.835	0.898	0.625	0.906	0.889	0.903	0.862	0.907
		F	T	0.818	0.920	0.606	0.920	0.865	0.925	0.835	0.925
		F	F	0.825	0.917	0.622	0.929	0.875	0.921	0.852	0.927
	35	T	T	0.838	0.740	0.434	0.740	0.859	0.758	0.824	0.758
		T	F	0.845	0.727	0.445	0.740	0.870	0.744	0.841	0.750
		F	T	0.814	0.775	0.422	0.775	0.837	0.791	0.803	0.791
		F	F	0.825	0.776	0.442	0.795	0.852	0.792	0.828	0.800
Strong	20	T	T	0.829	0.891	0.307	0.891	0.883	0.910	0.818	0.910
		T	F	1.007	0.765	0.433	0.888	1.042	0.791	0.996	0.816
		F	T	0.796	0.936	0.295	0.936	0.864	0.943	0.800	0.943
		F	F	0.819	0.950	0.754	1.004	0.884	0.959	1.020	0.982
	35	T	T	0.767	0.774	0.235	0.774	0.791	0.807	0.735	0.808
		T	F	1.087	0.680	0.412	0.838	1.117	0.712	1.073	0.736
		F	T	0.703	0.857	0.216	0.857	0.739	0.880	0.686	0.880
		F	F	0.766	0.893	0.677	1.008	0.789	0.903	0.887	0.940

^aT = Working model specified correctly. F = Working model misspecified by excluding the quadratic term $Z_{2,ij}^2$.

^bRatio comparing multilevel approach to corresponding comparison method.

4 |. APPLICATION TO CHNS

We applied the proposed method to data from the CHNS. Starting in 2009, CHNS collected fasting blood samples on participants age seven years or older, providing data on a variety of cardiovascular and nutrition biomarkers⁸. For our analysis, we are interested in estimating the mean trajectory of triglycerides (mg/dL) as measured via fasting blood samples, both continuous (mg/dL) and dichotomized (high triglycerides defined as ≥ 150 mg/dL), adjusted for sex and age in 2009 (the first wave that collected fasting blood samples). Fasting blood samples were collected during 2009 and 2015 study waves, and so analysis was restricted to those two study years. The analysis was restricted to participants who were from the nine provinces included in the study in 2009, were adults (at least 18 years old) in 2009, and participated in the 2009 and/or 2015 wave of data collection (13,370 study participants). However, 7,225 individuals from this sample did not participate in either the 2009 or 2015 wave, and an additional 1,444 individuals who participated in both waves did not provide a valid fasting blood sample for either 2009 and/or 2015. In particular, there were 7,141 individuals in the analytic sample who were missing biomarker data for one wave, and 1,528 individuals missing biomarker data for both the 2009 and 2015 waves, resulting in missing biomarker data for 38.1% of data records in the analytic sample.

For the purposes of this example analysis, the proposed method accounted for within-individual clustering only (i.e., resulting in clusters with a size of 2 data records per cluster), and ignored higher levels of clustering (Section 5 will discuss the extension of the proposed method for more than one level of clustering). For the working models for missingness and the outcome, we considered individual-level variables, household-level variables, community-level variables, and study design variables; see Table 5 for a complete list of covariates included in the working models. While some covariates, such as time-invariant variables and variables that could be calculated based on the study design, were available for all records for all individuals in the analytic sample, time-varying variables were missing for waves for which the individual, household, or community of residence did not participate in data collection. In addition, some participants refused to provide data for variables at some waves (i.e., variable-level missingness). Since the focus of this example is to handle missing data on the response variable (i.e., triglycerides), and since most individuals had data for these covariates from other waves, missing data on time-varying auxiliary variables were handled in the following way: (1) if the covariate was reported in other waves of data collection, then the missing covariate was imputed (i.e., filled-in) as the value of the variable from the closest wave in which the variable was observed, and (2) if the individual did not report the covariate at any wave, then the individual was dropped from the analytic sample; 381 individuals (2.8% of the analytic sample) were dropped due to having no observed data for at least one of the time-varying auxiliary variables at any wave, resulting in a final sample size of 12,989 participants.

TABLE 5.

List of covariates included in the working models for CHNS data analysis, organized by individual-level, household-level, community-level, and study design variables

Individual	Household	Community	Design
• Time since 2009 • Sex • Age in 2009 • Education level • Current marital status • Current employment status • Body mass index • Waist circumference • Current smoking status • Current alcohol consumption • Average dietary intake of nutrients from 3 daily 24-hour dietary recalls • MET-hours per week of physical activity from different lifestyle activities (including interactions with time)	• Total gross household income • Total household expenses • Household income from different sources • Composite score summarizing assets owned by at least one household member	• Components of the urbanization index9  – Population density  – Economic activity  – Traditional markets  – Modern markets  – Transportation infrastructure  – Sanitation  – Communications  – Housing  – Education  – Diversity  – Health infrastructure  – Social services	• Province • City/county

The final regression models of interest were the linear regression model E[triglycerides|time, sex, age] = β₀ + β₁time + β₂sex + β₃age and the logistic regression model logit{P(high triglycerides|time, sex, age)} = β₀ + β₁time + β₂sex + β₃age, where continuous triglycerides (mg/dL) and dichotomized triglycerides (≥ 150 mg/dL) were the outcome variables for the linear and logistic regressions respectively, and the predictor variables were time since 2009, sex, and age in 2009. These final regression models were estimated using available case analysis, the marginal approach ignoring clustering, and the proposed multilevel approach (i.e., using the same methods as in the simulation study). For the proposed multilevel approach, the working models for missingness and the outcome variables were specified as a logistic mixed effect model and generalized linear mixed effect model (linear mixed effect model for continuous triglycerides and logistic mixed effect model for dichotomized triglycerides) respectively, with a random intercept for the individual, and fixed effects for the covariates listed in Table 5 and the specified interactions; standard errors were estimated using the proposed estimator for the asymptotic covariance matrix introduced in (8). For the marginal approach (i.e., ignoring clustering), the marginal working model for missingness was specified as a logistic regression model with only fixed effects including the same fixed effects as included in the multilevel working model, and the marginal working model for the outcome was specified as a linear regression model for continuous triglycerides and logistic regression model for dichotomized triglycerides with only fixed effects including the same fixed effects as included in the multilevel working models; standard errors were estimated using a bootstrap procedure. Table 6 presents the regression coefficients and standard errors based on all three methods for both outcomes. All methods suggest that triglycerides were higher for older individuals, higher for men, and lower in 2015 than 2009, based on models for both continuous triglycerides (mg/dL) and high triglycerides (≥ 150 mg/dL). Most estimated associations for the available case approach were attenuated compared to the proposed multilevel approach, especially for the estimated associations of age and time with continuous triglycerides, and for the estimated association of time with dichotomized triglycerides. In addition, standard errors for the marginal approach were similarly or less precise than the standard errors for the proposed multilevel approach, which was consistent with the results from the simulation study in Section 3.

TABLE 6.

Regression coefficient estimates and standard errors from models for triglycerides (mg/dL) and high triglycerides (≥ 150 mg/dL) in the CHNS, using proposed multilevel approach, marginal approach, and available case analysis

		Triglycerides (mg/dL)		High triglycerides (≥ 150 mg/dL)
Method	Effect	Estimate	SE	Estimate	SE
Multilevel	Intercept	163.29	2.120	−0.563	0.030
	Age in 2009 (years)	0.195	0.066	0.006	0.001
	Women	−24.744	2.208	−0.311	0.038
	Time since 2009 (years)	−2.863	0.293	−0.037	0.005
Marginal	Intercept	162.15	2.942	−0.569	0.042
	Age in 2009 (years)	0.188	0.071	0.005	0.001
	Women	−23.929	2.311	−0.308	0.039
	Time since 2009 (years)	−2.856	0.390	−0.037	0.007
Available Case	Intercept	162.04	1.738	−0.586	0.030
	Age in 2009 (years)	0.129	0.072	0.006	0.001
	Women	−23.536	2.160	−0.293	0.037
	Time since 2009 (years)	−2.255	0.267	−0.026	0.005

Abbreviations: SE, standard error.

5 |. DISCUSSION

This research extended the doubly robust approach for handling missing outcome data in semi-parametric regression introduced by Scharfstein et al.⁵ to the case with clustered, and thereby correlated, data. The new approach estimates separate hierarchical working models for the missingness mechanism and the outcome, with random effects specified to account for within-cluster correlation for each model. A set of estimating equations were proposed, where the estimating equations are averaged across unknown random effects. This approach was shown to have the double robustness property, and was shown in simulation studies to be generally more precise than the approach ignoring clustering in the data.

We derived the asymptotic covariance matrix for the proposed doubly robust estimator ${\widehat{\mathit{\beta }}}_{\mathit{m}}$, and proposed an empirical covariance estimator based on these asymptotic results. However, an alternative approach could be to estimate the covariance matrix using a bootstrap approach. Nonparametric bootstrap sampling approaches for variance estimation with clustered data have been described elsewhere, where the recommended bootstrap sampling approach involves randomly sampling the highest level clusters with replacement, and then selecting all data records within each randomly sampled cluster from this highest level¹⁰. Further research is needed to verify the performance of a bootstrap approach for variance estimation for this proposed doubly robust estimator.

The proposed method accounts for within-cluster correlation by including random cluster-specific effects in the working models, with an assumed distribution for the random effects. However, an alternative approach could have instead incorporated cluster-specific fixed effects¹¹. There are a couple key advantages for using the random effects modeling approach employed in the proposed method. First, the CHNS data considered in Section 4 contained a large number of clusters with comparatively few data records per cluster (i.e., data were clustered within 12,989 individuals with 2 records per cluster). However, maximum likelihood estimation may be unstable and may not be statistically consistent for a model with fixed effects for such a large number of relatively small clusters¹². On the other hand, using a random effects modeling approach reduces the number of unknown parameters estimated by maximum likelihood estimation, and allows prediction of cluster-specific random effects to “borrow” information from the average (i.e., marginal) distribution, where the amount of “borrowing” for each cluster depends on cluster size (with smaller clusters “borrowing” more)^13,14. Also, a random effects framework can easily accommodate cluster-specific regression coefficients in addition to a cluster-specific intercept (e.g., a cluster-specific slope for time when modeling longitudinal data). One notable disadvantage of the random effects modeling approach employed in the proposed method is that it requires additional distributional assumptions about the random effects, which are not required for a comparable fixed effects modeling approach. Although it is not possible to verify the assumption that the working distribution for the random effects is specified correctly, the sensitivity of the working model to these distributional assumptions for the random effects can be tested^15,16. In practice, a convenient choice for the working distribution of the random effects would be a normal distribution, since assuming normally distributed random effects would allow the use of Gauss-Hermite quadrature to estimate integrals (e.g., for maximizing the observed data likelihoods, for solving the proposed estimating equations in (4)), which is generally simpler and faster to implement than alternative approaches such as the EM algorithm or Markov Chain Monte Carlo. However, note that the asymptotic properties of the estimator ${\widehat{\mathit{\beta }}}_{\mathit{m}}$ hold regardless of whether the true random effects are normally distributed (as long as at least one of the working models [R_j, a_j|Z_j] and/or [Y_j, b_j|Z_j] is specified correctly). Exploratory simulation studies have shown a benefit in precision for the effect estimates of interest when both the random effects distribution for the missingness and outcome model were specified correctly, but future research should further explore this in detail.

Hierarchical working models have been employed elsewhere to adjust for bias due to informative missing data or confounding in statistical analyses of clustered data. Kasim and Raudenbush¹⁷ have developed a two-level linear imputation model for normally-distributed data that can be used with fully conditional specification imputation methods, which has been implemented in the mice package in R¹⁸. In addition, random effects models have been used to estimate propensity scores to adjust for unmeasured cluster-level confounding when estimating causal effects^19,20. The methods proposed in this research have further contributed to this growing literature by employing hierarchical working models to model both missingness and a regression outcome in a doubly robust approach to adjust for bias due to informatively missing data.

The approach proposed here addresses missing data in the outcome variable for a semi-parametric regression. However, there may be cases with missing data on the predictor variables for the regression model of interest and/or auxiliary variables used in the hierarchical working models. One possibility for handling this situation could be to impute any missing predictor or auxiliary variables using a model that accounts for correlation due to clustering, use these imputed data to estimate the doubly robust regression estimator described here in the presence of missing outcome data, and then obtain standard errors using multiple imputation³ or a bootstrap approach²¹. However, although this approach would be robust to misspecification of the imputation model for the outcome variable (i.e., the working model for Y ), it would not be robust to misspecification of the imputation model for the other missing variables.

For illustration, we specified the hierarchical working models for the missingness mechanism and the outcome as generalized linear mixed effect models with a cluster-specific random intercept. More general models could be used to increase the chance that the working model(s) are specified correctly. For example, higher-order polynomial terms, interaction terms, or splines could be included as fixed effects in the working models. Additional random effects could also be included in the working models. However, specification of higher-dimensional random effects will generally be more computationally intensive, both for estimating the parameters of the hierarchical working models and for averaging the final set of estimating equations across the random effects to estimate S_m(β). Generally, specification of the working models can be viewed as a trade-off between specifying models that are general enough to make it more likely that the model is correctly specified and simple enough to be computationally feasible.

Although doubly robust estimators, such as the estimator presented here, can protect against bias due to a misspecified outcome model if the missingness model is specified correctly (and vice versa), it should be noted that simulation results from previous research²² have illustrated situations where methods that depend on only a missingness model (e.g., inverse probability weighting) or only an outcome model (e.g., imputation) performed better than doubly robust estimators when both models are misspecified, which highlights the importance of carefully specifying working models that are as plausible as possible. In this research, we used fully parametric working models for both missingness and the outcome variable. However, an alternative could be to instead specify non-parametric working models for both missingness and the outcome variable. In the case of independent data, previous research has shown that if the estimators for the non-parametric working models converge at faster than n^−1/4 rates, then the asymptotic behavior of the resulting doubly robust estimator would be the same as if the working models were correctly specified parametric models (e.g., $\sqrt{n}$-consistent and asymptotically normal)^23,24. Therefore, assessing the statistical properties of the proposed method for doubly robust estimation with missing multilevel data using non-parametric working models is an important topic for future research.

The statistical derivations and simulation studies presented in this paper involve two-level data (e.g., longitudinal data for independently sampled study participants, cross-sectional data collected on all individuals within a sample of households). However, many large cohort studies contain data consisting of more than two levels. For example, the CHNS collected longitudinal data on all people living in households included in the cohort, and these households were clustered within neighborhoods, which were further clustered within cities/counties. Extending the approach described in this paper to data with an arbitrary number of levels of clustering is straightforward in theory. One could fit hierarchical working models with a vector of random effects for each level of clustering. Then the final set of estimating equations S_m(β) would be obtained by averaging across all random effects from the hierarchical working models. Assuming that the entire set of random effects (for all levels of clustering) are independent between the two working models, then the double robustness property would still hold. However, in practice increasing the dimension of the random effects in either working model would increase the computational burden, both for estimating the hierarchical working models and for averaging the final set of estimating equations across the random effects to estimate S_m(β). Therefore, for datasets with many levels of clustering (e.g., CHNS), it may be more reasonable to carefully select just a few levels of clustering that are most important to account for in either working model (e.g., the levels of clustering that are hypothesized to induce the most correlation after conditioning on the observed covariates), and/or to include fixed effects for observed covariates that help explain the within-cluster correlation for levels of clustering for which no random effects are included (e.g., include fixed effects for household income to help account for within-household correlation, include community-level variables to help account for within-community correlation).

One key assumption required for this method to be doubly robust is that the random effects for the working models for the missingness mechanism and the outcome need to be independent of each other. If the random effects from both working models are correlated, then misspecification of one of the working models (e.g., ignoring an important covariate, specifying the wrong functional form for a covariate, specifying the wrong link function) would necessarily misspecify the other working model. Therefore, when the random effects from both models are in fact correlated, the proposed method would only produce unbiased results when both working models are specified correctly, and therefore would no longer possess the double robustness property. Extending this methodology to the case with correlated random effects is a topic for future research.

In the simulation studies presented in Section 3 and Web Appendix C in the Supplementary Materials, the proposed method was generally less precise when the missingness model was correctly specified and the outcome model was misspecified than when the outcome model was correctly specified. In addition, previous research has shown that the doubly robust estimator of Scharfstein et al.⁵, from which our proposed method was derived, is inefficient when the outcome model is misspecified²⁵. For the case with independent data, some doubly robust methods have been proposed that have improved efficiency, particularly for this scenario where the missingness model is correctly specified and the outcome model is misspecified^26,27. Extending our proposed methodology to improve the efficiency in this case is not straightforward, and so this is another topic for future research.