Abstract
Motivation
Inter-protein (interfacial) contact prediction is very useful for in silico structural characterization of protein–protein interactions. Although deep learning has been applied to this problem, its accuracy is not as good as intra-protein contact prediction.
Results
We propose a new deep learning method GLINTER (Graph Learning of INTER-protein contacts) for interfacial contact prediction of dimers, leveraging a rotational invariant representation of protein tertiary structures and a pretrained language model of multiple sequence alignments. Tested on the 13th and 14th CASP-CAPRI datasets, the average top L/10 precision achieved by GLINTER is 54% on the homodimers and 52% on all the dimers, much higher than 30% obtained by the latest deep learning method DeepHomo on the homodimers and 15% obtained by BIPSPI on all the dimers. Our experiments show that GLINTER-predicted contacts help improve selection of docking decoys.
Availability and implementation
The software is available at https://github.com/zw2x/glinter. The datasets are available at https://github.com/zw2x/glinter/data.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Proteins perform functions by interacting with other molecules or forming protein complexes. As a result, the full characterization of protein–protein interactions with structural details is crucial to atom-level understanding of protein functions. The in silico structural characterization of protein complexes, or quaternary protein structure prediction, is a longstanding challenge in computational structural biology. Given individual protein chains (and possibly their structures), interfacial contact prediction aims to predict which pairs of residues on the protein surface are geometrically close to each other after the protein chains bind together. Interfacial contacts may facilitate generating and filtering docking decoys (Baldassi et al., 2014; Geng et al., 2020; Hopf et al., 2014; Ovchinnikov et al., 2014), and reveal important biophysical properties and evolutionary information of protein interfaces (Uguzzoni et al., 2017). They are also useful for the redesign of protein–protein interfaces (Laine and Carbone, 2015) and prediction of binding affinity (Vangone and Bonvin, 2015).
Co-evolution analysis by global statistical methods (Burger and van Nimwegen, 2008; Weigt et al., 2009) has been used for inter-protein contact prediction. A recent study (Cong et al., 2019) showed that co-evolution-based in silico protein–protein interaction screening methods produced more true protein–protein interactions than high-throughput experimental techniques. Nevertheless, accurate co-evolution analysis needs a large number of sequence homologs and thus, may not work well on a large portion of heterodimers for which it is very challenging to find sufficient number of interacting paralogs (interlogs) (Bitbol et al., 2016; Gueudré et al., 2016; Zeng et al., 2018). On the other hand, protein language models, which are trained on individual protein sequences or multiple sequence alignment (MSAs), are shown to perform similarly as or better than global statistical methods on intra-chain contact prediction when few sequence homologs are available (Rao et al., 2021; Rives et al., 2021). It was shown before that a deep learning model trained by individual protein chains works fine on protein complex contact prediction (Zeng et al., 2018; Zhou et al., 2018). Therefore, we hypothesize that a deep language model trained on individual protein chains may also generalize well to protein–protein interactions, reducing the required number of interlogs. Protein language models are also much faster since they require only one-time forward computation during inference and thus, more suitable for proteome-scale screening of protein–protein interactions.
RaptorX ComplexContact (Zeng et al., 2018; Zhou et al., 2018) possibly is the first deep learning method for interfacial contact prediction. It is mainly developed for heterodimers, although can be used for homodimers. Nevertheless, its deep models are purely trained on individual protein chains instead of protein complexes. Further, ComplexContact does not make use of any (experimental or predicted) structures of constituent monomers of a dimer. Recently, some deep learning methods are developed specifically for contact prediction of a homodimer, e.g. DNCON_inter (Quadir et al., 2021) and DeepHomo (Yan and Huang, 2021), both using ResNet originally implemented in RaptorX (Wang et al., 2017). In addition to evolution information, DeepHomo uses docking maps, native intra-chain contacts, and experimental structural features derived from monomers to achieve state-of-the-art performance. However, it is slow in calculating docking maps and thus, cannot scale well to proteome-scale prediction. Some deep learning methods also use learned representations of tertiary structures, including voxels (Derevyanko and Lamoureux, 2019; Townshend et al., 2019) and radial/point cloud representations on protein surfaces (Dai and Bailey-Kellogg, 2021; Gainza et al., 2020; Sverrisson et al., 2020). Meanwhile, some representations include anisotropy information in the structures (Fout et al., 2017; Pittala and Bailey-Kellogg, 2020) while others do not.
Given the tremendous progress in protein structure prediction (Jing and Xu, 2020; Jumper et al., 2021; Wang et al., 2017; Xu, 2019; Xu et al., 2021) and the fast growing number of protein sequences, it is important to leverage predicted structures of constituent monomers and large sequence corpus to produce accurate, proteome-scale interfacial contact predictions. An interfacial contact prediction method shall effectively extract coevolution signals from a small number of interlogs, and make use of predicted structures of constituent monomers. Here, we propose a new supervised deep learning method GLINTER for interfacial contact prediction that integrates representations learned from (experimental and predicted) monomer structures and attentions generated by the MSA Transformer (ESM-MSA) (Rao et al., 2021) from interlogs of the dimer under prediction. GLINTER applies to both heterodimers and homodimers, outperforming ComplexContact, DeepHomo and BIPSPI on the 13th and 14th CASP-CAPRI datasets. The contacts predicted by GLINTER may also improve the ranking of the HDOCK-generated docking decoys (Yan et al., 2017). Further, our method runs very quickly, which makes it suitable for proteome-scale study.
2 Materials and methods
2.1 Network architecture
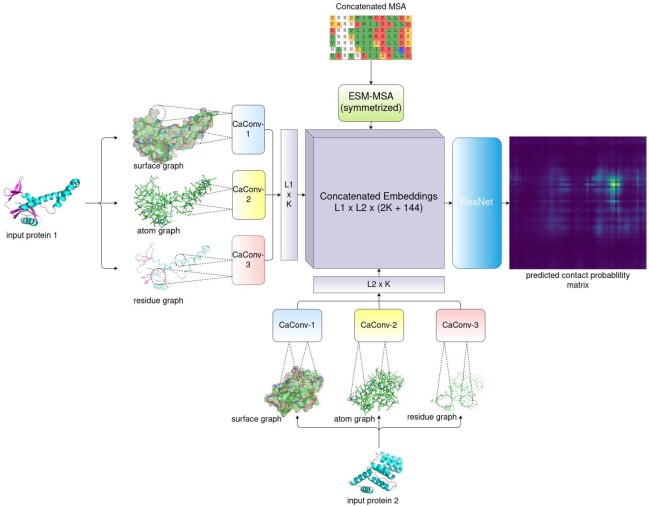
As shown in Figure 1, our network, denoted as GLINTER, consists of two major modules: a Siamese graph convolutional network (GCN) (Hashemifar et al., 2018) and a 16-block ResNet (He et al., 2016). The GCN extracts local features from three types of graphs derived from monomer structures. The ResNet takes as input the outputs of the GCN module and the attention weights generated by the MSA Transformer (Rao et al., 2021) and yields interfacial contact prediction. One ResNet block has two convolutional layers, each with 96 filters and a 3×3 kernel. ELU and BatchNorm are used in each block. ResNet is connected to a fully connected layer and a softmax layer for contact probability prediction.
Fig. 1.
Overview of the GLINTER architecture. L1and L2 are the lengths of the two protein chains, K is the number of channels in a CaConv layer and 144 is the total number of heads in the row attention weights generated by Facebook’s MSA Transformer (Rao et al., 2021)
At each graph convolution layer (denoted as CaConv), we calculate the message for a graph edge and node as follows. For an edge e, we feed its feature and the features of its two ends to a subnetwork to generate a message. For a node q, we first aggregate all messages of its adjacent nodes using max pooling, and then pass the result to a subnetwork to generate a message of q, i.e. gq=g(maxv∈Nqf([xq,xv,e(q,v)])) where xq is the feature of node q, v is a node in the neighborhood Nq of q, xv is the feature of v, e(q,v) is the feature of edge (q, v) and the non-linear functions g and f are two fully connected layers of 128 hidden units with BatchNorm and ReLU.
Both coordinates and normals are used to represent the geometric properties of a monomer structure (Sverrisson et al., 2020). We standardize the geometric features so that they are invariant to the coordinate system used by the monomer structure. While calculating an message for any node q (i.e. computation of f), all the adjacent nodes of q are first translated using q as the origin, and then rotated using its predefined local reference frame (Pagès et al., 2019; Sanyal et al., 2020). The standardized features are then concatenated with other features to form the actual inputs of function f.
We use a separate graph convolution network (GCN) module to process each graph. When multiple graphs are used for a monomer, the outputs of all its GCN modules are concatenated to form a single output vector of this monomer. The outputs of two monomers are then outer-concatenated to form a pairwise representation of this dimer. When the ESM row attention weight is used, the attention matrix generated by Facebook’s MSA Transformer is concatenated to the pairwise representation, which is then fed to the ResNet for interfacial contact probability prediction.
2.2 Features
Graph representation of protein structures
We build three different graphs from one protein structure: residue graph, atom graph and surface graph. In a residue graph, a node is a residue represented by its CA atom, and there is an edge between two residue nodes if and only if the Euclidean distance between their CA atoms is within a certain cutoff, e.g. 8 Å. In an atom graph, a node is a heavy atom or a residue represented by its CA atom, and there is one edge between one residue node and one atom node if and only if their Euclidean distance is within a certain cutoff.
We use Reduce (Word et al., 1999), MSMS (Sanner et al., 1996) and trimesh (Dawson-Haggerty,M et al., 2019) to construct the triangulated surface of a protein structure (detailed in Supplementary File). The surface can be essentially interpreted as a mesh enclosing the protein. Two neighboring triangles in the surface share either one edge or at least one vertex. In a surface graph, one node represents one residue or one vertex on the triangulated surface. There is one edge between one residue node and one triangle vertex if and only if their Euclidean distance is within a certain cutoff. It takes only a few seconds to build a surface graph and thus, our method scales well on large-scale prediction (Cong et al., 2019).
Features
Supplementary Table S2 summarizes all the features. The geometric features of a residue node include its coordinates and a local reference frame derived from the N-CA-C plane. As shown in Supplementary Figure S3, it uses the CA-C bond as the x-axis, the vector perpendicular to the plane formed by the N-CA and CA-C bonds as the z-axis, and their cross-product as the y-axis. Such a representation is rotation invariant and thus, may generalize well without data augmentation in contrast to the network that is not rotation invariant. The other features of a residue node include position-specific scoring matrix (PSSM), residue solvent accessible surface areas (summation of the solvent accessible surface areas of all atoms in the residue), the one-hot encoding of amino acid type, and the sequence index of the residue divided by the protein sequence length (which is used to provide order information for neural network architectures that are order invariant) (Jing and Xu, 2020).
In an atom graph, an edge has a binary feature called ‘edge type’. It is equal to 1 if the nodes of this edge belong to the same residue. An atom is encoded by a 10-dimensional 1-hot vector, indicating four backbone atom types (CA, N, C, O) and six side chain atom types (CB, C, N, O, S, H).
In a surface graph, we use the coordinates and normals generated by MSMS as the features of a triangle vertex (Gainza et al., 2020), which indicate the contour and orientation of some local patches on the surfaces. Normals are initially computed by MSMS, then validated by trimesh’s default protocol.
Coevolution signals generated by Facebook’s MSA transformer (Rao et al., 2021)
We use the row attention weights generated by the MSA Transformer as interfacial co-evolution signals. We build a joint MSA for a heterodimer using the protocol proposed by ComplexContact (Zeng et al., 2018). For a homodimer, we simply concatenate each sequence in the MSA with itself. We then select a diverse set of sequences from the joint MSA as the input of the MSA Transformer. That is, we filter the MSA with HHfilter (Steinegger et al., 2019) and assign Henikoff weights to sequences, as detailed in the Supplementary File. We further symmetrized the generated inter-chain attentions, following the MSA Transformer’s protocol (Rao et al., 2021).
2.3 Datasets
Following DeepHomo (Yan and Huang, 2021), we say there is one true contact between two residues (of two monomers) if in the experimental complex structure, the minimal distance between their respective heavy atoms is less than 8 Å. We define the interfacial contact density of a given dimer by N/(L1L2), where N is the number of inter-protein contacts and L1 and L2 are the respective lengths of the constituent monomers.
CASP-CAPRI data
We use all 32 dimers (23 homodimers and 9 heterodimers) with at most 1000 residues in the 13th and 14th CASP-CAPRI datasets 40 as our test set. We do not include the dimers with more than 1000 residues since Facebook’s MSA Transformer cannot handle such a large protein. To avoid redundancy between our training and test sets and to fairly compare GLINTER with recently published methods, we do not use the 11th and 12th CASP-CAPRI data. We run HHblits on the ‘uniclust30_2016_09’ database to build MSAs for individual chains and then concatenate two MSAs to form a joint MSA for a heterodimer using the method described in ComplexContact (Zeng et al., 2018). We use monomer (bound) experimental structures as inputs since their unbound structures are unavailable. We also tested the 3D structure models of individual chains predicted by AlphaFold (Jumper et al., 2020; Senior et al., 2020) in CASP13 and 14, except for T0974s2 which did not have a predicted 3D model. The median interfacial contact density of this dataset is 1.79%. Calculated by FreeSASA (Mitternacht, 2016), the median buried solvent accessible surface area (SASA) of this dataset is 2507Å2.
3D complex data
Our training set has 5306 homodimers and 1036 heterodimers derived from 3DComplex (Levy et al., 2006). We do not include the dimers with more than 1000 residues due to MSA Transformer’s limit (Rao et al., 2021). We say two dimers are at most x% similar, if the maximum sequence identity between their constituent monomers is no more than x% and build a joint MSA as described in the previous subsection.
The median interfacial contact density of the training set is 0.76%. The median buried SASA of the training set is 2393.Å2
PDB2018 data
We build two more test sets from the complexes released to PDB after January 1, 2018. One test set (denoted as ‘HomoPDB2018’) has 165 homodimers and the other one (denoted as ‘HeteroPDB2018’) has 72 heterodimers. We define homodimers and heterodimers in the same way as the 3DComplex data. We exclude dimers similar to the training set, judged by MMseqs2 E-value < 1. We cluster dimers using the 40% sequence identity threshold and also remove dimers with interfacial contact density < 0.7%, which is slightly lower than the median interfacial contact density of the training set. The medians of the buried SASAs of ‘HomoPDB2018’ and ‘HeteroPDB2018’ are 2557 and 2346 Å2, respectively. The medians of the interfacial contact densities of ‘HomoPDB2018’ and ‘HeteroPDB2018’ are 2.41% and 3.52%, respectively. It should be noted that although we remove dimers similar to our training set, there may be some redundancy between our test dimers and the training sets used by the other competing methods. Therefore, the estimated performance of the competing methods on the PDB2018 data may be overly optimistic.
2.4 Training and evaluation
We use weighted cross-entropy as the loss function since the interfacial contact density is very small (the median of the training set is 0.76%). We initially trained our network on a small training subset using weights 5, 10, 50 and 100 and found that the weight 5 yields the best average top-10 precision in the first few epochs. So in the formal training, we set the weight of a contact to be five times that of a non-contact. We trained our deep models using Adam as the optimizer (Kingma et al., 2014), with the hyperparameters β1=0.9,β2=0.9999,ϵ=1e−8. The learning rate is initialized to 0.0001 and reduced by half every four epochs. All models are trained for 20 epochs on two Titan X GPUs, with minibatch size 1 on each GPU. It takes 20–40 min to train one epoch. For a given hyperparameter setting, we select the model with the best top-10 precision on the validation data as the final model.
Since our deep network is rotation invariant, we do not augment the training set by rotating a monomer multiple times. Nevertheless, we randomly rotate a monomer once before training to prevent our deep network from learning unexpected artifacts in the dataset. For a heterodimer, we use both of the orders of its two proteins in training. For evaluation, we predict two contact maps for one heterodimer by exchanging the order of its two proteins, and then compute the geometric average of the two predicted contact map probability matrices as the final prediction.
We evaluate contact prediction in terms of top k precision where k=10,25,50,L/10 and L/5 and L is the length of the shorter protein in a dimer. When the number of native contacts is less than k, we still use k as the denominator while computing the top k precision. Inter-chain contact maps are more sparse than intra-chain contact maps, so we evaluate a smaller number of predicted inter-chain contacts.
2.5 Methods to compare
We compare GLINTER with DeepHomo, ComplexContact and BIPSPI. DeepHomo is a ResNet-based method developed for only homodimers. ComplexContact is a sequence-only and ResNet-based method developed mainly for heterodimers. Both DeepHomo and ComplexContact take as input the coevolution information computed by CCMpred (Seemayer et al., 2014) while GLINTER does not. BIPSPI works for both homodimers and heterodimers and can take both structures and MSAs as input.
3 Results
We test our method with the bound experimental structures while comparing it with BIPSPI, DeepHomo and ComplexContact, as mentioned in Section 2.5. We also study the impact of the quality of predicted structures on our method.
3.1 Evaluation of interfacial contact prediction
Performance on the CASP-CAPRI data
As shown in Table 1, tested on the 23 test homodimers, GLINTER has 54% top 10 precision and 51% top L/10 precision where L is the sum of the two monomer protein sequence lengths, while DeepHomo has 30% top 10 precision and 27% top L/10 precision. Tested on the nine heterodimers, GLINTER has 44% top 10 precision and 48% top L/10 precision, while ComplexContact has 14% top 10 precision and 14% top L/10 precision. Even using the monomer structures predicted by AlphaFold-1 and AlphaFold-2 as input, GLINTER has 43% top 10 precision on the homodimers and 24% top 10 precision on the heterodimers.
Table 1.
Average contact prediction precision (%) on the CASP-CAPRI and PDB data
| HomoCASP | HeteroCASP | HomoPDB | HeteroPDB | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of top predictions | 10 | L10 | L5 | 10 | L10 | L5 | 10 | L10 | L5 | 10 | L10 | L5 |
| BIPSPI (native) | 16 | 16 | 14 | 11 | 11 | 14 | 20 | 21 | 19 | 18 | 18 | 19 |
| DH (native) | 30 | 27 | 23 | 24 | 25 | 24 | ||||||
| CC (none) | 14 | 14 | 11 | 14 | 13 | 14 | ||||||
| GLINTER (native) | 54 | 51 | 47 | 44 | 48 | 37 | 48 | 48 | 47 | 47 | 47 | 46 |
| GLINTER (pred) | 43 | 40 | 37 | 24 | 30 | 23 | ||||||
Note: ‘Native’ means the experimental monomer structures are used. ‘None’ means that tertiary structures are not used at all. ‘Pred’ means the monomer structures predicted by AlphaFold are used. HomoCASP represents the set of 23 homodimers in the CASP-CAPRI data. HeteroCASP represents the set of nine heterodimers in the CASP-CAPRI data. For the PDB2018 test sets (HomoPDB and HeteroPDB), only the native monomer structures are used. ‘DH’ represents DeepHomo and ‘CC’ represents ComplexContact. In each column, the entry of the best performance is in bold.
Performance on the PDB2018 data
As shown in Table 1, tested on the 165 HomoPDB2018 homodimers, GLINTER has 48% top 10 precision, while BIPSPI and DeepHomo have 20 and 24% top 10 precision, respectively. Tested on the 72 HeteroPDB2018 targets, GLINTER has 47% top 10 precision, while BIPSPI and ComplexContact have 18 and 14% top 10 precision, respectively. See detailed results in Supplementary Tables S5 and S6.
In summary, GLINTER consistently outperforms DeepHomo and ComplexContact by a large margin no matter which test sets are evaluated and whether experimental or predicted monomer structures are used.
3.2 Ablation study
We train the GLINTER models under eight different settings (different sets of input features). Supplementary Tables S3 and S4 show their test results with monomer experimental structures and AlphaFold-predicted monomer structures, respectively. We have studied the following eight settings: ‘Residue’, ‘Residue+ESM’, ‘Residue+Atom’, ‘Residue+Atom+ESM’, ‘Residue+Surface’, ‘Residue+Surface+ESM’, ‘Residue+Atom+Surface’ and ‘Residue+Atom+Surface+ESM’ models. Here, ‘Residue’, ‘Atom’ and ‘Surface’ represent the residue, atom and surface graphs, respectively. ‘ESM’ means that the ESM row attention weights are used. Using the ESM row attention weights does not change the network architecture, but increases the input dimension of the first ResNet block, as shown in Figure 1.
To evaluate the contribution of the ESM row attention weights, we test a sequence-only model called ‘ESM-Attention’ that uses only the ESM row attention weights as input. As shown in Supplementary Figure S1, its major module is a 2D ResNet with the same architecture as the one used in the Residue+ESM model.
To evaluate the contribution of the graph convolution module, we develop a sequence-structure-hybrid model denoted as ‘CNN+ESM-Attention’, which uses an 1D convolutional network (CNN) and the same set of input features. Similar to the Residue+ESM model, the CNN+ESM-Attention model consists of two major modules: a Siamese 1D CNN and a ResNet. The 1D CNN has four convolution layers (each with 128 filters and kernel size 5) and the ResNet is the same as that used in the Residue+ESM model (Supplementary Fig. S2). Both the ESM-Attention and the CNN+ESM-Attention models are trained on the same dataset using the same protocols as the GLINTER models.
Contribution of the graph convolution module
As shown in Table 2 and Supplementary Table S3, the CNN+ESM-Attention model has similar performance as the ESM-Attention model. The best CNN+ESM-Attention model has 35% top-10 precision and 24% top-L/10 precision, while the ESM-Attention model has 31% top-10 precision and 29% top-L/10 precision. In contrast, the Residue+ESM model has 43% top-10 precision and 42% top-L/10 precision, which suggests that the residue graph (derived from monomer structures) used by GLINTER is indeed very helpful for interfacial contact prediction.
Table 2.
Average interfacial contact precision (%) of the ESM-Attention, CNN+ESM-Attention and Residue+ESM models on the CASP-CAPRI data
| No. of top predictions | 10 | 25 | 50 | L10 | L5 |
|---|---|---|---|---|---|
| ESM-attention | 31 | 27 | 24 | 29 | 28 |
| CNN+ESM-attention | 35 | 28 | 20 | 24 | 34 |
| Residue+ESM | 43 | 37 | 34 | 42 | 32 |
Note: The ESM-Attention model only uses MSAs as inputs, while the CNN+ESM-Attention and Residue+ESM models use MSAs and experimental monomer structures as inputs.
Dependency on distance cutoff
The distance cutoff used to define graph edges is an important hyperparameter. According to our observation, a model with a larger distance cutoff tends to have a lower training loss, although its prediction performance may not be as good. A model with a smaller distance cutoff may have a higher training loss and much worse prediction performance. As shown in Table 3 and Supplementary Table S3, the top k precision of GLINTER models increases along with the distance cutoff until reaching the optimal value. For example, the top-10 precision of the Residue+Atom model increases from 22 to 33% as the distance cutoff increases from 4 to 6 Å, and then decreases to 27% when the distance cutoff is 8 Å. This saturation effect on the distance cutoffs is also observed in Townshend et al. (2019).
Table 3.
Average top-10 interfacial contact precision (%) of the ‘Residue+Atom’ and ‘Residue+Surface’ models on the CASP-CAPRI data when experimental monomer structures are used
| 8,4 | 8,6 | 8,8 | 8,10 | |
|---|---|---|---|---|
| Residue+atom | 22 | 33 | 27 | 30 |
| Residue+surface | 33 | 34 | 33 | 33 |
Note: The first row shows the distance cutoffs used to define graph edges. For example, ‘8,6’ for ‘Residue+Atom’ indicates that the residue graph and atom graph use 8 and 6 Å to define edges, respectively.
Different types of graphs may rely on distance cutoffs differently. For example, the top 10 precision of the Residue+Surface model is around 33% when the distance cutoff defining the surface graph ranges from 4 to 10 Å, while the precision of the ‘Residue+Atom’ model changes a lot with respect to the distance cutoff. Here, we determine the optimal distance cutoff using the experimental monomer structures, which may not have the optimal performance when predicted monomer structures are used.
Dependency on the quality of predicted monomer structures
GLINTER models are trained with monomer experimental structures. Here, we study their prediction performance when the AlphaFold-predicted monomer structures are used. We use the lower TMscore (Zhang and Skolnick, 2005) of the two constituent monomer models to measure the structure quality of a dimer under test. We exclude the test dimers without any correct top k predicted contacts when their native structures are used as input. Since there are only dozens of test targets, we divide them into four groups according to their TMscores: low quality (0.2 ≤ TMscore < 0.5), acceptable quality (0.5 ≤ TMscore < 0.7), medium quality (0.7 ≤ TMscore < 0.9) and high quality (0.9 ≤ TMscore < 1.0).
Supplementary Figure S6 shows that even trained on bound experimental structures, our methods work well on predicted structures with medium or high quality (i.e. TMscore > 0.7). When the predicted monomer structures have lower quality (TMscore < 0.7), GLINTER models perform better with experimental structures than predicted structures. By comparing Supplementary Figure S6D and E, we find that the ESM row attention weight may not be able to reduce the precision gap incurred by predicted structures. This suggests that the ESM row attention weight derived purely from MSAs may not necessarily improve the robustness of our structure-based models.
Contribution of the ESM row attention weight
As shown in Table 1 and Supplementary Table S3, on the 32 dimer targets, the ESM-Attention model has top 10 and L/10 precision 31 and 29%, respectively, greatly outperforming BIPSPI, which has top 10 and L/10 precision 15 and 14%, respectively. That is, even though the MSA Transformer is pre-trained with the MSAs of single-chain protein sequences, it works for inter-chain contact prediction. Over the nine heterodimer targets, the top 10 precision of ComplexContact and ESM-Attention is 14 and 28%, respectively. As shown in Supplementary Tables S3 and S4, no matter whether native or predicted monomer structures are used the ESM row attention weight consistently improves the performance of GLINTER models, which confirms that coevolution signals are very useful for inter-chain contact predictions.
Figure 2A compares the performance of the ESM-Attention model (which is a sequence-only model) and the Residue+Atom+Surface model (which is a structure-only model) when the native structures are used. They have similar overall performance, but perform very differently on individual test targets, which suggests that the ESM row attention weight and structure information are highly complementary to each other. On the majority of test targets, the Residue+Atom+Surface+ESM model outperforms the ESM-Attention model (Fig. 2B) and the Residue+Atom+Surface model (Fig. 2C). Figure 2A and B differs only in the y-axis by an ESM feature, so their comparison shows the impact of the ESM features. Figure 2A and C differs only in the x-axis by Residue+Atom+Surf, so their comparison shows the impact of the Residue+Atom+Surf features. Detailed performance comparison among the three models is shown in Supplementary Table S1. A case study on target T0997 is in Supplementary File.
Fig. 2.
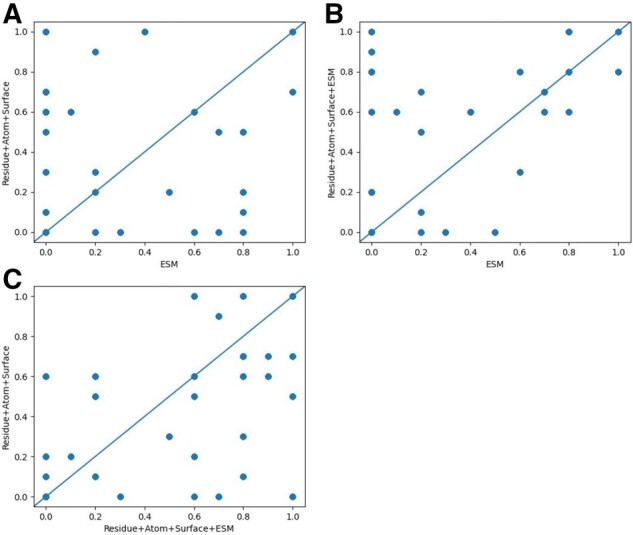
Comparison of top-10 precision of three models: ESM, Residue+Atom+Surface and Residue+Atom+Surface+ESM. (A) compares Residue+Atom+Surface and ESM, (B) compares Residue+Atom+Surface+ESM and ESM, and (C) compares Residue+Atom+Surface and Residue+Atom+Surface+ESM.
Dependency on the depth of MSAs
It is known that intra-chain contact prediction precision correlates with the depth of MSAs denoted as Meff (defined in Supplementary File). Here, we study the impact of MSA depth on interfacial contact prediction when the ESM row attention weight is used. To remove the impact of inaccurate predicted structures, here, we test GLINTER models with native monomer structures. Supplementary Figure S7 shows that there is certain correlation (R2=0.3093) between the number of correct top-10 predictions by the ESM-Attention model and the ln(Meff) of the input MSA.
3.3 Application to selection of docking decoys
A simple application of predicted interfacial contacts is to select the docking decoys. We use the top k (k = 10, 25, 50) contacts predicted by the Residue+Atom+Surface+ESM model to rank the docking decoys generated by HDOCK. The quality of a docking decoy is calculated by comparing it with its experimental complex structure using MMalign (Mukherjee and Zhang, 2009). For each target, we select top N decoys ranked by the predicted interfacial contacts and define their highest TMscore as the ‘TMscore of the top N decoys’. In Figure 3, the y-axis shows the average TMscore of the top N decoys of all the test dimers. Generally speaking, predicted contacts may improve the quality of top decoys by 5-8%. Except when N≤10, generally speaking using more top predicted contacts may select better decoys than using only top 10 predicted contacts.
Fig. 3.
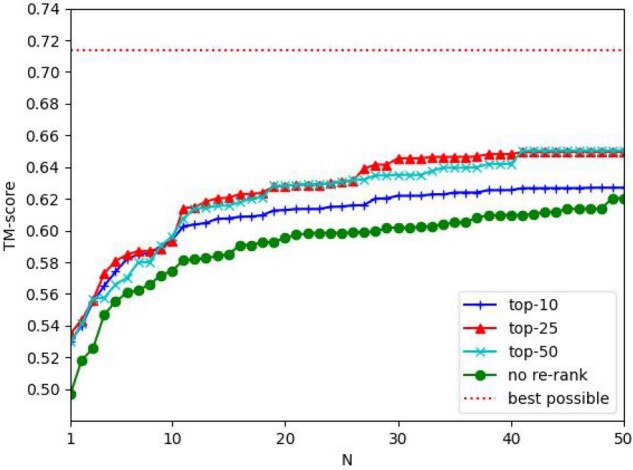
The average quality (measured by TMscore) of the selected decoys by top predicted contacts. The x-axis is the number of top decoys selected. In the legend, ‘top-10’, ‘top-25’ and ‘top-50’ represent that top 10, 25 and 50 predicted contacts are used to select docking decoys, respectively. ‘best decoy’ indicates the quality of the best decoys generated by HDOCK
4 Conclusion
We have presented an interfacial contact prediction method, GLINTER, that predicts inter-protein contacts by integrating attention information generated by protein language models and graph modeling of monomer (experimental and predicted) structures. The attention may capture evolutionary and coevolutionary information encoded in MSA. We demonstrate that GLINTER outperforms existing methods and even if trained with experimental structures, it generalizes well to predicted structures. The interfacial contacts predicted by our method may help improve selection of docking decoys. Our ablation study shows that the attention information and structural features are complementary and important for interfacial contact prediction. The features used by GLINTER can be calculated very efficiently and GLINTER is applicable to both heterodimers and homodimers. Therefore, potentially GLINTER is applicable to the proteome-scale study of protein–protein interactions and complexes.
Funding
This work was supported by National Institutes of Health [R01GM089753 to J.X.].
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Ziwei Xie, Toyota Technological Institute at Chicago, Chicago, IL 60637, USA.
Jinbo Xu, Toyota Technological Institute at Chicago, Chicago, IL 60637, USA.
References
- Baldassi C. et al. (2014) Fast and accurate multivariate Gaussian modeling of protein families: predicting residue contacts and protein-interaction partners. PLoS One, 9, e92721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bitbol A.-F. et al. (2016) Inferring interaction partners from protein sequences. Proc. Natl. Acad. Sci. USA, 113, 12180–12185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burger L., van Nimwegen E. (2008) Accurate prediction of protein–protein interactions from sequence alignments using a Bayesian method. Mol. Syst. Biol., 4, 165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cong Q. et al. (2019) Protein interaction networks revealed by proteome coevolution. Science, 365, 185–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai B., Bailey-Kellogg C. (2021) Protein interaction interface region prediction by geometric deep learning. Bioinformatics, 37, 2580–2588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson-Haggerty,M. et al. (2019) Trimesh. https://github.com/mikedh/trimesh
- Derevyanko G., Lamoureux G. (2019) Protein–protein docking using learned three-dimensional representations. bioRxiv, 738690. doi:10.1101/738690.
- Fout A. et al. (2017) Protein interface prediction using graph convolutional networks. Adv. Neural Inf. Process. Syst., 6533–6542. [Google Scholar]
- Gainza P. et al. (2020) Deciphering interaction fingerprints from protein molecular surfaces using geometric deep learning. Nat. Methods, 17, 184–192. [DOI] [PubMed] [Google Scholar]
- Geng C. et al. (2020) iScore: a novel graph kernel-based function for scoring protein–protein docking models. Bioinformatics, 36, 112–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gueudré T. et al. (2016) Simultaneous identification of specifically interacting paralogs and interprotein contacts by direct coupling analysis. Proc. Natl. Acad. Sci. USA, 113, 12186–12191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashemifar S. et al. (2018) Predicting protein–protein interactions through sequence-based deep learning. Bioinformatics, 34, i802–i810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K. et al. (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 770–778.
- Hopf T.A. et al. (2014) Sequence co-evolution gives 3D contacts and structures of protein complexes. eLife, 3, e03430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing X., Xu J. (2021) Fast and effective protein model refinement by deep graph neural networks. Nat Comput Sci, 1, 462–469. 10.1038/s43588-021-00098-9. [DOI] [PMC free article] [PubMed]
- Jumper J. et al. (2020) High accuracy protein structure prediction using deep learning. Fourteenth Crit. Assess. Tech. Protein Struct. Predict., 22, 24. [Google Scholar]
- Jumper J. et al. (2021) Highly accurate protein structure prediction with AlphaFold. Nature, 596, 583–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma D.P. et al. (2014) Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
- Laine E., Carbone A. (2015) Local geometry and evolutionary conservation of protein surfaces reveal the multiple recognition patches in protein–protein interactions. PLoS Comput. Biol., 11, e1004580.vol. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy E.D. et al. (2006) 3D complex: a structural classification of protein complexes. PLoS Comput. Biol., 2, e155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitternacht S. (2016) FreeSASA: an open source C library for solvent accessible surface area calculations. F1000Res, 5, 189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee S., Zhang Y. (2009) MM-align: a quick algorithm for aligning multiple-chain protein complex structures using iterative dynamic programming. Nucleic Acids Res., 37, e83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ovchinnikov S. et al. (2014) Robust and accurate prediction of residue–residue interactions across protein interfaces using evolutionary information. eLife, 3, e02030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagés G. et al. (2019) Protein model quality assessment using 3D oriented convolutional neural networks. Bioinformatics, 35, 3313–3319. [DOI] [PubMed] [Google Scholar]
- Pittala S., Bailey-Kellogg C. (2020) Learning context-aware structural representations to predict antigen and antibody binding interfaces. Bioinformatics, 36, 3996–4003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quadir F. et al. (2021) DNCON2_Inter: predicting interchain contacts for homodimeric and homomultimeric protein complexes using multiple sequence alignments of monomers and deep learning. Sci Rep, 11, 12295. 10.1038/s41598-021-91827-7 [DOI] [PMC free article] [PubMed]
- Rao R. et al. (2021) MSA Transformer. bioRxiv 2021.02.12.430858. doi:10.1101/2021.02.12.430858.
- Rives A. et al. (2021) Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. USA, 118, e2016239118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanner M.F. et al. (1996) Reduced surface: an efficient way to compute molecular surfaces. Biopolymers, 38, 305–320. [DOI] [PubMed] [Google Scholar]
- Sanyal S. et al. (2020) ProteinGCN: protein model quality assessment using Graph Convolutional Networks. bioRxiv, 04.06.028266. doi:10.1101/2020.04.06.028266.
- Seemayer S. et al. (2014) CCMpred–fast and precise prediction of protein residue–residue contacts from correlated mutations. Bioinformatics, 30, 3128–3130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senior A.W. et al. (2020) Improved protein structure prediction using potentials from deep learning. Nature, 577, 706–710. [DOI] [PubMed] [Google Scholar]
- Steinegger M. et al. (2019) HH-suite3 for fast remote homology detection and deep protein annotation. BMC Bioinformatics, 20, 473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strodthoff N. et al. (2020) UDSMProt: universal deep sequence models for protein classification. Bioinformatics, 36, 2401–2409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sverrisson F. et al. (2020) Fast end-to-end learning on protein surfaces. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 15272–15281.
- Townshend R. et al. (2019) End-to-end learning on 3D protein structure for interface prediction. Adv. Neural Inf. Process. Syst., 32, 15642–15651. [Google Scholar]
- Uguzzoni G. et al. (2017) Large-scale identification of coevolution signals across homo-oligomeric protein interfaces by direct coupling analysis. Proc. Natl. Acad. Sci. USA, 114, E2662–E2671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vangone A., Bonvin A.M. (2015) Contacts-based prediction of binding affinity in protein–protein complexes. eLife, 4, e07454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S. et al. (2017) Accurate de novo prediction of protein contact map by ultra-deep learning model. PLoS Comput. Biol., 13, e1005324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigt M. et al. (2009) Identification of direct residue contacts in protein-protein interaction by message passing. Proc. Natl. Acad. Sci. USA, 106, 67–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Word J.M. et al. (1999) Asparagine and glutamine: using hydrogen atom contacts in the choice of side-chain amide orientation 1 1Edited by J. Thornton. J. Mol. Biol., 285, 1735–1747. [DOI] [PubMed] [Google Scholar]
- Xu J. (2019) Distance-based protein folding powered by deep learning. Proc. Natl. Acad. Sci. USA, 116, 16856–16865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu,J. et al. (2021) Improved protein structure prediction by deep learning irrespective of co-evolution information. Nature Machine Intelligence, 3, 601–609. 10.1038/s42256-021-00348-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan Y. et al. (2017) HDOCK: a web server for protein–protein and protein–DNA/RNA docking based on a hybrid strategy. Nucleic Acids Res., 45, W365–W373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan Y., Huang S.-Y. (2021) Accurate prediction of inter-protein residue-residue contacts for homo-oligomeric protein complexes. Brief. Bioinform, 22. 10.1093/bib/bbab038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng H. et al. (2018) ComplexContact: a web server for inter-protein contact prediction using deep learning. Nucleic Acids Res., 46, W432–W437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2005) TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res., 33, 2302–2309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T.-M. et al. (2018) Deep learning reveals many more inter-protein residue–residue contacts than direct coupling analysis. bioRxiv 10.1101/240754. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.