Abstract
The importance of studying the health impacts of exposure mixtures is increasingly being recognized, but such research presents many methodological and interpretation difficulties. We used Bayesian g-computation to estimate effects of a simulated public health action on exposure mixtures and birth weights in Milwaukee, Wisconsin, in 2011–2013. We linked data from birth records with census-tract–level air toxics data from the Environmental Protection Agency’s National Air Toxics Assessment model. We estimated the difference between observed and expected birth weights that theoretically would have followed a hypothetical intervention to reduce exposure to 6 airborne metals by decommissioning 3 coal-fired power plants in Milwaukee County prior to 2010. Using Bayesian g-computation, we estimated a 68-g (95% credible interval: 25, 135) increase in birth weight following this hypothetical intervention. This example demonstrates the utility of our approach for using observational data to evaluate and contrast possible public health actions. Additionally, Bayesian g-computation offers a flexible strategy for estimating the effects of highly correlated exposures, addressing statistical issues such as variance inflation, and addressing conceptual issues such as the lack of interpretability of independent effects.
Keywords: air toxics, air pollution, Bayesian methods, causal inference, g-computation, metals
Abbreviations
- BMA
Bayesian model averaging
- CrI
credible interval
- MCMC
Markov chain Monte Carlo
- NATA
National Air Toxics Assessment
- PIP
posterior inclusion probability
Editor’s note: An invited commentary on this article appears on page 2658, and the authors’ response appears on page 2662.
Many determinants of human health are naturally clustered. Nutrients cluster in vegetables; exposure to stressors and toxins correlates with poverty; genes are inherited on chromosome segments; and multiple environmental chemical pollutants arise from food packaging, personal care products, tobacco smoke, and vehicle emissions. Environmental epidemiology, in particular, is increasingly concerned with quantifying the health impacts of complex exposure mixtures (1, 2). Such study is complicated by the presence of highly correlated, high-dimensional, or sparse exposure data which can yield imprecise or invalid statistical results (3, 4). Much of the methodological development in mixtures relates to these statistical challenges (5, 6).
While the statistical problems of mixtures have been a useful focal point for progress, there has been a lesser focus on developing the inferential framework which would address the public health questions of interest. These questions emphasize potentially measurable health impacts of interventions, such as “How much could we have improved health in a city if we had intervened on sources of multiple specific pollutants, compared with no intervention?”. Causal inferential questions can directly inform public health action and yield answers that are more interpretable than conventional approaches to exposure mixtures. The results correspond to a simple comparison of 2 hypothetical interventions on multiple exposures versus a conventional approach reporting multidimensional exposure-response surfaces or multiple independent association measures. Despite these virtues, little has been done to bridge mixtures methods with causal inference to ask public-health–relevant study questions from difficult mixtures data (7, 8).
A potentially useful framework for asking these causal questions with mixtures is g-computation, which can map statistical models to explicit comparisons of public health actions. Applications of g-computation often include target parameters that extend past standard statistical model parameters, such as static plans (e.g., what happens when everyone is treated (9)), dynamic plans (e.g., the optimal time to treat (10)), joint treatments (e.g., what happens when multiple treatments are given (11)), and generalized impact fractions (e.g., who to treat and at what level (12)). However, such work has not often been applied to settings with the challenges that occur in mixtures research, such as correlated, continuous exposures with no natural contrasts (e.g., “treated versus untreated”).
Toward these ends, we propose and demonstrate an approach that leverages methodological developments in mixtures methods to ask questions in a causal framework (13). As our example, we address associations between metal mixtures present in coal-fired power plant emissions (e.g., mercury, arsenic) and infant birth weight. These metals are known to be detrimental to fetal development (14), and such emissions have been associated with birth outcomes (15–17). However, estimation of the effects of decommissioning such power plants in the absence of natural experiments is not straightforward (18). Here we demonstrate how such effects can be estimated using data on coal-fired power plant emissions and Bayesian g-computation. We estimate the difference in average birth weight following a hypothetical intervention to reduce exposure to 6 airborne metals by decommissioning 3 coal-fired power plants (hereafter called “coal plants”) in Milwaukee, Wisconsin, in 2010. While we seek to answer this question as accurately as possible with existing data, the primary contribution of this work is to demonstrate the unique data and modeling considerations of addressing causal questions involving correlated mixtures.
METHODS
Data
Our study population comprised all live births that occurred in Milwaukee from January 1, 2011, to December 31, 2013. The study was conducted in coordination with the Milwaukee Health Department and under the ethical oversight of the University of Wisconsin-Milwaukee. The maternal residential address on the birth certificate was geocoded to the 2010 US Census tract, which was used to link the address to data on airborne metal exposure. Information on birth weight and all covariates was obtained from vital records data. Starting from 30,248 live births, we excluded births that could not be matched to a 2010 census tract within the Milwaukee city boundaries (n = 2,174). We further excluded 971 births with missing data on covariates, for a final sample size of 27,103.
From the Environmental Protection Agency’s National Air Toxics Assessment (NATA) 2011 (19, 20), we obtained modeled, census-tract–level data on ambient concentrations of the following airborne metals for the year 2011: mercury compounds, selenium compounds, beryllium compounds, organic and inorganic arsenic compounds, hexavalent chromium, and nickel compounds. The NATA uses emissions data collected from federal to local levels, including point, area, and mobile pollutant sources, along with weather data. For simplicity, we refer to the model-predicted airborne exposure levels, corresponding to one of the 219 census tracts in Milwaukee, as “measured” exposures.
Statistical methods
We quantified bivariate relationships between the 6 metals considered in our analysis with Spearman rank correlation coefficients.
Target trial.
Our goal was to estimate effects of a reduction in airborne metal exposures that would occur as a consequence of an intervention to deactivate all 3 coal plants in Milwaukee (Figure 1). Though infeasible, we can conceptualize our study question as a target randomized trial (21) in which we recruit all Milwaukee women who become pregnant between April 2010 and about April 2013. Among the recruited women who give birth, we would record the birth weight. In the “standard of care” arm, we would follow the natural course (i.e., no intervention on exposures). In the intervention arm (requiring a doppelganger Milwaukee), we would intervene to decommission the 3 coal plants that existed in Milwaukee as of January 1, 2010, while replacing them with clean power sources (with no effects on birth weight). The target parameter would then be the mean difference in birth weight between study arms.
Figure 1.
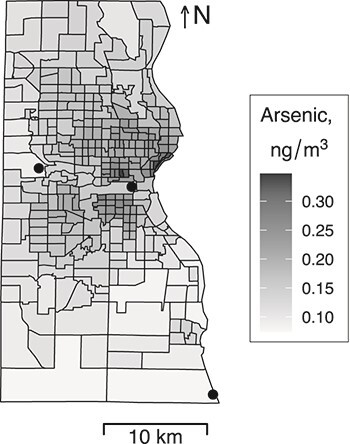
Estimated (National Air Toxics Assessment (19, 20)) ambient arsenic concentrations in Milwaukee County, Wisconsin, by US Census tract, 2011. Black dots represent the locations of the 3 coal-fired power plants in operation in Milwaukee County during the study period.
We hypothesize that much of the effect of such an intervention would result from consequent reductions in pollution, specifically metals, so the target trial can be approximated as a reduction in coal plant metal emissions. We used emissions inventory data included with NATA 2011 and NATA 2005 data (reported under the Wisconsin Air Toxics Rule (22)) to determine which of the metal air toxics included in NATA 2011 could be plausibly attributable to coal plant emissions. We identified 6 metals that demonstrated 1) a high (40%–99%) proportion of total emissions in Milwaukee County attributable to the 3 coal plants and 2) a consistent proportion of total emissions across both NATA years, so that the NATA 2011 data could better represent airborne metal exposures from coal plants incurred during the prenatal period spanning over the course of more than 3 years.
We operationalized the “intervention” arm of the target trial as a proportional reduction in exposure to each of the 6 identified metals, relative to the observed or “natural value” of exposure (23). This was required because the airborne metals also arose from other pollution sources. For each metal, this proportion was equal to the sum of the reported NATA 2011 emissions from the 3 coal plants divided by the total reported emissions in Milwaukee County. For example, we estimated that 91% of local chromium emissions were from coal plants. This implies that an individual with an observed exposure of 0.5 ng/m3 would have an “intervention” exposure of 0.5 ng/m3 × (1 − 0.09) = 0.045 ng/m3. The intervention is represented by a joint reduction in exposure to all 6 metals. The analyst did not have access to data on maternal location, and thus we necessarily assumed uniform reductions across the study area. All nonexposure covariates were kept fixed across possible interventions. We used scatter plots to assess the extent to which our intervention metal values were within the range of observed values.
Bayesian g-computation.
We evaluated the relationships between the 6 metals of interest and birth weight using Bayesian g-computation (13). Under the assumptions discussed below, this approach can 1) estimate independent or joint effects of exposure mixture components in terms of exposure-response functions and 2) estimate the effects of hypothetical interventions on exposure sources that may emit multiple adverse exposures.
For time-fixed exposures such as ours, the Bayesian g-computation algorithm (described elsewhere in detail (13)) consists of the following steps: 1) fit a Bayesian linear model (the “statistical model”) with birth weight as the outcome and including terms for the 6 airborne metal exposures and adjustment variables; 2) use the model parameters from step 1 to predict birth weight under each intervention; and 3) estimate the mean difference in predicted average birth weight between interventions.
To address potential confounding, in the statistical model we adjust for maternal race/Hispanicity (indicator variables for non-Hispanic Black, non-Hispanic White, Hispanic White, and other), maternal smoking during pregnancy (yes or no), maternal marital status (yes or no), and maternal age at birth (quadratic polynomial). We also adjust for a nonconfounder, child’s sex, to improve precision.
Standard statistical models often favor parsimonious models over complex but potentially more accurate models, to enhance interpretability (24). Bayesian g-computation does not rely on directly interpreting model coefficients, so models can be made more potentially complex by including, for example, many product terms. Such models risk overfit, however, and it is uncertain which nonlinear terms are important. We use Bayesian model averaging (BMA) to account for model uncertainty and avoid overfitting (25). This algorithm starts with a “full model” from which possible “submodels” (e.g., models in which some coefficients are set to 0) are explored stochastically. We implement this approach using Markov chain Monte Carlo (MCMC (26)) methods, which simulate the posterior and allow a potentially different submodel to be fitted in each simulation iteration. Fully Bayesian inference for model parameters is then performed by averaging over the MCMC iterations, resulting in a weighted average of submodels with weights proportional to the submodel posterior probability. Our full model includes an intercept and 83 terms comprising all main terms for the 6 metals and 7 covariates, as well as all 2-way product terms for interaction between continuous variables (all metals and maternal age) and all other variables (including “self-interaction” quadratic terms). The basic model form is given by
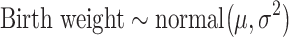 |
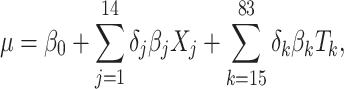 |
(1) |
where the 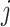 terms represent all main-term coefficients (
terms represent all main-term coefficients (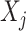 refers to exposures and confounders) plus a quadratic term for maternal age and the
refers to exposures and confounders) plus a quadratic term for maternal age and the 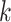 terms represent product terms (
terms represent product terms (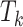 refers to product terms for the interaction between exposures and confounders, and quadratic terms for exposures). The
refers to product terms for the interaction between exposures and confounders, and quadratic terms for exposures). The 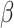 ’s represent model coefficients,
’s represent model coefficients, 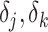 are discrete (1/0) parameters representing inclusion/exclusion from the model, and
are discrete (1/0) parameters representing inclusion/exclusion from the model, and 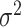 is the variance of the error term. The model is hierarchical, allowing
is the variance of the error term. The model is hierarchical, allowing 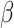 to shrink toward j- and k-specific means. We standardize all continuous variables (including birth weight) to have a mean value of 0 and a standard deviation of 1.
to shrink toward j- and k-specific means. We standardize all continuous variables (including birth weight) to have a mean value of 0 and a standard deviation of 1.
The posterior means of 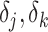 terms are interpreted as posterior inclusion probabilities (PIP) for each
terms are interpreted as posterior inclusion probabilities (PIP) for each 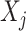 or
or 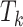 , which is the posterior probability that the coefficient is nonzero. We group coefficients into 2 groups (main or product terms) and set higher prior skepticism for product terms, relative to main effect terms. All priors for our analyses are given in Web Table 1 (available at https://doi.org/10.1093/aje/kwab053).
, which is the posterior probability that the coefficient is nonzero. We group coefficients into 2 groups (main or product terms) and set higher prior skepticism for product terms, relative to main effect terms. All priors for our analyses are given in Web Table 1 (available at https://doi.org/10.1093/aje/kwab053).
The final step of Bayesian g-computation is to contrast predicted birth weight under the “natural course” (no intervention) scenario with predicted birth weight under exposure levels corresponding to the hypothetical intervention. With point-exposure data, g-computation is similar to marginalizing a model-based target parameter over the empirical distribution of covariates (27). Bayesian g-computation yields a full posterior distribution of the target parameter, which in our example accounts for model uncertainty. Further description is available in Web Appendix 1.
We took 40,000 MCMC draws over 8 independent chains, including 500 burn-in iterations on each chain that were discarded. We used standard MCMC convergence and mixing diagnostics (28). We report posterior means and 95% credible intervals (a Bayesian counterpart to confidence intervals).
Sensitivity analyses.
In sensitivity analyses, we fitted several alternative Bayesian models that assessed the influence of quadratic terms, the hierarchical structure, model selection priors, and forcing certain variables into the model. Further description is available in Web Appendix 2. We also fitted conventional adjusted linear models for birth weight for each metal individually (“single-pollutant models”) and all metals together (“multipollutant model”), which included main terms of confounders/exposures and a quadratic term for maternal age. We fitted these latter models using maximum likelihood for computational efficiency and because a difference from the Bayesian approach would be minimal in this simple setting.
To assess whether the direction or precision of the findings was sensitive to our operationalization of the hypothetical intervention (and to reduce model extrapolation), we additionally used Bayesian g-computation to estimate the expected mean birth weight from the 10th to the 90th empirical percentiles of the 6 exposures of interest (e.g., the intervention “50th percentile” means that all 6 metals were set to the sample medians). Further details are given in Web Appendix 3.
Simulation analyses
Because our primary analysis relied on predictions at low exposure levels, we performed a small simulation analysis to assess the potential impacts of model extrapolation contrasting BMA, Bayesian hierarchical modeling, and maximum likelihood approaches with g-computation. Simulation methods are given in Web Appendix 4. Briefly, in 1,000 simulated data sets of  , we simulated a random normal outcome with a mean that is a linear function of 2 continuous, correlated exposures (X1, X2) and 3 continuous confounders, as well as all 2-way product terms. We estimated the expected outcome if we could set both exposures either to 15.0 (denoted Y(15)), close to the population mean (𝔼(X1) ≈ 𝔼(X2) ≈ 15), or to 1.0 (denoted Y(1)), which was outside the range of the observed exposures (thus requiring model extrapolation). We compared point estimates of the expected outcomes and the mean difference between these outcomes (similar to our example above with coal plants) in terms of bias, Monte Carlo standard deviation, and mean squared error. Illustrative code with which to replicate our simulation analyses is available on GitHub (29).
, we simulated a random normal outcome with a mean that is a linear function of 2 continuous, correlated exposures (X1, X2) and 3 continuous confounders, as well as all 2-way product terms. We estimated the expected outcome if we could set both exposures either to 15.0 (denoted Y(15)), close to the population mean (𝔼(X1) ≈ 𝔼(X2) ≈ 15), or to 1.0 (denoted Y(1)), which was outside the range of the observed exposures (thus requiring model extrapolation). We compared point estimates of the expected outcomes and the mean difference between these outcomes (similar to our example above with coal plants) in terms of bias, Monte Carlo standard deviation, and mean squared error. Illustrative code with which to replicate our simulation analyses is available on GitHub (29).
RESULTS
Mothers of the 27,103 infants included the study were predominantly Black (46%), unmarried (65%), and nonsmokers (83%) (Table 1). The median birth weight was 3,232 g, and the proportion of births with low birth weight (<2,500 g) was 10%, higher than the 2011 US average of 6.3% (30).
Table 1.
Demographic, Birth Weight, and Exposure Characteristics of 27,103 Live Births, Milwaukee, Wisconsin, 2011–2013
| Characteristic | No. of Births | % | Median (IQR) |
|---|---|---|---|
| Maternal race/ethnicity | |||
| Non-Hispanic White | 6,800 | 25.1 | |
| Non-Hispanic Black | 12,333 | 45.5 | |
| Non-Hispanic, other race | 6,954 | 25.7 | |
| Hispanic, any race | 1,016 | 3.7 | |
| Married mother | 9,373 | 34.6 | |
| Any maternal smoking during pregnancy | 4,511 | 16.6 | |
| Female child sex | 13,298 | 49.1 | |
| Preterm birth (<37 weeks) | 2,881 | 10.6 | |
| Low birth weight (<2,500 g) | 2,760 | 10.2 | |
| Very low birth weight (<1,500 g) | 597 | 2.2 | |
| Maternal age at birth, years | 27 (22–31) | ||
| Birth weight, g | 3,232 (2,892–3,572) | ||
| Gestational age at birth, weeks | 39 (38–40) | ||
| NATA 2011 metals exposure, ng/m3 | |||
| Mercury compounds | 1.60 (1.50–1.70) | ||
| Selenium compounds | 0.50 (0.46–0.56) | ||
| Beryllium compounds | 0.09 (0.07–0.11) | ||
| Arsenic compounds | 0.18 (0.15–0.22) | ||
| Hexavalent chromium | 0.09 (0.08– 0.12) | ||
| Nickel compounds | 1.24 (0.80–2.87) |
Abbreviations: IQR, interquartile range; NATA, National Air Toxics Assessment.
Three pairs of metals had correlation coefficients of ρ > 0.7, and the rest were more modestly correlated. Arsenic and beryllium levels were the most highly correlated (ρ = 0.94) (Figure 2). The proposed intervention to decommission coal plants in the Milwaukee area would result in joint exposure values that were often outside the range of the observed data, while joint percentiles of exposures (used in sensitivity analyses) were always in the range of the observed exposures (Web Figure 1).
Figure 2.
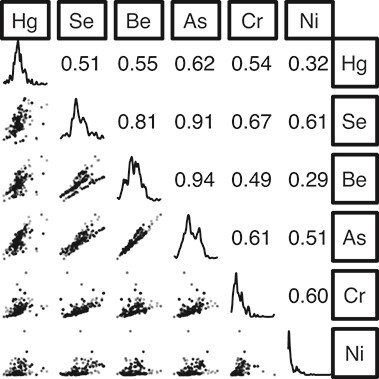
Bivariate scatter plots, univariate kernel density plots, and Spearman correlation matrix for a hypothetical intervention to reduce exposure to 6 airborne metals by decommissioning 3 coal-fired power plants, Milwaukee County, Wisconsin, 2011. Hg, mercury; Se, selenium; Be, beryllium; As, arsenic; Cr, chromium; Ni, nickel.
Bayesian g-computation
In our primary analysis using BMA, we estimated an increase in the average birth weight of 68 g (95% credible interval (CrI): 25, 135) following the hypothetical intervention to decommission the 3 Milwaukee coal plants, corresponding to a reduced proportion of low birth weight (<2,500 g) from 10.2% in the study population to 8.6% (Table 2, Web Figure 2).
Table 2.
Estimated Birth Weightsa (Bayesian g-Computation) for 27,103 Live Births Under a Hypothetical Intervention to Decommission 3 Coal-Fired Power Plants and Mean Difference Between the Natural Course of Events and the Intervention, Milwaukee, Wisconsin, 2011–2013
| Model b , c , d | No Intervention | Decommissioning of Power Plants | Mean Difference | |||
|---|---|---|---|---|---|---|
| Mean BW, g | 95% CrI e | Mean BW, g | 95% CrI e | BW Difference, g | 95% CrI e | |
| Primary analysis | ||||||
| A. All terms, hierarchical, selection | 3,191 | 3,184, 3,198 | 3,259 | 3,215, 3,326 | 68 | 25, 135 |
| Sensitivity analyses | ||||||
| B. Main terms only, hierarchical, selection | 3,191 | 3,184, 3,198 | 3,260 | 3,217, 3,327 | 69 | 27, 136 |
| C. All terms, hierarchical, relaxed selection | 3,191 | 3,184, 3,198 | 3,259 | 3,214, 3,330 | 68 | 24, 139 |
| D. All terms, hierarchical, aggressive selection | 3,191 | 3,184, 3,198 | 3,257 | 3,209, 3,326 | 66 | 19, 134 |
| E. All terms, hierarchical, smoothing spline on maternal age | 3,191 | 3,184, 3,198 | 3,257 | 3,214, 3,320 | 66 | 24, 129 |
| F. All terms, hierarchical, selection with t-distribution slab prior | 3,191 | 3,184, 3,198 | 3,254 | 3,210, 3,313 | 63 | 20, 122 |
| G. All terms, hierarchical, no selection on confounder main terms | 3,191 | 3,184, 3,198 | 3,231 | 3,188, 3,300 | 40 | 0, 109 |
| H. All terms, hierarchical, no selection on any main term | 3,191 | 3,184, 3,198 | 3,319 | 3,219, 3,419 | 128 | 29, 228 |
| I. No selection, nonhierarchical, main terms only | 3,191 | 3,184, 3,198 | 3,320 | 3,221, 3,419 | 129 | 31, 228 |
| J. No selection, hierarchical | 3,191 | 3,184, 3,198 | 3,432 | 2,966, 3,897 | 241 | −224, 706 |
| K. No selection, hierarchical with uniform priors | 3,191 | 3,184, 3,198 | 3,432 | 2,967, 3,896 | 241 | −223, 705 |
| L. No selection, nonhierarchicalf | 3,191 | 3,184, 3,198 | 3,772 | 2,675, 4,872 | 581 | −516, 1,681 |
| M. Maximum likelihood | 3,191 | 3,184, 3,199 | 3,768 | 2,627, 4,901 | 577 | −561, 1,707 |
Abbreviations: BW, birth weight; CrI, credible interval.
a Estimates are given as the posterior mean value and its 95% CrI over 36,000 Markov chain Monte Carlo iterations across 8 independent chains, except for the maximum likelihood model (model M), in which 95% confidence intervals were estimated using quantiles of the nonparametric bootstrap distribution across 10,000 iterations. Variables included in each model included standardized (to have a mean of 0 and a standard deviation of 1) variables for each metal, standardized maternal age at birth (years; continuous), maternal race/ethnicity (4 categories: non-Hispanic White, Hispanic White, non-Hispanic Black, and non-Hispanic any other race), maternal smoking during pregnancy (yes/no), maternal married status (yes/no), and female child sex (yes/no). Prior distributions for models A–L are given in Web Table 1.
b As described in the text. Models included main terms for all variables and all first-order interaction terms unless otherwise noted.
c Main terms and interaction terms given separate, hierarchical normal priors unless otherwise noted (see Table 1 for prior distributions).
d Bayesian model averaging or “selection” using a “spike-and-slab” prior, where the spike is a point mass at 0 and the slab has a normal, hierarchical prior unless otherwise noted (see Table 1 for prior distributions).
e Ninety-five percent CrIs given by the 2.5th and 97.5th percentiles of the estimated posterior distribution, except in model M (95% confidence intervals), where percentiles are from the nonparametric bootstrap distribution.
f Model coefficients given independent standard normal priors.
Sensitivity analyses
Our results were robust to priors on model selection and hierarchical variance, as well as the functional form of maternal age. In contrast, results varied when the model was “forced” to include certain (or all) variables. A model with main terms only provided inference similar to that of our main analysis. When all main terms (exposures and confounders) were forced into the primary model (with variable selection), the estimated mean difference increased from 68 g to 128 g, and the width of the 95% credible interval doubled (95% CrI: 29, 228). Without model averaging, the estimated mean difference was larger and much less precise (241 g, 95% CrI: −224, 706). Upon removal of hierarchical priors, the estimated mean difference increased further to 581 g, which was similar to the point estimate obtained using maximum likelihood (577 g). The 95% credible intervals for all analyses without model averaging fully contained the 95% credible intervals of all of the analyses that included model averaging, demonstrating consistency across approaches even with highly variable point estimators.
The differences among statistical models were much smaller in sensitivity analyses using interventions that were within the range of the observed data (10th–90th percentiles of the observed empirical exposure distributions, Web Figure 3). Results were qualitatively similar to those from the main analysis and demonstrated that precision losses at the tails of the exposure distribution were smaller when using BMA (Figure 3).
Figure 3.
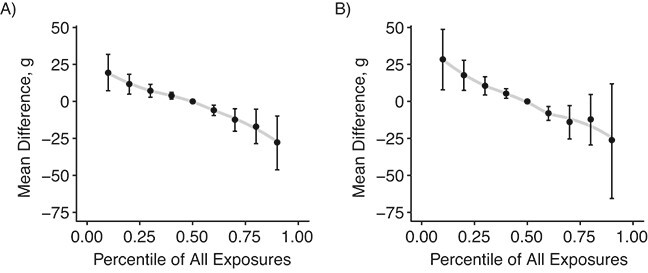
Posterior mean difference (points) and 95% credible intervals (bars) for contrasts between population interventions in which all individuals have arsenic, beryllium, chromium, mercury, nickel, and selenium exposures simultaneously set to a percentile of their observed values, where the referent intervention is to set all exposures to the population median values (medians are given in Table 1). A) Results from the primary model with Bayesian model averaging (model A in Table 3); B) results from the hierarchical Bayesian model with no selection (model J in Table 3). Scatter plot smoothing lines (gray) are shown for visual reference.
BMA coefficients
Among the metals, the main term for chromium had the highest posterior inclusion probability (PIP = 0.64, Web Table 2). Except for a product term for the interaction between maternal age at birth and smoking (PIP = 0.99), all product terms had PIPs less than 0.1, and most PIPs were 0. PIPs that accounted for inclusion of any term including a metal were very similar to PIPs for main term coefficients. A main term for at least one of arsenic and beryllium (the most highly correlated exposures) was included in 79% of the models. Main terms for 5 of the 6 metals were negative, indicating a reduction in birth weight with increasing levels of each metal, which can be roughly interpreted as independent associations (due to the low PIPs of product terms). Parameter estimates for metals in non-Bayesian, single-pollutant models were less variable than those in adjusted models and maintained a consistent effect direction, in contrast with the highly variable (as expected due to exposure correlation) results from the non-Bayesian multipollutant model (Web Tables 3 and 4). Parameter estimates were much more variable without (versus with) BMA (Web Table 5).
Simulation
In our simulated example, patterns of precision were similar to our data example, where BMA resulted in much lower standard errors than maximum likelihood or other Bayesian approaches (Table 3). The BMA approach yielded lower mean squared error for the target parameter than all other approaches while incurring some bias relative to the maximum likelihood approach.
Table 3.
Results of a Simulation Comparing Bias, Variation, and Squared Error Loss of 3 Bayesian Approaches and 1 Maximum Likelihood Approach to g-Computation
| Model |
Sample Size
(n) |
Bias × 100 a |
MCSD × 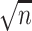 b b
|
RMSE c | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y (15,15) | Y (1,1) | PA MD | Y (15,15) | Y (1,1) | PA MD | Y (15,15) | Y (1,1) | PA MD | ||
| BMA | 100 | −18.1 | 16.6 | 34.8 | 5.8d | 2.3d | 5.6d | 0.6d | 0.3d | 0.7d |
| Full—hierarchical | 100 | −0.8d | 262.1 | 262.9 | 5.8 | 43.8 | 44.5 | 0.6 | 5.1 | 5.2 |
| Main terms—hierarchical | 100 | −85.1 | 444.0 | 529.1 | 5.6 | 47.1 | 47.1 | 1.0 | 6.5 | 7.1 |
| Full—maximum likelihood | 100 | −1.4 | −7.4d | −6.0d | 9.3 | 65.1 | 64.9 | 0.9 | 42.4 | 42.1 |
| BMA | 1,000 | −10.9 | −4.2 | 6.7 | 6.1d | 5.8d | 7.1d | 0.2 | 0.2d | 0.2d |
| Full—hierarchical | 1,000 | −0.6 | 46.1 | 46.7 | 6.1 | 58.7 | 59.2 | 0.2 | 1.9 | 1.9 |
| Main terms—hierarchical | 1,000 | −84.9 | −30.0 | 54.8 | 6.0 | 66.6 | 66.7 | 0.9 | 2.1 | 2.2 |
| Full—maximum likelihood | 1,000 | −0.3d | 0.9d | 1.1d | 8.4 | 60.6 | 60.4 | 0.1d | 3.7 | 3.6 |
| BMA | 10,000 | −0.6 | −2.5 | −1.9 | 10.0 | 15.6d | 14.9d | 0.1 | 0.2d | 0.2d |
| Full—hierarchical | 10,000 | −0.7 | 6.7 | 7.4 | 6.8 | 59.0 | 59.1 | 0.1 | 0.6 | 0.6 |
| Main terms—hierarchical | 10,000 | −85.1 | −79.4 | 5.6 | 6.1d | 67.7 | 67.9 | 0.9 | 1.0 | 0.7 |
| Full—maximum likelihood | 10,000 | 0.1d | 1.5d | 1.4d | 8.5 | 60.3 | 60.5 | 0.0d | 0.4 | 0.4 |
Abbreviations: BMA, Bayesian model averaging; MCSD, Monte Carlo standard deviation; MD, mean difference; PA, population average; RMSE, root mean squared error.
a Bias from true value (truth: 𝔼[Y1,1)] = 0.55, 𝔼[Y(15)] = 14.55, MD = 𝔼[Y(1)] − 𝔼[Y(15)] = 14.00), where 𝔼[Y(15)] = expected population average outcome if setting x1 = x2 = 15.
b Standard deviation of point estimates (Bayesian posterior mean or maximum likelihood estimate) scaled by the square root of the sample size.
c Square root of the mean squared error, given by 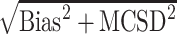 .
.
d Best-performing method for each statistic at a given sample size.
DISCUSSION
Using Bayesian g-computation, we estimated a 68-g (95% CrI: 25, 135) increase in birth weight following a hypothetical intervention to decommission 3 coal plants, and hence reduce exposure to 6 airborne metals, in Milwaukee County. We demonstrated the utility of this approach for using observational data to directly evaluate policy choices and contrast possible public health actions (including inaction) when appropriate data are available. While we found the magnitude of the association to be sensitive to some modeling assumptions, we demonstrated a useful framework and identified the data and modeling needs for estimating effects of interventions in environmental data, where many correlated exposures may influence health and many effects of public health interest necessarily extend to exposure levels outside the range of the data.
As in most statistical approaches to mixtures, we included exposures simultaneously to account for confounding of the effect of one metal by another. The potential of such copollutant confounding is a classical problem of exposure mixtures and gives rise to the need for multipollutant models. Coefficients from such models are cumbersome or even illogical to interpret: a unit change in birth weight associated with a unit change in exposure, holding constant other exposures, many of which arise from the same source (31). Interpretation of individual coefficients is further complicated when product terms are included. For example, model selection may indicate that a product term should be kept while a main term from that product is removed from the model, which is anathema to direct interpretation of coefficients (32). In our approach, model parameters need not be interpretable. Bayesian g-computation requires an underlying multipollutant model, similar to other approaches to estimating joint effects within a mixture, such as quantile g-computation (33) and Bayesian kernel machine regression (34). Bayesian g-computation extends these approaches to a myriad of statistical models and allows effect estimation for realistic interventions in which exposures will be affected to different extents.
Our findings are consistent with the expected toxicity of the metals we explored, though the independent, metal-specific findings were imprecise (a fundamental problem of correlated exposures). Much of the prior epidemiologic investigation of these airborne metals and birth outcomes has not considered them within a mixture. Of studies that did consider mixtures (35–38), results did not clearly indicate whether any given metal was a particular “bad actor” after accounting for other metals, whether certain combinations were particularly harmful, or whether a certain pollution source was to blame. Differences in study objectives and methodology make it difficult to quantitatively compare our findings with this prior literature. More relevant are natural experiments. Our estimates are similar in magnitude to the decrease in birth weight observed following the replacement of nuclear power plants in the Tennessee Valley in the 1980s with increased output of local coal plants (39) and are generally consistent with improvement in other birth outcomes following closures of coal plants in California (17) and New Jersey (16).
Under all models and priors assessed, we obtained point estimates for the effect of our hypothetical intervention in the same direction, with variable levels of precision. The magnitude of the association was sensitive to model parsimony, regardless of whether this was achieved by excluding product terms a priori or using BMA. In simulations, the mean squared error was orders of magnitude better for our approach than for the standard parametric g-formula using maximum likelihood at all sample sizes considered—this advantage comes by trading small biases for large reductions in variance. While bias is unknown in our coal plant example, the simulations provide some assurance that the variance improvement that comes from using BMA (relative to other approaches) is not coming at the expense of large biases from the modeling procedure.
Aside from model specification, there are a number of necessary assumptions for interpreting data analytical results as causal effects. We focus on 4 of these: exchangeability, positivity, measurement error, and treatment variation irrelevance.
Exchangeability includes selection bias and confounding. Results may be subject to selection bias if exposure or some cause of exposure also results in pregnancy loss (40). Such biases manifest similarly to loss to follow-up in a target trial, and correction would require information on how airborne metals and other study covariates affect fetal loss. Additionally, any of our exposures of interest could be serving as proxies for other unexplored factors that affect birth weight (i.e., there may be residual confounding), such as airborne lead and cadmium, which did not meet our selection criteria based on data quality. Knowledge or data about sources of selection bias or unmeasured confounders could be used in Bayesian sensitivity analyses (41, 42) or to estimate alternative parameters such as a survivor average causal effect (43), both of which are potentially useful extensions of our approach.
Positivity states that there is a nonzero probability (density) that exposure can take on all values implicit under the intervention of interest in infinite samples. Petersen et al. (44) distinguished nonpositivity from a similar, finite-sample condition referred to as sparsity, which ensures that the intervention values of exposure are observed in the analytical sample in all strata of confounders. Formally, our analysis meets the positivity criterion because metal exposures can (in principle) take on any nonnegative value. However, our observed correlation matrix suggests that our data are subject to sparsity. Historically, such correlation has been considered only in the context of independent effects: the effects of one exposure while holding the others constant (e.g., the linear multipollutant model in Web Table 4). Sparsity manifests in variance inflation of independent effects, though prior evidence suggests that highly correlated exposures can actually improve variance for joint effects (33). Intuitively, if exposures covary, the data will contain more observations consistent with the interventions “high joint exposure” or “low joint exposure”—our approach simply mapped “low joint exposure” onto a potential real-world intervention. These prior results suggest that even if the underlying model is challenged by exposure correlation, the overall joint effect estimate may not be. Thus, for pragmatic and conceptual reasons, we focused on questions about joint rather than independent effects.
Because parametric models can interpolate and extrapolate, nonsparsity is not a necessary assumption in our analysis or in related approaches using the parametric g-formula, unlike semiparametric methods such as inverse probability weighting (45–48). Rather, this assumption is replaced by the assumption of correct model specification. This tradeoff in assumptions may be beneficial in terms of making progress in causal inference approaches in environmental epidemiology. In the case of highly correlated exposures, estimation of joint effects may not be strongly affected by sparsity, and the use of inverse probability weighting or doubly robust methods (49) can provide useful alternative approaches that yield a triangulation of evidence due to differing assumptions. In environmental settings that are not subject to sparsity due to multiple pollutant sources, correlation may be low enough to justify exchangeability, or g-computation with standard mixture approaches to reducing mean squared error may still be used at the cost of requiring stronger modeling assumptions. Care must be taken, however, by assessing the impacts of modeling assumptions. Our simulations demonstrate that BMA can yield biased but low mean-squared-error estimates in spite of using a highly flexible model to achieve model accuracy. This result was especially pronounced when extrapolating to intervention values of exposure outside the range of the data. Tabular analysis and scatter plots help identify model extrapolation, but we know of no model fit diagnostics that extend outside of the range of available data. By reducing overfit, BMA seems well-suited to such analyses; but, as with other assumptions underlying causal inference, model accuracy outside the range of the data is untestable in the data set at hand. Thus, one can perform, as we did, sensitivity analyses for modeling and prior assumptions, secondary analyses that reduce extrapolation, and simulations that mimic the scientific question.
Environmental studies relying on area exposure estimates, like ours, are particularly subject to exposure measurement error. We used an air pollution model of each census tract (NATA) to represent person-level exposure. While NATA 2011 validity is supported by favorable comparisons with air measurements (50–53) and demonstrated model improvements over subsequent years (54), there are uncertainties in model performance across pollutants and across geographic regions (55). Furthermore, we used NATA 2011 data to represent exposure across 3 years. Additionally, we operationalized interventions on a coal plant using homogenous, proportional decreases in metal exposures across space and time. The accuracy of this operationalization affects how well our results map onto expected effects of real-world interventions, but not internal validity.
The treatment variation irrelevance assumption raises issues similar to measurement error: We may be able to estimate the effect of reducing our exposures of interest, but that may not map directly onto the effect of decommissioning if there are unanticipated economic or environmental impacts from switching energy sources that subsequently affect birth weight. We assumed that airborne metals arose only from local coal plants instead of more distal sources. Coal emissions probably spread beyond the 20-mile (32-km) length of Milwaukee (56, 57), though only 1 other coal plant exists in the counties adjacent to Milwaukee. Approaches for estimating impacts of interventions on mixtures could be greatly improved by better interfaces between causal inference and exposure sciences.
Bayesian g-computation provides a unifying framework with which to leverage the strengths of innovative statistical models for analyzing mixtures data, such as hierarchical modeling and BMA. Our approach allows for complex model fit while preserving precision and yields an overall joint impact of the mixture on health that is straightforward to communicate. Further, our results demonstrate the immense potential of the use of causal effect estimation approaches to supplement the evidence obtained from natural experiments. When data exist to estimate exposure values before and after a potential intervention, this approach is a useful addition to increase our understanding of the effects of exposure mixtures on human health.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Epidemiology, Gillings School of Global Public Health, University of North Carolina, Chapel Hill, North Carolina, United States (Alexander P. Keil); Department of Environmental Health and Engineering, Bloomberg School of Public Health, Johns Hopkins University, Baltimore, Maryland, United States (Jessie P. Buckley); Department of Epidemiology, Bloomberg School of Public Health, Johns Hopkins University, Baltimore, Maryland, United States (Jessie P. Buckley); and Department of Environmental Health Sciences, Joseph J. Zilber School of Public Health, University of Wisconsin-Milwaukee, Milwaukee, Wisconsin, United States (Amy E. Kalkbrenner).
This work was supported by the National Institutes of Health (grants R01 ES029531 and R01 ES030078).
Conflict of interest statement: none declared.
REFERENCES
- 1. Braun JM, Gennings C, Hauser R, et al. What can epidemiological studies tell us about the impact of chemical mixtures on human health? Environ Health Perspect. 2016;124(1):A6–A9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Carlin DJ, Rider CV, Woychik R, et al. Unraveling the health effects of environmental mixtures: an NIEHS priority. Environ Health Perspect. 2013;121(1):A6–A8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Chadeau-Hyam M, Campanella G, Jombart T, et al. Deciphering the complex: methodological overview of statistical models to derive OMICS-based biomarkers. Environ Mol Mutagen. 2013;54(7):542–557. [DOI] [PubMed] [Google Scholar]
- 4. MacLehose RF, Dunson DB, Herring AH, et al. Bayesian methods for highly correlated exposure data. Epidemiology. 2007;18(2):199–207. [DOI] [PubMed] [Google Scholar]
- 5. Hamra GB, Buckley JP. Environmental exposure mixtures: questions and methods to address them. Curr Epidemiol Rep. 2018;5(2):160–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Stafoggia M, Breitner S, Hampel R, et al. Statistical approaches to address multi-pollutant mixtures and multiple exposures: the state of the science. Curr Environ Health Rep. 2017;4(4):481–490. [DOI] [PubMed] [Google Scholar]
- 7. Urman R, Garcia E, Berhane K, et al. The potential effects of policy-driven air pollution interventions on childhood lung development. Am J Respir Crit Care Med. 2020;201(4):438–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Garcia E, Urman R, Berhane K, et al. Effects of policy-driven hypothetical air pollutant interventions on childhood asthma incidence in southern California. Proc Natl Acad Sci U S A. 2019;116(32):15883–15888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Robins JM, Hernán MA, Brumback BA. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. [DOI] [PubMed] [Google Scholar]
- 10. Cain LE, Robins JM, Lanoy E, et al. When to start treatment? A systematic approach to the comparison of dynamic regimes using observational data. Int J Biostat. 2010;6(2):Article 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Howe CJ, Cole SR, Mehta SH, et al. Estimating the effects of multiple time-varying exposures using joint marginal structural models: alcohol consumption, injection drug use, and HIV acquisition. Epidemiology. 2012;23(4):574–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Westreich D, Edwards JK, Rogawski ET, et al. Causal impact: epidemiological approaches for a public health of consequence. Am J Public Health. 2016;106(6):1011–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Keil AP, Daza EJ, Engel SM, et al. A Bayesian approach to the g-formula. Stat Methods Med Res. 2018;27(10):3183–3204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Rahman A, Kumarathasan P, Gomes J. Infant and mother related outcomes from exposure to metals with endocrine disrupting properties during pregnancy. Sci Total Environ. 2016;569-570:1022–1031. [DOI] [PubMed] [Google Scholar]
- 15. Ha S, Hu H, Roth J, et al. Associations between residential proximity to power plants and adverse birth outcomes. Am J Epidemiol. 2015;182(3):215–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Yang M, Chou S-Y. The impact of environmental regulation on fetal health: evidence from the shutdown of a coal-fired power plant located upwind of New Jersey. J Environ Econ Manag. 2018;90:269–293. [Google Scholar]
- 17. Casey JA, Karasek D, Ogburn EL, et al. Retirements of coal and oil power plants in California: association with reduced preterm birth among populations nearby. Am J Epidemiol. 2018;187(8):1586–1594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Rich DQ. Accountability studies of air pollution and health effects: lessons learned and recommendations for future natural experiment opportunities. Environ Int. 2017;100:62–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Weinhold B. Pollution portrait: the fourth National-Scale Air Toxics Assessment. Environ Health Perspect. 2011;119(6):A254–A257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Scheffe RD, Strum M, Phillips SB, et al. Hybrid modeling approach to estimate exposures of hazardous air pollutants (HAPs) for the National Air Toxics Assessment (NATA). Environ Sci Technol. 2016;50(22):12356–12364. [DOI] [PubMed] [Google Scholar]
- 21. Hernán MA, Robins JM. Using big data to emulate a target trial when a randomized trial is not available. Am J Epidemiol. 2016;183(8):758–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Wisconsin State Legislature . Wisconsin Administrative Code. Chapter NR 445: Control of Hazardous Pollutants. 2016. https://docs.legis.wisconsin.gov/code/admin_code/nr/400/445. Published March 2016. Accessed November 21, 2020.
- 23. Young JG, Herńan MA, Robins JM. Identification, estimation and approximation of risk under interventions that depend on the natural value of treatment using observational data. Epidemiol Method. 2014;3(1):1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Buckley JP, Doherty BT, Keil AP, et al. Statistical approaches for estimating sex-specific effects in endocrine disruptors research. Environ Health Perspect. 2017;125(6):670131–670137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Herring AH. Nonparametric Bayes shrinkage for assessing exposures to mixtures subject to limits of detection. Epidemiology. 2010;21(suppl 4):S71–S76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Plummer M. rjags: Bayesian Graphical Models using MCMC. (R package, version 4-6). Vienna, Austria: R Foundation for Statistical Computing; 2016. https://cran.r-project.org/package=rjags. Accessed October 29, 2019. [Google Scholar]
- 27. Muller CJ, MacLehose RF. Estimating predicted probabilities from logistic regression: different methods correspond to different target populations. Int J Epidemiol. 2014;43(3):962–970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Gelman A. Bayesian Data Analysis. 3rd ed. Boca Raton, FL: CRC Press; 2014. [Google Scholar]
- 29. Keil AP. CIRL-UNC/bgf_airtoxics. https://github.com/CIRL-UNC/bgf_airtoxics. Published April 19, 2021. Accessed April 19, 2021.
- 30. Womack LS, Rossen LM, Martin JA. Singleton low birthweight rates, by race and Hispanic origin: United States, 2006–2016. NCHS Data Brief. 2018;306:1–8. [PubMed] [Google Scholar]
- 31. Snowden JM, Reid CE, Tager IB. Framing air pollution epidemiology in terms of population interventions, with applications to multipollutant modeling. Epidemiology. 2015;26(2):271–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Greenland S. Modeling and variable selection in epidemiologic analysis. Am J Public Health. 1989;79(3):340–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Keil AP, Buckley JP, O’Brien KM, et al. A quantile-based g-computation approach to addressing the effects of exposure mixtures. Environ Health Perspect. 2020;128(4):047004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Bobb JF, Valeri L, Henn BC, et al. Bayesian kernel machine regression for estimating the health effects of multi-pollutant mixtures. Biostatistics. 2015;16(3):493–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Govarts E, Remy S, Bruckers L, et al. Combined effects of prenatal exposures to environmental chemicals on birth weight. Int J Environ Res Public Health. 2016;13(5): Article 495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Kim SS, Meeker JD, Carroll R, et al. Urinary trace metals individually and in mixtures in association with preterm birth. Environ Int. 2018;121(1):582–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Deyssenroth MA, Gennings C, Liu SH, et al. Intrauterine multi-metal exposure is associated with reduced fetal growth through modulation of the placental gene network. Environ Int. 2018;120:373–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Woods MM, Lanphear BP, Braun JM, et al. Gestational exposure to endocrine disrupting chemicals in relation to infant birth weight: a Bayesian analysis of the HOME Study. Environ Health. 2017;16:Article 115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Severnini E. Impacts of nuclear plant shutdown on coal-fired power generation and infant health in the Tennessee Valley in the 1980s. Nat Energy. 2017;2(4):Article 17051. [Google Scholar]
- 40. Kinlaw AC, Buckley JP, Engel SM, et al. Left truncation bias to explain the protective effect of smoking on preeclampsia: potential, but how plausible? Epidemiology. 2017;28(3):428–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. McCandless LC, Gustafson P, Levy A. Bayesian sensitivity analysis for unmeasured confounding in observational studies. Stat Med. 2007;26(11):2331–2347. [DOI] [PubMed] [Google Scholar]
- 42. Robins JM, Rotnitzky A, Scharfstein DO. Sensitivity analysis for selection bias and unmeasured confounding in missing data and causal inference models. In: Statistical Models in Epidemiology, the Environment, and Clinical Trials. New York, NY: Springer Publishing Company; 2000:1–94. [Google Scholar]
- 43. Tchetgen Tchetgen EJ. Identification and estimation of survivor average causal effects. Stat Med. 2014;33(21):3601–3628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Petersen ML, Porter KE, Gruber S, et al. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. 2012;21(1):31–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Neugebauer R, van der Laan M. Nonparametric causal effects based on marginal structural models. J Stat Plan Inference. 2007;137(2):419–434. [Google Scholar]
- 46. Hernán MA, Robins JM. Estimating causal effects from epidemiological data. J Epidemiol Community Health. 2006;60(7):578–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Kang JDY, Schafer JL. Demystifying double robustness: a comparison of alternative strategies for estimating a population mean from incomplete data. Stat Sci. 2007;22(4):523–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Taubman SL, Robins JM, Mittleman MA, et al. Intervening on risk factors for coronary heart disease: an application of the parametric g-formula. Int J Epidemiol. 2009;38(6):1599–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Haneuse S, Rotnitzky A. Estimation of the effect of interventions that modify the received treatment. Stat Med. 2013;32(30):5260–5277. [DOI] [PubMed] [Google Scholar]
- 50. Payne-Sturges DC, Burke TA, Breysse P, et al. Personal exposure meets risk assessment: a comparison of measured and modeled exposures and risks in an urban community. Environ Health Perspect. 2004;112(5):589–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Pratt GC, Palmer K, Wu CY, et al. An assessment of air toxics in Minnesota. Env Health Perspect. 2000;108(9):815–825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Rosenbaum AS, Axelrad DA, Woodruff TJ, et al. National estimates of outdoor air toxics concentrations. J Air Waste Manag Assoc. 1999;49(10):1138–1152. [DOI] [PubMed] [Google Scholar]
- 53. Department of Environmental Protection, State of New Jersey . Comparison of 1996 NATA results to measured concentrations in outdoor air in New Jersey. Trenton, NJ: Department of Environmental Protection, State of New Jersey; 2001. https://www.state.nj.us/dep/airmon/airtoxics/natavmon.htm. Accessed November 19, 2020. [Google Scholar]
- 54. Garcia E, Hurley S, Nelson DO, et al. Evaluation of the agreement between modeled and monitored ambient hazardous air pollutants in California. Int J Environ Health Res. 2014;24(4):363–377. [DOI] [PubMed] [Google Scholar]
- 55. Xue Z, Jia C. A model-to-monitor evaluation of 2011 National-Scale Air Toxics Assessment (NATA). Toxics. 2019;7(1):Article 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Gorle JMR, Sambana NR. Dispersion modeling of thermal power plant emissions on stochastic space. Theor Appl Climatol. 2016;124(3):1119–1131. [Google Scholar]
- 57. Rodríguez Martín JA, Nanos N. Soil as an archive of coal-fired power plant mercury deposition. J Hazard Mater. 2016;308:131–138. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


