AIPW: An R Package for Augmented Inverse Probability–Weighted Estimation of Average Causal Effects

Abstract

An increasing number of recent studies have suggested that doubly robust estimators with cross-fitting should be used when estimating causal effects with machine learning methods. However, not all existing programs that implement doubly robust estimators support machine learning methods and cross-fitting, or provide estimates on multiplicative scales. To address these needs, we developed AIPW, a software package implementing augmented inverse probability weighting (AIPW) estimation of average causal effects in R (R Foundation for Statistical Computing, Vienna, Austria). Key features of the AIPW package include cross-fitting and flexible covariate adjustment for observational studies and randomized controlled trials (RCTs). In this paper, we use a simulated RCT to illustrate implementation of the AIPW estimator. We also perform a simulation study to evaluate the performance of the AIPW package compared with other doubly robust implementations, including CausalGAM, npcausal, tmle, and tmle3. Our simulation showed that the AIPW package yields performance comparable to that of other programs. Furthermore, we also found that cross-fitting substantively decreases the bias and improves the confidence interval coverage for doubly robust estimators fitted with machine learning algorithms. Our findings suggest that the AIPW package can be a useful tool for estimating average causal effects with machine learning methods in RCTs and observational studies.

Abbreviations:

AIPW

augmented inverse probability weighting

ATE

average treatment effect

CI

confidence interval

EAGeR

Effects of Aspirin in Gestation and Reproduction

GAM

generalized additive model

GLM

generalized linear model

MSE

mean squared error

OR

odds ratio

RCT

randomized controlled trial

RD

risk difference

RR

risk ratio

SE

standard error

TMLE

targeted maximum likelihood estimation

Machine learning methods are increasingly being used to estimate cause-effect relationships. Numerous examples exist, including use of random forests, gradient boosting, or a combination of learners (e.g., stacking) for propensity score weighting, stratification, or matching, or use of marginal standardization with a regression-based estimator (1–6). However, there is a growing body of theoretical and simulation evidence suggesting that without some form of statistical bias correction, using machine learning methods to estimate causal effects can result in high bias, high mean squared error (MSE), and less-than-nominal 95% confidence interval (CI) coverage (7–11).

In contrast, doubly robust estimators possess a statistical bias correction property (12) and are thus less susceptible to problems with bias, MSE, and CI coverage when machine learning methods are used. Hence, when estimating causal effects with machine learning methods, doubly robust estimators, such as targeted maximum likelihood estimation (TMLE) or augmented inverse probability weighting (AIPW), should be used (9–11, 13, 14). Several software programs that implement doubly robust estimators are currently available in a number of different programming languages, including SAS (SAS Institute, Inc., Cary, North Carolina) (15), Stata (StataCorp LLC, College Station, Texas) (16), R (R Foundation for Statistical Computing, Vienna, Austria) (17–21), Python (22), and MATLAB (23). However, only a handful of them enable use of machine learning methods (17, 18, 20). Additionally, most share important limitations known to either affect the performance of doubly robust estimation or lower their relevance to epidemiologists. Most importantly, these limitations include 1) the inability to implement sample-splitting or cross-fitting for effect estimation and 2) the estimation of effects on a single scale of measurement (e.g., additive effects). To address these limitations, we developed the AIPW package, which implements AIPW (24) for a binary exposure in the R programming environment (25). Compared with other packages for implementing doubly robust estimators via machine learning methods, the AIPW package

1. allows different covariate sets to be specified for the exposure and outcome models, which may be important when analyzing data from randomized controlled trials (RCTs);

2. obtains appropriate standard errors (SEs) for estimates of the average treatment effect (ATE) by implementing k-fold cross-fitting;

3. relies on a user-friendly parallel processing framework for computationally heavy tasks; and

4. enables estimation directly from the fitted objects from existing doubly robust implementations (e.g., tmle (17) or tmle3 (18)) in the R programming language.

In this paper, we illustrate the AIPW estimator and how to use it in our package. Additionally, we highlight the differences between various software implementations of these estimators in R, including AIPW, CausalGAM (19), npcausal (20), tmle (17), and tmle3 (18).

METHODS

Motivation and data-generating mechanisms

Here we outline the data sets motivating our illustration of AIPW and the use of the AIPW package. We rely on the Effects of Aspirin in Gestation and Reproduction (EAGeR) Trial, a multicenter RCT of the effect of daily low-dose aspirin on pregnancy outcomes in women at high risk of miscarriage. The EAGeR investigators recruited 1,228 women aged 18–40 years who were attempting to become pregnant. Details on the EAGeR Trial and its data are provided elsewhere (26–29).

We simulate 2 different data sets from EAGeR to illustrate the use of the AIPW package. We use a simulation approach because 1) the actual data are not publicly available and 2) true exposure effects are known in simulation settings. Data are generated on the basis of the causal relationships depicted in Figure 1.

Figure 1.

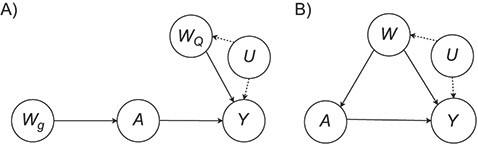
Causal diagrams for a randomized controlled trial (A) and an observational study (B). A, binary treatment assignment/exposure; U, unmeasured confounders; W, confounders; W_g, confounder(s) that affect(s) the treatment assignment; W_Q, baseline prognostic covariates; Y, outcome.

Figure 1A illustrates a data-generating mechanism for an RCT in which the treatment A is assigned conditionally on the basis of a measured covariate 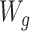. For example, in a study designed to explore the impact of aspirin on pregnancy outcomes in women with previous pregnancy losses, one may decide to randomize to aspirin versus placebo 1:1 for women with only 1 prior pregnancy loss but elect to randomize 3:1 for women with more than 1 prior pregnancy loss. Similarly, Figure 1B illustrates a simple causal diagram for an observational study of the relationship between an exposure A (e.g., whether a given woman took aspirin during the study’s follow-up), an outcome of interest Y (e.g., an indicator of whether live birth occurred during follow-up), and a set of confounders of the exposure-outcome relationship W.

To construct data sets governed by the data-generating mechanisms in Figure 1, we sampled (with replacement) baseline covariates from the EAGeR data. For the simulated AIPW (n = 1,228; Figure 1A), A denotes the binary treatment assignment, Y is the binary outcome, and 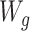represents the covariate that affects the treatment assignment, which in our case was deemed to be the eligibility stratum indicator, sampled with replacement from the EAGeR Trial. Similarly, 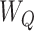is a set of baseline prognostic covariates, which were also sampled with replacement from the EAGeR Trial, and includes the number of prior pregnancy losses, age, number of months of trying to conceive prior to randomization, body mass index (weight (kg)/height (m)²), and mean arterial blood pressure (denoted 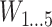, respectively). Our simulated treatment A was generated such that 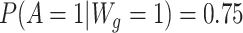and . 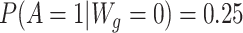The outcome Y was simulated from a logistic regression model defined as

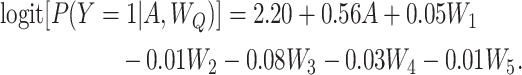The above model defines the treatment effect via a conditional odds ratio (OR) of 1.75. In our simulated setting, this yielded true marginal effects of 0.13, 1.29, and 1.71 on the risk difference (RD), risk ratio (RR), and OR scales, respectively (Table 1, row 1). We used the correctly specified parametric regression model in a sample of 1 million observations to obtain the estimate of the true effects to serve as our parameters of the true causal effect parameter values.

Table 1.

Estimated Average Treatment Effects in a Simulated Randomized Controlled Trial Based on the EAGeR Trial

Software Package	Effect Estimate
	Risk Difference (SE a )	95% CI	Risk Ratio (SE)	95% CI	Odds Ratio (SE)	95% CI
True estimateb	0.132 (N/A)	N/A	1.285 (N/A)	N/A	1.708 (N/A)	N/A
AIPW c , d	0.136 (0.033)	0.070, 0.201	1.305 (0.068)	1.143, 1.490	1.727 (0.136)	1.323, 2.253
CausalGAM	0.134 (0.033)	0.070, 0.198	N/A	N/A	N/A	N/A
npcausal c , d	0.133 (0.035)	0.065, 0.201	N/A	N/A	N/A	N/A
tmle c , d	0.135 (0.026)	0.083, 0.186	1.306 (0.054)	1.176, 1.451	1.719 (0.107)	1.394, 2.121
tmle3 c , d , e	0.138 (0.034)	0.071, 0.205	1.310 (0.070)	1.141, 1.503	1.764 (0.140)	1.339, 2.323

Abbreviations: AIPW, augmented inverse probability weighting; CI, confidence interval; EAGeR, Effects of Aspirin in Gestation and Reproduction; GAM, generalized additive model; N/A, not applicable; SE, standard error.

^a All SEs in the table were calculated via asymptotic estimation (using the delta method).

^b The estimates of true causal effect parameter values were generated by the correctly specified parametric regression model with a sample size of 1 million (Figure 1A).

^c SuperLearner was used for AIPW, npcausal, and tmle, and sl3 was used for tmle3. Algorithms included gam, earth, ranger, and XGBoost.

^d We used 10-fold cross-fitting for AIPW, npcausal, tmle, and tmle3. (The tmle package only supports cross-fitting in the outcome model.)

^e Three different estimations were done for tmle3, since it can only output 1 type of estimand per estimation.

For the simulated observational study governed by the data-generating mechanism in Figure 1B, A, Y, and W denote a binary exposure, a binary outcome, and a set of binary, categorical, and continuous confounders (i.e., the aforementione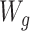d and 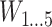), respectively. The propensity score model used to generate A was defined as

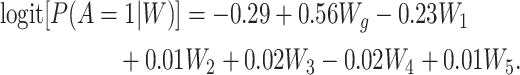Similarly, the outcome Y was simulated from an outcome model defined as

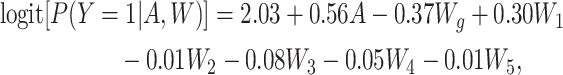such that the true conditional OR for the exposure-outcome relationship was 1.75. This yielded true marginal effects of 0.13, 1.36, and 1.70 on the RD, RR, and OR scales, respectively, which were again obtained using the approach described above.

Realizations of both of these data sets are included in the AIPW package and can be obtained using the data(eager_sim_rct) and data(eager_sim_obs) functions.

Basic implementation of AIPW

The AIPW package was developed to estimate treatment effects of a binary exposure. Such effects include ATEs commonly targeted in observational studies, which include intention-to-treat effects when a randomization indicator is available. These effects can be defined on the RD, RR, and OR scales (30) as

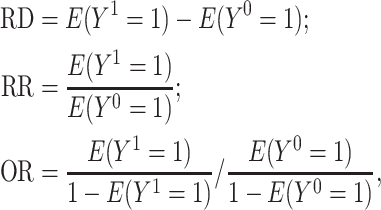where 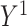and 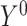denote the potential outcomes that would be observed if the exposure were set to 1 and 0, respectively.

Under consistency, exchangeability, positivity, and no interference, the average of potential outcomes that would be observed under 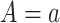is identified as the average of estimated outcomes, that is, 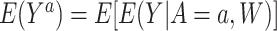, which for simplicity we denote 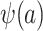. Several estimators can be constructed by combining predictions from the propensity score model with predictions from the outcome model. These predictions can be obtained from parametric regression, such as logistic regression. However, machine learning methods can also be used when these predictions are combined via a doubly robust estimator such as AIPW. This is because double robustness can yield estimators with low bias and valid SEs, even when the propensity score and outcome model estimators have high bias and no generally valid method for obtaining SEs (7–11).

Under the data-generating mechanism depicted in Figure 1A, the propensity score predictions should be obtained conditional on 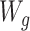(i.e., 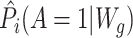), which could be used for constructing an inverse probability weighting (IPW) estimator (31, 32), such as

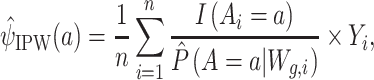(1)

where 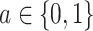and i represents the ith observation. For improved performance, the estimated propensity scores can be truncated, which the AIPW package implements by default at the 2.5th percentile (33).

Alternatively, outcome model predictions 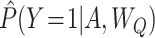can be used to construct a g-computation estimator (31, 34), defined as

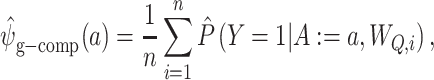(2)

where the := symbol denotes that we set each individual’s value for A in the sample to the argument’s value a. This equation represents the average of predictions from the outcome model by setting 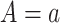over each confounder level.

When the propensity score model or the outcome model is used alone to estimate ATEs, they must in general be built from correct parametric models. In contrast, one can use both the propensity score and the outcome models together in an AIPW estimator (12, 19, 24, 34, 35) as follows:

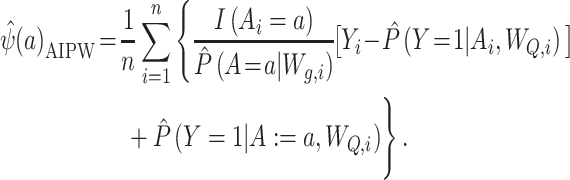(3)

A TMLE estimator of the same quantities can also be constructed using alternative techniques (14, 17).

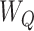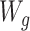As with the TMLE estimator, missing outcome data can be accounted for with the AIPW package if the covariate set W (i.e., both and ) enables one to assume that outcomes are missing at random conditional on W (see Web Appendix 1, available at https://doi.org/10.1093/aje/kwab207) (17, 36).

As long as either the outcome model or the exposure model is correctly specified, consistent estimates of the mean potential outcome can be obtained, that is, the doubly robust property of AIPW (37). Additionally, because of certain statistical properties of doubly robust estimators (10), one can use machine learning methods to quantify the exposure and outcome models while minimizing the slow convergence rates (i.e., large MSE) and overfitting problems that typically characterize use of machine learning methods with sample-splitting or cross-fitting (10, 11). Web Figure 1 shows the implementation of cross-fitting used in the AIPW package, as well as a general illustration of the relationship between sample-splitting and cross-fitting.

SEs for the AIPW on the RD scale can be constructed by taking the standard deviation of the estimated efficient influence function evaluated at each observation (38). Similarly, SE estimates for the estimated RR and OR can be constructed using the delta method. All derivations are provided in Web Appendix 2.

Package implementation

The AIPW package can easily be used to obtain ATE estimates on the RD, RR, and OR scales in several different ways. Using the simulated RCT data provided in the package, Web Appendix 3 provides some example code that could be used to obtain the results presented in Table 1, row 2.

The AIPW package was developed with the object-oriented programming design via the R6 class (39, 40). Similar to TMLE, the AIPW function can employ the SuperLearner stacking algorithm (41, 42). In the example code in Web Appendix 3, we combine 4 learners via stacking, including generalized additive model (GAM) (gam package) (43), multivariate adaptive regression splines (earth) (44), random forests (ranger) (45), and extreme gradient boosting (XGBoost) (46) to fit the propensity score and outcome models. Additionally, the AIPW function enables k-fold cross-fitting, which can provide more accurate SE estimates when machine learning methods are used (10, 47). Users must specify the 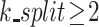argument to enable cross-fitting for the AIPW. This AIPW_SL object is then fitted with the stored arguments using fit(), as depicted on line 20 of Web Appendix 3, and the results are summarized using the summary() function (line 22). The propensity score can be truncated using the g.bound argument in summary(): Propensity scores lower than g.bound or higher than 1 − g.bound are set to g.bound or 1 − g.bound, respectively. For comparison, results from corresponding software implementations are also provided in Table 1.

Full details on using AIPW are available from the Comprehensive R Archive Network (48) and in our GitHub repository (49). This includes details on a range of scenarios that may be encountered with data in RCTs or observational studies, as well as options in the AIPW package that can be used to tailor analyses. In addition, methods for obtaining ATEs among the treated and among controls, along with their SEs, are described online and in the package help documentation (50).

Performance evaluation via a simulation study

To evaluate the performance of our AIPW package and compare it with existing implementations of doubly robust estimators, we conducted a simulation study in observational study data. A sample of 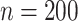from the observational data-generating mechanism (Figure 1B) is provided with the AIPW package. We used this data-generating mechanism to evaluate and compare AIPW and other doubly robust implementations in the R programming language (i.e., CausalGAM, npcausal, tmle, and tmle3) (17–20). Two thousand Monte Carlo simulations, each with a sample size of 200 observations, were conducted. Because CausalGAM does not support estimation of effects on the multiplicative scale, we only evaluated the performance for the RD scale. Performance was evaluated via estimated bias (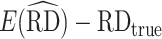) and MSE (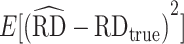) for the point estimates, as well as mean 95% CI width (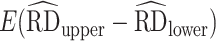) and 95% CI coverage (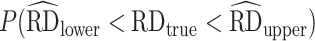) for the asymptotic SEs (51). We also provide information on mean run time (in seconds; sequentially, without parallel processing) per Monte Carlo run.

To explore the performance of different estimators, we conducted 5 sets of analyses. First, the true outcome and propensity score models (generalized linear models (GLMs)) were used to estimate the RD in all 5 packages along with g-computation (via the true outcome model) and stabilized inverse probability weighting (via the true propensity score model). Second, only GAMs (gam) were used to estimate the RD without cross-fitting in each of the 5 packages implementing doubly robust estimators. Third, GAMs were used with 10-fold cross-fitting for the AIPW, npcausal, tmle, and tmle3 packages, the only 4 packages that enable implementation of cross-fitting. Fourth, we used SuperLearner to stack gam, earth, ranger, and XGBoost into 1 meta-algorithm (41, 42, 52, 53) for RD estimation in AIPW, npcausal, tmle, and tmle3 without cross-fitting. Because CausalGAM only supports GAMs, we could not evaluate this package with the stacked metalearner. Lastly, we repeated the latter AIPW and TMLE analyses but this time with 10-fold cross-fitting, using the AIPW, npcausal, tmle, and tmle3 packages. Simulations were conducted in R (version 3.6.2), and details about the models used for estimation (e.g., tuning parameters) are provided in the GitHub repository (54).

RESULTS

Table 1 presents the ATE estimates from the 4 doubly robust packages in the example RCT data provided with the package. When estimated via the AIPW package, we obtained RD_AIPW = 0.136 (95% CI: 0.070, 0.201) for the ATE if all subjects were treated versus untreated. Similarly, the corresponding RR and OR obtained from the AIPW package were 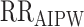 = 1.305 (95% CI: 1.143, 1.490) and  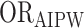= 1.727 (95% CI: 1.323, 2.253). Additionally, despite the differences in implementation and estimation, the other packages yielded estimates that were consistent with those obtained from AIPW. Estimates from all packages were close to the true estimates.

Performance results from our simulations are shown in Table 2. In general, among 2,000 simulated observational data sets, each with a sample size of 200, there was no substantive difference in the bias and MSE between any of the packages used. As expected, the biases from the estimators using GLMs and GAMs were similar but were generally lower than the bias from estimators using SuperLearner. Among packages using GAMs, we observed that CausalGAM yielded a bias about twice that of AIPW, npcausal, tmle, and tmle3. Among the packages enabling SuperLearner without cross-fitting, the bias of AIPW and tmle was about twice that of npcausal and tmle3. In terms of 95% CIs, the coverage was less than nominal (i.e., 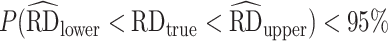) without cross-fitting except when correct parametric models were used, while the coverage improved to nominal when cross-fitting was enabled. Notably, cross-fitting in our setting largely improved the performance of the AIPW package, especially when using SuperLearner—its bias decreased from −0.009 to −0.002 and 95% CI coverage increased from 93.0% to 95.6%—which are comparable to its performance using the true GLMs (bias = −0.002 and 95% CI coverage = 94.8%).

Table 2.

Performance of the AIPW Software Package in Estimating the Average Treatment Effect (Risk Difference) in a Simulated Observational Study Based on the EAGeR Trial^a

Method and Software Package	Bias (SE)	MSE	Mean 95% CI   Width	95% CI   Coverage (SE), %b	Mean Run Time,   seconds
True model: GLM + no cross-fitting
G-computation	−0.002 (0.002)	0.005	0.271	94.8 (0.5)	1.82
IPW	−0.002 (0.002)	0.005	0.280	95.8 (0.4)	0.01
AIPW	−0.002 (0.002)	0.005	0.268	94.8 (0.5)	0.36
CausalGAM	−0.003 (0.002)	0.005	0.267	94.8 (0.5)	0.07
npcausal	−0.002 (0.002)	0.005	0.267	94.6 (0.5)	0.24
tmle	−0.002 (0.002)	0.005	0.261	94.4 (0.5)	0.29
tmle3	−0.002 (0.002)	0.005	0.268	94.8 (0.5)	0.31
GAMs + no cross-fitting
AIPW	−0.002 (0.002)	0.005	0.261	93.8 (0.5)	1.16
CausalGAM	−0.004 (0.002)	0.005	0.266	92.7 (0.6)	0.19
npcausal	−0.002 (0.002)	0.005	0.260	93.9 (0.5)	0.98
tmle	−0.002 (0.002)	0.005	0.257	94.0 (0.5)	0.86
tmle3	−0.002 (0.002)	0.005	0.261	93.9 (0.5)	4.54
GAMs + k = 10 cross-fitting
AIPW	−0.002 (0.002)	0.005	0.310	96.6 (0.4)	7.92
npcausal	−0.002 (0.002)	0.006	0.319	96.5 (0.4)	3.55
tmlec	−0.002 (0.002)	0.005	0.272	95.6 (0.5)	5.15
tmle3	−0.002 (0.002)	0.005	0.308	96.5 (0.4)	7.51
SuperLearnerd + no cross-fitting
AIPW	−0.009 (0.002)	0.005	0.246	93.0 (0.6)	14.65
npcausal	−0.005 (0.002)	0.005	0.232	90.3 (0.7)	21.71
tmle	−0.009 (0.002)	0.005	0.251	93.8 (0.5)	13.44
tmle3	−0.005 (0.002)	0.005	0.246	92.2 (0.6)	36.76
SuperLearnerd + k = 10 no cross-fitting
AIPW	−0.002 (0.002)	0.005	0.281	95.6 (0.5)	128.48
npcausal	−0.004 (0.002)	0.005	0.285	95.5 (0.5)	183.54
tmlec	−0.006 (0.002)	0.005	0.266	94.5 (0.5)	43.38
tmle3	−0.004 (0.002)	0.005	0.272	95.2 (0.5)	48.52

Abbreviations: AIPW, augmented inverse probability weighting; CI, confidence interval; EAGeR, Effects of Aspirin in Gestation and Reproduction; GAM, generalized additive model; GLM, generalized linear model; IPW, inverse probability weighting; MSE, mean squared error; SE, standard error.

^a Simulations were conducted with a sample size of 200 and 2,000 Monte Carlos simulations; the true risk difference was 0.128. Numbers in parentheses show Monte Carlo SEs for the performance indicator estimates.

^b Asymptotic SEs were used for CI calculation in AIPW, CausalGAM, tmle, and tmle3. The CIs for G-computation and IPW were obtained via 200 bootstraps and sandwich estimators, respectively.

^c Cross-fitting was conducted in the outcome model only because of its implementation.

^d SuperLearner was used for tmle and AIPW, and sl3 was used for tmle3. Algorithms included gam, earth, ranger, and XGBoost.

Web Figure 2 shows the pairwise comparisons of the ATE estimates from the simulation results using GLMs in Table 2. Panels on the diagonal are the distributions of estimates, and the lower triangular area includes pairwise scatterplots of all estimates. In the scatterplot panels, vertical and horizontal lines both depict 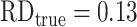. Estimates near the intersection of the true RD lines are less biased from both methods compared in the scatterplot. Interestingly, the estimates are highly correlated between the singly robust estimators (Pearson’s correlation between g-computation and inverse probability weighting = 0.99) and among doubly robust estimators (Pearson’s correlations ≥ 0.97), respectively; however, the correlations between singly and doubly robust estimators are only moderate (Pearson’s correlation = 0.44). Similarly, Web Figure 3 shows the pairwise comparisons of the ATE estimates derived using GAMs and SuperLearner in Table 2; all packages also yielded highly correlated estimates despite the different estimation methods. Simulation results for RR and OR estimates are presented in Web Table 1 and Web Figures 4 and 5.

DISCUSSION

In this paper, we have presented a new R implementation of the AIPW estimator, by means of the AIPW package. This package provides flexible implementation of the AIPW estimator via stacking (e.g., SuperLearner with parametric and machine learning algorithms). Designed for RCTs and observational studies, the AIPW package can provide average causal effect estimates for a binary exposure on the RD, RR, and OR scales, as well as support various features such as cross-fitting, parallel processing, and allowing different covariate sets for the exposure and outcome models.

For convenience, we summarized the key functionality of the AIPW package and its comparisons with CausalGAM, npcausal, tmle, and tmle3 in Table 3. Comparing the 2 packages implementing AIPW, the AIPW package is more flexible than CausalGAM because it supports estimations on multiplicative scales, models using stacking machine learning algorithms via SuperLearner (52) or sl3 (53), and cross-fitting. Compared with tmle and tmle3, the AIPW package holds similar features; additionally, it supports using the fitted tmle and tmle3 objects as input for AIPW estimation.

Table 3.

Comparison of R^a Software Packages That Implement Doubly Robust Estimators

Software Package	Package Characteristic
	Version Evaluated	Doubly Robust Estimator	Available Model	Cross-Fitting?	Different Covariate Sets?	Exposure Type	Propensity Score Truncation?	Outcome Type	Missing Data Support	ATE Estimate Scale	SE Type	Parallel Processing?
AIPW	0.6.3.1	AIPW	SuperLearner	Yes	Yes	Binaryb	Yes	Binary and  continuous	Missing  outcome	RD, RR, OR	Asymptotic	Yes
CausalGAM	0.1-4	AIPW	GAMs	No	Yes	Binary	Yes	Binary and  continuous	No	RD	Asymptotic,  sandwich,  bootstrap	No
npcausal	0.1.0	AIPW	SuperLearner	Yes	Yesc	Binary,  categorical,  continuous	No	Binary and  continuous	Missing  outcome	RD	Asymptotic	No
tmle	1.4.0.1	TMLE	SuperLearner	Yes	Yesd	Binaryb	Yes	Binary and  continuous	Missing  outcome	RD, RR, OR	Asymptotic	No
tmle3	0.1.7	TMLE	SuperLearner	Yes	Yes	Binary,  categorical,  continuous	Yes	Binary and  continuous	Missing  outcome	RD, RR, OR	Asymptotic	Yes

Abbreviations: AIPW, augmented inverse probability weighting; ATE, average treatment effect; GAM, generalized additive model; OR, odds ratio; RD, risk difference; RR, risk ratio; SE, standard error; TMLE, targeted maximum likelihood estimation.

^a R Foundation for Statistical Computing, Vienna, Austria.

^b Continuous and categorical exposures can be used but need to be dichotomized (17).

^c Users need to manually input propensity scores for different covariate sets.

^d When the support of different covariate sets is enabled, tmle uses only a generalized linear model for estimation.

Indeed, while they are often used in observational data, doubly robust estimators can be important when analyzing data from RCTs; in fact, they can be asymptotically efficient under essentially no assumptions. In such a setting, researchers may often wish to adjust for covariates to increase the efficiency of the unconditional intention-to-treat effect (55–58). However, when adjusting for covariates, one may inadvertently introduce misspecification biases, thus detracting from one of the major benefits of randomization (56, 57). Notably, use of doubly robust estimators can help one avoid such biases for RCTs, because the data-generating mechanism for treatment allocations (i.e., randomization stratum) is known by investigators.

Adjustment for covariates in an RCT via doubly robust estimation requires considering different covariate sets for the propensity score and outcome models. For instance, covariates that were not used to assign treatment generally need not be included in the exposure model, even though they might be included in the outcome model. The AIPW package easily allows specification of different covariate sets for the outcome and exposure models, and can thus be used for doubly robust estimation in RCTs. In addition, the AIPW package enables model specification using machine learning methods, which can help one avoid the strict assumptions imposed by parametric models.

With the observational data, our simulation study showed performance of the AIPW package comparable to that of other packages. Indeed, excellent performance was observed even with a relatively small sample size (n = 200). Performance would be expected to improve as the sample size increased (10).

Cross-fitting yielded major improvements in bias and 95% CI coverage of doubly robust methods in our simulation study, in line with a growing body of literature (7–11). Intuitively, sample-splitting or cross-fitting can be used to mitigate overfitting. If cross-fitting is not used, the same data would be used twice for 2 different tasks—once for estimating nuisance quantities (i.e., propensity scores and outcome model predictions) and once for averaging over them to form the estimator (8, 47). Mathematically, cross-fitting (along with consistency of nuisance estimators, at any rate) ensures that a so-called empirical process term is asymptotically negligible—without sample-splitting, one would need to rely on unverifiable assumptions about the true model that may not hold with high-dimensional data (59). Hence, complex machine learning methods should be accompanied by sample-splitting or cross-fitting for effect estimation.

Many machine learning methods, along with cross-validation, sample-splitting, or cross-fitting procedures, often rely on pseudo–random number generators to complete the estimation procedure. With such procedures, reproducibility can be attained by setting “seeds” that determine the exact settings in which the pseudo–random number generators operate. Unfortunately, this can make the results from a given study highly dependent on the value of the selected seed, particularly when cross-fitting is used. There are several options available that reduce the extent to which results depend upon a selected seed value. These include using a higher number of folds for cross-fitting, repeating the cross-fitting procedure iteratively in a given data set (8, 60), or, if one is willing to make unverifiable assumptions (i.e., the Donsker condition), avoiding cross-fitting entirely (59).

At present, the AIPW package relies on a single application of cross-fitting, which may result in seed dependence. Future versions of the package will include options for an iterative cross-fitting procedure. However, users concerned about seed dependence in the current package could select a large number of cross-fitting folds to mitigate this potential issue.

Theoretically, AIPW and TMLE estimators are asymptotically equivalent. Differences between the two arise only because of finite sample differences. These relationships are presented in Web Figures 2–5 with a sample size of 200 from 2,000 Monte Carlo samples. It also provides a degree of validation for our AIPW package by comparing it with existing, well-known, doubly robust R programs.

Our implementation of AIPW estimation is based on a particularly well-studied estimator (12, 24, 50). However, it is important to note that there are several different variations of the AIPW estimator that are distinct from the one we use. Some of these are known to perform better in certain settings, such as when there are potential near-positivity violations (36, 61). Our use of propensity score truncation alleviates some of the concerns raised by such positivity violations, yet researchers should be aware of the existence of alternative AIPW estimation methods.

Future planned implementations for the AIPW package include supporting categorical exposures by incorporating missing-data mechanisms (17, 36) and an iterative cross-fitting procedure (8, 60). The run time of the AIPW package depends on the algorithms included in the stacked learner and the implementation of stacking. Our preliminary (and unvalidated) findings suggest that the sl3 package is faster than SuperLearner (53). For convenience, we find that using SuperLearner for small jobs and sl3 for more complex models tends to optimize run time (53). Furthermore, to optimize run time, we have enabled use of parallel processing packages available in R. Given that the AIPW package is hosted on GitHub (49), future maintenance (e.g., bug reporting) can be requested on GitHub issues.

Altogether, doubly robust estimators are a powerful tool for investigating cause-effect relationships with machine learning methods. The novel AIPW package addresses the limitations of existing programs implementing doubly robust estimators and helps epidemiologists conduct causal inference with flexible machine learning methods.