Strengthening Health Services Research Using Target Trial Emulation: An Application to Volume-Outcomes Studies

Abstract

The number of operations that surgeons have previously performed is associated with their patients’ outcomes. However, this association may not be causal, because previous studies have often been cross-sectional and their analyses have not considered time-varying confounding or positivity violations. In this paper, using the example of surgeons who perform coronary artery bypass grafting, we describe (hypothetical) target trials for estimation of the causal effect of the surgeons’ operative volumes on patient mortality. We then demonstrate how to emulate these target trials using data from US Medicare claims and provide effect estimates. Our target trial emulations suggest that interventions on physicians’ volume of coronary artery bypass grafting operations have little effect on patient mortality. The target trial framework highlights key assumptions and draws attention to areas of bias in previous observational analyses that deviated from their implicit target trials. The principles of the presented methodology may be adapted to other scenarios of substantive interest in health services research.

Abbreviations

CABG

coronary artery bypass grafting

Policy-makers often consider whether medical services should be regionalized to expert providers or specialized centers. Although regionalized services would be less readily available for some patients, the quality of health care might increase if clinicians became more adept due to frequently treating the same conditions. In fact, patient advocacy organizations have suggested that health-care systems withhold credentialing, unless “the hospitals and their surgeons do [the operations] often enough to keep their skill level up” (1). In addition to considering such minimum mandates, it would also be important to learn whether outcomes are inferior among surgeons who opt to decrease their typical operative volumes in order to take on other responsibilities.

Health services researchers have previously studied the relationship between the frequency with which clinicians perform a specific health-care task (their “volume” of this task) and the outcomes of their patients. For example, in various studies, Medicare patients who developed serious conditions had lower mortality when admitted to hospitals that more frequently treated those conditions (2); radiologists who more frequently interpreted diagnostic mammograms had better performance (3); and Medicare patients who underwent an operation had lower mortality when the surgeon performed the operation more frequently (4).

However, the above findings are hard to interpret, because many studies were cross-sectional and ignored time-varying confounding (e.g., a surgeon’s poor postoperative outcomes—including patient deaths or other complications—may affect physicians’ decisions about future referrals to them) or common positivity violations (e.g., instructing surgeons to follow an unrealistic intervention in which they must perform many more operations than usual). In addition, the interpretations of the findings often conflate effects of 2 different interventions: 1) the effect of assigning a patient to select a physician with a certain volume and 2) the effect of assigning a physician to a certain volume. Each type of intervention would require its own separate study.

Here we describe a method for studying interventions on surgeons’ operative volumes. To demonstrate this with an example, we choose the volume of coronary artery bypass grafting (CABG) operations, which has been inconsistently associated with lower patient mortality (4–6). We first specify 4 hypothetical randomized trials (“target trials”) of increasing complexity in which surgeons are assigned to a specific CABG volume. In addition to avoiding common biases, the target trial specification also reveals how certain interventions may be impractically extreme and therefore difficult to implement. (For example, an intervention may be unfeasible if it were to require a cardiothoracic surgeon to perform an extra 20 CABG operations per year at the expense of another cardiothoracic surgeon.) We then emulate each of these target trials using observational data from the Medicare program. This application shows the generality of the target trial methodology, which here is tailored to the characteristics of a common subject in health services research: the effect of changing the provider’s volume onfuture patient outcomes.

SPECIFICATION OF THE TARGET TRIALS

With sufficient resources and cooperation, it would be hypothetically possible to enroll cardiothoracic surgeons in a randomized trial. We would include surgeons who have performed at least 1 CABG operation during each of 2 consecutive intervals of, say, 90 days, and who are willing and able to alter their operative volume (e.g., rural surgeons without an adequate number of nearby colleagues might find it unethical to reduce their operative volume and thereby leave their patients untreated). We could then assign these surgeons to perform a particular number of operations for patients seeking a first-time CABG operation.

However, it would be unrealistic to simply assign surgeons to an arbitrary volume of operations. Participants who perform 1 or 2 operations quarterly, perhaps because they have other obligations, may not be logistically able to suddenly perform 20 operations in a quarter-year. Therefore, we will restrict our target trials to only those that compare strategies under which surgeons increase or decrease their operative volume relative to their prebaseline volume. The surgeons may remove or add activities unrelated to their CABG operative volume at their own discretion. For example, surgeons randomized to perform 2 additional CABG operations per interval may reduce the number of hours dedicated to administrative or research tasks.

For all trials, we consider 1 or more 90-day intervals during which surgeons must perform their assigned number of operations and then a subsequent 90-day interval during which the outcome is evaluated. For each surgeon, the outcome is the 90-day all-cause mortality risk among their patients who underwent an operation in the 90-day interval after the surgeon’s completion of the intervention. Surgeons who do not perform any operations during this interval are considered lost to follow-up. Target trial 1 compares strategies sustained for 1 interval only. Target trial 2 compares strategies sustained over several intervals. Target trials 3 and 4 are modifications of trials 1 and 2 that take into account practical constraints in the number of available patients.

Target trial 1: single-interval intervention

We randomly assign each eligible surgeon to perform a number of CABG operations during the baseline interval k = 0 that is equal to the surgeon’s operative volume during the prebaseline interval k = −1 plus a random number 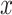that can take values in 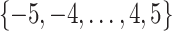. This 11-arm trial is represented by the causal directed acyclic graph in Figure 1.

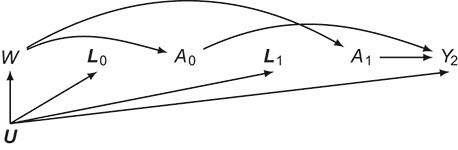
Figure 1.

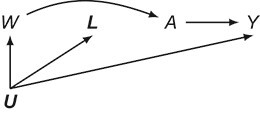
Causal directed acyclic graph corresponding to target trial 1. For each surgeon, 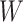is operative volume during interval 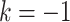, L_k is a vector of covariates during 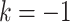(e.g., surgeon characteristics, average patient characteristics, average hospital characteristics, and mortality risk), 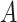is operative volume during 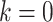(under full adherence to assignment), 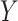is the 90-day mortality risk of patients who underwent an operation during 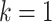, and U is a vector of unmeasured covariates. Directed edges between , L_k, and 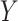are omitted for simplification.

Target trial 2: sustained intervention

Target trial 2 is the same as the previous trial, except that the assigned number of CABG operations is to be maintained during 4 consecutive 90-day intervals k = 0, 1, 2, 3. To allow for vacations, travel to conferences, or patient cancelations, surgeons are allowed to deviate from their assigned number during one of the 4 intervals. The first 2 intervals of this 11-arm trial are represented by the causal directed acyclic graph in Figure 2.

Figure 2.

Causal directed acyclic graph corresponding to target trial 2. For each surgeon, 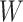is operative volume during interval 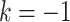; L_k is a vector of covariates during period 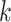(e.g., surgeon characteristics, average patient characteristics, average hospital characteristics, and mortality risk during the prior interval), with 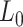also including time-fixed surgeon and hospital covariates; 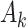is operative volume during period 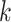; 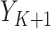is the 90-day mortality risk of patients who underwent an operation during interval 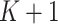; and U is a vector of unmeasured covariates. Directed edges between 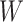, L_k, and 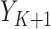are omitted for simplification.

Target trials 3 and 4: interventions to accommodate constraints in number of patients

Target trials 1 and 2 assume no constraints in the number of patients that can be assigned to each surgeon. However, in reality, the restructuring of operative volumes implied by these trials may not be feasible. There may not be a sufficiently large number of eligible patients whose date of operation can be modified to accommodate all of the surgeons who were assigned to perform more operations (surgical simulation is yet to become realistic enough to compensate for any shortfall in the assigned operative volume). Furthermore, it would be unethical to intervene by decreasing the number of CABG operations performed within regions in which surgeons are scarce.

Target trials 3 and 4 address this practical problem by keeping the number of patients approximately equal to the number of patients who had a CABG operation performed by the participating surgeons in the prebaseline interval. Specifically, target trial 3 (target trial 4) resembles target trial 1 (target trial 2), with the following modification. Surgeons are again assigned to perform a number of CABG operations per interval equal to their prebaseline value plus a random number x (ranging from −5 to 5). However, in these trials, surgeons who performed more operations than the median prebaseline volume of all surgeons are assigned to change their volume by (−1 × x) operations, while below-median surgeons are assigned to change their volume by x operations. For scenarios requiring below-median surgeons to reduce their volume below zero (i.e., for x < 0), we assign them to perform zero operations and randomly redistribute their patients to above-median surgeons (for details, see Web Appendix 1, available at https://doi.org/10.1093/aje/kwab170). In summary, this strategy redistributes patients from higher-volume surgeons to lower-volume surgeons (for x > 0) or vice versa (for x < 0), depending on the intervention arm.

Causal estimands

The aim of these trials may be to estimate the intention-to-treat effect, that is, the effect of assignment to each volume on postoperative mortality had all surgeons completed the follow-up, or the per-protocol effect (7), that is, the effect that would have been observed had all surgeons adhered to their assigned intervention and had complete follow-up.

Statistical analysis

To estimate the intention-to-treat effect, we could nonparametrically estimate the 90-day risk of mortality among operations performed by each surgeon during the interval subsequent to the completion of the intervention, π, and then compare this mean mortality risk among surgeons assigned to each of the 11 arms indexed by x, 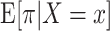. However, given the large number of strategies, we can obtain more precise estimates of 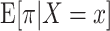by, for example, assuming the logistic regression model for a binomial random variable:

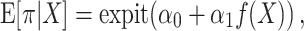where 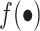denotes a flexible functional form such as restricted cubic splines. We would need to assume that the parametric interpolation across interventions is reasonable and that discontinuous jumps in the effect on postoperative mortality of incremental changes to operative volume do not exist.

If there was incomplete follow-up, such that not all surgeons performed an operation in the interval subsequent to completion of the intervention (leaving the outcome unobserved), we would adjust for potential selection bias by adding baseline covariates to the outcome regression and then standardizing to the distribution of these covariates in the overall population. Baseline covariates would include surgeon characteristics (age, sex, calendar time of meeting eligibility criteria in 90-day blocks since January 1, 2012), surgeon’s hospital characteristics (i.e., CABG operative volume), and patient characteristics (proportions of patients with a history of acute myocardial infarction, atrial fibrillation, chronic kidney injury, chronic obstructive pulmonary disease, congestive heart failure, diabetes, stroke or transient ischemic attack, and dementia; proportion of patients with elective hospital admission; average hospital proportion of Medicare patients; and proportion of patients who died within 90 days postoperatively after undergoing an operation during the prior interval (if no operations were performed in an interval, this proportion would be set to 0). Restricted cubic splines could be used to flexibly model all continuous covariates.

To estimate the per-protocol effect for target trial 1, we would additionally exclude the surgeons who did not adhere to their assigned strategy. We could then adjust for baseline prognostic factors associated with adherence by including them as covariates in the outcome regression and standardizing to the distribution of these covariates in the overall population (as described above in the adjustment for loss to follow-up).

To estimate the per-protocol effect for target trial 2 (which includes several intervals), instead of entirely excluding surgeons who did not adhere to their assigned strategy, we would censor them when they deviated from their assigned strategy. We could then we estimate (stabilized) inverse probability weights (as described in Web Appendix 2) to adjust for baseline and postbaseline (time-varying) covariates that may be associated with adherence and loss to follow-up (8, 9). The time-varying covariates L_k include the surgeon’s hospital characteristics (i.e., CABG operative volume) and patient characteristics (proportions of patients with a history of acute myocardial infarction, atrial fibrillation, chronic kidney injury, chronic obstructive pulmonary disease, congestive heart failure, diabetes, stroke or transient ischemic attack, and dementia; proportion of patients with elective hospital admission; average hospital proportion of Medicare patients; interval number; and proportion of patients who died within 90 days postoperatively after undergoing an operation during the prior interval (if no operations were performed in an interval, this proportion would be set to 0).

The analyses for target trials 3 and 4 mirror those of target trials 1 and 2, respectively.

A nonparametric bootstrap procedure with 1,000 resamples can be used to estimate 95% confidence intervals for the effect estimates in all trials.

EMULATION OF THE TARGET TRIALS

Conducting these target trials would be logistically challenging, for several reasons. For example, referring physicians may not agree to have their patients randomly assigned to a surgeon with whom they are not familiar. Surgeons likewise may not agree to forfeit the professional satisfaction or payment associated with randomization to an arm with lower operative volumes. However, we can attempt to emulate these target trials using observational data (8).

Our data source is the entire population of fee-for-service Medicare beneficiaries during the period January 1, 2011–September 30, 2016, who were ≥65 years of age and had not previously undergone a CABG operation (Web Table 1). Observation units for each surgeon were partitioned into 90-day discrete time intervals. Nationally, 85% of CABG operations among patients aged 65 years or older are estimated to be paid for by fee-for-service Medicare coverage (9).

Eligibility criteria

Surgeons were identified using a unique provider identification number designated by the “primary operator” field of the inpatient Medicare data, and subspecialty was classified by the surgeon specialty identifier in the Medicare Data on Provider Practice and Specialty File (10). This information was used to emulate the eligibility criteria as specified in the target trial (i.e., cardiothoracic surgeons who have performed at least 1 CABG operation for Medicare patients during each of 2 consecutive 90-day intervals).

Strategies

We emulated the same strategies as those described above for the target trials.

Treatment assignment

Each surgeon’s 90-day operative volume, defined as the number of CABG operations performed in the Medicare inpatient claims file, was recorded at the end of each interval (i.e., at the beginning of the kth interval, a surgeon’s operative volume over the prior 90-day interval was counted). Each surgeon was assigned to the intervention arm they were observed to have followed.

We assumed conditional randomization by adjusting for the following baseline covariates: surgeon’s age, surgeon’s sex, prebaseline operative volume, calendar time of meeting eligibility criteria (in 90-day blocks since January 1, 2012), and average total number of hospital beds at the surgeon’s hospital(s). The American Hospital Association Annual Survey of Hospitals was used to determine the characteristics of included hospitals. Surgeon and hospital characteristics were obtained from the Medicare Data on Provider Practice and Specialty File and the American Hospital Association Annual Survey of Hospitals, respectively. Average patient comorbidity information was obtained from the Medicare Master Beneficiary Summary File (11). A longer-term cumulative measure of operative volume was unavailable in the data; as such, we assumed that the other covariates were sufficient to approximately emulate conditional randomization. Given that there was no substantive basis for structural violations of positivity and the majority of covariates were continuous, we assumed that any violations of positivity were random.

Follow-up

For each eligible individual, follow-up begins at treatment assignment and extends for up to four 90-day intervals, plus 90 days during which the outcomes are measured.

Outcome

Patient mortality was assessed by linkage with the Medicare Vital Status File, which integrates information from Medicare claims data, family members, the Railroad Retirement Board, and the Social Security Administration.

Causal contrast

We estimated the observational analog of per-protocol effects.

Statistical analysis

The per-protocol analysis of the observational data is the same as that of the target trials, with the following modifications. First, because surgeons may meet eligibility criteria more than once, sequential trials will be emulated (each with a different time 0). Second, because in the emulation of target trials 2 and 4 all individuals have data compatible with all strategies in the first interval, each individual will have as many copies (clones) as strategies their data are compatible with (12, 13). Each clone is censored at the time of deviation from their assigned treatment strategy. An example of this censoring procedure is presented in Web Table 2. Risk differences are presented with each intervention arm, compared with the arm in which surgeons maintain their baseline volume. Software code for this analysis is available on GitHub (14).

Sensitivity analyses

Rather than arbitrarily setting the mortality to 0 when no operations were performed in an interval, we required surgeons to perform at least 1 operation during each interval in a sensitivity analysis for target trial 2 (see Web Appendix 3).

ESTIMATES FROM MEDICARE DATA

The baseline characteristics of the 2,338 eligible surgeons, their patients, and the hospitals in which they performed the operations are displayed in Table 1. Surgeon operative volume ranged from 0 to 41 operations, and the mean volume was 8.1 operations during the prebaseline interval. The 95th and 99th percentiles were 15 and 21 operations, respectively. Because of the higher variance associated with higher operative volume, the proportion of surgeons who followed the sustained strategies was lower among those with high prebaseline operative volumes than among those with lower volumes. (In a simplifying example, with operative volume following a Poisson distribution, the expected variance for surgeons performing, on average, 1 or 10 prebaseline operations would be 1 or 10, respectively. As such, surgeons with higher prebaseline operative volumes would be less likely to sustain the same number of operations per interval.) There did not appear to be nonrandom violations of positivity, as described in Web Appendix 4 and Web Tables 3 and 4.

Table 1.

Characteristics (During the 6 Months Prior to Baseline) of 2,338 Eligible Surgeons Who Performed Coronary Artery Bypass Grafting for Medicare Beneficiaries, United States, 2012–2016

Characteristic	No.	Mean (SD)
Surgeon characteristics
No. of CABG operations per 90 days		8.1 (6.3)
Age, years		50.6 (9.0)
Female sexa	86 (3.7)
Hospital characteristics
Total no. of hospitals	1,035
No. of CABG operations per 90 days		29.2 (24.1)
No. of beds		506.1 (324.7)
Proportion of patients with Medicare		0.4 (0.1)
Case mix characteristics
Total no. of patients	37,991
Age, years		74.2 (3.2)
Chronic conditions (surgeon-specific proportion)
Acute myocardial infarction		0.1 (0.2)
Dementia		0.1 (0.1)
Atrial fibrillation		0.2 (0.2)
Chronic kidney disease		0.3 (0.2)
Chronic obstructive pulmonary disease		0.3 (0.2)
Congestive heart failure		0.4 (0.3)
Diabetes mellitus		0.5 (0.3)
Stroke or transient ischemic attack		0.2 (0.2)

Abbreviations: CABG, coronary artery bypass grafting; SD, standard deviation.

^a Values are expressed as number (%).

The estimates of the mean 90-day mortality risk under each strategy are summarized in Table 2, Table 3, and Figure 3. The risk differences for each strategy were compared with a strategy in which surgeons maintained their baseline volume (i.e., a trial in which x = 0). We estimated that, had all surgeons increased their CABG operative volume by 5 for one 90-day interval as in target trial 1 (or a full year, as in target trial 2), the expected mortality would subsequently be 5.7% (4.8% in trial 2), as compared with 6.2% (5.5% in trial 2) had all surgeons instead decreased their volume by 5.

Table 2.

Estimated Risks of 90-Day Surgeon-Specific Mortality Among Surgeons Performing Coronary Artery Bypass Grafting for Medicare Beneficiaries Under Different Interventions on Surgeon Volume, United States, 2012–2016

Assignment   x	Target Trial 1 a		Target Trial 2 a		Target Trial 3 b		Target Trial 4 b
	ME, %	95% CI	ME, %	95% CI	ME, %	95% CI	ME, %	95% CI
−5	6.2	5.9, 6.5	5.5	3.9, 9.1	6.1	5.8, 6.4	4.3	2.6, 17.5
−4	6.2	5.9, 6.4	5.3	4.1, 6.8	6.0	5.8, 6.3	4.8	2.9, 14.8
−3	6.1	5.9, 6.3	5.4	4.5, 6.9	6.0	5.8, 6.2	5.4	3.5, 11.7
−2	6.0	5.8, 6.2	5.7	4.7, 7.6	6.0	5.8, 6.1	5.9	4.3, 9.8
−1	6.0	5.8, 6.1	5.9	4.9, 7.5	5.9	5.8, 6.1	6.0	4.8, 8.4
0	5.9	5.8, 6.1	6.1	5.1, 7.8	5.9	5.8, 6.1	6.2	5.1, 7.8
1	5.8	5.7, 6.0	6.3	5.0, 9.5	5.9	5.7, 6.0	6.6	5.2, 8.4
2	5.8	5.6, 5.9	6.3	4.6, 9.9	5.9	5.7, 6.0	6.7	4.9, 9.3
3	5.7	5.6, 5.9	5.8	4.0, 9.7	5.8	5.7, 6.0	6.4	4.8, 8.9
4	5.7	5.5, 5.8	5.2	3.7, 11.8	5.8	5.7, 6.0	6.0	4.7, 9.1
5	5.7	5.5, 5.8	4.8	3.6, 16.0	5.8	5.7, 6.0	6.3	5.1, 12.1

Abbreviations: CABG, coronary artery bypass grafting; CI, confidence interval; ME, mortality estimate.

^a In target trials 1 and 2, x denotes an addition of CABG operations for 1 (trial 1) or 4 (trial 2) 90-day interval(s).

^b In target trials 3 and 4, x denotes an addition of CABG operations for below-baseline surgeons and a subtraction for above-baseline surgeons for 1 (trial 3) or 4 (trial 4) 90-day interval(s).

Table 3.

Estimated Risk Difference in 90-Day Surgeon-Specific Mortality (%) Among Surgeons Performing Coronary Artery Bypass Grafting for Medicare Beneficiaries Under Different Interventions on Surgeon Volume, Relative to Maintaining Baseline Volume (x = 0), United States, 2012–2016

Assignment   x	Target Trial 1 a		Target Trial 2 a		Target Trial 3 b		Target Trial 4 b
	RD	95% CI	RD	95% CI	RD	95% CI	RD	95% CI
−5	0.3	0.1, 0.6	−0.7	−3.0, 3.0	0.2	−0.1, 0.4	−1.9	−3.9, 11.6
−4	0.3	0.1, 0.5	−0.8	−3.0, 0.8	0.1	−0.1, 0.3	−1.4	−3.7, 8.4
−3	0.2	0.1, 0.4	−0.7	−2.9, 0.8	0.1	−0.1, 0.3	−0.8	−2.9, 5.5
−2	0.1	0.1, 0.2	−0.4	−1.9, 1.2	0	0.0, 0.2	−0.3	−1.9, 3.3
−1	0.1	0.0, 0.1	−0.2	−1.2, 0.8	0	0.0, 0.1	−0.2	−1.0, 1.5
0	0	Referent	0	Referent	0	Referent	0	Referent
1	−0.1	−0.1, 0.0	0.2	−0.8, 2.2	0	−0.1, 0.1	0.4	−0.9, 1.7
2	−0.1	−0.2, −0.1	0.2	−1.6, 3.6	0	−0.1, 0.0	0.6	−1.4, 3.4
3	−0.2	−0.3, 0.1	−0.3	−2.5, 3.8	−0.1	−0.1, 0.0	0.2	−1.9, 3.2
4	−0.2	−0.3, −0.1	−0.9	−3.2, 6.0	−0.1	−0.1, 0.0	−0.2	−2.2, 3.1
5	−0.2	−0.4, −0.1	−1.3	−3.1, 10.2	−0.1	−0.1, 0.0	0.1	−1.6, 6.4

Abbreviations: CABG, coronary artery bypass grafting; CI, confidence interval; RD, risk difference.

^a In target trials 1 and 2, x denotes an addition of CABG operations for 1 (trial 1) or 4 (trial 2) 90-day interval(s).

^b In target trials 3 and 4, x denotes an addition of CABG operations for below-baseline surgeons and a subtraction for above-baseline surgeons for 1 (trial 3) or 4 (trial 4) 90-day interval(s).

Figure 3.

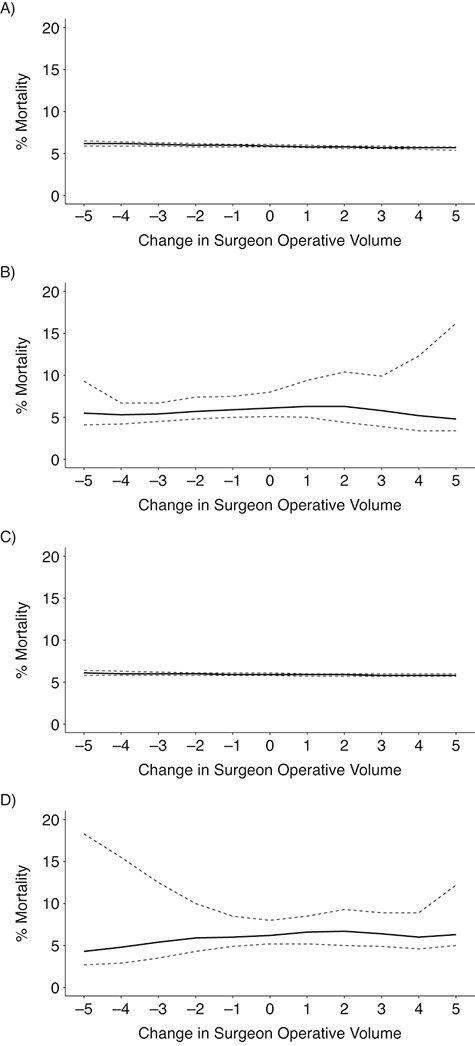
Estimated risks of 90-day surgeon-specific mortality among surgeons performing coronary artery bypass grafting for Medicare beneficiaries, United States, 2012–2016. The graph depicts results for the emulation of target trial 1 (A), target trial 2 (B), target trial 3 (C), and target trial 4 (D). Dashed lines, pointwise 95% confidence intervals.

Alternatively, we estimated that, had 5 CABG operations from above-median surgeons been reassigned to below-median surgeons for one 90-day interval as in target trial 3 (or a full year, as in target trial 4), the expected mortality would be 6.1% (4.3% in trial 4), as compared with 5.8% (6.3% in trial 4) had 5 operations been reassigned from below-median surgeons to their above-median volume counterparts.

Estimates were similar in the sensitivity analysis for the emulation of target trial 2 in which surgeons were required to perform at least 1 operation in all intervals (Web Table 5). Lack of adjustment for time-varying covariates changed point estimates by as much as 0.2 percentage points in target trials 2 and 4, while lack of adjustment for both time-varying and baseline covariates changed point estimates by as much as 1.7 percentage points in target trial 2 and 0.8 percentage points in target trial 4.

DISCUSSION

We used Medicare data to emulate 4 target trials of interventions on surgeons’ CABG operative volumes. Our estimates suggested little effect of these interventions on patient mortality, both during a single 90-day interval (trials 1 and 3) and over a calendar year (trials 2 and 4)—except potentially in cases of more extreme restructuring of referral patterns. Using the approach described in this paper, policy-makers may be better able to judge whether a redistribution of operations among surgeons is a worthwhile endeavor when counterbalanced by access to care and other logistical considerations.

Previous investigators have described an association between physicians’ volumes and better patient outcomes (2–4), with studies specific to CABG operations having conflicting results (4–6). However, a causal interpretation of these findings is not straightforward, because these analyses were cross-sectional, did not consider positivity violations, disregarded real-world constraints on implementation, and did not adjust for time-varying confounding.

In contrast, we used longitudinal data to emulate target trials that assign surgeons to a volume that depends on their prebaseline volume (thus preventing positivity violations). We emulated realistic target trials that, furthermore, account for realistic constraints in the number of patients available for implementation (by considering interventions which reassign cases from lower-volume to higher-volume surgeons or vice versa). Finally, we adjusted for time-varying confounding when considering interventions sustained over 1 year.

Our analysis had several limitations. First, because surgeons were not, in fact, randomized, the effect estimates may have been confounded. However, in sensitivity analyses, the unadjusted estimates were not drastically different from the adjusted ones. Since we adjusted for a large number of available covariates that may contribute to referral patterns and performance of future operations (including past outcomes and characteristics of prior patients), the general similarity of unadjusted estimates suggested that confounding is not likely to be a major source of bias. Second, our estimates were averaged over the entire population of eligible surgeons who performed services for Medicare, under the assumption that all would have been willing to participate in the trial. Thus, our effect estimates may not be transportable to a population of surgeons with a different distribution of prebaseline volumes or other characteristics. Third, the interventions compared in our target trials did not specify how surgeons alter activities that are unrelated to CABG operative volume, which might of be of interest for practical implementation. Fourth, we underestimated the total operative volume of surgeons because about 15% of operations performed were not done for fee-for-service Medicare beneficiaries.

In summary, we outlined and applied a method that estimates the expected outcome of requiring a surgeon to increase or decrease their existing volume of CABG operations. Specifying a realistic causal question and making potential biases explicit will help researchers implement and interpret analyses of sufficiently well-defined interventions on operative volume. When health services research involves substantive interest in intervening on physicians’ patient volumes, this article demonstrates how the target trial framework can be used to guide the analysis and interpret the results. This overall methodological approach can be modified for application to other operations and nonsurgical questions.