ZERO-INFLATED QUANTILE RANK-SCORE BASED TEST (ZIQRANK) WITH APPLICATION TO SCRNA-SEQ DIFFERENTIAL GENE EXPRESSION ANALYSIS

Abstract

Differential gene expression analysis based on scRNA-seq data is challenging due to two unique characteristics of scRNA-seq data. First, multimodality and other heterogeneity of the gene expression among different cell conditions lead to divergences in the tail events or crossings of the expression distributions. Second, scRNA-seq data generally have a considerable fraction of dropout events, causing zero inflation in the expression. To account for the first characteristic, existing parametric approaches targeting the mean difference in gene expression are limited, while quantile regression that examines various locations in the distribution will improve the power. However, the second characteristic, zero inflation, makes the traditional quantile regression invalid and underpowered. We propose a quantile-based test that handles the two characteristics, multimodality and zero inflation, simultaneously. The proposed quantile rank-score based test for differential distribution detection (ZIQRank) is derived under a two-part quantile regression model for zero-inflated outcomes. It comprises a test in logistic modeling for the zero counts and a collection of rank-score tests adjusting for zero inflation at multiple prespecified quantiles of the positive part. The testing decision is based on an aggregate result by combining the marginal p-values by MinP or Cauchy procedure. The proposed test is asymptotically justified and evaluated with simulation studies. It shows a higher precision-recall AUC in detecting true differentially expressed genes (DEGs) than the existing methods. We apply the ZIQRank test to a TPM scRNA-seq data on human glioblastoma tumors and exclusively identify a group of DEGs between neoplastic and nonneoplastic cells, which are heterogeneous and have been proved to be associated with glioma. Application to a UMI count scRNA-seq data on cells from mouse intestinal organoids further demonstrates the capability of ZIQRank to improve and complement the existing approaches.

1. Introduction.

Differential gene expression analysis is one of the most commonly performed tasks for RNA-seq data with a broad set of applications, such as identifying genes associated with a tumor, understanding phenotypic variation, as well as many others [Costa-Silva, Domingues and Lopes (2017), Zhang et al. (2014)]. The traditional RNA-seq experiments measure mRNA transcript abundance averaged over thousands or millions of cells which have proven useful in many studies. However, a gene may express at substantially different levels in different subgroups of cells, and the bulk experiments fail to take account of this cell-specific information [Korthauer et al. (2016)]. As a crucial technology advance, single cell RNA-sequencing (scRNA-seq) measures mRNA transcript abundance in individual cells and enables us to study the gene-specific expression heterogeneity across cells. This is important for understanding cancer progression and discovering novel cell types [Buettner et al. (2015), Hong et al. (2013), Patel et al. (2014), Ramsköld et al. (2012), Treutlein et al. (2014), Trombetta et al. (2014)].

Many methods have been proposed to identify differentially expressed genes (DEGs) in scRNA-seq data. Comprehensive reviews can be found in Soneson and Robinson (2018) and Molin, Baruzzo and Camillo (2017). A good scRNA-seq analysis tool should be tailed for two unique features of scRNA-seq data. First, due to biological and technical cell-to-cell variability, a given gene’s expression is often unobserved in a large fraction of cells, which leads to zero inflation in expression level [Kharchenko, Silberstein and Scadden (2014)]. Several mixture methods have been developed to accommodate the zero-inflated nature of scRNA-seq data, leading to substantively improved power compared to more traditional bulk RNA-seq models, such as the once-popular DESeq2 [Love, Huber and Anders (2014)]. For example, MAST [Finak et al. (2015)] uses logistic regression to model the zero inflation and a Gaussian linear model to model the positive continuous part. Monocle [Trapnell et al. (2014)] fits the data with a generalized additive model (GAM) and accounts for the dropout events using the tobit model. Second, scRNA-seq data is highly heterogeneous due to both the population and cellular heterogeneity. For example, several works [Birtwistle et al. (2012), Dobrzyński et al. (2012, 2014), Kærn et al. (2005), Singer et al. (2014)] report multimodal distributions of scRNA-seq gene expressions. This is probably a result of the multiple stable states among expressed genes [Birtwistle et al. (2012)] or comes from a series of biological processes. For example, when a tumor suppressor gene is overexpressed in some cells, it will be slightly adjusted back by another biological process in the human body. Such a negative feedback that causes oscillations has been observed in several studies [Kærn et al. (2005), Monk (2003)], which may lead to multiple modes in scRNA-seq gene expressions [Dobrzyński et al. (2012, 2014)]. The hidden heterogeneity in the scRNA-seq data could be more complex than the existence of multiple modes which is inherited from the bulk RNA-seq level. For example, Song et al. (2017) reports several eQTLs that only affect the upper tails of gene expressions. Although many aforementioned models consider the inflated zero counts, they rely on parametric models, such as the Gaussian model, which might not be sufficient to capture the heterogeneity in the scRNA-seq data. The scDD method proposed by Korthauer et al. (2016) utilizes a conjugate Dirichlet process mixture (DPM) of normal distributions to handle the hidden heterogeneity, but fails to accommodate more than two cell conditions and cannot incorporate confounding covariates, which are important considerations for gene expression analyses.

In this paper, we propose a two-part quantile regression model, which fully incorporates the zero-inflated and heterogeneous nature of scRNA-seq data while allowing adjustment of covariates. Quantile regression [Koenker and Bassett (1978)] models the conditional distribution of an outcome without any parametric likelihood specification and is hence a promising nonparametric alternative to detect DEGs with complex and heterogeneous associations. It also offers the flexibility to incorporate confounders. Several earlier works using quantile regression to test genetic associations [Song et al. (2017), Wei et al. (2016)] report discoveries in both GWAS and eQTL studies. These genetic association tools from direct quantile regression, however, do not account for zero inflation. The computation algorithm and theoretical results of quantile regression are built upon the assumption that the conditional distribution of outcomes is absolutely continuous. Since the existence of zero inflation violates the assumption, quantile regression often fails to produce reliable estimations, and inferences by these existing quantile-based tools may not be valid. Moreover, direct quantile regression cannot capture the dependence of zero proportions on the cell condition and covariates, leading to biased estimations. Thus, these direct quantile-based methods may suffer from the biases, resulting in uncontrolled false positives or underpowered testing. As a remedy, Zhang et al. (2020) use logistic regression for the zero inflation and apply quantile regression to the scRNA-seq data at shifted quantiles with perturbation to break the probability mass at zero. Though perturbation is a convenient numerical treatment, it could introduce extra noise into the analysis. To address the existing challenges, we propose a rank-score test adjusting the bias caused by zero inflation based on the proposed two-part quantile model, and we establish its asymptotic properties. Finally, we detect DEGs by combining the marginal p-values of the logistic regression for zero counts and the novel rank-score tests over a sequence of quantiles of nonzero expressions. We establish the asymptotic dependence structure of these marginal tests and incorporate it when combining the p-values. This proposed differential test is named zero-inflated quantile rank-score based test (ZIQRank).

Details of ZIQRank are presented in Section 2. Simulation studies to compare it with QRank, linear regression and existing differential expression analysis methods for bulk and scRNA-seq data can be found in Section 3. It is shown that ZIQRank has a well-controlled false positive rate and a higher precision-recall AUC than the competing methods. In Section 4, we apply the proposed method to a non-UMI TPM scRNA-seq data about glioblastoma in the conquer (consistent quantification of external rna-seq data) repository [Soneson and Robinson (2018)] and identify a group of genes that are differentially expressed between neoplastic and nonneoplastic cells. Previous biological investigations warrant the roles of those genes in diagnosis, progression or suppression of glioma. In Section 5, we further use ZIQRank to study a UMI count scRNA-seq data about cells from mouse intestinal organoids. We conclude the paper in Section 6. Technical proofs are relegated to the Supplementary Material [Ling et al. (2021)].

2. Proposed methods.

2.1. Notations in scRNA-seq data analysis.

A scRNA-seq data consists of a random sample of n cells. For each cell, we sequence J genes. As a result, we have an n × J gene expression matrix Y, whose entry Y_i,j denotes the expression level of the j th gene in the i th cell. We then denote the primary covariates of interest, cell conditions, as a q-dimensional vector C_i. The differential gene expression analysis is to identify genes whose cell-level expressions depend on the cell conditions C. In addition, we collect a set of additional cell characteristics, including the intercept, for example, patient from whom a cell is collected, potentially related clinical features and sequencing information, and we denote them as a p-dimensional vector Z_i. Throughout the paper, we denote Q_Yi,j (τ | X_i) as the τth conditional quantile of Y_i,j given X_i, where ${\text{X}}_i={\left({\text{Z}}_i^{\top },{\text{C}}_i^{\top }\right)}^{\top }$

2.2. Zero-inflated quantile regression model for individual gene expression.

We decompose the conditional distribution of the expression Y_i,j as

$$P\left(Y_{i,j}\le y\mid {\mathbf{\text{X}}}_i\right)=P\left(Y_{i,j}=0\mid {\mathbf{\text{X}}}_i\right)+P\left(Y_{i,j}\le y\mid {\mathbf{\text{X}}}_i,Y_{i,j}>0\right)P\left(Y_{i,j}>0\mid {\mathbf{\text{X}}}_i\right)I(y>0),$$

where P(Y_i,j = 0 | X_i) is the probability of no expression of the j th gene in the ith cell, while P(Y_i,j ≤ y | X_i, Y_i,j > 0) is the conditional distribution of expression level, given that the j th gene is expressed in the ith cell. Following the decomposition, we consider a two-part model for the zero-inflated expression. First, we model P(Y_i,j >0 | X_i) by a logistic regression model,

$$\text{logit}\left\{P\left(Y_{i,j}>0\mid {\mathbf{\text{X}}}_i\right)\right\}={\mathbf{\text{Z}}}_i^{\top }{\mathit{\zeta }}_j+{\mathbf{\text{C}}}_i^{\top }{\mathit{\gamma }}_j,$$ (1)

where exp(γ _j) is the odds-ratio for observing nonzero expression of the j th gene associated with cell conditions C. Next, we model the conditional distribution P(Y_i,j ≤ y | X_i, Y_i,j > 0) using a linear quantile regression model,

$$Q_{Y_{i,j}}\left(\tau \mid {\mathbf{\text{X}}}_i,Y_{i,j}>0\right)={\mathbf{\text{Z}}}_i^{\top }{\mathit{\alpha }}_j(\tau )+{\mathbf{\text{C}}}_i^{\top }{\mathit{\beta }}_j(\tau ),$$ (2)

where β_j(τ) depicts how the τth quantile of nonzero expression of the j th gene differs by cell conditions C and α_j(τ) captures the contribution of the remaining covariates. Due to the nonparametric nature of quantile regression, the proposed two-part quantile model is a generalization of the MAST method. As the model is proposed for analyzing each gene independently, we focus on the j th gene in the rest of Section 2, and we omit the subscript j in all the notations for a simpler presentation.

The quantile coefficients β(τ) and α(τ) can be estimated by minimizing the following loss function:

$$\underset{\mathit{\alpha },\mathit{\beta }}{\text{min}}\sum _{i=1}^n{\rho }_{\tau }\left\{Y_i-{\mathbf{\text{Z}}}_i^{\top }\mathit{\alpha }-{\mathbf{\text{C}}}_i^{\top }\mathit{\beta }\right\}I\left(Y_i>0\right),$$ (3)

where ρ_τ(u) = u{τ − I (u < 0)} is the quantile loss function. Due to the correlation between the indicator I (Y_i > 0) and the loss function ${\rho }_{\tau }\left\{Y_i-{\mathbf{\text{Z}}}_i^{\top }\mathit{\alpha }-{\mathbf{\text{C}}}_i^{\top }\mathit{\beta }\right\}$, the existing quantile regression inference tools cannot be applied directly. In addition, those inference tools, if applied directly, will underestimate the uncertainty that the “positive subset” is observed by chance and lead to biased tests. In the subsequent section we adapt the rank-score test (Gutenbrunner et al. (1993)) to the proposed zero-inflated quantile model. The rank-score test is robust and computationally efficient. Hence, it is the desired inference tool for genetic associations. In the case of no zero inflation, Song et al. (2017) have numerically shown that the traditional rank-score test has a well-controlled Type I error on the GTEx multitissue gene expression data.

2.3. Rank-score test of β(τ) with zero inflation.

Let ${\tilde{\text{C}}}_i={\text{C}}_i\cdot I\left(Y_i>0\right)$ and ${\tilde{\text{Z}}}_i={\text{Z}}_i\cdot I\left(Y_i>0\right)$ as the nominal variables of the cell conditions and remaining covariates. It follows that ${\tilde{\text{C}}}_{n\times q}={\left({\tilde{\text{C}}}_1,\dots ,{\tilde{\text{C}}}_n\right)}^{\top }$ , ${\tilde{\text{Z}}}_{n\times p}={\left({\tilde{\text{Z}}}_1,\dots ,{\tilde{\text{Z}}}_n\right)}^{\top }$ are the design matrix associated with ${\tilde{\text{C}}}_i$ ’s and ${\tilde{\text{Z}}}_i$ ’s. We further denote ${\tilde{\text{C}}}^{\ast }=\left(I-\tilde{\text{Z}}{\left({\tilde{\text{Z}}}^{\top }\tilde{\text{Z}}\right)}^{-1}{\tilde{\text{Z}}}^{\top }\right)\tilde{\text{C}}$, where I is the n × n identity matrix. This orthogonal transformation ensures the asymptotic independence between ${\tilde{\text{C}}}^{\ast }$ and $\tilde{\text{Z}}$.

We construct a rank score for β(τ) = 0 by

$${\mathbf{\text{S}}}_{n,\tau }^Q=n^{-\frac{1}{2}}\sum _{i=1}^n{\psi }_{\tau }\left\{Y_i-{\widetilde{\mathbf{\text{Z}}}}_i^{\top }{\widehat{\mathit{\alpha }}}_n(\tau )\right\}I\left(Y_i>0\right){\widetilde{\mathbf{\text{C}}}}_i^{*},$$ (4)

where ψ_τ (u) = τ − I (u < 0) is the piecewise first derivative of the quantile loss function ρ_τ (u), ${\widehat{\mathit{\alpha }}}_n(\tau )$ is the minimizer of (3) with β = 0 and ${\tilde{\text{C}}}_i^{\ast }$ is the ith row of ${\tilde{\text{C}}}^{\ast }$. By design, ${\text{S}}_{n,\tau }^Q$ measures the independent contribution of C onto the τth quantile of Y. When $\mathit{\beta }(\tau )=0,{\text{S}}_{n,\tau }^Q$ is close to a vector of zeros. We also note that the zero-positive uncertainty is incorporated into the rank score (4).

Finally, with ${\text{V}}_{n,\tau }=n^{-1}\tau (1-\tau ){\tilde{\text{C}}}^{\ast }{}^{\top }{\tilde{\text{C}}}^{\ast }$, we define the rank-score test statistic at the τth quantile as

$$T_{\tau }^Q={\mathbf{\text{S}}}_{n,\tau }^{Q\top }{\mathbf{\text{V}}}_{n,\tau }^{-1}{\mathbf{\text{S}}}_{n,\tau }^Q.$$ (5)

Under the conditions outlined in the Appendix, we establish the asymptotic distribution of $T_{\tau }^Q$ in the following theorem.

THEOREM 1. Under Assumptions 1–4 in the Appendix, as n → ∞, we have:

1. At a fixed τ, given β(τ) = 0, define

   $${\widetilde{\mathbf{\text{S}}}}_{n,\tau }^Q=n^{-\frac{1}{2}}\sum _{i=1}^n{\psi }_{\tau }\left\{Y_i-{\widetilde{\mathbf{\text{Z}}}}_i^{\top }{\widehat{\mathit{\alpha }}}_n(\tau )\right\}I\left(Y_i>0\right){\widetilde{\mathbf{\text{C}}}}_i,$$

   we have

   $${\widetilde{\mathbf{\text{S}}}}_{n,\tau }^Q\stackrel{d}{\to }N\left(0,{\Sigma }_{\tau }\right),$$

   where

   $${\Sigma }_{\tau }=\tau (1-\tau )\left\{\mathbb{E}\left({\widetilde{\mathbf{\text{C}}}}_i{\widetilde{\mathbf{\text{C}}}}_i^{\top }\right)-\mathbb{E}\left({\widetilde{\mathbf{\text{C}}}}_i{\widetilde{\mathbf{\text{Z}}}}_i^{\top }\right)\mathbb{E}{\left({\widetilde{\mathbf{\text{Z}}}}_i{\widetilde{\mathbf{\text{Z}}}}_i^{\top }\right)}^{-1}\mathbb{E}\left({\widetilde{\mathbf{\text{Z}}}}_i{\widetilde{\mathbf{\text{C}}}}_i^{\top }\right)\right\}=\tau (1-\tau ){\Sigma }_0.$$

   Replacing ${\tilde{\text{C}}}_i$ with ${\check{\text{C}}}_i={\tilde{\text{C}}}_i-\mathbb{E}\left({\tilde{\text{C}}}_i\mid {\tilde{\text{Z}}}_i\right)$ the decorrelated version ${\check{\text{S}}}_{n,\tau }^Q$ has the same asymptotic distribution but ${\Sigma }_0=\mathbb{E}\left({\check{\text{C}}}_i{\check{\text{C}}}_i^{\top }\right)$.
2. At a fixed τ, given β(τ) = 0, we have

   $$T_{\tau }^Q\stackrel{d}{\to }{\chi }_q^2.$$
3. Let ${\text{S}}_n^Q=\left({\text{S}}_{n,{\tau }_1}^Q,\dots ,{\text{S}}_{n,{\tau }_K}^Q\right)$ be a vector of rank-score statistics on a sequence of quantile levels 0 < τ₁ < · · · < τ_K < 1. Given β(τ₁) = · · · = β(τ_K) = 0, we have

   $${\mathbf{\text{S}}}_n^Q\stackrel{d}{\to }N(0,\Sigma ),$$

   where the (k, k)th diagonal block of Σ is ${\tau }_k\left(1-{\tau }_k\right)\mathbb{E}\left({\check{\text{C}}}_i{\check{\text{C}}}_i^{\top }\right)$ which can be approximated by V_n,τk; the (k, l)th off-diagonal block is $\left(\text{min}\left\{{\tau }_k,{\tau }_l\right\}-{\tau }_k{\tau }_l\right)\mathbb{E}\left({\check{\text{C}}}_i{\check{\text{C}}}_i^{\top }\right)$ which can be approximated by $n^{-1}\left(\text{min}\left\{{\tau }_k,{\tau }_l\right\}-{\tau }_k{\tau }_l\right){\tilde{\text{C}}}^{\ast \top }{\tilde{\text{C}}}^{\ast }$

All proofs in this section are deferred to Section A of the Supplementary Material [Ling et al. (2021)].

REMARK. The proposed rank-score test correcting zero-inflation biases has two major differences compared to the standard one. First, the rank-score statistic (4), in fact, is computed based on the subset of data with positive Y_i’s. Second, to correct the biases caused by zero inflation in testing, we incorporate the zero-positive uncertainty in estimating the variance of the rank score by introducing the zero-truncated nominal covariates. Technically, $\mathbb{E}\left({\tilde{\text{C}}}_i{\tilde{\text{C}}}_i^{\top }\right)=\mathbb{E}\left\{{\text{C}}_i{\text{C}}_i^{\top }P\left(Y_i>0\mid {\text{X}}_i\right)\right\}$. As a consequence, V_n,τ implicitly incorporates a “propensity score” of each cell, compensating the variability caused by the random status of the gene being observed or not.

2.4. Stepwise algorithm of ZIQRank test in scRNA-seq data.

In differential gene expression analysis, we are interested in testing whether the distribution of the expression level of a gene differs according to the cell conditions C. Following the two-part quantile regression model (1) and (2), the task translates into the following global null hypothesis:

$$H_0:\mathit{\gamma }=0\text{ \& }\mathit{\beta }(\tau )=0\forall \tau \in (0,1).$$ (6)

To test the global null hypothesis, we propose a stepwise test procedure, where we first marginally construct a test statistic for γ and the proposed rank-score test statistics (Section 2.3) for β(τ) on a grid of quantile levels. We then combine the marginal p-values while taking the correlations of the marginal test statistics into account. We call the proposed test zero-inflated quantile rank-score based test (ZIQRank). We describe the following three steps to implement ZIQRank.

Step 1. Construct a logistic regression test for γ : Conduct any asymptotically valid test, that is, Wald test, Rao’s score test or likelihood-ratio test, based on the estimated logistic regression model (1). Denote the test statistic as T ^L and the p-value as p^L.

Step 2. Construct the proposed rank-score test that corrects zero inflation on a sequence of quantile levels: Following Theorem 1(b), we can compute the p-values $p_{{\tau }_k}^Q$ associated with $T_{{\tau }_k}^Q$, k = 1, … , K at quantile levels 0 < τ₁ < · · · < τ_K < 1. Selection of the grid of quantile levels will be elaborated in Section 2.5.1.

Step 3. Combination of marginal p-values: Combine the marginal p-values by MinP [Lee, Wu and Lin (2012), He et al. (2017)] or Cauchy combination test [Liu and Xie (2020)]. Compared to the joint χ² test, the two procedures are more appropriate for sparse strong signals which is a characteristic of scRNA-seq data. The choice between MinP and Cauchy tests on specific data will be discussed in Section 2.5.2.

$T_{\text{ZIQRank-MinP }}=\text{min}\left\{p^L,p_{{\tau }_1}^Q,\dots ,p_{{\tau }_K}^Q\right\}$: It uses the minimum p-value as the test statistic and derives the final p-value by resampling based on the dependence structure of the marginal test statistics. The null hypothesis will be rejected if it is unlikely to observe an even smaller minimum p-value. Let $q_{\text{min}}^L$ denote the (1 − T_ZIQRank-MinP)th percentile of the distribution of T ^L and $q_{\text{min}}^Q$ denote the (1 − T_ZIQRank-MinP)th percentile of the distributions of $T_{{\tau }_k}^Q$, k = 1, … , K, which are all ${\chi }_q^2$. The p-value based on T_ZIQRank-MinP is

$$\begin{gathered} P\left\{\exists T_{{\tau }_k}^Q\ge q_{\text{min}}^Q,k=1,\dots ,K\text{ or }{T}^L\ge q_{\text{min}}^L\mid H_0\right\} \\ =1-P\left\{T^L<q_{\text{min}}^L\mid H_0\right\}P\left\{\forall T_{{\tau }_k}^Q<q_{\text{min}}^Q,k=1,\dots ,K\mid H_0\right\} \\ =1-\left(1-T_{\text{ZIQRank-MinP}}\right)P\left\{\forall T_{{\tau }_k}^Q<q_{\text{min}}^Q,k=1,\dots ,K\mid H_0\right\}, \end{gathered}$$

where the first equality is based on the asymptotic independence between T^L and $T_{\tau }^Q$ (Section A.1 of the Supplementary Material [Ling et al. (2021)]). The joint probability $P\left\{\forall T_{{\tau }_k}^Q<q_{\text{min}}^Q,k=1,\dots ,K\mid H_0\right\}$ can be computed via resampling ${\text{S}}_{n,{\tau }_k}^Q$ ’s from the joint limiting distribution of ${\text{S}}_n^Q$ under the null hypothesis (Theorem 1(c)) and calculating the realizations of $T_{{\tau }_k}^Q$ with the help of V_n,τk’s, k = 1, … , K.

$T_{\text{ZIQRank-Cauchy }}={\widehat{r}}_n\text{ tan}\left\{\left(0.5-p^L\right)\pi \right\}+{\sum }_{k=1}^K{w}_k\text{ tan}\left\{\left(0.5-p_{{\tau }_k}^Q\right)\pi \right\}$, where ${\widehat{r}}_n$ is the observed proportion of zero in Y_i’s and

$$w_k=\left(1-{\widehat{r}}_n\right)\frac{{\tau }_{k}I\left({\tau }_k\le 0.5\right)+\left(1-{\tau }_k\right)I\left({\tau }_k>0.5\right)}{{\sum }_{k=1}^K\left\{{\tau }_{k}I\left({\tau }_k\le 0.5\right)+\left(1-{\tau }_k\right)I\left({\tau }_k>0.5\right)\right\}},$$

that is, the sum of all weights is 1, and the p-values associated with central quantiles are assigned with larger weights while those on extreme tails have smaller weights: It uses the weighted average of p-values. After tangent transformation of the p-values, the aggregate statistic follows standard Cauchy distribution under the null hypothesis, regardless of the dependence structure of the marginal test statistics. The p-value based on T_{ZIQRank-Cauchy} is

$$1-{\Phi }_{\text{Cauchy}}\left(T_{\text{ZIQRank-Cauchy}}\right).$$

REMARK. ZIQRank is an omnibus test, which aggregates all signals of association between the gene expression and cell condition together, regardless of the magnitude and direction. A small p-value indicates that the gene shows differences in either zero proportions or quantiles of the positive part at some levels, or both. When the data is nonnormal, such as the zero-inflated scRNA-seq gene expression, combining signals over quantile processes is often more efficient in detecting the difference in comparison to the mean-based approaches, as it captures more heterogeneity among different groups. Similar power gain was reported in Zhao and Xiao (2014).

2.5. Practical considerations of implementing ZIQRank.

2.5.1. Selection of the grid of quantile levels.

One issue that affects the testing performance is the selection of a quantile grid. Without prior knowledge or preference, the entire distribution is of interest; thus, a grid covering all typical quantiles is required. Note that if one aims to test whether a particular region is different among distributions, for example, the tail differences, one can specify a grid within the interested interval.

Next, the number of quantiles should be chosen with care. More quantiles might introduce more significant signals but might also incorporate extra noise. When computing resources are adequate, a tuning process to achieve a satisfactory power while keeping Type I error controlled is encouraged. Note that the number of quantile levels cannot exceed the number of the positive observations of the gene, that is, $K<\left(1-{\widehat{r}}_n\right)n$. Otherwise, the marginal tests will be highly correlated, and the Type I error might be inflated.

2.5.2. Choice between MinP and Cauchy combination tests.

MinP and Cauchy combination methods use “local” and “global” principles, respectively, to combine p-values, and they have advantages in different scenarios.

When the data has a high degree of heterogeneity, the MinP test will be more powerful because it makes the decision based on the most significant signal. Otherwise, the Cauchy test will be preferred since it pools the uniformly significant or insignificant signals together. This point will be demonstrated by comparing the data characteristics and results of simulation studies (Section 3) and real data applications (Sections 4 and 5).

In addition, the MinP test is robust to the extent of zero inflation because all the p-values, from either logistic or quantile tests, are treated equally. By the Cauchy test, however, the result from the logistic component will dominate if the gene expression is highly zero-inflated. This point will be illustrated by comparing the simulation study with cell condition only (Section 3.1) and the simulation study with additional covariates (Section 3.2).

Finally, because there is no need to estimate the joint probability by resampling based on the dependence structure of marginal test statistics, the Cauchy test is easier to implement and more computationally efficient. When computing resources are limited, the Cauchy test will be preferred.

2.5.3. Default settings of ZIQRank in practice.

It is practically helpful to specify a default setting of ZIQRank. We recommend a dense quantile grid τ = 0.05, 0.1, … , 0.95 for continuous scRNA-seq data (e.g., non-UMI TPM). The grid distributes over the quantile support (0, 1) evenly and thoroughly, helping to fully capture the distributional difference, and it is conservative for most scRNA-seq data which are usually very big. For count data (e.g., UMI count), to ensure reliable estimations and valid inferences, a jittering uniformly distributed with a lower limit 0 and upper limit 1 should be added, that is, the rank-score (4) becomes ${\text{S}}_{n,\tau }^Q=n^{-\frac{1}{2}}{\sum }_{i=1}^n{\psi }_{\tau }\left\{W_i-{\tilde{\text{Z}}}_i^{\top }{\widehat{\mathit{\alpha }}}_n(\tau )\right\}I\left(Y_i>0\right){\tilde{\text{C}}}_i^{\ast }$, where W_i = Y_i + U and U ~ (0, 1). Machado and Santos Silva (2005) guarantee that ZIQRank is still valid. To compromise with potential spurious signals by jittering, a less dense but commonly used grid in quantile analysis τ = 0.1, 0.25, 0.5, 0.75, 0.9 is recommended.

Considering the heterogeneity in most scRNA-seq data, the MinP test is recommended as the default setting for p-value combination. The Cauchy test will be chosen if the data is less heterogeneous. The rule for heterogeneity is simple and fast to implement. Across genes, calculate: (1) the number of crossings of the quantile functions and (2) the coefficient of variation (CV) of nonzero quantile differences between cell conditions. If medians of both measures are larger than 1, the data is considered heterogeneous.

In the following numerical studies, we will use the default setting of ZIQRank (with the default grid and default combination method) to compare with existing approaches. The other combination method will also be examined, but for illustration purposes only.

3. Simulation.

In this section, we investigate the finite sample performance of ZIQRank in comparisons with existing methods through two simulation studies. Both studies aim to identify DEGs between two cell conditions. The first simulation study only considers the cell conditions without adjusting confounding covariates, named as “unadjusted analysis”. The second one includes one additional covariate, named as “adjusted analysis”.

For comparison, we choose eight competing methods: (1) QRank, (2) QRank with MinP test, (3) QRank with Cauchy test, (4) linear regression, (5) MAST, (6) Monocle, (7) scDD and (8) DESeq2. Each of them serves as a representative of one group of approaches, given the underlying model and characteristics. QRank is a direct quantile-based method ignoring zero inflation and using a joint χ² test. QRanks with MinP/Cauchy tests are presented to remove the effect of various p-value combination methods. However, applying the three QRanks directly to the zero-inflated scRNA-seq data is not viable. On the simulated data their estimations failed in 21 genes (out of 10,000), and we observed inflated false positive rates (nearly 25%). To make QRanks applicable in this work, we manually add a small random perturbation to the probability mass at zero to create “pseudo-continuous” data. MAST and Monocle are parametric scRNA-seq approaches, using Gaussian linear or generalized additive model for the positive part, and consider zero inflation in the models. scDD is a nonparametric Bayesian method to detect the difference between two cell conditions and cannot adjust additional covariates. DESeq2 is a commonly used method for bulk RNA-seq data, assuming negative binomial distribution, and does not consider zero inflation.

3.1. Simulation of unadjusted analysis.

3.1.1. Setting of the unadjusted analysis.

The simulated data are generated following the simulation framework in scDD R package with modifications. scDD simulates the data for two cell conditions, which mimics the gene expression distributions in a human embryonic stem cell scRNA-seq data, and generates both DEGs and null genes (NGs). Based on the starting data, scDD could cluster and simulate four scenarios of DEGs: (1) traditional differential expression (DE), (2) differential proportion of cells within each component (DP), (3) differential modality (DM) and (4) both differential modality and different component means within each condition (DB). Figure 1 plots the density and quantile functions for the four DEG scenarios. DE shows a unimodal distribution in density plot and a homogeneous difference in quantile plot, while DP, DM and DB have more than one mode in density plots and demonstrate heterogeneity in quantile differences. Additionally, the two quantile functions in DP form a spindle shape, and those in DB cross at some central quantiles which are two typical types of differential distribution with minimal mean differences but substantial differences in quantiles. Apart from the overall performance, we aim to examine ZIQRank on each of the four types of DEGs, especially those with multimodal distributions.

FIG. 1.

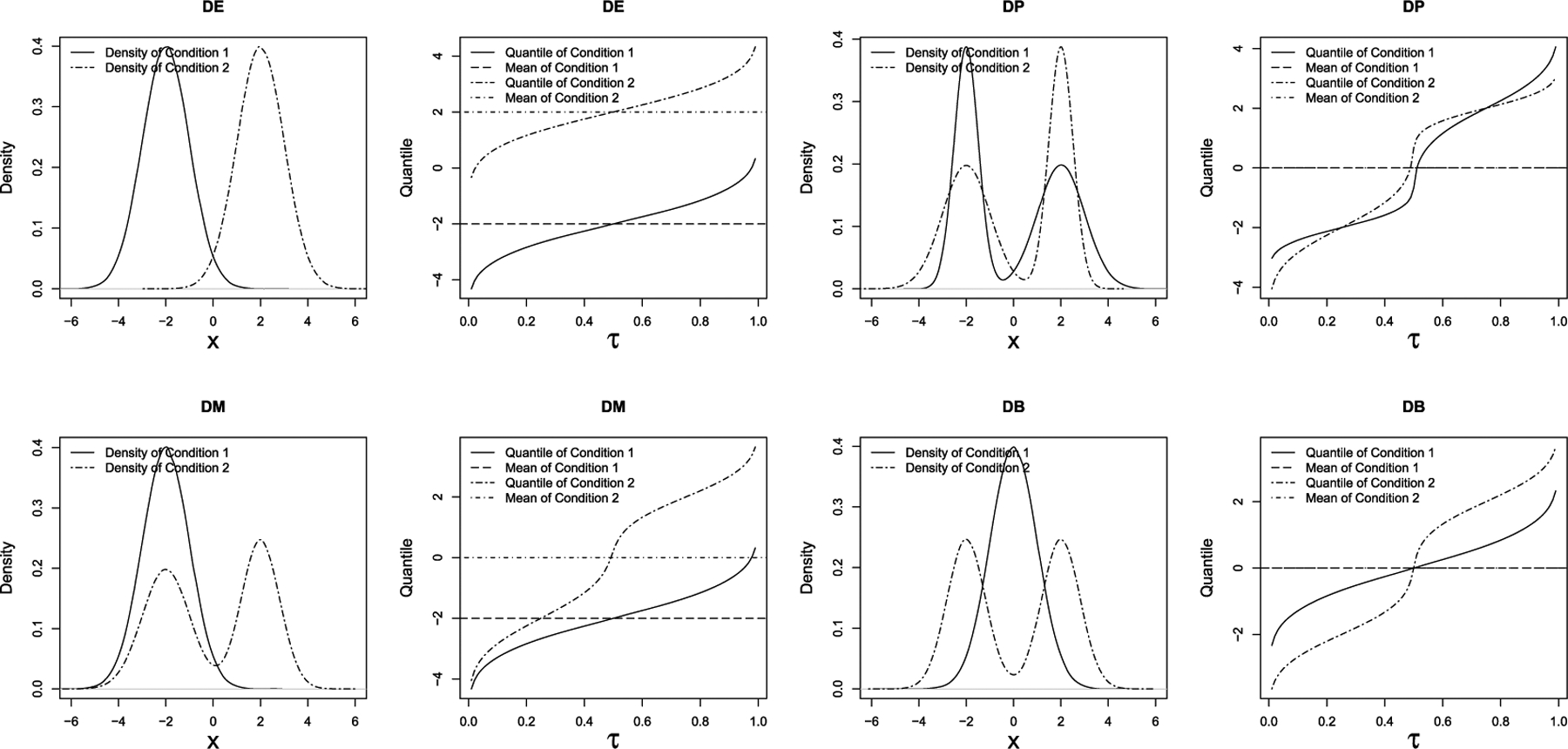
Density and quantile functions of the four scenarios of differential distributions: DE, traditional differential expression (top left); DP, differential proportion (top right); DM, differential modality (bottom left); DB, both differential modality and different component means (bottom right).

However, based on the human embryonic stem cell starting data, scDD generates DEGs with similar percentages of zeros between the two conditions. To introduce extra zero inflation and more differentiated zero rates between conditions, we simulate DEGs, using scDD, then further convert a certain percentage of the lowest nonzero expressions of each DEG to zero. The rationale is that the dropouts of scRNA-seq data are usually due to low gene expression. The selected proportions of the lowest nonzero values for conversion to zero follow a uniform distribution with a lower limit 0 and an upper limit 25%. We do not impose an extra zero inflation more than 25% to keep the specific shapes of DE, DP, DM and DB.

For each simulated dataset, 10,000 genes are simulated for two conditions with a sample size of 200 cells each. Eight thousand NGs are simulated. Two thousand genes are simulated as DEGs, with 500 for each of the four DEG scenarios. Logarithmic transformation is applied to the simulated data. To confirm that the simulated data represents the human embryonic stem cell scRNA-seq data, we plot and compare: (1) the dropout rates vs. mean and (2) mean vs. variance across genes (Figure S1). It shows that the synthetic data captures and even exaggerates the zero-inflated nature of the real data, and it does a satisfactory job in recapitulating the mean-variance relationship. Thus, this simulation is reliable.

ZIQRank with τ = 0.05, 0.1, … , 0.95 quantile grid and MinP procedure is the default, since the simulated data is continuous and highly heterogeneous (median of number of crossings between quantile functions = 6, median of CV of quantile difference > 1, shown in Figure S2a). The existing methods and ZIQRank are applied to each simulated dataset. Genes are considered as DEGs when the corresponding adjusted p-values using the Benjamini– Hochberg (BH) procedure are less than 0.05. Precision, defined as the number of true positive calls among all positive calls, and recall, defined as the number of true positive calls among all the true DEGs, are calculated. They are summarized into precision-recall (PR) curve and area under the curve (AUC). Also, stratified recall is calculated for each of the four DEG scenarios. Stratified precision cannot be calculated, since all the methods, except scDD, cannot classify the positive calls into the four DEG scenarios. False positive rate (FPR), defined as the number of false positive calls among all NGs, is calculated. The simulation process is repeated 10 times, and the results are summarized using means and standard deviations (sd) of the number of DEGs detected and the number of true DEGs detected. We present the boxplots of AUCs under PR curves and display the boxplots of stratified recalls and FPRs over the 10 simulation runs.

3.1.2. Results of the unadjusted analysis.

ZIQRank has the largest numbers of detected DEGs (1878.10) and correctly detected DEGs (1838.80) (Table 1). Even when the precision-recall trade-off is considered, it yields the highest AUC 0.99 (Figures 2a and S3a). In all of the four DEG scenarios, ZIQRank works best with the highest recall rates (Figure 2b).

TABLE 1.

Summary statistics of the number of DEGs detected and the number of correctly detected DEGs by ZIQRank and existing methods, with adjusted p-value less than 0.05, in unadjusted simulation study

Method	nDEG	sd	ntrueDEG	sd
ZIQRank-MinP	1878.10	9.34	1838.80	9.41
ZIQRank-Cauchy	1390.00	21.84	1375.10	21.28
QRank	1636.40	17.91	1600.20	16.11
QRank-MinP	1825.40	16.71	1802.30	15.10
QRank-Cauchy	1278.60	16.02	1268.10	15.73
linear	1365.60	20.35	1349.00	18.74
MAST	1586.80	8.73	1578.10	8.89
Monocle	1255.20	24.59	1236.90	23.48
scDD	1656.50	15.62	1643.30	13.50
DESeq2	1215.60	25.06	1215.40	25.10

FIG. 2.

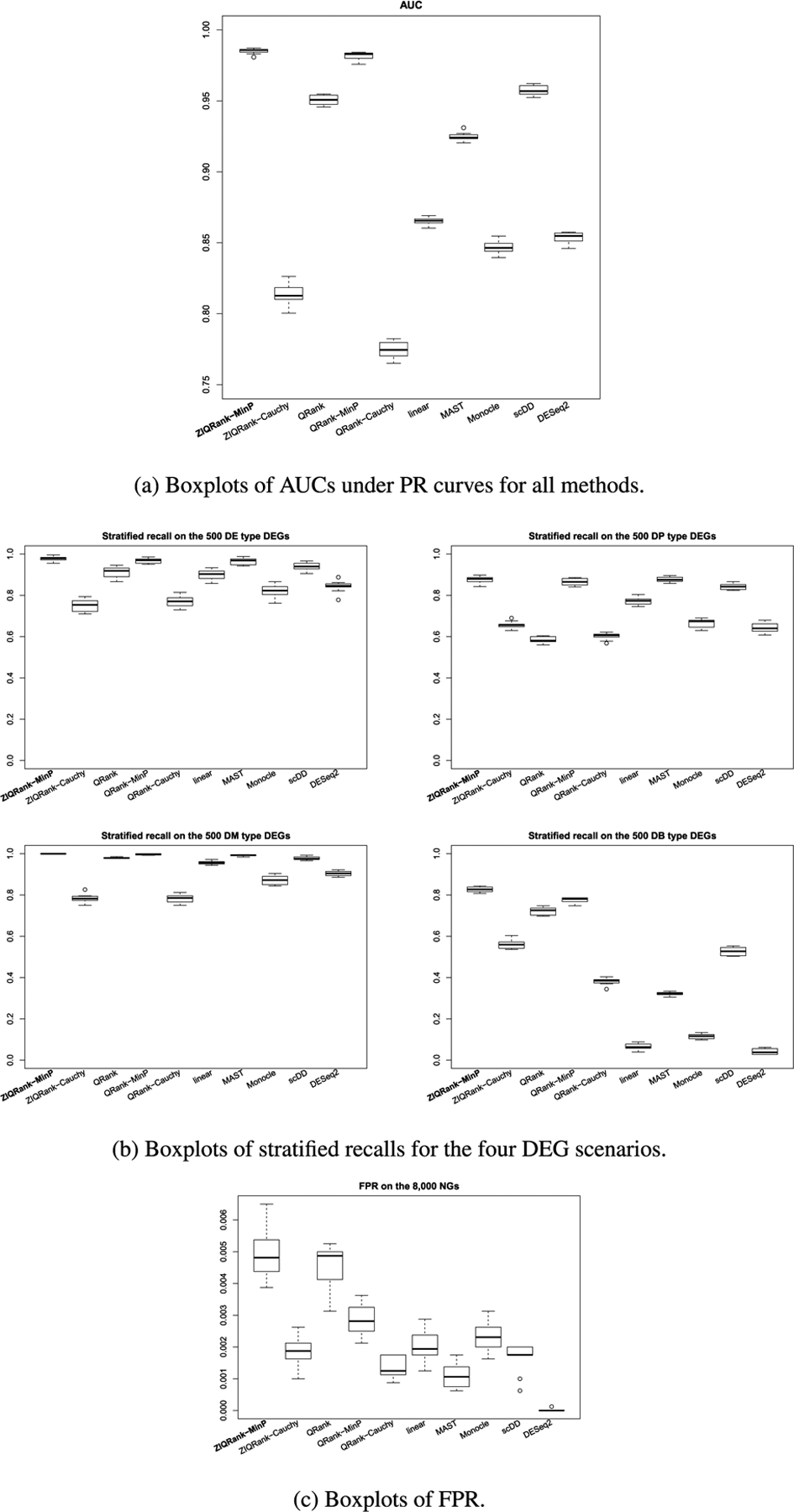
Performance of ZIQRank and existing methods in the unadjusted analysis.

The first runner-up is QRank-MinP, which detects 1802.30 true DEGs and has an AUC of 0.98. The outstanding performance is expected, as MinP test is good at picking the most significant signal in the heterogeneous data. Though the AUCs are close, ZIQRank surpasses QRank-MinP in terms of power, especially for DB scenario (DB recall of ZIQRank vs. QRank-MinP = 83% vs. 78%). Thus, we can infer that modeling zeros is beneficial by incorporating the signal from different zero proportions between conditions and amplifying the signals on the nonzero part, especially further separating the crossed distribution functions of DB-type DEGs.

All other methods have inferior AUCs (AUC of scDD = 0.96, QRank = 0.95, MAST = 0.92, etc.). Almost all methods provide satisfactory results for DE and DM scenarios, with stratified recalls higher than 80%. DE and DM scenarios have a clear mean difference between the two conditions, which can be detected by both parametric and nonparametric methods. For DP and DB scenarios, especially DB, ZIQRank has much higher recalls than the parametric methods. This is because the parametric approaches target detection of location/mean difference, which is minimal in DP and DB scenarios, while ZIQRank aims to detect quantile difference, which is substantial in the two scenarios.

Though ZIQRank has the highest FPR (Figure 2c), it is still well controlled below 0.01.Its PR curve and highest AUC also suggest a tolerable false discovery rate (FDR = 1-precision Therefore, though it does not dominate in all aspects, ZIQRank has a nonnegligible value improving the power and complementing the existing methods with controlled false positives.

Overall, ZIQRank performs best in detecting DEGs in terms of PR-AUC in the unadjusted analysis. It improves and complements the existing methods in identifying DP and DB-type multimodal DEGs, without undermining the power in identifying those DEGs with differences, while keeping false positives controlled.

3.2. Simulation of adjusted analysis.

3.2.1. Setting of the adjusted analysis.

We further compare the performance of ZIQRank with other methods by including one additional covariate. Similar to Section 3.1.1, we first use scDD R package to generate 10,000 genes for two conditions with 200 cells each, including 8000 NGs and 2000 DEGs from the four DEG scenarios. Denote the logarithmic transformed expression as Y_i,j for the j th gene in the ith cell. Then, we add one cell-level covariate Z_i into the simulation by $Y_{i,j}^{\prime }=Y_{i,j}+{\alpha }_j{Z}_i$, where α_j is the covariate effect on the j th gene. Z_i is simulated from a normal distribution with mean 5 and sd 1.5. α_j is assigned to be zero for randomly selected 75% of the simulated genes; for the remaining genes, α_j is simulated from a uniform distribution with a lower limit of 0 and an upper limit of 0.25. Following the same procedure in Section 3.1.1, we generate extra zero inflation by further converting a certain percentage of the lowest nonzero expressions to zero. Similarly, the mean-zeros and mean-variance plots (Figure S1) verify that the simulated data is a fair representation of the human embryonic stem cell scRNA-seq data.

ZIQRank with τ = 0.05, 0.1, … , 0.95 quantile grid and MinP procedure is still the default (data is continuous and highly heterogeneous, with median of number of crossings between quantile functions = 6, median of CV of quantile difference > 1 by Figure S2b). scDD is excluded, as it cannot handle confounding covariates. Genes are considered as DEGs when the BH adjusted p-values are less than 0.05. The numbers of DEGs detected, the PR curves with AUCs, stratified recalls and FPRs are summarized over 10 simulation runs.

3.2.2. Results of the adjusted analysis.

ZIQRank is the most powerful method, as it has the largest number of correctly detected DEGs (1825.10) (Table 2). It also produces the highest AUC (0.98) (Figures 3a and S3b). Again, it achieves the highest stratified recalls for all four types of DEGs (Figure 3b).

TABLE 2.

Summary statistics of the number of DEGs detected and the number of correctly detected DEGs by ZIQRank and existing methods with adjusted p-value less than 0.05, in adjusted simulation study

Method	nDEG	sd	ntrueDEG	sd
ZIQRank-MinP	1862.50	15.57	1825.10	11.69
ZIQRank-Cauchy	1784.40	8.45	1750.20	7.63
QRank	1997.80	21.89	1611.60	9.45
QRank-MinP	2103.80	32.41	1809.40	12.64
QRank-Cauchy	1547.70	20.65	1472.20	7.36
linear	1351.50	21.92	1335.40	19.29
MAST	1561.60	14.81	1553.60	15.65
Monocle	1220.80	28.62	1203.20	28.80
DESeq2	1193.90	27.41	1193.70	27.42

FIG. 3.

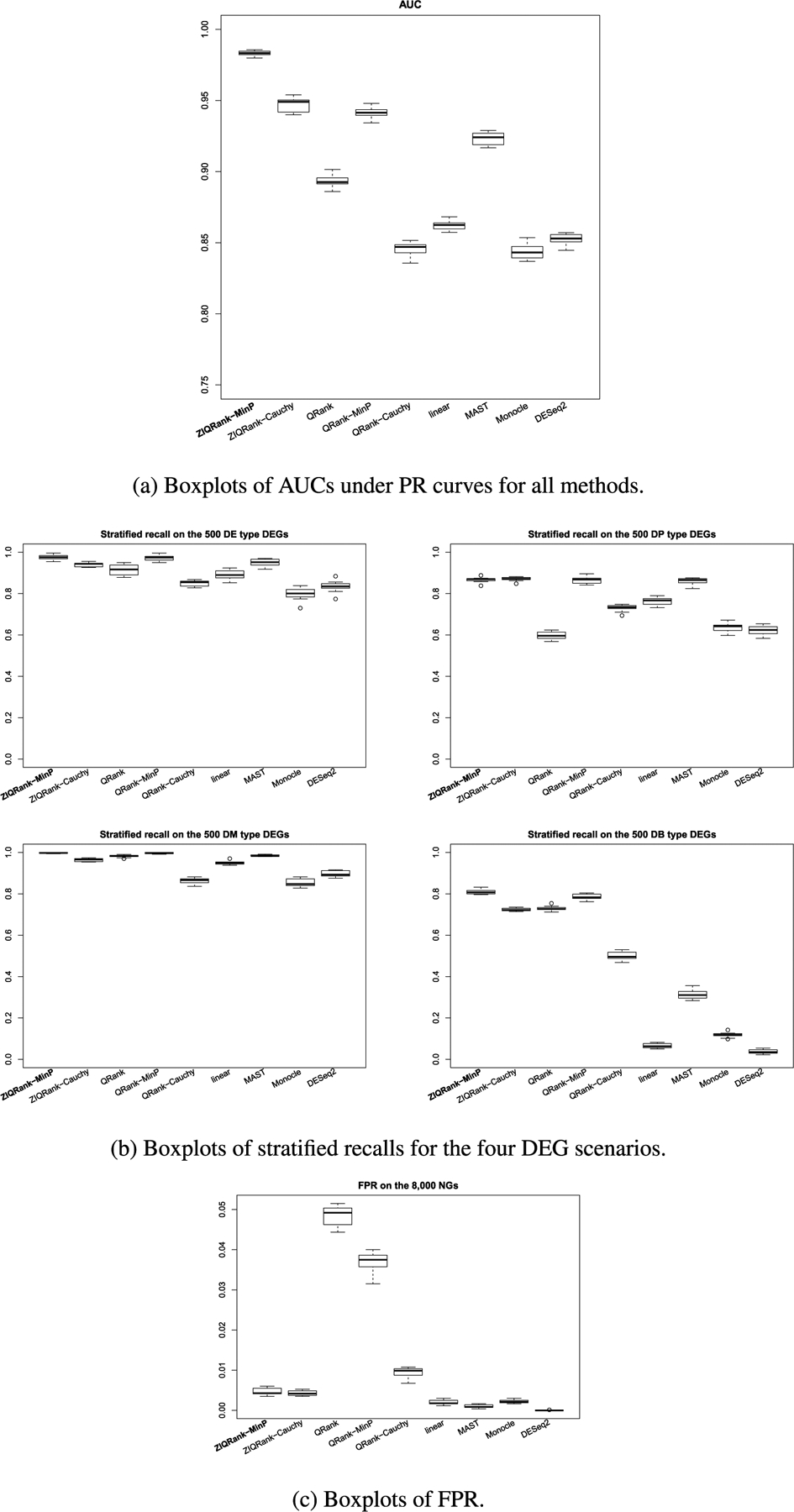
Performance of ZIQRank and existing methods in the adjusted analysis.

With a covariate associated with zero proportions and nonzero expressions, we observe more obvious drawbacks of QRanks. The AUCs of QRank, QRank-MinP and QRank-Cauchy are 0.89, 0.94 and 0.85, with excessive false positives shown by their low precisions and high FPRs (Figure 3c). MinP combination helps QRank to boost power, but still inferior to ZIQRank, especially for DB scenario (DB recall of ZIQRank vs. QRank-MinP = 81% vs. 78%). The uncontrolled false positives and lower testing power confirm the benefits of modeling inflated zeros when using quantile-based methods in the adjusted analysis.

All other methods have lower AUCs (AUC of MAST = 0.92, etc.). For DE and DM scenarios with a substantial mean difference, all methods work well with recall rates higher than 80%. For DP and DB scenarios, especially DB, with a small difference in mean and large differences in quantiles, ZIQRank dominates the parametric methods.

Note that the performance of ZIQRank-Cauchy improves from the unadjusted analysis (unadjusted vs. adjusted AUC = 0.81 vs. 0.95). As discussed in Section 2.5.2, this is because Cauchy test is sensitive to the signals from the zero proportion (shown by larger prevalence of significant logistic p-values than that in unadjusted analysis, Figure S4b vs. S4a).

To sum up, similar to the unadjusted analysis, ZIQRank performs best in terms of PR-AUC in the adjusted analysis. When confounding covariates exist, it still improves and enriches the competing methods by identifying highly heterogeneous DEGs, sustaining the power in identifying DEGs with mean differences, while keeping false positives controlled.

4. Analysis of scRNA-seq data about human glioblastoma.

4.1. Data source and analysis settings.

In this section, we illustrate the performance of ZIQRank in detecting DEGs between neoplastic and nonneoplastic cells, using one scRNA-seq data from a human glioblastoma multiforme study Darmanis et al. (2017) (GSE84465). The dataset was downloaded from conquer repository [Soneson and Robinson (2018)]. 3584 cells from both the tumor core and the peritumoral brain were sequenced using Smart-seq2 protocol, including 1091 neoplastic cells and 2493 nonneoplastic cells. Cells were collected from four patients, named S1, S2, S4 and S6. There are 487 cells from S1, 1169 cells from S2, 1540 cells from S4 and 388 cells from S6.

We apply the following preprocessing steps to the data before analysis: (1) Take the average of TPM of the same gene within each cell; (2) Delete the gene if it has positive expressions for one cell condition–only; (3) Remove the gene if its zero inflation rate is higher than 97.5%, and (4) Take the logarithmic transformation of TPM, that is, log(TPM + 1). After the preprocessing, the dataset includes 22,970 genes.

We consider two ways to analyze the data; one is unadjusted analysis, considering only the two cell conditions, and the other is adjusted analysis, which includes a cell-level covariate, the patient to whom the cells belong. All approaches used in simulation studies are applied to the data, except DESeq2. DESeq2 cannot be applied here due to its great demand for computing resources, which exceeds our maximum capacity. Also, its performance is demonstrated to be worse than other methods in our simulation studies (Section 3). ZIQRank with τ = 0.05, 0.1, … , 0.95 quantile grid and Cauchy test is the default, given the data is continuous and lacks heterogeneity (median of number of crossings between quantile functions = 1, median of CV of quantile difference < 1, shown in Figure S5a).

4.2. Evaluation of Type I error.

Before analyzing the data using different methods, we evaluate their Type I errors on the real scRNA-seq data. Using the preprocessed data, we permute the covariates (cell condition, patient ID) jointly at the cell level to create 50 permuted datasets. The permutation maintains the association between the cell-level covariates but removes the association between the cell condition and gene expression. Therefore, the permuted datasets are supposed to have no DEGs, and genes with small p-values are considered false positives. We calculate the Type I error as the proportion of genes with nominal p-values of less than 0.01. This evaluation procedure on real data is borrowed from Soneson and Robinson (2018). The Type I error evaluated is essentially a similar concept as FPR with BH procedure in Section 3 but uses different criteria to determine the false positives. We use nominal p-values in real data because, unlike simulated data, the true p-value distribution in real data is unknown and may heavily impact the BH adjusted p-values.

As Figure 4 shows, in both analyses Monocle has a slightly inflated Type I error, while all other methods keep Type I error well-controlled with around 1% genes having p-values smaller than 0.01. Thus, the results of all approaches, except Monocle, are trustworthy in the following analyses.

FIG. 4.

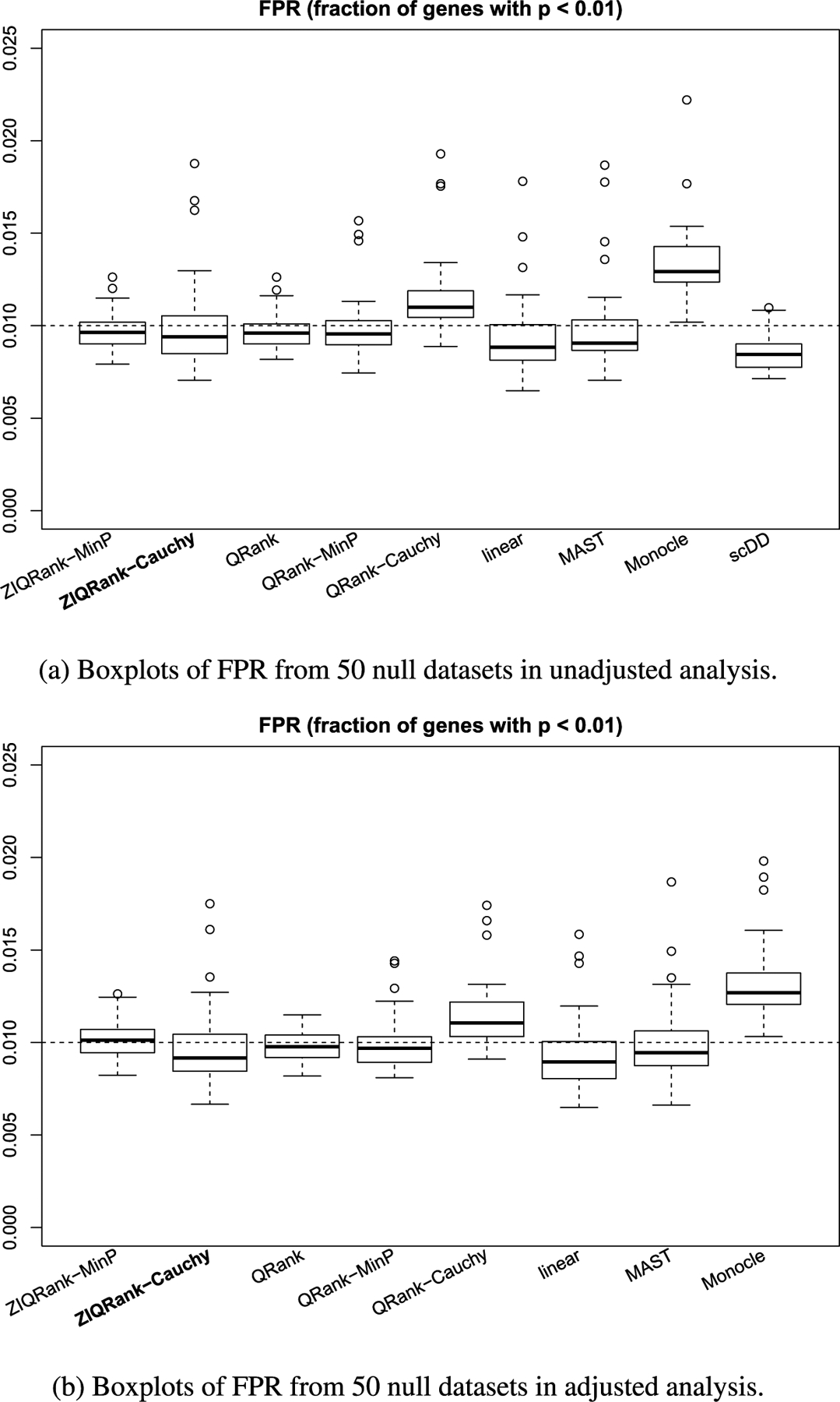
Type I error control of ZIQRank and competing methods in analyzing GSE84465.

4.3. Results on detecting DEGs.

We analyze the preprocessed data to identify DEGs using the various methods. The genes with BH adjusted p-values less than 0.01 are considered to be DEGs between neoplastic and nonneoplastic cells. Table 3 provides the numbers of DEGs detected by all approaches in both unadjusted and adjusted analyses.

TABLE 3.

Number of DEGs between neoplastic and nonneoplastic cells detected by ZIQRank under the six settings and competing methods on GSE84465 for both unadjusted and adjusted analyses

Method	Unadjusted analysis	Adjusted analysis
ZIQRank-MinP	15,537	12,764
ZIQRank-Cauchy	16,425	13,777
QRank	12,968	11,792
QRank-MinP	14,670	13,589
QRank-Cauchy	14,267	13,014
linear	14,239	12,345
MAST	16,367	13,696
Monocle	13,791	12,027
scDD	16,817	-

In the unadjusted analysis, scDD identifies the most DEGs (16,817), and ZIQRank detects the second most DEGs (16,425). In the adjusted analysis, ZIQRank detects the largest number of DEGs (13,777). QRank-Cauchy only detects 14,267 and 13,014 DEGs, showing that modeling zeros helps the quantile-based tests to capture more signals. All methods detect fewer DEGs in the adjusted analysis compared to the unadjusted analysis. This indicates that the covariate adjustment is necessary when analyzing GSE84465 to reduce false positive genes, due to the confounding effect. Therefore, the interpretation of detected DEGs in the following is based on the adjusted analysis, and we can conclude that ZIQRank has an improved power of identifying DEGs over the others.

Further, to evaluate the various methods, we compare their detected genes to the functional genes in the established pathways, de novo pathway and secondary pathway (map05214 of KEGG PATHWAY, Kanehisa and Goto (2000)). Amplification, deletion or mutation of the genes in the two paths affect the progression or suppression of glioma. Those genes are considered to be the critical DEGs between neoplastic and nonneoplastic cells based on biological mechanisms. Twenty genes from the two pathways are contained in the preprocessed GSE84465 data. ZIQRank detects all of the 20 genes, with the oncogenes, EGFR and CDK4, the tumor suppressors, ARF and Rb and several others, Shc, Grb2, E2F, GADD45, assigned with super small adjusted p-values that approach 0. The oncogenes, PDGF, PDGFR and MDM2, tumor suppressor PTEN and the rest, TGFα, IGF-1, Raf, mTOR, CDK6, POLK, etc. are also detected by ZIQRank with quite small adjusted p-values at the level of 10⁻³. The competing approaches miss several of the critical genes in the two pathways. The mean-based approaches, MAST, Monocle and linear regression, fail to detect Raf, POLK and CDK6, and the uncorrected quantile-based method, QRank, fails to detect mTOR and CDK6.

Next, ZIQRank exclusively identifies 136 DEGs, while the existing methods fail to detect them. Previous biological investigations show that some of those genes are differentially expressed between neoplastic and regular cells and play important roles in diagnosis, progression or suppression of glioma. For example, CHD4 is proved to be overexpressed in glioma cells and is a potent suppressor of glioma (McKenzie et al. (2019)). We examine the expression profiles of those genes and identify the pattern that highlights ZIQRank’s better detection performance. Figure 5 shows the quantile and violin plots of four representative genes (UBR1, PCDHA4, PHLPP1 and UBE2D3). The four genes share a similar distributional pattern, having a subtle mean difference between the neoplastic and nonneoplastic conditions but possessing substantial differences in quantiles. The two quantile functions either cross or form a spindle shape. Note that the four genes can be classified as DB or DP scenarios, as described in simulation studies (Section 3). The fundamental properties of ZIQRank can explain its improved power in detecting the two types of DEGs compared to the previous approaches. ZIQRank does not make any particular parametric assumptions on the gene expression (e.g., Gaussian or negative binomial distribution), but captures the quantile differences at various locations of the expression distribution and detects higher-order associations between the cell condition and gene expression.

FIG. 5.

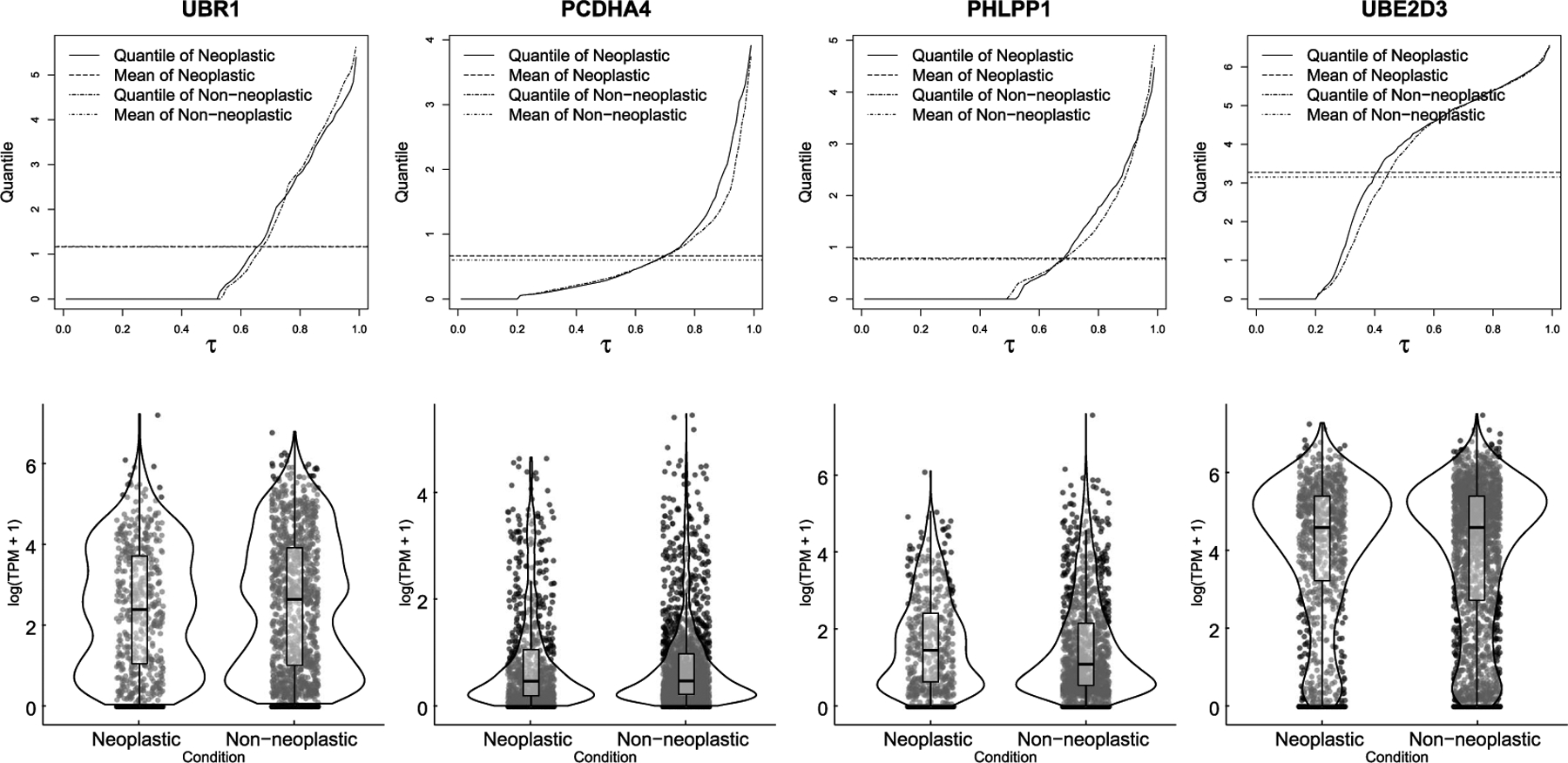
Quantile and violin plots of four DEGs detected by ZIQRank exclusively on GSE84465.

For UBR1, the quantile functions of the two cell conditions cross at quantile level 75% with neoplastic cells having higher quantile values below the crossing point, indicating a 75% chance of overexpression in neoplastic cells. This is consistent with the findings by Uhlen et al. (2010) and Fazi et al. (2015) that the expression of UBR1 is moderately higher in glioma cells. The quantile functions of PCDHA4 form a typical spindle shape, which indicates a proportion difference (DP) in high expression state. We divide the gene expression of PCDHA4 into high expression state and low expression state using the cutoff of 1.5 in log-transformed TPM. There is a higher proportion of the neoplastic cells in high expression state (13.74%), compared to the nonneoplastic ones (9.95%), with a p-value of 0.001 by χ² test. The overexpression of PCDHA4 in glioma cells is supported by Uhlen et al. (2010), and PCDHA4 also plays a vital suppression role in other cancers (Tombolan et al. (2016)). The violin plot of PHLPP1 shows a distributional pattern of DB scenario with the neoplastic cells having two modes and the nonneoplastic cells having only one mode. PHLPP1 in neoplastic cells have larger quantile values at higher percentages and smaller quantile values at lower percentages (1.36 at quantile level 0.75 and 0.00 at quantile level 0.5), as compared to nonneoplastic cells (1.10 at quantile level 0.75 and 0.07 at quantile level 0.5). This is a typical example of the tumor suppressor’s negative feedback process discussed in Section 1, and Teng et al. (2016) confirmed that PHLPP1 plays a vigorous suppression role in the inflammatory response of glioma. For UBE2D3, we define the expression in log-transformed TPM above 2.6 to be high expression state, and we observe that the proportion of neoplastic cells in high expression state is 64.80%, higher than that of nonneoplastic cells (60.41%), with a p-value of 0.014 by χ² test. Obacz et al. (2019) confirm the overexpression of UBE2D3 and point out that it controls the recruitment of myeloid cells to glioma.

Besides studying the four representative genes from a biological perspective, we define their quantile effect sizes associated with ZIQRank and numerically illustrate the advantages of ZIQRank over the others on such heterogeneous genes. The effect size, Δ, is defined as the total area between the two cell conditions’ quantile functions. Since the total area under the quantile function curve equals the mean, the quantile effect size is comparable to mean-based methods. For example, the mean difference of UBR1 is 0.01, but Δ_UBR1 = 0.09, supporting that ZIQRank, is more capable of differentiating the complex distributions.

Once a gene is identified, post hoc analyses on the quantile specific p-values and zero proportion p-value also shed light on how the gene expression distribution differs by conditions. The p-values help depict whether the difference is focused at upper or lower tails or a particular part of the distribution or whether zero proportions are significantly different between two conditions. For example, rank-score tests on PHLPP1 give small p-values on the 0.3th–0.7th quantiles of the nonzero expression, corresponding to the area between the two crossing points of quantile functions (Figure 5). Moreover, if one aims to confirm the regional difference statistically, one can choose a quantile grid within the area of interest and use ZIQRank again, as suggested in Section 2.5.1.

In conclusion, ZIQRank improves the power of detecting DEGs, and it complements the existing approaches by identifying additional heterogeneous genes. Those genes uniquely detected by ZIQRank are numerically meaningful due to their substantial quantile differences between cell conditions. Moreover, supported by literature, they are biologically crucial by revealing complex biological mechanisms.

4.4. Comparisons on computational performance.

Due to the gigabyte size level of scRNA-seq data, computational complexity is a critical measure of scRNA-seq analysis methods. We compare ZIQRank to the existing differential methods by recording the time and memory used in analyzing GSE84465. As presented in Table 4, the time consumed by ZIQRank is 34 min which is comparable to MAST. scDD is the fastest only because we use its fast procedure, while its standard setting is beyond our computing resources. Moreover, scDD cannot be applied in the general adjusted analysis. In terms of memory, ZIQRank entails the least resource of 3G, whereas Monocle, MAST and scDD need 5G, 6G and 8G, respectively, and DESeq2 needs more than 32G.

TABLE 4.

Time and memory required by ZIQRank and existing differential analysis methods to analyze GSE84465

Method	Time	Memory
ZIQRank	34 min	3G
MAST	31 min	6G
Monocle	66 min	5G
scDD	12 min	8G
DESeq2	-	>32G

5. Analysis of scRNA-seq data about cells from mouse intestinal organoids.

5.1. Data source and analysis settings.

We also demonstrate the advantages of ZIQRank on UMI count data, which is sequenced by CEL-Seq protocol and has different properties from the TPM data in Section 4: (1) the zero values are due to low counts that follow Poisson or overdispersed Poisson distributions, and (2) the data are zero-inflated integers in nature. The dataset was contributed by a study of cells from mouse intestinal organoids Grün et al. (2015) (GSE62270-GPL17021) and downloaded from conquer repository. A total of 2891 cells were collected, including 1547 marker-positive cells and 1344 randomly extracted cells from whole intestinal organoids. We preprocess the data following similar steps, except that we take the average of UMI counts,but round to preserve integers and do not take logarithmic transformation. After the preprocessing, the dataset includes 14,545 genes.

We consider unadjusted analysis only, since there are no cell-level covariates other than cell conditions. All methods used in simulation studies are applied to the data, including DESeq2 (our computing resource can handle it on the relatively small data). As DESeq2 assumes negative binomial distribution, it has been popular to analyze such count sequencing data. We also use the count version of Monocle which assumes negative binomial as well. ZIQRank with τ = 0.1, 0.25, 0.5, 0.75, 0.9 quantile grid and Cauchy test is the default, given the data is count and lacks heterogeneity (median of number of crossings between quantile functions = 0, median of CV of quantile difference < 1, shown in Figure S5b).

5.2. Evaluation of Type I error.

We permute the cell conditions to create 50 null datasets and calculate the Type I error by the proportion of genes with nominal p-values less than 0.01 within each set. As Figure 6 shows, all methods except Monocle have Type I error controlled with around 1% genes having p-values smaller than 0.01.

FIG. 6.

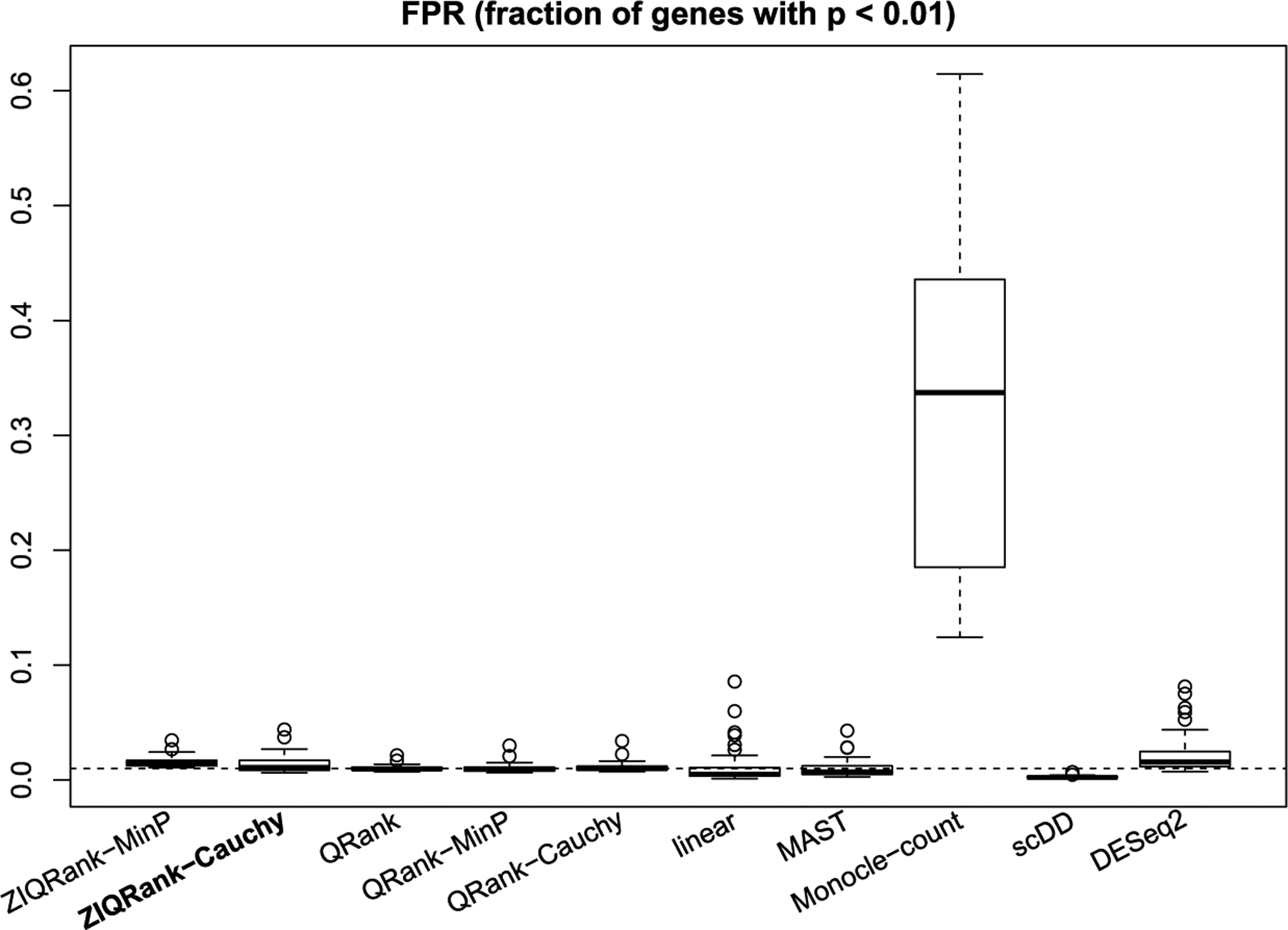
Type I error control (by boxplots of FPR from 50 null datasets in unadjusted analysis) of ZIQRank and competing methods in analyzing GSE62270-GPL17021.

5.3. Results on detecting DEGs.

We analyze the preprocessed data to identify DEGs using the various methods. The genes with BH adjusted p-values less than 0.01 are considered to be DEGs between marker-positive and randomly extracted cells. Table 5 provides the numbers of DEGs detected by all approaches in the unadjusted analysis. We exclude Monocle-count in the following comparisons, as it has exceedingly inflated Type I error. ZIQRank detects the most DEGs (10,117). As QRank-Cauchy only detects 6436 DEGs, we can confirm that modeling zeros is also rewarding for UMI count data, where zeros are due to low counts following Poisson overdispersed Poisson distributions. MAST detects the second most DEGs (9915), still inferior to ZIQRank because its Gaussian assumption for the nonzero part is inadequate for the complex count distributions. DESeq2 detects the least DEGs (4821), as it misses the inflated zeros, even though it uses negative binomial distribution. Thus, for UMI count data, we can also conclude that ZIQRank has an improved power of identifying DEGs compared to the others. There is no established pathway to further evaluate the detected genes, given that the cells were collected based on markers but not phenotypes.

TABLE 5.

Number of DEGs between marker-positive and randomly extracted cells from mouse intestinal organoids detected by ZIQRank and competing methods on GSE62270-GPL17021

Method	Unadjusted analysis
ZIQRank-MinP	9661
ZIQRank-Cauchy	10,117
QRank	5769
QRank-MinP	6443
QRank-Cauchy	6436
linear	5850
MAST	9915
Monocle-count	10,263
scDD	8245
DESeq2	4821

ZIQRank exclusively identifies 75 DEGs, which have substantial quantile differences between the marker-positive and randomly extracted cells but negligible mean differences. Their patterns are similar to those in Figure 5, and thus omitted.

To sum up, on UMI count data, ZIQRank can also improve and enrich the existing methods by detecting more genes with heterogeneous associations with cell conditions.

5.4. Comparisons on computational performance.

We compare ZIQRank to the existing differential methods by recording the time and memory used in analyzing GSE62270-GPL17021. As presented in Table 6, ZIQRank is the fastest and still the most economical, using only six min and 2G. Since a smaller quantile grid is used, both time and memory are improved, as compared in Table 4. Monocle-count is the first runner-up, entailing eight min and 3.5G. Its drastic improvement from Table 4 is due to the different assumed models, tobit for continuous data and negative binomial for count data, and the difference in corresponding estimation algorithms. As expected, DESeq2 is the slowest, using 44 min, and requires the most memory of 10G.

TABLE 6.

Time and memory required by ZIQRank and existing differential analysis methods to analyze GSE62270-GPL17021

Method	Time	Memory
ZIQRank	6 min	2G
MAST	13 min	4G
Monocle-count	8 min	3.5G
scDD	8 min	6G
DESeq2	44 min	10G

6. Conclusion and discussion.

In this paper, we have proposed a zero-inflated quantile rank-score test (ZIQRank) based on a two-part quantile regression model to detect differentially expressed genes in scRNA-seq data. The two-part framework models the probability of zero counts by logistic regression and models the nonzero expression intensity by quantile regressions. A new rank-score test tailored for the two-part quantile regression model was proposed. The ZIQRank test then marginally constructs a logistic regression test statistic on the zero counts and the novel rank-score test statistics at multiple quantiles of nonzero expressions. Finally, it combines the marginal tests using MinP or Cauchy procedures with the incorporation of test dependency.

The two-part quantile model considers inflated zeros and allows a comprehensive assessment of differentially expressed genes’ distributions without the restrictions of parametric likelihoods. Both are essential considerations for scRNA-seq analysis, given the zero-inflated and heterogeneous nature of scRNA-seq data. In both simulation studies and real applications, we have shown that ZIQRank outperforms the existing methods in identifying differentially expressed genes in scRNA-seq data. With Type I error well controlled, it improves the power and complements existing methods by revealing extra heterogeneous genes with substantial quantile differences but negligible mean differences among cell conditions. By design, the ZIQRank test can easily incorporate confounding covariates, and it is easy to implement and computationally efficient. Hence, it is a generic and practical inference tool for scRNA-seq data. The ZIQRank test can be applied to other zero-inflated data with complex distributional attributes, such as microbiome data.

Results, simulation settings and data examples of this paper are quite consistent with current benchmarking papers. Soneson and Robinson (2018) provide a comprehensive comparison of differential expression analysis methods using the PowSim R package to simulate data and a subset of conquer database as real data examples. Wang et al. (2019) evaluate the performance of several selected methods by using the scDD R package and one scRNA-seq data in Islam et al. (2011). We demonstrate the performance of the proposed ZIQRank using modified scDD R package and two scRNA-seq data in conquer. Though our paper focused on a different angle, the overlapped part has a very similar conclusion that there is a trade-off between the true positive rate and precision of calling DEGs. Methods with a higher true positive rate tend to show a lower precision due to their introducing false positives, whereas methods with a high precision show a low true positive rate due to identifying few DEGs.

There are various directions to extend ZIQRank. First, the current ZIQRank uses a default setting based on the data characteristics, and its optimal performance can be achieved by tuning the grid of quantile levels. As a progression, one may consider estimating the entire quantile process and construct a global simultaneous test. The construction of such a test statistic and its asymptotic theory needs to re-established. Second, the current test is conducted on individual genes separately. We can further enhance the power by incorporating the neighboring correlated genes or external functional information into the test.

APPENDIX: CONDITIONS OF THEOREM 1

Theorem 1 relies on the following sufficient conditions.

ASSUMPTION 1. The observations {(X_i, Y_i); i = 1, … , n} are i.i.d. from a joint distribution P , where x_i is a p-dimensional vector of covariates including the cell condition c_i.

ASSUMPTION 2. For any τ ∊ (0, 1), the conditional distribution function of Y_i’s, given Y_i > 0, $\left\{F_i=F_{Y_i\mid Y_i>0}\left(\cdot \mid {\text{X}}_i\right)\right\}$, are absolutely continuous, with continuous densities {f_i} uniformly bounded away from 0 and ∞ at $\left\{F_i^{-1}\left(\tau \mid {\text{X}}_i\right)\right\}$ with a bounded first-order derivative, i = 1, … , n.

ASSUMPTION 3. Eigenvalues of $\mathbb{E}\left({\tilde{\text{C}}}_i{\tilde{\text{C}}}_i^{\top }\right)$ and $\mathbb{E}\left({\tilde{\text{Z}}}_i{\tilde{\text{Z}}}_i^{\top }\right)$ are bounded away from 0 and ∞.

ASSUMPTION 4. There exists a positive constant b such that $f_i\left(F_i^{-1}\left(\tau \mid {\text{X}}_i\right)\right)=b$ for all i.

Practically, the four assumptions easily hold or won’t affect the performance of ZIQRank for most scRNA-seq data.

Assumption 1 means that the scRNA-seq data is collected randomly, not longitudinally.

Assumptions 2–3 are modified standard regularity conditions (Koenker (2005), Wang and He (2007)) to assure the validity of linear quantile regression and quantile rank score test on the positive part. For scRNA-seq data, Assumption 2 implies that every conditional quantile of the nonzero gene expression is uniquely defined, which is satisfied by most commonly used distributions, such as those from the exponential family. Assumption 3 suggests that covariates used in the model are neither redundant (hence, no collinearity issue) nor prone to outliers, which is a minimal requirement in most regression models.

Assumption 4 postulates a homoscedasticity condition on the nonzero gene expressions of scRNA-seq data. It is a technical assumption, useful for theory derivation. In practice, the rank score is quite robust against deviation from it (Wang (2009), Wei et al. (2006)).