High dimensional mediation analysis with latent variables

Abstract

We propose a model for high dimensional mediation analysis that includes latent variables. We describe our model in the context of an epidemiologic study for incident breast cancer with one exposure and a large number of biomarkers (i.e., potential mediators). We assume that the exposure directly influences a group of latent, or unmeasured, factors which are associated with both the outcome and a subset of the biomarkers. The biomarkers associated with the latent factors linking the exposure to the outcome are considered “mediators.” We derive the likelihood for this model and develop an expectation-maximization algorithm to maximize an L1-penalized version of this likelihood to limit the number of factors and associated biomarkers. We show that the resulting estimates are consistent and that the estimates of the nonzero parameters have an asymptotically normal distribution. In simulations, procedures based on this new model can have significantly higher power for detecting the mediating biomarkers compared with the simpler approaches. We apply our method to a study that evaluates the relationship between body mass index, 481 metabolic measurements, and estrogen-receptor positive breast cancer.

1 |. INTRODUCTION

In epidemiology, a mediation model aims to explain how an exposure (E) is associated with an outcome (Y). Traditionally, the model proposes that the exposure influences a single mediating variable (M), which, influences the outcome. More advanced models propose that the exposure influences a small set of mediating variables (M = (M₁,...,M_p)), which, in turn influence the outcome (VanderWeele and Vansteelandt, 2014; Assi et al., 2015; Steen et al., 2017). Here, we consider the scenario where the set of (putative) mediators is large and a study aims to identify the true set of mediators and to describe the underlying mediation model. Our motivation is an estrogen-receptor positive (ER+) breast cancer case-control study that measured body mass index (BMI) and 481 serum metabolites. The objective is to identify those metabolites that mediate the well-established relationship between high BMI and an increased risk of ER+ breast cancer (Moore et al., 2018).

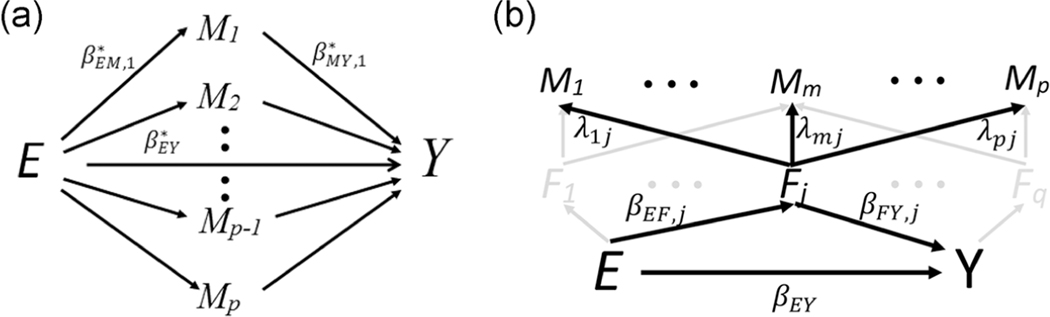
In most discussions of mediation, the presumption is that the exposure directly influences a subset of conditionally independent mediators (Figure 1A), with more recent discussions (Daniel et al., 2015) allowing the mediators to be causally ordered (Figure 2A). Here, following our beliefs about the underlying biology, we presume that the exposure directly influences a group of conditionally independent latent, or unmeasured, factors (F = (F₁,...,F_q)) which, in turn, influence both a subset of “mediating” biomarkers and the outcome (Figure 1B). In our motivating breast cancer study, for example, we might expect BMI to reduce the level of the sex hormone-binding globulin (SHBG) protein (Calle and Kaaks, 2004), which increases the availability of many of the measured hormones listed in Table 1 and the unmeasured, carcinogenic, hormones (i.e., estrogens) that cause breast cancer. In this example, the factor is a well-defined but unmeasured protein level. A more heuristic example might be evaluating the relationship between poverty, metabolites, and cancer, where poverty influences a number of distinct factors (e.g., consumption of specific foods, hours of sleep, proximity to sources of pollution, etc) that are each known to affect the levels of multiple metabolites and the risk of cancer.

FIGURE 1.

Causal graphs of the mediation models. A, Traditional mediation analysis where the exposure influences the biomarkers. B, Latent-variable mediation analysis where the exposure influences a set of q latent, or unmeasured, factors and those factors influence both the biomarkers and the outcome. To simplify the figure, we highlight the arrows and notation for only a single factor. In the sparse scenario, we expect most effects to be 0 (i.e., λ, β_EY, and β_FY, are usually 0). We define the p × q matrix, Λ, so that the m, jth entry is λ_mj

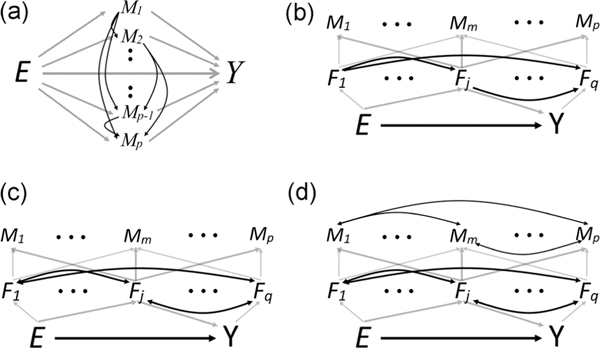
FIGURE 2.

Alternative causal graphs of the mediation models. A, Causally ordered mediation analysis where the exposure influences the biomarkers. B, Latent-variable mediation analysis where the exposure influences a set of q causally ordered latent factors. C, Latent-variable mediation analysis where the exposure influences a set of q bidirectionally connected latent factors. D, Latent-variable mediation analysis where the exposure influences a set of q bidirectionally connected latent factors and those factors influence bidirectionally connected biomarkers

TABLE 1.

Metabolites linking BMI and breast cancer

Metabolite	Loading (λmj)
5α-Pregnan-3β,20-α-diol monosulfate (2)	0.46
5α-Pregnan-3β,20-α-diol disulfate	0.49
Etiocholanolone glucuronide	0.49
16α-Hydroxydehydroepiandrosterone 3-sulfate	0.51
Epiandrosterone sulfate	0.60
Androsterone sulfate	0.61
4-Androsten-3β,17-β-diol monosulfate (2)	0.61
Pregnen-diol disulfate	0.63
4-Androsten-3β,17-α-diol monosulfate (3)	0.64
5α-Androstan-3β,17-β-diol disulfate	0.65
21-Hydroxypregnenolone disulfate	0.65
Pregnen steroid monosulfate	0.65
4-Androsten-3β,17-β-diol monosulfate (1)	0.67
4-Androsten-3β,17-β-diol disulfate (2)	0.70
4-Androsten-3β,17-β-diol disulfate (1)	0.70
Dehydroisoandrosterone sulfate (DHEA-S)	0.75

This list includes those metabolites that were strongly affected (γ > 0.4) by the factor mediating increased BMI and ER+ breast cancer in PLCO.

Our goal is to formalize the latent variable model for mediation depicted in Figure 1B. We specify an L1-penalized version of the corresponding likelihood, propose an extension of the expectation-maximization (EM) algorithm used for sparse factor analysis (Hirose and Yamamoto, 2014; Srivastava et al., 2017) to obtain the maximum-likelihood estimates, and show that these estimates have the “oracle” property (Zou, 2006). We develop our estimation procedure for data from cohorts and retrospectively collected case-control studies. Furthermore, we show that accounting for latent variables, when the proposed model holds, can significantly increase a study’s power to detect “mediating” biomarkers (i.e., those biomarkers influenced by the mediating factors). Importantly, we note that our model is a simplification. The graph describing the true relationship between the exposure, biomarkers, and outcome is likely more complicated, where in addition to unmeasured confounders, the mediating factors can be causally ordered (Figure 2B), the graph can include bidirectional edges and cycles (Figure 2C), and the graph can include edges directly connecting the biomarkers (Figure 2D).

We note that the models in Figures 1B, 2B, and 2C are not distinguishable without imposing additional restrictions (Bai and Li, 2012) on the latent variables (e.g., conditional independence). Therefore, our independent factors are constructs of the model and we caution against the interpretation of the indirect effects through any specific factors. Nevertheless, with more modest assumptions, we can estimate and interpret the total indirect effect through all factors.

These methods extend procedures that handle latent factors affecting a small set of biomarkers (Muthén and Asparouhov, 2015; Albert et al., 2016) and add to the literature exploring high dimensional mediators. Zhang et al. (2016) model how epigenetic changes mediate the relationship between smoking and reduced lung function, assuming smoking directly affects methylation levels (i.e., Figure 1A). Huang and Pan (2016) test whether the expression levels of specific sets of genes mediate the relationship between miR-223 and glioblastoma by rotating the biomarkers and testing the resulting conditionally independent components. Chen et al. (2018) identify brain regions, from functional magnetic resonance imaging (fMRI) images, that link thermal response and self-reported pain by identifying orthogonal linear combinations of the biomarkers (i.e., fMRI voxels), known as “directions of mediation.” We contrast these methods with our own approach further in Section 6.

The remainder of the paper is organized as follows. In Section 2, we describe the statistical model and the proposed EM algorithm. In Section 3, we state the theoretical properties of the resulting estimates. In Section 4, we describe two alternative approaches for identifying mediating biomarkers and estimating relevant parameters. In Section 5, we study the properties of the estimates obtained using the different approaches and apply our method to the motivating study of breast cancer. Section 6 concludes with a brief discussion.

2 |. LATENT-VARIABLE MEDIATION ANALYSIS

2.1 |. Overview

Our first goal is to propose a mediation model, where mediators are latent variables (Figure 1B). Our second goal is to provide a procedure to estimate the parameters in this model.

2.2 |. Mediation model

We index subjects in the study by i, i = 1,...,N, and assume that the relationship between the exposure (E_i), factors (F_i), biomarkers (M_i), and outcome (Y_i) can be described by the directed acyclic graph in Figure 1B. Moreover, although not pictured, we allow for a set of baseline covariates (X_i) that can influence E_i, F_i, and Y_i. We then define ${\mathit{F}}_i(e)={\left(F_{i1}(e),\dots ,F_{iq}(e)\right)}^{\prime }$, where F_ij (e) is the value of the jth factor in subject i if E_i is set to e and $Y_i\left(e,{\mathit{F}}_i\left(e^{\prime }\right)\right)$ is the value of Y_i if E_i is set to e and the vector of factors F_i is set to ${\mathit{F}}_i\left(e^{\prime }\right)$. We further assume that sequential ignorability (Imai et al., 2010) holds, or more specifically, that

$$\left\{Y_i(e,\mathit{f}),{\mathit{F}}_i\left(e^{\prime }\right)\right\}⫫E_i\mid {\mathit{X}}_i=\mathit{x}$$ (1)

$$Y_i(e,\mathit{f})⫫{\mathit{F}}_i\left(e^{\prime }\right)\mid E_i=e^{\prime },{\mathit{X}}_i=\mathit{x}.$$ (2)

We note that, in contrast to standard models, our mediators are latent variables (Albert et al., 2016). These latent variables are unlikely to individually match up with the underlying, conditionally independent biologic variables (e.g., F₁ is the unmeasured level of SHBG in the motivating example and is conditionally independent of all other mediating factors). In reality, it is more likely that there is a set (B = (B_i1,...,B_iq)) of interrelated biologic mediators (e.g., levels of SBHG, insulin, and cytokines) and the independent factors represent weighted combinations of these biological quantities (e.g., $F_j={\sum }_j^{\prime }{w}_j^{\prime }{B}_{ij}^{\prime }$). This truth suggests that we should focus and interpret the combined (i.e., through all factors) indirect effect defined in Equation (5), as opposed to factor or path specific indirect effects.

We can now partition the total effect (TE) of changing the exposure from e to e′ into the natural direct effect (NDE) and natural indirect effect (NIE): TE = NDE + NIE, where the indirect effect passes through those pathways captured by the latent factors:

$$\text{TE}=E\left[Y_i\left\{e^{\prime },\mathit{F}\left(e^{\prime }\right)\right\}-Y_i\{e,\mathit{F}(e)\}\right],$$ (3)

$$\text{NDE}=E\left[Y_i\left\{e^{\prime },\mathit{F}(e)\right\}-Y_i\{e,\mathit{F}(e)\}\right],$$ (4)

$$\text{NIE}=E\left[Y_i\left\{e^{\prime },\mathit{F}\left(e^{\prime }\right)\right\}-Y_i\left\{e^{\prime },\mathit{F}(e)\right\}\right].$$ (5)

For binary Y_i, we focus on the mediation effects defined on the odds ratio scale (VanderWeele and Vansteelandt, 2014), where OR_TE = OR_NDE × OR_NIE,

$${\text{OR}}_{\text{TE}}=\frac{P\left[Y_i\left\{e^{\prime },\mathit{F}\left(e^{\prime }\right)\right\}=1\right]}{1-P\left[Y_i\left\{e^{\prime },\mathit{F}\left(e^{\prime }\right)\right\}=1\right]}/\frac{P\left[Y_i\{e,\mathit{F}(e)\}=1\right]}{1-P\left[Y_i\{e,\mathit{F}(e)\}=1\right]},$$

$${\text{OR}}_{\text{NDE}}=\frac{P\left[Y_i\left\{e^{\prime },\mathit{F}(e)\right\}=1\right]}{1-P\left[Y_i\left\{e^{\prime },\mathit{F}(e)\right\}=1\right]}/\frac{P\left[Y_i\{e,\mathit{F}(e)\}=1\right]}{1-P\left[Y_i\{e,\mathit{F}(e)\}=1\right]},$$

and

$${\text{OR}}_{\text{NIE}}=\frac{P\left[Y_i\left\{e^{\prime },\mathit{F}\left(e^{\prime }\right)\right\}=1\right]}{1-P\left[Y_i\left\{e^{\prime },\mathit{F}\left(e^{\prime }\right)\right\}=1\right]}/\frac{P\left[Y_i\left\{e^{\prime },\mathit{F}(e)\right\}=1\right]}{1-P\left[Y_i\left\{e^{\prime },\mathit{F}(e)\right\}=1\right]}.$$

We note that it has already been demonstrated (Albert et al., 2016) that these effects are not generally (e.g., nonparametrically) identifiable when the mediators are factors. However, these effects are identifiable under the parametric model represented in Figure 1B and discussed in the next section. Moreover, these effects are identifiable even without assumptions (e.g., independence) about the factors as discussed in Web Appendix A. Finally, path-specific or factor-specific indirect effects are not well-defined because the models of Figures 1b, 2a, 1b and 2c are not distinguishable.

2.3 |. Parametric assumptions

Recall our notation. For subject i, i = 1, ..., N, let E_i be the exposure, Y_i be the outcome, and ${\mathit{M}}_i={\left(M_{i1},\dots ,M_{ip}\right)}^{\prime }$ be a vector of biomarkers with p > > N, and ${\mathit{F}}_i={\left(F_{i1},\dots ,F_{iq}\right)}^{\prime }$ be a vector of q latent mediators with q < < p. We assume that the distribution of Y_i belongs to an exponential family,

$$f\left(Y_i;{\zeta }_i,{\psi }_Y\right)=\exp \left[\left\{Y_i{\zeta }_i-b\left({\zeta }_i\right)\right\}/a\left({\psi }_Y\right)+c\left(Y_i,{\psi }_Y\right)\right]$$ (6)

with

$${\zeta }_i={\gamma }_Y+{\beta }_{EY}{E}_i+{\mathit{\beta }}_{FY}^{\prime }{\mathit{F}}_i.$$ (7)

We also assume that F_i and M_i are normally distributed:

$${\mathit{F}}_i={\mathit{\beta }}_{EF}{E}_i+{\mathit{e}}_{f,i}\text{with}{\mathit{e}}_{f,i}\sim N\left(0,I_q\right),$$ (8)

where I_q is the q by q identity matrix and

$$\begin{gathered} {\mathit{M}}_i={\mathit{\gamma }}_M+\text{Λ}{\mathit{F}}_i+{\mathit{e}}_{m,i}\text{with}{\mathit{e}}_{m,i}\sim N\left(0,{\text{Ψ}}^2\right), \\ {\text{Ψ}}^2=diag\left({\psi }_1^2,\dots ,{\psi }_p^2\right). \end{gathered}$$ (9)

Under retrospective sampling (i.e., for case-control data), we rely on the additional assumption that $E\sim N\left({\gamma }_E,{\sigma }_E^2\right)$. We note that ${\mathit{\beta }}_{\text{EF}}={\left({\beta }_{\text{EF},1},\dots ,{\beta }_{\text{EF},q}\right)}^{\prime }$ and ${\mathit{\beta }}_{\text{FY}}={\left({\beta }_{FY,1},\dots ,{\beta }_{FY,q}\right)}^{\prime }$ are vectors of length q, Λ is a p × q matrix and the (m, j)th element, denoted by λ_mj, represents the effect of the jth factor on the mth biomarker. Moreover, we define “mediating” biomarkers to be the set {m: ${\sum }_j\left|{\beta }_{\text{EF},j}{\beta }_{\text{FY},j}{\lambda }_{mj}\right|\ne 0$} and therefore, when trying to identify the mediators, select the set $\left\{m:{\sum }_j\left|{\widehat{\beta }}_{\text{EF},j}{\widehat{\beta }}_{\text{FY},j}{\widehat{\lambda }}_{mj}\right|\ne 0\right\}$.

The proposed setup accommodates outcomes from a variety of distributions, but for ease of exposition we focus on outcomes from either a binomial or a normal distribution. For a continuous Y we assume ${\psi }_Y={\sigma }_Y^2$, $b\left({\zeta }_i\right)={\zeta }_i^2/2$ and $c\left(Y_i,{\psi }_Y\right)=-1/2\left\{Y_i/{\sigma }_Y^2+\log \left(2\pi {\sigma }_Y^2\right)\right\}$ Equation (6) simplifies to

$$Y_i={\gamma }_Y+{\beta }_{EY}{E}_i+{\mathit{\beta }}_{FY}^{\prime }{\mathit{F}}_i+e_{y,i}\text{with}{e}_{y,i}\sim N\left(0,{\sigma }_y^2\right).$$ (10)

In this scenario, the pathway specific effects can be related to model parameters by

$$\text{TE}=\left({\mathit{\beta }}_{\text{EF}}^{\prime }{\mathit{\beta }}_{\text{FY}}+{\beta }_{\text{EY}}\right)\left(e^{\prime }-e\right),$$

$$\text{NDE}={\beta }_{\text{EY}}\left(e^{\prime }-e\right),$$

$$NIE={\mathit{\beta }}_{\text{EF}}^{\prime }{\mathit{\beta }}_{\text{FY}}\left(e-e^{\prime }\right)$$

and we note that these effects are identifiable. Similar conclusions were drawn by Albert et al. (2016) in the case of a single latent mediator. For a binary Y we assume ${\psi }_Y=1$ and $b\left({\zeta }_i\right)=\log \left\{1+\exp \left({\zeta }_i\right)\right\}$ and rewrite Equation (6) in logistic form, $P\left(Y_i=1;{\zeta }_i,{\psi }_Y\right)=\exp \left({\zeta }_i\right)/\left\{1+\exp \left({\zeta }_i\right)\right\}$. When the outcome is rare, we can approximate the pathway-specific effects on the OR scale by ${\text{OR}}_{\text{NDE}}\approx \exp \left\{{\beta }_{\text{EY}}\left(e^{\prime }-e\right)\right\}$ and ${\text{OR}}_{\text{NIE}}\approx \exp \left\{{\mathit{\beta }}_{\text{EF}}^{\prime }{\mathit{\beta }}_{\text{FY}}\left(e^{\prime }-e\right)\right\}$, with modifications available to accommodate matched case-control studies (VanderWeele and Tchetgen Tchetgen, 2016) or interactions between the factors and exposure (VanderWeele and Vansteelandt, 2014).

In Web Appendix E, we consider extensions of Models (6–9) to accommodate additional covariates and extend the estimation procedure and theory presented to this setting. To estimate the vector of parameters $\mathit{\theta }={\left({\gamma }_Y,{\mathit{\beta }}_{FY},{\beta }_{EY},{\psi }_Y,{\mathit{\beta }}_{EF},{\mathit{\gamma }}_M,\text{Λ},{\text{Ψ}}^2\right)}^{\prime }$ using the observed data, $\left(Y_i,{\mathit{M}}_i,E_i\right)$ for i = 1, ...,N, we first assume q, the number of latent factors, is known. In Section 2.5, we discuss how to choose q in practice.

2.4 |. Likelihood

Under prospective sampling, we derive the joint likelihood of (Y_i, M_i, F_i) and (Y_i, M_i) while conditioning on E_i to avoid modeling the distribution of the exposure. Under retrospective sampling (i.e., case-control data), we derive the joint likelihood of (Y_i, E_i, M_i, F_i) and (Y_i, E_i, M_i).

2.4.1 |. Prospective likelihood

Here the full data likelihood for (Y, M, F) is

$$L_P^F(\mathit{\theta })=\prod _{i=1}^{N}f\left(Y_i,{\mathit{M}}_i,{\mathit{F}}_i\mid E_i;\mathit{\theta }\right),$$ (11)

where f is the product of the densities defined by Equations (6–9),

$$\begin{gathered} f\left(Y_i,{\mathit{M}}_i,{\mathit{F}}_i\mid E_i;\mathit{\theta }\right)=f_Y\left(Y_i\mid {\mathit{F}}_i,E_i;{\gamma }_Y,{\mathit{\beta }}_{\text{FY}},{\beta }_{\text{EY}},{\psi }_Y\right) \\ \times f_M\left({\mathit{M}}_i\mid {\mathit{F}}_i;{\mathit{\gamma }}_M,\text{Λ},{\text{Ψ}}^2\right)f_F\left({\mathit{F}}_i\mid E_i;{\mathit{\beta }}_{\text{EF}}\right). \end{gathered}$$ (12)

We use f_M, f_Y, and f_F to denote implied distribution of M, Y, and F, respectively. However, the factors F_i are not observed. The likelihood for the observed data, (Y_i, M_i), is therefore

$$L_P^O(\mathit{\theta })=\prod _{i=1}^N\underset{\mathit{F}}{\int }f\left(Y_i,{\mathit{M}}_i,{\mathit{F}}_i\mid E_i;\mathit{\theta }\right)d\mathit{F}.$$ (13)

Although $L_P^O(\mathit{\theta })$ does not have a closed form in general, we show in the Web Appendix B that $L_P^O(\mathit{\theta })$ is the product of normal distributions when Y_i is normally distributed.

2.4.2 |. Retrospective likelihood

Under retrospective sampling, N₁ cases and N₀ controls are drawn from the population of cases and controls, respectively, and biomarkers and exposures are observed (N₁ + N₀ = N). The corresponding likelihood is

$$\begin{gathered} L_R^F(\mathit{\theta })=\prod _{t\in \text{case}}f\left(E_i,{\mathit{M}}_i,{\mathit{F}}_i{Y}_i=1;\mathit{\theta }\right) \\ \times \prod _{t\in \text{control}}f\left(E_i,{\mathit{M}}_i,{\mathit{F}}_i\mid Y_i=0;\mathit{\theta }\right). \end{gathered}$$ (14)

Here, we assume $E_i\sim N\left({\gamma }_E,{\sigma }_E^2\right)$ in the overall population. Although closed forms of the conditional distributions of (E_i, M_i, F_i) are generally not available, they can be approximated well when the outcome is rare in the general population, that is,

$$\begin{gathered} P(Y_i=1\mid E_i,{\mathit{F}}_i;{\gamma }_Y,{\beta }_{EY},{\mathit{\beta }}_{\text{FY}}) \\ =\frac{\exp \left({\gamma }_Y+{\beta }_{EY}{E}_i+{\mathit{\beta }}_{\text{FY}}^{\prime }{\mathit{F}}_i\right)}{1+\exp \left({\gamma }_Y+{\beta }_{EY}{E}_i+{\mathit{\beta }}_{\text{FY}}^{\prime }{\mathit{F}}_i\right)} \\ \approx \exp \left({\gamma }_Y+{\beta }_{EY}{E}_i+{\mathit{\beta }}_{\text{FY}}^{\prime }{\mathit{F}}_i\right) \end{gathered}$$ (15)

Under the rare disease assumption, the distribution of (E_i, M _i, F_i) in controls is approximately equal to the distribution in the general population. Thus, under Models (6–9)

$$\begin{gathered} f(E_i,{\mathit{M}}_i,{\mathit{F}}_i\mid Y_i=0;\mathit{\theta })\approx f\left(E_i,{\mathit{M}}_i,{\mathit{F}}_i;\mathit{\theta }\right) \\ =\varphi \left(E_i,{\mathit{M}}_i,{\mathit{F}}_i;{\mathit{\mu }}_0,{\text{Σ}}_{E,M,F}\right), \end{gathered}$$ (16)

where $\varphi \left(.;{\mathit{\mu }}_0,{\text{Σ}}_{E,M,F}\right)$ is a multivariate normal distribution with mean μ and covariance matrix Σ_E,M,F. The covariance matrix Σ_E,M,F is defined in the Web Appendix B.2 and ${\mathit{\mu }}_0={\left({\mu }_E,{\mathit{\mu }}_M,{\mathit{\mu }}_F\right)}^{\prime }$. Note that, Σ_E,M,F is a function of the parameters used in Models (6–9). The distribution of (E_i, M_i, F_i) in cases under Model (15) is

$$f\left(E_i,{\mathit{M}}_i,{\mathit{F}}_i\mid Y_i=1;\mathit{\theta }\right)\approx \varphi \left(E_i,{\mathit{M}}_i,{\mathit{F}}_i;{\mathit{\mu }}_1,{\text{Σ}}_{E,M,F}\right)$$ (17)

where

$$\begin{array}{c}{\mu }_1={\left({\mu }_E^1,{\mathit{\mu }}_M^1,{\mathit{\mu }}_F^1\right)}^{\prime }={\left({\mu }_E,{\mu }_M,{\mu }_F\right)}^{\prime }\\ +{\text{Σ}}_{E,M,F}{\left({\beta }_{EY},{\mathbf{0}}^{\prime },{\mathit{\beta }}_{FY}^{\prime }\right)}^{\prime }\end{array}$$

Note that the distributions of (E_i, M_i, F_i) in cases and controls differ only in their means.

Based on the above approximations, the likelihood for the full data (E_i, M_i, F_i) is

$$\begin{gathered} L_R^F(\mathit{\theta })=\prod _{t\in \text{case}}\varphi \left(E_i,{\mathit{M}}_i,{\mathit{F}}_i;{\mathit{\mu }}_1,{\text{Σ}}_{E,M,F}\right) \\ \times \prod _{t\in \text{controls}}\varphi \left(E_i,{\mathit{M}}_i,{\mathit{F}}_i;{\mathit{\mu }}_0,{\text{Σ}}_{E,M,F}\right). \end{gathered}$$ (18)

and the likelihood for the observed data is therefore easily shown to be

$$\begin{gathered} L_R^O(\mathit{\theta })=\prod _{t\in \text{case}}\varphi \left(E_i,{\mathit{M}}_i;{\mathit{\mu }}_{1;M,E},{\text{Σ}}_{M,E}\right) \\ \times \prod _{t\in \text{controls}}\varphi \left(E_i,{\mathit{M}}_i;{\mathit{\mu }}_{0;M,E},{\text{Σ}}_{M,E}\right), \end{gathered}$$ (19)

where ${\mu }_{1;E,M}={\left({\mu }_E^1,{\mathit{\mu }}_M^1\right)}^{\prime }$, ${\mu }_{0;E,M}={\left({\mu }_E,{\mathit{\mu }}_M\right)}^{\prime }$, and ${\text{Σ}}_{E,M}$ is the appropriate submatrix of Σ_E,M,F. The effects of the exposure and the latent factors on the outcome are thus completely captured by the difference between the means of (E_i, M_i) in cases and controls.

2.5 |. Penalty to induce sparsity in the factors, F

To introduce sparseness in the factors F and the number of biomarkers associated with those factors, we maximize the penalized log-likelihood

$$\begin{array}{c}\text{PLL}(\mathit{\theta })=\log \left\{L^O(\mathit{\theta })\right\}-{\rho }_{1N}\sum _{j=1}^{q}P\left({\beta }_{FY,j}\right)\\ -{\rho }_{2N}\sum _{j=1}^{q}P\left({\beta }_{EF,j}\right)-{\rho }_{3N}\sum _{m=1}^p\sum _{j=1}^{q}P\left({\lambda }_{mj}\right),\end{array}$$ (20)

where $L^O(\mathit{\theta })$ is the likelihood defined in (13) or (19) and P(·) is the chosen penalty function. We use the adaptive lasso penalty, where $P(\phi )=\frac{|\phi |}{\left|{\widehat{\phi }}^0\right|}$ and ${\widehat{\phi }}^0$ is a square root consistent estimate of φ, but other options, such as SCAD or MC+ (Fan and Li, 2001; Zhang, 2010), are possible. In practice, we let ${\widehat{\beta }}_{\text{EF},j}^0$, ${\widehat{\beta }}_{\text{FY},j}^0$ and ${\widehat{\lambda }}_{mj}^0$ be initial estimates from the observed likelihood L^O (θ). We allow the penalties (ρ_1N, ρ_2N, ρ_3N) to differ for each type of association. The penalized log-likelihood estimator ${\widehat{\mathit{\theta }}}_P$ is defined as

$${\widehat{\mathit{\theta }}}_P\equiv {\widehat{\mathit{\theta }}}_P\left({\rho }_{1N},{\rho }_{2N},{\rho }_{3N}\right)=\arg \underset{\theta }{\max }\text{PLL}(\mathit{\theta }).$$ (21)

Because ${\widehat{\mathit{\theta }}}_P$ cannot be expressed in a closed from, we develop an (EM) algorithm building upon the methods for sparse factor analysis (Hirose and Yamamoto, 2014; Srivastava et al., 2017). Although the EM algorithm is a significant contribution of this paper, we provide details in Web Appendix C to keep the main text focused.

In practice, we specify the total number of factors, q_max, to be 40 and choose values of ρ_1N, ρ_2N, and ρ_3N that minimize the extended Bayes information criterion (EBIC; Chen and Chen, 2008) defined as $\text{EBIC}=-2l\left\{{\widehat{\theta }}_P\left({\rho }_{1N},{\rho }_{2N},{\rho }_{3N}\right)\right\}+\log (N)df+2\gamma \log (\tau )$, where $l(\widehat{\mathit{\theta }})$ is the observed log-likelihood (Equations (13) or (19)), df is the number of parameters with nonzero estimates, and τ is the number of possible models with df nonzero parameters. We generally suggest that users start with a value of q_max that is likely to exceed the true number of factors influencing the biomarkers. In practice, we set γ = 0.5 in Equation (21). EBIC tends to outperform the more traditional selection criteria AIC and BIC in previous high dimensional settings (Chen and Chen, 2008; Srivastava et al., 2017) and in our simulations.

3 |. THEORETICAL PROPERTIES OF THE ESTIMATES

We highlight key properties of the model, the EM algorithm, and the estimates, ${\widehat{\mathit{\theta }}}_P$, with proofs in the Supporting Information (see Web Appendix D). First, we show that the parameters θ are identifiable under the following condition for factor analysis presented in Anderson and Rubin (1956),

Condition 1.

If any row of the loading matrix Λ is deleted, there remain two disjoint submatrices of rank q.

Proposition 1 (Identifiability).

If Condition 1 holds, then θ is identifiable, and Λ, β_FY, β_EF are identifiable up to an orthogonal rotation.

We note that the products of parameters $\text{Λ}{\text{Λ}}^{\prime },{\Vert {\mathit{\beta }}_{\text{FY}}\Vert }^2={\mathit{\beta }}_{\text{FY}}^{\prime }{\mathit{\beta }}_{\text{FY}},{\Vert {\mathit{\beta }}_{\text{EF}}\Vert }^2={\mathit{\beta }}_{\text{EF}}^{\prime }{\mathit{\beta }}_{\text{EF}}$ and mixed products $\text{Λ}{\mathit{\beta }}_{\text{FY}},\text{Λ}{\mathit{\beta }}_{\text{EF}}$ and ${\beta }_{\text{EF}}^{\prime }{\mathit{\beta }}_{\text{FY}}$ are uniquely identified. The identifiability of these terms is crucial when estimating direct and indirect effects (Section 2.2).

Our second property, building upon previous work of Hirose and Yamamoto (2014), Srivastava et al. (2017), states the properties the EM algorithm.

Proposition 2 (Convergence of the EM algorithm).

With each iteration of the proposed EM algorithm, the penalized log-likelihood (20) does not decrease,

$$\text{PLL}\left({\widehat{\mathit{\theta }}}^k\right)\le \text{PLL}\left({\widehat{\mathit{\theta }}}^{k+1}\right),k\ge 1,$$

and the sequence of EM estimates ${\widehat{\mathit{\theta }}}^k$ converges to a local maximum ${\widehat{\mathit{\theta }}}_P^{\ast }$.

Our third property, building upon work of Zou (2006), is that the resulting estimates, ${\widehat{\mathit{\theta }}}_P={\left({\widehat{\theta }}_{P1},\dots ,{\widehat{\theta }}_{PW}\right)}^{\prime }$, where W is the total number of parameters, have the oracle property. Let θ be the vector of all parameters (see Section 2.3), A = {j|θ_j ≠ 0} index the set of parameters not equal to 0, ${\widehat{A}}_N=\left\{j\mid {\widehat{\theta }}_{Pj}\ne 0\right\}$ index the set of parameters with nonzero estimates; based on our dataset of N subjects and let ${\widehat{\mathit{\theta }}}_P^S=\left\{{\widehat{\theta }}_{Pj}:j\in A\right\}$ be the vector of estimates for the nonzero parameters ${\mathit{\theta }}^S=\left\{{\theta }_j:j\in A\right\}$.

Proposition 3 (Oracle Property).

Suppose that ${\rho }_{kN}/\sqrt{N}\to 0$ and ${\rho }_{kN}\to \infty$ for k ∈ {1, 2, 3}. Then we obtain

1. consistency of the selection of nonzero effects:

   $$\underset{N\to \infty }{\lim }P\left({\widehat{A}}_N=A\right)=1,$$ (22)
2. asymptotic normality for the nonzero effects:

   $$\underset{N\to \infty }{\lim }\sqrt{N}\left({\widehat{\mathit{\theta }}}_P^S-{\mathit{\theta }}^S\right){\to }_{d}N\left(0,{\mathbb{I}}_{{\widehat{\theta }}^S}^{-1}\right),$$ (23)

   where ${\mathbb{I}}_{{\theta }^s}$ is Fisher’s information matrix for the true model (i.e., excluding zero coefficients).

4 |. ALTERNATIVE METHODS TO IDENTIFY SUBSETS OF MEDIATORS

Here, we propose two alternative, two-step approaches to identify the subset of “mediating” biomarkers. Recall for latent variable mediation analysis (LVMA), we identify the mediating biomarkers to be the set $\left\{m:{\sum }_j\left|{\widehat{\beta }}_{EF,j}{\widehat{\beta }}_{FY,j}{\widehat{\lambda }}_{mj}\right|\ne 0\right\}$.

4.1 |. Individual marker mediation analysis (IMA)

We first consider testing each biomarker individually using Sobel’s test (Sobel, 1982). For a continuous outcome, we can test biomarker m by fitting two linear regression models

$$Y_i={\gamma }_Y^{\ast }+{\beta }_{\text{MY},m}^{\ast }{M}_{m,i}+{\beta }_{\text{EY},m}^{\ast }{E}_i+{\mathrm{ϵ}}_Y^{\ast }$$

$$M_{m,i}={\gamma }_M^{\ast }+{\beta }_{\text{EM},m}^{\ast }{E}_i+{ϵ}_{M,m}^{\ast }$$

and then calculating the P value, p_m, for the test statistic $Z_m={\widehat{\beta }}_{\text{MY},m}^{\ast }{\widehat{\beta }}_{\text{EM},m}^{\ast }/{\widehat{\sigma }}_{\beta \beta }$, where ${\widehat{\sigma }}_{\beta \beta }^2$ is the estimated variance of the product ${\widehat{\beta }}_{\text{MY},m}^{\ast }{\widehat{\beta }}_{\text{BM},m}^{\ast }$ and is calculated using the Taylor-Series expansion (Sobel, 1982). Logistic regression would be used when Y is binary. We can then identify the set of “mediating” biomarkers as those with a P value below a specified threshold.

4.2 |. Two-step mediation analysis (TMA)

We next consider a two-step approach where, in the first step, we identify the latent factors underlying the biomarkers and, in the second step, we test whether each of those latent factors are mediators. Specifically, in the original-version (TMAO), we first perform sparse factor analysis on M, ignoring E and Y :

$$\arg \underset{\text{Λ},{\text{Ψ}}^2}{\max }\left[\sum _{i=1}^N\log \left\{\varphi \left({\mathit{M}}_i;\text{Λ},{\text{Ψ}}^2\right)\right\}-\rho \sum _{m=1}^p\sum _{j=1}^q\frac{\left|{\lambda }_{mj}\right|}{\left|{\widehat{\lambda }}_{mj}^0\right|}\right],$$ (24)

where $\varphi \left(\cdot ;\text{Λ},{\text{Ψ}}^2\right)$ is a multivariate normal distribution with mean 0 and variance $\text{Λ}{\text{Λ}}^{\prime }+{\text{Ψ}}^2$ and obtain our estimated factors $\left({\widehat{F}}_{i1},\dots ,{\widehat{F}}_{iq}\right)={\widehat{\text{Λ}}}^{\prime }{\left({\widehat{\text{Λ}}\widehat{\text{Λ}}}^{\prime }+{\widehat{\text{Ψ}}}^2\right)}^{-1}{\mathit{M}}_i$. Again, we choose the penalty, ρ, which minimizes the EBIC. In the second step, we use Sobel’s test (Sobel, 1982), to individually test each of the estimated factors. The “mediating” biomarkers are those with a nonzero loading on the selected factors.

In a modified version (TMAR), we perform sparse factor analysis (24) on M_R, where the jth row of M_R are residuals after regressing the jth row of M on E. Specifically, we substitute M_R for M in Equation (24) to obtain ${\widehat{\text{Λ}}}_R$ and ${\widehat{\text{Ψ}}}_R$, and then let ${\left({\widehat{F}}_{i1},\dots ,{\widehat{F}}_{iq}\right)}^{\prime }={\widehat{\text{Λ}}}_R^{\prime }{\left({\widehat{\text{Λ}}}_R{\widehat{\text{Λ}}}_R^{\prime }+{\widehat{\text{Ψ}}}_R^2\right)}^{-1}{\mathit{M}}_i$. Under prospective sampling, M, Y, and E need to be centered by their corresponding sample means because intercepts of are not identifiable directly from M or M_R by these two approaches. Under retrospective sampling, M and the exposure E are centered by their means in the controls. TMAR is conceptually similar to the mediation approach proposed by Huang and Pan (2016) and to surrogate variable analysis (Leek and Storey, 2007); that it is M_R, not M, that is accurately described by factor analysis.

4.2.1 |. Remarks

TMAO and TMAR are computationally faster than the full joint model LVMA and, for TMAO, it is straight-forward to calculate P values for the tested factors. However, by ignoring E and Y, less information is available for identifying factors and, ultimately, detecting mediators. Second, TMAO incorrectly assumes independence of factors. TMAR, or allowing for correlated factors (Hirose and Yamamoto, 2014), attempts to handle this issue, but these methods perform poorly in small samples. Third, in case-control studies, the assumption that the biomarkers are normally distributed is violated and Section 2.4.2 shows that much of the information is contained in the difference between the group means. Fourth, by not explicitly modeling the latent variables, the terms, β_EY and ${\mathit{\beta }}_{\text{EF}}^{\prime }{\mathit{\beta }}_{\text{FY}}$ used to estimate the direct and indirect effects are biased because the imputed mediators contain measurement error (Carroll et al., 2006; le Cessie et al., 2012; Valeri et al., 2014).

5 |. SIMULATIONS

5.1 |. Data generation

We compared the properties of LVMA, IMA, and TMA (O and R) in simulated data with N = 300 or N = 500 observations. We assumed that there were fifteen factors (q = 15) each affecting twenty unique biomarkers, M. The first factor was a mediator (i.e., β_EF,1 ≠ 0 and β_FY,1 ≠ 0), the next four factors were associated only with E (i.e., β_EF,j ≠ 0 and β_FY,j = 0 for j = 2,...,5) and the last ten factors were associated with neither E nor Y (i.e., β_EF,j = 0 and β_FY,j = 0 for j = 6,...,15). We then added an additional ninety independent normally distributed biomarkers so that p = 390. Data were simulated based on the model in Section 2.3, with binary outcomes assuming a logistic link and continuous outcomes assuming normality. For case-control studies, we sampled an equal number of cases and controls (i.e., N₁ = N₀ = 150 or N₁ = N₀ = 250) from a larger population prospectively simulated. We varied the effect of the exposure on the mediating factor (β_EF,1 ∈ {0.4, 0.5}), the effect of exposure-related factors on their constituent biomarkers (λ₁ ∈ {0.25, 0.3}), and the effect of exposure-unrelated factors on their constituent biomarkers (λ₀ ∈ {0.4, 0.5}). Here, λ_mj = λ₁ if j ≤ 5 (when λ_mj ≠ 0) and λ_mj = λ₀ if 6 ≤ j ≤ 15 (when λ_mj ≠ 0). Other parameters/distributions were set as follows: β_EY = β_FY,1 = 0.3, β_EF,2 = ··· = β_EF,5 = 0.7, γ_M,1 = ··· = γ_M,p = 0.5, ${\psi }_1^2=\cdots ={\psi }_p^2=1$, γ_Y = 4.6 (i.e., P(Y = 1|E = 0, F₁ = 0) = 0.01 for binary outcomes), and E∼N (0.5, 1). In Web Appendix F, we describe the simulation setup and corresponding results for scenarios when there are no latent variables and the exposure directly affects individual biomarkers.

For each parameter and sample size combination, we simulated 1000 datasets. Then we applied each of the four methods and calculated the average number of true positives (TPs) selected, the average number of false positives (FPs) selected, and the average estimate of the conditional exposure effect, β_EY. Here, the biomarker m is a “true positive” (TP) if it is identified as a mediator and ${\sum }_j\left|{\beta }_{\text{EF},j}{\beta }_{\text{FY},j}{\lambda }_{mj}\right|\ne 0$. It is a “false positive” (FP) if it is identified as a mediator but ${\sum }_j\left|{\beta }_{\text{EF},j}{\beta }_{\text{FY},j}{\lambda }_{mj}\right|=0$. For valid comparison between LVMA and the other methods, we selected P value thresholds for these methods so that the FP remained constant. Note, the requirement for a biomarker to be “selected” as a mediator is defined in Section 2. For IMA, TMAO, and TMAR, we estimated the conditional exposure effect as the coefficient for the exposure in a model for the outcome that also included all selected biomarkers or factors.

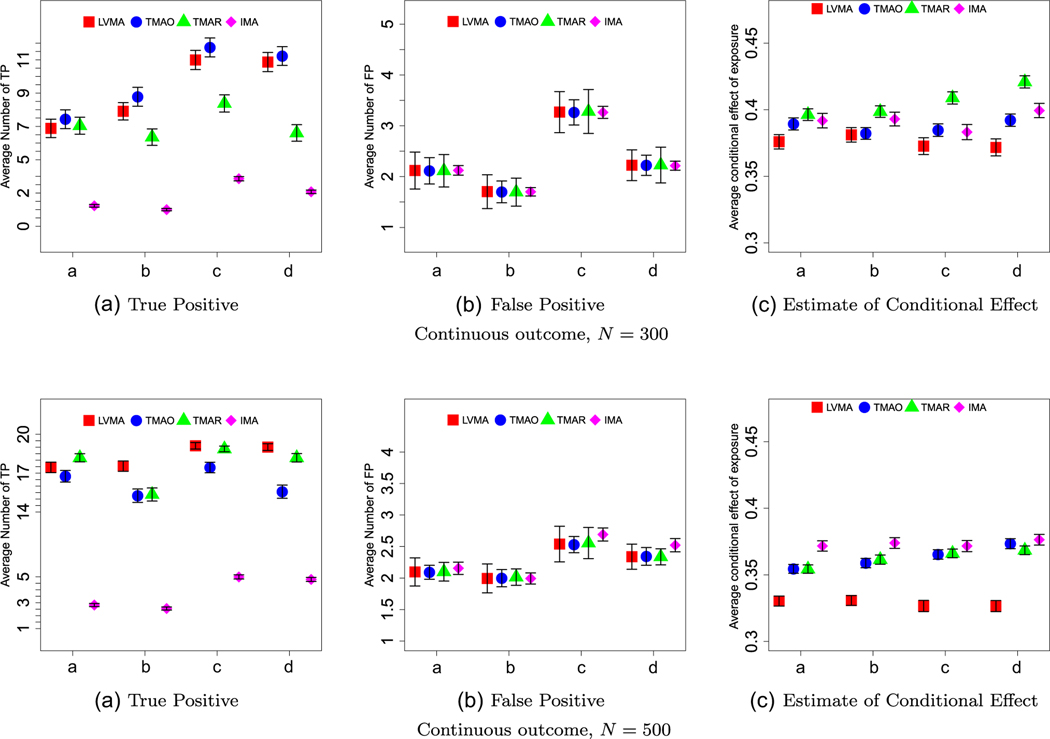
5.2 |. Results

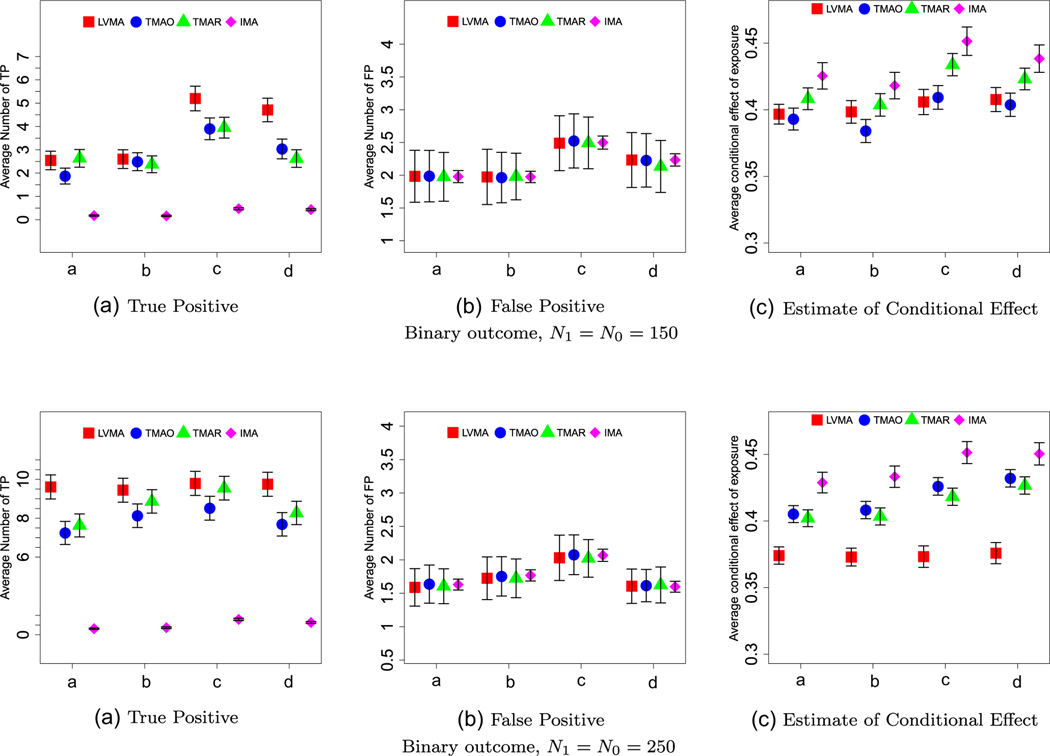
We summarize our results in Figures 3. First, for most settings, LMVA tended to have, the largest TP rate (panels (A) of Figures 3-5). Recall, we chose significance thresholds for the other three methods so that the average FP rate (see panels (B) of Figures 3-5) was similar across methods. TMAR and TMOR tended to perform similarly. The one exception is that TMAR performed poorly when we reduced the effect of exposure-related factors to λ₁ = 0.25 (see Figure 5). IMA consistently performed poorly (e.g., on average it had four-five times lower TP rate). The latter reinforces the need to use some form of latent variable analysis when the exposure does not directly affect biomarkers individually.

FIGURE 3.

Continuous outcome and large factor effects (λ₁ = 0.3). The panels, labeled A-C, show the average number of true positives (TP), the average number of false positives (FP), and the average estimate of the direct effect for the four methods (red = LVMA; blue = TMAO; green = TMAR; purple = IMA) and for four scenarios (a: β_EF,1 = 0.4, λ₀ = 0.4; b: β_EF,1 = 0.4, λ₀ = 0.5; c: β_EF,1 = 0.5, λ₀ = 0.4; d: β_EF,1 = 0.5, λ₀ = 0.5) based on 1000 simulations. Top and bottom panel are for studies with N = 300 and N = 500 subjects, respectively. The whiskers show two standard errors around the average estimates.

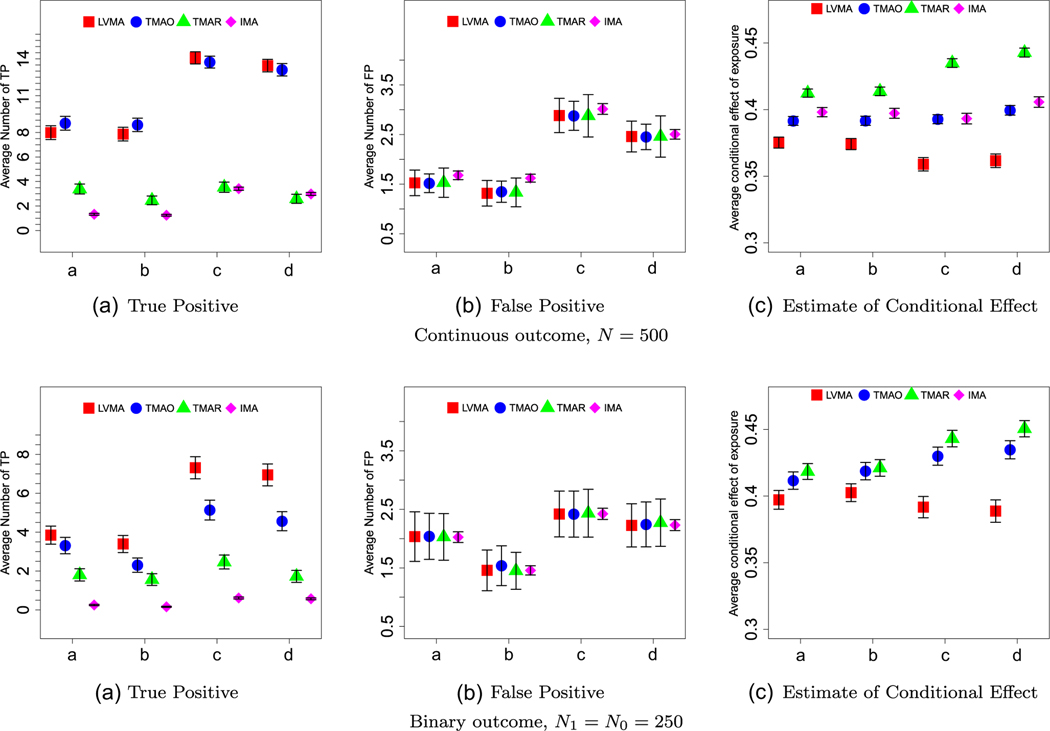
FIGURE 5.

Small factor effects (λ₁ = 0.25). The panels, labeled A-C, show the average number of true positives (TP), the average number of false positives (FP), and the average estimate of the direct effect for the four methods (red = LVMA; blue = TMAO; green = TMAR; purple = IMA) and for four scenarios (a: β_EF,1 = 0.4, λ₀ = 0.4; b: β_EF,1 = 0.4, λ₀ = 0.5; c: β_EF,1 = 0.5, λ₀ = 0.4; d: β_EF,1 = 0.5, λ₀ = 0.5) based on 1000 simulations. Top and bottom panel are for studies with continuous and binary outcomes, respectively (N = 500). The whiskers show two standard errors around the average estimates.

The pronounced when the effect of factors on associated biomarkers is small (Figure 5) and when the outcome was a binary variable (Figures 4 and 5). When comparing TMAO to TMAR, neither clearly performed better. Their relative performance strongly depends on sample size, with TMAR performing better as the sample sizes increased and the effect of the exposure could be better estimated. This advantage was further magnified when the effects of the factor on the biomarkers increased.

FIGURE 4.

Binary outcome and large factor effects (λ₁ = 0.3). The panels, labeled A-C, show the average number of true positives (TP), the average number of false positives (FP), and the average estimate of the direct effect for the four methods (red = LVMA; blue = TMAO; green = TMAR; purple = IMA) and for four scenarios (a: β_EF,1 = 0.4, λ₀ = 0.4; b: β_EF,1 = 0.4, λ₀ = 0.5; c: β_EF,1 = 0.5, λ₀ = 0.4; d: β_EF,1 = 0.5, λ₀ = 0.5) based on 1000 simulations. Top and bottom panel are for studies with N = 300 and N = 500 subjects, respectively. The whiskers show two standard errors around the average estimates.

As expected, TMAR, TMAO, and IMA produced biased estimates of the conditional effect of exposure; compare the results in panel (C) of Figures 3-5 to the true direct effect, β_EF = 0.3. Although LVMA had smaller bias, the estimates of the conditional effect of exposure using LVMA still exceeded 0.35 in most scenarios. When we increased the sample size or the effect size so that TP = 20 (see Web Figures 5, 8, and 21), the bias in LVMA, but not for the other methods, disappeared.

LVMA was robust to the number of specified factors (see Web Figures 11 and 12). Therefore, in practice, we suggest specifying a relatively large number of factors. Furthermore, we found that using EBIC was slightly preferable to using AIC or BIC, but the two two-step methods, TMAO and TMAR, were far more sensitive to the choice of selection criteria (see Web Figures 5-10). LVMA was also robust to violations of the assumption that the error terms for the biomarkers were normally distributed (see Web Figures 13-18). Finally, when we decreased exposure effects on nonmediating factors to β_EF,2 = ··· =β_EF,5 = 0.4, the TP of LVMA, TMAO, and TMAR become similar. Web Figures 19-21 shows that, if we also decrease the effect of the mediating factors on the biomarkers to λ₁ = 0.25, LVMA regains its advantages. Note, in this latter setting the exposure becomes important for identifying factors.

5.3 |. Data example

Our motivating study aims to identify metabolites that mediate the known relationship between high BMI and the increased risk of ER+ breast cancer. This study, nested inside the prostate, lung, colorectal, and ovarian cancer screening study (PLCO), includes 410 (ER+) breast cancers and 410 controls matched on study age (±2 years), date of blood collection (±3 months), and hormone therapy use at baseline. The study collected serum samples at the first follow-up visit, 1-year after baseline, and using these specimen, measured 481 known serum metabolites (<kDA). Metabolite levels were log transformed. Details on the study are in Moore et al. (2018).

We modeled the data using LVMA with q_max = 40 factors adjusting for the three matching variables (see Web Appendix E). The model identified only a single factor associated with both BMI (${\widehat{\beta }}_{\text{EF},1}$ = 0.035) and risk of breast cancer (${\widehat{\beta }}_{\text{FY},1}$ = 0.14). This factor had 111 nonzero loadings but only 16 of these loadings had an absolute value larger than 0.4, with the majority of remaining metabolites having loadings below 0.01. In Table 1, we list these 16 metabolites. In Web Figure 22, we display loadings for all metabolites from LVMA and standard factor analysis. Of interest, many of these metabolites are products of estrogen metabolism, suggesting estrogen metabolism does partially explain why increased BMI is associated with increased risk of ER+ breast cancer. However, most of the effect of BMI was not mediated by this factor. When estimating the TE, NDE, and NIE on the OR scale, we find OR_TE = exp(0.039), OR_NDE = exp(0.034), and OR_NIE = exp(0.005) suggesting that the estrogen pathways explains only a small fraction of the TE of BMI.

We also applied TMAO, TMAR, and IMA to the data, adjusting for the matching variables. TMAO and TMAR did not detect statistically significant factors mediating the relationship between BMI and the risk of ER+ breast cancers (Web Figures 23 and 24). Similarly, IMA did not identify statistically significant metabolites mediating the relationship (Web Figure 25). Further details are in Web Appendix G.

6 |. DISCUSSION

We proposed a latent variable model for high dimensional mediation analysis (LVMA). Our theoretical results show that the model parameters are identifiable, and LVMA estimates those parameters that have the so-called oracle properties of consistency and efficiency. Our simulation results further show that using LVMA, when appropriate, can significantly increase the number of discovered mediators. LVMA, by considering all variables simultaneously, efficiently estimates all parameters in the model. Specifically, using LVMA, we better estimate the mediating factors by using additional information about the exposure and outcome, as opposed to only using the information about the biomarkers. However, under model misspecification, such as when the exposure directly affects individual biomarkers, the assumption of latent variables can reduce the power to detect such biomarkers.

We highlight a couple of features of our method. First, we extend current literature on mediation analysis with a single latent mediator (Muthén and Asparouhov, 2015; Albert et al., 2016) to handle multiple latent mediators. Second, although some recent studies have started exploring penalized structural equation modeling (Jacobucci et al., 2016), these methods were not designed to handle the p > > n setting. Third, we extend our mediation model and, more generally, sparse factor analysis to accommodate case-control sampling.

None of the previously published methods (Boca et al., 2013; Huang and Pan, 2016; Zhang et al., 2016; Zhao and Luo, 2016; Chen et al., 2018 explicitly assumed the latent structure illustrated in Figure 1, but two methods did so implicitly. Huang and Pan (2016) take an approach similar to TMAR but do not impose any sparsity on the factors. Their objective is also fundamentally different as they are testing whether the set of all biomarkers are mediators as opposed to trying to identify the subset that is mediators. Chen et al. (2018) aims to identify linear combinations of biomarkers that are associated with both the exposure and outcome. However, their approach does not allow for factors that are only associated with the exposure or the outcome. Therefore, the biomarkers associated with only one of those variables get mistakenly included in the “direction of mediation.”

Several problems remain to be addressed in future work. Our latent model in (6–9) does not detect the existence of biomarkers that directly mediate the effect of E on Y. As evidenced by a large number of nonzero loadings in our application, the shrinkage of loadings for unrelated biomarkers may not be satisfactorily using EBIC. Some of our assumptions could also be violated in real-world examples. The factors need not be independent conditional on the exposure; the biomarkers need not be normally distributed; for retrospective sampling, the exposure needs to be normally distributed. We note the latter may be accommodated by the semiparametric approach based on Qin (1998) but that the discussion is beyond the scope of this paper. Despite these limitations, we believe the newly proposed LVMA offers a novel important tool for detecting biological mediators.