Combined Model of Aggregation and Network Diffusion Recapitulates Alzheimer's Regional Tau-Positron Emission Tomography

Abstract

Background: Alzheimer's disease involves widespread and progressive deposition of misfolded protein tau (τ), first appearing in the entorhinal cortex, coagulating in longer polymers and insoluble fibrils. There is mounting evidence for “prion-like” trans-neuronal transmission, whereby misfolded proteins cascade along neuronal pathways, giving rise to networked spread. However, the cause–effect mechanisms by which various oligomeric τ species are produced, aggregate, and disseminate are unknown. The question of how protein aggregation and subsequent spread lead to stereotyped progression in the Alzheimer brain remains unresolved.

Materials and Methods: We address these questions by using mathematically precise parsimonious modeling of these pathophysiological processes, extrapolated to the whole brain. We model three key processes: τ monomer production; aggregation into oligomers and then into tangles; and the spatiotemporal progression of misfolded τ as it ramifies into neural circuits via the brain connectome. We model monomer seeding and production at the entorhinal cortex, aggregation using Smoluchowski equations; and networked spread using our prior Network-Diffusion model.

Results: This combined aggregation-network-diffusion model exhibits all hallmarks of τ progression seen in human patients. Unlike previous theoretical studies of protein aggregation, we present here an empirical validation on in vivo imaging and fluid τ measurements from large datasets. The model accurately captures not just the spatial distribution of empirical regional τ and atrophy but also patients' cerebrospinal fluid phosphorylated τ profiles as a function of disease progression.

Conclusion: This unified quantitative and testable model has the potential to explain observed phenomena and serve as a test-bed for future hypothesis generation and testing in silico.

Impact statement

The presented aggregation-network-diffusion model exhibits all hallmarks of tau progression in human patients; it accurately captures not just the spatial distribution of empirical regional tau and atrophy but also patients' cerebrospinal fluid phosphorylated tau profiles. Thus, it serves to fill a theoretical gap between microscopic biophysical processes and empirical macroscopic measurements of pathological patterns in Alzheimer's disease. This unified quantitative and testable model has the potential to explain observed phenomena and serve as a test-bed for future hypothesis generation and testing in silico.

Introduction

Alzheimer's disease (AD) involves widespread and progressive deposition of amyloid beta ($A\beta$ from now on) protein in cortical plaques and of protein tau (τ) in tangles (Braak and Braak, 1991; Thal et al., 2002). The τ-protein is mostly found within neurons and promotes the assembly and stabilization of microtubules. In Alzheimer's patients, microtubule-associated τ undergoes hyperphosphorylation, losing its stabilizing function, and eventually aggregating into neurofibrillary tangles. Misfolded τ then propagates through neuronal pathways and coagulates, first in longer polymers and then as insoluble neurofibrillary tangles. Neurofibrillary τ tangles appear first in the locus coeruleus, then in the entorhinal cortex; then, they spread into the hippocampus, amygdala, temporal lobe, basal forebrain, and association areas, in that order (Braak and Braak, 1991). A wealth of evidence suggests that metastable, soluble oligomers formed early in the aggregation process and small fibril fragments are the predominant toxic species (Cárdenas-Aguayo et al., 2014; Gerson and Kayed, 2013).

The cause–effect mechanisms by which various oligomeric τ species are produced, aggregate, and disseminate, and how they cause neurodegeneration and symptomatology, are poorly understood. Preclinical studies have shown that pathological τ exhibits prion-like features: First, pathological τ species are capable of seeding, that is, they can serve as templates for misfolding of physiological τ species, initiating the formation of pathological τ tangles. Second, the induction of hyperphosphorylated τ seeds in circumscribed brain regions of rodents elicits the spread of pathological τ to anatomically connected regions rather than simple diffusion to spatially adjacent regions (Franzmeier et al., 2020). Many important questions in Alzheimer's research remain unresolved: How does protein aggregation and subsequent spread lead to stereotyped progression in the Alzheimer brain? Why do misfolded τ oligomers selectively target certain specific structures? How cross-sectional AD τ deposition patterns are related to brain networks, and how the latter govern the development and spread of τ pathology are important clinical and biological questions (Franzmeier et al., 2020).

Since almost all our understanding of these mechanisms comes from animal or in vitro studies, it is very challenging to apply or test them directly in humans. Hence, in this article, we approach these questions by using mathematical network modeling, and we test whether they can recapitulate in vivo measurements in human brains. Many biophysical models are available of how proteins aggregate, driven by destabilization of the native protein to yield partially folded intermediates with increased aggregation propensity (Gillam and MacPhee, 2013). These include the “heteromer” (Prusiner et al., 1990) and nucleated polymerization (NPM) (Masel et al., 1999). Protein conformational change is typically described as “monomer activation” (Morris et al., 2009). Subsequent fibrillation follows a nucleation-elongation process. Small, oligomeric species may then form by association of the partially folded protein units and proceed to assemble into larger, fibrillar aggregates, which, in turn, associate into mature fibril-like amyloid structures (Gillam and MacPhee, 2013; Serpell et al., 1997). The protein aggregation literature is extensive, and numerous recent reviews describe our current understanding of amyloid fibril structure (Eisenberg and Jucker, 2012; Serpell et al., 1997), mechanism of toxicity (Eisenberg and Jucker, 2012; Walsh and Selkoe, 2007), and the aggregation process (Wetzel, 1996).

Although mathematical models have been explored in related prion disease (Morris et al., 2009; Serpell et al., 1997), they have been scarce in Alzheimer's and dementia. Recent work is beginning to fill this gap, but it is focusing mainly on $A\beta$ (Achdou et al., 2013; Bertsch et al., 2017; Franchi and Lorenzani, 2016; Franchi and Lorenzani, 2017; Gillam and MacPhee, 2013; Murphy and Pallitto, 2000). See Carbonell et al. (2018) for a thorough review. Kinetic and thermodynamic descriptions of protein aggregation were reviewed by Morris et al. (2009), and mathematical models were reviewed in Gillam and MacPhee (2013).

Some early work incorporated classical spatial diffusion in prion aggregation models (Payne and Krakauer, 1998), in truncated Smoluchowski equations (Bertsch et al., 2017), and in NPM model (Matthäus, 2006). The latter also explored network spread on “toy” connectomes but not real data. A network model loosely based on protein aggregation as a process of epidemic spread was proposed and successfully validated on amyloid positron emission tomography (PET) data of Alzheimer patients (Iturria-Medina et al., 2014). A reaction-diffusion model incorporated a simplified two-species protein aggregation with anisotropic diffusion within the brain (Weickenmeier et al., 2019). However, spatial diffusion might not be the most appropriate model along fibers, since active axonal transport is commonly expected for τ transmission. A follow-up study (Fornari et al., 2019) added a network process (Raj et al., 2012; Raj et al., 2015) by using a simplified logistic growth model loosely related to protein aggregation.

Introducing a novel joint aggregation-network-diffusion model

In this article, we develop and empirically validate the mathematical machinery capable of encapsulating the entire gamut of τ etiology and progression, using parsimonious bottom-up biophysical modeling, as illustrated in Figure 1, of three processes: τ monomer production; subsequent aggregation into oligomers and tangles; and the spatiotemporal progression of misfolded τ as it ramifies into neural circuits. All model parameters are global and region-invariant. We hypothesized that this parsimonious model, which we call aggregation-network-diffusion (AND) model, can explain experimental findings of the spatiotemporal evolution of Alzheimer-associated τ in human brains.

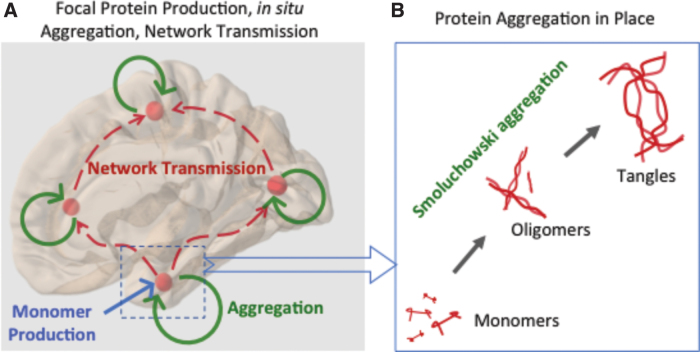
FIG. 1.

Illustration of the mechanisms and processes being modeled in this article. (A) Monomer production is assumed at a focal “seed” region, here entorhinal cortex. Aggregation into oligomers and finally tangles occurs in situ (B) and will be modeled via Smoluchowski aggregation theory. The local processes then spread into wider brain regions via axonal projections due to active transport and trans-neuronal transmission—here, they will be modeled by the NDM applied to the human brain connectome. Note that although monomer production is focal, all other processes are capable of occurring everywhere in the brain. NDM, Network Diffusion Model. Color images are available online.

Aggregation

Following (Achdou et al., 2013; Bertsch et al., 2017; Franchi and Lorenzani, 2016; Franchi and Lorenzani, 2017), we model the aggregation of τ polymers using Smoluchowski equations (Smoluchowski, 1917), a system of infinite discrete differential equations (without diffusion) for the study of rapid coagulation of aerosols. Smoluchowski's theory was previously extended to cover polymerization, aggregation of colloidal particles, formation of stars and planets, as well as biological populations, and it was successfully applied to the agglomeration of $A\beta$ amyloid (Achdou et al., 2013; Murphy and Pallitto, 2000).

Network diffusion

To model trans-neuronal spread, we extended our previous network-diffusion model (Raj et al., 2012; Raj et al., 2015), which was shown to recapitulate the classic spatial patterns of AD-related atrophy. This model approximates the trans-neuronal transmission of misfiled proteins as simple diffusive spread along axonal projections.

We hypothesized that this model will recapitulate the spatiotemporal evolution of τ, and predict the time course of the evolution of various oligomeric species. We validated it against empirical data from Alzheimer patients' regional atrophy and τ-PET scans. We evaluated several formulations of how the kinetics of protein aggregation and network diffusion varies according to oligomer size, and we showed that for each formulation, there exist parameter ranges within which the AND model recapitulated the empirical spatiotemporal pattern of AD. Using fluid biomarkers from patients, we also successfully predicted phosphorylated τ profiles as a function of disease progression. To our knowledge, this is the first report of an empirically validated complete biophysical model of both protein aggregation and trans-neuronal spread in AD.

Materials and Methods

Extracting anatomic connectivity graph

Connectomes were extracted from a dataset of 69 healthy subjects' structural MRI (T1) and diffusion-weighted MRI (dMRI) scans acquired and processed previously (Kuceyeski et al., 2013; Raj et al., 2015); details are portrayed in Supplementary Data S2. The number of streamlines between region i and j average over subjects was recorded as $c_{i,j}$, giving the full canonical the 86 × 86 connectivity matrix $C=\left\{c_{i,j}\right\}$.

Alzheimer's subject scans

Imaging data were obtained from two sources: AD neuroimaging initiative (ADNI)—117 AD, 156 late mild cognitive impairment (LMCI), and 148 early mild cognitive impairment (EMCI); and a published study at Yonsei University (Hanna et al., 2016)—128 patients (53 AD, 52 amnestic MCI, aMCI; 23 non-amnestic MCI, naMCI) and 67 matched controls. Freesurfer regional volumes and PET tracer uptake pipelines were applied (see Supplementary Data S2 for details) to achieve individual subjects' 86-region volumetrics and PET SUVr.

Ethics statement

All human data used here were approved by relevant institutional review boards, as described in prior reports (Kuceyeski et al., 2013), http://adni.loni.usc.edu and (Hanna et al., 2016).

Statistical analysis and model validation on empirical neuroimaging data

We applied the AND model on C, setting the starting pattern of τ to zero everywhere except a single “seed” region. The AND model was numerically solved by using MATLAB's ode45 solver, using Euler iterations of order (4,5). The time increment was set at 0.01. The simulation data were compared against empirical imaging-derived regional data (Korea cohort for τ-PET and ADNI cohort for atrophy), each of size 86 × 1. The metric of validation was the Pearson's correlation statistic R and its p-value. There are 16 multiple comparisons reported, not counting those in Supplementary Data since they are from secondary or post hoc analyses. All reported significant findings survive Bonferroni correction due to their extremely small p-values. Hence, we are reporting uncorrected p-values only. Parameter fitting was achieved by grid search, recording the best Pearson's R over model time.

Proposed AND model

Please refer Supplementary Data S3 for relevant mathematical notation and a review of Smoluchowski aggregation theory. To jointly model the separate processes of production, aggregation, and network-wide ramification of τ, we first replace the spatial diffusion term in Equation (4) of Supplementary Data with a graph diffusion process. Let $\Gamma$ be the weighted graph representing the human brain connectome, $V\left(\Gamma \right)$ the set of the vertices of $\Gamma$, and ${\Delta }_{\Gamma }$ its Laplacian matrix (Supplementary Data S2). Hence, we redefine Smoluchowski equations on vector-valued quantities, such that ${\tau }_m\left(v_i,t\right)$ denotes the molar concentration of soluble τ polymers of length m at the i-th vertex $v_i\in V\left(\Gamma \right)$ (i.e., at the i-th grey matter structure) at time t, with $1\le m\le M$ and $i=1,\dots ,\left|V\left(\Gamma \right)\right|=N$. We have capped the infinite Smoluchowski series to a small number M, as once aggregates reach a certain size they become tangles and exit reaction kinetics. Oligomers of length $\ge Meqnoopen\left(fibrils\right)$ are denoted by ${\tau }_M\left(v_i,t\right)$ and may be thought as tangles, clinically observable through T807-PET (Xia et al., 2013) or Flortaucipir-PET (Hanna et al., 2016) or MRI-derived regional atrophy (Vemuri et al., 2008; Whitwell et al., 2008).

The proposed model has the following components:

(a) Monomer production is defined as the generation of seeding- and aggregation-competent species of monomeric τ, for example, that has been hyperphosphorylated and cleaved from microtubules and is now undergoing reaction kinetics to form aggregates and undergo trans-neuronal transmission. It does not refer to healthy τ monomers that are produced and available ubiquitously within the brain. Initial intra-cellular phosphorylation of monomeric misfolded τ, mislocating to the somatodendritic compartment, will be represented by a production function $f_{\tau }\left(v,t\right):V\left(\Gamma \right)\times \left[0,\infty \right)\to ℛ$ for $t\ge 0$, $v\in V\left(\Gamma \right)$:

$$f_{\tau }\left(v_i,t\right)=\left\{\begin{array}{cc}{f}_{\tau }\left(t\right)& v_i=v_{seed}\\ 0& otherwise\\ \end{array}\right.,where{f}_{\tau }\left(t\right)=\frac{t}{{\sigma }_f}exp\left(-\frac{t}{{\sigma }_f}\right)$$

for a single seed region $v_{seed}\in V\left(\Gamma \right)$. $f_{\tau }$ is a Gamma-shaped function, with ${\sigma }_f=25$ to approximate a 25-year process—an arbitrary but realistic choice.

(b) Aggregation. Misfolded τ monomers undergo in situ agglomeration into oligomers and tangles. The evolution of the system satisfied by $\tau =\left({\tau }_1,\dots ,{\tau }_M\right)$ is described by Smoluchowski equations on $\Gamma$. If $t\ge 0$ and $v\in V\left(\Gamma \right)$, then

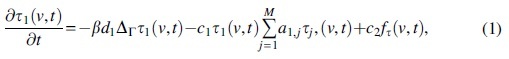
The first term is described in (c) next, whereas $c_1,c_2$ are positive aggregation and monomer production rates, respectively. For oligomers $1<m\le M$:

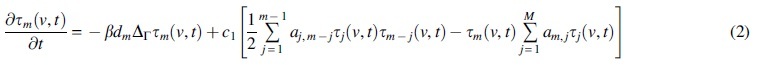
The constants $a_{j,k}$are reaction kinetic rates for the aggregation of two polymers of lengths $jandk$. Finally, the evolution of tangles is given by

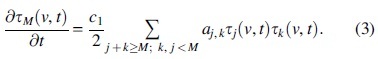
Initial conditions: At $t=t_0$, we assert ${\tau }_m\left(v,t_0\right)={\tau }_{0,m}\left(v\right)=0,\forall v\in V\left(\Gamma \right)$. This starting condition represents a healthy brain with no pathology.

(c) Network transmission. Postproduction transmission of oligomeric τ through neural pathways via trans-neuronal transmission (Clavaguera et al., 2009; Frost and Diamond, 2010; Iba et al., 2015; Jucker and Walker, 2013) is modeled via the Network Diffusion Model (NDM) (Raj et al., 2012; Raj et al., 2015), that is, by diffusion in $\Gamma$. This is given in Equations (1) and (2) depicted earlier by the graph diffusion term $\frac{\partial {\tau }_m\left(v,t\right)}{\partial t}=-\beta d_m{\Delta }_{\Gamma }{\tau }_m\left(v,t\right)$, where ${\Delta }_{\Gamma }$ is the graph Laplacian operator, and d_m is the diffusivity constant for the m-th oligomer. Please note that this involves a Laplacian operator that operates on the entire set of regional variables $\left\{{\tau }_m\left(v_i,t\right)\right\},\forall v_i\in V\left(\Gamma \right),$hence it should be read as defined in Supplementary Data (“Notation”). We have introduced a global rate of network “transmissibility” β.

Section Supplementary Data S4 contains important mathematical proofs of AND like existence, uniqueness, and boundedness of solutions.

Aggregation and diffusion rate parameters

For the sake of universality and parsimony, we assume that throughout the brain the rates of aggregation and transmission of oligomers are the same, but they are dependent on oligomer length. Hence, we impose a simple scaling behavior on $a_{mj}$ under two plausible regimes: (1) based on thermodynamic arguments,

$$a_{mj}=\frac{{\sigma }_{agg}^2}{mj}$$

and (2) based on empirical in vitro fitting data on amyloids, a Gamma-shaped expression (Gillam and MacPhee, 2013)

$$a_{mj}=\frac{mj}{{\sigma }_{agg}^2}exp\left(-\frac{mj}{{\sigma }_{agg}^2}\right),$$

where the ${\sigma }_{agg}$ is a positive scaling constant. Based on similar arguments, we define a scaling behavior of the diffusivity rates as:

$$d_m=1∕m,d_m=\frac{m}{{\sigma }_{diff}}exp\left(-\frac{m}{{\sigma }_{diff}}\right)$$

where ${\sigma }_{diff}$ is a scale parameter. Instead of imposing a hard constraint $d_M=0$ (tangles are immobile), the Gamma function ensures that large m diffusivity is close to zero.

Cerebrospinal fluid τ component

We model the accumulation of τ in cerebrospinal fluid (CSF) compartment by assuming that all τ species diffusing through the network do so by entering the extracellular pool in transit. A portion of this transiting species will be cleared out to CSF. Since the proportion of each species in the extracellular pool depends on their diffusivity, we predict the total τ from all regions, weighted by each oligomer's diffusivity rate:

Results

The proposed AND model's theoretical properties were rigorously derived in Supplementary Data S1.

Oligomer sizes were quantized for convenience

For the sake of computational load, convenience, and interpretability, and without loss of generality, we have lumped oligomers into only five bins, such that m can take the following values: 1 (monomer), 2, 3, 4, and 5 (tangle). Each bin should be considered a lumped average of several adjacent lengths, for example, $m=4$ can be considered an average of oligomers of length 30 to 40. This quantization scheme is arbitrary but not a limitation of the method, and it is done primarily for convenience and interpretability.

Free model parameters and their nominal (default) values are listed in Table 1 for convenience; please refer Methods for their definition and context.

Table 1.

List of Free Model Parameters and Their Nominal Values

Parameter name	Symbol	Nominal value (a.u.)
Oligomeric τ of size m	${\tau }_m$
Seed region	$v_{seed}$	$v_{EC}\left(entorhinal\right)$
Time scale of monomer production function $f_{\tau }\left(t\right)$	${\sigma }_f$	25
Network diffusivity/transmission rate for oligomer of size m	dm
Scaling constant that governs the relationship between dm and oligomer size m	${\sigma }_{diff}$	1
Global network “transmissibility” constant, governing relative propensity to aggregate in situ versus spread over network	$\beta$	1
Global constant relating aggregation rate to network diffusivity	c 1	1
Global constant relating monomer production rate to network diffusivity	c 2	0.05
Reaction kinetic rates for the aggregation of two polymers of lengths $jandk$	$a_{j,k}$
Scaling constant that governs the relationship between $a_{j,k}$ and oligomer sizes $j,k$	${\sigma }_{agg}$	2

Some variables are shown for context (shaded) but they are not free parameters themselves.

Temporal evolution

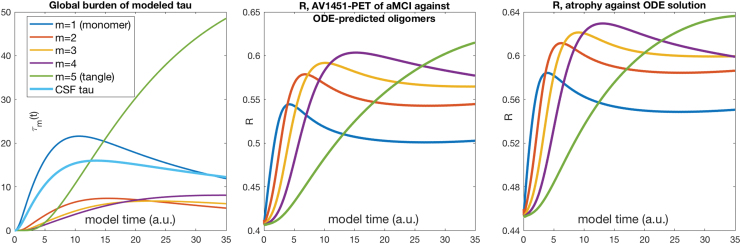
Figure 2 shows the temporal evolution of total ${\tau }_m$ oligomers, $m=1,2,3,4,5$, over model time, which has arbitrary units. As expected, the monomer levels are the first to rise, followed by oligomers of increasing length. The predicted concentration of CSF τ [Eq. (4)] is shown. Each oligomer exhibits a distinct plateau and eventually begins to decline, due to two factors. First, the monomer production itself declines as per Gamma-shaped production function $f_{\tau }\left(t\right)$, limited by the availability of intact protein and the loss of neurons, both of which serve to limit the available pool of cleavable protein. Second, Smoluchowski aggregation causes progressively larger oligomers leading to tangles, which takes active oligomers out of circulation. Thus, tangles show a slow increase while oligomers decrease. These aspects closely track the empirical data currently available on CSF-derived total τ (Dickerson and Wolk, 2013; Jack Jr et al., 2010; Trojanowski et al., 2010).

FIG. 2.

Left: Temporal evolution of τ oligomers over time, totaled over the entire brain, for oligomers of length $m=1,2,3,4,5$. As designed, monomers are the first to rise from zero, slowly giving way to higher oligomers. Tangles ($m=M=5$ here) are the last to develop, and last to reach steady state or fall back. The temporal sequencing of peak deposition clearly and strongly follows the sequence of oligomer length: $m=1,2,3,4,5$. Middle: Similarity index (Pearson's R) of the AND model against Korea study's empirical aMCI τ distribution, over model time t. Right: Similarity index of the AND model against ADNI study's empirical LMCI atrophy distribution, over model time t. ADNI, Alzheimer's disease neuroimaging initiative; AND, aggregation-network-diffusion. Color images are available online.

The Pearson similarity between the regional distribution of each oligomer at model time t between $t=0$ and $t=t_{max}=15$ and the (static) empirical 18F-AV1451 regional τ pattern is shown. The temporal sequencing of peak similarity suggests that monomer ($m=1$) is the first to peak, followed by $m=2,3,4,5$, in order. Here, we chose the aMCI and LMCI groups because they are the most pathologically active. Curves for AD groups in both studies give similar results and are not shown.

Although the results just cited used default choices of $a_{mj}$ and d_m, we implemented other functional forms noted in Methods (Supplementary Fig. S1), but AND dynamics did not change appreciably and the overall correspondence with empirical data was quite comparable.

Using AND model as a simulator for hypothesis generation

We showcased the ability of AND as a computational test-bed for generating new mechanistic hypotheses in Figure 3: how the total tangle burden ${\Sigma }_i{\tau }_M\left(i,t\right)$ depends on monomer production rate c₂ and network transmissibility β. We expect a complex and nonlinear relationship between initial conditions and final tangle pathology. We found that higher production rates yield higher τ burden, but not linearly but sub-linearly. Three different transmissibility regimes are shown, with β low, mid, and high. Tangle burden is limited at low β, and almost linear against c₂ at high β. We fitted power laws and found that the exponent of the power law was always less than 1 (Table 2). Specifically: low transmissibility regime had exponent 0.72, mid: 0.80, and high: 0.88.

FIG. 3.

Using the AND model as a simulator for hypothesis generation. In this example, we explore how the brain-wide total tangle burden would depend on the rate of monomer production in the initial seed region (here, entorhinal cortex), and whether tangle burden would be rate-limited by network transmissibility. (A) Evolution of total tangle burden ${\Sigma }_i{\tau }_M\left(i,t\right)$ over model time t, for various levels of the rate of monomer production. Clearly, higher production rates yield higher τ burden. (B) Maximum τ burden against production rate, indicating a strong sub-linear relationship. Three curves represent different transmissibility regimes, governed by parameter $\beta$: low, mid, and high. Tangle burden is limited at low transmissibility, and almost linear against production rate at high transmissibility. (C) Model time at which the peak tangle burden was achieved, versus production rate, indicating an inverse relationship between tangle growth duration and both monomer production rate and network transmissibility. Color images are available online.

Table 2.

Linear and Power Law Fitting of the Tangle Versus Monomer Production Rate Curves of Figure 3B

Transmissibility	Linear fit RMSE	Power law RMSE	Power law exponent
Low $\left(\beta =0.1\right)$	3.45	0.65*	0.72
Mid $\left(\beta =1\right)$	4.12	1.51*	0.80
High $\left(\beta =10\right)$	3.52	1.42*	0.88

Significant reductions of RMSE compared with linear fits are indicated by asterisk ^*. Power law exponent refers to symbol $\alpha$ in a power law given by $tangle=prodrat{e}^{\alpha }$. $\alpha <1$ denotes sub-linear growth. The exponent is close to 1 (linear growth) in the high transmissibility regime, and sub-linear in the low transmissibility regime, suggesting that transmissibility constrains tangle growth.

RMSE, root mean square error.

These power laws fitted the data significantly better than linear fits, as measured by the root mean square error. Panel C plots the model time at which the peak tangle burden was achieved, indicating that low transmissibility allows τ tangle pathology in the brain to settle quickly at (lower) steady-state levels, but higher rates of monomer production take longer duration to (higher) steady-state tangle burden. These findings demonstrate that network transmission plays a crucial role in brain-wide pathology ramification, and it greatly amplifies the effect of in situ production/aggregation.

Spatiotemporal evolution and its validation on regional τ and atrophy data

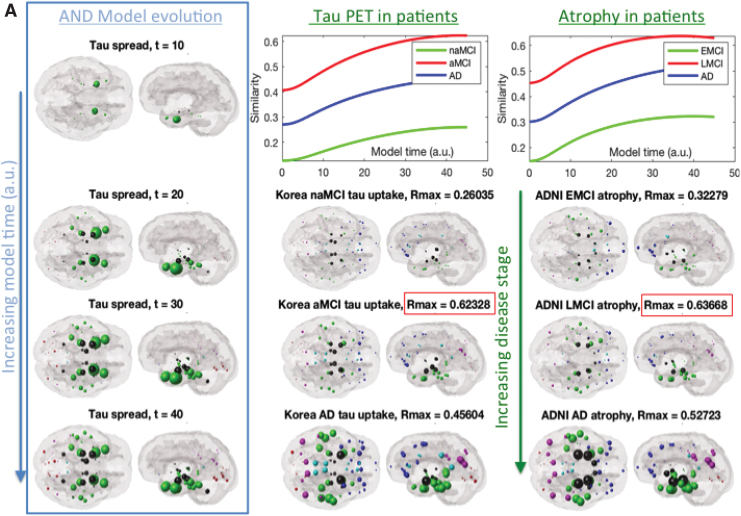
Figure 4 shows the evolution of regional AND-predicted ${\tau }_M$alongside empirical regional Flortaucipir-PET and atrophy, which is a close surrogate of τ (Vemuri et al., 2008; Whitwell et al., 2008). The AND model successfully recapitulates the spatiotemporal time course of τ progression: starting in entorhinal cortex (EC), increasing pathology in temporal cortices, then subcortical pathology in hippocampus and amygdala, followed by parietal and posterior cortices; in rough agreement with the ordered stages: naMCI/EMCI to aMCI/LMCI to AD. Please note, model time and disease stages are not implied to have a one-to-one correspondence. Similarity, scores between model and empirical distributions are shown in the R vs t curves.

FIG. 4.

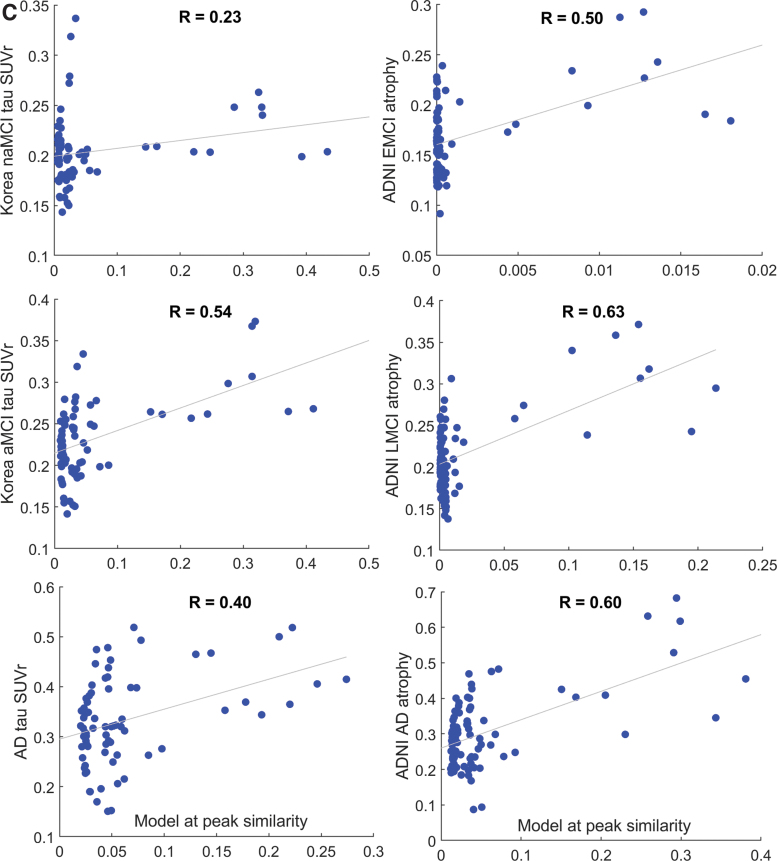
(A) Glass brain rendering of theoretical AND-predicted regional τ distribution (left column) and its comparison with empirical τ measured from regional Flortaucipir-PET scans of patients (middle column) and regional atrophy obtained from a different cohort of patients in the ADNI study (right column). Sphere color is by lobe: blue = frontal, purple = parietal, red = occipital, green = temporal, black = sub-cortical, and cyan = cingulate. Similarity scores (Pearson's R) between the model and empirical data are shown as a function of model time t in the top row (green = naMCI and EMCI; red = aMCI and LMCI; blue = AD). Here, we have chosen a model time window that is clinically relevant and interesting; however, please note that at further model times all correlation curves decline and eventually reach a plateau. For illustration purposes we have arranged both model and empirical data in increasing disease order, shown by vertical arrows. However, model time (which has arbitrary units) and disease stages are not implied to have a one-to-one correspondence. The best match between model and empirical regional data were found for the preclinical stages (aMCI and LMCI, respectively, denoted in red boxes), implying that the predictive ability of the AND model is likely to be the highest before clinical dementia has set in. The nonamnestic or early MCI groups (naMCI, EMCI) give the lowest correlation with the AND model at all model times, compared with the aMCI and AD groups. This is plausible, given the heterogeneity and sub-clinical manifestation among those subjects. (B) Scatter plots corresponding to peak R from (A). The right-most dots represent the seed region, in this case the EC. The distribution of the scatterplots suggests that the model is capable of a relatively wide distribution of regional values, with the seed region the highest, as expected. (C) Since the model is not normally distributed and its value at the seed point is unusually high, we also want to confirm that the R stated earlier are not being driven by the seed points. Hence, the correlation plots were repeated, this time excluding the seed points. Interestingly, the Pearson's R values are not substantially reduced. Note that the x-axis is slightly different from B, since the peak R is no longer achieved at the same model time. AD, Alzheimer's disease; EC, entorhinal cortex; EMCI, early MCI; LMCI, late MCI; MCI, mild cognitive impairment; aMCI, amnestic MCI; naMCI, non-amnestic MCI. Color images are available online.

Since the best fits were achieved aMCI and LMCI, the predictive ability of AND is highest before clinical dementia has set in—precisely the type of patient who may benefit most from it. Alzheimer's patients give moderate model fits, and naMCI and EMCI cohorts show poor fits. Latter subjects are very early, have nonamnestic dementia, or are possibly very heterogenous. That aMCI and LMCI data are a fit better than AD suggests that the AND model is capturing phases where active pathology transmission is ongoing; many recent authors have suggested that by the time of onset of full Alzheimer's, pathology might have reached a plateau, with further changes related only to cell loss and functional deficits (Jack Jr et al., 2010).

At the peak of the R-t curves, all fits are significant at $p=0.05$. At late time points, the similarity curves reach a plateau even though the tangle pathology keeps rising, since the similarity measure here is Pearson correlation, which is insensitive to overall scale. R-t curves begin at 0.4 for aMCI and 0.27 for AD at t = 0, since even without any network diffusion, the seeding location (ERC in this case) is correlated to its (future) τ deposition.

Robust correlation analysis

Scatter plots of the peak R shown in Figure 4 are not distributed normally; this is not surprising, since most graph models involve non-Gaussian connection weights, with some nodes and edges dominating over others. Pearson's R was previously used in prior NDM and other graph theoretic papers. However, several additional analyses were performed, including robust (skipped) correlations and seed-exclusion (Supplementary Data S1 and Figure 4C).

Comparison with network diffusion only

The AND simulation was compared with the classic NDM in Supplementary Figure S3. The regional topography given by each model is roughly similar, whereas the concentration profiles among brain regions over time are quite different. The NDM models a passive diffusion process, hence pathology is not created; in contrast AND starts with no initial pathology, and it slowly builds up pathology over time as a result of protein aggregation.

Sensitivity to model parameters, seed location, and connectome topology

A detailed analysis is now provided of various model parameters, seed location, and algorithmic choices. We also establish whether the model is specific to the human connectome, in comparison to random connectomes. Supplementary Data S1 explores the effect of three key parameters from the model—${\sigma }_{agg},{\sigma }_{diff},c_1$. Supplementary Figure S4 shows that model performance is quite insensitive to a wide parameter range, yet some parameters are better than others. This indicates that AND is an identifiable model. We repeated this analysis for four combinations of model choices noted earlier, arising from the two definitions of aggregation constants $a_{mj}$ and diffusivity rates d_m. All choices are capable of yielding similar performance at some parameter value. Note that thorough evaluation of kinetic parameters involving oligomeric species evolution is not possible at this time due to the absence of experimental data on reaction kinetics.

Connectome randomization

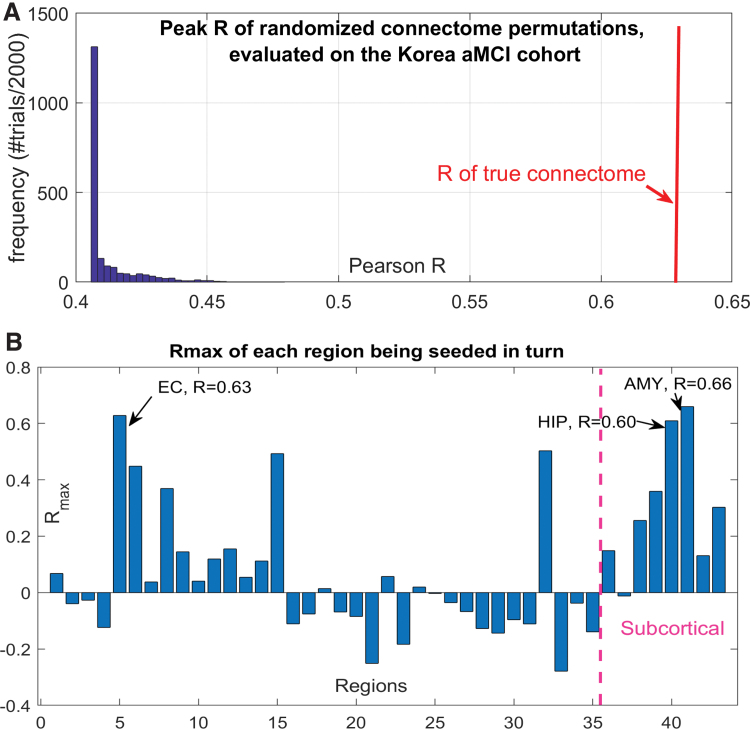
We wish to preclude the possibility that reported results are due to our choice of ERC seeding rather than due to the connectome, which we have placed at the center of the entire model. Therefore, we repeated AND simulations 2000 times, each time randomly scrambling the upper triangular portion of the true connectome. Randomized connectomes thus preserved connectivity values, but not the network topology. There is a hard lower limit at 0.4, which reflects the correlation between EC seed and regional τ. Figure 5 confirms that there are very few cases with higher R than true connectome's AND result, which is several standard deviations away from the center of the random distribution. Fisher's R-to-z transform confirms that the true result is highly significant (p < 10⁻⁶). Thus, AND applied to random networks does not recapitulate AD topography, and the connectome is a key mediator of AND-modeled processes.

FIG. 5.

AND simulations at different seedings and connectomes. (A) Histogram of peak Pearson's R achieved by AND over 2000 trials of randomly scrambled connectivity matrices. For comparison, the true network's R is shown by the vertical red line. (B) Bar chart of repeated seeding of each region in turn. For each seed region, peak Pearson's R over model time, corresponding to the correlation between model and amnestic MCI τ positron emission tomography data from the Korea cohort, is shown. EC, amygdala and hippocampus are the three best seed regions; EC is the best cortical seed. AMY, amygdale; HIP, hippocampus. Color images are available online.

Putamen seeding

It is possible that a different seeding location than ERC might also fit empirical data. Supplementary Data S1 shows results from an alternative seeding at the putamen, which is not, in fact, considered a plausible site of pathology initiation in AD. As expected, putamen-seeding was found not to be a good model of τ patterns in mature Alzheimer's subjects ($R=0.16$ with putamen seeding, vs. $R=0.45$ for EC-seeding), (Supplementary Fig. S5). However, putamen seeding was somewhat better for early MCI and mixed etiology groups, where many subjects might have a different, frontal or striatal etiologic origin.

Repeated seeding

Next, we wish to establish quantitatively whether other regions are equally plausible seed regions. Hence, we simulated AND model repeatedly, for each region acting as a seed in turn. We seeded regions bilaterally; for example, left and right amygdala are reported as a single seed region. These results are contained in Figure 5 and reveal that EC, amygdala, and hippocampus are the three best seed regions. Although all three are considered highly involved in AD, we speculate that the amygdala result is somewhat inflated due to the possibility of over-estimating its connectivity and conflating it with that of EC/hippocampus. Nonetheless, that a completely regionally unbiased modeling exercise was able to recapitulate the top seed regions known in AD strengthens the impact of AND and suggests that EC seeding is not only sensitive but may also be specific to AD.

Validation against ADNI CSF p-τ assay

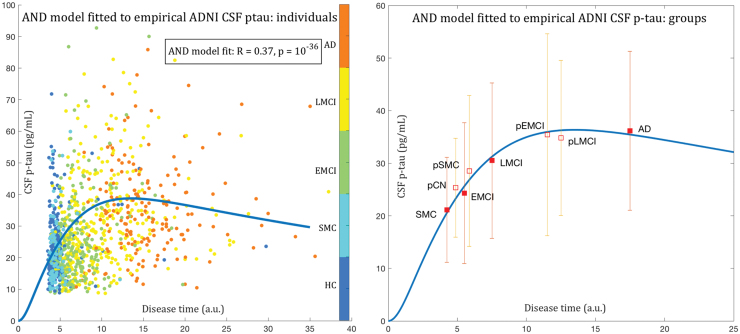
Finally, we validated the AND model's second important prediction, of the concentration of τ accumulated in the CSF, per Equation (4), on ADNI's CSF protein immunoassay biomarkers. We first organized ADNI subjects in increasing order of disease severity using logistic regression, as described in Supplementary Data S2. Using this common disease axis as “time,” we compared the AND's CSF τ prediction over t with empirical CSF data, after rescaling to the model time range of 0 to 40 using a scaling and a shift parameter.

As shown in Figure 6, predicted CSF τ fits very well to empirical ADNI CSF p-τ data. It correctly predicts both the rapid initial rise and eventual decline of CSF τ levels as the disease progresses. This result is, therefore, an excellent computational explanation for the observed changes in CSF-derived phosphorylated τ over disease duration (Dickerson and Wolk, 2013; Jack Jr et al., 2010; Trojanowski et al., 2010). It is noteworthy that even healthy subjects have significant levels of p-τ in the ADNI cohort (mean 20.0 pg/mL), because the cognitively normal group is elderly, age-matched to the disease groups in ADNI, and it is expected to have aging-related p-τ accumulation. The AND model correctly predicts this behavior, since it starts at zero and rises during early disease.

FIG. 6.

Fitting model CSF τ to empirical CSF p-τ. Left: After rescaling the model CSF τ curve from Figure 1 (left), we plot the empirical p-τ concentrations from each ADNI subject on the same model time axis. Each ADNI subject was placed on this time axis using the z-score of the logistic regression described in text, after rescaling it to fit in the model time range of 0 to 40. Each dot is a single subject, color-coded as shown. Healthy and SMC subjects are at the left and AD at the right. The fitted model yielded $R=0.37,p<10^{-36}$, which is highly significant. Right: Summarizing individuals into diagnostic groups (CN, SMC, EMCI, LMCI, AD) and their progressive counterparts (i.e., those CN that were found to have moved since baseline to either MCI or AD; or those MCI who moved to AD). The group means are shown in square boxes, and error bars show ±1 standard deviation. The progressive cases are assigned a “time” value that is the average of their baseline diagnosis and their converted diagnosis—that is, interpolated between the filled boxes. The model-predicted CSF τ evolution gives a very good fit to empirical data. Most importantly, it correctly predicts both the rapid initial rise and the eventual decline of CSF τ levels as the disease progresses. CN, cognitively normal; CSF, cerebrospinal fluid; SMC, subjective memory complaint. Color images are available online.

Discussion

The AND exhibits all hallmarks of τ progression seen in human patients and it explains many experimental findings in AD. Figure 4 shows that the model is significantly predictive of the spatial patterning of both regional τ-PET and MRI-derived atrophy, giving highly significant Pearson correlations of around R = 0.63 in LMCI or aMCI cases, and slightly lower R = 0.45 in mature AD cases. Interestingly, the model fit is far poorer for EMCI or naMCI cases, many of which have a heterogeneous etiology that may not be related to AD progression. That the fit to AD cases is slightly worse than for LMCI is suggestive of the well-known plateauing effect seen in pathology as disease progresses.

We showed that the AND model only succeeds when it is simulated using the human connectome. When the connectome is randomly scrambled, it fails to recapitulate empirical regional AD patterns (Fig. 5). Hence, our strong results cannot be due to chance or due to the high level of atrophy and τ present at the seed location in EC. Instead, brain network topology is a key mediator of AD pathology transmission. Although these results rely on a specific regional parcellation (Desikan-Killiany), prior uses of network diffusion modeling suggest that we may expect roughly similar spatial results using other parcellations and connectomes, for example, Raj et al. (2012). The model is specifically effective when seeded at EC, rather than putamen (Supplementary Fig. S5) or most other regions (Fig. 5B). Repeated seeding indicated that the best seed locations are amygdala, EC, and hippocampus, in order. The best cortical seed was the EC. These regions are well known as prominent and early sites of τ pathology in AD. The fact that their role was revealed via a completely regionally unbiased analysis shows that AND correctly recapitulates the essential properties of the AD pathological process. This also supports a role for AND as an effective quantitative test-bed for future hypothesis generation and testing.

In addition to giving regional predictions of τ, AND was also strikingly successful in correctly predicting the temporal behavior of phosphorylated τ accumulated in the CSF—Figure 6. The model was not only able to give a highly significant fit to individual p-τ levels across the entire cohort, but it also matched the average levels of each diagnostic group quite accurately. Most importantly, it was able to correctly capture the initial rapid rise in CSF τ levels, its plateauing in MCI subjects; and eventual slow decline in mature AD cases. These are all hallmarks of numerous empirical CSF τ studies, and our novel contribution is to explain this behavior using theoretical modeling.

As shown in Figure 3, we explored in silico the behavior of brain-wide tangle burden as a function of both monomer production rate in the entorhinal cortex and network transmissibility of oligomeric τ. We found that network transmission of τ is, by far, the more critical process, since it governs the long-term rate of brain-wide pathology ramification, greatly amplifying the effect of local protein production and aggregation. It is already known that exogenously seeded τ elicits a conformation-specific templated ramification of pathological τ that is independent of the amount of injectate (Holmes et al., 2014; Iba et al., 2013; Walker et al., 2013). Our previous network modeling of mouse tauopathy data had also found that the model's performance was not dependent on the amount, type, or location of injected τ (Mezias et al., 2017), supporting the same notion. Further, many additional factors are known to affect τ transmissibility, for example, neuronal activity, ApoE4 (Harris et al., 2010; Kamenetz et al., 2003; Oddo et al., 2003; Wu et al., 2016), and microglial activity (Hopp et al., 2018; Maphis et al., 2015; Yuan et al., 2016) are all strong regulators of extracellular transmission of amyloid and τ. Our result favoring a key role of transmissibility is consistent with therapeutic targeting of transmissibility via such actors (Soeda and Takashima, 2020).

Applications and implications

Historically, neurodegenerative research has relied on the “selective vulnerability” hypothesis to explain why we see stereotyped spatial patterns, positing that certain brain regions and cell types are especially vulnerable to AD. Our results support the alternate view that selective vulnerability is not essential for explaining spatial patterns—that network transmission by itself is sufficient—a far more parsimonious explanation. As modelers are well aware, parsimony does not always mean correct. However, invoking Occam's razor, we conclude that beyond the initial seeding event at EC or other specific areas there is no requirement of difference between ROIs in their vulnerability to τ or its propagation.

This does not exclude the possibility that various sources of regional vulnerability may mediate ongoing network-based vulnerability, including: differential patterns of insults governed by genetic, molecular, metabolic, or oxidative factors (Saxena and Caroni, 2011); different functional networks sharing similar genetic susceptibility (Franzmeier et al., 2020), synchronous neural activity, region-specific functional loads, or some as yet unknown structural, metabolic, and physiological aspect of neural network biology (Saxena and Caroni, 2011); or early metabolic activity in the default network (Buckner et al., 2005; de Haan et al., 2012). The notion that diverse mechanisms by which molecular dysfunction can interact with the neural architecture is now known as “molecular nexopathy” (Warren et al., 2013). Addressing these possibilities would require local profiles of protein expression within mathematical models—an aspect that has so far been addressed only superficially; see, for example, Acosta et al. (2018), Fornari et al. (2019), Pandya et al. (2019).

A computational test-bed

The presented AND model unifies structural biochemical processes at the microscopic scales with local and long range trans-neuronal transmission processes at the macroscopic scales in a single, quantitative, and testable model. Its biological value is that besides providing a simple computational model for τ propagation, it further strengthens the hypothesis that the diffusion of hyperphosphorilated τ follows the connectivity patterns. This was previously shown at the network level for a simple model of spread (Raj et al., 2012) but not for a fuller model that also involves protein aggregation. Therefore, this approach can serve as an effective bridge between theoretical studies, bench science, and human imaging studies. Formal models such as ours can serve as computational test-beds, to test preliminary new theories, quickly identifying the most relevant hypotheses or rejecting those less likely to lead to new insights. These could complement detailed experimental or clinical studies, and they can be used for reducing experimental costs or for overcoming structural difficulties.

Many future and follow-up explorations can be catalyzed by the presented approach:

First, current models of protein aggregation involve kinetic and aggregation parameters that must be estimated from detailed in vitro experimental data on reaction kinetics. Unfortunately, kinetics in solution or suspension do not frequently capture the complex environments and the pathological milieu of proteins in tissue in vivo. Our AND model provides a new opportunity to obtain parameter fits to real in vivo human and especially to detailed transgenic mouse data on reaction and aggregation rates.

Second, the AND model can open up the possibility of testing competing models of protein aggregation in terms of their ability to reproduce not only in situ kinetics of oligomerization, but also the brain-wide ramification via trans-neuronal transmission. Apart from Smoluchowski aggregation, several alternative models have been proposed, including the classic nucleation models. Although extensive experimental data are available on the basis of which the suitability of various aggregation models has previously been assessed (Gillam and MacPhee, 2013), these data typically come from in vitro reactions and it is unclear whether the same conclusions can be reached using in vivo data. The proposed AND model can fill this gap.

Third, the AND model provides a realistic avenue for understanding the pathophysiological progression of degenerative pathologies in a wide array of degenerative diseases, including Alzheimer's, Parkinson's, ALS, frontotemporal dementia, etc. Although human imaging does not give oligomeric data, CSF biomarkers do. Thus, a model like ours, which is able to provide a mathematical link between monomeric and oligomeric species to measurable plaques and tangles, can be an important addition to the burgeoning field of neurodegeneration.

Limitations and future work

In this study, we chose focal seeding location, at ERC or elsewhere. It is possible that in some real cases τ seeding might be a diffuse event. The focality of seeding (monomer production) is not an inherent limitation of the model—indeed, we could have chosen any other site, or diffuse seeding everywhere. Our current choice was motivated by Braak histopathological evidence of initial seeding in highly circumscribed areas, particularly ERC. The DTI-derived human connectomes cannot infer directionality of connections, an important limitation given that protein transmission is likely to be a directional process. Although we considered the entorhinal cortex as the most plausible seed region in this article, other regions are implicated even earlier in the AD process, for example, locus coeruleus, which is not covered in our MR or PET scans.

The proposed model may benefit from extension to multiple protein species (e.g., $A\beta$ and τ in AD) and their interactions. In this study, a template connectome was used instead of individual subjects' own connectomes. This choice removes potential confounds due to variability in connectomes and promotes the stability, interpretability, and ability to generate mechanistic insights and hypotheses. Further, individual variability in subjects' connectomes does not appear to impart network spread models with enhanced predictive ability—as previously shown (Powell et al., 2018). Nonetheless, we acknowledge the need to explore individual heterogeneity and the ability to predict future states of individual patients. We assume that internally within each ROI the behavior of τ is homogeneous, that is, free mixing. This is, of course, only true up to a size limit, but reasonable given that the model is only evaluated against average PET or atrophy signal across all the voxels within a ROI.

A note on the time axis in our results is also in order. The reader may reasonably expect that the correct temporal sequence as understood clinically (healthy<naMCI<aMCI<AD) should be reflected in the model's fitted time t. In general, this was not the case, for two reasons. First, a full quantitative fitting of the time axis in our model would require individual data and not group data with longitudinal follow-up, and advanced model inference procedures (Markov Chain Monte Carlo or variational Bayesian inference); this is the subject of ongoing development in our lab but outside current scope. Second, our chosen performance metric is Pearson's correlation, which is insensitive to the overall scale of the model or the data. Since the subgroups aMCI and AD are primarily different in overall severity rather than the relative spatial patterning, the use of correlation is not very good at capturing the expected disease sequence. In the current article, our focus was on the plausibility and reasonableness of the model, its group-level validation, and resulting biological insights. The accommodation of individual connectomes and other sources of heterogeneity, the resolution of time in our model, and its inference in individuals longitudinally will be the focus of future studies.

These limitations of empirical validation require caution in over-interpreting our results. It is the nature of in silico modeling that its conclusions warrant experimental verification. Finally, although we presented substantial comparisons with alternative models, we note that conclusively proving a presented model is “better” than all other alternatives is an impossibility, and this will always remain a work in progress.

Conclusions

We proposed a parsimonious mathematical model of monomer production, aggregation into oligomers, and the network-based progression of misfolded τ in AD brains. Bidirectional protein transmission was modeled through projection fibers via Network-Diffusion. This combined AND model unifies structural biochemical processes at the microscopic scales with local and long-range trans-neuronal transmission processes at the macroscopic scales in a single, quantitatively testable model. To our knowledge, this is the first theoretical model of protein aggregation and network transmission to be successfully tested on empirical macroscopic PET data.

Authors' Contributions

A.R., B.F., and V.T.: conceived the study, developed the mathematical model, and wrote the article. A.R.: implemented the model, validated on human imaging data, generated results, and performed statistical analysis. X.G.: performed CSF biomarker analysis. H.C., J.Y.C., Y.H.R., and C.H.L.: performed human imaging, study enrollment, consenting, image processing, quality checks, and helped improve the article.

Author Disclosure Statement

No competing financial interests exist.

Funding Information

A.R. was supported by NIH grant number R01NS092802, RF1AG062196, and R56AG064873. H.C., Y.H.R., J.Y.C., and C.H.L. were supported by Yonsei University College of Medicine Grant number 6-2015-0076 and National Research Foundation of Korea Grant number 2015R1C1A2A01054507. B.F. was supported by the University of Bologna, funds for selected research topics, by MAnET Marie Curie Initial Training Network, and by GNAMPA of INdAM (Istituto Nazionale di Alta Matematica “F. Severi”), Italy, and by PRIN of the MIUR, Italy.

Supplementary Material

Supplementary Data S1

Supplementary Data S2

Supplementary Data S3

Supplementary Data S4

Supplementary Figure S1

Supplementary Figure S2

Supplementary Figure S3

Supplementary Figure S4

Supplementary Figure S5

Supplementary Table S1

Supplementary Table S2