Deciphering how naturally occurring sequence features impact the phase behaviors of disordered prion-like domains

Abstract

Prion-like low complexity domains (PLCDs) have distinctive sequence grammars that determine their driving forces for phase separation. Here, we uncover the physicochemical underpinnings of how evolutionarily conserved compositional biases influence the phase behavior of PLCDs. We interpret our results in the context of the stickers-and-spacers model for phase separation of associative polymers. We find that tyrosine is a stronger sticker than phenylalanine whereas arginine is a context dependent auxiliary sticker. In contrast, lysine weakens sticker-sticker interactions. Increasing the net charge per residue destabilizes phase separation while also weakening the strong coupling between single-chain contraction in dilute phases and multi-chain interactions that give rise to phase separation. Finally, glycine and serine residues act as non-equivalent spacers, thus making glycine vs. serine contents an important determinant of the driving forces for phase separation. The totality of our results leads to a set of rules that enable comparative estimates of composition-specific driving forces for PLCD phase separation.

Graphical Abstract

Biomolecular condensates enable spatial and temporal organization of biochemical reactions that control key cellular processes such as division ¹, signaling ², transcriptional regulation ³, and stress response ⁴. In the latter, stress granule formation and dissolution are regulated by reversible phase transitions that are driven by a network of heterotypic protein-RNA interactions and homotypic protein-protein interactions ^{5, 6, 7}. Many of the protein components of stress granules and other ribonucleoprotein bodies are RNA-binding proteins that feature tandem RNA-binding domains and intrinsically disordered prion-like low complexity domains (PLCDs) ^{8, 9}. Mutations within PLCDs can cause neurodegenerative diseases such as Amyotrophic Lateral Sclerosis (ALS) ^{10, 11}. The consequences of these mutations can be assessed by leveraging and building on our growing understanding of how sequence features contribute to the driving forces for phase separation in PLCDs ^{12, 13, 14}. Here, we uncover rules and heuristics that lay the foundation for comparative assessments of phase behavior across a range of PLCDs.

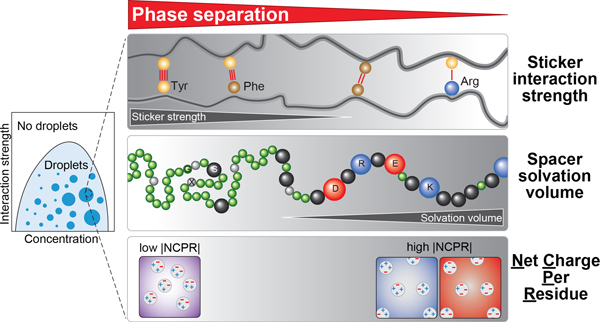
PLCDs are biological instantiations of associative polymers that can be described using a stickers-and-spacers framework ^{13, 15, 16, 17}. Stickers provide cohesive interactions for reversible, non-covalent crosslinks. Spacers provide scaffolds for stickers, and determine the effective solvation volume (v_es), which is defined as the average volume per residue that is set aside for interactions with the solvent ^{16, 17, 18, 19, 20}. Referenced against an ideal chain, for which v_es is zero, the sequence-specific v_es can be positive or negative. A positive value for v_es points to favorable solvation of residues, on average, whereas negative values imply desolvation. Changes to spacers can alter the magnitude and sign of v_es, thereby influencing the driving forces for phase separation and material properties of condensates ^{15, 17, 19, 20}.

While the stickers-and-spacers framework is readily applicable to synthetic polymers such as ionomers where charged groups are clearly delineated from uncharged groups ²¹, PLCDs are finite-sized heteropolymers. This makes it difficult to know the identities of stickers vs. spacers, the strengths of different types of stickers, and the effects of spacers. In a recent study, the stickers-and-spacers framework was applied to model the phase behavior of the PLCD from isoform A of human hnRNPA1, referred to hereafter as the WT A1-LCD or A1-LCD ¹³. Aromatic residues, specifically Tyr and Phe, were shown to be the primary stickers that form reversible non-covalent crosslinks. The main finding was that the valence (number) of stickers and their patterning along the linear sequence determine the interplay among sticker-sticker, sticker-spacer, and spacer-spacer interactions that leads to condensates that dissolve above an upper critical solution temperature (UCST) ¹³. Further, the intramolecular residue-residue interactions that determine the dimensions of individual PLCD chains in dilute solutions were found to be equivalent to intermolecular interactions that drive phase separation ^{13, 22}. This “strong coupling” between interactions that determine conformational and phase equilibria of PLCDs was attributed to the uniform distribution of aromatic stickers along the linear sequence ¹³. Importantly, the feature of strong coupling becomes useful for efficient computational calculations of full phase diagrams ^{22, 23, 24}.

The previous studies raise several questions that remain unanswered: (1) Are Tyr and Phe residues equivalent to one another as stickers? (2) Are all non-aromatic residues equivalent to one another as generic spacers or do the complex compositions of PLCDs point to modulations of phase behavior by the physicochemical properties of different residues? (3) Are there sequence features that can weaken the strong coupling between interactions that determine contraction of single chains in dilute phases and multi-chain interactions? In what follows, we answer these questions through a combination of investigations that are motivated by observations we make regarding evolutionarily conserved amino acid compositions among A1-LCD homologs. We explore the differences between Tyr vs. Phe residues as stickers, the contributions of charged residues as spacers and / or auxiliary stickers, and the differences between Gly and Ser residues as spacers. We obtain a physicochemical rationalization for the conserved biases and covarying trends across A1-LCD homologs. We find that the coupling between the determinants of single-chain dimensions and the driving forces for phase separation can be disrupted by altering the net charge per residue (NCPR). PLCDs across FET family proteins have similar compositional biases; therefore, the rules that emerge from our findings can be used for quantitative predictions of how compositional biases drive phase separation across a wide range of PLCDs.

Results

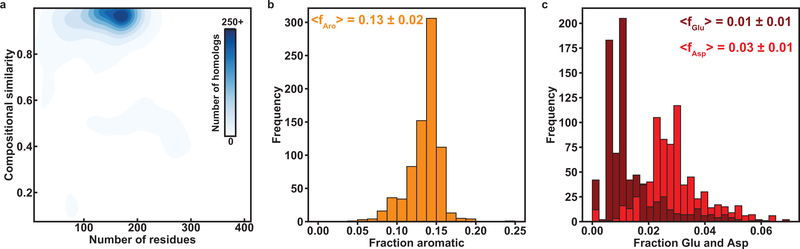
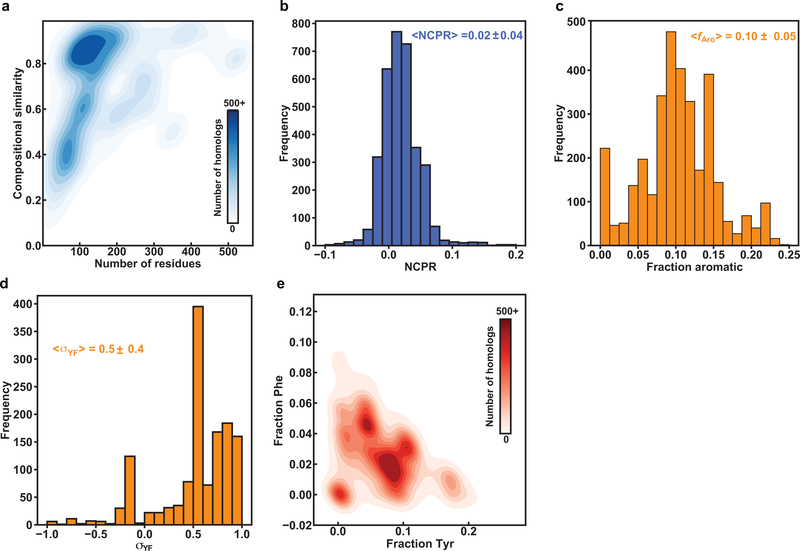
If Tyr and Phe residues are equivalent as stickers and if the only requirement of a spacer is that it not be Tyr or Phe, we would expect only the valence and patterning of Tyr / Phe residues in the sequence to be conserved. To assess if this expectation is valid, we quantified the amino acid composition of A1-LCD (Fig. 1a) and analyzed the extent to which compositions are conserved across 848 PLCDs drawn from orthologs and paralogs (referred to hereafter as homologs) within the hnRNPA1 family (Extended Data Fig. 1). Sequences for PLCDs of hnRNPA1 were drawn from proteomes of unrelated organisms and include species that diverged ~750 M years ago ²⁵. Despite this large evolutionary distance, we find that compositional biases are similar across PLCDs from homologous proteins (Extended Data Fig. 1). This suggests that there are conserved compositional preferences that contribute to the sequence grammar underlying the driving forces for phase separation of PLCDs. Accordingly, we pursued systematic investigations aimed at uncovering the physicochemical principles that underlie the conserved compositional biases across A1-LCD homologs.

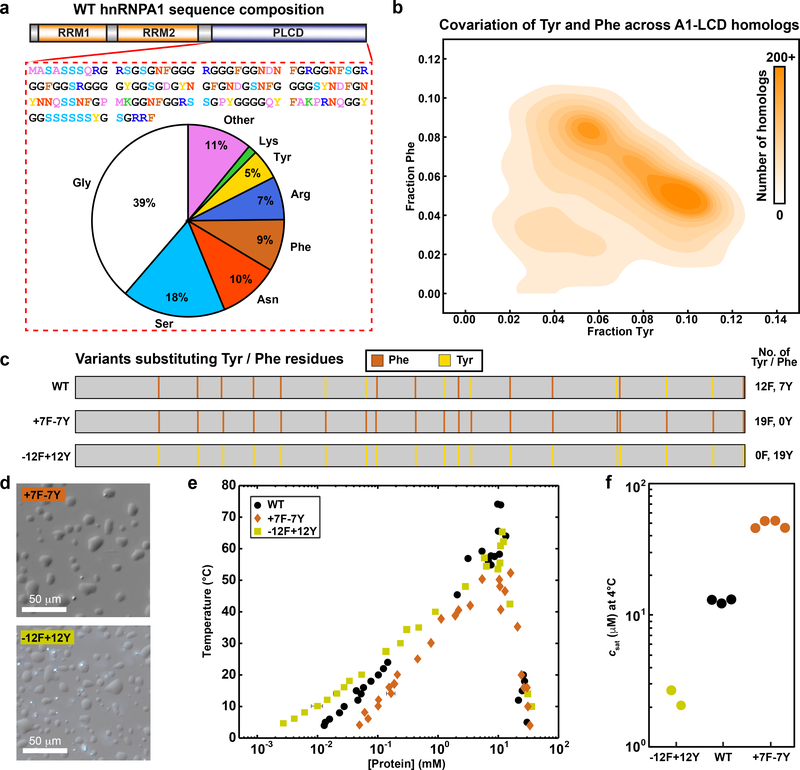
Fig. 1: Compositional analysis and covariation of aromatic content of hnRNPA1.

(a) Amino acid sequence and compositional statistics for the PLCD from isoform a of hnRNPA1 – referred to in the text as A1-LCD. (b) 2D histogram quantifying covariations in fractions of Tyr versus Phe residues across PLCDs. (c) Diagram of aromatic content type and placement in variants. Numbers next to each schematic indicate the number of residues of a certain type. Vertical bars in the schematics indicate the positions of Phe (brown) and Tyr (yellow) residues. (d) Differential interference contrast (DIC) images showing dense liquid droplets. Solution conditions were 20 mM HEPES, 150 mM NaCl, pH 7.0. (e) Binodals of A1-LCD variants as a function of temperature in 20 mM HEPES, 150 mM NaCl, pH 7.0. (f) A1-LCD variant saturation concentrations measured at 4°C.

Impact of Tyr versus Phe on the driving forces for phase separation.

The fraction of aromatic residues across A1-LCD homologs is narrowly distributed around a mean value of 0.13 (Extended Data Fig. 1). Further analysis shows that the fractions of Phe and Tyr residues vary considerably across A1-LCD homologs. Interestingly, there is a negative correlation between the fractions of Phe and Tyr residues across 770 of the 848 sequences (see details in the Supplementary Methods) indicating a covariation between the fractions of Phe and Tyr (Fig. 1b). The observed anticorrelation between Tyr and Phe contents, together with the conservation of overall Tyr / Phe contents, could imply that Tyr and Phe are physicochemically interoperable. Alternatively, it could reflect a natural titration of stickers of different strengths, while keeping the valence roughly the same. To test these hypotheses, we generated variants of the A1-LCD that replaced all Tyr with Phe, or all Phe with Tyr residues (Fig. 1c, Supplementary Table 1). All variants have the same length and maintain the background of A1-LCD. The designations used in Fig. 1c reflect the numbers of Tyr / Phe residues that were added or removed.

We expressed and purified the variants (Supplementary Fig. 1) and characterized their temperature-dependent phase behaviors in vitro. Just like A1-LCD ¹⁷, the two variants form condensates giving rise to dense droplets at pH 7.0 and 20°C in the presence of 150 mM NaCl (Fig. 1d). Sedimentation assays ^{13, 26} were used to measure coexisting dilute and dense phase concentrations as a function of temperature and cloud point measurements were used to estimate the locations of critical points ²⁷. Fig. 1e shows the measured coexistence curves and cloud points for the aromatic variants. The WT A1-LCD has 12 Phe and 7 Tyr residues distributed uniformly along the sequence (Fig. 1c). In the −12F+12Y variant, all Phe residues of the WT are replaced with Tyr residues. This increases the width of the two-phase regime, although the apparent critical point and the dense phase concentration stay roughly the same as those of the WT (Fig. 1e). The two-phase regime widens due to a shifting of the left arm of the binodal to lower concentrations. This indicates that substituting Phe with Tyr residues enhances the driving forces for phase separation without causing discernible changes to the concentrations of dense phases. In the variant +7F−7Y, all Tyr residues were replaced with Phe. In contrast to the −12F+12Y variant, the width of the two-phase regime narrows for +7F−7Y, indicating that Phe stickers weaken the driving forces for phase separation of A1-LCD when compared to Tyr stickers (Fig. 1e, 1f).

Extracting thermodynamic parameters from the temperature dependence of saturation concentrations.

To test whether we could systematically alter the phase behavior of A1-LCD by modulating Tyr vs. Phe contents, we created variants that contain Tyr and Phe residues at different ratios (Fig. 2a). Additions or deletions of Tyr / Phe residues were achieved either by replacing Gly / Ser spacers with the residues of interest or substituting deleted residues with Gly / Ser residues while preserving the overall balance of Gly and Ser. We measured coexistence curves for variants designated as −9F+6Y, −8F+4Y, and −9F+3Y. We quantified the driving forces for phase separation in terms of saturation concentrations (c_sat) at individual temperatures (Fig. 2b) and the relative positions of the low concentration arms of binodals with respect to one another (Supplementary Fig. 2a). For a given construct and temperature, c_sat is the threshold concentration above which the system separates into coexisting dense and dilute phases.

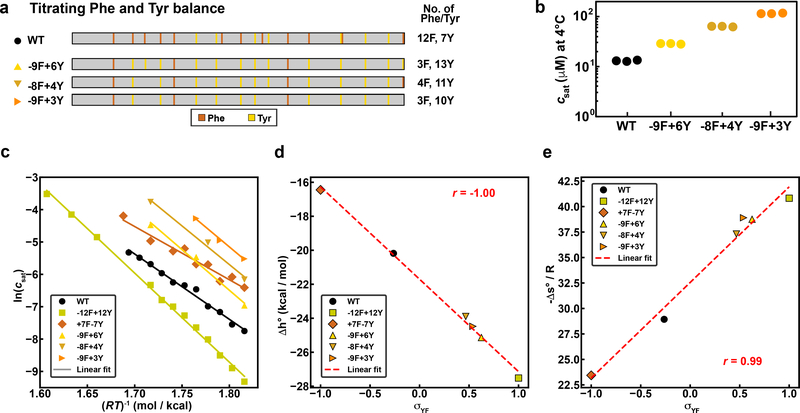
Fig. 2: Aromatic residue type and content influences balance of entropic and enthalpic contributions to phase separation.

(a) Diagram of aromatic content type and placement in variants. (b) A1-LCD variant saturation concentrations measured at 4°C. Solution conditions were 20 mM HEPES, 150 mM NaCl, pH 7.0. (c) Results from van’t Hoff analysis of select A1-LCD aromatic variants. Each data point is an average saturation concentration taken from at least 3 measurements at the given temperature. (d) Inferred values of Δh° plotted against σ_YF for all A1-LCD aromatic variants used in this study. Solid lines are linear fits to the data. Estimates for Δh°(d) and –Δs°/R (e) extracted from the van’t Hoff analysis. Red dashed lines are the linear fits to the data. Here, R= 0.00199 kcal/mol*K.

Overall, our measurements indicate that Tyr is a stronger sticker than Phe. This was previously observed in the context of cation-π interactions ¹⁵ but is also valid for PLCDs where π-π interactions are the primary drivers for phase separation. We used a van’t Hoff analysis method ²⁸ to extract apparent enthalpies (slopes) and entropies (intercepts) from plots of ln(c_sat) versus (RT)⁻¹ (see details in the Methods). The inferred parameters quantify the changes in standard state molar enthalpies (Δh°) and molar entropies (Δs°) associated with the transfer of PLCD molecules from the dilute to the dense phase (Fig. 2c). Replacing all Phe residues with Tyr (−12F+12Y) resulted in larger negative (favorable) Δh° values compared to the A1-LCD. Conversely, replacing all Tyr residues with Phe (+7F-7Y) reduced the enthalpic driving forces for phase separation (Fig. 2d). Shifting the balance between Tyr and Phe resulted in intermediate Δh° and Δs° values with a linear dependence on the Tyr versus Phe contents (Fig. 2d, 2e). In this analysis, we use a parameter defined as ${\sigma }_{YF}=\left(\frac{f_Y-f_F}{f_Y+f_F}\right)$ where f_Y and f_F are the fractions of Tyr and Phe, respectively. Note that σ_YF takes values of −1 for f_Y = 0, 0 for f_F = f_Y, and +1 for f_F = 0.

The entropy changes (Δs°) associated with the transfer of PLCD molecules from the dilute to dense phase are always unfavorable (Fig. 2e) in UCST phase behavior. The values of Δs° combine contributions from the gain / loss of solvent entropy, conformational entropy, the entropy of mixing, and the overall translational and rotational entropies. Overall, results from the van’t Hoff analysis highlight the interplay between enthalpy and entropy whereby variants defined by large, favorable changes in enthalpy are opposed by entropic penalties. This result suggests that stronger sticker-sticker interactions will restrict the degrees of freedom for molecules in the dense phase.

Comparative assessments of the role of charged residues on phase behavior.

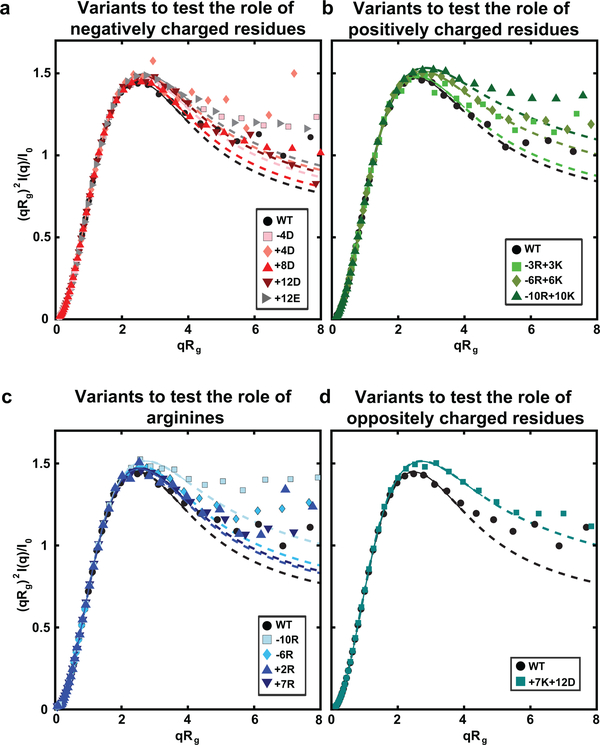
Analysis of the overall compositional biases across A1-LCD homologs showed that the NCPR values are narrowly distributed around a mean value of +0.04 (Fig. 3a). Further, there is a clear preference for Arg over Lys, with their contents being narrowly distributed around mean values of 0.06 and 0.02, respectively (Fig. 3b). Similarly, the Asp and Glu contents are narrowly distributed around mean values of 0.03 and 0.01, suggesting a slight preference for Asp over Glu (Extended Data Fig. 1). These compositional analyses become relevant in light of previous findings that highlight the role of Arg as a sticker ¹⁵, the relative weakness of Lys as a sticker ^{15, 29, 30, 31, 32}, and the contributions of charged residues as destabilizers of phase separation because they can act as solvation-promoting spacers^{19, 20} that repel one another if the NCPR is high ³³. Based on the observed compositional biases and resulting hypotheses, we designed several variants to probe the roles of different types of charged residues on A1-LCD phase separation, keeping their patterning in the sequence uniform. Titrations of charge content and asymmetry do not cause significant changes to the intrinsic disordered nature of the A1-LCD (Supplementary Fig. 3).

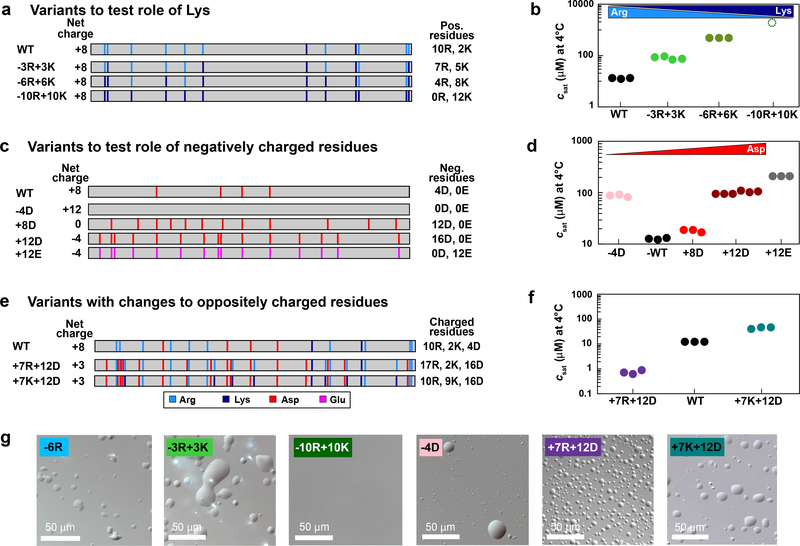
Fig. 3: Role of charged residues in PLCD phase separation.

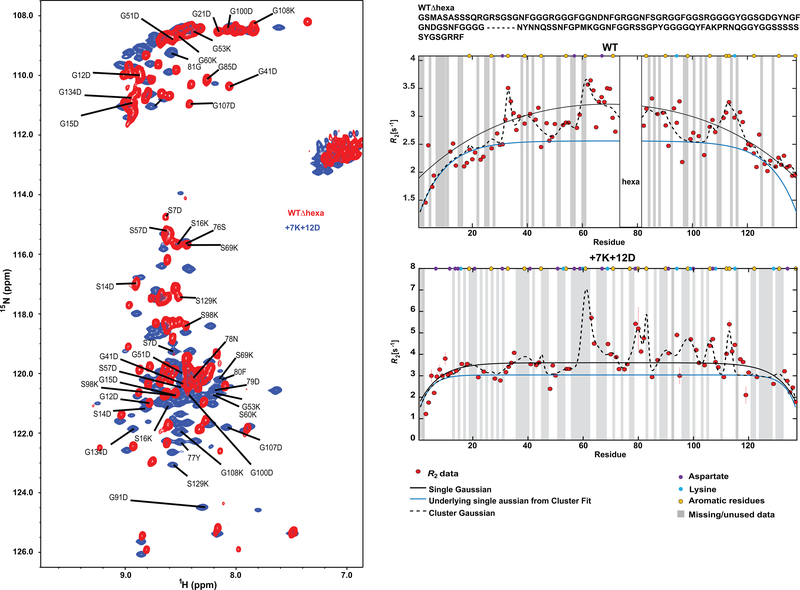
(a) Distribution of NCPR values and (b) distributions of fractions of Arg and Lys residues across A1-LCD homologs. Numerical values are mean values of the respective distribution ± the standard deviations. (c) Diagram of Arg/Lys content and placement across variants that test the role of Arg residues. Numbers next to each schematic indicate the number of Arg residues. Vertical bars in the schematics indicate the position of Arg residues (light blue). (d) Saturation concentrations of variants from (c) measured at 4°C. Solution conditions were 20 mM HEPES, 150 mM NaCl, pH 7.0. For binodals of variants see Supplementary Fig. 2. (e) Tyr and Phe sidechain planes of ¹³C-resolved ¹H^aromatic-¹H^aliphatic NOESY spectrum show NOEs between sidechain protons of Tyr/Phe and H^δ protons of Arg. Degenerate Arg H^δ proton resonances are shown as strips of (H)CC(CO)NH spectrum. A single (H)CC(CO)NH strip (corresponding to G63/N62) corresponds to the upfield carbon NOE resonance frequency. The other NOEs could not be unambiguously assigned. NMR spectra of A1-LCD Δhexa were recorded at 40°C to enable high enough concentrations without phase separation.

Three variants that removed (−10R, −6R) or added (+7R) Arg residues were used to assess whether Arg residues contribute as auxiliary stickers (Fig. 3c). The −10R construct showed a substantial reduction in the driving force for phase separation, with an increased c_sat at 4°C and a corresponding shift in the binodal (Fig. 3d, Supplementary Fig. 2b). This observation is in line with previous work that identified Arg residues as drivers of phase separation ^{15, 31}. Surprisingly, the −6R variant shows a slight increase in the width of the two-phase regime compared to WT, whereas phase separation is significantly destabilized for +7R (Fig. 3d). Together, these data suggest that Arg residues contribute as auxiliary stickers within PLCDs, but these contributions are context-dependent resulting in non-trivial relationships between Arg content, context, and the driving forces for phase separation.

Sticker-sticker interactions are detectable as nuclear Overhauser enhancements (NOEs) in nuclear magnetic resonance (NMR) spectra even in the absence of phase separation ¹³. NOEs are the result of magnetization transfer between nuclei through space and imply that physical distances between the nuclei are, at least transiently, within 5 Å of one another. Based on the established equivalence between cohesive interactions within single chains and the driving forces for multi-chain phase behavior of A1-LCD variants ¹³, we assessed the presence of Arg-Phe / Tyr NOEs in NMR spectra in the dilute phase. At 40°C, with the system in a single homogenous phase, we used a concentration of 800 μM in the NMR sample, which was high enough to observe NOEs between aromatic sidechain protons of Phe / Tyr and arginine H^δ protons (Fig. 3e). This supports the expectation that Arg residues interact with Phe / Tyr acting as auxiliary stickers within PLCDs.

Next, we quantified the implications of the observed preference for Arg over Lys by titrating the Arg vs. Lys contents using A1-LCD variants designated as −3R+3K, −6R+6K, and −10R+10K (Fig. 4a). While Arg possesses a delocalized pi system around its guanidinium functional group, Lys contains a more chemically simple primary amine. As a result, despite Arg and Lys being positively charged, they are different, both in terms of the types of non-covalent bonds they form and in terms of their free energies of solvation ^{34, 35 36}. Accordingly, we expect there to be differences in phase behavior across the variants ^{15, 30, 31, 32, 37, 38}. As expected, substituting Arg with Lys weakens the driving forces for phase separation (Fig. 4b). Replacement of all Arg residues with Lys (−10R+10K) resulted in the abrogation of phase separation in the concentration range up to 2.3 mM. Taken together with results for the −10R variant, our data suggest that Lys residues in the A1-LCD context appear to destabilize phase separation by increasing v_es of spacers and removing the contributions of Arg as auxiliary stickers.

Fig. 4: Role of charged residues in PLCD phase separation.

(a) Diagram of Arg / Lys content and placement across variants that test the role of Lys residues. (b) Saturation concentrations of variants from (a) measured at 4°C. (c) Diagram of Asp/Glu content and placement in variants that test the role of negatively charged residues. (d) Saturation concentrations of variants from (c) measured at 4°C. (e) Diagram of Arg, Lys, Asp, and Glu content and placement in variants that test the role of oppositely charged residues. (f) Saturation concentrations of variants from (e) measured at 4°C. (g) DIC images showing dense droplets for select variants from Fig. 3 and 4. Solution conditions were 20 mM HEPES, 150 mM NaCl, pH 7.0. For binodals of variants see Supplementary Fig. 2.

To assess the impact of acidic residues on phase separation, we added 8 or 12 Asp residues to generate variants +8D and +12D, or 12 Glu residues to generate +12E (Fig. 4c). Increasing the Asp or Glu contents beyond that of the WT sequence leads to substantial weakening of the driving forces for phase separation (Fig. 4d). Based on these results, we hypothesized that increasing the charge content, without compensatory electrostatic attractions, destabilizes phase separation through increased effective solvation volumes and electrostatic repulsions. Unlike the divergent effects of Arg and Lys, Asp and Glu affect phase behavior in a similar manner. Specifically, the +12D and +12E variants have similar phase behaviors, though the +12E variant has a slightly higher c_sat, which we attribute to the higher steric bulk of Glu over Asp. Interestingly, substitution of the four native Asp residues with Gly / Ser, as in variant −4D, also weakened the driving forces for phase separation (Fig. 4d). This points to a buffering role of the native Asp residues whereby they partially compensate for the excess positive charge in the system.

To test the hypothesis that electrostatic attractions offset the destabilizing effects of high v_es, we characterized the phase behavior for variants +7R+12D and +7K+12D (Fig. 4e). Indeed, the destabilizing effects seen in +7R and +12D are offset and overcome in the +7R+12D variant, which is close to being electroneutral (Fig. 4f). This effect also prevails for the +7K+12D variant. NMR experiments for the +7K+12D variant (Extended Data Fig. 2, 3) support our assessment that Lys and Asp residues do not act as stickers. Instead, they modulate the driving forces for phase separation through a combination of high v_es, electrostatic interactions, and weakening of attractive interactions among primary and auxiliary stickers. Finally, comparison of the phase behavior for +7R+12D and +7K+12D shows that a combination of near electroneutrality and the presence of context dependent auxiliary sticker effects of Arg contribute to the enhanced driving forces for phase separation in +7R+12D when compared to the A1-LCD (Fig. 4f). In summary, all variants (except −10R+10K) were able to undergo phase separation (Fig. 4g). However, the sequence variations in this set of A1-LCD variants modulated the saturation concentration by more than three orders of magnitude (Fig. 3d, 4b, 4d and 4f). Accordingly, we sought a framework to understand the molecular underpinnings of these sequence-dependent changes to the driving forces for phase separation.

Application of a mean-field model explains the data for charge variants.

Based on the preceding analysis we hypothesized that electroneutrality might be important for enhancing the driving forces for phase separation (Fig. 5a). According to this hypothesis, the WT sequence with a net charge of +8 should have an unfavorable balance of charged residues. We assessed the impact of net charge by plotting the measured log₁₀(c_sat) values against the NCPR for a series of variants with identical numbers and linear patterning of Tyr / Phe stickers but changes to charged residues (Fig. 5b). We performed this analysis using data collected at 4°C. The plot of log₁₀(c_sat) versus NCPR at 4°C has a putative V-shaped profile (Fig. 5a, 5b) indicating the possibility that c_sat is at its lowest value for electroneutral systems (NCPR ≈ 0). However, differences between Arg and Lys variants lead to significant deviations from the putative V-shaped profile (Fig. 5b). Specifically, for equivalent NCPR values, we find that increasing the number of Arg residues lowers c_sat below the apparent V-shape whereas decreasing the number of Arg residues increases c_sat. In contrast, increasing the number of Lys residues increases c_sat (+7K+12D, −3R+3K, and −6R+6K) to extents that cannot be explained by deviations from electroneutrality.

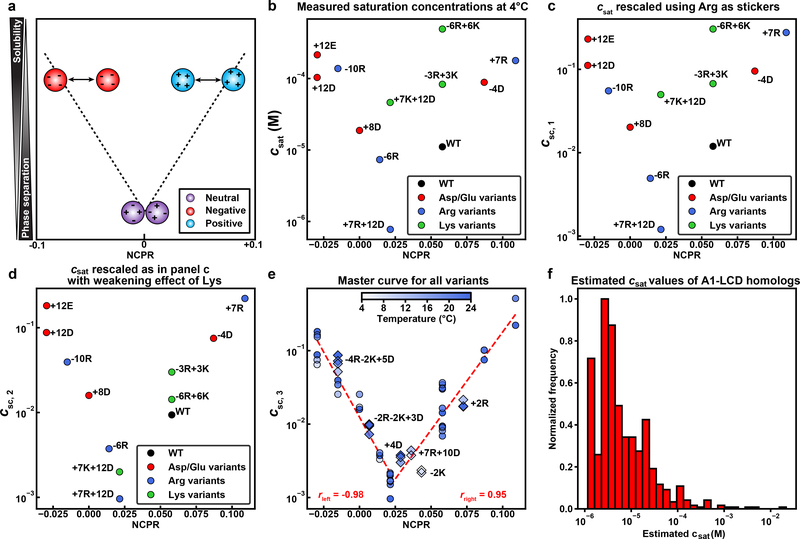
Fig. 5: NCPR modulates A1-LCD phase separation.

(a) Diagram illustrating the expected effect of net charge on driving force for phase separation. (b) c_sat values from data measured at 4 °C, plotted against NCPR for a subset of the sequence variants. Each data point is an average saturation concentration taken from at least 3 measurements at the given temperature. (c) Results of rescaling c_sat to account for the effects of Arg stickers. (d) Results of rescaling that accounts for the destabilizing effects of Lys in addition to accounting for the effects of Arg stickers. (e) Results of rescaling data using the approaches that lead to panels (b) and (c) combined with an accounting for the temperature-dependent variations to c_sat. The result is a master curve onto which all csat data for all measured temperatures collapse. The legends show the Pearson r-values that quantify the negative and positive linear correlations of the left and right arms, respectively. Variants not used for parameterization of the mean-field model were generated and their data shown as diamonds. (f) Histogram of calculated c_sat values for 770 PLCDs from the set of 848 sequences derived from hnRNPA1 homologs. These c_sat values were calculated using the mean-field model that yields c_sc,3 in (e).

We reasoned that Arg residues are context-dependent auxiliary stickers, whereas Lys residues weaken attractive interactions ^{15, 39}. To test this hypothesis, we used a generalized mean-field stickers-and-spacers model ³⁹ that considers the types, valence, and strengths of stickers. Using this model, we rescaled the c_sat values at 4°C using $c_{\text{sc},1}=c_{\text{sat}}\left({\lambda }_{aa}{n}_a^2+2{\lambda }_{aR}{n}_a{n}_R\right)$ where n_a and n_R are the numbers of Tyr / Phe and Arg residues, respectively. We used this mean-field model in a regression analysis where we fix λ_aa = 1 and obtained λ_aR. The resultant value of λ_aR = +1.69 reflects the positive cooperativity ³⁹ of Arg and its role as an enhancer of the driving forces for phase separation. The choice of λ_aa = 1 was made because the Tyr / Phe ratio and positioning of these residues do not change in the variants studied here.

To account for outliers in the plot of c_sc,1 against NCPR (Fig. 5c), we modeled the destabilizing effects of Lys using a further rescaling $c_{\text{sc},2}=c_{\text{sat}}\left[n_a^2\left({\lambda }_{aa}+3{\lambda }_K{n}_K\right)+n_a{n}_R\left(2{\lambda }_{aR}+6{\lambda }_K{n}_K\right)\right]$. Here, n_K is the number of Lys residues in the sequence. Regression analysis, performed by setting λ_aa = 1 and λ_aR = +1.69, yields λ_K = −0.0479. Here, the minus sign points to unfavorable contributions of Lys due to negative cooperativity ³⁹. With this rescaling, all data points at 4°C collapse onto two arms of a single V-shaped plot (Fig. 5d). Finally, we accounted for the changes to c_sat with temperature using $\exp \left[-\left(\frac{T-T_0}{m}\right)\right]\ast \left[n_a^2\left({\lambda }_{aa}+3{\lambda }_K{n}_K\right)+n_a{n}_R\left(2{\lambda }_{aR}+6{\lambda }_K{n}_K\right)\right]$. This yields a master curve for c_sc,3 versus NCPR (Fig. 5e) where we set T₀ = 277 K and directly obtained the value of m to be 8.26 K from the dilute arms of the binodals of the relevant variants (see SI for a detailed description of the mean-field stickers-and-spacers model).

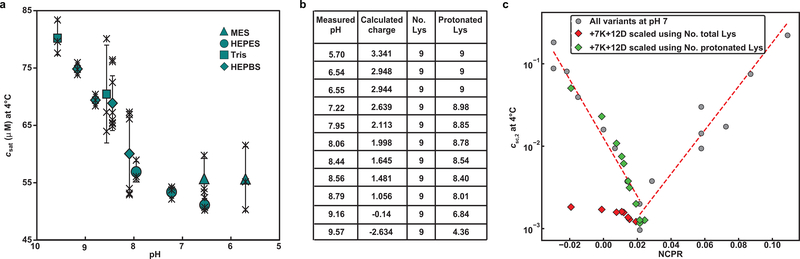
To test predictions made by the master curve, we generated six additional variants (marked as diamonds in Fig. 5e) whose NCPR values fill in gaps along the V-shaped master curve. Binodals for these new variants are shown in Supplementary Fig. 4. Importantly, without any further reparameterization, we find that the measured c_sat values for the new variants are readily rescaled to coincide with predictions from the V-shaped master curve (Fig. 5e). The V-shape results from the destabilizing effects of increased net charge. However, we find that the minimum in the V-shaped profile is located at a small positive value of NCPR as opposed to zero. To test for the possibility that the theoretical and actual NCPR values might be different due to shifted pK_a values of ionizable residues, we measured the pH dependence of phase separation for the +7K+12D variant. All data points collapse onto the V-shaped master plot when we rescale the measured c_sat values by estimating the expected numbers of protonated Lys residues as the entities that weaken sticker-sticker interactions (Extended Data Fig. 5). These observations suggest that the minimum of the V-shaped plot coincides with truly positive NCPR values.

Overall, our analysis, captured in the master curve for c_sc,3, highlights the role of mean-field electrostatic interactions in modulating the driving force for phase separation for fixed valence and patterning of Tyr / Phe residues. The model, specifically the expression for c_sc,3 and the values obtained for the λ coefficients, allow us to predict values for c_sat at 4°C for PLCD sequences derived from homologs of hnRNPA1 (Fig. 5f; see details in Methods). We restricted the analysis to PLCDs that were 100–200 residues long to ensure that changes to chain length do not confound the application of our mean-field model. Our model predicts values for c_sat that span up to three orders of magnitude, demonstrating how subtle changes to amino acid compositions are likely to impact the driving forces for PLCD phase separation.

Assessing the correlation between single-chain dimensions and c_sat.

Previous work on A1-LCD showed that increasing the number of aromatic residues while maintaining the uniform linear distribution of these stickers leads to increased chain contraction in the dilute phase and lowering of c_sat ¹³. The converse is true when the number of aromatic stickers is reduced ¹³. We asked if the correlation between single-chain dimensions and c_sat is preserved across the range of variants studied here.

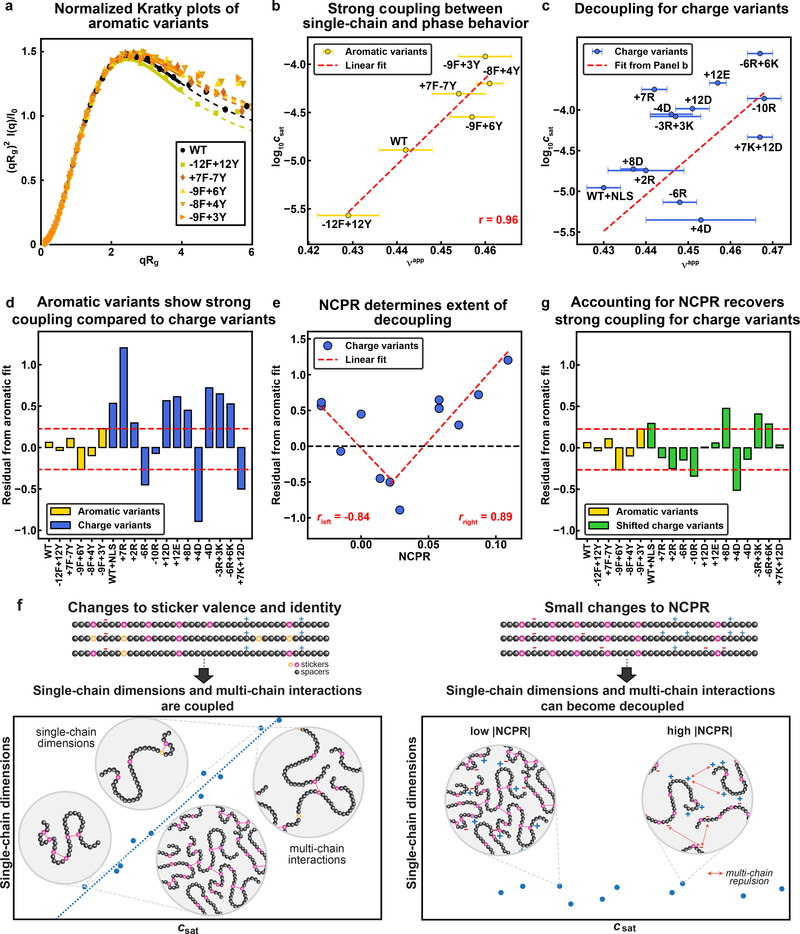
We collected size exclusion chromatography-coupled small-angle X-ray scattering data for dilute solutions of most of the variants (Fig. 6a, Extended Data Fig. 5, Supplementary Fig. 5). We extracted apparent scaling exponents ν^app (Supplementary Table 2) from the scattering data using an empirical molecular form factor ⁴⁰. We obtain a strong positive correlation between log₁₀(c_sat) and ν^app for the aromatic variants (Fig. 6b) with a Pearson r-value of 0.96. However, this correlation is abolished for the variants that alter net charge or the overall charge content (Fig. 6c). Instead, the data show that c_sat can be lowered or increased by up to two orders of magnitude without altering ν^app. Based on the results in Fig. 5e, which show that mean-field electrostatic effects can alter the driving forces for phase separation, we undertook the following analysis: First, we used linear regression to extract parameters from Fig. 6b that quantify the correlation between log₁₀(c_sat) at 4°C and ν^app for the aromatic variants. We used these parameters to assess the correlation between log₁₀(c_sat) and ν^app for the charge variants. Residuals from this linear regression analysis are shown in Fig. 6d. This analysis reveals a V-shaped profile when the residuals are plotted against the NCPR (Fig. 6e). The implication is that mean-field, intermolecular electrostatic interactions can enable a decoupling of the driving forces for single-chain contraction and the driving forces for phase separation. Specifically, increases to the NCPR can impact the collective interactions among PLCDs without having a significant impact on single-chain dimensions as quantified by ν^app (Fig. 6f).

Fig. 6: Mean-field electrostatic effects can disrupt the strong coupling between driving forces for single-chain contraction and phase separation.

(a) Normalized Kratky plot of SEC-SAXS data for aromatic variants of A1-LCD. Solid lines are fits to an empirical molecular form factor (MFF). Dashed lines show the predicted behavior at larger q values, where the experimental data are noisy. (b) Correlation between log₁₀(c_sat) and inferred values of ν^app for the aromatic variants. Red dashed line is the linear fit to the data. (c) Correlation between log₁₀(c_sat) and inferred ν^app values for the charge variants. The dashed line is the linear fit of the aromatic variants from (b). (d) Residuals from the correlation in (b) for all variants. Data for charge variants are shown using unmodified and shifted c_sat values as in (c) and (e), respectively. Red dashed lines indicate the bounds of the aromatic residuals. (e) Residuals from the correlation in (b) versus NCPR for the charge variants. Red dashed lines show two linear fits, i.e., for the variants whose NCPR is less than or equal to that of the +7K+12D variant and greater than or equal to that of the +7K+12D variant on the left and right, respectively. (f) Residuals from the linear correlation of log₁₀(c_{sat, shift}) vs. ν^app for charge variants. Here, c_{sat, shift} refers to the c_sat values that are shifted based on the linear fits in (e). Red dashed lines indicate the bounds of the aromatic residuals. (g) Schematic showing strong coupling of single-chain dimensions and driving force for phase separation across variants titrating sticker strength and valence, but the potential for decoupling for variants with small changes to NCPR. Error bars associated with ν^app values in (b) and (c) represent uncertainty from fitting SAXS data to MFFs. Saturation concentrations were measured independently at least 3 times for each variant.

We accounted for the effects of mean-field electrostatic repulsions by rescaling the measured c_sat values according to the NCPR of each variant and parameters obtained from the pair of linear fits in Fig. 6e. Specifically, we shifted c_sat using log₁₀(c_sat,shift) = log₁₀(c_sat) – (aQ + b). Here, Q is the NCPR of the variant of interest, and a and b are fitting parameters. If the NCPR is less than +0.0214, the parameters are a = −19.7 and b = −0.0273, whereas when the NCPR is greater than +0.0214, a = 21.1 and b = −0.989. The NCPR-based rescaling of c_sat values leads to a recovery of the one-to-one correspondence between ν^app and c_sat (Fig. 6e, 6g). These results imply that the interactions that disrupt strong coupling must have the duality of being weak enough to have negligible influence on single-chain dimensions ^{41, 42}, and yet be collectively strong enough to impact multichain interactions and hence the driving forces for phase separation. Our quantitative understanding of the origins of the decoupling and our ability to account for it in terms of the NCPR values will allow us to continue using parameters derived from analysis of single-chain dimensions ^{23, 24}, with suitable NCPR-based corrections, to infer interaction potentials for sequence- or architecture-specific simulations of phase behavior ^{13, 16}.

Spacers contribute to phase behavior through their effective solvation volumes.

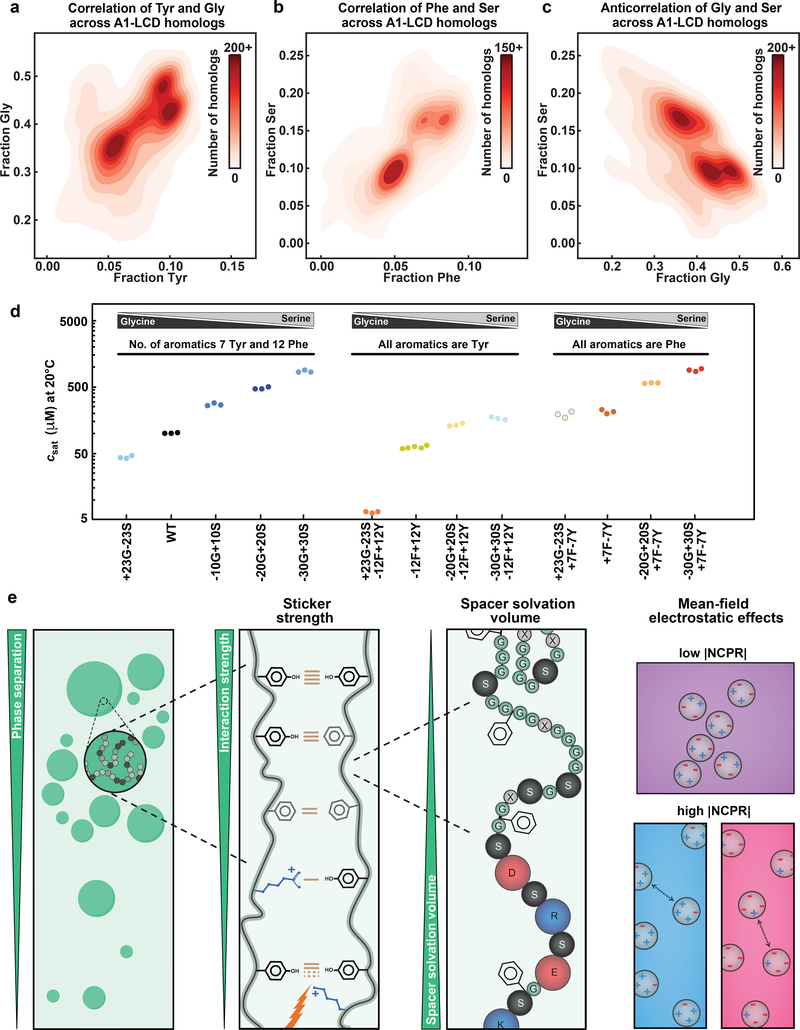
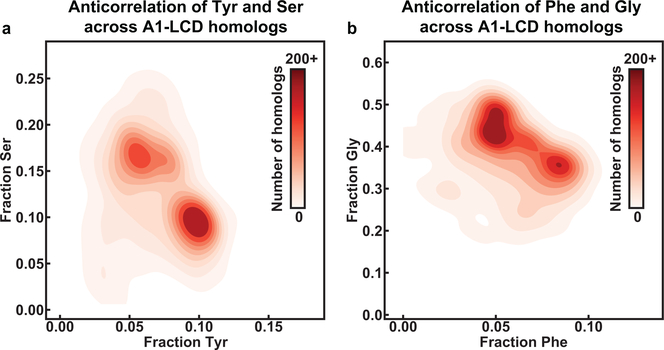
In the stickers-and-spacers formalism, spacers contribute to the driving forces for phase separation through their impact on the v_es of polymers ¹⁸. For a given sequence, the value of v_es will be influenced by a combination of the steric bulk and the intrinsic free energy of solvation of spacer residues ^{17, 19}. While increasing the charge content provides a direct route to increasing v_es through increased favorability of solvation ^{19, 20}, changing Gly to Ser, Asn to Gln or Ser to Thr should increase v_es through increased steric bulk ⁴³. Conversely, changing Ser / Asn / Gln to Gly should decrease v_es. If the polar residues Gly, Ser, Thr, Asn, and Gln contribute mainly as spacers, then substitutions that increase v_es should have a destabilizing effect on phase separation, whereas substitutions that decrease v_es should stabilize phase separation. Gly and Ser residues are by far the most abundant residue types in the A1-LCD, its homologs, and PLCDs in general. Interestingly, the broad distribution of σ_YF values for A1-LCD homologs reflects covariations between Tyr / Phe and Gly / Ser contents. Indeed, analysis of PLCDs derived from 770 of the 848 homologs (see details in the SI) of hnRNPA1 shows interesting covariation patterns (Fig. 7a–c). Specifically, we observe positive correlations between the fractions of Gly and Tyr as well as the fractions of Ser and Phe, respectively (Fig. 7a, 7b). We also observe a negative correlation between the fractions of Gly and Ser (Fig. 7c) and these derive from the negative correlations between the fractions of Tyr and Ser as well as Phe and Gly, respectively (Extended Data Fig. 6).

Fig. 7: Gly and Ser are spacers with different effective solvation volume.

(a-c) 2D histograms quantifying covariations in fractions of Tyr versus Gly (a), Phe versus Ser (b), and Ser versus Gly (c) residues across A1-LCD homologs. (d) A1-LCD variant saturation concentrations measured at 20°C. Gly vs. Ser content is titrated in the WT A1-LCD (left), in the background of the variant in which all aromatic residues are Tyr (middle), or in the background of the variant in which all aromatic residues are Phe (right). (e) Cartoon highlighting the hierarchy of physicochemical effects underlying the driving force of phase separation encoded in the evolutionarily conserved composition of PLCDs. Cohesive interactions between disordered chains made up of sticker and spacer residues (beads of grey shades) result in condensates (green droplets). Tyr-Tyr, Tyr-Phe and Phe-Phe interactions have, in order, decreasing pairwise interaction strengths. Arg residues act as auxiliary stickers with aromatic residues if the NCPR is favorable. Lys residues weaken sticker-sticker interactions via 3-body effects. Glycine, serine and charged residues are spacer residues that modulate the driving forces for phase separation through their effects on the v_es of spacers. The higher the v_es, the weaker is the driving force for phase separation. The NCPR of PLCDs affects phase separation via mean-field electrostatic effects, modulating the saturation concentration by up to three orders of magnitude. NCPR values close to electroneutrality favor phase separation whereas unbalanced charges increase solubility and weaken phase separation.

To make sense of trends observed in the compositional and covariation analyses, we generated A1-LCD variants in which we assessed whether Gly and Ser are equivalent spacers by replacing all Ser residues with Gly (+23G−23S) or replacing increasing numbers of Gly with Ser residues (−10G+10S, −20G+20S, −30G+30S) (Supplementary Fig. 6). We attempted to purify a variant in which all Gly residues were replaced with Ser, but this variant was not stable. We also performed Gly vs. Ser titrations in the background of −12F+12Y, which replaces all Phe with Tyr, and in the background of +7F−7Y, which replaces all Tyr with Phe, to address potential effects of Tyr / Gly and Phe / Ser covariation.

Increasing the Ser content beyond that of the WT sequence (−10G+10S, −20G+20S, −30G+30S) weakens the driving forces for phase separation (Fig. 7d, Supplementary Fig. 6). This is consistent with the prediction ^{16, 17, 19, 20} that increasing v_es through changes to spacer residues weakens the driving forces for phase separation. Conversely, replacing all Ser residues with Gly (+23G−23S) enhances the driving forces for phase separation. This observation is consistent with the expectation that Ser to Gly substitutions lower the v_es of A1-LCD, thereby enhancing the driving forces for phase separation. Our titrations suggest that Gly and Ser residues therefore act as true spacers, and their different effects on phase behavior are consistent with changes that modulate v_es. Interestingly, replacement of Ser residues with Gly in the context of a variant in which all aromatic residues were Tyr (+23G−23S−12F+12Y) strengthened phase separation strongly while the effect was smaller in the context of the variant in which all aromatic residues were Phe (+23G−23S+7F−7Y; Fig. 7d). Further, the effects from replacement of Gly with Ser residues in these contexts tended to be saturable, in that replacing additional Gly with Ser residues did not have further effects on phase behavior.

We also investigated the effects of other polar residues specifically Asn, Gln, and Thr (Extended Data Fig. 7). This was achieved using the following variants: −14N-4Q+18G where we replaced all 14 Asn and 4 Gln residues with Gly, −14N+14Q where we replaced all 14 Asn residues with Gln, and −23S+23T where we replaced all 23 Ser residues with Thr (Extended Data Fig. 7). The expectation was that v_es should decrease for −14N-4Q+18G vis-à-vis A1-LCD, whereas v_es should increase for the variants −14N+14Q and −23S+23T, respectively. Accordingly, when compared to WT A1-LCD, phase separation should be destabilized for variants −14N+14Q and −23S+23T and stabilized for variant −14N-4Q+18G. These expectations were borne out in measurements of the temperature dependence of the binodals and c_sat (Extended Data Fig. 7). Notice that replacing Asn / Gln with Gly leads to higher critical temperatures, and this is one of the hallmarks of reducing v_es ¹⁹ (Extended Data Fig. 7). We conclude that Gly, Ser, Asn, Gln and Thr residues contribute as bona fide spacers and differences in their effects on phase separation can be attributed to differences they engender for v_es of A1-LCDs.

Discussion

Intrinsically disordered PLCDs are prominent drivers of biomolecular condensates ^{10, 44, 45}. Given their abundance in RNA-binding proteins ⁴⁶, there is considerable interest in understanding the roles of PLCDs in protein function and assembly ⁴⁷. Here, we used a combination of experiments and novel analyses to uncover a set of readily deployable rules that underlie the driving forces for phase separation of PLCDs.

We find that Tyr and Phe are energetically non-equivalent stickers, with Tyr-Tyr interactions being measurably stronger than Tyr-Phe and Phe-Phe interactions. The measured saturation concentrations of A1-LCD variants increase as the magnitude of the NCPR increases. Analysis of compositional biases across homologs of A1-LCDs also reveals a clear preference for Arg over Lys. Through systematic titrations, we find that Arg plays the role of a context-dependent auxiliary sticker whereas Lys has a destabilizing effect on A1-LCD phase separation. Further, we find that negatively charged residues destabilize phase separation due to their large and positive effective solvation volumes.

We developed and deployed a mean-field model to generate a master curve that explains how the combination of the numbers of Tyr / Phe stickers, the numbers of Arg / Lys residues, the NCPR, and the solution temperature contribute to the driving forces for phase separation of PLCDs (Fig. 5e,f). Interestingly, the optimum NCPR that maximizes the driving forces for phase separation of A1-LCD and designed variants thereof is ≈+0.02. The preference for excess positive charge combined with the preference for Arg over Lys, points to the importance of networks of Arg-π interactions ⁴⁸. It could also be a reflection of the preferential condensation of solution anions around cationic residues ⁴⁹. The mean-field model cannot be used for assessing differences such as the changes from Tyr to Phe or vice versa while keeping the rest of the sequence fixed. This is because the sticker-sticker interactions are treated in an averaged sense. However, the rules inferred here can be captured and deployed in a model for LASSI ¹⁶ or PIMMS ¹³ based simulations of PLCDs. These simulations reproduce the entire spectrum of measured phase behaviors for A1-LCD variants and the results are to be presented elsewhere ⁵⁰.

We also investigated the effects of changes to proposed spacer residues on the driving forces for phase separation. If the identities, valence, and patterning of stickers remain unchanged, then changes to spacer residues will impact phase separation by altering v_es through their contributions to steric bulk and intrinsic free energies of solvation. Increased charge contents titrate the effect of increasing v_es by making the free energy of solvation more favorable. Increasing the steric bulk of spacers destabilizes phase separation whereas decreasing the steric bulk results in stabilization. Changes to stickers have stronger effects than changes to spacers as previously reported ⁵¹, but given the high spacer content of PLCDs, changing their identity and thus v_es can have considerable effects. Interestingly, the effects of increasing Ser over Gly contents are saturable in variants with only one type of aromatic residue. This indicates that a heterogeneous composition of Tyr / Phe stickers is important for achieving tunability of phase behavior through changes to v_es achieved by making changes to spacers ¹⁹.

Our bioinformatics analysis reveals positive correlations between Tyr and Gly as well as Phe and Ser content (Fig. 7a, 7b). We also observe concomitant negative correlations between Tyr and Phe (Fig. 1b), Gly and Ser (Fig. 7c), Tyr and Ser, and Phe and Gly (Extended Data Fig. 6), respectively. Taken together with the rules that emerge from our measurements of the driving forces for phase separation of PLCDs, we surmise that the driving forces for phase separation may be evolutionarily modulated through compositional covariations. One possible explanation for why these covariations exist comes from the observation that a particularly high Gly content seems to mimic polyglycine-like behavior ^{52, 53} within certain A1-LCD backgrounds. Specifically, increasing the Gly-to-Ser ratio in a construct where all the Tyr residues were replaced with Phe unexpectedly caused an increase in c_sat at lower temperatures and a steeper dilute arm of the binodal. In comparison, similar substitutions in the WT construct or in a construct where all Phe were replaced with Tyr resulted in decreased c_sat at all temperatures and relatively unchanged slopes. We hypothesize that the decreased sticker-strength of the Phe-dominated construct allows the relatively long Gly tracts to function as competing stickers that can generate dynamically arrested phases ⁵⁴, a feature that derives from the tendency of uninterrupted polyglycine molecules to self-associate with one another ^{52, 53}. This effect appears to be avoided in naturally occurring sequences by replacing Gly with Ser in sequences that are rich in Phe.

Previous observations regarding the correlation between single-chain dimensions in dilute phases and measured saturation concentrations, which we have referred to as strong coupling, have proven to be an important tool for computing and analyzing phase diagrams from single-chain simulations of coil-to-globule transitions ^{22, 23, 24, 55, 56, 57, 58}. This is because the assumption of strong coupling enables one to infer properties of the dense phase from simpler measurements of chain dimensions in the dilute phase. Here, we show that the driving forces for single-chain contraction and multi-chain phase separation can be decoupled if the magnitude of the NCPR increase is just enough to impact multi-chain interactions and not the dimensions of single chains (Fig. 6f).

Natural PLCDs are finite-sized heteropolymers with hidden complexities. These systems are distinct from effective homopolymeric systems such as resilin-like polypeptides that have been used to query the impact of specific types of stickers using host-guest systems ⁵⁹. Recent work ⁵⁹ used linear regression models to assess how the transition temperature at a fixed protein concentration changes in response to different amino acid substitutions. The insights, which parallel some of our findings, are useful for guiding engineering efforts of artificial, homopolymer IDPs with desired properties.

Are the rules extracted from our studies of A1-LCD variants transferable to PLCDs from other RNA-binding proteins, of the FET family (where FET stands for FUS, EWS and TAF15)? We begin to answer this question by generating a curated database of ~3,000 PLCDs from homologs of FUS / FET family proteins ^{60, 61}. The pairwise compositional similarities between these sequences and A1-LCD were on par with those observed for A1-LCD homologs. This suggests that the compositional biases uncovered for PLCDs across homologs of hnRNPA1 are preserved across PLCDs from homologs of FUS family proteins (Extended Data Fig. 8). Intriguingly, unlike the PLCDs from homologs of hnRNPA1, the PLCDs from homologs of FUS / FET family proteins show a stronger bias toward Tyr over Phe (Extended Data Fig. 8). This suggests that the driving forces for condensate formation might be evolutionarily tuned by titrating σ_YF in PLCDs from homologs of hnRNPA1, whereas the tuning in PLCDs across homologs of other FET family proteins is achieved by titrating the Tyr content. The tuning of sticker valence is also achievable through alternative splicing whereby splice variants feature different numbers of Gly-Tyr motifs ⁶². It is likely that the material properties of condensates such as stress granules that feature a diversity of PLCDs might be influenced by networks of heterotypic interactions where the PLCD-specific variations in σ_YF and Tyr content might enable the tuning of relative strengths of sticker-sticker interactions.

Methods

Details regarding the amino acid sequences of each designed variant, protein expression and purification, sample preparations for and collection of NMR, SAXS, and microscopy data are described in the Supplementary Information. Details of the bioinformatics analyses and mean-field stickers-and-spacers model are also provided in the Supplementary Information.

Measurements to construct binodals:

Phase separation was induced by adding NaCl to a final concentration of 150 mM. Dilute and dense phase concentrations were determined as a function of temperature using a centrifugation method ^{13, 26}. Briefly, phase separation of the sample was induced, and the dilute and dense phase were separated via centrifugation. Protein concentrations were determined by suitable dilutions of the samples and measurements of their absorbance at 280 nm. Points on the binodal above 30°C were determined via cloud point measurements using static light scattering as previously described ^{13, 27}. Briefly, phase separation of the sample was induced, and the dilute and dense phase were separated via centrifugation. Most of the dilute phase was removed and the remaining sample was heated above the critical point to enter the one-phase regime. 2 μL were removed with a positive displacement pipette and diluted to determine the protein concentration. 18 μL of the sample was transferred to a temperature equilibrated quartz DLS cuvette and the static light scattering was monitored as a function of temperature (temperature ramp 0.4°C/min) using a Wyatt NanoStar DLS instrument. The temperature at which the light scattering signal increases marks the transition of the one-phase regime into the two-phase regime. Cloud points at relatively lower temperatures/concentrations showed good agreement with coexistence points determined by centrifugation.

van’t Hoff analysis:

The chemical potentials of the dilute and dense phases can be written as μ_dilute=μ°_dilute + RTln(c_dilute/c_ref) and μ_dense=μ°_dense + RTln(c_dense/c_ref), respectively. Here, μ°_dilute and μ°_dense are the standard state chemical potentials of the PLCD molecules in the dilute and dense phases, respectively. Our measurements reveal that the concentrations of PLCD molecules in the dense phase show a weak dependence on temperature and on the sequence / compositions of the different variants. Accordingly, we set the reference concentration to be 0.03 M, which is also the approximate value of c_dense irrespective of temperature or the variant. This assumption is valid away from the critical point. At equilibrium, μ_dilute= μ_dense. Rearranging the equations for chemical potentials using the assumptions summarized thus far, we obtain the expression Δμ° = RTln(c_dilute/c_ref), where Δμ° = μ°_dense – μ°_dilute. The difference in standard state chemical potentials Δμ° quantifies the change in standard state free energies associated with transferring PLCD molecules from the dilute to dense phase. Assuming temperature independent values for standard state enthalpies (Δh°) and entropies (Δs°), we obtain the van’t Hoff equation ⁶³ according to which:

$$\begin{gathered} \mathrm{\Delta }{\mu }^{°}=\mathrm{\Delta }{h}^{°}-T\mathrm{\Delta }{s}^{°}=RT\ln \left(\frac{c_{\text{dilute}}}{c_{\text{ref}}}\right)=RT\ln \left(\frac{c_{\text{sat}}}{0.03\text{M}}\right) \\ \Rightarrow \ln \left(\frac{c_{\text{sat}}}{0.03\text{M}}\right)=\frac{\mathrm{\Delta }{h}^{°}}{RT}-\frac{\mathrm{\Delta }{s}^{°}}{R} \end{gathered}$$ (1)

Here, R = 0.001987 kcal/mol*K is the ideal gas constant. According to Equation (1), the slope of a plot of ln(c_sat/c_ref) versus (RT)⁻¹, providing it is linear, will yield an estimate of the change in standard state enthalpy (Δh°) and the intercept quantifies the standard state entropy (Δs°) associated with transferring PLCD molecules across the phase boundary between coexisting dilute and dense phases. Supplementary Fig. 7 shows the linear fits and associated parameters for all variants.

Data and Code availability

NMR assignments of A1-LCD +7K+12D are available from the BMRB at accession code ID 50739. All expression plasmids are available from T.M. under a material transfer agreement with St. Jude Children’s Hospital. Code needed to reproduce the results, SAXS data, CD data, experimental binodals, pH-dependent measurements, sequences used in the bioinformatics analysis, and estimated saturation concentrations of PLCD homologs are available at https://github.com/Pappulab/ PLCD-Data-Repository-and-Analysis-Routines.

Extended Data

Extended Data Figure 1: Compositional analysis of PLCDs from homologs of hnRNPA1.

(a) 2D histogram quantifying the joint distribution of lengths of PLCDs derived from homologs of hnRNPA1 and the compositional similarities, in terms of cosine values, to A1-LCD. (b) Distribution of fractions of aromatic residues (Tyr, Phe, and Trp). (c) Distributions of fractions of Glu and Asp residues. Numerical values are mean values of the respective distribution ± the standard deviations.

Extended Data Figure 2: ¹H,¹⁵N HSQC spectrum of the A1-LCD variant +7K+12D.

The plot on the right is an expansion of a crowded area of the spectrum (indicated by a box on the left). Spectra were collected in homogenous samples in the absence of phase separation. The lack of chemical shift dispersion indicates that the protein remains primarily disordered. Despite the significant overlap, 80% of the amide chemical shifts were assigned to their respective amino acid residues (i.e., 110 of the 135 non-proline residues).

Extended Data Figure 3: Aromatic residues are the main stickers in A1-LCD variant +7K+12D.

Panel on the left shows an overlay of ¹H,¹⁵N HSQC spectra of WT A1-LCD Δhexa variant (missing residues 259–264, red) as reported in (Martin et al. ¹³) and of A1-LCD variant +7K+12D (blue). The amino acid substitutions result in large-scale changes in resonance frequencies across the spectrum compared to the A1-LCD Δhexa. This may be expected due to the high number of charged amino acid substitutions and their widespread distribution. The panel on the right shows ¹⁵N R₂ relaxation profiles for WT A1-LCD Δhexa (top) and the +7K+12D variant (bottom). The R₂ relaxation rates are sensitive to differences in local dynamics due to intramolecular interactions. The solid black profile represents a pure Gaussian fit, whereas the black dashed fit represents multiple regions of enhanced relaxation centered at aromatic residues (yellow) with the blue line representing the underlying Gaussian profile from this fit with a persistence length of 7.8 amino acid residues. R₂ rates for +7K+12D show clusters of enhanced rates in similar sequence positions as the WT, with an additional cluster found in the hexapeptide region that is deleted in the WT and where two aromatic residues are located. This is consistent with the aromatic residues remaining stickers. These data support our prediction that Lys and Asp residues do not act as stickers. Instead, they modulate the driving forces for phase separation through a combination of increased effective solvation volume, electrostatic repulsions, and weakening attractive interactions among primary and auxiliary stickers.

Extended Data Figure 4: Measured pH-dependence of c_sat validates the prediction that the minimum value for c_sat is realized at positive values of NCPR.

(a) Saturation concentration of A1-LCD +7K+12D was measured at 4°C as a function of pH. Individual data points are shown as black crosses, the mean as green symbols, vertical lines represent the standard deviation. (b) Table summarizing the theoretical net charge of A1-LCD +7K+12D and the number of Lys residues that are calculated to be protonated at each pH. (c) Measured c_sat values for +7K+12D were rescaled using the equation for c_sc,2. Here, we compare the c_sc,2 values when we account for all nine Lys residues (red diamonds) or only the number of protonated Lys residues (green diamonds). The latter conform to the master curve, whereas the former deviate significantly from the master curve.

Extended Data Figure 5: Kratky plot of the raw SEC-SAXS of A1-LCD variants.

Data are shown for variants testing the roles of (a) negatively charged residues, (b) positively charged residues, (c) arginines, and (d) oppositely charged residues. Data were logarithmically smoothed into 40 bins. Solid lines are fits to system-specific empirical molecular form factors (MFF).

Extended Data Figure 6: Compositional analysis of aromatic stickers and Gly/Ser spacers.

(a) 2D histogram quantifying the joint distribution of the fractions of Tyr and Ser across PLCDs from 770 homologs of hnRNPA1. (b) 2D histogram quantifying the joint distribution of the fractions of Phe and Ser across PLCDs from 770 homologs of hnRNPA1. The solution conditions for all experiments were 20 mM HEPES, 150 mM NaCl, pH 7.0.

Extended Data Figure 7: Examining the effects of other spacer residues on A1-LCD phase behavior.

(a) Diagram of variants to understand the contributions of Asn, Gln and Thr to effective solvation volumes of A1-LCD. In variant −14N-4Q+18G, the role of Asn and Gln residues in comparison to Gly spacers is assessed. In variants −14N+14Q and −23S+23T, residues with similar intrinsic free energies of solvation but different steric bulk are substituted. Vertical bars in the schematics indicate the position of residue types, namely Asn (red), Gln (yellow), Gly (green), Ser (black) and Thr (purple). (b) Measured binodals of A1-LCD variants from (a) as a function of temperature. (c) A focused view on the dilute arms (saturation concentrations) of the binodals in (b). The solution conditions for all experiments were 20 mM HEPES, 150 mM NaCl, pH 7.0.

Extended Data Figure 8: Compositional biases in PLCDs drawn from homologs of the FUS / FET family of proteins.

(a) 2D histogram quantifying the distributions of lengths of PLCDs from FUS / FET family homologs and their compositional similarities to WT A1-LCD. (b) Histogram of the distribution of NCPR values; (c) Histogram of fraction of aromatic residues (Tyr, Phe, and Trp); (d) distribution of Tyr versus Phe asymmetries for LCDs from FUS / FET family homologs; numerical values are mean values of the respective distribution ± the standard deviation. (e) 2D histogram quantifying covariations in fractions of Tyr versus Phe residues across PLCDs.