Understanding Förster Resonance Energy Transfer in the Sheet Regime with DNA Brick-Based Dye Networks

Abstract

Controlling excitonic energy transfer at the molecular level is a key requirement for transitioning nanophotonics research to viable devices with the main inspiration coming from biological light-harvesting antennas that collect and direct light energy with near-unity efficiency using Förster resonance energy transfer (FRET). Among putative FRET processes, point-to-plane FRET between donors and acceptors arrayed in two-dimensional sheets is predicted to be particularly efficient with a theoretical 1/r⁴ energy transfer distance (r) dependency versus the 1/r⁶ dependency seen for a single donor–acceptor interaction. However, quantitative validation has been confounded by a lack of robust experimental approaches that can rigidly place dyes in the required nanoscale arrangements. To create such assemblies, we utilize a DNA brick scaffold, referred to as a DNA block, which incorporates up to five two-dimensional planes with each displaying from 1 to 12 copies of five different donor, acceptor, or intermediary relay dyes. Nanostructure characterization along with steady-state and time-resolved spectroscopic data were combined with molecular dynamics modeling and detailed numerical simulations to compare the energy transfer efficiencies observed in the experimental DNA block assemblies to theoretical expectations. Overall, we demonstrate clear signatures of sheet regime FRET, and from this we provide a better understanding of what is needed to realize the benefits of such energy transfer in artificial dye networks along with FRET-based sensing and imaging.

Graphical Abstract

INTRODUCTION

Technology development often turns to biological processes for inspiration as nature displays many desirable capabilities that cannot yet be emulated.^1–3 Light harvesting by plants and other species with subsequent photosynthetic conversion of this energy to a chemically storable form is one such prime example. Light harvesting in nature is carried out by specialized 3D structures that absorb light and then transport it to a reaction center (RC) where photosynthesis takes place.⁴ A key part of these structures are the networks of organic pigments that effect the energy transport, with the best known example perhaps being the Fenna–Matthews–Olson (FMO) complex of green sulfur bacteria that consists of 24 bacteriochlorophyll a pigments organized on a protein scaffold.⁵ The superb efficiency of these networks (>99% for the FMO complex) have inspired biomimetic efforts with potential applications to solar energy collection,⁶ biosensing,⁷ spectroscopic characterization,⁸ optical data storage,⁹ and even optically based quantum computing.¹⁰ However, the artificial systems tested to date are generally much simpler and less ordered than their natural counterparts, and their performance has not yet achieved comparable efficiency.^11,12

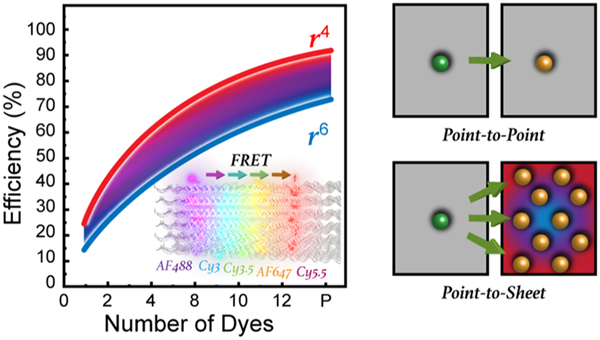
The primary form of energy transfer (ET) in photosynthesis is near-field dipole-mediated Förster resonance energy transfer (FRET).^7,12,13 FRET is well understood, but what is still not appreciated is how photosynthetic organisms are able to collect and move energy using multiple FRET steps with near-unity efficiency. Putative contributors to such efficiency include the ability derived over eons of evolutionary selection to position the optically active donor (D) and acceptor (A) components at exactly the right distances from each other with sub-nanometer precision to maximize FRET. Optimized spacing is critical given FRET’s inherent inverse sixth power ET dependency over D–A separation distance (1/r⁶). D–A stoichiometry is also optimized while each chromophore is positioned with exquisite control over relative orientation to achieve efficient dipole coupling. Nature further utilizes multiple, redundant ET pathways in well-ordered two- and three-dimensional arrays of closely spaced chromophores to achieve high-efficiency long-range transfer. The latter is intriguing, as it suggests the possibility of point D-to-A plane or even plane-to-plane D–A FRET processes, i.e., FRET in the sheet regime.^14–19 FRET between a single point D and multiple A dyes positioned in a plane should ideally manifest a 1/r⁴ ET dependency; this results in a more gradual falloff in ET efficiency as a function of D–A distance than the steeper 1/r⁶ process seen with single D–A FRET processes (see Supporting Information (SI) Figure S9 for a visual plot of this difference). Silbey has previously suggested the presence of such a change in exponential dependency for multichromophore FRET systems in the context of temperature and disorder.²⁰ The improvement arises from the cumulative summation of all possible transfer pathways and, if the fluorophores are appropriately positioned to maximize the effect, should provide for more efficient FRET over significantly longer distances.

Our goal in this paper is to better understand some of the key variables that enable Förster transfer in the sheet regime in real systems. Our focus is on systems of discrete donors and acceptors and not on physically continuous systems such as graphene, metallic absorbers, or surfaces, other 2D materials, or larger (metallic) plasmonic nanoparticle surfaces whose optoelectronic properties are still not fully characterized and where more complex processes may potentially be involved.^21–26 Beyond designing improved FRET networks, this work is also relevant to FRET-based applications such as fluorescent imaging and characterization of cellular membranes and probing of ligand–receptor interactions.^14,27–32

Despite strong interest in the sheet regime and possible payoffs for downstream applications,^33–35 robust experimental formats to quantitatively validate assumptions about point-to-plane and plane-to-plane FRET have remained elusive. Among the challenges facing a thorough investigation are (i) the D–A dyes must each be arrayed in a tight planar format with respect to each other; (ii) the number of dyes present per plane should be adjustable; (iii) there needs to be flexibility in the choice of the D and A dyes; (iv) the interplanar separation must be controllable with nanometer resolution; (v) the ability to characterize the individual dye positions, freedom of movement, and orientations should be available; (vi) the experimental scaffold hosting the dyes must be relatively rigid to minimize inter- and intraplanar movement; and, perhaps most importantly, (vii) the dye-hosting scaffold should be assembled in a facile manner, with good yield, reproducibility, inherent modularity, and affordability. Experimental approaches such as layer-by-layer (LBL) assembly have provided access to some of these desired properties;^33,36,37 however, achieving a plurality, let alone a majority in any one system, remained impossible until the advent of structural DNA nanotechnology.

DNA nanotechnology now allows for the self-assembly of almost any prescribed 3D nanoscale structure with reasonable yield and excellent fidelity.^38,39 Not only can incredibly complex, reconfigurable structures be designed with open source software and assembled from commercially sourced oligonucleotides in a one-pot reaction, they can also be site-specifically labeled with a wide variety of different organic dyes at known nucleotide positions with sub-nanometer precision.⁴⁰ To probe FRET in the sheet regime, we utilize the DNA brick design approach to create a rectangular block architecture consisting of 24 helices that incorporate from 2 to 5 DNA planes with each displaying from 1 to 12 D, A, or intermediary relay dyes; see Figure 1. FRET processes in the blocks were evaluated across multiple geometries displaying variable dye numbers, separation distances, and spectral properties using both steady-state and time-resolved spectroscopy. Idealized numerical FRET simulations were used to develop a detailed theoretical expectation of sheet regime behavior. This, together with FRET simulations that incorporated dye position and orientation information obtained from atomistic molecular dynamics (MD) modeling, was then used to interpret the experimental measurements. Overall, the results demonstrate more efficient directional photonic energy transport by approaching a point dipole-to-plane regime with as little as 4–8 A dyes depending upon dyes and structural configuration.

Figure 1.

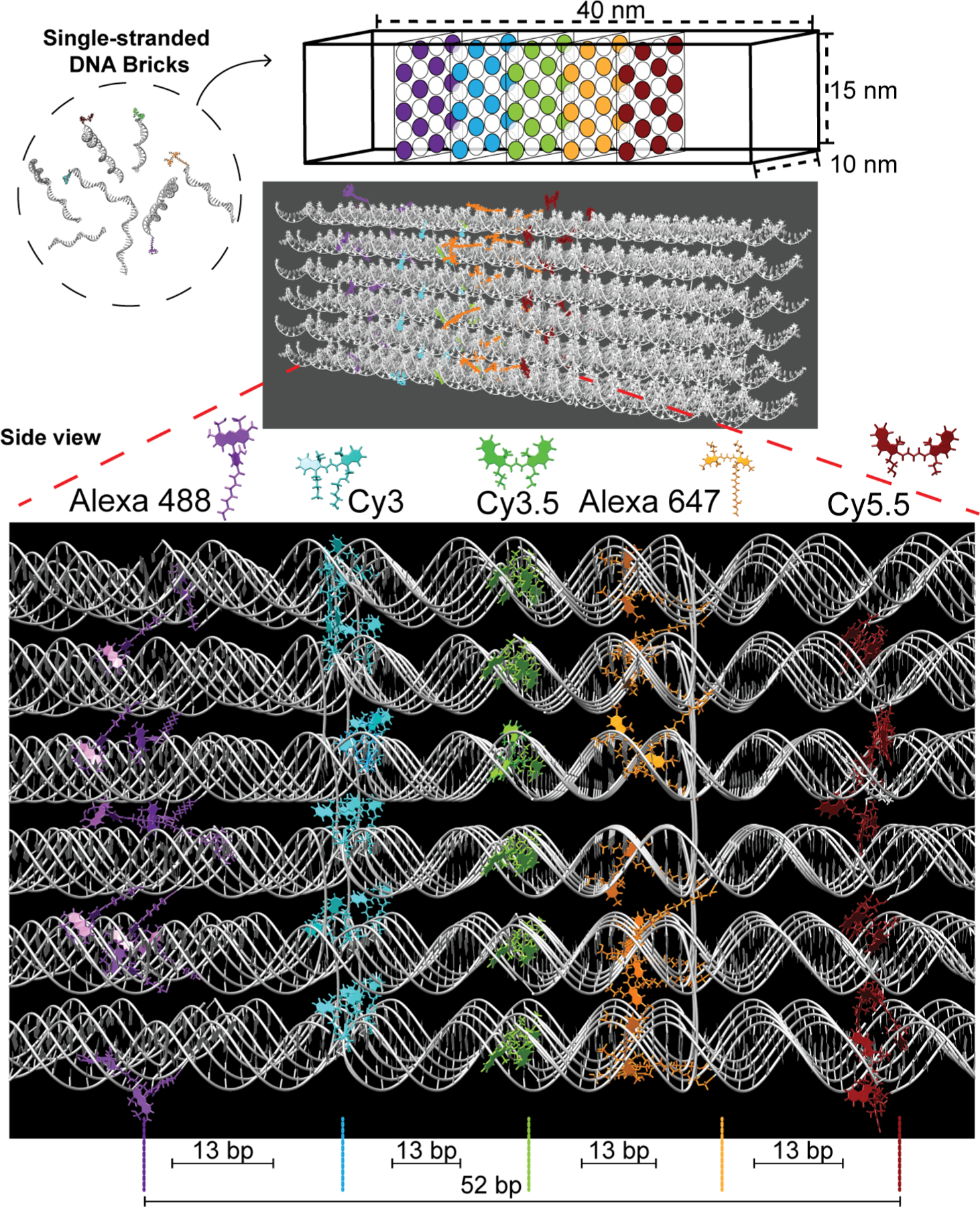
Schematic of the rectangular dye-labeled DNA block. Top: The DNA block self-assembles from ssDNA bricks into a prescribed 10 × 15 × 40 nm cuboidal structure shown schematically and as rendered by Chimera. Below: An enlarged side view highlighting the positioning of the five 2D planes arranged with an inter dye-plane separation of 13 bp. Each plane can display from 1 up to 12 dye copies with each dye positioned on alternating helices. The planes display Alexa 488, Cy3, Cy3.5, Alexa 647, and Cy5.5, respectively, to yield the full sequential initial D → relay → terminal A FRET cascade. See Figure S1 for a side view of the DNA block and a description of the helix numbering and dye positioning/numbering schemes.

RESULTS AND DISCUSSION

DNA Block Design, Donor–Acceptor Dye Pairs, and Confirmation of Assembly.

Details of the DNA block assembly, spectroscopy, and modeling are available in the Experimental Section and the SI. Although many different variants of DNA-based nanostructures are now available,^38,39 the DNA brick approach was selected as it accesses most of the desirable experimental attributes detailed above. In this assembly, a pool of orthogonal single-stranded (ss) DNA strands, referred to as bricks, bearing unique sequence domains (called voxels) hybridize via domain complementarity to form a large three-dimensional molecular lattice or “canvas”. Arbitrary shapes and structures can be “carved out” of this molecular canvas by identifying the voxels that make up the desired structure and using the corresponding subset of brick strands.⁴¹

As depicted schematically in Figures 1 and S1, a rectangular DNA block was chosen as the working scaffold. This assembled as a 6H × 4H × 104B (H = helices and B = bases) cuboid with estimated dimensions of 10 × 15 × 40 nm. Based on initial (unpurified) formation yields of similar cuboidal structures described in Ke et al., namely ones with specifications of 6H × 6H × 128B (∼22% formation yield) and 4H × 4H × 128B (26%), we expected our DNA block to assemble with comparable efficiency.⁴¹ More pertinently, this DNA block contains 6 × 4 × 8 voxels with each voxel consisting of a 13 base pair (bp) double-stranded (ds) DNA domain.⁴² Here, each voxel can potentially be used for end-coupling 1 dye molecule within the DNA block. The final structure was created using CaDNAno (Figure S2), and the required 131 brick strands were obtained commercially (see Table S1).^41,42

A series of 5 parallel vertical planes were designated within the center portion of the DNA block as shown in Figure 1, to each occupy a virtual 2D sheet or plane with a nominal interplanar distance of 13 bp or ca. 4.5 nm (1 voxel). Within each plane, dye sites were located on alternating helices starting near the center of the block and moving outward with a spacing of ca. 5.5 nm between dye tethering locations in that plane as estimated from design parameters (see Figure S1 for dye position definitions).⁴¹ This yielded 60 overall dye tethering sites, allowing for the placement of 1 to 12 dyes within each of the 5 planes (annotated as D1–D12 per plane; see Figure S1c). Note that a D followed by an integer, as in D12, indicates a dye position, while all other instances of the letter D indicate the word “donor”, unless otherwise stated. Critically, the dye spacing within and between planes was also designed such that the dyes should not physically interact with each other and potentially cause self-quenching, which typically occurs when the dye–dye distances are less than 2 nm. This was based on incorporating results from several previous studies where dye freedom of movement at a particular DNA location was studied in detail.^43,44 The dye planes are identical; each dye within a plane aligns with dyes in the other planes along the helical axis and only the inter dye–plane separation alters with a periodicity of 13 bp. This implies that each plane of dyes experiences a similar localized DNA/structural environment. It is important to note that these estimated inter- and intradye spacings do not account for any potential contributions from the length of the chemical linkers used to attach the dyes to the DNA.

The five organic dyes utilized are drawn from the cyanine (Cy) and Alexa Fluor (Alexa or AF) families and include Alexa 488 (AF488 or A488), Cy3, Cy3.5, Alexa 647 (AF647 or A647), and Cy5.5. Individual dye-labeled brick strands were obtained for site-specific incorporation into the assemblies as specified in the SI. This dye set was chosen based on its spectral overlap, robustness, ability to be incorporated into oligonucleotides during synthesis, and extensive use and experience based on previous DNA photonic wire configurations.^45–49 Figure 1 shows each dye structure and their designated plane positions relative to each other at scale except for the Alexa 647 dye, which is at 0.7× scale due to its extended attachment linker length. DNA-attachment chemistry for each dye is presented in Figure S3. Alexa 488, Cy3.5, and Cy5.5 were attached at the 5′ end, whereas Cy3 and Alexa 647 were tethered at the 3′ end of their brick strands. The AF488/647 attachment incorporates an extended 6/12 carbon linker, respectively, while the Cy dyes have 3 carbon linkers. In the role of FRET D’s and A’s (see Table 1 and Figure 2a), when the 5 dyes are placed in each plane in a manner aligning their absorption/emission across the visible spectrum, the design realizes 4 sequential primary D → A FRET pairs (i: Alexa 488 → Cy3, ii: Cy3 → Cy3.5, iii: Cy3.5 → Alexa 647, and iv: Alexa 647 → Cy5.5; → = FRET step). The estimated Förster distance (R₀, D–A separation corresponding to 50% FRET efficiency; eq 5, below) values for these pairs are in the 6.0–6.4 nm range (see Table 1), suggesting that the corresponding FRET efficiency (E_FRET; eq 3b, vide infra) for a single D–A of each pair should be >85% when placed at the nominal ∼4.5 nm separation distance r. The same configuration also gives rise to a number of secondary longer spectral range FRET pairs between alternating or two-plane spacing configurations (v: Alexa 488 → Cy3.5, vi: Cy3 → Alexa 647, and vii: Cy3.5 → Cy5.5). Although R₀ values for these secondary pairs are in a similar 5.8–6.1 nm range (Table 1), E_FRET for a single D–A in these pairs should be less than <9% when placed at the ∼9 nm separation corresponding to two-plane spacing. In sequential D–A systems assembled on linear structures, almost all FRET is expected to occur through nearest-neighbor interactions.⁵⁰ Overall, this combination of 5 dye planes with sequential spectral alignment allows for evaluation of several FRET configurations including point D-to-A plane, D plane-to-point A, and arrays of multiple planes including alternating planes; the numbers of dyes present in each plane can also be varied independently of the other planes.

Table 1.

Selected Photophysical and FRET Properties of the Organic Dye Fluorophores

fluorophore or donor	quantum yielda	ext. coeff (M−1 cm−1)	λmax abs (nm)	λmax em (nm)	R0 in nm with designated donorb
					Alexa 488	Cy3	Cy3.5	Alexa 647	Cy5.5
Alexa 488	0.47	70 000	495	518	4.2	6.0	5.8	4.7	4.2
Cy3	0.38	150 000	550	566		5.2	6.1	6.1	5.5
Cy3.5	0.61	150 000	592	611			5.7	6.4	6.1
Alexa 647	0.48	250 000	647	674				6.1	6.4
Cy5.5	0.30	190 000	676	714					6.0

^aQY of dyes obtained based on comparison to corresponding Fluorescein, Cresyl Violet, Rhodamine 640 (Rhodamine 101), Rhodamine 6G, and Rhodamine 800 (LD 800) standards. Uncertainty of QY ± 0.05.

^bR₀ were calculated assuming dynamic dipoles (κ² = 2/3) and n = 1.33. Uncertainty of values is ±10%.

Figure 2.

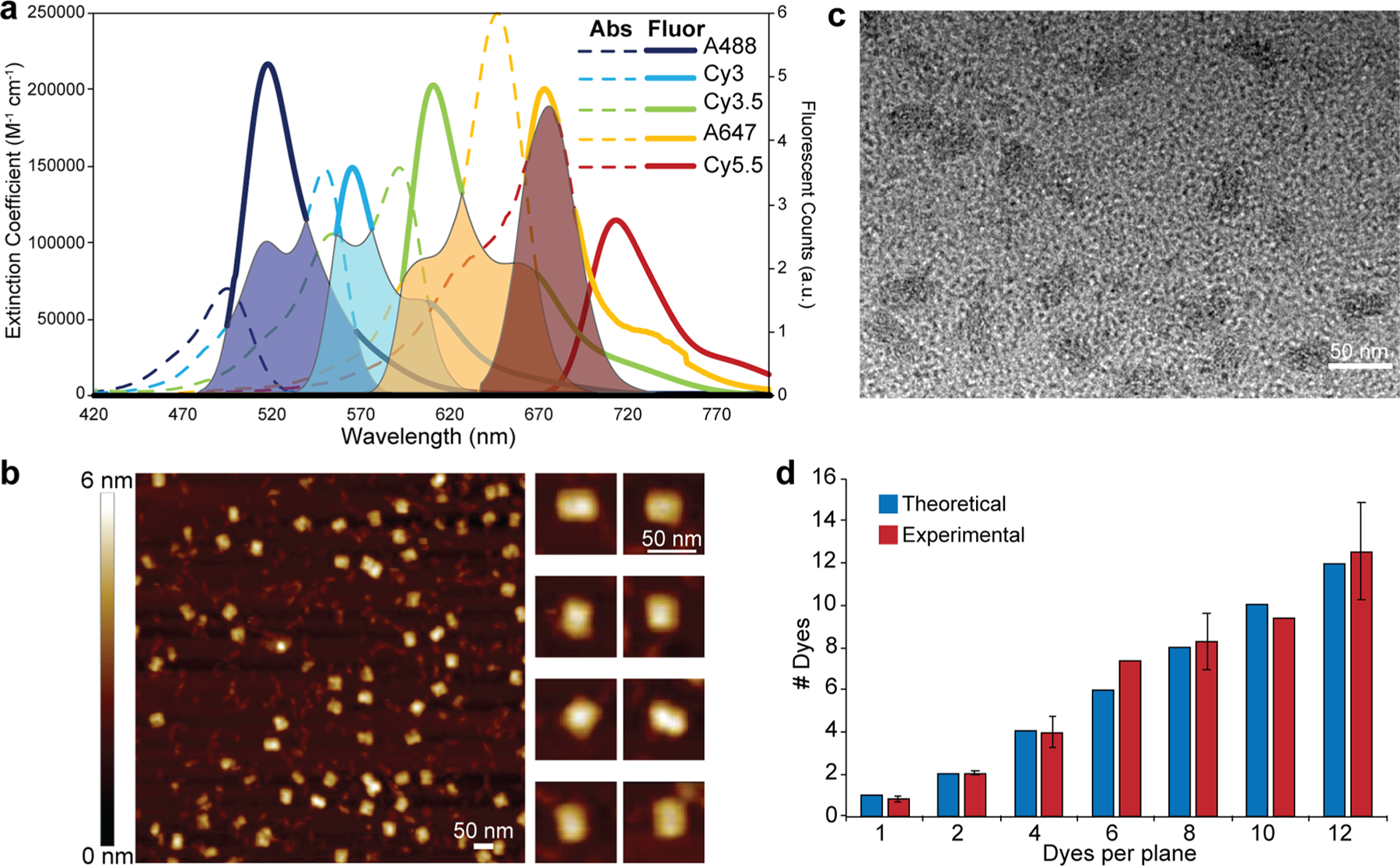
Overview of FRET cascade spectral properties and characterization of the DNA block assembly. (a) Absorption spectra scaled by extinction coefficient overlaid on the fluorescence spectra scaled to the corresponding quantum yield determined by area for the Alexa 488, Cy3, Cy3.5, Alexa 647, and Cy5.5 dyes. Putative spectral overlaps are shown as shaded portions for the four primary D → A FRET pairs: i, AF488 → Cy3 (navy blue), ii, Cy3 → Cy3.5 (cyan), iii, Cy3.5 → AF647 (yellow), iv, AF647 → Cy5.5 (red). (b) Atomic force microscopy (AFM) micrograph of the purified DNA block. Right side shows a gallery of representative higher-resolution images of the block structure. (c) Transmission electron microscopy (TEM) micrograph of the purified DNA blocks (stained with 0.7% uranyl formate). Block structures assume both horizontal and perpendicular configurations when dried on the AFM and TEM grids, hence the different sizes in the AFM and TEM micrographs. (d) Comparison of theoretical and experimentally measured dye incorporation efficiency in various DNA block configurations.

DNA block assembly and subsequent purification was confirmed by agarose gel electrophoresis and microscopy. Representative agarose gel electropherograms showed the separation of unincorporated ssDNA brick strands from the assembled DNA block in the unpurified sample, with quantifiable removal (>99%) of the free ssDNA strands over three rounds of ultracentrifugal filtration (Figure S4). By measuring the band intensity representing formed DNA blocks as a fraction of the intensity of the entire electropherogram lane, we estimated the initial formation yield to be ∼25%, which is comparable to previously reported yields.⁴¹ Representative atomic force microscope (AFM) and transmission electron microscope (TEM) micrographs of purified DNA block samples (Figure 2b,c) reflect consistent formation of the structure with dimensions close to those predicted. To characterize dye incorporation efficiency, we measured the absorbance of purified structures containing increasing ratios of a single dye species. We note that DNA strand incorporation efficiency has been studied for DNA origami structures,^51,52 but equivalent studies have yet to be realized for DNA brick-based assemblies. Comparing the dye absorbance normalized by the 260 nm DNA absorbance (to correct for the number of total DNA structures) with the predicted value for the estimated number of dyes that should be present, we find that for Cy3 and A647 the dye incorporation is near ideal (98 ± 9.0% incorporation, Figure 2d). This also confirmed the ability to control the dye stoichiometry in different block assemblies.

FRET Characterization in the DNA Block Assemblies.

Arranging from 1 to 12 dyes per plane in up to 5 sequential planes provides for >10¹⁸ potential dye-labeled DNA block combinations. Our studies focused on configurations that addressed specific questions of interest, utilizing >100 different assemblies. Steady-state fluorescence spectroscopy, time correlated single photon counting (TCSPC) lifetime fluorescence, and TCSPC lifetime anisotropy measurements were all used to characterize FRET in these structures. Of particular interest was the dye-labeled structure’s capacity to access the sheet regime as a coupled light-harvesting energy transfer system in experiments where assemblies were formed in parallel with an increasing number of dyes per plane. Similar FRET data were also used to experimentally determine the physical separation between individual dyes in the same plane and between dye planes, i.e., intraplane dye spacing (a) and interplane spacing (c), respectively.

Figure 3 shows representative steady-state fluorescence spectra collected from experimental structures displaying the indicated number of dyes per plane (1, 2, 4, 8, and 12, respectively) as each downstream A was added into the DNA block and compared across parallel assemblies with sequentially increasing numbers of labeled planes included. The cartoon above each depicts the configuration present in the final fully labeled 5-plane configuration along with the descriptive nomenclature used. The evolution of spectra as the D → A dye cascade is built up with addition of each downstream plane manifests a similar overall appearance (see Figure 3a–f, Figure S6). For example, in the Figure 3d series displaying 8 dye copies per plane (designated 8/8) the initial 8 Alexa 488 D photoluminescence (PL) is significantly quenched by the addition of 8 Cy3s to the adjacent A plane with the Cy3 PL significantly enhanced by FRET. Sensitized Cy3 plane emission now acting as D is, in turn, significantly quenched by the addition of a downstream Cy3.5 A plane and so on until all dyes are present. Figure 3f plots a series of spectra collected from an assembly designed to form an optical D–A pyramidal (denoted as P) or funnel arrangement of dyes. Here, the initial Alexa 488 D plane has all 12 dye copies present, the adjacent Cy3 A plane only has 10 dyes, and each subsequently added A plane after that has 2 less copies of dye than its predecessor D plane. Dyes were removed from the outer portion of each plane in a stepwise manner to sculpt the central pyramid shape based on a large initial Alexa 488 D dye base with each subsequent plane narrowing down to the terminal Cy5.5’s centrally placed 4-dye apex.

Figure 3.

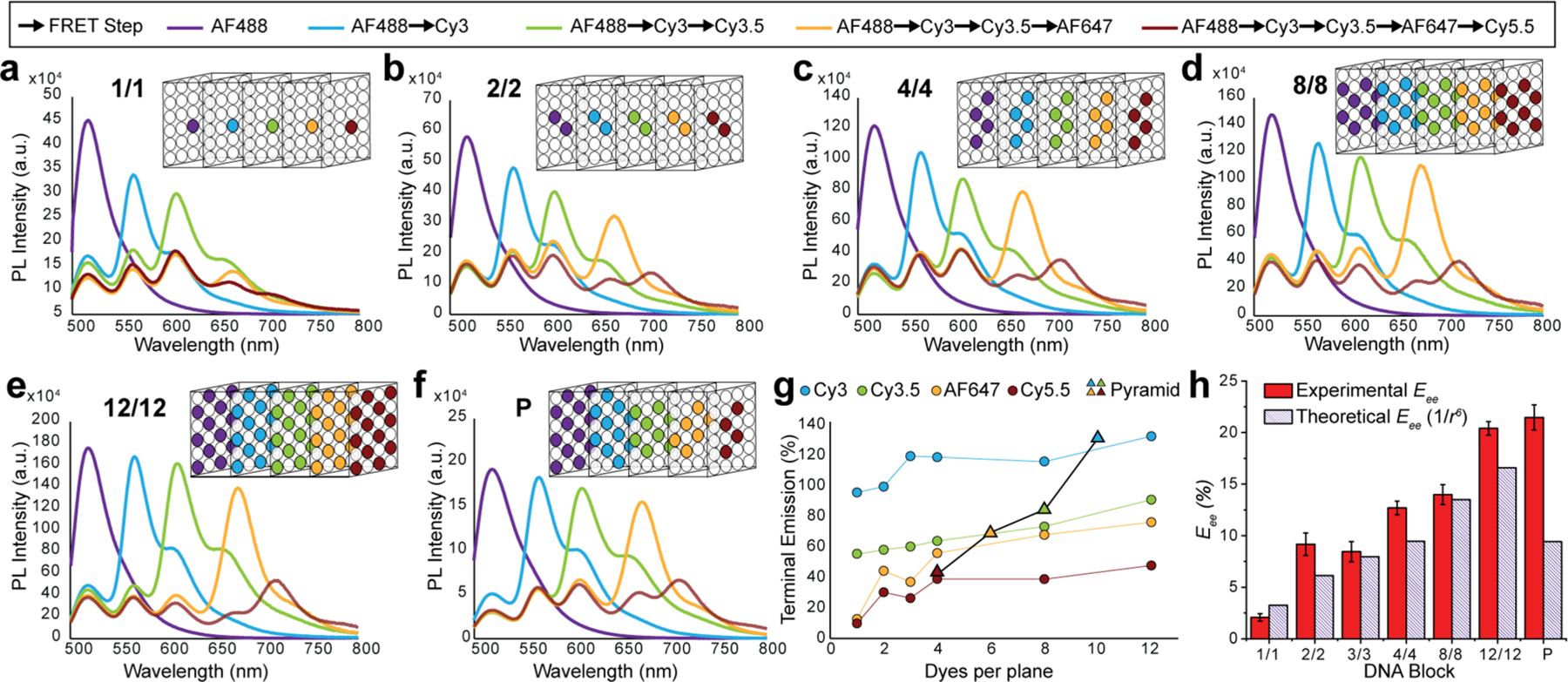
Steady-state fluorescence characterization of DNA blocks incorporating increasing ratios of dyes per plane. DNA blocks assembled with 1, 2, 4, 8, and 12 copies of each dye per plane are shown in panels (a)–(e), respectively. Each panel shows the evolution of spectra collected as each downstream A dye was added to the next plane in parallel assemblies. Nomenclature indicates the number of copies of each dye type incorporated in the structure, while the box structure schematically depicts this for the final plane-to-plane configuration. Descriptive nomenclature is based on the number of copies of a given dye present in each plane. DNA position on a plane is invariant, i.e., dye 1 will be on the same helix merely 13 bp laterally shifted on a different brick strand independent of the dye plane chosen. Similarly, the position for multiple dye copies was also kept unchanged; that is, when there are 4 dye copies in a plane, those 4 dyes will be in position 1 through 4 in all the 5 dye planes. A DNA block with 4 dye copies present in each plane or 4–4–4–4–4 is then abbreviated to the 4/4 shown (c). Figure S5 and Tables S2–S8 specify the brick strands used for the insertion of the 5 dyes into the DNA block. Corresponding data for the DNA block with 3 copies of each dye is found in Figure S6. (f) Data from a pyramid (P) structure assembled with 12 AF488, 10 Cy3, 8 Cy3.5, 6 AF647, and 4 Cy5.5 dyes. Dyes in each plane were removed from the outer edges inward in each successive plane to yield a pyramidal configuration with a large AF488 D base plane that constricts into a central terminal Cy5.5 apex plane. (g) Overview of terminal emission (TE) in panels (a)–(g) as each successive A plane is added. TE designates how much the PL of a dye plane is enhanced relative to the initial AF488 D when that dye is added as the terminal A versus increases in the number of dyes per plane. Pyramid data have the corresponding dye plane from which data were drawn highlighted and are plotted by dye number present. (h) Experimentally determined end-to-end efficiency (E_ee) estimated from steady-state fluorescence collected from fully labeled block assemblies (AF488 → Cy5.5) as the number of dye copies per plane is increased. Theoretical E_ee assumes each D–A pair has a 1/r⁶ E_FRET distance dependency.

Figure 3g presents a simplified overview of the cumulative spectral changes across all the systems as the number of dyes per plane is increased from 1 to 12. To provide a comparative overview, we utilize a metric called terminal emission (TE [%]), which is defined as the total emission counts detected from a wavelength corresponding to the final terminal emitter A dye present when the DNA block is excited at 466 nm as normalized to a DNA block containing the same number of A488 dyes only. Since increases in TE reflect increasing amounts of light being propagated through the system, it serves as a simple normalized comparator of relative efficiency across all systems while both plane occupancy and dye numbers are built up at each ET step. Increasing the number of dyes per plane improves TE, with the initial increases from 1 to 4 dyes having the greatest effect and an observed plateauing in efficiency as the number of dyes increases from 4 to 12. Values derived from the pyramid structure (Figure 3f) are also plotted on this graph as a function of the number of dyes present when acting as the terminal A. Interestingly, pyramid TE values are in line with the 12/12 densest-labeled block structure, while decreasing the total number of dyes present by 20 or one-third in comparison. Tables of TE and E_FRET (eq 4) values for all structures are available in the SI (Tables S9, S10).

Changes in E_FRET for structures with multiple ET steps in series are best characterized by looking at changes in end-to-end efficiency (E_ee), which, for the case of the fully labeled DNA block, reflects the conditional probability that an exciton created on an initial Alexa 488 D arrives at a terminal Cy5.5 A and is estimated with

$$E_{\text{ee}}=100\times \frac{\left[f\times \frac{{\Phi }_{\text{AD}}}{Q_{\text{A}}}\right]}{\left(\frac{{\Phi }_{\text{D}}}{Q_{\text{D}}}\right)}$$ (1)

Here, Φ_AD is the A emission (Cy5.5) in the presence of all the dyes, Φ_D is the emission of the D (AF488) only, while Q_A and Q_D are the quantum yields of the AF488 D and Cy5.5 A, respectively. E_ee requires a correction factor, f, that incorporates individual E_FRET (Table S10) and respective extinction coefficients to account for the percentage of downstream dyes other than AF488 that are excited at the 466 nm wavelength.⁵³ This factor is calculated with

$$f=P\left(\text{AF}488,n\right)=\frac{\left[d_{\text{AF}488}\right]\times {ϵ}_{d_{\text{AF}488}}^{466\text{nm}}}{\sum \left[d_i\right]\times {ϵ}_{d_i}^{466\text{nm}}}$$ (2)

where d represents the dye, i = (AF488, Cy3, Cy3.5, AF647, Cy5.5), n is the number of dye copies per plane, [d_i] is the relative dye concentration, and ${ϵ}_{d_i}^{\lambda }$ is the extinction coefficient of the dye at the excitation wavelength used (466 nm in our measurements).

As highlighted in Figure 3h, E_ee values over the total 5-dye plane separation distance of ∼32 nm increased from 2% for the 1/1 assembly to ∼23% as seen in both the 12/12 and pyramidal dye configurations. Theoretical E_ee values are coplotted for comparison and were determined assuming that each dye pair is acting as a classical or single D–A FRET pair following the expected 1/r⁶ exponential decay (eqs 3 and eq 7, below) under conditions of dynamic dipole coupling (dye positions were determined experimentally as described below). For all cases except the 1/1 structure, experimental values were greater than the theoretical value, suggesting the possibility that deviations from point dipole–dipole interactions might be occurring. Note that the 1/1 case is particularly susceptible to any formation yield issues since structures with a dye missing will have an efficiency close to zero. We assign E_ee improvements over the expected r⁶ values (∼30% on average) to a small sheet regime improvement in each transfer step, which then accumulates in a multiplicative manner over the four transfer steps (vide infra). Performance of the DNA blocks as a light-harvesting unit, analysis of their stepwise ET, and an example of multi-D to single A FRET, with metrics including antenna gain (AG) and anywhere-to-end efficiency (E_ae), are available in the SI (Figure S7). In brief, we note that the efficiency of the DNA blocks as an antenna is greater than most other linear systems, but is only about half that seen in previously described dendrimeric and concentric multiFRET systems displaying far denser dye arrangements.^46,49,54

Characterization of dye positions and, more importantly, their relative separation(s) within the DNA blocks were determined by TCSPC fluorescence lifetime analysis to minimize concentration and inner filter effects.^12,55 E_FRET from single D → A pairs in these structures was utilized to estimate r_i, the dye–dye distance (using eq 4, below and with R₀ values taken from Table 1) with a value of 2/3 assumed for dynamic dipole orientation (κ²). These same experimental values were used to define the plane-to-plane distances, c, yielding Cy3–Cy3.5 = 6.1 ± 0.2 nm; Cy3.5–AF647 = 6.9 ± 0.5 nm; Cy3–AF647 = 9.9 ± 0.9 nm; and Cy3.5–Cy5.5 = 9.0 ± 0.9 nm. Deviations from the nominally predicted interplanar value of 4.5 nm and also for intraplanar spacing are discussed in more detail below.

Within the design of the DNA block, multiple D moieties in a single plane are also expected to undergo homogeneous FRET (homoFRET) with each other.^54,56,57 Fluorescence lifetime anisotropy analysis was used to confirm the presence of homoFRET and estimate a, the average distance between dyes in the same plane. Anisotropy analysis provides insight into the dye’s rotational diffusion and freedom of movement; the anisotropy of the dyes within the assembled block should be greater than for freely diffusing dye labeled DNA strands. Analyzing data collected on Cy3 anisotropy kinetics confirmed this and showed that the dyes arranged in the block are more static with respect to dipole reorientation (see Figure S8 and Table S11). As dye density increases within a given plane, the dyes are also capable of undergoing more homoFRET, which should also decrease the anisotropy decay time. Analyzing the anisotropy curves and their respective decay times allowed us to determine an average intraplane dye distance, a, of 5.6 ± 0.5 nm.¹³ We note that this value is almost identical to the 5.5 nm predicted from the design parameters. Since the dyes were conjugated to the same helices in the block, we assume that this distance remains unmodified in the other dye planes except for the contributions of the various dye linkers.

Theoretical Predictions versus Experimental Results.

Förster Theory and the Sheet Limit.

For a discrete D–A dye pair interacting in the Förster regime, the energy transfer rate (k_FRET) and FRET efficiency (E_FRET) are given, respectively, by the well-known formulas

$$k_{\text{FRET}}=\frac{1}{{\tau }_{\text{D}}}{\left(\frac{R_0}{r}\right)}^6$$ (3a)

$$E_{\text{FRET}}=\frac{100\%}{1+{\left(\frac{r}{R_0}\right)}^6}$$ (3b)

where τ_D is the lifetime of a D exciton in the absence of A’s and r is the distance between the chromophores.^12,13,58 FRET efficiency is typically measured from the D’s emission (Φ_D) in the presence/absence of A or equivalently the D’s excited-state lifetime (τ) in the same configuration with

$$E_{\text{FRET}}=100\times \left(1-\frac{{\Phi }_{\text{DA}}}{{\Phi }_{\text{D}}}\right);\hspace{0.17em}100\times \left(1-\frac{{\tau }_{\text{DA}}}{{\tau }_{\text{D}}}\right)$$ (4)

R₀ is the Förster distance corresponding to the D–A separation where E_FRET = 50% and is defined as

$$R_0={\left[\frac{9\ln 10{\kappa }^2{Q}_{\text{D}}J}{128{\pi }^5{N}_{\text{A}}{n}^4}\right]}^{1/6}$$ (5)

where Q_D is the D quantum yield, N_A is Avogadro’s number, n is the index of refraction of the medium, and J is the overlap integral (units of M⁻¹ cm⁻¹ nm⁴). The dipole orientation factor κ² is defined by

$${\kappa }^2={\left[\sin {\theta }_{\text{D}}\sin {\theta }_{\text{A}}\cos \varphi -2\cos {\theta }_{\text{D}}\cos {\theta }_{\text{A}}\right]}^2$$ (6)

where the angles θ_D, θ_A, and ϕ specify the relative orientation approximated by 2/3). In the static limit, the dipoles are of the D–A transition dipoles.^12,59 Applied pairwise, eqs 3 are also relevant to more generalized situations with multiple dyes in the Förster regime (spaced sufficiently far apart). For this situation of a single D interacting with multiple nonequivalent A’s, a more phenomenological formula for the energy transfer efficiency (E_ET) that could be used is:

$$E_{\text{ET}}=\frac{1}{1+{\left[{\sum }_i{\left(\frac{R_0}{r_i}\right)}^{\alpha }\right]}^{-1}}$$ (7)

Here the exponent, α, is modified as we transition from a point-to-point to a point-to-plane regime.^{14–19,60,61} Alternatively, for the special case of a single D in front of a planar sheet of A’s, we have from eq 3a that:

$$k_{\text{DAsheet}}=\frac{1}{{\tau }_{\text{D}}}\sum _i{\left(\frac{{R_0}^2}{{r_{\left|\right|i}}^2+{R_{\min }}^2}\right)}^3$$ (8)

where R_min is the perpendicular distance from the D to the A plane (c in our system) and r_∥i is the distance projected parallel in the A plane to the ith acceptor. Equation 8 reduces to an especially simple form when a large number of A’s are present and they are close enough together to be regarded as a continuum. In this case, the summation can be approximated by an integral, and eq 8 reduces to the sheet limit:^62,63

$$k_{\text{DAsheet}}\cong \frac{1}{{\tau }_{\text{D}}}{\int }_0^{\infty }{\left(\frac{{R_0}^2}{{r_{\left|\right|}}^2+{R_{\min }}^2}\right)}^3{\rho }_{\text{A}}2\pi r\hspace{0.17em}\text{d}r=\frac{1}{{\tau }_{\text{D}}}{\left(\frac{{R_0}^{2\text{D}}}{R_{\min }}\right)}^4$$ (9)

where ρ_A is the A concentration (in number of A’s per unit area) and $R_0^{2\text{D}}$ is defined as

$$R_0^{2\text{D}}\equiv R_0^{3/2}{\left(\frac{\pi {\rho }_{\text{A}}}{2}\right)}^{1/4}$$ (10)

The corresponding expression for ET efficiency then becomes

$$E_{\text{DAsheet}}=\frac{100\%}{1+{\left(\frac{R_{\min }}{R_0^{2\text{D}}}\right)}^4}$$ (11)

The sheet formulas in eq 9 and eq 11 are neatly parallel to those for the dye pair in eqs 3, and they show that the sheet’s gain in efficiency due to its multiple paths is expressed in two ways, namely, a falloff as the fourth power of distance rather than the steeper sixth power of ordinary FRET (Figure S9) and an increase in the characteristic D–A FRET distance from R₀ to $R_0^{2\text{D}}$ (with the increase observed as long as a ≤ 1.25R₀).

Simulations of Ideal Sheet Behavior with Discrete Dyes.

To address the question of when do arrangements of multiple discrete A’s begin to act more like a continuous planar distribution, we utilize the formula provided by eq 7 to perform FRET simulations of ideal dye arrangements involving a single D and multiple A’s arranged in a plane. In this ideal dye arrangement, all dyes are present and active, all dye locations are precisely known, and the dipole orientation factor κ² is in either the dynamic or static limit. The ideal assumption of R₀ being the same for all dye pairs happens only in the dynamic limit when the dipoles are able to reorient rapidly in any direction on the time scale of FRET (here κ² is again assumed to have any orientation, but reorient only slowly on the time scale of the FRET. For this situation, numerous FRET efficiency calculations are made, using a Monte Carlo approach, with each having a different random selection of dipole orientations for the dyes.^43,64,65 Averaging over the ensemble then yields an estimate for efficiency in the static limit.

Key variables to be explored in our system include the D–A R₀, the distance between the D and A plane (c), dye-to-dye spacing in the A plane or A plane density (a), and the total number of A’s in a plane since the magnitude and ratios of these variables will determine the transition from point-to-point to point-to-plane ET. Consider first the transfer efficiency of an ensemble of isolated dye pairs with a given D–A distance r. By rewriting eq 3b as

$$\log \left(\frac{100}{E}-1\right)=\alpha \hspace{0.17em}\log \left(\frac{r}{R_0}\right)$$ (12)

a log–log plot of 100/E – 1 versus r/R₀ provides the ET exponent from the slope. For discrete D–A point-to-point FRET, a straight line with a slope of 6 is expected assuming that R₀ is the same for all pairs in the ensemble. Using this, numerical simulation does indeed confirm the exponent (α) of 6 expected from Förster theory; see Figure S10. For simulating a single D interacting with a proximal A plane, the sheet approximations described by eq 9 and eq 11 assume the A plane is continuous and infinite, conditions that can never be fully satisfied by an array of discrete dyes, whether in reality or in numerical simulation. We thus use a symmetric hexagonal lattice with as many as 66 A dyes (with an intraplane dye spacing of a) placed at a distance c opposite a single centrally located D as depicted schematically in Figure 4a. Here R_min = c, since the single D is lined up directly in front of the central A. Because the number of dyes at a distance r_∥ from the central A grows only linearly while their individual FRET contributions fall off as $\frac{1}{{\left(R_{\min }^2+r_{||}^2\right)}^3}$, we expect that the full-size array should provide an excellent approximation to the infinite sheet unless R_min ≫ r_∥. Using the Cy3.5 → AF647 D–A pair (Figure S9) and assuming that the dynamic dipole approximation is valid, we arrange the 66 A’s in various combinations of interplane dye (c) and intraplane (a) dye spacing with the results summarized in Figure 4b. This plot format is somewhat unconventional but functionally serves to provide extensive insight. The x-axis, normalized by R₀, shows that the R_min distance at which the sheet regime is approached depends on the E_FRET of the particular D–A pair. On the left side of Figure 4b, where (log(c/R₀) < 0), the D and A planes are very close together; high E_FRET is expected. On the right side (log(c/R₀) > 0) lower E_FRET is expected. The more interesting aspect of this plot is how this combines with the a/c ratios to determine the ET exponential. The a/c ratio correlates the A density to the distance from the D. One can imagine that at large a/c ratios, ≥1.5, the A dyes are so separated that they all appear as independent chromophores to the D. This is apparent in the dotted section of the lines, which converge in the bottom-left of the plot where the classical Förster single D–A process is obeyed and an exponent of 6 is realized (highlighted by the blue bounding box). Situations are also evident where the sheet model of eq 11 and its exponent of 4 are obtained, namely, when a/c is less than ∼0.8 (full lines, which are generally found in the upper-right of Figure 4b and highlighted by the red bounding box). For 0.8 < a/c < 1.5 (dashed lines), neither limit provides a good approximation. The transition is most easily followed when c = R₀ and one examines the change in slopes along the vertical black dotted line. When a is 10 or 20 nm, the a/c regime is >1.5 and α is clearly 6. As a decreases to 3 or 2 nm, the a/c regime is <0.5 and α = 4, while intermediate a values result in a transition of α between 6 and 4. Though this simulation generally represents an infinite plane, it was observed that when a/c is less than about 0.2, an increase in slope is observed that is a size effect resulting from it no longer accurately representing an infinite A array. The outcome of this approach is an information-rich visual methodology to plot and compare the R₀, a, and c variables and how their different combinations shift the dependency of ET efficiency as described by the α exponent.

Figure 4.

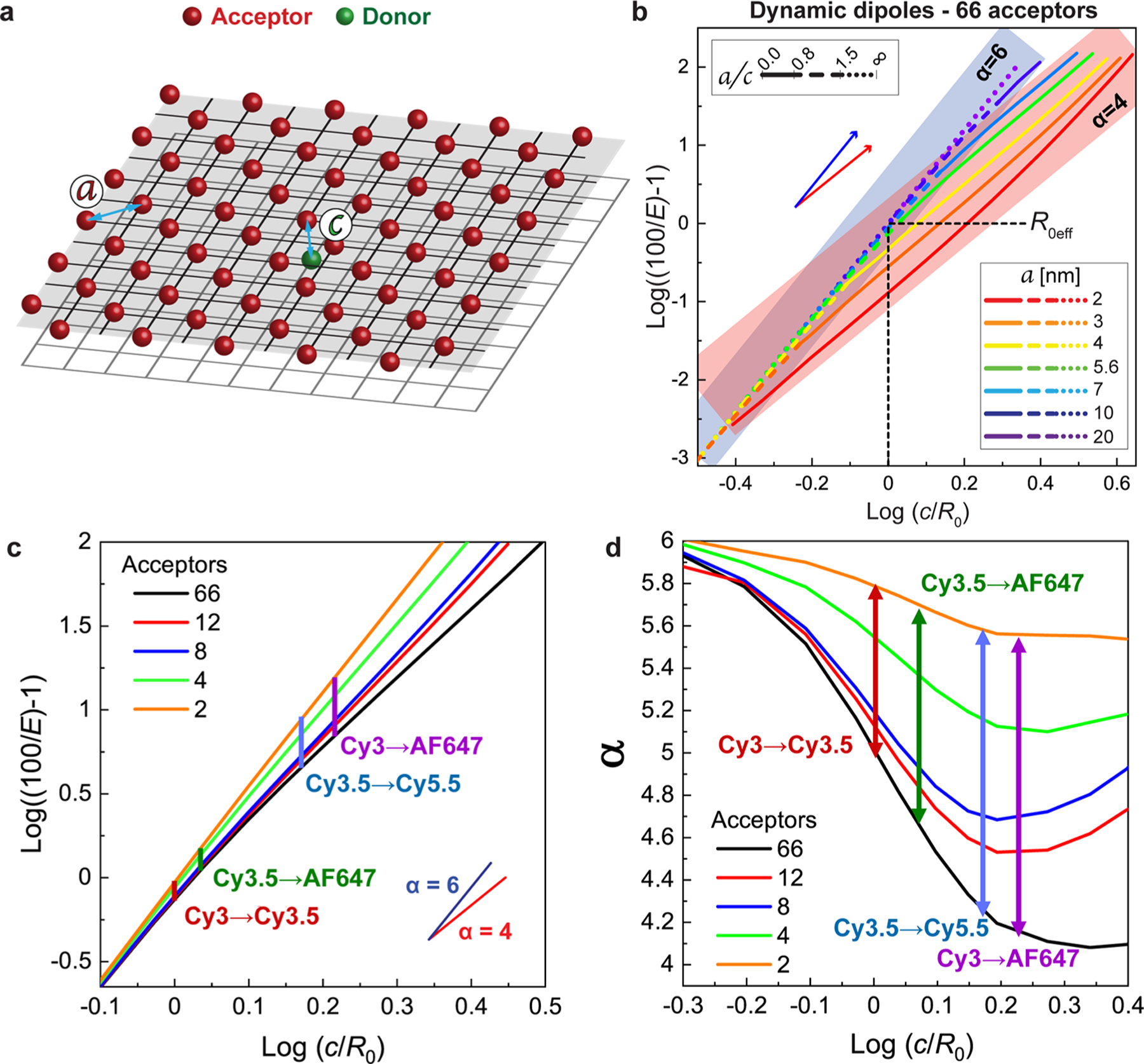
FRET simulations for a single donor with a sheet of acceptors. (a) Simulated arrangement of a single D (green sphere) and a hexagonal 2D array of 66 A’s (red spheres) in a planar-sheet arrangement. The central D is located on a planar sheet underneath the A-sheet. a designates the intraplane dye distance and c is the interplanar distance. (b) Log–log plot of E_FRET with Cy3.5 and AF647 as the D–A pair versus c/R₀ assuming dynamic dipoles between the single D (green) on the bottom plane and the sheet of 66 A’s. Values of a varied as indicated while utilizing R₀ = 6.4 nm, though the lines are equally representative of any equivalent a/R₀ ratio. The slope following the point-to-point Förster formalism (α = 6) is shown as the translucent blue band, and the point-to-plane model with an α = 4 is shown as a red band, thereby highlighting the regimes obeyed by different a/c lattice arrangements. (c) Log graph of ET efficiency as a function of log(c/R₀) obtained from Monte Carlo simulations. The curves represent varying A number for a = 5.6 nm, which was determined experimentally. Vertical lines indicate the varying D–A dye systems at their experimentally determined log(c/R₀) values. (d) E_ET exponential value, α, as a function of log(c/R₀). Curves obtained by determining the derivatives from (c). Vertical lines represent the varying D–A dye systems at their experimentally determined log(c/R₀) values.

An additional way of looking at the results of Figure 4b is to define an effective value of R₀, termed R_0eff, as the value of c when E_FRET = 50%; this quantity can be read directly from Figure 4b with the intersection points along the horizontal black dotted line giving the values of $\log \left(\frac{R_{0\text{eff}}}{R_0}\right)$ for any given value of a/c. The increased energy transfer distance in the sheet limit should manifest as both a smaller exponent and a larger R_0eff, i.e., the transition from R₀ toward $R_0^{2\text{D}}$ (Figure S10). Two additional variables were investigated in a similar manner, the total number of A dyes and the dynamic vs static limit of dipole orientations. Experimentally the structures we prepared had fewer A dyes of a given type than the 66 of Figure 4b that approximate the infinite sheet, and this will introduce significant finite size effects in the experiments. To examine this in an ideal case, we computed versions of Figure 4b in which there is one D but only 2, 4, 8, and 12 acceptors (see Figures S10, S11). In these simulations, slope changes continue to be observed, but the minimum slope is larger and only trends toward the slope of 4 of the infinite-plane result. In the case of the dynamic vs static limit, the static limit creates deviations from the individual D–A R₀, due to the fixed κ², which in turn means that the slopes can vary continuously in all cases. This suggests that although enhanced ET will be observed, no matter what the dimensions of an experimental array are, a clean signature of a sheet-regime α of 4 may not be seen.

Sheet Behavior in the DNA-Scaffolded Structures.

TCSPC analyses of D lifetimes were utilized to estimate E_ET in the four Cy3 → Cy3.5, Cy3.5 → A647, Cy3 → A647, and Cy3.5 → Cy5.5 single D systems as their respective A-ratios increased from 1 to 12; see Figures S12 and S13 and Tables S12 and S13. From these measurements, we derived transfer efficiencies and compared the results with those obtained from modeling. Other dye-pair combinations were inaccessible due to limitations in the TCSPC system’s laser wavelengths available for excitation. Modeling undertaken was of two types, the first being focused on the presumed ensemble version of the DNA block utilizing the equations presented in previous sections (i, “idealized”), while the second utilized molecular dynamics (MD) to try to capture various nonidealities of the actual experimental system (ii, “nonideal”). In either case, from comparisons with experiment we look to draw conclusions about the extent to which the DNA block nanostructure has allowed us to access the sheet regime experimentally and to realize its enhancements of FRET range and E_ET. The four chosen experimental D–A pairs cover a range of c/R₀ and a/c ratios, allowing us to explore pertinent configurations where ET is no longer defined by a point-to-point process and approaches the point-to-plane regime.

i. Idealized Modeling.

Here, we assume the dyes are all present as designed with a 100% formation yield and with 1 to 66 A’s in the A plane. In addition, we take them to be ideally positioned with a = 5.6 nm as determined experimentally and assume the dynamic dipole approximation is valid. On this basis, the relevant simulation results are as summarized in Figure 4c. Also shown in these plots as vertical lines are the range of values obtained as the number of A’s is varied from 1 to 66 for the c/R₀ values estimated from experiment for each dye pair, namely, 1.00, 1.62, 1.07, and 1.48 for Cy3 → Cy3.5, Cy3 → A647, Cy3.5 → A647, and Cy3.5 → Cy5.5, respectively (see Table 1 for R₀ values and the FRET characterization section above for c values). From Figure 4c it is evident that as the number of A’s decreases, the lines approach the expected α = 6 slope, while for large numbers of A’s the slope approaches α = 4, but only when log(c/R₀) ≥ 0.2, or in other words c > 1.6 × R₀. In between these limits we have the experimental realizations with 1–12 A’s, and we expect intermediate slopes. In particular, as the number of A’s varies, the assemblies with single-plane separations (Cy3 → Cy3.5 and Cy3.5 → A647) are predicted to have smaller variations in α (from 5.8 to 5.0), while the assemblies with two-plane separations (Cy3 → A647 and Cy3.5 → Cy5.5) should exhibit greater variations (5.6 to 4.5). These differences are due to the particular a/c ratios, with the smaller α values achieved in the two-plane cases (a/c = 0.56 and 0.62 for Cy3 → A647 and Cy3.5 → Cy5.5, respectively), allowing the off-center A’s to make a relatively larger contribution than for the single-plane cases (a/c ratios of 0.92 and 0.82 for Cy3 → Cy3.5 and Cy3.5 → A647, respectively). The derivatives of the curves in Figure 4c are presented in Figure 4d, correlating directly with the α exponents. Most importantly, from the illustrative plots in Figure 4d, it can be seen for the two-plane cases (Cy3 → A647 and Cy3.5 → Cy5.5) that have 12 A’s that the systems are approaching the theoretical sheet limit with α near 4.

Utilizing the dye positions afforded by the ideal DNA block nucleotide positions (Figure 1 and Figure S1), a dye-position matrix was obtained that provides an r_i value for each D–A pair (eq 7). This assumed that (i) R₀ is unmodified between D–A pairs of the same dye (this necessitates dynamic dipoles) and (ii) dyes in the same plane are all at the same R_min distance (i.e., ignoring positional variance). Analyzing this in conjunction with eq 7 and the respective α values determined in Figure 4d allows us to compare the predicted E_ET values for each of these same D₍₁₎ → A_(n) systems to those experimentally determined. Figure 5a,c highlights this comparison for the Cy3₍₁₎ → Cy3.5_(n) and Cy3.5₍₁₎ → AF647_(n) adjacent plane systems, respectively, while Figure 5b,d present equivalent data for the Cy3₍₁₎ → AF647_(n) and Cy3.5₍₁₎ → Cy5.5_(n) alternating or two-plane spacing configurations, respectively. In these plots, the dotted lines provide guides for applying eq 7 with α = 4, 5, or 6. These comparisons highlight the transition in α as a function of A number (experimental and predicted values are available in Table S14) and how the systems transition from a point-to-point interaction at an A ratio of 1 to the equivalent of a point-to-plane at the highest ratios. We also note that the predicted values correlate well with the experimental results showing no tendency toward systematically over- or under-estimating the values across the different D–A systems.

Figure 5.

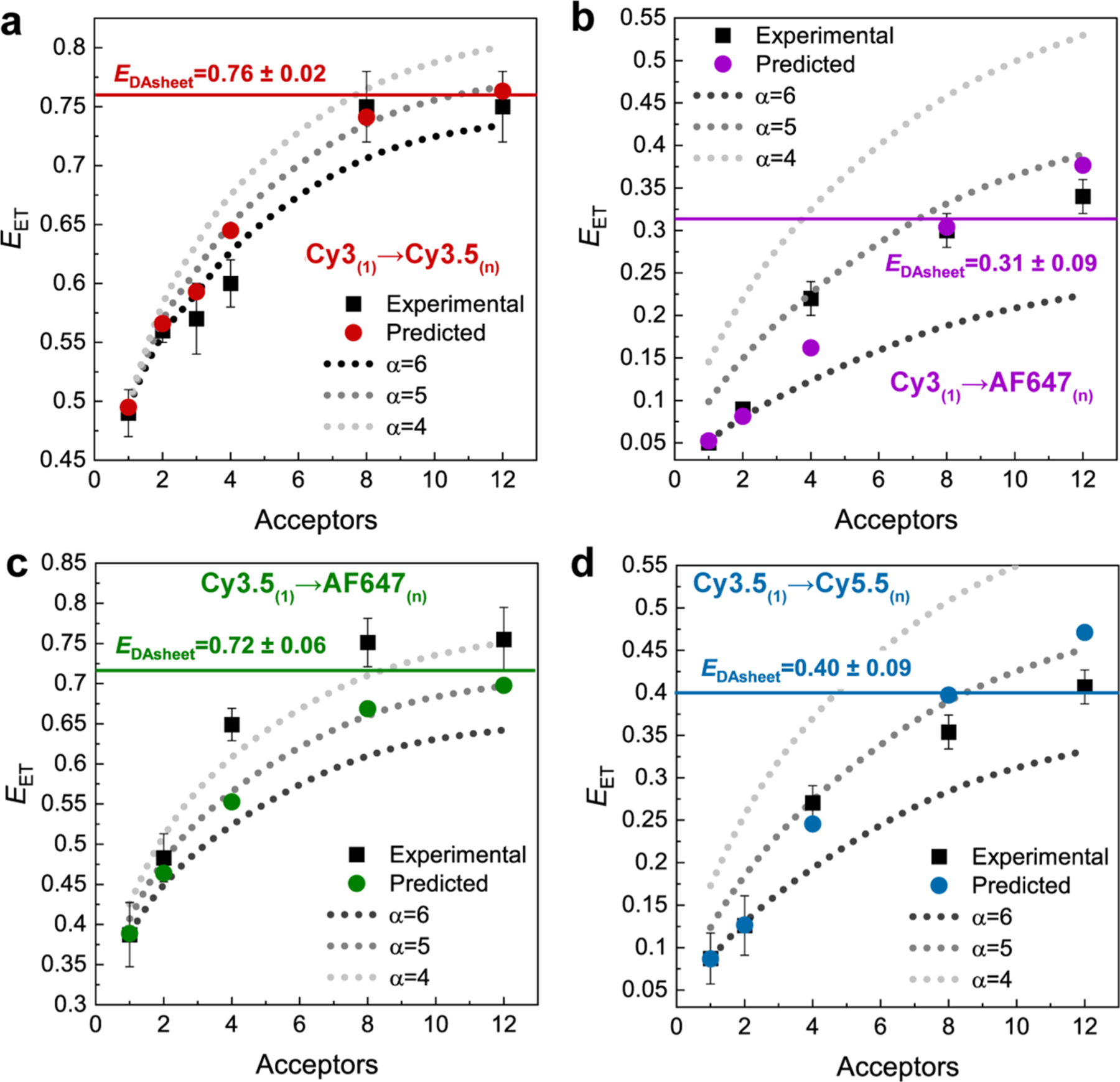
Characterization of a single donor to multiple acceptors distributed in a plane. Experimental and predicted E_ET values for (a) Cy3 → Cy3.5, (b) Cy3 → A647, (c) Cy3.5 → A647, and (d) Cy3.5 → Cy5.5 versus A number. Predicted values are based on using the α value shown in Figure 4d. The dashed curves are guides for α = 4, 5, or 6. Experimental values were determined by TCSPC.

A key point from this analysis was to observe where the increasing A presence causes ET to begin to exhibit sheet behavior. What is apparent in all four data sets is that while 2-A remains indistinguishable from an α = 6 point-to-point regime, at 4-A all but the Cy3 → Cy3.5 experimental data set lies on or above the α = 5 curve. Since all D–A pairs have a/c < 1 (see above), they should be capable of accessing the sheet regime. We also determined the $R_0^{2\text{D}}$ values using the known R for each D–A pair and the ρ_A (A concentration unit area) as a function of the a value and then using eq 9 with R_min = c found the predicted E_DAsheet values; the latter are shown as the horizontal lines in Figure 5 and are also listed in Table 2. The maximum observed experimental energy transfer (obsd max E_ET) and the predicted E_DAsheet overlap in all four cases suggested that all four D–A pairs clearly begin to access the “sheet” regime.

Table 2.

Select Energy Transfer Parameters for the D–A Pairs^a

	Cy3→Cy3.5	Cy3→AF647	Cy3.5→AF647	Cy3.5→Cy5.5
log(c/R0)	0.00	0.21	0.03	0.17
range of αb	5.80–5.12	5.58–4.52	5.75–4.98	5.58–4.56
$R_0^{2\text{D}}$ [nm]	8.1	8.1	8.7	8.1
E DAsheet	0.76 ± 0.02	0.31 ± 0.09	0.72 ± 0.06	0.40 ± 0.09
obsd max EETc	0.75 ± 0.03	0.34 ± 0.02	0.75 ± 0.04	0.40 ± 0.02

^a→ denotes a FRET step.

^bα values are from 2 to 12 A’s (and do not include the 66 A’s, black curve) as based on Monte Carlo simulations and a = 5.6 nm as shown in Figure 4d.

^cMaximum observed experimental energy transfer observed with 12 A’s shown in Figure 5.

From the above experiments we can estimate that the increase in E_ET in a 12 A system for a single plane transfer goes from 0.69 ± 0.04 assuming a point-to-point process up to 0.73 ± 0.03 when functioning in the sheet regime. At first pass, this appears to be only a minor increase of ∼6%. If, however, we return to the experiments presented in Figure 3, we observe that the 12/12 DNA block had a 23% increase in E_ee over what would be expected if all E_ET was point-to-point (α = 6). Considering that the 12/12 DNA block undergoes four sequential ET steps, if we improve each transfer to an efficiency of 0.73 instead of 0.69, then we would expect a 26% increase in E_ee, which is well in line with the value we observed experimentally. This serves as additional support that we have accessed the sheet regime in the DNA block systems with 12 A’s and effectively highlights that even in the cases of minor improvement in E_ET for a single step, over multiple ET steps it can become quite significant.

Although obsd max E_ET values are presented for the maximum 12-A configuration values in Table 2, it is apparent that the 8-A systems already function within the sheet regime for all D–A pairs. This suggests that assuming appropriate c/R₀ ratios of 1–2.5 and a/c ratios of 0.2–1, respectively, 8-As could also access point-to-plane equivalent ET regimes. Although the ET efficiencies are in line with point-to-plane regimes, deviations from prediction were observed (e.g., the Cy3.5 → A647 data set has higher experimental ET than predicted, while Cy3.5 → Cy5.5 mostly falls below expectation). It is partly for this reason that we next turned to an MD-informed model to probe the more complex potential contributions of dye-linker length, the effect of dipole orientation (i.e., static vs dynamic limits), and other DNA structural nonidealities.

ii. Nonideal Modeling.

In this section we perform more realistic FRET simulations that incorporate MD-derived information about the dye positions and orientations as a way of accounting for three particular nonidealities present in the DNA block experiments: (i) Distortions and fluctuations in the dye positions due to the flexibility of the DNA scaffold and the linkers that attach the dyes, (ii) anisotropic distributions (including fluctuations) of dipole orientation, and (iii) less than ideal formation yield. For the last factor, we previously estimated dye incorporation efficiency to be 98 ± 9.0%, and so for the present analysis we regard formation yields as ≥90%.

The approach used to estimate the dye positions and orientations in the DNA block from MD simulation is detailed in the SI. Because of the computational burden associated with simulating the large DNA block (run time of ∼1 month on a large CPU cluster), we did not perform separate simulations for each of the many different dye combinations that were studied experimentally. Instead we included in a single simulated structure one dye of each type (see Figure 6a for a frame from this simulation) and then extrapolated to find the positions/orientations of those same dyes at any other equivalent locations in a manner explained in the SI. In this way, we obtained time histories for the location and orientation of every dye, and we assume that the 1 μs simulation duration is sufficient to fully explore the phase space of the actual DNA block in equilibrium. We then incorporate this information into FRET simulations by assuming that any variations in position and orientation are slow on the time scale of the FRET. This is analogous to our ideal static dipole simulations discussed earlier (see Figures S10, S11) in which we employed a Monte Carlo algorithm; only here the dye positions and orientations are determined by sampling the MD histories. Accumulating many such results for different samplings and then averaging over the ensemble gives the simulated FRET efficiency for the given dye configuration. Finally, to represent nonideal formation efficiencies, in some simulations we simply assume the probability of any given dye being present to be 90% rather than the ideal 100%.

Figure 6.

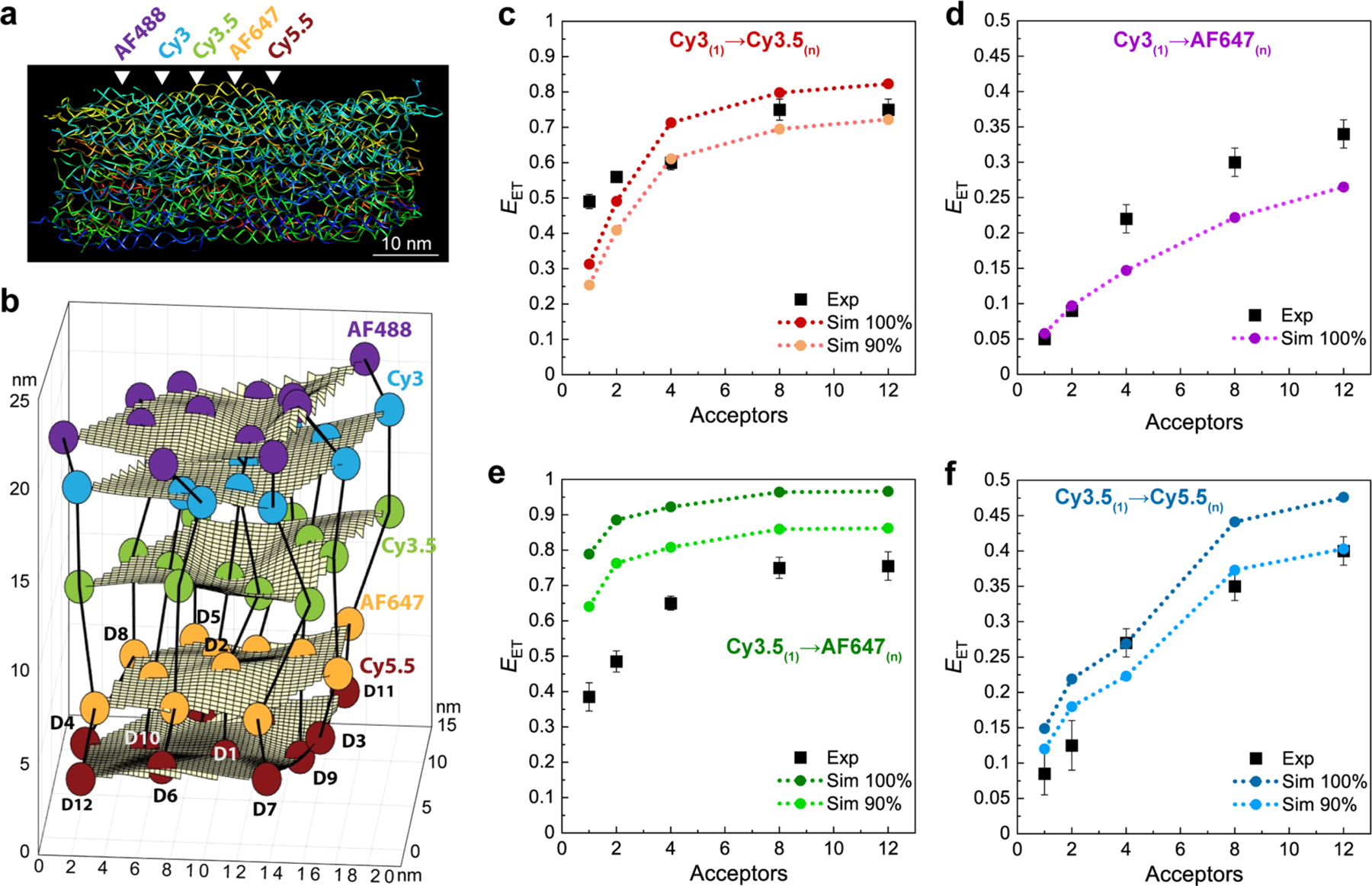
Experimental efficiencies versus MD-based FRET simulations. (a) Frame from an atomistic MD simulation showing the constituent DNA strands and emphasizing structural distortions associated with thermal fluctuations. White arrowheads approximate the location of the 5 dye planes within the DNA block. (b) Dye positions as estimated from the MD simulation with the small spheres represent the dyes (D1–D12, see Figure S1) with their colors matching those in Figure S2. In the ideal crystal the planes would be flat and the vertical lines (that approximate every other constituent duplex) would be straight. The axes dimensions are in nm. Comparisons of experimental efficiencies to the MD-based FRET simulations as the A number is increased in DNA-organized dye assemblies for (c) Cy3₍₁₎ → Cy3.5_(n), (d) Cy3₍₁₎ → AF647_(n), (e) Cy3.5₍₁₎ → AF647_(n), and (f) Cy3.5₍₁₎ → Cy5.5_(n).

Before comparing the FRET simulations with experiment, we look first at the average dye positions in the fully labeled DNA block as obtained from MD simulation (see Figure 6b). It is evident that in simulation the block is properly formed with the dyes in the desired order; however, significant distortions from a regular lattice are also apparent. In Table 3, the MD-determined average interdye distances are compared with the a and c values derived from experiment under a number of idealized assumptions as discussed earlier. We see that the average MD-derived a values are not much different from the distances derived earlier from anisotropy measurements, with the exception of the A647 plane. The interplane distances (c) between Cy3 and Cy3.5 and AF647 on the central helix are also similar to what was assumed previously; however, the MD-derived distances between the Cy3.5 and both AF647 and Cy5.5 are significantly smaller. In addition, the structure shows considerable thermal fluctuations about these averages, though no significant collective motions are apparent. Not surprisingly, given the orientation of the DNA duplexes relative to the programmed dye planes (see Figure S1), the fluctuations in position are much greater within planes than between planes. With respect to the D-to-A distances r_i, Figures S14–S17 show the MD-computed distributions for the 12 D–A pairs and κ² averages in the different D₍₁₎ → A_(1–12) configurations. From these plots, it is apparent that the distributions and their averages are somewhat nonuniform. For the corresponding information on the dipole orientation factors (κ²), Table 3 gives the average values for the four dye pairs of interest; these are seen to be different from the dynamic dipole value (2/3 or ∼0.67), sometimes smaller, sometimes larger, though overall the change is minimal with at most a ≤ 2.5% difference over the full range of 0 to 4. Functionally at the ensemble level, the changes in κ² resulted in minimal differences between the idealized and MD-determined ET efficiencies. Overall, these plots suggest more dye organization than would be seen in random distributions.

Table 3.

Experimental and MD-Derived Parameters for Selected D–A Pairs^a

	Cy3→Cy3.5	Cy3→AF647	Cy3.5→AF647	Cy3.5→Cy5.5
c(exptl) [nm]	6.1	9.9	6.9	9.0
c(MD) [nm]	6.3	10.0	4.0	7.9
a(exptl) [nm]	5.6	5.6	5.6	5.6
a(MD) [nm]	5.8	5.0	5.0	5.7
κ 2 *	0.72	0.61	0.77	0.57

^a→ denotes a FRET step. c = distance between D and A plane, a = acceptor plane density

^*Average κ² between D₍₁₎ → A_(n).

Comparisons between experimental E_ET values and values predicted from the MD-based FRET simulations for the four dye pairings Cy3₍₁₎ → Cy3.5_(n), Cy3₍₁₎ → AF647_(n), Cy3.5₍₁₎ → AF647_(n), and Cy3.5₍₁₎ → Cy5.5_(n), with n ranging from 1 to 12, are shown in Figure 6c–f, respectively. The dashed lines in these plots are predicted best fits either assuming all dyes are present and active at 100% assembly or alternatively with reduced formation yields of 90%. In all cases the trend of efficiency increasing with the presence of more A’s is apparent. Generally, the agreement is quite good, especially when nonideal formation yield is considered. The exception to this is in Figure 6e for the Cy3.5₍₁₎ → AF647_(n) system, where experiment and simulation show significant disagreement unless the formation yield is lowered by another 10% to around 80%. We believe that the far longer AF647 linker and some of the uncertainties arising from it may be contributing to the disagreement in this case. More interesting is that the simulations show the largest discrepancy from experiment for the Cy3₍₁₎ → AF647_(n) structures (Figure 6d), and since the simulations in this case fall below experiment, this difference cannot be accounted for by formation yield issues but rather suggests this to be an excellent example where the benefits of accessing the sheet regime are manifest.

MD values for c, a, and κ² were also compared by degrees along with the experimentally determined values as seen in Table 3. Each variable was modified individually with the other variables retaining the ideal values, and equivalent graphs as seen in Figure 5 were created for each iteration (see Figure S18). Average relative E_ET errors were compared to the experimental values. Here, relatively small changes in a and κ² result in minor adjustments, either positive or negative, to the idealized model’s fit to the experimental data. When c was considerably different, namely, for the Cy3.5 → AF647 and Cy3.5 → Cy5.5 systems, this resulted in substantially worse fits. Some further analyses in this regard along with related discussion can be found in the SI (Figure S19). Overall, the MD analysis provides important insight that the dye linkers and in particular the longest one— that of the A647 dye— are perhaps the biggest contributors to the observed deviations seen in the plots of Figure 6c–f rather than just assembly and formation issues.

CONCLUSIONS

An understanding of FRET in the sheet regime and how it is affected by various nonidealities is not just an academic exercise, but can inform real-world applications. Sheet regime effects become critical for quantitatively interpreting FRET microscopy of cellular membranes where one typically monitors dye-labeled D moieties interacting with membranes labeled with numerous lipophilic A dyes (or displaying some endogenous receptor/protein that can similarly act as the A sheet) in order to gather information about ligand–receptor interaction dynamics, vesicle formation, membrane biomolecular sensing events, etc.^14,27–32 The density of fluorophores in such confines can make interpretation of ET and subsequent distance estimates complex. Moreover, it is in just such situations where changing the 1/r^α exponent value from 6 to 4 can significantly alter estimated separation distances and assumptions of viable FRET sensing ranges. Other areas where a better understanding of sheet regime FRET can be beneficial are in light harvesting, photonic wires, and optical devices that look to optimize stepwise E_FRET and E_ee.^{3,46,49,66–68} Indeed, that sheet-like architectures are common in high-efficiency biological light-harvesting antennas suggests that careful attention to the details of the sheet design could well benefit solar concentrators, dye-sensitized solar cells, and other solar energy conversion technologies.^69,70 The interesting and somewhat unexpected properties demonstrated by the pyramid design further suggest that the number of dyes required could be functionally reduced and the light energy efficiently concentrated to an apex point.

We have previously investigated hybrid photonic wire constructs where a central quantum dot (QD) donor was surrounded by multiple DNAs displaying sequentially arranged relay-A dyes at various increasing distances from the central QD.^45,47 However, analysis and modeling of the FRET processes observed in those structures, along with subsequent similarly assembled constructs,⁷¹ confirmed that they acted as linear photonic wires and did not manifest any sheet regime properties despite the presence of multiple concentric arrangements of A around the central QD. Moreover, modifying such QD-centric configurations with multiple A’s placed closer to each other allowed them to drive a concentric multistep FRET process around the QD rather than sheet-like behavior.^71–73 Here, dye integration into a 3D DNA brick nanostructure serves to demonstrate the latter’s capability as a versatile and modular template for studying FRET while also allowing access to the sheet regime. A first basic conclusion arises from the experimental confirmation that properly spaced zero-dimensional A’s can act as an equivalent to a continuous 2D sheet A. Benefits of accessing the sheet regime arise not only from the change in exponent (from α = 6 to α = 4) but with an increase in the effective R₀ value (R_0eff) that can approach as much as twice the ordinary R₀. Critically, accessing the sheet regime provides ET enhancement only if the proper D–A and planar density/spacing is maintained. To realize enhancements, the a/c ratio should be between 0.2 and 1.0, i.e., the A’s density should be greater than the R_min. The maximum benefit achievable by decreasing a/c is, however, limited by the total number of A’s present. For example, experimental data suggest that under the right conditions sheet regime effects begin to come into play at ca. 4-A, with the relative enhancement plateauing at about 8-A’s. However, it is fair to note that our experiments only explore up to 12-A and the simulations show much more pronounced outcomes for the 66-A scenario. Another important benefit to consider is that the payoff for minimizing the α exponential is obtained in conditions when ordinary single-pair D–A FRET is inefficient (c/R₀ ratios of 1 to 2.5).

In addition to providing an improved understanding of the sheet regime, the foregoing conclusions from ideal simulations are useful for designing dye networks that effectively exploit the sheet regime. However, the nonidealities of real systems (e.g., precise dye positions and orientations) mean that these rules should be regarded as no more than rough guidelines with respect to actual performance. From experiment, a first unsurprising observation is that one sees E_FRET rise when even just one extra A is added. This is mainly due to the addition of another channel for excitonic transport; if an A is missing or dark, having a second A will be especially consequential. The latter, in essence, provides a redundant pathway for the exciton. As more A’s are added, E_FRET continues to rise as the sheet enhancements become increasingly apparent. However, detecting this unambiguously is nontrivial, as is evidenced by the ideal FRET simulations of Figure 5. The clearest cases are in Figure 5b and d, where dye placement skips an intermediary plane so that the value of c is large, a/c is reduced, and sheet behavior is favored as noted above. This argument is supported by the agreements between experiment and the MD-based simulations in Figure 6c–f. Among other things, these agreements are a basis for saying that the MD-based model provides a reasonably accurate representation of the actual system and that we can then make reliable predictions based on it.

The experimental access to the sheet regime provided by the DNA brick approach suggests that this may be an effective platform for building light-harvesting antennas.⁴¹ Indeed, as shown in Figures 6b and S14–S17, the effects are quite tolerant to quasi-planar arrangements that do not strictly fall into a flat plane or rigid lattice structure; however, it is not clear if this tolerance is a universal feature or will be design dependent. This contrasts from what is typically found with protein scaffolds or achieved in alternative dye-labeled DNA nanostructure designs that purposely focus on rigidity.⁴³ There are also alternative methods for making DNA structures more rigid, e.g., by cross-linking or adding exogenous intercalating agents, and these could potentially contribute to improving the DNA approach if rigidity is needed.^74,75 Absent these measures, we explored experimentally the antenna processes using the native DNA block design with the results shown in Figures 3, S7, S8, and S20. The performance was especially good when full dye sheets were maintained throughout the block; however, one can also use the “Lego” aspect of the DNA bricks to create antennas that provide focusing as in the current pyramidal design or, alternatively, the previously described dendrimers.⁴⁶ Further analyses and some discussion of the intriguing reasons why the pyramidal configuration performs with the same efficiency as the 12/12 block arrangement despite having one-third fewer dyes is presented in Figure S20. Overall, accessing the sheet regime provides a way of increasing excitonic energy transfer efficiency and can contribute to improved performance in nanoscale FRET-based devices assembled from a variety of materials beyond discrete dyes,⁶⁸ with our experimental design showing up to a 35% increase in ET efficiency for a single step and a > 20% increase across four sequential transfer steps.

EXPERIMENTAL SECTION

Materials.

All DNA strands required to assemble a dye-free DNA block structure were purchased from Integrated DNA Technologies in lyophilized form in microtiter well plates and reconstituted in DNase- and RNase-free water. DNA oligonucleotides modified with Alexa 488, Cy3, and Alexa 647 were purchased from Integrated DNA Technologies, while Cy3.5- and Cy5.5-labeled oligonucleotides were purchased from Operon. All dye-labeled oligos were also reconstituted in DNase- and RNase-free water before use.

Assembly and Purification of DNA Block Structures.

The block nanostructures were synthesized following the protocol reported earlier.⁴¹ For each dye configuration, the corresponding DNA strands are specified in Tables S2–S8 which can be cross-referenced with the master DNA sequence in Table S1 using the index diagram shown in Figure S5. The unpurified DNA strands, dissolved in DNase- and RNase-free water, were mixed at equimolar final concentration of 100 nM for each strand in 1 × TE buffer (50 mM Tris + 1 mM EDTA, pH 7.9, adjusted with acetic acid) supplemented with 40 mM MgCl₂ (TE+Mg). The structures were annealed in a PCR thermocycler using a 72 h annealing ramp. The ramp consists of two distinct steps: first a fast-cooling step from 80 to 60 °C at a rate of 3 min/°C, which was followed by a relatively slower cooling ramp from 60 to 25 °C at a rate of 2 h/°C. The samples were purified with 100 kDa molecular weight cutoff (MWCO) Amicon filters using the following procedure: the filter column was first rinsed with buffer by loading 400 μL of TE+Mg and centrifuged at 12000g for 1 min. After discarding the eluate, a 300 μL sample was loaded into the column and centrifuged for 5 min at 9000g. After discarding the eluate, 300 μL of buffer was added to the same column and the process was repeated three times. Sample was eluted from the column by inverting it into a fresh 2 mL vial and centrifuged at 1000g for 3 min. The samples purified with the Amicon filter were subsequently tested using agarose gel electrophoresis, and this revealed that less than 1% of unincorporated oligonucleotides remained in the sample after three rounds of filtration. Each construct was assembled, purified, and analyzed separately.

Physical Characterization of the DNA Block Structure.

AFM imaging was performed using a Multimode AFM (Bruker) in tapping in air mode. A 10 μL amount of purified DNA block sample (at ∼5 nM) was deposited on a freshly cleaved mica disc and allowed to adsorb for 30–60 s. After that, the mica was rinsed with molecular biology grade water and dried using N₂ gas.^76,77 High-resolution transmission electron microscopy (HRTEM) was performed on a JEOL TEM 2010F electron microscope operating at 200 kV. For TEM imaging, the samples were adsorbed on glow-discharged carbon-coated TEM grids (400 mesh, Ted Pella).⁷⁸ Postdeposition, the grids were stained with a 0.7% uranyl formate solution in 25 mM NaOH.

Steady-State Spectroscopic Characterization of the DNA Block Structures.

Steady-state fluorescent spectra were collected at room temperature under ambient conditions in a Horiba Nanolog spectrometer (Horiba Jobin Yvon) equipped with a 450 W xenon lamp and a thermoelectrically cooled R928PMT detector (range 200–850 nm) or on a multifunction microtiter plate reader (Tecan Infinite MR 1000 Pro). Absorption spectra of each dye were measured for samples in a 10 mm path length cuvette using an Agilent 8453 diode array UV–vis spectrophotometer.

Fluorescence Lifetimes and Anisotropy Characterization.

Excited-state fluorescence lifetimes (τ) and lifetime anisotropies were measured with a TCSPC technique using a Becker-Hickl SPC-630 board.^45,79,80 The excitation laser was a 80 MHz 7 ps pulsed 532 nm frequency-doubled diode-pumped Nd:YVO4 laser (High-Q pico-TRAIN). Sample fluorescence was sent through a polarizer set to the magic angle for lifetime determinations and then filtered using a monochromator. The polarizers were adjusted to the pertinent parallel and perpendicular settings to obtain the anisotropy measurements.