Abstract
This study proposes a decision support system (DSS) that integrates GIS, analytics, and simulation methods to help develop a priority-based distribution of COVID-19 vaccines in a large urban setting. The methodology applies novel hierarchical heuristic-simulation procedures to create a holistic algorithm for prioritising the process of demand allocation and optimising vaccine distribution. The Melbourne metropolitan area in Australia with a population of over five million is used as a case study. Three vaccine supply scenarios, namely limited, excessive, and disruption, were formulated to operationalise a two-dose vaccination program. Vaccine distribution with hard constraints were simulated and then further validated with sensitivity analyses. The results show that vaccines can be prioritised to society’s most vulnerable segments and distributed using the current logistics network with 10 vehicles. Compared with other vaccine distribution plans with no prioritisation, such as equal allocation of vaccines to local government areas based on population size or one on a first-come-first-serve basis, the plans generated by the proposed DSS ensure prioritised vaccination of the most needed and vulnerable population. The aim is to curb the spread of the infection and reduce mortality rate more effectively. They also achieve vaccination of the entire population with less logistical resources required. As such, this study contributes to knowledge and practice in pandemic vaccine distribution and enables governments to make real-time decisions and adjustments in daily distribution plans. In this way any unforeseen disruptions in the vaccine supply chain can be coped with.
Keywords: Logistics and Supply Chain, COVID-19 vaccine distribution, Two-dosage vaccination, Heuristics, GIS, Capacity allocation, Simulation
1. Introduction
The Coronavirus Disease 2019 (COVID-19) is one of the major global pandemics since the outbreaks of SARS in 2002 and MERS in 2012 (Wu and McGoogan, 2020). As of January 2021, COVID-19 has infected over 85 million people in 190 countries and resulted in the death of more than 1.8 million globally (BBC News, 2020). To reduce the risk of infection and fatalities, many governments are now administering plans to roll out mass vaccination of their citizens. On December 11, 2020, the U.S. Food and Drug Administration (FDA) issued the first emergency use authorisation for a vaccine developed by pharmaceutical companies. The emergency use authorisation allows the COVID-19 Vaccines to be distributed in the U.S. (FDA, 2021). Other countries, such as Australia, also granted approvals for the use of different vaccines and begun mass inoculation to protect their nationals against the COVID-19 virus. Owing to the unprecedented scale of infection, hundreds of thousands of doses of vaccine need to be administered at hospitals and vaccine centres in a short period of time (Department of Health, Australian Government, 2020a). While mathematical models can help optimise the allocation and distribution of vaccines, the uncertainty of supply and the huge size of the problem render an exact solution infeasible, especially when decision has to be made in a very short period time under uncertainty. Given these challenges and the complexity of vaccine supply chains, governments will benefit from evidence-based planning to help optimise vaccine allocation and distribution processes. Simply put, it is a race against time.
The supply of COVID-19 vaccines is limited at the beginning of the production cycle. It would then be difficult for most governments to meet the huge demand for vaccines, and be able to mass vaccinate the populace within a time threshold with finite resources. Allocation of vaccine also needs to be prioritised based on different levels of susceptibility, exposure and accessibility to vaccine centres (Centers for Disease Control and Prevention, 2020). Furthermore, due to other stringent supply chain constraints, such as an extreme cold storage requirement and a short shelf life, proper planning and formulation of distribution strategy are needed to maximise usage and minimise waste. A standard sequential-planning approach to formulating delivery strategy may be ill-suited for COVID-19 vaccines (McKinsey & Company, 2020). All sorts of uncertainties where the allocation and distribution planning process need to be considered, may arise. An integrated approach with multiple supply scenarios must be embraced to help formulate the appropriate strategies and dispensing policies for the vaccine supply chain to achieve the best possible outcome.
Once the vaccine is available, each and every individual needs to be vaccinated to protect against COVID-19 (Docherty et al., 2020). However, not all individuals are equally susceptible since some are more susceptible than others. Furthermore, not all individuals could be inoculated due to a supply constraint of vaccines during the initial production cycle. Hence, allocation and dispensing of vaccines require priority-based planning which schedules inoculation of the populace based on susceptibility and exposure levels. Population at risk to COVID-19 is also influenced by the environment or context in which they live. Higher density areas are at an elevated risk given the likelihood of community transmission. Many studies (Suleyman et al., 2020, Zhou et al., 2020) have identified other vital risk factors, such as age and chronic health conditions. The conditions have significantly contributed to higher COVID-19 related mortality. Allocation and dispensing of vaccines in pandemics investigated in most previous studies, however, have considered these criteria individually rather than holistically (Deo et al., 2020). Given the projected limited supply of vaccines during the initial production cycle, it is imperative to design an allocation technique that takes into account multi-factored contexts within which vaccines can be inoculated to the people needing them the most, on a large scale.
Age (Medlock and Galvani, 2009), chronic medical conditions (Kee et al., 2007) and exposure (Persad et al., 2020, McMorrow et al., 2019, Uscher-Pines et al., 2006) are vital factors, which need to be integrated when prioritising people for vaccination. There are only a few studies that have aggregated these critical factors into a finer spatial scale to generate a prioritisation scheme. In particular, co-morbidity of the population, such as high blood pressure and chronic health conditions (e.g., cancers, diabetes), are not yet fully integrated into estimating the susceptibility of people to COVID-19 at a disaggregate level. Given the availability of co-morbidity data, a new risk index estimating susceptibility levels needs to be generated by aggregating mortality risk factors at a geographic scale. This will help formulate an equitable and effective vaccine distribution plan to remove any potential risk faced by the most vulnerable groups.
There is also an urgency to formulate an optimised supply network to distribute vaccines from the centralised warehouse to hospitals or medical centres where the vaccines will be administered. Previous studies have shown that operational constraints such as multi-dose vaccination, storage requirement, shorter expiry date upon opening, higher cost of wastage, and variegated vaccination needs of vulnerable community groups can pose significant logistics challenges at the downstream vaccine supply chain (Abrahams and Ragsdale, 2012). Storage capacity at vaccine centres can also influence distribution efficiency (Shittu et al., 2016). Previous studies have investigated various factors, such as transport and storage capacity (Lee et al., 2011), consolidation (Brown et al., 2014), scheduling preferences of patients, scheduling inconvenience (Abrahams and Ragsdale, 2012), and cold or non-cold chain transportation (Lin et al., 2020) when examining vaccine supply chain performance. However, to date there is no comprehensive study which simultaneously integrates these factors in a single unified solution framework. Given the complexity of a time-sensitive COVID-19 vaccine supply chain, a robust holistic approach needs to be developed to optimise the priority-based distribution of vaccines to the wider community. To meet such a need, this study proposes a two-stage scheme to prioritise the allocation of vaccine packs and then develop an efficient plan for the distribution of COVID-19 vaccines. The scheme is then tested and validated through simulation with scenario analysis using Melbourne, the second largest city in Australia with over 5 million residents (Australian Bureau of Statistics, 2020), as a study area.
This study makes several both theoretical and practical contributions to the subject matter. First of all, empirical analysis using Melbourne as a study corroborates some of the vaccine allocation strategies put forward by recent studies such as Chen et al. (2020) and Foy et al. (2021). Next, the study is the first attempt to combine demand prioritisation and efficient distribution arrangement in a single framework making it a truly practical decision support system for COVID vaccination planners and decision makers. The system is designed to incorporate short delivery time window, extreme cold storage requirement, capacity constraint and demand uncertainties in the downstream vaccine supply chain. Finally, the framework combines different tools and algorithms to automate the entire process and produce outcomes in a reasonable timeframe. This novel approach enables decision-makers to generate operational plans in real time to support in situ operational decisions. Real-time decision-making capability is critical to maximising the effectiveness and efficiency of the COVID-19 vaccination program.
The remainder of paper is as follows. A literature review on pandemic vaccine allocation and distribution planning studies is given in Section 2 to help identify the research gap. Section 3 describes the problem in detail and the assumptions involved. Section 4 presents the solution approach and the framework. The application of the proposal framework to a real case study is provided in Section 6. Section 7 discusses the results with a focus on the robustness of the algorithm based on sensitivity analysis. Section 8 provides managerial insights of this study. The article concludes in Section 9 with a discussion on the key contributions and implications of the study, its limitations and the direction for future research.
2. Related works
First reported in December 2019 in Wuhan City, Hubei Province of mainland China, the COVID-19 disease was quickly transmitted to other parts of the world (WHO, World Health Organization, 2020a). Despite its relatively low case fatality rate, the disease is highly contagious and spreads rapidly within and between populations. Governments throughout the world have enforced severe measures, such as self-isolation, wearing of masks, social distancing, quarantine and even partial or total lockdown of cities and countries, to control the diffusion of the virus (Anderson et al., 2020). Nonetheless, many people have been infected or deceased in the pandemic. As such, tremendous global effort has been invested in developing a vaccine to mitigate the risk of infection.
Although COVID-19 infects people of all ages, evidence suggests that two groups of people are at higher risk of being infected by the disease. According to a situation report issued by the World Health Organisation (WHO, World Health Organization, 2020b), the two groups are older people (i.e., those over 60 years of age) and those with underlying medical conditions (such as cardiovascular disease, diabetes, chronic respiratory disease, and cancer). The risk of severe disease gradually increases with age starting from around 40 years. As such, most of the studies on COVID-19 vaccine allocation strategies focus on reduction of mortality and morbidity rates (Chen et al., 2020, Foy et al., 2021). Since supply of the COVID-19 vaccine will be limited at the beginning, an effective prioritisation scheme to allocate the vaccines to the most needed populace will be critical if the vaccination program is to succeed.
In view of the importance of vaccine prioritisation and distribution during a pandemic crisis such as COVID-19, relevant works will be reviewed according to two major themes: (1) prioritisation of vaccine allocation; and (2) optimisation of vaccine distribution.
2.1. Prioritisation of vaccine allocation
Prioritising the allocation of a vaccine against an epidemic or pandemic such as COVID-19 to prevent the disease from spreading is of great importance to many governments, especially when the population of the infected area is large and vaccination facilities are limited. The determination of who gets the vaccine first can be a very difficult task (Persad et al., 2020). Epidemic vaccine prioritisation (EVP) as well as efficient distribution of vaccines to those needing it most, in order to prevent the infectious diseases spreading constitute the most important healthcare challenges in large urban areas. Appropriate EVP not only can reduce mortality and healthcare expenses but also minimise political destabilisation and claims of injustice (Uscher-Pines et al., 2006). EVP can be based on groups, such as healthcare personnel and long-term care facility residents, as well as geographical areas, such as densely populated metropolitan areas (Gamchi et al., 2020). Allocation decisions can be ethically and logistically complex, given the limited and uncertain supply of vaccines and the competing priority groups with distinct risk profiles and vaccine acceptability (Huang et al., 2017).
Careful design of a vaccine prioritisation strategy is a crucial public policy challenge (Buckner et al., 2020). Prioritisation of vaccine allocation must be empirically and objectively determined (Bubar et al., 2020). For example, Chen et al. (2020) used clinical and demographic indicators, for instance age, to prioritise vaccination. With the help of an age-structured simulation model, the researchers concluded that older groups should be given priority due to their vulnerability. Govindan et al. (2020) divided community residents into four groups based on the risk level of their immune system (namely, very sensitive, sensitive, slightly sensitive, and normal) and two indicators (age and pre-existing diseases, such as diabetes, heart problems, or high blood pressure). Furthermore, they are required to observe the regulations of their class to prevent a sudden surge in demand in the healthcare system. Such arrangements would help manage demand in a healthcare supply chain and break down or decelerate the virus chain. Buccieri and Gaetz (2013) emphasised the ethical dimensions of vaccine prioritisation. They opined that during an epidemic or pandemic, such as the pH1N1 influenza in 2009, homeless people who generally have poor health should be given priority for vaccination. Medlock and Galvani (2009) used different demographic variables, mortality or incidence rates and age groups to prioritise vaccination. They concluded that the elderly and school children should be given priority because of their vulnerability. Others focus on the groups subject to high risk due to direct contact. Uscher-Pines et al. (2006) prioritised different groups including hospital service workers, people at high risk and hospitalised cases. Deo et al. (2020) used socioeconomic characteristics as the basis of prioritisation and contended that frontline healthcare workers and people in the 60+ age group, with moderate or severe comorbidities, or low income should be given priority. Research by Kee et al. (2007) in South Korea concluded that, in addition to patients with specific illnesses such as chronic diseases, people over the age of 65 years should be given priority for vaccination. Similarly, Persad et al. (2020) prioritised vaccination for healthcare workers, essential workers and people in high-transmission settings, people with medical vulnerabilities such as diabetes, pulmonary disease, cardiac disease, and obesity. In another study, McMorrow et al. (2019) argued that adults, children with tuberculosis disease, HIV-infected adults and pregnant women should receive the vaccine first. In the same vein, Abbasi et al. (2020) prioritised vaccination using a segmentation system which deals with allocation of vaccine to medical centres based on the priority of individuals who registered their request for vaccine in a medical centre. The mathematical model proposed is generic and can take any possible prioritisation as input. For the case study, however, only age group is used for prioritisation as an illustration.
Our review shows that most studies have focused on socioeconomic characteristics and age for prioritising epidemic vaccination. Geographical aspects as well as comorbidities of the population, such as high blood pressure, cancers, diabetes are given less priority. Owing to the limited supply of vaccines especially during the early stages of vaccination, it may not be possible to vaccinate the population in all geographical areas at the same time. Prioritisation based on geographical areas is equally important due to differences in the exposure to physical contact, socio-economic status, co-morbidity outcomes and remoteness. Gamchi et al. (2020) used an infected–recovered model and a bi-objective vehicle routing problem method to prioritise city districts and citizens of Tehran for COVID-19 vaccine distribution. Prioritisation of city districts was based on priority groups, such as pregnant women and children under six months of age. However, no location-based method was used to prioritise areas. Also, the geographical scale used for vaccine distribution was very large and general. To be practical, a finer geographical scale has to be employed to accurately prioritise areas and the populace for vaccine distribution. In another study, Acharya and Porwal (2020) used a comprehensive set of social, economic, and epidemiological variables as well as availability of healthcare facilities to identify high-risk areas in India. Again, however, the geographical scale of the entire country was selected thus limiting the practical use of the outcome. Also, the importance or the weight of each indicator in the prioritisation has not been specified. In Australia, Liu and Xian (2020) used health and demographic indicators (e.g., age, cancer, and other clinical variables) to classify communities at high risk of certain diseases to conduct the corresponding therapeutic measures. The prioritisation is again very general and applicable on a national scale leading to the conclusion that a major city such as Melbourne is not considered a high-risk area in most of its metropolitan area. Obviously, for vaccination against a pandemic such as COVID-19, a much smaller scale, for instance local areas, should be used to achieve a more precise prioritisation in order to be practical.
Previous studies on vaccine allocation have shed light on prioritisation. Keeling and White (2011) used the SIR (susceptible–infectious–recovered) model to target vaccination against H1N1 influenza virus in Great Britain. The population was prioritised by age, level of risk of disease prevalence, and epidemiological characteristics of high-risk groups. Epidemiological scenarios were tested with different onset times for the start of vaccination, different numbers of districts initially infected, and different levels of transmission heterogeneity in each district. They concluded that targeting of vaccination towards regions experiencing high levels of infection would generally reduce the total number of cases. Araz et al. (2012) used mathematical modelling to prioritise counties in Arizona, U.S.A for vaccine distribution against the A/H1N1 pandemic in 2009. Four different prioritisation strategies, including pro rata, sequential by population, sequential by peak, and reverse sequential by peak, were examined. Adoption of a pro rata policy, i.e., distributing according to population size, was regarded as the most effective strategy. Venkatramanan et al. (2019) used mobility and travel time patterns as well as influenza epidemic seasonal intensity patterns to model vaccine allocation across the states of the USA. Greedy optimisation algorithm method was used to model the allocation problem. The population was divided into groups, including susceptible, exposed, infected, recovered, and vaccinated and modelled separately. Under this classification, the southern and southeastern states were identified as of high priority for vaccine allocation. Chen et al. (2020) used an age-structured SAPHIRE model and the standard least squares model parameter estimation method to evaluate the outcome of various vaccine allocation policies. They concluded that with constant daily supply of limited amount of vaccine, allocating them to the oldest group first would be most effective to reduce mortality rate. With increase in constant daily supply, more vaccines could be allocated to the younger groups to help reduce infection rate.
Table B.1 in Appendix B summarises the reviewed literature on prioritisation of vaccination. It reveals that only a few studies have used “individual medical condition” as an indicator for vaccine prioritisation (Liu and Xian, 2020). Also, location and geographical distribution of the vaccine has not been considered especially at a finer spatial granularity within a large metropolitan city. Furthermore, the time of distribution, the location and the capacity of vaccine centres as well as the target groups were only taken into account in a few studies. These inadequacies would need to be addressed in order to develop a practical and effective allocation plan to prioritise COVID-19 vaccination.
2.2. Optimisation of vaccine distribution
In addition to prioritisation of vaccine allocation, an efficient and effective distribution of vaccines to the populace is equally important to successfully mitigate risk and prevent the transmission of diseases to the wider community. The goal is to ensure that there would be adequate vaccines shipped to the medical centres in time to meet demand while ensuring the capacity of the centres would not be exceeded. Owing to the huge demand, the COVID-19 vaccines are unlikely to be supplied to any country at once in large quantity. They would likely be supplied in batches to maintain a sustainable and equitable replenishment system to meet the global needs. The extreme cold storage requirement and short shelf life of the vaccines, together with the limited dispensing capacity of vaccine centres, could also impede the supply of the vaccines to effectively inoculate people within the expected time threshold.
The fact that the vaccines have to be stored in extremely low temperatures and, once thawed, must be administered within several hours has created tremendous difficulties in distribution. It implies that the thawed vaccines can only be delivered from the central storage location to the vaccine centres within a narrow time widow and must be used almost immediately. Unpredictable and dynamic emergency situations can also pose critical challenges when implementing a planned distribution strategy. These situations can include simultaneous random arrival of many people, even with prior booking for different time slots, at a vaccine centre waiting for inoculation, thereby increasing the risk of person-to-person transmission. Furthermore, ’no-shows’ of people with prior bookings at a vaccine centre can lead to possible waste of precious vaccines which cannot be frozen again for future use. All these variables and constraints will need to be considered when designing the vaccine distribution system to ensure practicality and success.
There are significant differences in determining optimal vaccine distribution arrangements between normal and pandemic vaccination due to demand, scale, exposure, time–space thresholds and other operating constraints in the latter. Most studies on typical vaccine supply chain are based on a cost-efficiency argument and the effectiveness of procurement, allocation and distribution to provide vaccination to a wider population. For example, using simulation and mathematical modelling, Lee et al. (2011) explored the impact of a newly introduced vaccine on the existing vaccine supply chain and concluded that additional transport and storage capacity would be required to effectively distribute the new vaccine. Abrahams and Ragsdale (2012) considered scheduling preferences of patients and argued that operational management challenges, such as multi-dose vaccine packages, rapid spoilage upon opening, high cost of wastage, and unique vaccination needs of patients, could all seriously compromise the effectiveness of vaccine distribution. Based on the method used by Lee et al., 2011, Brown et al., 2014 explored how the introduction of the new vaccine could affect cost and availability in the downstream vaccine supply chain. The results indicated that consolation of distribution levels to streamline the distribution process could be the best option in terms of cost and efficiency.
Storage capacity can also affect downstream vaccine supply chain performance. For example, through scenario testing using simulation, Shittu et al. (2016) analysed the impact of variances in vaccine supply and demand in Nigeria. They concluded that proper redesign of existing vaccine supply chain could be crucial to improving capacity utilisation. Similarly, Lee et al. (2011) examined the efficiency of an existing multi-tiered vaccine supply chain in Mozambique in comparison with an alternative distribution design through simulation. The results revealed that, by delivering directly from national depot to district stores in each province and then to health centres without going through the provincial stores, the alternative distribution design tends to increase availability of vaccines and reduce logistics costs. These analyses suggest that proper distribution design of the downstream vaccine supply chain can improve utilisation of storage capacity. Subsequently, the overall distribution efficiency and effectiveness of vaccination program will improve.
Owing to short supply and huge demand commonly for vaccines as well as time–space constraints, most studies on pandemic vaccine supply chains focus on prioritising allocation of vaccines to the neediest in the populace as discussed previously. Nevertheless, rapid distribution of medical supplies plays a crucial role in the effectiveness and efficiency of disaster response, hence the overall performance of the healthcare system (Al Theeb and Murray, 2017, Dessouky et al., 2013). Therefore, upon determination of the priority groups for vaccination, delivery of vaccine to the targeted groups becomes primarily an assignment problem (Gamchi et al., 2020). Studies on distribution of vaccines and other medical supplies in humanitarian aid settings mainly focus on a few aspects. They include vehicle routing with different minimisation objectives, such as total distribution time (Özdamar and Demir, 2012), distribution cost (Balcik et al., 2008), unsatisfied demand or unserved victim (Özdamar and Yi, 2008, Tan et al., 2009), and evacuation time (Tan et al., 2009). Mathematical modelling is commonly adopted in these studies. For example, Al Theeb and Murray (2017) presented a multi-objective model considering commodity delivery, victim evacuation, and relief workers assignment. Li et al. (2016) developed a model to optimise the medicine distribution routes by minimising the total cost of refrigeration storage, transportation, and vehicle fixed costs. Vehicle routing is critical in healthcare services when resources are inadequate, and the demand is geographically spreading (Harper et al., 2005, Syam and Côté, 2010). There are studies on applying the vehicle routing problem (VRP) in the distribution planning of healthcare-related products. For example, Moghadam and Seyedhosseini (2010) presented a specific VRP to reduce the unmet demand in drug distribution. Ceselli et al. (2014) considered a double channel distribution problem, including the distribution centre and routing strategies, to distribute vaccines or drugs in an emergency. Despite the critical importance of time in a pandemic vaccine distribution system such as that required for COVID-19, the objectives of minimising distribution time and unmet demand remain unchanged. As such, the VRP approach to optimise assignment and vehicle routing is still relevant and applicable.
Despite the frequent occurrence of epidemics and pandemics in the last two decades such as SARS, pH1N1, MERS, studies that aim at designing and building an efficient distribution network to deliver the vaccines to those who need them most are relatively limited (Abrahams and Ragsdale, 2012, Brown et al., 2014, Buccieri and Gaetz, 2013, Medlock and Galvani, 2009). Table B.2 - Appendix B summarises the reviewed literature on optimisation of distribution of vaccines and medical supplies. Revealed here is a lack of research on building an efficient distribution network that takes into account priority demand allocation, waiting time of and staff levelling, as well as vehicle routing to ensure that the vaccines will be effectively delivered to the neediest people. Furthermore, these studies usually only investigate certain aspects of the distribution problem and have not fully incorporated the multitude of factors and constraints affecting the optimisation of a vaccine supply chain to mitigate infection risk. The need for a holistic approach to designing a pandemic vaccine supply chain is more critical in the case of COVID-19 in view of its profound global healthcare and economic impacts.
3. Problem description
The COVID-19 vaccine is being produced by several companies using different technologies and storage requirements. A robust logistics system must be established to make the vaccine supply chain as efficient as possible. The Pfizer vaccine, in particular, is highly vulnerable to contamination and requires storage at an extremely low temperature. Even when refrigerated at the correct temperature, it is only effectively useable for a period of about two weeks. The mRNA-based technology required to produce the vaccine is only used at Pfizer’s plants which are in the United States, Belgium and Germany. At this stage, Pfizer vaccines can only be supplied from these manufacturing plants via airfreight. Australia is planning to secure 10 million doses to cover five million Australians in 2021 once the vaccine is approved by the Therapeutic Goods Administration under the federal Department of Health (Department of Health, Australian Government, 2020a).
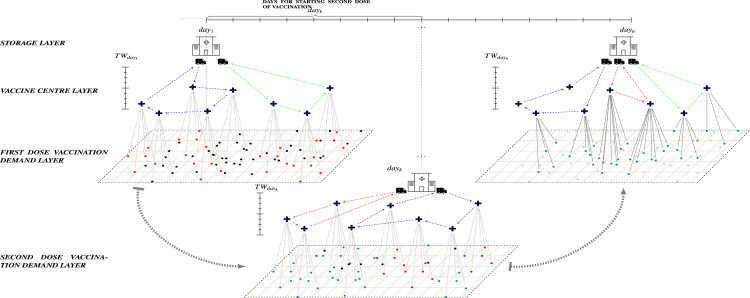
To develop an efficient COVID-19 vaccine supply chain in Australia, it is important to consider a range of constraints within which vaccines will have to be allocated to vaccine centres (VCs) for mass inoculation. Vaccines need to be manufactured on short notice in large quantities and delivered on a long haul from overseas. The vaccines need to be stored in refrigerated warehouses/vehicles and then distributed across large geographic catchments within a restricted time window. Owing to the limited supply of vaccines at the beginning, allocation has to be prioritised based on certain criteria to get the vaccine to the most needed populace first. This is essential if the effectiveness of controlling the virus infection is to be maximised. Furthermore, the vaccine is required to be injected twice with one dose initially, followed by a booster shot three weeks later. Missing out on the second dose can significantly reduce the protection of the recipient. The timing is critical as the second dose must be injected 21 days later in order to get the best result. Other factors, such as different packaging of vaccines, capacity of delivery vehicles, serving capacity and random arrival of participants at VCs, no-shows, short shelf life of vaccines upon thawing and WHO multiple-dose vaccine vial policy, etc., can pose significant challenges in the daily routing and scheduling of delivery vehicles. These constraints pose a complex distribution problem in the vaccine supply chain as shown in Fig. 1.
Fig. 1.
Problem definition: On each day, available vaccines need to be distributed from cooler storage to the within a certain time window (). On , people who have already received the first dose will become top priority to receive the second dose of vaccine. Each , based on type, has specific service capacity. The plus symbols indicate the locations of the , and the black dots indicate the locations of people. The black dots show the population who are waiting to receive their first vaccination dose. The red dots indicate the high priority demands in each suburb assigned for receiving their first dose of the vaccine. The green dots indicate people who are due to receive the second dose of vaccination on the day. The grey coloured dots show the people who have received both doses of vaccine. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
An effective and efficient vaccine supply chain requires a solution approach which would integrate the following practical assumptions and the underlying constraints. The vaccine packages are imported and stored in a centralised Government Designated Deep Cold Storage (GDDCS) facility and then distributed to the at which participants would arrive to receive vaccination.
-
–
The vaccines are sequentially delivered in packages to the from the GDDCS on daily basis.
-
–
Two doses of vaccine need to be dispensed to each recipient with 21 days interval.
-
–
Vaccine packs are distributed among facilities to sequentially serve population segmented on various priority levels.
-
–
The vaccine shelf life at fridge temperature is 6 days.
-
–
The capacity of is flexible which can be increased to double capacity from the original capacity by calling more medical staff.
-
–
The duration of vaccination per person ranges from 8 to 12 minutes.
-
–
All vaccine packs received and opened at must be used within the same day in 7 hours.
-
–
Vaccine delivery at the per day is set for 3-hour time window.
Within these assumptions, this study aims to develop a mathematical model to effectively distribute the vaccine packages. To achieve this aim, the following questions have to be answered:
-
–
Who needs to take the vaccine first to minimise the risk of infection? (Stage I)
-
–
Which are the areas with high level of susceptibility to COVID-19? (Stage I)
-
–
What is the daily assignment and schedule to efficiently distribute vaccines to population based on priority levels to the nearest ? (Stage II)
-
–
What is the best amount of vaccine packs to be assigned to each to minimise vaccine degradation? (Stage II)
-
–
What is the best capacity (number of staff required for vaccination) in each to minimise service waiting time? (Stage II)
-
–
What is the best daily assignment vaccine packs and routing of vehicles with minimum required couriers from GDDCS to the ? (Stage II)
Appendix G shows the mathematical formulation of the problem which comprises two models, namely assignment model Appendix G.1, capacity allocation model Appendix G.2. While these optimisation models can help identify an optimal arrangement of vaccine allocation and distribution for small size problem, the amount of calculation increases exponentially when the problem size increases. Real-time application becomes infeasible as the computation time becomes exceedingly long (see Appendix I). For a city with millions of people such as Melbourne waiting for vaccination, these models become impractical in helping healthcare planners to allocate and distribute vaccines on a daily basis. An efficient algorithm amalgamating mathematical modelling and heuristic that can produce a good enough solution in a relatively short period of time has to be employed instead. As such, the problem is reformulated as a math-heuristic algorithm using an integrated approach combining the three aspects of the problem — assignment, capacity allocation.
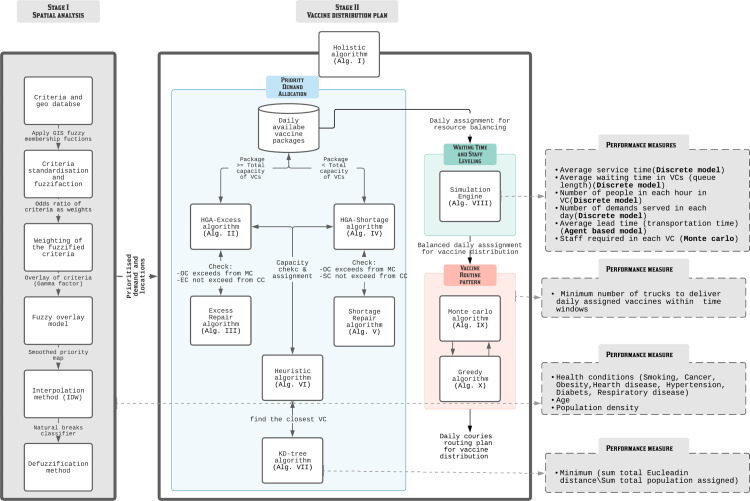
A framework to obtain a solution to this problem on a daily basis using the Holistic algorithm Alg. III is shown in Fig. 2 which comprises two stages. The first stage is to prioritise the allocation of vaccines to the neediest based on nine key prioritisation criteria identified from the literature. A geodatabase and fuzzy logic are used to spatially prioritise areas of vaccination demand in the study area. The second stage consists of three sub-stages to form a holistic system incorporating demand allocation, capacity balancing and vehicle routing to generate an efficient distribution plan. In allocating the priority demand determined in the first stage, eight hierarchical heuristic algorithms are integrated to obtain the daily assignments from the central storage location of vaccines to the where the vaccines are dispensed. A simulation engine is then used to simulate the many possible scenarios, such as mass random arrival of participants, to achieve the best resource balancing at the in terms of participant waiting time and vaccination staff levelling. Finally, the balanced daily assignments will be distributed to the through efficient vehicle routing to be obtained through heuristics including Monte Carlo and greedy algorithms. Various performance measures, such as average waiting and service time, number of trucks for delivery and total travelling distance, are used at each sub-stage to ensure the best outcome is obtained. Fig. 1 illustrates the proposed problem of this study.
Fig. 2.
Solution method framework. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
4. Solution approach
As shown in the solution method framework (Fig. 2), the objective of Stage I is to identify, locate, and prioritise people who are in need of vaccination by screening attributes including health condition, age, and population density of the locale using spatial analytical method. Once the daily priority demands for vaccine are determined, demands for the individual will be assigned considering the waiting time and the best serving capacity at the . After that, the optimal vehicle routes from the GDDCS to the will be calculated. These challenges are to be overcome in Stage II as described in the section below.
This integration exponentially escalates the complexity level of the problem (Pardalos, 1993) meaning that no commercial solver/method would be able to optimally solve the problem in an exact method with reasonable computational time. As such, an integrated hierarchical GIS-heuristic-simulation approach incorporated with heuristics to help generate semi-optimal daily vaccination plans in relatively short period of time is proposed. It addresses the problem covering all the five modelling concepts to be solved using eight algorithms and measured by seven system performance improvement indices.
4.1. Stage I- Spatial analysis
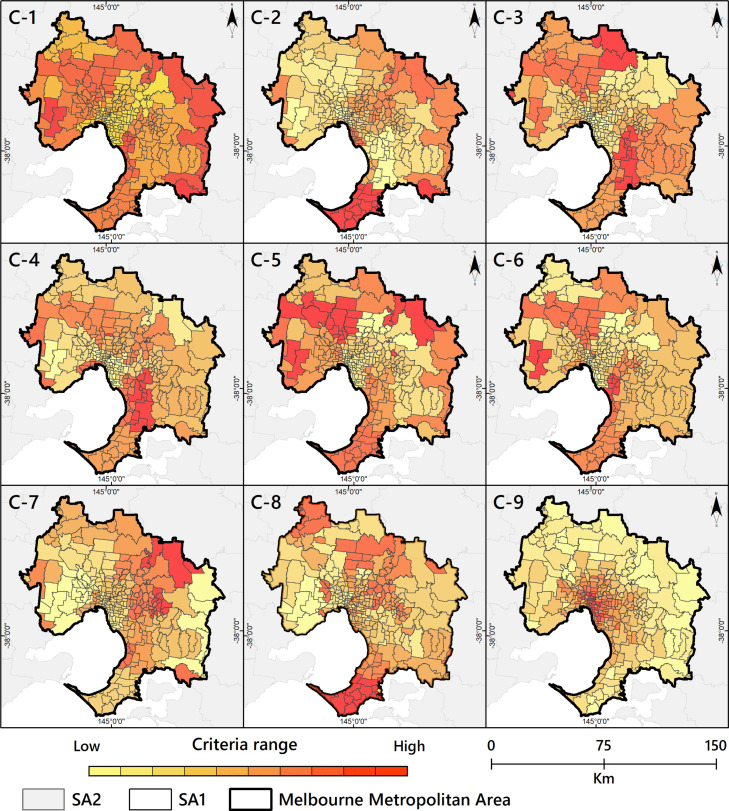
In Stage I, the first step is to prepare a geodatabase. Nine key criteria identified from the literature are used to spatially prioritise areas of vaccination demand (Table C.2). The fuzzy logic method is used to standardise the scale of each criterion (see Appendix D.3). Criteria weights obtained from the literature (Table C.2) are applied to the criteria layer in the GIS geodatabase. How each criterion dispersed on the GIS geodatabase of the Melbourne metropolitan area is depicted separately in Fig. C.2.
Fig. C.2.
Criteria map; C-1: Smoking C-2: Cancer; C-3: Obesity; C-4: Heart disease; C-5: Hypertension, C-6: Diabetes; C-7: Respiratory disease; C-8: Ageing; C-9: Population density.
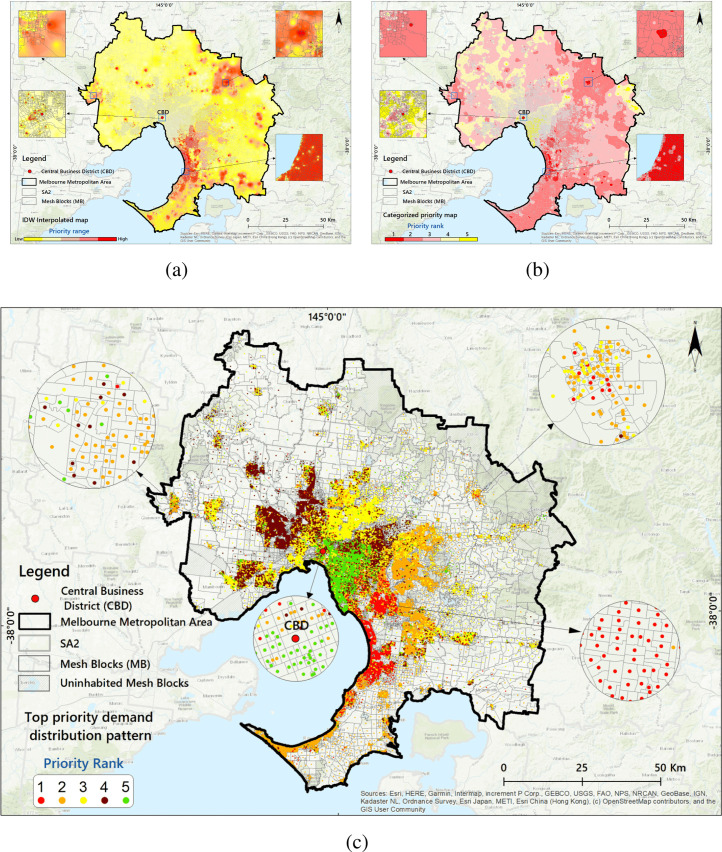
To apply each of the weighted criteria and extract an output with priority values, the fuzzy overlay function is used to overlay the criteria layers in GIS (see Appendix D for more details). Since the scale of the original survey data is in ‘mesh blocks’,1 the Inverse distance weighting (IDW) method interpolation method is applied to delineate the prioritised values (Fig. 3(a)).
Fig. 3.
Priority areas for vaccination; 3(a): IDW-interpolated map based on Fuzzy method by priority ranges; 3(b): Defuzzified ranking of areas in order of priority for vaccination; 3(c): Top priority demand distribution pattern within the SA1 centroids.(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In the final step, the linguistic fuzzy values (Fig. 3(a)) are converted to numerical interval values as input for Stage II. A defuzzification process is performed using the ‘reclassify’ approach in GIS (Fig. 3(b)). The final outputs of Stage I are the top priority demand locations and scores (Fig. 3(c)).
4.2. Stage II-Distribution pattern analysis
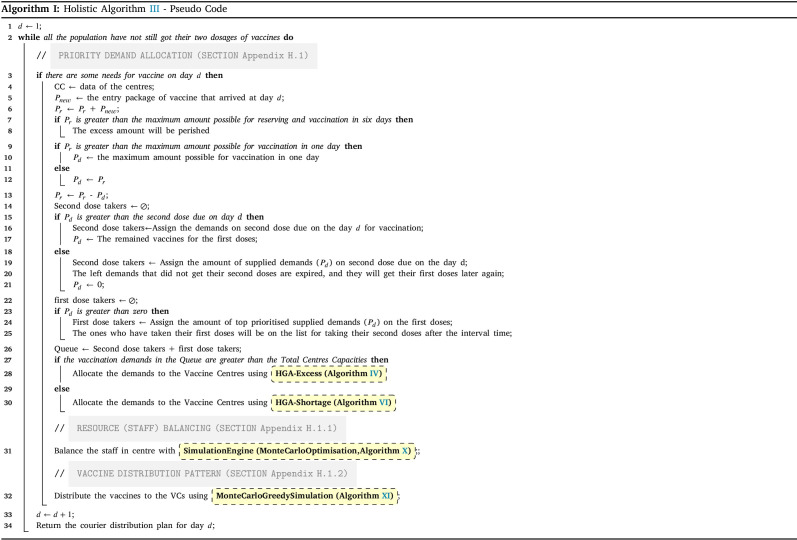
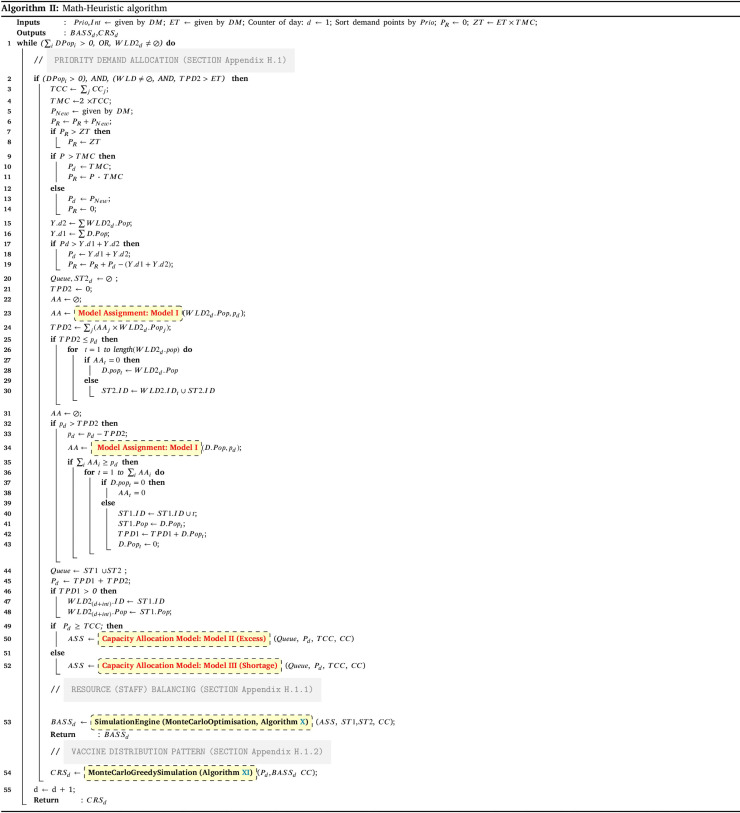
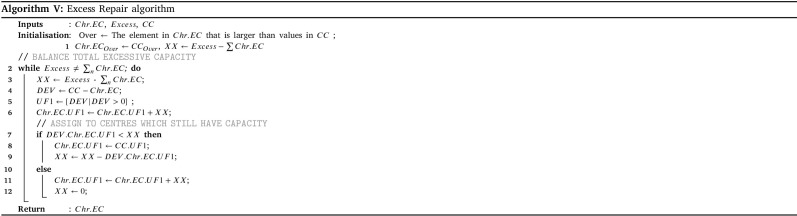
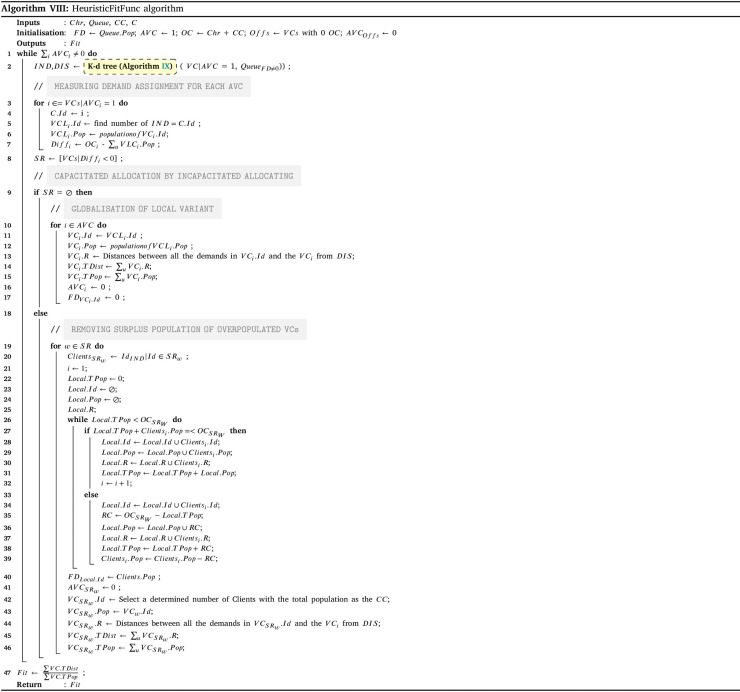
Stage II includes three main subsections as Priority demand allocation (Subsection Appendix H.1; Fig. 2-blue area), Resource (staff) balancing (simulation-optimisation) (subsection Appendix H.1.1; Fig. 2-green area), and vaccine distribution pattern (subsection Appendix H.1.2; Fig. 2-red area) that all integrated in the Holistic algorithm III. Using other inputs, the algorithm follows the three main steps to generate the best daily values for the decision variable as the Balanced Vaccine Allocation of day , and as the daily couriers vaccine distribution pattern through designed sequential progressive iterations (see Table A.1 for the nomenclature and Appendix H for detailed explanations).
In below, the pseudo-code for the holistic algorithm is provided. It contains iterations for each day. The iteration continues until all demands get both doses (line 2). On each day, the data of the centres will be given for any update (line 4). In addition, each day a package of vaccines will be received (line 5). Regardless of its amount, it aggregates on the reserved vaccines () from previous days (line 6). Next, if the reserved vaccines become larger than the maximum reserve capacity (line 7), the excess vaccines will be perished and minus from the reserved vaccines (line 8). If the number of reserved vaccines is less than the maximum capacity () of the day, the total amount will be prepared for the day vaccination. Otherwise, a part of the vaccines as the amount of TMC will be separated and prepared for the vaccination in the day, and the rest of them will be reserved for the next days (line 9–12). The prepared vaccines will first be assigned to the second dose due of the day. Whatever is left from the second dose, will be assigned to the leftover first doses demands. If the prepared vaccines are less than the second doses due of the day, some of the demands cannot get their second dose on time, hence, their vaccine cycle will be expired, thus, they should take their first doses again (line 15–21). Whoever gets his first dose, will be on the queue for taking their second dose after the interval time (line 22–24).
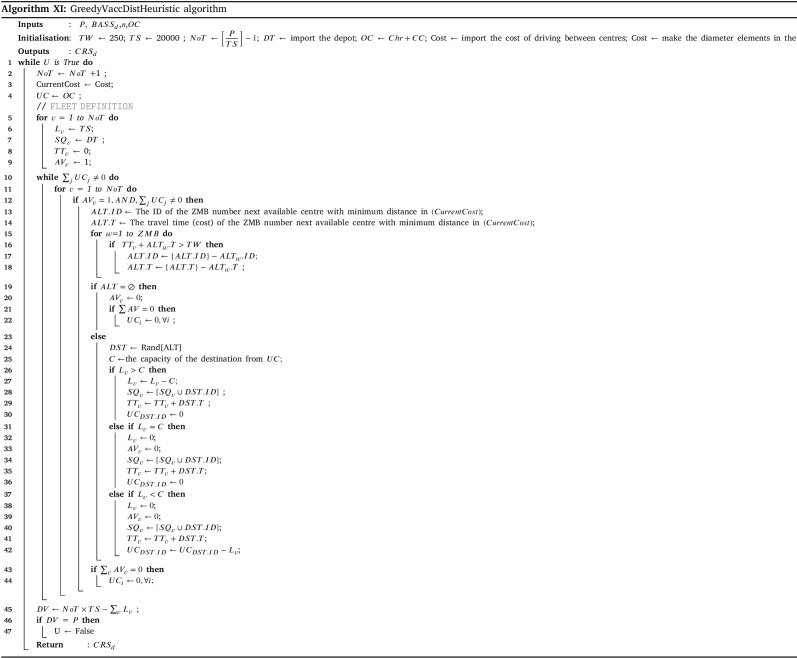
The amount of prepared vaccines determines which distribution strategy to choose. If the amount exceeds the total intrinsic capacity of the centres (TCC), the centre should operate over their capacity; otherwise, they can work under their capacity. The HGA-Excess algorithm IV and HGA-Shortage algorithm VI are developed to address the allocation of vaccines regarding the chose strategy (line 25–29). After the allocation of vaccines among the centres, Algorithm X balance the staff of the centres (line 30). Lastly, the Algorithm XI plans the distribution of vaccine to the centre with refrigerated trucks (line 31).
5. Numerical experiment
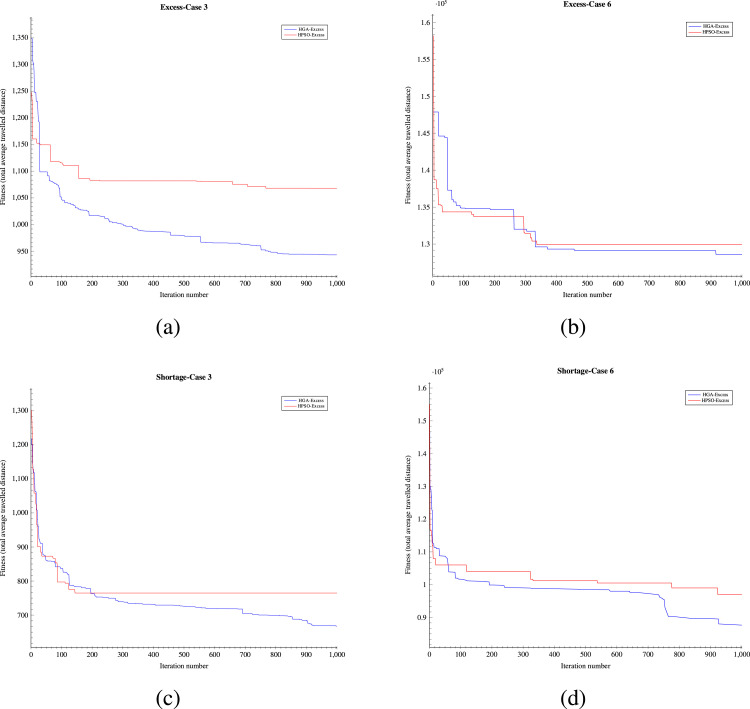
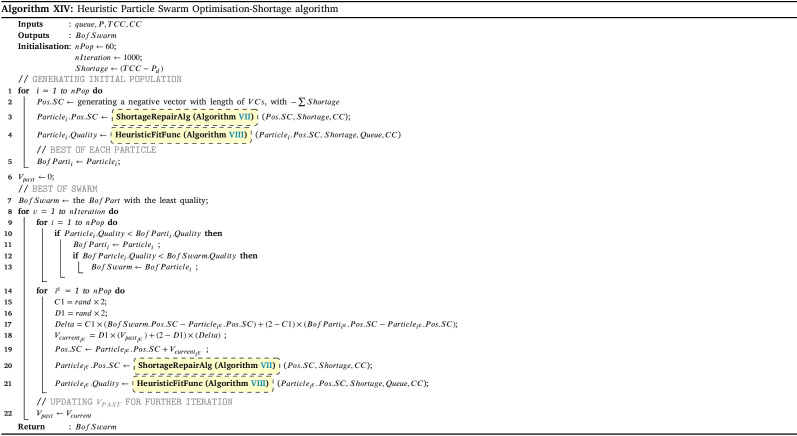
To assess the effectiveness of the developed solution approach, sets of numerical experiments are designed using various sample problems. The proposed solution approach’s performance III strongly relies on the three algorithms of HGA-Excess IV, HGA Shortage VI (including the Heuristic and Repair algorithms (Algs. VIII, V and VII which are embedded), and Monte Carlo algorithm XII (which the greedy algorithm XI is included). We have compared the performance of both the HGA-Excess and HGA-Shortage algorithms with the developed counterpart Heuristic Particle Swarm Optimisation (HPSO) algorithms (see Appendix I.2 - Algs. XIII and XIV). The performance of the Monte Carlo greedy algorithm has been evaluated by Bodaghi et al. (2020). To ensure that variations of the algorithm inputs are captured in the fitness value, each case is repeated and analysed for thirty iterations. The algorithms are coded in MATLAB and run on a PC with a 3.8 GHz CPU with 16 GB RAM. The mean and standard deviation of thirty runs in several cases are presented in Appendix I.2 - Table I.2 as follows.
The results in Appendix I.2 - Table I.2 indicate that the outcomes of the both HGA-Excess and Shortage algorithms can outperform the relative HPSO algorithms by at least 3.26% in the case 8 - Excess and 1.99% in case 4 - Shortage.
Appendix I.2 - Fig. I.1 illustrates another comparison as the convergence graph for solving Cases 3 Appendix I.2 - Figs. 1(a), 1(c) and 6 Appendix I.2 - Figs. 1(b), 1(d) in the numerical example with both methods after 1000 iterations. The computation time is 7321.2 s. Using the above instances explained, the suggested HGA-Excess and HGA-Shortage algorithms’ performance is validated. The figures indicate that the HGA algorithm can obtain better outcomes in the same scenarios within a certain period of time.
Fig. I.1.
Convergence comparison; Fig. 1(a): Convergence plot of day 1 in Case 3 with HGA-Excess; Fig. 1(b): Convergence plot of day 1 in Case 6 with HGA-Excess; Fig. 1(c): Convergence plot of day 1 in Case 3 with HGA-Shortage; Fig. 1(d): Convergence plot of day 1 in Case 6 with HGA-Shortage.
6. Case study area
6.1. Characteristics and properties
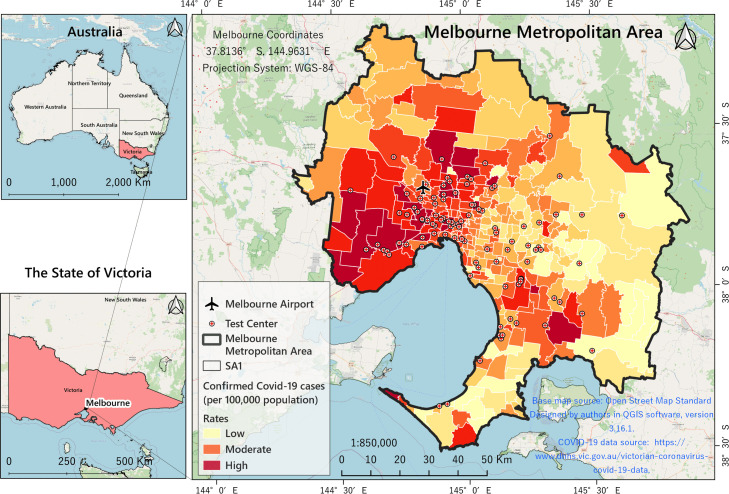
In this research, the Greater Melbourne Metropolitan Area (GMMA) is chosen as the study area. The GMMA is located in the southern part of the state of Victoria in Australia occupying an area of 9991.51 km (Fig. C.1). With a population of 5.078 million (2.3% annual growth rate), the GMMA is considered the second most populous urban area in Australia (ABS, 2020, DHHS, 2020). The average population density was calculated to be 1,618 people per km using mesh SA1 population data (DHHS, 2020). The inner city, with an average density of 3,700 people per km, has the highest population density. The median age of people in the GMMA is 36 years and people aged 65 years and over constitute 14.0% of the population. Melbourne is a very multicultural place and most of its residents are non-indigenous (94%). The first confirmed case of COVID-19 in Australia was identified on 25 January 2020, in the GMMA, when a man who had returned from Wuhan, China, tested positive for the virus (DHHS, 2020). From that date to the last date of this study period (24/08/2021), 21,526 people were infected with the coronavirus in the GMMA. Fig. C.1 shows the GMMA location by Statistical Areas Level 1 (SA1) and the COVID-19 infection as at 24/08/2021. Just as the virus itself is highly variable and complex, its spread in geographical terms is highly dynamic and unstable. Appendix C - Fig. C.1, which is drawn based on DHHS data, shows that the western, southeastern and northeastern areas of the GMMA have experienced higher rates (active cases per 100,000) of infection since the outbreak.
Fig. C.1.
Spatial location of GMMA by SA1 boundaries and Empirical Bayesian Smoothed (EBS) COVID-19 rates.
6.2. Criteria and weights
For prioritisation of vaccine allocation, the required criteria are derived and assembled from a comprehensive investigation and a thorough review of the literature and meta-analysis studies. Previous epidemiological meta-analysis studies have confirmed the role of these selected variables in increasing the risk of death following coronavirus infection. As such, allocating vaccines in priority to people meeting these criteria would be more effective to curb the infection. These criteria include epidemiological risk factors such as individual and Socio-physiological characters of vulnerable groups in the GMMA. They can be categorised into nine types based on health conditions (C-1:C-7), ageing (C-8), and population density (C-9) as documented in Appendix C.
These criteria increase the risk of death upon infection with the virus, although it does not mean that anyone who has one of these characteristics will be infected. Nevertheless, they are appropriate and important factors in prioritising vaccination. As weighting is a crucial step in FL-GIS prioritisation process, we use Odds Ratios (OR), a measure of association between exposure and an outcome commonly adopted in meta-analysis studies, as the weight of the criteria. As described in the following steps, the weights obtained from the literature review are applied to create the criteria maps. Table C.2 shows the selected criteria (symbolised by the letter C) by definition, weights, meta-analysis references and data source.
6.3. Data and geodatabase
In this study we used three types of dataset. The first dataset is related to the information of SA1 population, people with confirmed COVID-19 disease and 104 test centres. The disease data were recorded in SA1 (postcodes) level from 25 January 2020 to 24 September 2020 by the Department of Health and Human Services (DHHS), State Government of Victoria, Australia. There have been 18,816 people infected with the virus in Melbourne, of which 518 were active. Fig. C.1 shows the EBS2 rates of COVID-19 per 100,000 for the GMMA (high range = 1048 and low range = 8.3). The second type of dataset is administrative and statistical boundaries (SA2 and SA1) GIS vector format which are obtained from the Spatial Department of the Victorian State Government and Australian Bureau of Statistics (ABS, 2020). In addition, Open Street Standard Map is used to introduce the study area. These spatial data are used in FL-GIS visualisation process Appendix D.3. The third type of dataset includes information concerning nine selected criteria. This dataset is the basis of FL-GIS model application and is compiled from the available databases, and Victorian state government resources, which have been tabulated in details in Table B.1.
Priority areasFig. 3(a) shows the output map of the FL-GIS method based on the IDW method (see Appendix D.3 for details). As shown on the map, different areas of the city are clustered with high priority (red), moderate (yellow) and low priority (green). In terms of areal coverage, 3347.81 km fall in high and 6643.63 km on moderate and low priority range categories. Based on this split, 33.5% of the city area is given a higher priority of vaccination.
Fig. 3(b) shows the classified (defuzzified) priority ranked map. On this map, the GMMA is classified into five priority areas (catchments) based on priority values obtained from the applied FL-GIS method. According to this map, 419,780 (9.35%) people live in priority area 1 (red coloured), 888,771 (19.79%) in catchment 2 (orange coloured), 1,100,286 (24.51%) in catchment 3 (yellow coloured), 1,175,488 (26.18%) in catchment 4 (light green coloured) and 904,441 (20.14%) in catchment 5 (dark green coloured) respectively (based on 2016 census data). Population calculations based on the 2016 census data also show that 1,308,551 people, equivalent to 29.15% of the city population, are in the high priority of vaccination. About 41% of the GMMA postcodes are located in catchments 1 and 2 with high-ranged priority areas. Fig. 3(c) delineates the mesh blocks areas and related priorities. In this study, the GMMA’s COVID-19 test centres Appendix C - Fig. C.1 are assumed to be the vaccine centres Appendix C - Table C.1.
7. Results and discussion
In this section, two scenarios of vaccine supply distribution have been analysed to evaluate the performance of the proposed solution framework in generating vaccine distribution patterns under different circumstances. The parameter settings have been tuned before computational analysis in the below scenarios:
7.1. Scenario I - Limited daily supply (supply shortage )
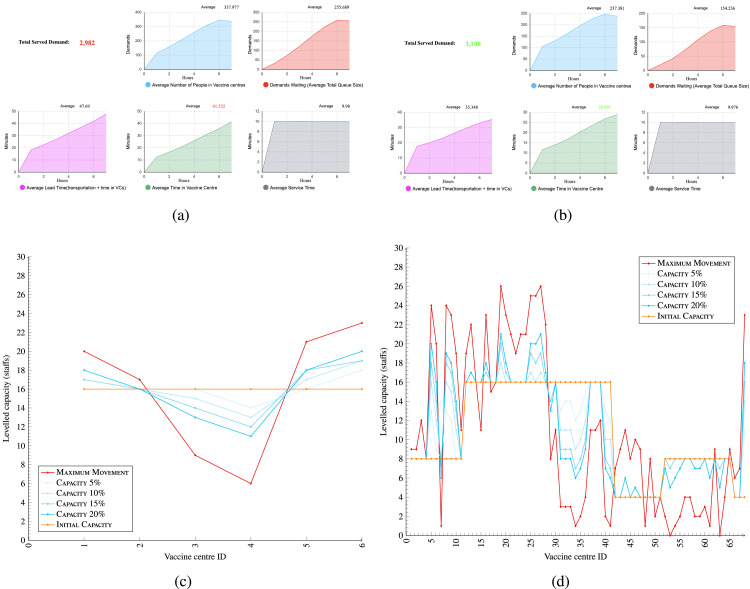
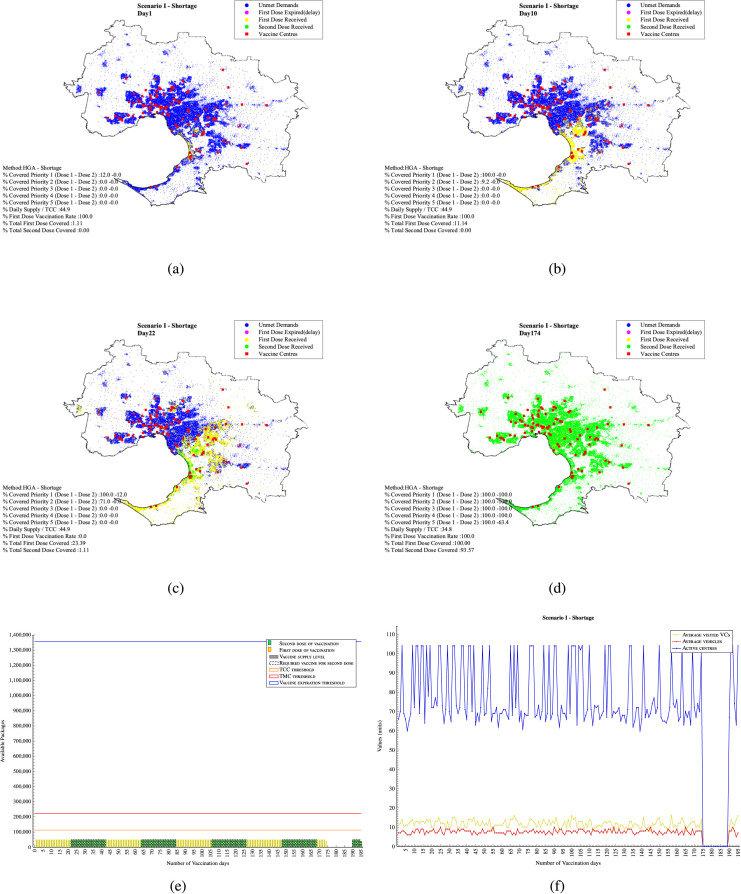
In this scenario, it is assumed that vaccine supplies are limited to 50,000 doses per day which is 44.9% of the original total capacity of the VCs at 113,000. Appendix F - Fig. F.1 shows the output of applying simulation engine in one day for staff balancing (reallocation) in the vaccine centres. The initial capacity allocation in Stage II has been calculated based on the direct Euclidean distance between the demands and the VCs as and VC capacities. In some cases, however, not all the assigned demand could serve since the VCs capacity considered in the is not enough to finish all the vaccinations within the 7 hours. For instance, in Day 1-VCs type A, only 2,982 from the entire 3,108 assigned population could be served within 7 working hours. The average time in vaccine centres with current vaccination capacities is 41’:53 minutes which exceeds the 30 minutes allowed Appendix F - Fig. 1(a). There is, however, another factor that should be taken into consideration, which is the last time the people left their homes to be served. In this case it is assumed that after 5.5 hour from the beginning of the vaccination, demand population has a maximum 1.5 hours lead time to spend on the road and the allocated VC.
Fig. F.1.
Simulation - Performance indicators - Fig. 1(a) shows before and Fig. 1(b) shows after applying the staff levelling optimisation in the simulation engine in a group in one day.
Appendix F - Fig. 1(b) visualises the best capacity in each VCs type A. Considering the new updated capacities, the key performances have been improved and cover the entire 3,108 assigned population Appendix F - Fig. 1(b). Appendix F - Fig. 1(d) shows an example of results of staff optimisation with 68 vaccine centres.
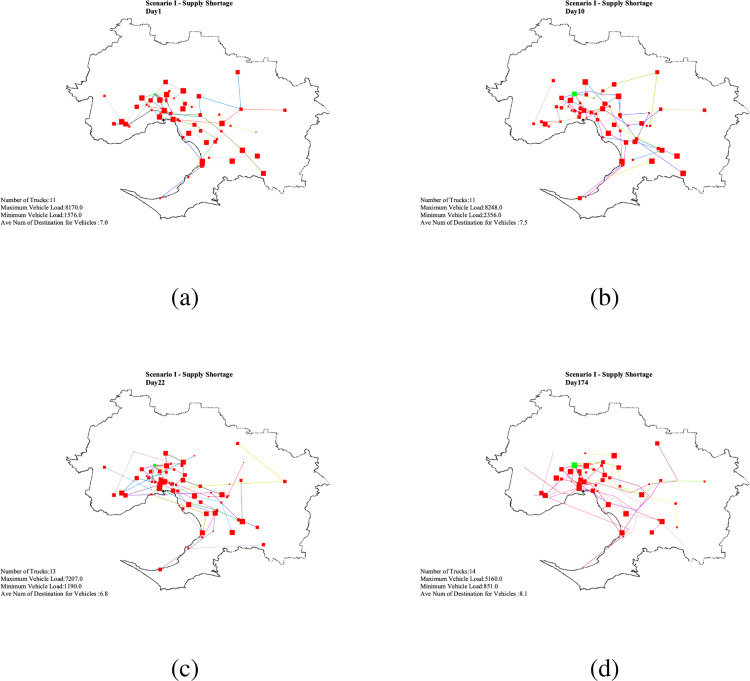
The daily balanced coverage plan for Days 1, 10 and 22 are plotted in Appendix F - Figs. 2(a) , 2(b) and 2(c) respectively. Results show that in this scenario 1.11% of the demand population can be vaccinated on the first day of vaccination (accounts for 12% of top priority demand population 1). On Day 10, 100% of the daily supplied vaccines have been used for vaccination of cumulative total 11.14% of the top priority demand population. 9.2% of top priority demand 2 have also been served. Appendix F - Fig. 2(b).
Fig. F.2.
Scenario I- Daily vaccination coverage.(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
By Day 22, 23.39% of the total population have received their first dose of the vaccination (Appendix F - Fig. 2(c) - (yellow dots)) which are those population areas ranked as top first (red spots), or second (orange spots) in Fig. 3(c). Considering the 21-day vaccination gap assumption, these people are due to receive their second dose of the vaccine. Since there is a shortage in the daily vaccine supply, all vaccines are used to vaccinate 1.11% of the population who received their vaccines on the first day (green dots) with 0% assignment for vaccination of new first dose demand. The maximum load of vaccination on this day is 1,806 while the average number of people vaccinated is 480 in all the VCs with 74% . Results also indicate that, on this day, 13 trucks as a minimum are required to timely distribute the vaccines to the active VCs with 7,207 and 1,190 vaccines as the maximum and the minimum load, respectively, within the daily three-hour time window each visiting 6.8 VCs on average.
In this scenario, 100% of all the people who have received their first dose of vaccine and 93.57% received their second dose in 174 days Appendix F - Fig. 2(d). The remaining 6.43% will need to wait until their due date which starts on Day 190. Therefore, there will be no vaccination between Day 174 and Day 190. The vaccination of the remaining population will finish by Day 195 (as low priority people would receive their first dose between Day 169 and Day 174).
Appendix F - Fig. 2(e) shows the daily vaccine supply and capacity thresholds. Fig. 2(f) shows the daily assignment required. The blue lines indicate the number of required active VCs, while the red and yellow lines show the average number of required vehicles (trucks) and visited VCs per day, respectively. The average number of vehicles required to distribute the vaccines is around 8 trucks per day visiting around 10 VCs. As shown in Appendix F - Fig. 2(f), there is always a shortage in capacity reflected as fluctuations in the number of daily required VCs. The total computational time for this was 6956 s. In Appendix F - Fig. 2(d), it is mentioned that there will not be any need for vaccination from Day 175 to Day 190. From Day 190 onward, some VCs and vehicles will still be required to serve the remaining second dose takers.
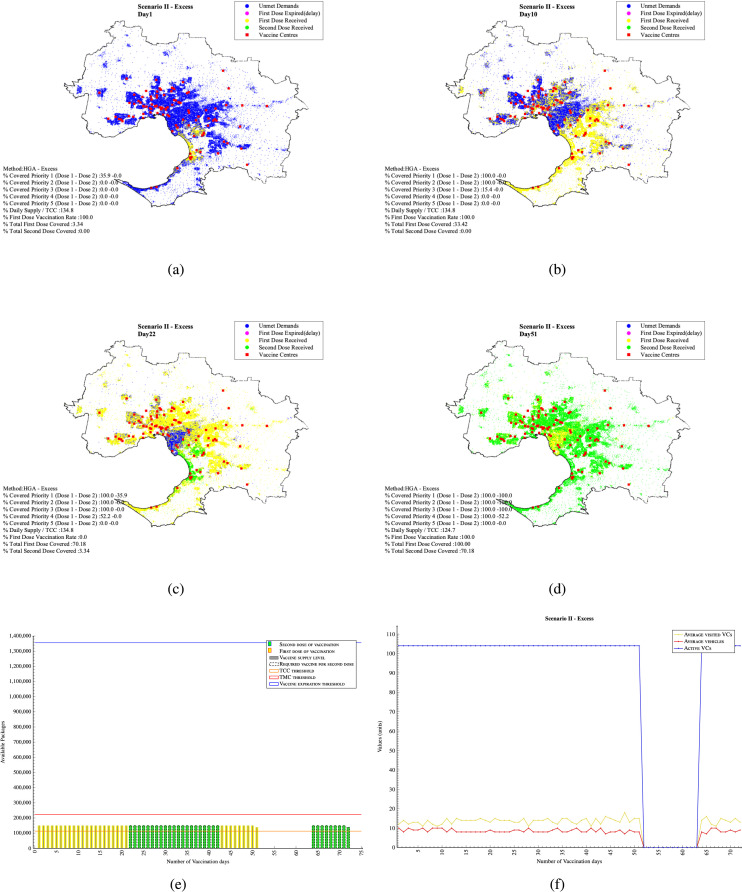
7.2. Scenario II - Excessive daily supply (excessive supply )
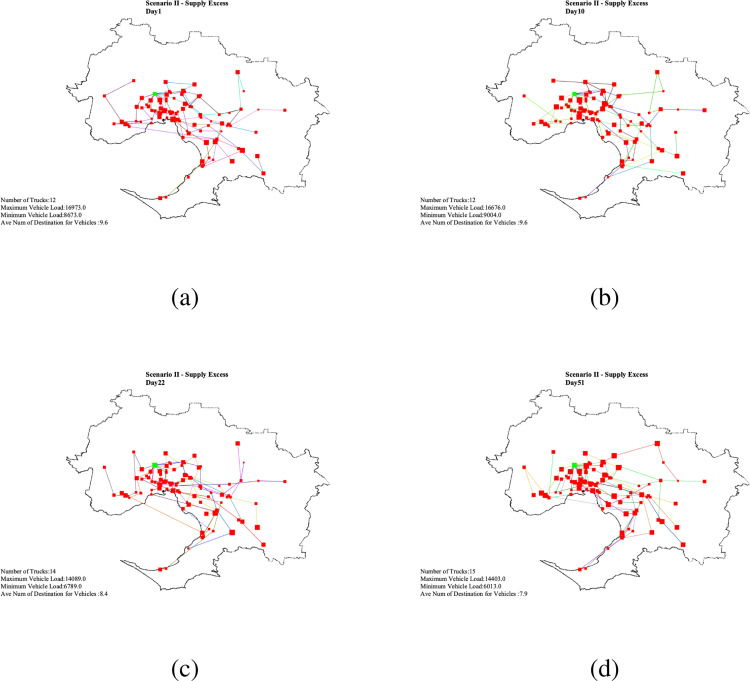
In this scenario, it is assumed that the supply is limited to 150,000 vaccines per day. This daily constant vaccine supply is greater than the total original capacity (113,000 per day) of all . Whenever there is a demand yet the supply is sufficient, the are assumed to work with a capacity increase which can be twice the size of the original capacity maximum. In this case, the are planned to work with 34.8% over capacity. As a result, considering the excess in the amount of available vaccines, 3.34% of top priority population can be covered on the first day of vaccination Appendix F - Fig. 3(a). In 10 days, 33.43% of the population is covered Appendix F - Fig. 3(b). On Day 21, almost 70.18% of the demand received their first dose of the vaccine. Day 22 is the due date for those 3.34% people vaccinated on Day 1 to receive their second dose Appendix F - Fig. 3(c). In this scenario, by Day 51, 100% of the people will have received their first dosage, and 70.18% received their second dosage. It means that there is no population left to receive the first dose of vaccine and no population is due to be vaccinated from Day 51 to Day 64. The remaining 29.82% who received their first vaccination dose in the period Days 42 to 51 should wait until their due date starts from Days 64 to 72. The results was obtained in 5984 s. The daily distribution plan for the above-mentioned Days is plotted in Appendix F - Fig. F.5.
Fig. F.3.
Scenario II- Daily assignment plan.
Fig. F.5.
Scenario II - Daily vaccine distribution routing plan .
7.3. Resilience analysis
The presented supply chain is designed to implement plans of Vaccination by the opinion of DM. Yet, unanticipated events may change the distribution process unlike what it is planned. The most significant ones are vaccine supply disruption and drop in capacity of some (or all) centres. Such disruptions are very likely to happen in the vaccine supply chain (Lemmens et al., 2016). Hence, a resilient and flexible system is necessary to survive from such disruptions. In this section, two stress tests are arranged to evaluate the resiliency of the supply chain under the disruptions. The aim of the experiment is to assess the system performance during and after disruptions, quantifying ”time to survive (TTS)” and “time to recover (TTR)” (Ciancimino et al., 2012, Dominguez et al., 2014). The TTRs for disruptions are presumed in the examples. To analyse the system’s performance each day, the accumulated vaccinated target demands in the scenario and the optimal plan will be compared (Hausman, 2004).
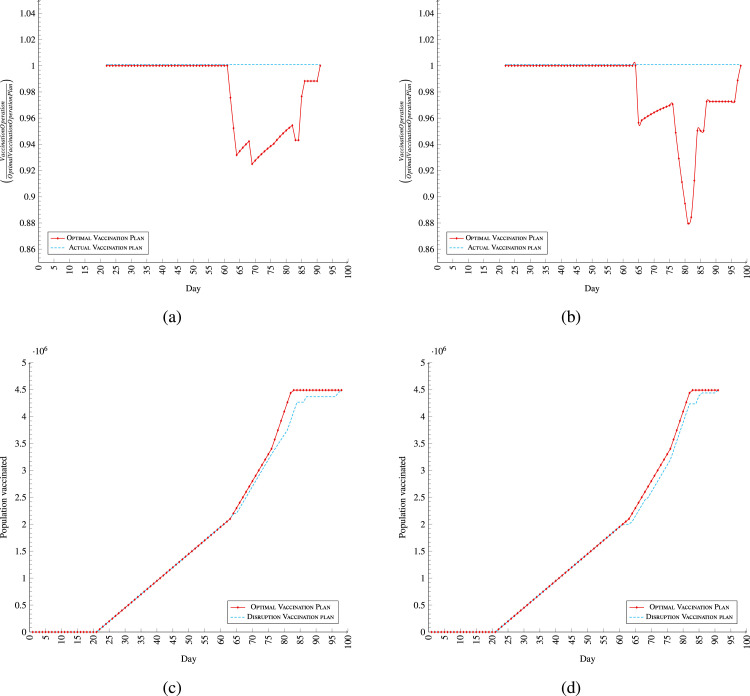
A DM’s assumptive optimal plan is to supply and vaccinate the target demands in the following order. In the first 21 days, 50,000 demands are supplied their vaccines for their first doses of vaccination. From Day 22 to 41, 100,000 vaccines, from Day 42 to 63, 150,000 vaccines and Days 64 and 65, 222,600 vaccines are supplied for first and second dosage demands. Day 63 gets 143,566 vaccines to finish the rest of the first dosages and respond to its second dosages. For the rest of the plan, 100,000 vaccines daily are received until the full coverage of second dosages and finish the vaccination process at day 88 (Fig. 4(a)).
Fig. 4.
Resilience analysis comparison bar charts.
7.3.1. Supply disruption
In this scenario, the process supposed to be as optimal plan, but after day 56, the supply confront some disruptions, which disrupted the vaccination process. The fluctuation in supply happens from Day 56, when a package of 1,500,000 is received. This amount exceeds the vaccine expiration limit threshold (blue line). Considering the presumed characteristics of the vaccines, the received package can be used for a maximum of six days at maximum level TMC. The amount of vaccines over the blue line cannot be used in the next six days become perished. As a result, with no supply from Days 57 to 63, the received vaccines cover the demands for both dosages until Day 62 (Fig. 5(a)).
Fig. 5.
Resilience analysis; optimal and actual plan comparison. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Those demands whose second dosage due are on Days 62, 63 and 69 to receive are expired because of no supply and no reserved vaccine, subsequently, they need to repeat their first dosages with the next earliest supply. Such shortage in supply is considered disruption for the vaccination operation. The system absorbs the expiration disruptions as it is noted in (Fig. 5(a)). As soon as the supply recovers from the deviation, the performance starts to recover the drop in vaccination rate. (Fig. 5(a) - day 64). Those people who need to repeat their first vaccination will receive their second vaccination 21 days later on Days 85, 86 and 91 (Fig. 4(c) supply disruption-:red line border — Day 91 is due for second dose for demands expire on Day 69) (Fig. 4(c)). Hence, the process become eight days longer than what it is in the optimal plan to adapt with the disruptions. Fig. 5, Fig. 5 depict the performance of the system for both the supply disruption scenario and the optimal plan based on each day. As it is shown in Fig. 5(d), disruptions are absorbed by the system on the days that the scenario deviates from the optimal plan.
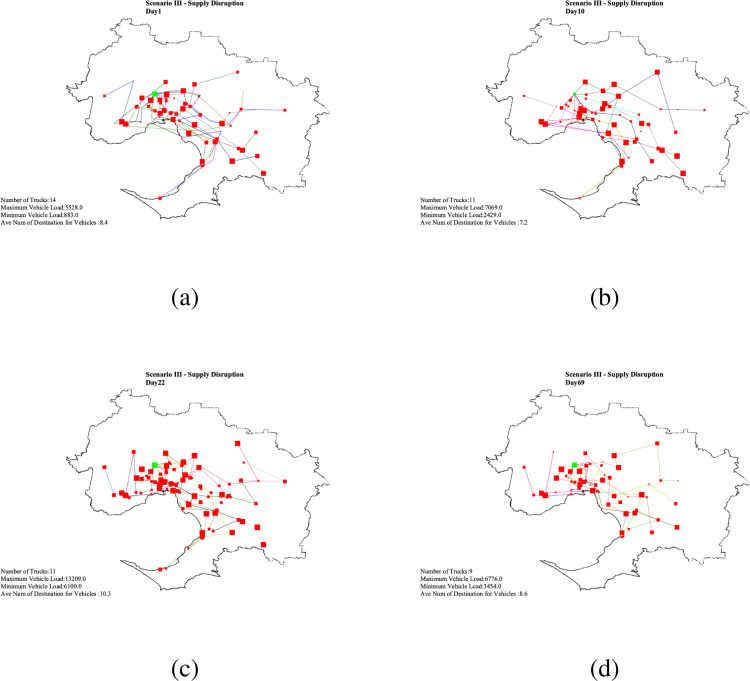
The TTS, the maximum time that the system match supply with demand after a disruption (Simchi-Levi and Simchi-Levi, 2020), is always greater than TTR (Golan et al., 2020). It is obvious from the supply disruption scenario that soon after recovering from the disruption, the system match the demands with the input supply. Because the system match demands with supply instead of matching supply with demands, the system is rigidly resilient for supply disruption (Fig. F.6 for daily vaccine disruption routing plan).
Fig. F.6.
Scenario III - Daily vaccine distribution routing plan .
7.3.2. Capacity drop disruption
This section evaluates the resiliency of the system for the disruption of capacity drop of the VCs. The drop of capacity can have any reason in the supply chain. Regardless of the reasons, we assess the performance of the system under the designed stress test. The optimal operation plan is explained in Section 7.3. It is assumed that the daily supply of vaccine to be the same as the optimal plan. Two disruptions from drop in capacities happen in this scenario. The drops can be for drop in one VC or more. The first one happens from day 56 to day 60, which the total capacities drops to 70,000 from 111,300. The other one, happens on Day 65 when the total capacity drops to zero (Fig. 4(b)). The four-stage of resilience – plan, absorb, recover, adapt – provided by NAS to respond such adverse events over time (Linkov et al., 2014) is visible in the (Fig. 5(b)). This scenario takes 15 days longer than the optimal plan. And for the rest of days after the optimal plan, the supply considered to be matching with the demands, to avoid mixing capacity drop disruption with supply disruption.
The responses of system to the disruptions confirm resiliency. After the drop in capacity get back to full operation, the performance starts to adapt with the new situation after the disruption through matching demands with the supply (Fig. 5(b)). This concludes that the TTS of the supply chain is absolutely greater than the TTR (Golan et al., 2020, Simchi-Levi and Simchi-Levi, 2020).
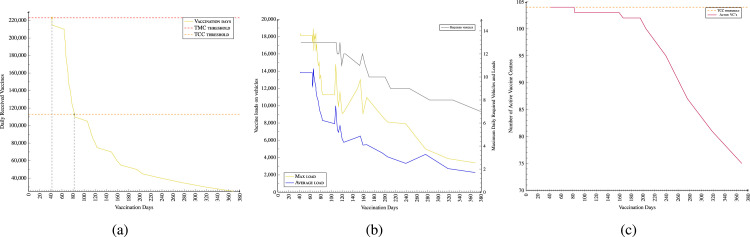
7.4. Sensitivity analysis on supply
Based on the number of daily supply packages and required days for vaccinations in Fig. 6, a sensitivity analysis is also examined. The results indicate that serving demands with maximum allowed capacity of 226,000 vaccines per day (TMC threshold - red line), the entire GMMA’s vaccination could finish in 42 days. On average, 82 days are required to vaccinate the entire population of the GMMA working with the original TCC capacity threshold (green line) (Fig. 6(a)). The number of required daily active centres () has a direct relation with the number of received vaccines. The more vaccine received, the shorter is the vaccination period, and the higher is the number of VCs required to actively serve the population daily (Fig. 6(c) - orange line). Fig. 6(b) indicates the results that having a shorter vaccination period requires a higher number of vehicles (gray line) on average loading more amount of vaccines (blue line) to supply to the VCs within the three-hour time window from the central GDDCS.
Fig. 6.
Sensitivity analysis- Fig. 6(b) shows the vaccine supply-vaccination days trade-off; Fig. 6(b) shows results for required number of vehicles and related loads. Fig. 6(b) shows the number of average required active vaccine centres — vaccination days trade-off. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
8. Managerial implications
This study provides evidence-based management insights to support both operational and strategic decision making in the vaccine rollout process. The solutions and plans generated in this study can inform the current ‘COVID-19 Vaccine National Rollout Strategy’ through a well-informed, geo-targeted and prioritised approach to the implementation of three-phase vaccine rollout program in Australia. The potential limits estimated by the model can be used as benchmarks by the Department of Health to guide evidence-based operational planning and execution of the vaccination program. Knowing the constraints, network capacity and thresholds under different scenarios is important to mitigate risks of community transmission through the deployment of prevention strategies. Agencies responsible for vaccine rollout would be able to generate efficient solutions across plausible supply scenarios, namely limited, excessive and disruption (the DM’s plan in resilience analysis section), within a reasonable computational time. The proposed centralised distribution system will allow the government agencies to have a full visibility, control and coordination of the supply network in Melbourne. In this section, management implications onto both operational and strategic decisions on vaccine rollout across the populace are discussed.
-
–
Spatially integrated prioritisation: Vaccination should provide the equitable protection from COVID-19 of all people living in Australia. However, given the limited and uncertainty of vaccine supplies, prioritisation may an effective strategy to ensure the vaccines are first inoculated to most vulnerable groups. The prioritisation groups ready for vaccination, segmented by locations and risk levels, provide an efficient and safe allocation mechanism for the government agency to reduce the risk of infection and associated mortality. Static policies with prioritisation of demand in the allocation of limited supply of vaccines can significantly reduce mortality and infection rates when compared to the situation with no prioritisation of demand or where the allocation is driven by population size (Chen et al., 2020, Foy et al., 2021). In addition, the spatially integrated vaccination strategy, prioritising both exposure risk and neighbourhood, would reduce infection risk and prevent community transmission when compared to a strategy that prioritises merely based on age alone (Brown et al., 2014).
-
–
Priority-based daily allocation of vaccines: The daily vaccine allocation plans will equip the Department of Health to manage vaccine stock levels, ensuring an efficient coordination, tracking and timely allocation of vaccines to locations where they are most needed. Vaccine allocation schedules are generated to help the Department to make nuanced decision on daily allocation of vaccines across the distribution network. Knowing the minimum number of days needed to vaccinate population with the first and second dose or both across different locations will help setting up benchmarks for monitoring the efficiency of vaccine allocation and dispensing. In all scenarios, all the people in the priority 1 can be vaccinated with the first dose of vaccine within 10 days; the entire population in Victoria can be vaccinated with the first dose within 174 days maximum (average 82 days); and the majority (average 73.5%) vaccinated with the second dose. The daily allocation plan provides empirical evidence to guide the execution of the ‘phased approach to COVID-19’ as planned by the ’Centers for Disease Control and Prevention’ (CDC) in the USA based on four prioritised groups for initial vaccination: healthcare personnel, non-healthcare essential workers, adults with high-risk medical conditions, and people over 65 years of age. The simulation results in Fig. F.1, Fig. 6, and 6(c), for instance, can guide health planners to make informed decision on determining daily vaccine requirements as well as staff capacity utilisation, number of daily active vaccine centres, daily required vehicles and loads, across the demand nodes. The allocation tool is versatile and scalable as it allows additional vaccines to be allocated to support ‘ring-fencing’ to reduce community transmission from rapidly emerging clusters.
-
–
Integrated and distributed vaccine supply chain: The logistics of vaccine distribution is complex and atypical, which require specific storage, transportation and allocation requirements of different vaccines. In the 2021–22 federal budget, the Australian Government has allocated almost A $234 million for vaccine distribution, cold storage and purchase of consumables. The two-stage approach, combining prioritisation of demand allocation with heuristic algorithm, has generated optimal daily vaccine distribution routing plans (Fig. F.4, Fig. F.5, Fig. F.6). These plans would enhance the analytic capability of government agencies as well as private logistics providers to provide a complete spatial coverage whilst minimising transportation costs. Further, estimated number of refrigerated vehicles required to distribute the vaccines can make the operations relatively efficient and easy to manage. Logistics providers assigned with the distribution tasks will benefit from knowing the minimum number of trucks required to timely distribute vaccines to active VCs with known maximum and the minimum load within the daily three-hour time window. The use of centralised distribution network will enable the Health Department to manage information visibility across the vaccine supply chain, material control (track and trace) and the supply agility to shift resources to optimise need-based vaccine distribution. Vaccine allocation and centralised distribution can be embedded as a secured integrated web-based distributed system to include purchasing, ordering, storing through to allocation, distribution and inoculation of vaccines via designated vaccination centres.
-
–
Decision-support system tool with visualisation capability: The DSS, integrating spatially analysis with heuristics and simulation approach, provides a relatively more practical toolkit than outputs from pure optimisation through mathematical modelling. This is because of the NP-hard nature of the problem, which can render finding an optimal solution impossible in large cases. The simulation approach integrated with various heuristics permits a quick analysis of the likely outcomes of a proposed allocation and distribution system. This is due to, firstly, unforeseen fluctuations in vaccine supply, and secondly, the effect of re-allocating limited resources to achieve the set objectives, which may change with time and uncertainty). The visual outputs from GIS-based analysis enable non-technical planners and health experts to visualise the complexity of multi-tiered vaccine supply chain and the likely impact of their decisions on the effectiveness and efficacy of vaccination allocation and physical distribution. DSS may also render the visual interface more user-friendly and valuable in practice. Five major catchments in Melbourne will help health advisers in spatial planning to differentiate COVID-19 risk levels and exposure by localities. This geo-targeted approach can assist policymakers in formulating effective spatially-integrated health policies and operational plans to create priority-based zoning to enhance spatial accessibility to vaccine centres. The delineation of catchment areas will also enable transport providers to effectively distribute vaccines whilst keeping the delivery cost low. Again, this functionality provides valuable insights for healthcare experts to readily evaluate the pros and cons of certain policy options prior to making the final decision.
Fig. F.4.
Scenario I - Daily vaccine distribution routing plan.
9. Conclusion
This study developed an integrated platform, combining prioritisation of demand with assignment and daily distribution of vaccine packs to vaccine centres in Melbourne. Priority groups and vulnerable areas were identified and mapped for vaccine allocation and distribution. A FL-GIS integrated model is developed to delineate priority areas for vaccination in the GMMA using key risk factors. A holistic algorithm, amalgamating several heuristics to allocate the prioritised demand, compute daily assignment, balance waiting time, calculate staff resource utilisation, and optimise vehicle routes. It is the first attempt to provide an alternative based on a holistic algorithm to the traditional optimisation approach in generating the best solution to the problem within an acceptable computational time within the bounds of various constraints and uncertainties. By combining both demand prioritisation with assignment and distribution in a single platform, the chance of finding the best arrangement has improved when compared to handling the two tasks separately.
The results of the FL-GIS and IDW method and adding priority values to mesh blocks level (Stage I) show improvement in accuracy, readability and expressiveness. Melbourne is delineated into five main catchments based on spatially weighted ranks, which enables the population at risk to be calculated by priority value. This mapped output is then used in Stage II to identify the best sites for the establishment of vaccine centres.
The methodology developed in this study has several merits. First is the determination of appropriate weights of each of the criteria to map the priority groups in Melbourne. The different weights applied to the criteria embed varying risk levels to COVID-19 reflect situations such as the risk of death from COVID- 19 is twice as high in the elderly as in smokers. This additional step improves the guidelines for prioritisation of vaccines to the neediest and disadvantaged. Second is the visual analytic capability to spatially represent the vaccine allocation and scheduling by locations. Visual outputs are simpler to comprehend, relatively easier to integrate in healthcare plans and practically operational to support in-situ decision-making during crisis. Finally, the algorithm and model are generic, interoperable and adaptable to different cities and regions. It is a versatile decision support tool that helps find the most efficient vaccine distribution arrangement.
There are, however, limitations of this study. Firstly, the current COVID-19 test centres are assumed to be vaccine centres for the case study. Recent media release indicates the possibility of using General Practitioners or pharmacies to be vaccine administrating units. The addition of these units with varying capacities may provide much wider coverage and necessitate a new vaccine allocation schedule due to the reconfiguration of the vaccine supply network. Secondly, mesh blocks, instead of individuals, are used to prioritise demand for vaccination. This is due to the lack of access to highly confidential individual level information. The use of a web-portal however will enable people to self-report their personal details and make it accessible to the Health Department to be used for vaccine allocation. In recent days, vaccines are re-allocated to areas which are at higher risk of community transmission by the Government. Further, the use of centroids of mesh blocks may not represent the weighted centre of population, which may affect the routing and scheduling. If information on the exact locations of individuals and their health conditions were known, prioritisation at mesh block level could be easily refined at an individual level. Through the web portal, government agency can obtain the individual level details for demand prioritisation and allocation of vaccines based on scheduled appointments. Finally, co-morbidity data on health at a smaller geographic scale could enable health agency to identify and prioritise spatial pockets of acute health challenges. The design of the DSS is driven by a centralised distribution and vaccination program, which is currently in place in Australia, that controls and regulation the procurement, storage, allocation and dispensing of vaccines to population. Future research will build a DSS to support a decentralised model to operate in a multi-agency decision-support structure with specific tasks and responsibilities assigned to each agency.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Mesh blocks are the smallest geographical area defined by the ABS (2017) and form the building blocks for the larger regions of the Australian Statistical Geography Standard (ASGS). All other statistical areas or regions are built up from or, approximated by whole mesh blocks. They broadly identify land use such as residential, commercial, primary production and parks, etc. The ASGS boundaries by areas can be ordered as SA4, SA3, SA2, SA1 (suburbs), and mesh blocks). Most mesh blocks contain 30 to 60 dwellings.
Empirical Bayesian Smoothed (EBS) is a technique employed for smoothing and preventing bias in raw rates (Marek et al., 2014) EBS balances event rates, especially for areas with limited populations (Nyadanu et al., 2019).
Appendix A. Nomenclature
Table A.1.
Nomenclature; list of sets, indices, parameters, and decision variables.
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| Suffix for excessive capacity of related variable; | Suffix for location ID of population of related variable; | ||
| Suffix for population of related variable; | Position (chromosome) of particle in a shortage strategy; | ||
| The quality (fitness) of the particle (individual); | Suffix for the initial results; | ||
| Suffix for total distance of related variable; | Suffix for total population of related variable; | ||
| Probability rate of Monte Carlo selection process; | Set of assigned demand points (equal to decision variable of Assignement model); |
||
| Set of Average distance of demands and allocated ; | Set of IDs of the available from the current position of truck ; | ||
| Set of travel times to available from the current position of truck ; | Demand assignment of day to ; | ||
| Truck availability for next destination; binary parameter; | Set of numbers of active vaccine centres; | ||
| Balanced capacity assignment of the service centres ; | Maximum movements in staff re-allocation; | ||
| Balanced distribution; | The particle with best quality (fitness) in the last set of particles; | ||
| The particle with overall best quality (fitness); | Assigned capacity of VCs in the for simulation; | ||
| Allocated capacity to the centre ; | A random coefficient number in Delta in Alg. XI; | ||
| Set of Original capacities of the ; | Current capacity of vaccine distribution ; | ||
| Capacity difference; | Chromosome; | ||
| Set of numbers (ID) of the pre allocated Demands to a centre; | The distance between centre to centre ; | ||
| Couriers distribution of day within time window ; | Unchanged cost in process of the Alg. IX; | ||
| Counter for vaccination day; | The Euclidean distance between centre and demand ; | ||
| Set of coordinates of Demand point ; | A random coefficient number in in Alg. XI; | ||
| Dynamic capacity difference; | Distance of particle from Bofparticle and Bofswarm; | ||
| Difference of centres’ capacity from constraint; | Remaining capacity of ; | ||
| Set of distances from allocated demand points to a centre; | Distance between the demand and ; | ||
| The Euclidean distance between centre and demand ; | Decision maker; | ||
| Population of the demand point (in each day ) ; | ID number of the next destination of truck in day ; | ||
| Central vaccine storage place (depot); | Delivered vaccines to in day ; | ||
| Individual with the least amount of fitfuncion; | Expiration time of vaccine packages; | ||
| Excessive load; | Set of locations’ IDs with no unmet demand; | ||
| Fitness ; | Counter for offsprings of the crossover; | ||
| , | index of demand points; | ID number of ; | |
| Individual for crossover; | Selected particles for muting by mutation 1; | ||
| Selected particles for muting by mutation 2; | Set of IDs (numbers) of centre corresponding the allocating demands point; |
||
| Interval gap for receiving second dose of vaccine; | Counter for demands for the assignment model; | ||
| Load of vehicle ; | Prefix for local variables (Set of demand points temporary allocated to ); |
||
| Levelled capacity of ; | Set of IDs (numbers) of the ; | ||
| Maximum capacity of ; | The individual that has been muted by mutation 1; | ||
| The individual that has been muted by mutation 2; | Set pf Population of IDs of demands for assignment model; | ||
| Set of IDs (numbers) of the Demand points; | Number parent particles for crossover; | ||
| Next generation of results; | Number of iteration for the GA; | ||
| Nominated for serving demand; | Number of individuals to get mutated by the mutation 1; | ||
| Number of individuals to get mutated by the mutation 2; | Number of trucks in day to distribute vaccines; | ||
| Population of initial results in HGA Alg.s; | Overall capacity of ; | ||
| with zero overall capacity; | The first child of parent 1 and parent 2; | ||
| The second child of parent 1 and parent 2; | Over populated centres; | ||
| New received package; | Package of vaccines of day ; | ||
| Reserved vaccines; | The individual that is a parent for the crossover; | ||
| Another individual for parenting in the crossover; | The particle I in the swarm; | ||
| Chance of being parent for the individuals in a generation; | Peak dynamic capacity difference; | ||
| Mutation probability rate 1; | Mutation probability rate 2; | ||
| The individual in the generation; | Priority ranking of mesh block area centroid; | ||
| Set of demand points’ IDs waiting for vaccination of the day; | Distance between all the demands and their nearest centre; | ||
| Accuracy measure index; | Remaining capacity; | ||
| Euclidean distance between demand and nearest centre; | The number of supply for the assignment model; | ||
| A counter for centres; | Set of vaccine distribution sequences; | ||
| Chance of selecting centre in the chromosome; | Shortage load; | ||
| Set of sequence of truck visiting ; | Surplus population in overpopulation of (iteration); | ||
| Set of demands’ numbers as Service takers (first dose vaccination); | Set of demands’ numbers as Service takers (second dose vaccination); |
||
| A counter for demand points; | Total centres capacity; | ||
| Total capacity difference; | Total maximum capacity of ; | ||
| Top priority demand layer 1 (first dose vaccination); | Top priority demand layer 2 (second dose vaccination); | ||
| Vehicle (truck) capacity; | Travel time of truck from current to the next ; | ||
| Time window for vaccine delivery; | A Boolean variable to terminate the loop in the Alg. IX; | ||
| Undelivered vaccine demand of ; | that can change during the process of Alg. IX; | ||
| Set of not working with full of excess capacity centres; | Index of couriers trucks; | ||
| A counter for the trucks; | current speed for changing; | ||
| Speed of changing in the last generation; | Total distance of the allocated demands to the centre ; | ||
| Total population of the allocated demands to the centre ; | Vaccine centre’s load; | ||
| Valley dynamic capacity difference; | vehicle sequence with minimum travel time; | ||
| Population of the assigned demand point ; | Index of the centre that has been selected for muting; | ||
| Set of number of demands as waiting list (second dose vaccination) on day ; | Allocated population of point to centre ; | ||
| Decision variable of the assignment model; | Sum of chromosomes with less excess amount; | ||
| Total maximum daily required demand for dose 1; | Total maximum daily required demand for dose 2; | ||
| Sum of chromosomes with less shortage amount; | A counter for crossover operation; | ||
| Number of allowed set of destinations collection; | Vaccine expiration threshold; |
Appendix B. Related works
Table B.1.
A selective summary of most recent literature on pandemic vaccine supply chain.
| Authors | Objectives | Methodology | Variables | Priority group |
|---|---|---|---|---|
| Uscher-Pines et al. (2006) | To review national pandemic influenzas prioritisation plans | Descriptive statistics | Vaccine and antiviral priority groups, group rankings, goals of pharmaceutical interventions, the inclusion of scenarios and population size | Healthcare workers, essential service providers, people at high risk, children, elderly, key decision-makers, influenzas cases, hospitalised cases and unvaccinated |
| Kee et al. (2007) | To assess the level of influenza vaccine coverage, to understand the driving forces and barriers to vaccination and determine vaccination interventions for the South Korean population | Cross-sectional descriptive statistics | Demographic data, Vaccination rate, Factors associated with vaccination | The priority groups recommended for annual vaccination includes persons aged 65 years, persons with chronic illness such as chronic cardiopulmonary disease, diabetes, chronic liver disease and malignancy, residents of long-term care facilities, healthcare personnel and pregnant women. |
| Medlock and Galvani (2009) | To evaluate current vaccine allocation policies and to determine the optimal strategy | Age-structured Simulation model | Number of mortalities, contact rates, the duration of the infectious period, years of life lost, weighing deaths by the expected remaining years of life for different ages, contingent valuation, cost associated with vaccination, cost associated with illness and valued death. | 17 age groups (ages 0, 1 to 4; 5 to 9; 10 to 14; ; 70 to 74; and 75 and older). |
| Keeling and White (2011) | To targeting vaccination against novel infections: risk, age and spatial structure for pandemic influenza in Great Britain | SIR (susceptible,infectious, recovered) model | Age groups (5–14 years old and then 15–24 years old), regions, risk-groups, time periods to vaccination | Most affected regions of the country where the virus is most prevalent should be given priority |
| Araz et al. (2012) | To geographic prioritisation of distributing pandemic vaccines (Arizona, USA) | Geospatial and demographically-structured model, mathematical modelling | Age groups, number of people in county, vaccine Efficacy, vaccination rate, transmission probability, Vaccine Supply Data | Areas with high population size being the priority |
| Lee et al. (2012) | To determine optimal vaccination allocation policies during the H1N1 pandemic in Mexico | Non-Linear Dynamic mathematical model | The age distribution of the population, age specific vaccine efficacy, hospitalisation rates, | 6 age groups (1 0–5 yr, 2 6–12 yr, 3 13–19 yr, 4 20–39 yr, 5 40–59 yr, 6 60 yr) |
| Buccieri and Gaetz (2013) | To evaluate ethical pandemic planning policies | Mixed method (Descriptive statistics and interviews) | Gender, demographic factors, fear of infection, lack of concern, access to community-based clinics, access to a regular doctor, promotional campaign. | Homeless individuals in Toronto |
| Huang et al. (2017) | To explore the optimal allocation of several vaccine types to certain priority groups. | Optimisation model | The five priority groups and regions were taken as input. | Pregnant women, infants (0–3 years old); people between ages of 4–24; and adults at high risk and infant care givers. |
| Takahashi et al. (2017) | Toe targeting at-risk areas to vaccination against the measles in the African Great Lakes region | Sensitivity analysis, generalised additive models (GAMs) | Vaccinated and unvaccinated population variables, population age, | Some areas had never been vaccinated and were ’hot spots’ in terms of risk of disease and thus given priority for vaccination |
| Lessler et al. (2018) | To map cholera burden in sub-Saharan Africa and assess how geographical targeting could lead to more efficient interventions and vaccination | Descriptive statistics and Bayesian mapping | Population variables, disease data, | Countries located in central and east Africa (at high risk of disease) should be given priority |
| McMorrow et al. (2019) | To prioritise between different influenza vaccine risk groups | Descriptive statistics | Socio-economic variables, Rates of influenza, Vaccine efficacy, | Pregnant women, HIV-infected adults aged 15–64 years, Children aged 6–23 months, Adults aged 65 years, Healthcare workers, Adults and children with TB and chronic illnesses. |
| Venkatramanan et al. (2019) | To optimise spatial allocation of seasonal influenza vaccine under temporal constraints, USA | Greedy optimisation algorithm | Population, Airline flows, Commuter flows, Disease dynamics, population mobility | Southern and southeastern states of the United States were identified as priority centres |
| Acharya and Porwal (2020) | To provide vulnerability index for identification of vulnerable regions in India in terms of COVID-19 epidemic prevalence | Descriptive statistics and mapping | The comprehensive socioeconomic, epidemiological and availability of healthcare variables | Central and eastern regions are a priority |
| Chen et al. (2020) | To determine the optimal allocation policies for the COVID-19 vaccine. | Age-structured Simulation model | The number of individuals in each of the seven compartments, the population size, the transmission rate, the contact rate, the discount factor of the transmission rate, the average time (from exposed to infectious, from pre-symptomatic infectious to symptomatic infectious, from symptomatic infectious to recovered, from ascertained infectious to isolation, from isolation to recovered), the fraction of ascertainment in each age group, the level of permitted economic activities, the amount of vaccination allocated to each age group. | Seven compartments (susceptible, exposed, Pre-symptomatic infectious, un-ascertained infectious, ascertained infectious, isolated, and removed) and five age group (0–17, 18–44, 45–64, 65–74 and 75+). |
| Deo et al. (2020) | To examine the challenges of COVID-19 vaccine distribution | Descriptive statistics, Multi-parameter model | Age, co-morbidity, income and profession | 60 Plus Years, Moderate or severe comorbidities, Frontline healthcare and other essential workers, Low Income |
| Gamchi et al. (2020) | To prioritisation of Tehran city districts and individuals for vaccine distribution | Infected–recovered (SIR) model and bi-objective vehicle routing problem (VRP) method | Number of susceptible individuals, Number of infected individuals, Number of recovered individuals, Disease transmission rate, Natural death rate, Fixed cost of immunisation, Total available doses of required vaccine, Vaccination time in regions, Distance between regions, etc. | Areas in which ratio of Pregnant women is high, Areas where ratio of children under 6 months of age is high |
| Liu and Xian (2020) | To identify and locate potentially vulnerable demographic groups in terms of epidemic prevalence against the transmission of COVID-19 disease | COVID-19 Susceptibility Index | Age, cancer, diabetes, cardiovascular disease, obesity and lung disease | Vulnerable segments of the population are generally situated away from capital cities |
| Persad et al. (2020) | To prioritise access to COVID-19 vaccines | Descriptive statistics | None | Healthcare workers; other essential workers and people in high-transmission settings; and people with medical vulnerabilities associated with poorer COVID-19 outcomes, such as diabetes, pulmonary disease, cardiac disease, and obesity. |
Table B.2.
A selective summary of most recent literature on optimisation of vaccine distribution design. .
| Authors | Objectives | Methodology | Assumptions | Findings |
|---|---|---|---|---|
| Balcik et al. (2008) | To deliver relief supplies from local distribution centre(LDC) to beneficiaries affected by disasters efficiently using a vehicle-based last mile distribution system | A mixed integer programming model that determines delivery schedules for vehicles and equitably allocates resources, based on supply, vehicle capacity, and delivery time restrictions | Location of the LDC is predetermined. Its capacity is sufficient to serve its service region | Number of nodes, routes and partial-allocation options, penalty costs, LDC-supply and vehicle capacities, vehicles’ characteristics, etc. can make the problem very complex and difficult to find a preferred solution. |
| Medlock and Galvani (2009) | To determine optimal vaccine allocation for five outcome measures: deaths, infections, years of life lost, contingent valuation, and economic costs. | A mathematical model parametrised with survey-based contact data and mortality data from influenza pandemics | Limited supply of vaccines; Vaccinate the most valued based on age structure but not risk or occupation; Nonlinear constrained optimisation. | Optimal vaccination is achieved by prioritisation of schoolchildren and adults aged 30 to 39 years. Consideration of age-specific transmission dynamics is paramount in the desired allocation of influenza vaccines. |
| Lee et al. (2011) | To examine the impacts of new vaccines on existing vaccine supply chain in terms of storage or transport capacity. | Discrete-event simulation model based on HERMES and deterministic mathematical equation-based model (EBM models to simulate introducing various new vaccines to a district in Thailand | Children would present to clinics for immunisation when they reach the appropriate age | New vaccine introduction can exceed refrigerator space transport cold space at district and sub-district levels As such, additional storage capacity at the provincial level would be required. |
| Abrahams and Ragsdale (2012) | To design a decision support tool for clerical staff in a healthcare clinic using a familiar, affordable, and accessible software platform. | A binary integer programming model and a genetic algorithm solution technique with conventional scheduling approaches | Multiple vaccines; Single time slot of constant duration; All patients receive the needed vaccines; Number of patients is less than or equal to the number of available time slots; Single patient queue and a single server | Computational results show that significant cost savings can be achieved with the decision support system while simultaneously considering scheduling preferences of patients and mitigating scheduling inconvenience. |
| Özdamar and Demir (2012) | To develop transportation plans of the last mile delivery and pick-up problem in large-scale disaster relief | A hierarchical cluster and route procedure (HOGCR) for coordinating vehicle routing in large-scale post-disaster distribution and evacuation activities | Operational logistics plans are devised based on estimates of deliveries and evacuations necessary information such as population is known with certainty | The proposed optimisation approach can obtain in 15 min CPU time solutions within a percentage deviation of less than 12% from a strong lower bound for large-scale relief networks. |
| Dessouky et al. (2013) | To help design an efficient pharmaceutical supply chain with strategic locations to place warehouses and inventories and optimal routes for distribution vehicles | Mathematical models to solve facility location and vehicle routing problems in the context of a response to a large-scale emergency | The plans need to be flexible enough to accommodate contingencies of daily operations. They must consider the stochastic nature of the problem, such as uncertain demand, traffic conditions, etc. | Analysis using a hypothetical anthrax emergency in Los Angeles County shows the approach can help design a effective pharmaceutical supply chain to meet urgent needs. |
| Brown et al. (2014) | To explore different potential redesigns of the Benin vaccine supply chain and how they would compare with simply adding refrigerators and freezers to the current vaccine supply chain. | A discrete-event simulation model called HERMES (Highly Extensible Resource for Modelling Event-Driven Supply Chains) | Demand for vaccines is modelled stochastically at each location through vaccination sessions Data are drawn from a Poisson distribution around the expected number of patients from yearly census estimates | Operational costs can be reduced while vaccine availability increased by streamlining the distribution system from four to three levels. |
| Ceselli et al. (2014) | To determine the efficient distribution of vaccines or drugs through the simultaneous and coordinated use of distribution centres and vehicles | A mathematical model to solve a combined location and routing problem. An exact algorithm based on column generation with three different types of columns and branch-and-bound is devised to find the best solution. | Once a delivery site is visited, all people assigned to it will get the drugs within a very short time. Assignment of delivery sites to distribution centres is known beforehand. All vehicles travel at the same speed | Results of numerical experiments show that the proposed algorithm is able to quickly find the optimal value in most of the instances. |
| Li et al. (2016) | To minimise the overall cost (including refrigeration storage cost, vehicle fixed cost, and transportation cost) of medicine distribution in a certain region | A transport-distance-constrained local community medicine distribution route optimising model is established and solved using a tabu-search-based algorithm | Not stated. | Simulated results show that the proposed algorithm is able to obtain an optimum distribution scheme cost with minimum transportation cost. |
| Shittu et al. (2016) | To explore the effects of variance in supply of and demand for vaccines in Nigeria on storage capacity requirements | An improved discrete-event simulation model based on HERMES | Monthly requirements are independent random variables. Any required vaccines not available are back ordered and delivered as soon as possible | More vaccine storage capacity is needed than is currently available to cope with the variation; Situation can be improved with proper redesign of the vaccine supply chain. |
| Gamchi et al. (2020) | To distribute vaccines among different regions to control the spread of communicable diseases in the aftermath of a disaster | A bi-objective mathematical model to simultaneously minimise the total social cost incurred by infected individuals before and after vaccination as well as the cost of assigning appropriate vehicles to routes considering their capacity | The epidemic process follows the SIR model before receiving the vaccines; Vaccine demand for each priority group in each region should be fully satisfied; One vehicle only serves one particular route | With only limited amounts of vaccines, considering high-risk groups as priority groups would help practitioners effectively assign the available vaccine doses. This will help to minimise the social cost incurred by infected individuals. |
Appendix C. Case study area and criteria
-
–
Smoking (C-1): Current smoking groups (especially men over 65 years old) have a higher risk (OR = 2.51) of developing critical COVID-19-related illness or death (Zheng et al., 2020a)
-
–
Cancer (C-2): People who have any critical and advanced type of cancers are at higher risk (OR = 3.04) of mortality from COVID-19 infection (Parohan et al., 2020a)
-
–
Obesity (C-3): Obesity defined as a body mass index (BMI) ¿ 25 (BMI ¿ 30 is severe obesity). Based on previous meta-analysis studies, obesity is associated with significant morbidity and excess mortality factor (OR = 3.68) for critical illness and death following COVID-19 infection (Hussain et al., 2020a)
-
–
Heart disease (C-4): Heart (cardiovascular) disease can greatly affect the prognosis of the illness and the death risk (OR = 2.19) of the patients infected (Zheng et al., 2020a)
-
–
Hypertension (C-5): Hypertension (high blood pressure) is a global health problem associated with increased risk of death following COVID-19 infection (Lu et al., 2020a)
-
–
Diabetes (C-6): Diabetes is one of the leading causes of morbidity and mortality throughout the world (Takahashi et al., 2017) and positively correlated with COVID-19 mortality (Lu et al., 2020b)
-
–
Respiratory disease (C-7): Respiratory diseases can also greatly affect the prognosis of the illness and the risk of death (OR = 2.15) of patients in critical illness (Zheng et al., 2020a)
-
–
Ageing (C-8): People who are 65 years old or more constitute the most vulnerable groups with the highest risk of death upon infection (OR = 6.01) (Zheng et al., 2020b)
-
–
Population density (C-9): Higher population density might be responsible for more interaction as well as COVID-19 transmission (Mishra et al., 2020, Sarkar, 2020)
Table C.1.
Greater Metropolitan Melbourne Area COVID test centres (assumed to be vaccine centres) and capacities.
| Type | Category | Quantity | CC (vaccines) | Staffs (per day) | |
|---|---|---|---|---|---|
| 1 | Community Health Respiratory Clinic | A | 11 | 1000 | 8 |
| 2 | Drive-through Facility | B | 30 | 2000 | 16 |
| 3 | GP Respiratory Clinic | C | 10 | 500 | 4 |
| 4 | Hospital Respiratory Clinic | D | 14 | 1000 | 8 |
| 5 | Pathology Collection Centre | E | 28 | 500 | 4 |
| 6 | Private GP clinic | F | 3 | 300 | 2 |
| 7 | Walk-through clinics | G | 8 | 800 | 6 |
Criteria
See Fig. C.2.
Table C.2.
Criteria used for the prioritisation of the city areas for vaccination in the most epidemiological studies. Previous epidemiological meta-analysis studies have been used to calculate the weight of criteria.
| Sym. | Factors (criteria) | Definition | Weight | Meta-analysis source | Data source |
|---|---|---|---|---|---|
| People aged over 18 who are current smokers (Daily smoker ratio) | Proportion of adult (18+ years) population, by smoking status (in percent) | 2.51 | Zheng et al. (2020b) | ABS (2020) | |
| Cancer incidence per 1,000 population | The total number of malignant cancers (rate) | 3.04 | Parohan et al. (2020b) | DHHS (2020) | |
| People reporting being obese (ratio) | Proportion of adult (18+ years) population, who were overweight (pre-obese or obese) (in percent) | 3.68 | Hussain et al. (2020b) | VHISS (2017) | |
| People reporting heart disease (ratio) | People reporting heart disease (in percent) | 5.19 | Zheng et al. (2020b) | DHHS (2020) | |
| People reporting high blood pressure (Hypertension ratio) | People reporting high blood pressure (in percent) | 3.32 | Lu et al. (2020b) | DHHS (2020) | |
| People reporting type 2 diabetes (ratio) | The percentage of people who have type 2 diabetes (in percent) | 3.73 | Lu et al. (2020b) | DHHS (2020) | |
| People reporting respiratory disease (ratio) | The percentage of people who reported having current respiratory disease | 5.15 | Zheng et al. (2020b) | DHHS (2020) | |
| The people aged over 65 years (ratio) | The ratio of people 60 and over to total population | 6.06 | Zheng et al. (2020b) | ABS (2020) | |
| Population density (per sq.km) | Persons per square kilometre (per sq.km) | 2.49 | Mishra et al. (2020) | Sarkar (2020) |
Appendix D. Fuzzy GIS approach materials
D.1. Phase I: FL-GIS spatial model
D.1.1. Fuzzy Logic
Upon preparing the initial data, a geodatabase was generated using the ArcCatalog environment which is one of the plugins of ArcGIS 10.7 software (ESRI, Redlands, CA, USA). The geodatabase includes points (city location and test centres), linear (roads) and polygonal features (Mesh block, SA1 and SA2 boundaries). The Geocentric Datum of Australia (GDA2020) coordinate system was used for country and regions level as official and reference system. The projection system was used for SA2 and SA1 map layers in GIS. This projection coordinate system enables researchers to create a map that accurately shows distances, areas or directions (Shabanikiya et al., 2020, Pishgar et al., 2020) and is suitable for use between E and S where the study area is located. Upon creating the geodatabase, we defined SA1 level as the base map for all analyses. Since most of the city data are collected at the SA1 level, this level permits more appropriate analysis (compared to the SA2 and mesh block levels) and implementation of FL-GIS model. Finally, all the data of the selected criteria were joined to the SA1 level map and groundwork was laid for further analysis.
Spatial related features often do not have clearly defined boundaries, and concepts can better be expressed with degrees of membership to a fuzzy set than with a binary (1 or 0) classification (Kainz, 2007). In fuzzy logic, the classes are defined as sets. The theory of fuzzy sets was introduced by Zadeh (1965). In conventional logic, the degree to which an individual (z) being a member or not of a given set (A) is expressed by the membership function . The membership function can take the value 0 or 1 as shown below in an example of a set being an interval :
| (D.1) |
where () and () define the exact boundaries of the set (A) (Malczewski, 1999). Mathematically, a fuzzy set (A) is defined as follows (Gorsevski et al., 2006):
If (z) denotes a space of objects, then the fuzzy set (A) in (Z) is the set of ordered pairs
| (D.2) |
where the membership function is referred to as the “degree of membership of (z) in (A)”. The higher the membership value of , the more z belongs to the set. The various fuzzy membership functions are defined in FL (Burrough et al., 2015). Several membership function integrated with GIS includes Gaussian, Large, Small, MSLarge, MSSmall, Near and Linear (ESRI, 2020). As will be explained below, we used the Linear method for the fuzzification of the criteria maps.
D.2. Standardisation of criteria layers and weighing of criteria
Data normalisation is an essential part of any MCDM process (Jahan and Edwards, 2015). This approach usually converts criteria with different measurement units to a common scale in the interval [0–1] (Pavličić, 2001). The fuzzy sets have a high capability in normalising spatial data and they are compatible with Geographic Information Systems (Ribeiro et al., 2014). Due to the different scale of each criterion (e.g. rate, percentage and count) (Table C.2), fuzzy membership functions were applied to standardise the criteria maps (fuzzification) using the spatial analytical tool in GIS. We tested different membership functions and found that the fuzzy linear function gave the best results. The fuzzy linear transformation function applies a linear function between the user-specified minimum and maximum values (Raines et al., 2010):
| (D.3) |
where min and max are user inputs. Anything below the minimum will be assigned a 0 (definitely not a member) and anything above the maximum a 1 (definitely a member) (ESRI, 2020). Upon fuzzification of the criteria maps, weights extracted from previous studies (Table C.2) were applied to the criteria fuzzy maps by using the raster calculator in GIS as below:
| (D.4) |
D.3. The fuzzy overlay model
The final step in prioritising urban areas for vaccination is to implement fuzzy overlay of criteria maps using GIS. The overlay type lists the methods available to combine the data based on FL in GIS. Five methods are available, namely fuzzy And, fuzzy Or, fuzzy Product, fuzzy Sum, and fuzzy Gamma (Abdulrazzaq et al., 2020). In this study, the fuzzy gamma type is used. The fuzzy gamma type is an algebraic product of fuzzy product and fuzzy sum, which are both raised to the power of gamma. The generalised function is as follows (ESRI, 2020):
| (D.5) |
| (D.6) |
where is a user input variable selected from the range [0, 1]. We tested different values (0, 0.50, 0.75 and 0.90). Finally, 0.90 was chosen as an efficient value to be applied in the overlay of criteria maps.
D.4. Interpolation (IDW) and defuzzification
The interpolation method often chosen by geoscientists is Inverse distance weighted (IDW) implemented in GIS (Lu and Wong, 2008). Inverse distance weighted (IDW) interpolation determines cell values using a linearly weighted combination of a set of sample points. The IDW method can be viewed as a process of minimising a deviation function between the expected value and the sample values (Li et al., 2020). After overlapping, the values obtained from the previous step were joined onto the residential mesh blocks by zonal statistics in GIS. The IDW method was used to obtain more accurate results in logical representation and eliminate the distortion of the final output map. The results was a smoothed weighted map that became the basis for the areal prioritisation.
Defuzzification is the process of conversion of aggregated fuzzy set into one crisp value (Van Leekwijck and Kerre, 1999). In the final step of FL-GIS modelling, defuzzifying the overlaid output map (standardised and weighted) was carried out to convert the fuzzy set values to numeric values with clearly defined boundaries using the natural break classifier and converted into a conventional final priority map. In all the analyses, cell size for raster (image format file in GIS) maps is defined as 30 × 30 metre. The final numeric classified output map was prepared to introduce areas in the prioritisation of vaccination.
Appendix E. Algorithms chromosomes
E.1. Definitions
Centre Capacity (): A vaccine centre has a certain initial capacity indicating the original daily capacity (). Total Centre Capacity () is the summation of all centres’ capacities to cover demands . Fig. E.1 depicts the structure of its solution space as chromosome.
Fig. E.1.
Fixed chromosome for VCs.
Maximum Capacity (): It is assumed that the centres can serve at maximum double their original capacities (); Total Maximum Capacity () is the summation of all centres’ maximum capacities , and . Daily distributing packages of vaccines could be maximum be at Total Maximum Capacity level as , accordingly ().
Overall Capacity (): A Vaccine centre could serve amount of vaccines per day. The of each could vary in the range of zero to (). is the difference of a centre’s overall capacity to its original capacity. Put simply, the amount of vaccines that the is serving demands related to its initial capacity of (). Hence, depending on the amount of distributing vaccines the Total Overall Capacity () of centres can be more or less than (). In cases that the vaccines are distributed to all the Vaccine Centres for vaccination, could be equal to available daily package ().
E.2. Solution space structure design (Chromosomes)
The amount of , determines which algorithm of capacity allocation to proceed, or .
E.2.1. HGA-Excess solution space ()
If the distributing vaccines is more than , then HGA-Excess must keep the amount of different capacity of each centre in the range of 0 to . In other words, at least some of the centres must work over their . No centre works more than twice its and no centre works under its .
In HGA-Excess, we define ;
Lemma E.1
When , the different amount of capacity of each centre ( ), related to its original capacity ( ), is a positive number and is less than its ( )
Proof
Given , it can be concluded that . The different amount of vaccines for serving relating to , which here defined as , defines as (). When, , then . Since , it can be assumed that . This equation can be written as . Since and , it can be assumed that . The solution space of the problem, hence, can be stated as which is a positive number and less that its . for centre to will be computed by HGA-Excess algorithm IV. The Excess Repair Algorithm algorithm V ensures the solutions in always within the range if mentioned solution space. □
The HGA-Excess generates the elements in chromosome in a way that the distance between centres and their assigned demands is minimal. The solution space structure can be shown as follows in Fig. E.2:
Fig. E.2.
Excessive chromosome structure for .
E.2.2. HGA-Shortage solution space ()
In HGA-shortage, we define ;
Lemma E.2
When , the different amount of capacity of each centre ( ), related to its initial capacity ( ), is a negative number and more than its
Proof
Given , it can be concluded that , then . Since , it can be assumed that . The equation can be written as . Since and , it can be assumed that , which is the solution space if the problem is in this condition. If the distributing vaccines is less than , then HGA-Shortage algorithm VI keeps the amount of different capacity of each centre in the range of to zero and the Shortage Repair Algorithm VII is designed for this job. In this condition, at least some of the centres must work under their thresholds. None of the works more than its . □
The HGA-Shortage optimises the elements in chromosome. It balances the and hence in a way that the distance between active centres, , and their assigned demands be minimised. The chromosome structure can be shown as follows in Fig. E.3:
Fig. E.3.

Shortage chromosome structure for .
Appendix F. Result visualisation
Appendix G. Problem formulation (Math-Heuristic Alg. II)
The proposed problem can be formulated using the Math-heuristic algorithm. The pseudo-code of the proposed algorithm in shown in Algorithm II below:
G.1. Assignment model I
| (G.1) |
| (G.2) |
| (G.3) |
| (G.4) |
| (G.5) |
Where is number of demand points. denotes the population of the points, and defines the number of supply. is a Binary decision variable which returns 1 if the point is assigned, and zero otherwise.
G.2. Capacity allocation model
Shortage model - Model II:
| (G.6) |
| (G.7) |
| (G.8) |
| (G.9) |
| (G.10) |
Where is number of centres and is an integer decision variable defining allocated capacity to the centre , and is an integer variable of population of the point is allocated to the centre . defines matrix of distances. is the vector of the population of the demand points, and is the vector of the capacities for the centres.
Excess model - Model III:
| (G.11) |
| (G.12) |
| (G.13) |
| (G.14) |
| (G.15) |
Objective function (G.6) minimises the total distance of all allocation of the points to the centres.
Appendix H. Holistic algorithm details (Alg. III) sub-algorithms
Stage II includes three main subsections as Priority demand allocation (Appendix H.1; Fig. 2-blue area), Resource (staff) balancing (simulation-optimisation) (Appendix H.1.1; Fig. 2-green area), and vaccine distribution pattern (Appendix H.1.2; Fig. 2-red area) that all integrated in the Holistic algorithm III.
The proposed Holistic algorithm (Alg. III) is an heuristic solution approach integrating eight hierarchical heuristic algorithms as shown in Fig. 2. The Holistic algorithm comprises three main sub-steps, including Priority Demand Allocation (Alg. III -Line 2), Waiting Time and Resource Balancing (Alg. III -Line 57), and Vaccine Distribution Routing Pattern (Alg. III -Line 58). To answer the key question of “how many doses of the vaccine should be supplied to each VC today?”, the output from Stage I will be used as input for the Holistic algorithm in Stage II. The algorithm is run on a daily basis to develop a vaccine allocation, assignment and delivery plan.
H.1. Priority demand allocation
The first loop defines the extend time horizon to receive new vaccine packages by checking “if there are yet demands to receive either the first or the second dose of vaccination?” (Alg. III -Line 1). Based upon the amount of vaccine packages supplied each day, a set of three conditions is applied to determine the allocation. Firstly, have all the first dose vaccine-takers been served? Secondly, is there at least one demand waiting to receive its second dose of vaccination? Thirdly and lastly, is the earliest time for people on the waiting list to receive their second dose beyond the expiry date of the vaccines? If none of all three conditions are met, no new package will be supplied as it will be a waste (Alg. III -Line 2). Otherwise, there is a need to place an order for new packages.
On each day, there might be excess packages that must be used within the following days (six days in this study) before expiry (Alg. III-Lines 5:6). The excess vaccines will remain in storage and will be added to packages to be received on the following day (Alg. III-Lines 7:13). The daily distributing amount of vaccines must not exceed total available demands of the day. If this happens, the excess amount of vaccines is stored during the next days (Alg. III -Lines 13:17). If so, demands of the day () which is due to receive the second dose of vaccination () will be pushed to the top of the priority list ()(Alg. III -Lines 18:40). The condition in line 20 checks if there is any demand on vaccine for second dose for the day . In this situation, the is assumed to perform with up to 200% of the original vaccination capacity () as maximum capacity . When there are demands for a second dose that have not been satisfied on their due day, they will be expired and prepared to take another first dose on earliest further days. (Alg. III-Lines 38:40). If the supplied package sizes exceed the amount of , the remaining ones could be used to serve the top priority people to receive their first dose (Alg. III-Lines 41:58).
When the daily supplied vaccine packages exceed the total vaccination capacity () of the , the Holistic algorithm calls for (Alg. III -Line 54).
HGA-Excess is designed for the situation when the supplied daily package is greater than or equal to the . The HGA-Shortage algorithm (Alg. VI) is designed for the situation when the supplied daily package is smaller than the (Alg. III-Line 56). In this situation, some might not be assigned to serve demand on the same day. Instead, adjacent in the dense priority demand locations will set to work with an increased level. In the situation when the daily package equals , all the will work with their original .
Heuristic Genetic Algorithm-Excess:
The Heuristic Genetic Algorithm-Excess (Alg. IV) HGA-Excess is designed for when there is excess in daily supplied vaccine packages. The HGA-Excess includes a Genetic loop with two reinforcing ROULETTEWHEEL modules built in as SHORT-DISTFUNC (Alg. IV-Line 8) and LONG-DISTFUNC (Alg. IV-Line 20). HGA-Excess has chromosome which indicates the excess over centre capacity () when the distributed package is more than .
Lemma H.1
When , the different amount of capacity of each centre ( ), related to its original capacity ( ), is a positive number and is less than its ( ).
Proof
See Appendix E.2.1 for the proof of lemma and detailed chromosome structure. □
The role of the HeuristicFitFunc is to return the fitness of the called chromosome and also the assignment of the demands in the queue to each based on the ’ capacity from the chromosome. The ExcessRepairAlg (Alg. V) is called to ensure that avoid assignment exceeds from , and not exceed from . In excess, (Alg. V) ensures that of the could be zero or greater than zero and less or equal to (the sent to the related loop for next assignments). Using a developed ROULLETEWEEL, the SHORT-DISTFUNC module maximises the capacity of the closest to the top dense demand areas. In this case, assignments with less average distance have higher chance of being selected to increase the and serve demands. The LONG-DISTFUNC module (Alg. IV-Line 20) works, reversely. The ROULLETEWEE module finds the best of bests and weakest of weaks by devoting score to based on their Total distance and Total population of one previous assignment. Crossover function is considered to ensure that results does not trap into local optima and distribute the high score chromosome entire the solution space. (see E.2.1, E.2.2 for the chromosome structure visualisation.)
Heuristic Genetic Algorithm-Shortage:
The HGA-Shortage algorithm (Alg. VI) has similar steps as the HGA-Excess algorithm (Alg. IV) as the k-site selection problem, in which k can be dynamic. The main difference is that it is specifically designed to generate allocation plans when there is shortage in the number of daily supplied Vaccine Packages. The chromosome has negative values.
Lemma H.2
When , the different amount of capacity of each centre ( ), related to its initial capacity ( ), is a negative number and more than its .
Proof
See Appendix E.2.2 for the proof of lemma and detailed chromosome structure. □
In this algorithm, if an element in the chromosome gets the highest absolute amount possible, the related gets the overall capacity of zero VI-Line 16) to avoid serving any demand point. As the result, in some cases not all the will be open in that day due to package shortage. The generated pattern ( chromosome) will send to HeuristicFitFunc (Alg. VIII for calculating the fitness function.
SHORT-DISTFUNC module of HGA-Shortage (Alg. VI-Line 8) has a negative chromosome as input which needs to convert to positive to ease the calculation (Alg. VI-Line 9). The ROULETTEWHEEL function (Alg. VI-Line 13) selects the elements with less value (higher scores) in the chromosome (Alg. VI-Line 17). The function weakens the amount of the element in related chromosome to reinforce the of the . The ShortageRepairAlg (Alg. VII) repairs the by ensuring that of the could only be zero (no package assigned to that ) or greater than zero (the sent to the related loop for next assignments). The repaired chromosome is sent to HeuristicFitFunc (Alg. VIII) for choose the best pattern with higher performance index as fitness function. LONG-DISTFUNC module (Alg. VI-Line 19) performing the same steps vice-versa by weakening the score of the most furthest to the demand points. It weakens a weak element of the chromosome to reduce and consequently the overall capacity () of assigned . ROULETTEWHEEL and CROSSOVER modules perform as it is in HGA-Excess.
The Heuristic Fitness Algorithm (Alg. VIII) is designed for capacitated allocation interacting with the K-d tree (Alg. IX). indicates centres original capacity of all the . The chromosome shows the overall service capacity of the all the (see Appendix E.1).
In the kd-tree demands and centres have been classified into and meaning that demands that have at least one uncovered population. The output of the K-d tree algorithm is, hence, local variables () which needs to be globalise to synchronise this to the entire vaccine supply network plan of day by updating the dependent variables (Alg. VIII-Line 11:15, and 42:46). first need to be classified using a binary variable; 1 if the centre has not been assigned any demands yet, and 0 otherwise (the has been assigned a demand population equals to its overall capacity () (Alg. VIII -Lines 16 and 41). Demands in gets their number of uncovered population. Initially, it is equal to the considered the population of demands. Any time a part or whole of population of a demand covered by a , its related will be updated with remained population for further loops (Alg. VIII - line 17 and 40). The incapacitated covered demand points indexed in need to be identified in a separated list ().
Incapacitated allocation of the entire population of a demand point to its closes might cause over-assigned of some centres. For each , K-d tree allocates the yet uncovered demands () to the in list. In this process, K-d tree algorithm count the population of centres in “for loop” (Alg. IX-Line 1). Since K-d tree algorithm is not originally designed to run capacitated assignments, there could always be some that become over-assigned. Put simply, the total demand population that K-d tree algorithm allocates to the , could be higher than its overall capacity (Alg. VIII -Line 8). In this case, the algorithm locates the overpopulated , their already assigned demands points, and the population of the demands points. In some cases, hence, the demand point’s population can be only partially allocated to (s) while rest of will be called later for assignment in further iterations. In these cases, HeuristicFitFunc distributes the priority population, and allocate only a part of the population to avoid overpopulation in the .
The excessive assigned demands () to the by incapacitated assignment of the kd-tree algorithm first needs to be identified (Alg. VIII-Lines 3:7), to be stored (Alg. VIII -Line 8), and later to be repaired and globalised (Alg. VIII-Lines 18:46) to create the final performance index of fitness (Alg. VIII-Line 47). There are, however, situation with no excessive demands (i.e, in the last loop of the ‘while’ in Alg. VIII-Line 1. In this case the and variable can be directly globalised without need to repair (Alg. VIII-Lines 9:17).
The loop of allocating continues until all the uncovered demands served.
The k-d tree algorithm (Alg. IX) finds the nearest neighbour of for each demand points (Friedman et al., 1983, Ram and Sinha, 2019). It this study the is considered one since each demand must only visit one .
H.1.1. Resource (staff) levelling (Simulation-Optimisation)
In this section the second step of Stage II as Resource (Staff) Balancing is explained (Fig. 2 - green area). The Priority Demand Allocation Step generates a daily assignment plan of top priority demands (first and second dose vaccine takers) into the capacitated . The ratio of total Euclidean-based distance by the total assigned population is considered as the system performance index.
Obtaining the results for some performance measures such as average service time, average waiting time in (queue length), congestion, average lead time (transportation time), average number of people in each hour in centres, total number of demand served in each day, and staff required in is only possible using the simulation engine. The simulation engine runs on a daily basis by considering the assignment plan generated in the previous step, aiming to improve the entire system’s performance by monitoring the above mentioned performances. The simulation engine consists of two interacting agent-based and discrete processes based-modelling (discrete event simulation) models having been designed in this step (Alg. III -Line 44). Agent-based modelling is developed to model the transportation demands to (lead time index). Process-based modelling (discrete event simulation) is integrated to model the queue systems to find the rest of the service performance measures (Breuer, 2000).
Algorithm X is developed to improve the computational performance of the simulation-optimisation process in very large cases. The heuristic examines the 5%, 10%, 15%, and 20% reallocation levels for the with the highest positive and negative differences between the current capacity assigned in and the best theoretical capacity as maximum movement (). The heuristic then subtracts one from the maximum (Alg X - line 13) and increases the minimum value by one (Alg X - line 14). The process repeats until the 5% is complete (Alg X - line 12) for 10%C, 15%C, and 20%C scenarios (Alg X - line 7). These capacities will be used as scenario variables in the Monte Carlo simulation approach to define the optimal capacity reallocation as follows.
Finally, a Monte Carlo simulation-optimisation approach is developed on the simulation engine to reach an optimal staff distribution pattern aiming to minimise the objective function of , where is the original capacity for each , is the levelled capacity of the .
The objective function is considered for the productivity and cost of the capacity. The more demands served within the restricted time and service constraints, the more value the objective function obtains. Conversely, there is a cost of capacity which is considered as being subject to time and performance () constraints as mentioned above.
In the process of simulation, the time between arrivals intervals will be exponentially distributed with the average of time between arrivals 7 hours (the maximum time for a Pfizer vaccine to be used after defrosting). The service time is assumed to be uniformly distributed from 8 to 12 minutes as queue system in the process-based model. The impact of the lead time is screened in the agent-based model. Actual transportation time has been obtained by Integrated GIS data in Anylogic 8.1 Software.
It is possible to make some changes on the branches’ capacity for at least some of these branches within a certain range. To guarantee that the last demand will have enough time for transportation time and be served, it was assumed that he/she will leave home at least one hour before closing the . The vaccine centres have been organised into groups in order to improve the computational time of simulation. It is also assumed that there is a penalty of waiting more than 30 minutes to be served in each . All the demands assigned must be served on that day. Given the above-mentioned settings, the Simulation optimises the number of staff required in each in each day. The output of this step hence would be a daily balanced assignment plan of (Alg III -Line 48).
H.1.2. Vaccine distribution pattern
The last step of Stage II is named Vaccine Distribution Pattern (Fig. 2). Given the daily balanced assignment vaccination plan, the vaccines need to be distributed from a central deep-cold storage (Melbourne Airport is assumed to be the central GDDCS depot (Appendix F - green points) to complete the entire vaccine delivery supply. There is a limit on the number of specified couriers. It is also assumed that there is a maximum 3-hour delivery time limit to distribute the vaccines to the before open at 9 A.M.
GreedyVaccDistHeuristic (Alg. XI) is designed for the purpose of distributing the package among the , while no truck takes longer than the predefined time window. It is a main returning loop. In each iteration of the loop, a Greedy approach distributes the required daily package from . Every iteration that the main loop could not distribute the package in the time window, it adds another truck to the fleet in order to decrease the maximum tour time of trucks (Alg. XI -Line 2). The main loop continues until the fleet delivers all the vaccines in less than the time window (Alg. XI -Lines 45:47).
It is assumed that all the trucks are heterogeneous with certain reefer container capacity. The greedy algorithm starts with minimum possible trucks required for delivery. Based on the ratio of the total required packages to deliver to and truck full capacity, the minimum number of required trucks is calculated as the main input of the Greedy algorithm. In each iteration, for each truck, the Greedy algorithm starts assigning one of the top combinations nearest the vaccine centre to the nearest vaccine centre up until the time window allows the assignment (Alg. XI -Lines 10:44). Once the truck reaches its time window, it is removed from the available list of trucks to avoid its further transportation (Alg. XI -Lines 19:20). If all the trucks are removed from the available truck list and there are still uncovered vaccine centres, the Greedy algorithm restarts the entire assignment by increasing the number of available trucks by one (Alg. XI -Lines 21:22). The process continues until all the vaccine centres’ demands are satisfied within the maximum allowed time window of 3 hours.
The proposed GreedyVaccDistHeuristic algorithm XI provides significant benefits that can solve the parallel vaccine distribution pattern. However, due to the complexity of the problem, this method might get stuck in a local optimum. To further improve this method and to overcome the informational uncertainties, and to minimise the bias against deliveries with long travel times in distributing vaccines, we have customised the Monte Carlo method to deal with this problem. The structure of this method is similar to the GreedyVaccDistHeuristic heuristic algorithm except for the decision-making process to select which vehicle is going to cover the next . Nonetheless, it can be challenging to determine the appropriate level of randomness and number of iterations. Once a list of capable nodes with capable vehicles is identified, the as next destination with the lowest travel time is selected to undertake the service delivery in the GreedyVaccDistHeuristic method. The difference here is that, in an iterative loop, instead of selecting the nearest with the least travel time, a list of all close by destination are sorted based on their estimated actual travel time. of with least travel time are then screened. Afterwards, in each assignment one is randomly selected from the screened list. By introducing randomness into the process of identifying the local optimal choice and repeating this process for a predefined number of iterations, the vaccine distribution plan may improve the GreedyVaccDistHeuristic method. Algorithm XII delineates the process of applying the Monte Carlo heuristics method on the GreedyVaccDistHeuristic algorithm.
Appendix I. Validations
I.1. Performance comparison of the Holistic Alg. III and Math-heuristic Alg. II
The performance of the Math-heuristic algorithm (Alg. II) and Holistic algorithm (Alg. III) are compared in Table I.1.
As the results show, the Holistic algorithm (Algorithm III) outperforms the Math-heuristic algorithm (Algorithm II) in almost all the large size cases. In this study, hence, we have implied the Holistic algorithm (Algorithm III) in our case study analysis.
I.2. Comparison numerical experiment of HGA Algs. IV, & VI and HPSO Algs. XIII, & XII
Table I.1.
Performance comparison table of the Holistic Alg. III and Math-heuristic Alg. II (The presented computational time of Total alg. II and Total alg. III include the demand assignment computation and the capacity allocation computation.)
 |
Table I.2.
Numerical experiment results; comparison of the HGA and HPSO based methods; A 3600 s time limit termination criterion has been set for each run. is the ratio of the network elements used to generate test scenarios as the numerical experiment cases.The results are mean () and standard deviation () of thirty runs, respectively.
 |
I.3. Robustness check
In evaluating the performance in terms of the robustness of the HGA-E algorithm and HGA-S algorithm, we test each of them on the data of the Melbourne city on the supply of 1,000,000 vaccines with TCC of 1,500,000 for HGA-E and 750,000 for HGA-S. We repeat each run 10 times. In each run, 60 chromosomes are generated as the initial population of genetic algorithms (Zhang et al., 2020). The resulted average distance of the tests are provided in Table I.3. The t-test is performed to check if there is a significant difference among the obtained results for each algorithm (Owais and Osman, 2018). The statistical test shows no significant difference in results as the null hypothesis is accepted at the significant level of 0.05 for both algorithms. The test indicates that both HGA-E and HGA-S algorithms are robust.
Table I.3.
Robustness performance evaluation of the HGA-E algorithm and HGA-S algorithm.
| Test | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Average distance | HGA-E | 5.051 | 4.983 | 5.032 | 5.09 | 5.032 | 5.032 | 5.108 | 5.122 | 5.081 | 4.95 | 5.0481 |
| HGA-S | 5.362 | 5.387 | 5.424 | 5.291 | 5.271 | 5.387 | 5.203 | 5.458 | 5.387 | 5.387 | 5.3557 | |
References
- Abbasi, B., Fadaki, M., Kokshagina, O., Saeed, N., Chhetri, P., 2020. Modeling Vaccine Allocations in the COVID-19 Pandemic: A Case Study in Australia. Working Paper, SSRN, https://ssrn.com/abstract=3744520 or https://ssrn.com/abstract=3744520 10.2139/ssrn.3744520. [DOI]
- Abdulrazzaq, Z.T., Agbasi, O.E., Aziz, N.A., Etuk, S.E., 2020. Identification of potential groundwater locations using geophysical data and fuzzy gamma operator model in Imo, Southeastern Nigeria. 10 (8), 188–188, 10.1007/s13201-020-01264-6. [DOI]
- Abrahams A.S., Ragsdale C.T. A decision support system for patient scheduling in travel vaccine administration. Decis. Support Syst. 2012;54(1):215–225. [Google Scholar]
- ABS . ABS; 2017. victorian-population-health-survey-2017-vhiss: Report. URL https://discover.data.vic.gov.au/dataset/victorian-population-health-survey-2017-vhiss. [Google Scholar]
- ABS . 2020. Greater melbourne population, 29. URL https://www.abs.gov.au/statistics/people/population/regional-population/2018-19. [Google Scholar]
- Acharya R., Porwal A. A vulnerability index for the management of and response to the COVID-19 epidemic in India: an ecological study. 2020;8(9):e1142–e1151. doi: 10.1016/S2214-109X(20)30300-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al Theeb N., Murray C. Vehicle routing and resource distribution in postdisaster humanitarian relief operations. Int. Trans. Oper. Res. 2017;24(6):1253–1284. [Google Scholar]
- Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Araz O.M., Galvani A., Meyers L.A. Geographic prioritization of distributing pandemic influenza vaccines. 2012;15(3):175–187. doi: 10.1007/s10729-012-9199-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Australian Bureau of Statistics . 2020. Regional population. URL https://www.abs.gov.au/statistics/people/population/regional-population/latest-release#capital-cities. [Google Scholar]
- Balcik B., Beamon B.M., Smilowitz K. Last mile distribution in humanitarian relief. J. Intell. Transp. Syst. 2008;12(2):51–63. [Google Scholar]
- BBC News . 2020. Covid-19 pandemic: Tracking the global coronavirus outbreak. URL https://www.bbc.com/news/world-51235105. [Google Scholar]
- Bodaghi B., Shahparvari S., Fadaki M., Lau K.H., Ekambaram P., Chhetri P. Multi-resource scheduling and routing for emergency recovery operations. Int. J. Disaster Risk Reduct. 2020;50 doi: 10.1016/j.ijdrr.2020.101780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breuer L. Univ., Mathematik/Informatik; 2000. Operator-Geometric Solutions For The M/G/K Queue And Its Variants. [Google Scholar]
- Brown S.T., Schreiber B., Cakouros B.E., Wateska A.R., Dicko H.M., Connor D.L., Jaillard P., Mvundura M., Norman B.A., Levin C., et al. The benefits of redesigning benin’s vaccine supply chain. Vaccine. 2014;32(32):4097–4103. doi: 10.1016/j.vaccine.2014.04.090. [DOI] [PubMed] [Google Scholar]
- Bubar K.M., Kissler S.M., Lipsitch M., Cobey S., Grad Y., Larremore D.B. 2020. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buccieri K., Gaetz S. Ethical vaccine distribution planning for pandemic influenza: Prioritizing homeless and hard-to-reach populations. 2013;6(2):185–196. [Google Scholar]
- Buckner J.H., Chowell G., Springborn M.R. 2020. Optimal dynamic prioritization of scarce COVID-19 vaccines. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrough P.A., McDonnell R., McDonnell R.A., Lloyd C.D. Oxford University Press; 2015. Principles of geographical information systems. [Google Scholar]
- Centers for Disease Control and Prevention . 2020. When vaccine is limited, who gets vaccinated first? URL https://www.cdc.gov/coronavirus/2019-ncov/vaccines/recommendations.html. [Google Scholar]
- Ceselli A., Righini G., Tresoldi E. Combined location and routing problems for drug distribution. Discrete Appl. Math. 2014;165:130–145. [Google Scholar]
- Chen X., Li M., Simchi-Levi D., Zhao T. 2020. Allocation of COVID-19 vaccines under limited supply. [Google Scholar]
- Ciancimino E., Cannella S., Bruccoleri M., Framinan J.M. On the bullwhip avoidance phase: the synchronised supply chain. Eur. J. Oper. Res. 2012;221(1):49–63. [Google Scholar]
- Deo, S., Manurkar, S., Krishnan, S., Franz, C., 2020. COVID-19 vaccine: Development, access and distribution in the Indian context. 378, 16–16.
- Department of Health, Australian Government . 2020. Covid-19 vaccine and treatment strategy. URL https://www.health.gov.au/initiatives-and-programs/covid-19-vaccine-and-treatment-strategy. [Google Scholar]
- Dessouky M., Ordóñez F., Jia H., Shen Z. Patient Flow. Springer; 2013. Rapid distribution of medical supplies; pp. 385–410. [Google Scholar]
- DHHS . 2020. Victoria Government report; Victorian Coronavirus (COVID-19) data. URL https://www.dhhs.vic.gov.au/victorian-coronavirus-covid-19-data. [Google Scholar]
- Docherty A.B., Harrison E.M., Green C.A., Hardwick H.E., Pius R., Norman L., Holden K.A., Read J.M., Dondelinger F., Carson G. 2020. Features of 20 133 UK patients in hospital with covid-19 using the ISARIC WHO Clinical Characterisation Protocol: prospective observational cohort study 369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dominguez R., Cannella S., Framinan J.M. On bullwhip-limiting strategies in divergent supply chain networks. Comput. Ind. Eng. 2014;73:85–95. [Google Scholar]
- ESRI . 2020. ArcGIS Desktop Help. URL https://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-analyst-toolbox/how-fuzzy-membership-works.htm. [Google Scholar]
- FDA . FDA; 2021. U.S. Food and Drug Administration: Report. URL https://www.fda.gov/ [Google Scholar]
- Foy B.H., Wahl B., Mehta K., Shet A., Menon G.I., Britto C. Comparing COVID-19 vaccine allocation strategies in India: A mathematical modelling study. Int. J. Infect. Dis. 2021;103:431–438. doi: 10.1016/j.ijid.2020.12.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J.H., Bentley J.L., Finkel R.A. An algorithm for finding best matches in logarithmic expected time. ACM Trans. Math. Softw. (TOMS) 1983;1983(23):435–44209–226. [Google Scholar]
- Gamchi N.S., Torabi S.A., Jolai F. 2020. A novel vehicle routing problem for vaccine distribution using SIR epidemic model; pp. 1–34. [Google Scholar]
- Golan M.S., Jernegan L.H., Linkov I. Trends and applications of resilience analytics in supply chain modeling: systematic literature review in the context of the COVID-19 pandemic. Environ. Syst. Decis. 2020;40:222–243. doi: 10.1007/s10669-020-09777-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorsevski P.V., Jankowski P., Gessler P.E. An heuristic approach for mapping landslide hazard by integrating fuzzy logic with analytic hierarchy process. 2006;35:121–146. [Google Scholar]
- Govindan K., Mina H., Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: A case study of coronavirus disease 2019 (COVID-19) Transp. Res.Part E. Logist. Transp. Rev. 2020;138 doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper P.R., Shahani A., Gallagher J., Bowie C. Planning health services with explicit geographical considerations: a stochastic location–allocation approach. Omega. 2005;33(2):141–152. [Google Scholar]
- Hausman W.H. The Practice Of Supply Chain Management: Where Theory And Application Converge. Springer; 2004. Supply chain performance metrics; pp. 61–73. [Google Scholar]
- Huang, H.-C., Singh, B., Morton, D.P., Johnson, G.P., Clements, B., Meyers, L.A., 2017. Equalizing access to pandemic influenza vaccines through optimal allocation to public health distribution points. 12 (8), e0182720–e0182720, 10.1371/journal.pone.0182720. [DOI] [PMC free article] [PubMed]
- Hussain A., Bhowmik B., do Vale Moreira N.C. 2020. COVID-19 and diabetes: Knowledge in progress, pp. 108142–108142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussain A., Mahawar K., Xia Z., Yang W., Shamsi E.-H. Obesity and mortality of COVID-19. Meta-analysis. Obes. Res. Clin. Pract. 2020 doi: 10.1016/j.orcp.2020.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Jahan A., Edwards K.L. A state-of-the-art survey on the influence of normalization techniques in ranking: Improving the materials selection process in engineering design. Mater. Des. (1980-2015) 2015;65:335–342. [Google Scholar]
- Kainz W. 2007. Fuzzy logic and GIS. [Google Scholar]
- Kee S.Y., Lee J.S., Cheong H.J., Chun B.C., Song J.Y., Choi W.S., Jo Y.M., Seo Y.B., Kim W.J. Influenza vaccine coverage rates and perceptions on vaccination in South Korea. 2007;55(3):273–281. doi: 10.1016/j.jinf.2007.04.354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J., White P.J. Targeting vaccination against novel infections: risk, age and spatial structure for pandemic influenza in great britain. 2011;8(58):661–670. doi: 10.1098/rsif.2010.0474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee B.Y., Assi T.-M., Rookkapan K., Wateska A.R., Rajgopal J., Sornsrivichai V., Chen S.-I., Brown S.T., Welling J., Norman B.A., et al. Maintaining vaccine delivery following the introduction of the rotavirus and pneumococcal vaccines in thailand. PLoS One. 2011;6(9) doi: 10.1371/journal.pone.0024673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S., Golinski M., Chowell G. Modeling optimal age-specific vaccination strategies against pandemic influenza. 2012;74(4):958–980. doi: 10.1007/s11538-011-9704-y. [DOI] [PubMed] [Google Scholar]
- Lemmens S., Decouttere C., Vandaele N., Bernuzzi M. A review of integrated supply chain network design models: Key issues for vaccine supply chains. Chem. Eng. Res. Des. 2016;109:366–384. [Google Scholar]
- Lessler, J., Moore, S.M., Luquero, F.J., McKay, H.S., Grais, R., Henkens, M., Mengel, M., Dunoyer, J., M’Bangombe, M., Lee, E.C., Djingarey, M.H., Sudre, B., Bompangue, D., Fraser, R.S.M., Abubakar, A., Perea, W., Legros, D., Azman, A.S., 2018. Mapping the burden of cholera in sub-Saharan Africa and implications for control: an analysis of data across geographical scales. 391 (10133), 1908–1915, 10.1016/S0140-6736(17)33050-7, URL http://www.sciencedirect.com/science/article/pii/S0140673617330507. [DOI] [PMC free article] [PubMed]
- Li Z., Ma Z., Shi W., Qian X. Research on medicine distribution route optimization for community health service institutions. Math. Probl. Eng. 2016;2016 [Google Scholar]
- Li Z., Zhang X., Zhu R., Zhang Z., Weng Z. Integrating data-to-data correlation into inverse distance weighting. 2020;24(1):203–216. [Google Scholar]
- Lin Q., Zhao Q., Lev B. Cold chain transportation decision in the vaccine supply chain. Eur. J. Oper. Res. 2020;283(1):182–195. [Google Scholar]
- Linkov I., Bridges T., Creutzig F., Decker J., Fox-Lent C., Kröger W., Lambert J.H., Levermann A., Montreuil B., Nathwani J., et al. Changing the resilience paradigm. Nature Clim. Change. 2014;4(6):407–409. [Google Scholar]
- Liu C., Xian A. 2020. Identifying vulnerable populations in Australia using the COVID-19 susceptibility index. URL https://www.actuaries.digital. [Google Scholar]
- Lu G.Y., Wong D.W. An adaptive inverse-distance weighting spatial interpolation technique. 2008;34(9):1044–1055. [Google Scholar]
- Lu L., Zhong W., Bian Z., Li Z., Zhang K., Liang B., Zhong Y., Hu M., Lin L., Liu J. 2020. A comparison of mortality-related risk factors of COVID-19, SARS, and MERS: A systematic review and meta-analysis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu L., Zhong W., Bian Z., Li Z., Zhang K., Liang B., Zhong Y., Hu M., Lin L., Liu J., et al. A comparison of mortality-related risk factors of COVID-19, SARS, and MERS: A systematic review and meta-analysis. J. Infect. 2020 doi: 10.1016/j.jinf.2020.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malczewski J. John Wiley & Sons; 1999. GIS And Multicriteria Decision Analysis. [Google Scholar]
- Marek L., Pászto V.t., Tucek P. Modern Trends In Cartography. Springer; 2014. BayesIan mapping of medical data; pp. 489–505. [DOI] [Google Scholar]
- McKinsey & Company . 2020. The COVID-19 vaccines are here: What comes next? URL https://www.mckinsey.com/industries/public-and-social-sector/our-insights/the-covid-19-vaccines-are-here-what-comes-next. [Google Scholar]
- McMorrow, M.L., Tempia, S., Walaza, S., Treurnicht, F.K., Ramkrishna, W., Azziz-Baumgartner, E., Madhi, S.A., Cohen, C., 2019. Prioritization of risk groups for influenza vaccination in resource limited settings – A case study from South Africa. 37 (1), 25–33, 10.1016/j.vaccine.2018.11.048, URL http://www.sciencedirect.com/science/article/pii/S0264410X18315731. [DOI] [PMC free article] [PubMed]
- Medlock, J., Galvani, A.P., 2009. Optimizing influenza vaccine distribution. 325 (5948), 1705–1708. [DOI] [PubMed]
- Mishra S.V., Gayen A., Haque S.M. COVID-19 And urban vulnerability in India. Habitat Int. 2020;103 doi: 10.1016/j.habitatint.2020.102230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moghadam B., Seyedhosseini S. A particle swarm approach to solve vehicle routing problem with uncertain demand: A drug distribution case study. Int. J. Ind. Eng. Comput. 2010;1(1):55–64. [Google Scholar]
- Nyadanu S.D., Pereira G., Nawumbeni D.N., Adampah T. Geo-visual integration of health outcomes and risk factors using excess risk and conditioned choropleth maps: a case study of malaria incidence and sociodemographic determinants in Ghana. BMC Public Health. 2019;19(1) doi: 10.1186/s12889-019-6816-z. 514–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owais M., Osman M.K. Complete hierarchical multi-objective genetic algorithm for transit network design problem. Expert Syst. Appl. 2018;114:143–154. [Google Scholar]
- Özdamar L., Demir O. A hierarchical clustering and routing procedure for large scale disaster relief logistics planning. Transp. Res.Part E. Logist. Transp. Rev. 2012;48(3):591–602. [Google Scholar]
- Özdamar L., Yi W. Greedy neighborhood search for disaster relief and evacuation logistics. IEEE Intell. Syst. 2008;23(1):14–23. [Google Scholar]
- Pardalos P.M. World Scientific; 1993. Complexity In Numerical Optimization. [Google Scholar]
- Parohan M., Yaghoubi S., Seraji A., Javanbakht M.H., Sarraf P., Djalali M. 2020. Risk factors for mortality in patients with Coronavirus disease 2019 (COVID-19) infection: a systematic review and meta-analysis of observational studies, pp. 1–9. [DOI] [PubMed] [Google Scholar]
- Parohan M., Yaghoubi S., Seraji A., Javanbakht M.H., Sarraf P., Djalali M. Risk factors for mortality in patients with coronavirus disease 2019 (COVID-19) infection: a systematic review and meta-analysis of observational studies. Aging Male. 2020:1–9. doi: 10.1080/13685538.2020.1774748. [DOI] [PubMed] [Google Scholar]
- Pavličić D. Normalization affects the results of MADM methods. Yugosl. J. Oper. Res. 2001;11(2):251–265. [Google Scholar]
- Persad, G., Peek, M.E., Emanuel, E.J., 2020. Fairly Prioritizing Groups for Access to COVID-19 Vaccines. 324 (16), 1601–1602, 10.1001/jama.2020.18513. [DOI] [PubMed]
- Pishgar, E., Fanni, Z., Tavakkolinia, J., Mohammadi, A., Kiani, B., Bergquist, R., 2020. Mortality rates due to respiratory tract diseases in Tehran, Iran during 2008–2018: a spatiotemporal, cross-sectional study. 20 (1), 1–12. [DOI] [PMC free article] [PubMed]
- Raines, G.L., Sawatzky, D.L., Bonham-Carter, G.F., Incorporating expert knowledge: New fuzzy logic tools in ArcGIS 10. 49, 8–13.
- Ram, P., Sinha, K., 2019. Revisiting kd-tree for nearest neighbor search. In: Proceedings Of The 25th ACM SIGKDD International Conference On Knowledge Discovery & Data Mining, pp. 1378–1388.
- Ribeiro R.A., Falcao A., Mora A., Fonseca J.M. Fif: A fuzzy information fusion algorithm based on multi-criteria decision making. Knowl.-Based Syst. 2014;58:23–32. [Google Scholar]
- Sarkar S.K. Covid-19 susceptibility mapping using multicriteria evaluation. Disaster Med. Public Health Prep. 2020:1–17. doi: 10.1017/dmp.2020.175. [DOI] [PubMed] [Google Scholar]
- Shabanikiya, H., Hashtarkhani, S., Bergquist, R., Bagheri, N., VafaeiNejad, R., Amiri-Gholanlou, M., Akbari, T., Kiani, B., 2020. Multiple-scale spatial analysis of paediatric, pedestrian road traffic injuries in a major city in North-Eastern Iran 2015–2019. 20 (1), 722–722, 10.1186/s12889-020-08911-2. [DOI] [PMC free article] [PubMed]
- Shittu E., Harnly M., Whitaker S., Miller R. Reorganizing Nigeria’s vaccine supply chain reduces need for additional storage facilities, but more storage is required. Health Aff. 2016;35(2):293–300. doi: 10.1377/hlthaff.2015.1328. [DOI] [PubMed] [Google Scholar]
- Simchi-Levi D., Simchi-Levi E. We need a stress test for critical supply chains. Harv. Bus. Rev. 2020;28 [Google Scholar]
- Suleyman, G., Fadel, R.A., Malette, K.M., Hammond, C., Abdulla, H., Entz, A., Demertzis, Z., Hanna, Z., Failla, A., Dagher, C., 2020. Clinical characteristics and morbidity associated with coronavirus disease 2019 in a series of patients in metropolitan Detroit. 3 (6), e2012270–e2012270. [DOI] [PMC free article] [PubMed]
- Syam S.S., Côté M.J. A location–allocation model for service providers with application to not-for-profit health care organizations. Omega. 2010;38(3–4):157–166. [Google Scholar]
- Takahashi, S., Metcalf, C.J.E., Ferrari, M.J., Tatem, A.J., Lessler, J., 2017. The geography of measles vaccination in the African Great Lakes region. 8 (1), 15585–15585, 10.1038/ncomms15585. [DOI] [PMC free article] [PubMed]
- Tan Q., Huang G.H., Wu C., Cai Y., Yan X. Development of an inexact fuzzy robust programming model for integrated evacuation management under uncertainty. J. Urban Plan. Dev. 2009;135(1):39–49. [Google Scholar]
- Uscher-Pines, L., Omer, S.B., Barnett, D.J., Burke, T.A., Balicer, R.D., 2006. Priority Setting for Pandemic Influenza: An Analysis of National Preparedness Plans. 3 (10), e436–e436, 10.1371/journal.pmed.0030436. [DOI] [PMC free article] [PubMed]
- Van Leekwijck, W., Kerre, E.E., 1999. Defuzzification: criteria and classification. 108 (2), 159–178.
- Venkatramanan, S., Chen, J., Fadikar, A., Gupta, S., Higdon, D., Lewis, B., Marathe, M., Mortveit, H., Vullikanti, A., 2019. Optimizing spatial allocation of seasonal influenza vaccine under temporal constraints. 15 (9), e1007111–e1007111, 10.1371/journal.pcbi.1007111. [DOI] [PMC free article] [PubMed]
- 2017. Victorian Population Health Survey 2017 - VHISS, Victoria government. URL.
- WHO, World Health Organization . 2020. Origin of SARS-CoV-2. URL https://www.who.int/publications/i/item/origin-of-sars-cov-2. [Google Scholar]
- WHO, World Health Organization . 2020. Coronavirus disease 2019 (COVID-19): Situation report, 51. URL https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200311-sitrep-51-COVID-19.pdf. [Google Scholar]
- Wu Z., McGoogan J.M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention. JAMA. 2020;323(13):1239–1242. doi: 10.1001/jama.2020.2648. [DOI] [PubMed] [Google Scholar]
- Zadeh, L.A., 1965. Fuzzy sets. 8 (3), 338–353.
- Zhang L.L., Gang D., Jun W., Yujie M. Joint production planning, pricing and retailer selection with emission control based on Stackelberg game and nested genetic algorithm. Expert Syst. Appl. 2020;161 [Google Scholar]
- Zheng Z., Peng F., Xu B., Zhao J., Liu H., Peng J., Li Q., Jiang C., Zhou Y., Liu S. 2020. Risk factors of critical & mortal COVID-19 cases: A systematic literature review and meta-analysis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Z., Peng F., Xu B., Zhao J., Liu H., Peng J., Li Q., Jiang C., Zhou Y., Liu S., et al. Risk factors of critical & mortal COVID-19 cases: A systematic literature review and meta-analysis. J. Infect. 2020 doi: 10.1016/j.jinf.2020.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Xiang J., Wang Y., Song B., Gu X. 2020. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. [DOI] [PMC free article] [PubMed] [Google Scholar]