Abstract
The mechanistic pathways linking genetic polymorphisms and complex disease traits remain largely uncharacterized. At the same time, expansive new transcriptome data resources offer unprecedented opportunity to unravel the mechanistic underpinnings of complex disease associations. Two-stage strategies involving conditioning on a single, penalized regression imputation for transcriptome association analysis have been described for cross-sectional traits. In this manuscript, we propose an alternative two-stage approach based on stochastic regression imputation that additionally incorporates error in the predictive model. Application of a bootstrap procedure offers flexibility when a closed form predictive distribution is not available. The two-stage strategy is also generalized to longitudinally measured traits, using a linear mixed effects modeling framework and a composite test statistic to evaluate whether the genetic component of gene-level expression modifies the biomarker trajectory over time. Simulations studies are performed to evaluate relative performance with respect to type-1 error rates, coverage, estimation error, and power under a range of conditions. A case study is presented to investigate the association between whole blood expression for each of five inflammasome genes with inflammatory response over time after endotoxin challenge.
Keywords: Biomarker response, genome-wide association studies, multiple imputation, repeated measures, transcriptome-wide association studies
1. Introduction
Transcriptome-wide association studies (TWAS) aim to unravel the mechanisms of association between genotypes and complex traits, and specifically to characterize the mediating roles of cell and tissue-specific gene expression. While genome-wide association studies (GWAS) generally reveal a multitude of single-nucleotide polymorphism (SNP) and gene-level associations with complex traits, the mechanistic underpinnings of a large majority of these associations remain uncharacterized. An overarching analytic challenge in this setting arises from the fact that GWAS include data on genotypes and traits but do not typically involve the collection of transcriptome data. At the same time, the emergence of several independent and expansive transcriptome data resources that include data on both genotype and gene expression offer a new opportunity for interrogating the mediating role of gene expression.
Recent studies describe approaches for analyzing cross-sectional traits in this setting using single regression imputation.1-4 Briefly, this involves: (i) application of penalized regression to arrive a model between genotype and expression; (ii) predicting unobserved expression based on this model in a distinct data resource; and (iii) evaluating association between predicted expression and the observed trait. Further extensions allow for consideration of meta-analysis summary statistics1,4,5 and include methods for multiple tissue eQTLs.6-9 While single imputation is a reasonable strategy, extensive statistical and epidemiological literature favors the application of multiple imputation for missing data, specifically, emphasizing the importance of accounting for error in prediction.10-20
In this article, we consider a multiple stochastic regression imputation (mSRI) approach for integrated transcriptome analysis of both cross-sectional and longitudinal traits. Similar to single regression imputation, this approach accounts for features being measured on distinct samples of individuals across data resources, while mSRI also accounts for uncertainty in prediction. Statistical inference is performed based on asymptotic normal theory and multiple imputations. A case study is presented to examine the associations between whole blood (WB) expression for five inflammasome genes and non-linear biomarker response over time during endotoxin challenge. We consider data arising from the Genetics of Evoked Response to Niacin and Endotoxemia (GENE) study, an NIH-sponsored investigation of the genomics of inflammatory and metabolic responses during low-grade endotoxemia,21-26 and independently generated transcriptome data from the Genotype-Tissue Expression (GTEx) Program.27 Simulation studies are provided to illustrate power, coverage, estimation error and type-1 error rates under a range of conditions.
2. Material and methods
2.1. Model
Let where denotes the T × 1 vector of responses for subject i, i = 1, … , N. Further suppose for each subject i: Xi is a T × q design matrix for expression of q expression values across T time points, where expression is measured on one or more genes and/or cell or tissue types; zi is an s × 1 column vector of SNPs; Wi is a T × p design matrix for time, encoding p−1 basis functions for a polynomial, spline, or similar smooth fit over time and a column of 1’s corresponding to an intercept term; and Ui is a T × p* design matrix for the random effects. Note that we remove the notational dependency of T on subject i for simplicity of presentation.
To begin, we let Ui = 1T to include only random intercepts for each individual and consider a single gene expression at baseline so that Xi = 1T xi where xi is a scalar observation of expression. Finally, we assume that the trait and expression values are normally distributed after appropriate transformation. In this case, we have the following two models of association
| (1) |
| (2) |
where f(·) is a fixed and known function, , , , bi⊥εi and all subjects independent of each other. In the examples provided below, we let the components of Wi be natural spline basis functions for time, inclusive of an intercept. Two treatments of Vi are considered: one represents the full model and includes all time by expression interactions, given by Vi = Wi; the second represents the reduced model with just a main effect for expression is represented by setting Vi equal to a column of 1’s.
Two distinct data resources are available. For n1 subjects in the first data set, yi and zi are observed, as well as the design matrices, Wi, Vi, and Ui, while xi is unobserved. For the n2 subjects in the second data set, xi and zi are observed, while yi is unobserved. Here N = n1 + n2, i.e. all subjects are in either the first or second data set. The observed data are represented by: {(yi, Wi, Vi, Ui, zi)i∈[1,n1], (xi′, zi′)i′∈[n1+1,N]}. Two-stage estimation involves first fitting the model of equation (2) using the observed data from data set 2, {(xi′, zi′)i′∈[n1+1,N]} to arrive at parameter estimates and a corresponding predictive model for expression given genotypes. In turn, an imputed expression can be derived based on this estimated model, and used in place of the unobserved expression in data set 1. The parameter of primary interest for examining the association between gene expression and the trait is γ of equation (1).
2.2. Estimation via stochastic regression imputation
In order to address both missing expression values and the uncertainty in prediction, we propose mSRI in which imputations represent conditional draws from the predictive distribution of plausible values.28,29 A draw from the predictive distribution includes the mean imputation component as well as a stochastic component given by a random normal deviate with mean 0 and variance equal to the predictive variance of the fitted values from the stage 1 model fit. Formally, we let be an estimate of the mean component f(·) in equation (2) and define for i ∈ [1, n1], where and ζi∣zi is the variance of . In the second stage, we replace xi with for i ∈ [1, n1] to fit the model of equation (1) and denote the resulting estimate of γ by . Multiple draws from the predictive distribution yields multiple estimates, , where B is the number of draws. In turn, these parameter estimates can be combined and evaluated using multiple imputation strategies,28,29 as described in more detail below. First, we consider derivations of the predictive distribution used for imputation.
The particular functional form of f(·) in equation (2) will determine the predictive distribution from which is drawn. To begin, consider the usual linear model, given by
| (3) |
and the corresponding least squares estimator , where . In this case, it is straightforward to show the predictive variance for a fitted value with z = z* is given by30
| (4) |
More generally, in order to accommodate a large number of potentially correlated SNPs, an alternative penalized regression approach, such as Least Absolute Shrinkage and Selection Operator (LASSO),31 Elastic Net32 or Ridge Regression,33 can be used to fit the linear model of equations (2) and (3). In the case of ridge regression, a closed-form estimate of α is given by , where λ is the penalty parameter, and the predictive variance conditional on λ can therefore be derived analytically; however, a closed-form solution to minimizing the objective function in LASSO and elastic net is not generally available. In this case, a bootstrap approach can be used to generate the predictive distribution.
The bootstrap procedure includes repeatedly sampling with replacement n2 pairs from data set 2, (xi′, zi′)i′∈[n1+1,N] and fitting the model of equation (2). Repeating this B times, where B is a large number, results in a sample of parameter estimates, . In turn, each of these estimates can be used to yield a predicted expression for each individual in data set 1, given by , … , for i ∈ [1, n1] and corresponding estimates of the coefficients for expression, , … , . For computational efficiency, the bootstrap can be combined with the multiple imputation approach described above. In this case, each iteration involves both sampling n2 pairs from (xi′, zi′)i′∈[n1+1,N] and drawing n1 stochastic components based on the predictive variance. A step-by-step summary of the approach is provided below.
2.3. Statistical inference
A special case of the model of equation (1) is the univariate or cross-sectional setting, in which and Vi = Ui = 1 are scalars, the design matrix for time, Wi, is a column of 1’s for the intercept, and bi + ϵi is replaced with a single measurement error term. In this case, the parameter of interest, γ, will also be a scalar, and we can apply well-established multiple imputation techniques for computing a combined estimate across multiply imputed data sets and making inference based on the t-distribution.28 Briefly, a combined test statistic is given by
| (5) |
where , is the average of the within imputation variance of the estimate of γ, and is the between imputation variance of the estimates of γ. It can be shown that TmSRI has a t-distribution with degrees of freedom given by
| (6) |
For the longitudinal setting, we propose a composite Wald test statistic for null hypothesis of no expression effect, H0 : γ = 0, given by
| (7) |
where S is the variance-covariance matrix of . To test the null of no time by expression interaction, we replace with , defined as γ without the first element, i.e. the vector of all coefficients for interactions between expression and the basis elements for time. Asymptotic theory tells us that in large sample settings, the statistic R has a central χ2 distribution with p degrees of freedom where p is the number of elements of γ. Moreover, the Wald statistic is asymptotically equivalent to a likelihood ratio test statistic comparing the full model of equation (1) to a reduced model with γ = 0.
For each of the estimates , … , , a corresponding Wald test statistic can be generated. Let these be denoted , … , , respectively. Methods for combining multiply imputed χ2-test statistics generated via bootstrap for hypothesis testing are described in Little and Rubin28 and Kim-Hung et al.34 and involve calculating the pooled estimate
| (8) |
where , the sample variance of times (1 + B−1), is given by
| (9) |
and is the sample mean. The reference distribution for is as B → ∞, and in finite samples, we make inference assuming an F distribution on p and p−3/Bw degrees of freedom where .34
2.4. Summary approach
A step-by-step summary of the mSRi approach for integrated transcriptome association analysis is given below.
-
Determine the functional form of f(·) in equation (2) relating genotype to expression.
Repeat steps 2–4 for b = 1, … , B:
- Derive a predicted expression, , for each individual in data set 1 by either:
- Drawing from a closed form predictive distribution: Let for i ∈ [1, n1], where and ζi∣zi is defined as the predictive variance, for example equation (4) for the simple linear regression setting; OR
- Bootstrapping to arrive at a sample from the predictive distribution: Sample with replacement n2 pairs (xi′, zi′) from data set 2 and let where is the estimate of f(·) from the bootstrap sample.
Fit the model of equation (1), replacing the unobserved expression, xi, with the stochastic regression imputed from step 2.
- Record:
- the expression coefficient estimate ;
- the corresponding variance-covariance matrix S; and
- in the case of longitudinal data, the composite test statistic R of equation (7).
Calculate the pooled test statistic of equation (5) (for the univariate setting) or equation (8) (for the longitudinal setting), and compare to the associated distribution to arrive at a corresponding p-value.
3. Examples
3.1. Simulation study
A simulation study is performed to evaluate estimation error, type-1 error rates and power under a range of plausible conditions. To begin, we consider the setting in which a single SNP with minor allele frequency = 0.20 is assumed to have an additive association with expression, represented by the parameter α. We further assume an association between expression and a cross-sectional trait, represented by the parameter γ. In both cases, linear models are assumed with variance parameters given by and , respectively. Sample sizes are set equal to n1 = 175 for the GWAS study and n2 = 450 for the TWAS study, 1000 simulations are performed per condition, and 40 bootstrapped samples are used for the mSRI approach. We refer to the complete null as the situation in which there exists no association between the SNP and expression nor an association between expression at the trait (α/σδ = 0 and γ/σε = 0, respectively). Coverage is the proportion of 95% confidence intervals that cover the true parameter value used for the simulation. Under the complete null, coverage is equal to one minus the type-1 error rate. Finally, estimation error is defined as the difference between the estimated parameter, , for association between expression and the trait and the true value used for the simulation. The expectation of this quantity is the bias in the estimator.
Simulation results under the simple (partial) null of no association between SNP and expression for a range of expression-trait effect sizes are provided in Figure 1. Here we see that under the complete null (both effect sizes = 0), conditional mean imputation (CMI) has appropriate type-1 error control (nominal level of 0.05) and coverage while mSRI is conservative with an error rate of 0 and coverage of 100% (Figure 1(a)). For increasing effect sizes, CMI continues to exhibit approximate control of type-1 error rates while coverage based on 95% confidence intervals declines to 91% for larger expression-trait association effects. mSRI, on the other hand, is consistently conservative for both type-1 error and coverage. Estimation error is substantial in both cases, with slightly larger variability for CMI compared to mSRI (Figure 1(b)). These results suggest that inference will largely be correct under the null for both CMI and mSRI, with higher, though generally acceptable, error rates for CMI. In both cases, the estimated effect sizes should be viewed with caution. Moreover, confidence interval estimates are conservative for mSRI but do not provide appropriate coverage with CMI.
Figure 1.
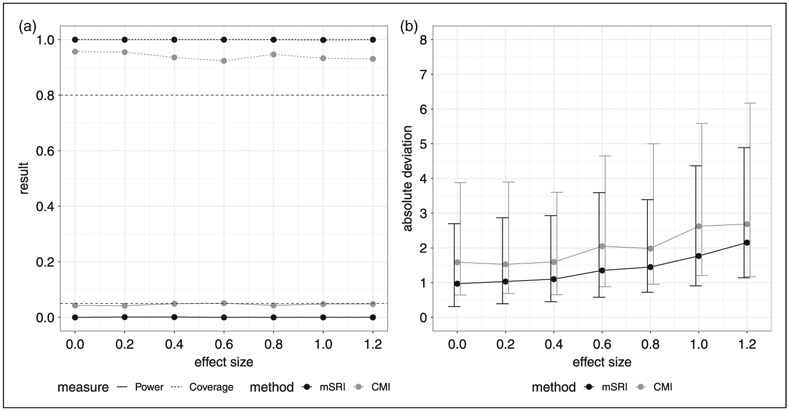
Simulation results for mSRI and CMI under the null of no SNP-expression association for a range of expression-trait effect sizes. Type-1 error is estimated as the proportion of simulations for which the test statistic H0: γ = 0 is significant at the 0.05 level. Coverage is the proportion of 95% confidence intervals that cover the true parameter value used for the simulation – under the complete null, coverage is the same as one minus the type-1 error rate. Estimation error is defined as the difference between the estimated parameter for association between expression and the trait and the true value used for the simulation (=0 in this example). (a) Power (type-1 error rate) and coverage. (b) Absolute deviation (median and IQR).
Power for a range of alternative effect sizes for the expression-trait association is provided in Figure 2. For moderate SNP-trait association effects (Figure 2(b) and (c); α/σδ = 0.6 and 0.8), estimated power is greater for mSRI compared to CMI across all ranges of the expression-trait association effects (γ/σε = 0.2–1.2). For a smaller SNP-trait association effect (Figure 2(a); α/σδ = 0.2), CMI has slightly higher estimated power than mSRI for small expression-trait association effects (γ/σε = 0.2–0.4), and overall the differential in power is smaller. Coverage is consistently lower for CMI compared to mSRI, and again decreases to lower than one minus the nominal level for CMI as the expression-trait association increases. The impact of model misspecification with respect to the error distribution for expression and the trait is also illustrated in Figure 3 under a moderate SNP-expression effect (α/σδ = 0.6). Power of CMI is notably greater than mSRI in the context of misspecification of the expression distribution (Figure 3(a)), while a corresponding differential in type-1 error (0.063 and 0.024 for CMI and mSRI, respectively) is also observed. Coverage based on 95% confidence intervals range from 0.975 to 0.992 for mSRI and from 0.895 to 0.940 for CMI. In the context of misspecification of the trait distribution, the results are more similar to those observed under correct specification, with a consistent and expected decrease in power for both CMI and mSRI.
Figure 2.
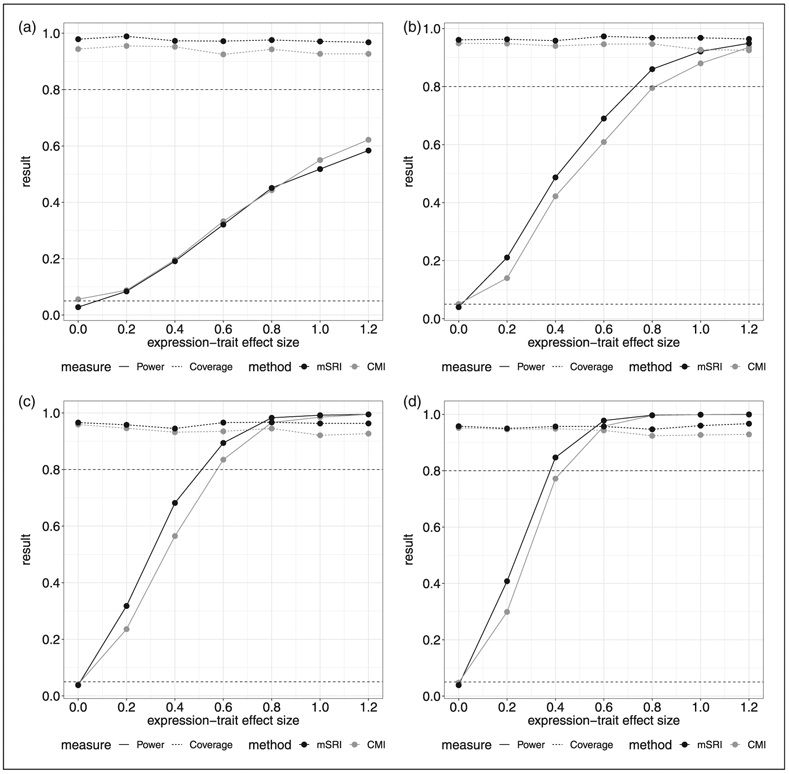
Estimated power and coverage for mSRI and CMI under a range of alternative effect sizes for the SNP-expression and expression-trait associations. Power is the estimated proportion of significant tests at the 0.05 level when the effect size is non-zero. Coverage is the proportion of 95% confidence intervals that cover the true parameter value used for the simulation.
(a) SNP-expression effect size: α/σδ = 0.4. (b) SNP-expression effect size: α/σδ = 0.6. (c) SNP-expression effect size: α/σδ = 0.8. (d) SNP-expression effect size: α/σδ = 1.0.
Figure 3.
Misspecified models have a moderate SNP-expression effect (α/σδ = 0.6) and the error terms are assumed to follow a log normal distribution while normality is assumed in the model fitting procedure. (a) Misspecified error distribution for expression, (b) misspecified error distribution for the trait.
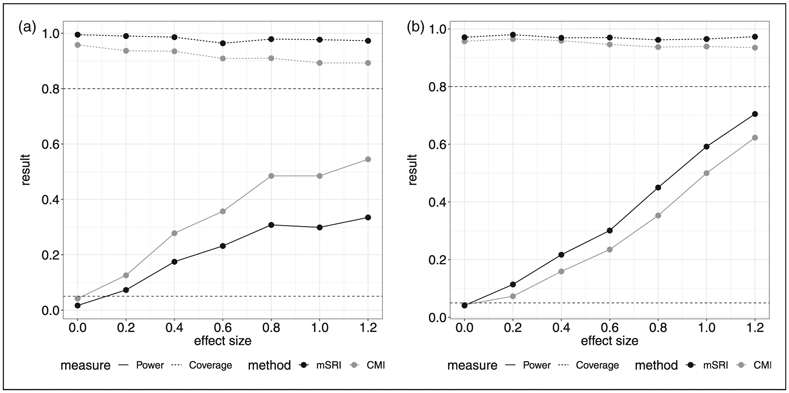
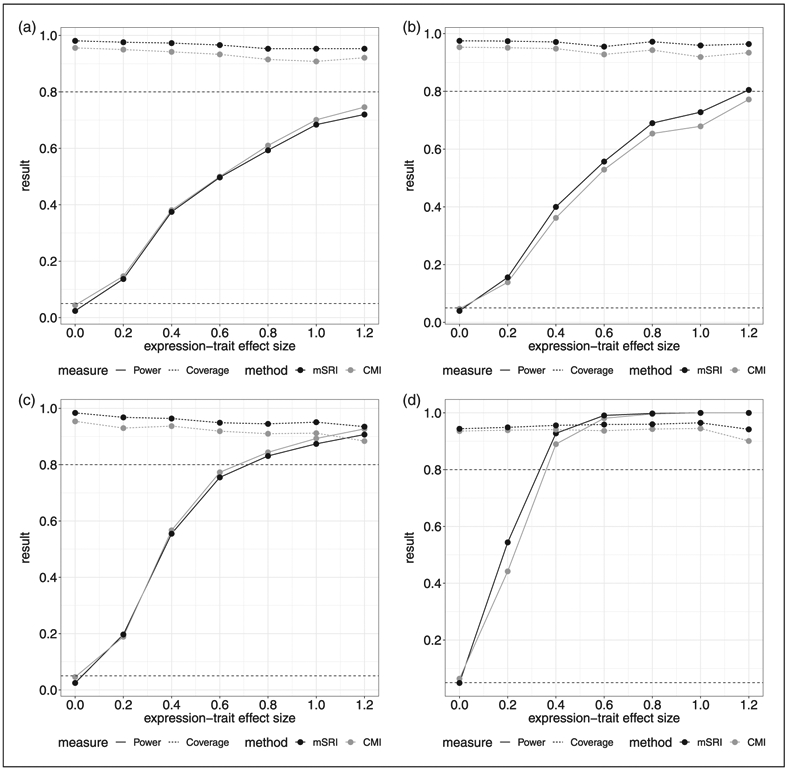
Two additional simulations are performed based on the inflammasome gene SNPs associated with WB IL1RN expression (rs3917296, rs315952, and rs55910638) and WB Caspase 1 (CASP1) expression (rs3917365, rs3917243, rs3917296, rs3181052, and rs55910638) in the case study below. In these simulations, we sample with replacement from the genotype data observed in the GENE study and GTEx project, preserving within individual links, to achieve corresponding sample sizes of n1 = 175; 400 and n2 = 450; 650. Assumed SNP-expression effect estimates are based on fitting a linear model and given by −0.277, −0.164 and −0.205, respectively, with residual standard deviation given by σδ = 1.514 for IL1RN expression and 0.160, −0.096, −0.228, −0.109, and −0.161 respectively, with residual standard deviation given by σδ = 1.262 for CASP1 expression. Type-1 error, power and coverage are provided in Figures 4 and 5. The results for sample sizes of n1 = 175 and n2 = 450 (Figures 4(a) and (c) and 5(a) and (c)) are fairly consistent with the previous findings for small SNP-expression associations. The power differential between mSRI and CMI becomes more pronounced for the larger SNP-expression sample size of n2 = 650 (Figures 4(b) and (d) and 5(b) and (d)). Power increases for both approaches as the expression-trait sample size increases to n1 = 300; however, coverage for CMI declines more significantly to less than 90%. We also note that the results for the two genes investigated are fairly consistent.
Figure 4.
Simulation results based on three inflammasome gene SNPs (rs3917296, rs315952, rs55910638) associated with WB IL1RN expression. Assumed SNP-expression effect estimates are −0.277, −0.164 and −0.205, respectively, with residual standard deviation given by σδ = 1.514. (a) n1 = 175; n2 = 450, (b) n1 = 175; n2 = 650, (c) n1 = 300; n2 = 450, (d) n1 = 175; n2 = 650; SNP-expression effect sizes based on two-times observed estimates.‡
‡In panel (d), effect sizes of all three SNPs are doubled. Genotype data are sampled with replacement from the observed data in the GENE study and GTEx project, preserving within individual links, to achieve corresponding sample sizes.
Figure 5.
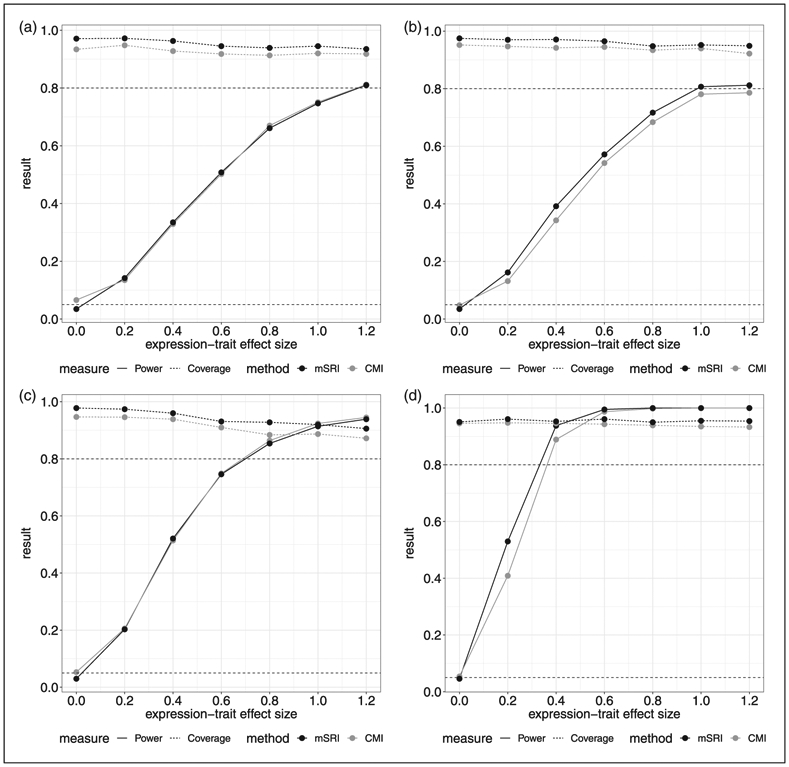
Simulation results based on five inflammasome gene SNPs (rs3917365, rs3917243, rs3917296, rs3181052, rs55910638) associated with WB CASP1 expression. Assumed SNP-expression effect estimates are 0.160, −0.096, −0.228, −0.109, and −0.161 respectively, with residual standard deviation given by σδ = 1.262. (a) n1 = 175; n2 = 450, (b) n1 = 175; n2 = 650, (c) n1 = 300; n2 = 450, (d) n1 = 175; n2 = 650; SNP-expression effect sizes based on two-times observed estimates.‡
‡In panel (d), effect sizes of all five SNPs are doubled. Genotype data are sampled with replacement from the observed data in the GENE study and GTEx project, preserving within individual links, to achieve corresponding sample sizes.
3.2. Case study: Inflammasome gene expression and evoked inflammatory response
As activation of innate immunity is a fundamental pathophysiological process in cardiometabolic disease and complex inflammatory disorders, our understanding of the genetic underpinnings of these evoked inflammatory biomarkers provides clinically relevant impact toward development of novel prognostic markers and therapeutic targets in complex diseases. In this report, we consider data arising from the Genetics of Evoked Response to Niacin and Endotoxemia (GENE) study, an NIH-sponsored investigation of the genomics of inflammatory and metabolic responses during low-grade endotoxemia.21-23 A total of 294 individuals were genotyped at baseline and monitored during a 48 h hospital visit after an endotoxin challenge. A subset of n1 = 193 Caucasians are used for analysis. Multiple clinical variables including temperature and five plasma biomarkers were recorded repeatedly over time in increments of 1 to 12 h. Our application is focused on interleukin-1 receptor agonist (IL-1RA) response, which was measured at 0, 1, 2, 4, 6, 12 and 24 h after the endotoxin challenge. The NIH-sponsored GTEx data are used for the transciptome reference panel. These data include whole-genome sequencing data and RNAseq on WB for 449 donors,27 and a subset of n2 = 334 Caucasians are used for analysis.
Our interrogation focuses on six inflammasome loci – namely, interleukin 1 receptor type 1 (IL1R1), interleukin 1 alpha (IL1A), interleukin 1 beta (IL1B), interleukin 1 receptor antagonist (IL1RN), CASP1 and NLR family Pyrin domain containing 1 (NLRP1) – to characterize the potential mediating role of WB expression on time-varying IL-1RA response to stimulus. We consider 133 typed SNPs within ±5 Kb of the start and stop locations of these six genes that are available in both GENE and GTEx. Single mean imputation is used to address the small degree of missing SNP data, with implications described in the Discussion section below. Each SNP is transformed to have mean 0 and standard deviation 1 prior to model fitting, and a log base 2 transformation is applied to normalized WB expression. Separate models are fitted for each gene expression via LASSO, using the complete set of 133 SNPs, for variable selection. The results subset of SNPs is then used for analysis. The implications of using a first stage variable selection are described in the Discussion section below. Expression of WB IL1A expression is not considered as it is zero inflated and violates the linear model assumptions of equations (1) and (2). Finally, the trait IL-1RA is naturally log transformed prior to analysis to meet model assumptions.
The results of applying mSRI to evaluate the association between expression of each inflammasome gene and IL-1RA response are given in Tables 1 and 2. A total of 133 SNPs within six inflammasome genes are used as input into a LASSO analysis and leave-one-out cross-validation is performed to select the penalty parameter. SNPs with non-zero LASSO coefficient estimates for WB expression are reported. Corresponding least squares coefficient estimates and associated p-values are provided in Table 1. SNPs that are selected as associated with the five WB inflammasome expressions are within four gene regions (IL1R1, IL1B, IL1RN, and NRLP1). All SNPs fall within the indicated protein coding gene with the exception of rs3917365 which is located within than 1 Kb from the start location of IL1B.
Table 1.
Inflammasome gene SNPs association with WB gene expression.
| Coefficient estimates (p) for WB expression |
||||||||
|---|---|---|---|---|---|---|---|---|
| Gene | SNPa | chr | Coordinate | IL1R1 | IL1B | IL1RN | CASP1 | NLRP1 |
| intercept | 11.284 | 10.286 | 12.289 | 12.343 | 13.250 | |||
| IL1R1 | rs3917243 | 2 | 102774988 | · | · | · | −0.096 | · |
| · | · | · | (0.205) | · | ||||
| rs3917296 | 2 | 102784833 | −0.303 | · | −0.277 | −0.228 | −0.158 | |
| (0.002) | · | (<0.001) | (0.002) | (0.020) | ||||
| IL1B | rs3917365 | 2 | 113586469 | · | · | · | 0.160 | · |
| · | · | · | (0.023) | · | ||||
| IL1RN | rs3181052 | 2 | 113886049 | · | −0.226 | · | −0.110 | · |
| · | (0.016) | · | (0.116) | · | ||||
| rs315952 | 2 | 113890304 | · | · | −0.164 | · | · | |
| · | · | (0.049) | · | · | ||||
| NLRP1 | rs55910638 | 17 | 5404270 | · | · | −0.205 | −0.161 | · |
| · | · | (0.014) | (0.022) | · | ||||
WB: whole blood; IL1R: 1interleukin 1 receptor type 1; IL1B: interleukin 1 beta; IL1RN: interleukin 1 receptor antagonist; CASP1: Caspase 1; NLRP1: NLR Family Pyrin Domain Containing 1.
A total of 133 SNPs within six inflammasome genes are used as input into the LASSO analysis and leave-one-out cross-validation is performed to select the penalty parameter. SNPs with non-zero LASSO coefficient estimates for WB expression are reported.
Table 2.
WB inflammasome gene expression association with induced biomarker response.
| ΔIL-1RAa |
IL-1RA trajectoryb |
|||||
|---|---|---|---|---|---|---|
| Coef | test stat (tdf) | df | p- | Test stat () | p | |
| IL1R1 | 0.791 | 1.293 | 41.40 | 0.102 | 14.533 | 0.024 |
| IL1B | −0.284 | −0.210 | 53.06 | 0.583 | 2.603 | 0.857 |
| IL1RN | 0.385 | 1.201 | 49.82 | 0.118 | 5.995 | 0.424 |
| CASP1 | 0.367 | 1.143 | 51.21 | 0.129 | 5.254 | 0.512 |
| NLRP1 | −0.118 | −0.010 | 39.48 | 0.504 | 14.533 | 0.024 |
IL1R1: 1interleukin 1 receptor type 1; IL1B: interleukin 1 beta; IL1RN: interleukin 1 receptor antagonist; CASP1: Caspase 1; NLRP1: NLR Family Pyrin Domain Containing 1; IL-1RA: interleukin 1 receptor antagonist.
Univariate analysis based on change from baseline to peak value of IL-1RA.
Longitudinal analysis based on repeated measure of IL-1RA. Wald statistic corresponding to test for expression by time interaction. Results are based on 40 stochastic regression imputations. Reported statistics correspond to , which are asymptotically χ2 with 6 degrees of freedom.
For the univariate analysis, the trait is defined as change from baseline to peak IL-1RA value and hypothesis testing focuses on the test of whether predicted expression is associated with this univariate trait. For the longitudinal analysis, a linear mixed effects modeling framework with natural splines is used to model IL-1RA flexibly over time. Knots at times 1, 2, 4, 5 and 8 with boundaries at 0.5 and 18 are assumed (resulting in six parameters for time), and random person-specific intercepts are included in the model. Fixed effects for the six interactions between time components and predicted expression are also included. A visual display of the observed and model-based predicted IL-1RA trajectories is given in Figure 6. Predicted lines are based on the model for WB IL1R1 expression with values set equal to the 25th and 75th percentiles of observed WB IL1R1 expression in the GTEx data. In the context of the longitudinal data, hypothesis testing focuses on whether there is an overall interaction between expression and time on the biomarker response. Test statistics and corresponding p-values for expression-trait association are given in Table 2. Results are based on 40 stochastic regression imputations. This analysis is unable to identify an association between genetically predicted expression and change from baseline to peak in IL-1RA; however, there is the suggestion of an association between both IL1R1 and NLRP1 expression (expression × time interaction) and IL-1RA when leveraging the full range of the observed biomarker data over time.
Figure 6.
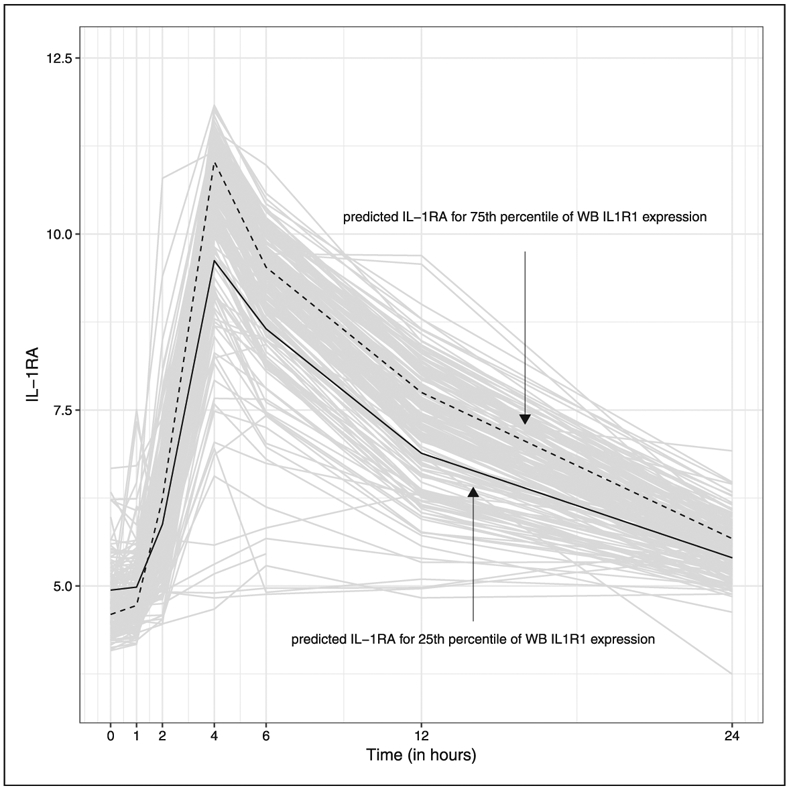
Observed and predicted IL-1RA over time by WB IL1R1 expression. A linear mixed effects modeling framework with natural splines is used to model IL-1RA flexibly over time. Predicted lines are based on the model for WB IL1R1 expression with values set equal to the 25th and 75th percentiles of observed WB IL1R1 expression in the GTEx data.
3.3. Some remarks on compute times
One drawback of multiple imputation as compared to a single imputation procedure is the associated computational burden. Performance with respect to speed will depend largely on the number of imputations, sample size, and model complexity. In Table 3, we report the mean central processing unit (CPU) times for computing test statistics and corresponding p-values based on CMI and mSRI across 1000 evaluations according to the simulation scenario described in Figure 2. The number of bootstrap imputations ranges from 20 to 100, and the sample sizes are varied as indicated. Times are reported in second and are based on application with a 2.9 GHz Intel Core i7 processor using the microbenchmark() function in R. Application of a more complex model fitting approach, such as penalized regression, involving a cross-validation procedure, results in a marked increase in computational burden. For example, in the data example above, the average CPU time across 1000 evaluations for a single fit of LASSO using glmnet() in R with 10-fold cross-validation is 3.9556 s. The user CPU increases to 139.0149 seconds for a single application of leave-one-out cross-validation. Notably, it is straightforward to parallelize these operations, resulting in an increase in the overall required CPU, as additional resources are needed to parse the parallel jobs, while offering overall savings in clock time.
Table 3.
Computation timesa for CMI and mSRI.
| mSRI |
||||||
|---|---|---|---|---|---|---|
| Sample sizes | CMI | B = 20 | B = 40 | B = 60 | B = 80 | B = 100 |
| n1 = 175; n2 = 450 | 0.0018 | 0.0418 | 0.0860 | 0.1258 | 0.1637 | 0.2153 |
| n1 = 350; n2 = 900 | 0.0023 | 0.0467 | 0.0908 | 0.1390 | 0.1833 | 0.2249 |
mSRI: multiple stochastic regression imputation; CMI: conditional mean imputation.
Times are reported in seconds as the mean across 1000 evaluations using the microbenchmark() function in R. Results are based on application with a 2.9 GHz Intel Core i7 processor and the conditions described in the simulation scenarios of Figure 2.
4. Discussion
In this study, we present an mSRI approach for transcriptome association analysis that serves as an alternative to conditional mean imputation. The primary contribution of mSRI is that, similar to CMI, it provides a platform for integrating features measured on distinct samples of individuals across data resources, while mSRI additionally accounts for uncertainty in prediction. We also extend this strategy to evaluate the modifying role of predicted expression on non-linear biomarker trajectories. Our simulation studies suggest comparable performance of the two approaches with respect to power and type-1 error rates under the null of no SNP-expression association (Figure 1(a)), and under relatively small SNP-expression association effect sizes (Figure 2(a), Figures 4(b), (d) and Figures 5(b), (d)). However, estimated power is greater for mSRI compared to CMI with more moderate SNP-expression effects (Figure 2(b) to (d)) and with larger SNP-expression sample sizes (Figures 4(b), (d) and Figures 5(b), (d)). Both strategies exhibit increasing deviations in effect estimates from the true values as the expression-trait effect size increases (Figure 1(b)), although this is more pronounced in CMI. Appropriate coverage is achieved under a range of alternative models for mSRI, while coverage is lower than one minus the confidence level with CMI (Figures 2 to 5). In summary, these results suggest that under the correct model specification: (i) both strategies are appropriate for hypothesis testing; (ii) mSRI tends to have greater power; (iii) point estimates are not reliable for either strategy; (iv) and interval estimates are valid for mSRI but are not valid for CMI.
In the example provided, we used LASSO with leave-one-out cross-validation for variable selection prior to applying CMI and mSRI. A first-stage variable selection is one approach to addressing the large number of SNPs (133 in our example) and high-degree of linkage disequilibrium (LD) typical in TWAS applications. In our data example, this resulted in the identification of six SNPs associated with five WB inflammasome gene expressions. The observed cross-talk is expected given the shared influences of these genes on inflammation; however, the significance of this result is difficult to evaluate given the high degrees of correlation among SNPs and expression profiles. Moreover, much of the literature on SNP-expression associations is based on univariate analysis.35 An alternative penalized regression approach, such as the elastic net,32 or an ensemble learner approach, such as random forests,36,37 could also be used at this stage and could result in higher predictive performance. Importantly, first-stage variable selection introduces an additional layer of prediction error that can be accounted for using the same approach described herein. However, the computational burden for multiple imputation would be considerable, particularly if using leave-one-out cross-validation as described above. Moreover, application of penalized regression with 10-fold cross-validation or other perturbations in the data, yields vastly different SNP sets and numbers of SNPs selected (results not shown), rendering the results of both CMI and mSRI difficult to interpret. An alternative strategy is to first reduce dimensionality using LD pruning38 in order to ensure model identifiability as we have described previously.26 Notably, all results based on first stage variable selection are valid but need to reported as conditional on the selected SNP set.
In the application presented, we used only typed SNPs, i.e. those that were present on the associated array platform, although we do apply a single mean imputation for the small amount of missing SNP data in our example. More generally, mSRI can be applied to 1000 Genomes imputed data, i.e. to SNPs that are imputed based on sequencing information on an independent sample of individuals with common ancestry.39 An application of CMI to imputed SNP data has been described, for example in Gamazon et al.1 without accounting for the associated predictive uncertainty. The proposed mSRI approach could be extended to further account for this SNP-level uncertainty, although the computational burden associated with repeated application of SNP level imputation would be fairly large. Imputing SNPs based on 1000 Genomes data, however, yields as many as 10 times the number of imputed SNPs as typed SNPs, and thus accounting for associated error is worthy of further consideration.
In this study, we also demonstrate the opportunity for unraveling interactions between expression and time on non-linear biomarker trajectories. We derive a composite Wald statistic for this setting and use the result of Li et al.40 to combine statistics across multiply imputed data sets. Improvements to the approach of Li et al.40 are currently being developed (personal communication with Xiao-Li Meng, paper under review) and application is straightforward. Finally, we emphasize that the transcriptome association approach we describe captures association of the genetic component of expression with the trait. Unmeasured confounding and reverse causality are generally concerns relating to the non-genetic component of expression and the trait. However, in order to conclude causal mediation the SNPs must be “valid” instruments, i.e.: (i) the SNPs must be associated with expression; (ii) the SNPs must have no “direct” effect on the trait, i.e. an effect via another pathway; and (iii) there must not be confounding between the SNPs and the trait, e.g. by population substructure.41,42 Integration with recent methods in causal inference that allow for incorporation of some valid and some invalid instruments43-45 is a direction of future research. Methods for considering the potential modifying roles of clinical and demographic factors on SNP-expression associations, as well as evaluating the transportability between GWAS and TWAS data resources, would also advance the broader applicability of these methods.
Acknowledgments
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Support for this research was provided by NIH/NIGMS R15 GM126485 and R01 GM127862.
Footnotes
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- 1.Gamazon ER, Wheeler HE, Shah KP, et al. A gene-based association method for mapping traits using reference transcriptome data. Nat Genet 2015; 47: 1091–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mancuso N, Shi H, Goddard P, et al. Integrating gene expression with summary association statistics to identify genes associated with 30 complex traits. Am J Hum Genet 2017; 100: 473–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gusev A, Ko A, Shi H, et al. Integrative approaches for large-scale transcriptome-wide association studies. Nat Genet 2016; 48: 245–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barbeira AN, Dickinson SP, Bonazzola R, et al. Exploring the phenotypic consequences of tissue specific gene expression variation inferred from GWAS summary statistics. Nat Commun 2018; 9: 1825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hormozdiari F, Gazal S, van de Geijn B, et al. Leveraging molecular quantitative trait loci to understand the genetic architecture of diseases and complex traits. Nat Genet 2018; 50: 1041–1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li G, Jima D, Wright FA, et al. HT-eQTL: integrative expression quantitative trait loci analysis in a large number of human tissues. BMC Bioinformatics 2018; 19: 95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li G, Shabalin AA, Rusyn I, et al. An empirical Bayes approach for multiple tissue eQTL analysis. Biostatistics 2018; 19: 391–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ongen H, Brown AA, Delaneau O, et al. Estimating the causal tissues for complex traits and diseases. Nat Genet 2017; 49: 1676–1683. [DOI] [PubMed] [Google Scholar]
- 9.Gamazon ER, Segre AV, van de Bunt M, et al. Using an atlas of gene regulation across 44 human tissues to inform complex disease- and trait-associated variation. Nat Genet 2018; 50: 956–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Spiegelman D, McDermott A and Rosner B. Regression calibration method for correcting measurement-error bias in nutritional epidemiology. Am J Clin Nutr 1997; 65(4 Suppl): 1179S–1186S. [DOI] [PubMed] [Google Scholar]
- 11.Berglund L Regression dilution bias: tools for correction methods and sample size calculation. Ups J Med Sci 2012; 117: 279–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Brakenhoff TB, van Smeden M, Visseren FLJ, et al. Random measurement error: why worry? An example of cardiovascular risk factors. PLoS ONE 2018; 13: e0192298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wood AM, White IR, Thompson SG, et al. Correcting for multivariate measurement error by regression calibration in meta-analyses of epidemiological studies. Stat Med 2009; 28: 1067–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rosner B, Spiegelman D and Willett WC. Correction of logistic regression relative risk estimates and confidence intervals for random within-person measurement error. Am J Epidemiol 1992; 136: 1400–1413. [DOI] [PubMed] [Google Scholar]
- 15.Rosner B, Willett WC and Spiegelman D. Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error. Stat Med 1989; 8: 1051–1069. [DOI] [PubMed] [Google Scholar]
- 16.Cole SR, Chu H and Greenland S. Multiple-imputation for measurement-error correction. Int J Epidemiol 2006; 35: 1074–1081. [DOI] [PubMed] [Google Scholar]
- 17.Guo Y and Little RJ. Regression analysis with covariates that have heteroscedastic measurement error. Stat Med 2011; 30: 2278–2294. [DOI] [PubMed] [Google Scholar]
- 18.Guo Y, Little RJ and McConnell DS. On using summary statistics from an external calibration sample to correct for covariate measurement error. Epidemiology 2012; 23: 165–174. [DOI] [PubMed] [Google Scholar]
- 19.Keogh RH and White IR. A toolkit for measurement error correction, with a focus on nutritional epidemiology. Stat Med 2014; 33: 2137–2155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bartlett JW and Keogh RH. Bayesian correction for covariate measurement error: a frequentist evaluation and comparison with regression calibration. Stat Methods Med Res 2018; 27: 1695–1708. [DOI] [PubMed] [Google Scholar]
- 21.Ferguson JF, Patel PN, Shah RY, et al. Race and gender variation in response to evoked inflammation. J Transl Med 2013; 11: 63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ferguson JF, Ryan MF, Gibney ER, et al. Dietary isoflavone intake is associated with evoked responses to inflammatory cardiometabolic stimuli and improved glucose homeostasis in healthy volunteers. Nutr Metab Cardiovasc Dis 2014; 24: 996–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ferguson JF, Meyer NJ, Qu L, et al. Integrative genomics identifies 7p11.2 as a novel locus for fever and clinical stress response in humans. Hum Mol Genet 2015; 24: 1801–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Qian J, Nunez S, Kim S, et al. A score test for genetic class-level association with nonlinear biomarker trajectories. Stat Med 2017; 36: 3075–3091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ferguson JF, Shah RY, Shah R, et al. Activation of innate immunity modulates insulin sensitivity, glucose effectiveness and pancreatic β-cell function in both African ancestry and European ancestry healthy humans. Metab Clin Exp 2015; 64: 513–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Qian J, Ray E, Brecha RL, et al. A likelihood-based approach to transcriptome association analysis. Stat Med 2019; 38: 1357–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lonsdale J, Thomas J, Salvatore M, et al. The Genotype-Tissue Expression (GTEx) project. Nat Genet 2013; 45: 580–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Little RJA and Rubin DB. Statistical analysis with missing data. New York: John Wiley & Sons, 2002. [Google Scholar]
- 29.Enders C Applied missing data analysis. New York: Gilford Press, 2010. [Google Scholar]
- 30.Weisberg S Applied linear regression, 3rd ed. Hoboken NJ: Wiley, 2005. [Google Scholar]
- 31.Tibshirani R Regression shrinkage and selection via the lasso. J R Stat Soc Series B (Methodological) 1996; 58: 267–288. [Google Scholar]
- 32.Zou H and Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc, Series B 2005; 67: 301–320. [Google Scholar]
- 33.Hoerl AE and Kennard RW. Ridge regression: biased estimation for nonorthogonal problems. Technometrics 1970; 12: 55–67. [Google Scholar]
- 34.Kim-Hung Li TER, Xiao-Li Meng and Rubin DB. Significance levels from repeated p-values with multiply-imputed data. Stat Sinica 1991; 1: 65–92. [Google Scholar]
- 35.Battle A, Brown CD, Engelhardt BE, et al. Genetic effects on gene expression across human tissues. Nature 2017; 550: 204–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Breiman L Random forests. Mach Learn 2001; 45: 5–32. [Google Scholar]
- 37.Bureau A, Dupuis J, Falls K, et al. Identifying SNPS predictive of phenotype using random forests. Genet Epidemiol 2005; 28: 171–182. [DOI] [PubMed] [Google Scholar]
- 38.Laurie CC, Doheny KF, Mirel DB, et al. Quality control and quality assurance in genotypic data for genome-wide association studies. Genet Epidemiol 2010; 34: 591–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Auton A, Brooks LD, Durbin RM, et al. A global reference for human genetic variation. Nature 2015; 526: 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Li KH, Meng XL, Raghunathan TE, et al. Significance levels from repeated p-values with multiply-imputed data. Statistica Sinica 1991; 1: 65–92. [Google Scholar]
- 41.Davey Smith G and Hemani G. Mendelian randomization: genetic anchors for causal inference in epidemiological studies. Hum Mol Genet 2014; 23: 89–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Burgess S, Small DS and Thompson SG. A review of instrumental variable estimators for Mendelian randomization. Stat Methods Med Res 2017; 26: 2333–2355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kang H, Zhang A, Cai TT, et al. Instrumental variables estimation with some invalid instruments and its application to Mendelian randomization. J Am Stat Assoc 2016; 111: 132–144. [Google Scholar]
- 44.Bao Y, Clarke PS, Smart M, et al. Assessing the robustness of sisVIVE in a Mendelian randomization study to estimate the causal effect of body mass index on income using multiple SNPs from understanding society. Stat Med 2019; 38: 1529–1542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wang X, Jiang Y, Zhang NR, et al. Sensitivity analysis and power for instrumental variable studies. Biometrics 2018; 74: 1150–1160. [DOI] [PubMed] [Google Scholar]


