Consciousness is supported by near-critical slow cortical electrodynamics

Significance

What changes in the brain when we lose consciousness? One possibility is that the loss of consciousness corresponds to a transition of the brain’s electric activity away from edge-of-chaos criticality, or the knife’s edge in between stability and chaos. Recent mathematical developments have produced tools for testing this hypothesis, which we apply to cortical recordings from diverse brain states. We show that the electric activity of the cortex is indeed poised near the boundary between stability and chaos during conscious states and transitions away from this boundary during unconsciousness and that this transition disrupts cortical information processing.

Abstract

Mounting evidence suggests that during conscious states, the electrodynamics of the cortex are poised near a critical point or phase transition and that this near-critical behavior supports the vast flow of information through cortical networks during conscious states. Here, we empirically identify a mathematically specific critical point near which waking cortical oscillatory dynamics operate, which is known as the edge-of-chaos critical point, or the boundary between stability and chaos. We do so by applying the recently developed modified 0-1 chaos test to electrocorticography (ECoG) and magnetoencephalography (MEG) recordings from the cortices of humans and macaques across normal waking, generalized seizure, anesthesia, and psychedelic states. Our evidence suggests that cortical information processing is disrupted during unconscious states because of a transition of low-frequency cortical electric oscillations away from this critical point; conversely, we show that psychedelics may increase the information richness of cortical activity by tuning low-frequency cortical oscillations closer to this critical point. Finally, we analyze clinical electroencephalography (EEG) recordings from patients with disorders of consciousness (DOC) and show that assessing the proximity of slow cortical oscillatory electrodynamics to the edge-of-chaos critical point may be useful as an index of consciousness in the clinical setting.

What are the dynamical properties of electric brain activity that are necessary for consciousness, and how are those properties disrupted during unconscious states such as anesthesia, generalized seizures, coma, and vegetative states?

One possibility, which is suggested by a large body of recent evidence, is that the electrodynamics of the conscious brain are poised near some sort of phase transition or “critical point” and that this near-critical behavior supports the vast flow of information through the brain during conscious states (1, 2). A critical point refers to the knife’s edge in between different phases of a system (e.g., liquid to solid water) or types of dynamical states (e.g., laminar to turbulent airflow). It is widely believed that electrodynamics of both micro- and macroscale cortical networks are poised near some critical point or perhaps near several critical points, because power-law statistics, which are a key signature of criticality (3), are consistently identified in recordings of neural electrodynamics (4, 5). And such critical behavior is known to have important computational benefits, because critical and near-critical systems tend to have a high capacity for encoding and transmitting information (6–9). For these reasons, it is widely believed that being poised at—or at least near (10–12)—criticality of some form endows neural populations with a high capacity for encoding and communicating information (4, 5, 12, 13), particularly during conscious states (1, 2). Conversely, because signatures of cortical criticality have been observed to disappear or diminish during unconscious states (4, 14, 15), it may be that a transition of cortical activity away from some critical point is what underlies the disruption to cortical information processing during unconscious states (2).

Although the existing evidence supports this conjectured relationship between criticality, cortical information processing, and conscious vs. unconscious brain states, prior empirical work has, for the most part, relied on the detection of power-law statistics in neural electrodynamics, most typically in the form of “neuronal avalanches” or bursts of electric activity whose sizes follow a power-law distribution, to infer neural criticality during conscious states and a loss of criticality during unconscious states (16). But the detection of power-law statistics alone cannot specify the type of critical point a system is poised at, because power-law statistics appear across many types of phase transitions (3). Moreover, neuronal avalanches can arise in noncritical neural systems (17), and neural networks can display several unique dynamical critical points, only one of which is the phase transition that gives rise to neuronal avalanches (18). Although some prior studies have attempted to use metrics other than power-law statistics to assess the relationship between neural criticality and consciousness (19–21), the precise form of criticality under consideration has largely remained mathematically unspecified (16), which leaves open the fundamental question: What, exactly, is the phase transition (or transitions) near which cortical electrodynamics seem to operate during conscious states? Put another way, what, from a mathematical perspective, are the dynamical phases that lie on either side of the critical point(s) near which waking brain dynamics operate?

Terms like “order” and “disorder” have commonly been used to describe the phases on either side of neural criticality, but these terms are imprecise unless they are defined relative to the breaking of a specific form of mathematical symmetry, where the “ordered” phase of a system is the symmetry-broken phase (in the way that ice is the ordered phase of water relative to the freezing critical point, because water loses its translational and rotational symmetry at this phase transition)—see SI Appendix, Supplementary Note 1 for a more detailed discussion of this point. Imprecise use of terms like order and disorder can also be misleading in the context of neural criticality. For example, chaos, which is defined as exponential sensitivity to small perturbations, is often used interchangeably with disorder in the literature on neural criticality (16), but chaos is in fact the ordered phase of dynamical systems because it corresponds to the breaking of the topological supersymmetry present in all dynamical systems (22) (SI Appendix, Supplementary Note 1). This inconsistency and lack of mathematical specificity in definitions of neural criticality may underlie the apparent variability of prior results relating criticality to different brain states, where, for example, some purported metrics of criticality seem to suggest that seizures constitute a departure from criticality while others seem to suggest that seizures are in fact critical phenomena (23). If, as has been proposed (1), the disruption to cortical information processing during unconscious states is mediated by an excursion of cortical electrodynamics away from some sort of critical point during these states, then mathematically precise identification of this critical point (or points) may be crucial for improving both our theoretical and clinical grasp on the neural correlates of consciousness.

Here, we provide direct empirical evidence for the hypothesis (24) that during conscious states, cortical electrodynamics—and specifically low-frequency cortical electrodynamics—operate near a mathematically well-defined critical point known as edge-of-chaos criticality or the phase transition from stable to chaotic dynamics. We additionally provide evidence that slow cortical oscillations may specifically operate on the chaotic side of this critical point during normal waking states. Many systems (6–9, 25, 26), including deep neural networks (25), echo state networks (8), and neuromorphic nanowire networks (26), have been shown to exhibit their highest capacity for information processing precisely at this specific critical point. In line with this well-replicated phenomenon, we show that excursions of low-frequency cortical oscillations away from this critical point during generalized seizures and γ-aminobutyric acid agonist (GABAergic) anesthesia induce a loss of information in cortical dynamics as well as a loss of consciousness. We moreover show that lysergic acid diethylamide (LSD), a 5-HT${}_{2A}$ receptor agonist characterized as a hallucinogen or “psychedelic,” may tune slow cortical dynamics closer to the edge-of-chaos critical point relative to normal waking states, which increases the information richness of cortical activity. Finally, we provide preliminary evidence that low-frequency cortical electrodynamics return to the vicinity of this critical point as patients with disorders of consciousness (DOC) regain awareness, which suggests that assessing the proximity of cortical dynamics to edge-of-chaos criticality may be useful as an approach to track patient awareness. We provide Matlab (R2020a) code for our analysis in the hopes of facilitating further basic and translational research along these lines.

Results

Mean-Field Dynamics.

To empirically assess whether cortical dynamics operate near the edge-of-chaos critical point during conscious states and whether this underpins the information richness of cortical dynamics during conscious states (Fig. 1), we must first assess varying levels of chaoticity and information richness in a model of cortical electrodynamics and then test whether real data agree with the model’s predictions. The reason we must first analyze a model is because a system’s level of stability can be detected with certainty only in a simulation, where noise and initial conditions can be precisely controlled. For this reason, it is generally agreed (27) that empirical evidence of varying levels of chaos in a biological system requires comparison of real data to an accurate model of the biological system of interest. Toward that end, we assessed the mean-field model of macroscale cortical electrodynamics developed by Steyn-Ross, Steyn-Ross, and Sleigh (28), which is based on the earlier model developed by Liley et al. (29, 30), because it has been shown to successfully model the low-frequency macroscale cortical electrodynamics of waking conscious (28), generalized seizure (28, 31, 32), and GABAergic anesthesia (28, 33) states and thus can be compared to real recordings of large-scale cortical electrodynamics across these diverse brain states. The model also includes gap junction coupling between cortical interneurons, which recent empirical work in zebrafish has shown is an important mechanism for the maintenance of criticality in electric neural activity (34). Using this model, we generated 10-s simulations of macroscale cortical electrodynamics corresponding to waking conscious, generalized seizure, and GABAergic anesthesia states (using parameter ranges identified in past studies) (Materials and Methods). We also performed a parameter sweep on the model to generate dynamics from 773 additional states, some of which may fall outside the physiological bounds for what may be considered waking, seizure, or anesthesia, to more broadly assess the relationship between proximity to edge-of-chaos criticality and information richness (Materials and Methods). For each parameter configuration of the model, we estimated the largest Lyapunov exponent of the deterministic component of the model’s dynamics (i.e., with the model’s noise inputs turned off) (Materials and Methods). The largest Lyapunov exponent is a mathematically formal measure of chaoticity: A largest Lyapunov exponent of 0 corresponds to edge-of-chaos criticality, a positive largest Lyapunov exponent corresponds to chaos, and a negative largest Lyapunov exponent corresponds to periodicity. Note that exact calculation of largest Lyapunov exponents is usually impossible, but that simulated systems allow for accurate estimation of Lyapunov exponents, by assessing how quickly initially similar simulations diverge (Materials and Methods). We furthermore chose to assess the information richness of the model’s stochastic dynamics (i.e., with noise inputs turned on) using three variants of Lempel–Ziv complexity (Materials and Methods), as this measure has been repeatedly shown to track level of consciousness (35) (see also discussion in ref. 35 of purported dissociations between Lempel–Ziv complexity and conscious vs. unconscious brain states). As a measure of compressibility (36), Lempel–Ziv complexity quantifies the amount of nonredundant information in a time series, as compressibility is mathematically lower bounded by the amount of unique information in a signal (37).

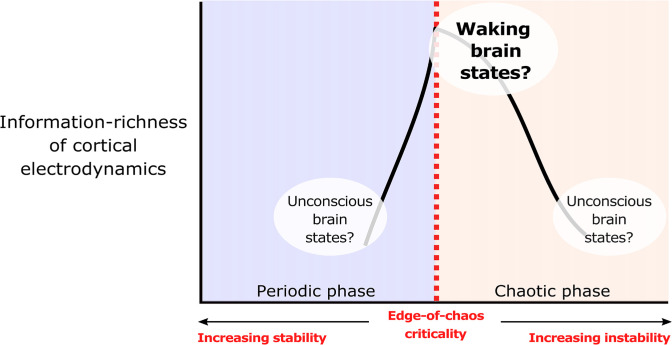
Fig. 1.

Hypothesized relationship between consciousness, edge-of-chaos criticality, and cortical information processing. We suggest that the electrodynamics of the cortex may be poised near the edge-of-chaos critical point during conscious states and transition away from this specific critical point during unconscious states. According to this hypothesis, transitions of cortical electrodynamics away from this critical point—either into the chaotic phase (leading to dynamical instability) or into the periodic phase (leading to hyperstability)—should disrupt cortical information processing and induce unconsciousness. In other words, we should expect to see an inverse-U relationship between chaoticity and information processing in the cortex, with cortical dynamics during conscious states near the top of this inverse U (i.e., in the near-critical, information-rich regime), and we should moreover expect to see cortical dynamics during unconscious states at either the bottom right of this inverse U (i.e., the unstable, information-poor regime) or at the bottom left of this inverse U (i.e., the hyperstable, information-poor regime) (1, 2, 22). Such an inverse-U relationship between chaoticity and information processing has been observed in many other dynamical systems (6–9), but remains to be empirically observed in the brain.

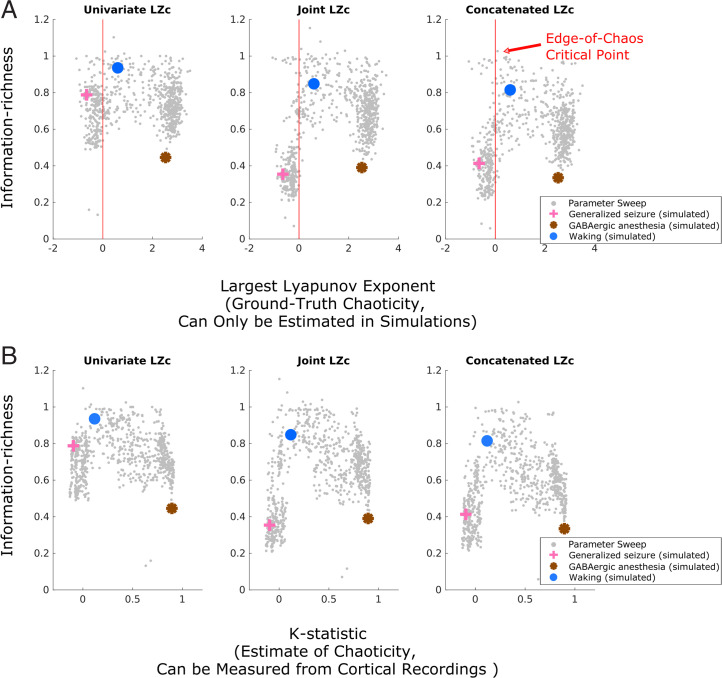
Consistent with the prediction that the cortex generates information-rich dynamics during conscious states by operating near the edge-of-chaos critical point, we found that the Lempel–Ziv complexity of the model’s simulated electrodynamics (with noise inputs) was maximal when the deterministic component of its dynamics were poised near this critical onset of chaos (red vertical line in Fig. 2A) and that the model’s simulation of the conscious, waking state was near this critical, information-rich regime. Importantly, the model specifically placed waking, conscious cortical dynamics on the chaotic side of this critical edge (blue circle in Fig. 2A) [note that, although some parameter configurations on the periodic side of the phase transition likewise yielded information-rich dynamics, Steyn-Ross et al. (28) found that parameters in the range of physiological realism for normal waking states generally produce weakly chaotic electrodynamics]. Moreover, as predicted, the model exhibited an inverse-U relationship between chaoticity and information richness, with the amount of information generated by its dynamics falling both in the chaotic phase (bottom right of the inverse U) and in the periodic phase (bottom left of the inverse U), similar to what has been shown in many other systems (6–9, 38). Importantly, we found a similar relationship between Lempel–Ziv complexity and this critical point in three other noise-driven dynamical systems for which ground-truth chaoticity could be calculated with even greater accuracy (SI Appendix, Fig. S1). To quantitatively confirm this qualitative result, we used Simonsohn’s two-lines statistical test of a U-shaped relationship, which accepts a null hypothesis of no U-shaped relationship if either of two opposite-sign regression lines (one for high and one for low values of the x variable) are statistically insignificant—see Simonsohn (39) for details on this test. The two-lines test failed to reject the null hypothesis no U-shaped relationship between largest Lyapunov exponents and univariate, joint, or concatenated Lempel–Ziv complexity in the mean-field model (Table 1). Finally, we note that the mean-field model specifically placed GABAergic anesthesia in the strongly chaotic/unstable phase and placed generalized seizures in the periodic/stable phase, even though both simulated states led to information loss (Fig. 2A) and increased spectral power at low frequencies (SI Appendix, Figs. S2–S4).

Fig. 2.

Predictions relating brain states, information processing, and the criticality of low-frequency cortical electrodynamics and the testability of those predictions in real data. (A) We calculated both the largest Lyapunov exponent (ground-truth instability) and Lempel–Ziv complexity (information richness) of 10-s mean-field simulations of low-frequency cortical electrodynamics during waking conscious (blue circle), generalized seizure (pink cross), and GABAergic anesthesia (brown asterisk) states. We also performed a parameter sweep of the mean-field model to more generally assess the relationship between the information richness of its dynamics and the proximity of those dynamics to this critical point (Materials and Methods); each small gray dot represents the result of a single 10-s simulation with a unique parameter configuration that did not correspond to a biologically specific brain state. We found that all three measures of information richness peak near the edge-of-chaos critical point (red vertical line) and that the simulated waking conscious dynamics are near this critical, information-rich regime. Importantly, waking cortical dynamics are here predicted to lie on the unstable side of this critical point. All three information measures drop in both the chaotic/unstable phase (positive largest Lyapunov exponent), where GABAergic anesthesia cortical dynamics are predicted to lie, and the periodic/stable phase (negative largest Lyapunov exponent), where generalized seizure dynamics are predicted to lie. (B) The modified 0-1 chaos test (Materials and Methods), when applied to the low-pass filtered simulated dynamics of the mean-field model, accurately tracks the chaoticity of those dynamics and is able to recapitulate the ground-truth inverse-U relationship between chaoticity and information richness. This validates the ability of the modified 0-1 chaos test to empirically evaluate these specific predictions relating consciousness, information processing, and the proximity of low-frequency cortical electrodynamics to the edge-of-chaos critical point in real cortical recordings.

Table 1.

Results of Simonsohn’s two-lines test of a U-shaped relationship (39)

Simonsohn’s two-lines test results
	Regression line 1	Regression line 2
Simulation data
LLE vs. univariate LZc	b = 0.1, z = 5.65, P < 10–4	b = –0.06, z = –5.44, P < 10–4
LLE vs. joint LZc	b = 0.4, z = 11, P < 10–4	b = –0.08, z = –8.39, P < 10–4
LLE vs. concatenated LZc	b = 0.29, z = 8.89, P < 10–4	b = –0.08, z = –6.98, P < 10–4
K vs. univariate LZc	b = 0.71, z = 11.76, P < 10–4	b = –0.28, z = –11.99, P < 10–4
K vs. joint LZc	b = 1.79, z = 25.4, P < 10–4	b = –0.32, z = –11.66, P < 10–4
K vs. concatenated LZc	b = 1.49, z = 21.49, P < 10–4	b = –0.36, z = –12.62, P < 10–4
Empirical data
K vs. univariate LZc	b = 0.26, z = 10.74, P < 10–4	b = –1.03, z = –8.42, P < 10–4
K vs. joint LZc	b = 0.12, z = 1.99, P = 0.137	b = –1.38, z = –6.55, P < 10–4
K vs. concatenated LZc	b = 0.33, z = 6.01, P < 10–4	b = –1.25, z = –10, P < 10–4

The test confirmed the U-shaped relationship (across different states of the mean-field model of cortical electrodynamics) between all three measures of Lempel–Ziv complexity (LZc) and chaoticity, as measured by both ground-truth largest Lyapunov exponents (LLE) and the K statistic of the modified 0-1 chaos test. The test also confirmed the U-shaped relationship (across subjects) in our cortical recordings between chaoticity, as measured by the K statistic, and both univariate and concatenated Lempel–Ziv complexity. P values were Bonferroni corrected for multiple comparisons against the same set of either LLE or K statistic values.

Such predictions of varying degrees of chaoticity in real biological systems have historically been difficult to test, but recent mathematical developments in nonlinear time-series analysis now allow for accurate detection of chaoticity from noisy time-series data. In particular, the modified 0-1 chaos test has emerged as a robust measure of chaoticity from noisy recordings (27, 40–44) (Materials and Methods). Given a recorded time series, the 0-1 chaos test outputs a statistic K, which estimates the degree of chaoticity of a (predominantly) deterministic signal on a scale from 0 to 1; lower values indicate periodicity and higher values indicate chaos. To specifically assess the chaoticity of low-frequency cortical electrodynamics (as simulated in the mean-field model), we low-pass filtered all time-series data in this study before applying the modified 0-1 chaos test. While low-pass filter cutoffs of neural electrophysiology recordings are often selected at canonical frequency bands, recent work has shown that this approach can result in data with spurious oscillations when no such neural electrodynamic oscillations are present and can moreover obfuscate natural but meaningful variance in oscillation frequencies across channels, subjects, and species; for these reasons, to select low-pass filter cutoffs in the 1- to 6-Hz range for every channel in every trial, we used the data-driven “Fitting Oscillations and One Over F” (“FOOOF”) algorithm, which helps identify real channel-specific oscillations and their respective frequencies based on neural power spectra (45). We then applied the modified 0-1 chaos test to these low-pass filtered signals. Note that a minority of channels for which no oscillations were identified in the 1- to 6-Hz range were excluded from chaoticity analysis (SI Appendix, Table S1) (see Materials and Methods for more details). Importantly, we verified that the majority of signals analyzed in this paper were generated by predominantly deterministic processes (SI Appendix, Tables S4 and S5), which is a key assumption of the modified 0-1 chaos test. Finally, where applicable, our statistical analyses included these selected low-pass filter frequencies as a covariate, to ensure that our results are driven by the stability of low-frequency cortical oscillations, rather than by their frequencies.

Confirming the ability of the modified 0-1 chaos test to detect varying levels of chaoticity from real time-series data, we found that its K statistic, when applied to the model’s simulated dynamics (with noise inputs turned on) after low-pass filtering using the FOOOF algorithm, was strongly correlated with the ground-truth largest Lyapunov exponent of the deterministic component of the mean-field model’s dynamics (which can be estimated only in simulations) (r = 0.84, P < 10^–4, Bonferroni corrected for multiple chaos estimation tests [SI Appendix, Table S6]; and partial correlation ρ = 0.82, P < 10^–4 after controlling for selected low-pass filter frequencies, Bonferroni corrected for multiple chaos estimation tests [SI Appendix, Table S7]). Moreover, this correlation was robust to high levels of both white measurement noise (i.e., equal power at all frequencies f) and pink measurement noise (i.e., 1/f noise, or noise power inversely proportional to frequency) (SI Appendix, Tables S6 and S7). The K statistic of these low-pass filtered signals was likewise correlated with the stochastic Lyapunov exponents of the model (i.e., with Lyapunov exponents calculated for partially stochastic simulations with identical noise inputs) (r = 0.83, P < 10^–4; and partial correlation ρ = 0.81, P < 10^–4 after controlling for selected low-pass filter frequencies). Moreover, the K statistic was able to recapitulate the inverse-U relationship between chaoticity and Lempel–Ziv complexity in the model, as shown qualitatively in Fig. 2B. As was the case for the ground-truth largest Lyapunov exponents, Simonsohn’s two-lines test quantitatively confirmed the inverse-U relationship between the K statistic and univariate, joint, and concatenated Lempel–Ziv complexity (Table 1). These results indicate that we can use the 0-1 test’s K statistic to directly empirically test the above-mentioned predictions relating consciousness, information richness, and cortical chaoticity relative to the edge-of-chaos critical point in real recordings of macroscale cortical electrodynamics.

Cortical Electrodynamics Confirm Mean-Field Predictions.

We therefore applied the modified 0-1 chaos test to low-frequency activity extracted from surface electrocorticography (ECoG) recordings of the cortical electrodynamics of two macaques and five human epilepsy patients during normal waking states, of two macaques and three human epilepsy patients under GABAergic (propofol or propofol and sevoflurane) anesthesia, and of two human epilepsy patients experiencing generalized seizures; we further applied this test to magnetoencephalography (MEG) recordings of the cortical electrodynamics of a third human epilepsy patient experiencing a generalized seizure. We also applied the 0-1 chaos test to the low-frequency component of MEG recordings of the cortical electrodynamics of 16 human subjects under the influence of either a saline placebo or LSD, as psychedelics are the only known compounds to reliably increase the information richness of cortical electrodynamics (1, 2, 46, 47) and are thought to do so by tuning cortical dynamics closer to some critical point (2, 48, 49). Psychedelics therefore allow us to test a specific and counterintuitive prediction of this chaos vs. information-processing framework: If cortical electrodynamics during normal waking states do indeed lie on the chaotic side of the edge-of-chaos critical point (as the mean-field model predicts), then psychedelics should, counterintuitively, increase the information richness of cortical activity by reducing the chaoticity of cortical dynamics, as those dynamics approach the edge-of-chaos critical point from the chaotic side of the phase transition (where normal waking dynamics are predicted to lie).

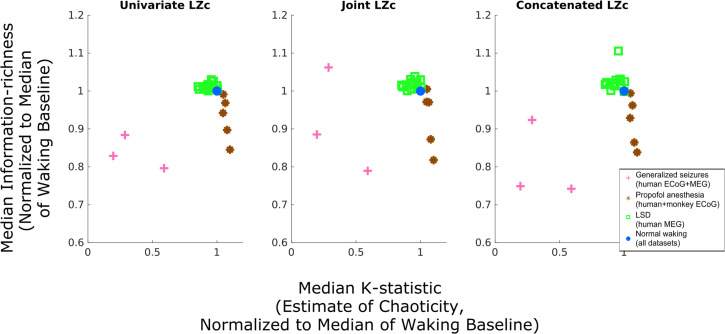
Confirming our predictions, our empirical analysis yielded an inverse-U relationship between chaoticity and information richness (as measured by three variants of Lempel–Ziv complexity) in our recordings of cortical electrodynamics, with conscious states at the top of this inverse U, as shown qualitatively in Fig. 3. To confirm this result quantitatively, we applied Simonsohn’s two-lines test to the median of each subject’s K statistic and Lempel–Ziv complexity over all trials from their altered states (seizure, anesthesia, LSD), normalized to their own normal waking baseline (as shown in Fig. 3). The test failed to reject the null hypothesis of no inverse-U relationship between the normalized K statistic and both univariate and concatenated Lempel–Ziv complexity, but not joint Lempel–Ziv complexity (Table 1). Moreover, as predicted, our within-subject analyses showed significant increases in chaoticity coinciding with significant drops in Lempel–Ziv complexity in the anesthesia state, small but significant reductions in chaoticity coinciding with significant increases in Lempel–Ziv complexity in the LSD state, and significant reductions in both chaoticity and Lempel–Ziv complexity during generalized seizures (SI Appendix, Fig. S5). Furthermore, we observed that the degree of reduction in chaoticity during the LSD state relative to placebo (assessed by normalizing each subject’s median K statistic during the LSD state by the subject’s median during the normal waking state, as in Fig. 3) was significantly correlated with subjects’ behavioral ratings (Materials and Methods) of the intensity of the LSD experience (partial correlation ρ = 0.55, P = 0.033, controlling for differences between placebo and LSD states in the median frequency at which signals were low-pass filtered). Importantly, even though there was a significant correlation between relative low-frequency spectral power (i.e., total power under the frequency selected for low-pass filtering, divided by total power under 45 Hz) in the mean-field model (ρ = 0.55, P < 0.001), an analysis of covariance (ANCOVA) analysis revealed that neither low-frequency filter cutoff nor relative spectral power under that cutoff significantly explained the empirically observed variance of chaoticity estimates, whereas brain state did—both for chaoticity estimates normalized to subjects’ normal waking baselines (F = 90.644, P = 0.001) and for nonnormalized chaoticity estimates (F = 43.477, P = 0.001) (SI Appendix, Tables S2 and S3). This result suggests that the chaoticity of cortical electrodynamics may offer unique insights about brain states and neural information processing over and above the insights offered by their spectral properties. Importantly, we found a similar overall inverse-U trend between chaoticity and information richness when using fixed low-pass filter frequency cutoffs rather than channel-specific oscillation frequencies, although with less consistent results for any given brain state (SI Appendix, Fig. S7), which highlights the importance of data-driven selection of frequency cutoffs. Furthermore, our analyses of surrogate time series not only suggest that low-frequency cortical electrodynamics are predominantly deterministic, but also show no difference in the level of stochasticity of cortical dynamics across brain states (SI Appendix, Tables S5 and S6), which suggests that these between-condition differences were likely driven by changes in the relative stability of cortical dynamics as predicted, rather than by changing levels of intrinsic noise in cortical networks. Finally, we compared the low-frequency power spectral densities of our real and simulated cortical electrodynamics and observed spectral changes that were consistent across our real and simulated data (SI Appendix, Figs. S2–S4), which lends further support to the model’s prediction of increased or decreased chaoticity relative to the edge-of-chaos critical point in these different states.

Fig. 3.

Transitions of low-frequency cortical electrodynamics away from the edge-of-chaos critical point induce a loss of information in cortical dynamics during unconscious states. We applied the modified 0-1 chaos test to ECoG and MEG recordings from humans and macaques across different brain states to empirically assess the predicted relationship between proximity to edge-of-chaos criticality, consciousness, and the information richness of cortical dynamics. Here, each marker represents the median estimated chaoticity and information richness of cortical dynamics across each individual subject’s trials, normalized to the median of the subject’s normal waking baseline. The observed inverse-U relationship between stability and information richness, with cortical dynamics during conscious states at the top of this inverse U, validates the prediction that cortical dynamics operate near the edge-of-chaos critical point during conscious states, transition deeper into the chaotic/unstable phase under GABAergic anesthesia, and transition into the periodic/stable phase during generalized seizures. These results support our hypothesis that these transitions away from edge-of-chaos criticality during unconscious states induce a loss of information in electrical cortical activity. Moreover, the counterintuitive reduction of chaoticity coinciding with increased information richness in the LSD state supports our prediction that waking cortical dynamics operate on the chaotic side of this critical point. See SI Appendix, Fig. S5 for statistical analysis of within-subject results and SI Appendix, Fig. S6 for a plot of all subjects’ nonnormalized chaoticity estimates.

Edge-of-Chaos Criticality Is a Potential Clinical Index of Consciousness.

The above findings support the hypothesis that the low-frequency electrodynamics of the cortex during conscious states are poised near the edge-of-chaos critical point and specifically operate on the chaotic side of this phase transition. This implies that use of the modified 0-1 chaos test (or other chaoticity tests) to assess the proximity of slow cortical oscillations to edge-of-chaos criticality, or to the unstable side of this phase transition, may be clinically useful as a tool for monitoring depth of anesthesia or diagnosing and monitoring emergence from disorders of consciousness—a group of conditions for which additional biomarkers are sorely needed (50). Toward that end, we here introduce a time-series estimate c of proximity to edge-of-chaos criticality, based on a nonlinear transformation of the K statistic (Materials and Methods). Our measure c includes a parameter α, set between 0 and 1, such that c will approach 1 as the K statistic approaches α and will approach 0 as the K statistic approaches either 0 (periodicity) or 1 (chaos). In other words, our measure c will assign low values for clearly periodic dynamics (K statistic near zero) and clearly chaotic dynamics (K statistic near one) and will assign high values to dynamics that are neither clearly periodic nor clearly chaotic (K statistic near α). Note that α values nearer to 0 will likely bias our criticality measure to assign higher values to systems on the periodic side of the edge-of-chaos critical point, while α values nearer to 1 will likely bias our measure to assign higher values to systems within the chaotic phase (although in general the overall relationship between ground-truth chaoticity, α, and c will vary on a system-by-system basis). To test the diagnostic utility of this criticality measure c, we applied our chaos analysis pipeline (i.e., low-pass filtering at a frequency determined by the FOOOF algorithm followed by application of the modified 0-1 chaos test) to clinical EEG data recorded from four traumatic brain injury patients as they recovered consciousness (Materials and Methods). Degree of consciousness was assessed using the Glasgow Coma Scale (GCS) as part of conventional bedside neurobehavioral testing. Following prior work (51, 52), data were split into conscious and unconscious states based on the verbal and motor subscores of the GCS. Patients were considered conscious if either their GCS verbal subscore was greater than or equal to four (meaning that they could answer questions) or if their motor subscore was greater than or equal to five (meaning that they displayed clearly purposeful movement). We considered patients unconscious if their verbal subscore was less than four and motor subscore was less than five, although we note that this criterion cannot differentiate between unconsciousness and unresponsiveness/disconnectedness.

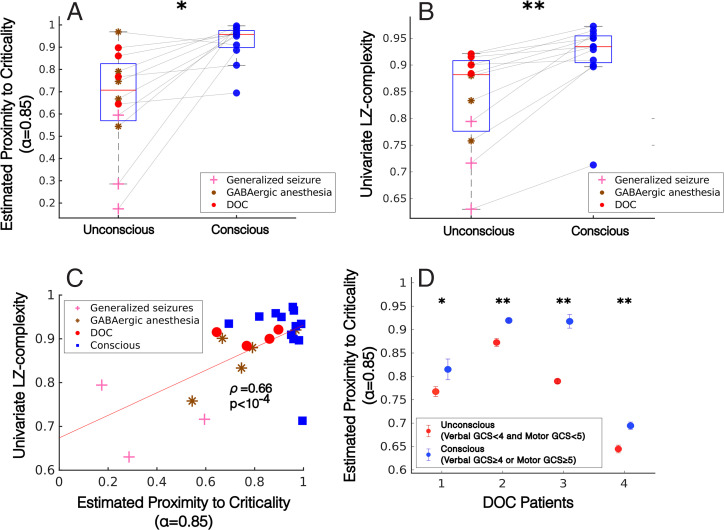
To test the utility of our criticality measure as an index of consciousness, we converted the median (unnormalized) K statistics of these four patients in their unconscious and conscious states, along with the median K statistics of our five anesthesia subjects and three generalized seizure subjects in their waking and unconscious states, to our criticality estimate c, using 19 unique values of its parameter α ranging from 0.05 to 0.95 in steps of 0.05. For each value of α, we performed a cross-subject, right-tailed Wilcoxon rank-sum test to compare estimates of proximity to edge-of-chaos criticality in conscious versus unconscious states. Before correcting for multiple comparisons, estimates of criticality were significantly higher during conscious states for all α values between 0.65 and 0.85; after conservative Bonferroni correction, c at α = 0.85 remained significantly higher across subjects during conscious states than during unconscious states (P < 10^–4 before Bonferroni correction, P = 0.016 after Bonferroni correction) (SI Appendix, Fig. S8) (Fig. 4A). Note that, as mentioned above, an α of 0.85 will likely bias our criticality measure c to assign higher values to dynamics on the chaotic side of the edge-of-chaos critical point, and so the finding of higher values of c during conscious states, with α set to 0.85, may be considered additional evidence that slow cortical oscillations are weakly chaotic during waking states. See SI Appendix, Fig. S9 for a bivariate plot of unnormalized chaoticity estimates versus criticality estimates for each subject and brain state. A cross-subject Wilcoxon rank-sum test revealed no significant difference in the median low-pass filter frequencies selected by the FOOOF algorithm in conscious vs. unconscious states (P = 0.795), while right-tailed Wilcoxon rank-sum tests showed that, across subjects, consciousness corresponded to significantly higher values of univariate Lempel–Ziv complexity (P = 0.003) (Fig. 4B) and concatenated Lempel–Ziv complexity (P = 0.0265) (SI Appendix, Fig. S10) but not joint Lempel–Ziv complexity (P = 0.107) (SI Appendix, Fig. S10). Furthermore, after controlling for the median frequency at which signals were low-pass filtered across these 12 subjects (4 DOC patients, 5 anesthesia subjects, and 3 generalized seizure subjects), our criticality measure c (at α = 0.85) was significantly correlated with cross-trial median univariate Lempel–Ziv complexity (partial correlation ρ = 0.66, P < 10^–4) (Fig. 4C) and concatenated Lempel–Ziv complexity (ρ = 0.66, P < 10^–4) but not with joint Lempel–Ziv complexity (ρ = 0.36, P = 0.093) (SI Appendix, Fig. S10); these correlations support the hypothesis that proximity to the edge-of-chaos critical point mediates the information richness of cortical electrodynamics as well as consciousness. Finally, we used a one-tailed block bootstrap test (block size = 30 s of data), which controls for the nonindependence of successive timepoints by preserving local time-series autocorrelations, to test for within-subject increases in c as patients recovered consciousness. We found significant increases in c for all four DOC patients (Fig. 4D), which supports the potential diagnostic utility of this criticality measure. Significant within-subject increases in univariate Lempel–Ziv complexity were also observed within all four DOC patients as they regained consciousness, but not in joint or concatenated Lempel–Ziv complexity (SI Appendix, Fig. S11).

Fig. 4.

Low-frequency criticality predicts consciousness. (A) Using our time-series measure of criticality (derived from the 0-1 chaos test) (Materials and Methods), we estimated the proximity of low-frequency cortical dynamics to edge-of-chaos criticality in 12 subjects for whom data were available from both conscious and unconscious states (namely, 5 GABAergic anesthesia subjects, 3 generalized seizure subjects, and 4 DOC patients). Our criticality measure includes a parameter α, which we here set to 0.85, based on our parameter analysis (SI Appendix, Fig. S8). Estimates of proximity to edge-of-chaos criticality were significantly higher (P < 10^–4 before Bonferroni correction for comparisons at multiple values of α, and P = 0.0157 after Bonferroni correction) in conscious states than in unconscious states (significance was tested using a right-tailed Wilcoxon rank-sum test). (B) Cross-trial, within-subject medians of univariate Lempel–Ziv complexity were significantly higher (P = 0.003) during conscious states than during unconscious states. See SI Appendix, Fig. S6 for comparisons using joint and concatenated Lempel–Ziv complexity. (C) Across the waking (blue square) and nonwaking (red circle) states of all 12 subjects exhibiting transitions between consciousness and unconsciousness, cross-trial medians of estimated proximity to edge-of-chaos criticality (with α = 0.85) were significantly correlated with cross-trial medians of univariate Lempel–Ziv complexity (partial correlation ρ = 0.66, P < 10^–4, controlling for median frequency at which signals were low-pass filtered). See SI Appendix, Fig. S10 for comparisons using joint and concatenated Lempel–Ziv complexity. (D) As was the case for our cross-subject analysis (A), our within-subject, cross-trial analysis revealed significant increases in our criticality measure (with α = 0.85) in four DOC patients as they recovered consciousness. Significance was assessed using a left-tailed overlapping block bootstrap test (which controls for dependencies across data points by preserving local time-series autocorrelations) with a block size of three trials (30 s of recording), to test against the null hypothesis that median estimated proximity to criticality during conscious states is not greater than median estimated proximity to criticality during unconscious states. Circles correspond to cross-trial medians, and error bars indicate SE of the median (estimated by taking the SD of a bootstrap distribution of sample medians) *P < 0.05, **P < 0.01.

Discussion

In this paper, we present empirical evidence that during conscious states, the cortex generates information-rich activity by tuning its low-frequency electrodynamics toward the mathematically specific critical point separating periodicity and chaos. Our evidence was based on the application of the recently modified 0-1 chaos test to neural electrophysiology data. Many systems, including deep neural networks (25), have been shown to exhibit their highest information-processing capacity when poised near this transition from periodicity to chaos (6–9, 26, 38), likely because dynamics near this critical point optimally balance stability with flexibility and responsiveness to inputs (53).

We further present evidence that transitions of low-frequency cortical electrodynamics away from the edge-of-chaos critical point—either into the chaotic phase, as our evidence suggests is the case for GABAergic anesthesia, or into the periodic phase, as our evidence suggests is the case for generalized seizures—precipitate a loss of information richness in cortical dynamics, thus resulting in unconsciousness. These results are consistent with previous findings of a loss of empirical signatures of criticality during these states of unconsciousness (4, 14, 15), but go beyond prior analyses in specifying whether dynamics in these states are subcritical or supercritical with respect to a specific, mathematically well-defined critical point (in this case, the edge-of-chaos critical point). Finally, we present evidence that LSD is increasing the Lempel–Ziv complexity of cortical activity while stabilizing (i.e., reducing the chaoticity of) low-frequency cortical electrodynamics and that the degree of this stabilization correlates with the subjective intensity of the LSD experience. To the degree to which we also believe that approaching the edge-of-chaos critical point should increase Lempel–Ziv complexity—which we support with simulations of both the cortex (Fig. 2) and three other dynamical systems (SI Appendix, Fig. S1)—this result supports prior findings suggesting a transition closer to criticality in the LSD state (48). Importantly, this result constitutes our primary empirical evidence that waking low-frequency cortical electrodynamics specifically lie on the chaotic side of the edge-of-chaos critical point, as it implies that LSD is tuning slow cortical dynamics toward edge-of-chaos criticality from the chaotic side of the edge. However, we note that we observed increased variance in the K statistic near criticality (SI Appendix, Fig. S12), and that the K statistic is sensitive to choices of preprocessing steps (SI Appendix, Tables S6 and S7 and Fig. S12), which raises the potential risk of misclassifying waking cortical dynamics as lying on the periodic or on the chaotic side of the edge-of-chaos critical point. Thus, despite our observation of reduced chaoticity in the LSD state (Fig. 3 and SI Appendix, Fig. S5), it will be imperative to replicate this observation in other cortical recordings from subjects experiencing psychedelic states and to develop additional or improved tools for estimating the chaoticity of cortical dynamics (see below).

Our finding that waking slow cortical dynamics may specifically operate on the chaotic side of this phase transition supports the decades-old conjecture that the waking brain’s large-scale electrodynamics might be at least weakly chaotic (54–61). Historically, this hypothesis has been difficult to test, owing to the shortcomings of classic chaos detection algorithms—limitations that are largely (but not fully) overcome by the time-series analysis tools utilized here (27). Although our empirical results are in accord with the large body of modeling literature showing that biologically realistic simulations of neural networks are frequently chaotic (at all spatial scales) (54–65), our results may appear to contradict prominent work in artificial intelligence research, which has largely focused on nonchaotic neural systems, owing to the failure of some learning algorithms to converge in chaotic recurrent neural networks (RNNs) (66). Importantly, however, this is not a universal phenomenon, as a number of training algorithms (66–72), including several biologically realistic algorithms based on Hebbian learning (73–75), have been shown to successfully converge in chaotic RNNs. Moreover, there are possible benefits to neural networks being poised on the chaotic side of this phase transition. For example, it has been analytically shown that while the memory and decodability of recurrent networks are highest at the edge-of-chaos critical point, these computational capacities decay more slowly in the chaotic phase than they do in the periodic phase (76). Thus, in the absence of fine tuning of parameters (which is difficult to achieve in both real and artificial neural systems), high memory and input decodability are more easily attainable on the chaotic side of this phase transition (76). Additionally, it has been shown that some amount of chaos is not only useful (72), but also in some cases necessary (75), for some RNNs to learn complex target functions, because weak chaoticity can expand neural networks’ dynamical repertoire. Finally, although it has often been assumed that chaos inevitably disrupts the consistency of input–output mappings required for computation in some RNNs (77, 78), it is now recognized that weakly chaotic systems in general (79–82), and weakly chaotic RNNs in particular (72), can generate consistent responses to their inputs. However, because input–output consistency generally breaks down in strongly chaotic systems (79, 80), it is likewise computationally reasonable for waking cortical electrodynamics to remain only weakly chaotic, in the vicinity of the edge-of-chaos critical point.

Beyond the known benefits of being poised on the chaotic side of the edge-of-chaos critical point, the possibility that waking low-frequency cortical electrodynamics are weakly chaotic may additionally explain a number of empirical results regarding the variability of neural activity and how that variability relates to attention and conscious perception. A salient feature of chaotic RNNs is their ability to transiently stabilize their dynamics in response to external or feedback signals (65–67, 69, 83), which appears to be important for their trainability (65–67, 69). Indeed, this ability to temporarily stabilize in response to inputs is a general and well-established feature of chaotic systems (84). If normal waking cortical dynamics are weakly chaotic as our evidence suggests, then this feature of chaotic systems might explain several key empirical findings regarding the trial-by-trial variability of neuronal activity. In general, biological neural dynamics exhibit significant variation across trials (85–87), which has been linked in both simulation (65, 69) and empirical (88) studies to chaos. But, just as in artificial RNNs (65–67, 69), the trial-by-trial variability of real neural dynamics has been empirically shown to drop after the onset of a sensory stimulus (89, 90); this suggests that in some cases, sensory stimuli might transiently stabilize real neural dynamics, just as they do in simulated chaotic RNNs (65–67, 69, 83). Similarly, the finding that trial-by-trial neural variability is lower when stimuli are consciously perceived (91, 92) might suggest that weaker chaos—i.e., chaotic dynamics closer to the edge-of-chaos critical point—can support successful conscious perception, perhaps owing to the more robust transmission of information nearer to this critical point. Finally, because attention also appears to reduce this trial-by-trial neural variability (93), it may be that attentional mechanisms can transiently stabilize local, weakly chaotic neural dynamics, pulling them closer to the edge-of-chaos critical point—and thereby facilitate the transmission of the attended information. These possibilities warrant further empirical investigation, which we hope will be aided by the time-series analysis tools described here.

Despite our evidence that low-frequency cortical activity during waking states may operate on the chaotic side of the edge-of-chaos critical point, as well as the known benefits of weak chaoticity, the question of what “side” of this critical point normal waking brain dynamics operate near, and how this might vary across different parts of the brain, is far from settled. First, we note that in our mean-field simulations, dynamics apparently on the periodic side of this critical point likewise yielded high values of Lempel–Ziv complexity (Fig. 2), and so neural dynamics on the periodic side of this phase transition may be as information rich as dynamics on the chaotic side. Additionally, there are some neural circuits, such as the suprachiasmatic nucleus, whose functioning crucially depends on their ability to produce highly regular oscillations (94), which would make weak chaoticity (or even edge-of-chaos criticality) likely unfavorable. Moreover, the computations of some other neural circuits, such as the CA3 region of the hippocampus, are thought to resemble those of a Hopfield network (95), which depends on the ability of the network’s dynamics to converge to a stable fixed-point attractor (96), therefore ruling out chaos (although we note that chaotic neural networks have also been shown to support associative memory storage, similar to Hopfield networks) (97). Thus, the question of whether the normal waking brain’s dynamics operate on the periodic or the chaotic side of the edge-of-chaos critical point, and how this might vary across different neural circuits and brain areas, will need to be investigated further in future research.

Our finding—that slow cortical electrodynamics may be operating on the chaotic side of the edge-of-chaos critical point during waking states—may appear to conflict with prior reports suggesting that the waking brain may operate on the ordered side of some phase transition. As noted in our Introduction, this apparent inconsistency likely lies in imprecise and/or inconsistent definitions of “criticality,” order, and disorder in the literature on neural criticality. In the context of phase transitions, terms such as order and disorder are meaningful only when used with reference to the breaking of some specific form of mathematical symmetry: Ice water is ordered precisely because it lacks the rotational and translational symmetries of liquid water, ferromagnets are ordered because their magnetic spins lack rotational symmetry, and chaotic systems are ordered because they lack de Rham or topological supersymmetry. It is for this reason that terms more specific than criticality, order, and disorder should be used when studying phases and phase transitions and why it is likewise important to utilize mathematical tools that are precisely tailored for assessing proximity to a particular type of critical point (rather than using less specific tools, such as power-law statistics, detrended fluctuation analysis, phase coherence, etc.). Because we were interested in specifically studying the edge-of-chaos critical point, which has long been associated with optimal computation and information processing (Introduction), we studied neural dynamics using the K statistic of the modified 0-1 chaos test, which directly tracks the quantity of interest (i.e., largest Lyapunov exponents). That said, we note that it is possible, and even likely, that normal waking brain dynamics operate near several distinct critical points, only one of which is the edge-of-chaos critical point, which would potentially allow the brain to flexibly transition between different types of activity states as needed (28). Indeed, in the mean-field model analyzed here, normal waking brain activity is modeled as being poised near four critical points (namely, a Turing bifurcation, a Hopf bifurcation, the onset of chaos, and a transition from a high-firing phase to a low-firing phase), and anesthesia is modeled as a phase transition across only one of these critical points (from a high-firing to a low-firing phase) (28).

Although both our simulation and empirical work focused on the chaoticity of low-frequency cortical electrodynamics, it would be fruitful to repeat our analyses in other frequency bands in future work. In particular, it will be important to further explore potential contributions of the varying chaoticity of alpha (8- to 12-Hz) waves, as cortical electrodynamics in this frequency range exhibit marked changes in anesthesia (98), disorders of consciousness (99), and psychedelic states (100). At present, it is difficult to predict how this framework will extend to other higher-frequency bands or whether the chaoticity of higher-frequency processes can be meaningfully disentangled from the chaoticity of low-frequency processes.

We note that our finding of increased low-frequency instability during GABAergic anesthesia may appear to conflict with a prior report by Solovey et al. (101) of increased stability in the cortical dynamics of macaques during propofol anesthesia. This seeming discrepancy rests on differing notions of stability, as well as different assumptions about data: Solovey et al. (101) defined stability in terms of the eigenvalues of regression matrices estimated from ECoG recordings, a notion of stability that indicates only that a process will not diverge to infinity and further assumes that data are both linear and stochastic (an assumption not supported by our analyses) (SI Appendix, Tables S4 and S5). In contrast, we assessed stability in terms of chaos, or sensitivity to perturbations/inputs, and also used time-series analysis tools that do not assume linearity and therefore capture features of data that cannot by definition be captured by linear analysis tools such as autoregressive models. It is also worth noting that two of the four ECoG datasets used in the report by Solovey et al. (101) were the same as the macaque anesthesia data used here (data were downloaded from the same repository) (Materials and Methods), and yet we found robust increases in instability in the anesthetized state for these two macaques, as we did in our three human anesthesia subjects (Fig. 2 and SI Appendix, Fig. S5).

While the finding that GABAergic anesthetics destabilize low-frequency cortical electrodynamics may be counterintuitive, we found that known correlates of anesthetic depth—namely, delta (1- to 4-Hz) power (102, 103), multiscale sample entropy (104), and spectral slope (105, 106)—all changed in the simulation of anesthesia cortical electrodynamics in ways that are consistent with prior empirical results (SI Appendix, Fig. S13). In addition, recent recordings of extracellular potentials have shown that desflurane, a GABAergic anesthetic, increases the trial-by-trial variability of neuronal spike timing (107), which, given both the empirical (88) and simulation-based (65) evidence of a relationship between spike-timing variability and chaos (see above), accords with the hypothesis that GABAergic anesthetics induce a transition to strong chaos. That said, we point out that some functional magnetic resonance imaging studies have found reduced temporal variability of the blood oxygenation level-dependent (BOLD) signal during GABAergic anesthesia (108, 109), while others have found increased variability of BOLD signals in some regions but decreases in others (110); however, we note that the relationship between the chaoticity of low-frequency cortical electrodynamics and the variability of the BOLD signal is unclear and warrants investigation. Finally, it has been predicted that strongly chaotic low-frequency cortical electrodynamics during GABAergic anesthesia should disrupt the coherence between electric cortical oscillations at low frequencies (28), which has been empirically confirmed for occipital, frontal, and frontal–occipital electrode pairs, but not for right–left temporal electrodes (111), although we point out that phase coherence is at best only an indirect correlate of chaoticity (given the well-known ability of chaotic oscillators to synchronize given particular network structures) (112).

In an attempt to facilitate potential translational applications of this framework, we developed a time-series measure c of proximity to edge-of-chaos criticality, based on a transformation of the K statistic of the 0-1 chaos test. We found that c was significantly higher in conscious states than in diverse states of unconsciousness and likewise was significantly correlated with the Lempel–Ziv complexity of cortical electrodynamics (Fig. 4). That said, we note that despite the significant increase in c in all four DOC patients as they regained consciousness, estimates of low-frequency chaoticity were significantly higher (within subject) during unconsciousness in only three of four of the patients (similar to the GABAergic anesthesia state) and were significantly lower during unconsciousness in the fourth patient (similar to generalized seizures) (SI Appendix, Fig. S11). This may imply that disorders of consciousness constitute a heterogeneous set of conditions with respect to the stability of cortical electrodynamics, a possibility we hope to explore more fully in future work. We further note that the distributions of both this measure c and univariate Lempel–Ziv complexity in conscious vs. unconscious states were partially overlapping (Fig. 4), even though both measures displayed consistent within-subject increases from unconscious to conscious states (Fig. 4 and SI Appendix, Figs. S5 and S11). This suggests that these measures may perhaps best be used as within-patient indexes of recovery of consciousness rather than as cross-sectional biomarkers. Additionally, we point out one important limitation in our analysis of DOC patients, which is the potential confounding effect of drugs administered to the patients: Patients were occasionally administered several painkillers and anesthetics on the same day as GCS assessments and EEG data collection (SI Appendix, Table S8) (Materials and Methods). We were unable to ascertain the precise timing of drug administration relative to behavioral assessments and, as such, we cannot rule out the possibility that observed differences in cortical stability/criticality in unconscious states versus conscious states in these DOC patients were possibly driven by the effects of these drugs on their slow cortical electrodynamics. Moreover, our sample size of DOC patients who regained consciousness was small (n = 4), and so the utility of our criticality measure c as an index of consciousness in patients with disorders of consciousness warrants validation in a larger dataset. Along the same lines, if this framework is to be used in the aid of diagnosis, then it will be imperative to develop additional methods for estimating changing levels of chaoticity in cortical electrodynamics. This might be achieved, for example, by observing the consistency of cortical responses to external stimuli (e.g., in response to transcranial magnetic stimulation), which should degrade as cortical electrodynamics become strongly chaotic—a possibility we plan to explore in future work.

Finally, we note that it would be fruitful to further study neural computation near the edge-of-chaos critical point on a more theoretical level. While important advances have been made along these lines, for example in establishing relationships between this critical point and the trainability of deep neural networks (25), the memory capacity and decodability of recurrent networks (76), information complexity (6–9), and Bayes-optimal perceptual categorization (113), much theoretical work remains to be done to understand the implications of these findings for neural computation. If the slow electrodynamics of the cortex during conscious states are poised near this critical point, as our work suggests, then improving our theoretical understanding of computation and information flow at the onset of chaos will also improve our understanding of how, precisely, neural information processing is disrupted in unconsciousness.

Materials and Methods

Mean-Field Model of Slow Cortical Electrodynamics.

We here study the mean-field model of Steyn-Ross, Steyn-Ross, and Sleigh (28). The model allows for straightforward manipulation of both the strength and balance of postsynaptic inhibition and excitation, which have long been thought to be key in tuning neural dynamics to chaotic (62), critical (114), and information-rich (114) states. Furthermore, the model is unique in its inclusion of gap junction coupling between inhibitory interneurons, which recent empirical work in zebrafish has shown are also likely important for tuning neural dynamics toward and away from criticality (34).

The model simulates GABAergic anesthesia (e.g., propofol or sevoflurane) as an increase in cortical inhibition coupled with a mild decrease in gap junction coupling between inhibitory interneurons, based on findings that GABAa agonists (115), and GABAergic anesthetics more specifically (116), inhibit gap junction communication (115, 116) and that these compounds also increase postsynaptic inhibition by prolonging inhibitory postsynaptic potentials (117). The model treats waking conscious states as a balance between excitation and inhibition, with strong gap junction coupling between inhibitory interneurons, which yields weak chaos (near edge-of-chaos criticality) in the model’s deterministic component (Fig. 2A), arising from interacting Turing (spatial) and Hopf (temporal) instabilities. Finally, a strong reduction of inhibitory gap junction coupling results in a Hopf bifurcation that produces periodic dynamics reminiscent of whole-of-cortex, generalized seizures (28). This is consistent with observations of increased seizure frequency following either genetic ablation (118) or drug-induced reduction (119) of gap junction coupling between inhibitory interneurons. See SI Appendix, Supplementary Methods for model equations and parameters and for details on how ground-truth largest Lyapunov exponents of the model were calculated.

Lempel–Ziv Complexity.

Lempel–Ziv complexity is a measure of the size of a signal following Lempel–Ziv compression and thus tracks the amount of nonredundant information in a signal (36). To compute Lempel–Ziv complexity, a continuous recording must first be discretized. Following prior work (46, 120), we binarized both our simulated and recorded data by thresholding at the mean of the signal’s instantaneous amplitude, which is the absolute value of the analytic signal. We then computed three measures of Lempel–Ziv complexity: 1) the median univariate Lempel–Ziv complexity across all recorded channels (“univariate LZc”); 2) the joint Lempel–Ziv complexity between all channels, using the method described by Zozor et al. (121); and 3) the Lempel–Ziv complexity of all channels concatenated, timepoint by timepoint, into a single string, following the method described by Schartner et al. (46, 120). Typically, Lempel–Ziv complexity is then normalized to provide a single value between 0 and 1. We compared several different normalization approaches and found that the approach most robust against changes to a signal’s spectral profile was to divide the Lempel–Ziv complexity of a signal by the Lempel–Ziv complexity of a phase-randomized surrogate of that signal (SI Appendix, Fig. S14), following Brito et al. (122); note that phase-randomized surrogates were generated independently for each channel-x trial in all recordings for the calculation of the Lempel–Ziv complexity measures. All measures of Lempel–Ziv complexity reported in this paper were normalized in this fashion and were calculated for data low-pass filtered at 45 Hz. Data were low-pass filtered at 45 Hz to avoid potential confounds introduced by muscle activity at higher frequencies.

Extracting Low-Frequency Cortical Activity.

The mean-field model described above specifically simulates the low-frequency (< 4-Hz) component of macroscale electric cortical oscillations. To compare the model results against real data, we therefore extracted the low-frequency component of both our simulated and real cortical signals. Although different frequencies of cortical electrodynamics have historically been studied at fixed, canonical frequency bands, with choices of oscillation center frequencies and bandwidths varying across studies, there is growing evidence that these center frequencies and bandwidths vary considerably as a function of age, brain state, subject, and species and that low-pass filtering at fixed canonical frequencies can therefore produce spurious oscillations where no oscillations exist (45). Given that our analyses span diverse brain states, species, and imaging modalities, it was important to identify subject-, trial-, and channel-specific neural oscillation frequencies. We therefore identified low-frequency neural activity for each channel, for each trial, using the recently developed FOOOF algorithm, which automatically parameterizes neural signals’ power spectra (45). The algorithm fits a neural power spectrum as a linear combination of the background 1/f component with oscillations at specific frequencies that rise above this background 1/f component as peaks in the power spectrum. The algorithm fits the spectral power P as

$$P=L+{\displaystyle \sum _{n=0}^N{G}_N},$$ [1]

where L is the background 1/f power spectrum, and each G_n is a Gaussian fit to a peak rising above the 1/f background,

$$G_n=a*\mathit{exp}\left(\frac{-{(F-c)}^2}{2w^2}\right),$$ [2]

where a is a given oscillation’s amplitude, c is its center frequency, w is its bandwidth, and F is a vector of input frequencies. The 1/f background component L is modeled as an exponential in semilog-power space (i.e., with log-power values as a function of linear frequencies):

$$L=b-\mathit{log}(k+F^{\chi }),$$ [3]

where b is a broadband power offset, χ is the spectral slope, k controls the “knee” at which the 1/f power spectrum bends, and F is a vector of input frequencies.

To specifically extract the low-frequency component of neural oscillations, we set the input frequency range F to 1 to 6 Hz. The FOOOF algorithm then identifies the center frequencies and bandwidths of putative oscillations that rise above the 1/f background within this frequency range. For all channels-x trials in our data, we extracted the lowest-frequency oscillation identified by the algorithm, by low-pass filtering at the high-frequency end of the bandwidth of the slowest identified oscillation. If the FOOOF algorithm failed to identify any oscillation in the 1- to 6-Hz range for a particular channel in a particular trial, then data for that channel in that trial were excluded from further analysis of chaoticity. See SI Appendix, Table S1 for the percentage of channels that were thus excluded from chaoticity estimates for each subject and brain state. Across all datasets, the mean frequency selected using this approach was 3.27 Hz, with a SD of 0.48 Hz. We then low-pass filtered all signals using EEGLAB’s two-way least-squares finite impulse response low-pass filtering, where the filter order was set to 3 × $\frac{\text{sampling}\hspace{0.17em}\text{rate}}{\text{lowpass}\hspace{0.17em}\text{frequency}\hspace{0.17em}\text{cutoff}}$ (the default of EEGLAB). Note that using the FOOOF algorithm improved our ability to track chaoticity in the mean-field model of cortical electrodynamics, where the ground-truth chaoticity is known (SI Appendix, Tables S6 and S7), and that estimates of the chaoticity of data low-pass filtered using the FOOOF algorithm were stable across different simulations compared to alternative methods (SI Appendix, Fig. S12), which validates its utility in tracking chaoticity in real low-frequency cortical electrodynamics.

The Modified 0-1 Test for Chaos.

The 0-1 chaos test was developed by Gottwald and Melbourne (40) as a simple tool for testing whether a discrete-time system is chaotic, using only a single time series recorded from that system. Gottwald and Melbourne (41) provided an early modification to the test, which made it more robust against measurement noise. Dawes and Freeland (43) added additional modifications to the test, improving its ability to distinguish between chaotic dynamics and strange nonchaotic or quasiperiodic dynamics. The modified test outputs a statistic K as an estimate of chaoticity. As the length of a time series is increased, K will approach 1 for chaotic systems and will approach 0 for periodic systems, and it will track degree of chaos for finite-length time series (40–43). See SI Appendix, Supplementary Methods for a mathematically detailed description of the test.

The 0-1 test is designed to track chaos in discrete-time systems, and thus signals recorded from non–time-discrete processes (like neural electrodynamics) must first be transformed into discrete-time signals before application of the test (42). Two approaches have been proposed for time discretization prior to application of the test: downsampling (42) and taking all local minima and maxima of a continuous signal (44). We used the latter approach for all datasets (real and simulated), as it yielded best correspondence to the ground truth in our simulations (SI Appendix, Tables S6 and S7).

A Time-Series Estimate of Proximity to Edge-of-Chaos Criticality.

With an eye toward clinical applications of this edge-of-chaos criticality framework in the study of unconsciousness, we here introduce a time-series estimate of proximity to the edge-of-chaos critical point, based on the K statistic outputted by the modified 0-1 chaos test (see above). This measure c is defined as follows:

$$c=\{\begin{array}{ll}\frac{K}{\alpha }\hfill & K<\alpha \hfill \\ 1-\frac{K-\alpha }{1-\alpha }\hfill & K\ge \alpha \hfill \end{array},$$ [4]

where K is the output of the 0-1 chaos test and α is a parameter that takes on a value between 0 and 1. This criticality measure c will approach 1 as K approaches α and will approach 0 as K approaches either 0 (periodicity) or 1 (strong chaos). As noted in Results, precise choice of α may bias c toward either periodic near-critical or chaotic near-critical dynamics (i.e., to dynamics on either the stable or the unstable side of the edge-of-chaos critical point), and thus the optimal value of α for potential clinical assessments of consciousness using c will need to be determined by further empirical work.

Empirical Data.

Previously published cortical recordings from psychedelic states (100) and generalized seizures (123, 124) were reanalyzed in this work (see SI Appendix, Supplementary Methods for more details). In addition to these previously described datasets, surface ECoG recordings from three human epilepsy patients given propofol anesthesia prior to surgical resection of their epileptic focus were analyzed. Data were collected at the University of California, Irvine, Medical Center. Patients provided informed and written consent in accordance with the local ethics committees of the University of California, Irvine (University of California, Irvine Institutional Review Board Protocol no. 2014-1522) and University of California, Berkeley (University of California, Berkeley Committee for the Protection of Human Subjects Protocol no. 2010-01-520), which approved the study. Data were also collected from four traumatic brain injury patients admitted at the University of California, Los Angeles (UCLA) Ronald Reagan University Medical Center intensive care unit. The UCLA institutional review board approved the study, and informed consent was obtained according to local regulations. See SI Appendix, Supplementary Methods for more details.

Data Availability

Anonymized summary statistics/values required to recreate the figures and statistical analyses of this paper have been deposited in Figshare (https://figshare.com/articles/software/Consciousness_is_supported_by_near-critical_cortical_electrodynamics/12949355) (DOI: 10.6084/m9.figshare.12949355). Previously published data were used for this work (https://doi.org/10.1371/journal.pone.0022561, https://doi.org/10.1016/j.cmpb.2010.08.011).