Mutation bias shapes the spectrum of adaptive substitutions

Significance

How do mutational biases influence the process of adaptation? A common assumption is that selection alone determines the course of adaptation from abundant preexisting variation. Yet, theoretical work shows broad conditions under which the mutation rate to a given type of variant strongly influences its probability of contributing to adaptation. Here we introduce a statistical approach to analyzing how mutation shapes protein sequence adaptation. Using large datasets from three different species, we show that the mutation spectrum has a proportional influence on the types of changes fixed in adaptation. We also show via computer simulations that a variety of factors can influence how closely the spectrum of adaptive substitutions reflects the spectrum of variants introduced by mutation.

Abstract

Evolutionary adaptation often occurs by the fixation of beneficial mutations. This mode of adaptation can be characterized quantitatively by a spectrum of adaptive substitutions, i.e., a distribution for types of changes fixed in adaptation. Recent work establishes that the changes involved in adaptation reflect common types of mutations, raising the question of how strongly the mutation spectrum shapes the spectrum of adaptive substitutions. We address this question with a codon-based model for the spectrum of adaptive amino acid substitutions, applied to three large datasets covering thousands of amino acid changes identified in natural and experimental adaptation in Saccharomyces cerevisiae, Escherichia coli, and Mycobacterium tuberculosis. Using species-specific mutation spectra based on prior knowledge, we find that the mutation spectrum has a proportional influence on the spectrum of adaptive substitutions in all three species. Indeed, we find that by inferring the mutation rates that best explain the spectrum of adaptive substitutions, we can accurately recover the species-specific mutation spectra. However, we also find that the predictive power of the model differs substantially between the three species. To better understand these differences, we use population simulations to explore the factors that influence how closely the spectrum of adaptive substitutions mirrors the mutation spectrum. The results show that the influence of the mutation spectrum decreases with increasing mutational supply ($N\mu$) and that predictive power is strongly affected by the number and diversity of beneficial mutations.

The spectrum of adaptive substitutions is a distribution of types of changes fixed in adaptation. A systematic empirical picture of the spectrum of adaptive substitutions is beginning to emerge from methods of identifying and verifying individual adaptive changes at the molecular level. The most familiar method is the retrospective analysis of adaptive species differences, often in cases where multiple substitutions target the same protein, e.g., changes to photoreceptors involved in spectral tuning (1), changes to adenosine triphosphatase (ATPase) involved in cardiac glycoside resistance (2), or changes to hemoglobin involved in altitude adaptation (3). Other retrospective analyses focus on cases of recent local adaptation, such as the repeated emergence of antibiotic-resistant bacteria (4, 5) or herbicide-resistant plants (6). In addition, experimental studies of adaptation in the laboratory provide large and systematic sets of data on the spectrum of adaptive substitutions (7, 8). While the first two types of studies tend to focus on specific target genes, the third approach, combined with genome sequencing, casts a much broader net, covering the entire genome. Such data were rare just 15 y ago, but they are now sufficiently abundant—cataloging thousands of adaptive events—that accounting for the species-specific spectrum of adaptive substitutions represents an important challenge.

One aspect of this challenge is to understand the role of mutation in shaping the spectrum of adaptive substitutions. Systematic studies of the distribution of mutational types in diverse organisms (9–17) have demonstrated the presence of a variety of biases, including transition bias and GC:AT bias, as well as CpG bias and other context effects (for review, see ref. 18). At the same time, multiple studies have now shown that adaptive substitutions are enriched for mutationally likely changes (5, 19–27). For instance, the influence of a mutational bias favoring transitions is evident in the evolution of antibiotic resistance in Mycobacterium tuberculosis (5). Likewise, the evolution of increased oxygen affinity in hemoglobins of high-altitude birds shows a tendency to occur at CpG hotspots (24).

Such studies have shown effects of specific types of mutation bias using statistical tests for asymmetry, i.e., tests for a significant excess of a mutationally favored type, relative to a null expectation of parity. A more general question is how strongly the entire mutation spectrum shapes the spectrum of adaptive substitutions. That is, the entire mutation spectrum reflects (simultaneously) all relevant mutation biases, because it describes the relative rates of the different mutation types. Mutation spectra have been experimentally characterized in a diversity of species (9–17), and these universally reveal some form of mutation bias in that the different mutation types do not occur with the same relative rates. Such biased mutation spectra shape the spectra of adaptive substitutions to some degree that is, in principle, quantifiable and measurable.

Here, we provide an approach to answer this more general question, based on modeling the spectrum of missense mutations underlying adaptation as a function of the nucleotide mutation spectrum. More specifically, we use negative binomial regression to model observed numbers of adaptive codon-to-amino-acid substitutions as a function of codon frequencies and per-nucleotide mutation rates, which we estimate from published data on mutation frequencies. This modeling framework allows us to measure the influence of mutation bias on adaptive evolution in terms of the regression coefficient associated with the mutation spectrum.

We separately apply this approach to three large datasets of missense changes associated with adaptation in Saccharomyces cerevisiae, Escherichia coli, and M. tuberculosis. We find that, in each case, the regression on the mutation spectrum is significant, with a regression coefficient close to 1 (proportional effect) and significantly different from zero (no effect). This indicates that mutational biases play an important role in determining which mutations, among those that are beneficial, underlie molecular adaptation. Whereas the ability to predict the spectrum of adaptive substitutions differs substantially among the three species, in each case we find that experimentally determined mutation spectra provide better model fits than the vast majority of randomized mutation spectra, confirming the relevance of empirical mutation spectra outside of the controlled conditions in which they are typically measured. Moreover, we show that by inferring the optimal mutational spectrum based on the spectrum of adaptive substitutions, we can accurately recover species-specific patterns of mutational bias previously documented via mutation-accumulation experiments or patterns of neutral diversity. Finally, we use simulations of a population model to explore the possible reasons for differences in predictability of the spectrum of adaptive substitutions. As expected, the impact of the mutation spectrum decreases as the total mutation supply ($N\mu$) increases. However, other factors are important, such as the size and heterogeneity (in adaptive value) of the set of adaptive mutations.

Results

Data and Model.

We curated a list of previously reported missense substitutions associated with adaptation for each of three species: S. cerevisiae, E. coli, and M. tuberculosis (Fig. 1 A and B and Methods). Note that “substitution” here refers to an evolutionary change, whereas we restrict the term “mutation” to mutational changes or categories, following the definitions provided in SI Appendix. For S. cerevisiae, the substitutions were associated with adaptation to high salinity (28), low glucose (28), and rich media (29), as well as the genetic stress of gene knockout (30); for E. coli, the substitutions were associated with adaptation to temperature stress during laboratory evolution (8); for M. tuberculosis, the substitutions were identified in clinical isolates resistant to one or more of 11 antibiotics or antibiotic classes (5). Whereas the M. tuberculosis dataset is composed entirely, or almost entirely, of bona fide adaptive changes that have been experimentally verified to confer antibiotic resistance (5), the datasets for S. cerevisiae and E. coli are likely contaminated with hitchhikers, i.e., mutations that are not drivers of adaptation, but reached a high frequency due to linkage with a driver. Below, we first present our results under the assumption that substitutions in each dataset are exclusively adaptive and then use simulations to assess the robustness of our conclusions to various degrees of contamination.

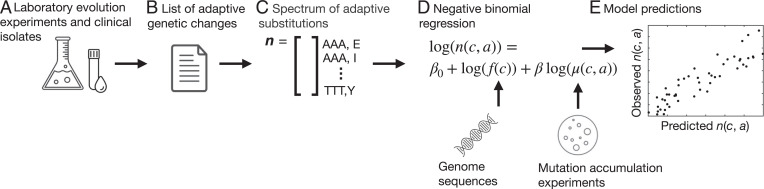
Fig. 1.

Workflow. (A and B) We use data from laboratory evolution experiments (E. coli and S. cerevisiae) and clinical isolates (M. tuberculosis) (A) to curate a list of genetic changes associated with adaptation for each species (B). (C) From each list of adaptive changes, we construct the spectrum of adaptive substitutions n. Each element in this spectrum $\mathbf{n}(c,a)$ corresponds to one of the 354 distinct changes from codon c to amino acid a that can be produced by a single-nucleotide mutation under the standard genetic code, and tallies the number of adaptive events for a specific codon-to-amino-acid change. (D) We perform negative binomial regression to model the influence of mutation bias on the spectrum of adaptive events, using codon frequencies derived from genome sequences and experimentally characterized mutation spectra. (E) We use the fitted model to predict the spectrum of adaptive substitutions.

Each dataset consists of a list of events of putatively adaptive missense substitution, each of which can be defined by a specific initial and final genomic state. For example, the substitution defined by a G →C transversion in the second position of codon 315 of katG in M. tuberculosis, which changes Ser (AGC) to Thr (ACC), confers resistance to the antibiotic isoniazid (31). In our dataset, we observe 445 independent instances of adaptation via this specific genomic alteration; for the sake of brevity we describe this as observing 445 “events” corresponding to this specific adaptive “path.” Here, to define a spectrum of adaptive substitutions, we further aggregate these adaptive missense substitutions into types of changes. Possible types of changes include nucleotide-to-nucleotide, codon-to-codon, codon-to-amino-acid, and amino acid-to-amino acid changes, each of which results in a different level of aggregation of the mutational events. We focus on codon-to-amino-acid changes, which we track only by the initial codon and final amino acid of the substitution, without regard to the specific gene or amino acid position where the substitution occurred. Given that there are 354 such types of codon-to-amino-acid changes allowed by the standard genetic code, the spectrum of adaptive substitutions for each species is a 354-element vector n, where each element $\mathbf{n}(c,a)$ is a count of the number of events of single-nucleotide changes from codon c to amino acid a (Fig. 1C and Methods). Table 1 reports the total number of mutational paths and events, as well as the number of nonzero elements in the spectrum of adaptive substitutions (out of 354) for each dataset.

Table 1.

Data and negative binomial regression

	Data		Influence of mutation spectrum
Species	Paths	Events	β	$p_{\beta }$
S. cerevisiae	534	713	1.05 ±0.08	$<{10}^{-16}$
E. coli	492	602	0.98 ±0.14	$<{10}^{-11}$
M. tuberculosis	283	4,413	0.85 ±0.23	$<{10}^{-3}$

Shown are the observed numbers of paths and events for adaptive changes in the three datasets, along with calculated values for the mutation coefficient β (with SE) and its P value.

Our goal is to quantify how strongly the mutation spectrum shapes the spectrum of adaptive substitutions. To do so, we specify a phenomenological model that treats each element in the spectrum of adaptive substitutions as the product of the starting codon frequency and the relevant mutation rate, raised to an exponent β representing the degree of mutational influence, e.g., β  =  0 would indicate no influence. More specifically, we model the expected number $\mathbb{E}[\mathbf{n}(c,a)]$ of adaptive substitutions from codon c to amino acid a as being directly proportional to the genomic frequency f(c) of codon c [i.e., f(c) is the number of times codon c appears in protein-coding regions of the genome divided by the total number of codons in protein-coding regions of the genome] and the total mutation rate $\mu (c,a)$ of codon c to codons for amino acid a raised to the power of β, as follows:

$$\mathbb{E}[\mathbf{n}(c,a)]\propto f(c)\mu {(c,a)}^{\beta }.$$ [1]

Taking the logarithm of this equation gives

$$\log \mathbb{E}[\mathbf{n}(c,a)]={\beta }_0+\log f(c)+\beta \log \mu (c,a),$$ [2]

where β₀ is the logarithm of the constant of proportionality (Methods and SI Appendix). This formulation allows us to estimate β₀ and β from our observed datasets using negative binomial regression, which is appropriate for counts data that are overdispersed (32), as is the case for the observed spectra of adaptive substitutions.

Given the form of this regression, β represents a coefficient of mutational influence, capturing the effect of the entire mutation spectrum on the entire spectrum of adaptive substitutions. An inferred value of $\beta =0$ indicates that $\mathbb{E}[\mathbf{n}(c,a)]$ does not depend on $\mu (c,a)$, implying that the mutation spectrum has no influence on the spectrum of adaptive substitutions; when $\beta =1,\hspace{0.17em}\mathbb{E}[\mathbf{n}(c,a)]$ is directly proportional to $\mu (c,a)$, indicating a strong influence of the mutation spectrum on the spectrum of adaptive substitutions; values of β between 0 and 1 indicate an intermediate influence.

Population-genetic theory and prior simulation studies suggest a variety of factors likely to influence β, including population size, absolute mutation rates, fitness landscape architecture, and whether adaptation is short-term or long-term (33–36). In particular, prior results suggest that the supply of beneficial mutations will often influence β.

When new mutations are sufficiently rare, beneficial mutations sweep through the population one at a time, resulting in the so-called origin-fixation (37) or strong-selection-weak-mutation (SSWM) (38) regime. In this regime, the substitution rate is directly proportional to the mutation rate, implying $\beta \approx 1$ (33, 37). When the beneficial mutation supply is high, multiple adaptive mutations may compete against each other, resulting in “clonal interference” (39). Due to clonal interference, late-arising mutant alleles with larger selection coefficients may prevent the fixation of early-arising alleles favored by mutation, decreasing the influence of mutation bias (33, 35) and leading to an expected reduction in β.

Mutation Bias Strongly Influences Adaptation in Three Distinct Species.

To what extent does the mutation spectrum influence the outcome of adaptive evolution? To answer this question, we used empirical mutation spectra generated in prior studies from mutation-accumulation experiments or patterns of neutral diversity. These prior studies were carried out independently of the studies used to characterize the spectrum of adaptive substitutions. The three species differ substantially in their mutation spectra (SI Appendix, Fig. S1A). M. tuberculosis shows the greatest heterogeneity, with a 14.7-fold range of rates, whereas S. cerevisiae and E. coli have smaller ranges of 5.6- and 4.7-fold, respectively. The species also differ substantially in the rates of individual types of nucleotide mutations; e.g., the rate of G →C transversion is 2.1-fold higher in S. cerevisiae than in E. coli (SI Appendix, Fig. S1B), whereas the rate of A →T transversions is 2.5-fold higher in S. cerevisiae (SI Appendix, Fig. S1C) and 2.9-fold higher in E. coli (SI Appendix, Fig. S1D) than in M. tuberculosis.

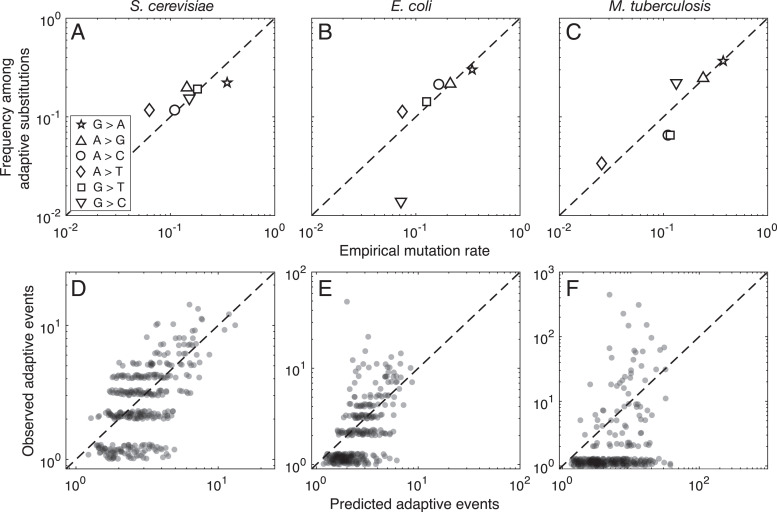
Our first observation is that, when we reduce the adaptive missense substitutions to the six types of underlying nucleotide mutations, the distribution closely follows the mutation spectrum for each species (Fig. 2 A–C). Specifically, the correlation coefficients between the mutation rates of the six mutation types and their frequencies among adaptive substitutions are 0.83 (P = 0.041), 0.91 (P = 0.012), and 0.93 (P = 0.008) for S. cerevisiae, E. coli, and M. tuberculosis, respectively. However, this naive comparison ignores potentially confounding effects of the genetic code and codon usage, where in particular the three species differ substantially in their patterns of codon usage (SI Appendix, Fig. S1 E–G). For example, GAA (Glu) is the most frequent codon in S. cerevisiae (frequency 0.045) and the second most frequent codon in E. coli (frequency 0.039), but it appears less frequently in M. tuberculosis (frequency 0.016). Thus, we might expect adaptive GAA →AAA (Glu →Lys) changes to occur more frequently in S. cerevisiae and E. coli than in M. tuberculosis, merely by merit of the greater frequency of GAA in the former two species. To account for this type of influence, we apply negative binomial regression to the codon-based model described above (Eq. 2). The results, shown in Table 1, reveal a strong and statistically significant influence of mutation bias in all three species, with each of the 95% confidence intervals containing β  =  1 (proportional effect), and excluding β  =  0 (no effect). Specifically, for S. cerevisiae, $\beta =1.05$ (95% CI, 0.89 to 1.21); for E. coli, $\beta =0.98$ (95% CI, 0.71 to 1.25); and for M. tuberculosis, $\beta =0.85$ (95% CI, 0.31 to 1.37), so that in all three species, differences in mutation rates produce approximately proportional changes in the spectrum of adaptive substitutions. Whereas such strong mutational effects are typically associated with neutral evolution, theory (33, 35, 36, 40), prior evidence (5, 19–27), and our simulations (below) indicate that such effects are possible even when all fixations are selective. What this suggests about the roles of mutation and selection is addressed further in Discussion.

Fig. 2.

Predicted and observed substitutions at the nucleotide and codon-to-amino-acid levels. (A–C) The frequency of nucleotide changes among adaptive substitutions is plotted as a function of the empirical mutation rate for (A) S. cerevisiae, (B) E. coli, and (C) M. tuberculosis. The symbols correspond to the six different types of point mutations (A, Inset). (D–F) The predicted spectra of adaptive substitutions are shown in relation to the observed spectra of adaptive substitutions for (D) S. cerevisiae, (E) E. coli, and (F) M. tuberculosis. See SI Appendix, Table S3 for model predictions using codon frequencies alone. For visualization purposes, a pseudocount of one event and a jitter of range [0,0.3] were added to both the observed and predicted numbers of events in D–F. The dashed diagonal lines indicate y = x.

Prior work has uncovered an enrichment of transition mutations in the M. tuberculosis dataset, which was attributed to the high transition–transversion ratio in the mutation spectrum of this species (5). We therefore wondered whether the entire mutation spectrum provides a better model fit than just the transition–transversion ratio. To find out, we used a likelihood-ratio test to compare two nested models that differ in the mutation term: a model that uses only the transition–transversion ratio and a model that uses both the transition–transversion ratio and the rest of the mutation spectrum (Methods). For all three species, we find that the model using both the transition–transversion ratio and the rest of the mutation spectrum provides significantly better fits and that $\beta \approx 1$ on both terms of the regression (SI Appendix, Table S2).

Having seen the influence of the mutation spectrum on the spectrum of adaptive substitutions, we can also ask to what extent the mutation spectrum, the pattern of codon usage, and the structure of the standard genetic code are jointly sufficient to explain the spectrum of adaptive substitutions observed in each species. Fig. 2 D–F shows the observed frequency of each type of codon-to-amino-acid change in relation to its predicted frequency under our fitted models. We observe from Fig. 2 D–F that despite the mutation spectrum having its maximum theoretically predicted influence ($\beta \approx 1$) in each species, the predictive power of our model nonetheless differs substantially among the three species, with the correlation between predicted and observed frequencies dropping dramatically from 0.68 in S. cerevisiae, to 0.41 in E. coli, to only 0.16 in M. tuberculosis. While all of these correlations are statistically significant (Table 2), it is clear that the predictive power of a model depending only on mutation rates, codon frequencies, and the structure of the standard genetic code differs between these three species, an observation that we will return to shortly.

Table 2.

Model predictions

	Prediction model		Spectrum elements
Species	Correlation [CI]	$P_{\text{corr}}$	Nonzero	Entropy
S. cerevisiae	$0.68\hspace{0.17em}[0.62,0.73]$	$<{10}^{-16}$	265	0.91
E. coli	$0.41\hspace{0.17em}[0.31,0.49]$	$<{10}^{-14}$	176	0.80
M. tuberculosis	$0.16\hspace{0.17em}[0.05,0.26]$	0.003	111	0.53

Shown are the Pearson correlations between observed and predicted spectra of adaptive substitutions, their 95% confidence intervals and P values, the number of nonzero elements in the spectrum of adaptive substitutions (out of 354), and the entropy of the spectrum of adaptive substitutions normalized so that uniformity corresponds to an entropy of 1.

Randomization Tests Confirm the Relevance of Empirical Mutation Spectra for Adaptive Evolution.

The species-specific mutation spectra employed above reflect either 1) mutation-accumulation experiments under laboratory conditions in the absence of selection (S. cerevisiae, E. coli), or 2) putatively neutral single-nucleotide polymorphisms in natural populations (M. tuberculosis). The observation that the 95% confidence interval for the inferred values of the coefficient of mutational influence β includes one in all three species highlights the relevance of these species-specific mutation spectra for adaptive evolution.

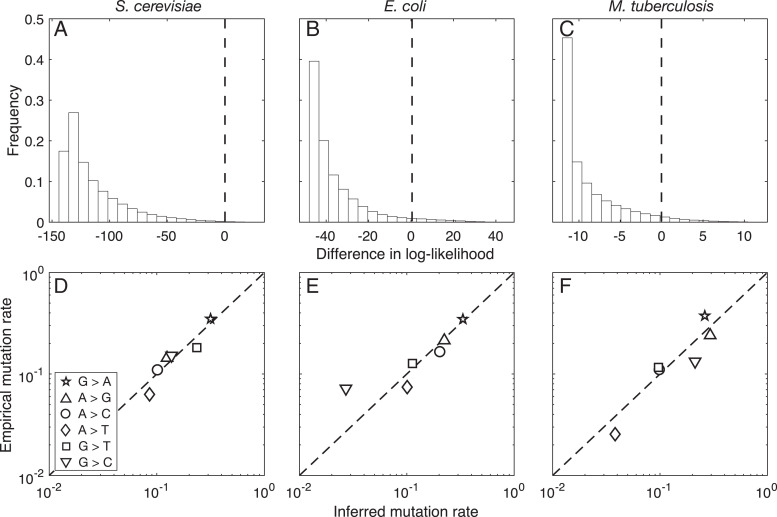
To explore the relevance of precise estimates of the mutation spectrum more thoroughly, we repeated our regression above 10⁶ times for each species, each time using a randomized mutation spectrum instead of the empirical spectrum (each randomized spectrum was generated by drawing six random uniform numbers and then normalizing the sum to 1). We then calculated the difference between the log-likelihood of the model fit with the randomized mutation spectrum and the log-likelihood of the model fit with the empirical mutation spectrum. When this difference is positive, the fit using the randomized mutation spectrum explains the spectrum of adaptive substitutions better than the fit using the empirical mutation spectrum, and when this difference is negative the empirical mutation spectrum provides the better explanation. Fig. 3 A–C shows that the empirical mutation spectra almost always explain the spectra of adaptive substitutions better: Randomly generated spectra outperform the observed spectrum with frequency 0.002 for S. cerevisiae, 0.037 for E. coli, and 0.042 for M. tuberculosis. While so far we have attempted to predict the spectrum of adaptive substitutions based on experimentally characterized mutation spectra, the strong relationship between the mutational and adaptive spectra in these three species suggests that it might also be possible to estimate the mutation spectrum from the spectrum of adaptive substitutions. To do this, we again fitted a negative binomial model but treated the rates of the six possible types of single-nucleotide mutations as free parameters, which we estimated using maximum likelihood. Fig. 3 D–F shows that the inferred mutation spectra strongly resemble the experimentally characterized mutation spectra, with Pearson correlation coefficients of 0.945 ($P=0.004$) for S. cerevisiae, 0.960 (P = 0.002) for E. coli, and 0.837 (P = 0.038) for M. tuberculosis. Thus, it is possible to accurately recover species-specific mutation spectra directly from species-specific spectra of adaptive substitutions.

Fig. 3.

Empirical mutation rates explain the spectrum of adaptive substitutions better than randomized rates. In A–C, the white bars show the distribution of log-likelihood differences for randomized vs. empirical mutation rates for (A) S. cerevisiae, (B) E. coli, and (C) M. tuberculosis. A value of 0 (dashed vertical line) means that a randomized rate performs as well as the empirical mutation rate. The fraction of randomized rates providing a better model fit than the empirical rates (i.e., right of 0) is 0.2%, 3.7%, and 4.2% for A, B and C, respectively. Data are based on 10⁶ randomized rates. Note that A–C have different limits on their horizontal axes. In D–F, the empirical mutation rate is shown in relation to the inferred mutation rate on a double-logarithmic scale for (D) S. cerevisiae, (E) E. coli, and (F) M. tuberculosis. Symbol types correspond to D, Inset. The dashed diagonal line indicates y = x.

What Factors Influence the Predictive Power of the Model?

Although the analysis above reveals a statistically significant and approximately directly proportional contribution of mutational biases to the spectrum of adaptive substitutions for all three datasets, there is considerable variation in the strength of the correlation between the predicted and observed spectra of adaptive substitutions, with this correlation being strongest and most significant for S. cerevisiae and weakest and least significant for M. tuberculosis (Table 2 and Fig. 2 D–F).

One immediate hypothesis is that this variation in predictive power is driven by differences in the completeness of our estimates of the spectrum of adaptive substitutions. Even though our datasets include hundreds to thousands of adaptive events per species, a substantial fraction of the 354 possible types of codon-to-amino-acid changes are missing from the spectrum for each species (Table 2), a situation that likely arises due to both finite sample size effects and the limited diversity of distinct adaptive paths under a specific ecological circumstance (e.g., only a limited number of mutations confer resistance to any given antibiotic). Indeed, we note that at a qualitative level, the smaller the number of missing codon-to-amino-acid changes, the stronger the correlation between predicted and observed spectra of adaptive substitutions (Table 2). Moreover, when we aggregate the adaptive substitutions into just six types of distinct nucleotide changes, all six types are well represented and there is a strong correlation with the mutation spectrum for all three species (Fig. 2 A–C).

To evaluate the influence of this kind of sampling effect on the predictive power of our model, we first simulated random data under the codon model assuming β  =  1, sampling adaptive events according to their expected frequencies, based on the empirical codon frequencies and mutation spectrum of each species, but restricting the sampled events to the observed set of nonzero elements for each species-specific spectrum of adaptive substitutions. We then used negative binomial regression to fit this simulated spectrum of adaptive substitutions and measured the correlation between the simulated spectrum of adaptive substitutions and the spectrum of adaptive substitutions predicted by the fitted model. We repeated this process 10³ times for each species to obtain a distribution of correlations. These distributions are shown in SI Appendix, Fig. S2. On average, the correlations decreased from S. cerevisiae (0.76) to E. coli (0.75) to M. tuberculosis (0.61), suggesting that sampling effects are partly responsible for differences in model fits between the three species. However, SI Appendix, Fig. S2 also shows that the correlations for these simulated datasets are considerably stronger than those obtained with models fitted to the observed spectra of adaptive substitutions, and the decrease is far less dramatic than the drop from 0.68 to 0.41 to 0.16 noted above (triangles in SI Appendix, Fig. S2). This suggests that factors other than sampling effects also modulate the predictive power of our modeling framework.

To address a combination of additional factors, we turned to population-genetic simulations of evolution in a haploid genome, with variable parameters for population size N, mutation rate μ, and fraction of beneficial mutations B. The model genome consists of 500 codons subject to neutral synonymous mutations and nonneutral missense mutations, where a fraction B of missense mutational paths are beneficial, with a positive selection coefficient drawn from an exponential distribution, and other missense paths are deleterious, with effects drawn from a reflected gamma distribution (Methods). Note that the inclusion of both advantageous and deleterious mutations allows our simulations to capture both the effects of interference between multiple advantageous mutations (clonal interference) (39, 41) and the effects of selection against linked deleterious alleles (i.e., background selection) (42). We implemented the simulations in SLiM v3.4 (43). For each run of the simulation, we recorded the identity of all adaptive mutations on the first sequence to reach fixation, repeating this process 1,000 times to produce a simulated spectrum of adaptive substitutions similar in size to our empirical datasets. For each combination of N, μ, and B, we simulated 50 datasets and analyzed them using negative binomial regression (Methods).

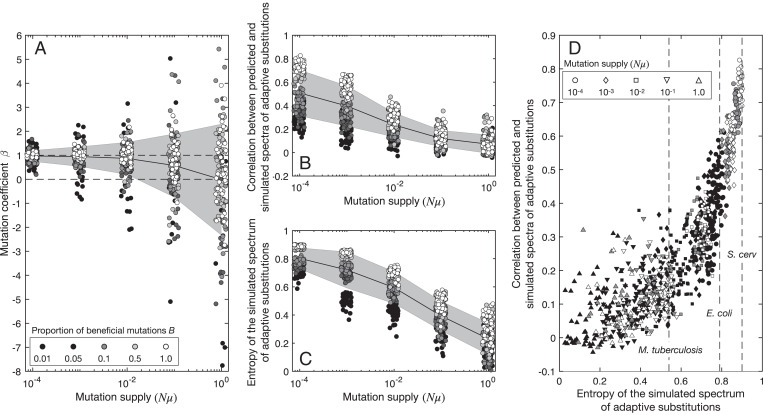
Previous theoretical work suggests that mutational supply $N\mu$ will modulate the influence of mutational biases on the spectrum of adaptive substitutions (33–36, 44). In particular, the simplest effect of increasing $N\mu$ is that multiple beneficial mutations are typically simultaneously present in the population, competing with each other, so that the adaptive mutation that ultimately fixes in the population is determined more by selective differences between these segregating mutations than by which beneficial mutation becomes established in the population first. This expectation is confirmed by Fig. 4A, which shows the inferred values of β relative to $N\mu$ for different proportions of beneficial mutations B. At the lowest mutation supply, β is approximately one, reflecting the direct proportionality expected for the origin-fixation regime (33, 37). As the mutation supply increases, β tends toward zero, reflecting a diminished influence of the mutation spectrum on adaptation. At the same time, the distribution of estimates for β becomes more dispersed (Fig. 4A), and the individual estimates become both less significant and less certain, as indicated by increasing average P values and increasingly large confidence intervals (SI Appendix, Fig. S3). Similarly, the predictive power of the model decreases with increasing mutation supply, as measured by a decreasing average correlation between the predicted and simulated spectra of adaptive substitutions (Fig. 4B).

Fig. 4.

Evolutionary simulations show mutation supply and mutational target size jointly modulate the predictive power of our model. (A) The inferred mutation coefficient β as a function of $N\mu$ for five different values of B, the fraction of beneficial mutations (the same color scheme for B is used in all panels). Dashed horizontal lines are drawn at β  =  0 and β  =  1 to indicate no influence and proportional influence of the mutation spectrum on the spectrum of adaptive substitutions, respectively. (B and C) Pearson’s correlation coefficient between predicted and simulated spectra of adaptive substitutions as a function of $N\mu$ for five different values of B (B) and entropy of simulated spectra of adaptive substitutions as a function of $N\mu$ for five different values of B (C). In A–C, the black lines show the mean and the gray areas show the SD. (D) Pearson’s correlation coefficient between predicted and simulated spectra of adaptive substitutions is shown in relation to the entropy of the simulated spectra of adaptive substitutions for different levels of mutation supply. The dashed vertical lines show the entropy of the spectrum of adaptive substitutions for each of our three study species.

The fraction of beneficial mutations B also influences the predictive power of the fitted models, but in a somewhat more surprising manner. Intuitively, one might think that increasing the proportion of beneficial mutations would decrease predictive power, as increasing B effectively increases the beneficial mutational supply, allowing increased competition between simultaneously segregating beneficial mutations. However, Fig. 4 A and B shows the opposite pattern. At low and intermediate levels of mutation supply, the largest values of B (white dots) yield the best correlations, the lowest values of B (black dots) yield the worst correlations, and intermediate values of B (gray dots) are intermediate. At high mutation supply, all of the correlations are poor regardless of B.

A potential explanation for this unexpected effect of B relates to the way that biases in nucleotide mutations have relatively broad effects, in the sense that changing a single nucleotide mutation rate will affect the rates of ∼60 codon-to-amino-acid changes. Because nucleotide mutational biases thus enrich broad classes of codon-to-amino-acid changes, they will tend to perform poorly in predicting distributions of adaptive events when those distributions are highly concentrated on a small set of codon-to-amino-acid changes. Increasing B expands the set of possible beneficial mutations to cover more diverse types of changes at various genomic sites, and this effect may be expected to improve the correlation of predicted and observed changes. Indeed, weak correlations due to this effect might arise, not only from having relatively few available adaptive paths in a given selective environment (small B), but also from limited sampling density, or even from a broad and well-sampled distribution of adaptive substitutions that is nonetheless heavily skewed toward a small number of strongly favored changes.

To quantify both the breadth of the adaptive spectrum (i.e., the distribution of events across the nonzero elements of the spectrum of adaptive substitutions) and its effects on the predictive power of our model, we calculated the entropy of observed and simulated spectra of adaptive substitutions, normalized so that the entropy has a minimum value of 0 when all adaptive events correspond to a single codon-to-amino-acid change and a maximum value of 1 when the adaptive events are uniformly distributed across all possible codon-to-amino-acid changes (Methods). Fig. 4C shows that the entropy decreases as mutation supply increases and that for any level of mutation supply, a lower proportion of beneficial mutations likewise decreases the entropy. To determine whether these patterns of decreasing entropy are sufficient to explain differences in the predictive power of our model across the range of model parameters, we plotted the correlation between predicted and simulated spectra of adaptive substitutions against the entropy of the simulated spectrum of adaptive substitutions (Fig. 4D). We see that increasing entropy, via either a decreased mutation supply or an increased proportion of beneficial mutations, increases the correlation between simulated and predicted spectra of adaptive substitutions. These observations from the evolutionary simulations are qualitatively similar to our empirical observation that as the entropy of the spectrum of adaptive substitutions increases from M. tuberculosis to E. coli to S. cerevisiae, there is a corresponding increase in the correlation between predicted and observed spectra of adaptive substitutions (Table 1). Indeed, the correlations for our three empirical datasets are well within the range of what we would expect from our simulations given their respective entropies (Fig. 4D).

To summarize, the results from our evolutionary simulations show that the predictive power of our model is strongest when the mutation supply is low and the mutational target size is large. However, we note that predictive power might also be influenced by other factors not included in our simulations, e.g., heterogeneity in the mutation rate across the genome, such as that caused by local sequence context (15, 45–50).

Assessing Possible Effects of Contamination.

A key assumption of the analysis above is that the events used to populate the spectrum of adaptive codon-to-amino-acid changes represent adaptive substitutions. While this is likely the case for the M. tuberculosis dataset, because these mutations have been shown experimentally to confer antibiotic resistance (5), we now consider the possibility that some fraction of observations in the S. cerevisiae and E. coli datasets represent contamination such as hitchhikers. If contaminants reflect the mutation spectrum more than genuine adaptive changes, this will exaggerate the correspondence with mutational predictions. Using the method of Tenaillon et al. (8), based on the observed dN / dS ratio (Methods), we estimate these proportions to be ∼24% and ∼13% for S. cerevisiae and E. coli, respectively.

To assess the influence of contamination up to, and even beyond, these estimated levels, we randomly remove a fraction q of events, sampled according to the species-specific empirical mutation spectrum. This procedure simulates the removal of a hypothetical contaminant fraction of size q under the worst-case scenario in which the nucleotide changes in the contaminant fraction mirror the mutation spectrum. As shown in SI Appendix, Fig. S4, even under the assumption that 40% of the events are contaminants, we observe a strong and statistically significant influence of mutation bias on adaptive evolution. In fact, we estimate that for S. cerevisiae and E. coli, levels of contamination of ∼65% and ∼44%, respectively, would be required to increase the P value of β to the point where the influence of mutation bias would no longer be significant.

Discussion

A growing body of evidence suggests that specific mutation biases influence the types of genetic changes involved in adaptation (5, 19–27), consistent with a small body of theoretical work on how biases in the introduction of variation—both low-level mutational biases and higher-level systemic biases—are expected to influence adaptive evolution (33, 35, 36, 40). Yet a general approach for quantifying this influence was missing. Here, we have developed and applied such a general approach to assess how the entire mutation spectrum shapes the spectrum of adaptive substitutions. It uses negative binomial regression to model the spectrum of adaptive substitutions as a function of codon frequencies and the mutation spectrum, measuring the influence of mutation in terms of a single statistic—the coefficient of mutational influence β.

This statistic takes on a value of zero when the mutation spectrum has no influence, a value of one for a proportional influence, and intermediate values for intermediate degrees of influence. Applying this framework to large datasets from S. cerevisiae, E. coli, and M. tuberculosis, we find a clear signal that the mutation spectrum strongly shapes the spectrum of adaptive substitutions. Specifically, the inferred values of β are not significantly different from one in any species. This result holds even when we account for the contamination by hitchhikers that is likely present in the datasets for S. cerevisiae and E. coli.

Our approach also illustrates how the spectrum of adaptive substitutions may be interrogated to reveal clues about the genetic basis of adaptation. We used our fitted models to predict the spectrum of adaptive substitutions in each species and uncovered variation in their predictive capacity, decreasing from S. cerevisiae to E. coli to M. tuberculosis. Using evolutionary simulations, we uncovered multiple potential sources of this variation. Specifically, we found that the degree to which the mutation spectrum is a good predictor of the spectrum of adaptive substitutions depends on how the adaptive events are distributed among all possible codon-to-amino-acid changes, with reduced predictive capacity associated with distributions concentrated on a small number of codon-to-amino-acid changes. Factors that affect the degree of concentration include dataset size, population-genetic conditions, diversity of selective environments, and the genetic architecture of adaptive traits. Importantly, population-genetic conditions that modulate the influence of mutation bias on adaptation, such as mutation supply, and nonpopulation-genetic conditions, such as the diversity of environmental conditions included in the dataset, can affect the predictive capacity of our model in similar ways.

While additional work is needed to disambiguate these various causes of differing model fits between species, our results are consistent with known facts concerning the population-genetic conditions, as well as the environmental conditions and mutational target sizes for adaptive mutations for the three species studied here. M. tuberculosis has one of the lowest mutation supplies of all bacteria (51), a small population size upon infection (52), and the 11 antibiotics considered here target specific gene products (5). For example, Rifampicin targets the beta subunit of bacterial RNA polymerase, and only a small handful of mutations to the rpoB gene that encodes this subunit cause resistance (53). Thus, while the population-genetic conditions of M. tuberculosis are more likely similar to origin-fixation dynamics than to clonal interference dynamics, and the set of observations is large, the mutational target size for antibiotic resistance is small. In contrast, E. coli experiences clonal interference due to a relatively higher mutation supply (54), but adaptation to temperature stress involves a larger mutational target (8, 55). Similarly, S. cerevisiae experiences clonal interference due to a high mutation supply (29), but because the data we study include adaptation to several environmental conditions, the mutational target size is large. Thus, the inferred influence of mutation bias on adaptation in these three species, increasing from M. tuberculosis to E. coli to S. cerevisiae, is consistent with our findings from evolutionary simulations that mutation supply and mutational target size modulate the influence of mutation bias on adaptation. However, it may also be the case that the diminished influence of mutation bias in M. tuberculosis, relative to E. coli and S. cerevisiae, results from differences in the way the data were collected (clinical isolates vs. laboratory evolution experiments).

The three species studied here also share several important features that suggest a need for similar studies across a greater diversity of population-genetic conditions. For example, all of the data analyzed here were obtained either from clonally reproducing experimental populations (E. coli and S. cerevisiae) or, in the case of M. tuberculosis, from natural populations with little or no recombination (52, 56, 57). This absence of recombination amplifies both the role of background selection (42) and the degree of interference between selected alleles (41), and it remains an open question whether mutational biases in practice play as large a role in sexual populations. Another important population-genetic commonality across the datasets studied here is the low degree of genetic diversity prior to the onset of selection, so that adaptation likely proceeds in all three systems from new mutations rather than standing genetic variation. This low initial diversity is the result of either the experimental setup in the case of E. coli and S. cerevisiae or the low worldwide nucleotide diversity empirically observed for M. tuberculosis (56), which is likely due to repeated bottlenecks at transmission events as well as other factors (58).

The discovery that mutation biases strongly shape the spectrum of adaptive substitutions has implications for several other related issues in evolutionary genetics. First, it has implications for the predictability of evolution (59–61), because it shows that mutationally favored types of changes are more likely to contribute to evolutionary adaptation, an effect that is both large and readily predictable from prior data on the relevant mutation spectrum. When the spectrum of adaptive substitutions is compared to the mutation spectrum, we see a significant correlation (of variable strength) for the spectrum of codon-to-amino-acid changes and a consistently strong correlation for the six types of nucleotide changes. This can be understood as an effect of aggregation. Many previous studies based on laboratory evolution experiments show that aggregating distinct genomic paths of adaptation by functional criteria (e.g., shared gene, operon, or functional category) highlights predictable effects that are presumably effects of selection (8), although effects of mutation are also evident at the gene level (44). The extreme aggregation of distinct genomic changes into just six types of nucleotide changes also reveals a highly predictable effect, but it is an effect of mutation rather than selection, because the criterion of aggregation is the mutational type. At the opposite extreme of aggregation—particular nucleotide changes at specific genomic coordinates—mutation bias is unlikely to be predictive of the genetic changes that cause adaptation.

Second, the discovery of a direct influence of mutation bias on evolutionary adaptation parallels recent reports that driver mutations in cancer reflect the underlying biases of cancer-associated mutational processes, including exogenous effects of ultraviolet (UV) light and tobacco exposure and endogenous effects of DNA mismatch repair and APOBEC activity (62–64). The increased predictability of such changes, due to mutational effects, can inform rational drug design, as has been suggested for drugs for leukemia, prostate cancer, breast cancer, and gastrointestinal stromal tumors (26). The same may be true for designing antibiotic treatments for mycobacteria, which evolve multidrug resistance via a sequence of mutations, several of which interact epistatically, such that only a subset of possible mutational trajectories to multidrug resistance is possible (65).

Finally, the broadest context for the present work is a debate about the role of so-called “internal” causes in shaping the course of evolution. Arguments dating back to the origins of theoretical population genetics emphasize selection as the sole directional force in evolution, with mutation treated as a weak and ineffectual pressure due to the smallness of mutation rates (66–68). Haldane (66) concluded that mutation can influence the course of evolution only under neutral evolution or when mutation rates are unusually high. Accordingly, strong effects of mutation bias have been historically associated with neutral evolution (69). However, more recent theoretical work has shown that this classic way of thinking depends on the assumption that evolution begins with abundant standing genetic variation, so that mutation acts only as a frequency-shifting force and not as a source of genetic novelty (33). When the dynamics of an evolutionary process depend on events that introduce novel variants, biases in the introduction process, such as toward particular nucleotide changes, systematically influence which types of genetic changes are involved in adaptation (33, 70).

A variety of statistical frameworks assume a proportional influence of the mutation spectrum on the spectrum of adaptive substitutions, including those for quantifying selection pressures on proteins. For example, the ratio of nonsynonymous to synonymous mutations (dN/dS)—a commonly used statistical test to detect proteins undergoing adaptation—is often corrected to account for the mutation spectrum (54, 71). Implicit in this accounting is the assumption that the mutation spectrum influences neutral and adaptive mutations in the same way. Our finding that the mutation spectrum can be directly inferred from the spectrum of adaptive substitutions provides empirical support for this assumption, at least for the species and evolutionary conditions considered here.

Some have responded to the theory of mutation-biased adaptation by arguing that such an influence is unlikely, on the grounds of requiring sign epistasis or unusually small population sizes (72). However, modeling here and in other work shows that mutation bias can influence adaptation across a range of conditions, including in the absence of sign epistasis and when conditions induce clonal interference among concurrent mutations (35). More broadly, while theoretical arguments are surely helpful for sharpening our understanding, ultimately the prevalence and magnitude of the mutational influence on adaptation is an empirical question, and the impact of mutational biases on adaptation has now been shown for several different types of mutations, in a range of systems from bacteriophage to birds to somatic evolution in human cancers (5, 19–27).

This growing body of work on mutation-biased adaptation provides a basis to reconsider certain long-standing claims about how variational properties influence the evolutionary process. For instance, evo-devo arguments about bias or constraint relate evolutionary patterns to tendencies of developmental variation, but the causal nature of this link, in terms of population-genetic principles, is typically unspecified (73, 74). Likewise, a significant body of neostructuralist work on “findability” or “self-organization,” going back at least to Kauffman (75), emphasizes the tendency of evolution to prefer structures common in abstract state spaces, e.g., in regard to RNA folds (76) or regulatory circuit motifs (77). Recent work on mutation-biased adaptation provides a rigorous body of theory and evidence establishing how tendencies of variation may act as dispositional causes in evolution, suggesting a previously missing population-genetic basis for these long-standing claims. Our results contribute to the empirical case that mutational biases, which are more accessible to study at the level of population genetics, have a strong and measurable impact on adaptive evolution.

Methods

Data.

Our modeling framework is built around three key quantities, which are specific to each species: a spectrum of adaptive substitutions n, a table of codon frequencies f, and a mutation spectrum μ. These are all constructed using empirical data, as described below.

Spectrum of adaptive substitutions.

We curated a list of missense mutations associated with adaptation from the published literature for each of three species: S. cerevisiae, E. coli, and M. tuberculosis. For each mutation, these lists specify a genomic coordinate, nucleotide change, amino acid substitution, and literature reference (Datasets S1–S3). We refer to each unique combination of genomic coordinate and nucleotide change as a mutational path and each instance of adaptive change along a mutational path as an adaptive event. The number of adaptive events per mutational path is also reported in Datasets S1–S3.

For S. cerevisiae, the adaptive events were reported in four studies, each of which considered one or more environmental or genetic challenges, including high salinity (28), low glucose (28), rich media (29), and gene knockout (30). The list contains 713 adaptive events across 534 mutational paths (Dataset S1).

For E. coli, the adaptive events were reported in a single study of 115 replicate populations adapting to temperature stress (8). The list contains 602 adaptive events across 492 mutational paths (Dataset S2).

For M. tuberculosis, the adaptive events were reported in a single study of the influence of mutation bias on adaptation to antibiotic stress (5). The underlying mutational paths were derived from two separate meta-analyses of the literature on antibiotic resistance (one performed for the study and another previously published) (4), with each mutational path required to pass stringent tests for conferring antibiotic resistance. A total of 11 antibiotics or antibiotic classes were considered: rifampicin, ethambutol, isoniazid, ethionamide, ofloxacin, pyrazinamide, streptomycin, kanamycin, pyrazinamide, fluoroquinolones, and aminoglycosides. The adaptive events were inferred from a phylogenetic reconstruction of public M. tuberculosis genomes. We merged the adaptive events from the two meta-analyses. The resulting list contains 4,413 adaptive events across 283 mutational paths (Dataset S3). Analyzing the adaptive events from the two meta-analyses separately (SI Appendix, Table S1) produced qualitatively similar results to those reported in Table 1.

For each species, we constructed the spectrum of adaptive substitutions n from the list of adaptive events described above, assigning each adaptive event to its respective codon-to-amino-acid change. Each element $\mathbf{n}(c,a)$ of the spectrum of adaptive substitutions therefore tallies the number of adaptive events that changed codon c to amino acid a. Note the adaptive events tallied for any codon-to-amino-acid change often reflect more than one genomic coordinate and/or nucleotide change (i.e., different mutation paths). These spectra are reported in Dataset S4.

Codon frequencies.

We used the tables of codon frequencies reported in the Codon Usage Database (78), found via query to an exact match to S. cerevisiae, E. coli, and M. tuberculosis. These frequencies are reported in Dataset S5 and shown in SI Appendix, Fig. S1 E–G.

Empirical mutation spectra.

For S. cerevisiae and E. coli, we used mutation rates derived from mutation-accumulation experiments, as reported in figure 3 of ref. 15 and table 3 of ref. 14, respectively. For E. coli, we corrected the mutation rates for GC content, following ref. 12. For S. cerevisiae, the rates were already corrected (15). For M. tuberculosis, we used mutation rates derived from single-nucleotide polymorphism data (5) (Dataset S6). We restricted our analysis to synonymous mutations in the third codon position and corrected the rates for GC content in that position. We also corrected for the probability that each type of mutation causes a synonymous change. For instance, of all the possible synonymous mutations in the third position allowed by the standard genetic code, 23% are G/C →A/T transitions, whereas only 12% are G/C →C/G transversions.

These spectra are reported in Dataset S7 and shown in SI Appendix, Fig. S1A. We used these estimated mutation rates to define a total codon-to-amino-acid mutation rate $\mu (c,a)$ for each of the 354 codon-to-amino-acid changes allowed by the standard genetic code, summing the rates of all point mutations in codon c that lead to amino acid a. For example, the probability of the mutation from codon CAC to glutamine (Q) is the sum of the probabilities of point mutations C →A and C →G, since both mutations in the third position of CAC lead to codons for glutamine (Q).

Transition–Transversion Ratio vs. the Full Mutation Spectrum.

The influence of the mutation spectrum can be partitioned into an overall transition–transversion bias and biases among different types of transitions and transversions. The model that considers only the contribution of the species-specific transition–transversion bias is given by

$$\log \mathbb{E}[\mathbf{n}(c,a)]={\beta }_0+\log f(c)+{\beta }_{\text{ti/tv}}\log {\mu }_{\text{ti/tv}}(c,a).$$ [3]

As in Eq. 2, β₀ is the logarithm of the constant of proportionality and f(c) is the genomic frequency of codon c. The mutation term ${\mu }_{\text{ti/tv}}(c,a)$ is defined only by the species-specific transition–transversion ratio and thus assigns one rate to all transitions and one (different) rate to all transversions. The corresponding regression coefficient is ${\beta }_{\text{ti/tv}}$.

The complete model contains all of the terms of the model above (Eq. 3), with an additional mutation term ${\mu }_{\text{rest}}(c,a)$ that accounts for the rest of the mutation spectrum [such that ${\mu }_{\text{ti/tv}}(c,a){\mu }_{\text{rest}}(c,a)=\mu (c,a)$], along with its respective regression coefficient ${\beta }_{\text{rest}}$. This complete model is given by

$$\log \mathbb{E}[\mathbf{n}(c,a)]={\beta }_0+\log f(c)+{\beta }_{\text{ti/tv}}\log {\mu }_{\text{ti/tv}}(c,a)+{\beta }_{\text{rest}}\log {\mu }_{\text{rest}}(c,a).$$ [4]

As in our main analyses, we used negative binomial regression to estimate the regression coefficients. Because the two models are nested, we compared their performance using a likelihood-ratio test (SI Appendix, Table S2).

Entropy of the Spectrum of Adaptive Substitutions.

The spectrum of adaptive substitutions n describes the number of adaptive events per codon-to-amino-acid change. We calculate the entropy H of this spectrum as

$$H=\frac{-{\displaystyle \sum _{i=1}^{m}p}(n_i)\log p(n_i)}{\log (m)},$$ [5]

where $p(n_i)$ is the proportion of adaptive events that correspond to the ith codon-to-amino-acid change, and m = 354 is the number of codon-to-amino-acid changes allowed by the standard genetic code.

Evolutionary Simulations.

We used SLiM v3.4 for the evolutionary simulations (43). We ran each simulation until the first fixation event, repeating this process 1,000 times and recording each beneficial mutation that went to fixation. We performed 50 replicates per combination of the parameters N, μ, and B. Each of the 1,000 simulations per replicate used the same initial population, which comprised N copies of a nucleotide sequence of length $L=1,500$ (i.e., 500 codons), randomly generated using the codon frequencies for S. cerevisiae.

All sequences in the initial population were assigned a fitness of one. The fitness effects assigned to each of the possible codon-to-amino-acid changes from each of the 500 codons were drawn at random from a distribution of fitness effects and were held constant across the 1,000 simulations per replicate.

A unique distribution of fitness effects was constructed for each replicate, such that synonymous mutations were neutral, a fraction B of missense codon-to-amino-acid changes were beneficial, and a fraction $1-B$ of missense codon-to-amino-acid changes were deleterious. The fitness effects of beneficial codon-to-amino-acid changes were drawn from an exponential distribution with density

$$f_b(x)=\lambda e^{-\lambda x},$$ [6]

where $\lambda =33.33$, so that the expected advantageous selection coefficient was 0.03. The fitness effects of deleterious codon-to-amino-acid changes were drawn from a gamma distribution with density

$$f_d(x)=\frac{x^{(a-1)}{e}^{-(x/s)}}{s^a\hspace{0.17em}\mathrm{\Gamma }(a)},$$ [7]

where a = 0.4 and s = 0.15, so that the magnitude of the expected deleterious selection coefficient was twice the advantageous one (79). For sequences with more than one mutation, we summed the effects of the individual mutations. SI Appendix, Fig. S5 shows representative distributions of fitness effects for different proportions of beneficial mutations B.

Each simulation proceeded until a single sequence went to fixation and any beneficial mutations were recorded. Our simulations thus correspond to single-step adaptive walks, extending prior theoretical work considering just a few possible adaptive mutations (19, 33) into a codon-based model of a whole gene with thousands of possible mutations. Single-step adaptive walks are particularly germane to the M. tuberculosis data, in which antibiotic resistance is often strongly associated with single mutations. Multistep walks are also relevant for long-term evolution, but they would require further assumptions about the structure of the fitness landscape. In each generation t, N sequences were chosen from the population at generation t – 1 with replacement and with a probability proportional to their fitness. Mutations were introduced according to the product of the genome-wide mutation rate μ and the per-nucleotide mutation rate defined by the mutation spectrum for S. cerevisiae, with each mutation affecting fitness as defined at the onset of the simulation.

Contamination Estimates.

For each type of mutation, we calculated the number of synonymous and nonsynonymous sites for each possible codon, and we estimated the total number of synonymous and nonsynonymous sites in the genome by taking into account the codon usage patterns of S. cerevisiae and E. coli (SI Appendix, Fig. S1 E and F). We then calculated dN/dS ratios among all substitutions in the adapted lines correcting for the mutation rates of each type of mutation (SI Appendix, Fig. S1A). Following ref. 8, we estimated the proportion of adaptive nonsynonymous mutations from such ratios as $y=(x-1.0)/x$, where x is the estimated dN/dS ratio (4.24 and 7.76 for S. cerevisiae and E. coli, respectively). Finally, we estimated the fraction of hitchhikers in our datasets as $1-y$.

Data Availability

All study data are included in this article and/or SI Appendix. The scripts used to analyze these data and to run the evolutionary simulations can be found at GitHub, https://github.com/alejvcano/Mutbias2022.