Abstract
Dendritic spines are membranous protrusions that receive essentially all excitatory inputs in most mammalian neurons. Spines, with a bulbous head connected to the dendrite by a thin neck, have a variety of morphologies that likely impact their functional properties. Nevertheless, the question of whether spines belong to distinct morphological subtypes is still open. Addressing this quantitatively requires clear identification and measurements of spine necks. Recent advances in electron microscopy enable large-scale systematic reconstructions of spines with nanometer precision in 3D. Analyzing ultrastructural reconstructions from mouse neocortical neurons with computer vision algorithms, we demonstrate that the vast majority of spine structures can be rigorously separated into heads and necks, enabling morphological measurements of spine necks. We then used a database of spine morphological parameters to explore the potential existence of different spine classes. Without exception, our analysis revealed unimodal distributions of individual morphological parameters of spine heads and necks, without evidence for subtypes of spines. The postsynaptic density size was strongly correlated with the spine head volume. The spine neck diameter, but not the neck length, was also correlated with the head volume. Spines with larger head volumes often had a spine apparatus and pairs of spines in a post-synaptic cell contacted by the same axon had similar head volumes. Our data reveal a lack of morphological subtypes of spines and indicate that the spine neck length and head volume must be independently regulated. These results have repercussions for our understanding of the function of dendritic spines in neuronal circuits.
Keywords: dendritic spines, electron microscopy, plasticity, pyramidal cells
1 |. INTRODUCTION
Dendritic spines, small neuronal appendages that mediate essentially all excitatory transmission in the brain, were discovered by Cajal more than a century ago (Cajal, 1904), who first described them as composed of a “ball-like” spine head and a “lightly stained” spine neck (reviewed in Yuste, 2010). However, due to the limited resolution of the light microscope, these findings were controversial and not confirmed until the development of electron microscopy (EM), which allowed imaging of dendritic spines with nanoscale resolution (Gray, 1959). Recent advances in EM have enabled systematic reconstructions of brain tissues, providing large numbers of high-resolution 3D spine structures (Dorkenwald et al., 2019; Kasthuri et al., 2015; Lee et al., 2019; Motta et al., 2019). Given the small size of spines, 3D ultrastructural reconstructions are particularly important since the border between the head and neck can appear very differently when viewed from different angles (Arellano et al., 2007).
The question of whether spines belong to different morphological subtypes or represent a continuum is still controversial (Pchitskaya & Bezprozvanny, 2020), and part of the problem lies on the lack of a clear definition of what constitutes the spine neck. Peters and Kaiserman-Abramof examined spines of rat neocortex, proposing the distinction between three types of spines: stubby, mushroom, and thin spines (Peters & Kaiserman-Abramof, 1970). They defined stubby spines as short, thick spines without a clear neck, mushroom spines as spines with thick necks that expand into a large end-bulb, and thin spines as spines with slender necks that expand into a small oval or rounded end-bulb. This classification has been widely adopted and used by almost every study on spines at the optical microscope level (Arellano et al., 2007). However, no clear borderline was noted between these three types and a continuum and unimodal distribution of the spine’s morphological parameters has been reported in many quantitative studies since then (Arellano et al., 2007; Loewenstein et al., 2015; Peters & Kaiserman-Abramof, 1970; Tønnesen et al., 2014). A more precise way to distinguish between stubby, mushroom, or thin spines is the analysis of the joint distributions of neck versus head morphological parameters. While some studies find multimodal distributions when plotting neck versus head morphological parameters (Harris et al., 1992), others have found unimodal distributions (Arellano et al., 2007), so the conundrum of whether spines belong to different subtypes or not still remains.
Recently, analyses of large-scale connectomics datasets of mouse cortex have enabled systematic measurements of synaptic size (Motta et al., 2019) and spine head volume (Dorkenwald et al., 2019) and differentiated two subtypes of spines: small and large. However, the data showed significant overlap in sizes between these two groups. Thus, the question of whether dendritic spines are divided into distinct types or constitutes a continuum is still undecided (Berry & Nedivi, 2017; Rochefort & Konnerth, 2012). This controversy is essentially confounded by the lack of methods to define and measure spine necks objectively, since the proposed distinction between different spine subtypes depends critically on the dimensions of the neck.
To address this issue head-on, in this study we focus on the morphological analysis of the spine necks and develop an objective method to measure them. We analyze an ultrastructural dataset from mouse neocortex and introduce computer vision algorithms to show that the vast majority of spines present a clear morphological separation between head and neck. Then, we analyze morphological parameters of the neck and head to examine whether distinct types of spines can be detected, finding instead unimodal and continuous distribution of spine parameters. We also find a lack of correlation between the spine neck length and the spine head volume, indicating that the two compartments are independently regulated. Finally, we describe correlations between spine morphological properties, including the post-synaptic densities (PSD) and spine apparatus (SA), and spine head volumes. Our results confirm a lack of distinct morphological classes of spines and have implications for the spine development and function.
2 |. METHODS
2.1 |. Ultrastructural dataset
In this paper, we analyzed a set of 4,223 dendritic spines of layer 6 pyramidal cells (at the apical dendrite level in layer 5) from the somatosensory cortex of a young adult mouse, published in Kasthuri et al. (2015). The EM data was acquired using automated ultrastructural technology with nanometer resolution (Figure 1). The detailed methodology to reconstruct spines in three dimensions is described in Kasthuri et al. (2015). Neuronal processes in this image dataset were segmented using VAST, a computer-assisted manual space-filling segmentation and annotation program (Berger et al., 2018). VAST allows coloring images at multiple scales of resolution, to organize the results in a flexible annotation framework, and to export results for 3D visualization and analysis. Each spine was represented by a triangle mesh in an “OBJ” format which includes a list of 3D vertices followed by a list of faces formed by the vertices (Figure 2a). A detailed spreadsheet for 1,700 synapses, that describes synapse position, axon ID, dendrite ID, and biological details, such as if the spine consists an SA and PSD size, is provided by Kasthuri et al. (2015). The IDs of the pre- and post-synaptic partners enabled us to find pairs of spines that create dual connection between the same pre- and post-synaptic neurons.
FIGURE 1.
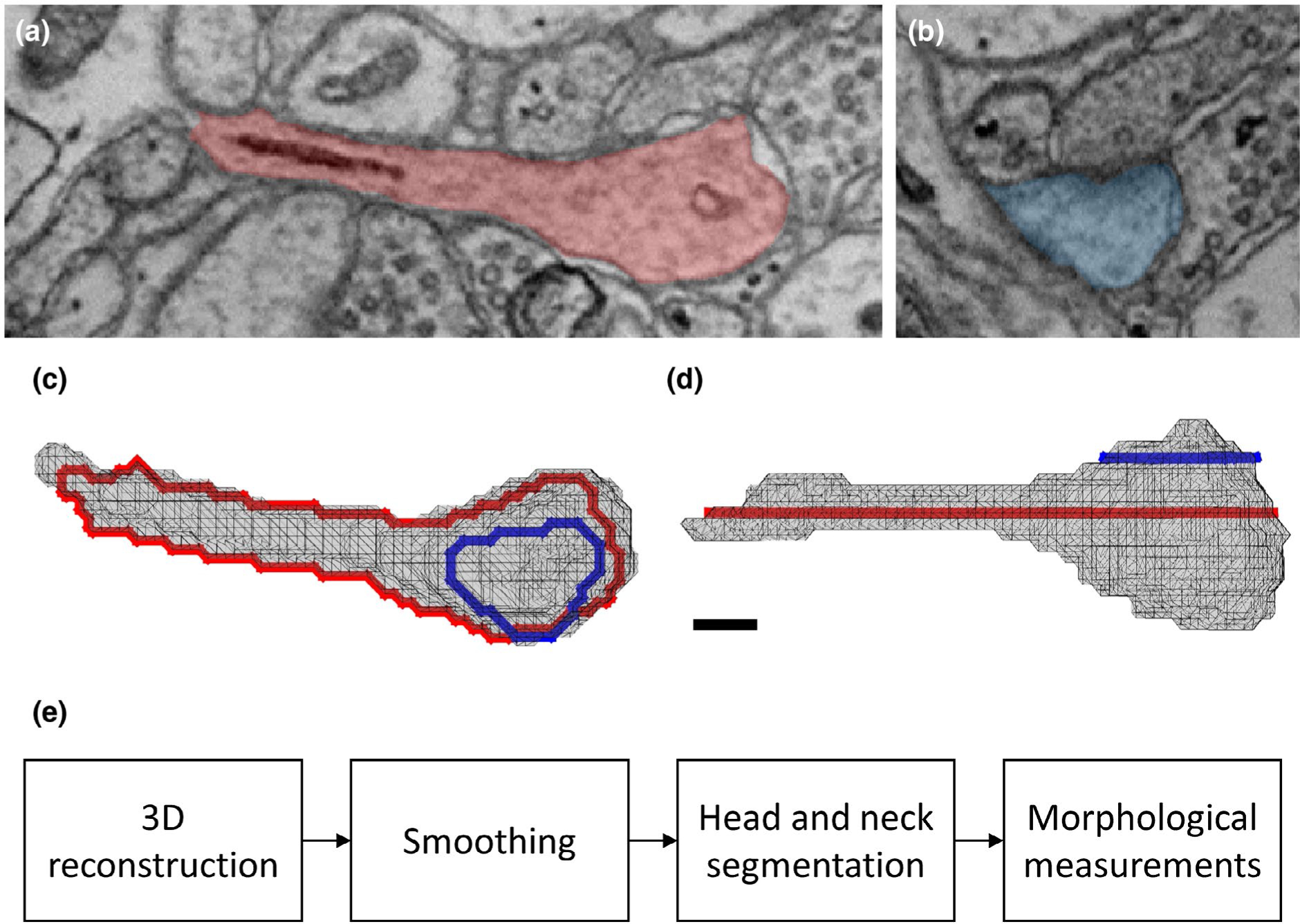
Ultrastructural 3D reconstruction and analysis. (a-b) Two sections from the EM stacks of the same spine. The spines are shaded in red (a) and blue (b). A synapse between the spine head and axonal above can be seen in (b). (c-d) Reconstructed triangle mesh of the same spine, from a top (c) and a side view (d). The frame of the spine shown in (a) is colored in red, and the frame of the spine shown in (b) in blue. Scale bar: 100 nm. Spine ID: Kasthuri_3316. Coordinates: 5,812, 8,354, slices: 1,203 (a) and 1,208 (b). (e) Workflow diagram, describing the algorithm
FIGURE 2.
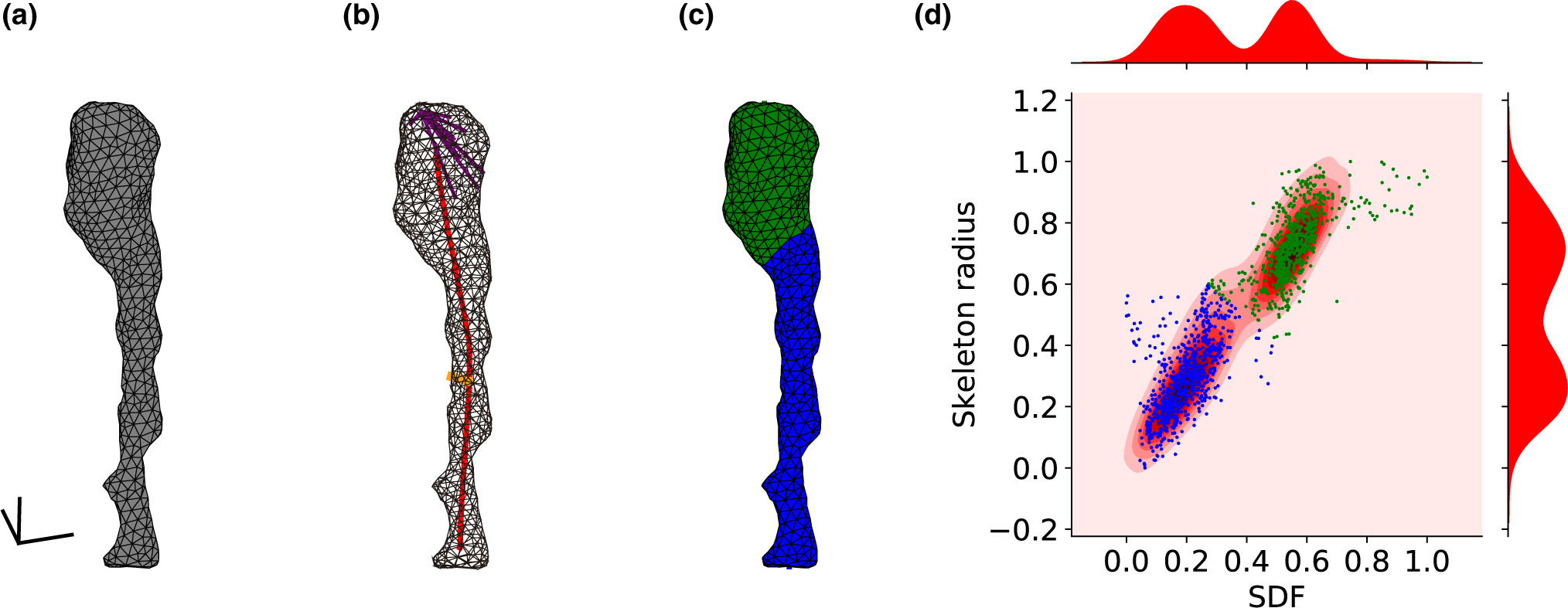
Computational separation of spine head and neck. (a) Triangle mesh of a spine surface, scale bar: 100 nm. (b) The centerline skeleton line is colored in red. An example of the “skeleton radius” is colored in orange. An example of rays in a 60° cone for measuring the SDF colored in purple. (c) The head (green) and neck (blue) were classified according to the SDF and “skeleton radius” values. The centerline curve was extended and divided into neck length (blue) and head length (green). Parameters values are: spine volume: 0.006 μm3, head volume: 0.004 μm3, spine surface area: 0.268 μm2, head surface area: 0.141 μm2, spine length: 0.854 μm, neck length: 0.596 μm, neck diameter: 0.072 μm, head sphericity: 0.864. (d) Scatter plot of faces SDF and “skeleton radius” values. Each dot represents a single face of the spine. Distributions of SDF and “skeleton radius” on top and right. Faces were clustered using Gaussian Mixture Model. Hartigan’s dip-test p-values are under .001, indicating bimodality. The spine ID: Kasthuri_4643
2.2 |. Spine selection
The full dataset included 4,223 spines, of which 3,138 spines that had two clear segments—head and neck—were processed for future analysis. The discarded cases included two spines that were connected to each other and cases of additional segments caused by a bulge or swelling on the spine head or neck. We discarded an additional 140 spines, in cases where it was impossible to draw a clear centerline skeleton over the neck and head, mainly as a result of complex geometry. Overall, the total number of morphologically analyzed spines was 2,998.
For the PSD size analysis, we used a subset of 1,700 synapses from the dataset where the PSD size was known. From these synapses: 273 were on dendritic shafts and 229 were labeled as “Unknown,” resulting in 1,198 confirmed synapses on spines. The intersection between the 2,998 spines that we morphologically analyzed and the 1,198 spines where the PSD size was measured led us to a dataset of 888 spines.
Finally, for the spine apparatus (SA) analysis, spines were manually scored as having an SA or not. From the 1,700 synapses of the datasheet, there were 530 spines with SA, 307 spines without SA, 315 spines indicated as “uncertain,” and 548 spines indicated as “N/A.” The intersection between the 2,998 spines that were morphologically analyzed and this SA data subset led to 401 spines with SA, and 220 spines without SA.
2.3 |. Morphological analysis
In our first analysis stage, Laplacian smoothing, each vertex in a mesh covering each spine was replaced by the average of its neighbors (that share an edge). This was applied to compensate for the quantization effect caused by the EM sectioning process. Next, small isolated components that contain less than 17 faces were removed. Shape Diameter Function (SDF) and Mesh Skeletons were then calculated using the “Triangulated Surface Mesh Segmentation” and “Triangulated Surface Mesh Skeletonization” packages from the Computational Geometry Algorithms Library (CGAL) 5.0.2, https://www.cgal.org (Shapira et al., 2008; Tagliasacchi et al., 2012). To this end, data were converted from “OBJ” to “OFF” format. SDF measurement were done by averaging 25 rays beams in a cone of 60° projecting to the opposite spine surface (purple rays in Figure 2b). The SDF is a pose-independent method that matters for this dataset because of the tortuous nature of spines. The “skeleton radius” is the distance from each face to the closest point along the mesh skeleton (orange line in Figure 2b). These algorithms, normalized between 0 and 1, were then used for the segmentation between the head and neck, and later, for measurements of the spine morphological parameters.
For the segmentation of spines into head and neck, we used two local parameters for each face, the SDF and the “skeleton radius” values, as well as a spatial parameter, the dihedral angle between neighboring faces. The energy-function algorithm applied a graph-cut-based algorithm that combines fast changes on SDF and “skeleton radius” values as natural candidates for segment boundaries and geometric criterion in adjacent facets, sharing a sharp and concave edge (CGAL “Triangulated Surface Mesh Segmentation” package). The parameters used in this algorithm were the number of clusters of 2 and smoothing-lambda of 0.1.
Branched spines, in which the spine neck splits into two different heads, were severed into main and side branches. The neck of the main branch included the mutual trunk, from the dendritic shaft to the branching point, while the neck of the side branch started at the branching point. In the dataset, branched spines were defined as two separated objects, and were analyzed separately. Branched spines (10.06% of spines in the dataset), which had shorter neck length of the side branches (13.93% on average) were included in the analysis.
2.4 |. Morphological parameter measurements
The volume of spines was calculated using the signed tetrahedral volumes summarizing algorithm (Zhang & Chen, 2001):
| (1) |
where (xi1, yi1, zi1), (xi2, yi2, zi2), and (xi3, yi3, zi3) are the coordinates of the vertices of face i. This algorithm requires a closed mesh and face normals pointed to the same inner or outer direction (the order of the face vertices, clockwise or counterclockwise, indicates the normal). Thus, for calculating the spine head volume, after computationally severing the head, the hole was filled by connecting the border faces to the center point of the hole, considering the neighbor faces to find the correct direction of the normals.
For measuring spine length, we summed the length of the skeleton center line and the extension to the spine surface, in the direction of the vector of the last two vertices, in the two edges. For measuring spine’s neck length separately, each vertex among the centerline was labeled as “head” or “neck” according to the major of its belonged vertices. Summarizing the “neck” segments gives us the neck length.
The spine head sphericity was calculated by Equation (2):
| (2) |
where V is the spine head volume and A is the area. In a perfect ball, the sphericity equals 1.
2.5 |. Statistical analysis
The Hartigan’s dip-test of unimodality (Hartigan & Hartigan, 1985) was applied to examine whether data are unimodal distributed. Since the Hartigan test was designed for a 1-dimensional dataset, for considering mutually two parameters, we tested the unimodality on 18 projections of 10° rotations of the 2-dimensional dataset (Schelling & Plant, 2020). 10,000 pairs of spines were randomly sampled from the entire database using the Python “random.choices()” function. Kolmogorov–Smirnov (KS) test for two samples was used to compare two empirical cumulative distribution function (CDF) with a two-tailed p-value.
2.6 |. Code accessibility
The CGAL scripts were written in C++; the other codes were written in Python 3.7 using the libraries: numpy 1.17.4, scipy 1.5.4, scikit-learn 0.23.1, and unidip 0.1.1. All the data is publicly available at the Columbia University Academic Commons site (https://doi.org/10.7916/d8-tdqd-dh88). VAST program, the EM stacks, and the segmentation are available at (https://lichtman.rc.fas.harvard.edu/vast/). Codes used in this paper are publicly available at the Columbia University Neurotechnology Center’s GitHub page (https://github.com/NTCColumbia/Ultrastructural-analysis-of-dendritic-spine-head-and-neck-).
3 |. RESULTS
3.1 |. Computational separation of spine head and neck
We first explored the morphological identity of the spine neck. To do so, we segmented spine structures into head and neck using their morphological properties. To this end, we divided the surface of the spine into a triangular mesh, and, for each face of the spine surface, two geometrical parameters, the SDF and the “skeleton radius,” were calculated. The SDF and the “skeleton radius” are complementary morphological parameters, and the combination of both distributions enabled a robust segmentation between the head and neck, as evident visually in a bimodal distribution of values (Figure 2d). The cluster with the lower value of average SDF was labeled as “neck” (blue) and the other cluster was labeled as “head” (green). Manual examination of the connecting point between the dendritic shaft and the spine neck in the EM data confirmed the automatic head and neck segmentation in 97.9% of the analyzed spines (3,073/3,138). To quantify the extent of the separation between head and neck for every spine, we tested whether the distributions of the SDF and the “skeleton radius” values were unimodal. Disproving unimodality implies a bimodal or higher-order distribution, with a clear clustering into two groups: the head and the neck faces. Statistical tests were applied to examine if the separation between head and neck was significant. The Hartigan’s dip-test revealed that 88.44% (3,717/4,203) of spines had a bimodal distribution of SDFs, and 74.87% (3,147/4,203) of spines had a bimodal distribution of “skeleton radius” values (p-value < .05, Hartigan’s dip-test). Mutual SDF and “skeleton radius” 2-dimensional Hartigan’s dip-test (see Methods) led to 95.12% (3,998/4,203) of the spines demonstrating statistically significant bimodal distributions. To find the exact border between head and neck we used a graph-cut algorithm with an energy minimization function, taking into account the SDF and “skeleton radius” values, as well as the convexity of the mesh surface. The border was often in sharp dihedral angles between neighboring faces, which occur between the head and neck. In 74.33% of the spines, the two clusters of faces led to two segments, one for head faces and the other for the neck faces. In 1% of spines there was only a single cluster, meaning that there was no clear separation between head and neck. In the rest of the spines, the two clusters led to more than two segments. These cases included cases of two spines that were connected to each other and cases of additional segments caused by a bulge or swelling on the spine head or neck. We concluded that most spines can be rigorously separated into a head and neck. For the rest of the study, focused on the morphological analysis of spine necks, we analyzed only spines consisted of clear two segments (3,138/4,223 spines).
3.2 |. A continuum of spines morphological parameters
We then proceed to build a dataset of different morphological variables for each spine. First, we measured three basic morphological parameters of the entire spine: its volume, surface area, and length. The spine surface area was measured by adding all the triangle mesh areas of the spine. The volume of the spine was calculated using the signed tetrahedral volumes algorithm (Zhang & Chen, 2001). The spine’s length was obtained by measuring the extended centerline skeleton (Figure 2c). The separation between the spine head and neck enabled us to also measure “head volume,” “neck length,” and “neck diameter.” To measure head volume, since the algorithm for volume measurements requires a closed volume, we first filled the hole created by the cutting of the neck with a simple plane, followed by calculating the volume of the new closed spine head mesh. To measure neck length, we used similar methods as with total spine lengths. Each vertex along the skeleton centerline was labeled as “head” or “neck” according to most of its faces (Figure 2c). Thus, we integrated the lengths of the neck-labeled centerline vertices. In contrast to previous methods that measure Euclidean or Geodesic distances either manually or semi-automatically with user mediation (Jorstad et al., 2014, 2018), our method is an automatic approach for measuring of the spine neck along the center of the 3D spine, considering also head position. Finally, to measure neck diameter, we first computed the value of the radius at each vertex along the skeleton centerline by averaging the shortest distance between the face center and the centerline skeleton line for all faces belonging to each vertex (see orange line in Figure 2b, as example of a neck radius for a specific face). Then, we averaged these values along all the vertices and doubled this value to compute the neck diameter. This method for measuring spine neck dimensions provided reliable results even for non-round (elliptic) neck cross-sections. As neck radius was perpendicular to the centerline skeleton it was not affected by the 2D section-cutting or projection angle.
Using this analysis pipeline, we created a database of measured values of spine’s morphological parameters (Figure 3a–g). Inspection of the distributions for each of the morphological parameters revealed skewed unimodal functions, with no clear bi- or multimodality. To explore this in depth, and test if spines could be classified into different morphological subtypes, we plotted data along pairs of variables, including “spine volume,” “spine surface area,” and “spine length” (Figure 4a), and “head volume,” “neck length,” and “neck diameter” (Figure 4b). Visual inspection still failed to show clear multimodal distributions. This was confirmed with the 3-dimensional Hartigan’s dip-test, finding a continuous and unimodal distribution. The lack of multimodality in the morphological parameters disproves the existence of distinct spine types. We concluded that, in our dataset, spines displayed a continuum distribution of morphologies.
FIGURE 3.
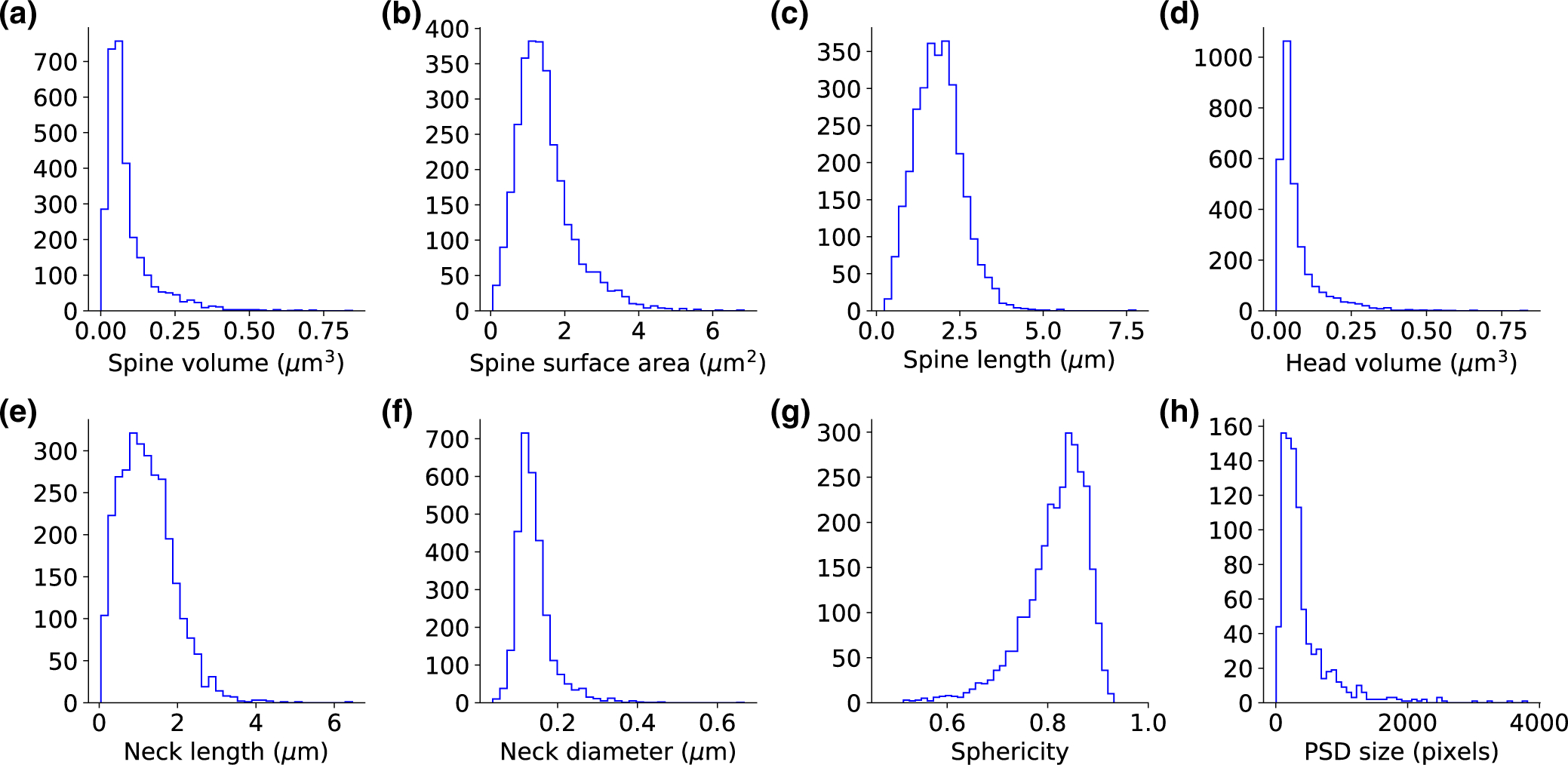
Unimodality of spine morphological parameters. (a-c) The morphological parameters of the entire spine. (d-f) The morphological parameters for the separated head and neck. (g) The sphericity of the head volumes. The dataset includes 2,998 spines. (h) Post-synaptic density size distribution, a dataset of 888 spines
FIGURE 4.
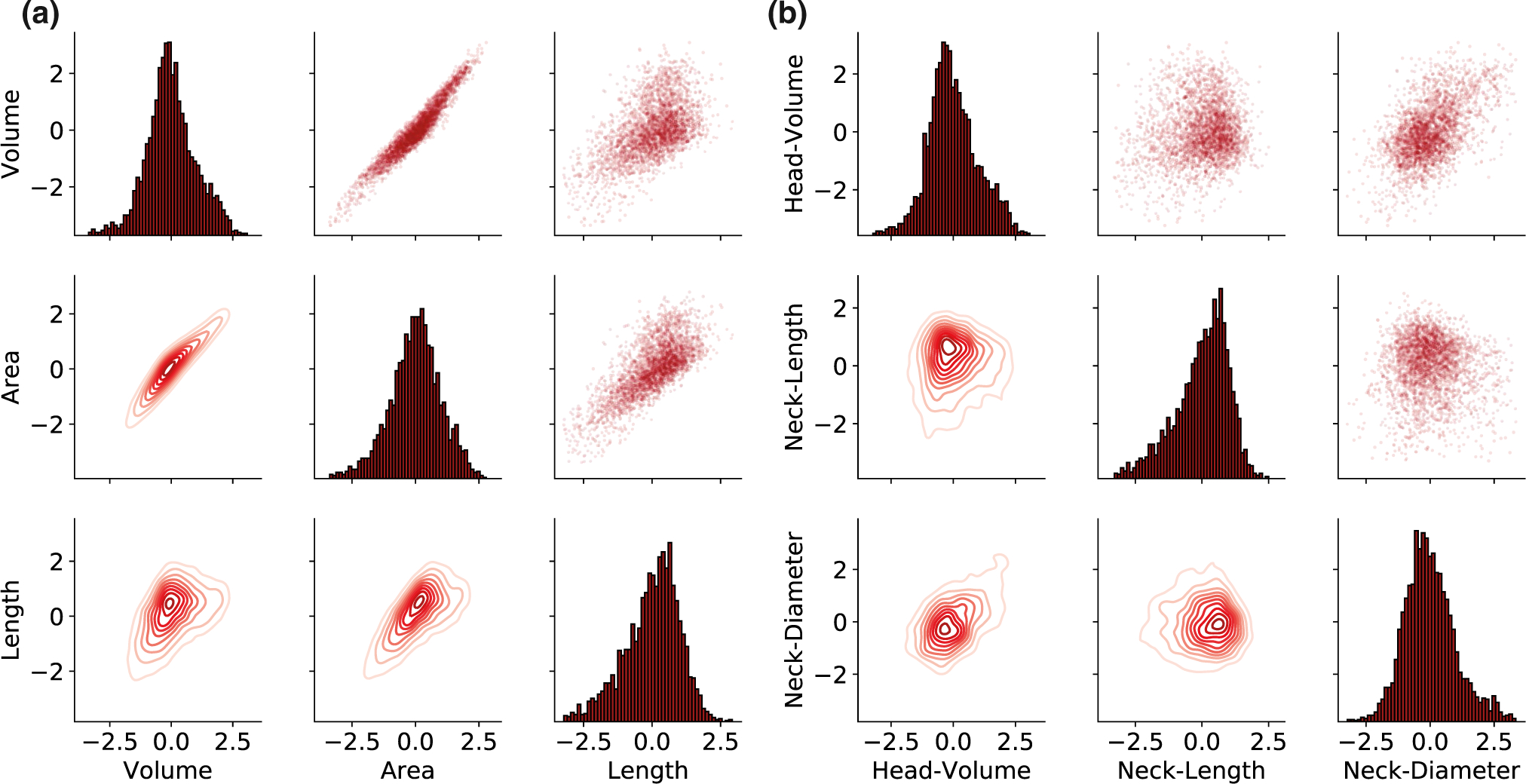
Continuous distribution of spine morphological parameters. The pair-plot presents in the upper and lower triangles the pairwise relationships of the morphological parameters of all the spines. The marginal distribution of each parameter can be shown on the diagonal. (a) For the three basic parameters of the entire spine. (b) For neck and head parameters after segmentation. The data were logarithmic z-scored and the outliers (above 3 STD) were removed
3.3 |. Correlations between spine morphological parameters
The morphological ratio between head and neck affects the electrical and biochemical isolation of the spine (Araya et al., 2006). Previous studies in living tissue have reported no correlation between spine head and neck parameters (Araya et al., 2014; Tønnesen et al., 2014). Studies in fixed tissue have found weak correlations between head volume and neck diameter in chemically fixed spines, but not in cryo-fixed spines (Arellano et al., 2007; Bartol et al., 2015; Tamada et al., 2020). We used our dataset and analysis pipeline to explore this issue with a larger number of ultrastructural reconstructed spines (Figure 5). Our results confirmed the existence of a strong correlation between head volume and neck diameter (Figure 5a, p < .001, n = 2,998), a weak negative correlation between neck diameter and neck length (Figure 5b, p < .001, n = 2,998), and a lack of a significant correlation between head volume and neck length (Figure 5c, p = .3482, n = 2,998).
FIGURE 5.
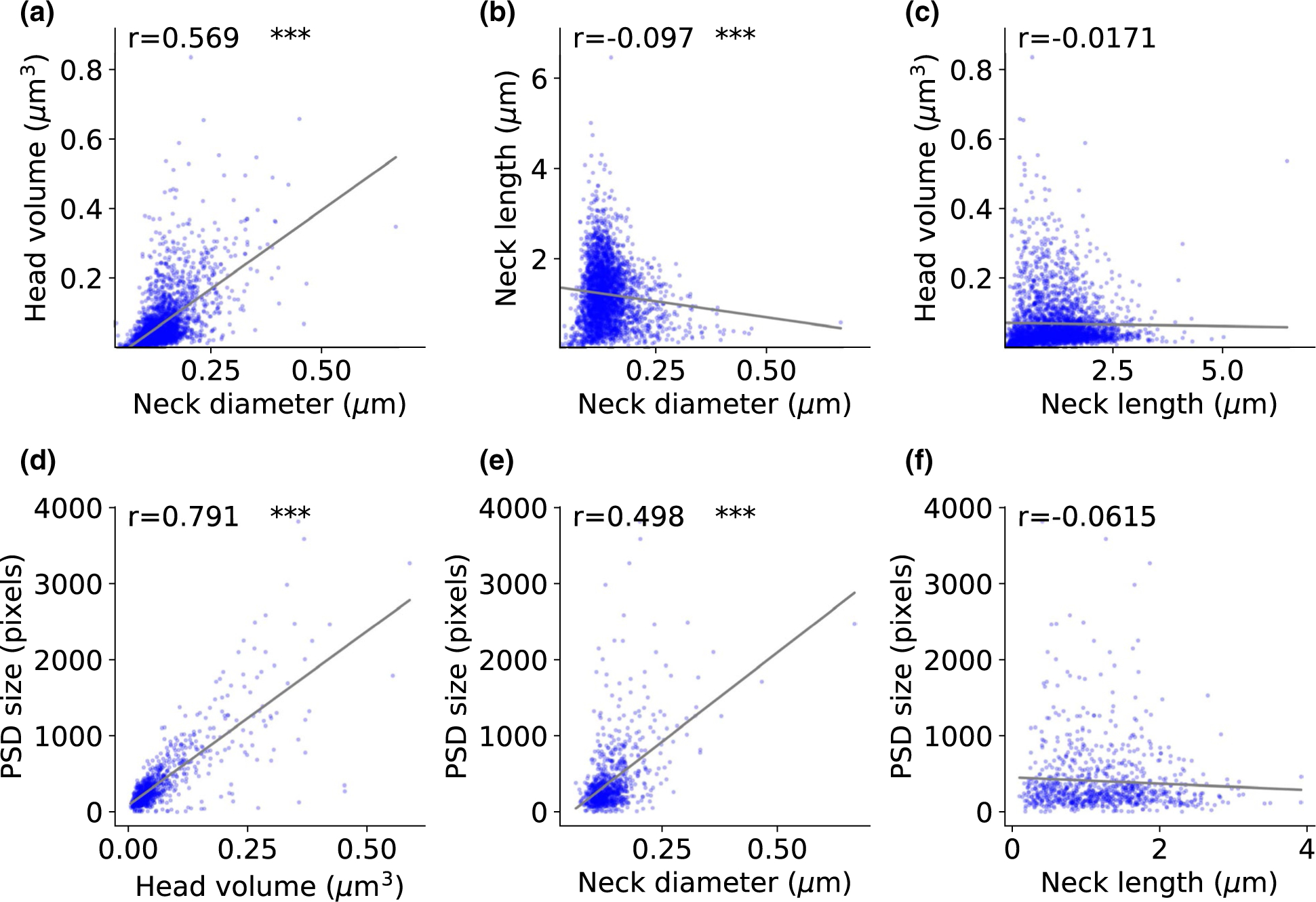
Correlation between spine head and neck morphological variables. (a-c) Correlation between head and neck morphologies (2,998 spines). (d-f) Correlation between head volume, neck length, and neck diameter and post-synaptic density size (888 spines). The correlation coefficients (Spearman) are indicated for each graph. The asterisks indicate statistical significance ***p < .001. Two-sided p-value for a hypothesis test whose null hypothesis is that the slope is zero, using Wald Test with t-distribution of the test statistic
In addition, to investigate the relationship between biological properties and physical dimensions of the spines, we analyzed the postsynaptic density (PSD) size and presence or absence of a spine apparatus (SA), as a function of the measured spine morphology. In agreement with previous studies (Arellano et al., 2007; Holler et al., 2021), the PSD size presented a long-tailed unimodal distribution (Figure 3h) and was strongly correlated with the spine head volume (Figure 5d, p < .001, n = 888). The PSD size also correlated with the spine neck diameter (Figure 5e, p < .001, n = 888), but not correlated with the spine neck length (Figure 5f, p = .0671, n = 888). We then examined the relationship between the presence of an SA and spine morphology. Spines with SA had higher head volumes and neck diameters than spines without SA (Figure 6a). We found also no clear correlation between head volume and neck length only in spines with SA or only in spines without SA (Figure 6b). Cumulative distribution functions showed a significant difference in head volume (Figure 6c, KS test p < .001) and neck diameter (Figure 6e, KS test p < .001) between spines with and without SA. Consistent with our finding that neck length and head volume are not significantly correlated (Figure 5c), we also saw no differences in neck length between the presence and absence of SA (Figure 6d, KS test p = .3677).
FIGURE 6.
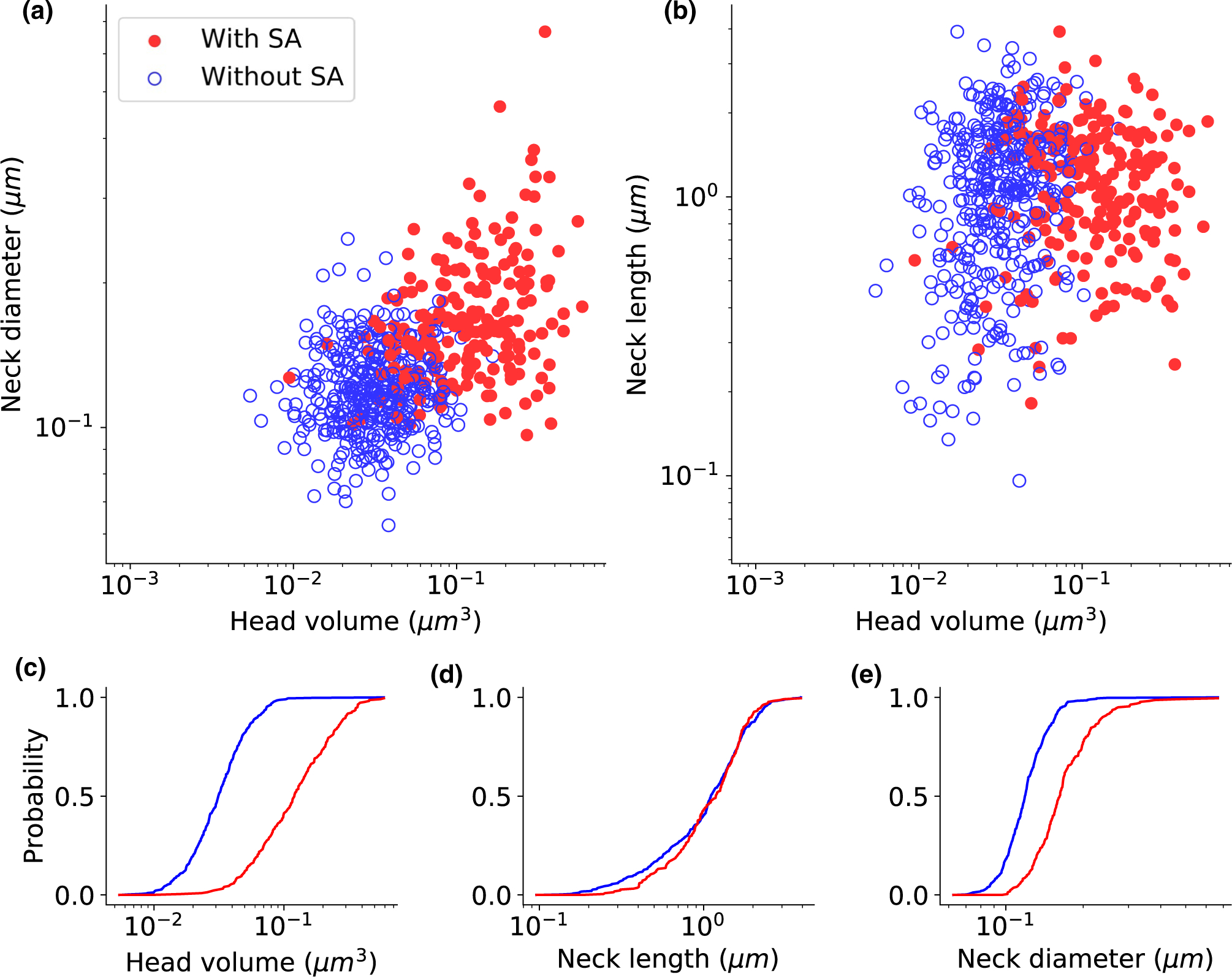
Spine apparatus is present in larger spines. Spine apparatus as a function of head volume and neck diameter (a), and head volume and neck length (b). Full red circles indicate the spine with spine apparatus, and empty blue circles indicate the spine without spine apparatus. (c-e) The empirical cumulative distribution function of the spines with spine apparatus (red) and without spine apparatus (blue). Kolmogorov–Smirnov test p-values: (c) p < .001, (d) p = .3677, and (e) p < .001. Spine apparatus indicated as “uncertain” or “N/A” in the spreadsheet were not included, resulted in 401 spines with spine apparatus, and 220 spines without spine apparatus
Finally, we examined the morphological relationship between two spines that create “dual connection,” meaning spine pair that share the same pre- and post-synaptic neurons. To determine the morphological similarity between these spines, we calculated the difference and the ratio of the morphological parameters of dual connection spines. We compared these distributions to the difference and ratio of any two spines, randomly chosen from the entire dataset. To examine whether the underlying probability distributions of the two empirical CDF curves differ, the Kolmogorov–Smirnov test was used. The differences between the morphological parameter values showed the same distribution as those found in random spines pairs (Figure 7a–c, KS test p = .5448, .7437, .0711, respectively). For neck length and neck diameter, the ratio between the dual connection spines also resembled those from random spines pairs (Figure 7e–f, KS test p = .5967, .0602). However, the ratios between head volumes in dual connection spines were significantly lower than those of two random spines (Figure 7d, KS test p = .0038). Only one of the 41 dual connection spines analyzed above arose from a branched spine, so the similarity between spine head volumes was not due to branched spines. These results are in line with previous studies that reported a correlation in head volumes between the two spines of a dual connection (Bartol et al., 2015; Dorkenwald et al., 2019; Kasthuri et al., 2015; Motta et al., 2019).
FIGURE 7.
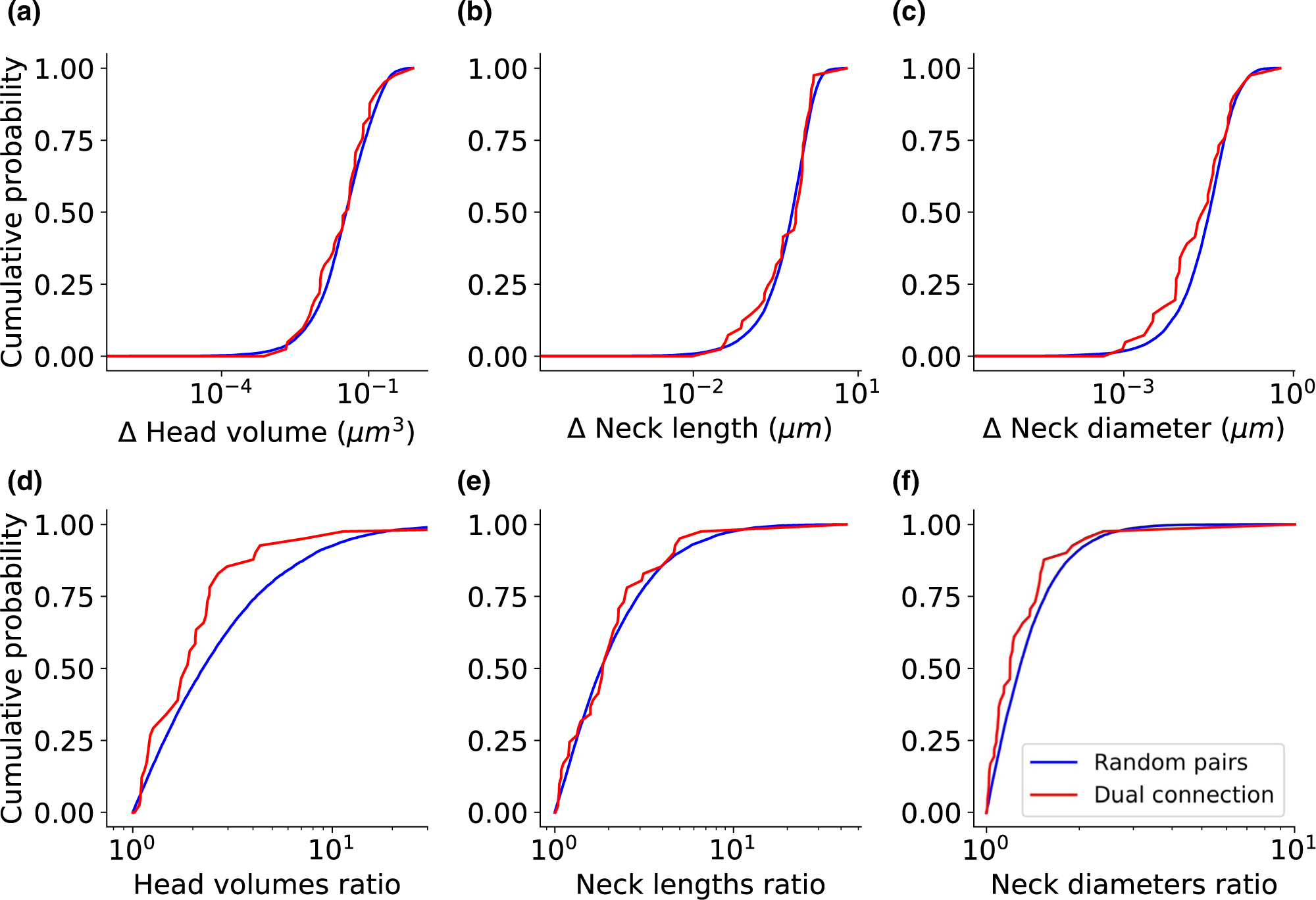
Dual connection spines have similar head volumes. The empirical cumulative distribution function of the difference between two spines (a-c) and the ratio between two spines (d-f) belong to the dual connection (red), compared to two random spines from the entire database (blue). Kolmogorov–Smirnov test p-values: (a) p = .5448, (b) p = .7437, (c) p = .0711, (d) p = .0038, (e) p = .5967, and (f) p = .0602. The dataset includes 41 dual connection pairs
4 |. DISCUSSION
Dendritic spines display a large morphological heterogeneity of head and neck dimensions. These differences likely have functional meaning, as the neck can cause a biochemical and electrical isolation between the spine head and the dendritic shaft (Yuste, 2010). Since spines regulate most excitatory communication between neurons, this diversity could enrich the computational capabilities of the brain. Here, using an objective head and neck separation algorithm, we showed that the vast majority of spines have a clear head and neck. Based on this, we developed methods to measure the spine head volume, neck length, and neck diameter. All these morphological parameters present a continuum distribution in our dataset, in agreement with previous proposals that spines do not belong to different morphological subtypes. Finally, we examined the correlation between the morphological parameters and the relationship between them and the PSD size and SA and detect correlations between spine volume and neck width, PSD size, and presence of SA, but find no correlation between neck length and head volume.
4.1 |. Objective identification of spine necks
Although the spine’s head and neck dimensions determine its electrical and chemical activity (Bell et al., 2019; Lagache et al., 2019; Segev & Rall, 1998; Yuste, 2013), the definition of head and neck and the exact border between them has been difficult in the past. Previous studies measured the head and neck manually or using algorithms with arbitrary cutoffs that required a large number of corrections by a human annotator (Arellano et al., 2007; Benavides-Piccione et al., 2002; Dorkenwald et al., 2019; Motta et al., 2019). In this study, we developed an automatic algorithm to separate between head and neck, confirming that spine neck is real and that, in the vast majority of spines, one can separate the head and neck in a statistically significant manner.
4.2 |. A continuum of spine morphologies
Given the great variety of spine morphologies, an open question in the field is whether spines belong to different morphological subtypes. The common nomenclature of Peters and Kaiserman-Abramof classified spines into three types, stubby, mushroom, and thin (Peters & Kaiserman-Abramof, 1970). Their description of stubby spines, without a well-defined neck, may be a consequence of the limited spatial resolution of optical microscopy (Tønnesen et al., 2014). Consistent with this, in our dataset “stubby” spines without a clear neck are very rare, approximately 1%. In addition, Kaiserman-Abramof’s “thin” spines were originally named after their “slender stalk,” but without taking into account the variety of neck lengths, so one could question the validity of that term. Following Peters and Kaiserman-Abramof visual classification, semi-supervised learning and a decision tree have also been used to classify spines into these same types: stubby, mushroom, and thin (Basu et al., 2018; Harris et al., 1992; Janoos et al., 2009; Rodriguez et al., 2008; Shi et al., 2014). On the other hand, unsupervised morphology-based clustering of dendritic spines from human cortical pyramidal neurons uncovered at least six separate groups of spines (Luengo-Sanchez et al., 2018).
Our analysis, using computer vision methods to measure spine necks on ultrastructural data, reveals a clear continuum distribution of the morphological parameters, without any evidence of separate subtypes (Figure 4). Statistical tests applied to these data, the same that proved the morphological difference between spine neck and heads, do not reject the unimodal hypothesis, meaning that we cannot prove the existence of distinct types of spines. This conclusion is of course limited to our dataset and our measured variables, so we cannot rule out the possibility that in different datasets, or with different morphological measurements, one could identify different subtypes of spines. The spine morphological parameters present a skewed distribution with a small number of high values (Figure 3). Also, even logarithmic-scale plot reveals a spread and non-Gaussian distributions (Figure 4). The existence of spines with extreme values in one of the morphological parameters could hint at the possible existence of distinct types of spines (for example, see the right blip in the bottom histogram in Figure 4b). Because of this, cluster analysis methods may indicate the existence of distinct spine types, even though the continuum distribution of the parameters. However, in our hands, statistical tests of the clustering, based on the bootstrap approach (Hennig & Lin, 2015; Kimes et al., 2017), and Hartigan’s dip-test of unimodality failed to verify the existence of distinct spine types. Of course, we cannot rule out that larger datasets, with more spines that have extreme morphological values, could provide statistical evidence for the existence of different subtypes of spines. Also, different morphological subtypes of spines could still exist but have overlapping morphological parameters. For example, the boundaries between spines subtypes could be blurred as a result of the dynamic morphological transition between spine types (Bourne & Harris, 2007; Harris et al., 1992; Hering & Sheng, 2001), leading to a unimodality in cluster analysis. While all these possibilities are theoretically possible, the simplest interpretation of our results that spines represent a continuum of morphologies, without any clear subtypes.
4.3 |. Functional considerations
Studying the morphological parameters of dendritic spines may shed light on their functional role. For example, the lack of correlation between head volume and neck length (Figure 5c) points out that different biological mechanisms must govern the development of the spine head and neck. As one possibility, the fact that spines could reach out to connect with axons that running close-by may dictate spine length, and could explain the lack of correlation of neck length with head size. Also, the similarity in head volume between dual connection spines, but not in neck length (Figure 7), implies different functional roles of the head and neck during synaptic plasticity. The correlation between the presence of SA and head volume was reported (Dorkenwald et al., 2019), but, in addition, here we show also a significant relationship between SA and neck diameter (Figure 6). This could be interpreted as if the large size of the head, together with a thick neck, enables the insertion of the SA from the dendritic shaft into the spine head.
Although our dataset is significantly larger than previous ones, our analysis is limited to spines from pyramidal cells from the mouse somatosensory cortex (Kasthuri et al., 2015). More studies are needed to strengthen our results, and answer whether dendritic spine morphologies are continuous or form subtypes, and the extent of correlation between morphological parameters. Future studies could expand and compare the results to other species and brain regions, particularly examining the difference between mice and humans. While EM reconstruction of spines have nanometer resolution, they reflect a fixed structure, representing snapshots of spines in morphological transition that could bias towards a misleadingly static view of spine morphology. Moreover, the fixation method could introduce confounding differences. For example, spine morphology analysis using EM after cryo-fixation revealed similar spine head volume and neck length values, but overall thinner spine necks diameter (~30% less), as compared with standard chemical fixation (Tamada et al., 2020). Because of this, super-resolution microscopy in living samples should be considered to characterize the dynamic structures of spines and tracking structure changes. Finally, analysis methods can be subject to further improvements. Current tools for morphological analysis of spines, such as SpineJ—a wavelet-based custom-made ImageJ plugin (Levet et al., 2020), enable semi-automatically measurements of the neck length, neck diameter, and head area from a 2D image. Our algorithm could also enable measuring super-resolution microscopy data of living neurons. This could provide an additional test of the morphological parameters measurements, especially comparing living tissue with compared to cryo- or chemical fixation.
As a final thought, the rich diversity of spine morphologies is likely not accidental but must enrich the neuronal circuit function. Because of this, the computational advantages of adding such complexity could be explored in models. Artificial neural networks with realistic architecture could be built, not only to model brain circuits but in addition, to explore improvements of existing computational algorithms, following a brain-inspired strategy.
ACKNOWLEDGMENTS
We thank Victor Cornejo and members of the Yuste Lab for useful advice and comments. Supported by the NINDS (R01NS110422; R34NS116740). This material is based upon work supported by, or in part by, the U. S. Army Research Laboratory and the U. S. Army Research Office under contract number W911NF-12-1-0594 (MURI). N.O. and R.Y. conceived the project. N.K. and D.B. performed experiments and N.O. and R.Y. wrote the paper. N.O., N.K. and D.B. analyzed the data. J.L. discussed results and edited the paper. R.Y. and J.L. assembled and directed the team and secured funding and resources.
Footnotes
CONFLICT OF INTEREST
The authors declare no conflict of interest.
REFERENCES
- Araya R, Jiang J, Eisenthal KB, & Yuste R (2006). The spine neck filters membrane potentials. Proceedings of the National Academy of Sciences, 103, 17961–17966. 10.1073/pnas.0608755103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Araya R, Vogels TP, & Yuste R (2014). Activity-dependent dendritic spine neck changes are correlated with synaptic strength. Proceedings of the National Academy of Sciences, 111, E2895–E2904. 10.1073/pnas.1321869111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arellano JI, Benavides-Piccione R, DeFelipe J, & Yuste R (2007). Ultrastructure of dendritic spines: Correlation between synaptic and spine morphologies. Frontiers in Neuroscience, 1, 131–143. 10.3389/neuro.01.1.1.010.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartol TM, Bromer C, Kinney J, Chirillo MA, Bourne JN, Harris KM, & Sejnowski TJ (2015). Nanoconnectomic upper bound on the variability of synaptic plasticity. eLife, 4, 1–18. 10.7554/eLife.10778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu S, Saha PK, Roszkowska M, Magnowska M, Baczynska E, Das N, Plewczynski D, & Wlodarczyk J (2018). Quantitative 3-D morphometric analysis of individual dendritic spines. Scientific Reports, 8, 1–13. 10.1038/s41598-018-21753-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell M, Bartol T, Sejnowski T, & Rangamani P (2019). Dendritic spine geometry and spine apparatus organization govern the spatio-temporal dynamics of calcium. Journal of General Physiology, 151, 1017–1034. 10.1085/jgp.201812261 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benavides-Piccione R, Ballesteros-Yáñez I, DeFelipe J, & Yuste R (2002). Cortical area and species differences in dendritic spine morphology. Journal of Neurocytology, 31, 337–346. [DOI] [PubMed] [Google Scholar]
- Berger DR, Seung HS, & Lichtman JW (2018). VAST (Volume Annotation and Segmentation Tool): Efficient manual and semi-automatic labeling of large 3D image stacks. Frontiers in Neural Circuits, 12, 1–15. 10.3389/fncir.2018.00088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berry KP, & Nedivi E (2017). Spine dynamics: Are they all the same? Neuron, 96, 43–55. 10.1016/j.neuron.2017.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourne J, & Harris KM (2007). Do thin spines learn to be mushroom spines that remember? Current Opinion in Neurobiology, 17, 381–386. 10.1016/j.conb.2007.04.009 [DOI] [PubMed] [Google Scholar]
- Cajal SRY (1904). Textura del sistema nervioso del hombre y de los vertebrados. Madrid: Nicolas Moya. [Google Scholar]
- Dorkenwald S, Turner NL, Macrina T, Lee K, Lu R, Wu J, Bodor AL, Bleckert AA, Brittain D, Kemnitz N, & Silversmith WM (2019). Binary and analog variation of synapses between cortical pyramidal neurons. bioRxiv, 2019.12.29.890319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray EG (1959). Electron microscopy of synaptic contacts on dendrite spines of the cerebral cortex. Nature, 183, 1592–1593. 10.1038/1831592a0 [DOI] [PubMed] [Google Scholar]
- Harris KM, Jensen FE, & Tsao B (1992). Three-dimensional structure of dendritic spines and synapses in rat hippocampus (CAI) at postnatal day 15 and adult ages: Implications for the maturation of synaptic physiology and long-term potentiation. Journal of Neuroscience, 12, 2665–2705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartigan JA, & Hartigan PM (1985). The dip test of unimodality. Annals of Statistics, 13, 70–84. [Google Scholar]
- Hennig C, & Lin CJ (2015). Flexible parametric bootstrap for testing homogeneity against clustering and assessing the number of clusters. Statistics and Computing, 25, 821–833. 10.1007/s11222-015-9566-5 [DOI] [Google Scholar]
- Hering H, & Sheng M (2001). Dentritic spines: Structure, dynamics and regulation. Nature Reviews Neuroscience, 2, 880–888. 10.1038/35104061 [DOI] [PubMed] [Google Scholar]
- Holler S, Köstinger G, Martin KAC, Schuhknecht GFP, & Stratford KJ (2021). Structure and function of a neocortical synapse. Nature, 591, 111–116. [DOI] [PubMed] [Google Scholar]
- Janoos F, Mosaliganti K, Xu X, Machiraju R, Huang K, & Wong STC (2009). Robust 3D reconstruction and identification of dendritic spines from optical microscopy imaging. Medical Image Analysis, 13, 167–179. 10.1016/j.media.2008.06.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorstad A, Blanc J, & Knott G (2018). NeuroMorph: A software toolset for 3D analysis of neurite morphology and connectivity. Frontiers in Neuroanatomy, 12, 1–12. 10.3389/fnana.2018.00059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorstad A, Nigro B, Cali C, Wawrzyniak M, Fua P, & Knott G (2014). NeuroMorph: A toolset for the morphometric analysis and visualization of 3D models derived from electron microscopy image stacks. Neuroinformatics, 13, 83–92. 10.1007/s12021-014-9242-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasthuri N, Hayworth KJ, Berger DR, Schalek RL, Conchello JA, Knowles-Barley S, Lee D, Vázquez-Reina A, Kaynig V, Jones TR, Roberts M, Morgan JL, Tapia JC, Seung HS, Roncal WG, Vogelstein JT, Burns R, Sussman DL, Priebe CE, … Lichtman JW (2015). Saturated reconstruction of a volume of neocortex. Cell, 162, 648–661. 10.1016/j.cell.2015.06.054 [DOI] [PubMed] [Google Scholar]
- Kimes PK, Liu Y, Neil Hayes D, & Marron JS (2017). Statistical significance for hierarchical clustering. Biometrics, 73, 811–821. 10.1111/biom.12647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagache T, Jayant K, & Yuste R (2019). Electrodiffusion models of synaptic potentials in dendritic spines. Journal of Computational Neuroscience, 47(1), 77–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Turner N, Macrina T, Wu J, Lu R, & Seung HS (2019). Convolutional nets for reconstructing neural circuits from brain images acquired by serial section electron microscopy. Current Opinion in Neurobiology, 55, 188–198. 10.1016/j.conb.2019.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levet F, Tønnesen J, Nägerl UV, & Sibarita JB (2020). SpineJ: A software tool for quantitative analysis of nanoscale spine morphology. Methods, 174, 49–55. 10.1016/j.ymeth.2020.01.020 [DOI] [PubMed] [Google Scholar]
- Loewenstein Y, Yanover U, & Rumpel S (2015). Predicting the dynamics of network connectivity in the neocortex. Journal of Neuroscience, 35, 12535–12544. 10.1523/JNEUROSCI.2917-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luengo-Sanchez S, Fernaud-Espinosa I, Bielza C, Benavides-Piccione R, Larrañaga P, & DeFelipe J (2018). 3D morphology-based clustering and simulation of human pyramidal cell dendritic spines. PLoS Computational Biology, 14, e1006221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motta A, Berning M, Boergens KM, Staffler B, Beining M, Loomba S, Hennig P, Wissler H, & Helmstaedter M (2019). Dense connectomic reconstruction in layer 4 of the somatosensory cortex. Science, 366(6469), eaay3134. 10.1126/science.aay3134 [DOI] [PubMed] [Google Scholar]
- Pchitskaya E, & Bezprozvanny I (2020). Dendritic spines shape analysis—Classification or clusterization? Perspective. Frontiers in Synaptic Neuroscience, 12, 1–11. 10.3389/fnsyn.2020.00031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters A, & Kaiserman-Abramof IR (1970). The small pyramidal neuron of the rat cerebral cortex. The Perikaryon, dendrites and spines. The American Journal of Anatomy, 127, 321–355. 10.1002/aja.1001270402 [DOI] [PubMed] [Google Scholar]
- Rochefort NL, & Konnerth A (2012). Dendritic spines: From structure to in vivo function. EMBO Reports, 13, 699–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez A, Ehlenberger DB, Dickstein DL, Hof PR, & Wearne SL (2008). Automated three-dimensional detection and shape classification of dendritic spines from fluorescence microscopy images. PLoS ONE, 3(4), e1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schelling B, & Plant C (2020). Dataset-Transformation: Improving clustering by enhancing the structure with DipScaling and DipTransformation. Knowledge and Information Systems, 62, 457–484. 10.1007/s10115-019-01388-5 [DOI] [Google Scholar]
- Segev I, & Rall W (1998). Excitable dendrites and spines: Earlier theoretical insights elucidate recent direct observations. Trends in Neurosciences, 21, 453–460. 10.1016/S0166-2236(98)01327-7 [DOI] [PubMed] [Google Scholar]
- Shapira L, Cohen-Or D, & Shamir A (2008). Consistent mesh partitioning and skeletonisation using the shape diameter function. The Visual Computer, 24, 249–259. 10.1007/s00371-007-0197-5 [DOI] [Google Scholar]
- Shi P, Huang Y, & Hong J (2014). Automated three-dimensional reconstruction and morphological analysis of dendritic spines based on semi-supervised learning. Biomedical Optics Express, 5, 1541. 10.1364/BOE.5.001541 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliasacchi A, Alhashim I, Olson M, & Zhang H (2012). Mean curvature skeletons. Computer Graphics Forum, 31, 1735–1744. 10.1111/j.1467-8659.2012.03178.x [DOI] [Google Scholar]
- Tamada H, Blanc J, Korogod N, Petersen CC, & Knott GW (2020). Ultrastructural comparison of dendritic spine morphology preserved with cryo and chemical fixation. eLife, 9, 1–15. 10.7554/eLife.56384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tønnesen J, Katona G, Rózsa B, & Nägerl V (2014). Spine neck plasticity regulates compartmentalization of synapses. Nature Neuroscience, 17(5), 678–685. 10.1038/nn.3682 [DOI] [PubMed] [Google Scholar]
- Yuste R (2010). Dendritic spines. Cambridge: MIT press. [Google Scholar]
- Yuste R (2013). Electrical compartmentalization in dendritic spines. Annual Review of Neuroscience, 36, 429–449. 10.1146/annurev-neuro-062111-150455 [DOI] [PubMed] [Google Scholar]
- Zhang C, & Chen T (2001). Efficient feature extraction for 2D/3D objects in mesh representation. IEEE International Conference on Image Processing, 3, 935–938. [Google Scholar]


