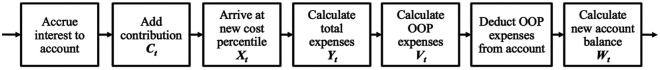Abstract
Background. Health savings accounts (HSAs) are tax-advantaged savings accounts available only to households with high-deductible health insurance. This article provides initial answers to two questions: 1) How should a household budget for its annual HSA contributions? 2) Do current contribution limits provide households with the flexibility to use HSAs efficiently? To answer these questions, we formulate the household’s problem as one of determining a contribution strategy for minimizing total expected discounted medical costs. Methods. We use the 2002–2014 Medical Expenditure Panel Survey to develop a novel data-driven model for forecasting a household’s health care costs based on its current cost percentile and other characteristics. A dynamic policy, in which the contribution each year brings the HSA balance up to a household-specific threshold, is derived. This is compared to a simpler static policy in which the target HSA balance is simply the plan’s out-of-pocket maximum, with contributions in any year capped by a limit. Results. We find that: 1) the dynamic policy can save a household up to 19% in costs compared to the static one that is a proxy for typical contribution behavior; and 2) the recommended contribution amounts for 9% to 11% of households in a given year materially exceed what is currently allowed by the federal government. Conclusions. The dynamic policy derived from our data-analytic framework is able to unlock significant tax savings for health care consumers. To allow all households to use HSAs in a tax-efficient manner, a two-tiered contribution policy is needed: Allow unlimited contributions up to some balance, and then impose restrictions thereafter. The resulting impact on overall tax receipts is estimated to be well below what is currently allowed by legislation.
Keywords: consumer-driven health care, health care cost forecasting, health savings accounts, HSA
Health savings accounts (HSAs) are tax-advantaged savings vehicles available to people enrolled in high-deductible health plans (HDHPs), health plans with higher deductibles and therefore greater consumer cost-sharing than other plans. HSAs allow annual pretax contributions and tax-free withdrawals to pay for qualified out-of-pocket (OOP) medical expenses. The unused HSA balance carries over year to year, and the funds may be invested and accrue interest over time. HSAs were introduced by the 2003 Medicare Modernization Act to complement HDHPs as a strategy for curbing rising health care costs. The pairing of HDHPs and HSAs was based on the hypothesis that assigning individuals the responsibility for a greater portion of their health care costs may incentivize them to be more prudent in their health care spending. Each year, HSA account holders must decide how much money to contribute to their HSA, up to an annual contribution limit set by the federal government.
Like most health plans, HDHPs are characterized by the following parameters: 1) the consumer must cover annual costs up to a certain deductible; 2) the consumer must cover a coinsurance rate (percentage) of costs above the deductible; and 3) the total annual OOP payments is capped by some OOP maximum. HDHPs are generally distinguished from other plans by their higher deductibles and lower premiums. In particular, HSA-qualifying HDHPs must meet a federally mandated minimum deductible level ($1,300 for individuals, $2,600 for families in 2017) and maximum OOP max value ($6,550 for individuals, $13,100 for families in 2017). These plans may be adopted either on an individual or family basis (though each family member must carry their own individual HSA), and plan parameters vary widely. For example, for family plans in 2017, the proportion of plans with deductibles in the ranges of {$2,000-$2,999, $3,000-$3,999, $4,000-$4,999, $5,000-$5,999, $6,000+} were {13%, 35%, 15%, 14%, 23%}. 1
While the merit of HDHPs as a health care cost containment strategy continues to be the subject of debate, 2 HDHP/HSA adoption has grown rapidly since their introduction, and they have commanded the attention of employers as a cost-curbing mechanism. HDHP plan enrollment has grown from about 1 million in 2005 to over 20 million in 2016, 3 and from 8% of the workforce in 2009 to 24% in 2015. 4 Additionally, a 2018 survey found that 70% of large employers offered at least one HDHP, up from 60% just one year prior. 5
In the face of this rapid adoption, a key conclusion of a recent comprehensive review of HDHPs is that there is a lack of tools to assist consumers in decision making with regard to such plans. 6 To fill this gap, this article addresses a key question for HSA adopters: How should a household budget for its HSA contributions from year to year? To our knowledge, this is the first article to examine this question. Additionally, the article also seeks to address a related question faced by policy makers: Do current contribution limits provide all households with the flexibility to use HSAs efficiently, and if not, which alternative should be adopted by policy makers?
Regarding the first question, we model a household as relying upon its HSA to cover OOP expenses over a 30-year period, and therefore seeking to balance excessive pretax HSA contributions against posttax expenditures due to insufficient HSA balance. We hence seek the contribution amount that minimizes the household’s total expected discounted expenditures throughout the contribution period. We consider two types of policies and use simulations to evaluate their relative performance.
Regarding the second question, the federal government imposes an annual contribution limit on both individuals and households. i We assess whether the current limits enable households to adhere to the best performing contribution policy examined in the first question. If not, we examine how the government should relax this limit, and whether the resulting impact on tax receipts would exceed what is currently allowed.
Analyzing the questions above requires a model for the evolution of household medical expenditures from year-to-year. We develop a cost evolution model for this purpose whose performance is competitive with leading commercial models. While there is considerable literature on modeling ii health care costs, 11 a novel aspect of our approach is to model the transitions of a household’s health care cost percentile from one year to the next rather than model actual costs directly. We discuss the advantage of this approach in Methods.
Methods
Data Description
Our dataset is from the Medical Expenditure Panel Survey, 12 a set of large-scale surveys of families and individuals drawn from a nationally representative subset of households in the United States. It is based on an overlapping panel design in which data on medical expenditures (and other information) are collected for two consecutive calendar years from each household. Henceforth, panel will refer to year pair . We limited our dataset to individuals who were in-scope iii throughout the survey period, and for whom the relevant covariate values (described below) were present. This excluded less than 10% of all individuals.
As the unit of analysis, we used Health Insurance Eligibility Units (HIEUs), “sub-family relationship units constructed to include adults plus those family members who would typically be eligible for coverage under the adults’ private health insurance family plans.” For panel , let be the cost percentile transition for the ith HIEU. Collecting these percentile pairs across panels produced the dataset used to calibrate our cost evolution models.
We divided the dataset into three samples: Training (Panels 7 to 14, corresponding to year pairs {2002, 2003} through {2009, 2010}), validation (Panels 15 and 16, corresponding to year pairs {2010, 2011} and {2011, 2012}), and test (Panels 17 and 18, corresponding to year pairs {2012, 2013} and {2013, 2014}). The training set was used to estimate all model parameters described below, and exploratory analyses were performed on the validation set to arrive at the chosen model. The chosen model was then refit to the combined training and validation datasets, and then used to predict the second year costs in the test set. All data preparation and model estimation was performed using SAS.
We develop two versions of the cost evolution model described further below: basic and expanded. The basic version uses a small set of covariates and is well suited for long-term planning as it does not require modeling the evolution of a large set of demographic and clinical variables. The expanded version includes a broader set of covariates and is well suited for generating more accurate short-term predictions that could have other applications as well. The covariates are the following:
Basic model: Household size, percentage of individuals within the HIEU of each insurance type (private, public, private + public, uninsured*). The values marked with an asterisk (*) denote the baseline values within each group.
Expanded model: This model additionally includes the following: % of individuals within the household of each sex (male, female*), age group (0-19, 20-39*, 40-59, 60+), race (White*, Black, American Indian/Alaskan Native, Asian/Native Hawaiian/Pacific Islander, Multiple races), perceived health status (excellent*, very good, good, fair, poor), perceived mental health status (excellent*, very good, good, fair, poor), region (West*, East, South, North), % of individuals not receiving help or supervision with instrumental activities of daily living (IADLs), % of individuals not receiving help or supervision with activities of daily living (ADLs), % of individuals without any functional limitations.
Overall, our 2002–2014 dataset includes 176,205 individuals belonging to 90,359 HIEUs. The final training, validation, and test sets contained 57,701, 15,818, and 16,840 HIEU pairs, respectively.
Problem Formulation
In year t, a HSA-eligible plan can be characterized by three parameters: A deductible , a coinsurance rate c (percentage of expenses exceeding covered by the household), and a maximum limit on household OOP expenses for that year.
The household begins each year t in health state with initial account balance (with initial values and at the beginning of year 1). The account balance increases by the investment return rate and the household’s pretax contribution is added to the account. The household then transitions to a new health state , incurs actual total expenses , and is responsible for OOP expenses , which are deducted from the savings account. Therefore,
| (1) |
| (2) |
If the current account balance is insufficient to cover these expenses (i.e., ), the household must pay the difference directly. The difference is paid with after-tax dollars, so if the marginal tax rate for the household is , the pretax value of this payment is , where . In each year, the deductible and OOP maximum values are increased by the health care cost inflation rate : and . This process repeats in year through year , the number of years in the contribution period. These dynamics are illustrated in Figure 1.
Figure 2.
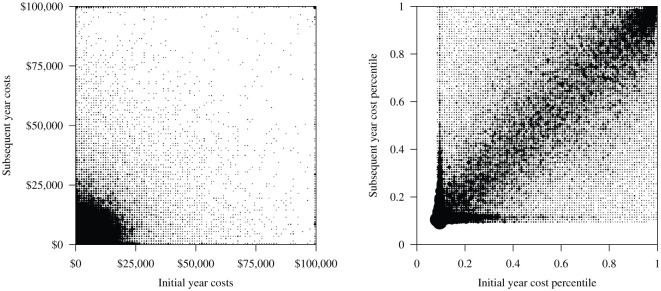
Scatter plots of year to year cost transitions. X-axis represents costs in year and the y-axis represents year for . The size of each point is proportional to the number of households in each group. Left: Actual costs (truncated at $100,000); correlation between a households costs in two consecutive years is 0.39; Right: Cost percentiles; correlation 0.70. Roughly 9% of households have zero costs, as reflected in the plot.
A household has the freedom to select a contribution amount for years , and the most economic choice is the one that minimizes the total expected discounted cost (in pretax dollars):
| (3) |
where is the household’s discount factor and is the household’s discount rate.
The health state is the percentile for the household’s total medical costs in year , and is a measure of how costly the household is when compared to all other households in the nation. is a continuous random variable , where and represent the least costly (healthiest) and most costly (sickest) households, respectively. The costs represent total payments to medical providers by the health plan and the household. The evolution of and from year to year are driven by the cost evolution model that is described later.
To select the investment return rate for the HSA, we observe that the 30-year annualized rates of return on the 10-year US treasury note and the S&P 500 index are about 6% and 10%, respectively. 13 A HSA adopter is likely to invest in a moderately conservative long-term asset allocation, so we choose a rate of 8% corresponding to a 50/50 split between equities and treasuries. We also choose a discount rate iv of This represents the return on money outside of the tax-advantaged HSA, assuming a marginal tax rate of 25%. Finally, the health care cost inflation rate is estimated to be 3.4%, based on a statistical analysis presented later.
Candidate Contribution Policies
We investigate two types of contribution policies in this article. The first is a dynamic policy that optimizes (3) over a long time horizon ( ). It has a closed form solution that can be used to approximate the optimal policy for the finite horizon setting. The second policy is a simpler static one that strives to cover the OOP maximum in each year, subject to an annual contribution limit.
Dynamic Policy
The contribution in each period depends on the current account balance and health cost percentile . The idea is to maintain the HSA balance at a level that is no less than some household-specific threshold , hence the contribution that is required in year is
| (4) |
Intuitively, should be set high enough so that it will cover the household’s OOP expenditures in year with a specific desired probability. The desired probability level strikes a balance between the benefit of having sufficient funds to cover OOP costs against the cost of excessive contributions. This level is mathematically determined from the calculations in the supplementary material:
| (5) |
Static Policy
The household contributes the amount that brings its HSA balance up to the OOP maximum in a given year, capped by some annual maximum contribution value :
| (6) |
The rationale is that in the absence of a personalized predictive cost model, a reasonable strategy would be to strive to cover all OOP expenses from within the HSA. This is intuitively more conservative than the dynamic policy. The annual maximum contribution value may represent the government’s maximum allowable annual contribution or other budgetary constraints.
Cost Evolution Model
Our model for producing year to year forecasts of household health care costs uses as predictors: 1) the household’s health care costs in the prior year and 2) demographic information and a set of self-reported health variables v described in Data Description. The use of prior year costs is based on evidence that their use alone can perform almost as well as models that employ a broader set of clinical/demographic variables.7,9,18,19 Furthermore, using more than one year of prior information has been shown to add little predictive power. 20
Rather than directly predict cost or some transformation of it, a novel aspect of our approach is to model the transitions of a household’s health care cost percentile from one year to the next. vi The rationale for modeling percentiles rather than actual costs is apparent from Figure 2: The presence of a linear association among cost percentiles in two consecutive years is apparent in the right panel. Indeed, the correlation among consecutive year percentile values is 0.70, much higher than the corresponding correlation among actual costs in consecutive years (0.39).
Figure 1.
A schematic description of the sequence of events within a period .
Specifically, we propose a four-stage model for evolving costs: 1) a binary outcome model for the event that a household incurs zero cost in the current year (a nonnegligible percentage of households have zero cost in a given year); 2) conditional on having positive costs, a continuous parametric model for the household’s cost percentile; 3) a mapping from cost percentile to actual cost; and 4) inflation adjustment of actual costs from year to year.
Some of the models can incorporate either the basic or the expanded covariates described in Data Description. We report out-of-sample performances for both versions, and use the basic one to study the two key questions.
Zero Cost Model
In any given year, a fraction of households incur zero cost. We employ logistic regression to estimate the probability that a household with prior year cost percentile and covariates will have zero cost in the current year. The independent variables used in the model are , , and . The last variable is included because exploratory analyses suggest a quadratic relationship between and .
Percentile Transitions
Conditional on incurring positive costs in year , the household’s cost percentile is
| (6) |
where is the percentile of the cost distribution conditional on having positive costs. To model a household’s transition from cost percentile in year to in year , we use mixtures of truncated Gamma distributions. Since the Gamma distribution is nonnegative while percentile values fall in the range of , it is necessary to truncate the distribution to . The truncated probability density function is
| (7) |
where and are the density and cumulative distribution functions for the Gamma distribution with shape and scale parameters .
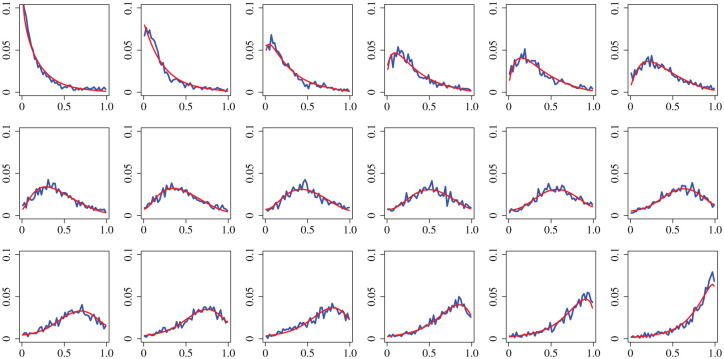
The rationale for the Gamma distribution can be seen from Figure 3. Each subplot shows the empirical probability density of conditional on a particular value of , that is, . For example, the upper-left plot is conditional on , and the one to its right is conditional on , and so forth. The smooth fits overlayed onto each plot represent our fitted mixture model, which closely resembles the empirical density. Incidentally, previous studies have found that Gamma mixtures are good for modeling health care costs.22,23
Figure 3.
Plots of the empirical probability density for . The upper-left plot is , and the one to its right is , and so forth. The lower-right plot is . The x-axis is and the y-axis is the probability density. The fitted mixture Gamma distributions are overlayed.
The mixture we use has to accommodate both the positive and negative skews on display in Figure 3. Since the skew of a Gamma distribution is positive, its reflection has negative skew. We therefore use a mixture of a truncated Gamma and a reflected truncated Gamma distribution to model cost percentile transitions:
| (8) |
Setting recovers a pure truncated Gamma distribution, while setting yields a reflected one. Values in between these two extremes provide varying degrees of skew. Given that the skew of the plots in Figure 3 shifts from positive to negative as increases, we model as a linear function of . The shape and scale parameters and are modeled as linear functions of the same independent variables used in the zero cost model.
Distribution of Nonzero Expenditures
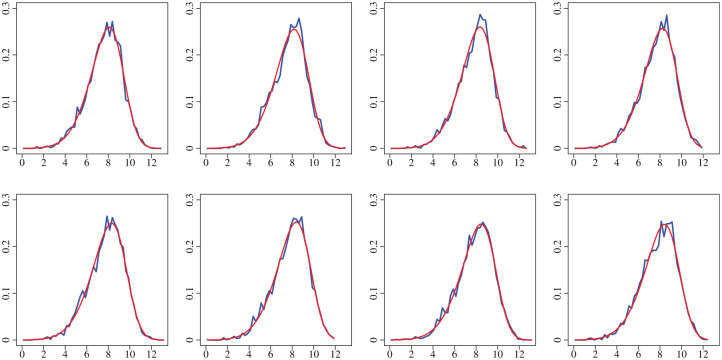
To map the conditional percentile in year to a corresponding dollar value, we need a model for the distribution of positive costs. Figure 4 displays the empirical probability densities for log household health care costs conditional on positive spending. A fitted skew-normal distribution is overlayed onto each subplot, providing a remarkably good visual fit. We therefore model the positive costs with a log-skew-normal distribution (that is, its logarithm has a skew-normal distribution).
Figure 4.
Plots of the empirical probability density for the logarithm of the nonzero household expenditures. The upper left plot is for the nonzero costs in the second year of panel 7, and the bottom right is for panel 14. The x-axis is log(Yt) and the y-axis is the probability density. Details of the panel data are given in Data Description under Methods. Fitted skew-normal distributions are overlayed.
Let us denote the cumulative distribution function of the log-skew-normal distribution for positive costs in year as , where is a collection of three parameters that define the skew-normal distribution. The inverse function of therefore maps to the corresponding actual cost
| (9) |
Cost Parameter Evolution and Inflation Estimation
For planning over long horizons, we need to account for the evolution of costs from year to year, including inflation. We therefore require a model for the evolution of the parameters in over time. Exploratory analyses suggest that the maximum likelihood estimate for the components in increase linearly from year to year. We therefore model each component of linearly in time.
To estimate the health care cost inflation rate , in each year of the data, the households were sorted into 100 equally sized bins by expenditure. For the jth bin and the tth year, we computed the mean expenditure for the bin. We then fitted the linear model to the data. The estimated value for is 3.4%.
Evaluation of Model Performance
We test the performance of our cost evolution model against ones employed in industry. The comparative studies by the Society of Actuaries24,25,26 report performances for these models in terms of out-of-sample (prospective) and mean absolute prediction error (MAPE). vii We therefore evaluate the accuracy of our model’s cost prediction for household in year ,
| (10) |
using the same metrics for comparison. We also calculate the predictive ratio, the ratio of the sum of predictions divided by the sum of actual expenditures. For , higher values are better, while for MAPE, lower values are better, and for predictive ratio, values closest to 1 are best. In order to limit the impact of outliers, we adopt the approach used in the comparative studies to truncate the forecast year expenditure values at $100,000 and $250,000.
Recall that measures how much variance a model (linear regression or otherwise) explains relative to the straw rule of using the average response as the one-size-fits-all prediction. For our model, we report , MAPE and predictive ratio on the out-of-sample data in the 2013–2014 test panels. Since the predictions are made for household observations that were not used to develop the model, they are not sensitive to overfitting by complex models the way that their in-sample counterparts are.
Evaluation of Contribution Policies
To compare the performances of the static and dynamic policies, we simulate the total expected discounted cost under each of these policies over a 30 year contribution period.
The results are calculated for an HSA-eligible family plan with a $3,500 deductible, $12,500 OOP maximum, and 20% coinsurance rate. viii We focus on family plans because individual and family plans have different federal requirements on their HDHP parameters (minimum deductible, maximum OOP max). As such, we assume a family of size of 2.8 (the average size of family units of 2 or more individuals). ix We further restrict attention to private (employer-sponsored) insurance holders, as this is the population most likely to use HDHPs, and therefore we assume all participants are covered by private health insurance.
Since the health care inflation rate and investment return rate are really time-varying random variables, we try to account for this qualitatively by using a basic random walk to capture their evolution over time: In each simulation of the 30-year contribution period, we randomly sample initial values for each of these parameters from within a range of ±50% of the default ( , ). Then in each year, each parameter is either increased by 5%, decreased by 5%, or left unchanged, with equal chance for each outcome.
The policies that we considered are the following: 1) dynamic policy; 2) static policy with annual contribution limit of $2,000 (static $2,000); 3) static $4,000; and 4) static $6,450. x We use the static $2,000 policy as the comparison benchmark because it is close to the median annual contribution for HSAs with nonzero account balances, 27 and as such serves as a proxy for common HSA contribution behavior. Household costs are simulated using the basic model because modeling the evolution of household covariates in the expanded model is beyond the scope of this article. All computations were performed in R 3.3.2.
We also perform sensitivity analyses on the results as different parameters are varied. First, we focus on the parameters of the HDHP that vary the most in the marketplace. Specifically we examine the nine pair-wise combinations of deductible values ($2,500, $3,500, $4,500) with OOP maximum values ($7,500, $10,000, $12,500). xi Second, we separately assess sensitivity to the discount rate by examining three discount rate values (4%, 6%, 8%).
Assessment of Tax Impact and Federal Contribution Limit
To determine if adopting the dynamic policy would lead to total contribution amounts exceeding what the federal contribution limit allows for over 30 years, we examine the distribution of inflation-adjusted contributions over this timeframe. To take a conservative approach in this analysis, we focus on households on the high end of the contribution spectrum. Specifically, we assume an initial cost percentile of and the highest marginal tax rate of 40%. We also take the highest deductible ($4,500) and OOP maximum ($12,500) values from our sensitivity analysis. These parameter choices yield the highest consumer cost burden, which requires the highest levels of HSA contributions. If the inflation-adjusted sum is less than what is allowed, then the dynamic policy’s long-term tax impact will be within what is currently budgeted by legislation.
We also analyze the proportion of annual contributions that exceed the federal annual limit. A high proportion would indicate that the current federal limit needs to be raised to enable households to take full advantage of the dynamic policy. We perform this analysis using our default parameters of deductible ($3,500) and OOP maximum ($12,500). For this analysis, using $3,500 rather than $4,500 represents a more conservative approach, since it leads to a lower proportion of limit-exceeding contributions.
Results
Performance of Cost Evolution Model
Table 1 compares our basic and expanded models to the commercial models detailed in the comparative studies.24–26 On the basis of , we see that our parsimonious models are superior to those in the first study. 24 Compared to the more sophisticated models evaluated in the other two studies, our models’ performances are in the middle of the range when truncation is applied at $250,000, and are at the high end when truncation applied at $100,000. Of course, for our HSA application, it suffices to truncate at the much lower level of the OOP maximum. On the basis of MAPE, our models’ performances are at the better end of the range in the comparison studies.
Table 1.
Out-of-Sample Model Performance Comparison
| Model | Cap at $250,000 | Cap at $100,000 | |
|---|---|---|---|
| R 2 | Expanded model | 23.9% | 30.3% |
| Basic model | 22.0% | 27.6% | |
| Methods in (24) | N/A a | 14.0% to 19.8% | |
| Methods in (25) | 20.5% to 29.1% | 21.5% to 33.1% | |
| Methods in (26) | 11.9% to 27.7% b | N/A a | |
| MAPE | Expanded model | 79.0% | 78.1% |
| Basic model | 80.0% | 79.1% | |
| Methods in (24) | N/A a | N/A c | |
| Methods in (25) | 78.3% to 86.6% | 76.1% to 85.2% | |
| Methods in (26) | 89.1% to 107.5% | N/A a | |
| Predictive ratio | Expanded model | 97.8% | 101.8% |
| Basic model | 96.1% | 100.1% |
MAPE, mean absolute prediction error
Not reported in this study.
Results based on out-of-the-box models without further recalibration.
MAPE values in this study were not normalized to a relative scale and were therefore not comparable.
Performance of Contribution Policies
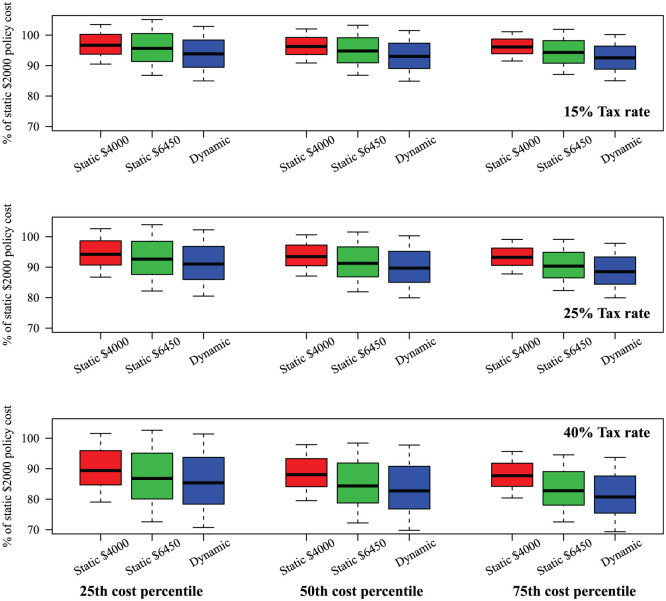
Figure 5 presents boxplots representing the costs of the static $4,000, static $6,450, and the dynamic policies as a percentage of the cost of the static $2,000 policy. Each boxplot summarizes the distribution of outcomes across 10,000 simulations of the 30-year contribution period. The columns represent initial cost percentile ( ) values of 0.25, 0.50 and 0.75, while the rows represent marginal tax rates of 15%, 25%, and 40%. Figures 6 and 7 present the results of the sensitivity analysis on plan parameters and discount rate. Figure 8 shows how the mean total discounted costs for the static $2,000 and dynamic policies vary with and with tax rate. The main qualitative results are the following:
Figure 5.
Boxplots of the expected discounted costs for the static policies with contribution limits of $4,000 and $6,450, and the dynamic policy. Costs are expressed as % of the cost of the static $2,000 policy. Columns: The left, middle, and right columns display results for the 25th, 50th, and 75th initial cost percentiles , respectively. Rows: The top, middle, and bottom rows represent marginal tax rates of 15%, 25%, and 40%, respectively.
Figure 6.
Sensitivity analysis to changes in health plan parameters. Other parameters held at: Initial cost percentile , 25% tax rate. Columns: The left, middle, and right columns displays results for deductible values of $2,500, $3,500, and $4,500, respectively. Rows: The top, middle, and bottom rows represent OOP maximum values of $7,500, $10,000, and $12,500, respectively.
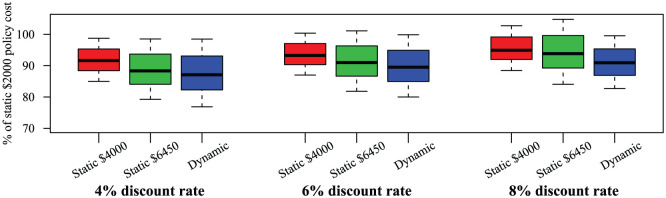
Figure 7.
Sensitivity analysis to changes in discount rate. Other parameters held at: Initial cost percentile , 25% tax rate, $3,500 deductible, $12,500 OOP maximum.
Figure 8.
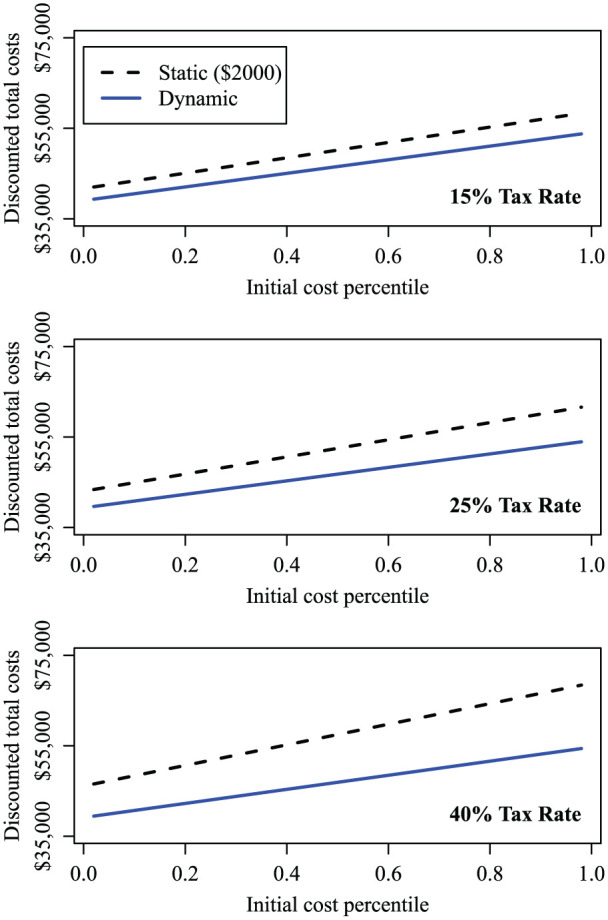
Mean discounted total costs of the static $2,000 policy and the dynamic policy, as tax rate and initial cost percentile vary.
Both the dynamic and static $6,450 policies consistently outperform the static $2,000 one. For example, at a marginal tax rate of 40% and , the dynamic policy costs 19% less than the static $2,000 one (based on median performance), with the static $6,450 policy not far behind (Figure 5).
The dynamic policy has just a moderate edge over the static $6,450 one, around 2 to 3 percentage points lower based on median performance (Figure 5).
The cost advantage of the dynamic and static $6,450 policies over the static $2,000 ones rises with marginal tax rate. For example, at , for marginal tax rates of 15%, 25%, and 40%, the dynamic policy is about 7%, 10%, and 17% less costly than the static $2,000 policy, respectively, based on median performance (Figure 5).
The advantage the dynamic policy has over the static $2,000 one is not sensitive to the parameters that define the HDHP. Across the nine combinations of deductible and OOP maximum tested, the cost advantage was 8% to 11% based on median performance, about the same as those for the default plan parameter values (Figure 6).
The advantage the dynamic policy has over the static $2,000 policy decreases moderately as the discount rate rises. When the discount rate doubles from 4% to 8%, the cost advantage of the dynamic policy fell from 13% to 9% (Figure 7).
The initial cost percentile significantly impacts the total costs of all policies. For example, at a marginal tax rate of 25%, the mean costs under the dynamic policy for is 17% greater than for , while the equivalent cost differential for the static $2,000 policy is 20% (Figure 8).
The impact of the marginal tax rate on total costs is highest for the static $2,000 policy, falls as contribution limit rises, and is negligible for the dynamic policy. For the static $2,000 policy, with , a 40% marginal tax rate results in 15% greater costs than at the 15% tax rate, while for the dynamic policy, this difference is 1%. This is because the dynamic save-up-to threshold is allowed to be as high as the OOP maximum, thereby keeping tax penalties to a minimum (Figure 8).
Tax Impact and Implications of Federal Contribution Limit
We compute the distribution of inflation-adjusted contributions over 30 years. The 25th, 50th, and 75th percentiles are $50,100, $71,400, and $96,300, respectively, in 2013 dollars. These are all significantly lower than the 2013 federal limit of
We compute the proportion of annual contributions that exceed the federal annual limit, for combinations of initial cost percentiles (0.25, 0.50, 0.75) with tax rates (15%, 25%, 40%). We find that 9% to 11% of households in a given year have recommended contributions that exceed the federal limit. For these households, the mean amount ranges from $10,100 to $10,300 in 2013 dollars.
Discussion
Taking advantage of the strong correlation between a household’s cost percentiles in consecutive years, the 1-year predictive accuracy of our cost evolution model is on par with leading industrial models. A key difference is that our model uses variables whose evolution is easy to track, making it possible to project a household’s cost over a long horizon. By contrast, the objective of the industrial models is to generate short-term forecasts using clinical variables that evolve stochastically over time. We use the results produced by our model to answer the two questions posed in the introduction:
How Should a Household Budget for Its HSA Contributions?
Our recommended dynamic policy and the static $6,450 one both incur substantially lower costs than our proxy for common contribution behavior (the static policy with a $2,000 contribution limit). The cost advantage is explained as follows. In the first few years following HSA adoption, there is a risk that the account will have insufficient funds to cover OOP expenses. By recommending that the household make a substantial contribution in year 1, the dynamic policy optimizes against this risk. Similarly, the static $6,450 limit policy makes large contributions in the first several years to quickly bring the balance up to the OOP max, thereby reducing this risk substantially. By contrast, the static $2,000 policy grows the balance more slowly, and is at greater risk of account insufficiency early on. The same phenomenon applies in years immediately following large expenditures, when the account is depleted. The dynamic and static $6,450 policies can quickly replenish the account, while the $2,000 policy requires more years to do so.
Our results suggest that while the dynamic policy is the most cost efficient among the ones examined, the static $6,450 policy is a worthy alternative. In the absence of personalized analytic guidance, the latter policy is a sensible strategy: Households outside the top tax brackets can capture most of the cost savings of the dynamic policy while still operating within the federal contribution limit. Our findings also indicate that insufficient annual contributions can result in substantially higher total costs.
The advantage the dynamic policy has over the static policies holds true across a range of parameter values, and is greatest for households with lower discount rates—those who place greater weight on future outcomes.
Should Policy Makers Revisit the Current Federal Contribution Limits for HSAs?
The last portion of our results suggest that 9% to 11% of households in a given year will need to make a HSA contribution that materially exceeds the current federal contribution limit. To allow these households to make full efficient use of HSAs, we propose an alternative to the current approach of capping annual contributions: Permit households to contribute to their HSA without limit up to a certain account balance (the limit-free balance), and then impose an annual limit on contributions thereafter. The limit-free balance could be set equal to each plan’s OOP maximum. This two-tiered approach allows households to quickly save up to the threshold recommended by the dynamic policy. Importantly, our results suggest that the resulting impact on overall tax receipts will be well below what is currently allowed by legislation.
To our knowledge, this is the first article to develop rigorous guidelines for HSA contributions, and we view it as a promising first step. To improve the accuracy of the model, future research should examine some of the possible extensions described below.
Health care costs during retirement. We might also factor into our objective health care costs during retirement, during which no contributions are made. For this objective, a preferred policy is likely to be a hybrid of the dynamic policy (to cover current costs) and a fixed contribution component (to cover estimated retirement costs), with the goal of attaining an account balance at the end of the contribution period that is sufficient to cover costs during retirement. We can leverage the modeling framework developed here to analyze this type of policy.
HSA withdrawals for nonmedical expenses. A reviewer correctly pointed out that a household can withdraw money from its HSA for nonmedical expenses. Such a withdrawal would trigger a penalty on top of the tax due on the withdrawal amount, so our current model prohibits negative contribution amounts. This can be relaxed by developing an additional model for predicting whether a withdrawal may be needed, as a function of the household’s wealth and spending needs. Fitting such a model requires gathering additional household financial data, which we leave for future research. If the current dynamic policy is operationalized to provide contribution recommendations, we advise that users contribute the minimum of what is recommended and the amount they anticipate would not be needed for other purposes.
Impact of HSAs and high-deductible plans on expenditure distribution. In this article, we did not attempt to model this because the Medical Expenditure Panel Survey dataset only has limited information about the insurance plan parameters of individuals, and only up to 2001 (before the implementation of HSAs). In the future our model could be recalibrated to data from households with multi-year enrollment in HDHPs. The results of the RAND Health Insurance Experiment suggest that increased cost sharing reduces the likelihood of visiting a physician, but has a smaller effect on the costliness per episode of care. 28 We hypothesize the effect might appear as an increase in the probability of zero costs, and/or as a shifting of the overall yearly cost distribution curve to the left.
Switching to a low-deductible health plan. Some households have access to both HDHPs and low-deductible plans, and may choose to switch between them. Under this scenario, the optimal policy may be of the form xii : If the household’s current cost percentile is below a certain level, use a HDHP and contribute the amount (4) to a HSA; otherwise, select the low-deductible plan. Further exploration of the choice between high- and low-deductible plans is left for future research, possibly along the direction discussed above.
Time-dependent covariates in cost prediction. Our cost evolution model uses time-fixed covariates to produce long-term forecasts, whereas leading industrial models use the most recently available values of time-dependent variables to forecast a little ahead in time. To incorporate these variables into our model for long-term planning, we need to have a way to simulate the evolution of these variables over time. This itself is a complex problem that is worthy of a separate research question. We note however that the short-term predictive performance of our model is already on par with the industrial ones. Hence, feeding a household’s most recent covariate values into our model should provide contribution recommendations that approximate the more sophisticated model.
We anticipate that our policy (or a version of it built atop more elaborate versions of the same models) could in the future be turned into a web application that consumers can use to determine contributions on an annual basis. While the details of such an implementation are outside the scope of this article, we imagine the application would operate as follows: The user would be requested to submit parameter values such as household size, prior year health care spending, marginal tax rate, and current health savings account balance. The application would then display the recommended contribution amount.
To conclude, we have developed a new analytical framework for modeling a HSA balance over time. We used this model to formulate a contribution policy that enables a household to optimize their expected discounted costs. With the growth trend in consumer-driven health plans, we expect that evidence-based modeling will play an increasing role in consumer health care financial planning.
Supplemental Material
Supplemental material, DS_10.1177_2381468318809373 for Health Savings Accounts: Consumer Contribution Strategies and Policy Implications by David J. Lowsky, Donald K. K. Lee and Stefanos A. Zenios in MDM Policy & Practice
Acknowledgments
We thank our reviewers for their excellent suggestions that significantly improved the article.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
The author(s) received no financial support for the research, authorship, and/or publication of this article.
Author Note: DKKL is now affiliated with Goizueta Business School, Emory University, Atlanta, Georgia.
Supplemental Material: The online supplementary materials for this article are available on the Medical Decision Making Policy & Practice website at http://journals.sagepub.com/home/mpp.
In 2013, the household limit was $6,450, and for 2017 it is $6,750. Individuals aged 55 and older and not enrolled in Medicare are allowed to make additional annual contributions of up to $1,000.
Machine learning methods have also been applied to predict expected health care costs.7-10 However, for our problem it is necessary to model the cost distribution instead, given that the optimal dynamic policy is a critical fractile solution.
“In-scope” is defined as being a member of the US civilian noninstitutionalized population. We further include individuals who were born or died at some point during the survey period.
We also performed an analysis of the sensitivity of results to discount rate (see Results).
Self-reported health variables, including perceived health status, have been shown to be a valuable predictor of health care costs.14-17
This is a continuous version of a similar approach for modeling transitions among discrete cost states: Low, Medium, High, and Very High. 21
MAPE is expressed as a fraction of the mean out-of-sample costs.
The relative performance of the policies was insensitive to the deductible amount or OOP maximum, per the results of our sensitivity analysis reported in Results.
Family size is modeled as a continuous covariate in our cost evolution models.
The 2013 federal annual contribution limit was $6,450.
We selected $2,500 as the lowest deductible and $12,500 as the highest OOP maximum. These correspond to the lowest and highest federal allowable limits, respectively, for all HSA-eligible plans in 2013.
This follows from applying policy iteration once to the Bellman equation in the supplementary material used to derive (4).
Contributor Information
David J. Lowsky, Independent Researcher, Santa Monica, CA.
Donald K. K. Lee, Yale University, New Haven, CT
Stefanos A. Zenios, Graduate School of Business, Stanford University, Stanford, CA
References
- 1. Claxton G, Rae M, Long M, Damico A, Foster G, Whitmore H. 2017 Employer Health Benefits Survey. San Francisco: Kaiser Family Foundation and Health Research & Educational Trust; 2017. [Google Scholar]
- 2. Committee on Child Health Financing. High-deductible health plans. Pediatrics. 2014;133(5):e1461–e1470. [DOI] [PubMed] [Google Scholar]
- 3. America’s Health Insurance Plans. 2016 Survey of Health Savings Account—High Deductible Health Plans. Washington, DC: America’s Health Insurance Plans; 2017. [Google Scholar]
- 4. Islam I. Trouble ahead for high deductible plans? [updated October 7, 2015; cited November 25, 2017]. Available from: http://healthaffairs.org/blog/2015/10/07/trouble-ahead-for-high-deductible-health-plans/
- 5. Butler L, Verona J. The State of Employee Benefits. Charleston: BenefitFocus; 2018. [Google Scholar]
- 6. Bundorf MK. Consumer-directed health plans: a review of the evidence. J Risk Insur. 2016;83(1):9–41. [Google Scholar]
- 7. Bertsimas D, Bjarnadóttir MV, Kane MA, et al. Algorithmic prediction of health-care costs. Oper Res. 2008;56(6):1382–92. [Google Scholar]
- 8. Lahiri CB, Agarwal N. Predicting healthcare expenditure increase for an individual from Medicare data. In: Proceedings of the ACM SIGKDD Workshop on Health Informatics, New York City;2014. Available from: http://cci.drexel.edu/hi/hi-kdd2014/morning_5.pdf [Google Scholar]
- 9. Sushmita S, Newman S, Marquardt J, et al. Population cost prediction on public healthcare datasets. In: Proceedings of the 5th International Conference on Digital Health; May 18-20, 2015; Florence, Italy. [Google Scholar]
- 10. Tamang S, Milstein A, Sørensen HT, et al. Predicting patient “cost blooms” in Denmark: a longitudinal population-based study. BMJ Open. 2017;7(1):e011580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Mihaylova B, Briggs A, O’Hagan A, Thompson SG. Review of statistical methods for analysing healthcare resources and costs. Health Econ. 2011;20(8):897–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Agency for Healthcare Research and Quality. Medical Expenditure Panel Survey, 2002-2014. Available from: http://www.meps.ahrq.gov/mepsweb/ [PubMed]
- 13. Damodaran A. Annual returns on stock, T. Bonds and T. Bills: 1928-current [updated January 5, 2018; cited October 10, 2018]. Available from: pages.stern.nyu.edu/∼adamodar/New_Home_Page/datafile/histretSP.html [Google Scholar]
- 14. Miilunpalo S, Vuori I, Oja P, Pasanen M, Urponen H. Self-rated health status as a health measure: the predictive value of self-reported health status on the use of physician services and on mortality in the working-age population. J Clin Epidemiol. 1997;50(5):517–28. [DOI] [PubMed] [Google Scholar]
- 15. DeSalvo KB, Fan VS, McDonell MB, Fihn SD. Predicting mortality and healthcare utilization with a single question. Health Serv Res. 2005;40(4):1234–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Wherry LR, Burns ME, Leininger LJ. Using self-reported health measures to predict high-need cases among Medicaid-eligible adults. Health Serv Res. 2014;49(Suppl 2):2147–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Boscardin CK, Gonzales R, Bradley KL, Raven MC. Predicting cost of care using self-reported health status data. BMC Health Serv Res. 2015;15(1):406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ash A, Zhao Y, Ellis R, Kramer M. Finding future high-cost cases: comparing prior cost versus diagnosis-based methods. Health Serv Res. 2001;36(6):194–206. [PMC free article] [PubMed] [Google Scholar]
- 19. Robst J. Comparing methods for identifying future high-cost mental health cases in Medicaid. Value Health. 2012;15(1):198–203. [DOI] [PubMed] [Google Scholar]
- 20. Cohen S, Ezzati-Rice T, Yu W. The utility of extended longitudinal profiles in predicting future health care expenditures. Med Care. 2006;44(5):I45–I53. [DOI] [PubMed] [Google Scholar]
- 21. Guo X, Gandy W, Coberley C, Pope J, Rula E, Wells A. Predicting health care cost transitions using a multidimensional adaptive prediction process. Popul Health Manag. 2015;18(4):290–9. [DOI] [PubMed] [Google Scholar]
- 22. Deb P, Burgess JF. A quasi-experimental comparison of econometric models for health care expenditures. Available from: http://econ.hunter.cuny.edu/wp-content/uploads/sites/6/RePEc/papers/HunterEconWP212.pdf
- 23. Malehi AS, Pourmotahari F, Angali KA. Statistical models for the analysis of skewed healthcare cost data: a simulation study. Health Econ Rev. 2015;5(1):11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Cumming RB, Knutson D, Cameron BA, Derrick B. A Comparative Analysis of Claims-based Methods of Health Risk Assessment for Commercial Populations. Schaumburg (IL): Society of Actuaries; 2002. [Google Scholar]
- 25. Winkelman R, Mehmud S. A Comparative Analysis of Claims-Based Tools for Health Risk Assessment. Schaumburg (IL): Society of Actuaries; 2007. [Google Scholar]
- 26. Hileman G, Steele S. Accuracy of Claims-Based Risk Scoring Models. Schaumburg (IL): Society of Actuaries; 2016. [Google Scholar]
- 27. Fronstin P. HSA balances, contributions, distributions, and other vital statistics—A first look at data from the EBRI HSA database on the 10th anniversary of the HSA. Employee Benefit Research Institute Research Brief. 2014;400:1–30. [Google Scholar]
- 28. Newhouse J. Consumer-directed health plans and the RAND health insurance experiment. Health Aff (Millwood). 2004;23(6):107–13. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material, DS_10.1177_2381468318809373 for Health Savings Accounts: Consumer Contribution Strategies and Policy Implications by David J. Lowsky, Donald K. K. Lee and Stefanos A. Zenios in MDM Policy & Practice