Probing Side-Chain Dynamics in Proteins by NMR Relaxation of Isolated ¹³C Magnetization Modes in ¹³CH₃ Methyl Groups

Abstract

The dynamics of methyl-bearing side chains in proteins were probed by ¹³C relaxation measurements of a number of ¹³C magnetization modes in selectively ¹³CH₃-labeled methyl groups of proteins. We first show how ¹³C magnetization modes in a ¹³CH₃ spin-system can be isolated using acute-angle ¹H radio-frequency pulses. The parameters of methyl-axis dynamics, a measure of methyl-axis ordering $S_{\text{axis}}^2$ and the correlation time of fast local methyl-axis motions (τ_f), derived from ¹³C relaxation in ¹³CH₃ groups are compared with their counterparts obtained from ¹³C relaxation in ¹³CHD₂ methyl isotopomers. We show that in high-molecular-weight proteins, excellent correlations are obtained between the [¹³CHD₂]-derived $S_{\text{axis}}^2$ values and those extracted from relaxation of the ¹³C magnetization of the I = 1/2 manifold in ¹³CH₃ methyls. In smaller proteins, a certain degree of anticorrelation is observed between the $S_{\text{axis}}^2$ and τ_f values obtained from ¹³C relaxation of the I = 1/2 manifold magnetization in ¹³CH₃ methyls. These parameters can be partially decorrelated by inclusion in the analysis of relaxation data of the I = 3/2 manifold ¹³C magnetization.

Graphical Abstract

INTRODUCTION

Protein side-chain motions are one of the principal determinants of conformational entropy of protein structures^1,2 and play a significant role in molecular recognition events.^3,4 Methyl groups have long been recognized as unique probes of molecular motions and have played a special role in NMR studies of protein side-chain dynamics, providing important insights into the dynamics and thermodynamics of many biochemical processes.^5,6 The use of ¹³C spin relaxation in ¹³CH₃ methyl moieties for the extraction of dynamics parameters, however, is fraught with difficulties, as the interpretation of ¹³C relaxation in these methyl isotopomers is complicated by interference effects between dipolar fields created by the three magnetically equivalent proton spins that lead to a non-single-exponential decay of the NMR signal.^7,8 In contrast, ¹³C relaxation in ¹³CHD₂ methyl isotopomers^9,10 or relaxation of ²H nuclei in ¹³CH₂D-^11–13 or ¹³CHD₂-labeled^10,13,14 methyl groups present much more favorable alternatives. While relaxation of ²H nuclei in ¹³CH₂D- and ¹³CHD₂-methyls, which is governed almost exclusively by quadrupolar interactions, provides the most robust probe of methyl-axis dynamics,¹⁵ NMR experiments that quantify ¹³C spin relaxation in ¹³CHD₂ methyls are generally more sensitive.^10,15 The quantitative interpretation of ¹³C relaxation in ¹³CHD₂ methyl isotopomers is well established.^9,10,15 The use of ¹³CH₃ methyls as probes for side-chain dynamics, however, has indisputable advantages in that no special (deuterium-containing) types of isotopic labels are required and the starting sensitivity of NMR experiments targeting ¹³CH₃ methyls is two- to three-fold higher than those for ¹³CH₂D- and ¹³CHD₂-labeled methyl groups.¹⁶

Recently, we demonstrated the utility of acute (<90°)-angle ¹H radio frequency (RF) pulses in a variety of NMR applications that target ¹³CH₃ methyl groups in selectively ¹³CH₃-labeled and otherwise perdeuterated proteins. In particular, we showed that more efficient and sensitive selection of ¹H and ¹³C transitions belonging to the I = 1/2 manifolds of ¹³CH₃ groups, which effectively reduces the complexity of a ¹³CH₃ spin system to the simpler case of its AX(¹³C–¹H) counterpart, can be achieved with ¹H RF pulses adjusted to ~42°.¹⁷ A special case of acute angle pulses, the “magic-angle” (54.7°) ¹H pulse, was shown to simplify and improve the sensitivity of NMR experiments that quantify the amplitudes of methyl three-fold symmetry axis motions in the case of small- to intermediate-sized proteins.¹⁸ We further demonstrated that the transfer of magnetization to and from the slow-relaxing ¹³C transitions of ¹³CH₃ methyl groups can be optimized by carefully adjusting the angles of the ¹H pulses in INEPT¹⁹ transfer schemes.²⁰ This optimized transfer scheme was applied to methyl ¹³C Carr–Purcell–Meiboom–Gill (CPMG)^21,22 relaxation dispersion experiments recorded on the slow-relaxing ¹³C transitions, significantly increasing the information content of the CPMG relaxation dispersion profiles in cases where the exchange process involved high-molecular-weight species (large protein complexes or partially aggregated states).

Here, we probe the dynamics of methyl-bearing side chains in proteins by separating groups of ¹³C magnetization modes in ¹³CH₃-methyls using a variety of acute-angle ¹H RF pulses and measuring their NMR spin relaxation properties, namely transverse (R₂) and longitudinal (R₁) relaxation rates. Two parameters that describe methyl-axis dynamics—the order parameter squared of the methyl three-fold symmetry axis, $S_{\text{axis}}^2$, that reports on the amplitudes of methyl-axis motions and the correlation time of fast local methyl-axis motions, τ_f, that occurs on the picosecond time scale (including the rotation of the methyl group around its three-fold symmetry axis)—are extracted from relaxation rates of groups of ¹³C magnetization modes in ¹³CH₃ methyls of a {U-[²H]; Ileδ1-[¹³CH₃]; Leu,Val-[¹³CH₃, ¹²CD₃]}-labeled (ILV-{¹³CH₃}) sample of the protein ubiquitin at 25 and 5 °C (MW = 8.5 kDa) and a {U-[²H]; Ileδ1-[¹³CH₃]}-labeled (Iδ1-{¹³CH₃}) sample of the high-molecular-weight enzyme malate synthase G (MSG, MW = 82 kDa) at 37 °C. The ¹³CH₃-derived reporters of methyl-axis dynamics were compared with their counterparts derived from ¹³C relaxation rates in ¹³CHD₂ methyl isotopomers using samples of the two proteins with the same labeling schemes, where the ¹³CH₃ methyl groups were substituted for those of the ¹³CHD₂ variety.

METHODS

Details regarding sample expression, purification, and isotope labeling; NMR spectroscopy; and data analysis are provided in the Supporting Information.

RESULTS AND DISCUSSION

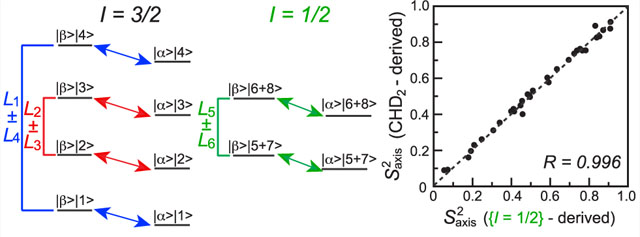
The energy-level diagram of a ¹³CH₃ methyl spin system is shown in Figure 1, with the ¹³C transitions that are the main focus of the present work shown by diagonal arrows. The diagram consists of one manifold with spin I = 3/2 and two manifolds with I = 1/2. In the macromolecular limit, transverse spin-relaxation rates of the inner ¹³C transitions of the I = 3/2 manifold and those of the I = 1/2 manifolds are generally slower ($R_{2,\text{C}}^{\text{S}}$, shown with red and green arrows for the I = 3/2 and I = 1/2 manifolds, respectively; Figure 1), while the rates of the outer ¹³C transitions of the I = 3/2 manifold are faster ($R_{2,\text{C}}^{\text{F}}$; blue arrows). By the “modes” of ¹³C magnetization in this work, we denote classes of ¹³C transitions (described by ¹³C spin operators C₊ = |α⟩⟨β| and C₋ = |β⟩⟨α|), as well as the corresponding spin-order groups (populations; described by ¹³C spin operators C_z = (1/2)(|α⟩⟨α| − |β⟩⟨β|)). These six ¹³C magnetization modes are differentiated by the eight ¹H polarization states |n⟩⟨n|, where the term |n⟩ is a linear combination of |i, j, k⟩, i, j, k ∈{α, β} (Figure 1), and are given by

$$\begin{array}{l}{L}_1+L_4\equiv C_{\pm ,z}(|1\rangle \langle 1|+|4\rangle \langle 4|)\\ L_2+L_3\equiv C_{\pm ,z}(|2\rangle \langle 2|+|3\rangle \langle 3|)\\ L_5+L_6\equiv \frac{1}{\sqrt{2}}{C}_{\pm ,z}(|5\rangle \langle 5|+|7\rangle \langle 7|+|6\rangle \langle 6|+|8\rangle \langle 8|)\\ L_1-L_4\equiv C_{\pm ,z}(|1\rangle \langle 1|-|4\rangle \langle 4|)\\ L_2-L_3\equiv C_{\pm ,z}(|2\rangle \langle 2|-|3\rangle \langle 3|)\\ L_5-L_6\equiv \frac{1}{\sqrt{2}}{C}_{\pm ,z}(|5\rangle \langle 5|+|7\rangle \langle 7|-|6\rangle \langle 6|-|8\rangle \langle 8|)\end{array}$$ (1)

Figure 1.

Energy level diagram of the ¹³CH₃ (AX₃) spin-system of a methyl group. Single-quantum ¹³C transitions are shown by diagonal arrows. The slow- and fast-relaxing ¹³C (R_2,C) transitions are distinguished by the superscripts “S” and “F”, respectively. The spin quantum numbers, I, of the three manifolds are specified below the energy-level diagram. The slow- and fast-relaxing ¹³C transitions of the I = 3/2 manifold are colored in red and blue, respectively, while the transitions of the I = 1/2 manifold are colored in green. Various ¹³C magnetization modes isolated in the NMR experiments are denoted by L_i ± L_j (i,j ∈ {1–6}) and shown using the same coloring scheme. All 16 eigenstates are denoted by |m⟩|n ⟩ , where |m⟩ is the state of the ¹³C spin, m ∈ {α, β}, and the eight ¹H eigenstates |n⟩ are described by linear combinations of |i, j, k⟩ (i, j, k ∈ {α, β}) as shown below the diagram.

Relaxation decay of the modes that include raising or lowering ¹³C spin operators (C_±) is described by transverse (R₂) rates, while the longitudinal rates (R₁) describe the relaxation of the modes involving longitudinal ¹³C operators (C_z). Further, we define the subset of ¹³C magnetization modes that involves the sums of the ¹H states (the first three modes in eq 1) as “in-phase” modes and those that involve the differences of ¹H states as “antiphase” modes.

Theoretical expressions for R₂ and R₁ spin relaxation rates of ¹³C magnetization modes in a ¹³CH₃ methyl group, calculated for intra-methyl interactions using the basis set in eq 1, are presented in the Supporting Information. Here, we only include the relaxation matrix (eq 2) that describes contributions to the R₂ and R₁ rates arising from dipolar interactions with “external” proton spins (¹H spins outside of a given methyl moiety), as these so-called “spin-flipping” rates are central to the content of the present work.

$$\frac{\text{d}}{\text{d}t}\left[\begin{array}{l}{L}_1+L_4\hfill \\ L_2+L_3\hfill \\ L_5+L_6\hfill \\ L_1-L_4\hfill \\ L_2-L_3\hfill \\ L_5-L_6\hfill \end{array}\right]=-k_{\text{HH}}^{\text{ext}}\left[\begin{array}{cccccc}1& -1& 0& 0& 0& 0\\ -1& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& -1& 0\\ 0& 0& 0& -1& 11/3& 0\\ 0& 0& 0& 0& 0& 2/3\end{array}\right]\left[\begin{array}{l}{L}_1+L_4\hfill \\ L_2+L_3\hfill \\ L_5+L_6\hfill \\ L_1-L_4\hfill \\ L_2-L_3\hfill \\ L_5-L_6\hfill \end{array}\right]$$ (2)

where $k_{\text{HH}}^{\text{ext}}=\left(\frac{3}{20}\right){\left(\frac{{\mu }_0}{4\pi }\right)}^2{\sum }_{\text{ext}}\frac{6{ħ}^2{\gamma }_H^4{\tau }_{\text{C}}}{r_{hh\text{ext}}^6};$ μ₀ is the vacuum permeability constant; γ_H is the gyromagnetic ratio of proton spins; r_hhext is the distance from methyl protons to an external proton spin, with the sum running over all external proton spins in the protein molecule; and τ_C is the global molecular rotational correlation time. Note that only the spectral density function at zero frequency, J(0), is considered here, and the order parameter of the interactions with external proton spins is assumed to be unity.

Extraction of the parameters of methyl-axis dynamics from ¹³C relaxation measurements in ¹³CH₃ methyl groups using ¹H-detected NMR experiments is hampered by (1) pervasive cross-correlations (interference) between dipolar fields created by the three magnetically equivalent ¹H spins (¹³C–¹H/¹³C–¹H and ¹H–¹H/¹H–¹H dipole–dipole cross-correlated relaxation) that lead to cross-relaxation between individual ¹³C magnetization modes, resulting in non-single-exponential decay of coherences of interest;^7,8 and (2) dipolar interactions of methyl protons with external ¹H spins. The latter contributes to (i) auto-relaxation of ¹³C magnetization, which is difficult to quantitatively account for even when a high-resolution 3D structure of a protein is available; and (ii) cross-relaxation between ¹³C magnetization modes that likewise results in non-single-exponential signal decay. In this work, the problem of “cross-talk” (cross-relaxation) between ¹³C magnetization modes is alleviated by sequestering groups of ¹³C modes of interest so that only these modes are present at the start of the relaxation delays. Meanwhile, the effects of auto-relaxation from spin-flips are mitigated by either (i) isolation of ¹³C magnetization that is not affected by spin-flips (in-phase mode of the I = 1/2 manifold, L₅ + L₆), or (ii) corrections applied to the measured relaxation rates that are based on experimental differences between the rates of the antiphase and in-phase inner ¹³C modes of the I = 3/2 manifold, (L₂ − L₃) and (L₂ + L₃). Note that both auto- and cross-relaxation arising from ¹H spin-flips are significantly reduced by high levels of deuteration of protein samples.

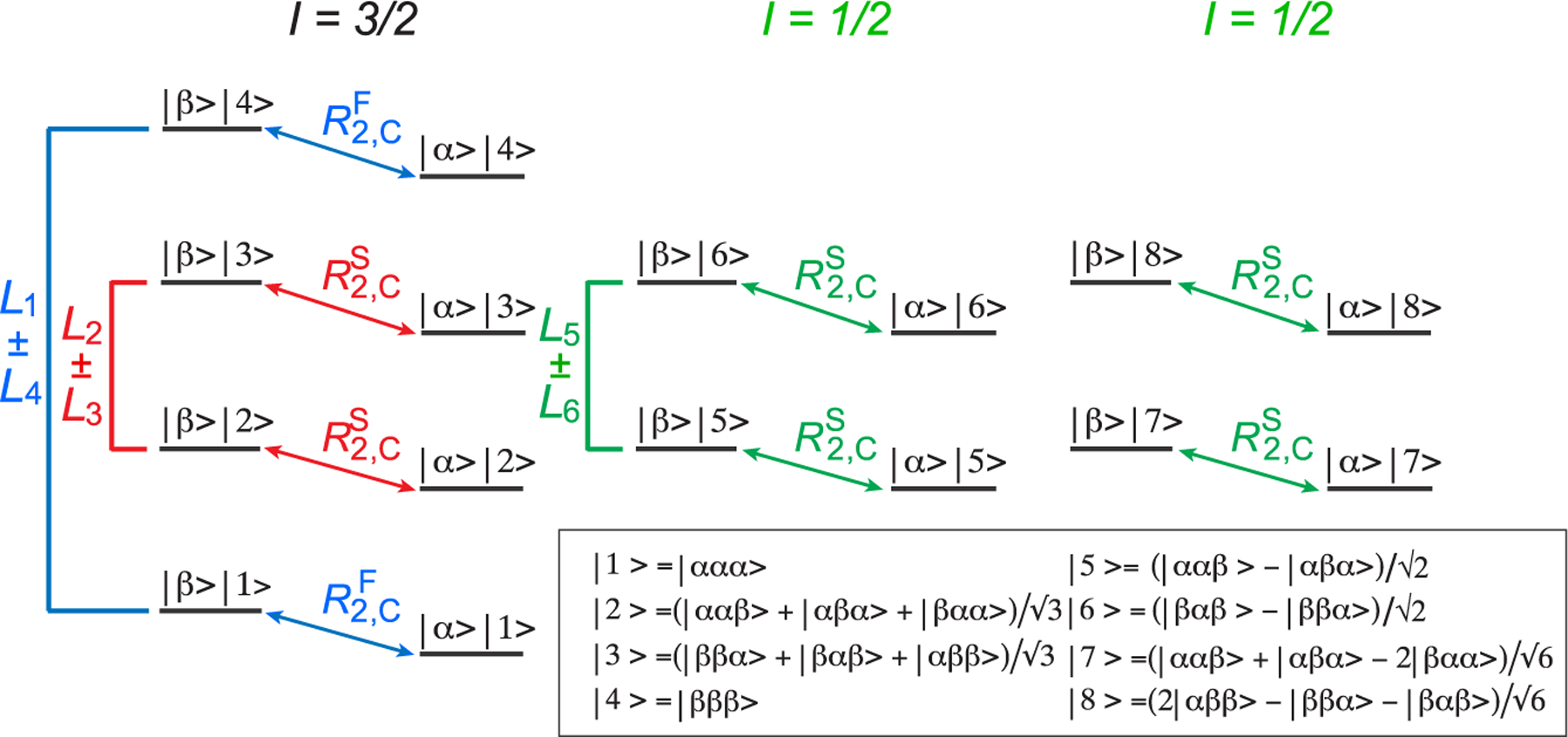
As in-phase ¹³C magnetization of the I = 1/2 manifold (L₅ + L₆) is “immune” to interactions with external ¹H spins (the third row and column of the relaxation matrix in eq 2), we first concentrate on the isolation and measurement of the R₂ and R₁ relaxation rates of the (L₅ + L₆) mode using the acute-angle pulse-based methodology described earlier.¹⁷ Figure 2 shows the pulse scheme for the measurements of R_1ρ and R₁ relaxation rates of the (L₅ + L₆) ¹³C magnetization mode. The interested reader is referred to our previous publication in ref 17 for details of (L₅ + L₆) sequestration from the rest of ¹³C magnetization. Briefly, the inner slow-relaxing multiple-quantum ¹³C–¹H transitions are isolated first by the initial 2τ_b “purge” element of the scheme, after which a ¹H pulse with flip angle α = sin⁻¹(2/3) = 41.8° (shown in green in Figure 2) is applied to eliminate the inner transitions of the I = 3/2 manifold. Subsequently, the remaining fast-relaxing ¹H transitions and ¹H triple-quantum coherences are eliminated by the second 2τ_b purge element (enclosed together with the first one in the solid green box in Figure 2) and the “filtering” element with a 2τ_c duration (enclosed in the dashed green box in Figure 2), respectively. Following the application of a ¹H_y pulse that polarizes only the ¹H transitions of the I = 1/2 manifold, the rest of the scheme in Figure 2 is the same as that commonly employed for ¹³C relaxation measurements in AX(¹³C–¹H) spin-systems (e.g., that of a ¹³CHD₂ methyl group). The measurements of R₂ and R₁ relaxation rates are thus performed on magnetization terms of the type C_±(|5⟩⟨5| + |6⟩⟨6| + |7⟩⟨7| + |8⟩⟨8|) and C_z(|5⟩⟨5| + |6⟩⟨6| + |7⟩⟨7| + |8⟩⟨8|), respectively (eq 1). Using the experiment shown in Figure 2, average (L₅ + L₆) R₂ values of 4.2 and 7.5 s⁻¹ are obtained for ILV-{¹³CH₃}-labeled ubiquitin at 25 and 5 °C, respectively; the corresponding (L₅ + L₆) R₁ values are 2.9 and 4.1 s⁻¹, respectively. Average (L₅ + L₆) R₂ and R₁ values of 12.1 and 0.95 s⁻¹, respectively, are obtained for ILV-{¹³CH₃}-labeled MSG (37 °C).

Figure 2.

Pulse scheme for the measurement of R_1ρ and R₁ relaxation rates of the ¹³C magnetization mode (L₅ + L₆) (I = 1/2 manifold) in ¹³CH₃ methyl groups. All narrow and wide rectangular pulses are applied with flip angles of 90° and 180°, respectively, along the x-axis unless indicated otherwise. For ILV-{¹³CH₃}-labeled samples, the ¹H and ¹³C carrier frequencies are positioned at 0.5 and 20 ppm, respectively, in the center of the Ileδ1-Leu-Val methyl region; for Iδ1-{¹³CH₃}-labeled samples, the ¹H and ¹³C carrier frequencies are set to 0.7 and 12 ppm, respectively. All ¹H and ¹³C pulses are applied with the highest possible power, while ¹³C WALTZ-16 decoupling²³ is achieved using a 2 kHz field. The ¹H pulse colored in green is applied with flip angle α equal to sin⁻¹(2/3) = 41.8°. Delays are τ_a = 1/(4J_HC) = 2.0 ms; τ_b = 1/(8J_HC) = 1.0 ms; τ_c = 1/(12J_HC) = 0.67 ms; δ = 300 μs; and ζ = 1/(2π × B_SL) – (4/π) × pwc,^24,25 where B_SL is the strength of ¹³C spin-lock field (Hz) applied along the x-axis, “pwc” is the length of the ¹³C 90° (high power) pulse. T is a variable relaxation delay. The durations and strengths of the pulsed-field gradients (ms; G/cm) are as follows: g1 = (1; 25), g2 = (0.4; 15), g3 = (0.3; 12), g4 = (0.35; 15), g5 = (0.2; 20), g6 = (1.2; −15), g7 = (0.4; 12), g8 = (0.2; 35), g9 = (0.5; 12), g10 = (0.4; 12), g11= (0.053; −35), g′= (1.2; 12), and g″= (0.8; 10). The phase cycle is as follows: ϕ1 = x; ϕ2 = 2(y), 2(−y); ϕ3 = 2(x), 2(−x); ϕ4 = y, −y; ϕ5 = 4(x), 4(−x); ϕ6 = 2(x), 2(−x); ϕ7 = x, −x; ϕ8 = x; receiver phase = 2(x, −x), 2(−x, x). Quadrature detection in t₁ is achieved in a Rance-Kay mode^26,27 by recording a pair of data sets for each value of t₁ corresponding to (ϕ8, g8) and (−ϕ8, −g8). The phase ϕ7 is incremented by 180° along with the phase of the receiver for each complex t₁ point.²⁸

The parameters of methyl-axis dynamics (order parameters of the methyl three-fold symmetry axis, $S_{\text{axis}}^2$, and correlation times of local methyl-axis motions, τ_f) derived from ¹³CH₃ methyl-labeled samples (see SI “Materials and Methods” for details of data analysis) are compared with their counterparts derived from ¹³C relaxation of ¹³CHD₂ methyls of ubiquitin and MSG shown in Figures 3 and 4, respectively. Although good correlations are obtained for most methyl sites for the values of $S_{\text{axis}}^2$ in ubiquitin (τ_C = 5 and 11 ns at 25 and 5 °C, respectively, in D₂O solvent), a subset of around six sites showed notably poorer agreement at both temperatures (Figure 3A and C). Better correlations are generally obtained for τ_f, with only around four methyl sites exhibiting the highest τ_f values notably overestimated in the (L₅ + L₆)-derived data set (Figures 3B and D). The disagreements between the two sets of $S_{\text{axis}}^2$ data can be traced to the lower sensitivity of the (L₅ + L₆) R₂ rates toward $S_{\text{axis}}^2$ compared to that of ¹³C R₂ in the ¹³CHD₂ methyl groups. Figure S1 (SI) compares the contour plots or theoretical R₂ and R₁ rates of the (L₅ + L₆) mode with those of the ¹³C nuclei in ¹³CHD₂ methyls as a function of [$S_{\text{axis}}^2$; τ_f] for τ_C = 5 ns. It can be readily appreciated from these plots that since the R₂ of (L₅ + L₆) is dependent on both $S_{\text{axis}}^2$ and τ_f, these two parameters of dynamics can become significantly anti-correlated. As a consequence, a small error in R₁ (and hence τ_f) can result in a relatively large error of opposite sign in $S_{\text{axis}}^2$ (the two most prominent cases of such a correlation in ubiquitin are labeled in Figure 3). Simulations show that for five of the six methyl sites with the largest disagreements in $S_{\text{axis}}^2$ values in Figures 3A and C, a “correction” of the measured R₁ rate by only a few percent (on the order of 0.10–0.12 s⁻¹ in absolute values) is sufficient to “restore” the agreement between the (L₅ + L₆)-derived and ¹³CHD₂-derived $S_{\text{axis}}^2$ values. The physical origin of the lower sensitivity of the (L₅ + L₆) R₂ rates toward $S_{\text{axis}}^2$ and the ensuing anti-correlations between $S_{\text{axis}}^2$ and τ_f lie in the contributions to these rates from intramethyl ¹H–¹H interactions at zero frequency in the limit where the auto-relaxation spectral density is not equal to the cross-correlated relaxation one (see expressions for relaxation rates in SI), which is notably absent from ¹³C R₂ rates in ¹³CHD₂ isotopomers.

Figure 3.

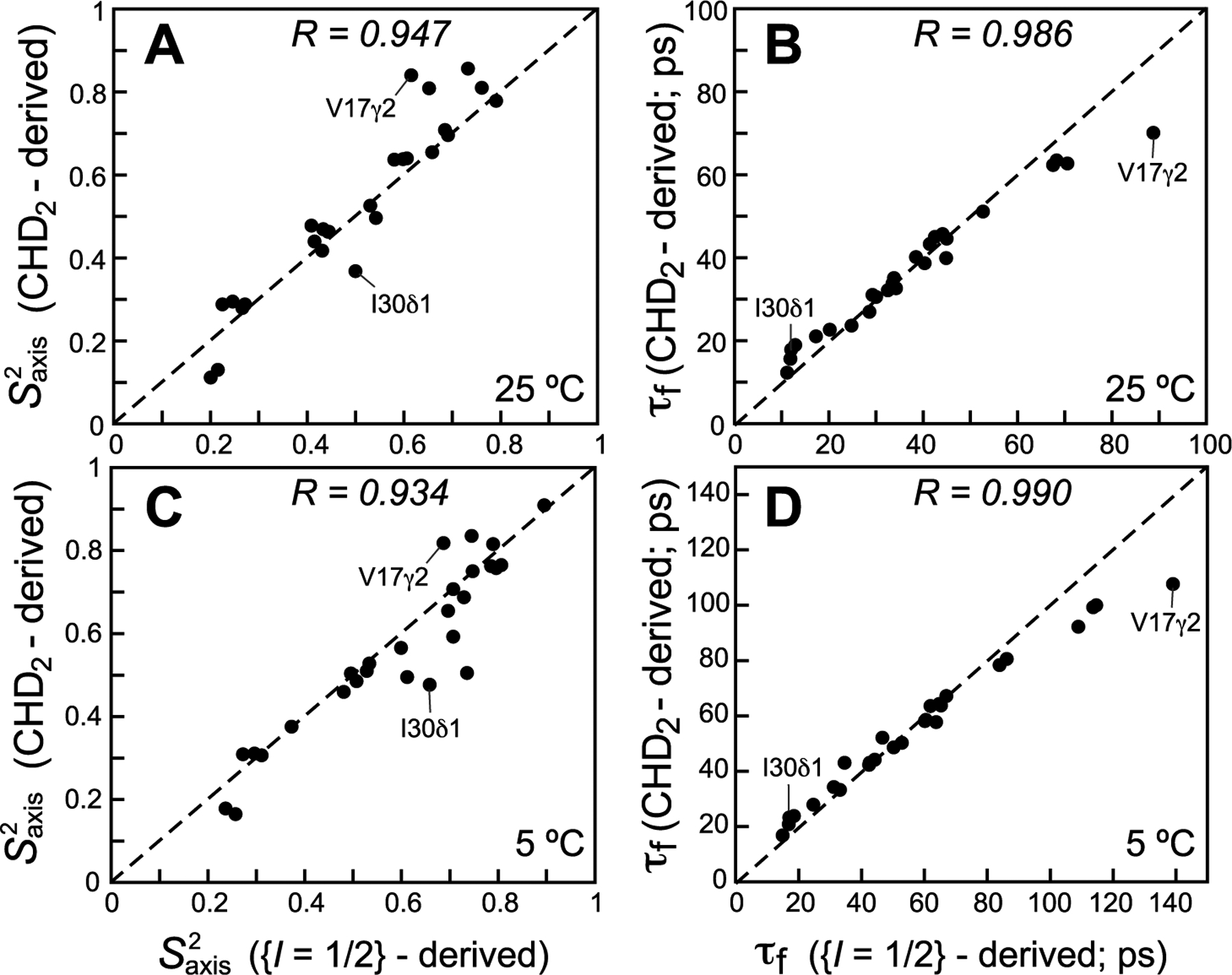
Correlation plots comparing methyl-axis dynamics parameters derived from ¹³C relaxation measurements of the (L₅ + L₆) magnetization mode (I = 1/2 manifold) in ¹³CH₃ methyls using the scheme in Figure 2 (x-axes) with those derived from ¹³C relaxation in ¹³CHD₂ methyls (y-axes) for ILV-labeled samples of ubiquitin at 25 °C (upper row; (A) $S_{\text{axis}}^2$ and (B) τ_f; 29 correlations) and 5 °C (lower row; (C) $S_{\text{axis}}^2$ and (D) τ_f; 30 correlations). All data were collected at 600 MHz. The data for the L50δ2 and L56δ2 methyl sites were excluded from the plots because of large exchange contributions to their R₂ values. Linear correlation coefficients are shown at the top of each plot. Dashed lines are drawn at y = x.

Figure 4.

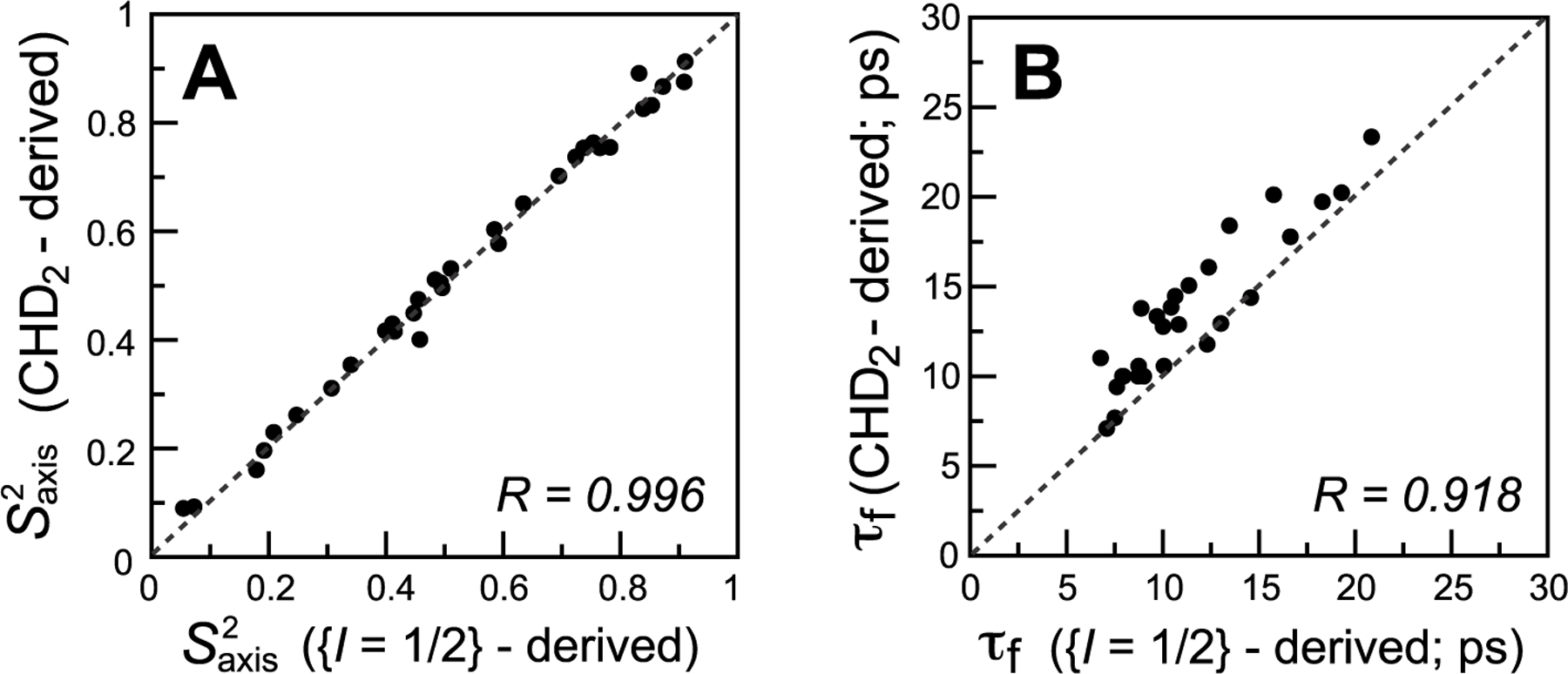
Correlation plots comparing methyl-axis dynamics parameters derived from ¹³C relaxation measurements of the (L₅ + L₆) magnetization mode (I = 1/2 manifold) in ¹³CH₃ methyls using the scheme in Figure 2 (x-axes) with those derived from ¹³C relaxation in ¹³CHD₂ methyls (y-axes) for Ileδ1-labeled samples of MSG at 37 °C (600 MHz). (A) $S_{\text{axis}}^2$ and (B) τ_f (ps). Linear correlation coefficients are shown at the lower right corner of each plot. Dashed lines are drawn at y = x. A total of 33 correlations are included in panel A, and 27 correlations in panel B with 6 correlations showing the lowest $S_{\text{axis}}^2$ values excluded from the plot.

In larger protein molecules such as MSG, with τ_C = 46 ns (assumed isotropic) at 37 °C in D₂O, the (L₅ + L₆) R₂ and R₁ rates are separated in their information content in the sense that R₂ reports almost exclusively on $S_{\text{axis}}^2$, while R₁ is dependent exclusively on τ_f. This is a direct consequence of the (near) equality of the auto- and cross-correlated relaxation spectral density functions in the limit where τ_C ≫ τ_f. Therefore, the sensitivity of the (L₅ + L₆) R₂ rates with respect to $S_{\text{axis}}^2$ is “restored” in this case, and the agreement between the (L₅ + L₆)-derived $S_{\text{axis}}^2$ values and their ¹³CHD₂-derived counterparts is excellent for almost all Ileδ1 methyl sites in MSG (Figure 4A; see SI “Materials and Methods” for experimental details of the relaxation measurements). The contour plots of theoretical (L₅ + L₆) relaxation rates are compared with the ¹³C rates in ¹³CHD₂ isotopomers as a function of [$S_{\text{axis}}^2$; τ_f] for τ_C = 60 ns in Figure S2 (SI). As the τ_C value of MSG is strongly dependent on the protein concentration in the NMR sample (ranging from ~46 ns for a 0.5 mM sample to ~64 ns for a 1.1 mM sample), we have chosen, for the purposes of illustration, to make the plots for a τ_C value closer to the upper limit of this range.

The correlations obtained between the two sets of τ_f data for MSG (Figure 4B) are notably inferior to those for smaller proteins (cf. Figure 4B and Figure 3B and D). This is not surprising considering the large contributions of ¹H–¹H dipolar interactions to the (L₅ + L₆) R₁ rates, whereas ¹³C R₁ rates in ¹³CHD₂ methyls are not affected by these interactions. The worst agreement between the two sets of τ_f data is noted for methyl sites with the lowest $S_{\text{axis}}^2$ values (where the part of the spectral density that accounts for local motions is the largest). Therefore, six such methyl sites were eliminated from the plot in Figure 4B. We note that the systematic underestimation of τ_f values derived from the (L₅ + L₆) rates compared to their ¹³CHD₂-derived counterparts (apparent in Figure 4B) is unlikely to arise from differences in dynamics between ¹³CH₃ and ¹³CHD₂ methyl isotopomers (as the same trend is not observed for ubiquitin in Figures 3B and D) and is probably an artifact of the modeling of the spectral density function (see SI for details).

In an attempt to improve the agreement between the (L₅ + L₆)-derived and ¹³CHD₂-derived measures of methyl-axis dynamics for small- to medium-sized proteins, we explored the possibility of using the relaxation properties of other ¹³C magnetization modes in a ¹³CH₃ spin system. The fast-relaxing (outer) ¹³C transitions (shown in blue in Figure 1) and the corresponding spin orders (L₁ ± L₄) present a potentially attractive choice because of (1) the steep dependence of (L₁ ± L₄) R₂ rates on $S_{\text{axis}}^2$ (see Figure S1; the lower row of panels shows the contour plots of (L₁ + L₄) R₂/R₁ as a function of [$S_{\text{axis}}^2$;τ_f]) and (2) the absence of contributions from intramethyl ¹H–¹H interactions at zero frequency to (L₁ ± L₄) R₂/R₁ rates (see expressions for the relaxation rates in the SI). Note that both R₂ and R₁ rates of the antiphase magnetization (L₁ − L₄) are predicted to be very similar to those of the in-phase (L₁ + L₄) magnetization for deuterated proteins (down to very short distances to external ¹H spins, ~2.5 Å). However, both auto- and cross-relaxation rates of the (L₁ ± L₄) mode have contributions from spin flips (eq 2). Although the contributions to R₂ from spin flips are not predicted to exceed a few percent of the total rate in deuterated protein samples (a maximal value of ~6% is calculated for the shortest effective distance to an external ¹H spin in deuterated ILV-{¹³CH₃}-ubiquitin), the R₁ rates are affected more significantly—up to ~40% of the total rate for ubiquitin at 5 °C. In larger proteins the size of MSG, spin flips are predicted to dominate the (L₁ ± L₄) R₁ rates (>50% of the total), making them practically uninterpretable. Nevertheless, as long as the rate of spin flips does not dominate the longitudinal relaxation decay, and individual ¹³C magnetization modes are isolated prior to the relaxation delay, minimizing the effect of cross-relaxation between different modes, these contributions can be approximately corrected for. Indeed, close inspection of the expressions for relaxation rates of all magnetization modes (see SI) shows that the difference between the rates of decay (R₂ or R₁) of the antiphase and in-phase inner magnetization modes of the I = 3/2 manifold, (L₂ − L₃) and (L₂ + L₃), respectively, represents the most accurate measure of spin-flipping rates in the macromolecular limit (see eqs S5.1 and S5.2 and Figure S3 in the SI). According to eq 2, this difference is $\Delta =R_{(L2-L3)}-R_{(L2+L3)}\approx (8/3)k_{\text{HH}}^{\text{ext }}$. Once estimated experimentally from the R_(L2−L3) and R_(L2+L3) rates, the value of Δ can then be scaled by a factor of 3/8 to be used as a correction for spin flips for R₂/R₁ rates of the (L₁ ± L₄) mode. Note that rather than relying on an estimation of distances to external protons from the protein structure, such a correction is entirely based on the relaxation properties of a ¹³CH₃ spin system.

The pulse schemes designed for the isolation and relaxation measurements of the (L₁ ± L₄) and (L₂ ± L₃) ¹³C magnetization modes in ¹³CH₃ methyls are shown in Figures 5 and 6, respectively, and rely on the use of acute-angle ¹H pulses. Both schemes start with selection of fast-relaxing multiple-quantum ¹³C–¹H magnetization using purge elements of duration 4τ_b (enclosed in solid blue and red boxes in Figures 5 and 6, respectively). In the scheme for (L₁ ± L₄) selection in Figure 5, this element is followed by a ¹H_y pulse applied with a flip angle β equal to the “magic” angle cos⁻¹(1/√3) = 54.7° (shown in blue), which selectively polarizes the outer ¹H magnetization states (|1⟩⟨1| and |4⟩⟨4|, Figure 1; see SI for details) so that magnetization terms of the type C_±(|1⟩⟨1| ± |4⟩⟨4|) and C_z(|1⟩⟨1| ± |4⟩⟨4|) can be generated for R₂ and R₁ measurements, respectively. In the experiment for the selection of (L₂ ± L₃) in Figure 6, the selection of fast-relaxing multiple-quantum ¹³C–¹H magnetization is followed by a ¹H_y 90° pulse to polarize all the ¹H states of the I = 3/2 manifold(|1⟩⟨1|, |2⟩⟨2|, |3⟩⟨3| and |4⟩⟨4|; Figure 1), which is followed by selection of the desired ¹H states (|2⟩⟨2|, |3⟩⟨3|) by a “filtering” element of 2τ_c duration (enclosed in a dashed red box in Figure 6) and subsequent generation of the magnetization terms C_±(|2⟩⟨2| ± |3⟩⟨3|) and C_z(|2⟩⟨2| ± |3⟩⟨3|) for R₂ and R₁ measurements, respectively. Note that to maximize the transfer of magnetization from ¹³C coherences of the type C_±,z(|2⟩⟨2| − |3⟩⟨3|) to the slow-relaxing component of the multiple-quantum ¹³C–¹H magnetization C_±(|2⟩⟨3| + |3⟩⟨2|), a ¹H pulse with flip angle γ = sin⁻¹(√8/27) = 33° is applied (shown in red in Figure 6; see the SI for details), followed by a purge element 2τ_b that selects for the slow-relaxing part of the (multiple-quantum) magnetization before the t₁ evolution period.

Figure 5.

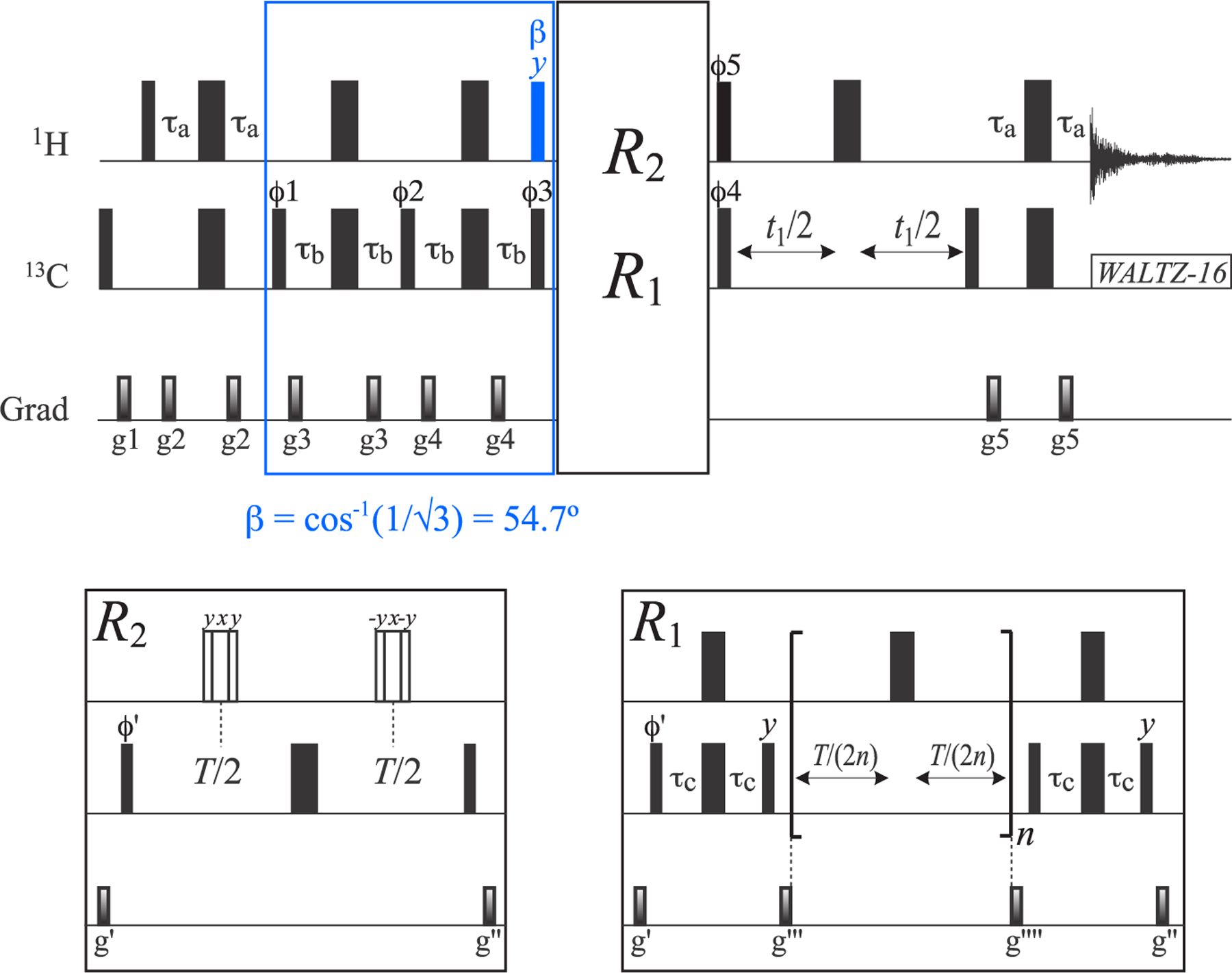
Pulse scheme for the measurement of R₂ and R₁ relaxation rates of the outer ¹³C magnetization modes of the I = 3/2 manifold (L₁ ± L₄) in ¹³CH₃ methyl groups. All the parameters of the scheme (including delays) are the same as described in Figure 2. The ¹H pulse shown in blue is applied with the flip-angle β = cos⁻¹(1/√3) = 54.7°. “Open” ¹H pulses in R₂ measurements are composite pulses of the 90°–240°–90° variety²⁹ that are applied with the phase-cycling indicated in the figure. Only the scheme for in-phase (L₁ + L₄) R₁ measurements is shown as used in practice. The durations and strengths of the pulsed-field gradients(ms; G/cm) are as follows: g1 = (1; 25), g2 = (0.4; 15), g3 = (0.3; 12), g4 = (0.35; 12), g5 = (0.4; 15), g′ = (1.2; 20), g″ = (0.8; 15), g‴ = (0.8; 20), and g⁗ = (0.6; 20). The phase cycle is as follows: ϕ1 = 2(x), 2(−x); ϕ2 = x, −x; ϕ3 = 4(x), 4(−x); ϕ4 = x, −x; ϕ5 = 4(x), 4(−x); ϕ′ = 4(x), 4(−x); and = receiver phase of (x,−x,−x,x, −x,x,x,−x). Quadrature detection in t₁ is achieved via States-TPPI²⁸ incrementation of ϕ4.

Figure 6.

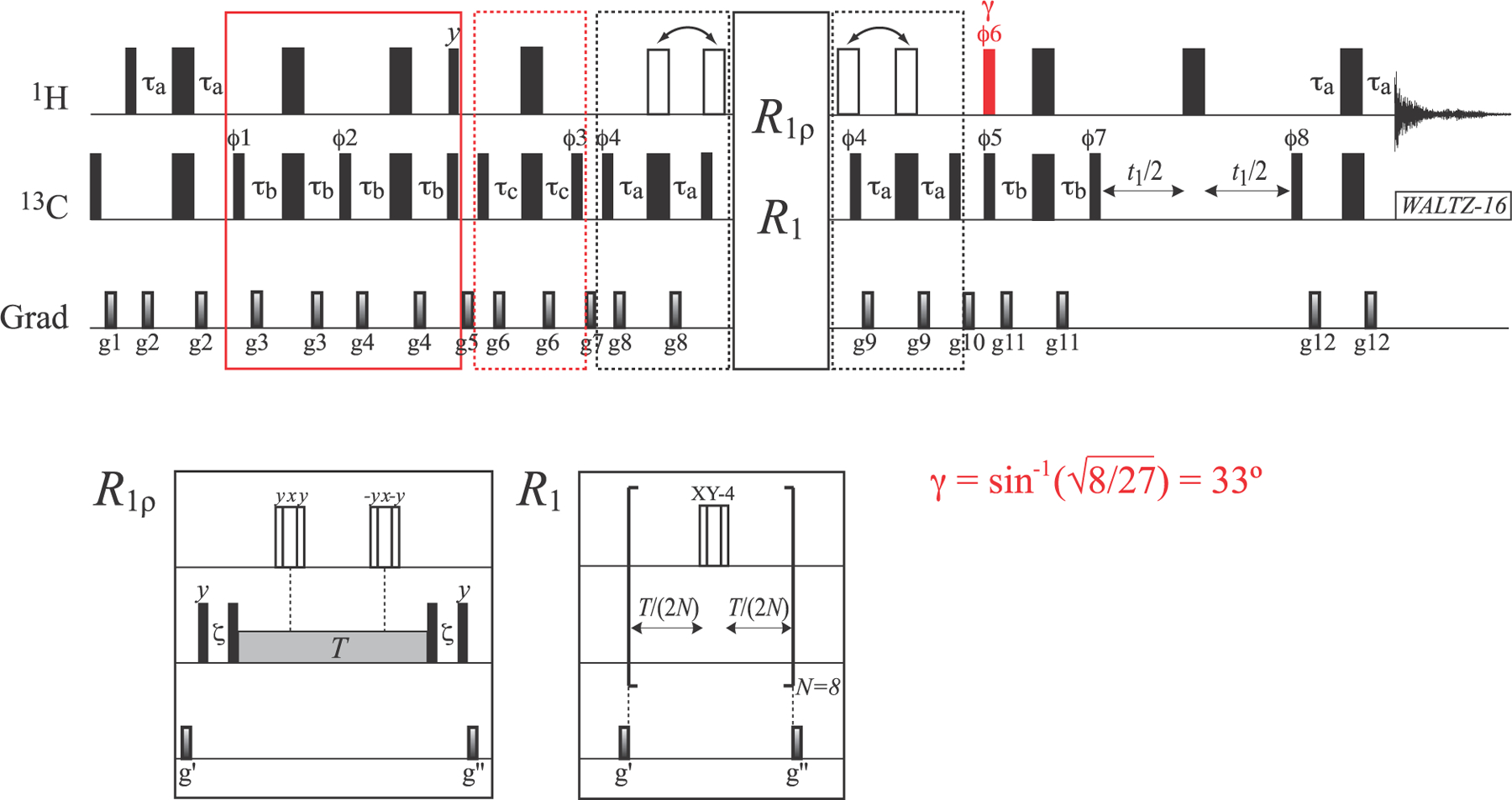
Pulse scheme for the measurement of the R_1ρ and R₁ relaxation rates of the inner ¹³C magnetization mode of the I = 3/2 manifold (L₂ ± L₃). All the parameters of the scheme (including delays) are the same as in Figure 2. The ¹H pulse shown in red is applied with flip angle γ = sin⁻¹(√8/27) = 33°. “Open” ¹H 180° pulses of the main scheme (in the elements enclosed in dashed black boxes before and after the relaxation delays) are applied either simultaneously with ¹³C 180° pulses (for in-phase measurements; L₂ + L₃) or outside the 2τ_a elements (for antiphase measurements; L₂ − L₃) as indicated by arrows above the scheme. “Open” ¹H pulses in the R₂ and R₁ measurements are composites pulses of the 90°–240°–90° variety²⁹ that are applied using the phase-cycling indicated in the figure for the R_1ρ measurements, and XY-4 phase-cycling^30,31 for R₁ measurements. Note that a total of eight ¹H π-pulses (N = 8) is used for R₁ measurements to avoid artifacts due to fast pulsing. The durations and strengths of pulsed-field gradients (ms; G/cm) are as follows: g1 = (1.0; 25), g2 = (0.4; 15), g3 = (0.3; 20), g4 = (0.35; 25), g5 = (1.4; 12), g6 = (0.2; 20), g7 = (0.8; 20), g8 = (0.5; 20), g9 = (0.4; 20), g10 = (1.0; 20), g11 = (0.3; 12), g12 = (0.5; 15), g′ = (0.8; 25), and g″ = (0.6; 20). The phase cycle is as follows: ϕ1 = 2(x), 2(−x); ϕ2 = x, −x; ϕ3 = 2(x), 2(−x); ϕ4 = 2(x), 2(−x) for antiphase (L₂ − L₃) measurements and 2(y), 2(−y) for in-phase (L₂ + L₃) measurements; ϕ5 = x, −x; ϕ6 = 4(x), 4(−x); ϕ7 = y, −y; ϕ8 = x; and receiver phase = (x,−x,−x,x, −x,x,x,−x). Quadrature detection in t₁ is achieved via the States³² incrementation of ϕ8.

It is worth emphasizing that relaxation measurements of the (L₁ ± L₄) and (L₂ ± L₃) magnetization modes (Figures 5 and 6, respectively) are more technically demanding by far than those of the (L₅ ± L₆) magnetization mode in Figure 2. One of the underlying difficulties arises from cross-relaxation between the (L₁ ± L₄) and (L₂ ± L₃) modes, which is induced by spin-flips (eq 2) that make the relaxation decay of these terms non-single-exponential for at least some methyl sites. Although perdeuteration of NMR samples mitigates this effect, it cannot be eliminated completely. Therefore, care should be exercised not to extend relaxation delays to excessively large values. Further, in the measurement of (L₁ ± L₄) R₂ rates (Figure 5), we have chosen not to apply a spin-lock RF field to (1) avoid problems associated with large values of the ¹H–¹³C scalar couplings operative for the outer (fast-relaxing) ¹³C transitions (3¹J_CH ~ 380 Hz; the 2 kHz spin-lock field, typically employed in other experiments, may be only marginally sufficient for couplings of this magnitude; note that the “free-precession” R₂ values should not be affected by the differences between in-phase (L₁ + L₄) and antiphase (L₁ − L₄) R₂ rates as these are predicted to be very small in deuterated proteins); and (2) mitigate the effect of spin flips, which are expected to be reduced as the cross-relaxing components of the magnetization are secular in the absence of the RF field. In addition, ¹H 180° pulses applied during relaxation delays to eliminate methyl ¹³C CSA and ¹³C–¹H dipolar cross correlations in the measurements involving antiphase magnetization, i.e., (L₁ − L₄) or (L₂ − L₃), have to be implemented as composite pulses with the phase cycling as described in Figures 5 and 6. Using the pulse scheme in Figure 5, average (L₁ ± L₄) R₂ rates of 12.5 and 24.3 s⁻¹ were obtained for ILV-{¹³CH₃}-labeled ubiquitin at 25 and 5 °C, respectively, while the corresponding average R₁ rates were 3.8 and 4.2 s⁻¹, respectively. The average (L₂ + L₃) R₂ and R₁ rates were 4.3 and 3.3 s⁻¹, respectively, at 25 °C, and 7.0 and 6.0 s⁻¹ at 5 °C, while their antiphase counterparts (L₂ − L₃) had average values of 6.4 and 5.4 s⁻¹, respectively, at 25 °C and 11.4 and 10.3 s⁻¹, respectively, at 5 °C. The (L₁ ± L₄) R₂ and R₁ rates of all methyl sites were corrected (on a site-specific basis) by the experimental value of $k_{\text{HH}}^{\text{ext }}=(3/8)\Delta$, where Δ is the difference between the R₂/R₁ rates of the antiphase (L₂ − L₃) and in-phase (L₂ + L₃) modes as described above. The average corrections employed for the R₂ and R₁ rates were 0.79 and 0.78 s⁻¹, respectively, at 25 °C, and 1.64 and 1.62 s⁻¹, respectively, at 5 °C.

By themselves, the thus-corrected relaxation rates of the (L₁ ± L₄) modes are not (on average) as good measures of methyl-axis dynamics as those of the (L₅ + L₆) ¹³C magnetization. Although it may be tempting to include the (corrected) (L₁ ± L₄) relaxation rates in the analysis only for those methyl sites that show the worst agreement between the two sets of dynamics parameters in Figure 3, we prefer to do so for all ILV methyl groups of ubiquitin since in the absence of the “benchmark” set of ¹³CHD₂-derived parameters [$S_{\text{axis}}^2$; τ_f] it would not be possible to know a-priori which methyl sites are compromised (where $S_{\text{axis}}^2$ is anticorrelated with τ_f). Note that the (L₂ + L₃) rates are not included in the analysis directly as, in the absence of spin flips, the (L₂ + L₃) relaxation rates are very similar (to within experimental errors) to those of the (L₅ + L₆) mode and, therefore, are not expected to provide additional information on methyl-axis dynamics.

Figure 7 shows correlation plots comparing methyl-axis dynamics parameters derived from ¹³C relaxation of the (L₅ + L₆) mode (I = 1/2 manifold) complemented with the R₂/R₁ rates of (L₁ ± L₄) in ¹³CH₃ methyl groups with those derived from ¹³C relaxation in ¹³CHD₂ isotopomers of ubiquitin. A notable improvement is observed in the quality of the correlations for $S_{\text{axis}}^2$ at both temperatures (Figures 7A and C) compared to the plots where only the (L₅ + L₆) data are used (cf. Figures 3A and C). The agreement in τ_f is likewise ameliorated for the four methyl sites with the highest τ_f values (Figures 7B and D). Note that inclusion of the (L₁ ± L₄) R₂/R₁ data in the analysis (see SI “Materials and Methods”), increases the number of degrees of freedom in the fit from zero to two, providing additional information content that at least partially overcomes correlations between $S_{\text{axis}}^2$ and τ_f.

Figure 7.

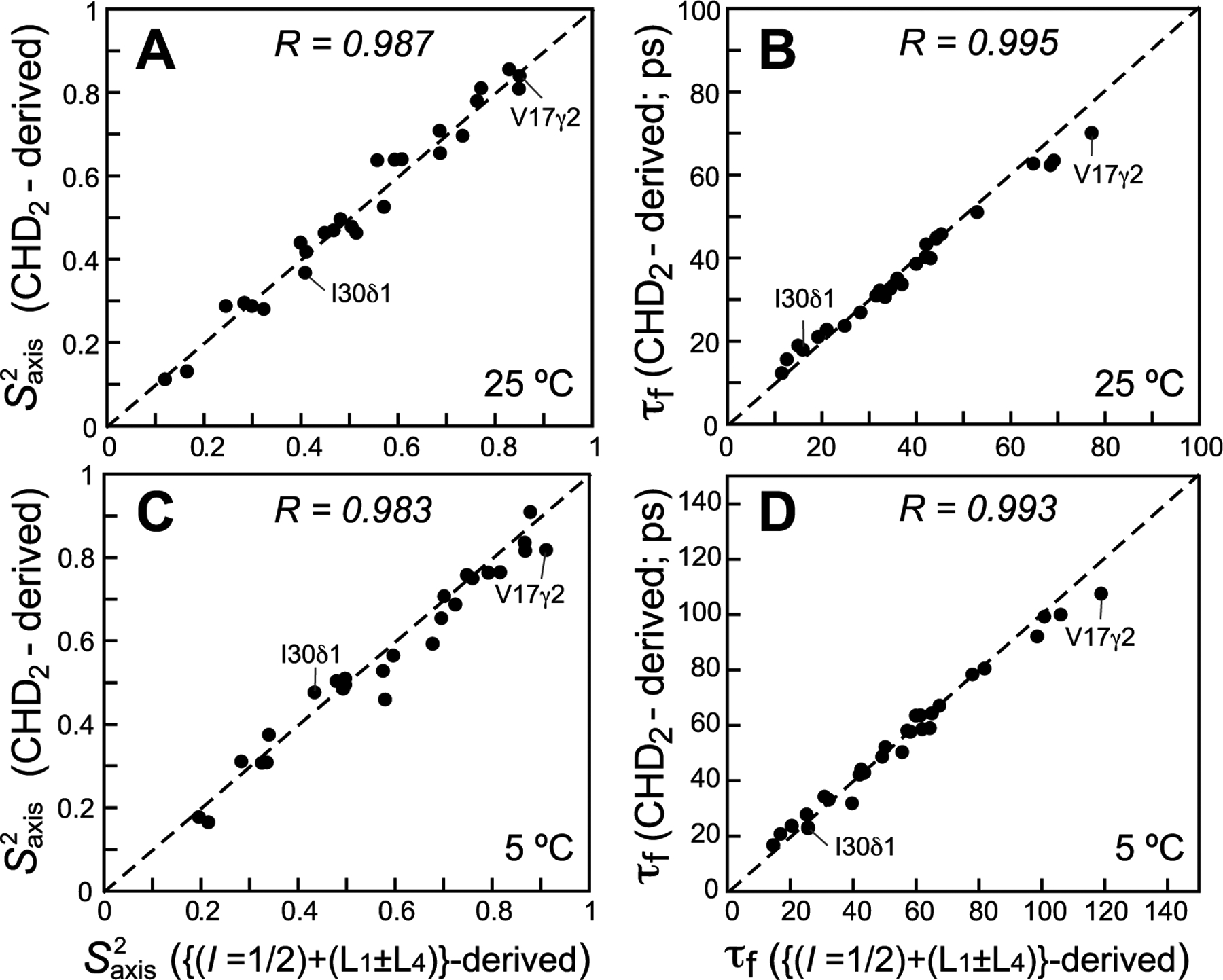
Correlation plots comparing methyl-axis dynamics parameters derived from ¹³C relaxation of the (L₅ + L₆) mode complemented with ¹³C relaxation of (L₁ ± L₄) in ¹³CH₃ methyls (x-axes) with those derived from the ¹³C relaxation in ¹³CHD₂ methyls (y-axes) for an ILV-labeled sample of ubiquitin at 25 °C (upper row; (A) $S_{\text{axis}}^2$ and (B) τ_f; 29 correlations) and 5 °C (lower row; (C) $S_{\text{axis}}^2$ and (D) τ_f; 30 correlations). All data were collected at 600 MHz. Linear correlation coefficients are shown at the top of each plot. Dashed lines are drawn at y = x.

In the absence of relaxation, experiments for the measurement of R_1ρ and R₁ relaxation rates of the (L₅ + L₆) magnetization mode (Figure 2) are predicted to be around threefold less sensitive than the experiments designed for relaxation measurements in ¹³CHD₂ methyl isotopomers.¹⁷ As discussed previously, transverse relaxation during the 4τ_b and 2τ_a periods in the pulse scheme of Figure 2, and slower longitudinal ¹H relaxation in ¹³CHD₂ methyls during recovery delays, can increase or reduce this factor, respectively.¹⁷ These predictions are borne out in this work, with sensitivity ratios for the two types of experiments of 0.42 and 0.38 measured for ubiquitin and MSG, respectively, for the first point of the relaxation series (T = 0) when using a recovery delay of 1.5 s. In the absence of relaxation, the sensitivity of the experiments selecting for the (L₁ ± L₄) and (L₂ ± L₃) magnetization modes in Figures 5 and 6, respectively, is related to that selecting for the (L₅ + L₆) mode in Figure 2 in a ratio of 2.68:1.04:1.0, where the sensitivity enhancement of the experiment in Figure 2 by √2 is taken into account. However, as both experiments that target the I = 3/2 manifold modes (Figures 5 and 6) start with the selection of the fast-relaxing methyl coherences and, in the case of the experiment in Figure 5, the fast-relaxing ¹H coherences are included during signal detection (the acquisition period), these experiments are less tolerant to transverse relaxation. While the measured ratio of sensitivities is 1.95:0.88:1.0 for ubiquitin at 5 °C, we predict that the sensitivity of both experiments in Figures 5 and 6 will be significantly lower for much larger proteins than that of the experiment in Figure 2.

Numerical simulations of sensitivity of the relaxation rates obtained in the experiments described here to mis-settings of the ¹H acute-angle pulses show that R₂(R_1ρ) relaxation rates measured in the experiment in Figure 2 (the selection of the (L₅ + L₆) magnetization modes) are quite sensitive to inaccuracies of the pulse with flip angle α. The relative sensitivity of the extracted R₂ rates is predicted to be inversely proportional to the global molecular correlation time τ_C; changes of ~1.5% in the R₂ rate per one degree of α-angle mis-setting are obtained for MSG (τ_C ~ 46 ns), and values of ~2.5% and ~2.8% per degree are obtained for ubiquitin at 25 and 5 °C, respectively (τ_C ~ 5 and 11 ns, respectively). R₁ rates obtained in the same experiment (Figure 2) are relatively less sensitive to the mis-calibration of the α-pulse, with values of less than ~0.5% per degree predicted for the whole range of τ_C values studied here. It is worth noting that the ¹H 90° “purging” pulse applied to “in-phase” magnetization (L₅ + L₆) immediately before the relaxation delay (the inset in Figure 2) substantially mitigates these effects. In contrast, both R₂ and R₁ relaxation rates of the (L₁ ± L₄) magnetization modes (pulse scheme in Figure 5) are quite insensitive to the mis-setting of the β-angle, with relative sensitivities of only ~0.2% and ~0.1% per degree obtained for R₂ and R₁ rates in ubiquitin (5 °C), respectively. Note that relaxation rates of the (L₂ ± L₃) magnetization modes (pulse scheme in Figure 6) should not depend on the mis-setting of angle γ, as this angle is not used for the selection proper of the (L₂ ± L₃) modes and is optimized solely to improve the sensitivity of the experiment.

CONCLUSIONS

In summary, we have described the dynamics of methyl-bearing side-chains in proteins by ¹³C relaxation measurement of a number of modes (classes) of ¹³C magnetization in selectively ¹³CH₃-labeled methyl groups of otherwise deuterated proteins. We first show how the ¹³C magnetization modes whose NMR relaxation properties, transverse (R₂) and longitudinal (R₁) spin relaxation rates, bear information on the methyl-axis dynamics in ¹³CH₃ methyl groups, can be isolated using acute-angle ¹H RF pulses. The parameters of methyl-axis dynamics ($S_{\text{axis}}^2$, a measure of the amplitudes of the methyl-axis motions, and τ_f, the correlation time of the fast local methyl-axis motions) derived from ¹³C relaxation in ¹³CH₃ methyls are compared with their counterparts derived from ¹³C relaxation in ¹³CHD₂ methyl isotopomers. We show that excellent correlations between the [¹³CHD₂]-derived $S_{\text{axis}}^2$ values and those extracted from relaxation of ¹³C magnetization of the I = 1/2 manifold in ¹³CH₃ methyls can be obtained in larger proteins. In ¹³CH₃ methyls of smaller proteins, a certain degree of anti-correlation is observed between $S_{\text{axis}}^2$ and τ_f values obtained from ¹³C relaxation of the I = 1/2 manifold magnetization. This correlation can be (partially) removed by inclusion in the analysis of ¹³C relaxation data acquired on the I = 3/2 manifold magnetization modes.