Abstract
Generating a novel and optimized molecule with desired chemical properties is an essential part of the drug discovery process. Failure to meet one of the required properties can frequently lead to failure in a clinical test which is costly. In addition, optimizing these multiple properties is a challenging task because the optimization of one property is prone to changing other properties. In this paper, we pose this multi-property optimization problem as a sequence translation process and propose a new optimized molecule generator model based on the Transformer with two constraint networks: property prediction and similarity prediction. We further improve the model by incorporating score predictions from these constraint networks in a modified beam search algorithm. The experiments demonstrate that our proposed model, Controlled Molecule Generator (CMG), outperforms state-of-the-art models by a significant margin for optimizing multiple properties simultaneously.
Keywords: molecule optimization, drug discovery, sequence to sequence, self-attention, neural networks
1. INTRODUCTION
Drug discovery is an expensive process. According to Dimasi et al. [8], the estimated average cost to develop a new medicine and gain FDA approval is $1.4 billion. Among this amount, 40% of it is spent on the candidate compound generation step. In this step, around 5,000 to 10,000 molecules are generated as candidates but 99.9% of them will be eventually discarded and only 0.1% of them will be approved to the market. This inefficient nature of the candidate generation step serves as motivation to design an automated molecule search method. However, finding target molecules with the desired chemical properties is challenging because of two reasons. First, an efficient search is not possible because the search space is discrete to the input [22]. Second, the search space is too large that it reaches up to 1060 [28]. As such, this task is currently being tackled by pharmaceutical experts and takes years to design. Therefore, this paper aims to accelerate the drug discovery process by proposing a deep-learning (DL) model that accomplishes this task effectively and quickly.
Recently, many methods of molecular design have been proposed [3, 5, 10, 12, 14, 23, 27, 32, 33, 42]. Among them, Matched Molecular Pair Analysis (MMPA) [13] and Variational Junction Tree Encoder-Decoder (VJTNN) [21] formulated molecular property optimization as a problem of molecular paraphrase. Just as a Natural Language Process (NLP) model produces paraphrased sentences, when a molecule comes in as an input to these models, another molecule with improved properties is generated by paraphrase. Although MMPA was the first to try this approach, it is not effective unless many rules are given to the model [21]. To mitigate this problem, Jin et al. [21] proposed VJTNN, an end-to-end molecule optimization model without the need for rules. By efficiently encoding and decoding a molecule with graphs and trees, it is the current state-of-the-art (SOTA) model for optimizing a single property (hereby referred to as a single-objective optimization task). However, it cannot optimize multiple properties at the same time (a multi-objective optimization task) because the model inherently optimizes only one property. As noted by Shanmugasundaram et al. [34] and Vogt et al. [39], the actual drug discovery process frequently requires balancing of multiple properties.
With these motivations, we propose a new DL-based end-to-end model that can optimize multiple properties in one model. By extending the preceding problem formulation, we consider the molecular optimization task as a sequence-based controlled paraphrase (or translation) problem. The proposed model, controlled molecule generator (CMG), learns how to translate the input molecules given as sequences into new molecules as sequences that best reflect the newly desired molecule properties. Our model extends the Transformer model [38] that showed its effectiveness in machine translation. CMG encodes raw sequences through a deep network and decodes a new molecule sequence by referencing that encoding and the desired properties. Since we represent the desired properties as a vector, this model inherently can consider multiple objectives simultaneously. Moreover, we present a novel loss function using pre-trained constraint networks to minimize generating invalid molecules. Lastly, we propose a novel beam search algorithm that incorporates these constraint networks into the beam search algorithm [26].
We evaluate CMG using two tasks (single-objective optimization and multi-objective optimization) and two analysis studies (ablation study case study)1. We compare our model with six existing approaches including the current SOTA, VJTNN. CMG outperforms all baseline models in both benchmarks. In addition, our model is trained once and evaluated for all tasks, which shows practicality and generality. The ablation study not only shows the effectiveness of each sub-part, but demonstrates the superiority of CMG itself without the sub-parts. Lastly, the case study demonstrates the practicality of our method through the target affinity optimization experiment using an actual experimental drug molecule.
Contribution
The contributions of this paper are summarized as below;
A new formulation of the multi-objective molecule optimization task as a sequence-based controlled molecule translation problem
A new self-attention based molecule translation model that can reflect the multiple desired properties through constraint networks
New loss functions to incorporate the pre-trained constraint networks
A novel beam search algorithm using the pre-trained constraint networks
2. RELATED WORK
Molecule property optimization:
Molecule property optimization models can be divided into two types depending on the data representation: sequence representations and graph representations. One of the earlier approaches using sequence representations utilizes encoding rules [40], while the recent ones [12, 23, 33] are based on DL methods that learn to reconstruct the input molecule sequence. This is related to our work in terms of the input representation, but they offer subpar performance when compared to the SOTA models. Another group of research uses graph representations conveying structural information [4, 6, 19, 24, 31]. Among them, VJTNN [21] and MMPA [6, 9, 13] are closely related to our work because they formulate the molecule property optimization task as a molecule translation problem. From the model perspective, MMPA is a rule-based model and VJTNN is a supervised DL model. Although our approach is also based on a DL method, there is a big difference in practical use cases. A single VJTNN model is capable of optimizing a single property, while CMG can optimize multiple properties by using the controlled decoder. With these differences, we formulate the molecule property optimization task as a “controlled” molecule “sequence” translation problem. Other molecule generation methods include Junction Tree Variatinal Auto Encoder (JT-VAE) [20], Variational Sequence-to-Sequence (VSeq2Seq) [1, 12], Graph Convolutional Policy Network (GCPN) [43], and Molecule Deep Q-Networks (MolDQN) [44].
Natural Language Generation Model:
Our model is inspired by the recent success in molecule representation using the self-attention technique [36]. By adopting the BERT [7] architecture to represent molecule sequences, their model becomes the SOTA in the drug-target interaction task. In terms of the model architecture, our work is related to Transformer [38] because we extend it to be applicable to the molecule optimization task. There is a controlled text generation model [17] in NLP domain. It is related to ours because they feed the desired text property as one of the inputs. However, all of these methods are designed for NLP tasks, therefore, they cannot be directly applied to molecule optimization tasks for two reasons. Firstly, the similarity constraint of the molecule optimization is an important feature, however, a typical NLP model can’t reflect this. Secondly, NLP models take categorical properties while ours is designed for numerical ones, which is more realistic in a molecule optimization.
Transfer learning:
DL-based transfer learning by pre-training has been applied to many fields such as computer vision [11, 30], NLP [16], speech recognition [18, 25], and health-care applications [35]. They are related to ours because we also pre-train the constrained networks and transfer the weights to the main model.
3. CONTROLLED MOLECULE GENERATOR
3.1. Problem Definition
Given an input molecule X, its associated molecule property vector pX, and the desired property vector pY, the goal is to generate a new molecule Y with the property pY with the similarity of . Note that δ is a similarity threshold and the similarity measure is Tanimoto molecular similarity over Morgan fingerprints [29]. Formally, for two Morgan fingerprints, FX and FY, where both of them are binary vectors, the Tanimoto molecular similarity is .
3.2. Model Overview
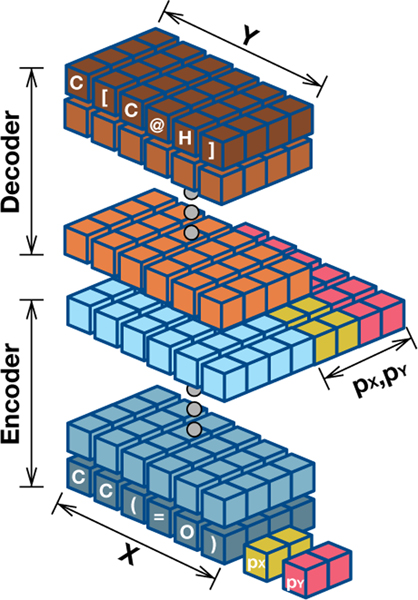
Our model extends the Transformer [38] to a molecular sequence by incorporating molecule properties and additional regularization networks. Inspired by the previous success in applying the self-attention mechanism to represent a molecule sequence [36], we treat each molecule just like a sequence. However, this NLP technique cannot be directly applied, because the structure of the molecular sequence differs from natural languages, where the hierarchy is a letter-word-sentence. Not only that, there is no training data available that is collected for the molecule translation task, while there are ample datasets in the NLP domain. To fill these gaps, we propose the controlled molecule generation model (Figure 1) and present how we gather the training data for this network (Section 4.1). We optimize CMG using three loss functions as briefly shown in Figure 1a. In addition, we propose two constraint networks (Section 3.4, Figure 3), the property prediction network and the similarity prediction network to train the model more accurately. Lastly, we also present how we modify the beam search algorithm [26] to best exploit the existing auxiliary networks, as briefly shown in Section 3.5 and Figure 1b.
Figure 1:
Controlled Molecule Generator (CMG) at training and prediction.
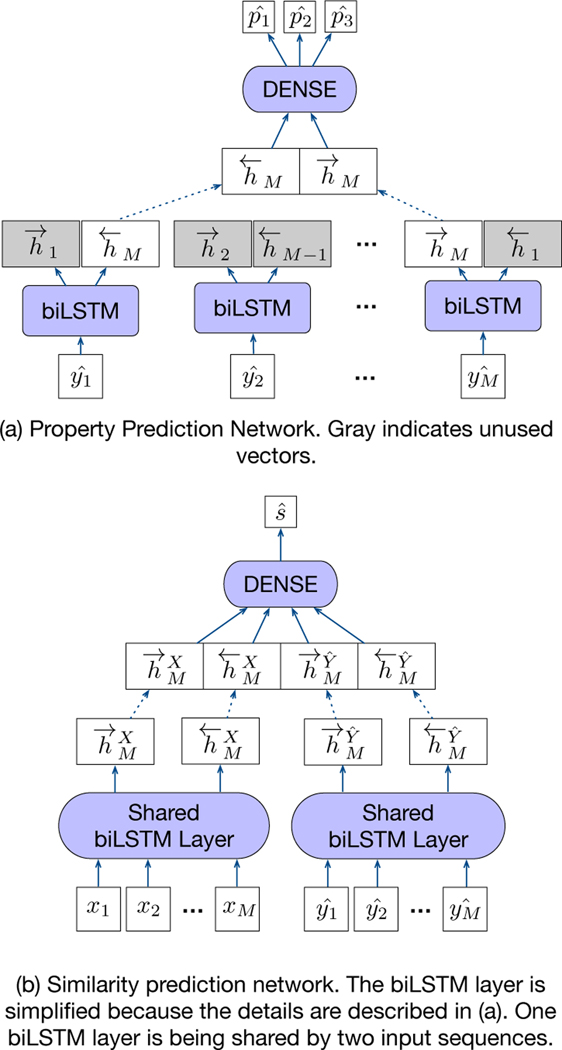
Figure 3:
Two Constraint Networks.
3.3. Molecule Translation Network
We apply two modifications to the Transformer model [38]. First, unlike Transformer which uses word embeddings, we use character embeddings because the molecule sequence is comprised of characters representing atoms or structure indicators. To mark the beginning and the end of a sequence, we add “[BEGIN]” token at the first position of the sequence and “[END]” token at the last. Another modification is that we add chemical property awareness to the hidden layer of the Transformer model. We enrich token vectors of the last encoder by concatenating property vectors to each of the token vectors as shown in Figure 2. Formally, let zi be the token vectors in the last encoder. Then, the new encoding vector becomes , where k represents the number of properties. Although it might be seen as a simple method, this empirically shows the best result among other types of configurations, such as property embeddings, disentangled encodings (property and non-property encodings), and concatenating property differential information instead of providing two raw vectors. The cost function of this network is the cross entropy between the target (yi) and predicted molecule (). Therefore, it is formally defined as,
where θT denotes all parameters of the Transformer and N, M,V represent the number of training samples, the length of a sequence, and the size of the vocabulary, respectively.
Figure 2:
The molecule translation network.
3.4. Constraint Networks
We hypothesize that the cost function of the Transformer network () is not enough to teach the generating model, because the error signals from this loss function can hardly capture the valuable information, such as if a predicted sequence pertains to the desired property or if it satisfies the similarity constraint. With this motivation, we add two constraint networks as follows.
3.4.1. Property Prediction Network.
The property prediction network (PropNet) takes the predicted molecule sequence () as an input (on the top of Figure 3). The left-to-right LSTM [15] layer and the right-to-left one encode input vectors () into hidden vectors, and , respectively. Since the last vectors for each direction summarize the sequence, they are concatenated and fed into a dense network with two hidden layers. With the predicted property, and the desired property (pY) from the input, we can create a loss function, which will enrich error signals by adding property awareness in predicting a molecule. This is formally written as,
We pre-train PropNet using molecules in the training set, and the properties are calculated using a third-party library. Once pretrained, the parameters are transferred to the CMG network and frozen when training the CMG.
3.4.2. Similarity Prediction Network.
The input of the similarity prediction network (SimNet) is composed of the predicted molecule sequence () and the input molecule sequence (xi) (on the bottom of Figure 3). We posit that adding estimated similarity error signals to the loss function could be useful for satisfying the similarity requirement because this is relatively direct information in the generation modeling. We employ one layer of BiLSTM for SimNet, which is shared by two different inputs. Two inputs ( and xi) is passed to the BiLSTM layer to produce each corresponding feature vector, and (M indicates the last token index). We concatenate these two feature vectors as (, ) , so that the next two dense networks can capture the similarity between the two. After applying two-layered dense network, we get the binary prediction () whether the two input molecules are similar or not according to the threshold δ. With this prediction () and the label (sn), we can create the last loss function, formally written as
We transfer the pre-trained SimNet weights into the CMG model and freeze the SimNet weights when training the CMG network.
3.4.3. CMG Loss Function.
By combining all cost functions (, , ), we can obtain the CMG loss function as
where λp and λs are weight parameters.
3.5. Modified Beam Search with Constraint Networks
When generating a sequence from CMG at testing, there is no gold output sequence that it can reference. Therefore we need to sequentially generate tokens until we encounter the “[END]” token, like other sequence-based algorithms. At this process, a typical way
Algorithm 1.
Modified Beam Search
| 1: | Input: Candidate molecules: , Corresponding beam scores: Input molecule: X Desired property vector: pY |
| 2: | for i = 1 to b do |
| 3: | |
| 4: | |
| 5: | |
| 6: | |
| 7: | |
| 8: | end for |
| 9: | best_index ← arg maxsi |
| 10: | Output: Cbest_index |
is the beam search, where the model maintains top b number of best candidate sequences when predicting each token. When all candidate sequences are complete and ready, the model outputs the best candidate in terms of a beam score, a cumulative log-likelihood score for a corresponding candidate. However, the standard beam search does not account for the multi-objective nature of our task. For example, there is a possibility that low ranked molecules could be closer to the desired properties than the top molecule selected by the beam search. Therefore, we propose a modified beam search algorithm (Algorithm 1) using our constraint networks. For the property evaluation, we first get the predicted property of each candidate and get the absolute difference from the desired property (Line 3–4 in Algorithm 1). Since this difference is desired to be small, we calculate the property evaluation score (spn) by subtracting them from one (Line 5 in Algorithm 1). The property could have multiple values, therefore, we take an average of all elements of this difference vector. For the similarity evaluation, we get the predicted similarity between the input X and each candidate Ci (Line 6 in Algorithm 1). Since we expect a candidate should be similar (label 1) to the input, we regard the predicted similarity as the raw score from SimNet. By adding these two predicted scores to the original beam scores, we obtain the modified beam scores (Line 7 in Algorithm 1). With this new score, we can select the best candidate (Line 9–10 in Algorithm 1)
3.6. Diversifying the Output
Unlike other variational models (VSeq2Seq and VJTNN), CMG encodes a fixed vector that is able to generate a single output for one input. In order to diversify the output for a fixed input, we re-parameterize the desired vector, (p1,p2,p3), as random variable by adding a Gaussian noise with a user-specified variance, ∼ N (pk,σk). For example, if the desired property vector is (p1, p2, p3), we feed (p1 + α, p2 + β, p3 + γ), where α, β and γ are samples drawn from N (0, σ1), N (0, σ2), and N (0, σ3).
4. EXPERIMENTS
We compare CMG with state-of-the-art molecule optimization methods in the following tasks. Single Objective Optimization (SOO): This task is to optimize an input molecule to have a better property while preserving a certain level of similarity between the input molecule and the optimized one. Since developing a new drug usually starts with an existing molecule [2], this task serves as a good benchmark. Multi-Objective Optimization (MOO): This task reflects a more practical scenario in drug discovery, where modifying an existing drug involves optimizing multiple properties simultaneously, such as similarity, lipophilicity scores, drug likeness scores, and target affinity scores. Since improving one property might often result in sacrificing other properties, this task is harder than a single-objective optimization task. To present multifaceted aspects of CMG, we additionally perform the following experiments. Ablation Study: For ablation study, we report the validity of the constraint networks both in training testing phases. Case Study: To evaluate the effectiveness of CMG, we present the result of an actual drug optimization task with an existing molecule in an experimental phase. More precise information regarding the reproducibility can be found in the supplementary material.
4.1. Datasets
Since CMG is based on sequence translation, we need to appropriately curate the dataset.
Training Set for CMG:
We use the ZINC dataset [37] (249,455 molecules) and the DRD2 related molecule dataset (DRD2D) [27] (25,695 molecules), which result in 260,939 molecules for our experiments. This is the same set of molecules on which Jin et al. [21] used to evaluate their model (VJTNN). From these 260k molecules, we exclude molecules that appear in the development and the test set of VJTNN, resulted in 257,565 molecules. With these molecules, we construct training datasets by selecting molecule pairs (X,Y) with the similarity is greater than or equal to 0.4, following the same procedure in [6, 21]. Jin et al. [21] used the small portion of these pairs by excluding all property-decreased molecule pairs. The main difference from their curation processes is that we don’t have to exclude many property-decreased molecule pairs because our model can extract useful information even from them. By doing this, we provide a more ample dataset to a deep model, so that it could be helpful in finding more useful patterns. As a result, the number of pairs in training data is significantly bigger than theirs. Among all possible pairs (257K × 257K = 67B), we select 10,827,615 pairs that satisfies similarity condition (≥ 0.4). With the same similarity condition, Jin et al. [21] gathered less than 100K due to additional constraints of training sets, which is only property increased molecule pairs can be used as training data. As previous works [21, 23] did, we pre-calculate the three chemical properties of all molecules (pX and pY ) in the training set: Penalized logP (PlogP) [23] is a measure of lipophilicity of a compound, specifically, the octanol/water partition coefficient (logP) penalized by the ring size and synthetic accessibility. Drug likeness (QED) is the quantitative estimate of drug-likeness proposed by Bickerton et al. [2] and Dopamine Receptor (DRD2) is a measure of molecule activity against a biological target, the dopamine type 2 receptor.
Training Set for PropNet:
Among 260,939 molecules, we excluded all molecules in the test sets of the two tasks; single-objective optimization, multi-objective optimization. The number of these remained molecules is 257,565. We construct the dataset for PropNet by arranging all molecules as inputs and the corresponding three properties as outputs. We randomly split this into the training and validation sets with a ratio of 8:2.
Training Set for SimNet:
We use a subset of all 10,827,615 pairs in the CMG training set due to the simpler network configuration of SimNet. When sub-sampling pairs, we tried to preserve the proportion of the similarity in the CMG dataset to best preserve the original data distribution. The reason behind this effort is that preserving the similarity distribution could possibly contribute to the SimNet accuracy although SimNet only uses binary labels. In addition, we try to preserve the similar/not-similar ratio to be about to the same. By sampling about 10% of data, we gathered 997,773 number of pairs and the ratio of the positive samples is 49.45%. We randomly split this into the training and validation set with a ratio of 8:2.
4.2. Pre-Training of Constraint Networks
We pre-train the two constraint networks using the training sets described in Section 4.1. We choose the pre-trained PropNet that recorded the mean square error of 0.0855 and the the pre-trained SimNet of 0.9759 accuracy through the best model evaluated on each corresponding development set. The pre-trained weights of the two networks are transferred to the corresponding part in the CMG model and frozen when training CMG and predicting a new molecule using it. The details of the configuration is described in the supplement material.
4.3. Single Objective Optimization
The first task is the single objective optimization task proposed by Jin et al. [20]. The goal is to generate a new molecule with an improved single property score under the similarity constraint (δ = 0.4). We used the same development and test sets provided by Jin et al. [20]. Our model is trained once and evaluated for all tasks (SOO, MOO and the case study).
Baselines:
We compare CMG with the following baselines; MMPA, JT-VAE, GCPN, VSeq2Seq, MolDQN, and VJTNN introduced in Section 2. Since Jin et al. [21] ran and reported almost all of the baseline methods on the single property optimization task (PlogP improvement task) with the same test sets, we cite their experiment results. For MolDQN, which is published after VJTNN, we referenced the scores from MolDQN paper [44].
Metrics:
Since the task is to generate a molecule with an improved PlogP value, we measure an average of raw increments and its standard deviation among valid molecules with the similarity constraint met. Following the VJTNN procedure [21], one best molecule is selected among 20 generated molecules. We also measure the diversity defined by Jin et al. [21]. Although this diversity measure has been used by previous researches, it is limited in that it encourages the outputs to have low similarity around the threshold. However, this could be beneficial in a practical situation where the model needs to generate various molecules around the similarity threshold.
Result:
After we train the model we generate new molecules by feeding input molecules and desired chemical properties to the trained model. As discussed in Section 3.6, we add offsets to desired properties so that the output can be diversified. Since the number of generated samples for each input is set to 20, we use the desired property vector of {XP log P, 0.0, 0.0} with a total of 20 combinations of (α,β,γ) that are sampled from the user-defined distributions. We select the best model using the development set, and the test set performance of that model is reported in the left part of Table 1. In the PlogP optimization task, CMG outperforms all baselines including the current SOTA, VJTNN, in terms of both the average improvement and the diversity by a large margin. Considering the two recently proposed methods (MolDQN and VJTNN) are competing in 0.18 difference, CMG surpasses the current SOTA by 0.37 improvement. The same trend can be found in the diversity comparison. For QED and DRD2 cases, however, CMG underperforms the others (the scores are in the supplemental material). The primary reason is that the CMG model is trained once for the MOO task. This model is then re-used and evaluated on the SOO tasks. More specifically, the proportions of improved QED and DRD2 pairs in the training set are just 5.9% and 0.08%, respectively. Therefore, when optimizing solely for QED or DRD2, CMG could not fully extract the useful information from the training set. Since our model is trained once for all tasks (SOO, MOO, and the case study), this small portion of information can negatively impact certain single property optimizations, such as QED and DRD2. However, considering SOO is less practical in drug discovery, the focus should be on the MOO results.
Table 1:
Single and multi objective optimization performance comparison on the penalized logP task. For the single one, MolDQN results are from [44], and the scores of other baselines are from [21]. The reported scores of the multi objective optimization task is a success rate. CMG outperforms the baselines in both of the two tasks.
| Single Obj. Opt. | Multi Obj. Opt. | |||
|---|---|---|---|---|
| Method | Improvement | Diversity | All Samples | Sub Samples |
| MMPA | 3.29 ± 1.12 | 0.496 | - | - |
| JT-VAE | 1.03 ± 1.39 | - | - | - |
| GCPN | 2.49 ± 1.30 | - | - | - |
| VSeq2Seq | 3.37 ± 1.75 | 0.471 | - | - |
| MolDQN | 3.37 ± 1.62 | - | - | 0.00% |
| VJTNN | 3.55 ± 1.67 | 0.480 | 3.56% | 4.00% |
| CMG | 3.92 ± 1.88 | 0.545 | 6.98% | 6.00% |
4.4. Multi Objective Optimization
We set up a new benchmark, multi-objective optimization (MOO) because the actual drug discovery process frequently requires balancing of multiple compound properties [34, 39]. In this task, we jointly optimize three chemical properties for a given molecule. We set up the success criteria of the generated molecules in the MOO task as follows:
sim(X,Y) ≥ 0.4
PlogP improvement is at least 1.0
QED value is at least 0.9
DRD2 value is over 0.5
We created the above four conditions by combining the existing single optimization benchmarks from VJTNN [21] as one simultaneous condition2.
To create the development set of this task, we merge all three different development sets provided by VJTNN, consisting of 1,038 molecules. Among those molecules, we exclude any molecules that already satisfy the above criteria. Then, the final development set contains 985 molecules. We perform the same procedure for the test set, which reduces the number of molecules to 2,365.
Baselines:
For this task, we include the top two baselines (MolDQN and VJTNN) from the SOO task. While MolDQN can perform the MOO task by simply modifying the reward function, VJTNN can’t perform as it is because it is designed for a single property optimization. Here are how we prepare those baselines for the MOO task.
-
MolDQN: The reward function of MolDQN for this task is defined as
The first four terms represent the exact goal of the task, and the last four terms provide continuous information about the goals. Unlike VJTNN and CMG that require mere evaluation of the trained models, MolDQN should be re-trained from the beginning for each test sample, which requires significant time. Therefore, evaluating MolDQN for all 2,365 samples requires 2,365 times of training that is estimated as more than three months with a 96-CPUs server.
Therefore, we sub-sample the test set (n = 50) while preserving the original distribution3 and we use it for the proxy evaluation of MolDQN. For each input, we generate 60 samples after training the model (with exploration rate set to zero) and report success if at least one of them satisfies the success criteria defined above.
VJTNN: We sequentially optimize an input molecule using three trained models from VJTNN (models for PlogP, QED, and DRD2). Firstly, the PlogP model generates 20 molecules for an input molecule. We select the most similar molecules that satisfy PlogP criteria. Then, we repeat this process for QED and DRD2 models using the output of a preceding model as an input. Finally, we report success if any output of DRD2 model satisfies the success criteria.
Result:
We only compare VJTNN for all samples due to the infeasible running time of MolDQN as mentioned above. As the right part of Table 1 shows, CMG is almost two times more successful in this task. The sub-sample experiment shows similar performance for VJTNN and ours, while MolDQN is not able to generate any successful samples.
4.5. Ablation Study
To illustrate the effect of the two constraint networks and the modified beam search, we present the result of the ablation study in Table 2. We use the MOO task for this comparison, and the result of VJTNN is also included for the reference. It’s worthwhile to note that CMG without any constraint networks and the modified beam search still outperforms VJTNN by 1.77% point. The component with the biggest contribution is SimNet that improves the performance by 0.72% point from the model without it. Another interesting thing is the success rates of the last two models in Table 2 are identical. The possible explanation is that if a model is trained without any constraint networks, the neurons generating candidate molecules could not properly convey any information about similarity and properties that can be exploited in the modified beam search.
Table 2:
Ablation study on the Multi Objective Optimization task. MBS is modified beam search, PNet is PropNet, and SNet is SimNet. It’s worthy to note that CMG without any constraints networks and the modified beam search still outperforms VJTNN in the MOO task.
| Method | Success Rate | ± | |||
|---|---|---|---|---|---|
|
| |||||
| VJTNN | 3.56 | −3.42 | |||
|
| |||||
| PNet | SNet | MBS | |||
| CMG | ☑ | ☑ | ☑ | 6.98 | − |
| ☑ | ☑ | □ | 6.72 | −0.26 | |
| □ | ☑ | ☑ | 6.77 | −0.21 | |
| ☑ | □ | ☑ | 6.26 | −0.72 | |
| □ | □ | ☑ | 5.33 | −1.65 | |
| □ | □ | □ | 5.33 | −1.65 | |
4.6. Case Study
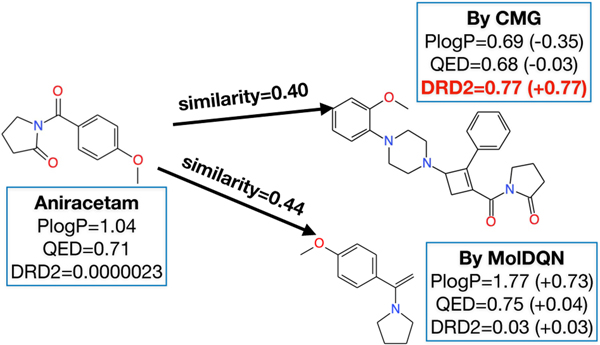
The purpose of this case study is to test how well a model can maintain other properties unchanged when optimizing one property. Therefore, we try to improve only the Dopamine D2 receptor (DRD2) score, and keep other properties unchanged as much as possible. We performed this case study using an actual drug that is under the experimental stage targeting DRD2. From Drugbank [41], we first enlist all DRD2 targeting drugs that are in either experimental or investigational stages. Among these 28 drugs, we select the lowest DRD2 scored drug, named Aniracetam (COC1=CC=C(C=C1)C(=O)N1CCCC1=O) for this study. The goal is to improve DRD2 score with minimum perturbation of other properties. This can be seen as SOO, however it’s a MOO, because DRD2 should be increased while others need to be unchanged.
Baselines:
Since one VJTNN model optimizes one property, we just run the DRD2 VJTNN model trained by Jin et al. [21] by feeding Aniracetam. For MolDQN, the reward function becomes simpler as .
Result:
In Figure 4, we compare the molecules generated by MolDQN (C=C(c1ccc(OC) cc1)N1CCCC1) and ours (COc1ccccc1N1 CCN(C2CC(C(=O)N3CCCC3=O)=C2c2ccccc2)CC1), excluding the result of VJTNN, because VJTNN didn’t generate valid (sim(X,Y) ≥ 0.4) molecules. In terms of the predicted DRD2 scores, our molecule reached 0.77 whereas MolDQN’s molecule only recorded 0.03. For the other two properties which should be unchanged, our molecule seems to be stable with changes in PlogP by −0.35 and QED by −0.03 when compared with the MolDQN molecule that showed larger changes especially in PlogP. Although one case study cannot prove the general superiority of CMG, it consistently outperforms other baselines in all benchmarks (SOO, MOO, and the case study).
Figure 4:
A case study: The molecule produced by CMG has a better DRD2 score while keeping other properties less perturbed. On the other hand, the molecule produced by MolDQN is less improved in terms of DRD2 score, and more perturbed in terms of the other two. We exclude the result of VJTNN because it didn’t generate any valid (sim(X, Y) ≥ 0.4) molecules.
5. CONCLUSION
This paper proposes a new controlled molecule generation model using the self-attention based molecule translation model and two constraint networks. We pre-train and transfer the weights of the two constraint networks so that they can effectively regulate the output molecules. Not only that, we present a new beam search algorithm using these networks. Experimental results show that CMG outperforms all other baseline approaches in both single-objective optimization and multi-objective optimization by a large margin. Moreover, the case study using an actual experimental drug shows the practicality of CMG. In the ablation study, we present how each sub-unit contributes to model performance. It’s worth to note that our model is trained once and evaluated for all tasks (SOO, MOO and the case study), which shows practicality and generalizability.
Supplementary Material
CCS CONCEPTS.
Computing methodologies → Neural networks.
ACKNOWLEDGEMENTS
This work was supported by the National Science Foundation award IIS-#1838200, National Institute of Health award 1K01LM012924, AWS Cloud Credits for Research program, and Google Cloud Platform research credits
Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, or republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from permissions@acm.org.
Footnotes
Code and data are available at https://github.com/deargen/cmg
For the PlogP improvement, we set a hard number of 1.0 instead of measuring the magnitude of improvements to transform the criteria into a binary condition.
When sub-sampling, we tried to preserve the proportion of the PlogP values to best get unbiased samples.
Contributor Information
Bonggun Shin, Deargen Inc. Seoul, South Korea.
Sungsoo Park, Deargen Inc. Seoul, South Korea.
JinYeong Bak, SungKyunKwan University, Suwon, South Korea.
Joyce C. Ho, Emory University, Atlanta, GA, USA
REFERENCES
- [1].Bahdanau Dzmitry, Cho Kyunghyun, and Bengio Yoshua. 2014. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473 (2014). [Google Scholar]
- [2].Bickerton G Richard, Paolini Gaia V, Besnard Jérémy, Muresan Sorel, and Hopkins Andrew L. 2012. Quantifying the chemical beauty of drugs. Nature chemistry 4, 2 (2012), 90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Bjerrum Esben Jannik and Threlfall Richard. 2017. Molecular generation with recurrent neural networks (RNNs). arXiv preprint arXiv:1705.04612 (2017). [Google Scholar]
- [4].Dai Hanjun, Dai Bo, and Song Le. 2016. Discriminative embeddings of latent variable models for structured data. In International conference on machine learning. 2702–2711. [Google Scholar]
- [5].Dai Hanjun, Tian Yingtao, Dai Bo, Skiena Steven, and Song Le. 2018. Syntax-directed variational autoencoder for structured data. arXiv preprint arXiv:1802.08786 (2018). [Google Scholar]
- [6].Dalke Andrew, Hert Jerome, and Kramer Christian. 2018. mmpdb: An open-source matched molecular pair platform for large multiproperty data sets. Journal of chemical information and modeling 58, 5 (2018), 902–910. [DOI] [PubMed] [Google Scholar]
- [7].Devlin Jacob, Chang Ming-Wei, Lee Kenton, and Toutanova Kristina. 2018. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 (2018). [Google Scholar]
- [8].DiMasi Joseph A, Grabowski Henry G, and Hansen Ronald W. 2016. Innovation in the pharmaceutical industry: new estimates of R&D costs. Journal of health economics 47 (2016), 20–33. [DOI] [PubMed] [Google Scholar]
- [9].Dossetter Alexander G, Griffen Edward J, and Leach Andrew G. 2013. Matched molecular pair analysis in drug discovery. Drug Discovery Today 18, 15–16 (2013), 724–731. [DOI] [PubMed] [Google Scholar]
- [10].Ertl Peter, Lewis Richard, Martin Eric, and Polyakov Valery. 2017. In silico generation of novel, drug-like chemical matter using the LSTM neural network. arXiv preprint arXiv:1712.07449 (2017). [Google Scholar]
- [11].Ghifary Muhammad, Kleijn W Bastiaan, Zhang Mengjie, Balduzzi David, and Li Wen. 2016. Deep reconstruction-classification networks for unsupervised domain adaptation. In European Conference on Computer Vision. Springer, 597–613. [Google Scholar]
- [12].Gómez-Bombarelli Rafael, Wei Jennifer N, Duvenaud David, Hernández-Lobato José Miguel, Sánchez-Lengeling Benjamín, Sheberla Dennis, Aguilera-Iparraguirre Jorge, Hirzel Timothy D, Adams Ryan P, and Aspuru-Guzik Alán. 2018. Automatic chemical design using a data-driven continuous representation of molecules. ACS central science 4, 2 (2018), 268–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Griffen Ed, Leach Andrew G, Robb Graeme R, and Warner Daniel J. 2011. Matched molecular pairs as a medicinal chemistry tool: miniperspective. Journal of medicinal chemistry 54, 22 (2011), 7739–7750. [DOI] [PubMed] [Google Scholar]
- [14].Guimaraes Gabriel Lima, Sanchez-Lengeling Benjamin, Outeiral Carlos, Farias Pedro Luis Cunha, and Aspuru-Guzik Alán. 2017. Objective-reinforced generative adversarial networks (organ) for sequence generation models. arXiv preprint arXiv:1705.10843 (2017). [Google Scholar]
- [15].Hochreiter Sepp and Schmidhuber Jurgen. 1997. Long short-term memory. Neural computation 9, 8 (1997), 1735–1780. [DOI] [PubMed] [Google Scholar]
- [16].Howard Jeremy and Ruder Sebastian. 2018. Universal language model fine-tuning for text classification. arXiv preprint arXiv:1801.06146 (2018). [Google Scholar]
- [17].Hu Zhiting, Yang Zichao, Liang Xiaodan, Salakhutdinov Ruslan, and Xing Eric P. 2017. Toward controlled generation of text. In Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR.org, 1587–1596. [Google Scholar]
- [18].Jaitly Navdeep, Nguyen Patrick, Senior Andrew, and Vanhoucke Vincent. 2012. Application of pretrained deep neural networks to large vocabulary speech recognition. (2012). [Google Scholar]
- [19].Jin Wengong, Barzilay Regina, and Jaakkola Tommi. 2018. Junction tree variational autoencoder for molecular graph generation. arXiv preprint arXiv:1802.04364 (2018). [Google Scholar]
- [20].Jin Wengong, Coley Connor, Barzilay Regina, and Jaakkola Tommi. 2017. Predicting organic reaction outcomes with weisfeiler-lehman network. In Advances in Neural Information Processing Systems. 2607–2616. [Google Scholar]
- [21].Jin Wengong, Yang Kevin, Barzilay Regina, and Jaakkola Tommi. 2019. Learning multimodal graph-to-graph translation for molecular optimization. ICLR (2019). [Google Scholar]
- [22].Kirkpatrick Peter and Ellis Clare. 2004. Chemical space. [Google Scholar]
- [23].Matt J Kusner Brooks Paige, and Hernández-Lobato José Miguel. 2017. Grammar variational autoencoder. In Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR.org, 1945–1954. [Google Scholar]
- [24].Li Yibo, Zhang Liangren, and Liu Zhenming. 2018. Multi-objective de novo drug design with conditional graph generative model. Journal of cheminformatics 10, 1 (2018), 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Lu Xugang, Tsao Yu, Matsuda Shigeki, and Hori Chiori. 2013. Speech enhancement based on deep denoising autoencoder.. In Interspeech. 436–440. [Google Scholar]
- [26].Medress Mark F., Franklin S Cooper Jim W. Forgie, Green CC, Klatt Dennis H., O’Malley Michael H, Neuburg Edward P, Newell Allen, Reddy DR, Ritea B, et al. 1977. Speech understanding systems: Report of a steering committee. Artificial Intelligence 9, 3 (1977), 307–316. [Google Scholar]
- [27].Olivecrona Marcus, Blaschke Thomas, Engkvist Ola, and Chen Hongming. 2017. Molecular de-novo design through deep reinforcement learning. Journal of cheminformatics 9, 1 (2017), 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Polishchuk Pavel G, Madzhidov Timur I, and Varnek Alexandre. 2013. Estimation of the size of drug-like chemical space based on GDB-17 data. Journal of computer-aided molecular design 27, 8 (2013), 675–679. [DOI] [PubMed] [Google Scholar]
- [29].Rogers David and Hahn Mathew. 2010. Extended-connectivity fingerprints. Journal of chemical information and modeling 50, 5 (2010), 742–754. [DOI] [PubMed] [Google Scholar]
- [30].Rothe Rasmus, Timofte Radu, and Van Gool Luc. 2015. Dex: Deep expectation of apparent age from a single image. In Proceedings of the IEEE international conference on computer vision workshops. 10–15. [Google Scholar]
- [31].Samanta Bidisha, De Abir, Ganguly Niloy, and Gomez-Rodriguez Manuel. 2018. Designing random graph models using variational autoencoders with applications to chemical design. arXiv preprint arXiv:1802.05283 (2018). [Google Scholar]
- [32].Sanchez-Lengeling Benjamin, Outeiral Carlos, Guimaraes Gabriel L, and Aspuru-Guzik Alán. 2017. Optimizing distributions over molecular space. An objective-reinforced generative adversarial network for inverse-design chemistry (ORGANIC). (2017). [Google Scholar]
- [33].Segler Marwin HS, Kogej Thierry, Tyrchan Christian, and Waller Mark P. 2018. Generating focused molecule libraries for drug discovery with recurrent neural networks. ACS central science 4, 1 (2018), 120–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Shanmugasundaram Veerabahu, Zhang Liying, Kayastha Shilva, de la Vega de Leon Antonio, Dimova Dilyana, and Bajorath Jurgen. 2016. Monitoring the progression of structure–activity relationship information during lead optimization. Journal of medicinal chemistry 59, 9 (2016), 4235–4244. [DOI] [PubMed] [Google Scholar]
- [35].Shin Bonggun, Chokshi Falgun H, Lee Timothy, and Choi Jinho D. 2017. Classification of radiology reports using neural attention models. In 2017 International Joint Conference on Neural Networks (IJCNN). IEEE, 4363–4370. [Google Scholar]
- [36].Shin Bonggun, Park Sungsoo, Kang Keunsoo, and Ho Joyce C. 2019. SelfAttention Based Molecule Representation for Predicting Drug-Target Interaction. In Proceedings of the 4th Machine Learning for Healthcare Conference (Proceedings of Machine Learning Research), Vol. 106. PMLR, 230–248. [Google Scholar]
- [37].Sterling Teague and Irwin John J. 2015. ZINC 15–ligand discovery for everyone. Journal of chemical information and modeling 55, 11 (2015), 2324–2337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Vaswani Ashish, Shazeer Noam, Parmar Niki, Uszkoreit Jakob, Jones Llion, Gomez Aidan N, Kaiser Łukasz, and Polosukhin Illia. 2017. Attention is all you need. In Advances in neural information processing systems. 5998–6008. [Google Scholar]
- [39].Vogt Martin, Yonchev Dimitar, and Bajorath Jurgen. 2018. Computational method to evaluate progress in lead optimization. Journal of medicinal chemistry 61, 23 (2018), 10895–10900. [DOI] [PubMed] [Google Scholar]
- [40].Weininger David. 1988. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. Journal of chemical information and computer sciences 28, 1 (1988), 31–36. [Google Scholar]
- [41].Wishart David S, Feunang Yannick D, Guo An C, Lo Elvis J, Marcu Ana, Grant Jason R, Sajed Tanvir, Johnson Daniel, Li Carin, Sayeeda Zinat, et al. 2018. DrugBank 5.0: a major update to the DrugBank database for 2018. Nucleic acids research 46, D1 (2018), D1074–D1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Yang Xiufeng, Zhang Jinzhe, Yoshizoe Kazuki, Terayama Kei, and Tsuda Koji. 2017. ChemTS: an efficient python library for de novo molecular generation. Science and technology of advanced materials 18, 1 (2017), 972–976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].You Jiaxuan, Liu Bowen, Ying Zhitao, Pande Vijay, and Leskovec Jure. 2018. Graph convolutional policy network for goal-directed molecular graph generation. In Advances in neural information processing systems. 6410–6421. [Google Scholar]
- [44].Zhou Zhenpeng, Kearnes Steven, Li Li, Zare Richard N, and Riley Patrick. 2019. Optimization of molecules via deep reinforcement learning. Scientific reports 9, 1 (2019), 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.