Anharmonic Vibrational Analysis of Biomolecules and Solvated Molecules Using Hybrid QM/MM Computations

Abstract

Quantum mechanics/molecular mechanics (QM/MM) calculations are applied for anharmonic vibrational analyses of biomolecules and solvated molecules. The QM/MM method is implemented into a molecular dynamics (MD) program, GENESIS, by interfacing with external electronic structure programs. Following the geometry optimization and the harmonic normal-mode analysis based on a partial Hessian, the anharmonic potential energy surface (PES) is generated from QM/MM energies and gradients calculated at grid points. The PES is used for vibrational self-consistent field (VSCF) and post-VSCF calculations to compute the vibrational spectrum. The method is first applied to a phosphate ion in solution. With both the ion and neighboring water molecules taken as a QM region, IR spectra of representative hydration structures are calculated by the second-order vibrational quasi-degenerate perturbation theory (VQDPT2) at the level of B3LYP/cc-pVTZ and TIP3P force field. A weight-average of IR spectra over the structures reproduces the experimental spectrum with a mean absolute deviation of 16 cm^–1. Then, the method is applied to an enzyme, P450 nitric oxide reductase (P450nor), with the NO molecule bound to a ferric (Fe^III) heme. Starting from snapshot structures obtained from MD simulations of P450nor in solution, QM/MM calculations have been carried out at the level of B3LYP-D3/def2-SVP(D). The spin state of Fe^III(NO) is likely a closed-shell singlet state based on a ratio of N–O and Fe–NO stretching frequencies (ν_N–O and ν_Fe–NO) calculated for closed- and open-shell singlet states. The calculated ν_N–O and ν_Fe–NO overestimate the experimental ones by 120 and 75 cm^–1, respectively. The electronic structure and solvation of Fe^III(NO) affect the structure around the heme of P450nor leading to an increase in ν_N–O and ν_Fe–NO.

1. Introduction

Vibrational spectroscopy is one of the valuable methods to elucidate molecular mechanisms for biological functions.¹ Since molecular vibrational states are highly sensitive to intermolecular interaction, the time-resolved spectrum provides atomically detailed information on biomolecules. Advanced spectroscopic methods, such as resonance Raman,^2,3 infrared (IR) difference,⁴ and two-dimensional IR,⁵ have further made it feasible to measure the spectrum arising from local structures of biomolecules. These techniques have been used, for example, to reveal conformational changes,^4,6 the structure of recognition sites,^7,8 and intermediate species in enzymatic reactions.⁹ However, extensive efforts such as mutation and isotope studies are needed to assign the observed vibrational bands and relate the spectrum with biomolecular structures. Therefore, theoretical calculations that predict the vibrational spectrum with reliable accuracy are of great importance.

Anharmonic vibrational calculations have significantly advanced in recent decades.¹⁰⁻¹² Because the conventional harmonic approximation has limited accuracy, it is necessary to incorporate the anharmonicity of the potential energy surface (PES) for quantitative purposes. The second-order vibrational perturbation theory (VPT2)¹²⁻¹⁴ based on a harmonic solution is widely used in conjunction with the quartic force field (QFF). Vibrational self-consistent field (VSCF)^15,16 and post-VSCF methods,¹⁶⁻²³ together with PES generation techniques using electronic structure calculations,²⁴⁻³⁰ have been developed as a solver of the vibrational Schrödinger equation for general polyatomic molecules. Yagi et al.^31,32 have extended VSCF based on the quasi-degenerate perturbation theory (VQDPT), and developed a suite of programs, SINDO,³³ to generate the PES and solve the VSCF equations. Hanson-Heine et al.³⁴ have extended a partial Hessian approach^35,36 for VPT2 calculations for large molecular systems. Bowman and co-workers^37,38 have proposed to use normal modes localized to a water molecule, and performed vibrational configuration interaction (VCI) calculations for water clusters and ice. Methods to transform normal coordinates to local coordinates are also actively studied.³⁹⁻⁴⁷ These methods are applicable to molecules with a single minimum (or a few minima) in the gas phase.

Vibrational calculations for complex systems remain a challenge, because (1) the system visits many minima with different frequencies in finite temperature, and (2) the solvent/protein environment needs to be considered. We have recently developed a weight-averaged method,⁴⁸⁻⁵⁰ which incorporates the former effect using classical molecular dynamics (MD) simulations and vibrational calculations based on the ab initio PES. In this method, MD simulations are first carried out to sample a large number of structures in the target system. Then, the trajectory is analyzed to extract relevant local structures and their statistical weights, and the vibrational calculations are carried out for each local structure to obtain its spectrum. Finally, the spectra are averaged using the weights of local structures to yield a total spectrum. The method has been used to calculate the IR and Raman spectra of a sphingomyelin bilayer^48,51 and the IR spectrum of Nylon6 with different humidity.⁴⁹

In the present study, we combine anharmonic vibrational calculations with a quantum mechanical/molecular mechanical (QM/MM) method to incorporate the effect of solvent/protein environment on the vibrational spectrum. The QM/MM method, first proposed in seminal papers by Warshel, Levitt, and Karplus,^52,53 is a multiscale model, which treats a local region of chemical interest by the electronic structure theory (QM) and the surrounding environment by molecular mechanics force field (MM).⁵⁴⁻⁶³ Although QM/MM has been extensively used to study enzymatic reactions, it has also been employed to compute the vibrational spectrum of biomolecules. Cui and Karplus⁶⁴ have derived an analytical Hessian for QM/MM and carried out normal-mode analyses. Tavan and co-workers⁶⁵⁻⁶⁸ have combined instantaneous normal-mode analyses (INMA) with QM/MM. However, these methods neglect the effect of anharmonicity. Anharmonic vibrational calculations combined with QM/MM are still scarce; the only report so far, to the best of our knowledge, is the work by Ringer and MacKerell,⁶⁹ in which VPT2 calculations have been carried out for nitrile probes in solution using QM/MM calculations. Here, we report VQDPT2 calculations based on a PES derived from QM/MM calculations.

The QM/MM method is implemented in many MD programs. The implementation in CHARMM, which was originally combined with semiempirical electronic structure methods,⁵⁵ has been extended to interface with external ab initio programs (CADPACK,⁷⁰ Q-Chem,⁷¹ and TURBOMOLE⁷²) and DFTB.⁷³⁻⁷⁵ AMBER also includes the QM/MM method.^54,76,77 Recently, a portable interface⁷⁸ has been developed and combined with FIREBALL⁷⁹ and TeraChem.⁸⁰ Other QM/MM-MD programs are also found in the literature: NAMD,^81,82 Dynamo,^83,84 etc. In addition, QM/MM calculations are available in electronic structure programs (Gaussian,⁸⁵ Q-Chem,⁸⁶ deMon2k,⁸⁷ Platypus,⁸⁸ etc.) and by interface programs (ChemShell⁸⁹ and PUPIL⁹⁰).

Following these works, we have implemented the QM/MM method into GENESIS^91,92 (Generalized-Ensemble Simulation System). A QM/MM module in GENESIS interfaces QM programs (Gaussian, Q-Chem, TeraChem, and DFTB+⁹³) with MM calculations based on the CHARMM force field.⁹⁴ An efficient method to optimize the geometry, which is necessary prior to vibrational calculations, is also implemented on the basis of a limited memory version of Broyden–Fletcher–Goldfarb–Shanno (L-BFGS-B) developed by Zhu et al.⁹⁵⁻⁹⁷ and a macro-/microiteration scheme.⁹⁸ A partial Hessian of a local region of the system is computed by numerical differentiations to obtain normal coordinates. Then, the anharmonic PES is generated in terms of the normal coordinates by combining GENESIS with SINDO, which is then used for solving the VSCF equations to obtain the spectrum.

We first describe an overview of the QM/MM method in Section 2, and the vibrational analysis based on the QM/MM potential in Section 3. Pilot applications are carried out for a phosphate ion in solution and P450 nitric oxide reductase (P450nor). The computational details and the results are given in Sections 4 and 5, respectively. Concluding remarks and outlooks are given in Section 6.

2. Overview of the QM/MM Method

2.1. QM/MM Potential

The QM/MM method divides a system into a QM region of particular interest and an MM region that provides its surrounding environment. The nuclei and electrons are considered explicitly in the QM region, while the MM region is described in terms of atoms defined in a molecular force field. The electrons are treated quantum mechanically by solving the following Schrödinger equation in atomic units

1

2

where i, a, and m are indices for electrons, nuclei, and MM atoms, respectively, and Z_a and q_m are the charge of nuclei and MM atoms, respectively. r_XY denotes a distance between X and Y. Note that |Ψ_e⟩ and E_e are the functions of coordinates of nuclei (R_a) and MM atoms (R_m)

3

4

Then, the potential energy of the system is written as

5

where V^QM is the QM energy defined as

6

and V_LJ^QM/MM and V^MM are the Lennard-Jones interaction between nuclei and MM atoms and the classical force field for MM atoms, respectively.

7

8

The derivative of the potential with respect to R_a and R_m gives the forces acting on nuclei and MM atoms

9

10

The first term in the right-hand side of eq 10 represents the electrostatic interaction between the MM charge and the electron density of the QM region, which can be rewritten in terms of the electric field, E_m(77)

11

In eqs 5, 9, and 10, V^QM, ∇_aV^QM, and E_m are calculated using an external QM program, whereas other terms are calculated by GENESIS.

2.2. Link Atom Method

Many QM/MM applications require setting QM and MM boundaries cutting covalent bonds of a molecule, in particular, when dealing with large biomolecules. For this purpose, we have implemented the link atom method.^54,55,57 In this method, (1) the QM atom (nuclei) at the boundary (Q₁) is terminated by a hydrogen atom, and (2) MM charges in the vicinity of the boundary are excluded in QM calculations to avoid overpolarization of the electron density (see Figure 1a). There are two options to exclude the charges: one is only the charge of the MM atom at the boundary (M₁), and the other is that of a group of MM atoms that M₁ belongs to. Note that the group is defined in the CHARMM force field. The MM potential includes bonded terms between QM and MM atoms at the boundary as shown in Figure 1b. We follow the implementation in CHARMM, where all possible combinations of QM and MM atoms are included for bond (V_b) and angle (V_a) terms, whereas the interaction between M₃ – Q₁ and M₂ – Q₂ is included, but that between M₁ – Q₃ is not for 4-site terms (V₁₄) such as dihedral, improper, and (ϕ, ψ) grid-based energy correction map (CMAP) terms.

Figure 1.

(a) Schematic illustration of QM and MM boundary. A hydrogen atom is added to the QM atom at the boundary (Q₁), and the MM charges are excluded in the vicinity of the link hydrogen atom (open circles). (b) Bonded terms between QM and MM atoms included in the MM potential.

In the presence of link hydrogen atoms, the QM energy becomes a function of their coordinates, R_L

12

To remove the dependency on the position of link atoms, we introduce constraint to the position of the hydrogen atom.^57,76,99 Let us place the hydrogen atom along a bond between Q₁ and M₁ with a distance d from Q₁

13

where R^Q = (R_x^Q, R_y, R_z^Q) and R^M = (R_x, R_y^M, R_z) are the position of Q₁ and M₁, respectively, and r₁ is a distance between Q₁ and M₁. Then, the gradient of the QM energy is obtained by a chain rule

14

where X is either Q or M. From eq 14, the gradient at Q₁ and M₁ is obtained as

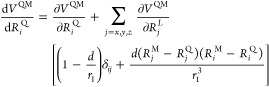15

16

where δ_ij is the Kronecker delta.

Further details on the implementation of QM/MM in GENESIS are given in Section 1 of the Supporting Information (SI).

3. Vibrational Analysis Based on the QM/MM Potential

3.1. Geometry Optimization and Normal Coordinates of a Partial System

Let us assume that a local region of the system that yields the spectrum in question is known (denoted VIB region): for example, reactant/product species in enzymatic reactions, hydrogen bonds in a protein, and so on. Then, the QM region is taken to be the VIB region as well as some surrounding molecules to account for the nearest neighbor interaction that affects the vibrational states of the VIB region.

The geometry is first optimized for the QM region and a part of the MM region. An efficient optimizer is implemented using an L-BFGS-B code developed by Zhu et al.⁹⁵⁻⁹⁷ in terms of Cartesian coordinates. Furthermore, the macro-/microiteration scheme is implemented following Kästner et al.⁹⁸ This scheme optimizes the geometry in two loops of cycle. The outer loop (macroiteration) is the usual cycle for all atoms, whereas the inner loop (microiteration) optimizes only the MM atoms keeping the QM atoms fixed. In the microiteration, the electrostatic interaction between QM and MM atoms is approximated using charges of QM atoms, q_a, as

17

Note that, in the presence of link atoms, the sum over MM atoms excludes MM atoms in the vicinity of the link hydrogen in which the charge is removed. The charges of QM atoms are derived, for example, from the electrostatic potential (ESP) obtained from QM calculations in the macroiteration.^100,101 The scheme drastically reduces the computational cost, because the MM atoms are optimized in microiteration without requiring QM calculations. However, the approximation in eq 17 becomes less accurate as MM atoms move more. For a compensation for such deviations, the gradient of MM atoms is corrected as

18

19

where R₀ denotes coordinates of the system in macroiteration. The correction recovers the gradient of the QM energy at R = R₀ and makes the gradient in macro- and microiterations consistent with each other.

Once the geometry optimization is converged, a partial Hessian matrix^35,36 is computed for VIB atoms in 3N_v dimension, where N_v is the number of VIB atoms. The Hessian is obtained from numerical differentiations as

20

where x_a denotes 3N_v Cartesian components of VIB atoms, δ is a step-size of numerical differentiations, and g_a(±δ_a′) is the ath component of the gradient at (x_a′ ± δ). QM calculations are required at 6N_v points to construct the Hessian matrix, which is processed in MPI parallel. Then, the Hessian is mass-weighted and diagonalized to obtain normal coordinates (Q_i) and harmonic frequencies (ω_i)

21

22

where m_a and x_a^eq are the atomic mass and coordinates at the equilibrium structure, respectively, and M is a diagonal matrix with M_aa′ = δ_aa′m_a.

3.2. Anharmonic Vibrational Calculations

The vibrational Hamiltonian is written in terms of the normal coordinates as

23

where f is the number of modes, and V⁽ⁿ⁾ is the so-called n-mode representation of the potential energy surface (nMR-PES),¹⁰² in which the PES is expanded in terms of mode coupling and truncated at the nth order

24

Note that the PES is a function of coordinates of all atoms, but that the coordinates of atoms out of the VIB region (X) are fixed to the equilibrium geometry

25

In other words, the present method neglects the motion of atoms out of the VIB region.

The nMR-PES can be generated using the techniques matured in the field of vibrational calculations.^{24−26,29,30,103−105} Multiresolution PES²⁹ is a composite of grid potentials²⁷ and QFF.²⁸ QFF is written in the form of nMR as

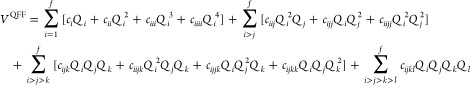26

The third- and fourth-order coefficients are generated by numerical differentiations of the gradient (see Section 2 in Supporting Information). The number of grid points to compute 3MR- and 4MR-QFF accumulated over all coupling order is, respectively, given as

27

28

The grid potential is based on the harmonic oscillator discrete variable representation (HO–DVR). The number of energy points needed for generating nMR grid potential is

29

where M_g is the number of grid points along each coordinate. Note that the grid potentials of the low-order coupling (n′ < n) are generated simultaneously by setting one of the grid point to be the origin, i.e., by taking M_g to be an odd number. Although the number of grid points scales steeply with respect to n and f, it may be reduced by selecting the mode of interest such that f < 3N_v and by varying the size of grid according to the strength of coupling terms.

These grid points are generated by SINDO, and the QM/MM energy and gradients at the points are calculated by GENESIS in conjunction with a QM program. The loop over grid points is parallelized by MPI. The information is used to generate the multiresolution nMR-PES; in the present study, we combine 3MR-QFF and 1MR-grid PES. The PES is subsequently used for solving the vibrational Schrödinger equation by VSCF and post-VSCF methods. Details on VSCF and VQDPT2 methods are described in Section 3 of the Supporting Information.

4. Computational Details

4.1. Phosphate Ion in Solution

H₂PO₄^– was prepared in a box of water (48.6 × 48.6 × 48.6 ų) by the solvation utility in VMD.¹⁰⁶ The total number of atoms was 11 747. Then, the all-atom MD simulation was performed using spdyn of GENESIS 1.2.2. The force field parameters for H₂PO₄^– and water were, respectively, those in the previous work¹⁰⁷ and TIP3P.¹⁰⁸ Following a 1000-step minimization and an equilibration NPT run for 1.0 ns, a production NVT run was carried out for 10.0 ns. The leapfrog algorithm was used for integration with a time step of 2.0 fs. SHAKE¹⁰⁹ and SETTLE¹¹⁰ were used to constrain the bond length involving hydrogen atoms. A Langevin thermostat and barostat¹¹¹ were used to control the target temperature and pressure at 300 K and 1 atm, respectively. The long-range electrostatic interaction was calculated using the smooth particle mesh Ewald (PME) method.^112,113 The non-bonded interaction was reduced to zero between 10 and 12 Å employing a switching function. The neighbor list was updated every 20 fs. The trajectory was saved every 10 ps, and the resulting 1000 snapshots were used for the analysis.

The snapshots were classified in terms of the number of water molecules near H₂PO₄^– (N_wat). The water molecule was judged to be “near” when the oxygen atom of a water molecule was within 3.5 Å in distance of any of the oxygen atoms of H₂PO₄^–. The number of snapshot structures (N_ss) for each N_wat is shown in Table 1 indicating a distribution of N_wat in the range 9–16. Then, one representative snapshot was selected for each class of N_wat by k-means clustering method with respect to a root-mean square deviation (RMSD) of all atoms of H₂PO₄^–. The snapshot was employed as an initial structure of the QM/MM optimization. QM/MM calculations were performed combining a development version of GENESIS/atdyn with Gaussian09.⁸⁵ The QM region was set to H₂PO₄^– and the neighboring water molecules, so that the number of QM atoms was 7 + 3N_wat. DFT calculations were performed at the level of B3LYP/cc-pVTZ.^114−116

Table 1. Number of MD Snapshots Classified in Terms of the Number of Water Molecules around H₂PO₄^–

Nwata	9	10	11	12	13	14	15	16
Nssb	21	70	194	268	264	135	39	9

^aThe number of water molecules, where the oxygen atom is within 3.5 Å of any of the oxygen atoms of H₂PO₄^–.

^bThe number of MD snapshots classified by N_wat.

The geometry was optimized relaxing the atoms within 10 Å of H₂PO₄^– and fixing the others. The optimization was performed using the macro-/microiteration scheme with the Merz–Singh–Kollman charge.^100,101 The convergence threshold was set to 0.36 and 0.54 kcal mol^–1 Å^–1 for the RMS and maximum gradient, respectively. The optimization converged after 110 cycles on average and 183 cycles in maximum.

The vibrational analysis was performed for the optimized geometry taking H₂PO₄^– as a VIB region. For the calculation of a partial Hessian, 42 points of gradients were required. After the normal-mode analysis, 3MR-QFF and 1MR-grid PES (with 11 grid points to each coordinates) were constructed in 21 normal coordinates of H₂PO₄^–. The generation of 3MR-QFF and 1MR-grid PES required 925 points of gradients and 211 points of energies, respectively. Then, VSCF and VQDPT2 were carried out using the harmonic oscillator basis functions up to n = 10. The quasidegenerate space in VQDPT2 was selected using N_gen = 1 and k = 4. The PES generation and VQDPT2 calculations were carried out using SINDO. The dipole moment surface was constructed from 1MR-grid points and used for calculating the IR intensity. The IR spectrum was constructed by a convolution of vibrational bands constructed by Lorentz functions of 40 cm^–1 width (see Section 4 of the Supporting Information). Finally, the IR spectra for each N_wat were weight-averaged using N_ss/N_tot as a weight, where N_tot is the total number of snapshots (=1000).

4.2. P450 Nitric Oxide Reductase (P450nor)

The structure was taken from a recent X-ray crystal structure¹¹⁷ (PDBID 5Y5H), which contains P450nor with a NO molecule bound to a ferric iron (Fe^III) and crystal water molecules. First, the missing residues of the N terminus were added using GaussView5.0.¹¹⁸ The hydrogen atoms and protons were added to the system using UCSF Chimera.¹¹⁹ His96 and Glu361 were protonated based on pK_a values at pH 6.5 estimated by PROPKA3.1.^120,121 The CHARMM36 (c36)⁹⁴ force field was used for the protein and ions, and TIP3P for water molecules. The parameters for a heme–NO unit were set as follows: (1) By considering the unit as a ferrous heme–NO⁺, the heme was described by the c36 force field for a ferrous heme, and the atomic charges of N and O atoms were set to +1.272e and −0.272e, respectively. (2) Other parameters for the NO (the N–O bond function and the vdW parameters) were taken from the previous study on myoglobin.^122,123 (3) The parameters for an Fe–NO bond function were set to r_eq = 1.670 Å, k_r = 350.0 kcal mol^–1 Å^–2; those for N_por–Fe–N (N_por is a nitrogen atom of porphyrin) and Fe–N–O angle functions were set to θ_eq = 90.0°, k_θ = 100.0 kcal mol^–1 rad^–2, and θ_eq = 158.0°, k_θ = 8.0 kcal mol^–1 rad^–2, respectively, and those for a X–Fe–N–Y dihedral function (X and Y denote an arbitrary atom type) were set to δ = 0.0°, n = 4, k_φ = 0.05 kcal mol^–1.

The MD simulation was first carried out fixing heavy atoms of P450nor and crystal water molecules using NAMD 2.12.⁸¹ The energy was minimized for 5000 steps in vacuum to relax the position of hydrogen atoms. The resulting structure is referred to as XtalV. Next, a simulation box of 120 × 113 × 101 ų in size was constructed adding 38 284 water molecules, 116 Na⁺, and 110 Cl^–. Then, three simulations were carried out each for 3 ns in NVT, NPT, and NVT conditions. A Langevin thermostat and the Nosé–Hoover Langevin piston methods^124,125 were used to control the temperature at 300 K and the pressure at 1 atm, respectively. The size of the box was relaxed to 115.2 × 108.5 × 97.0 ų after the NPT simulation. The last snapshot of these simulations is referred to as XtalW.

Then, the crystal structure (P450nor and water molecules) was gradually relaxed in a series of NVT simulations using harmonic positional restraints. The force constants, initially set to 5.0 and 2.0 kcal mol^–1 Å^–2 for the backbone and the others, respectively, were reduced to zero in 9 steps for 27.0 ns (see Table S1 in the Supporting Information). Then, the system was further equilibrated for 10.0 ns without restraint, followed by a production run for 70.0 ns. The temperature was controlled at 300 K with Bussi thermostat.¹²⁶ The equilibration runs with restraint were carried out with a time step of 2.0 fs using the velocity Verlet integrator, whereas the 10 ns equilibration and the 70 ns production runs were performed using r-RESPA integrator¹²⁷ with a time step of 2.5 fs. The long-range electrostatic interaction was calculated using the smooth PME method.^112,113 The non-bonded interaction was reduced to zero between 10 to 12 Å using a switching function. All bonds involving hydrogen atoms were kept rigid using SHAKE¹⁰⁹ and SETTLE.¹¹⁰ These simulations were performed using spdyn of GENESIS 1.1.6. The snapshot structures of the production run were classified into five clusters using the k-means clustering method by fitting the structure to nitrogen atoms of the heme and measuring the RMSD of Fe, N, and O atoms. The representative structures, i.e., the center of each cluster, were found to be the snapshot at 27.27, 33.59, 35.70, 45.20, and 65.53 ns, which are referred to as NVT1, NVT2, NVT3, NVT4, and NVT5, respectively.

QM/MM calculations were performed starting from the seven snapshots, XtalV, XtalW, and NVT1–5, using a development version of GENESIS/atdyn. A QM subsystem consisted of a heme–NO unit and a side chain of Cys352 (79 atoms). The QM and MM boundary was set between C_α and C_β atoms of Cys352. The distance between a QM boundary atom and a link H atom was set to 1.0 Å. The charge of group atoms near the MM boundary was excluded in QM calculations. DFT calculations were performed at the level of BP86 or B3LYP-D3 (B3LYP hybrid functional and the D3 version of Grimme’s dispersion with Becke–Johnson damping¹²⁸) using Gaussian09, and ωB97M-V¹²⁹ using Q-Chem 4.4. The def2-SVPD¹³⁰ basis functions were used for seven atoms (four N atoms of porphyrin, a S atom of Cys352, and NO), and the def2-SVP¹³¹ basis sets for other atoms [denoted def2-SVP(D)]. The ωB97M-V calculation was also carried out using larger basis sets, def2-TZVPPD¹³⁰ for Fe, the atoms bound to Fe, and NO, and def2-TZVP¹³¹ for the others [denoted def2-TZVP(PD)]. The spin multiplicity was set to singlet. In addition to a closed-shell singlet (cs-1et) state, an open-shell singlet (os-1et) state was also calculated by a spin-unrestricted Kohn–Sham (KS) method. The initial guess orbitals for the os-1et state were prepared by combining KS orbitals obtained for the heme, the NO ligand, and the side chain of Cys352 by specifying the charge/spin multiplicity as −1e/doublet, 0e/doublet, and −1e/singlet, respectively. An MM subsystem consisted of the remaining part of the protein and water molecules excluding the ions.

The geometry was optimized for the whole protein and water molecules within 20 Å of NO keeping the other atoms fixed. The optimization was performed using the macro-/microiteration scheme based on the Merz–Singh–Kollman ESP charges^100,101 by setting the atomic radii for Fe and H to 1.3 and 1.0 Å, respectively. A convergence threshold was set to 0.30 and 0.45 kcal mol^–1 Å^–1 for the RMS and maximum gradients, respectively. The optimization converged after 154 cycles on average and 219 cycles in maximum.

The vibrational analysis was performed setting four atoms as a VIB region; Fe, N, and O atoms of NO, and S of Cys352. For the computation of a partial Hessian, 25 points of gradients were required. After the normal-mode analysis, 3MR-QFF and 1MR-grid PES (with 11 grid points to each coordinates) were constructed for 9 normal modes excluding 3 modes related to the motion of the S atom. The generation of 3MR-QFF and 1MR-grid PES required 181 points of gradients and 91 points of energies, respectively. Then, VSCF and VQDPT2 calculations were carried out using the harmonic oscillator basis functions up to n = 10. The quasidegenerate space in VQDPT2 was selected using N_gen = 1 and k = 4. The PES generation and the VQDPT2 calculations were carried out using SINDO.

QM cluster calculations without the MM environment were also carried out for reference. The geometry of the QM subsystem was taken from the X-ray crystal structure. The position of C_β atom of Cys352 and a dihedral angle, C_β–S–Fe–N_A (N_A is one of the nitrogen atoms of a heme group), were frozen during the geometry optimization to avoid rotation of a heme plane around an Fe–S axis. The geometry optimization and the vibrational calculations were performed in the same way as above.

5. Results

5.1. Phosphate Ion in Solution

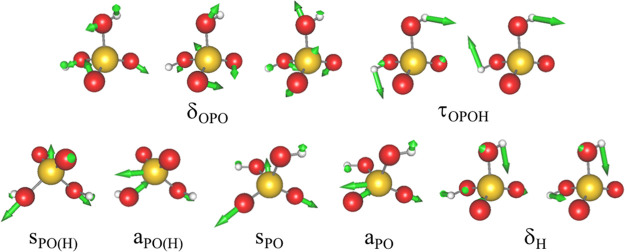
The previous studies^66,132 have reported a strong solvation effect in the vibrational spectrum of H₂PO₄^– in solution. Comparison of the spectrum in the gas phase and solution has shown that P–O stretching modes (s_PO and a_PO in Figure 2) are red-shifted by 50–170 cm^–1, whereas P–O–H bending and P–OH stretching modes (δ_H and s_PO(H)/a_PO(H), respectively, in Figure 2) are blue-shifted by 120–150 cm^–1. The large spectral shift arises from strong hydrogen bonds (HBs) formed between the ion and water molecules, which require an accurate treatment by QM methods. Thus, H₂PO₄^– serves as a test case to assess the accuracy of the proposed method.

Figure 2.

Vibrational modes of phosphate ion (H₂PO₄^–). δ_OPO, OPO bending modes; τ_OPOH, OPOH torsion; s_PO(H) and a_PO(H), symmetric and asymmetric P–OH stretching modes of hydroxyl groups; s_PO and a_PO, symmetric and asymmetric P–O stretching modes; δ_H, POH bending mode.

From the MD trajectory, the number of water molecules around H₂PO₄^– (N_wat) was found to be distributed in the range 9–16 with N_wat = 12 and 13 being the most abundant, as shown in Table 1. QM/MM optimized structures for N_wat = 12 and 13, shown in Figure 3, indicate that the PO^– bond accepts three water molecules whereas the hydroxyl group accepts one and donates to another water molecule. Thus, the current QM/MM calculation with N_wat = 9–16 takes into account the HB interaction between H₂PO₄^– and water molecules in the first solvation shell and some in the second solvation shell at the DFT level.

Figure 3.

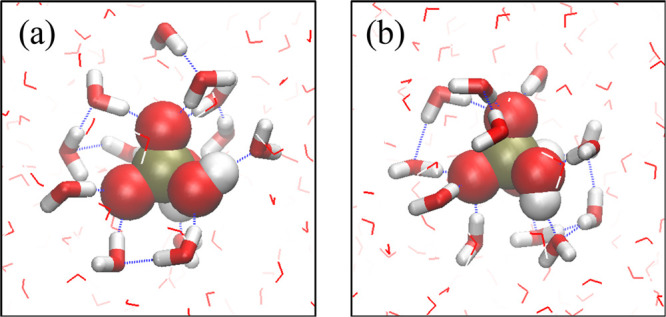
Optimized structures for (a) N_wat = 12 and (b) N_wat = 13. H₂PO₄^– and highlighted water molecules are QM atoms, whereas the surrounding other water molecules are MM atoms. Hydrogen bonds are indicated by blue broken lines, which are drawn when r_OO < 3.2 Å and θ_OHO > 130°.

IR spectra obtained by the harmonic approximation for a QM/MM system with N_wat = 12 (QM/MM-12) and H₂PO₄^– in the gas phase are shown in Figure 4e and 4f, respectively. The solvation of H₂PO₄^– causes a drastic change in the spectrum as reported in the previous studies.^66,132 The prominent peak shifts, i.e., the red-shift of a_PO and s_PO and the blue-shift of δ_H, a_PO(H), and s_PO(H), are clearly seen in the present result as well. Furthermore, peak positions of τ_OPOH are found to be dramatically shifted by more than 500 cm^–1. This is because the formation of HBs restricts the motion of hydroxyl groups and makes the torsional motion rigid and stiff. Such behavior is similar to bulk water, where the rotational motion of water molecules is restricted by HBs giving rise to libration bands around 400–700 cm^–1.

Figure 4.

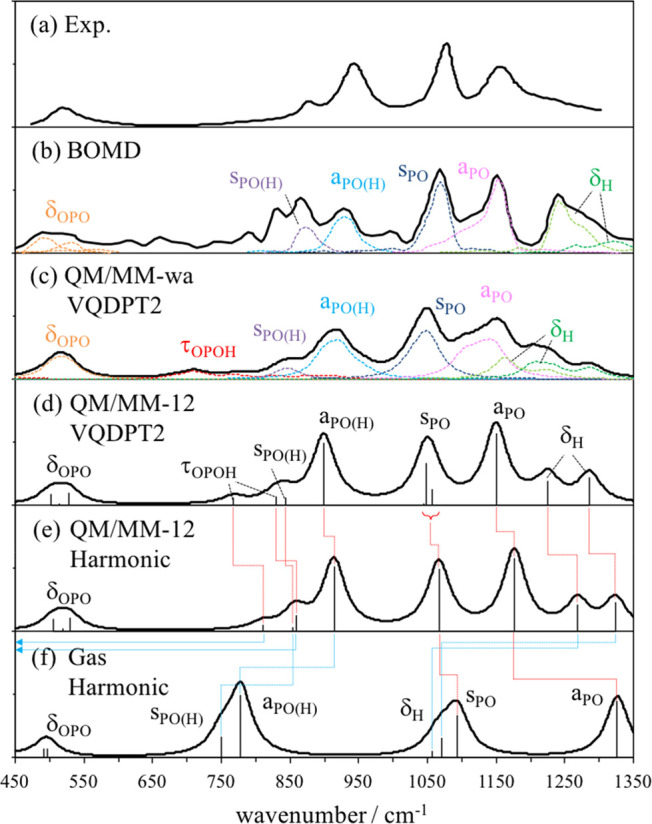
(a) Experimental IR spectrum of H₂PO₄^– in solution.⁶⁶ (b) IR spectrum obtained by Born–Oppenheimer (BO) MD based on the B3LYP-D/TZV2P level in the previous work.¹³² IR spectra calculated by QM/MM in this work: (c) weight-average of VQDPT2 spectra over N_wat = 9–16, (d) VQDPT2 for N_wat = 12, and (e) harmonic calculation for N_wat = 12. (f) Harmonic spectrum of H₂PO₄^– isolated in the gas phase. The spectrum is constructed using Lorentz functions with a width of 40 cm^–1.

To further investigate the strong solvation effect, we have calculated the vibrational frequency of H₂PO₄^– using the polarizable continuum model (PCM)¹³³ and a QM/MM model which takes only H₂PO₄^– as a QM region (QM/MM-0). The results are listed in Table 2. Although PCM is capable of predicting the direction of the shift of P–O and P–OH stretching modes, the amount of shift is insufficient. Furthermore, δ_H and τ_OPOH are shifted to an opposite direction. The mean absolute deviation (MAD) is 200.5 cm^–1 compared to QM/MM-12. In QM/MM-0, the result is significantly improved predicting the shift of δ_H and τ_OPOH in the right direction and reducing the MAD to 21.3 cm^–1. Nonetheless, QM/MM-0 is semiquantitative yielding a maximum deviation of 52.9 cm^–1 for s_PO. Therefore, it is essential to take not only H₂PO₄^– but also the water molecules as a QM region to account for the effect of HBs on the vibrational states of H₂PO₄^–.

Table 2. Fundamental Frequencies of H₂PO₄^– Obtained by the Harmonic Approximation and VQDPT2 for an Isolated System (Gas), PCM with Water as Solvent (PCM), a QM/MM System with and without 12 Water Molecules in the QM Region (QM/MM-12 and QM/MM-0, Respectively), and a Weight-Average over 9–16 Water Molecules (QM/MM-wa), together with the Experimental Results.

	gas	PCM	QM/MM-0	QM/MM-12		QMMM-wa
mode	harmonic	harmonic	harmonic	harmonic	VQDPT2	VQDPT2	exptla
δOPO	429.8	441.5	505.9	505.6	502.5	517	521
	492.2	481.8	540.0	519.0	513.7	517	521
	497.6	492.8	552.7	529.8	527.3	517	521
τOPOH	203.5	190.1	774.6	810.5	768.0	713
	313.3	275.1	864.7	858.5	829.3	713
sPO(H)	750.1	770.3	841.5	854.1	843.2	848	879
aPO(H)	778.2	789.7	894.9	914.0	899.0	922	944
sPO	1093.9	1090.4	1119.4	1066.5	1048.5	1051	1077
aPO	1326.6	1275.4	1206.6	1176.5	1149.9	1145	1156
δH	1056.4	1020.3	1250.1	1268.7	1225.8	1211	1213
	1071.0	1040.3	1309.1	1324.0	1285.9	1283

^aref (66).

Comparison of VQDPT2 and harmonic spectra in Figure 4d and 4e shows that the anharmonicity makes the frequency of all modes lower, although the overall shape of the spectrum looks similar. Nevertheless, it is notable that the size of anharmonic correction differs by the character of modes. δ_H and τ_OPOH make a larger shift than others, whereas δ_OPO hardly shows any shift. Thus, the scaling of harmonic frequencies by a single factor is not appropriate. It is also interesting to note that Fermi splitting is found for s_PO, which is due to the resonance between a fundamental of s_PO and an overtone of δ_OPO. The splitting makes the bandwidth slightly broader in VQDPT2 than in the harmonic spectrum.

The weight-average over N_wat = 9–16 (QM/MM-wa) smears out a peaky structure in a spectrum of QM/MM-12, as shown in Figure 4c and 4d. It is notable that the frequency of δ_H and τ_OPOH is distributed in an extremely wide range, which is a consequence of the motion of hydrogen atoms being sensitive to the hydration structure of H₂PO₄^–. Note that the broadening makes it difficult to identify the peak position of δ_H and τ_OPOH in the total spectrum. It is also interesting to see that the relative intensity of s_PO and a_PO is reversed in Figure 4c and 4d. Although a_PO has larger intensity than s_PO for each cluster, the frequency of a_PO fluctuates more than that of s_PO. Thus, the weight-average yields the band of a_PO broader in frequency and smaller in intensity than that of s_PO.

Figure 4a and 4b shows the experimental spectrum⁶⁶ and the theoretical one obtained in the previous study,¹³² respectively. The previous study carried out Born–Oppenheimer MD (BOMD) at the B3LYP-D level with TZV2P basis sets and obtained the spectrum by a Fourier transform of ensemble-averaged autocorrelation functions of the dipole moment. The two methods reproduce the experimental spectrum with similar quality, which is encouraging given that the computational techniques are totally different. One of the conclusions of the BOMD study was that the use of a nonpolarizable MM force field for water molecules (i.e., TIP3P) is inadequate for predicting the IR spectrum of H₂PO₄^– in solution. The present result is in line with this finding. We observe that treating all water molecules at the MM level incurs a large error in the calculated frequency (see QM/MM-0 in Table 2) and that the inclusion of water molecules in the QM region is important for quantitative purposes. Nonetheless, some improvements are worth mentioning. The previous work shows a sharp dip between a_PO and δ_H, and a prominent peak of δ_H, whereas the present result shows a smooth shoulder in the range 1200–1300 cm^–1 that resembles the experimental feature. Also, τ_OPOH was not identified in the previous work. These shortcomings may be due to a limited sampling time (56 ps) in the BOMD simulation. In the present study, we performed a sampling of the hydration structure for 10 ns and a clustering in terms of N_wat. This procedure, albeit at the MM level, yields essential HB structures between H₂PO₄^– and water molecules that contributes to the spectrum, and leads to a smooth convergence of the spectrum with respect to the number of snapshot as small as 8 (one for each N_wat = 9–16). The result suggests that the weight-average approach⁵⁰ combining a structural sampling using MD and vibrational calculations of IR spectra using VQDPT2 and QM/MM is a promising approach to simulate the IR spectrum of solvated molecules.

5.2. P450 Nitric Oxide Reductase (P450nor)

P450nor is a heme enzyme isolated from the fungus Fusarium oxysporum that reduces a nitric oxide (NO) to a nitrous oxide (N₂O) with electrons transferred from a nicotinamide adenine dinucleotide (NADH). The mechanism of the NO reduction has been extensively studied by spectroscopy^117,134,135 and theoretical calculations.^136,137 The initial step of the reaction is a binding of NO to a ferric iron (Fe^III) of the heme group, which is characterized by N–O and Fe–NO stretching modes.^138−141 Here, we study these vibrations by VQDPT2 based on QM/MM.

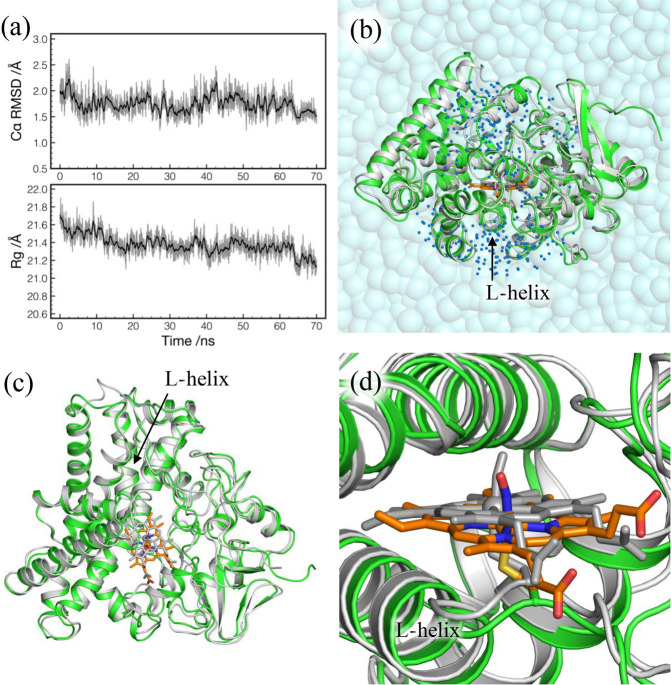
Figure 5a plots the RMSD from the crystal structure and the radius of gyration (R_g) obtained from the MD trajectory of the production run. Both RMSD and R_g are found to be stable, suggesting that the structure of P450nor is well-maintained during the MD simulation. The RMSD is obtained as 1.74 ± 0.19 Å, and the R_g, which is 21.06 Å at the crystal structure, is slightly increased to 21.38 ± 0.12 Å.

Figure 5.

(a) RMSD from the X-ray crystal structure (top) and the radius of gyration (R_g) (bottom) as a function of simulation time in the production run. RMSD is calculated for C_α atoms of residues 4–403. R_g is obtained using backbone heavy atoms of residues 4–403 with mass weighting. (b) QM/MM optimized geometry of P450nor for NVT4 (colored) superimposed with the X-ray crystal structure (gray). The two structures are fit by C_α atoms of residues 4–403. Water molecules within 20 Å of NO (blue dots) are relaxed in QM/MM calculations. (c) Top view of part b without water molecules. (d) Close view of part b around the heme group with NO.

The results of QM/MM calculations are listed in Table 3. The RMSD for XtalV and XtalW is as small as 0.26 and 0.22 Å, respectively, confirming that the optimized structures are close to the crystal structure. On the other hand, RMSD for NVT is obtained in the range 1.24–1.87 Å, indicating that the optimized structure for NVT corresponds to the one relaxed in solution. The structure of NVT4 is compared with the crystal structure in Figure 5b,c. Although NVT4 is slightly expanded in accordance with the increase in R_g, and loop regions show some deviations, the overall structure of NVT4 matches well with the crystal structure without undergoing conformational changes or unfolding. Nevertheless, it is notable that the heme group is significantly shifted as shown in Figure 5d. The distance between Fe atoms of the crystal and NVT4 structures is 1.52 Å. A similar shift is observed for all the NVT snapshots, and thus, the shift is a general trend of P450nor in solution. Figure 5d also shows that the orientation of NO around the Fe–S axis is different between the crystal and NVT4 structures. In fact, NO is oriented in many different ways in NVT1–5, as evident from the dihedral angles, ϕ_{NA–Fe–N–O} and ϕ_{Cβ–S–N–O}, listed in Table 3. The result implies that NO rotates around the Fe–S axis in the absence of NADH.

Table 3. RMSD from the Crystal Structure and Geometric Parameters in the Active Site of P450nor [Bond Lengths (r in Å), Bond Angles (θ in deg), and Dihedral Angles (ϕ in deg)], and the N–O and Fe–NO Stretching Vibrations [Harmonic (ω) and VQDPT2 (ν) Frequencies Both in cm^–1] Obtained from QM Cluster and QM/MM Calculations Together with Experimental Values.

	cs-1eta								os-1eta
	Gasc	XtalV	XtalW	NVT1	NVT2	NVT3	NVT4	NVT5	NVT4	exptlb
Cα RMSDd		0.26	0.22	1.24	1.72	1.87	1.72	1.47	1.72
rFe–NO	1.672	1.680	1.672	1.659	1.665	1.654	1.653	1.661	1.697	1.67
rN–O	1.149	1.146	1.143	1.139	1.140	1.138	1.137	1.137	1.144	1.15
rFe–S	2.282	2.287	2.301	2.305	2.296	2.319	2.310	2.316	2.297	2.33
θFe–N–O	158.6	155.7	158.3	164.7	161.9	167.6	165.0	164.6	163.3	157.9
ϕNA–Fe–N–Oe	48.2	46.3	52.9	46.4	99.5	120.3	130.8	122.6	129.7	60.3
ϕCβ–S–N–O	57.3	55.7	63.3	39.3	93.0	115.0	125.3	123.3	123.8	71.4
ωN–O	1936.5	1946.2	1967.6	1998.1	1988.9	2008.9	2017.4	2011.6	1974.4
νN–O	1894.7	1913.4	1932.1	1966.2	1956.8	1975.4	1984.7	1981.5	1929.3	1853
ΔN–Of	(41.8)	(32.8)	(35.5)	(31.9)	(32.1)	(33.5)	(32.7)	(30.1)	(45.1)
ωFe–NO	603.5	605.1	607.2	633.7	614.9	620.9	628.4	617.8	417.3
νFe–NO	595.3	587.7	585.6	617.4	596.2	600.5	610.9	600.0	327.2	530
ΔFe–NOf	(8.2)	(17.4)	(21.6)	(16.3)	(18.7)	(20.4)	(17.5)	(17.8)	(90.1)

^aClosed-shell singlet (cs-1et) and open-shell singlet (os-1et) states.

^bStructural parameters are from X-ray crystal structure¹¹⁷ and frequencies from resonance Raman spectra in solution.¹³⁵

^cA QM cluster calculation in the gas phase without the MM region.

^dThe RMSD from the X-ray crystal structure calculated for C_α atoms of residues 4–403.

^eN_A is one of the nitrogen atoms of a heme.

^fThe difference between harmonic and VQDPT2 frequencies (Δ = ω – ν).

The harmonic (ω) and VQDPT2 (ν) frequencies are also listed in Table 3. The shift in the frequency due to anharmonicity on average over the seven snapshots in the cs-1et state is found to be 32.7 ± 1.5 and 18.5 ± 1.7 cm^–1 for the N–O and Fe–NO stretching modes, respectively. The ratio between VQDPT2 and harmonic frequencies for the N–O stretching mode, ν_N–O/ω_N–O, is obtained as 0.984, which is larger than 0.961 used in the previous study to correct the harmonic frequency.¹³⁷

Interestingly, ν_N–O increases as 1913.4, 1932.1, and 1956.8–1984.7 cm^–1 for XtalV, XtalW, and NVT1–5, respectively, as the solvation is incorporated in the model. Such a drastic blue shift may be surprising given that NO is a hydrophobic molecule that does not directly interact with water molecules. The result has inspired us to carry out a QM cluster calculation without the MM environment (denoted Gas in the following), which yield 1894.7 cm^–1 for ν_N–O and a similar geometry to XtalV. Figure 6 shows plots of a bond angle between Fe–N–O (ν_Fe–N–O) and an Fe–S bond length (r_Fe–S) as a function of ν_N–O for Gas, XtalV, XtalW, and NVT1–5. It is notable that the increase in ν_N–O correlates with an expansion of θ_Fe–N–O and an elongation of r_Fe–S. The behavior is consistent with the so-called thiolate trans effect,¹³⁸ where the ligation of thiolate to Fe^III(NO) induces an occupation of antibonding orbitals of Fe–NO and N–O that makes Fe–NO and N–O bonds weak and an Fe–N–O angle bent (see Section 5 of the Supporting Information for details). These results suggest that the solvation of P450nor elongates r_Fe–S and weakens the thiolate trans effect, thereby inducing a strengthening of N–O bond and an increase in ν_N–O.

Figure 6.

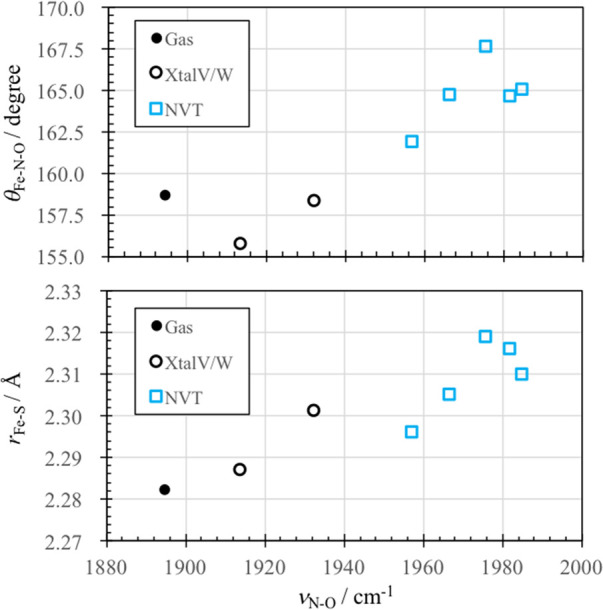
Fe–N–O bond angle (θ_Fe–N–O) and the Fe–S bond length (r_Fe–S) as a function of the NO stretching frequency (ν_N–O) calculated by QM cluster (gas) and QM/MM (XtalV, XtalW, and NVT).

Fe^III(NO) has another spin state, os-1et state, where the radical electrons of NO and Fe remain unpaired, but have an antiparallel spin so that the total system is singlet. The os-1et state is known to be close in energy to the cs-1et state.^136,137,139 Thus, we have repeated the same calculation for the os-1et state starting from NVT4. The results are also listed in Table 3. It is notable that ν_N–O and ν_Fe–NO are both decreased in the os-1et state compared to those in the cs-1et state. This is because the radical electron of NO occupies a π* orbital of NO and reduces the d → π* back-donation, and hence, the N–O and Fe–NO bonds are both weakened. The decrease in ν_N–O, obtained as 55.5 cm^–1, is consistent with the previous QM/MM calculation by Riplinger et al.¹³⁷

ν_N–O and ν_Fe–NO have been measured at 1853 and 530 cm^–1, respectively, by the resonance Raman spectroscopy for P450nor in solution.¹³⁵ However, the calculated ν_N–O and ν_Fe–NO for NVT1–5 in the cs-1et state, which are 1973 and 605 cm^–1 on average, overestimate the experiment by 120 and 75 cm^–1, respectively. In view of such a deviation, we have extended the size of a QM region to include residues and water molecules nearby the heme group, but found that it has little effect on the frequencies (data shown in Table S2 of the Supporting Information). In the os-1et state, ν_N–O is decreased to 1929.2 cm^–1, and thus, the deviation is reduced to 76.2 cm^–1. However, ν_Fe–NO is also decreased to 327.2 cm^–1 and deviates from the experiment by −202.8 cm^–1. Note that the ratio of ν_N–O/ν_Fe–NO is obtained as 3.25 and 5.90 for the cs-1et and os-1et states, respectively. Judging from the corresponding value for the experiment (3.49), it is plausible that the spin state of Fe^III(NO) is the cs-1et state in the experimental condition.

On the basis of these findings, we have carried out QM/MM calculations with the same QM region for NVT4 in the cs-1et state using different DFT functionals and basis sets. The results are listed in Table 4. The pure functional, BP86, gives ν_N–O as 1881.3 cm^–1 in agreement with the experimental value of 1853 cm^–1. However, ν_N–O/ν_Fe–NO is obtained as 3.09. Furthermore, the variation in the geometry (r_Fe–S and ν_Fe–N–O) from B3LYP-D3 to BP86, which indicates a weakening of the thiolate trans effect, is inconsistent with the decrease in ν_N–O. Thus, the agreement of ν_N–O using BP86 may be fortuitous. We also employed ωB97M-V, which is one of the latest density functionals developed by Mardirossian and Head-Gordon.¹²⁹ As shown in Table 4, both ν_N–O and ν_Fe–NO are increased compared to B3LYP-D3 resulting in a larger deviation from the experiment. Nonetheless, ν_N–O/ν_Fe–NO is obtained as 3.27 and 3.20 using the def2-SVP(D) and def2-TZVP(PD) basis sets, and the variations in the geometry and frequency are consistent with each other. Considering that cs-1et and os-1et states lie close in energy,¹³⁹ multiconfigurational methods, which can describe the two states on an equal footing, may be needed for the electronic structure calculations. Furthermore, it may be necessary to treat multiple PESs and their coupling terms in the vibrational calculation to achieve quantitative accuracy.

Table 4. Representative Geometric Parameters in the Active Site of P450nor [Bond Lengths (r in Å), Bond Angles (θ in deg)], and the N–O and Fe–NO Stretching Vibrations (ν in cm^–1) Obtained from QM/MM Calculations^a Using Different DFT Functionals and Basis Sets Together with Experimental Values.

	BP86	B3LYP-D3	ωB97M-V
	def2-SVP(D)c	def2-SVP(D)c	def2-SVP(D)c	def2-TZVP(PD)d	exptlb
rFe–NO	1.655	1.653	1.643	1.641	1.67
rN–O	1.160	1.137	1.121	1.115	1.15
rFe–S	2.337	2.310	2.298	2.300	2.33
θFe–N–O	170.0	165.0	167.5	170.0	158
νN–O	1881.3	1984.7	2097.5	2054.6	1853
νFe–NO	608.0	610.9	641.1	642.0	530

^aThe snapshot is taken from NVT4, and the spin state is set to cs-1et.

^bStructural parameters are from X-ray crystal structure¹¹⁷ and frequencies from resonance Raman spectra in solution.¹³⁵

^cdef2-SVPD for the atoms bound to Fe and NO, and def2-SVP for the others.

^ddef2-TZVPPD for Fe, the atoms bound to Fe, and NO, and def2-TZVP for the others.

6. Summary and Outlook

An anharmonic vibrational method based on a PES from hybrid QM/MM computations is developed for vibrational analyses of biomolecules and solvated molecules. For this purpose, we have implemented into GENESIS an interface for QM/MM calculations and methods to facilitate the normal-mode analysis: the geometry optimization (L-BFGS-B minimizer and macro-/microiteration scheme) and a numerical differentiation scheme to derive a Hessian matrix for a local region. Using the resulting vibrational coordinates, multiresolution nMR-PESs are generated from the QM/MM energy and gradient at grid points, and the PES is used for VSCF and VQDPT2 calculations to obtain the anharmonic vibrational spectrum.

The method is first applied to a phosphate ion in solution. The strong solvation effect is incorporated by treating not only the phosphate ion but also neighboring water molecules as a QM region at the B3LYP/cc-pVTZ level. The calculated spectrum demonstrates a characteristic red-shift of the P–O stretching frequency, and a blue-shift of the P–OH stretching and POH bending frequencies. The calculated band positions agree with experiment with a mean absolute deviation of 16 cm^–1. The present calculation also reproduces the shape of the spectrum by taking a weight-average of IR spectra over relevant hydration structures. Second, the method is applied to a NO molecule bound to a ferric (Fe^III) heme of P450nor. The spin state of Fe^III(NO) is suggested to be a cs-1et state based on a ratio ν_N–O/ν_Fe–NO calculated for cs- and os-1et states. The absolute values of ν_N–O and ν_Fe–NO deviate from the experiment by ∼100 cm^–1, which may be due to imbalance in the QM and MM interaction or deficiency in DFT to describe the electronic structure of Fe^III(NO).

Applications of the proposed vibrational analysis method extend to a wide range. Hydrogen-bonded systems are relevant above all: for example, internal water molecules in a protein, proton transfer systems, amide modes of polypeptides and proteins, etc. To treat such systems, not only the explicit treatment of hydrogen-bonded molecules by QM calculations but also the use of advanced force fields that incorporate polarizability and charge transfer is a promising direction. These subjects will be the scope of future works.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b01193.

• Implementation of QM/MM in GENESIS, QFF coefficients by numerical differentiations, VSCF and VQDPT2 methods, bandwidth of Lorentz functions, equilibration protocol of P450nor, orbital diagram of FeIII(NO), QM/MM calculations of P450nor with extended QM region(PDF)

This research is partially supported by the “Molecular Systems”, “iTHES”, “Integrated Lipidology”, and “Dynamic Structural Biology” projects in RIKEN (to Y. Sugita), the Center of innovation Program from Japan Science and Technology Agency, JSPS KAKENHI Grant JP26220807 and JP26119006 (to Y. Sugita), and JSPS KAKENHI Grant JP16H00857 (to K. Yagi). We used a supercomputer system, HOKUSAI, provided by the RIKEN Information Systems Division.

The authors declare no competing financial interest.