Role of internal loop dynamics in antibiotic permeability of outer membrane porins

Significance

Antibiotic resistance in Gram-negative pathogens has been identified as an urgent threat to human health by the World Health Organization. The major challenge with treating infections by these pathogens is developing antibiotics that can traverse the dense bacterial outer membrane (OM) formed by a mesh of lipopolysaccharides. Effective antibiotics permeate through OM porins, which have evolved for nutrient diffusion; however, the conformational states of these porins regulating permeation are still unclear. Here, we used molecular dynamics simulations, free energy calculations, Markov-state modeling, and whole-cell accumulation assays to provide mechanistic insight on how a porin shifts between open and closed states. We provide a mechanism of how Gram-negative bacteria confer resistance to antibiotics.

Abstract

Gram-negative bacteria pose a serious public health concern due to resistance to many antibiotics, caused by the low permeability of their outer membrane (OM). Effective antibiotics use porins in the OM to reach the interior of the cell; thus, understanding permeation properties of OM porins is instrumental to rationally develop broad-spectrum antibiotics. A functionally important feature of OM porins is undergoing open–closed transitions that modulate their transport properties. To characterize the molecular basis of these transitions, we performed an extensive set of molecular dynamics (MD) simulations of Escherichia coli OM porin OmpF. Markov-state analysis revealed that large-scale motion of an internal loop, L3, underlies the transition between energetically stable open and closed states. The conformation of L3 is controlled by H bonds between highly conserved acidic residues on the loop and basic residues on the OmpF β-barrel. Mutation of key residues important for the loop’s conformation shifts the equilibrium between open and closed states and regulates translocation of permeants (ions and antibiotics), as observed in the simulations and validated by our whole-cell accumulation assay. Notably, one mutant system G119D, which we find to favor the closed state, has been reported in clinically resistant bacterial strains. Overall, our accumulated ∼200 µs of simulation data (the wild type and mutants) along with experimental assays suggest the involvement of internal loop dynamics in permeability of OM porins and antibiotic resistance in Gram-negative bacteria.

Antibiotic resistance is a major concern in the treatment of bacterial infections (1–3). Design of antibiotics targeting Gram-negative bacteria is particularly challenging due to the presence of an outer membrane (OM) containing lipopolysaccharide glycolipids. The OM provides a major permeation barrier against the uptake of various substrates, including antibiotics (2, 4–11). Due to the low permeability of the OM, essential nutrients for the bacteria typically diffuse into the cell through a variety of general diffusion, β-barrel OM porins (6). Several OM porins have been shown to also be the main pathways for penetration of antibiotics into Gram-negative bacteria (6, 12).

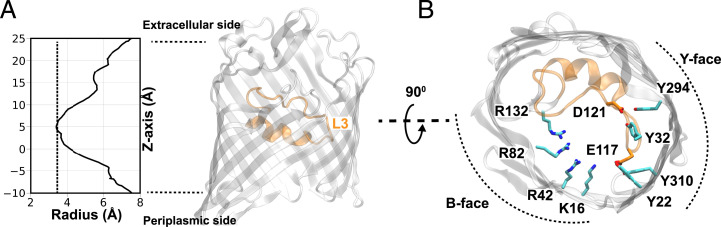
The general diffusion OM porins are typically organized into trimeric β-barrel structures with multiple loops connecting individual β-strands in each monomer. Of particular functional interest is a long internal loop (L3) that folds into the lumen of the monomeric β-barrels and forms a constriction region (CR) within the porin. The CR significantly narrows the pore (Fig. 1A) and acts as a major permeation barrier (13). Additionally, the CR contains many charged and polar residues, including acidic residues on the L3 loop and a cluster of tyrosine and basic residues on two opposite sides of the barrel wall (termed here as Y and B face, respectively) (Fig. 1B). The nature and organization of the B-face and Y-face residues will determine their interaction with the L3 loop and therefore, are expected to influence the dynamics of L3 and thus, the permeation properties of the porin.

Fig. 1.

Structural features of OmpF in E. coli. (A) The monomeric radius profile [calculated using the program HOLE (31)] of the crystal structure of OmpF [PDB code 3POX (26)]. A molecular representation of a single monomer of OmpF is shown highlighting the internal loop L3 (orange) that constricts the pore. (B) A top-down view of OmpF showing that two acidic residues of L3 (D121 and E117) form hydrogen bonds with residues in the Y face. A cluster of basic residues (B face) on the opposite side of the Y face is hypothesized to facilitate the movement of L3 to further narrow the pore.

A remarkable feature of many OM porins is their ability to undergo spontaneous conformational transitions between macroscopically distinct “open” and “closed” states. Functionally relevant conformational transitions in OM transport proteins are often active processes, coupled to and driven by an external energy input, such as the transmembrane voltage change (14–18). However, in OM porins, thermal fluctuations seem to be the main source for such conformational changes (19–24). The most abundant OM porin in Escherichia coli, OmpF, is an ideal model to study such conformational changes. OmpF is known for spontaneously fluctuating between highly stable conducting (open) and less stable nonconducting (closed) states, as observed in electrophysiological measurements under a low electric voltage (21, 22, 25). Notably, spontaneous fluctuations between conducting and nonconducting states have also been observed at 0 mV for OmpC, a close homolog of OmpF, where a KCl concentration gradient was used to drive ion diffusion (19). The asymmetric voltage-dependent inactivation of OmpC was not affected by mutations in these experiments, suggesting different molecular mechanisms for the spontaneous and voltage-dependent gating processes. However, the molecular mechanism by which OmpF undergoes these transitions is still not well understood.

We expect that the internal loop, L3, might play a direct role in the open–closed transitions in OmpF due to its location within the CR. Several of the acidic residues in L3, including E117 and D121, interact with tyrosine residues of the Y face in the crystal structure of OmpF (Protein Data Bank [PDB] code 3POX) (Fig. 1A) (26). It has been observed in a previous molecular dynamics (MD) study that L3 leaves the Y face to transiently interact with the B face, thereby narrowing the pore (27). These results led to the hypothesis that L3 movement could be responsible for controlling open–closed transitions of the pore. However, due to the short duration of the simulations and the nonphysiological conditions (vacuum) used in that computational study, structural support for this hypothesis remained lacking. The role of L3 conformational dynamics in permeability of OM porins remains an open subject. Notably, it is reported that the movement of L3 may not be critical to “voltage gating” of OM porins, a process occurring at voltages of 100 mV or more (28–31). However, this does not exclude the possibility that L3 can be involved in the open–closed transition at low or zero external voltage.

As a support for the latter hypothesis, mutations to disrupt the hydrogen bonds between L3 and Y face in OmpC, a homologous protein to OmpF, have been reported to increase closed-state visiting frequency of the porin under no voltage conditions in electrophysiology experiments (19). Furthermore, mutation of B-face residues to uncharged or negatively charged residues in OmpF showed an increase in substrate permeation (32–34), possibly as a result of reduced attraction of L3 to the B face, shifting the equilibrium toward the open state. Moreover, the crystal structure of a clinically relevant mutant of OmpF, G119D (35), suggested that adding a negative charge to L3 can potentiate its attraction toward the B face, thereby further reducing the pore size (SI Appendix, Fig. S1) as compared with the wild type (WT) and therefore, shifting the porin toward the closed state. This shift resulted in decreased permeability of the mutant to substrates such as carbohydrates and antibiotics (35). Strikingly, this mutant porin was shown to confer colicin N resistance to clinical strains of E. coli (35).

The aim of this study is to provide atomistic insight into the mechanisms controlling the equilibrium between open and closed states of OmpF using extended MD simulations, which are used to construct a Markov-state model (MSM) for the process. MSMs are a class of model used to describe the long-timescale dynamics of molecular systems and to obtain the thermodynamic and kinetic information about dynamic processes from MD simulations (36). Using MSMs, we find that large-scale motion of L3 controls the equilibrium between conducting and nonconducting states of OmpF. Further analysis using the transition path theory (TPT) (37) revealed that transitions between open and closed states occur in two steps: 1) movement of E117 to the B face to initiate the transition from the open state and 2) movement of D121 to the B face that drives a large-scale movement of L3 to mediate complete closure of the pore.

The significant effect of pore narrowing in the closed state on OmpF permeability is examined by electrophysiology simulations, in which ionic currents are shown to be substantially reduced in the closed state, and by free energy calculations indicating the presence of a higher-energy barrier against permeation of an antibiotic. Furthermore, simulations of charge-reversal mutants of B-face residues key in our proposed mechanism show a significant decrease in the probability of the closed state. This agrees with the increased accumulation observed for several antibiotics in our whole-cell assays, in which we expressed the mutant porins. Furthermore, previous experiments also report an increase in substrate permeability of these mutants (32–34). According to our model, these mutations reduce the attraction of E117 or D121 to the B face, thereby reducing the closed-state probability. Overall, our results provide mechanistic details on how thermal motion of an internal loop controls a dynamic equilibrium between open and closed states, thereby regulating permeability of OM porins.

Results

Dynamics of L3 Mediate OmpF Conformational Transitions.

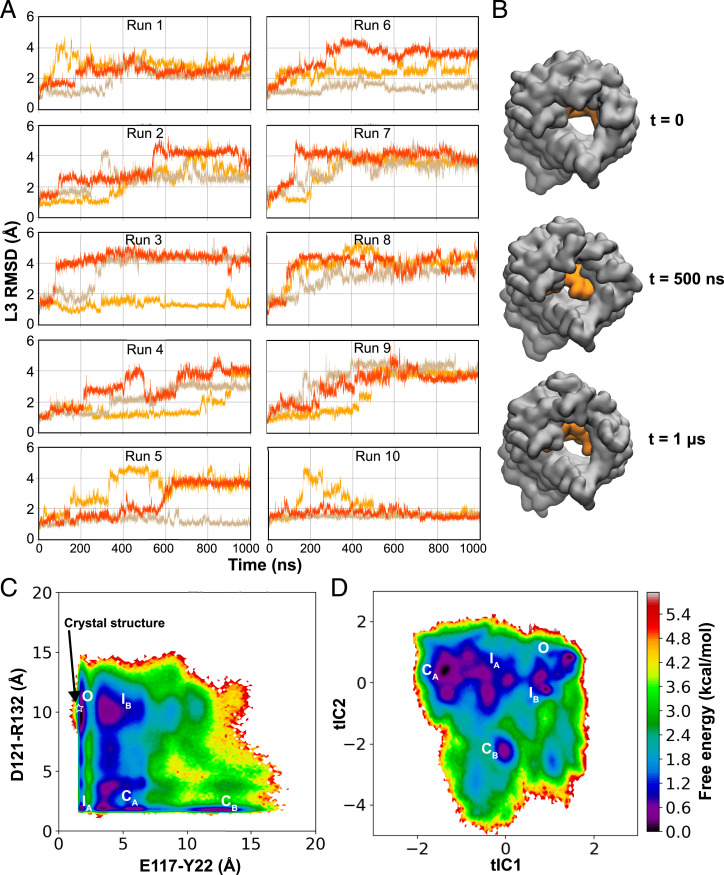
To extensively sample multiple conformations of L3 that could lead to functionally distinct states, we performed 10 independent replicas of MD simulation, each for 1 µs, starting from the crystal structure of the OmpF trimer (PDB code 3POX) (26) embedded in a lipid bilayer. In multiple replicas, the root mean square deviation (RMSD) of L3 (backbone atoms) was observed to reach values greater than 4 Å from the crystallized state, indicating a large-scale motion of this loop (Fig. 2A). This large-scale motion of L3 was accompanied with widening and narrowing of the CR in the pore (Fig. 2B), suggesting its potential role in regulating open–closed transitions of OmpF. The structural deviation of L3 from its initial conformation, which was even observed in the early phase of a few replicas, was seemingly unexpected because the crystal structure represents a thermodynamically stable configuration. However, since we performed our MD simulations at a more relevant biological temperature (310 K) (38) as opposed to the relatively low temperature (296 K) at which OmpF was crystallized (26), the observed rapid structural deviation of L3 was reasonable.

Fig. 2.

Dynamics and the conformational landscape of L3. (A) Time evolution of RMSD of loop L3 (after aligning the barrel residues to the crystal structure) in each monomer (shown in a different color) in all 10 replicas (runs 1 to 10). (B) Conformation of L3 (shown in orange) of a single monomer at different time points along a representative trajectory of membrane-embedded OmpF. L3 appears to close and reopen the pore during the trajectory. (C) The free energy landscape for L3 dynamics in OmpF, reweighted by the stationary distribution, is projected onto the space formed by the E117–Y22 and D121–R132 closest distances (optimal indicators of the slowest process) (more details are in Materials and Methods). Conformational states corresponding to energetic minima are represented as O, I_A, I_B, C_A, and C_B, representing open, intermediate, and closed states (details are in the text). The white star indicates the crystal structure of OmpF (PDB code 3POX). (D) Free energy landscape projected onto the top two tICA eigenvectors. The five conformational states (identified from the free energy projection onto E117–Y22 and D121–R132 distances) are mapped onto this surface.

To probe the key amino acids contributing to the loop’s dynamics, we calculated the root mean square fluctuation (RMSF) of the Cα atom of each residue in L3 (SI Appendix, Fig. S2). We found that residues 116 to 123 are the most flexible with Cα RMSF greater than 2 Å in at least one of the monomers of any simulation replica. The largest fluctuation was observed in the residue G120, located at the tip of the L3 loop, with a maximum RMSF of 5.2 Å (SI Appendix, Fig. S2). A high flexibility for G120 has also been reported in a previous MD simulation study (39).

During our simulations, the dynamics of L3 residues resulted in differential hydrogen-bonding patterns with two opposite faces (Y and B faces) of the β-barrel wall. A total of 26 hydrogen bonds can be defined based on either 1) high occurrence probability (occurrence >25%) or 2) long lifetime (maximum lifetime >50 ns), suggesting their importance in the transition of L3 between different conformational states.

To identify key conformational states of L3 and kinetics of state transitions, we constructed an MSM by featurizing our trajectory data using the distances of these 26 hydrogen-bond pairs. Since these distances are uncorrelated between monomers (SI Appendix, Fig. S3), indicating no significant monomer–monomer cooperativity, the trajectory of each monomer can be considered independently, resulting in an aggregate of 30 µs (10 independent runs × 3 monomers × 1 µs). We then performed time-lagged independent components analysis (tICA) on this dataset for dimensionality reduction and kept the top five tICAs, which sufficiently describe slow transitions of the system (SI Appendix, Figs. S4 and S5). The tICA space was then discretized into 1,000 microstates, which were used to build an MSM with a lag time of 2 ns (Materials and Methods has more details; SI Appendix, Figs. S5 and S6).

To reveal key conformational states, we evaluated the free energy landscape, reweighted by the stationary distribution obtained from an MSM. To identify physically meaningful metrics to project this landscape, we evaluated the correlation of each distance feature with the second eigenvector of the transition probability matrix (TPM) (SI Appendix, Fig. S7) since it has been established that features correlated to this eigenvector optimally describe the slowest transitions of the system (40). We then projected the reweighted free energy landscape onto the features with the greatest positive or negative correlation (E117–Y22 and D121–R132 distances) (SI Appendix, Fig. S7), corresponding to breakage and formation of hydrogen bonds, respectively. From the free energy landscape (Fig. 2C), we identified five distinct conformational states corresponding to energy minima. These five states also correspond to minima in the MSM reweighted free energy landscape projected onto the first two tICA eigenvectors (Fig. 2D), indicating that these states are not simply a result of the choice of representative metrics.

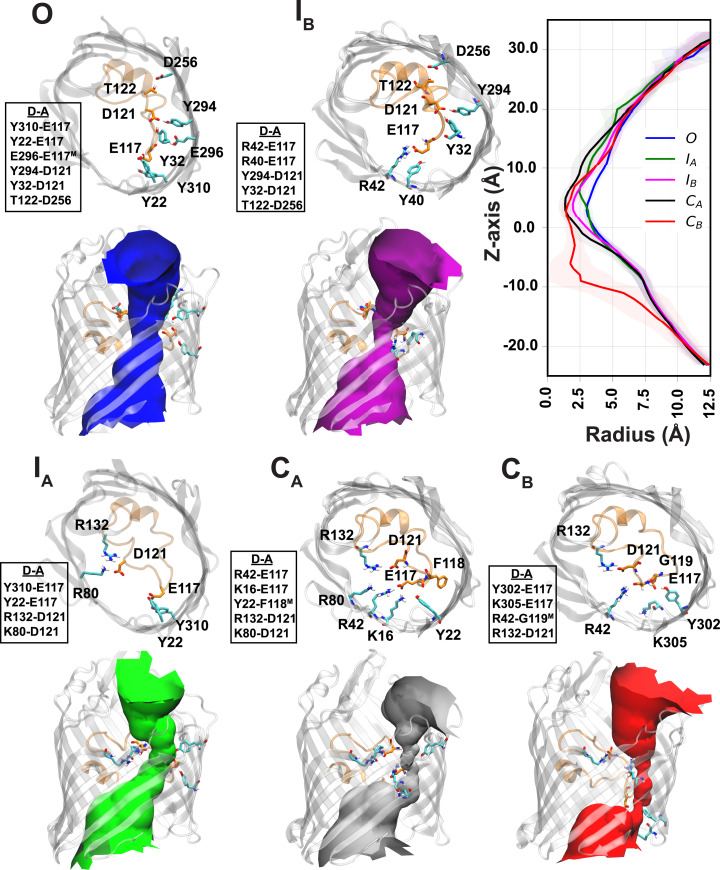
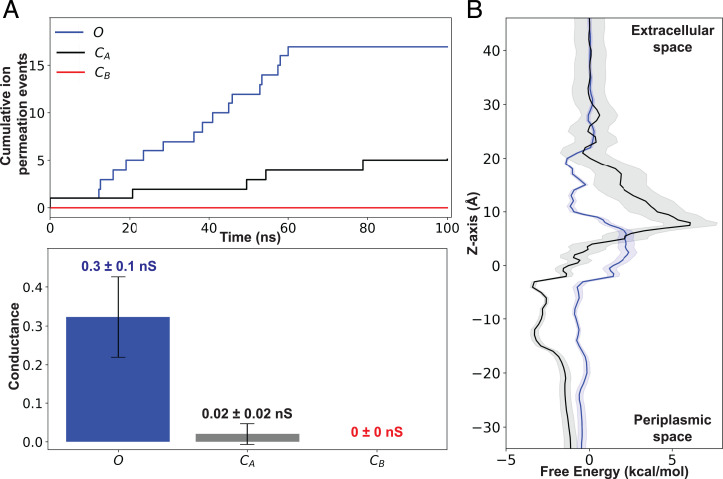
To evaluate the functional characteristics of these conformational states, we computed the pore radius profile of each state using the HOLE program (31) (Fig. 3). Based on the calculated pore bottleneck radius, we identified distinct functional states: an open state (O) with the widest bottleneck radius of 3.0 ± 0.2 Å and two closed states (C_A, C_B) with the narrowest bottleneck radii of 1.3 ± 0.5 and 1.4 ± 0.4 Å, respectively. Additionally, two intermediate states (I_A, I_B) with bottleneck radii of 2.4 ± 0.3 and 1.9 ± 0.6 Å, respectively, were also identified. To further characterize these states, five replicas of constant electric-field simulations (corresponding to an electric potential difference of 100 mV) were performed independently on representative structures of the OmpF monomer for each of the O, C_A, and C_B states (Fig. 4A). These simulations revealed the largest conductance of 0.3 ±0.1 nS for the O state and virtually zero conductance for the two closed states: 0.02 ±0.02 nS for the C_A state and 0 nS for the C_B state (Fig. 4A). These values are in good agreement with previous electrophysiology experiments reporting conductances of 0.31 and 0.03 to 0.05 nS for the open and closed states for a single monomer of OmpF, respectively (22).

Fig. 3.

Structural characteristics of the conformational states in OmpF. The figure shows top-down snapshots of the five conformational states (O, I_A, I_B, C_A, and C_B) highlighting hydrogen bonds with >20% occurrence probability between the most fluctuating residues of L3 (SI Appendix, Fig. S2) and the barrel residues. The abbreviation “D-A” here refers to the donor–acceptor pair of the hydrogen bond. The ensemble distribution of distances of each hydrogen bond for the conformational states can be seen in SI Appendix, Fig. S8. The pore profiles [determined using the program HOLE (31)] of the conformational states are depicted with different colors in the side view of the pore. The mean (solid lines) and SD (shaded regions) of the radius profile calculated using HOLE (31) are shown for each conformational state.

Fig. 4.

Effect of the open–closed transition of OmpF on permeation of ions and antibiotics. (A, Upper) The cumulative net number of channel-crossing events by ions (Cl^–and Na⁺) tracked over the time course of a representative MD simulation for O (blue), C_A (black), and C_B (red) states. (A, Lower) Mean and SD of conductance for O (blue), C_A (black), and C_B (red) states determined using five independent constant electric-field simulations for each state. (B) Mean (solid) and SD (shaded) of the free energy for permeation of fosfomycin through O (blue) and C_A (black) states. Free energies were calculated using all the 94 MCPS BEUS windows and projected along the z coordinate of the antibiotic center of mass (C.O.M.), relative to the membrane C.O.M.

Now, to characterize antibiotic permeation properties in different conformational states of OmpF, we performed two independent bias-exchange umbrella sampling (BEUS) (41–45) simulations of fosfomycin, an antibiotic known to permeate OmpF (46), in the O and C_A OmpF conformations obtained from the MSM analysis. The protein backbone was restrained during these simulations to prevent significant deviation from the conformational state to be investigated (O or C_A state). The initial seeds for these BEUS simulations were obtained using a Monte Carlo–based pathway search (MCPS) algorithm we recently developed specifically to improve sampling of the position and orientation of antibiotics during permeation through OM porins (47). The free energy profiles obtained from the BEUS simulations revealed a significantly larger energetic barrier, corresponding to a lower permeability, for the C_A vs. the O state (Fig. 4B), which can be attributed primarily to a smaller radius of the former at the CR. Thus, our results show that the conformation of L3 is of direct consequence to the permeation of ions and molecular systems, such as antibiotics.

Beyond regulating antibiotic permeation through opening and closing the porin, L3 residues might also directly interact with permeating antibiotics. In a previous study (47), in which we compared the permeation of positively charged and neutral antibiotic derivatives through OmpF, we found favorable electrostatic interactions between positively charged antibiotics and D113. Notably, however, this residue is not in the L3 tip that shows the largest conformational changes during the open–closed transition of OmpF. In the present study, we observe that during its translocation through the O state of OmpF, fosfomycin interacts noticeably with S125; however, in the C_A state, the antibiotic interacts mainly with E117 and T124. Such direct interactions between L3 and the permeating antibiotic are expected to be antibiotic specific and may even have opposite effects in other compounds with different molecular structures and charges. However, the steric occlusion of the L3 conformation in the closed state is a general effect that is expected to impede the translocation of all molecular species across the CR in OmpF.

Distinct Open–Closed Transitions Mediated by Acidic Residues, E117 and D121.

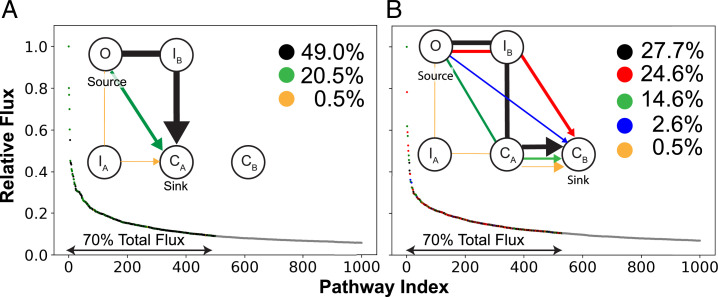
Two distinct processes play major roles in the observed dynamics of L3 in OmpF: the O to C_A transition, with a mean first-passage time (MFPT) of 4.6 ± 0.1 µs, and the significantly slower O to C_B transition, with an MFPT of 40.5 ± 2.0 µs. To obtain mechanistic insight on the two processes, pathways of conformational transitions from O to C_A and from O to C_B were identified separately using TPT (37, 48, 49). The two processes were analyzed by grouping their pathways according to conformational states visited, which allowed us to identify key intermediates. We found that in half of the pathways involved in both processes, initial transitions are from O to the intermediate state I_B (Figs. 3 and 5). These transitions are primarily mediated by movement of E117 a short distance (∼ 2.5 Å) from the Y face to the B face, where it interacts with R42 and Y40 (Figs. 2C, 3, and 5). In comparison, direct O to C_A transitions are mediated by movement of both E117 and D121 from the Y face to the B face. These transitions have a lower likelihood since D121 needs to travel a larger distance (∼ 10 Å) to reach its new interaction partners, R132 and R80 (Figs. 2C, 3, and 5). Pathways involving an initial movement of only D121 (and not E117) to the B face (O to I_A transition) have negligible total fluxes.

Fig. 5.

Dominant conformational transition pathways in WT OmpF. The pathways (A) from O to C_A and (B) from O to C_B identified from the TPT are ranked according to their flux relative to the highest-flux path. The paths representing the top 70% of the total flux are grouped according to the intermediate conformational states visited and color coded black, red, green, blue, or orange according to the pathway group. The flux sum for all paths belonging to each pathway group is depicted. Schematic of each pathway group for (A, Inset) O to C_A and (B, Inset) O to C_B transitions. The width of the arrow approximates the flux sum of each group.

After reaching the intermediate state I_B (observed in half of the transitions), movement of D121 from the Y to B face triggers a large-scale motion of the entire L3 loop toward the B face and completes closure of the pore (transitions to either C_A or C_B) (Figs. 3 and 5). This D121-mediated loop movement is preserved in transitions from I_B to either C_A or C_B. However, transition to C_B requires additional movement of E117 (along the pore axis and toward the periplasmic space) to interact with K305 and Y302 located below the B face (SI Appendix, Fig. S9A), which elongates the narrow region of the pore. The downward movement of E117 is accompanied by partial unfolding of the α-helical portion of L3 and conformational restriction of the backbone torsion of a proline residue P116 at the tip of the loop (SI Appendix, Fig. S9). This offers a possible explanation for the slow timescale of the processes involving the formation of C_B. Overall, our analysis suggests that pore closure generally occurs in two key steps: 1) E117 movement to the B face (R42 and K16) mediating the initial transition out of the O state and 2) D121 movement to the B face (R132) mediating large-scale motion of L3, leading to closure of the pore.

Our mechanism for open–closed transitions could be generalized to OM porins of Enterobacteriaceae, such as OmpC and PhoE in E. coli, OmpK36 of Klebsiella pneumoniae, and OmpE36 from Enterobacter cloacae, since these porins share a similar architecture with OmpF and conserve key residues involved in the conformational transitions (SI Appendix, Fig. S10). However, our mechanism should not be generalized to porins with multiple internal loops, such as the OccK and OccD family in Pseudomonas aeruginosa, since the open–closed transitions of these porins might involve the motion of multiple loops (50, 51).

Mutations Regulating Dynamics of the Loop Determine OM Permeability to Antibiotics.

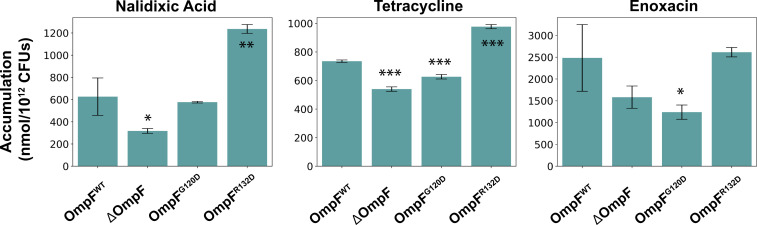
Many of the key residues in the identified open–closed transition are shown to be important for permeation through OM porins of Enterobacteriaceae in our own and previous experiments. In our whole-cell assays (details in SI Appendix), we compared the accumulation of various antibiotics (nalidixic acid, tetracycline, and enoxacin) in E. coli BW26678 (parental strain) with a strain containing a point mutation of a key B-face residue (R132) to a negatively charged side chain in OmpF, E. coli OmpF^R132D. These three antibiotics have all been previously shown with whole-cell accumulation and liposome-swelling assays to permeate the OM when WT OmpF is expressed (52–54). We found a statistically significant increase in the accumulation of the two negatively charged antibiotics, nalidixic acid and tetracycline, for cells expressing the mutant (Fig. 6). However, accumulation values of the zwitterionic enoxacin (at physiological pH) were not significantly altered, possibly because the accumulation of enoxacin through WT OmpF is already saturated (note the substantially higher accumulation values for this compound in Fig. 6). The higher accumulation of other zwitterionic antibiotics has also been described before (55) and might be due to differential engagement of these drugs with other uptake/efflux mechanisms.

Fig. 6.

Accumulation values of three different antibiotics in WT E. coli BW26678 (parental strain) and three modified strains, including complete deletion of the ompF locus, E. coli OmpF ^G120D, and E. coli OmpF^R132D. Accumulation values are reported in nanomoles per 10¹² colony-forming units (CFUs). Data shown represent the average of three independent experiments. Error bars represent the SD of the data. Statistical significance was determined by a two-sample Welch’s t test (one-tailed test, assuming unequal variance) relative to accumulation values in the WT strain. Statistical significance is indicated with asterisks. *P < 0.05; **P < 0.01; ***P < 0.001.

Previous experiments including liposome swelling assays, radiolabeled substrate uptake assays, and antibiotic susceptibility measurements have also shown that mutation of key B-face residues in OmpF to uncharged or negative residues (R42S, K16D, R132A, and R132D) significantly increases permeation of various substrates, including carbohydrates and antibiotics (32–34). Additionally, mutation of a conserved basic residue, K16, in OmpC to a negatively charged residue (K16D) in electrophysiology measurements showed significant increase in the probability of open, conducting states (20). The rationale previously given for the increased substrate permeation was that these mutations either 1) decreased the bulkiness of the CR, thereby increasing the pore radius, or 2) altered substrate–protein interactions to facilitate permeation (32, 34). Our study, however, suggests an alternative hypothesis; these mutations increase permeation by altering the equilibrium between open and closed states. In particular, the K16D or R42S mutations would hinder the initial transition of OmpF out of the open state by reducing E117 attraction to the B face. The R132A or R132D mutations would hinder the large-scale motion of L3 by reducing D121 attraction to the B face. Both sets of mutations would decrease the probability of pore closure transitions, leading to an increased likelihood of the open state.

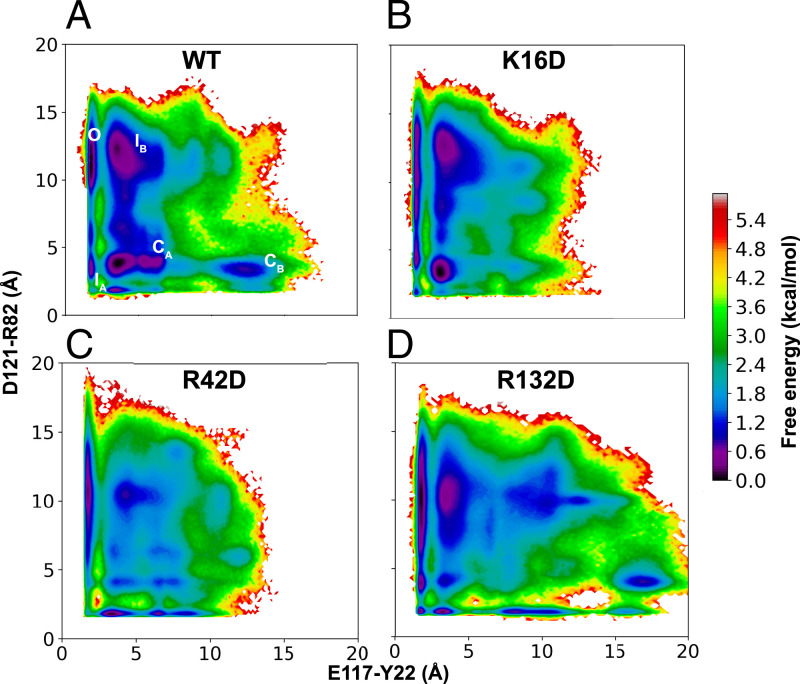
To test this hypothesis, we built three mutant systems, R42D, K16D, and R132D, in all three monomers of the crystal structure of the OmpF trimer (PDB code 3POX) (26). Using these three mutant structures as starting points, 10 independent 1-µs simulations were performed for each mutant. Simulation trajectories were then used to build an independent MSM for each mutant system following the same procedure as for the WT. We evaluated the free energy landscapes, reweighted by the stationary distribution obtained from the MSM, for each mutant. To compare the results, free energy landscapes of WT and mutant systems were projected onto the distance features, E117–Y22 and D121–R82 (Fig. 7). D121–R82 was used as a distance feature instead of D121–R132 since the R132D mutation abolishes a favorable interaction between these sites. In the K16D and R42D systems, an increased energetic barrier compared with the WT system was observed for the O to I_B transition (Fig. 7 B and C). This supports the hypothesis that a negative charge at residue 16 or 42, the interaction site of E117 upon transition to the B face in WT, hinders the initial transition out of the O state (Figs. 2 and 5). In the R132D system, the energetic barrier for the O to I_B transition was not substantially altered (Fig. 7D) since this mutation does not affect the movement of E117. Regardless, in each mutant system, at least one closed-state probability was significantly lowered compared with the WT (Fig. 7), in accordance with our hypothesis that both D121 and E117 movements are necessary for closed-state formation.

Fig. 7.

Conformational landscape of L3 in the WT, K16D, R42D, and R132D OmpF simulations. (A) The free energy landscape for the WT OmpF, reweighted by the stationary distribution, is projected onto the E117–Y22 and D121–R82 distance features. The conformational states identified in Fig. 2 C and D are mapped onto this landscape. (B–D) Free energy landscapes for K16D, R42D, and R132D OmpF. The free energy error for each system can be seen in SI Appendix, Fig. S13.

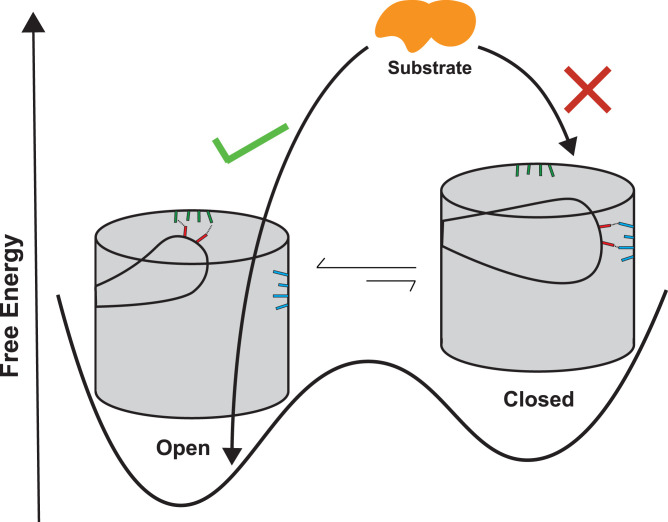
In general, the proposed model suggests that the permeability of OmpF depends on the dynamic equilibrium between the open and closed conformations of the pore (Fig. 8). This is in contrast to the typical understanding of the pore as a rigid body permeating substrates (56, 57). An example of how a shift in dynamic equilibrium impacts permeability has been previously captured in the clinically relevant G119D mutant of OmpF. The crystal structure of the OmpF^G119D (35) shows that the introduced negative charge on L3 increases attraction of the loop to the B face, thus stabilizing the pore in a narrower state than in the WT structure (SI Appendix, Fig. S1). The loop movement reduces the pore radius compared with the open WT crystal structure (SI Appendix, Fig. S1). After further relaxing the mutant crystal structure in microsecond-scale MD simulations (in multiple replicates) followed by MSM analysis, we find additional shifts in equilibrium toward the closed state (SI Appendix, Fig. S11). We identify two structurally distinct closed states on the conformational landscape of L3 (bottleneck radii of 0.9 ± 0.3 and 1.8 ± 0.3 Å) for this mutant. These shifts in equilibrium relate to the significantly decreased permeability of the G119D mutant to substrates, such as carbohydrates and antibiotics (35). Strikingly, the reduced permeability of this mutant porin was shown to confer colicin N resistance to clinical strains of E. coli (35).

Fig. 8.

A schematic model summarizing the impact of open–closed transitions of the loop L3 on the substrate permeability of OmpF. Cartoon representations of open and closed states are shown with their relative free energies. Acidic, basic, and polar residues that stabilize the L3 loop in its alternative conformations are highlighted in red, blue, and green, respectively. Substrates are shown to readily pass through the open but not through the closed state.

To generalize the idea that a negative charge can shift L3 dynamics, we built another mutant system, G120D, and applied our approach of microsecond-scale MD simulations (in multiple replicates) and MSM analysis to this mutant. Each energetically stable state found for G120D exhibits a narrower pore (bottlenecks of 2.3 ± 0.6, 1.2 ± 0.6, and 1.0 ± 0.6 Å, respectively, for the three identified stable states) than the open state of WT OmpF (SI Appendix, Fig. S12). To verify experimentally the potential effect of the G120D mutation on antibiotic permeation, as suggested by our simulations, we compared the accumulation of the three antibiotics in E. coli BW26678 (parental strain) with a strain containing the G120D point mutation in OmpF, E. coli OmpF ^G120D. We found a statistically significant decrease in the accumulation of tetracycline and enoxacin for cells expressing the mutant (Fig. 6). However, we did not observe a significant decrease in accumulation of nalidixic acid, possibly because nalidixic acid is markedly smaller than the other two antibiotics and could still permeate through narrower porins. In general, our study suggests that regulation of the dynamic equilibrium between open and closed states of OM porins could be a mechanism by which Gram-negative bacteria become resistant to antibiotics.

Concluding Remarks.

OM porins form the main pathway for exchange of material between the environment and the intracellular compartment in Gram-negative bacteria. Due to their central role in transport, OM porins are a key factor in determining antimicrobial resistance of a large number of bacteria. Using extensive MD simulations to construct an MSM, we characterize the open–closed-state transitions in OmpF, the archetypal OM porin in E. coli. From the MSM combined with structural analysis of the involved states, we find that large-scale motion of an internal loop, L3, controls the transition of OmpF between open and closed states. The transitions captured during multimicrosecond simulations of membrane-embedded OmpF are primarily mediated by 1) the shift of E117 to a cluster of basic residues (B face) causing an initial departure from the open state and 2) movement of D121 to the B face driving large-scale motion of L3 and completing closure of the pore. Further narrowing of the pore upon the formation of the closed state has clear effects on the translocation of permeants through the pore. In the closed state, the ionic currents are substantially reduced, and the barrier against movement of antibiotics across the channel is significantly increased. The observed mechanism may be generalized to several other Gram-negative porins with similar architecture and conserved key residues involved in open–closed transitions (SI Appendix, Fig. S10). Supported by the altered antibiotic accumulation inside E. coli in our experiment and previous experiments (32–34), microsecond-scale simulations of mutants of key B face and L3 residues show a decreased or increased probability for the closed state, respectively. Based on these results, a simple model can be put forward in which open–closed transitions mediated by L3 movement impact substrate permeability of OM porins (Fig. 8). This model could offer a perspective on the mechanisms by which OM porins mediate antibiotic resistance in Gram-negative bacteria.

Materials and Methods

Markov-State Analysis.

OmpF trimer (PDB code 3POX) (26) was embedded using CHARMM-GUI (58) in a DMPC (1,2-dimyristoyl-sn-glycero-3-phosphocholine) membrane buffered with TIP3P water (59) and 0.15 M NaCl and protonated in accordance with previous studies (60–62). The system was used for 10 independent 1-µs MD simulations in NAMD (63, 64) using CHARMM36m (65) and CHARMM36 (66) force-field parameters, particle mesh Ewald (PME) (67), and constant pressure/temperature (68, 69). Then, an MSM was built from the trajectory data using pyEmma (70). The trajectories were featurized using 26 residue–residue distance pairs, which were then reduced to the space of the slowest five tICA eigenvectors (40, 71–73) to decrease finite sampling error (74) and discretized using k-means clustering into 1,000 microstates based on VAMP-2 (variational approach for Markov processes) score analysis (75) (SI Appendix, Fig. S5). A maximum likelihood, reversible MSM was constructed with a lag time of 2 ns based on convergence of implied timescales (SI Appendix, Fig. S6). The free energy landscape weighted by the stationary distribution obtained from the MSM was then projected onto the features with greatest correlation to the second eigenvector of the MSM (E117–Y22 and D121–R132 distances) (Fig. 2 C and D) according to a previously established protocol (40). We used this free energy landscape to lump our microstates into five macrostates (O, I_A, I_B, C_A, C_B) depending on whether the microstate lies within a free energy minima (defined using an energy cutoff of 1.2 kcal/mol) shown in Fig. 2 C and D. To obtain kinetic information, MFPTs for the O–C_A and O–C_B transitions were evaluated. Uncertainties are determined using a Bayesian estimated MSM. The TPT module in pyEmma (70) was used to identify the conformational transitions by choosing the O and C_A/C_B states as the source and sink, respectively, and identifying the pathways connecting them.

Conductance Calculations.

Conductance was calculated by performing simulations with a constant electric field in five independent replicas for each of the three different OmpF states (O, C_A, C_B) derived from MSM analysis, each simulated for 100 ns under a membrane potential of 100 mV. During these simulations, the protein heavy atoms were restrained (k = 0.1 kcal mol⁻¹ Å⁻²) to maintain the respective conformational state (O, C_A, or C_B). Ionic current (I) was computed by counting the number of ions that cross the porin over a time interval τ, and conductance (C) was then calculated as $\text{C}=\frac{\text{I}}{\text{V}}$.

Antibiotic Permeation Free Energy Calculations.

To investigate the energetics of permeation of fosfomycin [parameterized using CHARMM general force field (76–78)] in the open and closed states, two independent sets of BEUS simulations (41–45) were performed starting from the O and C_A states. The initial seeds for these BEUS simulations were obtained using an MCPS algorithm (47). The reaction coordinate included 1-Å windows except for the CR (Z = –3 to 12 Å) , where 0.5-Å windows were used (94 windows in total for each system). To obtain reference free energies, we extended the reaction coordinate into the extracellular and periplasmic spaces by at least 10 Å away from the protein; 30 ns of BEUS simulations were then performed using the distance between the drug and the protein as the collective variable (until convergence), during which the protein backbone was restrained. The last 20 ns were used in evaluating the free energy using a nonparametric variation of the weighted histogram analysis method (79), proposed by Bartels (80) and implemented by Moradi and Tajkhorshid (45).

Accumulation Assay.

The accumulation assay was performed in triplicate as outlined elsewhere (12, 81) for OmpF WT and designed mutants. OmpF mutants were constructed using established protocols (82, 83) (SI Appendix has details).

Data Availability

Representative structures for MSMs for the WT and mutants of OmpF, structure (PDB/PSF) files of the models, and simulation trajectories have been deposited in Zenodo (https://zenodo.org/record/5790144#.Yd6-Iy-B1O4) (84). Simulation trajectories were collected using NAMD. Visualization and analysis were performed using VMD and pyEmma. All of these software packages are publicly available. All other data are included in the manuscript and/or SI Appendix.