Kinetics of Phenol Escape from the Insulin R₆ Hexamer

Abstract

Therapeutic preparations of insulin often contain phenolic molecules, which can impact both pharmacokinetics and shelf life. Thus understanding the interactions of insulin and phenolic molecules can aid in designing improved therapeutics. In this study, we use molecular dynamics to investigate phenol release from the insulin hexamer. Leveraging recent advances in methods for analyzing molecular dynamics data, we expand on existing simulation studies to identify and quantitatively characterize six phenol binding/unbinding pathways for wildtype and A10 Ile → Val and B13 Glu → Gln mutant insulins. A number of these pathways involved large-scale opening of the primary escape channel, suggesting that the hexamer is much more dynamic than previously appreciated. We show that phenol unbinding is a multipathway process, with no single pathway representing more than 50% of the reactive current and all pathways representing at least 10%. We use the mutant simulations to show how the contributions of specific pathways can be rationally manipulated. Predicting the net effects of mutations is more challenging because the kinetics depend on all the pathways, demanding quantitatively accurate simulations and experiments.

Graphical Abstract

Introduction

The primary therapeutic for diabetes management is the protein hormone insulin. Both the pharmacokinetics and the shelf life of insulin depend on equilibria between conformational and oligomeric states. Insulin is typically a hexamer in therapeutic formulations, a dimer in the blood, and a monomer when bound to its receptor;^1,2 therapeutic formulations require cold storage and transport to suppress off-pathway equilibria that lead to fibrillation.^3–5 Much effort is directed toward modulating insulin’s equilibria to achieve therapeutics with desired properties.⁶ For example, the widely used fast-acting diabetes therapeutics lispro (Pro^B28 → Lys^B28, and Lys^B29 → Pro^B29)⁷ and aspart (Pro^B28 → Asp^B28)⁸ destabilize the insulin dimer. In contrast, slow-acting basal insulin analogs like glargine⁹ and detemir^10,11 function by either decreasing insulin solubility or adsorption in the body.¹² Longer-acting insulin analogs are also being developed,^13,14 but such formulations are often expensive and complicated. To enable rational design of improved insulin mutants and analogs, better understanding of insulin equilibria at the molecular level is needed.

In the present study, we focus on the insulin hexamer. The hexamer exists in three conformational states that are designated T₆, T₃R₃, and R₆ for the contributing monomer conformational states.^15–17 Each monomer consists of a 21-amino acid A chain joined to a 30-amino acid B chain by two interchain disulfide bonds (Cys^A7-Cys^B7 and Cys^A20-Cys^B19). Each A chain contains an intrachain disulfide bond (Cys^A6-Cys^A11) and two α helices: Gly^A1 - Ser^A9 and Leu^A13 - Asn^A21. Each B chain has a single α helix, and this secondary structure element differs in length depending on whether the monomer is in the T or R state. It spans Ser^B9 - Cys^B19 in the T state and Phe^B1 - Cys^B19 in the R state.¹⁸ The hexamer can be viewed as a trimer of dimers, with the dimer interface made up of the B-chain α helix and an anti-parallel β sheet (Phe^B24-Tyr^B26) from each monomer.

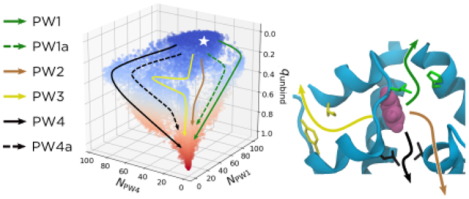
The T₆ and R₆ states of the hexamer have markedly different dissociation kinetics. The T₆ state dominates under physiological conditions² and dissociates to dimers in minutes.¹⁹ By contrast, the lifetime of the R₆ state is hours to days.¹⁹ Therapeutic formulations often contain phenol because it prolongs their shelf lives by shifting the equilibrium to R₆,²⁰ which presumably suppresses dissociation and in turn off-pathway equilibria. The phenol binds in pockets that are formed in R₆ between the A chains of one insulin dimer and the Gly^B1 - Gly^B8 segments from an adjacent dimer.¹⁵ The X-ray crystal structure of the phenol-bound human insulin R₆ hexamer (PDB ID 1ZNJ)²¹ suggests that when bound, each phenol forms two hydrogen bonds, one with the backbone carbonyl oxygen of Cys^A6 and one with the backbone amide NH of Cys^A11, and interacts with His^F5, among other residues in the binding pocket (Figure 1).^15,22 These pockets are absent from T₆.

Figure 1:

The solvated and equilibrated crystal structure for the R₆ insulin hexamer. (A) The full hexamer, with phenols being shown in magenta/pink. The protein is colored to correspond with the other panels. (B) The cyan protein chains from (A), labelled as chains A, B, F, G, and H. For a full description of the protein nomenclature, see the Supplemental Information. Sidechains are shown that define the phenolic binding pocket. Some specific sidechains are highlighted as follows: Ile^A10 and His^F5 (green), Leu^A13 and Leu^H17 (black), Ile^A2 and Tyr^A19 (yellow), Cys^A6 and Cys^A11 (orange), and Phe^B25 (brown). Other residues involved in the binding pocket and escape pathways are shown in white. We omit hydrogens for clarity. (C) The configuration in (B) represented to show the two hydrogen bonds formed by the −OH in the phenol, one with the backbone carbonyl oxygen of Cys^A6 and one with the backbone amide NH of Cys^A11.

Compared to the hexamer dissociation timescales, the phenol unbinding timescale is relatively fast. Existing NMR data suggest that phenol unbinding and rebinding occur on the sub-millisecond timescale.²³ This fast equilibrium is somewhat surprising, as the R₆ binding pockets bury the phenols nearly completely.^15,24 In this case, the crystal structure is not sufficient to predict the timescales of phenol escape, and we must consider the dynamics of the protein.

NMR data indicate that Ile^A10 serves as an essential “gatekeeper” residue, whose flexibility is required for the binding/unbinding of phenolic ligands.²³ Two subsequent molecular dynamics studies in which external forces were used to accelerate phenol escape^25,26 identified three pathways for unbinding. Abrams and Vashisth²⁶ call these pathways PW1, PW2, and PW3, and we use this nomenclature throughout our paper. PW1 is a gate-pushing mechanism, where the phenol pushes through the gatekeeper residues Ile^A10 and His^F5 (green in Figure 1). By contrast, PW2 is as a gate-hopping mechanism, with the phenol passing through an existing escape channel between Ile^A10/His^F5 and Leu^A13/Leu^H17 (black in Figure 1). Finally, PW3 is an unrelated pathway, where the phenol moves back through the A chain and escapes through the A chain and the β sheet dimeric interface, interacting with Ile^A2 and Tyr^A19 (yellow in Figure 1).

While the pathways in these simulations suggest possible mechanisms of phenol unbinding, applying external forces can significantly bias the dynamics.²⁷ Consequently, it is difficult to determine the significance of the pathways and to estimate their kinetics. To address this issue, here, we exploit recent advances in computational methods for estimating kinetic statistics from an ensemble of short, unbiased simulations^28,29 to compute free energies, escape and rebinding probabilities (commmittors), and reactive currents for phenol unbinding from the R₆ hexamer. By combining these quantities, we are able to characterize six unbinding pathways quantitatively and determine their relative weights. All pathways contribute significantly to unbinding/binding rates, highlighting the importance of methods that naturally account for a diversity of mechanisms,^28,29 in contrast to traditional rate theories.^30,31

In addition to providing quantitative insights, our simulations reveal qualitatively new dynamics. We observe a large-scale opening of the primary channel for phenol escape and delineate six pathways for phenol unbinding. Based on our observations, we identify and model two mutations that we expect to impact the dynamics. We find that one mutation (B13 Glu→Gln) encourages phenol unbinding, and the other (A10 Ile→Val) discourages it. The relative weights of our six pathways are dramatically affected for both mutations, with the preferred wildtype (WT) pathway becoming sparsely populated for the B13 Glu→Gln mutation. We thus demonstrate how molecular dynamics simulations can inform the design of therapeutics with improved properties.

Methods

System setup.

All systems were prepared using CHARMM-GUI, version 3.0 for the wild-type (WT) simulations, and version 3.2 for the mutant simulations.^32–34 The crystal structure for wildtype (WT), phenol-bound human insulin R₆ hexamer was retrieved from the Protein Data Bank (PDB ID 1ZNJ).²¹ All ions (including the two Zn²⁺ ions and two Cl⁻ ions bound within the hexamer) and 331 crystallographic water molecules were retained. Six of the seven phenols in the structure were included in the simulations; following the procedure in ref. 26, the seventh phenol, located adjacent to one of the bound Cl⁻ ions, was deleted.²⁶ Missing Thr residues at the C-termini of the six insulin B chains were added, along with hydrogen atoms. We refer to the A and B chains of the six insulin monomers as chains A through L, with nomenclature specifics given in the Supplemental Information. CHARMM parameter files for phenol were generated from the phenol Structure Data File (SDF) available from the RCSB and the CHARMM General Force Field.³⁵ Protonation states were chosen by using the PROPKA3 algorithm.^36,37 The edited crystal structure was solvated in a (8.2 nm)³ box of TIP3P water³⁸. To neutralize the system at a concentration of 150 mM KCl, 53 K⁺ and 43 Cl⁻ additional ions were added³⁹. There was a total of 51,064 atoms.

Equilibration.

All simulations were performed using GROMACS 2019.4⁴⁰ patched with PLUMED 2.5.3,^41–43 using the CHARMM36m force field.^44–46 Unless otherwise noted, simulations were carried out in the isochoric isothermal (NVT) ensemble at 303.15 K using a Langevin thermostat⁴⁷ with a 2 fs timestep and a friction constant of 10 ps⁻¹ applied to all atoms. This friction constant was chosen to be as weak as possible, while still maintaining the correct temperature, so as to minimally perturb the dynamics. The LINCS algorithm⁴⁸ was used to constrain all bonds to hydrogen. The particle-mesh Ewald method⁴⁹ was used to calculate electrostatic forces, accounting for periodic boundary conditions, with a cutoff distance of 1.2 nm. The Lennard-Jones interactions were smoothly switched off from 1.0 to 1.2 nm through the built-in GROMACS force-switch function. We used VMD⁵⁰ for molecular visualization.

To relax each system following its preparation, we used the steepest descent algorithm to minimize the energy until the maximum force felt by the system was below 1000 kJ/mol nm. We then equilibrated the system for 100 ps in the NVT ensemble with a 1 fs timestep, followed by 10 ns in the NPT ensemble at 1 bar using the Parrinello-Rahman barostat,⁵¹ with a 2 fs timestep and time constant of 5.0 ps. For the energy minimization and equilibration above, harmonic restraints were used to stabilize the positions of all non-hydrogen protein atoms. The system was equilibrated further for 1 ns in the NPT ensemble without position restraints, and the average box size was determined to be (7.96 nm)³. This box size was used for all further simulations. The system was equilibrated once more without position restraints for 3 ns in the NVT ensemble. The resulting equilibrated structure was used to initialize further simulations as described below.

Comparison of phenols.

Although in principle all six phenols are equivalent, in practice their behaviors may differ owing to asymmetries in the initial structure. To determine if this was the case, we used Adiabatic-Bias Molecular Dynamics (ABMD) implemented in PLUMED 2.5.3^41–43,52 to drive their dissociation from the WT hexamer. This method uses a half-harmonic potential, moved in a ratchet-and-pawl like mechanism, to trap natural fluctuations toward a specific target in collective variable (CV) space. It thus tends to bias the dynamics more gently than alternatives. Specifically, we used ABMD because we previously observed ABMD to successfully drive insulin dimer dissociation without melting otherwise stable α helices, in contrast to steered molecular dynamics.⁵³

Our first guesses for CVs to control phenol dissociation were the six distances d_n, where 1 ≤ n ≤ 6 denotes the identity of the phenol being released. Specifically, d_n is the distance between the geometric center of the non-hydrogen atoms of phenol n and the Zn²⁺ ion bound closest to it. We biased the six d_ns independently but simultaneously; since the timing of events in ABMD simulations depends on the specific fluctuations that occur, this led to simulations where varying numbers of the phenols dissociated with no externally imposed order. A total of 276 such simulations were performed (each run for 5 ns with structures saved every 10 ps): 20 simulations for each of nine equally spaced force constants ranging from 20 to 28 kJ/(mol nm), inclusive, and 48 simulations for both 29 and 30 kJ/(mol nm).

For these simulations, phenols were considered dissociated if the number of non-hydrogen atom contacts between them and the protein dropped below five. Phenol 4 was released in all 276 simulations, while phenol 3 was released in only 150/276 simulations. Furthermore, for the 77 simulations where all phenols were released, phenol 4 was released either first or second in 74/77 simulations, while phenol 3 was released either fifth or sixth in 42/77 simulations. This suggested that phenol 4 and phenol 3 are the ligands that are most and least easily released, respectively. To ensure that our results were not specific to any particular feature of initial structure, we investigated the release of each of these two phenols following the procedure described below. However, because we found that the results for them were nearly identical, we present only those for phenol 4.

Generation of starting structures.

To generate starting structures for the unbiased trajectories used for later analyses, we again used ABMD, this time to explore various mechanisms of phenol release for a single phenol (phenol 4), as opposed to all six phenols at once. This time, the bias was placed on just d₄. Initially, 120 simulations were performed (each run for 5 ns with structures saved every 5 ps): 30 simulations for each of the four force constants 12.5, 15.0, 17.5, and 20.0 kJ/(mol nm). Through visual analysis of these trajectories, three CVs were initially chosen to represent the dominant features observed: N_A10, N_A13, and RMSD_P. N_A10 and N_A13 are the number of non-hydrogen atom contacts between phenol 4 and either Ile^A10 (green in Figure 1) or Leu^A13 (black in Figure 1), respectively. RMSD_P is the distance root-mean-squared deviation (RMSD) between the α carbons of residues in the phenolic binding pocket compared to their position in the crystal structure. The distance RMSD is defined by first calculating the pairwise distances between all atoms in a selection for a reference structure, then calculating those same distances for each frame of the simulation, and finally calculating the root mean squared difference of these pairwise distances. The binding pocket residues, pictured in green, orange, black, and white in Figure 1, were defined to be the residues most often interacting with phenol both in its crystallographic binding pocket and along the different observed pathways of dissociation. These 22 binding pocket residues, following the naming convention described in the Supplemental Information, are as follows: Cys^A6, Ser^A9-Tyr^A14, Leu^A16, Glu^A17, His^B10, Leu^B11, Ala^B14, Phe^F1, Val^F2, His^F5, Leu^F6, Leu^G13, Tyr^G14, Glu^G17, Leu^H17, Val^H18, and Glu^H21. It should be noted that while N_A10 and N_A13 proved sufficient to categorize our initial sampling, we also present analysis based on other contact-based CVs that we subsequently developed to better capture the unbinding pathways.

When building this ABMD data set, we wanted to fully explore unbinding pathways. To do this, we wanted multiple trajectories to sample all populated areas in our CV space of N_A10, N_A13, and RMSD_P. By doing this, not only did we ensure starting structures that sampled all relevant pathways, but we also decreased the possible correlation between starting structures for our unbiased simulations. From our initial set of ABMD simulations, we observed pathways similar to PW1, PW2, and PW3 as identified by Vashisth and Abrams in ref. 26, although only a handful of trajectories followed PW1, and only one pathway followed PW3. To supplement the PW1 data, we ran an extra 30 ABMD simulations, each of length 5 ns with force constant k = 12.5 kJ/(mol nm), starting from a structure from a previous ABMD run that ended approximately halfway along PW1. We supplement the PW3 data later, in the unbiased data set. Furthermore, we saw a number of trajectories where RMSD_P spiked from approximately 0.5 Å to approximately 3–4 Å. As discussed in the Results and Discussion, this corresponds to a channel opening mechanism, where two dimers rotate away from one another, exposing more of the phenol directly to solvent. To sample this behavior further, we identified two trajectories that led to channel opening but without phenol release and ran 30 extra ABMD simulations starting from each of these configurations. Each of these trajectories was 5 ns with a force constant of k = 12.5 kJ/(mol nm). In total, we thus supplemented our initial data set with 90 additional ABMD simulations, to create a data set of 210 ABMD trajectories.

State definitions.

To measure binding and unbinding statistics, one needs to define both the bound and free states. The CVs we used to do this include RMSD_P, as previously defined, and N_PW1, N_PW4, N_Prot, and N_HP, which we define here. N_PW1 and N_PW4 can be viewed as extensions of the previously defined N_A10 and N_A13, chosen to more fully describe the unbinding behavior in our simulations. N_PW1 is the number of non-hydrogen atom contacts between phenol and residues Ile^A10 and His^F5 (green in Figure 1). Residue His^F5, like Ile^A10, helps to define Pathway 1 as in ref. 26. Similarly, N_PW4 is the number of non-hydrogen atom contacts between phenol and residues Leu^A13 and Leu^H17 (black in Figure 1). Residue Leu^H17, along with Leu^A13, helps to define Pathway 4 (PW4), a pathway similar to but distinct from ones previously characterized that we discuss in Results and Discussion. Finally, N_Prot is the total number of non-hydrogen atom contacts between the phenol and the protein, while N_HP is the two-step rolling average of the number of hydrogen bonds between the phenol and both the backbone carbonyl of Cys^A6 and the backbone amide nitrogen of Cys^A11. For this CV, we defined a hydrogen bond as a distance of less than 4 Å between the non-hydrogen atoms of the donor (D) and acceptor (A) and a D-H-A angle less than 60° out of line.

The free state is defined so that N_PW1 < 2, N_PW4 < 2, and N_Prot < 5. The bound state is defined by N_Prot > 540, N_HP > 1, and ${{\sum }_{\text{CV}}{\left(\text{CV}-{\mu }_{\text{CV}}\right)}^2/\left(2{\sigma }_{\text{CV}}\right)}^2\le 1$ for CV = N_PW1, N_PW4, and RMSD_P. Here, μ_CV and σ_CV represent the average and standard deviation of the corresponding CV as defined from a 10 ns unbiased simulation. For N_PW1, N_PW4, and RMSD_P, the means were 52.503, 31.924, and 0.0872 Å, and the standard deviations were 5.023, 5.264, and 0.0223 Å, respectively.

DGA data set.

Our goal is to estimate equilibrium and dynamical quantities through the Dynamical Galerkin Approximation (DGA).^28,29 Using this technique, dynamical statistics like the committor, reactive current, and reaction rate can be calculated from an ensemble of unbiased trajectories. The essential idea is that we cast quantities of interest as solutions to operator equations involving this transition operator, the operator that determines the statistics of the dynamics. In general, the solutions are subject to boundary conditions involving both the bound and free states, defined in the previous section. We approximate the solutions through a basis expansion, choosing our basis so that it captures all of the movements important for phenol binding/unbinding. This enables us to represent the action of the transition operator through its inner products with the basis functions; in turn, these can be estimated from averages over unbiased trajectories. This approach can be thought of as an extension of Markov State Models (MSMs)^54–58 that directly yields statistics for a specified reaction.

To generate the unbiased trajectories needed for DGA, we first defined a 10 × 10 × 10 grid in cylindrical coordinates that fully covers the area of CV space sampled by our ABMD data set (N_A10 = r cosθ, N_A13 = r sinθ, and RMSD_P). Specifically, r varied between 3 and 50 contacts, θ varied between 0 and 90°, and z varied between 0.08 and 0.38 Å. The structure from the ABMD data set closest to each of these 1000 grid points was found, leading to 326 unique structures (as the ABMD sampling is not uniform in this space, many grid points had duplicate structures; see Supplemental Figure S1). From each one of these unique structures, we launched two independent 40 ns unbiased simulations and saved structures every 10 ps. Of these 652 trajectories, only three trajectories partially or fully sampled PW3 as defined by Vashisth and Abrams 26. To supplement the sampling of that pathway, from these three trajectories, we selected a total of 20 structures that captured various features of PW3. From each of these 20 structures, two independent 40 ns simulations were launched. Thus, our total unbiased data set consisted of 692 trajectories of length 40 ns, for an aggregate simulation time of 27.68 μs.

DGA basis choice.

As described earlier, DGA solves operator equations for dynamical statistics by expanding them in terms of a set of basis functions. In this work, we chose the modified pairwise distance form described in ref. 29. To construct the appropriate pairwise distances, we first included those between two carbons on opposite sides of the escaping phenol and our 22-atom binding pocket of α carbons described earlier (protein-ligand distances). We also included the pairwise distances between the α carbons of the side chains themselves (protein-protein distances) to account for protein rearrangements. To account for movement along PW3, which involves residues not in the binding pocket, we added the protein-protein and protein-ligand distances between the phenol and the α carbons for residues Ile^A2/Tyr^A19 (yellow in Figure 1), and Phe^B25 (brown in Figure 1), as suggested by both ref. 26 and our preliminary results. Additionally, to capture movements of side chains along Pathways 1 and 2, we added the protein-protein and protein-ligand distances between the phenol and C_γ atoms from residues Ile^A10, Leu^A13, His^F5, and Leu^H17. Finally, we added one constant basis function, which improved the numerical solutions. Combining these distances led to a 299-dimensional basis set, a summary of which is shown in Supplementary Table S1.

For each point in our unbiased data set, we measured the minimum distance in the space of the 298 pairwise distances to points in both the bound and free states. Using these distances, we followed the procedure in ref. 29 to construct the smoothing function h(x), the guess function(s) ψ(x), and the smoothed basis functions ϕ_i(x). These basis functions were then orthogonalized using singular value decomposition. A key choice in applying DGA is the time interval for the transition operator, termed the “lag time.” We found most statistics to be insensitive to the lag time over ranges tested (Supplemental Figure S2) and report results for a lag time of 500 ps unless otherwise noted because it yielded convergence of estimates with a minimum of apparent statistical error (Supplemental Figure S2). The exceptions were rate constants and their ratios. Based on the convergence of our estimates for the relative weights of pathways (Supplemental Figure S2), we use lag times between 500 ps and 1.25 ns for rates and their ratios. We discuss further details of these calculations in the Supplemental Information.

Mutants.

A similar workflow to the above was followed for both insulin mutants studied, A10 Ile→Val and B13 Glu→Gln. Details on system generation using CHARMM-GUI^32–34 and workflow for these mutants are given in the Supplemental Information.

Results and Discussion

The goal of this study was to probe the dynamics of phenol release from the R₆ insulin hexamer to understand how the release mechanism(s) could be altered by mutations. To do this, as described in detail in Methods, we employed a pipeline of multiple simulation techniques. First, we used an array of Adiabatic-Bias Molecular Dynamics (ABMD) simulations to create a large, diverse data set of driven dissociation events. From this, we discovered a small set of physically meaningful collective variables (CVs) that can be best used to visualize the results: RMSD_P describes the distance RMSD (referenced to the crystal structure) of the 22 residues determined to be in the phenolic binding pocket, while N_PW1, N_PW3, and N_PW4 describe the number of non-hydrogen atom contacts between the released phenol and gatekeeper residues along pathway (PW) 1 (Ile^A10 and His^F5, green in Figure 1), PW3 (Ile^A2 and Tyr^A19, yellow in Figure 1), and PW4 (Leu^A13 and Leu^H17, black in Figue 1), respectively. To escape via each of these pathways, the phenol must pass between the side chains of its two gatekeeper residues. We do not consider an analogous N_PW2 because there are no specific gatekeeper residues for PW2.

We then ran short (40 ns) unbiased simulations starting from a selection of partially unbound structures from the ABMD data set and used Dynamical Galerkin Approximation (DGA)^28,29 to estimate long-time statistics from the resulting short trajectories. Using this method, we compute free energies, escape versus rebinding probabilities (committors), and reactive currents. Combining these statistics allows us to to delineate six pathways and their transition states. DGA furthermore enables us to estimate the relative weights for the unbinding pathways and rates, providing insights into kinetics that go beyond the free energies by themselves. Below, we first describe the simulations for WT insulin, followed by those for the A10 Ile→Val and B13 Glu→Gln mutants.

Driven simulations reveal channel opening and six dissociation pathways.

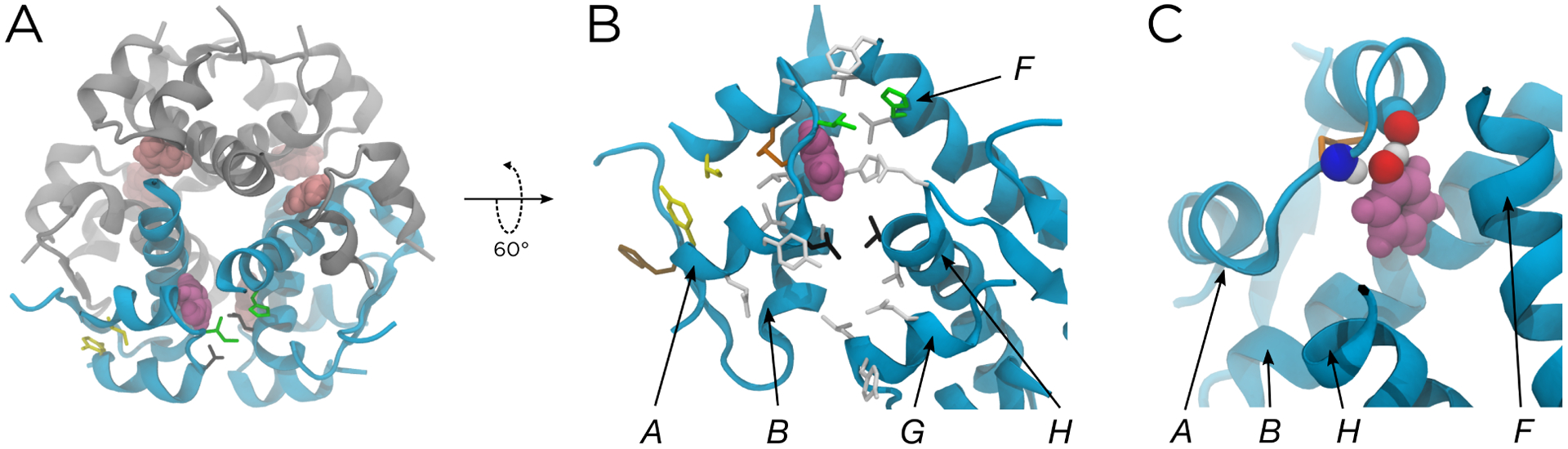
When visually analyzing the ABMD simulations with driven phenol release, we were able to distinguish six unbinding pathways. Three of these pathways (PW1, PW2, and PW3) were previously reported by Vashisth and Abrams,²⁶ while the other three (PW1a, PW4, PW4a) are reported here for the first time. An essential feature of two of these pathways (PW1a and PW4a) is a large-scale widening of the primary escape channel (indicated by cyan coloring in Figure 2A) that results from two adjacent insulin dimers twisting away from one another. This behavior is discussed in depth in the following section. In addition, while we explicitly discuss the driven ABMD simulations in this section, the same six pathways with the same molecular characteristics are further supported by the unbiased simulations and our quantitative analysis of them.

Figure 2:

Results from the ABMD simulations. (A) The structure of the hexamer, with the phenolic escape channel closed (top) and open (bottom). The chains that form the phenolic binding pocket are shown in cyan; other chains are shown in gray. The released phenol is shown in purple, with other phenols shown in pink. (B) The six unbinding pathways, shown both structurally (top) and as a function of N_PW1 and N_PW4 (bottom). The structures shown correspond to the solid data points, and represent the k-medoids cluster centers along each pathway. The solid protein cartoons correspond to the starting structure for each set of driven simulations, and the translucent spheres are the non-hydrogen atoms of the phenols from the cluster centers, all aligned to the A chain backbone of the starting structure. The translucent lines in the bottom panels represent the data used to generate the k-medoids clusters. The cyan chains in the top panels are the same as those in (A). Non-hydrogen atoms of gatekeeper side chains along PW1 (green, Ile^A10 and His^F5), PW3 (yellow, Ile^A2 and Tyr^A19), and PW4 (black, Leu^A13 and Leu^H17) are also shown in the top panels. The configuration of the escape channel is indicated above each panel. For PW2 and PW3, the channel can be either open or closed.

We tested a variety of CVs for their utility in visualizing the six unbinding pathways. As noted earlier, three of the best that we found were N_PW1, N_PW3, and N_PW4, the numbers of non-hydrogen contacts between the phenol and the gatekeeper residues for PW1, PW3, and PW4, respectively. We determined the gatekeeper residues based on the previous literature and our analysis of the ABMD trajectories. The gatekeeper residues for PW1 are Ile^A10 and His^F5; these were identified by both Swegat et al.²⁵ and Vashisth and Abrams²⁶ and were confirmed by our own simulations. The gatekeeper residues for PW3 are Ile^A2 and Tyr^A19; these were identified by Vashisth and Abrams²⁶ and confirmed by our own simulations. The gatekeeper residues for PW4 are Leu^A13 and Leu^H17. Vashisth and Abrams²⁶ note these residues in conjunction with PW2, but we designate them as gatekeeper residues for PW4 in this study because the phenol passes between them only along PW4 (versus near them along PW2). We present most of our results in terms of N_PW1 and N_PW4 because they provide the best separation of all six pathways when projected to two dimensions.

To visualize these pathways, we first identified three ABMD trajectories that corresponded to each pathway other than PW3. We then identified the section of each trajectory that corresponded to phenol unbinding and used k-medoids clustering in the 298-dimensional set of pairwise distances described in Methods to identify 60 cluster centers per pathway. For PW3, we had only one ABMD trajectory (as noted in Methods, we addressed this issue through additional unbiased simulations), so we generated only 20 cluster centers. Regardless, the cluster centers were used to understand the characteristics of each observed pathway. Structural and CV representations of the six unbinding pathways are shown in Figure 2B.

As shown in the left panel of Figure 2B, PW1 consists of the green phenol moving upwards toward the green gatekeeper residues, Ile^A10 and His^F5, then pushing through them and escaping into the solvent. This corresponds to the green loop in the CV representation. As discussed in the Methods, the bound state exists where N_PW1 ≈ 53 and N_PW4 ≈ 32. Starting from there, PW1 loops down and outward to N_PW1 ≈ 85 and N_PW4 ≈ 10, corresponding to the phenol approaching the green gatekeeper residues. As the phenol pushes through these residues and escapes into the solvent, both N_PW1 and N_PW4 decrease to zero.

By contrast, PW4 proceeds in the opposite direction, with the gray phenol passing through the black gatekeeper residues, Leu^A13 and Leu^H17. This leads to the black loop in the CV representation, where the system moves from the bound state to N_PW1 ≈ 10 and N_PW4 ≈ 85 as the phenol approaches the gatekeeper residues. As the phenol pushes through those residues and escapes into the solvent, both N_PW1 and N_PW4 decrease to zero. While PW1 was described in previous simulation studies,^25,26 PW4 is presented for the first time in this work.

Both PW1 and PW4 occur with a closed escape channel, with each gatekeeper residue remaining in close proximity to its position in the crystal structure. However, very similar pathways can occur with an open escape channel, as the H and F chains twist away from the A chain. This large-scale protein motion, seen in Figure 2A, leads to the change in the binding pocket seen in the right panel of Figure 2B. Here, the separation between both the green residues and the black residues is increased, meaning they no longer function as gates. For example, along the PW1-like pathway, the phenol still interacts with Ile^A10, but His^F5 is shifted far enough away to allow a layer of water between the side chain and the phenol. We refer to this pathway as PW1a. Similarly, along the PW4-like pathway, the phenol interacts with Leu^A13 but not Leu^H17. We refer to this pathway as PW4a. In the CV representations, both of these pathways are associated with smaller loops in the bottom panels of Figure 2B, consistent with the contacts coming from only one gatekeeper residue. Both of these pathways are described for the first time in this work.

Finally, we also observed PW2 and PW3 in our driven simulation data set. These are illustrated in the middle panel of Figure 2B. PW2 is a gate-hopping mechanism, where the brown phenol escapes by hopping between the green and black gatekeeper residues. In Figure 2B, this is moving out of the plane of the paper, directly toward the reader. In contrast, along PW3, the yellow phenol moves toward the yellow gatekeeper residues, Ile^A2 and Tyr^A19, before pushing through them and escaping into the solvent. Both of these pathways were described by Vashisth and Abrams,²⁶ but we add an important clarification: along both of these pathways, the escape channel can be either closed or open. However, since PW2 involves an escape through a channel that exists in the crystal structure and PW3 involves escape through an unrelated channel, neither of these two pathways are particularly affected by the opening/closing of the escape channel. For a discussion of the sequence of release of the six phenols and its relation to the experimentally observed cooperativity of phenol binding to the insulin hexamer,^59,60 see Supplemental Figure S3 and associated text in Supplemental Information.

Further characterization of the channel opening.

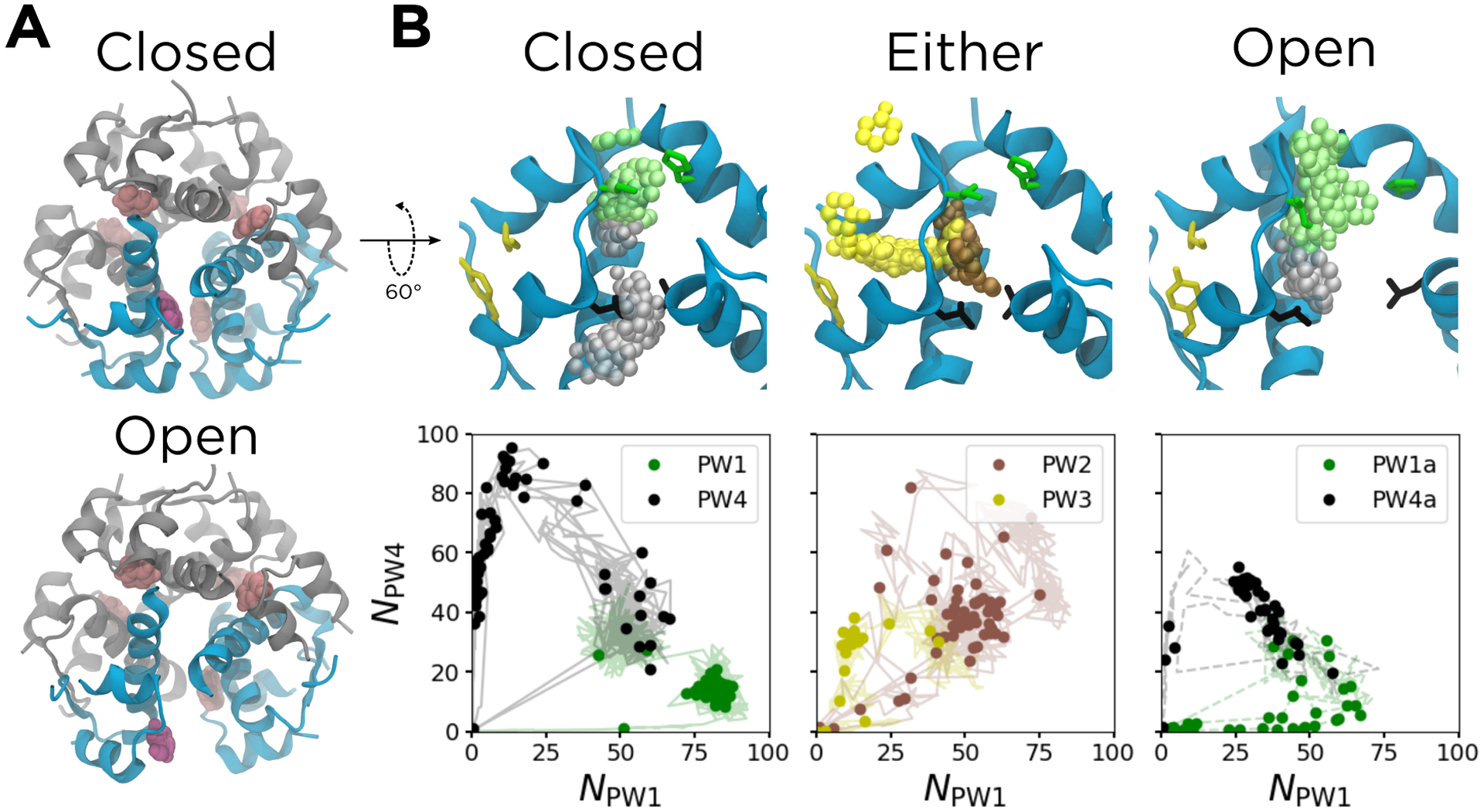
The observed channel opening was not an artifact of the ABMD bias, as we also found it in many of our unbiased simulations seeded with a closed channel. Furthermore, by analyzing our unbiased simulations, we can correlate the channel opening with the rotation of the α helices on the dimeric interface, a conformational transition previously found to be accessible to the insulin dimer.^53,61 In Figure 3A, we quantify channel opening by measuring the average of RMSD_P, which is a distance RMSD that quantifies how much the phenolic binding pocket structurally deviates from the binding pocket present in the crystal structure. This quantity was also compared to the average of Φ_α,BD, the pseudodihedral angle of the α helices on the dimeric interface of chains B and D (shown in orange in Figure 3B), as defined in ref. 53.

Figure 3:

Measures of flexibility of the phenolic binding pocket. The bound state is marked by the white star, and the unbound state is marked by the white dashed lines. The circle and square represent the partially-open escape channel with the phenol bound and partially unbound, respectively. The triangle represents a PW3 intermediate in which the A chain is partially melted. (A) The distance RMSD of the 22 binding pocket residues as a function of N_PW1 and N_PW4. Contours spacing is 0.5 Å. (B) The pseudodihedral angle between the α helices at the dimer interface between chains B and D, Φ_α,BD, as a function of N_PW1 and N_PW4. Contour spacing is 1°. (C) Hexameric (left) and binding pocket (right) structures showing the closed-to-open transition indicated by the star and circle in (A) and (B), respectively. Chains B and D are shown in orange, while chains F and H are shown in blue.

The bound state, marked by the white star in Figure 3A and located at N_PW1 ≈ 53 and N_PW4 ≈ 32, is characterized by a relatively low average RMSD_P of approximately 0.1 Å. The phenolic binding pocket in this state is quite similar to the one in the crystal structure. Across the space defined by N_PW1 and N_PW4, RMSD_P is highly correlated with Φ_α,BD. The BD dimer, along with the dimer defined by the interface made of chains F and H (shown in blue in Figure 3B), makes up the primary escape channel for the phenol studied. The average of Φ_α,FH is nearly identical to Figure 3B, so is omitted for clarity. Both have a value of approximately 132° in the bound state (Figure 3B). As discussed previously, this leads to both the green gatekeeper residues (Ile^A10 and His^F5) and the black gatekeeper residues (Leu^A13 and Leu^H17) remaining in close proximity, acting as closed gates that define the boundaries of the escape channel.

Moving from the star to circle to square in Figure 3A, RMSD_P increases from 0.1 to 0.2 to 0.3Å, corresponding to a three degree rotation of the α helices on the dimer interfaces. Structurally, this dimeric rotation leads to separation of the four gatekeeper residues that define the edges of the phenolic escape channel, as seen in the right panels in Figure 3C. Specifically, again moving from star to circle to square, the average separation of the α carbons of Leu^A13 and Leu^H17 increases from 0.8 to 1.2 to 1.4 Å, and the average separation of the α carbons of Ile^A10 and His^F5 increases from 0.8 to 0.9 to 1.2 Å (Supplemental Figure S4A). While the circle and square both correspond to structures with an partially open escape channel, the square represents a slightly more dramatic channel opening that is paired with the breaking of the hydrogen bonds between the phenol and both the backbone carbonyl of Cys^A6 and the backbone amide nitrogen of Cys^A11; although the phenol is still located in the binding pocket, it is more loosely bound (Supplemental Figure S4B). Overall, this channel opening, found in both our biased and unbiased simulations, is also consistent with the displacements observed in the lowest frequency modes of a normal mode analysis of an elastic network representation of the hexamer (Supplemental Figure S5), suggesting that this flexibility is an intrinsic feature of the structure. The channel opening allows for increased penetration of solvent closer to the phenol and decreased steric occlusion by the side chains.

Finally, the point marked by the triangle in Figure 3 has a RMSD_P between 0.5 – 1.0 Å higher than those for the points marked by the square and the circle. This corresponds to the melting of the A-chain C-terminal α helix along PW3, as the phenol escapes through the A chain (Supplemental Figure S4C). As this helix melts, the PW1 and PW4 gatekeeper residues separate even further (Figure 3B and Supplemental Figure S4A); although this motion affects the binding pocket, it occurs after the phenol is no longer in it.

Combining the potential of mean force, committor, and reactive current enables quantitative characterization of transition states and intermediates.

DGA can be used to estimate the relation between the sampled distribution and the stationary distribution and in turn potentials of mean force (PMFs). However, the true power of DGA is in the ability to combine these free energies with estimates for dynamical statistics like the committor, reactive current, and rate. The committor describes the probability of proceeding to a product state before returning to a reactant state. By explicitly defining bound and unbound states (see Methods), we can thus calculate the unbinding committor, q_unbind, that describes, at every point in our unbiased data set, the probability of proceeding to the unbound state before returning to the bound state. This is, by construction, the perfect reaction coordinate to track phenol unbinding, as it measures the likelihood of phenol unbinding regardless of pathway. By definition, transition states have q_unbind = 0.5. By projecting q_unbind into various CV spaces, we can distinguish molecular rearrangements (e.g., those giving rise to the metastable states that we identify on a PMF) that increase the probability of unbinding from those that do not.

Another useful quantity is the reactive current, which describes how trajectories that lead to phenol unbinding flow through each point in a CV space. Just like a diagram of fluxes between clusters of states in a Markov State Model,^54–58 a plot of the reactive current can give a sense of the populations of different pathways. Here, as established by recent work,²⁹ we represent the reactive current, J_unbind, as a vector field. An advantage to this representation is that it can be compared directly with the PMF and commmittor as functions of the same CVs. By combining these statistics, we can characterize the transition states and intermediates along the six pathways. J_unbind can furthermore be used to determine their relative weights; integration of J_unbind yields the rate.

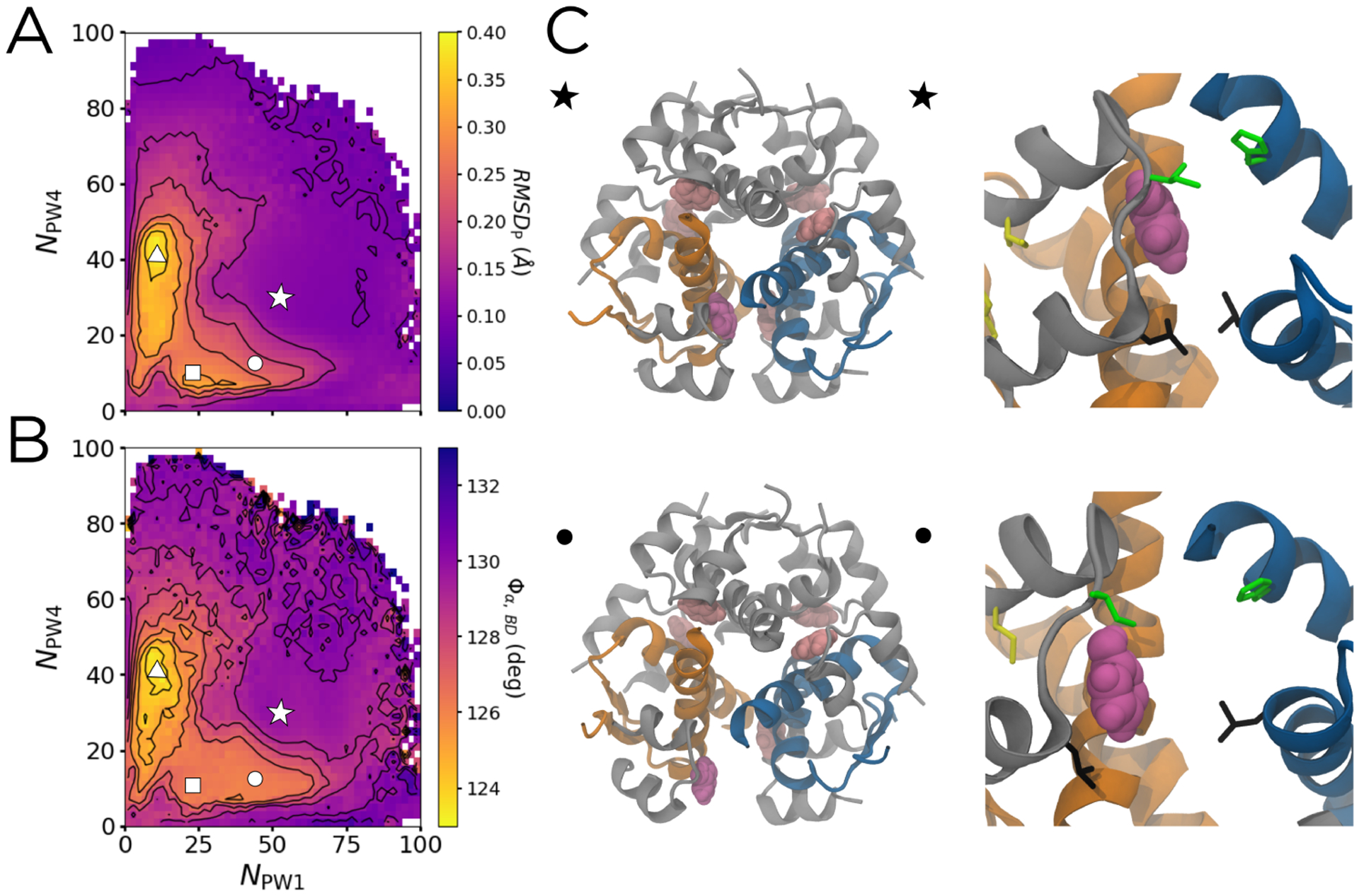
We show the free energy, committor, and reactive current projected onto N_PW1 and N_PW4 in Figure 4. The unbound state (bottom left corner in Figure 4A) is set to be the zero of free energy. The DGA-generated PMF is in good agreement with one independently generated through Replica Exchange Umbrella Sampling (Supplemental Figure S6), suggesting that the unbiased trajectories cover the space sufficiently to draw quantitative conclusions. The bound state with energy 4.5 k_BT is marked by a white star at N_PW1 ≈ 53 and N_PW4 ≈ 32. As discussed in the Introduction, this state involves the phenol making one hydrogen bond with the backbone carbonyl of Cys^A6 and one with the backbone amide NH of Cys^A11. We find that in this state, His^F5 is rotated outward toward the solvent, with the ring pointing away from the phenol (see Figure 2B and 3C). The free energetic shoulder directly to the right of the star involves a side chain ring flip of this histidine, so that it is instead facing inward, toward the phenol, which increases the number of contacts between the phenol and the histidine ring. This is consistent with a previous ¹H-NMR study that suggested the presence of an unidentified aromatic ring-flip,²³ and a computational study which proposed His^H5 as one of the residues that could undergo such a flip.²⁶

Figure 4:

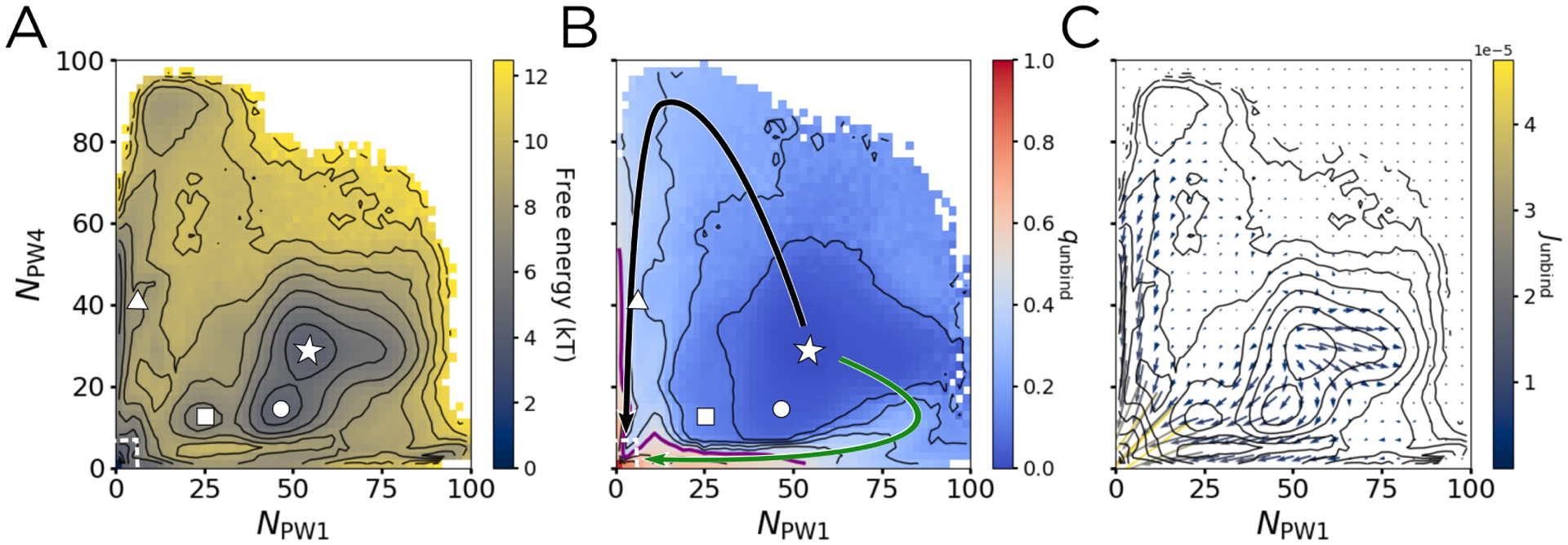
The potential of mean force (PMF), unbinding committor (q_unbind), and unbinding reactive current (J_unbind) projected on N_PW1 and N_PW4. The points marked by the star, circle, square, and triangle are the same as in Figure 3, with the unbound state outlined by the dashed white box. (A) The PMF, with contours spaced by 1k_BT. (B) q_unbind, with contours spaced by 0.1 and the q_unbind = 0.5 surface marked in purple. Arrows showing PW1 (green) and PW4 (black) are overlaid. (C) J_unbind binned into a 22 × 22 grid spanning from 0 to 100 in both N_PW1 and N_PW4. The results shown are smoothed with a Gaussian filter, using a kernel with standard deviation of 1 bin. Contours are the same as in (A) to aid in comparison.

The point marked by a circle in 4A corresponds to a free energy basin, confirming that the channel opened state is energetically stable. Furthermore, this transition only involves a free energy barrier of about 1 k_BT, suggesting that these structures can readily interconvert. Corroborating this idea, all of these areas have an average q_unbind of less than 0.1 (Figure 4B), meaning that both the channel opening and the histidine ring-flip do not markedly increase the probability of escape before returning to the bound state. Interestingly, the channel opening itself does not lead to a marked increase in q_unbind. This suggests that while channel opening may play a part in phenol unbinding, such a motion alone is not enough to allow the phenol to escape. The point marked by the square, which corresponds to the phenol breaking its hydrogen bonds to the channel-opened structure, also lies in a free energetic basin, one separated from the channel-opened bound state by a barrier of about 3 k_BT. This barrier is three times as high as the one for channel opening. and also corresponds to a 0.1 increase in q_unbind. The breaking of the hydrogen bonds to Cys^A6 and Cys^A11 thus slightly increases the probability of successful unbinding, while the channel opening by itself does not.

As discussed earlier, this projection effectively separates PW1 and PW4, marked by the solid black and green arrows in Figure 4B. Comparing these arrows to the PMF in Figure 4A, one finds the barriers for PW1 and PW4 to be 4–5 k_BT and 5–6 k_BT, respectively, significantly lower than the 20–30 k_BT barriers found by Vashisth and Abrams.²⁶ Our free energy barriers change very little when projected into a three-dimensional space that further separates PW1 and PW4 (Supplemental Figure S7). Vashisth and Abrams estimate free energies by applying Jarzynski’s equality to steered molecular dynamics simulations, which we would expect to overestimate barriers because such simulations will only rarely sample trajectories with protein fluctuations that anticipate the phenol motion. By contrast, our unbiased trajectories, as well as our independent Replica Exchange Umbrella Sampling (Supplemental Figure S6), capture these dynamics.

Additionally, comparing Figure 4 to Figure 3, it is clear that there is very little opening of the escape channel inherent along either PW1 or PW4, as the average RMSD_P along these pathways stays below 0.1 Å. Instead, the phenol is directly pushing through the adjacent gatekeeper residues. However, this projection does not allow us to fully distinguish PW2, PW3, PW1a, and PW4a because they partially overlap (see Figure 2B). At the same time, the area through which they pass has the highest magnitude of reactive current (Figure 4C), suggesting that that the dominant binding pathways lie in this region. To distinguish these pathways, we introduce a third dimension.

Three-dimensional projections show that competing pathways are similarly populated.

Since the unbinding committor q_unbind tracks phenol unbinding across all pathways, we use it as the third dimension on which to project our data. From our unbiased data set, we visually identify four trajectories for each of our six unbinding pathways. These trajectories are shown in Figure 5A with coloring consistent with Figure 2B. We also show the full unbiased data set, colored to show q_unbind and with arrows representing the six pathways overlaid in Figure 5B. A structural representation of these pathways is shown in Figure 5C.

Figure 5:

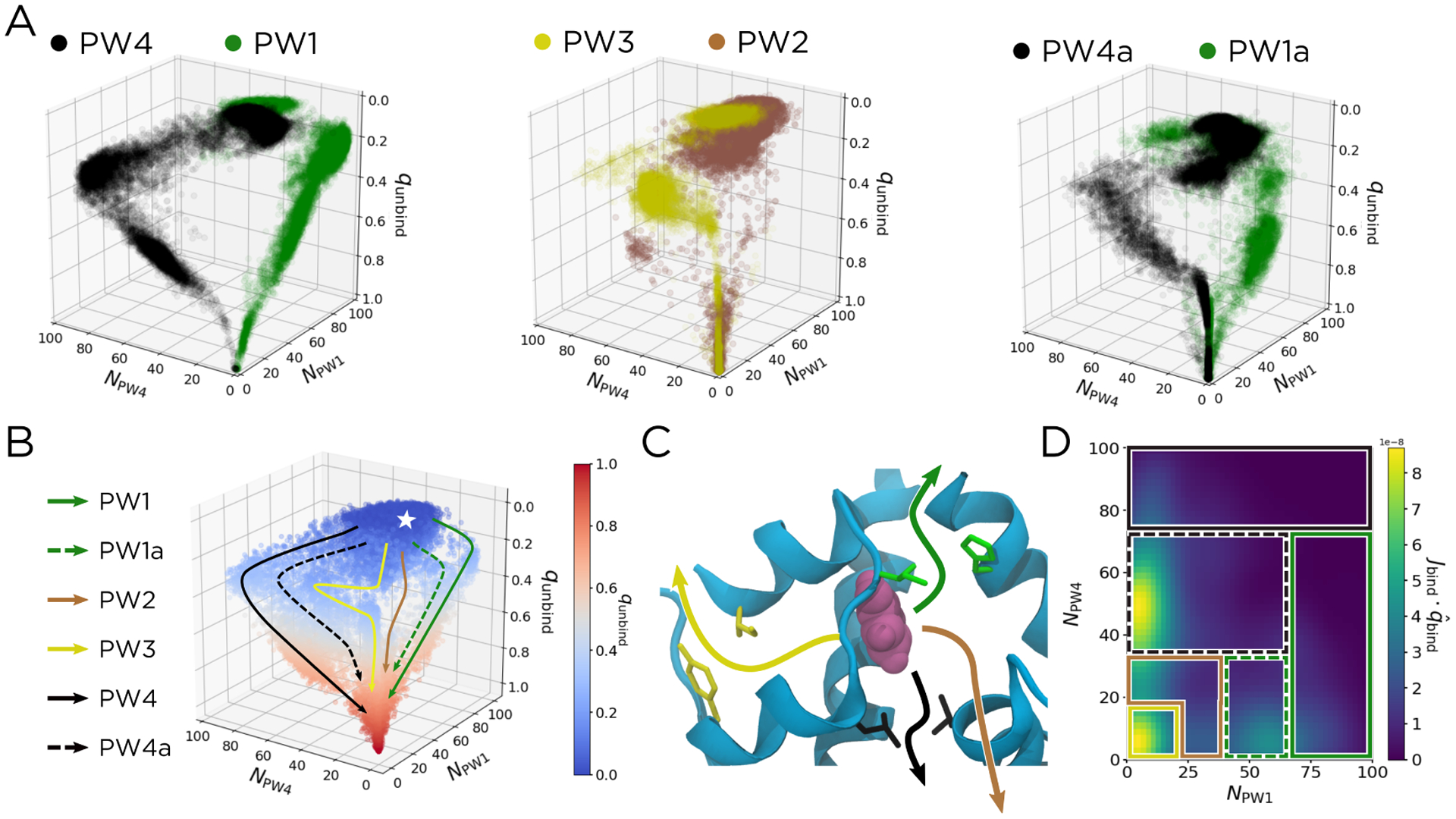
Pathways can be more readily distinguished in the space of N_PW1, N_PW4, and q_unbind. (A) Scatter plots of trajectories along each of our six pathways. From the unbiased data set, we identify four trajectories that correspond to each pathway, which are shown for PW1/PW4 (left), PW2/PW3 (middle), and PW1a/PW4a (right), mirroring the conventions used in Figure 2B. (B) A scatter plot of q_unbind for all the unbiased data. Six pathways are overlaid and labelled. The bound state is represented by the white star. (C) Structural representation of the unbinding pathways in (B). The dashed arrows in (B) correspond to the similarly-colored solid arrows in (C), except with the escape channel being opened as in Figure 3. (E) The q_bind component of J_bind, taken at q_bind = 0.63. The patches corresponding to each pathway are overlaid, using the coloring and line styles from (B).

As shown in Figures 5A and 5B, using q_unbind as the third dimension clearly separates the six pathways. The q_unbind = 0.5 surface (gray points in Figure 5B) is the transition state ensemble, as structures in this region have an equal probability of proceeding to the unbound state as they do of returning to the bound state. Notably, for PW1/PW1a and PW4/PW4a, this does not occur until after N_PW1 and N_PW4 have reached their respective maxima along each pathway. The transition states thus occur when the phenol is just outside the gatekeeper residues, and the numbers of contacts with those residues have started to decrease. In contrast, for PW3, the q_unbind = 0.5 surface occurs just as the phenol maximizes its contacts with Ile^A2 and Tyr^A19, the PW3 gatekeeper residues (Supplemental Figure S8). Since PW2 encompasses all gate-hopping mechanisms and the phenol can be closer to the gatekeeper residues for PW1 or those for PW4, its transition state is comparatively structurally diverse.

We can also use DGA to calculate the relative weight of each unbinding pathway. To do this, we adapt the method described in ref. 29, using the binding reactive current J_bind projected into the space of N_PW1, N_PW4, and q_bind. For this calculation only, we use kinetic statistics for binding as opposed to unbinding, as this slightly improved our ability to distinguish the six pathways (Supplemental Figure S9). We choose as a dividing surface the plane corresponding to q_bind = 0.63, as this best separates the reaction pathways (Supplemental Figure S10). We then partition this surface into patches that encompass the pathways (Figure 5D). By binning the reactive current in the direction of q_bind across these patches, one can calculate the relative weight of each pathway as the ratio of the reactive current in each patch compared to the total reactive current flowing through the dividing surface. We provide exact definitions of the patches, as well as a discussion of the parameters used to calculate and smooth J_bind, in the Supplemental Information. Using this method, we determined the relative weights of the six identified pathways (Table 1). These relative weights are robust to changes in the sampling distribution (Supplemental Table S2) and choice of dividing surface (Supplemental Figure S11).

Table 1:

Relative weights of unbinding mechanisms for WT insulin and the A10 Ile→Val and B13 Glu→Gln mutations.

Pathway	WT (%)	A10 (%)	B13 (%)
PW1	11.2	4.3	19.0
PW1a	11.2	7.8	16.0
PW2	16.3	16.7	14.1
PW3	12.6	8.7	7.1
PW4	13.7	18.4	26.7
PW4a	35.0	44.2	17.2

The pathway with the clear plurality of reactive current (35.0%) is PW4a (dashed black arrow), which corresponds to an unbinding mechanism with an open channel, where the phenol closely passes by Leu^A13 as it leaves the binding pocket. While this is the most likely unbinding mechanism, all of the other pathways are significantly populated (ranging from 11% to 17%). Furthermore, the preference for mechanisms with an open escape channel is relatively mild, with the PW1/PW4 percentage being 24.9% compared to the PW1a/PW4a percentage being 46.2%. As a note, as defined in this study, PW2 and PW3 can have either a closed or open escape channel. So while channel opening does play a role in the overall phenol unbinding process, the majority (53.8%) of unbinding events occur through pathways that do not necessarily involve channel opening. As we discuss further below, the manifestly multipathway nature of the unbinding process makes it challenging to predict how point mutations will impact phenol unbinding.

A10 and B13 mutations alter the preferred pathway and the binding/unbinding rates.

As discussed in the Introduction, there is much interest in designing insulin mutants and analogs for the management of diabetes, including those which might slow the unbinding of phenol. To this end, we simulated two mutants: A10 Ile→Val and B13 Glu→Gln. The A10 Ile→Val mutation is one of the three sequence differences between human and bovine insulin; since Ile^A10 is one of the gatekeeper residues for PW1/PW1a, we expected its mutation to affect the rate of phenol release. The B13 Glu→Gln mutation removes negative charges from the center of the hexamer and stabilizes the R state, as evidenced by the fact that it leads to the formation of T₃R₃ hexamers even in the absence of zinc.⁶² Given the stabilization of the R state, we expected the B13 Glu→Gln mutation to stabilize the R₆ hexamer and impact channel opening.

We performed simulations analogous to those above for human insulin with each of these mutations separately and determined their effects on the unimolecular rate constants of unbinding and binding, k_unbinding and k_binding, as well as the corresponding ratio, K = k_unbinding/k_binding (Table 2 and Supplemental Figure S12). We also calculated the relative weights for the six unbinding pathways for each mutant (Table 1). Note that k_binding is a unimolecular rate constant that does not include the contribution from diffusion, which we expect to be less sensitive to mutations, and consequently K differs from an experimentally measured dissociation constant in that it is a ratio of unimolecular rates. Rate constants that account for diffusion are discussed in the Supplementary Information, with results in Supplemental Figure S13 and Supplemental Table S3. These estimates provide good quantitative agreement with available experimental values for dissociation constants,⁶³ indicating that DGA yields accurate results. Here, we focus on unimolecular rate constants because we expect them to have fewer sources of error. The binding and unbinding inverse unimolecular rate constants for WT insulin and the two mutants are in the range 0.11–0.31 μs, which is consistent with the expected sub-millisecond phenol unbinding timescale predicted from existing NMR data.²³

Table 2:

The inverse unimolecular unbinding rate constant, $k_{\text{unbinding}}^{-1}$, the inverse unimolecular binding rate constant $k_{\text{binding}}^{-1}$ and their ratio (K = k_unbinding/k_binding). Ranges derive from taking lag times between 500 ps and 1.25 ns.

Statistic	WT	A10	B13
$k_{\text{unbinding}}^{-1}(\mu s)$	0.16 – 0.28	0.21 – 0.37	0.17 – 0.27
$k_{\text{binding}}^{-1}(\mu s)$	0.13 – 0.20	0.12 – 0.18	0.16 – 0.26
K	0.70 – 0.83	0.40 – 0.48	0.97 – 0.99

We first describe the A10 Ile→Val mutation. We find that the A10 Ile→Val mutation has almost no affect on the phenol binding rate constant, while slightly decreasing the unbinding rate constant (increasing the timescale of unbinding). This, in turn, leads to a 42–43% decrease in the ratio K compared to WT insulin. To understand how this mutation, which decreases the size of the A10 side chain, inhibits phenol dissociation, we examine the relative weights for the six pathways (Table 1). Because A10 is a gatekeeper for PW1/PW1a, we expected the A10 Ile→Val mutation to impact the weights of these pathways most strongly, and indeed this is the case. The decreases in the relative weights of these pathways are corroborated by increases in the free energies and decreases in the unbinding committors and reactive current in associated regions (Supplemental Figure S14). Intermediate structures along these pathways are less likely, and when they do occur, they are less likely to lead to the unbound state. The preferred binding pathway remains PW4a, although the relative weights of PW2 and PW4 are all higher than for WT.

Our calculations indicate that the B13 Glu→Gln mutation, while having little effect on phenol unbinding, slows phenol binding. As a result, there is a 19–39% increase in K compared to WT. As seen in Table 1, this mutation leads to a dramatic decrease in relative weight for PW4a, the preferred unbinding mechanism for both WT and A10 Ile→Val insulins. This is paired with a corresponding increase in relative weight for both PW1 and PW4, the two mechanisms that explicitly do not include any channel-opening and instead involve the phenol pushing through gatekeeper residues, as well as an increase in relative weight for PW1a, which does involve channel opening. This agrees with our calculations that, after the mutation, the energetic benefit of channel opening is approximately 10 kJ/mol greater along PW1a than along PW4a (Supplemental Figure S15). The mutation thus discourages PW4a more than PW1a. The overall shift in relative weight away from PW4a is further corroborated by the PMF, committor, and reactive current (Supplemental Figure S14): areas of CV space along PW4a are 2 k_BT higher in free energy compared to the same areas for WT insulin.

Beyond the shifting relative weights between pathways, the overall effect of the mutation is to destabilize the bound state and increase K. Molecularly, this can be explained by the more favorable interactions the mutated B13 residue can make with the rest of the protein in the free state, particularly with Ser^B9 and His^B10 (Supplemental Table S4). This prediction agrees with existing experimental data for this mutated species. Dunn and coworkers⁶³ used UV/Vis spectroscopy and a three-state allosteric model to determine the dissociation constant for WT insulin to be 1.8 × 10⁻⁴ ± 1 × 10⁻⁴ M, and that for the B13 mutant to be 2.5 × 10⁻⁴ ± 1 × 10⁻⁴ M, meaning that the mutation caused a 39% increase. Assuming that the main impact of the mutation is on the protein dynamics and not diffusion, this is in agreement with our estimates, which predict a 19–39% increase in K upon B13 Glu→Gln mutation.

For both mutations, there are at least four pathways which each represent at least 10% of the overall reactive current, and no one mechanism ever makes up more than 50%, similar to our findings for WT insulin. As a result, the effects of a mutation on certain pathways can be compensated by those on others. For example, when the A10 Ile→Val mutant discouraged unbinding through PW1 and PW1a, the absolute amount of reactive current flowing through PW4 increased (Supplemental Figure S14). Indeed, the multipathway nature of unbinding is the main takeaway from our simulations, and it suggests that future mutation and ligand design studies of the insulin R₆ hexamer need to target multiple pathways at once.

Solvation of phenol and its binding pocket.

Given the interplay between the pathways and channel opening, we characterized the solvation of the phenol and select residues by calculating radial distribution functions of water around those species as a function of committor value (Supplemental Figure S16). In all cases (WT, A10 Ile→Val, B13 Glu→Gln), the phenol becomes more solvated as it leaves the binding pocket. In general, the radial distribution functions around gatekeeper and pocket residues do not change dramatically as a function of committor. However, we do observe slight changes for three residues: Ile^A2 (a gatekeeper for PW3), Ile^A10 (a gatekeeper for PW1/PW1a), and His^B10 (a pocket residue that also defines the binding site for the Zn²⁺ ions). The increase in solvation of Ile^A10 and His^B10 comes early in the release process, whereas that for Ile^A2 occurs as the phenol escapes.

We also computed radial distribution functions of water for different RMSD_P values, tracking channel opening (Supplemental Figure S17). These data reveal that the gatekeeper residues near the phenol escape channel (Ile^A10, His^F5, Leu^A13, and Leu^H17) all become more solvated upon channel opening. The other residues considered are affected less by channel opening. Interestingly, while channel opening does not significantly affect the solvation of Glu^B13 in WT insulin, it does lead to increased solvation for Glu^B13 in the B13 Glu→Gln mutant insulin.

Finally, Bagchi and co-workers have argued that water molecules confined in the central cavity stabilize the hexamer.^64,65 To examine whether the dynamics that we observe can facilitate exchange of water molecules between the cavity and the bulk, we defined the cavity waters as those within 6 Å of the center of mass of the two Zn²⁺ ions and calculated their MSD over 1 ns (right panels in Supplemental Figures S16 and S17). For comparison, we measure an MSD over 1 ns of 35 nm² for bulk waters in our simulations. The MSD of the waters in the cavity shows very little dependence on committor and is generally less than 10 nm², meaning that these waters are confined regardless of the dissociation of phenol. By contrast, the MSD of waters in the cavity increases as RMSD_P increases, indicating that channel opening facilitates exchange of solvent between the cavity and the bulk.

Conclusions

Diabetes management can be improved through both the introduction of insulin analogs with modulated pharmacokinetics, as well as delivery preparations that can facilitate transport and storage. Because phenol stabilizes the R₆ insulin hexamer, understanding the phenol unbinding mechanism can inform the design of improved therapeutics. Here, we use molecular dynamics simulations to investigate this mechanism for WT and two mutant insulins. We expand on existing simulation studies by Swegat et al.²⁵ and Vashisth and Abrams²⁶ to identify and quantitatively characterize six phenol binding/unbinding pathways. A number of these pathways involved large-scale opening of the primary escape channel, suggesting that the hexamer is much more dynamic than previously appreciated. Methods that we recently introduced^28,29 enable us to determine the intermediates, transition states, and relative weights of the pathways. For WT insulin, a pathway in which the channel opens and phenol passes between Leu^A13 and Leu^H17 (PW4a) represents 40% of the reactive current, but each of the other pathways represents at least 10% of the reactive current. Phenol unbinding/binding is thus a multipathway process.

Our simulations of mutants show that it is possible to rationally control the prevalence of pathways and the overall unbinding kinetics. The A10 Ile→Val mutant reduced the contributions from pathways for which this residue is a gatekeeper (PW1 and PW1a) and decreased phenol unbinding; the B13 Glu→Gln mutation stabilized the phenol-free state and thus led to increased phenol unbinding. However, because other pathways than those targeted can compensate, the overall effects on rates can be challenging to predict without quantitative simulations like those presented here. By combining computation and experiment, it may be possible to target multiple pathways to achieve larger shifts in kinetics.