The effect of renewable energy incorporation on power grid stability and resilience

Abstract

Contemporary proliferation of renewable power generation is causing an overhaul in the topology, composition, and dynamics of electrical grids. These low-output, intermittent generators are widely distributed throughout the grid, including at the household level. It is critical for the function of modern power infrastructure to understand how this increasingly distributed layout affects network stability and resilience. This paper uses dynamical models, household power consumption, and photovoltaic generation data to show how these characteristics vary with the level of distribution. It is shown that resilience exhibits daily oscillations as the grid’s effective structure and the power demand fluctuate. This can lead to a substantial decrease in grid resilience, explained by periods of highly clustered generator output. Moreover, the addition of batteries, while enabling consumer self-sufficiency, fails to ameliorate these problems. The methodology identifies a grid’s susceptibility to disruption resulting from its network structure and modes of operation.

The drive toward renewable energy production in new building developments can make microgrids susceptible to outages.

INTRODUCTION

Conventional power grids are dominated by small numbers of centrally located, high-output generators. However, many countries are experiencing a rapid shift toward renewable generation. For example, the United Kingdom has seen the renewable share of production rise from 6.9% in 2010 to 37.1% in 2019 (1). Renewable generators such as photovoltaic (PV) and wind power are low-output and intermittent. This small-scale generation is often distributed across and embedded within power grids in large numbers. Household generation forms a key component of such grid integration of renewables and may include the ability to store the power they produce and to supply it back upstream to the grid. The resulting network is highly distributed, bidirectional, and mutable, with generators coming on- and off-line and households adopting the role of consumers or producers as daily and seasonal usage, and meteorological conditions vary. With the uptake in renewable production set to continue in line with initiatives such as “net zero” (2) and the Paris agreement (3), understanding how this increased complexity affects network dynamics and function is an important challenge with implications for grid control strategies and future smart grid design.

The resilience and dynamics of conventional power grids have been extensively researched. Of particular interest is their resilience to cascading failures, phenomena whereby an initial fault propagates throughout a network, causing large-scale disruption (4). Cascades have been described mathematically using threshold models (5), which identified critical operating regimes within which network-wide failures can occur. Using steady-state flow–based modeling, the severity of these cascades was found to be power-law distributed (6), with networks having highly heterogeneous power flow shown to be particularly fragile (7, 8). Modeling of blackouts in large-scale power grids (9, 10) has revealed some of the characteristics that drive cascade severity and abruptness, such as the centrality of the initial failure and the network size. Methods to optimize the structure of power grids for resilience against cascades have also been investigated (11, 12). It has been shown that adding interdependencies between different power grids can increase each grid’s resilience to blackouts (12, 13). However, increasing interdependency has also been shown to increase the probability of systemic failures (13). Another important requirement of power grids is to maintain stable operation despite fluctuations in frequency, voltage, and demand. In electrical engineering, this is often investigated using transient stability analysis (14). In the broader field of complex systems, grid stability has been interrogated using the so-called swing equation: a nonlinear oscillator model of power dynamics (15). Its behavior has been characterized using the master stability function (16), and its dynamical impact upon the function of country-scale power grids has been modeled numerically and analytically (17, 18). Paradoxically, the addition of new lines to a power grid can cause instability (19).

These studies have focused on large-scale and conventional transmission networks, rather than highly distributed, renewable-dominated microgrids (20) that are the focus here. Microgrid designs have been shown to boost self-sufficiency (21). It has also been shown that an increased distribution of power generation can aid synchronization (22, 23) and resilience (24, 25). In addition, the effect of self-healing policies based on redundant, activatable links has been investigated (26, 27). However, these issues have not been addressed together with the impact of realistic supply and demand variability. The effective level of distribution will change over the course of a day. The objective of this paper is to determine the dependence of network resilience on key previously unconsidered spatiotemporal features associated with small-scale renewable-integrated power grids. This is achieved by marrying network architecture and power flow dynamics with fluctuations in renewable generation and consumer demand, informed by exploiting PV generation and household consumption data. We provide a framework in which to analyze microgrids and show that increased uptake of renewable generators can adversely affect grid robustness since their power outputs are highly clustered in time, despite their spatially distributed nature. This results in grids handling large power flows, rendering them fragile to catastrophic failures. Moreover, conventional usage of household batteries, commonly used to boost grid self-sufficiency, offers only limited improvements to resilience.

RESULTS

Grid coupling and stability

To capture important transient dynamics that can cause network failure in real power grids, and the emergent power-balancing and stabilizing properties of these networked systems, steady-state approaches are inappropriate. Power grids must be synchronized to the grid reference frequency Ω (typically 2π × 50 Hz in Europe, most of Asia, and Africa and 2π × 60 Hz in North America), drift from which will cause damage and failure. We use the so-called swing equation (15, 28, 29) to describe the deviation θ_i(t) of the phase angle from Ω of each network node i = 1…n, comprising a network of size n

$$\frac{{\mathrm{d}}^2{\mathrm{\theta }}_i}{{\mathrm{d}\mathit{t}}^2}+\mathrm{\gamma }\frac{\mathrm{d}{\mathrm{\theta }}_i}{\mathrm{d}\mathit{t}}=P_i-\mathrm{\kappa }{\displaystyle \sum _{j=1}^n}{A}_{\mathit{ij}}\text{sin}({\mathrm{\theta }}_i-{\mathrm{\theta }}_j)$$ (1)

and from which the power flow on a network edge connecting i and j is computed as

$$f_{\mathit{ij}}=\mathrm{\kappa } \text{sin} ({\mathrm{\theta }}_i-{\mathrm{\theta }}_j)$$ (2)

A full derivation and description of Eqs. 1 and 2 is given in the Supplementary Materials; briefly, network nodes are modeled as rotating machines and Eq. 1 expresses the balance of inertial, dissipative, and transmitted electrical power at each node. Power generation/consumption on each network node is denoted by a suitably defined P_i(t), which will be informed by power usage data as detailed in Materials and Methods. Transmission is encapsulated by the network adjacency matrix A_ij and coupling parameter κ, while γ scales inertial damping. For simplicity, γ and κ are assumed to be order one constants as in (29). In contrast to large-scale power transmission grids, the topologies of smaller-scale grids are highly variable and lack commonly agreed design principles to ensure stable operation under their changing composition associated with renewable generation. Hence, throughout this paper, we use ensembles of synthetic Watts-Strogatz networks (30) with random rewiring parameter q ∈ [0,1] and varying consumer/generator composition to extract general results.

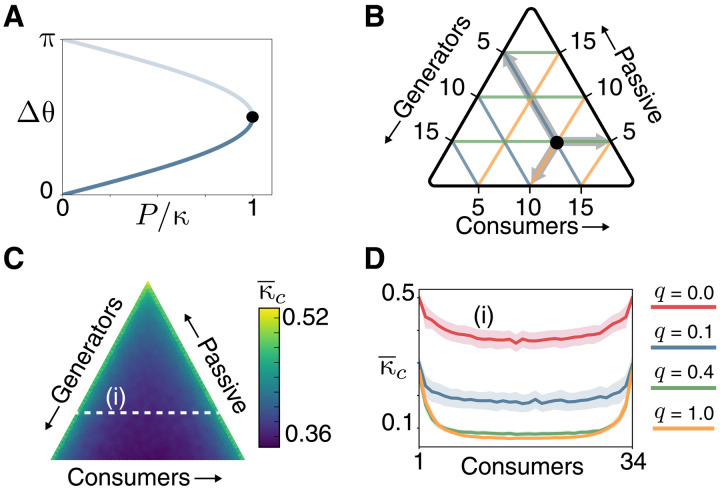
To inform and motivate the results that follow, we first consider an elementary network comprising two coupled nodes, one generating power with constant output, P₁ = P, and the other with power consumption P₂ = − P. A stability analysis shows that, in this case, the two fixed points of Eq. 1 annihilate at a saddle-node bifurcation at a critical value of the coupling constant κ_c = P. Stable networks require κ_c/P ≤ 1. Hence, the system requires a coupling capacity κ equal to at least the total power flowing through the network for stable synchronous operation. Minimizing κ_c is desirable from a grid design perspective: The lower the value of κ_c, the less excess capacity is required for the grid to maintain synchrony and hence stable operation. Figure 1A illustrates the bifurcation diagram that results as the parameter P/κ changes. The lower and upper branches are the loci of the stable/unstable fixed points of Eq. 1, respectively, and these coalesce where P/κ = 1, which defines pa_c. For this simple illustrative example, the steady states and critical capacity can be determined analytically; however, for realistic power grids and, in particular, for those with heterogeneous generation/consumption characteristics considered here, κ_c must be obtained numerically (see Materials and Methods).

Fig. 1. Variation in the critical coupling.

(A) Bifurcation diagram of the elementary two-node network coupling a single generator to a consumer. The phase difference between the two nodes is Δθ = θ₁ − θ₂. The dark and light blue lines denote stable and unstable fixed points of Eq. 1, respectively, and the black dot indicates the saddle node bifurcation occurring at the critical value κ_c = P. (B) Diagrammatic example of the configuration simplex for networks with n = 20 nodes. The black dot is a network with 5 generators, 10 consumers, and 5 passive nodes, or (n₊, n₋, n_p) = (5,10,5). (C) Mean critical coupling capacity ${\overline{\mathrm{\kappa }}}_c$ as a function of node configuration for lattice networks with n = 50. Each point is averaged over 200 lattice realizations. The cross section (i) is plotted in (D), which shows that ${\overline{\mathrm{\kappa }}}_c$ is minimized when the number of consumers is equal to the number of generators. Colored lines in (D) show the equivalent sections for Watts-Strogatz networks with increasing q.

Figure 1 (B and C) summarizes the dependence of grid operating capacity, as encoded by κ_c, on network structure and generator/consumer composition. For a given network realization of size n and architecture defined through mean edge degree $\overline{K}$ and rewiring parameter q ∈ [0,1], consumer/generator variation is interrogated by defining n₊ generator, n₋ consumer, and n_p passive nodes, allocated to random locations, and constrained by n₊ + n₋ + n_p = n. Figure 1B shows a representation of this node composition space for a particular example network; subsequent results are projected onto corresponding simplexes. Each generator has output P_i = P_max/n₊, while for consumers P_i = −P_max/n₋ so that consumption and generation is balanced; this constraint will be relaxed later to model the network’s ability to import, export, or store power. The mean critical coupling ${\overline{\mathrm{\kappa }}}_c$, normalized by P_max, for ensembles of 200 realizations of lattice networks (q = 0) is projected onto a simplex in Fig. 1C. Figure 1D shows equivalent results corresponding to a section of the simplex in Fig. 1C for different network structures. Grid synchrony is promoted where lower values of ${\overline{\mathrm{\kappa }}}_c$ are obtained, and this is minimized in the central regions of the simplex where the numbers of generators and consumers are commensurate. Moreover, Fig. 1D demonstrates that ${\overline{\mathrm{\kappa }}}_c$ is minimized in the central regions across the entire class of Watts-Strogatz networks. It also shows that ${\overline{\mathrm{\kappa }}}_c$ values decrease as q increases, indicating that networks with more topological randomness are easier to synchronize. For instance, Fig. 1D shows that a lattice (q = 0) with only one consumer will require a critical coupling capacity of half the maximum power in the network, whereas an equivalent small-world network (q = 0.1) requires only around a quarter of the maximum power. The q = 0.1 system is therefore inherently easier to synchronize. Coupling parameter values can be rescaled to give quantities in kilowatts to gauge the typical maximum power values that a system can handle. This reveals an approximate lower bound of 18.3 kW (see the Supplementary Materials). Subsequent data analysis will show that typical power values handled by a microgrid are around 13 kW. The coupling capacity κ is therefore likely to be in excess of the maximum power and any critical values κ_c as expected and means that power grids will not in general spontaneously desynchronize during normal operation. However, desynchronizations will be shown to play an important role during cascading failures. Making networks less susceptible to desynchronization is therefore desirable from a resilience perspective.

Resilience to cascades

The preceding results suggest that uptake of renewable energy in the grid, corresponding to increasingly distributed power generation, can lead naturally to improved grid function insofar as synchrony is concerned. However, to function, grids must be resilient to transient shocks, such as line failures or overloads, not captured by these steady-state analyses. These failures can cascade through the grid, causing widespread power outages and damage.

To investigate the importance of these transient features in modern microgrids, we use a dynamic model of cascades based on Eq. 1 to evaluate their resilience as a function of consumer/generator composition. We consider disruptions by two mechanisms. The first is through the power on any edge exceeding a prescribed maximum capacity α that it can carry, termed an overload failure. The second is through the absolute value of the phase difference on an edge exceeding the 1-Hz safety threshold (see the Supplementary Materials) whereupon the network undergoes a desynchronization failure. In either case, the edge where the fault occurs is removed and the voltages and associated power flows readjust according to Eq. 1. Edges on which subsequent faults occur continue to be removed until the cascade ceases through a new equilibrium being attained or the network collapses entirely. A cascade is initiated by removing the edge on which the power is greatest. This maximum power flow is denoted α_*. The proportion S of surviving edges after such a cascade provides a convenient measure of network resilience; S = 1 or 0 indicates complete resilience or failure, respectively. A critical capacity value α_c can be assigned for which half of the edges in the network survive the cascade, i.e., S = 1/2. The α_c value will be used subsequently to characterize the power in kilowatts that edges are required to carry for the network to be resilient to overloading failure.

Figure 2 (A and B) shows the dependence of the proportion of failures F due to overloads (green) or desynchronizations (orange) and the fraction of surviving edges S (blue) on the normalized capacity α/α_*. The networks have the same size n = 60, but Fig. 2A has a surfeit of consumers over generators, whereas these are equal for Fig. 2B; in either case, there are no passive nodes. The vertical red line denotes the mean value of the normalized critical capacity $\overline{\mathrm{\rho }}={\overline{\mathrm{\alpha }}}_c/{\overline{\mathrm{\alpha }}}_{*}$ for this network configuration. The curves for the failures have similar characteristic shapes for either configuration, but different magnitudes. Generally, overload failures are prevalent, but there is a range of α values for which desynchronization failures dominate when the network composition favors consumers. This will invariably be the case in real networks at certain times of the day as generation and consumption vary. Figure 2C shows the dependence on α/α_* of the mean cascade duration $\overline{T}$, defined as being the interval between the removal of the edge with flow α_* and attaining a new equilibrium of Eq. 1, or failing entirely, for the two cases of network composition. The values of $\overline{T}$ show slight differences between the two cases at small values of α. This regime corresponds to networks with high susceptibility to complete failure, with all edges failing once the network is perturbed. The principal cause of failure in these cases is attributable to overloads and occurs so rapidly that an equilibrium of Eq. 1 cannot be accessed following the triggering event. As α increases, both curves rise steeply to a peak value in the 20 to 30s range at the value of ${\overline{\mathrm{\alpha }}}_c/{\mathrm{\alpha }}_{*}$, which coincides with the value for which half of the network remains intact. The results in Fig. 2C are for the case of γ = 1, but these peak values are approximately constant across the entire range of realistic parameter values (see fig. S2). The cause of the failures here is approximately equally apportioned between overloads and desynchronizations. With further increase of α, $\overline{T}$ declines and then saturates to a value independent of network composition. The sizes of the cascades in this regime are all small, being small perturbative fluctuations that do little damage to the network. Figure 2C therefore demonstrates that catastrophic cascades occur very rapidly, while less damaging cascades occur on a slower time scale (see fig. S3 for further examples). Countermeasures against the most damaging cascades must therefore be preventative, highlighting the importance of boosting network resilience.

Fig. 2. Impact of cascading failures as a function of network edge capacity.

The proportion P of surviving edges, and failures F due to overloads and desynchronizations are shown as functions of α/α_* for an ensemble of small-world networks with n = 60 and (n₊, n₋, n_p) = (15,45,0) in (A) and (n₊, n₋, n_p) = (30,30,0) in (B). The critical points $\overline{\mathrm{\rho }}$ are marked by the vertical sections (i) and (ii) in each case. (C) shows $\overline{T}$, the mean duration of cascades as a function of α/α_* for the same networks.

The fraction S of edges surviving a cascade as a function of edge capacity follows a sigmoidal profile, as demonstrated in Fig. 2 (A and B), revealing a threshold capacity (at the point of inflection) at which the system transitions from complete failure to resilience. The lower this threshold value of edge capacity, the more resilient the network. The normalized location of the inflection point ρ = α_c/α_* is therefore a natural metric to gauge the resilience of an ensemble of networks, and it will later allow for a convenient means of incorporating real power data. The lower the value of ρ, the greater the resilience. An equivalent metric was used in (25); however, the analysis was not dynamical as here. Rather, the networks relaxed via a sequence of quasi-equilibria to a new equilibrium state following the removal of overloaded edges. This implicitly assumed that the time scale of equilibration is sufficiently short to accommodate the new power flows. However, we have seen in Fig. 2 that these transient reconfigurations can lead to additional failure through desynchronization. Moreover, these cascades occur on a time scale that is much shorter than those on which the network changes because of diurnal or meteorological variations.

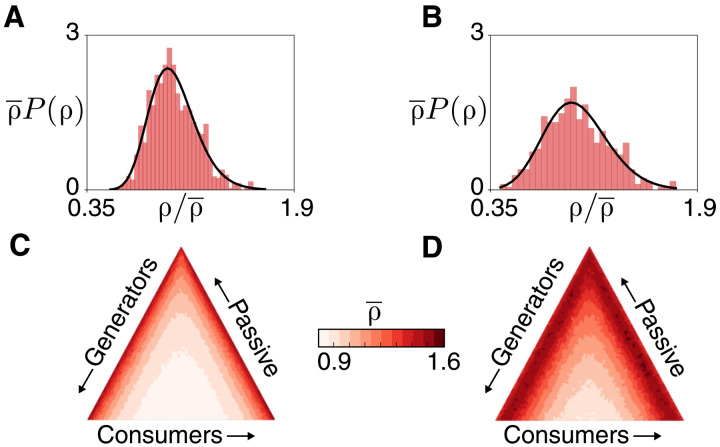
Using realizations of networks of size n = 100 with equal number of consumers and generators as examples produces distributions of ρ observed across an ensemble of network realizations of lattice (Fig. 3A) and small-world type (Fig. 3B). In both cases, the probability density of ρ is accurately described by a log-normal distribution as shown by the full line, as was found in (25). The log-normal distribution is characterized by the mean and variance, and these values depend on the node composition and topological structure of the network. To visualize this dependence, we project the mean value of ρ onto a network composition simplex, as shown in Fig. 1C, to provide a resilience landscape. That shown in Fig. 3C is for a regular lattice and shows that the most resilient node configuration occurs in the central region of the simplex, the least resilient being found in a narrow band at the simplex’s lateral edges, corresponding to an imbalance between consumers and generators of power. The most advantageous configurations are located at the bottom-center of the simplex, where the number of passive nodes is small: Recall that this was also the case for κ_c (Fig. 1C). Figure 3D for the small-world network (q = 0.1) exhibits qualitatively similar behavior to the regular lattice, but with some important distinctions. The value of $\overline{\mathrm{\rho }}$ is raised everywhere, and the region of low resilience near the simplex’s edge has broadened into the interior. The most resilient configurations remain those with small numbers of passive nodes. These behaviors maintain for smaller systems; networks with only n = 50 nodes display the same simplex morphologies as those with n = 100 (see fig. S5). As topological randomness increases to q = 1, giving Poisson networks, the region of low resilience spreads even further into the interior (see fig. S4). Nevertheless, across the entire range of q, the most resilient region of the simplex remains the bottom-center, with the least resilient configurations being in the peripheral regions.

Fig. 3. Variation in resilience with generator-consumer numbers.

(A and B) Distributions of the normalized critical capacity ρ = α_c/α_* for a lattice (q = 0) and a small-world (q = 0.1, $\overline{K}=4$) network, respectively, both with equal numbers of consumers and generators (n₊ = n₋ = 50). (C and D) Simplexes for lattice and small-world networks. In all cases, n = 100 and the ensemble size is 200.

The dynamical model considered here predicts different resilience characteristics for particular (25), which found that most resilient networks lie in the middle of the simplex, implying an advantage of having passive nodes in the network’s compositional mix. This disparity is of importance when considering the impact of dynamic changes in network composition over a day and across different seasons on a network’s susceptibility to disruption. This is explored in the next section.

Power usage trajectories in microgrids

Having established an operational space in which resilience is quantified, the next task is to model how a small network of renewable power generators and consumers, referred to as a microgrid (20), traverses this terrain as diurnal and seasonal conditions change. This is informed with power consumption and generation data to define P_i(t) in Eq. 1 and, hence, the node composition of the network at any instant. Consumption of approximately 5000 households in the London area was recorded by UK Power Networks with a resolution of 30 min over a 2-year period (31), and PV power generation from 100 separate panels with 10-min resolution was obtained over a year (32). The net power on each network node is given by P_i(t) = g_i(t) − c_i(t), where g_i(t) and c_i(t) denote generation and consumption time series drawn from the dataset (see Materials and Methods). The vector P(t) ∈ ℝⁿ with components P_i(t) then determines the power supply and demand of the microgrid at time t. The microgrid is connected to the external grid via a point of common coupling (PCC), modeled as a single additional node that imports power in response to demand or exports power generated in excess of requirement.

To map these data onto the configuration space of the simplex, we define, by analogy with the discrete variables (n₊, n₋, n_p), the power generation/consumption densities (η₊, η₋, η_p). For a given snapshot in time t, these are defined by

$${\mathrm{\eta }}_{+}≔\frac{1}{n \text{max}(\mathbf{P})}{\displaystyle \sum _{x\in {\mathbf{P}}^{+}}}x$$ (3)

and

$${\mathrm{\eta }}_{-}≔\frac{1}{n \text{min}(\mathbf{P})}{\displaystyle \sum _{x\in {\mathbf{P}}^{-}}}x$$ (4)

where P⁺ and P⁻ contain only the positive and negative contributions to P, respectively, and η_p = 1 − η₊ − η₋. Note that the dependence on t has been suppressed for notational brevity in the above definitions. The values (η₊, η₋, η_p) define a set of coordinates for a point on the consumer/generation simplex. These coordinates vary as P(t) changes with time. The daily variability in household power demand thus causes the microgrids to sweep a trajectory through the (η₊, η₋, η_p) simplex.

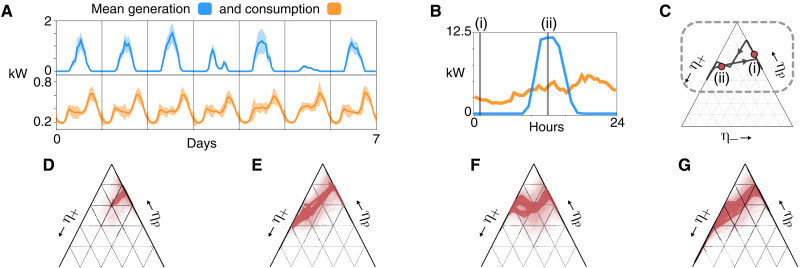
Figure 4A shows the mean power generation (blue) and consumption (orange) measured in kilowatt-hour (kWh) for a week in autumn. Power consumption is low during the night, rising to a morning peak, then declining to a fairly constant value throughout the daytime, before rising again to a principal peak in the evening. PV generation of power is only significant during the middle third of the day, at which time local demand is not especially high. Figure 4B is the daily power profile during a day in September for a network comprising 25 houses and 100% PV uptake, i.e., all 25 houses are equipped with PV generation. The vertical lines denote midnight (i) and midday (ii). At midnight, there is no generation but still significant overall consumption of power. The data reveal that this is due to a few high consumers with a large number of passive nodes (i.e., houses of net zero power), so the configuration lies at the top-right of the simplex as shown in Fig. 4C. By midday, there are large numbers of generators, few consumers, but still a high proportion of passives. The network has now moved to the top-left of the simplex. So as the day progresses, there is an oscillation between the right- and left-hand extremities of the simplex.

Fig. 4. Daily variations in household power demand and generation.

(A) Mean PV generation and household consumption for an example week in autumn. Shaded area shows 1 SD from the mean. (B) Total power generation (blue) and consumption (orange) in a model microgrid of n = 50 nodes in autumn over a day with network nodes defined by data in (A) with all nodes equipped with PV generation. (C) Trajectory in the simplex corresponding to (B), with power generation/consumption densities (n₊, n₋, n_p) defined by Eqs. 3 and 4. Points (i) and (ii) indicate midnight and midday, respectively. (D to G) Mean simulated weekly trajectories in the region of the simplex indicated by the dashed box in (C) for an ensemble of 50 model microgrids with generation and consumption data as in (B). All grids have n = 50. (D) Winter, 50% PV uptake; (E) winter, 100% PV uptake; (F) summer, 50% PV uptake; (G) summer, 100% PV uptake.

We consider a network of size n = 50 and simulate the grid response using the data as described above for different levels of PV uptake. Figure 4D shows the mean trajectories over an ensemble of 50 such networks during winter for the case of 50% PV uptake. The trajectories are confined to a small region of the simplex and do not gain access to its left-hand side, whereas a full traversal of across the simplex occurs in the 100% PV uptake case, as shown in Fig. 4E. The summer trajectories are shown for a network with 50% PV uptake in Fig. 4F, which traverses the simplex, and this can be contrasted with those for the case of 100% uptake in Fig. 4G—note the substantial excursion along the η₊ axis during this season. For the base case of 0% uptake, the trajectories never leave the upper right boundary of the simplex, since the number of generators never changes. These trajectories simply oscillate on the η_p axis as household demand fluctuates. Figure 4 (D to G) demonstrates that trajectories venture into the center of the simplex at higher uptake levels, reflecting the increasing numbers of generators. For 100% uptake, the trajectories complete a full traversal to the left-hand side as they become more dominated by generators. These excursions become more prominent during the summer because of the higher PV output (see fig. S6 for more examples). Nevertheless, in all cases, the network operates principally in the peripheral regions of the landscape where resilience is poorest. The following section uses these trajectories in conjunction with the above results to simulate when network failures occur, and their causes, as the resilience terrain is traversed throughout the day.

Daily variability of synchrony and resilience in microgrids

We are now able to track the time dependence of resilience as the grid’s form and function changes. Both the critical coupling κ_c and the critical capacity α_c display temporal variations, which indicate that the performance of a power grid is not simply a fixed feature of the network but depends on power usage and therefore on time and season.

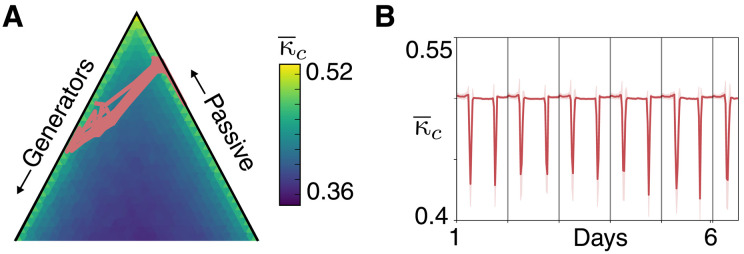
The mean weekly trajectory of 50 regular lattice microgrid realizations, each with 50 houses in the summer and 100% PV uptake, shows clear daily oscillations in the critical coupling capacity κ_c that describes the minimal coupling required to achieve grid synchrony (Fig. 5). The value remains approximately constant for large parts of the day, with a small peak evident during the morning, and then two brief minima as the network traverses the simplex in each direction, these being associated with the morning and evening peaks in power consumption (see Fig. 4, A and C). These minima coincide with power consumption and generation characteristics being such that the grid is balanced, i.e., trajectories approach the center of the simplex. Figure 1D demonstrates that ${\overline{\mathrm{\kappa }}}_c$ is minimized, rendering networks more synchronizable, in these interior regions of the simplex where the numbers of effective generators and consumers are commensurate. Of note is the significant deviation from the mean near these transition points, highlighting that particular grids will be especially susceptible at these points. The simulations underlying Fig. 5 concern a regular lattice structure; although the amplitude of oscillations is typically reduced, the above-described features hold for less regular topologies (see the Supplementary Materials). The narrow downward spikes in Fig. 5B reveal that microgrids spend fleetingly little time in the advantageous interior region. This is due to the time disparity between periods of high consumer and generator activity. As shown in Fig. 2, desynchronization plays an important role in driving edge failures during cascades. Increasing the time spent in the central region should therefore be an important consideration for future grid control schemes.

Fig. 5. Changes in critical coupling capacity over time.

(A) Weekly trajectory through the ${\overline{\mathrm{\kappa }}}_c$ simplex of a microgrid network with q = 0 and n = 50 houses in the summer, with 100% PV uptake. (B) Corresponding values of ${\overline{\mathrm{\kappa }}}_c$ during the weekly trajectory plotted as a time series. Shaded regions indicate 1 SD from the mean.

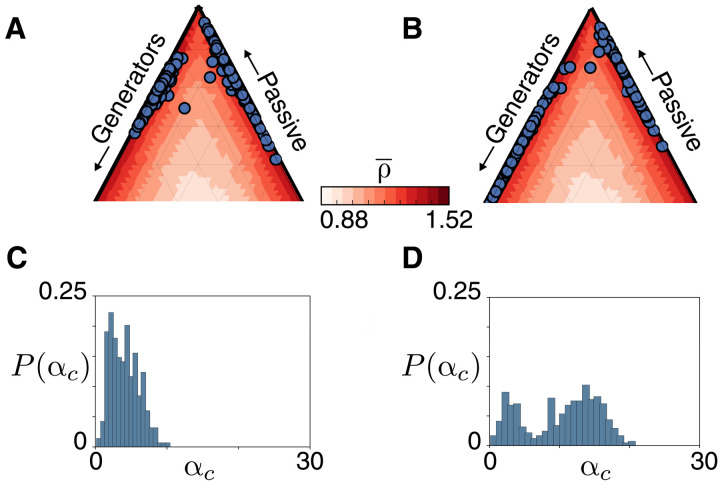
To determine how these daily variations affect grid resilience, cascading failures are randomly triggered in ensembles of microgrids at some point during their trajectories. The triggering probability is chosen to make cascades more likely to occur when grids are handling high volumes of power (see Materials and Methods). The points of failure are then recorded on the simplex. Figure 6 (A and B) shows the case for a sample of cascade simulations with different PV uptake on lattice networks during summer. For both cases, failures are concentrated near the boundary of the simplex, as would be expected because of the inadequate temporal distribution of power generation/usage over the grid.

Fig. 6. Effect of PV generation on microgrid resilience.

(A and B) Points of failure for ensembles of 500 lattice microgrid realizations of size n = 50 and with 50% and 100% renewable uptake, respectively, during the summer. (C and D) Corresponding distributions of the critical capacity α_c from each of these failure points.

For each failure event, the critical capacity that would be required to survive the cascade α_c = ρα_* in kilowatts is obtained from the log-normal resilience distribution computed above, but where α_* is now defined as the maximum flow specified by the power time series data at the time where the cascade was initiated. The distribution of α_c shown in Fig. 6 (C and D) reveals that higher uptake of PV significantly decreases grid resilience during the summer, with grid connections requiring significantly higher rating α_c to survive potential cascading failure. This is attributable to the high power generation during the day, which must be shunted to the PCC. The increased concentration of generators at these times acts to push the trajectories further down the >left-hand side of the simplex into regions of lower resilience. The distribution of α_c becomes bimodal during the summer in the case of high PV uptake, with peaks corresponding to failures occurring on each side of the simplex. The smaller mode is associated to those less damaging cascades occurring in the evening, when the grids exhibit heterogeneous demand; the larger mode corresponds to those that arise during high PV output. The emergence of a larger, more damaging mode for high PV uptake also occurs for more random networks with q > 0 (see fig. S11). The critical line capacities α_c required to survive the cascades about this larger mode are in the range 5 to 15 kW. Since the line ratings of connections in low-voltage transmission grids are typically 4 to 15 kW (33), microgrids with high PV uptake are operating at close to their critical capacity during summer months.

These results demonstrate that the high temporal variability in power flow characteristics counteracts the stabilizing effect of increased distribution of generation associated with grids containing high numbers of renewable generators. Control strategies that address this daily and seasonal temporality are therefore necessary. We will discuss this in the next section.

Impact of batteries on resilience

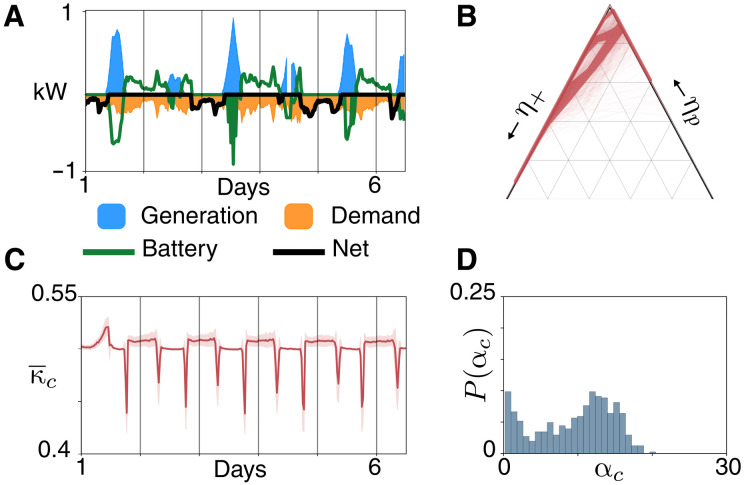
Battery storage forms a natural candidate to affect a spreading of spikes in PV generation and thereby to ameliorate the temporal volatility of usage and generation highlighted above. Figure 7 shows how the resilience of microgrids examined in the previous section (Fig. 4) is affected by the addition of batteries. Each house in the network with a PV generator is equipped with a battery, based on the Tesla Powerwall 2 (34), typical of present-day commercially available household batteries. These batteries are designed to only optimize for individual household self-sufficiency. As solar generation and consumer demand varies, the battery linearly charges or discharges to smooth out the net demand; see Materials and Methods for a full description of the battery model. An example time series for an individual house is shown in Fig. 7A; note that the house becomes self-sufficient (i.e., P_i = 0) for large parts of the week. This increase in passivity is reflected in Fig. 7B, showing the mean weekly trajectory for an ensemble of 50 microgrids corresponding to those shown in Fig. 4G (i.e., each with 100% PV uptake and summer conditions) but now incorporating batteries on each generator. The trajectory is largely confined to the simplex edges, and particularly to the left-hand side, reflecting the self-sufficiency now introduced by the PV-battery pair and the excess daytime production. Unfortunately, while beneficial for individual households, this is problematic from a network resilience perspective, as it constrains the grid dynamics to precisely the regions with the highest values of ${\overline{\mathrm{\kappa }}}_c$ and $\overline{\mathrm{\rho }}$. We also see that the daily oscillations in ${\overline{\mathrm{\kappa }}}_c$ and bimodality of α_c observed in Figs. 5B and 6D are retained. In the latter case, the mean value of the critical capacity α_c is only marginally reduced, while in the former, the maximum value of the mean critical coupling strength actually increases. To boost resilience, a battery operating scheme should ideally act to manipulate trajectories further into the lower-central regions of the simplex. These regions are associated with higher resilience for networks across the full range of q. However, Fig. 7 shows that present-day household battery operation does not achieve this. Further simulations reveal that this type of battery is also ineffective at boosting resilience during the winter months and for lower levels of PV uptake (see fig. S12).

Fig. 7. Impact of household batteries.

(A) Weekly trajectory of a house equipped with PV panels and a battery during the summer. (B) Simplex trajectory of a microgrid consisting of such battery- and PV-equipped houses in the summer. (C) Corresponding values of mean critical coupling ${\overline{\mathrm{\kappa }}}_c$ over the week. (D) Results of the resilience experiment for the ensemble in (B).

DISCUSSION

This paper has addressed the resilience characteristics of electrical microgrids, which are of increasing importance as housing stock is replaced and developed afresh, and as the power that supplies these, and existing, dwellings moves toward carbon-neutral renewable generation and storage. The ad hoc way that these developments are established prompts questioning whether there are favorable network architectures or dynamic control strategies that can flexibly accommodate changes in usage and generation throughout the day and across the seasons while remaining resilient to failure. Initial steps for answering some of these issues were tackled by assuming that a network’s response to an outage, caused by a power carrying edge being overloaded, could be determined through the power distribution relaxing via a sequence of quasi-equilibrium states, when these exist (25). While informative, this approach neglects transient processes that can occur on power networks that can further affect performance. Following (17), we remedy this by incorporating the dynamics described by the swing Eq. 1, which, in addition to predicting when and where power overloads occur, also accounts for desynchronization of the local AC power supply from the external grid. In this way, a fitness landscape is established whereby the resilience of a network, with given composition of consumers, producers, and net passive users of power, can be determined for overloading and desynchronization faults.

These landscapes provide values of the grid coupling κ_c required for stable operation, together with the power line ratings α_c required to survive a cascade, for networks of any consumer-generator configuration. Regions of greatest robustness are located in the central regions of the landscapes, corresponding to grids operating with roughly equal proportions of generators and consumers on-line at a given time. Combining these landscapes with household data for power consumption and generation reveals the paths that microgrids trace as they traverse these terrains. The analysis shows that microgrids spend most of their time operating in the least favorable regions of the robustness landscape, across all ranges of PV uptake. This is due to a supply-demand discrepancy, meaning microgrids are alternately dominated by either consumption or generation. The grids therefore spend fleetingly little time in the center of the simplex and are therefore unable to exploit the robustness advantages that increased distribution intuitively ought to provide. Increased uptake of PV can cause microgrids to operate at critical values α_c that are at the upper end of modern line ratings. These grids would be able to operate normally but would be extremely fragile to cascading failures. The installation of household battery storage, while increasing consumer self-sufficiency, does little to ameliorate this resilience problem.

In conclusion, this paper has shown that increased installation of distributed renewable generation and household storage can lead to a lack of robustness. This highlights the importance of developing new control strategies for future microgrids. In particular, battery usage could be adjusted to push grids into the more favorable regions of the robustness landscape. Today’s commercially available household batteries, such as those modeled here, are not designed to dispatch energy back upstream into the network. Instead, they optimize only for individual household self-sufficiency. This mode of operation was reported to be economically inefficient (35), and our work establishes that it fails to mitigate undesirable vulnerabilities introduced by the increasingly variable and distributed nature of modern power generation. Nascent technologies such as vehicle-to-grid (36) show promising abilities to balance renewable power systems (37) and can be used together with energy management control systems to form so-called virtual power plants (38). It is vital that any such future control schemes also take into account the dynamical properties of the network to ensure the resilience of future power grids.

MATERIALS AND METHODS

Computation of κ_c

The critical coupling κ_c for a given power network is evaluated by finding stable fixed points of Eq. 1 for a range of κ values. These fixed points satisfy

$$P_i-\mathrm{\kappa }{\displaystyle \sum _{i=1}^n} \text{sin}({\mathrm{\theta }}_i-{\mathrm{\theta }}_j)=0$$ (5)

for all nodes i = 1, …, n and are computed via numerical integration of Eq. 1. Since no stable fixed points exist for κ < κ_c, the critical coupling can therefore be readily identified as the value of κ beneath which time-stepping fails to converge on a steady state satisfying Eq. 5. Other methods to identify κ_c based on numerical continuation are also available but may, in practice, be more computationally intensive because of the presence of multiple parallel branches of stable solutions.

Network cascade model

This paper uses cascading failures as a means to gauge the resilience of power networks. Algorithm 1 is used to compute these cascading failures in a given power network G = (𝒱, E, P, α), with n = ∣𝒱∣ nodes, m = ∣E∣ edges, power vector P, and edge capacities α.

Algorithm 1 Dynamic cascade

Input: A network G = (𝒱, E, P, α).

Output: Fraction of surviving edges S

1: Find steady state θ^* by integrating Eq. 1

2: Delete an edge

3: Find all connected components H ∈ G and their node phase vectors θ_ℋ

4: S ≔ 0

5: for all H ∈ G do

6:        S = S + NETMON(H, θ_H, α)

7: end for

8: S = S/∣E∣

The dynamical cascade algorithm used here is adapted from the steady-state Motter-Lai process (7), which has previously been used to investigate network resilience as a function of edge capacity (17, 25, 39, 40). The algorithm monitors the network after some initial failure, removing edges that become overloaded or that drift too far from the grid reference frequency Ω. The procedure begins by finding the steady-state power flow pattern of the network using Eq. 1, giving a vector of node phase angles θ and frequencies ω. The greatest power flow on any edge in this initial steady state is labeled α_* and is the minimum edge capacity required for normal operation. The edge carrying this greatest power is then deleted, serving as a model of overloading line failure. The network (or networks, if it has fragmented into separate connected components) is then monitored using the function in Algorithm 2. This function continues to time-step Eq. 1 while removing any edge e with power flow f_e > α and removing any nodes i where ω_i > 1 Hz to mimic the typical tolerances of the U.K. power grid (41). The function also detects any new connected components formed as the network breaks down, which are then monitored by recursively calling Algorithm 2; note the recursive step at line 19. The cascade finishes when all remaining network components are within the frequency and capacity tolerances. The fraction S of surviving edges is then returned. A small adaptation to Algorithm 2 provides the total cascade time, and the fractions of edges failing by either desynchronization or overload. This cascade scheme is repeated for a range of edge capacity values α, producing profiles of the type shown in Fig. 2. The critical value α_c at which S = 1/2, and thus the resilience measure ρ = α_c/α_*, is determined using a bisection method. The distribution of ρ values for networks of a given composition of generators to consumers is then obtained by repeating this cascade procedure over an ensemble of Watts-Strogatz network realizations of fixed rewiring q and node composition (n₊, n₋, n_p) placed uniformly at random.

Algorithm 2 Network monitor function

1: function NETMON(G, θ, α)

2:    Surviving edges S ≔ 0

3:    Balance supply and demand in G

4:    while Finished == False do

5:          Time-step Eq. 1

6:          if frequency exceeds tolerance then

7:          return S = 0

8:          end if

9:          if steady state found then

10:        return S = number of edges in G

11:        end if

12:        if edge flow f_e exceeds α on any edge e then

13:        Finished = True

14:    end if

15:    end while

16:    Delete all overloaded edges

17:    Find all connected components H ∈ G and their node phase vectors θ_H

18:    for all H ∈ G do

19:        S = S + NETMON(H, θ_H, α)

20:    end for

21:    return S

22: end function

Microgrid model

Household power consumption and PV panel generation time series data are used to construct random models of microgrids. These datasets contain U.K. household power demand and PV panel output data at up to 10-min resolution. Each dataset covers at least a full year, allowing microgrids to be modeled for different seasons in a temperate climate.

The microgrids are modeled as networks of size n, wherein n − 1 nodes are houses and the remainder is the PCC, which connects the microgrid to the external grid. Each of the houses is prescribed a time series of power demand c_i(t), drawn uniformly at random from the dataset. A random subset of the houses is also chosen to additionally be equipped with PV generation; these houses are prescribed a time series of generation g_i(t) drawn uniformly at random from the PV dataset. The fraction of houses with PV is referred to as the uptake. The net power generated by each house is then P_i(t) = g_i(t) − c_i(t). Surplus power generated by PV units will flow through the PCC to be supplied back upstream to the external grid. If there is a deficit within the microgrid, with household demand outstripping local PV production, then power from the external grid will flow in through the PCC. The PCC is therefore modeled as behaving variably as a source or sink, serving to balance supply and demand.

Battery model

Batteries are modeled on the Tesla Powerwall 2, a common domestic battery currently being installed in renewable housing developments. They have a maximum charge and discharge rate of 5 kW and a maximum storage capacity of around 14 kWh (34). Their usage in microgrids is modeled by assuming that each household injects any surplus power produced via PV units into their battery. At other times, when a household’s consumption outstrips its PV generation, the house first uses any power stored in the battery before taking any power from the microgrid. Each battery-equipped house i then has net power production P_i(t) = g_i(t) − c_i(t) − b_i(t), where b_i(t) is the battery’s rate of charge in kilowatts.

Data-driven cascade model

Microgrids constructed as above trace daily trajectories through the node configuration simplex as usage and generation patterns vary. Each point on the simplex has a resilience distribution calculated using the network cascade model outlined above. Exploiting the log-normal distribution of ρ in this way obviates the need for prohibitively intensive direct simulation, as the ability of a network to survive a failure therefore depends on where in the simplex the microgrid happens to be at the onset of failure. To investigate this, the maximum power flow P_max occurring within a microgrid is tracked throughout the course of a week as it travels through the simplex, producing a time series of maximum power flow. A cascading failure is then chosen to occur randomly at some time t, with a probability p proportional to the maximum power at that time P_max(t), where

$$p=\frac{P_{\text{max}}(t)}{{\sum }_{t\prime \in \mathrm{T}} P_{\text{max}}(t\prime )}$$ (6)

and T is the set of time points over the week. This probability is very low, except during times of high power usage. If a cascade is triggered, then the grid’s location in the simplex is recorded. A value of ρ is then sampled from that simplex point’s resilience distribution, given the value of $\overline{\mathrm{\rho }}$ and the variance for that network’s log-normal distribution. This is then used to calculate the edge capacity volume α_c = ρα_* required for at least half of the network to remain functional. This experiment is then repeated for an ensemble of microgrid realizations for a given time of year and level of PV uptake, producing a distribution of α_c values as shown in Fig. 6A.

The objective of these experiments is not to derive a realistic distribution describing the likelihood of a cascade occurring. See, for example, (18) for an analysis along those lines. Instead, the objective here is to evaluate the ability of the system to survive a cascade should one occur. The probability in Eq. 6 is therefore designed to make cascades more likely to occur when grid connections are handling heavy loads, and microgrid realizations that do not enter a cascade are discarded.

Supplementary Materials

This PDF file includes:

Supplementary text

Equations S1 to S19

Figs. S1 to S12

References